Прямая и ломаная линии | Математика
Прямая линия
Прямая линия есть кратчайшее расстояние между двумя точками.
Свойства прямой. a) Положение прямой линии вполне определяется теми двумя точками, между которыми она проведена.
Это свойство зависит от того, что b) между двумя точками можно провести только одну прямую линию, ибо между двумя точками существует только одно кратчайшее расстояние.
Определение прямой линии, вытекающее из непосредственного усмотрения ее свойства, некоторые называют аксиомой. Это понятие о прямой линии называют иногда основным.
В прямой линии нужно отличить ее положение и ее длину.
Прямую линию можно неопределенно продолжать в обе стороны.
Две точки определяют прямую линии не только в тех точках, которые лежат между ними, но и в тех точках, которые получаются, если неопределенно продолжать прямую линию в обе стороны.
c) Две прямые линии пересекаются в одной точке, ибо точка их пересечения находится на конце прямой линии.
d) Через одну точку можно провести бесчисленное множество прямых линий.
Все линии на чертеже 5 проходят через общую точку A.
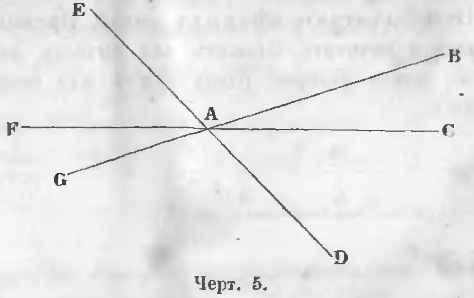
e) Если две прямые имеют две общие точки, то они совпадают всеми остальными точками.
f) Расстояние между двумя точками определяется длиной прямой линии, их соединяющей.
Равные прямые. Две прямые линии, имеющие одинаковую длину, называются равными. Линии AB с CD (черт. 6) будут равными линиями.

Равные прямые совпадают при наложении друг на друга.
Сравнение прямых линий
Чтобы сравнить две данные прямые AB и CD по длине (черт. 7) накладывают линию CD на линию AB так, чтобы точка C совпадала с точкой A.
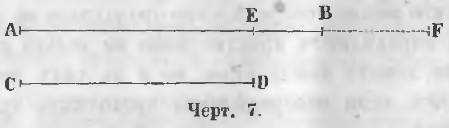
Здесь могут быть три случая:
Если точка D упадет в точку E, находящуюся между A и B, линия CD меньше AB.
Если точка D упадет в точку B, линия CD равна AB.
Если точка D упадет в точку F, находящуюся на продолжении линии AB, линия CD больше AB.
Сложение и вычитание прямых линий. Прямые линии можно складывать и вычитать. Сложить или вычесть линии значит найти линию, длина которой равна сумме или разности длин данных линий.
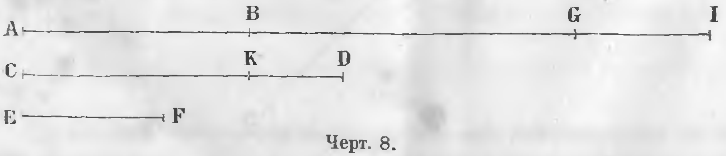
Чтобы сложить прямые линии AB, CD, EF (черт. 8), продолжают линию AB и от точки B откладывают линию BG, равную CD, от точки G линию GI равную EF. Линия AI равна сумме всех этих трех линий.
Чтобы найти разность линий CD и AB, откладывают на линии CD от точки C линию CK, равную AB, тогда линия KD равна разности линий CD и AB.
KD = CD — AB.
Отношение двух прямых линий
Сравнивая две прямые линии по длине, определяют их взаимное отношение. При этом сравнении имеет значение линия, называемая общей мерой двух линий.
Общая мера двух линий есть такая линия, которая содержится целое число раз в обеих линиях.
При определении взаимного отношения двух прямых линий по длине, могут встретиться два случая:
Когда эти линии имеют общую меру.
Когда они ее не имеют.
В первом случае они называются соизмеримыми, во втором — несоизмеримыми. В первом случае отношение двух линий выражается каким-нибудь рациональным, т. е. целым или дробным числом; во втором оно не может быть точно выражено ни целым, ни дробным числом.
Если две прямые линии соизмеримы, то находят их общую меру.
Определение общей меры двух линий
Общая мера двух линий большей AB и меньшей CD (черт. 9) не может быть больше линии CD. Удостоверимся сначала, не будет ли меньшая линия CD этой общей мерой.
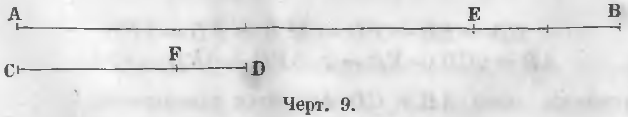
Для этого накладывают меньшую линию на большую и определяют, сколько раз она уложится в большей. Если она укладывается ровное число раз, например, m раз, тогда отношение двух линий выражается этим целым числом m.
Действительно, тогда
AB = m * CD и AB/CD = m.
Если же она не укладывается ровное число раз, то последовательно накладывают линию CD до тех пор, пока не получится остатка EB меньшего CD.
Положим, линия CD уложилась в AB два раза и получился еще остаток EB. Общая мера линий AB и CD не может быть более остатка EB.
Действительно, из равенства
видно, что общая мера линий AB и CD должна содержаться равное число раз в линии EB. Она может или равняться линии EB или быть меньше ее.
Отсюда заключение:
Общая мера двух линий AB и CD должна быть общей мерой меньшей линии и остатка EB.
Отыскивая общую меру CD и EB, поступаем по предыдущему. Откладываем линию EB на линии CD до тех пор, пока не получится остатка FD, меньшего линии EB. Общая мера CD и EB будет по предыдущему заключению общей мерой EB и FD.
Линию FD снова откладываем по линии EB. Пусть линия FD отложится на линии EB ровно два раза, тогда линия FB и будет этой общей мерой.
Связь между линиями выразится рядом равенств:
AB = 2CD + EB
CD = EB + FD
EB = 2FD
откуда
CD = EB + FD = 2FD + FD = 3FD
AB = 2CD + EB = 2 * 3FD + 3FD = 8FD.
Отношение линий AB и CD выразится равенством:
AB/CD = 8FD/3FD = 8/3.
Мы видим, что при нахождении общей меры нужно поступать точно так же, как при нахождении общего наибольшего делителя между целыми числами. Отсюда
Правило нахождения общей меры двух линий. Чтобы найти общую меру, нужно меньшую линию наложить на большую, первый остаток на меньшую, второй остаток на первый, и поступить так до тех пор, пока последний остаток не уложится ровное число раз в предпоследнем.
Чтобы найти отношение двух линий, нужно при помощи общей меры выразить обе линии и потом найти частное этих выражений.
2-й случай: две прямые линии несоизмеримы. Если две линии несоизмеримы, мы никогда не получим такого остатка, который содержался бы в предпоследнем остатке целое число раз. В этом случае определяют отношение прямых линий с каким угодно приближением. Для этого разделив меньшую линию на n равных частей, накладывают это часть CE на большую линию AB (черт. 10). Положим, что эта часть повторяется в большей линии m раз и еще получается остаток FB меньше CE.

Из равенств
AB = mCE + FB
CD = nCE
имеем
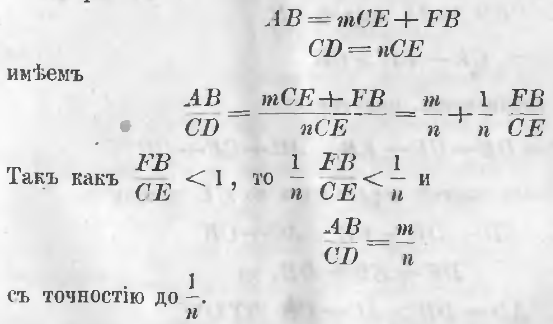
Так как n можно увеличивать произвольно, то и отношение длин двух прямых можно выразить с каким угодно приближением.
(См. о несоизмеримости диагонали квадрата с его стороной).
Измерение линий. Измерить линию значит найти ее отношение к другой линии, принятой за единицу. Это отношение называют длиной данной линии. Длина линии всегда выражается в каких-нибудь единицах.
Ломаные линии
Две линии ACB и ADB (черт. 11), соединяющие концы прямой AB, называются ломаными. При этом линия ACB называется внутренней, а линия ADB внешней ломаной линией.
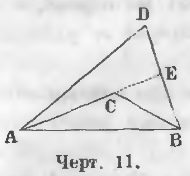
Теорема 1. Внешняя ломаная больше внутренней.
Даны две ломаные линии: внешняя ADB и внутренняя ACB (черт. 11).
Требуется доказать, что ADB больше ACB или
AD + DB > AC + CB.
Доказательство. Продолжим линию AC до пересечения с линией DB в точке E.
Линия ADE как ломаная больше прямой AE.
AD + DE > AC + CE
Ломаная линия CEB больше прямой CB
CE + EB > CB
Сложив эти неравенства, получим:
AD + DE + CE + EB > AC + CE + CB
Вычтя из обоих частей неравенства по CE, получим:
AD + DE + EB > AC + CB
Так как DE + EB = DB, то
AD + DB > AC + CB.
Что и требовалось доказать.
Теорема 2. Сумма пересекающихся частей ломаных больше суммы непересекающихся.
Даны пересекающиеся ломаные ABC и ADC (черт. 12), AD и BC их пересекающиеся части.
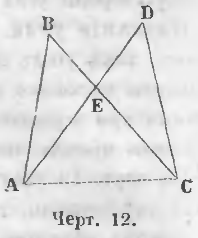
Требуется доказать, что
AD + BC > AB + DC.
Доказательство. Из того, что ломаная AEB больше прямой AB и ломаная CED больше прямой DC вытекают неравенства:
AE + BE > AB
ED + EC > DC
Сложив их, находим:
AE + BE + ED + EC > AB + DC
Так как
AE + ED = AD
BE + EC = BC
то
AD + BC > AB + DC
Что и требовалось доказать.
Линии: прямая, кривая, ломаная. Замкнутые и незамкнутые линии
Линия – это геометрическая фигура, образованная множеством точек, последовательно расположенных друг за другом.
Любую линию можно представить как след от точки, перемещающейся по данному пути. Например, грифель карандаша при прикосновении к бумаге оставляет на ней точку (1), но если грифелем провести по бумаге, то получится линия – последовательность точек, расположенных друг за другом (2):

Геометрические линии не имеют толщины.
Виды линий
Геометрические линии делятся на три вида:
| Линия | Пример |
|---|---|
| Прямая |
|
| Ломаная |
|
| Кривая |
|
Замкнутые и незамкнутые линии
Ломаные линии и кривые линии могут быть как замкнутыми, так и незамкнутыми. Замкнутая линия – это линия, у которой начало совпадает с концом (концы соединены друг с другом).
Самой простой геометрической фигурой, образованной замкнутой ломаной линией, является треугольник:

Все остальные многоугольники (четырёхугольник, пятиугольник, шестиугольник и т. д.) тоже являются замкнутыми ломаными линиями.
Самым распространённым примером замкнутой кривой линии является окружность:

Незамкнутая линия – это линия, у которой конец не совпадает с началом (концы линии не соединены друг с другом):

1.Мотивация к учебной деятельности. Цель: включение учащихся в учебную деятельность и определение содержательных рамок урока. | Учитель создаёт благоприятный психологический настрой на работу. Знает, что класс участвовал в проекте «Успешное чтение», все прочли книгу «Робинзон Крузо». На доске, справа висит яркий рисунок попугая ?, слева висит портрет Крузо и рисунок лестницы. | Ученики обращают внимание на все изображения на доске. Интересуются, мнением учителя о прочитанной книги. Узнают лестницу к хижине Крузо. | Личностные: положительное отношение к учебной деятельности. Регулятивные: самостоятельное установление причинно-следственной связи. Коммуникативные: планирование учебного сотрудничества с учителем, со сверстниками. | 2. Создание проблемной ситуации. Цель: Организовать актуализацию знаний учащихся. | Учитель: В романе «Приключения Робинзона Крузо» Робинзон сам рассказывает историю своей жизни. Мы знакомимся с героем задолго до того, как он попадает на остров. Робинзон Крузо оказывается единственным выжившим в результате кораблекрушения. Как же он решает жить дальше? Что берёт с потерпевшего крушение корабля на остров Робинзон Крузо? Почему именно этими вещами автор считает необходимым снабдить своего героя? Робинзон оказывается на острове, где ему предстоит провести много-много лет. Автор создает яркие картины южной природы, подчеркивает своеобразие каждого времени года. Каким же видит Робинзон Крузо необитаемый остров? Картину острова, жилища, изображаем с помощью линий. Какую линию представляет собой лестница в хижину? После изображения ломаной формулируем тему урока. Учитель на рисунке выделяет тропинку от хижины до огорода и между грядками виде отрезков(цветным мелом). Можем узнать сколько метров её длина? Учитель. Робинзон оказывается на острове, где ему предстоит провести много-много лет. Автор создает яркие картины южной природы, подчеркивает своеобразие каждого времени года. Каким же видит Робинзон Крузо необитаемый остров? Как относится к деньгам? Что думает о тех деньгах, которые находит на корабле? Нужны ли они ему? Сообщения о валюте страны и перевод её в денежные единицы России. Что поддерживает Робинзона Крузо в его одиночестве? Как он оценил своё положение? Что считает добром, а что злом? Проанализировали список поступков, составленный самим Робинзоном. Учитель: Робинзон Крузо старается утешить себя тем, «что могло бы случиться и хуже, и противопоставлял злу добро». Труд, религия, терпение, благоразумие, здравый смысл спасло Робинзона, он «работал не покладая рук». Учитель: Разум, трудолюбие, оптимизм, вера в Бога помогают найти выход из самой сложной ситуации, в которую попадает человек. Человек начинает свою жизнь на острове с почти примитивного состояния и столь же примитивных занятий. Он вводит новое летоисчисление. | Ученики рассказывают историю жизни Робинзона Крузо до того момента, как он попал на остров. Робинзоном безраздельно овладела страсть к обогащению сверх меры, считавшаяся в XVII веке самой губительной для человека. Ради наживы Робинзон способен даже торговать людьми, забыв христианские заповеди. За это и был жестоко наказан. Все рушится тогда, когда Крузо решает купить рабов в Гвинеи. Это является заслуженной карой за антигуманное, противоречащее природе человека поведение. «Мне по-прежнему суждено было самому быть виновником всех моих несчастий, благоразумием я никогда не отличался:». Ученики перечисляют предметы, которые кажутся герою необходимыми на острове, подкрепляя ответ цитатами. Параллельно на доске и в тетрадях выполняются рисунки объектов построенных Робинзоном на острове. хижина-параллелепипед; приставная лестница землянка-вход изображён виде прямоугольника; огород с выращенными овощами- прямоугольник; рисовое поле-прямоугольник; Ученики подбирают цитаты с описанием острова. Картина острова (на доске) добавляется изображением гор, солнца, забором и близкими друзьями — пятницей, козой. Учащиеся повторяют изученные на прошлом уроке виды линий. Пытаются чертить вне острова. Получают – ломаную. Говорят, что она сама себя пересекает. Делают вывод: длина ломаной = сумме длин её частей(отрезков). Предлагают измерить каждый отрезок и сложить( 1см=1м) В учебнике на стр.13 рассматривают рисунок 1.18 и читают определение длины ломаной. Ученики подбирают цитаты с описанием острова. Проанализировали список поступков, составленный самим Робинзоном. Учащиеся рассказывают как Робинзон пробует вести своё хозяйство, приспосабливается к жизни на острове, они воспроизводят мельчайшие подробности жизни героя на острове. В частности, со слов автора подробно описывают процесс изготовления того или иного предмета. Один из учеников вспоминает, что Робинзон спас книгу: Коран. Что такое летоисчисление! | Личностные: положительное отношение с обучению; понимают важность бережного отношения к здоровью; Оценивает поступки героя художественного произведения; Регулятивные: самостоятельно обнаруживают и формулируют учебную проблему; Выдвигают версии решения проблемы; Коммуникативные: планируют совместную деятельность с учителем и сверстниками; Развивают умение точно и грамотно выражать свои мысли; Слушают и понимают речь других. Познавательные: Анализируют объекты с целью выявления признаков; Самостоятельно определяют способ решения проблемы поискового характера. Предметные: Знают определение отрезка, прямой, прямоугольника, параллелепипеда меры длины. | 3.Решение учебной задачи. Цель: построение и фиксация новых знаний. | Постройте в тетради ломаную по следующему описанию. Учебник №22. Начертите в тетради какую-нибудь ломаную с вершинами в узлах сетки и «продиктуйте её соседу» Где в классной комнате, на каких предметах видите ломаные? В каких единицах длины могут быть выражены звенья ломаной? А ступеньки лестницы в хижину?(это звенья) Ломаная -границы грядок? | Выполняют в тетради. На интерактивной доске проверяем (учитель готовит заранее). Отмечают, что похоже на игру «морской бой». Обращают внимание на каркасные модели многогранников.(покрашенные в другой цвет рёбра образуют замкнутые и не замкнутые ломаные).Считают количество рёбер, находят длины ломаных. Перечисляют меры длины. В см. В м и см. | Личностные: умение распределять внимание Регулятивные: Коммуникативные: | 4.Первичное закрепление. Цель: Формировать у обучающихся способности к новому способу действий. | Рассмотреть рисунок (изображены ломаные), заполнить таблицу. Таблицы на партах. Работаем в парах. Выполняем задания по уровням. 1 уровень: №8 тетрадь тренажер. 2 уровень; №16 тетрадь тренажер. Что не получалось? Что не увидели в ломаной? | Обсуждают, заполняют таблицу.
Выполняют в тетрадях. Первому уровню, после попыток предлагается каркасная модель и учащиеся находят решение. Сложно работать без модели в руках. Сложно, если не покрашены звенья ломаной. Нет концов у звеньев ломаной. | Личностные: адекватно реагируют на трудности и не боятся сделать ошибку; Регулятивные: работают по плану, сверяют свои действия с целью, исправляют ошибки; Владеют общими приёмами решения задач; оценивают качество и уровень усвоения ими материала; Коммуникативные: слушают и слышат, сотрудничают с учителем и сверстниками; видят разницу двух высказанных версий; | 5.Включение в систему знаний и повторение. Цель: использование приобретённых знаний в практической деятельности и повседневной жизни. | Зачем мы изучили ломаную? Где знания о ней могут пригодиться? Какой путь будет короче? | Робинзон Крузо отмерял равные отрезки, сплетал и получил лестницу. Если бы звенья были разной длины, то лестница не получилась бы. Путь к океану можно изобразить ломаной из нескольких звеньев, а можно одним отрезком звеном- соединим начало первого звена и конец последнего. Так можно и дорогу в школу начертить- ломаная(заходить в дворы домов) или одним отрезком! Путь –одним отрезком! | Личностные: Регулятивные: Коммуникативные: | 5.Рефлексия учебной деятельности. Цель: зафиксировать новое содержание, оценить собственную деятельность на уроке. | Давайте скажем что нового и полезного мы узнали на уроке? Было интересно … Я понял, что … Теперь я могу … У меня получилось … Меня удивило … Я попробую … Домашнее задание: Рисунок места обитания Робинзона Крузо завершить-раскрасить, дать название. Оценка по ИЗО. Определить день для сдачи работы учителю ИЗО. Учебник: п.2 , №23, №24. По желанию: сообщение о летоисчислении. | Учащиеся подводят итоги, вспомнив поставленные цели и задачи. Учащиеся приобретают навык рефлексии результатов деятельности. | Личностные: Регулятивные: Коммуникативные: |
Урок математики по теме «Части прямой. Ломаная». 5-й класс
Тип урока: урок по типу ОНЗ (открытие новых знаний).
Формы организации познавательной деятельности:
- Фронтальная
- Парная
- Индивидуальная
Цель урока: направлена на формирование следующих универсальных учебных действий
Личностные УУД: Формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний.
Метапредметные УУД:
Регулятивные:
- понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и оценивать свои достижения
Познавательные:
- формировать навыки изображения прямой и её частей, а также ломаной; знать общие и отличительные особенности изучаемых линий; познакомить с разными способами обозначения прямой и луча; научить правильно обозначать прямую, её части и ломаную линию; формировать умение применять полученные знания при решении практических задач.
Коммуникативные:
- воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.
Задачи:
- Формирование и развитие наблюдательности и внимания;
- Умение выделять существенные признаки геометрической фигуры;
- Формировать умение сравнивать линии, отмечая при этом сходные и различные признаки и свойства.
I. Орг. момент.
Здравствуйте, ребята! Сегодня мы продолжаем изучать разнообразный мир линий. Мир о котором древнегреческий математик Евклид сказал: “Точка есть то, что не имеет частей.
Линия же – длина без ширины. Прямая линия есть та, которая равно расположена по отношению к точкам на ней”.
II. Активизация учебной деятельности.
Разгадайте ребус и попробуйте сформулировать тему урока.
Д: Отрезок.
У: Правильно, отрезок. А кто может сказать — что такое отрезок?
Д: Отрезок-это часть прямой, у которой есть начало и конец.
У: Молодцы! Как вы думаете, ребята, что мы сегодня будем изучать на уроке, с какими линиями познакомимся?
Ребята высказывают разные предположения: “Прямую”, “Отрезок”, “Части прямой”.
Формулируется тема урока.
У: Верно, сегодня мы с вами будем изучать “Части прямой. …”. Но это только часть темы. Вторую часть темы, мы “откроем” выполняя практическое задание.
У: Что означает в переводе с латинского слово “linea”?
У: Какие виды линий вы знаете?
У: — Назовите, где мы в жизни можем увидеть различные линии?
У: Язык линий понятен людям всей земли. Линии окружают нас повсюду. Это линия горизонта, дороги, молний и многие другие.
III. Открытие нового знания.
У:Перегните лист бумаги. Какая линия получится?
У:Где вам приходилось наблюдать в природе прямыелиниии?
У:С помощью какого инструмента мы строим прямые линии в тетради?
Д: Прямую линию можно построить с помощью линейки.
У:
Мне посоветовала мама,
Вести свою дорогу прямо.
Как сделать линию прямой
— Никак не получается.
Фломастер у меня хромой,
Или рука сбивается?
А вот с линейкой по листу
Так просто провести черту.
Смотрите, ровная какая,
Это линия – ПРЯМАЯ.
У: Ребята, попробуйте сформулировать определение прямой.
Д: Прямая линия бесконечна, изобразить всю прямуюневозможно.Эта линия без самопересечений. У неё нет ни начала, ни конца. Строится прямая линия с помощью линейки.
У: Кто знает, как обозначают прямую?
Д: Прямую обозначают двумя заглавными буквами латинского алфавита. Этими буквами обозначают две точки, через которые проходит прямая.
У: Правильно. А как ещё можно обозначить прямую?
Д: Прямую можно обозначать одной прописной буквой латинского алфавита.
У: Давайте проверим, как вы умеете выполнять задания и строить прямые. Какой инструмент вам потребуется для построения прямой линии?
Д: Линейка, карандаш.
У: Молодцы! Будьте внимательны. Возьмите в руки линейку и карандаш и точно выполните следующие задания.
У: Отметьте в тетради точку А. Проведите через точку А три прямых. Проведите через эту точку ещё одну прямую. Сколько таких прямых можно провести?
Д: Через одну точку можно провести очень много прямых.
У: Отметьте в тетради точки В и С. Проведите через эти точки прямую. Проведите через эти точки несколько других, отличных от первой, прямых. Сколько прямых можно провести через две точки?
Д: Через две точки можно провести только одну прямую.
У: Отметьте в тетради точки Р и К. Проведите через них прямую РК. Отметьте напрямой РК ещё три точки и обозначьте их М, N и Е. Какие геометрические фигуры получились?
Д: Получились отрезки.
У: Что такое отрезок?
Д: Отрезок – это часть прямой, у которой есть начало и конец.
У:Как обозначают отрезок?
Д: Отрезок обозначают двумя заглавными латинскими буквами.
У: Сколько отрезков получилось на рисунке? Запишите в тетради получившиеся отрезки.
У:Постройте прямую и отметьте на ней точку О. На какие фигуры разбила прямую точка О? Найдите в учебнике как называются эти части прямой?
Д: Точка О разбила прямую на лучи.
У: Сколько лучей с началом в точке О получилось?
Д: Получилось два луча.
У: Что такое луч?
Д: Луч – это часть прямой. У неё есть начало и нет конца. Луч можно продлить только в одну сторону.
У:О новой фигуре разносится весть: Конца в ней пусть нет, но начало-то есть! И солнце, тихонько взойдя из-за туч, Сказало: “Друзья! Назовем его луч!”
У: Найдите в учебнике как обозначают луч?
Д: Луч обозначают двумя заглавными буквами латинского алфавита. На первом месте всегда пишут обозначение начала луча.
У: Запишите все возможные обозначения лучей с началом в точке Р, в предыдущем задании.
У: Отметьте в тетради точки А, В, С, К, не лежащие на одной прямой. Соедините их по порядку. Какая линия получилась?
Д: Получилась кривая линия. Ломаная.
У:
Верно. Узри, что мир полон ломаных линий,
И чтобы увидеть прямые лучи,
Сумей провести чрез себя ту прямую,
Что свяжет земное с небесным в пути.
У: “Ломаная” — это продолжение темы урока. А поможет нам узнать о такой линии верный помощник – учебник.
У: Чем являются точки А, В, С, К – для ломаной? Прочитайте в учебнике.
Д: Эти точки – вершины ломаной.
У: Чем являются отрезки АВ, ВС, СК – для ломаной?
Д: Отрезки – это стороны или звенья ломаной.
IV. Практическая работа в парах
Выполняется работа с взаимопроверкой
У: Отметьте точку А и отсчитайте от неё 5 клеточек вправо и 4 клеточки вверх. Отметьте точку В и поведите отрезок АВ.
У: Отсчитайте от точки А 2 клетки влево и 3 клетки вверх. Отметьте точку С и проведите отрезок СВ.
У: Назовите построенную ломанную. Карандашом другого цвета проведите ещё какую-нибудь ломаную с вершинами в точках А, В и С. Назовите её.
У: Постройте ломаную из 2 звеньев. “Продиктуйте” её соседу по парте.
У: В некотором городке всего три попарно пересекающиеся прямолинейные улицы. На каждом перекрёстке установлен светофор. Сколько всего светофоров в этом городке? Было решено проложить новую улицу, пересекающую все старые и не проходящую через уже имеющиеся перекрёстки. Сколько придётся установить светофоров? А если прокладка улиц в городке будет продолжена таким же образом, можно ли сказать сколько будет светофоров в городке с 10 улицами?
Д: Всего 3 светофора.
Д: Если проложить ещё одну улицу, то нужно установить ещё 3 светофора.
Д: Если улиц будет 10, то светофоров – 45.
IV. Закрепление изученного.
У: Молодцы. Каждая пара успешно справилась со всеми заданиями. Ну а теперь покажите, что каждый из вас может справиться с заданиями самостоятельно.
Самостоятельная работа в рабочих тетрадях стр. 58 № 10, 11, 12 с последующей самопроверкой по слайдам. Ребята, допустившие ошибки при выполнении задания проговаривают, где они допустили ошибку, какую, почему.
№ 10. Постройте точки пересечения прямыхb, c и d. Обозначьте их. (Рисунок 1)
№ 11. Через точку пересечения прямых а и b проведите прямую с. (Рисунок 2)
№ 12. Проведите прямые АВ, ВС и АС. Проведите ещё одну прямую, пересекающую каждую из этих прямых. (Рисунок 3)
V. Итоги урока. Рефлексия.
- Что нового я сегодня узнал?
- Что мне понравилось на уроке?
- О чём я ещё хочу узнать?
- Что у меня получилось хорошо?
- Над чем мне ещё нужно поработать?
Информационные материалы:
- Дорофеев Г. В. Математика 5; учебник / Г. В. Дорофеев и др. — М.: Просвещение;
- Дорофеев Г. В. Математика 5; дидактические материалы / Г. В. Дорофеев и др.-М.: Просвещение;
- Буминович Е. А. Рабочая тетрадь/ Е. А. Буминович и др. – М.: Просещение;
- Интернет-ресурсы. Ребус. Приношу извинения автору – не запомнила сайт и автора. Большое спасибо за предоставленный материал.
Прямая. Части прямой. Ломаная. (5 класс)
Инфоурок › Математика ›Презентации›Презентация по математике на тему: Прямая. Части прямой. Ломаная. (5 класс)Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:3 сентября Классная работа Тема урока: 1.2 Прямая. Части прямой. Ломаная. Прямая. Отрезок и луч.
2 слайд Описание слайда:
Описание слайда:Устная работа Как можно разложить в две коробки 11 карандашей? В двух корзинах 20 белых грибов. Сколько грибов может оказаться в каждой корзине? В классе 9 мальчиков и 16 девочек. Сколько всего учеников в классе? У продавца было 23 кг орехов. Он продал 18 кг. Сколько килограммов орехов у него осталось?
3 слайд Описание слайда:
Описание слайда:Устная работа какая линия является самой важной на плоскости? 700+350 — А 900+420 — Р 1200-700 — К 220-800 — Я 1300+800 — М 1500-600 — О 750+410 — Я 1700 1320 1160 2100 1050 1400
4 слайд Описание слайда:
Описание слайда:Изучение нового материала Построение прямой. Определение прямой. Прямая – незамкнутая линия, неограниченно продолжается в обе стороны. Проводя прямую, мы показываем лишь ее часть.
5 слайд Описание слайда:
Описание слайда:Изучение нового материала 3. Обозначение прямой.
6 слайд Описание слайда:
Описание слайда:Изучение нового материала 4. Практическая работа. 1) Постройте прямую k. Отметьте на прямой точки А, В, D. Отметьте точки М и С, не лежащие на прямой k. Сколько существует точек, лежащих на прямой k ? Не принадлежащих прямой k? Сделайте вывод. 2) Отметьте точку О. Проведите через точку О прямую а. Проведите через точку О прямую b. Сколько прямых можно провести через точку о? Сделайте вывод. 3) Отметьте точки А и В. Проведите через них прямую. Сколько прямых можно провести через две данные точки? Сделайте вывод.
7 слайд Описание слайда:
Описание слайда:Изучение нового материала 5. Понятие луча. На прямой АВ отметим точку О. Эта точка делит прямую на две части. Каждую из них называют лучом. Луч – часть прямой, ограниченная с одной стороны. Обозначают лучи, так же как и прямые двумя буквами, но в отличие от прямой тут важен порядок, на первое место всегда ставят начало луча, а на второе любую точку этого луча.
8 слайд Описание слайда:
Описание слайда:Изучение нового материала Сколько лучей на данном рисунке? Подсказка: Каждая точка – это начало двух лучей
9 слайд Описание слайда:
Описание слайда:Изучение нового материала 6. Понятие отрезка. На прямой k отметим две точки А и В. Часть прямой, ограниченная данными точками, называется отрезком. Отрезок обозначают так : АВ или ВА.
10 слайд Описание слайда:
Описание слайда:Изучение нового материала Отрезок – часть прямой, ограниченная с двух сторон.
11 слайд Описание слайда:
Описание слайда:Физкультминутка
12 слайд Описание слайда:
Описание слайда:Закрепление изученного материала Учебник № 15 № 16 № 17 № 18 № 23 № 25
13 слайд Описание слайда:
Описание слайда:Домашнее задание Учебник – п. 1.2 прочитать. Рабочая тетрадь — № 9, 10, 11, 12, 13.

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-129803
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийКонспект урока»геометрические линии и фигуры Прямая, кривая,ломаная, отрезок»(7 класс)
Конспект урока по математике. Класс 7. Дата ____________
Тема: Геометрические линии и фигуры: прямая, кривая, ломаная, отрезок, луч.
Цель: формирование у учащихся знаний о разновидностях линий.
Задачи:
– учить различать прямую, кривую, луч и ломаную линии;
– формировать умение чертить разные виды линий;
– развивать память, логическое мышление, воображение, внимание, мелкую моторику;
– воспитывать аккуратность при работе.
Ход урока
Приветствие, проверка готовности к уроку
Посмотрите внимательно на картинку, что вы видите? Правильно, все линии и они очень разные. Сегодня на уроке мы узнаем, как называется каждая из этих линий. Тема урока: «Линии. Прямая, кривая, ломаная, луч».
На столах у каждого лежит веревочка, возьмите ее и бросьте на стол, скажите, она похожа на линию? А на какую линию? Правильно получилась кривая линия.
Начертите кривую линию в своей тетради и назовите ее. А теперь снова возьмите веревочку и натяните ее, и у нас получилась прямая линия.
Так же начертите и подпишите. Из этой веревочки могут получаться любые линии, например ломаная. Посмотрите, какая линия ломаная и сделайте ее из своих веревочек.
Теперь занесите результат в тетрадь. Посмотрите внимательно, чем отличается кривая линия от ломаной. Ломаная линия состоит из палочек, отрезков, полосок. Они должны быть под углом, они образуют угол. – Теперь снова вытяните веревочку. У прямой линии нет конца, а если мы возьмем ножницы и разрежем прямую в двух местах, то у нас получится отрезок. У нас получился отрезок прямой и два луча. Это луч, луч имеет только начало.
Физ минутка.
Топай, Мишка,
Хлопай, Мишка.
Приседай со мной, братишка.
Руки вверх, вперед и вниз.
Улыбайся и садись.
Уч. Стр 69 № 218, 219,220
Физ минутка для глаз.
Конспект по организации образовательной деятельности «Линия: прямая, кривая, ломаная».
Направление
«Дошкольное и дополнительное образование»
Сапрыкина Ольга Юрьевнавоспитатель дошкольной группы МАОУ «Лабазинская средняя общеобразовательная школа» Курманаевского района Оренбургской области
Конспект по организации образовательной деятельности
«Линия: прямая, кривая, ломаная».
2.Методы и приёмы реализации содержания ОД
Сюрпризный момент — сказочный гость, проблемная ситуация, загадки, беседа, рассказ воспитателя в сопровождении мультимедийной презентации, продуктивная работа детей,
динамическая пауза под музыкальное сопровождение, игра – перевоплощение.
3.
Интеграция образовательных областей.
«Социально-коммуникативное развитие», «Познавательное развитие» (формирование целостной картины мира), «Физическое развитие», «Художественное творчество».
4.
Вид детской деятельности.
-игровая;
-коммуникативная;
-двигательная;
-продуктивная;
-предпосылки учебной деятельности.
5.
Возрастная группа.
Подготовительная.
6.
Цель
развитие интеллектуально-творческих способностей детей через освоение ими логико-математических представлений и способов познания.
6.1
Задачи воспитания
Приобщать к культуре общения.
Воспитывать доброжелательное отношение друг к другу.
Прививать интерес к играм, требующим умственного напряжения, интеллектуального усилия;
Способствовать стремлению к достижению положительного результата, настойчивости и находчивости.
Воспитывать чувство товарищества, взаимопомощи и сотрудничества.
6.2
Задачи развития
Развивать воображение, эмпатию, креативность мышления (умение гибко, оригинально мыслить);
логическое мышление, внимание, конструктивные способности.
6.3
Задачи обучения
Повторить с детьми названия основных плоских и объёмных геометрических тел: круг, квадрат, прямоугольник, треугольник, трапеция, шар, сфера, куб, цилиндр, пирамида, конус.
Познакомить детей с понятием линия, её видами; упражнять в использовании линейки как предмета для проведения прямых линий.
7
Планируемые результаты
Сформированность интегративных качеств личности ребёнка.
7.1
Личностные
Овладевший средствами общения и способами взаимодействия со взрослыми и сверстниками:
-Любознательный, активный;
— эмоционально отзывчивый;
-способный управлять своим поведением и планировать свои действия;
-соблюдающий элементарные общепринятые нормы и правила поведения;
-способный к совместному творчеству.
7.2
Интеллектуальные
Овладевший необходимыми умениями и навыками в образовательной области «Познание» (формирование элементарных математических представлений):
-знаком с плоскими геометрическими фигурами: точкой, различными линиями, квадратом, кругом, треугольником, прямоугольником, овалом; объемными телами: шаром, кубом, цилиндром, параллелепипедом, конусом, пирамидой.
-умеет группировать предметы и фигуры по признаку формы; определять форму окружающих предметов; видоизменять фигуры;
создавать модели предметов из геометрических фигур.
7.3
Физические
Овладевший необходимыми умениями и навыками в образовательной области «Физическая культура»:
— имеет физическое развитие, соответствующее возрастным нормативным показателям; у него сформированы основные физические качества, потребность в физической активности, движении
8.
Организация среды для проведения образовательной деятельности
Герой «Волшебный Карандаш», дверь разрезная с 9 секторами, набор плоских и объёмных геометрических фигур, плакаты с изображением различных видов линий, геометрических фигур; линейки, проволока.
9.
Подготовка к образовательной деятельности в режимные моменты.
-Поиск геометрических фигур в окружающей обстановке на улице и в помещении;
-Поиск геометрических фигур в произведениях искусства;
-Рисование картин из разных геометрических фигур, линий;
-Просмотр забавных мультфильмов про точку, линии;
-Заучивание стихотворений и загадок про геометрические фигуры;
— игра «Узнай фигуры на ощупь»; настольная игра «Геометрическая мозаика».
-изготовление поделок из геометрических тел.
Сценарий образовательной деятельности.
1
Вводная часть
1.1
Введение в тему (сюрпризный момент)
Ребята, у меня для вас СЮРПРИЗ! К нам сегодня КТО-ТО пришёл в гости. Он прячется вот за этой дверью (на доске прикреплено изображение двери, разрезанное на 9 пронумерованных квадратов, за которым «спрятался» Волшебный карандаш).
1.2
Мотивация деятельности детей
(проблемная ситуация)
Воспитатель: Гость сказал, что дверь волшебная, и откроется только тем, кто сможет отгадать трудные загадки.
1.3
Целеполагание
(с помощью педагога дети формулируют цель своей деятельности).
Воспитатель: Что же нам делать? Как открыть эту дверь?
Дети: постараемся отгадать.
Воспитатель: Ребята, я верю, что вы справитесь с заданиями, и мы скоро увидим таинственного гостя!
2.
Основная часть.
Актуализация ранее приобретённых знаний
Каждая отгаданная загадка будет приоткрывать нам девятую часть двери. Слушайте загадку №1:
1.
Нет углов у меня
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья?
Назовите вы меня! Круг.
(Воспитатель после каждого правильного ответа демонстрирует геометрическую фигуру, чтобы повторить отличительные свойства каждой, и снимает квадрат с номером ).
2.
Три моих стороны
Могут разной быть длины.
Где стороны встречаются –
Угол получается.
Что же вышло? Посмотри!
Ведь углов-то тоже три.
На меня вы посмотрите,
Мое имя назовите. Треугольник.
3.
Четыре угла и четыре сторонки,
Похожи точно родные сестренки.
В ворота его не закатишь, как мяч,
И он за тобою не пустится вскачь.
Фигура знакома для многих ребят.
Его вы узнали? Ведь это … Квадрат.
4.
Вы подумайте, скажите …
Только помнить вы должны:
Стороны фигуры этой
Противоположные равны. Прямоугольник.
5.
Треугольник подпилили
И фигуру получили:
Два тупых угла внутри
И два острых – посмотри.
Не квадрат, не треугольник,
А похож на многоугольник. Трапеция.
6.
Как его нам не вертеть
Равных граней ровно шесть.
С ним в лото сыграть мы сможем,
Только будем осторожны:
Он не ласков и не груб,
Потому что это… куб.
7.
Вновь беремся мы за дело,
Изучаем снова тело:
Может мячиком он стать
И немного полетать.
Очень круглый, не овал.
Догадались? Это… шар..
8.
Египтяне их сложили
И так ловко смастерили,
Что стоят они веками.
Догадайтесь, дети, сами
Что же это за тела,
Где вершина всем видна?
Догадались? Из-за вида
Всем известна… пирамида.
9.
Присмотрись, стоит ведро —
Сверху крышка, снизу дно.
Два кружка соединили
И фигуру получили.
Как же тело называть?
Надо быстро отгадать. Цилиндр.
Воспитатель: Молодцы, ребята, вы справились!
Поздороваемся с гостем! Кто это? Правильно, волшебный карандаш!
-Как вы думаете, откуда он к нам пришёл? (Дети: из волшебной страны, где живут геометрические фигуры).
Воспитатель: Как называется такая страна? (Дети: Геометрия).
Динамическая пауза.
Воспитатель:
-Ребята, карандаш очень устал стоять за дверью, он хочет размяться и потанцевать. Потанцуем вместе с ним?
Звучит «Песенка весёлого карандаша», воспитатель показывает движения, а дети повторяют.
Добывание (сообщение и приятие нового знания)
Весёлый карандаш: Молодцы, ребята! Вы угадали, я из страны Геометрия. Много геометрических фигур вы знаете, да только обидно мне, что не знакомы вы с моей маленькой подружкой- точкой. А ведь она раньше всех появилась в стране Геометрия! А знакомы ли вы с линиями? (отрицательные ответы детей). Буду рад вас с ними познакомить.
Но прежде расскажу историю: сначала грустную, а потом очень весёлую. Хотите послушать? Ну слушайте!
1. Мультимедийная презентация темы: «Линия: прямая, кривая, ломаная»:
«Сказка о точке и карандаше».
Однажды налетел сильный ураган, и я оказался в странном месте. Это была белая пустыня, следовательно, вокруг было пусто. И вот тут я услышал тихий детский плач. Я посмотрел вокруг – никого. А когда наклонился к ногам, то увидел рядом маленькую точку. (Слайд 2)
Я спросил её, почему она плачет. Точка ответила, что ей ужасно одиноко. У неё нет ни мамы, ни папы, ни бабушек с дедушками, ни подруг.
Я задумался, как же ей помочь.
-Ребята, а что сделали бы вы в этом случае? (варианты ответов).
Молодцы! А я в тот момент придумал вот что (Слайд 3): нарисовал ей подружку, а потом провел под ними линию, чтобы точкам можно было бегать по ней и играть в салочки, догонялки, бегать наперегонки.
— Вы любите эти игры? (Да!)
Так в стране геометрия помимо одинокой точки, появилась другая точка и линия.
-Ребята, посмотрите, какая она? (Дети: прямая). Верно, у неё нет ни начала, ни конца. Она бесконечна. Поэтому подружки – точки бегали по ней, бегали, играли –играли …
Потом им стало скучно и неинтересно. Они попросили новых подружек и дорожку, но не прямую, а извилистую, кривую. Я выполнил их просьбу и нарисовал….. (Слайд 4). Что это? (Линия). Какая?
Так появилась новая жительница страны Геометрии — Кривая линия.
Точки были в восторге. Они вместе со мной начали прыгать из стороны в сторону. (Слайд 5). И я неожиданно для себя начертил ещё одну линию. Кто догадается, как она называется? Ломаная! Кажется, будто прямую переломили в разных местах, и вот что получилось!
А потом я решил населить страну Геометрию другими фигурами. Догадайтесь, какая это фигура? (Слайды 6,7,8,9).
Теперь в стране Геометрия проживает много разных фигур, и они приглашают нас к себе в гости.
Физминутка «Превращения»
Ребята, а вы любите волшебство? Я знаю волшебные слова, при помощи которых дети превратятся в наших новых знакомых! С какими геометрическими фигурами мы познакомились на занятии? (Точка, прямая, кривая, ломаная).
Итак, произносим волшебные слова: «Волшебство скорей явись – каждый в точку (прямую, кривую, ломаную) превратись! (дети садятся на корточки, обхватывают колени руками, головы прижимают к коленям – это точки). Затем изображают прямую, кривую и ломаную.
Закрепление нового материала
Игра «Угадай фигуру» (на закрепление)
Продуктивная деятельность (индивидуальная и групповая работа)
Ребята, у меня в руках чудесная проволочка. Я могу из неё складывать разные геометрические фигуры. Угадайте, что это? (прямая, кривая, ломаная).
Воспитатель: Ребята, карандаш хочет научить своих братьев рисовать так же, как и он? Поможем ему? Тогда возьмите карандаши и повторяйте за мной (на доске и на листочках рисуем точку). Держите карандаши правильно, чтобы они вас слушались. Иначе получится не так, как надо. Давайте проведём прямую линию через эту точку (дети на листочках чертят от руки линию) Покажите друг другу, что у вас получилось. Это прямая линия или нет? (всё криво, не ровно).
Но что же нам поможет начертить прямую линию? (линейка). Воспитатель показывает, как начертить при помощи линейки прямую на доске.
А теперь вы начертите прямую на листочках. Покажите, что у вас получилось.
От руки начертим кривую.
А ломаную изобразим при помощи счётных палочек. Посоветуйтесь друг с другом и придумайте, как это сделать (работа в группах.)
Карандаш с воспитателем проходит и смотрит. Что у ребят получилось.
3.
Итог ОД.
Ребята, Весёлый карандаш очень рад, что вы научили его младших братьев рисовать точки и проводить линии.
Пусть похлопают в ладоши те ребята, чьи карандаши сумели начертить прямую линию.
А теперь потопают ножками те, у кого отлично получилась кривая.
А теперь пожмут друг другу руки те группы, которые правильно сложили из палочек ломаную.


