Рациональная функция — Википедия
Материал из Википедии — свободной энциклопедии
 Пример рациональной функции от одной переменной: f(x)=x2−3x−2×2−4{\displaystyle f(x)={\frac {x^{2}-3x-2}{x^{2}-4}}}
Пример рациональной функции от одной переменной: f(x)=x2−3x−2×2−4{\displaystyle f(x)={\frac {x^{2}-3x-2}{x^{2}-4}}} 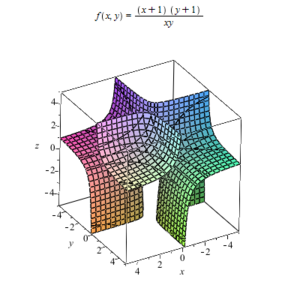 Пример рациональной функции от двух переменных
Пример рациональной функции от двух переменныхРациональная функция — это функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются многочлены. К этому виду может быть приведено любое рациональное выражение[⇨], то есть алгебраическое выражение, без радикалов.
Рациональной функцией называется функция вида
- Pn(x1,…,xn)Qm(x1,…,xm){\displaystyle {\frac {P_{n}(x_{1},\dots ,x_{n})}{Q_{m}(x_{1},\dots ,x_{m})}}}
где Pn(x1,…,xn){\displaystyle P_{n}(x_{1},\dots ,x_{n})}, Qm(x1,…,xm){\displaystyle Q_{m}(x_{1},\dots ,x_{m})} — многочлены от любого числа переменных.
Такая функция определена во всех точках, кроме тех, в которых знаменатель Qm(x1,…,xm){\displaystyle Q_{m}(x_{1},\dots ,x_{m})} обращается в ноль.
Частным случаем являются рациональные функции одной переменной:
- R(x)=P(x)Q(x){\displaystyle R(x)={\frac {P(x)}{Q(x)}}}, где P(x){\displaystyle P(x)} и Q(x){\displaystyle Q(x)} — многочлены.
Другим частным случаем является отношение двух линейных функций — дробно-линейная функция.
Рациональное выражение[править | править код]
Рациональное выражение — алгебраическое выражение, не содержащее радикалов. Другими словами, это одна или несколько алгебраических величин (чисел и переменных), соединённых между собой знаками арифметических действий: сложения, вычитания, умножения и деления, возведения в целую степень и знаками последовательности этих действий (обычно скобками различного вида).
Например:
- x+x−1{\displaystyle x+x^{-1}}
- xy−z−3{\displaystyle {\frac {x}{y-z^{-3}}}}
Любое рациональное выражение может быть приведено к виду рациональной функции.
Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если это не так.
Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби
Pn(x)Qm(x)=Pn−m′(x)+Pm−1″(x)Qm(x){\displaystyle {\frac {P_{n}(x)}{Q_{m}(x)}}=P’_{n-m}(x)+{\frac {P_{m-1}^{»}(x)}{Q_{m}(x)}}}
Любую рациональную дробь многочленов с вещественными коэффициентами можно представить как сумму рациональных дробей, знаменателями которых являются выражения (x−a)k{\displaystyle (x-a)^{k}} (a{\displaystyle a} — вещественный корень Q(x){\displaystyle Q(x)}) либо (x2+px+q)k{\displaystyle (x^{2}+px+q)^{k}} (где x2+px+q{\displaystyle x^{2}+px+q} не имеет действительных корней), причём степени k{\displaystyle k} не больше кратности соответствующих корней в многочлене Q(x){\displaystyle Q(x)}. На основании этого утверждения основана теорема об интегрируемости рациональной дроби. Согласно ей, любая рациональная дробь может быть интегрирована в элементарных функциях, что делает класс рациональных дробей весьма важным в математическом анализе.
C этим связан метод выделения рациональной части в первообразной от рациональной дроби, который был предложен в 1844 году М. В. Остроградским[1].
- ↑ M. Ostrogradsky. De l’intégration des fractions rationnelles. — Bulletin de la classe physico-mathématique de l’Académie impériale des sciences de Saint-Pétersbourg. — 1845. — Vol. IV. — Col. 145—167, 286—300.
Рациональное выражение — это… Что такое Рациональное выражение?
- Резольвента
- Пресная вода
Смотреть что такое «Рациональное выражение» в других словарях:
РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., a2 + b, x/(y z2) … Большой Энциклопедический словарь
рациональное выражение — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Например, a2 + b, х/(у z2). * * * РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ, алгебраическое выражение, не содержащее… … Энциклопедический словарь
Рациональное выражение — алгебраическое выражение, не содержащее радикалов, например a2 + b, х/(у z3). Если входящие в Р. в. буквы считать переменными, то Р. в. задаёт рациональную функцию (См. Рациональная функция) от этих переменных … Большая советская энциклопедия
РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебрарическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., а2 + b, х/(y z2) … Естествознание. Энциклопедический словарь
ВЫРАЖЕНИЕ — первичное математическое понятие, под которым подразумевают запись из букв и чисел, соединённых знаками арифметических действий, при этом могут быть использованы скобки, обозначения функций и т.п.; обычно В формула млн. её часть. Различают В (1)… … Большая политехническая энциклопедия
РАЦИОНАЛЬНОЕ — (Rational; Rational) термин, используемый для описания мыслей, чувств и действий, согласуемых с разумом; установка, базирующаяся на объективных ценностях, полученных в результате практического опыта.«Объективные ценности устанавливаются в опыте… … Словарь по аналитической психологии
РАЦИОНАЛЬНОЕ ПОЗНАНИЕ — субъективный образ объективного мира,полученный с помощью мышления. Мышление – активный процесс обобщенного и опосредованного отражения действительности, обеспечивающий открытие на основе чувственных данных ее закономерных связей и их выражение … Философия науки и техники: тематический словарь
УРАВНЕНИЕ, РАЦИОНАЛЬНОЕ — Логическое или математическое выражение, основанное на (рациональных) предположениях о процессах. Такие уравнения отличаются от эмпирических уравнений тем, что их параметры получаются в результате дедуктивных выводов из теоретических… … Толковый словарь по психологии
РАЦИОНАЛЬНЫЙ — РАЦИОНАЛЬНЫЙ, рациональная, рациональное; рационален, рациональна, рационально. 1. прил. к рационализм (книжн.). Рациональная философия. 2. Вполне разумный, обоснованный, целесообразный. Он внес рациональное предложение. Рациональное… … Толковый словарь Ушакова
РЕЗОЛЬВЕНТА — 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения… … Математическая энциклопедия
Рациональные выражения. Общая теория.
Рациональные выражения.
! Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
Например
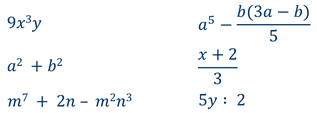
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Например
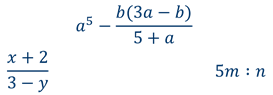
Целые и дробные выражения называют рациональными выражениями.

! Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Например

Напомним, что целые выражения имеют смысл при любых значениях переменных.
! Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.
Дробное выражение при некоторых значениях переменных может не иметь смысла.
Например
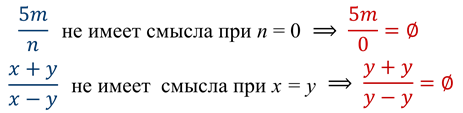
Чтобы найти значение рационального выражения, надо:
1) подставить числовое значение переменной в данное выражение;
2) выполнить все действия.
!Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.
Как вы уже знаете, выражение вида  называется дробью.
называется дробью.
Дробь, числитель и знаменатель которой многочлены, называют
Например
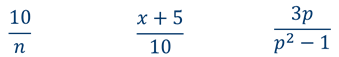
Итоги:
Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Чтобы найти значение рационального выражения, надо:
1) Подставить числовое значение переменной в данное выражение;
2) Выполнить все действия.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.
Преобразование рациональных выражений
Рациональные выражения и дроби — краеугольный пункт всего курса алгебры. Те, кто научатся работать с такими выражениями, упрощать их и раскладывать на множители, по сути смогут решить любую задачу, поскольку преобразование выражений — неотъемлемая часть любого серьёзного уравнения, неравенства и даже текстовой задачи.
В этом видеоуроке мы посмотрим, как грамотно применять формулы сокращённого умножения для упрощения рациональных выражений и дробей. Научимся видеть эти формулы там, где, на первый взгляд, ничего нет. Заодно повторим такой нехитрый приём, как разложение квадратного трёхчлена на множители через дискриминант.
Как вы уже наверняка догадались по формулам за моей спиной, сегодня мы будем изучать формулы сокращенного умножения, а, точнее, не сами формулы, а их применение для упрощения и сокращения сложных рациональных выражений. Но, прежде чем переходить к решению примеров, давайте познакомимся ближе с этими формулами или вспомним их:
- ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$ — разность квадратов;
- ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ — квадрат суммы;
- ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$ — квадрат разности;
- ${{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)$ — сумма кубов;
- ${{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)$ — разность кубов.
Еще хотел бы отметить, что наша школьная система образования устроена таким образом, что именно с изучением этой темы, т.е. рациональных выражений, а также корней, модулей у всех учеников возникает одна и та же проблема, которую я сейчас объясню.
Дело в том, что в самом начале изучения формул сокращенного умножения и, соответственно, действий по сокращению дробей (это где-то 8 класс) учителя говорят что-то следующее: «Если вам что-то непонятно, то вы не переживайте, мы к этой теме еще вернемся неоднократно, в старших классах так точно. Мы это еще разберем». Ну а затем на рубеже 9-10 класса те же самые учителя объясняют тем же самым ученикам, которые так и не знают, как решать рациональные дроби, примерно следующее: «А где вы были предыдущие два года? Это же изучалось на алгебре в 8 классе! Чего тут может быть непонятного? Это же так очевидно!».
Однако обычным ученикам от таких объяснений нисколько не легче: у них как была каша в голове, так и осталась, поэтому прямо сейчас мы разберем два простых примера, на основании которых и посмотрим, каким образом в настоящих задачах выделять эти выражения, которые приведут нас к формулам сокращенного умножения и как потом применять это для преобразования сложных рациональных выражений.
Сокращение простых рациональных дробей
Задача № 1
\[\frac{4x+3{{y}^{2}}}{9{{y}^{4}}-16{{x}^{2}}}\]
Первое, чему нам нужно научиться — выделять в исходных выражениях точные квадраты и более высокие степени, на основании которых мы сможем потом применять формулы. Давайте посмотрим:
\[9{{y}^{4}}={{3}^{2}}\cdot {{y}^{4}}={{3}^{2}}\cdot {{\left( {{y}^{2}} \right)}^{2}}={{\left( 3{{y}^{2}} \right)}^{2}}\]
\[16{{x}^{2}}={{2}^{4}}\cdot {{x}^{2}}={{\left( {{2}^{2}} \right)}^{2}}\cdot {{x}^{2}}={{\left( {{2}^{2}}\cdot x \right)}^{2}}={{\left( 4{{x}^{2}} \right)}^{2}}\]
Перепишем наше выражение с учетом этих фактов:
\[\frac{4x+3{{y}^{2}}}{{{\left( 3{{y}^{2}} \right)}^{2}}-{{\left( 4x \right)}^{2}}}=\frac{4x+3{{y}^{2}}}{\left( 3{{y}^{2}}-4x \right)\left( 3{{y}^{2}}+4x \right)}=\frac{1}{3{{y}^{2}}-4x}\]
Ответ: $\frac{1}{3{{y}^{2}}-4x}$.
Задача № 2
Переходим ко второй задаче:
\[\frac{8}{{{x}^{2}}+5xy-6{{y}^{2}}}\]
Упрощать тут нечего, потому что в числителе стоит константа, но я предложил эту задачу именно для того, чтобы вы научились раскладывать на множители многочлены, содержащие две переменных. Если бы вместо него был написанный ниже многочлен, как бы мы разложили его?
\[{{x}^{2}}+5x-6=\left( x-… \right)\left( x-… \right)\]
Давайте решим уравнение и найдем $x$, которые мы сможем поставить вместо точек:
\[{{x}^{2}}+5x-6=0\]
\[D=25-4\cdot \left( -6 \right)=25+24=49\]
\[\sqrt{D}=7\]
\[{{x}_{1}}=\frac{-5+7}{2}=\frac{2}{2}=1\]
\[{{x}_{2}}=\frac{-5-7}{2}=\frac{-12}{2}=-6\]
Мы можем переписать трехчлен следующим образом:
\[{{x}^{2}}+5xy-6{{y}^{2}}=\left( x-1 \right)\left( x+6 \right)\]
С квадратным трехчленом мы работать научились — для этого и нужно было записать этот видеоурок. А что делать, если кроме $x$ и константы присутствует еще $y$? Давайте рассмотрим их как еще одни элементы коэффициентов, т.е. перепишем наше выражение следующим образом:
\[{{x}^{2}}+5y\cdot x-6{{y}^{2}}\]
\[a=1;b=5y;c=-6{{y}^{2}}\]
\[D={{\left( 5y \right)}^{2}}-4\cdot \left( -6{{y}^{2}} \right)=25{{y}^{2}}+24{{y}^{2}}=49{{y}^{2}}\]
\[\sqrt{D}=7y\]
\[{{x}_{1}}=\frac{-5y+7y}{2}=y\]
\[{{x}_{2}}=\frac{-5y-7y}{2}=\frac{-12y}{2}=-6y\]
Запишем разложение нашей квадратной конструкции:
\[\left( x-y \right)\left( x+6y \right)\]
Итого если мы вернемся к исходному выражению и перепишем его с учетом изменений, то получим следующее:
\[\frac{8}{\left( x-y \right)\left( x+6y \right)}\]
Что нам дает такая запись? Ничего, потому что его не сократить, оно ни на что не умножается и не делится. Однако как только эта дробь окажется составной частью более сложного выражения, подобное разложение окажется кстати. Поэтому как только вы видите квадратный трехчлен (неважно, отягощен он дополнительными параметрами или нет), всегда старайтесь разложить его на множители.
Нюансы решения
Запомните основные правила преобразования рациональных выражений:
- Все знаменатели и числители необходимо раскладывать на множители либо через формулы сокращенного умножения, либо через дискриминант.
- Работать нужно по такому алгоритму: когда мы смотрим и пытаемся выделить формулу сокращенного умножения, то, прежде всего, пытаемся все перевести в максимально возможную степень. После этого выносим за скобку общую степень.
- Очень часто будут встречаться выражения с параметром: в качестве коэффициентов будут возникать другие переменные. Их мы находим по формуле квадратного разложения.
Таким образом, как только вы видите рациональные дроби, первое, что нужно сделать — это разложить и числитель, и знаменатель на множители (на линейные выражения), при этом мы используем формулы сокращенного умножения или дискриминант.
Давайте посмотрим на пару таких рациональных выражений и попробуем их разложить на множители.
Решение более сложных примеров
Задача № 1
\[\frac{4{{x}^{2}}-6xy+9{{y}^{2}}}{2x-3y}\cdot \frac{9{{y}^{2}}-4{{x}^{2}}}{8{{x}^{3}}+27{{y}^{3}}}\]
Переписываем и стараемся разложить каждое слагаемое:
\[4{{x}^{2}}={{2}^{2}}\cdot {{x}^{2}}={{\left( 2x \right)}^{2}}\]
\[6xy=2\cdot 3\cdot x\cdot y=2x\cdot 3y\]
\[9{{y}^{2}}={{3}^{2}}\cdot {{y}^{2}}={{\left( 3y \right)}^{2}}\]
\[8{{x}^{3}}={{2}^{3}}\cdot {{x}^{3}}={{\left( 2x \right)}^{3}}\]
\[27{{y}^{3}}={{3}^{3}}\cdot {{y}^{3}}={{\left( 3y \right)}^{3}}\]
Давайте перепишем все наше рациональное выражение с учетом этих фактов:
\[\frac{{{\left( 2x \right)}^{2}}-2x\cdot 3y+{{\left( 3y \right)}^{2}}}{2x-3y}\cdot \frac{{{\left( 3y \right)}^{2}}-{{\left( 2x \right)}^{2}}}{{{\left( 2x \right)}^{3}}+{{\left( 3y \right)}^{3}}}=\]
\[=\frac{{{\left( 2x \right)}^{2}}-2x\cdot 3y+{{\left( 3y \right)}^{2}}}{2x-3y}\cdot \frac{\left( 3y-2x \right)\left( 3y+2x \right)}{\left( 2x+3y \right)\left( {{\left( 2x \right)}^{2}}-2x\cdot 3y+{{\left( 3y \right)}^{2}} \right)}=-1\]
Ответ: $-1$.
Задача № 2
\[\frac{3-6x}{2{{x}^{2}}+4x+8}\cdot \frac{2x+1}{{{x}^{2}}+4-4x}\cdot \frac{8-{{x}^{3}}}{4{{x}^{2}}-1}\]
Давайте рассмотрим все дроби.
Первая:
\[3-6x=3\left( 1-2x \right)\]
\[2{{x}^{2}}+4x+8=2\left( {{x}^{2}}+2x+{{2}^{2}} \right)\]
Вторая:
\[{{x}^{2}}+4-4x={{x}^{2}}-4x+2={{x}^{2}}-2\cdot 2x+{{2}^{2}}={{\left( x-2 \right)}^{2}}\]
Третья:
\[8-{{x}^{3}}={{2}^{3}}-{{x}^{3}}=\left( 2-x \right)\left( {{2}^{2}}+2x+{{x}^{2}} \right)\]
\[4{{x}^{2}}-1={{2}^{2}}\cdot {{x}^{2}}-{{1}^{2}}={{\left( 2x \right)}^{2}}-{{1}^{2}}=\left( 2x-1 \right)\left( 2x+1 \right)\]
Перепишем всю конструкцию с учетом изменений:
\[\frac{3\left( 1-2x \right)}{2\left( {{x}^{2}}+2x+{{2}^{2}} \right)}\cdot \frac{2x+1}{{{\left( x-2 \right)}^{2}}}\cdot \frac{\left( 2-x \right)\left( {{2}^{2}}+2x+{{x}^{2}} \right)}{\left( 2x-1 \right)\left( 2x+1 \right)}=\]
\[=\frac{3\cdot \left( -1 \right)}{2\cdot \left( x-2 \right)\cdot \left( -1 \right)}=\frac{3}{2\left( x-2 \right)}\]
Ответ: $\frac{3}{2\left( x-2 \right)}$.
Нюансы решения
Итак, чему мы только что научились:
- Далеко не каждый квадратный трехчлен раскладывается на множители, в частности, это относится к неполному квадрату суммы или разности, которые очень часто встречаются как части кубов суммы или разности.
- Константы, т.е. обычные числа, не имеющие при себе переменных, также могут выступать активными элементами в процессе разложения. Во-первых, их можно выносить за скобки, во-вторых, сами константы могут быть представимы в виде степеней.
- Очень часто после разложения всех элементов на множители возникают противоположные конструкции. Сокращать эти дроби нужно крайне аккуратно, потому что при из зачеркивании либо сверху, либо снизу возникает дополнительный множитель $-1$ — это как раз и есть следствие того, что они противоположны.
Решение сложных задач
\[\frac{27{{a}^{3}}-64{{b}^{3}}}{{{b}^{2}}-4}:\frac{9{{a}^{2}}+12ab+16{{b}^{2}}}{{{b}^{2}}+4b+4}\]
Рассмотрим каждое слагаемое отдельно.
Первая дробь:
\[27{{a}^{3}}={{3}^{3}}\cdot {{a}^{3}}={{\left( 3a \right)}^{3}}\]
\[64{{b}^{3}}={{2}^{6}}\cdot {{b}^{3}}={{\left( {{2}^{2}} \right)}^{3}}\cdot {{b}^{3}}={{\left( {{2}^{2}}\cdot b \right)}^{3}}={{\left( 4b \right)}^{3}}\]
\[{{\left( 3a \right)}^{3}}-{{\left( 4b \right)}^{3}}=\left( 3a-4b \right)\left( {{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}} \right)\]
\[{{b}^{2}}-{{2}^{2}}=\left( b-2 \right)\left( b+2 \right)\]
Вторая:
\[9{{a}^{2}}={{3}^{2}}\cdot {{a}^{2}}={{\left( 3a \right)}^{2}}\]
\[16{{b}^{2}}={{4}^{2}}\cdot {{b}^{2}}={{\left( 4b \right)}^{2}}\]
\[12ab=3\cdot 4ab=3a\cdot 4b\]
Весь числитель второй дроби мы можем переписать следующим образом:
\[{{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}}\]
Теперь посмотрим на знаменатель:
\[{{b}^{2}}+4b+4={{b}^{2}}+2\cdot 2b+{{2}^{2}}={{\left( b+2 \right)}^{2}}\]
Давайте перепишем все рациональное выражение с учетом вышеизложенных фактов:
\[\frac{\left( 3a-4b \right)\left( {{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}} \right)}{\left( b-2 \right)\left( b+2 \right)}\cdot \frac{{{\left( b+2 \right)}^{2}}}{{{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}}}=\]
\[=\frac{\left( 3a-4b \right)\left( b+2 \right)}{\left( b-2 \right)}\]
Ответ: $\frac{\left( 3a-4b \right)\left( b+2 \right)}{\left( b-2 \right)}$.
Нюансы решения
Как мы еще раз убедились, неполные квадраты суммы либо неполные квадраты разности, которые часто встречаются в реальных рациональных выражениях, однако не стоит их пугаться, потому что после преобразования каждого элемента они практически всегда сокращаются. Кроме того, ни в коем случае не стоит бояться больших конструкций в итогом ответе — вполне возможно, что это не ваша ошибка (особенно, если все разложено на множители), а это автор задумал такой ответ.
В заключение хотелось бы разобрать еще один сложных пример, который уже не относится напрямую к рациональным дробям, однако он содержит все то, что ждет вас на настоящих контрольных и экзаменах, а именно: разложение на множители, приведение к общему знаменателю, сокращение подобных слагаемых. Вот именно этим мы сейчас и займемся.
Решение сложной задачи на упрощение и преобразование рациональных выражений
\[\left( \frac{x}{{{x}^{2}}+2x+4}+\frac{{{x}^{2}}+8}{{{x}^{3}}-8}-\frac{1}{x-2} \right)\cdot \left( \frac{{{x}^{2}}}{{{x}^{2}}-4}-\frac{2}{2-x} \right)\]
Сначала рассмотрим и раскроем первую скобку: в ней мы видим три отдельных дроби с разными знаменателями поэтому первое, что нам необходимо сделать — это привести все три дроби к общему знаменателю, а для этого каждый из них следует разложить на множители:
\[{{x}^{2}}+2x+4={{x}^{2}}+2\cdot x+{{2}^{2}}\]
\[{{x}^{2}}-8={{x}^{3}}-{{2}^{2}}=\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)\]
Перепишем всю нашу конструкцию следующим образом:
\[\frac{x}{{{x}^{2}}+2x+{{2}^{2}}}+\frac{{{x}^{2}}+8}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}-\frac{1}{x-2}=\]
\[=\frac{x\left( x-2 \right)+{{x}^{3}}+8-\left( {{x}^{2}}+2x+{{2}^{2}} \right)}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\]
\[=\frac{{{x}^{2}}-2x+{{x}^{2}}+8-{{x}^{2}}-2x-4}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\frac{{{x}^{2}}-4x-4}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\]
\[=\frac{{{\left( x-2 \right)}^{2}}}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\frac{x-2}{{{x}^{2}}+2x+4}\]
Это результат вычислений из первой скобки.
Разбираемся со второй скобкой:
\[{{x}^{2}}-4={{x}^{2}}-{{2}^{2}}=\left( x-2 \right)\left( x+2 \right)\]
Перепишем вторую скобку с учетом изменений:
\[\frac{{{x}^{2}}}{\left( x-2 \right)\left( x+2 \right)}+\frac{2}{x-2}=\frac{{{x}^{2}}+2\left( x+2 \right)}{\left( x-2 \right)\left( x+2 \right)}=\frac{{{x}^{2}}+2x+4}{\left( x-2 \right)\left( x+2 \right)}\]
Теперь запишем всю исходную конструкцию:
\[\frac{x-2}{{{x}^{2}}+2x+4}\cdot \frac{{{x}^{2}}+2x+4}{\left( x-2 \right)\left( x+2 \right)}=\frac{1}{x+2}\]
Ответ: $\frac{1}{x+2}$.
Нюансы решения
Как видите, ответ получился вполне вменяемый. Однако обратите внимание: очень часто при таких масштабных вычислениях, когда единственная переменная оказывается лишь в знаменателе, ученики забывают, что это знаменатель и он должен стоял внизу дроби и пишут это выражение в числитель — это грубейшая ошибка.
Кроме того, хотел бы обратить ваше отдельное внимание на то, как оформляются такие задачи. В любых сложных вычислениях все шаги выполняются по действиям: сначала отдельно считаем первую скобку, потом отдельно вторую и лишь в конце мы объединяем все части и считаем результат. Таким образом мы страхуем себя от глупых ошибок, аккуратно записываем все выкладки и при этом нисколько не тратим лишнего времени, как это может показаться на первый взгляд.
До новых встреч!
Смотрите также:
- Как выполнять сокращение рациональных дробей без ошибок? Простой алгоритм на примере пяти различных задач.

- Дробно-рациональные выражения

- Как сдать ЕГЭ по математике

- Пробный ЕГЭ 2012. Вариант 12 (без логарифмов)

- Метод интервалов: случай нестрогих неравенств

- Тест по задачам B14: легкий уровень, 1 вариант

Рациональные выражения
Вопросы занятия:
· вспомнить, какие выражения называют рациональными;
· поговорить об основном свойстве дробей;
· вспомнить, как выполняют действия над рациональными дробями.
Материал урока
Прежде, чем мы начнём говорить о рациональных выражениях, стоит вспомнить такие понятия, как «целые выражения» и «дробные выражения».
Итак, целые выражения – это выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля.
Например, целыми являются выражения:

Любое целое выражение можно представить многочленом.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Т.е. дробные выражения – это выражения, составленные из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на выражения с переменными.
Например, дробными будут выражения:

Напомним, что значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.
Область определения целого выражения – любые значения переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.
Например, целое выражение:
 имеет
смысл при любых действительных
имеет
смысл при любых действительных  ,
,
 ,
,
 и
и
 .
.
Дробное же выражение при некоторых значениях переменных может не иметь смысла.
Область определения дробного выражения – все значения переменных, при которых делители этого выражения не равны нулю.
Например, дробное
выражение  не
имеет смысла при
не
имеет смысла при  .
Так как в этом случае в знаменателе получится нуль. А мы помним, что на нуль
делить нельзя. При всех же остальных значениях переменных это выражение имеет
смысл.
.
Так как в этом случае в знаменателе получится нуль. А мы помним, что на нуль
делить нельзя. При всех же остальных значениях переменных это выражение имеет
смысл.
Целые и дробные выражения называют рациональными выражениями.

Определение.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Например,

Чтобы найти значение рационального выражения, надо:
1) подставить числовое значение переменной в данное выражение;
2) выполнить все действия.
Задание.
Найти значение дроби:
а)  ,
при
,
при  ;
б)
;
б)  ,
при
,
при  ;
в)
;
в)  ,
при
,
при  .
.
Первое выражение:  .
Подставим указанное значение
.
Подставим указанное значение  в
выражение. Выполним действия. В результате получим,
в
выражение. Выполним действия. В результате получим,

Переходим ко второму дробному выражению  .
Нужно найти его значение при
.
Нужно найти его значение при  .
Значит, подставим указанное значение вместо а. Выполним все действия по
порядку. Получим,
.
Значит, подставим указанное значение вместо а. Выполним все действия по
порядку. Получим,

И третье дробное выражение:  .
Найдём его значение при
.
Найдём его значение при  .
Подставим указанное значение. Выполним действия. Получим,
.
Подставим указанное значение. Выполним действия. Получим,

Заметили, в знаменателе получился нуль? Разве мы можем
делить на нуль? Правильно! Значит, выражение:  не
имеет смысла при
не
имеет смысла при  ,
так как на нуль делить нельзя.
,
так как на нуль делить нельзя.
Как вы уже знаете, выражение вида  называется
дробью.
называется
дробью.
Определение.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Например, выражения:

являются рациональными дробями.
Область определения рациональной дроби – все значения переменных, при которых знаменатель не равен нулю.
Задание.
Указать область определения следующих рациональных дробей:
а)  ;
б)
;
б)  .
.
Итак, первый пример: 
 ,
т.е. все числа, кроме
,
т.е. все числа, кроме  и
и
 .
.И второй пример:  .
Область определения данной дроби все действительные числа, так как знаменатель
.
Область определения данной дроби все действительные числа, так как знаменатель  ни
при каких а
ни
при каких а
Рассмотрим равенство:  .
.
Это равенство верно при всех допустимых значениях
переменной, т.е. при всех  ,
кроме
,
кроме  и
и
 .
.
Такое равенство называют тождеством.
Определение.
Тождество – это равенство, верное при всех допустимых значениях входящих в него переменных.
Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.
Замену одного такого выражения другим называют тождественным преобразованием выражения.
Справедливо следующее тождество:  ,
если
,
если  ,
где
,
где  и
и
 –
не равные нулю многочлены.
–
не равные нулю многочлены.
Рассмотрим равенство:  .
.
Это равенство верно при всех допустимых значениях
переменной  ,
т.е. при всех
,
т.е. при всех  кроме
кроме
 и
и
 .
Так как
.
Так как  .
.
Перейдём к основному свойству рациональной дроби.
Итак, основное свойство рациональной дроби сводится к тому, что:
Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.
Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.
Задание.
Привести дроби к новому знаменателю:
а)  к
знаменателю
к
знаменателю  ;
б)
;
б)  к
знаменателю
к
знаменателю  .
.
Первая рациональная дробь:  .
Её нужно привести к знаменателю
.
Её нужно привести к знаменателю  .
Не трудно заметить, что
.
Не трудно заметить, что  –
это
произведение
–
это
произведение  .
Значит, мы должны умножить дробь на
.
Значит, мы должны умножить дробь на  .
Напомним, что для того чтобы значение дроби не изменилось, нужно и числитель, и
знаменатель умножить на одно и то же число. Тогда получаем дробь:
.
Напомним, что для того чтобы значение дроби не изменилось, нужно и числитель, и
знаменатель умножить на одно и то же число. Тогда получаем дробь:

Множитель:  называют
дополнительным множителем к числителю и знаменателю дроби
называют
дополнительным множителем к числителю и знаменателю дроби  .
.
Вторая дробь:  .
Её нужно привести к новому знаменателю
.
Её нужно привести к новому знаменателю  .
Для этого числитель и знаменатель дроби нужно умножить на выражение:
.
Для этого числитель и знаменатель дроби нужно умножить на выражение:  .
Выполним умножение. Получим дробь:
.
Выполним умножение. Получим дробь:

Задание.
Сократить дроби:
а)  ;
б)
;
б)  .
.
Рассмотрим первую рациональную дробь. Числитель
состоит из произведения  ,
,
 и
и
 ,
знаменатель из произведения
,
знаменатель из произведения  ,
,
 и
и
 .
Дробь можно сократить на общий множитель
.
Дробь можно сократить на общий множитель  .
В итоге получим дробь,
.
В итоге получим дробь,

Вторая рациональная дробь:  .
В числителе вынесем общий множитель
.
В числителе вынесем общий множитель  за
скобку. Сократим дробь на общий множитель
за
скобку. Сократим дробь на общий множитель  .
В результате получим,
.
В результате получим,

Перейдём к действиям над рациональными дробями. Давайте вспомним, какие действия можно выполнять над рациональными дробями и по каким правилам.
Итак, правило сложения рациональных дробей с одинаковыми знаменателями:
Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.
В буквенном виде это правило записывают так:

где  ,
,
 и
и
 –
многочлены, причём
–
многочлены, причём  –
не равный нулю многочлен. Это правило справедливо при сложении любого числа
дробей.
–
не равный нулю многочлен. Это правило справедливо при сложении любого числа
дробей.
Например, найдём сумму
дробей  .
.
Видно, что у первой и второй рациональных дробей один и тот же знаменатель. Воспользуемся правилом сложения рациональных дробей с одинаковыми знаменателями. Сложим их числители, а знаменатель оставим тем же. Получим,

Вычитание рациональных дробей с одинаковыми знаменателями выполняется аналогично сложению.
Вспомним правило вычитания рациональных дробей с одинаковыми знаменателями.
Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.
В буквенном виде это правило записывают так:

где  ,
,
 и
и
 –
многочлены, причём
–
многочлены, причём  –
не равный нулю многочлен.
–
не равный нулю многочлен.
Рассмотрим пример. Найти разность дробей  .
.
Дроби имеют одинаковые знаменатели. Значит, можем
смело воспользоваться правилом вычитания рациональных дробей с одинаковыми
знаменателями. Из числителя первой дроби вычтем числитель второй дроби,
знаменатель оставим прежним. Сократим числитель и знаменатель дроби на
выражение  .
В итоге получим,
.
В итоге получим,

Сложение и вычитание рациональных дробей с разными знаменателями выполняется аналогично сложению и вычитанию дробей с одинаковыми знаменателями, но предварительно нужно дроби привести к общему знаменателю.

где  ,
,
 ,
,  и
и
 –
многочлены, причём
–
многочлены, причём  ,
,
 –
не равные нулю многочлены.
–
не равные нулю многочлены.
Вспомним алгоритм приведения дробей к наименьшему общему знаменателю:
1) разложить на множители знаменатель каждой дроби;
2) найти дополнительный множитель каждой дроби. Он равен произведению тех множителей знаменателей остальных дробей, которые не содержатся в знаменателе этой дроби;
3) домножить числитель и знаменатель каждой дроби на её дополнительный множитель.
Задание.
Представить в виде дроби:
 .
.
Знаменатели дробей представлены в виде одночленов.
Разложим знаменатель последней дроби на множители, применяя формулу разности
квадратов. Затем приведём дроби к общему знаменателю. Общим знаменателем трёх
дробей является выражение  .
Значит, дополнительным множителем к первой дроби будет выражение
.
Значит, дополнительным множителем к первой дроби будет выражение  ,
а дополнительным множителем ко второй дроби:
,
а дополнительным множителем ко второй дроби:  .
Тогда получим,
.
Тогда получим,

Теперь дроби имеют одинаковые знаменатели. А значит,
можем воспользоваться правилом сложения рациональных дробей с одинаковыми
знаменателями. Упростим числитель, получившейся дроби. Обратите внимание, в
числителе можем вынести общий множитель 2 за скобки. Сократим числитель и
знаменатель на выражение  .
В результате, получим дробь:
.
В результате, получим дробь:

Умножение рациональных дробей выполняется аналогично умножению обыкновенных дробей.
Вспомним правило умножения рациональных дробей.
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
В буквенном виде это правило записывают так:

где  ,
,
 ,
,  и
и
 –
многочлены, причём
–
многочлены, причём  ,
,
 –
не равные нулю многочлены.
–
не равные нулю многочлены.
Это правило выполняется и когда произведение трёх и более рациональных дробей.
Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.
Рассмотрим пример. Выполнить умножение рациональных дробей:
 .
.
Воспользуемся правилом и умножим числитель первой дроби на числитель второй дроби, знаменатель первой дроби на знаменатель второй дроби. Сократим дробь. В результате получим:

Теперь вспомним, как выполняется возведение рациональной дроби в степень.
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
В буквенном виде это правило записывают так:

где 𝒂, 𝒃
– многочлены, причём  .
.
Рассмотрим пример. Возведём в 4-ую степень
дробь  .
.
Воспользуемся правилом возведения рациональной дроби в степень. Получим дробь,

Обратите внимание, что и числовой множитель в числителе мы также возводим в степень.
Деление рациональных дробей сводится к делению обыкновенных дробей.
Вспомним правило деления рациональных дробей:
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
В буквенном виде это правило записывают так:

где 𝒂, 𝒃,
𝒄
и 𝒅
– многочлены, причём  ,
,
 и
и
 .
.
Прежде чем выполнять деление рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате деления.
Рассмотрим пример. Выполнить деление рациональных дробей:
 .
.
Воспользуемся правилом деления рациональных дробей.
Т.е. первую дробь умножим на дробь обратную второй или, что то же самое
числитель первой дроби умножим на знаменатель второй дроби, а знаменатель
первой дроби умножим на числитель второй дроби. Заметим, в числителе дроби мы
можем вынести  за
скобку, а в знаменателе: 3 за скобку. Затем сократим числитель и знаменатель
получившейся дроби на
за
скобку, а в знаменателе: 3 за скобку. Затем сократим числитель и знаменатель
получившейся дроби на  и
на выражение
и
на выражение  .
В результате получим дробь:
.
В результате получим дробь:

Итоги урока
На этом уроке мы разобрали тему «рациональные выражения». Вспомнили, какие выражения называют рациональными. Поговорили об основном свойстве дробей. И вспомнили, как выполняют действия над рациональными дробями.
Опорный конспект по алгебре «Рациональные выражения» (9 класс)
Рациональные выражения
Целые выражения – это выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля.
Например, целыми являются выражения:
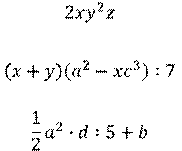
Любое целое выражение можно представить многочленом.
Дробные выражения – это выражения, составленные из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на выражения с переменными.
Например, дробными будут выражения:
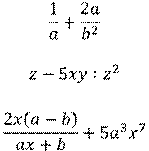
Напомним, что значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.
Область определения целого выражения – любые значения переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.
Например, целое выражение: 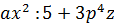 имеет смысл при любых действительных
имеет смысл при любых действительных  ,
, 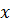 ,
, 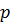 и
и 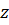 .
.
Дробное же выражение при некоторых значениях переменных может не иметь смысла.
Область определения дробного выражения – все значения переменных, при которых делители этого выражения не равны нулю.
Например, дробное выражение 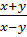 не имеет смысла при
не имеет смысла при 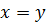 . Так как в этом случае в знаменателе получится нуль. А мы помним, что на нуль делить нельзя. При всех же остальных значениях переменных это выражение имеет смысл.
. Так как в этом случае в знаменателе получится нуль. А мы помним, что на нуль делить нельзя. При всех же остальных значениях переменных это выражение имеет смысл.
Целые и дробные выражения называют рациональными выражениями.

Определение.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Например,
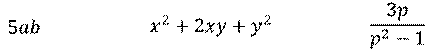
Чтобы найти значение рационального выражения, надо:
1) подставить числовое значение переменной в данное выражение;
2) выполнить все действия.
Задание.
Найти значение дроби:
а)  , при
, при 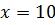 ; б)
; б) 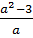 , при
, при 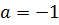 ; в)
; в) 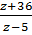 , при
, при 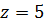 .
.
Первое выражение:  . Подставим указанное значение
. Подставим указанное значение 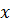 в выражение. Выполним действия. В результате получим,
в выражение. Выполним действия. В результате получим,
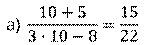
Переходим ко второму дробному выражению 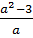 . Нужно найти его значение при
. Нужно найти его значение при 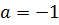 . Значит, подставим указанное значение вместо а. Выполним все действия по порядку. Получим,
. Значит, подставим указанное значение вместо а. Выполним все действия по порядку. Получим,
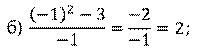
И третье дробное выражение: 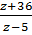 . Найдём его значение при
. Найдём его значение при 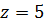 . Подставим указанное значение. Выполним действия. Получим,
. Подставим указанное значение. Выполним действия. Получим,

Определение.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Например, выражения:
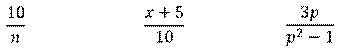
являются рациональными дробями.
Область определения рациональной дроби – все значения переменных, при которых знаменатель не равен нулю.
Задание.
Указать область определения следующих рациональных дробей:
а) 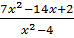 ; б)
; б) 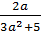 .
.
Итак, первый пример: 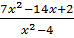 . Область определения данной дроби: все действительные числа, кроме тех, при которых знаменатель
. Область определения данной дроби: все действительные числа, кроме тех, при которых знаменатель 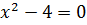 , т.е. все числа, кроме
, т.е. все числа, кроме 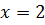 и
и 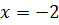 .
.
И второй пример: 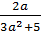 . Область определения данной дроби все действительные числа, так как знаменатель
. Область определения данной дроби все действительные числа, так как знаменатель 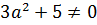 ни при каких а.
ни при каких а.
Рассмотрим равенство: 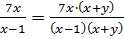 .
.
Это равенство верно при всех допустимых значениях переменной, т.е. при всех 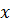 , кроме
, кроме 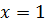 и
и 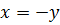 .
.
Такое равенство называют тождеством.
Определение.
Тождество – это равенство, верное при всех допустимых значениях входящих в него переменных.
Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.
Замену одного такого выражения другим называют тождественным преобразованием выражения.
Справедливо следующее тождество: 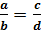 , если
, если 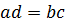 , где
, где  и
и  – не равные нулю многочлены.
– не равные нулю многочлены.
Рассмотрим равенство: 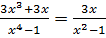 .
.
Это равенство верно при всех допустимых значениях переменной 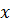 , т.е. при всех
, т.е. при всех 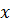 кроме
кроме 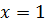 и
и 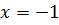 . Так как
. Так как 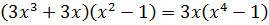 .
.
Основное свойство рациональной дроби сводится к тому, что:
Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
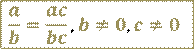
Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.
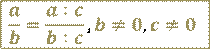
Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.
Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.
Задание.
Привести дроби к новому знаменателю:
а) 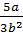 к знаменателю
к знаменателю  ; б)
; б) 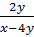 к знаменателю
к знаменателю 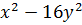 .
.
Первая рациональная дробь: 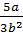 . Её нужно привести к знаменателю
. Её нужно привести к знаменателю  . Не трудно заметить, что
. Не трудно заметить, что  – это произведение
– это произведение 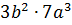 . Значит, мы должны умножить дробь на
. Значит, мы должны умножить дробь на 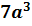 . Напомним, что для того чтобы значение дроби не изменилось, нужно и числитель, и знаменатель умножить на одно и то же число. Тогда получаем дробь:
. Напомним, что для того чтобы значение дроби не изменилось, нужно и числитель, и знаменатель умножить на одно и то же число. Тогда получаем дробь:
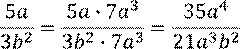
Множитель: 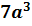 называют дополнительным множителем к числителю и знаменателю дроби
называют дополнительным множителем к числителю и знаменателю дроби 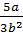 .
.
Вторая дробь: 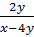 . Её нужно привести к новому знаменателю
. Её нужно привести к новому знаменателю 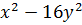 . Для этого числитель и знаменатель дроби нужно умножить на выражение:
. Для этого числитель и знаменатель дроби нужно умножить на выражение: 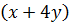 . Выполним умножение. Получим дробь:
. Выполним умножение. Получим дробь:
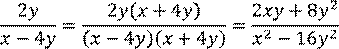
Задание.
Сократить дроби:
а) 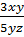 ; б)
; б) 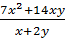 .
.
Рассмотрим первую рациональную дробь. Числитель состоит из произведения 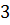 ,
, 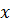 и
и 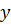 , знаменатель из произведения
, знаменатель из произведения 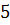 ,
, 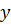 и
и 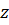 . Дробь можно сократить на общий множитель
. Дробь можно сократить на общий множитель 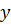 . В итоге получим дробь,
. В итоге получим дробь,
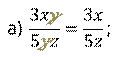
Вторая рациональная дробь: 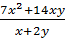 . В числителе вынесем общий множитель
. В числителе вынесем общий множитель 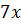 за скобку. Сократим дробь на общий множитель
за скобку. Сократим дробь на общий множитель  . В результате получим,
. В результате получим,
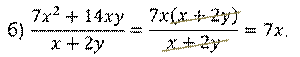
Перейдём к действиям над рациональными дробями. Давайте вспомним, какие действия можно выполнять над рациональными дробями и по каким правилам.
Правило сложения рациональных дробей с одинаковыми знаменателями:
Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.
В буквенном виде это правило записывают так:
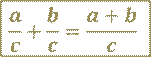
где 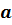 ,
, 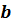 и
и 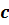 – многочлены, причём
– многочлены, причём 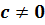 – не равный нулю многочлен. Это правило справедливо при сложении любого числа дробей.
– не равный нулю многочлен. Это правило справедливо при сложении любого числа дробей.
Например, найдём сумму дробей 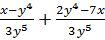 .
.
Видно, что у первой и второй рациональных дробей один и тот же знаменатель. Воспользуемся правилом сложения рациональных дробей с одинаковыми знаменателями. Сложим их числители, а знаменатель оставим тем же. Получим,
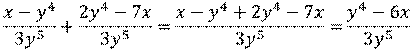
Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.
В буквенном виде это правило записывают так:

где 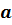 ,
, 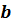 и
и 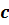 – многочлены, причём
– многочлены, причём 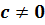 – не равный нулю многочлен.
– не равный нулю многочлен.
Рассмотрим пример. Найти разность дробей  .
.
Дроби имеют одинаковые знаменатели. Значит, можем смело воспользоваться правилом вычитания рациональных дробей с одинаковыми знаменателями. Из числителя первой дроби вычтем числитель второй дроби, знаменатель оставим прежним. Сократим числитель и знаменатель дроби на выражение 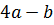 . В итоге получим,
. В итоге получим,
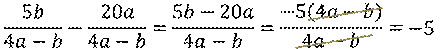

где 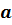 ,
, 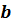 ,
, 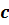 и
и 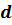 – многочлены, причём
– многочлены, причём 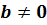 ,
, 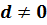 – не равные нулю многочлены.
– не равные нулю многочлены.
Вспомним алгоритм приведения дробей к наименьшему общему знаменателю:
1) разложить на множители знаменатель каждой дроби;
2) найти дополнительный множитель каждой дроби. Он равен произведению тех множителей знаменателей остальных дробей, которые не содержатся в знаменателе этой дроби;
3) домножить числитель и знаменатель каждой дроби на её дополнительный множитель.
Задание.
Представить в виде дроби:
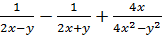 .
.
Знаменатели дробей представлены в виде одночленов. Разложим знаменатель последней дроби на множители, применяя формулу разности квадратов. Затем приведём дроби к общему знаменателю. Общим знаменателем трёх дробей является выражение 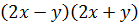 . Значит, дополнительным множителем к первой дроби будет выражение
. Значит, дополнительным множителем к первой дроби будет выражение 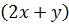 , а дополнительным множителем ко второй дроби:
, а дополнительным множителем ко второй дроби: 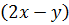 . Тогда получим,
. Тогда получим,
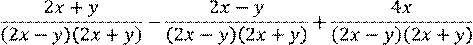
Теперь дроби имеют одинаковые знаменатели. А значит, можем воспользоваться правилом сложения рациональных дробей с одинаковыми знаменателями. Упростим числитель, получившейся дроби. Обратите внимание, в числителе можем вынести общий множитель 2 за скобки. Сократим числитель и знаменатель на выражение 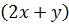 . В результате, получим дробь:
. В результате, получим дробь:
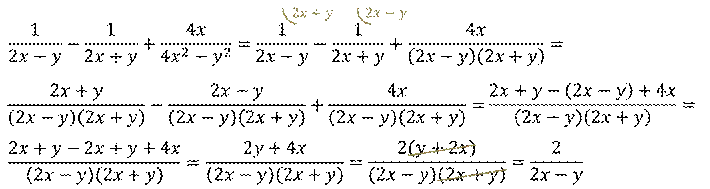
Умножение рациональных дробей выполняется аналогично умножению обыкновенных дробей.
Вспомним правило умножения рациональных дробей.
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
В буквенном виде это правило записывают так:
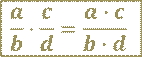
где 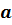 ,
, 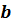 ,
, 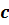 и
и 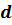 – многочлены, причём
– многочлены, причём 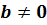 ,
, 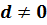 – не равные нулю многочлены.
– не равные нулю многочлены.
Это правило выполняется и когда произведение трёх и более рациональных дробей.
Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.
Рассмотрим пример. Выполнить умножение рациональных дробей:
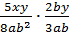 .
.
Воспользуемся правилом и умножим числитель первой дроби на числитель второй дроби, знаменатель первой дроби на знаменатель второй дроби. Сократим дробь. В результате получим:
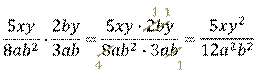
Теперь вспомним, как выполняется возведение рациональной дроби в степень.
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
В буквенном виде это правило записывают так:
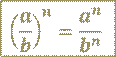
где 𝒂, 𝒃 – многочлены, причём 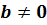 .
.
Рассмотрим пример. Возведём в 4-ую степень дробь  .
.
Воспользуемся правилом возведения рациональной дроби в степень. Получим дробь,
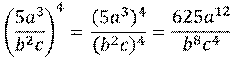
Обратите внимание, что и числовой множитель в числителе мы также возводим в степень.
Деление рациональных дробей сводится к делению обыкновенных дробей.
Вспомним правило деления рациональных дробей:
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
В буквенном виде это правило записывают так:
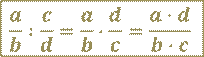
где 𝒂, 𝒃, 𝒄 и 𝒅 – многочлены, причём 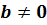 ,
, 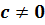 и
и 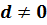 .
.
Прежде чем выполнять деление рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате деления.
Рассмотрим пример. Выполнить деление рациональных дробей:
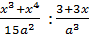 .
.
Воспользуемся правилом деления рациональных дробей. Т.е. первую дробь умножим на дробь обратную второй или, что то же самое числитель первой дроби умножим на знаменатель второй дроби, а знаменатель первой дроби умножим на числитель второй дроби. Заметим, в числителе дроби мы можем вынести 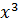 за скобку, а в знаменателе: 3 за скобку. Затем сократим числитель и знаменатель получившейся дроби на
за скобку, а в знаменателе: 3 за скобку. Затем сократим числитель и знаменатель получившейся дроби на 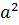 и на выражение
и на выражение 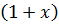 . В результате получим дробь:
. В результате получим дробь:
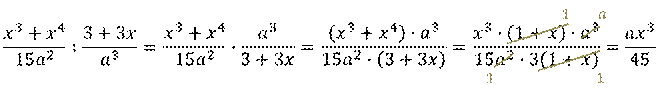
РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — это… Что такое РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ?
- РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ
- РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., a2 + b, x/(y — z2).
Большой Энциклопедический словарь. 2000.
- РАЦИОНАЛЬНАЯ ФУНКЦИЯ
- РАЦИОНАЛЬНОЕ ЧИСЛО
Смотреть что такое «РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ» в других словарях:
Рациональное выражение — Рациональное выражение алгебраическое выражение, не содержащее радикалов. Другими словам, это одна или несколько алгебраических величин (чисел и букв), соединённых между собой знаками арифметических действий: сложения, вычитания, умножения… … Википедия
рациональное выражение — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Например, a2 + b, х/(у z2). * * * РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ, алгебраическое выражение, не содержащее… … Энциклопедический словарь
Рациональное выражение — алгебраическое выражение, не содержащее радикалов, например a2 + b, х/(у z3). Если входящие в Р. в. буквы считать переменными, то Р. в. задаёт рациональную функцию (См. Рациональная функция) от этих переменных … Большая советская энциклопедия
РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебрарическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., а2 + b, х/(y z2) … Естествознание. Энциклопедический словарь
ВЫРАЖЕНИЕ — первичное математическое понятие, под которым подразумевают запись из букв и чисел, соединённых знаками арифметических действий, при этом могут быть использованы скобки, обозначения функций и т.п.; обычно В формула млн. её часть. Различают В (1)… … Большая политехническая энциклопедия
РАЦИОНАЛЬНОЕ — (Rational; Rational) термин, используемый для описания мыслей, чувств и действий, согласуемых с разумом; установка, базирующаяся на объективных ценностях, полученных в результате практического опыта.«Объективные ценности устанавливаются в опыте… … Словарь по аналитической психологии
РАЦИОНАЛЬНОЕ ПОЗНАНИЕ — субъективный образ объективного мира,полученный с помощью мышления. Мышление – активный процесс обобщенного и опосредованного отражения действительности, обеспечивающий открытие на основе чувственных данных ее закономерных связей и их выражение … Философия науки и техники: тематический словарь
УРАВНЕНИЕ, РАЦИОНАЛЬНОЕ — Логическое или математическое выражение, основанное на (рациональных) предположениях о процессах. Такие уравнения отличаются от эмпирических уравнений тем, что их параметры получаются в результате дедуктивных выводов из теоретических… … Толковый словарь по психологии
РАЦИОНАЛЬНЫЙ — РАЦИОНАЛЬНЫЙ, рациональная, рациональное; рационален, рациональна, рационально. 1. прил. к рационализм (книжн.). Рациональная философия. 2. Вполне разумный, обоснованный, целесообразный. Он внес рациональное предложение. Рациональное… … Толковый словарь Ушакова
РЕЗОЛЬВЕНТА — 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения… … Математическая энциклопедия

