Расстояние между точками [wiki.eduVdom.com]
Пусть на плоскости хОу даны две точки: А1 с координатами х1, у1 и А2 с координатами х2, у2. Выразим расстояние между точками А1 и А2 через координаты этих точек.
Рассмотрим сначала случай, когда х1 ≠ х2 и у1 ≠ у2. Проведем через точки А1 и А2 прямые, параллельные осям координат, и обозначим точку их пересечения буквой А (рис. 1).
Рис.1
Расстояние между точками А и А1 равно |y1 — у2|, а расстояние между точками А и А2 равно |х1 — х2|. Применяя к прямоугольному треугольнику АА1А2 теорему Пифагора, получим: $$ А_1А_2^2 = АА_1^2 + АА_2^2 \,\text{, откуда }\, \\ d = sqrt{ (x_1 — x_2}^2 + (y_1 — y_2)^2 \,\,\,(1) $$ , где d — расстояние между точками А1 и А2.
Хотя формула (1) для расстояния между точками выведена нами в предположении х1 ≠ х2, y1 ≠ y2, она остается верной и в других случаях. Действительно, если 1 = х2, у1<sub> ≠ у<sub>2, то d равно |у1 — y2|. Тот же результат дает и формула (1). Аналогично рассматривается случай, когда x1 ≠ x2, y1 = y2. При x1 = x2, y1 = y2 точки А1 и А2 совпадают и формула (1) дает d = 0 .
Пример 1. Найти расстояние между точками А(-1; -2) и В(-4; 2).
Решение. По формуле (1) имеем: $$ d = AB = \sqrt{(-4 + 1)^2 +(2 + 2)^2 } = \sqrt{ 9 + 16 } = \sqrt{25} = 5 \,\,. $$
Математика. Расстояние между двумя точками. Теорема Пифагора
Внимание! Данный сайт не обновляется. Новая версия: shatalov.suДата создания: 2009-01-22 00:00:57
Последний раз редактировалось: 2012-02-08 08:43:58
Это первый урок из раздела Математика. Надеюсь мы закончим вводный курс к моменту начала публикации в рассылке выпусков по directX. Вполне вероятно, что получится закончить математический вводный курс гораздо раньше: тем не слишком много и они не сказать чтобы сложные. Приступим.
Координатные пространства
В большинстве примеров будет использоваться трёхмерное координатное пространство. Возможны два варианта трёхмерного пространства: ось z уходит вглубь листа и наоборот. Это продемонстрировано на рис. 1.
Мы всегда будем пользоваться первым. Выбор этот не произвольный. Дело в том, что как раз такое представление пространства используется в DirectX. А вот если бы мы использовали OpenGL, тогда бы выбрали второй вариант.
Расстояние между двумя точками
В начале рассмотрим самый простой случай — точка на координатной прямой (рис.2а). Расстоянием до точки M от начала координат будет значение координаты данной точки — x. Для кракткости используют форму — M(x).
рис.2б: на координатной прямой заданы две точки А и B с координатами x1, x2 — A(x1), B(x2). Расстояние между ними можно найти вычтя значение второй координаты из первой.
Dx = x2 — x1
Здесь Dx — расстояние между двумя точками, которое в математике обычно обозначается Δx, где Δ читается как — дельта.
рис.2в: мы добавили ещё одну ось. Здесь рассматривается случай, когда отрезки между точками параллельны осям. На плоскости заданы четыре точки: A(x1,y3), B(x2,y3), C(x3,y1), D(x3,y2)
Расстояниями между точками будут:Dx = x2 — x1 Dy = y2 — y1
Теперь рассмотрим ситуацию когда отрезок проведённый между двумя точками не параллелен осям координат — рис.3:
Здесь, на координатной плоскости задана точка M(x,y), где x, y имеют конкретные значения, возможно: x = 5, y = 4.
Расстояние между точками O(0,0), M(x,y) находится по теореме Пифагора из прямоугольного треугольника, где d — гипотенуза, а x, y — катеты.
d2 = x2 + y2
Если первая точка находится не в начале координат (рис.3б), то формула нахождения расстояния между точками A(1,y1), B(x2,y2) следующая:
Ну и последний случай, две точки расположены в пространстве (рис.4). Их координаты — A(x1,y1,z1), B(x2,y2,z2). Небольшое замечание: соответствуюище координаты имеют названия. x — абсцисса точки, y — ордината, z — аппликата. Координаты точки — упорядочены. Это значит, что нелья менять их местами и всегда нужно записывать сначала x, затем y и только потом z.
Прежде чем спроецировать координаты на оси, нужно опустить перпендикуляр на соответствующую плоскость. На рисунке, из точек опускается перпендикуляр на плоскость xz. Ординаты (y1 и y2) точек в данном случае — это перпендикуляры опущенные из соответствующих точек на плоскость xz.
Формула для нахождения расстояния между точками в пространстве мало отличается от формулы для нахождения расстояния между точками на плоскости:
Дополнительное упражнение к пятому выпуску рассылки
Для данного упражнения вам понадобится включить заголовочный файл math.h.
Напишите программу, где пользователь вводит координаты, куда нужно переместить обьект. Программа подсчитывает расстояние на которое переместился пользователь. Для хранения расстояния используйте отдельную переменную.
Пользователь вводит координаты через запятую: 12,21,3.4.
Заметьте, что в английском, используется десятичная точка, а не запятая. Поэтому следующий оператор присвоит переменной 0, а не 0.5:
Использование запятой вместо точки может стать причиной труднообнаруживаемых ошибок.
Операция извлечения (>>) может считывать больше одного значения за раз. Для этого вам понадобится определить переменную типа char, например — helper:
cin >> a >> helper >> b;
Для нахождения корня квадратного используйте фукнцию sqrt(). В скобки вставьте выражение, чей квадратный корень вам нужно найти: d = d + sqrt(Dx*Dx + Dy*….).
Если возникнут вопросы или сложности с выполнением задания пишите мне e-mail. Попытаемся разобраться.
Расстояние между параллельными прямыми / Соотношения между сторонами и углами треугольника / Справочник по геометрии 7-9 класс
Теорема
| Все точки каждой из двух параллельных прямых равноудалены от другой прямой. |
Доказательство:
Рассмотрим параллельные прямые  и
и 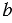 .
.

Отметим точку А на прямой  и проведем из этой точки перпендикуляр АВ к прямой
и проведем из этой точки перпендикуляр АВ к прямой 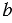 .
.
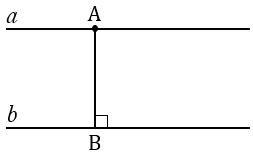
Отметим точку Х на прямой  и докажем
и докажем
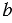 равно АВ. Проведем из точки Х перпендикуляр ХУ к прямой
равно АВ. Проведем из точки Х перпендикуляр ХУ к прямой 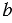 .
.
ХУ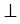
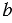 , следовательно, ХУ
, следовательно, ХУ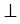
 (т.к. прямая перпендикулярная к одной из параллельных прямых перпендикулярна и ко второй из них).
(т.к. прямая перпендикулярная к одной из параллельных прямых перпендикулярна и ко второй из них).
Рассмотрим 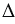
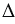 АХУ:
АХУ: 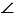 В =
В =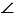 Х = 900, т.е.
Х = 900, т.е. 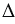 АВУ и
АВУ и 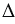 АХУ прямоугольные, АУ — общая гипотенуза,
АХУ прямоугольные, АУ — общая гипотенуза, 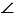 1 =
1 = 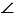 2 (т.к. они накрест лежащие при пересечении параллельных прямых
2 (т.к. они накрест лежащие при пересечении параллельных прямых  и
и 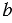 секущей АУ), следовательно,
секущей АУ), следовательно, 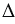 АВУ =
АВУ =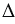 АХУ (по гипотенузе и острому углу), ХУ = АВ.
АХУ (по гипотенузе и острому углу), ХУ = АВ.Точка Х находится на расстоянии АВ от прямой 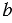 , а так как эту точку мы выбрали произвольно, все точки каждой из двух параллельных прямых
, а так как эту точку мы выбрали произвольно, все точки каждой из двух параллельных прямых  и
и 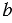 равноудалены от другой прямой. Что и требовалось доказать.
равноудалены от другой прямой. Что и требовалось доказать.
Из доказанной выше теоремы следует, что расстояние между параллельными прямыми
Замечание 1
| Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от нее, лежат на прямой параллельной данной. |
Доказательство:
Дано: прямая 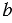 , А, С
, А, С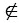
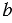 , АВ
, АВ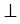
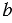 , СE
, СE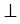
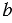 , АВ = СЕ.
, АВ = СЕ.Доказать: А, С
 и
и  .
.
Доказательство:
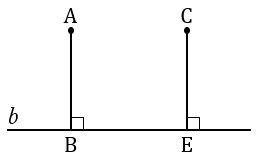
По аксиоме параллельных прямых через точку А проходит единственная прямая параллельная прямой 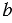 . Проведем через точку А прямую
. Проведем через точку А прямую  параллельную
параллельную 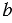

По теореме, доказанной выше, все точки, лежащие на прямой  равноудалены от точек прямой
равноудалены от точек прямой 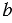 .
.
Предположим, что точка С не лежит на прямой  , тогда расстояние от точки С до прямой
, тогда расстояние от точки С до прямой 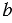 будет больше или меньше, чем расстояние АВ.
будет больше или меньше, чем расстояние АВ.

Но по условию АВ = СЕ, следовательно, получили противоречие, значит, наше предположение неверно и А, С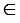
 , при этом по построению
, при этом по построению  . Что и требовалось доказать.
. Что и требовалось доказать.
Замечание 2
| Множество всех точек плоскости, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от нее, есть прямая, параллельная данной прямой. |
Доказательство:
Пусть  — данная прямая, d — данное расстояние. Отметим на прямой
— данная прямая, d — данное расстояние. Отметим на прямой  произвольную точку А и проведем отрезок АВ длины d так, что АВ
произвольную точку А и проведем отрезок АВ длины d так, что АВ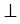
 , через точку В по аксиоме параллельных прямых проходит единственная прямая параллельная прямой
, через точку В по аксиоме параллельных прямых проходит единственная прямая параллельная прямой  . Проведем через точку В прямую
. Проведем через точку В прямую 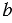 параллельную
параллельную  .
.
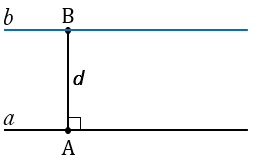
По доказанной выше теореме все точки прямой 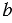 находятся на расстоянии d от прямой
находятся на расстоянии d от прямой  , т.е. все эти точки принадлежат искомому множеству. В силу обратной теоремы любая точка искомого множества лежит на прямой
, т.е. все эти точки принадлежат искомому множеству. В силу обратной теоремы любая точка искомого множества лежит на прямой 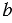 . Значит, прямая
. Значит, прямая 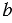 является геометрическим местом всех точек, удовлетворяющих данному условию. Что и требовалось доказать.
является геометрическим местом всех точек, удовлетворяющих данному условию. Что и требовалось доказать.
Геометрическое место точек, удовлетворяющих данному условию — множество всех точек, удовлетворяющих какому-либо условию.
Расстояния и теорема Пифагора
Договорившись о системе координат, можно определить расстояние между двумя точками. В одномерном пространстве расстояние между двумя точками — это длина соединяющего их отрезка. Рассмотрим точки P и Q. Расстояние между ними, которое мы обозначим как d (Р, Q), будет вычисляться как абсолютная величина разности: d (Р, Q)=|P-Q|.
Мы помним, что абсолютная величина числа равна положительному значению этого числа. Например, |3|=3 и |-3|=3. Для того, чтобы расстояние было определено однозначно, необходимо, чтобы d (Р, Q)=d (Q,P), то есть величина расстояния между точками не должна зависеть от порядка перечисления этих точек.
Кроме того, расстояние всегда должно быть положительной величиной. Именно поэтому расстояние вычисляют с помощью модуля. Например, расстояние между точками 4 и 9 будет определяться не как: 4-9=-5, а по нашему определению: d (4,9)=|4-9|=|-5|=5.
Давайте посмотрим, как определяется расстояние между двумя точками в двумерном пространстве, то есть между точками на плоскости. Предположим, что у нас есть две точки P и Q, координаты которых заданы как (a, b) и (c, d).
Расположив обе точки на декартовой плоскости, мы можем построить прямоугольный треугольник РОQ. Длины катетов этого треугольника известны: РО=c-a и OQ=d-b.
Чтобы найти значение гипотенузы РQ, применим теорему Пифагора:
$(PQ)^2=(PO)^2+(OQ)^2=(c-a)^2+(d-b)^2$, откуда $d(PQ) =\sqrt {(c-a)^2+(d-b)^2}$.
Таким образом, мы получили формулу для вычисления расстояния между двумя любыми точками на плоскости. Например, расстояние между точками Р (3, 5) и Q(-2,7) в соответствии с этой формулой вычисляется так:
$d(PQ) =\sqrt {(-2-3)^2+(7-5)^2}=\sqrt {(-5)^2+(2)^2}=\sqrt {25+4}=\sqrt {29}$.
 Посмотрим, что произойдет в трехмерном пространстве. Предположим, что мы хотим вычислить расстояние между точками Р (a, b, c) и Q(d, e, f).
Посмотрим, что произойдет в трехмерном пространстве. Предположим, что мы хотим вычислить расстояние между точками Р (a, b, c) и Q(d, e, f).
Здесь мы также будем опираться на теорему Пифагора, но применим ее в два последовательных этапа.
Расстояние, которое нам нужно найти, является диагональю в параллелепипеде (это фигура, похожая на обувную коробку). Два прямоугольных треугольника, к которым мы будем применять теорему Пифагора, закрашены на рисунке разными цветами. Фиолетовый треугольник расположен горизонтально, желтый — вертикально. В фиолетовом треугольнике значения катетов таковы: |d-a| и |e-b|. Поэтому длина гипотенузы вычисляется как $(d-a)^2+(e-b)^2$
Рассмотрим теперь желтый прямоугольный треугольник. Длину одного из двух его катетов мы только что рассчитали. Другой катет, вертикальный, имеет длину |f-c|. Вновь применим теорему Пифагора и получим искомое значение гипотенузы: $\sqrt{[ \sqrt{(d-a)^2+(e-b)^2}]^2+(f-c)^2}=\sqrt{(d-a)^2+(e-b)^2+(f-c)^2}$.
Таким образом, мы получили формулу для вычисления расстояния между двумя любыми точками трехмерного пространства:
$d(PQ)=\sqrt{(d-a)^2+(e-b)^2+(f-c)^2}$.
Например, расстояние между точками Р (2, -1,6) и Q(1, 5, 3) будет равно:
$d(PQ)=\sqrt{(1-2)^2+(5-(-1))^2+(3-6)^2}=\sqrt{(-1)^2+6^2+(-3)^2}=\sqrt{1+36+9}=\sqrt{46}$.
Этот способ определения расстояния между точками можно применять к пространствам любого измерения. Обычно для n-мерного пространства
расстояние между точками $Р (x_1, x_2,…, x_n)$ и $Q(y_1, y_2, …, y_n)$ задается формулой:
$d(PQ)=\sqrt{(x_1-y_1)^2+…+(x_n-y_n)^2}$.
Заметим, что применяя теорему Пифагора для получения формул для вычисления расстояния между двумя точками в двух- и трехмерном про-странствах, мы получили обобщение данной теоремы для n-мерных пространств, где n>2.
Материалы по теме:
Поделиться с друзьями:
 Загрузка…
Загрузка…Расстояние от точки до прямой. Расстояние между параллельными прямыми
Этот видеоурок будет полезен тем, кто хочет самостоятельно изучить тему «Расстояние от точки до прямой. Расстояние между параллельными прямыми». В ходе урока вы сможете узнать о том, как можно рассчитать расстояние от точки до прямой. Затем учитель даст определение расстояния между параллельными прямыми.
В текущем уроке мы познакомимся с понятием «расстояние» в целом. Также мы конкретизируем данное понятие в случае вычисления расстояния между двумя точками, точкой и прямой, параллельными прямыми
Рассмотрим рисунок 1. На нём изображены 2 точки А и В. Расстоянием между двумя точками А и В является отрезок, имеющий концы в заданных точках, то есть отрезок АВ
Рис. 1. АВ – расстояние между точками
Примечательно, что расстоянием нельзя считать кривую или ломаную линии, соединяющих две точки. Расстояние – это кратчайший путь от одной точки к другой. Именно отрезок АВ является наименьшим из всех возможных линий, соединяющие точки А и В
Рассмотрим рисунок 2, на котором изображена прямая а, и точка А, не принадлежащая данной прямой. Расстоянием от точки А до прямой будет длина перпендикуляра АН.

Рис. 2. АН – расстояние между точкой и прямой
Важно заметить, что АН – кратчайшее расстояние, так как в треугольнике АМН данный отрезок является катетом, а произвольный иной отрезок, соединяющий точку А и прямую а (в данном случае – это АМ) будет являться гипотенузой. Как известно, катет всегда меньше гипотенузы
Обозначение расстояния: 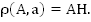
Рассмотрим параллельные прямые a и b, изображённые на рисунке 3
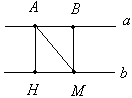
Рис. 3. Параллельные прямые a и b
Зафиксируем две точки на прямой a и опустим из них перпендикуляры на параллельную ей прямую b. Докажем, что если 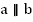 ,
, 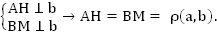
Проведём отрезок АМ для удобства доказательства. Рассмотрим полученные треугольники АВМ и АНМ. Поскольку 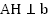 , а
, а 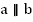 , то
, то 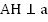 . Аналогично,
. Аналогично, 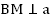 . У данных прямоугольных треугольников (
. У данных прямоугольных треугольников (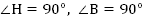 ) сторона АМ – общая. Она является гипотенузой в обоих треугольниках. Углы АМН и АМВ являются внутренними накрестлежащими при параллельных прямых АВ и НМ и секущей АМ. По известному свойству,
) сторона АМ – общая. Она является гипотенузой в обоих треугольниках. Углы АМН и АМВ являются внутренними накрестлежащими при параллельных прямых АВ и НМ и секущей АМ. По известному свойству, 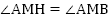 .
.
Из всего выше изложенного следует, что 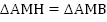 . Из равенства треугольников следует, что АН = ВМ
. Из равенства треугольников следует, что АН = ВМ
Итак, мы доказали, что на рисунке 3 отрезки АН и ВМ равны. Это значит, что расстоянием между параллельными прямыми является длина их общего перпендикуляра, при чём выбор перпендикуляра может быть произвольным. Таким образом, 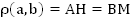
Верно и обратное утверждение: множество точек, которые находятся на одном и том же расстоянии от некоторой прямой, образуют прямую, параллельную данной
Закрепим наши знания, решим несколько задач
Пример 1: Задача 272 из учебника «Геометрия 7-9». Автор — Атанасян Л.С.
В равностороннем треугольнике АВС проведена биссектриса АD. Расстояние от точки D до прямой АС равно 6 см. Найти расстояние от точки А до прямой ВС

Рис. 4. Чертёж к примеру 1
Решение:
Равносторонним треугольником называется треугольник с тремя равными сторонами (а значит, и с тремя равными углами, то есть – по 600). Равносторонний треугольник является частным случаем равнобедренного, поэтому все свойства, присущие равнобедренному треугольнику, распространяются и на равносторонний. Поэтому АD – не только биссектриса, но ещё и высота, стало быть AD ⊥BC
Поскольку расстояние от точки D до прямой АС – это длина перпендикуляра, опущенного из точки D на прямую АС, то DH – данное расстояние. Рассмотрим треугольник АНD. В нём угол Н = 900, так как DH – перпендикуляр к АС (по определению расстояния от точки до прямой). Кроме этого, в данном треугольнике катет DH лежит против угла  , поэтому AD =
, поэтому AD = 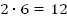 (см) (По свойству)
(см) (По свойству)
Расстояние от точки А до прямой ВС – это длина опущенного на прямую ВС перпендикуляра. По доказанному AD ⊥BC, значит,  .
.
Ответ: 12 см.
Пример 2: Задача 277 из учебника «Геометрия 7-9». Автор — Атанасян Л.С.
Расстояние между параллельными прямыми a и b равно 3 см, а расстояние между параллельными прямыми a и c равно 5 см. Найдите расстояние между параллельными прямыми b и c
Решение:

Рис. 5. Чертёж к примеру 2 (первый случай)
Поскольку 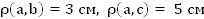 , то
, то 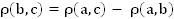 = 5 – 3 = 2 (см).
= 5 – 3 = 2 (см).
Однако данный ответ неполный. Существует и другой вариант расположения прямых на плоскости:

Рис. 6. Чертёж к примеру 2 (второй случай)
В данном случае  .
.
Ответ: 2 см, 8 см.
Рекомендованные ссылки на ресурсы интернет
- Единая коллекция цифровых образовательных ресурсов (Источник).
- Репетитор по математике (Источник).
Рекомендованное домашнее задание
- № 280, 283. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. под редакцией Тихонова А. Н. Геометрия 7-9 классы. М.: Просвещение. 2010 г.
- Сумма гипотенузы СЕ и катета СК прямоугольного треугольника СКЕ равна 31 см, а их разность равна 3 см. найдите расстояние от вершины С до прямой КЕ
- На основании АВ равнобедренного треугольника АВС взята точка М, равноудалённая от боковых сторон. Докажите, что СМ – высота треугольника АВС
- Докажите, что все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной