Расстояние между точками на плоскости и в пространстве Модуль вектора, его направляющие углы и косинусы. Координаты орта вектора. » Аналитическая геометрия f(x)dx.Ru
п.1. Расстояние между точками на плоскости и в пространстве.
Мы выведем формулу расстояния между любыми двумя точками в пространстве. Случай на плоскости будет следовать из общей формулы как частный случай.
Рассмотрим предварительно частный случай. Пусть вектор коллинеарный какой-нибудь координатной оси, например, Ох.
рис.1.
Расстояние между точками А и В равно:
. (1)
Ординаты и аппликаты точек А и В в этом случае равны:
, .
Формула, аналогичная формуле (1) имеет место и в случаях, когда или .
Рассмотрим теперь общий случай расположения точек А и В в пространстве относительно системы координат Охуz.
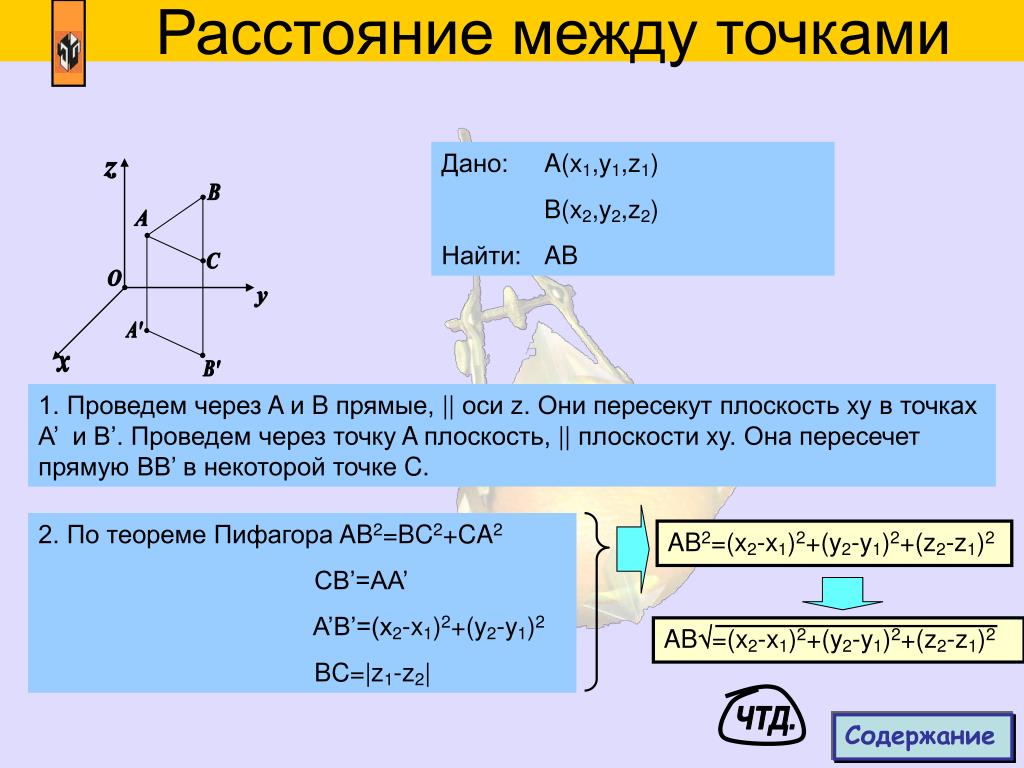
Пусть и – две произвольные точки пространства. Проведем через точки А и В плоскости параллельные координатным плоскостям. Эти 6 плоскостей высекают прямоугольный параллелепипед. См. рис.2.
Проведем через точки А и В плоскости параллельные координатным плоскостям. Эти 6 плоскостей высекают прямоугольный параллелепипед. См. рис.2.
рис.2.
Из прямоугольного треугольника ADC по теореме Пифагора , а из прямоугольного треугольника АВС:
.
Так как точки А, D, С лежат в плоскости перпендикулярной оси Оz, то , т.к. , то .
Точки В, С, D лежат в плоскости перпендикулярной оси Оу, поэтому и , откуда следует, что .
Теперь, по формулам, аналогичным формуле (1), имеем:
,
,
,
откуда следует равенство:
.
Таким образом мы доказали следующую теорему.
Теорема. Пусть и . Тогда
. (2)
Следствие. Пусть и . Тогда
.
п.2. Модуль вектора, его направляющие углы и косинусы. Координаты орта вектора.
Теорема. (О модуле вектора.)
Модуль вектора равен корню квадратному из суммы квадратов его координат.
Иначе, если , то
. (3)
Доказательство. Пусть . Тогда равны их модули и их декартовые координаты: и
, , .
Подставляя в формулу (2), получаем (3), ч.т.д.
Теорема доказана.
Обозначим углы между вектором и координатными осями: , , .
Определение. Углы между вектором и координатными осями называются направляющими углами вектора.
рис.3.
Пусть . По теореме о вычислении проекции вектора на ось, имеем: , , . Отсюда следует:
, , , (4)
. (5)
Из последнего равенства следует, что орт вектора , т.е. вектор единичной длины и сонаправленный с имеет декартовые координаты:
. (6)
(6)
А т.к. , то по теореме о модуле вектора, получаем:
, откуда следует
. (7)
Возможно найдутся ответы здесь:
Расстояние между двумя точками
Расстояние между двумя точками является мерой соединяющего их отрезка.
Мы можем рассчитать эту меру с помощью аналитической геометрии.
Расстояние между двумя точками на плоскости
На плоскости точка полностью определена, зная связанную с ней упорядоченную пару (x, y).
Чтобы узнать расстояние между двумя точками, мы сначала представим их в декартовой плоскости, а затем вычислим это расстояние.
Примеры:
1) Какое расстояние между точкой A (1.1) и точкой B (3.1)?
d (A, B) = 3 — 1 = 2
2) Каково расстояние между точкой A (4.1) и точкой B (1,3)?
Обратите внимание, что расстояние между точкой A и точкой B равно гипотенузе прямоугольного треугольника с катетами 2 и 3.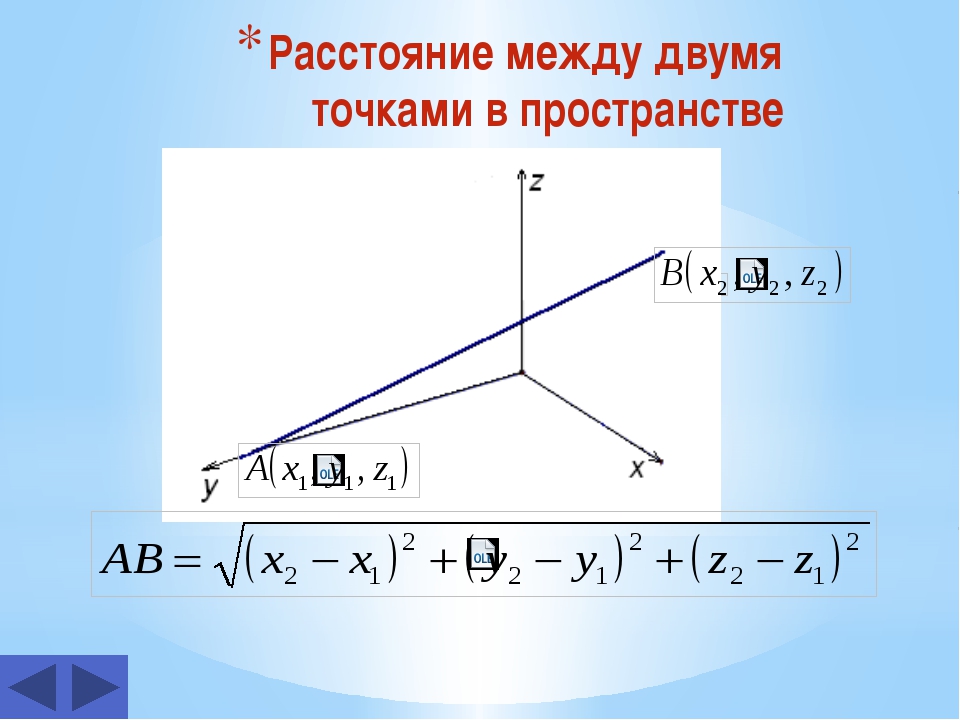
Итак, мы будем использовать теорема Пифагора для расчета расстояния между заданными точками.
[d (A, B)]2 = 32 + 22 = √13
Формула расстояния между двумя точками на плоскости
Чтобы найти формулу расстояния, мы можем обобщить расчет, сделанный в примере 2.
Для любых двух точек, таких как A (x1гг1) и B (x2у2), у нас есть:
Чтобы узнать больше, прочтите также:
- плоская геометрия
- Декартов план
- прямой
Расстояние между двумя точками в пространстве
Мы используем трехмерную систему координат для представления точек в пространстве.
Точка полностью определена в пространстве, когда с ней связана упорядоченная тройка (x, y, z).
Чтобы найти расстояние между двумя точками в пространстве, сначала мы можем представить их в системе координат, а оттуда выполнить вычисления.
Пример:
Каково расстояние между точкой A (3,1,0) и точкой B (1,2,0)?
В этом примере мы видим, что точки A и B принадлежат плоскости xy.
Расстояние будет определяться следующим образом:
[d (A, B)]2 = 12 + 22 = √5
Формула расстояния между двумя точками в пространстве
Чтобы узнать больше, прочтите также:
- Пространственная геометрия
- Линейное уравнение
- Математические формулы
Решенные упражнения
1) Точка A принадлежит оси абсцисс (ось x) и равноудалена от точек B (3.2) и C (-3.4). Каковы координаты точки А?
См. ОтветПоскольку точка A принадлежит оси абсцисс, то ее координата равна (a, 0). Итак, нам нужно найти значение a.
(0 — 3)2 + (к — 2)2 = (0 + 3)2 + (до -4)2
От 9 + до 2 — 4а +4 = 9 + а2 — 8 + 16
4-й = 12
а = 3
(3.0) — координаты точки А.
2) Расстояние от точки A (3, a) до точки B (0.2) равно 3. Вычислить значение ординаты a.
См. Ответ32 = (0 — 3)2 + (2 — а)2
9 = 9 + 4 — 4а + а2
В2 — 4-й +4 = 0
а = 2
3) ЭНЭМ — 2013 г.
В последние годы на телевидении произошла настоящая революция с точки зрения качества изображения, звука и интерактивности со зрителем. Это преобразование связано с преобразованием аналогового сигнала в цифровой сигнал. Однако во многих городах до сих пор нет этой новой технологии. Стремясь донести эти преимущества до трех городов, телевизионная станция намеревается построить новую передающую вышку, которая отправляет сигнал на антенны A, B и C, которые уже существуют в этих городах. Расположение антенн представлено в декартовой плоскости:
Вышка должна быть расположена на одинаковом расстоянии от трех антенн. Правильное место для строительства этой башни соответствует координатной точке
а) (65; 35)
б) (53; 30)
в) (45; 35)
г) (50; 20)
д) (50; 30)
Правильная альтернатива e: (50; 30)
Смотрите также: расстояние между двумя точками упражнения
4) ЭНЕМ — 2011 г.
Район города планировался в плоском районе с параллельными и перпендикулярными улицами, ограничивающими кварталы одинакового размера. В следующей декартовой координатной плоскости эта окрестность расположена во втором квадранте, а расстояния в
В следующей декартовой координатной плоскости эта окрестность расположена во втором квадранте, а расстояния в
оси даны в километрах.
Прямая линия уравнения y = x + 4 представляет собой планирование маршрута подземной линии метро, которая будет пересекать окрестности и другие районы города.
В точке P = (-5,5) расположена государственная больница. Сообщество попросило комитет по планированию спланировать станцию метро так, чтобы расстояние от нее до больницы, измеренное по прямой линии, не превышало 5 км.
а) (-5,0)
б) (-3,1)
в) (-2,1)
г) (0,4)
д) (2.6)
Правильная альтернатива b: (-3,1).
Смотрите также: упражнения по аналитической геометрии
Расстояние от точки до отрезка
Расстоянием от точки до отрезка является либо перпендикуляр, опущенный из этой точки на отрезок, либо минимальное расстояние от точки до одного из концов отрезка.
Если треугольник, вершинами которого является данная точка и концы заданного отрезка, является тупоугольным (проверка на тупоугольность проводится рассмотрением знака скалярного произведения соответствующих векторов, построенных на сторонах треугольника (кос тупого угла отрицательный))(т. е. из данной точки невозможно опустить перпендикуляр на данный отрезок), то расстоянием от точки до отрезка считается минимальное расстояние от данной точки, до одного из концов отрезка. Оно определяется с помощью формулы:
Если все же перпендикуляр опустить возможно, то расстоянием от точки до отрезка считается длина этого перпендикуляра. Ее можно определить двумя способами:
1) посчитав площадь треугольника по двум формулам (полувысота на сторону и полупроизведение сторон на синус угла между ними) мы можем выразить высоту как:
h = (AC • AB • sin (AC, AB)) / BC ;
2) можем определить координаты точки пресечения отрезка с перепендикуляром, опущенным из данной точки на отрезок и посчитать расстояние между двумя точками.
(1)(x — x1)(y2 — y1) = (y — y1)(x2 — x1)
(2) (x — k)(x2 — x1) = — (y — l)(y2 — y1)
Если (x2 — x1) = 0, то решение:
x = x1
y = l.
Если (y2 — y1) = 0, то решение:
y = y1
x = k.
В остальных случаях (пусть (x2 — x1) = α, (y2 — y1) = β):
x = (α / β) (y — y1) + x1
y = ((α2 / β)y1 + α (k — x
Краткосрочный план урока по теме » Расстояние между точками в пространстве»
Краткосрочный план
Раздел долгосрочного плана: 10. 3В
3ВПрямоугольная система координат и векторы в пространстве
Школа: НИШ ФМН г Астаны.
Дата:
ФИО учителя: Косова Г.П.
Класс:
Количество присутствующих:
отсутствующих:
Тема урока
Расстояние между двумя точками в пространстве
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
10.4.2 уметь находить расстояние между двумя точками в пространстве
Цели урока
Повторить формулу расстояния между двумя точками на плоскости, построение токи в прямоугольной системе координат пространства. Вывести формулу расстояния между точками в пространстве. Находить расстояния между точками в пространстве при решении задач.
Критерии успеха
Учащийся
записывает формулу расстояния между двумя точками в пространстве;
применяет формулу расстояния между двумя точками в пространстве при решении задач.

Языковые цели
Учащиеся будут:
использовать терминологию трехмерного пространства, чтобы описать операции с векторами.
Лексика и терминология, специфичная для предмета:
вектор
плоскость
коллинеарные векторы
условие коллинеарности векторов
координатные оси
координаты вектора
Полезные выражения для диалогов и письма:
Координаты проекции точки на…
Координаты вектора…
Длина вектора…
Привитие ценностей
Учащиеся должны участвовать в диалоге с учителем и одноклассниками, развивая коммуникативные навыки.
В результате работы на уроке развиваем творческие способности, ответственность, умение слушать, наблюдать, делать выводы.
Межпредметные связи
Применение в физике при описании физических процессов
Навыки использования ИКТ
Работа с презентацией
Предварительные знания
Умеют изображать на плоскости прямоугольную систему координат в пространстве;
умеют определять координаты точки в пространстве;
знают и умеют применять расстояние между точками на плоскости.
Ход урока
Запланированные этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока
10 мин
Организационный момент ( готовность учащихся к работе)
Повторение предыдущего материала. Решаем задачи по презентации, повторяя следующие теоретические вопросы:
Расстояние между точками на плоскости;
Деление отрезка пополам на плоскости;
Определение координат точки в прямоугольной системе координат в пространстве
Определение координат вектора по координатам начала и конца вектора (акцентируем внимание учащихся: чтобы найти координаты вектора, необходимо от соответствующих координат конца отнять соответствующие координаты начала)
Задача: Дан куб с ребром, равным 4. Определите координаты его вершин.
Определите координаты его вершин.
После повторения расстояния между точками на плоскости и координат точки в пространстве, естественно спросить о теме урока учащихся.
. Совместно формулируем цели урока и критерии оценивания.
Дополнительные задачи на повторение ( если располагаете временем и возможностями конкретного класса)
1. Найдите на оси ординат точку, равноудаленную от точек (-1;1) и (3;5)
Ответ: (0;4)
2. В треугольнике АВС с вершинами в точках А(2;-1), В(-1;3), С(-3;1) проведена медиана AD. Найдите длину этой медианы.
Ответ: 5.
Презентация
Слайды:
14
Середина урока
10 мин
5 мин
15 мин
Изучение нового материала (После детальной актуализации знаний, учащиеся самостоятельно выводят формулу расстояния между точками в пространстве).

Получили формулу и обобщаем формулу для расстояния между точками в пространстве.
Решение задач на применение формулы с постепенным усложнением.
Решение задач индивидуально. Взаимопроверка и обсуждение решения в парах. Если возникают вопросы в парах, то обсуждение выводим на доску и совместно приходим к решению.
1. А(3;-2;-4). Найдите сумму расстояний от точки А до оси Оу и от точки А до плоскости хОz.
Ответ: 7.
3. Координаты точек: А(4; -3; 2), В(-1; -5; 4). Найдите сумму координат точки С, лежащей на оси Оу и равноудаленной от точек А и В.
Ответ: -3,25.
4. Найдите расстояние от точки (1; 2; -3) до начало координат.
Ответ:
5. На оси Ох найдите точку С(х; 0; 0), равноудаленную от двух точек А(1; 2; 3) и В(-2; 1; 3).
Ответ: С(0;0;0)
6. Точка В(-6; -3; 8). Точка С – основание перпендикуляра ВС, проведенного к оси Оу. D – основание перпендикуляра ВD, проведенного к плоскости хОz. Найдите сумму расстояний ВС и ВD.
Точка В(-6; -3; 8). Точка С – основание перпендикуляра ВС, проведенного к оси Оу. D – основание перпендикуляра ВD, проведенного к плоскости хОz. Найдите сумму расстояний ВС и ВD.
Ответ: 13.
7.. Докажите, что ABCD — прямоугольник, если А(4; –2; 2), В(6; 1; –4), С(0; –1; –7), D(–2; –4; –1).
Презентация
Слайды:
13-16
Слайды:
17-18
Конец урока
2 мин
2 мин
1 мин
Домашняя работа:
В(-7; 4; -3). Найдите сумму расстояний от точки В до оси Ох и от точки В до плоскости уОz.
2. А(1; 7; –1), В(–4; 5; –5), С(2; –1; 1).
а) Найдите координаты вершины D параллелограмма ABCD.
б) На оси аппликат найдите точку, равноудаленную от точек В и С.
Рефлексия:
Учащиеся на стикерах отвечают на вопросы:
Чему научился за сегодняшнем уроке?
Что не получается и вызывает трудности при решении задач. Над чем еще необходимо поработать?
Учитель комментирует работу учащихся.
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
Здоровье и соблюдение техники безопасности
Подборка достаточного количества задач с постепенным усложнением. Комментарии решений, ответы на поставленные вопросы, анализ собственной деятельности на уроке.
Фронтальная беседа по теоретическим вопросам. Работа в парах, комментарии своих действий при решении задач.
Использование физминуток и активных методов работы.
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
1:
2:
Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
1:
2:
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
Расстояние между двумя точками.
 Середина отрезка. Координаты середины отрезка. Тема 4
Середина отрезка. Координаты середины отрезка. Тема 41. Тема 1-11. Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Уравнение прямой на плоскости.
Раздел III. Аналитическая геометрияТема 1-11.
Расстояние между двумя точками. Середина
отрезка. Координаты середины отрезка.
Уравнение прямой на плоскости. Уравнение
прямой в пространстве. Уравнение
плоскости. Расстояние от точки до плоскости.
Расстояние между плоскостями. Расстояние
от точки до прямой на плоскости. Расстояние
от точки до прямой в пространстве. Угол
между плоскостями. Угол между прямой и
плоскостью
2. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Расстояние между двумя точками — этодлина отрезка, что соединяет эти точки.
• Формула вычисления расстояния между двумя
точками A(xa, ya) и B(xb, yb) на плоскости:
AB = √(xb — xa)2 + (yb — ya)2
• Формула вычисления расстояния между двумя
точками A(xa, ya, za) и B(xb, yb, zb) в пространстве:
AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2
3.
 Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек. Середина отрезка — это точка, которая
Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек. Середина отрезка — это точка, котораялежит на отрезке и находится на равном
расстоянии от конечных точек.
• Формула вычисления координат середины
отрезка с концами A(xa, ya) и B(xb, yb) на
плоскости:
x a + xb
ya + yb
xc =
yc =
2
2
• Формула вычисления координат середины
отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в
пространстве:
xa + xb
ya + yb
za + zb
xc =
yc =
zc =
2
2
2
4. Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Прямая (прямая линия) — этобесконечная линия, по которой
проходит кратчайший путь между
любыми двумя её точками.
• Любую прямую на плоскости можно
задать уравнением прямой первой степени
вида
A x + B y + C = 0,
где A и B не могут быть одновременно равны
нулю.

5. Уравнение прямой с угловым коэффициентом
• Общее уравнение прямой при B≠0 можнопривести к виду
y = k x + b,
где k — угловой коэффициент равный тангенсу
угла, образованного данной прямой и
положительным направлением оси ОХ.
6. Уравнение прямой в отрезках на осях
• Если прямая пересекает оси OX и OY вточках с координатами (a, 0) и (0, b), то она
может быть найдена используя
формулу уравнения прямой в отрезках
x
a
+
y
b
=1
7. Уравнение прямой, проходящей через две различные точки на плоскости
• Если прямая проходит через две точкиA(x1, y1) и B(x2, y2), такие
что x1 ≠ x2 и y1 ≠ y2 то уравнение
прямой можно найти, используя
следующую формулу
x -x1
x2 -x1
=
y -y1
y2 — y1
8. Параметрическое уравнение прямой на плоскости
• Параметрические уравнения прямой могутбыть записаны следующим образом
x = l t +x0
y = m t + y0
где (x0, y0) — координаты точки лежащей на
прямой,
{l,m} — координаты направляющего вектора
прямой.

9. Каноническое уравнение прямой на плоскости
• Если известны координаты точки A(x0, y0)лежащей на прямой и направляющего
вектора n ={l;m}, то уравнение прямой
можно записать в каноническом виде,
используя следующую формулу
x -x0
l
=
y — y0
m
10. Уравнение прямой, проходящей через две различные точки в пространстве
• Если прямая проходит через две точкиA(x1,y1,z1) и B(x2,y2,z2), такие что
x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2 то уравнение
прямой можно найти используя
следующую формулу
x -x1
x2 -x1
=
y -y1
y2 -y1
=
z -z1
z2 — z1
11. Параметрическое уравнение прямой в пространстве
• Параметрические уравнения прямой могутбыть записаны следующим образом
x = l t +x0
y = m t + y0
z = n t + z0
где (x0, y0, z0) — координаты точки лежащей на
прямой,
{l; m; n} — координаты направляющего вектора
прямой.
12. Каноническое уравнение прямой в пространстве
• Если известны координаты точки A(x0, y0, z0)лежащей на прямой и направляющего
вектора n={l;m;n}, то уравнение прямой
можно записать в каноническом виде,
используя следующую формулу
x -x0
l
=
y -y0
m
=
z -z0
n
13.
 Прямая как линия пересечения двух плоскостей • Если прямая является пересечением двух
Прямая как линия пересечения двух плоскостей • Если прямая является пересечением двухплоскостей, то ее уравнение можно задать
следующей системой уравнений
A1x + B1y + C1z + D1 = 0
A2x + B2y + C2z + D2 = 0
при условии, что не имеет место равенство
A1
A2
=
B1
B2
=
C1
C2
.
14. Плоскость — есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.
Плоскость — есть поверхность, полностьюсодержащая, каждую прямую,
соединяющую любые её точки.
• Любую плоскость можно
задать уравнением плоскости первой
степени вида
Ax+By+Cz+D=0
где A, B и C не могут быть одновременно
равны нулю.
15. Уравнение плоскости в отрезках
• Если плоскость пересекает оси OX, OY и OZ вточках с координатами (a, 0, 0), (0, b, 0) и (0,
0, с), то она может быть найдена, используя
формулу уравнения плоскости в отрезках
x
a
+
y
b
+
z
c
=1
16.
 Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали • Чтобы составить уравнение плоскости, зная
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали • Чтобы составить уравнение плоскости, знаякоординаты точки плоскости M(x0, y0, z0) и
вектора нормали плоскости n = {A; B; C} можно
использовать следующую формулу.
A(x — x0) + B(y — y0) + C(z — z0) = 0
17. Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
• Если заданы координаты трех точекA(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3),
лежащих на плоскости, то уравнение
плоскости можно найти по следующей
формуле
x — x1 y — y1 z — z1
x2 — x1 y2 — y1 z2 — z1
x3 — x1 y3 — y1 z3 — z1
=0
18. Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
Расстояние от точки до плоскости —равно длине перпендикуляра,
опущенного из точки на плоскость.
• Если задано уравнение плоскости Ax + By +
Cz + D = 0, то расстояние от точки M(Mx, My,
Mz) до плоскости можно найти, используя
следующую формулу:
|A·Mx + B·My + C·Mz + D|
d=
√A2 + B2 + C2
19.
 Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую. Расстояние между плоскостями — равно
Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую. Расстояние между плоскостями — равнодлине перпендикуляра, опущенного с
одной плоскости на другую.
• Если заданы уравнения параллельных
плоскостей Ax + By + Cz + D1 = 0 и
Ax + By + Cz + D2 = 0, то расстояние между
плоскостями можно найти, используя
следующую формулу
|D2 — D1|
d=
√A2 + B2 + C2
20. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Расстояние от точки до прямой — равнодлине перпендикуляра, опущенного из
точки на прямую.
• Если задано уравнение прямой Ax + By + C = 0,
то расстояние от точки M(Mx, My) до прямой
можно найти, используя следующую формулу
|A·Mx + B·My + C|
d=
√A2 + B2
21. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Расстояние от точки до прямой —равно длине перпендикуляра,
опущенного из точки на прямую.

• Если s = {m; n; p} — направляющий вектор
прямой l, M1(x1, y1, z1) — точка лежащей на
прямой, тогда расстояние от точки
M0(x0, y0, z0) до прямой l можно найти,
используя формулу
d=
|M0M1×s|
|s|
• Двугранный угол между плоскостями равен углу
образованному нормальными векторами этих
плоскостей.
• Двугранный угол между плоскостями равен углу
образованному прямыми l1 и l2, лежащими в
соответствующих плоскостях и перпендикулярными
линии пересечения плоскостей.
• Если заданы уравнения плоскостей A1x + B1y + C1z +
D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между
плоскостями можно найти, используя следующую
формулу
|A1·A2 + B1·B2 + C1·C2|
cos α =
√A12 + B12 + C12√A22 + B22 + C22
23. Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Угол между прямой и плоскостью — это уголмежду прямой и ее проекцией на эту
плоскость.
• Если в пространстве заданы направляющий
вектор прямой L s = {l; m; n} и уравнение
плоскости Ax + By + Cz + D = 0, то угол
между этой прямой и плоскостью можно
найти используя формулу
|A·l+B· m+C· n|
sin φ =
√A2 + B2 + C2 · √l2 + m2 + n2
Расчет евклидова расстояния с помощью NumPy / Хабр
В этом руководстве мы рассмотрим, как рассчитать евклидово расстояние между двумя точками в Python с помощью Numpy.
Что такое евклидово расстояние?
Евклидово расстояние — это фундаментальная метрика расстояния, относящаяся к системам в евклидовом пространстве.
Евклидово пространство — это классическое геометрическое пространство, с которым вы знакомитесь на уроке математики, обычно связанное с 3 измерениями. Хотя его также можно приписать к любой неотрицательной целочисленной размерности.
Евклидово расстояние — кратчайшая прямая между двумя точками в евклидовом пространстве.
Название происходит от Евклида, который широко известен как «отец геометрии», так как это было единственное пространство, которое люди в то время обычно задумывали. Со временем в физике и математике наблюдались различные типы пространства, такие как пространство Аффин.
Учитывая этот факт, евклидово расстояние не всегда является наиболее полезной метрикой для отслеживания при работе со многими размерностями, мы сосредоточимся на 2D и 3D евклидовом пространстве для расчета евклидова расстояния.
Вообще говоря, евклидова расстояние широко используется в разработке 3D-миров, а также алгоритмов машинного обучения, которые включают в себя метрики расстояния, такие как K-ближайшие соседи. Как правило, евклидово расстояние будет представлять, насколько похожи две точки данных, предполагая, что некоторая кластеризация на основе других данных уже была выполнена.
Математическая формула
Математическая формула расчета евклидова расстояния между 2 точками в 2D пространстве:
Формула легко адаптируется к 3D-пространство, а также к любому размеру:
Общая формула может быть упрощена до:
Острый глаз может заметить сходство между евклидовым расстоянием и теоремой Пифагора:
На самом деле существует связь между ними — евклидовое расстояние рассчитывается с помощью теоремы Пифагора, учитывая декартовы координаты двух точек.
Из-за этого евклидова расстояние иногда называют расстоянием Пифагора, хотя прежнее название гораздо более известно.
Примечание: Две точки являются векторами, но выход должен быть скалярным.
Мы будем использовать NumPy для расчета этого расстояния для двух точек, и один и тот же подход используется для 2D и 3D пространств:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
ax.scatter(0, 0, 0)
ax.scatter(3, 3, 3)
plt.show()Расчет евклидова расстояния в Python с помощью NumPy
Во-первых, нам нужно будет установить библиотеку NumPy:
$ pip install numpyТеперь давайте импортируем его и настроим две наши точки с декартовыми координатами (0, 0, 0) и (3, 3, 3):
import numpy as np
# Initializing the points
point_1 = np.array((0, 0, 0))
point_2 = np.array((3, 3, 3))Вместо того, чтобы выполнять расчет вручную, мы будем использовать вспомогательные методы NumPy, чтобы сделать его еще проще!
np. Что равно 27. Осталось все, что получить квадратный корень из этого числа: Это приводит к: В истинном питоновом духе это можно сократить до одной строки: И вы даже можете вместо этого использовать встроенные методы pow() и sum() математического модуля Python, хотя они требуют, чтобы вы немного поработали с вводом, который удобно абстрагируется с помощью NumPy, так как функция pow() работает только со скалярами (каждый элемент в массиве индивидуально) и принимает аргумент — в какой степени вы увеличиваете число. Этот подход, однако, интуитивно больше похож на формулу, которую мы использовали раньше: Это также приводит к: np.linalg.norm() Функция np.linalg.norm() представляет математическую норму. По сути, нормой вектора является его длина. Эта длина не обязательно должна быть евклидовым расстоянием, а может быть и другими расстояниями. Евклидово расстояние-это норма L2 вектора (иногда известная как евклидова норма), и по умолчанию функция norm() использует L2 — параметр ord имеет значение 2. Если бы вы установили для параметра ord какое-то другое значение p, вы бы рассчитали другие p-нормы. Например, норма L1 вектора-это расстояние Манхэттена! Имея это в виду, мы можем использовать функцию np.linalg.norm() для легкого и гораздо более чистого вычисления евклидова расстояния, чем использование других функций: Это приводит к печати расстояния L2/евклида: Нормализация L2 и нормализация L1 широко используются в машинном обучении для нормализации входных данных. np.dot() Мы также можем использовать точечное произведение для расчета евклидова расстояния. В математике точечное произведение является результатом умножения двух векторов равной длины, а результатом является единственное число — скалярное значение. Из-за возвращаемого типа его иногда также называют «скалярным продуктом». Эту операцию часто называют внутренним произведением для двух векторов. Для расчета точечного произведения между 2 векторами вы можете использовать следующую формулу: С помощью NumPy мы можем использовать функцию np.dot(), передавая два вектора. Если мы вычислим точечное произведение разницы между обеими точками с той же разницей — мы получим число, которое находится в зависимости от евклидова расстояния между этими двумя векторами. Извлечение квадратного корня из этого числа дает нам расстояние, которое мы ищем: Конечно, вы также можете сократить это до однострочного: В Python есть встроенный метод в математическом модуле, который вычисляет расстояние между 2 точками в трехмерном пространстве. Однако это работает только с Python 3.8 или более поздней версии. math.dist()принимает два параметра, которые являются двумя точками, и возвращает евклидово расстояние между этими точками. Примечание: Обратите внимание, что две точки должны иметь одинаковые размеры (т.е. оба в 2d или 3d пространстве). Теперь, чтобы вычислить Евклидово расстояние между этими двумя точками, мы просто заправляем их в метод thedistdist(): Данная метрика используется во многих контекстах в интеллектуальном анализе данных, машинном обучении и ряде других областей и является одной из фундаментальных метрик расстояния. \({\color{red}{\textbf{Факт 1. Про векторы}}}\) \(\qquad \blacktriangleright\) сумма этих векторов \(\vec{a}+\vec{b}=\{x_1+x_2;y_1+y_2;z_1+z_2\}\) \(\qquad \blacktriangleright\) разность этих векторов \(\vec{a}-\vec{b}=\{x_1-x_2;y_1-y_2;z_1-z_2\}\) \(\qquad \blacktriangleright\) произведение вектора на число \(\lambda
\vec{a}=\{\lambda x_1;\lambda
y_1;\lambda z_1\}\)
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), а точка \(O\) — середина отрезка \(AB\), то \(O\) имеет координаты \[O\left(\dfrac{x_1+x_2}2;\dfrac{y_1+y_2}2;\dfrac{z_1+z_2}2\right)\] \({\color{red}{\textbf{Факт 2. Про скалярное произведение}}}\) \(\bullet\) Справедливы следующие утверждения: I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: \[(\vec{a}, \vec{b})=0 \quad\Leftrightarrow\quad
\vec{a}\perp \vec{b}\] II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: \[|\vec{a}|=\sqrt{(\vec{a},
\vec{a})}\] III. Переместительный закон: \[(\vec{a}, \vec{b})=(\vec{b},
\vec{a})\] IV. Распределительный закон: \[(\vec{a}+\vec{b},
\vec{c})=(\vec{a}, \vec{c})+(\vec{b}, \vec{c})\] V. \({\color{red}{\textbf{Факт 3. Про уравнение плоскости}}}\) \({\color{red}{\textbf{Факт 4. Когда мы знаем расстояния по горизонтали и по вертикали между двумя точками, мы можем вычислить расстояние по прямой следующим образом: расстояние = √ a 2 + b 2 Представьте, что вы знаете расположение двух точек (A и B), как здесь. Какое расстояние между ними? Мы можем провести линии вниз от A и вдоль от B, чтобы получился прямоугольный треугольник. И с небольшой помощью Пифагора мы знаем, что: a 2 + b 2 = c 2 Теперь отметьте координаты точек A и B. x A означает координату x точки A Горизонтальное расстояние a равно (x A — x B ) Расстояние по вертикали b равно (y A — y B ) Теперь мы можем найти c (расстояние между точками): Начнем с: c 2 = a 2 + b 2 Поместите в вычисления для a и b: c 2 = (x A — x B ) 2 + (y A — y B ) 2 Неважно, в каком порядке расположены точки, потому что возведение в квадрат удаляет любые негативы: А вот еще пример с некоторыми отрицательными координатами. (Примечание √136 можно дополнительно упростить до 2√34, если хотите) Перетащите точки: Отлично работает в 3 (и более!) Измерениях. Возвести в квадрат разность для каждой оси, затем сложить их и извлечь квадратный корень: Расстояние = √ [(x A — x B ) 2 + (y A — y B ) 2 + (z A — z B ) 2 ] Учитывая две точки $ (x_1, y_1) $ и $ (x_2, y_2) $, напомним, что их
расстояние по горизонтали друг от друга составляет $ \ Delta x = x_2-x_1 $, а их
расстояние по вертикали друг от друга составляет $ \ Delta y = y_2-y_1 $. (Фактически,
слово «расстояние» обычно означает «положительное расстояние». $ \ Delta
x $ и $ \ Delta y $ — это расстояний со знаком , но это ясно из
контекст.) Фактическое (положительное) расстояние от одной точки до другой.
длина гипотенузы прямоугольного треугольника с катетами $ | \ Delta
x | $ и $ | \ Delta y | $, как показано на рисунке 1.2 = 16 $.
Теперь мы видим, что это круг с радиусом 4 и центром $ (1, -2) $,
который легко построить графиком.
$ \ квадрат $ Пр. 1.2.1 Найдите уравнение окружности радиуса 3 с центром в точке: (отвечать) Пр. 1.2.2 Для каждой пары точек $ A (x_1, y_1) $ и $ B (x_2, y_2) $ найти (i) $ \ Delta x $
и $ \ Delta y $ при переходе от $ A $ к $ B $, (ii) наклон линии, соединяющей
$ A $ и $ B $, (iii) уравнение прямой, соединяющей $ A $ и $ B $, в виде
$ y = mx + b $, (iv) расстояние от $ A $ до $ B $, и (v) уравнение
круг с центром в $ A $, проходящий через $ B $. Пр. 1.2.6 Найдите стандартное уравнение круга, проходящего через $ (- 2,1) $.
и касательная к прямой $ 3x-2y = 6 $ в точке $ (4,3) $. Эскиз.
(Подсказка: линия, проходящая через центр круга и точку касания
перпендикулярна касательной.)
(отвечать) К настоящему времени вы и Дельфиниус, возможно, уже получили представление о том, как определять местоположение точек, проводя линию от начала координат и затем ища прямоугольный треугольник.Разместим в нашем пространстве еще одну зеленую точку на расстоянии d от начала координат: Если смотреть в сторону исходной точки из некоторой точки положительного угла x -ось показывает другой прямоугольный треугольник: Линия c такая же, как и раньше, а расстояние d мы уже описали. Теперь мы куда-то идем, потому что можем заменить c : Если извлечь квадратный корень из обеих частей: d — это расстояние.В этом примере d — это расстояние от начала координат до второй точки. Начало координат можно записать как (0, 0, 0). Если мы включим эту информацию «0»: Дельфиниус, будучи умным дельфином, любит, чтобы результаты были как можно более общими. Допустим, у нас есть две произвольные точки в пространстве, и мы хотим узнать расстояние между ними. Одна из точек находится в ( x 1, y 1, z 1).Другая точка находится в ( x 2, y 2, z 2). Вместо расстояния от начала координат в (0, 0, 0) у нас есть расстояние от точки ( x 1, y 1, z 1). Уравнение расстояния d : Теперь рассмотрим два примера Дельфиниуса, чтобы проверить математику. Эти две точки находятся на оси z , и расстояние между ними равно 6. Как насчет использования уравнения? Что, если бы мы поменяли местами точки? Из-за возведения в квадрат, какая точка равна «1», а какая — «2», значения не имеет. Мы используем уравнение, которое дает нам расстояние между двумя точками: Мы разработали уравнение расстояния и провели некоторые вычисления.Что может сделать дельфина счастливее? Исходная точка — это место, где x , y и z равны нулю. Гипотенуза — самая длинная сторона прямоугольного треугольника. Теорема Пифагора связывает длины сторон прямоугольного треугольника. Используя теорему Пифагора, мы нашли расстояние между двумя произвольными точками в трехмерном пространстве. Для двух точек с координатами ( x 1, y 1, z 1) и ( x 2, y 2, z 2) расстояние d равно Обычно в двухмерном пространстве каждая точка в пространстве определяется двумя параметрами: координатой x и координатой y. Прежде чем вы научитесь определять расстояние между двумя точками 3D, вы должны знать базовую формулу расстояния, которая приведена ниже. Рассматривая две точки M (x1, y1) и N (x2, y2) на данной координатной оси, вы можете найти расстояние между ними по формуле: Шаги, чтобы найти расстояние между двумя точками: Во-первых, вам нужно взять координаты двух точек, таких как (x1, y1) и (x2, y2). Затем вы должны использовать формулу расстояния, которая равна √ [(x2 — x1) ² + (y2 — y1) ²]. Теперь вам нужно рассчитать расстояние по вертикали и горизонтали между двумя точками. Затем вы должны возвести в квадрат оба значения, полученные из (x2 — x1) и (y2 — y1). Теперь все, что вам нужно сделать, это сложить оба значения, что выглядит как (x2 — x1) 2 + (y2 — y1) 2. Наконец, вам нужно найти квадратный корень из полученного значения. В итоге вы получите расстояние между двумя точками на координатной плоскости. Следующее исследование можно расширить, чтобы определить расстояние между двумя точками в пространстве. Мы можем определить расстояние между двумя точками в 3D, используя приведенную ниже формулу. А пока обратитесь к рис. (изображение будет загружено в ближайшее время) Из точек P и Q нужно провести плоскости, параллельные координатной плоскости. Тогда вы получите прямоугольный параллелепипед с диагональю PQ. Как видно на рисунке, ∠PAQ образует прямой угол. Это позволяет нам применить теорему Пифагора в треугольнике PAQ. Итак, теперь вы получаете PQ2 = PA2 + AQ2. . .{2}} \] \ [AB = \ sqrt {16 + 144 + 36} \] Наконец, AB = 14; Таким образом, расстояние между точками A и B равно 14. Калькуляторы, представленные ниже, можно использовать для определения расстояния между двумя точками на двухмерной плоскости или трехмерном пространстве. Их также можно использовать для определения расстояния между двумя парами широты и долготы или двумя выбранными точками на карте. Используйте этот калькулятор, чтобы найти расстояние между двумя точками на 2D-координатной плоскости. Используйте этот калькулятор, чтобы найти расстояние между двумя точками в трехмерном координатном пространстве. Используйте этот калькулятор, чтобы найти кратчайшее расстояние (большой круг / воздушное расстояние) между двумя точками на поверхности Земли. Щелкните карту ниже, чтобы установить две точки на карте и найти кратчайшее расстояние (большой круг / воздушное расстояние) между ними.После создания маркер (маркеры) можно переместить, щелкнув и удерживая, а затем перетащив их. Point 1: [‘ + lat1 + ‘,’ + lon1 + ‘] Установите другой маркер на карте, чтобы рассчитать расстояние. Установите два маркера на карте, чтобы рассчитать расстояние между ними. Расстояние в 2D координатной плоскости: Расстояние между двумя точками на двухмерной координатной плоскости можно найти с помощью следующей формулы расстояния d = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2 , где (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух задействованных точек.Порядок точек не имеет значения для формулы, если выбранные точки совпадают. Например, учитывая две точки (1, 5) и (3, 2), либо 3, либо 1 могут быть обозначены как x 1 или x 2 , если используются соответствующие значения y: Использование (1, 5) как (x 1 , y 1 ) и (3, 2) как (x 2 , y 2 ): Использование (3, 2) как (x 1 , y 1 ) и (1, 5) как (x 2 , y 2 ): В любом случае результат будет одинаковым. Расстояние в трехмерном координатном пространстве: Расстояние между двумя точками на трехмерной координатной плоскости можно найти с помощью следующей формулы расстояния d = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2 + (z 2 — z 1 ) 2 , где (x 1 , y 1 , z 1 ) и (x 2 , y 2 , z 2 ) — это трехмерные координаты двух задействованных точек.Как и в двухмерной версии формулы, не имеет значения, какая из двух точек обозначена (x 1 , y 1 , z 1 ) или (x 2 , y 2 , z 2 ), если в формуле используются соответствующие точки. Учитывая две точки (1, 3, 7) и (2, 4, 8), расстояние между точками можно найти следующим образом: Есть несколько способов найти расстояние между двумя точками на поверхности Земли. Формула Хаверсина: Формулу гаверсинуса можно использовать для определения расстояния между двумя точками на сфере с учетом их широты и долготы: В формуле гаверсинуса d — это расстояние между двумя точками по большому кругу, r — радиус сферы, & directphi; 1 и & Stratocaster; 2 — это широты двух точек, а λ 1 и λ 2 — долготы двух точек, все в радианах. Формула гаверсинуса работает, находя расстояние по большому кругу между точками широты и долготы на сфере, которое можно использовать для аппроксимации расстояния на Земле (поскольку оно в основном сферическое). Большой круг (также ортодромия) сферы — это самый большой круг, который можно нарисовать на любой данной сфере. Он образован пересечением плоскости и сферы через центральную точку сферы. Расстояние по дуге большого круга — это кратчайшее расстояние между двумя точками на поверхности сферы. Результаты с использованием формулы гаверсинуса могут иметь погрешность до 0,5%, потому что Земля — не идеальная сфера, а эллипсоид с радиусом 6 378 км (3963 мили) на экваторе и радиусом 6 357 км (3950 миль). Формула Ламберта: Формула Ламберта (формула, используемая вычислителями выше) — это метод, используемый для вычисления кратчайшего расстояния по поверхности эллипсоида.Когда он используется для аппроксимации Земли и расчета расстояния на поверхности Земли, он имеет точность порядка 10 метров на тысячи километров, что более точно, чем формула гаверсинуса. Формула Ламберта выглядит следующим образом: , где a — экваториальный радиус эллипсоида (в данном случае Земли), σ — центральный угол в радианах между точками широты и долготы (найденный с использованием такого метода, как формула гаверсинуса), f — сглаживание Земля, а также X и Y развернуты ниже. Где P = (β 1 + β 2 ) / 2 и Q = (β 2 — β 1 ) / 2 В приведенных выше выражениях β 1 и β 1 представляют собой приведенные широты с использованием следующего уравнения: загар (β) = (1 — f) загар (& Straightphi;) , где & Stratocaster; широта точки. Обратите внимание, что ни формула гаверсинуса, ни формула Ламберта не дают точного расстояния, потому что невозможно учесть все неровности на поверхности Земли. % PDF-1.5
%
1 0 объект
>>>
эндобдж
2 0 obj
> поток
2014-11-25T02: 35: 55 + 05: 302014-11-25T02: 35: 58 + 05: 302014-11-25T02: 35: 58 + 05: 30Adobe InDesign CS5 (7.0) 2
2# The last step is to get the square root and print the Euclidean distance
distance = np.sqrt(sum_square)
print(distance)5.196152422706632from math import *
distance = np.sqrt(sum(pow(a-b, 2) for a, b in zip(point_1, point_2)))
print(distance)5. 196152422706632
196152422706632distance = np.linalg.norm(point_1-point_2)
print(distance)5.196152422706632
# Take the difference between the 2 points
diff = point_1 - point_2
# Perform the dot product on the point with itself to get the sum of the squares
sum_square = np. dot(diff, diff)
# Get the square root of the result
distance = np.sqrt(sum_square)
print(distance)
dot(diff, diff)
# Get the square root of the result
distance = np.sqrt(sum_square)
print(distance)distance = np.sqrt(np.dot(point_1-point_2, point_1-point_2))
print(distance)5.196152422706632Использование встроенной системы math.dist()
import math
distance = math.dist(point_1, point_2)
print(distance)5. 196152422706632
196152422706632Заключение
Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), то вектор \(\overrightarrow{AB}\) имеет координаты \[\overrightarrow{AB} = \{x_2-x_1;y_2-y_1;z_2-z_1\}\]
\(\bullet\) Если в пространстве заданы два вектора \(\vec{a}
=\{x_1;y_1;z_1\}\) и \(\vec{b}=
\{x_2;y_2;z_2\}\), то:
\(\bullet\) Длина вектора \(\vec{a}=\{x;y;z\}\) обозначается \(|\vec{a}|\) и вычисляется по формуле \[|\vec{a}|=\sqrt{x^2+y^2+z^2}\]
\(\bullet\) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
\(\bullet\) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: \[{\large{(\vec{a},
\vec{b})=|\vec{a}|\cdot|\vec{b}|\cdot\cos \angle (\vec{a},
\vec{b})}}\] На рисунке показано, что такое угол между векторами: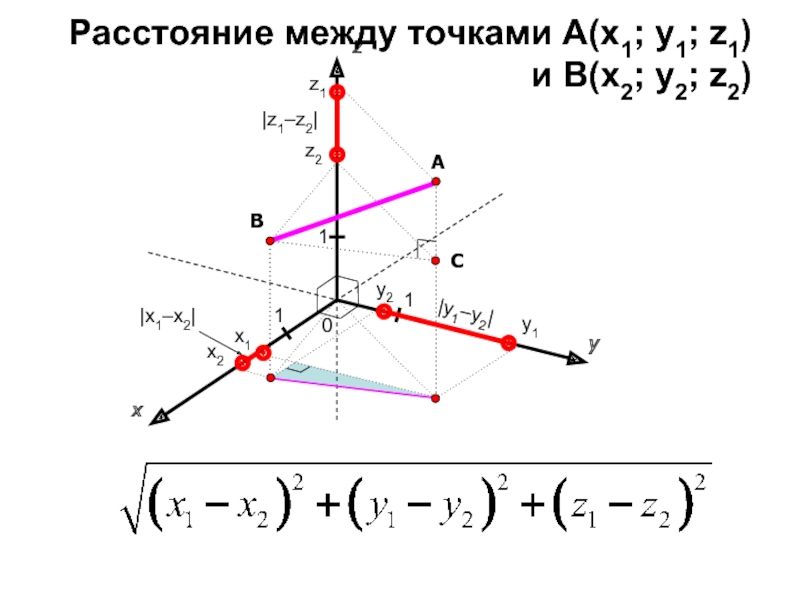 2_2}}}}\]
2_2}}}}\]
\(\bullet\) Если \(\vec{n}=\{a;b;c\}\) – нормаль к плоскости, то уравнение плоскости имеет вид \[ax+by+cz+d=0\] Для того, чтобы найти \(d\), нужно подставить в уравнение плоскости вместо \(x, y, z\) координаты любой точки, лежащей в этой плоскости.
Пример: если \(\vec{n}=\{1;2;3\}\) – нормаль к плоскости, \(O(4;5;6)\) – точка из плоскости, то справедливо: \(1\cdot 4+2\cdot 5+3\cdot
6+d=0\), откуда \(d=-32\), следовательно, уравнение плоскости имеет вид \(x+2y+3z-32=0\).
\(\bullet\) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть \(A(1;0;0), \
B(0;3;4), \ C(2;0;5)\) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: \[\begin{cases}
1\cdot a+0\cdot b+0\cdot c+d=0\\
0\cdot a+3\cdot b+4\cdot c+d=0\\
2\cdot a+0\cdot b+5\cdot c+d=0\end{cases} \quad\Rightarrow\quad
\begin{cases}
d=-a\\
3b+4c-a=0\\
a+5c=0\end{cases}\quad\Rightarrow\quad \begin{cases} d=-a\\
a=-5c\\
b=-3c\end{cases}\quad\Rightarrow\quad\begin{cases}a=-5c\\
b=-3c\\
d=5c\end{cases}\] Следовательно, уравнение плоскости имеет вид: \[-5c\cdot x-3c\cdot y+c\cdot z+5c=0\] Можно разделить обе части на \(c\), так как \(c\ne 0\) (иначе \(a=b=c=d=0\)), следовательно, уравнение плоскости имеет вид \[-5x-3y+z+5=0\]
 2}}\]
2}}\]
\(\bullet\) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости. Расстояние между 2 точками
Краткое объяснение

y A означает координату y точки A Примеры
Пример 1
Введите значения: Пример 2
Введите значения: Пример 3
 .. все еще работает:
.. все еще работает: Введите значения: Попробуйте сами
Три или более измерения
Пример: расстояние между двумя точками (8,2,6) и (3,5,7) составляет:
= √ [(8−3) 2 + (2−5) 2 + (6−7) 2 ] = √ [5 2 + (−3) 2 + (−1) 2 ] = √ (25 + 9 + 1) = √35 Что примерно равно 5. 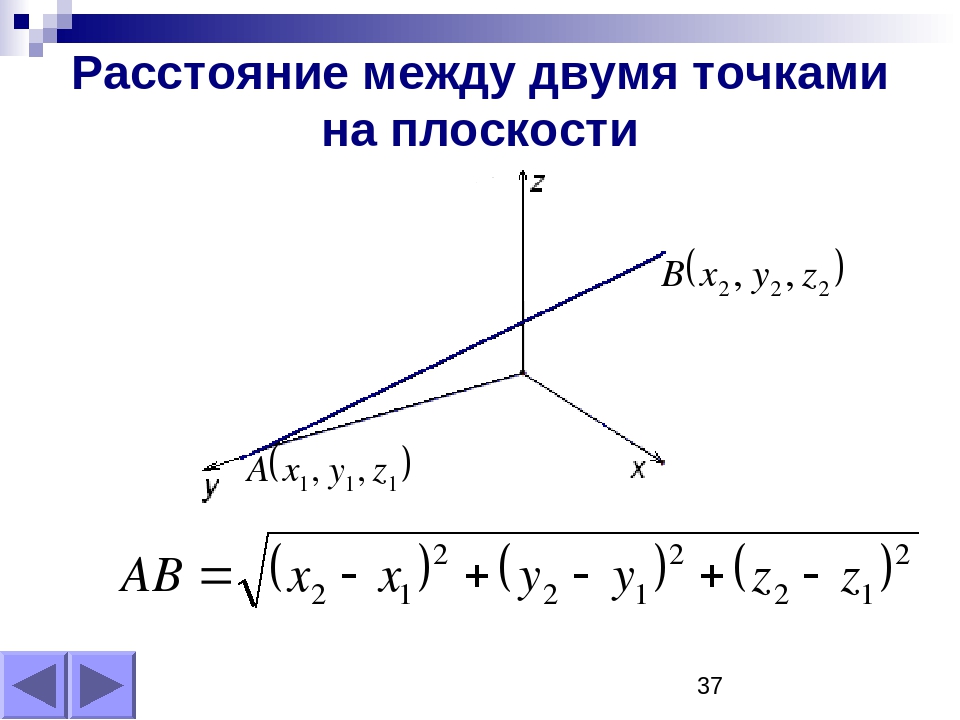 9
9 1,2 Расстояние между двумя точками; Круги
Упражнения 1.2
 2-8лет = 0 $.
2-8лет = 0 $. Определение расстояния между двумя точками в трехмерном пространстве
Вторая точка в трехмерном пространстве
 А как насчет z 2? Это длина точки d в направлении z , составляющая линию, параллельную оси z . Этот отрезок линии образует угол 90o с плоскостью x — y . От Пифагора:
А как насчет z 2? Это длина точки d в направлении z , составляющая линию, параллельную оси z . Этот отрезок линии образует угол 90o с плоскостью x — y . От Пифагора: Расстояние между двумя точками в трехмерном пространстве

Пример: Найдите расстояние между двумя точками (0, 0, 3) и (0, 0, -3).

Пример: Найдите расстояние между (-1, 2, -5) и (1, -2, 5).
Краткое содержание урока
Расстояние между двумя точками 3D
Формула расстояния между двумя точками
 Вам потребуется пара координатных осей, чтобы определить точное положение точки на плане. Комбинация координат x и y выражается в виде упорядоченной пары, например, (x, y). Итак, координаты точки, скажем M, можно выразить как M (x, y). Эта упорядоченная пара (x, y) дает вам координаты точки.
Вам потребуется пара координатных осей, чтобы определить точное положение точки на плане. Комбинация координат x и y выражается в виде упорядоченной пары, например, (x, y). Итак, координаты точки, скажем M, можно выразить как M (x, y). Эта упорядоченная пара (x, y) дает вам координаты точки. Расстояние по горизонтали (x2 — x1) представляет точки на оси x, а расстояние по вертикали (y2 — y1) обозначает точки на оси y.
Расстояние по горизонтали (x2 — x1) представляет точки на оси x, а расстояние по вертикали (y2 — y1) обозначает точки на оси y. Расстояние между двумя точками в 3D
 1. Здесь точки P (x1, y1, z1) и Q (x2, y2, z2) относятся к системе прямоугольных осей OX, OY и OZ.
1. Здесь точки P (x1, y1, z1) и Q (x2, y2, z2) относятся к системе прямоугольных осей OX, OY и OZ. Distance Calculator
Distance Calculator
2D-калькулятор расстояния
Трехмерный калькулятор расстояний
Расстояние по широте и долготе
Расстояние на карте

Расстояние в системе координат
d = √ (3-1) 2 + (2-5) 2 = √2 2 + (-3) 2 = √4 + 9 = √13 d = √ (1-3) 2 + (5-2) 2 = √ (-2) 2 + 3 2 = √4 + 9 = √13 
d = √ (2 — 1) 2 + (4 — 3) 2 + (8-7) 2 = √1 2 + 1 2 + 1 2 = √3 Расстояние между двумя точками на поверхности Земли
 Ниже приведены две общие формулы.
Ниже приведены две общие формулы. у столба. Из-за этого формула Ламберта (формула эллипсоидальной поверхности) более точно аппроксимирует поверхность Земли, чем формула гаверсинуса (формула сферической поверхности).
у столба. Из-за этого формула Ламберта (формула эллипсоидальной поверхности) более точно аппроксимирует поверхность Земли, чем формула гаверсинуса (формула сферической поверхности).
 сделал: FD0105EE1920681180838212EDF7EDC9xmp.did: FB7F11740720681188C68A053A992F47 Стойкость: pdf
сделал: FD0105EE1920681180838212EDF7EDC9xmp.did: FB7F11740720681188C68A053A992F47 Стойкость: pdf iid: 1812D3880B20681188C68A053A992F472014-07-10T10: 10: 14 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 1812D3880B20681188C68A053A992F472014-07-10T10: 10: 14 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: FFAF01E31120681188C68A053A992F472014-07-10T10: 57: 50 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: FFAF01E31120681188C68A053A992F472014-07-10T10: 57: 50 + 05: 30 Adobe InDesign 7.0 /; / метаданные
 iid: BFAB4F1A1620681188C68A053A992F472014-07-10T11: 25: 53 + 05: 30Adobe InDesign 7.0 /; / метаданные
iid: BFAB4F1A1620681188C68A053A992F472014-07-10T11: 25: 53 + 05: 30Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 96257E0A1A20681188C68A053A992F472014-07-10T11: 54: 04 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 96257E0A1A20681188C68A053A992F472014-07-10T11: 54: 04 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 1AAE8C3A1F20681188C68A053A992F472014-07-10T12: 31: 12 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 1AAE8C3A1F20681188C68A053A992F472014-07-10T12: 31: 12 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 0AA38E402720681188C68A053A992F472014-07-10T13: 28: 38 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 0AA38E402720681188C68A053A992F472014-07-10T13: 28: 38 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 0BD5B1BC3F20681188C68A053A992F472014-07-10T16: 23: 55 + 05: 30Adobe InDesign 7.0 /; / метаданные
iid: 0BD5B1BC3F20681188C68A053A992F472014-07-10T16: 23: 55 + 05: 30Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 540B609E0D2068118083CFA8A33D2D302014-07-12T10: 23: 53 + 05: 30Adobe InDesign 7.0 /; / метаданные
iid: 540B609E0D2068118083CFA8A33D2D302014-07-12T10: 23: 53 + 05: 30Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 7FC722CC182068118083CFA8A33D2D302014-07-12T11: 43: 54 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 7FC722CC182068118083CFA8A33D2D302014-07-12T11: 43: 54 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 9E71BBFF222068118083CFA8A33D2D302014-07-12T12: 56: 56 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 9E71BBFF222068118083CFA8A33D2D302014-07-12T12: 56: 56 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 368E21972B2068118083CFA8A33D2D302014-07-12T14: 28: 04 + 05: 30 Adobe InDesign 7.0 / метаданные
iid: 368E21972B2068118083CFA8A33D2D302014-07-12T14: 28: 04 + 05: 30 Adobe InDesign 7.0 / метаданные 0 /; / метаданные
0 /; / метаданные iid: 2A82754A392068118083EA641D5118F62014-08-30T04: 07: 56 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 2A82754A392068118083EA641D5118F62014-08-30T04: 07: 56 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: AD07790E482068118083EA641D5118F62014-08-30T06: 18: 34 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: AD07790E482068118083EA641D5118F62014-08-30T06: 18: 34 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 / метаданные
0 / метаданные iid: D3DA278E1C2068118083E5D3E04E85182014-09-10T11: 59: 09 + 05: 30Adobe InDesign 7.0 /; / метаданные
iid: D3DA278E1C2068118083E5D3E04E85182014-09-10T11: 59: 09 + 05: 30Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 712BAE452068118083E5D3E04E85182014-09-10T12: 25: 45 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 712BAE452068118083E5D3E04E85182014-09-10T12: 25: 45 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 957A2F973D2068118083E5D3E04E85182014-09-10T15: 55: 37 + 05: 30Adobe InDesign 7.0 /; / метаданные
iid: 957A2F973D2068118083E5D3E04E85182014-09-10T15: 55: 37 + 05: 30Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 03F7E8B61B2068118083CAA9B67E85842014-10-10T00: 01: 15 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 03F7E8B61B2068118083CAA9B67E85842014-10-10T00: 01: 15 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 92A257661D2068118083CAA9B67E85842014-10-10T00: 13: 19 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 92A257661D2068118083CAA9B67E85842014-10-10T00: 13: 19 + 05: 30 Adobe InDesign 7.0 /; / метаданные 0 /; / метаданные
0 /; / метаданные iid: 1205533E282068118083D9D6A60ECCA12014-11-14T03: 53: 47 + 05: 30 Adobe InDesign 7.0 /; / метаданные
iid: 1205533E282068118083D9D6A60ECCA12014-11-14T03: 53: 47 + 05: 30 Adobe InDesign 7.0 /; / метаданные 015 0 Тд
(Мини-урок SpringBoard, Блок геометрии 1) Tj
/ T1_0 1 Тс
-0.006 Tw 12 0 0 12 36 747.0601 Tm
(Расстояние и середина в трех измерениях \ (продолжение \)) Tj
/ CS1 CS 1 SCN
/ GS1 GS
0 Tw 13 0 0 13 36 710,3151 Tm
(ПРАКТИКА) Tj
/ CS0 cs 0,717 0,66 0,666 0,786 scn
/ GS0 гс
/ T1_2 1 Тс
11,5 0 0 11,5 36 691,8151 тм
[(F) 19 (o) 12 (re) -6 (a) 2 (c) 6 (hp) -5 (a) 9 (ir o) 12 (fp) -9 (o) 12 (in) 19 ( ts, f) -10 (дюйм) 4 (dt) -6 (h) 4 (e di) 3 (s) 5 (t) -6 (a) 9 (n) 4 (c) -1 (ea) 9 (n) 4 (dt) -6 (h) 4 (em) 2 (i) 1 (d) 12 (p) -9 (o) 12 (in) 19 (tb) -9 (et) -3 (w ) 8 (e) -5 (e) 1 (nt) -6 (h) 4 (et) -3 (w) 8 (og) -5 (i) 7 (v) 8 (e) 1 (np) — 9 (o) 12 (дюйм) 19 (ц.)] TJ
/ T1_3 1 Тс
0,279 Tw / Span >> BDC
0 -1,565 TD
() Tj
ЭМС
0,574 0 Тд
(1.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (0, 0, 0 \) a) 9 (n) 4 (d \ (3, 4, 12 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
/ T1_5 1 Тс
-0,042 Tc 0,042 Tw [(1) -33 (3;) — 42 ()] ТДж
0 Tc 0 Tw () Tj
-0,003 Tc 0,003 Tw 0 -1,217 TD
[(mi) 3 (d) 5 (p) -10 (oi) 11 (n) -4 (t) -3 ()] TJ
/ T1_6 1 Тс
0 Tc 0 Tw (5) Tj
/ T1_5 1 Тс
-0,022 Tc 0,022 Tw [(\ () 36 (1,5) 10 (,) — 22 (2,) — 22 (6) 3 (\))] ТДж
/ CS0 cs 0.
015 0 Тд
(Мини-урок SpringBoard, Блок геометрии 1) Tj
/ T1_0 1 Тс
-0.006 Tw 12 0 0 12 36 747.0601 Tm
(Расстояние и середина в трех измерениях \ (продолжение \)) Tj
/ CS1 CS 1 SCN
/ GS1 GS
0 Tw 13 0 0 13 36 710,3151 Tm
(ПРАКТИКА) Tj
/ CS0 cs 0,717 0,66 0,666 0,786 scn
/ GS0 гс
/ T1_2 1 Тс
11,5 0 0 11,5 36 691,8151 тм
[(F) 19 (o) 12 (re) -6 (a) 2 (c) 6 (hp) -5 (a) 9 (ir o) 12 (fp) -9 (o) 12 (in) 19 ( ts, f) -10 (дюйм) 4 (dt) -6 (h) 4 (e di) 3 (s) 5 (t) -6 (a) 9 (n) 4 (c) -1 (ea) 9 (n) 4 (dt) -6 (h) 4 (em) 2 (i) 1 (d) 12 (p) -9 (o) 12 (in) 19 (tb) -9 (et) -3 (w ) 8 (e) -5 (e) 1 (nt) -6 (h) 4 (et) -3 (w) 8 (og) -5 (i) 7 (v) 8 (e) 1 (np) — 9 (o) 12 (дюйм) 19 (ц.)] TJ
/ T1_3 1 Тс
0,279 Tw / Span >> BDC
0 -1,565 TD
() Tj
ЭМС
0,574 0 Тд
(1.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (0, 0, 0 \) a) 9 (n) 4 (d \ (3, 4, 12 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
/ T1_5 1 Тс
-0,042 Tc 0,042 Tw [(1) -33 (3;) — 42 ()] ТДж
0 Tc 0 Tw () Tj
-0,003 Tc 0,003 Tw 0 -1,217 TD
[(mi) 3 (d) 5 (p) -10 (oi) 11 (n) -4 (t) -3 ()] TJ
/ T1_6 1 Тс
0 Tc 0 Tw (5) Tj
/ T1_5 1 Тс
-0,022 Tc 0,022 Tw [(\ () 36 (1,5) 10 (,) — 22 (2,) — 22 (6) 3 (\))] ТДж
/ CS0 cs 0. 717 0,66 0,666 0,786 сбн
/ GS0 гс
/ T1_3 1 Тс
0 Tc 0,279 Tw / Span >> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(2.) Tj
/ T1_2 1 Тс
0,26 Tw / Span >> BDC
() Tj
ЭМС
(\ (4,) Tj
/ T1_6 1 Тс
0 Tw 2.62 0 Td
(2) Tj
/ T1_2 1 Тс
[(3, 6 \) a) 9 (n) 4 (d \ (1, 0, 17 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-1,368 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 79.3097 605.3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,872 л
24,281 7,872 л
24,281 7,31 л
7,274 7,31 л
4.343 -3,878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_7 1 Тс
11,5 0 0 11,5 86,1534 602,5631 тм
(139) Tj
/ T1_5 1 Тс
1,652 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-9,686 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(3.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (6, 5, 4 \) a) 9 (n) 4 (d \ (10, 9, 8 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 78,7897 554,0242 см
0 0 мес.
1,575 0,823 л
4.
717 0,66 0,666 0,786 сбн
/ GS0 гс
/ T1_3 1 Тс
0 Tc 0,279 Tw / Span >> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(2.) Tj
/ T1_2 1 Тс
0,26 Tw / Span >> BDC
() Tj
ЭМС
(\ (4,) Tj
/ T1_6 1 Тс
0 Tw 2.62 0 Td
(2) Tj
/ T1_2 1 Тс
[(3, 6 \) a) 9 (n) 4 (d \ (1, 0, 17 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-1,368 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 79.3097 605.3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,872 л
24,281 7,872 л
24,281 7,31 л
7,274 7,31 л
4.343 -3,878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_7 1 Тс
11,5 0 0 11,5 86,1534 602,5631 тм
(139) Tj
/ T1_5 1 Тс
1,652 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-9,686 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(3.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (6, 5, 4 \) a) 9 (n) 4 (d \ (10, 9, 8 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 78,7897 554,0242 см
0 0 мес.
1,575 0,823 л
4. 065 -2.72 л
6.84 7,872 л
19,469 7,872 л
19,469 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_9 1 Тс
11,5 0 0 11,5 86,3522 551,2717 тм
(48) ТД
/ T1_5 1 Тс
1,168 -0,04 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(4.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (1, 1, 1 \) a) 9 (n) 4 (d \ (10, 10, 10 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
К 1 0 0 1 79.1897 г. 501,3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,5 7,873 л
24,5 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_10 1 Тс
11,5 0 0 11,5 86,2522 498,5631 тм
(243) Ти
/ T1_5 1 Тс
1,734 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(5.) Tj
/ T1_2 1 Тс
0,26 Tw / Span >> BDC
() Tj
ЭМС
(\ () Tj
/ T1_6 1 Тс
0 Tw (2) Tj
/ T1_2 1 Тс
(4,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(5,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
[(19 \) a) 9 (n) 4 (d \ (8, 3, 12 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
1.
065 -2.72 л
6.84 7,872 л
19,469 7,872 л
19,469 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_9 1 Тс
11,5 0 0 11,5 86,3522 551,2717 тм
(48) ТД
/ T1_5 1 Тс
1,168 -0,04 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(4.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (1, 1, 1 \) a) 9 (n) 4 (d \ (10, 10, 10 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
К 1 0 0 1 79.1897 г. 501,3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,5 7,873 л
24,5 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_10 1 Тс
11,5 0 0 11,5 86,2522 498,5631 тм
(243) Ти
/ T1_5 1 Тс
1,734 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(5.) Tj
/ T1_2 1 Тс
0,26 Tw / Span >> BDC
() Tj
ЭМС
(\ () Tj
/ T1_6 1 Тс
0 Tw (2) Tj
/ T1_2 1 Тс
(4,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(5,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
[(19 \) a) 9 (n) 4 (d \ (8, 3, 12 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
1. 252 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 79,1897 450,0243 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
30,031 7,873 л
30.031 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_11 1 Тс
11,5 0 0 11,5 86,0334 447,2718 тм
(1169) Tj
/ T1_5 1 Тс
2,028 -0,04 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-10,761 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(6.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (5, 5, 18 \) a) 9 (n) 4 (d \ (5, 5,)] TJ
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(8 \)) Tj
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0.087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 79,0697 398,0243 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,5 7,873 л
24,5 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_12 1 Тс
11,5 0 0 11,5 86,1322 395,2718 тм
(676) Tj
/ T1_5 1 Тс
1,581 -0,04 тд
() Tj
/ T1_6 1 Тс
(5) Tj
/ T1_5 1 Тс
-0,039 Tc 0,039 Tw [(2) -17 (6;) — 39 ()] ТДж
0 Tc 0 Tw () Tj
-0,003 Tc 0,003 Tw -4,114 -1,217 Td
[(mi) 3 (d) 5 (p) -10 (oi) 11 (n) -4 (t) -3 ()] TJ
/ T1_6 1 Тс
0 Tc 0 Tw (5) Tj
/ T1_5 1 Тс
-0.
252 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 79,1897 450,0243 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
30,031 7,873 л
30.031 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_11 1 Тс
11,5 0 0 11,5 86,0334 447,2718 тм
(1169) Tj
/ T1_5 1 Тс
2,028 -0,04 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-10,761 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(6.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (5, 5, 18 \) a) 9 (n) 4 (d \ (5, 5,)] TJ
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(8 \)) Tj
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0.087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 79,0697 398,0243 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,5 7,873 л
24,5 7,31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_12 1 Тс
11,5 0 0 11,5 86,1322 395,2718 тм
(676) Tj
/ T1_5 1 Тс
1,581 -0,04 тд
() Tj
/ T1_6 1 Тс
(5) Tj
/ T1_5 1 Тс
-0,039 Tc 0,039 Tw [(2) -17 (6;) — 39 ()] ТДж
0 Tc 0 Tw () Tj
-0,003 Tc 0,003 Tw -4,114 -1,217 Td
[(mi) 3 (d) 5 (p) -10 (oi) 11 (n) -4 (t) -3 ()] TJ
/ T1_6 1 Тс
0 Tc 0 Tw (5) Tj
/ T1_5 1 Тс
-0. 032 Tc 0,032 Tw [(\ () 9 (5,) — 32 (5,) — 32 (5) 10 (\))] TJ
/ CS0 cs 0,717 0,66 0,666 0,786 scn
/ GS0 гс
/ T1_3 1 Тс
0 Tc 0,279 Tw / Span >> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(7.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (3, 6, 1 \) a) 9 (n) 4 (d \ (1, 6, 3 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 78,7897 345,3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
13,469 7,873 л
13,469 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_13 1 Тс
11,5 0 0 11,5 86,1022 342,5631 тм
(8) Tj
/ T1_5 1 Тс
0,641 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(8.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (9, 6, 3 \) a) 9 (n) 4 (d \ ()] TJ
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(9,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(6,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(3 \)) Tj
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
К 1 0 0 1 79.
032 Tc 0,032 Tw [(\ () 9 (5,) — 32 (5,) — 32 (5) 10 (\))] TJ
/ CS0 cs 0,717 0,66 0,666 0,786 scn
/ GS0 гс
/ T1_3 1 Тс
0 Tc 0,279 Tw / Span >> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(7.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (3, 6, 1 \) a) 9 (n) 4 (d \ (1, 6, 3 \))] TJ
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
q 1 0 0 1 78,7897 345,3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
13,469 7,873 л
13,469 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_13 1 Тс
11,5 0 0 11,5 86,1022 342,5631 тм
(8) Tj
/ T1_5 1 Тс
0,641 0,022 тд
() Tj
/ T1_8 1 Тс
(>> BDC
-1,826 -1,652 тд
() Tj
ЭМС
0,574 0 Тд
(8.) Tj
/ T1_2 1 Тс
0 Tw / Span >> BDC
() Tj
ЭМС
1.339 0 Тд
[(\ (9, 6, 3 \) a) 9 (n) 4 (d \ ()] TJ
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(9,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(6,) Tj
/ T1_6 1 Тс
(2) Tj
/ T1_2 1 Тс
(3 \)) Tj
/ CS2 CS 1 SCN
/ GS1 GS
/ T1_4 1 Тс
-0,087 -1,652 тд
(г) Tj
/ T1_5 1 Тс
() Tj
/ T1_6 1 Тс
(5) Tj
ET
/ PlacedGraphic BMC
ЭМС
К 1 0 0 1 79. 0697 293.3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,969 7,873 л
24.969 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_14 1 Тс
11,5 0 0 11,5 86,1322 290,5631 тм
(504) ТД
/ T1_5 1 Тс
1,622 0,022 тд
() Tj
/ T1_8 1 Тс
(> / ExtGState >>> / Subtype / Form >> stream
/ CS0 CS 0,717 0,66 0,666 0,786 SCN
1 Вт 4 М 0 Дж 0 Дж
/ GS0 гс
q 1 0 0 1 306 29,6339 см
0 0 мес.
5,412 0 9,8 4,388 9,8 9,8 в
9,8 15,212 5,412 19,6 0 19,6 в
-5,412 19,6 -9,8 15,212 -9.8 9,8 в
-9,8 4,388 -5,412 0 0 0 в
час
S
Q конечный поток
эндобдж
12 0 объект
>
эндобдж
9 0 объект
[/ ICCBased 68 0 R]
эндобдж
68 0 объект
> поток
HuTK tKKJI, t (4 K% ҹh5J # Ғ (H
wqyy ~ 3̙g
0697 293.3156 см
0 0 мес.
1,575 0,823 л
4.065 -2.72 л
6,84 7,873 л
24,969 7,873 л
24.969 7.31 л
7,274 7,31 л
4.343 -3.878 л
3,762 -3,878 л
0,987 0,071 л
0,182 -0,349 л
ж
Q
BT
/ T1_14 1 Тс
11,5 0 0 11,5 86,1322 290,5631 тм
(504) ТД
/ T1_5 1 Тс
1,622 0,022 тд
() Tj
/ T1_8 1 Тс
(> / ExtGState >>> / Subtype / Form >> stream
/ CS0 CS 0,717 0,66 0,666 0,786 SCN
1 Вт 4 М 0 Дж 0 Дж
/ GS0 гс
q 1 0 0 1 306 29,6339 см
0 0 мес.
5,412 0 9,8 4,388 9,8 9,8 в
9,8 15,212 5,412 19,6 0 19,6 в
-5,412 19,6 -9,8 15,212 -9.8 9,8 в
-9,8 4,388 -5,412 0 0 0 в
час
S
Q конечный поток
эндобдж
12 0 объект
>
эндобдж
9 0 объект
[/ ICCBased 68 0 R]
эндобдж
68 0 объект
> поток
HuTK tKKJI, t (4 K% ҹh5J # Ғ (H
wqyy ~ 3̙gОбъяснитель урока: точки, средние точки и расстояния в космосе
В этом объяснителе мы узнаем, как по формуле найдите координаты точки в 3D, расстояние между двумя точками в 3D и координаты средней и конечной точек в 3D.
Мы уже должны знать, как найти все это в двух измерениях. Любая точка в двух измерениях будет иметь 𝑥- и 𝑦-координату и может быть записана в форме (𝑥, 𝑦). Каждое из действительных чисел в упорядоченной паре представляет смещение этой точки от начала координат, другими словами, положительное или отрицательное расстояние от точки (0,0).
Любая точка в двух измерениях будет иметь 𝑥- и 𝑦-координату и может быть записана в форме (𝑥, 𝑦). Каждое из действительных чисел в упорядоченной паре представляет смещение этой точки от начала координат, другими словами, положительное или отрицательное расстояние от точки (0,0).
Если две точки 𝐴 и 𝐵 имеют координаты (𝑥, 𝑦) и (𝑥, 𝑦) соответственно, то мы можем вычислить их среднюю точку по формуле 𝑥 + 𝑥2, 𝑦 + 𝑦2.
Если две точки 𝐴 и 𝐵 имеют координаты (𝑥, 𝑦) и (𝑥, 𝑦) соответственно, то мы можем вычислить расстояние между ними, используя формулу расстояния, полученную из теоремы Пифагора, (𝑥 − 𝑥) + (𝑦 − 𝑦) .
В этом объяснителе мы исследуем, как мы можем расширить эти формулы, чтобы включить третью координату при работе с точками в трех измерениях.
Определение: координаты точки в трехмерном пространстве
Любая точка в трех измерениях будет иметь 𝑥-, 𝑦-,
и 𝑧-координаты и могут быть записаны в виде (𝑥, 𝑦, 𝑧). Каждое действительное число в упорядоченной тройке дает расстояние от начала координат, измеренное по соответствующей оси.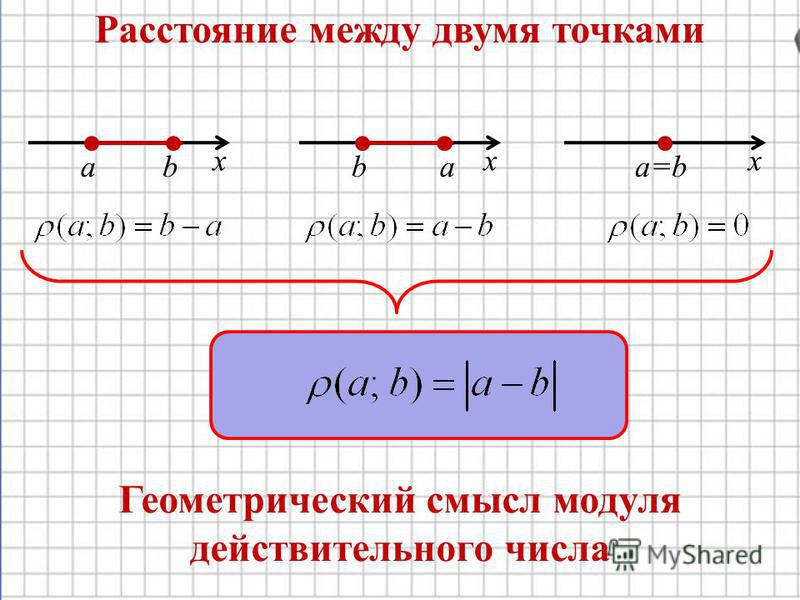
В нашем первом примере мы рассмотрим, в какой плоскости находится точка, одна из координат которой равна нулю.
Пример 1: Определение плоскости, в которой лежит заданная координата
В какой из следующих координатных плоскостей находится точка (−7, −8,0) ложь?
- 𝑥𝑦
- 𝑥𝑧
- 𝑦𝑧
Ответ
Мы знаем, что точка в 3D будет иметь 𝑥-, 𝑦- и 𝑧-координаты. В этом вопросе 𝑥 = −7, 𝑦 = −8 и 𝑧 = 0.
Поскольку-координата равна нулю, точка лежит на нулевом расстоянии от начала координат в 𝑧-направлении. Это означает, что он будет лежать в 𝑥𝑦-плоскости.Фактически, любая точка с координаты (𝑥, 𝑦, 0) будут лежать на этой плоскости.
Таким образом, мы можем заключить, что точка (−7, −8,0) лежит на 𝑥𝑦-плоскости.
Определение: три координатных плоскости
Любая точка с координатами (𝑥, 𝑦, 0) будет лежать на 𝑥𝑦-плоскости.
Аналогично, любая точка с координатами (𝑥, 0, 𝑧) будет лежать на
-плоскость, и любая точка с координатами (0, 𝑦, 𝑧) будет лежать на 𝑦𝑧-плоскости.
В следующем вопросе мы рассмотрим, как вычислить координаты точки в трех измерениях.
Пример 2: Нахождение координат заданной точки в 3D
Определите координаты точки 𝐴.
Ответ
Любая точка в трех измерениях будет иметь 𝑥-, 𝑦- и 𝑧-координаты и может быть записана в форме (𝑥, 𝑦, 𝑧).
Двигаясь от начала координат, мы перемещаемся на 3 единицы в положительном 𝑥-направлении, −3 единицы в направлении и, наконец, 3 единицы в направлении.
Это означает, что 𝑥 = 3, 𝑦 = −3 и 𝑧 = 3.
Координаты точки: (3, −3,3).
Напомним, что формула средней точки в двух измерениях просто говорит нам найти среднее значение двух точек. Мы находим среднее значение-координат и среднее значение 𝑦-координат. Теперь мы расширим эту идею до трех измерений, найдя также среднее значение 𝑧-координат.
Чтобы найти среднее значение любых двух чисел, мы складываем их, а затем делим их сумму на два.
Определение: Середина двух точек в трехмерном пространстве
Если две точки 𝐴 и 𝐵
имеют координаты (𝑥, 𝑦, 𝑧) и
(𝑥, 𝑦, 𝑧) соответственно, то
можно вычислить их среднюю точку, используя следующую формулу:
𝑥 + 𝑥2, 𝑦 + 𝑦2, 𝑧 + 𝑧2.
В нашем следующем примере мы будем использовать эту формулу для определения средней точки двух точек в пространстве.
Пример 3: Нахождение координат средней точки в 3D
Точки 𝐴 и 𝐵 имеют координаты (8, −8, −12) и (−8,5, −8) соответственно. Определите координаты средней точки.
Ответ
Чтобы найти среднюю точку двух точек в трех измерениях, мы будем использовать формулу для вычисления средней точки координат (𝑥, 𝑦, 𝑧) и (𝑥, 𝑦, 𝑧) : 𝑥 + 𝑥2, 𝑦 + 𝑦2, 𝑧 + 𝑧2.
Пусть точка 𝐴 имеет координаты (𝑥, 𝑦, 𝑧) , а точка 𝐵 имеет координаты (𝑥, 𝑦, 𝑧) .
Середина между точками 𝐴 и 𝐵 равна = 8 + (- 8) 2, −8 + 52, −12 + (- 8) 2 = 02, −32, −202 = 0, −32 , −10.
Координаты середины равны 0, −32, −10.
В нашем следующем примере мы будем использовать формулу средней точки для определения конечной точки с учетом средней точки из двух точек в пространстве и другой конечной точки.
Пример 4: Нахождение координат конечной точки отрезка линии с учетом координат средней точки и координат начальной точки
Учитывая, что точка (0,17, −10) является средней точкой 𝐴𝐵 и что 𝐴 (−19,7,14), какие координаты 𝐵?
Ответ
Чтобы найти середину двух точек в трех измерениях, мы будем использовать формулу для вычисления середины координат (𝑥, 𝑦, 𝑧)
и (𝑥, 𝑦, 𝑧) :
𝑥 + 𝑥2, 𝑦 + 𝑦2, 𝑧 + 𝑧2.
Мы знаем, что точка 𝐴 имеет координаты (−19,7,14) и пусть точка имеет координаты (𝑥, 𝑦, 𝑧). Середина между этими двумя точками имеет координаты (0,17, −10).
Подставляя эти значения в формулу, получаем (0,17, −10) = − 19 + 𝑥2,7 + 𝑦2,14 + 𝑧2.
Затем мы можем приравнять отдельные компоненты, получив для решения три уравнения.
Во-первых, координата дает нам 0 = −19 + 𝑥2.
Умножая обе части уравнения на 2, получаем 0 = −19 + 𝑥.
Итак, 19 = 𝑥.
Во-вторых, координата 𝑦 дает нам 17 = 7 + 2.
Умножая обе части уравнения на 2, получаем 34 = 7 + 𝑦.
Итак, 27 = 𝑦.
Наконец, координата 𝑧 дает нам −10 = 14 + 𝑧2.
Умножая обе части уравнения на 2, получаем −20 = 14 + 𝑧.
Итак, −34 = 𝑧.
Координаты точки: (19,27, −34).
В двух измерениях мы можем вычислить расстояние между двумя точками, используя адаптацию теоремы Пифагора.Это означает, что 𝑎 + 𝑏 = 𝑐,
где 𝑐 — длина самой длинной стороны прямоугольного треугольника, известной как гипотенуза.
Если две точки 𝐴 и 𝐵 имеют координаты (𝑥, 𝑦) и (𝑥, 𝑦) соответственно, то можно рассчитать расстояние между ними, используя следующую формулу: (𝑥 − 𝑥) + (𝑦 − 𝑦) .
Теперь мы рассмотрим, как мы можем вычислить расстояние между двумя точками в три измерения.
Рассмотрим трехмерную прямоугольную призму 𝐴𝐵𝐶𝐷𝐸𝐹𝐺𝐻, нарисованную ниже, и предположим, что мы хотим переместиться из самого нижнего левого переднего угла, 𝐴, в самый верхний правый задний угол, 𝐺.
Сначала рассмотрим треугольник 𝐴𝐵𝐹 в нижней части призмы. Теорема Пифагора говорит нам, что 𝐴𝐹 = 𝐴𝐵 + 𝐵𝐹.
Итак, 𝐴𝐹 = √𝑥 + 𝑦.
Теперь сделаем еще один треугольник 𝐴𝐹𝐺, основанием по и высотой.
Мы можем снова использовать теорему Пифагора, так что 𝐴𝐺 = 𝐴𝐹 + 𝐹𝐺. Подставляя длины 𝐴𝐹 и 𝐹𝐺, мы видим, что 𝐴𝐺 = √𝑥 + 𝑦 + 𝑧.
Следовательно, 𝐴𝐺 = √𝑥 + 𝑦 + 𝑧.
Определение: расстояние между двумя точками в трехмерном пространстве
Если две точки 𝐴 и 𝐵
имеют координаты (𝑥, 𝑦, 𝑧) и (𝑥, 𝑦, 𝑧) ,
соответственно, то мы можем вычислить расстояние между ними, используя следующую формулу: (𝑥 − 𝑥) + (𝑦 − 𝑦) + (𝑧 − 𝑧).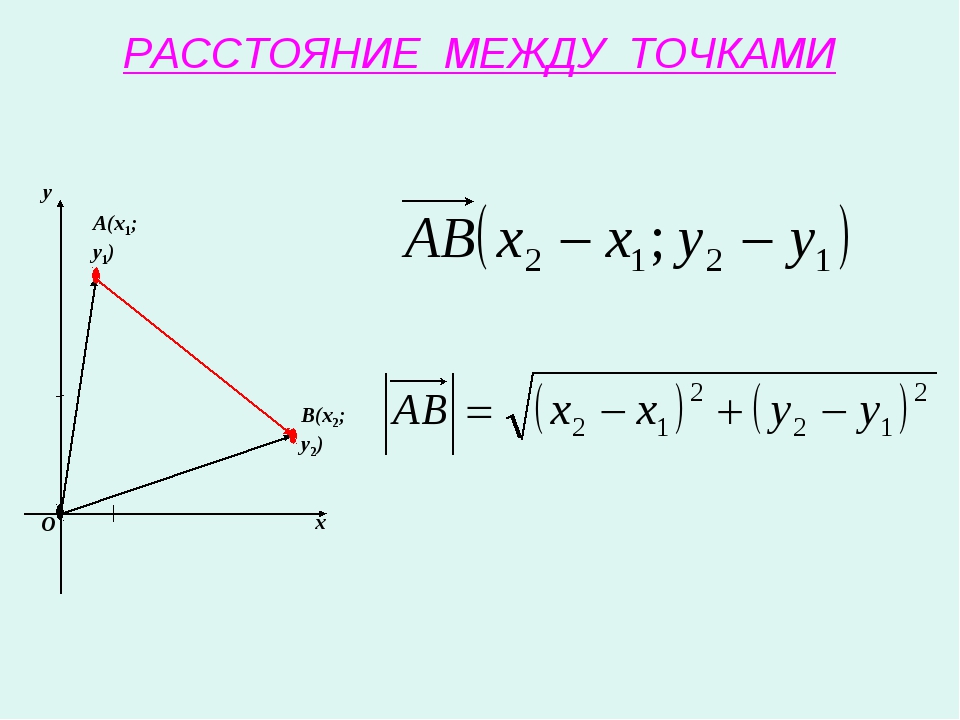
Это адаптация теоремы Пифагора в трех измерениях; мы находим сумму квадратов разницы между каждой координатой и затем извлекаем квадратный корень из этого ответа.
В последних двух вопросах мы вычислим кратчайшее расстояние между точкой и одной из осей, а также расстояние между двумя точками в пространстве.
Пример 5: Определение расстояния между двумя точками по их координатам в трех измерениях
Найдите расстояние между двумя точками 𝐴 (−7,12,3) и 𝐵 (−4, −1, −8).
Ответ
Чтобы вычислить расстояние между двумя точками в трех измерениях, мы будем использовать следующую формулу, где две точки 𝐴 и 𝐵 имеют координаты (𝑥, 𝑦, 𝑧) и (𝑥, 𝑦, 𝑧) соответственно: (𝑥 − 𝑥) + (𝑦 − 𝑦) + (𝑧 − 𝑧) .
Пусть точка 𝐴 имеет координаты (𝑥, 𝑦, 𝑧) , а точка имеют координаты (𝑥, 𝑦, 𝑧) .
Расстояние между ними = √ (−4 — (- 7)) + (- 1−12) + (- 8−3) = √ (3) + (- 13) + (- 11) = √9 + 169 + 121 = √299 .
Расстояние между двумя точками 𝐴 (−7,12,3) и 𝐵 (−4, −1, −8) составляет √299 единиц длины.
Пример 6: Определение расстояния между точкой и осью в 3D
Какое расстояние между точкой (19,5,5) и осью?
Ответ
Мы знаем, что любая точка будет лежать на оси 𝑥, если ее координата 𝑦 и координата 𝑧 равны нулю. Это означает, что мы можем определить точку на оси 𝑥 как (𝑥, 0,0).
Мы понимаем, что требуемое расстояние — это расстояние по перпендикуляру от точки до оси 𝑥, что означает проекцию точки на Ось будет в точке (19,0,0).
Расстояние между двумя точками можно рассчитать по формуле (𝑥 − 𝑥) + (𝑦 − 𝑦) + (𝑧 − 𝑧) следующим образом √ (19−19) + (5−0) + (5−0) = √0 + (5) + (5) = √50 = 5√2.
Расстояние между точка (19,5,5) и ось составляют 5√2 единиц длины.
Мы закончим это объяснение повторением некоторых ключевых моментов.
Ключевые точки
- Любая точка в трех измерениях имеет координаты, записанные в форме (𝑥, 𝑦, 𝑧).
- Если 𝑧-координата равна нулю, то мы знаем, что точка лежит в 𝑥𝑦-плоскости; если 𝑦-координата равна нулю, то мы знаем, что точка лежит в
𝑥𝑧-плоскость; и если 𝑥-координата равна нулю, то мы знаем, что точка лежит в-плоскости.

- Если и 𝑦-координата, и 𝑧-координата равны нулю, то точка лежит на оси; если и 𝑥-координата, и -координаты равны нулю, тогда точка лежит на оси; и если и 𝑥-координата, и 𝑦-координата равны равна нулю, то точка лежит на оси.
- Середина двух точек с координатами (𝑥, 𝑦, 𝑧) и (𝑥, 𝑦, 𝑧) лежит в точке 𝑥 + 𝑥2, 𝑦 + 𝑦2, 𝑧 + 𝑧2.
- Мы также можем использовать формулу средней точки для вычисления конечной точки линейного сегмента, учитывая среднюю точку и другую конечную точку.
- Расстояние между двумя точками с координатами (𝑥, 𝑦, 𝑧) и (𝑥, 𝑦, 𝑧) — это равно (𝑥 − 𝑥) + (𝑦 − 𝑦) + (𝑧 − 𝑧) .