Числовые выражения, преобразование числовых выражений

Числовые выражения, преобразование числовых выражений (рациональных и иррациональных). Друзья! В этой статье для вас представлено решение числовых рациональных и иррациональных выражений. Это несложные задания на ЕГЭ по математике, достаточно знать свойства степеней и корней. Ещё необходимо уметь работать с дробями (находить их сумму, разность, произведение, частное). Процесс решения такого задания занимает минуты две, не более. Не много теории:
Говоря простым (не математическим) языком рациональные выражения — это целые и дробные выражения. Ниже рассматриваются дробные выражения.
Алгебраическое выражение называется иррациональным, если в выражении, наряду с операциями сложения, вычитания, умножения и деления производится операция возведения в рациональную (не целую) степень.
Обыкновенная дробь – это отношение, вида:

*ОТНОШЕНИЕ это есть действие — ДЕЛЕНИЕ (в данном случае «a» делим на «b»).
Также может быть записано в виде: a/b или a:b (косая черта и знак «:» означает — деление). Примеры обыкновенных дробей:

Как видно, число 4 можно записать в виде дроби 4/1. Есть дроби которые можно сократить, например, 48/8 = 6. Некоторые можно представить как конечные десятичные дроби: ½ = 0,5 ¼ = 0,25.
Если имеем целое число с дробной частью (смешанная дробь) и нам необходимо выполнить действие, то её нужно представить в виде простой дроби. Как?
Имеем число вида:

Чтобы получить дробное равное ему число, целую часть умножаем на знаменатель и прибавляем числитель, результат записываем в числитель, знаменатель остаётся прежний:

Например:

Если нужно вычислить сумму (разность) двух дробей с разными знаменателями, необходимо дроби привести к такому виду, чтобы их знаменатели были равны:

*То есть мы получили общий знаменатель путём умножения числителя и знаменателя первой дроби на знаменатель второй и умножением числителя и знаменателя второй дроби на знаменатель первой. Я намеренно не упоминаю здесь наименьшее общее кратное, так как для некоторых, закончивших школу «давно», возможна перегрузка информацией.
Весь смысл действия в том, чтобы привести дроби к общему знаменателю, так как с разными знаменателями дроби складывать нельзя. Если же дроби имеют общий знаменатель, то результатом суммы дробей будет дробь с тем же знаменателем, а числители складывают.
Если нужно вычислить произведение двух дробей, то результатом будет дробь, числитель которой равен произведению числителей этих дробей, а знаменатель равен произведению знаменателей:

Если одну дробь необходимо разделить на другую, то данное действие сводится к произведению делимого и дроби обратной делителю:

*То есть, говоря простым языком, мы «переворачиваем» ту дробь на которую делим и деление заменяем умножением.
Свойства степени и корня можно посмотреть здесь.
Рассмотрим задания:

77387. Найдите значение выражения

Ответ: 8

77389. Найдите значение выражения

Ответ: 5

77391. Найдите значение выражения

Ответ: 10

77392. Найдите значение выражения

*В данной задаче не нужно вычислять произведения и затем отношение. Глядя на числа видно, что они прекрасно сокращаются. Достаточно произвести несложные преобразования и пример вычисляется устно.
Ответ: 10

86983. Найдите значение выражения

Упрощаем, используя формулу разности квадратов

и вычисляем:

Ответ: 702

61513. Найдите значение выражения

Ответ: 24

62385. Найдите значение выражения

Ответ: 2

62647. Найдите значение выражения

Ответ: 2

68141. Найдите

Определим числитель и знаменатель:

Числитель равен знаменателю. Это означает, что отношение равно единице:

Ответ: 1

26745. Найдите значение выражения

*Если корни имеют разные степени, то преобразования с внесением выражений под один корень выполнять нельзя. Требуется привести все корни к равной степени. Используем свойство:

Ответ: 1

77405. Найдите значение выражения

*На заключительном этапе использовали:

Ответ: 7
Полезным будет посмотреть статью с показательными выражениями.

26900. Найдите значение выражения

Посмотреть решение
77390. Найдите значение выражения

Посмотреть решение
26735. Найдите значение выражения

Посмотреть решение
26736. Найдите значение выражения

Посмотреть решение
26737. Найдите значение выражения

Посмотреть решение
26743. Найдите значение выражения

Посмотреть решение
26744. Найдите значение выражения

Посмотреть решение
26746. Найдите значение выражения

Посмотреть решение
26750. Найдите значение выражения

Посмотреть решение
26752. Найдите значение выражения

Посмотреть решение
На этом всё. Посмотрите, какие чудеса можно нарисовать простым карандашом.
Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Числовые и алгебраические выражения. Часть 2. Практика. Решение заданий
Задание 1 (алгебраические выражения)
Выберите алгебраические выражения:

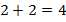
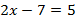



Решение
 является алгебраическим выражением (вместо
является алгебраическим выражением (вместо 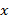 можно подставить какое-нибудь число и вычислить значение выражения).
можно подставить какое-нибудь число и вычислить значение выражения).
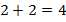 не является алгебраическим выражением, т.к. содержит знак равно
не является алгебраическим выражением, т.к. содержит знак равно  .
.
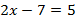 не является алгебраическим выражением, т.к. содержит знак равно
не является алгебраическим выражением, т.к. содержит знак равно 
 не является алгебраическим выражением, т.к. нельзя вычислить его значение (не имеет смысла).
не является алгебраическим выражением, т.к. нельзя вычислить его значение (не имеет смысла).
 является алгебраическим выражением (вместо
является алгебраическим выражением (вместо  можно подставить какие-нибудь числа и вычислить значение выражения).
можно подставить какие-нибудь числа и вычислить значение выражения).
 является и алгебраическим выражением, и числовым (его значение можно вычислить
является и алгебраическим выражением, и числовым (его значение можно вычислить 
Ответ:  .
.
Чему равно значение выражения 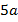 , если
, если  ? Подставим вместо
? Подставим вместо 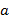 число 3 и посчитаем:
число 3 и посчитаем:  .
.
Так можно поступить с любым алгебраическим выражением – найти его значение при заданных значениях переменных.
Пример 5. Найти значение выражения 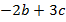
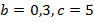 .
.Решение. Подставим значения переменных  в выражение:
в выражение:  .
.
Ответ:  .
.
Пример 6. Найти значение выражения 
 .
.Решение. Подставим значения переменных  в выражение:
в выражение:  .
.
Ответ:  .
.
Задание 2. Запишите формулу целых чисел, которые при делении на 9 дают остаток 2. Найдите количество таких чисел в пределах от 100 до 300.
Решение.
Пусть 
 делится на 9, то в его разложении на множители 9 было бы одним из них, т.е.
делится на 9, то в его разложении на множители 9 было бы одним из них, т.е.  . Т.к. число должно иметь остаток 2 при делении на 9, то тогда его можно записать так:
. Т.к. число должно иметь остаток 2 при делении на 9, то тогда его можно записать так:  .
.Первое такое число, большее 100, – это 101 (при 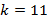 ), а последнее число – это 299 (при
), а последнее число – это 299 (при 
 .
.Ответ:  .
.
Заключение
На этом уроке мы познакомились с алгебраическими и числовыми выражениями, научились вычислять значение алгебраических выражений. На следующем уроке мы узнаем, как работать с алгебраическими выражениями.
Список рекомендованной литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, «Просвещение», 2017.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник. «Просвещение», 2014.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник. «Просвещение», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «yaklass.ru» (Источник)
- Интернет-портал «school-assistant.ru» (Источник)
- Интернет-портал «scienceland.info» (Источник)
Домашнее задание
- Найдите значения следующих числовых выражений:
 ;
; 
- Найдите значение алгебраического выражения
 , если
, если 
- Найдите
 от числа
от числа  .
.
Рациональные выражения. Задачи В11 ЕГЭ по математике
Часть 1.
Здесь смотрим части 2, 3, 4, 5
Разбор Задач №9 ЕГЭ по математике из открытого банка заданий
I. Преобразование числовых рациональных выражений
Задание 1.
Найдите значение выражения  .
.
Решение: + показать Ответ: 18. 
Задание 2.
Найдите значение выражения .
.Решение: + показать Ответ: 0,1. 

Задание 3.
Найдите значение выражения 
Решение: + показать
Задание 4.
Найдите значение выражения:  .
.
Решение: + показать Ответ: -24,32. 

II. Преобразование буквенных рациональных выражений
Задание 1.
Найдите значение выражения  .
.
Решение: + показать
Задание 2.
Найдите значение выражения  .
.
Решение: + показать
Задание 3.
Найдите значение выражения  .
.
Решение: + показать Раскладываем числитель на множители, пользуясь формулой разности квадратов: Ответ: -2. 
Задание 4.
Найдите значение выражения  .
.
Решение: + показать Раскладываем числитель и знаменатель на множители путем вынесения общего множителя за скобку: Ответ: 17. 
Задание 5.
Найдите значение выражения  .
.
Решение: + показать
Задание 6.
Найдите значение выражения  .
.
Решение: + показать Не выполняя действие во вторых скобках, сразу производим раскрытие скобок: Ответ: -8. 

Задание 7.
Найдите  , если
, если  при
при  .
.
Решение: + показать Ответ: 1. 
Задание 8.
Найдите  , если
, если  при
при  .
.
Решение: + показать Ответ: 0. 

Задание 9.
Найдите  , если
, если  .
.
Решение: + показать Делим обе части равенства на Ответ: -0,2.  =>
=> 

 :
:

Задание 10.
Найдите  , если
, если  .
.
Решение: + показать Тогда Ответ: 2.  =>
=> 

Задание 11.
Найдите значение выражения  , если
, если  ,
,  .
.
Решение: + показать
🙂 За улыбкой сюда –>+ показать
Надеюсь, вам было также интересно…


Вы можете пройти тест по заданиям 9 «Преобразования рациональных выражений».
Числовые и буквенные показательные выражения
Часть 3.
Здесь смотрим части 1, 2, 4, 5
Часть 1. Числовые показательные выражения
Задание 1.
Найдите значение выражения  .
.
Решение: + показать Мы воспользуемся следующими двумя правилами: Ответ: 9.  и
и 

Задание 2.
Найдите значение выражения  .
.
Решение: + показать Воспользуемся следующими правилами: Ответ: 63.  и
и 

Задание 3.
Найдите значение выражения ![Rendered by QuickLaTeX.com (\frac{4^{\frac{1}{6}}\cdot 4^{\frac{1}{9}}}{\sqrt[18]4})^9](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) .
.
Решение: + показать Ответ: 16. ![Rendered by QuickLaTeX.com (\frac{4^{\frac{1}{6}}\cdot 4^{\frac{1}{9}}}{\sqrt[18]4})^9=(\frac{4^{\frac{1}{6}+\frac{1}{9}}}{\sqrt[18]4})^9=(\frac{4^{\frac{5}{18}}}{\sqrt[18]4})^9=\frac{4^{\frac{5}{2}}}{\sqrt 4}=\frac{2^{2\cdot \frac{5}{2}}}{2}=\frac{32}{2}=16;](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Задание 4.
Найдите значение выражения  .
.
Решение: + показать
Задание 5.
Найдите значение выражения:  .
.
Решение: + показать Ответ: 216. 
Задание 6.
Найдите значение выражения  .
.
Решение: + показать Ответ: 49. 
Часть 2. Буквенные показательные выражения
Задание 1.
Найдите значение выражения  .
.
Решение: + показать Ответ: 3. 
Задание 2.
Найдите значение выражения  при
при  .
.
Решение: + показать Ответ: 1. 
Задание 3.
Найдите значение выражения  при
при  .
.
Решение: + показать Ответ: 33. 
Задание 4.
Найдите значение выражения  .
.
Решение: + показать Ответ: 0,8. 
Задание 5.
Найдите значение выражения  .
.
Решение: + показать Ответ: 2. 
Задание 6.
Найдите значение выражения  .
.
Решение: + показать Ответ: 3,5. 
Задание 7.
Найдите значение выражения  при
при  .
.
Решение: + показать При Ответ: -101. 



Задание 8.
Найдите значение выражения  , если
, если  .
.
Решение: + показать Ответ: 11. 
Задание 9.
Найдите значение выражения  при
при  .
.
Решение: + показать При Ответ: 180. 



Самое время передохнуть –> + показать
Не дрефь! Все будет хорошо!

Вы можете пройти тест «Преобразование показательных выражений»
План-конспект урока по математике (2 класс) на тему: Антипова Е.Р. Сценарий урока математики во 2 классе по теме «Составление и решение числовых выражений».
— У вас на парте лежат листки оценивания.
В них вы будите оценивать свою работу при помощи отметок.
Оцените себя
-Справился 5
-Сомневался 4
— Плохо справился 3
1) Устный счет. Решаем математический ребус.
49:7 | т |
8*5 | р |
7*3 | к |
32:8 | е |
4*3 | а |
Крыльев нет у этой птицы,
Но нельзя не подивиться.
Лишь распустит птица хвост
И поднимется до звёзд (Ракета).
— А кто догадался, почему именно ракета?
2) Завтра большой праздник – День космонавтики. Портрет Ю.А.Гагарина — а этот портрет знаком Вам. И первое задание связано с космосом. Я вам читаю текст, а вы ловите и записываете числа, которые услышали. Кто готов быть ловцом у доски?
9 марта этого года исполнилось 83 года со дня рождения первого космонавта планеты Юрия Алексеевича Гагарина. 12 апреля 1961 года Юрий Алексеевич Гагарин проложил дорогу к звёздам. Он стал первым человеком, совершившим полёт в космос. Впервые в истории человечества был выведен на орбиту вокруг Земли космический корабль «Восток» с человеком на борту. Всего 108 минут продолжался полёт, но Гагарин был ПЕРВЫМ кто доказал, что человек может работать в космосе.
-Какие числа вы услышали в моем рассказе.
— 9, 80, 12, 1961, 108.
— На какие группы можно разделить эти числа?
-С какими числами мы обычно работаем с Вами?
-Назовите эти числа. Подчеркните их одной чертой.
3)- Составьте примеры, чтобы в результате получились эти числа?
— Что общего у этих примеров? Докажите.
— Попробуйте назвать тему урока (Выражения). Какую запись называют выражением? Что значит найти значение выражения?
ТК по математике «Решение задач и числовых выражений» (1 класс)
Предмет: математика
Класс: 1
Тема урока Решение задач и числовых выражений
Тип урока урок закрепления (сказка — путешествие).
Цели урока закрепление знаний сложения и вычитания из числа 1 и 2, сформировать умение решать задачи изученных видов.
Задачи:
закрепить знание соответствующих случаев состава чисел; развивать математическую речь учащихся; совершенствовать мыслительные операции; формировать уважительное отношение друг к другу и толерантность при ведении диалога; воспитывать любовь к природе, к животным.
Планируемые образовательные результаты:
Предметные: уметь решать простые задачи изученных видов.
Регулятивные: уметь ставить цель с помощью учителя и составлять алгоритм действий в решении задач.
Познавательные: уметь сравнивать геометрические фигуры и определять признаки.
Коммуникативные: уметь выражать свою мысль, слушать товарища.
Личностные: проявлять интерес к предмету.
Организационная структура урока
Этап урока
Ход урока
Организационный момент
Громко прозвенел звонок,
Начинается урок.
Наши ушки на макушке,
Глазки широко раскрыты.
Слушаем, запоминаем,
Ни минуты не теряем.
Воспроизведение и коррекция опорных знаний учащихся. Актуализация знаний.
— Сегодня на уроке мы с вами отправляемся в гости. Посмотрите на экран.
Хоть сама и снег, и лед,
А уходит – слезы льет. (Зима) (К зимушке — зиме).
— Ребята, скажите, пожалуйста, какой праздник приближается? (Новый год).
— Да, это самый лучший праздник для взрослых и детей.
— До Нового года осталось вот столько дней (показать карточку с числом )
— Кто сможет прочитать это число?
— Какое это число? (двузначное)
— Какие цифры использованы для записи этого числа? (35)
— Назовите соседей числа 3 и 5 (2, 4; 4, 6)
— Какие это числа? (однозначные)
— Найдите сумму чисел 2 и 4 (6)
— Вычтите из 4 два (2)
— Вспомните пословицы, где встречается число 2
— Вспомните скороговорки с числом 2
Закончи пословицы:
Старый друг, лучше новых двух.
За двумя зайцами погонишься, ни одного не поймаешь.
— Отгадайте ребус по 2 л (подвал)
— Что такое подвал? (ответы детей)
— А как животные готовятся к зиме? (ответы детей)
— В течение осени одни животные запасают корм на зиму (белки, мыши), другие (медведь, барсук) — сильно жиреют, жир это тоже как бы запас на зиму, они уходят в спячку, третьи (зайцы, волки, лисы) никаких запасов не делают, они себе и зимой найдут пищу.
Приготовьте тетради.
Дети:
Я тетрадь свою открою и наклонно положу
Я друзья, от вас не скрою — ручку я вот так держу.
Сяду, прямо, не согнусь, за работу я возьмусь.
— Какое число написано у вас в тетрадях? (2)
— Внимание на доску (напоминаю, как правильно писать цифру 2): Начинают писать немного ниже середины верхней стороны клетки. Ведут линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию вниз к середине нижней стороны клетки. Вдоль нижней стороны клетки. Вдоль нижней стороны клетки пишут волнистую линию, ведя руку к правому нижнему углу клетки.
Минутка чистописания
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
— Ребята, в какое время года мы встречаем Новый год? (зимой)
— Зима прислала нам свой портрет и телеграмму, в которой вот что написано.
“Помогите, дети, лесная нечисть – Баба Яга, Кощей Бессмертный, Кикимора, Леший украли моих друзей: Деда Мороза и Снегурочку, а вместе с ними пропали и елка с игрушками и мешок с подарками. А без них наш праздник не состоится.”
— Грустное известие? Выручим Деда Мороза со Снегурочкой? Но для этого нам надо выполнить несколько заданий, которые приготовила для нас нечистая сила! Согласны?
1-е задание Бабы Яги.
Решите задачи:
1.Еж спросил ежа – соседа:
“Ты откуда, непоседа?”
— Запасаюсь я к зиме,
Видишь, яблоки на мне.
10 он уже принес,
Ну а два сосед унес.
Сколько яблок осталось у ежа? (8 яблок)
2.Опустился тихий вечер
Над тропинкою лесной.
Белка цокнула при встрече,
Поздоровалась со мной.
Заглянула мне в корзинку,
Где лежали 6 опят.
— Подари-ка мне корзинку,
Да 2 гриба, что в ней лежат.
Поделилась с белкой я,
Сколько грибов теперь у меня? (4 гриба)
3. Наступил долгожданный декабрь. Сначала зацвели 2 яблони, а потом 3 сливы. Сколько деревьев зацвело всего? (Зимой деревья не цветут, а весной бы их зацвело 5)
4. До царя Петра на Руси праздновали Новый год 1 марта, потом 1 сентября, царь Петр велел праздновать Новый год 1 января. Сколько раз назначалась дата празднования Нового года?
5. Следующее задание – математическая цепочка. Если вы ее решите верно, то узнаете, в какой стране родилась традиция отмечать Новый год.
— Первое слагаемое 6, второе 2, найдите сумму, вычесть из нее один, прибавить 2, уменьшить на 1, увеличить на 2, минус 1 (9)
8 Россия
10 Италия
9 Англия
— На уроке окружающего мира мы с вами говорили о том, что на нашей земле есть много стран: Англия – одна из них. Именно англичане решили отмечать Новый год, надеясь на изменения жизни к лучшему, исполнение всех своих желаний.
6. Что это записано? (показываю карточку с записью 1+2)
— Это числовое выражение
— Найдите его значение (3)
— Назовите числа, которые больше 3, но меньше 6 (4,5)
— Как можно получить число 5?
— Как можно прочитать это выражение? (1+2) (сумма чисел 1 и 2, первое слагаемое 1, второе слагаемое 2, 1 увеличить на 2, к 1 прибавить 2, 1 плюс 2)
7. Назовите, что написано на доске? (Неравенства) (проверьте, верные ли это неравенства?)
5<7, 8>6, 10<10
(10<10 неверно, надо поставить знак =)
— Что получилось? (равенство)
8. Расположите числа в порядке возрастания.
1 4 10 8 6 3 7 2
у ч м а и а в д
— Кто сможет прочитать запись, которая получится? Удачи вам.
Зима желает вам удачи. И вы молодцы, Деда Мороза и Снегурочку освободили. И прежде чем приступить к более сложным заданиям, немного отдохнем.
Первичное закрепление
— Все задания Бабы Яги мы выполнили, а следующие задания от Кощея.
— Давайте вспомним, как прибавить к числу 1 и 2, а как вычесть из числа 1 и 2?
— Посмотрите на экран. Что надо сделать? (решение примеров самостоятельно)
1+2 3+1 10-2
2+2 4+1 9-2
— Ребята посмотрите внимательно как получены вторые примеры в каждом столбике? Молодцы!
— Учебники закройте, уберите на край парты.
— Составьте задачу и решите ее. (вывешивается картинка с птицами у кормушки)

— Зачем надо птиц подкармливать зимой? Чем можно кормить птиц?
7. Работа с геометрическим материалом
Следующее задание для вас приготовил Леший. Посмотрите на доску.
— Что изображено под №1 (прямая)
— Что вы знаете о прямой?
— Что изображено под №2 (отрезок)
— Чем отличается отрезок от прямой?
— Что изображено под №3 (ломаная)
— Из чего состоит ломаная (из звеньев)
— Как называются концы каждого звена? (вершинами)
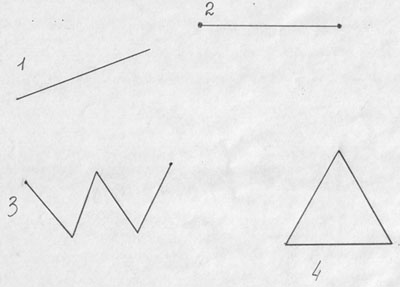
— Подумайте, что здесь лишнее? Почему? (прямая, у нее нет ни начала ни конца)
На доске – синие и красные большие и маленькие треугольники и четырёхугольники.
— Как можно одним словом назвать эти фигуры? ( Многоугольники)
— Разделите эти фигуры на две группы разными способами.
По цвету – синие и красные.
По размеру – большие и маленькие.
По форме – треугольники и четырёхугольники.
Творческое применение и добывание знаний в новой ситуации (проблемные задания) Итоги урока.
— Очень хорошо, отдает нам Леший ёлку. Но игрушек на ней нет. Что? А ну-ка тихо. Мне Кикимора что-то шепчет, подсказывает, что игрушки тут в классе и находятся в ваших конвертах. У одних будут шишки, у других шары, у третьих сосульки, у четвертых фонарики. Откройте конверты и достаньте игрушки. С обратной стороны для каждого из вас есть задание. Оно следующее: решить примеры с окошечком. Заполните пропуски так, чтобы получились верные равенства.
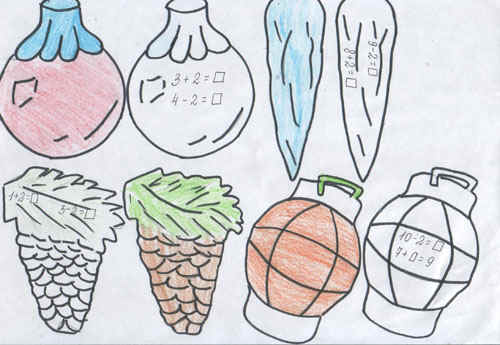
Проверяем (переворачиваю на доске игрушки на них правильное решение, дети проверяют)
Рефлексия (подведение итогов занятия)
Молодцы ребята! Сегодня вы хорошо потрудились, все задания выполнили, проявив при этом смекалку и находчивость. А Деда Мороза со Снегурочкой мы теперь будем ждать в гости на Новогоднее представление с большими подарками.
У р о к 67. РЕШЕНИЕ ЧИСЛОВЫХ ВЫРАЖЕНИЙ | Поурочные планы по математике 1 класс
У р о к 67. РЕШЕНИЕ ЧИСЛОВЫХ ВЫРАЖЕНИЙ
16.05.2013 6924 0У р о к 67. РЕШЕНИЕ ЧИСЛОВЫХ ВЫРАЖЕНИЙ
Цели урока: закреплять у учащихся знание состава изученных чисел; развивать навыки счета; формировать умение использовать понятия «увеличить», «уменьшить»; работать над развитием мышления учеников.
Ход урока
I. Организационный момент.
II. Каллиграфическая минутка.
10 10 10
9 8 7 9 8 7
III. Устный счёт.
Игра «Помоги Винни-Пуху и Пятачку»:
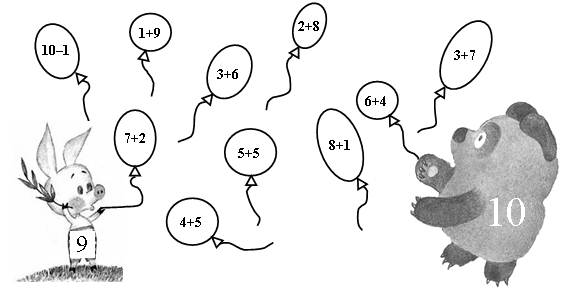
IV. Формирование умения использовать понятия «увеличить», «уменьшить».
Р а б о т а п о у ч е б н и к у.
Учитель предлагает учащимся рассмотреть рисунок (с. 7 учебника, часть 2).
– Что вы можете сказать о количестве ложек и мисок в верхнем ряду (не считая их)? (Их число одинаково.)
– Как вы об этом узнали? (Около каждой миски есть ложка.)
– Что можно сказать о количестве ложек и мисок в нижнем ряду? (Мисок больше, чем ложек. Ложек меньше, чем мисок.)
– Обоснуйте ваш ответ. (Около одной миски нет ложки, значит, ложек на одну меньше.)
Р а б о т а с р а з р е з н ы м м а т е р и а л о м.
– Положите в один ряд 6 квадратов.
– В другой ряд положите столько же кругов.
– Уберите 2 круга.
– Количество кругов уменьшилось (стало меньше) или увеличилось (стало больше)?
– Сколько кругов осталось у вас на партах? (4.)
– Сравните числа 4 и 6. (Четыре меньше шести на 2.)
– Положите на парту 7 красных треугольников.
– Ниже положите столько же синих треугольников.
– Сколько синих треугольников положили? (7.)
– Уменьшите число синих треугольников на 3.
– Что вы сделали? (Убрали 3 синих треугольника.)
– Почему убрали, а не добавили? (Потому что уменьшить – сделать меньше, а не больше.)
– Сколько синих треугольников у вас осталось? (4.)
Затем ученики могут предложить друг другу подобные задания.
Р а б о т а в т е т р а д я х.
Учащиеся выполняют с а м о с т о я т е л ь н о задания 1, 3 (с. 4 в тетради № 2) с последующей в з а и м о п р о в е р к о й.
В задании 1 закрашивают 2 треугольника, а кругов – на 3 больше.
В задании 3 ученики закрашивают 7 кругов, а треугольников – на 3 меньше, чем кругов.
– Количество кругов в первом задании увеличилось или уменьшилось?
– Увеличилось или уменьшилось число треугольников в задании 3?
V. Развитие навыков счета.
С этой целью выполняются задания 4 (с. 4 в тетради № 2) и 4 (с. 7 учебника, часть 2).
Задание 4 в тетради № 2 выполняется учащимися с объяснением: необходимо вставить пропущенные числа.
Например:
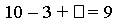
Из десяти вычесть три, получится семь. Значение данного выражения равно девяти. Чтобы получить 9, нужно к семи прибавить два. Значит, пропущено число 2.
Задание 4 (учебник, часть 2) ученики выполняют по вариантам с последующей ф р о н т а л ь н о й или с а м о п р о в е р к о й.
VI. Работа с геометрическим материалом.
Учащиеся выполняют задание 5 (с. 4 в тетради № 2): из треугольников и прямоугольников составляют квадрат заданной величины.
Затем можно предложить детям сравнить круги на рисунках (с. 7 учебника, часть 2, поля).
VII. Работа над развитием логического мышления учащихся.
В заключение урока учащиеся выполняют задачу на смекалку (с. 7 учебника, часть 2).
Это задание (на усмотрение учителя) можно включить в начало урока.
– Кто из детей старше всех? (Коля.)
– Объясните, почему так считаете. (Оля старше Вани, значит, Ваня не может быть старше Оли. Но Оля моложе Коли, то есть Коля старше Оли. Раз Коля старше Оли, значит, он будет старше Вани. Таким образом, самый старший – Коля, за ним – Оля, самый младший – Ваня.)
Здесь же дети могут выполнить задание 3 (с. 7 учебника, часть 2).
Однако если учитель считает, что на уроке необходимо уделить внимание работе над задачами, данное задание можно использовать и с такой целью. По рисункам дети составляют и решают задачу, повторяя ее составные части и обосновывая решения. (В таком случае работа над заданием 3 должна быть перенесена в предыдущую часть урока.)
VIII. Итог урока.
– Чем запомнился сегодняшний урок?
– Что особенно понравилось?
– А что бы вам хотелось изменить?
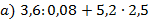 ;
; 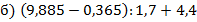
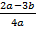 , если
, если 
 от числа
от числа  .
.