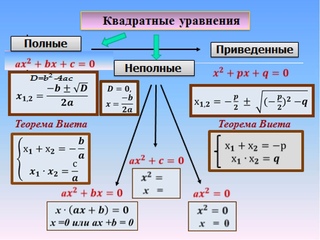
Квадратное уравнение

Квадратное уравнение

— это уравнение вида a x² + b x + c = 0, где a не равно 0.

Геометрический смысл

Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют точки пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.

Если коэффициент a положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.

Вывод формулы для решения квадратного уравнения

Формулу для решения квадратного уравнения a x ² + b x + c = 0 можно получить так:

• перенесем c в правую часть a x² + b x = — c
• умножим уравнение на 4a (2a x)² + 4a b x = — 4a c
• добавим b² к обоим частям (2a x)² + 4a b x + b² = b² — 4a c
• в левой части выделим полный квадрат (2a x + b)² = b² — 4a c
• извлечем квадратный корень 2a x + b = ± √b² — 4a c
• перенесем b в правую часть 2a x = — b ± √b² — 4a c
• разделим уравнение на 2a

  x =	-b ± √b2 — 4a c
  	2 a

Дискриминант квадратного уравнения

Дискриминантом

квадратного уравнения называют число равное D = b² − 4ac

Квадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта:

• при D > 0 корней два, и они вычисляются по формуле

  x1,2 =	-b ± √D
  	2 a

• при D = 0 корень один (два равных или совпадающих корня), кратности 2:
• при Dx_1,2 =  -b ± i√-D 2 a

Теорема Виета

Приведенным квадратным уравнением

называется уравнение, в котором коэффициент при x² равен единице. Такое уравнение может быть получено делением всего выражения на коэффициент a: x² + px + q = 0, где p = ba, q = ca

Сумма корней приведённого квадратного уравнения

x² + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
      x₁ + x₂ = -p,      x₁x₂ = q.

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле

ax² + bx + c = a(x — x₁)(x — x₂)

Примеры решения квадратных уравнений

Например. Найти корни квадратного уравнения: 2x² + 5x + 3 = 0
D = 5² — 4·3·2 = 25 — 24 = 1

x1 =  —5 + √1  = -1, 2·2

x2 =  —5 — √1  = -1 1 2·2 2

Упражнения. Квадратные уравнения.

Простое решение квадратных уравнений — Доктор Лом

Затем определяются корни:

х₁ = (-b + √D)/2a (684.0.2)

х₂ = (-b — √D)/2a (684.0.3)

Если дискриминант отрицательный, то уравнение не имеет решений, так как невозможно извлечь квадратный корень из отрицательного числа. Все запомнили? Ну до экзаменов запомните.

Как-то так было. Откуда взялся этот дискриминант и почему у уравнения возможны 2 корня, никто толком не объяснял, да и мне тогда было не интересно. Я запомнил только, что есть дискриминант и 2 корня, а значения этих параметров всегда можно посмотреть в учебнике или справочнике.

Не, ну для экзамена я конечно выучил и дискриминант и значения корней (хотя можно было просто написать «шпору»), вот только тупо заучить (списать из справочника или шпаргалки) и понять принцип расчета — это разные вещи.

Сейчас при расчете строительных конструкций иногда приходится решать квадратные уравнения, например нужно найти точку нулевых поперечных сил во втором пролете трехпролетной балки. Но сейчас даже знать про существование дискриминанта или справочников, где его значение указывается, вовсе необязательно. В сети полно онлайн-калькуляторов, в миг решающих квадратные уравнения, только подставляй значения коэффициентов.

Я так обычно и делал, но в последний раз чего-то захотел решить квадратное уравнение классическим способом. Полез в сеть посмотреть значение дискриминанта и корней и наткнулся на очень хороший ресурс, где решение квадратных уравнений разложено не просто по полочкам, но и вплоть до молекул, атомов, протонов и нейтронов. Ну то есть, я, когда хочу разжевать какую-то мысль, иногда перебарщиваю, но там все разжевано до состояния муки. Ниже я просто попробую слепить из той муки пирожки, ну а жарить пирожки вы будете уже сами. Итак:

1. Уравнение вида ax² + bx + c = 0 — это полное квадратное уравнение. Но если быть совсем уж точным, то более правильно писать такое уравнение так: ax² + bx¹ + cx⁰ = 0. чтобы не возникало сомнений, с — это свободный член или все-таки коэффициент?

2. Литеры а, b и с — это коэффициенты членов уравнения (Во как! И кстати при правильном написании полного квадратного уравнения

с— совсем не свободный член, как опрометчиво думают некоторые несознательные математики). Значения коэффициентов могут быть любыми: положительными, отрицательными; они могут быть = 1 или = 0.

3. Если b или(и) с = 0, то квадратное уравнение является неполным. Если а = 0, то это вообще не квадратное уравнение.

4. Неполные квадратные уравнения решаются в несколько простых приемов (что я раньше и делал, не особо задумываясь над глубоко математической сутью проделываемых операций).

4.1. При с = 0

Уравнение вида ax² + bx = 0 решается следующим образом:

ax² + bx = 0 (684. 1.1)

ax²/х + bx/х = 0/х (684.1.2)

ax + b = 0 (684.1.3)

ax + b — b = 0 — b (684.1.4)

ax = -b (684.1.5)

ax/a = — b/a (681.6)

х = -b/a (684.1.7)

Тут смысл в том, что ноль на сколько ни дели, все равно будет 0 и это очень помогает при решении неполных квадратных уравнений указанного вида. Впрочем, тут можно использовать и другой подход:

ax² + bx = 0 (684.1.1)

ax² + bx — bx = 0 — bх (684.1.7)

ax² = — bx (684.1.8)

ax²/x = — bx/x (684.1.9)

aх = -b (684.1.5)

ax/a = -b/a (681.1.6)

x = -b/a (684.1.7)

Но как ни крути, количество действий не уменьшается. Впрочем в классической записи уравнений будет немного меньше, так как в классической версии один член уравнения сразу переносится в другую часть уравнения с обратным знаком, а тут я просто расписал, почему это именно так. Тем не менее воспользуемся далее классической записью, чтобы сократить количество уравнений.

4.2. При b = 0

Уравнение вида ax² + c = 0 решается следующим образом:

ax² + с = 0 (684.2.1)

ax² = -с (684.2.2)

x² = -с/а (684.2.3)

х = √-с/a (684.2.4)

И тут мы впервые получаем корень из отрицательного числа, который невозможно извлечь, если в квадратном уравнении (684.2.1) коэффициенты с и а — положительные. Тут в принципе ничего странного. Просто как ни крути, но как умножить число само на себя (а это и есть квадрат числа), чтобы в итоге получилось отрицательное число, люди пока не придумали.

А такие числа раньше называли мнимыми, теперь — комплексными (видать, дедушка Фрейд повлиял).

И тут же мы получаем и второй корень уравнения:

х₂ = -√-с/a (684.2.5)

Все по той же вышеуказанной причине. Когда мы возводим отрицательное число в квадрат, т.е. умножаем само на себя, то получаем положительное число, ну а уж при умножении положительного числа самого на себя получить отрицательное число вообще не удается. Ну то есть 2·2 = 4 и (-2)·(-2)=4, соответственно, когда мы извлекаем квадратный корень из 4, то и 2 и -2 — правильный ответ.

Вот и получается, что квадратное уравнение вида ax² + c = 0 имеет два корня, а вещественные эти корни или нет, то для математики дело уже десятое.

4.3. Совсем неполное квадратное уравнение вида ax² = 0 имеет два вещественных корня, но при этом всегда х₁ = х₂ = 0

.

То есть решать это уравнение в принципе не нужно, ответ уже известен, но можно и расписать, мало ли чего:

ax² = 0 (684. 3.1)

ax²/а = 0/а (684.3.2)

x² = 0 (684.3.3)

х₁ = √0 = 0 (684.3.4)

х₂ = — √0 = -0 = 0 (684.3.5)

Тут конечно может возникнуть вопрос: а почему это -0 = 0, на каком основании? К сожалению я не настолько хорошо знаю математику, чтобы ответить на этот вопрос.

Ну а теперь самое интересное:

5. Есть еще один вид квадратных уравнений:

(ax + b)² + c = 0 (684.5.1)

С одной стороны уравнение такого вида полное, так как все коэффициенты членов не = 0. А с другой стороны в нем пока нет явного х² и ничто не мешает нам решить это уравнение по принципу решений уравнений вида (682.2.1):

(ax + b)² + c = 0 (684.5.1)

(ax + b)² = -c (684. 5.2)

ax₁ + b = √-c (684.5.3)

ax₂ + b = -√-c (684.5.3.1)

ax₁ = — b + √-c (684.5.4)

ax₂ = -b — √-c (684.5.4.1)

x₁ = (- b + √-c)/a (684.5.5)

x₂ = (-b — √-c)/a (684.5.5.1)

6. Все остальные квадратные уравнения являются полными, а чтобы их решить нужно помнить главное:

Решение полного квадратного уравнения сводится к выделению полного квадрата! Вот и все!!!

Тут конечно нужно пояснить, что такое полный квадрат. Полный квадрат — это выражение типа (ax + b)². Да-да, то самое, которое мы рассматривали в предыдущем пункте. А полный квадрат тут потому, что:

(a + b)² = (a + b)(a + b) = a² + ab + ba + b² = a² + 2ab + b² (684. 6.1)

Соответственно если мы добавим еще один множитель (и тут даже не важно для a или для b), то в принципе ничего не изменится:

(ax + b)² = (ax + b)(ax + b) = a²x² + 2abx + b² (684.6.2)

Т.е. члены исходного уравнения вида ax² + bx + c = 0 нужно так умножить-поделить на какое-то число или добавить-отнять какое-то число к(из) каждой части уравнения, чтобы привести его к нужному виду. Итак, пробуем:

ax²·a + bx· + c·a = 0 (684.6.3)

a²x² + аbx = — aс (684.6.4)

Пока все хорошо, вот только в таком виде у нас второй член уравнения abx в 2 раза меньше требуемого до полного квадрата, а если мы умножим все члены уравнения на 2, то у нас первый член уравнения a²x² станет в 2 раза больше, чем нам нужно. Что же делать?

А просто еще раз внимательно проанализировать формулу (684.6.2). Ведь что получается? Любой из членов мы можем умножать на любое количество коэффициентов. Т.е. для начала мы умножили а на х, но никто не запрещает умножить а еще и на такое число n, чтобы n² = 2n, в математическом виде это выглядит так:

(nax + b)² = n²a²x² + 2nabx + b² (684.6.2.1)

Почему n = 2, я подробно расписывать не буду (для этого есть формулы первого пункта). А в итоге получается, что мы должны все члены уравнения умножить на такое число у, которое равно у = n² = 2n = 2² = 2·2 = 4. Тогда

4a²x² + 4аbx = — 4aс (684.6.5)

Ну и теперь добавим к каждой части уравнения b², чтобы получить полный квадрат:

4a²x² + 4аbx + b² = b² — 4aс (684. 6.5)

Тогда 

(2ax + b)² = b² — 4ac (684.6.6) 

И используя формулы п.5 мы получим:

2ax₁ + b = √b² — 4ac (684.6.7.1)

2ax₂ + b = — √b² — 4ac (684.6.7.2)

2ax₁ = -b + √b² — 4ac (684.6.8.1)

2ax₂ = -b — √b² — 4ac (684.6..8.2)

x₁ = (-b + √b² — 4ac)/2a (684.6.9.1)

x₂ = (-b — √b² — 4ac)/2a (684.6.9.2)

Ну а если мы еще на стадии уравнения (684.6.6) заменим постоянное выражение b² — 4ac неким дискриминантом D, то запись уравнений (684.6.6 — 684.6.9) значительно сократится.

Сейчас, при большом объеме свободной памяти на жестком диске, наличии в компьютере функций «Ctrl+C», «Сtrl+V» и прочих весьма полезных функций, такая замена вовсе не обязательна. Но раньше, в эпоху гусиных перьев, перебоев с поставками чернил из-за очередной столетней войны в Европе и очередным повышением цен на бумагу это помогало экономить много времени, денег и нервов.

А самое главное — система образования была такая, что проще было заставить школяров заставить заучить некие, не вполне понятные формулы, чем долго и подробно объяснять, что, да как, да почему.

К XVII веку у меня вопросов нет, но обидно, что и сейчас принцип решения квадратных уравнений в школе излагают также, как и тогда.

Решение квадратных уравнений с помощью графиков функций. Алгебра, 8 класс: уроки, тесты, задания.

1.	Графическое решение Сложность: лёгкое	1
2.	Гипербола и прямая Сложность: лёгкое	2
3.	Квадратное уравнение Сложность: лёгкое	1
4.	Составление уравнения Сложность: среднее	2
5.	Количество корней уравнения Сложность: среднее	2
6.	Графическое решение неполного квадратного уравнения Сложность: среднее	2
7.	Решение задачи Сложность: сложное	3
8.	Графическое решение квадратного уравнения Сложность: сложное	3
9.	Графическое решение квадратного уравнения (5 способ) Сложность: сложное	3

Урок «Решение квадратных уравнений с параметром»

Министерство образования и науки Самарской области

Государственное автономное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов

САМАРСКИЙ ОБЛАСТНОЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

И ПЕРЕПОДГОТОВКИ РАБОТНИКОВ ОБРАЗОВАНИЯ

Итоговая работа

На курсах повышения квалификации

«Методические особенности обучения решению задач с параметром в условиях перехода к новым образовательным стандартам».

По ИОЧ ВБ 13.03.2017г-17.03.2017г

по теме:

« Квадратные уравнения с параметрами»

 

Выполнила:

Тихонова Надежда Викторовна,

Преподаватель математики

БГПОУ Сызранский «политехнический колледж»

 Сызрань 2017 г.

. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ

Уравнение вида ax2+bx+c=0, где a, b, c – числа, причем а≠0 называется

квадратным уравнением.

а – первый коэффициент, b – второй коэффициент, с – свободный член.

Например:

а) 2х2– 3х + 0,7 = 0

б) -0,9 х2+ 8 – 2 1/6х=0

Найти a, b, c?

Решим уравнение ax2+bx+c=0

а) если а=0, то уравнение имеет вид bx+c=0. Тогда x=-c|b

б) если а≠0, то уравнение имеет:

1) 2 различных корня х1≠х2, если Д>0,

2) 2 равных корня х1=х2, если Д=0

3) не имеет корней, если Д<0.

Рассмотрим примеры.

Пример №1. При каких значениях уравнение имеет 2 корня?

2х2+6х+b=0

Уравнение квадратное.

Найдем Д=36-4*2*b=36-8b. По условию задачи уравнение имеет 2 корня,

значит Д>0.

Решим неравенство 36-8b>0

-8b>-36

b<4,5.

Ответ: при b<4,5.

Пример № 2. При каких значениях имеет один корень?

3х2-6х+2v=0

Уравнение квадратное. Д=36-4*3*2v=36-24v.

Так как уравнение имеет один корень, то Д=0.

36-24v=0

24v=36

V=1,5.

Пример № 3. При каких t уравнение не имеет корней?

2×2-15x+t=0

Уравнение квадратное. Д=225-4*2t=225-8 t По условию Д<0, то

225-8t<0

-8t<-225

t>281/8.

Ответ: при t>281/8/

Пример № 4.

При каких значениях m равно один из корней уравнения равен нулю. х2 – 2х + 2m – 3 = 0

Решение: Если х = 0, то имеем:

02 – 2 . 0 + 2m – 3 = 0

2m = 3

m = 1,5

Проверим, не равняется ли второй корень уравнения нулю.

х = 0

х = 2

х2 – 2х = 0

Ответ: m = 1,5

При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0. Дело в том, что если этот коэффициент равен нулю, то уравнение превращается в линейное и решается по соответствующему алгоритму; если же этот коэффициент отличен от нуля, то имеем квадратное уравнение, которое решается по иному алгоритму. Дальнейшее решение зависит от дискриминанта.

 

Пример №.5

Решить уравнение х2 – (2р + 1)х + (р2 + р – 2) = 0

Решение: Здесь коэффициент перед х2 отличен от нуля, значит данное уравнение при любых значениях параметра является квадратным. Найдем дискриминант:

D = (2р + 1)2 – 4∙1(р2 + р – 2) = (4р2 + 4р + 1) – (4р2 + 4р – 8) = 4р2 + 4р + 1 – – 4р2 – 4р + 8 = 9

D > 0, значит квадратное уравнение имеет два решения

х1 = р + 2

х2 = р – 1

Ответ: при любых значениях р х1 = р + 2; х2 = р – 1

Пример № 6.

Решить уравнение рх2 +( 1 – р)х – 1 = 0

Решение: Мы не можем утверждать, что данное уравнение является квадратным. Рассмотрим контрольные (точки) значения р = 0, имеем два случая.

Если р=0, то получается уравнение вида 0∙х2 + х – 1 = 0, которое является линейным и имеет корень х = 1

Если р ≠0, то уравнение является квадратным, можно применять формулы корней квадратного уравнения.

D = (1 – р)2 – 4∙.р .(-1) = 1 – 2р + р2 + 4р = (1+ р)2

х1 = 1

х2 = –

Ответ: при р = 0 х = 1; при р ≠0 х1 = 1 х2 = –

 

Пример № 7

Решить уравнение: (а – 1)х 2 + 2(2а + 1)х + (4а + 3) = 0

Решение: здесь контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0.

Если а – 1 = 0, а = 1, уравнение имеет вид 0∙ х2 + 6х + 7 = 0 и является линейным. Корнем этого уравнения является х =

Если а–1 ≠ 0, а ≠ 0, уравнение является квадратным. Найдем его дискриминант.

D = (2∙(2а + 1))2 – 4(а – 1)(4а + 3) = 4(4а2 + 4а + 1) – 4(4а2 – а – 3) = 4(5а + 4)

Дальнейшие рассуждения зависят от значения дискриминанта.

Если D < 0, то квадратное уравнение не имеет корней; если D = 0, то уравнение имеет один корень, если D > 0, то уравнение имеет два корня.

Дискриминант обращается в нуль при а = – (можно сказать, что это – второе контрольное значение параметра; при переходе через него происходит качественное изменение уравнения – меняется число корней уравнения).

Если а < – , то D < 0 и следовательно, квадратное уравнение не имеет корней.

Если а > – , то если D > 0 и, значит квадратное уравнение имеет два корня:

х1 =

х2 =

Если а = – , то D = 0, то уравнение имеет единственное решение

х =

Ответ: при а = 1, х = – ;

при а = –, х = ;

при а < –, корней нет;

при а > –, х1 =

х2 =

Иногда задания сформулированы так, что искать корни нет необходимости.

Пример №8

При каких значениях m ровно один из корней х2+(m+3)х +|m| – 3 = 0

уравнения равен нулю.

Решение. Если нуль является корнем уравнения, квадратный трехчлен х2+(m+3)х +|m| – 3 при х = 0 обращается в нуль. 02+(m+3) .0 +|m| – 3 = 0

|m| – 3 = 0 m1 = 3 m2 = –3

Найдем второй корень при найденных значениях m.

Если m=3, то уравнение принимает вид х2+6х = 0; х1 = 0 х2 = –6

Если m= –3, то уравнение принимает вид х2 = 0, которое имеет два кратных корня, равных нулю.

Ответ: при m = 3

Пример №9

Сколько корней имеет уравнение 3х (х – 1) 2 = kх в зависимости от значения параметра k ?

Решение: 3х (х – 1) 2 = kх

3х (х – 1) 2 – kх = 0

х (3(х – 1) 2 – k) = 0

Один корень есть всегда – х0 = 0

Исследуем 3х 2 – 6х + 3 – k = 0

D = 32 – 3(3 – k) = 3k

а) Если k = 0, существует один корень х = 1;

б) Если k > 0, существуют два корня х1 = х2 = , но необходимо исследовать случай, когда один из корней равен 0. Это так, если k = 3;

в) Если k < 0, корней нет.

Ответ: уравнение 3х (х – 1) 2 = kх имеет при

1) k > 0

k ≠ 3 три корня;

2) k = 0 два корня

3) k = 3 два корня

4) k < 0 один корень.

Решение квадратных уравнений, формулы и примеры

Коэффициент называется старшим коэффициентом, а — свободным членом.

Если старший коэффициент , то квадратное уравнение (1) имеет вид и называется приведенным.

Чтобы квадратное уравнение (1) записать в виде (2), необходимо его левую и правую части поделить на старший коэффициент .

Решение квадратных уравнений с помощью дискриминанта

Если дискриминант , то квадратное уравнение (1) имеет два различных действительных корня:

   

Если дискриминант , то уравнение имеет два равных действительных корня (или корень кратности два)

   

Если дискриминант , то квадратное уравнение (1) действительных корней не имеет, то есть

   

Решение квадратных уравнений с помощью выделения полного квадрата

В левой части уравнения (2) выделим полный квадрат при помощи формулы сокращенного умножения «квадрат суммы/разности»:

   

Таким образом, уравнение (2) принимает вид:

   

или

   

Если выражение , то применим к левой части последнего равенства формулу «разность квадратов», в результате будем иметь:

   

Использовав тот факт, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю, придем к следующей совокупности линейных уравнений:

   

Если выражение , то уравнение запишется в виде

   

Оно имеет кратный корень .

В случае, когда , то квадратное уравнение \eqref{GrindEQ__1_} действительных корней не имеет: .

Решение квадратных уравнений с помощью теоремы Виета

Если приведенное квадратное уравнение \eqref{GrindEQ__2_} имеет корни и , то

   

Следствие. Таким образом, целые решения уравнения \eqref{GrindEQ__2_} являются делителями свободного коэффициента .

Решение квадратных уравнений способом переброски коэффициентов

Умножим левую и правую части уравнения (1) на старший коэффициент :

или .

В результате старший коэффициент умножается на свободный член, то есть как бы «перебрасывается» к нему.

Делаем замену

   

В результате получаем уравнение

   

которое является равносильным заданному уравнению (1). Его корни та находим, если это возможно, по теореме Виета (если нет, то вычисляем дискриминант).

Искомые решения исходного уравнения

   

Частные случаи квадратных уравнений

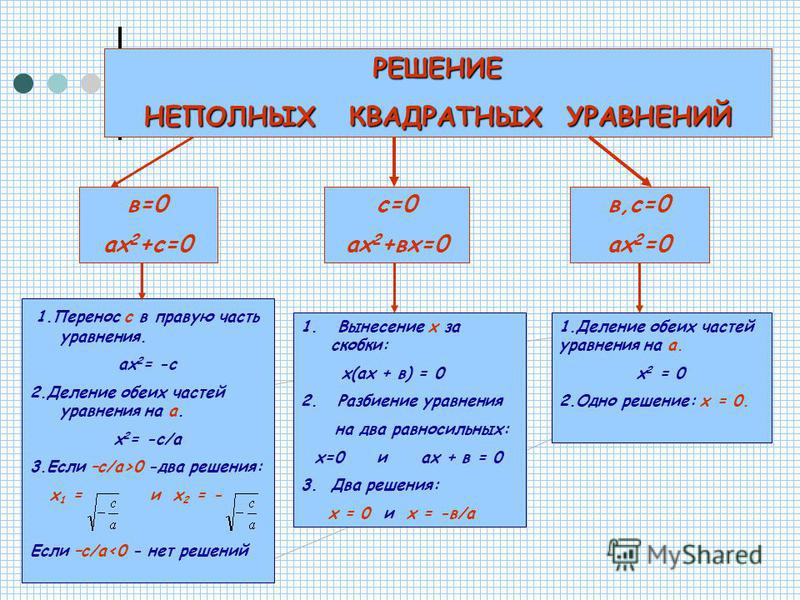
Если хотя бы один из коэффициентов или равен нулю, то уравнение (1) называется \textbf{неполным}.

Если , то уравнение (1) принимает вид: , его кратный корень .

Если , то уравнение (1) запишется в виде , откуда

   

Если права часть , то уравнение имеет два корня

   

В случае же, если , то уравнение корней не имеет: .

Если , то уравнение \eqref{GrindEQ__1_} принимает вид , откуда

   

то есть

   

Тренировочные задания на решение квадратных уравнений 8 класс

Loading…

Квадратные  уравнения 8 класс  алгебра

 

Учитель: Федулкина Т.А.

 

• Что такое квадратные уравнения. Виды уравнений.

Формула квадратного уравнения: ax²+bx+c=0,где a≠0, где x — переменная,  a,b,c — числовые коэффициенты.

 

Пример полного квадратного уравнения:

3x²-3x+2=0
x²-16x+64=0

Решение полных квадратных уравнений сводится к нахождению дискриминанта:

Формула дискриминанта:  D=b²-4aс

Если D>0, то уравнение имеет два корня и находим эти корни по формуле:

Если D=0, уравнение имеет один корень 

Если D<0, уравнение не имеет вещественных корней.

№1  x²-x-6=0

Записываем сначала, чему равны числовые коэффициенты a, b и c.

Коэффициент a всегда стоит перед x², коэффициент b  всегда перед переменной x, а коэффициент  c – это свободный член.
a=1,b=-1,c=-6
D=b²-4ac=(-1)²-4∙1∙(-6)=1+24=25

Дискриминант больше нуля, следовательно, у нас два корня, найдем их:

 Ответ: x₁=3; x₂=-2

№2  x²+2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
D=b²-4ac=(2)²-4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1

Ответ: x=-1

№3 7x²-x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
D=b²-4ac=(-1)²-4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.

Рассмотрим неполное квадратное уравнение:
ax²+bx=0, где числовой коэффициент c=0.

Пример как выглядят такие уравнения: x²-8x=0, 5x²+4x=0.

Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax²+bx=0  x(ax+b)=0  x₁=0 x₂=-b/a

№1  3x²+6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x₁=0      3x+6=0   3x=-6     x₂=-2

Ответ: x₁=0; x₂=-2

№2  x²-x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x₁=0
x₂=1

Ответ: x₁=0; x₂=1

Рассмотрим неполное квадратное уравнение:
ax²+c=0, где числовой коэффициент b=0.

Чтобы решить это уравнение, нужно записать так:
x²=c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом: корень квадратного уравнения

№1  x²+5=0
x²=-5, видно, что -5<0, значит нет решения.
Ответ: нет решения

№2 3x²-12=0
3x²=12
x²=12/3
x²=4
x₁=2

x₂=-2

Ответ: x₁=2; x₂=-2

 

2) Тренировочные задания на решение квадратных уравнений 8 класс  алгебра.

 

Задания для  устного решения:

 

1. Решите неполное квадратное уравнение:

 

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

2. Решите квадратное уравнение, используя теорему Виета:

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

3. Решите квадратное уравнение, используя формулу :

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

4. Найдите дискриминант квадратного уравнения по формуле D= :

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 

5. Сколько корней имеет квадратное уравнение, если D= равно:

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

3)Решить  квадратные  уравнения:

 

6. Решите квадратное уравнение:

1)	6)	11)	16)
2)	7)	12)	17)
3)	8)	13)	18)
4)	9)	14)	19)
5)	10)	15)	20)

 скачать файл

Дата публикации — 03. 12.2017

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k² − ac, а корни по формулам и .

Примеры

Решим квадратное уравнение x² + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.

Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.

n = 2k

Например, число 10 можно представить как 2 × 5.

10 = 2 × 5

В этом произведении k = 5.

---

Число 12 можно представить как 2 × 6.

12 = 2 × 6

В этом произведении k = 6.

---

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7.

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.

В уравнении x² + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = 3² − 1 × (−16) = 9 + 16 = 25

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x² + 6x − 16 = 0 являются числа 2 и −8.

В отличие от стандартной формулы для вычисления дискриминанта (D=b² − 4ac), в формуле D₁ = k² − ac не нужно выполнять умножение числа 4 на ac.

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

---

Пример 2. Решить квадратное уравнение 5x² − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−3)² − 5 × 1 = 9 − 5 = 4

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

---

Пример 3. Решить квадратное уравнение x² − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−5)² − 1 × (−24) = 25 + 24 = 49

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

---

Пример 5. Решить квадратное уравнение

Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k. Получается, что

Найдём дискриминант по формуле D₁ = k² − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .

Вычислим второй корень уравнения:

---

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax² + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

b = 2k

Заменим в уравнении ax² + bx + c = 0 коэффициент b на выражение 2k

ax² + 2kx + c = 0

Теперь вычислим дискриминант по ранее известной формуле:

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac

Вынесем в получившемся выражении за скобки общий множитель 4

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac = 4(k² − ac)

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k² − ac.

В выражении 4(k² − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k² − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k² − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

D₁ = k² − ac

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax² + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k² − ac)

Но ранее было сказано, что выражение k² − ac обозначается через D₁. Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Задания для самостоятельного решения

Задание 1. Решить уравнение:

Решение:

Ответ: 1; 0,6

Задание 2. Решить уравнение:

Решение:

Ответ:

Задание 3. Решить уравнение:

Решение:

Ответ: 1; −1,4

Задание 4. Решить уравнение:

Решение:

Ответ:

Задание 5. Решить уравнение:

Решение:

Ответ:

Задание 6. Решить уравнение:

Решение:

Ответ:

Задание 7. Решить уравнение:

Решение:

Ответ:

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Калькулятор квадратичных формул

Использование калькулятора

Этот онлайн-калькулятор представляет собой программа решения квадратного уравнения , которая решает полиномиальное уравнение второго порядка, такое как ax ² + bx + c = 0 для x, где a 0, используя квадратная формула .

Решение калькулятора покажет работу с использованием формулы корней квадратного уравнения для решения введенного уравнения для действительных и комплексных корней. 2 — 4ac> 0 \) Итак, существует два действительных корня.

Упростите радикал:

\ (x = \ dfrac {8 \ pm 2 \ sqrt {11} \,} {2} \)

\ (x = \ dfrac {8} {2} \ pm \ dfrac {2 \ sqrt {11} \,} {2} \)

Упростить дроби и / или знаки:

\ (x = 4 \ pm \ sqrt {11} \, \)

, который становится

\ (х = 7.2 — 4ac <0 \), значит, есть два комплексных корня.

Упростите радикал:

\ (x = \ dfrac {-20 \ pm 4 \ sqrt {15} \, i} {10} \)

\ (x = \ dfrac {-20} {10} \ pm \ dfrac {4 \ sqrt {15} \, i} {10} \)

Упростить дроби и / или знаки:

\ (x = -2 \ pm \ dfrac {2 \ sqrt {15} \, i} {5} \)

, который становится

\ (х = -2 + 1.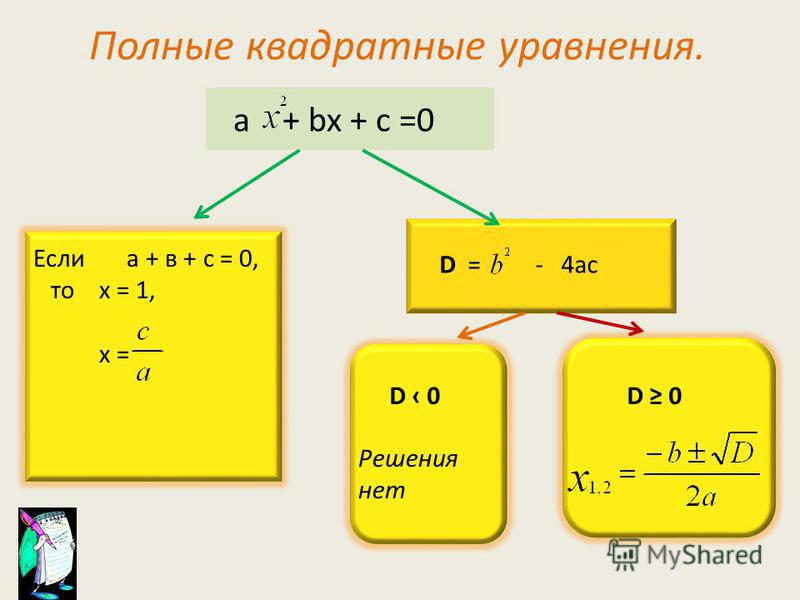 2} + bx + c = 0, потому что трехчлен в левой части нелегко вынести за скобки. Это не означает, что квадратное уравнение не имеет решения. На этом этапе нам нужно обратиться к прямому подходу квадратной формулы, чтобы найти решения квадратного уравнения или, проще говоря, определить значения x, которые могут удовлетворять уравнению.

Чтобы использовать квадратную формулу, квадратное уравнение, которое мы решаем, необходимо преобразовать в «стандартную форму», иначе все последующие шаги не будут работать.Цель состоит в том, чтобы преобразовать квадратное уравнение таким образом, чтобы квадратное выражение было изолировано с одной стороны уравнения, в то время как противоположная сторона содержала только ноль, 0.

Взгляните на диаграмму ниже.

В этом удобном формате числовые значения a, b и c легко идентифицируются! Зная эти значения, мы можем теперь подставить их в формулу корней квадратного уравнения, а затем найти значения x.

---

Квадратичная формула

• Где a, b и c — коэффициенты произвольного квадратного уравнения в стандартной форме, a {x ^ 2} + bx + c = 0.

При необходимости снизьте скорость. Будьте осторожны с каждым шагом, упрощая выражения. Здесь обычно случаются типичные ошибки, потому что учащиеся склонны «расслабляться», что приводит к ошибкам, которые можно было предотвратить, например, при сложении, вычитании, умножении и / или делении действительных чисел.

---

Примеры решения квадратных уравнений по квадратичной формуле

Пример 1 : Решите квадратное уравнение, приведенное ниже, с помощью квадратной формулы.

При осмотре очевидно, что квадратное уравнение имеет стандартную форму, поскольку правая часть равна нулю, а остальные члены остаются в левой части. Другими словами, у нас есть что-то вроде этого

Это здорово! Нам нужно просто определить значения a, b и c, а затем подставить их в формулу корней квадратного уравнения.

Вот и все! Возьмите за привычку всегда проверять решенные значения x обратно в исходное уравнение.

---

Пример 2 : Решите квадратное уравнение ниже, используя квадратную формулу.

Это квадратное уравнение абсолютно не в той форме, в которой мы хотим, потому что правая часть равна НЕ нулю. Мне нужно удалить это 7 с правой стороны, вычтя обе части на 7. Это решит нашу проблему. После этого решите относительно x как обычно.

Окончательные ответы: {x_1} = 1 и {x_2} = — {2 \ over 3}.

---

Пример 3 : Решите квадратное уравнение ниже, используя квадратную формулу.

Это квадратное уравнение выглядит как «беспорядок». У меня есть переменные x и константы по обе стороны уравнения. Если мы сталкиваемся с чем-то подобным, всегда придерживайтесь того, что мы знаем. Да, все дело в стандартной форме. Мы должны заставить правую часть равняться нулю. Мы можем сделать это в два этапа.

Сначала я вычту обе стороны на 5x, а затем прибавлю 8.

Необходимые нам значения:

a = — 1, b = — \, 8 и c = 2

---

Пример 4 : Решите квадратное уравнение ниже, используя квадратную формулу.

Что ж, если вы думаете, что Пример 3 — это «беспорядок», тогда он должен быть еще более «беспорядочным». Однако вскоре вы поймете, что на самом деле они очень похожи.

Сначала нам нужно выполнить некоторую очистку, преобразовав это квадратное уравнение в стандартную форму. Звучит знакомо? Поверьте, эта проблема не так плоха, как кажется, если мы знаем, что делать.

Напоминаю, что нам нужно что-то вроде этого

Следовательно, мы должны сделать все возможное, чтобы правая часть уравнения стала равной нулю.2} термин справа.

• Исключите член x с правой стороны.

• Удалите константу с правой стороны.

После получения правильной стандартной формы на предыдущем шаге теперь пора подставить значения a, b и c в формулу корней квадратного уравнения, чтобы найти x.

• Из преобразованной стандартной формы извлеките требуемые значения.

a = 1, b = — \, 4 и c = — \, 14

• Затем вычислите эти значения в формуле корней квадратного уравнения.

---

Практика с рабочими листами

---

Возможно, вас заинтересует:

Решение квадратных уравнений методом квадратного корня
Решение квадратных уравнений методом факторинга
Решение квадратных уравнений путем заполнения квадрата

Решение квадратных уравнений — квадратная формула, как решить квадратное уравнение?

Прежде чем приступить к изучению решения квадратных уравнений, давайте вспомним несколько фактов о квадратных уравнениях.Слово «квадратичный» происходит от слова «четырехугольник» и имеет значение «квадрат». Это означает, что в квадратном уравнении переменная повышена до 2 как член наибольшей степени. Стандартная форма квадратного уравнения задается уравнением ax ² + bx + c = 0, где a ≠ 0. Мы знаем, что любое значение (я) x, которое удовлетворяет уравнению, известно как решение (или) корень уравнения и процесс нахождения значений x, которые удовлетворяют уравнению ax ² + bx + c = 0, известен как решение квадратных уравнений.

Существуют различные методы решения квадратных уравнений. Но наиболее популярным методом является решение квадратных уравнений на множители. Давайте изучим все методы здесь подробно вместе с несколькими решенными примерами.

Как решать квадратные уравнения?

Решение квадратных уравнений означает поиск значения (или) значений переменной, которые удовлетворяют уравнению. Значения, которые удовлетворяют квадратному уравнению, известны как его корни (или) решения (или) нули.Поскольку степень квадратного уравнения равна 2, оно может иметь максимум 2 корня. Например, легко увидеть, что x = 1 и x = 2 удовлетворяют квадратному уравнению x ² — 3x + 2 = 0 (вы можете подставить каждое из значений в это уравнение и проверить). Таким образом, x = 1 и x = 2 являются корнями x ² — 3x + 2 = 0. Но как их найти, если они не заданы? Есть разные способы решения квадратных уравнений.

• Решение квадратных уравнений на множители
• Решение квадратных уравнений до квадрата
• Решение квадратных уравнений с помощью построения графиков
• Решение квадратных уравнений по квадратной формуле

Помимо этих методов, существуют некоторые другие методы, которые используются только в особых случаях (когда квадратное уравнение имеет пропущенные члены), как описано ниже.

Решение отсутствующих квадратных уравнений b

В квадратном уравнении ax ² + bx + c = 0, если член с b отсутствует, уравнение принимает вид ax ² + c = 0. Это можно решить, извлекая квадратный корень с обеих сторон. Процесс поясняется примерами ниже.

• x ² — 4 = 0 ⇒ x ² = 4 ⇒ x = ± √4 ⇒ x = ± 2
  Таким образом, корни уравнения равны 2 и -2.
• x ² + 36 = 0 ⇒ x ² = -36 ⇒ x = ± √ (-36) ⇒ x = ± 6i
  Таким образом, корни уравнения — 6i и -6i.
  (обратите внимание, что это мнимые (или) комплексные числа).

Решение отсутствующих квадратных уравнений c

В квадратном уравнении ax ² + bx + c = 0, если член с c отсутствует, уравнение принимает вид ax ² + bx = 0. Чтобы решить этот тип уравнения, мы просто выносим x из слева, установите каждый из множителей равным нулю и решите. Процесс поясняется примерами ниже.

• x ² — 5x = 0 ⇒ x (x — 5) = 0 ⇒ x = 0; х — 5 = 0 ⇒ х = 0; х = 5
  Таким образом, корни уравнения равны 0 и 5.
• x ² + 11x = 0 ⇒ x (x + 11) = 0 ⇒ x = 0; х + 11 = 0 ⇒ х = 0; х = -11
  Таким образом, корни уравнения равны 0 и -11.

Теперь мы изучим методы решения квадратных уравнений в каждом из вышеупомянутых методов.

Решение квадратных уравнений с факторингом

Решение квадратных уравнений путем разложения на множители — один из известных методов, используемых для решения квадратных уравнений.Пошаговый процесс решения квадратных уравнений путем факторизации объясняется вместе с примером, в котором мы решаем уравнение x ² — 3x + 2 = 0.

• Шаг — 1: Приведите уравнение в стандартную форму. т.е. переведите все члены в одну сторону (обычно в левую) уравнения так, чтобы другая сторона была равна 0.
  Уравнение x ² — 3x + 2 = 0 уже находится в стандартной форме.
• Шаг — 2: Разложите квадратное выражение на множители.Если вы хотите узнать, как разложить квадратное выражение на множители, щелкните здесь.
  Тогда получаем (x — 1) (x — 2) = 0.
• Шаг — 3: По нулевому свойству продукта установите каждый из коэффициентов равным нулю.
  x — 1 = 0 (или) x — 2 = 0
• Шаг — 4: Решите каждое из приведенных выше уравнений.
  х = 1 (или) х = 2

Таким образом, решения квадратного уравнения x ² — 3x + 2 = 0 равны 1 и 2. Этот метод применим только тогда, когда квадратное выражение факторизуемо.Если это НЕВОЗМОЖНО, то мы можем использовать один из других методов, как описано ниже.

Решение квадратных уравнений путем завершения квадрата

Завершение квадрата означает запись квадратного выражения ax ² + bx + c в форме a (x — h) ² + k (которая также известна как форма вершины), где h = -b / 2a и ‘ k ‘можно получить, подставив x = h в ax ² + bx + c. Пошаговый процесс решения квадратных уравнений путем заполнения квадрата объясняется вместе с примером, в котором мы собираемся найти решения уравнения 2x ² + 8x = -3.

• Шаг — 1: Приведите уравнение в стандартную форму.
  Складывая 3 с обеих сторон, получаем 2x ² + 8x + 3 = 0.
• Шаг — 2: Завершите квадрат с левой стороны.
  Тогда мы получаем 2 (x + 2) ² — 5 = 0. Если вы хотите знать, как заполнить квадрат, щелкните здесь.
• Шаг — 3: Решите его относительно x (нам придется извлекать квадратный корень с обеих сторон по пути).
  Складываем 5 с обеих сторон,
  2 (х + 2) ² = 5
  Делим обе стороны на 2,
  (х + 2) ² = 5/2
  Извлечение квадратного корня с обеих сторон,
  х + 2 = √ (5/2) = √5 / √2 · √2 / √2 = √10 / 2
  Вычитая 2 с обеих сторон,
  х = -2 ± (√10 / 2) = (-4 ± √10) / 2

Таким образом, корни квадратного уравнения 2x ² + 8x = -3 равны (-4 + √10) / 2 и (-4 — √10) / 2.

Решение квадратных уравнений с помощью построения графиков

Для решения квадратных уравнений путем построения графика мы сначала должны построить график квадратичного выражения (когда уравнение имеет стандартную форму) либо вручную, либо с помощью графического калькулятора. Тогда отрезок (точки) x графика (точка (точки), где график пересекает ось x) являются не чем иным, как корнями квадратного уравнения. Вот шаги для решения квадратных уравнений с помощью построения графиков, которые объясняются вместе с примером, в котором мы собираемся решить уравнение 3x ² + 5 = 11x.

• Шаг — 1: Привести стандартную форму.
  Вычитая 11x с обеих сторон, получаем 3x ² — 11x + 5 = 0.
• Step — 2: Постройте квадратичное выражение (слева).
  Изобразите квадратичную функцию y = 3x ² — 11x + 5 вручную или с помощью графического калькулятора (GDC).
  Вы можете увидеть график на шаге ниже.
• Шаг — 3: Определите точки пересечения по оси x.
  
• Step — 4: Координаты x точек пересечения с координатами x являются не чем иным, как корнями квадратного уравнения.
  Таким образом, решения квадратного уравнения 3x ² + 5 = 11x равны 0,532 и 3,135.

Посмотрев приведенный выше пример, мы можем увидеть, что метод построения графиков решения квадратных уравнений может не давать точных решений (т.е. он дает только десятичные приближения корней, если они иррациональны). т.е. если мы решим то же уравнение, завершив квадрат, мы получим x = (11 + √61) / 6 и x = (11 — √61) / 6.Но мы не можем получить эти точные корни графическим методом.

Что делать, если график вообще не пересекает ось абсцисс? Это означает, что квадратное уравнение имеет два комплексных корня. то есть метод построения графика НЕ ​​помогает найти корни, если они являются комплексными числами. Мы можем использовать формулу корней квадратного уравнения (которая объясняется в следующем разделе), чтобы найти корни любого типа.

Решение квадратных уравнений по квадратичной формуле

Как мы уже видели, предыдущие методы решения квадратных уравнений имеют некоторые ограничения, такие как метод факторизации полезен только тогда, когда квадратное выражение факторизуемо, метод построения графиков полезен только тогда, когда квадратное уравнение имеет действительные корни и т. Д.Но , решающий квадратные уравнения по квадратной формуле , преодолевает все эти ограничения и полезен для решения любого типа квадратного уравнения. Вот пошаговое объяснение решения квадратных уравнений по квадратной формуле вместе с примером, в котором мы будем находить решения квадратного уравнения 2x ² = 3x — 5.

• Шаг — 1: Привести стандартную форму.
  Тогда приведенное выше уравнение принимает вид 2x ² — 3x + 5 = 0.
• Шаг — 2: Сравните уравнение с ax ² + bx + c = 0 и найдите значения a, b и c.
  Тогда получаем a = 2, b = -3. и c = 5. 90 · 109
• Шаг — 3: Подставьте значения в формулу корней квадратного уравнения, которая говорит, что x = [-b ± √ (b² — 4ac)] / (2a). Тогда получаем
  x = [- (- 3) ± √ ((- 3) ² — 4 (2) (5))] / (2 (2))
• Шаг — 4: Упростить.
  x = [3 ± √ (9–40)] / 4
  = [3 ± √ (-31)] / 4
  = [3 ± i√ (31)] / 4

Таким образом, корни квадратного уравнения 2x ² = 3x — 5 равны [3 + i√ (31)] / 4 и [3 — i√ (31)] / 4.В четвертой формуле выражение b² — 4ac называется дискриминантом (обозначается D). т.е. D = b² — 4ac. Это используется для определения природы корней квадратного уравнения.

Природа корней с использованием дискриминанта

• Если D> 0, то уравнение ax ² + bx + c = 0 имеет два действительных и различных корня.
• Если D = 0, то уравнение ax ² + bx + c = 0 имеет только один действительный корень.
• Если D <0, то уравнение ax ² + bx + c = 0 имеет два различных комплексных корня.

Таким образом, используя дискриминант, мы можем найти количество решений квадратных уравнений, фактически не решая их.

Важные замечания по решению квадратных уравнений:

• Метод факторизации не может применяться, если квадратичное выражение НЕ факторизуемо.
• Метод построения графиков не может дать ни комплексных корней, ни точных корней, если квадратное уравнение имеет иррациональные корни.
• Заполнение метода квадратов и метода квадратных формул можно применять для решения любого типа квадратного уравнения.
• Корни квадратного уравнения также известны как «решения» или «нули».
• Для любого квадратного уравнения ax ² + bx + c = 0,
  сумма корней = -b / a
  произведение корней = c / a.

☛Связанные темы квадратных уравнений:

Часто задаваемые вопросы по решению квадратных уравнений

Что означает решение квадратных уравнений?

Решение квадратных уравнений означает нахождение его решений или корней.т.е. это процесс нахождения значений переменной, удовлетворяющих уравнению.

Как решать квадратные уравнения?

Есть разные способы решения квадратных уравнений. Но наиболее популярными способами являются «решение квадратных уравнений путем факторизации» и «решение квадратных уравнений с помощью квадратной формулы».

Какие 4 способа решить квадратное уравнение?

Есть 4 способа решения квадратных уравнений.

• с учетом факторинга
• , заполнив квадрат
• , построив график
• по квадратичной формуле

Как решить квадратные уравнения с помощью квадратной формулы?

Решения квадратного уравнения ax ² + bx + c = 0 даются квадратной формулой x = [-b ± √ (b² — 4ac)] / (2a). Итак, чтобы решить квадратное уравнение с использованием квадратной формулы, просто приведите уравнение в стандартную форму ax ² + bx + c = 0 и примените квадратную формулу.

Как проще всего решить квадратные уравнения?

Самый простой способ решения квадратных уравнений — это метод факторизации. Но не всегда квадратные выражения факторизуемы. В этом случае мы можем использовать формулу квадратов или метод завершающих квадратов.

Каковы шаги в решении квадратного уравнения до квадрата?

Чтобы решить квадратное уравнение ax ² + bx + c = 0, заполнив квадрат, преобразуйте ax ² + bx + c в форму a (x — h) ² + k, где h = -b / 2a а k получается заменой x = h в ax ² + bx + c.Тогда мы можем легко решить a (x — h) ² + k = 0, изолировав x. В этом процессе нам нужно будет извлечь квадратный корень с обеих сторон.

Как узнать, какой метод использовать при решении квадратных уравнений?

Мы можем решить квадратные уравнения любого типа, заполнив квадрат или квадратную формулу. Но если квадратичное выражение факторизуемо, то проще всего применить метод факторизации. Мы также можем решить эту проблему с помощью графического метода, но он дает только приближенные действительные корни (т.е., сложные корни в этом методе не найти).

Как решить квадратные уравнения факторингом?

Для решения квадратных уравнений путем факторизации сначала преобразуйте его в стандартную форму (ax ² + bx + c = 0). Затем разложите левую часть на множители, используя методы факторизации квадратичных выражений, установите каждый из множителей равным нулю, что приводит к двум линейным уравнениям, и, наконец, решите линейные уравнения.

Чем полезна форма с факторизацией при решении квадратных уравнений?

Если квадратное выражение в стандартной форме квадратного выражения в нем факторизуемо, то мы можем просто установить каждый коэффициент равным нулю и решить их.Решения — не что иное, как корни квадратного уравнения.

Как найти корни квадратных уравнений?

Корни квадратного уравнения ax ² + bx + c = 0 можно найти, используя формулу корней квадратного уравнения, которая говорит, что x = [-b ± √ (b² — 4ac)] / (2a). Кроме того, мы можем решить их, выполнив метод квадрата (или) факторизации (только если они факторизуемы).

Каковы этапы решения квадратных уравнений с помощью построения графиков?

Чтобы решить квадратные уравнения с помощью построения графиков, сначала примите стандартную форму ax ² + bx + c = 0.Затем изобразите квадратичное выражение ax ² + bx + c. Найдите, где график пересекает ось x. Координата x точки пересечения с координатами x — это не что иное, как решения квадратного уравнения.

Какой метод лучше всего подходит для решения квадратных уравнений?

Лучший метод решения квадратных уравнений — это факторинг. Но когда факторизация невозможна, мы решаем их, используя формулу корней квадратного уравнения x = [-b ± √ (b² — 4ac)] / (2a). Если у вас есть графический калькулятор, то метод построения графиков будет самым простым способом найти десятичное приближение корней (однако мы не можем найти точные корни).2 — 4ac}} {2a} $

Число D = b ² — 4ac называется «дискриминантом» . 2-32 $ $ y = 2 (x-3) (x + 5) $ y-перехват на
$ (0, -30) $ вершина при
$ (- 1, -32) $ x-перехватов на
$ (3, 0) $ и $ (- 5, 0) $

Парабола

График квадратного уравнения называется параболой .
Если a> 0, то его вершина указывает вниз:

Если a <0, то его вершина указывает вверх: Если a = 0, график не парабола, а прямая линия.

Вершина параболы равна $ x = — \ frac {b} {2a} $.

Формулы Виета

Если x ₁ и x ₂ являются корнями квадратного уравнения ax ² + bx + c = 0 затем:
$ x_1 + x_2 = — \ frac {b} {a} $
$ x_1x_2 = \ frac {c} {a} $
Эти формулы называются формулами Виета .
Мы можем найти корни x ₁ и x ₂ квадратного уравнения, решив совместные уравнения.

Задачи на квадратные уравнения

Задача 1. Решите уравнение:
x ² — 4 = 0
Решение: x ² — 4 = (x — 2) (x + 2)
(x — 2) (x + 2 ) = 0
x — 2 = 0 или x + 2 = 0
Корни равны x = 2 или x = -2

Решение 2: a = 1, b = 0, c = -4
D = 0 ² — 4 ⋅ 1 ⋅ (-4) = 16
$ x_1 = \ frac {-b — \ sqrt {D}} {2a} = \ frac {- 0 — \ sqrt {16}} {2 \ cdot 1} = \ frac {-4} {2} = -2 $
$ x_2 = \ frac {-b + \ sqrt {D}} {2a } = \ frac {- 0 + \ sqrt {16}} {2 \ cdot 1} = \ frac {4} {2} = 2 $

---

Задача 2. Решите уравнение:
3x ² + 4x + 5 = 0
Решение: дискриминант D = 4 ² — 4⋅3⋅5 = 16-60 = -44 Итак, квадратное уравнение не имеет реальных корней.

---

Задача 3. Решите уравнение:
x ² + 4x — 5 = 0; х =?
Решение: Дискриминант 4 ² — (-4⋅1⋅5) = 16 + 20 = 36> 0
Уравнение имеет 2 действительных корня: $ \ frac {-4 \ pm \ sqrt {36} } {2}
долларов США x = 1 или x = -5

---

Задача 4. Решите уравнение:
x ² + 4x + 4 = 0; х =?
Решение: Дискриминант 4 ² — (4⋅1⋅4) = 16-16 = 0
Итак, есть одно реальное решение: $ x = \ frac {-4} {2} $
x = -2

---

Задача 5. Решите уравнение:
x ² — 13x + 12 = 0
Корни: 1, 12

---

Задача 6. Решите уравнение:
8x ² — 30x + 7 = 0
Корни: 3.2 + 11c + 24 = 0 Tiger Algebra Solver

Пошаговое решение:

Шаг 1:

Попытка разложить на множители путем разделения среднего члена

1.1 Факторинг c ² + 11c + 24

Первый член равен , C ² его коэффициент равен 1.
Средний член, + 11c, его коэффициент равен 11.
Последний член, «константа», равен +24

Шаг-1: Умножьте коэффициент первого члена на константу 1 • 24 = 24

Шаг-2: Найдите два множителя 24, сумма которых равна коэффициенту среднего члена, который равен 11.

650
+

	-24	+	-1	=	-25
	-12	+	-2		=
	-8	+	-3	=	-11
	-6	+	-4	=	-4	=50		—	-4	+	-6	=	-10
	-3	+	-8	=	-11							-12	=	-14
	-1	+	-24	=	-25
	1	+	24	=	25
	9050					14
	3	+	8	=	11	Вот и все

Шаг 3: Перепишите два множителя полинома, найденные в среднем члене выше, 3 и 8
c ² + 3c + 8c + 24

Шаг 4: сложите первые 2 члена, извлекая аналогичные множители:
c • (c + 3)
Сложите последние 2 члена, извлекая общие множители:
8 • (c + 3)
Шаг 5: сложите четыре члена шага 4:
(c + 8) • (c + 3) 90 209 Какое является желаемое разложение на множители

Уравнение в конце шага 1:

 (c + 8) • (c + 3) = 0
 

Шаг 2:

Теория — Корни продукта:

2. 1 Произведение нескольких членов равно нулю.

Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.

Теперь мы решим каждый член = 0 отдельно

Другими словами, мы собираемся решить столько уравнений, сколько членов есть в произведении.

Любое решение члена = 0 также решает продукт = 0.

 
 Решение уравнения с одной переменной: 
 
 2.2 Решите: c + 8 = 0 
 
 Вычтите 8 из обеих частей уравнения: 
 c = -8 
 
 
 
 Решение уравнения с одной переменной: 
 
 2.3 Решение: c + 3 = 0 
 
 Вычтем 3 из обеих частей уравнения: 
 c = -3 
 
 
 
 Дополнение: решение квадратного уравнения напрямую 
 
 Решение c  2  + 11c + 24 = 0 напрямую 
 Ранее мы разложили этот многочлен на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
 
 Парабола, поиск вершины: 
 3. 1 Найдите вершину y = c  2  + 11c + 24
 Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы.То есть, если парабола действительно имеет два реальных решения.
 Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
 Для любой параболы Ac  2  + Bc + C c-координата вершины задается как -B / (2A).В нашем случае координата c равна -5,5000
 Подставив в формулу параболы -5,5000 для c, мы можем вычислить координату y: 
 y = 1,0 * -5,50 * -5,50 + 11,0 * -5,50 + 24,0 
 или y = — 6.250
 Парабола, графическая вершина и пересечения по оси X: 
 Корневой график для: y = c  2  + 11c + 24 
 Ось симметрии (пунктирная линия) {c} = {- 5.50} 
 Вершина в точке {c, y } = {-5.50, -6.25} 
 c -Перехваты (корни): 
 корень 1 в {c, y} = {-8.00, 0.00} 
 корень 2 в {c, y} = {-3.00, 0.00}
 Решите квадратное уравнение, заполнив квадрат 
 3.2 Решение c  2  + 11c + 24 = 0, заполнив квадрат.
 Вычтем 24 из обеих частей уравнения: 
 c  2  + 11c = -24
 Теперь умный бит: возьмите коэффициент при c, равный 11, разделите на два, получив 11/2, и, наконец, возведите в квадрат. это дает 121/4
 Добавьте 121/4 к обеим частям уравнения: 
 В правой части мы имеем: 
 -24 + 121/4 или, (-24/1) + (121/4) 
. общий знаменатель двух дробей равен 4. Сложение (-96/4) + (121/4) дает 25/4 
 Таким образом, сложив обе части, мы, наконец, получаем: 
 c  2  + 11c + (121/4) = 25 / 4
 При сложении 121/4 левая часть превратилась в полный квадрат: 
 c  2  + 11c + (121/4) = 
 (c + (11/2)) • (c + (11/2)) = 
 (c + (11/2))  2  
 Вещи, которые равны одному и тому же, также равны друг другу.Поскольку 
 c  2  + 11c + (121/4) = 25/4 и 
 c  2  + 11c + (121/4) = (c + (11/2))  2  
, то по закону транзитивность, 
 (c + (11/2))  2  = 25/4
 Мы будем называть это уравнение уравнением. # 3.2.1
 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
 Обратите внимание, что квадратный корень из 
 (c + (11/2))  2  равен 
 (c + (11/2))  2/2  = 
 (c + (11/2))  1  = 
 c + (11/2)
 Теперь, применяя принцип квадратного корня к уравнению. # 3.2.1 получаем: 
 c + (11/2) = √ 25/4
 Вычтем 11/2 с обеих сторон, чтобы получить: 
 c = -11/2 + √ 25/4
 Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное 
 c  2  + 11c + 24 = 0 
 имеет два решения: 
 c = -11/2 + √ 25/4 
 или 
 c = -11/2 — √ 25 / 4
 Обратите внимание, что √ 25/4 можно записать как 
 √ 25 / √ 4, что равно 5/2 
 Решите квадратное уравнение с помощью квадратичной формулы 
 3.3 Решение c  2  + 11c + 24 = 0 по квадратичной формуле.
 Согласно квадратичной формуле, c, решение для Ac  2  + Bc + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как: 
   
 — B ± √ B  2  -4AC 
 c = ———————— 
 2A
 В нашем случае A = 1 
 B = 11 
 C = 24
 Соответственно B  2  — 4AC = 
 121 — 96 = 
 25
 Применение формулы корней квадратного уравнения:
 -11 ± √ 25 
 c = —————— 
 2
 Можно ли упростить √ 25?
 Да! Разложение 25 на простые множители равно 
 5 • 5 
 Чтобы можно было удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i. е. второй корень).
 √ 25 = √ 5 • 5 = 
 ± 5 • √ 1 = 
 ± 5
 Итак, теперь мы смотрим на: 
 c = (-11 ± 5) / 2
 Два реальных решения:
 c = (-11 + √25) / 2 = (- 11 + 5) / 2 = -3,000
 или:
 c = (- 11-√25) / 2 = (- 11-5) / 2 = -8,000
 Было найдено два решения: 
 c = -3
 c = -8
 Квадратное уравнение 
 Стандартная форма квадратного уравнения:
 ax  2  + bx + c = 0, где a ≠ 0
 В уравнении a, b и c — константы, а x — переменная.Степень уравнения 2 (показатель степени при x) делает уравнение квадратичным. Квадратные уравнения этой формы могут быть решены относительно x, чтобы найти корни уравнения, которые являются точкой (точками), где уравнение равно 0. Корни также могут называться нулями.
 Решение квадратных уравнений 
 Существует несколько различных методов решения квадратного уравнения. Ниже приведены несколько из них.
 Квадратные уравнения вида ax 
 2  + c = 0
 Квадратное уравнение без члена x  1  решить относительно просто. Нам не нужно множить или использовать квадратную формулу (обсуждается позже). Все, что нам нужно сделать, это выделить x, как если бы мы пытались найти x в любом уравнении, а затем извлечь квадратный корень из константы.
 Пример
 Учитывая x  2  — 4 = 0, найти x:
 х  2  = 4
 x = & pm; = & pm; 2
 Одна из ключевых вещей, которые нам нужно помнить при решении квадратных уравнений, это то, что x может принимать как положительные, так и отрицательные значения, поскольку и -2 × -2, и 2 & times 2 = 4.это также означает, что если bot a и c положительны или отрицательны, реальных решений нет, поскольку невозможно извлечь квадратный корень из отрицательного числа без использования мнимых чисел.
 Использование факторинга 
 Решение уравнений с использованием факторизации основывается на использовании одного из свойств 0. Если произведение двух чисел или выражений равно 0, то по крайней мере одно из выражений должно быть равно 0. Это позволяет нам разделить множители и установить их равными. до 0 индивидуально, чтобы найти решение (я) уравнения.
 Примеры
 1. Решите 2x  2  — 8x = 0:
 2x (x — 4) = 0
 Мы можем разделить это и решить для 2x = 0 и x — 4 = 0:
 2x = 0
 х = 0
 и
 х — 4 = 0
 х = 4
 Уравнение имеет два решения: x = 0 и x = 4.
 2. Решить x  2  — 4x + 4 = 0:
 x  2  — 4x + 4 = (x — 2)  2  = 0
 x — 2 = & pm; 0
 х = 2
 В этом случае, даже если мы извлекаем квадратный корень, 0 не является ни положительным, ни отрицательным, поэтому есть только одно решение.Это всегда будет иметь место в уравнениях, которые можно разложить на множители в форме (x — c)  2 , поэтому, как только вы начнете распознавать эти уравнения в их развернутой форме, x  2  — 2cx + c  2 , вы ‘ Я смогу решить их относительно быстро.
 3. Решить x  2  — x — 6 = 0:
 x  2  — x — 6 = (x — 3) (x + 2) = 0
 х — 3 = 0
 х = 3
 и
 х + 2 = 0
 х = -2
 Два решения уравнения: x = 3 и x = -2.
 Используя формулу корней квадратного уравнения 
 Термины «квадратная формула» и «квадратное уравнение» иногда используются как синонимы, но их не следует путать. Квадратичная формула относится к формуле, используемой для решения квадратных уравнений:
 Квадратичную формулу можно рассматривать как метод «грубой силы» для решения квадратных уравнений, поскольку ее можно использовать для решения любого квадратного уравнения в стандартной форме, как и все приведенные выше примеры.Однако, в зависимости от конкретного квадратного уравнения, часто бывает проще использовать такой метод, как разложение на множители, завершение квадрата или какой-либо другой метод, где это возможно, до использования формулы квадратичного. При этом сама квадратная формула относительно проста в использовании, если уравнение имеет стандартную форму.
 Все a, b и c в квадратной формуле являются константами и относятся к коэффициентам стандартной формы квадратного уравнения:
 топор  2  + bx + c
 Чтобы решить квадратное уравнение с помощью формулы корней квадратного уравнения, нам нужно просто подставить коэффициенты уравнения в формулу.
 Пример
 Решить 7x  2  — 13x + 6 = 0:
 В приведенном выше уравнении a = 7, b = -13 и c = 6. Подставляя их в формулу корней квадратного уравнения:
 x = и x =
 Хотя квадратичная формула утомительна, она очень эффективна, поскольку позволяет нам решать любое квадратное уравнение, если мы выражаем его в стандартной форме.
 В квадратной формуле выражение под знаком квадратного корня, b  2  — 4ac, называется дискриминантом.Стоит отметить, что если:
 b  2  — 4ac = 0, есть только одно решение
 b  2  — 4ac> 0, есть два реальных решения
 б  2  — 4ac
 Еще один метод решения квадратных уравнений — завершение квадрата.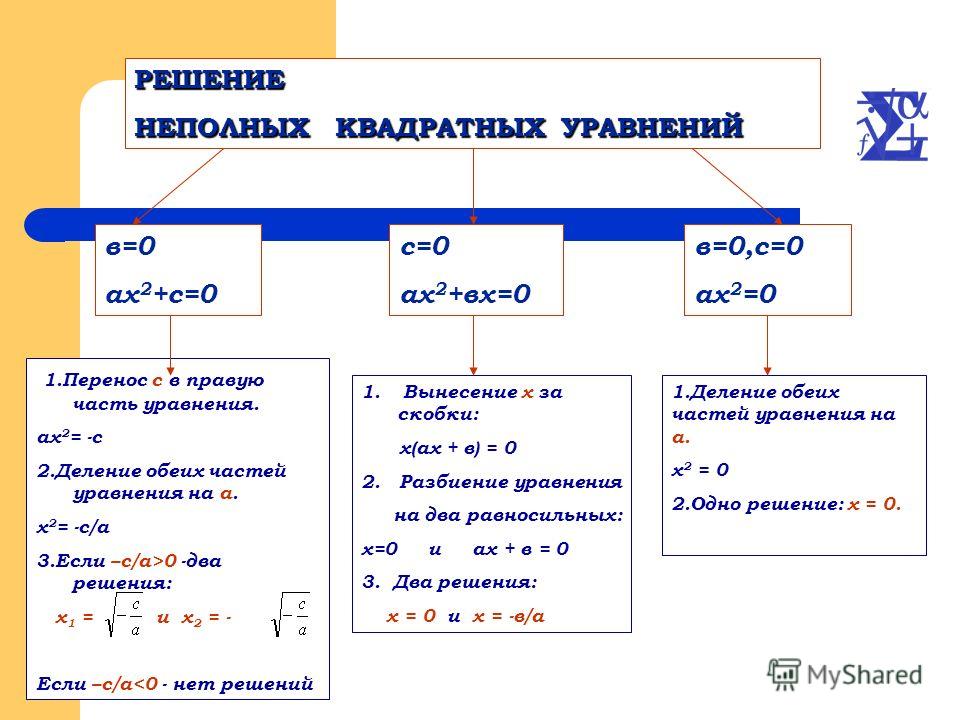
 
 Квадратичная формула — объяснения и примеры 
 К настоящему времени вы знаете, как решать квадратные уравнения с помощью таких методов, как завершение квадрата, разность квадрата и формула трехчлена полного квадрата.
 В этой статье мы узнаем, как  решать квадратные уравнения, используя два метода,  а именно квадратную формулу     и графический метод    . Прежде чем мы углубимся в эту тему, давайте вспомним, что такое квадратное уравнение.
 Что такое квадратное уравнение? 
 Квадратное уравнение в математике определяется как многочлен второй степени, стандартная форма которого — ax  2  + bx + c = 0, где a, b и c — числовые коэффициенты, а a 0.
 Термин вторая степень означает, что по крайней мере один член в уравнении возведен в степень двойки. В квадратном уравнении переменная x является неизвестным значением, для которого нам нужно найти решение.
 Примеры квадратных уравнений: 6x² + 11x — 35 = 0, 2x² — 4x — 2 = 0, 2x² — 64 = 0, x² — 16 = 0, x² — 7x = 0, 2x² + 8x = 0 и т. Д. В этих примерах вы можете заметить, что в некоторых квадратных уравнениях отсутствуют члены «c» и «bx».
 Как пользоваться формулой корней квадратного уравнения? 
 Предположим, что ax  2  + bx + c = 0 — наше стандартное квадратное уравнение.Мы можем вывести формулу корней квадратного уравнения, заполнив квадрат, как показано ниже.
 Выделите член c в правой части уравнения
 ax  2  + bx = -c
 Разделите каждый член на a.
 x  2  + bx / a = -c / a
 Выразить в виде полного квадрата 
 x  2  + b x / a + (b / 2a)  2  = — c / a + (b / 2a)  2 
 (x + b / 2a)  2  = (-4ac + b  2 ) / 4a  2 
 (x + b / 2a) = ± √ (-4ac + b  2 ) / 2a
 x = — b / 2a ± √ (b  2  — 4ac) / 2a
 x = [- b ± √ (b  2  — 4ac)] / 2a …… ….(Это квадратная формула)
 Наличие плюса (+) и минуса (-) в квадратной формуле означает, что существует два решения, например:
 x  1  = (-b + √b2 — 4ac) / 2a
 AND,
 x  2  = (-b — √b2 — 4ac) / 2a
 Два вышеуказанных значения x известны как корни квадратного уравнения. Корни квадратного уравнения зависят от природы дискриминанта. Дискриминант является частью формулы корней квадратного уравнения в виде b  2  — 4 ac.Квадратное уравнение имеет два разных действительных корня дискриминанта.
 Когда значение дискриминанта равно нулю, тогда уравнение будет иметь только один корень или решение. А если дискриминант отрицательный, то квадратное уравнение не имеет действительного корня.
 Как решать квадратные уравнения? 
 Давайте решим несколько примеров задач, используя формулу корней квадратного уравнения.
   Пример 1  
 Используйте формулу корней квадратного уравнения, чтобы найти корни x  2  -5x + 6 = 0.
  Решение 
 Сравнение уравнения с общей формой ax  2  + bx + c = 0 дает
 a = 1, b = -5 и c = 6
 b  2  — 4ac = ( -5) 2-4 × 1 × 6 = 1
 Подставляем значения в формулу корней квадратного уравнения
 x  1  = (-b + √b2-4ac) / 2a
 ⇒ (5 + 1) / 2
 = 3
 x  2  = (-b — √b2-4ac) / 2a
 ⇒ (5 — 1) / 2
 = 2
   Пример 2  
 Решите квадратное уравнение ниже используя квадратную формулу:
 3x  2  + 6x + 2 = 0
  Решение 
 Сравнение задачи с общей формой квадратного уравнения ax  2  + bx + c = 0 дает
 a = 3 , b = 6 и c = 2
 x = [- b ± √ (b  2  — 4ac)] / 2a
 ⇒ [- 6 ± √ (6  2  — 4 * 3 * 2)] / 2 * 3
 ⇒ [- 6 ± √ (36-24)] / 6
 ⇒ [- 6 ± √ (1 2)] / 6
 x  1  = (-6 + 2√3) / 6
 ⇒ — (2/3) √3
 x  2  = (-6– 2√3) / 6
 ⇒ — (4/3) √3
   Пример 3  
 Решить 5x  2  + 6x + 1 = 0
  Решение 
 Сравнивая квадратное уравнение, получаем
 a = 5, b = 6, c = 1
 Теперь примените квадратную формулу:
 x = −b ± √ (b  2  — 4ac) 2a
 Подставьте значения a, b и c
 ⇒ x = −6 ± √ (6  2  — 4 × 5 × 1) 2 × 5
 ⇒ x = −6 ± √ (36-20) 10
 ⇒ x = −6 ± √ (16) 10
 ⇒ x = −6 ± 410
 ⇒ x = — 0. 2, −1
   Пример 4  
 Решить 5x  2  + 2x + 1 = 0
  Решение 
 Коэффициенты:
 a = 5, b = 2, c = 1
 В этом случае дискриминант отрицательный:
 b  2  — 4ac = 2  2  — 4 × 5 × 1
 = −16
 Теперь примените формулу корней квадратного уравнения;
 x = (−2 ± √ −16) / 10
 ⇒√ (−16) = 4
, где i — мнимое число √ − 1
 ⇒x = (−2 ± 4i) / 10
 Следовательно, x = −0.2 ± 0,4i
   Пример 5  
 Решить x  2  — 4x + 6,25 = 0
  Решение 
 Согласно стандартной форме квадратного уравнения ax  2  + bx + c = 0, мы можем это наблюдать;
 a = 1, b = −4, c = 6,25
 Определите дискриминанты.
 b  2  — 4ac = (−4)  2  — 4 × 1 × 6,25
 = −9 ………………. (отрицательный дискриминант)
 ⇒ x = — (- 4) ± √ (−9) / 2
 ⇒ √ (−9) = 3i; где i — мнимое число √ − 1
 ⇒ x = (4 ± 3i) / 2
 Следовательно, x = 2 ± 1. 5i
 Как построить квадратное уравнение? 
 Чтобы построить квадратное уравнение, выполните следующие действия:
 Для квадратного уравнения перепишите уравнение, приравняв его к y или f (x)
 Выберите произвольные значения x и y для построения кривой
 Теперь изобразите функцию.
 Считайте корни там, где кривая пересекает или касается оси x.
 Решение квадратных уравнений с помощью построения графиков 
 Построение графиков — это еще один метод решения квадратных уравнений.Решение уравнения получается путем считывания отрезков x на графике.
  При решении квадратных уравнений графическим методом есть три возможности: 
 Уравнение имеет один корень или решение, если отрезок графика по оси x равен 1.
 Уравнение с двумя корнями имеет 2 точки пересечения x
 Если нет x-точек пересечения, то уравнение не имеет реальных решений.
 Давайте изобразим несколько примеров квадратных уравнений. В этих примерах мы нарисовали наши графики с помощью графического программного обеспечения, но чтобы вы хорошо поняли этот урок, нарисуйте свои графики вручную.
   Пример 1  
 Решите уравнение x  2  + x — 3 = 0 графическим методом
  Решение 
 Наши произвольные значения показаны в таблице ниже:
 x- точки пересечения равны  x   =  1,3 и  x =  –2,3. Следовательно, корни квадратного уравнения x = 1.3 и x = –2,3
   Пример 2  
 Решите уравнение 6x — 9 — x  2  = 0.
  Решение 
 Выберите произвольные значения x.
 Кривая касается оси x в точке x = 3. Следовательно, 6  x  — 9 —  x   2  = 0 имеет одно решение (x = 3).
   Пример 3  
 Решите уравнение x  2  + 4x + 8 = 0 графическим методом.
  Решение 
 Выберите произвольные значения x.