Так как \( \displaystyle \sin \left( \frac{\pi }{2} \right)=1\)
Но ты же внимательно читал мои пространные рассуждения, не так ли? И ты ведь не напишешь такую чушь? И ты понял, в чем здесь подвох?
А подвох вот в чем:
\( \displaystyle \frac{\pi }{2}\approx \frac{3,14}{2}>1\)
А мы помним, что если правая часть тригонометрического уравнения больше \( \displaystyle 1\) (или меньше \( \displaystyle -1\)), то такое уравнение решений не имеет в принципе!!
Второе рассуждение тем более ересь: \( \displaystyle \arcsin \left( \frac{\pi }{2} \right)\) надо понимать как угол, синус которого равен \( \displaystyle \frac{\pi }{2}\).
А ну-ка попытайся в таблице найти такой угол, синус которого равен \( \displaystyle \frac{\pi }{2}\)?!
Не нашёл? То-то же!
В общем, из того, что \( \displaystyle \sin \left( \frac{\pi }{2} \right)=1\) никак не следует, что и \( \displaystyle \arcsin \left( \frac{\pi }{2} \right)=1\)!!
Из этого только следует, что \( \displaystyle \arcsin 1=\frac{\pi }{2}\)!
4. {n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
{n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
5. \( \displaystyle cos\left( x \right)=1\)
И снова по определению (теперь для уравнения другого вида)
\( \displaystyle x=\pm arccos1+2\pi n,~n\in Z\)
Чему равен угол, косинус которого равен \( \displaystyle 1\)?
Этот угол равен\( \displaystyle 0\)!
\( \displaystyle x=\pm 0+2\pi n,~n\in Z\)
Тогда нет смысла прибавлять или вычитать ноль, всё равно это ноль.
\( \displaystyle x=2\pi n,~n\in Z\)
Получили формулу, которая есть в таблице решений тригонометрических уравнений!
Ответ: \( \displaystyle x=2\pi n,~n\in Z\)
6. \( \displaystyle cos\left( x \right)=-\frac{1}{\sqrt{2}}\)
По определению:
\( \displaystyle x=\pm \arccos \left( -\frac{1}{\sqrt{2}} \right)+2\pi n,~n\in Z\)
Прежде всего вынесем «минус» по правилам для арккосинуса:
\( \displaystyle x=\pm \left( \pi -\arccos \left( \frac{1}{\sqrt{2}} \right) \right)+2\pi n,~n\in Z\)
Вот так и никак иначе выносится минус, запомни это!
Теперь арккосинус.
Не во всех таблицах есть значение \( \displaystyle \frac{1}{\sqrt{2}}\), но во всех есть \( \displaystyle \frac{\sqrt{2}}{2}\)!!!
А теперь, внимание, ловкость рук и никакого мошенничества!
\( \displaystyle \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}=\frac{\sqrt{2}}{2}\)Единица деленная на корень из двух равно корень из двух деленное на два!
Я не зря выделил это замечание жирным шрифтом, запомни это тождество хорошенько! Оно спасёт тебя в очень многих случаях!!
Итак, чему же равен угол, косинус которого равен \( \displaystyle \frac{1}{\sqrt{2}}\)(или одно и то же \( \displaystyle \frac{\sqrt{2}}{2}\))?
Верно, это угол \( \displaystyle \frac{\pi }{4}\).
Тогда:
\( \displaystyle x=\pm \left( \pi -\text{ }\!\!~\!\!\text{ }\frac{\pi }{4} \right)+2\pi n,~n\)
\( \displaystyle x=\pm \left( \frac{4\pi }{4}-\text{ }\!\!~\!\!\text{ }\frac{\pi }{4} \right)+2\pi n,~n\in Z\)
\( \displaystyle x=\pm \frac{3\pi }{4}+2\pi n,~n\in Z\)
Ответ: \( \displaystyle x=\pm \frac{3\pi }{4}+2\pi n,~n\in Z\)
7. \( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
\( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
\( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
Ещё один пример-обманка! Хотя данное уравнение решения имеет, ибо:
\( \displaystyle \frac{\pi }{4}=\frac{3,14}{4}<1\)
Тогда по определению:
\( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
Но из этого никак не следует, что \( \displaystyle \arccos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{\sqrt{2}}{2}\)!!!!!!
Запомни, арккосинус – это угол, его аргумент (начинка) – это число, а выход – угол!!!
Ты когда-нибудь встречал в своей практике такой странный угол как \( \displaystyle \frac{\sqrt{2}}{2}\)?!
Вот и я нет. Поэтому оставим как есть!
Поэтому оставим как есть!
Ответ: \( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
8. \( \displaystyle cos\left( x \right)=-\sqrt{2}\)
Всё просто: \( \displaystyle -\sqrt{2}<-1\)
… и решений данное уравнение не имеет.
9. \( \displaystyle tg\left( x \right)=\sqrt{2}\)
Запишем по определению:
\( \displaystyle x=arctg\sqrt{2}+\pi n,~n\in Z\)
\( \displaystyle arctg\sqrt{2}\) – не табличное значение, поэтому ответ сохраняем неизменным.
Обрати внимание, что в отличие от уравнений с синусом и косинусом, здесь мне не уже важно, какое у меня число стоит в правой части уравнения.
10. \( \displaystyle ctg\left( x \right)=-\sqrt{3}\)
Снова по определению:
\( \displaystyle x=arсctg\left( -\sqrt{3} \right)+\pi n,~n\in Z\)
Без проблем выносим минус из арккотангенса:
\( \displaystyle x=\pi-arcctg\left( \sqrt{3} \right)+\pi n,~n\in Z\)
Вычисляем: котангенс какого угла равен \( \displaystyle \sqrt{3}\)?
Это угол \( \displaystyle \frac{\pi }{6}\).
Ответ: \( \displaystyle x=\pi-\frac{\pi }{6}+\pi n = \frac{5\pi}{6}+\pi n,~n\in Z\).
11. \( \displaystyle ctg\left( x \right)=1\)
По формуле: \( \displaystyle x=arcctg1+\pi n,~n\in Z\).
Котангенс какого угла равен \( \displaystyle 1\)?
Это угол \( \displaystyle \frac{\pi }{4}\).
Ответ: \( \displaystyle x=\frac{\pi }{4}+\pi n,~n\in Z\).
Ну как, материал не кажется тебе слишком сложным? Я надеюсь, что нет. Теперь давай порешаем для закрепления чуть более сложные задачки.
Отбор корней при решении тригонометрических уравнений
Отбор корней при решении тригонометрических уравнений
Математика
Областное государственное бюджетное учреждение
дополнительного профессионального образования
«Курский институт развития образования»
ОГБУ ДПО КИРО
ТЕМА: Отбор корней при решении тригонометрических уравнений.
Работу выполнили:
Сколодова Л.В.
Новиков В. В.
Холодова Н. И.
18.12 2017год
Г. Курск
Решение тригонометрических уравнений — важный раздел в математике. Успешное её изучение невозможно без умения решать тригонометрические уравнения. Для успешного решения тригонометрических уравнений необходимо знать не только формулы и методы решения этих уравнений, но и правильно отбирать корни на заданном промежутке или при других дополнительных условиях. Но основной мотив углублённого изучения данной темы – это то, что одно из заданий, а именно №13, экзаменационной работы ЕГЭ «Решить тригонометрическое уравнение и выполнить отбор корней, удовлетворяющих условию».
Цель работы: Изучить различные способы отбора корней в тригонометрических уравнениях.
Задачи:
$1üрассмотреть различные типы заданий, содержащие тригонометрические уравнения, где необходимо выполнить отбор корней, классифицировать их;
$1üопределить наиболее рациональный способ отбора корней для каждого типа заданий;
$1üрассмотреть примеры решения уравнений и систем уравнений, где необходимо выполнить отбор корней;
При отборе корней в процессе решения тригонометрических уравнений обычно используют один из следующих способов.
Арифметический способ. Перебор значений целочисленного параметра и вычисление корней приходиться в случаях, когда требуется отобрать корни, принадлежащие заданному промежутку или некоторому условию.
Алгебраический способ отбора корней наиболее удобен в тех случаях, когда последовательный перебор значений параметров приводит к вычислительным трудностям, промежуток для отбора корней большой, значения обратных тригонометрических функций, входящих в серии решений, не являются табличными. Для этого решают неравенство относительно неизвестного целочисленного параметра и вычисления корней.
Геометрический способ. В последние годы в учебниках используются разные модели к иллюстрации решения простейших тригонометрических уравнений с применением тригонометрического круга, графика тригонометрической функции или числовой прямой.
а) Тригонометрическую окружность удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 , или в случае, когда значения обратных тригонометрических функций, входящих в серию решений, не являются табличными.
б) При изображении решении простейших тригонометрических уравнений иногда используют графики простейших тригонометрических функций. Для нахождения решения тригонометрического уравнения при этом подходе требуется построение «кусочка» графика.
в) Числовую прямую удобно использовать при отборе корней на промежутке, длина которого превосходит 2 .
Процессе обучения решению задач, в которых требуется отобрать корни тригонометрического уравнения, следует обсудить разные способы выполнения этого действия, а также выяснить случаи, когда тот или иной способ может оказать наиболее удобным или наоборот непригодным.
Рассмотрим один конкретный пример с использованием всех вышеуказанных способов:
а) Решить уравнение:
б) Найти все корни этого уравнения, принадлежащие отрезку
Решение.
а) Используя формулу косинуса двойного угла и формулу приведения, запишем уравнение в виде:
Решаем квадратное уравнение относительно ,
Отсюда
Уравнение так как
Из уравнения х = .
Отметим, что решение уравнения
х= или х= .
б) отберем корни уравнения, принадлежащие отрезку
1. Арифметический способ.
Пусть . Подставляя k =… , получаем
. Отрезку принадлежит корень .
Пусть . Подставляя k =… , получаем . Отрезку принадлежит корень .
Отрезку принадлежат корни
Ответ: а) ;
в)
2. Алгебраический способ.
Отберем корни, принадлежащие отрезку . Решаем двойное неравенство.
Пусть .
Тогда
.
Пусть .
Тогда
.
Отрезку принадлежат корни
3. Геометрический способ.
1. Корни уравнения изображаются точками А и В, отрезок изображен жирной дугой (см. рис.). В указанном отрезке содержаться два корня уравнения:
у
А
-П х
-3П
В
2. Корни, принадлежащие отрезку , отберем по графику у= . Прямая пересекает график в двух точках, абсциссы которых принадлежат отрезку , Так как период функции y = равен , то эти абсциссы равны ; .
Корни, принадлежащие отрезку , отберем по графику у= . Прямая пересекает график в двух точках, абсциссы которых принадлежат отрезку , Так как период функции y = равен , то эти абсциссы равны ; .
у
$13. Рассмотрим отбор корней с помощью координатной прямой.
у= . //////////////// /////////////////
Отрезку принадлежат корни
Ответ: а) х = .
б)
А теперь рассмотрим более сложные уравнения, которые решаются здесь различными способами.
№1. а) Решите уравнение .
б) Найдите все корни, принадлежащие отрезку .
Решение:
а) ОДЗ : sinx > 0 ( )
;
;
4sinxcosx = 2 sinx;
4sinxcosx — 2 sinx = 0;
2sinx(2cosx — ) =0;
Решая последнее уравнение получаем корни:
sinx = 0 или .
Учитывая ОДЗ, получаем корни уравнения:
б) С помощью числовой окружности отберём корни на указанном отрезке:
Получим число .
Ответ: ; б) .
№2. Дано уравнение log– cosx (1 – 0,5 sinx) = 2.
а) Решите уравнение.
б) Найдите корни уравнения, принадлежащие отрезку [14π; 16π].
Решение:
$1a) ОДЗ: — 1os x 0;
log – cos x ( 1 – 0,5 sin x) = log – cos x cos2 x,
1 – 0,5 sin x = cos 2 x,
1 – 0,5 sin x – cos 2 x = 0,
sin 2 x – 0,5 sin x = 0,
sin x ( sin x – 0,5) = 0,
sin x = 0 или sin x = 0,5
х=πn, nÎZ, x = + 2πn, n ÎZ, x = + 2πn, nÎ Z.
учитывая ОДЗ, получаем, что х=πn, nÎZ, и x = , nÎZ не являются корнями уравнения ( cosx = 1, и — 1osx
б) Найдем корни уравнения на заданном промежутке геометрическим способом:
х =
Ответ: а) х = nÎZ, б) .
№ 3. Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
а) Ограничения на x:
Для таких x:
б) Отбор корней произведем с помощью единичной окружности.
Ответ: а) nÎZб) .
№ 4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение.
а) Перейдём к системе:
Решаем уравнение системы
Получаем:
С учётом всех ограничений
б) С помощью числовой окружности отберём корни, принадлежащие указанному отрезку Получим число
Отбор корней может быть обоснован и любым другим способом: с помощью графика, решения двойных неравенств и т. п.
п.
Ответ: а) б) .
№ 5. Дано уравнение
а) Решите уравнение.
б) Найдите его корни, принадлежащие отрезку
Решение.
а) Найдем ограничения на:
Для таких
б) Отбор корней сделаем путем перебора подходящих значений n
Из серии корней
Заметим, что отрицательные значения здесь не подойдут. Значение n=0 тоже не подходит, так как
При n = 1: . Докажем, что 4.
Для этого достаточно доказать:
Действительно,
При n = 2:
При n = 3:
Этот корень уже не подходит. Дальнейшие поиски корней из этой серии смысла не имеют.
Из серии корней
При отрицательных значениях несложно понять, искомых корней не будет.
При n = 1:
Корень не подходит.
При n = 2:
При n = 3:
Но
Корень не подходит, дальнейшие поиски просто излишни.
Ответ: а) б)
№ 6. Дано уравнение
а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие промежутку
Решение:
а) Последовательно получаем:
Покажем, что , k, nÎZ при k = 6n — 2 .
Действительно,
Итак, решениями заданного уравнения являются числа вида: .
Эти же числа можно представить также в виде
б) Отбор корней:
Ответ: а) б)
№ 7. а) Решите уравнение:
б) Укажите корни этого уравнения,
принадлежащие отрезку [ ]
Решение:
а) Запишем исходное уравнение в виде:
Заметим, что выражение, стоящее под знаком логарифма, приравнено к единице, поэтому исследовать ОДЗ не требуется.
Для решения полученного тригонометрического уравнения используем формулу косинуса двойного угла
откуда получаем
Обозначая t = cosx, имеем:
Откуда или .
Вернемся к исходной переменной.
Уравнение корней не имеет, поскольку косинус не больше 1.
Из уравнения находим: или ,
nÎZ.
б) С помощью числовой окружности отберём корни, принадлежащие отрезку
Получим числа: .
Ответ: а) , nÎZ; б) .
№ 8. а) Решите уравнение
б) Найдите все корни на промежутке
Решение:
а) Обратим внимание на то, что правая часть заданного уравнения есть ограниченная функция. В частности,
Следовательно, такие же ограничения следует наложить и на левую его часть. То есть
Из-за ограниченности функции косинус будем иметь:
а последнее неравенство истинно только при выполнении условия
Решим его:
Таким образом, мы установили, что , и это равенство выполняется при .
Теперь оценим сверху и снизу выражение:
Тогда левая часть уравнения будет иметь вид:
Таким образом, левая часть уравнения может принять единственное значение, равное 1.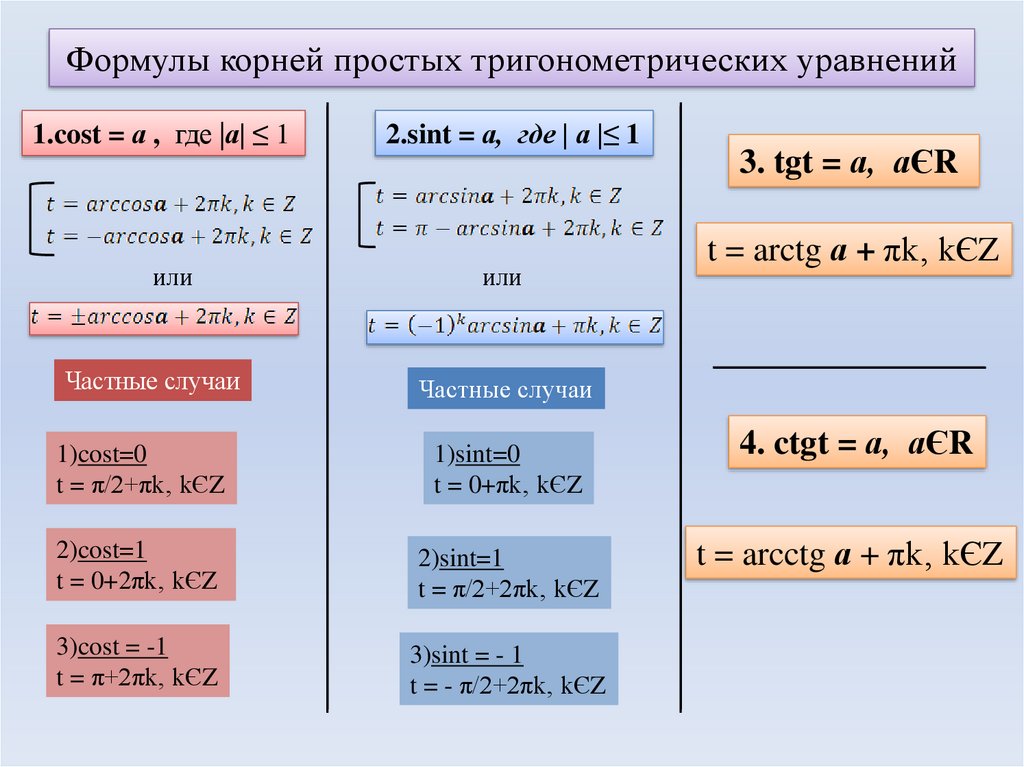 Поскольку это так, то и правая часть уравнения обязана быть равной 1 хотя бы при некоторых значениях переменной , являющихся решениями уравнения . Если такие числа найдутся, то уравнение будет иметь решение. Если же их не будет, то у уравнения решений не будет.
Поскольку это так, то и правая часть уравнения обязана быть равной 1 хотя бы при некоторых значениях переменной , являющихся решениями уравнения . Если такие числа найдутся, то уравнение будет иметь решение. Если же их не будет, то у уравнения решений не будет.
Нами были найдены корни уравнения
Ими являются числа вида .
Теперь мы ищем решения уравнения . Последнее равенство имеет место, если
Найдем значения , при которых серии решений и совпадут. Для этого найдем их значения, принадлежащие промежутку
Из серии
При n = 0 x1=
При n = 1 x2 =
При n = 2 x3 =
При n = 3 x = >2p.
Из серии :
При n = 0 x4 =
При n = 1 x5 =
При n = 2 x6 =
При n = 3 x = >2p
Как видим, общие решения двух уравнений, указанных выше, имеются, они равны числам вида .
б) При отборе корней уравнения решим двойное неравенство , решая далее, получаем , где m = — 1, m = 0, mÎZ. При найденных целых m получим:
Ответ: а) ; б)
Задания для самостоятельного решения:
$11) а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащего отрезку
$12) Дано уравнение
а) Решите уравнение.
б) Найдите корни на промежутке
$13)
а) Решите уравнение
б) Найдите все корни на промежутке
$14) а) Решите уравнение
б) Найдите все его корни, принадлежащие отрезку
$15) ) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
$16) Дано уравнение
а) Решите уравнение.
б) Укажите корни, принадлежащие интервалу (−5; 1).
Симметрия корней и оптимизация ответов в тригонометрии
Внимание! Еще одна часть видеоурока находится ниже!
Когда вы решаете квадратное уравнение относительно синуса или косинуса, то в ответе получается много отдельных множеств, работать с которыми крайне неудобно. Поэтому сегодня мы научимся объединять их, научимся искать симметрию в наборах корней и упрощать себе ответы, а, следовательно, и работу с множествами.
На самом деле существует два способа упростить решение квадратных тождеств. Назовем их условно геометрическим и алгебраическим. Алгебраический подход рассказывается в школе, но большинство учеников пропускают этот способ мимо ушей. Поэтому сегодняшний видео урок будет состоять из двух частей: второй — целиком посвященной геометрическому подходу, когда мы отмечаем корни на тригонометрическом круге, и первой части — в ней рассказывается о формулах понижения степеней. Итак, начнем.
Алгебраический подход
Сейчас мы будем использовать только алгебраический подход. {2}}=a\]
{2}}=a\]
\[\left[ \begin{align}& f=\sqrt{a} \\& f=-\sqrt{a} \\\end{align} \right.\]
\[a\ge 0\]
Решаем уравнение, чтобы найти корни тригонометрического выражения:
\[\cos x=\sqrt{\frac{3}{4}}\]
\[\cos x=\frac{\sqrt{3}}{2}\]
\[x=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+2\pi n\]
В контексте нашего сегодняшнего урока все числа принадлежат множеству целых чисел.
\[\cos x=-\sqrt{\frac{3}{4}}\]
\[\cos x=-\frac{\sqrt{3}}{2}\]
\[x=\pm \arccos \left( -\frac{\sqrt{3}}{2} \right)+2\text{ }\!\!\pi\!\!\text{ }k\]
\[x=\pm \left( \text{ }\!\!\pi\!\!\text{ }-\frac{\pi }{6} \right)+2\text{ }\!\!\pi\!\!\text{ }k\]
\[x=\pm \frac{5\text{ }\!\!\pi\!\!\text{ }}{6}+2\text{ }\!\!\pi\!\!\text{ }k\]
Вот мы и получили два множества. Давайте отметим эти числа на тригонометрической окружности и найдем корни:
Все наше множество сводится к четырем точкам. А теперь заметим, что $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ и $-\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$ симметричны относительно начала координат. В этом легко убедиться, если вычесть из одного числа другое. Например:
В этом легко убедиться, если вычесть из одного числа другое. Например:
\[\frac{\text{ }\!\!\pi\!\!\text{ }}{6}-\left( -\frac{5\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\text{ }\!\!\pi\!\!\text{ }\]
Другими словами, расстояние между этими числами по окружности равно $\text{ }\!\!\pi\!\!\text{ }$.
То же самое можно сказать про $-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ и $\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$ — они симметричны друг другу относительно начала координат или, другими словами, можно сказать, что они лежат на одном диаметре. Если идти по нашей окружности, то расстояние между ними будет равно $\text{ }\!\!\pi\!\!\text{ }$, а это значит, что если мы возьмем точку $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$, а потом шагнем от нее на $\text{ }\!\!\pi\!\!\text{ }$, то получим точку $-\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$. Потом еще шагнем на $\text{ }\!\!\pi\!\!\text{ }$ — снова попадем в точку $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$, но уже $+2\text{ }\!\!\pi\!\!\text{ }$. {2}}x=1\]
{2}}x=1\]
Опять же используем наши выкладки и избавляемся от квадрата:
\[\sin x=1\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }n\]
И второе уравнение:
\[\sin x=-1\]
\[x=-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}\text{+}2\text{ }\!\!\pi\!\!\text{ }k\]
Отмечаем эти числа на тригонометрической окружности:
Из рисунка становится очевидно, что эти точки лежат на одном диаметре — он является осью $Oy$, осью синусов. Это значит, чтобы получить из\[\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}+2\text{ }\!\!\pi\!\!\text{ }n\]\[-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }k\], достаточно шагнуть из точки $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ до $-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ на $\text{ }\!\!\pi\!\!\text{ }$. Таким образом мы объединяем два множества корней и получаем:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n˜˜˜˜˜˜\]
Пример №3
\[{{\sin }^{2}}x=\frac{1}{2}\]
Снова считаем по нашим выкладкам:
\[\sin x=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\]
\[\sin x=\frac{\sqrt{2}}{2}\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\frac{3\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
Переходим ко второму выражению:
\[\sin x=-\frac{\sqrt{2}}{2}\]
\[x=-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }l\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\left( -\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)+2\text{ }\!\!\pi\!\!\text{ }m\]
\[x=\text{ }\!\!\pi\!\!\text{ }+\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }m\]
\[x=\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }m\]
Вот мы и получили четыре набора корней. Давайте отметим их:
Давайте отметим их:
Еще очень важно, что между $\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$ и $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$ угол равен 90°. Также и между $\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}$ и $-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$ угол равен 90°. Наконец, и между $\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$и $\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}$ угол тоже равен 90°. Это значит, что все четыре точки мы можем свести к одной точке вида\[\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\frac{\text{ }\!\!\pi\!\!\text{ }n}{2}\].
На первый взгляд эта конструкция, все эти вычисления могут показаться очень сложными. Геометрический подход, действительно, понимают не все ученики. Однако стоит немного потренироваться, и вы будете щелкать квадратные уравнения как орешки.
Ключевые моменты
Решая уравнения, квадратные относительно синуса или косинуса, вы постоянно будете натыкаться на громоздкие ответы, работать с которыми (например, для отбора корней) совершенно невозможно. Однако при желании можно значительно упростить эти конструкции. И сегодня мы поговорим о двух методах упрощения:
Однако при желании можно значительно упростить эти конструкции. И сегодня мы поговорим о двух методах упрощения:
- Графический — отмечаем ответы на тригонометрическом круге и пытаемся найти закономерности.
- Алгебраический — переходим от квадратного уравнения к линейному с помощью формул понижения степеней.
Вы можете использовать любой прием — ответ получится один и тот же. Кому-то (например, мне) удобнее отмечать точки на тригонометрическом круге, а кому-то проще раз и навсегда запомнить формулы понижения степени (которые, кстати, совсем несложные).
Симметрия корней на тригонометрическом круге
Тут все банально. Решаем равенство, отмечаем полученные корни на круге, а затем ищем какую-нибудь закономерность в их расположении. Например, корни могут отстоять друг от друга на половину исходного периода, либо располагаться симметрично относительно начала координат.
Формулы понижения степеней
Это уникальная фишка, которая работает только в тригонометрических уравнениях. Уравнения, квадратные относительно синуса или косинуса, легком сводятся к равносильным линейным. Все, что для этого потребуется — формулы косинуса двойного угла:
Уравнения, квадратные относительно синуса или косинуса, легком сводятся к равносильным линейным. Все, что для этого потребуется — формулы косинуса двойного угла:
\[\cos 2x=2\cos 2\text{ }x-1;\]
\[\cos 2x=1-2\sin 2x.\]
Смотрите также:
- Однородные тригонометрические уравнения: общая схема решения
- Учимся расщеплять ответы в тригонометрических уравнениях
- Решение задач B6: №362—377
- Геометрическая вероятность
- Пробный ЕГЭ по математике 2015: 2 вариант
- Задача B2 на проценты: вычисление полной стоимости покупки
Тригонометрическое уравнение с выборкой корней. Задание С1
В этой статье я хочу показать вам решение тригонометрического уравнения с выборкой корней. Но, самое главное, я хочу предостеречь вас от одного неравносильного перехода, который может возникнуть при решении тригонометрического неравенства.
Итак, задание такое:
1. Решите уравнение:
.
2. Найдите корни, принадлежащие промежутку
Это классическое распадающееся уравнение.
Произведение двух множителей равно нулю, когда хотя бы один из них равен нулю, а второй при этом существует.
Наше уравнение равносильно совокупности двух систем:
Вместо второй системы мы получили одно уравнение, так как первый множитель существует при всех действительных значениях , и ограничений на ОДЗ нет.
Решим уравнения системы:
,
Это однородное тригонометрическое уравнение первой степени. Разделим обе части уравнения на . (Проверим, что корни уравнения не являются корнями исходного уравнения — если , то , и левая часть не равна нулю).
Помним, что уравнение является частью системы
и его корни должны удовлетворять неравенству
.
Вот в этом месте нужно быть очень внимательными!
Правильное решение.
Решим неравенство. Левая часть неравенства обращается в ноль при . Эти точки разбивают тригонометрический круг на два промежутка — зеленый и красный, на каждом из которых левая часть неравенства сохраняет знак:Чтобы выяснить, какой именно знак, возьмем произвольную точку, принадлежащую, например, красной дуге. Пусть это будет точка, соответствующая повороту на 0 радиан.
Левая часть неравенства обращается в ноль при . Эти точки разбивают тригонометрический круг на два промежутка — зеленый и красный, на каждом из которых левая часть неравенства сохраняет знак:Чтобы выяснить, какой именно знак, возьмем произвольную точку, принадлежащую, например, красной дуге. Пусть это будет точка, соответствующая повороту на 0 радиан.
, поэтому во всех точках красной дуги выполняется неравенство .
Итак, нас устраивают корни уравнения которые расположены на красной дуге.
Расположим на тригонометрическом круге числа и . Если принять во внимание, что число 1 чуть-чуть меньше, чем , то, число поставим чуть-чуть не доходя до , а число 2 чуть-чуть не доходя до :
Мы видим, что корень удовлетворяет условию , а корень 2 — не удовлетворяет.
Теперь найдем корни, которые принадлежат промежутку :
Это числа
Ответ: 1. ;
2.
Неверное решение.
Если мы будем решать неравенство тем же способом, что решали уравнение , то есть разделим обе части на , то получим неравенство, не равносильное исходному:
Решение этого неравенства на тригонометрическом круге выглядит так:
Мы получили решение, отличное от предыдущего. При этом решении получится, что число 2 является корнем исходного уравнения.
При этом решении получится, что число 2 является корнем исходного уравнения.
В чем причина ошибки? Когда мы делили обе части неравенства на , мы не учли, что может быть меньше нуля. При делении на положительное число знак неравенства не меняется, а при делении на отрицательное, меняется на противоположный.
Строго говоря, при делении на мы получили такое неравенство:
В этом неравенстве знак левой части меняется в корнях числителя, то есть в корнях уравнения , и в корнях знаменателя, то есть в корнях уравнения , что для нас уже совершенно лишнее. Поэтому мы получили неверное решение.
И.В. Фельдман, репетитор по математике.
Тригонометрические уравнения. Повторение. Отбор корней.
Название предмета Алгебра и начала анализа.
Класс 10
УМК А.Г. Мордкович и др. «Алгебра и начала анализа», 10 класс, (профильный уровень), М. «Мнемозина», 2014г.
Уровень обучения Профильный
Тема урока Тригонометрические уравнения. Повторение. Отбор корней
Общее количество часов, отведенное на изучение данной темы 10
Место урока в системе уроков по теме 9.
Цель урока Обобщить и систематизировать теорию о способах решения тригонометрических уравнений, виды уравнений, способы отбора корней
Задачи урока
Образовательные:
повторить решение простейших уравнений, основные тригонометрические формулы, основные формулы тригонометрических уравнений;
закрепить умения применять данные формулы не только в знакомой, но в модифицированной и незнакомой ситуациях.
Развивающие
развивать умения самостоятельного решения уравнений связанных с выбором алгоритма решения уравнений;
содействовать развитию устойчивого интереса к математике с помощью математической строгости умозаключения;
ознакомить с логическими приемами мышления.

Воспитательные:
воспитать чувство ответственности, формировать навыки самооценки;
содействовать желанию расширить и углубить знания, полученные на уроке,
содействовать повышению грамотности устной и письменной речи учащихся.
Планируемые результаты
Обучающиеся должны уметь: находить корни тригонометрических уравнений, уметь решать уравнения как простейшие (из ЕГЭ базового уровня), так и более сложных уравнений (из ЕГЭ профильного уровня) использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчетов по формулам.
Техническое обеспечение урока проектор, компьютер, экран.
Содержание урока.
1. Организационный момент: вступительное слово учителя, в котором подчеркивается значение, материала повторяемой темы, сообщается цель и план урока (1 мин. )
)
Тема “Решение тригонометрических уравнений» актуальна, умение решать тригонометрические уравнения позволит вам справиться с заданиями ЕГЭ за курс средней школы. Будьте активны, внимательны, помогайте друг другу вспомнить, все то, что вы изучали на уроках алгебры и началах анализа ранее.
2.Актуализация опорных знаний. Обучающиеся по очереди выходят к доске и решают предложенные задания.
Блиц опрос:
Найдите , если Ответ: 4
Найдите , если Ответ: -7
Найдите значение выражения Ответ: -24
Найдите значение выражения Ответ: -1,5
Найдите значение выражения Ответ: -6
Решите уравнение В ответе напишите наибольший отрицательный корень.
Ответ: -1
Решение уравнений:
Решите уравнение cos x = x2 + 1
Указание учителя, каким способом удобно решить это уравнение?
Указание учителя, дискриминант получается не очень хороший, это не означает, что допущена ошибка.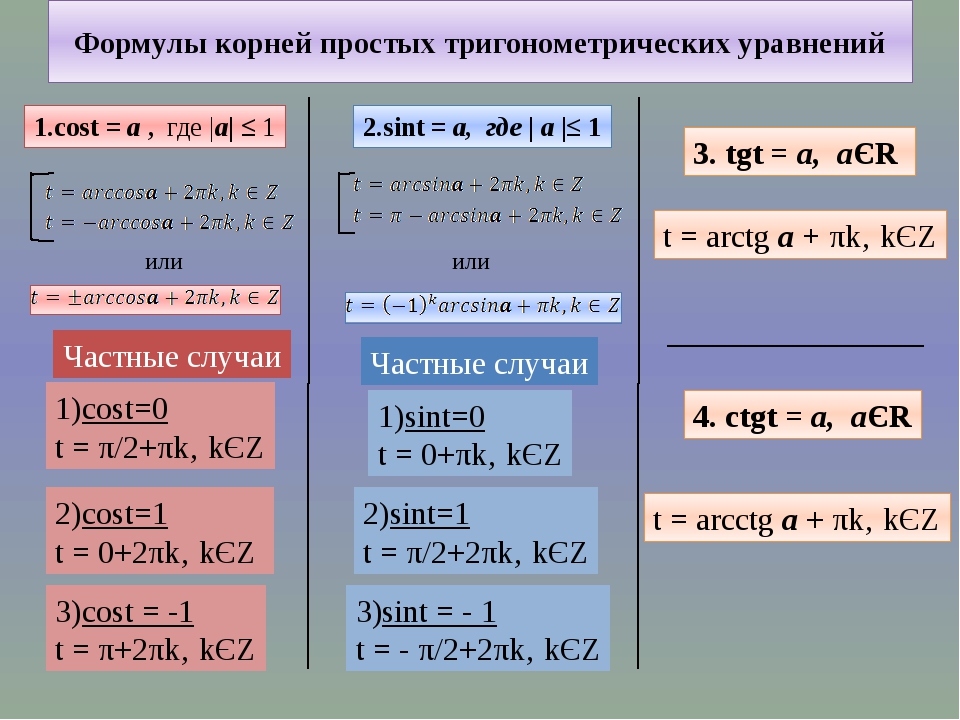 Продолжайте работать.
Продолжайте работать.
3.) Решите уравнение
Указание учителя, обратите внимание на знаменатель и тангенс.
4.) а.)Решите уравнение cos 2x + = 0,75
б.) Укажите корни этого уравнения, принадлежащие отрезку Произвести отбор с помощью единичной окружности.
в.) Произвести отбор корней с помощью графика функции на отрезке
5.) Решите уравнение . Укажите корни, принадлежащие отрезку
Указание учителя. Данное уравнение решить двумя способами:
Привести к общему знаменателю
Используя формулу
Какой способ вам показался более легким? Что для этого надо помнить
6.) Найти ошибку в решении ученика, если она есть
Дополнительные задания:
Найти все значения х, при которых выполняется равенство: производная
функции y= sin2x — x равна нулю, принадлежащие отрезку
Решите уравнение .
 Укажите корни, принадлежащие отрезку .
Укажите корни, принадлежащие отрезку .Решить уравнение: 6cos2x – 7cosx – 5 = 0. Укажите его корни, принадлежащие отрезку .
Решите уравнение
а) Решите уравнение cos 2x — cos ( — 1 = 0
б.) Укажите корни этого уравнения, принадлежащие отрезку
6.) Решить уравнение: 4sin2x – 12sinx + 5 = 0. Укажите его корни, принадлежащие отрезку .
7.) Решите уравнение 2 sin2 х + 3 cos х -3 =0.
б )Укажите его корни, принадлежащие отрезку .
Итог урока.
Учитель: Подведем итоги урока.
Сегодня на уроке мы вспомнили формулы решения тригонометрических уравнений, рассмотрели общие подходы решения тригонометрических уравнений, закрепили навыки и проверили умения решать тригонометрические уравнения, познакомились с новыми способами отбора корней с помощью графика.
Вывод:
Смотрите внимательно на уравнение.

Определите, нужно ли что то исключить из решения, используя условие.
Делайте полные обоснования при решении уравнения и отборе корней.
Выбирайте удобный способ отбора корней.
Фронтальным опросом вместе с учащимися подводятся итоги урока:
Что нового узнали на уроке?
Испытывали ли вы затруднения при решении уравнений?
Какие из способов решения тригонометрических уравнений из рассмотренных оказались наиболее трудными?
Какие пробелы в знаниях выявились на уроке?
Какие проблемы у вас возникли по окончании урока?
Методы решения тригонометрических уравнений
Методы решения
тригонометрических уравнений
1. Решение
простейших тригонометрических уравнений
Решение
простейших тригонометрических уравнений
2. Решение тригонометрических уравнений разложением на множители
3. Решение тригонометрических уравнений сводящихся к квадратным уравнениям
4. Решение тригонометрических уравнений преобразованием суммы тригонометрических функций в произведение
5. Решение тригонометрических уравнений преобразованием произведения тригонометрических функций в сумму
6. Решение тригонометрических уравнений с применением формул понижения степени
7. Решение тригонометрических уравнений как однородное
8. Решение тригонометрических уравнений с помощью введения вспомогательного аргумента
9. Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки
10. Решение
тригонометрических уравнений с помощью замены неизвестного
Решение
тригонометрических уравнений с помощью замены неизвестного
11. Решение тригонометрических уравнений с помощью оценки левой и правой частей уравнения (метод оценок)
12. Решение тригонометрических уравнений содержащих тригонометрические функции под знаком радикала
1. Решение простейших тригонометрических уравнений
По определению арифметического квадратного корня перейдем к равносильной системе уравнений.
Ответ:
2. Решение тригонометрических уравнений разложением на множители
или
или решений нет
Отметим полученные решения и
область определения на тригонометрическом круге.
Решением уравнения является:
Ответ:
3. Решение тригонометрических уравнений
сводящихся к квадратным уравнениям
Пусть , тогда
или
Т.к.
при , то корней нет.
Ответ:
4. Решение тригонометрических уравнений преобразованием
суммы тригонометрических функций в произведение
или
Ответ: ;
5. Решение
тригонометрических уравнений преобразованием
Решение
тригонометрических уравнений преобразованием
произведения тригонометрических функций в сумму
а) Найдем область определения функции.
Областью определения данного уравнения является:
б) Решим данное уравнение.
Ответ:
6. Решение тригонометрических уравнений с
применением формул понижения степени
Пусть , тогда
или
Т. к.
к.
при , то корней нет.
Ответ:
7. Решение тригонометрических уравнений как однородное
Однородное уравнение – это уравнение, в котором каждое слагаемое имеет одну и туже степень.
, где
— действительные числа. — показатель однородности.
Если , то и , что противоречит основному тригонометрическому тождеству, значит . Разделим обе части на , получим
Ответ:
8. Решение тригонометрических уравнений с помощью
введения вспомогательного аргумента
Т. к. , то корни есть.
к. , то корни есть.
Разделим обе части уравнения на , получим
Т. к. и , то существует такой угол , что , а , тогда получим
Ответ:
Теория.
1) если , то уравнение однородное.
2) если и (то есть хотя бы одно из чисел или не равно 0), то разделим обе части уравнения на , получим
Т. к. и , то существует такой угол , что , тогда
а) если, т. е. , то корней нет.
в) если, т. е. , тогда
Т. к. , то корней нет.
к. , то корней нет.
9. Решение тригонометрических уравнений с помощью
универсальной тригонометрической подстановки
(1)
(2)
При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения корнями данного уравнения.
Проверка.
Если , тогда
— не верно, значит , не является корнями исходного уравнения.
Ответ:
10. Решение
тригонометрических уравнений
Решение
тригонометрических уравнений
с помощью замены неизвестного
Уравнение вида решается следующей заменой , , ,
Способ I
Пусть , , , , получим
или
(3)
Разделим на , получим
Т. к. , при , то корней нет.
Ответ:
Теория.
, при
Доказательство:
Шесть способов решения уравнения (3).
1. применение формулы .
2. через .
3. привести к однородному уравнению второй степени.
4. способ введения вспомогательного аргумента.
5. с помощью неравенства , при .
6. метод оценки левой и правой частей уравнения.
Способ II
или
Разделим на , получим
Т.
к. , при , то корней нет.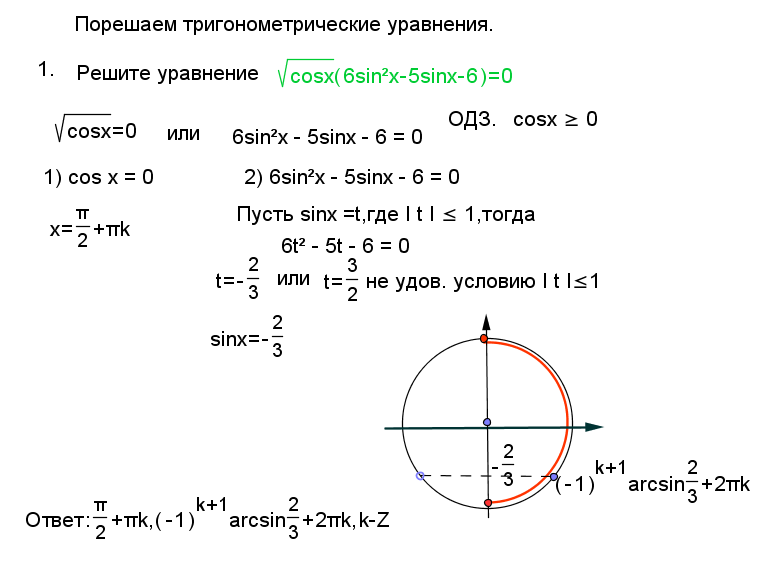
Ответ:
11. Решение тригонометрических уравнений с помощью оценки
левой и правой частей уравнения (метод оценок)
12. Решение тригонометрических уравнений содержащих
тригонометрические функции под знаком радикала
Пример №1
Решим уравнение 2.
или
Отметим поученные решения и условие 1 на тригонометрическом круге.
Ответ: ,
Пример №2
Решим уравнение 2.
Решим квадратное уравнение относительно.
и то корней нет.
Отметим поученные решения и условие 1 на тригонометрическом круге.
Ответ:
тригонометрические уравнения (типовые задания 13(С1))
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ПодробнееЛогарифмические неравенства
Логарифмические неравенства 1. 1. Решите неравенство: Решим неравенство:. 2. 2. Решите неравенство: Найдём значения, при которых определены обе части неравенства: Для таких получаем: Тогда исходное неравенство
1. Решите неравенство: Решим неравенство:. 2. 2. Решите неравенство: Найдём значения, при которых определены обе части неравенства: Для таких получаем: Тогда исходное неравенство
1. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
КЛАССИФИКАЦИЯ УРАВНЕНИЙ 1 Алгебраические уравнения: рациональные (содержат только целые степени неизвестной) и иррациональные (содержат дробные степени неизвестной) ) Показательные и логарифмические (неизвестная
ПодробнееРАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Оглавление РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ I Рациональные алгебраические уравнения Равносильность уравнений Равносильность уравнений на множестве Равносильность
ПодробнееИррациональные неравенства
Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного
ПодробнееГотовим к ЕГЭ хорошистов и отличников
А. Г. КОРЯНОВ, А.А. ПРОКОФЬЕВ Готовим к ЕГЭ хорошистов и отличников Лекции Москва Педагогический университет «Первое сентября» 0 Анатолий Георгиевич Корянов, Александр Александрович Прокофьев Материалы
Г. КОРЯНОВ, А.А. ПРОКОФЬЕВ Готовим к ЕГЭ хорошистов и отличников Лекции Москва Педагогический университет «Первое сентября» 0 Анатолий Георгиевич Корянов, Александр Александрович Прокофьев Материалы
Теоретический материал.
0.5 Логарифмические уравнения и неравенства. Используемая литература:. Алгебра и начала анализа 0- под редакцией А.Н.Колмогорова. Самостоятельные и контрольные работы по алгебре 0- под редакцией Е.П.Ершова
ПодробнееТригонометрические уравнения. 2
И. В. Яковлев Материалы по математике MathUs.ru Тригонометрические уравнения. В статье «Тригонометрические уравнения. 1» мы рассмотрели стандартные методы решения весьма простых тригонометрических уравнений.
ПодробнееФДП МАТЕМАТИКА ЕГЭ 2012
Корянов АГ, Прокофьев АА Тригонометрические уравнения: методы решений и отбор корней ФДП МАТЕМАТИКА ЕГЭ 0 Тригонометрические уравнения: методы решений и отбор корней (типовые задания С) Прокофьев АА, СОДЕРЖАНИЕ
Подробнее УД 373: / ISBN ББ 22. 1я721. в.., 2018 ISBN
1я721. в.., 2018 ISBN
УД 373:51.171 64 64 в, я ава.. 10 11 /… : Э, 018. 160. (. ). ISBN 978504093535, 10 11. П ё. П ё,. П 1011,,. УД 373:51 ББ.1я71 ISBN 978504093535 в.., 018. «Иаьв «Э», 018 СОДЕРЖАНИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА,
ПодробнееНеравенства С3, С5. Подготовка к ЕГЭ 2011.
Неравенства С С Подготовка к ЕГЭ 0 (материал для лекции для учителей 8040) Прокофьев АА aaprokof@yanderu Основные способы решения: Задачи С Решение неравенства на промежутках Упрощение неравенства и сведение
ПодробнееИррациональные уравнения
Иррациональные уравнения Уравнения, в которых переменная содержится под знаком корня, называются иррациональными. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному
ПодробнееИррациональные уравнения и неравенства 2
Иррациональные уравнения и неравенства Оглавление Иррациональные уравнения Метод возведения обеих частей уравнения в одну и ту же степень Задание Задание Задание Замена иррационального уравнения смешанной
ПодробнееГлава 1 Действительные числа(10ч)
Дата Название изучаемой Контроль Характеристика основных видов деятельности Тема урока Тип урока Форма контроля Требования к результатам (предметным и метапредметным) Учащийся научится Учащийся сможет
Подробнее Тригонометрические уравнения. 1
1
И. В. Яковлев Материалы по математике MathUs.ru Тригонометрические уравнения. 1 В данной статье рассматриваются самые простые виды тригонометрических уравнений. Методы решения таких уравнений стандартны
ПодробнееТема 5 Рациональные системы уравнений
Тема 5 Рациональные системы уравнений F ( x, x,…, ) 0, F ( x, x,…, ) 0, Система уравнений вида где… Fk ( x, x,…, ) 0, F i( x, x,…, ), i,…, k, некоторые многочлены, называется системой рациональных
ПодробнееТригонометрические уравнения
И. В. Яковлев, А. Г. Малкова. Подготовка к ЕГЭ по математике. Материалы сайта http://www.ege-study.ru Тригонометрические уравнения В данной статье мы расскажем об основных типах тригонометрических уравнений
ПодробнееИррациональные уравнения и неравенства 3
Иррациональные уравнения и неравенства Оглавление 4 Метод исключения радикалов в иррациональном уравнении умножением на сопряженный множитель Задание 7 4 5 Выделение полного квадрата (квадрата двучлена)
ПодробнееТригонометрические уравнения
Тригонометрические уравнения Определение. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций. Простейшими тригонометрическими уравнениями являются
Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций. Простейшими тригонометрическими уравнениями являются
Логарифмические уравнения
И В Яковлев Материалы по математике MathUsru Логарифмические уравнения и неравенства Логарифмические уравнения и неравенства это уравнения и неравенства, в которых переменная величина находится под знаком
ПодробнееМЕТОДИЧЕСКОЕ ПОСОБИЕ
ВОЕННО-ТЕХНИЧЕСКИЙ КАДЕТСКИЙ КОРПУС Дисциплина: «Математика, основы информатики и вычислительной техники» МЕТОДИЧЕСКОЕ ПОСОБИЕ для кадет Тема: Уравнения и неравенства с параметрами. Преподаватель: Молоткова
ПодробнееТема 3. Алгебраические выражения.
13.Модуль. Композиция линейной функции и модуля, квадратичной функции и модуля, дробно-линейной функции и модуля. Линейная функция с двумя модулями. Тема 3. Алгебраические выражения. 1. Алгебраические
Линейная функция с двумя модулями. Тема 3. Алгебраические выражения. 1. Алгебраические
Решение уравнений в целых числах
Решение уравнений в целых числах Линейные уравнения. Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.
Подробнее4.6. Иррациональные уравнения
4.6. Иррациональные уравнения Иррациональным уравнением называют уравнение, содержащее под знаком радикала переменную, относительно которой оно решается. Областью допустимых значений уравнения являются
ПодробнееМАТЕМАТИКА ЕГЭ 2011 (типовые задания С3)
Корянов АГ, Прокофьев АА Методы решения неравенств с одной переменной МАТЕМАТИКА ЕГЭ типовые задания С Методы решения неравенств с одной переменной Корянов А Г, г Брянск, korynov@milru Прокофьев АА, г
ПодробнееСПРАВОЧНИК ПО МАТЕМАТИКЕ
1. СВОЙСТВА СТЕПЕНЕЙ 1. Если степени с одинаковыми основаниями перемножаются, то основание остаётся тем же самым, а показатели складываются: a m a n a m`n. Если степени с одинаковыми основаниями делятся,
СВОЙСТВА СТЕПЕНЕЙ 1. Если степени с одинаковыми основаниями перемножаются, то основание остаётся тем же самым, а показатели складываются: a m a n a m`n. Если степени с одинаковыми основаниями делятся,
; ctg α = 1 sin 2 α = 1 + ctg2 α
Министерство науки и образования Российской Федерации Московский Государственный Университет Геодезии и Картографии Т. М. Королёва, Е. Г. Маркарян, Ю. М. Нейман ПОСОБИЕ ПО МАТЕМАТИКЕ ДЛЯ ПОСТУПАЮЩИХ В
Подробнее— его дробную часть). Вычислить 2 2
0 0 ( день) класс Задача ( балл) Решить неравенство,, 8, Решение Бесконечная сумма в правой части неравенства представляет собой сумму бесконечной убывающей геометрической прогрессии с первым членом b,
ПодробнееЯгубов.РФ. Решение. 2
Данное пособие по математике предназначено для учителей выпускающих класс общеобразовательных школ и ориентировано на подготовку учащихся старшей школы к решению задач по теме «Уравнения» и в частности
Подробнее {n}} \ cdot 1+ \ pi n, ~ n \ in Z \)Так как \ (\ displaystyle \ sin \ left (\ frac {\ pi} {2} \ right) = 1 \)
Но ты же внимательно читал мои пространные рассуждения, не так ли? И ты ведь не напишешь такую чушь? И ты понял, в чем здесь подвох?
А подвох вот в чем:
\ (\ displaystyle \ frac {\ pi} {2} \ приблизительно \ frac {3,14} {2}> 1 \)
А мы помним, что если правая часть тригонометрического уравнения больше \ (\ displaystyle 1 \) (или меньше \ (\ displaystyle -1 \)), то такое уравнение решений не имеет в принципе !!
Второе рассуждение тем более ересь: \ (\ displaystyle \ arcsin \ left (\ frac {\ pi} {2} \ right) \) надо понимать как угол, синус которого равенство \ (\ displaystyle \ frac {\ pi} { 2} \).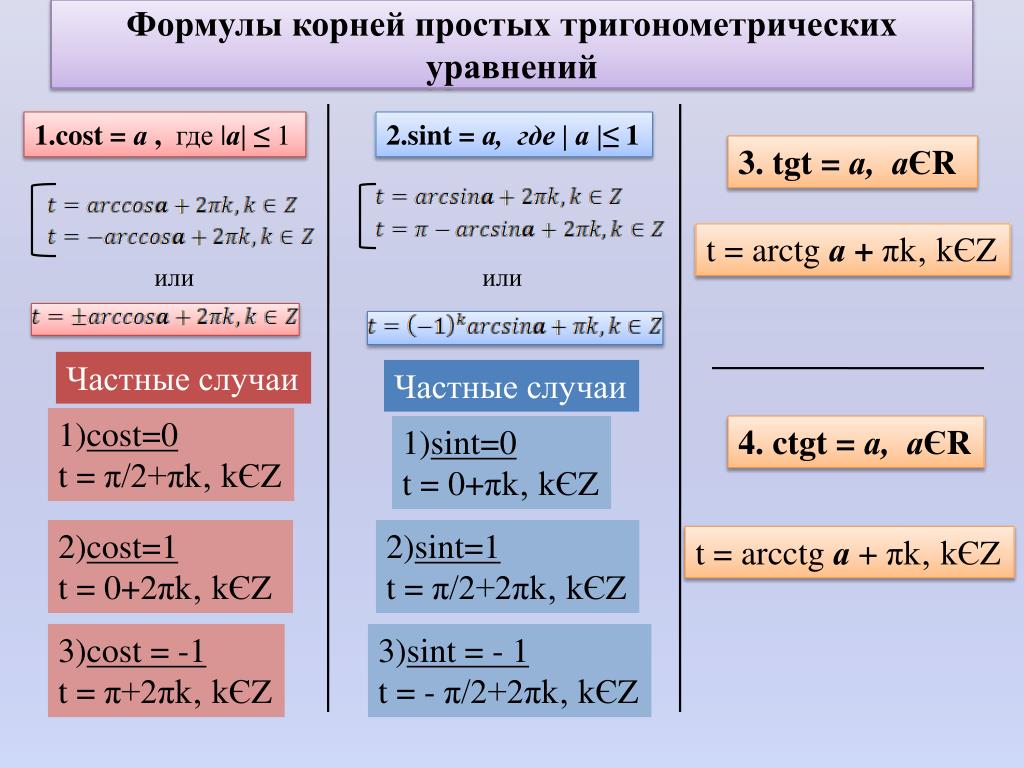 {n + 1 }} \ arcsin \ left (0,1 \ right) + \ pi n, ~ n \ in Z \)
{n + 1 }} \ arcsin \ left (0,1 \ right) + \ pi n, ~ n \ in Z \)
5.\ (\ displaystyle cos \ left (x \ right) = 1 \)
И снова по определению (теперь для уравнения другого вида)
\ (\ displaystyle x = \ pm arccos1 + 2 \ pi n, ~ n \ in Z \)
Чему равенство угол, косинус которого равенство \ (\ displaystyle 1 \)?
Этот угол равенства \ (\ displaystyle 0 \)!
\ (\ displaystyle x = \ pm 0 + 2 \ pi n, ~ n \ in Z \)
Тогда нет смысла прибавлять или вычитать ноль, всё равно это ноль.
\ (\ displaystyle x = 2 \ pi n, ~ n \ in Z \)
Получили формулу, которая есть в таблице решений тригонометрических уравнений!
Ответ : \ (\ displaystyle x = 2 \ pi n, ~ n \ in Z \)
6.\ (\ displaystyle cos \ left (x \ right) = — \ frac {1} {\ sqrt {2}} \)
По определению:
\ (\ displaystyle x = \ pm \ arccos \ left (- \ frac {1} {\ sqrt {2}} \ right) +2 \ pi n, ~ n \ in Z \)
Прежде всего вынесем «минус» по правилам для арккосинуса:
\ (\ displaystyle x = \ pm \ left (\ pi — \ arccos \ left (\ frac {1} {\ sqrt {2}} \ right) \ right) +2 \ pi n, ~ n \ in Z \)
Вот так и никак иначе выносится минус, запомни это!
Теперь арккосинус.
Не во всех таблицах есть значение \ (\ displaystyle \ frac {1} {\ sqrt {2}} \), но во всех есть \ (\ displaystyle \ frac {\ sqrt {2}} {2} \)! !!
А теперь, внимание, ловкость рук и никакого мошенничества!
\ (\ displaystyle \ frac {1} {\ sqrt {2}} = \ frac {\ sqrt {2}} {\ sqrt {2} \ cdot \ sqrt {2}} = \ frac {\ sqrt {2 }} {2} \)Единица деленная на корень из двух равно корень из двух деленное на два!
Я не зря выделил это замечание жирным шрифтом, запомни это тождество хорошенько! Оно спасёт тебя в очень многих случаях !!
Итак, чему же равен угол, косинус которого равен \ (\ displaystyle \ frac {1} {\ sqrt {2}} \) (или одно и то же \ (\ displaystyle \ frac {\ sqrt {2}} { 2} \))?
Верно, это угол \ (\ displaystyle \ frac {\ pi} {4} \).
Тогда:
\ (\ displaystyle x = \ pm \ left (\ pi — \ text {} \! \! ~ \! \! \ Text {} \ frac {\ pi} {4} \ right) + 2 \ pi n, ~ n \)
\ (\ displaystyle x = \ pm \ left (\ frac {4 \ pi} {4} — \ text {} \! \! ~ \! \! \ Text {} \ frac {\ pi} {4} \ right) +2 \ pi n, ~ n \ in Z \)
\ (\ displaystyle x = \ pm \ frac {3 \ pi} {4} +2 \ pi n , ~ n \ in Z \)
Reply : \ (\ displaystyle x = \ pm \ frac {3 \ pi} {4} +2 \ pi n, ~ n \ in Z \)
7. \ (\ displaystyle cos \ left (x \ right) = \ frac {\ pi} {4} \)
\ (\ displaystyle cos \ left (x \ right) = \ frac {\ pi} {4} \)
\ (\ displaystyle cos \ left (x \ right) = \ frac {\ pi} {4 } \)
Ещё один пример-обманка! Хотя данное уравнение решения имеет, потому что:
\ (\ displaystyle \ frac {\ pi} {4} = \ frac {3,14} {4} <1 \)
Тогда по определению:
\ (\ displaystyle x = \ pm \ arccos \ left (\ frac {\ pi} {4} \ right) +2 \ pi n, ~ n \ in Z \)
Но из этого никак не следует , что \ (\ displaystyle \ arccos \ left (\ frac {\ text {} \! \! \ Pi \! \! \ Text { }} {4} \ right) = \ frac {\ sqrt {2}} {2} \) !!!!!!
Запомни, арккосинус — это угол, его аргумент (начинка) — это число, а выход — угол !!!
Ты когда-нибудь встречался в своей практике такой странный угол как \ (\ displaystyle \ frac {\ sqrt {2}} {2} \) ?!
Вот и я нет. Поэтому оставим как есть!
Поэтому оставим как есть!
Ответ : \ (\ displaystyle x = \ pm \ arccos \ left (\ frac {\ pi} {4} \ right) +2 \ pi n, ~ n \ in Z \)
8 . \ (\ displaystyle cos \ left (x \ right) = — \ sqrt {2} \)
Всё просто: \ (\ displaystyle — \ sqrt {2} <- 1 \)
. .. и решений данное уравнение не имеет.
9. \ (\ displaystyle tg \ left (x \ right) = \ sqrt {2} \)
Запишем по определению:
\ (\ displaystyle x = arctg \ sqrt {2} + \ pi n, ~ n \ in Z \)
\ (\ displaystyle arctg \ sqrt {2} \) — не табличное значение, поэтому ответ сохраняем сохранить.
Обрати внимание, что в отличие от уравнения с синусом и косинусом, здесь мне не уже важно, какое у меня число стоит в правой части уравнения.
10. \ (\ displaystyle ctg \ left (x \ right) = — \ sqrt {3} \)
Снова по определению:
\ (\ displaystyle x = arсctg \ left (- \ sqrt { 3} \ right) + \ pi n, ~ n \ in Z \)
Без проблем выносим минус из арккотангенса:
\ (\ displaystyle x = \ pi-arcctg \ left (\ sqrt {3} \ right) + \ pi n, ~ n \ in Z \)
Вычисляем: котангенс какого угла равенства \ (\ displaystyle \ sqrt {3} \)?
Это угол \ (\ displaystyle \ frac {\ pi} {6} \).
Ответ : \ (\ displaystyle x = \ pi- \ frac {\ pi} {6} + \ pi n = \ frac {5 \ pi} {6} + \ pi n, ~ n \ in Z \).
11. \ (\ displaystyle ctg \ left (x \ right) = 1 \)
По формуле: \ (\ displaystyle x = arcctg1 + \ pi n, ~ n \ in Z \).
Котангенс какого угла равенства \ (\ displaystyle 1 \)?
Это угол \ (\ displaystyle \ frac {\ pi} {4} \).
Ответ : \ (\ displaystyle x = \ frac {\ pi} {4} + \ pi n, ~ n \ in Z \).
Ну как, материал не кажется тебе слишком сложным? Я надеюсь, что нет. Теперь давай порешаем для закрепления чуть более сложные задачки.
Отбор корней при решении тригонометрических соотношений
Отбор корней при решении тригонометрических уравнений
Математика
Областное государственное бюджетное учреждение
дополнительного профессионального образования
«Курский институт развития образования»
ОГБУ ДПО КИРО
ТЕМА: Отбор корней при решении тригонометрических уравнений.
Работу выполнили:
Сколодова Л.В.
Новиков В. В.
Холодова Н. И.
18.12 2017год
Г. Курск
Решение тригонометрических правил — важный раздел в математике. Успешное изучение невозможно без умения решать тригонометрические уравнения. Для успешного решения тригонометрических правил необходимо знать не только формулы и методы решения этих уравнений, но и правильно отбирать корни на заданном промежутке или при других дополнительных условиях.«Решить тригонометрическое уравнение и выполнить отбор корней, удовлетворяющих условию».
Цель работы: Изучить различные способы отбора корней в тригонометрических уравнениях.
Задачи:
$ 1üрассмотреть различные типы заданий, содержащие тригонометрические уравнения, где необходимо выполнить отборней, классать;
$ Определить наиболее рациональный способ отбора корней для каждого типа заданий;
$ 1üрасс посмотреть примеры решения уравнений и систем, где необходимо выполнить отбор корней;
При отборе корней в процессе решения тригонометрических параметров используют один из следующих способов.
Арифметический способ . Перебор значений первого и вычисление корней приходиться в случаях, когда требуется отобрать корни, принадлежащие заданному промежутку или некоторому условию.
Алгебраический способ отбора корней наиболее удобен в тех случаях, когда последовательный перебор параметров приводит к вычислительным трудам, промежуток для отбора корней большой, значения обратных тригонометрических функций, входящих в серии, не обозначены табличными.Для этого решают неравенство относительно неизвестного целочисленного задания и вычисления корней.
Геометрический способ. В последние годы в учебниках используются разные модели решения простейших тригонометрических уравнений с применением тригонометрического круга, графика тригонометрической функции или числовой прямой.
а) Тригонометрическую окружность удобно использовать при отборе корней на промежутке, длина которого не превосходит 2, или в случае, когда значения обратных тригонометрических функций, входящих в серию решений, не предусмотрены табличными.
б) При изображении решения простейших тригонометрических используются иногда используют графики простейших тригонометрических функций. Для нахождения решения тригонометрического уравнения при этом подходе требуется построение «кусочка» графика.
в) Числовую прямую удобно использовать при отборе корней на промежутке, длина которого превосходит 2.
Процессе обучения задач, в которых требуется отобрать различные варианты выполнения этого тригонометрического уравнения, следует обсудить разные способы выполнения, а также случаи, когда тот или иной способ может использоваться чаще или наоборот непригодным.
Рассмотрим один конкретный пример с использованием всех вышеуказанных способов:
а) Решить уравнение:
б) Найти все корни этого уравнения, принадлежащие отрезку
Решение.
а) Используя формулу косинуса двойного угла и формулу приведения, запишем уравнение в виде:
Решаем квадратное уравнение относительно,
Отсюда
Уравнение так как
Из уравнения х =.
Отметим, что решение уравнения
х = или х =.
б) отберем корни уравнения, принадлежащие отрезку
1. Арифметический способ.
Пусть. Подставляя k =… , получаем
. Отрезку принадлежит корень.
Пусть. Подставляя k =… , получаем. Отрезку принадлежит корень.
Отрезку принадлежат корни
Ответ: а);
в)
2.Алгебраический способ.
Отберем корни, принадлежащие отрезку. Решаем двойное неравенство.
Пусть.
Тогда
.
Пусть.
Тогда
.
Отрезку принадлежат корни
3. Геометрический способ.
1 . Корни уравнения изображаются точками А и В , отрезок изображен жирной дугой (см.рис.). В указанном отрезке содержаться два корня уравнения:
у
А
-П х
-3П
Â
2. Корни, принадлежащие отрезку, отберем по графику у =. Прямая пересекает график в двух точках, абсциссы, которые принадлежат отрезку, Так как период функции y = равенство, то эти абсциссы равны; .
Корни, принадлежащие отрезку, отберем по графику у =. Прямая пересекает график в двух точках, абсциссы, которые принадлежат отрезку, Так как период функции y = равенство, то эти абсциссы равны; .
у
13 долларов США. Рассмотрим отбор корней с помощью координатной прямой.
у =. /////////////////////////////////
Отрезку принадлежат корни
Ответ: а) х =.
б)
А теперь рассмотрим более сложные уравнения, которые решаются различными способами.
№1. а) Решите уравнение.
б) Найдите все корни, принадлежащие отрезку.
Решение:
а) ОДЗ: sinx> 0 ()
;
;
4sinxcosx = 2 sinx;
4sinxcosx — 2 sinx = 0;
2sinx (2cosx -) = 0;
Решая последнее уравнение получаем корни:
sinx = 0 или.
Учитывая ОДЗ, получаем корни уравнения:
б) С помощью числовой окружности отберём корни на указанном отрезке:
Получим число.
Ответ:; б).
№2. Дано уравнение log — cos x (1 — 0,5 sinx) = 2.
а) Решите уравнение.
б) Найдите корни уравнения, принадлежащие отрезку [14π; 16π].
Решение:
$ 1а) ОДЗ: — 1os x 0;
log — cos x (1 — 0,5 sin x) = log — cos x cos 2 x,
1 — 0,5 sin x = cos 2 x,
1 — 0,5 sin x — cos 2 x = 0,
грех 2 х — 0,5 грех х = 0,
грех х (грех х — 0,5) = 0,
грех х = 0 или грех х = 0,5
х = πn, nÎZ, x = + 2πn, n ÎZ, x = + 2πn, nÎ Z.
учитывая ОДЗ, получаем, что х = πn, nÎZ, и x =, nÎZ не являются коренными уравнениями (cosx = 1, и — 1osx
б) Найдем корни уравнения на заданном промежутке геометрическим способом:
х =
Ответ: а) х = nÎZ, б).
№ 3. Дано уравнение
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
а) Ограничения на x :
Для таких x :
б) Отбор корней произведем с помощью единичной окружности.
Ответ: а) n Î Z б).
№ 4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение.
а) Перейдём к системе:
Решаем уравнение системы
Получаем:
С учётом всех ограничений
б) С помощью числовой окружности отберём корни, принадлежащие указанному отрезку Получим число
Отбор корней может быть обоснован любым другим способом: с помощью графика, решения двойных неравенств и т.п.
Ответ: а) б).
№ 5. Дано уравнение
а) Решите уравнение.
б) Найдите его корни, принадлежащие отрезку
Решение.
а) Найдем на ограничения:
Для таких
б) Отбор корней сделаем путем перебора подходящих значений n
Из серии корней
Заметим, что отрицательные значения здесь не подойдут. Значение n = 0 тоже не подходит, так как
При n = 1:.Докажем, что 4.
Для этого достаточно доказать:
Действительно,
При п = 2:
При п = 3:
Этот корень уже не подходит. Дальнейшие поиски корней из этой серии смысла не имеют.
Из серии корней
При отрицательных значениях несложно понять, искомых корней не будет.
При п = 1:
Корень не подходит.
При п = 2:
При п = 3:
Но
Корень не подходит, дальнейшие поиски просто излишни.
Ответ: а) б)
№ 6. Дано уравнение
а) Решите уравнение.
б) Укажите корни уравнения, длинные промежутки
Решение:
а) Последовательно получаем:
Покажем, что, k , n Î Z при k = 6 n — 2.
Действительно,
Итак, решения заданного уравнения являются числами вида:.
Эти же числа можно представить также в виде
б) Отбор корней:
Ответ: а) б)
№ 7. а) Решите уравнение:
б) Укажите корни этого уравнения,
принадлежащие отрезку []
Решение:
а) Запишем исходное уравнение в виде:
Заметим, что выражение, стоящее под знаком логарифма, приравнено к единице, поэтому исследовать ОДЗ не требуется.
Для решения полученного тригонометрического уравнения использовать формулу косинуса двойного угла
откуда получаем
Обозначая t = cos x , имеем:
Откуда или.
Вернемся к исходной переменной.
Уравнение корней не имеет, поскольку косинус не больше 1.
Из уравнения находим: или,
n Î Z .
б) С помощью числовой окружности отберём корни, принадлежащие отрезку
Получим числа:.
Ответ: а), n Î Z ; б).
№ 8. а) Решите уравнение
б) Найдите все корни на промежутке
Решение:
а) Обратим внимание на то, что правая часть заданного уравнения есть ограниченная функция. В частности,
Следовательно, такие же ограничения следует наложить и на левую его часть.То есть
Из-за ограниченности функции косинус будем иметь:
а последнее неравенство истинно только при выполнении условия
Решим его:
Таким образом, мы установили, что, и это выполнено выполняется при.
Теперь оценим сверху и снизу выражение:
Тогда левая часть уравнения будет иметь вид:
Таким образом, левая часть уравнения может принять единственное значение, равное 1, равное 1, хотя бы при некоторых значениях стандартных, существующих решений уравнения.Если такие числа найдутся, то уравнение будет иметь решение. Если же их не будет, то у уравнения решений не будет.
Нами были найдены корни уравнения
Ими являются числа вида.
Теперь мы ищем решения уравнения. Последнее равенство имеет место, если
Найдем значения, при которых серии решений и совпадение. Для этого найдем их значения, принадлежащие промежутку
Из серии
При n = 0 x 1 =
При n = 1 x 2 =
При n = 2 x 3 =
При n = 3 x => 2p.
Из серии:
При n = 0 х 4 =
При n = 1 x 5 =
При n = 2 x 6 =
При n = 3 x => 2p
Как видим, общие решения двух указанных выше, имеются, они равны числам вида.
б) При отборе корней уравнения решим двойное неравенство, решая далее, получаем, где m = — 1, m = 0, mÎZ. При найденных целых м получим:
Ответ: а); б)
Задания для самостоятельного решения:
$ 11) а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащего отрезку
$ 12) Дано уравнение
а) Решите уравнение.
б) Найдите корни на промежутке
$ 13)
а) Решите уравнение
б) Найдите все корни на промежутке
$ 14) а) Решите уравнение
б) Найдите все его корни, принадлежащие отрезку
$ 15)) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
$ 16) Дано уравнение
а) Решите уравнение.
б) Укажите корни, принадлежащие интервалу (−5; 1).
Тригонометрическое уравнение с выборкой корней. Задание С1
В этой статье я хочу показать вам решение тригонометрического уравнения с выборкой корней. Но, самое главное, хочу предостеречь вас от одного неравносильного перехода , который может возникнуть при решении тригонометрического неравенства.
Итак, задание такое :
1. Решите уравнение:
.
2. Найдите корни, принадлежащие промежутку
Это классическое распадающееся уравнение.
Произведение двух множителей равно нулю, когда хотя бы один из них равенство нулю, а второй при этом существует.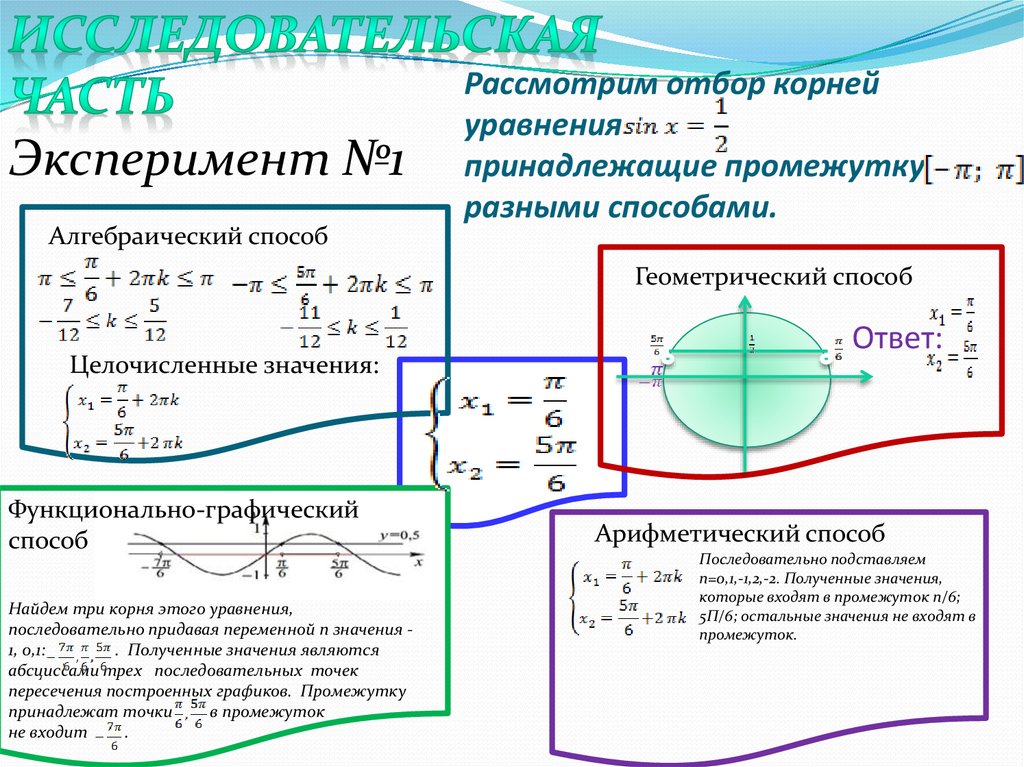
Наше уравнение равносильно совокупности двух систем:
Вместо второй системы мы получили одно уравнение, так как первый множитель существует при всех действительных значениях, и ограничения на ОДЗ нет.
Решим уравнения системы:
,
Это однородное тригонометрическое уравнение первой степени.Разделим обе части уравнения на. (Проверим, что корни уравнения не являются корнями исходными уравнениями — если, то, и левая часть не равна нулю).
Помним, что уравнение является частью системы
и его корни должны удовлетворять неравенству
.
Вот в этом месте нужно быть очень внимательными!
Правильное решение.
Решим неравенство. Левая часть неравенства обращается в ноль при.Эти точки разбивают тригонометрический круг на два промежутка — зеленый и красный, на каждом из которых левая часть поддерживает знак: Чтобы определить какой именно знак, возьмем произвольную точку, принадлежащую, например, красную дуге.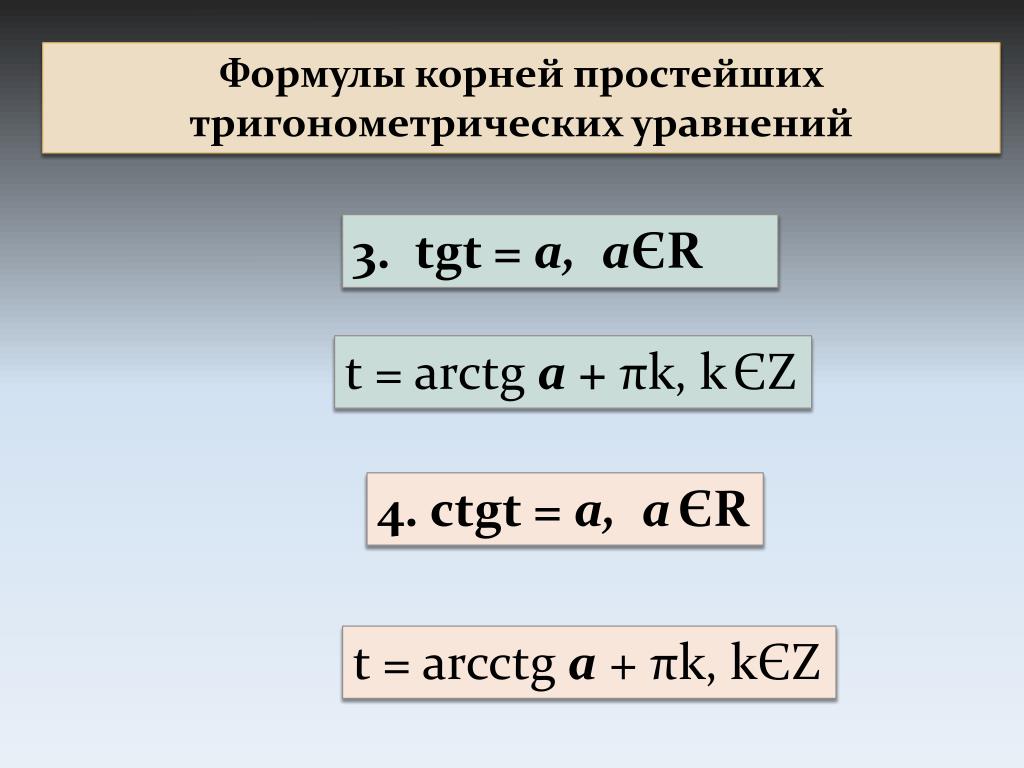 Пусть это будет точка, соответствующая повороту на 0 радиан.
Пусть это будет точка, соответствующая повороту на 0 радиан.
, поэтому во всех точках красной дуги выполняется неравенство.
Итак, нас устраивают корни уравнения, расположенные на красной дуге.
Расположим на тригонометрическом круге числа и.Если принять во внимание, что число 1 чуть-чуть меньше, чем, то, число поставим чуть-чуть не доходя до, а число 2 чуть-чуть не доходя до:
Мы видим, что корень удовлетворяет условию, а корень 2 — не удовлетворяет.
Теперь найдем корни, которые занимают промежуток:
Это числа
Ответ: 1.;
2.
Неверное решение.
Если мы будем решать неравенство тем же способом, то есть разделим обе части на, то получим неравенство, не равносильное исходному:
Решение этого неравенства на тригонометрическом круге выглядит так:
Мы получили решение, отличное от предыдущего.При этом решении получится, что число 2 является корнем исходного уравнения.
В чем причина ошибки? Когда мы делили обе части неравенства на, мы не учли, что может быть меньше нуля. При делении на положительное число знак неравенства не меняется, а при делении на отрицательное число меняется на противоположный.
Строго говоря, при делении на мы получили такое неравенство:
В этом неравенстве знак левой части меняется в корнях числителя, то есть в корнях уравнения, и в корнях знаменателя, то есть в корнях уравнения, что для нас уже совершенно лишнее.Поэтому мы получили неверное решение.
И.В. Фельдман, репетитор по математике.
Методы решения тригонометрических уравнений
Методы решения
тригонометрических уравнений
1. Решение простейших тригонометрических уравнений
2. Решение тригонометрических уравнений разложением на множители
3. Решение
тригонометрических уравнений приводящихся к квадратным уравнениям
Решение
тригонометрических уравнений приводящихся к квадратным уравнениям
4. Решение тригонометрических преобразованием суммы тригонометрических функций в произведение
5. Решение тригонометрических преобразованием произведений тригонометрических функции в сумме
6. Решение тригонометрических уравнений с применением формул понижения степени
7. Решение тригонометрических уравнений как однородное
8. Решение тригонометрических элементов с помощью вспомогательного аргумента
9. Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки
10. Решение тригонометрических уравнений с помощью замены неизвестного
11. Решение тригонометрических уравнений с помощью оценки левой и правой частей уравнения (метод оценок)
12. Решение
тригонометрических равных тригонометрические функции под знаком
радикала
Решение
тригонометрических равных тригонометрические функции под знаком
радикала
1. Решение простейших тригонометрических уравнений
По определению арифметического квадратного корня перейдем к равносильной системе уравнений.
Ответ:
2. Решение тригонометрических уравнений разложением на множители
или
или решений нет
Отметим полученные решения и область определения на тригонометрическом круге.
Решением уравнения является:
Ответ:
3. Решение тригонометрических
формулы
Решение тригонометрических
формулы
сводящихся к квадратным уравнениям
Пусть , тогда
или
Т.к.
при , то корней нет.
Ответ:
4. Решение тригонометрических преобразований
сумма тригонометрических функций в произведении
или
Ответ: ;
5. Решение
тригонометрических преобразований
Решение
тригонометрических преобразований
произведений тригонометрических функций в сумме
а) Найдем область определения функции.
Областью определения данного уравнения является:
б) Решим данное уравнение.
Ответ:
6.Решение тригонометрических уравнений с
применение формул понижения степени
Пусть , тогда
или
Т. к.
к.
при , то корней нет.
Ответ:
7. Решение тригонометрических уравнений как однородное
Однородное уравнение — это уравнение, в котором слагаемое имеет одну и туже степень.
, где
— действительные числа. — показатель однородности.
Если , то и , что противоречит основному тригонометрическому тождеству, значит . Разделим обе части на , получим
Ответ:
8.Решение тригонометрических уравнений с помощью
введение вспомогательного аргумента
Т. к. , то корни есть.
к. , то корни есть.
Разделим обе части уравнения на , получим
Т. к. и , то существует такой угол , что , а , тогда получим
Ответ:
Теория.
1) если , то уравнение однородное.
2) если и (то есть хотя бы одно из чисел или не равно 0), то разделим обе части уравнения на , получим
Т. к. и , то существует такой угол , что , тогда
а) если, т.е. , то корней нет.
в) если, т. е. , тогда
Т. к. , то корней нет.
к. , то корней нет.
9. Решение тригонометрических уравнений с помощью
универсальной тригонометрической подстановки
(1)
(2)
При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения корнями данного уравнения.
Проверка.
Если , тогда
— не верно, значит , не является корнями исходного уравнения.
Ответ:
10. Решение
тригонометрических уравнений
Решение
тригонометрических уравнений
с помощью замены неизвестного
Уравнение вида решается следующая заменой , , ,
Способ I
Пусть , , , , получим
или
(3)
Разделим на , получим
Т.к. , при , то корней нет.
Ответ:
Теория.
, при
Доказательство:
Шесть способов решения уравнения
(3).
1. Применение формулы .
2. через .
3. приведению к однородному уравнению второй степени.
4. способ введения вспомогательного аргумента.
5. с помощью неравенства , при .
6. метод оценки левой и правой частей уравнения.
Способ II
или
Разделим на , получим
Т.к. , при , то корней нет.
Ответ:
11. Решение тригонометрических уравнений с помощью оценки
левая и правая части уравнения (метод оценок)
12. Решение
тригонометрических равных
Решение
тригонометрических равных
тригонометрические функции под знаком радикала
Пример №1
Решим уравнение 2.
или
Отметим поученные решения и условие 1 на тригонометрическом круге.
Ответ: ,
Пример №2
Решим уравнение 2.
Решим квадратное уравнение относительно .
и то корней нет.
Отметим поученные решения и условие 1 на тригонометрическом круге.
Ответ:
тригонометрические уравнения (типовые задания 13 (С1))
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ПодробнееЛогарифмические неравенства
Логарифмические неравенства 1. 1. Решите неравенство: Решим неравенство :. 2. 2. Решите неравенство: Найденные значения, при которых обе части неравенства получают:
Подробнее
1. Решите неравенство: Решим неравенство :. 2. 2. Решите неравенство: Найденные значения, при которых обе части неравенства получают:
Подробнее
1. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
КЛАССИФИКАЦИЯ УРАВНЕНИЙ 1 Алгебраические уравнения: рациональные (содержат только целые степени неизвестной) и иррациональные (содержат дробные степени неизвестной)) Показательные и логарифмические (неизвестная
) ПодробнееРАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Оглавление РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ I Рациональные алгебраические уравнения Равносильность уравнения Равносильность уравнения на множестве Равносильность
ПодробнееИррациональные неравенства
Иррациональные неравенства Неравенства, называемые иррациональными Основными методами решения иррациональных неравенств являются методическими сведениями исходного
ПодробнееГотовим к ЕГЭ хорошистов и отличников
А. Г. КОРЯНОВ, А.А. ПРОКОФЬЕВ Готовим к ЕГЭ хорошистов и отличников Лекции Москва Педагогический университет «Первое сентября» 0 Анатолий Георгиевич Корянов, Александр Александрович Прокофьев
Г. КОРЯНОВ, А.А. ПРОКОФЬЕВ Готовим к ЕГЭ хорошистов и отличников Лекции Москва Педагогический университет «Первое сентября» 0 Анатолий Георгиевич Корянов, Александр Александрович Прокофьев
Теоретический материал.
0.5 Логарифмические уравнения и неравенства. Используемая литература :. Алгебра и начала анализа 0- под редакцией А.Н.Колмогорова. Самостоятельные и контрольные работы по алгебре 0-под редакцией Е.П.Ершова
ПодробнееТригонометрические уравнения. 2
И. В. Яковлев Материалы по математике MathUs.ru Тригонометрические уравнения. В статье «Тригонометрические уравнения. 1 мы рассмотрели стандартные методы решения весьма простых тригонометрических уравнений.
ПодробнееФДП МАТЕМАТИКА ЕГЭ 2012 г.
Корянов АГ, Прокофьев АА Тригонометрические уравнения: методы решений и отбор корней ФДП МАТЕМАТИКА ЕГЭ 0 Тригонометрические уравнения: методы решений и отбор корней (типовые задания С) Прокофьев АА, СОДЕРЖАНИЕ
Подробнее УД 373: / ISBN ББ 22. 1я721. в .., 2018 ISBN
1я721. в .., 2018 ISBN
УД 373: 51.171 64 64 в, я ава .. 10 11 / …: Э, 018. 160. (.). ISBN 9785040
Неравенства С3, С5. Подготовка к ЕГЭ 2011.
Неравенства С Подготовка к ЕГЭ 0 (материал для лекции для учителей 8040) Прокофьев АА aaprokof @ yanderu Основные решения: Задачи Решение неравенства на промежутках Упрощение неравенства и сведение
ПодробнееИррациональные уравнения
Иррациональные уравнения Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.Решение иррациональных уравнений сводится к переходу от иррационального к рациональному
ПодробнееИррациональные уравнения и неравенства 2
Иррациональные уравнения и неравенства Оглавление Иррациональные уравнения Метод возведения частей уравнения в одну и ту же степень Задание Задание Задание Замена иррационального уравнения смешанной
ПодробнееГлава 1 Действительные числа (10ч)
Дата Название изучаемой Контроль Характеристика основных видов деятельности Тема урока Типа Форма контроля Требования к результатам (предметным и метапредметным) Учащийся научится Учащийся сможет
Подробнее Тригонометрические уравнения. 1
1
И. В. Яковлев Материалы по математике MathUs.ru Тригонометрические уравнения. 1 В данной статье самые простые виды тригонометрических уравнений. Методы решения таких систем стандартны
ПодробнееТема 5 Рациональные системы уравнений
Тема 5 Рациональные системы уравнений F (x, x, …,) 0, F (x, x, …,) 0, Система уравнений вида где …Fk (x, x, …,) 0, F i (x, x, …,), i, …, k, некоторые многочлены, называется системой рациональных
ПодробнееТригонометрические уравнения
И. В. Яковлев, А. Г. Малкова. Подготовка к ЕГЭ по математике. Материалы сайта http://www.ege-study.ru Тригонометрические уравнения В данной статье мы расскажем об основных типах тригонометрических уравнений
ПодробнееИррациональные уравнения и неравенства 3
Иррациональные уравнения и неравенства Оглавление 4 Метод исключения радикалов в иррациональном уравнении умножением на сопряженный множитель Задание 7 4 5 Выделение полного двурата (квадратаучлена)
ПодробнееТригонометрические уравнения
Тригонометрические уравнения Определение. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций. Простейшими тригонометрическими уравнениями являются
Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций. Простейшими тригонометрическими уравнениями являются
Логарифмические уравнения
И В Яковлев Материалы по математике MathUsru Логарифмические уравнения и неравенства Логарифмические уравнения и неравенства это уравнения и неравенства, в переменная величина находится под знаком
ПодробнееМЕТОДИЧЕСКОЕ ПОСОБИЕ
ВОЕННО-ТЕХНИЧЕСКИЙ КАДЕТСКИЙ КОРПУС Дисциплина: «Математика, основы информатики и вычислительной техники» МЕТОДИЧЕСКОЕ ПОСОБИЕ для кадет Тема: Уравнения и неравенства с предписаниями.Преподаватель: Молоткова
ПодробнееТема 3. Алгебраические выражения.
13.Модуль. Композиция линейной функции и модуля, квадратичной функции и модуля, дробно-линейной функции и модуля. Линейная функция с двумя модулями. Тема 3. Алгебраические выражения. 1. Алгебраические
Линейная функция с двумя модулями. Тема 3. Алгебраические выражения. 1. Алгебраические
Решение уравнений в целых числах
Решение уравнений в целых числах Линейные уравнения.Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.
Подробнее4.6. Иррациональные уравнения
4.6. Иррациональные уравнения Иррациональным уравнением уравнение, используемое под радикала переменную, относительно которое решается. Областью допустимых значений уравнения являются
ПодробнееМАТЕМАТИКА ЕГЭ 2011 (типовые задания С3)
Корянов АГ, Прокофьев АА Методы решения неравенств с одной стандартной МАТЕМАТИКА ЕГЭ типовые задания С Методы решения неравенств с одной моделью Корянов А Г, г Брянск, korynov @ milru Прокофьев АА, г
ПодробнееСПРАВОЧНИК ПО МАТЕМАТИКЕ
1. СВОЙСТВА СТЕПЕНЕЙ 1. В степени с одинаковыми основаниями перемножаются, то основание остаётся тем же самым, а показатели складываются: a m a n a m`n. Если степени с одинаковыми основаниями делятся,
СВОЙСТВА СТЕПЕНЕЙ 1. В степени с одинаковыми основаниями перемножаются, то основание остаётся тем же самым, а показатели складываются: a m a n a m`n. Если степени с одинаковыми основаниями делятся,
; ctg α = 1 sin 2 α = 1 + ctg2 α
Министерство науки и образования Российской Федерации Московский Государственный Университет Геодезии и Картографии Т. М. Королёва, Е. Г. Маркарян, Ю. М.Нейман ПОСОБИЕ ПО МАТЕМАТИКЕ ДЛЯ ПОСТУПАЮЩИХ В
Подробнее— его дробную часть). Вычислить 2 2
0 0 (день) класс Задача (балл) Решить неравенство ,, 8, Решение Бесконечная сумма в правой части неравенства представляет собой сумму бесконечной убывающей геометрической прогрессии с первым членом b,
ПодробнееЯгубов.РФ. Решение. 2
Основное пособие по математике предназначено для учителей выпускающих классобразовательных школ и ориентировано на подготовку учащихся старшей школы к решению задач по теме «Уравнения» и в частности
Подробнее Урок 46. однородные тригонометрические уравнения — Алгебра и начала математического анализа — 10 класс
однородные тригонометрические уравнения — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №46. Однородные тригонометрические уравнения.
Перечень вопросов, рассматриваемых в теме:
1) Однородные тригонометрические уравнения первой и второй степени.
2) Рассмотреть решение тригонометрических соотношений с помощью универсальной тригонометрической подстановки.
3) Рассмотреть решение более сложных тригонометрических уравнений.
Глоссарий по теме
- Арккосинусом число называется такое число α, что:. Арккосинус числа m обозначают:.
- Арксинусом называется такое число α, что: и числа. Арксинус числа m обозначают:.
- Арктангенсом числа m называется такое число α, что: и. Арктангенс числа m обозначают:.
- Арккотангенсом числа n называется такое число α, что: и.Арккотангенс числа n обозначают:
- Уравнение вида:
называется однородным.
Здесь f и g произвольные функции, коэффициенты.
6. Универсальная тригонометрическая подстановка — это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента:
Основная литература:
Колягин Ю. М., Ткачева М. В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М .: Просвещение, 2014.
Дополнительная литература:
Шахмейстер А.Х. Тригонометрия. М. 2014, 712 с.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Мы уже знаем, как решены простейшие тригонометрические уравнения, а также тригонометрические уравнения, которые могут быть сведены к квадратным, дробно-рациональным или алгебраическим степени выше второго с помощью замены переменных. Но это лишь маленькое количество тригонометрических уравнений. Как, например, быть в том случае, когда тригонометрическое уравнение выглядит, например, так:
Но это лишь маленькое количество тригонометрических уравнений. Как, например, быть в том случае, когда тригонометрическое уравнение выглядит, например, так:
.
Для этого нам нужно рассмотреть некоторые вспомогательные решения уравнений, а также формулы преобразования тригонометрических выражений.
Задание:
Как Вы думаете, какие факты и формулы мы будем использовать при решении этого уравнения?
Ответ: определение тангенса, формулу синуса двойного аргумента.
1. Итак, рассмотрим однородное тригонометрическое уравнение.
Напомним определение однородного уравнения
Определение
Уравнение вида:
называется однородным.
Здесь f и g произвольные функции, коэффициенты.
В зависимости от значения показателя n, мы можем получить однородное уравнение первой, второй или более высокой степени.
Например, уравнение является однородным, а уравнение однородным не является.
2. Теперь перейдем к рассмотрению однородных тригонометрических уравнений.
Если функции f и g это синус и косинус одного и того же аргумента, то мы получим тригонометрическое однородное уравнение.
Рассмотрим сначала однородное тригонометрическое уравнение первой степени.
Запишем его в общем виде: (1).
Разделим это уравнение на (или на) и получим: .
Решать такие уравнения мы умеем:,.
Заметим, что, решая это уравнение, мы выполняли деление уравнения на выражение с изменением.Так как это действие не является равносильным, не потеряли ли мы корни.
Если, то. То есть при подстановке в уравнение (1) таких значений х, при которых оно не обращается в верное числовое равенство, а значит такие х корнями исходные уравнения не являются, и значит наше действие не к потере корней.
Рассмотрим конкретный пример.
Пример 1.
Решить уравнение:
Решение:
.
Ответ:
Решим теперь однородное тригонометрическое уравнение второй степени
Общий вид такого уравнения:
(2)
Так же, как и уравнение (1), разделим его на наибольшую степень косинуса х.
Так же, как и при решении уравнения (1), мы должны убедиться в том, что при делении уравнения на уравнении мы не потеряли корней. Это не произойдет в том случае, если.
После деления мы получили квадратное уравнение относительно тангенса х, которое и решаем известными способами.
.
При решении этого уравнения мы можем ввести новую переменную, но можем это и не делать.
.
В зависимости от значения дискриминанта этого квадратного уравнения оно может иметь от 0 до 2 корней. И, соответственно, исходное уравнение может иметь две серии решений, одну или ни одной.
Рассмотрим пример.
Пример 2.
Решить уравнение:
Решение:
.
.
Ответ:.
Даже если исходное тригонометрическое уравнение второй степени не является однородным, можно его преобразовать к такому виду.
Рассмотрим это сначала на примере уравнения второй степени.
Пример 3.
Решить уравнение:
Решение:
Сначала умножим 3 на тригонометрическую единицу, то есть на выражение
(. Мы получим:
Мы получим:
Теперь преобразуемное полученное:
Теперь решим полученное однородное уравнение:
.
.
Ответ :.
3. Теперь рассмотрим, как можно привести к однородному уравнению вида
, то есть левая часть которого является однородной первой степени, а в правой стоит число.
Рассмотрим это на примере.
Пример 4.
Решение:
Используем три формулы двойного аргумента:
Подставим их в исходное уравнение и домножим на гонометрическую единицу 2, стоящую в правой части.
.
.
Ответ :.
Заметим, что подобное аргумент уравнения можно решить и по-другому, применимо формулу вспомогательного средства:
Рассмотрим решение примера 4 способом.
Пример 4-а.
Решение:
Преобразуем левую часть:
Ответ:
Мы видим, что результат, полученный при работе способами, кажется разным. На самом деле в тригонометрии одно и то же число может быть записано разными способами.
На самом деле в тригонометрии одно и то же число может быть записано разными способами.
Можно сказать, что первый способ в этом случае приводит к более короткому и красивому результату.
Решите уравнение
Решение:
В такие записи уравнение не является однородным.
Используем формулу синуса двойного аргумента.
Теперь уравнение однородное.
Решим его.
,.
Ответ:.
Решить уравнение
1) с помощью формулы вспомогательного аргумента
Решение
Ответ:
2) с помощью формулы синуса и косинуса
двойногоОтвет:
3) Решите уравнение:
Решение
Ответ:
.Рассмотрим теперь решение тригонометрических уравнений с использованием универсальной тригонометрической подстановки.
Она называется универсальной, так как позволяет уравнение вида
(*), где рациональная функция, свести к рациональному алгебраическому уравнению.
Универсальная тригонометрическая подстановка — это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента:
То есть если сразу обозначить, то видение (*) примет:.А так как сама функция F является рациональным, то и получающееся уравнение будет рациональным алгебраическим.
Рассмотрим пример 5.
Решить уравнение.
Решение:
Область определения исходного уравнения:
Преобразуем исходное уравнение:
или
Используем универсальную тригонометрическую подстановку.
Если, то получим уравнение:
Решим его.
, .
Ответ: .
Заметим, что когда мы используем универсальную тригонометрическую подстановку, у нас появляется тангенс половинного угла, который не всегда определен. Поэтому мы можем потерять корни. Нужно проверить.
Поэтому мы можем потерять корни. Нужно проверить.
определен для всех.
Так как эти числа, не принадлежат области исходного уравнения, то мы не потеряем корней.
Решите уравнение
Рассмотрим уравнение решения
(**)
Решение:
Найдем область допустимых значений:
Теперь используем универсальную аргументную подстановку и формулугенсацию суммы.
Область допустимых значений полученного уравнения уже, чем исходного:
.
Решим полученное уравнение:
.
Необходимо проверить те числа, которые выпали из области определения после использования универсальной тригонометрической подготовки.
Это числа вида.
Подставим π в (**): верное равенство. Это означает, что числа вида тоже являются решениями исходного уравнения.
Таким образом, получается ответ.
.
Ответ:.
Примеры и разбор решения заданий тренировочного модуля
№ 1.
Даны уравнения.
Запишите номера однородных соотношений
Ответ: однородными являются 1), 5), 7) и 8) уравнения.
№ 2.
Даны уравнения.
Распределите их по группам в зависимости от того, являются они однородными или не являются.
+ +Однородные уравнения | Неоднородные уравнения |
№ 3.
Даны уравнения.
Выделите уравнения, которые могут быть приведены к однородному
000
000
000
000
000000
000
000
000
000
000
000
000
000
000
№ 4.
Автоматически заполняемый кроссворд.
Решите уравнения. Укажите значение k, при котором его корень становится больше.
1)
k = 1
Слово МИНУС
2)
k = 1
Слово КОРЕНЬ
3)
k = 2
Слово РАВЕНСТВО
9000 9000 Простей № 5. тригонометрические уравнения, которые получаются при решении данного уравнения
Ответ: 16
№ 6.
Подчеркните простейшее тригонометрическое уравнение вида, которое получается при решении данного уравнения
1)
2)
3)
4)
5)
Ответ: 3
№7.
Выберите из списка простейшие тригонометрические уравнения, которые получаются при решении данного уравнения.
1)
2)
3)
4)
5)
6)
Ответ: 25
№ 8 .
Решите уравнение
Перетащите в ответные составляющие
1)
2)
3)
4)
5)
6)
Ответ:
№
Автоматически заполняемый кроссворд
Решите уравнения. Определите, сколько корней имеет каждое из этих уравнений на интервале (-π; π).
Определите, сколько корней имеет каждое из этих уравнений на интервале (-π; π).
Ответ: 4
Слово ПРОМЕЖУТОК
Ответ: 20
Слово ОТРЕЗОК
Ответ: 8
Слово ИНТЕРВАЛ
№ 10.*
Заполните пропуски в решении.
Растащите вспомогательные элементы по пропускам
Домножим второе и третье слагаемые на ____________
____ + _____
Разделим уравнение на ___________
___ + ____- 1 = 0
После решения
Получим ответ:
Элементы для перетаскивания
второе третье
тригонометрическую единицу
0003
0003
0003
0003
0003
0003
0003 единицу
Разделим уравнение на
Получим ответ:
№ 11.* АЗК
Решите уравнение. Впишите в формулу ответа правильные коэффициенты.
Ответ:
№ 12. **
Решите уравнение.
Выберите серии, из которых состоит решение
1)
2)
3)
4)
5)
6)
7)
Ответ: 3, 5, 6
№ 13. **
Автоматически заполняемый кроссворд
Выберите номер наименьшего положительного корня
1) 1
2)
3)
4)
5)
6)
6)
Ответ: 2
Слово РЕШЕНИЕ
Выберите номер наименьшего положительного корня
1) 1
2)
3)
4)
5)
6)
7)
Решение:
Умножим второе и третье слагаемые на тригонометрическую единицу:
Разделим уравнение на
Вспомогательное уравнение:
Оно имеет единственное кооперативное уравнение рень t = 1
Ответ: 5
Слово ТРИГОНОМЕТРИЯ
Выберите правильный ответ
1) 1
2)
3)
4)
)7)
Ответ: 4
Слово АЛГЕБРА
№ 14. ** АЗК
** АЗК
Решите уравнение. Впишите в формулу ответа правильные коэффициенты.
Решение:
Разделим обе части уравнения на
Введем новую переменную:.
Вспомогательное уравнение:
Так как t неотрицательное, то t = 1.
Поэтому
1)
2)
3)
Ответ:
Проверочная работа:
№ 1.
А) Автоматически заполняемый кроссворд
Решите уравнение. Введите значения коэффициентов
Ответ:
1) a = 1 слово ТРИГОНОМЕТРИЯ
2) b = 12 слово КОСИНУС
3) c = 1 слово МИНУС
4) d = 2 слово КВАДРА2Т 9000 Ответ :
Б) Автоматически заполняемый кроссворд
Решите уравнение. Введите значения коэффициентов
Ответ:
1) a = 1 слово УРАВНЕНИЕ
2) b = 6 слово СИНУС
3) c = 1 слово СТЕПЕНЬ
4) d = 2 слово ТОЖДЕСТВО
Ответ :
№ 2.
А) Решите уравнение. Выберите самый большой отрицательный корень.
Б) Решите уравнение. Выберите наименьший положительный корень
Ответ:
№ 3.
А) Автоматически заполняемый кроссворд
Решите уравнение. Введите значения коэффициентов
Ответ: а = 30 слово ДЕЛИМОЕ, b = 2 ДЕЛИТЕЛЬ, c = 5 слово ЧАСТНОЕ
Б) Автоматически заполняемый кроссворд
уравните.Введите значения коэффициентов
Ответ: а = 18 слово МНОЖИТЕЛЬ, b = 2 слово ПРОИЗВЕДЕНИЕ, c = 3 слово УМНОЖЕНИЕ
Конспект урока обобщения и систематизации знаний по теме «Отбор корней при решении тригонометрических уравнений» 10 класс
Конспект урока по теме
«Отбор корней при решении тригонометрических уравнений»
Класс: 10
Профиль: информационно-технологический
Учитель: МБОУ г. Москва, ул.Мурманска СОШ № 31
Москва, ул.Мурманска СОШ № 31
Иванова Татьяна Ивановна
Урок обобщения и систематизации с использованием индивидуальной,
групповой и коллективной форм работы.
Мне приходиться делить свое время между
политикой и уравнениями. Однако уравнения, по – моему,
намного важнее, потому что политика существует
только для данного момента,
а уравнения будут существовать вечно.
А. Эйнштейн
Цели урока:
Образовано: повторить различные методы и способы отбора корней при решении тригонометрических уравнений.
Развивающая: развитие ЗУН по основному блоку алгебры «Решение уравнения», в частности «Решение тригонометрических уравнений».

Воспитательная: воспитывать у обучающихся умение работать в коллективе (в парах, в группах) при выполнении различных видов работ.
Пояснение: данный конспект является фрагментом обобщающего урока по теме «Решение тригонометрических уравнений».
Предметно-аналитический анализ ЕГЭ по математике показывает, что при решении тригонометрических условий обучающиеся испытывать затруднения, при выборе решения уравнения, так и при отборе его корней, поэтому в одном из последних уроков темы целесообразно обобщить методы отбора корней при решении уравнения . Данный компонент решения является одним из основополагающих моментов изучения темы.
Для успешного усвоения темы «Решение тригонометрических правил» и в свете методической темы «Индивидуальная образовательная траектория, как средство повышения качества обучения» отработка темы была построена следующим образом:
все учащиеся класса были разбиты на группы (по два человека), каждой из которых было дано индивидуальное задание. Задания отличаются по уровню сложности, что позволяет учащемуся индивидуально подобрать тему работы в зависимости от его интеллектуальных способностей.Своё заданиещиеся оформляет видеоматериалы, таким образом на момент окончания изучения темы формируется комплект презентаций, получает каждый ученик. Это позволит им повторить теорию и практические задания при подготовке к ЕГЭ.
Задания отличаются по уровню сложности, что позволяет учащемуся индивидуально подобрать тему работы в зависимости от его интеллектуальных способностей.Своё заданиещиеся оформляет видеоматериалы, таким образом на момент окончания изучения темы формируется комплект презентаций, получает каждый ученик. Это позволит им повторить теорию и практические задания при подготовке к ЕГЭ.
Тематика предложенных заданий была такова:
Числовая окружность;
Простейшие тригонометрические уравнения;
Решение с использованием новой новой;
Решение уравнения с помощью разложения на множители;
Однородные уравнения и к ним сводящиеся;
Решение решений с помощью равенства одноименных функций;
Решение с помощью вспомогательного угла;
Универсальная тригонометрическая подстановка;
Функциональные методы решения уравнений;
Функционально-графические методы решения решений.

Арифметический метод отбора корней;
Алгебраический метод отбора корней;
Геометрический метод отбора корней.
На уроке будет представлена работа учащихся по блоку «Отбор корней тригонометрического уравнения» и проведена самостоятельная работа по выбору способов и методов отбора корней при решениигонометрических уравнений.
Ход урока:
Вступительная речь учителя. Постановка цели урока и мотивация учебной деятельности учащихся. Презентация №1
Презентация № 2 по теме «Арифметический способ отбора корней при решении тригонометрических условий». Выступление ученицы 10 класса Котляревской Марии.
Презентация № 3 по теме «Алгебраический способ отбора корней при решении тригонометрических условий». Выступление ученицы 10 класса Борлуцкой Анастасии.
Презентация № 4 по теме «Отбор корней уравнения при использовании тригонометрического круга» Выступление ученицы 10 класса Новиковой Алины.

Групповая работа учащихся по решению уравнения и указанному способу выбора корней. Анализ полученных данных и определение оптимального качества отбора корней для конкретных уравнений. Презентация № 1
Домашнее задание в виде практикума размещенного по электронному адресу «Karaulege @ ya.ru »
Вступление учителя. (Презентация №1)
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических условий специфична. Тогда отбор корней осуществляется через ОДЗ уравнения. Использование универсальной тригонометрической подстановки требует проверки установленных серий корней.Кроме того отбор корней производится при наличии дополнительного задания типа С1 на ЕГЭ. Сегодня на уроке мы заслушаем выступления ваших одноклассников, которые обобщили результаты отбора корней при решении тригонометрических уравнений, а в конце урока Вам предстоит выполнить небольшую практическую работу по теме урока.
2. Презентация №2: Арифметический способ: перебор значений целочисленного запуска и вычисление корней тригонометрического уравнения.
Перебор значений целочисленного выполнения и вычисление корней приходится
выполнять в случаях, когда требуются отобрать корни, принадлежащие заданному промежутку или некоторому условию.
Решить уравнение: и его корни на промежутке
Приложение: Презентация по теме: Арифметический способ: перебор значений целочисленного управляющего и вычисление корней тригонометрического уравнения.
(автор: ученица 10-а класса)
В процессе просмотра всех презентаций учащимися анализируются способы решения уравнения и отбора корней. Кроме этого оговариваются плюсы и минусы предлагаемых методов отбора корней при решении тригонометрических уравнений.
3. Презентация №3: Алгебраический способ: решение неравенства относительно неизвестного целочисленного процесса и вычисление корней
Алгебраический способ отбора корней наиболее удобен в тех случаях, когда последовательный перебор параметров приводит к вычислительным
трудностей, пробоотборов корней большой и при решении задач с дополнительными условиями.
Решить уравнение: и найти его корни на промежутке
Приложение: Презентация по теме: Алгебраический способ: решение неравенства неизвестного целочисленного задачи и вычисление корней
тригонометрического уравнения.
(автор: ученица 10-а класса)
Презентация №4: Геометрический способ: отбор корней тригонометрического уравнения в числовой окружности
Тригонометрическую окружность удобно использовать при отборе корней на
9000 длина не 2 превосходит, или в случае, когда значения обратных тригонометрических функций, входящие в серию решений, не являютсятабличными.
Решить уравнение: и его корни на промежутке
Решить уравнение: и найти его корни на промежутке
Примечание: в данном уравнении анализируется удобство применения данного метода для случая, когда уравнения корни не являются табличными значениями.
(автор: ученица 10-а класса)
Индивидуальная работа по группам.
 Презентация №1
Презентация №1
Учащиеся класса во время урока разбиты на три группы, из предложенного решить одно и то же уравнение и выполнить отбор корней из предложенного промежутка определенным способом.
Решить уравнение и найти его корни на промежутке
различными способами:
1 группа перебором целочисленного программы;
2 группа решения двойного неравенства;
3 группа с помощью тригонометрического круга.
Вывод: так как при решении мы получаем две серии корней, рассматриваемый промежуток имеет длину не более, то наиболее является геометрический способ отбора корней. Следует указать при разборе заданий, что при решении каждый решающий выбирает способ отбора корней удобный для него лично.
Домашнее задание в виде практикума по теме «Решение тригонометрических условий» размещено по электронному адресу «Karaulege @ ya.RU».
Литература:
1.

 Укажите корни, принадлежащие отрезку .
Укажите корни, принадлежащие отрезку .
 1я721. в.., 2018 ISBN
1я721. в.., 2018 ISBN  1
1  1я721. в .., 2018 ISBN
1я721. в .., 2018 ISBN  1
1  однородные тригонометрические уравнения — Алгебра и начала математического анализа — 10 класс
однородные тригонометрические уравнения — Алгебра и начала математического анализа — 10 класс 


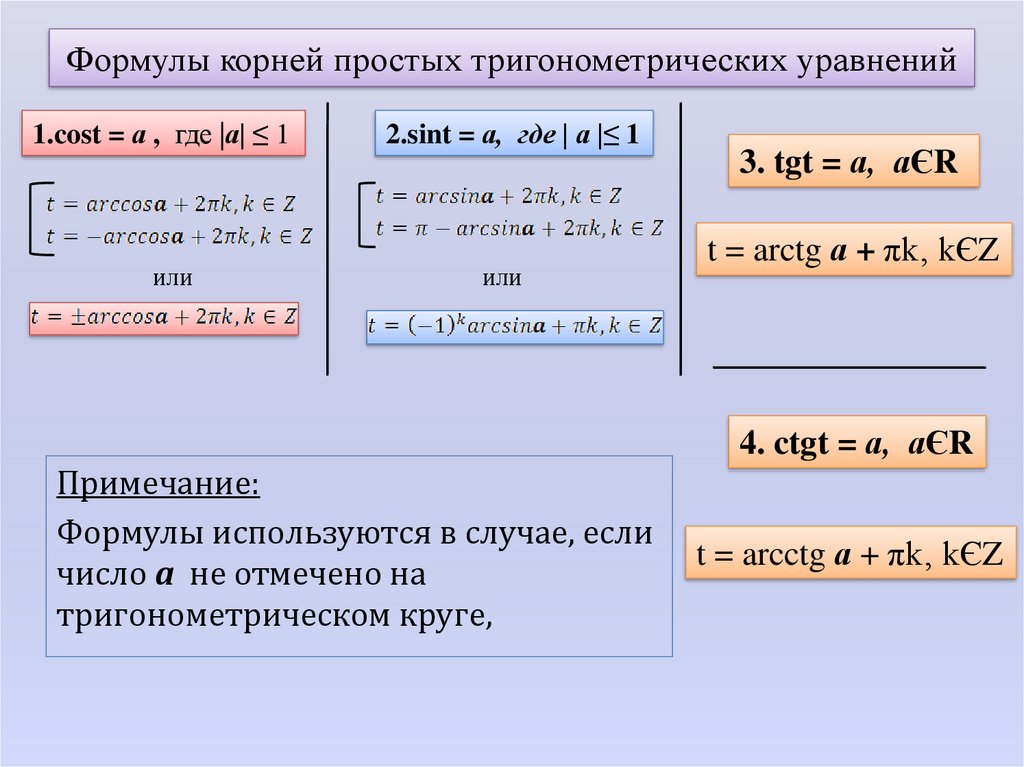 Презентация №1
Презентация №1