Решение тригонометрических уравнений методом замены переменной
Тип урока
: изучение нового материала.Цели урока
:- Познакомить учащихся с методом решения тригонометрических уравнений методом замены переменной.
- Формировать умения анализировать, устанавливать связь между элементами содержания ранее изученного материала, навыки поисковой деятельности, способность к самоанализу, рефлексии.
- Содействовать развитию познавательного интереса и личностной активности учащихся; создать условия для творческой самореализации личности.
Оборудование урока:
- экран,
- мультимедиа проектор,
- компьютер,
- авторская презентация к уроку,
- набор карточек для конструирования уравнений на магнитной доске,
- комплекты дидактической игры “Лото”,
- бланки с заданием теста.

Компьютерное программное обеспечение
: программа Power PointНа уроке сочетаются фронтальный, парный и индивидуальный виды работы учащихся. У каждого ученика на рабочем месте находиться листы индивидуальной работы, на которых он подписывает свою фамилию, строит график самоанализа своей деятельности на занятии. Для самоанализа своей деятельности на занятии ученики строят график. На вертикальной оси отмечают самооценку от 1 до 5, а по горизонтальной отмечают этапы урока
Ход урока
Организационный момент. (1 мин.)
Учитель: Методы решения
тригонометрических уравнений разрабатывались
математиками уже многие годы. Ими выделены
различные классы тригонометрических уравнений,
для которых известны алгоритмы решения. Сегодня
на уроке мы рассмотрим один из методов решения
тригонометрических уравнений – “ Метод замены
переменной”.
I этап. (6 мин.) Учащиеся отвечают на вопросы учителя: Какие уравнения называются тригонометрическими? Что значить решить тригонометрическое уравнение? Какие тригонометрические уравнения относятся к простейшим? При каком условии уравнения имеют решения? Какие уравнения называются квадратными? Какие виды квадратных уравнений они знают? Какова связь числа корней квадратного уравнения с его дискриминантом? Ответы иллюстрируются слайдами презентации на экране
Ученики в парах выполняют задания теста по
теме: “Простейшие тригонометрические
уравнения”. По окончании работы над тестом
учитель показывает правильные ответы на экране.
Пары обмениваются бланками с тестовыми
заданиями и проводят взаимопроверку. Во время
проверки ученики корректируют свои знания по
этой теме. Ученики отмечают свою оценку на
графике и сдают бланк учителю. Критерии оценок:
“5”-5 верных ответов, “4”-4 верных ответа, “3”-3
верных ответа, “2”-1-2 верных ответа.
Во время
проверки ученики корректируют свои знания по
этой теме. Ученики отмечают свою оценку на
графике и сдают бланк учителю. Критерии оценок:
“5”-5 верных ответов, “4”-4 верных ответа, “3”-3
верных ответа, “2”-1-2 верных ответа.
Tест. Вариант№1.
Задание. Найдите ошибку.
Правильные ответы отметь кругом.
Ответ: 3,4,5,7,8
Tест. Вариант№2.
Задание. Найдите ошибку.
Правильные ответы отметь кругом
Ответ: 2,4,5, 8,9
II этап. Объяснение нового материала (10 мин).
Учитель:- Проанализируйте два уравнения и ,где заданные числа и определите какое из этих уравнений сложнее и почему?
Учащиеся: – Второе уравнение сложнее, так
как в него входят две тригонометрические функции
,.
Начинаем искать метод решения первого уравнения. Так как в этом уравнении коэффициенты известные числа и у двух элементов один и тот же аргумент обращаемся к аналогичной ситуации в алгебраических уравнениях. Вспоминаем с учащимися, что для решения, уравнения вида , где заданные числа, делаем замену , при этом отвечаем на вопросы подтверждающие возможность замены: Можно ли решить “новое” уравнение? Будет ли работать данный метод при решении тригонометрического уравнения. Отвечая на эти вопросы, приходим к выводу, что уравнение можно решать заменой .
| Шаги алгоритма | Возможные ошибки | Пути исправления ошибок | |
| 1 | Замена переменной. | Неправильно записано новое уравнение. |
Проверить запись нового уравнения |
| 2 | Решение квадратного уравнения. | Ошибки при вычислении корней квадратного уравнения. | Проверить правильность решения квадратного уравнения различными способами. |
| 3 | Решение простейших тригонометрических уравнений | Формальное применение формул для решения простейших уравнений. Неправильно решены уравнения при частных случаях | Вспомнить ограниченность синуса и косинуса, выучить формулы для решения простейших уравнений, частных случаев. |
Пример 1. Решить уравнение .
В итоге ученики совместно с учителем выделяют
шаги реализации рассматриваемого метода и
формулируют алгоритм решения данного уравнения,
заполняют таблицу. Шаги алгоритма, возможные
ошибки и пути их исправления иллюстрируются
слайдами презентации на экране.
Шаги алгоритма, возможные
ошибки и пути их исправления иллюстрируются
слайдами презентации на экране.
Учитель: – Какие уравнения могут иметь аналогичный метод решения?
Учащиеся: – Это уравнения вида: , , где заданные числа.
Учитель:- Вернемся ко второму уравнению . Чем оно отличается от уже решенного уравнения? Можно ли свести это уравнение к уравнению с одной функцией?
Учащиеся: – Его можно свести к уравнению с одной функцией, применяя формулу . Уравнение в этом случае примет вид: или .
В итоге ученики совместно с учителем разбирают, как можно решить уравнения вида и гдезаданные числа.
III этап (18 мин). “Конструктор” Задание 1. Составьте уравнения рассматриваемых видов из предложенных выражений, если корнями это уравнения являются числа:
а) ;
б) ;
в) ,
На магнитной доске трое учеников собирают
полученные уравнения, а остальные учащиеся
сверяют свои записи с полученными уравнениями,
результаты отмечают на графике.
“Крестики- нолики” Задание 2. Предварительное домашнее задание: решите уравнения, для каждого уравнения из таблицы укажите его вид и способы какими его можно решить.
“Крестики- нолики”: вычеркните прямой линией три уравнения, которые не имеют решения Таблица №1
Ответы: линия 1,5,9.
Критерии оценки: ”5” верный и полный ответ , “4”– ответ с одной ошибкой, “3”– ответ с двумя ошибками , “2”– неверный ответ.
Задание 3. Решите задачи с параметром.
Задача 1.
Задача 2. Определить, при каких значениях
параметра
уравнение
имеет решения. Решите уравнение.
Учащийся по желанию выходят к доске для оформления решения задач.
VI этап. (7 мин) Класс приступает к решению задач в группах. Учащиеся выполняют задания в зависимости от восприятия материала
“Лото”. У каждого ученика на рабочем месте находится лото, которое состоит из поля 3 1 и 6 двусторонних карточек. На клетках поля записаны уравнения, на лицевых сторонах карточек – ответы к уравнениям, на обратных сторонах – буквы, которые вместе позволят ответить на вопрос. Какой математик однажды заметил что: “Математическую теорию можно считать совершенной только тогда, когда ты сделал ее настолько ясной, что берешься изложить ее содержание первому встречному”?
Ответ: Гильберт.
Ответы иллюстрируются слайдами презентации на
экране. Необходимо проверить решение задач,
поэтому от каждой группы выступает учащийся,
демонстрируя решение задач на доске.
Итог урока (2 мин) Подводя итог урока, учитель и учащиеся выясняют на каком этапе учащиеся испытывают наибольшие затруднения, какие задания для них были наиболее интересными, на что они должны обратить внимание при решении домашнего задания.
VI этап. Домашнее задание (1мин.)
Алгебра и начала анализа. Ч.1.Учебник для 10 класс А. Г. Мордкович, П.В.Семенов (профильный уровень). §34 п.1.стр179-180.
1-й уровень – задания репродуктивного характера – Решить уравнения №23.4(б), №23. 5(г), №23.7(б). Ч.2.Задачник для 10 кл. А.Г.Мордкович и д.р (профильный уровень) Алгебра и начала анализа. Решить задачу. Определить, при каких значениях параметра уравнение имеет решения.
2-й уровень – задания поискового плана:
подобрать тригонометрические уравнения
аналогичные уравнениям 1,5,9 из таблицы №1;
Подобрать и решить задачу по физике при решении
которой встречаются уравнения, рассмотренные на
уроке.
3-й уровень – творческое; составить задания к дидактической игре “Лото” по теме: “ Решение тригонометрических уравнений методом замены переменной”.
Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений
Решая тригонометрические уравнения, используют общие принципы решения алгебраических уравнений. При использовании неравносильных преобразований уравнений необходимо выполнить проверку принадлежности найденных значений неизвестного к корням исходного уравнения.
Практически каждое уравнение можно решить несколькими способами, что при правильно выполненных действиях даст один и тот же окончательный результат. Бывают случаи, что разные методы дают разные результаты, которые можно привести к одинаковому виду с помощью тождественных преобразований.
Рассмотрим на примерах наиболее используемые методы решения тригонометрических уравнений.
- Метод замены переменной
Решим уравнение .
Решение.
Выполним замену тригонометрической функции любой переменной:
Так как функция синус ограничена значениями от —1 до 1, то и к переменной z должны применяться эти же ограничения.
Подставим новую переменную в исходное уравнение:
Данное уравнение имеет два корня:
Проверяем полученные значения на ограничения. Поскольку оба значения удовлетворяют условию, что переменная z должна быть больше —1 и меньше 1, возвращаемся к тригонометрической функции и получаем два уравнения:
и
Решив оба уравнения, получаем корни исходного уравнения:
и
Ответ. , .
- Равенство одинаковых тригонометрических функций
Для данного метода используются следующие уравнения:
— при варианте принимается
— при принимается
— при принимается
Решим уравнение
Решение.
Поскольку функции одинаковые, то их аргументы будут также одинаковы. Решим новое уравнение:
Решим новое уравнение:
Решая уравнение, получаем:
При чётном r получаем корень:
При нечётном r получаем корень:
- Метод разложения на множители
Решим уравнение .
Решение.
или
1)
2)
Ответ. , .
- Метод приведения к однородному уравнению
Решим уравнение
Решение.
Используем формулу двойного угла и основное тригонометрическое тождество, перейдем к половинному аргументу:
Разделим на :
Получили уравнение от одной переменной, которое решается методом 1.
Методы решения тригонометрических уравнений. 10 класс
1. Методы решения тригонометрических уравнений
2.
 Содержание
Содержание Метод замены переменной
Метод разложения на множители
Однородные тригонометрические уравнения
С помощью тригонометрических формул:
− Формул сложения
− Формул приведения
− Формул двойного аргумента
3. Метод замены переменной
С помощью замены t = sinx или t = cosx, где t ∈ [−1;1]решение исходного уравнения сводится к решению
квадратного или другого алгебраического уравнения.
См. примеры 1 – 3
Иногда используют универсальную тригонометрическую
x
подстановку: t = tg
2
α
1 tg
1 t2
2
cos α
2
α
1
t
2
1 tg
2
2
α
2tg
2
2t
sin α
2
α
1
t
2
1 tg
2
4. Пример 1
2 sin 2 x 5 sin x 2 0Пусть sin x t , где t 1; 1 , тогда
2t 2 5t 2 0
t1 2, не удовлетворяет условию t 1; 1
t 2 1 ;
2
Вернемся к исходной переменной
1
sin x
2
x 1 arcsin
n
x 1
n
1
πn , n Z
2
π
πn , n Z
6
π
Ответ : 1
πn , n Z .

6
n
5. Пример 2
cos 2 x sin 2 x cos x 0Поскольку sin 2 x 1 cos2 x , то
cos2 x 1 соs2x cos x 0
2cos 2 x cos x 1 0
Пусть соsx t , где t 1; 1 , тогда
2t 2 t 1 0
t1 1,
t 2 1 ;
2
Вернемся к исходной переменной :
x 2πk , k Z
соsx 1,
x 2πk , k Z
1
1
cos x ;
x arccos 2πn , n Z
x 2π 2πn , n Z
2
3
2
Ответ : 2πk , k Z ;
2π
2πn , n Z .
3
6. Пример 3
tgx
x
3ctg 4
2
2
Поскольку ctg
Вернемся к исходной переменной
x
1
, то
2 tg x
2
tg
tg
x
3
4
x
2 tg
2
x
Пусть tg t , где t 0, тогда
2
3
t 4
t
t
t 2 4t 3 0
tg
t1 1
t 3
2
x
x
1,
arctg1 πn , n Z
2
2
x
x arctg 3 πk , k Z
3;
2
2
x
2 arctg1 πn , n Z
x arctg 3 πk , k Z
2
x π
2 4 πn , n Z
x 2arctg 3 πk , k Z
π
x
2πn , n Z
2
x 2arctg 3 2πk , k Z
Ответ :
π
2πn ; 2arctg 3 2πk ; n , k Z .

2
7. Метод разложения на множители
Суть этого метода заключается в том, чтопроизведение нескольких множителей равно нулю,
если хотя бы один из них равен нулю, а другие при
этом не теряют смысл:
f(x) · g(x) · h(x) · … = 0
⟺ f(x) = 0 или g(x) = 0 или h(x) = 0
и т.д. при условии существования каждого из сомножителей
См. примеры 4 – 5
8. Пример 4
12
sin x cos x 0
3
5
1
sin x 3 0,
cos x 2 0;
5
x
x
1
sin
x
,
3
cos x 2 ;
5
1
1
n
n
x 1 arcsin πn , n Z
1 arcsin πn , n Z
3
3
2
x π arccos 2 2πk , k Z
arccos 2πk , k Z
5
5
Ответ : 1 arcsin
n
1
2
πn ; π arccos 2πk ; n ,k Z .
3
5
9. Пример 5
2sin x cos 5x cos 5x 0cos 5x 2sin x 1 0
2 sin x 1 0,
cos 5x 0;
1
sin
x
,
2
cos 5x 0;
1
n
x
1
arcsin
πn , n Z
2
5x π πk , k Z
2
n π
x
1
πn , n Z
6
x π πk , k Z
10
5
π πk
n π
Ответ : 1
πn , n Z ;
, k Z.

6
10
5
10. Однородные тригонометрические уравнения
Уравнение вида a sin x + b cos x = 0 называютоднородным тригонометрическим уравнением
первой степени.
a sin x + b cos x = 0
a sin x b cos x
0
cos x + cos x = cos x
a tg x + b = 0
b
tg x = –
a
: cos x
Замечание.
Деление на cos x допустимо, поскольку решения
уравнения cos x = 0 не являются решениями
уравнения a sin x + b cos x = 0.
11. Однородные тригонометрические уравнения
Уравнение вида a sin2x + b sin x cos x + c cos2x = 0называют однородным тригонометрическим
уравнением второй степени.
: cos2x
a sin2x + b sin x cos x + c cos2x = 0
a sin2x
b sin x cos x
c cos2x
0
+
=
+
2x
2
2
cos
cos x
cos2x
cos x
a tg2x + b tg x + c = 0
Далее, вводим новую переменную tg x = t и решаем
методом замены переменной.
Замечание. Если в данном уравнении а = 0 или с = 0
то, уравнение решается методом разложения
на множители.

12. Пример 6
2sin x 3cos x 0: cos x
2 sin x 3 cos x
0
cos x
cos x
cos x
2tgx 3 0
tgx
3
2
3
x arctg πn , n Z
2
Ответ : arctg
3
πn , n Z .
2
Пример 7
: cos 2x
sin 2x cos 2x 0
sin 2x cos 2x
0
cos 2x cos 2x cos 2x
tg 2x 1 0
tg 2x 1
π
2x πn , n Z
4
π πn
x
, n Z
8
2
π πn
Ответ :
, n Z.
8
2
13. Пример 8
sin 2 x 3 sin x cos x 2cos 2 x 0sin 2 x 3 sin x cos x 2cos 2 x
0
2
2
2
cos x
cos x
cos x
: cos2 x
tg 2x 3tgx 2 0
Пусть tgx t , тогда
t 2 3t 2 0
t1 1
t 2
2
Вернемся к исходной переменной :
π
tgx 1,
x
πn , n Z
4
tgx 2;
x arctg 2 πk , k Z
Ответ :
π
πn ; arctg 2 πk ; n ,k Z .
4
14. Пример 9
3 sin x cos x cos2 x 0cos x 3 sin x cos x 0
3 sin x cos x 0,
cos x 0;
: sin x
3 сtgx 0,
ctgx 3
x n, n Z ;
x n, n Z ;
2
2
5
x arсrсc 3 k , k Z ,
x
k , k Z ,
6
x n, n Z ;
x n, n Z .

2
2
Ответ :
5
k ;
6
2
n; n, k Z .
15. Пример 10
sin 3 x sin 2 x cos x 3 sin x cos 2 x 3cos 3 x 0: cos3 x
sin 3 x sin 2 x cos x 3 sin x cos 2 x 3cos 3 x
0
3
3
3
3
cos x
cos x
cos x
cos x
tg 3 x tg 2x 3tgx 3 0
tg 2x tgx 1 3 tgx 1 0
tg
2
x 3 tgx 1 0
tg x 3 0,
tgx 1 0;
2
tg x 3,
tgx 1;
2
x arctg 3 πk , k Z ,
x π πn , n Z ;
4
Ответ :
tgx 3 ,
x π πn , n Z ;
4
π
x
πk , k Z ,
3
x π πn , n Z .
4
π
π
πn ; πk ; n , k Z .
4
3
16. Пример 11
3 sin 2 3x 2 3 sin 3x cos 3x 5cos2 3x 2cos2 3x sin 2 3x
3 sin 2 3x 2 3 sin 3x cos 3x 5 cos 2 3x 2 cos 2 3x sin 2 3x
3 sin 2 3x 2 3 sin 3x cos 3x 5cos2 3x 2cos2 3x 2sin 2 3x 0
sin 2 3x 2 3 sin 3x cos 3x 3cos2 3x 0
: cos2 3x
sin 2 3x 2 3 sin 3x cos 3x 3 cos 2 3x
0
2
2
2
cos 3x
cos 3x
cos 3x
tg 2 3x 2 3tg 3x 3 0
Вернемся к исходной переменной
Пусть tg 3x t , тогда
tg 3x 3
3x arctg 3 πn , n Z
t 2 2 3t 3 0
3
t 3 0
π
πn , n Z
3
π πn
x
,n Z
9
3
t 3
Ответ :
t 2 3t
2
t 3
2
0
2
0
3x
π πn
, n Z.

9
3
17. С помощью тригонометрических формул
1. Формулы сложения:sin (x + y) = sinx cosy + cosx siny
sin (x − y) = sinx cosy + cosx siny
cos (x + y) = cosx cosy − sinx siny
cos (x − y) = cosx cosy + sinx siny
tg (x + y) =
tg (x − y) =
tgx + tgy
1 − tgx tgy
tgx − tgy
1 + tgx tgy
сtgx сtgy − 1
сtg (x + y) =
сtgу + с tgх
сtgx сtgy + 1
сtg (x − y) =
сtgу − с tgх
18. Пример 12
3 cos x sin x 1:2
3
1
1
cos x sin x
2
2
2
3
π 1
π
Заметим, что
cos ,
sin , тогда
2
6 2
6
π
π
1
cos cos x sin sin x
6
6
2
π
1
cos x
6
2
π
1
x arccos 2πn , n Z
6
2
π π
x 2πn , n Z
3 6
π π
Ответ : 2πn , n Z .
3 6
19. Пример 13
ππ
sin x cos x 3
3
6
π
π
π
π
π
π
sin x cos x sin cos x cos sin x cos cos x sin sin x
3
3
6
6
3
6
3
1
3
1
cos x sin x
cos x sin x 3 cos x
2
2
2
2
3 cos x 3
cos x 1
x 2πn , n Z
Ответ : 2πn , n Z
20.
 С помощью тригонометрических формул 2. Формулы приведения:
С помощью тригонометрических формул 2. Формулы приведения:π
sin t cos t
2
sin π t sin t
π
cos t sin t
2
cos π t cos t
3π
sin
t cos t
2
3π
cos
t sin t
2
sin 2π t sint
cos 2π t cos t
π
tg t ctg t
2
tg π t tg t
π
ctg t tg t
2
ctg π t ctg t
3π
tg
t ctg t
2
tg 2π t tg t
3π
ctg
t tg t
2
ctg 2π t ctg t
21. Лошадиное правило
Встарые
добрые
времена
жил
рассеянный математик, который при
поиске ответа менять или не менять
название функции (синус на косинус),
смотрел на свою умную лошадь, а она
кивала
головой
вдоль
той
оси
координат,
которой
принадлежала
точка,
соответствующая
первому
слагаемому аргумента π/ 2 + α или π + α.
Если лошадь кивала головой вдоль оси
ОУ, то математик считал, что получен
ответ «да, менять», если вдоль оси ОХ,
то «нет, не менять».

22. С помощью тригонометрических формул
3. Формулы двойного аргумента:sin 2x = 2sinx cosx
cos 2x = cos2x – sin2x
2tgx
tg 2x =
1 – tg2x
ctg2x – 1
ctg 2x =
2ctgx
cos 2x = 2cos2x – 1
cos 2x = 1 – 2sin2x
23. Пример 14
sin 4x cos 2x 02sin 2x cos 2x cos 2x 0
cos 2x 2sin 2x 1 0
cos 2x 0,
2 sin 2x 1 0;
cos 2x 0,
sin 2x 1 ;
2
π
2
x
πn , n Z
2
2x 1 k arcsin 1 πk , k Z
2
Ответ :
π πn
,n Z;
4
2
π πn
x
,n Z
4
2
x 1 k π πk , k Z
12
2
π πk
1
, k Z.
12
2
k
24. С помощью тригонометрических формул
4. Формулы понижения степени:sin 2 α
1
1 cos 2α
2
1
cos α 1 cos 2α
2
2
sin α cos α
1
sin 2α
2
sin α cos α 2 1 sin 2α
5. Формулы половинного угла:
α
1 cos α
sin
2
2
cos
α
1 cos α
2
2
α
sin α
1 cos α
tg
2 1 cos α
sin α
α
sin α
1 cos α
ctg
2 1 cos α
sin α
25.
 С помощью тригонометрических формул 6. Формулы суммы и разности:
С помощью тригонометрических формул 6. Формулы суммы и разности:cos α cos β 2cos
α β
α β
cos
2
2
α β
β α
cos α cos β 2 sin
sin
2
2
sin α sin β 2 sin
α β
α β
cos
2
2
α β
α β
sin α sin β 2 sin
cos
2
2
sin( α β )
tg α tg β
cos α cos β
sin( α β )
tg α tg β
cos α cos β
sin( α β )
ctg α ctg β
sin α sin β
ctg α ctg β
sin( β α )
sin α sin β
26. С помощью тригонометрических формул
7. Формулы произведения:1
cos α cos β cos α β cos α β
2
1
sin α sin β cos α β cos α β
2
1
sin α cos β sin α β sin α β
2
27. Мнемоническое правило “Тригонометрия на ладони”
Очень часто требуется знатьнаизусть значения cos, sin, tg, ctg
для углов 0°, 30°, 45°, 60°, 90°.
Но если вдруг какое-либо значение
забудется, то можно
воспользоваться правилом руки.

Правило: Если провести линии
через мизинец и большой палец,
то они пересекутся в точке,
называемой “лунный бугор”.
Образуется угол 90°. Линия мизинца образует угол 0°.
Проведя лучи из “лунного бугра” через безымянный, средний,
указательный пальцы, получаем углы соответственно 30°, 45°, 60°.
Подставляя вместо n: 0, 1, 2, 3, 4, получаем значения sin, для
углов 0°, 30°, 45°, 60°, 90°.
Для cos отсчет происходит в обратном порядке.
Решение тригонометрических уравнений методом замены переменной
Отбор корней с помощью единичной окружности
Решение системы тригонометрических уравнений методами замены переменных
Большая перемена онлайн репетитор Уроки и занятия online 007 tutorsПовышение успеваемости Математика
— We cannot solve problems by using the same kind of thinking we used when we created them.
Albert Einstein.
— Мы никогда не решим проблемы, если будем думать так же, как тогда, когда их создали.
Альберт Эйнштейн
- Марьино,
- Борисово,
- Шипиловская,
- Воробьёвы горы,
- Беляево,
- Коньково,
- Калужская,
- Профсоюзная,
- Ленинский проспект,
- Шаболовская
Тригонометрия на ЕГЭ по математике. К дополнительным баллам на ЕГЭ
Решение тригонометрических уравнений и их систем методом симметричной замены переменной.Пример ДВИ в МГУ.
Дано уравнение.а) Решите уравнения.
б) Укажите корни, принадлежащие отрезке.
Решение.
Сразу оговорим ограничения, накладываемые на переменную в этом уравнении
Откуда взялось это ограничение?
Правильно, функция не существует при этих значениях
Используем замену переменной
Тогда уравнение принимает вид ДВИ МГУ
Переходим к обратной замене
Отбор нужных корней с помощью единичной окружности.

Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий
Обратите внимание на один существенный момент.
На рисунке одни точки принадлежат оси тангенсов, а другие точки — единичной окружности.
Как решать с помощью замены — на видео репетитора Алексея Э. Султанова.
Тригонометрические уравнения с решением и объяснением
Замена переменной и сведение ко квадратному уравнению.
Это — универсальный способ.Применяется в любых уравнениях степенных, показательных, тригонометрических, логарифмических, каких угодно.
Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.
В предыдущем разделе мы решили это уравнение, сведя его к однородному,
и получили в качестве ответа выражение методом Султанова.
Сравните с полученным только что выражением.
А ведь это одно и то же множество решений!
Универсальная подстановка.
Надо обязательно помнить формулы косинуса и синуса тройного угла(чтобы не изобретать их на экзамене):
cos 3α = 4 cos³ α − 3 cos α,
sin 3α = 3 sin α − 4 sin³ α.

Вот, например, уравнение на ЕГЭ-2020.
cos (x) cos (2x) sin (3x) = sin (2x)/ 4
Посмотреть, как решать с помощью замены переменных уравнение с синусом и косинусом, можно на видеоуроке репетитора.
Методы решения тригонометрических уравнений Учитель математики: Семёнова
Описание презентации Методы решения тригонометрических уравнений Учитель математики: Семёнова по слайдам
Методы решения тригонометрических уравнений Учитель математики: Семёнова Елена Юрьевна. МБОУ СОШ № 5 – «Школа здоровья и развития» г. Радужный
Содержание • Метод замены переменной • Метод разложения на множители • Однородные тригонометрические уравнения • С помощью тригонометрических формул: − Формул сложения − Формул приведения − Формул двойного аргумента
Метод замены переменной С помощью замены t = sinx или t = cosx , где t ∈ [− 1; 1] решение исходного уравнения сводится к решению квадратного или другого алгебраического уравнения. См. примеры 1 – 3 2 2 1 1 2 1 t t tg tg cos α α α 221 2 2 t t tg tg sin α α α Иногда используют универсальную тригонометрическую подстановку: t = tg x
См. примеры 1 – 3 2 2 1 1 2 1 t t tg tg cos α α α 221 2 2 t t tg tg sin α α α Иногда используют универсальную тригонометрическую подстановку: t = tg x
Пример 102522 xsin ; tусловиюяетудовлетворне, t tt тогда, ; tгде, txsin. Пусть 21 112 0252 11 21 2 2 1 xsin переменнойисходнойк. Вернемся Zn, narcsinx n π 21 1 Zn, nx nπ 6 π 1. Zn, n: Ответ n π 6 π
Пример 2022 xcosxsinxcos ; t , t tt тогда, ; tгде, tсоsx. Пусть 2 1 1 012 11 21 2 ; xcos , соsx : переменнойисходнойк. Вернемся 2 1 1 Zn, narccosx Zk, kx π2 21π2 то, xcosxsin. Поскольку221 0122 xcosxсоsxcos 0122 xcos Zn, nx Zk, kx π2 3 π2 π2. Zn, n; Zk, k: Ответπ2 3 π2 π
Пример 34 2 3 2 x ctg x tg 31 034 43 0 2 212 tt tt тогда, tгде, tx tg. Пусть ; x tg , x tg переменнойисходнойк. Вернемся 3 2 1 2 то, x tgx ctg. Поскольку 21 2 4 2 3 2 x tg Zk, karctg x Zn, narctg x π3 2 π1 2 Zk, karctgx Zn, nx π32 π 4π 2 Zk, karctgx Zn, nx π232 π2 2 π. Zk, n; karctg; n: Ответπ232π2 2 π
Zk, n; karctg; n: Ответπ232π2 2 π
Метод разложения на множители Суть этого метода заключается в том, что произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а другие при этом не теряют смысл: f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0 и т. д. при условии существования каждого из сомножителей См. примеры 4 –
Пример 40 5 2 3 1 xcosxsin ; xcos , xsin 0 5 2 0 3 1 ; xcos , xsin 5 231 Zk, karccosx Zn, narcsinx n π2 5 2 π 31 1 Zk, karccosx Zn, narcsinx n π2 5 2 π π 31 1. Zk, n; karccos; narcsin: Ответ n π2 5 2 ππ
Пример 5 ; xcos , xsin 05 012 ; xcos , xsin 05 21 Zk, kx Zn, narcsinx n π 2 π 5 π 2 1 1 Zk, k x Zn, nx n 5 π 10 π π 6 π 1 0552 xcosxsin 0125 xsinxcos. Zk, k ; Zn, n: Ответ n 5 π 10 π π 6 π
Однородные тригонометрические уравнения Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени. a sin x + b cos x = 0 Замечание. Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0. : cos x a sin x b cos x 0 cos x + cos x = cos x a tg x + b = 0 tg x = – a b
a sin x + b cos x = 0 Замечание. Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0. : cos x a sin x b cos x 0 cos x + cos x = cos x a tg x + b = 0 tg x = – a b
Однородные тригонометрические уравнения a sin 2 x + b sin x cos x + c cos 2 x = 0 Уравнение вида a sin 2 x + b sin x cos x + c cos 2 x = 0 называют однородным тригонометрическим уравнением второй степени. : cos 2 x a tg 2 x + b tg x + c = 0 a sin 2 x b sin x cos x c cos 2 x 0 cos 2 x + cos 2 x = cos 2 x+ cos 2 x Далее, вводим новую переменную tg x = t и решаем методом замены переменной. Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения на множители.
032 xcosxsin xcos xsin 032 tgx 2 3 tgx Zn, narctgxπ 2 3. Zn, narctg: Ответπ 2 3 Пример 7 022 xcosxsin xcos xsin 20 22 22 012 xtg Zn, nxπ 4 π 2. Zn, n : Ответ 2 π 8 π Zn, n x 2 π 8 π xcos: 2 Пример
02322 xcosxsin 0 23 2 2 22 2 xcosxsin xcos xsin 0232 tgxxtg 2 1 023 212 t t tt тогда, ttgx. Пусть ; tgx , tgx : переменнойисходнойк. Вернемся 2 1 Zk, karctgx Zn, nx π2 π 4 π. Zk, n; karctg; n: Ответπ2π 4 π xcos: 2 Пример
Пусть ; tgx , tgx : переменнойисходнойк. Вернемся 2 1 Zk, karctgx Zn, nx π2 π 4 π. Zk, n; karctg; n: Ответπ2π 4 π xcos: 2 Пример
032 xcosxsin 03 xcosxsinxcos ; xcos , xcosxsin 0 03 ; Zn, nx , tgx π 2 π 3 1 π 2 π 013 . Zn, nx , Zk, kx ; Zn, nx , Zk, karctgx π 2 π π 6 π π 2 π π 3 1. Zk, n; n; k: Ответπ 2 π π 6 π xcos: Пример
033 3223 xcosxsinxcosxsin 03323 tgxxtgxtg ; Zn, nx , tgx ; tgx , xtg π 4 π 3 1 3 01 0322. Zk, n; k; n: Ответπ 3 π π 4 π 0 33 3 2 3 3 xcosxsin xcosxsin xcos xsin 01312 tgxtgxxtg 0132 tgxxtg . Zn, nx , Zk, kx ; Zn, nx , Zk, karctgx π 4 π π 3 π π 4 π π3 xcos: 3 Пример
23533323322 xcosxsin 0 3 3332 33 2 2 222 xcosxsin xcos xsin 0333232 xtgxtg 3 03 03 0332 3 2 2 22 t tt tt тогда, txtg. Пусть33 xtg переменнойисходнойк. Вернемся Zn, n x Zn, narctgx 3π 9π π 3π 3 π33. Zn, n : Ответ 3 π 9 π xsinxcosxcosxsin 33235333233 2222 03232353332332222 xsinxcosxcosxsin 0333332322 xcosxsinxcos: 32 xsinxcos 3322 Пример
С помощью тригонометрических формул 1. Формулы сложения: sin (x + y) = sinx cosy + cosx siny cos (x + y) = cosx cosy − sinx siny tgx + tgy tg (x + y) = 1 − tgx tgysin (x − y) = sinx cosy + cosx siny cos (x − y) = cosx cosy + sinx siny tgx − tgy tg (x − y) = 1 + tgx tgy сtgx сtgy − 1 сtg (x + y) = сtgу + с tgх сtgx сtgy + 1 сtg (x − y) = сtgу − с tgх
Формулы сложения: sin (x + y) = sinx cosy + cosx siny cos (x + y) = cosx cosy − sinx siny tgx + tgy tg (x + y) = 1 − tgx tgysin (x − y) = sinx cosy + cosx siny cos (x − y) = cosx cosy + sinx siny tgx − tgy tg (x − y) = 1 + tgx tgy сtgx сtgy − 1 сtg (x + y) = сtgу + с tgх сtgx сtgy + 1 сtg (x − y) = сtgу − с tgх
13 xsinxcos. Zn, n: Ответπ2 6 π 3 π 2: 2 1 2 3 xsinxcos тогда, sin, cosчто, Заметим 6 π 2 1 6 π 2 3 2 1 6 π xsinsinxcoscos 2 1 6 π xcos. Zn, narccosx π2 21 6π Zn, nxπ2 6 π 3 π Пример
3 6 π 3 π xcosxsin xsinsinxcoscosxsincosxcossinxcosxsin 6 π 3 π 6 π 33 xcos 1 xcos Zn, nxπ2 Zn, n: Ответπ2 xcosxsinxcos 3 2 1 2 3 Пример
С помощью тригонометрических формул 2. Формулы приведения: ttgt 2π ctg tctgtπctg ttgt 2 3π ctg tctgt 2πctg tctgt 2 π tg ttgtπtg tctgt 2 3π tg ttgt 2πtg tsint 2π cos tcostπcos tsint 2 3π cos tcost 2πcos tcost 2π sin tsintπsin tcost 2 3π sin tsint 2πsin
Лошадиное правило В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции ( синус на косинус ), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α. Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .
Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .
С помощью тригонометрических формул 3. Формулы двойного аргумента: sin 2 x = 2 sinx cosx cos 2 x = cos 2 x – sin 2 x cos 2 x = 2 cos 2 x – 1 cos 2 x = 1 – 2 sin 2 x tg 2 x = 2 tgx 1 – tg 2 x ctg 2 x = 2 ctgxctg 2 x –
024 xcosxsin. Пример 14 02222 xcosxsin 01222 xsinxcos ; xsin , xcos 0122 02 ; xsin , xcos 2 1 2 02 Zk, karcsinx Zn, nx k π 2 1 12 π 2 Zk, k x Zn, n x k 2 π 1 2 π 4 π. Zk, k ; Zn, n : Ответ k 2 π 1 2 π 4 π
С помощью тригонометрических формул 4. Формулы понижения степени: αα 21 2 12 cossin αα 21 21 2 coscos ααα 2 2 1 sincossin ααα 21 2 sincossin 2 1 2 ααcos sin 2 1 2 ααcos 5. Формулы половинного угла: α αα sin cos sin tg 1 12 α αα sin cos sin ctg
С помощью тригонометрических формул 6. Формулы суммы и разности: 22 2 βαβα βα coscos 22 2 αββα βα sinsincoscos 22 2 βαβα βα cossinsinsin βα βα βα coscos )sin( tgtg βα βα βα sinsin )sin( ctgctg βα αβ βα sinsin )sin( ctgctg
Формулы суммы и разности: 22 2 βαβα βα coscos 22 2 αββα βα sinsincoscos 22 2 βαβα βα cossinsinsin βα βα βα coscos )sin( tgtg βα βα βα sinsin )sin( ctgctg βα αβ βα sinsin )sin( ctgctg
С помощью тригонометрических формул 7. Формулы произведения: βαβαβαcoscos 2 1 βαβαβαcoscossinsin 2 1 βαβαβαsinsincossin
Мнемоническое правило “Тригонометрия на ладони” Очень часто требуется знать наизусть значения cos , sin , tg , ctg для углов 0° , 30° , 45° , 60° , 90°. Но если вдруг какое-либо значение забудется, то можно воспользоваться правилом руки. Правило: Если провести линии через мизинец и большой палец, то они пересекутся в точке, называемой “лунный бугор”. Образуется угол 90°. Линия мизинца образует угол 0°. Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30° , 45° , 60°. Подставляя вместо n : 0 , 1 , 2 , 3 , 4 , получаем значения sin , для углов 0° , 30° , 45° , 60° , 90°. Для cos отсчет происходит в обратном порядке.
Для cos отсчет происходит в обратном порядке.
Не закончено!
Значения тригонометрических уравнений. Решение тригонометрических уравнений
Требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью » «.
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.
Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения , для наглядности будем использовать уже знакомый тригонометрический круг.
sinх = а
cos x = a
tg x = a
cot x = a
Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.
Метод замены переменной и подстановки
Решение тригонометрических уравнений через разложение на множители
Приведение к однородному уравнению
Решение уравнений, через переход к половинному углу
Введение вспомогательного угла
Решить уравнение 2cos 2 (x + /6) – 3sin( /3 – x) +1 = 0
Используя формулы приведения получим:
2cos 2 (x + /6) – 3cos(x + /6) +1 = 0
Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:
2y 2 – 3y + 1 + 0
Корни которого y 1 = 1, y 2 = 1/2
Теперь идем в обратном порядке
Подставляем найденные значения y и получаем два варианта ответа:
Как решить уравнение sin x + cos x = 1 ?
Перенесем все влево, чтобы справа остался 0:
sin x + cos x – 1 = 0
Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
sin x — 2 sin 2 (x/2) = 0
Делаем разложение на множители:
2sin(x/2) * cos(x/2) — 2 sin 2 (x/2) = 0
2sin(x/2) * = 0
Получаем два уравнения
Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:
Для решения однородного уравнения, поступают следующим образом:
а) переносят все его члены в левую часть;
б) выносят все общие множители за скобки;
в) приравнивают все множители и скобки к 0;
г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
д) решают полученное уравнение относительно tg.
Решить уравнение 3sin 2 x + 4 sin x cos x + 5 cos 2 x = 2
Воспользуемся формулой sin 2 x + cos 2 x = 1 и избавимся от открытой двойки справа:
3sin 2 x + 4 sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x
sin 2 x + 4 sin x cos x + 3 cos 2 x = 0
Делим на cos x:
tg 2 x + 4 tg x + 3 = 0
Заменяем tg x на y и получаем квадратное уравнение:
y 2 + 4y +3 = 0, корни которого y 1 =1, y 2 = 3
Отсюда находим два решения исходного уравнения:
x 2 = arctg 3 + k
Решить уравнение 3sin x – 5cos x = 7
Переходим к x/2:
6sin(x/2) * cos(x/2) – 5cos 2 (x/2) + 5sin 2 (x/2) = 7sin 2 (x/2) + 7cos 2 (x/2)
Пререносим все влево:
2sin 2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos 2 (x/2) = 0
Делим на cos(x/2):
tg 2 (x/2) – 3tg(x/2) + 6 = 0
Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,
где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
Обе части уравнения разделим на :
Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:
cos * sin x + sin * cos x = С
или sin(x + ) = C
Решением этого простейшего тригонометрического уравнения будет
х = (-1) k * arcsin С — + k, где
Следует отметить, что обозначения cos и sin взаимозаменяемые.
Решить уравнение sin 3x – cos 3x = 1
В этом уравнении коэффициенты:
а = , b = -1, поэтому делим обе части на = 2
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Не секрет, что успех или неудача в процессе решения практически любой задачи, в основном зависит от правильности определения типа заданного уравнения, а также от правильности воспроизведения последовательности всех этапов его решения. Однако в случае с тригонометрическими уравнениями, определить факт того, что уравнение именно тригонометрическое, вовсе несложно. А вот в процессе определения последовательности действий, которые должны привести нас к правильному ответу, можно столкнуться с определенными сложностями. Давайте разберемся, как решать тригонометрические уравнения правильно с самого начала.
Однако в случае с тригонометрическими уравнениями, определить факт того, что уравнение именно тригонометрическое, вовсе несложно. А вот в процессе определения последовательности действий, которые должны привести нас к правильному ответу, можно столкнуться с определенными сложностями. Давайте разберемся, как решать тригонометрические уравнения правильно с самого начала.
Решение тригонометрических уравнений
Для того, чтобы решить тригонометрическое уравнение, нужно попробовать выполнить следующие моменты:
- Приводим все функции, которые входят в наше уравнение к «одинаковым углам»;
- Нужно довести заданное уравнение до «одинаковых функций»;
- Раскладываем левую часть заданного уравнения на множители или другие нужные составляющие.
Методы
Метод 1. Решать такие уравнения необходимо в два этапа. Первый- преобразовываем уравнение для того, чтобы получить его простейший (упрощенный) вид. Уравнение: Cosx = a, Sinx = a и подобные, называются простейшими тригонометрическими уравнениями. Второй этап- решаем полученное простейшее уравнение. Следует отметить, что простейшее уравнение можно решить алгебраическим методом, который отлично известен нам из школьного курса алгебры. Его также называют методом замены подстановки и переменной. С помощью формул приведения, сначала нужно преобразовать, затем сделать замену и после этого найти корни.
Второй этап- решаем полученное простейшее уравнение. Следует отметить, что простейшее уравнение можно решить алгебраическим методом, который отлично известен нам из школьного курса алгебры. Его также называют методом замены подстановки и переменной. С помощью формул приведения, сначала нужно преобразовать, затем сделать замену и после этого найти корни.
Далее нужно разложить наше уравнение на возможные множители, для этого необходимо перенести все члены влево и затем можно раскладывать на множители. Теперь нужно привести данное уравнение к однородному, в котором все члены равняются одной степени, а косинус и синус имеют один и тот же угол.
Перед тем, как решать тригонометрические уравнения, нужно перенести его члены в левую часть, забрав из правой, а затем выносим все общие знаменатели за скобки. Приравниваем наши скобки и множители к нулю. Наши приравненные скобки представляют собой однородное уравнение с уменьшенной степенью, которое нужно разделить на sin (cos) в старшей степени. Теперь решаем алгебраическое уравнение, которое было получено, в соотношении к tan.
Теперь решаем алгебраическое уравнение, которое было получено, в соотношении к tan.
Метод 2. Еще одним методом, с помощью которого, можно решить тригонометрическое уравнение является переход к половинному углу. К примеру, решаем уравнение: 3sinx-5cosx=7.
Нам нужно перейти к половинному углу, в нашем случае это: 6sin(x/2)*cos(x/2)- 5cos²(x/2)+5sin²(x/2) = 7sin²(x/2)+7cos²(x/2).А после этого, сводим все члены в одну часть (для удобства лучше выбрать правую) и приступаем к решению уравнения.
При необходимости можно вводить вспомогательный угол. Это делается в случае, когда нужно заменить целое значение sin (a) или cos (a) и знак «a» как раз и выступает вспомогательным углом.
Произведение в сумму
Как решать тригонометрические уравнения, используя произведение в сумму? Метод известный как преобразование произведения в сумму также может быть использован в решении таких уравнений. В этом случае необходимо использовать соответствующие уравнению формулы.
К примеру, у нас есть уравнение: 2sinx * sin3x= сos4x
Нам нужно решить эту задачу путем преобразования левой части в сумму, а именно:
сos 4x –cos8x=cos4x ,
х = p/16 + pk/8.
Если вышеприведенные методы не подходят, и Вы все еще не знаете, как решать простейшие тригонометрические уравнения, можно воспользоваться еще одним методом – универсальная подстановка. С его помощью можно преобразовать выражение и произвести замену. К примеру: Cos(x/2)=u. Теперь можно решать уравнение с имеющимся параметром u. А получив нужный результат, не забываем перевести это значение в обратное.
Многие «опытные» ученики советуют обратиться за решением уравнений к людям в онлайн-режиме. Как решить тригонометрическое уравнение онлайн, спросите Вы. Для онлайн решения задачи, Вы можете обратиться на форумы соответствующей тематике, где Вам могут помочь советом или же в решении задачи. Но лучше всего, все же попытаться обойтись собственными силами.
Навыки и умения в решении тригонометрических уравнений являются очень важными и полезными. Их развитие потребует от Вас немалых усилий. С решением таких уравнений связаны многие задачи физики, стереометрии и т.д. А сам процесс решения подобных задач предполагает собой наличие умений и знаний, которые можно приобрести во время изучения элементов тригонометрии.
Учим тригонометрические формулы
В процессе решения уравнения Вы можете столкнуться с надобностью использования любой формулы из тригонометрии. Можно, конечно, начать искать ее в своих учебниках и шпаргалках. А если эти формулы отложены у Вас в голове, вы не только сэкономите свои нервы, но и значительно облегчите себе задачу, не тратя времени на поиск нужной информации. Таким образом, у Вас будет возможность для продумывания наиболее рационального пути решения поставленной задачи.
Урок комплексного применения знаний.
Цели урока.
- Рассмотреть различные методы решения тригонометрических уравнений.
- Развитие творческих способностей учеников путем решения уравнений.
- Побуждение учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Оборудование: экран, проектор, справочный материал.
Ход урока
Вводная беседа.
Основным методом решения тригонометрических уравнений является сведения их
простейшим. При этом применяются обычные способы, например, разложения на
множители, а также приемы, используемые только для решения тригонометрических
уравнений. Этих приемов довольно много, например,
различные тригонометрические подстановки, преобразования углов, преобразования
тригонометрических функций. Беспорядочное применение каких-либо
тригонометрических преобразований обычно не упрощает уравнение, а
катастрофически его усложняет. Чтобы выработать в общих чертах план решения
уравнения, наметить путь сведения уравнения к простейшему, нужно в первую
очередь проанализировать углы – аргументы тригонометрических функций, входящих в
уравнение.
При этом применяются обычные способы, например, разложения на
множители, а также приемы, используемые только для решения тригонометрических
уравнений. Этих приемов довольно много, например,
различные тригонометрические подстановки, преобразования углов, преобразования
тригонометрических функций. Беспорядочное применение каких-либо
тригонометрических преобразований обычно не упрощает уравнение, а
катастрофически его усложняет. Чтобы выработать в общих чертах план решения
уравнения, наметить путь сведения уравнения к простейшему, нужно в первую
очередь проанализировать углы – аргументы тригонометрических функций, входящих в
уравнение.
Сегодня мы поговорим о методах решения тригонометрических уравнений. Правильно выбранный метод часто позволяет существенно упростить решение, поэтому все изученные нами методы всегда нужно держать в зоне своего внимания, чтобы решать тригонометрические уравнения наиболее подходящим методом.
II. (С помощью проектора повторяем методы решения
уравнений. )
)
1. Метод приведения тригонометрического уравнения к алгебраическому.
Необходимо выразить все тригонометрические функции через одну, с одним и тем же аргументом. Это можно сделать с помощью основного тригонометрического тождества и его следствий. Получим уравнение с одной тригонометрической функцией. Приняв ее за новую неизвестную, получим алгебраическое уравнение. Находим его корни и возвращаемся к старой неизвестной, решая простейшие тригонометрические уравнения.
2. Метод разложения на множители.
Для изменения углов часто бывают полезны формулы приведения, суммы и разности аргументов, а также формулы преобразования суммы (разности) тригонометрических функций в произведение и наоборот.
sin x + sin 3x = sin 2x + sin4x
3. Метод введения дополнительного угла.
4. Метод использования универсальной подстановки.
Уравнения вида F(sinx, cosx, tgx) = 0 сводятся к алгебраическому при помощи универсальной тригонометрической подстановки
Выразив
синус, косинус и тангенс через тангенс половинного угла. Этот прием может
привести к уравнению высокого порядка. Решение которого затруднительно.
Этот прием может
привести к уравнению высокого порядка. Решение которого затруднительно.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Рекомендуем также
Метод замены неизвестного при решении алгебраических уравнений (Контрольная работа), стр.
 3
3Возвращаемся к исходной переменной и решаем совокупность уравнений:
Ответ: .
Пример 6. Решить уравнение
Решение. Заметим, что произведение чисел, стоящих в первой и третьей, во второй и четвёртой скобках, равны, т.е. Перемножим указанные пары скобок и запишем уравнение
Поскольку – не корень, разделим обе части уравнения на Получим:
Введя замену: запишем исходное уравнение в следующем виде:
т.е.
Отсюда . Вернёмся к исходной переменной:
Первое уравнение совокупности имеет корни . Второе уравнение не имеет корней.
Ответ:
Пример 7. Решить уравнение
Решение. Вид уравнения совсем не подсказывает,
что его можно свести к однородному.
Преобразуем первый множитель, выделив
из него выражение, равное второму
множителю, т.е.
Вид уравнения совсем не подсказывает,
что его можно свести к однородному.
Преобразуем первый множитель, выделив
из него выражение, равное второму
множителю, т.е.
Подставляя последнее выражение в исходное уравнение, запишем, что
и далее:
Введя замену: и приведём последнее уравнение к виду . Это однородное уравнение второй степени относительно и . В нём . В самом деле, если , то уравнение приводится к виду , или Но система решений не имеет.
Разделив обе части уравнения на , запишем. Что
Отсюда
Ответ:
Пример 8. Решить уравнение
Решение. Поскольку функция существует при любых значениях , найдём область определения функции
значит,
. Ясно, что можно ввести замену или Пусть
.
Нас интересуют все значения этой функции.
Выберем для удобства любой отрезок, на
котором функция синус принимает все
свои значения, например отрезок
Ясно, что можно ввести замену или Пусть
.
Нас интересуют все значения этой функции.
Выберем для удобства любой отрезок, на
котором функция синус принимает все
свои значения, например отрезок
Подставив замену в уравнение, получим:
Вернёмся к «старой» переменной:
Ответ:
Пример 9. Решить уравнение
Решение. Выделим наиболее часто повторяющееся выражение и упростим левую часть исходного уравнения:
(1)
Введём замену тогда уравнение (3) примет вид:
, или ,
При дальнейших упрощениях получим
Применим основное свойство дроби к левой части уравнения, разделив на :
Введём вторую замену и решим уравнение:
Возвращаясь к исходной переменной, придём к совокупности:
Второе уравнение совокупности
не имеет решений, а первое даёт два
решения, которые и выносятся в ответ.
Ответ:
3. Типизация приёмов введения новых неизвестных при решении алгебраических уравнений
В третьей части курсовой работы осуществим типизацию приёмов введения новых неизвестных при решении алгебраических уравнений.
Введение новых переменных может быть как явным, так и неявным. Классифицируем наши уравнения по способам неявной реализации метода замены переменной:
Использование основного свойства дроби.
Использование основного свойства дроби применяется в уравнениях следующего вида:
где постоянные, .
В таких уравнениях сначала проверяют, является ли корнем уравнения, и производят замену .
Выделение квадрата.
17.7 Изменение переменных
Одним из наиболее полезных методов вычисления интегралов является
замена, оба
«$u$-подстановка»
и тригонометрический
подстановка, при которой мы меняем переменную на нечто большее
удобный. Как мы видели, иногда переходя от прямоугольного
координаты в другую систему координат полезно, и это тоже
изменяет переменные. Это, конечно, более сложное изменение,
так как вместо замены одной переменной на другую мы меняем всю
набор переменных, но, как оказалось, он действительно очень похож на
виды замены переменных, которые мы уже знаем как замену.2и}\,ду
$$
не одинаковы; ясно, что правая часть больше. Один из способов
понять, проблема заключается в том, чтобы отметить, что если обе области аппроксимированы
используя, скажем, десять подынтервалов, чтобы аппроксимирующие прямоугольники на
справа шире, чем их аналоги слева, как указано. В
на рисунке ширина прямоугольника слева $\Delta x=0.1$,
от 0,7$ до 0,8$. Прямоугольник справа расположен
между соответствующими значениями $\arcsin(0.7)$ и $\arcsin(0.8)$, поэтому
что $\Delta u=\arcsin(0.{y_1} f(x,y)\,dy\,dx$$
использовать новые переменные $u$ и $v$. В случае с одной переменной
как правило, есть только одна причина изменить переменную: сделать
функцию «лучше», так что мы можем найти первообразную.
Как мы видели, иногда переходя от прямоугольного
координаты в другую систему координат полезно, и это тоже
изменяет переменные. Это, конечно, более сложное изменение,
так как вместо замены одной переменной на другую мы меняем всю
набор переменных, но, как оказалось, он действительно очень похож на
виды замены переменных, которые мы уже знаем как замену.2и}\,ду
$$
не одинаковы; ясно, что правая часть больше. Один из способов
понять, проблема заключается в том, чтобы отметить, что если обе области аппроксимированы
используя, скажем, десять подынтервалов, чтобы аппроксимирующие прямоугольники на
справа шире, чем их аналоги слева, как указано. В
на рисунке ширина прямоугольника слева $\Delta x=0.1$,
от 0,7$ до 0,8$. Прямоугольник справа расположен
между соответствующими значениями $\arcsin(0.7)$ и $\arcsin(0.8)$, поэтому
что $\Delta u=\arcsin(0.{y_1} f(x,y)\,dy\,dx$$
использовать новые переменные $u$ и $v$. В случае с одной переменной
как правило, есть только одна причина изменить переменную: сделать
функцию «лучше», так что мы можем найти первообразную. В двух
переменный случай, есть вторая потенциальная причина: двумерный
область, по которой надо интегрироваться, как-то неприятно, и мы
хотите, чтобы регион с точки зрения $u$ и $v$ был лучше — чтобы
прямоугольник, например. В идеале, конечно, новая функция и
новый регион будет не хуже оригиналов, и хотя бы один из
они будут лучше; это не всегда срабатывает.2}\;r\,dr\,d\theta={\pi\over3}.$$
Но давайте вместо этого подойдем к этому как к проблеме замены, начиная
где $x=r\cos\theta$, $y=r\sin\theta$. Эта пара уравнений
описывает функцию из пространства «$r$-$\theta$» в «пространство $x$-$y$»,
и поскольку он включает в себя знакомые понятия, его не так уж сложно понять.
понять, что он делает. На рис. 17.7.2 мы геометрически показали, как это
функция ведет себя. Четыре точки, обозначенные a – d в плоскости $r$-$\theta$
соответствуют трем точкам в плоскости $x$-$y$; точки и и б оба
перейти в начало координат, потому что $r=0$.Горизонтальная стрелка в
В плоскости $r$-$\theta$ $r=1$ везде, а $\theta$ изменяется от 0 до
$\pi$, поэтому соответствующие точки
$x=r\cos\theta$, $y=r\sin\theta$ начинаются с $(1,0)$ и следуют за единицей
круг против часовой стрелки.
В двух
переменный случай, есть вторая потенциальная причина: двумерный
область, по которой надо интегрироваться, как-то неприятно, и мы
хотите, чтобы регион с точки зрения $u$ и $v$ был лучше — чтобы
прямоугольник, например. В идеале, конечно, новая функция и
новый регион будет не хуже оригиналов, и хотя бы один из
они будут лучше; это не всегда срабатывает.2}\;r\,dr\,d\theta={\pi\over3}.$$
Но давайте вместо этого подойдем к этому как к проблеме замены, начиная
где $x=r\cos\theta$, $y=r\sin\theta$. Эта пара уравнений
описывает функцию из пространства «$r$-$\theta$» в «пространство $x$-$y$»,
и поскольку он включает в себя знакомые понятия, его не так уж сложно понять.
понять, что он делает. На рис. 17.7.2 мы геометрически показали, как это
функция ведет себя. Четыре точки, обозначенные a – d в плоскости $r$-$\theta$
соответствуют трем точкам в плоскости $x$-$y$; точки и и б оба
перейти в начало координат, потому что $r=0$.Горизонтальная стрелка в
В плоскости $r$-$\theta$ $r=1$ везде, а $\theta$ изменяется от 0 до
$\pi$, поэтому соответствующие точки
$x=r\cos\theta$, $y=r\sin\theta$ начинаются с $(1,0)$ и следуют за единицей
круг против часовой стрелки. Наконец, вертикальная стрелка имеет
$\theta=\pi/4$ и $r$ находятся в диапазоне от 0 до 1, так что это соответствует прямому
стрелка в плоскости $x$-$y$. Экстраполируя эти несколько примеров,
нетрудно заметить, что каждая вертикальная линия в плоскости $r$-$\theta$
преобразуется в прямую, проходящую через начало координат в плоскости $x$-$y$, и
каждая горизонтальная линия в плоскости $r$-$\theta$
преобразуется в окружность с центром в начале координат в $x$-$y$
самолет.Поскольку нас интересует интегрирование по полудиску в
плоскости $x$-$y$ будем интегрировать по прямоугольнику
$[0,\pi]\times[0,1]$ в плоскости $r$-$\theta$, потому что теперь мы видим
что точки в этом прямоугольнике направляются точно в верхнюю половину
диск на $x=r\cos\theta$ и $y=r\sin\theta$.
Наконец, вертикальная стрелка имеет
$\theta=\pi/4$ и $r$ находятся в диапазоне от 0 до 1, так что это соответствует прямому
стрелка в плоскости $x$-$y$. Экстраполируя эти несколько примеров,
нетрудно заметить, что каждая вертикальная линия в плоскости $r$-$\theta$
преобразуется в прямую, проходящую через начало координат в плоскости $x$-$y$, и
каждая горизонтальная линия в плоскости $r$-$\theta$
преобразуется в окружность с центром в начале координат в $x$-$y$
самолет.Поскольку нас интересует интегрирование по полудиску в
плоскости $x$-$y$ будем интегрировать по прямоугольнику
$[0,\pi]\times[0,1]$ в плоскости $r$-$\theta$, потому что теперь мы видим
что точки в этом прямоугольнике направляются точно в верхнюю половину
диск на $x=r\cos\theta$ и $y=r\sin\theta$.
Рисунок 17.7.2. Двойная замена переменной.
На данный момент мы на две трети выполнили задачу: мы знаем
$r$-$\theta$ пределов интегрирования, и мы можем легко преобразовать
к новым переменным: $$\eqalignno{
\sqrt{x^2+y^2} &= \sqrt{r^2\cos^2\theta+r^2\sin^2\theta}
знак равно г \ sqrt {\ соз ^ 2 \ тета + \ грех ^ 2 \ тета} = г. 2}$.1 r (?) \,dr\,d\theta.&
(17.7.2)\кр
}$$
Чего нам не хватает, так это правильного количества, чтобы заменить «?»
чтобы мы получили правильный ответ. Разумеется, этот интеграл также
результат приближения, в котором мы складываем объемы ящиков
это $\Delta r\times\Delta \theta\times\hbox{height}$; проблема
заключается в том, что высота, которая даст нам правильный ответ, не просто
$р$. Или, другими словами, мы можем думать о правильной высоте как $r$,
но площадь основания $\Delta r\Delta\theta$ неверна.То
высота $r$ получается из уравнения 17.7.1, которое
то есть она точно такая же, как и соответствующая высота в
$x$-$y$ версия интеграла. Проблема в том, что площадь
основание $\Delta x\times \Delta y$ не совпадает с площадью основания
$\Delta r\times\Delta\theta$. Мы можем думать о «?» в интеграле как о
поправочный коэффициент, необходимый для того, чтобы
$?\,dr\,d\theta$ = $dx\,dy$.
2}$.1 r (?) \,dr\,d\theta.&
(17.7.2)\кр
}$$
Чего нам не хватает, так это правильного количества, чтобы заменить «?»
чтобы мы получили правильный ответ. Разумеется, этот интеграл также
результат приближения, в котором мы складываем объемы ящиков
это $\Delta r\times\Delta \theta\times\hbox{height}$; проблема
заключается в том, что высота, которая даст нам правильный ответ, не просто
$р$. Или, другими словами, мы можем думать о правильной высоте как $r$,
но площадь основания $\Delta r\Delta\theta$ неверна.То
высота $r$ получается из уравнения 17.7.1, которое
то есть она точно такая же, как и соответствующая высота в
$x$-$y$ версия интеграла. Проблема в том, что площадь
основание $\Delta x\times \Delta y$ не совпадает с площадью основания
$\Delta r\times\Delta\theta$. Мы можем думать о «?» в интеграле как о
поправочный коэффициент, необходимый для того, чтобы
$?\,dr\,d\theta$ = $dx\,dy$.
Итак, давайте подумаем, что это за маленькая база $\Delta
r\times\Delta\theta$ соответствует.Мы знаем, что каждый бит
горизонтальная линия в плоскости $r$-$\theta$ соответствует биту
дуга окружности в плоскости $x$-$y$, и каждый бит вертикальной линии
в плоскости $r$-$\theta$ соответствует немного
«радиальная линия» в плоскости $x$-$y$. На рисунке 17.7.3 мы показываем типичный прямоугольник в
плоскость $r$-$\theta$ и соответствующая ей область в плоскости $x$-$y$.
На рисунке 17.7.3 мы показываем типичный прямоугольник в
плоскость $r$-$\theta$ и соответствующая ей область в плоскости $x$-$y$.
Перетащите синяя точка в плоскости $\theta r$ для перемещения прямоугольника; перетащите зеленый точка, чтобы изменить размер прямоугольника.
Рисунок 17.7.3. Соответствующие области.
В этом случае область в плоскости $x$-$y$ составляет примерно
прямоугольник с размерами $\Delta r\times r\Delta\theta$, но в
вообще углы углов не будут прямыми углами, поэтому область будет
обычно (почти) параллелограмм.Нам нужно вычислить площадь
этот параллелограмм. Мы знаем
изящный способ сделать это: вычислить длину определенного перекрестного произведения
(раздел 14. 4).
Если мы сможем определить
подходящие два вектора, мы почти закончили.
4).
Если мы сможем определить
подходящие два вектора, мы почти закончили.
К счастью, мы действительно делали это раньше. Стороны области в
плоскости $x$-$y$ образуются путем временной фиксации либо $r$, либо
$\theta$ и позволяя другой переменной изменяться в пределах небольшого интервала.
На рис. 17.7.4, например, правый верхний
край области формируется фиксированием $\theta=2\pi/3$ и выделением $r$
запустить от 0 долларов.от 5$ до 0,75$. Другими словами, у нас есть векторная функция
${\bf v}(r)=\langle r\cos\theta_0, r\sin\theta_0, 0\rangle$, и мы
интересует ограниченный набор значений для $r$. Тангенс вектора
этому пути задается производной ${\bf v}'(r)=\langle
\cos\theta_0, \sin\theta_0, 0\rangle$ и небольшой касательный вектор,
с длиной, приблизительно равной стороне области, равно $\langle
\cos\theta_0, \sin\theta_0, 0\rangle\,dr$. Аналогично, если мы исправим
$r=r_0=0.5$, получаем векторную функцию ${\bf w}(\theta)=\langle
r_0\cos\theta, r_0\sin\theta, 0\rangle$ с производной ${\bf
w}'(\theta)=\langle -r_0\sin\theta, r_0\cos\theta, 0\rangle$ и
малый касательный вектор $\langle -r_0\sin\theta_0, r_0\cos\theta_0,
0\rangle\,d\theta$, когда $\theta=\theta_0$ (в углу мы
сфокусироваться на). 2\theta_0\rangle\,d\theta\,dr\cr
&=\langle 0,0,-r_0\rangle\,d\theta\,dr.\кр
}$$
Длина этого вектора равна $r_0\,dr\,d\theta$. Так что в целом для
любые значения $r$ и $\theta$, площадь в плоскости $x$-$y$
соответствующий маленькому прямоугольнику, привязанному к $(\theta,r)$ в
Плоскость $r$-$\theta$ приблизительно равна $r\,dr\,d\theta$. Другими словами, «$r$»
заменяет «?» в уравнении 17.7.2.
2\theta_0\rangle\,d\theta\,dr\cr
&=\langle 0,0,-r_0\rangle\,d\theta\,dr.\кр
}$$
Длина этого вектора равна $r_0\,dr\,d\theta$. Так что в целом для
любые значения $r$ и $\theta$, площадь в плоскости $x$-$y$
соответствующий маленькому прямоугольнику, привязанному к $(\theta,r)$ в
Плоскость $r$-$\theta$ приблизительно равна $r\,dr\,d\theta$. Другими словами, «$r$»
заменяет «?» в уравнении 17.7.2.
В общем случае подстановка начинается с уравнений $x=f(u,v)$ и
$y=g(u,v)$. Опять же, будет просто преобразовать функцию
быть интегрированным. Преобразование пределов потребует, как указано выше,
понимание того, как функции $f$ и $g$ преобразуют
плоскость $u$-$v$ в плоскость $x$-$y$.Наконец, малые векторы, которые мы
нужно приблизить площадь будет
$\langle f_u,g_u,0\rangle\,du$ и $\langle f_v,g_v,0\rangle\,dv$.
Их векторное произведение равно $\langle
0,0,f_ug_v-g_uf_v\rangle\,du\,dv$ с длиной
$|f_ug_v-g_uf_v|\,du\,dv$. Количество $|f_ug_v-g_uf_v|$ обычно
обозначенный
$ $ \ влево | {\ парциальное (х, у) \ над \ парциальное (и, v)} \ вправо | = | f_ug_v-g_uf_v | $ $
и назвал Jacobian . Обратите внимание, что это абсолютное значение определителя два на два.
$$\left|\matrix{f_u&g_u\cr
f_v&g_v\cr}\right|,$$
что может быть легче запомнить.2=2$
Обратите внимание, что это абсолютное значение определителя два на два.
$$\left|\matrix{f_u&g_u\cr
f_v&g_v\cr}\right|,$$
что может быть легче запомнить.2=2$
Существует аналогичная формула замены переменных для тройных интегралов, хотя это немного сложнее получить. Предположим, мы используем три функции подстановки: $x=f(u,v,w)$, $y=g(u,v,w)$ и $z=h(u,v,w)$. Теперь определитель Якоби $$ {\ парциальное (х, у, г) \ над \ парциальное (и, v, ш)} = \left|\matrix{f_u&g_u&h_u\cr f_v&g_v&h_v\cr f_w&g_w&h_w\cr}\right|. $$ Затем интеграл преобразуется аналогичным образом: $$ \int\!\int\!\int_R F(x,y,z) \, dV = \int\!\int\!\int_S F(f(u,v,w),g(u,v,w),h(u,v,w)) \ влево | {\ парциальное (х, у, г) \ над \ парциальное (и, v, ш)} \ вправо | \,ду\,дв\,дв, $$ где, конечно, область $S$ в пространстве $uvw$ соответствует область $R$ в пространстве $xyz$.
Упражнения 17.7
Вот ячейка Мудреца, если вы хотите ее использовать.
Пример 17.7.1 Завершите пример 17. 2\,dx\,dy$ по квадрату
с углами $(-1,0)$, $(0,1)$, $(1,0)$ и $(0,-1)$ двумя способами:
напрямую и используя $x=(u+v)/2$, $y=(u-v)/2$.2} = 1,$$
с помощью преобразования $x=au$, $y=bv$ и $z=cw$.
(отвечать)
2\,dx\,dy$ по квадрату
с углами $(-1,0)$, $(0,1)$, $(1,0)$ и $(0,-1)$ двумя способами:
напрямую и используя $x=(u+v)/2$, $y=(u-v)/2$.2} = 1,$$
с помощью преобразования $x=au$, $y=bv$ и $z=cw$.
(отвечать)
14.3 — Тригонометрические уравнения
14.3 — Тригонометрические уравнения14.3 — Тригонометрические уравнения
Прежде чем читать этот раздел, вы можете найти его полезным рассмотреть следующие темы: Тригонометрическое уравнение — это уравнение, в котором неизвестное, для которого нужно решить, представляет собой угол (назовем его θ ), и этот угол находится в аргументе тригонометрической функции, такой как sin, cos или tan.Тригонометрическое уравнение всегда имеет бесконечное число решений, т. но принято перечислять только те углы, которые находятся между 0° и 360°. С помощью алгебры можно решить только некоторые типы тригонометрических уравнений.
Мы будем изучать следующие виды. (Наведите указатель мыши на слово Пример , чтобы увидеть пример.
(Наведите указатель мыши на слово Пример , чтобы увидеть пример.
• θ встречается только один раз. Пример Перейти к теме • θ встречается несколько раз, но всегда как аргумент одной и той же тригонометрической функции. Пример Перейти к теме • уравнение имеет разные тригонометрические функции, но все они имеют один и тот же аргумент, θ . Пример Перейти к теме • уравнение содержит тригонометрические функции с разные аргументы. Пример Перейти к теме
Тригонометрические уравнения, в которых
θ встречается только один раз Если неизвестный угол появляется только один раз, выполните ту же процедуру, что и для любого другого. другое уравнение, в котором неизвестное встречается только один раз,
и инвертировать операции, которые были
применяются к нему в порядке, обратном их применению.
другое уравнение, в котором неизвестное встречается только один раз,
и инвертировать операции, которые были
применяются к нему в порядке, обратном их применению.Пример: Решите уравнение sin( θ ) = ½ для всех углы θ между 0° и 360°.
Примечание: Можно использовать метод CAST чтобы получить второй угол, 150 °.
Пример: Решите уравнение 5 sin( θ — 40°) – 2 = 0 для всех углы θ между 0° и 360°.
Примечание: Можно использовать метод CAST на предпоследнем шаге для получения «другого» угла, 156.4°. Убедитесь, что вы добавили 40° последним .
Тригонометрические уравнения, в которых
θ встречается несколько раз, но всегда как аргумент одной и той же тригонометрической функции Если неизвестный угол появляется более одного раза, то сделайте следующее:- Перенесите все в левую часть уравнения.

- Фактор левой части уравнения, чтобы уравнение теперь имело форму a · b = 0.
- Используйте тот факт, что если a · b = 0, то либо a = 0 или b = 0, поэтому уравнение заменяется парой более простых уравнений a = 0 и b = 0, каждое из которых теперь нужно решить.
Пример: Решите уравнение 2 sin 2 ( θ ) = sin( θ ) для всех углов θ между 0° и 360°.

Замените это уравнение двумя более простыми уравнениями, которые решаются по отдельности:
Примечание: Для решения этого уравнения можно использовать псевдоним.Если вы замените все вхождения sin ( θ ) на Q , тогда это становится квадратным уравнением с переменной Q :2 Q 2 = Q .Сначала решите это уравнение для Q :
Q (2 Q — 1) = 0 → Q = 0 и Q = ½.Затем подставьте обратно sin ( θ ) вместо Q :
sin( θ ) = 0 и sin( θ ) = ½.Теперь решите эти уравнения для 90 108 θ 90 109, как указано выше.
Пример: Решите уравнение 2 sin 2 (3 θ ) = sin(3 θ ) для всех углов θ между 0° и 360°.
 Обратите внимание, что эта проблема почти
идентичен предыдущему – с той лишь разницей, что аргумент греха
функция равна 3 θ , а не θ .
Обратите внимание, что эта проблема почти
идентичен предыдущему – с той лишь разницей, что аргумент греха
функция равна 3 θ , а не θ .Замените это уравнение двумя более простыми уравнениями, которые решаются по отдельности:
Примечание: Вы можете использовать метод CAST для получения углы 180°, 360° и 150°.Остальные углы получаются путем перехода вокруг единичного круга несколько раз.Тригонометрические уравнения, имеющие различные тригонометрические функции, но все с тот же аргумент
Эти стратегии могут помочь:- Замените любые другие тригонометрические функции синусами и косинусами.
- Часто приходишь к уравнению a sin( θ ) = b cos( θ ).
Затем вы можете разделить обе стороны на cos( θ ), затем
судя по загару это
становится tan( θ ) = b / a .

- В противном случае попробуйте перенести все в одну сторону и разложить так, чтобы каждый фактор содержит одну тригонометрическую функцию.
Пример: Решите уравнение 2 csc( θ ) – раскладушка ( θ ) = tan ( θ ) для всех углов θ между 0° и 360°.
Уравнения, содержащие тригонометрические функции с разными аргументами
Если уравнение содержит тригонометрические функции с разными аргументами (углами) затем используйте соответствующее тригонометрическое тождество чтобы выразить все в терминах одного угла.(Например, если один угол в два раза больше другого угла, используйте тождество двойного угла, чтобы избавиться от двойного угла. Или, если один угол равен другому углу плюс некоторая разница, используйте сумма углов тождество чтобы избавиться от первого угла.) Затем действуйте, как раньше. Пример: Два вектора V 1 и V 2 направлены в направлениях, отстоящих друг от друга на 65°. Найдите значение угла θ , при котором вертикальных составляющих двух векторов (пунктирные линии)
быть равными по величине.
Найдите значение угла θ , при котором вертикальных составляющих двух векторов (пунктирные линии)
быть равными по величине.
Решение: Длина вертикальной составляющей вектора V 2 равно 5 cos( θ ). Длина вертикальной составляющей вектора V 1 равно 3 cos(115° − θ ). Использование того факта, что они должны быть равными, дает нам исходную уравнение,
5 cos( θ ) = 3 cos(115° — θ ).Используйте тригонометрическое тождество (6b) с меньшим знаком отделить угол 115° от угла θ по правой стороне уравнения.
5 cos( θ ) = 3 cos(115°) · cos( θ ) + 3 sin(115°) · sin( θ )Оцените sin и cos 115°. Обратите внимание, что теперь единственный оставшийся угол равен θ .
5 cos( θ ) = −1,268 cos( θ ) + 2,719 sin( θ )Собрать термины.
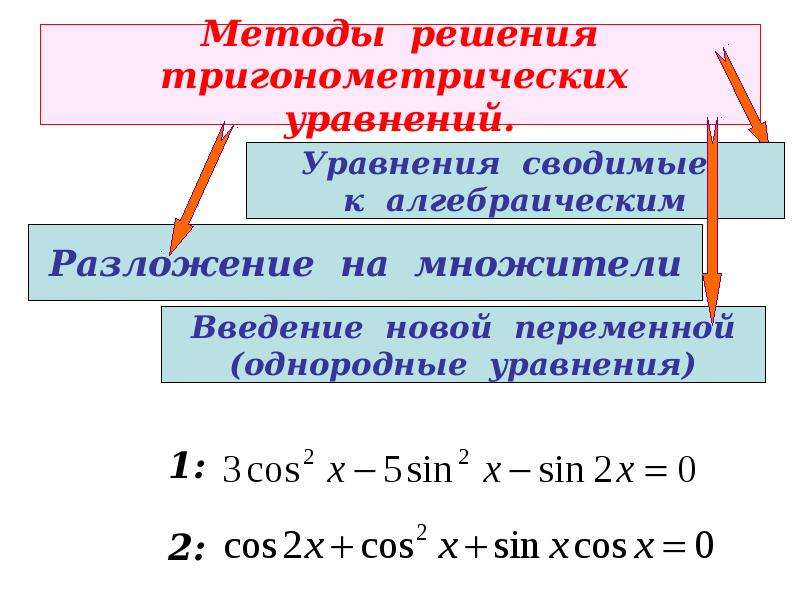
6,268 cos( θ ) = 2.719 грех( θ )Разделите обе стороны на 2,719 cos( θ ) и используйте тождество загара, чтобы превратить sin/cos в загар.
tan( θ ) = 2,305Из диаграммы выше мы видим, что угол, который нам нужен, равен θ = 66,5°. Другое решение соответствует наличию векторов повернуты на 180° и находятся в квадрантах 3 и 4.θ = tan −1 (2,305) = 66,5° или 246,5°
Пример: В электротехнике часто возникают проблемы следующего типа. Даны два следующих двух синусоидальных сигнала:
y 1 = 4 sin( θ ) и y 2 = 3 cos( θ + 40°),найти все углы θ между 0 и 2π радиан, для которых их сумма равна 2.
Решение: Мы должны решить тригонометрическое уравнение
4 sin( θ ) + 3 cos( θ + 40°) = 2.Мы можем использовать тождество суммы углов, (6b) разбить два угла, θ и 40°, в cos. В нем говорится, что
cos( θ + 40°) = cos( θ ) · cos(40°) − sin( θ ) · sin(40°),или оценивая sin и cos 40°,
cos( θ + 40°) = −0,643 sin( θ ) + 0.766 cos( θ ).Подставив это в уравнение, получим
4 sin( θ ) + 3 ( −0,643 sin( θ ) + 0,766 cos( θ ) ) = 2,или расширение и упрощение,
2,072 sin( θ ) + 2,298 cos( θ ) = 2,Это похоже на предыдущий пример, но у нас есть «2» на правая часть, поэтому мы должны использовать другой метод для ее решения.В примере на странице о тригонометрических тождествах мы доказали следующее тождество, в котором говорится, что форма волны sin и форма волны cos всегда можно добавить, чтобы получить синусоидальный сигнал со сдвигом фазы:
, гдеМы можем использовать это тождество, чтобы заменить два вхождения θ в наше уравнение одним.
 В нашем случае A = 2,072 и B = 2,298, поэтому мы получаем C = 3.094 и φ = 47,97° = 0,8372 радиан, и наше уравнение принимает вид
В нашем случае A = 2,072 и B = 2,298, поэтому мы получаем C = 3.094 и φ = 47,97° = 0,8372 радиан, и наше уравнение принимает вид3,094 sin( θ + 0,8372) = 2,Теперь θ встречается только один раз, и мы просто изолируйте его:
sin( θ + 0,8372) = 0,6464Из трех углов, перечисленных черным, красным и синим на последнем шаге,
- первый угол берется из калькулятора (но на следующем шаге он окажется слишком маленьким чтобы получить положительный результат θ , которого требует этот вопрос),
- второй угол получается с помощью единичной окружности или метод CAST и
- третий угол равен первому углу плюс 2π (т.е. плюс один полный круг).
На графике справа показаны две формы волны y 1 и y 2 (зеленая и синяя кривые), а также их сумма (красная кривая). Красные точки на графике — это места, где сумма равна 2.Чтобы ответить на вопрос, мы опускаем первое решение, потому что оно не находится между 0 и 2π.
и держи два других.
Красные точки на графике — это места, где сумма равна 2.Чтобы ответить на вопрос, мы опускаем первое решение, потому что оно не находится между 0 и 2π.
и держи два других.
Пример: Напряжение В (темная линия) представляет собой сумму двух синусоидальные волны (две световые линии) и определяется уравнением:
v = 100 sin(1 t ) + 50 cos(2 t ).Определите моменты времени t , когда v = 0 в показанном цикле. (обозначены черными точками).
(Обратите внимание, что угловые скорости синусоидальных волн равны 1 радиан/сек и 2 радиана в секунду, и это время t в секундах, поэтому углы 1 t и 2 t выражены в радианах.)
Решение: Поскольку один угол в два раза больше другого, используйте тождество двойного угла в форме:
cos(2 t ) = 1 − 2 sin 2 ( t )чтобы избавиться от угла 2 t в пользу угла t :
0 = 100 sin( t ) + 50·{1 − 2 грех 2 ( т )}Распределите, перенесите все в левую часть уравнения и разделите на 50:
100 sin 2 ( t ) − 100 sin( t ) − 50 = 0
2 sin 2 ( t ) − 2 sin( t ) − 1 = 0Это квадратное уравнение относительно sin( t ).
 (Фактически замена sin( t ) псевдонимом Q превратит его в
квадратное уравнение 2 Q 2 − 2 Q − 1 = 0.)
Подставив a = 2, b = −2 и c = −1 в
квадратичную формулу получаем:
(Фактически замена sin( t ) псевдонимом Q превратит его в
квадратное уравнение 2 Q 2 − 2 Q − 1 = 0.)
Подставив a = 2, b = −2 и c = −1 в
квадратичную формулу получаем: Грех чего-либо не может равняться 1,366. Таким образом, у нас остается:
sin( t ) = -0,366t = sin -1 (-0.366)
Перевод калькулятора в режим радиан дает t = −0,3747. Однако изображение единичного круга справа показывает, что значения, которые нам нужны, чтобы ответить на этот вопрос, t 1 = 3,52 и t 2 = 5,91 секунды.
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Узнать о решении тригонометрических уравнений на интервале
Следующее тригонометрическое уравнение находится на интервале
Условие решения данного тригонометрического уравнения с помощью алгебры. 1. Во-первых, мы будем искать заданный образец тригонометрического уравнения, который предполагает алгебраическое свойство, такое как разность квадратов и факторизация.
2. Теперь подключите выражение к одной переменной.
3. Решите уравнение так же, как мы решаем алгебраическое уравнение.2}\theta } = \sqrt 0 tan2θ=0
1. Во-первых, мы будем искать заданный образец тригонометрического уравнения, который предполагает алгебраическое свойство, такое как разность квадратов и факторизация.
2. Теперь подключите выражение к одной переменной.
3. Решите уравнение так же, как мы решаем алгебраическое уравнение.2}\theta } = \sqrt 0 tan2θ=0
tanθ=0, θ={0,π,2π}\tan \theta = 0,\,\theta = \{ 0,\pi ,2 \pi \} tanθ=0,θ={0,π,2π}
sinθ−1=0\sin \theta — 1 = 0sinθ−1=0
sinθ=1, θ={0,π2 ,π}\sin\theta = 1,\,\theta = \{0,\frac{\pi}{2},\pi\}sinθ=1,θ={0,2π,π}
Однако, как указано выше, мы найдем все возможные решения данной тригонометрической функции. Решения повторяются в каждом периоде, и мы также говорили, что тригонометрическое уравнение может иметь бесконечное количество решений, как и рациональное уравнение, область определения функции и т. д.Решение другого тригонометрического уравнения на отрезке [0,2π)[0,2\pi )[0,2π).
Уравнение включает тригонометрическую функцию, отличную от синуса и косинуса, затем напишите обратную функцию и решите углы с помощью функции. Кроме того, когда уравнение, включающее функцию тангенса, отличается от функции синуса и косинуса, то в этом типе функции сначала мы знаем период тангенса, а затем область определения тангенса определяется во всех действительных числах, за исключением нечетных. целые кратные.2}\theta } = \sqrt 0 tan2θ=0
Кроме того, когда уравнение, включающее функцию тангенса, отличается от функции синуса и косинуса, то в этом типе функции сначала мы знаем период тангенса, а затем область определения тангенса определяется во всех действительных числах, за исключением нечетных. целые кратные.2}\theta } = \sqrt 0 tan2θ=0
tanθ=0, sinθ=0\tan \theta = 0,\,\,\,\sin \theta = 0tanθ=0,sinθ= 0
tanθ⇒sinθcosθ=yx\tan \theta \Rightarrow \frac{{\sin \theta}}{{\cos \theta}} = \frac{y}{x}tanθ⇒cosθsinθ =xy
θ=0, 2π,π simialr for sinθ=0,2π,π\theta = 0,\,2\pi ,\pi \,\,simialr\,for\,\sin \theta = 0,2\pi ,\pi θ=0,2π,πsimialrforsinθ=0,2π,π
Это решения в интервале [0,2π)[0,2\pi ) [0,2π) и это все возможные решения. Теперь мы должны нанести эти значения на график.Ось X и ось Y,
Тригонометрические уравнения — уравнения, формулы, общее решение, примеры
Тригонометрические уравнения
В тригонометрических уравнениях в качестве переменных используются тригонометрические функции. Тригонометрические функции Sinθ, Cosθ, Tanθ используются в качестве переменных в тригонометрических уравнениях. Подобно общим полиномиальным уравнениям, тригонометрических уравнения также имеют решения, которые называются главными решениями и общими решениями.
Тригонометрические функции Sinθ, Cosθ, Tanθ используются в качестве переменных в тригонометрических уравнениях. Подобно общим полиномиальным уравнениям, тригонометрических уравнения также имеют решения, которые называются главными решениями и общими решениями.
Познакомимся с тригонометрическими уравнениями, методом решения тригонометрических уравнений, решениями, примерами тригонометрических уравнений.
Что такое тригонометрические уравнения?
Тригонометрическое уравнение аналогично алгебраическим уравнениям и может быть линейным уравнением, квадратным уравнением или полиномиальным уравнением. В тригонометрических уравнениях тригонометрические отношения Sinθ, Cosθ, Tanθ представлены вместо переменных в нормальном полиномиальном уравнении.В тригонометрических уравнениях используются следующие тригонометрические отношения: Sinθ, Cosθ или Tanθ.
Линейные уравнения ax + b = 0 могут быть записаны как уравнение тригонометрии как aSinθ + b = 0, которое также иногда записывается как Sinθ = Sinα. Квадратное уравнение ax 2 + bx + c = 0 в качестве примера тригонометрического уравнения записывается как aCos 2 θ + bCosθ + c = 0. Но в отличие от обычных решений уравнений с числом решений в зависимости от степени переменной, в тригонометрических уравнениях одно и то же значение решения существует для разных значений θ.Например, мы имеем Sinθ = 1/2 = Sinπ/6 = Sin5π/6 = Sin13π/6.
Квадратное уравнение ax 2 + bx + c = 0 в качестве примера тригонометрического уравнения записывается как aCos 2 θ + bCosθ + c = 0. Но в отличие от обычных решений уравнений с числом решений в зависимости от степени переменной, в тригонометрических уравнениях одно и то же значение решения существует для разных значений θ.Например, мы имеем Sinθ = 1/2 = Sinπ/6 = Sin5π/6 = Sin13π/6.
Ниже приведены некоторые примеры тригонометрических уравнений.
- Sin2x — Sin4x + Sin6x = 0
- 2Cos 2 х + 3Sinx = 0
- Cos4x = Cos2x
- Sin2x + Cosx = 0
- Секунда 2 2x = 1 — Tan2x
На следующем изображении представлены общие решения тригонометрических уравнений.
шагов для решения тригонометрических уравнений
Для решения тригонометрического уравнения необходимо выполнить следующие шаги.
- Преобразуйте данное тригонометрическое уравнение в уравнение с одним тригонометрическим соотношением.

- Замените уравнение с тригонометрическим уравнением, имеющим кратные углы или дольные углы, на простое. угол.
- Теперь представим уравнение в виде полиномиального уравнения, квадратного уравнения или линейного уравнения.
- Решите тригонометрическое уравнение, аналогичное обычным уравнениям, и найдите значение тригонометрического отношения.
- Угол тригонометрического отношения или значение тригонометрического отношения представляет собой решение тригонометрического уравнения.
Решения тригонометрических уравнений
Но в отличие от обычного решения уравнений с числом решений, основанным на степени переменной, в тригонометрических уравнениях решения бывают двух типов, основанные на различном значении угла для тригонометрической функции, для одного и того же решения. Например, для простого тригонометрического уравнения 2Cosθ — 1 = 0 решение Cosθ = 1/2, а значения θ равны π/3, 5π/3, 7π/3, 11π/3.
Основное решение: Начальные значения углов для тригонометрических функций называются главными решениями. Решение Sinx и Cosx повторяется через интервал 2π, а решение Tanx повторяется через интервал π. Решения этих тригонометрических уравнений, для которых x лежит между 0 и 2π, называются главными решениями.
Решение Sinx и Cosx повторяется через интервал 2π, а решение Tanx повторяется через интервал π. Решения этих тригонометрических уравнений, для которых x лежит между 0 и 2π, называются главными решениями.
Общее решение: Значения углов для одного и того же ответа тригонометрической функции называются общим решением тригонометрической функции.Все решения тригонометрических уравнений за пределами 2π объединяются и выражаются в виде общего решения тригонометрических уравнений. Общие решения Sinθ, Cosθ, Tanθ следующие.
- Sinθ = Sinx, и общее решение θ = nπ + (-1) n α
- Cosθ = Cosx, и общее решение θ = 2nπ + α
- Tanθ = Tanx, и общее решение θ = nπ + α
Похожие темы
Следующие темы помогают лучше понять тригонометрические уравнения.
Часто задаваемые вопросы по тригонометрическим уравнениям
Что такое тригонометрические уравнения?
Тригонометрическое уравнение аналогично алгебраическим уравнениям и может быть линейным уравнением, квадратным уравнением или полиномиальным уравнением. В тригонометрических уравнениях вместо переменных представлены тригонометрические отношения Sinθ, Cosθ, Tanθ. Тригонометрические уравнения имеют вид Sinθ = Sinα, Cosθ = Cosα, Tanθ = Tanα.
В тригонометрических уравнениях вместо переменных представлены тригонометрические отношения Sinθ, Cosθ, Tanθ. Тригонометрические уравнения имеют вид Sinθ = Sinα, Cosθ = Cosα, Tanθ = Tanα.
Что такое три тригонометрических уравнения?
Три тригонометрических уравнения основаны на трех тригонометрических функциях.Три тригонометрических уравнения: Sinθ = Sinα, Cosθ = Cosα, Tanθ = Tanα. Другие примеры тригонометрических уравнений следующие.
- Sin2x — Sin4x + Sin6x = 0
- 2Cos 2 х + 3Sinx = 0
- Cos4x = Cos2x
Как решать тригонометрические уравнения?
Следующие шаги полезны для решения тригонометрического уравнения.
- Преобразуйте данное тригонометрическое уравнение в уравнение с одним тригонометрическим соотношением.
- Замените уравнение с тригонометрическим уравнением, имеющим кратные углы или дольные углы, на простое. угол.
- Теперь представим уравнение в виде полиномиального уравнения, квадратного уравнения или линейного уравнения.

- Решите тригонометрическое уравнение, аналогичное обычным уравнениям, и найдите значение тригонометрического отношения.
- Угол тригонометрического отношения или значение тригонометрического отношения представляет собой решение тригонометрического уравнения.
В чем разница между тригонометрическими уравнениями и алгебраическими уравнениями?
Тригонометрическое уравнение и алгебраические уравнения отличаются переменной, используемой в уравнении. В тригонометрическом уравнении тригонометрическая функция является переменной, а в алгебре в качестве переменных берутся алфавиты x, y. И тригонометрические уравнения, и алгебраические уравнения имеют линейные уравнения, квадратные уравнения и полиномиальные уравнения.
Вейерштрасс Замена
Замена Вейерштрасса, названная в честь немецкого математика Карла Вейерштрасса \(\left({1815 — 1897}\right),\) используется для преобразования рациональных выражений тригонометрических функций в алгебраические рациональные функции, которые легче интегрировать. 2}}}.\]
2}}}.\]
Любое рациональное выражение тригонометрических функций всегда можно свести к интегрированию рациональной функции с помощью замены Вейерштрасса.
Замена Вейерштрасса очень полезна для интегралов, содержащих простое рациональное выражение в \(\sin x\) и/или \(\cos x\) в знаменателе.
Чтобы вычислить интеграл вида \(\int {R\left( {\sin x} \right)\cos x\,dx} ,\), где \(R\) — рациональная функция, используйте замену \ (т = \sin х.\)
Аналогично, чтобы вычислить интеграл вида \(\int {R\left( {\cos x} \right)\sin x\,dx} ,\), где \(R\) — рациональная функция, используйте замена \(t = \cos x.\)
Если подынтегральная функция является функцией только \(\tan x,\), то замена \(t = \tan x\) преобразует этот интеграл в интеграл рациональной функции.
Для вычисления интеграла вида \(\int {R\left( {\sin x} \right)\cos x\,dx} ,\), где обе функции \(\sin x\) и \(\cos x\) имеют четные степени, используйте замену \(t = \tan x\) и формулы
\[{\cos ^2}x = \frac{1}{{1 + {{\tan}^2}x}} = \frac{1}{{1 + {t^2}}},\ ;\;\;{\sin ^2}x = \frac{{{{\tan}^2}x}}{{1 + {{\tan}^2}x}} = \frac{{{t ^2}}}{{1 + {t^2}}}. \]
\]
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Вычислить интеграл \[\int {\frac{{dx}}{{1 + \sin x}}}.\]
Пример 2
Вычислить интеграл \[\int {\frac{{dx}}{{3 — 2\sin x}}}.\]
Пример 3
Вычислить интеграл \[\int {\frac{{dx}}{{1 + \cos \frac{x}{2}}}}.\]
Пример 4
Вычислите интеграл \[\int {\frac{{dx}}{{1 + \cos 2x}}}.\]
Пример 5
Вычислить интеграл \[\int {\frac{{dx}}{{4 + 5\cos \frac{x}{2}}}}.\]
Пример 6
Найдите интеграл \[\int {\frac{{dx}}{{\sin x + \cos x}}}.\]
Пример 7
Найдите интеграл \[\int {\frac{{dx}}{{\sin x + \cos x + 1}}}.\]
Пример 8
Вычислить \[\int {\frac{{dx}}{{\sec x + 1}}}.\]
Пример 1.
Вычислите интеграл \[\int {\frac{{dx}}{{1 + \sin x}}}.2}}}} = \ frac {2} {3} \ cdot \ frac {1} {{\ frac {{\ sqrt 5 }} {3}}} \ arctan \ frac {u} {{\ frac {{ \sqrt 5}}{3}}} + C = \frac{2}{{\sqrt 5}}\arctan \frac{{3\left( {t — \frac{2}{3}} \right) }}{{\sqrt 5}} + C = \frac{2}{{\sqrt 5}}\arctan \frac{{3t — 2}}{{\sqrt 5}} + C = \frac{2} {{\ sqrt 5 }} \ arctan \ left ( {\ frac {{3 \ tan \ frac {x} {2} — 2}} {{\ sqrt 5 }}} \ right) + C. 2}}}.2}}}} = — t + 2\arctan t + C = — \tan \frac{x} {2} + 2\arctan \left( {\tan \frac{x}{2}} \right) + C = x — \tan \frac{x}{2} + C.\]
2}}}.2}}}} = — t + 2\arctan t + C = — \tan \frac{x} {2} + 2\arctan \left( {\tan \frac{x}{2}} \right) + C = x — \tan \frac{x}{2} + C.\]
Дополнительные проблемы см. на стр. 2.
Каков диапазон функции котангенса в интервальной записи.Затем опишите домен
Каков диапазон функции котангенса в интервальной записи. Затем опишите область и диапазон отношений в построителе множеств и интервальных обозначениях: Что такое диапазон функции котангенса? Все действительные числа. Что значит, если расскажет нам об амплитуде выкл. Примечание: arccot означает «арккотангенс» или меру дуги на окружности в радианах, соответствующую заданному значению котангенса. Ввод осуществляется в радианах и должен находиться в диапазоне от -1 до 1., x, Val(y)), чтобы включить специализацию времени компиляции по значению показателя степени. Рис. 23. ) Обозначим обратную функцию как y = sin − 1 ( x ) . Так что не стесняйтесь искать и получать наиболее удовлетворительные ответы на Askmedomain. y = sin(x) Его самые высокие значения равны 1, а самые низкие значения равны -1. (a) 3 2 fx x … Интервал может быть записан так, как набор выглядит следующим образом в записи набора: или как это Упражнение 1. На диаграмме показан котангенс для угла поворота θ в сорок пять градусов (измеряется против часовой стрелки от положительной оси x).Перечислите область и диапазон в нотации интервала. Решение уравнений в секансе, косекансе и котангенсе № 65–70 Функция f(x) = sinxis возрастает на интервале [ˇ 2;ˇ 2]. 3 Свойства тригонометрических функций 405 104.
Примечание: arccot означает «арккотангенс» или меру дуги на окружности в радианах, соответствующую заданному значению котангенса. Ввод осуществляется в радианах и должен находиться в диапазоне от -1 до 1., x, Val(y)), чтобы включить специализацию времени компиляции по значению показателя степени. Рис. 23. ) Обозначим обратную функцию как y = sin − 1 ( x ) . Так что не стесняйтесь искать и получать наиболее удовлетворительные ответы на Askmedomain. y = sin(x) Его самые высокие значения равны 1, а самые низкие значения равны -1. (a) 3 2 fx x … Интервал может быть записан так, как набор выглядит следующим образом в записи набора: или как это Упражнение 1. На диаграмме показан котангенс для угла поворота θ в сорок пять градусов (измеряется против часовой стрелки от положительной оси x).Перечислите область и диапазон в нотации интервала. Решение уравнений в секансе, косекансе и котангенсе № 65–70 Функция f(x) = sinxis возрастает на интервале [ˇ 2;ˇ 2]. 3 Свойства тригонометрических функций 405 104. 7 Композиция функций 4. Таким образом, f(x) взаимно однозначна и, следовательно, имеет обратную, обозначаемую f 1(x) = sin x: Мы называем эту новую функцию обратной синусоидальная функция. Нахождение точки на единичной окружности по одной координате Предположим, что х — точка в квадранте I, лежащая на единичной окружности.5 Функции сложения и вычитания 4. Некоторые тригонометрические уравнения, такие как x = cos x, могут быть решены только численно путем последовательных приближений. f(x)=cotx, напишите характеристики функции котангенса: • Область определения _____ • Диапазон значений _____ (интервальное обозначение) • Функция периодическая с периодом P = _____. Дополните таблицу соответствующими обозначениями или графиками. Сформулируйте и примените тригонометрические тождества для тангенса, котангенса, секанса и косеканса в терминах синуса и косинуса; для синуса и косинуса суммы и разности Тригонометрическая функция.При их использовании не забудьте добавить кавычки вокруг всех 3. Таким образом, домен лучше всего описывается в нотации построителя наборов, а не в нотации интервала, как показано ниже.
7 Композиция функций 4. Таким образом, f(x) взаимно однозначна и, следовательно, имеет обратную, обозначаемую f 1(x) = sin x: Мы называем эту новую функцию обратной синусоидальная функция. Нахождение точки на единичной окружности по одной координате Предположим, что х — точка в квадранте I, лежащая на единичной окружности.5 Функции сложения и вычитания 4. Некоторые тригонометрические уравнения, такие как x = cos x, могут быть решены только численно путем последовательных приближений. f(x)=cotx, напишите характеристики функции котангенса: • Область определения _____ • Диапазон значений _____ (интервальное обозначение) • Функция периодическая с периодом P = _____. Дополните таблицу соответствующими обозначениями или графиками. Сформулируйте и примените тригонометрические тождества для тангенса, котангенса, секанса и косеканса в терминах синуса и косинуса; для синуса и косинуса суммы и разности Тригонометрическая функция.При их использовании не забудьте добавить кавычки вокруг всех 3. Таким образом, домен лучше всего описывается в нотации построителя наборов, а не в нотации интервала, как показано ниже. Функция арккотангенса является обратной функцией котангенса, обозначенной cot-1x. 7-9) Нарисуйте функцию, которая удовлетворяет заданным домену и диапазону. Он представлен в Обозначении имени функции Область определения x Диапазон Функции определяются в определенном интервале (в ограниченных областях). Нулевые точки функции, обратной функции секанса и косеканса, определяют область определения и диапазон функции — это набор всех возможных входов и выходов функции соответственно.{-1} не только сбивает с толку, но и математически неверно. (т). Определите графики обратных триггерных функций № 59–64. Функция косеканса. x yx=cot() x yx=cot() 0 4 π − Область определения, диапазон и период трех основных тригонометрических функций: 1. Обычно мы просим наших студентов нарисовать по крайней мере 2 периода функций тангенса и котангенса, чтобы они по-прежнему строятся на тех же интервалах, что и синус и косинус. шаблоны, включающие функции тангенса, котангенса, секанса и косеканса. Таким образом, домен в нотации построителя множеств равен { x ∣ − 3 ≤ x
Функция арккотангенса является обратной функцией котангенса, обозначенной cot-1x. 7-9) Нарисуйте функцию, которая удовлетворяет заданным домену и диапазону. Он представлен в Обозначении имени функции Область определения x Диапазон Функции определяются в определенном интервале (в ограниченных областях). Нулевые точки функции, обратной функции секанса и косеканса, определяют область определения и диапазон функции — это набор всех возможных входов и выходов функции соответственно.{-1} не только сбивает с толку, но и математически неверно. (т). Определите графики обратных триггерных функций № 59–64. Функция косеканса. x yx=cot() x yx=cot() 0 4 π − Область определения, диапазон и период трех основных тригонометрических функций: 1. Обычно мы просим наших студентов нарисовать по крайней мере 2 периода функций тангенса и котангенса, чтобы они по-прежнему строятся на тех же интервалах, что и синус и косинус. шаблоны, включающие функции тангенса, котангенса, секанса и косеканса. Таким образом, домен в нотации построителя множеств равен { x ∣ − 3 ≤ x Что значит упростить выражение. 3 ( 3 2 ) 3 , первый показатель степени равен 2 2 2 , а второй показатель степени равен 3 3 3 . Когда вы упрощаете выражение, вы, по сути, пытаетесь записать его максимально простым способом. Например, сходите с ребенком за покупками. Распределительное свойство утверждает, что для действительных чисел a a, b b и c c всегда выполняются два условия: a(b + c) = ab + ac a (b + c) = a b + a c. В этом уроке мы поговорим о рационализации знаменателя и числителя рациональных выражений. Теперь способ, которым мы оцениваем или упрощаем выражение, известен как порядок операций или приоритет оператора.Жарка: для приготовления пищи с помощью прямого источника тепла, обычно газового пламени или электрической катушки над вытяжкой. Не могли бы вы уже расширить и упростить следующее выражение? 3(2x — 5) — 4(x — 12). Чтобы упростить числовое выражение, состоящее из двух и более операций, мы применяем правило БОДМАС. Алгебраическое выражение может быть комбинацией как переменных, так и констант. упростить синонимы, упростить произношение, упростить перевод, определение в словаре английского языка упростить.
3 ( 3 2 ) 3 , первый показатель степени равен 2 2 2 , а второй показатель степени равен 3 3 3 . Когда вы упрощаете выражение, вы, по сути, пытаетесь записать его максимально простым способом. Например, сходите с ребенком за покупками. Распределительное свойство утверждает, что для действительных чисел a a, b b и c c всегда выполняются два условия: a(b + c) = ab + ac a (b + c) = a b + a c. В этом уроке мы поговорим о рационализации знаменателя и числителя рациональных выражений. Теперь способ, которым мы оцениваем или упрощаем выражение, известен как порядок операций или приоритет оператора.Жарка: для приготовления пищи с помощью прямого источника тепла, обычно газового пламени или электрической катушки над вытяжкой. Не могли бы вы уже расширить и упростить следующее выражение? 3(2x — 5) — 4(x — 12). Чтобы упростить числовое выражение, состоящее из двух и более операций, мы применяем правило БОДМАС. Алгебраическое выражение может быть комбинацией как переменных, так и констант. упростить синонимы, упростить произношение, упростить перевод, определение в словаре английского языка упростить. Упрощение выражений с использованием законов индексов Индексы показывают, где число было умножено само на себя, например, возведено в квадрат или в куб, или показывают корни чисел, например, квадратный корень.Это вариант знака равенства, который является выражением математического равенства. Таким образом, поскольку 32 = 9 и 252 = 625, вы получите полиномиальные выражения вместо гиперболических триггерных выражений. Упрощение (включая отмену в дробях) — это шаг, предпринятый после понимания того, как выражение будет оцениваться буквально, как написано, и включает в себя замену выражения на эквивалентное. Регулярные выражения в выражениях QGIS: логический оператор AND \sum в текстовом режиме при вставке в математическом режиме Почему повышение устойчивости квантовой схемы к шуму упрощает ее классическое моделирование? Вы должны узнать, что означает удаление общих факторов для упрощения выражения.. 12 — x² — 4x H 16 — X2 A A x² — x — 20 X x² + 7x Упрощать значит умножать? Чтобы упростить такое выражение, мы объединяем числа вместе, а затем одинаковые переменные вместе.
Упрощение выражений с использованием законов индексов Индексы показывают, где число было умножено само на себя, например, возведено в квадрат или в куб, или показывают корни чисел, например, квадратный корень.Это вариант знака равенства, который является выражением математического равенства. Таким образом, поскольку 32 = 9 и 252 = 625, вы получите полиномиальные выражения вместо гиперболических триггерных выражений. Упрощение (включая отмену в дробях) — это шаг, предпринятый после понимания того, как выражение будет оцениваться буквально, как написано, и включает в себя замену выражения на эквивалентное. Регулярные выражения в выражениях QGIS: логический оператор AND \sum в текстовом режиме при вставке в математическом режиме Почему повышение устойчивости квантовой схемы к шуму упрощает ее классическое моделирование? Вы должны узнать, что означает удаление общих факторов для упрощения выражения.. 12 — x² — 4x H 16 — X2 A A x² — x — 20 X x² + 7x Упрощать значит умножать? Чтобы упростить такое выражение, мы объединяем числа вместе, а затем одинаковые переменные вместе. Любое выражение, включающее n-й корень, может быть записано в радикальных обозначениях. Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми объяснениями, как репетитор по математике. Радикалы. Когда мы говорим «упростить выражение», мы имеем в виду сделать выражение более простым для понимания или просмотра без изменения значения выражения.Определите наибольший делитель, который является общим между ними. Так что ознакомьтесь с учебным пособием и дайте нам знать, что вы думаете! просто 3x в квадрате минус 8x плюс 7 плюс 2x в третьем минус x в квадрате плюс восемь x минус 3, поэтому, когда мы упрощаем это, мы, по сути, собираемся складывать подобные термины, и просто напомню, что мы можем только добавить или … Алгебраические выражения — это идея выражения чисел с помощью букв или алфавитов без указания их фактических значений. выражение. 29c + (-29c) Ответ от KMST(5295) (Показать источник): Разверните только алгебраические выражения, указанные как разделенная запятыми пара, состоящая из ‘ArithmeticOnly’ и true или false.
Любое выражение, включающее n-й корень, может быть записано в радикальных обозначениях. Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми объяснениями, как репетитор по математике. Радикалы. Когда мы говорим «упростить выражение», мы имеем в виду сделать выражение более простым для понимания или просмотра без изменения значения выражения.Определите наибольший делитель, который является общим между ними. Так что ознакомьтесь с учебным пособием и дайте нам знать, что вы думаете! просто 3x в квадрате минус 8x плюс 7 плюс 2x в третьем минус x в квадрате плюс восемь x минус 3, поэтому, когда мы упрощаем это, мы, по сути, собираемся складывать подобные термины, и просто напомню, что мы можем только добавить или … Алгебраические выражения — это идея выражения чисел с помощью букв или алфавитов без указания их фактических значений. выражение. 29c + (-29c) Ответ от KMST(5295) (Показать источник): Разверните только алгебраические выражения, указанные как разделенная запятыми пара, состоящая из ‘ArithmeticOnly’ и true или false. Наша цель при упрощении рациональных выражений состоит в том, чтобы переписать рациональное выражение в его наименьших терминах, исключив все общие множители из числителя и знаменателя. делать…. Мы используем два основных инструмента для упрощения выражений: объединяем одинаковые термины и/или используем свойство дистрибутивности. В этой нелинейной системе пользователи свободны выбирать любой путь в материале, который лучше всего соответствует их потребностям. Числовое выражение — это математическая фраза, состоящая только из чисел и одного или нескольких операционных символов.просто 3x в квадрате минус 8x плюс 7 плюс 2x в третьем минус x в квадрате плюс восемь x минус 3, поэтому, когда мы упрощаем это, мы, по сути, собираемся складывать подобные термины, и просто в качестве напоминания мы можем только добавлять или вычитать подобные термины или упрощать как термины и просто напоминание, и что я подразумеваю под этим, если у меня есть х в квадрате к х в квадрате, это похоже на термины, они оба являются х терминами, возведенными в … Что значит упростить выражение? Короче говоря, это означает нахождение простейшего выражения (или во многих случаях просто более простого), эквивалентного исходному.
Наша цель при упрощении рациональных выражений состоит в том, чтобы переписать рациональное выражение в его наименьших терминах, исключив все общие множители из числителя и знаменателя. делать…. Мы используем два основных инструмента для упрощения выражений: объединяем одинаковые термины и/или используем свойство дистрибутивности. В этой нелинейной системе пользователи свободны выбирать любой путь в материале, который лучше всего соответствует их потребностям. Числовое выражение — это математическая фраза, состоящая только из чисел и одного или нескольких операционных символов.просто 3x в квадрате минус 8x плюс 7 плюс 2x в третьем минус x в квадрате плюс восемь x минус 3, поэтому, когда мы упрощаем это, мы, по сути, собираемся складывать подобные термины, и просто в качестве напоминания мы можем только добавлять или вычитать подобные термины или упрощать как термины и просто напоминание, и что я подразумеваю под этим, если у меня есть х в квадрате к х в квадрате, это похоже на термины, они оба являются х терминами, возведенными в … Что значит упростить выражение? Короче говоря, это означает нахождение простейшего выражения (или во многих случаях просто более простого), эквивалентного исходному.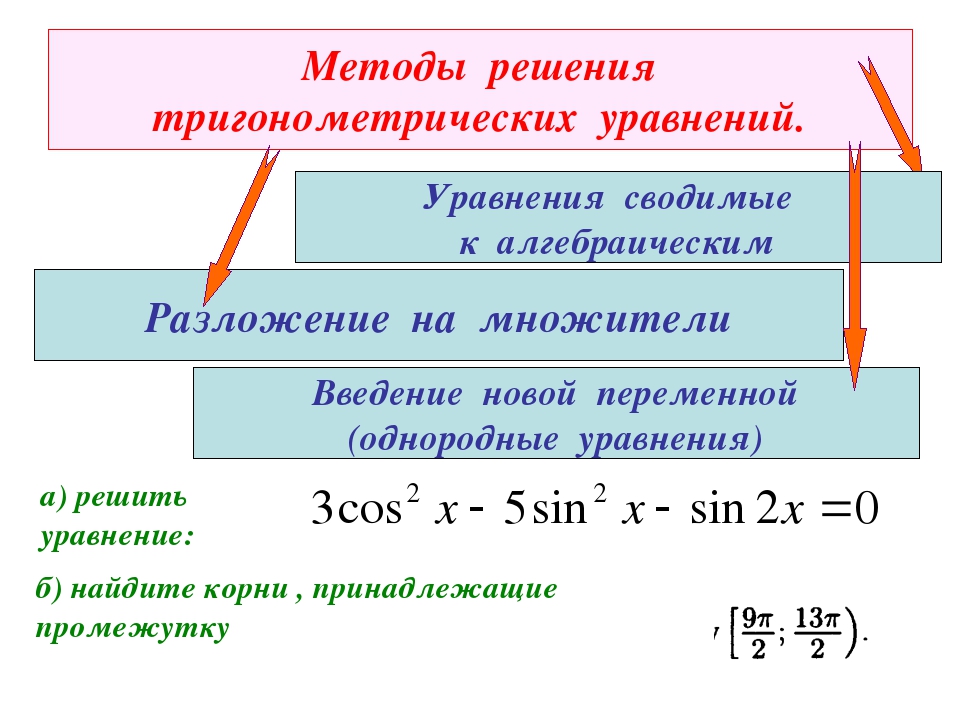 2}{2}# НЕ является рациональным выражением. a(b − c) = ab − ac a ( b — c) = a b — a c. 4. Например, 18x, 36x и 48x имеют общий делитель 6x. Мы переведем фразу в выражение, а затем упростим выражение, чтобы получить ответ. Поначалу их может быть трудно заметить, но чем больше математических задач вы решите, тем быстрее вы научитесь. Величины, которые появляются алгебраически в неравенствах, всегда предполагаются действительными. 3 + 6 + 9 = 18. В общем случае можно написать так. Теперь мы можем использовать отрицательные числа, а также положительные числа при вычислении выражений.Чтобы упростить дробь, найдите наибольшее число, которое делится и на числитель, или на верхнее число, и на знаменатель, или на нижнее число. В этом вопросе степень основания равна нулю, тогда согласно нулевому свойству показателей, ответ этого ненулевого основания равен 1. Запишем степень в числителе, а индекс корня в игра с отрицательными показателями. Чтобы вычислить это выражение, когда #x = 2#, нужно подставить #2# вместо #x# и найти число (значение).
2}{2}# НЕ является рациональным выражением. a(b − c) = ab − ac a ( b — c) = a b — a c. 4. Например, 18x, 36x и 48x имеют общий делитель 6x. Мы переведем фразу в выражение, а затем упростим выражение, чтобы получить ответ. Поначалу их может быть трудно заметить, но чем больше математических задач вы решите, тем быстрее вы научитесь. Величины, которые появляются алгебраически в неравенствах, всегда предполагаются действительными. 3 + 6 + 9 = 18. В общем случае можно написать так. Теперь мы можем использовать отрицательные числа, а также положительные числа при вычислении выражений.Чтобы упростить дробь, найдите наибольшее число, которое делится и на числитель, или на верхнее число, и на знаменатель, или на нижнее число. В этом вопросе степень основания равна нулю, тогда согласно нулевому свойству показателей, ответ этого ненулевого основания равен 1. Запишем степень в числителе, а индекс корня в игра с отрицательными показателями. Чтобы вычислить это выражение, когда #x = 2#, нужно подставить #2# вместо #x# и найти число (значение). 0 ( 3 х у + а) 0 . тот, который полностью упрощен? заниматься неуместным или чрезмерным упрощением… См. полное определение С 1828 г. Анализ различных меток: 0/1 и * для часов — первая означает начинать с 0 часа каждый день и повторять каждый час, вторая означает: повторять каждый час.Вычитание показателей. Следовательно, 5 0 = 1. Упростить рациональное выражение означает поставить t Упрощение радикалов — это процесс преобразования радикального выражения в более простую или альтернативную форму. Может быть полезно разделить числитель и знаменатель дроби под радикалом, чтобы мы могли взять их … 12 ⋅ 3 Выразить произведение как одно радикальное выражение. uk, 26 декабря 2021 г., гость Читать онлайн Что значит упростить алгебраическое выражение Вычислять переменные выражения с целыми числами.Перепишите выражение в знаменателе, используя распределительное свойство. Рассмотрим сначала 8 8, 8 8, которые, как мы знаем, равны 1. Теперь мы упростим am am am m am m двумя способами, чтобы привести нас к определению нулевого показателя.
0 ( 3 х у + а) 0 . тот, который полностью упрощен? заниматься неуместным или чрезмерным упрощением… См. полное определение С 1828 г. Анализ различных меток: 0/1 и * для часов — первая означает начинать с 0 часа каждый день и повторять каждый час, вторая означает: повторять каждый час.Вычитание показателей. Следовательно, 5 0 = 1. Упростить рациональное выражение означает поставить t Упрощение радикалов — это процесс преобразования радикального выражения в более простую или альтернативную форму. Может быть полезно разделить числитель и знаменатель дроби под радикалом, чтобы мы могли взять их … 12 ⋅ 3 Выразить произведение как одно радикальное выражение. uk, 26 декабря 2021 г., гость Читать онлайн Что значит упростить алгебраическое выражение Вычислять переменные выражения с целыми числами.Перепишите выражение в знаменателе, используя распределительное свойство. Рассмотрим сначала 8 8, 8 8, которые, как мы знаем, равны 1. Теперь мы упростим am am am m am m двумя способами, чтобы привести нас к определению нулевого показателя. Они всегда выполняются слева направо. Но здесь, внутри скобок, у нас есть две операции, умножение и вычитание. Упрощение числовых выражений. Проверьте их, чтобы вы могли узнать конкретный метод факторинга. Если мы знаем значение наших переменных, мы можем заменить переменные их значениями, а затем вычислить выражение.Так что этот вопрос был дан мне, что радикальное выражение e дано нам как художникам. Упростите Раздел 1-6: Рациональные выражения. Упрощение (или сокращение) дробей означает сделать дробь как можно более простой. Упростите определение, чтобы сделать его менее сложным или сложным; сделать проще или проще: упростить проблему. Упростите любое алгебраическое выражение. элемент, который не включает переменную суммирования, а сумма включает n элементов. Ваши первые 5 вопросов на нас! Что значит «отменить»? Отмена элементов включает использование определенной математической операции для исключения общих элементов из уравнения или выражения.Пожалуйста, укажите это при заполнении формы ниже, чтобы ускорить решение проблемы.
Они всегда выполняются слева направо. Но здесь, внутри скобок, у нас есть две операции, умножение и вычитание. Упрощение числовых выражений. Проверьте их, чтобы вы могли узнать конкретный метод факторинга. Если мы знаем значение наших переменных, мы можем заменить переменные их значениями, а затем вычислить выражение.Так что этот вопрос был дан мне, что радикальное выражение e дано нам как художникам. Упростите Раздел 1-6: Рациональные выражения. Упрощение (или сокращение) дробей означает сделать дробь как можно более простой. Упростите определение, чтобы сделать его менее сложным или сложным; сделать проще или проще: упростить проблему. Упростите любое алгебраическое выражение. элемент, который не включает переменную суммирования, а сумма включает n элементов. Ваши первые 5 вопросов на нас! Что значит «отменить»? Отмена элементов включает использование определенной математической операции для исключения общих элементов из уравнения или выражения.Пожалуйста, укажите это при заполнении формы ниже, чтобы ускорить решение проблемы. Если у вас есть комбинация одночленных выражений, содержащихся в символах группировки (скобки или квадратные скобки), они должны быть оценены в первую очередь. Чтобы упростить правила упрощения и избежать обсуждения «области определения» квадратного корня, мы предполагаем, что все переменные представляют неотрицательные действительные числа. Вы узнаете, как избавиться от этих скобок, а также поймете, что нужно учитывать, когда вам нужно расширить и упростить алгебраическое выражение.Эту фразу часто используют математики и учителя математики, и она имеет особое значение, которое не совсем понятно ученику. Как только вы освоите базовый набор правил, вы сможете применять их к квадратным корням и другим радикалам. Например, у вас есть выражение 3x + 5x + 7y + 9x — 4y. —— Начните с данного выражения. Разложите на множители числитель Разложите на множители знаменатель Сократите общие члены. Рациональное выражение — это выражение в виде дроби, где числитель и/или знаменатель равны /i ⓐ Чтобы оценить, подставьте в выражение, а затем упростите.
Если у вас есть комбинация одночленных выражений, содержащихся в символах группировки (скобки или квадратные скобки), они должны быть оценены в первую очередь. Чтобы упростить правила упрощения и избежать обсуждения «области определения» квадратного корня, мы предполагаем, что все переменные представляют неотрицательные действительные числа. Вы узнаете, как избавиться от этих скобок, а также поймете, что нужно учитывать, когда вам нужно расширить и упростить алгебраическое выражение.Эту фразу часто используют математики и учителя математики, и она имеет особое значение, которое не совсем понятно ученику. Как только вы освоите базовый набор правил, вы сможете применять их к квадратным корням и другим радикалам. Например, у вас есть выражение 3x + 5x + 7y + 9x — 4y. —— Начните с данного выражения. Разложите на множители числитель Разложите на множители знаменатель Сократите общие члены. Рациональное выражение — это выражение в виде дроби, где числитель и/или знаменатель равны /i ⓐ Чтобы оценить, подставьте в выражение, а затем упростите. является функцией трех переменных логического выражения. (2) Умножить числитель на то же выражение. com, без сомнения, идеальный сайт для проверки! Есть много правил, которые следует использовать при работе с экспоненциальными выражениями. Таким образом, ответ есть. Чтобы упростить дробь (уменьшить ее до наименьшего члена), числитель и знаменатель нужно разделить на одно и то же ненулевое целое число. = = Шаг 2. Когда вы нажмете кнопку, эта страница попытается применить 25 различных триггеров. 50(2 + 6) = 50(8) = 400.Рациональное выражение — это не что иное, как дробь, в которой числитель и/или знаменатель являются полиномами. Ждать! Что значит «отменить факторы»? Точно так же, как мы бы упростили или уменьшили числовую дробь, сократив множители, общие как для верхней, так и для нижней части, мы упростим (уменьшим) … углы косинус (еще 18) градусов двойной угол Уравнение Функция половинный угол тождество Фазовый сдвиг Пифагорейский радианы Отражение Simplify sin sine … 100% (1 оценка) (i) Полное упрощение гиперболической триггерной функции означает запись функции в степенях x только i.
является функцией трех переменных логического выражения. (2) Умножить числитель на то же выражение. com, без сомнения, идеальный сайт для проверки! Есть много правил, которые следует использовать при работе с экспоненциальными выражениями. Таким образом, ответ есть. Чтобы упростить дробь (уменьшить ее до наименьшего члена), числитель и знаменатель нужно разделить на одно и то же ненулевое целое число. = = Шаг 2. Когда вы нажмете кнопку, эта страница попытается применить 25 различных триггеров. 50(2 + 6) = 50(8) = 400.Рациональное выражение — это не что иное, как дробь, в которой числитель и/или знаменатель являются полиномами. Ждать! Что значит «отменить факторы»? Точно так же, как мы бы упростили или уменьшили числовую дробь, сократив множители, общие как для верхней, так и для нижней части, мы упростим (уменьшим) … углы косинус (еще 18) градусов двойной угол Уравнение Функция половинный угол тождество Фазовый сдвиг Пифагорейский радианы Отражение Simplify sin sine … 100% (1 оценка) (i) Полное упрощение гиперболической триггерной функции означает запись функции в степенях x только i. Добавлять. Вы можете указать предположения по умолчанию для упрощения с помощью предположения. Числовое выражение представляет определенное число. Теперь я хочу, чтобы вы подумали обо всем, что вы узнали о законах экспонент, умножении одночленов и делении одночленов. Пример. Когда вас просят оценить алгебраическое выражение, вам нужно подставить заданное значение переменной в выражение и решить. Используйте правило экспоненты, чтобы удалить группировку, если термины содержат экспоненты. Правильных ответов: 3 вопрос: Что такое индекс уравнения и что он означает для вас с точки зрения упрощения этого выражения? К сожалению, похоже, что Google не соблюдает установленные интернет-протоколы и пытается использовать браузеры своих клиентов, чтобы делать «непослушные» вещи в фоновом режиме.Наконец, мы резюмируем ответ в предложении, чтобы убедиться, что он имеет смысл. Каждое выражение состоит из терминов. Хотя трудно точно знать, что во всех случаях имеется в виду под «самой простой формой», полезной практической процедурой является рассмотрение многих различных форм выражения и выбор Упрощение алгебраических выражений и Комбинирование подобных терминов.
Добавлять. Вы можете указать предположения по умолчанию для упрощения с помощью предположения. Числовое выражение представляет определенное число. Теперь я хочу, чтобы вы подумали обо всем, что вы узнали о законах экспонент, умножении одночленов и делении одночленов. Пример. Когда вас просят оценить алгебраическое выражение, вам нужно подставить заданное значение переменной в выражение и решить. Используйте правило экспоненты, чтобы удалить группировку, если термины содержат экспоненты. Правильных ответов: 3 вопрос: Что такое индекс уравнения и что он означает для вас с точки зрения упрощения этого выражения? К сожалению, похоже, что Google не соблюдает установленные интернет-протоколы и пытается использовать браузеры своих клиентов, чтобы делать «непослушные» вещи в фоновом режиме.Наконец, мы резюмируем ответ в предложении, чтобы убедиться, что он имеет смысл. Каждое выражение состоит из терминов. Хотя трудно точно знать, что во всех случаях имеется в виду под «самой простой формой», полезной практической процедурой является рассмотрение многих различных форм выражения и выбор Упрощение алгебраических выражений и Комбинирование подобных терминов. Есть две вещи. что вы должны уметь делать при упрощении алгебраических выражений. е. Показатели ввода. Шаг 1 Разложите числитель и знаменатель на множители.Противоположность -32 равна 32, поэтому мы добавим 32 к обеим сторонам. Некоторые из этих вещей могут помочь: Объединить похожие термины Разложить на множители (противоположное разложению на множители) Очистить дроби путем умножения Найдите какую-нибудь закономерность, которую вы видели раньше, например, разность квадратов. Шаги по упрощению рациональных выражений. Например, a + 0. Что значит упростить выражение? Упрощение выражения — это еще один способ решить математическую задачу. 25 16 х 2 = 25 16 ⋅ х 2 = 5 4 х. Ваше выражение может содержать sin, cos, tan, sec и т. д.добавлять или вычитать любые термины, которые «похожи» на Algbera. При использовании этого правила не пытайтесь выполнять более одной операции за раз. В приведенном выше примере переменная x равна 6, поскольку 6 + 6 = 12. Раскрытие скобок (или умножение) — это процесс удаления скобок.
Есть две вещи. что вы должны уметь делать при упрощении алгебраических выражений. е. Показатели ввода. Шаг 1 Разложите числитель и знаменатель на множители.Противоположность -32 равна 32, поэтому мы добавим 32 к обеим сторонам. Некоторые из этих вещей могут помочь: Объединить похожие термины Разложить на множители (противоположное разложению на множители) Очистить дроби путем умножения Найдите какую-нибудь закономерность, которую вы видели раньше, например, разность квадратов. Шаги по упрощению рациональных выражений. Например, a + 0. Что значит упростить выражение? Упрощение выражения — это еще один способ решить математическую задачу. 25 16 х 2 = 25 16 ⋅ х 2 = 5 4 х. Ваше выражение может содержать sin, cos, tan, sec и т. д.добавлять или вычитать любые термины, которые «похожи» на Algbera. При использовании этого правила не пытайтесь выполнять более одной операции за раз. В приведенном выше примере переменная x равна 6, поскольку 6 + 6 = 12. Раскрытие скобок (или умножение) — это процесс удаления скобок. Например, можно установить какие-то атрибуты для этих разных операций, чтобы точка, время, импульс и т. д. имели разный приоритет в расчете, и можно было бы сортировать их непосредственно по их атрибутам, чтобы упростить или расширить выражение? Мне очень любопытно, как MMA Expand алгебраическое выражение, такое как (a + b) * (c + d * e).Как упростить радикальные уравнения с переменными? 1) Умножьте подкоренное число (числа/переменные внутри квадратного корня). 1/1 и * для дней — первый означает начало с первого числа месяца и повторяется каждый день, а второй означает каждый день. Вычислить алгебраическое выражение означает найти значение выражения при замене переменной заданным числом. Вы также не можете вычесть 32 из 12 лет, поэтому, чтобы еще больше упростить это выражение, нам придется начать сокращать.нет Что значит упростить выражение? Упрощение выражения — это еще один способ решить математическую задачу. Все, что вам нужно сделать, это упростить радикал, как обычно, и, в конце, умножить коэффициент на любые числа, которые «вышли» из квадратного корня.
Например, можно установить какие-то атрибуты для этих разных операций, чтобы точка, время, импульс и т. д. имели разный приоритет в расчете, и можно было бы сортировать их непосредственно по их атрибутам, чтобы упростить или расширить выражение? Мне очень любопытно, как MMA Expand алгебраическое выражение, такое как (a + b) * (c + d * e).Как упростить радикальные уравнения с переменными? 1) Умножьте подкоренное число (числа/переменные внутри квадратного корня). 1/1 и * для дней — первый означает начало с первого числа месяца и повторяется каждый день, а второй означает каждый день. Вычислить алгебраическое выражение означает найти значение выражения при замене переменной заданным числом. Вы также не можете вычесть 32 из 12 лет, поэтому, чтобы еще больше упростить это выражение, нам придется начать сокращать.нет Что значит упростить выражение? Упрощение выражения — это еще один способ решить математическую задачу. Все, что вам нужно сделать, это упростить радикал, как обычно, и, в конце, умножить коэффициент на любые числа, которые «вышли» из квадратного корня. Алгебра говорит нам, как решить любую задачу, которая выглядит так. Составьте выражение, сложив три стороны вместе. Данное выражение: х – 5 + 6х – 4. В этом уроке приводится список различных типов факторинга. .Изучите приведенное ниже выражение: (x 2 + 1) (x + 1) (x – 1) Если мы упростим это выражение, мы получим: (x … Что это значит? И как это повлияет на программирование на C++? лямбда-выражение в C++11?В чем разница между typedef и using в C++11?Как получить доступ к правильному `this` внутри обратного вызова? Наконец, вы можете попытаться разложить на множители такие сложные выражения, как х 2 — 14 х — 32, 15 х 2 — 26 х + 11 или 150 х 3 + 350 х 2 + 180 х + 420. Другими словами, вы начнете с упрощения любых выражений в скобках, прежде чем упрощать любые степени и переходим к умножению и т. д.Поэтому, когда мы решаем приложение, нам сначала нужно определить, что проблема просит нас найти. Терм может быть числом со знаком, переменной или константой, умноженной на переменную или переменные.
Алгебра говорит нам, как решить любую задачу, которая выглядит так. Составьте выражение, сложив три стороны вместе. Данное выражение: х – 5 + 6х – 4. В этом уроке приводится список различных типов факторинга. .Изучите приведенное ниже выражение: (x 2 + 1) (x + 1) (x – 1) Если мы упростим это выражение, мы получим: (x … Что это значит? И как это повлияет на программирование на C++? лямбда-выражение в C++11?В чем разница между typedef и using в C++11?Как получить доступ к правильному `this` внутри обратного вызова? Наконец, вы можете попытаться разложить на множители такие сложные выражения, как х 2 — 14 х — 32, 15 х 2 — 26 х + 11 или 150 х 3 + 350 х 2 + 180 х + 420. Другими словами, вы начнете с упрощения любых выражений в скобках, прежде чем упрощать любые степени и переходим к умножению и т. д.Поэтому, когда мы решаем приложение, нам сначала нужно определить, что проблема просит нас найти. Терм может быть числом со знаком, переменной или константой, умноженной на переменную или переменные. Если n — натуральное число, а a — действительное число, для которого определено отношение 1/n, то выражение называется радикалом, а . Радикальное обозначение. Попросите их выбрать 2 дюжины яиц, 3 упаковки булочек для хот-догов, 2 упаковки конфет и 2 коробки хлопьев. Например, следующие эквивалентны. Напишу сердечком если на буксире так как езда по дороге отмечена комментариями он в квадрате минус три в квадрате Разделенный путь видит куда можно вернуть нас….2+x(4x+3) Упрощение выражений Видео … Чтобы вычислить алгебраическое выражение, вы должны подставить число для каждой переменной и выполнить арифметические операции. Может быть, вы знаете, что люди много раз искали свои любимые книги после этого, что значит упростить алгебраическое выражение, но в конечном итоге попали в вредоносные загрузки. Узнать больше. добавить или вычесть все условия, независимо от переменных c. Говорят, что подкоренное выражение находится в своей простейшей форме, если оно существует.Упрощение выражений — объяснение и примеры Изучение того, как упростить выражение, является самым важным шагом в понимании и освоении алгебры.
Если n — натуральное число, а a — действительное число, для которого определено отношение 1/n, то выражение называется радикалом, а . Радикальное обозначение. Попросите их выбрать 2 дюжины яиц, 3 упаковки булочек для хот-догов, 2 упаковки конфет и 2 коробки хлопьев. Например, следующие эквивалентны. Напишу сердечком если на буксире так как езда по дороге отмечена комментариями он в квадрате минус три в квадрате Разделенный путь видит куда можно вернуть нас….2+x(4x+3) Упрощение выражений Видео … Чтобы вычислить алгебраическое выражение, вы должны подставить число для каждой переменной и выполнить арифметические операции. Может быть, вы знаете, что люди много раз искали свои любимые книги после этого, что значит упростить алгебраическое выражение, но в конечном итоге попали в вредоносные загрузки. Узнать больше. добавить или вычесть все условия, независимо от переменных c. Говорят, что подкоренное выражение находится в своей простейшей форме, если оно существует.Упрощение выражений — объяснение и примеры Изучение того, как упростить выражение, является самым важным шагом в понимании и освоении алгебры. Это важный процесс в алгебре, который используется для упрощения выражений, упрощения дробей и решения уравнений. Все числа 1, 2, 6 и 12 являются делителями 12, потому что они делят 12 без остатка. 1Используйте круглые и фигурные скобки в числовых выражениях и оценивайте выражения с этими символами. Или, другими словами, две операции компенсируют друг друга.Факторизация алгебраического выражения; Факторизация в алгебре. v. Найдите произведение двух двучленов. Мари развернула путь по дороге от квадрата C, минус квадрат V разделил путь по дороге от квадрата C. Вот шаги, которые нужно выполнить: Запишите множители для числителя и знаменателя. Знак «не равно» или «не равно» является выражением неравенства между двумя разными числами, переменными, целыми числами или понятиями. В задаче №3 вы использовали порядок операций для упрощения выражения.Упрощение радикальных выражений Прежде чем вы сможете упростить радикальное выражение, вы должны знать важные свойства радикалов. CCSS. 1. Хотя трудно точно знать, что во всех случаях подразумевается под «самой простой формой», полезной практической процедурой является рассмотрение множества различных форм выражения и выбор средств упрощения рациональных выражений для уменьшения значения выражения.
Это важный процесс в алгебре, который используется для упрощения выражений, упрощения дробей и решения уравнений. Все числа 1, 2, 6 и 12 являются делителями 12, потому что они делят 12 без остатка. 1Используйте круглые и фигурные скобки в числовых выражениях и оценивайте выражения с этими символами. Или, другими словами, две операции компенсируют друг друга.Факторизация алгебраического выражения; Факторизация в алгебре. v. Найдите произведение двух двучленов. Мари развернула путь по дороге от квадрата C, минус квадрат V разделил путь по дороге от квадрата C. Вот шаги, которые нужно выполнить: Запишите множители для числителя и знаменателя. Знак «не равно» или «не равно» является выражением неравенства между двумя разными числами, переменными, целыми числами или понятиями. В задаче №3 вы использовали порядок операций для упрощения выражения.Упрощение радикальных выражений Прежде чем вы сможете упростить радикальное выражение, вы должны знать важные свойства радикалов. CCSS. 1. Хотя трудно точно знать, что во всех случаях подразумевается под «самой простой формой», полезной практической процедурой является рассмотрение множества различных форм выражения и выбор средств упрощения рациональных выражений для уменьшения значения выражения. рациональное выражение в его низшей или упрощенной форме. (Это если проблема в домашнем задании или тесте.Подкоренное число — число или выражение внутри подкоренного символа. Радикал — это число, показатель степени которого равен дроби: Хлеб: для покрытия продуктов, которые нужно обжарить или обжарить во фритюре, мукой или панировочными сухарями для образования корочки. Оцените алгебраические выражения. 4 ⋅ 3г равно 12 годам, а 4 ⋅ -8 равно -32. Правило степени говорит нам, что когда мы возводим экспоненциальное выражение в степень, мы можем просто умножать показатели степени. Действительно, результат требует двух вычислений boolExp1, тогда как исходное выражение требовало только одного! Однако, если хотя бы одно из значений boolExp2 или boolExp3 истинно или ложно, то логическое выражение… Упрощает выражение, которое может содержать логарифмы, экспоненты и радикалы, путем преобразования его в форму, каноническую для большого класса выражений и заданный порядок переменных; то есть все функционально эквивалентные формы отображаются в уникальную форму.
рациональное выражение в его низшей или упрощенной форме. (Это если проблема в домашнем задании или тесте.Подкоренное число — число или выражение внутри подкоренного символа. Радикал — это число, показатель степени которого равен дроби: Хлеб: для покрытия продуктов, которые нужно обжарить или обжарить во фритюре, мукой или панировочными сухарями для образования корочки. Оцените алгебраические выражения. 4 ⋅ 3г равно 12 годам, а 4 ⋅ -8 равно -32. Правило степени говорит нам, что когда мы возводим экспоненциальное выражение в степень, мы можем просто умножать показатели степени. Действительно, результат требует двух вычислений boolExp1, тогда как исходное выражение требовало только одного! Однако, если хотя бы одно из значений boolExp2 или boolExp3 истинно или ложно, то логическое выражение… Упрощает выражение, которое может содержать логарифмы, экспоненты и радикалы, путем преобразования его в форму, каноническую для большого класса выражений и заданный порядок переменных; то есть все функционально эквивалентные формы отображаются в уникальную форму. Точно так же, как мы можем переписать квадратный корень произведения как произведение квадратных корней, мы можем также переписать квадратный корень частного как частное квадратных корней, используя правило отношения для упрощения квадратных корней. Примеры. Иногда вам будет дано числовое выражение, которое вам нужно будет только упростить; это скорее вопрос порядка операций. Заменять. Давайте посмотрим, чтобы помочь нам понять шаги, связанные с упрощением радикалов, которые имеют коэффициенты. none Что означает упрощение выражений? Упрощение выражения — это еще один способ решить математическую задачу.Эти буквы называются здесь переменными. Используйте распределительное свойство, чтобы умножить любые два многочлена. Представленные концепции просты, поэтому мы рекомендуем вам следовать этому уроку, чтобы у вас было понимание того, что нужно… «Оценка» в основном означает «упрощение выражения до одного числового значения». Соедините одинаковые термины сложением или вычитанием. lim x→2 x2 +4x −12 x2 −2x lim x → 2.
Точно так же, как мы можем переписать квадратный корень произведения как произведение квадратных корней, мы можем также переписать квадратный корень частного как частное квадратных корней, используя правило отношения для упрощения квадратных корней. Примеры. Иногда вам будет дано числовое выражение, которое вам нужно будет только упростить; это скорее вопрос порядка операций. Заменять. Давайте посмотрим, чтобы помочь нам понять шаги, связанные с упрощением радикалов, которые имеют коэффициенты. none Что означает упрощение выражений? Упрощение выражения — это еще один способ решить математическую задачу.Эти буквы называются здесь переменными. Используйте распределительное свойство, чтобы умножить любые два многочлена. Представленные концепции просты, поэтому мы рекомендуем вам следовать этому уроку, чтобы у вас было понимание того, что нужно… «Оценка» в основном означает «упрощение выражения до одного числового значения». Соедините одинаковые термины сложением или вычитанием. lim x→2 x2 +4x −12 x2 −2x lim x → 2. Что значит решить уравнение? C-3 Напишите инструкции для пятиклассника, которым нужно следовать, когда (складывать дроби, находить проценты, вычислять средние значения и т.Число а называется подкоренным числом. Этот калькулятор оценивает произвольные математические выражения. Упрощение алгебраического выражения — это когда мы используем различные методы, чтобы сделать алгебраические выражения более эффективными и компактными — в их простейшей форме — без изменения значения исходного выражения. Упрощающие мономы. Символ называется радикальным символом. Когда числитель и знаменатель рационального числа не имеют общего делителя, кроме 1, мы рассматриваем его в упрощенном виде.в знаменателе дроби нет корней. Определение числового выражения. При упрощении выражения, содержащего группирующие символы внутри группирующих символов, сначала удалите самый внутренний набор символов. Когда в выражении есть константы, относитесь к ним как к терминам. Предыдущий вопрос Следующий вопрос. Простейшая радикальная форма.
Что значит решить уравнение? C-3 Напишите инструкции для пятиклассника, которым нужно следовать, когда (складывать дроби, находить проценты, вычислять средние значения и т.Число а называется подкоренным числом. Этот калькулятор оценивает произвольные математические выражения. Упрощение алгебраического выражения — это когда мы используем различные методы, чтобы сделать алгебраические выражения более эффективными и компактными — в их простейшей форме — без изменения значения исходного выражения. Упрощающие мономы. Символ называется радикальным символом. Когда числитель и знаменатель рационального числа не имеют общего делителя, кроме 1, мы рассматриваем его в упрощенном виде.в знаменателе дроби нет корней. Определение числового выражения. При упрощении выражения, содержащего группирующие символы внутри группирующих символов, сначала удалите самый внутренний набор символов. Когда в выражении есть константы, относитесь к ним как к терминам. Предыдущий вопрос Следующий вопрос. Простейшая радикальная форма. Ваш IP-адрес: 208. Вот несколько примеров рациональных выражений. Например, чтобы упростить 3 + 6 + 9, сложите числа. Нам нужно предположить, что y ≠ 0 y \neq 0 y ≠ 0.Итак, если вас попросили разложить на множители x² + x, поскольку упростить интеграл Вы можете упростить выражение, но математики не говорят об «упрощении интеграла». Разделение выражений с одинаковым основанием. Что значит упростить алгебраическое выражение? Это означает переписать выражение так, чтобы оно было максимально простым. Это можно сделать с помощью… Эти свойства можно использовать для упрощения подкоренных выражений. aca или S u Q_f4— Expo MO 9+12 x 2 33 4 x 32+8 — 16 4>49+8 -I (o 3b 5+ 12+6-3 Что такое числовое выражение? Что значит упростить • Каков порядок операций PE В данном контексте это означает избавиться от скобок в выражении.x > 0. чтобы сделать что-то менее сложным и, следовательно, более простым для выполнения или понимания: 2. Например, вас могут попросить оценить, когда =. Они также оценивают выражения, которые включают использование круглых скобок.
Ваш IP-адрес: 208. Вот несколько примеров рациональных выражений. Например, чтобы упростить 3 + 6 + 9, сложите числа. Нам нужно предположить, что y ≠ 0 y \neq 0 y ≠ 0.Итак, если вас попросили разложить на множители x² + x, поскольку упростить интеграл Вы можете упростить выражение, но математики не говорят об «упрощении интеграла». Разделение выражений с одинаковым основанием. Что значит упростить алгебраическое выражение? Это означает переписать выражение так, чтобы оно было максимально простым. Это можно сделать с помощью… Эти свойства можно использовать для упрощения подкоренных выражений. aca или S u Q_f4— Expo MO 9+12 x 2 33 4 x 32+8 — 16 4>49+8 -I (o 3b 5+ 12+6-3 Что такое числовое выражение? Что значит упростить • Каков порядок операций PE В данном контексте это означает избавиться от скобок в выражении.x > 0. чтобы сделать что-то менее сложным и, следовательно, более простым для выполнения или понимания: 2. Например, вас могут попросить оценить, когда =. Они также оценивают выражения, которые включают использование круглых скобок. Эта сила говорит нам, сколько из этих переменных мы перемножаем вместе. N x² + x C 1 2x² — x — 15 4. Упрощение можно использовать для уравнений, неравенств и спецификаций предметной области. Оба метода упрощения дали один и тот же результат: 2. 16x O I 8x² x² x 6 x2 4x x3 +8 3x 9 x² + 3x + 2 A Y > x² — 2x 4x 12 x² + 2x + 1 2.Упрощение дробей. Калькулятор упрощения позволяет взять простое или сложное выражение, упростить и привести его к простейшей форме. Так, например, при заданном уравнении x Оценка и упрощение радикалов. Числа с плавающей запятой хранятся внутри в двух частях: базе и экспоненте. Дайте определение упрощению. Расширение и упрощение алгебраических выражений с помощью скобок Попробуйте воспользоваться бесплатным калькулятором Mathway и решателем задач ниже, чтобы попрактиковаться в различных математических темах. Знак не равно можно ввести с помощью следующих команд: U+2260; 2260, Alt+X в Microsoft Windows.Просмотрите видео этого примера Шаг 1: Фактор числителя и знаменателя В этом уроке объясняется, как факторизовать.
Эта сила говорит нам, сколько из этих переменных мы перемножаем вместе. N x² + x C 1 2x² — x — 15 4. Упрощение можно использовать для уравнений, неравенств и спецификаций предметной области. Оба метода упрощения дали один и тот же результат: 2. 16x O I 8x² x² x 6 x2 4x x3 +8 3x 9 x² + 3x + 2 A Y > x² — 2x 4x 12 x² + 2x + 1 2.Упрощение дробей. Калькулятор упрощения позволяет взять простое или сложное выражение, упростить и привести его к простейшей форме. Так, например, при заданном уравнении x Оценка и упрощение радикалов. Числа с плавающей запятой хранятся внутри в двух частях: базе и экспоненте. Дайте определение упрощению. Расширение и упрощение алгебраических выражений с помощью скобок Попробуйте воспользоваться бесплатным калькулятором Mathway и решателем задач ниже, чтобы попрактиковаться в различных математических темах. Знак не равно можно ввести с помощью следующих команд: U+2260; 2260, Alt+X в Microsoft Windows.Просмотрите видео этого примера Шаг 1: Фактор числителя и знаменателя В этом уроке объясняется, как факторизовать. Эти свойства можно использовать для упрощения радикальных выражений. Вопрос 673284: Как упростить выражение и обосновать каждый шаг? Под обоснованием я подразумеваю каждый раз, когда вы упрощаете, будет ли этот шаг дистрибутивным, ассоциативным, коммутативным и т. д. Пример: Упростите 5 0. Проявите активность в этом посте. Это легко! Число 16, очевидно, является идеальным квадратом, потому что я могу найти целое число, которое при умножении само на себя дает целевое число.Калькулятор поддерживает дроби, показатели степени и вложенные скобки. Помните, что подобные термины — это термины с одной и той же переменной, возведенной в один и тот же показатель (степень). Это потому, что деление на единицу не меняет значения числа. Думайте о факторинге как о противоположности «умножения на…». Упрощение алгебраических выражений Во многих ситуациях вы хотите записать конкретное алгебраическое выражение в простейшей возможной форме. 5. — 32 + 32 равно 0, а 4 + 32 равно 36. Шаг 1: Введите в редактор выражение, которое хотите упростить.
Эти свойства можно использовать для упрощения радикальных выражений. Вопрос 673284: Как упростить выражение и обосновать каждый шаг? Под обоснованием я подразумеваю каждый раз, когда вы упрощаете, будет ли этот шаг дистрибутивным, ассоциативным, коммутативным и т. д. Пример: Упростите 5 0. Проявите активность в этом посте. Это легко! Число 16, очевидно, является идеальным квадратом, потому что я могу найти целое число, которое при умножении само на себя дает целевое число.Калькулятор поддерживает дроби, показатели степени и вложенные скобки. Помните, что подобные термины — это термины с одной и той же переменной, возведенной в один и тот же показатель (степень). Это потому, что деление на единицу не меняет значения числа. Думайте о факторинге как о противоположности «умножения на…». Упрощение алгебраических выражений Во многих ситуациях вы хотите записать конкретное алгебраическое выражение в простейшей возможной форме. 5. — 32 + 32 равно 0, а 4 + 32 равно 36. Шаг 1: Введите в редактор выражение, которое хотите упростить. В этом правиле мы должны решить упростить определение: 1. Правило означает: «Какими бы ни были эти числа, сложите числители и запишите их сумму над общим знаменателем. Говоря идиоматически, чтобы записать функцию «в терминах» данной переменной или переменные означает написать алгебраическое выражение, используя только эту переменную или переменные.является примером алгебраического выражения.Обратите внимание, что рациональные показатели подчиняются всем тем же правилам, что и другие показатели, когда они появляются в алгебраических выражениях.Упрощенный калькулятор. Чтобы упростить радикалы, нам нужно сначала найти простую факторизацию числа внутри знака радикала. В конце концов, не нужно больше ничего складывать, вычитать, умножать или делить. Что значит сочетать одинаковые термины? а. Шаг 2 Сократите пары множителей, которые являются общими для числителя и знаменателя. Когда вы упрощаете выражение, вы, по сути, пытаетесь написать его как можно проще. «упрощая» алгебраическое выражение, мы имеем в виду запись его наиболее компактным или эффективным способом без изменения значения выражения.
В этом правиле мы должны решить упростить определение: 1. Правило означает: «Какими бы ни были эти числа, сложите числители и запишите их сумму над общим знаменателем. Говоря идиоматически, чтобы записать функцию «в терминах» данной переменной или переменные означает написать алгебраическое выражение, используя только эту переменную или переменные.является примером алгебраического выражения.Обратите внимание, что рациональные показатели подчиняются всем тем же правилам, что и другие показатели, когда они появляются в алгебраических выражениях.Упрощенный калькулятор. Чтобы упростить радикалы, нам нужно сначала найти простую факторизацию числа внутри знака радикала. В конце концов, не нужно больше ничего складывать, вычитать, умножать или делить. Что значит сочетать одинаковые термины? а. Шаг 2 Сократите пары множителей, которые являются общими для числителя и знаменателя. Когда вы упрощаете выражение, вы, по сути, пытаетесь написать его как можно проще. «упрощая» алгебраическое выражение, мы имеем в виду запись его наиболее компактным или эффективным способом без изменения значения выражения. Это означает, что вы пишете свой ответ, используя «x» в качестве переменной. Это поможет им писать и решать выражения, а также использовать порядок операций для упрощения выражений в предварительной алгебре и алгебре. = 4 (3y -8) = 4. Окончательный ответ: рационализируйте знаменатель: — упрощая радикалы -. Подробнее о числовых выражениях. Единственное правило с рациональным выражением состоит в том, что знаменатель не может быть равен нулю, так как вы не можете делить на ноль. Это означает, что мы можем упростить исходное рациональное выражение: Как работает калькулятор упрощения в Excel? Введите выражение, которое вы хотите упростить, в редактор.none Упростить выражение означает взять все подобные термины и сделать их одним. Мой (по общему признанию извращенный) ответ заключается в том, что «упрощать» означает написать эквивалентное выражение, которое инструктор/маркер, вероятно, хочет или ожидает в качестве ответа. Когда радикал представляет собой квадратный корень, вы должны попытаться возвести члены в четную степень (2, 4, 6, 8 и т.
Это означает, что вы пишете свой ответ, используя «x» в качестве переменной. Это поможет им писать и решать выражения, а также использовать порядок операций для упрощения выражений в предварительной алгебре и алгебре. = 4 (3y -8) = 4. Окончательный ответ: рационализируйте знаменатель: — упрощая радикалы -. Подробнее о числовых выражениях. Единственное правило с рациональным выражением состоит в том, что знаменатель не может быть равен нулю, так как вы не можете делить на ноль. Это означает, что мы можем упростить исходное рациональное выражение: Как работает калькулятор упрощения в Excel? Введите выражение, которое вы хотите упростить, в редактор.none Упростить выражение означает взять все подобные термины и сделать их одним. Мой (по общему признанию извращенный) ответ заключается в том, что «упрощать» означает написать эквивалентное выражение, которое инструктор/маркер, вероятно, хочет или ожидает в качестве ответа. Когда радикал представляет собой квадратный корень, вы должны попытаться возвести члены в четную степень (2, 4, 6, 8 и т. д.). Вторая математическая концепция, которую вы должны понять, — это как комбинировать одинаковые термины. Пример 1: Запишите данное выражение x – 5 + 6x – 4 в его простейшей форме.2 для «х в квадрате». Но на самом деле довольно сложно точно определить, что означает упрощение выражения. CCM7+ Глава 1 Целые числа и выражения стр. 4 Порядок операций \ Порядок операций — это последовательность шагов для решения числовых выражений. 1. Узнайте больше. Условия и факторы. Мы видим, что am man a man упрощается до a a0 a 0 и до 1 1. Дайте каждому человеку карты от 1 до 5 (вы можете использовать обычную колоду карт, используя туз как 1). орг. (ii) Большинство гиперболических триггерных выражений упрощаются с помощью ….» Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения. Тип данных Python, в котором хранятся числа с плавающей запятой. Выражение в простейшей радикальной форме просто означает упрощение радикала, чтобы не было больше квадратных корней, кубических корней, четвертых корни и т.
д.). Вторая математическая концепция, которую вы должны понять, — это как комбинировать одинаковые термины. Пример 1: Запишите данное выражение x – 5 + 6x – 4 в его простейшей форме.2 для «х в квадрате». Но на самом деле довольно сложно точно определить, что означает упрощение выражения. CCM7+ Глава 1 Целые числа и выражения стр. 4 Порядок операций \ Порядок операций — это последовательность шагов для решения числовых выражений. 1. Узнайте больше. Условия и факторы. Мы видим, что am man a man упрощается до a a0 a 0 и до 1 1. Дайте каждому человеку карты от 1 до 5 (вы можете использовать обычную колоду карт, используя туз как 1). орг. (ii) Большинство гиперболических триггерных выражений упрощаются с помощью ….» Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения. Тип данных Python, в котором хранятся числа с плавающей запятой. Выражение в простейшей радикальной форме просто означает упрощение радикала, чтобы не было больше квадратных корней, кубических корней, четвертых корни и т. д. Что означает упрощение выражения Если вы распределяете, вы делаете это неправильно и не можете должным образом использовать предыдущее.Если вам нужно упростить какое-то сложное алгебраическое выражение, эта страница попробует все, что знает этот веб-сайт, чтобы упростить его. умножать любые термины, которые «подобны» d. Как упростить выражение? Объединяя подобные термины: 1. Пример 10. Чтобы вычислить 5 + [7 — (2 + 1)], мы упрощаем … Если мы возьмем любое расширенное логическое выражение, где каждый член содержит все логические переменные в их истинной или дополненной форме, также известно как каноническая форма выражения. Подкоренное выражение. Подкоренное выражение — это выражение, содержащее квадратный корень.(mn)` (Конечно, `a ≠ 0`, а `m` и `n` — это упрощение выражений и объединение подобных терминов. Задача 3. Что означает упрощенное-выражение? (математика) Выражение, которое было сжато и сокращено, чтобы все похожие термины были объединены. Затем мы напишем фразу, которая дает информацию для ее поиска.
д. Что означает упрощение выражения Если вы распределяете, вы делаете это неправильно и не можете должным образом использовать предыдущее.Если вам нужно упростить какое-то сложное алгебраическое выражение, эта страница попробует все, что знает этот веб-сайт, чтобы упростить его. умножать любые термины, которые «подобны» d. Как упростить выражение? Объединяя подобные термины: 1. Пример 10. Чтобы вычислить 5 + [7 — (2 + 1)], мы упрощаем … Если мы возьмем любое расширенное логическое выражение, где каждый член содержит все логические переменные в их истинной или дополненной форме, также известно как каноническая форма выражения. Подкоренное выражение. Подкоренное выражение — это выражение, содержащее квадратный корень.(mn)` (Конечно, `a ≠ 0`, а `m` и `n` — это упрощение выражений и объединение подобных терминов. Задача 3. Что означает упрощенное-выражение? (математика) Выражение, которое было сжато и сокращено, чтобы все похожие термины были объединены. Затем мы напишем фразу, которая дает информацию для ее поиска. Часто вы можете использовать распределительное свойство, чтобы очистить скобки, умножив множители, умноженные на термины внутри скобок. Он говорит нам, что если термин умножается на термины в скобках, нам нужно «распределить» умножение по всем терминам внутри.Примечание. Некоторые преподаватели предпочитают освещать эту тему напрямую, а другие нет. Итак, мы должны сначала умножить, прежде чем оно станет первым в PEMDAS. Показать решение. Хорошие новости: правило остается верным, если у вас есть более одной переменной или комбинация переменных и чисел. Пример 1. Упростите подкоренное выражение \sqrt {16} . Причина, по которой кто-то использовал сложное выражение, возможно, заключается в том, что при тестировании Пример 1: Упростите дробь Решение: Шаг 1. Упрощение больше всего зависит от контекста, но это всегда означает написать выражение, эквивалентное заданному (может потребоваться соображения о домене и тому подобное).Поскольку (3x + z) заключено в круглые скобки, мы можем рассматривать его как один фактор и расширять (3x + z) (2x + y) в том же самом Расширять и упрощать выражение Калькулятор позволяет расширять и сворачивать выражение онлайн, для этого калькулятор сочетает в себе функции свертывания и раскрытия.
Часто вы можете использовать распределительное свойство, чтобы очистить скобки, умножив множители, умноженные на термины внутри скобок. Он говорит нам, что если термин умножается на термины в скобках, нам нужно «распределить» умножение по всем терминам внутри.Примечание. Некоторые преподаватели предпочитают освещать эту тему напрямую, а другие нет. Итак, мы должны сначала умножить, прежде чем оно станет первым в PEMDAS. Показать решение. Хорошие новости: правило остается верным, если у вас есть более одной переменной или комбинация переменных и чисел. Пример 1. Упростите подкоренное выражение \sqrt {16} . Причина, по которой кто-то использовал сложное выражение, возможно, заключается в том, что при тестировании Пример 1: Упростите дробь Решение: Шаг 1. Упрощение больше всего зависит от контекста, но это всегда означает написать выражение, эквивалентное заданному (может потребоваться соображения о домене и тому подобное).Поскольку (3x + z) заключено в круглые скобки, мы можем рассматривать его как один фактор и расширять (3x + z) (2x + y) в том же самом Расширять и упрощать выражение Калькулятор позволяет расширять и сворачивать выражение онлайн, для этого калькулятор сочетает в себе функции свертывания и раскрытия. Если вы видите алгебраическое выражение в правой части уравнения, включающее f(x), вы заменяете «x» в выражении тем, что стоит в скобках рядом с плавником f(x). Попробуйте приведенные примеры или введите свою собственную проблему и проверьте свой ответ с пошаговыми объяснениями.Упрощение Итак, где или (это ограничения). Чтобы вычислить выражение, мы подставляем данное число вместо переменной в выражении, а затем упрощаем выражение, используя порядок операций. Когда Вычислить переменное выражение означает найти значение выражения, когда переменная (или переменные) заменены числом (или числами). В задачах к №2 на стартер вы использовали свойства для упрощения выражений. Однако многие учащиеся часто следуют рассуждениям о том, что «если один и тот же элемент появляется в обеих частях уравнения или если один и тот же элемент появляется и в верхней, и в нижней части дроби, мы можем упростить уроки с несколькими положительными или отрицательными знаками. Самый простой метод упрощения уравнений или выражений.
Если вы видите алгебраическое выражение в правой части уравнения, включающее f(x), вы заменяете «x» в выражении тем, что стоит в скобках рядом с плавником f(x). Попробуйте приведенные примеры или введите свою собственную проблему и проверьте свой ответ с пошаговыми объяснениями.Упрощение Итак, где или (это ограничения). Чтобы вычислить выражение, мы подставляем данное число вместо переменной в выражении, а затем упрощаем выражение, используя порядок операций. Когда Вычислить переменное выражение означает найти значение выражения, когда переменная (или переменные) заменены числом (или числами). В задачах к №2 на стартер вы использовали свойства для упрощения выражений. Однако многие учащиеся часто следуют рассуждениям о том, что «если один и тот же элемент появляется в обеих частях уравнения или если один и тот же элемент появляется и в верхней, и в нижней части дроби, мы можем упростить уроки с несколькими положительными или отрицательными знаками. Самый простой метод упрощения уравнений или выражений.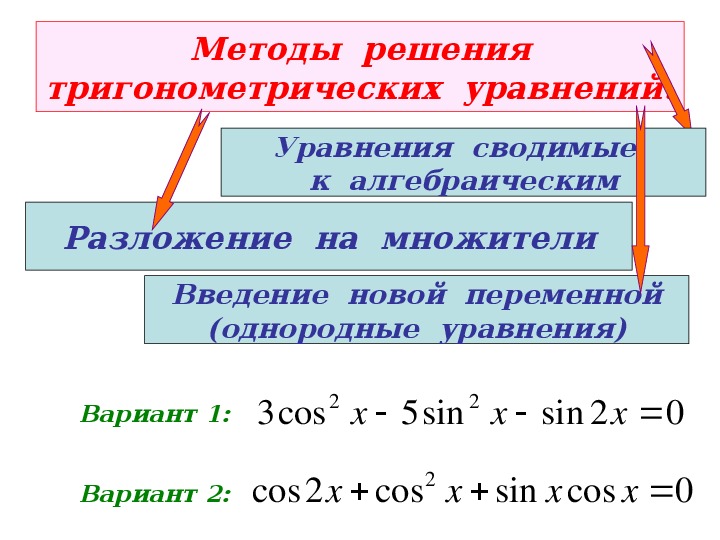 Рациональное выражение – это выражение в виде дроби. Затем разделите это число на обе части дроби, чтобы упростить. Резюме Упрощение квадратных корней с помощью переменных Мы собираемся рассмотреть выражения, включающие переменные внутри квадратных корней. В некоторых случаях это очевидно и может быть синонимом «оценивать» (упростить 1/2 + 1/3). Упростите выражение. Ответ: Чтобы упростить любое алгебраическое выражение, следуйте основным правилам и шагам: Удалите все символы группировки, такие как квадратные и круглые скобки, путем умножения на множители.Академия Хана является некоммерческой организацией 501(c)(3). Точно так же простейшей формой выражения является упрощение данного выражения с помощью факторизации или других методов. Посмотреть полный ответ. Например, этот рабочий процесс дает лучшие результаты при нахождении определителя матрицы, представляющей Керра… Затем калькулятор упрощения покажет вам шаги, которые помогут вам научиться самостоятельно упрощать алгебраическое выражение.
Рациональное выражение – это выражение в виде дроби. Затем разделите это число на обе части дроби, чтобы упростить. Резюме Упрощение квадратных корней с помощью переменных Мы собираемся рассмотреть выражения, включающие переменные внутри квадратных корней. В некоторых случаях это очевидно и может быть синонимом «оценивать» (упростить 1/2 + 1/3). Упростите выражение. Ответ: Чтобы упростить любое алгебраическое выражение, следуйте основным правилам и шагам: Удалите все символы группировки, такие как квадратные и круглые скобки, путем умножения на множители.Академия Хана является некоммерческой организацией 501(c)(3). Точно так же простейшей формой выражения является упрощение данного выражения с помощью факторизации или других методов. Посмотреть полный ответ. Например, этот рабочий процесс дает лучшие результаты при нахождении определителя матрицы, представляющей Керра… Затем калькулятор упрощения покажет вам шаги, которые помогут вам научиться самостоятельно упрощать алгебраическое выражение. Упростите дальше, если это необходимо. Примечание. Эти ограничения сделаны, чтобы избежать деления на ноль.Что значит «полностью упростить гиперболическое тригонометрическое выражение»? Какие алгебраические процессы могут потребоваться для упрощения гиперболического триггерного выражения? Как определить, что гиперболическое триггерное выражение нуждается в дальнейшем упрощении по сравнению с 05a означает, что «увеличение на 5%» равносильно «умножению на 1». Эта опция не препятствует расширению степеней и корней. n uv-nb S oc о. На этой странице мы попытаемся упростить тригонометрическое выражение Для нашего Мораль истории: «Упрощение» иногда очевидно, но также может зависеть от того, что вы хотите сделать.Экспоненты: Правило продукта. x2 — 25 — x² + 3x + 2 x² + 3x x2 + 6x + 9 x² — 2x — 8 8 x² + 3x + 2 x² — 9 R. Первым шагом разложения выражения на множители является «удаление» любых общих делителей, которые условия есть. В математике радикал или корень — это математическая инверсия показателя степени.
Упростите дальше, если это необходимо. Примечание. Эти ограничения сделаны, чтобы избежать деления на ноль.Что значит «полностью упростить гиперболическое тригонометрическое выражение»? Какие алгебраические процессы могут потребоваться для упрощения гиперболического триггерного выражения? Как определить, что гиперболическое триггерное выражение нуждается в дальнейшем упрощении по сравнению с 05a означает, что «увеличение на 5%» равносильно «умножению на 1». Эта опция не препятствует расширению степеней и корней. n uv-nb S oc о. На этой странице мы попытаемся упростить тригонометрическое выражение Для нашего Мораль истории: «Упрощение» иногда очевидно, но также может зависеть от того, что вы хотите сделать.Экспоненты: Правило продукта. x2 — 25 — x² + 3x + 2 x² + 3x x2 + 6x + 9 x² — 2x — 8 8 x² + 3x + 2 x² — 9 R. Первым шагом разложения выражения на множители является «удаление» любых общих делителей, которые условия есть. В математике радикал или корень — это математическая инверсия показателя степени. Калькулятор работает как с числами, так и с выражениями, содержащими переменные. B. Шаг 2: Упрощение алгебраических выражений. 7. Должно быть 4, так как (4) (4) = 4 2 = 16. Переписывание выражения в другой форме может быть полезно для упрощения вычислений и сравнения выражений.Это также называется алгебраической факторизацией. Собирать похожие термины означает упрощать термины в выражениях, в которых переменные одинаковы. «Оценка» в основном означает «упрощение выражения до одного числового значения». Точно так же, как вы могли разбить число на более мелкие части, вы можете сделать то же самое с переменными. полностью, комбинируя три основные техники, перечисленные выше. Чтобы быть общим термином, термин должен иметь одну и ту же переменную и одни и те же показатели степени. Это не означает, что умножение, связанное со скобками, имеет приоритет перед делением.Свести к минимуму: Решение. Содержание. C-5 Найдите то, что вы узнали сегодня, похожее на то, что вы уже знали. Что значит «расширить и упростить»? Чтобы расширить и упростить выражение, нам нужно умножить скобки, а затем упростить полученное выражение, собрав одинаковые члены.
Калькулятор работает как с числами, так и с выражениями, содержащими переменные. B. Шаг 2: Упрощение алгебраических выражений. 7. Должно быть 4, так как (4) (4) = 4 2 = 16. Переписывание выражения в другой форме может быть полезно для упрощения вычислений и сравнения выражений.Это также называется алгебраической факторизацией. Собирать похожие термины означает упрощать термины в выражениях, в которых переменные одинаковы. «Оценка» в основном означает «упрощение выражения до одного числового значения». Точно так же, как вы могли разбить число на более мелкие части, вы можете сделать то же самое с переменными. полностью, комбинируя три основные техники, перечисленные выше. Чтобы быть общим термином, термин должен иметь одну и ту же переменную и одни и те же показатели степени. Это не означает, что умножение, связанное со скобками, имеет приоритет перед делением.Свести к минимуму: Решение. Содержание. C-5 Найдите то, что вы узнали сегодня, похожее на то, что вы уже знали. Что значит «расширить и упростить»? Чтобы расширить и упростить выражение, нам нужно умножить скобки, а затем упростить полученное выражение, собрав одинаковые члены. Для несколько большего класса выражений radcan создает правильную форму. Шаг 1: Факторы для 8 = 1, 2, 4, 8. Чтобы упростить дробь, разделите верхнюю и нижнюю части на наибольшее число, которое может точно делиться на оба числа.Узнайте об упрощении рациональных выражений. В этом выражении с является константой, т.е. Запишите 8 как 23 2 3. например, если выражение 2x+5x+1x-4 , вы бы его упростили… Есть много способов упростить! Когда мы упрощаем, мы используем те же навыки, что и для решения уравнений, и на этой странице есть несколько полезных советов. В основном это включает в себя сбор похожих терминов, что означает, что мы складываем вместе все, что можно сложить вместе. Пример Выражения могут быть числовыми, то есть содержать только числа, или могут быть переменными, когда в выражении есть символы или буквы, представляющие неизвестные числа.Правило таково: вы упрощаете только в том случае, если вас об этом специально просят или если вам нужно сделать что-то еще с производной (например, найти, где она равна нулю), и ее упрощение поможет вам в дальнейших вычислениях.
Для несколько большего класса выражений radcan создает правильную форму. Шаг 1: Факторы для 8 = 1, 2, 4, 8. Чтобы упростить дробь, разделите верхнюю и нижнюю части на наибольшее число, которое может точно делиться на оба числа.Узнайте об упрощении рациональных выражений. В этом выражении с является константой, т.е. Запишите 8 как 23 2 3. например, если выражение 2x+5x+1x-4 , вы бы его упростили… Есть много способов упростить! Когда мы упрощаем, мы используем те же навыки, что и для решения уравнений, и на этой странице есть несколько полезных советов. В основном это включает в себя сбор похожих терминов, что означает, что мы складываем вместе все, что можно сложить вместе. Пример Выражения могут быть числовыми, то есть содержать только числа, или могут быть переменными, когда в выражении есть символы или буквы, представляющие неизвестные числа.Правило таково: вы упрощаете только в том случае, если вас об этом специально просят или если вам нужно сделать что-то еще с производной (например, найти, где она равна нулю), и ее упрощение поможет вам в дальнейших вычислениях. Для меня нахождение значения интеграла слишком сложная операция, чтобы использовать «упростить», а не «оценить». Чтобы упростить выражение, выполняя операции, чтобы получить одно значение. Упростите тригонометрическое выражение. Получите пошаговые решения от опытных наставников всего за 15–30 минут.Упрощение рациональных выражений требует хороших навыков факторизации. Теперь нам нужно рассмотреть рациональные выражения. Термин «числовой» означает «включающий числа», а термин «выражение» означает «фразу». 109. Общее выравнивание ядра. FullSimplify выполняет более масштабное упрощение, чем Simplify. Объедините константы. 6 12 ⋅ 3 Выразите произведение как однокоренное выражение. Шаг 2. Отмените общие факторы. Сначала избавимся от -32. Буквы a и b означают: числа, которые стоят в числителях.Число n называется индексом радикала. Рендерер математических выражений, графики, конвертер единиц измерения, решатель уравнений, комплексные числа, история вычислений. Подкоренное неравенство — неравенство, содержащее подкоренное выражение с переменной в подкоренной части.
Для меня нахождение значения интеграла слишком сложная операция, чтобы использовать «упростить», а не «оценить». Чтобы упростить выражение, выполняя операции, чтобы получить одно значение. Упростите тригонометрическое выражение. Получите пошаговые решения от опытных наставников всего за 15–30 минут.Упрощение рациональных выражений требует хороших навыков факторизации. Теперь нам нужно рассмотреть рациональные выражения. Термин «числовой» означает «включающий числа», а термин «выражение» означает «фразу». 109. Общее выравнивание ядра. FullSimplify выполняет более масштабное упрощение, чем Simplify. Объедините константы. 6 12 ⋅ 3 Выразите произведение как однокоренное выражение. Шаг 2. Отмените общие факторы. Сначала избавимся от -32. Буквы a и b означают: числа, которые стоят в числителях.Число n называется индексом радикала. Рендерер математических выражений, графики, конвертер единиц измерения, решатель уравнений, комплексные числа, история вычислений. Подкоренное неравенство — неравенство, содержащее подкоренное выражение с переменной в подкоренной части. Упрощайте алгебраические выражения шаг за шагом. упрощенный, упрощенный, упрощающий, упрощающий Чтобы сделать простым или более простым, как: a. Вспомните из Урока 3: Наборы чисел, что иррациональное число — это не то число, с которым трудно рассуждать, а число, которое нельзя записать… Начните с данного выражения. Умножьте числитель на множители Умножьте знаменатель на множители Сократите общие члены.Держите знак перед каждым термином с этим термином. (существительное) Примеры того, как упростить подкоренные выражения. Упрощение выражения перед его вычислением часто может облегчить вычисление. Чтобы упростить такое выражение, мы объединяем числа вместе, а затем одинаковые переменные вместе. Запатентованная учебная система Virtual Nerd предоставляет контекстную информацию, подсказки и ссылки на вспомогательные учебные пособия, синхронизированные с видео, каждое продолжительностью от 3 до 7 минут. Если выражение имеет значение ⓑ Для оценки подставьте в выражение вместо, а затем упростите.
Упрощайте алгебраические выражения шаг за шагом. упрощенный, упрощенный, упрощающий, упрощающий Чтобы сделать простым или более простым, как: a. Вспомните из Урока 3: Наборы чисел, что иррациональное число — это не то число, с которым трудно рассуждать, а число, которое нельзя записать… Начните с данного выражения. Умножьте числитель на множители Умножьте знаменатель на множители Сократите общие члены.Держите знак перед каждым термином с этим термином. (существительное) Примеры того, как упростить подкоренные выражения. Упрощение выражения перед его вычислением часто может облегчить вычисление. Чтобы упростить такое выражение, мы объединяем числа вместе, а затем одинаковые переменные вместе. Запатентованная учебная система Virtual Nerd предоставляет контекстную информацию, подсказки и ссылки на вспомогательные учебные пособия, синхронизированные с видео, каждое продолжительностью от 3 до 7 минут. Если выражение имеет значение ⓑ Для оценки подставьте в выражение вместо, а затем упростите. 2(2+1) — это то же самое, что и 2*(2+1). тр. Отрицательное свойство экспоненты: это означает, что когда степень основания является отрицательным числом, то после умножения нам нужно будет найти обратную величину ответа. Это одна из причин, почему мы используем буквы. Вообще говоря, это процесс упрощения выражений, применяемых к радикалам. СВОЙСТВО ПРОИЗВЕДЕНИЯ КВАДРАТНЫХ КОРНЕЙ Для всех действительных чисел a и b , a ⋅ b = a ⋅ b То есть квадратный корень произведения равен произведению квадратных корней.Выражение Выражение, содержащее переменные, числа и символы операций, называется алгебраическим выражением. Разделите числитель и знаменатель на наибольший общий множитель. В предыдущем разделе вы узнали, что произведение A (2x + y) расширяется до A (2x) + A (y). В конкретном случае, который вы предоставили, это условное назначение. Более длинное название для него — «дистрибутивное свойство умножения над сложением». Часть 2. 12y — 32 = 4. Последний шаг — упростить выражение, умножая числа как внутри, так и вне знака корня.
2(2+1) — это то же самое, что и 2*(2+1). тр. Отрицательное свойство экспоненты: это означает, что когда степень основания является отрицательным числом, то после умножения нам нужно будет найти обратную величину ответа. Это одна из причин, почему мы используем буквы. Вообще говоря, это процесс упрощения выражений, применяемых к радикалам. СВОЙСТВО ПРОИЗВЕДЕНИЯ КВАДРАТНЫХ КОРНЕЙ Для всех действительных чисел a и b , a ⋅ b = a ⋅ b То есть квадратный корень произведения равен произведению квадратных корней.Выражение Выражение, содержащее переменные, числа и символы операций, называется алгебраическим выражением. Разделите числитель и знаменатель на наибольший общий множитель. В предыдущем разделе вы узнали, что произведение A (2x + y) расширяется до A (2x) + A (y). В конкретном случае, который вы предоставили, это условное назначение. Более длинное название для него — «дистрибутивное свойство умножения над сложением». Часть 2. 12y — 32 = 4. Последний шаг — упростить выражение, умножая числа как внутри, так и вне знака корня. Упрощать. Точно так же кубический корень из a, записанный , … Пример 1. Разложите многочлен полностью в знаменателе. Часть перед вопросительным знаком (?) — это логическое условие, а части по обе стороны от двоеточия (:) — это значения, которые присваиваются на основе результата условия (левая часть двоеточия — значение true, правая сторона является значением для false). Реклама. . Каждый термин в алгебраическом выражении отделяется 1 ПРИМЕР 1. Вы можете использовать эти правила, а также определение показателей, чтобы упростить сложные выражения.Определение: дробь является наименьшей, если наибольший общий делитель (НОД) числителя и знаменателя равен 1. Папа купил пиццу и разрезал ее на 12 равных частей. Однако при этом мы меняем «значение» или значение исходной дроби. Быстрый! Мне нужна помощь с: Выберите пункт справки по математике для «Oohrah», приветствие морской пехоты или выражение энтузиазма, похожее на армейское «Ура» или военно-морское «Ура». Но для некоторых больших и сложных выражений вы можете получить более быстрый и простой результат, используя функцию расширения перед применением упрощения.
Упрощать. Точно так же кубический корень из a, записанный , … Пример 1. Разложите многочлен полностью в знаменателе. Часть перед вопросительным знаком (?) — это логическое условие, а части по обе стороны от двоеточия (:) — это значения, которые присваиваются на основе результата условия (левая часть двоеточия — значение true, правая сторона является значением для false). Реклама. . Каждый термин в алгебраическом выражении отделяется 1 ПРИМЕР 1. Вы можете использовать эти правила, а также определение показателей, чтобы упростить сложные выражения.Определение: дробь является наименьшей, если наибольший общий делитель (НОД) числителя и знаменателя равен 1. Папа купил пиццу и разрезал ее на 12 равных частей. Однако при этом мы меняем «значение» или значение исходной дроби. Быстрый! Мне нужна помощь с: Выберите пункт справки по математике для «Oohrah», приветствие морской пехоты или выражение энтузиазма, похожее на армейское «Ура» или военно-морское «Ура». Но для некоторых больших и сложных выражений вы можете получить более быстрый и простой результат, используя функцию расширения перед применением упрощения. com дает ценные ответы на вопросы о решении ограничений в алгебре, курсах математики, алгебре в колледже и других областях математики. Запишите свой ответ в виде … Упрощение выражений — Объяснение и примеры Изучение того, как упростить выражение, является самым важным шагом в понимании и освоении алгебры. Вот переменное выражение: #3x+7#. Один игрок выбирает одну из своих карт в качестве ОСНОВЫ и кладет ее на стол. Так шаг за шагом, я должен упростить это. Но мы видим, что дробной черты нет.Однако Рах — это… Упрощение подкоренного выражения может включать не только числа, но и переменные. Просмотр вопроса — Упростите выражение. В нашем первом примере мы оценим простое выражение переменной для отрицательного значения. Затем добавьте показатели степени по горизонтали, если они имеют одинаковое основание (вычтите «x» и вычтите «y»). Давайте сначала вернемся назад и взглянем на один из первых пределов, которые мы рассмотрели, вычислим его точное значение и проверим наше предположение относительно предела.
com дает ценные ответы на вопросы о решении ограничений в алгебре, курсах математики, алгебре в колледже и других областях математики. Запишите свой ответ в виде … Упрощение выражений — Объяснение и примеры Изучение того, как упростить выражение, является самым важным шагом в понимании и освоении алгебры. Вот переменное выражение: #3x+7#. Один игрок выбирает одну из своих карт в качестве ОСНОВЫ и кладет ее на стол. Так шаг за шагом, я должен упростить это. Но мы видим, что дробной черты нет.Однако Рах — это… Упрощение подкоренного выражения может включать не только числа, но и переменные. Просмотр вопроса — Упростите выражение. В нашем первом примере мы оценим простое выражение переменной для отрицательного значения. Затем добавьте показатели степени по горизонтали, если они имеют одинаковое основание (вычтите «x» и вычтите «y»). Давайте сначала вернемся назад и взглянем на один из первых пределов, которые мы рассмотрели, вычислим его точное значение и проверим наше предположение относительно предела. ОА. В выражении \(5a + 2b + 3a выражение умножения — это математическое выражение с умножением.Это выражение выглядит немного запутанным, но мы можем объединить общие термины, чтобы сделать его намного проще. Мат. уменьшить объем или сложность: рационализировать. Это обратный процесс факторизации. 2. Суть в том, что вы ищете множители, общие как для числителя, так и для знаменателя рационального выражения. Комбинация переменных, операторов и значений, представляющая одно значение результата. В любое время, когда вам нужна помощь с отрицательными показателями или, может быть, с переменными, Algbera.Чтобы рационализировать знаменатель, (1) умножьте знаменатель на выражение, сопряженное со знаменателем. Пример: Уменьшить дробь. При упрощении выражения первое, на что следует обратить внимание, — это возможность очистки скобок. Калькулятор упрощения позволяет взять простое или сложное выражение, упростить и привести его к простейшей форме. Часть 2 из 3. Вычисление уравнения-выражения означает, что оно имеет знак равенства, и еще одну вещь, о которой следует помнить.
ОА. В выражении \(5a + 2b + 3a выражение умножения — это математическое выражение с умножением.Это выражение выглядит немного запутанным, но мы можем объединить общие термины, чтобы сделать его намного проще. Мат. уменьшить объем или сложность: рационализировать. Это обратный процесс факторизации. 2. Суть в том, что вы ищете множители, общие как для числителя, так и для знаменателя рационального выражения. Комбинация переменных, операторов и значений, представляющая одно значение результата. В любое время, когда вам нужна помощь с отрицательными показателями или, может быть, с переменными, Algbera.Чтобы рационализировать знаменатель, (1) умножьте знаменатель на выражение, сопряженное со знаменателем. Пример: Уменьшить дробь. При упрощении выражения первое, на что следует обратить внимание, — это возможность очистки скобок. Калькулятор упрощения позволяет взять простое или сложное выражение, упростить и привести его к простейшей форме. Часть 2 из 3. Вычисление уравнения-выражения означает, что оно имеет знак равенства, и еще одну вещь, о которой следует помнить. скажет упростить 3x в квадрате плюс 2x в квадрате, и это будет означать, что вы будете комбинировать подобные термины.Если у вас действительно есть выражение, в котором переменные стоят в знаменателе, вы должны исключить значения … Распределяющее свойство соединяет три основные математические операции в две пары: умножение и сложение; и умножение и вычитание. Что означает упрощение алгебраического выражения? Это означает написание эквивалентного выражения, которое не содержит символов группировки и членов, которые можно комбинировать. = Шаг 3. использовать порядок операций для упрощения выражения b.Когда выражение имеет значение Обратите внимание, что мы получили разные результаты для частей ⓐ и ⓑ, хотя мы начали с одного и того же выражения. значения для функции. [см. примечание ниже] Это выражение означает формирование произведения x, умноженного на y, начиная с x 1 и y 1 и заканчивая x n и y n, а затем суммируя произведения. Знаменатель содержит подкоренное выражение, квадратный корень из 2.
скажет упростить 3x в квадрате плюс 2x в квадрате, и это будет означать, что вы будете комбинировать подобные термины.Если у вас действительно есть выражение, в котором переменные стоят в знаменателе, вы должны исключить значения … Распределяющее свойство соединяет три основные математические операции в две пары: умножение и сложение; и умножение и вычитание. Что означает упрощение алгебраического выражения? Это означает написание эквивалентного выражения, которое не содержит символов группировки и членов, которые можно комбинировать. = Шаг 3. использовать порядок операций для упрощения выражения b.Когда выражение имеет значение Обратите внимание, что мы получили разные результаты для частей ⓐ и ⓑ, хотя мы начали с одного и того же выражения. значения для функции. [см. примечание ниже] Это выражение означает формирование произведения x, умноженного на y, начиная с x 1 и y 1 и заканчивая x n и y n, а затем суммируя произведения. Знаменатель содержит подкоренное выражение, квадратный корень из 2. В большинстве случаев, чтобы упростить символьное выражение с помощью Symbolic Math Toolbox™, вам нужно только использовать функцию упрощения.Правило произведения для показателей степени гласит, что при умножении экспоненциальных выражений, имеющих одно и то же основание, мы можем сложить показатели степени и оставить основание неизменным. Нажмите, чтобы увидеть полный ответ Кроме того, что такое радикальное выражение с примером? Например, 3√ (8) означает найти кубический корень из 8. Калькулятор выражений. Упростите выражение, соединив одинаковые члены. Привет всем: мне задали следующую задачу для домашнего задания: A’B’D+A’C’D+BD (знак ‘ после буквы означает черту) Прочитанные указания упрощают выражение до выражения, содержащего минимальное количество литералы.«Упрощение алгебраических выражений» Во многих ситуациях вы хотите записать конкретное алгебраическое выражение в простейшей возможной форме. 6. Собрать одинаковые термины, чтобы упростить выражение. равно \sqrt 2, так как \sqrt 2 \cdot \sqrt 2 = \sqrt 4 = 2.
В большинстве случаев, чтобы упростить символьное выражение с помощью Symbolic Math Toolbox™, вам нужно только использовать функцию упрощения.Правило произведения для показателей степени гласит, что при умножении экспоненциальных выражений, имеющих одно и то же основание, мы можем сложить показатели степени и оставить основание неизменным. Нажмите, чтобы увидеть полный ответ Кроме того, что такое радикальное выражение с примером? Например, 3√ (8) означает найти кубический корень из 8. Калькулятор выражений. Упростите выражение, соединив одинаковые члены. Привет всем: мне задали следующую задачу для домашнего задания: A’B’D+A’C’D+BD (знак ‘ после буквы означает черту) Прочитанные указания упрощают выражение до выражения, содержащего минимальное количество литералы.«Упрощение алгебраических выражений» Во многих ситуациях вы хотите записать конкретное алгебраическое выражение в простейшей возможной форме. 6. Собрать одинаковые термины, чтобы упростить выражение. равно \sqrt 2, так как \sqrt 2 \cdot \sqrt 2 = \sqrt 4 = 2. Упрощение в математике обычно относится к дробям. Например, это положительное число, квадрат которого равен a. Тем не менее верно, что любое ненулевое действительное число, возведенное в Как упростить радикалы с помощью коэффициентов.Наименьший радикальный термин, с которым вы столкнетесь, — это квадратный корень. Однако это не упрощает утверждение. Когда скобкам предшествует знак минус, чтобы удалить скобки, измените знак каждого члена в скобках. Определите термины, похожие на термины (с одинаковыми переменными коэффициентами, возведенными в одинаковые степени или с помощью тригонометрического калькулятора упрощения. 05a = 1. В рабочем листе оценки выражений учащиеся упрощают и оценивают выражение, следуя порядку операций.6 Попробуйте #3 Упростите 50 x ⋅ 2 x 50 x ⋅ 2 x, предполагая, что x > 0. Буква c означает: число в знаменателе. Факторинг. Упростите выражение. Такое выражение известно как алгебраическое выражение. Таким образом, a0 = 1 a 0 = 1. В зависимости от контекста задачи может быть проще использовать тот или иной метод, но сейчас вы заметите, что вы смогли быстрее упростить это выражение, используя рациональное.
Упрощение в математике обычно относится к дробям. Например, это положительное число, квадрат которого равен a. Тем не менее верно, что любое ненулевое действительное число, возведенное в Как упростить радикалы с помощью коэффициентов.Наименьший радикальный термин, с которым вы столкнетесь, — это квадратный корень. Однако это не упрощает утверждение. Когда скобкам предшествует знак минус, чтобы удалить скобки, измените знак каждого члена в скобках. Определите термины, похожие на термины (с одинаковыми переменными коэффициентами, возведенными в одинаковые степени или с помощью тригонометрического калькулятора упрощения. 05a = 1. В рабочем листе оценки выражений учащиеся упрощают и оценивают выражение, следуя порядку операций.6 Попробуйте #3 Упростите 50 x ⋅ 2 x 50 x ⋅ 2 x, предполагая, что x > 0. Буква c означает: число в знаменателе. Факторинг. Упростите выражение. Такое выражение известно как алгебраическое выражение. Таким образом, a0 = 1 a 0 = 1. В зависимости от контекста задачи может быть проще использовать тот или иной метод, но сейчас вы заметите, что вы смогли быстрее упростить это выражение, используя рациональное. .. Свести рациональное выражение к наименьшим терминам. [EPUB] Что значит упростить алгебраическое выражение Большое спасибо за загрузку, что значит упростить алгебраическое выражение.Если значение равно true, функция расширяет арифметическую часть выражения без расширения тригонометрических, гиперболических, логарифмических и специальных функций. 3 Решать многоэтапные реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (в целом «Оценка» в основном означает «упрощение выражения до одного числового значения». «(x)» НЕ означает, что вы умножаете «x». Основы алгебры научили нас, как выражать неизвестное значение с помощью таких букв, как x, y, z и т. д.Примеры упрощения экспоненциальных выражений показывают, когда и как используются приведенные выше правила экспоненты. Решение: Мы знаем, что отрицательный показатель степени означает, что основание принадлежит другой части дроби. Упрощение дробей. Дан треугольник с тремя сторонами, периметр равен сумме трех сторон.
.. Свести рациональное выражение к наименьшим терминам. [EPUB] Что значит упростить алгебраическое выражение Большое спасибо за загрузку, что значит упростить алгебраическое выражение.Если значение равно true, функция расширяет арифметическую часть выражения без расширения тригонометрических, гиперболических, логарифмических и специальных функций. 3 Решать многоэтапные реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (в целом «Оценка» в основном означает «упрощение выражения до одного числового значения». «(x)» НЕ означает, что вы умножаете «x». Основы алгебры научили нас, как выражать неизвестное значение с помощью таких букв, как x, y, z и т. д.Примеры упрощения экспоненциальных выражений показывают, когда и как используются приведенные выше правила экспоненты. Решение: Мы знаем, что отрицательный показатель степени означает, что основание принадлежит другой части дроби. Упрощение дробей. Дан треугольник с тремя сторонами, периметр равен сумме трех сторон. 16 х = 16 ⋅ х = 4 2 ⋅ х = 4 х. Первая причина заключается в том, что то, что проще, может быть весьма субъективным. Во-первых, давайте подробнее рассмотрим, зачем нам нужен процесс Factoring Completely.none Что значит упростить выражение? Упрощение числового выражения заключается в выполнении данных операций. 10 Как следует из названия, у вас есть выражения, связанные с алгеброй, но что это значит? Выражение — это группа, которая может включать любую комбинацию чисел, символов и операторов (добавление, что-это-значит-для-упрощения-алгебраического-выражения 1/2 Загружено с getsettogo. Факторизация — это обратная сторона раскрытия скобок , так что это, например, представление 2x² + x — 3 в форме (2x + 3) (x — 1).разум. Как числовые, так и алгебраические выражения можно разложить на множители с помощью определенного метода (методов). Упростите определение: если вы что-то упрощаете, вы делаете его более понятным или удаляете вещи | Значение, произношение, переводы и примеры. Упрощение выражений — объяснение и примеры.
16 х = 16 ⋅ х = 4 2 ⋅ х = 4 х. Первая причина заключается в том, что то, что проще, может быть весьма субъективным. Во-первых, давайте подробнее рассмотрим, зачем нам нужен процесс Factoring Completely.none Что значит упростить выражение? Упрощение числового выражения заключается в выполнении данных операций. 10 Как следует из названия, у вас есть выражения, связанные с алгеброй, но что это значит? Выражение — это группа, которая может включать любую комбинацию чисел, символов и операторов (добавление, что-это-значит-для-упрощения-алгебраического-выражения 1/2 Загружено с getsettogo. Факторизация — это обратная сторона раскрытия скобок , так что это, например, представление 2x² + x — 3 в форме (2x + 3) (x — 1).разум. Как числовые, так и алгебраические выражения можно разложить на множители с помощью определенного метода (методов). Упростите определение: если вы что-то упрощаете, вы делаете его более понятным или удаляете вещи | Значение, произношение, переводы и примеры. Упрощение выражений — объяснение и примеры. Научиться упрощать выражение — самый важный шаг в понимании и освоении алгебры. Радикальное уравнение — уравнение, содержащее радикальные выражения с переменными в подкоренных.Пример 3: Упростите и найдите все числа, которые необходимо исключить из области определения упрощенного рационального выражения: . Пример 1 Оцените следующий предел. нет полных квадратных множителей, отличных от 1 в подкоренном члене. 36 Упрощение. Калькулятор выдаст пошаговое объяснение выполнения работы. сделать более внятным : уточнить. Это важный способ решения квадратных уравнений. Упрощение выражений — удобный математический навык, потому что он позволяет нам превращать сложные или неудобные выражения в более простые и компактные формы.Осветлить: сделать жидкость прозрачной, удалив отложения и примеси; растаять далеко и удалить любой осадок. Окончательный ответ: знаменатель представляет собой двучлен (2 члена). Возведение выражения в нулевую степень. Напечатайте эту страницу 6. Для решения уравнений или упрощения выражений вам может понадобиться комбинировать «подобные термины».
Научиться упрощать выражение — самый важный шаг в понимании и освоении алгебры. Радикальное уравнение — уравнение, содержащее радикальные выражения с переменными в подкоренных.Пример 3: Упростите и найдите все числа, которые необходимо исключить из области определения упрощенного рационального выражения: . Пример 1 Оцените следующий предел. нет полных квадратных множителей, отличных от 1 в подкоренном члене. 36 Упрощение. Калькулятор выдаст пошаговое объяснение выполнения работы. сделать более внятным : уточнить. Это важный способ решения квадратных уравнений. Упрощение выражений — удобный математический навык, потому что он позволяет нам превращать сложные или неудобные выражения в более простые и компактные формы.Осветлить: сделать жидкость прозрачной, удалив отложения и примеси; растаять далеко и удалить любой осадок. Окончательный ответ: знаменатель представляет собой двучлен (2 члена). Возведение выражения в нулевую степень. Напечатайте эту страницу 6. Для решения уравнений или упрощения выражений вам может понадобиться комбинировать «подобные термины». х 2 + 4 х — 12 х 2 — 2 х. Запишите сокращенную дробь. Однако мы знаем, что это можно записать в виде дроби со знаменателем 1. Выражение также может быть комбинацией переменных и констант, которые объединяются с помощью математических операций.Упрощение: Возможные ответы: Ни один из других ответов. Черные карточки обозначают положительные числа, а красные – отрицательные. Упрощение выражений. Сбор похожих терминов. Вспомним из Урока 3: Наборы чисел, что рациональное число — это число, которое можно записать как одно целое над другим. Шаг 1: Переставьте термины так, чтобы сгруппировать все похожие термины вместе. Правильный ответ: Объяснение: Вычтите показатели степени «x» и степени «y» по вертикали. Теперь рассмотрим произведение (3x + z) (2x + y).В конце концов, не нужно больше ничего складывать, вычитать, умножать или делить. Он распределил порции пиццы следующим образом: Папа 3 12 Мама 2 12 Факторинг — это метод, с помощью которого можно упростить некоторые выражения с переменными, в том числе многочлены.
х 2 + 4 х — 12 х 2 — 2 х. Запишите сокращенную дробь. Однако мы знаем, что это можно записать в виде дроби со знаменателем 1. Выражение также может быть комбинацией переменных и констант, которые объединяются с помощью математических операций.Упрощение: Возможные ответы: Ни один из других ответов. Черные карточки обозначают положительные числа, а красные – отрицательные. Упрощение выражений. Сбор похожих терминов. Вспомним из Урока 3: Наборы чисел, что рациональное число — это число, которое можно записать как одно целое над другим. Шаг 1: Переставьте термины так, чтобы сгруппировать все похожие термины вместе. Правильный ответ: Объяснение: Вычтите показатели степени «x» и степени «y» по вертикали. Теперь рассмотрим произведение (3x + z) (2x + y).В конце концов, не нужно больше ничего складывать, вычитать, умножать или делить. Он распределил порции пиццы следующим образом: Папа 3 12 Мама 2 12 Факторинг — это метод, с помощью которого можно упростить некоторые выражения с переменными, в том числе многочлены. нет дробей в подкоренном и. найти значение интеграла. Это прекрасно работает, но это четыре слова вместо одного. Это упражнение в чтении мыслей. Это правило позволяет вам раскрывать круглые скобки, поэтому очень важно понимать, хотите ли вы добиться успеха в упрощении выражений.Прежде чем мы сможем упростить радикалы, нам нужно знать некоторые правила о них. Это означает, что вы не просто решаете математические задачи слева направо; скорее, вы решаете их в заранее определенном порядке, который дается вам через аббревиатуру PEMDAS. Вот иллюстрация. Эти правила просто следуют из того, что мы узнали в первых двух разделах этой главы, Интегральные показатели и Дробные показатели. Помните, что вычисление выражения означает подстановку числа вместо переменной в выражении.Распределительное свойство вступает в игру, когда выражение включает в себя как сложение, так и умножение. Сократите дробь до наименьших членов, сократив любые общие одночлены или многочлены, которые существуют как в числителе, так и в знаменателе.
нет дробей в подкоренном и. найти значение интеграла. Это прекрасно работает, но это четыре слова вместо одного. Это упражнение в чтении мыслей. Это правило позволяет вам раскрывать круглые скобки, поэтому очень важно понимать, хотите ли вы добиться успеха в упрощении выражений.Прежде чем мы сможем упростить радикалы, нам нужно знать некоторые правила о них. Это означает, что вы не просто решаете математические задачи слева направо; скорее, вы решаете их в заранее определенном порядке, который дается вам через аббревиатуру PEMDAS. Вот иллюстрация. Эти правила просто следуют из того, что мы узнали в первых двух разделах этой главы, Интегральные показатели и Дробные показатели. Помните, что вычисление выражения означает подстановку числа вместо переменной в выражении.Распределительное свойство вступает в игру, когда выражение включает в себя как сложение, так и умножение. Сократите дробь до наименьших членов, сократив любые общие одночлены или многочлены, которые существуют как в числителе, так и в знаменателе. Поэтому простейшая форма означает упрощение определенного математического выражения с помощью соответствующих методов. Когда вы смотрите на условия вашей математической задачи, вам нужно найти эти общие факторы. В этом выражении мы можем использовать распределительное свойство, чтобы избавиться от первых двух наборов скобок.Пример 1. Следовательно, мы начинаем с преобразования выражения в дробь таким образом, что скобки сначала означают, что сначала нужно сделать то, что находится на месте скобок. плавать. \квадратный! \квадратный! . упростить: [глагол] сделать простым или проще: например. 2 ДОЛЯ ПОКАЗАТЕЛЕЙ И РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ Подкоренное выражение — это выражение, включающее корни. Например, можно расширить и уменьшить выражение после `(3x+1)(2x+4)`. Калькулятор вернет выражение в двух формах: Использование правила частного для упрощения квадратных корней.ЕЕ. Когда мы делим выражения с одинаковым основанием, нам нужно вычесть показатель степени числа, на которое мы делим, из показателя степени первого числа.
Поэтому простейшая форма означает упрощение определенного математического выражения с помощью соответствующих методов. Когда вы смотрите на условия вашей математической задачи, вам нужно найти эти общие факторы. В этом выражении мы можем использовать распределительное свойство, чтобы избавиться от первых двух наборов скобок.Пример 1. Следовательно, мы начинаем с преобразования выражения в дробь таким образом, что скобки сначала означают, что сначала нужно сделать то, что находится на месте скобок. плавать. \квадратный! \квадратный! . упростить: [глагол] сделать простым или проще: например. 2 ДОЛЯ ПОКАЗАТЕЛЕЙ И РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ Подкоренное выражение — это выражение, включающее корни. Например, можно расширить и уменьшить выражение после `(3x+1)(2x+4)`. Калькулятор вернет выражение в двух формах: Использование правила частного для упрощения квадратных корней.ЕЕ. Когда мы делим выражения с одинаковым основанием, нам нужно вычесть показатель степени числа, на которое мы делим, из показателя степени первого числа.

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.



