Дифференциальные уравнения с разделенными переменными

Многие студенты спрашивают «Как найти решение дифференциального уравнения?» Ответ возможно неординарен, но что Вы знаете о дифференциальных уравнениях (ДУ), их типах, какие распространенные схемы вычислений ДУ? С этого нужно начинать.
Сферы применения дифференциальных уравнений были в общем очерчены на предыдущем уроке. Здесь речь пойдет об одном из самых простых (в плане вычислений) типов ДУ первого порядка среди всех возможных уравнений что Вас ждут. Начнем с базовых понятий теории которые Вы должны знать и мы будем использовать в терминологии. Для одних это не нужно, потому что они ищут готовые ответы по дифференциальным уравнениям и думают, что таким образом решат все проблемы. Но это ошибка, потому что не знание элементарных понятий по теории ДУ сравнимо с тем, что Вы пытаетесь говорить, предварительно не изучив звуки и алфавит.
Дифференциальное уравнение первого порядка, которое можно записать формулой
N(х)dx+М(у)dy=0 (1)
называют уравнением с разделенными переменными.
Их не трудно обнаружить среди других уравнений, основной признак — множители при dx и dy являются функциями (константами), которые зависят только от х при множителе dx и у при dy.
Чтобы найти общее решение (общий интеграл) уравнения с разделенными переменными необходимо проинтегрировать уравнение (1)
Int(N(x), x) + Int(M(y),y) = С,

Для понимания дифференциальное уравнение (1) можно принимать, как условие равенства нулю полного дифференциала некоторой функции двух переменных U(x,y)

Отсюда следует что функция U(x,y)=С=const равна постоянной.
Дифференциальное уравнение вида
f₁(x)*g₁(y)dx+f₂(x)*g₂(y)dy=0 (2)
называют дифференциальным уравнением с разделяющимися переменными в симметричной форме.
В уравнении (2) коэффициенты при дифференциалах dx и dy является произведениями двух функций: одна зависит только от x, а вторая — от y. В области, где g1(y), f2(x) принимают отличные от нуля значения в уравнение с разделяющимися переменными (2) сводится к уравнению с разделенными переменными

Звучит как игра слов: разделенными, разделяющимися, однако между ними как видите есть маленькая разница, и теперь Вы ее знаете.
Рассмотрим типичные для практики задания на диф. уравнения первого порядка, которые в достаточно простой способ можно свести к уравнениям с разделенными переменными.

Пример 1 Решить дифференциальное уравнение
Решение:Имеем дифференциальное уравнение первого порядка, по теории его можно назвать уравнением с разделяющимися переменными или уравнением в дифференциалах. Для его упрощения сгруппируем слагаемые, содержащие dx, dy по разные стороны знака равенства

Далее выделим общие множители для каждой суммы и перепишем уравнение в дифференциалах в форме

После этого все, что содержит y переносим к dy, то же самое проделываем с множителями которые содержат переменную x.
В результате придем к дифференциальному уравнению с разделенными переменными

Теперь посмотрите почему данное уравнение называется уравнением с разделенными переменными? — Возле dx имеем функцию зависимую только от «икс», у dy — только от y.
Проинтегрируем дифференциальное уравнение

Выносим множители, чтобы при переменной в знаменателе стояли единицы. Также, чтобы в числителе получить дифференциалы знаменателя умножаем обе части на 2

Это позволяет упростить вычисления интеграла ДУ (после интегрирования получить логарифмы)

Константу рекомендуем внести в логарифм, для этого записывайте всегда ее в виде C₁=ln(C)

Чтобы раскрыть логарифмическое уравнение экспонируем (находим экспоненту) правую и левую сторону зависимости
(3)
Также выделяем значение функции

Конечная запись имеет двойной корень и является общим решением уравнения с разделяющимися переменными. Это не совсем хороший тон подавать ответ, лучше решение оставить в виде формулы (3), только тройку перенести в правую сторону.

 

Пример 2 Найти общий интеграл дифференциального уравнения
Решение:Имеем уравнение в дифференциалах первого порядка. Разделим в уравнении переменные, содержащиеся при dx, dy и перенесем их по разные стороны знака равенства

С первых скобок выносим общий для двух слагаемых множитель y за скобки

Далее разделим множители так, чтобы при dy получить функцию только от y, а при dx — функцию аргумента x. В результате получим дифференциальное уравнение с разделенными переменными

После интегрирования

получим корневую зависимость для y и арктангенс в результате вычисления интеграла по аргументу (правая сторона).

Общий интеграл можем оставить в такой форме или перенести артангенс в левую часть зависимости.
Так же можем записать решение дифференциального уравнения в виде зависимости y(x) (явном виде). Для этого возведем обе части к квадрату

и перенеся сталую в правую сторону, вычислим корень квадратный

Это и есть искомое решение дифференциального уравнения.

 

Пример 3 Решить дифференциальное уравнение
Решение:Данное ДУ первого порядка необходимо свести под правило решения уравнений с разделенными переменными. Для этого второе слагаемое, что со знаком минус, переносим в правую сторону от знака равенства

и разделяем переменные

Проинтегрируем левую и правую сторону зависимости

В результате придем к логарифмическому уравнению вида

И снова обращаем Ваше внимание на то что в таком виде как правило не записывают.
Целесообразно, для компактности конечного решения, постоянную вносить под логарифм, то есть в форме

Взяв экспоненту от правой и левой части формулы придем к конечному виду решения дифференциального уравнения

Как Вы могли убедиться примеры достаточно просты, методика вычислений ДУ з разделенными переменными легкая для изучения.

Пример 4 Решить дифференциальное уравнениеРешение: Одно из слагаемых (не содержит производной) переносим за знак равенства

и записываем уравнение в дифференциалах..

Следующим шагом сводим зависимость к дифференциальному уравнению с разделенными переменными.
Для заданного уравнения всего лишь перекрестным делением записываем корни в знаменатели

В таком виде можем интегрировать уравнения

Левая сторона содержит функцию которая при иртегрировании даст корневую зависимость, для правой стороны по формулам получим арксинус.

Выполняем манипуляции с корнем, чтобы получить зависимость вида y=y(x)

Решение дифференциального уравнения будет иметь вид

На этом вводный урок закончен и основные выводы Вы должны сделать самостоятельно.
Для закрепления темы рекомендуем самостоятельно решить несколько из следующих примеров.

Хотите верьте, а хотите — нет, но это самый простой тип дифференциальных уравнений, с которым Вам придетсяиметь дело на контрольной, экзаменах, практических занятиях, модулях. Это можно сказать важнейшая часть, поскольку сложные дифференциальные уравнения придется упрощать и сводить к уравнениям с разделенными переменными.
Схему вычислений должны заучить и знать на зубок — это один из основных методов решения сложных примеров на диф. уравнения.

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т. к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.

И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Что такое дифференциальные уравнения? | Наука в Сибири

Как известно, в современной науке, стремящейся к описанию наблюдаемых природных или общественных явлений, значительная роль принадлежит математике. Теория дифференциальных уравнений, являясь одним из крупных разделов математики, в то же время всегда была и остается тесно связанной с приложениями.

Рассматривая математику как способ проникновения в тайны окружающего нас мира, можно сказать, что основным приемом исследования является формирование и изучение математических моделей реальных явлений. Исследуя какие-либо явления, ученый в первую очередь создает математическую идеализацию или, иначе говоря, математическую модель.

Математическая модель есть не что иное, как запись основных законов, описывающих явление, в математической форме. И очень часто эти законы можно выразить в виде дифференциальных уравнений, соотношений между функциями и их производными: в приложениях функции обычно представляют изменяющиеся величины, а производные описывают скорость их изменения. Такое выражение допускают модели многих явлений механики сплошных сред, химических реакций, фундаментальных физических взаимодействий, биологических и экономических процессов и так далее.

Изучая полученные дифференциальные уравнения, исследователь извлекает полезные сведения о происходящих явлениях, часто может узнать их прошлое и предсказать будущее, получить качественные оценки происходящих в течение процесса изменений и даже открыть новые феномены, выдвинуть новые гипотезы, которые, быть может, приведут к более совершенным научным воззрениям и приоткроют завесу тайны окружающего мира. Таким образом, теория дифференциальных уравнений широко используется при решении научных проблем как для точной формулировки их содержания, так и для получения новых результатов.

Вместе с тем следует помнить, что математическая модель сама по себе является объектом и может обладать собственными свойствами, не имеющими отношения к моделируемому процессу. Модель не всегда адекватна конкретному явлению: так, например, из существования решения реальной задачи (существование наблюдаемого процесса обычно не вызывает сомнений ученых) не следует существование решения соответствующей математической задачи; или же может оказаться, что решений математической задачи много; или же решение неустойчиво к изменениям данных. Именно поэтому главной целью теории дифференциальных уравнений в первую очередь является изучение внутренне присущих свойств задач, сформулированных на языке дифференциальных уравнений: исследование их корректности, разрешимости, качественных и количественных характеристик решений, взаимосвязи и классификации. Несмотря на то, что изучением дифференциальных уравнений научное сообщество занимается уже несколько веков, цель эта в общем случае настолько трудна, что если некто наугад напишет произвольное дифференциальное уравнение, то с большой долей вероятности ни один математик в мире ничего не сможет про это уравнение сказать.

 

В настоящее время теория дифференциальных уравнений представляет собой обширную и широко разветвленную теорию, находящуюся в постоянном взаимодействии с другими науками. Приложения снабжают ее новыми проблемами, решая которые, теория дифференциальных уравнений обращается к остальным разделам математики, таким как алгебра, функциональный анализ, теория функций, геометрия, теория вероятностей, вычислительная математика. В то же время прогресс в перечисленных разделах математики неизбежно приводит к достижениям в теории дифференциальных уравнений, что опять же дает толчок развитию приложений. Другими словами, как писала академик Ольга Арсеньевна Олейник, теория дифференциальных уравнений «лежит на перекрестке математических дорог», служит мостом между чистыми и прикладными науками, показывает направление новым веяниям фундаментальной науки на пути к приложениям, одновременно стимулируя совершенствование математического аппарата с оглядкой на прикладные нужды. 

Фото и изображение предоставлены исследователем
 

Дифференциальные уравнения — Решение

Дифференциальные уравнения

Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.

  В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.

  Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:

 В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.

 

Тогда получаем:  — уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).

 

 

  Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

  Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

  Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

  Пример.

 — обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается .

 — обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается

 — дифференциальное уравнение в частных производных первого порядка.

  Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

 

Свойства общего решения.

 

  1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.

  2) При каких- либо начальных условиях х = х₀, у(х₀) = у₀ существует такое значение С = С₀, при котором решением дифференциального уравнения является функция у = j(х, С₀).

  Определение. Решение вида у = j(х, С₀) называется частным решением дифференциального уравнения.

  Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С₀), удовлетворяющего начальным условиям у(х₀) = у₀.

  Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)

  Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х₀, у₀) в области D, существует единственное решение  уравнения , определенное в некотором интервале, содержащем точку х₀, принимающее при х = х₀ значение j(х₀) = у₀, т. е. существует единственное решение дифференциального уравнения.

  Определение. Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

  Пример. Найти общее решение дифференциального уравнения .

Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

 Теперь интегрируем: 

   — это общее решение исходного дифференциального уравнения.

 

  Допустим, заданы некоторые начальные условия: x₀ = 1; y₀ = 2, тогда имеем

 При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).

 

 Определение. Интегральной кривой называется график y = j(x) решения дифференциального уравнения на плоскости ХОY.

  Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.

Особые решения не зависят от постоянной С.

  Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.

  Отметим, что не каждое дифференциальное уравнение имеет особые решения.

 

  Пример. Найти общее решение дифференциального уравнения:  Найти особое решение, если оно существует.

 Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0  можно получить из общего решения при С₁ = 0 ошибочно, ведь C₁ = e^C ¹ 0. 

 Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.

Дифференциальные уравнения первого порядка.

Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:

 

 Если такое соотношение преобразовать к виду  то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.

 

  Преобразуем такое выражение далее:

Функцию f(x,y) представим в виде:  тогда при подстановке в полученное выше уравнение имеем:

 

—         это так называемая дифференциальная форма уравнения первого порядка.

Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.

  

Уравнения вида y’ = f(x).

  Пусть функция f(x) – определена и непрерывна на некотором интервале

a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х₀ и у₀, то можно определить постоянную С.

 

Уравнения с разделяющимися переменными

  Определение. Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде

.

 

  Такое уравнение можно представить также в виде:

 

Перейдем к новым обозначениям

 

Получаем: 

 

 

 После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.

  Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.

 

 

  Пример. Найти общее решение дифференциального уравнения:

 

 

Интеграл, стоящий в левой части, берется по частям

 

—         это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.

 

Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.

 — верно

  Пример. Найти решение дифференциального уравнения  при условии у(2) = 1.

 

при у(2) = 1 получаем

Итого:  или  — частное решение;

   Проверка:  , итого

  — верно.

   Пример. Решить уравнение

  — общий интеграл

   — общее решение

 

  Пример. Решить уравнение

 

 

 Пример. Решить уравнение при условии у(1) = 0.

Интеграл, стоящий в левой части будем брать по частям

 

  Если у(1) = 0, то

   Итого, частный интеграл: .

  

  Пример. Решить уравнение .

 

 

 Для нахождения интеграла, стоящего в левой части уравнения см. Получаем общий интеграл:

  

 Пример. Решить уравнение

Преобразуем заданное уравнение:

 Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.

 

  Пример. Решить уравнение .

 

 

; ;

Допустим, заданы некоторые начальные условия х₀ и у₀. Тогда:

 Получаем частное решение

Однородные уравнения.

   Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

 

 Пример.  Является ли однородной функция 

 

 Таким образом, функция f(x, y) является однородной 3- го порядка.

  Определение. Дифференциальное уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

  Любое уравнение вида  является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

  Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

  Рассмотрим однородное уравнение

Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:

 Т.к. параметр t вообще говоря произвольный, предположим, что . Получаем:

 Правая часть полученного равенства зависит фактически только от одного аргумента , т. е.

Исходное дифференциальное уравнение таким образом можно записать в виде:

Далее заменяем y = ux, .

 

таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

 

Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

  Пример. Решить уравнение .

 Введем вспомогательную функцию u.

.

Отметим, что введенная нами функция u всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее .

Подставляем в исходное уравнение:

 

 Разделяем переменные:

 Интегрируя, получаем:

 Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

 

 Уравнения, приводящиеся к однородным.

   Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.

   Это уравнения вида .

Если определитель  то переменные могут быть разделены подстановкой

где a и b — решения системы уравнений

  Пример. Решить уравнение

Получаем

 Находим значение определителя .

Решаем систему уравнений

 Применяем подстановку  в исходное уравнение:

 

Заменяем переменную   при подстановке в выражение, записанное выше, имеем:

 Разделяем переменные:

 

 

Переходим теперь к первоначальной функции у и переменной х.

 

 Итого, выражение  является общим интегралом исходного дифференциального уравнения.

  

  В случае если в исходном уравнении вида  определитель  то переменные могут быть разделены подстановкой

  Пример. Решить уравнение

 Получаем

Находим значение определителя

Применяем подстановку

Подставляем это выражение в исходное уравнение:

 

Разделяем переменные:

Далее возвращаемся к первоначальной функции у и переменной х.

таким образом, мы получили общий интеграл исходного дифференциального уравнения.

Линейные уравнения.

   Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.

 

  P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

Линейные однородные дифференциальные уравнения.

  Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида

.

  Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.

 

  Общее решение: 

Линейные неоднородные дифференциальные уравнения.

  Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.

 Метод Бернулли.

(Якоб Бернулли (1654-1705) – швейцарский математик.)

    Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций .

  При этом очевидно, что  — дифференцирование по частям.

   Подставляя в исходное уравнение, получаем:

 Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

  Например, функция  может быть представлена как

 и т.п.

  Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение .

  Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

 

 

  Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение  с учетом того, что выражение, стоящее в скобках, равно нулю.

 

  Интегрируя, можем найти функцию v:

; ;

  Т.е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

  Подставляя полученные значения, получаем:

 

  Окончательно получаем формулу:

, С₂ — произвольный коэффициент.

Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.

Метод Лагранжа.

( Ларганж Жозеф Луи (1736-1813) — французский математик,  през. Берлинской АН, поч. чл. Пет. АН (1776)).

  Метод Лагранжа  решения неоднородных линейных дифференциальных уравнений еще называют методом  вариации произвольной постоянной.

   Вернемся к поставленной задаче:

 Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.

  Далее находится решение получившегося однородного дифференциального уравнения:

.

Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С₁ некоторой функцией от х.

  Тогда по правилам дифференцирования произведения функций получаем:

 

Подставляем полученное соотношение в исходное уравнение 

Из этого уравнения определим переменную функцию С₁(х):

Интегрируя, получаем:

 Подставляя это значение в исходное уравнение, получаем:

 .

 Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.

    При выборе метода решения линейных дифференциальных уравнений следует руководствоваться  простотой интегрирования функций, входящих в исходный интеграл.

   Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним результаты.

  Пример. Решить уравнение

 Сначала приведем данное уравнение к стандартному виду:

Применим полученную выше формулу:

 Уравнение Бернулли.

   Определение. Уравнением Бернулли называется уравнение вида

где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.

   Для решения уравнения Бернулли применяют подстановку , с помощью которой, уравнение Бернулли приводится к линейному.

  Для этого разделим исходное уравнение на yⁿ.

  

Применим подстановку, учтя, что .

Т.е. получилось линейное уравнение относительно неизвестной функции z.

Уравнения в полных дифференциалах (тотальные).

  Определение. Дифференциальное уравнение первого порядка вида:

называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции

  Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде:

  Таким образом, для решения надо определить:

1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;

2) как найти эту функцию.

 

Если дифференциальная форма является полным дифференциалом некоторой функции u, то можно записать:

Т.е. . 

Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:

Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется условием тотальности.

  Теперь рассмотрим вопрос о нахождении собственно функции u.

Проинтегрируем равенство :

Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т.к. при интегрировании переменная у полагается постоянным параметром.

  Определим функцию С(у).

Продифференцируем полученное равенство по у.

Откуда получаем:

Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.

Теперь определяем функцию С(у):

Подставляя этот результат в выражение для функции u, получаем:

 

Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:

 

 Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым формула была получена.

  Пример. Решить уравнение

 Проверим условие тотальности:

 

Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.

Определим функцию u.

;

Итого,

Находим общий интеграл исходного дифференциального уравнения:

 Уравнения вида y = f(y’) и x = f(y’).

 

  Решение уравнений, не содержащих в одном случае аргумента х, а в другом – функции у, ищем в параметрической форме, принимая за параметр производную неизвестной функции.

Для уравнения первого типа получаем: 

Делая замену, получаем:

В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.

  Общий интеграл в параметрической форме представляется системой уравнений:

 

Исключив из этой системы параметр р, получим общий интеграл и не в параметрической форме.

   Для дифференциального уравнения вида x = f(y’) с помощью той же самой подстановки и аналогичных рассуждений получаем результат:

 

Геометрическая интерпретация решений дифференциальных уравнений первого порядка.

 

 

  Как уже говорилось выше, линия S, которая задается функцией, являющейся каким- либо решением дифференциального уравнения, называется интегральной кривой уравнения

  Производная y’ является угловым коэффициентом касательной к интегральной кривой.

  В любой точке А(х, у) интегральной кривой этот угловой коэффициент касательной может быть найден еще до решения дифференциального уравнения.

Т.к. касательная указывает направление интегральной кривой еще до ее непосредственного построения, то при условии непрерывности функции f(x, y) и непрерывного перемещения точки А можно наглядно изобразить поле направлений кривых, которые получаются в результате интегрирования дифференциального уравнения, т.е. представляют собой его общее решение.

  Определение. Множество касательных в каждой точке рассматриваемой области называется полем направлений.

  С учетом сказанного выше можно привести следующее геометрическое истолкование дифференциального уравнения:

  1) Задать дифференциальное уравнение первого порядка – это значит задать поле направлений.

  2) Решить или проинтегрировать дифференциальное уравнение – это значит найти всевозможные кривые, у которых направление касательных в каждой точке совпадает с полем направлений.

  Определение. Линии равного наклона в поле направлений называются изоклинами.

 Численные методы решения дифференциальных уравнений.

  Известные методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции, однако эти методы применимы для очень ограниченного класса функций. Большинство уравнений, встречающихся при решении практических задач нельзя проинтегрировать с помощью этих методов.

  В таких случаях используются численные методы решения, которые представляют решение дифференциального уравнения не в виде аналитической функции, а в виде таблиц значений искомой функции в зависимости от значения переменной.

  Существует несколько методов численного интегрирования дифференциальных уравнений, которые отличаются друг от друга по сложности вычислений и точности результата.

  Рассмотрим некоторые из них.

 Метод Эйлера.

(Леонард Эйлер (1707 – 1783) швейцарский математик )

  Известно, что уравнение  задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке.

  Если взять последовательность точек х₀, х₁, х₂, …. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию. 

 y

  M₂  M₁  M₃

  При подстановке заданных начальных условий (х₀, у₀) в дифференциальное уравнение получаем угловой коэффициент касательной к интегральной кривой в начальной точке

  Заменив на отрезке [x₀, x₁] интегральную кривую на касательную к ней, получаем значение

  Производя аналогичную операцию для отрезка [x₁, x₂], получаем:

  Продолжая подобные действия далее, получаем ломаную кривую, которая называется ломаной Эйлера.

  Можно записать общую формулу вычислений:

  Если последовательность точек х_i выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу:

 Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета.

Суть метода состоит в том, что в формуле  вместо значения

 берется среднее арифметическое значений f(x₀, y₀) и f(x₁, y₁). Тогда уточненное значение:

 Затем находится значение производной в точке . Заменяя f(x₀, y₀) средним арифметическим значений f(x₀, y₀) и , находят второе уточненное значение у₁.

 Затем третье:

и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М₁ ломаной Эйлера.

  Аналогичная операция производится для остальных значений у.

 Подобное уточнение позволяет существенно повысить точность результата.

Дифференциальные уравнения высших порядков.

  Определение. Дифференциальным уравнением порядка n называется уравнение вида:

 В некоторых случаях это уравнение можно разрешить относительно y⁽ⁿ⁾:

 Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.

   Определение. Решение удовлетворяет начальным условиям , если

   Определение. Нахождение решения уравнения , удовлетворяющего начальным условиям , называется решением задачи Коши.

  Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

  Если функция (n-1) –й переменных вида в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по , то какова бы не была точка () в этой области, существует единственное решение  уравнения , определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

   Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.

  Рассмотрим подробнее методы нахождения решений этих уравнений.

 

Уравнения, допускающие понижение порядка.

  Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.

  Уравнения вида y⁽ⁿ⁾ = f(x).

  Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

 

 Пример. Решить уравнение  с начальными условиями x₀ = 0; y₀ = 1;

  Подставим начальные условия:

 Получаем частное решение (решение задачи Коши): .

  Ниже показана интегральная кривая данного дифференциального уравнения.

 

Решение дифференциальных уравнений — Информатика, информационные технологии

Дифференциальные уравнения являются основной формой представления математических моделей. Напомним, что уравнение, в котором неизвестная функция входит под знаком производной или дифференциала, называется дифференциальным уравнением. Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, то уравнение называется обыкновенным. Обыкновенное дифференциальное уравнение в общем случае содержит независимую переменную (X), неизвестную функцию (Y(X)) и ее производные (dY/dX) до n-го порядка и имеет вид

F(X, Y, Y¢, Y?, … , Y(n))=0.

Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.

Здесь мы рассмотрим технику решения обыкновенных дифференциальных уравнений с начальными условиями, т. е. таких, для которых известны значения искомой функции и ее производных (до n-1 порядка) при Х=0. Решение уравнений в такой постановке называется задачей Коши. Известно, что аналитическое решение дифференциальных уравнений возможно лишь в небольшом числе случаев. В остальных случаях оно доступно только с помощью численных методов. Самый простой из них – метод Эйлера. Суть метода применительно к уравнению первого порядка dY/dX=Y(X,Y) с начальными условиями Y(X0)=Y0поясняет рис. 11.3а.

Решением уравнения является такая функция Y(Х), которая, будучи подставленной в уравнение, превращает его в тождество. Само уравнение не известно. В начальных условиях задается только одна его точка Y(Х0). Разобьем весь диапазон интегрирования уравнения на участки с одинаковым шагом DХ и попытаемся найти значение искомой функции Y(Х) в точке Х1=Х0+DХ. Здесь искомая функция изображена линией с ординатами Y0,Y1,Y2,…, Yk+1 (пустые прямоугольники), а полученная по методу Эйлера – ломаной с ординатами Y0, Y1,Y2, …, Yk+1 (черные прямоугольники). Если DХ мало – можно полагать, что уравнение касательной к искомой функции в точке Х0 (прямая Y0Y1) не сильно отличается от Y(Х) на участке DХ (дуга Y0Y1). Найдем Y1

Y1=Y0+DY1=Y0+DХ?Tg(W0).

Тангенс W0равен значению производной функции Y(Х) в точке Х0, которую легко вычислить

TgW0=Y’0=Z(X0,Y0). И можем записать Y=Y0+DХ?Z(X0,Y0).

Следующий шаг – проведение касательной к Y(Х1), т.е. построение участка с тангенсом наклона, равным Z(X1,Y1). Однако поскольку нам известно не точное значение Y1, а приближенное Y1, проведем линию с тангенсом угла наклона, равным Z(X1,Y1). Тогда

Y 2=Y1+DХ?Z(Х1,Y1).

Отсюда можем получить рабочие формулы метода

Хk+1=Хk+DХ и Yk+1=Yk+DХ?Z(Хk,Yk).

Метод является весьма приблизительным (сравните вычисленную и настоящую функции на рисунке). Уменьшив шаг интегрирования DХ, можно добиться приемлемой погрешности. При DХ?0 решение сходится к точному.

На рис.3.3б и 3в представлены (в числовом и формульном виде) таблицы решения дифференциального уравнения (начальные условия Y(0)=1) вида:

Решение Y=exp(X2) такого простого уравнения известно, что позволит нам оценить точность вычислений в таблице. Здесь в ячейке В1 установлен шаг интегрирования 0,4, в В4 и С4 – начальные условия уравнения. Текущие значения номера шага и значения Х вычисляются аналогично предыдущему. В колонке Yэ находится решение по методу Эйлера, а в колонке Yт – предъявляется точное решение с непосредственным использованием функции exp(X2). Решение доведено до Х=1,96 (50 шагов). Видим (рис. 3.3б), что точное решение и решение, полученное с помощью метода Эйлера, достаточно близки. Это подтверждает и график на рис.3.3г, построенный также средствами Excel (тип диаграммы: “точечная”, вид: “Точечная диаграмма со значениями, соединенными отрезками без маркеров”). Дальнейшее снижение погрешности может быть достигнуто уменьшением шага интегрирования. Увеличение предела интегрирования может быть осуществлено, как и в предыдущем случае, копированием последней строки до достижения нужного значения аргумента Х.

	A	B	C	D
	DC=	0,04
			Р е ш е	н и е:
	Шаг	X	Yэ	Yт
				=EXP(B4^2)
	=A4+1	=B4+B$1	=C4+B$1*2*B4*C4	=EXP(B5^2)
	=A5+1	=B5+B$1	=C5+B$1*2*B5*C5	=EXP(B6^2)
			Рис. 3.3в

Конечно, при такой организации вычислений, к которой нам пришлось прибегнуть для интегрирования и решения дифференциальных уравнений, мы ограничены числом строк в рабочем листе Excel. И хотя мы можем продолжить вычисления на другом листе, нам вряд ли потребуется и такое число строк.

Как уже указывалось, метод Эйлера является самым простым (и самым грубым) средством решения дифференциальных уравнений. Здесь можно воспользоваться и более точными методами, например, методом Рунге-Кутта.

Тест. 3.3.1. Что мы получим при решении дифференциального уравнения? 1). число, 2). функцию.

4.

АППРОКСИМАЦИЯ

ЗАВИСИМОСТЕЙ

Задача аппроксимации возникает при необходимости аналитически описать явления, имеющие место в жизни и заданные в виде таблиц, содержащих значения аргумента/аргументов и функции. Если зависимость удается найти, можно сделать прогноз о поведении исследуемой системы в будущем и, возможно, выбрать оптимальное направление ее развития. Такая аналитическая функция (называемая еще трендом) может иметь разный вид и разный уровень сложности в зависимости от сложности системы и желаемой точности представления.

ЛИНЕЙНАЯ РЕГРЕССИЯ

Самый простой и популярной является аппроксимация прямой линией – линейная регрессия.

Пусть мы имеем фактическую информацию об уровнях прибыли Y в зависимости от размера X капиталовложений – Y(X). На рис. 4.1-1 показаны четыре такие точки М(Y,X). Пусть также у нас имеются основания предполагать, что зависимость эта линейная, т.е. имеет вид Y=А+ВX.Если бы нам удалось найти коэффициенты A и B и по ним построить прямую (например, такую, как на рисунке), в дальнейшем мы могли бы сделать осознанные предположения о динамике бизнеса и возможном коммерческом состоянии предприятия в будущем. Нас бы устроила прямая, находящаяся как можно ближе к известным точкам М(Y,X), т.е. имеющая минимальную сумму отклонений или сумму ошибок (на рисунке отклонения показаны пунктирами). Известно, что существует только одна такая прямая. Для решения этой задачи используют метод наименьших квадратов ошибок. Разность (ошибка) между известным значением Y1точки М1(Y1,X1) и значением Y(X1), вычисленным по уравнению прямой для того же значения X1, составит

D1= Y1– A – B•X1.

Такая же разность

для X=X2 составит D2= Y2– A – B•X2;

для X=X3 D3= Y3– A – B•X3;

и для X=X4 D4= Y4– A – B•X4.

Запишем выражение для суммы квадратов этих ошибок

Ф(A,В)=(Y1–A–B•X1)2+(Y2–A–B•X2)2+(Y3–A–B•X3)2+(Y4–A–B•X4)2

или сокращенно Ф(B,A)=a(Yi – A – BXi)2.

i=1

Здесь нам известны все X и Y и неизвестны коэффициенты A и B. Проведем искомую прямую так (т.е. выберем A и B такими), чтобы эта сумма квадратов ошибок Ф(A,B) была минимальной. Условиями минимальности являются известные соотношения

¶Ф(A,B)/¶A=0 и ¶Ф(A,B)/¶B=0.

Выведем эти выражения (индексы при знаке суммы опускаем):

¶[a(Yi–A–B•Xi)2]/¶A = a(Yi–A–B•Xi)(–1)

¶[a(Yi–A–B•Xi)2]/¶B = a(Yi–A–B•Xi)(–Xi).

Преобразуем полученные формулы и приравняем их нулю

2a(–Yi +B•Xi +A) = 0

2a(–Xi•Yi +B•Xi2 +A•Xi) = 0.

Сократим выражения на 2 и раскроем скобки. Тогда

–aYi + BaXi + Aa1 = 0

–aXi•Yi + BaXi2 +AaXi = 0.

Мы получили систему из двух линейных алгебраических уравнений, в которой неизвестными являются A и B, а сумма N единиц равна N (в нашем случае a1=4). Перенесем свободные члены в правую часть и для упрощения записи опустим индексы при знаке суммирования. Окончательно получим:

BaX + NA = aY

BaX2+AaX =aXY.

Решив эту систему с помощью любого известного метода линейной алгебры, получим

В=(N•aXY–aX•aY)/( N•aX2–X•aX), А=(N•aX2–aX•aX)/(N•aX2–aX•aX).

В случае, если величина Y зависит не от одного, а от нескольких параметров Y(x,z, …w), задача нахождения коэффициентов решается аналогично и называется задачей множественной регрессии.

Оценить функциональную близость (в линейном смысле) значений Х и Y можно с помощью коэффициента корреляции R, который находится по следующей формуле

R=(N•aXY – aX•aY)/( N•aX2–aX•aX • N•aY2–aY•aY ).

Cчитается что при R?0,3 наблюдается слабая линейная связь, при R= 0,3¸0,7 – средняя, при R³0,7 – сильная, при R³0,9 – весьма сильная связь, при R=1 – полная функциональная связь (все точки Y(X) лежат на одной прямой).

В Excel имеются функции для нахождения коэффициентов уравнения линейной регрессии.

u ЛИНЕЙН(известное Y; известное X) – вычисляет два коэффициента линейного уравнения регрессии для множества значений независимой переменной Х и зависимой переменной Y. Результат выводится в две смежные ячейки – сначала коэффициент при Х, затем – свободный член. Функция должна вводиться как функция обработки массива: выделяются две ячейки для результата, вводится функция и нажимаются клавиши Ctrl+Shift+Enter (вместо обычного Enter).

Пример. Если исходные данные расположены, как показано на рис. 4.1-2, и в C3:D3 введена функция {=ЛИНЕЙН(B2:B11;A1:A11)},результаты в C3 и D3 можно интерпретировать как коэффициенты линейного уравнения регрессии y=0,6364x+1,8. Таким образом, если нам понадобится вычислить ожидаемое значение прибыли Y в будущем, например, при капиталовложениях в сумме 20 единиц, нужно подставить их в найденную функцию Y=0,64+1,8*20=36,64.

u ТЕНДЕНЦИЯ(известное Y; известное X; новое X) – вычисляет ожидаемое новое значение Y для нового Х, если известны некоторые опытные значения X и Y и в предположении, что Х и Y зависят линейно.

	А	В	С	D
	Х	Y
			ЛИНЕЙН
			0,64	1,8
			ТЕНДЕНЦИЯ
				9,44
			4,5	4,66
			Ри	с.4.1.2

Пример: Исходные данные расположены (рис. 4.1-2) в C7 и C8, результаты – в

D7=ТЕНДЕНЦИЯ(B2:B11;A1:A11;G4)и

D8=ТЕНДЕНЦИЯ( B2:B11; A1:A11;G5).

Таким образом, при Х=12 ожидается Y=9,44, а при Х=4,5; Y=4,66.

Используя значения X и Y с помощью Excel, построим график, совмещенный с линией регрессии (линией тренда), как показано на рис.4.1.3.

@ В Excel имеется очень простой способ строить линейную аппроксимацию равноотстоящих значений аргумента. Для этого нужно выделить известные значения прогнозируемой величины и потянуть за маркер заполнения, удерживая правую кнопку мыши. Затем, из появившегося контекстного меню выбрать пункт Линейное приближение. В заполняемых клетках мы обнаружим значения, вычисленные системой для самостоятельно найденного ею линейного уравнения регрессии. На рис.4.1.4 исходными значениями являются 2, 4, 5. Остальные числа являются вычисленным прогнозом в предположении линейной связи аргументов в соответствии с найденным Excel уравнением. Здесь же (рис.10.1.5), при необходимости, можно выбрать и Экспоненциальное приближение.

		5	6,67	8,17	9,67	11,17	12,67	Рис. 4.1.4
		5	8,55	13,52	21,37	33,80	53,44	Рис. 4.1.5

С помощью средств деловой графики Excel можно не только построить необходимые кривые, но получить линии тренда и соответствующие им уравнения Y(X) (здесь y=1,5x+0,6667 для линейного закона, y=1,368e0,4581x– для экспоненты). Экспоненциальная аппроксимация обозначена прямоугольными точками, линейная – кружками. Исходные точки обведены овалом.

Статьи к прочтению:

Основные понятия дифференциальных уравнений от bezbotvy

Похожие статьи:

Дифференциальное уравнение Бернулли | Математика

Дифференциальное уравнение Бернулли — это уравнение вида

   

где n≠0,n≠1.

Это уравнение может быть преобразовано при помощи подстановки

   

в линейное уравнение

   

На практике дифференциальное уравнение Бернулли обычно не приводят к линейному, а сразу решают теми же методами, что и линейное уравнение — либо методом Бернулли, либо методом вариации произвольной постоянной.

Рассмотрим, как решить дифференциальное уравнение Бернулли  с помощью замены y=uv (метод Бернулли). Схема решения —  как и при решении линейных дифференциальных уравнений первого порядка.

Примеры. Решить уравнения:

1) y’x+y=-xy².

Это дифференциальное уравнение Бернулли. Приведем его к стандартному виду. Для этого поделим обе части на x: y’+y/x=-y². Здесь p(x)=1/x, q(x)=-1, n=2. Но для решения нам не нужен стандартный вид. Будем работать с той формой записи, которая дана в условии.

1) Замена y=uv, где u=u(x) и v=v(x) — некоторые новые функции от x. Тогда y’=(uv)’=u’v+v’u. Подставляем полученные выражения в условие: (u’v+v’u)x+uv=-xu²v².

2) Раскроем скобки: u’vx+v’ux+uv=-xu²v². Теперь сгруппируем слагаемые с v: [u’x+u]v+v’ux=-xu²v²   (I)          (слагаемое со степенью v, стоящее в правой части уравнения, не трогаем). Теперь требуем, чтобы выражение в скобках равнялось нулю: u’x+u=0. А это — уравнение с разделяющимися переменными u и x. Решив его, мы найдем u. Подставляем u=du/dx и разделяем переменные: x·du/dx=-u. Обе части уравнения умножаем на dx и делим на xu≠0:

   

   

(при нахождении u С берем равным нулю).

3) В уравнение (I) подставляем [u’x+u]=0 и найденную функцию u=1/x. Имеем уравнение: v’·(1/x)·x=-x·(1/x²)·v². После упрощения: v’=-(1/x)·v². Это уравнение с разделяющимися переменными v и x. Заменяем v’=dv/dx и разделяем переменные: dv/dx=-(1/x)·v². Умножаем обе части уравнения на dx и делим на  v²≠0:

   

(взяли -С, чтобы, умножив обе части на -1, избавиться от минуса). Итак, умножаем на (-1):

   

(можно было бы взять не С, а ln│C│ и в этом случае было бы v=1/ln│Cx│).

4) Так как y=uv, подставляем найденные функции u и v:

   

Ответ:

   

2) 2y’+2y=xy².

Убедимся в том, что это — уравнение Бернулли. Поделив на 2 обе части, получаем y’+y=(x/2) y². Здесь p(x)=1, q(x)=x/2, n=2. Решаем уравнение методом Бернулли.

1) Замена y=uv, y’=u’v+v’u. Подставляем эти выражения в первоначальное условие: 2(u’v+v’u)+2uv=xu²v².

2) Раскрываем скобки: 2u’v+2v’u+2uv=xu²v². Теперь сгруппируем слагаемые, содержащие v: [2u’+2u]+2v’u=xu²v² (II).  Требуем, чтобы выражение в скобках равнялось нулю: 2u’+2u=0, отсюда u’+u=0. Это — уравнение с разделяющимися переменными относительно u и x. Решим его и найдем u. Подставляем u’=du/dx, откуда du/dx=-u. Умножив обе части уравнения на dx и поделив на u≠0, получаем: du/u=-dx. Интегрируем:

   

3) Подставляем во (II) [2u’+2u]=0 и

   

Теперь подставляем v’=dv/dx и разделяем переменные:

   

Интегрируем:

   

Левая часть равенства — табличный интеграл, интеграл в правой части находим по формуле интегрирования по частям:

   

   

Подставляем найденные v и du по формуле интегрирования по частям имеем:

   

А так как

   

Сделаем С=-С:

   

   

4) Так как y=uv, подставляем найденные функции u и v:

   

Ответ:

   

3) Проинтегрировать уравнение x²(x-1)y’-y²-x(x-2)y=0.

Разделим на x²(x-1)≠0 обе части уравнения и слагаемое с y² перенесем в правую часть:

   

Это — уравнение Бернулли,

   

1) Замена y=uv, y’=u’v+v’u. Как обычно, эти выражения подставляем в первоначальное условие: x²(x-1)(u’v+v’u)-u²v²-x(x-2)uv=0.

2) Отсюда x²(x-1)u’v+x²(x-1)v’u-x(x-2)uv=u²v². Группируем слагаемые, содержащие v (v² — не трогаем):

[x²(x-1)u’-x(x-2)u]v+x²(x-1)v’u=u²v²      (III).    Теперь требуем равенства нулю выражения в скобках:  x²(x-1)u’-x(x-2)u=0,  отсюда x²(x-1)u’=x(x-2)u. В уравнении разделяем переменные u и x, u’=du/dx: x²(x-1)du/dx=x(x-2)u. Обе части уравнения умножаем на dx и делим на x²(x-1)u≠0:

   

В левой части уравнения — табличный интеграл. Рациональную дробь в правой части надо разложить на простейшие дроби:

   

При x=1:  1-2=A·0+B·1, откуда B=-1.

При x=0:  0-2=A(0-1)+B·0, откуда A=2.

   

ln│u│=2ln│x│-ln│x-1│. По свойствам логарифмов: ln│u│=ln│x²/(x-1)│, откуда u=x²/(x-1).

3) В равенство (III) подставляем [x²(x-1)u’-x(x-2)u]=0 и u=x²/(x-1). Получаем: 0+x²(x-1)v’u=u²v²,

   

v’=dv/dx, подставляем:

   

вместо С возьмем — С, чтобы, умножив обе части на (-1), избавиться от минусов:

   

Теперь приведем выражения в правой части к общему знаменателю и найдем v:

   

4) Так как y=uv, подставляя найденные функции u и v, получаем:

   

Ответ:

   

Примеры для самопроверки:

   

   

Показать решение

1) Убедимся, что это — уравнение Бернулли. Поделив на x обе части, имеем:

   

1) Замена y=uv, откуда y’=u’v+v’u. Эти y и y’ подставляем в первоначальное условие:

   

2) Группируем слагаемые с v:

   

Теперь требуем, чтобы выражение в скобках равнялось нулю и находим из этого условия u:

   

Интегрируем обе части уравнения:

   

3) В уравнение (*) подставляем [xu’ + 2u]=0 и u=1/x²:

   

Интегрируем обе части получившегося уравнения:

   

   

Обозначим С=3С1, получаем

   

4) Так как y=uv, то

   

Ответ:

   

2) Поделим обе части данного уравнения на x: y’+y/x=(lnx/x)·y². Это — уравнение Бернулли. Здесь p(x)=1/x, q(x)=lnx/x, n=2.
1) Замена y=uv, откуда y’=u’v+v’u. Эти y и y’ подставляем в условие: x(u’v+v’u)+uv=u²v²lnx.

2) xu’v+xv’u+uv=u²v²lnx. Группируем слагаемые с v: [xu’+u]v+xv’u=u²v²lnx  (**).   Теперь требуем равенства нулю выражения, стоящего в скобках: xu’+u=0. Из этого уравнения ищем u: xdu/dx=-u,  du/u=-dx/x. Теперь интегрируем:

   

3) Подставляем в (**) [xu’+u]=0 и u=1/x (сначала упростим): xv’u=u²v²lnx, отсюда xv’=uv²lnx,  xv’=(1/x)v²lnx,

   

   

Интеграл в левой части — табличный. Интеграл, стоящий в правой части равенства, находим по формуле интегрирования по частям. u=lnx, du=(lnx)’dx=(1/x)dx, dv=(1/x²)dx,

   

Теперь подставляем u,v и du в формулу интегрирования по частям:

   

   

Итак,

   

умножаем обе части на (-1):

   

   

4) Так как y=uv, то

   

Ответ:

   

 

Линейные дифференциальные уравнения первого порядка.

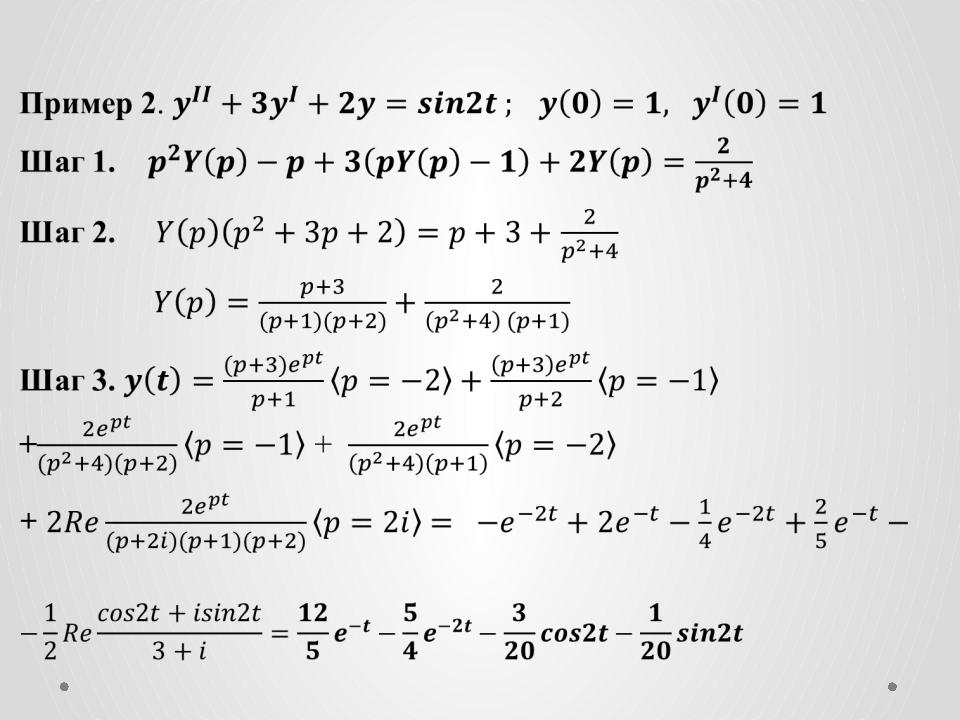2}$ те же рассуждения побуждают нас искать частное решение в виде  $y=\frac{a}{x}.$ Подставляя $y=\frac{a}{x}$ в уравнение, найдем постоянную $a.$     

 

 

 

 

Неявные дифференциальные уравнения

Определение и методы решения

Уравнение типа

\[F\влево({х,у,у’}\вправо) = 0,\]

, где \(F\) — непрерывная функция, называется неявным дифференциальным уравнением первого порядка.

Если это уравнение можно решить относительно \(y’,\), мы получим одно или несколько явных дифференциальных уравнений типа

\[y’ = f\left( {x,y} \right),\]

, которые можно решить методами, описанными в других разделах.

Далее предположим, что дифференциальное уравнение не может быть решено в явном виде, поэтому следует использовать другие методы. Основным приемом решения неявного дифференциального уравнения является метод введения параметра. Ниже мы покажем, как этот метод работает, чтобы найти общее решение для некоторых наиболее важных частных случаев неявных дифференциальных уравнений.

Здесь заметим, что общее решение может не охватывать все возможные решения дифференциального уравнения.Помимо общего решения, дифференциальное уравнение может иметь и так называемые сингулярные решения.

Более подробно мы рассмотрим это на странице Сингулярные решения дифференциальных уравнений.

Случай \(1.\) Неявное дифференциальное уравнение типа \(x = f\left( {y,y’} \right).\)

В этом случае переменная \(x\) выражается явно через \(y\) и производную \(y’).\) Введем параметр \(p = y’ = \frac{{dy} }{{dx}}.\) Продифференцируем уравнение \(x = f\left( {y,y’} \right)\) по \(y.\) Получается:

\[\frac{{dx}}{{dy}} = \frac{d}{{dy}}\left[ {f\left( {y,p} \right)} \right] = \frac{ {\partial f}}{{\partial y}} + \frac{{\partial f}}{{\partial p}}\frac{{dp}}{{dy}}.\]

Поскольку \(\frac{{dx}}{{dy}} = \frac{1}{p},\) последнее выражение можно записать следующим образом:

\[\frac{1}{p} = \frac{{\partial f}}{{\partial y}} + \frac{{\partial f}}{{\partial p}}\frac{{dp }}{{dy}}. \]

Получаем явное дифференциальное уравнение, общее решение которого дается функцией

\[г\влево( {у,р,С} \вправо) = 0,\]

, где \(C\) — константа.

Таким образом, общее решение исходного неявного дифференциального уравнения определяется в параметрической форме системой двух алгебраических уравнений:

\[\left\{ \begin{массив}{l} г\влево({у,р,С}\вправо) = 0\\ х = f\влево({у,р}\вправо) \конец{массив} \право..\]

Если параметр \(p\) можно исключить из системы, общее решение дается в явном виде \(x = f\left( {y,C} \right).\)

Случай \(2.\) Неявное дифференциальное уравнение типа \(y = f\left( {x,y’} \right).\)

Здесь мы рассматриваем аналогичный случай, когда переменная \(y\) является явной функцией \(x\) и \(y’). Введем параметр \(p = y’ = \frac{{dy} }{{dx}}\) и продифференцируем уравнение \(y = f\left( {x,y’} \right)\) по \(x.\) В результате имеем:

\[\frac{{dy}}{{dx}} = \frac{d}{{dx}}\left[ {f\left( {x,p} \right)} \right] = \frac{ {\partial f}}{{\partial x}} + \frac{{\partial f}}{{\partial p}}\frac{{dp}}{{dx}}\;\; \text{или}\;\;p = \frac{{\partial f}}{{\partial x}} + \frac{{\partial f}}{{\partial p}}\frac{{dp} {{dx}}. \]

Решая последнее дифференциальное уравнение, получаем алгебраическое уравнение \(g\left( {x,p,C} \right) = 0.\) Вместе с исходным уравнением они образуют следующую систему уравнений:

\[\left\{ \begin{массив}{l} г\влево({х,р,С}\вправо) = 0\\ у = f\влево({х,р}\вправо) \end{массив} \right.,\]

, которое является общим решением данного дифференциального уравнения в параметрической форме. В некоторых случаях, когда параметр \(p\) можно исключить из системы, общее решение можно записать в явном виде \(y = f\left( {x,C} \right).\)

Случай \(3.\) Неявное дифференциальное уравнение типа \(x = f\left( {y’} \right).\)

Здесь дифференциальное уравнение не содержит переменной \(y.\) Используя параметр \(p = y’ = \frac{{dy}}{{dx}},\), легко построить общее решение уравнения уравнение. Как \(dy = pdx\) и

\[dx = d\left[ {f\left( p \right)} \right] = \frac{{df}}{{dp}}dp,\]

, то выполняется следующее соотношение:

\[dy = p\frac{{df}}{{dp}}dp. \]

Интегрирование последнего уравнения дает общее решение в параметрической форме:

\[\left\{ \begin{массив}{l} y = \int {p\frac{{df}}{{dp}}dp} + C\\ х = f\влево( р \вправо) \конец{массив} \право..\]

Случай \(4.\) Неявное дифференциальное уравнение типа \(y = f\left( {y’} \right).\)

Уравнение такого типа не содержит переменной \(x\) и решается аналогично. Используя параметр \(p = y’ = \frac{{dy}}{{dx}},\), мы можем написать \(dx = \frac{{dy}}{p}.\) Тогда из уравнения следует, что

\[dx = \frac{{dy}}{p} = \frac{1}{p}\frac{{df}}{{dp}}dp.\]

Интегрирование последнего выражения дает общее решение исходного неявного уравнения в параметрической форме:

\[\left\{ \begin{массив}{l} х знак равно \ int {\ гидроразрыва {1} {p} \ гидроразрыва {{df}} {{dp}} dp} \\ y = f\влево( p \вправо) \конец{массив} \право..\]

См. решенные проблемы на стр. 2.

Введение в дифференциальные уравнения, часть 5

Введение в дифференциальные уравнения, часть 5

Введение в дифференциальные уравнения

Часть 5.

Символьные решения разделимых дифференциальных уравнений 90 087 В части 4 мы показали один из способов использования числовой схемы, метода Эйлера, для аппроксимации решений дифференциального уравнения.В предыдущих частях мы описали символьные решения конкретных дифференциальных уравнений. Оба представления — числовое и символьное — важны, и оба могут быть исследованы на различных уровнях сложности. В этом разделе мы опишем простой метод получения символических описаний для общего класса дифференциальных уравнений первого порядка.

К простейшим дифференциальным уравнениям относятся уравнения вида

dY/dt = f(t) ,

т. е. дифференциальные уравнения первого порядка, в которых правая часть не имеет явной зависимости от зависимой переменной Y .Для такого уравнения получить общее описание решений то же самое, что найти все первообразные f , т. е. то же самое, что вычислить неопределенный интеграл. Так, например, решения

dY/dt = cos(t)

составляют семейство функций Y вида

где C может быть любой константой. В более общем смысле поиск символьных описаний решений дифференциальных уравнений первого порядка сводится к вычислению одного или нескольких интегралов.

Мы опишем здесь метод вычисления символьных описаний решений большого класса дифференциальных уравнений, которые можно записать в виде

. Такие дифференциальные уравнения называются сепарабельными . Например, каждое из следующих дифференциальных уравнений разделимо:

dY/dt = cos(t)

dY/dt = Y ²

dY/dt = Y(t + 1)

С другой стороны, дифференциальное уравнение не является разделимым дифференциальным уравнением.

&nbsp

Первый пример

Прежде чем мы опишем процедуру решения в целом, давайте рассмотрим простой случай,

dY/dt = kY.

Вы, наверное, знаете, что это представляет собой экспоненциальный рост или спад в зависимости от того, является ли k положительным или отрицательным, и что семейство решений равно

. где C может быть любой реальной константой. Однако давайте забудем, что мы это знаем, и заново откроем это описание.

При обсуждении мы будем использовать тот факт, что начальные задачи для этого дифференциального уравнения имеют единственное решение. В частности, поскольку постоянная функция ноль является решением, любое другое решение никогда не бывает нулевым. Действительно, предположим, что Y является решением дифференциального уравнения, а Y(t ₀ ) равно нулю. Тогда Y является решением начальной задачи

dY/dt = ky и Y(t ₀ ) = 0,

Но функция постоянного нуля также является решением задачи с начальными значениями

dY/dt = kY и Y(t ₀ ) = 0.

Поскольку существует только одно решение задачи о начальных значениях, Y должно быть постоянной нулевой функцией.

Таким образом, нам нужно только описать решения, которые никогда не равны нулю. Предположим, что Y является таким ненулевым решением дифференциального уравнения dY/dt = kY . Затем

на все т . Думайте о левой части этого уравнения как о результате дифференцирования по цепному правилу

Мы также можем записать правую часть как производную

. Используя эти идентификаторы, Y должны удовлетворять

на все т .Так как две функции имеют одну и ту же производную для всех t ровно тогда, когда они отличаются на константу, мы должны иметь

для некоторых постоянных c и всех t . Теперь возводя в степень обе части этого уравнения, мы получаем

Поскольку Y(t) либо всегда положительно, либо всегда отрицательно, то либо Y(t) = e ^c e ^kt для всех t , либо Y(t) = -e ^c e ^кт для всех т .Если мы допустим, что C будет либо e ^c , либо -e ^c , то Y должно иметь вид

. Позволяя C быть любой отличной от нуля константой, мы опишем все ненулевые решения дифференциального уравнения. Если мы позволим C быть равным нулю, мы также получим постоянное нулевое решение в нашем описании.

Мнемоническое устройство

Теперь мы повторим это вычисление в мнемонической форме, которая облегчит запоминание шагов.Сначала перепишем дифференциальное уравнение в виде

Обратите внимание, что мы «разделили переменные». Теперь формально интегрируйте обе стороны. (Это шаг Цепного правила в исходном расчете.) Получаем

Выполняя указанные интегрирования, имеем

ln(|Y|) + константа = kt + константа

Комбинируя две константы, мы имеем

ln(|Y|) = kt + константа

В остальном расчет прежний.

Общий метод

В общем случае, если дифференциальное уравнение сепарабельно, мы можем разделить переменные

Тогда, если мы сможем вычислить интегралы

мы сводим задачу от задачи исчисления к задаче алгебры — решению для Y(t) .

Второй пример

Давайте попробуем это с дифференциальным уравнением dY/dt = 5Y ² . Конечно, одним из решений этого дифференциального уравнения является постоянная нулевая функция.

1. Объясните, почему решения уравнения dY/dt = 5Y ² либо тождественно равны нулю, либо никогда не равны нулю.
2. Пусть Y будет ненулевым решением уравнения dY/dt = 5Y ² . Покажите, что для некоторой константы c , Y должно удовлетворять

   на все т .

3. Пусть Y будет решением начальной задачи dY/dt = 5Y ² и Y(0) = 1

   покажите, что

   Y(t) = 1/(1 — 5t) .

Обратите внимание, что Y(t) приближается к бесконечности, поскольку t приближается к 1/5 слева. Ниже показано поле наклона для этого дифференциального уравнения с отображением этого конкретного решения.

Третий пример

В качестве последнего примера этого метода определения символьных решений мы рассмотрим дифференциальное уравнение

dY/dt = 2Y(2 — Y) .

Обратите внимание, что это наше дифференциальное уравнение из части 1, распространяющее слухи, где k и M равны 2 .

4. Есть два постоянных решения этого уравнения. Кто они такие?
5. Покажите, что если Y является решением этого дифференциального уравнения, то либо 2Y(2 — Y) равно нулю для всех значений t, , либо оно никогда не равно нулю.
6. Предположим, что Y является решением дифференциального уравнения таким, что 2Y(2 — Y) всегда положительно. Разделите переменные, чтобы получить

   Интегрируйте обе части, чтобы показать, что Y должны удовлетворять

7. Используйте свою систему компьютерной алгебры, чтобы найти общий вид решений дифференциального уравнения dY/dt = 2Y(2 — Y),

   и покажите, что описание на шаге 6 согласуется с описанием системы компьютерной алгебры.

8. Теперь предположим, что Y является решением таким, что Y(t) всегда строго больше, чем 2 . Повторите свой символический расчет. Будьте осторожны, что вы берете только журналы положительных величин. Можно ли по-прежнему представить решение в форме, описанной в шаге 6? Если да, то какой диапазон C с соответствует этим решениям?
9. Теперь предположим, что Y — это решение, при котором Y(t) всегда строго отрицательно.Повторите свой символический расчет. Опять же, будьте осторожны, что вы берете журналы только положительных величин. Можно ли по-прежнему представить решение в форме, описанной в шаге 6? Если да, то какой диапазон C с соответствует этим решениям?

---

Нахождение частного решения дифференциального уравнения, проходящего через заданную точку общего решения | Расчет

Шаги к нахождению частного решения дифференциального уравнения, проходящего через заданную точку общего решения

Шаг 1 : Подставьте заданную точку {eq}(a,b) {/eq} в выражение {eq}y=f(x)+C {/eq} для общего решения дифференциального уравнения. То есть заменить {eq}x {/экв} с {экв}а {/экв} и {экв}у {/eq} с {eq}b. {/экв}

Шаг 2 : Решите полученное уравнение для константы {eq}C. {/экв}

Шаг 3 : Подставьте это значение {eq}C {/eq} в общее уравнение. Это частное решение дифференциального уравнения.

Словарь для нахождения частного решения дифференциального уравнения, проходящего через заданную точку общего решения

Дифференциальное уравнение : Дифференциальное уравнение — это уравнение, в которое входят производные функции.{2x} {/eq} является решением дифференциального уравнения {eq}y’=2y {/экв}.

Общее решение дифференциального уравнения : Общее решение дифференциального уравнения — это решение, в котором используется неизвестная константа. Каждое другое значение константы — это другое решение.

Частное решение дифференциального уравнения : Частное решение дифференциального уравнения — это такое решение, которое не включает неизвестную константу. { п } я _ {j} = м , $$

$F$ отличен от нуля; натуральное число $ m $ называется порядком уравнения (1).

Регулярным решением является функция $ u $ определено в области $D$ где уравнение (1) задано, непрерывное вместе со своими частными производными, входящими в уравнение, и такое, что (1) выполняется тождественно. В теории уравнений в частных производных важны не только регулярные решения, но и решения, перестающие быть регулярными в окрестности изолированных точек или в окрестности многообразий специального типа; в частности, важны элементарные (фундаментальные) решения.{2} , $$

где коэффициенты $\alpha _{i}$, $ i = 1, \dots, n $, принять значения $1$, $ — 1 $, $ 0 $, а число отрицательных коэффициентов (показатель инерции) и число нулевых коэффициентов (дефект формы) являются аффинными инвариантами. Если все $ \alpha _ {i} = 1 $ или если все $ \alpha _ {i} = — 1 $, т.е. если форма $Q$ положительно или отрицательно определено, соответственно уравнение (3) называется эллиптическим в точке $x\inD$. {2} $$

для всех $x\in D$.{в} } . $$

Если для данного значения $ x \in D $, можно найти аффинное преобразование $ \lambda _ {i} = \lambda _ {i} ( \mu _ {i}, \dots, \mu _ {n} ) $, $ i = 1, \dots, n $, в результате чего форма, полученная из (5), содержит только $l$, $ 0 < l < n $, переменные $\mu$, тогда говорят, что уравнение (4) становится параболически вырожденным при $ x $. Если параболическое вырождение отсутствует и коническое многообразие

$$ \тег{6} k (\lambda _ {1}, \dots, \lambda _ {n}) = 0 $$

не имеет никаких реальных точек, кроме $\lambda _ {1} = \dots = \lambda _ {n} = 0 $, уравнение (4) называется эллиптическим в точке $x$.Уравнение (4) называется гиперболическим при $ x $ если в пространстве переменных $ \lambda _ {1}, \dots, \lambda _ {n} $ существует прямая $ \delta $ такое, что если принять его за координатную линию в новых переменных $\mu _ {1}, \dots, \mu _ {n} $ полученный аффинным преобразованием $\lambda_{1}, \dots, \lambda_{n}$, уравнение (6) будет иметь относительно меняющейся вдоль $\delta$ координаты ровно $м$ действительные корни (простые или кратные) при любом выборе остальных координат $\mu$. {i _ {n} } } , $$

векторное уравнение (1) называется системой уравнений в частных производных относительно неизвестных функций $ u _ {1}, \dots, u _ {M} $ или для неизвестного вектора $ u = ( u _ {1}, \dots, u _ {M} ) $.{ п } я _ {к} = м, $$

— квадратная матрица, форма порядка $ Nm $ относительно вещественных скалярных параметров $\lambda_{1}, \dots, \lambda_{n}$, известный как характеристический определитель системы (1). Классификация по типу системы (1) осуществляется по характеру (7) точно так же, как и для одного уравнения порядка $m$. Величины, появляющиеся в левой части уравнения (1), могут быть комплексными числами и функциями. Сложное дифференциальное уравнение в частных производных заменяется системой вещественных уравнений очевидным образом.

Уравнение в частных производных может вообще не иметь решения. Однако уравнения, используемые в практических приложениях, обычно имеют целые семейства решений. При выводе таких уравнений из общих законов явлений природы естественно возникают дополнительные условия на искомые решения. Нахождение регулярных решений, удовлетворяющих этим условиям, является основной задачей теории уравнений в частных производных. Характер таких условий во многом зависит от типа рассматриваемого уравнения.{ п } я _ {j} = л , \ \ л < м, $$

понимаются как соответствующие производные от $ u $ полученные как пределы изнутри $D$ в сторону $S$.

В такой общей постановке задача (8) еще далека от полного решения. Частные случаи этой задачи — т.е. более подробно изучены так называемые краевые задачи первого и второго порядка (см. задачу Дирихле и задачу Неймана) для случая линейных равномерно-эллиптических уравнений второго порядка.{п} $ несут дополнительные данные, и область определения решения существенно зависит от этих поверхностей. К ним относятся, например, задача Коши с начальными данными и характеристическая задача Коши (см. Характеристическая задача Коши). Краевые задачи для уравнений смешанного типа ставятся особым образом. В теории уравнений в частных производных большой интерес вызвал обширный класс смешанных задач. См. Смешанные и краевые задачи для гиперболических уравнений и систем; Смешанные и краевые задачи для параболических уравнений и систем.

Задача считается корректной в классическом смысле, если она имеет единственное решение, непрерывно зависящее от данных задачи. До недавнего времени задачи, не удовлетворяющие этому требованию, считались бессмысленными. С 1940-х годов широкий круг математических задач в физике, механике и технике сделал необходимым не только расширение понятия корректности задач, связанных с уравнениями в частных производных, но и расширение смысла понятия решения.Были введены так называемые обобщенные решения. Помимо вопроса о существовании и единственности точных решений задач, связанных с уравнениями в частных производных, важное значение в приложениях приобрели понятие аппроксимации решений и методы практических вычислений.

Исторически метод разделения переменных, или метод Фурье, и родственный ему метод интегральных преобразований (см. интеграл Фурье) были одними из первых методов вычисления решений классов уравнений в частных производных. Применение этого метода дало начало спектральной теории дифференциальных операторов.

Метод параметрикса, послуживший основой для метода потенциалов (ср. Потенциалы, метод), был разработан совсем недавно. Аппарат интегральных уравнений применяется в этом методе для исследования краевых задач эллиптических уравнений. К крупному развитию метода параметриксов можно отнести и методы теории функций комплексного переменного, успешно применяемые при изучении эллиптических уравнений с двумя независимыми переменными.См. Дифференциальные уравнения, методы с частными производными и комплексными переменными.

Если рассматриваемое уравнение в частных производных является уравнением Эйлера для задачи вариационного исчисления в большем количестве измерений, часто используется вариационный метод. Такой метод очень удобен, если уравнение Эйлера эллиптического типа. См. также Дифференциальное уравнение, парциальные, вариационные методы.

С 1930-х годов уравнения в частных производных широко исследуются методами функционального анализа, часто методом Шаудера и его дальнейшим развитием — методом априорных оценок. Использование этих методов позволяет установить существование слабых и сильных решений как для линейных, так и для классов нелинейных уравнений в частных производных. См. Дифференциальное уравнение, парциальные, функциональные методы; Сильное решение; Слабое решение.

Наиболее популярными методами вычисления приближенных решений уравнений в частных производных являются методы конечно-разностного исчисления. См. также Гиперболическое уравнение в частных производных, численные методы; Параболическое уравнение в частных производных, численные методы; Эллиптическое уравнение в частных производных, численные методы.

Ссылки

Бицадзе, «Уравнения математической физики», МИР (1980) (Перевод с русского) MR0581247 Zbl 0499.35002

[1]	Л. Берс, Ф. Джон, М. Шехтер, «Уравнения в частных производных», Interscience (1964) MR0163043 Zbl 0126.00207
A.V.V.V [2]
[3]	В. С. Владимиров, «Уравнения математической физики», МИР (1984) (пер. с русского) MR0764399 Zbl 0954.35001 zbl 0652.35002 ZBL 0695.35001 ZBL 0699.35.35001 ZBL 0699.35005 ZBL 0607.35001 ZBL 0506.35001 ZBL 0223.35002 ZBL 0231.35002 ZBL 0207.09101
[4]	R. Courant, D. Hilbert, «Методы математической физики. Частичные дифференциальные уравнения», 2 , (1965) (перевод с немецкого) MR0195654
[5]	AN Тихонов, А.А. Самарский, «Уравнения математической физики», Пергамон (1963) (Перевод с русского) MR0165209 Zbl 0111.29008

В последние годы произошла революция в теории уравнений в частных производных. Были введены многие важные методы, такие как решение с помощью псевдодифференциальных или интегральных операторов Фурье, ср. [а8].

Ссылки

[A1]	p.r. Гарабедиан, «Частичные дифференциальные уравнения», Wiley (1967) MR1657375 MR0943117 MR0162045 MR0176086 MR0129167 MR0120441 MR0060698 MR0054819 MR0046440 ZBL 0913. 35001 Збл 0124.30501 Збл 0133.04402 Збл 0096.06503 Збл 0058.08902 Збл 0050.10002
[а2]	А.В. Бицадзе, «Уравнения смешанного типа», Пергамон (1964) (Перевод с русского)
[a3]	А.В. Бицадзе, «Краевые задачи для эллиптических уравнений второго порядка», Северная Голландия, 1968. ) MR0304828 Збл 0209.40001
[а5]	В.П. Михайлов, «Уравнения в частных производных», МИР (1978) (перевод с русского) 1964) MR0181836 Zbl 0144.34903
[a7]	ИГ Петровский, «Обыкновенные дифференциальные уравнения», Prentice-Hall (1966) (пер. с рус.) MR0193298
В. Хёрмандер, «Анализ линейных дифференциальных операторов», 1-4 , Спрингер (1983-1985) MR2512677 MR2304165 MR2108588 MR1996773 MR1481433 MR1313500 MR1065993 MR1065136 MR0961959 MR0925821 MR0881605 MR0862624 MR1540773 MR0781537 MR0781536 MR0717035 MR0705278 Zbl +1178,35003 Zbl +1115,35005 Zbl +1062,35004 Zbl 1028. 35001 ZBL 0712.35001 ZBL 0687.35002 ZBL 0619.35002 ZBL 0619.35002 ZBL 0619.35001 ZBL 0612.35001 ZBL 0601.35001 ZBL 0521.35002 ZBL 0521.35001
D.	D.Гилбарг, Н.С. Trudinger, «Эллиптические уравнения в частных производных второго порядка», Springer (1977) MR0473443 Zbl 0361.35003

Как цитировать эту запись:
Дифференциальное уравнение в частных производных. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Differential_equation,_partial&oldid=51986

Дифференциальные уравнения. Определения. Орден, степень. Общие, частные и сингулярные решения.

Дифференциальные уравнения.Определения. Орден, степень. Общее, частное и единичное решения.

---

SolitaryRoad.com

Владелец сайта: Джеймс Миллер
 

---

[ Домой ] [ Вверх ] [ Информация ] [ Почта ]

---

Дифференциальные уравнения. Определения. Орден, степень. Общие, частные и сингулярные решения.

Определения

Защ. Дифференциальное уравнение. Дифференциальное уравнение – это уравнение, содержащее производные зависимая переменная по отношению к одной или нескольким или независимым переменным.Ниже приведены типичные примеры:

Когда используется только первая производная, уравнение часто записывается в терминах дифференциалы. Например 2) выше может быть написано

Защ. Обыкновенное дифференциальное уравнение. Дифференциальное уравнение, содержащее один независимая переменная. Производные, входящие в уравнение, являются обычными производными.

Защ.Уравнение в частных производных. Дифференциальное уравнение, содержащее два или более независимые переменные. Производные, встречающиеся в уравнении, являются частными производными.

Защ. Порядок дифференциального уравнения. Порядок старшей производной происходящее в уравнении. Уравнения 2) и 4) выше относятся к первому порядку, а уравнения 1) и 3) второго порядка.

Защ. Степень дифференциального уравнения. В общем случае степень высшего порядка производная, входящая в уравнение.Однако не каждое дифференциальное уравнение имеет степень. Если производные встречаются внутри радикалов или дробей, уравнение может не иметь степени. Если уравнение можно рационализировать и очистить от дробей относительно всех присутствующих производных, тогда его степень — это степень старшей производной, входящей в уравнение.

Пример. Уравнения 1), 2) и 4) выше имеют первую степень, а уравнение 3) — вторую. степень. Дифференциальное уравнение (y») ^2/3 = 2 + 3y’ может быть рационализировано путем возведения обеих сторон в куб получить (y») ² = (2 + 3y’ ) ³ .Таким образом, он второй степени.

Защ. Линейное дифференциальное уравнение. Линейное дифференциальное уравнение – это уравнение форма

, где a _i (x) являются функциями только от x. Это уравнение, в котором каждый член имеет первую степень зависимая переменная и ее производные.

Решения дифференциальных уравнений. Решением дифференциального уравнения является любое отношение без производных между участвующими переменными, которое сводит дифференциальное уравнение к личности.Решение может принять форму выражения зависимой переменной явно как функция независимой переменной (или переменных), как в y = f (x), или неявно как в отношении типа f(x, y) = 0,

Защ. Существенные константы. Набор констант называется существенным, если их нельзя заменить меньшее количество констант.

Решение содержит n существенных произвольных констант. Пример очень простого дифференциальное уравнение имеет вид

Решение такого уравнения включает n повторных интегрирований, где каждое интегрирование дает произвольная постоянная.Таким образом, решение содержит n существенных произвольных констант. Например, в уравнение

имеем после двойного интегрирования

            y = x ³ + C ₁ x + C ₂

Этот результат называется общим решением дифференциального уравнения. Любое решение, которое может быть полученное из него путем придания C ₁ и C ₂ частных значений, называется частным решением.

Общее решение дифференциального уравнения также называется примитивным.

Теорема. Общее решение или первообразная дифференциального уравнения порядка n всегда содержит ровно n существенных произвольных констант.

Сингулярные решения. В дополнение к общему решению дифференциальное уравнение также может иметь единственное решение. Сингулярное решение — это решение, которое невозможно получить, присваивая определенные значения произвольным константам общего решения. Это уравнение оболочки семейства кривых, представленных общим решением.Эта огибающая удовлетворяет дифференциальному уравнению потому что в каждой из его точек его наклон и координаты точки такие же, как у некоторого члена семейства кривых, представляющих общее решение.

 

Джеймс/Джеймс. Математический словарь

 

Наличие решений. Не каждое дифференциальное уравнение имеет решение. Например, там не может быть никакой вещественной функцией, удовлетворяющей дифференциальному уравнению

            (y’) ² + 1 = 0

Почему? Потому что для любой действительной функции левая часть уравнения будет больше или равен единице и, следовательно, не может быть равен нулю.На самом деле, лишь относительно небольшое число дифференциальных уравнений имеют решения. Из тех, что есть, лишь немногие могут быть решены в закрытой аналитической форме. Только некоторые могут быть решается в терминах элементарных функций (т. е. рациональных алгебраических, тригонометрических, экспоненциальных и логарифмические функции, знакомые по элементарному исчислению). Некоторые другие могут быть решены в термины высших трансцендентных функций. Для остальных необходимо использовать численное приближение такие методы, как представление степенных рядов.

Большинство дифференциальных уравнений возникают из задач физики, техники и естественных наук. Эти уравнения часто имеют определенные условия, называемые граничными или начальными условиями, связанные с их, что они должны удовлетворить. Тогда мы должны задаться вопросом не только о том, существует ли решение уравнения, но и о том, также, если он существует, он также будет удовлетворять указанным начальным условиям. Например, предположим, что мы хотите решить дифференциальное уравнение

 

            xy’ — 2y = 0

при начальном условии x = 0, y = 1. Общее решение уравнения

 

5)        y = Ax ²

, но проверка 5) показывает, что не существует значения A, удовлетворяющего начальным условиям.

Методы решения. Не существует общей процедуры решения дифференциального уравнения. Только несколько простых уравнений можно решить путем прямого интегрирования. Большинство уравнений решается методы, разработанные для конкретного типа уравнения. Каждый из различных типов имеет свои собственные метод решения. Как правило, чтобы решить уравнение, нужно уметь распознавать тип и вспомнить правильный метод ее решения.

Ссылки

1. Росс Р. Миддлмисс. Дифференциальное и интегральное исчисление.Глава. XXIX

2. Джеймс/Джеймс. Математический словарь.

3. Мюррей Р. Шпигель. Прикладные дифференциальные уравнения.

4. Джеймс Б. Скарборо. Дифференциальные уравнения и приложения.

5. Фрэнк Эйрес. Дифференциальные уравнения (Шаум).

6. Эшбах. Справочник по основам инженерии.

7. Эрл Рейнвилл. Элементарные дифференциальные уравнения.

Еще от SolitaryRoad.com:

Путь Истины и Жизни

Божье послание миру

Иисус Христос и Его Учение

Мудрые слова

Путь просветления, мудрости и понимания

Путь истинного христианства

Америка, коррумпированная, развратная, бессовестная страна

О честности и ее отсутствии

Критерием христианства человека является то, что он есть

Кто попадет в рай?

Высшее лицо

О вере и делах

Девяносто пять процентов проблем, с которыми большинство людей пришли от личной глупости

Либерализм, социализм и современное государство всеобщего благосостояния

Желание причинить вред, мотив поведения

Учение это:

О современном интеллектуализме

О гомосексуализме

О самодостаточной загородной жизни, приусадебном хозяйстве

Принципы жизни

Тематические пословицы, поучения, Цитаты. Общие поговорки. Альманах бедного Ричарда.

Америка сбилась с пути

Действительно большие грехи

Теория формирования характера

Моральное извращение

Ты то, что ты ешь

Люди как радиотюнеры — они выбирают и слушать одну длину волны и игнорировать остальные

Причина черт характера — по Аристотелю

Эти вещи идут вместе

Телевидение

Мы то, что мы едим — живем по дисциплине диеты

Избегание проблем и неприятностей в жизни

Роль привычки в формировании характера.

Истинный христианин

Что такое истинное христианство?

Личные качества истинного христианина

Что определяет характер человека?

Любовь к Богу и любовь к добродетели тесно связаны

Прогулка по одинокой дороге

Интеллектуальное неравенство между людьми и властью в хороших привычках

Инструменты сатаны.Тактика и Уловки, используемые Дьяволом.

О реакции на обиды

Настоящая христианская вера

Естественный путь – неестественный путь

Мудрость, Разум и Добродетель тесно связаны

Знание одно, мудрость другое

Мои взгляды на христианство в Америке

Самое главное в жизни это понимание

Оценка людей

Мы все примеры — хорошо это или плохо

Телевидение — духовный яд

Перводвигатель, который решает, «Кто мы есть»

Откуда берутся наши взгляды, взгляды и ценности?

Грех — дело серьезное.