Решение уравнений с модулем (часть 1)

Уравнения с модулем с решениями (часть 1)

перейти к содержанию

Свойства модуля (справочник)

1. Найдите корни уравнения

Решение

Так как и для любого , то . Поэтому и уравнение принимает вид , откуда . Условию удовлетворяет только число .

Ответ:

2. Найдите сумму корней уравнения

Решение

www.itmathrepetitor.ru Раскроем модуль. Для этого рассмотрим первый случай: . Тогда . Корнями этого уравнения являются числа и . После проверки остается только .

Второй случай: . Тогда , откуда . Условию удовлетворяет только .

Сумма корней равна

Ответ:

3. Найдите произведение корней уравнения .

Решение

Пусть , тогда , откуда или , то есть или . Первое уравнение имеет корни , второе уравнение корней не имеет, так как . Значит, произведение корней исходного уравнения равно .

Ответ:

4.

Найдите сумму корней уравнения

Решение

www.itmathrepetitor.ru , что равносильно при условии . Корнями первого уравнения совокупности являются числа и , корнями второго — числа и . Неравенству удовлетворяют только и . Значит, сумма корней исходного уравнения равна .

Ответ: 

5. Найдите разность между наибольшим и наименьшим корнями уравнения

Решение

. Пусть , тогда и , то есть или . Первое уравнение корней не имеет, так как . Из второго следует, что . Сумма этих корней равна .

Ответ: 

6. Найдите сумму корней уравнения

Решение

Уравнение равносильно совокупности , откуда  Избавимся от знаменателя: .

Ответ: 

7. Найдите сумму корней уравнения

Решение

www.itmathrepetitor.ru Уравнение равносильно совокупности , откуда . Сумма корней равна .

Ответ: 

8. Решите уравнение

Решение

Нули модулей равны и . Рассмотрим три случая: . Для каждого из них модули раскрываются с определенным знаком.

Первый случай.

, то есть — любое число. С учетом ограничения случая, .

Второй случай. 

. С учетом ограничения случая, корней нет.

Третий случай. 

, то есть корней нет.

Ответ: 

9. Найдите сумму корней уравнения

Решение

Нули модулей равны и . Рассмотрим три случая: . Для каждого из них модули раскрываются с определенным знаком.

Первый случай.

. Найденный корень удовлетворяет ограничению случая.

Второй случай. 

. С учетом ограничения случая, корней нет.

Третий случай. 

. Найденный корень удовлетворяет ограничению случая.

Сумма корней исходного уравнения равна .

Ответ: 

10. Найдите произведение корней уравнения

Решение

Уравнение равносильно совокупности , откуда . Произведение корней равно .

Ответ: 

смотрите раздел «Математика»

 

Урок 4: Уравнения с модулем

План урока:

Модуль числа

Решение уравнений с модулем

Уравнения с параметрами

 

Модуль числа

Напомним, что такое модуль числа.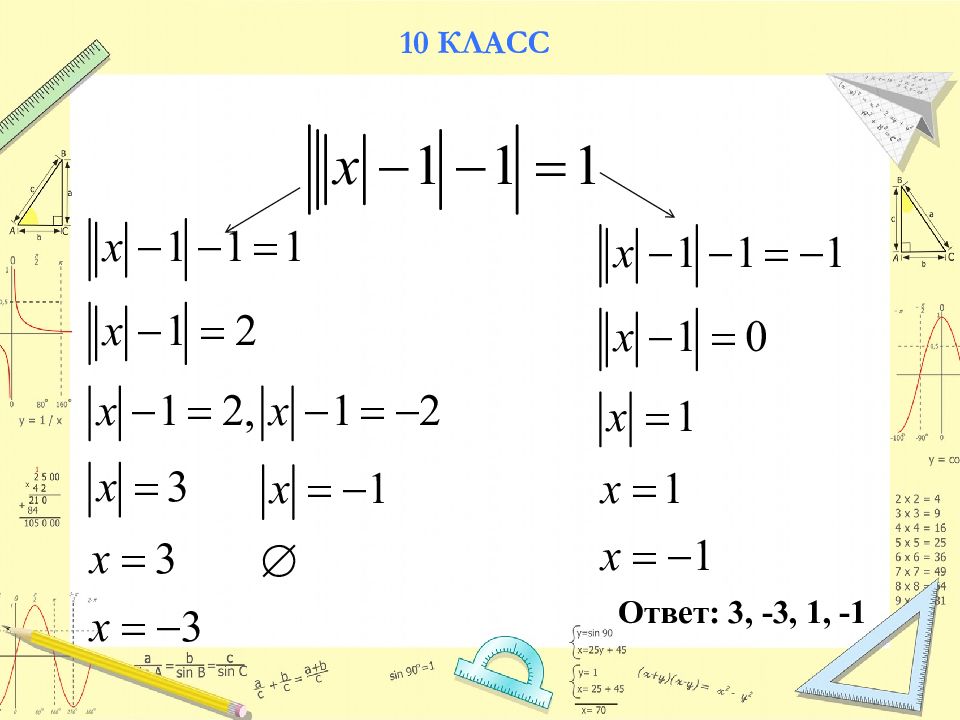 Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:

|9| = |– 9| = 9

|674| = |– 674| = 674

|2,536| = |– 2,536| = 2,536

Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:

Именно такое определение обычно и применяется в математике.

Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:

Также модуль возникает при извлечении квадратного корня из четной степени числа:

В частности, если n = 1, получим формулу:

Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:

Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:

В результате получилась «галочка».

Пример. Постройте график ф-ции у = |х² – 4х + 3|

Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х² – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:

Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х² – 4х + 3|, надо перевернуть эту часть графика:

Решение уравнений с модулем

Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число.

То есть уравнение имеет вид

|у(х)| = b

где b – какое-то число, а у(х) – произвольная ф-ция.

Если b< 0, то ур-ние корней не имеет, ведь модуль не может быть отрицательным.

 

Пример. Найдите корни ур-ния

|125x¹⁰ + 97x⁴– 12,56х³ + 52х² + 1001х – 1234| = – 15

Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.

Ответ: корни отсутствуют.

Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.

 

Пример. Решите ур-ние

|13х – 52| = 0

Решение.

Ясно, что подмодульное выр-ние равно нулю:

13х – 52 = 0

13х = 52

х = 4

Ответ: 4.

Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число.

Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:

|b| = b

|– b| = b

То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.

 

Пример. Решите ур-ние

|х| = 10

Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.

Ответ: 10; (– 10).

 

Пример. Решите ур-ние

|10х + 5| = 7

Решение. Исходное ур-ние разбивается на два других ур-ния:

10х + 5 = 7 или 10х + 5 = – 7

10х = 2 или 10х = – 12

х = 0,2 или х = – 1,2

Ответ: 0,2; (– 1,2).

 

Пример. Найдите корни ур-ния

|x²– 2х – 4| = 4

Решение. Снова заменим исходное равенство на два других:

x²– 2х – 4 = 4 или x²

– 2х – 4 = – 4

Имеем два квадратных ур-ния. Решим каждое из них:

x²– 2х – 4 = 4

x²– 2х – 8 = 0

D = b²– 4ас = (– 2)² – 4•1•(– 8) = 4 + 32 = 36

х₁ = (2 – 6)/2 = – 2

х₂ = (2 + 6)/2 = 4

Нашли корни (– 2) и 4. Решаем второе ур-ние:

x²– 2х – 4 = – 4

x²– 2х = 0

х(х – 2) = 0

х = 0 или х – 2 = 0

х = 0 или х = 2

Получили ещё два корня: 0 и 2.

Ответ: – 2, 4, 0, 2

Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:

|у(х)| = |g(x)|

Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.

 

Пример. Решите ур-ние

|x² + 2x– 1| = |х + 1|

Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:

x² + 2x– 1 = х + 1 или x² + 2x– 1 = – (х + 1)

х² + х – 2 = 0 или х² + 3х = 0

Решим 1-ое ур-ние:

х² + х – 2 = 0

D = b²– 4ас = 1² – 4•1•(– 2) = 1 + 8 = 9

х₁ = (1 – 3)/2 = – 1

х₂ = (1 + 3)/2 = 2

Теперь переходим ко 2-омуур-нию:

х² + 3х = 0

х(х + 3) = 0

х = 0 или х + 3 = 0

х = 0 или х = – 3

Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.

Ответ:(– 1), (– 2), 2, 0.

Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.

Пример. Найдите решение уравнения, содержащего модуль:

|х² + 3,5х – 20| = 4,5х

Решение. Рассмотрим два отдельных равенства:

х² + 3,5х – 20 = 4,5х илих² + 3,5х – 20 = – 4,5х

х² – х – 20 = 0 или х² + 8х – 20 = 0

Решим каждое из полученных квадратных ур-ний.

х² – х – 20 = 0

D = b²– 4ас = 1² – 4•1•(– 20) = 1 + 80 = 81

х₁ = (1 – 9)/2 = – 4

х₂ = (1 + 9)/2 = 5

х² + 8х – 20 = 0

D = b²– 4ас = 8² – 4•1•(– 20) = 64 + 80 = 144

х₃ = (– 8 – 12)/2 = – 10

х₄ = (– 8 + 12)/2 = 2

Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:

4,5х ≥ 0

Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.

Ответ: 2 и 5

Мы рассмотрели три случая, когда ур-ние имеет вид:

1. у(х) = b (b– это некоторая константа)
2. |у(х)| = |g(x)|
3. |у(х)| = g(x)

Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.

 

Пример. Найдите корни ур-ния

|x + 1| + |x– 4| = 6

Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:

Если отметить обе точки на прямой, то они образуют на ней 3 интервала:

Исследуем ур-ние на каждом из полученных промежутков.

Так как при х <– 1 оба подмодульные выр-ния отрицательны, то можно записать, что

|x + 1| = – (х + 1) = – х – 1

|x– 4| = – (х – 4) = – х + 4

Тогда ур-ние примет вид

|x + 1| + |x– 4| = 6

– х – 1 – х + 4 = 6

–2х = 3

х = – 1,5

Это значение удовлетворяет условию х <– 1, поэтому корень верный.

Далее изучим случай, когда х∊[– 1; 4). Здесь отрицательно только выражение x– 4, поэтому модули заменяются так:

|x + 1| = х + 1

|x– 4| = – (х – 4) = – х + 4

Ур-ние примет вид:

|x + 1| + |x– 4| = 6

x + 1 – x+ 4 = 6

5 = 6

Получили неверное тождество. Получается, что на промежутке [– 1; 4) корней нет.

При х ≥4 выр-ния х – 4 и х + 1 положительны, поэтому

|x + 1| = х + 1

|x– 4| = х – 4

Исходное ур-ние будет выглядеть так

|x + 1| + |x– 4| = 6

х + 1 + х – 4 = 6

2х = 9

х = 4,5

Найденный корень удовлетворяет условию х ≥4, поэтому он также должен быть включен в ответ.

 

Уравнения с параметрами

Изучим ур-ния:

5х = 10

5х = 15

5х = 20

Для решения каждого из них надо число справа поделить на 5 (множитель перед х). В итоге получаем значения х, равные 2, 3 и 4.

Теперь обозначим число в правой части буквой, например, как v. Тогда все эти ур-ния будут выглядеть одинаково:

5х = v

Решением таких ур-ний будет дробь v/5.

Надо понимать разный смысл, который мы вкладываем при этом в буквы х и v. Через х мы обозначили переменную, то есть ту величину, значение которой необходимо найти. Под буквой v подразумевалась заранее известная величина, то есть константа, которая известна заранее в каждом конкретном ур-нии. Такую величину называют параметром, а ур-ние 5х = v называют уравнением с параметром.

Изучая уравнение с параметром, мы рассматриваем не одно конкретное ур-ние, а сразу целую группу, или семейство ур-ний. Например, все ур-ния первой степени можно описать в виде

ах + b= 0

где х – это переменная величина, а числа а, b– это параметры. Для описания квадратного ур-ния в общем виде необходимы уже три параметра (а, b и с):

ах² + bx + c = 0

Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.

Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.

 

Пример. Решите ур-ние

х² – 2ах = 0

и найдите его корни при значении параметра а, равном 3.

Решение. Вынесем множитель х за скобки:

х² – 2ах = 0

х(х – 2а) = 0

х = 0 или х – 2а = 0

х = 0 или х = 2а

Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:

при а = 3х = 2•3 = 6

Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.

 

Пример. Решите ур-ние

р²х – 3рх = р² – 9

Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:

рх(р – 3) = (р – 3)(р + 3)

Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.

Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во

0•х•(0 – 3) = (0 – 3) (3 – 0)

0 = – 9

Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.

Если р – 3 = 0, то есть р = 3, получится следующее

3•х•0 = 0•(3 + 3)

0 = 0

Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.

Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим

В этом случае ур-ние имеет единственный корень.

Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.

Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.

 

Пример. Сколько корней имеет ур-ние

|х² – 6х + 5| = b

при различных значениях параметра b.

Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х² – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:

х² – 6х + 5 = 0

D = b²– 4ас = (– 6)² – 4•1•5 = 36 + 20 = 16

х₁ = (6 – 4)/2 = 1

х₂ = (6 + 4)/2 = 5

Итак, нули ф-ции – это точки 1 и 5. Найдем координату х₀ вершины параболы по формуле:

х₀ = –b/2a = 6/2 = 3

Подставив х₀ в квадратичную ф-цию найдем координату у₀ вершины параболы:

3² – 6•3 + 5 = 9 – 18 + 5 = – 4

Теперь построим квадратичную ф-цию:

Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:

Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:

При b< 0 прямая пролегает ниже графика. Общих точек у графиков нет, а потому ур-ние корней не имеет.

При b = 0 прямая у = 0 касается графика в 2 точках: (1; 0) и (5; 0). Получаем 2 корня.

Если 0 <b< 4, то прямая пересекает график в 4 точках.

При b = 4 прямая у = 4 касается перевернутой вершины параболы, а также пересекает ветви ещё в 2 точках. Итого 3 корня.

Наконец, при b>4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.

Ответ: нет корней при b< 0; 2 корня при b = 0 и b> 4; 3 корня при b = 4; 4 корня при 0 <b< 4.

Пример. При каком а ур-ние

х⁴ – (а + 2)х² + 3а – 3 = 0

имеет ровно 4 корня?

Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х²:

у² – (а + 2)у + 3а – 3 = 0 (1)

Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у₁ и у₂. Тогда, проводя обратную замену х² = у₁ и х² = у₂, мы получим два разных квадратных ур-ния, корни которых будут равны

Если же хоть один из двух корней, например, у₁, окажется равным нулю, то величины

Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у₁ будет отрицательным числом, то ур-ние

х² = у₁

вовсе не будет иметь решений, и тогда останется не более 2 корней.

Итак, решим ур-ние (1):

у² – (а + 2)у + 3а – 3 = 0

D = b²– 4ас = (– (а + 2))² – 4•1•(3а – 3) = (а + 2)² – 12 а + 12 =

= а² + 4а + 4 – 12а + 12 = а² – 8а + 16 = а² – 2•4•а + 4² = (а – 4)²

Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4)² положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.

Извлечем корень из дискриминанта:

Корни ур-ния (1) можно вычислить по формулам:

И у₁, и у₂ должны быть положительными величинами, однако у₁ меньше, чем у₂ (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:

Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство

|а – 4| = а – 4

Тогда имеем

а + 2 – (а – 4) > 0

6> 0

Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.

Если а < 4, то справедливо соотношение

|а – 4| = – (а – 4)

Тогда получится следующее:

а + 2 – |а – 4|> 0

а + 2 – (– (а – 4)) > 0

а + 2 + а – 4 > 0

2а > 2

а > 1

Итак, при условии, что а< 4, должно выполняться нер-во а > 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение

а > 4

можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).

Ответ: а∊(1; 4)∪(4; + ∞).

 

Пример. При каких параметрах а у ур-ния

х² – 2(а + 1)х + а² + 2а – 3 = 0

существует два корня, которые принадлежат интервалу (– 5; 5)?

Решение. Данное ур-ние является квадратным. Найдем его дискриминант:

D = b²– 4ас = (– 2(а + 1))² – 4•1•( а² + 2а – 3) = 4(а² + 2а + 1) – 4(а² + 2а – 3) =

= 4(а² + 2а + 1 – а²– 2а + 3) = 4•4 = 16

Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам

Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х₁) был больше – 5, больший (это х₂) – меньше – 5:

Значит, должны выполняться два нер-ва

х₁>– 5и х₂<5

а – 1 >– 5 и а + 3 < 5

а >– 4 и а < 2

Эти два нер-ва выполняются, если а∊(– 4; 2)

Ответ: (– 4; 2)

 

Конспект урока для 11 класса «Решение уравнений с модулем»

Схема конспекта урока

Педагог Черноусова Татьяна Георгиевна

Предмет алгебра Класс 11

Тема урока: Решение уравнений с модулем.

Цель урока: систематизировать и обобщить знания, умения и навыки решать уравнения с модулем.

Образовательные: обобщить и систематизировать знания учащихся о модуле и его свойствах; умения решать различные уравнения, содержащие модуль и уравнения, приводимые к уравнениям, содержащим модуль.

.

Развивающие цели: развивать творческую и мыслительную деятельность учащихся, навыки проектно-исследовательской деятельности, способствовать формированию навыков коллективной работы, развивать умение чётко и ясно излагать свои мысли.

Воспитательные цели: формирование интереса к предмету посредством вовлечения их в проектную деятельность, способствовать формированию навыков взаимодействия в малых группах.

Тип урока: урок систематизации знаний

Применяемые технологии: проектная

Оборудование: . компьютер, проектор, экран, карточки – задания, инструкция о работе над проектом, информационные мини-проекты учащихся, опросный лист, таблицы.

Предварительное задание: Найдите в интернете информацию: свойства модуля; геометрический смысл модуля. Подготовить информационные мини – проекты.

Ответы учащихся:

-Уравнения 1, 7, 10 можно решить на основании определения модуля.

-Уравнение 2 не имеет решений, так как модуль – величина неотрицательная.

Воспользоваться определением

модуля и рассмотреть 2 условия:

5). x -10 и x -1

По свойству модуля: получим уравнение, содержащее модуль

Постепенно раскрывать модули

Методом интервалов.

1). Найдём значения х, при которых значения выражений, стоящих под знаком модуля равны нулю.

2). Эти значения х разбивают ОДЗ на промежутки.

3). На каждом из полученных промежутков можно записать уравнение без знаков модуля. Получим

совокупность систем.

..

.

Критерии и нормы оценки знаний и умений обучающихся применительно к различным формам контроля знаний.

Составлены на основании письма Министерства Просвещения № 117 – М от 10.03.1977 и согласовано на ГМО учителей математики.

	Время	Деятельность учителя	Деятельность ученика
Слайд-1-2	1.Организационный момент 2.Актуализация знаний	1мин 3мин	«Просто «думать» не умеет никто. Думать можно только над конкретным вопросом. Умение решать задачи в большой мере сводится к обучению тому, над чем надо думать в ходе решения». Доктор педагогических наук, профессор М.Волович Ребята, приглашаю вас к сотрудничеству и предлагаю работать вместе на сегодняшнем уроке. Продолжаем учиться решать. Формируем математическую интуицию, которая поможет ориентироваться в способах решения уравнений. На уроке можно ошибаться, сомневаться, консультироваться. Дать самому себе установку: «Понять и быть тем первым, который увидит ход решения». На слайде записаны уравнения. Что записано? Как называются эти уравнения?	Приветствие учителя. Дежурный докладывает об отсутствующих. Уравнения. Уравнения, содержащие модуль .
слайд 3-5 мини-проекты Постановка проблемы		2мин 3мин	Итак тема нашего урока. Сформулируйте. Чем мы будем заниматься на уроке и какие поставим цели? Сегодня на уроке мы повторим теоретический материал о модуле и его свойствах, геометрический смысл модуля. Научимся решать уравнения, содержащие модуль. Поработаем над основными понятиями, встречающимися в данной теме. — Дайте определение модуля. — Объясните геометрический смысл модуля. — Назовите свойства модуля. — Чему равен ? — Чему равен ? 1) Можно ли свести решение данных уравнений к решению линейных уравнений? 2).Как бы вы сгруппировали данные уравнения по способам решения?( слайд 2-выше записаны уравнения с модулем). Работают в парах, заполняют таблицу. В ходе рассуждений сделали выводы: 1).Если f(x)=g(x) то есть указали способ решения уравнений 3 и 8. 2).Если то должно выполняться условие: , так как модуль величина неотрицательная, тогда по определению модуля То есть указали способ решения уравнений 4 и 9. Как же можно решить уравнение 5,12? Разве уравнение 11 имеет отношение к теме «Модуль»? А как же решить уравнение 6? Каковы ваши предложения по применению метода интервалов? .	Формулируют тему урока. Повторить, отработать, обобщить способы решения уравнений с модулем. Учащиеся показывают и рассказывают информационные мини- проекты
				Работают в парах .заполняют таблицу №	уравнения	Способ решения
1	1,7,10	На основании определения модуля
2	2	Не имеет решения
3	3,8	│f(x)│=│g(x)│f (x) =g(x)
4	4,9	g(x) ≥0, f(x)│=g(x), f(x)│=—g(x),
5	5,12	Определение модуля(два случая)
6	11	Свойство модуля=│х│
7	6	Метод интервалов
	3.Физкультминутка 4.Актуализация деятельности учащихся	1 мин	Немного отдохнем Ваша задача: решить предлагаемые уравнения, проанализировать способы их решения, провести классификацию уравнений, содержащих модуль по способам решения, составить таблицу « Решение уравнений, содержащих модуль». Провести защиту вашего проекта. (Вначале более простые примеры выбирают те учащиеся, которым труднее даётся предмет; более сложные примеры выбирают те учащиеся, у которых есть математические способности. После обмена примерами, более сильные учащиеся могут выступать в роли консультантов.) Каждой группе даются карточки с уравнениями (см приложение №1). Каждая группа получает инструкцию. Прежде, чем приступить к работе над проектом, внимательно ознакомьтесь с инструкцией.	Выполняют упражнение(звучит музыка) Работа в группах( 7 групп ) Решают уравнения
	5.Работа над проектом	20мин	Инструкция по работе над проектом. 1. Решить уравнения. 2. Проанализировать способы решения. 3. Провести классификацию данных уравнений: а) сгруппировать примеры по способам решения; б) определить, в чём заключается общий вид уравнений в каждой группе; в) дать название каждой группе уравнений. 4. Создать проект таблицы: « Решение уравнений, содержащих модуль». 5. Подготовить защиту проекта.	1группа-1,2,4 уравнения. 2 группа-3 ,13 ; 3 группа-12 ;9 4группа-10, 7; 5 группа-8 ,11 6 группа-5, 14 7группа- 6
	6.Защита проектов	10мин	Оценочный лист. (5-бальная система) Владеет докладчик терминологией, которую использует своём проекте
Смог докладчик проекта доказать, что разработанная группой структура самая оптимальная для решения поставленной задачи
Выполнила ли группа все поставленные перед ней задачи
Творческие способности докладчика
Оформление проекта
В процессе обсуждения участники других групп записывают само уравнение и название метода решения, дома их решают.
	7.Домашнее задание	1мин	Сформировать 2 группы (по3 человека), которые представят результаты исследования в виде презентации к следующему уроку. Задание на карточках.
	8 Рефлексия	1мин	Какая задача стояла перед нами в начале урока? Можно ли считать,что мы ее решили? Сможем ли мы теперь решать уравнения аналогичные данным? Заполните опросный лист(см приложение 2)	Учащиеся отвечают на вопросы, заполняют опорный лист

«Практикум решения уравнений с модулем»

Аттестационная работа слушателя курсов повышения квалификации по программе: «Проектная и исследовательская деятельность как способ формирования метапредметных результатов обучения в условиях реализации ФГОС»

Кугушева Наталья Ивановна

КГБ ПОУ «Минусинский сельскохозяйственный колледж» г. Минусинск, Красноярский край.

На тему:

Методическая разработка

«Практикум решения уравнений с модулем»

Краткая характеристика методической разработки

• Данная разработка может быть предложена обучающимся 9-11 классов, студентам 1 курса средне-специальных учреждений в рамках урочной деятельности и элективного курса.
• Изучение материала построено по принципу «от простого к сложному». В начале рассматриваются задания на преобразование выражений, содержащих модуль, затем простейшие уравнения с модулем.
• В рамках изучения темы, рассматриваются следующие вопросы: определение и свойства модуля; преобразования выражений, содержащих модуль; решение простейших уравнений с модулем; общие методы решения уравнений с модулем; метод интервалов.

Краткая характеристика КГБ ПОУ «Минусинского сельскохозяйственного колледжа»

• Колледж готовит студентов по специальностям: Механизация сельского хозяйства; Электрификация и автоматизация сельского хозяйства; Теплоснабжение и теплотехническое оборудование; Экономика и бухгалтерский учет; Технология хлебопечения, кондитерских и макаронных изделий.

• Отделение, на котором я работаю, образовалось при объединении колледжа с сельским профессиональным училищем, и готовит для сельского хозяйства рабочих по профессиям: тракторист-машинист сельскохозяйственного производства; повар-кондитер;

портной. Срок обучения на данном отделении 2года 10 месяцев.

Цель и задачи методической разработки

Цель: обобщение и систематизация знаний, связанных с определением и свойствами модуля.

Задачи:

• Повысить интерес к математике за счет дифференцированного подхода к решению математических заданий с модулем.
• Способствовать развитию практического опыта решения уравнений, неравенств и систем уравнений и неравенств, содержащих модули.
• Помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их применения.
• Формировать умение работать со справочной литературой, находить и использовать информацию в рекомендованных изданиях.

Формы работы

В процессе изучения темы «Решение уравнений с модулем» учащиеся могут включиться в такие виды деятельности, как:

• поиск и анализ необходимой информации, в том числе с помощью Интернета;
• работа в группах при составлении и решении заданий;
• устные выступления по способам решения с последующей дискуссией;
• оформление результатов деятельности в форме набора уравнений и неравенств, а также их систем или компьютерной презентации.

Основное содержание работы

Задание 1. Вспомнить или найти в справочной литературе определение модуля.

Модулем (абсолютной величиной) действительного числа называется само это число, если a≥ 0, и противоположное число – a , если a

Основное содержание работы

Задание 2. Работа в группе. Найдите и запишите свойства модуля.

• |a|≥0
• |a|=|-a|
• |a·b|=|a|·|b|
• |a:b|=|a|:|b|
• |a|²=a²
• |a-b| есть расстояние между точками a и b числовой оси.

Основное содержание работы

Презентация основных способов решения уравнений с модулем.

• По определению.
• Возведение обеих частей уравнения в квадрат.
• Замена переменной.
• «Раскрытие» модуля на промежутке знакопостоянства.
• Использования геометрического смысла модуля.

Основное содержание работы

Задание 3. Выбрать, к какому способу решения уравнений с модулем относится каждый из предложенных алгоритмов.

Алгоритм 1.

1. Решить уравнение | а | = а.

2. Решить уравнение | а | = -а.

3. Сделать проверку найденных корней.

4. Записать ответ.

Алгоритм 2.

1. Обозначить | х | = t .

2. Решить полученное уравнение относительно t .

3. Сделать замену на х.

4. Сделать проверку найденных значений х.

5. Записать ответ.

Основное содержание работы

Алгоритм 3.

1. Возвести левую и правую части уравнения в квадрат.

2. В полученном равносильном уравнении найти корни.

3. Сделать проверку. Записать ответ.

Алгоритм 4.

1. Найти нули всех подмодульных выражений,

расположить их по мере возрастания на числовой оси.

2. На полученных интервалах определить знак всех

подмодульных выражений и раскрыть модули по

определению.

3. Найти решение уравнения на каждом интервале.

4. Объединить эти решения. Записать ответ.

Основное содержание работы

Задание 4. Выясните, к какому способу

решения уравнений с модулем алгоритм не

предложен. Найдите к этому способу

соответствующие примеры. Составьте

алгоритм решения.

Задание 5. Подберите по 3 примера к каждому

из рассмотренных способов. Решите их,

объясняя каждый этап решения.

• Гайдуков И.И. Абсолютная величина. Пособие для учителей.Изд.2-е.М. «Просвещение»,1995.
• Семенко Е.А. Готовимся к ЕГЭ. Обобщающее повторение курса алгебры и начала анализа. Краснодар: «Просвещение — Юг»,2005, 1 часть.
• Сканави М.И. Сборник задач по математике для поступающих в вузы. М.: ООО «Издательский дом» ОНИКС 21 век.2003.
• Никольский С.М. Алгебра и начала анализа. Изд. «Просвещение», 2009.
• Под ред.Фальке Л.Я.Изучение сложных тем курса алгебры в средней школе. Пособие по математике. Изд.2-е.- М.: Народное образование; Илекса; Ставрополь: Сервисшкола, 2004.

Методы диагностики образовательных результатов

Если учащийся:

• принимал активное участие в практикумах,
• успешно выполнил индивидуальные домашние

задания,

• продемонстрировал умение использовать

справочную литературу,

• научился работать в группах,
• находить и использовать информацию в

рекомендованных изданиях.

То он набирает от 30 до 50 баллов (максимальное

количество 50 баллов) и получает зачет. Каждое

задание 10 баллов.

Перспективы развития исследовательской деятельности в профессиональной работе

1. Систематизация имеющегося материала по темам.

Корректировка групповых и домашних заданий,

используя приемы исследовательской деятельности.

2. Презентация образовательных результатов учащихся

на дистанционных и очных олимпиадах по математике

разного уровня (очная межрегиональная олимпиада

«Ищем Ломоносовых», международная дистанционная

олимпиада научно-образовательного центра

«Эрудит»).

3. Составление групповых и индивидуальных проектов

по математике со студентами 1-2 курсов Минусинского

сельскохозяйственного колледжа.

6.2.4. Модуль числа

Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 5.7k. Опубликовано 9 ноября 2013

Модулем числа а (записывают |a|) называют расстояние от начала отсчета до точки, соответствующей данному числу а.

Значение модуля любого числа неотрицательно. |3|=3; |-3|=3, т.к. расстояние от начала отсчета и до числа -3, и до числа 3 равно трем единичным отрезкам. Противоположные числа имеют равные модули. Модуль нуля равен нулю: |0|=0.

По определению модуля числа: |a|=a, если a≥0 и |a|=-a, если а<0. Читают: модуль неотрицательного числа равен самому этому числу; модуль отрицательного числа равен противоположному числу.

Примеры.

1. Вычислить: а) |5|-2; б) |-12| : 6; в) |-24| + |13|; г) |65|-|-45|.

Решение. а) |5|-2=5-2=3;

б) |-12| : 6=12 : 6=2;

в) |-24|+|13|=24+13=37;

г) |65|-|-45|=65-45=20.

2. Решить уравнение: а) |m|+4=10; б) 6-|x|=2.

Решение.

а) |m|+4=10;

|m|=10-4; из суммы вычли известное слагаемое;

|m|=6. Так как |-6|=6  и  |6|=6, то m=-6  или m=6.

Ответ: -6; 6.

б) 6-|x|=2.

|x|=6-2;

|x|=4, отсюда х=-4 или х=4.

Ответ: -4; 4.

3. Записать перечислением элементов множество целых чисел А, модуль которых меньше числа 5.

Решение. По определению модуля числа 5 искомые числа должны отстоять от начала отсчета как вправо, так и влево на расстояние, меньшее пяти единичных отрезков. В этом промежутке (показан штриховкой на рисунке) бесконечно много чисел, но нам нужно выбрать из них лишь все целые числа. Берем числа: -4, -3, -2, -1, 0, 1, 2, 3, 4. Числа -5 и 5 не подходят по условию.

Ответ:  множество А={-4, -3, -2, -1, 0, 1, 2, 3, 4}.

4. Записать перечислением множество натуральных чисел В, модуль которых меньше числа 5.

Решение. Из всех чисел, показанных на рисунке штриховкой, нам нужно выбрать натуральные, т.е. только те числа, которые употребляются при счете предметов. Ответ: B={1, 2, 3, 4}.

 

Внеклассный урок — Уравнения и неравенства с модулем

Уравнения и неравенства с модулем

Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.

Например, модулем числа 6 является 6, модулем числа –6 тоже является 6.

То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.

Обозначается так: |6|, |х|, |а| и т.д.

(Подробнее – в разделе «Модуль числа»).

 

Уравнения с модулем.

Пример 1. Решить уравнение

|10х – 5| = 15.

Решение.

В соответствии с правилом, уравнение равносильно совокупности двух уравнений:

│10х – 5 = 15
│10х – 5 = –15

Решаем:

│10х = 15 + 5 = 20
│10х = –15 + 5 = –10

↕

│х = 20 : 10
│х = –10 : 10

↕

│х = 2
│х = –1

Ответ: х₁ = 2, х₂ = –1.

Пример 2. Решить уравнение

|2х + 1| = х + 2.

Решение.

Поскольку модуль – число неотрицательное, то х + 2 ≥ 0. Соответственно:

х ≥ –2.

Составляем два уравнения:

│2х + 1 = х + 2
│2х + 1 = –(х + 2)

Решаем:

│2х + 1 =  х + 2
│2х + 1 = –х – 2

↕

│2х – х =  2 – 1
│2х + х = –2 – 1

↕

│х = 1
│х = –1

Оба числа больше –2. Значит, оба являются корнями уравнения.

Ответ: х₁ = –1, х₂ = 1.

 

Пример 3. Решить уравнение

  |х + 3| – 1
————— = 4
     х – 1

Решение.

Уравнение имеет смысл, если знаменатель не равен нулю – значит, если х ≠ 1. Учтем это условие. Наше первое действие простое – не просто освобождаемся от дроби, а преобразуем ее так, чтобы получить подмодульное выражение в чистом виде:

|х + 3| – 1 = 4 · (х – 1),

|х + 3| – 1 = 4х – 4,

|х + 3| = 4х – 4 + 1,

|х + 3| = 4х – 3.

Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.

Модуль числа есть неотрицательное число – то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:

4х – 3 ≥ 0

4х ≥ 3

х ≥ 3/4

Таким образом, у нас появилось второе условие: корень или корни уравнения должны быть не меньше 3/4.

В соответствии с правилом модуля составляем совокупность двух уравнений и решаем их:

│х + 3 = 4х – 3
│х + 3 = –(4х – 3)

↕

│ х + 3 = 4х – 3
│ х + 3 = –4х + 3

↕

│х – 4х = –3 – 3
│х + 4х = 3 – 3

↕

│х = 2
│х = 0

Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.

У нас было два условия: корень уравнения должен быть не меньше 3/4, но не может быть равен 1. То есть х ≠ 1, х ≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.

Ответ: х = 2.

 

Неравенства с модулем.

Пример 1. Решить неравенство:

|х — 3| < 4

Решение.

Правило модуля гласит:

|а| = а, если а ≥ 0.
|а| = –а, если а < 0.

Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая:
х – 3 ≥ 0 и х – 3 < 0.

1) При х – 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:

х – 3 < 4.

2) При х – 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

–(х – 3) < 4. Раскрыв скобки, получаем:

–х + 3 < 4.

Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:

│ х – 3 ≥ 0
│ х – 3 < 4

и

│ х – 3 < 0
│–х + 3 < 4

Решим их:

│х ≥ 3
│ х < 7

и

│х < 3
│х > –1

Итак, у нас в ответе объединение двух множеств:

3 ≤ х < 7  U  –1 < х < 3.

Определяем наименьшее и наибольшее значения. Это –1 и 7. При этом х больше –1, но меньше 7. Кроме того, х ≥ 3. Значит, решением неравенства является все множество чисел от –1 до 7, исключая эти крайние числа.

Ответ: –1 < х < 7.

Или: х ∈ (–1; 7).

 

Дополнения.

1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).

  

Выражение |х — 3| < 4 означает, что расстояние от точки х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа – к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.

При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:

–1 < х < 7.

 

2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:

–4 < х – 3 < 4.

Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число –4 являются границами решения неравенства.

Далее мы просто переносим влево и вправо число –3 с обратным знаком, оставляя х в одиночестве:

–4 + 3 < х < 4 + 3

–1 < х < 7.

 

Пример 2. Решить неравенство

|х – 2| ≥ 5

Решение.

Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны –3 и больше или равны 7. А значит, мы уже получили ответ.

Ответ: –3 ≥ х ≥ 7.

Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:

–5 ≥ х – 2 ≥ 5

–5 + 2 ≥ х ≥ 5 + 2

Ответ тот же: –3 ≥ х ≥ 7.

Или: х ∈ [–3; 7]

Пример решен.

 

Пример 3. Решить неравенство:

6х² – |х| – 2 ≤ 0

Решение.

Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х < 0. При х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:

6х² – х – 2 ≤ 0.

Теперь о втором случае: если х < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6х² – (–х) – 2 ≤ 0.

Раскрываем скобки:

6х² + х – 2 ≤ 0.

Таким образом, мы получили две системы уравнений:

│6х² – х – 2 ≤ 0
│ х ≥ 0

и

│6х² + х – 2 ≤ 0
│ х < 0

Надо решить неравенства в системах – а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.

Начнем с первого:

6х² – х – 2 = 0.

Как решается квадратное уравнение – см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:

х₁ = –1/2, х₂ = 2/3.

Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от  –1/2 до 2/3. Пишем объединение решений при х ≥ 0:
[–1/2; 2/3].

Теперь решим второе квадратное уравнение:

6х² + х – 2 = 0.

Его корни:

х₁ = –2/3, х₂ = 1/2.

Вывод: при х < 0 корнями исходного неравенства являются также все числа от –2/3 до 1/2.

Объединим два ответа и получим итоговый ответ: решением является все множество чисел от –2/3 до 2/3, включая и эти крайние числа.

Ответ: –2/3 ≤ х ≤ 2/3.

Или: х ∈ [–2/3; 2/3].

Двойной модуль как решать

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Как решить простейшее модульное уравнение или уравнение содержащее модуль?

Обычно решение сводится к системе :
Уравнения содержащие модуль

Сразу рассмотрим на примере решение уравнений.

Решите уравнение | x – 6| = 18.

Выражение стоящее под модулем приравниваем к 0:

Отмечаем 6 на координатной прямой, далее проверяем знак на каждом из получившихся интервалах.

На интервале (-∞; 6) возьмем число 0 и подставим
0-6=-6 получилось отрицательное число, значит на этом интервале будет знак “ – ”

На интервале (6;+∞) возьмем число 7 и подставим
7-6=1 получилось положительное число, значит на этом интервале будет знак “ + ”

Числовая прямая

Теперь решаем уравнения на каждом интервале.

(-∞; 6) здесь получился знак “ – ”, значит выражение под модулем поменяет знаки на противоположные:

Видно, что -12 лежит на интервале (-∞; 6) следовательно, является корнем уравнения.

(6;+∞) здесь получился знак “ + ”, значит выражение под модулем остается без изменения:

Видно, что 24 лежит на интервале (6;+∞) следовательно, является корнем уравнения.

Решите уравнение | 2x – 5 |- | 4 — x | = -18.

Выражения стоящие под модулем приравниваем к 0:

2x – 5 = 0 и 4 — x = 0
x=2,5 и x=4

Отмечаем x=2,5 и x=4 на координатной прямой, далее проверяем знак на каждом из получившихся интервалах.

На интервале (-∞; 2,5) возьмем число 0 и подставим в каждое выражение
2*0-5=-5 получилось отрицательное число, значит на этом интервале будет знак “ – ”
4-0=4 получилось положительное число, значит на этом интервале будет знак “ + ”

На интервале (2,5; 4) возьмем число 3 и подставим в каждое выражение
2*3-5=1 получилось положительное число, значит на этом интервале будет знак “ + ”
4-3=1 получилось положительное число, значит на этом интервале будет знак “ + ”

На интервале (4; +∞) возьмем число 5 и подставим в каждое выражение
2*5-5=5 получилось положительное число, значит на этом интервале будет знак “ + ”
4-5=-1 получилось отрицательное число, значит на этом интервале будет знак “ – ”

Теперь решаем уравнения на каждом интервале.

(-∞; 2,5) здесь получился знак “ – ” у выражения “ 2x – 5 ”, значит выражение под модулем поменяет знаки на противоположные и знак “ + ” у выражения “ 4 — x ”, значит выражение под модулем остается без изменения:

-2x + 5 — ( 4 — x ) = -18
-2x + 5 — 4 + x = -18
x=19
Видно, что 19 не лежит на интервале (-∞; 2,5) следовательно, не является корнем уравнения.

(2,5; 4) здесь получился знак “ + ” у обоих выражений, значит выражения под модулем останутся без изменений:

2x – 5 — ( 4 — x ) = -18
2x – 5 — 4 + x = -18
3x=-9
x=-3

Видно, что -3 лежит на интервале (2,5; 4) следовательно,не является корнем уравнения.

(4; +∞) здесь получился знак “ – ” у выражения “ 4 — x ”, значит выражение под модулем поменяет знаки на противоположные и знак “ + ” у выражения “ 2x – 5 ”, значит выражение под модулем остается без изменения:

2x – 5 — ( — 4 + x ) = -18
2x – 5 + 4 — x = -18
x=-17

Видно, что -17 лежит на интервале (4; +∞) следовательно,не является корнем уравнения.

Ответ: корней нет

Решите уравнение ||x|-3|=15.

Так как в правой части стоит простое число то распишем на два уравнения (раскроем внешний модуль):

Перенесем в обоих уравнениях -3 вправо, получим:

|x|=18
|x|=-12 (модуль не может равняться отрицательному числу, следовательно это уравнение не имеет решений)

Раскрываем модуль |x|=18

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Надеюсь, ты уже усвоил тему «Модуль числа» и таким образом уже частично готов к ЕГЭ по математике? 🙂

Если нет, срочно повтори эту тему. А если да, читай дальше.

Решение уравнений с модулем может быть самостоятельной задачей, но часто такие уравнения могут возникнуть при решении уравнений другого типа, например, квадратных.

Вот пример подобной ситуации:

Видно, что в правой части – квадрат числа :

Казалось бы, теперь достаточно просто убрать квадраты слева и справа, и получим линейное уравнение.

В таких ситуациях нужно быть предельно осторожным: ведь ты же помнишь простое правило:

Вот и появляется на сцене наш модуль:

Чтобы не теряться в таких случаях, давай разберемся, что из себя представляет решение уравнений с модулем.

Let’s dive right in. (Поехали!)

Решение уравнений с модулем вида |Х| = a

Уравнения такого вида решаем, основываясь на свойствах модуля, которые мы разобрали в теме «Модуль числа» .

Давай разбираться на примерах. Необходимо решить уравнение вида:

Это просто , если больше либо равно нулю, или , если меньше нуля.

То есть можно формализовано записать так:

А если вот такое уравнение:

Эти рассуждения можно было и обойти, вспомнив основное свойство модуля:

Модуль всегда положителен либо равен нулю!

Если обобщить разобранные выше примеры, то можно написать общее правило для решения уравнений вида :

Попробуем применить это правило для такого уравнения:

Выражение под знаком модуля изменилось, но на логике рассуждений это не отражается, поэтому давай решать уравнение, применяя наше правило:

В нашем примере под » » подразумевается » «, а значение . Зная это, получаем:

А если уравнение имеет вид:

Что-то меняется в рассуждениях? Конечно, нет! Ну, тогда давай решать его!

Уловил? Закрепим на примерах.

Примеры для самостоятельной работы

Решения примеров для самостоятельной работы

Точно так же как и в предыдущем примере уравнения с модулем могут возникнуть при решении уравнений другого типа, например, иррациональных.

Вот пример подобной ситуации:

Мы могли бы раскрыть скобки, перенести все в одну сторону, привести подобные и решить обычное квадратное уравнение (например, через дискриминант).

Но здесь удобнее поступить по-другому!

Заметим, что в правой части уравнения – формула сокращённого умножения квадрат суммы:

Тогда уравнение станет таким:

Казалось бы, теперь достаточно просто убрать квадраты слева и справа, и получим линейное уравнение.

Будь предельно осторожным: опять вспоминаем простое правило: ?

И опять на сцене наш модуль:

Чтобы не теряться в таких случаях, научимся решать уравнения с модулем (все три типа).

Три типа уравнений с модулем

1. Уравнения вида |X| = |a|

Большинство уравнений с модулем можно решить, используя одно только определение модуля. Например:

Решите уравнение:

Это просто , если , или , если .

Ответ:

Другой пример:

И правда, вспомним свойство №1:

, то есть модуль всегда неотрицателен.

Итак, мы выработали общее правило решения простейших уравнений с модулем:

Ещё примеры (как обычно, пробуй решить их сам, потом смотри решения):

Решения:​

2. Уравнения вида |X| = |Y|

Если начнём раскрывать модули по определению, натолкнёмся на множество проверок: какое число больше нуля, какое меньше; в итоге получим большую совокупность, которая затем упростится.

Но можно сделать так, чтобы сразу было всё кратко.

Для этого вспомним свойство модуля №7:

С помощью этого свойства можем избавляться от модулей:

Пример:

Решение:

Реши самостоятельно:

Ответы:

3. Уравнения вида |X| = Y

Отличие от первого типа уравнений в том, что в правой части тоже переменная. А она может быть как положительной, так и отрицательной.

Поэтому в её неотрицательности нужно специально убедиться, ведь модуль не может равняться отрицательному числу (свойство №1):

Пример:

Решение:

Если пропустить проверку на неотрицательность правой части, можно ошибочно написать в ответе сторонние корни, и таким образом потерять баллы. Давайте проверим: действительно ли надо выбросить корень ? Подставим его в исходное уравнение :

Теперь задачи для самостоятельного решения:

Ответы:

Решим квадратные уравнения и . Дискриминант у них одинаковый:

Итак, исходное уравнение равносильно системе

Ответ:

Метод интервалов в задачах с модулем

Пример:

Решение:

Рассмотрим первый модуль . По определению он раскрывается «с плюсом» (то есть выражение под модулем не меняется), если , и «с минусом» (то есть все знаки меняются на противоположные), если :

Аналогично и со вторым:

Проблема только в том, что теперь нам нужно рассмотреть очень много вариантов: по варианта для каждого модуля, итого четыре разных, но похожих друг на друга, уравнения.

Если модулей будет не два, а три, получится уже уравнений!

Можно ли как-то сократить количество вариантов?

Да, можно – ведь не все условия могут выполняться одновременно: и противоречат друг другу.

Поэтому нет смысла раскрывать второй модуль «с плюсом», если первый раскрыт «с минусом». Значит, здесь у нас на одно уравнение меньше.

Теперь систематизируем то, что мы только что выяснили, и разработаем последовательность действий в таких примерах:

1. Определим корни подмодульных выражений – такие , при которых выражения равны нулю:

2. Отметим корни выражений под модулями на числовой оси:

3. Подпишем у каждого из получившихся интервалов, какой знак принимает каждое из наших подмодульных выражений.

4. Для каждого интервала запишем и решим уравнение. Важно проследить, чтобы ответы соответствовали интервалу!

I. . Здесь оба модуля раскрываем «с минусом»:

-3″> – этот корень сторонний.

II. . Здесь первый модуль раскрываем «с плюсом», а второй – «с минусом»:

– этот корень попадает в «свой» интервал, значит, он подходит.

III. . Здесь оба модуля раскрываем «с плюсом»:

– этот корень тоже является решением.

Проверим полученные корни:

I. (корень и правда сторонний).

II. .

III. .

Ответ:

Примеры:

Решения:

Модуль в модуле

В некоторых уравнениях встречается «вложенный» модуль, то есть модуль какого-то выражения является частью подмодульного выражения, например:

Что делать в таком случае? Все банально: раскрывать модули. Но раскрывать их нужно по очереди. Какой будем раскрывать первым?

А это зависит от того, каким методом ты хочешь решить это уравнение. Рассмотрим два возможных варианта:

I. Данное уравнение является уравнением вида

В этом случае первый способ решения будет стандартным для такого типа:

– подмодульное выражение – в нашем примере это , то есть:

Получили два элементарных уравнения такого же типа, то есть:

Эти четыре числа и будут ответом, можешь проверить их подстановкой в исходное уравнение.

II. Есть ещё один, более универсальный способ, который подойдёт для любых задач, не попадающих ни в какой из стандартных типов.

Что это за метод?

Метод интервалов.

В этом случае нужно раскрывать модули начиная с самых «глубоких», то есть «внутренних». В нашем случае внутренним будет модуль, выделенный красным цветом:

Чтобы раскрыть его, надо рассмотреть 2 случая: и , то есть уравнение распадается на два уравнения:

Краткое изложение статьи и основные формулы

Уравнения с модулем делятся на три вида, каждый вид имеет свой подход к решению:

1. Уравнения вида

2. Уравнения вида .

3. Уравнения вида .

Теперь тебе слово.

Как тебе. про уравнения с модулем? Легкотня! )

Напиши внизу в комментариях помогла тебе наша статья или нет.

Расскажи о своем опыте решения уравнений с модулем, если он у тебя был.

Возможно у тебя есть вопросы. Или предложения.

Напиши в комментариях. Мы читаем все.

И удачи на экзаменах!

P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это – не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время.

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте – нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Я рекомендую использовать для этих целей наш учебник «YouClever» (который ты сейчас читаешь) и решебник и программу подготовки «100gia».

Условия их приобретения изложены здесь. Кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!

И в заключение.

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Комментарии

Спасибо огромное,повторил,сдал на отлично,Алексею нобелевскую по математике)

Марк, наши поздравления с отличной сдачей. Премию Алексею передам 🙂

нобелевские по математике не присуждаются .

Наградим поощрительной грамотой )

Добрый день! В пункте №3 Уравнения вида ∣x∣=y во втором примере: −2∣x+4∣=3−x, откуда дальше в решении появляется коэффициент 4 в правой части? −2∣x+4∣=3−4x Спасибо за ответ и Ваш чудесный и полезный сайт!

Роман, привет! Спасибо за замечания и слова благодарности. Очень ценно. Алексей Шевчук проверит и поправит, если там ошибка. Еще раз спасибо!

Роман, спасибо. Это была опечатка в условии.

А как решить такой пример 7|2-4|+4*-8

помогите,пожалуйста,решить уравнение дробь в модуле :числитель 13,296 знаменатель 3.71 минус модуль 0,4х минус4,7 модуль закрывается,далее от дроби минус 2,2 умножить на 1,4.Еще раз обращаю внимание: сама дробь в модуле И равно 8 Пожалуйста помогите

Здравствуйте, помогите пожалуйста решить такое уравнение |x-1|=2x+3

Спасибо большое . Сайт замечательный ,я смогла разобраться и понять материал . Создателям огромное спасибо ,их работа заслуживает высокого внимания . Перейду на родной язык: Danke schön. Ihre Arbeit ist wirklich wunderschön. Danke ein male.

Gern geschehen, Dascha! Bitte. International Mathematical Unterstützung zu Ihren Diensten ))

как по графику кусочно заданной функции записать уравнение, содержащее несколько модулей вида y=a|x|+b|x-8|+x+c? №23 ОГЭ систему составила y= -2x-4 . x 8 , а как перейти к другой записи уравнения

Очень хорошо разобрано и объяснено. И за советы спасибо)

Лера, жму руку! Спасибо за теплые слова. Удачи на всех экзаменах!

Решите уравнение ∣x∣=−3. разве может модуль равняться отрицательному числу

Джозеф, нет, не может, и в этом примере поясняется, почему.

Помогите решить |х|+|y-x|=2 Нужно расскрыть модуль и по получившимся ответам которых 4 как сказал препод

Виталий, в самом начале раздела «Метод интервалов в задачах с модулем» показано, как раскрывать сумму модулей. Принципиально это ничем не отличается от раскрытия одного модуля, просто будет больше комбинаций – 4 штуки, по 2 на каждый модуль: 1) x>=0, y>=x; 2) x =x; 3) . и так далее

Линейные уравнения ADS по модулю целых чисел 2

Подраздел 12.6.1 Уменьшение ряда, мод 2

Методы, которые мы изучали для решения систем уравнений до этого момента, могут быть применены к системам, в которых вся арифметика выполняется над другими алгебраическими системами, включая целые числа по модулю 2. Случай mod 2 станет особенно полезным в нашем более позднем исследовании теория кодирования.

При решении систем уравнений с арифметикой по модулю 2 элементарные операции со строками по-прежнему остаются фундаментальными.{n-m} \) разные решения.

Давайте посмотрим на пример, который сразу же переводится в матричную форму.

\ begin {уравнение *} \ begin {array} {r @ {} r @ {} r @ {} r @ {} r @ {} r @ {} r @ {} r @ {} r @ {} r @ {} r @ {} р@{}} x_1 & {} + {} & x_2 & & & {} + {} & x_4 & & & & & = 1 \\ x_1 & & & {} + {} & x_3 & & & {} + {} & x_5 & & & = 0 \\ & & x_2 & {} + {} & x_3 & & & & & {} + {} & x_6 & = 0 \\ \ end {массив} \ end {уравнение *}

Расширенная матрица системы

\ begin {уравнение *} \оставил( \ begin {array} {cccccc | c} 1 & 1 & 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ \ end {массив} \верно) \ end {уравнение *}

Шаги по уменьшению строк этой матрицы приведены ниже.Записи, по которым мы «делаем поворот», выделены жирным шрифтом, чтобы было легче идентифицировать основные переменные.

\ begin {уравнение *} \ begin {split} \оставил( \ begin {array} {cccccc | c} 1 & 1 & 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ \ end {массив} \ right) & \ overset {\ textrm {add} R_1 \ textrm {to} R_2} {\ text {} \ longrightarrow} \ text {} \оставил( \ begin {array} {cccccc | c} \ textbf {1} & 1 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ \ end {массив} \верно)\\ & \ text {} \ overset {\ textrm {add} R_2 \ textrm {to} R_1} {\ text {} \ longrightarrow} \ text {} \ left ( \ begin {array} {cccccc | c} \ textbf {1} & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & \ textbf {1} & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ \ end {массив} \верно) \\ & \ overset {\ textrm {add} R_2 \ textrm {to} R_3} {\ text {} \ longrightarrow} \ text {} \оставил( \ begin {array} {cccccc | c} \ textbf {1} & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & \ textbf {1} & 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ \ end {массив} \верно) \ end {split} \ end {уравнение *}

Обратите внимание, что в этот момент мы не можем повернуться к третьей строке, третьему столбцу, поскольку эта запись равна нулю.Поэтому мы переходим к следующему столбцу, делая \ (x_4 \) основным.

\ begin {уравнение *} \ begin {split} \ text {} & \ overset {\ textrm {add} R_3 \ textrm {to} R_2} {\ text {} \ longrightarrow} \ text {} \оставил( \ begin {array} {cccccc | c} \ textbf {1} & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & \ textbf {1} & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & \ textbf {1} & 1 & 1 & 1 \\ \ end {массив} \верно) \ end {split} \ end {уравнение *}

На этом сокращение строки завершено, и теперь мы можем идентифицировать набор решений.Имейте в виду, что, поскольку сложение — это вычитание, члены можно перемещать в любую сторону от знака равенства без изменения знака. Основными переменными являются \ (x_1 \ text {,} \) \ (x_2 \ text {,} \) и \ (x_4 \ text {,} \), а остальные три переменные свободны. Общее решение системы

\ begin {уравнение *} \ begin {array} {c} х_1 = х_3 + х_5 \\ х_2 = х_3 + х_6 \\ х_3 = х_3 \\ х_4 = 1+ х_5 + х_6 \\ х_5 = х_5 \\ х_6 = х_6 \\ \ end {массив} \ end {уравнение *}

С тремя свободными переменными существует \ (2 ^ 3 = 8 \) решений этой системы.Например, один из них получается установкой \ (x_3 = 1 \ text {,} \) \ (x_5 = 1 \ text {,} \) и \ (x_6 = 0 \ text {,} \), что дает \ ((x_1, x_2, x_3, x_4, x_5, x_6) = (0,1,1,0,1,0) \ text {.} \)

Мы можем проверить сокращение строки с помощью SageMath:

Калькулятор по модулю

[Примеры модификаций]

Этот калькулятор по модулю — удобный инструмент, если вам нужно найти результат операций по модулю. Все, что вам нужно сделать, это ввести начальное число x и целое число y , чтобы найти число по модулю r , согласно x mod y = r .Читайте дальше, чтобы узнать, что такое операции по модулю, как вычислить по модулю и как правильно использовать этот калькулятор.

Что такое операции по модулю?

Представьте себе часы, висящие на стене. Допустим, уже поздно — 23 часа. Вы задаетесь вопросом, во сколько вы проснетесь после 8 часов сна. Вы не можете просто прибавить 8 к 11, потому что нет такого времени, как 19 часов утра. Чтобы найти правильный ответ, вам нужно выполнить операцию по модулю (mod 12) — вы складываете эти два числа и продолжаете вычитать 12, пока не получите число меньше 12.В данном случае 7. Вы только что подсчитали, что проснетесь в 7 утра.

Операции по модулю в случае часов настолько интуитивно понятны, что мы их даже не замечаем. В математике есть много типов более сложных операций по модулю, которые требуют большего осмысления. Мы можем записать это:

x mod y = r

истинно, если такое целое число q (называемое частным ) существует, тогда:

y * q + r = x .

В противном случае число r — это остаток от деления, где x — — делимое , а y — — делитель .

Если определение по модулю вам не нравится, и вы все еще не знаете, как вычислить по модулю, взгляните на следующий абзац, и все должно стать кристально ясным.

Что такое сравнение по модулю?

Два числа a и b считаются равными по модулю n , когда их разность a - b целиком делится на n (так что (a - b) кратно n ).

Математически формула сравнения по модулю записывается как:

a ≡ b (мод. N)

и n называется модулем конгруэнции.

С другой стороны, вы можете сказать, что a и b считаются равными по модулю n , когда они оба имеют одинаковый остаток при делении на n:

мод n = r

b мод n = r

, где r — общий остаток.

Итак, проще говоря — совпадение по модулю происходит, когда два числа имеют одинаковый остаток после одного и того же делителя, например: 24 по модулю 10 и 34 по модулю 10 дают тот же ответ: 4.Следовательно, 24 и 34 сравнимы по модулю 10.

Давайте посмотрим на другой пример:

9 ≡ 21 (мод.6) ,

, потому что 21 - 9 = 12 делится на 6. Его также можно записать коротко как 6 | (21 - 9) . Или, что то же самое, 21 и 9 имеют одинаковый остаток, когда мы делим их на 6:

.

9 мод 6 = 3

21 mod 6 = 3

Как вычислить по модулю — пример

Рассчитать модуль вручную — несложная задача.Просто следуйте инструкциям ниже!

1. Начните с выбора начального числа (перед выполнением операции по модулю). Допустим, 250. Это наши дивиденды.
2. Выберите делитель. Возьмем 24. Операция, которую мы хотим вычислить, тогда 250 mod 24 ( 250% 24 , если используется другое соглашение).
3. Разделите одно число на другое, округляя в меньшую сторону: 250/24 = 10 . Это частное. Кроме того, вы можете рассматривать эту операцию как целочисленное деление на — тип деления, при котором нам не важна дробная часть результата.
4. Умножьте делитель на частное. Итак, в нашем примере это 10 * 24 = 240 .
5. Вычтите это число из вашего начального числа (делимого). Здесь: 250 - 240 = 10 .
6. Полученное число является результатом операции по модулю. Мы можем записать это как 250 mod 24 = 10 .

Как пользоваться нашим калькулятором модов? 10 mod 3 и другие примеры по модулю

Определить модуль с помощью нашего инструмента просто и удобно.Чтобы найти результат операций по модулю между целыми числами, вам необходимо:

1. Введите начальное число — делимое — в первое поле . Возьмем пример из предыдущего абзаца, поэтому введите 250.
2. Введите делитель . В нашем случае 24.
3. Тадааа! Наш калькулятор по модулю вернет вам результат — остаток! И это неудивительно, оно равно 10 — столько же, сколько мы рассчитывали раньше.

Ниже вы найдете несколько типичных запросов, касающихся модуля:

• 1 mod 1 = 0 (поскольку mod 1 всегда равен 0)
• 1 мод 2 = 1
• 1 мод 3 = 1
• 5 мод 2 = 1
• 5 мод 3 = 2
• 6 мод 3 = 0
• 7 мод 3 = 1
• 10 мод 3 = 1
• 18 мод 3 = 0
• 100 мод 3 = 1
• 100 мод 7 = 2

Если вы не видите здесь тот, который хотите найти, воспользуйтесь нашим калькулятором по модулю!

Модульная арифметика

Модульная арифметика — это, вообще говоря, арифметическая система для целых чисел, в которой числа «оборачивают» определенное число.Подведем итог тому, что мы узнали о различных представлениях операций по модулю — все приведенные ниже утверждения являются эквивалентами:

• A ≡ B (мод. C)
• A мод C = B мод C
• C | (А - В)
• A = B + K * C , где K — некоторое целое число

Мы также можем выполнять вычисления по модулю операций.

1. Модульное сложение и вычитание

(A + B) мод C = (A мод C + B мод C) мод C

(A - B) мод C = (A мод C - B мод C) мод C

Итак, сумма по модулю суммы двух чисел равна сумме по модулю этих чисел, вычисленных отдельно, а затем умноженной на делитель по модулю.Первый этап делается для того, чтобы избавиться от частной части, а затем снова используется операция mod. Взгляните на пример:

• А = 11, В = 7, С = 4

  (11 + 7) по модулю 4 = (11 по модулю 4 + 7 по модулю 4) по модулю 4

  левая часть уравнения: (11 + 7) mod 4 = 18 mod 4 = 2

  правая часть уравнения: (11 mod 4 + 7 mod 4) mod 4 = (3 + 3) mod 4 = 6 mod 4 = 2

Аналогично, вычисления аналогичны для вычитания.

2. Модульное умножение

(A * B) мод C = (A мод C * B мод C) мод C

Такое уравнение может быть полезно при работе с большими числами, и мы не можем сразу узнать модуль этого большого числа. Давайте посмотрим на тот же пример (A = 11, B = 7, C = 4) — можете ли вы найти результат 77 mod 4 на месте? 11 mod 4 и 7 mod 4 вычислить проще:

• (11 * 7) мод 4 = (11 мод 4 * 7 мод 4) мод 4

  левая часть уравнения: (11 * 7) mod 4 = 77 mod 4 = 1

  правая часть уравнения: (11 mod 4 * 7 mod 4) mod 4 = (3 * 3) mod 4 = 9 mod 4 = 1

3.100 мод 3 = (1 * 1) мод 3 = 1

Для некоторых конкретных случаев существуют даже более быстрые методы модульного возведения в степень (если B — степень двойки). Если вы хотите прочитать о них и попрактиковаться в модульной арифметике, ознакомьтесь с отличным учебником от Khan Academy под названием «Что такое модульная арифметика?»

Неопределенность определения по модулю

Слово modulo происходит от латинского слова modus , означающего меру. Обычно, когда мы используем слово по модулю , мы имеем в виду операцию по модулю , например, e.грамм. 11 по модулю 3 равно 2, поэтому нужно просто найти остаток. В строгом понимании, модуль означает:

.

По указанному модулю

или

A то же самое, что B по модулю C, за исключением различий, учитываемых или объясняемых C

Это определение, о котором мы писали в сравнении по модулю абзаца.

Однако по модулю используется не только в математическом контексте.Иногда вы можете услышать это в повседневном разговоре, где это, вероятно, означает игнорирование, не учет чего-либо, с должным учетом чего-то, например:

Дизайн был лучшим до сих пор, по модулю частей, которые все еще нуждаются в доработке.

Percent — символ операции по модулю

Операция по модулю часто используется в языках программирования. Для этого% — процент — используется для обозначения этой операции (или иногда оператор остатка для отрицательных чисел).Если вам интересно узнать о происхождении знака%, мы настоятельно рекомендуем вам прочитать небольшой абзац, который мы составили об истории знака процента.

Вам нужно быть осторожным, так как при учете отрицательных значений есть некоторая двусмысленность с определением по модулю. Для остатка есть два возможных варианта — отрицательный и положительный, и результат зависит от реализации на выбранном языке программирования.

Приложения по модулю

На первый взгляд они могут быть неочевидными, но существует множество применений модуло — от повседневной жизни до задач по математике и естествознанию!

1. Самый очевидный и известный пример — так называемая арифметика часов 🕞.Это может быть добавление часов, как в объяснении по модулю выше, или минут, или секунд! Никто не скажет, что «у вас осталось 40 минут 90 секунд », верно? Единственный вариант — выполнить операцию по модулю и найти частное и остаток — 60 * 1 + 30 = 90 . 41 минута 30 секунд звучит намного лучше.

2. Операции по модулю используются для вычисления контрольных сумм серийных номеров. Контрольные цифры используются в основном в длинных числах, и это цифры, вычисляемые алгоритмом.Они готовы сообщить вам о возникающих ошибках, например от опечаток. Вы можете найти применение по модулю в:

• Контрольные цифры GTIN, UPC, EAN используются для подтверждения целостности штрих-кода. В формуле для контрольных цифр используется модуль 10.
• Номера ISBN и ISSN , которые являются уникальными периодическими идентификаторами и идентификаторами книг, имеют модуль 11 или 10, а в формуле контрольной цифры применяется средний вес.
• IBAN — Номера международных банковских счетов — используйте модуль 97, чтобы проверить, правильно ли клиент ввел номер.
• NPI — Национальный идентификатор провайдера США использует операцию по модулю 10 для вычисления десятой цифры.

Поскольку контрольные цифры используются для выявления человеческих ошибок транскрипции, они часто используются для длинных серийных номеров. Другие примеры алгоритмов контрольных цифр с использованием операций по модулю:

• национальный идентификационный номер (например, в Исландии, Турции, Польше)
• фискальный идентификационный номер (Испания)
• идентификационный номер автомобиля (США)
• и многие, многие другие.

3. Он применяется во многих научных областях, таких как компьютерная алгебра, криптография, информатика или простая школьная математика — как в алгоритме Евклида для вычисления наибольшего общего множителя.

4. Modulo полезен, когда вам нужно что-то разделить. Примером из реальной жизни может быть разделение пиццы с друзьями или семьей.

Предположим, что в большой пицце для вечеринки 10 ломтиков, а вы — группа из трех человек.Сколько кусочков останется, если пиццу разделить поровну?

Это именно тот случай, когда вы можете использовать по модулю! 10 mod 3 = 1. Другими словами, 10, разделенное на 3, равняется 3, но остается 1 кусок 🍕. Это был не самый сложный пример, но мы надеемся, что вы видите полезность модуло.

Кстати , а вы видели нашу коллекцию калькуляторов пиццы? У нас есть удивительный калькулятор пиццы, который может помочь оценить, сколько пиццы вам нужно заказать, а также инструменты, помогающие сравнить размеры пиццы — если вы когда-нибудь задумывались, что лучше купить две пиццы среднего размера или одну большую, пиццу Калькулятор сравнения — беспроигрышный вариант.Также мы подготовили калькуляторы для тех, кто хочет испечь идеальную пиццу самостоятельно!

О нет. Мы проголодались. Давайте оставим это вкусное отвлечение и вернемся на Землю. Если вы заинтересованы в поиске более забавных приложений модульной арифметики, ознакомьтесь с этим сообщением в блоге betterexplained.com.

Решение квадратичных сравнений

Как вы решаете сравнения формы x ² ≡ a (mod m )? Другими словами, как найти квадратные корни в модульной арифметике?

Каждая книга по теории чисел, которую я видел, указывает на то, что общая проблема решения x ² ≡ a (mod m ) может быть сведена к решению частного случая, когда m — простое число, тогда тратится больше всего. времени, изучая этот частный случай подробно.Однако я не видел книги, в которой было бы полностью ясно, как именно свести общую проблему к проблеме простых модулей или как можно развернуть редукцию, чтобы получить решение исходной проблемы. Я постараюсь восполнить здесь пробелы.

В этих примечаниях мы будем предполагать, что m и a не имеют общих факторов.

Уменьшить общие модули до основных модулей мощности

Первый шаг в сокращении очевиден. Разложите модуль m на простые степени: m = p ₁ ^{e ₁} p ₂ ^{e ₂} … p _r ^{e _р} .Если сравнение x ² ≡ a (mod m ) имеет решение, это решение обязательно является решением каждого из основных степенных конгруэнций x ² ≡ a (mod p _i ^{e _i} ). И наоборот, если вы найдете решения для каждой из степенных конгруэнций простых чисел, вы можете использовать китайскую теорему об остатках для получения решения исходной проблемы.

Уменьшить основные модули мощности до основных модулей

Это та часть, которая часто не представлена ​​четко.Кроме того, степени двойки должны обрабатываться отдельно от степеней нечетных простых чисел, а первым иногда пренебрегают.

Для любого простого числа p , необходимое условие для x ² ≡ a (mod p ⁿ ), чтобы иметь решение, — x ² ≡ a (mod p ), чтобы найти решение. (Чтобы увидеть это, обратите внимание, что если x ² — a делится на p ⁿ , то оно, безусловно, делится на p .) Как ни удивительно, но это тоже достаточное условие.

Полномочия 2

Пусть a будет нечетным целым числом. (Поскольку мы предполагаем, что m и a являются относительно простыми, если m имеет степень 2 в качестве множителя, a должно быть нечетным.)

Во-первых, x ² ≡ a (mod 2) имеет решение, а именно x ≡ 1 (mod 2).

Далее, x ² ≡ a (mod 4) имеет решение тогда и только тогда, когда a ≡ 1 (mod 4), и в этом случае решения составляют x ≡ 1 (mod 4) и x 3 (мод 4).

Наконец, для n ≥ 3, x ² ≡ a (mod 2 ⁿ ) имеет четыре уникальных решения, если a ≡ 1 (mod 8), и никаких решений в противном случае.

Если a ≡ 1 (mod 8), то x ² ≡ a (mod 8) имеет четыре решения: 1, 3, 5 и 7. Решения для x ² ≡ a (mod 2 ⁿ ) для n > 3 можно найти с помощью процедуры ниже, которая начинается с каждого из решений (mod 8) и производит решения индукцией для более высоких степеней двойки.

Предположим, что x _k ² ≡ a (mod 2 ^k ) для k ≥ 3. По определению это означает, что x ² — a делится на 2 ^к . Если ( x ² — a ) / 2 ^k является нечетным, пусть i = 1. В противном случае пусть i = 0. Тогда x _{k +1} определено по x _k + i 2 ^{k -1} является решением для x _{k +1} ² ≡ a (mod 2 ^{k +1} ).

Степени нечетных простых чисел

Пусть p будет нечетным простым числом и пусть a будет любым целым числом, относительно простым с p . Затем существует процедура, основанная на лемме Гензеля, которая может принимать решение для x ² ≡ a (mod p ) и производить решения для x ² ≡ a (mod p ⁿ ) для n = 2, 3, 4 и т. д.

Предположим, что x _k является решением для x ² ≡ a (mod p ^k ) для некоторого k ≥ 1.Пусть y _k будет решением 2 x _k y _k ≡ 1 (mod p ^k ). Тогда x _{k +1} = x _k — ( x _k ² — a ) y _k является решением для x ² ≡ a (мод. p ^{k +1} ).

Приведенная выше процедура показывает, как построить одно решение для x ² ≡ a (mod p ⁿ ), но не говорит нам, есть ли другие решения.Далее мы покажем, что если мы найдем решение x, будет ровно одно другое решение — x . (Спасибо Немо за это доказательство.)

Предположим, что x ² = y ² ≡ a (mod p ⁿ ), где p является нечетным простым числом, а a является относительно простым относительно p . Тогда x ² — y ² ≡ ( x — y ) ( x + y ) ≡ 0 (mod p ⁿ ).Таким образом, p ⁿ делит продукт ( x + y ) ( x — y ), и поэтому p также делит продукт.

Если p разделить и x + y , и x — y , тогда p разделит их сумму и их разность, 2 x и -2 y . Поскольку p является нечетным простым числом, p не делит 2, и поэтому p делит как x , так и y .Теперь x ² ≡ a (mod p ⁿ ), и поэтому x ² = k p ⁿ + a для некоторых k . Если p разделить x , тогда p разделит x ² , и, следовательно, p разделит на , а p не будет относительно простым с p ⁿ . Следовательно, p не делит ни x , ни y .Отсюда следует, что p либо делит ( x + y ), либо ( x — y ), но не оба. Поскольку p ⁿ делит ( x + y ) ( x — y ), он делит только одно из ( x + y ) и ( x — y ). Следовательно, либо x ≡ y (mod p ⁿ ), либо x ≡ — y (mod p ⁿ ).Итак, если a имеет любой квадратный корень по модулю p ⁿ — назовите его x — тогда он имеет ровно два корня: x и — x .

Нечетные простые модули

Мы рассматриваем здесь только нечетные простые числа, потому что случай p = 2 рассматривался выше. Поэтому мы предполагаем, что p — нечетное простое число в этом разделе.

Если x ² ≡ a (mod p ) имеет решение, мы говорим, что a является «квадратичным модулем резерва p .«Если это сравнение не имеет решения, мы говорим, что x является« квадратичным модулем без остатка p ».

Сравнение x ² ≡ a (mod p ) либо не имеет решений, либо имеет два решения. Если x — решение, значит — x .

Критерий Эйлера гласит, что нечетное целое число, относительное простое к p , является квадратичным остатком (mod p ) тогда и только тогда, когда a ^{( p -1) / 2} ≡ 1 (mod p ).Этого факта достаточно, чтобы разрешить вопрос о том, является ли a квадратичным вычетом. Его можно использовать в практическом алгоритме с использованием быстрого возведения в степень. Однако существует обширная и красивая теория, называемая «квадратичной взаимностью», которая дополнительно исследует эту проблему и создает более эффективные алгоритмы.

Если a является квадратичным остатком (mod p ) и p ≡ 3 (mod 4), то a ^{( p +1) / 4} является решением для x ² ≡ a (мод. p. ).Если a ≡ 1 (mod 4), аналогичной формулы нет. В этом случае можно использовать алгоритм Тонелли-Шанкса. (Спасибо Аласдеру МакЭндрю за указание на этот алгоритм.)

3.3: Линейные сравнения — математика LibreTexts

Поскольку сравнения аналогичны уравнениям, естественно спросить о решениях линейных уравнений. В этом разделе мы обсудим линейные сравнения одной переменной и их решения. Начнем с определения линейных сравнений.

Конгруэнция вида \ (ax \ Equiv b (mod \ m) \), где \ (x \) — неизвестное целое число, называется линейной конгруэнцией по одной переменной.

Важно знать, что если \ (x_0 \) является решением линейного сравнения, то все целые числа \ (x_i \) такие, что \ (x_i \ Equiv x_0 (mod \ m) \) являются решениями линейного сравнения . Также обратите внимание, что \ (ax \ Equiv b (mod \ m) \) эквивалентно линейному диофантову уравнению, т.е. существует \ (y \) такое, что \ (ax-my = b \). Докажем теперь теоремы о решениях линейных сравнений.

Пусть \ (a, b \) и \ (m \) — такие целые числа, что \ (m> 0 \) и пусть \ (c = (a, m) \). Если \ (c \) не делит \ (b \), то сравнение \ (ax \ Equiv b (mod \ m) \) не имеет решений. Если \ (c \ mid b \), то \ [ax \ Equiv b (mod \ m) \] имеет точно \ (c \) инконгруэнтные решения по модулю \ (m \).

Как мы упоминали ранее, \ (ax \ Equiv b (mod \ m) \) эквивалентно \ (ax-my = b \). По теореме 19 о диофантовых уравнениях мы знаем, что если \ (c \) не делит \ (b \), то уравнение \ (ax-my = b \) не имеет решений.Также обратите внимание, что если \ (c \ mid b \), то существует бесконечно много решений, переменная \ (x \) которых задается как \ [x = x_0 + (m / c) t \] Таким образом, указанные выше значения \ (x \) являются решениями сравнения \ (ax \ Equiv b (mod \ m) \). Теперь нам нужно определить количество имеющихся у нас неконгруэнтных решений. Предположим, что два решения конгруэнтны, т.е. \ [x_0 + (m / c) t_1 \ Equiv x_0 + (m / c) t_2 (mod \ m). \] Таким образом, мы получаем \ [(m / c) t_1 \ Equiv (m / c) t_2 (mod \ m). \] Теперь заметим, что \ ((m, m / c) = m / c \) и, следовательно, \ [t_1 \ Equiv t_2 (mod \ c). \] Таким образом, мы получаем набор инконгруэнтных решений, заданных формулой \ (x = x_0 + (m / c) t \), где \ (t \) берется по модулю \ (c \).

Обратите внимание, что если \ (c = (a, m) = 1 \), то существует единственное решение по модулю m уравнения \ (ax \ Equiv b (mod \ m) \).

Найдем все решения сравнения \ (3x \ Equiv 12 (mod \ 6) \). Обратите внимание, что \ ((3,6) = 3 \) и \ (3 \ mid 12 \). Таким образом, имеется три инконгруэнтных решения по модулю \ (6 \). Мы используем алгоритм Евклида, чтобы найти решение уравнения \ (3x-6y = 12 \), как описано в главе 2. В результате мы получаем \ (x_0 = 6 \). Таким образом, три инконгруэнтных решения задаются формулами \ (x_1 = 6 (mod \ 6) \), \ (x_1 = 6 + 2 = 2 (mod \ 6) \) и \ (x_2 = 6 + 4 = 4 (mod \ 6) \).

Как мы упоминали ранее в замечании 2, сравнение \ (ax \ Equiv b (mod \ m) \) имеет единственное решение, если \ ((a, m) = 1 \). Это позволит нам говорить о модульных инверсиях.

Решение сравнения \ (ax \ Equiv 1 (mod \ m) \) для \ ((a, m) = 1 \) называется модульным обратным к \ (a \) по модулю m. Обозначим такое решение через \ (\ bar {a} \).

Модульное обратное к 7 по модулю 48 равно 7. Обратите внимание, что решение для \ (7x \ Equiv 1 (mod \ 48) \) есть \ (x \ Equiv 7 (mod \ 48) \).

Упражнения

1. Найдите все решения \ (3x \ Equiv 6 (mod \ 9) \).
2. Найдите все решения \ (3x \ Equiv 2 (mod \ 7) \).
3. Найдите обратное по модулю 13 2 и 11.
4. Покажите, что если \ (\ bar {a} \) является обратным к \ (a \) по модулю \ (m \) и \ (\ bar {b} \) является обратным к \ (b \) по модулю \ ( m \), то \ (\ bar {a} \ bar {b} \) является обратным к \ (ab \) по модулю \ (m \).

Авторы и авторство

• Доктор Виссам Раджи, доктор философии, Американский университет в Бейруте. Его работа была выбрана фондом Saylor Foundation Open Textbook Challenge для публичного выпуска по лицензии Creative Commons Attribution ( CC BY ).

% PDF-1.2 % 89 0 объект > эндобдж xref 89 333 0000000016 00000 н. 0000007009 00000 н. 0000009935 00000 н. 0000010150 00000 п. 0000010393 00000 п. 0000010779 00000 п. 0000010957 00000 п. 0000011305 00000 п. 0000011639 00000 п. 0000011931 00000 п. 0000012245 00000 п. 0000012595 00000 п. 0000012922 00000 п. 0000013251 00000 п. 0000013513 00000 п. 0000013834 00000 п. 0000014105 00000 п. 0000014402 00000 п. 0000014716 00000 п. 0000015123 00000 п. 0000015520 00000 н. 0000015817 00000 п. 0000016158 00000 п. 0000016528 00000 п. 0000016890 00000 п. 0000017218 00000 п. 0000017501 00000 п. 0000017841 00000 п. 0000018133 00000 п. 0000018453 00000 п. 0000018834 00000 п. 0000019196 00000 п. 0000019500 00000 н. 0000019846 00000 п. 0000020123 00000 п. 0000020330 00000 п. 0000020565 00000 п. 0000020780 00000 п. 0000020948 00000 н. 0000021118 00000 п. 0000021453 00000 п. 0000021736 00000 п. 0000022101 00000 п. 0000022447 00000 п. 0000022791 00000 п. 0000023124 00000 п. 0000023400 00000 п. 0000023719 00000 п. 0000023910 00000 п. 0000024259 00000 п. 0000024526 00000 п. 0000024578 00000 п. 0000024799 00000 п. 0000025285 00000 п. 0000025782 00000 п. 0000026041 00000 п. 0000026331 00000 п. 0000026619 00000 п. 0000026872 00000 н. 0000027088 00000 п. 0000027328 00000 н. 0000027626 00000 н. 0000027883 00000 п. 0000028136 00000 п. 0000028402 00000 п. 0000028700 00000 п. 0000028969 00000 п. 0000029089 00000 н. 0000029263 00000 п. 0000029446 00000 н. 0000029658 00000 п. 0000029825 00000 п. 0000030003 00000 п. 0000030276 00000 п. 0000030528 00000 п. 0000030777 00000 п. 0000031046 00000 п. 0000031098 00000 п. 0000031289 00000 п. 0000031522 00000 п. 0000031775 00000 п. 0000031827 00000 н. 0000031936 00000 п. 0000032189 00000 п. 0000032379 00000 п. 0000032558 00000 п. 0000032707 00000 п. 0000032985 00000 п. 0000033263 00000 н. 0000033542 00000 п. 0000033822 00000 п. 0000034071 00000 п. 0000034246 00000 п. 0000034612 00000 п. 0000034664 00000 п. 0000034869 00000 п. 0000035164 00000 п. 0000035409 00000 п. 0000035715 00000 п. 0000035952 00000 п. 0000036167 00000 п. 0000036421 00000 п. 0000036656 00000 п. 0000036826 00000 п. 0000037156 00000 п. 0000037491 00000 п. 0000037818 00000 п. 0000038079 00000 п. 0000038384 00000 п. 0000038718 00000 п. 0000038936 00000 п. 0000039390 00000 н. 0000039442 00000 п. 0000039581 00000 п. 0000039877 00000 п. 0000040179 00000 п. 0000040417 00000 п. 0000040705 00000 п. 0000040979 00000 п. 0000041229 00000 п. 0000041531 00000 п. 0000041790 00000 п. 0000042119 00000 п. 0000042366 00000 п. 0000042589 00000 п. 0000042765 00000 н. 0000043045 00000 п. 0000043291 00000 п. 0000043658 00000 п. 0000044013 00000 п. 0000044347 00000 п. 0000044715 00000 п. 0000045148 00000 п. 0000045513 00000 п. 0000045877 00000 п. 0000046141 00000 п. 0000046448 00000 н. 0000046626 00000 п. 0000046826 00000 п. 0000046994 00000 п. 0000047268 00000 п. 0000047568 00000 п. 0000047870 00000 п. 0000048198 00000 п. 0000048562 00000 н. 0000048881 00000 п. 0000049262 00000 п. 0000049448 00000 п. 0000049786 00000 п. 0000050119 00000 п. 0000050481 00000 п. 0000050717 00000 п. 0000051014 00000 п. 0000051244 00000 п. 0000051531 00000 п. 0000051711 00000 п. 0000051988 00000 п. 0000052225 00000 п. 0000052521 00000 п. 0000053198 00000 п. 0000053649 00000 п. 0000053987 00000 п. 0000054232 00000 п. 0000054474 00000 п. 0000054827 00000 н. 0000055118 00000 п. 0000055430 00000 п. 0000055728 00000 п. 0000056074 00000 п. 0000056353 00000 п. 0000056727 00000 н. 0000057207 00000 п. 0000057489 00000 п. 0000057733 00000 п. 0000057936 00000 п. 0000058201 00000 п. 0000058561 00000 п. 0000058859 00000 п. 0000059157 00000 п. 0000059209 00000 п. 0000059456 00000 п. 0000059813 00000 п. 0000060043 00000 п. 0000060386 00000 п. 0000060731 00000 п. 0000061079 00000 п. 0000061347 00000 п. 0000061634 00000 п. 0000061805 00000 п. 0000062062 00000 н. 0000062238 00000 п. 0000062588 00000 п. 0000063001 00000 п. 0000063344 00000 п. 0000063682 00000 п. 0000064058 00000 п. 0000064356 00000 п. 0000064666 00000 п. 0000064851 00000 п. 0000065134 00000 п. 0000065479 00000 п. 0000065755 00000 п. 0000066011 00000 п. 0000066376 00000 п. 0000066602 00000 п. 0000066788 00000 п. 0000067043 00000 п. 0000067422 00000 п. 0000067634 00000 п. 0000067960 00000 п. 0000068193 00000 п. 0000068434 00000 п. 0000068716 00000 п. 0000069004 00000 п. 0000069276 00000 п. 0000069503 00000 п. 0000069777 00000 п. 0000070779 00000 п. 0000071315 00000 п. 0000071601 00000 п. 0000071940 00000 п. 0000072259 00000 п. 0000072578 00000 п. 0000072880 00000 п. 0000073225 00000 п. 0000073453 00000 п. 0000073746 00000 п. 0000074050 00000 п. 0000074344 00000 п. 0000074617 00000 п. 0000074899 00000 н. 0000075082 00000 п. 0000075361 00000 п. 0000075659 00000 п. 0000075902 00000 п. 0000076105 00000 п. 0000076349 00000 п. 0000076590 00000 п. 0000076612 00000 п. 0000077477 00000 п. 0000077704 00000 п. 0000077934 00000 п. 0000078107 00000 п. 0000078293 00000 п. 0000078345 00000 п. 0000078439 00000 п. 0000078540 00000 п. 0000078796 00000 п. 0000079042 00000 н. 0000079275 00000 п. 0000079297 00000 п. 0000080195 00000 п. 0000080555 00000 п. 0000080906 00000 п. 0000081293 00000 п. 0000081616 00000 п. 0000081985 00000 п. 0000082306 00000 п. 0000082699 00000 н. 0000082985 00000 п. 0000083350 00000 п. 0000083673 00000 п. 0000084044 00000 п. 0000084276 00000 п. 0000084573 00000 п. 0000084995 00000 п. 0000085346 00000 п. 0000085563 00000 п. 0000085740 00000 п. 0000086041 00000 п. 0000086093 00000 п. 0000086367 00000 п. 0000086672 00000 н. 0000086931 00000 п. 0000087304 00000 п. 0000087497 00000 п. 0000087845 00000 п. 0000088231 00000 п. 0000088568 00000 п. 0000088916 00000 п. 0000089323 00000 п. 0000089666 00000 п. 00000

00000 п. 00000

00000 н. 00000 00000 п. 00000 00000 н. 0000091244 00000 п. 0000091532 00000 п. 0000092185 00000 п. 0000092630 00000 п. 0000092981 00000 п. 0000093244 00000 п. 0000093564 00000 п. 0000093862 00000 п. 0000094127 00000 п. 0000094433 00000 п. 0000094745 00000 п. 0000095098 00000 п. 0000095375 00000 п. 0000095690 00000 н. 0000096030 00000 н. 0000096395 00000 п. 0000096720 00000 н. 0000096996 00000 н. 0000097332 00000 п. 0000097623 00000 п. 0000097958 00000 п. 0000098276 00000 п. 0000098298 00000 н. 0000099112 00000 п. 0000099134 00000 п. 0000099902 00000 н. 0000100125 00000 н. 0000100393 00000 н. 0000100611 00000 н. 0000100663 00000 н. 0000100925 00000 н. 0000101018 00000 н. 0000101115 00000 н. 0000101357 00000 н. 0000101679 00000 п. 0000101922 00000 н. 0000101944 00000 н. 0000102773 00000 н. 0000102795 00000 н. 0000103657 00000 п. 0000103679 00000 н. 0000104515 00000 н. 0000104719 00000 н. 0000104741 00000 н. 0000105531 00000 н. 0000007064 00000 н. 0000009912 00000 н. трейлер ] >> startxref 0 %% EOF 90 0 объект > эндобдж 420 0 объект > поток HWhCB @ H ҫ0 0I! «C @ j! @ (Gp (tT @ Efgf9 {v {ｿ}

.