Разбор и решение задания №6 ОГЭ по математике
Уравнения, неравенства и их системы
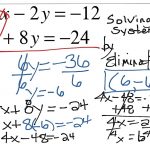В шестом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными.
Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию.
Ответом в задании №6 является целое число или конечная десятичная дробь.
Теория к заданию №6
Ниже я привел теорию по решениям линейных и квадратных уравнений:
Схема решения, правила и алгоритм действий при
Схема решения, правила и порядок действий при решении квадратного уравнения:
В трех типовых вариантах я разобрал данные случаи — в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем — решение полного квадратного уравнения с вычислением дискриминанта.
Разбор типовых вариантов задания №6 ОГЭ по математике
Первый вариант задания (линейные уравнения)
Найдите корень уравнения:
10 ( x — 9 ) = 7
Решение:
Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.
Для начала следует раскрыть скобки: 10x — 90 = 7
Затем переносим 90 в правую часть (не забываем поменять знак):
10x = 7 + 90
10x = 97
Затем делим обе части на 10:
x = 9,7
Ответ: 9,7
Второй вариант задания (неполные квадратные уравнения)
Решите уравнение:
3 x² + 12 x = 0
Решение:
Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:
x ( 3 x + 12 ) = 0
Произведение множителей тогда равно нулю, когда один из множителей равен нолю:
x = 0
или
3 x + 12 = 0
3 x = -12
x = -4
Так как в ответе просят указать наименьший корень, то это -4.
Ответ: -4
Третий вариант задания (квадратные уравнения)
Решите уравнение:
8 x² — 10x + 2 = 0
Решение:
Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:
4 x² — 5x + 1 = 0
Далее вычисляем дискриминант:
D = b² — 4ac
D = 5² — 4 •4•1 = 9
Вычисляем корни:
x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25
x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1
Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25
Ответ: 0,25
Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)
Решите уравнение:
7х — 9 = 40
Решение:
В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой — всё, что известно переносим в правую часть, всё, что неизвестно — оставляем в левой. Далее выполняем необходимое арифметическое действие.
Решение:
7х — 9 = 40
Переносим 9 в правую часть (не забываем про смену знака):
7х = 40 + 9, что эквивалентно
7х = 49
х в нашем случае — это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:
х = 49/7, откуда
х = 7
Ответ: 7
Пятый вариант задания (рациональные уравнения)
Найдите корень уравнения:
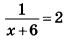
Решение:
Прежде всего, исключим корень, который не входит в ОДЗ:
x+6≠0 → х≠–6
Далее решаем уравнение.
Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает вид пропорции:
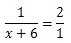
Применим правило пропорции. Перемножим между собой крайние ее члены и средние:
1·1=(х+6)·2
Выполним умножение в левой части уравнения и раскроем скобки справа:
1=2х+12
Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:
2х+12=1
Переносим 12 из левой части в правую:
2х=1–12
2х=–11
Находим корень:
х=–11/2=–5,5
ОДЗ это значение не исключает, поэтому оно является искомым результатом.
Ответ: –5,5
Шестой вариант задания(рациональные уравнения)
Найдите корень уравнения:
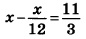
Решение:
Обе части уравнения приводим к единому знаменателю 12:
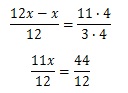
Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем:
11х=44
х=44:11
х=4
Ответ: 4
Разбор и решение задания №3 ОГЭ по математике
Числовые неравенства, координатная прямая
Теория к заданию №3
Для того, чтобы переводить дроби из обыкновенного вида в десятичный, необходимо выполнить деление столбиком.
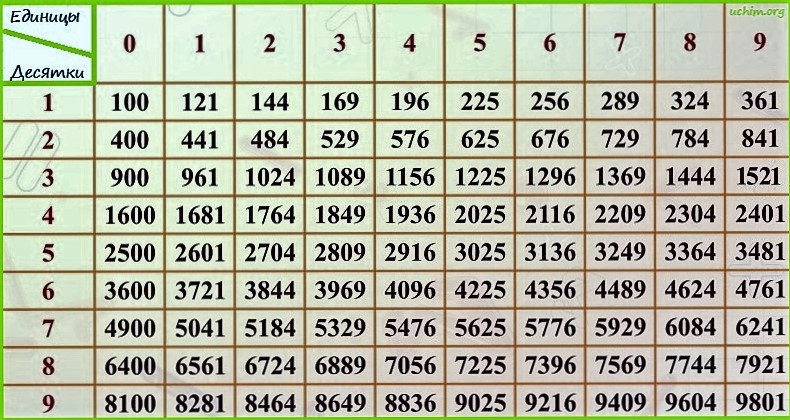
Для успешного вычисления примерного значения корня достаточно иметь представления о вычисляемых подкоренных выражениях, а для этого необходимо хорошо знать таблицу квадратов натуральных чисел!
Таблица квадратов натуральных чисел
В заданиях на определение знака выражения я рекомендую подставлять числа и вычислять выражение — подробная инструкция по этому методу изложена в третьем варианте.
Разбор типовых вариантов задания №3 ОГЭ по математике
Первый вариант задания
Какое из следующих чисел заключено между числами 8 / 3 и 11 / 4 ?
- 2,7
- 2,8
- 2,9
- 3
Решение:
В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:
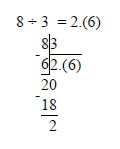
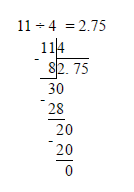
Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75.
Ответ: 1 (2,7)
Второй вариант задания
Какое из данных чисел принадлежит промежутку [ 6 ; 7 ] ?
- √6
- √7
- √38
- √50
Решение:
Для решения этого задания достаточно представлять себе значения чисел меньше и больше заданного, корни которых подлежат вычислению.
- Рассмотрим √6. √4 — это 2, √9 — это 3, значит √6 лежит в промежутке между 2 и 3
- Рассмотрим √7. Ситуация аналогична √6. √4 — это 2, √9 — это 3, значит √6 лежит в промежутке между 2 и 3
- Рассмотрим √38. Ближайшее вычисляемое число меньше 38 — 36, √36 = 6, ближайшее вычисляемое число больше 38 — 49, √49 = 7, значит √38 лежит между 6 и 7
- Рассмотрим √50. Ближайшее вычисляемое число меньше 50 — 49, √49 = 7, ближайшее вычисляемое число больше 50 — 64, √64 = 8, значит √50 лежит между 7 и 8
Значит, нам подходит третий вариант ответа — √38.
Ответ: 3
Третий вариант задания
На координатной прямо отмечены числа a и b:
Какое из приведенных утверждений для этих чисел неверно:
- ab²<0
- a — b > 0
- a + b < 0
- ab < 0
Решение:
Для удобства решения необходимо оценить данные нам числа. Из координатной прямой видно, что a > 0, так как расположено справа от ноля, а b < 0, так как расположено слева. К тому же, b значительно более удалено от ноля, а значит больше по модулю.
Для удобства, исходя из вышеизложенных рассуждений, примем a = 1, а b = -2.
Теперь подставим значения в данные неравенства:
1 • (-2)² = 4 > 0
Значит, утверждение неверно.
1 — (-2) = 3 > 0
Утверждение верно.
1 + (-2) = -1 < 0
Утверждение верно.
1 • (-2) = -2 < 0
Утверждение верно.
Следовательно, правильный ответ первый.
Ответ: 1
Демонстрационный вариант ОГЭ 2019
На координатной прямой отмечена точка А:
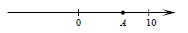
Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?
- 181/16
- √37
- 0,6
- 4
Решение:
Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду.
Оцениваем 181/16 — можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.
Оцениваем √37 — самое близкое значение, из которого вычисляется квадратный корень — это 36, значит √37 — это 6 и что-то еще, что вычислять нам не обязательно. Данное значение нам подходит, так как лежит чуть правее середины отрезка 0-10, как и точка А.
Посмотрим на вариант 0,6 — это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет.
Вариант с ответом 4 также не подойдет по вышеуказанной причине.
Ответ: 2
Четвертый вариант задания
Одно из чисел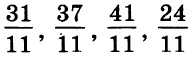 
отмечено на прямой точкой.
Какое это число?
Решение:
Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат.
Итак, выделяем целые части:
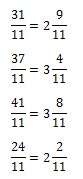
Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.
Ответ: 2
Пятый вариант задания
На координатной прямой точки А, В, С и D соответствуют числам -0,201; -0,012; -0,304; 0,021.
Какой точке соответствует число -0,304?
1) А 2) В 3) С 4) D
Решение:
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304<–0,201<–0,012.
В итоге имеем возрастающий ряд: –0,304; –0,201; –0,012; 0,021.
Поскольку стрелка положительного направления на координатной прямой направлена вправо, то А<B<C<D. Следовательно, А=–0,304; В=–0,201; С=–0,012; D=0,021. Значит, числу –0,304 соответствует точка А.
Ответ: 1
Разбор и решение задания №20 ОГЭ по математике
Анализ геометрических высказываний
В 20 задании из приведенных утверждений необходимо выбрать одно или несколько правильных. Утверждения из общего теоретического курса геометрии, поэтому, какие-то определенные рекомендации здесь дать нельзя, кроме как полного повторения теоретического курса. Другое дело, что если вы точно не знаете какое-либо утверждение, то решить задачу можно наоборот — выбирая и отсеивая неправильные. Это задание не имеет какого либо подхода к решению, однако ниже я привел несколько разобранных задач.
Разбор типовых вариантов задания №20 ОГЭ по математике
Первый вариант задания
Какие из следующих утверждений верны?
- Все диаметры окружности равны между собой.
- Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
- Любые два равносторонних треугольника подобны.
Решение:
Все диаметры окружности всегда равны между собой — это даже интуитивно понятно. Что касается второго утверждения, то оно неверно — вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно — треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны.
Ответ: 1,3.
Второй вариант задания
Какие из следующих утверждений верны?
- Все высоты равностороннего треугольники равны.
- Существуют три прямые, которые проходят через одну точку.
- Если диагонали параллелограмма равны, то он является ромбом.
Решение:
Первое утверждение верно, так как у равностороннего треугольника все стороны равнозначны, а значит и все элементы, проведенные к ним, тоже. Второе утверждение тоже верно, так как нет ограничений на количество произвольных прямых, проходящих через одну точку. Третье утверждение неверно — если диагонали равны, то это либо прямоугольник, либо квадрат.
Ответ: 1,2.
Третий вариант задания
Какие из следующих утверждений верны?
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
- Любой прямоугольник можно вписать в окружность.
- Через заданную точку плоскости можно провести единственную прямую.
Решение:
Первое утверждение верно из общих свойств треугольника — сумма двух сторон всегда больше третьей. Второе утверждение тоже верно — действительно, любой прямоугольник можно вписать в окружность. Третье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку.
Демонстрационный вариант ОГЭ 2019
Укажите номера верных утверждений.
- Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
- Треугольник со сторонами 1, 2, 4 существует.
- Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
- В любом параллелограмме диагонали равны.
Решение:
Проанализируем каждое из утверждений:
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Да, такое утверждение в геометрии есть, с дополнением » и только одну» :
«Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой, и причем только одну.»
2) Треугольник со сторонами 1, 2, 4 существует.
Для существования треугольника должно выполняться следующее правило:
Сумма двух сторон всегда больше третьей. В данном случае это не так, так как 1 + 2 < 4
3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
Действительно, ромб — параллелограмм с равными сторонами, если у него один из углов будет равен 90°, а значит и все остальные, то тогда он станет квадратом.
4) В любом параллелограмме диагонали равны.
Нет, такого утверждения в геометрии нет, они равны только в квадрате и прямоугольнике.
Ответ: 1,3
Четвертый вариант задания
Какое из следующих утверждений верно?
1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом.
2) Смежные углы всегда равны.
3) Каждая из биссектрис равнобедренного треугольника является его высотой.
Решение:
Проанализируем каждое утверждение.
1) Это утверждение верно, поскольку равенство и перпендикулярность диагоналей является одним из свойств именно квадрата.
2) Это утверждение неверно. Основание – соответствующая теорема, которой утверждается, что смежные углы в сумме имеют 1800, т.е. дополняют друг друга до развернутого угла. Следовательно, равенство смежных углов может иметь место только в случае, если достоверно известно, что один из них прямой.
3) Утверждение неверно. Высотой является только биссектриса, опущенная на основание равнобедренного треугольника.
Ответ: 1
Пятый вариант задания
Какое из следующих утверждений верно?
1) Если угол острый, то смежный с ним угол также является острым.
2) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
Решение:
Выполняем анализ утверждений.
1) Согласно теореме о смежных углах, их сумма всегда равна 1800. Это означает, что любой из смежных углов является разностью 1800 и величины 2-го смежного угла. Если первый смежный угол острый, значит, второй равен разности 1800 и острого угла (т.е. угла, меньшего 900), которая в любом случае окажется больше 900. А угол, больший 900, по определению тупой. Итак, утверждение неверно.
2) Одно из свойств ромба заключается в том, что его диагонали перпендикулярны. Однако и диагонали квадрата тоже пересекаются под прямым углом. Но поскольку квадрат является частным случаем ромба, то и в этом противоречия заданному утверждению нет. Т.е. в целом утверждение верно.
3) Одно из основных св-в касательных к окружности заключается в том, что касательная всегда перпендикулярна к радиусу, проведенному из центра этой окружности в точку касания. Оно противоречит заданному утверждению, поэтому утверждение неверно.
Ответ: 2
Разбор и решение задания №15 ОГЭ по математике
Практические задачи по геометрии
15 задание — применение знания геометрии в окружающем мире. Самые распространенные задания — на прямоугольные треугольники и вычисление расстояния по теореме Пифагора, а также определение положения стрелок в градусах. Итак, перейдем к рассмотрению примеров.
Разбор типовых вариантов задания №15 ОГЭ по математике
Первый вариант задания
Какой угол (в градусах) образуют минутная и часовая стрелки часов в 18:00?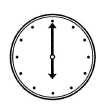
Решение:
Данный пример несложный — стрелки образуют прямую, а значит, угол равен 180 градусов.
Ответ: 180
Второй вариант задания
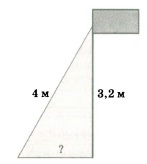
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,2 метра от земли. Длина троса равна 4 метра. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.
Решение:
Так как на чертеже — прямоугольный треугольник, применяем теорему Пифагора:
4² = 3,2² + x²
16 = 10,24 + x²
x² = 16 — 10,24
x² = 5,76
x = √5,76
x = 2,4 метра
Ответ: 2,4 метра
Третий вариант задания
Какой угол (в градусах) описывает минутная стрелка за 4 минуты?
Решение:
Вначале найдем сколько в одной минуте градусов — так как в круге 60 минут и 360 градусов, то:
360 / 60 = 6 градусов — в одной минуте
В 4 минутах, соответственно:
6 • 4 = 24 градуса
Ответ: 24
Демонстрационный вариант ОГЭ 2019
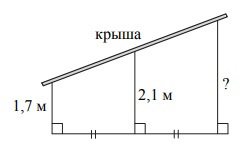
Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,7 м, высота средней опоры 2,1 м. Найдите высоту большой опоры. Ответ дайте в метрах.
Решение:
В данном задании необходимо применить знания из геометрии, а именно:
«Средняя линия трапеции равна среднему арифметическому двух оснований.»
Нам известна средняя линия — средняя опора, и малое основание — малая опора.
Из этих данных находим большее основание большую опору):
( Малое основание + Большее основание ) / 2 = Средняя линия
( 1,7 + Большее основание ) / 2 = 2,1
Можем переписать в виде уравнения, где х — Большее основание
( 1,7 + х ) / 2 = 2,1
Решая, получаем:
х = 2,5 (м)
Ответ: 2,5
Четвертый вариант задания
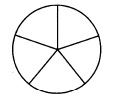
На рисунке изображено колесо с пятью спицами.
Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 600?
Решение:
Из рисунка видно, что кол-во секторов, на которые колесо разделяется спицами, равно кол-ву спиц. Добавив еще одну спицу, получим еще один сектор. И так далее. Поэтому в произвольной ситуации число спиц и число секторов колеса всегда будет равно.
В колесе, которое нам предлагается рассмотреть, углы между любой парой спиц равны (по условию =600). Значит, колесо разделено на одинаковые сектора. Полный круг колеса составляет угол в 3600. Если каждый сектор равен 600, то всего имеется секторов
3600 : 600 = 6.
Поскольку число секторов и спиц совпадает, то и число спиц равно 6.
Ответ: 6
Пятый вариант задания
Проектор полностью освещает экран А высотой 50 см, расположенный на расстоянии 100 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 150 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
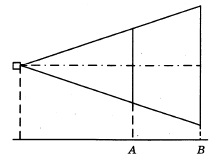
Решение:
Малый экран, с линиями, показывающими полное его освещение проектором, образует т.н. малый треугольник. Соответственно, большой экран образует аналогичный треугольник, который назовем большим.
Т.к. экраны расположены параллельно между собой, то малый и большой треугольники подобны (у них боковые стороны являются продолжением друг друга, третьи стороны параллельны, следовательно, образуемые в треугольниках соответствующие углы равны). Если так, то соответствующие стороны и другие элементы треугольников пропорциональны. В нашем случае АС пропорционально КВ, а PD пропорционально PN:
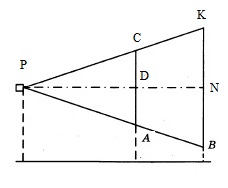
Тогда составим пропорцию:
АС : КВ = PD : PN.
Применив правило пропорции (произведение крайних ее членов = произведению средних), выразим искомую величину PN (миним.расстояние от проектора до большого экрана):
PN = KB ·PD / AC.
По условию КВ=150 см (величина большого экрана), PD=100 см (расстояние от проектора до малого экрана), АС=50 см (величина малого экрана).
Вычислим PN:
PN = 150 · 100 / 50 = 300 (см).
Ответ: 300
Разбор и решение задания №17 ОГЭ по математике
Окружность, круг и их элементы
В 17 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.
По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Ответом в задании 17 является целое число или конечная десятичная дробь.
Теория к заданию №17
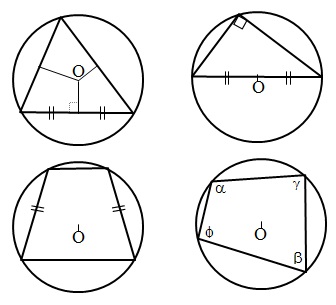
Несмотря на то, что в задании №17 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность».
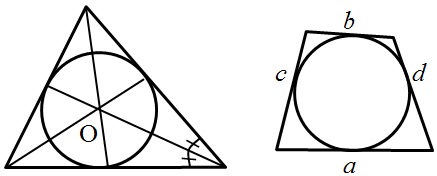
Начнем рассмотрение с понятия вписанная окружность:
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
- Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d
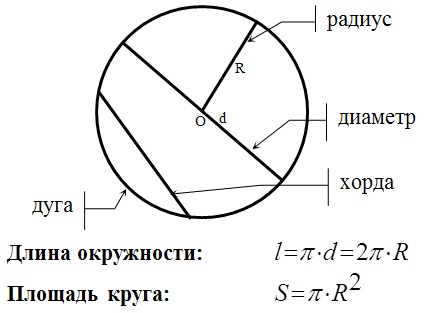
Длинна окружности и площадь:
Касательная и секущая:
- Касательная – прямая, имеющая с окружностью одну общую точку.
- Секущая – прямая, имеющая с окружностью две общие точки.
Описанная окружность и её свойства:
- Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
- Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
- Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
- Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.
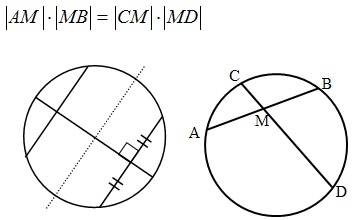
Хорда – отрезок, соединяющий две точки окружности.
- Диаметр, делящий хорду пополам, перпендикулярен хорде.
- В окружности равные хорды равноудалены от центра окружности.
- Отрезки пересекающихся хорд связаны равенством:
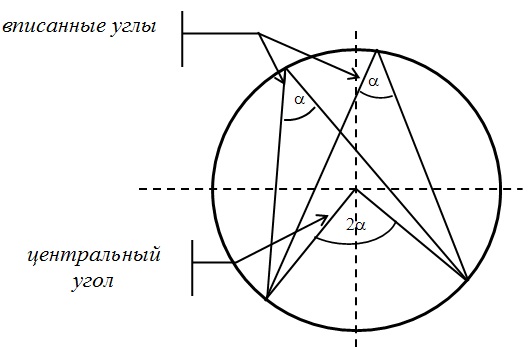
Центральный и вписанный углы:
Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.
Разбор типовых вариантов заданий №17 ОГЭ по математике
Первый вариант задания
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
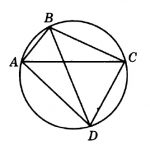
Решение:
Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:
∠ABD = 92 — 60 = 32
Ответ: 32°
Второй вариант задания
Касательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах.
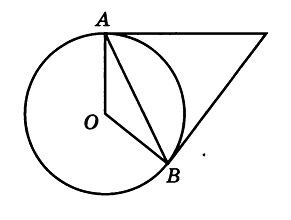
Решение:
Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:
(180 — 2) / 2 = 89°
Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.
Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:
90 — 89 = 1°
Ответ: 1
Третий вариант задания
В треугольнике ABC известно, что AC = 16, BC = 12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
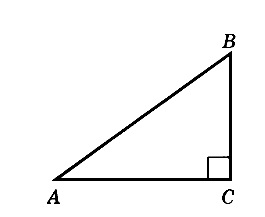
Решение:
Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом.
По теореме Пифагора найдем гипотенузу AB:
AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400
AB = √400 = 20
Гипотенуза равна 20, значит радиус — 10.
Ответ: 10
Демонстрационный вариант ОГЭ 2019
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.
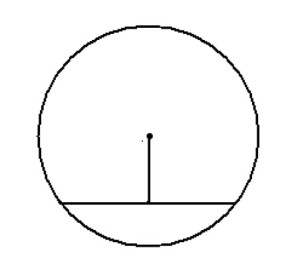
Решение:
Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:
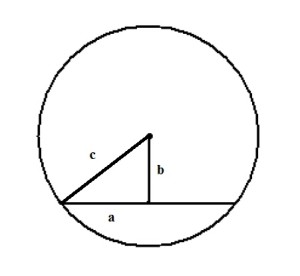
Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a:
a² + b² = c²
a² = c² — b² = 13² — 5² = 169 — 25 = 144
Откуда
а = √144 = 12
Но а — лишь половина хорды, поэтому вся хорда равна 2 • а = 24
Ответ: 24
Четвертый вариант задания
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 10. Найдите ВС, если АС=16.
Решение:
Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 900, и, следовательно, ∆АСВ прямоугольный.
Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора
АС2+ВС2=АВ2 (1)
По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20.
Тогда из (1) получим:
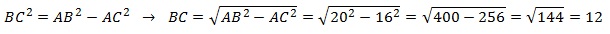
Ответ: 12
Пятый вариант задания
Треугольник АВС вписан в окружность с центром в точке О. Найдите угол АСВ, если угол АОВ равен 1130. Ответ дайте в градусах.
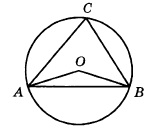
Решение:
Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=1130.
Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=1130, то угол АСВ равен
0,5 · ᴗАВ = 0,5 · 1130 = 56,50.
Ответ: 56,5
Разбор и решение задания №18 ОГЭ по математике
Треугольники, четырёхугольники, многоугольники и их элементы
В 18 задании нас ждут задачи с четырехугольниками, а именно трапецией, ромбами и произвольными параллелограммами. Необходимо знать формулы вычисления площади всех вышеперечисленных четырехугольников, а также их свойства.
В демонстрационном варианте ОГЭ предлагается задание, связанное с нахождением площади фигуры.
Как найти площадь треугольника, трапеции, параллелограмма, круга и сектора?
С одной стороны, мы знаем соответствующие формулы. Для выполнения большинства заданий этого будет вполне достаточно, но иногда надо проявить и определенную сообразительность. В некоторых случаях будет разумно представить
заданную геометрическую фигуру как сумму или как разность более простых фигур. Безусловно, площадь измеряется в соответствующих единицах. Например, если длины сторон фигуры заданы в сантиметрах, то вычисляемая площадь автоматически измеряется в квадратных сантиметрах. Чтобы не загромождать условие задачи информацией, которая при ее решении фактически не используется, единицы измерения, если они не существенны, не указаны.
Ответом в задании 16 является целое число или конечная десятичная дробь.
Теория к заданию №18
Приступим к разбору теории.
Выпуклый четырехугольник:
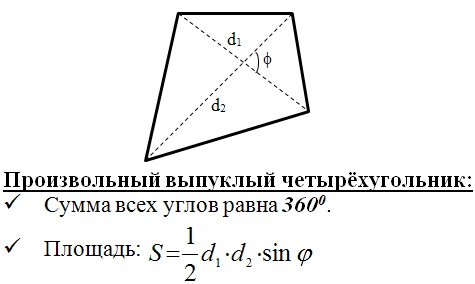
Правильный многоугольник:
- Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
- Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.
Ниже я привожу формулы для вычисления элементов произвольного правильного многоугольника:
Разберем пример четырехугольника — ромб.
Параллелограмм, все стороны которого равны называется ромбом.
- Диагональ ромба является его осью симметрии.
- Диагонали взаимно перпендикулярны.
- Диагонали являются биссектрисами углов.
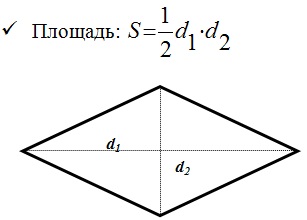
Трапеция:
Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.
Ниже я разобрал типовые примеры 11 задания. Давайте приступим к их рассмотрению.
Разбор типовых вариантов задания №18 ОГЭ по математике
Первый вариант задания
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.
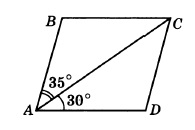
Решение:
Найдем угол BAD — это сумма углов, на которые диагональ делит этот угол, поэтому:
∠BAD = 35° + 30° = 65°
Вспоминаем, что в параллелограмме противоположные углы равны, а соседние в сумме дают 180°.
Значит:
∠ABC = ∠ADC = 180 — 65 = 115°
∠BAD = ∠BCD = 65°
Так как нас просят найти меньший угол, то это 65.
Ответ: 65
Второй вариант задания
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основаниям равен 45°. Найдите площадь трапеции.
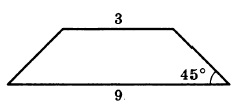
Решение:
Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:
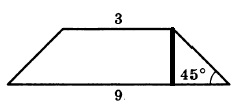
После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный — потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.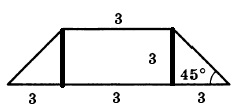
Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.
Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:
( 9 — 3 ) / 2 = 3
А так как треугольники равнобедренные, то и высота равна 3.
Отсюда можем найти площадь:
S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18
Ответ: 18
Третий вариант задания
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
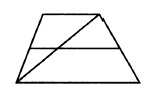
Решение:
Средняя линия трапеции является еще и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны:
10 / 2 = 5
11 / 2 = 5,5
Так как нас просят найти больший из отрезков, то ответ 5,5.
Ответ: 5,5
Демонстрационный вариант ОГЭ 2019
Найдите площадь трапеции, изображённой на рисунке.
Решение:
Для решения необходимо помнить и знать формулу для вычисления площади трапеции, а это
«полусумма оснований умноженная на высоту»
Непонятно, зачем нам дана информация о значениях длин отрезков, тем не менее решение выглядит так:
- Верхнее основание равно 7
- Нижнее основание равно 9 + 12 = 21
- Полусумма (21 + 7) / 2 = 14
- Высота равна 12
Таким образом, площадь равна 14 • 12 = 168 см²
Ответ: 168
Четвертый вариант задания
Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь ромба.
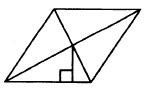
Решение:
Площадь ромба будем искать по формуле:
S=ah,
где a – сторона ромба, h– высота, опущенная на сторону а.
По условию а=4.
Найдем h. Для этого рассмотрим ∆ОКС и ∆АРС:
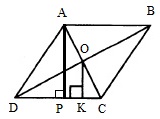
Здесь ОК || АР, причем ОК проходит через середину АС (т.к. АВСD ромб, то его диагонали в т.О делятся пополам). Значит, ОК – ср.линия ∆АРС. Поэтому АР=2ОК. Т.к. пор условию ОК=1, то АР=2·1=2. Т.о., h=АР=2.
Отсюда получаем:
S=4·1=4.
Ответ: 4
Пятый вариант задания
Найдите величину острого угла параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 410. Ответ дайте в градусах.
Решение:
Т.к. АК биссектриса, то углы ВАК и КАD равны. Обозначим ∠ВАК через х.
Поскольку АВСD параллелограмм, то ∠В+∠А=1800. Т.к. АК биссектриса, то ∠А=2х. Тогда ∠В=1800–2х.
Рассм. ∆АВК:
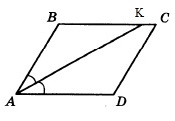
По теореме о сумме углов треуг-ка ∠ВАК+∠В+∠ВКА=1800.
По условию ∠ВКА = 410.
Отсюда получаем:
х+ 1800–2х+410=1800
х–2х=1800–1800–410
–х=–410
х=410
Значит, искомый (острый) ∠А=2·410=820
Ответ: 82
Разбор и решение задания №13 ОГЭ по математике
Расчеты по формулам
Перейдем к рассмотрению тестового задания ОГЭ по математике — задания №13. В данном задании нам необходимо поработать с формулами — либо просто подставить значения в формулу и провести вычисления, либо вначале выразить неизвестную величину, а затем произвести подстановку.
Итак, рассмотрим конкретные типовые примеры.
Разбор типовых вариантов задания №13 ОГЭ по математике
Первый вариант задания
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
Решение:
Выразим сопротивление R:
R = P / I2
Подставим значения в полученную формулу:
R = 224 / 42 = 224 / 16 = 14 ом
Ответ: 14
Второй вариант задания
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле:
С = 6000 + 4100•n,
где n — число колец, установленных в колодце.
Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.
Решение:
В данном случае выражать из формулы нам ничего не требуется, поэтому подставим в данную форму лу значение n = 7:
С = 6000 + 4100•7 = 6000 + 28700 = 34700
Ответ: 34700
Третий вариант задания
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле:
T = 2 • √l
где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Решение:
Выразим из формулы l, для этого возведем обе части в квадрат, получим:
T ² = 4 • l ,
тогда:
l = T ² / 4
Подставляя значения из условия, получаем:
l = 3 ² / 4 = 9 / 4 = 2,25
Ответ 2,25
Демонстрационный вариант ОГЭ 2019
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой
tF = 1,8 • tC + 32,
где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
Какая температура по шкале Фаренгейта соответствует -25° по шкале Цельсия?
Решение:
Подставляем значение -25 в формулу:
tF = 1,8 • (-25) + 32 = -45 + 32 = -13
Ответ: -13
Четвертый вариант задания
Закон Кулона описывает взаимодействие между двумя электрическими зарядами. Закон можно записать в виде
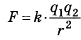
где F — сила взаимодействия в ньютонах, q1 и q2 — величины зарядов в кулонах, k — коэффициент пропорциональности в Н·м2/Кл2, а r — расстояние между зарядами в метрах. Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9·109 Н·м2/Кл2, q2=0,004 Кл, r=600 м, F=0,4 Н.
Решение:
Поскольку искомая величина стоит в формуле справа и не является результирующей), необходимо преобразовать эту формулу. Результатом преобразования в данном случае должно стать уравнение, в котором слева будет зафиксировано искомое q1, а справа – все остальные величины, фигурирующие в начальной формуле.
Для удобства преобразования сначала поменяем местами левую и правую части начальной формулы:
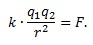
Далее r2 из знаменателя слева переносим в числитель справа, а k и q2 из числителя слева – в знаменатель справа. Получим:
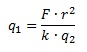
Результат мы получим в кулонах, как и требуется по условию. Основание для этого утверждения таково: т.к. все величины в условии даны в единицах СИ, то и результат будет получен только в СИ, а в этой системе единицей измерения эл.заряда является кулон (Кл).
Подставим в полученную формулу числовые данные из условия и вычислим искомую величину:
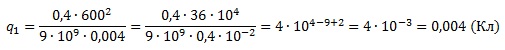
Ответ: 0,004
Пятый вариант задания
Площадь четырёхугольника можно вычислить по формуле
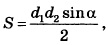
где d1 и d2 – длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1=13, sinα=3/13, а S=25,5.
Решение:
Т.к. искомая величина является в формуле частью выражения справа, то ее необходимо выразить через остальные величины. Тогда получим:
В полученную формулу подставим числовые данные из условия и вычислим искомую диагональ:
Ответ: 17