Уравнения с параметром, формулы и примеры
Определение и формулы уравнений с параметром
ОПРЕДЕЛЕНИЕ Уравнением вида с неизвестными и параметрами называется уравнением с параметрами.Например.
ОПРЕДЕЛЕНИЕРешить уравнение, содержащее параметры, это значит, для каждой допустимой системы значений этих параметров найти множество всех решений заданного уравнения.
Два уравнения с параметрами называются эквивалентными, если при всякой допустимой системе значений параметров имеют одно и то же множество решений.
Для уравнения с параметром особым или контрольным значением параметра называется такое значение, при котором обращается в нуль коэффициент при неизвестном.
При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.
Линейное уравнение
записанное в общем виде, можно рассматривать как уравнение с параметрами, где является неизвестной величиной, а — параметры.
Для линейного уравнения (1) особым значением параметра есть значение .
Рассмотрим два случая значения указанного параметра (параметр равен своему особому значению и отличен от него).
Случай 1а. Если , то при любой паре параметров и уравнение (1) имеет единственное решение
Случай 2а. Если , то уравнение (1) принимает вид:
А тогда значение является особым значением параметра . Поэтому рассмотрим далее два случая этого параметра:
Случай 1b. При уравнение решений не имеет: .
Случай 2b. При уравнение принимает вид
Решением последнего является любое действительное число, то есть .
Примеры решения задач
ПРИМЕР 1| Задание | Решить уравнение |
| Решение | Определим контрольные значения параметра, то есть такие значения, при которых коэффициент при неизвестной величине обращается в нуль, то есть необходимо найти решение уравнения . Его решениями являются значения и . При полученных значениях параметра деление обеих частей уравнения на коэффициент при неизвестной невозможно. Но если , , то деление возможно.
Для нахождения решения заданного уравнения разобьем множество всех допустимых значений параметра на следующие случаи: 1) ; 2) ; 3) , .
1) При заданное уравнение принимает вид
Полученное уравнение решений не имеет (см. случай 1b), поскольку умножение любого числа на нуль в результате дает нуль. Итак, имеем, что . 2) При решаемое уравнение записывается в виде
Его решением является любое действительное число (случай 2b): . 3) При , левую и правую часть исходного уравнения можно поделить на коэффициент при неизвестной . В итоге получаем
Откуда, после сокращения числителя и знаменателя на , находим корень
|
| Ответ | Если ,то уравнение решений не имеет; если , то ; если , , то |
| Задание | Решить иррациональное уравнение |
| Решение | Для нахождения корней заданного уравнения возведем обе его части в квадрат, а в конце выполним проверку полученных решений, для предотвращения появления сторонних решений. Исходное уравнение запишем в виде:
Решаем полученное квадратное уравнение. Его дискриминант:
В зависимости от знака дискриминанта, полученное квадратное уравнение может иметь два различных действительных корня, кратный корень или вовсе действительных корней не иметь: 1) :
2) :
3) . Сделаем проверку: 1) подставляем в полученное уравнение значения . Для имеем:
Рассмотрим возможные случаи знака подмодульного выражения: — если . В пересечении с неравенством , для которого получен корень, имеем, что . В этом случае
а равенство принимает вид:
Таким образом, является корнем исходного уравнения для . — если . В пересечении с имеем, что . В этом случае модуль раскрывается со знаком «минус»:
равенство записывается в виде:
То есть для решений нет. Для будем иметь:
Левая часть последнего равенства принимает неположительные значения (то есть ), а правая строго положительна: . Поэтому равенство не может быть верным, а, значит, значение не является корнем заданного уравнения. 2) :
Получили неверное равенство, значит, значение не является решением исходного уравнения. |
| Ответ |
ru.solverbook.com
Уравнения с параметром | LAMPA
Исследование квадратного трёхчлена
Часто уравнение с параметром удаётся привести к квадратному. В таких задачах нужно найти значения параметра, при которых корни лежат на некотором промежутке. Для решения подобных примеров необходимо произвести анализ расположения корней. Чтобы определить взаимное расположение границ промежутка и корней уравнения, следует воспользоваться следующими утверждениями:
- Чтобы число ppp находилось между корнями квадратичной функции f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c, необходимо и достаточно, чтобы выполнялось условие a⋅f(p)<0a\cdot f(p)\lt 0a⋅f(p)<0;
- Чтобы число ppp было меньше корней квадратичной функции f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c, необходимо и достаточно, чтобы {D≥0,a⋅f(p)>0,p<−b2a;\begin{cases} D\ge 0{,}\\ a\cdot f(p)\gt 0{,}\\ p\lt -\frac{b}{2a}{;}\end{cases}⎩⎪⎨⎪⎧D≥0,a⋅f(p)>0,p<−2ab;
- Чтобы число ppp было больше корней квадратичной функции f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c, необходимо и достаточно, чтобы {D≥0,a⋅f(p)>0,p>−b2a.\begin{cases} D\ge 0{,}\\ a\cdot f(p)\gt 0{,}\\ p\gt -\frac{b}{2a}{.}\end{cases}⎩⎪⎨⎪⎧D≥0,a⋅f(p)>0,p>−2ab.
Для использования приведённых выше утверждений не нужно непосредственно вычислять корни уравнения.
При каких значениях параметра aaa оба корня уравнения x2+ax−1=0x^2+ax-1=0x2+ax−1=0 меньше 3?
Воспользуемся утверждением, приведённым выше, для f(x)=x2+ax−1f(x)=x^2+ax-1f(x)=x2+ax−1. Система примет вид: {D>0,1⋅f(3)>0,3>−a2⋅1.\begin{cases} D\gt 0{,}\\ 1\cdot f(3)\gt 0{,}\\ 3\gt -\frac{a}{2\cdot 1}{.}\end{cases}⎩⎪⎨⎪⎧D>0,1⋅f(3)>0,3>−2⋅1a.D=a2+4>0,D=a^2+4\gt 0,D=a2+4>0,Первое условие выполняется автоматически. Запишем два других условия:1⋅f(3)>0⇔32+a⋅3−1=3a+8>0⇔a>−83,1\cdot f(3)\gt 0 \,\,\,\,\Leftrightarrow \,\,\,\, 3^2+a\cdot 3-1=3a+8\gt 0\,\,\,\,\Leftrightarrow \,\,\,\,a\gt -\frac{8}{3},1⋅f(3)>0⇔32+a⋅3−1=3a+8>0⇔a>−38,3>−a2⇔a>−6.3\gt -\frac{a}{2}\,\,\,\,\Leftrightarrow \,\,\,\,a\gt -6.3>−2a⇔a>−6.
Взяв наиболее сильное из этих условий, получим a>−83a\gt -\frac{8}{3}a>−38.
Ответ: (−83;+∞)(-\frac{8}{3}; +\infty )(−38;+∞).
Параметр как равноправная переменная
Несмотря на то, что выше параметр рассматривался как фиксированное, но неизвестное число, можно считать его равноправной переменной.
При каких aaa уравнение a+a+sinx=sinx\sqrt{a+\sqrt{a+\sin x}}=\sin xa+a+sinx=sinx имеет решения?
Обозначим sinx=t\sin x = tsinx=t. Исходное уравнение примет вид a+a+t=t\sqrt{a+\sqrt{a+t}}=ta+a+t=t. С учётом ∣t∣≤1|t|\le 1∣t∣≤1 это уравнение равносильно системе: {a+t=(t2−a)2,1≥t≥0,t2≥a.\begin{cases} a+t=(t^2-a)^2{,}\\ 1\ge t\ge 0{,}\\ t^2\ge a{.}\end{cases}⎩⎪⎨⎪⎧a+t=(t2−a)2,1≥t≥0,t2≥a.
Уравнение удобно представить как квадратное относительно aaa. Получим a2−a(2t2+1)+t4−t=0⇔(a−t2−t−1)(a−t2+t)=0⇔a^2-a(2t^2+1)+t^4-t=0\,\,\Leftrightarrow \,\,(a-t^2-t-1)(a-t^2+t)=0\,\,\Leftrightarrowa2−a(2t2+1)+t4−t=0⇔(a−t2−t−1)(a−t2+t)=0⇔⇔[a=t2+t+1,a=t2−t.\Leftrightarrow \,\,\left[\begin{array}{l} a=t^2+t+1{,}\\ a=t^2-t{.}\end{array}\right.⇔[a=t2+t+1,a=t2−t.
Так как t2≥at^2\ge at2≥a и 1≥t≥01\ge t\ge 01≥t≥0, то t2−a+t+1>0t^2-a+t+1\gt 0t2−a+t+1>0. Поэтому первое равенство совокупности не может выполняться. Тогда выполняется второе, и исходная система равносильна такой: {a=t2−t,1≥t≥0,t2≥a.⇔{a=t2−t,1≥t≥0.\begin{cases} a=t^2-t{,}\\ 1\ge t\ge 0{,}\\ t^2\ge a{.}\end{cases}\,\,\,\,\Leftrightarrow \,\,\,\,\begin{cases} a=t^2-t{,}\\ 1\ge t\ge 0{.}\end{cases}⎩⎪⎨⎪⎧a=t2−t,1≥t≥0,t2≥a.⇔{a=t2−t,1≥t≥0.
Условие t2≥at^2\ge at2≥a выполняется автоматически при a=t2−ta=t^2-ta=t2−t и t≥0t\ge 0t≥0.
lampa.io
Линейные уравнения с параметром
Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где \(p(a)\) и \(q(a)\)- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все \(x\) при всех значениях параметра \(a\). Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение:
\(x=\frac{q(a)}{p(a)}\) при \(p(a)≠0.\) Если же \(p(a)=0\) и \(q(a)=0\), то решением данного уравнения является любое число. И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:Пример 1
Решить уравнение \(ax-5a=7x-3\) при всех возможных \(a\).
Перенесем все одночлены с \(x\) влево, а оставшиеся члены – вправо. И вынесем \(x\) за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случайОтвет: При \(a=7\) \(x∈∅;\)
при \(a≠7\) \(x=\frac{5a-3}{a-7}.\)
Пример 2
Найдите все \(a\), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число.
Раскроем скобки и перенесем все члены, содержащие \(x\), влево, а остальные – вправо. $$ax-6x+5x=-5a+4+a^2$$ Приведем подобные: $$ax-x=a^2-5a+4$$ И вынесем за скобку \(x\) и разложим квадратный многочлен на множители: $$x(a-1)=a^2-5a+4$$ $$x(a-1)=(a-1)(a-4)$$ Первый случай: \((a-1)=0\),т.е. \(a=1\) $$x*0=(a-1)(a-4)$$ $$x*0=0.$$ Решением уравнения будет любое число.Второй случай: \((a-1)≠0\), т.е. \(a≠1\) $$x=\frac{(a-1)(a-4)}{a-1}=a-4.$$ Решением данного уравнения будет одно число \(x=a-4\).
Ответ: \(a=1.\)
Пример 3
Решите уравнение \(\frac{x}{5a+x}-\frac{5a+x}{x-5a}=\frac{100a^2}{25a^2-x^2}.\)
Из ОДЗ видно, что \(5a+x≠0\) и \(x-5a≠0,\) таким образом, \(x≠±5a.\) Приведем уравнение к общему знаменателю \(x^2-25a^2\) и умножим на него все уравнение: $$x^2-5ax-x^2-10ax-25a^2=-100a^2$$ $$-15ax=-75a^2$$ $$ax=5a^2.$$После преобразований получили линейное уравнение.
Первый случай: \(a=0.\) Получаем уравнение \(0*x=0.\) Решениями этого уравнения будет любое число, кроме \(x=0\) (ОДЗ \(x≠±5a\)).
Второй случай: \(a≠0.\) Выражаем \(x=\frac{5a^2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ.
Ответ: При \(a=0\) решениями уравнения будут все действительные числа, кроме \(x=0.\) Если \(a≠0,\) то решений нет.
sigma-center.ru
Один из методов решения уравнений с параметром
Уравнениями с параметром называются уравнения, у которых коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами.
Решить уравнение с параметром – это значит:
а) исследовать, при каких значениях параметров уравнение имеет корни и при каких не имеет;
б) выяснить количество корней при различных значениях параметров;
в) найти все выражения для корней.
Уравнения с параметром весьма различны по структуре:
Моя работа посвящена отысканию метода решения уравнений с параметрами вида
F(xn; p2) =0
В основе этого метода лежит взгляд на параметр, как на переменную, т.е. уравнение F(xn;p?)=0 можно рассматривать как квадратное относительно параметра р.
Задача 1. Пусть нужно решить уравнение с параметром
Преобразуем данное уравнение
Это уравнение 4-й степени относительно х, причём содержит и . Как его решить? Но заметим, что это уравнение является квадратным относительно , т.е. вида . Применим наш метод:
1. Перепишем уравнение в виде
, т.е. рассмотрим его как квадратное относительно .
2. Найдем корни уравнения по формуле корней квадратного уравнения:
3. Далее используем графический метод. В системе координат построим параболы , и ,
4. Найдём точки пересечения графиков функций. Для этого приравняем
, отсюда , т.е. точка пересечения единственная .
5. По рисунку видно, что горизонтальная прямая не имеет общих точек с параболами, если она проходит ниже , т.е.
при данное уравнение не имеет корней
при уравнение имеет единственный корень
при уравнение имеет два корня т.к. прямая имеет две точки пересечения с параболой , отсюда , ,
при и — три корня
при
при
при и уравнение имеет четыре корня
Этот метод не является универсальным, но во многих случаях является весьма результативным и позволяет решать уравнения повышенной сложности, второй степени и выше.
Задача 2. Определить число корней уравнения в зависимости от параметра а х4-10х3-2(а-11)х2+2(5а + 6)х +2а + а2 =0 (1)
Решение. Уравнение является квадратным относительно параметра а. Перепишем (1) в виде (2)
Найдём дискриминант
Решая уравнение (2), находим
Построим в системе координат (х; а) графики функций
и (рис 2)
Найдем точки пересечения графиков функций. Для этого приравняем отсюда . Далее рассуждая аналогично, как и в задаче 1, получим
Ответ: если , уравнение корней не имеет;
если один корень;
если , уравнение имеет два корня;
если три корня;
если - четыре корня.
Задача 3. Найти все значения параметра р, при которых уравнение (3)
имеет ровно три решения.
Решении. Уравнение (3) является квадратным относительно р. Перепишем его в виде
Найдем корни уравнения
В системе координат (х; р) построим параболы
и (рис.2)
Данное уравнение имеет три решения при тех значениях параметра р, при которых горизонтальная прямая имеет три точки пересечения с параболами. Таким образом, уравнение (3) имеет три решения в следующих случаях:
1) прямая проходит через вершину одной параболы и пересекает другую в двух точках. Это возможно, когда т.е. при уравнение имеет три решения;
2) прямая проходит через точку пересечения парабол. Найдём абсциссу точки пересечения парабол, для этого решим уравнение
Если то т.е. при прямая пересекает параболы в трех точках, значит, исходное уравнение имеет три корня.
Ответ:
Задача 4. При каких значениях параметра а существует единственная пара (х; у), удовлетворяющая уравнению
(4)
Решение: Уравнение – квадратное относительно х.
(5)
1. Контрольным значением параметра является число , при котором уравнение (5) примет вид отсюда . Видно, что в этом случае решениями уравнения будут все пары , т.е. при исходное уравнение имеет бесконечное множество решений.
2. Пусть . Дискриминант уравнения (5)
Если т.е. , то , исходное уравнение имеет решение только тогда, когда , а — единственное решение.
Если же , исходное уравнение относительно х имеет решение при любом у.
Ответ: .
Задача 5. Решите уравнение
(6)
относительно х
Решение. Уравнение является квадратным относительно р. Перепишем уравнение (6) в виде
(7)
Дискриминант квадратного уравнения (7)
Решая (7), получим
Здесь возможны случаи.
1. Уравнение (6) имеет четыре корня, если
Решая систему, получаем . Таким образом, при уравнение (6) имеет четыре корня ,
2. Уравнение (6) имеет три корня, если
Решая систему, получим Значит, при уравнение (6) имеет три корня
3. Уравнение (6) имеет два корня, если
Решая систему, получим , значит, при этих значениях параметра р уравнение (6) имеет два корня
4. Уравнение (6) имеет один корень, если
Решая систему, получим . Следовательно, при решением уравнения (6) будет .
5. Уравнение (5) не имеет корней, если
Ответ: если — корней нет;
если
если ;
если
если
Этот метод не является универсальным, но во многих случаях является весьма результативным и позволяет решать уравнения повышенной сложности. Иногда трудно предвидеть будет ли применение этого метода результативным, но такие уравнения существуют и поэтому его надо знать.
Например, с помощью этого метода можно решить следующие уравнения:
из сборника для подготовки к ЕГЭ.
из сборника Сканави
и другие.
urok.1sept.ru
Решение уравнений с параметром. Видеоурок. Алгебра 9 Класс
На этом уроке мы рассмотрим решение различных уравнений с параметром.
Когда один футболист хочет отдать другому «пас на ход», он должен решить уравнение: с какой силой и под каким углом нужно отдать пас, чтобы другой футболист успел к мячу.
Рассмотрим упрощенную модель: футболист  отдает мяч по прямой, а футболист
отдает мяч по прямой, а футболист  бежит по заданной прямой
бежит по заданной прямой  с заданной постоянной скоростью. При этом скорость и направление паса футболист
с заданной постоянной скоростью. При этом скорость и направление паса футболист 

Рис. 1. Иллюстрация к рассматриваемой задаче
Можем перевести эту задачу на математический язык: при каких начальных параметрах паса (скорости и угла) расстояние  мяч пройдет за то же время, что и футболист пробежит расстояние
мяч пройдет за то же время, что и футболист пробежит расстояние  ? Тогда:
? Тогда:


Но  – гипотенуза прямоугольного треугольника
– гипотенуза прямоугольного треугольника  ,
,  – катет, поэтому они связаны соотношением:
– катет, поэтому они связаны соотношением:

Получаем:
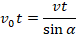
Откуда:

Мы нашли скорость паса при заданном угле. Можем найти угол при заданной скорости паса:

Это примеры простейших уравнений с параметром. В первом случае параметром выступает угол, а скорость – это неизвестная. Во втором – наоборот.
Можно рассмотреть похожую задачу с противоположной целью: капитаны судов должны решать вопрос, какими должны быть скорости и направление движения, чтобы корабли не столкнулись.
Сегодня на уроке мы поговорим о технике решения уравнений и неравенств с параметром.
Принципиально новых алгоритмов и методов не появится – мы будем использовать уже полученные нами навыки. Но при этом взглянем на решение уравнений и неравенств чуть шире и сделаем акцент на некоторых нюансах. Начнем с решения самых простых – линейных уравнений.
Вспомним, что любое линейное уравнение можно привести к виду 
 и
и  – некоторые числа.
– некоторые числа.Это общий вид, и он нам удобен, поскольку описывает целый класс уравнений. Так вот, эти числа,  и
и  , еще называют параметрами. Соответственно, уравнение
, еще называют параметрами. Соответственно, уравнение  – это линейное уравнение с двумя параметрами:
– это линейное уравнение с двумя параметрами:  и
и  .
.
Смотрите: ничего нового, это все то же уравнение, алгоритм решения которого мы уже все знаем. Но есть нюансы. Решить уравнение с параметром – значит найти его корни при всевозможных значениях параметров. Мы знаем, что при  корнем уравнения будет:
корнем уравнения будет:

Но нужны решения при всех значениях параметров. Что же будет при  ? Если
? Если  , наше уравнение примет вид
, наше уравнение примет вид или просто
или просто  . Какие решения имеет это уравнение?
. Какие решения имеет это уравнение?
Если  , то получим правильное равенство. Значит, решением будут все действительные числа.
, то получим правильное равенство. Значит, решением будут все действительные числа.
Если же  , то равенство будет неверным. В таком случае уравнение не имеет решений.
, то равенство будет неверным. В таком случае уравнение не имеет решений.
Запишем ответ:
- Если
 , то:
, то:  .
. - Если
 и
и  , то
, то  (все действительные числа).
(все действительные числа). - Если
 и
и  , то
, то  (пустое множество, нет решений).
(пустое множество, нет решений).
Проанализируем решение. Мы действовали по известному нам алгоритму решений линейных уравнений.
Шаг 1. Перенести все слагаемые с неизвестной величиной  в одну сторону, остальные – в другую.
в одну сторону, остальные – в другую.
Шаг 2. Привести подобные слагаемые.
Шаг 3. Разделить на коэффициент при  .
.
Правда, первые два шага у нас уже были выполнены. При этом мы отдельно рассмотрели значение . Почему? Потому что при
. Почему? Потому что при  мы не можем совершить шаг 3: деление на ноль не определено.
мы не можем совершить шаг 3: деление на ноль не определено.
Этот принцип можно применить для решения любых уравнений и неравенств с параметром: мы действуем по стандартному алгоритму для данного типа математической модели, но на каждом шаге проверяем, не возникает ли недопустимых действий или других особенностей. С алгоритмами мы уже знакомы, так что посмотрим, какие могут возникать «особенности».
Задание 1. Решить уравнение при всех значениях параметра  :
:

Решение
Это линейное уравнение, поскольку неизвестная  стоит в первой степени. Действуем по алгоритму решения линейного уравнения.
стоит в первой степени. Действуем по алгоритму решения линейного уравнения.
Шаг 1. Перенести слагаемые с неизвестной в одну сторону, остальные – в другую:

Шаг 2. Привести подобные слагаемые. Для этого вынесем  за скобку:
за скобку:

Шаг 3. Нужно разделить на коэффициент при  . Но выражение
. Но выражение  может равняться 0, тогда мы не сможем выполнить деление. Поэтому нужно отдельно рассмотреть этот случай:
может равняться 0, тогда мы не сможем выполнить деление. Поэтому нужно отдельно рассмотреть этот случай:

Решим это квадратное уравнение, чтобы определить значения параметра:

Тогда:
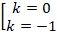
Итак, при  и
и 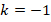 мы не можем выполнить 3 шаг нашего алгоритма. Подставим эти значения в уравнение и посмотрим, какой вид оно примет:
мы не можем выполнить 3 шаг нашего алгоритма. Подставим эти значения в уравнение и посмотрим, какой вид оно примет:
при  :
:


Уравнение не имеет решений.
при 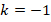 :
:


Решение – все действительные числа.
Если же  , то мы можем выполнить деление в уравнении:
, то мы можем выполнить деление в уравнении:

Или после упрощения:


Ответ: при  :
:  ; при
; при 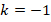 :
:  ; при
; при  и
и  :
:  .
.
Теперь перейдем к линейным неравенствам с параметром. Алгоритм их решения практически такой же, как и у уравнений. Только возникает еще одна особенность на последнем шаге: знак неравенства меняется на противоположный, если делим обе части неравенства на отрицательное выражение.
Задание 2. Решить неравенство при всех значениях параметра  .
.

Решение
Шаг 1. Здесь уже выполнен.
Шаг 2. Выносим за скобки  :
:

Шаг 3. Обе части неравенства нужно разделить на  . Но, во-первых, это выражение может быть равно
. Но, во-первых, это выражение может быть равно  , тогда результат деления будет не определен. Во-вторых, мы не знаем знак этого выражения. Соответственно, не знаем, изменится ли знак неравенства. Поэтому рассмотрим отдельные случаи.
, тогда результат деления будет не определен. Во-вторых, мы не знаем знак этого выражения. Соответственно, не знаем, изменится ли знак неравенства. Поэтому рассмотрим отдельные случаи.
1. Первый случай:

Решая это уравнение для параметра , получаем:
, получаем:

Рассмотрим его отдельно, подставив в неравенство:


Неравенство верное, значит, решение – все действительные числа.
2. Второй случай:

Решая неравенство, получим:

При этих значениях мы делим на положительное выражение:
мы делим на положительное выражение:

Знак неравенства не изменяется:

3) Третий случай:

Решая неравенство, получим:

В этом случае делим на отрицательное число, знак меняется на противоположный:

Ответ: при  ,
,  ; при
; при  ,
,  ; при
; при  ,
,  .
.
С решением еще одного линейного неравенства с параметром вы можете ознакомиться ниже.
Решение неравенства с параметром
Задание. Решить неравенство при всех значениях параметра  :
:

Мы уже решали аналогичное уравнение. После выполнения первых двух шагов алгоритма получаем:

Как и в решении предыдущего линейного неравенства, рассматриваем 3 случая:
-
 – при этом мы не можем выполнить деление, эти значения нужно рассмотреть отдельно.
– при этом мы не можем выполнить деление, эти значения нужно рассмотреть отдельно. -
 – в этом случае знак неравенства не изменится при делении.
– в этом случае знак неравенства не изменится при делении. -
 – в этом случае знак неравенства изменится на противоположный.
– в этом случае знак неравенства изменится на противоположный.
Для каждого случая нам нужно найти значения  , при которых выражение
, при которых выражение  больше, меньше или равно нулю. Это удобно сделать сразу:
больше, меньше или равно нулю. Это удобно сделать сразу:
1. Решения уравнения мы уже знаем:  или
или 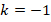 .
.
2 и 3. При решении неравенств для параметра  можем использовать метод интервалов. Корни соответствующего уравнения:
можем использовать метод интервалов. Корни соответствующего уравнения:  или
или 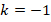 . Осталось расставить их на оси и определить знаки на интервалах (см. рис. 2).
. Осталось расставить их на оси и определить знаки на интервалах (см. рис. 2).

Рис. 2. Иллюстрация к заданию
То есть  при
при  ;
;  при
при  .
.
Со значениями параметра определились, переходим к решению исходного неравенства для  .
.
1. Отдельно рассматриваем случаи  и
и 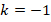 . При
. При  :
:


Неравенство верное, решение – любое действительное число. При 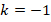 :
:


Неравенство неверное, решений нет.
2. При  знак неравенства не изменится при делении на
знак неравенства не изменится при делении на  :
:


3. При  знак неравенства изменится на противоположный:
знак неравенства изменится на противоположный:


Ответ: при  :
:  ; при
; при 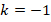 :
:  ; при
; при  :
:  ;
;  :
:  .
.
Теперь перейдем к решению квадратных уравнений с параметром. Мы изучали несколько способов решения квадратных уравнений, но для уравнений с параметром нам понадобится четкий алгоритм – решение с помощью дискриминанта.
Выделим особенности, которые могут возникнуть в ходе решения уравнения вида  . Во-первых, они могут возникнуть уже на этапе определения типа уравнения. Если
. Во-первых, они могут возникнуть уже на этапе определения типа уравнения. Если  , то полученное уравнение будет уже не квадратным, а линейным.
, то полученное уравнение будет уже не квадратным, а линейным.
Вторая особенность связана с дискриминантом. Помним, что в зависимости от знака дискриминанта квадратное уравнение имеет два или одно решение или вообще не имеет решений в действительных числах.
Итак, мы указали особенности, знаем общий алгоритм решения квадратных уравнений. Перейдем к практике.
Задание 3. Решить уравнение для всех значений параметра  :
:

Решение
Коэффициент при  равен
равен  , это точно квадратное уравнение. Вычисляем дискриминант:
, это точно квадратное уравнение. Вычисляем дискриминант:

Видим, что дискриминант зависит от параметра и его знак мы не можем однозначно определить. Рассматриваем отдельно возможные варианты:
- Если
 , то уравнение имеет два действительных корня.
, то уравнение имеет два действительных корня. - Если
 – один действительный корень.
– один действительный корень. - Если
 , то уравнение не имеет действительных корней.
, то уравнение не имеет действительных корней.
Найдем значения параметра, при которых выполняется каждое из этих условий:
1.



2.


3. 

Итак, при  уравнение имеет два корня. Находим их по известной формуле:
уравнение имеет два корня. Находим их по известной формуле:

Упростив выражение:


При уравнение имеет один корень:
уравнение имеет один корень:

При  уравнение не имеет действительных корней.
уравнение не имеет действительных корней.
Ответ: при  ,
,  ; при
; при ,
,  ; при
; при  ,
,  .
.
Задание 4. Решить уравнение для всех значений параметра  :
:

Решение
Обратим внимание на коэффициент при  . Он может быть равен нулю, и в этом случае уравнение будет не квадратным, а линейным. Эту ситуацию рассматриваем отдельно:
. Он может быть равен нулю, и в этом случае уравнение будет не квадратным, а линейным. Эту ситуацию рассматриваем отдельно:
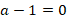

При получим линейное уравнение:
получим линейное уравнение:


Если же  , то уравнение будет квадратным. Вычисляем дискриминант:
, то уравнение будет квадратным. Вычисляем дискриминант:


Оцениваем знак дискриминанта. Можно, как и в предыдущем примере, решать уравнения и неравенства:



А можно сразу отметить, что  всегда неотрицательная величина. Т. е.
всегда неотрицательная величина. Т. е.  только при
только при  ; в остальных случаях это положительная величина.
; в остальных случаях это положительная величина.
Получаем, что при  уравнение имеет один корень:
уравнение имеет один корень:

В остальных случаях имеем два корня:

Рассмотрев корни по отдельности, выражение можем еще упростить:

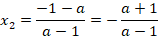
Ответ: при  ,
,  ; при
; при  ,
,  ; при
; при  и
и  ,
,  ,
,  .
.
Мы с вами разобрали основные задания с параметрами: решение линейных уравнений и неравенств, а также квадратных уравнений. Параметры могут встретиться и в более сложных типах уравнений и неравенств, а также их системах.
Но принцип их решения будет абсолютно такой же – действуем по известному алгоритму, на каждом шаге обращаем внимание на особенности: возможное деление на ноль, смену знака неравенства, извлечение корней, раскрытие модуля и пр.
Иногда для поставленной задачи нам не нужно находить общее решение уравнения, а нужно всего лишь узнать какую-то информацию о его корнях. Например, узнать количество корней уравнения или их расположение относительно некоторого фиксированного числа. В таком слу
interneturok.ru
Решение показательных уравнений с параметрами
Цели урока: Учащиеся должны знать способы решений уравнений вида – показательная функция и уметь применять при решении задач.
Ход урока.
Для первой группы учащихся выдавались следующие задания.
Для каждого значения a решить уравнения:
Задания для второй группы учащихся.
Указать число решений в зависимости от параметра а.
Третья группа решает уравнения, сводящиеся к квадратным.
Задание 1. Решить уравнение p · 4x – 4 · 2x + 1 = 0 и указать число решений в зависимости от параметра p.
Задание 2. При каких a уравнение 9x + (2a + 4) · 3x + 8a + 1 = 0 имеет единственное решение.
Задание 3. Указать число решений уравнения 49x + 2p · 7x + p2 – 1 = 0 в зависимости от параметра p.
Задание 4. При каких значениях p уравнение 4x – (5p – 3) · 2x + 4p2 – 3p = 0 имеет единственное решение.
Выступление первой группы – решение показательных уравнений вида
Докладывает лидер первой группы и привлекает к своему докладу участников этой группы. То есть диалог идёт ученик – ученик.
Решение исходного уравнения сводится к решению линейного уравнения с параметрами kx = b.
Если k = 0, b = 0, то 0 · x = 0, – любое действительное число.
Если k = 0, b ≠ 0, то 0 · x = b – нет решений.
Если k ≠ 0, то , один корень.
Задание 1. Решить уравнение .
Докладчик решает у доски с комментариями, остальные записывают в тетрадях.
Значит уравнение (1) можно представить в виде (a – 1)(a + 4)x = (a – 1)(a – 1)(a – 3).
Исследуем полученное уравнение:
Ответ:
На этом выступление первой группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 1.
Выступление второй группы – решение уравнений вида
Докладывает лидер второй группы и привлекает к обсуждению этого вопроса всех учащихся. Исходное уравнение равносильно уравнению ax2 + bx + c1 = c0, или ax2 + bx + c = 0.
Далее идёт диалог ученик–ученик.
- Какое уравнение получили? – Это уравнение степени не выше второй.
- При a = 0, bx + c = 0, получили линейное уравнение, которое может иметь одно решение, не иметь корней, или иметь бесконечное множество решений.
- При a ≠ 0, ax2 + bx + c = 0, квадратное уравнение.
- От чего зависит число решений квадратного уравнения? – Число решений квадратного уравнения зависит от дискриминанта. Если D = 0 то квадратное уравнение имеет одно решение. Если D > 0, то два решения. Если D < 0, то решений нет.
Задание 1. Решить уравнение .
Данное уравнение равносильно (a – 1)x2 + 2(a + 3)x + a + 2 = 0.
Ответ:
На этом выступление второй группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 2.
Выступление третьей группы – решение уравнений вида af2(x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.
Слово предоставляется выступающему от третьей группы. Он докладывает, что их группа решала уравнения вида: (1) af2(x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.
Исходное уравнение (1) равносильно
Далее докладчик задаёт вопросы, а учащиеся отвечают на них.
При каких условиях уравнение (1) имеет один корень?
- При a = 0 уравнение (2) становится линейным, значит может иметь только один корень, и он должен быть положительным.
- Если D = 0, уравнение (2) имеет один корень, и он должен быть положительным.
- Если D > 0, уравнение (2) имеет два корня, но они должны быть различных знаков.
- Если D > 0, уравнение (2) имеет два корня, но один из низ нуль. А второй положительный.
При каких условиях уравнение (1) имеет два корня?
Исходное уравнение имеет два корня, если уравнение (2) имеет два корня и оба они положительны.
При каких условиях уравнение (1) не имеет корней?
- Если D < 0, то исходное уравнение не имеет корней.
- Если D ≥ 0.
а) Уравнение (2) имеет один корень, но он отрицательный.
б) Уравнение (2) имеет два корня, но они оба отрицательные.
в) Уравнение (2) имеет два корня. Но один из них нуль, а другой – отрицательный.
Результаты обсуждения этого вопроса заносятся в таблицу.
Далее докладчик решает на доске и класс вместе с ним.
Задание 1. Решить уравнение p · 4x – 4 · 2x + 1 = 0 и указать число решений в зависимости от параметра p.
Ответим на вопрос: При каких значениях p уравнение (1) имеет один корень?
- Если одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t < 0 – нет решений.
- . Это необходимое условие того, чтобы был единственный корень в уравнении (1). Достаточность нужно проверить.
одно решение - Если p ≠ 0, D > 0.
Уравнение будет иметь единственное решение при условии. Что дискриминант уравнения (2) есть число положительное, но корни при этом имеют различные знаки. Эти условия достигаются с помощью теоремы Виета. Чтобы корни квадратного трёхчлена были действительными и имели различные знаки, необходимо и достаточно выполнение соотношений.
Итак, уравнение (1) имеет единственное решение при p ≤ 0, p = 4.
Теперь остаётся ответить на вопрос. При каких условиях исходное уравнение (2) имеет два решения? Это возможно, если уравнение (2) имеет два корня и оба они положительны. По теореме Виета для того, чтобы корни квадратного трёхчлена были действительными и при этом оба были положительными, необходимо и достаточно выполнение соотношений.
Исходное уравнение имеет два корня при 0 < p < 4.
Осталось выяснить при каких значениях p исходное уравнение не имеет корней. Это возможно в двух случаях. Если D < 0, и если D > 0, то уравнение (2) имеет корни, но они оба отрицательны.
Итак, D < 0, 16 – 4p < 0, p > 4. При p > 4 – нет решений. Второе условие равносильно следующим соотношениям.
Значит уравнение (1) не имеет решений при p > 4.
Ответ:
- При p = 4, p ≤ 0 одно решение.
- При 0 < p < 4 два решения.
- При p > 4 нет решений.
На этом выступление третьей группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 3.
Домашнее задание.
Задание 1. Найти все значения параметра a, при которых уравнение (a – 3) · 4x – 8 · 6x + (a +3) 9x = 0 не имеет корней.
Задание 2.Указать число решений уравнения p · 2x + 2–x – 5 = 0 в зависимости от параметра p.
Задание 3. Выяснить при каких значениях a уравнение . имеет решения, найти эти решения.
Задание 4. Найти все значения p при которых уравнение (p – 1) · 4x – 4 · 2x + (p + 2) = 0 имеет хотя бы одно решение.
Задание 5. Указать число решений уравнения a · 12|x| = 2 – 12–|x| в зависимости от параметра a.
urok.1sept.ru
Алгебраические уравнения высших степеней с параметрами
1.1. Общая методическая концепция решения уравнений с параметрами
Пусть дано уравнение F(x, a) = 0, (1)
если ставится задача для каждого значения а А решить уравнение (1) относительно х, т.е. получить уравнение
х = f(a), (2)
то уравнение (1) называется уравнением с неизвестным х и параметром а. А – область изменения параметра. Принято считать, что А – множество действительных чисел. Решить уравнение (1) – значит решить множество уравнений, которые получаются из уравнения (1) при а R. Сделать это можно, если по некоторому признаку разбить множество А на подмножества и решить заданное уравнение на каждом из них. Значения а называются контрольными.
1.2. Использование параметра как равноправной переменной
Некоторые уравнения бывает целесообразно решать, рассматривая их как уравнение именно относительно параметра, который фигурирует в условии, а не относительно искомой переменной. Этот путь эффективен, в частности, в тех случаях, когда степень переменной относительно высока, а степень параметра равна двум.
Пример 1. Решить уравнение с параметром.
2x3 – (а+2)х2 – ах + а2 = 0 (1)
Решение: Данное уравнение можно рассматривать как квадратное относительно параметра а, переписав его в виде:
а2 – х(х+1)а – 2х2 + 2х3 = 0 (2)
Найдем дискриминант D.
D = х2 (х+1)2 – 8(х3 – х2) = х4 — 6х3 + 9х2 = х2(х2 — 6х + 9) = х2(х — 3)2.
D = х2(х — 3)2
Найдем корни уравнения (2).
; а2 = 2х.
Получим уравнение (а – х2 + х)(а – 2х) = 0 равносильное исходному уравнению, которое ещё в свою очередь равносильно совокупности
Рассмотрим уравнение х2 – х – а = 0, D = 1 – 4а.
D = 0 при а = -1/4 один корень х = 1/2
D < 0 при а < — 1/4 корней нет
D > 0 при а > -1/4 два корня
Рассмотрим уравнение х = а/2, при а = -1/4, х = -1/8.
Выбираем ответ.
Ответ: при а > -1/4 три корня: х1 = а/2,
при а = -1/4 два корня: х1 = -1/8; х2 = ½
при а < — 1/4 один корень: х = а/2.
Упражнения
Решить уравнения.
- 2x4 – (а+2)х3 – (а – 1)х2 + (а2 – 1) = 0;
- x4 + 6х3 + (4 – 2а)х2 – (6а + 1)х + а2 + а = 0;
- х3 + (2а – 3)х2 + (а2 – 4а + 2)х – а2 + 2а = 0;
- х3 — (2а + 3)х2 + (а2 + 4а + 2)х – а2 – 2а = 0.
1.3. Графический способ решения уравнений с параметрами
Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. В самом деле, поскольку параметр «равен в правах» с переменной, то ему, естественно можно выделить и свою координатную ось. Таким образом, возникает координатная плоскость (х; а). Рассмотрим примеры.
Пример 1. В зависимости от параметра а определить число корней уравнения.
x4 – 10х3 – 2(а — 11)х2 + 2(5а + 6)х + 2а + а2 = 0;
Решение. Рассмотрим это уравнение как квадратное относительно а.
а2 + 2а(1 + 5х – х2) + (х4 – 10х3 + 22х2 + 12х) = 0;
Найдем дискриминант
D/4 = 1 + 25х2 + х4 + 10х – 10х3 – 2х2 – х4 + 10х3 – 22х2 – 12х = х2 – 2х +1 = = (х – 1)2
Найдем а1 и а2 ; а1 = х2 -5х – 1 + х – 1 = х2 — 4х – 2;
а2 = х2 -5х – 1 — х + 1 = = х2 – 6х.
Теперь обращаемся к координатной плоскости (х; а).
х2 — 4х – 2 = х2 – 6х, 2х = 2, х = 1, а(1) = -5.
Ответ: если а < -9, то нет решений;
если а = -9, то одно решение;
если -9 < a < -6, то два решения;
если а = -6 или а = -5, то три решения;
если -6 < а < -5 или а > -5, то четыре решения.
Упражнения
Найти все значения параметра а, при каждом из которых уравнение имеет три решения.
- (х2 – 12а)2 – 24х2 + 32х + 96а = 0;
- (2х2 – а)2 – 24х2 + 16х + 4а = 0;
- (2х2 – а)2 = 13х2 + 6х – 2а = 0.
1.4. Использование свойств функций для решения алгебраических уравнений
На выпускных экзаменах за курс средней школы встречаются уравнения с параметром, решение которых связано с использованием четности функций. Напомним определение четности функции.
Определение. Функция f(x) называется четной, если f(-x) = f(x) для любого х из области определения этой функции. График четной функции симметричен относительно оси ординат. У четной функции область определения симметрична относительно начала координат.
Пример 1. Может ли при каком-нибудь значении а уравнение
2х8 – 3ах6 + 4х4 – ах2 = 5 иметь 5 корней?
Решение. Обозначим f(x) = 2х8 – 3ах6 + 4х4 – ах2. f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х0 – тоже, х = 0 не является корнем данного уравнения (0 ≠ 5). Следовательно, число корней у этого уравнения при любом действительном а четно, поэтому 5 корней оно иметь не может.
Ответ: не может.
Пример 2. При каком значении а уравнение х10 – а|х| + a2 – а = 0 имеет единственное решение?
Решение. Обозначим f(x) = х10 – а|х| + a2 – а, f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х0 – тоже. Значит для единственности решения необходимо, чтобы х0 = 0. В этом случае из уравнения получим: a2 – а = 0, а = 0 или а = 1. Проверим достаточность каждого из полученных значений параметра а,
при а = 0, х10 = 0, т.е. х = 0 единственное решение.
при а = 1, х10 — |x| = 0. Корнями являются числа ± 1, 0.
Ответ: при а = 0 уравнение имеет единственное решение.
Упражнения
- Может ли при каком-нибудь а уравнение 2х6 – х4 – ах2 = 1 иметь три корня?
- Может ли при каком-нибудь а уравнение 2х6 – 2ах4 + 3х2 = 4 иметь пять корней?
- При каком значении а уравнение имеет единственное решение?
1.5. Метод замены
Как мы уже знаем, что рациональное и быстрое решение уравнения зависит от замены переменной. Рассмотрим примеры, для решения которых нужны специальные замены, которые приводят как раз к быстрому решению уравнений.
Пример 1. Решить уравнение (х + 2а)(х +3а)(х + 8а)(х + 12а) = 4а2х2,
где а – параметр.
Решение. Данное уравнение относится к уравнению вида
(х + а)(х +b)(х + c)(х + d) = Eх2 (см. п. 2.5 (3))
Используя специфику решения такого уравнения, будем иметь:
(х2 + 14ах +24а2)( х2 + 11ах +24а2) = 4а2х2
Если а = 0, то х = 0.
Обратно, если а ≠ 0, то х ≠ 0.
Разделим обе части этого уравнения на а2х2, будем иметь
В полученном уравнении сделаем подстановку и получим уравнение (у + 14)(у + 11) = 4, у2 + 25у + 150 = 0, у1 = — 15, у2 = — 10.
Таким образом, получим два уравнения
и
Решим первое уравнение х2 + 15ах + 24а2 = 0, D = 129a2, х1,2
Решим второе уравнение х2 + 10ах + 24а2 = 0, D = 4a2
х3 = -6а, х4 = -4а
Ответ: если а = 0, то х = 0
если а ≠ 0, то х1,2, х3 = -6а, х4 = -4а
Упражнения
- Найдите все действительные значения величины а, при которых уравнение х(х +1)(х + а)(х + 1 + а) = а2 имеет четыре действительных корня.
- Решить уравнение х4 + а4 – 3ах3 + 3а2х = 0.
- При каких значениях а уравнение (х2 – 2х)2 — (а + 2)(х2 – 2х) + 3а – 3 = 0 имеет четыре корня?
- Решить уравнение (х + а)(х + 2а)(х + 3а)(х + 4а) = 3а4
urok.1sept.ru
 .
.