Урок алгебры в 10-м классе по теме «Уравнения, содержащие переменную под знаком модуля»
Цели урока: создать условия для:
образовательные:
- обобщения и закрепления умений решать уравнения с переменной под знаком модуля;
- промежуточного контроля и оценки качества усвоения учащимися способов решения уравнений;
развивающие:
- формирования устной и письменной речи, познавательной активности, творческих способностей учащихся;
- развития логического мышления;
воспитательные:
- воспитание навыков самоконтроля;
- воспитание ответственного отношения к учебному труду.
Тип урока: обобщения и закрепления знаний и умений.
Ход урока
I. Определение темы и цели урока
Совместно с учащимися формулируем тему урока;
Совместно с учащимися ставим цели и задачи урока;
Определяем основные этапы урока.
Для этого обратиться к учащимся с вопросами:
Решением каких уравнений мы занимались на предыдущих уроках?
Что нужно знать для этого?
Каким образом можно это закрепить , проверить?
II. Обобщение и систематизация знаний
1. Учитель: Сформулируйте определение модуля числа.
Ученики: Модулем действительного
числа х называется само это число, если х ≥ 0, и
противоположное ему число, если х < 0, т.е.
2. Учитель: Основные свойства модуля числа?
Ученики: Для любых действительных чисел х и у :
2 = х2;
3. Учитель: Решение уравнения вида
Ученики: Уравнение
4. Учитель: Решение уравнения вида
Ученики: Т.к. то
5. Учитель: Решение уравнения видаУченики: Уравнения такого вида решаются методом разбиения на промежутки. Для этого надо: 1) найти нули выражений, стоящих под знаком модуля; 2) разбить ОДЗ переменной на промежутки, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак; 3) на каждом из полученных промежутков решить уравнение с учётом определения модуля. Объединение решений на указанных промежутках и составляет все решения данного уравнения.
6. Учитель: Решение уравнения, в котором под знаком модуля находится выражение, содержащее модуль?
Ученики: Надо сначала освободиться от внутренних модулей, а затем в полученных уравнениях раскрыть оставшиеся модули.
III. Устная работа
Учащиеся выполняют задания устно, комментируя своё решение.
1. Раскрыть знак модуля:
а) б)
Решение:
а)
б)
в)
2. Найти множество решений уравнения:
а) б) в) г)
Решение:
а) х+5=1 или х+5=-1
х=-4 х=-6
Ответ: -6; -4.
б) т.к. при любом х, а -7, то уравнение решений не имеет.
Ответ:
в)
2-8х = 0
х=0,25
Ответ: 0,25
г)
Решений нет
Ответ:
IV. Закрепление умений учащихся решать уравнения
4 ученика решают на доске, остальные в тетрадях. Затем сверяют решения, при необходимости исправляют ошибки. Работающие у доски отвечают на возникающие вопросы.
1) .
Решение: Данное
уравнение равносильно совокупности систем:
Ответ: 1,5; .
2) .
Решение:
Ответ: ; 1; 3.
3)
Решение:
3х+4 = 0, х = -;
х-3 = 0, х = 3.
1) х < , тогда данное уравнение равносильно уравнению:
-3х – 4 + 2·(3-х) = 16 -3х-4+6-2х = 16 -5х = 14 х = -2,8 — является корнем уравнения.2) , тогда 3х + 4 +2· (3 - х) = 16 3х + 4 + 6 – 2х = 16 х = 6 – не является корнем уравнения.
3) х > 3, тогда 3х + 4 + 2·(х – 3) = 16 х = 3,6 – является корнем уравнения.
Ответ: -2,8; 3,6.
4) = 4.
Решение: Данное уравнение равносильно совокупности двух систем:
Вторая система решений не имеет. Первая система равносильна совокупности двух систем: х = 0.
Ответ: 0.
V. Самостоятельная работа (разноуровневая)
Самостоятельная письменная работа в трёх уровнях с последующей сдачей учителю. Ученик может выбрать любой из трёх уровней.
Первый уровень оценивается оценкой «3», второй – оценкой «4», третий – «5».
I уровень
Решить уравнения:
а) ;
б)
II уровень
Решить уравнения:
а) ;
б)
III уровень
Решить уравнения:
а) ;
б) Найти сумму корней уравнения:
VI. Постановка домашнего задания
1. Решить уравнения:
а) х2 = ;
б) ;
в)
г)
* д) Найти сумму целых решений уравнения
VII. Итоги урока
Какими навыками, умениями овладели?
Какими понятиями, приёмами воспользовались при решении уравнений?
Решение каких уравнений вам показалось сложным?
Чему надо уделить особое внимание?
urok.1sept.ru
Рівняння з модулями. Приклади
«Розв’язати рівняння з модулями» або «Знайти усі розв’язки рівняння з модулями» – одні з найпопулярніших завдань в шкільному курсі математики, та на першому курсі у ВУЗах при вивченні модулів. Завдання легко зводяться до звичайних рівнянь при знанні правил, а вони досить прості. При розкритті модуля потрібно знайти точки в яких підмодульна функція приймає нульове значення. Дійсну вісь розбити знайденими точками на інтервали та встановити знаки функції на кожному з них. Дальше розкривають модулі за правилом:
Якщо підмодульна функція додатна, то модулі розкривають без змін. Якщо від’ємна, то розкриваючи модуль функцію беруть зі знаком мінус.
Все це напряму випливає з означення модуля числа:
Після обчислень перевіряють, чи належить розв’язок розглядуваному інтервалі чи ні. В такий спосіб відсівають зайві результати.
Для наочності перейдемо до обчислень.
Приклад 1. Знайти розв’язок рівняння
Розв’язання: Задане завдання є найпростішим типом рівнянь з модулями. В першу чергу рівняння містить модуль один раз та змінна входить лінійно.
Знаходимо точку, в якій вираз під знаком модуля перетворюється в нуль
Справа від цієї точки вираз під модулем приймає додатне значення, зліва – від’ємне.
Розкриваючи модуль, отримаємо два рівняння з умовами на невідому
Знаходимо розв’язки
Такого типу рівняння з модулем можна розв’язати графічним методом. В результаті отримаємо наступний вигляд функцій
Приклад 2. Знайти корені рівняння
Розв’язання: Розв’язуємо за схемою попереднього прикладу.
Знаходимо точки в яких модулі перетворюються в нуль.
Обидві точки розділяють дійсну вісь на інтервали.
Позначаємо знаки підмодульних функцій на знайдених інтервалах. Знаки встановлюємо простою підстановкою точок з інтервалу
Для зручності можете позначати інтервали графічно, декому це дуже допомагає, однак можна обійтися лише наведеними вище записами.
Розкриваємо модулі, враховуючи знаки та знаходимо розв’язки.
Останній розв’язок не має змісту, оскільки не належить проміжку на якому його знаходимо. Таким чином рівняння задовільняють значення
Графік модуль-функцій наведено нижче, точки їх перетину і є розв’язком.
Приклад 3. Знайти розв’язок рівняння
Розв’язання: Знаходимо точки, які розбивають вісь на області знакосталості
Визначаємо знаки підмодульних функцій на цих областях
Розкриваємо модулі та обчислюємо
Другий і третій розв’язки не належать проміжку, отже рівнянню відповідає лише x=-4.
Графіки модулів зображено графічно
Приклад 4. Знайти розв’язок рівняння
Розв’язання: Маємо квадратний тричлен, який зводиться до розв’язування двох рівнянь
Розв’язуємо кожне з квадратних рівнянь. Дискримінант у них буде однаковий
Знаходимо корені першого рівняння
та другого
Позначені корені рівняння не належать області, на якій шукали розв’язок. Остаточно отримали два корені рівняння з модулем
На графіку модуль-функції розв’язок є перетином з віссю Ox
Приклад 5. Визначити корені рівняння
Розв’язання: Точка x=-4 ділить область на інтервали
На першому інтервалі отримаємо квадратне рівняння
на другому відповідно нас
yukhym.com
Рівняння з модулями
Тема уроку. Рівняння з модулями
Мета уроку: формувати навики розв’язування рівнянь з модулями, вміння висловлювати і обґрунтовувати свою думку, розвивати логічне мислення, навики самостійної роботи і роботи в парі
Тип уроку: урок формування вмінь і навичок
Обладнання: мультимедійна дошка, картки для роботи в парах
Хід уроку
І. Організаційний момент
ІІ. Повідомлення теми уроку
Тема уроку. Рівняння з модулями
Якщо хочете навчитися плавати, то сміливо заходьте у воду, а якщо хочете навчитися розв’язувати рівняння, то розв’язуйте їх!
Саме ці слова американського видатного математика, педагога Джорджа Пойа будуть епіграфом до нашого уроку.
Ми з вами продовжуємо розв’язувати різні види рівнянь з модулями; вчимося обґрунтовувати свою думку; працювати, довіряючи один одному; відточуємо свої вміння розв’язувати цікаві логічні завдання.
ІІІ. Актуалізація опорних знань
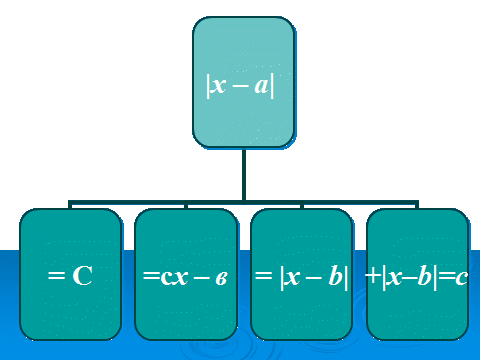1. На початку уроку повторимо вивчені види рівнянь. Проведемо для цього ’’Аукціон рівнянь’’. На діаграмі, перед нами чотири види рівнянь .
1) Вашій увазі пропонується перше рівняння виду: | x – a | = C.
– Хто бажає презентувати дане рівняння?
Відповіді учнів:
Якщо С < 0, то рівняння розв’язку немає, виходячи із означення модуля.
Якщо С > 0, то рівняння має два корені.
Якщо С = 0, то рівняння має один корінь.
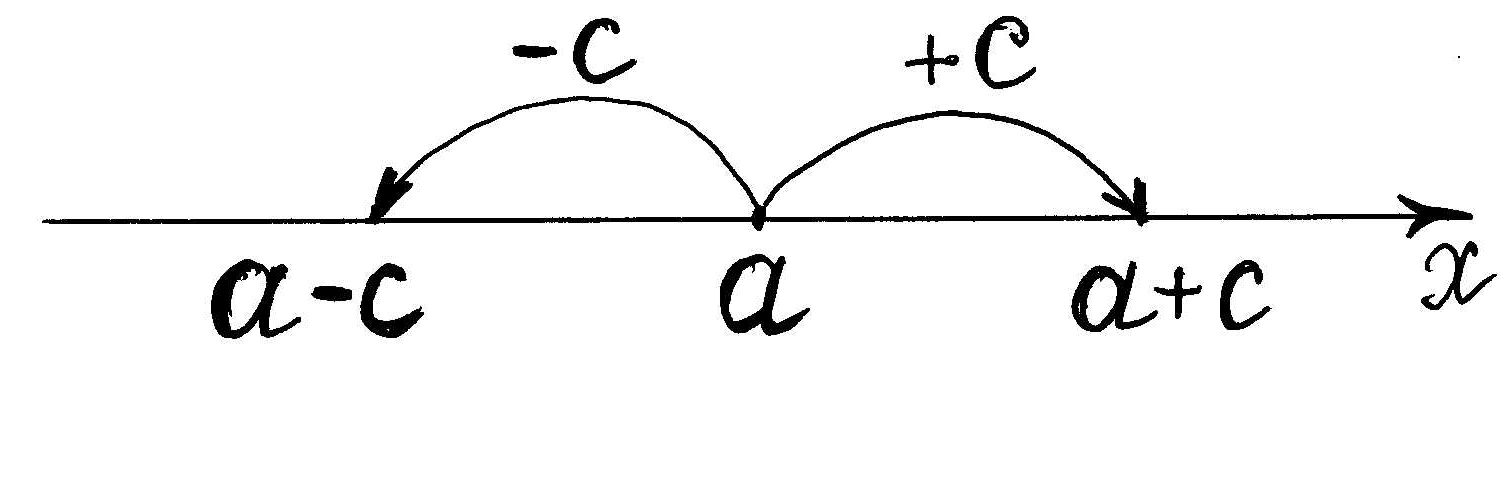
– Геометричний зміст даного рівняння
2) Рівняння виду | x – a | = c x – b .
Учні вказують на умову, при якій існують розв’язки даного рівняння:
c x – b 0.
3) Рівняння виду | x – a | = | x – b |
– Це рівняння полюбляє квадрати, бо його ліва і права частини невід’ємні.
4) Четвертий вид рівняння: | x – a | + | x – b | = C .
Підготуйте дане рівняння до аукціону.
Відповіді учнів:
Якщо С < 0, то рівняння розв’язків немає, бо сума двох невід’ємних чисел є число невід’ємне.
Якщо С < | b – a
Якщо С > | b – a |, то рівняння має два розв’язки.
Якщо С = | b – a |, то розв’язків безліч, х a; b.
Геометричний зміст.
5) Підведемо підсумок аукціону.
Яке з рівнянь кому найлегше розв’язувати, а яке найскладніше ?
IV. Розв’язування вправ.
Розглянемо завдання, які пропонуються випускникам під час проходження ЗНО з математики .
а) Чи правильно розкрито модуль ?
1. | x 4 + 3 | = x 4 + 3.
2. | 2 – | = + 2.
3. | x – 5 | = 5 – x, x > 5.
4. | x + 3 | = – x + 3, x < – 3.
5. | x 2 – 10x + 26 | = x 2 – 10x + 26.
Правильні відповіді:
1. Так. 2. Ні. 3. Ні. 4. Ні. 5. Так.
(Всі відповіді подаються дітьми з обґрунтуванням).
б) Встановити відповідність між рівняннями і їх коренями.
Перші три рівняння взяті з вашої домашньої роботи, отже, заразом перевіримо, як ви справилися з ними вдома, а два останні ви розв’язуєте зараз. На виконання завдання відводимо 5 хвилин.
1. | – x + 2 | = x – 2. A. x = – 1
2. | – x – 3 | = | x + 3 | Б. x 2
3. | x + 3,8 | + | 4 – x | = 6,5 B. x R
4. | x 2 – 1 | + | 4x + 4 | = 0 Г. x = 1; 2
5. | 2x – 3 | – 1 = 0 Д. x
Правильні відповіді:
1 – Б 2 – В 3 – Д 4 – А 5 – Г
(Всі відповіді подаються дітьми з обґрунтуванням).
в) Робота в парах.
1 пара: Розв’яжіть рівняння і знайдіть суму його коренів:
| – x – 3 | + | 5 – x | = 10.
2 пара: Розв’яжіть рівняння і знайдіть його найменший додатний корінь:
| 10 – | 6 – 4x || = 4.
3 пара: Розв’яжіть рівняння і знайдіть найбільший його корінь:
| 3x – 5 | = | 2x + 4 |.
4 пара: Розв’яжіть рівняння і знайдіть добуток його коренів:
|| 2x – 1 | – 3 | = x – 1.
Перевірка роботи в парах (слайд 21):
1. 2 2. 3 3. 9 4. 5
Кожному числу поставте у відповідність букву.
А | Б | К | Л | О | П | Р |
3 | 6 | 2 | 5 | 4 | 7 | 9 |
Отримаємо слово КАРЛ.
Карл Теодор Вільгельм Вейєрштрас – так звати видатного німецького математика, який вніс великий вклад у розвиток вищої математики. А для нас з вами має велике значення, що саме цей вчений в 1841 році вперше ввів знак модуля, який ми використовуємо і по цей час. Хто захоче більше дізнатися про цікаве в житті видатних математиків можете взяти в бібліотеці дуже цікаву книгу «Математичні мініатюри», автор О. І. Баран (слайд 22-23).
А ми з вами продовжуємо працювати далі.
г) Модуль і параметр.
Розв’яжіть рівняння :
1. | 3x – 12 | + | 2x + c | = 0.
Розв’язання:
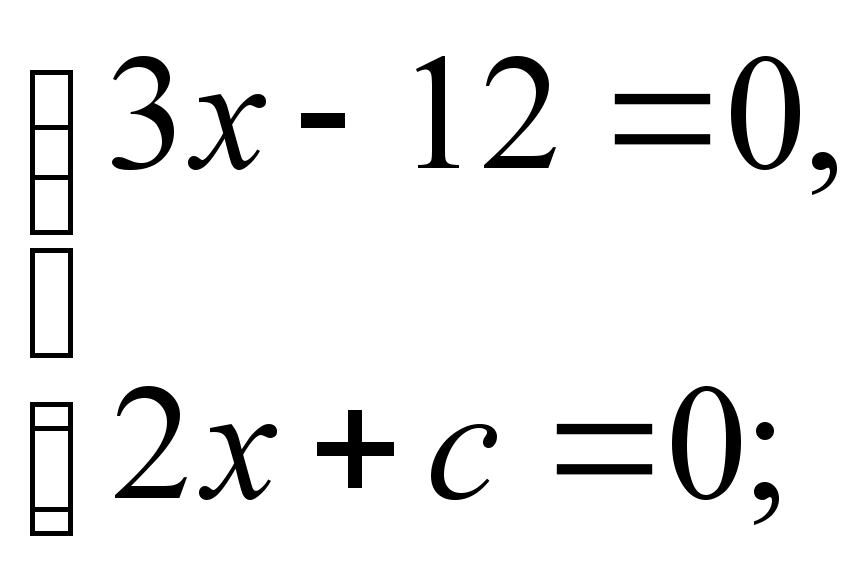
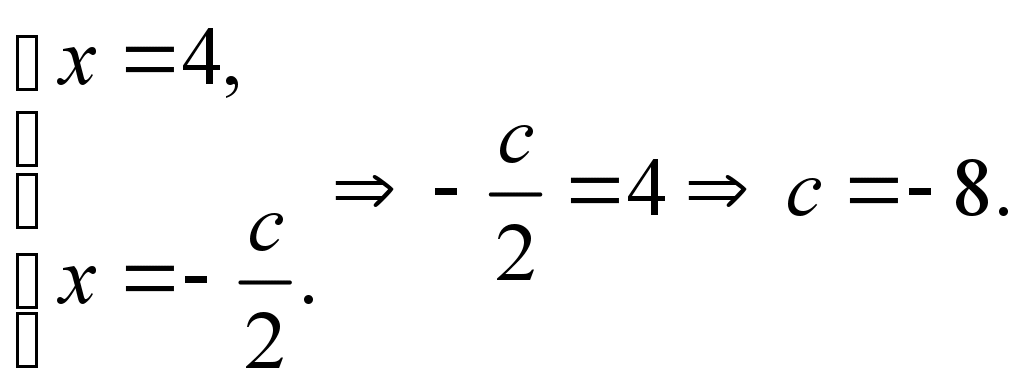
Відповідь: Якщо с = – 8, то рівняння має розв’язок, х = 4;
якщо с – 8, то рівняння коренів немає.
2. | x – b | = x – 2.
Розв’язання:
ОДЗ: х – 2 0,
х 2.
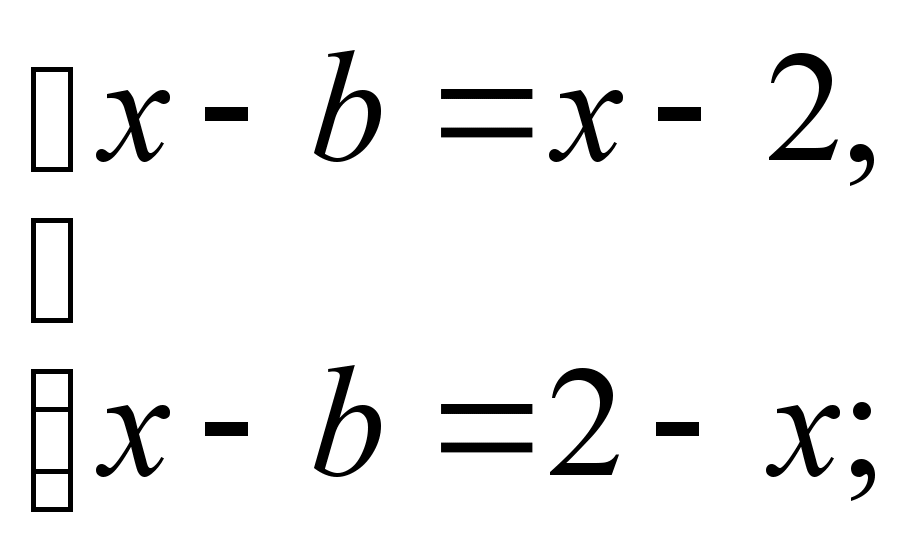
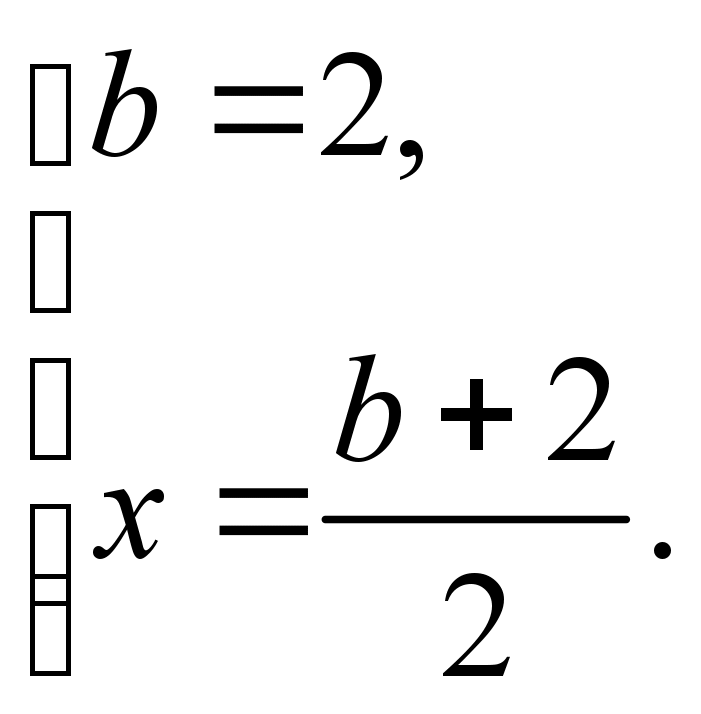
Відповідь: Якщо b < 2, то х ;
якщо b = 2, то х 2;
якщо b > 2, то х =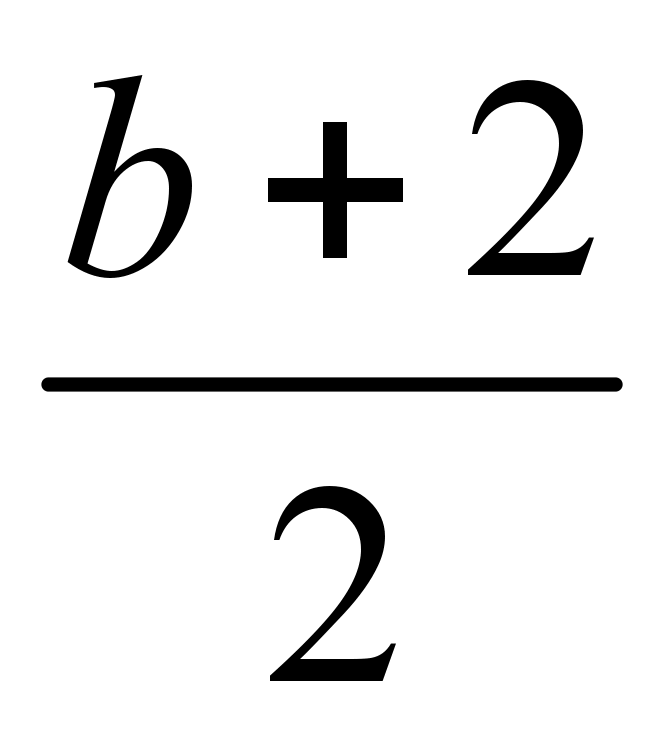 
.
V. Задачі від мудрої сови (слайд 26-30).
1. Знайдіть невідоме число:
11 2 20
7 9 5
5 3 ? (7)
2. Знайдіть невідоме слово:
КРІТ 1 < х < 3 КІТ
КРОЛИК 2 < х < 5 ? (КРИК)
3. Знайдіть невідоме число:
КОНКУРС 5х – 1 = 3х + 3 49
ТИР 7х + 6 = 8х + 2 81
ПАРК 6х – 2 = 16 ?
Додаткові завдання:
1. | x – 2009 | + | 2009 – x | = 2010
2. ||||x| – 5 | – 2 | – 5 | = 3
3. |x – | x – | x – 5 ||| = 4
VІ. Підсумок уроку
Яке з рівнянь з модулями викликає найбільше проблем?
Чому?
А яке з вивчених рівнянь вам подобається?
Чому?
Над яким видом рівняння ви бажаєте попрацювати на наступному уроці?
VІІ. Домашнє завдання
Розв’язати рівняння:
1. | 6x + 2 | = 4 – 5x
2. | x – 2 | + | x + 2 | = 5
3. || 5 – x | – x + 2 | + x = 10
4. | x + a | = x + 5
Література
1. Апостолова Г. В. Хитромудрий модуль. – К.: «Факт», 2004. – 256 с.
2. Ліпчевський Л. В. Задачі з модулями. Програма спецкурсу
3. Мерзляк А. Г., Полянський В. Б., Якір М. С.Алгебра: Підручник для класів з поглибленим вивченням математики. – Х.: Гімназія, 2008. – 368 с.
4. Харік О. Ю. Матеріали для факультативних занять, спецкурсів, гуртків. Математика 5 – 7. – Х.: Вид. група «Основа», 2008. – 143, 1 с. – (Б-ка журн. «Математика в школах України»; Вип.. 8 (68)).
vseosvita.ua
уравнение по алгебре с модулями. 10 класс. 10 класс. решите уравнение с модулями! с пояснением
|2x-1|=3. Рассмотрим 2 ситуации: 1) когда х>= 0. Тогда просто снимаем знак модуля, получается 2х-1=3 2х=4 х=2 2) когда х<0. Тогда снимаем знак модуля, меняя все знаки части, которой была под модулем на противоположные, получается: -2х+1=3 -2х=2 2х=-2 х=-1.
списывать чужие решения .. где гарантия. что оно верное.. . 0 пользы. постарайся разобраться и это станет твоим Знанием: Решение неравенств, используя определение модуля. Существует несколько способов решения неравенств, содержащих модуль. Рассмотрим некоторые из них. 1) Решение неравенства с помощью геометрического свойства модуля. tutoronline.ru›blog/neravenstva-s-modulem.aspx копия ещё Уравнения и неравенства с модулем на централизованном тестировании Абсолютная величина и её свойства. Простейшие уравнения и неравенства с модулем. Графическое решение уравнений и неравенств с модулем. Иные способы решения уравнений и неравенств с модулем. Метод раскрытия модулей. CoolReferat.com›Уравнения_и_неравенства_с_модулем…
touch.otvet.mail.ru