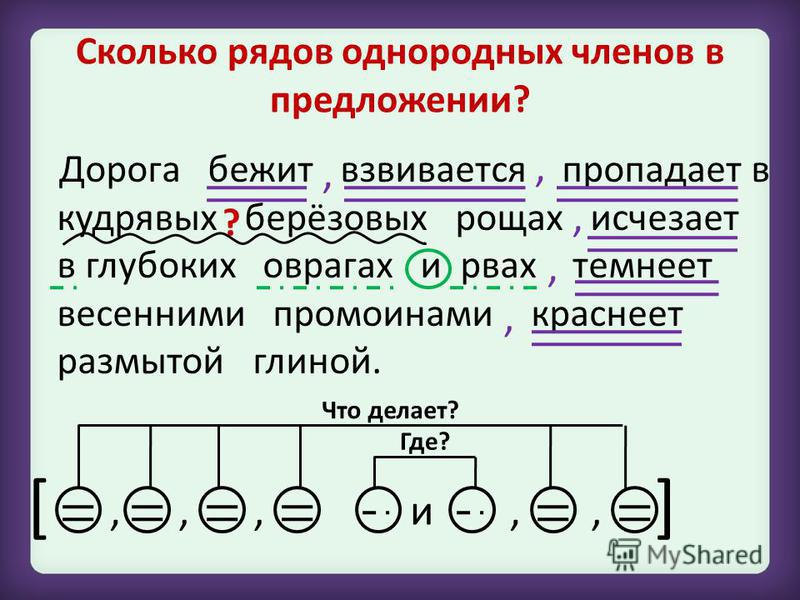
Однородные члены предложения. Схема предложения с однородными членами. Режим дня.
Урок русского языка в 4 классе
Тема: Однородные члены предложения. Схема предложения с однородными членами. Режим дня.
Цели урока:
Закрепить понятие «однородные члены предложения».
Уметь разбирать простое предложение с однородными членами.
Уметь ставить запятые в простых предложениях с однородными членами (без союзов, с союзами и, а, но).
Воспитывать бережное отношение к своему здоровью, соблюдая режим дня.
Закрепить знания учащихся о гигиенических нормах и культуре поведения.
Оборудование:
Схемы предложений с однородными членами предложений.
Филворд
Индивидуальные карточки
Тест-контроль
Лист достижений
Мультимедиапроектор
Ход урока
І.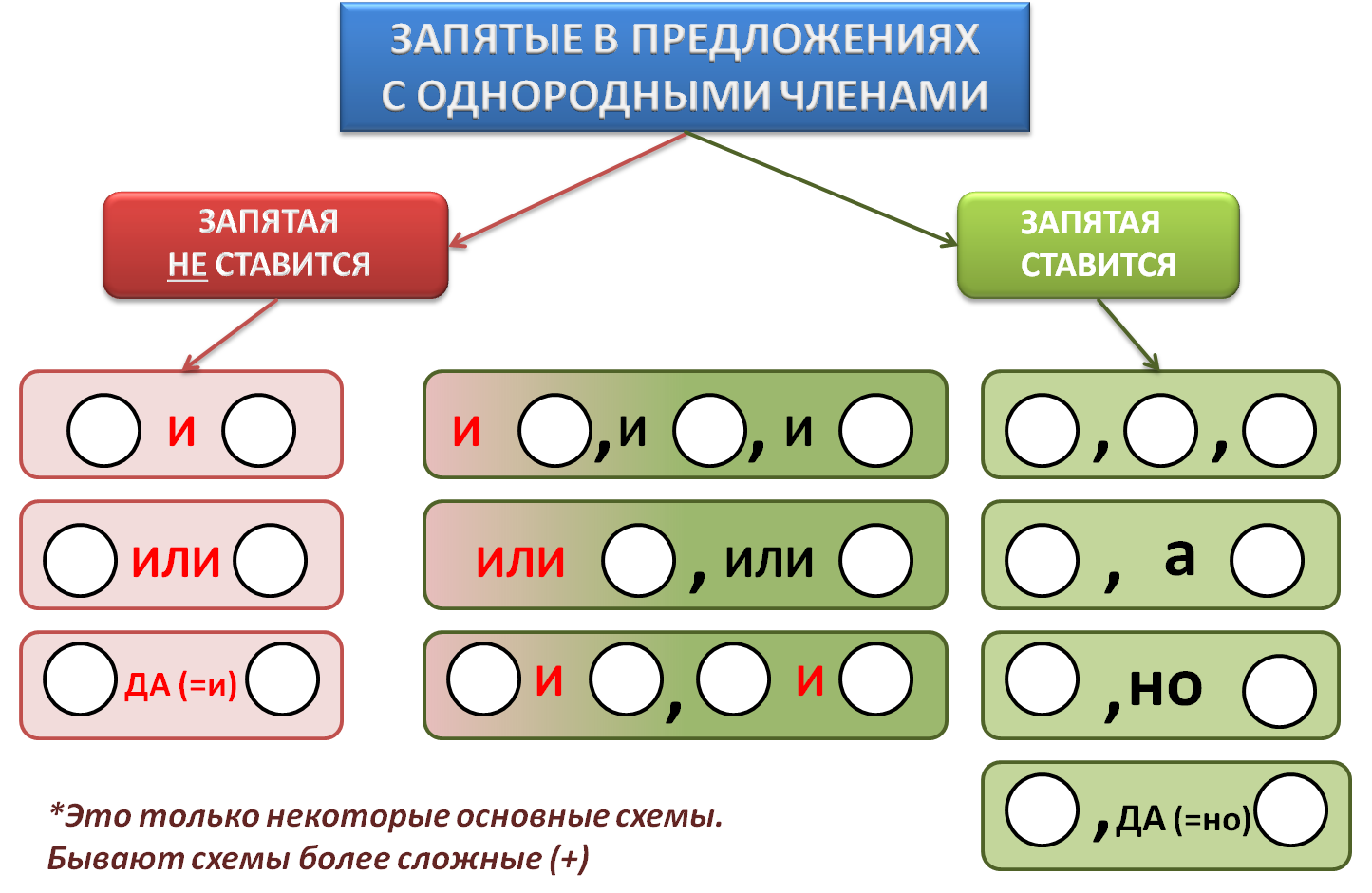 Организационный момент.
Организационный момент.
Приветствие. Создание эмоционального настроя
ІІ. Актуализация опорных знаний.
Чистописание
Зрительно-слуховой диктант. (слайд 1 )
Слова: утро, обед, пробежка, причесать, умыть, зарядка, ванна, друзья.
В слове утро — найдите согласный, твёрдый, звонкий и непарный звук и запишите эту букву.
В слове обед — найдите и запишите ударный гласный звук в корне.
В слове пробежка — найдите парный согласный в корне.
В слове причесать -выделите безударный гласный в приставке.
В слове умыть — найдите согласный, твёрдый, звонкий, непарный звук и запишите эту букву.
В слове зарядка — найдите парный согласный в корне слова.
В слове ванна — найдите удвоенную согласную.
В слове друзья — найдите и запишите букву, обозначающую два звука.

А теперь соедините все буквы и прочитайте, что получилось.
(слайд № 2)
Р + Е + Ж + И + М Д + Н + Я = РЕЖИМ ДНЯ.
Продолжим минуту чистописания подобными словосочетаниями: Утренняя зарядка, ослепляющая улыбка, красивая осанка.
Девиз: Я здоровье сберегу, сам себе я помогу! (слайд 3)
ІІІ. Определение темы урока
(слайд 4) Прочитав стихотворение, определить тему урока.
Слова есть в предложениях,
Не очень внешне схожие,
Но, полномочия на них
Все поровну возложены.
И подчеркнуть их в предложении нужно одинаково,
И между ними правильно
Должны расставить знаки мы.
Шагают вереницею они за словом главным,
Оно ими командует и за собой их тянет.
Наверное, узнали вы,
Слова те благородные —
И это члены предложения,
Какие? … (Однородные)
слайд 5 (Тема урока)
Определение целей урока (слайд 6 – 9)
Цели урока:
1. Вспомнить признаки однородных членов предложения .
Вспомнить признаки однородных членов предложения .
2. Повторить правило о расстановке знаков препинания при однородных членах .
3. Упражняться в умении находить однородные члены в предложении и составлять предложения.
IV. Повторение изученного
Филворд . Работа в группах. (слайд 10)
Одно из слов показать, чтобы дети поняли принцип работы.
(слайд 11) ключ к филворду
Словарная работа.
Записать слова: завтрак, молоко, зарядка, стакан, бутерброд, гантели, восемь, ужин, обед, кисель, посуда, язык . Определить словарные слова. Поставить в них ударение, подчеркнуть непроверяемые буквы.
Составление рассказа «Режим дня» с использованием опорных слов и картинок (слайд 12)
Примерный вариант рассказа.
Я встаю в 8 часов утра. Умываюсь, делаю зарядку с гантелями, убираю постель. На завтрак я ем кашу, выпиваю стакан молока и съедаю бутерброд с сыром. Затем иду в школу. В школе я изучаю русский язык, математику, окружающий мир. Время в школе бежит очень быстро. Я иду домой. Отдыхаю, потом делаю уроки. Вечером приходит с работы мама. Она готовит вкусный ужин. Я ужинаю, помогаю маме убрать со стола. Мою посуду. Перед сном я читаю интересные книги и детские журналы. После чищу зубы и ложусь спать в десять часов.
5. Выделенные предложения записать и разобрать по членам предложения и по частям речи.
— На какой вопрос отвечают однородные члены предложения?
— Каким членом предложения они являются?
— К какому члену предложения они относятся?
— Какой частью речи выражены однородные члены предложения?
— С какой интонацией они произносятся?
6. Сделать вывод о признаках однородных членов предложения (слайд 13)
Однородные члены предложения:
Отвечают на один и тот же вопрос
Являются одним членом предложения
Относятся к одному и тому же члену предложения
Обычно выражены одной и той же частью речи
Произносятся с перечислительной интонацией
ФИЗМИНУТКА (слайд 14)
Вам, мальчишки и девчонки,
Приготовила вопросы !
Если мой совет хороший,
Вы похлопайте в ладоши.
Раз! Два! (руки над головой)
На неправильный совет
Говорите: нет, нет, нет. (повороты головы)
Постоянно нужно есть
Для зубов для ваших
Фрукты, овощи, омлет,
Творог, простоквашу.
Если мой совет хороший,
Вы похлопайте в ладоши.
(Дети хлопают в ладоши.)
Не грызите лист капустный,
Он совсем, совсем не вкусный,
Лучше ешьте шоколад,
Вафли, сахар, мармелад.
Это правильный совет?
Нет, нет, нет. (Дети хором.)
Блеск зубам чтобы придать,
Нужно крем сапожный взять.
Выдавить полтюбика
И почистить зубики.
Это правильный совет?
Нет, нет, нет. . .(Дети хором.)
Навсегда запомните,
Милые друзья.
Не почистив зубы,
Спать идти нельзя.
Если мой совет хороший,
Вы похлопайте в ладоши.
(Дети хлопают в ладоши.)
Зубы вы почистили
И идёте спать.
Захватите булочку
Сладкую в кровать.
Это правильный совет?
Нет, нет, нет.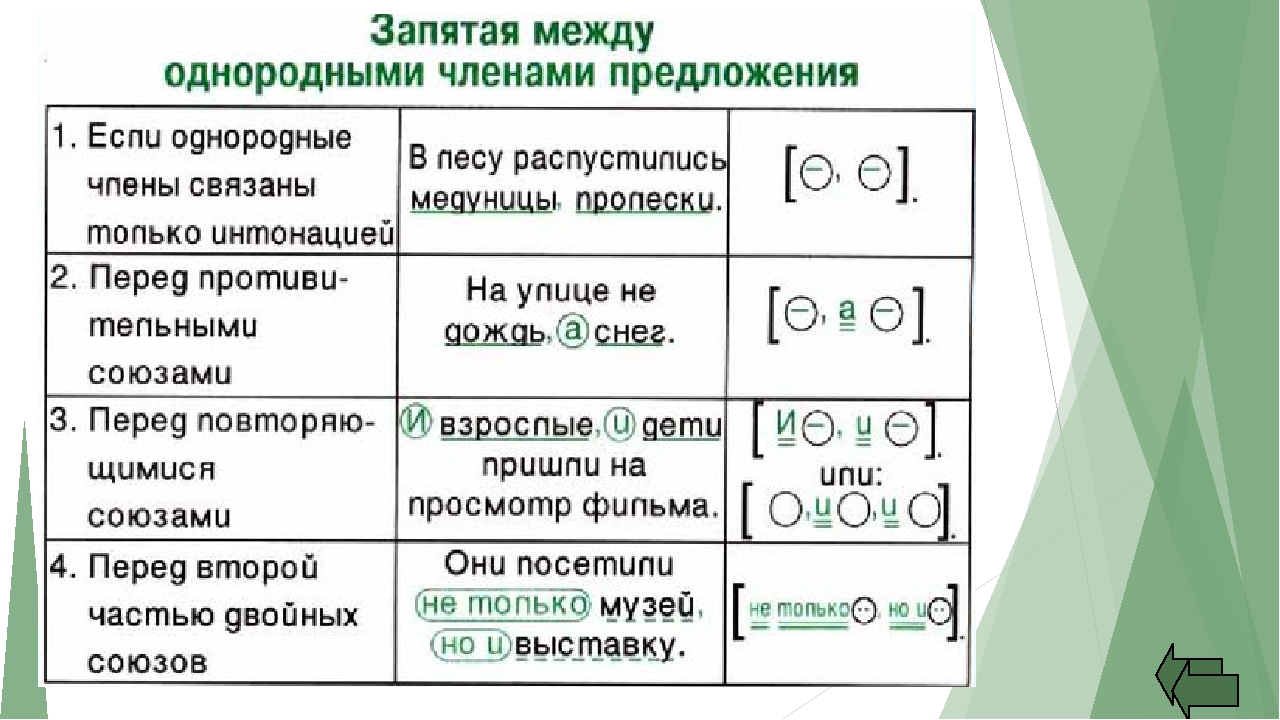 (Дети хором.)
(Дети хором.)
Чтобы зубы укреплять,
Полезно гвозди пожевать.
Это правильный совет?
Нет, нет, нет. (Дети хором.)
Запомните совет полезный,
Не стоит грызть предмет железный.
Если мой совет хороший,
Вы похлопайте в ладоши.
(Дети хлопают в ладоши.)
V. Формирование новых знаний.
1. Возвращение по гиперссылке к слайду 9. Повторение целей урока.
2. Возвращение по гиперссылке к слайду 15
3. Знакомство со схемами соединения и разделения однородных членов предложения.
Ключ:
1. Если однородные члены предложения соединены между собой союзом и, то запятая между ними не ставится.
2. Если между однородными членами предложения нет союзов и они произносятся с перечислительной интонацией, то между ними ставится запятая.
3. Если между однородными членами предложения есть союз а или но, то перед союзом ставится запятая.
4. Если между однородными членами предложения многократно употребляется союз и, то между ними ставится запятая.
5. Если между однородными членами предложения многократно употребляется союз или, то между ними ставится запятая.
4. Закрепление новых знаний. (слайд 16)
1.Подобрать к схемам соответствующие предложения с однородными членами.
2.Записать схему с многократно повторяющимися союзами или и соответствующее предложение предложение в тетрадь.
— В русской речи много пословиц о здоровье, здоровом образе жизни. Какие пословицы о здоровье вы знаете? (слайд 17)
VI. Формирование практических знаний, умений, навыков.
ТЕСТ-КОНТРОЛЬ. ( 2 мин. )
Взаимопроверка теста по ключу (слайд 18)
Индивидуальная работа по карточкам. (3 мин.)
VII. Формирование информационной компетентности. Рефлексия.
А теперь мы с вами поработаем в листе достижений.
Подпишите его (слайд 19). Принцип работы следующий:
Если об изученном вопросе вы можете сказать: «Отлично владею информацией», то помечаете этот пункт зелёным цветом.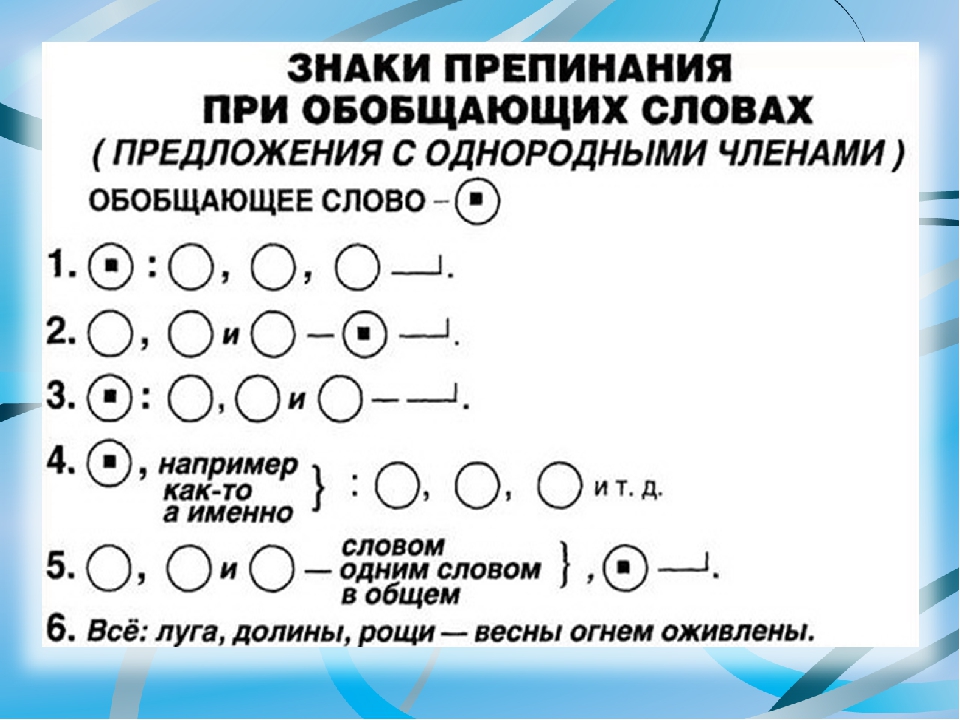
Если об изученном вопросе вы можете сказать: «Понятно, но не полностью», то помечаете этот пункт жёлтым цветом.
Если об изученном вопросе вы можете сказать: «Затрудняюсь в ответе», то помечаете этот пункт красным цветом.
Отвечать мы будем на следующие вопросы (слайд 20):
Лист достижений_________________________________
Фамилия имя
______
класс
1
ЗНАЮ признаки однородных членов предложения
2
УМЕЮ находить в тексте однородные члены предложения
3
УМЕЮ правильно расставлять знаки препинания
4
УМЕЮ определять их синтаксическую роль (каким членом предложения является)
5
УМЕЮ составлять схемы предложений с однородными членами
— Скажите, какой цвет преобладает в ваших ответах?
Если зелёный – вы полностью справились с задачами урока.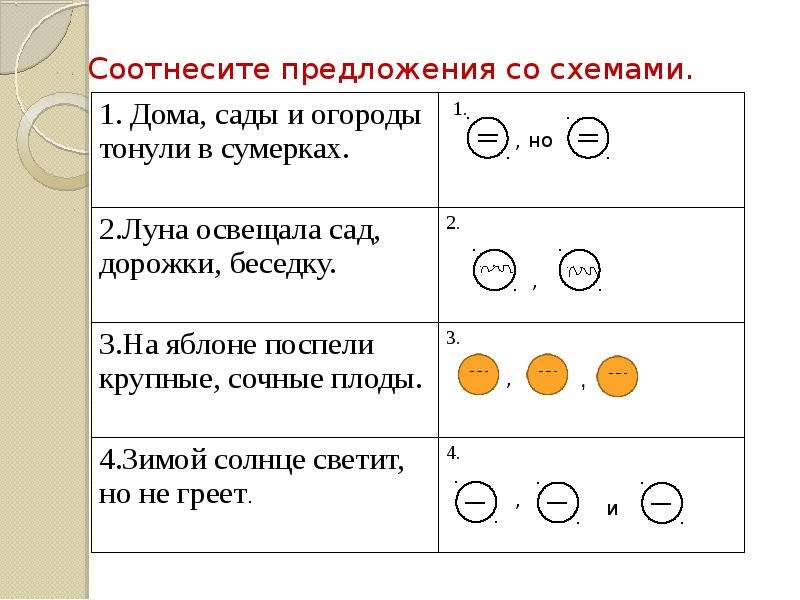
Если жёлтый – вы хорошо справились, но следует уделить внимание некоторым вопросам.
Ну а если красный – нужно остановиться на этой теме ещё раз.
VIII. Итог урока. (слайд 21)
Назовите тему сегодняшнего урока.
Какие знаки препинания ставятся между однородными членами предложения?
Когда не ставятся знаки препинания между однородными членами предложения?
О чём важном для здоровья человека мы сегодня с вами говорили?
Для чего нужно выполнять режим дня?
Итоговая беседа
Режим дня следует строго соблюдать: вовремя завтракать, обедать, ужинать, ложиться спать, гулять и отдыхать, внимательно слушать на уроках, чтобы не отставать по предметам.
IX. Домашнее задание. (слайд 22)
Составить и записать 5 предложений с однородными членами и подобрать к ним соответствующие схемы; повторить словарные слова.
-Урок окончен. Спасибо за работу! (слайд 23)
Спасибо за работу! (слайд 23)
ПРИЛОЖЕНИЕ
Вставь, где необходимо, запятые // Ф.И._________________________
НАШ ЛЕС.
В нашем лесу растут сосна ель береза осина дуб ольха. В лесу мы собираем землянику и ежевику. В лесу растут рыжики маслята подберезовики опята. В лесу живут и волки и лисицы и зайцы и белки. Летом в лесу мы часто видим бревна на постройку изб и сараев. Наши кустари делают из дерева ложки корыта колеса телеги сани.
__________________________________________________________________________
Вставь, где необходимо, запятые Ф.И._________________________
БЕЛКА.
У белки мягкая шерсть чуткие стоячие уши быстрые глаза и проворные цепкие лапы. Она очень быстро скачет с ветки на ветку прыгает с вершины дерева на землю не падает. Белка принадлежит к грызунам и питается древесными почками зернами орехами семенами еловых и сосновых шишек.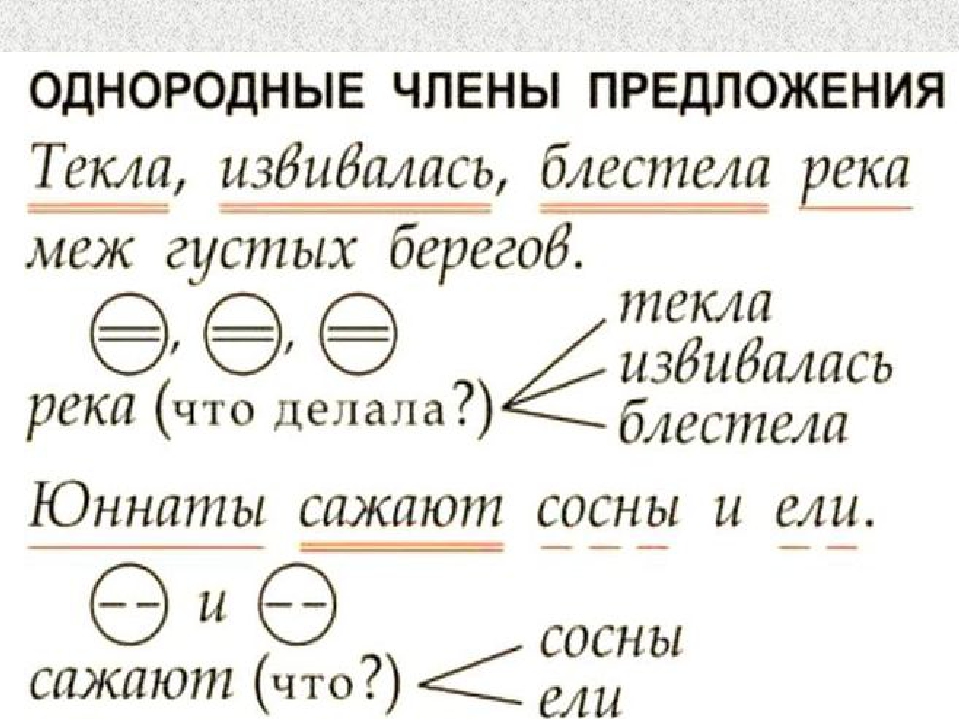 Зубы у белки стираются но вскоре опять подрастают.
Зубы у белки стираются но вскоре опять подрастают.
__________________________________________________________________________
Вставь, где необходимо, запятые // Ф.И._________________________
О ВОЛКЕ.
Волк для деревни — первый враг и разбойник. Он ходит бродит около скота. Выследит овцу накинется сзади вцепится зубами в горло и зарежет. Волк дик жаден и труслив.
_________________________________________________________________________
Вставь, где необходимо, запятые // Ф.И._________________________
ПОМОЩНИКИ.
Коля Костя и Миша приехали в лагерь на день раньше всего отряда. Им дали задание: приготовить помещение к приезду мальчиков и девочек. Когда они приехали в лагерь, в доме уже мыли полы вытирали пыль. Ребята стали помогать: носили воду перетаскали с чердака все койки тюфяки и матрацы. Расставили в порядке столы стулья и тумбочки. Нарвали цветов и поставили их на столах и на окнах в банках с водой. Ребята устали но были довольны своей работой.
Расставили в порядке столы стулья и тумбочки. Нарвали цветов и поставили их на столах и на окнах в банках с водой. Ребята устали но были довольны своей работой.
Тест-контроль
ОДНОРОДНЫЕ ЧЛЕНЫ ПРЕДЛОЖЕНИЯ
1. Члены предложения называются однородными, если…
1) отвечают на один и тот же вопрос;
2) относятся к одному и тому же члену предложения.
3) состоят из одних и тех же частей речи;
4) пишутся с одной и той же орфограммой.
2. Какие члены предложения бывают однородными?
1) Подлежащие;
2) Сказуемые;
3) Второстепенные члены.
3. Как связаны между собой однородные члены предложения?
1) Интонацией перечисления;
2) Союзами;
3) Предлогами.
4. Выбери союзы.
1)и 2) из 3) а 4) на 5) но 6) над
5. В каком случае между однородными членами предложения ставится запятая?
В каком случае между однородными членами предложения ставится запятая?
1) Если однородные члены связаны интонацией перечисления;
2) Если однородные члены связаны союзами а, но;
3) Если однородные члены связаны союзом и.
6. В каком случае между однородными членами предложения не ставится запятая?
1) Если однородные члены связаны союзами а, но.
2) Если однородные члены связаны союзом и.
7. Перед какими союзами между однородными членами всегда ставится запятая?
1)а 2) но 3)и
Филворд
Утренний приём пищи
Жидкий продукт детского питания, который еженедельно вы получаете в школе
комплекс упражнений после сна утром
Посуда для жидкости из которой пьют воду, молоко и т.д.
Хлеб + сыр + колбаса
Снаряд для укрепления мышц рук
Цифра
Вечерний приём пищи
Дневной приём пищи
Жидкий сладкий напиток на основе крахмала
Набор предметов для приёма или приготовления пищи
Название урока: русский …….
 .
.
Источники:
http://www.google.com.ua/search?aq=f&sourceid=chrome&ie=UTF-8&q=%D0%BA%D0%BE%D0%BB%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D1%8F+%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BE%D0%BA –коллекция картинок
1. Однородные члены предложения, знаки препинания при них
Здравствуй, мой друг. Я очень рад нашей новой встрече. И сегодня мы будем изучать однородные члены предложения, правила постановки знаков препинания между ними.
Однородными членами предложения называются члены, которые относятся к одному слову и отвечают на один вопрос. Однородными могут быть все члены предложения.
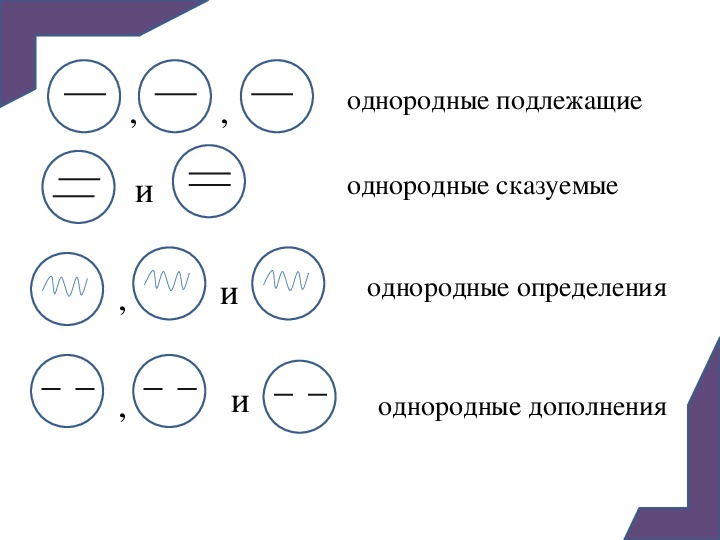
Однородные подлежащие.
Маша и Витя встретились случайно.
Грибы и ягоды росли на поляне в изобилии.
Однородные сказуемые.
Я одновременно слушаю и пишу.
Ласточки кружатся над озером и ловят мошек.
Однородные дополнения.
Мы увидели тебя и маму ещё возле магазина.
Я люблю булочки и пирожки.
Однородные определения.
Ветер гнал жёлтые и красные листья клёнов по улице.
Нежные и трепетные слова мама произнесла в день рождения своей мамы.
Однородные обстоятельства.
Я быстро и чётко проговорил слово.
Грибы росли быстро и всюду.
Знаки препинания при однородных членах
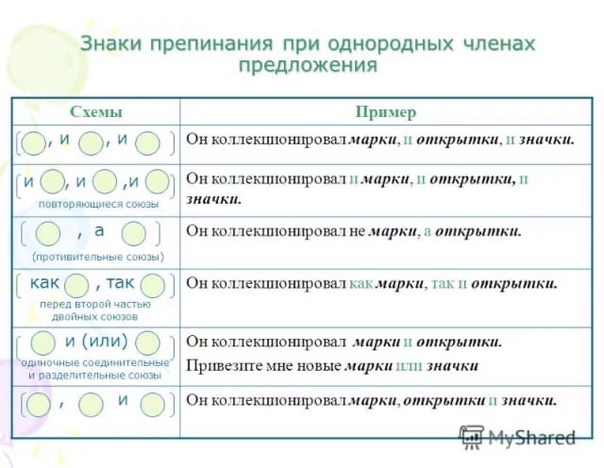
Если однородные члены предложения соединены без союзов, то между ними всегда ставится запятая.
Дома, улицы, переулки мелькали из окна машины со скоростью человеческой мысли.
О, О, О
Запятая ставится и перед союзами А, НО, которые связывают однородные члены.
Не высокий, а низкий клён рос возле дома со стороны улицы.
О, а О
Он подошёл ближе, но всё равно не смог прочитать объявление.
О, но О
Запятая не ставится, если между однородными членами один раз употребляется союз и.
Мел и губка лежали возле доски.
О и О
Коты и собаки не любят друг друга.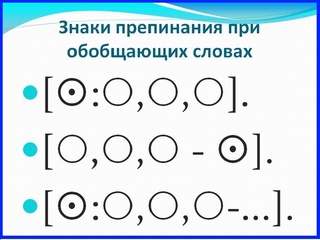
О и О
Союз И может связывать однородные члены, которые повторяются.
Мальчики и девочки, взрослые и дети прыгнули с палубы в море.
О и О, О и О
Я читал и Пушкина, и Лермонтова, и Державина.
И О, и О, и О
В схемах однородные члены обозначаются заглавной буквой О. Схемы помогают лучше понять, какие знаки препинания необходимо ставить при однородных членах предложения.
Обрати внимание!
1. Однородными называются такие члены предложения, которые отвечают на один вопрос и относятся к одному слову.
2. Могут быть однородными и главные, и второстепенные члены предложения.
3. Запятая при однородных членах обязательно ставится перед союзами а, но, а при союзе и — только если он повторяется.
Однородные члены предложения. (8 класс)
1. Однородные члены предложения 8 класс
5klass.netПЛАН
1.Понятие об однородности членов
предложения
2.Знаки препинания при союзах
а) одиночных
б) повторяющихся
в) составных
3.
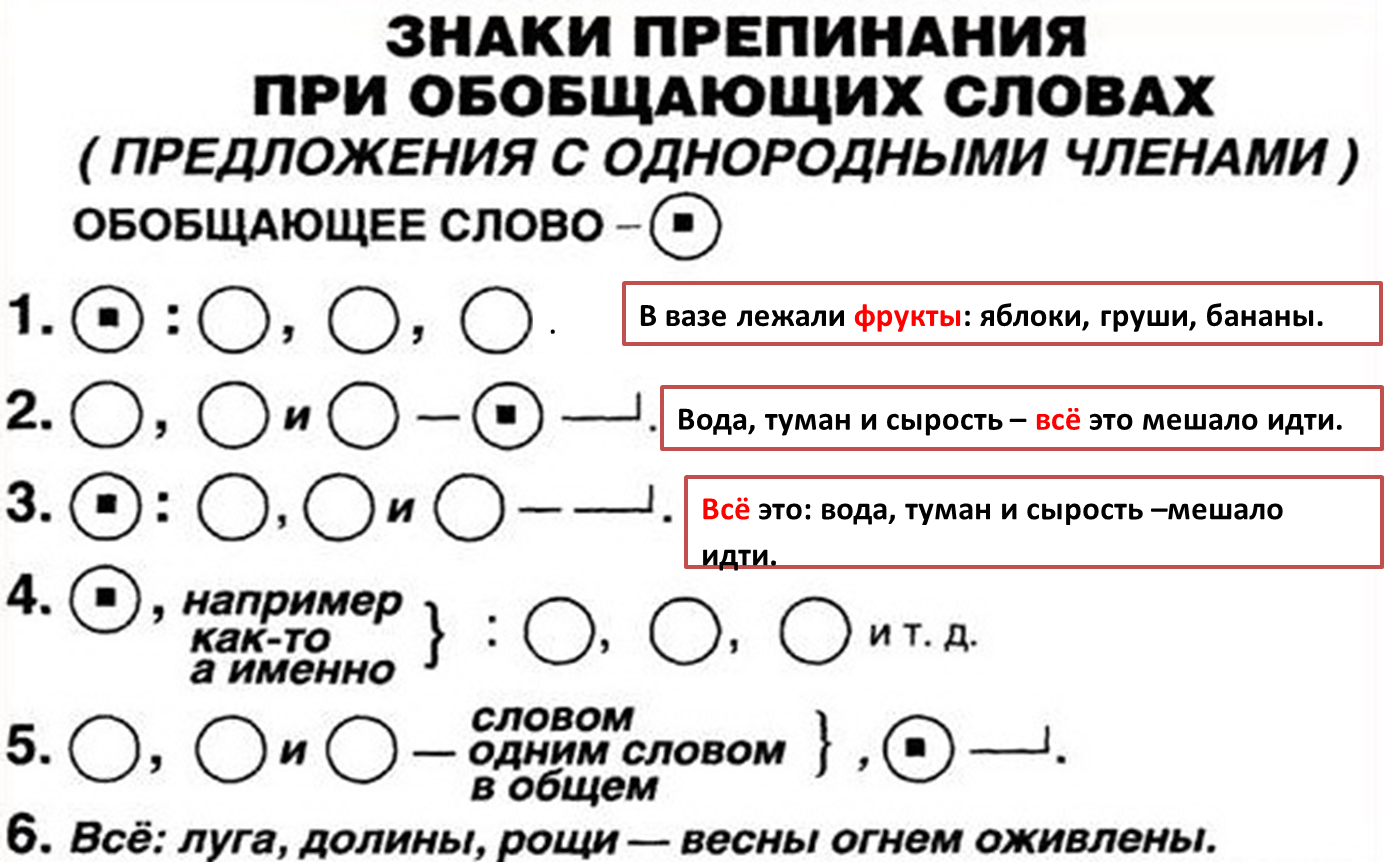 Определения
Определенияа) однородные
б) неоднородные
4. Обобщающие слова при однородных
членах
Знак однородности в схемах
(внутри – символ члена
предложения)
Однородными могут
быть любые члены
предложения:
4. Признаки однородности
• К однородным членампредложения задается один и
тот же вопрос
• Они равноправны и независимы
• Присутствует интонация
перечисления
• Связаны интонацией или
интонацией и союзом
5. Выразительно прочтите, запишите, подчеркните однородные члены, составьте схему предложений
Как я люблю свои березы,Свои леса, свои луга, и ночи летние, и грозы,
И зиму с стужей, и снега!
Люблю я речки серебристой
Хрустально-нежный
разговор
И травки бархатный,
С цветами скромными
ковер.
6. Проверка
Как я люблю свои березы,Свои леса, свои луга, и ночи летние, и грозы,
И зиму с стужей, и снега!
Люблю я речки серебристой
Хрустально-нежный
разговор
И травки бархатный,
душистый,
С цветами скромными
ковер.
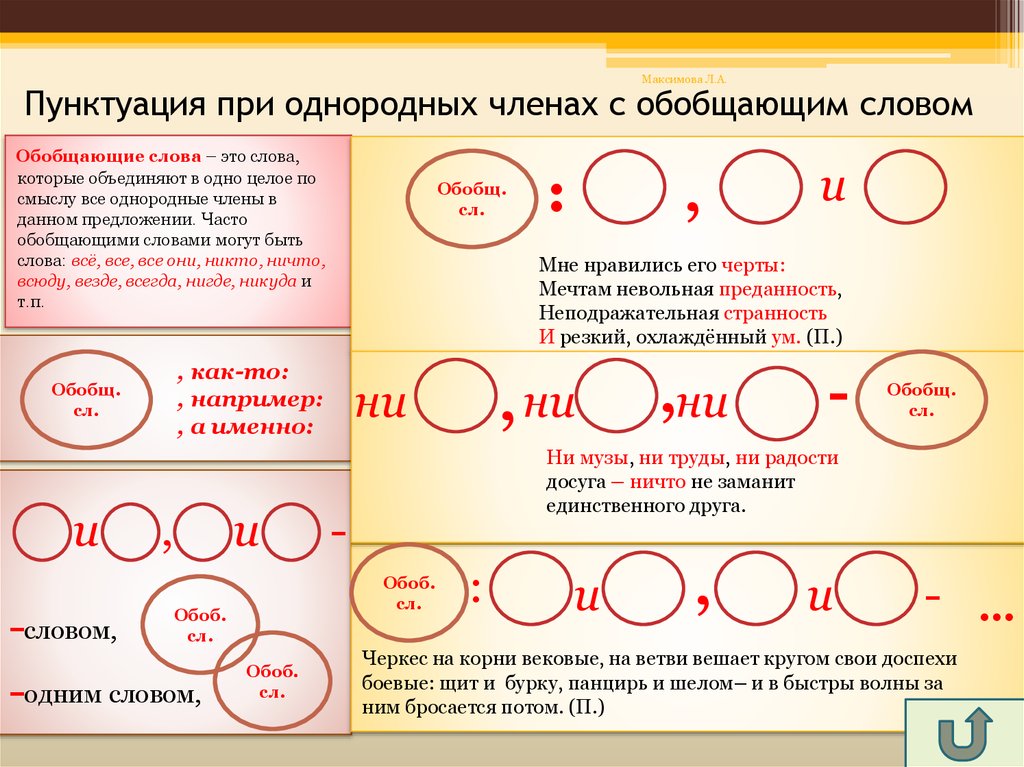
7. Определите, какому предложению соответствует схема. Докажите.
— ——
—
—
—
—
Определите, какому предложению
соответствует схема. Докажите.
—
и
—
9. Пунктуация при однородных членах предложения
Прочтите схемы, придумайте предложения1)
и
и
2) Не только
но и
Не путать со сложносочинённым предложением:
и
10. Пунктуация при однородных членах предложения 1.Одиночные союзы
и
или
либо
да = и
соединительные
союзы
но
а
однако
зато
да = но
противительные
союзы
Спишите, расставляя знаки препинания.
Составьте схемы предложений.
1. Я часто ходил смотреть на величавую реку и
просиживал долгие часы на каменной скамье.
2. Девушка была грациозно сложена , но не
вполне ещё развита.
3. Молодость не кипела в Гагине ключом , а
светилась тихим светом.
4. Ася училась прекрасно была чрезвычайно
понятлива , однако не хотела подойти под
общий уровень , упрямилась , глядела букой.
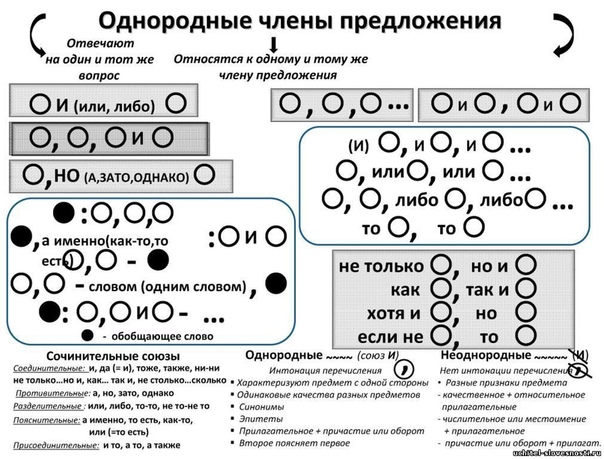
5. Луна пристально глядела на город , и он
чувствовал этот взгляд и стоял чутко и мирно.
12. 2.Повторяющиеся
иили
не то
ни
и
и
или
не то
ни
В цельных выражениях (фразеологических
оборотах) с повторяющимися союзами запятая не
ставится
ни
ни
Спишите, расставляя знаки препинания.
Составьте схемы предложений.
1. Однажды сидел я на своей любимой скамье и
глядел то на реку , то на небо то на виноградники.
2. Отец долго глядел мне в глаза не то испытующим ,
3. Часа четыре мы провели вместе : или сидели на
диване , или расхаживали перед домом.
4. И тут свободно потекли наши речи не то горячие ,
не то задумчивые , не то восторженные , но всегда
неясные речи русского человека.
5. На другой день Ася проснулась ни свет ни заря.
Определите значения
фразеологических оборотов
Ни то ни сё
Посредственный
Ни свет ни заря
Очень рано
И так и сяк
С разных сторон
Ни рыба ни мясо
Нечто среднее
Ни днём ни ночью
Нет покоя в любое
время суток
Ни дать ни взять
Действительно
Ни жив ни мёртв
Сильно напуган
Ни два ни полтора
15.
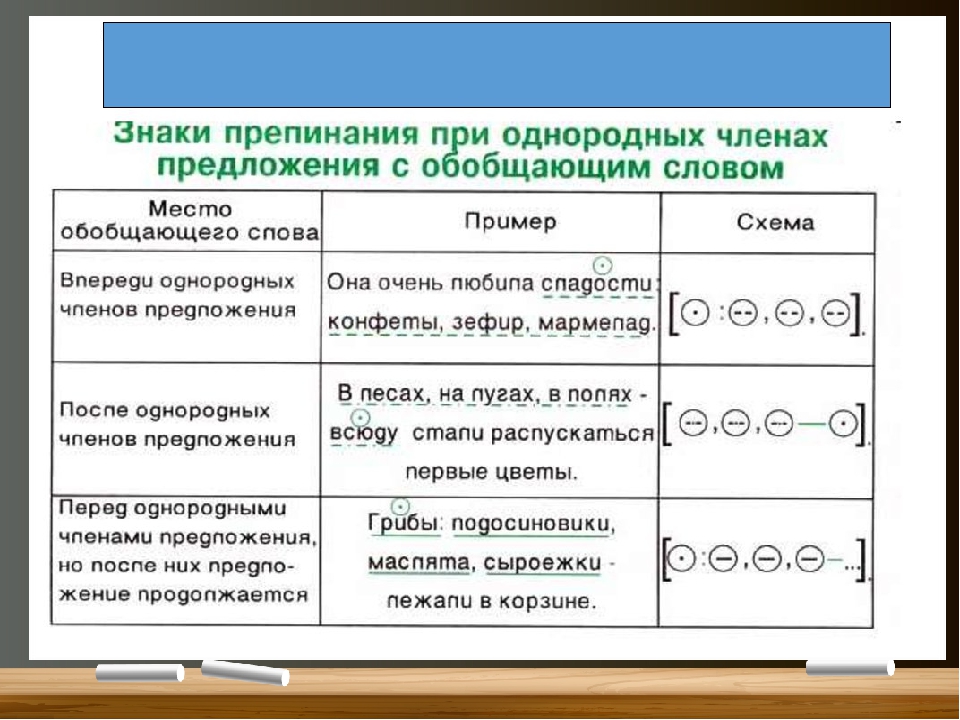 3.Составные не только
3.Составные не толькокак
но и
так и
Спишите, расставляя знаки препинания.
Составьте схемы предложений.
1. Барышни в пансионе не только не любили
Асю но и язвили и кололи её, как только
могли.
2. Любовь Аси как радовала так и смущала
меня.
17. Определения 1.Однородные
Не зависят друг от друга
Интонация перечисления
Возможность постановки союза И между
ними
Или качественные, или относительные
прилагательные
Отличительные признаки разных
предметов
Эпитеты
Синонимы
Могут стоять после определяемого слова
Противопоставление при одном слове
Часто соединяются по схеме
«прилагательное + причастный оборот»
18. Докажите, что в этих предложениях определения однородные.
1) Приятный, нежный голосок птичкизвенел не умолкая.
2) Темные, плотно стоящие ели
отражались в воде.
3) Собака смотрела на зловещий,
красный круг луны.
4) Я всегда любил наблюдать трудовую,
хлопотливую жизнь скворцов.
19. Определения 2. неоднородные
• Поясняет первое слово всегословосочетания
• Характеризует предмет с разных
сторон: материал и впечатление, размер
и цвет, форма и возраст и т.д.
прилагательное
• Нельзя поставить между ними союз «и»
• Не ставится запятая
20. Найдите однородные и неоднородные определения. Докажите.
1) Это единственное решение трудной? математической задачи.
2) И очи синие ?, бездонные цветут на
дальнем берегу.
3) Наш путь преградила небольшая ?
горная речонка.
4)Тонкий ? лунный свет создает
странное ,? пугающее впечатление.
Спишите, расставляя знаки препинания.
Составьте схемы предложений.
1. Дом с своей ветхой резьбой и
острой черепичной кровлей казался
огромной , сгорбленной птицей.
2. В тёмной , холодной глубине реки
колыхались и дрожали звёзды.
Однородные
3. Несколько мгновений спустя лицо
Аси побледнело и приняло
сосредоточенное , печальное
выражение.

4. Дорога к развалине вилась по скату
узкой лесистой долины.
Неоднородные
22. Обобщающие слова при однородных членах
Любишь всё : каждую травинку ,поникшую от росы или согретую
солнцем , каждое деревце над озером ,
трепещущее в безветрии листьями ,
каждое плывущее по бледному и
высокому небу облако.
:
,
,
.
Везде: на стенах, над дверью, у окна –
висели связки сухой травы.
Далекие гулы повторяют и рев, и
треск, и шум, и гром – все звуки моря.
1)
Везде
2)
—
:
…..
—
все …….
Спишите, расставляя знаки препинания.
Составьте схемы предложений.
1. Всё : тонкий запах смолы по лесам , крик и
стук дятлов , немолчная болтовня светлых
ручейков – слились в одно общее чувство.
2. В темноте ни гор , ни дороги – ничего не
было видно.
3. Алый тонкий свет севшего солнца лежал
повсюду : на зелёных лозах , на высоких
тычинках , на сухой земле.

4. Ася и Гагин вдвоём несли большой поднос с
сахаром , ягодами и хлебом.
Где нужно поставить
ТЕСТ
1-запятую, 2-тире, 3-двоеточие?
а) В знакомой хижине огонёк 1) то трепетал 2) то
снова гас.
б) Иван Никифорович был 3) ни жив 4) ни мёртв.
в) Татьяна верила преданьям простонародной
старины 5) и снам 6) и карточным гаданьям 7) и
предсказаниям луны.
г) Стол 7) кресла 8) стулья 9) всё было самого
тяжёлого 10) беспокойного свойства.
д) Всюду 11) вверху 12) и внизу 14) пели жаворонки.
Конспект урока «Однородные члены предложения. Схема предложения с однородными членами. Режим дня.» 4 класс
Урок русского языка в 4 классе
Тема: Однородные члены предложения. Схема предложения с однородными членами. Режим дня.
Цели урока:
Закрепить понятие «однородные члены предложения».
Уметь разбирать простое предложение с однородными членами.

- Уметь ставить запятые в простых предложениях с однородными членами (без союзов, с союзами и, а, но).
Воспитывать бережное отношение к своему здоровью, соблюдая режим дня.
Закрепить знания учащихся о гигиенических нормах и культуре поведения.
Оборудование:
Схемы предложений с однородными членами предложений.
Филворд
Индивидуальные карточки
Тест-контроль
Лист достижений
Мультимедиапроектор
Ход урока
І. Организационный момент.
Приветствие. Создание эмоционального настроя
ІІ. Актуализация опорных знаний.
Чистописание
Зрительно-слуховой диктант. (слайд 1 )
Слова: утро, обед, пробежка, причесать, умыть, зарядка, ванна, друзья.
В слове утро — найдите согласный, твёрдый, звонкий и непарный звук и запишите эту букву.
В слове обед — найдите и запишите ударный гласный звук в корне.

В слове пробежка — найдите парный согласный в корне.
В слове причесать -выделите безударный гласный в приставке.
В слове умыть — найдите согласный, твёрдый, звонкий, непарный звук и запишите эту букву.
В слове зарядка — найдите парный согласный в корне слова.
В слове ванна — найдите удвоенную согласную.
В слове друзья — найдите и запишите букву, обозначающую два звука.
А теперь соедините все буквы и прочитайте, что получилось.
(слайд № 2)
Р + Е + Ж + И + М Д + Н + Я = РЕЖИМ ДНЯ.
Продолжим минуту чистописания подобными словосочетаниями: Утренняя зарядка, ослепляющая улыбка, красивая осанка.
Девиз: Я здоровье сберегу, сам себе я помогу! (слайд 3)
ІІІ. Определение темы урока
(слайд 4) Прочитав стихотворение, определить тему урока.
Слова есть в предложениях,
Не очень внешне схожие,
Но, полномочия на них
Все поровну возложены.
И подчеркнуть их в предложении нужно одинаково,
И между ними правильно
Должны расставить знаки мы.
Шагают вереницею они за словом главным,
Оно ими командует и за собой их тянет.
Наверное, узнали вы,
Слова те благородные —
И это члены предложения,
Какие? … (Однородные)
слайд 5 (Тема урока)
Определение целей урока (слайд 6 – 9)
Цели урока:
1. Вспомнить признаки однородных членов предложения .
2. Повторить правило о расстановке знаков препинания при однородных членах .
3. Упражняться в умении находить однородные члены в предложении и составлять предложения.
IV. Повторение изученного
Филворд . Работа в группах. (слайд 10)
Одно из слов показать, чтобы дети поняли принцип работы.
(слайд 11) ключ к филворду
Словарная работа.
Записать слова: завтрак, молоко, зарядка, стакан, бутерброд, гантели, восемь, ужин, обед, кисель, посуда, язык .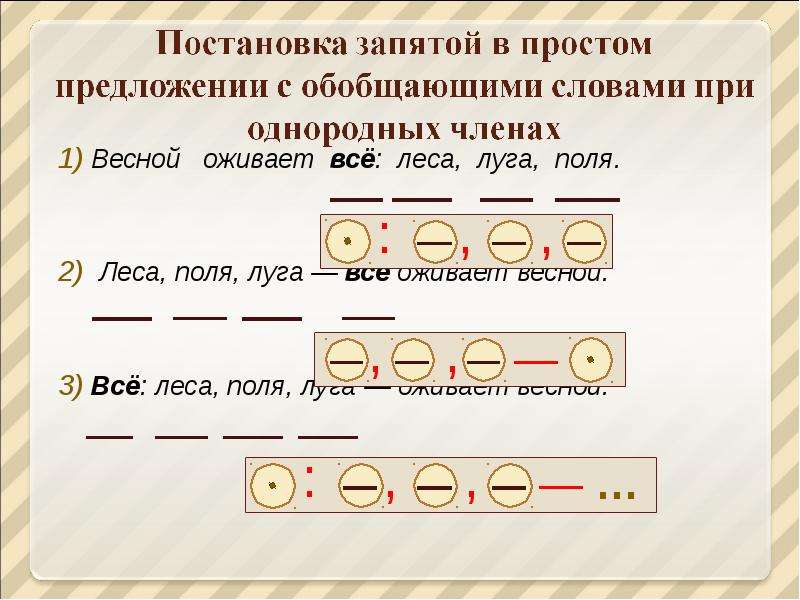 Определить словарные слова. Поставить в них ударение, подчеркнуть непроверяемые буквы.
Определить словарные слова. Поставить в них ударение, подчеркнуть непроверяемые буквы.
Составление рассказа «Режим дня» с использованием опорных слов и картинок (слайд 12)
Примерный вариант рассказа.
Я встаю в 8 часов утра. Умываюсь, делаю зарядку с гантелями, убираю постель. На завтрак я ем кашу, выпиваю стакан молока и съедаю бутерброд с сыром. Затем иду в школу. В школе я изучаю русский язык, математику, окружающий мир. Время в школе бежит очень быстро. Я иду домой. Отдыхаю, потом делаю уроки. Вечером приходит с работы мама. Она готовит вкусный ужин. Я ужинаю, помогаю маме убрать со стола. Мою посуду. Перед сном я читаю интересные книги и детские журналы. После чищу зубы и ложусь спать в десять часов.
5. Выделенные предложения записать и разобрать по членам предложения и по частям речи.
— На какой вопрос отвечают однородные члены предложения?
— Каким членом предложения они являются?
— К какому члену предложения они относятся?
— Какой частью речи выражены однородные члены предложения?
— С какой интонацией они произносятся?
6. Сделать вывод о признаках однородных членов предложения (слайд 13)
Сделать вывод о признаках однородных членов предложения (слайд 13)
Однородные члены предложения:
Отвечают на один и тот же вопрос
Являются одним членом предложения
Относятся к одному и тому же члену предложения
Обычно выражены одной и той же частью речи
Произносятся с перечислительной интонацией
ФИЗМИНУТКА (слайд 14)
Вам, мальчишки и девчонки,
Приготовила вопросы !
Если мой совет хороший,
Вы похлопайте в ладоши.
Раз! Два! (руки над головой)
На неправильный совет
Говорите: нет, нет, нет. (повороты головы)
Постоянно нужно есть
Для зубов для ваших
Фрукты, овощи, омлет,
Творог, простоквашу.
Если мой совет хороший,
Вы похлопайте в ладоши.
(Дети хлопают в ладоши.)
Не грызите лист капустный,
Он совсем, совсем не вкусный,
Лучше ешьте шоколад,
Вафли, сахар, мармелад.
Это правильный совет?
Нет, нет, нет.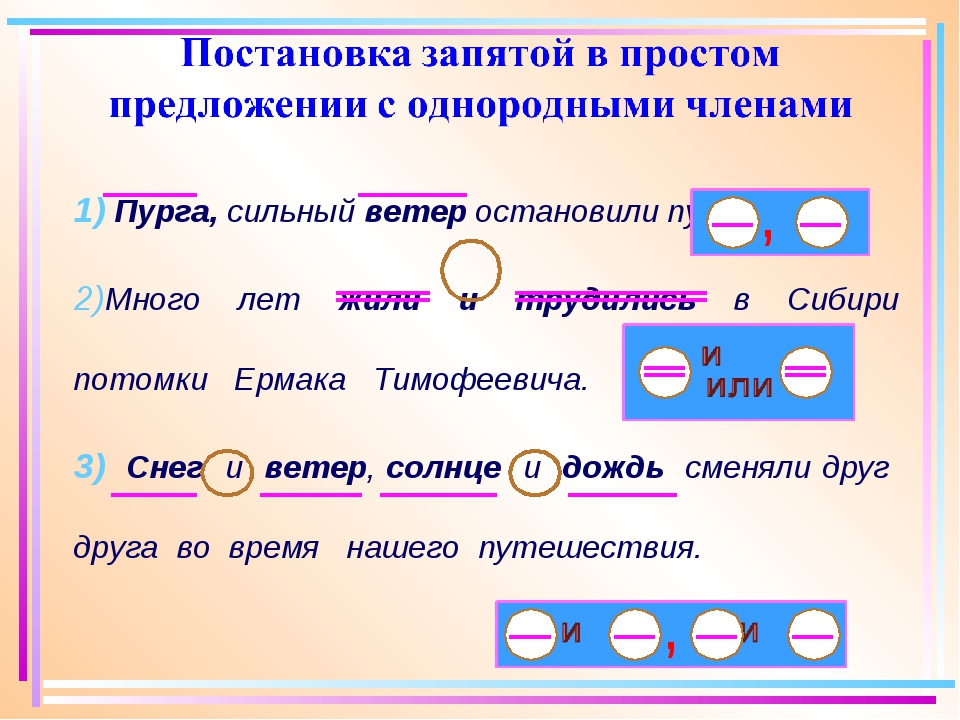 (Дети хором.)
(Дети хором.)
Блеск зубам чтобы придать,
Нужно крем сапожный взять.
Выдавить полтюбика
И почистить зубики.
Это правильный совет?
Нет, нет, нет. . .(Дети хором.)
Навсегда запомните,
Милые друзья.
Не почистив зубы,
Спать идти нельзя.
Если мой совет хороший,
Вы похлопайте в ладоши.
(Дети хлопают в ладоши.)
Зубы вы почистили
И идёте спать.
Захватите булочку
Сладкую в кровать.
Это правильный совет?
Нет, нет, нет. (Дети хором.)
Чтобы зубы укреплять,
Полезно гвозди пожевать.
Это правильный совет?
Нет, нет, нет. (Дети хором.)
Запомните совет полезный,
Не стоит грызть предмет железный.
Если мой совет хороший,
Вы похлопайте в ладоши.
(Дети хлопают в ладоши.)
V. Формирование новых знаний.
1. Возвращение по гиперссылке к слайду 9. Повторение целей урока.
2. Возвращение по гиперссылке к слайду 15
3. Знакомство со схемами соединения и разделения однородных членов предложения.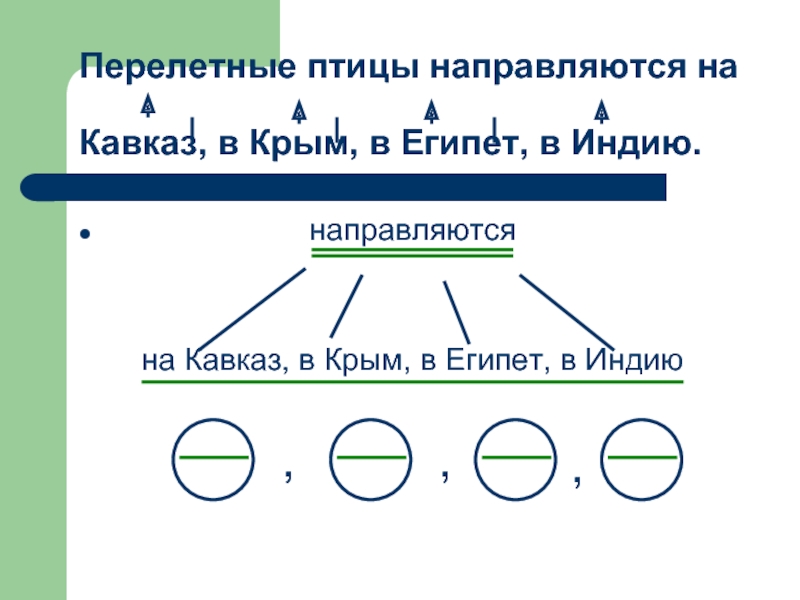
Ключ:
1. Если однородные члены предложения соединены между собой союзом и, то запятая между ними не ставится.
2. Если между однородными членами предложения нет союзов и они произносятся с перечислительной интонацией, то между ними ставится запятая.
3. Если между однородными членами предложения есть союз а или но, то перед союзом ставится запятая.
4. Если между однородными членами предложения многократно употребляется союз и, то между ними ставится запятая.
5. Если между однородными членами предложения многократно употребляется союз или, то между ними ставится запятая.
4. Закрепление новых знаний. (слайд 16)
1.Подобрать к схемам соответствующие предложения с однородными членами.
2.Записать схему с многократно повторяющимися союзами или и соответствующее предложение предложение в тетрадь.
— В русской речи много пословиц о здоровье, здоровом образе жизни. Какие пословицы о здоровье вы знаете? (слайд 17)
VI. Формирование практических знаний, умений, навыков.
Формирование практических знаний, умений, навыков.
ТЕСТ-КОНТРОЛЬ. ( 2 мин. )
Взаимопроверка теста по ключу (слайд 18)
Индивидуальная работа по карточкам. (3 мин.)
VII. Формирование информационной компетентности. Рефлексия.
А теперь мы с вами поработаем в листе достижений.
Подпишите его (слайд 19). Принцип работы следующий:
Если об изученном вопросе вы можете сказать: «Отлично владею информацией», то помечаете этот пункт зелёным цветом.
Если об изученном вопросе вы можете сказать: «Понятно, но не полностью», то помечаете этот пункт жёлтым цветом.
Если об изученном вопросе вы можете сказать: «Затрудняюсь в ответе», то помечаете этот пункт красным цветом.
Отвечать мы будем на следующие вопросы (слайд 20):
Лист достижений_________________________________
Фамилия имя
______
класс
1
ЗНАЮ признаки однородных членов предложения
2
УМЕЮ находить в тексте однородные члены предложения
3
УМЕЮ правильно расставлять знаки препинания
4
УМЕЮ определять их синтаксическую роль (каким членом предложения является)
5
УМЕЮ составлять схемы предложений с однородными членами
— Скажите, какой цвет преобладает в ваших ответах?
Если зелёный – вы полностью справились с задачами урока.
Если жёлтый – вы хорошо справились, но следует уделить внимание некоторым вопросам.
Ну а если красный – нужно остановиться на этой теме ещё раз.
VIII. Итог урока. (слайд 21)
Назовите тему сегодняшнего урока.
Какие знаки препинания ставятся между однородными членами предложения?
Когда не ставятся знаки препинания между однородными членами предложения?
О чём важном для здоровья человека мы сегодня с вами говорили?
Для чего нужно выполнять режим дня?
Итоговая беседа
Режим дня следует строго соблюдать: вовремя завтракать, обедать, ужинать, ложиться спать, гулять и отдыхать, внимательно слушать на уроках, чтобы не отставать по предметам.
IX. Домашнее задание. (слайд 22)
Составить и записать 5 предложений с однородными членами и подобрать к ним соответствующие схемы; повторить словарные слова.
-Урок окончен. Спасибо за работу! (слайд 23)
ПРИЛОЖЕНИЕ
Вставь, где необходимо, запятые // Ф.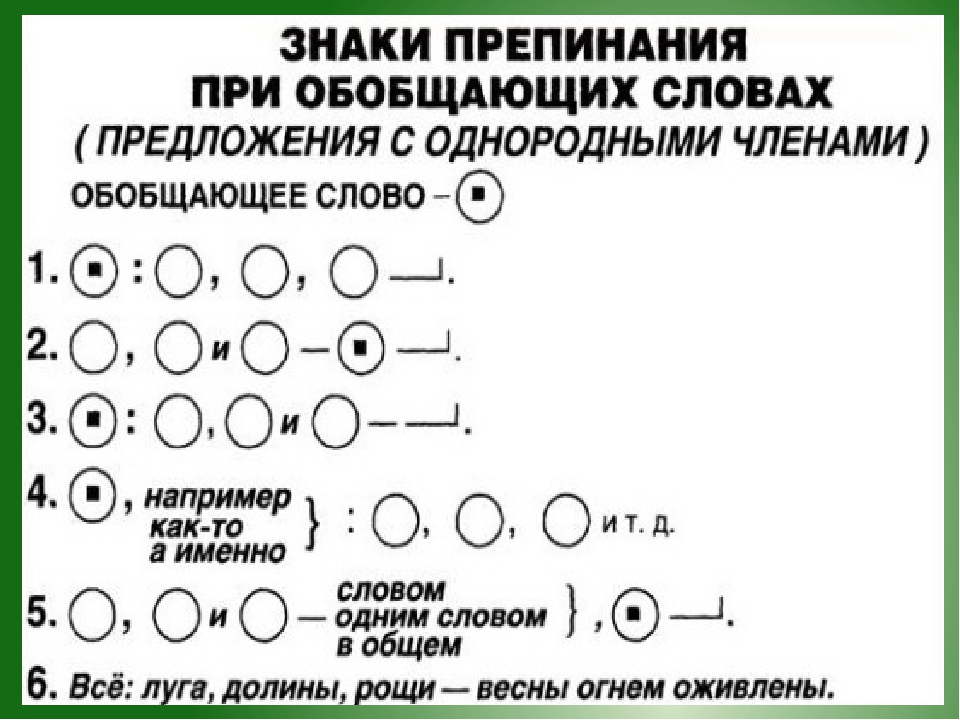 И._________________________
И._________________________
НАШ ЛЕС.
В нашем лесу растут сосна ель береза осина дуб ольха. В лесу мы собираем землянику и ежевику. В лесу растут рыжики маслята подберезовики опята. В лесу живут и волки и лисицы и зайцы и белки. Летом в лесу мы часто видим бревна на постройку изб и сараев. Наши кустари делают из дерева ложки корыта колеса телеги сани.
__________________________________________________________________________
Вставь, где необходимо, запятые Ф.И._________________________
БЕЛКА.
У белки мягкая шерсть чуткие стоячие уши быстрые глаза и проворные цепкие лапы. Она очень быстро скачет с ветки на ветку прыгает с вершины дерева на землю не падает. Белка принадлежит к грызунам и питается древесными почками зернами орехами семенами еловых и сосновых шишек. Зубы у белки стираются но вскоре опять подрастают.
__________________________________________________________________________
Вставь, где необходимо, запятые // Ф.И._________________________
О ВОЛКЕ.
Волк для деревни — первый враг и разб…
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
Однородные члены предложения (обобщение)
8 класс
Тема: Однородные члены предложения (обобщение)
Цели:
Организовать деятельность учащихся по обобщению и систематизации знаний об однородных членах предложения на материале произведений о природе, о системе знаков препинания в предложениях с однородными членами; по разграничиванию однородных и неоднородных определений.
Создать условия для формирования умения составлять предложения с однородными членами;
для развития у учащихся умения структурировать учебную информацию, определять способ действия, позволяющий осмыслить особенности построения и пунктуации предложений с однородными членами;.
Углубить практические навыки постановки знаков препинания при однородных членах.
Развивать умение пользоваться синтаксическими конструкциями с однородными членами в речи, интонационно правильно произносить такие предложения.
Воспитывать любовь к родному краю, природе.
Тип урока: урок обобщения и систематизации знаний, совершенствования умений и навыков.
Оборудование: мультимедийный проектор, презентация, раздаточный материал (тесты).
Эпиграф
«С русским языком можно творить чудеса. Нет ничего такого в жизни и в нашем сознании, что нельзя было бы передать русским словом. Звучание музыки, блеск красок, игру света, шум и тень садов, неясность сна, тяжкое громыхание грозы, детский шепот и шорох морского гравия. Нет таких звуков, образов и мыслей, для которых не нашлось бы в нашем языке точного выражения»
К.Паустовский.
Ход урока
Организационный этап
Слово учителя:
-Здравствуйте, садитесь.
Я рада видеть, что у вас всё готово к уроку, и сами вы настроены на серьёзное общение.
Сегодняшний урок я хочу начать с эпиграфа. Это слова К.Паустовского. Прочитаем их.
3. Работа над эпиграфом
1.) Орфографическая «минутка»
— Объяснить написание слов с не/ни.
— О/е после шипящих.
— Окончания прилагательных.
2. ) «Четвертое лишнее»
— Эпиграф состоит из 4 –ех предложений. Найдите среди них 4 –ое лишнее.(3 предложение, т.к все остальные безличные, а 3 –е двусоставное)
— А в чем особенность 3-го предложения? Чем оно осложнено? (однородными членами)
4. Объявление темы
-Сформулируйте тему нашего урока.
Однородные члены предложения.
5. Постановка целей.
Постановка целей.
— Сегодня мы приведем наши знания об однородных членах в систему, проверим, чему вы научились и , может быть, узнаем что-то новое.
6. Синтаксическая «пятиминутка»
— Давайте вернемся к нашему эпиграфу. 4 –е лишнее — предложение особое и «опасное». Что соединяет союз «и» в этом предложении? (Однородные члены)
— Такую ли функцию выполняет союз «и» во 2 и 4 предложениях? (Да)
7. Задание на сопоставление и определение функции союза «И». Отработка пунктуационных навыков.
Образец для наблюдения:
Все весны дыханием согрето, все кругом и любит и поет.(А.К.Толстой)
В ярком золоте день утопает,
И ручьи по оврагам шумят.
Выборочный диктант ( 1вариант – выписать сложные предложения, 2 вариант – предложения с однородными членами)
Ночью ветер злится и стучит в окно. (А.Фет)
(А.Фет)
Ночь прошла под большой чистой луной и к утру лег первый мороз.(М.Пришвин)
В ярком золоте день утопает и ручьи по оврагам шумят. (И.Никитин)
На дворах и домах снег лежит полотном и от солнца блестит разноцветным ковром.( И.Никитин)
Проверьте себя
— Найдите определения в 3-ем предложении. Какие они? (Неоднородные.) Почему?
8.Актуализация знаний, сформированных на предыдущих уроках.
— На протяжении нескольких занятий предметом нашего внимания были предложения с однородными членами. И сейчас я приглашаю вас на игру «Блеф-клуб». Кстати, назовите мне лексическое значение этого слова (учащиеся определяют лексическое значение слова «блеф»).
Вашему вниманию предлагаются утверждения, которые могут быть правильными или ошибочными. Моя задача — ввести вас в заблуждение. Я блефую. Ваша же задача — не поддаться на мои уловки. Если вы согласны с утверждением, то поднимаете руку и исправляете меня, а если согласны – то молчите.
Я блефую. Ваша же задача — не поддаться на мои уловки. Если вы согласны с утверждением, то поднимаете руку и исправляете меня, а если согласны – то молчите.
Итак, я утверждаю:
Синтаксис – это раздел науки о языке, который изучает части речи.
Однородными называются члены предложения, соединенные подчинительной связью..
Однородные члены предложения относятся к одному и тому же слову в предложении.
4) Однородные члены отвечают на разные вопросы.
5) однородные члены являются только определениями.
6) Однородные члены могут быть разными членами предложения.
7) Однородные члены предложения равноправны по отношению друг к другу и связываются подчинительной связью.
— Мы повторили признаки второстепенных членов. Все ли мы вспомнили?
(слайд с признаками второстепенных членов)
Признаки однородных членов
Относятся к одному и тому же слову;
Отвечают на один и тот же вопрос;
Являются одинаковыми членами предложения;
Равноправны по отношению друг к другу и связываются сочинительной связью;
Произносятся с интонацией перечисления.
8.Обобщение и систематизация знаний.
1) Схематический диктант
Задание 1. Расставьте знаки препинания при однородных членах, составьте схемы предложений.( К доске выходит один ученик с предложениями, составляет на доске схемы, объясняет знаки препинания)
И вспомнил я отцовский дом ущелье наше и кругом в тени рассыпанный аул.
Щеки румяны и полны и смуглы.
Ни смех ни говор твой веселый не прогнали темных дум.
Небо стало заволакиваться не то тучами не то туманом.
Им приходилось как землю рыть так и камни обтесывать.
Виднелись равнины или далекие горы.
Как я люблю свои березы
Свои леса свои луга
И ночи летние и грозы
И зиму с стужей и снега.
9. Физкультминутка
Повторение понятия «обобщающее слово». Пунктуация предложений с обобщающим словом.
Задание: объясните, почему в одном случае после слова багаж нет знака препинания, а в другом – есть. Почему в одном примере после слова картонку нет запятой, а в другом – есть?
Дама сдавала в багаж Диван, Чемодан, Саквояж, Картину, Корзину, Картонку И маленькую собачонку. | Носильщик 15 –й номер Везет на тележке багаж: Диван, Чемодан. Саквояж, Картину, Корзину, Картонку, А дальше ведут собачонку. С.Маршак |
Задание 2. Я предлагаю вам поработать с понятием «Обобщающее слово». Что это такое?
Спишите предложение, расставьте знаки препинания. Составьте схему на доске.
Все сверкало, искрилось, переливалось: стволы берез и сосен, листья травы, самый воздух, вода лесных озер.
— Перестройте предложение так, чтобы изменились знаки.(Устно)
10. Творческое задание.
1. Задание: осложнить предложения, составляя поочередно с каждым членом отдельный ряд однородных членов.
вариант. Вдоль дорожек зацвели тюльпаны.
2 вариант. Над цветами кружатся пчелы.
11. Проверка усвоения знаний.
Задание: Списать предложения, решая орфографические и пунктуационные задачи. Построить схемы однородных членов.
Построить схемы однородных членов.
Мой са… с каждым днем ув…да…т;
П…мят он п…ломан и пуст,
Хоть пышно ещ… д…цв…тает
Настурций (в)нем огне(н,нн)ый куст.
А.Майков
Чере…чур с…леная в…да (М,м)ертвого моря убивает все ж…вое
и рыб и р…стительные орг…низмы (М.И.Ильин)
Отг…в…рила роща з…л…тая
Б….резовым в…селым языком.(С.Есенин)
12. «Словесный натюрморт»
— А сейчас закройте глаза, а я вам прочитаю стихотворение Георгия Оболдуева. На что оно похоже?
— Из чего состоит это стихотворение? (из распространенных однородных членов)
13. Рефлексия.
— Используя однородные члены предложения опишите свое состояние по готовности к контрольной работе.
Красный- не готов, ничего не понимаю.
Желтый – еще бы чуть-чуть!
Зеленый – я уверен в своих силах.
14. Домашнее задание:
На 1-4 балла: выписать из «Евгения Онегина» 4 предложения с однородными членами.
На 5 -8 баллов: выписать из «Евгения Онегина» 5-6 предложений с однородными членами, подчеркнуть их как члены предложения, составить схемы.
На 9-10 баллов: Составить словесный натюрморт, используя только однородные члены предложения.(по аналогии), или центон по теме «Зима».
Карточки «Однородные члены предложения»
Подчеркните однородные члены предложения. Назовите автора сказок, из которых взяты эти предложения.
1. Ветер по морю гуляет и кораблик подгоняет.
2. И царица хохотать,
И плечами пожимать,
И подмигивать глазами,
И прищелкивать перстами.
3. Положила иль не жить, иль царевну погубить.
Вставьте буквы, подчеркните однородные члены предложения
Бледно-серое небо св..тлело, х..лодело, с..нело.
В..сёлые г..лоса, шутки и смех разн..сились по долине.
Каштанка л..знула незнакомцу руку и заскулила ещё жалос..нее.
Туристы ежегодно путешествуют по Дн..пру, Бугу, Х..ролу.
Туризм от каждого требует выд..ржки, мужества, дисц..плины.
Подчеркните однородные члены предложения, расставьте знаки препинания и, если нужно, союзы
Этот путь короткий очень трудный.
В нашем лесу растут ель сосна осина и берёза.
В берёзовых рощах сосновых борах под раскидистыми елями растёт белый гриб.
В любом лесу могут встретиться сыроежки с красными жёлтыми белыми шляпками.
Дети, поддерживайте чистоту и порядок везде!
Дополните предложения однородными членами, подчеркните их, расставьте знаки препинания
В вазе на столе лежали разные фрукты …
Посуда, а именно … была невымыта.
В словах мы выделили их части …
С базара мы принесли … зеленые овощи.
В магазине покупают … красивую мебель.
Раскройте скобки, подчеркните однородные члены предложения, составьте схему однородных членов
Для дальнего путешествия они запаслись (провизия, тёплая одежда, бельё).
Ежегодно в больших городах Украины (Одесса, Киев, Харьков) проходит много фестивалей (песни, танцы и народные ремесла).
Школьники принесли в живой уголок (ёж, черепаха, кролик).
На пришкольном участке есть (картофель, капуста, морковь).
Восстановите пословицы с помощью однородных членов предложения, подчеркните их как члены предложения. Расставьте запятые.
На смелого собака лает а трусливого …
Без нитки и … шубу не сшить.
… и труд все перетрут.
Чужой земли мы не хотим но и своей не …
Пей … а правду режь.
Однородные продукты: определение и обзор — видео и стенограмма урока
Что такое однородный продукт?
Однородный продукт — это продукт, который невозможно отличить от конкурирующих продуктов от разных поставщиков. Другими словами, продукт имеет практически те же физические характеристики и качество, что и аналогичные продукты других поставщиков. Один продукт легко заменить другим. Для покупателя это означает, что вы не можете отличить продукт от компании ABC от продукта от компании XYZ.
Когда вы покупаете продукт, который оказывается однородным, это означает, что все версии продукта служат одной и той же цели, и вам вряд ли будет важно, какую из них вы используете. Следовательно, если вы ходите по магазинам, чтобы купить «лучший» продукт, единственной разницей будет цена. Этот термин обычно применяется к сельскохозяйственной продукции, металлам и товарам на основе энергии. Например, когда вы покупаете пакет зеленых яблок, вы, вероятно, не знаете, откуда они и кто их выращивал, и вам, вероятно, все равно.Вы основываете свой выбор только на цене.
Например, когда вы покупаете пакет зеленых яблок, вы, вероятно, не знаете, откуда они и кто их выращивал, и вам, вероятно, все равно.Вы основываете свой выбор только на цене.
Напротив, гетерогенный продукт — это продукт, который легко отличить от конкурирующих продуктов и который нельзя легко заменить друг на друга. Как покупатель, это означает, что вы должны решить, какие функции наиболее важны для вас. Например, физические характеристики аналогичных товаров могут различаться у разных поставщиков. Это означает, что реклама, торговые марки, упаковка, гарантии и элементы дизайна, такие как цвет, размер и форма, будут влиять на ваше решение.Фактические цены, вероятно, будут значительно отличаться от одного продукта к другому, потому что поставщики могут сделать свой продукт отличным от конкурентов.
Например, для покупателей Ford Mustang легко отличить от Chevrolet Camaro, даже если оба являются автомобилями и выполняют одну и ту же базовую функцию. Такие вещи, как реклама, лояльность к бренду, имидж и внешний вид, будут влиять на решение покупателя. Сама по себе цена, вероятно, не будет самым важным фактором при принятии решения о покупке.
Сама по себе цена, вероятно, не будет самым важным фактором при принятии решения о покупке.
Эффективная схема совместного использования разделенного секрета, основанная на линейных однородных отношениях повторяемости
Схемы совместного использования нескольких частей — это схемы, которые имеют многостороннюю структуру доступа. Набор участников этих схем разделен на несколько частей, и все участники одной части играют равноценную роль. Один тип такой структуры доступа — это разделенная структура доступа, а другой — иерархическая структура доступа. Мы предлагаем эффективную схему разделенного мультисекретного обмена, основанную на линейных однородных рекуррентных (LHR) отношениях.На этапе построения общие секреты скрыты в некоторых терминах линейной однородной рекуррентной последовательности. На этапе восстановления общие секреты получают путем решения тех условий, в которых общие секреты скрыты. Когда глобальный порог равен, наша схема может снизить вычислительную сложность схем разделения секрета с экспоненциального времени до полиномиального. Безопасность предлагаемой схемы основана на пороговой схеме Шамира, т.е. наша схема идеальна и совершенна.Более того, в предлагаемой схеме эффективно разделять мультисекретность и изменять разделяемые секреты.
Безопасность предлагаемой схемы основана на пороговой схеме Шамира, т.е. наша схема идеальна и совершенна.Более того, в предлагаемой схеме эффективно разделять мультисекретность и изменять разделяемые секреты.
1. Введение
Шамир [1] и Блейкли [2] предложили схемы разделения порогового секрета в 1979 году. Их схемы были основаны на алгоритме интерполяции Лагранжа и линейной проективной геометрии соответственно. В схеме разделения порогового секрета ( t , n ) секреты могут совместно использоваться участниками, и любой или несколько участников могут восстановить общие секреты путем объединения своих долей, поскольку количество участников больше или равно количеству участников (пусть будет набор участников, где является th участником в наборе) может построить квалифицированное подмножество.Менее чем участники не могут получить общие секреты, поскольку менее чем участники не могут построить квалифицированное подмножество. Если участники какого-либо неквалифицированного подмножества не могут получить какую-либо информацию об общих секретах, тогда схема называется совершенной схемой . Мы называем схему разделения секрета идеальной схемой , когда каждый участник держит долю до тех пор, пока общий секрет. Схемы порогового разделения секрета, предложенные Шамиром и Блейкли, представляют собой лишь особые случаи, когда все участники имеют одинаковые полномочия.Многие приложения [3, 4] были разработаны на основе схемы разделения секрета. Это причина того, что схема разделения секретов по-прежнему популярна.
Мы называем схему разделения секрета идеальной схемой , когда каждый участник держит долю до тех пор, пока общий секрет. Схемы порогового разделения секрета, предложенные Шамиром и Блейкли, представляют собой лишь особые случаи, когда все участники имеют одинаковые полномочия.Многие приложения [3, 4] были разработаны на основе схемы разделения секрета. Это причина того, что схема разделения секретов по-прежнему популярна.
1.1. Связанные работы
Схемы разделения порогового секрета имеют много ограничений в некоторых условиях. Следовательно, последовательно предлагались и другие структуры доступа. Шамир предложил схему разделения секрета с взвешенным порогом [1]. Построение этой схемы простое: возьмите пороговую схему и дайте каждому участнику столько долей, сколько его вес.Тем не менее, полученная схема уже не идеальна. В 1987 году Ито и др. впервые предложил схему для достижения разделения секрета на общую структуру доступа [5]. Симмонс первым предложил структуру многостороннего доступа [6].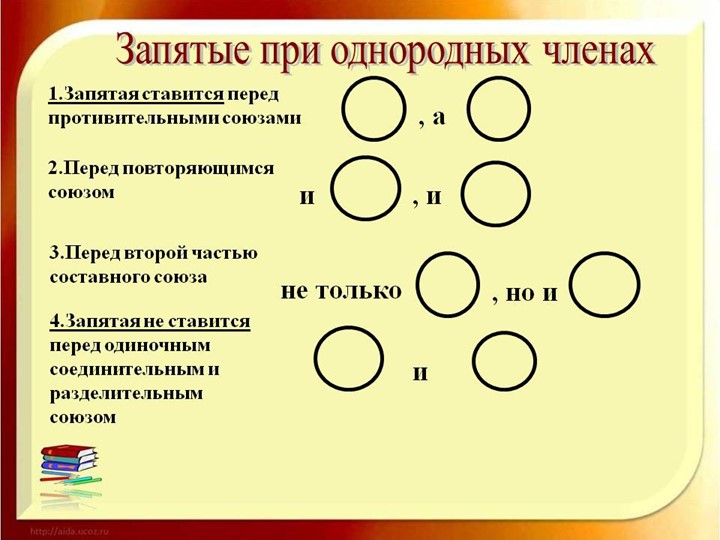 Брикелл предложил метод построения идеальной схемы разделения секрета для многоуровневых и разделенных структур доступа [7], но он неэффективен. Определение разделенной структуры доступа можно найти в Разделе 2.2.2. Вычислительная сложность и размер дискового пространства обычно используются для измерения эффективности схемы.Скорость передачи информации обычно используется для измерения эффективности схемы разделения секрета. Поэтому, чтобы повысить эффективность схемы разделения секрета, многие исследователи сосредоточились на изучении конкретных семейств структур доступа, таких как структуры доступа на основе графов [8], взвешенные пороговые структуры доступа [9], двусторонние структуры доступа [10–10]. 12], трехсторонние структуры доступа [13, 14] и пороговые структуры доступа [15]. В частности, Фаррас и Мартл-Фарр дали полную характеристику идеальных многосторонних структур доступа [16].Схему многостороннего совместного использования секретов можно разделить на два типа. Одна из них — это схема разделения секретов, а другая — иерархическая схема разделения секретов.
Брикелл предложил метод построения идеальной схемы разделения секрета для многоуровневых и разделенных структур доступа [7], но он неэффективен. Определение разделенной структуры доступа можно найти в Разделе 2.2.2. Вычислительная сложность и размер дискового пространства обычно используются для измерения эффективности схемы.Скорость передачи информации обычно используется для измерения эффективности схемы разделения секрета. Поэтому, чтобы повысить эффективность схемы разделения секрета, многие исследователи сосредоточились на изучении конкретных семейств структур доступа, таких как структуры доступа на основе графов [8], взвешенные пороговые структуры доступа [9], двусторонние структуры доступа [10–10]. 12], трехсторонние структуры доступа [13, 14] и пороговые структуры доступа [15]. В частности, Фаррас и Мартл-Фарр дали полную характеристику идеальных многосторонних структур доступа [16].Схему многостороннего совместного использования секретов можно разделить на два типа. Одна из них — это схема разделения секретов, а другая — иерархическая схема разделения секретов.
Недавно было проведено несколько исследований по структуре разделенного доступа [17–19]. Tassa et al. предложили два типа схем разделения секрета на основе двумерной интерполяции Лагранжа [20]. Хотя некоторые из существующих схем оказались идеальными, указанные методы неэффективны.Фаррас и Мартл-Фарр использовали матроиды и целочисленные полиматроиды для изучения разделенной структуры доступа [16, 19], и с помощью матроидов и целочисленных полиматроидов легко определить, являются ли схемы разделения секрета идеальными или нет. Проблема того, как разработать схему для реализации разделенной структуры доступа, может рассматриваться как проблема того, как найти представление матроида из представления связанного с ним полиматроида [21]. Chen et al. [21] предложили схему разделения секрета, основанную на общем полиматроиде и кодах Габидулина, но эта схема также предназначена для получения невырожденных матриц.Позже Чен и др. [22] дал другой метод, основанный на идее Брикелла [7], и эта схема также требовала проверки многих матриц на невырожденность. Но Фаррас и Мартл-Фарр [16, 19] показали, что остается открытым вопрос о том, существуют ли эффективные алгоритмы для получения представлений многочастных матроидов из представлений связанных с ними полиматроидов в целом. Разделенная структура доступа особенно полезна в некоторых приложениях. Например, компания разделена на несколько отделов.Решение этой компании требует одобрения хотя бы нескольких человек в каждом отделе. То есть решение требует сотрудничества всех отделов, и в нем должно быть задействовано минимальное количество сотрудников в каждом отделе.
Но Фаррас и Мартл-Фарр [16, 19] показали, что остается открытым вопрос о том, существуют ли эффективные алгоритмы для получения представлений многочастных матроидов из представлений связанных с ними полиматроидов в целом. Разделенная структура доступа особенно полезна в некоторых приложениях. Например, компания разделена на несколько отделов.Решение этой компании требует одобрения хотя бы нескольких человек в каждом отделе. То есть решение требует сотрудничества всех отделов, и в нем должно быть задействовано минимальное количество сотрудников в каждом отделе.
Машхади и Дехкорди впервые представили отношения линейной однородной повторяемости (LHR) для пороговой схемы разделения секрета [23]. Позже они ввели линейные неоднородные рекуррентные отношения (LNHR) в схему разделения секрета [24]. Но участники имеют равные полномочия, и квалифицированное подмножество удовлетворяет схемам Машхади и Дехкордис.Юань и др. [25] представили отношения LHR к иерархической схеме разделения секрета. Они снизили вычислительную сложность иерархических схем разделения секрета с экспоненциального времени до полиномиального времени () (в [25] оно отличается от нашей схемы). Но не существует схемы, которая реализует схему разделения секрета за полиномиальное время. Таким образом, в этой статье мы в основном обсуждаем разделенную структуру доступа.
Они снизили вычислительную сложность иерархических схем разделения секрета с экспоненциального времени до полиномиального времени () (в [25] оно отличается от нашей схемы). Но не существует схемы, которая реализует схему разделения секрета за полиномиальное время. Таким образом, в этой статье мы в основном обсуждаем разделенную структуру доступа.
1.2. Наш вклад
Мотивация нашей схемы состоит в том, чтобы разработать эффективную схему совместного использования секрета со структурами доступа, которые являются более общими, чем структуры порогового доступа.Одним из ключевых вкладов является введение отношений LHR в разделенную структуру доступа, которая делит степень полинома на низкие степени некоторых полиномов, и каждая низкая степень равна фиксированному порогу отсека минус один. В предлагаемой схеме разделенная структура доступа реализована с помощью линейных однородных рекуррентных (LHR) соотношений. Отношения LHR подходят для разделенной структуры доступа, поскольку у нее есть возможность связать каждую ячейку с различным полиномом. Другой ключевой вклад — снижение вычислительной сложности схем разделения секретов с экспоненциального времени до полиномиального (). В нашей схеме легко разделить мультисекретность. Каждый участник владеет долей, равной тайне. Безопасность предлагаемой схемы основана на пороговой схеме Шамира.
Другой ключевой вклад — снижение вычислительной сложности схем разделения секретов с экспоненциального времени до полиномиального (). В нашей схеме легко разделить мультисекретность. Каждый участник владеет долей, равной тайне. Безопасность предлагаемой схемы основана на пороговой схеме Шамира.
Остальная часть этого документа организована следующим образом. Раздел 2 вводит базовые знания о линейных однородных рекуррентных отношениях и схеме разделения секрета.В разделе 3 представлена предлагаемая схема. В разделе 4 мы анализируем безопасность предложенной схемы. В разделе 5 обсуждаются некоторые важные свойства предложенной схемы и ее характеристики. Наконец, раздел 6 подводит наш вывод.
2. Предварительные знания
В этом разделе, прежде всего, мы вводим основные математические знания, используемые в предлагаемой схеме. Подробное описание линейных однородных рекуррентных соотношений можно найти в [24–28]. Мы также даем краткое описание идеальной схемы, идеальной схемы и структуры доступа с отсеками.
2.1. Линейные однородные рекуррентные отношения
Теорема 1 (Ричард [26]). Позвольте быть последовательность целых чисел, и пусть быть различными корнями следующего характеристического уравнения линейного однородного рекуррентного отношения с постоянными коэффициентами: где, выбирается над GF ( q ) (), и является большим простым числом.
Если — кратный корень характеристического уравнения (1), то часть общего решения этого рекуррентного соотношения, соответствующая, задается как
Пусть.Итак, мы можем получить
Общее решение рекуррентного соотношения находится где-то.
Следствие 1. Если, то общее решение рекуррентного соотношения находится где
Определение 2 (Ричард [26]). Позвольте быть бесконечной последовательности чисел. Его производящая функция определяется как бесконечный ряд: коэффициент при in является th членом. Таким образом, действует как заполнитель для. Конечную последовательность можно рассматривать как бесконечную последовательность, в которой все, кроме конечного числа членов, равны 0. Следовательно, каждая конечная последовательность имеет производящую функцию: которая является многочленом.
Следовательно, каждая конечная последовательность имеет производящую функцию: которая является многочленом.
Теорема 2 (Ричард [26]). Предположим, что последовательность LHR {} определена как (1), а характеристическое уравнение имеет разные корни с кратностями, где. Тогда производящая функция последовательности {} iswhere является полиномиальной функцией от степени не выше. Таким образом, мы можем получить, где есть полиномиальная функция от степени не выше. Наоборот, для таких многочленов существует последовательность, удовлетворяющая линейному однородному рекуррентному соотношению с постоянными коэффициентами порядка типа (1), производящая функция которой задается формулой (5).
2.2. Схемы совместного использования секретов
В следующем разделе мы дадим определение идеальной схемы и идеальной схемы, а также будет перечислена иерархическая структура доступа.
2.2.1. Совершенная схема и идеальная схема
Определение 3. A ( t , n ) пороговая схема разделения секрета на M , где — совместно используемое секретное пространство, — это набор случайных входных данных, а () — это разделяемое пространство удовлетворяет следующим двум условиям: (1) Для всех A M и t , где — подмножество участников, — количество участников в подмножестве, обозначает информацию об акциях. должны быть получены участниками подмножества, а — энтропия.(2) Для всех и,. Если, то схема называется совершенной схемой .
должны быть получены участниками подмножества, а — энтропия.(2) Для всех и,. Если, то схема называется совершенной схемой .
Определение 4 (Tassa and Dyn [20]). Позвольте обозначить набор возможных долей для участника. Информационная скорость схемы определяется следующим образом: где обозначает размер совместно используемого секрета и обозначает размер долей, сохраненных участником. Если, схема называется идеальной схемой.
2.2.2. Комментируемая структура доступа
используется для обозначения общего количества участников в наборе, т.е.е.,. В схеме разделения секрета набор разделен на непересекающиеся части, то есть, и. Участники одного купе играют равноценную роль. Пусть будет порог купе. В купе присутствуют участники, где и. Квалифицированное подмножество разделенной пороговой схемы разделения секрета содержит, по крайней мере, участников из отсека, где и. В предлагаемой схеме предполагается, что глобальный порог равен. Раздельная структура доступа представлена по номеру
3.
 Предлагаемая схема
Предлагаемая схема Наша схема основана на линейных однородных рекуррентных соотношениях. При разделенном разделении секрета набор участников разделен на разделы, и общие секреты могут быть восстановлены только в том случае, если количество участников из любого раздела больше или равно фиксированному пороговому значению раздела, а общее количество участников больше, чем глобальный порог. В нашей схеме мы это предполагаем. Предлагаемая схема состоит из трех этапов, т.е.е., фаза инициализации, фаза строительства (фаза генерации доли и фаза распределения доли) и фаза восстановления. Основная идея предложенной схемы поясняется следующим образом. Система состоит из нескольких участников и дистрибьютора. Дистрибьютор генерирует отношение LHR с разными корнями, где — номер непересекающегося отсека. Затем распространитель выбирает общие секреты и скрывает общие секреты в некоторых терминах этой последовательности LHR. Сложность нашей схемы состоит в том, как сгенерировать это отношение LHR. Восстановление общих секретов осуществляется путем решения общего члена последовательности LHR {}. Затем участники, которые хотят восстановить общие секреты, должны получить те термины, в которых общие секреты скрыты.
Восстановление общих секретов осуществляется путем решения общего члена последовательности LHR {}. Затем участники, которые хотят восстановить общие секреты, должны получить те термины, в которых общие секреты скрыты.
3.1. Фаза инициализации
В предлагаемой схеме предположим, что разделенная структура доступа является монотонной, то есть, если существует и (структура доступа),, и, то мы можем получить. Ито и др. представили, что если структура доступа монотонна, то существует идеальная схема разделения секрета для структуры доступа [29].
Для предлагаемой схемы требуется общедоступная доска объявлений. Любой человек имеет право читать или загружать содержимое с общественной доски объявлений. Только законные участники системы могут публиковать информацию в каталоге и изменять или обновлять опубликованный контент в соответствии со своими собственными разрешениями.
Предлагаемая схема основана на соотношении LHR над, где — большое простое число, а — конечное поле.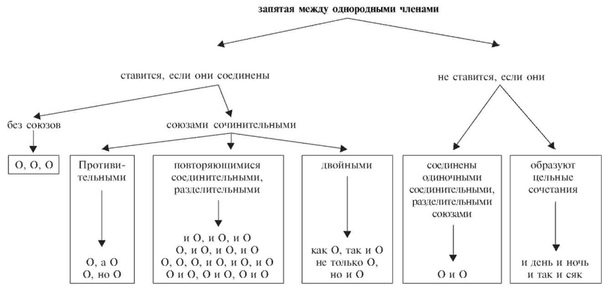 обозначает общие секреты, которые могут быть разделены между участниками.Дистрибьютор выбирает в качестве входящего участника, где (это гарантирует, что мы можем скрыть общие секреты в первых элементах последовательности) и. обозначает -й участник в отсеке, где. Затем дистрибьютор публикует объявление на общественной доске объявлений.
обозначает общие секреты, которые могут быть разделены между участниками.Дистрибьютор выбирает в качестве входящего участника, где (это гарантирует, что мы можем скрыть общие секреты в первых элементах последовательности) и. обозначает -й участник в отсеке, где. Затем дистрибьютор публикует объявление на общественной доске объявлений.
3.2. Этап построения
Дилер выполняет следующие шаги для создания долей, распределения долей и сокрытия общих секретов в первых условиях: (1) Дилер выбирает различные целые числа, каждое из которых не равно нулю и соответствует количество непересекающихся отсеков участников.(2) Крупье выбирает разные многочлены. Обозначим через разные полиномы. Степень полинома равна и является фиксированным порогом отсека, то есть, когда глобальный порог равен и. (3) вычисляет и отправляет долю в отсек частным образом в защищенном канале, где и. Этот участник сохраняет свою долю. (4) После того, как все доли были отправлены участникам через, где дилер вычисляет Let (5) После того, как общий термин получен, дилер продолжает вычисление. Затем скрывает общие секреты в этих условиях. (6) Дилер вычисляет, где. (7) Дилер публикует и на общедоступной доске объявлений.
Затем скрывает общие секреты в этих условиях. (6) Дилер вычисляет, где. (7) Дилер публикует и на общедоступной доске объявлений.
Замечание 1. Из шага (3), приведенного выше, мы знаем, что многочлен соответствует отделению, и участники отделения, равные или превышающие его, могут восстановить полином, объединив свои доли.
Замечание 2. Из теоремы 1 мы можем определить, что это общее решение отношения LHR со степенью, а корни характеристического уравнения этого отношения LHR равны.Кратность корня.
3.3. Фаза восстановления
Если участники квалифицированного подмножества хотят восстановить совместно используемые секреты, они должны сначала восстановить полиномы. На этапе построения мы знаем, что порядок полинома равен. равно фиксированному порогу отсека, и только участники отсека могут восстановить полином. Поскольку порядок равен, нам нужно большее или равное количество участников в отсеке для восстановления полинома.
Итак, эти участники квалифицированного подмножества содержат по крайней мере участников из подмножества, где. Предположим, что подмножество удовлетворяет этим условиям. Участник подмножества может получить долю каждого участника путем обмена в защищенном канале. Предположим, что участники квалифицированного подмножества хотят восстановить общие секреты. В подмножестве участники из отсека объединяют акции, где. Используя эти доли, эти участники могут определить полином, где.После того, как все полиномы были получены из теоремы 1 и общедоступных параметров на публичной доске объявлений, участники подмножества могут определить общее решение рекуррентного отношения, то есть
Предположим, что подмножество удовлетворяет этим условиям. Участник подмножества может получить долю каждого участника путем обмена в защищенном канале. Предположим, что участники квалифицированного подмножества хотят восстановить общие секреты. В подмножестве участники из отсека объединяют акции, где. Используя эти доли, эти участники могут определить полином, где.После того, как все полиномы были получены из теоремы 1 и общедоступных параметров на публичной доске объявлений, участники подмножества могут определить общее решение рекуррентного отношения, то есть
Из (17) участники подмножество может вычислить. На шаге (6) этапа построения участники подмножества могут получить общие секреты с помощью, где.
3.4. Пример
В этом разделе мы приводим пример, показывающий, как дилер распределяет секреты на этапе строительства, а участники восстанавливают общие секреты на этапе восстановления.
3.4.1. Фаза инициализации
(1) Предположим, что набор участников разделен на две непересекающиеся части и, то есть, и let. Пусть и. (2) случайным образом выбирает два общих секрета, где простое число. Установить больше.
Пусть и. (2) случайным образом выбирает два общих секрета, где простое число. Установить больше.
3.4.2. Этап построения
(1) выбирает два значения. (2) случайным образом выбирает два многочлена. Пусть и. (3) распределяет долю на-го участника в, где и. Эти акции перечислены следующим образом: (4) Пусть. Затем вычисляет.(5) вычисляет. (6) издает, и.
3.4.3. Фаза восстановления
Прежде чем участники смогут восстановить общие секреты, они должны сначала восстановить два полинома. Для и квалифицированное подмножество должно включать не менее двух участников из и трех участников из. Эти участники восстанавливают общие секреты, обмениваясь своими акциями. Допустим два участника из и три участника из. Два полинома восстанавливаются следующим образом. (1) Во-первых, мы показываем, как восстанавливается многочлен с помощью.Для двух точек (3, 7) и (5, 11) полином можно определить по (2). Во-вторых, полином восстанавливается по. Для трех точек (7, 17), (9, 9) и (10, 8) полином может быть определен по формуле (3) Из общедоступных значений эти участники могут получить Примечание: из Раздела 3. 4.2, Построение На этапе мы знаем, что участники подмножества получают доли через, а участники подмножества получают доли, соответственно. Таким образом, участники могут только выздоравливать, а участники только выздоравливать.(4) Эти участники вычисляют. (5) Из публичных ценностей эти участники могут получить два общих секрета с помощью следующего уравнения: так.
4.2, Построение На этапе мы знаем, что участники подмножества получают доли через, а участники подмножества получают доли, соответственно. Таким образом, участники могут только выздоравливать, а участники только выздоравливать.(4) Эти участники вычисляют. (5) Из публичных ценностей эти участники могут получить два общих секрета с помощью следующего уравнения: так.
4. Анализ безопасности
В этом разделе мы проанализируем, что неквалифицированное подмножество не может получить общие секреты, и докажем, что общедоступные значения не могут утечь никакой информации об общих секретах. Сначала мы дадим следующее предложение.
Предложение 1. Если — кратный корень характеристического уравнения отношения LHR и общее решение этого отношения LHR дается следующим образом, то его коэффициент может быть определен по начальным значениям путем решения линейной системы уравнений, где.
Из (17) мы знаем, что когда участники неквалифицированного подмножества хотят восстановить общие секреты, они должны восстановить каждый многочлен,.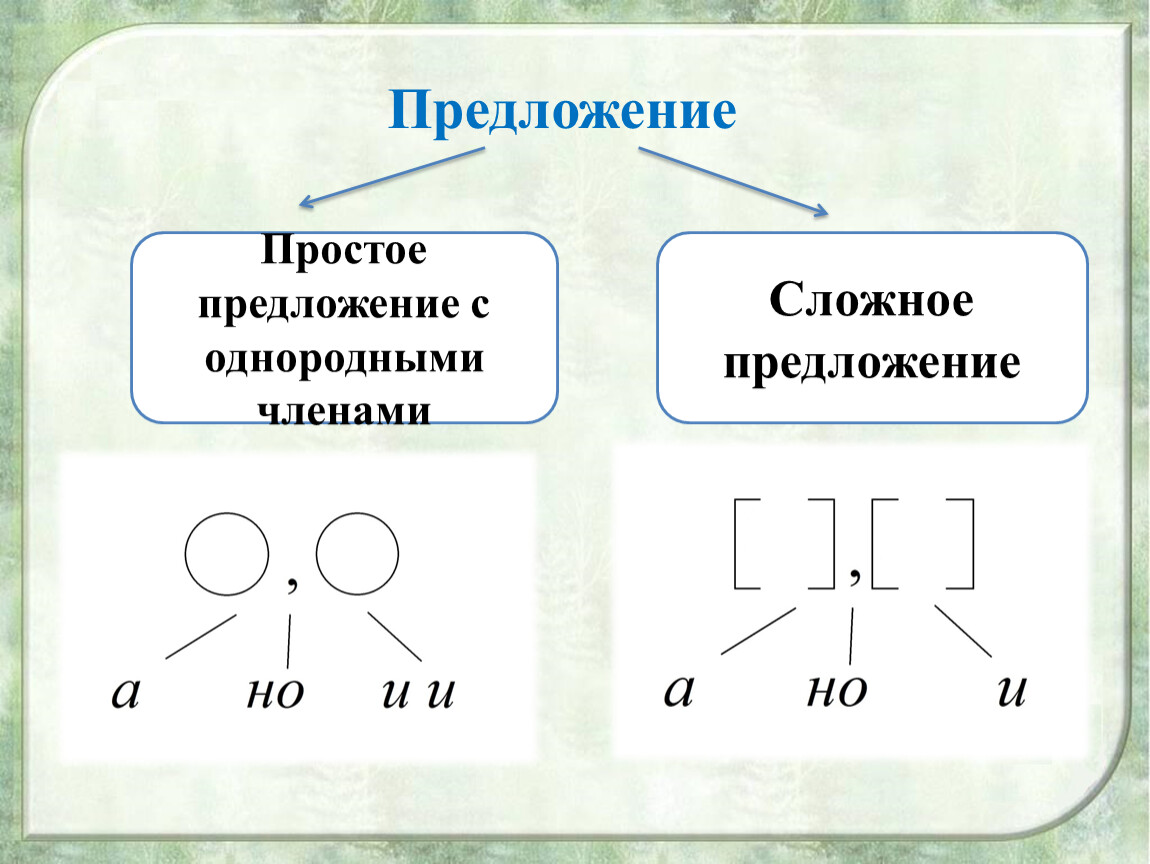 Предположим, что количество участников находится в неквалифицированном подмножестве. Если общее количество участников в неквалифицированном подмножестве равно, где, то существует ситуация, когда количество участников, содержащихся в некотором отсеке, равно.
Предположим, что количество участников находится в неквалифицированном подмножестве. Если общее количество участников в неквалифицированном подмножестве равно, где, то существует ситуация, когда количество участников, содержащихся в некотором отсеке, равно.
Теорема 3. Общий член линейного однородного рекуррентного отношения безопасен для неквалифицированных участников тогда и только тогда, когда полином безопасен для неквалифицированных участников.
Доказательство. Во-первых, мы даем анализ того, что публичные ценности не пропускают никакой информации об общих секретах. Из общедоступных значений можно определить характеристическое уравнение отношения LHR в соответствии с теоремой 1. Если задано отношение LHR, то можно определить характеристическое уравнение этого отношения LHR и найти корень характеристического уравнения. Таким образом, публичные ценности не пропускают никакой информации, кроме характеристического уравнения отношения LHR.Из (4) имеем: По следствию 1, также является общим членом отношения LHR со степенью, где порядок многочлена равен. Мы предположили, что неквалифицированное подмножество содержит участников, а out of is in (пусть случайные члены будут). Предположим, что общий член линейного однородного рекуррентного отношения со степенью безопасен для неквалифицированных участников. Из вышесказанного мы знаем, что общественная ценность не содержит никакой информации, кроме характеристического уравнения. Если многочлен со степенью не является безопасным для неквалифицированных участников, то есть точки могут определять многочлен со степенью.Из (5) мы также заключаем, что значения могут определять общий член линейного однородного рекуррентного отношения со степенью. Это противоречит нашему предположению. () Предположим, что многочлен со степенью безопасен для неквалифицированных участников. Если общий член линейного однородного рекуррентного отношения со степенью не является безопасным для неквалифицированных участников, то случайные члены () могут определять общий член линейного однородного рекуррентного отношения. Согласно (24), мы выбираем разные члены, а затем можем получить разные точки многочлена.
Мы предположили, что неквалифицированное подмножество содержит участников, а out of is in (пусть случайные члены будут). Предположим, что общий член линейного однородного рекуррентного отношения со степенью безопасен для неквалифицированных участников. Из вышесказанного мы знаем, что общественная ценность не содержит никакой информации, кроме характеристического уравнения. Если многочлен со степенью не является безопасным для неквалифицированных участников, то есть точки могут определять многочлен со степенью.Из (5) мы также заключаем, что значения могут определять общий член линейного однородного рекуррентного отношения со степенью. Это противоречит нашему предположению. () Предположим, что многочлен со степенью безопасен для неквалифицированных участников. Если общий член линейного однородного рекуррентного отношения со степенью не является безопасным для неквалифицированных участников, то случайные члены () могут определять общий член линейного однородного рекуррентного отношения. Согласно (24), мы выбираем разные члены, а затем можем получить разные точки многочлена. Поскольку степень случайного многочлена равна, мы можем сказать, что точки могут определять случайный многочлен со степенью. Это противоречит нашему предположению, поэтому, когда участники неквалифицированного подмножества хотят получить общие секреты, наша схема безопасна. Каждая акция отправляется через защищенный канал, поэтому мы не обсуждаем утечку акций.
Поскольку степень случайного многочлена равна, мы можем сказать, что точки могут определять случайный многочлен со степенью. Это противоречит нашему предположению, поэтому, когда участники неквалифицированного подмножества хотят получить общие секреты, наша схема безопасна. Каждая акция отправляется через защищенный канал, поэтому мы не обсуждаем утечку акций.
5. Обсуждение
В нашей схеме каждый участник владеет только одной долей для восстановления секретов во всем процессе восстановления.В этом разделе, во-первых, мы доказываем, что наша схема идеальна и идеальна, а также показываем, что распространение нескольких секретов эффективно. Во-вторых, мы сравниваем популярные схемы с нашей схемой.
5.1. Производительность
Сначала покажем, что предложенная схема идеальна. Итак, мы должны доказать, что для всех,. Эквивалентно, мы требуем, чтобы для любых общих секретов и, где, и распределялись с помощью отношения линейной однородной рекуррентности (LHR) ().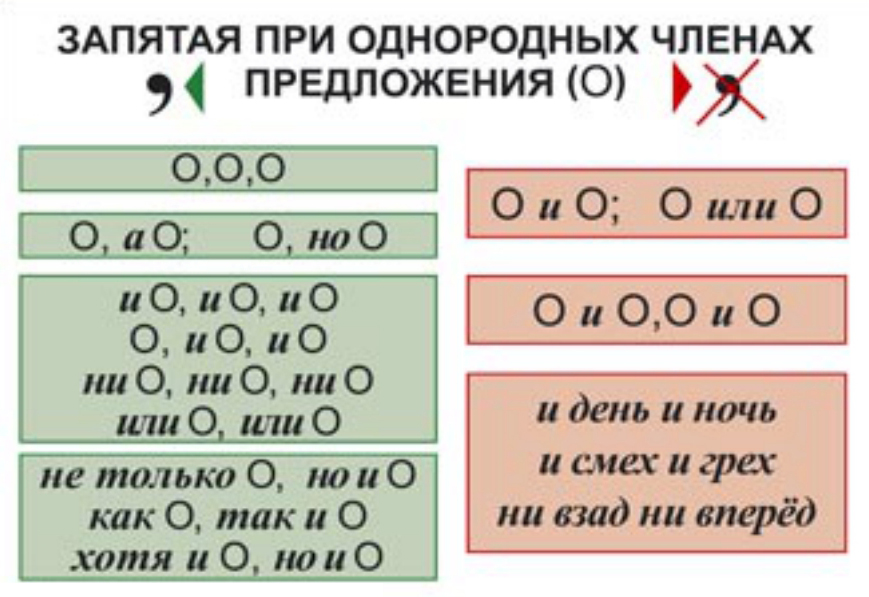 Используем для обозначения линейного однородного рекуррентного отношения.Другой распределяется через линейное однородное рекуррентное соотношение (LHR) (). Поскольку количество участников в подмножестве равно, существует ситуация, когда количество участников, содержащихся в некотором отсеке, меньше порогового значения. Мы предполагаем, что участники подмножества могут восстановить все многочлены, кроме. Предположим, что две линейные однородные рекурсивные (LHR) последовательности и удовлетворяют следующим условиям, то есть
Используем для обозначения линейного однородного рекуррентного отношения.Другой распределяется через линейное однородное рекуррентное соотношение (LHR) (). Поскольку количество участников в подмножестве равно, существует ситуация, когда количество участников, содержащихся в некотором отсеке, меньше порогового значения. Мы предполагаем, что участники подмножества могут восстановить все многочлены, кроме. Предположим, что две линейные однородные рекурсивные (LHR) последовательности и удовлетворяют следующим условиям, то есть
Степени многочленов и равны.Поскольку мы можем определить все многочлены, кроме и, если мы можем восстановить два многочлена и, то и можно определить. Таким образом, мы можем определить общие секреты и. Поскольку мы можем добраться куда угодно и является участником.
Из характеристики матрицы Вандермонда мы можем сделать вывод. Единственного решения (28) не существует. Вероятности определения вектора и вектора равны. Поскольку в предложенной схеме, когда определяются полиномы, можно определять общие секреты. Итак, вероятности определения и равны, т. Е. Так. Поэтому предлагаемая схема идеальна.
Итак, вероятности определения и равны, т. Е. Так. Поэтому предлагаемая схема идеальна.
В нашей схеме доля каждого участника публикуется на публичной доске объявлений, и доля каждого участника выбирается поверх. Каждый участник должен владеть только одной долей, и общие секреты выбираются поверх. Итак, каждая доля равна длине каждого секрета. Поэтому предлагаемая схема идеальна.
По соображениям безопасности или по определенным требованиям мы должны изменить общие секреты.Процесс изменения общих секретов описывается следующим образом. (1) выбирает новые общие секреты (2) вычисляет, где (3) обновляет на общедоступной доске объявлений, где
Из приведенного выше процесса мы знаем, что вычислительные затраты равны низкий, чтобы изменить общие секреты.
5.2. Эффективность
Когда глобальный порог велик, обычно требуется много вычислений для получения пар точек полинома. Поскольку порядок полинома также может быть таким, вычисление полинома с большой степенью требует много времени.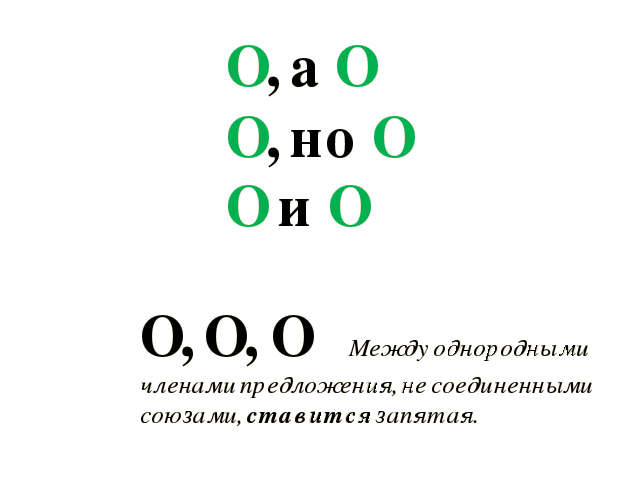 В нашей схеме мы делим глобальный порог на маленькие пороги, где. Каждому порогу соответствует полином со степенью. Поскольку в предлагаемой схеме глобальный порядок разделен на небольшие низкие пороги, эффективно получать оценки на этих полиномах низкого порядка. Когда порог равен, вычислительная сложность обычно выше, чем. До того, как была предложена схема иерархического разделения секрета [25], вычислительная сложность схем разделения секрета на несколько частей была экспоненциальной по времени.Юань и Янг [25] снизили вычислительную сложность иерархической схемы разделения секрета с экспоненциального времени до полиномиального (в [25] оно отличается от нашей схемы, а в нашей схеме обычно меньше, чем в [25]), но вычислительная сложность нашей схемы может снизиться до. Таким образом, вычислительная эффективность схемы разделения секрета лучше, чем вычислительная эффективность иерархической схемы разделения секрета, когда два типа схем разделения секрета основаны на отношениях LHR.В недавно популярной схеме разделения секретов [21] также необходимо получить невырожденные матрицы, и эта вычислительная сложность является экспоненциальной по времени.
В нашей схеме мы делим глобальный порог на маленькие пороги, где. Каждому порогу соответствует полином со степенью. Поскольку в предлагаемой схеме глобальный порядок разделен на небольшие низкие пороги, эффективно получать оценки на этих полиномах низкого порядка. Когда порог равен, вычислительная сложность обычно выше, чем. До того, как была предложена схема иерархического разделения секрета [25], вычислительная сложность схем разделения секрета на несколько частей была экспоненциальной по времени.Юань и Янг [25] снизили вычислительную сложность иерархической схемы разделения секрета с экспоненциального времени до полиномиального (в [25] оно отличается от нашей схемы, а в нашей схеме обычно меньше, чем в [25]), но вычислительная сложность нашей схемы может снизиться до. Таким образом, вычислительная эффективность схемы разделения секрета лучше, чем вычислительная эффективность иерархической схемы разделения секрета, когда два типа схем разделения секрета основаны на отношениях LHR.В недавно популярной схеме разделения секретов [21] также необходимо получить невырожденные матрицы, и эта вычислительная сложность является экспоненциальной по времени. По сравнению с популярной схемой [21], вычислительная сложность нашей схемы составляет полиномиальное время (). Таким образом, наша схема более эффективна, чем существующие популярные схемы разделения секретов. Но наша схема требует больше публичных ценностей, чем существующая популярная схема разделения секретов [21].
По сравнению с популярной схемой [21], вычислительная сложность нашей схемы составляет полиномиальное время (). Таким образом, наша схема более эффективна, чем существующие популярные схемы разделения секретов. Но наша схема требует больше публичных ценностей, чем существующая популярная схема разделения секретов [21].
6.Заключение
В этой статье, основанной на линейных однородных рекуррентных соотношениях, мы предлагаем разделенную мультисекретную схему совместного использования. Доказано, что предложенная схема безупречна и идеальна. Безопасность нашей схемы основана на пороговой схеме Шамира. Каждый полином соответствует разному подмножеству участников, и степень полинома равна порогу отсека минус один, т. Е. Мы делим полином -й степени на разные полиномы и сумму степеней разных полиномов. равно .Распространять или восстанавливать общие секреты более эффективно, используя некоторые полиномы с низкими степенями, чем распределять / восстанавливать общие секреты, используя полином с большой степенью, то есть вычислительная сложность снижается с экспоненциального времени до. Более того, наша схема эффективна, когда мы разделяем мультисекретность. В частности, когда мы хотим изменить общие секреты, мы можем обнаружить, что предложенная схема более эффективна, чем существующие популярные многосекретные схемы совместного использования, которые не были основаны на линейных однородных рекуррентных отношениях.В предлагаемой схеме каждому участнику необходимо владеть только одной акцией всего процесса. Ограничение нашей схемы состоит в том, что нашей схеме нужно больше общественных ценностей.
Более того, наша схема эффективна, когда мы разделяем мультисекретность. В частности, когда мы хотим изменить общие секреты, мы можем обнаружить, что предложенная схема более эффективна, чем существующие популярные многосекретные схемы совместного использования, которые не были основаны на линейных однородных рекуррентных отношениях.В предлагаемой схеме каждому участнику необходимо владеть только одной акцией всего процесса. Ограничение нашей схемы состоит в том, что нашей схеме нужно больше общественных ценностей.
Доступность данных
Никакие данные не использовались для подтверждения результатов исследования.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Эта работа была поддержана Национальным фондом естественных наук Китая в рамках гранта No.61897069.
Новая схема форсирования для поддержания насыщенной частицами однородной и изотропной турбулентности: Physics of Fluids: Vol 25, No.
 8
8I. ВВЕДЕНИЕ
Раздел:
ВыборВверх страницыABSTRACTI.INTRODUCTION << II.MATHEMATICAL DESCRIPTION ... III. МОДЕЛИРОВАНИЕ И УСЛОВИЯ ... IV.РЕЗУЛЬТАТЫ V. РЕЗЮМЕ И ВЫВОДЫ С СТАТИСТИКОЙ, стационарная однородная изотропная турбулентность (HIT) дает нам возможность изучать турбулентность в отсутствие граничных условий и переноса турбулентности.HIT - ценный инструмент, потому что он позволяет нам изолировать и, следовательно, изучать определенные аспекты турбулентного потока. Кроме того, его можно использовать при разработке моделей для прогнозирования статистических характеристик турбулентности. Важно отметить, что HIT не может быть обнаружен естественным путем, и его даже очень трудно получить экспериментально. Тем не менее, есть успешные эксперименты, такие как проведенный Контом-Белло и Коррсином 3 3. Г. Конт-Белло и С. Коррсин, «Простая эйлерова временная корреляция полнополосных и узкополосных сигналов скорости в сгенерированных сеткой, изотропная турбулентность », Ж. Жидкий мех. 48 (02), 273–337 (1971). https://doi.org/10.1017/S0022112071001599 с помощью статических сеток. С другой стороны, очень легко получить разумное приближение к HIT с помощью компьютерного моделирования, и после новаторского исследования Райли и Паттерсона 13 13. Дж. Дж. Райли и Г. С. Паттерсон, «Диффузионные эксперименты с численно интегрированной изотропной турбулентностью», Phys. Жидкости 17 (2), 292 (1974). https://doi.org/10.1063/1.1694714 является предметом исследования более трех десятилетий.В отсутствие какого-либо производственного механизма однородная и изотропная турбулентность будет затухать из-за диссипативного эффекта вязкости. Поэтому объемные силы, в терминах схемы вынуждающего воздействия, могут быть добавлены в уравнение импульса жидкости, если должна поддерживаться статистическая стационарность. Лундгрен 11 11. Т.С. Лундгрен, «Линейно-вынужденная изотропная турбулентность», Технический отчет 2, DTIC Document, 2003. предложил схему форсирования турбулентности, которая уравновешивает скорость рассеивания жидкости и турбулентную кинетическую энергию для создания стационарного, однородного и изотропного турбулентного потока путем добавления постоянной массовой силы в физическом пространстве.
Жидкий мех. 48 (02), 273–337 (1971). https://doi.org/10.1017/S0022112071001599 с помощью статических сеток. С другой стороны, очень легко получить разумное приближение к HIT с помощью компьютерного моделирования, и после новаторского исследования Райли и Паттерсона 13 13. Дж. Дж. Райли и Г. С. Паттерсон, «Диффузионные эксперименты с численно интегрированной изотропной турбулентностью», Phys. Жидкости 17 (2), 292 (1974). https://doi.org/10.1063/1.1694714 является предметом исследования более трех десятилетий.В отсутствие какого-либо производственного механизма однородная и изотропная турбулентность будет затухать из-за диссипативного эффекта вязкости. Поэтому объемные силы, в терминах схемы вынуждающего воздействия, могут быть добавлены в уравнение импульса жидкости, если должна поддерживаться статистическая стационарность. Лундгрен 11 11. Т.С. Лундгрен, «Линейно-вынужденная изотропная турбулентность», Технический отчет 2, DTIC Document, 2003. предложил схему форсирования турбулентности, которая уравновешивает скорость рассеивания жидкости и турбулентную кинетическую энергию для создания стационарного, однородного и изотропного турбулентного потока путем добавления постоянной массовой силы в физическом пространстве. Этот метод запускает все режимы волнового числа энергетического спектра одновременно. Другие схемы избегают этого, вызывая определенные волновые числа, которые обычно представляют собой низкие волновые числа энергетического спектра, такие как предложенный Эсвараном и Поупом. 6 6. В. Эсваран и С. Б. Поуп, «Исследование воздействия в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi.org/10.1016/0045-7930(88)-8 Метод Эсварана и Папы 6 6.В. Эсваран и С. Б. Поуп, «Исследование воздействия в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi.org/10.1016/0045-7930(88)-8 предполагает использование псевдоспектральной структуры. Идея их схемы принуждения состоит в том, чтобы поддерживать постоянную общую диссипацию жидкости за счет использования статистически независимых случайных процессов для каждого волнового числа. Эти случайные процессы, которые также удовлетворяют непрерывности, снабжают энергией несколько первых мод волновых чисел жидкости за счет заданной дисперсии и интегрального временного масштаба турбулентности.
Этот метод запускает все режимы волнового числа энергетического спектра одновременно. Другие схемы избегают этого, вызывая определенные волновые числа, которые обычно представляют собой низкие волновые числа энергетического спектра, такие как предложенный Эсвараном и Поупом. 6 6. В. Эсваран и С. Б. Поуп, «Исследование воздействия в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi.org/10.1016/0045-7930(88)-8 Метод Эсварана и Папы 6 6.В. Эсваран и С. Б. Поуп, «Исследование воздействия в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi.org/10.1016/0045-7930(88)-8 предполагает использование псевдоспектральной структуры. Идея их схемы принуждения состоит в том, чтобы поддерживать постоянную общую диссипацию жидкости за счет использования статистически независимых случайных процессов для каждого волнового числа. Эти случайные процессы, которые также удовлетворяют непрерывности, снабжают энергией несколько первых мод волновых чисел жидкости за счет заданной дисперсии и интегрального временного масштаба турбулентности. 14 14. К. Розалес и К. Менево, «Линейное воздействие в численном моделировании изотропной турбулентности: реализации физического пространства и свойства сходимости», Phys. Жидкости 17 , 095106 (2005). https://doi.org/10.1063/1.2047568 Стоит упомянуть, что когда энергия подается на этих первых нескольких малых волновых числах, временные флуктуации очень высоки. 9,14 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J.Жидкий мех. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022 14. С. Розалес, К. Менево, «Линейное воздействие в численном моделировании изотропной турбулентности: реализация физического пространства и свойства сходимости», Phys. Жидкости 17 , 095106 (2005). https://doi.org/10.1063/1.2047568 Воспользовавшись сохраненной статистикой, обеспечиваемой принудительной однородной и изотропной турбулентностью, Сквайрс и Итон, 16 16.
14 14. К. Розалес и К. Менево, «Линейное воздействие в численном моделировании изотропной турбулентности: реализации физического пространства и свойства сходимости», Phys. Жидкости 17 , 095106 (2005). https://doi.org/10.1063/1.2047568 Стоит упомянуть, что когда энергия подается на этих первых нескольких малых волновых числах, временные флуктуации очень высоки. 9,14 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J.Жидкий мех. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022 14. С. Розалес, К. Менево, «Линейное воздействие в численном моделировании изотропной турбулентности: реализация физического пространства и свойства сходимости», Phys. Жидкости 17 , 095106 (2005). https://doi.org/10.1063/1.2047568 Воспользовавшись сохраненной статистикой, обеспечиваемой принудительной однородной и изотропной турбулентностью, Сквайрс и Итон, 16 16. К. Д. Сквайрс и Дж. К. Итон, «Реакция частиц и изменение турбулентности при изотропной турбулентности. Phys.Жидкости А 2 , 1191 (1990). https://doi.org/10.1063/1.857620 Squires and Eaton, 17 17. К. Д. Сквайрс, Дж. К. Итон, «Преимущественная концентрация частиц за счет турбулентности», Phys. Жидкости А 3 (5), 1169 (1991). https://doi.org/10.1063/1.858045 и Boivin et al. 2 2. М. Бойвин, О. Симонин и К. Д. Сквайрс, «Прямое численное моделирование модуляции турбулентности частицами в изотропной турбулентности», J. Fluid Mech. 375 (1), 235–263 (1998).https://doi.org/10.1017/S0022112098002821 среди других выполнили исследования, связанные с двусторонней связанной принудительной турбулентностью, чтобы изучить дисперсию частиц и модуляцию турбулентности. Недавно это утверждали Lucci et al. , 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J.
К. Д. Сквайрс и Дж. К. Итон, «Реакция частиц и изменение турбулентности при изотропной турбулентности. Phys.Жидкости А 2 , 1191 (1990). https://doi.org/10.1063/1.857620 Squires and Eaton, 17 17. К. Д. Сквайрс, Дж. К. Итон, «Преимущественная концентрация частиц за счет турбулентности», Phys. Жидкости А 3 (5), 1169 (1991). https://doi.org/10.1063/1.858045 и Boivin et al. 2 2. М. Бойвин, О. Симонин и К. Д. Сквайрс, «Прямое численное моделирование модуляции турбулентности частицами в изотропной турбулентности», J. Fluid Mech. 375 (1), 235–263 (1998).https://doi.org/10.1017/S0022112098002821 среди других выполнили исследования, связанные с двусторонней связанной принудительной турбулентностью, чтобы изучить дисперсию частиц и модуляцию турбулентности. Недавно это утверждали Lucci et al. , 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J. Fluid Mech. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022, что существующие схемы принуждения могут иметь прямое влияние на поведение спектра двусторонней связи.Луччи и др. 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J. Fluid Mech. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022 перечислите три возможные причины, которые делают исследование принудительной турбулентности с использованием текущих схем нагнетания и двусторонней связи «некорректным»: (а) форсирование первых нескольких мод с низким волновым числом в спектральном пространстве. создает большие флуктуации временной эволюции кинетической энергии турбулентности, которые могут иметь тот же порядок величины, что и эффект двусторонней связи; (b) форсирование выполняется в физическом пространстве, где все режимы волнового числа запускаются как Lundgren 11 11.Т. С.
Fluid Mech. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022, что существующие схемы принуждения могут иметь прямое влияние на поведение спектра двусторонней связи.Луччи и др. 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J. Fluid Mech. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022 перечислите три возможные причины, которые делают исследование принудительной турбулентности с использованием текущих схем нагнетания и двусторонней связи «некорректным»: (а) форсирование первых нескольких мод с низким волновым числом в спектральном пространстве. создает большие флуктуации временной эволюции кинетической энергии турбулентности, которые могут иметь тот же порядок величины, что и эффект двусторонней связи; (b) форсирование выполняется в физическом пространстве, где все режимы волнового числа запускаются как Lundgren 11 11.Т. С. Лундгрен, «Линейно вынужденная изотропная турбулентность», Технический отчет 2, DTIC Document, 2003. предлагает, искажает перераспределение энергии, и, следовательно, влияние частиц на E (κ, t ) не может быть определено количественно; и (c) из-за триадных взаимодействий невозможно исследовать модификацию нелинейной передаточной функции, T (κ, t ), и, следовательно, энергетического спектра жидкости в режимах волновых чисел, где действует форсирование. Позже показано, что их выводы справедливы для схемы принуждения, предложенной Лундгреном, 11 11.Т. С. Лундгрен, «Линейно вынужденная изотропная турбулентность», Технический отчет 2, документ DTIC, 2003 г., поскольку нелинейная передаточная функция влияет на все волновые числа. Фактически нелинейная передаточная функция может быть выражена как T (κ, t ) = 2 (ν f κ 2 — A ) E (κ, t ), где коэффициент A — постоянная воздействия.
Лундгрен, «Линейно вынужденная изотропная турбулентность», Технический отчет 2, DTIC Document, 2003. предлагает, искажает перераспределение энергии, и, следовательно, влияние частиц на E (κ, t ) не может быть определено количественно; и (c) из-за триадных взаимодействий невозможно исследовать модификацию нелинейной передаточной функции, T (κ, t ), и, следовательно, энергетического спектра жидкости в режимах волновых чисел, где действует форсирование. Позже показано, что их выводы справедливы для схемы принуждения, предложенной Лундгреном, 11 11.Т. С. Лундгрен, «Линейно вынужденная изотропная турбулентность», Технический отчет 2, документ DTIC, 2003 г., поскольку нелинейная передаточная функция влияет на все волновые числа. Фактически нелинейная передаточная функция может быть выражена как T (κ, t ) = 2 (ν f κ 2 — A ) E (κ, t ), где коэффициент A — постоянная воздействия. Таким образом, эта константа влияет на все волновые числа энергетического спектра, но также показано, что более общие схемы форсирования могут избежать этой трудности, по крайней мере, для невынужденных волновых чисел.Цель этой статьи — представить новую схему принуждения, которая позволяет избежать трех ограничений, предложенных Lucci et al. 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J. Fluid Mech. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022 Это позволяет избежать влияния схемы форсирования на нелинейную передаточную функцию для всех волновых чисел, но сохраняет реализацию в физическом пространстве.Используя новую схему принуждения, прямое численное моделирование (DNS) принудительного HIT на периодическом кубическом ящике 128 3 (длиной L b = 0,128 м), полностью связанном с частицами с числами Стокса 0,07 и 3,45 при числе Тейлора Рейнольдса 35,4, чтобы оценить относительную эффективность текущей схемы форсирования как на статистическом, так и на теоретическом уровне.
Таким образом, эта константа влияет на все волновые числа энергетического спектра, но также показано, что более общие схемы форсирования могут избежать этой трудности, по крайней мере, для невынужденных волновых чисел.Цель этой статьи — представить новую схему принуждения, которая позволяет избежать трех ограничений, предложенных Lucci et al. 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J. Fluid Mech. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022 Это позволяет избежать влияния схемы форсирования на нелинейную передаточную функцию для всех волновых чисел, но сохраняет реализацию в физическом пространстве.Используя новую схему принуждения, прямое численное моделирование (DNS) принудительного HIT на периодическом кубическом ящике 128 3 (длиной L b = 0,128 м), полностью связанном с частицами с числами Стокса 0,07 и 3,45 при числе Тейлора Рейнольдса 35,4, чтобы оценить относительную эффективность текущей схемы форсирования как на статистическом, так и на теоретическом уровне. Чтобы выяснить влияние новой схемы воздействия на жидкость и частицы, в этой статье исследуются спектры когерентности между текущей схемой воздействия как с жидкостью, так и с двусторонней связью.Рассмотренные результаты также используются для определения того, является ли влияние воздействия на жидкость и двустороннюю связь статистически значимым. Кроме того, анализ и результаты Abdelsamie and Lee 1 1. AH Abdelsamie and C. Lee, « Затухающая и стационарная турбулентность в изотропной турбулентности, насыщенной частицами: механизм модуляции турбулентности, Физ. Жидкости 24 (1), 015106 (2012). https://doi.org/10.1063/1.3678332 пересмотрены. Они исследуют временную эволюцию кинетической энергии турбулентности в вынужденной турбулентности с помощью спектральной схемы форсирования Эсварана и Поупа. 6 6. В. Эсваран и С. Б. Поуп, «Исследование воздействия в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi.
Чтобы выяснить влияние новой схемы воздействия на жидкость и частицы, в этой статье исследуются спектры когерентности между текущей схемой воздействия как с жидкостью, так и с двусторонней связью.Рассмотренные результаты также используются для определения того, является ли влияние воздействия на жидкость и двустороннюю связь статистически значимым. Кроме того, анализ и результаты Abdelsamie and Lee 1 1. AH Abdelsamie and C. Lee, « Затухающая и стационарная турбулентность в изотропной турбулентности, насыщенной частицами: механизм модуляции турбулентности, Физ. Жидкости 24 (1), 015106 (2012). https://doi.org/10.1063/1.3678332 пересмотрены. Они исследуют временную эволюцию кинетической энергии турбулентности в вынужденной турбулентности с помощью спектральной схемы форсирования Эсварана и Поупа. 6 6. В. Эсваран и С. Б. Поуп, «Исследование воздействия в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi. org/10.1016/0045-7930(88)-8 Они предположили, что во времена меньших, чем интегральная шкала принуждения, одноточечный, одноразовый член двусторонней связи «существенно изменяется под воздействием принуждения. схема », особенно для легких частиц (числа Стокса, St, , константа турбулентной кинетической энергии при заданном значении.Эта статья состоит из четырех разделов. Раздел описывает структуру флюидной фазы и форсирование HIT. В разделе представлены модели и условия этого исследования. В разделе сравнивается и оценивается относительная эффективность новой схемы принуждения с точки зрения трех ограничений, обсуждаемых Lucci et al. 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J. Fluid Mech. 650 (2010), 5–55 (2010).https://doi.org/10.1017/S0022112009994022 Наконец, разд. Обобщены основные выводы этой работы.
org/10.1016/0045-7930(88)-8 Они предположили, что во времена меньших, чем интегральная шкала принуждения, одноточечный, одноразовый член двусторонней связи «существенно изменяется под воздействием принуждения. схема », особенно для легких частиц (числа Стокса, St, , константа турбулентной кинетической энергии при заданном значении.Эта статья состоит из четырех разделов. Раздел описывает структуру флюидной фазы и форсирование HIT. В разделе представлены модели и условия этого исследования. В разделе сравнивается и оценивается относительная эффективность новой схемы принуждения с точки зрения трех ограничений, обсуждаемых Lucci et al. 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J. Fluid Mech. 650 (2010), 5–55 (2010).https://doi.org/10.1017/S0022112009994022 Наконец, разд. Обобщены основные выводы этой работы.III. МОДЕЛИРОВАНИЕ И УСЛОВИЯ
Раздел:
Выбрать верх страницы АБСТРАКТЫ. ВВЕДЕНИЕII.МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ … III.МОДЕЛИРОВАНИЕ И УСЛОВИЯ … << IV.РЕЗУЛЬТАТЫ V. РЕЗЮМЕ И ВЫВОДЫ ССЫЛКА СОСТАВЛЯЮЩИЕ СТАТЬИ
ВВЕДЕНИЕII.МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ … III.МОДЕЛИРОВАНИЕ И УСЛОВИЯ … << IV.РЕЗУЛЬТАТЫ V. РЕЗЮМЕ И ВЫВОДЫ ССЫЛКА СОСТАВЛЯЮЩИЕ СТАТЬИ ящик = 0,128 м) были выполнены при кинематической вязкости жидкости ν f = 1.47 × 10 −5 м 2 с −1 и плотность жидкости ρ f = 1,17 кгм −3 с объемной долей частиц 1,37 × 10 −5 , что соответствует 223, 520 частицы. Рассматриваемые в данной работе частицы являются сферическими и упругими с фиксированным диаметром d p = 67,6 мкм. Этот диаметр гарантирует, что частицы намного меньше микромасштаба Колмогорова, который составляет d p / η κ = 0.1. Плотность частиц варьировалась следующим образом: 150 кгм -3 , 2500 кгм -3 , 8000 кгм -3 и 12000 кгм -3 для получения частиц с разными числами Стокса. Соответствующее число Стокса ( St ) частиц составляет St = 0,07, St = 1,12, St = 3,45 и St = 5,15.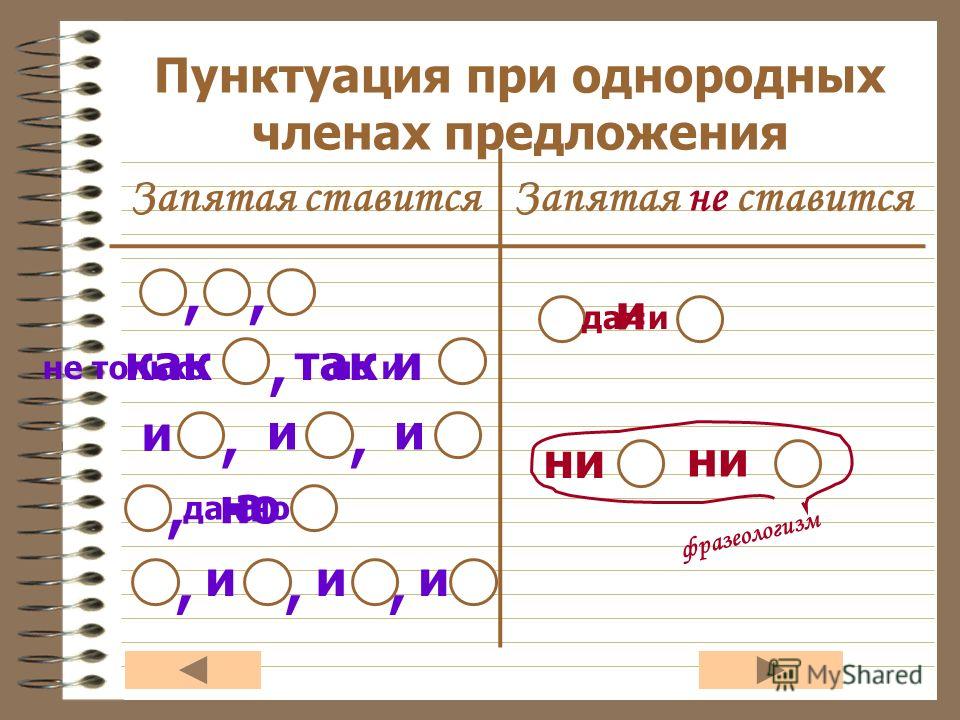 Обратите внимание, что уровни кинетической энергии турбулентности оставались постоянными и составляли примерно 6,52 × 10 −3 м 2 с −2 .Число Тейлора Рейнольдса, Re λ равно 35,4. Статистика постобработки была собрана после 10 интегральных шкал времени и дискретизирована для 20 интегральных шкал времени. Обратите внимание, что κ определяется как 2π n / L box , где n — волновое число, а расстояние между длинами волн составляет 49,1 м -1 .
Обратите внимание, что уровни кинетической энергии турбулентности оставались постоянными и составляли примерно 6,52 × 10 −3 м 2 с −2 .Число Тейлора Рейнольдса, Re λ равно 35,4. Статистика постобработки была собрана после 10 интегральных шкал времени и дискретизирована для 20 интегральных шкал времени. Обратите внимание, что κ определяется как 2π n / L box , где n — волновое число, а расстояние между длинами волн составляет 49,1 м -1 .
V. РЕЗЮМЕ И ВЫВОДЫ
Раздел:
ВыбратьВверху страницыABSTRACTI.INTRODUCTIONII.MATHEMATICAL DESCRIPTION … III.МОДЕЛИРОВАНИЕ И ПОДГОТОВКА … IV.РЕЗУЛЬТАТЫ V. РЕЗЮМЕ И ВЫВОДЫ << ССЫЛКИ НА СТАТЬИ Целью данной работы было проверить пригодность и оценить производительность недавно предложенной схемы форсирования для однородной и изотропной турбулентности, нагруженной частицами. Ввиду проблем, с которыми столкнулись предыдущие моделирования, с тремя ограничениями, касающимися HIT с вынужденными частицами, обсужденными Lucci et al. 9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J.Жидкий мех. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022. Новая схема была оценена с использованием как теории, так и статистики моделирования DNS для моделирования вынужденной турбулентности с частицами. Нелинейная передаточная функция была исследована, чтобы определить, на какие режимы волнового числа влияет схема форсирования. Теоретический анализ показал, что новая предложенная схема влияет только на T (κ, t ) на тех режимах волнового числа, где действует форсирование.Таким образом, дополнительный эффект частиц может быть определен количественно при всех других волновых числах. Воздействие на E (κ, t ) из-за частиц с промежуточными и высокими волновыми числами возможно, потому что на передаточную функцию не влияет непосредственно за пределами диапазона воздействия. Напротив, при выполнении аналогичного анализа с линейным воздействием Лундгрена, 11 11.
9 9. Ф. Луччи, А. Ферранте и С. Эльгобаши, «Модуляция изотропной турбулентности частицами размера Тейлора в масштабе длины», J.Жидкий мех. 650 (2010), 5–55 (2010). https://doi.org/10.1017/S0022112009994022. Новая схема была оценена с использованием как теории, так и статистики моделирования DNS для моделирования вынужденной турбулентности с частицами. Нелинейная передаточная функция была исследована, чтобы определить, на какие режимы волнового числа влияет схема форсирования. Теоретический анализ показал, что новая предложенная схема влияет только на T (κ, t ) на тех режимах волнового числа, где действует форсирование.Таким образом, дополнительный эффект частиц может быть определен количественно при всех других волновых числах. Воздействие на E (κ, t ) из-за частиц с промежуточными и высокими волновыми числами возможно, потому что на передаточную функцию не влияет непосредственно за пределами диапазона воздействия. Напротив, при выполнении аналогичного анализа с линейным воздействием Лундгрена, 11 11. Т.С. Лундгрен, «Линейно-вынужденная изотропная турбулентность», Технический отчет 2, документ DTIC, 2003. показано, что передаточная функция была затронута вообще волновые числа, так что влияние частиц не может быть четко определено количественно.
Т.С. Лундгрен, «Линейно-вынужденная изотропная турбулентность», Технический отчет 2, документ DTIC, 2003. показано, что передаточная функция была затронута вообще волновые числа, так что влияние частиц не может быть четко определено количественно. Спектры пространственной когерентности между двусторонней связью и скоростью жидкости, между воздействием и скоростью жидкости, а также между воздействием и двусторонней связью были исследованы с целью определения коэффициентов взаимной корреляции для каждой моды волновых чисел. Спектры пространственной когерентности показывают, что воздействие умеренно коррелирует с частицами в диапазоне волновых чисел, которые оно действует (менее 0,17), но быстро падает до очень низких значений корреляции (менее 0,001) за пределами диапазона воздействия; последний фактически равен нулю с точностью до ошибки вычислений.Аналогичным образом было показано, что форсирование не влияет на скорость жидкости за пределами рабочего диапазона. Кроме того, была исследована фаза комбинированных перекрестных спектров между воздействием и флюидом, а также между воздействием и частицами. Результаты показывают, что вне рабочего диапазона форсирования фаза этих спектров случайным образом колеблется в пределах ± 180 °. Это указывает на то, что при этих волновых числах воздействие не коррелирует ни с жидкостью, ни с частицами. С другой стороны, фаза перекрестного спектра между жидкостью и частицами изменяется от 0o до 180o с увеличением волновых чисел.Это означает, что жидкость непосредственно влияет на частицы при низких волновых числах, но при больших волновых числах частицы взаимодействуют с структурами жидкости и вызывают движение жидкости.
Результаты показывают, что вне рабочего диапазона форсирования фаза этих спектров случайным образом колеблется в пределах ± 180 °. Это указывает на то, что при этих волновых числах воздействие не коррелирует ни с жидкостью, ни с частицами. С другой стороны, фаза перекрестного спектра между жидкостью и частицами изменяется от 0o до 180o с увеличением волновых чисел.Это означает, что жидкость непосредственно влияет на частицы при низких волновых числах, но при больших волновых числах частицы взаимодействуют с структурами жидкости и вызывают движение жидкости.
 Преимущество этой схемы принуждения над схемой принуждения Эсварана и Папы 6 6. В. Эсваран и С. Б. Поуп, «Исследование принуждения в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi.org/10.1016/0045-7930(88)-8 заключается в том, что схема находится в физическом пространстве. Коды, которые реализованы в физическом пространстве, не нуждаются в преобразовании Фурье величин, тем самым сокращая время вычислений при моделировании.
Преимущество этой схемы принуждения над схемой принуждения Эсварана и Папы 6 6. В. Эсваран и С. Б. Поуп, «Исследование принуждения в прямом численном моделировании турбулентности», Comput. Жидкости 16 (3), 257–278 (1988). https://doi.org/10.1016/0045-7930(88)-8 заключается в том, что схема находится в физическом пространстве. Коды, которые реализованы в физическом пространстве, не нуждаются в преобразовании Фурье величин, тем самым сокращая время вычислений при моделировании.(PDF) Обзор схем зеленого планирования для однородных и гетерогенных сотовых сетей
2
, контролирующих как межуровневые, так и внутриуровневые помехи.Установка HetNet
обеспечивает дополнительную гибкость в экологическом планировании, позволяя
достичь дальнейшего энергосбережения при передаче, например,
, выполняя совместное планирование между двумя уровнями для
, координируя их помехи и, в свою очередь, улучшая EE.
Некоторые ранние исследования уже показали обнадеживающие
результатов зеленого планирования в HetNets [6], [7].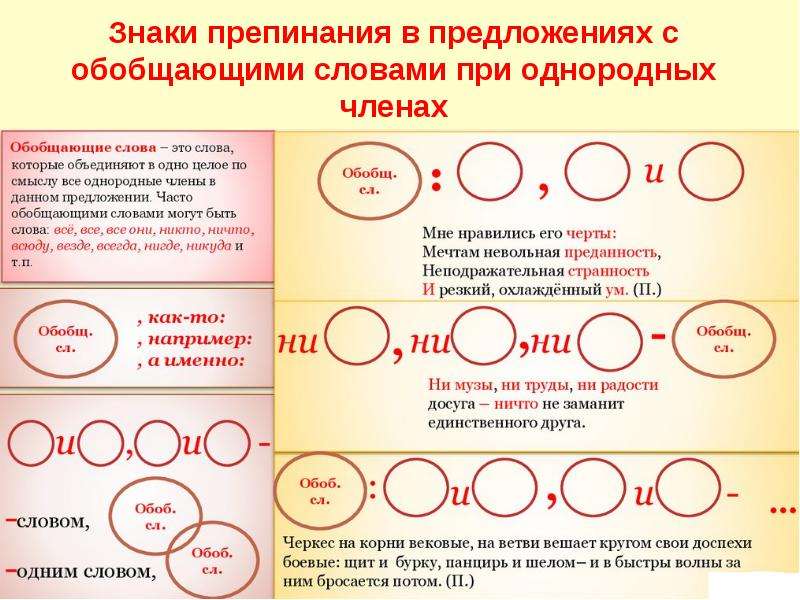
Однако мы считаем, что весь потенциал зеленого schedul-
ing для дальнейшего улучшения EE в будущей сети связи
работает, т.е.е. плотные небольшие сотовые сети, которые еще предстоит разблокировать.
Таким образом, мы предоставляем здесь подробный обзор схем зеленого планирования
для мобильных сетей и появляющихся HetNets путем выявления и классификации текущих тенденций в зеленом планировании и
с обобщением основных результатов существующих работ. Основываясь на последнем
, мы сначала определяем будущие проблемы для зеленого плана
, а затем предлагаем свои мысли и идеи по их решению.
Остальная часть статьи организована следующим образом. В Разделе II,
мы представляем модель системы и структуру, общие
для существующих исследований зеленого планирования. Раздел III описывает
различных существующих подходов к зеленому планированию. Ключевые результаты
этих подходов обобщаются и анализируются,
, а затем моделируются как одноуровневые сценарии, так и сценарии HetNet
в качестве иллюстрации эффективности схем зеленого планирования
в Разделе IV.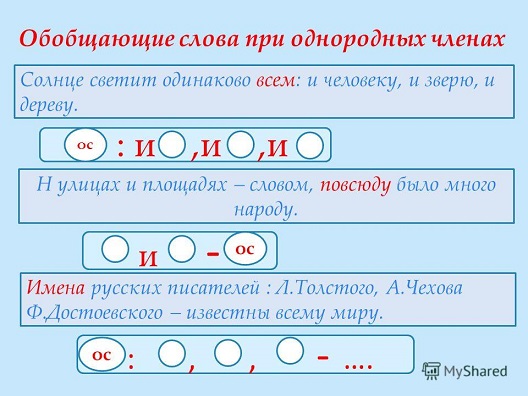 Проблемы и будущие направления в планировании зеленого
Проблемы и будущие направления в планировании зеленого
обсуждаются в Разделе V, за которым следуют важные заключительные замечания
.
II. SY ST EM MO DE L
Зеленое планирование направлено на достижение EE в дополнение к SE.
При зеленом планировании EE часто измеряется отношением скорости передачи
к соответствующей используемой мощности. Исследования
зеленого планирования в основном рассматривают сеть нисходящего канала с ортогональным частотным мультиплексированием (OFDMA)
с частотным разделением каналов
с единственной BS или M-скоординированными BS.Каждая BS имеет доступ к
совместно используемому спектру N поднесущих для обслуживания пользователей в пределах своего радиодиапазона
. Как BS, так и пользовательское оборудование (UE) оснащены
одной антенной. Наличие идеального состояния канала
информации (CSI) часто предполагается в процессе планирования зеленого
.
Энергетическая эффективность системы, EE, определяемая как отношение общей скорости передачи
к общей потребляемой мощности, может быть
выражено как [4]
EE, Rtotal
Ptotal
= PM
m = 1 PK
k = 1 Rk (m)
PM
m = 1 PN
n = 1 ∆mpn
m + Pfix
, (1)
, где Rk (m) представляет собой суммарную ставку пользователей, обслуживаемых
BS m. Экологичное планирование направлено на максимальное увеличение числа передаваемых
Экологичное планирование направлено на максимальное увеличение числа передаваемых
битов на каждый джоуль потребления энергии. Потребляемая мощность
состоит из двух частей: мощности передачи
pn
и рабочей мощности Pfix и ∆maccounts для
, зависящего от радиочастоты (RF) крутизны BS m. В (1),
,, количество Pfix захватывает рабочую потребляемую мощность
, включая мощность цепи, систему охлаждения, мощность для транзитных соединений
,и другие.Вышеупомянутая формула также действительна
для сценария малых ячеек с соответствующими настройками [4].
Цель зеленого планирования состоит в том, чтобы найти конкретное расписание пользователей
и распределение мощности таким образом, чтобы EE было максимальным
, учитывая некоторые ограничения по мощности, скорости, качеству услуги
(QoS) и т. Д. отметил, что в большинстве из
существующих работ по зеленому планированию для систем с несколькими ячейками [2] предполагается, что
[5] — [10], CSI, доступна на всех BS.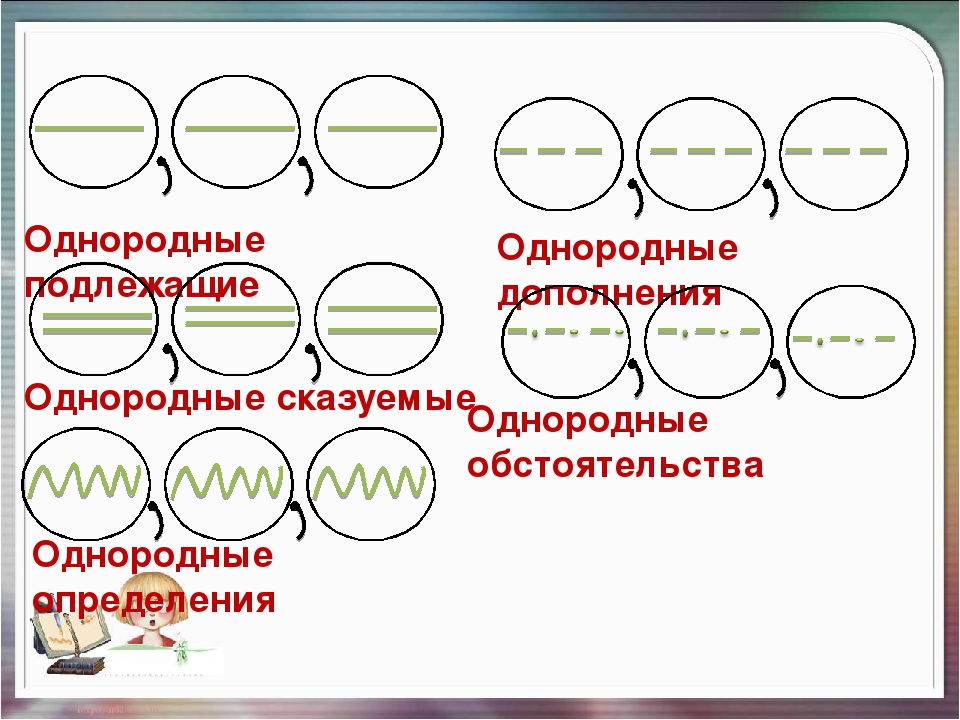 Это
Это
неявно соответствует скоординированному сценарию, в котором BS
имеют достаточно возможностей обратного рейса для обмена этой CSI. Как
для систем с одной сотой, CSI доступен только в каждой отдельной соте
для принятия решения о планировании [11], [12].
III. GRE EN СХЕМЫ ПЛАНИРОВАНИЯ
В исследовании зеленого планирования обычно используется информация о состоянии канала
для снижения мощности передачи при сохранении рабочих характеристик.В литературе были разработаны различные методы
для различных ограничений и сценариев. Мы
классифицируем существующие исследования по различным ограничениям
, а затем по сценариям, как показано на рис. 1. Первый след из
исследовательских работ обычно накладывает ограничение на мощность передачи
при разработке методов зеленого планирования [5] , [7],
[9]. Чтобы уловить требования к минимальной скорости передачи в системе
, исследовательские работы на втором треке совместно рассматривают
ограничений мощности и скорости [2], [6], [8], [11], [12]. Помимо мощности и скорости
Помимо мощности и скорости
, третье направление исследований фокусируется на
зеленого планирования с учетом справедливости, которое направлено на обеспечение
сбалансированных ставок среди пользователей [10], [13].
В то время как большинство существующих работ рассматривают традиционную сеть макросотов
в качестве своего сценария, в некоторых недавних работах
начали сосредотачиваться на предложении схем зеленого планирования для
развивающегося сценария HetNet. В случае многосотовых макро-сетей
BS могут выполнять скоординированное планирование зеленого, т.е.е.
BS могут координировать свою передачу для улучшения своего EE. Сценарий
HetNet более сложен из-за задействования
двух уровней. В идеале, при разработке схемы планирования
, которую можно интерпретировать как полную координацию между двумя уровнями, следует совместно учитывать помехи между внутри сотами и между
межсотовыми ячейками. Однако из-за сложности моделирования,
Однако из-за сложности моделирования,
многие существующие работы в HetNet согласованы лишь наполовину, т.е.е.
разработка схем зеленого планирования только для малых сот
с учетом помех от макроуровня в модели своей системы
. Для каждого трека исследования и сценария
мы представляем несколько важных работ ниже.
A. Зеленое планирование с ограничением мощности
Для сотовых сетей, использующих одну и ту же частоту, максимальная мощность передачи
для каждой BS устанавливается для управления помехами для других сот.Эта максимальная мощность передачи часто равна
, полученная на этапе планирования с целью обеспечить необходимое покрытие
без чрезмерных помех для других
соседних сот. Традиционно максимальная мощность передачи
делится поровну на каждой поднесущей в системе OFDMA.
Однако, когда состояние канала известно, соответствующая мощность передачи
может быть вычислена в процессе оптимизации EE
, так что максимальная мощность передачи может фактически использоваться не обязательно. Сумма запланированной мощности на каждой
Сумма запланированной мощности на каждой
поднесущей не должна превышать максимальную мощность передачи для
каждой BS. Учитывая ограничение мощности и знание CSI,
ограниченное зеленое планирование мощности назначает ресурсы с течением времени
, чтобы максимизировать EE системы.
Учебные группы студентов: однородные или неоднородные?
«Хорошо, ребята, сегодня мы будем учиться в группах. Каждой группе нужен математик, ведущий, писатель / редактор и иллюстратор.Вы решаете, кто что делает. Вы рассмотрите лучшие способы решения полиномиальных задач. Вытащите инструкцию и рубрику для этого задания. Как группа, ваша задача — создать одностраничный пошаговый процесс, которому кто-то может следовать, чтобы прийти к решению. У вас есть 15 минут, чтобы выполнить это задание в соответствии с заданной мной рубрикой. На старт, внимание, марш!»
Учитель, который дает эти инструкции, затем тратит следующие 15 минут на прогулку по классу, анализируя прогресс каждой группы и задавая вопросы, чтобы помочь отдельным группам прояснить свое мышление.
Группировка звучит так просто. В приведенном выше примере мы не видим того, как учитель организовал учеников в группы для достижения наилучших результатов. Некоторые преподаватели твердо убеждены в том, что учитель должен смешивать группы так, чтобы в каждой группе были представлены ученики всех уровней (разнородная группа учеников), в то время как другие считают, что учитель должен организовать учеников по уровням способностей (однородная группировка учеников). Роберт Марцано, Дебра Пикеринг и Джейн Поллок объясняют в книге « Классная инструкция, которая работает» (первое издание), что у обоих методов есть преимущества в зависимости от того, что хочет делать учитель.
Определение целей
Если целью группового обучения является помощь учащимся, испытывающим трудности, исследование показывает, что разнородные группы могут помочь больше всего. С другой стороны, если цель состоит в том, чтобы стимулировать группы со средними способностями к обучению на высоких уровнях, однородное группирование было бы лучше.
Я усвоил это как учитель, когда одна из моих одаренных и талантливых учениц по секрету сказала мне, что она действительно ненавидит все время находиться в разнородных группах (она говорила это по-другому), потому что по умолчанию другие члены группы ожидали она должна быть лидером, организовывать дела и делать всю работу.
Это был переломный момент для меня, потому что он заставил меня понять, что я не группирую студентов для повышения уровня обучения. Я использовал группировку в основном как инструмент управления дисциплиной, и на самом деле моя попытка увеличить вовлеченность студентов полностью обернулась. Всегда следя за тем, чтобы «умные» студенты и учащиеся, испытывающие трудности, были поровну разделены на группы, я фактически ограничивал участие студентов фактическими лидерами групп.
Выбор лучшего
Из-за этого прозрения я помню, как пообещал, что буду и дальше дифференцировать свое обучение, также ища способы дать ученикам старших классов сложные и увлекательные учебные задания. Я пообещал прекратить использовать «хороших детей» в надежде, что часть их «доброты» отразится на других учениках. Интересный случай произошел, когда я сгруппировал студентов по способностям. Сформировались новые структуры лидерства, и студенты, которые раньше никогда не участвовали активно в группах, внезапно продемонстрировали навыки и креативность, о которых я даже не подозревал.
Я пообещал прекратить использовать «хороших детей» в надежде, что часть их «доброты» отразится на других учениках. Интересный случай произошел, когда я сгруппировал студентов по способностям. Сформировались новые структуры лидерства, и студенты, которые раньше никогда не участвовали активно в группах, внезапно продемонстрировали навыки и креативность, о которых я даже не подозревал.
Студенты умны и могут легко понять, что мы делаем на самом деле. Учащиеся в наших классах знают, когда их группируют в основном для наставничества и исправления менее способных учеников и… большую часть времени они возмущены этим. Мы также можем отметить их, когда мы формируем группы исключительно в целях дисциплины, помещая спокойных, послушных учеников в каждую группу, чтобы отделить и успокоить непослушных. Моя дочь Мерседес, которая попадает в обе указанные выше категории, сказала, что, когда учителя делают это с ней, она не учится, и это не доставляет удовольствия ни ей, ни другим ученикам. Возможно, чаще всего ученики достаточно сообразительны, чтобы подыгрывать, когда понимают, что группировка — это не более чем рутинный способ провести время и вообще не имеет реальной учебной цели.
Возможно, чаще всего ученики достаточно сообразительны, чтобы подыгрывать, когда понимают, что группировка — это не более чем рутинный способ провести время и вообще не имеет реальной учебной цели.
Если есть выбор, учащиеся предпочитают учиться в группах своих сверстников и друзей (однородные группы), но они также ценят возможность узнавать что-то новое и учиться у других членов класса. Это требует, чтобы мы доверяли учащимся принимать правильные решения и требовали от них ответственности за соблюдение норм обучения в группах.
По мнению Марцано, Пикеринга и Поллока, эффективное обучение в группах должно включать как минимум следующие элементы:
- В работе должен участвовать каждый член группы.
- У каждого человека есть допустимая работа с известным уровнем завершения.
- Каждый участник вкладывается в выполнение задачи или учебной цели.
- Каждый член подотчетен индивидуально и коллективно.
Помните, что столы не прикреплены к полу — мы можем смешивать вещи в разнородные и однородные группы интересными и творческими способами: по цвету глаз, леворукости или праворукости, предпочитаемым начинкам для пиццы, количеству братьев и сестер, музыкальным предпочтениям и т. Д. пол, национальность, длина волос, шнурки для обуви, генетические особенности, стили обучения и т. д.
Д. пол, национальность, длина волос, шнурки для обуви, генетические особенности, стили обучения и т. д.
Стратегия гейтинга на основе модели для изоляции гомогенных субпопуляций в гетерогенной популяции одиночных клеток
Abstract
Стратегия стробирования на основе модели разработана для сортировки ячеек и анализа популяций отдельных ячеек. Стратегия, названная CCAST, для кластеризации, классификации и сортировки дерева, определяет стратегию стробирования для изоляции однородных субпопуляций от гетерогенной популяции отдельных ячеек с использованием представления дерева решений на основе данных, которое может применяться к сортировке ячеек.Поскольку CCAST не полагается на экспертные знания, он устраняет человеческую предвзятость и изменчивость при определении стратегии стробирования. Он сочетает в себе любой алгоритм кластеризации с измерениями силуэта для определения лежащих в основе однородных субпопуляций, а затем применяет методы рекурсивного разделения для создания дерева решений, которое определяет стратегию стробирования. CCAST обеспечивает оптимальную стратегию сортировки ячеек путем автоматизации выбора маркеров стробирования, соответствующих пороговых значений стробирования и последовательности стробирования; все эти параметры обычно определяются вручную.Несмотря на то, что CCAST оптимизирован для сортировки ячеек, его можно применять для идентификации и анализа однородных субпопуляций среди разнородных данных отдельных ячеек. Мы применяем CCAST к данным по отдельным клеткам как из линий клеток рака груди, так и из нормального костного мозга человека. По данным клеточной линии рака молочной железы SUM159 CCAST указывает по крайней мере пять различных состояний клеток на основе двух поверхностных маркеров (CD24 и EPCAM) и обеспечивает стратегию сортировки по воротам, которая дает более однородные субпопуляции, чем сообщалось ранее.Применительно к нормальным данным о костном мозге CCAST показывает эффективную стратегию стробирования Т-клеток без предварительного знания основных подтипов Т-клеток и маркеров, которые их лучше всего определяют.
CCAST обеспечивает оптимальную стратегию сортировки ячеек путем автоматизации выбора маркеров стробирования, соответствующих пороговых значений стробирования и последовательности стробирования; все эти параметры обычно определяются вручную.Несмотря на то, что CCAST оптимизирован для сортировки ячеек, его можно применять для идентификации и анализа однородных субпопуляций среди разнородных данных отдельных ячеек. Мы применяем CCAST к данным по отдельным клеткам как из линий клеток рака груди, так и из нормального костного мозга человека. По данным клеточной линии рака молочной железы SUM159 CCAST указывает по крайней мере пять различных состояний клеток на основе двух поверхностных маркеров (CD24 и EPCAM) и обеспечивает стратегию сортировки по воротам, которая дает более однородные субпопуляции, чем сообщалось ранее.Применительно к нормальным данным о костном мозге CCAST показывает эффективную стратегию стробирования Т-клеток без предварительного знания основных подтипов Т-клеток и маркеров, которые их лучше всего определяют. По данным нормального костного мозга CCAST также выявляет два основных подтипа зрелых B-клеток, а именно CD123 + и CD123- клетки, которые не были обнаружены ручным гейтированием, но демонстрируют различные внутриклеточные сигнальные ответы. В более общем плане, структура CCAST может использоваться для других биологических и небиологических типов данных большой размерности, которые представляют собой смеси неизвестных гомогенных субпопуляций.
По данным нормального костного мозга CCAST также выявляет два основных подтипа зрелых B-клеток, а именно CD123 + и CD123- клетки, которые не были обнаружены ручным гейтированием, но демонстрируют различные внутриклеточные сигнальные ответы. В более общем плане, структура CCAST может использоваться для других биологических и небиологических типов данных большой размерности, которые представляют собой смеси неизвестных гомогенных субпопуляций.
Сведения об авторе
Сортировка гомогенных субпопуляций в гетерогенной популяции одиночных клеток позволяет проводить последующую характеристику конкретных типов клеток, например геномное профилирование конкретных типов клеток. В этом исследовании предлагается стратегия стробирования, управляемая данными, CCAST, для отделения гомогенных субпопуляций от гетерогенной популяции отдельных клеток, не полагаясь на экспертные знания, тем самым устраняя человеческую предвзятость и изменчивость. Полностью автоматизированным способом CCAST идентифицирует соответствующие маркеры стробирования, иерархию стробирования и разделы, которые изолируют однородные субпопуляции клеток. CCAST оптимизирован для сортировки клеток, но может применяться для идентификации и анализа однородных субпопуляций. Показано, что CCAST идентифицирует более однородные субпопуляции рака груди в SUM159 по сравнению с предыдущими стратегиями сортировки. Применительно к данным о единичных клетках нормального костного мозга CCAST предлагает эффективную стратегию выхода Т-клеток, не полагаясь на экспертные знания; на В-клетках он обнаруживает новую характеристику подтипов зрелых В-клеток, не выявленных при ручном гейтинге.
CCAST оптимизирован для сортировки клеток, но может применяться для идентификации и анализа однородных субпопуляций. Показано, что CCAST идентифицирует более однородные субпопуляции рака груди в SUM159 по сравнению с предыдущими стратегиями сортировки. Применительно к данным о единичных клетках нормального костного мозга CCAST предлагает эффективную стратегию выхода Т-клеток, не полагаясь на экспертные знания; на В-клетках он обнаруживает новую характеристику подтипов зрелых В-клеток, не выявленных при ручном гейтинге.
Образец цитирования: Anchang B, Do MT, Zhao X, Plevritis SK (2014) CCAST: Стратегия гейтинга на основе модели для выделения гомогенных субпопуляций в гетерогенной популяции одиночных клеток.PLoS Comput Biol 10 (7): e1003664. https://doi.org/10.1371/journal.pcbi.1003664
Редактор: Шэн Чжун, Калифорнийский университет, Сан-Диего, Соединенные Штаты Америки
Поступило: 26 августа 2013 г . ; Одобрена: 25 апреля 2014 г .; Опубликовано: 31 июля 2014 г.
; Одобрена: 25 апреля 2014 г .; Опубликовано: 31 июля 2014 г.
Авторские права: © 2014 Anchang et al. Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Финансирование: Эта работа финансировалась грантом NCI U54 CA149145 и Дарственным фондом Гэри М. Глейзера. Финансирующие организации не играли никакой роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.
Введение
Понимание гетерогенности рака становится все более важным для понимания прогрессирования рака и преодоления терапевтической резистентности [1] — [4]. Среди клеток, составляющих одну опухоль, обычно наблюдаются различные типы гетерогенности, включая генетическую [5], [6], эпигенетическую [7] и фенотипическую гетерогенность [3], [4]. Хотя технологические проблемы ограничили нашу способность полностью охарактеризовать внутриопухолевую гетерогенность, в последние годы характеристика гетерогенных популяций клеток на уровне одной клетки с использованием данных многомерной флуоресценции и масс-проточной цитометрии в сочетании с новыми вычислительными инструментами значительно улучшила наше понимание степень клеточной неоднородности [8], [9].Более того, сортируя однородные субпопуляции, исследователи могут измерять и сравнивать геномные и другие функциональные свойства различных субпопуляций. Однако, несмотря на высокую пропускную способность этих измерений отдельных ячеек, современные методы сортировки определенных субпопуляций ячеек основываются на низкоразмерном, часто определяемом пользователем процессе, известном как стробирование. Стробирование на машине для сортировки клеток с активацией флуоресценции (FACS) обычно относится к ручному процессу, выполняемому путем последовательного выбора областей из двумерных графиков, которые отображают экспрессию двух маркеров одновременно во всех клетках.
Среди клеток, составляющих одну опухоль, обычно наблюдаются различные типы гетерогенности, включая генетическую [5], [6], эпигенетическую [7] и фенотипическую гетерогенность [3], [4]. Хотя технологические проблемы ограничили нашу способность полностью охарактеризовать внутриопухолевую гетерогенность, в последние годы характеристика гетерогенных популяций клеток на уровне одной клетки с использованием данных многомерной флуоресценции и масс-проточной цитометрии в сочетании с новыми вычислительными инструментами значительно улучшила наше понимание степень клеточной неоднородности [8], [9].Более того, сортируя однородные субпопуляции, исследователи могут измерять и сравнивать геномные и другие функциональные свойства различных субпопуляций. Однако, несмотря на высокую пропускную способность этих измерений отдельных ячеек, современные методы сортировки определенных субпопуляций ячеек основываются на низкоразмерном, часто определяемом пользователем процессе, известном как стробирование. Стробирование на машине для сортировки клеток с активацией флуоресценции (FACS) обычно относится к ручному процессу, выполняемому путем последовательного выбора областей из двумерных графиков, которые отображают экспрессию двух маркеров одновременно во всех клетках. Стратегия стробирования часто основывается на экспертной оценке выбора маркеров стробирования, порядка стробирования и точек отсечения для идентификации каждой стробируемой области; эта оценка часто основана на субъективном анализе с использованием таких пакетов, как flowJo и FlowCore [10]. Хорошо задокументировано, что незначительные различия в стратегии стробирования могут привести к существенно разным количественным выводам [11], [12]. Мы представляем стратегию стробирования, оптимизированную для сортировки ячеек. Поскольку наша стратегия стробирования основана на полученных данных, мы утверждаем, что она оптимальна по сравнению со стратегией стробирования, полученной вручную, которая может быть предвзятой и сильно изменчивой.В своей работе мы проводим различие между алгоритмами стробирования, которые оптимизированы для сортировки отдельных ячеек и анализа гетерогенной популяции данных отдельных ячеек. Несмотря на то, что наша стратегия стробирования оптимизирована для сортировки ячеек, она также имеет значение при использовании при анализе данных о населении на уровне отдельных ячеек.
Стратегия стробирования часто основывается на экспертной оценке выбора маркеров стробирования, порядка стробирования и точек отсечения для идентификации каждой стробируемой области; эта оценка часто основана на субъективном анализе с использованием таких пакетов, как flowJo и FlowCore [10]. Хорошо задокументировано, что незначительные различия в стратегии стробирования могут привести к существенно разным количественным выводам [11], [12]. Мы представляем стратегию стробирования, оптимизированную для сортировки ячеек. Поскольку наша стратегия стробирования основана на полученных данных, мы утверждаем, что она оптимальна по сравнению со стратегией стробирования, полученной вручную, которая может быть предвзятой и сильно изменчивой.В своей работе мы проводим различие между алгоритмами стробирования, которые оптимизированы для сортировки отдельных ячеек и анализа гетерогенной популяции данных отдельных ячеек. Несмотря на то, что наша стратегия стробирования оптимизирована для сортировки ячеек, она также имеет значение при использовании при анализе данных о населении на уровне отдельных ячеек.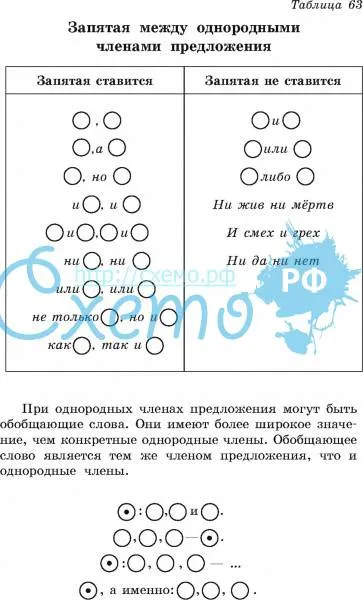
При анализе популяции отдельных клеток было разработано несколько алгоритмов стробирования, чтобы уменьшить технические, биологические и человеческие источники вариаций, участвующих в идентификации и анализе кластеров схожих субпопуляций клеток [8], [9], [13] — [17] ].Башашати и Бринкман предоставляют всесторонний обзор инструментов анализа данных проточной цитометрии (FCM) [18]. Совсем недавно в проекте FlowCAP-II [12] сравнивались точность и воспроизводимость нескольких алгоритмов стробирования с точки зрения идентификации кластеров ячеек. Все алгоритмы стробирования, включая наш, имеют некоторую форму алгоритма кластеризации, который используется для определения однородных субпопуляций в качестве основного компонента. Многие алгоритмы неконтролируемой кластеризации учитывают неопределенность в распределении кластеров, моделируя данные как смеси параметрических распределений [18].Хотя для анализа данных FCM были разработаны параметрические модели смеси [14], ошибки вычислений, а также ошибки оценки при кластеризации все еще могут возникать из-за выбросов и асимметрии данных, которые могут не отражать исходные допущения параметрической модели. В качестве альтернативы мы предлагаем модифицированную версию непараметрического многомерного подхода к моделированию смеси Benaglia et al. [19] для кластеризации данных FCM, где наша модификация включает использование мер силуэта.Этот алгоритм кластеризации обрабатывает неопределенность относительно того, к какому кластеру должно быть отнесено событие, а также неопределенность в количестве базовых состояний ячеек в гетерогенной родительской популяции и делает небольшие предварительные предположения о структуре базовой модели или не делает их вообще. Кроме того, мы реализуем альтернативный алгоритм кластеризации, а именно иерархическую кластеризацию [20], чтобы показать, что результаты нашей стратегии стробирования не зависят от конкретного используемого метода кластеризации. Целью нашего исследования является не обеспечение оптимальной стратегии кластеризации, а предоставление оптимальной стратегии стробирования для сортировки однородных субпопуляций клеток с учетом любого разумного алгоритма кластеризации.
В качестве альтернативы мы предлагаем модифицированную версию непараметрического многомерного подхода к моделированию смеси Benaglia et al. [19] для кластеризации данных FCM, где наша модификация включает использование мер силуэта.Этот алгоритм кластеризации обрабатывает неопределенность относительно того, к какому кластеру должно быть отнесено событие, а также неопределенность в количестве базовых состояний ячеек в гетерогенной родительской популяции и делает небольшие предварительные предположения о структуре базовой модели или не делает их вообще. Кроме того, мы реализуем альтернативный алгоритм кластеризации, а именно иерархическую кластеризацию [20], чтобы показать, что результаты нашей стратегии стробирования не зависят от конкретного используемого метода кластеризации. Целью нашего исследования является не обеспечение оптимальной стратегии кластеризации, а предоставление оптимальной стратегии стробирования для сортировки однородных субпопуляций клеток с учетом любого разумного алгоритма кластеризации.
Обычно игнорируемая область при изучении популяций отдельных клеток — это определение оптимальной стратегии стробирования для сортировки клеток. Сортировка ячеек для последующего анализа зависит не только от идентификации кластеров, но и от стратегии стробирования, которая определяется маркерами стробирования, порогами и последовательностью. Для ручного стробирования на машине FACS типичные стратегии стробирования организованы как генеалогическое древо. Например, из зрелых клеток костного мозга лимфоциты блокируются из родительских клеток, и из этих ворот блокируются Т-клетки или В-клетки, и из этих ворот блокируются определенные типы Т-клеток и В-клеток [9]. .В частности, сортировка Т-клеток эквивалентна выделению популяции CD4 + / CD8 +; пользователь сначала выделял лимфоциты, затем извлекал клетки CD3 + и оттуда рисовал ворота вокруг субпопуляций с положительным и положительным по CD4 и CD8. Этот подход предполагает предварительное знание базового набора маркеров, которые определяют типы клеток, иерархию стробирования и относительные границы для выделения представляющих интерес чистых субпопуляций клеток. Выбор этих параметров, основанный исключительно на литературе и точке зрения человека, привносит систематическую ошибку и вариабельность и может привести к заражению субпопуляций клеток.Мы делаем этот процесс управляемым данными и полностью автоматизированным, применяя технику рекурсивного разделения, которая генерирует дерево решений, представляющее воспроизводимую стратегию стробирования для всех представляющих интерес субпопуляций.
Выбор этих параметров, основанный исключительно на литературе и точке зрения человека, привносит систематическую ошибку и вариабельность и может привести к заражению субпопуляций клеток.Мы делаем этот процесс управляемым данными и полностью автоматизированным, применяя технику рекурсивного разделения, которая генерирует дерево решений, представляющее воспроизводимую стратегию стробирования для всех представляющих интерес субпопуляций.
Признавая текущую зависимость от человеческой точки зрения и интуиции при ручном стробировании, Рэй и Пайн [17] недавно разработали стробирующую структуру, которая имитирует человеческую перспективу при анализе данных FCM на основе математической карты многомерного ландшафта данных. Они предлагают гибкие шаблоны для конкретных образцов для извлечения интересующих объектов, которые могут иметь необычные формы и распределения.Альтернативный подход Ли и др. [21] использует метод обучения передачи в сочетании с принципом разделения с низкой плотностью; Этот подход переносит экспертные знания по обучению наборов данных FCM на новые данные. Более недавнее исследование Aghaeepour et al. [22] разработал вычислительную структуру с контролируемым обучением, которая автоматически выявляет подмножества клеток, которые сильно коррелируют с клиническим исходом, и идентифицирует соответствующий набор маркеров для стробирования. В последующем исследовании Aghaeepour et al. [22] разработал вычислительный инструмент RchOptimyx [23], который использует методы динамического программирования и оптимизации из теории графов для построения клеточной иерархии, обеспечивая стратегию стробирования для идентификации целевых популяций до желаемого уровня чистоты. Кто-то может возразить, что наша работа больше всего похожа на RchOptimyx. Однако, как будет показано позже, RchyOptimyx предоставляет несколько подходов для стробирования конкретной субпопуляции, тогда как наш подход направлен на поиск единой оптимальной стратегии стробирования полностью автоматизированным способом, не полагаясь на качественную оценку.
Более недавнее исследование Aghaeepour et al. [22] разработал вычислительную структуру с контролируемым обучением, которая автоматически выявляет подмножества клеток, которые сильно коррелируют с клиническим исходом, и идентифицирует соответствующий набор маркеров для стробирования. В последующем исследовании Aghaeepour et al. [22] разработал вычислительный инструмент RchOptimyx [23], который использует методы динамического программирования и оптимизации из теории графов для построения клеточной иерархии, обеспечивая стратегию стробирования для идентификации целевых популяций до желаемого уровня чистоты. Кто-то может возразить, что наша работа больше всего похожа на RchOptimyx. Однако, как будет показано позже, RchyOptimyx предоставляет несколько подходов для стробирования конкретной субпопуляции, тогда как наш подход направлен на поиск единой оптимальной стратегии стробирования полностью автоматизированным способом, не полагаясь на качественную оценку.
Мы представляем алгоритм, названный CCAST для дерева кластеризации, классификации и сортировки, для выявления и сортировки однородных субпопуляций из гетерогенной родительской популяции с использованием представления дерева решений для стратегии стробирования, которое можно использовать для сортировки однородных субпопуляций клеток. Стратегия стробирования, полученная из CCAST, основана на данных, полностью автоматизирована и не полагается на экспертные знания. Хотя CCAST оптимизирован для сортировки ячеек, CCAST также имеет значение при применении к анализу данных путем фильтрации и повторного обучения дерева решений для получения более однородных субпопуляций.Кроме того, при использовании для анализа данных CCAST может идентифицировать новые субпопуляции среди начальных кластеров. Мы применяем CCAST к популяциям одноклеточных измерений рака груди и нормального костного мозга человека. В клеточной линии рака молочной железы SUM159 CCAST выявляет по крайней мере 5 различных состояний клеток на основе двух поверхностных маркеров (CD24 и EPCAM). Применительно к данным о нормальном костном мозге CCAST показывает эффективную стратегию стробирования Т-клеток. Кроме того, CCAST выявляет два новых подтипа зрелых B-клеток, которые не были обнаружены с помощью ручного стробирования, но демонстрируют отличное внутриклеточное сигнальное поведение.
Стратегия стробирования, полученная из CCAST, основана на данных, полностью автоматизирована и не полагается на экспертные знания. Хотя CCAST оптимизирован для сортировки ячеек, CCAST также имеет значение при применении к анализу данных путем фильтрации и повторного обучения дерева решений для получения более однородных субпопуляций.Кроме того, при использовании для анализа данных CCAST может идентифицировать новые субпопуляции среди начальных кластеров. Мы применяем CCAST к популяциям одноклеточных измерений рака груди и нормального костного мозга человека. В клеточной линии рака молочной железы SUM159 CCAST выявляет по крайней мере 5 различных состояний клеток на основе двух поверхностных маркеров (CD24 и EPCAM). Применительно к данным о нормальном костном мозге CCAST показывает эффективную стратегию стробирования Т-клеток. Кроме того, CCAST выявляет два новых подтипа зрелых B-клеток, которые не были обнаружены с помощью ручного стробирования, но демонстрируют отличное внутриклеточное сигнальное поведение.
Результаты
Мы демонстрируем производительность CCAST на смоделированных и фактических популяциях данных отдельных ячеек. Подробная информация об алгоритме CCAST представлена в разделе «Материалы и методы». На рисунке 1 CCAST кратко представлен в виде блок-схемы вместе с его приложением к смоделированным данным. Вкратце, начиная с совокупности данных одной ячейки (рисунок 1A), CCAST выполняет алгоритм кластеризации ячеек для идентификации групп похожих ячеек (рисунок 1B). Кластеризация может выполняться разными способами.Мы реализуем непараметрическую модель смеси, обозначенную как «npEM» (см. «Материалы и методы»), но показываем, что другие алгоритмы кластеризации, такие как иерархическая кластеризация (HCLUST), создают аналогичные стратегии стробирования в рамках CCAST. После того, как кластеры ячеек (также известные как «типы ячеек») установлены, CCAST выводит стратегию стробирования, которая представлена деревом решений (рис. 1C), где узлы указывают маркеры стробирования и их пороги (также известные как «точки разделения») в качестве ребер.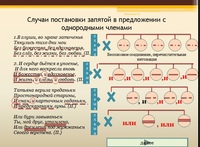 . Конечные листья дерева решений представляют собой конечные стробированные субпопуляции.Часто конечное количество закрытых популяций больше, чем количество кластеров клеток. Когда это происходит, некоторые субпопуляции захватывают клетки только из одного кластера, а другие захватывают клетки из нескольких кластеров. Для субпопуляций, которые содержат клетки из нескольких кластеров, все, кроме клеток из доминирующего кластера, удаляются, а CCAST повторно обучается на оставшейся популяции, обеспечивая более надежную стратегию стробирования, поскольку на нее меньше влияют «заражающие» клетки (рис. 1D).Окончательное дерево решений можно использовать для сортировки ячеек (рисунок 1E) или анализа данных (рисунок 1F). Хотя это не показано на рисунке 1, возможно, что один кластер может быть распределен по нескольким субпопуляциям, где каждая субпопуляция содержит только клетки из этого кластера; в этих случаях в кластере может быть больше субпопуляций, чем получено с помощью алгоритма кластеризации.
. Конечные листья дерева решений представляют собой конечные стробированные субпопуляции.Часто конечное количество закрытых популяций больше, чем количество кластеров клеток. Когда это происходит, некоторые субпопуляции захватывают клетки только из одного кластера, а другие захватывают клетки из нескольких кластеров. Для субпопуляций, которые содержат клетки из нескольких кластеров, все, кроме клеток из доминирующего кластера, удаляются, а CCAST повторно обучается на оставшейся популяции, обеспечивая более надежную стратегию стробирования, поскольку на нее меньше влияют «заражающие» клетки (рис. 1D).Окончательное дерево решений можно использовать для сортировки ячеек (рисунок 1E) или анализа данных (рисунок 1F). Хотя это не показано на рисунке 1, возможно, что один кластер может быть распределен по нескольким субпопуляциям, где каждая субпопуляция содержит только клетки из этого кластера; в этих случаях в кластере может быть больше субпопуляций, чем получено с помощью алгоритма кластеризации. Эта функция и все другие упомянутые функции CCAST показаны ниже.
Эта функция и все другие упомянутые функции CCAST показаны ниже.
Рис. 1. Блок-схема CCAST и анализ смоделированного набора данных.
A Данные цитометрии, представленные трехмерной диаграммой рассеяния смоделированных данных FCM, показывающей экспрессию 3 маркеров во всех клетках. B Кластерный анализ дает пять типов ячеек с цветовой кодировкой, обозначенных как типы ячеек 1, 2, 3, 4 и 5. C Сгенерировано исходное дерево решений CCAST, показывающее субпопуляции в конечных узлах. Узлы 9, 10 и 11 содержат клетки одного типа и считаются чистыми субпопуляциями. Узлы 5, 6 и 8 содержат смесь типов ячеек. D Окончательное дерево решений CCAST, полученное после фильтрации данных путем удаления загрязняющих ячеек в узлах со смешанными типами ячеек. Это дерево можно использовать для сортировки ячеек или анализа данных. E 2D диаграмма разброса исходных (нефильтрованных) данных, показывающая 5 кластеров с цветовой кодировкой и оцененные пороговые значения с соответствующими цветовыми порогами для сортировки 5 совокупностей состояний ячеек.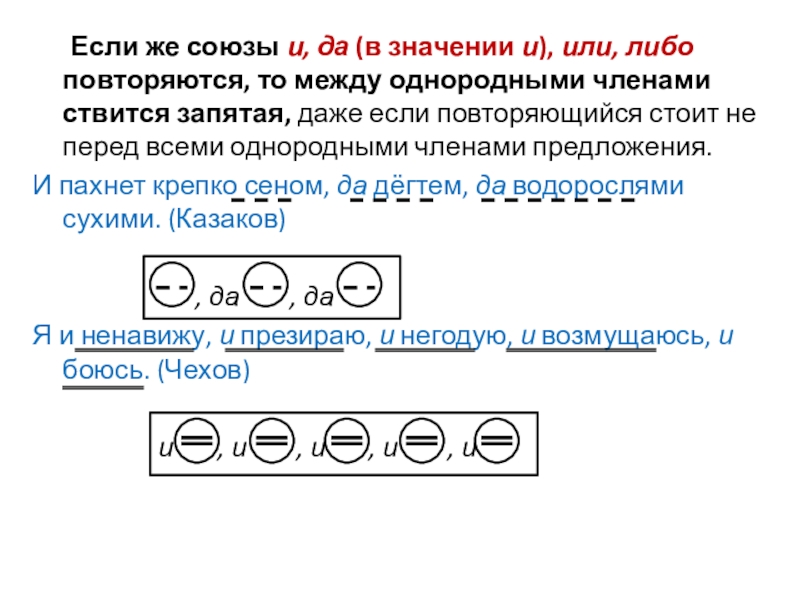 Обратите внимание, что субпопуляции могут быть отсортированы с использованием только маркера 1 и маркера 2, хотя изначально для идентификации типов клеток использовались три маркера. F Гистограмма трех маркеров в каждой подгруппе, полученных с использованием окончательного дерева CCAST на отфильтрованных данных. G 2D-диаграмма разброса отфильтрованных данных, полученных из CCAST, показывающая, что анализ, полученный на основе иерархической (справа) кластеризации, в сравнении с npEM (слева) аналогичен.
Обратите внимание, что субпопуляции могут быть отсортированы с использованием только маркера 1 и маркера 2, хотя изначально для идентификации типов клеток использовались три маркера. F Гистограмма трех маркеров в каждой подгруппе, полученных с использованием окончательного дерева CCAST на отфильтрованных данных. G 2D-диаграмма разброса отфильтрованных данных, полученных из CCAST, показывающая, что анализ, полученный на основе иерархической (справа) кластеризации, в сравнении с npEM (слева) аналогичен.
https://doi.org/10.1371/journal.pcbi.1003664.g001
Мы реализовали CCAST как пакет R, и он был доступен в виде zip-файла в Приложении.
CCAST устойчив к алгоритму кластеризации, что подтверждается смоделированными данными
Чтобы проиллюстрировать основные свойства CCAST, мы применили его к смоделированному набору данных из 850 отдельных ячеек, состоящих из смеси 5 типов ячеек, как показано на рисунке 1A. На каждой отдельной ячейке измеряется 3 маркера; распределения значений маркеров для каждого типа ячеек обобщены в дополнительной таблице S1. Мы выбрали 100, 300, 150, 100, 200 значений выражения вектора ячеек для каждого типа ячеек соответственно. На рис. 1В показан трехмерный график разброса измерений ячеек с цветовой кодировкой 5 типов ячеек; из этого рисунка автоматически не видно, как оптимально отсортировать эти 5 кластеров. На рис. 1C показано первое дерево решений, полученное с помощью CCAST, на основе всего набора данных; это дерево разделило данные на 5 кластеров, о чем свидетельствуют листовые узлы (5, 6, 9, 10 и 11) дерева.Узлы 9, 10 и 11 представляют чистые субпопуляции кластеров 4, 3 и 5 соответственно; узел 8 показывает смесь кластеров 1 и 4; в узлах 5 и 6 преобладают ячейки из кластеров 2 и 1 соответственно. После того, как CCAST удалил загрязняющие клетки из субпопуляций, которые имеют более одного кластера, и повторно запустил алгоритм дерева решений, он сгенерировал окончательное дерево решений на рисунке 1D.
На каждой отдельной ячейке измеряется 3 маркера; распределения значений маркеров для каждого типа ячеек обобщены в дополнительной таблице S1. Мы выбрали 100, 300, 150, 100, 200 значений выражения вектора ячеек для каждого типа ячеек соответственно. На рис. 1В показан трехмерный график разброса измерений ячеек с цветовой кодировкой 5 типов ячеек; из этого рисунка автоматически не видно, как оптимально отсортировать эти 5 кластеров. На рис. 1C показано первое дерево решений, полученное с помощью CCAST, на основе всего набора данных; это дерево разделило данные на 5 кластеров, о чем свидетельствуют листовые узлы (5, 6, 9, 10 и 11) дерева.Узлы 9, 10 и 11 представляют чистые субпопуляции кластеров 4, 3 и 5 соответственно; узел 8 показывает смесь кластеров 1 и 4; в узлах 5 и 6 преобладают ячейки из кластеров 2 и 1 соответственно. После того, как CCAST удалил загрязняющие клетки из субпопуляций, которые имеют более одного кластера, и повторно запустил алгоритм дерева решений, он сгенерировал окончательное дерево решений на рисунке 1D. Также обратите внимание, что эти субпопуляции были стробированы с использованием только двух маркеров, хотя были измерены 3 маркера.На рисунке 1E показано применение окончательного дерева решений (рисунок 1D) ко всему набору данных. Когда эта стратегия стробирования была применена к отфильтрованному набору данных для последующего анализа, полученные субпопуляции показаны на рисунке 1F, представлены столбчатыми диаграммами экспрессии маркеров и помечены соответствующими кластерами клеток. На рисунке 1G показано применение стратегии стробирования с использованием оцененных пороговых значений для всех данных с использованием иерархической кластеризации вместо кластеризации «npEM». Сходные разделы 2D-данных означают, что использование другого алгоритма кластеризации приводит к аналогичным однородным субпопуляциям.
Также обратите внимание, что эти субпопуляции были стробированы с использованием только двух маркеров, хотя были измерены 3 маркера.На рисунке 1E показано применение окончательного дерева решений (рисунок 1D) ко всему набору данных. Когда эта стратегия стробирования была применена к отфильтрованному набору данных для последующего анализа, полученные субпопуляции показаны на рисунке 1F, представлены столбчатыми диаграммами экспрессии маркеров и помечены соответствующими кластерами клеток. На рисунке 1G показано применение стратегии стробирования с использованием оцененных пороговых значений для всех данных с использованием иерархической кластеризации вместо кластеризации «npEM». Сходные разделы 2D-данных означают, что использование другого алгоритма кластеризации приводит к аналогичным однородным субпопуляциям.
CCAST является воспроизводимым, что подтверждается данными цитометрии Т-клеточной массы
Далее мы демонстрируем применимость CCAST к фактическому набору гематопоэтических данных, полученному в исследовании Bendall et al. [9]. В этом исследовании был проанализирован нормальный костный мозг на уровне отдельных клеток с использованием массовой цитометрии (MCM), которая представляет собой недавно разработанную высокопроизводительную технологию для маркировки отдельных клеток металл-хелатными антителами, которые снижают эффект аутофлуоресценции. Привлекательность этого конкретного исследования заключается в том, что гематопоэтические клетки имеют хорошо установленный набор клональных маркеров, определяющих стадии их дифференцировки.В этом исследовании нестимулированные и стимулированные мононуклеарные клетки периферической крови человека (PBMC) от здорового донора были проанализированы с использованием тринадцати параметров поверхности, а именно: CD45, CD45RA, CD19, CD11b, CD4, CD8, CD34, CD20, CD33, CD123, CD38, CD90 и CD3. Кроме того, было измерено 18 внутриклеточных сигнальных молекул. Процесс ручного стробирования и характеристика основных клеточных популяций показаны на Рисунке S5 приложения [9].
[9]. В этом исследовании был проанализирован нормальный костный мозг на уровне отдельных клеток с использованием массовой цитометрии (MCM), которая представляет собой недавно разработанную высокопроизводительную технологию для маркировки отдельных клеток металл-хелатными антителами, которые снижают эффект аутофлуоресценции. Привлекательность этого конкретного исследования заключается в том, что гематопоэтические клетки имеют хорошо установленный набор клональных маркеров, определяющих стадии их дифференцировки.В этом исследовании нестимулированные и стимулированные мононуклеарные клетки периферической крови человека (PBMC) от здорового донора были проанализированы с использованием тринадцати параметров поверхности, а именно: CD45, CD45RA, CD19, CD11b, CD4, CD8, CD34, CD20, CD33, CD123, CD38, CD90 и CD3. Кроме того, было измерено 18 внутриклеточных сигнальных молекул. Процесс ручного стробирования и характеристика основных клеточных популяций показаны на Рисунке S5 приложения [9]. Одна часть этого исследования была сосредоточена на подмножестве Т-клеток, которое включало наивные CD4 + и CD8 + Т-клетки и зрелые CD4 + и CD8 + Т-клетки.Анализ индуцированных внутриклеточных сигнальных ответов в этих субпопуляциях по сравнению с нестимулированным контролем основывался на вручную определяемом процессе стробирования.
Одна часть этого исследования была сосредоточена на подмножестве Т-клеток, которое включало наивные CD4 + и CD8 + Т-клетки и зрелые CD4 + и CD8 + Т-клетки.Анализ индуцированных внутриклеточных сигнальных ответов в этих субпопуляциях по сравнению с нестимулированным контролем основывался на вручную определяемом процессе стробирования.
Чтобы продемонстрировать надежность CCAST, мы рассматриваем подмножество данных из исследования Bendall et al. [9], чтобы прозрачно оценить как погрешность, так и воспроизводимость наших результатов. Мы фокусируемся на субпопуляции Т-клеток из 20 000 клеток, которые были вручную разделены на 4 подтипа (см. Рисунок 1 в Bendall et al. [9] для схемы ручного стробирования). Здесь мы объединяем эти вручную введенные данные о Т-клетках, а затем закрываем эти данные, удаляя все предыдущие сведения о типах клеток или метках маркеров. Затем мы случайным образом разделяем эти данные на обучающий и тестовый набор по 10 000 ячеек каждая. Графики парного разброса по всем 13 маркерам без меток показаны на рисунке 2. Мы применяем CCAST к обучающим данным, чтобы получить окончательное дерево решений, показанное на рисунке 3A. Эти результаты показывают, что 4 различных гомогенных состояния клеток можно легко выделить с помощью только 2 из 13 измеренных маркеров, а именно маркера 5 и маркера 2.Затем мы провели анализ чувствительности к параметрам дерева решений, а именно к оптимальной высоте дерева, обозначенной L, и точкам разделения (см. Материалы и методы). Сначала мы задаемся вопросом: что произойдет с чистотой однородных подгрупп, если мы увеличим уровень сокращения дерева решений L? На рисунке S1A в дополнительном документе показано точно такое же дерево решений, что и на рисунке 3A, после увеличения L до 3 или более уровней. Фактически, анализ L-чувствительности с смоделированными трехмерными данными (описанный выше) показал, что увеличение L выше 4 дает ожидаемые 5 однородных групп, но уменьшает ожидаемое количество клеток в группе (результаты не показаны).
Графики парного разброса по всем 13 маркерам без меток показаны на рисунке 2. Мы применяем CCAST к обучающим данным, чтобы получить окончательное дерево решений, показанное на рисунке 3A. Эти результаты показывают, что 4 различных гомогенных состояния клеток можно легко выделить с помощью только 2 из 13 измеренных маркеров, а именно маркера 5 и маркера 2.Затем мы провели анализ чувствительности к параметрам дерева решений, а именно к оптимальной высоте дерева, обозначенной L, и точкам разделения (см. Материалы и методы). Сначала мы задаемся вопросом: что произойдет с чистотой однородных подгрупп, если мы увеличим уровень сокращения дерева решений L? На рисунке S1A в дополнительном документе показано точно такое же дерево решений, что и на рисунке 3A, после увеличения L до 3 или более уровней. Фактически, анализ L-чувствительности с смоделированными трехмерными данными (описанный выше) показал, что увеличение L выше 4 дает ожидаемые 5 однородных групп, но уменьшает ожидаемое количество клеток в группе (результаты не показаны). CCAST автоматически определяет L на основе однородности субпопуляций (материалы и методы). Затем мы выполнили начальный анализ, чтобы оценить диапазон значений точек разделения в оптимальном дереве решений. В частности, мы выполнили метод страт-выборки с заменой, чтобы сгенерировать 200 наборов данных начальной загрузки с тем же размером выборки, что и обучающие данные. Мы запустили CCAST на этих выборках, чтобы сгенерировать 200 деревьев решений с разными точками разделения. Иерархия и выбранные маркеры для этих образцов начальной загрузки были точно такими же, как показано на рисунке 3A.Мы показываем доверительные интервалы точек разделения по минимальным и максимальным оценкам границ из нашего бутстрап-анализа (см. Диапазон, расположенный рядом с оценками точек разделения на рисунке 3A). Обратите внимание, что мы не смогли рассчитать нормальные доверительные интервалы для этих оценок точек разделения из-за многомодального характера распределений точек разделения (рис. 3B). Чтобы проверить производительность CCAST, мы применили CCAST к тестовым данным, используя дерево решений, полученное из обучающего набора (рисунок 3A). После фильтрации данных окончательное дерево решений для тестового набора данных показано на дополнительном рисунке S1B.Обратите внимание, что все оценки точки разделения лежат в пределах ранее оцененных доверительных интервалов, показанных на рисунке 3A. Кроме того, иерархия дерева остается прежней. Этот результат демонстрирует, что CCAST дает надежные оценки точки разделения и может давать воспроизводимые результаты. Наконец, мы сравниваем результат CCAST до (рис. 3C) и после фильтрации данных (рис. 3D). На рисунке 3C показан двухмерный график разброса двух маркеров, которые разделяют обучающие данные на 4 кластера. Хотя есть убедительные доказательства наличия 4 кластеров, очевидно, что сортировка популяции в желтом кластере без загрязнения зеленых клеток будет сложной задачей.На рисунке 3D показаны результаты после применения CCAST к обучающим данным для анализа данных. Обратите внимание на чистые субпопуляции после применения этапа фильтрации данных CCAST. Следовательно, помимо обеспечения стратегии стробирования, CCAST также может создавать более однородное представление исходных данных для анализа данных.
CCAST автоматически определяет L на основе однородности субпопуляций (материалы и методы). Затем мы выполнили начальный анализ, чтобы оценить диапазон значений точек разделения в оптимальном дереве решений. В частности, мы выполнили метод страт-выборки с заменой, чтобы сгенерировать 200 наборов данных начальной загрузки с тем же размером выборки, что и обучающие данные. Мы запустили CCAST на этих выборках, чтобы сгенерировать 200 деревьев решений с разными точками разделения. Иерархия и выбранные маркеры для этих образцов начальной загрузки были точно такими же, как показано на рисунке 3A.Мы показываем доверительные интервалы точек разделения по минимальным и максимальным оценкам границ из нашего бутстрап-анализа (см. Диапазон, расположенный рядом с оценками точек разделения на рисунке 3A). Обратите внимание, что мы не смогли рассчитать нормальные доверительные интервалы для этих оценок точек разделения из-за многомодального характера распределений точек разделения (рис. 3B). Чтобы проверить производительность CCAST, мы применили CCAST к тестовым данным, используя дерево решений, полученное из обучающего набора (рисунок 3A). После фильтрации данных окончательное дерево решений для тестового набора данных показано на дополнительном рисунке S1B.Обратите внимание, что все оценки точки разделения лежат в пределах ранее оцененных доверительных интервалов, показанных на рисунке 3A. Кроме того, иерархия дерева остается прежней. Этот результат демонстрирует, что CCAST дает надежные оценки точки разделения и может давать воспроизводимые результаты. Наконец, мы сравниваем результат CCAST до (рис. 3C) и после фильтрации данных (рис. 3D). На рисунке 3C показан двухмерный график разброса двух маркеров, которые разделяют обучающие данные на 4 кластера. Хотя есть убедительные доказательства наличия 4 кластеров, очевидно, что сортировка популяции в желтом кластере без загрязнения зеленых клеток будет сложной задачей.На рисунке 3D показаны результаты после применения CCAST к обучающим данным для анализа данных. Обратите внимание на чистые субпопуляции после применения этапа фильтрации данных CCAST. Следовательно, помимо обеспечения стратегии стробирования, CCAST также может создавать более однородное представление исходных данных для анализа данных.
Рисунок 2. Визуализация 13 маркеров в гетерогенной популяции Т-клеток.
Эти диаграммы разброса 13 × 13 показывают попарное распределение 13 маркеров (немаркированных) на клетку из объединенных данных отдельных клеток 4 подтипов Т-клеток.Первичные данные были опубликованы Bendall et al. [9].
https://doi.org/10.1371/journal.pcbi.1003664.g002
Рис. 3. CCAST применяется для анализа отдельных Т-клеток.
A Стратегия стробирования CCAST, основанная на немаркированных данных Т-клеток на рисунке 2, постфильтрация, показывающая, что 4 типа клеток могут быть получены с использованием только маркера 5 и маркера 2 с маркером 5 в качестве корневого узла. Точки разделения вместе с минимальным-максимальным диапазоном для каждой точки разделения предоставляются на каждом узле. B Графики гистограммы для точки разделения выборки для каждого узла получены с помощью самонастройки. Мультимодальный характер распределений затрудняет вычисление истинных доверительных интервалов для оценок точки разделения. C Результат CCAST без фильтрации, представленный как двухмерная диаграмма разброса для 4 типов ячеек, каждый из которых имеет цветовую кодировку; Обратите внимание, что блокировка ячеек желтого цвета, скорее всего, приведет к загрязнению ячеек зеленого цвета. D Результат CCAST с фильтрацией, представленной в виде двухмерной диаграммы разброса 4 чистых типов ячеек с цветовой кодировкой каждого типа ячеек.Обратите внимание, что все загрязняющие клетки, смешанные с различными кластерами, были удалены. Для целей ручного стробирования сравнение двух схем C и D обеспечивает визуальную оценку ожидаемых уровней загрязнения при сортировке субпопуляций. E Стратегия стробирования CCAST для всех типов Tcell с метками показывает, что ключевыми маркерами стробирования являются маркеры CD4 и CD45RA. F 2D график разброса для четырех типов меченых Т-клеток на основе CD4 и CD45RA.
https: // doi.org / 10.1371 / journal.pcbi.1003664.g003
CCAST обеспечивает эффективную стратегию гейтинга для Т-клеток
Используя набор данных Т-клеток, описанный выше, мы показываем, что наша стратегия стробирования, полученная с помощью CCAST, воспроизводит результаты ручного стробирования, описанные в Bendall et al. [9], не полагаясь на экспертные знания. На рисунке 3E показано, что CCAST выделяет 4 различных состояния Т-клеток, используя только 2 из 13 измеренных маркеров поверхности. Эти два маркера оказались CD4 и CD45RA. На рис. 3F показано распределение 4 подтипов меченых Т-клеток на основе экспрессии CD4 и CD45A.Этот результат демонстрирует, что CCAST может идентифицировать 2 из 13 маркеров, которые, как известно, наиболее релевантны для идентификации интересующих подтипов, не полагаясь на предварительные знания о подтипах или маркерах, которые, как известно, определяют их. Более того, для анализа данных CCAST предоставляет более однородные субпопуляции, отфильтровывая контаминирующие клетки; аналогичный шаг не выполнялся в анализе с ручной синхронизацией [9].
CCAST выявляет дополнительные подтипы B-клеток в объединенных вручную контролируемых субпопуляциях
Затем мы применили CCAST только к контролируемым вручную субпопуляциям B-клеток Bendall et al. исследование [9]. В этом исследовании подтипами B-клеток, контролируемыми вручную, были: ранние Pre-B I клетки, поздние Pre-B II клетки, незрелые B-клетки, наивные зрелые CD38mid B-клетки и зрелые CD38low B-клетки (см. Рисунок 1 в Bendall и др. [9]). Чтобы проверить существование этих 5 основных субпопуляций B-клеток, мы выполнили иерархическую кластеризацию с пороговым значением 5 кластеров на объединенных данных B-клеток с ручным вводом, которые состояли из примерно 17000 клеток. График силуэта на рисунке 4A демонстрирует убедительные доказательства наличия 5 кластеров.На рис. 4В показана стратегия стробирования, полученная из CCAST, в виде дерева решений, посредством которого 5 различных типов клеток могут быть выделены с использованием только 4 из 13 поверхностных маркеров (а именно CD45, CD34, CD38 и CD123) только с 3 уровнями ветвления. Анализ перекрестной классификации между подтипами, полученными из CCAST, и подтипами, введенными вручную, резюмирован в виде тепловой карты на рисунке 4C. На основании рисунка 4С мы прогнозируем, что субпопуляции, включающие клетки типа 1, 4, 3 и 5, полученные из CCAST, являются преимущественно незрелыми клетками B, зрелыми CD38low B, Pre B II и Pre B I соответственно.Однако нет четкого однозначного соответствия между подтипами, производными от CCAST, и подтипами, стробируемыми вручную. В частности, фиг. 4C демонстрирует убедительные доказательства смешения подтипов зрелых B-клеток в клетках CCAST типов 2 и 4. Тепловые карты на фигуре 4D демонстрируют свидетельства двух различных типов клеток, полученных из CCAST, соответствующих типам клеток 2 и 4. которые считались одной основной популяцией, а именно зрелыми В-клетками CD38low, путем ручного стробирования. Основываясь на экспрессии поверхностных маркеров, наиболее разительным различием между типами клеток 2 и 4 является экспрессия CD123, сигнальной молекулы, которая способствует пролиферации и дифференцировке в линиях кроветворных клеток и связана с лейкемией волосатых клеток [24].На Фигуре 5A представлены тепловые карты индуцированных BCR, IFNa, FTL3, IL3, IL7 и SCF внутриклеточных сигнальных ответов в 5 подтипах B-клеток, полученных из CCAST, по сравнению с нестимулированным контролем. Для сравнения с результатами Bendall et al. [9] индукция сигнализации рассчитывалась с использованием разности среднего масштабированного значения arcsinh нестимулированного состояния и среднего масштабированного значения arcsinh стимулированного состояния; кроме того, только 13 поверхностных маркеров использовались для прогнозирования типов клеток в стимулированных условиях с использованием дерева решений из нестимулированных контролей.Разница рассчитывается как разница абсолютных кратных изменений. Стимуляция BCR, IFNa, IL7 и SCF индуцирует сильную внутриклеточную передачу сигналов через B-клетки на разных стадиях развития. Тепловая карта на рисунке 5B представляет тепловые карты BCR, IFNa, FTL3, IL3, IL7 и SCF-индуцированных внутриклеточных сигнальных ответов для различных подтипов B-клеток, полученных в результате ручного стробирования в [9]. В клетках, закрытых вручную, самые сильные различия в передаче сигналов ограничиваются зрелыми B-клетками, особенно связанными с P38 и Ki67.В клетках, управляемых CCAST, стимуляция BCR вызывает сильные различия в передаче сигналов PLC-gamma2, STAT3, h4, S6, CREB; Стимуляция IL7 изменяет передачу сигналов ERK1 / 2 и P38, INFalpha изменяет передачу сигналов STAT3; и SCF индуцирует изменения в передаче сигналов P38. В целом, по сравнению с типами клеток, контролируемыми вручную, типы клеток, производных от CCAST, демонстрируют больше различий в стимулированной индуцированной передаче сигналов, предположительно из-за того, что субпопуляции, регулируемые с помощью CCAST, более однородны. Наконец, в качестве отступления отметим, что CCAST производит 7 гомогенно закрытых субпопуляций, 3 из которых принадлежат к клеточному типу 3, предполагая, что этот тип клеток может быть более гетерогенным, чем предполагает алгоритм кластеризации.
Рисунок 4. CCAST применен к одноклеточному анализу В-клеток.
A Силуэтный график, демонстрирующий 5 типов B-клеток. B Стратегия гейтирования CCAST для типов В-клеток на основе маркеров CD45, CD34, CD38 и CD123 с использованием 3 уровней гейтирования. Предполагаемые диапазоны для переменных точки разделения представлены на каждом узле. Примечание. Celltype 3 распределен по трем закрытым популяциям. C Тепловая карта перекрестной классификации введенных вручную и предсказанных CCAST типов B-клеток указывает на убедительные доказательства того, что наиболее распространенные зрелые B-клетки CD38low включают смесь других подтипов (Celltype 2 и 4). D Тепловые карты демонстрируют свидетельства двух производных различных состояний зрелых В-клеток, соответствующих клеточным типам 2 и 4, в основном на основе CD123 (метка выделена красным).
https://doi.org/10.1371/journal.pcbi.1003664.g004
Рисунок 5. Поведение сигналов в подтипах B-клеток для CCAST и стратегии ручного стробирования.
A Тепловая карта BCR, IFNa, FTL3, IL3, IL7 и SCF, индуцированных внутриклеточных сигнальных ответов в 5 подтипах B-клеток, производных от CCAST, по сравнению с таковыми из нестимулированного контроля. B Тепловая карта BCR, IFNa, FTL3, IL3, IL7 и SCF, индуцированных внутриклеточными сигнальными ответами в пяти подтипах B-клеток, полученными из ручных ворот в Bendall et al. [9], по сравнению с нестимулированным контролем. Более высокая разница подразумевает более сильный сигнал в типе ячеек, производных от CCAST, по сравнению с типом ячеек с ручным стробированием.
https://doi.org/10.1371/journal.pcbi.1003664.g005
CCAST идентифицирует по крайней мере пять различных типов клеток в линии клеток рака молочной железы SUM159
Мы применили CCAST примерно к 1 миллиону клеток линии клеток рака молочной железы SUM159 (тройной отрицательный).Мы провели первичный FACS-анализ на клеточной линии SUM159 для этого исследования на основе экспрессии EPCAM, CD24 и CD44 (см. Материалы и методы). Чтобы оценить вероятное количество кластеров ячеек в SUM159, мы запустили кластерный алгоритм npEM, предполагая 10 кластеров, на случайной подвыборке из примерно 3000 ячеек и получили 5 кластеров. Используя иерархическую кластеризацию с отсечением 5 кластеров по всему набору данных SUM159, CCAST произвел стратегию стробирования, показанную на рисунке 6. CCAST идентифицировал 9 однородных субпопуляций, обозначенных как P1 – P9, в конечных узлах дерева на рисунке 6. .Аналогичная реализация на flowJo, показывающая 9 однородных кластеров, показана на дополнительном рисунке S2. На рисунке 7A суммированы результаты процесса оценки для всей статистики точек разделения на всех внутренних узлах дерева решений CCAST. Корневой узел, соответствующий EPCAM, показывает один глобальный максимум, указывающий на сильную точку разделения. Узлы 3, 4, 8, 9, 13 и 14 имеют четкие естественные максимумы, указывающие на оптимальное разбиение данных на явно 9 субпопуляций, каждая из которых соответствует 9 одномодовым гистограммам в конечных узлах дерева.Соответствующие гистограммы для всех 9 субпопуляций с интервалами стандартного отклонения для каждого маркера показаны на рисунке 7B. Многомерный тест Т-квадрата Хотеллинга показал значительные различия между парами групп (p-значение: 0), указывая на то, что эти девять девяти субпопуляций статистически отличаются друг от друга. Интересно, что CCAST разделяет кластер 1 на субпопуляции P5, P6 и P8; он также разбивает кластер 3 на субпопуляции P3, P4 и P7.
Рисунок 6. Стратегия стробирования CCAST на линии клеток рака молочной железы SUM159.
Стратегия стробирования CCAST для клеточных линий рака молочной железы SUM159 выделяет 5 чистых состояний клеток (по 9 ячейкам) на основе CD24 и EPCAM. Визуализация этих 5 субпопуляций явно не очевидна из графиков двухосного бокового рассеяния (SSC) и биомаркеров. Оценки точек разделения (пунктирные красные линии) проходят через контурный график плотности (оранжевый) на распределенных данных, обеспечивая визуальное свидетельство подходящих отсечений через бимодальные контуры. Обратите внимание, что линии точек разделения для узлов 3 и 4 сконцентрированы на массе нулевой точки; это указывает на то, что существует несколько клеток с нулевыми значениями экспрессии для окрашивания EPCAM или CD24, но с более высокими значениями экспрессии по сравнению с CD44.
https://doi.org/10.1371/journal.pcbi.1003664.g006
Рисунок 7. Анализ CCAST результатов SUM159 по раку груди.
A Результаты процесса оценки для всей статистики точек разделения во всех внутренних узлах на рисунке 6. Корневой узел, соответствующий EPCAM, показывает один локальный максимум и один глобальный максимум. Сбор данных из этого глобального максимума дает 9 различных субпопуляций. Узлы 3, 4, 8, 9, 13 и 14 имеют четкие естественные максимумы, указывающие на оптимальное разделение данных на эти 9 однородных субпопуляций (см. Рисунок 6), соответствующие 9 столбчатым диаграммам в B . B Столбчатые диаграммы 9 гомогенных субпопуляций с фиг. 6 по всем 3 маркерам со стандартными интервалами отклонения для каждого маркера. Значения на столбцах с левой стороны каждого графика соответствуют минимальному значению для всех трех значений высоты столбцов. Каждая боковая панель дает представление об относительной разнице между высотой штанги. В главном заголовке каждого графика показан соответствующий интервал листового узла на дереве на рисунке 6. Прогнозируемые типы ячеек 3 и 1 соответствуют P3, P4, P7 и P5, P6, P8, соответственно, указывая на более однородные субпопуляции, чем ожидалось.Гистограммы показывают наличие по крайней мере 5 различных субпопуляций, то есть P1, P2, P5, P7 и P9. C Gupta et al. Стратегия стробирования [3] выделила 3 клеточных состояния (базальное, стволовое и просветное) с использованием EPCAM в качестве основного маркера. Далее они используют CD24, чтобы отсортировать эти 3 состояния. Мы также автоматически идентифицируем EPCAM как основной маркер, но используем комбинацию нескольких разделений из CD24 и EPCAM для получения 9 однородных бинов. D Сравнение прогнозируемых субпопуляций рака молочной железы при сравнении CCAST и Gupta et al.Стратегия стробирования [3] показывает потенциальные доказательства загрязнения после сортировки. Этот анализ показал, что субпопуляция CCAST P9 явно представляет собой смесь базальных, стволовых и просветных субпопуляций из Gutpa et al. [3]. Уникальные субпопуляции CCAST P1 и P2 даже не были идентифицированы Gupta et al. [3].
https://doi.org/10.1371/journal.pcbi.1003664.g007
Затем мы сравниваем результаты стратегии стробирования, полученной из CCAST, на SUM159 со стратегией стробирования, определенной вручную Гуптой и др. [3] на той же клеточной линии. Gupta et al. идентифицировал три клеточных состояния (стволовые, базальные и просветные клетки) в SUM159 на основе трех маркеров (EPCAM, CD24 и CD44). Основываясь на предшествующих знаниях, стволовые клетки были определены как CD44-high, CD24-neg и EPCAM-low; базальные клетки были определены как CD44-high, CD24-neg и EPCAM-neg; а люминально-подобные клетки были определены как CD44-низкий, CD24-высокий и EPCAM-высокий. Рисунок 7C воспроизводит Gupta et al. [3] стратегия стробирования для файла FCM проанализирована на рисунке 6.Gupta et al. Стратегия сначала блокирует клетки на основе высокого и низкого уровня EPCAM, а затем контролирует стволовые, просветные и базальные субпопуляции, основанные исключительно на низком и высоком уровне CD24, как показано на Фигуре 7C. Таблица перекрестной классификации наших 9 субпопуляций и 3 Gutpa et al. Состояния клеток (обозначенные как стволовые, просветные и базальные субпопуляции) показаны на рисунке 7D. Этот анализ показывает, что базальная субпопуляция, идентифицированная Gupta et al. стробирование — это комбинация всех состояний ячеек, производных от CCAST.Кроме того, анализ предполагает, что смесь популяций базальных, стволовых и люминальных клеток из группы Gupta et al. Сортировка фактически соответствует одной подгруппе CCAST P9. Эти результаты предполагают, что специфический анализ клеточного типа, предоставленный Gupta et al. мог отражать поведение одного типа ячеек. The Gupta et al. Анализ мог бы быть более информативным, если бы он исследовал отдельные субпопуляции, такие как P1, P2, P5 и P7.
Наконец, для экспериментальной проверки мы применили нашу стратегию стробирования, полученную из CCAST, на линии клеток SUM159 в реальном времени на машине FACS.Дополнительный рисунок S3 показывает результат сортировки этой независимой копии; мы можем восстановить 5 различных субпопуляций, полученных из CCAST, в режиме реального времени.
CCAST отличается от RchyOptimyx
Мы сравниваем применение алгоритмов CCAST и RchyOptimyx с данными FCM линии клеток рака молочной железы SUM159. Как кратко описано во введении, RchyOptimyx обеспечивает стратегию стробирования для идентификации целевых популяций на различных уровнях чистоты [23]. На SUM159 RchyOptimyx изначально генерирует 27 субпопуляций для анализа.Поскольку не существует переменной клинического исхода для фильтрации по этим 27 предсказанным фенотипам с использованием алгоритма RchyOptimyx, мы выбрали только те фенотипы, которые соответствуют комбинации CD24 и EPCAM для сравнения с CCAST. Напомним, что CCAST привел к 9 гомогенным субпопуляциям, которые можно охарактеризовать только с помощью этих 2 маркеров. Основываясь на использовании только EPCAM и CD24, RchyOptimyx дал 12 субпопуляций, которые могут быть нацелены с помощью различных стратегий стробирования, как показано на рисунке приложения S4.Другими словами, RchyOptimyx предоставляет несколько возможных путей к определенной субпопуляции; для сравнения, CCAST предлагает только один путь для нацеливания на однородные субпопуляции, тем самым обходя любую дополнительную интерпретацию выходных данных RchyOptimyx для выбора стратегии стробирования. Базовый формализм RchyOptimyx и CCAST различен, но полное описание этих различий выходит за рамки данного анализа.
Обсуждение
Мы представили основанную на модели стратегию стробирования, CCAST, для сортировки однородной субпопуляции из гетерогенной популяции отдельных клеток, не полагаясь на экспертные знания.Чтобы определить иерархическую схему двумерного стробирования для сортировки однородных ячеек, мы предлагаем CCAST как новый подход, который решает три ключевых и часто игнорируемых вопроса: (1) Как выбрать оптимальные маркеры для стробирования? (2) Каков оптимальный порядок маркеров для сортировки? (3) Как мы оцениваем отрезки маркеров для рисования ворот? Ответы на эти вопросы обычно решаются субъективно и предвзято, что очень затрудняет получение точных выводов из полученных отсортированных данных.CCAST — это автоматизированная и беспристрастная стратегия, требующая минимального опыта человека, для оптимизации стробирования данных отдельных ячеек. Хотя CCAST оптимизирован для сортировки клеток, его можно применять для анализа очищенных субпопуляций среди данных разнородных отдельных клеток.
Во всех применениях CCAST в исследовании мы показываем, что можно охарактеризовать и выделить типы клеток на основе подмножества измеренных маркеров. Применительно к данным о нормальном костном мозге CCAST показывает эффективную стратегию стробирования Т-клеток.CCAST также продуцировал альтернативную стробирующую структуру для B-клеток, которая произвела новую характеристику зрелых B-клеток в клетки CD123 + и CD123-. Возможность выделить важные клеточные субпопуляции на основе ограниченных маркеров особенно важна, поскольку технологии высокопроизводительной цитометрии увеличивают количество маркеров, которые они могут измерять, и потребуются новые подходы для оптимального выбора важных маркеров набора для стробирования. Следовательно, CCAST не только предоставляет соответствующий набор маркеров, оптимизированную схему стробирования и снижает потребность в человеческом опыте, но также может уменьшить количество антител, необходимых для сортировки клеток.
Мы также обосновали необходимость CCAST как автоматически генерируемой схемы стробирования, которая не полагается на предварительные знания о состояниях клеток или релевантности маркеров на линии клеток рака молочной железы SUM159. На этой клеточной линии Gutpa et al. проверил гипотезу о том, что раковые клетки могут переходить в любое из нескольких возможных состояний клеток, которые проявляют важные функциональные свойства [3]. Это исследование было направлено на демонстрацию доказательств фенотипического переключения между состояниями стволовых, базальных и просветных клеток молочной железы, которые определялись CD24 и EPCAM.Установление убедительных доказательств переходов между состояниями клеток потребует наличия чистых состояний клеток в начале, однако чистая сортировка не очевидна для схемы ручного стробирования, использованной в исследовании. В независимом исследовании фенотипического переключения состояний раковых клеток Zapperi и Porta [4] дали альтернативную интерпретацию Gupta et al. на основе сценария несовершенного маркера. Анализ CCAST также позволяет сделать вывод о неоднородных субпопуляциях в соответствии с Gutpa et al. и предоставил альтернативные, более однородные состояния клеток с использованием альтернативной стратегии гейтирования, основанной на тех же маркерах, а именно CD24 и EPCAM.CCAST идентифицирует по крайней мере 5 различных состояний клеток рака молочной железы в SUM159 и автоматически сортирует эти чистые состояния клеток (рис. 6), используя только два поверхностных маркера, а именно EPCAM и CD24. Эти субпопуляции требуют дальнейших исследований для подтверждения концепции переключения фенотипа в клетках рака груди, предложенной Gupta et al. этюд.
CCAST дает возможность оптимальным и непредвзятым образом отсортировать уникальные базовые неизвестные состояния ячеек из гетерогенной родительской популяции с использованием схемы стробирования, основанной на представлении дерева решений.CCAST идентифицирует однородные субпопуляции клеток, используя непараметрическое распределение смеси. Хотя также можно использовать несколько других алгоритмов кластеризации, CCAST может обрабатывать неизвестное количество истинных кластеров без математической оптимизации функции распределения. Коэффициенты силуэта используются для оптимизации субпопуляций ячеек, а метод рекурсивного разделения полных данных с учетом состояний ячеек используется для создания оптимального дерева решений для выделения различных интересующих субпопуляций.Разделение происходит после этапа выбора маркера, который зависит от статистики непараметрического теста, что делает его полностью управляемым данными. CCAST также обеспечивает доверительный интервал для отсечки маркеров с учетом возможной изменчивости в распределении маркеров. Для будущего методологического улучшения CCAST как для вычислительных затрат, так и для уровня отсечения L, можно было бы рассмотреть многостороннее разбиение на каждом узле вместо использования двоичного разбиения. Другое методологическое направление могло бы заключаться в использовании доверительных интервалов для дальнейшего улучшения деревьев решений; в частности, методы, предложенные Katz et al. [25] может быть адаптирован для CCAST.
Таким образом, CCAST представляет собой полностью автоматизированную структуру модели для определения стратегии стробирования для выделения субпопуляций из данных отдельных клеток с большей однородностью по сравнению с процедурами стробирования вручную. В более общем плане, структура CCAST может использоваться для других биологических и небиологических типов данных большой размерности, включающих смесь неизвестных гомогенных субпопуляций.
Материалы и методы
Алгоритм CCAST
CCAST формализует процесс стробирования отдельных ячеек в виде статистической модели и предоставляет простую несмещенную иерархическую двумерную схему стробирования с соответствующим набором пороговых значений маркеров для стробирования гомогенной субпопуляции клеток с учетом данных FCM.Далее мы описываем различные этапы непараметрической модели модели CCAST применительно к данным отдельной ячейки. Типичный набор данных FCM включает одновременные количественные измерения сигналов нескольких биомаркеров отдельных клеток. Эти измерения могут быть основаны на флуоресценции или атомной массе. Данные хранятся в файлах стандарта проточной цитометрии (FCS) в виде фрейма данных со строками, представляющими клетки или события, и столбцами, соответствующими интересующим маркерам. В настоящее время мы предполагаем, что данные уже были скомпенсированы для корректировки спектрального перекрытия во время генерации данных и предварительно обработаны с использованием стандартных шагов предварительной обработки при анализе данных FCM для удаления ложных событий.Затем данные преобразуются с использованием рекомендованной функции Arcsinh [9], которая может обрабатывать как положительные, так и отрицательные значения выражений.
CCAST применяет непараметрические многомерные модели конечного смешения или иерархическую кластеризацию для идентификации субпопуляций ячеек.
Преобразованные данные FCM визуализируются как облако точек большого размера из ячеек, где каждая ячейка является точкой в облаке, а каждый маркер представлен как одно измерение в облачном пространстве. Различные подобласти облаков с высокой плотностью отражают обилие конкретных субпопуляций клеток, которые нелегко определить в большом измерении.Первая цель — идентифицировать клетки, которые принадлежат к одной и той же субпопуляции клеток, то есть к типу клеток или состоянию.
Мы предлагаем модификацию подхода к непараметрическому многомерному моделированию смеси, предложенного Benaglia et al. [19] для выявления гомогенных субпопуляций клеток среди данных отдельных клеток. Этот конкретный алгоритм модели смеси представляет собой EM-подобный алгоритм для непараметрического моделирования конечной смеси, реализованный в пакете mixtools R [19]. Он оценивает многомерное распределение смеси из многомерных случайных векторов.Предполагается, что векторы имеют независимые координаты, при условии, что известно, из какого компонента смеси они происходят, однако их функции плотности остаются полностью неопределенными. Назначение случайных векторов наиболее вероятному компоненту смеси выполняется путем максимизации апостериорных вероятностей. Этот алгоритм очень гибкий и может обрабатывать любое количество компонентов смеси и любое количество векторных координат многомерных наблюдений. Следуя [19] спецификации и аннотациям модели, мы обозначаем векторы измерения ячеек как состоящие из координат маркера.Мы предполагаем, что они представляют собой выборку из конечной смеси произвольных распределений, каждое из которых является независимым, в зависимости от субпопуляции, из которой оно взято. Кроме того, поскольку некоторые маркеры могут совместно экспрессироваться в некоторых субпопуляциях клеток, мы также можем позволить одинаковое распределение наборов маркеров. Обозначим через набор, которому принадлежит th маркер, где с равным общему количеству наборов. Плотность каждого из них может быть записана как (1) где функция обозначает неизвестное одномерное условие функции плотности в пространстве параметров, и все они положительны и в сумме равны единице.Таким образом, в целях согласованности мы используем индексы для обозначения отдельной уникальной ячейки, субпопуляции ячеек, координаты маркера и набора маркеров соответственно. В целом, мы не знаем априори, какие наборы маркеров определяют определенные субпопуляции клеток. В этом случае мы предполагаем, что более общая модель с уравнением 1 становится
.(2) Оценка всех параметров модели в уравнении 1 основана на EM-подобном алгоритме [19], реализованном в пакете mixtools R с использованием функции «npEM». Подобно алгоритму EM, эта функция определяет случайную величину Бернулли, указывающую, что ячейка принадлежит состоянию ячейки Следовательно, и полные данные становятся Мы сначала инициализируем все параметры модели Для каждой итерации
- 1. E-step : Апостериорные вероятности присвоения ячейки конкретному условию состояния данных задаются выражением,
(3)
- 2. M-step : Доля состояний ячеек определяется как,
(4) для
- 3. KDE-step : Для любого реального значения выражения непараметрическая оценка плотности для некоторого параметра полосы пропускания и функции плотности ядра определяется выражением,
(5) Вышеупомянутый алгоритм является детерминированным, и на практике первая итерация включает только M-шаг с матрицей, полученной с помощью детерминированного алгоритма, такого как k. — означает алгоритм кластеризации, который присваивает каждой ячейке уникальное состояние ячейки.Обратите внимание, что шаг KDE зависит от плотности ядра и определяемой пользователем полосы пропускания. Следуя рекомендациям [19], используется стандартная функция нормальной плотности и простое правило зависящей от плотности полосы пропускания, заданное как (6), где и — стандартное отклонение и межквартильный диапазон объединенных данных. Этот метод может либо завышать, либо недооценивать пропускную способность. Обновленный итерационный подход, который изменяет полосу пропускания для каждого компонента смеси, также реализован в пакете mixtools R.Обратите внимание, что также можно использовать любой другой алгоритм кластеризации.
CCAST оптимизирует дерево решений, максимизируя размер однородных кластеров.
На практике дерево решений может быть очень большим, что делает его использование почти невозможным для ручного стробирования. Для практических целей мы предлагаем завершить дерево после того, как мы определили все состояния ячеек как максимальные по крайней мере в одном из листовых узлов во время процесса разделения. Это вводит новый параметр L, соответствующий желаемому уровню обрезки.Обратите внимание, что этот параметр будет зависеть от точности предполагаемого кластерного распределения данных. Затем мы выполняем следующее:
- Шаг 1. Для каждого листового узла в дереве мы выбираем только ячейки, соответствующие максимальному состоянию ячейки.
- Шаг 2. Оцените новое дерево решений по обновленным данным с максимальной высотой L.
- Шаг 3. Рекурсивно повторяйте шаги 1) и 2), пока мы не получим чистые состояния ячеек в конечных узлах.
Этот процесс обеспечивает максимально возможный размер выборки для всех гомогенных состояний клеток одновременно. Обратите внимание, что в конце можно получить больше однородных интервалов, чем ожидалось. Это может указывать на возможность появления новых кластеров, что потребует дальнейшего подтверждения. Также обратите внимание, что удаленные точки данных во время процесса обновления также могут быть помещены в дополнительную корзину для дальнейшего исследования.
CCAST доступен в виде пакета R.
Алгоритм CCAST был реализован в виде пакета R с примерами и документацией.Он доступен в виде zip-файла в дополнительной информации.
FACS-анализ SUM159
Клетки Sum 159 культивировали в среде Ham F12 с добавлением 5% телячьей сыворотки, инсулина (5 мкг / мл), гидрокортизона, Pen / Strep / L-глутамина. Клетки выращивали при 37 ° C в инкубаторе с 5% CO2. Исходные аликвоты клеток замораживали в 10% ДМСО и 90% FBS и хранили в жидком азоте -80 ° C. Клетки сначала размораживали во флаконах Т25 и позволяли им размножаться в культуре в течение двух недель перед сортировкой (размножали во флаконах Т75).В день сортировки клетки трипсинизировали, промывали PBS и окрашивали антителами, специфичными для следующих маркеров клеточной поверхности человека: EPCAM (ESA) -FITC (AbD Serotec, MCA1870F), CD24-PE (BD Biosciences), CD44-APC ( BD Biosciences), CD49f-PerCP / Cy5.5 (Biolegend). Примерно 1 × 107 клеток инкубировали с антителом (20 мкл антитела на миллион клеток) в течение 15 минут при комнатной температуре в PBS с 1% BSA. Несвязавшееся антитело смывали, и клетки анализировали с помощью специального сканера FACScan Stanford и Cytek, обновленного (Beckman Center, Stanford), не более чем через один час после окрашивания.Сортировку клеток проводили на BD Aria II (Beckman Center, Stanford). Необработанные данные доступны в дополнительном наборе данных S1 в виде файла FCS.
Вспомогательная информация
Алгоритм S1.
Алгоритм CCAST, реализованный в виде пакета R. Алгоритм, названный CCAST для кластеризации, классификации и сортировки дерева, определяет и изолирует однородные субпопуляции ячеек из разнородных данных отдельных ячеек оптимальным и беспристрастным образом, используя представление дерева решений, которое может применяться для сортировки ячеек и анализа данных.
https://doi.org/10.1371/journal.pcbi.1003664.s001
(GZ)
Рисунок S1.
Анализ высоты дерева решений CCAST (L) на данных обучения. A Стратегия стробирования CCAST, основанная на данных обучения немеченых Т-клеток, показывает точно такое же дерево решений, как на рисунке 3A, после увеличения L до 3 или более уровней. B Стратегия стробирования CCAST, основанная на немаркированных данных теста Т-клеток, показывает, что все оценки точек разделения лежат в пределах предполагаемых доверительных интервалов, показанных на рисунке 3A, полученных из данных обучения.
https://doi.org/10.1371/journal.pcbi.1003664.s003
(TIF)
Рисунок S4.
Анализ RchyOptimyx на линии клеток рака груди. Реализация инструмента RchyOptimyx на линии клеток рака молочной железы SUM159 дала 12 субпопуляций, определенных на EPCAM и CD24. Эти группы населения могут быть нацелены на различные стратегии стробирования, проиллюстрированные здесь как Стратегия 1–12.
https://doi.org/10.1371/journal.pcbi.1003664.s006
(TIF)
Таблица S1.
Смоделированные данные одной ячейки для CCAST. Мы смоделировали 850 измерений экспрессии клеток на 3 маркерах из смеси 5 состояний, чей глобальный паттерн экспрессии отражает прогрессирование состояния клетки. Клеточный тип 1 характеризуется как «низкий», «низкий», «высокий». Тип ячейки 2 характеризуется как «высокий низкий», «низкий средний», «высокий», тип ячейки 3 характеризуется как «средний», «средний», «высокий», тип ячейки 4 характеризуется как «низкий высокий», «низкий высокий». , «Высокий» и Celltype 5 характеризуется как «высокий», «высокий», «высокий».Мы используем различные нормальные распределения для количественной оценки этих состояний клеток.
https://doi.org/10.1371/journal.pcbi.1003664.s007
(TIF)
Благодарности
Мы благодарим доктора Шона Бендалла за ценные обсуждения и помощь в получении общедоступных наборов данных из Bendall et al. [9].
Вклад авторов
Эксперимент задумал и спроектировал: BA SKP. Проведены эксперименты: БА МТД СКП. Проанализированы данные: БА СКП.Внесенные реактивы / материалы / инструменты для анализа: БА МТД XZ SKP. Написал статью: БА СКП. Разработано программное обеспечение, используемое в анализе: BA.
Ссылки
- 1. Поляк К. (2011) Неоднородность при раке груди. Дж. Клин Инвест 121: 3786–3788.
- 2. Longo LT (2012) Неоднородность опухоли и персонализированная медицина. N Engl J Med 366: 956–957.
- 3. Гупта П.Б., Филлмор С.М., Цзян Дж., Шапира С.Д., Тао К. и др. (2011) Стохастические переходы состояний приводят к фенотипическому равновесию в популяциях раковых клеток.Ячейка 146: 633–644.
- 4. Zapperi S, La Porta CAM (2012) Происходит ли фенотипическое переключение раковых клеток? Случай несовершенных маркеров стволовых клеток рака. Научные отчеты 2: 441.
- 5. Терпенни П., Эллард С. (2007) Глава 8. В: Элементы медицинской генетики Эмери. 13-е издание. Атланта: Elsevier Limited.
- 6. Слэйд I, Мюррей А., Хэнкс С., Кумер А., Уокер Л. и др. (2011) Гетерогенность семейной медуллобластомы и вклад мутаций PTCh2 и SUFU зародышевой линии в спорадическую медуллобластому.Fam Cancer 10 (2): 337–42.
- 7. Хэн Х. Х., Бремер С. В., Стивенс Дж. Б., Е К. Дж., Лю Дж. И др. (2009) Генетическая и эпигенетическая гетерогенность рака: геном-ориентированная перспектива. J Cell Physiol 220 (3): 538–47.
- 8. Цю П., Саймондс Э.Ф., Бендалл С.К., Гиббс К.Д. мл., Бруггнер Р.В. и др. (2011) Извлечение клеточной иерархии из данных высокоразмерной цитометрии с помощью SPADE. Природная биотехнология 29 (10): 886–891.
- 9. Bendall SC, Simonds EF, Qiu P, Amir ED, Krutzik PO, et al.(2011) Одноклеточная масс-цитометрия дифференциальных иммунных и лекарственных реакций в континууме кроветворения человека. Science 332 (6030): 687–696.
- 10. Эллис Б., Хааланд П., Хане Ф., Ле Меур Н., Гопалакришнан Н. (2013) Flowcore: Основные структуры для данных проточной цитометрии. Пакет R версии 1.24.2.
- 11. Герценберг Л.А., Джеймс Т., Мур В.А., Герценберг Л.А., Паркс Д.Р. (2006) Интерпретация данных проточной цитометрии: руководство для озадаченных. Иммунология природы 7: 681–685.
- 12. Aghaeepour N, Finak G; Консорциум FlowCAP; DREAM Consortium, Hoos H, et al. (2013) Критическая оценка методов анализа данных автоматической проточной цитометрии. Природные методы 10 (3): 228–238.
- 13. Boedigheimer MJ, Ferbas J (2008) Подход моделирования смеси к данным проточной цитометрии. Цитометрия А 73 (5): 421–9.
- 14. Пайн С., Ху Х, Ван К., Россин Э., Лин Т., Майер Л. и др. (2009) Автоматический анализ данных многомерной проточной цитометрии.PNAS 106 (21): 8519–24.
- 15. Finak G, Bashashati A, Brinkman R, Gottardo R (2009) Объединение компонентов смеси для идентификации клеточной популяции в проточной цитометрии. Достижения в области биоинформатики 2009: 247646.
- 16. Ло К., Хане Ф., Бринкман Р., Готтардо Р. (2009) flowClust: пакет биопроводников для автоматического стробирования данных проточной цитометрии. BMC Bioinformatics 14 (10): 145.
- 17. Ray S, Pyne S (2012) Вычислительная структура для имитации человеческого взгляда на анализ данных проточной цитометрии.PLoS ONE 7 (5): e35693.
- 18. Башашати А., Бринкман Р. Р. (2009) Обзор методов анализа данных проточной цитометрии. Успехи в биоинформатике 2009: 584603.
- 19. Benaglia T, Chauveau D, Hunter DR (2009) EM-подобный алгоритм для полу- и непараметрической оценки в многомерных смесях. Журнал вычислительной и графической статистики 18: 505–526.
- 20. Маллнер Д. (2013) fastcluster: быстрые иерархические процедуры агломеративной кластеризации для R и Python.Journal of Statistical Software 53 (9): 118 Доступно: http://www.jstatsoft.org/v53/i09/. По состоянию на 8 июля 2014 г.
- 21. Ли Дж., Стулман Л., Скотт С. (2011) Передача обучения для автоматического стробирования данных проточной цитометрии. Труды семинара и конференции JMLR 27: 155–166.
- 22. Aghaeepour N, Chattopadhyay PK, Ganesan A, O’Neill K, Zare H, et al. (2012) Ранние иммунологические корреляты защиты от ВИЧ могут быть идентифицированы с помощью компьютерного анализа сложных многомерных анализов проточной цитометрии Т-клеток.Биоинформатика 28 (7): 1009–1016.
- 23. Агаипур Н., Джалали А., О’Нил К., Чаттопадхьяй П.К., Родерер М. и др. (2012) RchyOptimyx: Оптимизация клеточной иерархии для проточной цитометрии. Цитометрия Часть A 81 (12): 1022–1030.
- 24. Del Giudice I, Matutes E, Morilla R, Morilla A, Owusu-Ankomah K и др. (2004) Диагностическая ценность CD123 при В-клеточных нарушениях с волосатыми или ворсинчатыми лимфоцитами. haematologica 89 (3): 303–308.
- 25. Кац Г., Шабтай А., Рокач Л., Офек Н. и др.. (2012) ConfDTree: Улучшение деревьев решений с использованием доверительных интервалов. ICDM, Компьютерное общество IEEE 339–348.
- 26. Rousseeuw PJ (1987) Силуэты: графическое пособие для интерпретации и проверки кластерного анализа. Журнал вычислительной и прикладной математики 20: 53–65.
- 27. Hothorn T, Hornik K, Zeileis A (2006) Несмещенное рекурсивное разбиение: структура условного вывода. Журнал вычислительной и графической статистики 15: 651–674.
- 28. Штрассер Х., Вебер С. (1999) Об асимптотической теории статистики перестановок. Математические методы статистики 8: 220–250.
Однородные и гетерогенные облака: как выбрать гибридное облако — BMC Software
Когда дело доходит до облака, вам нужно принять множество решений. Выбор облачной стратегии начинается с определения общедоступных, частных или гибридных сред. Многие организации выбирают оба варианта — гибридное облако.
Но это еще не конец решения. После того, как вы решите следовать стратегии гибридного облака, вы также должны решить, использовать ли среду гибридного облака: однородную или гетерогенную.
Что это значит? Давайте разберемся.
Основы гибридного облака
Выбор однородного или гетерогенного облака основан на стратегии гибридного облака. Итак, давайте кратко рассмотрим три основных облачных среды. Общедоступное облако — это облачные вычисления, предоставляемые через Интернет. Частное облако — это облачные вычисления, предназначенные для вашей единственной организации, а не для других, и могут быть локальными или удаленными через вашего поставщика.
Гибридное облако представляет собой сочетание этих двух сред. Это то, что выбирает большинство организаций в своей облачной стратегии. Гибрид позволяет вам воспользоваться следующими преимуществами:
Выбрав гибридное облако, вы должны принять другое решение: однородное или гетерогенное.
Загрузить сейчас: Электронные книги ITIL 4 Best Practice
Эти новые электронные книги ITIL 2020 освещают важные элементы передовых практик ITIL 4.Быстро понять ключевые изменения и действенные концепции, написанные участниками ITIL 4.
Что такое однородное облако?
Проще говоря, однородное облако — это облако, в котором все от одного поставщика. Этот единственный поставщик предоставляет как доступ к общедоступному облаку, так и предложения, а также любое частное облако, которое у вас может быть, как локально, так и за пределами площадки.
С технической точки зрения, однородное облако — это облако, в котором весь программный стек, от гипервизора (удаленного поставщика облака) до различных промежуточных уровней управления и до портала конечного пользователя, предоставляется одним поставщиком.
Многие корпоративные провайдеры предлагали этот подход, но он выпал с рынка много лет назад. Традиционно варианты гибридного облака представляли собой просто стеки программного обеспечения, которые вы запускали локально, которые также интегрировались с общедоступным облаком. Это изменилось. Поставщики облачных услуг теперь выпускают физические устройства — оборудование. Однако недавние попытки Azure и AWS нацелены на возрождение однородного облака.
Что такое разнородное облако?
Гетерогенное облако, с другой стороны, объединяет общедоступные и частные компоненты от нескольких поставщиков, либо по адресу:
- На разных уровнях, например, инструмент управления от одного поставщика, управляющий гипервизором от другого
- Тот же уровень, где один инструмент управления управляет несколькими гипервизорами
Например, вы должны выбрать поставщика общедоступного облака, такого как Azure, GCP или AWS, а затем связать его с частным предложением, например, от VMware, CloudStack или OpenStack.
Однородное облако: плюсы и минусы
Аргумент в пользу однородных сред состоит в том, что, поскольку все поставляется предварительно интегрированным, их легче настроить, а если что-то пойдет не так, есть только одна ответственная сторона — «кому придется свернуть шею», как поговорка имеет это. Но у однородного облака гораздо больше преимуществ.
Преимущества однородного облака
- По сути, под ключ, с готовой функциональностью
- Легче установить и настроить
- Легче с точки зрения эксплуатации и управления.Поскольку общедоступная и частная части принадлежат одному поставщику, они предназначены для совместной работы.
- Услуги, такие как аварийное восстановление, безопасность, управление и мониторинг, являются встроенными и охватывают обе среды
- Дешевле, потому что локальная часть поставляется в виде оборудования для подключения или предварительно собранной стойки
- Талантам требуются специальные навыки только для этого провайдер
Это много преимуществ! Но есть один существенный недостаток — привязка к поставщику.
Недостатки однородной облачности
Простота использования часто означает, что ее сложнее покинуть.Предоставляя такую большую власть одному поставщику, пользователи оказываются во власти коммерческой и технической стратегии этого поставщика. Уйти от этого поставщика, независимо от причины, становится рискованно, дорого и сложно, особенно для стратегий безопасности и управления.
В сельском хозяйстве это известно как монокультура, то есть выращивается только одна культура. На первый взгляд это привлекательная идея, поскольку фермеры могут специализироваться и использовать эффект масштаба. Проблема в том, что любое заболевание, мороз, засуха или другое событие, которое влияет на этот урожай, может уничтожить весь урожай.Чтобы снизить этот риск, фермеры пытаются сеять несколько разных культур в качестве страховки от потери всего урожая.
Те же аргументы применимы и в ИТ. Преимущество ИТ-монокультуры заключается в том, что каждый может специализироваться на инструментах одного поставщика, а администраторам легко прикрывать друг друга.
Обратные стороны немного отличаются: с технической стороны функции будут доступны, когда — и если — поставщик решит их разработать. Настоящая боль часто возникает с коммерческой стороны, потому что, как только пользователи «привязаны» к стратегии одного поставщика, у них не будет выхода, если этот поставщик решил изменить свою структуру ценообразования таким образом, что приведет к увеличению затрат.
Гетерогенное облако: привязка к управлению
Гетерогенные архитектуры пытаются обойти этот эффект привязки, вводя компоненты от многих различных поставщиков и распределяя их использование в соответствии с общим набором стратегий. Это дает вам значительно больший контроль над облачной архитектурой — если это то, что нужно вашей организации или с чем может справиться ваша зрелость ИТ.
Однако в какой-то момент вам, вероятно, потребуется ввести единый компонент управления.
Защитники однородного подхода, основанного на использовании одного поставщика, противодействуют обвинениям в привязке, указывая на то, что такая конвергенция на едином уровне управления просто перемещает блокировку вверх по стеку, но по-прежнему оставляет пользователей на милость поставщика услуг. тот один компонент.
Ложная эквивалентность между блокировкой платформы и предполагаемой блокировкой управления — это изящный риторический трюк, но на самом деле он не работает. Вот почему:
- Поставщики средств управления должны идти в ногу с темпами развития управляемых платформ. В противном случае они рискуют отстать от конкурентов со стороны других поставщиков разнородных систем управления. Любая попытка хищнического ведения бизнеса будет пресечена в зародыше по той же причине.
- Уйти от пакетов управления проще, чем сменить гипервизоры или облачных провайдеров. Причина в том, что смена платформы почти гарантированно вызовет сбой, если она не будет предпринята очень тщательно. И наоборот, замена платформы управления даже при очень коротком предупреждении, безусловно, будет болезненной для ИТ-отдела и вызовет задержки в доставке новых запросов, но не повлияет на рабочие нагрузки, которые уже выполняются на базовых платформах.
Итак, сторонники гетерогенного облака ценят прямой контроль над архитектурой. Но больший контроль по сути означает еще два компонента, с которыми вам нужно решить, справитесь ли вы:
- Повышенная сложность. Больше контроля над любой моделью общего облака означает, что вам нужно иметь дело с XYZ. Даже если вашей организации требуется такой контроль и присущая ей сложность, вам также придется оценить, достаточно ли зрелая ваша ИТ-организация для этой сложности.
- Высококвалифицированный талант. Чтобы более тесно поддерживать более сложную среду, вам нужен талант с очень специфическими навыками. Эти навыки также не должны зависеть от программного обеспечения: специалисту по AWS может быть сложно поддерживать продукты и услуги других поставщиков.
Чтобы справиться с этой сложностью и найти нужных специалистов, вам может потребоваться нанять более продвинутых облачных архитекторов, что может занять время и дороже из-за недостатка ИТ-навыков. (Это причина того, что облачные сертификаты являются одними из самых высокооплачиваемых.) Это также может означать, что вам необходимо обучить или сертифицировать персонал, который у вас уже есть.
Как выбрать между двумя
Cloud Миграция и управление — это нелегкие решения. Вы захотите рассмотреть конкретные входы и выходы, которые мы изложили в этой статье, например:
- Ваши организационные потребности (бизнес-результаты), которые вы ожидаете от облака сегодня и в будущем
- Стоимость и ресурсы
- Независимо от того, требуется ли вам больше контроля с точки зрения архитектуры
- Зрелость вашей ИТ-среды
- Талант ваших облачных инженеров и архитекторов
Дополнительные ресурсы
Для получения дополнительной информации по этой теме посетите блог BMC Multi-Cloud или прочтите эти статьи:
Эти сообщения принадлежат мне и не обязательно отражают позицию, стратегию или мнение BMC.
Обнаружили ошибку или есть предложение? Сообщите нам об этом по электронной почте blogs@bmc.

 .
.