Синус меньше a
Рассмотрим решение тригонометрических неравенств вида синус меньше a (sinx<a) на единичной окружности.
Синус — это ордината точки. Соответственно, sinx=a в точках пересечения единичной окружности и прямой y=a. Часть окружности, расположенная выше прямой y=a, соответствует значениям синуса, большим a. Поскольку мы решаем неравенство sinx<a, его решениям будет соответствовать часть окружности, расположенная ниже прямой y=a. Рассмотрим несколько вариантов взаимного расположения прямой y=a и единичной окружности.
1) sinx<a при 0<a<1
Основная задача здесь — правильно определить точки пересечения прямой и окружности. Первая точка находится легко — это arcsina. Для определения второй точки рассуждаем так: так как sin<a, нам нужна часть окружности под прямой y=a. Значит, из первой точки во вторую идем нижним путем, то есть по часовой стрелке. Но при движении по часовой стрелке угол уменьшается. От arcsina мы дошли до 0, а дальше пошли отрицательные углы (точнее, сам угол положительный, а минус — всего лишь знак обхода от нуля по часовой стрелке). Таким образом мы доходим до -п, и переходим за него ровно на arcsina. Поскольку мы прошли п и еще arcsina, мы к п прибавляем arcsina. А так как движение шло по часовой стрелке, то перед суммой ставим знак минус.
Мы нашли только один интервал, на котором sinx<a. Чтобы учесть все решения (а таких интервалов — бесконечное множество), с учетом периодичности синуса к каждому из концов интервала прибавляем 2пn, где n — целое число (то есть n принадлежит Z).
Если неравенство нестрогое, точки пересечения окружности и прямой закрашиваем, а затем включаем в решение (круглую скобку заменяем на квадратную).
2) sinx<-a при 0<a<1
Первая точка arcsin(-a)=-arcsina. Чтобы попасть во вторую, идем нижним путем, то есть по часовой стрелке. До п, точнее до -п, не доходим на arcsina. Поэтому вторая точка — (п-arcsina).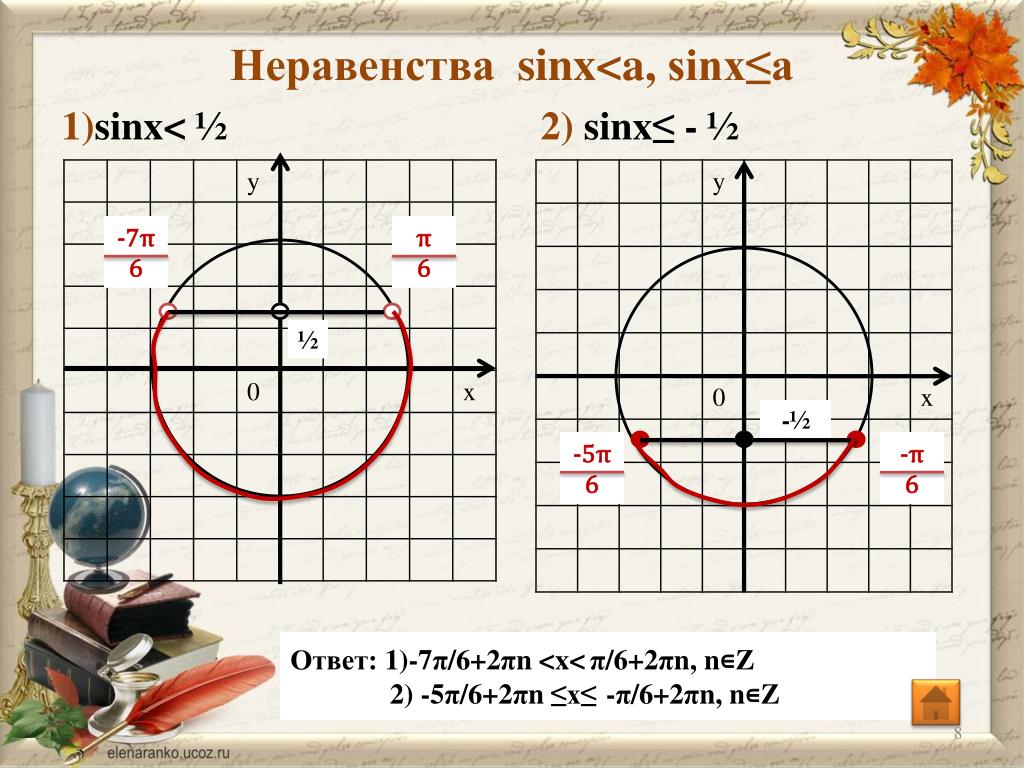
Для нестрого неравенства точки закрашиваем и включаем в ответ (с квадратной скобкой вместо круглой).
3) sinx<0
В этом случае удобнее решение записывать не от нуля до -п, а от п до 2п. Для нестрогого неравенства- квадратные скобки, закрашенные точки.
4) sinx<1
И в этом случае тоже удобнее выбирать положительные точки. Решением данного неравенства являются все x, кроме п/2+2пn. Чтобы записать это в виде промежутка, надо определить его концы. Если первую точку взять п/2, то во вторую мы попадем через полный оборот окружности, то есть п/2+2п=5п/2. К обоим концам прибавляем 2пn.
В этом случае никакие точки не исключаются, а значит, x — любое число:(-∞;+∞).
В этом случае единственной точкой на окружности, удовлетворяющей данному условию, является точка -п/2. С учетом периодичности синуса решение данного неравенства — множество точек вида x=-п/2+2пn, где n — целое число.
7) sinx<a при a>1
Окружность в этом случае целиком лежит ниже прямой y=a, а значит, решением данного неравенства является любое значение x: (-∞;+∞).
8) sinx< -a при a>1
Окружность целиком лежит выше прямой y=a, а значит, нет ни одного x, удовлетворяющего условию неравенства. Значит, решений нет.
И в заключении, рассмотрим пример.
Решить неравенство sinx<-1/2
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) |
|
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) |
|
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.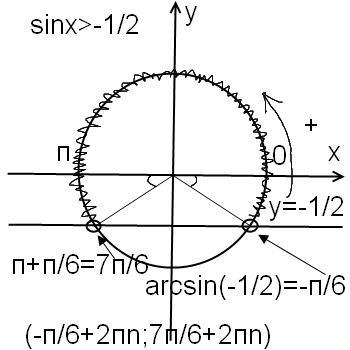 ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
sinx 1 2 решить неравенство
Вы искали sinx 1 2 решить неравенство? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решить неравенство sinx 1 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «sinx 1 2 решить неравенство».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как sinx 1 2 решить неравенство,решить неравенство sinx 1 2. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и sinx 1 2 решить неравенство. Просто введите задачу в окошко и нажмите «решить» здесь (например, sinx 1 2 решить неравенство).
Где можно решить любую задачу по математике, а так же sinx 1 2 решить неравенство Онлайн?
Решить задачу sinx 1 2 решить неравенство вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте.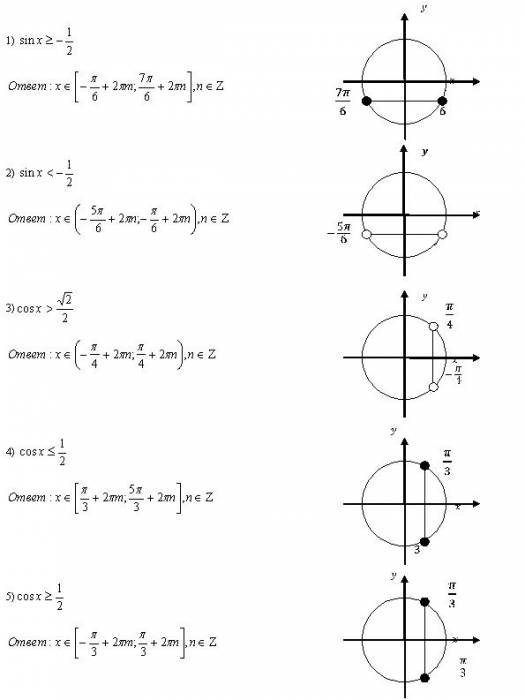 3*x+6
3*x+6
x/5-2
[src]
[src]
sin(x-3*pi/4)>=(-sqrt(2))*1/2
(неравенство)
2cos(pi/4-x/2)>=sqrt(3)
В неравенстве неизвестная
x
Решить неравенство!
Примеры
Шаг 1. Введите неравенство
Вы ввели:
Загрузка..
Быстрый ответ 2:
Подробное решение:
Решение неравенства на графике:
© Контрольная работа РУ — калькуляторы онлайн
Дано неравенство:
Чтобы решить это нер-во — надо сначала решить
соотвествующее ур-ние:
Решаем:
Дано уравнение
— это простейшее тригонометрическое ур-ние
Разделим обе части ур-ния на 2
Ур-ние превратится в
Это ур-ние преобразуется в
Или
, где n — любое целое число
Перенесём
в правую часть ур-ния
с противоположным знаком, итого:
Разделим обе части полученного ур-ния на
Данные корни
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
Возьмём например точку
=
=
подставляем в выражение
/ 1 pi \
| — — + — + 4*pi*n|
|pi 10 6 | ___
2*cos|— — ——————| >= \/ 3
| 1 1 |
\4 2 /
/1 pi \ ___
2*cos|— + — — 2*pi*n| >= \/ 3
\20 6 /
но
/1 pi \ ___
2*cos|— + — — 2*pi*n|
\20 6 /
Тогда
не выполняется
значит одно из решений нашего неравенства будет при:
_____
/ \
——-•——-•——-
x1 x2
2 cos (− + ) ≥
𝑥
2
𝜋
4
3‾
√
𝑥 ∈
{
−4 atan
(
+
2 (1 − )
2‾
√
−
− 2 + 2
+ 2
6‾
√
2‾
√
3‾
√
2‾
√
3 − 2
‾‾‾‾‾‾
√
−
− 2 + 2
6‾
√
2‾
√
2 cos (− + ) ≥
𝑥
2
𝜋
4
3‾
√
2 cos (− + ) =
𝑥
2
𝜋
4
3‾
√
2 cos (− + ) =
𝑥
2
𝜋
4
3‾
√
sin ( + ) =
𝑥
2
𝜋
4
3‾
√
2
+
= 2𝜋𝑛 + asin ( )
𝑥
2
𝜋
4
3‾
√
2
+
= 2𝜋𝑛 − asin ( ) + 𝜋
𝑥
2
𝜋
4
3‾
√
2
+
= 2𝜋𝑛 +
𝑥
2
𝜋
4
𝜋
3
+
= 2𝜋𝑛 +
𝑥
2
𝜋
4
2𝜋
3
𝜋
4
= 2𝜋𝑛 +
𝑥
2
𝜋
12
= 2𝜋𝑛 +
𝑥
2
5𝜋
12
1
2
= 4𝜋𝑛 +
𝑥
1
𝜋
6
= 4𝜋𝑛 +
𝑥
2
5𝜋
6
= 4𝜋𝑛 +
𝑥
1
𝜋
6
= 4𝜋𝑛 +
𝑥
2
5𝜋
6
= 4𝜋𝑛 +
𝑥
1
𝜋
6
= 4𝜋𝑛 +
𝑥
2
5𝜋
6
≤
𝑥
0
𝑥
1
=
−
𝑥
0
𝑥
1
1
10
(4𝜋𝑛 + ) + −
𝜋
6
1
10
4𝜋𝑛 −
+
1
10
𝜋
6
2 cos (− + ) ≥
𝑥
2
𝜋
4
3‾
√
𝑥 ≤ 4𝜋𝑛 +
𝜋
6
𝑥 ≥ 4𝜋𝑛 +
∧ 𝑥 ≤ 4𝜋𝑛 +
𝜋
6
5𝜋
6
0
5
10
15
20
-20
-15
-10
-5
-2.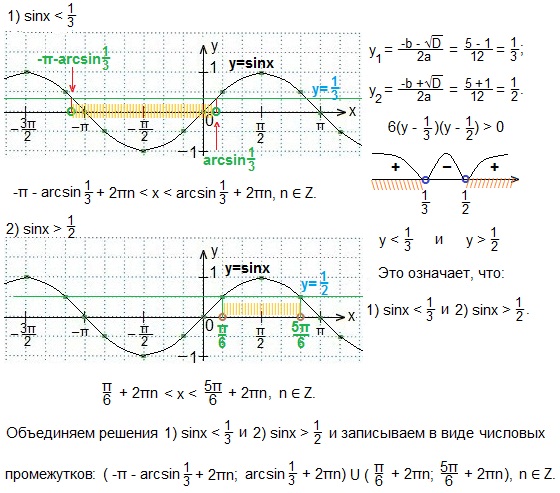 5
5
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
Solutions
2*cos(pi/4 — x/2)
sqrt(3)
0.551839464882943
2.6254180602006683
Яндекс.Директ
HC5.RU
Горные лыжи, Ботинки, Сноуборды!
18+
Яндекс.Директ
WAZZUP24.COM
Интеграция WhatsApp и Битрикс24
06.04.2020, 19:41
Стр. 1 из 1
Решение тригонометрических неравенств
Задача 1.
Решить неравенство cos x > 1/2.
Решение.
По определению косинуса cos x – это абсцисса точки единичной окружности. Чтобы решить неравенство cos x > 1/2, нужно выяснить, какие точки единичной окружности имеют абсциссу, большую 1/2.
Абсциссу, равную 1/2, имеют две точки единичной окружности М1 и М2.
Точка М1 получается поворотом точки Р (0; 1) на угол -π/3, а также на углы -π/3 + 2πn, где n = +/-1, +/-2, …; точка М2 – поворотом на угол π/3, а также на углы π/3 + 2πn, где n = +/-1, +/-2, …
Абсциссу, большую 1/2, имеют все точки М дуги единичной окружности, лежащие правее прямой М1М2. Таким образом, решениями неравенства cos x > 1/2 являются все числа х из промежутка -π/3 < х < π/3.
Ответ. Все решения данного неравенства – множество интервалов π/3 + 2πn < х < π/3 + 2πn, n € Z.
Задача 2.
Решить неравенство cos x ≤ 1/2.
Решение.
Абсциссу,
не большую 1/2, имеют все точки дуги
М1ММ2 единичной
окружности. Поэтому решениями неравенства
cos x ≤ 1/2 являются числа х, которые
принадлежат промежутку π/3 ≤ х ≤ 5π/3.
Поэтому решениями неравенства
cos x ≤ 1/2 являются числа х, которые
принадлежат промежутку π/3 ≤ х ≤ 5π/3.
Ответ. Все решения данного неравенства – множество отрезков π/3 + 2πn ≤ х ≤ 5π/3 + 2πn, n € Z.
Задача 3.
Решить неравенство sin x ≥ -1/2.
Решение.
Ординату, не меньшую -1/2, имеют все точки дуги М1ММ2 единичной окружности. Поэтому решениями неравенства sin x ≥ -1/2 являются числа х, принадлежащие промежутку -π/6 ≤ х ≤ 7π/6. Все решения данного неравенства – множество отрезков -π/6 + 2πn ≤ х ≤ 7π/6 + 2πn, n € Z.
Отметим, что все точки окружности, лежащие ниже прямой М1М2, имеют ординату, меньшую -1/2. Поэтому все числа х € (-5π/6; -π/6) являются решениями неравенства sin x < -1/2.
Ответ. Все решения этого неравенства – интервалы (-5π/6 + 2πn; -π/6 + 2πn), n € Z.
Задача 4.
Решить неравенство cos (x/4 – 1) ≤ -(√2/2).
Решение.
Обозначим x/4 – 1 = у. Решая неравенство cos у ≤ -(√2/2), находим 3π/4 + 2πn ≤ у ≤ 5π/4 + 2πn, n € Z.
Заменяя у = x/4 – 1, получаем 3π/4 + 2πn ≤ x/4 – 1 ≤ 5π/4 + 2πn, откуда 1 + 3π/4 + 2πn ≤ x/4 ≤ 1 + 5π/4 + 2πn, 4 + 3π + 8 πn ≤ х ≤ 4 + 5π + 8 πn, n € Z.
Ответ. 4 + 3π + 8 πn ≤ х ≤ 4 + 5π + 8 πn, n € Z.
Текст задания:
Решите тригонометрические уравнения
Решите тригонометрические неравенства
1) | 7) ctg2x — ctgx — 2 ≤ 0; |
2) | 8) |
3) | 9) |
4) -2 ≤ tgx < 1; | 10) 4sinxcosx(cos2x — sin2x) < sin6x; |
5) 2sin2x — 5sinx + 2 > 0; | 11) sinxsin3x ≥ sin5xsin7x; |
6) | 12)
sinx +
sin2x +
sin3x >
0. |
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
уметь:
— Вычислять производные и первообразные элементарных функций, используя справочные материалы;
— Исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
— Вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
— Решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Решение тригонометрических уравнений и неравенств (урок обобщения и систематизации знаний в 11-м классе вечерней школы)
Цели урока:
- систематизация знаний, умений и навыков решения тригонометрических уравнений и неравенств;
- развитие логического мышления, умений анализировать, сравнивать, обобщать; развитие математической речи учащихся;
- воспитание уверенности в себе; воспитание культуры общения, умения работать в коллективе, группе.
Оборудование:
- карточки-задания для каждого участника;
- задания для капитанов команд — - «цветик-семицветик»;
- карточки-задания для консультантов;
- плакат “Решение простейших тригонометрических уравнений и неравенств”.
Форма проведения: урок – КВН
Ход урока
Класс разбит на 3 команды, выбраны капитаны, в
каждой команде есть консультант, который ведёт
контроль за правильностью решения примеров.
1. Разминка: (устно)
Найти значение выражения: (правильный ответ – 1 балл)
Составить неравенство и указать его решение: (правильный ответ – 2 балла)
2. Конкурс-блиц: (1 задание – 1 балл)
Решить уравнения:
1. sin x = -1
cos x = 1
tg x = 0
arcsin 3x =
cos 2x = 2
2. sin x = 0
cos x = -1
tg x = 1
arccos 4х =
2sin x = 4
3. sin x = 1
cos x = 0
tg x = -1
arctg 2x =
sin 4x = 2
Решить неравенство:
1. sin x < -1 2. cos x > 1 3. sin x > 1
Самопроверка, с использованием плаката “Решение простейших тригонометрических уравнений и неравенств” (Приложение 1).
3. Конкурс команд:
Каждому учащемуся из команды предлагается задание, состоящее из двух тригонометрических уравнений и одного неравенства. Работа выполняется по индивидуальным карточкам-заданиям трёх уровней сложности.
(зелёная карточка – 4 балла; синяя – 5 баллов; красная – 6 баллов)
Решить уравнение:
- 2cos 3x + 1 = 0
- 1 + 2sin 2x = 0
- tg=1
- tg = 1
- 3tg
- sin
- 2cos
- sin
- ctg
- cos x = —
- sin =
- sin 3x·cos x – cos 3x·sin x = 0
- cos 3x·cos x — sin 3x·sin x = 0
- sin 5x·cos x – cos 5x·sin x =
- cos 5x·cos x + sin 5x·sin x =
- cos 2x·cos x — sin 2x·sin x = 1
- cos 3x·cos x — sin 3x·sin x =
- coscos x + sin x·sin =
- 2sin2 x – 2cos x =
- 2cos2 x + 2 sin x = 2,5
- 3cos2 x + 7sin x – 5 = 0
- cos2 x + 6sin x – 6 = 0
- 5sin2 x + cos x – 1 = 0
- 2sin2 x + 5cos x = 4
- 5sin2 + 8cos (? + x) = 0
- sin2— 3cos (4? + x) = 4
- 4sin2 x – 4sin x + 1 = 0
- 2sin2 x + 5cos x + 1 = 0
- 2sin2 x + 11cos x — 7 = 0
- 5sin2 x + cos x — 1 = 0
- 2sin2 x + 7cos x + 2 = 0
- 3tg3 x – 3tg x = 0
- 2 — cos2 x + sin x = 0
- sin x + cos x = 0
- sin x + cos x = 0
- sin x +cos x = 0
- sin 2x + cos 2x = 0
- sin 2x — cos 2x = 0
- sin 2x = 2 sin2 x
- sin 2x — 2sin2 x = 0
- 2sin2 (? — x) = cos 2x
- sin 2x + cos 2x = 1
- sin= sin x
- sin= cos x
- cos x = 2 cos
- sin x +cos x = 2
- sin x – cos x = 1
- sin x +cos x = 1
Решить неравенство:
- sin x ?
- tg x ? —
- cos x ?
- tg x > -1
- cos x >
- sin x ?
- 2sin x > -1
- 2cos x < —
- ctg x < 1
- -2cos x > 1
- tg 2x ?
- 3tg 3x >
- tg ? -1
- cos 2x < -0,5
- sin 2x < -0,5
- sin 4x >
- sin (x + ) >
- cos<
- tg (x + ) > 1
- tg
- 2cos
- 2sin
- 2cos
- 3tg
1 команда |
2 команда |
3 команда |
| №1 Решить уравнения: 1. 2. 2sin2 x – 2cos x = Решить неравенство: sin x ? |
№1 Решить уравнения: 1. 1 + 2sin 2x = 0 2. 2cos2 x + 2 sin x = 2,5 Решить неравенство: tg x ? — |
№1 Решить уравнения: 1. tg=1 2. 3cos2 x + 7sin x – 5 = 0 Решить неравенство: cos x ? |
| №2 Решить уравнения: 1. tg = 1 2. cos2 x + 6sin x – 6 = 0 Решить неравенство: tg x > -1 |
№2 Решить уравнения: 1. 3tg 2. 5sin2 x + cos x – 1 = 0 Решить неравенство: cos x > |
№2 Решить уравнения: 1. sin 2. 2sin2 x + 5cos x = 4 Решить неравенство: sin x ? |
| №3 Решить уравнения: 1. cos x = — 2. 2sin2 x + 5cos x + 1 = 0 Решить неравенство: -2cos x > 1 |
№3 Решить уравнения: 1. sin = 2. 2sin2 x + 11cos x — 7 = 0 Решить неравенство: tg 2x ? |
№3 Решить уравнения: 1. ctg 2. 4sin2 x – 4sin x + 1 = 0 Решить неравенство: ctg x < 1 |
| №4 Решить уравнения: 1. 2. 5sin2+8cos(? +x) = = 0 Решить неравенство: 2sin x > -1 |
№4 Решить уравнения: 1. sin 2. sin2-3cos (4?+x) = 4 Решить неравенство: 2cos x < — |
№4 Решить уравнения: 1. sin 3x·cos x – cos 3x·sin x = = 0 2. 5sin2 x + cos x — 1 = 0 Решить неравенство: 3tg 3x > |
| №5 Решить уравнения: 1. sin 5x·cos x – cos 5x·sin x = = 2. 2sin2 x + 7cos x + 2 = 0 Решить неравенство: tg ? -1 |
№5 Решить уравнения: 1. cos 5x·cos x+sin 5x·sin x = 2. 3tg3 x – 3tg x = 0 Решить неравенство: cos 2x < -0,5 |
№5 Решить уравнения: 1. cos 2x·cos x — sin 2x·sin x =1 2. 2 — cos2 x + sin x = 0 Решить неравенство: sin 2x < -0,5 |
| №6 Решить уравнения: 1. cos 3x·cos x — sin 3x·sin x = = 2. sin x + cos x = 0 Решить неравенство: sin 4x > |
№6 Решить уравнения: 1. cos 3x·cos x-sin 3x·sin x = 0 2. sin x + cos x = 0 Решить неравенство: sin (x + ) > |
№6 Решить уравнения: 1. + sin x·sin= 2. sin x +cos x = 0 Решить неравенство: cos< |
| №7 Решить уравнения: 1. sin 2x + cos 2x = 0 2. sin= sin x Решить неравенство: tg (x + ) > 1 |
№7 Решить уравнения: 1. sin 2x — cos 2x = 0 2. sin= cos x Решить неравенство: tg |
№7 Решить уравнения: 1. sin 2x = 2 sin2 x 2. cos x = 2 cos Решить неравенство: 2cos |
| №8 Решить уравнения: 1. sin 2x — 2sin2 x = 0 2. sin x +cos x = 2 Решить неравенство: 2sin |
№8 Решить уравнения: 1. 2sin2 (? — x) = cos 2x 2. sin x – cos x = 1 Решить неравенство: 2cos |
№8 Решить уравнения: 1. sin 2x + cos 2x = 1 2. sin x +cos x = 1 Решить неравенство: 3tg |
4. Конкурс капитанов:
Капитаны работают у доски. Им предлагается оторвать один лепесток «цветика-семицветика» (Приложение 2) с заданием (правильный ответ – 3 балла)
Решить уравнение:
- sin 2x = 2 sin2 x
- 3sin 2x + 7cos 2x = 0
- (cos x + sin x)2 = cos 2x
- 1 – 2sin 2x = 6cos2 x
- sin x – cos x = 2
- 7sin 2x + 2cos2x – 6 = 0
- sin x + cos x =
5. Конкурс консультантов: (правильный
ответ – 4 балла)
Конкурс консультантов: (правильный
ответ – 4 балла)
Решите систему уравнений:
1. 2. 3.
6. Конкурс эрудитов:
Пока команды готовят вопросы друг для друга, слушаем сообщение об истории развития учения о тригонометрических функциях (Приложение 3).
Вопросы: (правильный ответ – 2 балла)
- Кем и когда были составлены первые тригонометрические таблицы?
- Что больше сos 35° или cos 50°?
- Что больше sin 50° или sin 55°?
Итоги урока: Подсчитываем количество баллов, набранных командами и каждым учащимся. Каждому учащемуся команды-победительницы + 1 балл. Ученикам, набравшим:
10 и более баллов – «5» (отлично);
7–9 баллов – «4» (хорошо);
4–6 баллов – «3» (удовлетворительно).
Домашнее задание:
Решите систему уравнений:
1. 2. 3.
Рефлексия: вопрос классу: «Оцените своё самочувствие на уроке, поставив какой-либо значок на графике функции у = sin х, изображенной на отвороте доски. Где вы себя ощущали: на гребне волны синусоиды или во впадине?»
Решение простейших тригонометрических неравенств | Подготовка к ЕГЭ по математике
Часть 1.(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
,
,
,
,
где – один из знаков , .
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , меньшие – левее точки на оси косинусов.
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до .
Обратите внимание, многие, назвав первую точку вместо второй точки указывают точку , что неверно!
Становится видно, что неравенству удовлетворяют следующие значения
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , большие или равные – правее точки , включая саму точку.
Тогда выделенные красной дугой аргументы отвечают тому условию, что .
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси синусов
Все значения , большие или равные – выше точки , включая саму точку.
«Транслируем» выделенные точки на тригонометрический круг:
Пример 4.
Решить неравенство:
Решение:
Кратко:
или все , кроме
Пример 5.
Решить неравенство:
Решение:
Неравенство равносильно уравнению , так как область значений функции –
Пример 6.
Решить неравенство:
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
Если не очень понятно, загляните сюда –>+ показать
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен
А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.
Поэтому
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
4. Решить неравенство:
Ответ: + показать
5. Решить неравенство:
Ответ: + показать
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
Основные тригонометрические неравенства
Неизвестная переменная (угол): \ (x \)
Набор целых чисел: \ (\ mathbb {Z} \)
Целое число: \ (n \)
Набор действительных чисел: \ (\ mathbb {R} \)
Действительное номер: \ (a \)
Тригонометрические функции: \ (\ sin x, \) \ (\ cos x, \) \ (\ tan x, \) \ (\ cot x \)
Обратные тригонометрические функции: \ (\ arcsin a, \) \ (\ arccos a, \) \ (\ arctan a, \) \ (\ text {arccot} a \)
- Неравенство, включающее тригонометрические функции от неизвестного угла, называется тригонометрическим неравенством.
- Следующие \ (16 \) неравенства относятся к основным тригонометрическим неравенствам:
\ (\ sin x \ gt a \), \ (\ sin x \ ge a \), \ (\ sin x \ lt a \), \ (\ sin x \ le a \),
\ (\ cos x \ gt a \), \ (\ cos x \ ge a \), \ (\ cos x \ lt a \), \ (\ cos x \ ле а \),
\ (\ тан х \ gt а \), \ (\ тан х \ ге а \), \ (\ тан х \ lt а \), \ (\ тан х \ ле а \),
\ (\ cot x \ gt a \), \ (\ cot x \ ge a \), \ (\ cot x \ lt a \), \ (\ cot x \ le a \).
Здесь \ (x \) — неизвестная переменная, \ (a \) может быть любым действительным числом. - Если \ (\ left | a \ right | \ ge 1 \), неравенство \ (\ sin x \ gt a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ lt -1 \), решением неравенства \ (\ sin x \ gt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
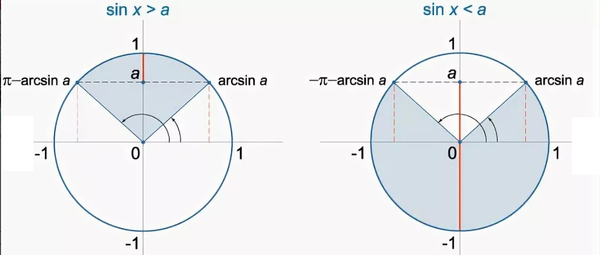
- Для \ (- 1 \ le a \ lt 1 \) решение неравенства \ (\ sin x \ gt a \) выражается в виде
\ (\ arcsin a + 2 \ pi n \ lt x \ ) \ (\ lt \ pi — \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (1 \)). - Если \ (a \ gt 1 \), неравенство \ (\ sin x \ ge a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ le -1 \), решением неравенства \ (\ sin x \ ge a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Случай \ (a = 1 \)
\ (x = \ pi / 2 +2 \ pi n, \) \ (n \ in \ mathbb {Z} \) - Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ sin x \ ge a \) включает граничные углы и имеет вид
\ (\ arcsin a + 2 \ pi n \ le x \) \ (\ le \ pi — \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (1 \)). - Если \ (a \ gt 1 \), решением неравенства \ (\ sin x \ lt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Если \ (a \ le -1 \), неравенство \ (\ sin x \ lt a \) не имеет решений: \ (x \ in \ emptyset \)
- Для \ (- 1 \ lt a \ le 1 \) решение неравенства \ (\ sin x \ lt a \) лежит в интервале
\ (- \ pi — \ arcsin a + 2 \ pi n \ lt x \) \ (\ lt \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (2 \)). - Если \ (a \ ge 1 \), решением неравенства \ (\ sin x \ le a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Если \ (a <-1 \), неравенство \ (\ sin x \ le a \) не имеет решений: \ (x \ in \ emptyset \)
- Случай \ (a = -1 \)
\ (x = — \ pi / 2 + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) - Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ sin x \ le a \) находится в интервале
\ (- \ pi — \ arcsin a + 2 \ pi n \ le x \) \ (\ le \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (2 \)).
- Если \ (a \ ge 1 \), неравенство \ (\ cos x \ gt a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ lt -1 \), решением неравенства \ (\ cos x \ gt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Для \ (- 1 \ le a \ lt 1 \) решение неравенства \ (\ cos x \ gt a \) имеет вид
\ (- \ arccos a + 2 \ pi n \ lt x \) \ (\ lt \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (3 \)). - Если \ (a \ gt 1 \), неравенство \ (\ cos x \ ge a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ le -1 \), решением неравенства \ (\ cos x \ ge a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Случай \ (a = 1 \)
\ (x = 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) - Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ cos x \ ge a \) выражается формулой
\ (- \ arccos a + 2 \ pi n \ le x \) \ (\ le \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (3 \)). - Если \ (a \ gt 1 \), неравенство \ (\ cos x \ lt a \) верно для любого действительного значения \ (x \): \ (x \ in \ mathbb {R} \)
- Если \ (a \ le -1 \), неравенство \ (\ cos x \ lt a \) не имеет решений: \ (x \ in \ emptyset \)
- Для \ (- 1
Неравенство \ (\ cos x \ le a \)
- Если \ (a \ ge 1 \), решением неравенства \ (\ cos x \ le a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Если \ (a \ lt -1 \), неравенство \ (\ cos x \ le a \) не имеет решений: \ (x \ in \ emptyset \)
- Случай \ (a = -1 \)
\ (x = \ pi + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \)- Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ cos x \ le a \) записывается как
\ (\ arccos a + 2 \ pi n \ le x \) \ (\ le 2 \ pi — \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (4 \)).
Неравенства вида \ (\ tan x \ gt a, \) \ (\ tan x \ ge a, \) \ (\ tan x \ lt a, \) \ (\ tan x \ le a \)
Рисунок 5.
Рисунок 6.
Неравенство \ (\ tan x \ gt a \)
- Для любого действительного значения \ (a \) решение строгого неравенства \ (\ tan x \ gt a \) имеет вид
\ (\ arctan a + \ pi n \ lt x \) \ (\ lt \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (5 \)).Неравенство \ (\ tan x \ ge a \)
- Для любого действительного значения \ (a \) решение неравенства \ (\ tan x \ ge a \) выражается в виде
\ (\ arctan a + \ pi n \ le x \) \ (\ lt \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (5 \)).Неравенство \ (\ tan x \ lt a \)
- Для любого значения \ (a \) решение неравенства \ (\ tan x \ lt a \) записывается в виде
\ (- \ pi / 2 + \ pi n \ lt x \) \ ( \ lt \ arctan a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (6 \)).Неравенство \ (\ tan x \ le a \)
- Для любого значения \ (a \) неравенство \ (\ tan x \ le a \) имеет следующее решение:
\ (- \ pi / 2 + \ pi n \ lt x \) \ (\ le \ arctan a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (6 \)).Неравенства вида \ (\ cot x \ gt a, \) \ (\ cot x \ ge a, \) \ (\ cot x \ lt a, \) \ (\ cot x \ le a \)
Рисунок 7.
Рисунок 8.
Неравенство \ (\ cot x \ gt a \)
- Для любого значения \ (a \) решение неравенства \ (\ cot x \ gt a \) имеет вид
\ (\ pi n \ lt x \ lt \ text {arccot} a + \ pi n , \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (7 \)).Неравенство \ (\ cot x \ ge a \)
- Нестрогое неравенство \ (\ cot x \ ge a \) имеет аналогичное решение:
\ (\ pi n \ lt x \ le \ text {arccot} a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (7 \)).Неравенство \ (\ cot x \ lt a \)
- Для любого значения \ (a \) решение неравенства \ (\ cot x \ lt a \) лежит на открытом интервале
\ (\ text {arccot} a + \ pi n \ lt x \) \ (\ lt \ pi + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (8 \)).
Неравенство \ (\ cot x \ le a \)
- Для любого значения \ (a \) решение нестрогого неравенства \ (\ cot x \ le a \) находится в полуоткрытом интервале
\ (\ text {arccot} a + \ pi n \ le x \) \ (\ lt \ pi + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (8 \)).
Неравенства вида \ (\ sin x \ gt a, \) \ (\ sin x \ ge a, \) \ (\ sin x \ lt a, \) \ (\ sin x \ le a \)
Фигура 1.
Фигура 2.
Неравенство \ (\ sin x \ gt a \)
Неравенство \ (\ sin x \ ge a \)
Неравенство \ (\ sin x \ lt a \)
Неравенство \ (\ sin x \ le a \)
Неравенства вида \ (\ cos x \ gt a, \) \ (\ cos x \ ge a, \) \ (\ cos x \ lt a, \) \ (\ cos x \ le a \)
Рисунок 3.
Рисунок 4.
Неравенство \ (\ cos x \ gt a \)
Неравенство \ (\ cos x \ ge a \)
Неравенство \ (\ cos x \ lt a \)
Математическая сцена — Тригонометрические функции — Более сложные уравнения и неравенства
Математическая сцена — Тригонометрические функции — Более сложные уравнения и неравенства — Урок 5 2008 Rasmus ehf | Триггерные функции | Печать |
Пример 1
Решите уравнение sin x = cos x и тогда неравенство
грех x> cos x на интервале 0 x <2.
Из единичного круга мы видим, что sin x и cos x может иметь одно и то же значение только в двух местах, в x = / 4 и х = 5/4 (45 и 225 ).
Уравнение sin x = cos x также может быть решено путем деления на cos x.
тангенс х = 1
x = загар −1 (1)
х = 45 ∙ /180 + к ∙
x = / 4 + k ∙ (k — любое целое число, положительное или отрицательное)
Если мы положим k = 0 и k = 1, мы получим решения / 4 (45 ) и /4 + = 5/4 (45 + 180 = 225 ).
Решить неравенство sin x> cos x нам нужно увидеть, что больше sin x или cos x на интервалах между решениями / 4 и 5/4. Решения можно увидеть, если нарисовать графики f (x) = sin x и g (x) = cos Икс. График sin x лежит над графиком cos x на интервале / 4 x 5x / 4 (см. Заштрихованную область на диаграмме).
sin x cos x на интервале / 4 x 5x / 4.
Пример 2
Решить уравнение sin x ∙ cos x = 0 и тогда неравенство
sin x ∙ cos x> 0 на интервале 0 x <2.
Неравенство не имеет решение, когда sin x или cos x принимают значение 0. Это происходит с интервалом 90.
Решения уравнение sin x ∙ cos x = 0 на интервале 0 x <2, следовательно, равны 0, / 2 и 3/2 (0 , 90 , 180 и 270 ).
Решение sin x
∙ cos x> 0 можно найти, посмотрев на единичный круг. Нам нужно найти
где sin x, умноженный на cos x, положителен. Другими словами sin x и cos x имеют
иметь один и тот же знак, оба будут
положительный или оба отрицательный. Это происходит в первом и третьем квадранте. В
решения поэтому Мы также можем увидеть это по
построение графика Решите уравнение sin x
∙ cos x — sinx = 0 и тогда выполняется неравенство sin x ∙ cos x
— sin x> 0 на интервале 0 x <2. sin x ∙ cos x — sinx = 0 sin x (cos x — 1) = 0 Нам нужно
разложить уравнение на множители, взяв sin x за скобки. Уравнение имеет решения
когда sin x = 0 или когда скобка, (cos x — 1) = 0. грех х = 0 x = 0 или (180 ). или cos x — 1 = 0 cos x = 1 х = 0 Единственные решения
уравнение поэтому 0 и. Неравенство греха
x ∙ cos x — sin x> 0 можно переписать как sin x (cos x — 1)
> 0, Теперь полезно сделать
таблицу знаков и посмотрите знаки sin x и cos x — 1. Мы видим, что оба фактора
отрицательный на интервале Теперь давайте посмотрим, как это подходит
в с графиком Заштрихованная область над x
ось показывает где Найти все решения уравнения cos 2 x — cos x = 0. cos 2 x — cos
х = 0 cos x ∙ (cos x — 1) = 0 Решения можно найти, когда cos x = 0 или cos x — 1 = 0 cos x = 0 x = / 2 или 3/ 2 (90 или 270 ) х = / 2 + к ∙ или cos
х — 1 = 0 cos x = 1 х = 0 + к ∙ 2 = к ∙ 2 Все решения укладываются в шаблон x = / 2 +
к ∙ Найти все решения уравнения sin 2 x — 5 sin x + 4 = 0. Это квадратное уравнение с sin x в качестве
Переменная. Таким образом, мы можем найти sin x, используя формулу корней квадратного уравнения. a = 1, b = −5 og c = 4. Синус мы не можем принять значение 4, поэтому нам не нужно рассматривать sin x =
4. Другая возможность — sin x = 1, которая имеет решение
/ 2 (90 ). Таким образом, полное решение: х
= / 2 +
к ∙ 2 Решите уравнение sin 5x = грех х . Одна из возможностей состоит в том, что
положение 5x на единичной окружности
совпадает с положением x и поскольку эта позиция повторяется с интервалом в 360, мы получаем следующее
уравнение: 1) 5x = x + к ∙ 360 4x = к ∙ 360 х = к ∙ 90 Мы показываем эту возможность в
диаграмму. Приходит вторая возможность
из того, что 5x = 180 — x + к ∙ 360 6x = 180 + k ∙ 360 x = 30 + k ∙ 60 Это решение показано на
диаграмма справа. Но мы замечаем, что первое решение содержится в
второе решение, поэтому достаточно дать второе решение х = 30 + к ∙ 60 Решите уравнение cos 2x =
cos x на интервале 0 x <2. 1) Сначала рассмотрим
возможность того, что x и 2x находятся в одной позиции на единичной окружности. 2x = x + k ∙ 2 х = к ∙ 2 х = 0 Вычесть
x с обеих сторон уравнения, а затем выберите k = 0 (k = 1 дает 2, что находится за пределами интервала 2) Приходит вторая возможность
по факту 2x = −x
+ к ∙ 2 3x = к ∙ 2 х = к ∙ 2/ 3 Это дает решения 2/3 (120 )
для k = 1 и 4 /3 (240 ) для k = 2.
итого полное решение: Решите уравнение tan 3x =
загар 2x. Уравнения Тана во многих
способов самый простой из триггерных уравнений, так как есть только возможность
Считайте, что повторяется с интервалом 180 . 3х = х + к ∙ 180 2x = к ∙ 180 x = k ∙ 90 или х = к ∙ / 2 Попробуйте тест 5 по триггерам. В разделах \ ref {TheUnitCircle}, \ ref {CircularFunctions} и совсем недавно \ ref {ArcTrig} мы решили некоторые основные уравнения, включающие тригонометрические функции.Ниже мы резюмируем методы, которые мы использовали до сих пор. Обратите внимание, что мы используем нейтральную букву `$ u $ ‘в качестве аргумента \ footnote {См. Комментарии в начале раздела \ ref {TrigGraphs} для обзора этой концепции. Стратегии решения основных уравнений с тригонометрическими функциями Используя приведенные выше рекомендации, мы можем легко решить \ (\ sin (x) = \ frac {1} {2} \) и найти решение \ (x = \ frac {\ pi} {6} + 2 \ pi k \) или \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Как мы решаем что-то вроде \ (\ sin (3x) = \ frac {1} {2} \)? Поскольку это уравнение имеет вид \ (\ sin (u) = \ frac {1} {2} \), мы знаем, что решения принимают вид \ (u = \ frac {\ pi} {6} + 2 \ pi k \) или \ (u = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \).Поскольку аргумент синуса здесь \ (3x \), мы имеем \ (3x = \ frac {\ pi} {6} + 2 \ pi k \) или \ (3x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Чтобы решить для \ (x \), мы разделим обе части \ footnote {Не забудьте также разделить \ (2 \ pi k \) на \ (3 \)!} Этих уравнений на \ (3 \) и получаем \ (x = \ frac {\ pi} {18} + \ frac {2 \ pi} {3} k \) или \ (x = \ frac {5 \ pi} {18} + \ frac {2 \ pi} {3} k \) для целых чисел \ (k \). Пример \ (\ PageIndex {1} \): Решите следующие уравнения и проверьте свои ответы аналитически.{2} (х) = 4 \) Решение \ [\ begin {array} {rclr} \ cos \ left (2 \ left [\ frac {5 \ pi} {12} + \ pi k \ right] \ right) & = & \ cos \ left (\ frac {5 \ pi} {6} + 2 \ pi k \ right) & \\ [3pt] & = & \ cos \ left (\ frac {5 \ pi} {6} \ right) & \ text {(период косинуса равен \ (2 \ pi $)} \\ [3pt] & = & — \ frac {\ sqrt {3}} {2} & \\ \ end {array} \] Аналогично находим \ (\ cos \ left (2 \ left [\ frac {7 \ pi} {12} + \ pi k \ right] \ right) = \ cos \ left (\ frac {7 \ pi} { 6} + 2 \ pi k \ right) = \ cos \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {\ sqrt {3}} {2} \).Чтобы определить, какое из наших решений лежит в \ ([0,2 \ pi) \), мы подставляем целые числа в \ (k \). Сохраняемые нами решения основаны на значениях \ (k = 0 \) и \ (k = 1 \) и равны \ (x = \ frac {5 \ pi} {12} \), \ (\ frac {7 \ pi} {12} \), \ (\ frac {17 \ pi} {12} \) и \ (\ frac {19 \ pi} {12} \). Используя калькулятор, построим графики \ (y = \ cos (2x) \) и \ (y = — \ frac {\ sqrt {3}} {2} \) над \ ([0,2 \ pi) \) и исследуйте, где пересекаются эти два графика. \ [\ frac {1} {3} x- \ pi = \ frac {\ pi} {4} + 2 \ pi k \ quad \ text {или} \ quad \ frac {1} {3} x- \ pi = \ frac {3 \ pi} {4} + 2 \ pi k \] Чтобы решить \ (\ frac {1} {3} x- \ pi = \ frac {\ pi} {4} + 2 \ pi k \), мы сначала добавляем \ (\ pi \) к обеим сторонам \ [\ frac {1} {3} x = \ frac {\ pi} {4} + 2 \ pi k + \ pi \] Распространенная ошибка — рассматривать термины `$ 2 \ pi k $ ‘и` $ \ pi $’ как « похожие » термины и пытаться объединить их, когда это не так.\ footnote {Вы понимаете, почему?} Однако мы можем объединить члены `$ \ pi $ ‘и` $ \ frac {\ pi} {4} $’, чтобы получить \ [\ frac {1} {3} x = \ frac {5 \ pi} {4} + 2 \ pi k \] Теперь мы закончим, умножив обе части на \ (3 \), чтобы получить \ [x = 3 \ left (\ frac {5 \ pi} {4} + 2 \ pi k \ right) = \ frac {15 \ pi} {4} + 6 \ pi k \] Решение другого уравнения \ (\ frac {1} {3} x- \ pi = \ frac {3 \ pi} {4} + 2 \ pi k \) дает \ (x = \ frac {21 \ pi} {4} + 6 \ pi k \) для целых чисел \ (k \). Чтобы проверить первую группу ответов, мы заменяем, объединяем строковые термины и упрощаем. \ [\ begin {array} {rclr} \ csc \ left (\ frac {1} {3} \ left [\ frac {15 \ pi} {4} + 6 \ pi k \ right] — \ pi \ right) & = & \ csc \ left (\ гидроразрыв {5 \ pi} {4} + 2 \ pi k — \ pi \ right) & \\ [3pt] & = & \ csc \ left (\ frac {\ pi} {4} + 2 \ pi k \ right) & \\ [3pt] & = & \ csc \ left (\ frac {\ pi} {4} \ right) & \ text {(период косеканса равен \ (2 \ pi $)} \\ & = & \ sqrt {2} & \\ \ end {array} \] Семейство \ (x = \ frac {21 \ pi} {4} + 6 \ pi k \) проверяет аналогично. \ begin {center} \ begin {tabular} {cc} \ includegraphics [width = 2in] {./ IntroTrigGraphics / TrigEquIneq01.jpg} & \ hspace {0.75 дюймов} \ includegraphics [width = 2in] {./ IntroTrigGraphics / TrigEquIneq02.jpg} \\ $ y = \ cos (2x) \) и \ boldmath \ (y = — \ frac {\ sqrt {3}} {2} \) & \ hspace {0,75 дюйма} \ (y = \ frac {1} {\ sin \ left (\ frac {1} {3} x- \ pi \ right)} \) и \ boldmath \ (y = \ sqrt { 2} \) \\ \ end {tabular} \ end {center} \ item Поскольку \ (\ cot (3x) = 0 \) имеет форму \ (\ cot (u) = 0 \), мы знаем \ (u = \ frac {\ pi} {2} + \ pi k \ ), поэтому в этом случае \ (3x = \ frac {\ pi} {2} + \ pi k \) для целых чисел \ (k \).Решение относительно \ (x \) дает \ (x = \ frac {\ pi} {6} + \ frac {\ pi} {3} k \). Проверяя наши ответы, получаем \ [\ begin {array} {rclr} \ cot \ left (3 \ left [\ frac {\ pi} {6} + \ frac {\ pi} {3} k \ right] \ right) & = & \ cot \ left (\ frac {\ pi} {2} + \ pi k \ right) & \\ [3pt] & = & \ cot \ left (\ frac {\ pi} {2} \ right) & \ text {(период котангенса равен \ (\ pi $)} \\ [3pt] & = & 0 & \\ \ end {array} \] Когда \ (k \) пробегает целые числа, мы получаем шесть ответов, соответствующих от \ (k = 0 \) до \ (k = 5 \), которые лежат в \ ([0, 2 \ pi) \): \ (x = \ frac {\ pi} {6} \), \ (\ frac {\ pi} {2} \), \ (\ frac {5 \ pi} {6} \), \ (\ frac { 7 \ pi} {6} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {11 \ pi} {6} \).Чтобы подтвердить это графически, мы должны быть осторожны. На многих калькуляторах нет функциональной кнопки для котангенса. & = & 4 & \\ \ end {array} \] То же самое верно и для семейства \ (x = \ frac {2 \ pi} {3} + \ pi k \). Решения, лежащие в \ ([0,2 \ pi) \), берутся из значений \ (k = 0 \) и \ (k = 1 \), а именно \ (x = \ frac {\ pi} {3} \), \ (\ frac {2 \ pi} {3} \), \ (\ frac {4 \ pi} {3} \) и \ (\ frac {5 \ pi} {3} \). \ end {tabular} \ end {center} \ item Уравнение \ (\ tan \ left (\ frac {x} {2} \ right) = -3 \) имеет вид \ (\ tan (u) = -3 \), решением которого является \ (u = \ arctan (-3) + \ пи к \). Следовательно, \ (\ frac {x} {2} = \ arctan (-3) + \ pi k \), поэтому \ (x = 2 \ arctan (-3) + 2 \ pi k \) для целых чисел \ (k \). Для проверки отметим \ [\ begin {array} {rclr} \ tan \ left (\ frac {2 \ arctan (-3) + 2 \ pi k} {2} \ right) & = & \ tan \ left (\ arctan (-3) + \ pi k \ right) & \\ [3pt] & = & \ tan \ left (\ arctan (-3) \ right) & \ text {(период касательной равен \ (\ pi $)} \\ [3pt] & = & -3 & (\ text {См. Теорему} \ ref {arctangentcotangentfunctionprops}) \\ \ end {array} \] Чтобы определить, какой из наших ответов лежит в интервале \ ([0,2 \ pi) \), нам сначала нужно получить представление о значении \ (2 \ arctan (-3) \).Хотя мы могли бы легко найти приближение с помощью калькулятора, \ footnote {Ваш инструктор сообщит вам, если вы должны отказаться от аналитического маршрута на этом этапе и использовать ваш калькулятор. А если серьезно, что это было бы забавно?} Мы продолжаем аналитически. Поскольку \ (- 3 <0 \), отсюда следует, что \ (- \ frac {\ pi} {2} <\ arctan (-3) <0 \). Умножение на \ (2 \) дает \ (- \ pi <2 \ arctan (-3) <0 \). Теперь мы можем спорить, какое из решений \ (x = 2 \ arctan (-3) + 2 \ pi k \) лежит в \ ([0,2 \ pi) \).Для \ (k = 0 \) мы получаем \ (x = 2 \ arctan (-3) <0 \), поэтому мы отбрасываем этот ответ и все ответы \ (x = 2 \ arctan (-3) + 2 \ pi k \) где \ (k <0 \). Затем обратим внимание на \ (k = 1 \) и получим \ (x = 2 \ arctan (-3) + 2 \ pi \). Начиная с неравенства \ (- \ pi <2 \ arctan (-3) <0 \), складываем \ (2 \ pi \) и получаем \ (\ pi <2 \ arctan (-3) +2 \ pi < 2 \ пи \). Это означает, что \ (x = 2 \ arctan (-3) + 2 \ pi \) лежит в \ ([0,2 \ pi) \). \ [\ begin {array} {rclr} \ sin \ left (2 \ left [\ frac {1} {2} \ arcsin (0.87) + \ pi k \ right] \ right) & = & \ sin \ left (\ arcsin (0.87) + 2 \ pi k \ right) & \\ [3pt] & = & \ sin \ left (\ arcsin (0.87) \ right) & \ text {(период синуса равен \ (2 \ pi $)} \\ [3pt] & = & 0.87 & (\ text {См. Теорему} \ ref {arccosinesinefunctionprops}) \\ \ end {array} \] Для семейства \ (x = \ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87) + \ pi k \) получаем \ [\ begin {array} {rclr} \ sin \ left (2 \ left [\ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87) + \ pi k \ right] \ right) & = & \ sin \ left (\ pi — \ arcsin (0.87) + 2 \ pi k \ right) & \\ [3pt] & = & \ sin \ left (\ pi — \ arcsin (0.87) \ right) & \ text {(период синуса равен \ (2 \ pi $)} \\ [3pt] & = & \ sin \ left (\ arcsin (0. & = & 0.87 & (\ text {См. Теорему} \ ref {arccosinesinefunctionprops}) \\ \ end {array} \] Чтобы определить, какое из этих решений лежит в \ ([0,2 \ pi) \), нам сначала нужно получить представление о значении \ (x = \ frac {1} {2} \ arcsin (0.87) \ ). Еще раз, мы могли бы использовать калькулятор, но здесь мы применяем аналитический подход.По определению \ (0 <\ arcsin (0.87) <\ frac {\ pi} {2} \), так что умножение на \ (\ frac {1} {2} \) дает нам \ (0 <\ frac { 1} {2} \ arcsin (0.87) <\ frac {\ pi} {4} \). Начиная с семейства решений \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi k \), мы используем те же аргументы, что и в нашем решении для числа \ ref {arctanin02pi} выше и найти только решения, соответствующие \ (k = 0 \) и \ (k = 1 \), лежащие в \ ([0,2 \ pi) \): \ (x = \ frac {1} {2} \ arcsin ( 0.87) \) и \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi \).Затем мы переходим к семейству \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) + \ pi k \) для целых чисел \ (k \). Здесь нам нужно получить лучшую оценку \ (\ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) \). Из неравенства \ (0 <\ frac {1} {2} \ arcsin (0.87) <\ frac {\ pi} {4} \) сначала умножаем на \ (- 1 \), а затем прибавляем \ (\ frac {\ pi} {2} \), чтобы получить \ (\ frac {\ pi} {2}> \ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87)> \ frac {\ pi} {4} \) или \ (\ frac {\ pi} {4} <\ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) <\ frac { \ pi} {2} \).Продолжая обычные рассуждения, мы находим единственные решения, лежащие в \ ([0,2 \ pi) \), соответствующие \ (k = 0 \) и \ (k = 1 \), а именно \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) \) и \ (x = \ frac {3 \ pi} {2} - \ frac {1} {2} \ arcsin ( 0,87) \). В общем, мы нашли четыре решения для \ (\ sin (2x) = 0.87 \) in \ ([0,2 \ pi) \): \ (x = \ frac {1} {2} \ arcsin (0.87) \), \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi \), \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0. \ hspace {0,75 дюйма} \ includegraphics [width = 2in] {./ IntroTrigGraphics / TrigEquIneq06.jpg} \\ $ y = \ tan \ left (\ frac {x} {2} \ right) \) и \ boldmath \ (y = -3 \) & Каждая из задач в примере \ ref {TrigEqnEx1} содержала одну тригонометрическую функцию. Если уравнение включает две разные тригонометрические функции или если уравнение содержит одну и ту же тригонометрическую функцию, но с разными аргументами, нам нужно будет использовать тождества и алгебру, чтобы привести уравнение к той же форме, что и приведенные на странице \ pageref {trigeqnstrategy1}. Мы повторяем здесь совет, данный при решении систем нелинейных уравнений в разделе \ ref {NonLinear} — когда дело доходит до решения уравнений, включающих тригонометрические функции, полезно просто попробовать что-нибудь. Далее мы сосредоточимся на решении неравенств, связанных с тригонометрическими функциями. Поскольку эти функции непрерывны в своих доменах, мы можем использовать технику знаковых диаграмм, которую мы использовали в прошлом, для решения неравенств. \ Footnote {См. Страницу \ pageref {firstsigndiagram}, Пример \ ref {polygraphex}, page \ pageref { rationalsigndiagram}, page \ pageref {algebraicsigndiagram}, Пример \ ref {expineq} и Пример \ ref {logineq} для обсуждения этого метода.} Пример \ (\ PageIndex {2} \): Решите следующие неравенства на \ ([0,2 \ pi) \). Выразите свои ответы, используя интервальную нотацию, и проверьте свои ответы графически. Решение Решение.{2} (x) = 0 \) или \ (3 \ sin (x) — 1 = 0 \). Решая для \ (\ sin (x) \), мы находим \ (\ sin (x) = 0 \) или \ (\ sin (x) = \ frac {1} {3} \). Решение первого уравнения — \ (x = \ pi k \), где \ (x = 0 \) и \ (x = \ pi \) — два решения, которые лежат в \ ([0,2 \ pi) \). Чтобы решить \ (\ sin (x) = \ frac {1} {3} \), мы используем функцию арксинуса, чтобы получить \ (x = \ arcsin \ left (\ frac {1} {3} \ right) + 2 \ pi k \) или \ (x = \ pi — \ arcsin \ left (\ frac {1} {3} \ right) + 2 \ pi k \) для целых чисел \ (k \). Здесь мы находим два решения, лежащих в \ ([0,2 \ pi) \), как \ (x = \ arcsin \ left (\ frac {1} {3} \ right) \) и \ (x = \ пи — \ arcsin \ left (\ frac {1} {3} \ right) \).2 \) и найдите \ (x \) — координаты точек пересечения этих двух кривых. Некоторое дополнительное масштабирование требуется около \ (x = 0 \) и \ (x = \ pi \), чтобы убедиться, что эти две кривые действительно пересекаются четыре раза. \ Footnote {Обратите внимание, что мы \ textit {не} считаем точку \ ((2 \ pi, 0) \) в нашем наборе решений, поскольку \ (x = 2 \ pi \) не находится в интервале \ ([0,2 \ pi) \). В следующих решениях помните, что, хотя \ (x = 2 \ pi \) может быть решением уравнения, оно не учитывается среди решений в \ ([0,2 \ pi) \).2 — u — 2 & = & 0 & \ text {Пусть \ (u = \ tan (x) \).} \\ (u + 1) (u — 2) & = & 0 & \\ \ end {array} \] Это дает \ (u = -1 \) или \ (u = 2 \). Поскольку \ (u = \ tan (x) \), мы имеем \ (\ tan (x) = -1 \) или \ (\ tan (x) = 2 \). Из \ (\ tan (x) = -1 \) мы получаем \ (x = — \ frac {\ pi} {4} + \ pi k \) для целых чисел \ (k \). (2u — 1) (u — 1) & = & 0 & \\ \ end {array} \] Это дает \ (u = \ frac {1} {2} \) или \ (u = 1 \). Поскольку \ (u = \ cos (x) \), мы получаем \ (\ cos (x) = \ frac {1} {2} \) или \ (\ cos (x) = 1 \). Решая \ (\ cos (x) = \ frac {1} {2} \), мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac { 5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Из \ (\ cos (x) = 1 \) мы получаем \ (x = 2 \ pi k \) для целых чисел \ (k \). Ответы, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {3} \) и \ (\ frac {5 \ pi} { 3} \).3-2u-2 = 0 \) равно \ (u = 1 \). Поскольку \ (u = \ cos (x) \), мы получаем \ (\ cos (x) = 1 \), поэтому \ (x = 2 \ pi k \) для целых чисел \ (k \). Единственное решение, которое лежит в \ ([0,2 \ pi) \), — это \ (x = 0 \). Построение графиков \ (y = \ cos (3x) \) и \ (y = 2- \ cos (x) \) на одном и том же наборе осей над \ ([0,2 \ pi) \) показывает, что графики пересекаются в что выглядит как \ ((0,1) \), как требуется. \ [\ begin {array} {rclr} \ sin (2x) & = & \ sqrt {3} \ cos (x) & \\ 2 \ sin (x) \ cos (x) & = & \ sqrt {3} \ cos (x) & \ text {(Поскольку \ (\ sin (2x) = 2 \ sin (x) \ cos (x) \).)} \\ 2 \ sin (x) \ cos (x) — \ sqrt {3} \ cos (x) & = & 0 & \\ \ cos (x) (2 \ sin (x) — \ sqrt {3}) & = & 0 & \\ \ end {array} \] , откуда получаем \ (\ cos (x) = 0 \) или \ (\ sin (x) = \ frac {\ sqrt {3}} {2} \). Из \ (\ cos (x) = 0 \) получаем \ (x = \ frac {\ pi} {2} + \ pi k \) для целых чисел \ (k \).Из \ (\ sin (x) = \ frac {\ sqrt {3}} {2} \) мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac {2 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Пример \ (\ PageIndex {4} \): Выразите домен следующих функций, используя нотацию с расширенным интервалом.\ footnote {Подробную информацию об этой нотации см. на странице \ pageref {extendedinterval}.} Решение \ item Чтобы найти область значений \ (f (x) = \ csc \ left (2x + \ frac {\ pi} {3} \ right) \), мы перепишем \ (f \) в терминах синуса как \ (f (x) = \ frac {1} {\ sin \ left (2x + \ frac {\ pi} {3} \ right)} \). Поскольку функция синуса определена везде, наша единственная проблема — нули в знаменателе.Решая \ (\ sin \ left (2x + \ frac {\ pi} {3} \ right) = 0 \), получаем \ (x = — \ frac {\ pi} {6} + \ frac {\ pi} {2} k \) для целых чисел \ (k \). В нотации конструктора множеств наш домен \ (\ left \ {x: x \ neq — \ frac {\ pi} {6} + \ frac {\ pi} {2} k \, \ text {для целых чисел \ ( k $} \ right \} \). Чтобы помочь визуализировать область, мы следуем старой мантре «Если сомневаешься, записывай!» Мы получаем \ (\ left \ {x: x \ neq — \ frac {\ pi } {6}, \ frac {2 \ pi} {6}, — \ frac {4 \ pi} {6}, \ frac {5 \ pi} {6}, — \ frac {7 \ pi} {6} , \ frac {8 \ pi} {6}, \ ldots \ right \} \), где мы сохранили знаменатели \ (6 \) повсюду, чтобы помочь увидеть закономерность.Изобразив ситуацию на числовой прямой, имеем Действуя так же, как на странице \ pageref {extendedinterval} в разделе \ ref {roundfunctionsbeyond}, мы позволяем \ (x _ {\ mbox {\ tiny \ (k $}}} \) обозначать \ (k $ th число, исключенное из домен, и у нас есть \ (x _ {\ mbox {\ tiny \ (k $}} = — \ frac {\ pi} {6} + \ frac {\ pi} {2} k = \ frac {(3k-1) \ pi} {6} \) для целых чисел \ (k \). Мы можем проверить наш ответ, подставив значения \ (k \), чтобы убедиться, что он соответствует нашей диаграмме. \ item Поскольку области \ (\ sin (x) \) и \ (\ cos (x) \) — все действительные числа, единственное беспокойство при нахождении области \ (f (x) = \ frac {\ sin (x)} {2 \ cos (x) — 1} \) является делением на ноль, поэтому мы устанавливаем знаменатель равным нулю и решаем. Из \ (2 \ cos (x) — 1 = 0 \) получаем \ (\ cos (x) = \ frac {1} {2} \), так что \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac {5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \).Используя обозначение конструктора множеств, доменом является \ (\ left \ {x: x \ neq \ frac {\ pi} {3} + 2 \ pi k \, \ text {and} \, x \ neq \ frac {5 \ pi} {3} + 2 \ pi k \, \ text {для целых чисел \ (k $} \ right \} \) или \ (\ left \ {x: x \ neq \ pm \ frac {\ pi} {3}, \ pm \ frac {5 \ pi} {3}, \ pm \ frac {7 \ pi} {3}, \ pm \ frac {11 \ pi} {3}, \ ldots \ right \} \ ), так что у нас В отличие от предыдущего примера, у нас есть \ textit {два} разных семейства точек для рассмотрения, и мы представляем два способа справиться с подобными ситуациями. Один из способов — обобщить то, что мы сделали в предыдущем примере, и использовать формулы, которые мы нашли в нашей работе с предметной областью, для описания интервалов.Для этого положим \ (a _ {\ mbox {\ tiny \ (k $}} = \ frac {\ pi} {3} + 2 \ pi k = \ frac {(6k + 1) \ pi} {3 } \) и \ (b _ {\ mbox {\ tiny \ (k $}} = \ frac {5 \ pi} {3} + 2 \ pi k = \ frac {(6k + 5) \ pi} {3}) \) для целых чисел \ (k \). Теперь цель состоит в том, чтобы записать область в терминах \ (a $ ‘s an \ (b $’ s. Мы находим \ (a _ {\ mbox {\ tiny \ (0 $}} = \ frac {\ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (1 $}} = \ frac {7 \ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (- 1 $}} = — \ frac {5 \ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (2 $}} = \ frac {13 \ pi} { 3} \), \ (a _ {\ mbox {\ tiny \ (- 2 $}} = — \ frac {11 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (0 $}) } = \ frac {5 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (1 $}} = \ frac {11 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (- 1 $}} = — \ frac {\ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (2 $}} = \ frac {17 \ pi} {3}) \) и \ (b _ {\ mbox {\ tiny \ (- 2 $}} = — \ frac {7 \ pi} {3} \). Второй подход к проблеме использует периодический характер \ (f \).Поскольку \ (\ cos (x) \) и \ (\ sin (x) \) имеют период \ (2 \ pi \), нетрудно показать, что функция \ (f \) повторяется каждые \ (2 \ pi \) единиц. \ footnote {Это не обязательно означает, что период \ (f \) равен \ (2 \ pi \). Касательная функция состоит из \ (\ cos (x) \) и \ (\ sin (x) \), но ее период составляет половину их периода. Читателю предлагается изучить период \ (f \).} Это означает, что если мы можем найти формулу для области на интервале длины \ (2 \ pi \), мы можем выразить всю область, переведя наш ответ слева и справа по оси \ (x \) — путем добавления целых чисел, кратных \ (2 \ pi \).Один из таких интервалов, который возникает в результате нашей работы в области, — это \ (\ left [\ frac {\ pi} {3}, \ frac {7 \ pi} {3} \ right] \). Часть домена здесь \ (\ left (\ frac {\ pi} {3}, \ frac {5 \ pi} {3} \ right) \ cup \ left (\ frac {5 \ pi} {3} , \ frac {7 \ pi} {3} \ right) \). Складывая целые числа, кратные \ (2 \ pi \), мы получаем семейство интервалов \ (\ left (\ frac {\ pi} {3} + 2 \ pi k, \ frac {5 \ pi} {3} + 2 \ pi k \ right) \ cup \ left (\ frac {5 \ pi} {3} + 2 \ pi k, \ frac {7 \ pi} {3} + 2 \ pi k \ right) \) для целых чисел \ (к \). Мы предоставляем читателю показать, что получение общих знаменателей приводит к нашему предыдущему ответу. \ item Чтобы найти область значений \ (f (x) = \ sqrt {1- \ cot (x)} \), сначала отметим, что из-за наличия члена \ (\ cot (x) \) , \ (x \ neq \ pi k \) для целых чисел \ (k \). Далее напомним, что для определения квадратного корня нам потребуется \ (1 — \ cot (x) \ geq 0 \). В отличие от неравенств, которые мы решили в примере \ ref {TrigIneqEx1}, здесь мы не ограничены заданным интервалом. Наша стратегия состоит в том, чтобы решить это неравенство над \ ((0, \ pi) \) (тот же интервал, который порождает фундаментальный цикл котангенса), а затем добавить целые числа, кратные периоду, в данном случае \ (\ pi \). В этом разделе вы: Рисунок 1 Египетские пирамиды, стоящие возле современного города. (кредит: Ойсин Малвихилл) Фалес Милетский (около 625–547 гг. до н.э.) известен как основоположник геометрии.Легенда гласит, что он рассчитал высоту Великой пирамиды в Гизе в Египте, используя теорию подобных треугольников , которую он разработал, измерив тень своего посоха. В предыдущих разделах этой главы мы рассматривали тригонометрические тождества.Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид. Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции. Во многом аналогично решению полиномиальных или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть.Часто мы решаем тригонометрическое уравнение на заданном интервале. Однако так же часто нас просят найти все возможные решения, и, поскольку тригонометрические функции являются периодическими, решения повторяются в течение каждого периода. Другими словами, тригонометрические уравнения могут иметь бесконечное количество решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предполагаем, что какое-либо решение является действительным. Период синусоидальной функции и косинусной функции равен 2π.2π. Другими словами, каждые 2π2π единицы повторяются значения y- . Если нам нужно найти все возможные решения, мы должны добавить 2πk, 2πk, где kk — целое число, к начальному решению. Вспомните правило, которое дает формат для определения всех возможных решений для функции с периодом 2π: 2π: Существуют аналогичные правила для указания всех возможных решений для других тригонометрических функций. Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Найдите все возможные точные решения уравнения cosθ = 12.cosθ = 12. Из единичного круга мы знаем, что Это решения в интервале [0,2π]. [0,2π]. Все возможные решения предоставлены , где kk — целое число. Найдите все возможные точные решения уравнения sint = 12.sint = 12. Решение для всех возможных значений t означает, что решения включают углы, превышающие период 2π.2π. Из рисунка 2 видно, что решениями являются π6π6 и 5π6,5π6. Но проблема в том, чтобы указать все возможные значения, которые решают уравнение. Следовательно, ответ , где kk — целое число. Для данного тригонометрического уравнения решить с помощью алгебры . Точно решите уравнение: 2cosθ − 3 = −5,0≤θ <2π.2cosθ − 3 = −5,0≤θ <2π. Используйте алгебраические методы для решения уравнения. Попробуй # 1 Решите в точности следующее линейное уравнение на интервале [0,2π): 2sinx + 1 = 0. [0,2π): 2sinx + 1 = 0. Когда нам задают уравнения, которые включают только одну из шести тригонометрических функций, их решения требуют использования алгебраических методов и единичного круга (см. Рисунок 2).Когда уравнение включает тригонометрические функции, отличные от синуса и косинуса, необходимо учитывать несколько факторов. Проблемы, связанные с величинами, обратными первичным тригонометрическим функциям, необходимо рассматривать с алгебраической точки зрения. Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен π, π, а не 2π.2π. Кроме того, область касательной — это все действительные числа, за исключением нечетных целых кратных π2, π2, если, конечно, проблема не накладывает свои собственные ограничения на область. Решите задачу точно: 2sin2θ − 1 = 0,0≤θ <2π. 2sin2θ − 1 = 0,0≤θ <2π. Поскольку эту проблему нелегко разложить на множители, мы решим ее, используя свойство квадратного корня. Во-первых, мы используем алгебру, чтобы выделить sinθ. Точно решите следующее уравнение: cscθ = −2,0≤θ <4π.cscθ = −2,0≤θ <4π. Нам нужны все значения θθ, для которых cscθ = −2cscθ = −2 в интервале 0≤θ <4π.0≤θ <4π. Поскольку sinθ = −12, sinθ = −12, обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах. Точно решите уравнение: tan (θ − π2) = 1,0≤θ <2π.tan (θ − π2) = 1,0≤θ <2π. Напомним, что касательная функция имеет период π.π. На интервале [0, π), [0, π) и под углом π4, π4 касательная имеет значение 1. Однако нам нужен угол (θ − π2). (Θ − π2) . Таким образом, если tan (π4) = 1, tan (π4) = 1, то На интервале [0,2π), [0,2π) имеем два решения: Попробуй # 2 Найдите все решения для tanx = 3.tanx = 3. Определите все точные решения уравнения 2 (tanx + 3) = 5 + tanx, 0≤x <2π.2 (tanx + 3) = 5 + tanx, 0≤x <2π. Мы можем решить это уравнение, используя только алгебру. Выделите выражение tanxtanx слева от знака равенства. На единичной окружности есть два угла, значение касательной которых равно −1: θ = 3π4−1: θ = 3π4 и θ = 7π4. Не все функции могут быть решены точно с использованием только единичной окружности.Когда мы должны решить уравнение с углом, отличным от одного из специальных углов, нам понадобится калькулятор. Убедитесь, что он установлен на правильный режим, градусы или радианы, в зависимости от критериев данной проблемы. Воспользуйтесь калькулятором, чтобы решить уравнение sinθ = 0,8, sinθ = 0,8, где θθ выражается в радианах. Убедитесь, что установлен режим радианы.Чтобы найти θ, θ, используйте функцию обратного синуса. На большинстве калькуляторов вам нужно будет нажать кнопку 2 ND , а затем кнопку SIN, чтобы вызвать функцию sin − 1sin − 1. На экране отображается sin − 1 (.sin − 1 (. Калькулятор готов к вводу в скобках. Для этой задачи мы вводим sin − 1 (0,8), sin − 1 (0,8)) и нажимаем ENTER. Таким образом, с точностью до четырех знаков после запятой, Решение Угол в градусах Обратите внимание, что калькулятор будет возвращать только угол в квадрантах I или IV для функции синуса, поскольку это диапазон обратного синуса. Другой угол получается с помощью π − θ.π − θ. Воспользуйтесь калькулятором, чтобы решить уравнение secθ = −4, secθ = −4, получив ответ в радианах. Мы можем начать с некоторой алгебры. Убедитесь, что РЕЖИМ установлен в радианах. Поскольку π2≈1,57π2≈1,57 и π≈3,14, π≈3,14, 1,8235 находится между этими двумя числами, поэтому θ≈1,8235θ≈1,8235 находится во втором квадранте. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор возвращает только угол в квадрантах I или II для функции косинуса, поскольку это диапазон обратного косинуса.См. Рисунок 2. Рисунок 2 Итак, нам также нужно найти меру угла в квадранте III. В квадранте III опорный угол равен θ’≈π − 1,8235≈1,3181. Θ’≈π − 1,8235≈1,3181. Другое решение в квадранте III: π + 1,3181≈4,4597.π + 1,3181≈4,4597. Решения: 1.8235 ± 2πk1.8235 ± 2πk и 4.4597 ± 2πk.4.4597 ± 2πk. Попробуй # 3 Решить cosθ = −0.2.cosθ = −0.2. Решение квадратного уравнения может быть более сложным, но, опять же, мы можем использовать алгебру, как и любое квадратное уравнение.Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция возводится в квадрат? Если представлена только одна функция и один из членов возведен в квадрат, подумайте о стандартной форме квадратичной функции. Замените тригонометрическую функцию переменной, например xx или u.u. Если после подстановки уравнение выглядит как квадратное уравнение, то мы можем использовать те же методы решения квадратичных уравнений для решения тригонометрических уравнений. Точно решите уравнение: cos2θ + 3cosθ − 1 = 0,0≤θ <2π.cos2θ + 3cosθ − 1 = 0,0≤θ <2π. Начнем с подстановки и замены cos θθ на x.x. Нет необходимости использовать замену, но это может облегчить визуальное решение проблемы. Уравнение нельзя разложить на множители, поэтому мы будем использовать квадратную формулу x = −b ± b2−4ac2a.х = −b ± b2−4ac2a. Заменить xx с cosθ, cosθ и решить. Таким образом, Обратите внимание, что используется только знак +. Это связано с тем, что мы получаем ошибку, когда решаем θ = cos − 1 (−3−132) θ = cos − 1 (−3−132) на калькуляторе, поскольку область определения функции обратного косинуса равна [−1,1 ]. [- 1,1]. Однако есть и второе решение: Эта конечная сторона угла лежит в квадранте I.Поскольку косинус также положителен в квадранте IV, второе решение — Решите уравнение точно: 2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π.2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π. Используя группировку, эту квадратичную величину можно разложить на множители. Либо сделайте настоящую замену, sinθ = u, sinθ = u, либо представьте ее, как мы множим: Теперь установите каждый множитель равным нулю. Затем найдите θ: sinθ ≠ 32, θ: sinθ ≠ 32, так как диапазон синусоидальной функции равен [−1,1]. [- 1,1]. Однако sinθ = 1, sinθ = 1, что дает решение π2.π2. Обязательно проверьте все решения в данном домене, так как некоторые факторы не имеют решения. Попробуй # 4 Решить sin2θ = 2cosθ + 2,0≤θ≤2π. Решите точно: Эта задача должна показаться вам знакомой, поскольку она похожа на квадратичную. Пусть sinθ = x.sinθ = x. Уравнение принимает вид 2×2 + x = 0,2×2 + x = 0. Начнем с факторинга: Установите каждый коэффициент равным нулю. Затем подставьте обратно в уравнение исходное выражение sinθsinθ вместо x.x. Таким образом, Решения в области 0≤θ <2π0≤θ <2π равны 0, π , 7π6,11π6. 0, π, 7π6,11π6. Если мы предпочитаем не заменять, мы можем решить уравнение, следуя той же схеме факторизации и установив каждый коэффициент равным нулю. Мы можем видеть решения на графике на рисунке 3. На интервале 0≤θ <2π, 0≤θ <2π график пересекает ось x- четыре раза в отмеченных решениях.Обратите внимание, что тригонометрические уравнения в квадратичной форме могут дать до четырех решений вместо ожидаемых двух, которые можно найти с помощью квадратных уравнений. В этом примере каждое решение (угол), соответствующее положительному значению синуса, даст два угла, которые приведут к этому значению. Рисунок 3 Мы также можем проверить решения на единичном круге на Рисунке 2. Решите квадратное по форме уравнение: 2sin2θ − 3sinθ + 1 = 0,0≤θ <2π. Мы можем факторизовать, используя группировку. Значения решения θθ можно найти на единичном круге: Попробуй # 5 Решите квадратное уравнение 2cos2θ + cosθ = 0.2cos2θ + cosθ = 0. Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, потому что они упрощают решение уравнений. Помните, что методы, которые мы используем для решения проблем, не совпадают с методами проверки личности. Здесь применяются основные правила алгебры, а не переписывание одной стороны идентичности для соответствия другой стороне. В следующем примере мы используем два тождества, чтобы упростить уравнение. Используйте тождества, чтобы точно решить тригонометрическое уравнение в интервале 0≤x <2π.0≤x <2π. Обратите внимание, что левая часть уравнения — это формула разности для косинуса. Из единичного круга на рисунке 2 мы видим, что cosx = 32cosx = 32, когда x = π6,11π6.x = π6,11π6. Точно решите уравнение, используя формулу двойного угла: cos (2θ) = cosθ. У нас есть три варианта выражения для замены двойного угла косинуса. Поскольку проще решать одну тригонометрическую функцию за раз, мы выберем тождество с двойным углом, включающее только косинус: Итак, если cosθ = −12, cosθ = −12, тогда θ = 2π3 ± 2πkθ = 2π3 ± 2πk и θ = 4π3 ± 2πk; θ = 4π3 ± 2πk; если cosθ = 1, cosθ = 1, то θ = 0 ± 2πk.θ = 0 ± 2πk. Точно решите уравнение, используя тождество: 3cosθ + 3 = 2sin2θ, 0≤θ <2π. 3cosθ + 3 = 2sin2θ, 0≤θ <2π. Если мы перепишем правую часть, мы можем записать уравнение через косинус: Наши решения: 2π3,4π3, π.2π3,4π3, π. Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими кратный угол, например sin (2x) sin (2x) или cos (3x) .cos (3x). Столкнувшись с этими уравнениями, вспомните, что y = sin (2x) y = sin (2x) — это горизонтальное сжатие с коэффициентом 2 функции y = sinx.y = sinx. На интервале 2π, 2π мы можем изобразить два периода y = sin (2x), y = sin (2x), в отличие от одного цикла y = sinx.y = sinx. Решите точно: cos (2x) = 12cos (2x) = 12 на [0,2π). [0,2π). Мы видим, что это уравнение является стандартным уравнением с углом, кратным углу.Если cos (α) = 12, cos (α) = 12, мы знаем, что αα находится в квадрантах I и IV. Хотя θ = cos − 112θ = cos − 112 даст решения только в квадрантах I и II, мы понимаем, что решения уравнения cosθ = 12cosθ = 12 будут в квадрантах I и IV. Следовательно, возможные углы равны θ = π3θ = π3 и θ = 5π3.θ = 5π3. Итак, 2x = π32x = π3 или 2x = 5π3,2x = 5π3, что означает, что x = π6x = π6 или x = 5π6.x = 5π6. Имеет ли это смысл? Да, потому что cos (2 (π6)) = cos (π3) = 12. cos (2 (π6)) = cos (π3) = 12. Есть еще возможные ответы? Вернемся к нашему первому шагу. В квадранте I 2x = π3,2x = π3, поэтому x = π6x = π6, как указано. Давайте снова вращаемся по кругу: , поэтому x = 7π6.x = 7π6. Еще один оборот дает x = 13π6> 2π, x = 13π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому оно не решение на [0,2π). [0,2π). В квадранте IV 2x = 5π3,2x = 5π3, поэтому x = 5π6x = 5π6, как указано. Давайте снова вращаемся по кругу: , поэтому x = 11π6.х = 11π6. Еще один оборот дает x = 17π6> 2π, x = 17π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому оно не решение на [0,2π). [0,2π). Наши решения: π6,5π6,7π6, 11π6.π6,5π6,7π6 и 11π6. Обратите внимание, что всякий раз, когда мы решаем задачу в форме sin (nx) = c, sin (nx) = c, мы должны обойти единичный круг nn раз. Теперь мы можем использовать все изученные нами методы для решения задач, связанных с применением свойств прямоугольных треугольников и теоремы Пифагора.Мы начнем с известной теоремы Пифагора, a2 + b2 = c2, a2 + b2 = c2, и смоделируем уравнение в соответствии с ситуацией. Используйте теорему Пифагора и свойства прямоугольных треугольников, чтобы смоделировать уравнение, которое соответствует задаче. Один из тросов, которыми центр колеса обозрения London Eye крепится к земле, необходимо заменить. Центр колеса обозрения находится на высоте 69,5 метров над землей, а второй якорь на земле находится в 23 метрах от основания колеса обозрения.Примерно какой длины кабель и каков угол подъема (от земли до центра колеса обозрения)? См. Рисунок 4. Рисунок 4 Используя предоставленную информацию, мы можем нарисовать прямоугольный треугольник. Мы можем найти длину кабеля с помощью теоремы Пифагора. Угол возвышения θ, θ, образованный вторым якорем на земле и тросом, идущим к центру колеса.Мы можем использовать касательную функцию, чтобы найти ее меру. Округлить до двух десятичных знаков. Угол возвышения составляет примерно 71,7∘, 71,7∘, а длина кабеля составляет 73,2 метра. . Правила безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы. Для лестницы любой длины основание должно находиться на расстоянии от стены, равном одной четвертой длины лестницы. Эквивалентно, если основание лестницы находится на расстоянии футов от стены фута, длина лестницы будет 4 на фута. См. Рисунок 5. Рис. 5 Сторона, примыкающая к θθ, равна a , а гипотенуза равна 4a.4а. Таким образом, Высота лестницы составляет 75,5∘75,5∘ с землей. Высота, на которой лестница касается стены, может быть найдена с помощью теоремы Пифагора: Таким образом, лестница касается стены на высоте 15a15a футов от земли. Всегда ли будут решения уравнений тригонометрических функций? Если нет, опишите уравнение, у которого не было бы решения. Объясните, почему да или почему нет. При решении тригонометрического уравнения, включающего более одной тригонометрической функции, всегда ли мы хотим попытаться переписать уравнение так, чтобы оно выражалось в терминах одной тригонометрической функции? Почему или почему нет? При решении линейных тригонометрических уравнений только с помощью синуса или косинуса, как мы узнаем, будут ли решения? Для следующих упражнений найдите все решения точно на интервале 0≤θ <2π.0≤θ <2π. Для следующих упражнений решите точно на [0,2π). [0,2π). 2cos (3θ) = — 22cos (3θ) = — 2 cos (2θ) = — 32cos (2θ) = — 32 2cos (π5θ) = 32cos (π5θ) = 3 Для следующих упражнений найдите все точные решения на [0,2π). [0,2π). сек (x) sin (x) −2sin (x) = 0sec (x) sin (x) −2sin (x) = 0 tan (x) −2sin (x) tan (x) = 0tan (x) −2sin (x) tan (x) = 0 2cos2t + cos (t) = 12cos2t + cos (t) = 1 2tan2 (t) = 3сек (t) 2tan2 (t) = 3сек (t) 2sin (x) cos (x) −sin (x) + 2cos (x) −1 = 02sin (x) cos (x) −sin (x) + 2cos (x) −1 = 0 tan2 (x) = — 1 + 2tan (−x) tan2 (x) = — 1 + 2tan (−x) 8sin2 (x) + 6sin (x) + 1 = 08sin2 (x) + 6sin (x) + 1 = 0 tan5 (x) = tan (x) tan5 (x) = tan (x) Для следующих упражнений решайте методами, указанными в этом разделе, точно на интервале [0,2π). [0,2π). sin (3x) cos (6x) −cos (3x) sin (6x) = — 0.9sin (3x) cos (6x) −cos (3x) sin (6x) = — 0.9 sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1 sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1 cos (2x) cosx + sin (2x) sinx = 1cos (2x) cosx + sin (2x) sinx = 1 6sin (2t) + 9sint = 06sin (2t) + 9sint = 0 9cos (2θ) = 9cos2θ − 49cos (2θ) = 9cos2θ − 4 cos (6x) −cos (3x) = 0cos (6x) −cos (3x) = 0 Для следующих упражнений решите точно на отрезке [0,2π). [0,2π). Если уравнения не учитываются, используйте формулу корней квадратного уравнения. tan2x − 3tanx = 0tan2x − 3tanx = 0 sin2x + sinx − 2 = 0sin2x + sinx − 2 = 0 sin2x − 2sinx − 4 = 0sin2x − 2sinx − 4 = 0 5cos2x + 3cosx − 1 = 05cos2x + 3cosx − 1 = 0 3cos2x − 2cosx − 2 = 03cos2x − 2cosx − 2 = 0 5sin2x + 2sinx − 1 = 05sin2x + 2sinx − 1 = 0 tan2x + 5tanx − 1 = 0tan2x + 5tanx − 1 = 0 cot2x = −cotxcot2x = −cotx −tan2x − tanx − 2 = 0 − tan2x − tanx − 2 = 0 Для следующих упражнений найдите точные решения на интервале [0,2π). sin2x − cos2x − sinx = 0sin2x − cos2x − sinx = 0 sin2x + cos2x = 0sin2x + cos2x = 0 sin (2x) −sinx = 0sin (2x) −sinx = 0 cos (2x) −cosx = 0cos (2x) −cosx = 0. 2tanx2 − sec2x − sin2x = cos2x2tanx2 − sec2x − sin2x = cos2x 1 − cos (2x) = 1 + cos (2x) 1 − cos (2x) = 1 + cos (2x). 10sinxcosx = 6cosx10sinxcosx = 6cosx −3sint = 15costsint − 3sint = 15costsint 4cos2x − 4 = 15cosx4cos2x − 4 = 15cosx 8sin2x + 6sinx + 1 = 08sin2x + 6sinx + 1 = 0 8cos2θ = 3−2cosθ8cos2θ = 3−2cosθ 6cos2x + 7sinx − 8 = 06cos2x + 7sinx − 8 = 0. 12sin2t + cost − 6 = 012sin2t + cost − 6 = 0 Для следующих упражнений точно алгебраически определите все решения тригонометрического уравнения, затем проверьте результаты, построив уравнение на графике и найдя нули. 6sin2x − 5sinx + 1 = 06sin2x − 5sinx + 1 = 0 8cos2x − 2cosx − 1 = 08cos2x − 2cosx − 1 = 0. 100tan2x + 20tanx − 3 = 0100tan2x + 20tanx − 3 = 0 2cos2x − cosx + 15 = 02cos2x − cosx + 15 = 0. 20sin2x − 27sinx + 7 = 020sin2x − 27sinx + 7 = 0 2tan2x + 7tanx + 6 = 02tan2x + 7tanx + 6 = 0 130tan2x + 69tanx − 130 = 0130tan2x + 69tanx − 130 = 0 Для следующих упражнений используйте калькулятор, чтобы найти все решения до четырех знаков после запятой. Для следующих упражнений решите уравнения алгебраически, а затем с помощью калькулятора найдите значения на интервале [0,2π).[0,2π). Округлить до четырех знаков после запятой. tan2x + 3tanx − 3 = 0tan2x + 3tanx − 3 = 0 6tan2x + 13tanx = −66tan2x + 13tanx = −6 tan2x − secx = 1tan2x − secx = 1 sin2x − 2cos2x = 0sin2x − 2cos2x = 0 2tan2x + 9tanx − 6 = 02tan2x + 9tanx − 6 = 0 4sin2x + sin (2x) secx − 3 = 04sin2x + sin (2x) secx − 3 = 0 Для следующих упражнений найдите все решения уравнений в точности на интервале [0,2π). [0,2π). csc2x − 3cscx − 4 = 0csc2x − 3cscx − 4 = 0 sin2x − cos2x − 1 = 0sin2x − cos2x − 1 = 0 sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0 3sec2x + 2 + sin2x − tan2x + cos2x = 03sec2x + 2 + sin2x − tan2x + cos2x = 0 sin2x − 1 + 2cos (2x) −cos2x = 1sin2x − 1 + 2cos (2x) −cos2x = 1 tan2x − 1 − sec3xcosx = 0tan2x − 1 − sec3xcosx = 0 sin (2x) sec2x = 0sin (2x) sec2x = 0 sin (2x) 2csc2x = 0sin (2x) 2csc2x = 0 2cos2x − sin2x − cosx − 5 = 02cos2x − sin2x − cosx − 5 = 0 1sec2x + 2 + sin2x + 4cos2x = 41sec2x + 2 + sin2x + 4cos2x = 4 У самолета достаточно бензина, чтобы долететь до города в 200 милях к северо-востоку от его текущего местоположения. Если пилот знает, что город находится в 25 милях к северу, на сколько градусов к северу от востока должен лететь самолет? Если погрузочная рампа размещена рядом с грузовиком на высоте 4 фута, а ее длина составляет 15 футов, какой угол образует аппарель с землей? Если погрузочная рампа расположена рядом с грузовиком на высоте 2 фута, а ее длина составляет 20 футов, то какой угол образует аппарель с землей? Женщина наблюдает за запущенной ракетой на высоте 11 миль. Если она стоит в 4 милях от стартовой площадки, под каким углом она смотрит вверх из горизонтали? Астронавт находится в запущенной ракете, которая сейчас находится на высоте 15 миль. Если мужчина стоит в 2 милях от стартовой площадки, под каким углом она смотрит на него сверху вниз из горизонтали? (Подсказка: это называется углом депрессии. Женщина стоит в 8 метрах от 10-метрового здания.Под каким углом она смотрит на вершину здания? Мужчина стоит в 10 метрах от 6-метрового дома. Кто-то наверху здания смотрит на него сверху вниз. Под каким углом смотрит на него человек? У здания высотой 20 футов есть тень длиной 55 футов. Какой угол подъема солнца? У здания высотой 90 футов есть тень длиной 2 фута. Какой угол подъема солнца? Прожектор на земле в 3 метрах от человека ростом 2 метра отбрасывает 6-метровую тень на стену в 6 метрах от человека.Под каким углом свет? Прожектор на земле в 3 футах от женщины ростом 5 футов отбрасывает тень 15 футов высотой на стену в 6 футах от женщины. Под каким углом свет? Для следующих упражнений найдите решение задачи со словами алгебраически. Затем воспользуйтесь калькулятором, чтобы проверить результат. Ответ округлите до десятых долей градуса. Человек выполняет стойку на руках, при этом его ноги касаются стены, а руки находятся на расстоянии 1,5 фута от стены.Если рост человека 6 футов, какой угол у его ступни со стеной? Человек выполняет стойку на руках, при этом ноги касаются стены, а руки находятся на расстоянии 3 футов от стены. Если рост человека 5 футов, какой угол у его ступни со стеной? 23-футовая лестница стоит рядом с домом. Если лестница соскользнет на расстоянии 7 футов от дома при недостаточном сцеплении с землей, под каким углом лестница должна быть расположена относительно земли, чтобы не поскользнуться? В этом разделе мы кратко рассмотрим элементарные методы, используемые для решения
уравнения и неравенства.Мы сосредоточимся на проблемах, которые могут появиться,
читатель может быть удивлен, увидев, как в игру вступают свойства функций
в этой секции. Этот раздел состоит из частей
Уравнения,
Неравенства,
Знаковые неравенства,
Двойные неравенства,
Разделение реальной линии и
(In) равенства с триггерными функциями. Рассмотрим уравнение с неизвестным размером x . Обычный способ
решение уравнений состоит в том, чтобы выделить x с одной стороны.В общем продолжаем
применив некоторые операции к обеим частям уравнения, что работает
во многих случаях, но иногда мы должны быть осторожны, что и является темой
этой части. Всем известно, что мы можем складывать или вычитать с обеих сторон
свободно, но при делении или умножении уравнения мы должны быть более
осторожно, так как это работает, только если мы не используем ноль для
деление / умножение. То, что не так широко понимается, — это еще один часто используемый прием.Во многих
уравнения, у нас есть функция, от которой мы хотим избавиться, например
уравнение ln ( x ) = 2 относится к этому типу. Большинство
эффективный трюк — применить (к обеим сторонам) функцию, обратную к одной
что мы хотим, чтобы функция и ее обратная функция исчезли, а затем отмените
друг с другом. Функция, обратная логарифму, — это экспонента, поэтому мы делаем e ln ( x ) = e 2 , Однако это не всегда так просто. Рассмотрим следующие два примера. Пример: Рассмотрим уравнение
arcsin ( x ) = π / 2. Применяем обратное
функция. sin [arcsin ( x )] = sin [π / 2], Теперь рассмотрим это уравнение: sin ( x ) = 1. Если мы
проделайте аналогичную процедуру, arcsin [sin ( x )] = arcsin [1], мы получаем неправильный ответ.Как это возможно? Тогда каков правильный ответ? Ключ к этому трюку — понятие обратной функции. Во-первых
Например, синус — это функция, обратная арксинусу на интервале
[-1,1].
Неужели х из этого интервала? В этом случае да, поскольку arcsin делает
не принимать никаких других значений, поэтому данное уравнение уже ограничивает x в правую часть. С другой стороны, arcsin — это не функция, обратная синусу, а только
синус ограничен.
Теперь нет гарантии, что x в уравнении
из этого региона, а для x из других регионов у нас разные
обратные функции. Поэтому поиск решения более сложен, и
на самом деле существует бесконечно много правильных решений
образуют π / 2 + 2 k π, где k — любое
целое число. У нас похожая проблема с корнями. Один из способов получить все решения: = 3, Это сработало, потому что квадрат — это функция, обратная квадратному корню на
интервал [0, ∞) и нет
другие x разрешены в данном уравнении. По-другому
не работает. x 2 = 16, Опять же, проблема в том, что для получения обратного квадрата нам нужно ограничить его до
[0, ∞),
но теперь у нас нет гарантии, что x в уравнении от этого
область, край. Правильный ответ здесь — 4 и 4. Пока у нас были проблемы с отсутствующими решениями. Также возможно получить
ложные решения. Фактически это опять же связано с проблемой с инверсией.
Мы меняем уравнение и находим решение нового, но как нам
знаете, что это тоже решение исходного уравнения? Это правда, если мы
также можно вернуться назад, от последней формы к первой (данной) форме
уравнение.Следовательно, операции, которые мы выполняем, также должны работать в
противоположное направление. Другими словами, если у нас есть две взаимные функции
инвертирует только где-то, то в одну сторону у нас проблемы и либо он
всплывает на пути к раствору, или может укусить нас на обратном пути. смотреть на
этот пример. (2- x 2 ) 1/2 = x , Вроде у нас два решения, но работает только одно, а именно x = 1. Обратите внимание, что такая проблема не возникает, когда мы работаем с
логарифм и экспонента, нас также устроит кубический корень и кубический
мощность и любая другая пара взаимно обратных функций, не требующая
ограничение. В других случаях мы должны быть очень осторожны, в частности, это
важно всегда проверять, что полученные нами решения действительно удовлетворяют
уравнение, которое нам было дано, в исходном виде. Универсального метода решения этих проблем не существует. Для популярных
функции мы помним, что происходит, например, мы должны помнить, что
квадратный корень из x 2 это не x , а
| x |.
Иногда, если у нас есть обратные функции только на части
реальная линия, это помогает разделить область, в которой мы решаем, на соответствующую
детали, см. соответствующий раздел ниже. С неравенством мы можем столкнуться со всеми проблемами, о которых говорилось выше, и некоторыми другими.
Опять же, мы можем прибавить / вычесть из обеих частей неравенства без
проблема, и все мы знаем, что при умножении / делении неравенства мы имеем
чтобы узнать о знаке числа, на которое мы умножаем / делим. Если это
число положительное, то мы сохраняем направление неравенства, но если оно
отрицательный, мы должны отменить его.Если в этот термин входит неизвестное, то
мы действительно не знаем знака, и мы должны решить неравенство несколько
раз, чтобы охватить все возможные ситуации, см. раздел «Разделение реальной линии». При применении некоторой функции к неравенству возникают две проблемы. Один о
отмена обратных функций, что вызывает те же проблемы, что и раньше.
Однако здесь мы должны быть осторожны уже при применении функции к
неравенство, потому что не каждую функцию можно применить к неравенствам.В
состояние простое. Могут применяться только монотонные функции; если
функция, которую мы применяем, возрастает, мы сохраняем неравенство как было; если
функция, которую мы применяем, уменьшается, тогда мы должны переключить направление
неравенство. Например, и логарифм, и экспонента являются возрастающими функциями.
везде.Таким образом, мы можем решить неравенство e x <5
применяя логарифм к обеим сторонам, не меняя направления, получаем
ln ( e x ) Для популярных функций у нас есть приемы решения неравенств. Если многочлены
вовлечены, мы можем использовать подход с помощью графиков или трюк, описанный в
часть Знаки неравенства. Рисунки также помогают при работе с тригонометрическими
функций, другой подход показан в последнем
часть здесь. Под знаковыми неравенствами мы понимаем неравенства, в которых одна сторона равна 0, а затем точное
значение выражения с другой стороны не имеет значения, важен только его знак.Эти неравенства могут быть решены довольно легко, если эта другая сторона может быть устранена.
выражается как произведение и / или соотношение простых терминов, потому что знак
продукт / соотношение можно легко определить по обозначениям его частей. Таким образом, это
достаточно, чтобы исследовать признаки отдельных факторов, а затем как-то
все вместе. Если повезет, каждое такое простое выражение будет непрерывным и как таковое
он меняет знаки контролируемым образом. Точнее, реальная линия разбивается на
несколько областей, в каждой из которых это выражение имеет только один знак, и
точки расщепления (где меняются знаки) — это именно те точки, где это
выражение равно нулю.Так как в каждом регионе знак один и тот же
везде, мы узнаем это, просто выбирая оттуда какую-то точку и
заменяя его. Например, x 2 — 1 равно нулю при -1 и 1, поэтому
вещественная прямая разбивается на области (−∞, −1), (- 1,1) и (1, ∞).
С первого раза мы
выберите, например, x = −2, подставьте и получите
3> 0, поэтому x 2 — 1 положительный на первом
области, аналогично узнаем, что это выражение отрицательно на втором
регион и позитив по последнему региону. Отсюда получаем процедуру решения знаковых неравенств. Сначала мы находим нулевые точки всех факторов. Затем мы используем их, чтобы разделить настоящие
линия в регионы. Для каждого региона мы находим признаки каждого фактора. Это
выполняется путем выбора некоторой точки внутри этой области и замены ее на
все факторы. Затем в каждом регионе мы складываем все признаки факторов
с помощью алгебры знаков и получить знаки всего выражения.Напоследок
На шаге собираем все области, где знак удовлетворяет заданному неравенству. Если
неравенство точное, мы используем открытые интервалы. Если в него входит равенство, то мы
включать конечные точки, но только если они не вызывают проблем в выражении. Для линейных факторов это становится еще проще, поскольку линейные факторы меняют только знак
один раз, в точке, где они равны нулю, поэтому для конкретного линейного фактора мы
просто отметьте точку, где он равен нулю, а затем везде будет один знак
справа, а другой слева.Чтобы найти, что есть что (
знаки идут — + или + -) мы просто
замените одну точку, кроме нулевой точки. Иногда мы разделяем не всю реальную строку, а только ее часть, это
происходит, когда некоторые числа запрещены выражениями в неравенстве.
Это случается не часто (обычно мы просто работаем с многочленами), но когда
бывает, что это не проблема, как вы увидите в следующем примере. Пример: Рассмотрим неравенство У нас есть одна проблема: логарифм принимает только положительные числа. Мы упорядочиваем эти точки, а затем проверяем, как они разделяют регион.
(−2, ∞)
где мы
за работой; в частности, мы видим, что x = −5 не падает
там, и поэтому это не имеет значения. Получаем области (−2, −1), (- 1,1 / 2), (1/2,1), (1,3) и (3, ∞). К
Для определения признаков в этих регионах воспользуемся таблицей. Мы хотим, чтобы выражение было положительным, поэтому правильные области
(−2, −1), (1/2,1) и (1,3).Так как неравенство также допускает ноль, проверяем
какие конечные точки этих трех интервалов не вызывают проблем. Мы видим, что −2
выпадает из-за логарифма, 1/2 и 1 равняются нулю в знаменателе, поэтому
единственное, что работает — 3. Ответ: (−2, −1) ∪ (1/2,1) ∪ (1,3]. Обратите внимание, что это неравенство также может быть решено, если сначала избавиться от
дробь, что означает, что мы хотели бы умножить обе части на
знаменатель.Но для этого нам нужно было бы исследовать возможные признаки
знаменатель, следовательно, нам пришлось бы разделить реальную линию и решить
несколько неравенств (см. раздел «Расщепление
реальная линия), скорее всего было бы намного хуже этого решения.
Определение знаков — обычно самый быстрый способ. Поэтому мы часто
преобразовать в этот тип и другие неравенства, например такие. Точки разделения 2 и 7, мы видим, что решение
(−∞, 2) ∪ (7, ∞). Двойное неравенство выглядит как эти два примера. Обычно существует два возможных способа решения таких двойных неравенств. Один
способ состоит в том, чтобы решить их оба одновременно, применяя операции ко всем трем
стороны. Иногда это легко сделать, например, с первым примером. Решение — интервал (−3,1).Однако второй пример выглядит не так привлекательно. Первый шаг был бы
быть умножить все стороны на знаменатель x + 3, но поскольку мы не знаем
его знак, нам пришлось бы разделить реальную линию и решить всю проблему
дважды. Мы покажем эту процедуру в части ниже, посвященной разделению реального
линии, вы увидите, что она немного длиннее. Второй возможный способ — просто решить каждое неравенство отдельно и
затем пересекаем решения (мы хотим, чтобы выполнялись оба неравенства).Это
часто проще, особенно если мы можем изменить два неравенства на знак
неравенства. Это был бы мой предпочтительный способ для второго примера. Отзывать
что знак «вверх ногами-ви» обозначает логическое «и». Часто мы оказываемся в ситуации, когда решаем (не) равенство, но шаг, который мы
собираемся сделать требует определенных знаний, которых у нас нет, а именно
признак некоторого выражения.Для этого есть две самые популярные причины:
мы хотим умножить / разделить неравенство на какое-либо выражение, или мы хотим
избавиться от абсолютного значения. Если это выражение включает неизвестные x , то мы не знаем его
знак. Затем нам нужно изучить обе возможности для знака, но каждый
решение будет работать только на той части реальной линии, где это
выражение имеет этот особый знак. Таким образом, мы фактически разделяем реальную линию
по нужному нам знаку и решаем проблему в каждой части отдельно,
в конце мы берем объединение частных решений.Однако учтите, что любые
результат, полученный при решении в одной конкретной области, действителен только в пределах
этот регион, то есть все части за пределами этого региона не должны приниматься во внимание
(другими словами, любое решение, которое мы получаем в конкретном регионе, должно быть
пересекались с этой областью, прежде чем мы будем использовать ее в дальнейшем). В качестве примера вернемся ко второму двойному неравенству выше. Нам бы хотелось
чтобы умножить все на x + 3, но для этого нам нужно
чтобы знать его знак, чтобы мы знали, следует ли переключать направление движения
неравенство.Есть две возможности, и нам нужно изучить обе. Мы видим
что выражение положительно для x > −3
и отрицательный для x <−3, что определяет области в
которые мы разделяем настоящие
линия. Затем решаем проблему в каждом регионе отдельно. Если у нас есть более сложные термины, мы найдем точки разделения для всех из них.
а затем сделайте универсальное разбиение реальной линии так, чтобы на каждой области
каждый хлопотный срок уже определен. Пример: Рассмотрим двойное неравенство Опять же, обратите внимание, как в каждой области мы пересекали полученное там решение.
с этой областью в конце мы использовали union для соединения всех решений. Здесь мы просто покажем один полезный трюк. Для первого равенства мы сначала заключаем, что в первом периоде
синуса у нас есть решение x = π / 2, затем добавляем периодичность: x = π / 2 + 2 k π. Второй пример работает аналогично. На картинке мы видим, что
решение описывается неравенствами π / 3 < x <4π / 3,
затем мы добавляем
периодичность: π / 3 + 2 k π < x <4π / 3 + 2 k π. Что делать, если аргумент триггерной функции каким-то образом трансформируется?
Рассмотрим неравенство
cos (2 x + 1) <1/2.Как мы решаем
это? Есть два популярных метода. Один из методов — это прямое использование изображения, но на этот раз нам нужно нарисовать график.
из cos (2 x + 1). Для опытного студента
это должно быть нетрудно догадаться (см. Преобразования и график
угадывание в функции — Обзор методов — Основные свойства реального
функции). Однако это может быть сложно, поэтому некоторые люди (например, я)
предпочитаю другой способ. Второй метод использует обычный график соответствующей триггерной функции и
сначала мы делаем вид, что в аргументе всего x .Мы находим
решение, как и раньше, но затем вместо x мы ставим
выражение в аргументе и решите относительно x . В нашем примере это будет
как это. Мы выразили ответ с помощью описания множества, а именно с помощью бесконечного
union, но, как вы можете видеть, как только у вас есть решение, описанное с помощью
неравенства, легко перейти на интервалы. Преимущество этого
метод заключается в том, что мы можем использовать его также для более общих преобразований, которые
трудно рисовать, например, решать такие неравенства:
0 ≤ загар ( x 2 +1) <1. Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже: Рассмотрим пример 6 на странице A30 в тексте Стюарта: «Найдите
все значения x в интервале
такой, что sin x = sin 2x.« Результат ввода этой функции в TI-89
решить функцию как «решить (sin (x) = sin (2x), x)» отображается на
верно. (Вы можете получить функцию решения, нажав
и выбрав «1: решить» (или набрав буквы). Калькулятор предоставил несколько решений (
стрелка вправо на линии решения указывает, что
есть еще решения на линии), но они
приближения.Это может быть, а может и не быть достаточно хорошим. Чтобы помочь TI-89 найти точные решения, мы можем
следуйте примеру 6 и поймите, что sin 2x = 2 sin
x cos x, что сводит все функции к одному и тому же
аргумент. Ввод «решить (sin (x) = 2sin (x) cos (x), x)» дает
результат показан справа. Что ж, хорошая новость в том, что TI-89 произвел точные
решения для этой версии уравнения.
0
f (x) = sin x ∙ cos x. Пример
3
Решение
f (x) = sin x ∙ cos x — sin x
sin x (cos x — 1)> 0, что согласуется с нашими расчетами.
Пример 4
Пример
5
Пример 6
грех x = грех (180 — х ). Это дает нам следующее решение: 
Пример
7
cos v = cos (−v).Тогда решение будет следующим:
0, 2 /3 и 4/3. Пример
8
Не забудьте использовать контрольный список, чтобы отслеживать свою работу. 10.7: Тригонометрические уравнения и неравенства
 } Каждой круговой функции для общности.
} Каждой круговой функции для общности.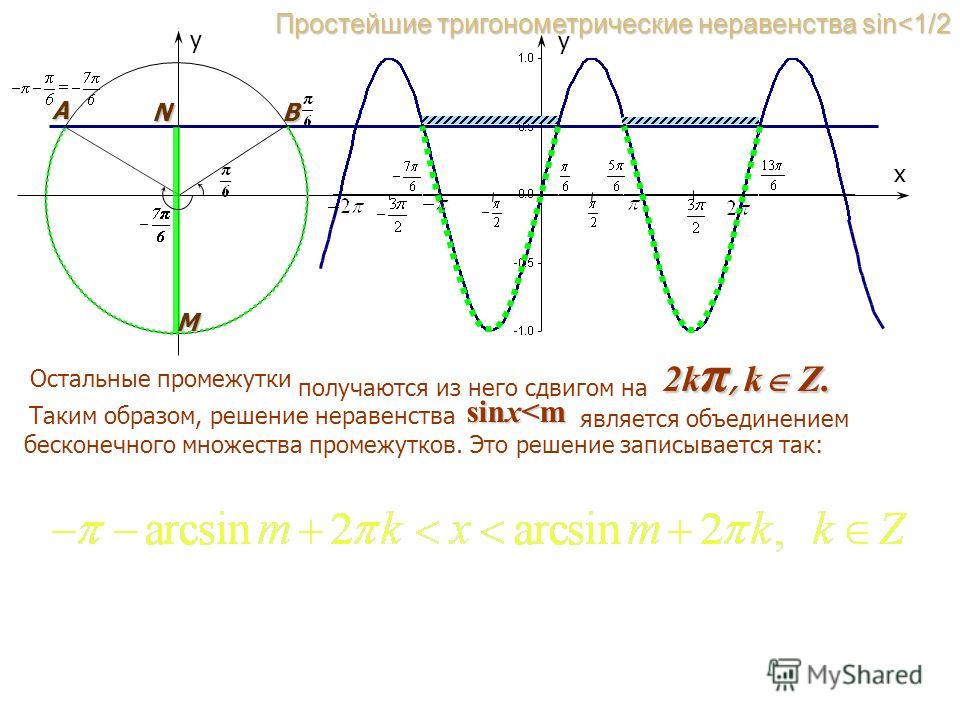 Это метод, использованный в примере ниже.
Это метод, использованный в примере ниже.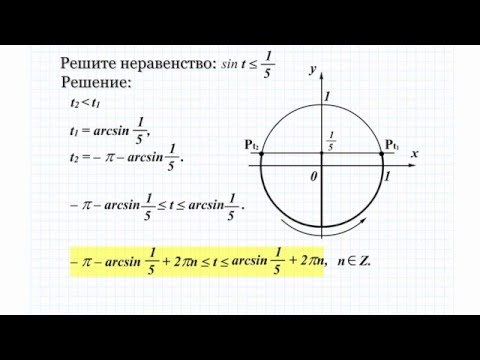 Мы видим, что \ (x \) — координаты точек пересечения соответствуют десятичным представлениям наших точных ответов.
Мы видим, что \ (x \) — координаты точек пересечения соответствуют десятичным представлениям наших точных ответов. Несмотря на бесконечное множество решений, мы обнаруживаем, что \ textit {none} из них лежат в \ ([0,2 \ pi) \). Чтобы проверить это графически, мы используем взаимное тождество, чтобы переписать косеканс как синус, и мы обнаруживаем, что \ (y = \ frac {1} {\ sin \ left (\ frac {1} {3} x- \ pi \ right )} \) и \ (y = \ sqrt {2} \) вообще не пересекаются на интервале \ ([0,2 \ pi) \).
Несмотря на бесконечное множество решений, мы обнаруживаем, что \ textit {none} из них лежат в \ ([0,2 \ pi) \). Чтобы проверить это графически, мы используем взаимное тождество, чтобы переписать косеканс как синус, и мы обнаруживаем, что \ (y = \ frac {1} {\ sin \ left (\ frac {1} {3} x- \ pi \ right )} \) и \ (y = \ sqrt {2} \) вообще не пересекаются на интервале \ ([0,2 \ pi) \). Мы выбираем \ footnote {Читателю предлагается увидеть, что произойдет, если вместо этого мы выбрали взаимное тождество \ (\ cot (3x) = \ frac {1} {\ tan (3x)} \). График на калькуляторе \ textit {выглядит} идентичным, но что происходит, когда вы пытаетесь найти точки пересечения?}, Чтобы использовать тождество частного \ (\ cot (3x) = \ frac {\ cos (3x)} {\ sin (3x)} \). Изобразив \ (y = \ frac {\ cos (3x)} {\ sin (3x)} \) и \ (y = 0 \) (ось \ (x \)), мы видим, что \ (x \ ) -координаты точек пересечения примерно совпадают с нашими решениями.{2} (x) = 4 \) происходит не из аргумента секанса, который есть просто \ (x \), а скорее из того факта, что секанс возводится в квадрат. Чтобы это уравнение выглядело как одна из форм, перечисленных на странице \ pageref {trigeqnstrategy1}, мы извлекаем квадратные корни, чтобы получить \ (\ sec (x) = \ pm 2 \). Преобразуя в косинусы, мы получаем \ (\ cos (x) = \ pm \ frac {1} {2} \). Для \ (\ cos (x) = \ frac {1} {2} \) мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac { 5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Для \ (\ cos (x) = — \ frac {1} {2} \) мы получаем \ (x = \ frac {2 \ pi} {3} + 2 \ pi k \) или \ (x = \ frac {4 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \).Если мы сделаем шаг назад и подумаем об этих семействах решений геометрически, мы увидим, что находим меры всех углов с опорным углом \ (\ frac {\ pi} {3} \). В результате эти решения могут быть объединены, и мы можем записать наши решения как \ (x = \ frac {\ pi} {3} + \ pi k \) и \ (x = \ frac {2 \ pi} {3} + \ pi k \) для целых чисел \ (k \). Чтобы проверить первое семейство решений, отметим, что, в зависимости от целого числа \ (k \), \ (\ sec \ left (\ frac {\ pi} {3} + \ pi k \ right) \) не всегда равно \ (\ sec \ left (\ frac {\ pi} {3} \ right) \).2 & \\ [3pt]
Мы выбираем \ footnote {Читателю предлагается увидеть, что произойдет, если вместо этого мы выбрали взаимное тождество \ (\ cot (3x) = \ frac {1} {\ tan (3x)} \). График на калькуляторе \ textit {выглядит} идентичным, но что происходит, когда вы пытаетесь найти точки пересечения?}, Чтобы использовать тождество частного \ (\ cot (3x) = \ frac {\ cos (3x)} {\ sin (3x)} \). Изобразив \ (y = \ frac {\ cos (3x)} {\ sin (3x)} \) и \ (y = 0 \) (ось \ (x \)), мы видим, что \ (x \ ) -координаты точек пересечения примерно совпадают с нашими решениями.{2} (x) = 4 \) происходит не из аргумента секанса, который есть просто \ (x \), а скорее из того факта, что секанс возводится в квадрат. Чтобы это уравнение выглядело как одна из форм, перечисленных на странице \ pageref {trigeqnstrategy1}, мы извлекаем квадратные корни, чтобы получить \ (\ sec (x) = \ pm 2 \). Преобразуя в косинусы, мы получаем \ (\ cos (x) = \ pm \ frac {1} {2} \). Для \ (\ cos (x) = \ frac {1} {2} \) мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac { 5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Для \ (\ cos (x) = — \ frac {1} {2} \) мы получаем \ (x = \ frac {2 \ pi} {3} + 2 \ pi k \) или \ (x = \ frac {4 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \).Если мы сделаем шаг назад и подумаем об этих семействах решений геометрически, мы увидим, что находим меры всех углов с опорным углом \ (\ frac {\ pi} {3} \). В результате эти решения могут быть объединены, и мы можем записать наши решения как \ (x = \ frac {\ pi} {3} + \ pi k \) и \ (x = \ frac {2 \ pi} {3} + \ pi k \) для целых чисел \ (k \). Чтобы проверить первое семейство решений, отметим, что, в зависимости от целого числа \ (k \), \ (\ sec \ left (\ frac {\ pi} {3} + \ pi k \ right) \) не всегда равно \ (\ sec \ left (\ frac {\ pi} {3} \ right) \).2 & \\ [3pt] 2} \) и \ (y = 4 \) подтверждают наши ответы.{2} (x)} \) и \ boldmath \ (y = 4 \) \\
2} \) и \ (y = 4 \) подтверждают наши ответы.{2} (x)} \) и \ boldmath \ (y = 4 \) \\ Продвижение \ (k \) к \ (2 \) дает \ (x = 2 \ arctan (-3) + 4 \ pi \). Еще раз, мы получаем из \ (- \ pi <2 \ arctan (-3) <0 \), что \ (3 \ pi <2 \ arctan (-3) + 4 \ pi <4 \ pi \).Поскольку это находится вне интервала \ ([0,2 \ pi) \), мы отбрасываем \ (x = 2 \ arctan (-3) + 4 \ pi \) и все решения вида \ (x = 2 \ arctan (-3) + 2 \ pi k \) для \ (k> 2 \). Графически мы видим, что \ (y = \ tan \ left (\ frac {x} {2} \ right) \) и \ (y = -3 \) пересекаются только один раз на \ ([0,2 \ pi) \) при \ (x = 2 \ arctan (-3) + 2 \ pi \ приблизительно 3,7851 \).
Продвижение \ (k \) к \ (2 \) дает \ (x = 2 \ arctan (-3) + 4 \ pi \). Еще раз, мы получаем из \ (- \ pi <2 \ arctan (-3) <0 \), что \ (3 \ pi <2 \ arctan (-3) + 4 \ pi <4 \ pi \).Поскольку это находится вне интервала \ ([0,2 \ pi) \), мы отбрасываем \ (x = 2 \ arctan (-3) + 4 \ pi \) и все решения вида \ (x = 2 \ arctan (-3) + 2 \ pi k \) для \ (k> 2 \). Графически мы видим, что \ (y = \ tan \ left (\ frac {x} {2} \ right) \) и \ (y = -3 \) пересекаются только один раз на \ ([0,2 \ pi) \) при \ (x = 2 \ arctan (-3) + 2 \ pi \ приблизительно 3,7851 \). 87) \ right) & \ text {($ \ sin (\ pi — t) = \ sin (t) $)} \\ [3pt]
87) \ right) & \ text {($ \ sin (\ pi — t) = \ sin (t) $)} \\ [3pt] 87) \) и \ (x = \ frac {3 \ pi} {2} — \ frac {1} {2} \ arcsin (0.87) \). Построив графики \ (y = \ sin (2x) \) и \ (y = 0.87 \), подтверждаем наши результаты.
87) \) и \ (x = \ frac {3 \ pi} {2} — \ frac {1} {2} \ arcsin (0.87) \). Построив графики \ (y = \ sin (2x) \) и \ (y = 0.87 \), подтверждаем наши результаты. Затем мы положим \ (f (x) = 2 \ sin (x) — 1 \) и отметим, что наше исходное неравенство эквивалентно решению \ (f (x) \ leq 0 \). Теперь посмотрим, где, если вообще, \ (f \) не определено, а где \ (f (x) = 0 \). Поскольку область определения \ (f \) — все действительные числа, мы можем немедленно приступить к поиску нулей \ (f \). Решая \ (f (x) = 0 \), мы имеем \ (2 \ sin (x) — 1 = 0 \) или \ (\ sin (x) = \ frac {1} {2} \). Здесь решениями являются \ (x = \ frac {\ pi} {6} + 2 \ pi k \) и \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ ( к \). Поскольку мы ограничиваем наше внимание \ ([0,2 \ pi) \), только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) нас беспокоят.Затем мы выбираем тестовые значения в \ ([0,2 \ pi) \), отличные от нулей, и определяем, является ли \ (f \) там положительным или отрицательным. Для \ (x = 0 \) имеем \ (f (0) = -1 \), для \ (x = \ frac {\ pi} {2} \) получаем \ (f \ left (\ frac {\ pi} {2} \ right) = 1 \) и для \ (x = \ pi \) получаем \ (f (\ pi) = -1 \). Поскольку наше исходное неравенство эквивалентно \ (f (x) \ leq 0 \), мы ищем, где функция отрицательна \ ((-) \) или \ (0 \), и получаем интервалы \ (\ left [0, \ frac {\ pi} {6} \ right] \ cup \ left [\ frac {5 \ pi} {6}, 2 \ pi \ right) \).Мы можем подтвердить наш ответ графически, увидев, где график \ (y = 2 \ sin (x) \) пересекает или находится ниже графика \ (y = 1 \).
Затем мы положим \ (f (x) = 2 \ sin (x) — 1 \) и отметим, что наше исходное неравенство эквивалентно решению \ (f (x) \ leq 0 \). Теперь посмотрим, где, если вообще, \ (f \) не определено, а где \ (f (x) = 0 \). Поскольку область определения \ (f \) — все действительные числа, мы можем немедленно приступить к поиску нулей \ (f \). Решая \ (f (x) = 0 \), мы имеем \ (2 \ sin (x) — 1 = 0 \) или \ (\ sin (x) = \ frac {1} {2} \). Здесь решениями являются \ (x = \ frac {\ pi} {6} + 2 \ pi k \) и \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ ( к \). Поскольку мы ограничиваем наше внимание \ ([0,2 \ pi) \), только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) нас беспокоят.Затем мы выбираем тестовые значения в \ ([0,2 \ pi) \), отличные от нулей, и определяем, является ли \ (f \) там положительным или отрицательным. Для \ (x = 0 \) имеем \ (f (0) = -1 \), для \ (x = \ frac {\ pi} {2} \) получаем \ (f \ left (\ frac {\ pi} {2} \ right) = 1 \) и для \ (x = \ pi \) получаем \ (f (\ pi) = -1 \). Поскольку наше исходное неравенство эквивалентно \ (f (x) \ leq 0 \), мы ищем, где функция отрицательна \ ((-) \) или \ (0 \), и получаем интервалы \ (\ left [0, \ frac {\ pi} {6} \ right] \ cup \ left [\ frac {5 \ pi} {6}, 2 \ pi \ right) \).Мы можем подтвердить наш ответ графически, увидев, где график \ (y = 2 \ sin (x) \) пересекает или находится ниже графика \ (y = 1 \).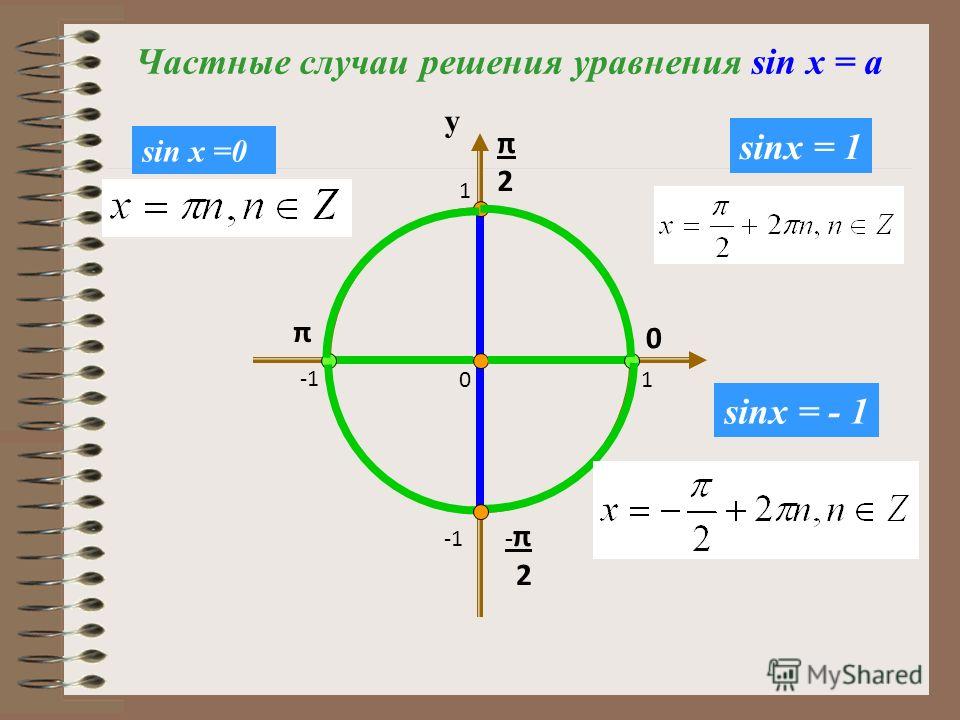 Для \ (2 \ sin (x) — 1 = 0 \) мы получаем \ (\ sin (x) = \ frac {1} {2} \), что дает \ (x = \ frac {\ pi} {6 } + 2 \ pi k \) или \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Из них только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) лежат в \ ([0,2 \ pi) \). Далее мы выбираем наши тестовые значения. Для \ (x = 0 \) находим \ (f (0) = -1 $; когда \ (x = \ frac {\ pi} {4} \) получаем \ (f \ left (\ frac {\ pi } {4} \ right) = 1 — \ frac {\ sqrt {2}} {2} = \ frac {2 — \ sqrt {2}} {2} $; для \ (x = \ frac {3 \ pi } {4} \) получаем \ (f \ left (\ frac {3 \ pi} {4} \ right) = -1 + \ frac {\ sqrt {2}} {2} = \ frac {\ sqrt { 2} — 2} {2} $; когда \ (x = \ pi \) имеем \ (f (\ pi) = 1 \), и, наконец, для \ (x = \ frac {7 \ pi} {4 } \) получаем \ (f \ left (\ frac {7 \ pi} {4} \ right) = -1 — \ frac {\ sqrt {2}} {2} = \ frac {-2 — \ sqrt { 2}} {2} \).Мы видим \ (f (x)> 0 \) на \ (\ left (\ frac {\ pi} {6}, \ frac {\ pi} {2} \ right) \ cup \ left (\ frac {5 \ pi} {6}, \ frac {3 \ pi} {2} \ right) \), так что это наш ответ. Мы можем использовать калькулятор, чтобы проверить, что график \ (y = \ sin (2x) \) действительно находится над графиком \ (y = \ cos (x) \) на этих интервалах.
Для \ (2 \ sin (x) — 1 = 0 \) мы получаем \ (\ sin (x) = \ frac {1} {2} \), что дает \ (x = \ frac {\ pi} {6 } + 2 \ pi k \) или \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Из них только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) лежат в \ ([0,2 \ pi) \). Далее мы выбираем наши тестовые значения. Для \ (x = 0 \) находим \ (f (0) = -1 $; когда \ (x = \ frac {\ pi} {4} \) получаем \ (f \ left (\ frac {\ pi } {4} \ right) = 1 — \ frac {\ sqrt {2}} {2} = \ frac {2 — \ sqrt {2}} {2} $; для \ (x = \ frac {3 \ pi } {4} \) получаем \ (f \ left (\ frac {3 \ pi} {4} \ right) = -1 + \ frac {\ sqrt {2}} {2} = \ frac {\ sqrt { 2} — 2} {2} $; когда \ (x = \ pi \) имеем \ (f (\ pi) = 1 \), и, наконец, для \ (x = \ frac {7 \ pi} {4 } \) получаем \ (f \ left (\ frac {7 \ pi} {4} \ right) = -1 — \ frac {\ sqrt {2}} {2} = \ frac {-2 — \ sqrt { 2}} {2} \).Мы видим \ (f (x)> 0 \) на \ (\ left (\ frac {\ pi} {6}, \ frac {\ pi} {2} \ right) \ cup \ left (\ frac {5 \ pi} {6}, \ frac {3 \ pi} {2} \ right) \), так что это наш ответ. Мы можем использовать калькулятор, чтобы проверить, что график \ (y = \ sin (2x) \) действительно находится над графиком \ (y = \ cos (x) \) на этих интервалах. {2} (x) = \ tan (x) + 3 \)
{2} (x) = \ tan (x) + 3 \) Чтобы решить \ (\ tan (x) = 2 \), мы используем функцию арктангенса и получаем \ (x = \ arctan (2) + \ pi k \) для целых чисел \ (k \). Из первого набора решений мы получаем \ (x = \ frac {3 \ pi} {4} \) и \ (x = \ frac {5 \ pi} {4} \) как наши ответы, которые лежат в \ ( [0,2 \ пи) \).2–3 u + 1 & = & 0 & \ text {Пусть \ (u = \ cos (x) \).} \\
Чтобы решить \ (\ tan (x) = 2 \), мы используем функцию арктангенса и получаем \ (x = \ arctan (2) + \ pi k \) для целых чисел \ (k \). Из первого набора решений мы получаем \ (x = \ frac {3 \ pi} {4} \) и \ (x = \ frac {5 \ pi} {4} \) как наши ответы, которые лежат в \ ( [0,2 \ пи) \).2–3 u + 1 & = & 0 & \ text {Пусть \ (u = \ cos (x) \).} \\ Отсюда получаем \ (\ sin (4x) = 0 \) или \ (\ sin (x) \) = 0. Решение \ (\ sin (4x) = 0 \) дает \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \), а решение \ (\ sin (x) = 0 \) — \ (x = \ pi k \) для целых чисел \ (k \). Второй набор решений содержится в первом наборе решений, \ footnote {Как всегда, если есть сомнения, запишите его!}, Поэтому наше окончательное решение для \ (\ cos (5x) = \ cos (3x) \) будет \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \). Есть восемь из этих ответов, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {4} \), \ (\ frac {\ pi } {2} \), \ (\ frac {3 \ pi} {4} \), \ (\ pi \), \ (\ frac {5 \ pi} {4} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {7 \ pi} {4} \).Наш график графиков \ (y = \ cos (3x) \) и \ (y = \ cos (5x) \) ниже (после некоторого осторожного увеличения) подтверждает это.
Отсюда получаем \ (\ sin (4x) = 0 \) или \ (\ sin (x) \) = 0. Решение \ (\ sin (4x) = 0 \) дает \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \), а решение \ (\ sin (x) = 0 \) — \ (x = \ pi k \) для целых чисел \ (k \). Второй набор решений содержится в первом наборе решений, \ footnote {Как всегда, если есть сомнения, запишите его!}, Поэтому наше окончательное решение для \ (\ cos (5x) = \ cos (3x) \) будет \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \). Есть восемь из этих ответов, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {4} \), \ (\ frac {\ pi } {2} \), \ (\ frac {3 \ pi} {4} \), \ (\ pi \), \ (\ frac {5 \ pi} {4} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {7 \ pi} {4} \).Наш график графиков \ (y = \ cos (3x) \) и \ (y = \ cos (5x) \) ниже (после некоторого осторожного увеличения) подтверждает это. Ответы, которые лежат в \ ([0,2 \ pi) \): \ (x = \ frac {\ pi} {2} \), \ (\ frac {3 \ pi} {2} \), \ ( \ frac {\ pi} {3} \) и \ (\ frac {2 \ pi} {3} \). Мы строим графики \ (y = \ sin (2x) \) и \ (y = \ sqrt {3} \ cos (x) \) и, после некоторого осторожного увеличения, проверяем наши ответы.
Ответы, которые лежат в \ ([0,2 \ pi) \): \ (x = \ frac {\ pi} {2} \), \ (\ frac {3 \ pi} {2} \), \ ( \ frac {\ pi} {3} \) и \ (\ frac {2 \ pi} {3} \). Мы строим графики \ (y = \ sin (2x) \) и \ (y = \ sqrt {3} \ cos (x) \) и, после некоторого осторожного увеличения, проверяем наши ответы. Решая последнее, мы получаем \ (x = — \ frac {\ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Только одно из этих решений, \ (x = \ frac {5 \ pi} {3} \), которое соответствует \ (k = 1 \), лежит в \ ([0,2 \ pi) \). Геометрически мы видим, что \ (y = \ cos (x) — \ sqrt {3} \ sin (x) \) и \ (y = 2 \) пересекаются только один раз, что подтверждает наш ответ.
Решая последнее, мы получаем \ (x = — \ frac {\ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Только одно из этих решений, \ (x = \ frac {5 \ pi} {3} \), которое соответствует \ (k = 1 \), лежит в \ ([0,2 \ pi) \). Геометрически мы видим, что \ (y = \ cos (x) — \ sqrt {3} \ sin (x) \) и \ (y = 2 \) пересекаются только один раз, что подтверждает наш ответ.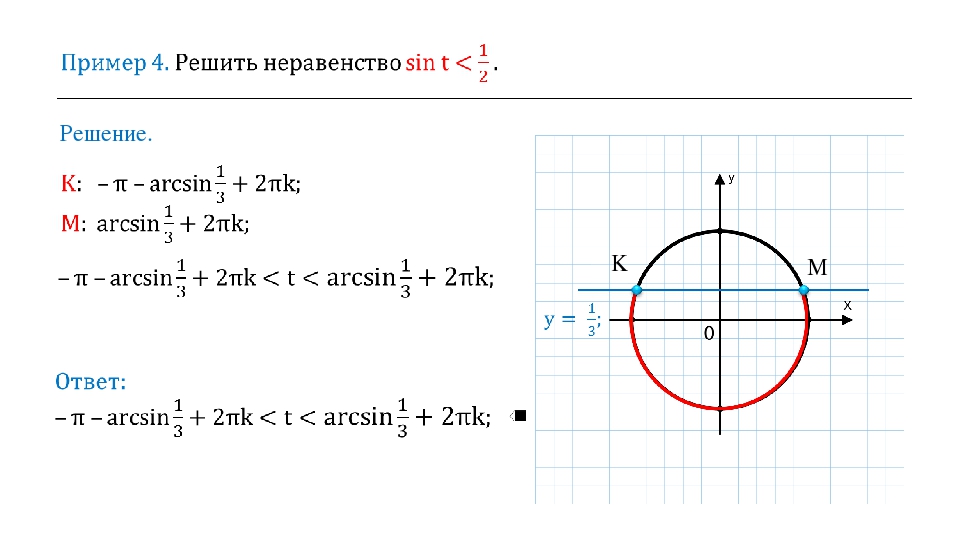 Интервалы, составляющие домен, имеют вид \ (\ left (x _ {\ mbox {\ tiny \ (k $}}), x _ {\ mbox { \ tiny \ (k + 1 $}} \ right) = \ left (\ frac {(3k-1) \ pi} {6}, \ frac {(3k + 2) \ pi} {6} \ right) \ ) как \ (k \) пробегает целые числа.{\ infty} \ left (\ dfrac {(3k-1) \ pi} {6}, \ dfrac {(3k + 2) \ pi} {6} \ right) \]
Интервалы, составляющие домен, имеют вид \ (\ left (x _ {\ mbox {\ tiny \ (k $}}), x _ {\ mbox { \ tiny \ (k + 1 $}} \ right) = \ left (\ frac {(3k-1) \ pi} {6}, \ frac {(3k + 2) \ pi} {6} \ right) \ ) как \ (k \) пробегает целые числа.{\ infty} \ left (\ dfrac {(3k-1) \ pi} {6}, \ dfrac {(3k + 2) \ pi} {6} \ right) \] {\ infty} \ left (\ frac {(6k + 1) \ pi} {3}, \ frac {(6k + 5) \ pi} {3} \ right) \ cup \ left (\ frac {(6k + 5) \ pi} {3}, \ frac {(6k + 7) \ pi} {3} \ right) \]
{\ infty} \ left (\ frac {(6k + 1) \ pi} {3}, \ frac {(6k + 5) \ pi} {3} \ right) \ cup \ left (\ frac {(6k + 5) \ pi} {3}, \ frac {(6k + 7) \ pi} {3} \ right) \] Положим \ (g (x) = 1 — \ cot (x) \) и приступим к построению знаковой диаграммы для \ (g \) на интервале \ ((0, \ pi) \), чтобы найти, где \ (g (х) \ geq 0 \). Отметим, что \ (g \) не определено для \ (x = \ pi k \) для целых чисел \ (k \), в частности, на концах нашего интервала \ (x = 0 \) и \ (x = \ Пи\). Далее ищем нули \ (g \). Решая \ (g (x) = 0 \), мы получаем \ (\ cot (x) = 1 \) или \ (x = \ frac {\ pi} {4} + \ pi k \) для целых чисел \ (k \) и только один из них, \ (x = \ frac {\ pi} {4} \), лежит в \ ((0, \ pi) \). Выбирая тестовые значения \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {\ pi} {2} \), получаем \ (g \ left (\ frac {\ pi} {6} \ right) = 1 — \ sqrt {3} \) и \ (g \ left (\ frac {\ pi} {2} \ right) = 1 \).{\ infty} \ left [\ dfrac {(4k + 1) \ pi} {4}, (k + 1) \ pi \ right) \]
Положим \ (g (x) = 1 — \ cot (x) \) и приступим к построению знаковой диаграммы для \ (g \) на интервале \ ((0, \ pi) \), чтобы найти, где \ (g (х) \ geq 0 \). Отметим, что \ (g \) не определено для \ (x = \ pi k \) для целых чисел \ (k \), в частности, на концах нашего интервала \ (x = 0 \) и \ (x = \ Пи\). Далее ищем нули \ (g \). Решая \ (g (x) = 0 \), мы получаем \ (\ cot (x) = 1 \) или \ (x = \ frac {\ pi} {4} + \ pi k \) для целых чисел \ (k \) и только один из них, \ (x = \ frac {\ pi} {4} \), лежит в \ ((0, \ pi) \). Выбирая тестовые значения \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {\ pi} {2} \), получаем \ (g \ left (\ frac {\ pi} {6} \ right) = 1 — \ sqrt {3} \) и \ (g \ left (\ frac {\ pi} {2} \ right) = 1 \).{\ infty} \ left [\ dfrac {(4k + 1) \ pi} {4}, (k + 1) \ pi \ right) \] Авторы и авторство
7.5 Решение тригонометрических уравнений — предварительное вычисление
Цели обучения
 Эта теория, основанная на пропорциях, имеет приложения в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол депрессии находят с помощью одинаковых треугольников.
Эта теория, основанная на пропорциях, имеет приложения в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол депрессии находят с помощью одинаковых треугольников. Решение линейных тригонометрических уравнений с синусом и косинусом
 Мы читаем уравнение слева направо по горизонтали, как предложение. Мы ищем известные закономерности, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Мы читаем уравнение слева направо по горизонтали, как предложение. Мы ищем известные закономерности, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах. Пример 1
Решение линейного тригонометрического уравнения с использованием функции косинуса
Решение
Пример 2
Решение линейного уравнения с синусоидальной функцией
Решение
Как это сделать

Пример 3
Решите тригонометрическое уравнение в линейной форме
Решение
Решение уравнений, содержащих одну тригонометрическую функцию
Пример 4
Решение задачи, связанной с одной тригонометрической функцией
Решение
 sinθ. Потом найдем углы.
sinθ. Потом найдем углы. Пример 5
Решение тригонометрического уравнения с использованием косеканса
Решение
Анализ
Пример 6
Решение уравнения с касательной
Решение
Пример 7
Определите все решения уравнения, содержащего касательную
Решение
 θ = 7π4.
θ = 7π4. Решение тригонометрических уравнений с помощью калькулятора
Пример 8
Использование калькулятора для решения тригонометрического уравнения с синусом
Решение
Анализ
Пример 9
Использование калькулятора для решения тригонометрического уравнения с секущей
Решение
 Теперь используйте функцию обратного косинуса.
Теперь используйте функцию обратного косинуса. Решение тригонометрических уравнений в квадратичной форме
Пример 10
Решение тригонометрического уравнения в квадратичной форме
Решение
 Пусть cosθ = x.cosθ = x. У нас
Пусть cosθ = x.cosθ = x. У нас Пример 11
Решение тригонометрического уравнения в квадратичной форме с помощью факторинга
Решение
Анализ
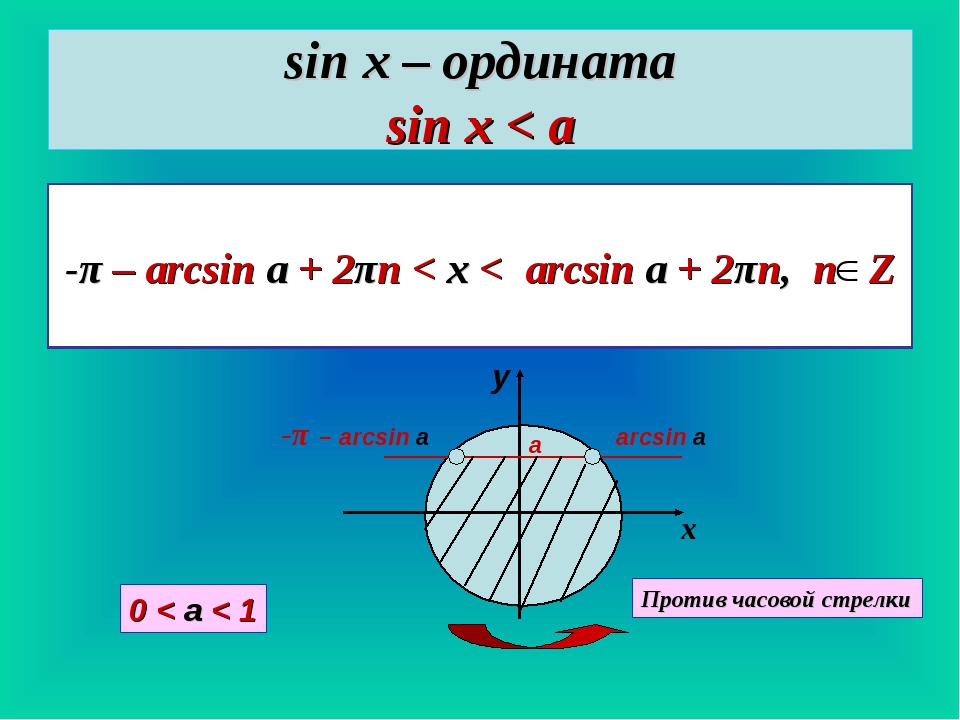 sin2θ = 2cosθ + 2,0≤θ≤2π.[Подсказка: сделайте замену, чтобы выразить уравнение только через косинус.]
sin2θ = 2cosθ + 2,0≤θ≤2π.[Подсказка: сделайте замену, чтобы выразить уравнение только через косинус.] Пример 12
Решение тригонометрического уравнения с помощью алгебры
Решение
Анализ
Пример 13
Решение тригонометрического уравнения, квадратичного по форме
 2sin2θ − 3sinθ + 1 = 0,0≤θ <2π.
2sin2θ − 3sinθ + 1 = 0,0≤θ <2π. Решение
Решение тригонометрических уравнений с использованием фундаментальных тождеств
Пример 14
Использование идентичностей для решения уравнения
Решение
Пример 15
Решение уравнения с использованием формулы двойного угла
 cos (2θ) = cosθ.
cos (2θ) = cosθ. Решение
Пример 16
Решение уравнения с использованием идентификатора
Решение
Решение тригонометрических уравнений с несколькими углами
 Такое сжатие графика приводит нас к выводу, что может быть в два раза больше перехватов или решений x для sin (2x) = 0sin (2x) = 0 по сравнению с sinx = 0. sinx = 0. Эта информация поможет нам решить уравнение.
Такое сжатие графика приводит нас к выводу, что может быть в два раза больше перехватов или решений x для sin (2x) = 0sin (2x) = 0 по сравнению с sinx = 0. sinx = 0. Эта информация поможет нам решить уравнение. Пример 17
Решение многоугольного тригонометрического уравнения
Решение

Решение задач прямоугольного треугольника
Пример 18
Использование теоремы Пифагора для моделирования уравнения
Решение
Пример 19
Использование теоремы Пифагора для моделирования абстрактной задачи
 Найдите угол, под которым лестница любой длины образует с землей, и высоту, на которой лестница касается стены.
Найдите угол, под которым лестница любой длины образует с землей, и высоту, на которой лестница касается стены. Решение
7.Упражнения из 5 частей
Устные
1. Алгебраический

 [0,2π). Ищите возможности использовать тригонометрические тождества.
[0,2π). Ищите возможности использовать тригонометрические тождества. Графический
Технологии

Расширения
Реальные приложения
93.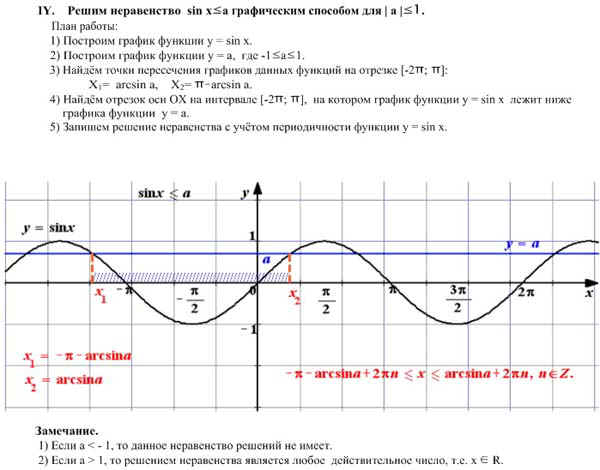 )
) Репетитор по математике — Экстра — Уравнения и неравенства
Репетитор по математике — Экстра — Уравнения и неравенства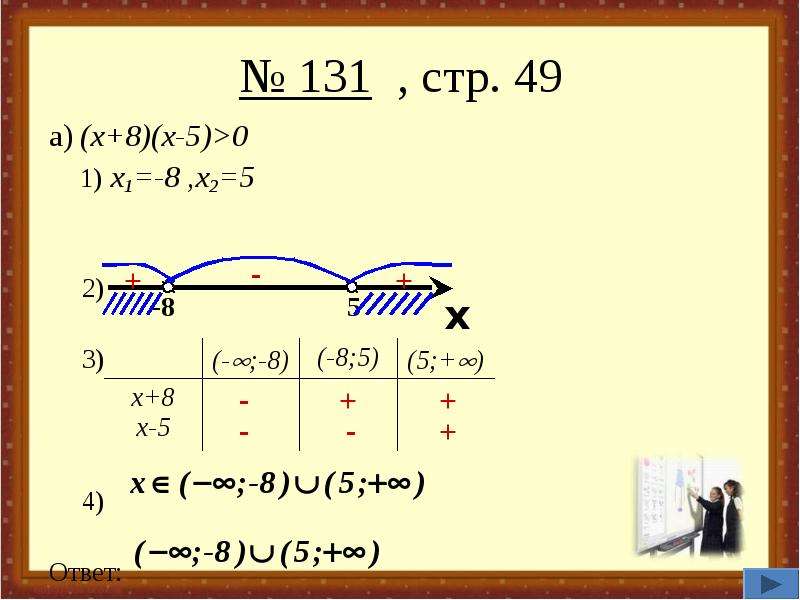
Уравнения
x = e 2 .
x = 1.
x = π / 2, Поэтому мы имеем дело с arcsin в регионе
где он обратим и формула работает.
Поэтому мы имеем дело с arcsin в регионе
где он обратим и формула работает.
[] 2 = 3 2 ,
x = 9.
[ x 2 ] 1/2 = 16 1/2 ,
x = 4.
[(2- x 2 ) 1/2 ] 2 = x 2 ,
2- x 2 = x 2 ,
2 x 2 = 2,
x 2 = 1,
x = 1, −1.
Неравенства
 И снова, иногда применяемая функция бывает только монотонной.
где-то и все становится еще интереснее.
И снова, иногда применяемая функция бывает только монотонной.
где-то и все становится еще интереснее. Знаковые неравенства

 В
соответствующее неравенство: x + 2> 0, поэтому с самого начала
мы ограничиваем наши вычисления до x > −2. Теперь приступим к обычному
алгоритм. Первые ноль баллов. Уравнения
3 — x = 0, x + 5 = 0, x — 1 = 0,2 x — 1 = 0, ln ( x + 2) = 0 есть решения x = 3, x = −5, x = 1, x = 1/2,
и x + 2 = 1, то есть х = -1.
В
соответствующее неравенство: x + 2> 0, поэтому с самого начала
мы ограничиваем наши вычисления до x > −2. Теперь приступим к обычному
алгоритм. Первые ноль баллов. Уравнения
3 — x = 0, x + 5 = 0, x — 1 = 0,2 x — 1 = 0, ln ( x + 2) = 0 есть решения x = 3, x = −5, x = 1, x = 1/2,
и x + 2 = 1, то есть х = -1. Двойное неравенство
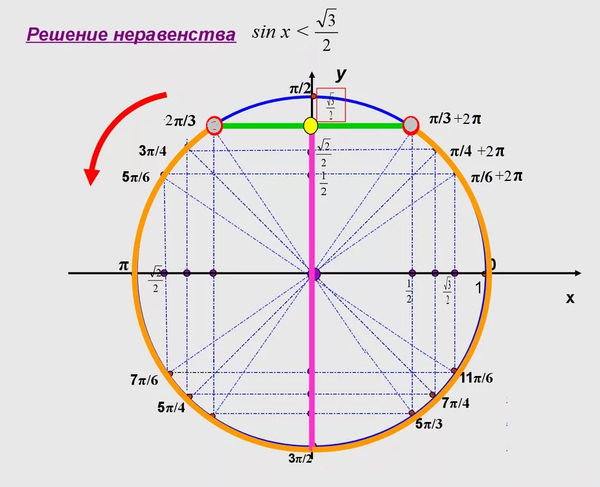
Разделение реальной строки

(In) равенство с триггерами
 Отправная точка здесь проста
(in) равенства типа sin ( x ) = 1 или
cos ( x ) <1/2. Лучший способ решить такие (не) равенства
заключается в использовании соответствующего графа. Наверное, самый простой способ - сначала
определить решение в течение одного периода, а затем добавить к нему периодичность.
Отправная точка здесь проста
(in) равенства типа sin ( x ) = 1 или
cos ( x ) <1/2. Лучший способ решить такие (не) равенства
заключается в использовании соответствующего графа. Наверное, самый простой способ - сначала
определить решение в течение одного периода, а затем добавить к нему периодичность.
Решите тригонометрические уравнения и неравенства в квадратичной форме
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105 Решение линейных неравенств


 2cos 3x + 1 = 0
2cos 3x + 1 = 0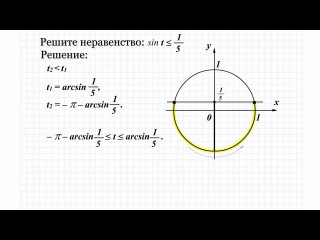 2cos
2cos coscos x +
coscos x +