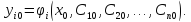Система линейных дифференциальных уравнений — Википедия
Материал из Википедии — свободной энциклопедии
Система линейных дифференциальных уравнений (СЛДУ) — система обыкновенных дифференциальных уравнений, которая является линейной относительно всех искомых функций yi(x){\displaystyle y_{i}(x)} и их производных всех порядков. Такую систему можно преобразовать к линейной системе первого порядка канонического вида, которую обычно и определяют, как СЛДУ.
Если в системе n{\displaystyle n} дифференциальных уравнений имеется производная yi(k+1),k>0{\displaystyle y_{i}^{(k+1)},k>0}, то можно добавить новую искомую функцию yn+1{\displaystyle y_{n+1}}, определяемую новым линейным уравнением yi(k)=yn+1{\displaystyle y_{i}^{(k)}=y_{n+1}}. Заменой yi(k+1)=yn+1′{\displaystyle y_{i}^{(k+1)}=y_{n+1}’} в остальных уравнениях производнаяyi(k+1){\displaystyle y_{i}^{(k+1)}} исключается из системы. Последовательное выполнение этих операций для линейной системы приводит к линейной системе первого порядка. В линейной системе каждую производную можно подстановкой исключить из всех уравнений кроме одного. Поэтому систему линейных дифференциальных уравнений обычно определяют, как систему вида [1]
- yj′=∑k=1npjk(x)yk+fj(x),j=1,2,…,n{\displaystyle y’_{j}=\sum _{k=1}^{n}{p_{jk}(x)y_{k}}+f_{j}(x),j=1,2,\dots ,n}
Линейное дифференциальное уравнение[править | править код]
Если дано линейное дифференциальное уравнение порядка n{\displaystyle n}
- y0(n)=∑k=0n−1pk(x)y0(k)+fj(x){\displaystyle y_{0}^{(n)}=\sum _{k=0}^{n-1}{p_{k}(x)y_{0}^{(k)}}+f_{j}(x)},
то описанным выше способом его можно преобразовать в систему n{\displaystyle n} уравнений следующего вида
- {y0′=y1y1′=y2⋯yn−2′=yn−2yn−1′=∑k=0n−1pk(x)yk+fj(x){\displaystyle {\begin{cases}y’_{0}=y_{1}\\y’_{1}=y_{2}\\\cdots \\y’_{n-2}=y_{n-2}\\y’_{n-1}=\sum _{k=0}^{n-1}{p_{k}(x)y_{k}}+f_{j}(x)\end{cases}}}
Общее решение однородной СЛДУ, получаемой приравниванием всех fj(x){\displaystyle f_{j}(x)} к нулю даётся формулами
- yj=∑k=1nCkyjk(x){\displaystyle y_{j}=\sum _{k=1}^{n}{C_{k}y_{jk}(x)}}
где yj1,yj2,…,yjn{\displaystyle y_{j1},y_{j2},\dots ,y_{jn}} — линейно независимые частные решения однородной системы, то есть такие, что определитель ||y(x)ij||≠0{\displaystyle ||y(x)_{ij}||\neq 0} хотя бы в одной точке. В случае постоянных коэффициентов p(x)jk=ajk{\displaystyle p(x)_{jk}=a_{jk}} частные решения однородной системы следует искать в виде
- yj(x)=(Aj0+Aj1x+⋯+Ajnk−1xnk−1)eλjx{\displaystyle y_{j}(x)=(A_{j0}+A_{j1}x+\dots +A_{jn_{k}-1}x^{n_{k}-1})e^{\lambda _{j}x}}
где Ajs{\displaystyle A_{js}} — неопределённые коэффициенты, λj{\displaystyle \lambda _{j}} — корни характеристического уравнения
- |a11−λa12⋯a1na21a22−λ⋯a2n⋮⋮⋱⋮an1an2⋯ann−λ|=0{\displaystyle {\begin{vmatrix}a_{11}-\lambda &a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}-\lambda &\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}-\lambda \end{vmatrix}}=0}
и nk{\displaystyle n_{k}} — кратность этих корней. Полный анализ всех возможных случаев производится методами линейной алгебры. Для решения СЛДУ с постоянными коэффициентами применяются также методы операционного исчисления.
- Степанов В. В., Курс дифференциальных уравнений, 9 изд., М.,1966
- Понтрягин Л.С., Обыкновенные дифференциальные уравнения, 4 изд., М., 1974.
44. Система линейных дифференциальных уравнений первого порядка. Фср однородной системы. Общее решение однородной системы.
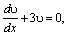
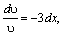 ln υ =–3x,υ=e–3x.
Подставляем
найденное значение υ в исходное
дифференциальное уравнение, получаем
уравнение с разделяющимися переменными:
ln υ =–3x,υ=e–3x.
Подставляем
найденное значение υ в исходное
дифференциальное уравнение, получаем
уравнение с разделяющимися переменными: .
Итак, общее решение данного уравнения
имеет вид:
.
Итак, общее решение данного уравнения
имеет вид: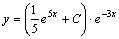 .
Найдем частное решение. Для этого
подставим начальные условия в
выражение для общего решения и найдем
С.
.
Найдем частное решение. Для этого
подставим начальные условия в
выражение для общего решения и найдем
С.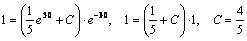 .
Частное решение имеет вид:
.
Частное решение имеет вид: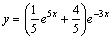
Линейное однородное
ОДУ:  .
.
Теорема о структуре общего решения линейного однородного уравнения:
Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y1(x), y2(x),…, yn(x) линейно независимые решения этого уравнения, то общее решение уравнения имеет вид
 ,
,
где C1,…,Cn — произвольные постоянные.
Фундаментальная система решений нормальной системы однородных линейных ОДУ с постоянными коэффициентами в случае простых действительных корней характеристического уравнения.
Нормальная линейная
однородная система n порядка с постоянными
коэффициентами — 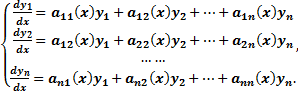 или
или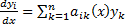 ,
,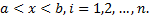 Коэффициенты линейных комбинаций
искомых функций постоянны. Эта система
в матричной форме
Коэффициенты линейных комбинаций
искомых функций постоянны. Эта система
в матричной форме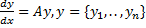 –матричная форма, где A-постоянная
матрица. Матричный метод: Из
характеристического уравнения
–матричная форма, где A-постоянная
матрица. Матричный метод: Из
характеристического уравнения  найдем различные корни
найдем различные корни 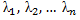 и для каждого корня
и для каждого корня  (с учетом его кратности) определим
соответствующее ему частное решение
(с учетом его кратности) определим
соответствующее ему частное решение 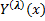 .
Общее решение имеет вид:
.
Общее решение имеет вид:  .
При этом 1) если
.
При этом 1) если 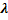 —
действительный корень кратности 1, то
—
действительный корень кратности 1, то 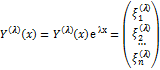 ,
где
,
где 
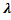 ,
то есть
,
то есть  .
2)
.
2)  – корень кратности
– корень кратности  ,
то соответствующее этому корню решение
системы ищут в виде вектора
,
то соответствующее этому корню решение
системы ищут в виде вектора
 (**), коэффициенты которого
(**), коэффициенты которого 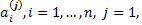 определяются из системы линейных
уравнений, получающихся приравнивание
коэффициентов при одинаковых степенях
x в результате подстановки вектора (**)
в исходную систему.
определяются из системы линейных
уравнений, получающихся приравнивание
коэффициентов при одинаковых степенях
x в результате подстановки вектора (**)
в исходную систему.
Фундаментальной
системой решений НЛОС называется
совокупность произвольных n линейно
независимых решений 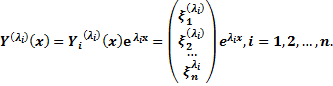
49
Система линейных дифференциальных уравнений — Википедия
Материал из Википедии — свободной энциклопедии
Система линейных дифференциальных уравнений (СЛДУ) — система обыкновенных дифференциальных уравнений, которая является линейной относительно всех искомых функций yi(x){\displaystyle y_{i}(x)} и их производных всех порядков. Такую систему можно преобразовать к линейной системе первого порядка канонического вида, которую обычно и определяют, как СЛДУ.
Определение
Если в системе n{\displaystyle n} дифференциальных уравнений имеется производная yi(k+1),k>0{\displaystyle y_{i}^{(k+1)},k>0}, то можно добавить новую искомую функцию yn+1{\displaystyle y_{n+1}}, определяемую новым линейным уравнением yi(k)=yn+1{\displaystyle y_{i}^{(k)}=y_{n+1}}. Заменой yi(k+1)=yn+1′{\displaystyle y_{i}^{(k+1)}=y_{n+1}’} в остальных уравнениях производнаяyi(k+1){\displaystyle y_{i}^{(k+1)}} исключается из системы. Последовательное выполнение этих операций для линейной системы приводит к линейной системе первого порядка. В линейной системе каждую производную можно подстановкой исключить из всех уравнений кроме одного. Поэтому систему линейных дифференциальных уравнений обычно определяют, как систему вида [1]
- yj′=∑k=1npjk(x)yk+fj(x),j=1,2,…,n{\displaystyle y’_{j}=\sum _{k=1}^{n}{p_{jk}(x)y_{k}}+f_{j}(x),j=1,2,\dots ,n}
Линейное дифференциальное уравнение
Если дано линейное дифференциальное уравнение порядка n{\displaystyle n}
- y0(n)=∑k=0n−1pk(x)y0(k)+fj(x){\displaystyle y_{0}^{(n)}=\sum _{k=0}^{n-1}{p_{k}(x)y_{0}^{(k)}}+f_{j}(x)},
то описанным выше способом его можно преобразовать в систему n{\displaystyle n} уравнений следующего вида
- {y0′=y1y1′=y2⋯yn−2′=yn−2yn−1′=∑k=0n−1pk(x)yk+fj(x){\displaystyle {\begin{cases}y’_{0}=y_{1}\\y’_{1}=y_{2}\\\cdots \\y’_{n-2}=y_{n-2}\\y’_{n-1}=\sum _{k=0}^{n-1}{p_{k}(x)y_{k}}+f_{j}(x)\end{cases}}}
Решение СЛДУ
Общее решение однородной СЛДУ, получаемой приравниванием всех fj(x){\displaystyle f_{j}(x)} к нулю даётся формулами
- yj=∑k=1nCkyjk(x){\displaystyle y_{j}=\sum _{k=1}^{n}{C_{k}y_{jk}(x)}}
где yj1,yj2,…,yjn{\displaystyle y_{j1},y_{j2},\dots ,y_{jn}} — линейно независимые частные решения однородной системы, то есть такие, что определитель ||y(x)ij||≠0{\displaystyle ||y(x)_{ij}||\neq 0} хотя бы в одной точке. В случае постоянных коэффициентов p(x)jk=ajk{\displaystyle p(x)_{jk}=a_{jk}} частные решения однородной системы следует искать в виде
- yj(x)=(Aj0+Aj1x+⋯+Ajnk−1xnk−1)eλjx{\displaystyle y_{j}(x)=(A_{j0}+A_{j1}x+\dots +A_{jn_{k}-1}x^{n_{k}-1})e^{\lambda _{j}x}}
где Ajs{\displaystyle A_{js}} — неопределённые коэффициенты, λj{\displaystyle \lambda _{j}} — корни характеристического уравнения
- |a11−λa12⋯a1na21a22−λ⋯a2n⋮⋮⋱⋮an1an2⋯ann−λ|=0{\displaystyle {\begin{vmatrix}a_{11}-\lambda &a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}-\lambda &\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}-\lambda \end{vmatrix}}=0}
и nk{\displaystyle n_{k}} — кратность этих корней. Полный анализ всех возможных случаев производится методами линейной алгебры. Для решения СЛДУ с постоянными коэффициентами применяются также методы операционного исчисления.
Примечания
Литература
- Степанов В. В., Курс дифференциальных уравнений, 9 изд., М.,1966
- Понтрягин Л.С., Обыкновенные дифференциальные уравнения, 4 изд., М., 1974.
Автономная система дифференциальных уравнений — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 марта 2013; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 марта 2013; проверки требует 1 правка.Автономная система дифференциальных уравнений (другое название: стационарная система дифференциальных уравнений) — частный случай системы дифференциальных уравнений, когда аргумент t{\displaystyle t} системы не входит явным образом в функции, задающие систему.
Автономная система в нормальном виде имеет вид:
dxkdt=fk(x1,…,xn),k=1,…,n{\displaystyle {\frac {dx_{k}}{dt}}=f_{k}(x_{1},…,x_{n}),\,k=1,…,n}
или в векторной записи:
dx¯dt=f¯(x¯){\displaystyle {\frac {d{\bar {x}}}{dt}}={\bar {f}}({\bar {x}})}
Любую систему дифференциальных уравнений можно свести к автономной, введя дополнительную вспомогательную функцию xn+1{\displaystyle x_{n+1}}, заменив ею аргумент t{\displaystyle t} там, где он входит явно, и дополнив систему ещё одним уравнением dxn+1dt=1{\displaystyle {\frac {dx_{n+1}}{dt}}=1}. Такая замена, однако, имеет преимущественно теоретическое значение, так как увеличивает размерность системы с n{\displaystyle n} на n+1{\displaystyle n+1}, что усложняет структуру семейства решений.
Если x¯=x¯(t){\displaystyle {\bar {x}}={\bar {x}}(t)} — решение автономной системы дифференциальных уравнений (в векторном виде), то эта функция остаётся решением и при сдвиге аргумента. Автономная система моделирует автономные процессы, то есть процесс, не подверженные внешним влияниям, и стационарные процессы, то есть процессы, установившиеся во времени. Все эти процессы полностью определяются начальными значениями переменных состояния, то есть x1,…,xn{\displaystyle x_{1},\dots ,x_{n}}, и не зависят от выбора начального значения аргумента t{\displaystyle t}.
- В. И. Арнольд. Обыкновенные дифференциальные уравнения.
35.1. Нормальная система дифференциальных уравнений
Система вида
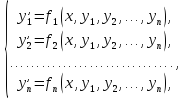
где
функции 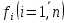 определены в некоторой
определены в некоторой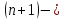 мерной
области
мерной
области 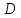 переменных
переменных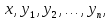 называетсянормальной
системой
называетсянормальной
системой  дифференциальных уравнений первого
порядкас
неизвестными функциями
дифференциальных уравнений первого
порядкас
неизвестными функциями 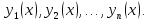
Число
уравнений, входящих в систему, называется порядком
нормальной системы. Решением нормальной
системы в
интервале 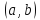 называется совокупность функций
называется совокупность функций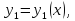
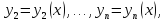 непрерывно
дифференцируемых в интервале
непрерывно
дифференцируемых в интервале  и обращающих вместе со своими производными
каждое уравнение нормальной системы в
тождество.
и обращающих вместе со своими производными
каждое уравнение нормальной системы в
тождество.
Задача
Коши для системы дифференциальных
уравнений первого порядка имеет
следующую формулировку. Найти решение 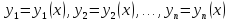 нормальной системы дифференциальных
уравнений первого порядка, удовлетворяющее
начальным условиям
нормальной системы дифференциальных
уравнений первого порядка, удовлетворяющее
начальным условиям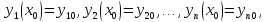 где
где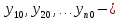 заданные
числа,
заданные
числа,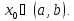
Теорема
Коши о существовании и единственности
решение задачи. Если
функции 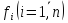 непрерывны
в окрестности точки
непрерывны
в окрестности точки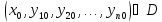 и имеют непрерывные частные производные
и имеют непрерывные частные производные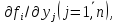 то
всегда найдется некоторый интеграл с
центром
то
всегда найдется некоторый интеграл с
центром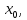 в котором существует единственное
решение нормальной системы дифференциальных
уравнений первого порядка, удовлетворяющее
заданным начальным условиям.
в котором существует единственное
решение нормальной системы дифференциальных
уравнений первого порядка, удовлетворяющее
заданным начальным условиям.
Общим решением нормальной системы называется совокупность функций
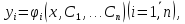 зависящих
от
зависящих
от 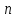 произвольных постоянных
произвольных постоянных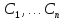 и
удовлетворяющих следующим условиям:
и
удовлетворяющих следующим условиям:
функции
 определены
в некоторой области изменения переменных
определены
в некоторой области изменения переменных  и имеют непрерывные частные производные
и имеют непрерывные частные производные
совокупность


для любых начальных условий из области
 где
выполняются условия теоремы Коши,
всегда найдутся такие значения
произвольных постоянных
где
выполняются условия теоремы Коши,
всегда найдутся такие значения
произвольных постоянных что будут справедливы равенства
что будут справедливы равенства
Частным решением нормальной системы дифференциальных уравнений первого порядка называется решение, полученное из общего при некоторых частных значениях произвольных постоянных.
Одним из методов решения нормальной системы дифференциальных уравнений первого порядка является сведение ее к решению одного или нескольких дифференциальных уравнений высших порядков – метод исключения.
35.2. Решение системы линейных дифференциальных уравнений с постоянными коэффициентами
Все сказанное выше верно и для частного случая нормальной системы дифференциальных уравнений, которая имеет вид

где
функции 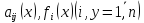 предполагаются непрерывными в некотором
интервале
предполагаются непрерывными в некотором
интервале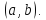 Если
все
Если
все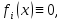 то
рассматриваемая система называется
однородной, в противном случае
неоднородной. Если
то
рассматриваемая система называется
однородной, в противном случае
неоднородной. Если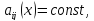
Первый метод. Составляем характеристическое уравнение
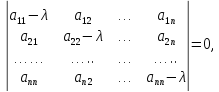
где  Раскрывая определитель, приходим к
алгебраическому уравнению степени
Раскрывая определитель, приходим к
алгебраическому уравнению степени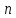 относительно
относительно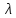 с действительными постоянными
коэффициентами, которое имеет
с действительными постоянными
коэффициентами, которое имеет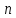 корней.
корней.
Если
корни характеристического уравнения
действительные и различные 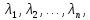
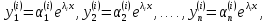
где
коэффициенты 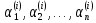 определяются из системы линейных
алгебраических уравнений
определяются из системы линейных
алгебраических уравнений
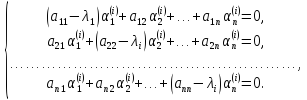
Все частные решения вида
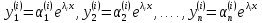
образуют фундаментальную систему решений.
Общее решение однородной системы с постоянными коэффициентами, получаемой из системы

при 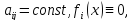 представляет
собой следующую совокупность функций,
являющихся линейной комбинацией решений
представляет
собой следующую совокупность функций,
являющихся линейной комбинацией решений


где 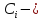 произвольные постоянные.
произвольные постоянные.
Рассмотрим пример. Найти общее решение однородной системы
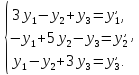
Характеристическое уравнение данной системы
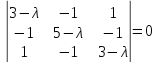
имеет
различные действительные корни 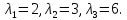 Для каждого из них составляем систему
Для каждого из них составляем систему
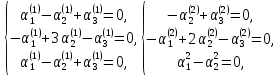
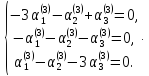
Так
как определители этих систем равны
нулю, то каждая из них имеет бесчисленное
множество решений. В данном случае можно
выбрать те решения, для которых  Тогда
получим следующие решения систем: если
Тогда
получим следующие решения систем: если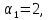 то
то
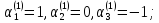
если 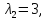 то
то
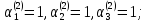
если  то
то
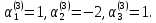
Это приводит к фундаментальной системе решений
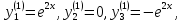
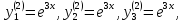

Линейная комбинация этих решений с учетом совокупности функций
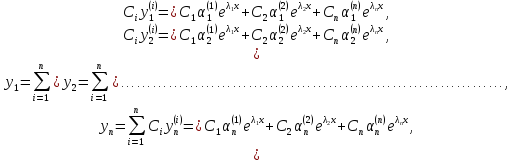
дает общее решение исходной системы

Второй
случай. Корни  характеристического
уравнения
характеристического
уравнения
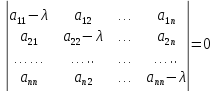
различные,
но среди них имеются комплексные.
Известно, что в этом случае каждой паре
комплексно – сопряженных корней  характеристического уравнения
соответствует пара частных решений
характеристического уравнения
соответствует пара частных решений

где  Коэффициенты
Коэффициенты определяются
из системы
определяются
из системы
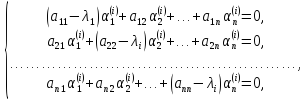
соответственно
для  и
и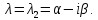 Коэффициенты
Коэффициенты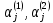 оказываются, как правило, комплексными
числами, а соответствующие им функции
оказываются, как правило, комплексными
числами, а соответствующие им функции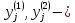 комплексными
функциями. Выделяя мнимую и действительную
части функций
комплексными
функциями. Выделяя мнимую и действительную
части функций и пользуясь тем, что для линейных
уравнений с действительными коэффициентами
и мнимая, и действительная части решения
также являются решениями, получаем пару
частных действительных решений однородной
системы.
и пользуясь тем, что для линейных
уравнений с действительными коэффициентами
и мнимая, и действительная части решения
также являются решениями, получаем пару
частных действительных решений однородной
системы.
Рассмотрим пример. Найти общее решение системы
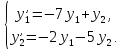
Характеристическое уравнение системы
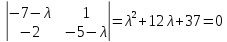
имеет
корни 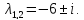 Получаем
Получаем
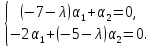
Корню 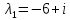 соответствует
система для вычисления
соответствует
система для вычисления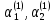

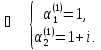
Согласно
формуле 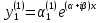 получаем
частное решение
получаем
частное решение
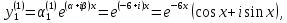
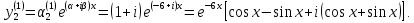
Взяв в отдельности действительные и мнимые части в решении, получим два решения в действительной форме, образующих фундаментальную систему решений системы
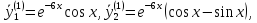
Тогда общее решение системы имеет вид
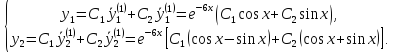
Третий
случай. Среди
корней 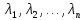 характеристического
уравнения имеются кратные. В этом случае
поступаем следующим образом. Пусть
характеристического
уравнения имеются кратные. В этом случае
поступаем следующим образом. Пусть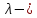 корень
кратности
корень
кратности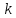 характеристического
уравнения. Тогда решение системы, для
которой
характеристического
уравнения. Тогда решение системы, для
которой соответствующее
этому
соответствующее
этому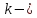 кратному
корню, ищем в виде
кратному
корню, ищем в виде
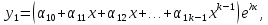

……………………………………………………………………………
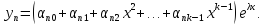
Числа  находим,
подставляя функции
находим,
подставляя функции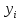 и
их производные
и
их производные в
исходную систему при указанных
ограничениях на
в
исходную систему при указанных
ограничениях на и
и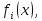 а
затем приравниваем коэффициенты при
одинаковых степенях
а
затем приравниваем коэффициенты при
одинаковых степенях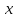 в
левых и правых частях полученных
равенств. В результате проведенных
действий из всех чисел
в
левых и правых частях полученных
равенств. В результате проведенных
действий из всех чисел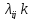 всегда
остаются в качестве свободных параметров,
которые принимаются за произвольные
постоянные.
всегда
остаются в качестве свободных параметров,
которые принимаются за произвольные
постоянные.
Рассмотрим пример. Найти общее решение системы
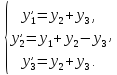
Характеристическое уравнение системы
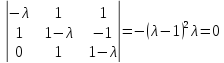
имеет
двукратный  и однократный
и однократный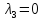 корни.
Двукратному корню
корни.
Двукратному корню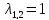 соответствует решение вида
соответствует решение вида

Коэффициенты 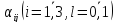 определяются из системы, полученной
подстановкой выражений для
определяются из системы, полученной
подстановкой выражений для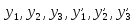 в исходную систему. После сокращения
на
в исходную систему. После сокращения
на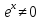 имеем
имеем

Приравнивая
коэффициенты при одинаковых степенях 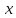 слева
и справа, получаем систему
слева
и справа, получаем систему
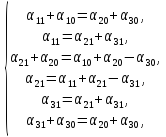
из которой находим, что
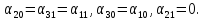
Числа 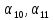 можно считать произвольными параметрами.
Обозначим их через
можно считать произвольными параметрами.
Обозначим их через и
и соответственно.
Тогда решение запишется в виде
соответственно.
Тогда решение запишется в виде

Корню 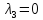 соответствует
решение
соответствует
решение

где
числа  определяется из системы
определяется из системы

Ее
решение  Следовательно,
соответствующее корню
Следовательно,
соответствующее корню
 решение
исходной системы имеет вид
решение
исходной системы имеет вид
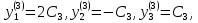
где 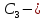 произвольная постоянная.
произвольная постоянная.
Общее решение исходной систему записывается в виде
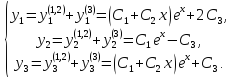
Если система неоднородная, то, зная общее решение вида
соответствующей
однородной системы, можно найти общее
решение исходной неоднородной системы
методом вариации произвольных постоянных  в
решении
в
решении

Общее
решение неоднородной системы всегда
можно записать в данном виде, заменив
произвольные постоянные  соответственно функциями
соответственно функциями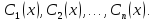 Эти функции определяются с помощью
данной неоднородной системы. В систему
подставляют
Эти функции определяются с помощью
данной неоднородной системы. В систему
подставляют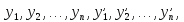 получают
линейную систему
получают
линейную систему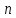 алгебраических
уравнений относительно
алгебраических
уравнений относительно решение
которой всегда существует и представимо
в виде
решение
которой всегда существует и представимо
в виде

где 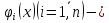 известные функции. Интегрируя эти
равенства, находим
известные функции. Интегрируя эти
равенства, находим
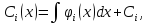
где произвольные постоянные.
Рассмотрим пример. Решить задачу Коши
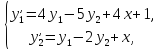
заданы
начальные условия 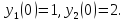
Найдем общее решение соответствующей однородной системы
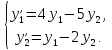
Корни
ее характеристического уравнения 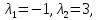 общее
решение ищем в виде
общее
решение ищем в виде
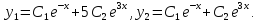
Пусть
в данном решении 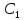 и
и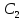 являются
неизвестными функциями
являются
неизвестными функциями и
и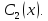 Потребуем, чтобы
Потребуем, чтобы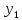 и
и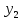 были
решением исходной системы. Находим
были
решением исходной системы. Находим
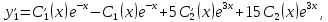
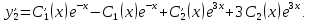
Подставляем
выражения для 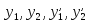 в исходную систему, приводим подобные
члены и получаем систему
в исходную систему, приводим подобные
члены и получаем систему
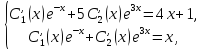
откуда
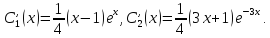
Проинтегрируем последние равенства
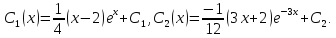
Подставляя 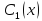 и
и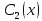 в равенства
в равенства вместо
вместо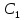 и
и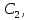 получаем
общее решение исходной неоднородной
системы
получаем
общее решение исходной неоднородной
системы

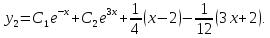
Используя
начальные условия, получим систему для
определения постоянных 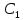 и
и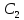 :
:
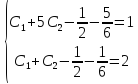
откуда 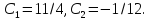
Решением задачи Коши будет следующее частное решение
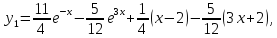
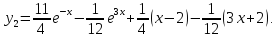
Контрольные вопросы
Что называют порядком нормальной системы?
Дать определение решению нормальной системы в заданном интервале?
Дать формулировку Задачи Коши для системы дифференциальных уравнений первого порядка.
Что называют общим решением нормальной системы?
Дать определение частного решения нормальной системы дифференциальных уравнений первого порядка.
Лекция №36. Применение аппарата дифференциальных уравнений в механике
36.1. Особенности составления дифференциальных уравнений в прикладных задачах.
36.2. Задачи, приводящие к решению дифференциальных уравнений.
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Решить систему ДУ
$\left\{\begin{array}{c} {\frac{dy_{1} }{dx} =3\cdot y_{1} -y_{2} } \\ {\frac{dy_{2} }{dx} =4\cdot y_{1} -y_{2} } \end{array}\right. $.
Систему решаем исключением неизвестной функции $y_{2} $.
Шаг 1. Из первого уравнения находим $y_{2} $: $y_{2} =-\frac{dy_{1} }{dx} +3\cdot y_{1} $.
Шаг 2. Подставляем $y_{2} $ во второе уравнение:
\[\frac{dy_{2} }{dx} =4\cdot y_{1} +\frac{dy_{1} }{dx} -3\cdot y_{1} ; \frac{dy_{2} }{dx} =\frac{dy_{1} }{dx} +y_{1} .\]Шаг 3. Дифференцируем первое уравнение по $x$: $\frac{d^{2} y_{1} }{dx^{2} } =3\cdot \frac{dy_{1} }{dx} -\frac{dy_{2} }{dx} $.
Шаг 4. Подставляем выражение, полученное на шаге 2, в выражение, полученное на шаге 3:
\[\frac{d^{2} y_{1} }{dx^{2} } =3\cdot \frac{dy_{1} }{dx} -\frac{dy_{1} }{dx} -y_{1} ; \frac{d^{2} y_{1} }{dx^{2} } -2\cdot \frac{dy_{1} }{dx} +y_{1} =0. \]Шаг 5. Решаем линейное однородное ДУ второго порядка с постоянными коэффициентами:
- характеристическое уравнение $k^{2} -2\cdot k+1=0$;
- корни характеристического уравнения $k_{1} =1$, $k_{2} =1$ — действительные, равные;
- искомая функция $y_{1} =C_{1} \cdot e^{x} +C_{2} \cdot x\cdot e^{x} $.
Шаг 6. Находим функцию $y_{2} $:
- производная $\frac{dy_{1} }{dx} =C_{1} \cdot e^{x} +C_{2} \cdot \left(e^{x} +x\cdot e^{x} \right)$;
- результат подстановки в выражение, полученное на шаге 1:
Общее решение данной системы:
\[y_{1} =C_{1} \cdot e^{x} +C_{2} \cdot x\cdot e^{x} ; y_{2} =2\cdot C_{1} \cdot e^{x} -C_{2} \cdot e^{x} +2\cdot C_{2} \cdot x\cdot e^{x} .\]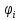 определены
в некоторой области изменения переменных
определены
в некоторой области изменения переменных 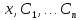 и имеют непрерывные частные производные
и имеют непрерывные частные производные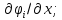
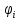
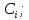
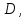 где
выполняются условия теоремы Коши,
всегда найдутся такие значения
произвольных постоянных
где
выполняются условия теоремы Коши,
всегда найдутся такие значения
произвольных постоянных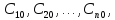 что будут справедливы равенства
что будут справедливы равенства