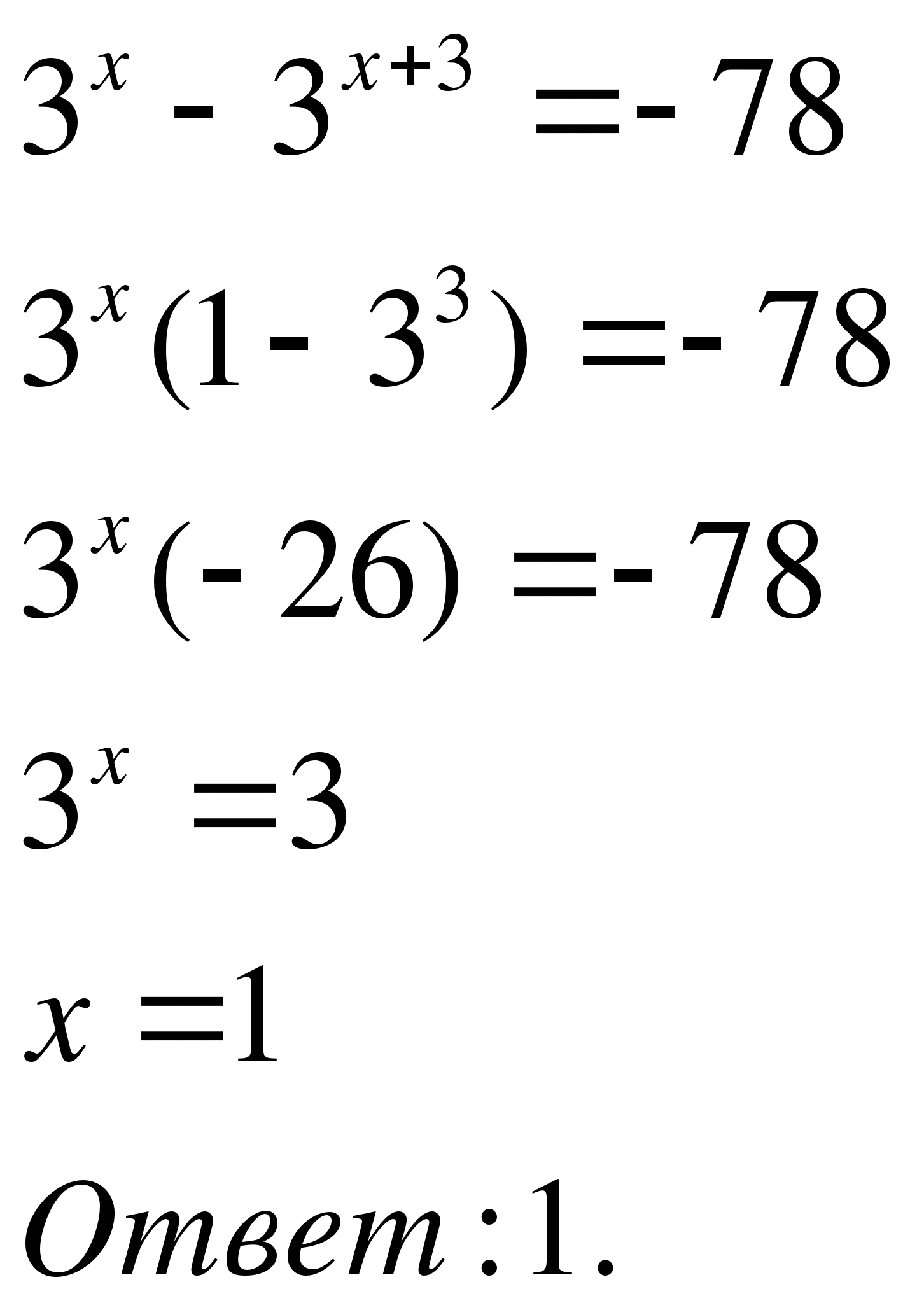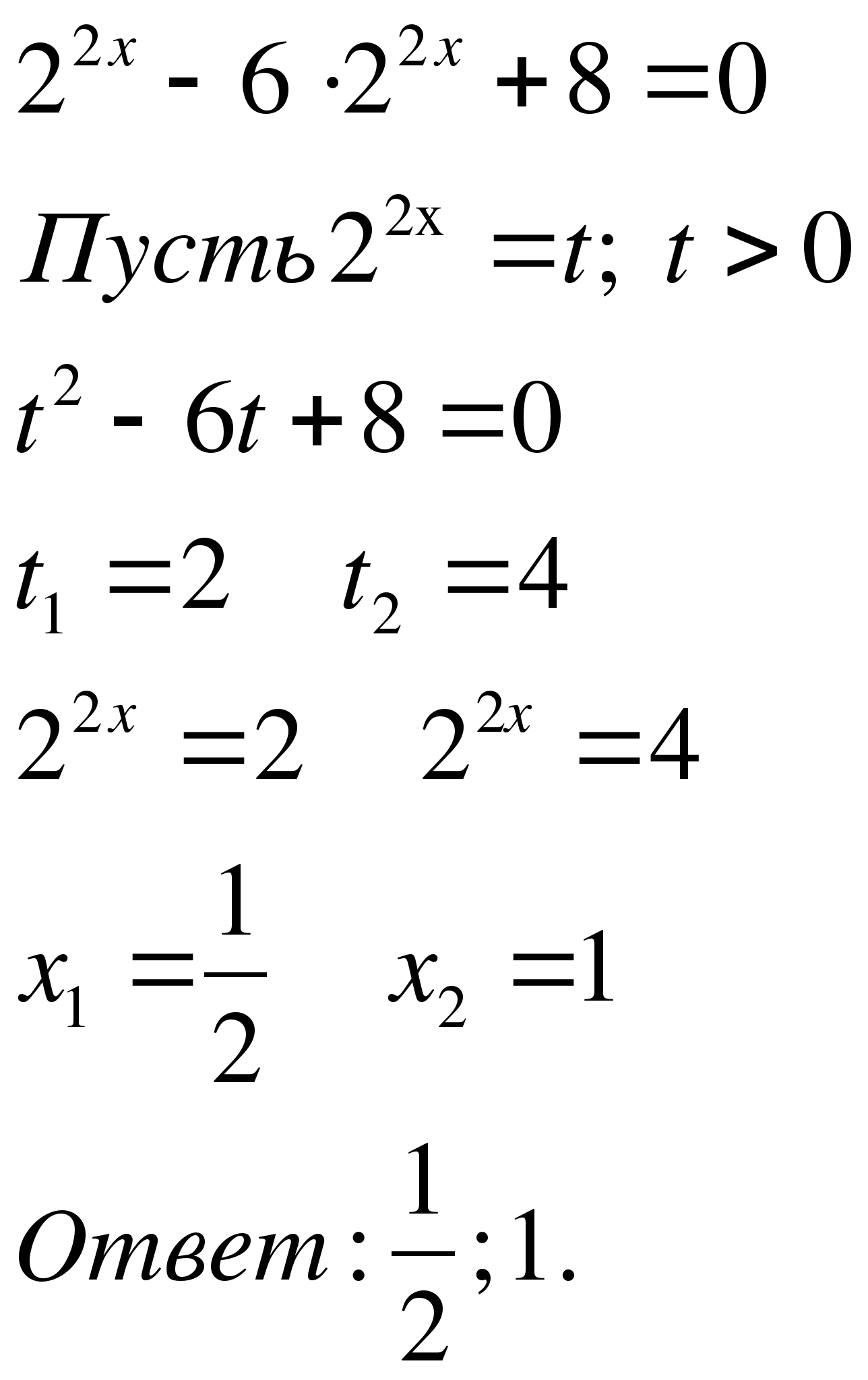Показательные уравнения и их системы
Показательные уравнения – уравнения, которые содержат неизвестное в показателе степени.
Уравнение вида: \(a^x = b, где\ a > 0, a ≠ 1\) называется простейшим показательным уравнением.
Методы решения показательных уравнений:
- В результате преобразований уравнение можно привести к виду \(a^{f(x)}=a^c\). Тогда применяем свойство: \(a^{f(x)}=a^c \Rightarrow f(x)=c\).
- При получении уравнения вида \( a ^{f(x)} = b \) используется определение логарифма, получим: \(f(x)=\log_a b\).
- В результате преобразований можно получить уравнение вида \(a^{f(x)}=b^{g(x)}\). Применяется логарифмирование: \(\log_ca^{f(x)}=\log_cb^{g(x)}\). Далее применяем свойство логарифма степени: \(f(x)\cdot \log_ca=g(x)\cdot \log_cb\). Выражаем и находим \(x\).
Пример 1. Решить уравнение: \(3^{x+1} + 3^x − 3^{ x−2} = 35\).
Решение: Метод решения уравнений такого вида – вынести за скобки степень с наименьшим показателем. В данном случае выносим \(3^{x-2}\) за скобки: \(3^{x−2} (3^3 + 3^2 − 1) = 35 \Rightarrow 3^{x−2}· 35 = 35 \Rightarrow 3^{x−2} = 1\).
Последнее равенство запишем как \(3^{x-2}=3^0\) и, ввиду монотонности показательной функции, заключаем, что \(x-2=0 \Rightarrow x=2\).
Ответ: 2.
Пример 2. Решить уравнение: \(4^{x} − 2^{x+1} − 8 = 0 \).
Решение: Перепишем уравнение следующим образом: \(2^{2x} − 2\cdot 2^{x} − 8 = 0 \). Вводя замену \(t=2^x\), получим квадратное уравнение относительно \(t\): \(t^2-2t-8=0\). Находим его корни: \(t_1=4, t_2=-2\). Остается сделать обратную замену. Уравнение \(2^ x = 4\) имеет единственный корень \(x = 2\). Уравнение \(2 ^x = −2\) корней не имеет, так как показательная функция \(y=2^x\) не может принимать отрицательных значений.
Ответ: 2.
Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.
Пример 3. Решить систему уравнений: \(\begin{cases} 2^{x+1}-3^y=-1,\\ 3^y-2^x=2. \\\end{cases}\)
Решение: Данная система равносильна системе \(\begin{cases} 2\cdot 2^{x}-3^y=-1\\ 3^y-2^x=2 \\\end{cases}\). Пусть \(2^x=u\ (u>0), 3^y=v \ (v>0)\), тогда получим: \(\begin{cases} 2u-v=-1 \\ v-u=2\\ \end{cases}\). Решим полученную систему методом сложения. Сложим уравнения: \(2u-v+v-u=-1+2 \Rightarrow u=1\). Тогда из второго уравнения получим, что \(v=2+u=2+1=3\). Переходим к обратной подстановке: \(\begin{cases} 2^x=1 \\ 3^y=3 \\ \end{cases} \Rightarrow \begin{cases} x=0 \\ y=1 \\ \end{cases} \).
Ответ: \((0;1)\).
| 1. |
Система логарифмического и линейного уравнений (определение логарифма)
Сложность: лёгкое |
3 |
| 2. |
Система показательного и линейного уравнений (нулевая степень)
Сложность: лёгкое |
6 |
| 3. | Система показательного и линейного уравнений Сложность: лёгкое | 5 |
| 4. |
Система уравнений (показательное уравнение)
Сложность: среднее |
4 |
| 5. |
Система показательных уравнений
Сложность: среднее |
4 |
| 6. |
Система показательных уравнений
Сложность: среднее |
7 |
| 7. |
Система показательных уравнений (теорема Виета)
|
5 |
| 8. |
Система показательных уравнений (десятичные дроби)
Сложность: среднее |
7 |
| 9. |
Система показательных уравнений (обыкновенные дроби)
Сложность: среднее |
8 |
| 10. |
Система показательных уравнений (сумма)
Сложность: среднее |
5 |
| 11. | Система логарифмических уравнений (сумма) Сложность: среднее | 9 |
| 12. |
Система логарифмических уравнений (определение логарифма)
Сложность: среднее |
|
| 13. |
Система показательного и логарифмического уравнений (обыкновенные дроби)
Сложность: среднее |
10 |
| 14. |
Система показательного и логарифмического уравнений (целые числа)
Сложность: среднее |
8 |
| 15. |
Система логарифмического и линейного уравнений (разность)
|
16 |
| 1. | Система логарифмического и линейного уравнений (определение логарифма) | 2 вид — интерпретация | лёгкое | 3 Б. | Решение системы уравнений. |
| 2. | Система показательного и линейного уравнений (нулевая степень) | 2 вид — интерпретация | лёгкое | 6 Б. | Решение системы линейного и показательного уравнений. |
| 3. | Система показательного и линейного уравнений | 2 вид — интерпретация | лёгкое | 5 Б. | Решение системы показательного и линейного уравнений. |
| 4. | Система уравнений (показательное уравнение) | 1 вид — рецептивный | среднее | 4 Б. | Трансцендентная система, содержит показательное уравнение. |
| 5. | Система показательных уравнений | 1 вид — рецептивный | среднее | 4 Б. | Система с двумя показательными уравнениями. |
| 6. | Система показательных уравнений | 2 вид — интерпретация | среднее | 7 Б. | Решение системы показательных уравнений. |
| 7. | Система показательных уравнений (теорема Виета) | 2 вид — интерпретация | среднее | 5 Б. | Решение системы показательных уравнений. |
| 8. | Система показательных уравнений (десятичные дроби) | 2 вид — интерпретация | среднее | 7 Б. | Решение системы показательных уравнений. |
| 9. | Система показательных уравнений (обыкновенные дроби) | 2 вид — интерпретация | среднее | 8 Б. | Решение системы показательных уравнений. |
| 10. | Система показательных уравнений (сумма) | 2 вид — интерпретация | среднее | 5 Б. | Решение системы показательных уравнений. |
| 11. | Система логарифмических уравнений (сумма) | 2 вид — интерпретация | среднее | 9 Б. | Решение системы логарифмических уравнений. |
| 12. | Система логарифмических уравнений (определение логарифма) | 2 вид — интерпретация | среднее | 9 Б. | Решение системы логарифмических уравнений. |
| 13. | Система показательного и логарифмического уравнений (обыкновенные дроби) | 2 вид — интерпретация | среднее | 10 Б. | Решение системы показательного и логарифмического уравнений. |
| 14. | Система показательного и логарифмического уравнений (целые числа) | 2 вид — интерпретация | среднее | 8 Б. | Решение системы показательного и логарифмического уравнений. |
| 15. | Система логарифмического и линейного уравнений (разность) | 2 вид — интерпретация | сложное | 16 Б. | Решение системы логарифмического и линейного уравнений. |
Тема: Показательная функция, уравнения,
неравенства и системы уравнений.
Цель: Обобщить и систематизировать ЗУН учащихся по теме
«Показательная функция, уравнения, неравенства и системы
уравнений».
Ход:
I. Оргмомент (2 мин)
Сегодня у нас урок решения показательных уравнений, неравенств и систем уравнений.
Главная ваша задача – показать свои знания и умения по решению показательных уравнений, неравенств и систем уравнений. Так же мы с вами потренируемся в данной теме по сдаче тестов в виде ЭГЕ (конечно в самом узком смысле).
II. Теоретическая часть (5 мин)
В это время 3 ученика садятся за компьютеры и отвечают на вопросы теста в электронном варианте (20 минут), а другие устно отвечают на вопросы:
Назовите область определения показательной функции. (множество всех действительных чисел)
Какие значения принимает показательная функция? (только положительные значения)
Что является областью значений показательной функции?
Является ли функция
 возрастающей? (нет)
возрастающей? (нет)Какие уравнения называются показательными? (показательными уравнениями называются уравнения, у которых неизвестное содержится в показателе степени)
Является ли показательная функция четной? (нет)
Сравните
 и
и  (
( возраст)
возраст)
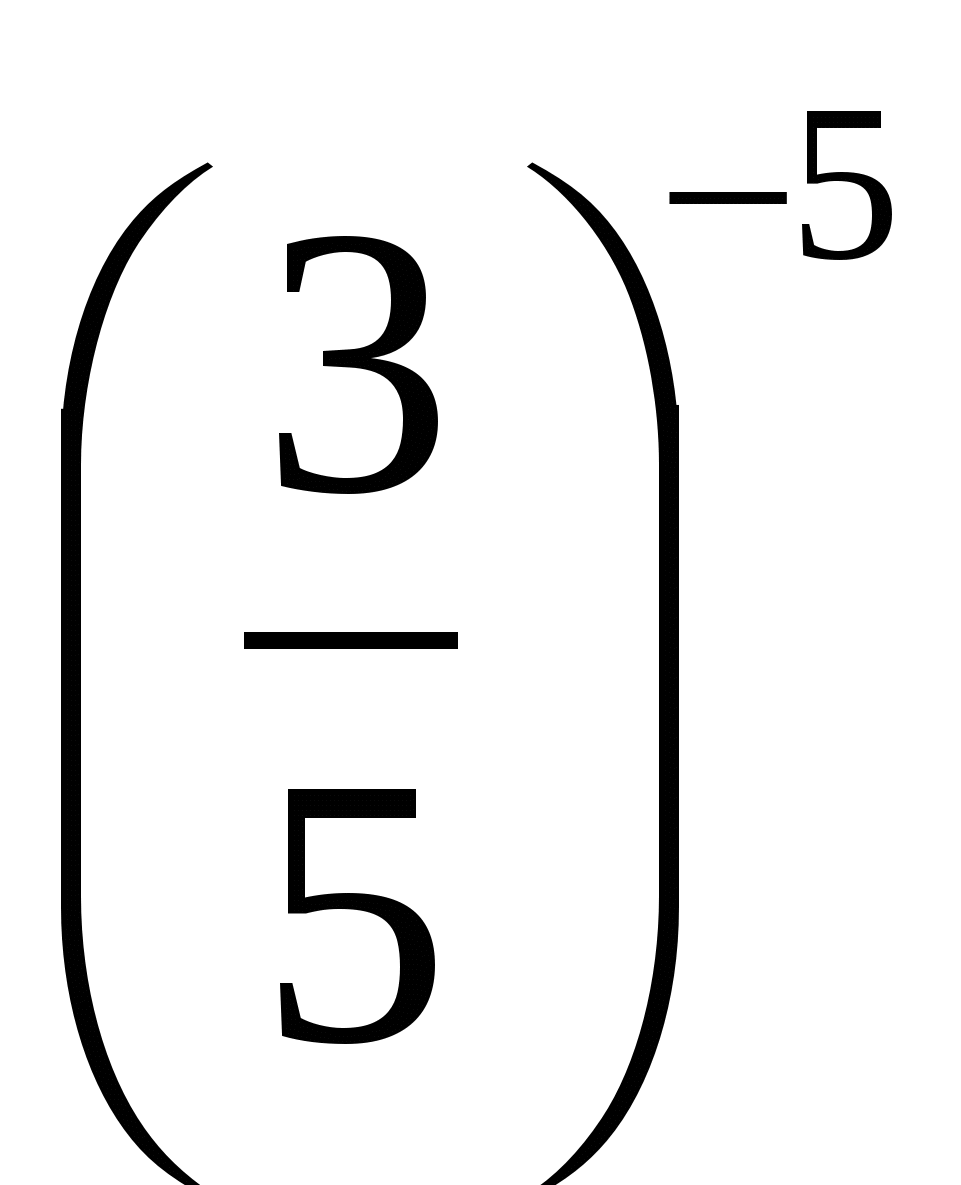 и
и 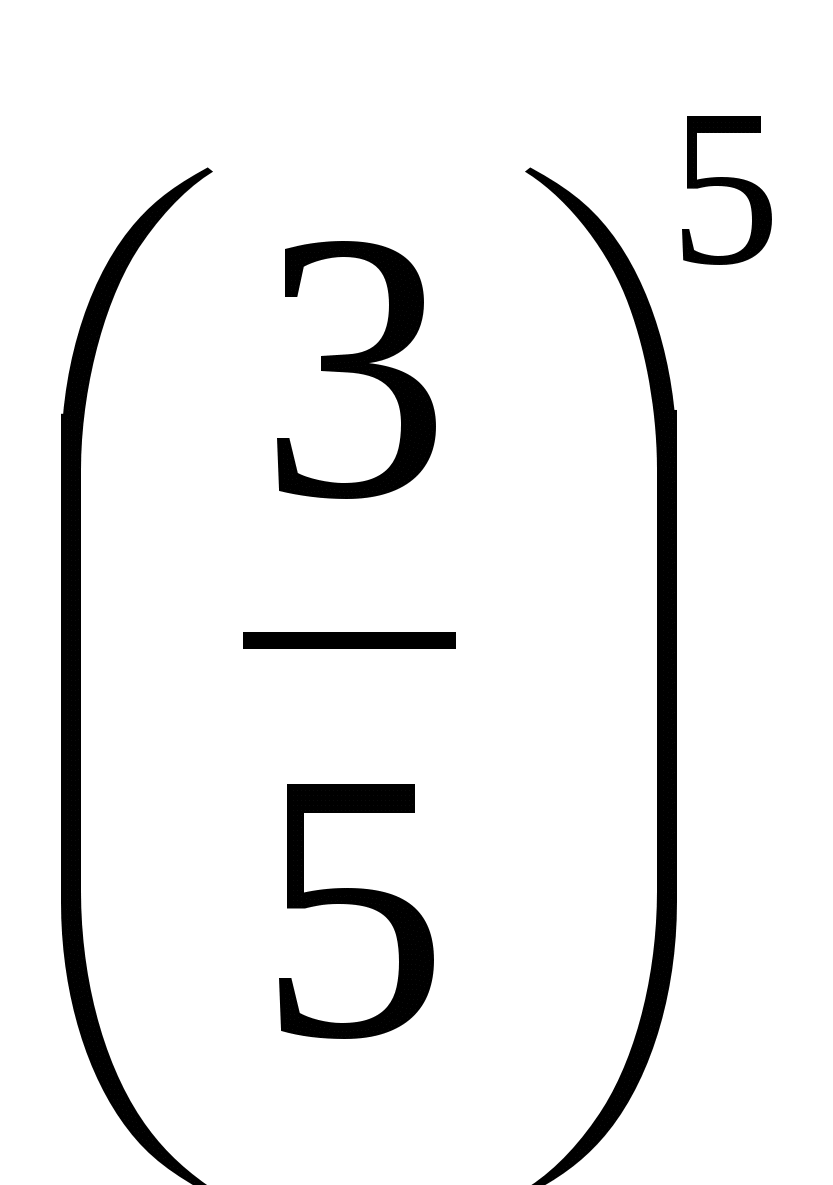 (
(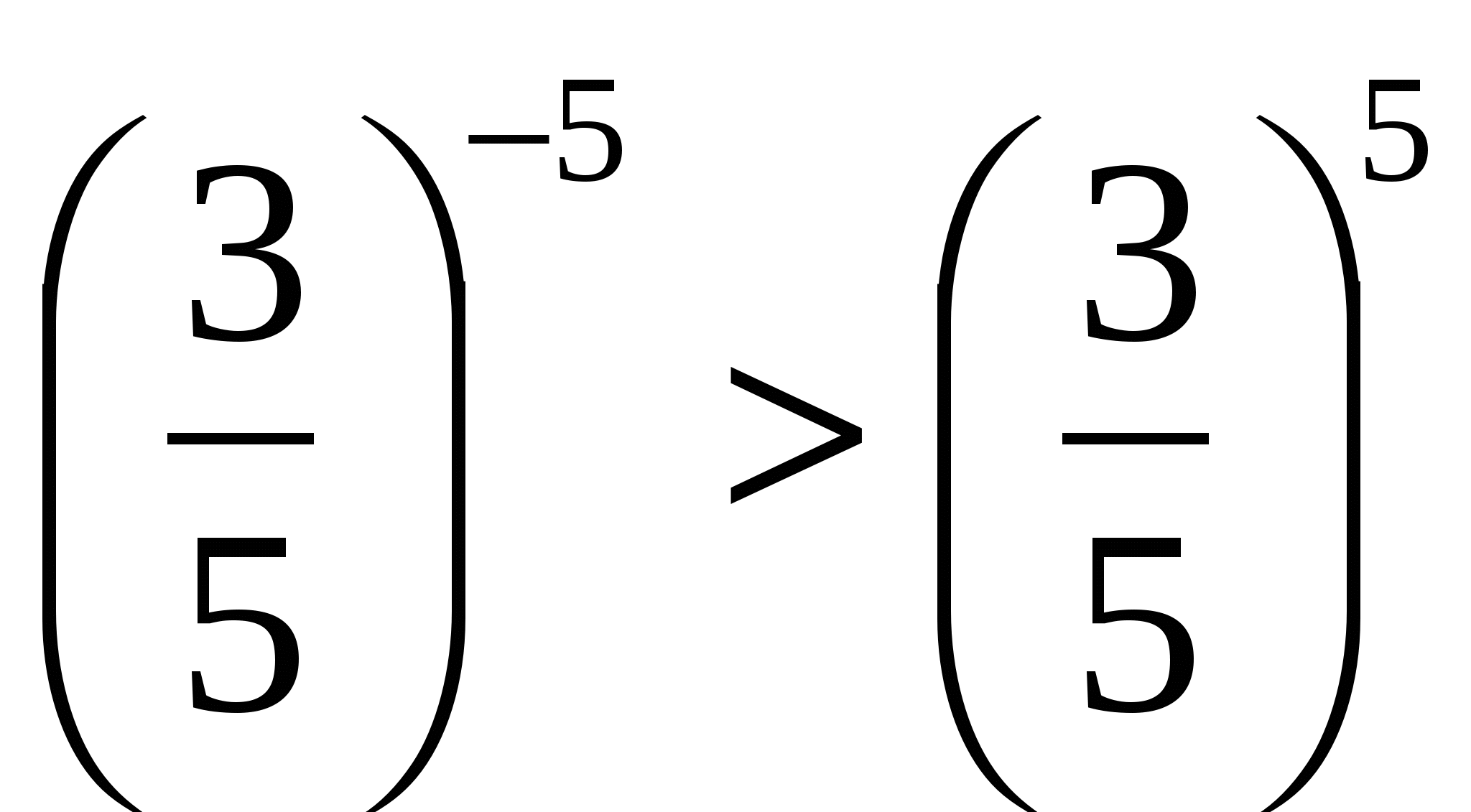 убывающая)
убывающая)
III. Самостоятельная работа (10 мин)
Каждому выдается карточка с заданиями с выбором ответов (2 варианта), потом проверяется правильность решения (правильные ответы вывешиваются на доске и дети проверяют свои решения). Работа оценивается и первая оценка выставляется в специально подготовленный список – в первую колонку.
I вариант
1. Укажите промежуток, которому принадлежит корень уравнения
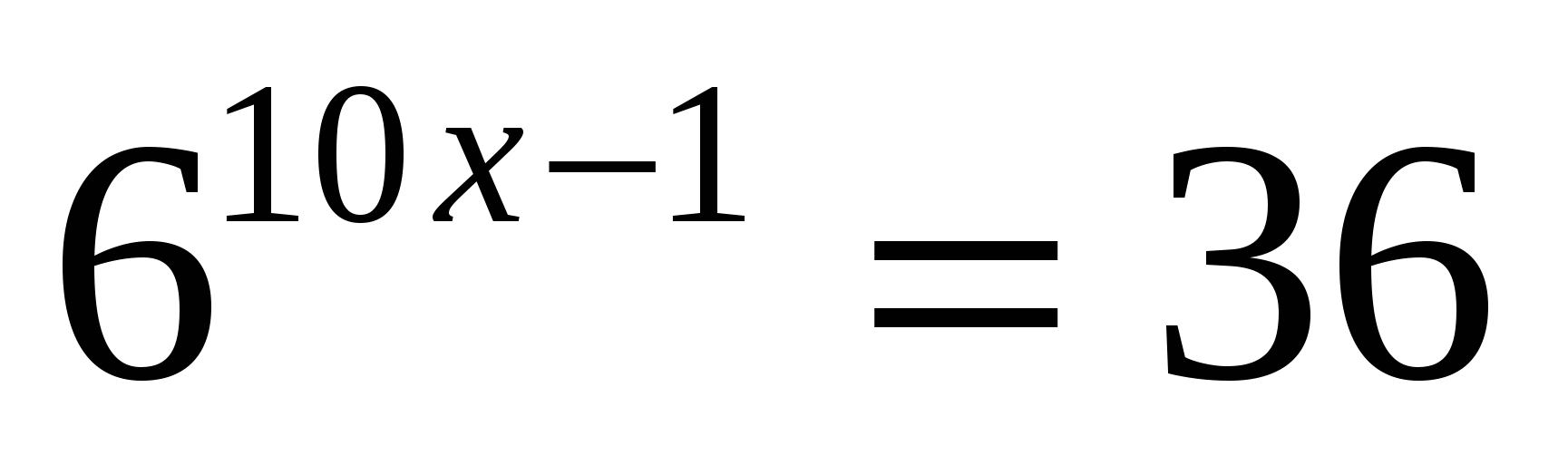
1) 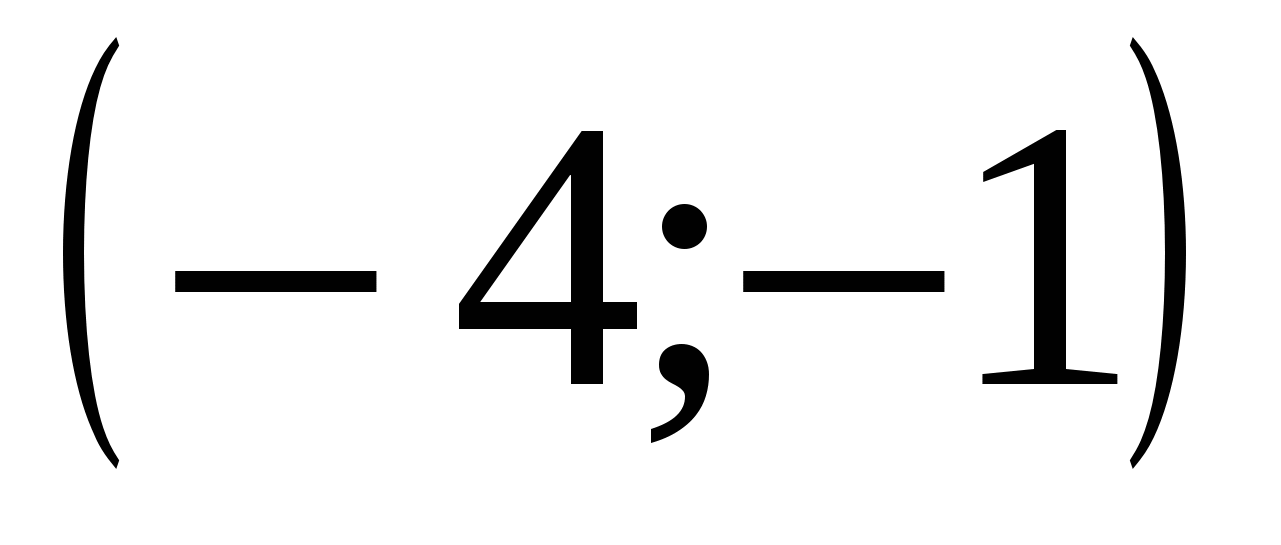 2)
2) 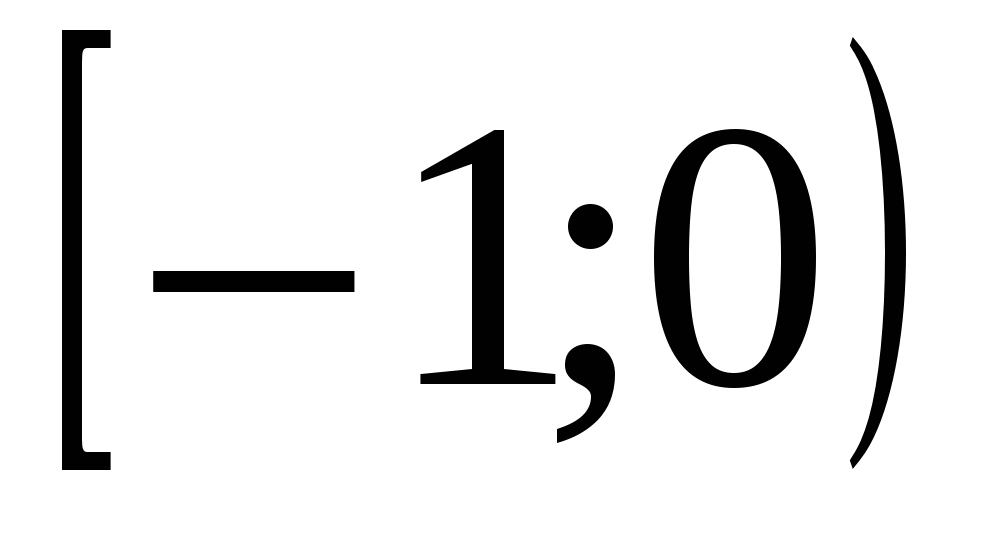 3)
3) 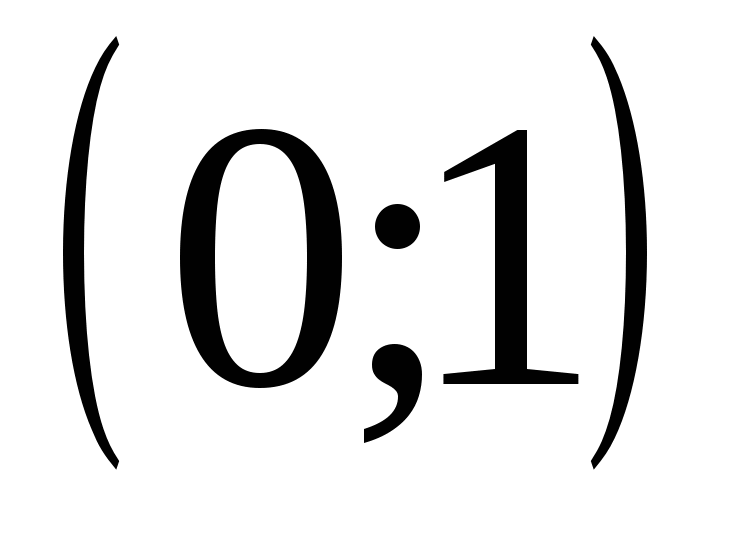 4)
4) 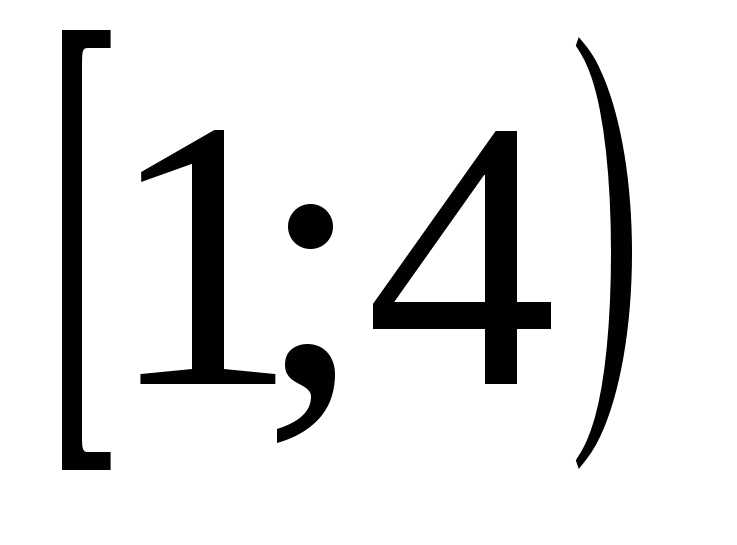
2. Найдите сумму корней уравнения 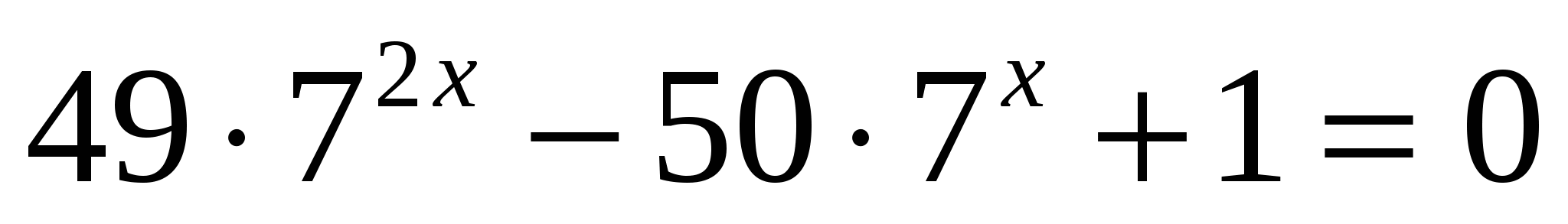
1) 1 2) 2 3) – 2 4) 50
3. Решить уравнение 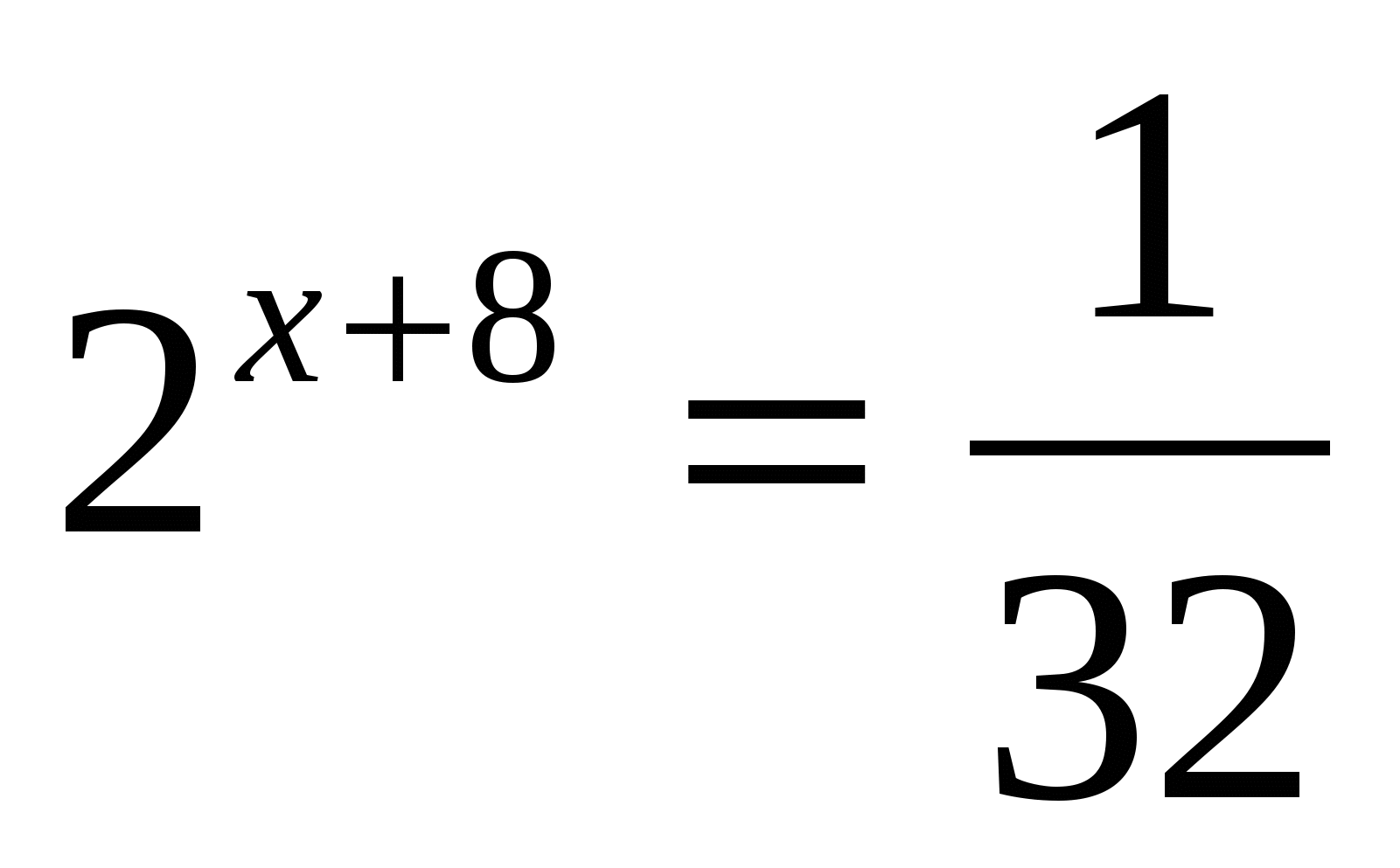
1) 12 2) – 12 3) – 13 4) 13
4. Решите неравенство 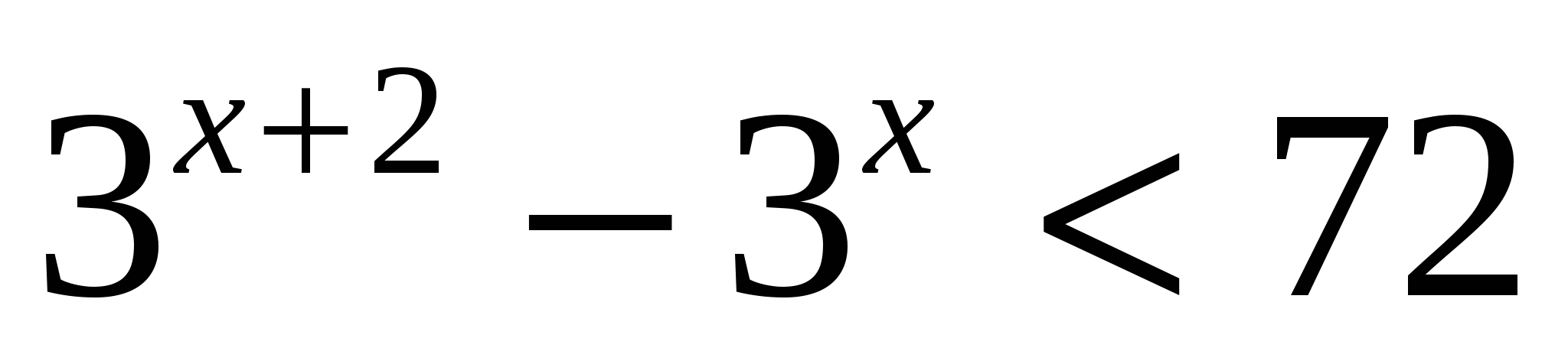
1) 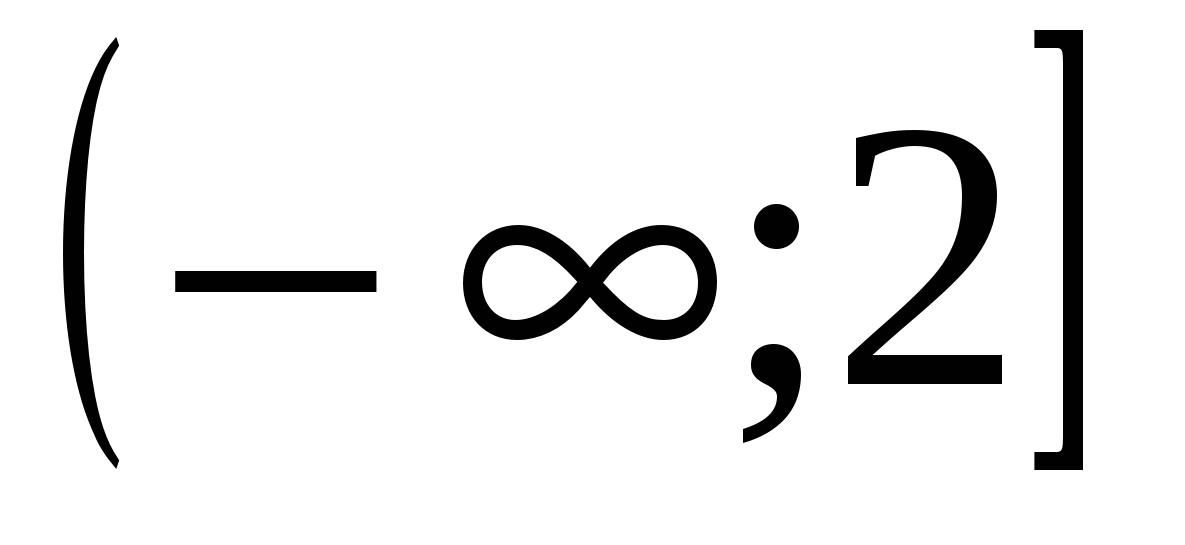 2)
2) 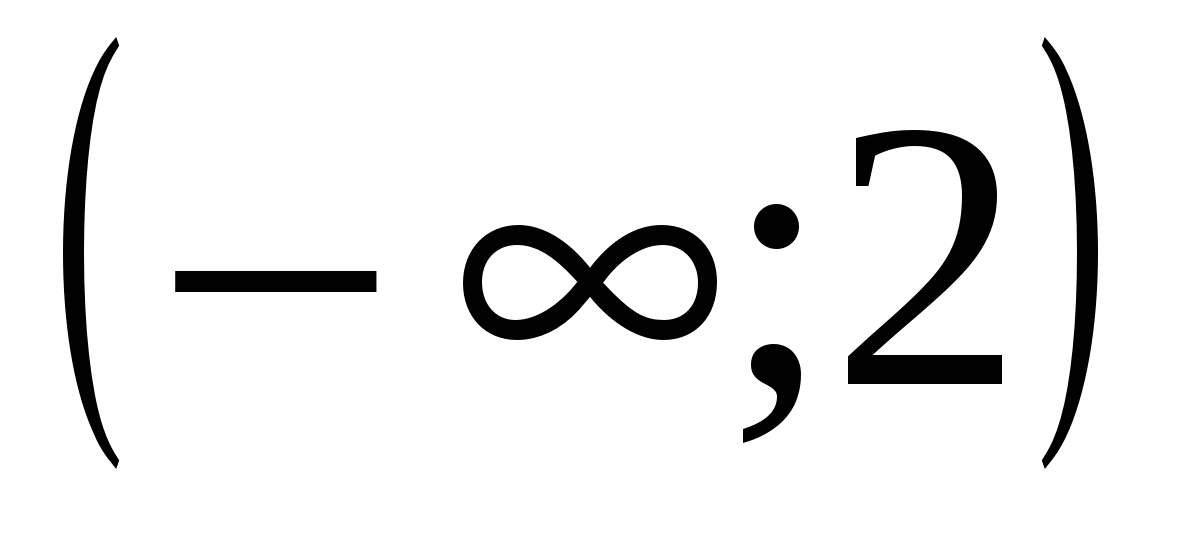 3)
3) 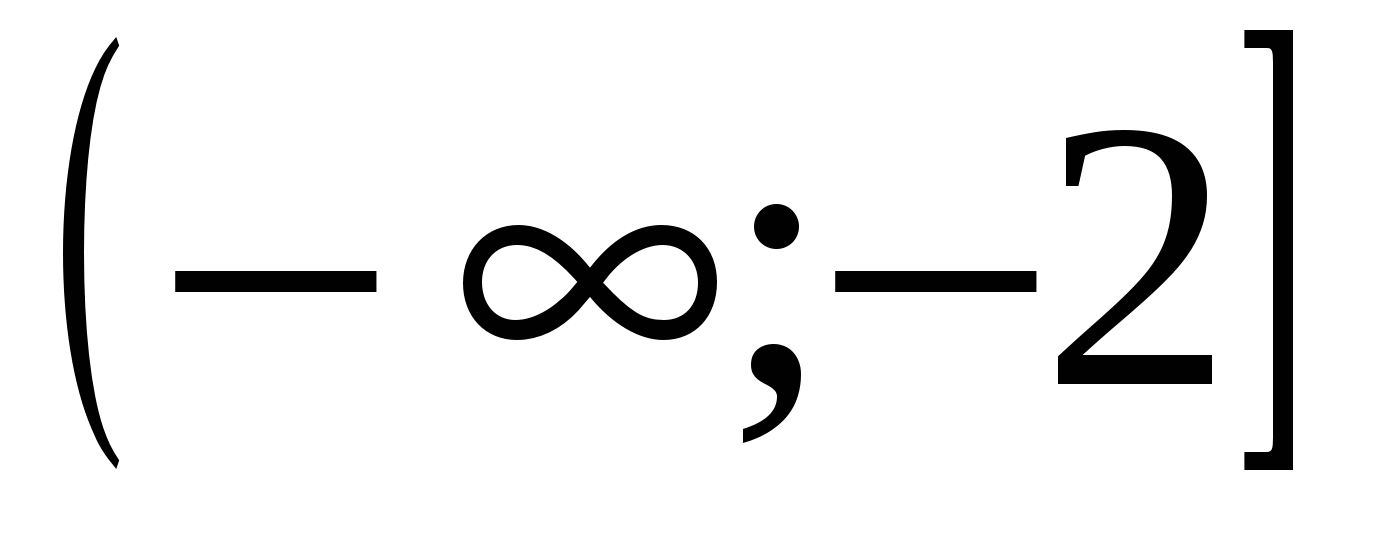
 4)
4) 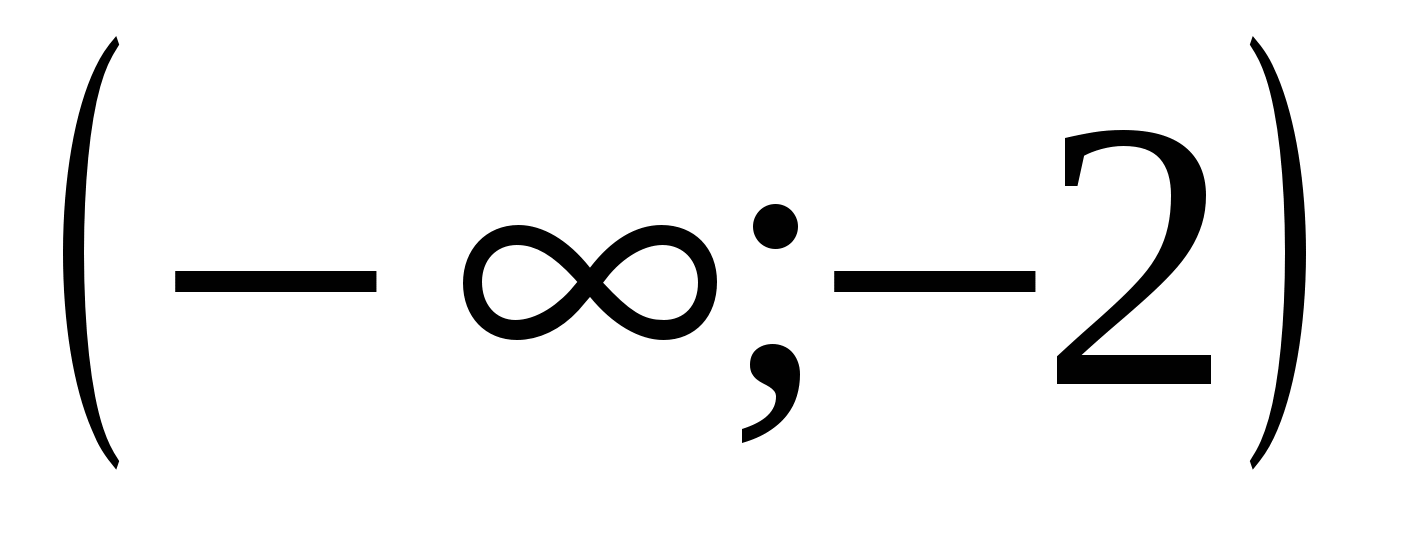
5. Найдите решение 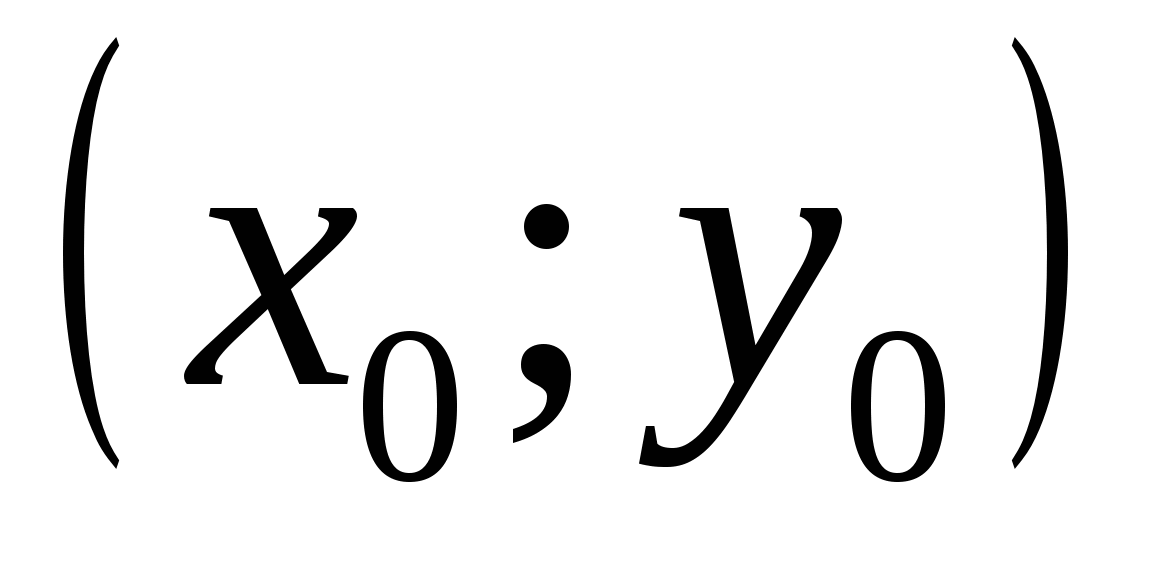 системы уравнений
системы уравнений 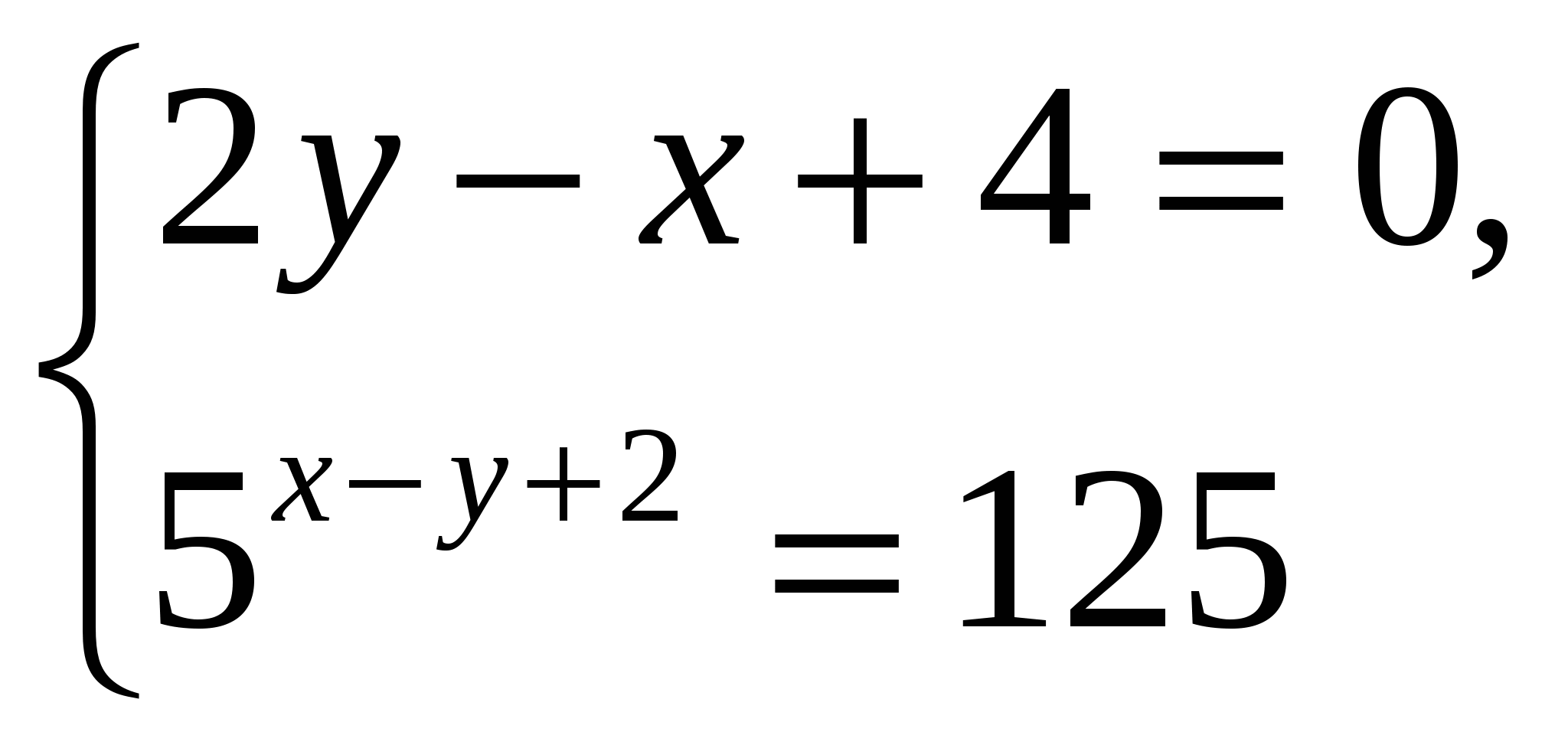 и
и
вычислите значение произведения 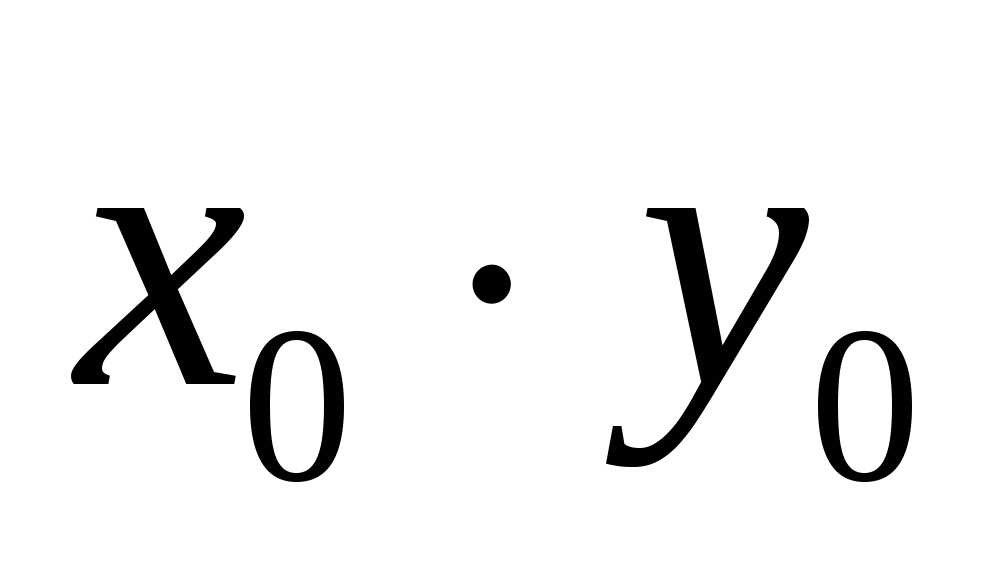
1) 6 2) 3 3) – 6 4) – 2
II вариант
1. Укажите промежуток, которому принадлежит корень уравнения
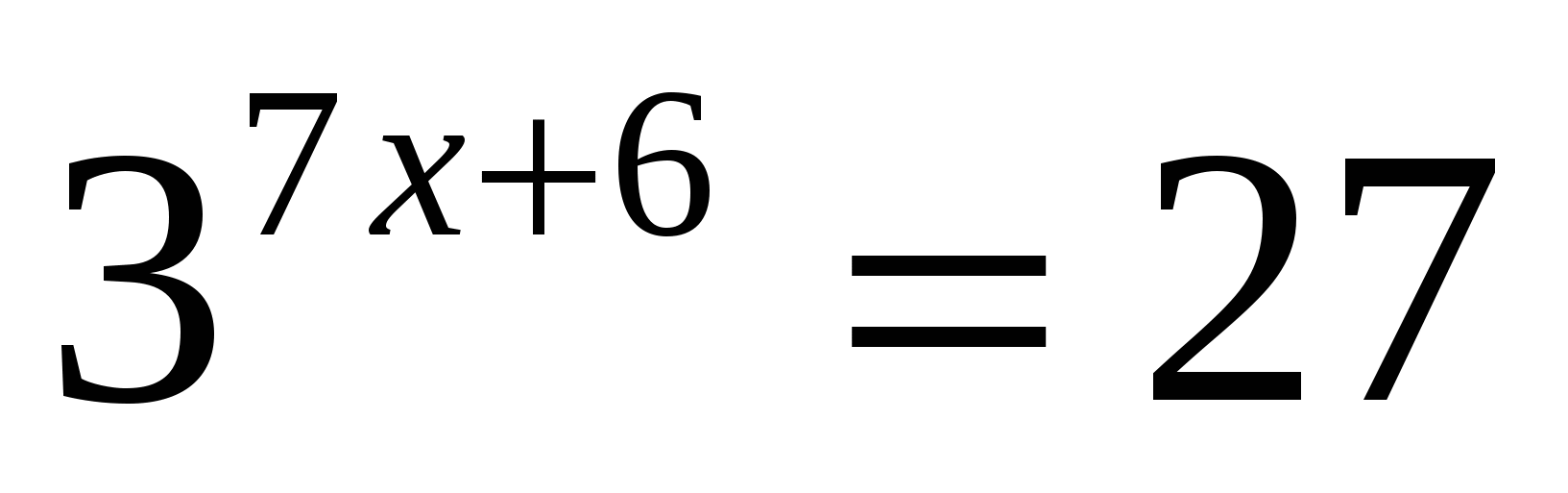
1) 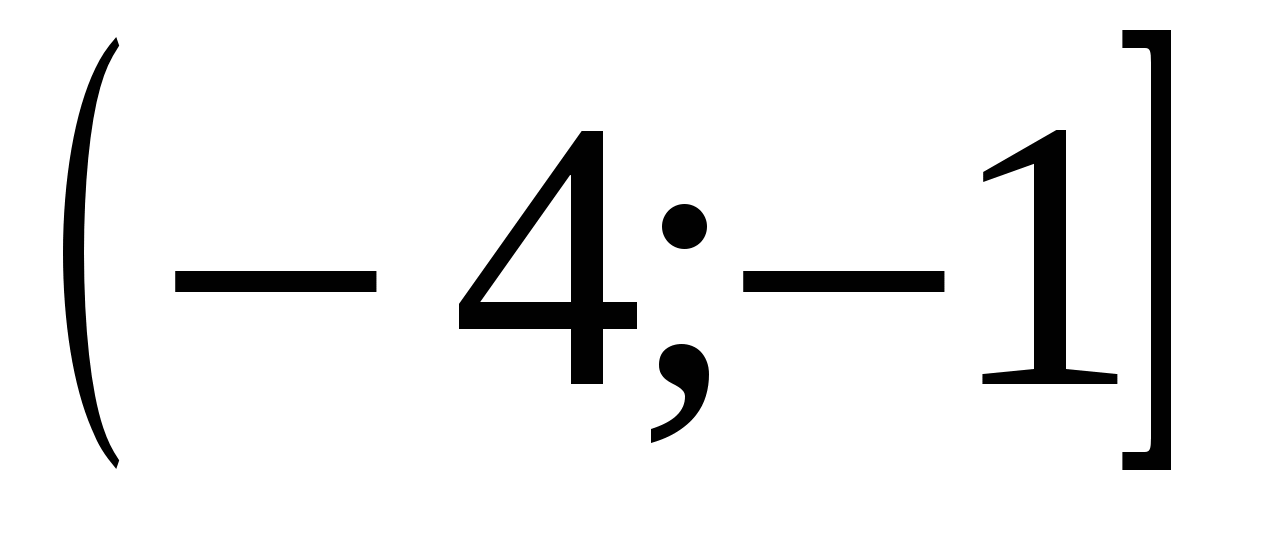 2)
2) 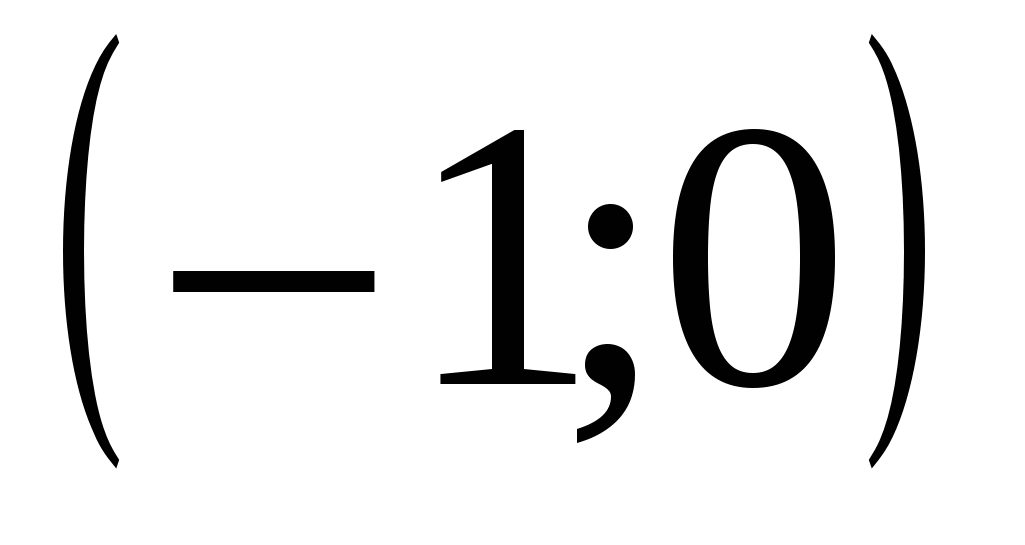 3)
3) 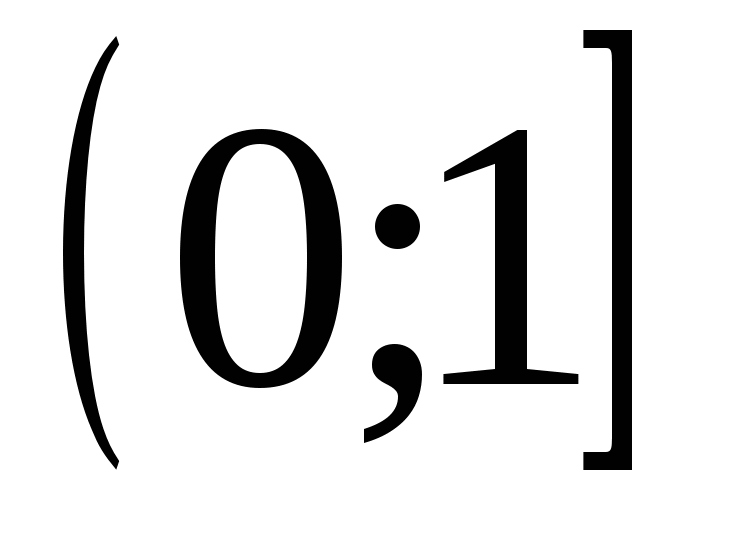 4)
4) 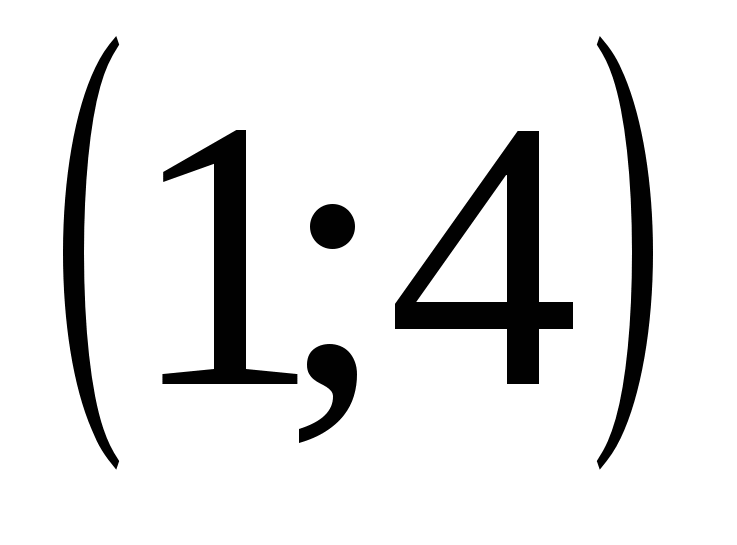
2. Найдите сумму корней уравнения 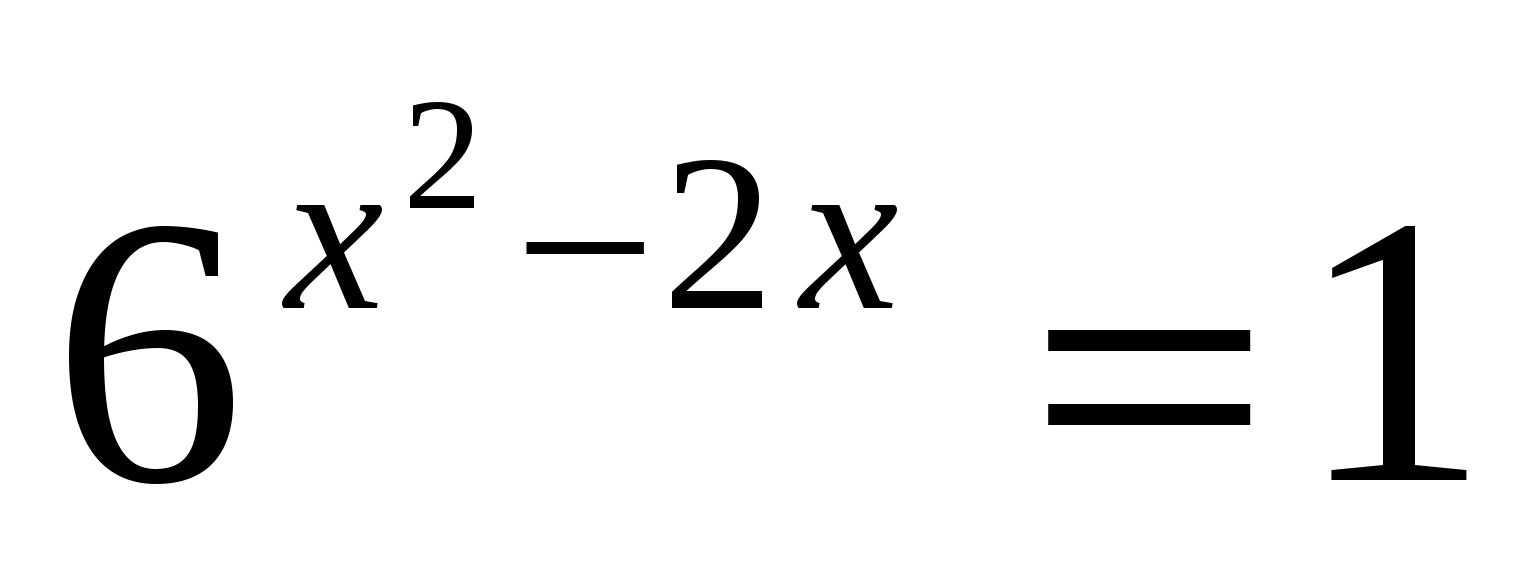
1) – 2 2) 0 3) 1 4) 2
3. Решить уравнение 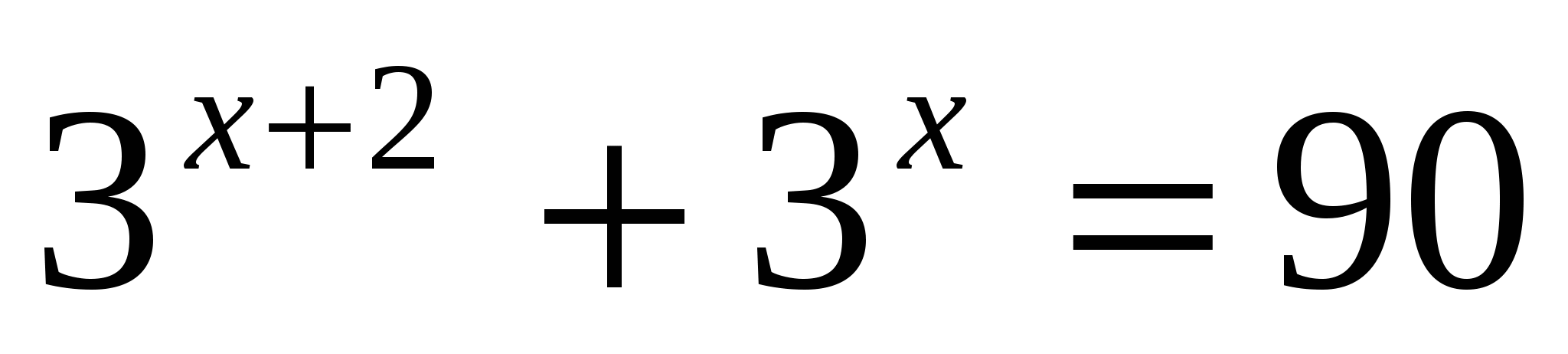
1) 0,2 2) 2 3) –2 4) 3
4. Решите неравенство 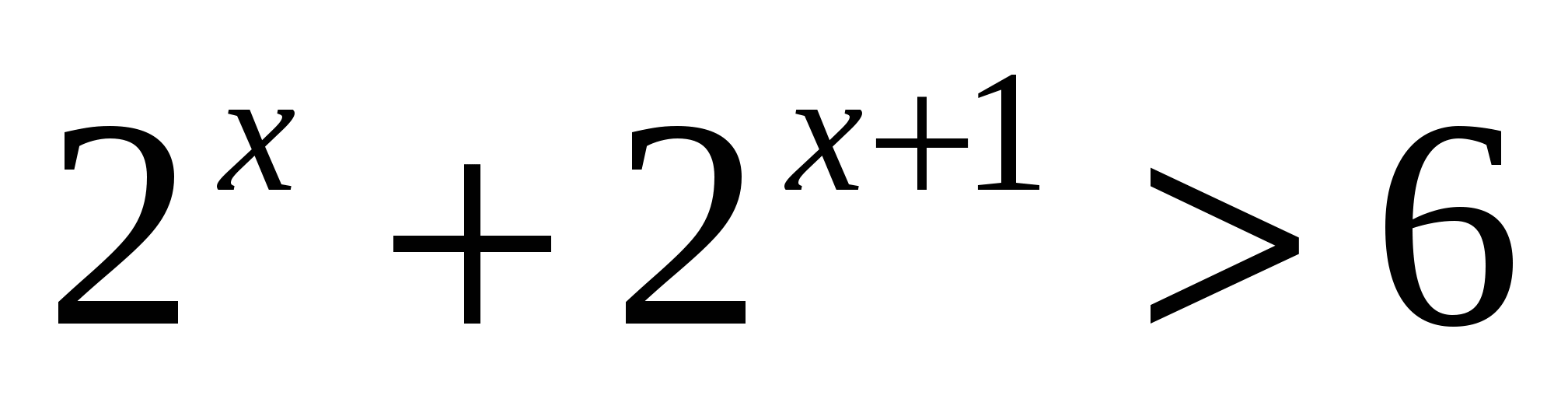
1) 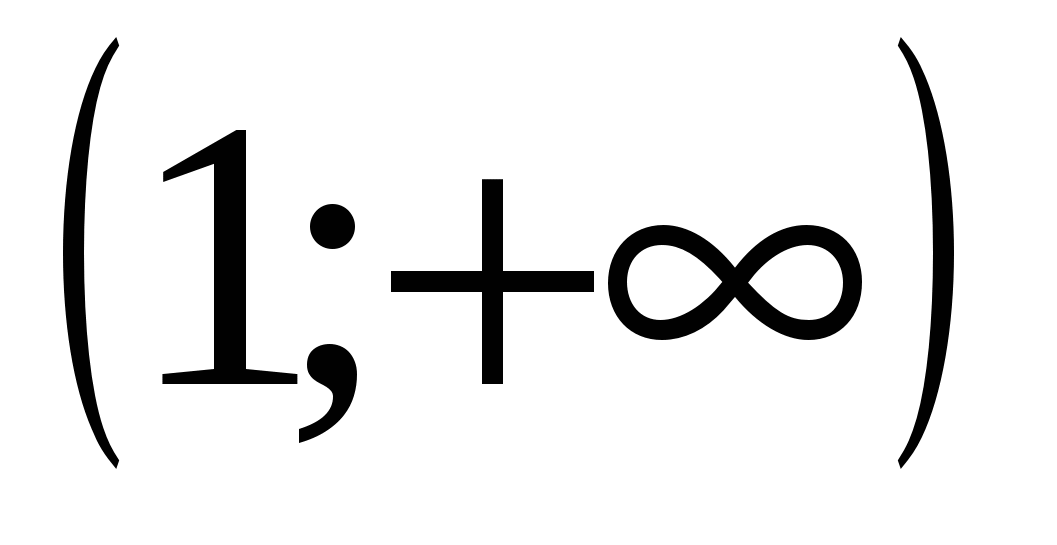 2)
2) 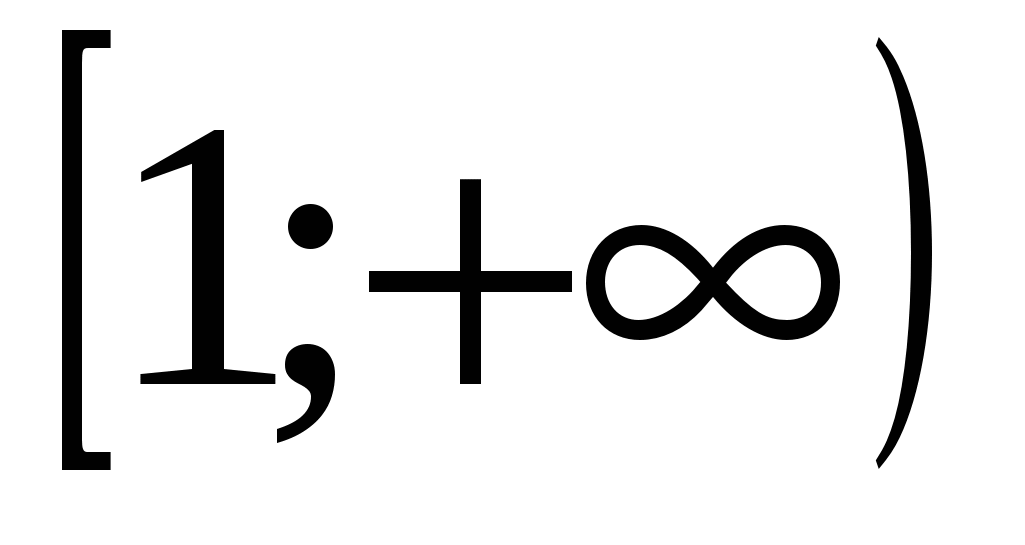 3)
3) 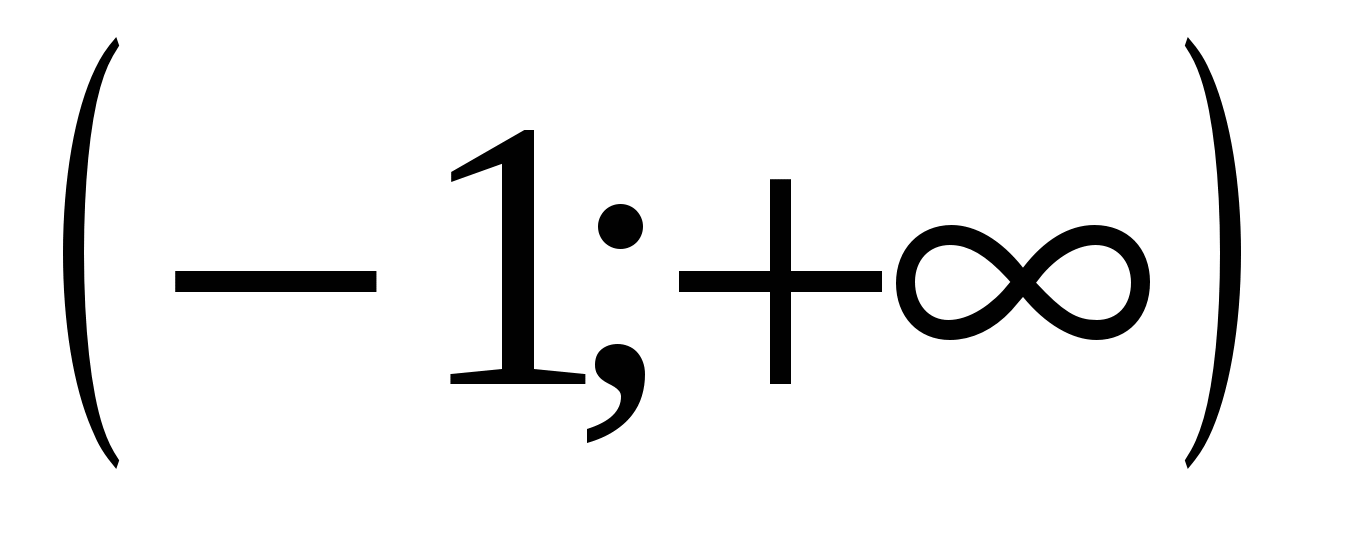

 4)
4) 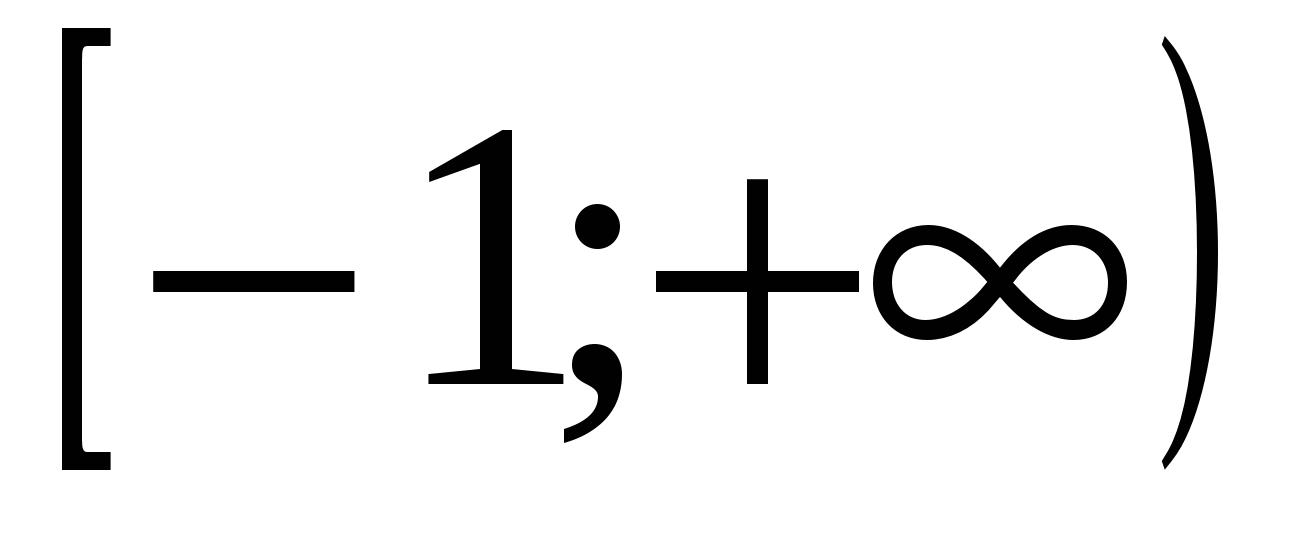
5. Найдите решение 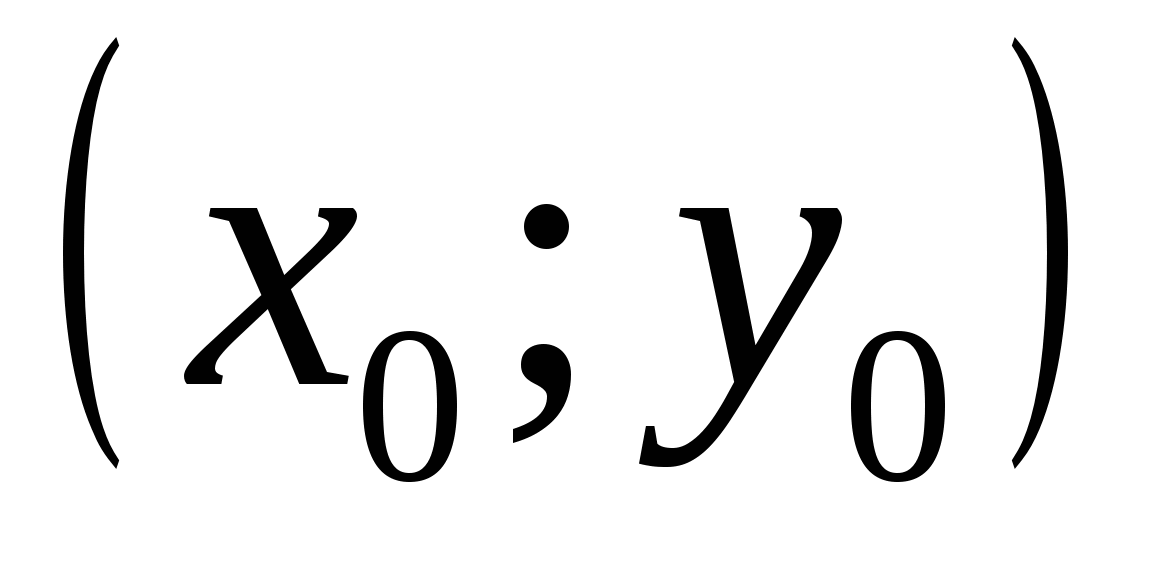 системы уравнений
системы уравнений 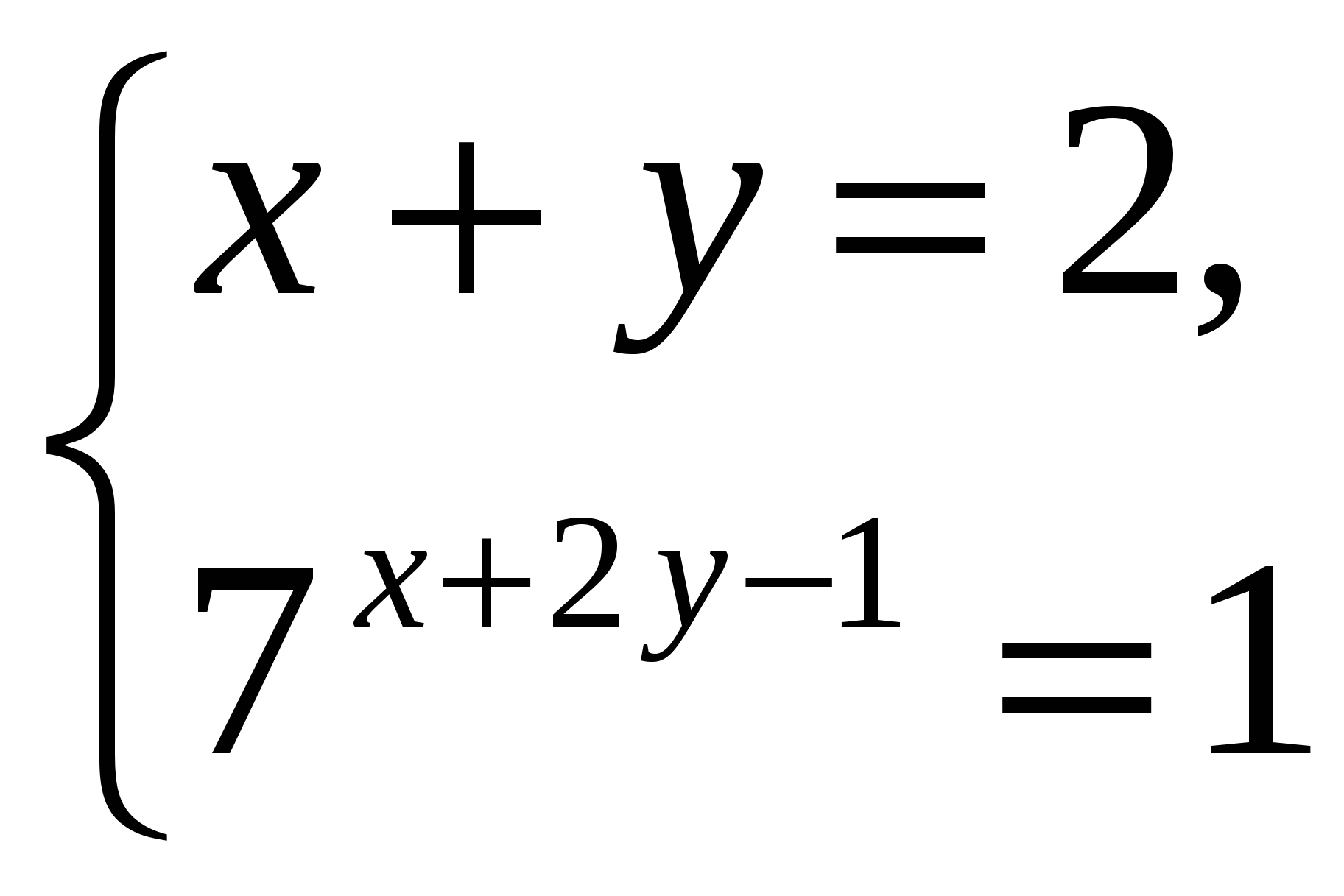 и вычислите
и вычислите
значение произведения 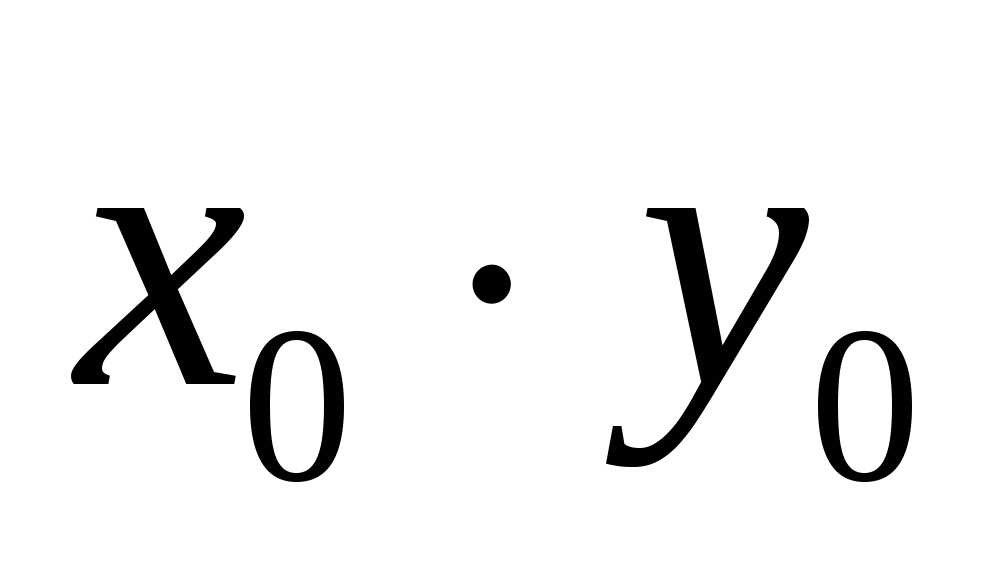
1) – 2 2) 2 3) – 3 4) 3
Решение:
I вариант
1. Укажите промежуток, которому принадлежит корень уравнения 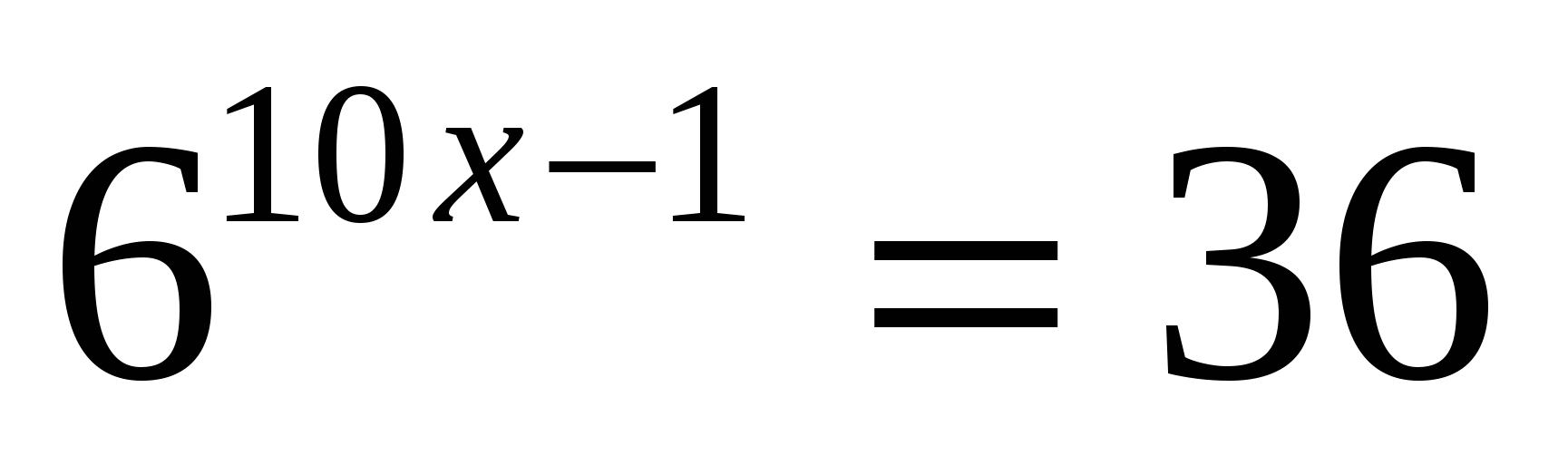
1) 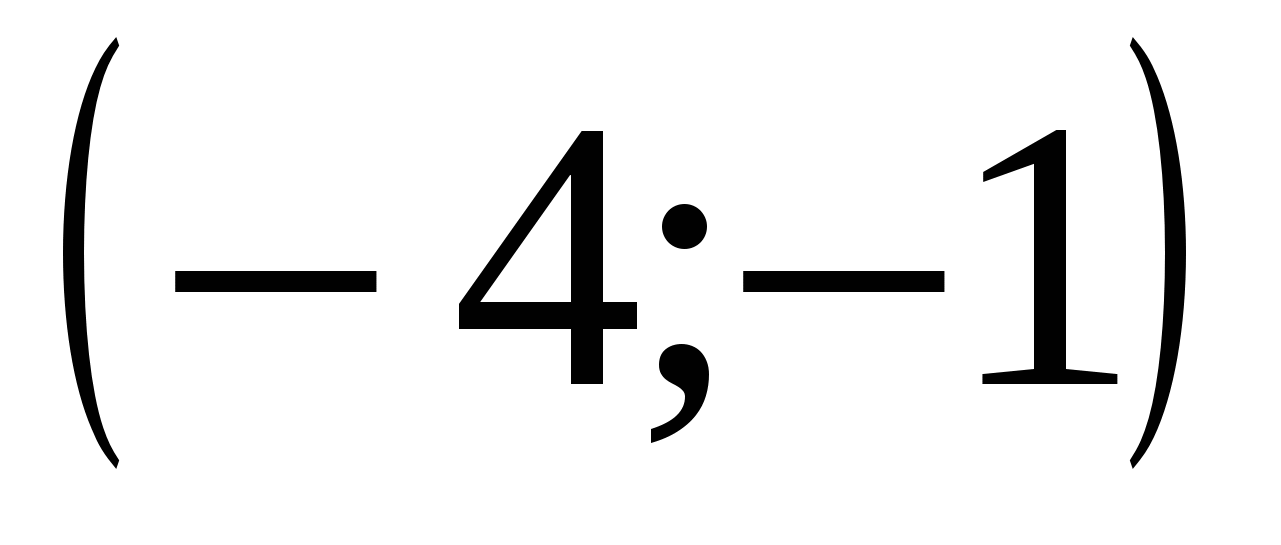 2)
2) 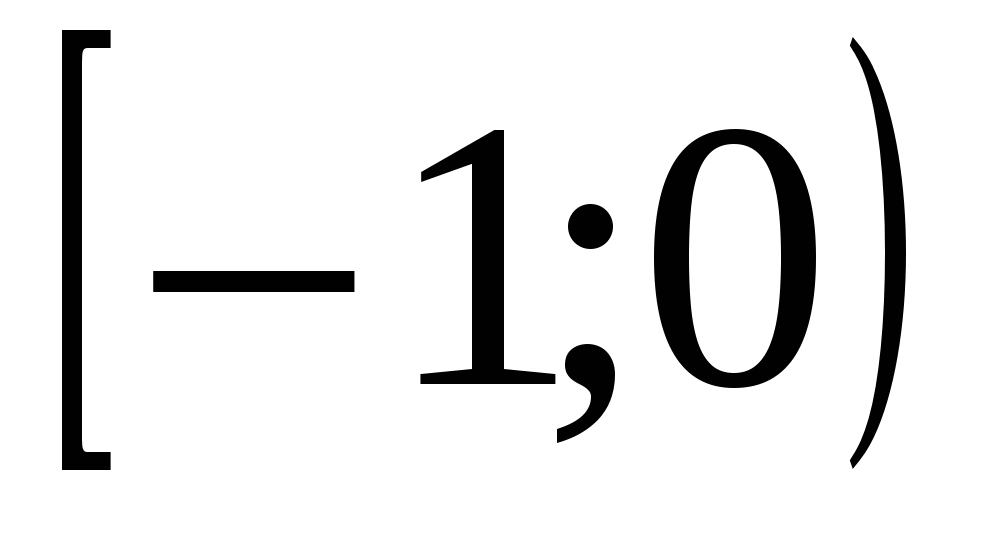 3)
3) 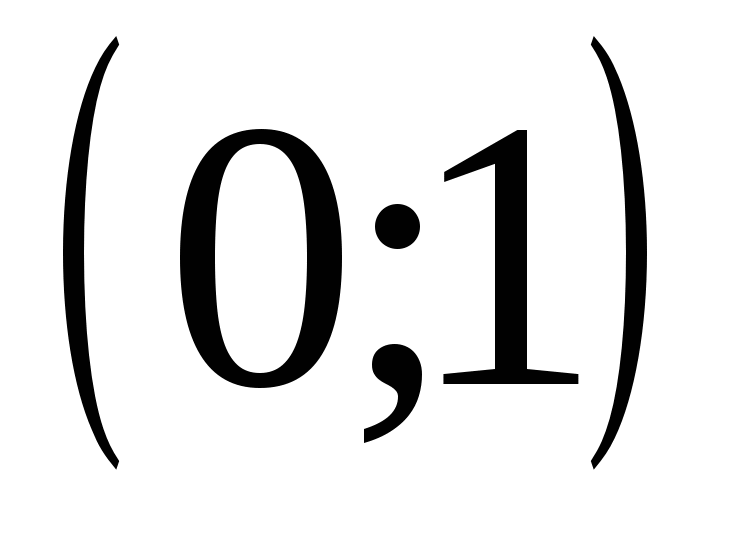 4)
4) 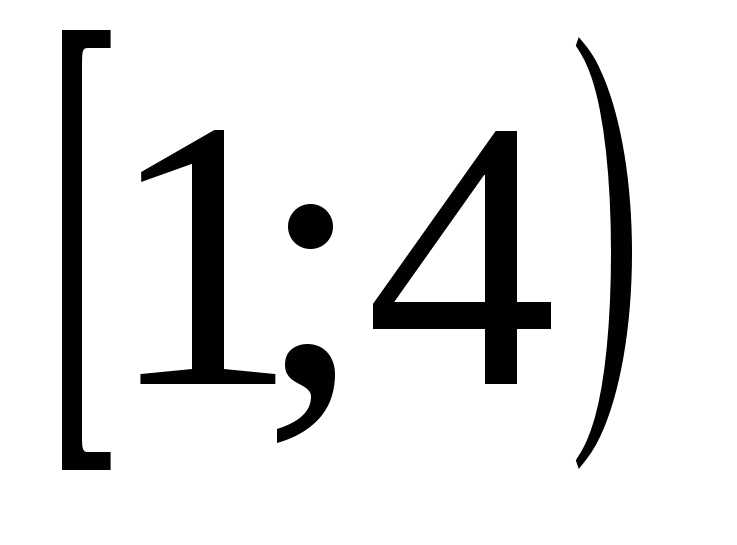

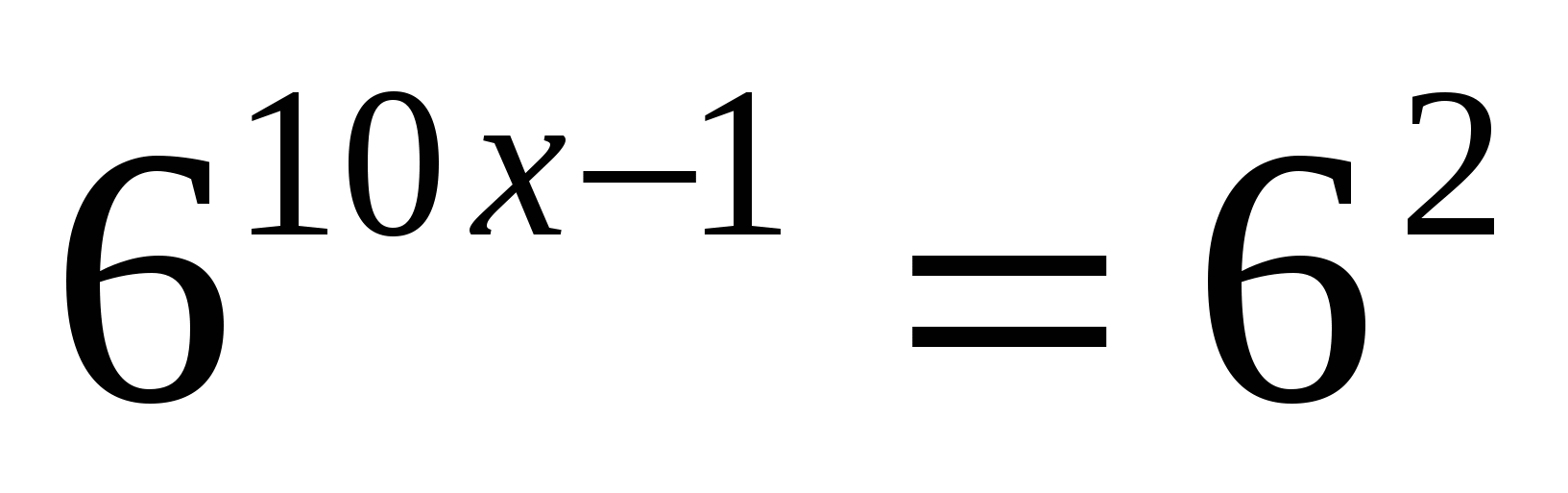
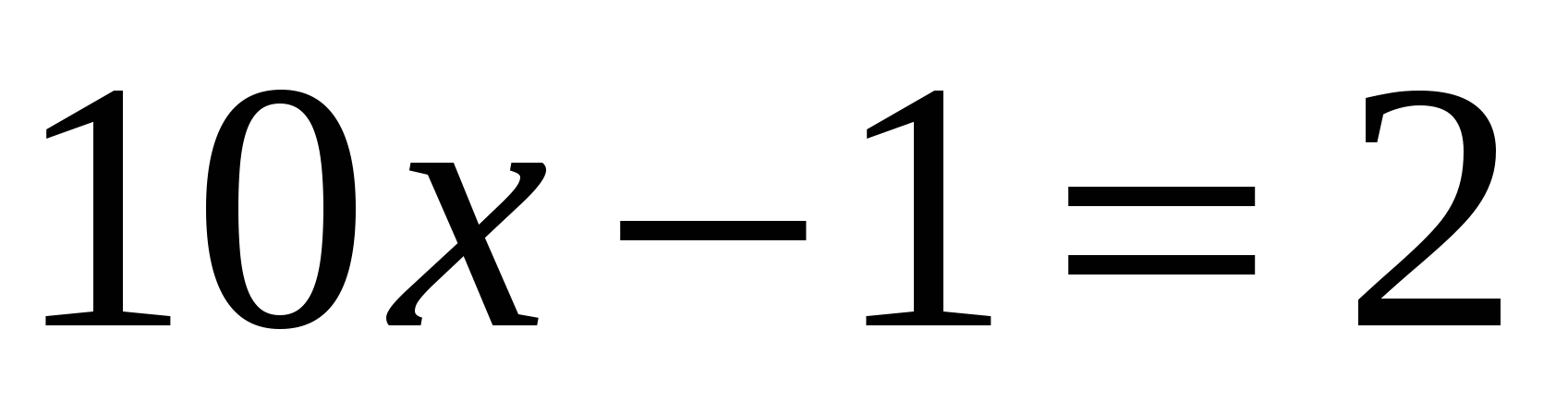
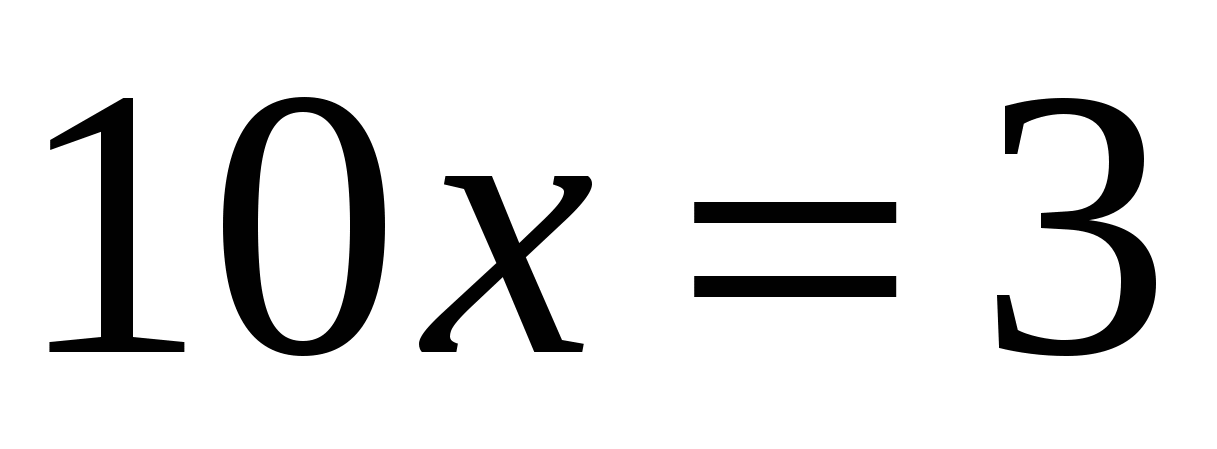
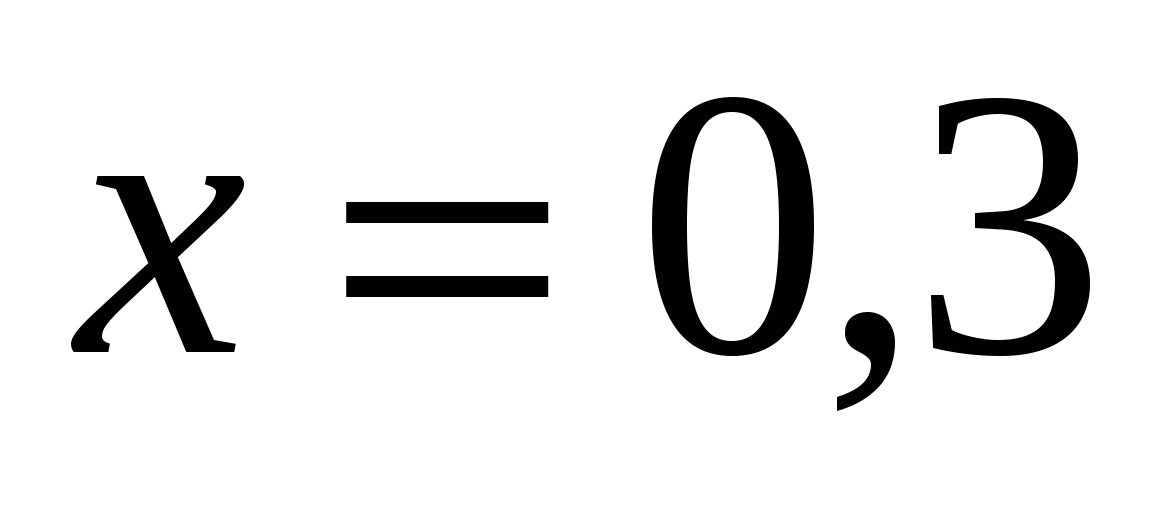
Ответ: 3
2. Найдите сумму корней уравнения 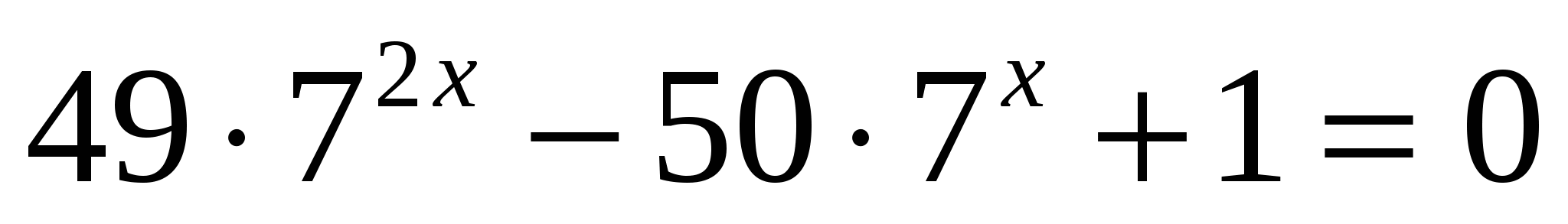
1) 1 2) 2 3) – 2 4) 50
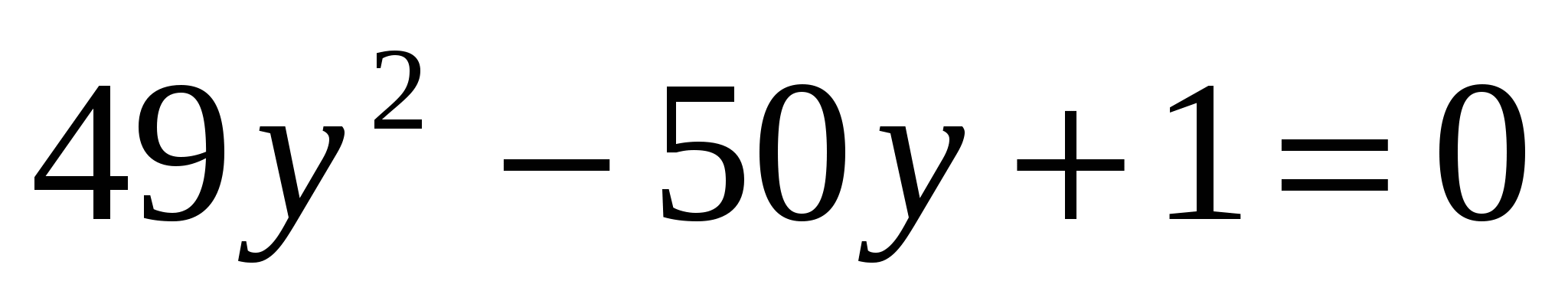
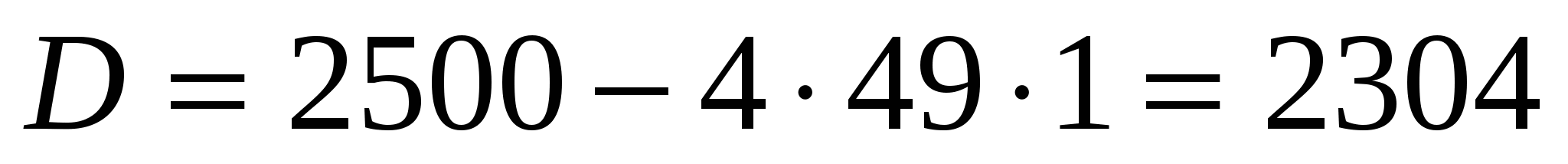
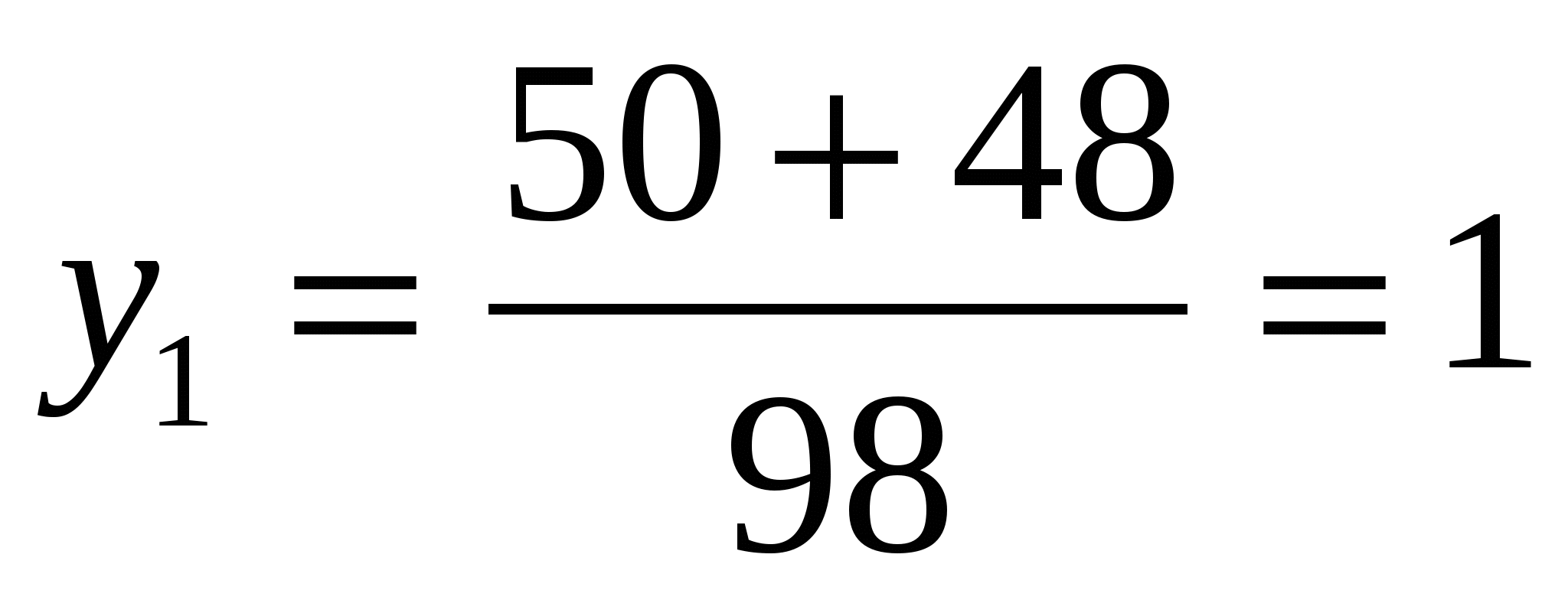
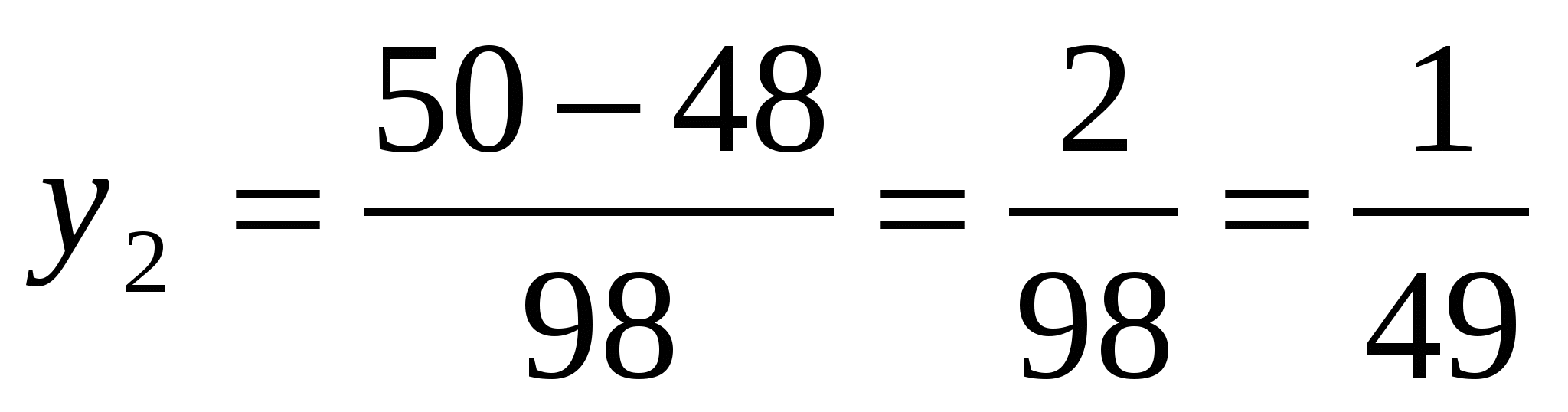
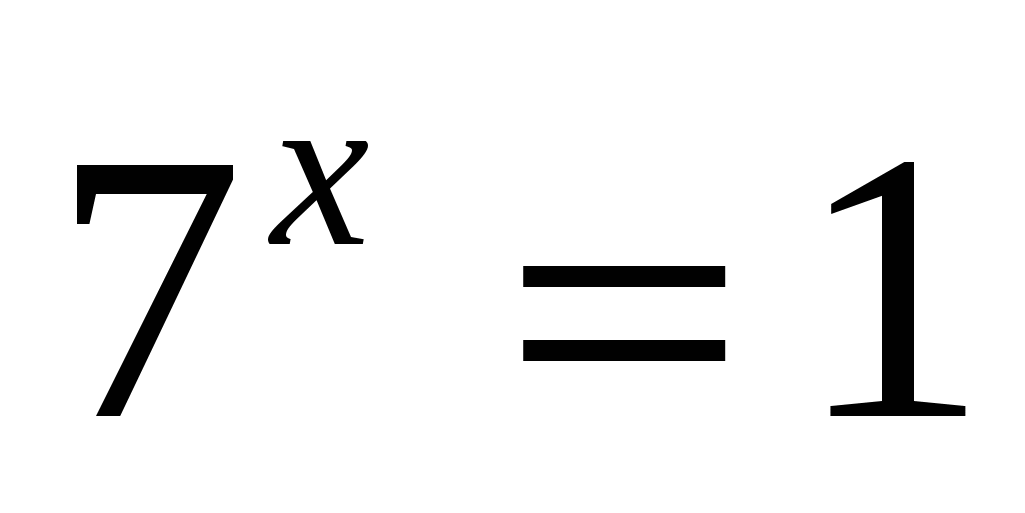
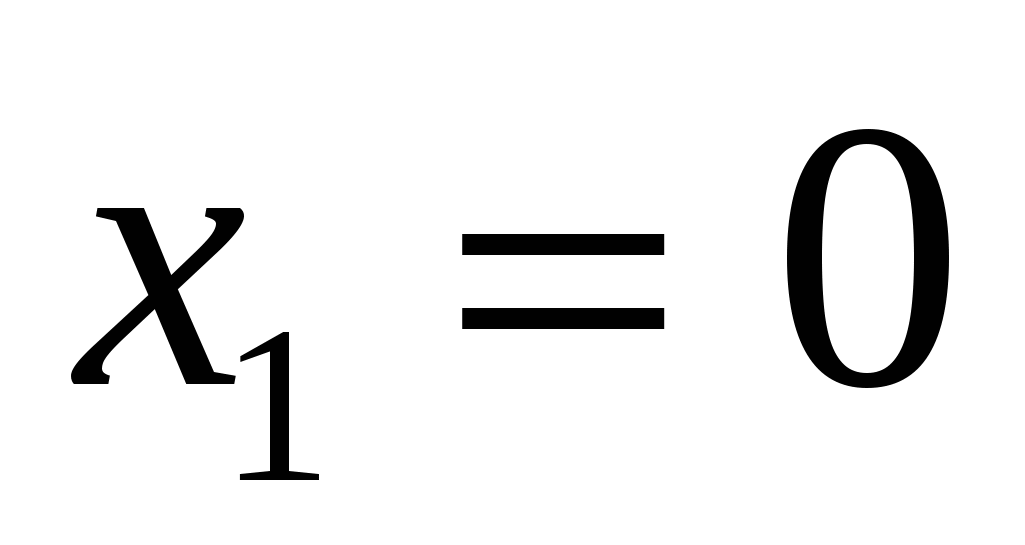
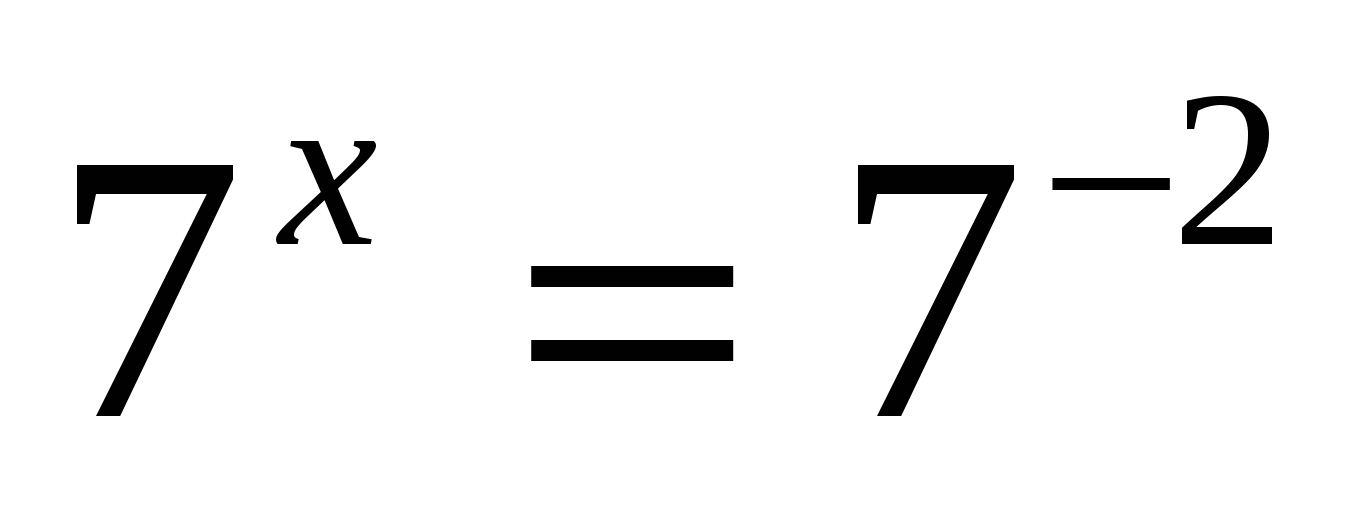
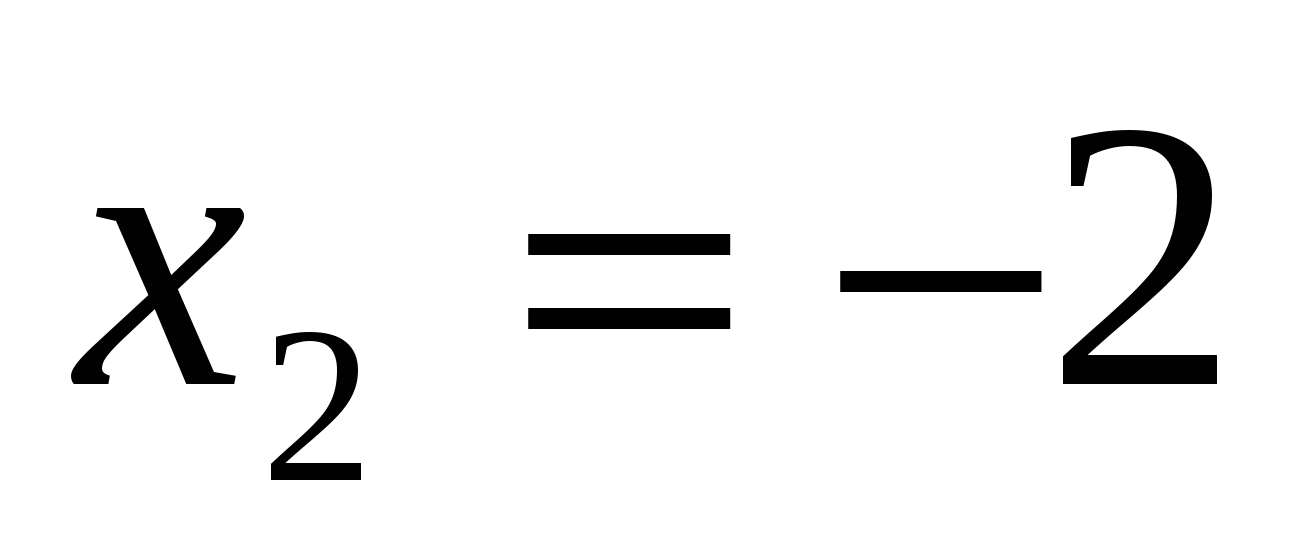
Ответ: 3
3. Решить уравнение 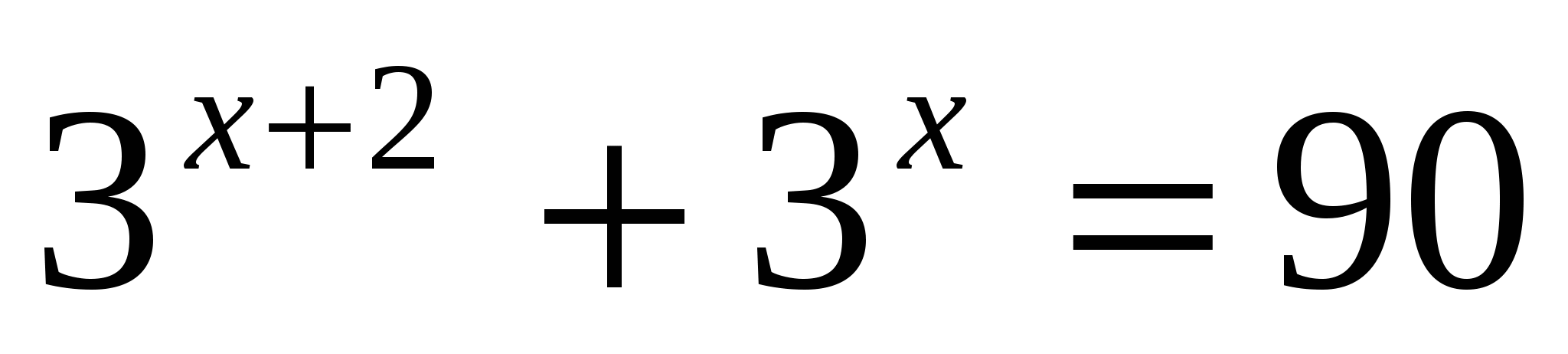
1) 0,2 2) 2 3) –2 4) 3
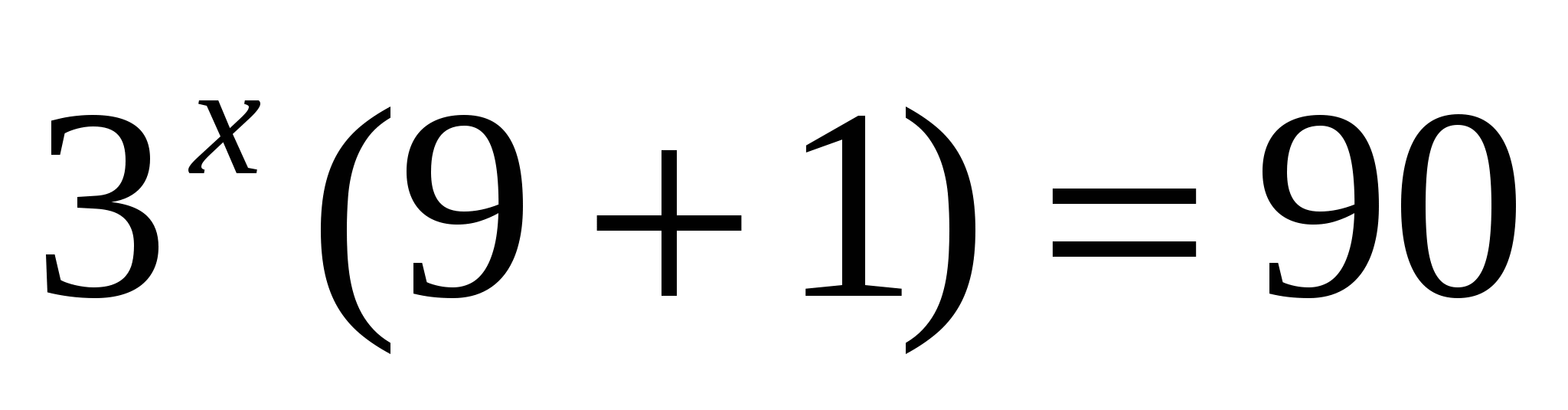
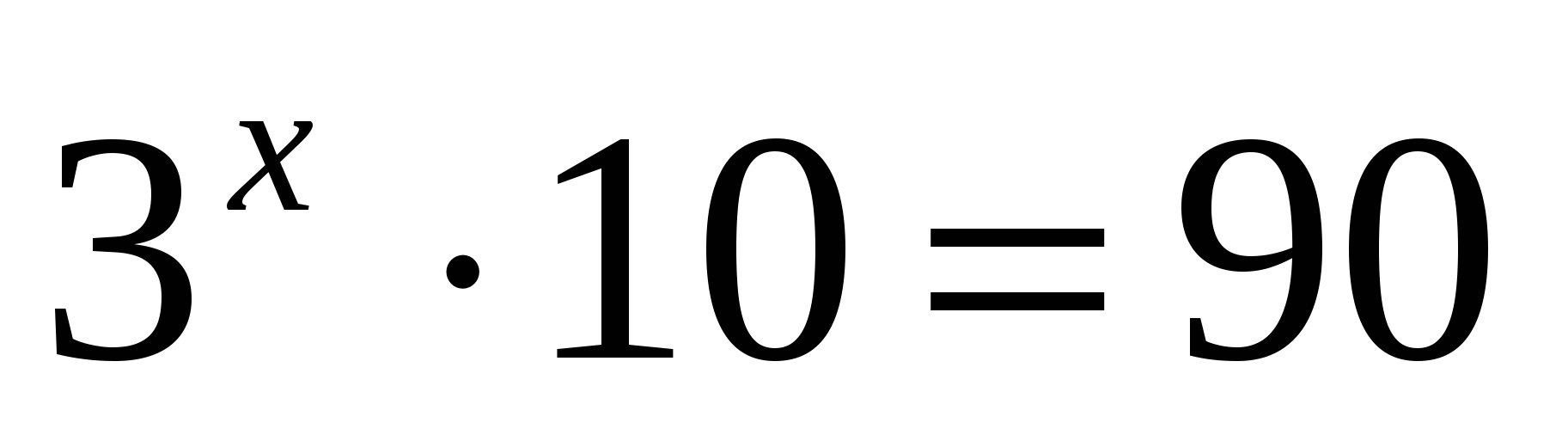
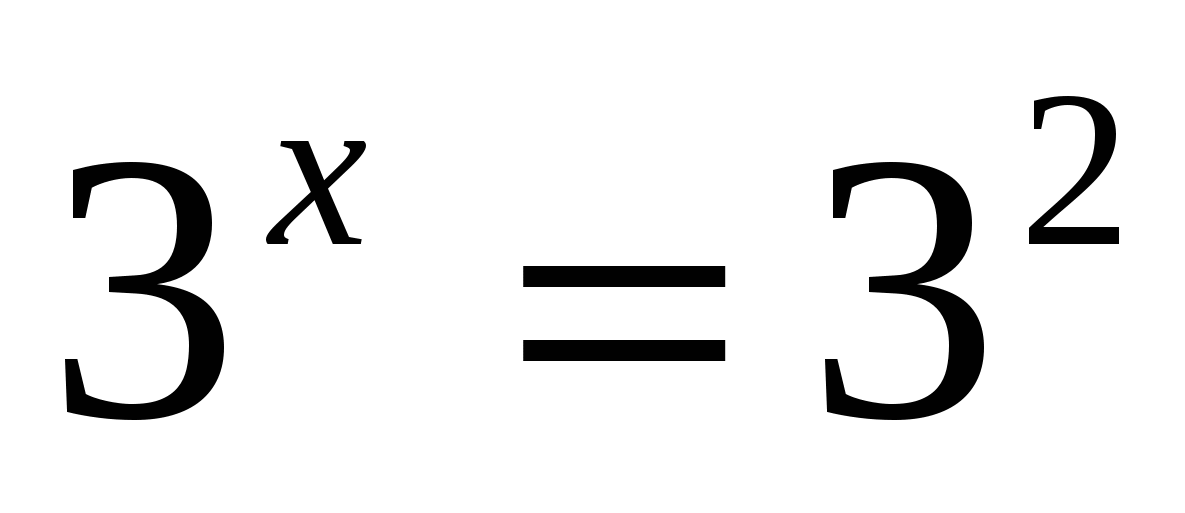
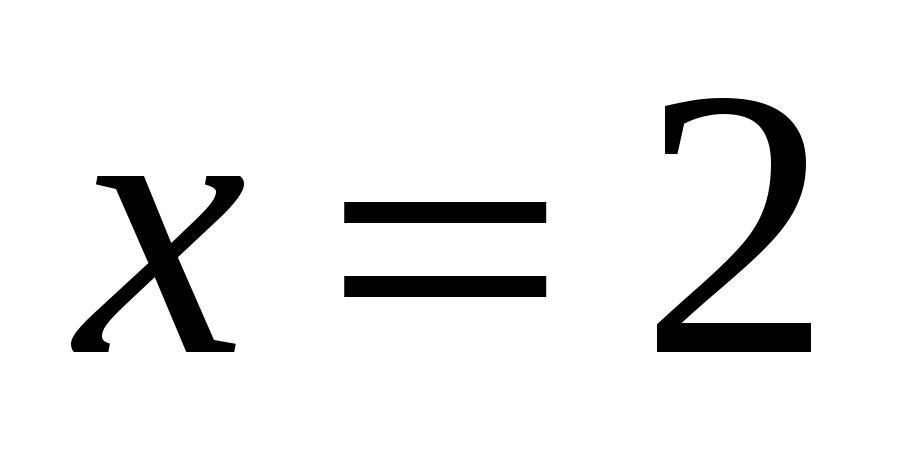
Ответ: 2
4. Решите неравенство 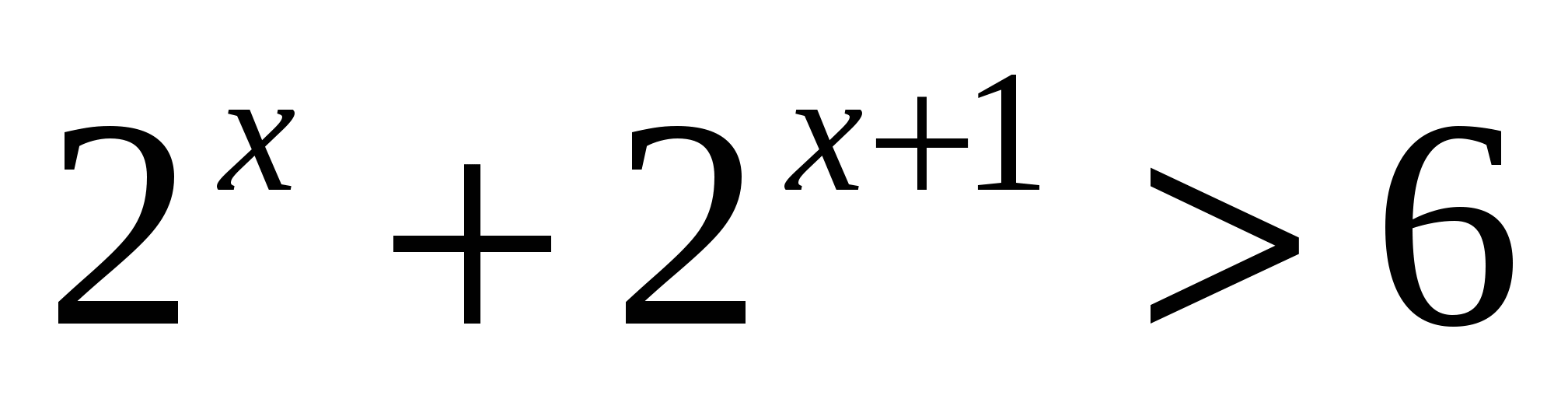
1) 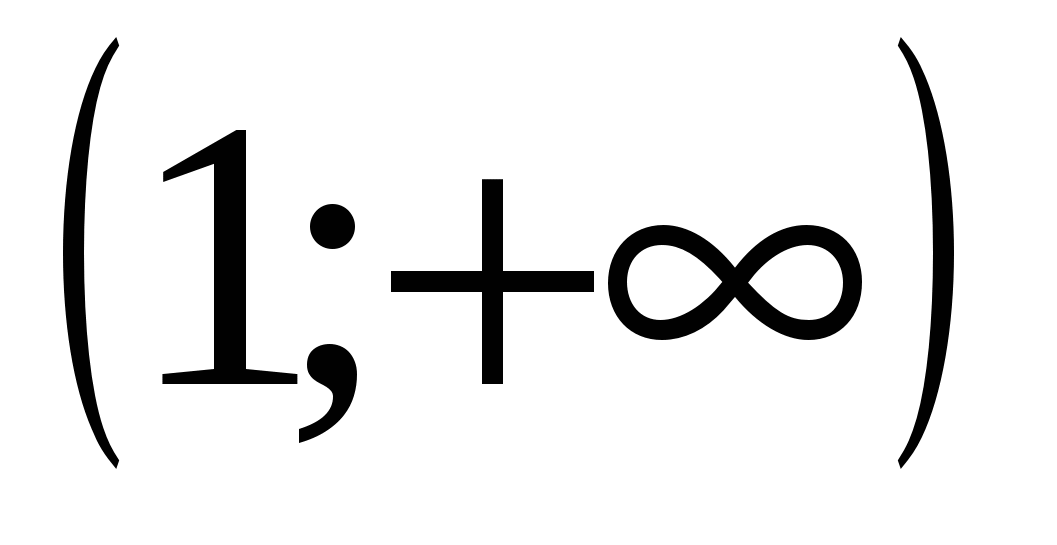 2)
2) 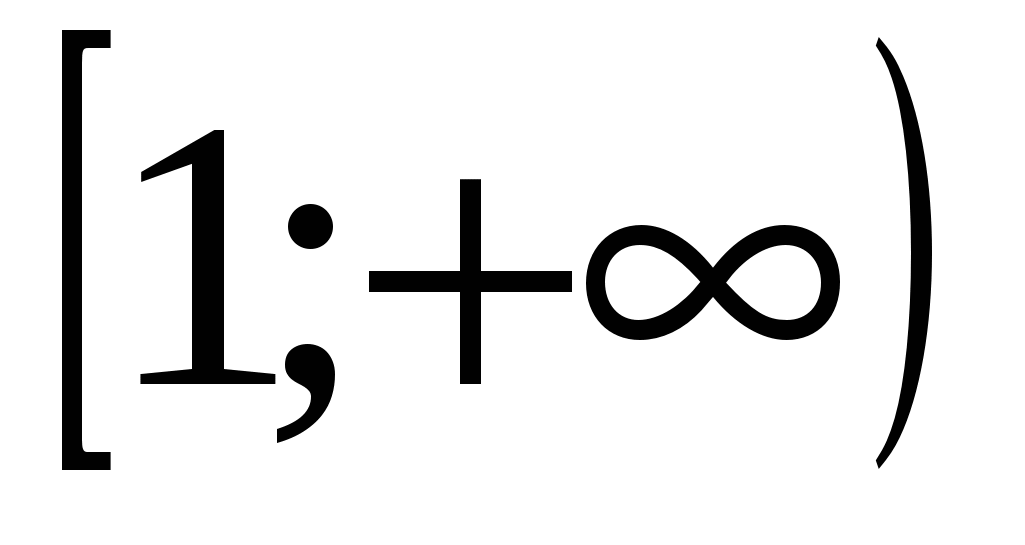 3)
3) 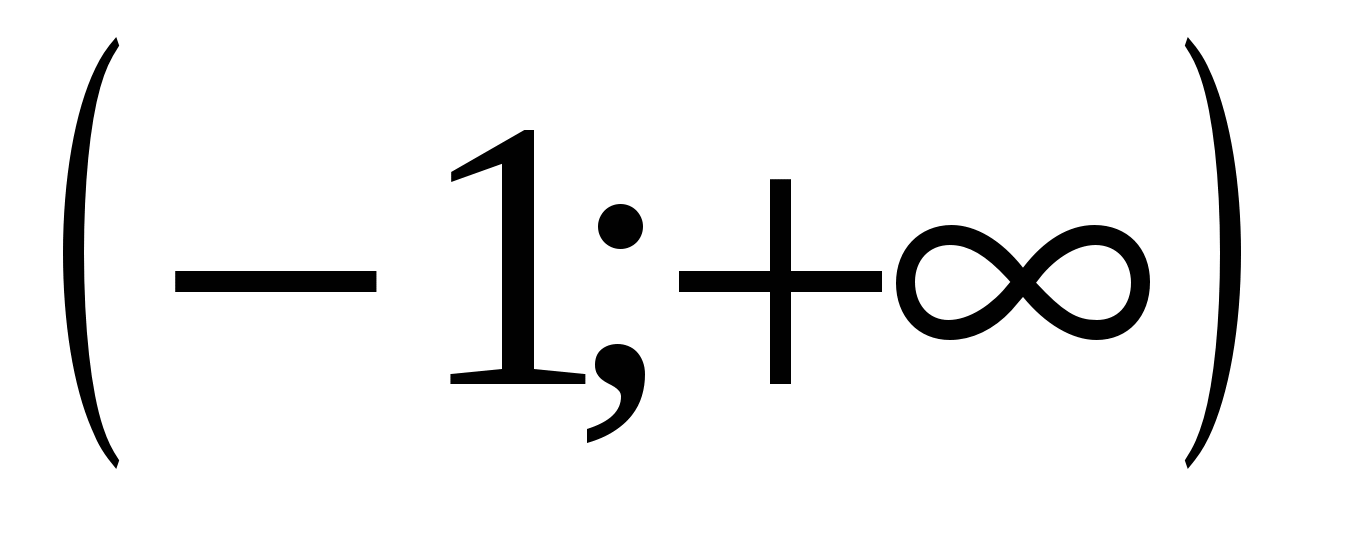

 4)
4) 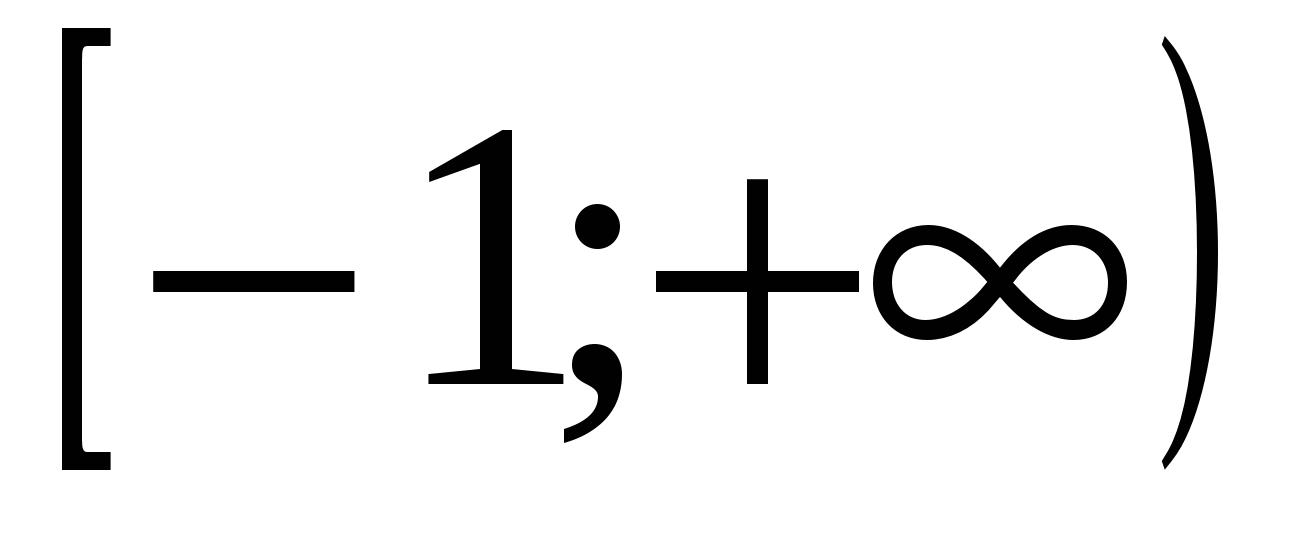
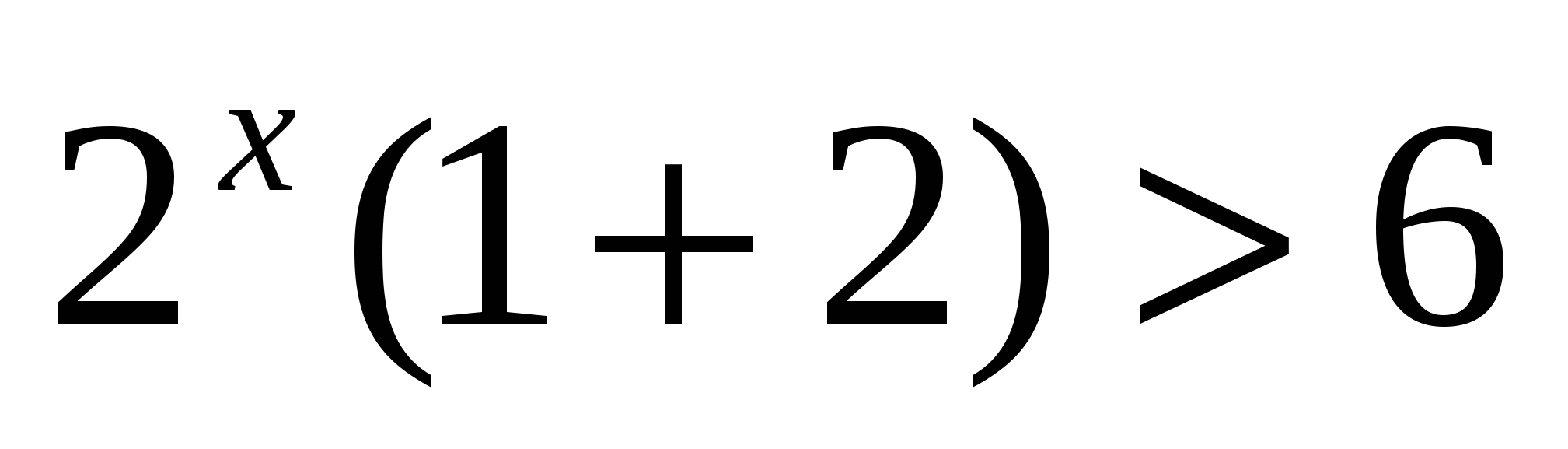
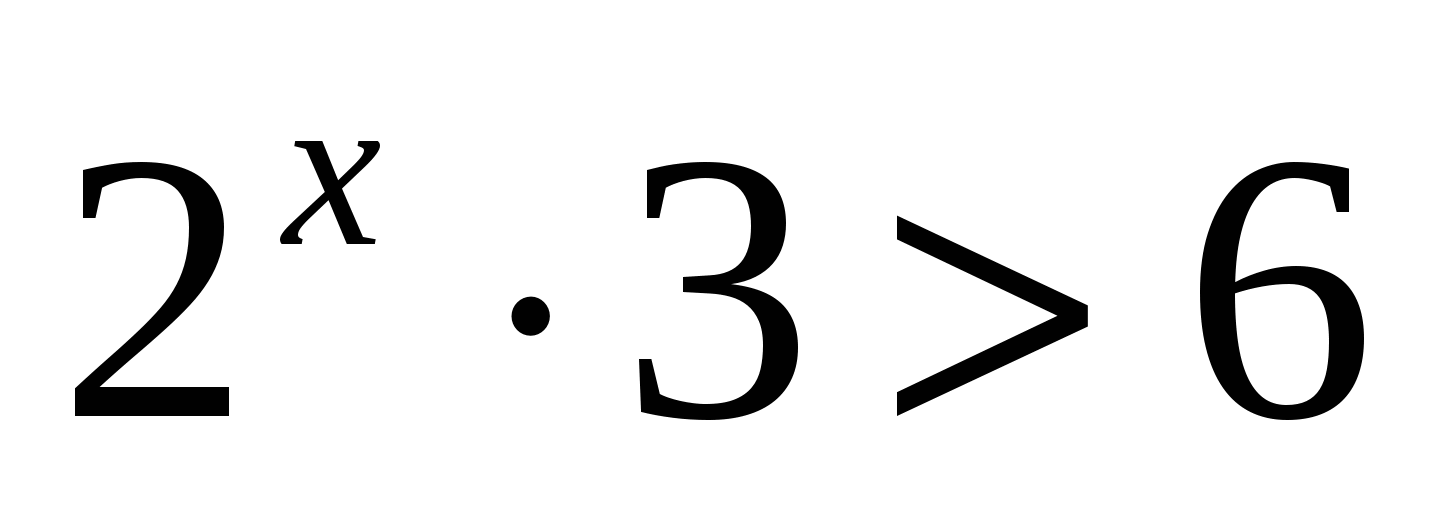
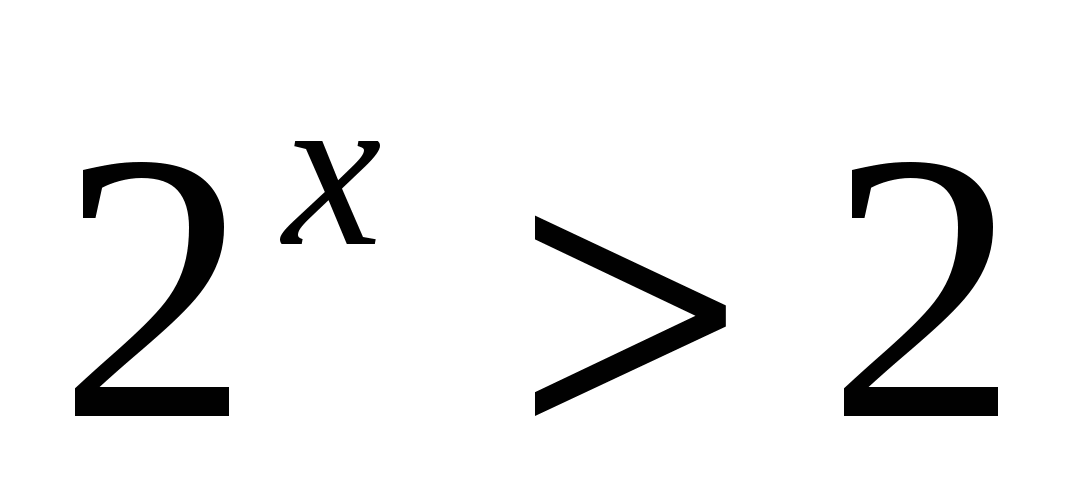
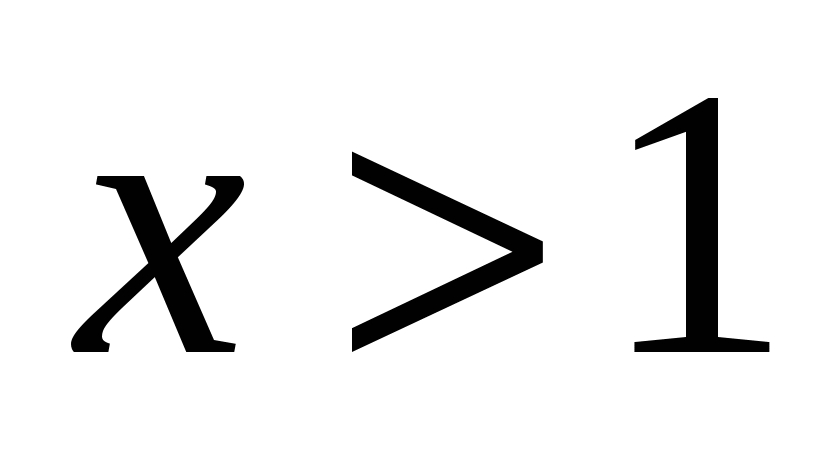
Ответ: 1
5. Найдите решение 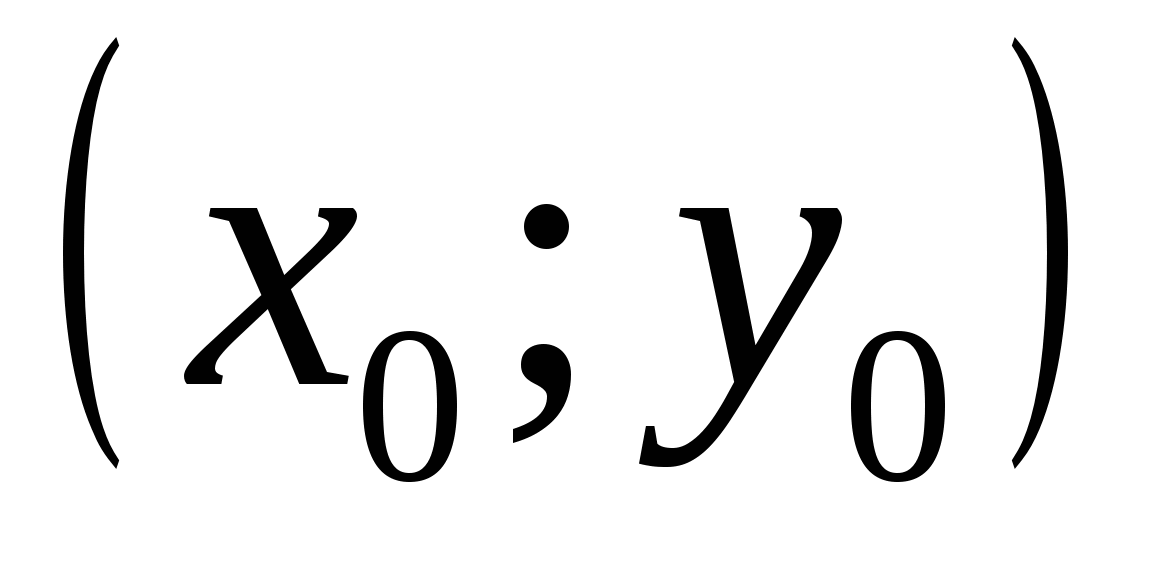 системы уравнений
системы уравнений 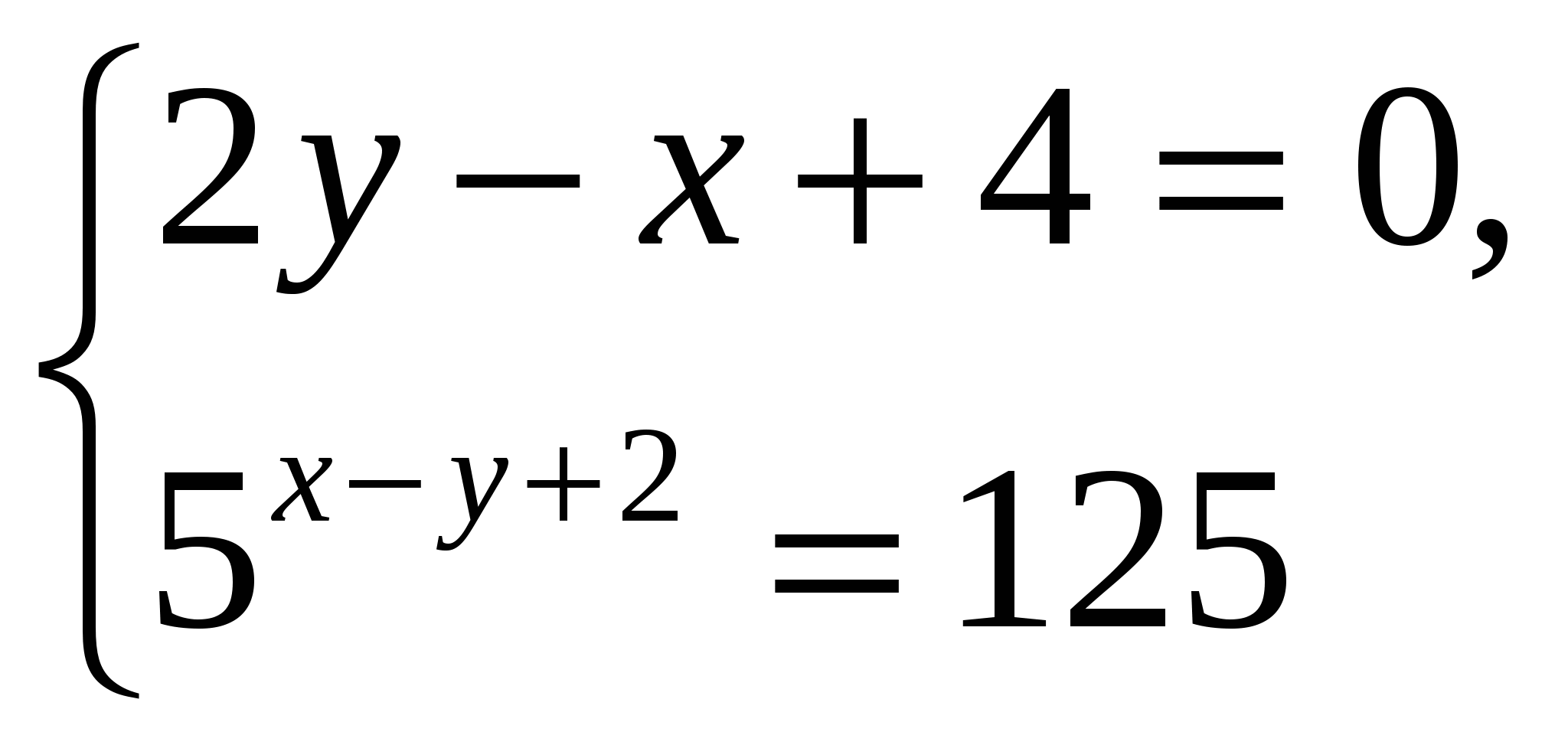 и вычислите значение произведения
и вычислите значение произведения 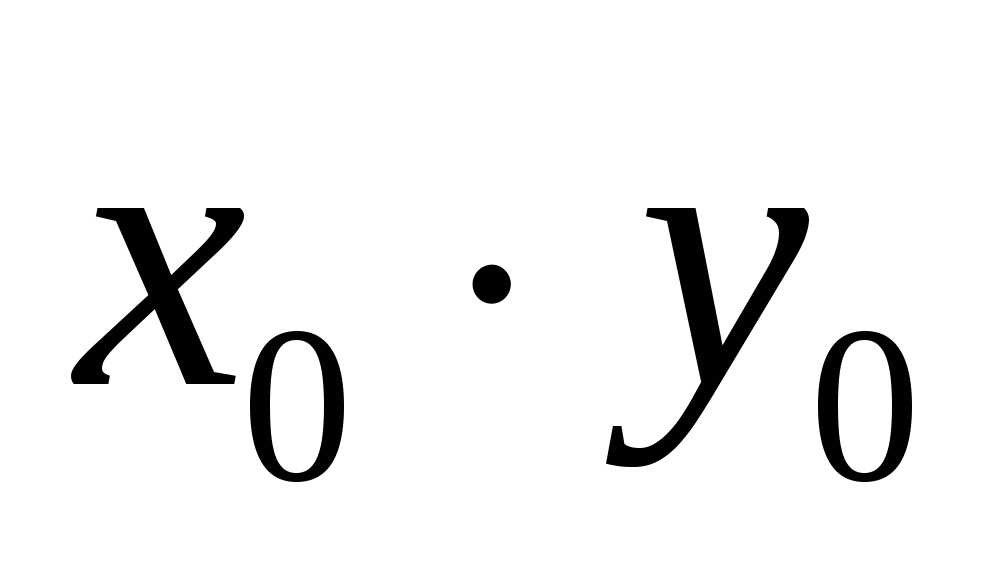
1) 6 2) 3 3) – 6 4) – 2
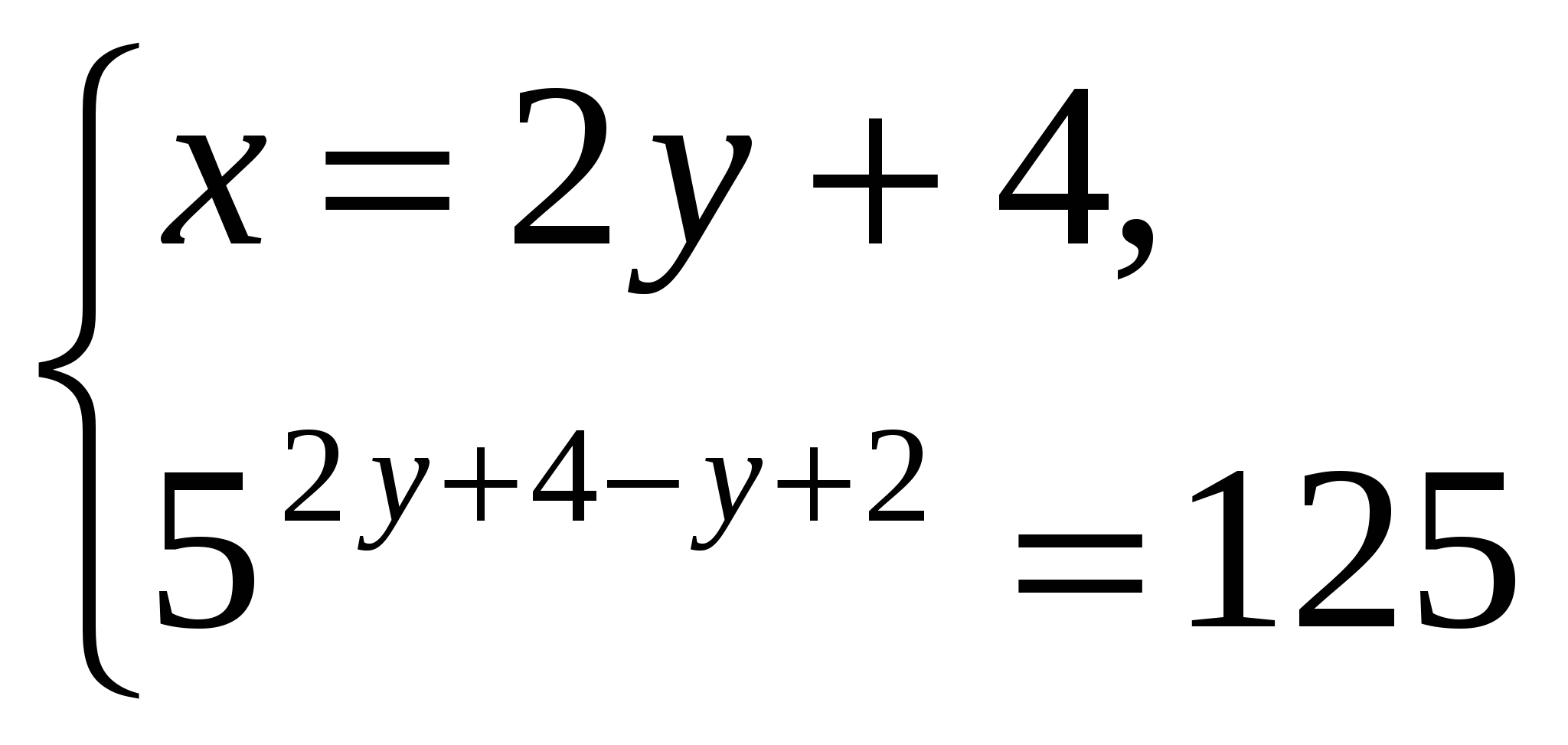
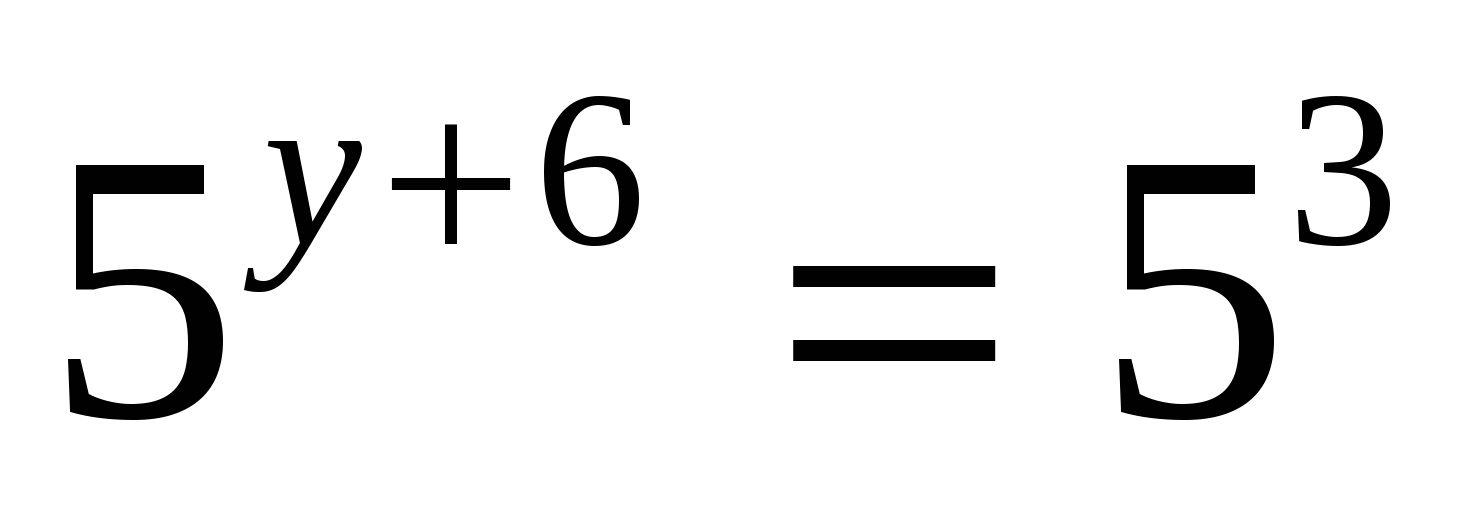
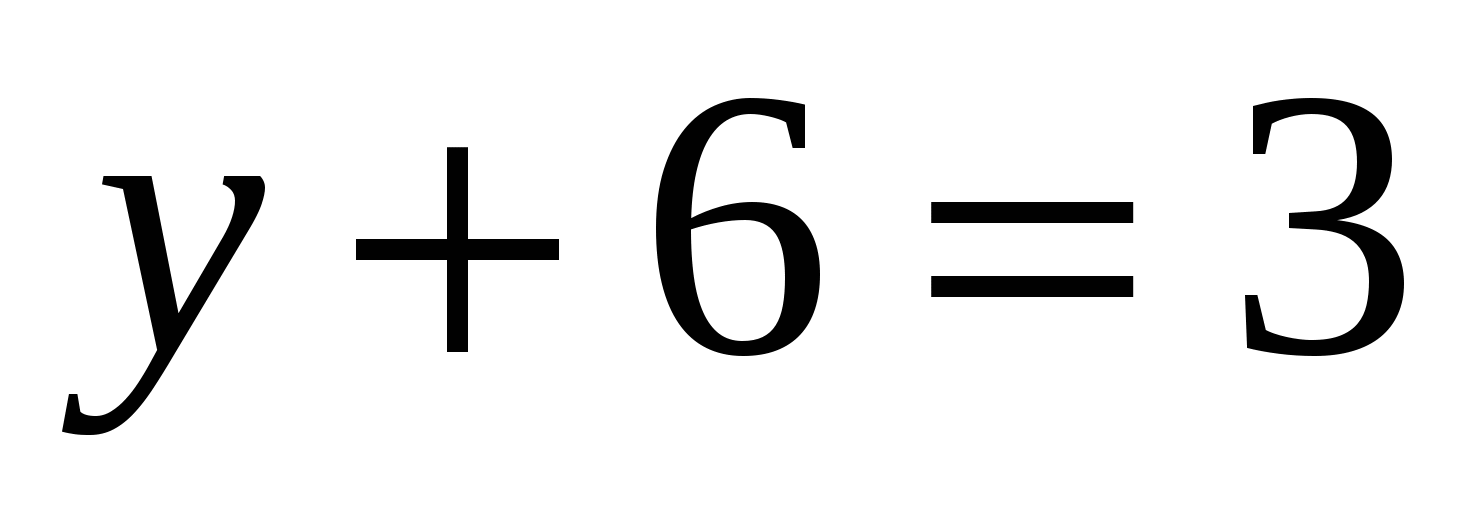
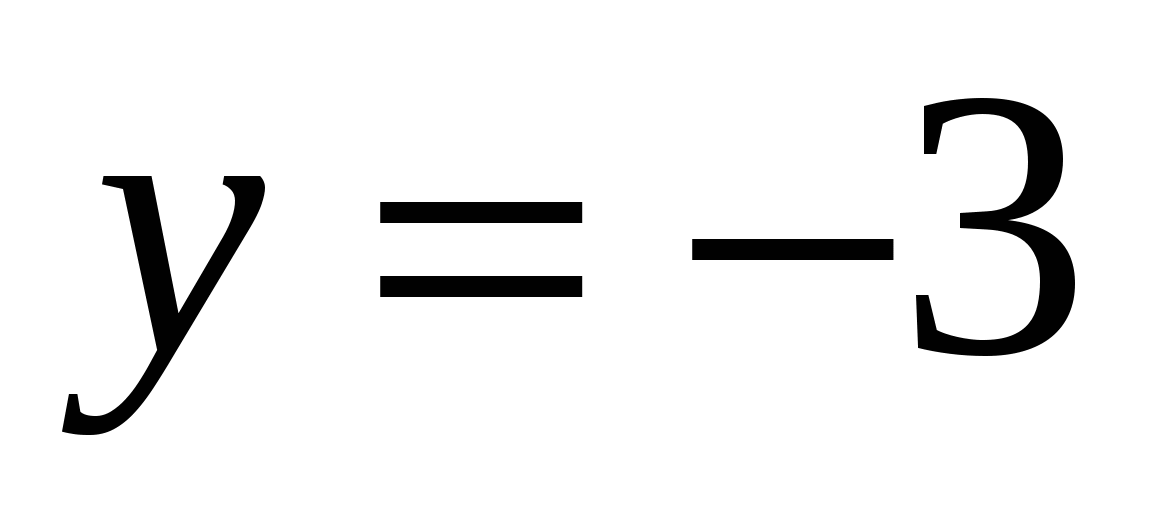
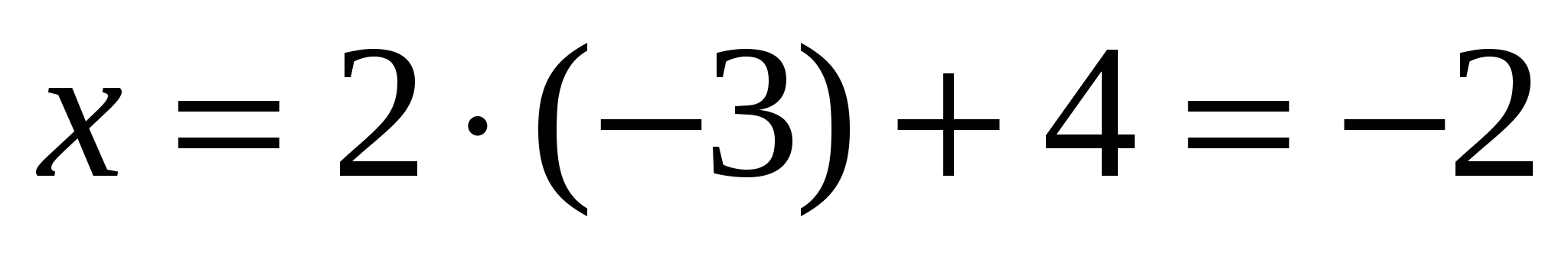
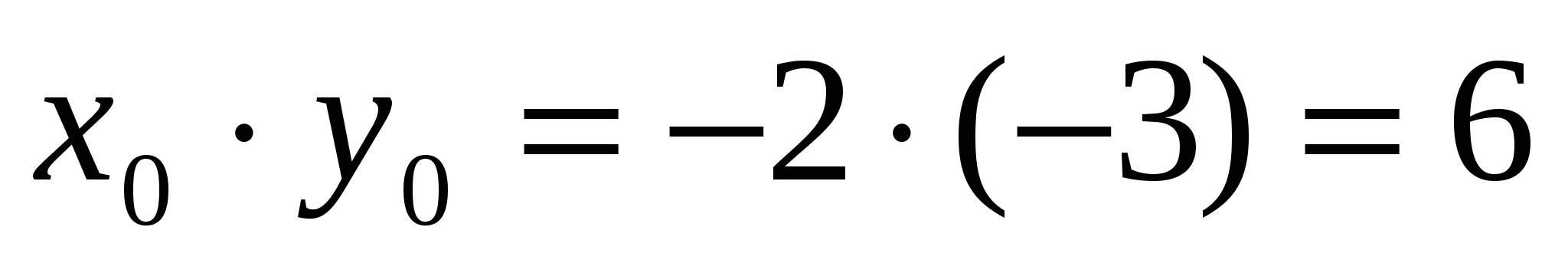
Ответ: 1
II вариант
1. Укажите промежуток, которому принадлежит корень уравнения 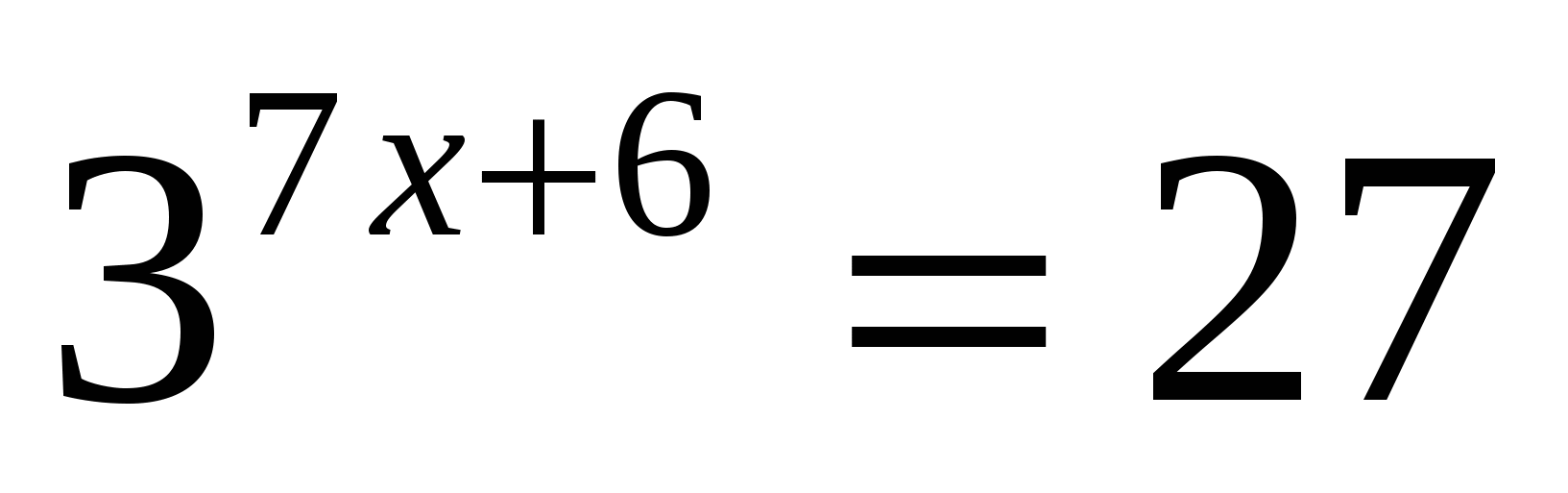
1) 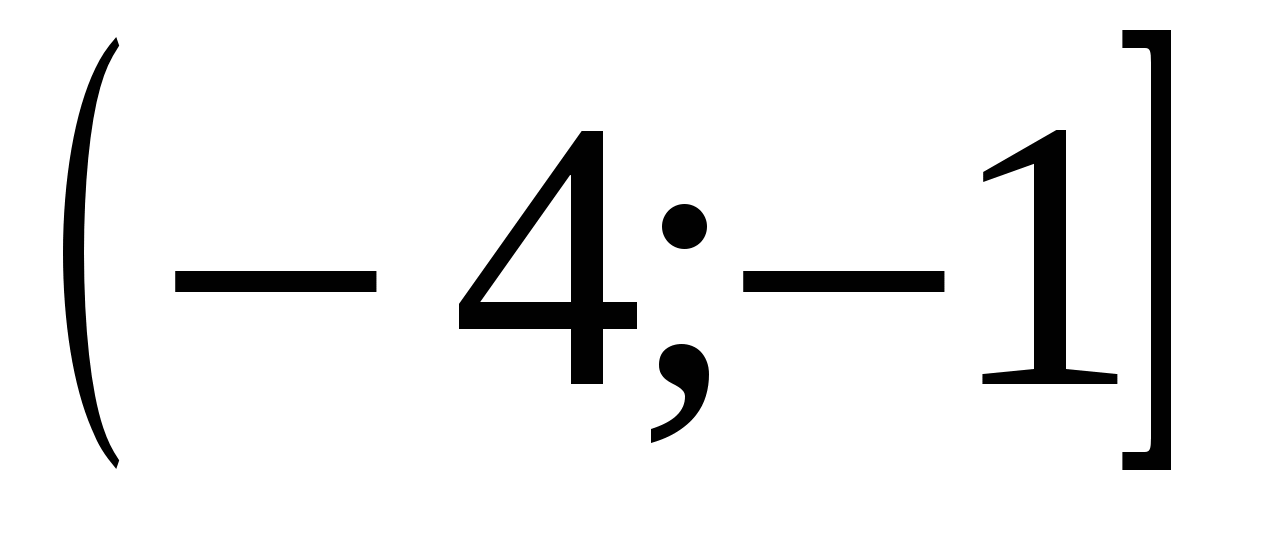 2)
2) 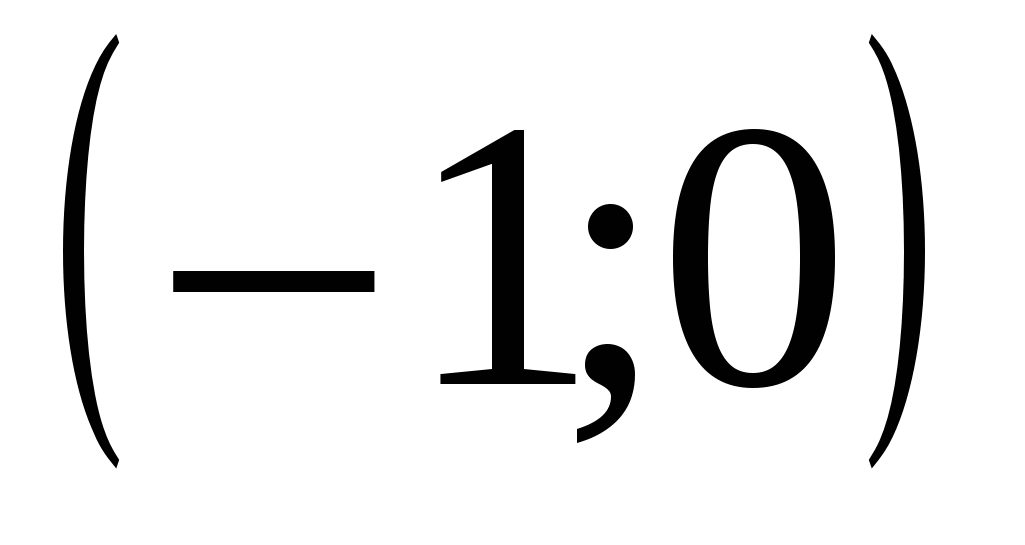 3)
3) 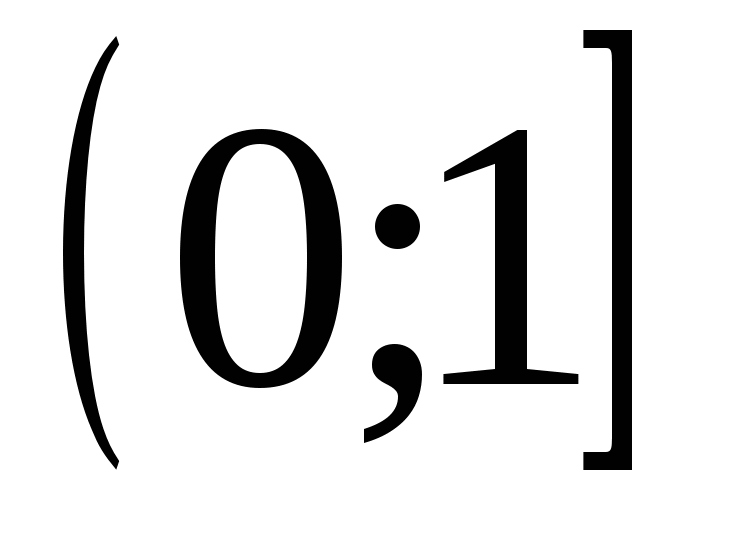 4)
4) 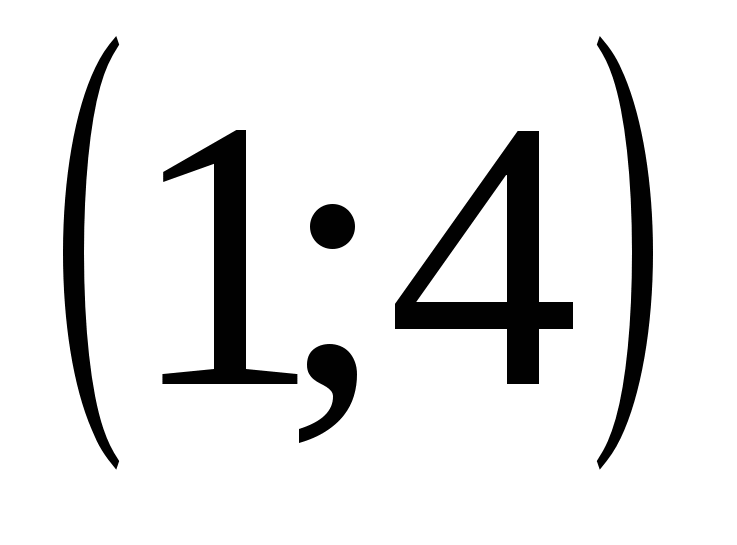

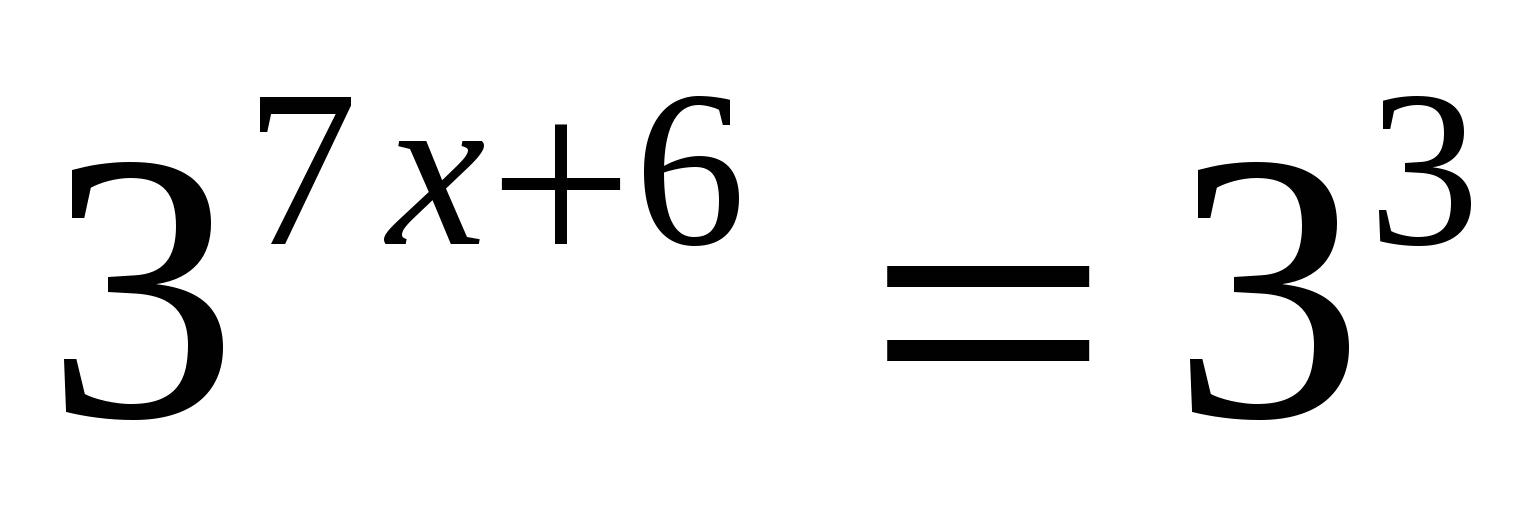
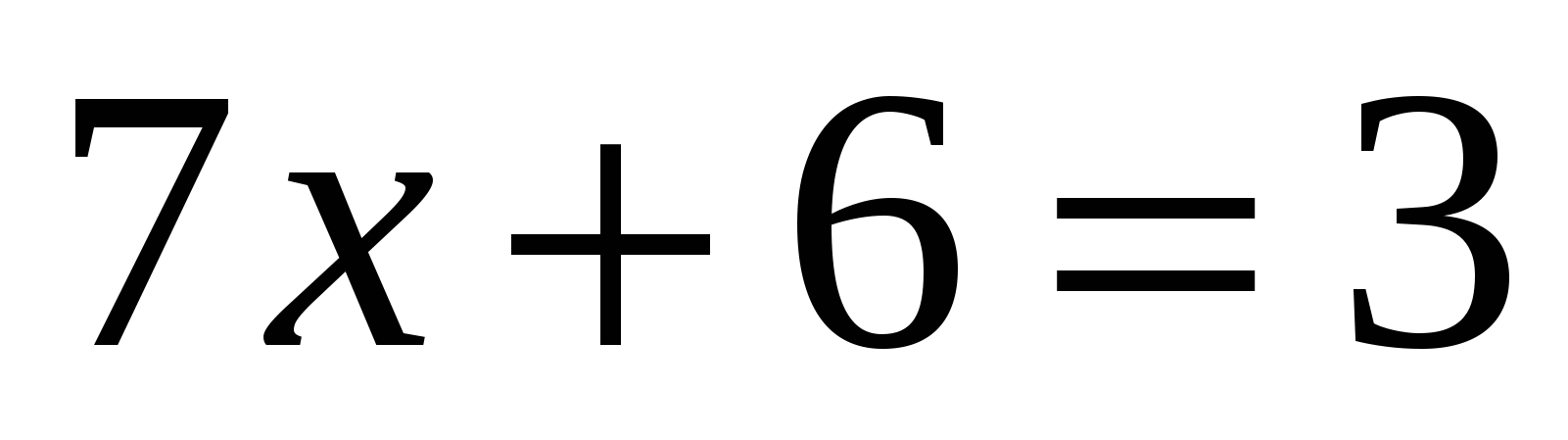
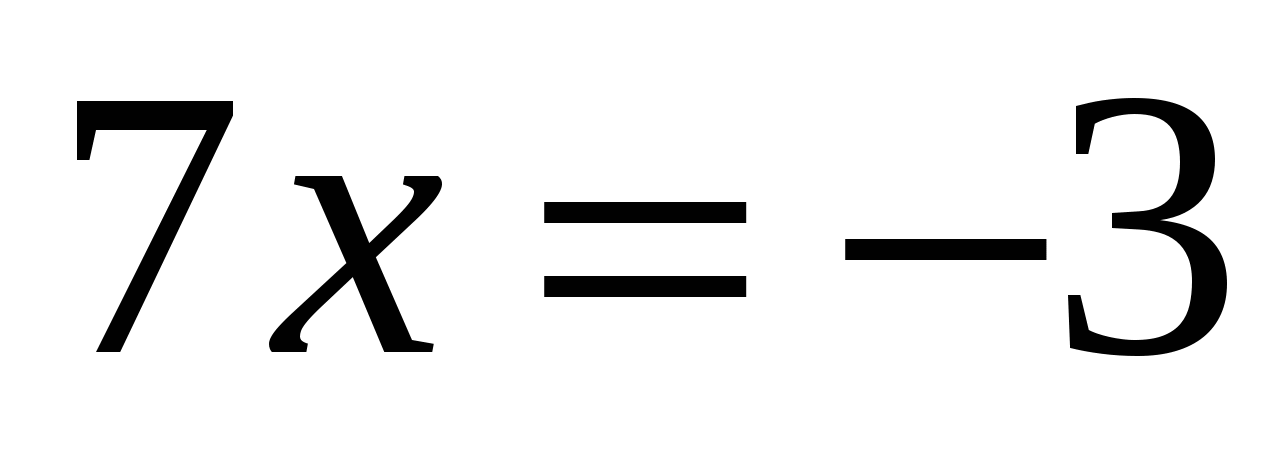
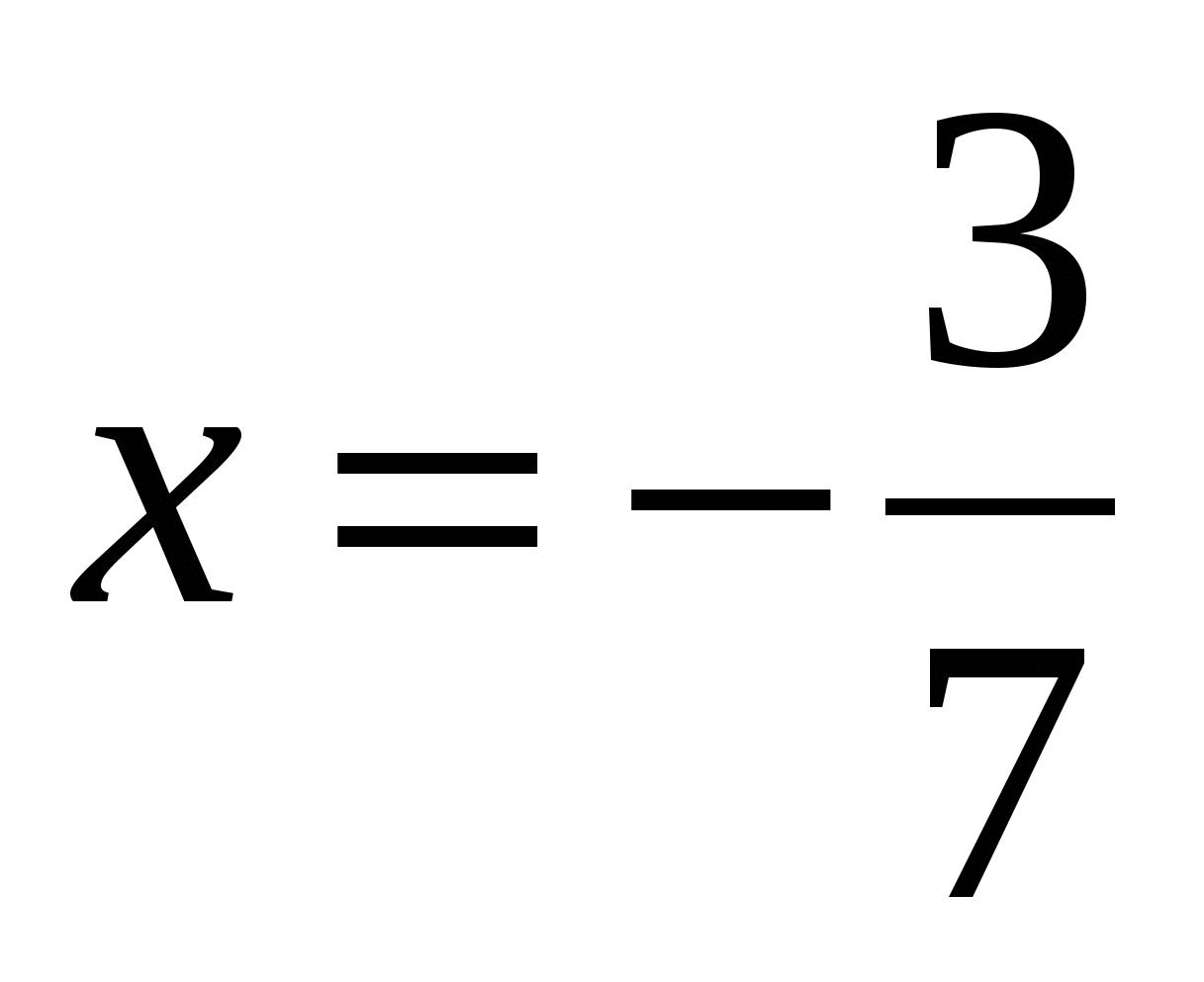
Ответ: 2
2. Найдите сумму корней уравнения 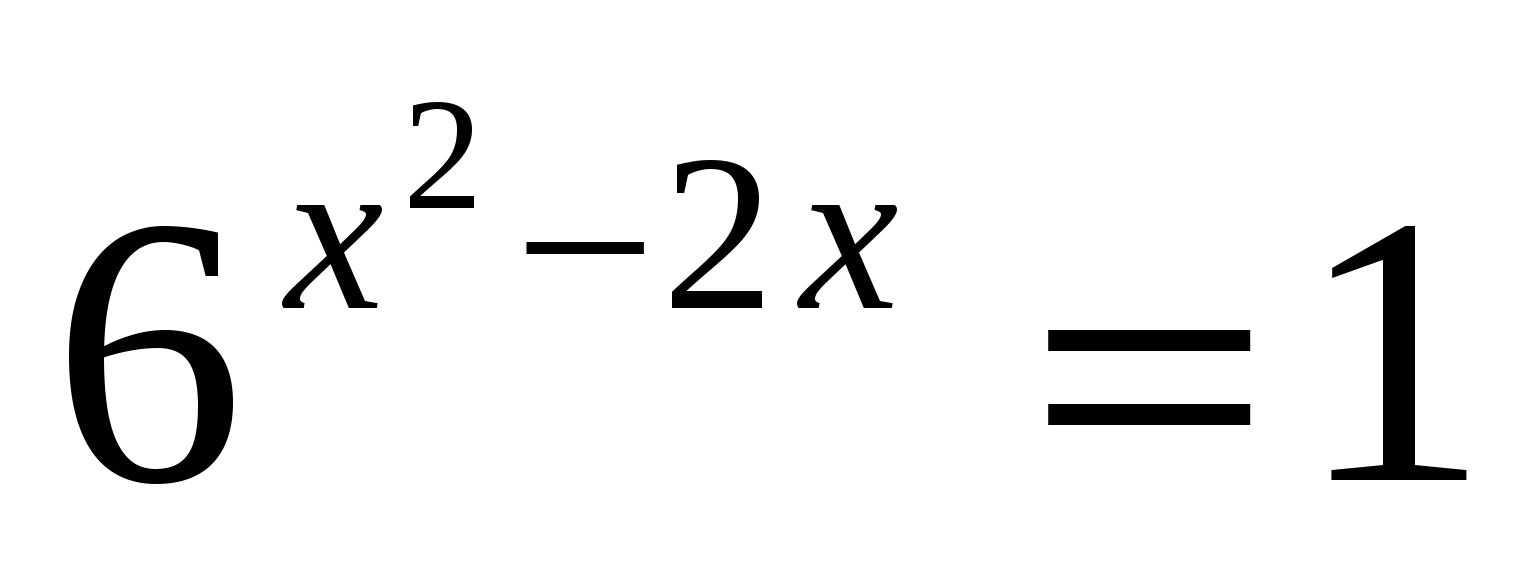
1) – 2 2) 0 3) 1 4) 2
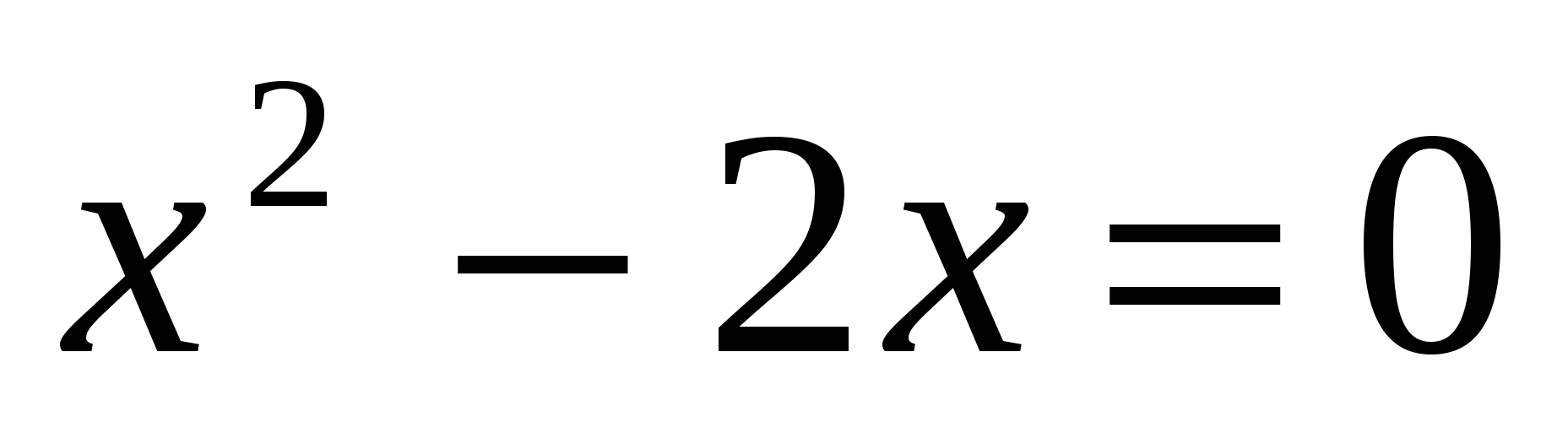
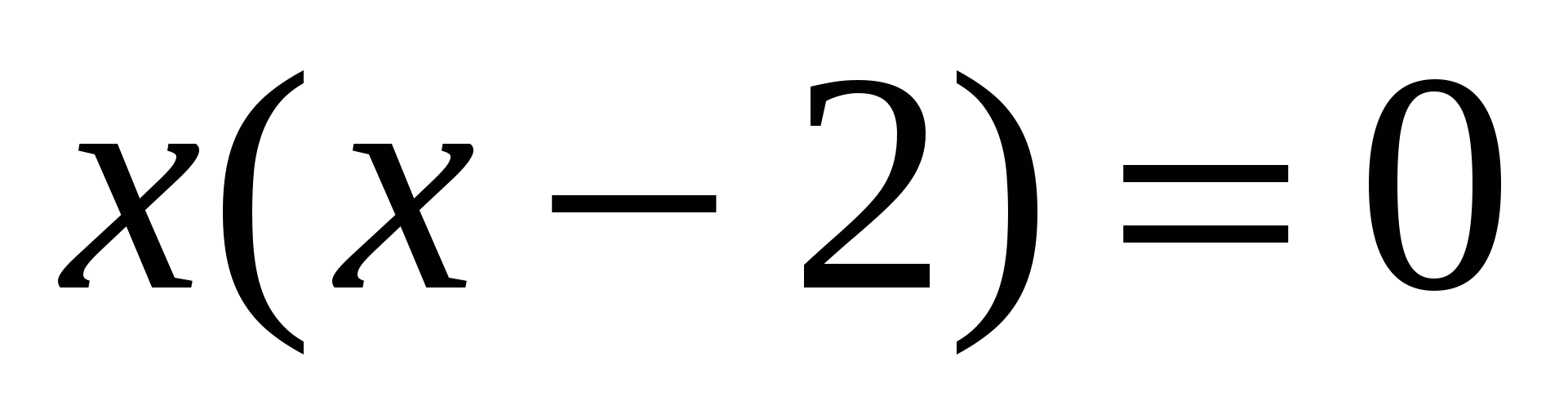
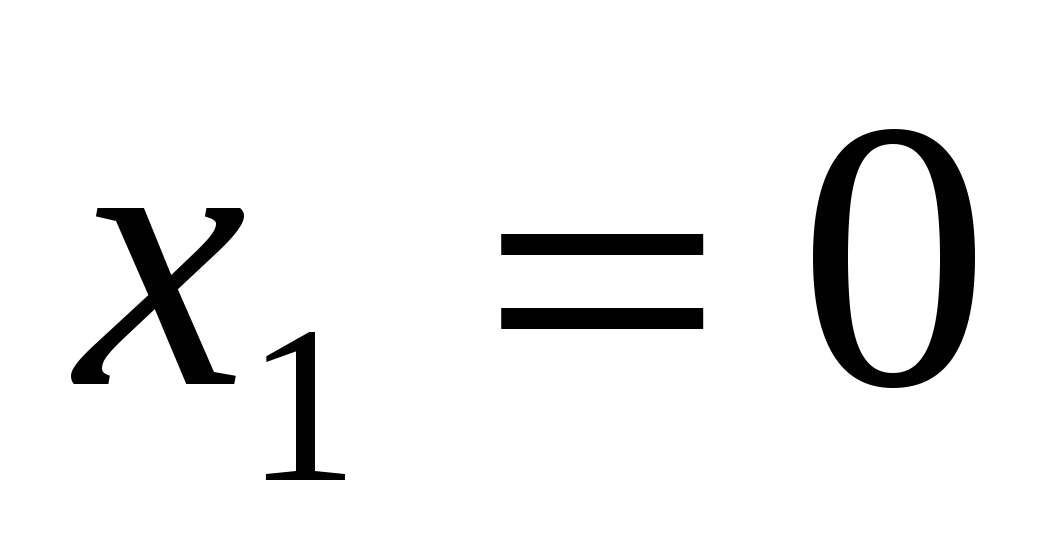
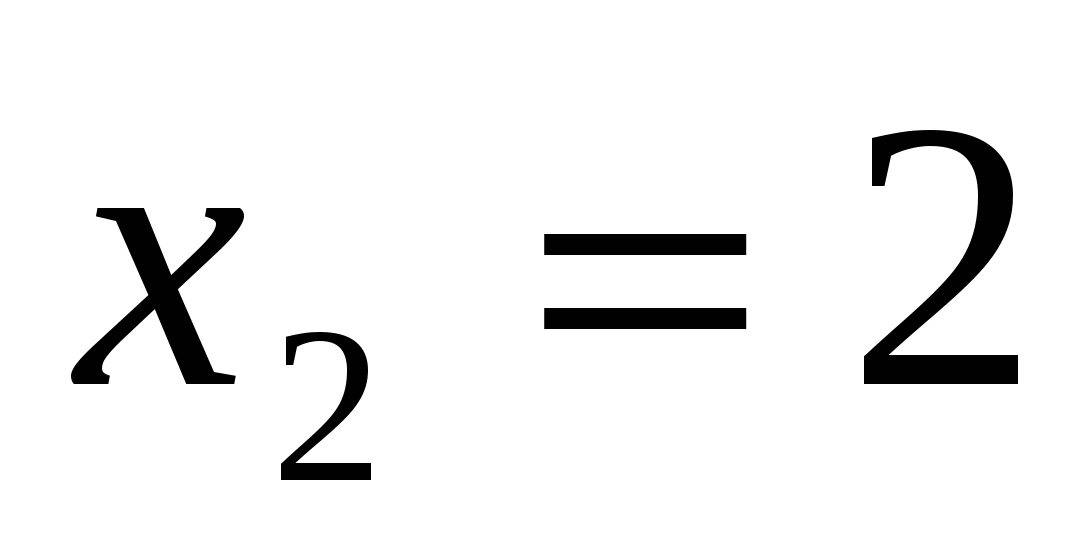
Ответ: 4
3. Решить уравнение 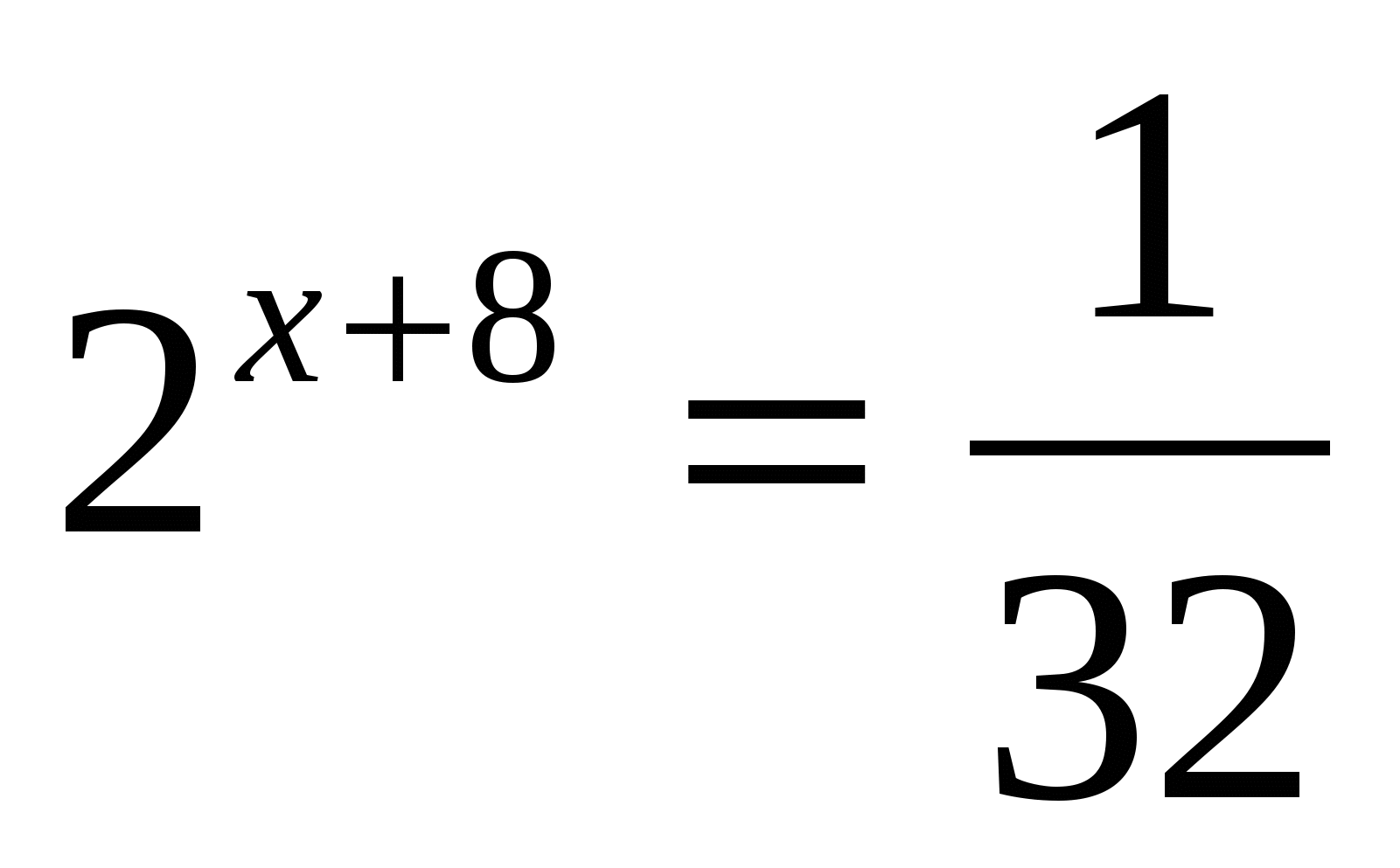
1) 12 2) – 12 3) – 13 4) 13
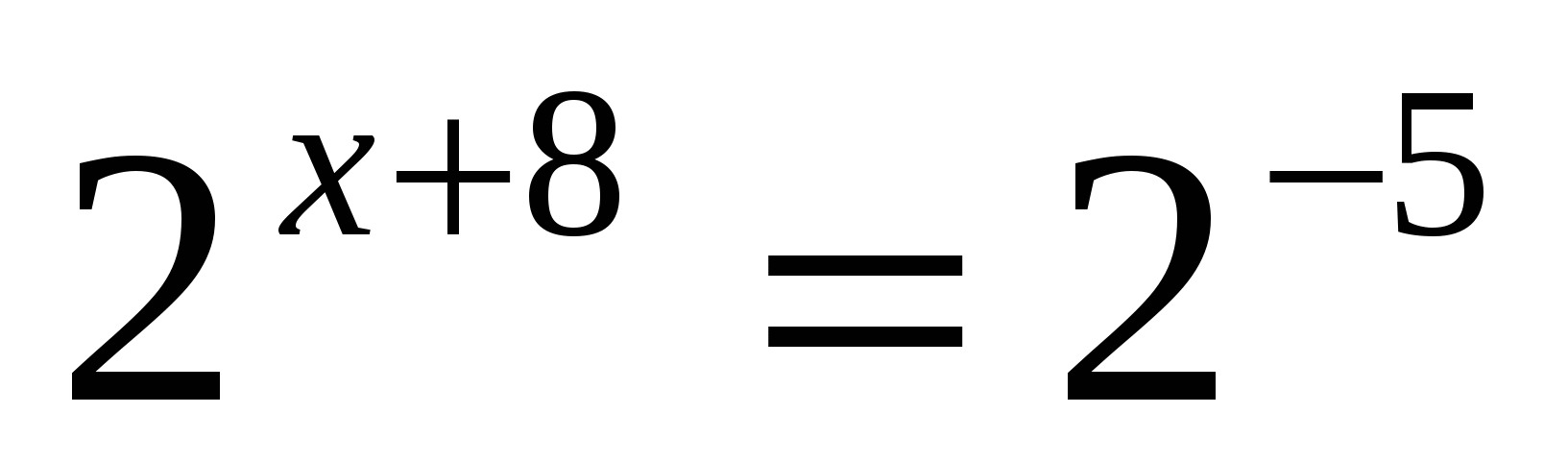
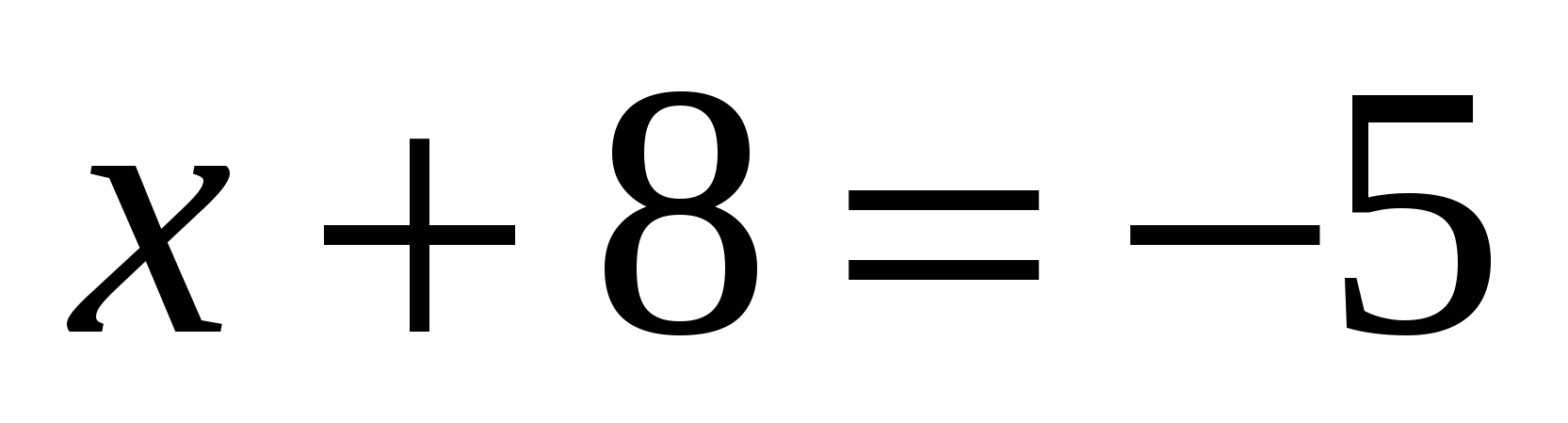
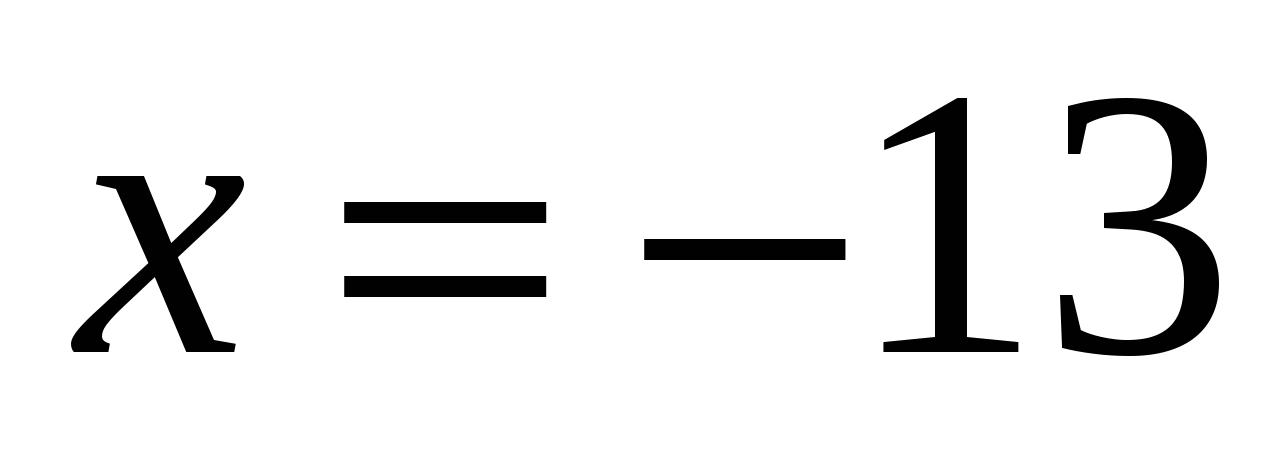
Ответ: 3
4. Решите неравенство 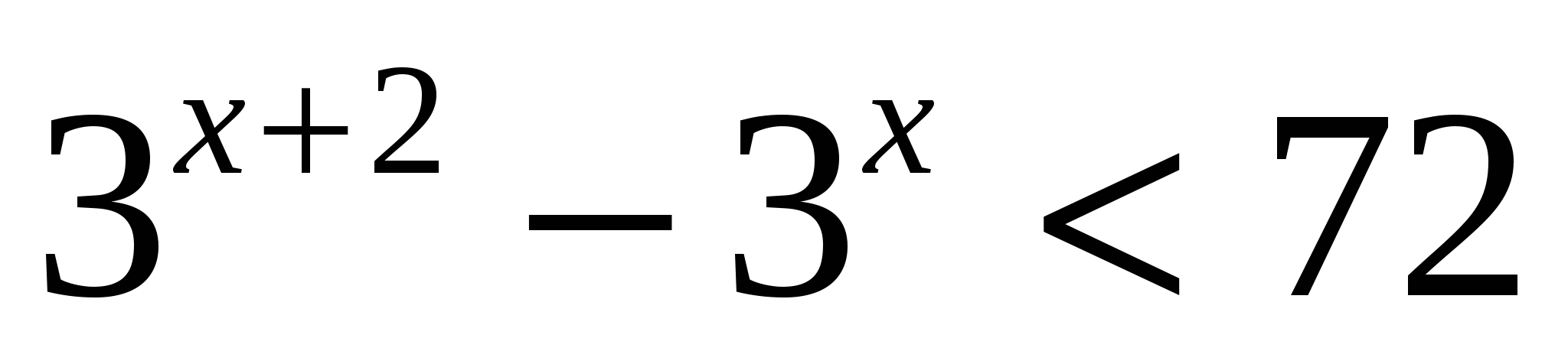
1) 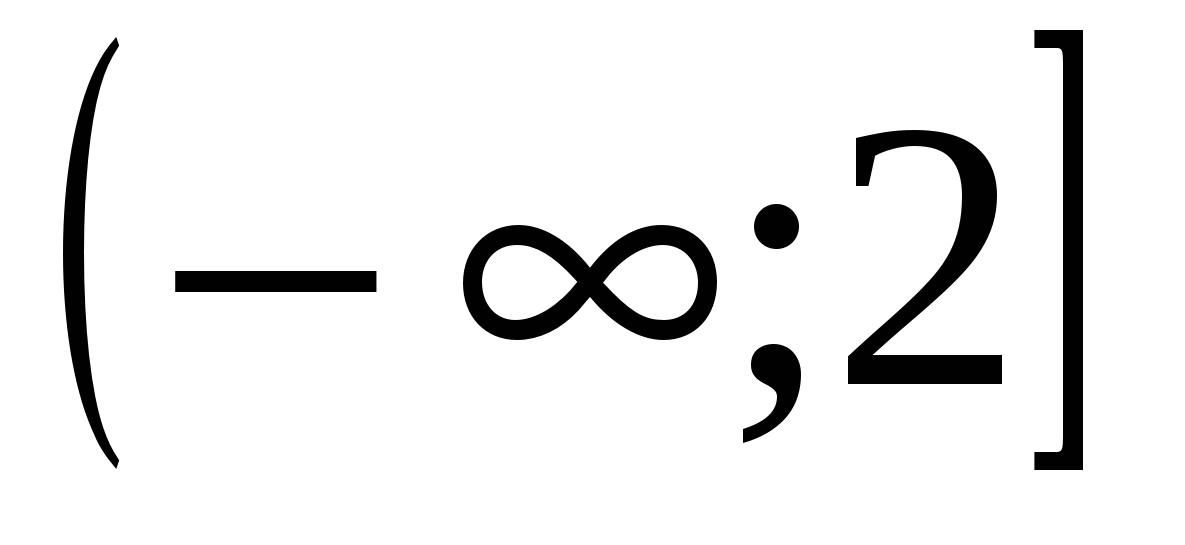 2)
2) 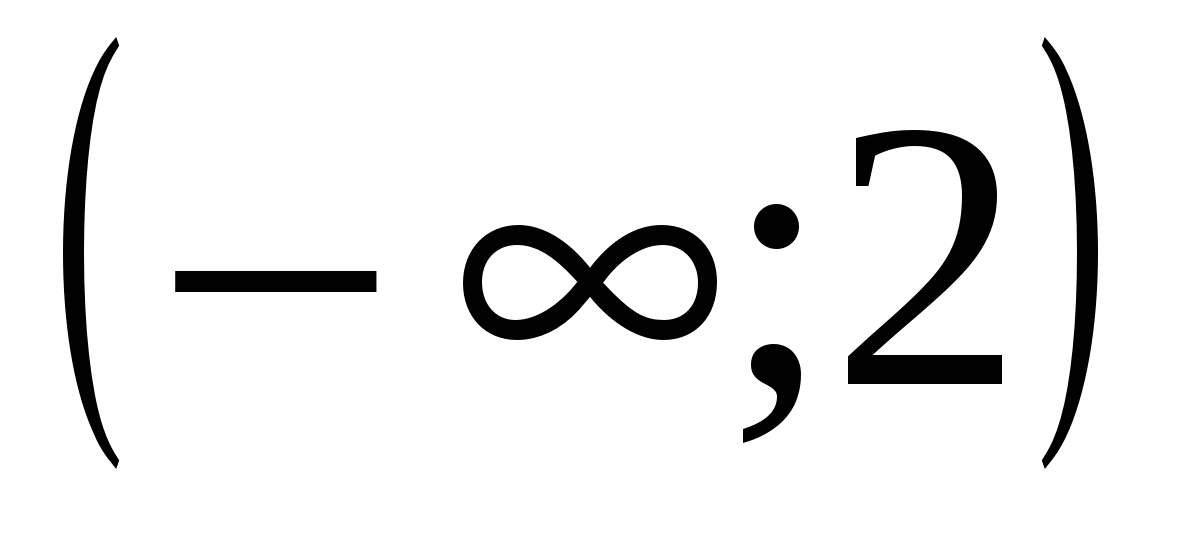 3)
3) 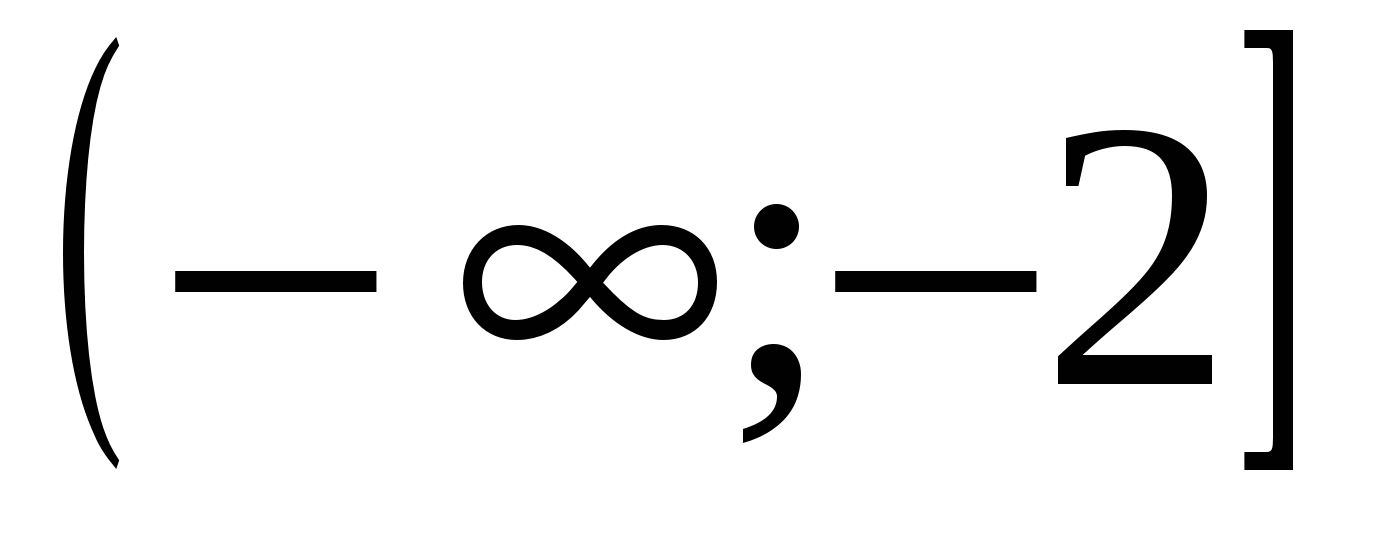
 4)
4) 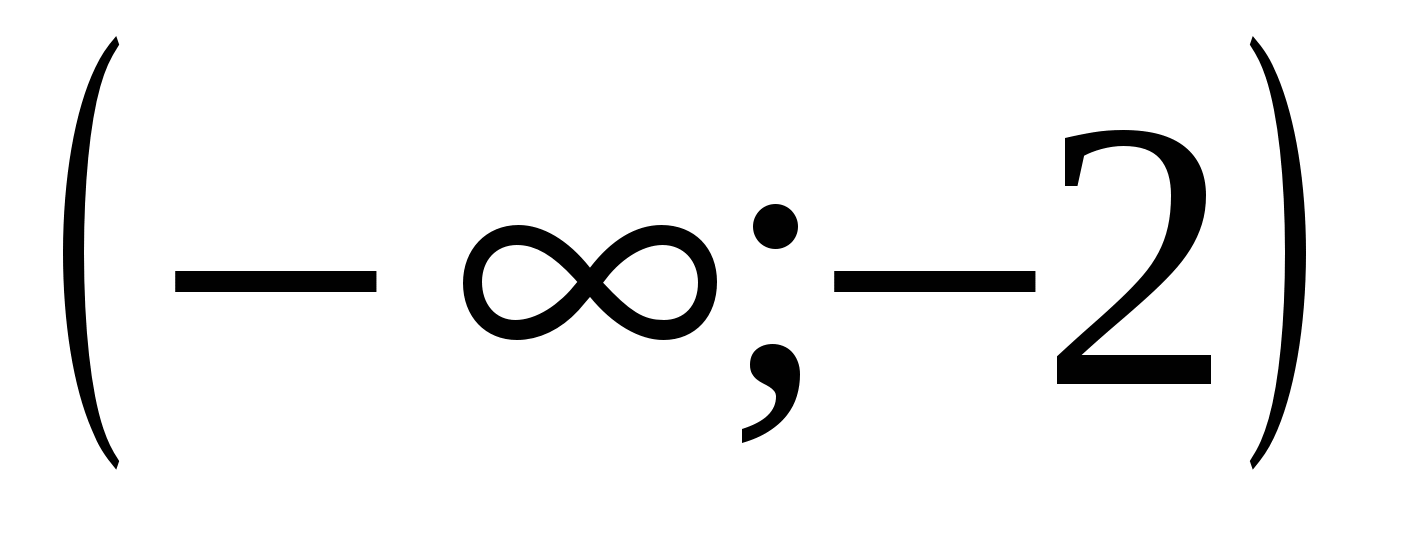
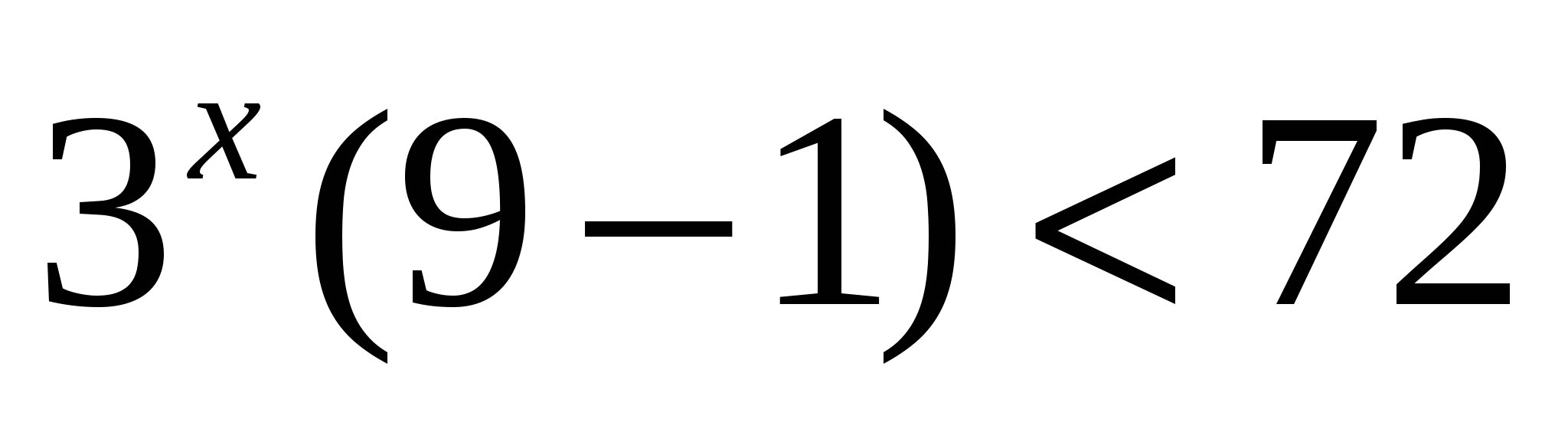
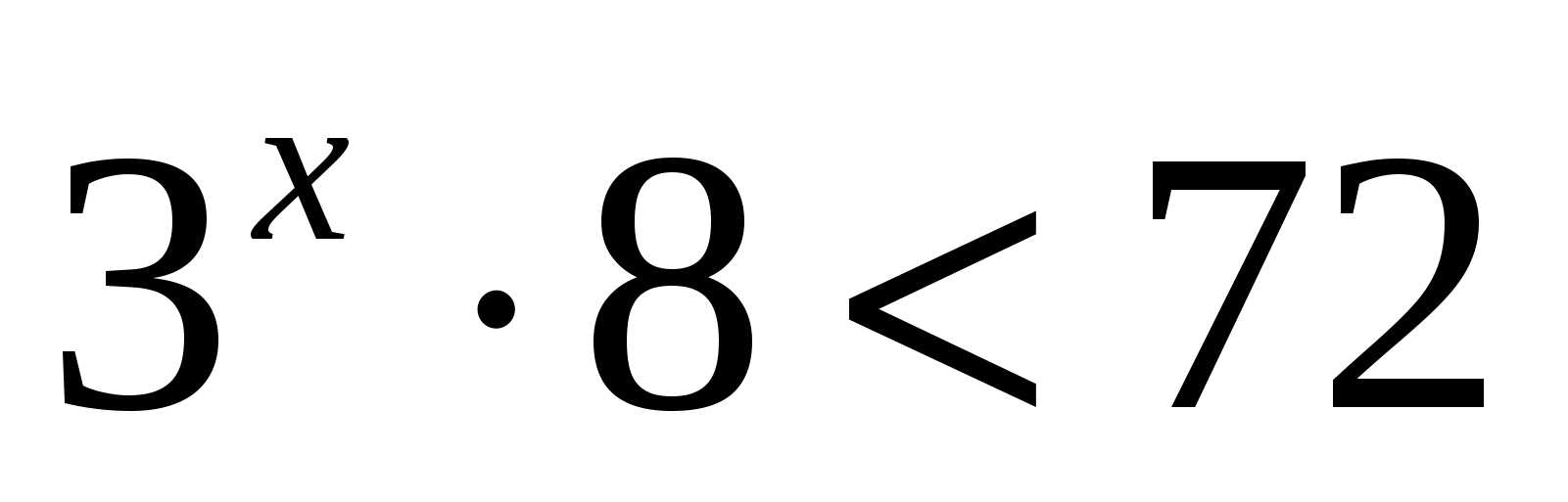
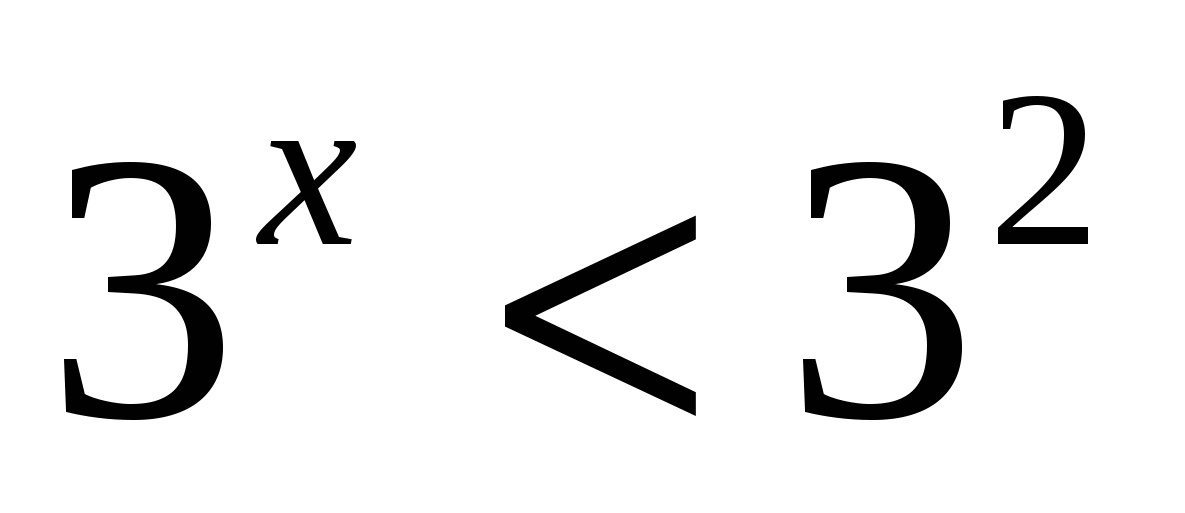
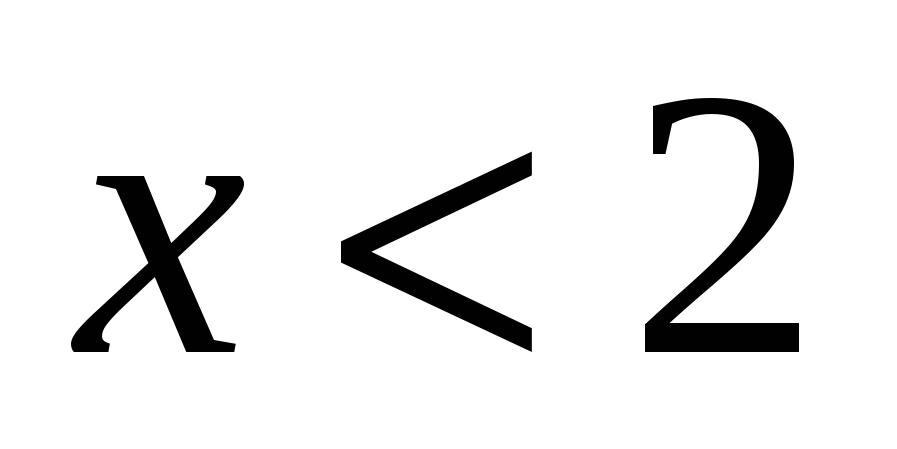
Ответ: 2
5. Найдите решение 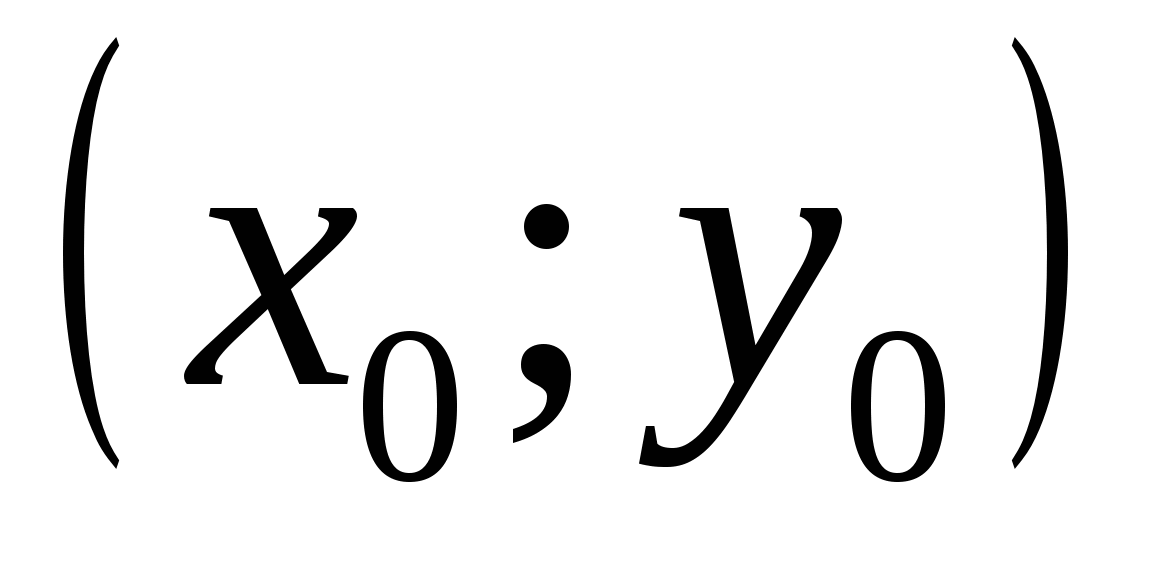 системы уравнений
системы уравнений 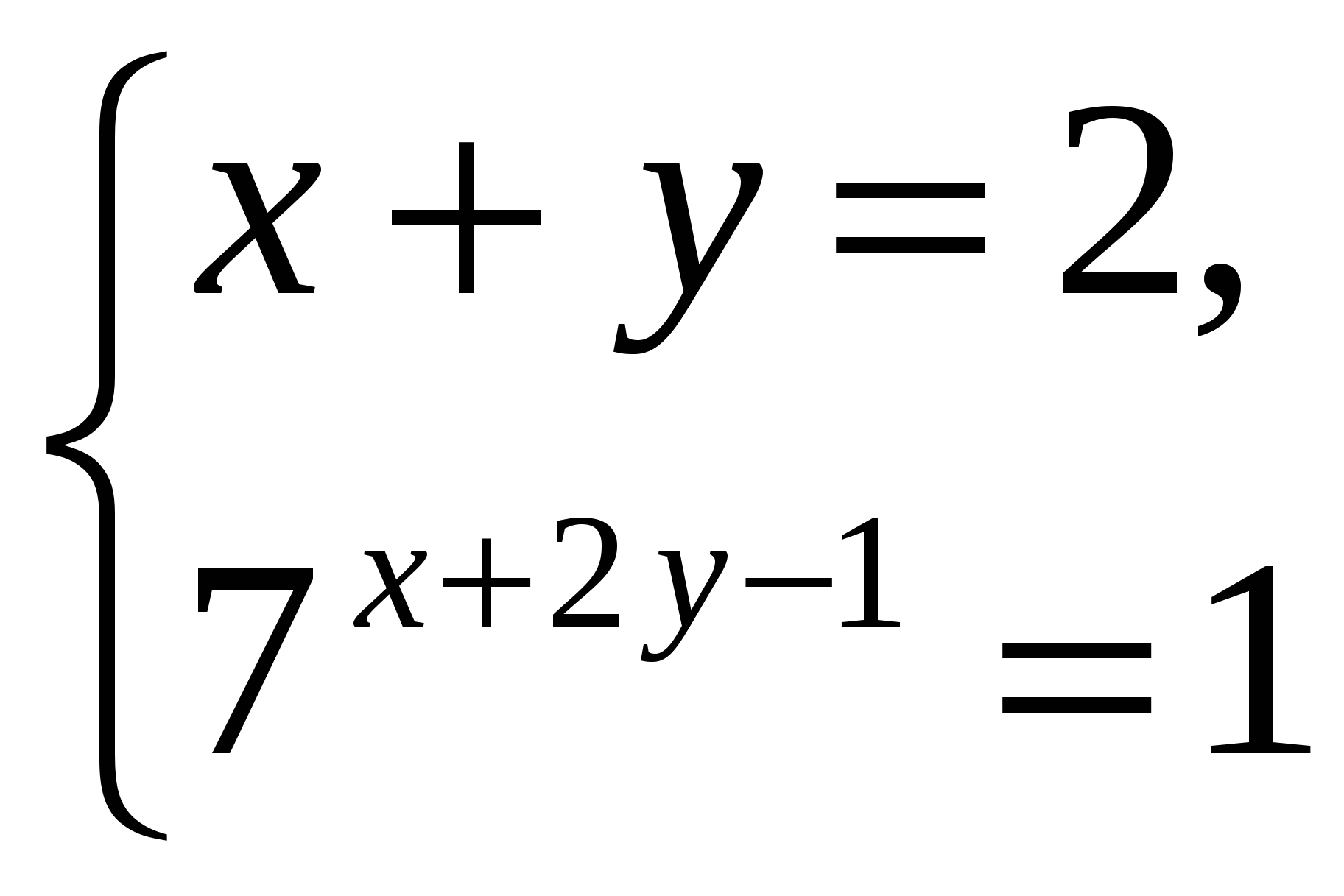 и вычислите значение произведения
и вычислите значение произведения 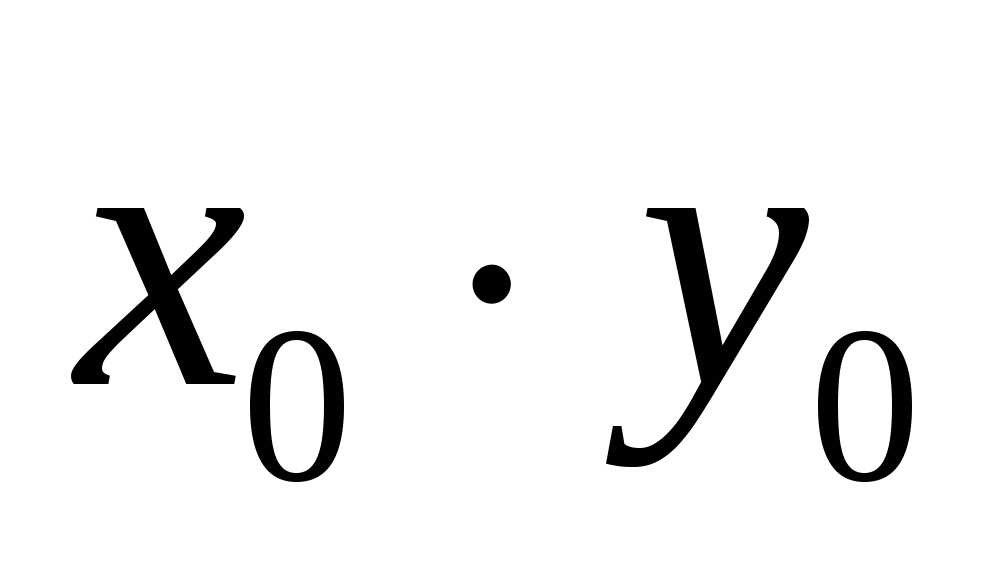
1) – 2 2) 2 3) – 3 4) 3
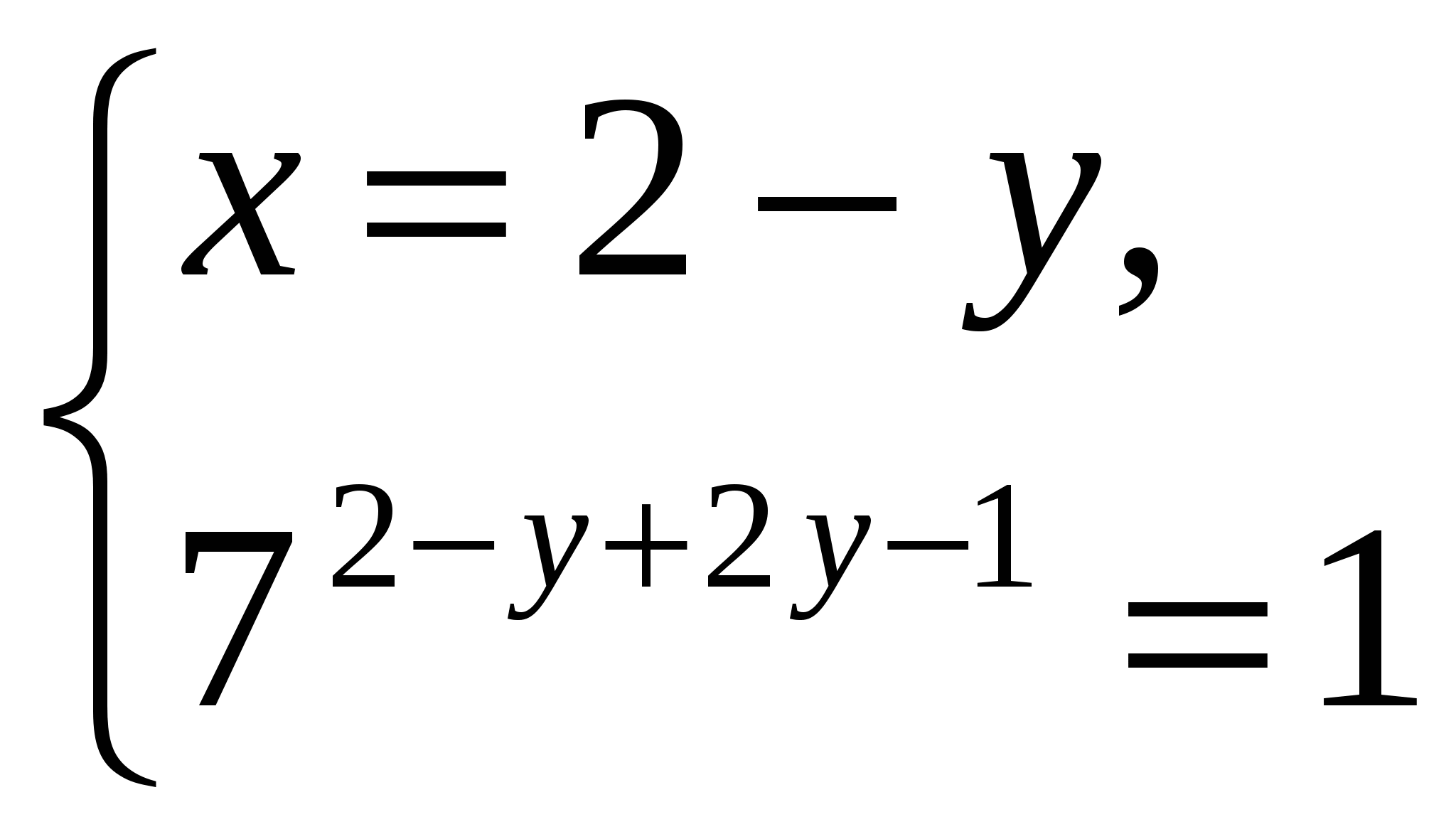
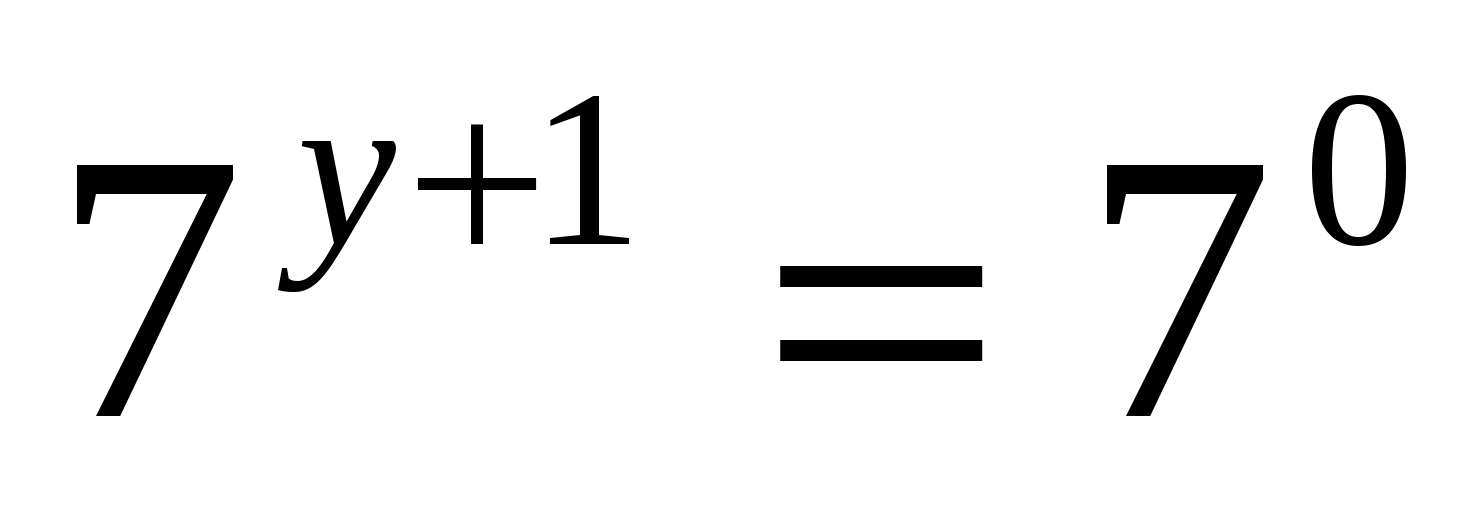
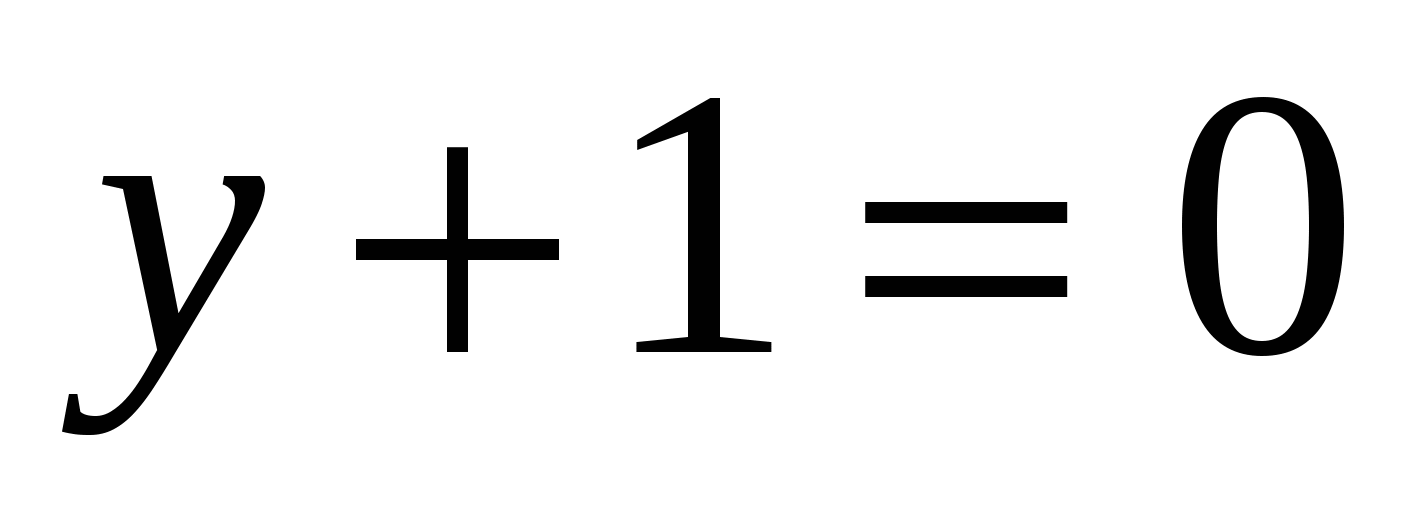
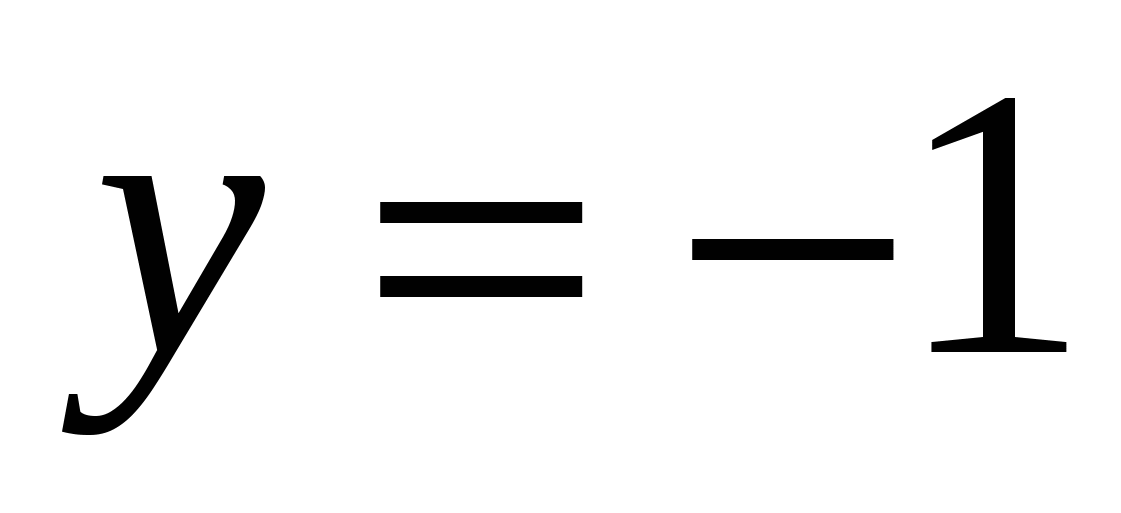
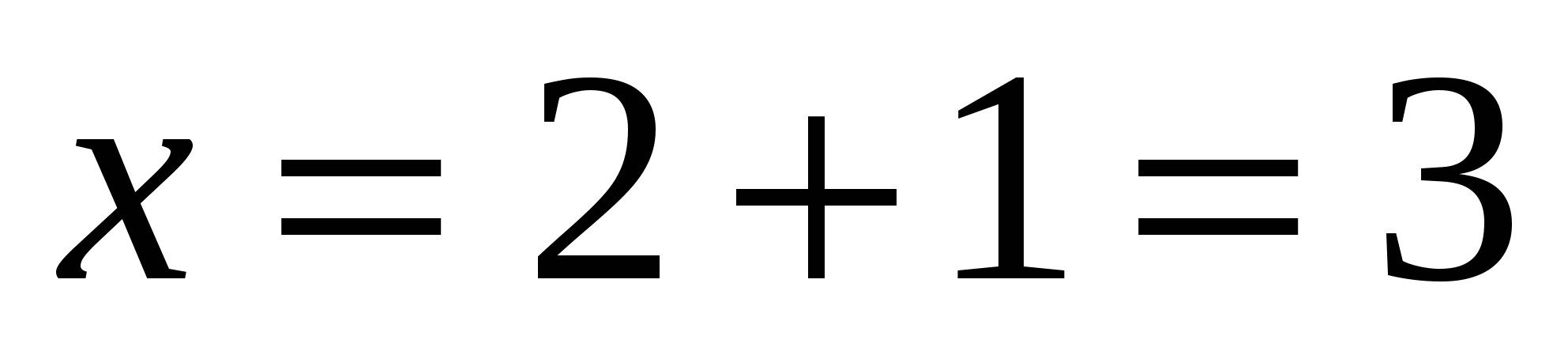
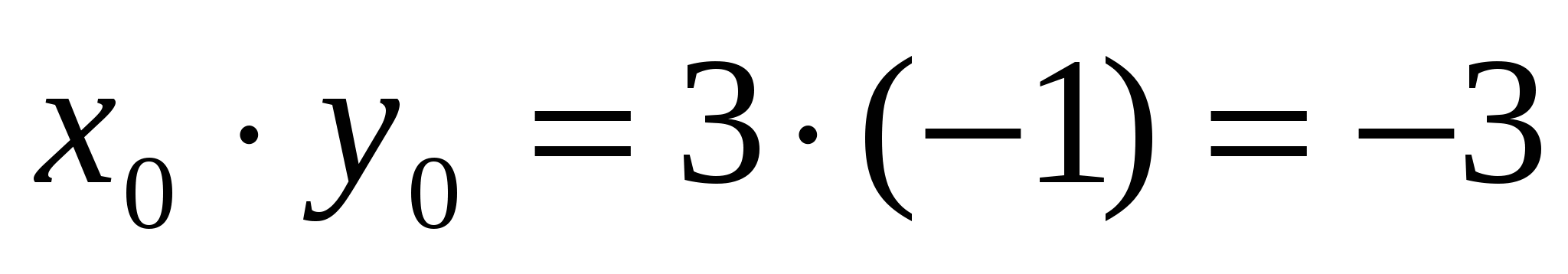
Ответ: 3
IV. Решение заданий (10 мин)
К доске вызывается 3 ученика (2 решают задания части В – остальные по вариантам, 1 решает задание С). В это время 3 ученика, сидящие за компьютером уступают место другим 3 ученикам. Оценки выставляются во вторую колонку.
1. Решите неравенство 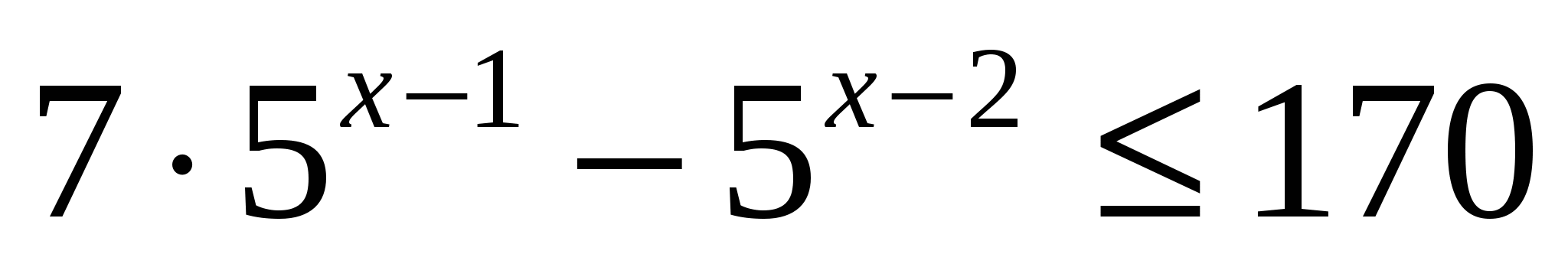 при
при 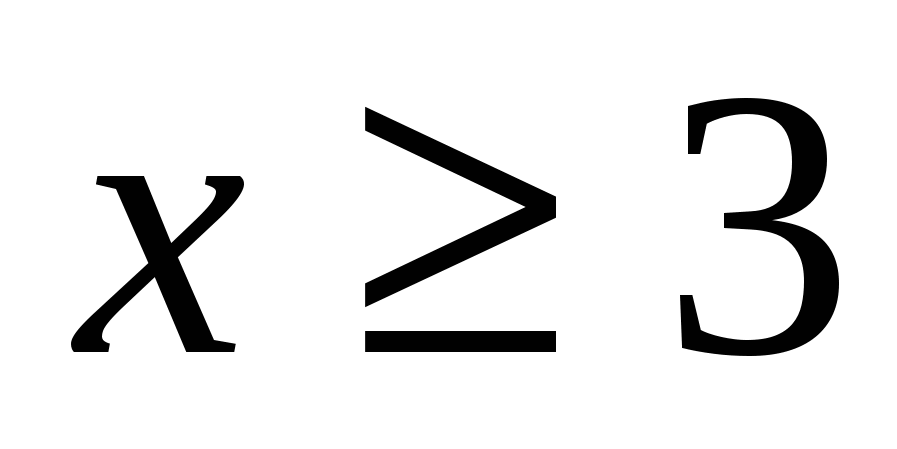
Решение: 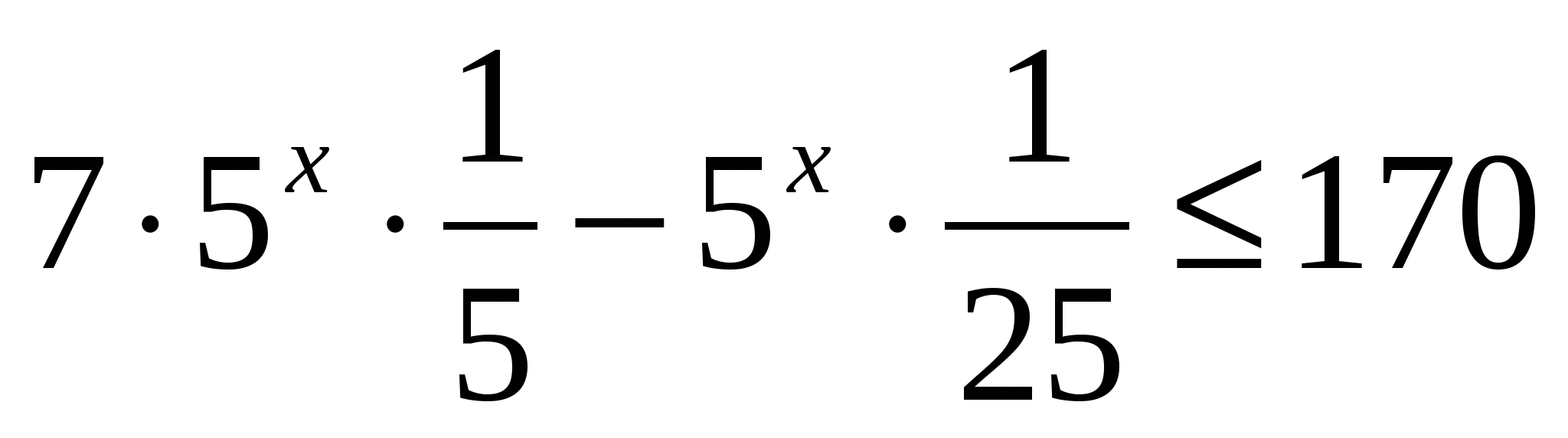
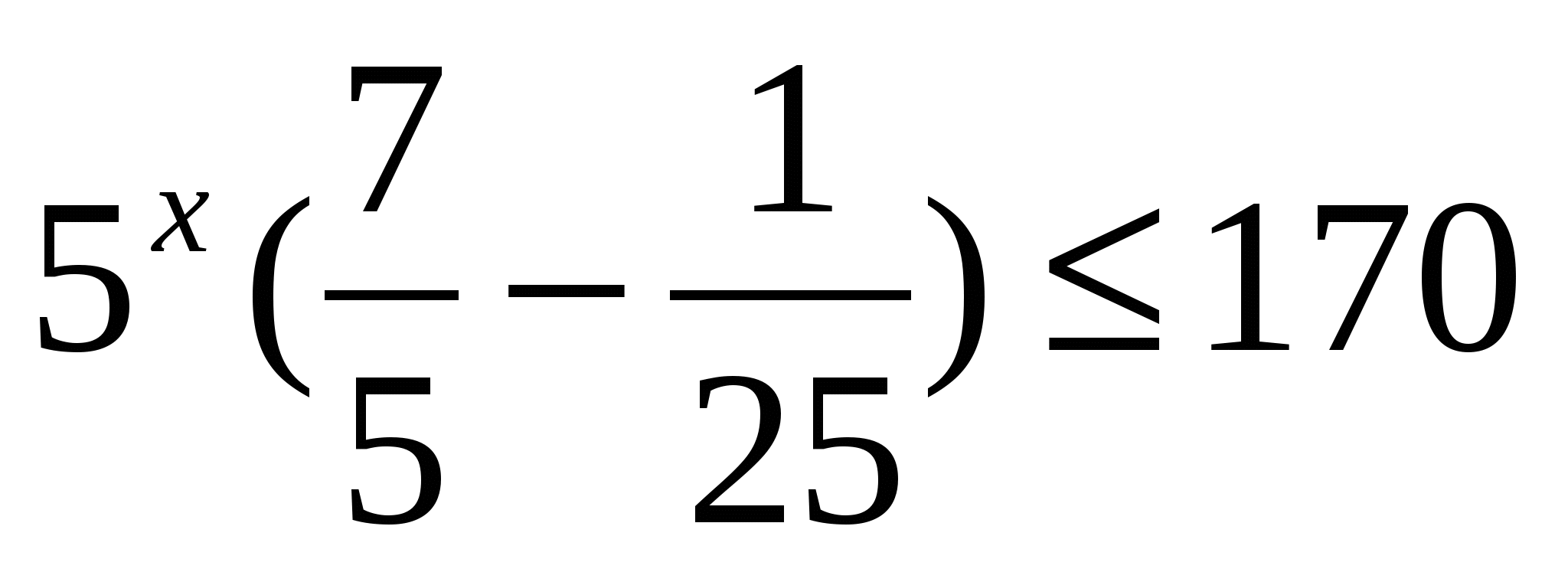
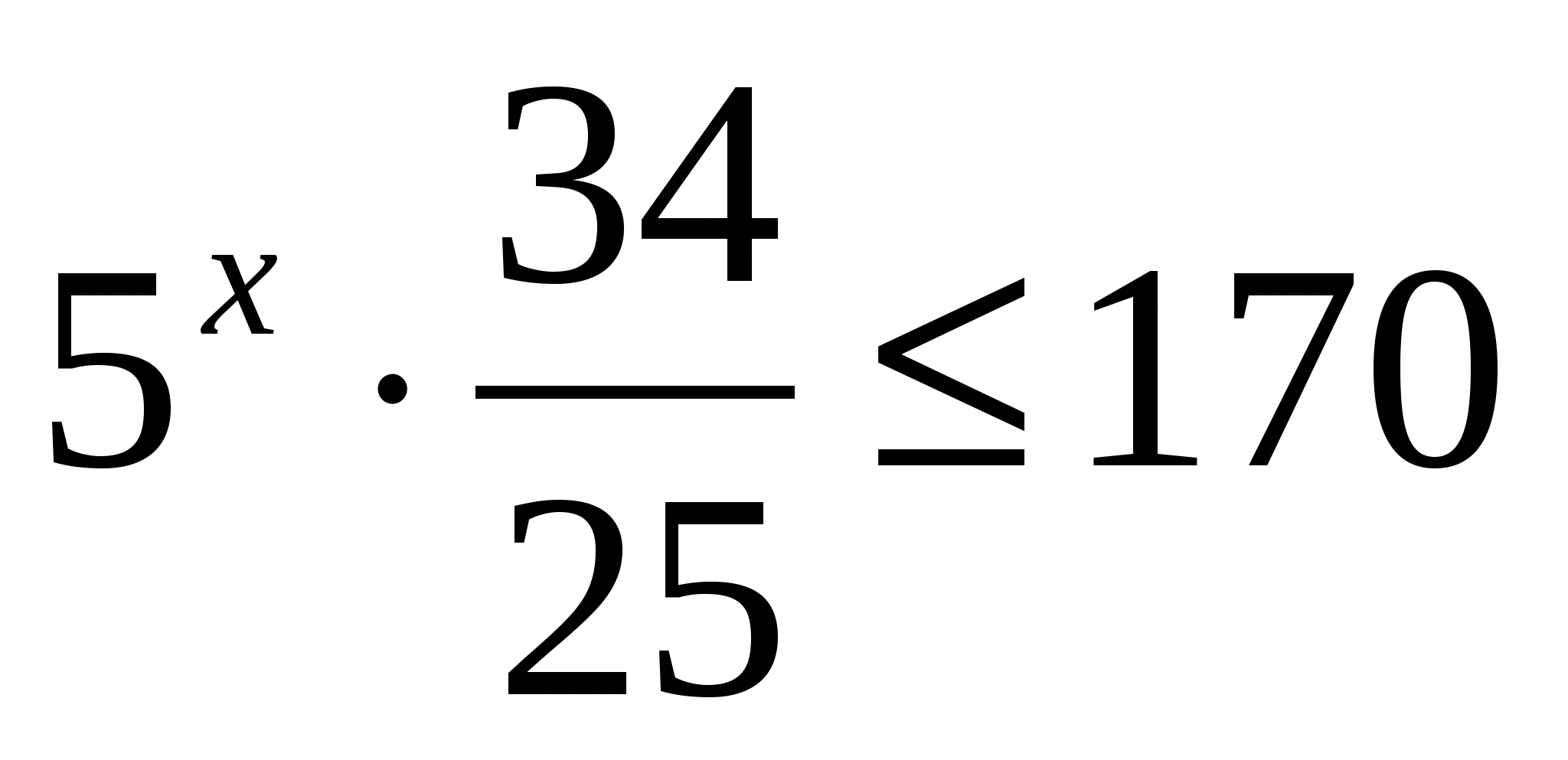
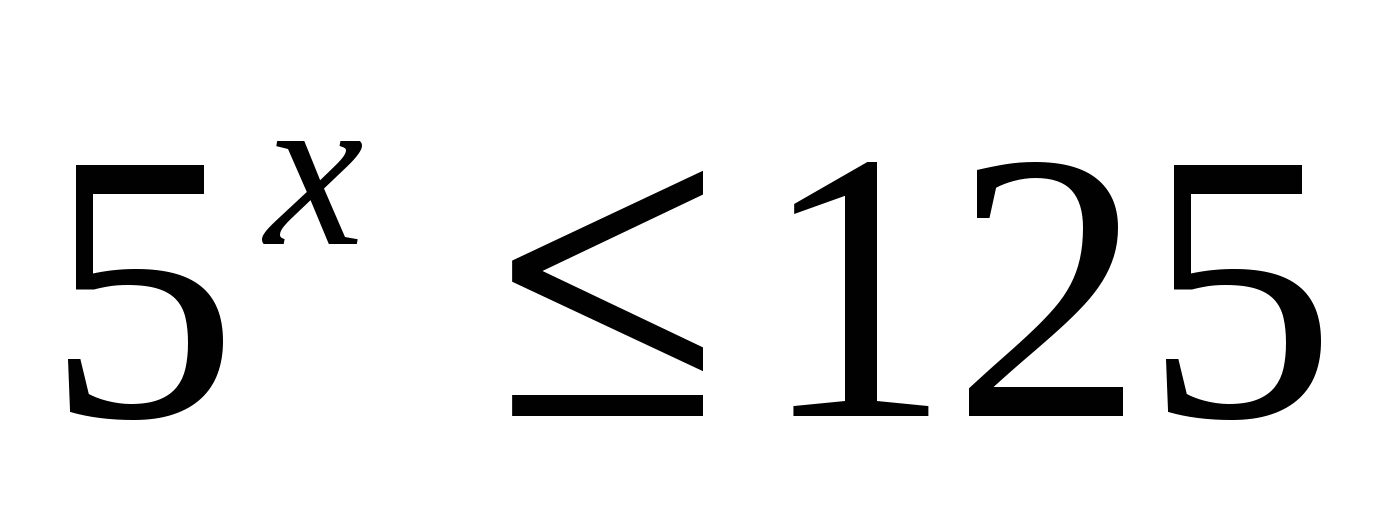
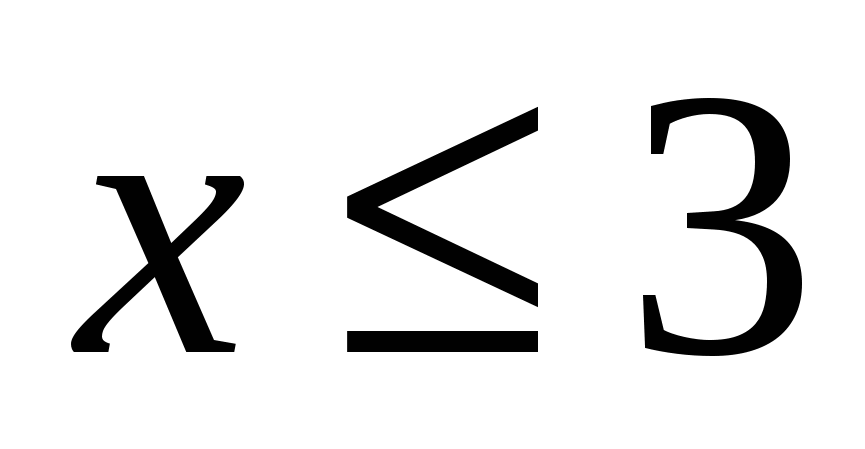
Ответ: 3
2. Найдите число целых отрицательных решений неравенства 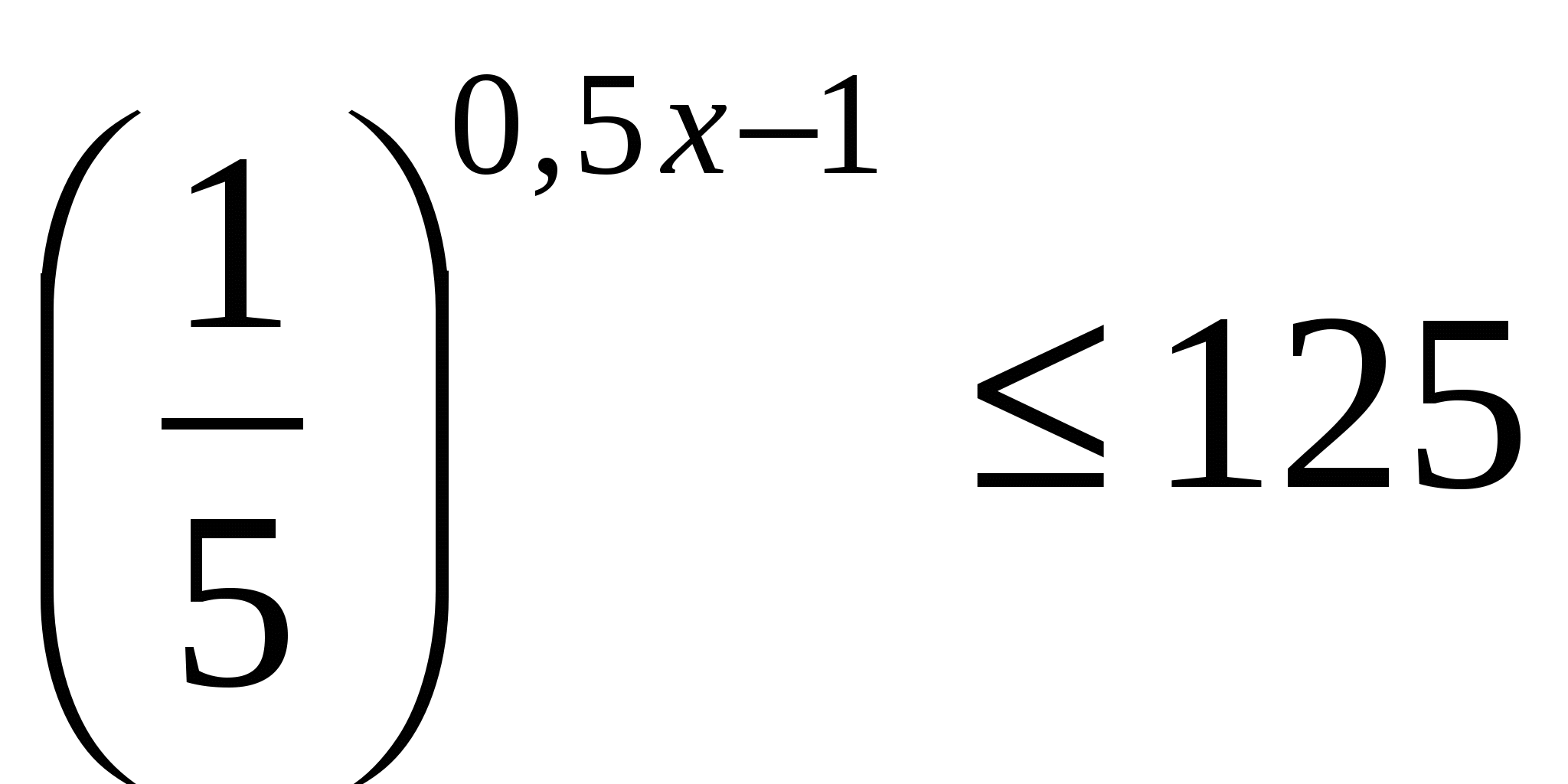
Решение: 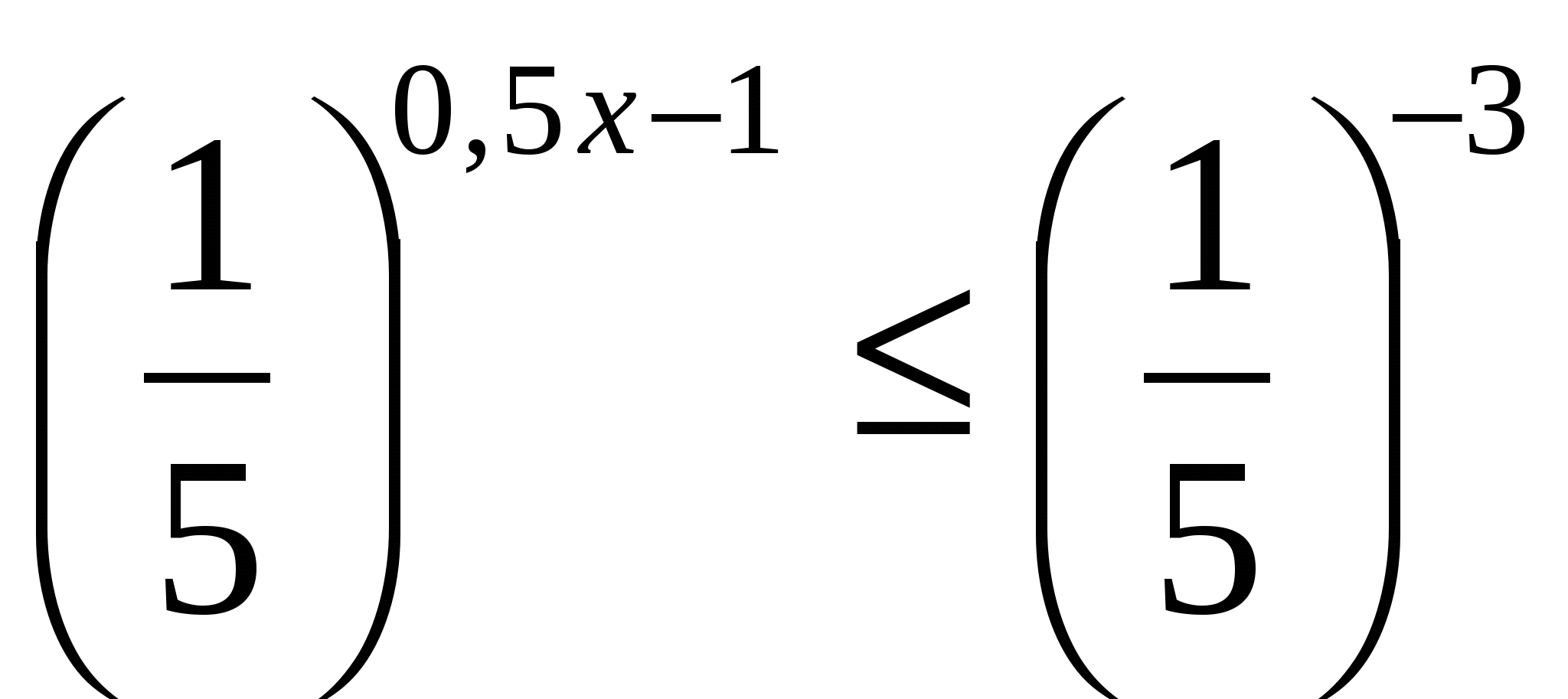
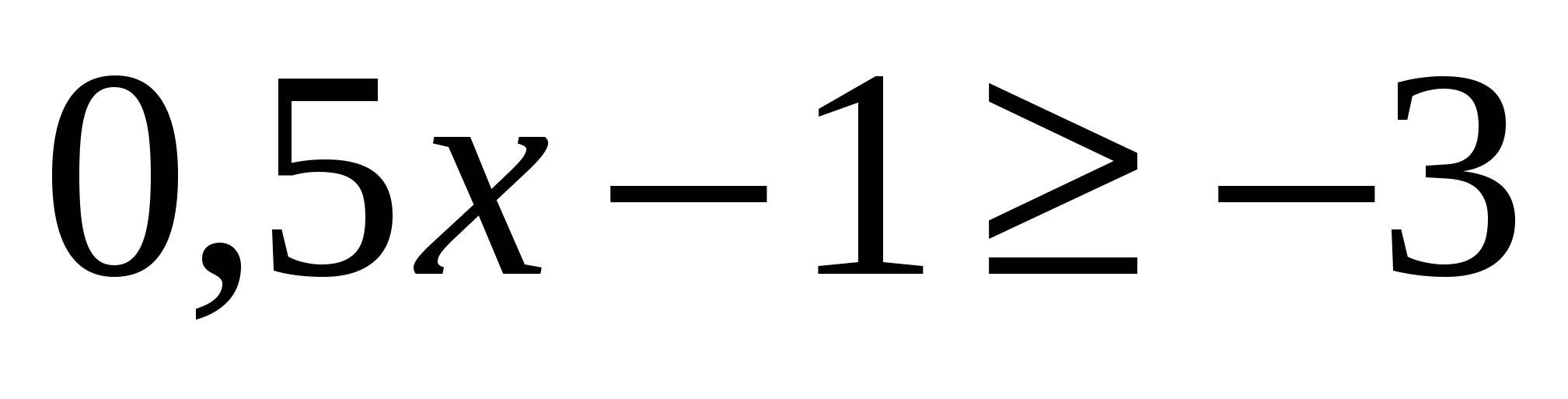
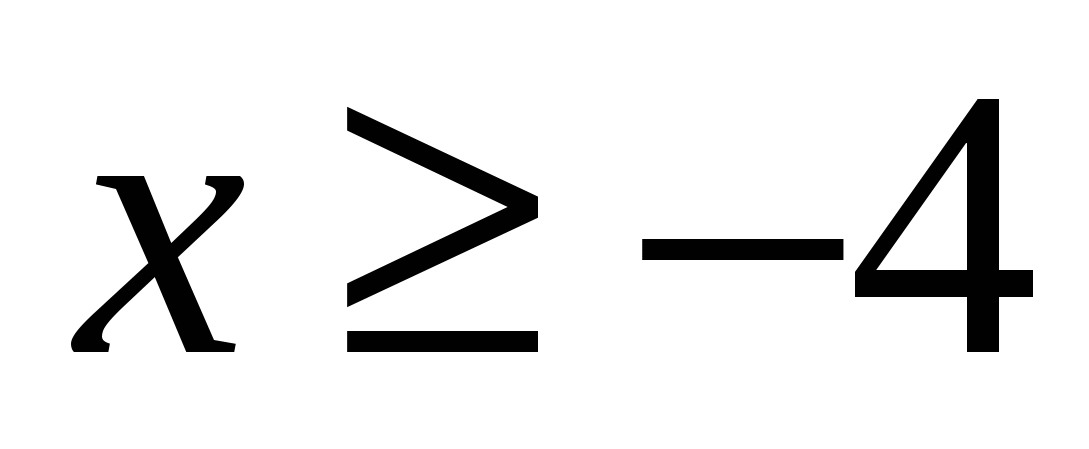
— 4; — 3; — 2; -1
Ответ: 4
3. Решите уравнение 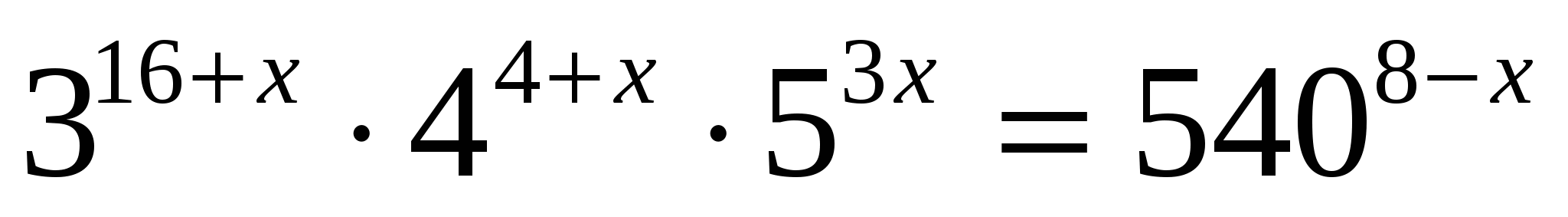
Решение:
1) Основания степеней в обеих частях уравнения разложим на простые
сомножители:
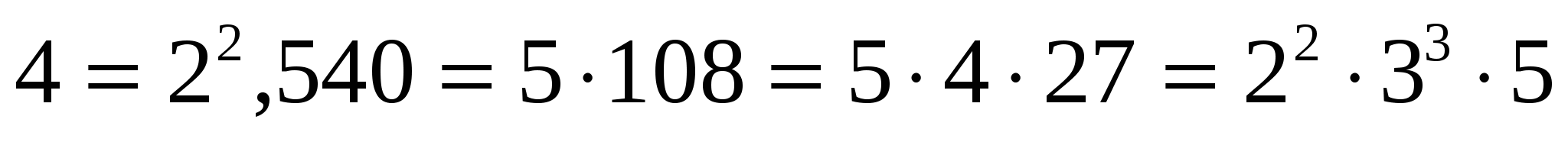
2) По правилам действий со степенями:
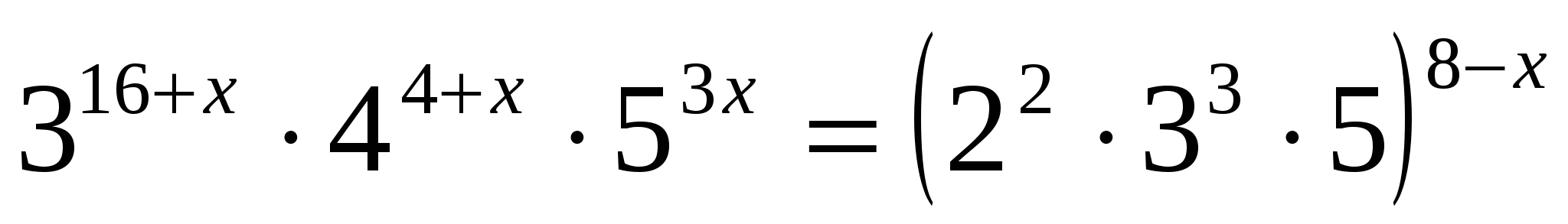
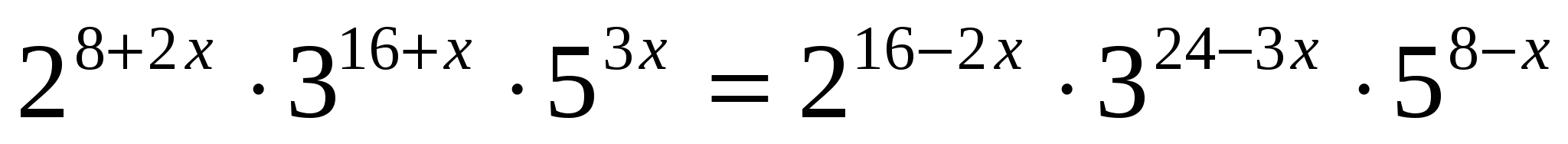
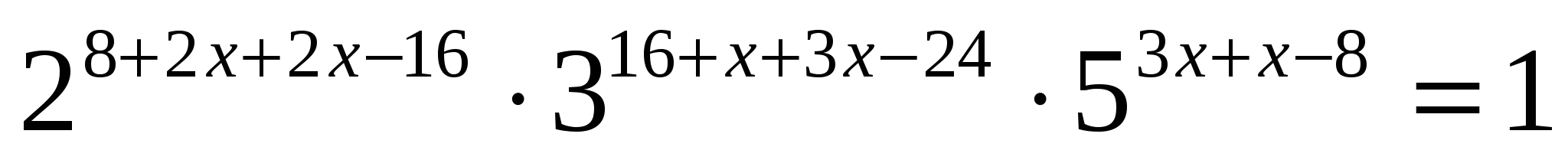
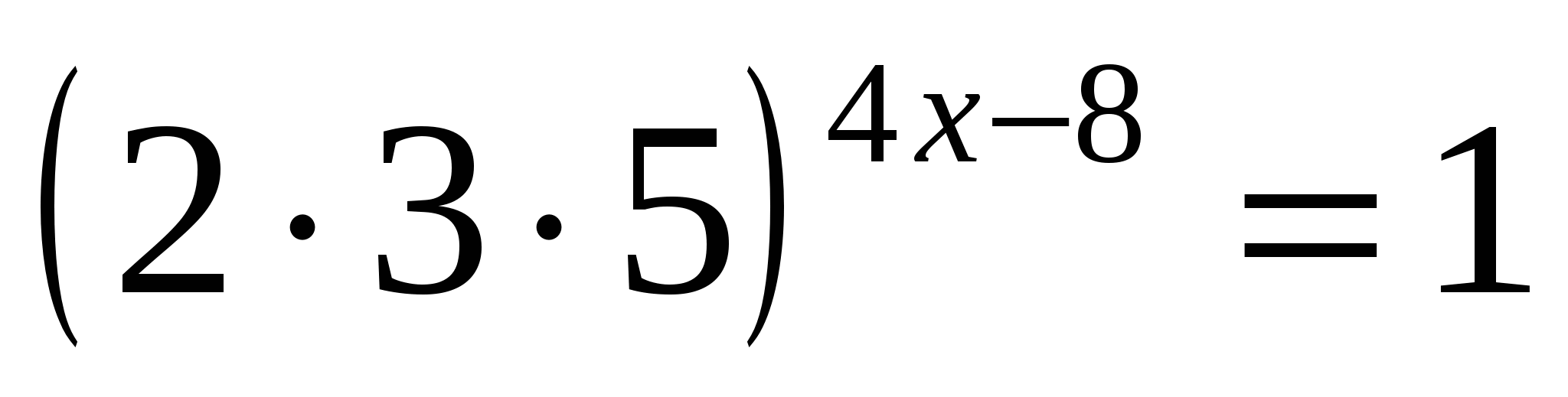
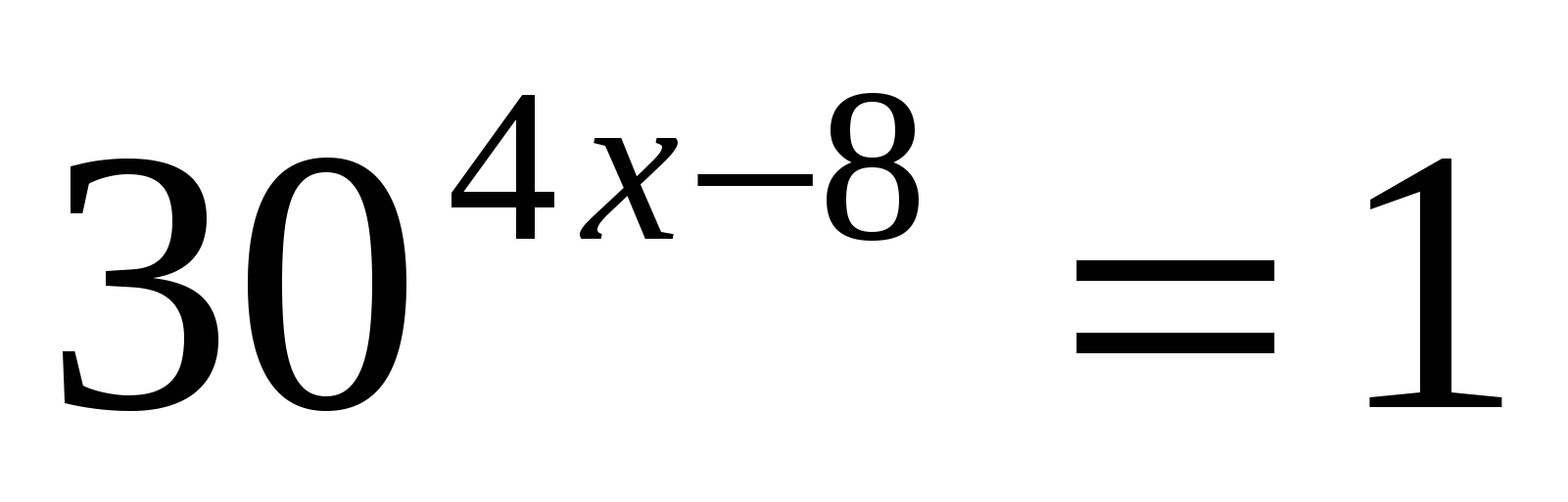
3) Значит, 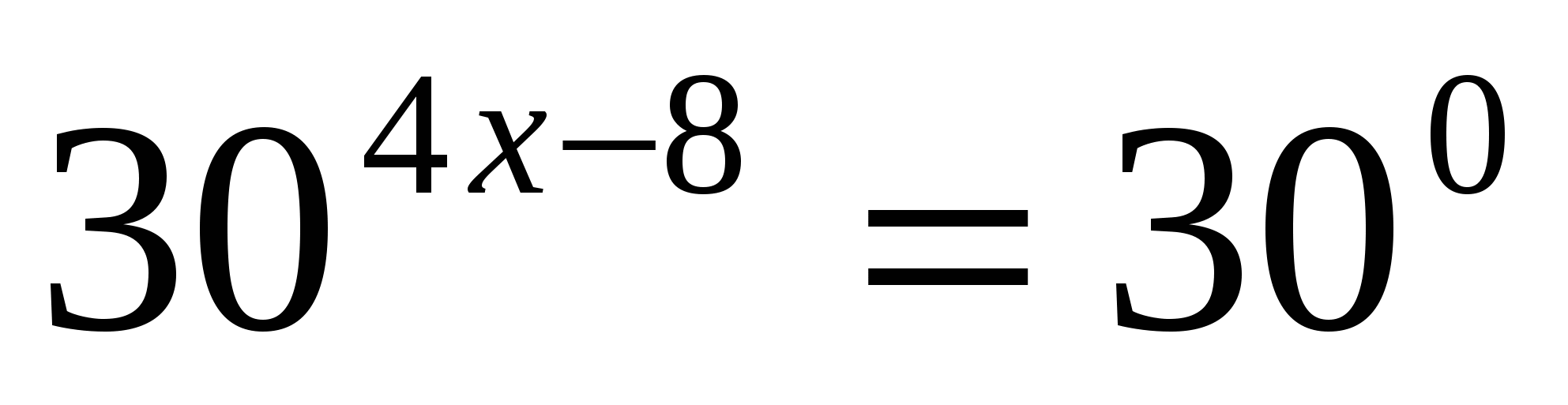 . Из свойств показательной функции следует, что
. Из свойств показательной функции следует, что
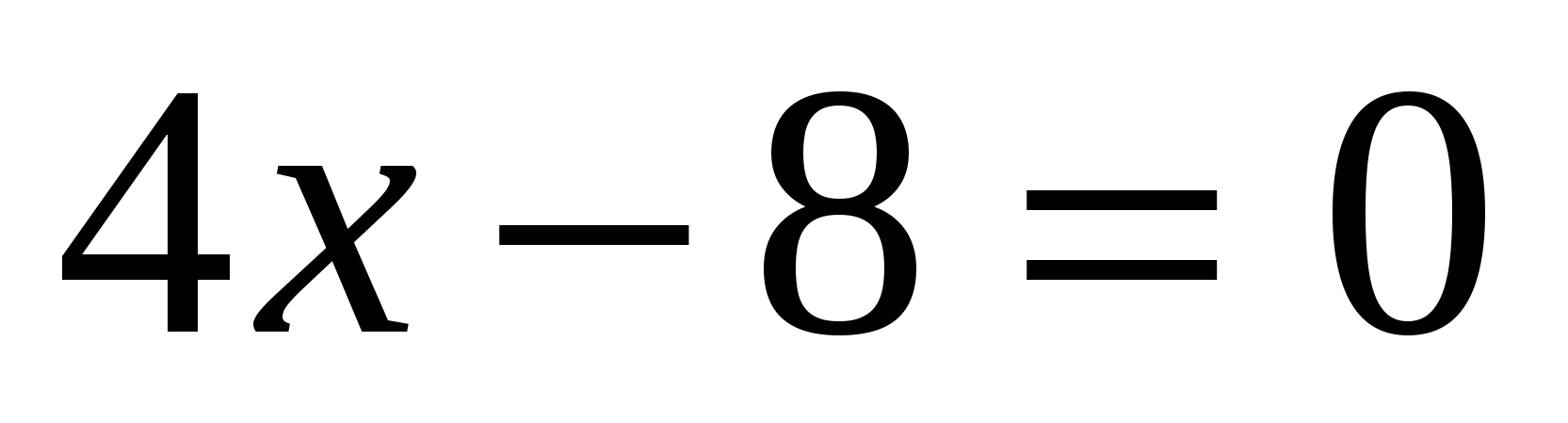 ;
; 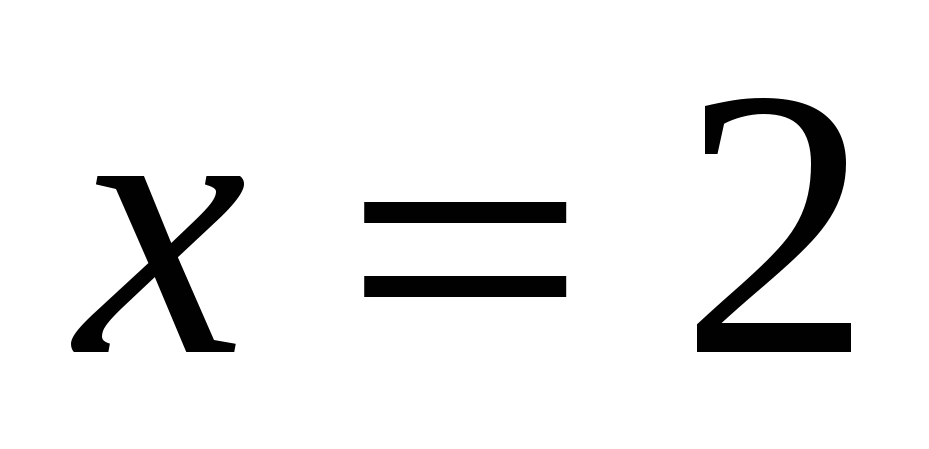 .
.
4) Так как все преобразования равносильные, то найденное число – корень
уравнения. Впрочем, нетрудно проверить его и подстановкой:
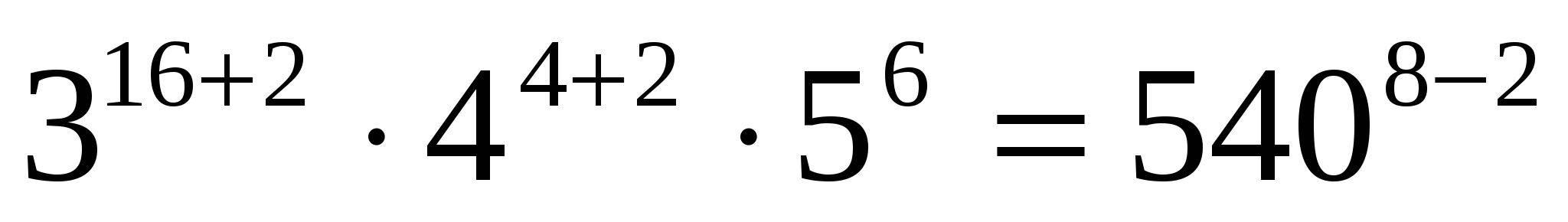
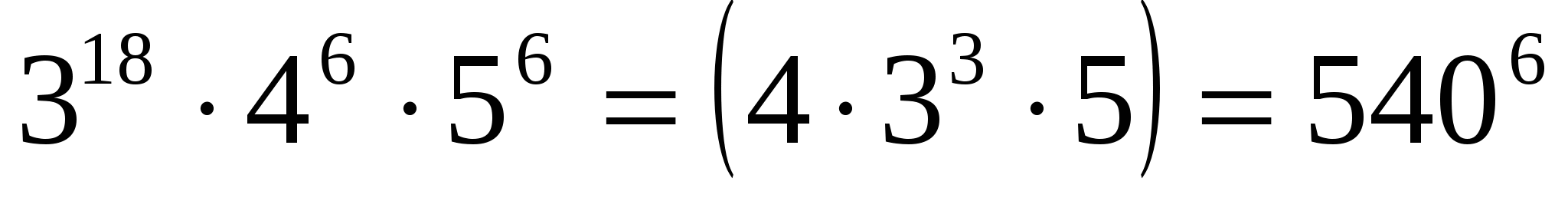
Ответ: 2.
V. Разгадать исторический факт (10 мин)
Класс делится на 3 группы и каждому раздается задание с буквой, решив которое ученик должен вставить букву на место, с которым совпадает ответ его задания. В результате на доске должны появиться ответы на 3 вопроса. Оцениваются ученики всей группы – оценка в третью колонку.
I. Решив уравнения, вы узнаете фамилию ученого, который вывел формулы, связывающие тригонометрические функции с показательной (ЭЙЛЕР)
Й
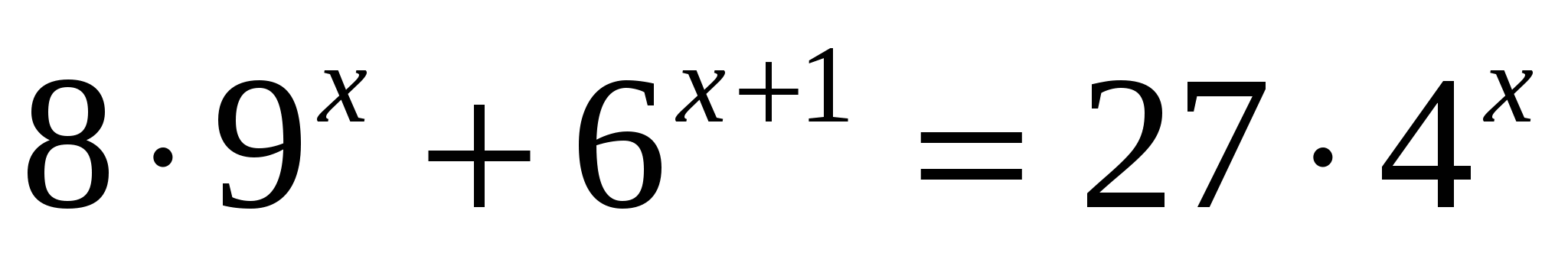
Е
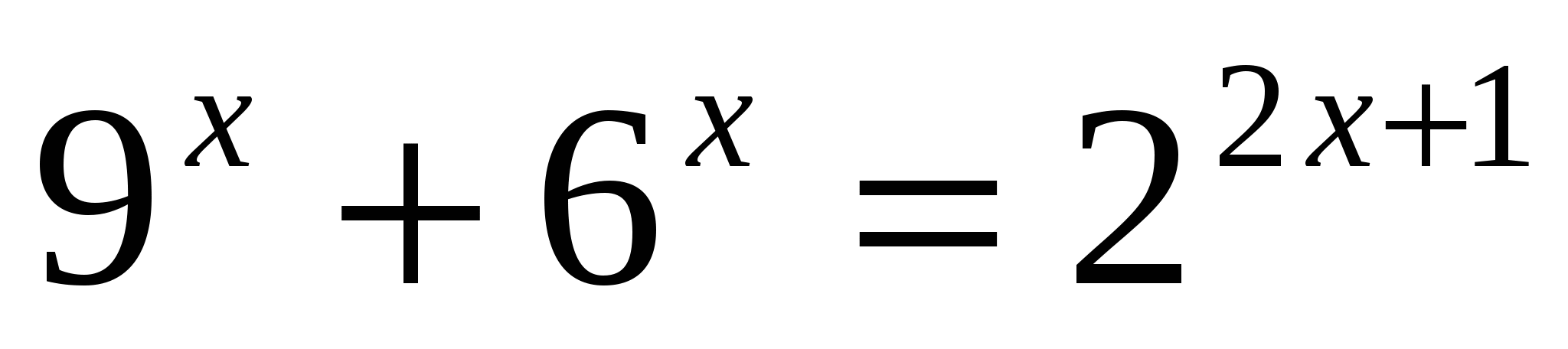
Э
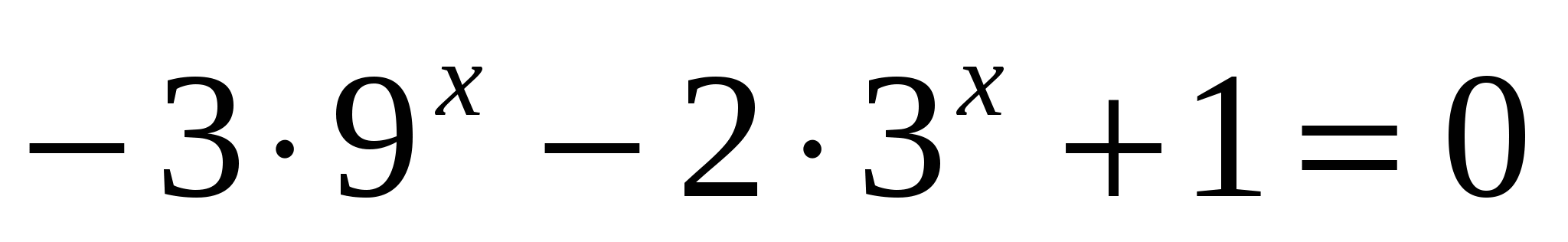
Р
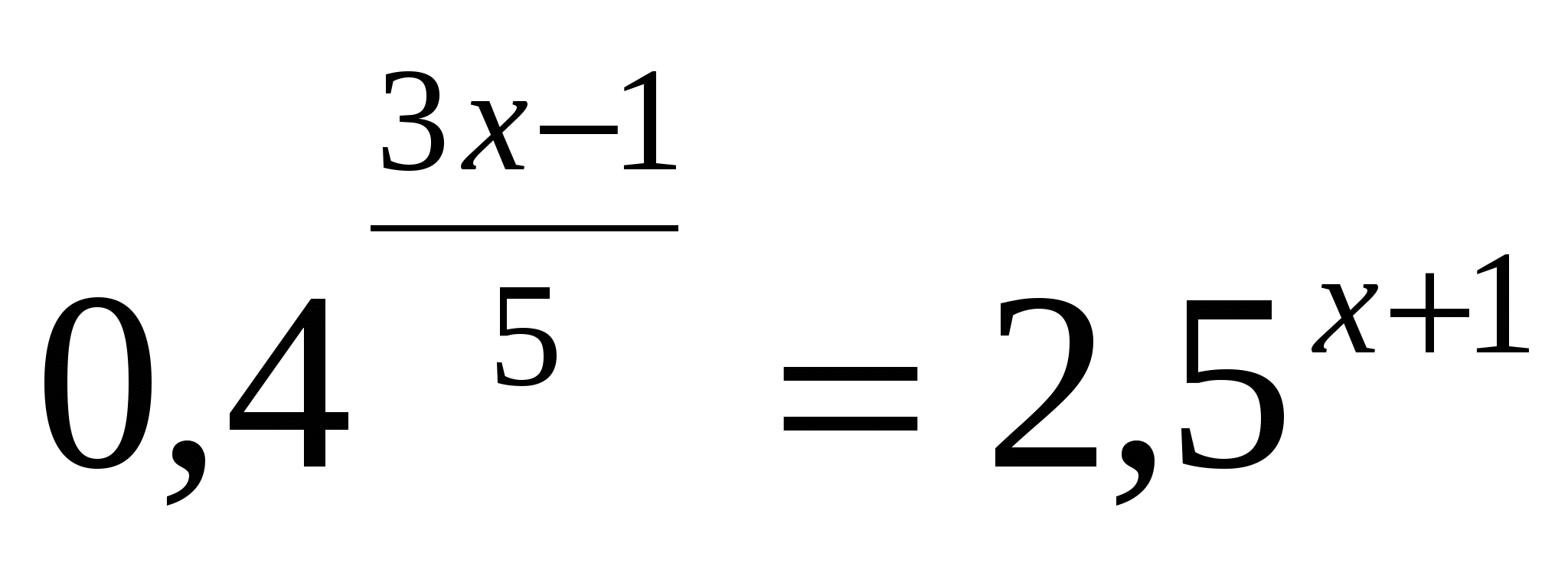
Л
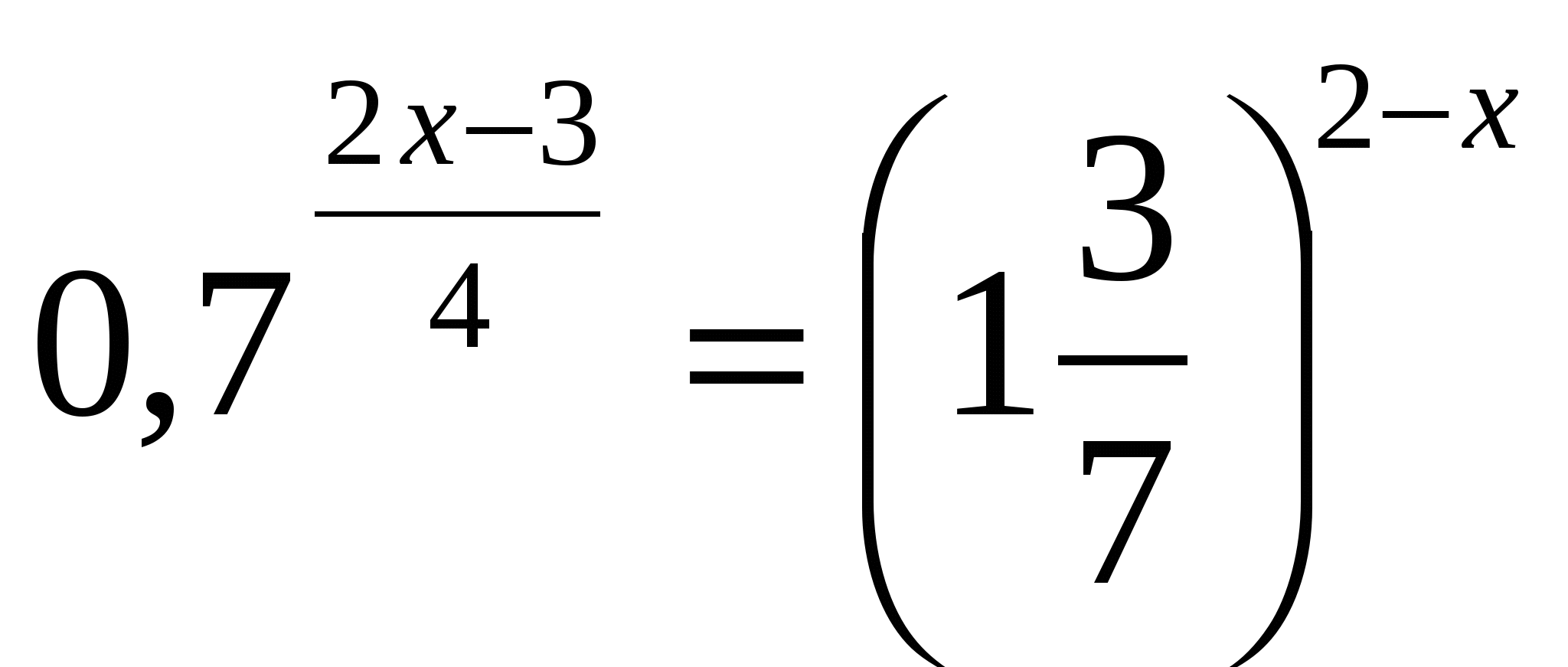
-1
1
2,5
0
-0,5
II. Решив эти уравнения, вы узнаете, у кого возникла идея о необходимости создания единой науки, изучающей процессы сохранения и переработки информации управления и контроля, для которой он предложил название «кибернетика», получившее общее признание (ВИНЕР)
Р
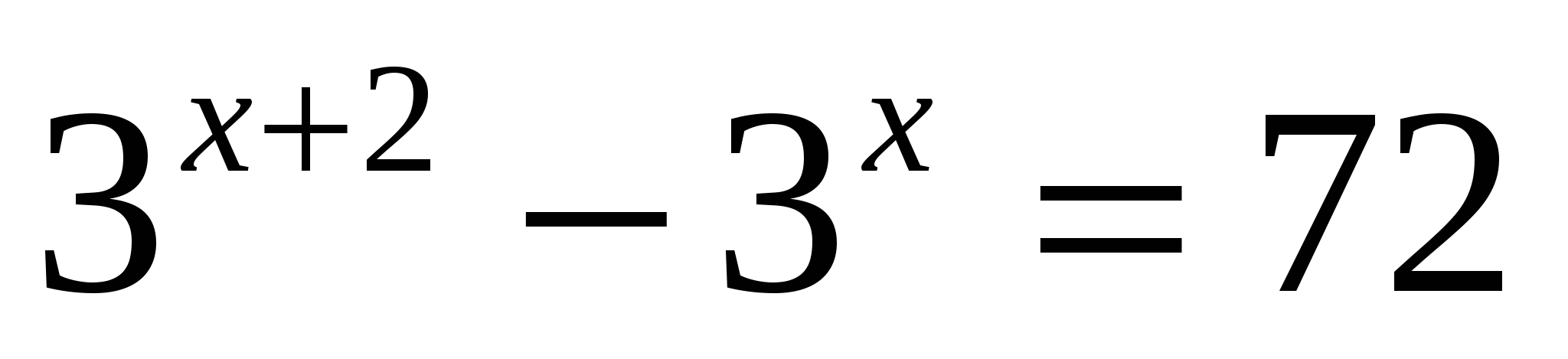
И
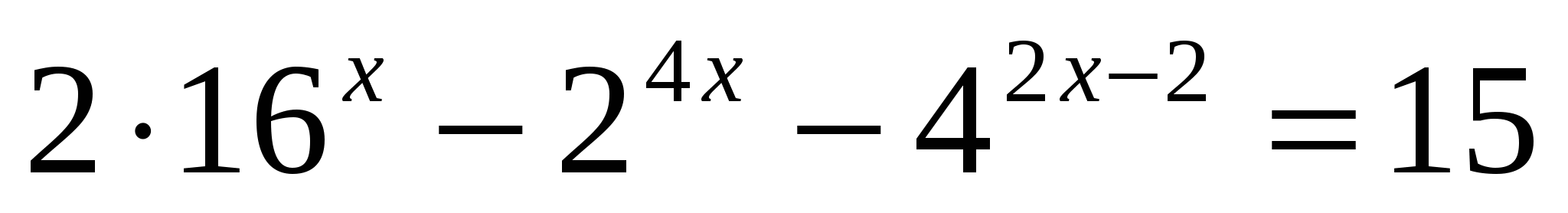
Е
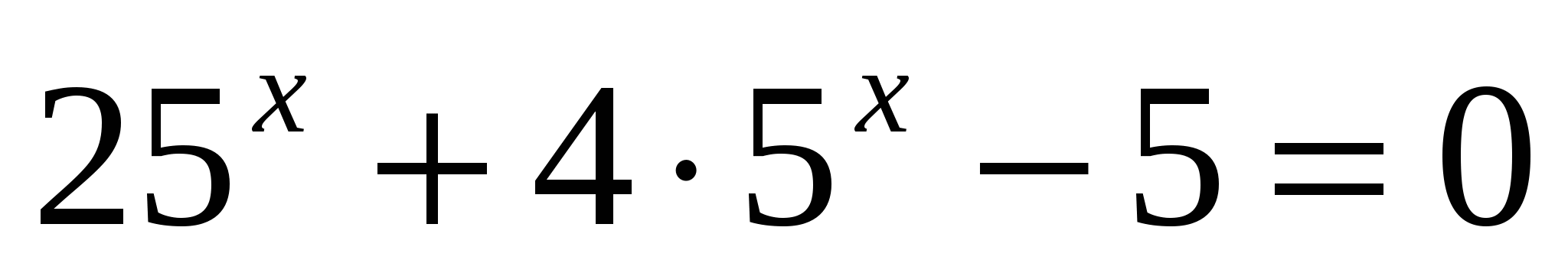
В
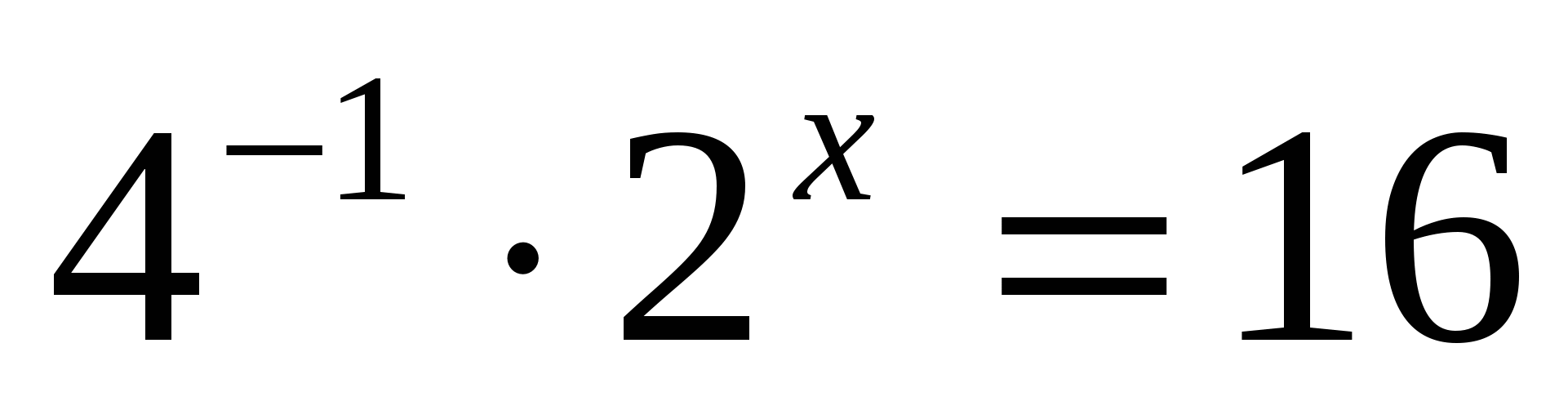
Н
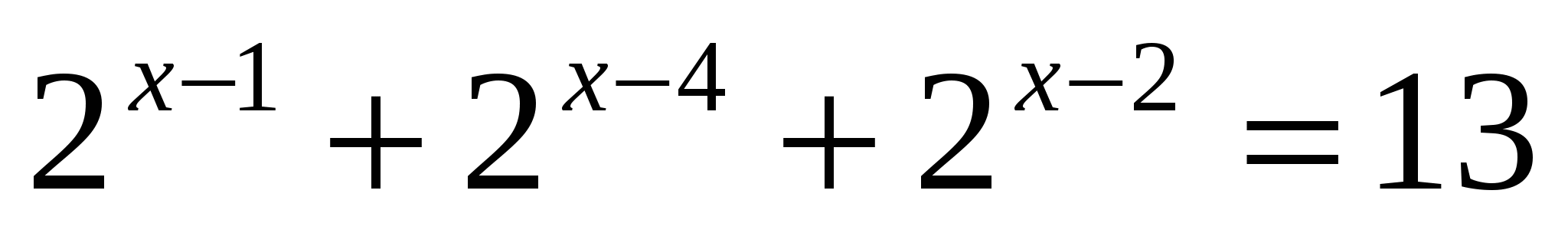
6
1
4
0
2
III. Решив неравенства, вы узнаете фамилию персидского и таджикского поэта, математика и философа, который в математическом трактате «О доказательствах задач алгебры и алмукабалы» дал систематическое изложение решения уравнений до третьей степени включительно (ХАЙЯМ)
А
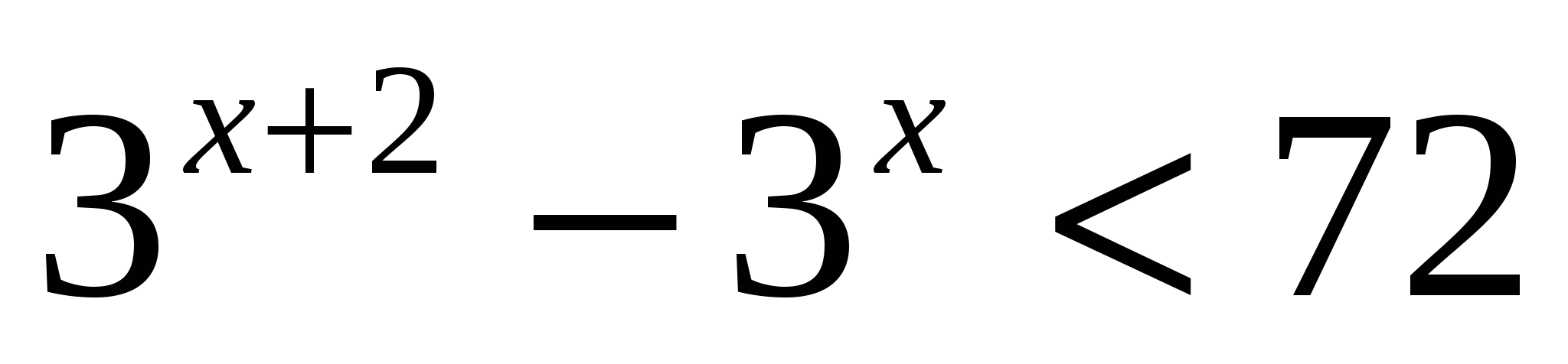
М
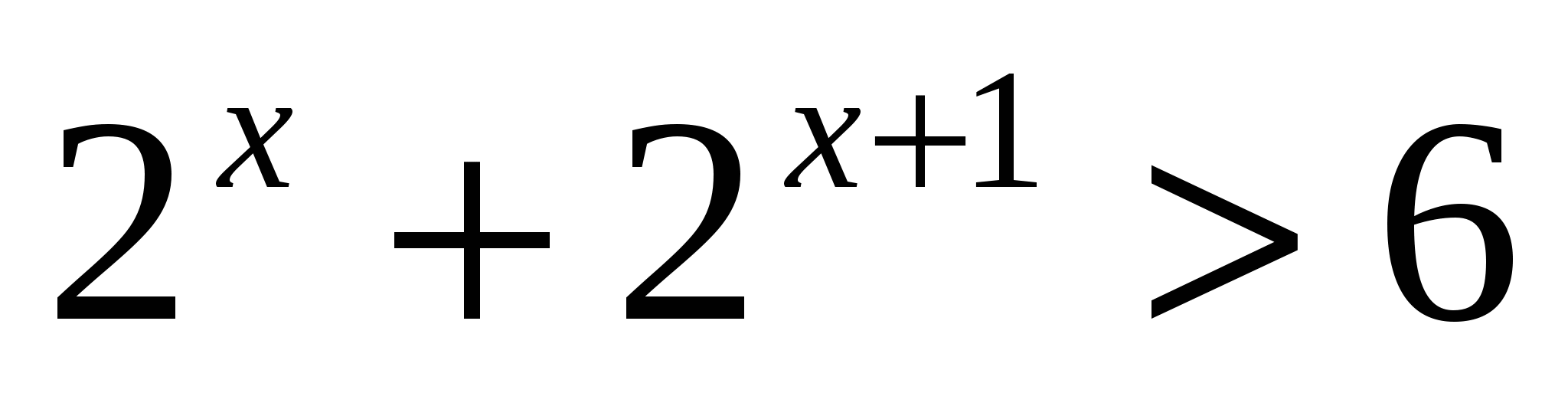
Я
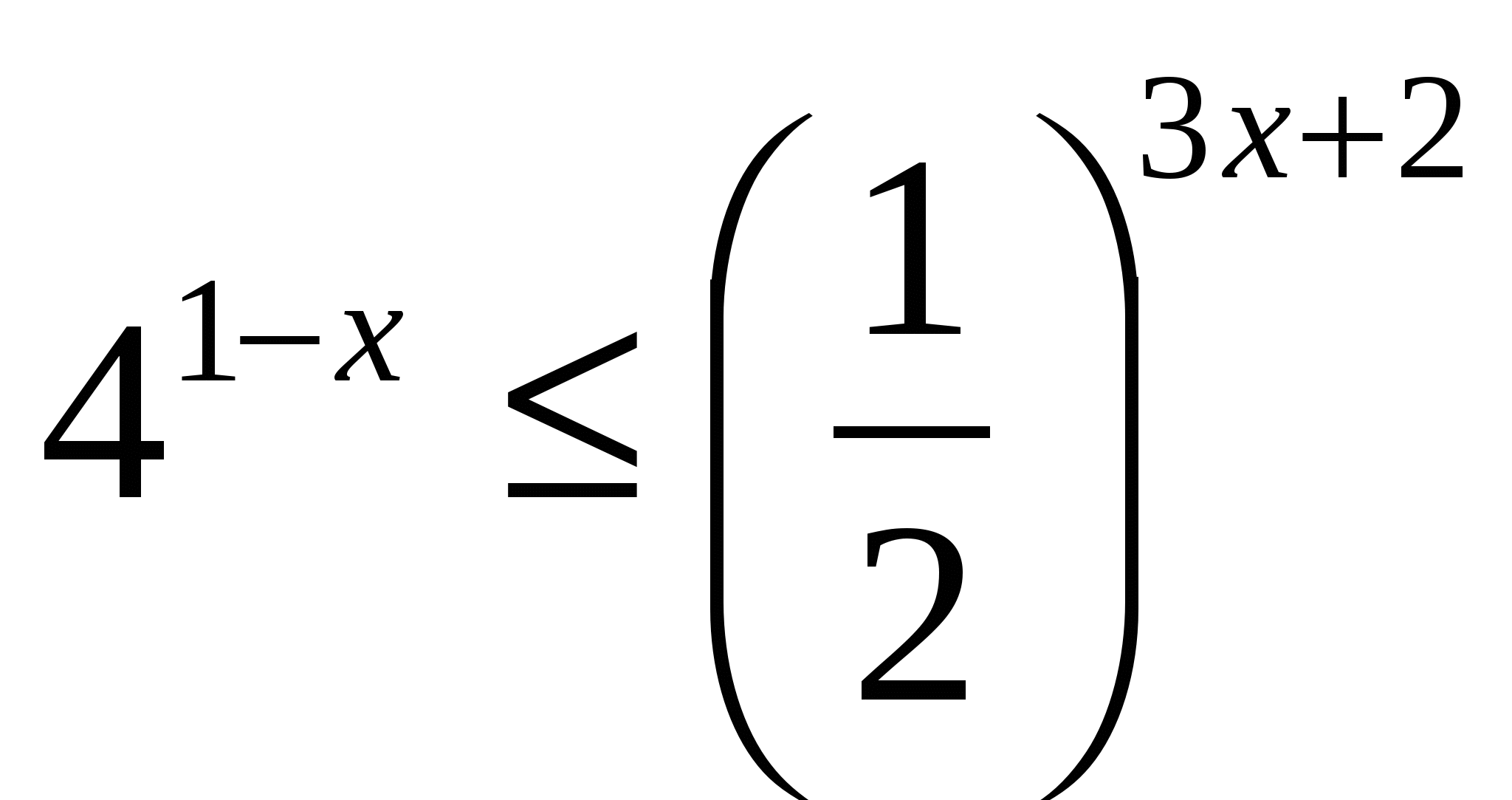
Х
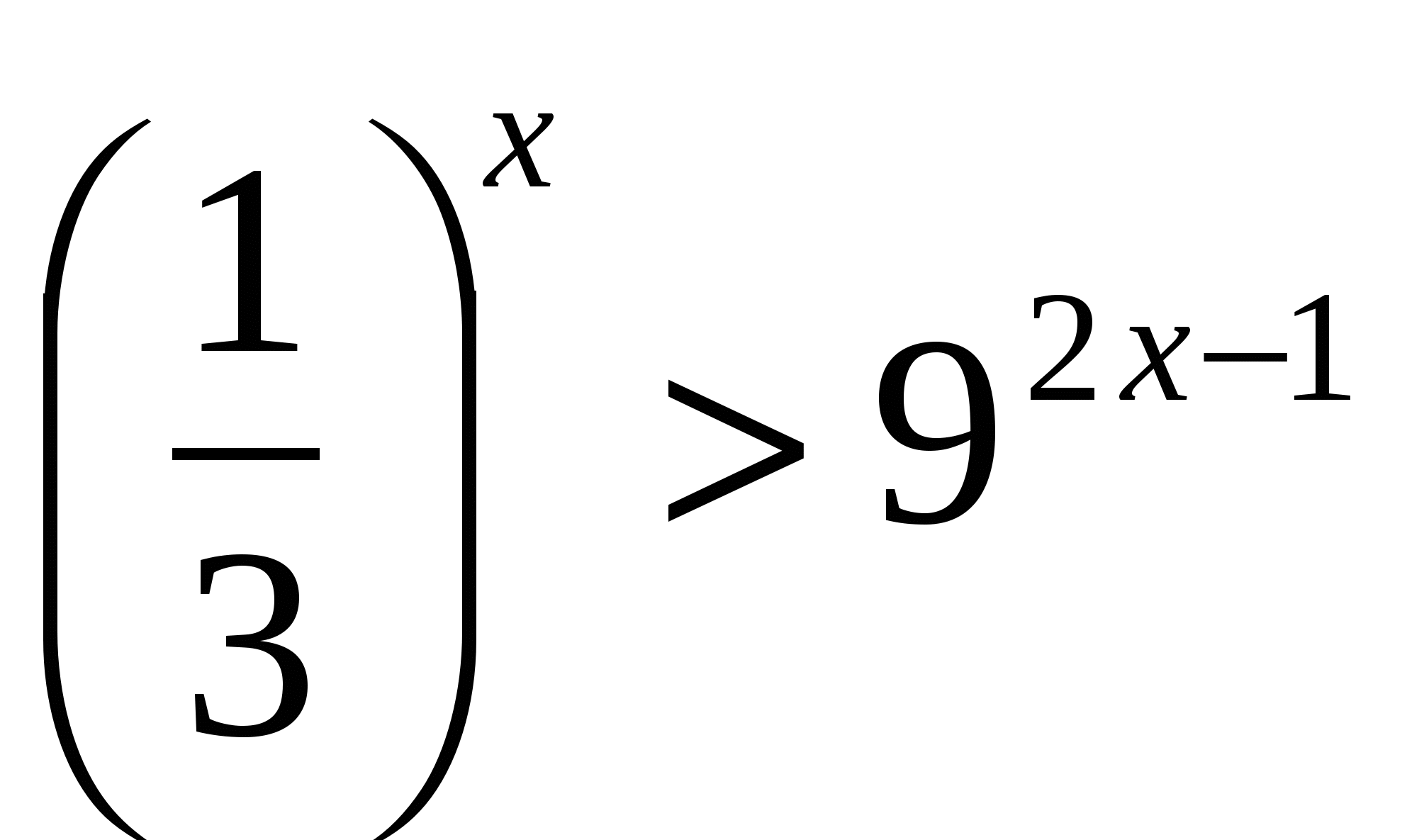
Й
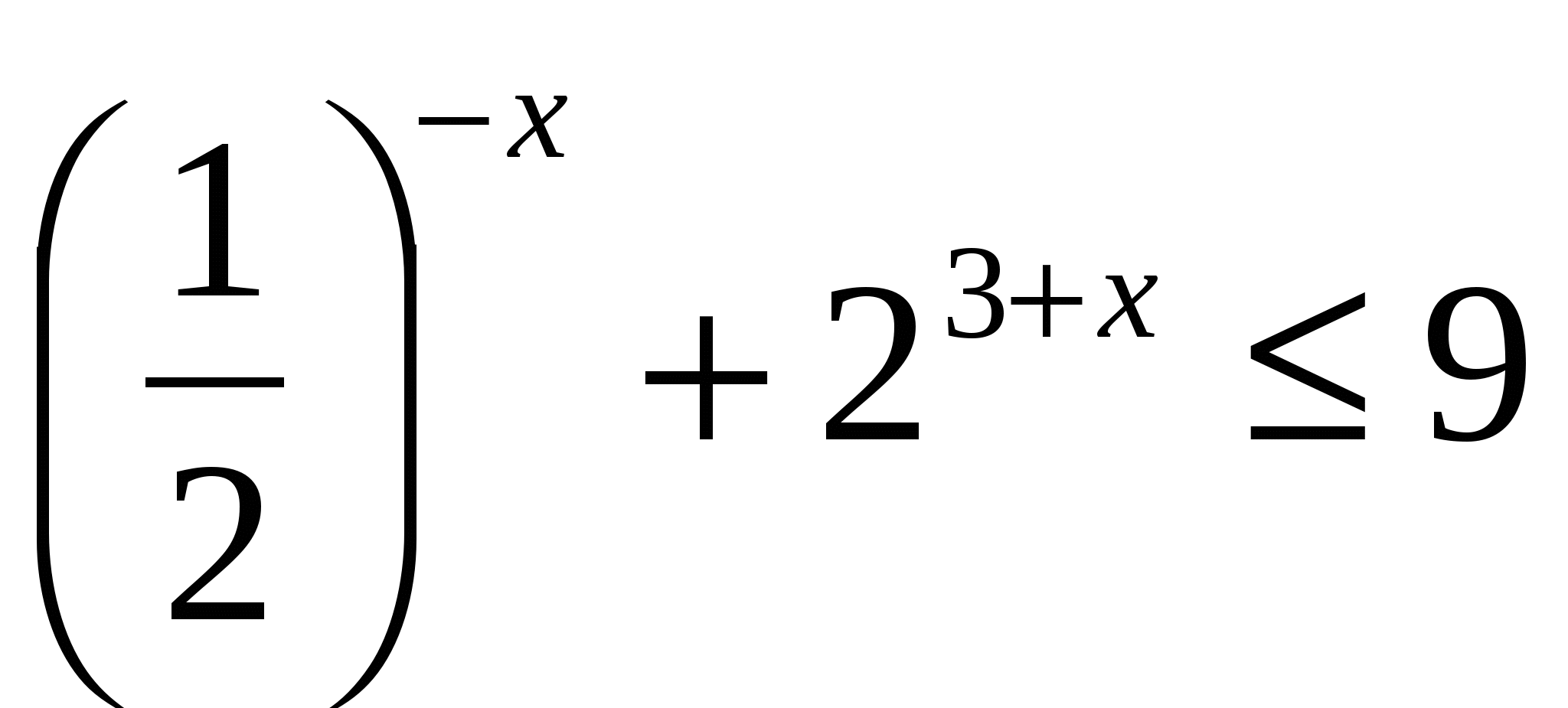
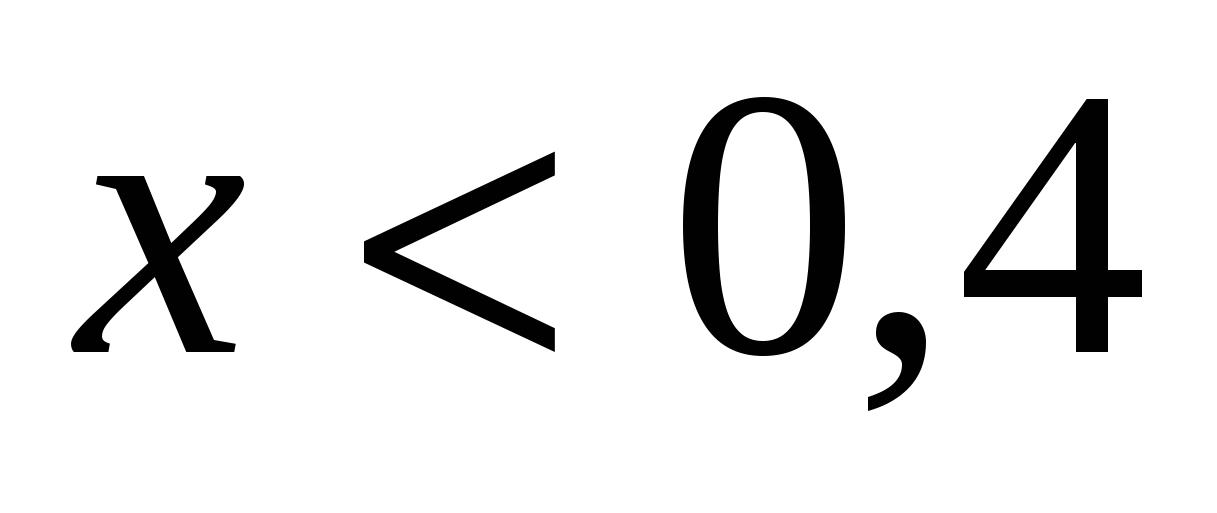
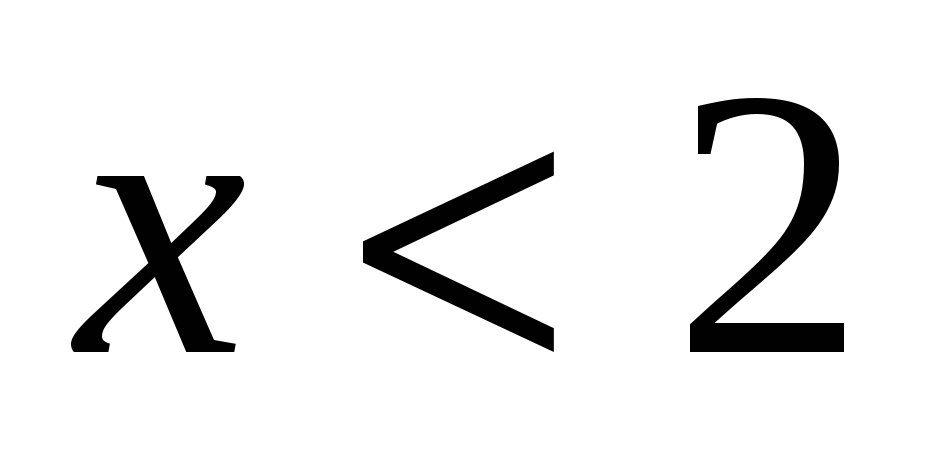
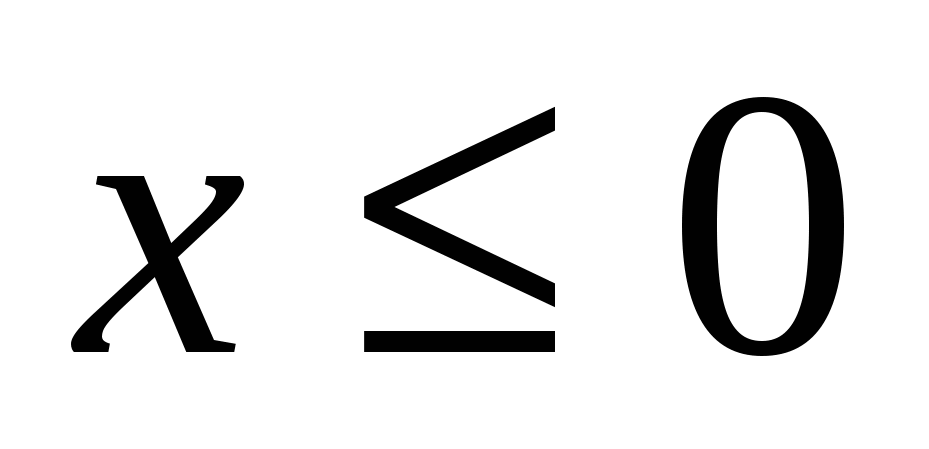
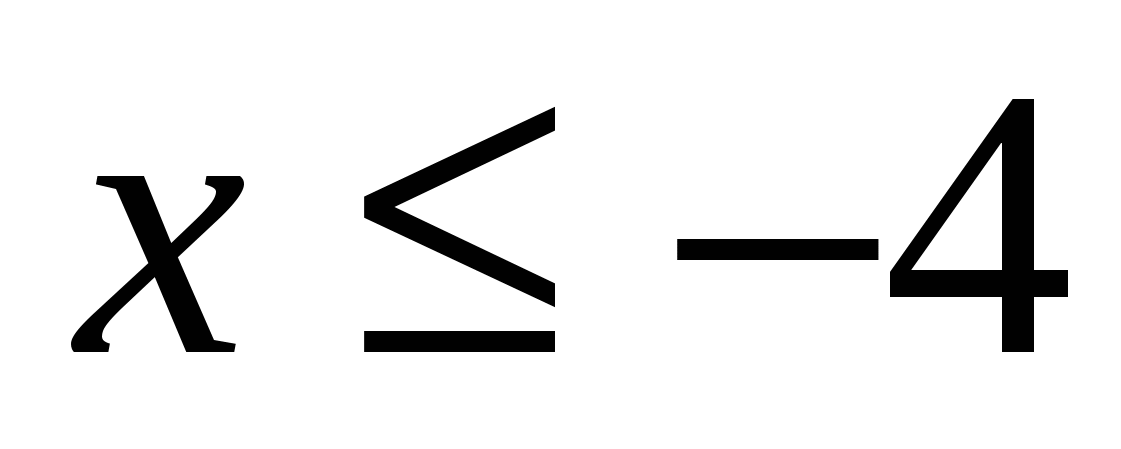
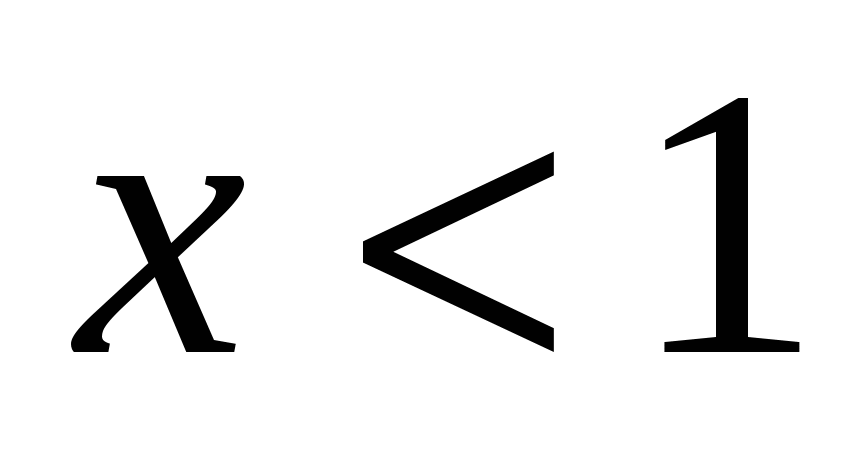
VI. Задания с карточками – домашнее задание, итог урока, выставление
оценок в журнал.
VII. Для дополнительного задания можно дать следующее задание из части С
Решите уравнение 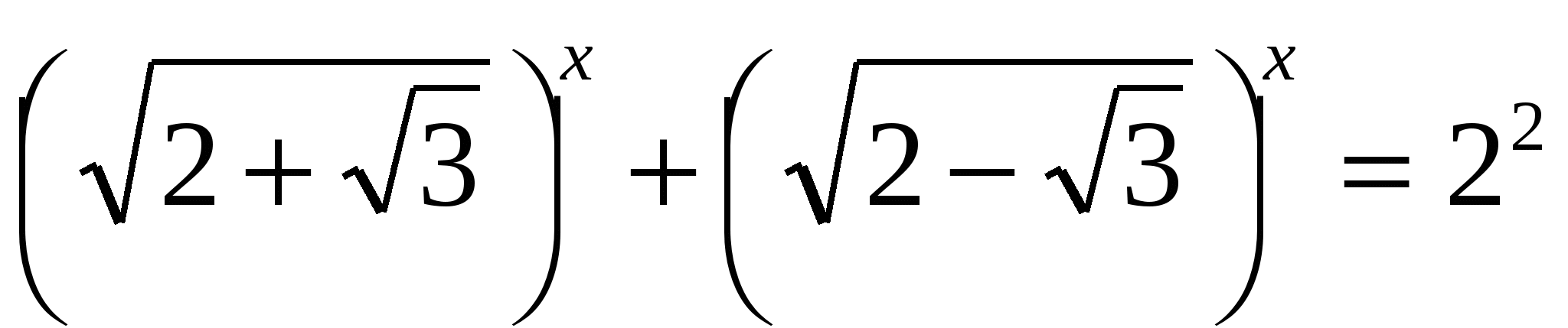
Решение: заметим, что 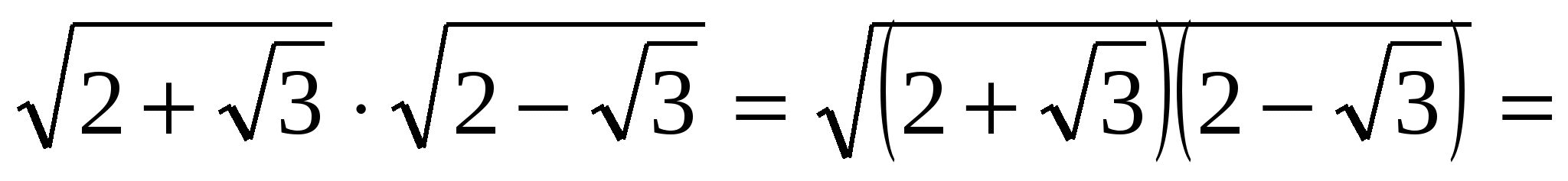
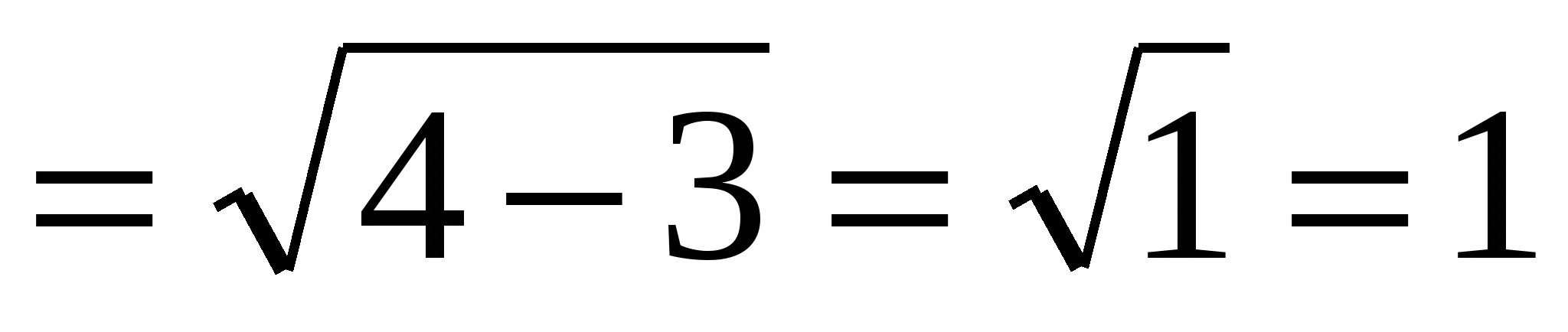 , следовательно,
, следовательно, 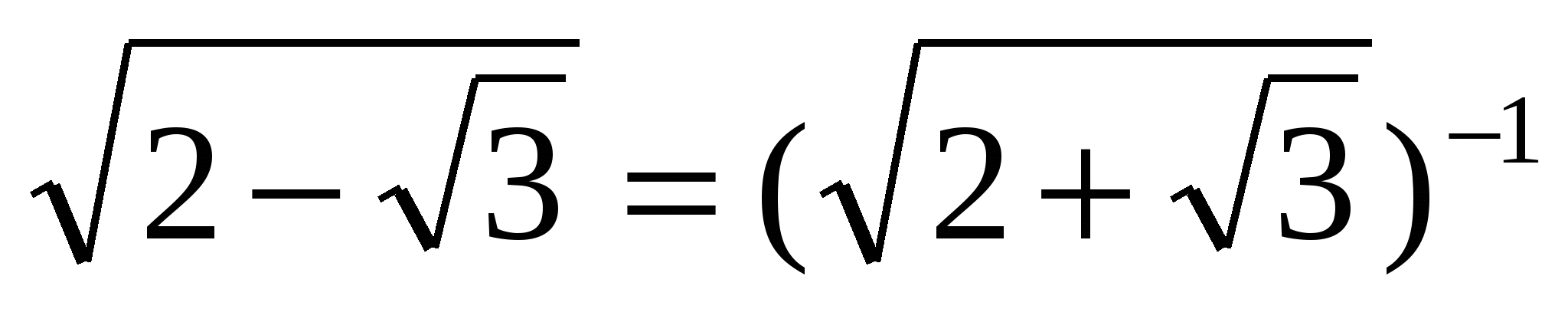 .
.
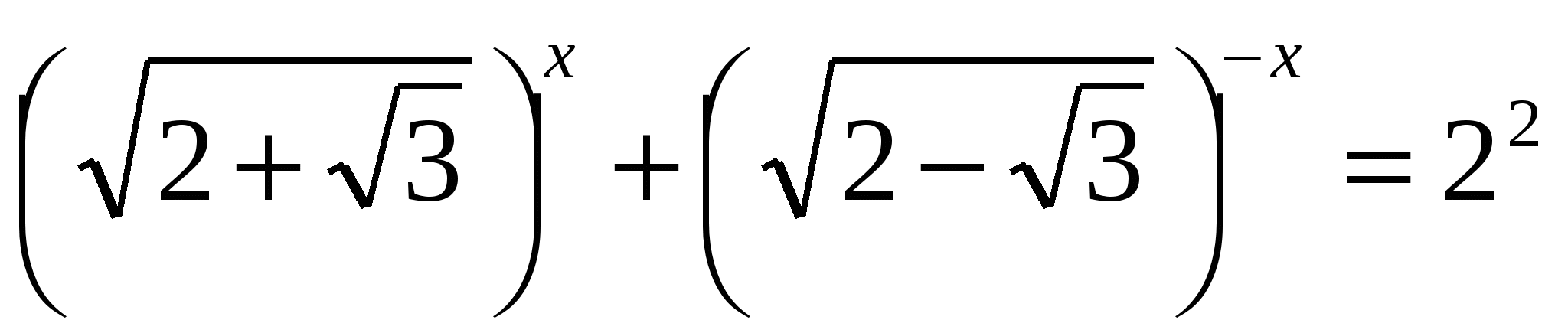
пусть 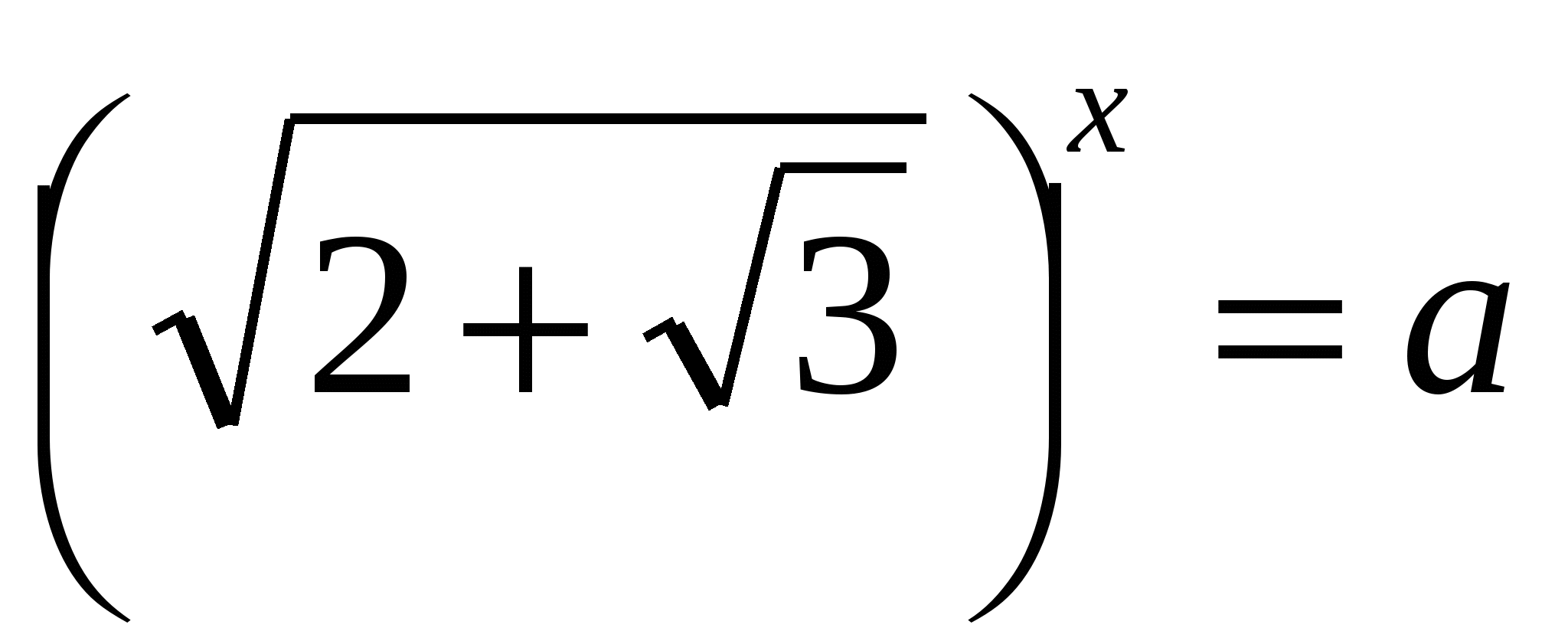 , тогда
, тогда 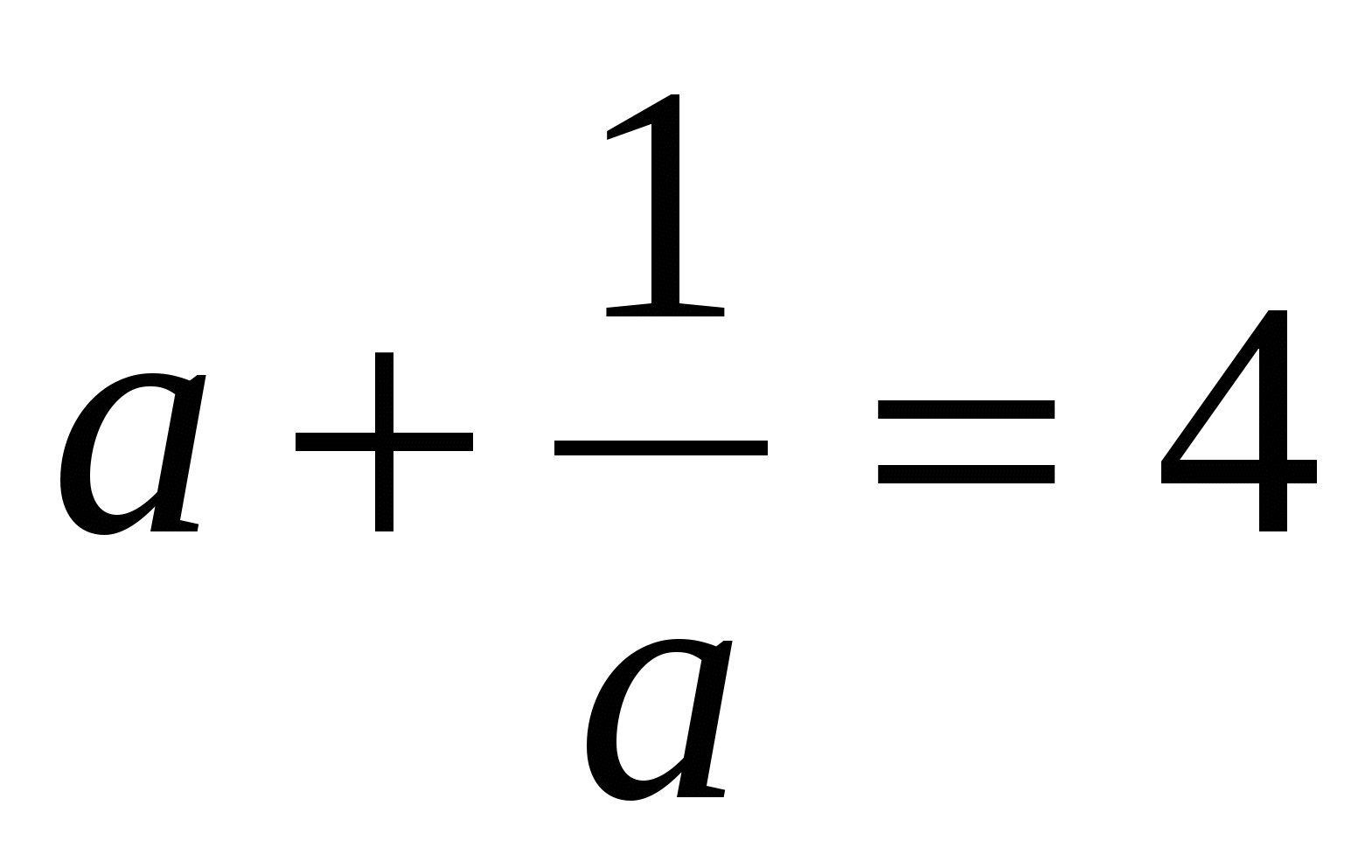
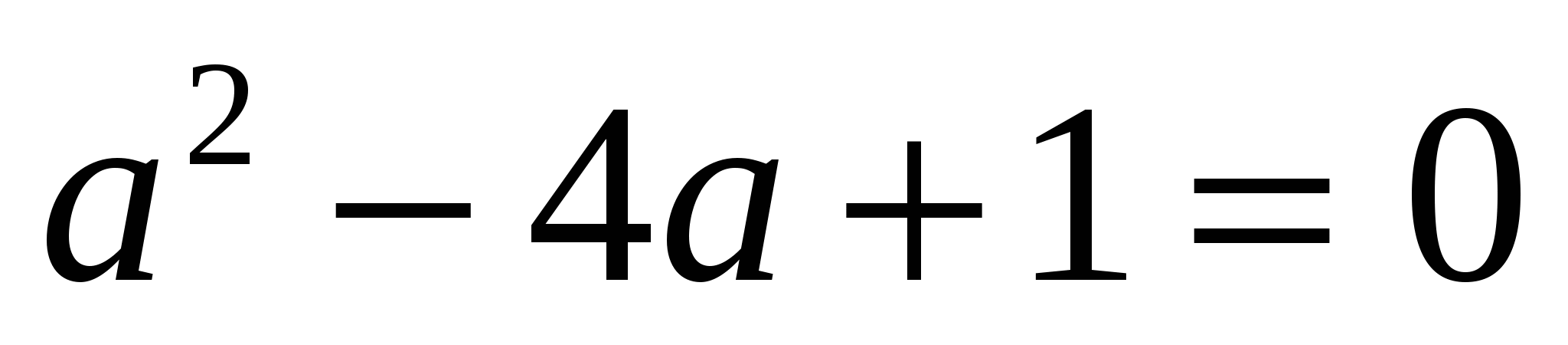
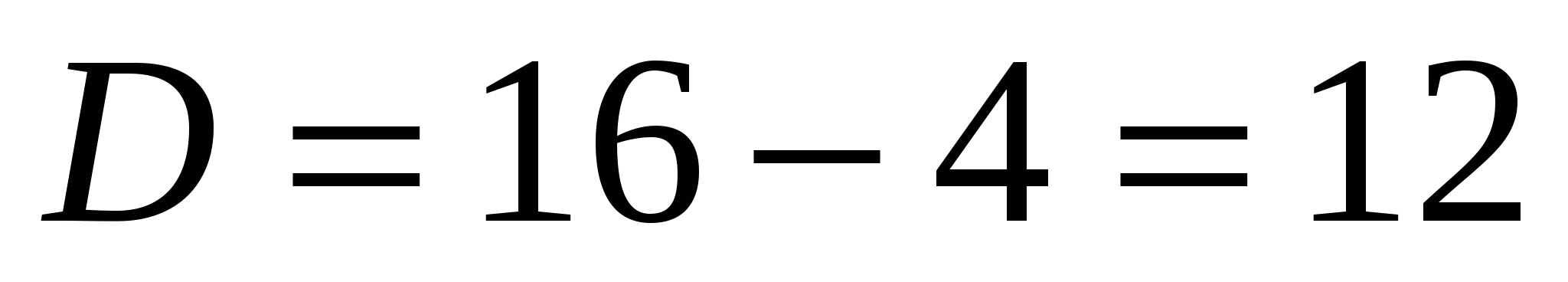
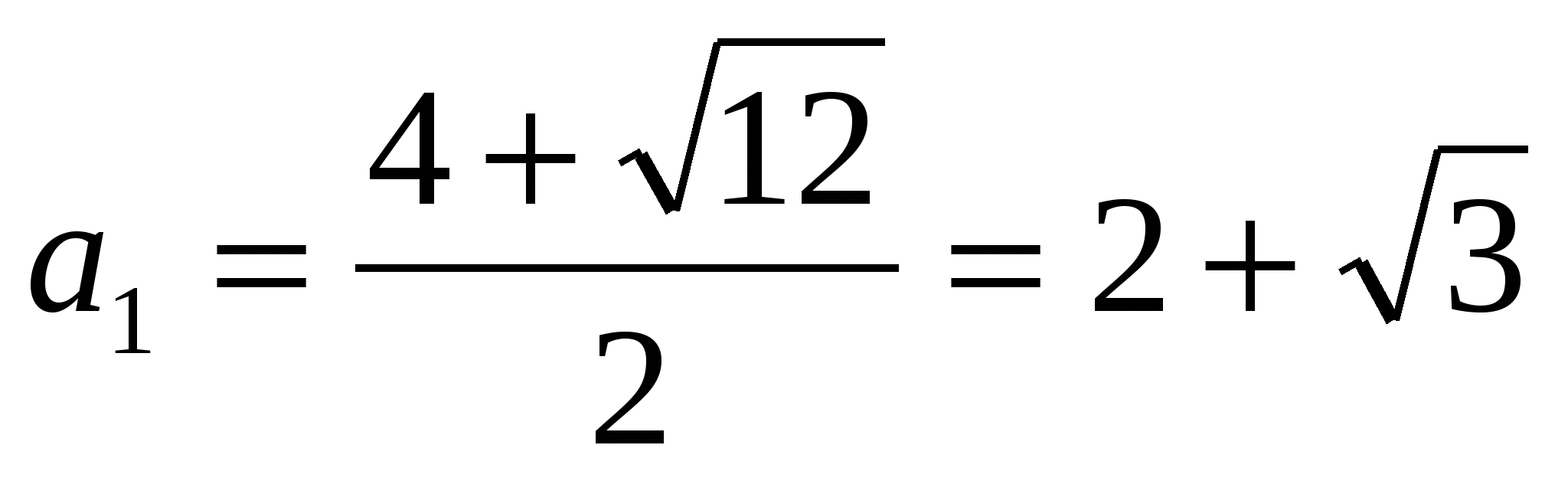
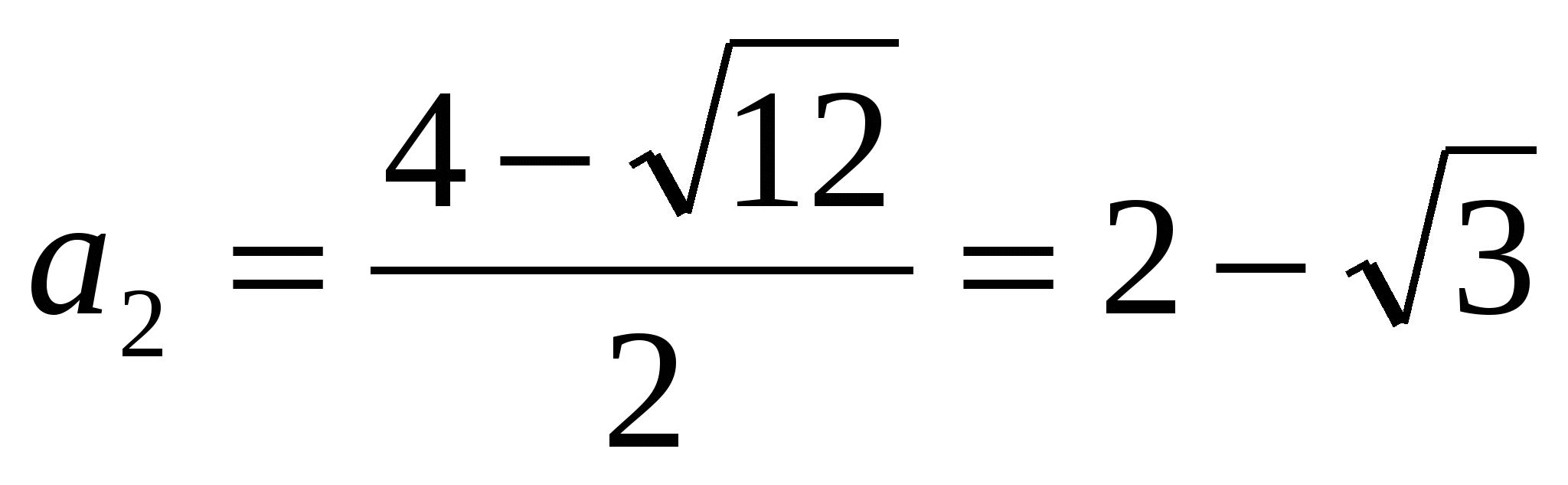
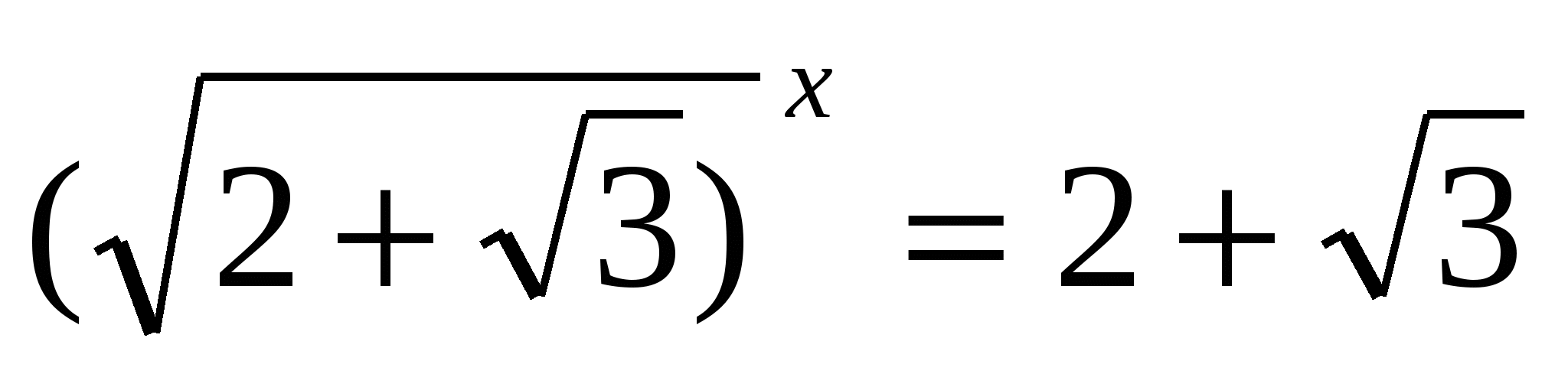
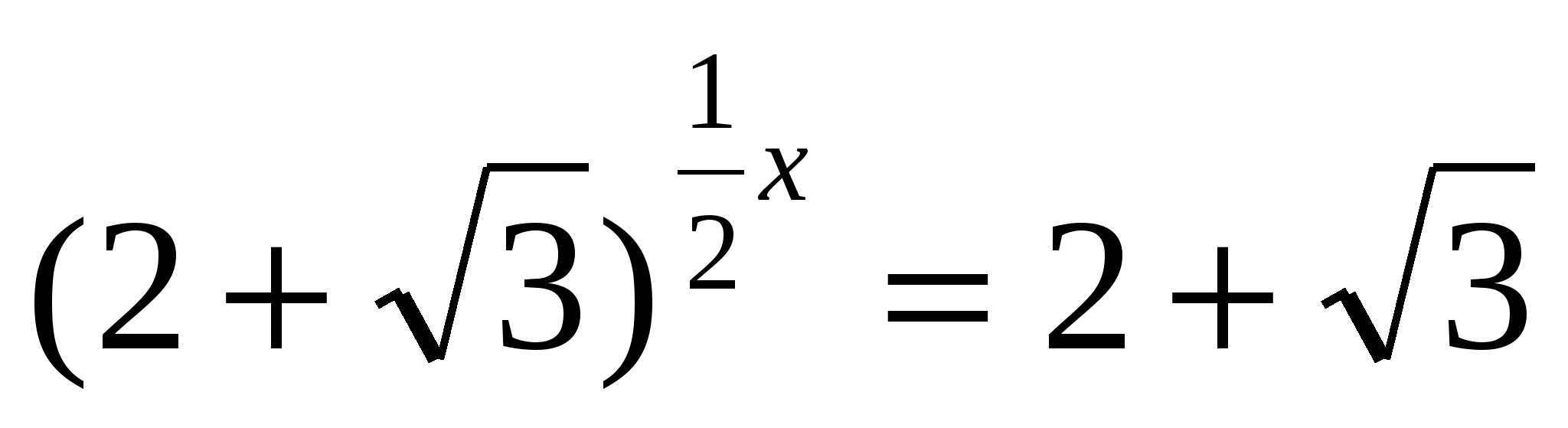
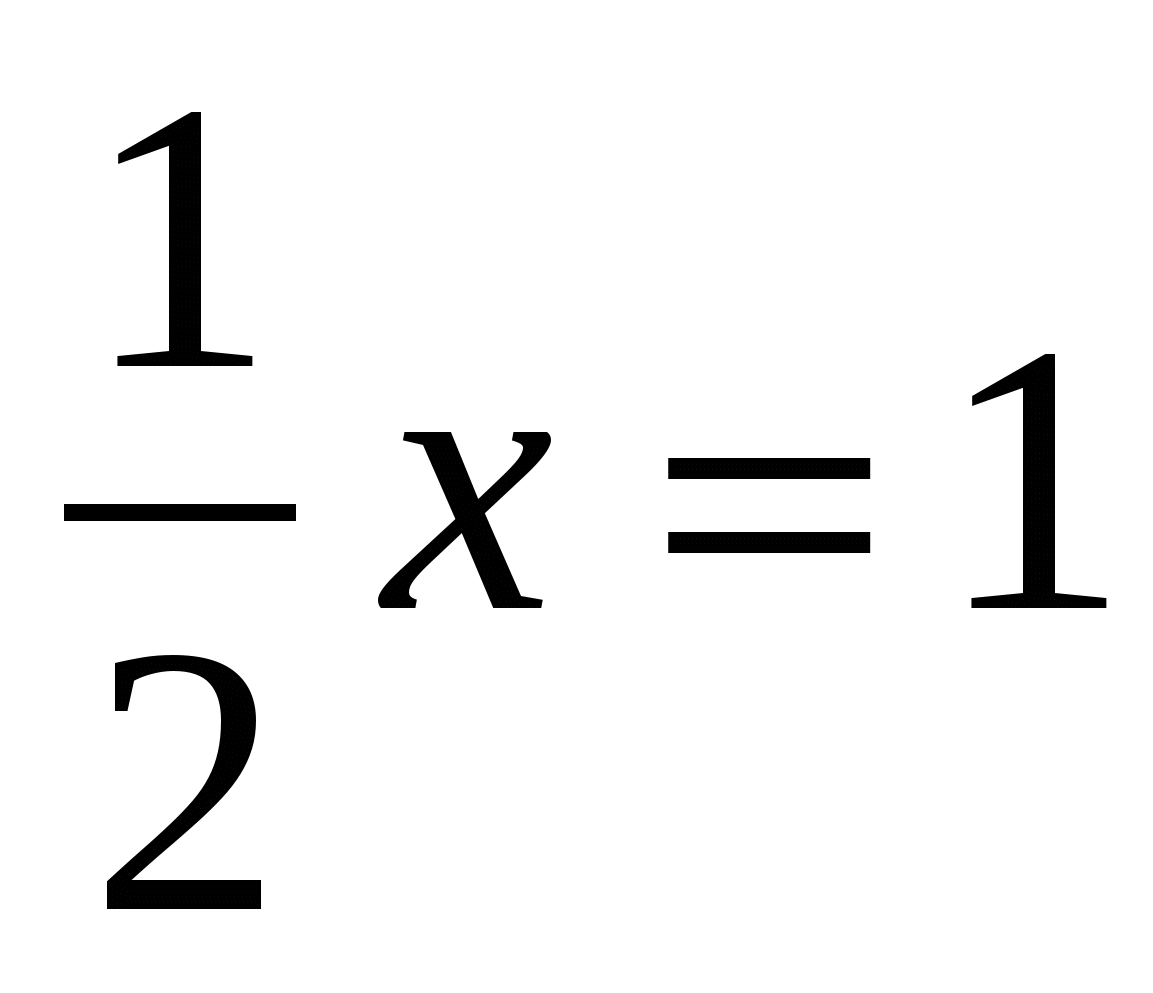
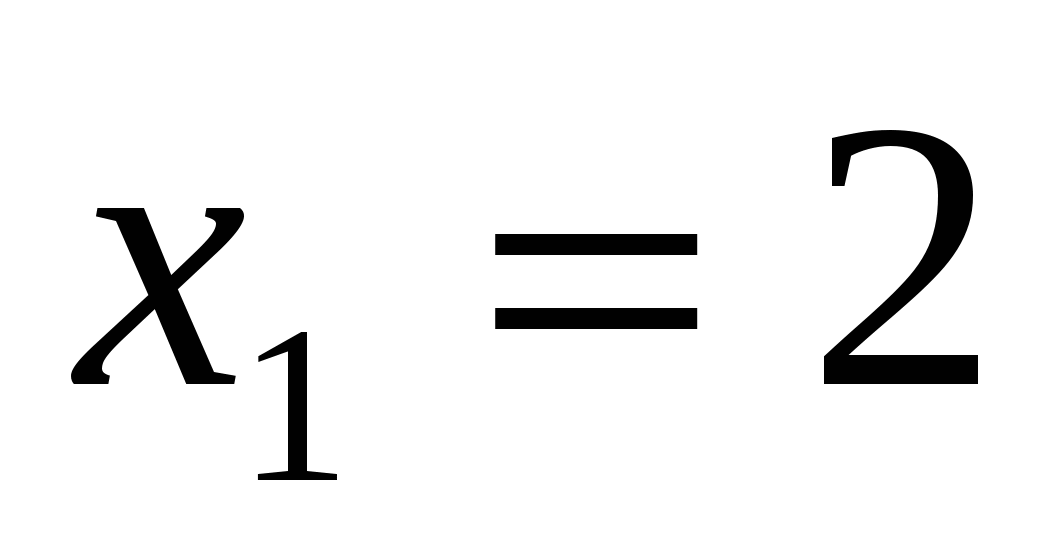
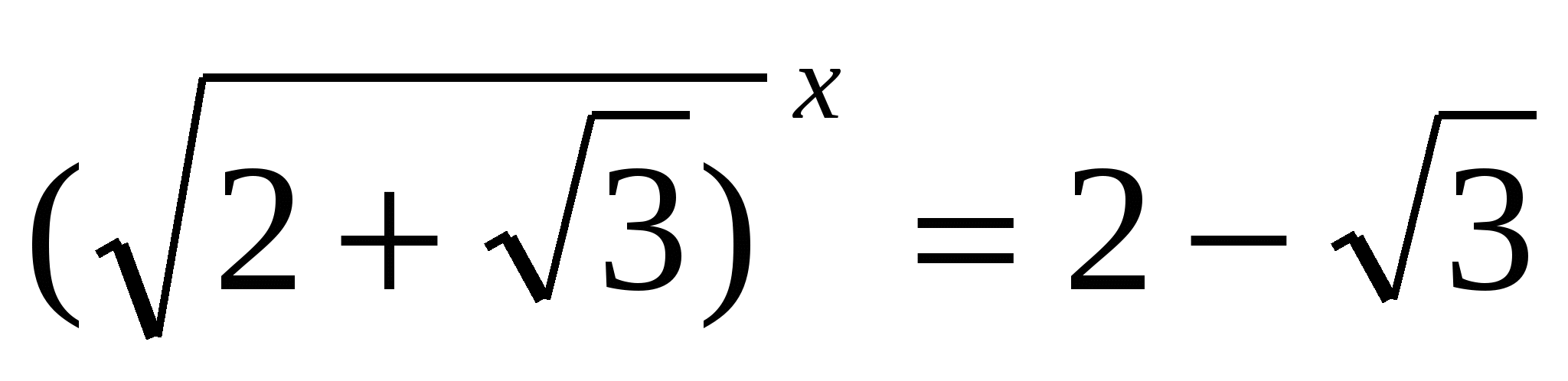
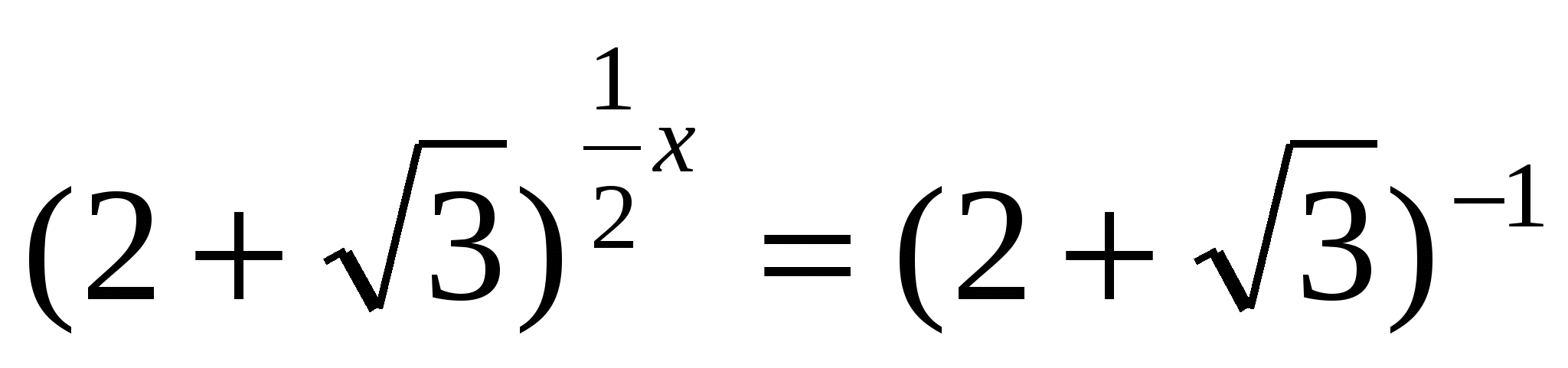
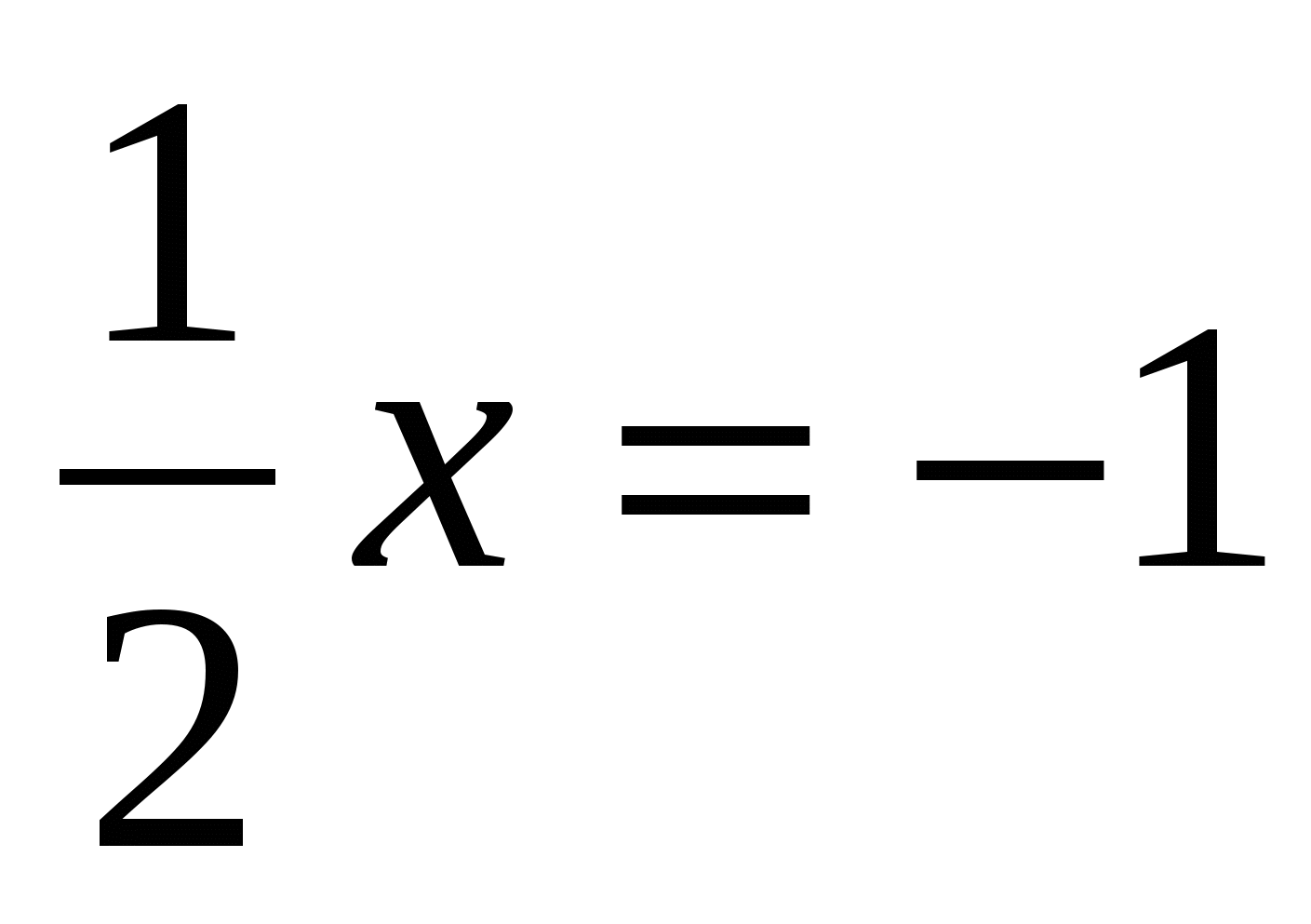
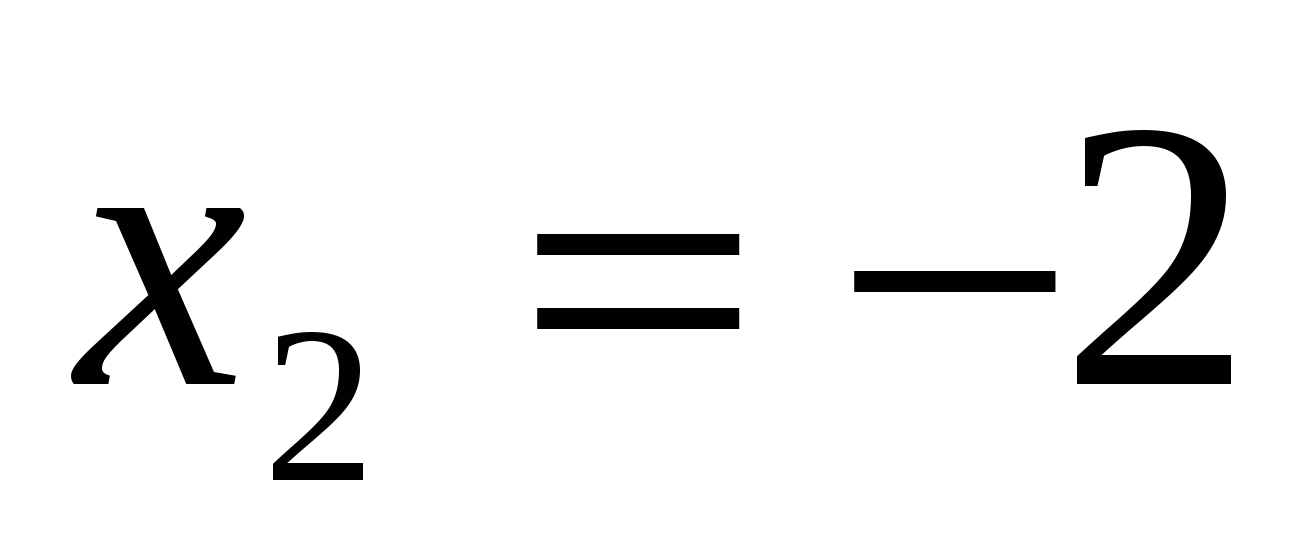
Ответ: 2; – 2
| 1. |
Система уравнений с применением теоремы Виета
Сложность: лёгкое |
3 |
| 2. |
Определение числа решений в системе по графикам
Сложность: лёгкое |
1 |
| 3. |
Взаимное расположение прямых — графиков линейных уравнений системы
Сложность: лёгкое |
1 |
| 4. |
Система иррациональных уравнений
Сложность: среднее |
3 |
| 5. |
Система, состоящая из иррациональных уравнений
Сложность: среднее |
4 |
| 6. |
Система логарифмических уравнений
Сложность: среднее |
3 |
| 7. |
Система уравнений (формула суммы кубов)
Сложность: среднее |
4 |
| 8. |
Система, состоящая из логарифмического и квадратного уравнений
Сложность: среднее |
6 |
| 9. |
Система, состоящая из иррационального и линейного уравнений
Сложность: среднее |
3 |
| 10. |
Система уравнений с взаимнообратными величинами
Сложность: среднее |
4 |
| 11. |
Система иррациональных уравнений
Сложность: среднее |
4 |
| 12. |
Система логарифмических уравнений
Сложность: среднее |
4 |
| 13. |
Система показательных уравнений с модулем
Сложность: среднее |
4 |
| 14. |
Система линейных уравнений (количество решений)
Сложность: среднее |
1 |
| 15. |
Система линейных уравнений с параметром, вычисление параметра, если система не имеет решения
Сложность: среднее |
1 |
| 16. |
Система линейных уравнений с параметром, вычисление параметра, бесконечное множество решений
Сложность: среднее |
3 |
| 17. |
Система уравнений
Сложность: сложное |
8 |
| 18. |
Система иррациональных уравнений
Сложность: сложное |
1 |
| 19. |
Составление уравнения параболы
Сложность: сложное |
3 |
Тема урока: «Решение показательных уравнений и систем уравнений»
10-А класс
Учитель: Чернцова И.П.
Цель урока: «Обобщение и систематизация знаний учащихся; закрепление умений решать показательные уравнения и системы уравнений»
Ход урока:
Сообщение темы и целей урока.
Проверка домашнего задания (на слайде):
№1 №2
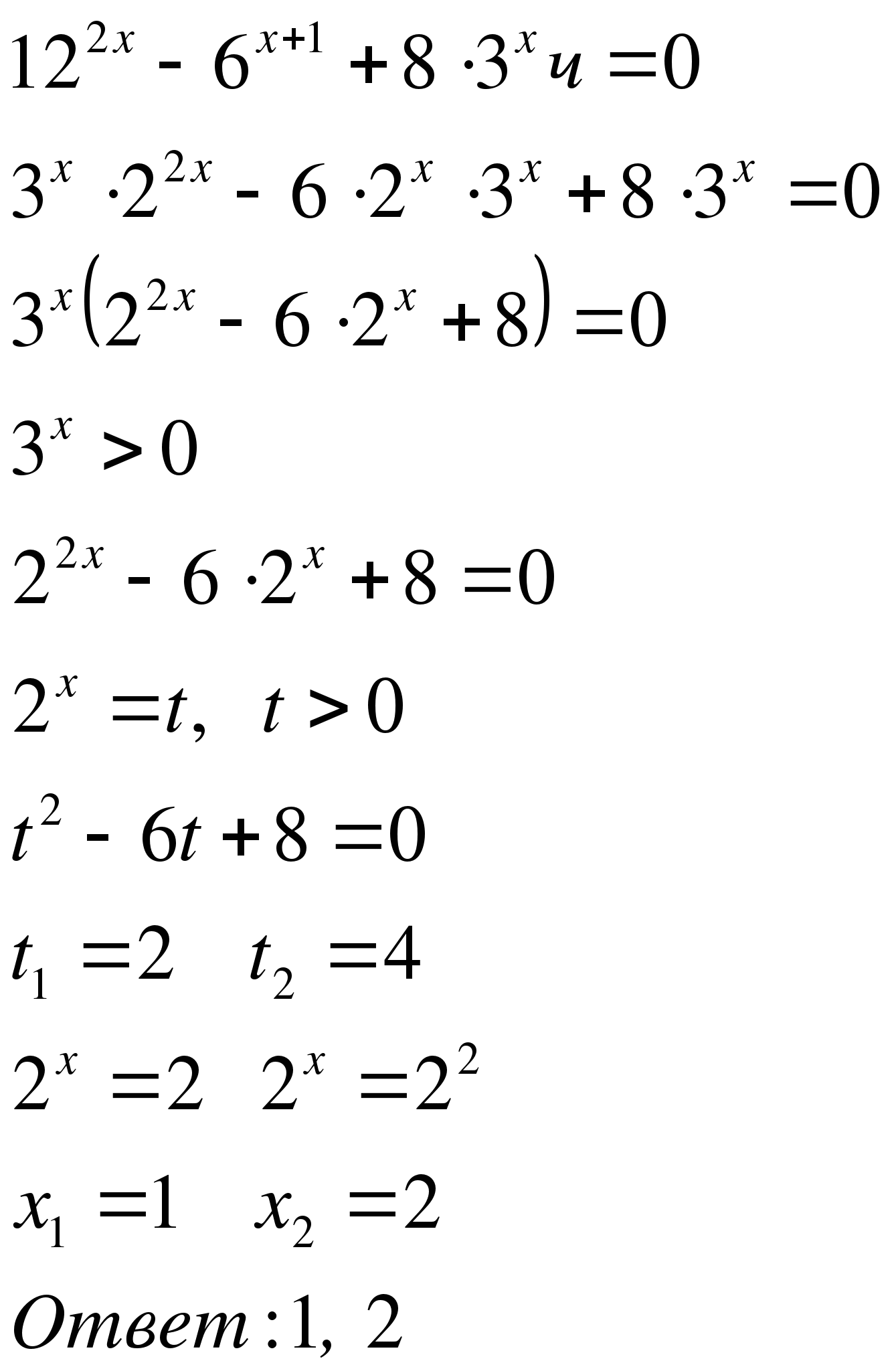
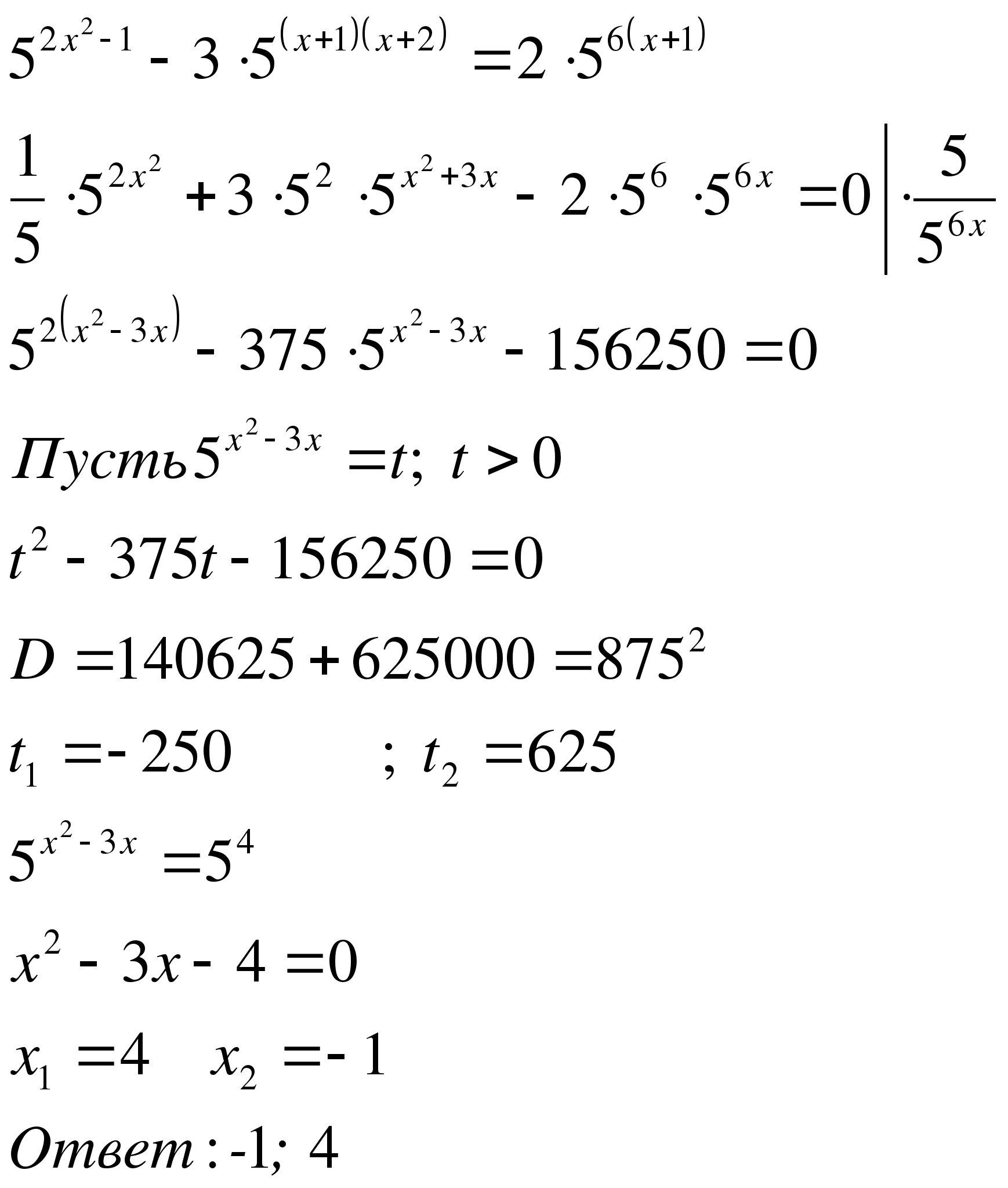
(не уд).
Повторение теоретического материала
Устная работа (на слайде):
Найти корень уравнения:
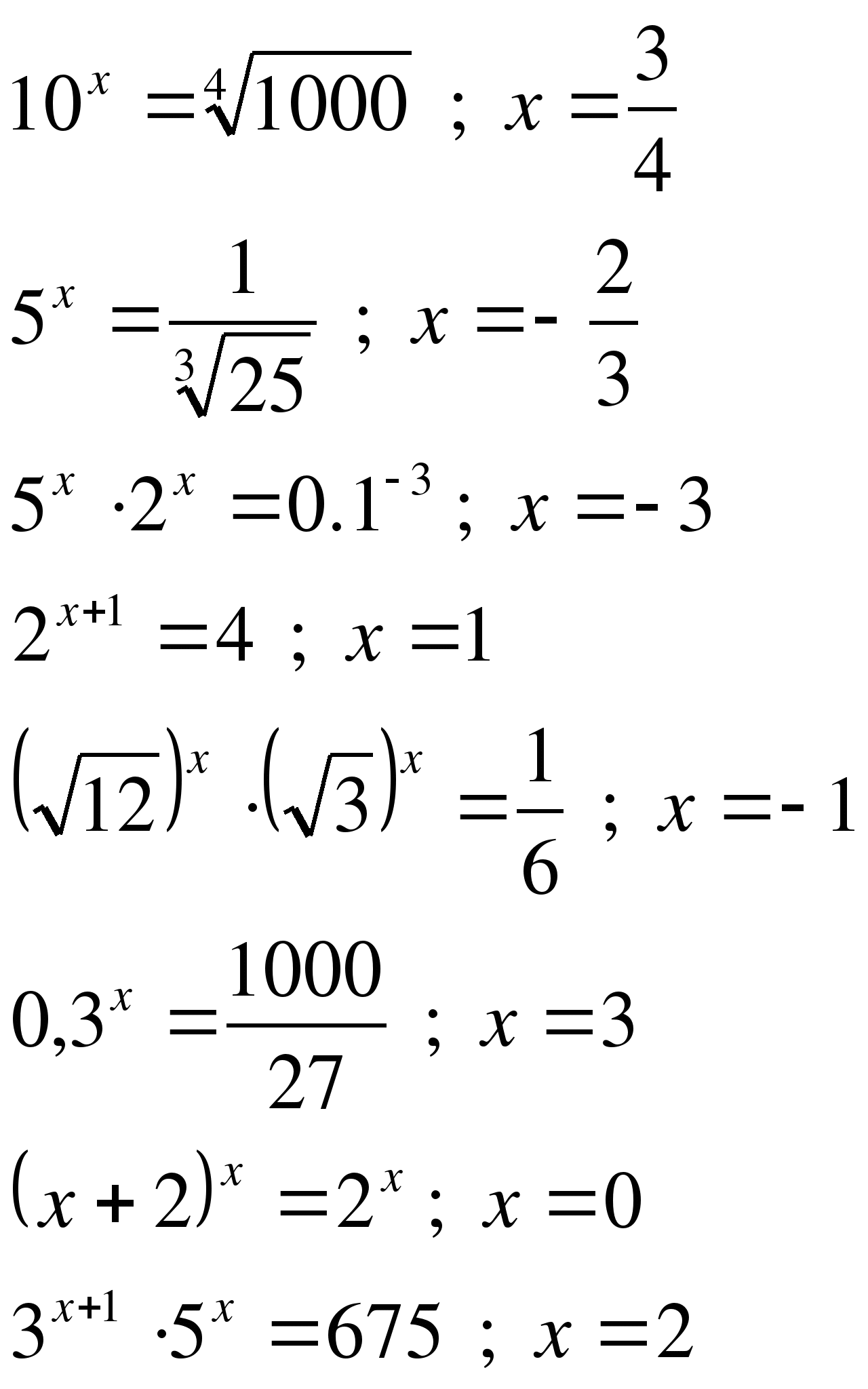







Найти координаты точки пересечения графиков функций:
а) 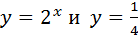
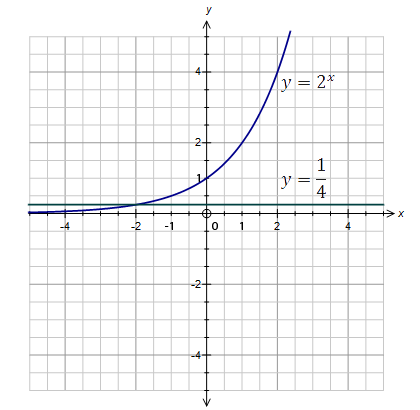
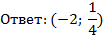
б) 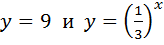
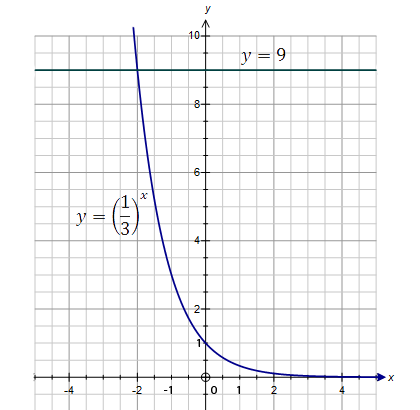
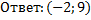
в) 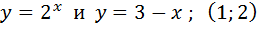 ;
;
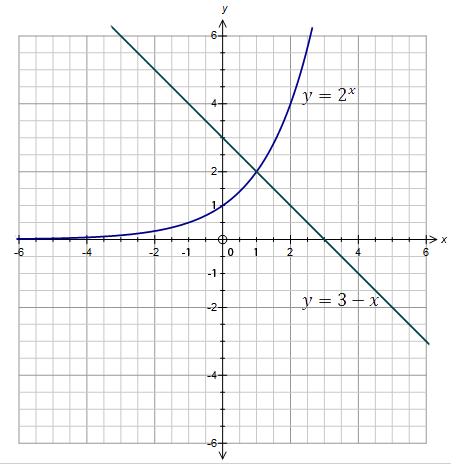
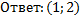
Письменные упражнения:
Решить систему уравнений:
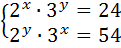
Решение:
Преобразуем: 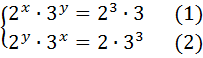
Перемножим уравнения (1) и (2):
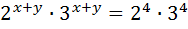
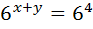
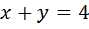
Поделим уравнения (1) и (2):
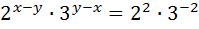
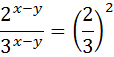
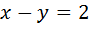
Данную систему сводим к эквивалентной ей системе:
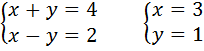
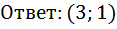
Выполним задание из учебника №686 (1):
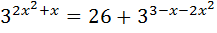
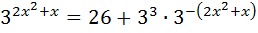
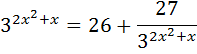
Введём новую переменную:
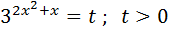
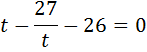
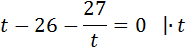
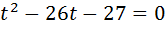
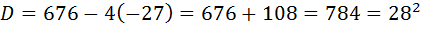
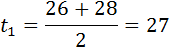
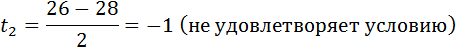
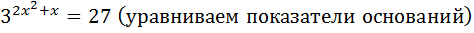
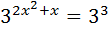
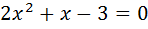
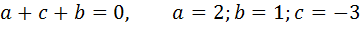
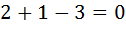
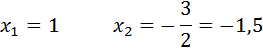
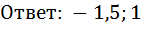
Самостоятельная работа. Взаимопроверка.
Проверка работы (на слайде):
№12.17 (а)

№12.17 (б)

№12.21 (а)

№12.21 (б)

И
 ндивидуальные работы по карточкам.
ндивидуальные работы по карточкам.Выполнить задание с параметрами.
-Молодцы, ребята! Цели нашего урока выполнены. Теперь запишите ваше домашнее задание:
№682
№685 (1, 2)
№690 (2)
№695(дополнительное задание).
И в завершение нашего урока, выполним тесты. Задания лежат у вас на столе. Приступайте к выполнению.
Ответы:
- № зад.
1
2
3
4
5
I
б
в
б
а
а
II
в
б
а
б
в
Вариант 1
1.Решите уравнение
А) В) С) D) Е)
2.Решите уравнение
А)1 В)0 С)-1 D) Е)0,5
3.Решите уравнение
А)5 В)2 С)-5 D) Е)-6
4.Решите уравнение =
А)-1,1 В)-1 С)-1,2 D) Е)0,1
5.Найдите сумму корней уравнения
А)8 В)7 С)1 D) Е)-1
6.Найдите произведение корней уравнения
А)26 В)25 С)5 D) Е)3
7.Найдите сумму х+y из системы уравнений
А)5 В)3 С)4 D) Е)7
8.Найдите произведение ху из системы уравнений
А)3 В)4 С)-3 D) Е) 6
9.Решите уравнение 3
А)-1 В)0,5 С)0 D) Е)-0,5
10.Найдите больший корень уравнения
А)3 В)2 С)-2 D) Е)4
Вариант 2
1.Решите уравнение
А) B) c) D)E)
2. Решите уравнение
A) 1 B) 0 C) -1 D) 2 E) 3
3. Решите уравнение
A) 2 B) 4 C) -4 D) 3 E) 1
4. Решите уравнения
A) B) C) D)-3 E)
5. Найдите произведения корней уравнения
A) 0 B) 2 C) 4 D) 3 E) -1
6. Найдите сумму корней уравнения
A) 0 B) 1 C) -1 D) 3 E) -3
7. Из системы уравнений
, найдите произведение xy.
A) 6 B) 3 C) 4 D) 2 E) -4
8. Найдите сумму x+yиз системы уравнений
A) 2 B) 0 C) 3 D) 5 E) 4
9. решите уравнение
A) 0.5 B)-1 C) 2 D) 0 E) 1
10. Найдите меньший корень уравнения
=6
A) -2 B) 2 C)-3 D) 1 E) 0
Вариант 3
Решите уравнение .
А) B) C) D) E)
2. Решите уравнение
A) 0 B)2 C)-1 D)1 E)-3
3.Решите уравнение .\
A) 1 B)0 C)2 D)-1,5 E)-2
4. Решите уравнение .
A)2,5 B)3,5 C)4,5 D)-4,5 E)-2,5
5. Найдите сумму корней уравнения
.
A)2 B)-1 C)0 D)1 E)3
6. Найдите произведение корней уравнения
.
A)-6 B)6 C)3 D)0 E)2
7. Найдите произведение xy из системы уравнений
.
A)5 B)6 C)3 D) 0 E)2
8. Найдите произведение xy из системы уравнений
.
A)4 B)6 C)3 D)2 E)2
9. Решите уравнение
.
A)-1 B)1 C)-2 D)0 E)2
10. Найдите меньший корень уравнения
A)4 B)0 C)2 D)-2 E)3
Вариант 4
1) Решите уравнение 3x =
A) B) C) D) E)
2 ) Решите уравнение += 4
A)1 B)-1 C)0 D)0,5 E)-0,5
3) Решите уравнение 5x+1 =)X-2
A)0,5 B)0 C)-0,5 D)-1 E)1
4)Решите уравнение =
A)3 B)1,5 C)4,5 D)2,5 E)2
5) Найдите сумму корней уравнения
*=0
A)6 B)-6 C)5 D)1 E)0
6) Найдите произведение корней уравнения
+ = 12
A)2 B)3 C)5 D)1 E)0
7) Найдите сумму x+y из системы уравнений
A)16 B)9 C)7 D)3 E)5
8) Найдите произведение x* y из системы уравнений
A)-3 B)3 C)6 D)2 E)-6
9) Решите уравнениe =0
A)1 B)-1 C)0 D)2 E)-2
10) Найдите больший корень уравнения
.
A)1 B)2 C)-1 D)3 E)4
Ответы
1
2
3
4
5
6
7
8
9
10
1
A
B
C
E
C
D
C
A
B
B
2
D
A
C
A
A
B
C
D
E
A
3
A
D
D
C
D
A
B
D
A
D
4
B
C
A
C
D
A
D
A
C
B
Инструкция:
Для 10 тестовых заданий:
9-10 правильных ответов оцениваются на «5»
7-8 – на «4»
5-6 – на «3»
Алгебра — Решение экспоненциальных уравнений
Пол Заметки ОнлайнНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы практики
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Логарифм Функции
- Решение логарифмических уравнений
- глав
- полиномиальных функций
- Системы уравнений
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений Уравнения
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- полиномиальных функций
- делительных полиномов
- Нули / корни полиномов
- графических полиномов
- В поисках нулей полиномов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- экспоненциальных функций
- Логарифм Функции
- Решение экспоненциальных уравнений
- Решение
- Предварительные
Ноты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы практики
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Логарифм Функции
- Общие графики
- глав
- Пределы
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений Уравнения
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- полиномиальных функций
- делительных полиномов
- Нули / корни полиномов
- графических полиномов
- В поисках нулей полиномов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- экспоненциальных функций
- Логарифм Функции
- Решение экспоненциальных уравнений
- Решение логарифмических уравнений
- приложений
- Системы Уравнений
- Линейные системы с двумя переменными
- Предварительные
экспоненциальных и логарифмических уравнений
Экспоненциальные и логарифмические уравнения
Экспоненциальное уравнение — это уравнение, в котором переменная появляется в показателе степени. Логарифмическое уравнение — это уравнение, которое включает логарифм выражения, содержащего переменную. Чтобы решить экспоненциальные уравнения, сначала посмотрите, можете ли вы записать обе части уравнения как степени одного и того же числа.Если вы не можете, возьмите общий логарифм обеих сторон уравнения, а затем примените свойство 7.
Пример 1
Решите следующие уравнения.
3 x = 5
6 x — 3 = 2
2 3 x — 1 = 3 2 x — 2

Деление обеих сторон на бревно 3,

Использование калькулятора для приближения,


Деление обеих сторон на бревно 6,

Использование калькулятора для приближения,

Использование дистрибутивного свойства,
3 x журнал 2 — журнал 2 = 2 x журнал 3 — 2 журнал 3
Сбор всех членов, включающих переменную, на одной стороне уравнения,
3 x log 2 — 2 x log 3 = log 2 — 2 log 3
Факторинг x ,
x (3 log 2 — 2 log 3) = log 2 — 2 log 3
Деление обеих сторон на 3 бревна 2 — 2 бревна 3,


Использование калькулятора для приближения,
x ≈ 12.770
Чтобы решить уравнение, включающее логарифмы, используйте свойства логарифмов, чтобы написать уравнение в форме log b M = N и затем изменить его на экспоненциальную форму, M = b N .
Пример 2
Решите следующие уравнения.
log 4 (3 x — 2) = 2
log 3 x + log 3 ( x — 6) = 3
log 2 (5 + 2 x ) — log 2 (4 — x ) = 3
log 5 (7 x — 9) = log 5 ( x 2 — x — 29)
log 4 (3 x — 2) = 2
Перейдите в экспоненциальную форму.

Проверьте ответ.

Это верное утверждение. Следовательно, решение составляет x = 6.
Перейдите в экспоненциальную форму.

Проверьте ответы.

Поскольку логарифм отрицательного числа не определен, единственным решением является x = 9.
log 2 (5 + 2 x ) — log 2 (4 — x ) = 3

Перейдите в экспоненциальную форму.

Использование свойства cross products,

Проверьте ответ.

Это верное утверждение. Следовательно, решение составляет x = 2,7.
Проверьте ответы.
Если x = 10,

Это верное утверждение.
Если x = –2,

Это похоже на правду, но журнал 5 (–23) не определен.Следовательно, единственное решение — x = 10.
Пример 3
Найти журнал 3 8.

Примечание: журнал 8 = журнал 10 8 и журнал 3 = журнал 10 3.
Использование калькулятора для приближения, 
Алгебра — Экспоненциальные функции
Пол Заметки ОнлайнНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы практики
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Экспоненциальные и логарифмические функции Введение
- Логарифм Функции
- глав
- полиномиальных функций
- Системы уравнений
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений Уравнения
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- полиномиальных функций
- делительных полиномов
- Нули / корни полиномов
- графических полиномов
- В поисках нулей полиномов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- экспоненциальных функций
- Логарифм Функции
- Предварительные
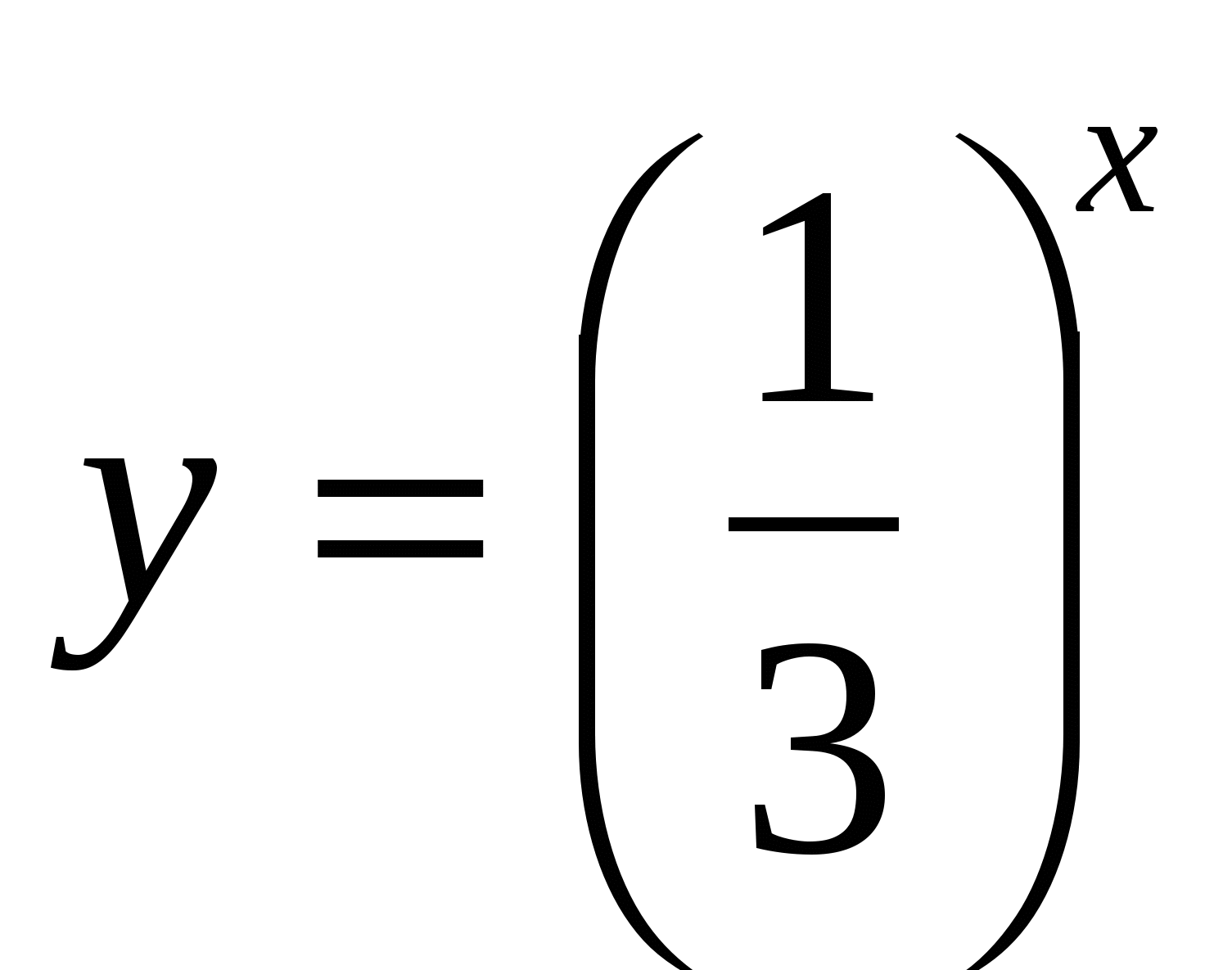 возрастающей? (нет)
возрастающей? (нет)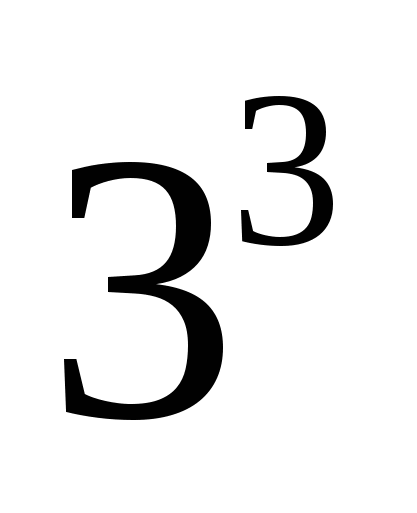 и
и 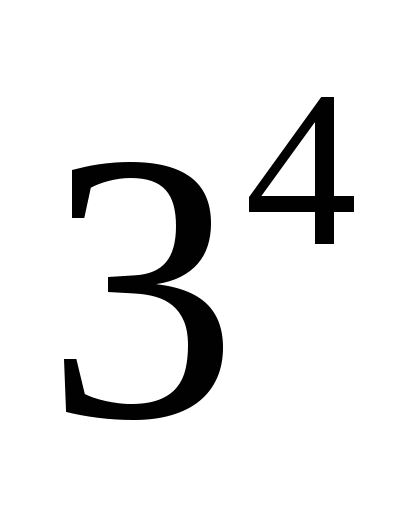 (
(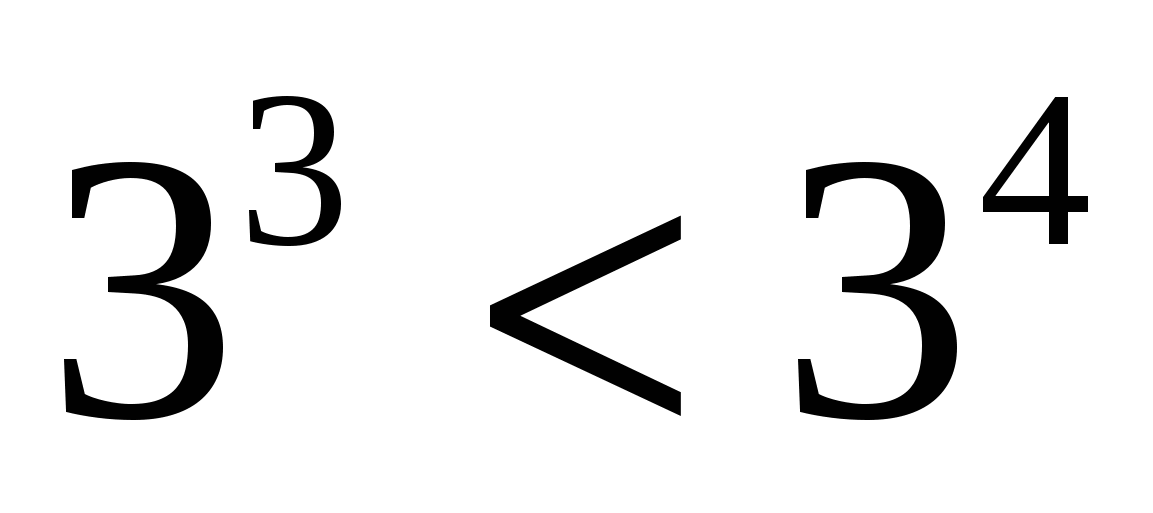 возраст)
возраст)