Сложение скоростей — это… Что такое Сложение скоростей?
При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
Классическая механика
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
Примеры
- Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, с которой её переносит пластинка за счёт своего вращения.
- Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
- Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.
Релятивистская механика
В XIX веке классическая механика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе осчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущимся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложение скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
Можно заметить, что в случае, когда , преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.
См. также
Литература
- Б. Г. Кузнецов Эйнштейн. Жизнь, смерть, бессмертие. — М.: Наука, 1972.
- Четаев Н. Г. Теоретическая механика. — М.: Наука, 1987.
dic.academic.ru
Сложение скоростей | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Сложение скоростей — с помощью данного закона определяется скорость движения тела относительно неподвижной системы отсчёта. Она равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы
Для того, чтоб было более понятно, как работает закон сложения скоростей, рассмотрим такой пример. Вагон движется со скоростью 50 км\ч (это будет ), в вагоне идет человек со скоростью 3 км\ч (это будет ), найти скорость человека относительно Земли.
У данной задачи будет два решения. Если человек будет идти по направлению движения вагона, то скорость человека относительно Земли будет 53 км\ч.
А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 км\ч.
В Формуле мы использовали :
— Конечная скорость тела
— Скорость тел в различных инерциальных системах отчета
xn--b1agsdjmeuf9e.xn--p1ai
Сложение скоростей — Википедия
Материал из Википедии — свободной энциклопедии
При рассмотрении сложного движения (когда точка или тело движется в одной системе отсчёта, а эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.
Классическая механика
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
- v→a=v→r+v→e.{\displaystyle {\vec {v}}_{a}={\vec {v}}_{r}+{\vec {v}}_{e}.}
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей[1].
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
Примеры
- Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).
- Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
- Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.
Релятивистская механика
В XIX веке физика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики (первая — Пространство-время теории Ньютона, вторая — принцип относительности), перенесёнными в новую область — теорию электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущемся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое, электродинамическим эффектам? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразований. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Специальная теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Одновременно специальная теория относительности кардинально изменяет представления о пространстве и времени. Правило сложения скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
vrel=v1+v21+v1v2c2.{\displaystyle v_{rel}={\frac {{v}_{1}+{v}_{2}}{1+{\dfrac {{v}_{1}{v}_{2}}{c^{2}}}}}.}
Можно заметить, что в случае, когда v/c→0{\displaystyle v/c\rightarrow 0}, преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что механика в специальной теории относительности сводится к механике Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом соотносятся специальная теория относительности и классическая механика — первая является обобщением второй.
См. также
Примечания
Литература
- Б. Г. Кузнецов Эйнштейн. Жизнь, смерть, бессмертие. — М.: Наука, 1972.
- Четаев Н. Г. Теоретическая механика. — М.: Наука, 1987.
wikipedia.green
Сложение скоростей — Википедия. Что такое Сложение скоростей
При рассмотрении сложного движения (когда точка или тело движется в одной системе отсчёта, а эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.
Классическая механика
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
- v→a=v→r+v→e.{\displaystyle {\vec {v}}_{a}={\vec {v}}_{r}+{\vec {v}}_{e}.}
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей[1].
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
Примеры
- Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).
- Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
- Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.
Релятивистская механика
В XIX веке физика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики (первая — Пространство-время теории Ньютона, вторая — принцип относительности), перенесёнными в новую область — теорию электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущемся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое, электродинамическим эффектам? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразований. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Специальная теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Одновременно специальная теория относительности кардинально изменяет представления о пространстве и времени. Правило сложения скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
vrel=v1+v21+v1v2c2.{\displaystyle v_{rel}={\frac {{v}_{1}+{v}_{2}}{1+{\dfrac {{v}_{1}{v}_{2}}{c^{2}}}}}.}
Можно заметить, что в случае, когда v/c→0{\displaystyle v/c\rightarrow 0}, преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что механика в специальной теории относительности сводится к механике Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом соотносятся специальная теория относительности и классическая механика — первая является обобщением второй.
См. также
Примечания
Литература
- Б. Г. Кузнецов Эйнштейн. Жизнь, смерть, бессмертие. — М.: Наука, 1972.
- Четаев Н. Г. Теоретическая механика. — М.: Наука, 1987.
wiki.sc
СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН — это… Что такое СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН?
- СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН
- СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН
-
— определяет связь между значениямискорости материальной точки по отношению к разл. системам отсчёта, движущимсядруг относительно друга. В нерелятивистской физике, когда рассматриваютсяскорости, малые по сравнению со скоростью света с, справедлив законсложения скоростей Галилея:

где u и u’ — скорости частицы в двух инерциалъных системах отсчётаК т К’ соответственно (система К’ движется относительно . со скоростью v). Если скорости движения близки к е, то ф-ла(1) неприменима и справедлив С. с. з. частной (специальной) относительноститеории:

где и
 — проекции скорости частицы в системе
— проекции скорости частицы в системе  отсчёта К(К’ )на направления параллельное и перпендикулярное к v.В пределе
отсчёта К(К’ )на направления параллельное и перпендикулярное к v.В пределе  и
и  ф-лы(2) переходят в (1). В случае, когда скорости и и v параллельны,(2) переписывается в виде
ф-лы(2) переходят в (1). В случае, когда скорости и и v параллельны,(2) переписывается в виде 
Из ф-лы (3), в частности, следует, что если и = с, то и и’= с независимо от в, т. е. абс. величина скорости света не зависитот движения системы отсчёта. Тот же вывод справедлив, разумеется, и припроизвольном направлении скоростей, когда надо пользоваться ф-лой (2).
В случае неравномерных относит. движений двух систем отсчёта, а такжепри наличии тяготения (т. е. в случае общей теории относительности)все приведённые соотношения справедливы в локально сопутствующих инерциальныхсистемах отсчёта
 , т. е. в таких бесконечно малых системах отсчёта, к-рые в данный моменти в данном месте неподвижны относительно рассматриваемых систем К кК’ соответствепно и в к-рых в этот момент нет сил ускорения и нет вращенияи деформаций, т. е. они локально инерциальны.
, т. е. в таких бесконечно малых системах отсчёта, к-рые в данный моменти в данном месте неподвижны относительно рассматриваемых систем К кК’ соответствепно и в к-рых в этот момент нет сил ускорения и нет вращенияи деформаций, т. е. они локально инерциальны.Лит. см. при ст. Относительности теория. И. Д. Новиков.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
- СЛЕД
- СЛОИСТЫЕ МАГНЁТИКИ
Смотреть что такое «СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН» в других словарях:
Закон — 1) необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие закон родственно понятию сущности. Существуют три основные группы законов: специфические, или частные (напр., закон сложения скоростей … Политология. Словарь.
ЗАКОН — необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие закон родственно понятию сущности. Существуют три основные группы законов: специфические, или частные (напр., закон сложения скоростей в… … Большой Энциклопедический словарь
ЗАКОН (в науке) — ЗАКОН, необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие закон родственно понятию сущности. Существуют три основные группы законов: специфические, или частные (напр., закон сложения… … Энциклопедический словарь
закон — а; м. 1. Нормативный акт, постановление высшего органа государственной власти, принятый в установленном порядке и имеющий юридическую силу. Кодекс законов о труде. З. о социальном обеспечении. З. о воинской обязанности. З. о рынке ценных бумаг.… … Энциклопедический словарь
ЗАКОН — (филос., науч.), необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие 3. родственно понятию сущности. Существуют три осн. группы 3.: специфические, или частные (напр., 3. сложения скоростей… … Естествознание. Энциклопедический словарь
Параллелограмм скоростей — геометрическое построение, выражающее закон сложения скоростей. Правило П. с. состоит в том, что при сложном движении (см. Относительное движение) абсолютная скорость точки представляется как диагональ параллелограмма, построенного на… … Большая советская энциклопедия
ПРОСТРАНСТВО И ВРЕМЯ — категории, обозначающие осн. формы существования материи. Пр во (П.) выражает порядок сосуществования отд. объектов, время (В.) порядок смены явлений. П. и в. осн. понятия всех разделов физики. Они играют гл. роль на эмпирич. уровне физ. познания … Физическая энциклопедия
АБЕРРАЦИЯ СВЕТА — в астрономии, изменение видимого положения светила на небесной сфере, обусловленное конечностью скорости света и движением наблюдателя вследствие вращения Земли (суточная А. с.), обращения Земли вокруг Солнца (годичная А. с.) и перемещения Солн.… … Физическая энциклопедия
ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ — физическая теория, рассматривающая пространственно временные закономерности, справедливые для любых физ. процессов. Универсальность пространственно временных св в, рассматриваемых О. т., позволяет говорить о них просто как о .св вах пространства… … Физическая энциклопедия
Специальная теория относительности — Почтовая марка с формулой E = mc2, посвящённая Альберту Эйнштейну, одному из создателей СТО. Специальная теор … Википедия
dic.academic.ru
Сложение скоростей Википедия
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
- v→a=v→r+v→e.{\displaystyle {\vec {v}}_{a}={\vec {v}}_{r}+{\vec {v}}_{e}.}
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей[1].
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
Примеры
- Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).
- Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
- Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.
В XIX веке физика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики (первая — Пространство-время теории Ньютона, вторая — принцип относительности), перенесёнными в новую область — теорию электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущемся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое, электродинамическим эффектам? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразований. Это нарушает принцип относительности, вернее, не поз
ruwikiorg.ru
Закон сложения скоростей. Часть 1.
Давайте в нескольких статьях рассмотрим подробно и внимательно закон сложения скоростей и решения задач, с использованием этого закона.
Для начала, вспомним, что часто мы наблюдаем довольно сложные типы движения, когда тело движется относительно системы отсчёта, которая в тоже время движется относительно Земли. И первая трудность здесь заключается в выборе подвижной и неподвижной систем отсчёта. Сегодня мы это и разберём. Если брать за неподвижную систему отсчета дерево, растущее на Земле (а чаще всего именно землю берут за неподвижную систему отсчёта), то довольно легко ввести другие системы отсчёта.
Попытаемся это сделать на следующих примерах:
1. Пассажир движется в движущемся автобусе (или по движущемуся эскалатору).
Здесь неподвижная система отсчета – Дерево, а подвижная система отсчета – автобус (эскалатор). И тогда
- скорость пассажира относительно автобуса (эскалатора) – скорость пассажира (Тела) Относительно Подвижной системы отсчета (автобуса; эскалатора) (ϑТоП),
- скорость пассажира относительно Земли (дерева) – скорость пассажира (Тела) Относительно неподвижной системы отсчета (Земли) (ϑТоЗ),
- скорость автобуса (эскалатора) – скорость Подвижной системы отсчета (автобуса; эскалатора) Относительно неподвижной (Земли) (ϑПоЗ).
2. Легковая машина и грузовик движутся по шоссе (даже не важно, в каком направлении).
В качестве неподвижной системы отсчета оставляем дерево, растущее на Земле, за подвижную систему отсчета возьмём грузовую машину. Тогда,
- скорость легковой машины относительно грузовой – скорость легковой машины (Тела) Относительно Подвижной системы отсчета (грузовой машины) (ϑТоП),
- скорость легковой машины относительно Земли (Дерева) – скорость легковой машины (Тела) Относительно неподвижной системы отсчета (Земли) (ϑТоЗ). Эту скорость показывает спидометр – прибор, для измерения скорости, который есть в каждой машине.
- скорость грузовой машины – скорость Подвижной системы отсчета (грузовой машины) Относительно неподвижной (Земли) (ϑПоЗ). Эту скорость показывает спидометр грузового автомобиля.
3. Лодка движется по реке.
Опять, в качестве неподвижной системы отсчета дерево, растущее на Земле. За неподвижную систему отсчета возьмём течение реки (чтобы это течение визуализировать, представьте опавший лист на поверхности воды). Тогда,
- скорость лодки относительно листка – скорость лодки (Тела) Относительно Подвижной системы отсчета (течения реки) (ϑТоП), т.е скорость лодки в стоячей воде,
- скорость лодки относительно Земли (дерева) – скорость лодки (Тела) Относительно неподвижной системы отсчета (Земли) (ϑТоЗ),
- скорость течения (листка) – скорость Подвижной системы отсчета (течения реки) Относительно неподвижной (Земли) (ϑПоЗ).
4. Падает капля дождя.
Опять, в качестве неподвижной системы отсчета дерево, растущее на Земле, подвижной системы отсчета – ветер (чтобы это визуализировать, представьте летящий оторвавшийся листок). Тогда,
- скорость капли относительно ветра – скорость капли (Тела) Относительно Подвижной системы отсчета (ветра) (ϑТоП),
- скорость капли относительно Земли (дерева) – скорость капли (Тела) Относительно неподвижной системы отсчета (Земли) (ϑТоЗ),
- скорость ветра – скорость Подвижной системы отсчета (ветра) Относительно неподвижной (Земли) (ϑПоЗ).
Разобравшись, с выбором систем отсчёта, введём и выучим закон сложения скоростей:
Скорость тела относительно неподвижной системы отсчета (ϑТоЗ) равна векторной сумме скорости тела относительно подвижной системы отсчета (ϑТоП) и скорости подвижной системы отсчета относительно неподвижной (ϑПоЗ).

При решении задач исходное выражение всегда будет в таком векторном виде. А вот как решать, приведённые выше задачи, это мы обсудим в следующих статьях.
Остались вопросы? Не знаете, как решать задачи на закон сложения скоростей?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru

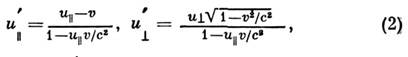
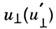 — проекции скорости частицы в системе
— проекции скорости частицы в системе 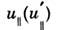 отсчёта К(К’ )на направления параллельное и перпендикулярное к v.В пределе
отсчёта К(К’ )на направления параллельное и перпендикулярное к v.В пределе 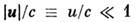 и
и 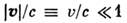 ф-лы(2) переходят в (1). В случае, когда скорости и и v параллельны,(2) переписывается в виде
ф-лы(2) переходят в (1). В случае, когда скорости и и v параллельны,(2) переписывается в виде 
 , т. е. в таких бесконечно малых системах отсчёта, к-рые в данный моменти в данном месте неподвижны относительно рассматриваемых систем К кК’ соответствепно и в к-рых в этот момент нет сил ускорения и нет вращенияи деформаций, т. е. они локально инерциальны.
, т. е. в таких бесконечно малых системах отсчёта, к-рые в данный моменти в данном месте неподвижны относительно рассматриваемых систем К кК’ соответствепно и в к-рых в этот момент нет сил ускорения и нет вращенияи деформаций, т. е. они локально инерциальны.