Сложные квадратные уравнения примеры с решением. Квадратные уравнения
Уравнение вида
Выражение D = b 2 — 4 ac называют дискриминантом квадратного уравнения. Если D = 0, то уравнение имеет один действительный корень; если D > 0, то уравнение имеет два действительных корня.
В случае, когда D = 0 , иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Используя обозначение D = b 2 — 4 ac , можно переписать формулу (2) в виде

Если b = 2 k , то формула (2) принимает вид:

где k = b / 2 .
Последняя формула особенно удобна в тех случаях, когда b / 2 — целое число, т.е. коэффициент
Пример 1: Решить уравнение 2 x 2 — 5 x + 2 = 0 . Здесь a = 2, b = -5, c = 2 . Имеем D = b 2 — 4 ac = (-5) 2- 4*2*2 = 9 . Так как D > 0 , то уравнение имеет два корня. Найдем их по формуле (2)

Итак x 1 =(5 + 3) / 4 = 2, x 2 =(5 — 3) / 4 = 1 / 2 ,
то есть x 1 = 2 и x 2 = 1 / 2 — корни заданного уравнения.
Пример 2: Решить уравнение 2 x 2 — 3 x + 5 = 0 . Здесь a = 2, b = -3, c = 5 . Находим дискриминант D = b 2 — 4 ac = (-3) 2- 4*2*5 = -31
Неполные квадратные уравнения. Если в квадратном уравнении ax 2 + bx + c =0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным . Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Пример 1: решить уравнение 2 x 2 — 5 x = 0 .
Имеем x (2 x — 5) = 0 . Значит либо x = 0 , либо 2 x — 5 = 0 , то есть x = 2.5 . Итак, уравнение имеет два корня: 0 и 2.5
Пример 2: решить уравнение 3 x 2 — 27 = 0 .
Имеем
Теорема Виета. Если приведенное квадратное уравнение x 2 + px + q =0 имеет действительные корни, то их сумма равна — p , а произведение равно q , то есть
x 1 + x 2 = -p ,
x 1 x 2 = q
(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).
», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.
Что называют квадратным уравнением
Важно!
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
- 5x 2 − 14x + 17 = 0
- −x 2 + x + = 0
- x 2 + 0,25x = 0
- x 2 − 8 = 0
Важно! Общий вид квадратного уравнения выглядит так:
A x 2 + b x + c = 0
«a », «b » и «c » — заданные числа.- «a » — первый или старший коэффициент;
- «b » — второй коэффициент;
- «c » — свободный член.
Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».
Давайте потренируемся определять коэффициенты «a », «b » и «c » в квадратных уравнениях.
| Уравнение | Коэффициенты |
|---|---|
| |
| x 2 − 8 = 0 |
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная
Запомните!
Чтобы решить квадратное уравнение нужно:
- привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
- использовать формулу для корней:
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.
X 2 − 3x − 4 = 0
Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду «ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .
Определим коэффициенты «a », «b » и «c » для этого уравнения.
x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
С её помощью решается любое квадратное уравнение.
В формуле «x 1;2 =
» часто заменяют подкоренное выражение
«b 2 − 4ac
» на букву «D
» и называют
дискриминантом
. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант ».
Рассмотрим другой пример квадратного уравнения.
x 2 + 9 + x = 7x
В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».
X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0
Теперь можно использовать формулу для корней.
X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.
Квадратное уравнение – решается просто! *Да
Формулы корней квадратных уравнений. Видеоурок. Алгебра 8 Класс
На данном уроке мы вспомним метод выделения полного квадрата, решим с помощью него несколько конкретных квадратных уравнений. Затем выведем общую формулу для корней квадратных уравнений.
Напомним, что квадратным уравнением называется уравнение вида:
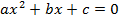 , причем
, причем 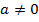
На прошлом уроке мы рассмотрели неполные квадратные уравнения и методы их решения. Сейчас мы поговорим о полных квадратных уравнениях, то есть уравнениях, в которых ни один из коэффициентов не равен 0 (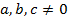 ).
).
Основной метод, который используется для выведения формул корней квадратных уравнений, – метод выделения полного квадрата. Мы уже изучали его в 7 классе, однако необходимо вспомнить его более подробно.
Рассмотрим несколько конкретных примеров квадратных уравнений, которые мы решим с помощью использования этого метода.
Пример 1
Решить квадратное уравнение: 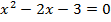 .
.
Решение:
Коэффициенты данного квадратного уравнения: 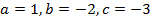 .
.
Для применения метода выделения полного квадрата воспользуемся следующей формулой: 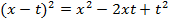 .
.
Метод выделения полного квадрата для данного примера состоит в том, чтобы подобрать число 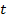 так, чтобы
так, чтобы  . Значит,
. Значит, 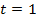 .
.
Получаем:
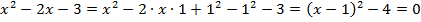
Данное уравнение можно решать двумя способами.
Способ 1
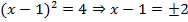 . Отсюда или:
. Отсюда или: 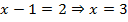 , или:
, или: 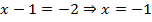 .
.
Ответ: .
.
Способ 2
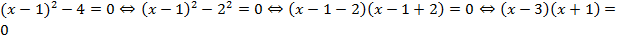 . Произведение равно 0 тогда и только тогда, когда хотя бы один из его множителей равен 0. Поэтому данное уравнение эквивалентно двум:
. Произведение равно 0 тогда и только тогда, когда хотя бы один из его множителей равен 0. Поэтому данное уравнение эквивалентно двум: 
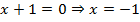 .
.Ответ: .
.
Мы рассмотрели метод выделения полного квадрата на частном примере. Давайте рассмотрим еще один, чуть более сложный пример, в котором старший коэффициент не будет равняться 1.
Пример 2
Решить квадратное уравнение: 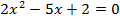 .
.
Решение:
Коэффициенты данного квадратного уравнения: 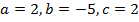
Прежде чем выделять полный квадрат, вынесем 2 за скобки в первых двух слагаемых: 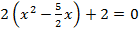 .
.
Теперь в скобках выделим полный квадрат. Опять же, необходимо подобрать  так, чтобы:
так, чтобы: 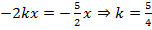 .
.
Получаем следующее уравнение:
 .
.
Отсюда:
 .
.
Отсюда: 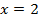 или
или 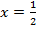 .
.
Ответ: 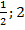 .
.
Разобрав конкретные примеры, можем перейти к получению общей формулы корней квадратного уравнения.
Итак, рассмотрим уравнение 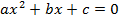 . Вынесем старший коэффициент за скобки в первых двух слагаемых:
. Вынесем старший коэффициент за скобки в первых двух слагаемых: 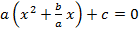 . Теперь выделим в скобочках полный квадрат:
. Теперь выделим в скобочках полный квадрат: 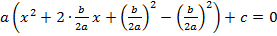 .
.
Далее:  .
.
Теперь поделим обе части уравнения на 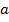 , так как знаем, что в квадратном уравнении
, так как знаем, что в квадратном уравнении 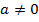 :
: 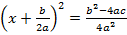 .
.
Выражение 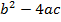 называется дискриминантом квадратного уравнения и обозначается буквой
называется дискриминантом квадратного уравнения и обозначается буквой 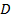 .
.
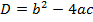
Пока мы будем считать, что в нашем уравнении 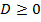 , то есть из него можно извлечь корень.
, то есть из него можно извлечь корень.
Тогда получаем:  . Или:
. Или:
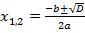 .
.
Это и есть формула для корней квадратного уравнения в общем виде.
Если расписать ее, то можно получить две формулы для каждого из корней:
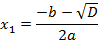
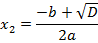
Если теперь мы вернемся к нашим примерам, то в уравнении 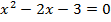 дискриминант равен:
дискриминант равен: 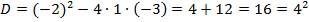 . Тогда:
. Тогда:
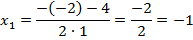
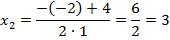
На этом уроке мы вспомнили метод выделения полного квадрата, разобрали решение конкретных квадратных уравнений с помощью этого метода. Кроме того, мы вывели формулу корней квадратного уравнения и узнали, что такое дискриминант.
На следующем уроке мы рассмотрим применение формул корней квадратных уравнений.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Прикладная математика (Источник).
- Bymath.net (Источник).
Домашнее задание
- № 427-429, Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. – М.: Просвещение. 2010 г.
- Решите уравнения: а)
 , б)
, б)  , в)
, в) , г)
, г)  .
. - Решите уравнения: а)
 , б)
, б)  , в)
, в)  .
.
Ещё одна формула для корней квадратных уравнений. Видеоурок. Алгебра 8 Класс
На данном уроке мы рассмотрим ещё одну формулу для корней квадратного уравнения. Эта формула применяется в тех случаях, когда коэффициент легко делится на 2.
Рассмотрим квадратное уравнение 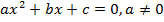 .
.
Мы уже знаем формулу для корней квадратного уравнения:  .
.
Рассмотрим случай, когда коэффициент 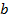 легко делится на 2. Тогда:
легко делится на 2. Тогда: 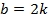 . Подставим это выражение в исходную формулу:
. Подставим это выражение в исходную формулу:
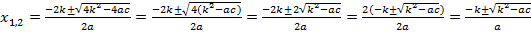 .
.
Если теперь обратно подставить  , то получим:
, то получим: 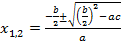 .
.
Основное преимущество этой формулы состоит в том, что она упрощает вычисления (в 2 или в 4 раза).
Если вернуться к исходному уравнению, то можно вспомнить о дискриминанте:  , тогда под корнем в этой формуле стоит выражение:
, тогда под корнем в этой формуле стоит выражение: 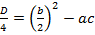 . Тогда ещё одна формула для корней квадратного уравнения выглядит следующим образом:
. Тогда ещё одна формула для корней квадратного уравнения выглядит следующим образом: 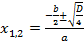 .
.
Рассмотрим несколько примеров на применение полученной формулы.
Пример 1
Решить уравнение: 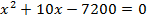 .
.
Решение
Выпишем коэффициенты данного уравнения: 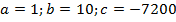 .
.
Теперь применим полученную формулу: 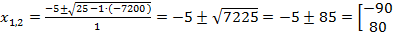 .
.
Ответ: 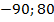 .
.
Рассмотрим ещё один пример.
Пример 2
Решить уравнение: 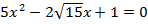 .
.
Решение
Выпишем коэффициенты данного уравнения: 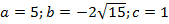 .
.
Теперь применим полученную формулу: 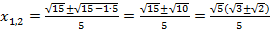 .
.
При желании можно сократить на 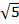 и числитель, и знаменатель. Однако в этом случае в знаменателе появится иррациональность, от которой обычно просят избавляться. Поэтому оставим ответ в таком виде.
и числитель, и знаменатель. Однако в этом случае в знаменателе появится иррациональность, от которой обычно просят избавляться. Поэтому оставим ответ в таком виде.
Ответ: 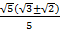 .
.
Теперь рассмотрим пример решения квадратного уравнения с параметром.
Пример 3
Решить уравнение: 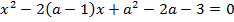 .
.
Решение
Перепишем данное уравнение в виде:  . В данном случае:
. В данном случае: 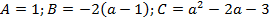 .
.
Теперь запишем полученную нами формулу для корней квадратного уравнения (несмотря на присутствие параметра, коэффициент 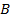 всё равно «хорошо» делится на 2).
всё равно «хорошо» делится на 2).
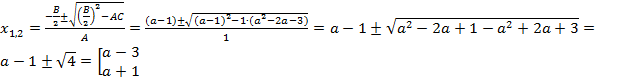 .
.
Ответ: 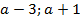 .
.
При решении данного уравнения могут возникать дополнительные вопросы.
Например:
1. Может ли у данного уравнения не быть корней? Ответ: нет, так как 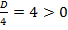 . То есть, наше уравнение всегда имеет два корня, причём различных.
. То есть, наше уравнение всегда имеет два корня, причём различных.
2. Может ли у данного уравнения быть один корень? Ответ: нет. См. пояснение к предыдущему вопросу. Можно ответить на этот вопрос по-другому: 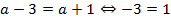 – невозможно.
– невозможно.
3. При каких значениях параметра 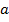 уравнение имеет 2 различных корня? Ответ: при всех значениях. См. пояснение к первому вопросу. Можно пояснить ответ на этот вопрос следующим образом:
уравнение имеет 2 различных корня? Ответ: при всех значениях. См. пояснение к первому вопросу. Можно пояснить ответ на этот вопрос следующим образом: 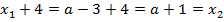 , то есть у уравнения всегда будет 2 корня, один из которых на 4 больше второго.
, то есть у уравнения всегда будет 2 корня, один из которых на 4 больше второго.
На этом уроке мы вывели и научились пользоваться ещё одной формулой для корней квадратного уравнения.
На следующем уроке мы познакомимся с теоремой Виета.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение. 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Домашнее задание
- Решить уравнение: а)
 ; б)
; б)  ; в)
; в)  .
. - Решить уравнение: а)
 ; б)
; б) .
. - № 449–452. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5-е изд. – М.: Просвещение, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал School.xvatit.com (Источник).
- Интернет-портал Edu.dvgups.ru (Источник).
- Интернет-портал Dpva.info (Источник).
НЕОБЫЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
НЕОБЫЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
Василенко А.М. 1Яковлева Е.А. 11
Поздина Н.Б. 11
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
«Уравнение – это золотой ключ, открывающий все математические сезамы»
С. Коваль
Математическое образование, получаемое в школе, очень важная часть жизни современного человека. Практически всё, что окружает нас так или иначе связано с математикой. Решение многих практических задач сводится к решению уравнений различных видов.
Уравнения – это наиболее объёмная тема всего курса алгебры. В прошлом учебном году на уроках алгебры мы познакомилась с квадратными уравнениями. Квадратные уравнения находят широкое применение при решении различных задач, как в области математики, так и в области физики и химии.
В школьном курсе математики изучается основные способы решения квадратных уравнений. Однако, имеются и другие приёмы решения квадратных уравнений, некоторые из которых позволяют быстро, рационально решать их.
Нами было проведено анкетирование среди 84 учащихся 8-9 классов по двум вопросам:
По результатам анкетирование были получены следующие результаты:
Проанализировав полученные результаты, мы пришли к выводу, что большинство учащихся используют при решении квадратных уравнений формулы корней с использование дискриминанта и недостаточно осведомлены о способах решения квадратных уравнений.
Таким образом, выбранная нами тема является актуальной.
Мы поставили перед собой цель: изучить нетрадиционные способы решения квадратных уравнений, познакомить учащихся 8 и 9 классов с различными способами решения, выработать умение выбирать рациональный способ решения квадратного уравнения.
Для достижения указанной цели нужно решить следующие задачи:
-
собрать информацию о различных способах решения квадратных уравнений,
-
освоить найденные способы решения,
-
составить программу для решения квадратных уравнений по формулам корней квадратного уравнения в Excel,
-
разработать дидактический материал для проведения урока или внеурочного мероприятия по нестандартным методам решения квадратных уравнений,
-
провести занятие «Необычные способы решения квадратных уравнений» с учащимися 8 – 9 классов.
Объект исследования: квадратные уравнения.
Предмет исследования: различных способы решения квадратных уравнений.
Считаем, что практическая значимость работы состоит в возможности использования банка приёмов и способов решения квадратных уравнений на уроках математики и внеурочной деятельности, а также в ознакомлении учащихся 8 — 9 классов с данных материалом.
ГЛАВА 1. НЕОБЫЧНЫЕ МЕТОДЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ-
- СВОЙСТВА КОЭФФИЦИЕНТОВ (a,b,c)
Метод основан на свойствах коэффициентов a,b,c:
-
Если a+b+c=0, то = 1, =
Пример:
-6х2 + 2х +4=0, то = 1, = = .
-
Если a – b+c=0, то = -1, = —
Пример:
2017х2 + 2001х +16 =0, то = -1, -.
-
- ЗАВИСИМОСТИ КОЭФФИЦИЕНТОВ (a,b,c)
Справедливы следующие зависимости коэффициентов a,b,c:
Если b=a2+1, c=a, то х1=-а; x2 = — .
Если b=-(a2+1), a=c, то x1=a; x2 =.
Если b=a2-1, c=-a, то x1=-a; x2 = .
Если b=-(a2-1), -a=c, то x1=a; x2 = — .
Решим следующие уравнения:
-
5x2 + 26x + 5 = 0
x1= -5
x2= — 0,2.
-
13x2 — 167x + 13 = 0
x1=13 x2=
-
14x2 + 195x — 14 = 0
x1= — 14 x2=
-
10x2 — 99x — 10 = 0
x1=10 x2=-0,1.
-
- «ПЕРЕБРОС» ГЛАВНОГО КОЭФФИЦИЕНТА
Коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Далее корни находятся по теореме Виета. Найденные корни делятся на ранее переброшенный коэффициент, благодаря этому мы находим корни уравнения.
Пример:
2х2 – 3х + 1 = 0.
«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 3у + 2 = 0.
Согласно теореме Виета
у1 = 2 , х1 = 2/2 , x1 = 1,
у2 = 1; x2 = 1/2; x2 = 0,5.
Ответ: 0,5; 1.
-
- ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ
Если в уравнении аx2 + bx + c = 0 перенести второй и третий члены в правую часть, то получим ax2 = –bx–c .
Построим графики зависимостей у = aх2 и у = –bx–c в одной системе координат.
График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая.
Возможны следующие случаи:
-
прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
-
прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;
-
прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Решим следующие уравнения:
1) х2 + 2х – 3 = 0
х2 = — 2х + 3
В одной системе координат построим график функции у =х2 и график функции у = — 2х+3. Обозначив абсциссы точек пересечения, получим ответ.
Ответ: х1= — 3, х2 =1.
2) х2 + 6х +9 = 0
х2 = — 6х — 9
В одной системе координат построим график функции у = х2 и график функции у = -6х — 9. Обозначив абсциссу точки касания, получим ответ.
Ответ: х= — 3.
3) 2х2 + 4х +7=0
2х2 = — 4х — 7
В одной системе координат построим график функции у =2х2 и график функции
у = — 4х — 7.
Парабола у =2х2 и прямая у = — 4х — 7 не имеют общих точек, следовательно уравнение не имеет корней.
Ответ: нет корней.
-
- РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ
Решим уравнение aх2 +bх+c=0:
-
Построим точки S(-b:2a,(a+c):2a)- центр окружности и точку А(0,1).
-
Провести окружность радиуса SA.
-
Абсциссы точек пересечения с осью Ох есть корни исходного уравнения.
При этом возможны три случая:
1) Радиус окружности больше ординаты центра (AS>SK, или R>), окружность пересекает ось Ох в двух точках..B(х1; 0) и D(х2;0), где х1 и х2 – корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SВ, или R = ), окружность касается оси Ох в точке B(х1; 0 ), где х1 – корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра (AS < SВ, или R < ), окружность не имеет общих точек с осью абсцисс, в этом случае уравнение не имеет решения.
а) AS > SВ или R > , б) AS = SВ или R = в) AS < SВ, или R < .
Два решения х1 и х2. Одно решение х1.. Не имеет решения.
Пример 1: 2х2 –8х + 6 = 0.
Решение: Определим координаты точки центра окружности по формулам:
у = = .
Проведём окружность радиуса SA, где А (0;1).
Ответ: х1 = 1 , х2 = 3.
Пример 2: х2 –6х + 9 = 0.
Решение: Найдём координаты S: x=3, y=5.
Ответ: x=3.
Пример 3: х2 + 4х + 5 = 0.
Решение: Координаты центра окружности: х= — 2 и y = 3.
Ответ: нет корней
-
- РЕШЕНИЕ С ПОМОЩЬЮ НОМОГРАММЫ
Номограмма (от греческого «nomos» – закон и грамма), графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.
Это старый и в настоящее время забытый способ решения квадратных уравнений, помещённый на стр. 83 сборника: Брадис В.М. «Четырехзначные математические таблицы». — М., “ДРОФА”, 2000. Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0 (см. Приложение 1).
Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам: ОВ = , АВ =
Полагая ОС = р, ЕD = q, ОЕ = а (все в см), из подобия треугольников САН и СDFполучим пропорцию откуда после подстановок и упрощений вытекает уравнение z2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.
Пример 1:z2 — 9z + 8 = 0.
На шкале p находим отметку -9, а на шкале q отметку 8. Проводим через эти метки прямую, которая пересекает кривую шкалу номограммы в отметках 1 и 8. Следовательно, корни уравнения 1 и 8.
Ответ: 1; 8.
Именно данное уравнение решено в таблице Брадиса стр. 83 (см. Приложение 1).
Пример 2: 2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение:
z2 — 4,5z + 1 = 0. Номограмма даёт корни z1 = 4 иz2 = 0,5.
Ответ: 4; 0,5.
Пример 3:x2 – 25x + 66 = 0
Коэффициенты p и q выходят за пределы шкалы. Выполним подстановку x = 5z, получим уравнение:
z2 – 5z + 2,64 = 0,
которое решаем посредством номограммы.
Получим z1 = 0,6 и z2 = 4,4,
откудаx1 = 5 z1 = 3,0 иx2 = 5 z2 = 22,0.
Ответ: 3; 22.
Пример 4: z2 + 5z – 6 = 0, номограмма даёт положительный корень z1=1, а отрицательный корень находим, вычитая положительный корень из — p, т.е. z2= — p –1= — 5 – 1= -6.
Z=1
Ответ: 1; -6.
Пример 5: z2 – 2z – 8 = 0, номограмма даёт положительный корень z1=4, а отрицательный равен z2= — p –4 =
Z=4
= 2 – 4= -2.
Ответ: 4; -2.
ГЛАВА 2. РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ПО ФОРМУЛАМ КОРНЕЙ С ПОМОЩЬЮ EXCELМы решили составить программу для решения квадратного уравнения с помощью Excel – это широко распространенная компьютерная программа. Нужна она для проведения расчётов, составления таблиц и диаграмм, вычисления простых и сложных функций. Она входит в состав пакета Microsoft Office.
Лист программы Excel, где отображены формулы:
Лист программы Excel, где показан конкретный пример решения квадратного уравнения x2 – 14x – 15 = 0:
ГЛАВА 3. СРАВНЕНИЕ РАЗНЫХ СПОСОБОВ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ|
Метод |
Плюсы |
Минусы |
|
Формула корней квадратного уравнения с использованием дискриминанта D и D1 |
Универсальность, т.к. можно использовать для решения абсолютно всех квадратных уравнений |
Громоздкий дискриминант, не входящий в таблицу квадратов |
|
Теорема Виета |
Быстрота решения в определённых случаях и экономия времени |
Если дискриминант не является полным квадратом целого числа. Не целые коэффициенты b и с. |
|
Выделение полного квадрата |
При правильном преобразовании в квадрат двучлена получаем квадратное уравнение неполного вида и следовательно быстрее находятся корни |
Сложность выделения полного квадрата при дробных коэффициентах уравнения |
|
Способ группировки |
Можно решить, не зная формул |
Не всегда среднее слагаемое удаётся разложить на подходящие слагаемые для группировки |
|
Графический способ |
Не требуется формул. Можно быстро узнать количество корней уравнения |
Приближённость решения |
|
Свойства коэффициентов a,b,c |
Быстрота решения. Для уравнений с большими коэффициентами |
Подходит только для некоторых уравнений |
|
«Переброс» главного коэффициента |
Быстрота решения, если корни целые |
Такие же как с помощью теоремы Виета |
|
Номограмма |
Наглядность Все, что требуется для решения–это номограмма |
Не всегда имеется с собой номограмма. Неточность решения |
|
Нахождение корней с помощью циркуля и линейки |
Наглядность |
Если координаты центра нецелые числа. Нахождении корней уравнений с большими коэффициентами |
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
Уолтер Варвик Сойер
В ходе работы мы собрали материал и изучили способы решения (нахождения корней) квадратных уравнений. Решение уравнений разными способами представлено в Приложении 2.
Изучая разные способы решения квадратных уравнений, мы сделали вывод, что для каждого уравнения можно подобрать свой наиболее эффективный и рациональный вариант нахождения корней. Каждый из способов решения уникален и удобен в определённых случаях. Некоторые способы решения позволяют сэкономить время, что немаловажно при решении заданий на ОГЭ, другие – помогают решить уравнение с очень большими коэффициентами. Мы постарались сравнить разные способы решения, составив таблицу, в которой отразили плюсы и минусы каждого из способов.
Нами разработан раздаточный материал. Познакомиться с банком заданий по теме можно в Приложении 3.
Используя Microsoft Excel, мы составили электронную таблицу, которая позволяет автоматически рассчитывать корни квадратного уравнения по формулам корней.
Мы провели урок, посвященный необычным способам решения квадратных уравнений, для учащихся 9 классов. Ученикам очень понравились способы, они отметили, что полученные знания пригодятся им в дальнейшем обучении. Результатом проведённого урока стали работы учащихся, в которых они представили различные варианты решения квадратных уравнений (см. Приложение 4).
Материал нашей работы можно рекомендовать для внеклассных и факультативных занятий по математике. Учителя могут использовать его для небольшого элективного курса «Необычные способы решение квадратных уравнений».
Материалом работы могут воспользоваться и те, кто любит математику и те, кто хочет знать о математике больше.
ЛИТЕРАТУРА-
Брадис В. М. «Четырехзначные математические таблицы для средней школы», М.: Дрофа, 2000.
-
Виленкин Н.Я. «Алгебра для 8 класса», М.: Просвещение, 2000.
-
Галицкий М.Л. «Сборник задач по алгебре», М.: Просвещение 2002.
-
Глейзер Г. И. «История математики в школе», М.: Просвещение, 1982.
-
Звавич Л.И. «Алгебра 8 класс», М.: Мнемозина, 2002.
-
Макарычев Ю.Н. “Алгебра 8 класс”, М.: Просвещение, 2015.
-
Плужников И. «10 способов решения квадратных уравнений» // Математика в школе. — 2000.- № 40.
-
Пресман А.А. «Решение квадратного уравнения с помощью циркуля и линейки»//М., Квант, №4/72, c.34.
-
Савин А.П. «Энциклопедический словарь юного математика»,
М.: Педагогика, 1989.
Интернет ресурсы:
http://revolution.allbest.ru/
http://mat.1september.ru/2001/42/no42_01.htm
ПРИЛОЖЕНИЕ 1«СБОРНИК БРАДИСА В.М.»
ПРИЛОЖЕНИЕ 2«РЕШЕНИЕ УРАВНЕНИЯ ВСЕМИ СПОСОБАМИ»
Исходноеуравнение: 4х2+3х -1 = 0.
1.Формула корней квадратного уравнения с использованием дискриминанта D
4х2+3х -1 = 0
D = b2 – 4ac = 9+16 = 25 > 0, => уравнение имеет два корня
x1,2 =
x1 ==
x2 ==-1
2.Теорема Виета
4х2+3х -1 = 0, поделим уравнение на 4, чтобы оно стало приведённым
х2+х -=0
+ =-
* =-
х1 = -1
х2 =
3. Метод выделения полного квадрата
4х2+3х -1 = 0
(4х2+2*2х *+)-1=0
(2х + )2 -=0
(2х + — )( 2х + + )=0, произведение =0, когда один из множителей=0
(2х — )=0 (2х +2)=0
х1 = х2 = -1
4. Способ группировки
4х2+3х -1 = 0
4х2+4х-1х-1=0
4х(х+1)-1(х+1)=0
(4х-1)( х+1)=0, произведение =0, когда один из множителей=0
(4х-1)=0 ( х+1)=0
х1 = х2 = -1
5. Свойства коэффициентов
4х2+3х -1 = 0
Если a — b+c=0, то = -1, = —
4-3-1=0, => = -1, =
6. Метод «переброски» главного коэффициента
4х2+3х -1 = 0
y2+3y — 4 = 0
Теорема Виета:
+ =- 3
* =- 4
y1 = -4
y2 = 1
Разделим найденные корни на главный коэффициент и получим корни нашего уравнения:
х1 = -1
х2 =
7. Способ решения квадратных уравнений с помощью циркуля и линейки
4х2+3х -1 = 0
Определим координаты точки центра окружности по формулам:
у = =
х1 = -1
х2 =
8. Графический способ решения
4х2+3х -1 = 0
4х2= — 3x + 1
В одной системе координат построим график функции у = 4х2и график функции
-3
у = — 3х+1. Обозначив абсциссы точек пересечения, получим ответ:
x
х1 = -1
=
9. С помощью номограммы
4х2+3х -1 = 0, разделим коэффициенты уравнения 1/на 4, получим уравнение
1/4
х2 +х -= 0.
Номограмма даёт положительный корень = ,
а отрицательный корень находим, вычитая положительный корень из — p, т.е.
x2= — p –=- -= -1.
10. Решение данного уравнения в EXCEL
ПРИЛОЖЕНИЕ 3«ДИДАКТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ ТЕМЫ
“РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ”»
10х2+ 2017х + 2007 = 0 -1 -200,7
-10х2+ 7х + 3 = 0 -1 0,3
354х2-52х -302 = 0 1 —
100х2-99х-1 = 0 1 -0,01
5х2+ 9х + 4 = 0 -1 -0,8
2017х2+ х -2016 = 0 -1
22х2+10х-12 = 0 -1
5432х2-3087х-2345 = 0 1 —
4х2+ 2х -6с = 0 1 -1,5
55х2-44х -11= 0 1 -0,2
6х2— 7х — 3 = 0 — , 1,5
4х2-17х-15 = 0 -0,75, 5
4271х2-4272х + 1 = 0 1,
3х2+10х + 7 = 0 -1, — 2
5х2— 11х + 2 = 0 2, 0,2
2х2— 11х + 15 = 0 2,5, 3
4х2+ 4х -3= 0 -1,5, 0,5
5х2 -12х + 7 = 0 1,4, 1
2х2+ 13х + 15 = 0 -1,5 -5
3х2-7х + 2 = 0 1/3 2
ПРИЛОЖЕНИЕ 4«РАБОТЫ УЧАЩИХСЯ»
Просмотров работы: 7773
 , б)
, б) 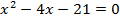 , в)
, в)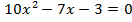 , г)
, г) 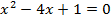 .
.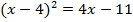 , б)
, б) 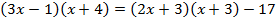 , в)
, в) 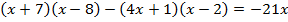 .
.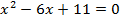 ; б)
; б) 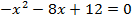 ; в)
; в)  .
.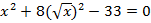 ; б)
; б)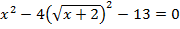 .
.