Основные формулы комбинаторики: размещения, перестановки, сочетания.
Комбинации из n элементов по m элементам, которые отличаются или самими элементами, или порядком их следования, называются размещениями.
Формула размещения:

Пусть имеются три буквы А, В и С. Составим всевозможные комбинации только из двух букв: АВ, ВА, АС, СА, ВС, СВ. Эти комбинации отличаются друг от друга только расположением букв или самими буквами.
Пример 1
На третьем курсе изучается 9 предметов. Сколькими способами можно составить расписание занятий на один день, если в учебный день разрешается проводить занятия только по четырем разным предметам?
Решение
Различных
способов составления расписания столько,
сколько существует четырехэлементных
комбинаций из девяти элементов, которые
отличаются друг от друга или самими
элементами, или их порядком, т.е. 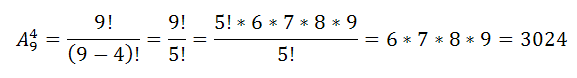
Ответ: 3024
Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Перестановки обозначаются Рn, где n — число элементов, входящих в перестановку.
Формула перестановки: Рn=n!
Пусть имеются три буквы А, В и С. Составим всевозможные комбинации из этих букв: ABC, АСВ, ВСА, ВАС, CAB, CBA. Эти комбинации отличаются друг от друга только расположением букв.
Пример 1
В турнире участвуют семь команд. Сколько вариантов распределения мест между ними возможно?
Решение: В итоговой таблице турнира команды будут отличаться занятыми местами, поэтому для подсчета вариантов распределения мест между ними воспользуемся формулой перестановки:
Р7=7!=1*2*3*4*5*6*7=5040
Ответ: 5040
Комбинации из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом, называются сочетаниями.
Формула сочетания:
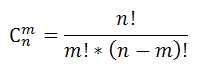
Пусть имеются три буквы А, В и С. Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС. Нетрудно увидеть, что их в два раза меньше, чем размещений из этих элементов. Пример 1
Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?
Решение:
Так
как путевки предоставлены в один
санаторий, то варианты распределения
отличаются друг от друга хотя бы одним
желающим. Поэтому число способов
распределения 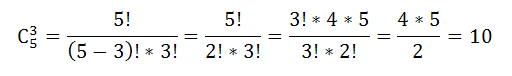
Виды случайных событий.
Случайным событием называется результат (исход) наблюдения какого-нибудь явления при выполнении некоторого комплекса условий (опыта).
Виды событий:
Элементарные события — возможно исключающие друг друга события опыта.
Невозможное событие — не может произойти в результате опыта.
Достоверное событие – в результате опыта обязательно произойдет.
Случайное событие – при осуществлении некоторых условий может произойти или не произойти.
Несовместные события – появление одного из них исключает появление других событий в одном и том же испытании.
Совместные события – в результате опыта могут появиться одновременно.
Равновозможные события – одинакова возможность появления в результате опыта.
Равносильные события – событие А влечет за собой событие В, а событие В влечет за собой событие А.
Алгебра событий.
Суммой (объединением) событий А и В называется событие С, состоящее в появлении события А или событие В или одновременно событий А и В. С=А+В
Произведением (пересечением) событий А и В называется событие С, состоящее в совместном появлении событий А и В. С=А*В
Разностью событий А и В называется событие С, состоящее в появлении событии А и не появлении события В. С=А-В
Классическое определение вероятности события. Свойства вероятности.
Вероятностью р события А называется отношение числа m-благоприятствующих случаев к числу всех возможных случаев n, образующих полную группу равновозможных несовместимых событий:
P
(A)=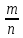
Свойства вероятности:
Число появления m-любого события входит в интервал 0<P<1.
Вероятность достоверного события равна 1.
Вероятность невозможного события равна 0.
Теоремы сложения вероятностей несовместных событий.
Теорема 1. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Доказательство: Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В.
Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m 1 + m2. Следовательно,
Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n.
Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончательно получим
Р (А + В) = Р (А) + Р (В).
Теорема 2. Сумма вероятностей событий А1 , А2 , …, Аn , образующих полную группу, равна единице:
Р (A1) + Р (А2) + … + Р (Аn) = 1.
Доказательство: Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то
Р (A1 + A2 + … + An) = 1. (*)
Любые два события полной группы несовместны, поэтому можно применить теорему сложения:
Сравнивая (*) и (**), получим
Р (А1) + Р (А2) + … + Р (Аn) = 1.
Пример: Консультационный пункт института получает пакеты с контрольными работами из городов А, В и С. Вероятность получения пакета из города А равна 0,7, из города В — 0,2. Найти вероятность того, что очередной пакет будет получен из города С.
Р е ш е н и е. События «пакет получен из города А», «пакет получен из города В», «пакет получен из города С» образуют полную группу, поэтому сумма вероятностей этих событий равна единице:
0,7 + 0,2 + p =1.
Отсюда искомая вероятность
р = 1 — 0,9 = 0,1.
Теорема 3. Сумма вероятностей противоположных событий равна единице:
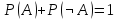
Доказательство:
Пусть дано А и 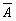 .
Тогда А+
.
Тогда А+ 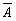 будет достоверным. Сумма достоверного
события равно 1. Тогда
будет достоверным. Сумма достоверного
события равно 1. Тогда
 .
.
З а м е ч а н и е 1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Таким образом, в силу предыдущей теоремы
p + q = l
З а м е ч а н и е 2. При решении задач на отыскание вероятности события А часто выгодно сначала вычислить вероятность противоположного события, а затем найти искомую вероятность по формуле

studfile.net
Формулы комбинаторики
Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N, состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.
Сформулируем следующие определения:
Размещения без повторения
Размещением без повторения из n элементов по m называется всякое упорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.Теорема 3. Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n. Записывают:
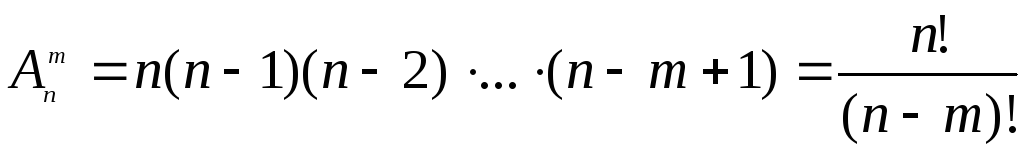
Перестановки без повторений
Перестановками из n элементов называются различные упорядочения множества N.
Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.
Теорема 4. Число различных перестановок без повторений вычисляется по формуле

Сочетания без повторений
Из определения следует, что два сочетания различаются только элементами, порядок не важен.
Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул:

Пример 1. В комнате 5 стульев. Сколькими способами можно разместить на них
а) 7 человек; б) 5 человек; в) 3 человека?
Решение: а) Прежде всего надо выбрать 5 человек
из 7 для посадки на стулья. Это можно
сделать 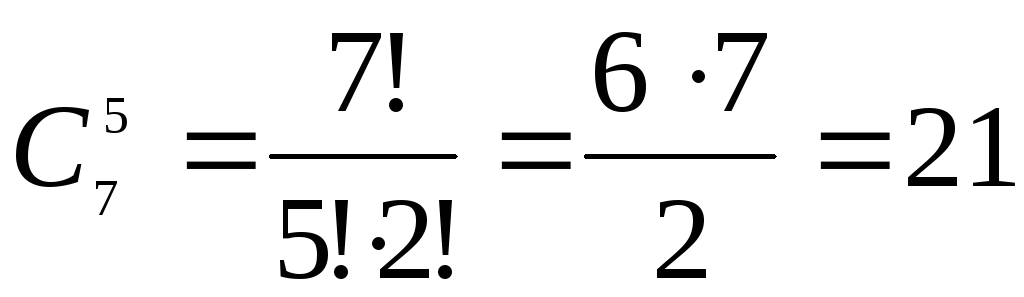 способом. С каждым выбором конкретной
пятерки можно произвести
способом. С каждым выбором конкретной
пятерки можно произвести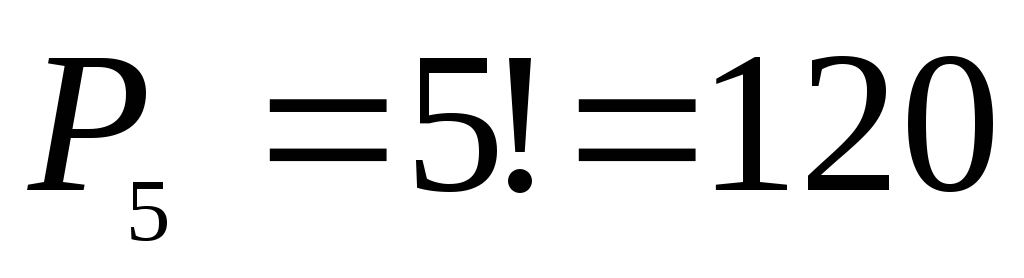 перестановок местами. Согласно теореме
умножения искомое число способов посадки
равно
перестановок местами. Согласно теореме
умножения искомое число способов посадки
равно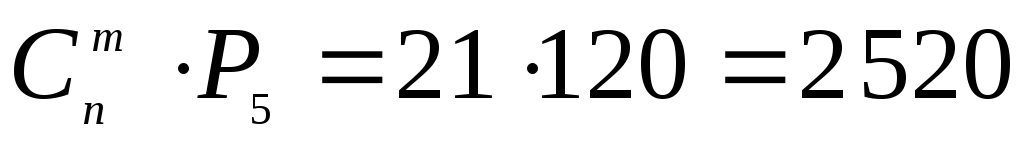 .
.
Замечание: Задачу можно решать, используя только
теорему произведения, рассуждая следующим
образом: для посадки на 1-й стул имеется
7 вариантов, на 2-й стул-6 вариантов, на
3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов
посадки 7 человек на 5 стульев равно  .
Решения обоими способами согласуются,
так как
.
Решения обоими способами согласуются,
так как
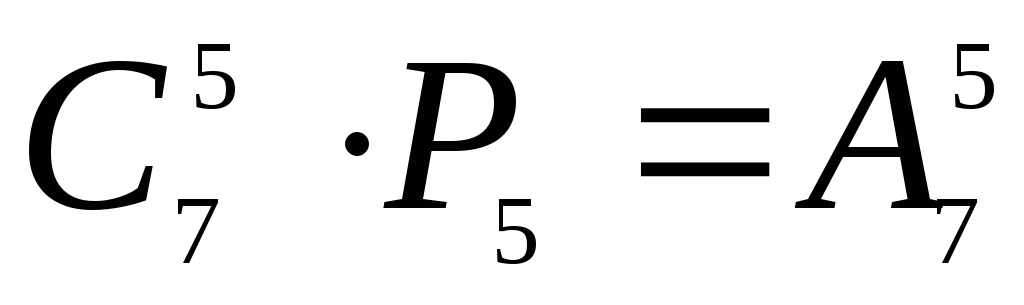
б) Решение очевидно
— 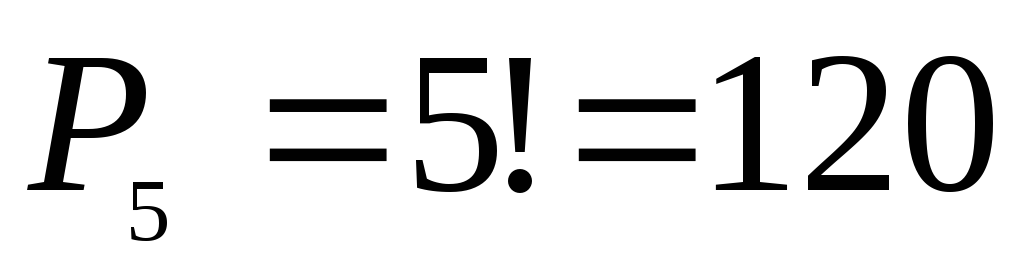
в)  — число выборов занимаемых стульев.
— число выборов занимаемых стульев.
 — число размещений
трех человек на трех выбранных стульях.
— число размещений
трех человек на трех выбранных стульях.
Общее число выборов
равно 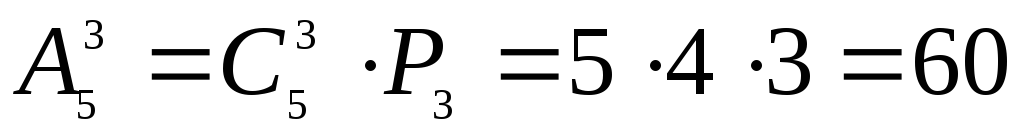 .
.
Не трудно проверить
формулы 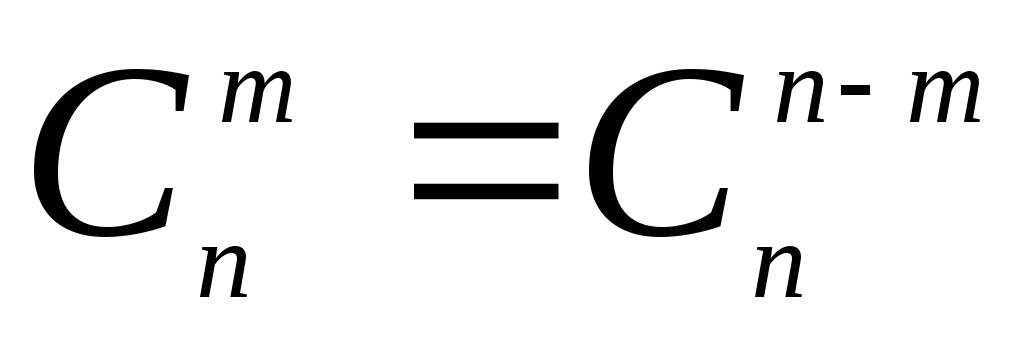 ;
;
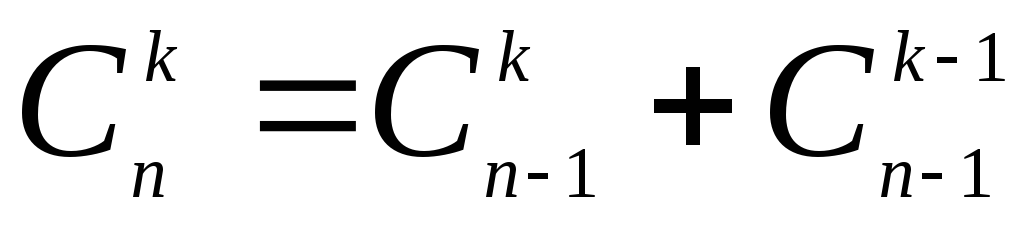 ;
;
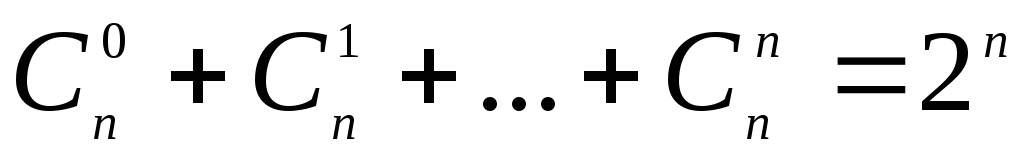 —
число всех подмножеств множества,
состоящего из n элементов.
—
число всех подмножеств множества,
состоящего из n элементов.
Размещения с повторением
Размещением с повторением из n элементов по m называется всякое упорядоченное подмножество множества N, состоящее из m элементов так, что любой элемент ожжет входить в это подмножество от 1 до m раз, либо вообще в нем отсутствовать.
Число
размещений с повторением обозначают 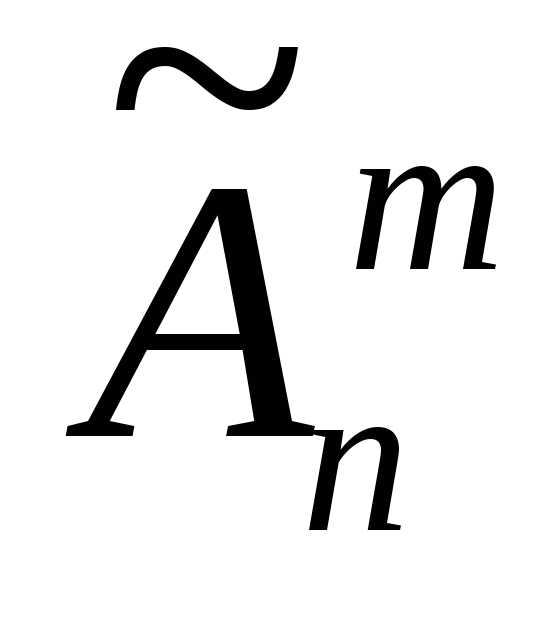 и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
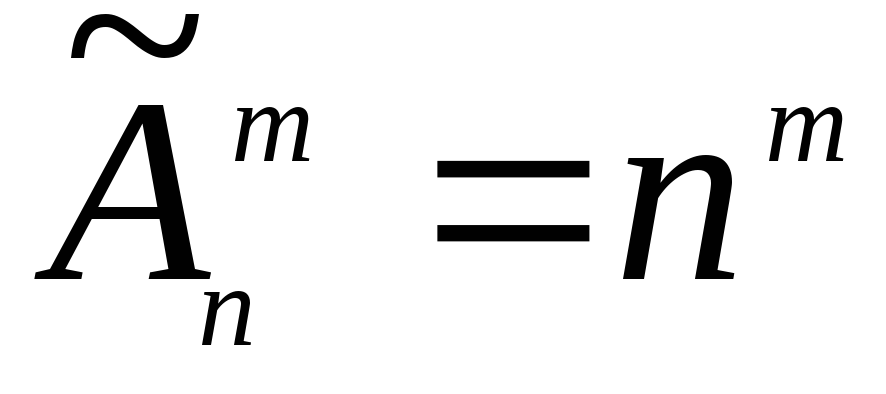
Пример 2.
Пусть дано множество из трех букв N
= {a,
b,
c}.
Назовем словом любой набор из букв,
входящих в это множество. Найдем
количество слов длиной 2, которые можно
составить из этих букв: 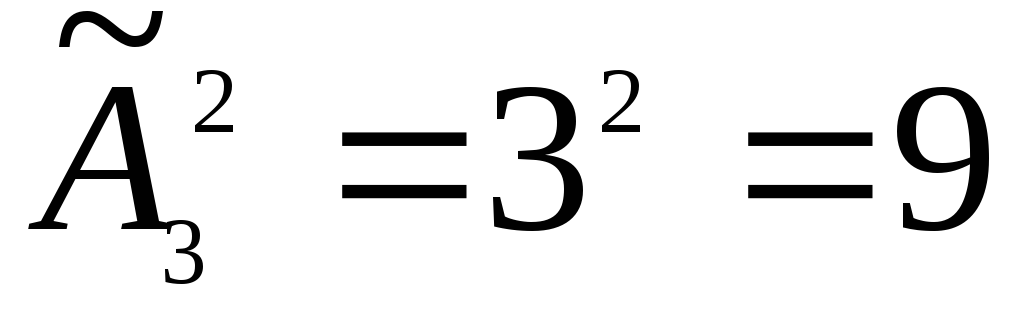 .
.
Замечание: Очевидно, размещения с повторением
можно рассматривать и при  .
.
Пример 3. Требуется из букв {a, b}, составить всевозможные слова длиной 3. Сколькими способами это можно сделать?
Ответ: 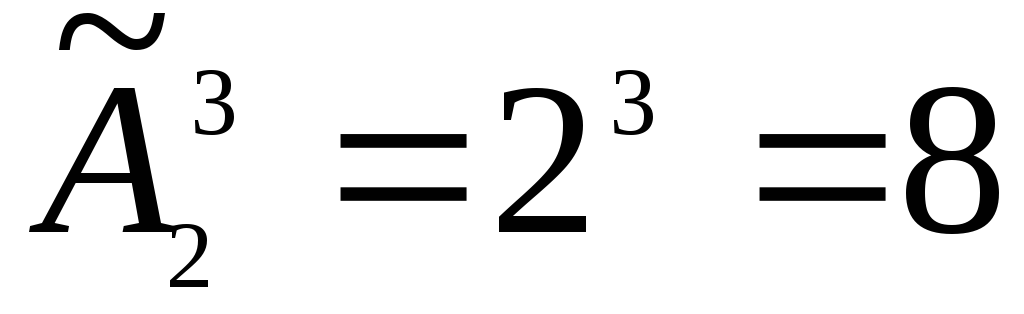
studfile.net
1.7. Основные формулы комбинаторики
При нахождении вероятностей в схеме классического определения широко используется комбинаторика, поэтому напомним наиболее употребительные определения и формулы для вычисления.
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества.
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
Рn = n!
Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.
Пример. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
Решение. Искомое число трехзначных чисел Р3 = 3! = 123 = 6.
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений
 .
.
Пример. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
Решение.
Искомое число сигналов  .
.
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний
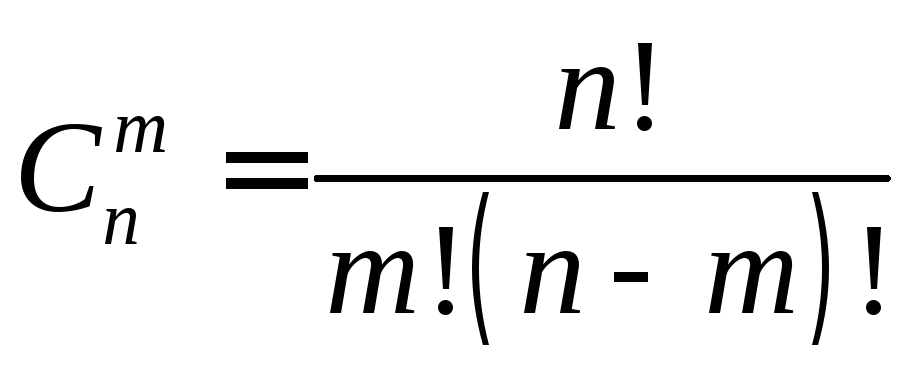 .
.
Пример. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Решение.
Искомое число способов 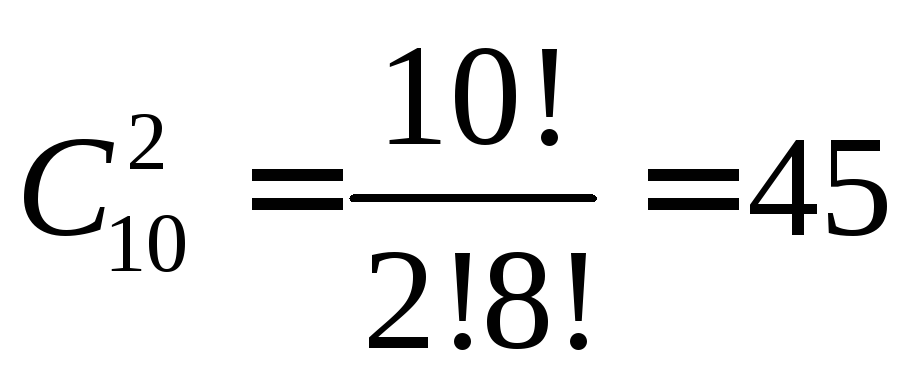 .
.
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

Замечание. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т. д., то число перестановок с повторениями
 ,
,
где n1 + n2 + … = n.
При решении задач комбинаторики используют следующие правила:
1. Правило суммы. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
2. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Приведем несколько примеров непосредственного вычисления вероятностей.
Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение. Обозначим через А событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
Р(А)=1/10.
Пример 2. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Решение. Обозначим через В событие – набраны две нужные цифры.
Всего можно набрать столько различных
цифр, сколько может быть составлено
размещений из десяти цифр по две, т.е. 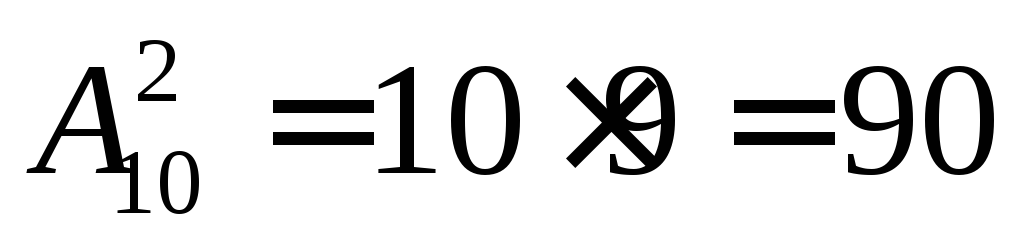 .
Таким образом, общее число возможных
элементарных исходов равно 90. Эти исходы
несовместны, равновозможны и образуют
полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность
равна отношению числа исходов,
благоприятствующих событию, к числу
всех элементарных исходов:
.
Таким образом, общее число возможных
элементарных исходов равно 90. Эти исходы
несовместны, равновозможны и образуют
полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность
равна отношению числа исходов,
благоприятствующих событию, к числу
всех элементарных исходов:
Р(В)=1/90.
Пример 3. Указать ошибку «решения» задачи: «Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4 (событие А)».
Решение. Всего возможны 2 исхода испытания: сумма выпавших очков равна 4, сумма выпавших очков не равна 4. Событию А благоприятствует один исход; общее число исходов равно двум. Следовательно, искомая вероятность
Р(А) = 1/2.
Ошибка этого решения состоит в том, что рассматриваемые исходы не являются равновозможными.
Правильное решение. Общее число равновозможных исходов испытания равно 66 = 36 (каждое число выпавших очков на одной кости может сочетаться со всеми числами очков другой кости). Среди этих исходов благоприятствуют событию А только 3 исхода: (1; 3), (3; 1), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность
Р(А) = 3/36 = 1/12.
Пример 4. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.
Решение. Общее число возможных элементарных
исходов испытания равно числу способов,
которыми можно извлечь 6 деталей из 10,
т. е. числу сочетаний из 10 элементов но
6 элементов ( ).
).
Определим
число исходов, благоприятствующих
интересующему нас событию А (среди шести взятых деталей 4 стандартных).
Четыре стандартные детали можно взять
на семи стандартных деталей  способами; при этом остальные 6 – 4 = 2
детали должны быть нестандартными;
взять же 2 нестандартные детали из 10 –
7 = 3 нестандартных деталей можно
способами; при этом остальные 6 – 4 = 2
детали должны быть нестандартными;
взять же 2 нестандартные детали из 10 –
7 = 3 нестандартных деталей можно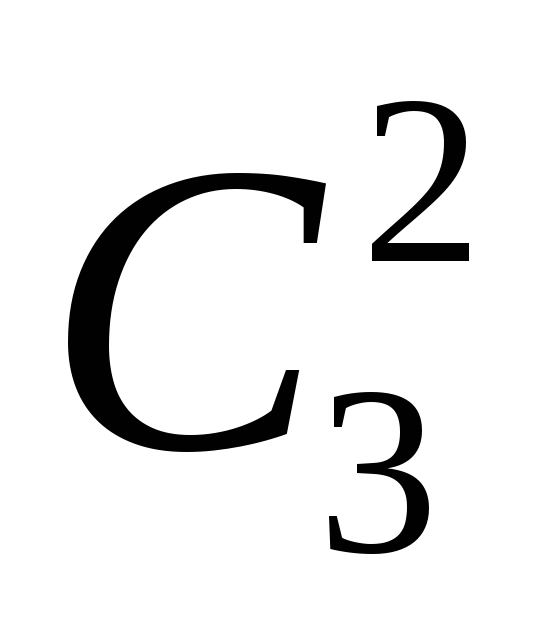 способами. Следовательно, число
благоприятствующих исходов равно
способами. Следовательно, число
благоприятствующих исходов равно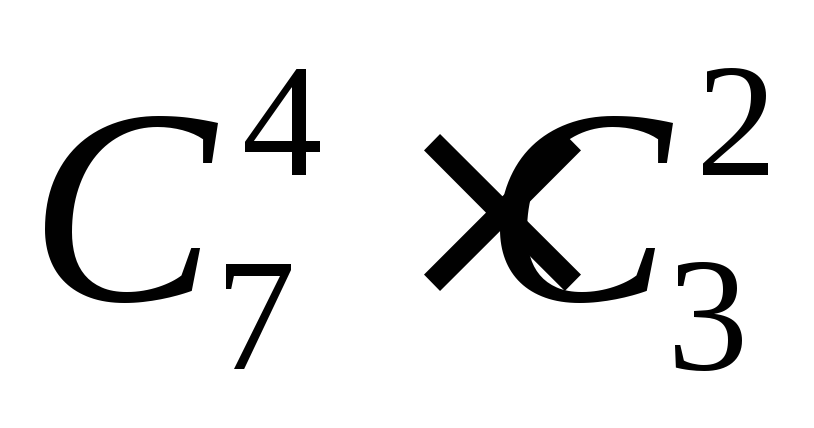 .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
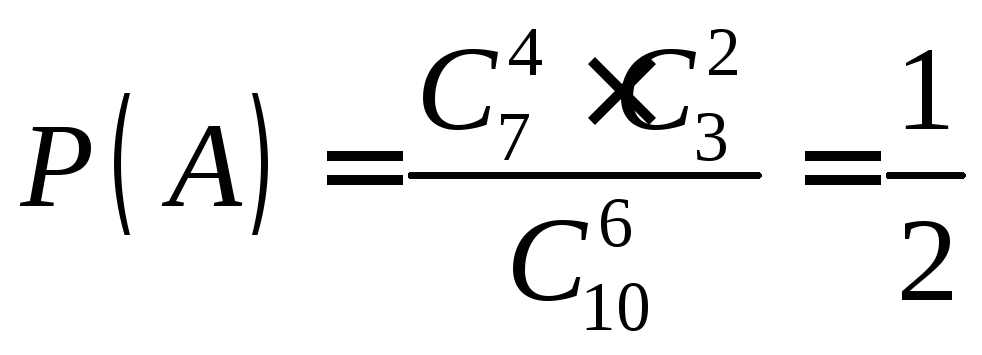
studfile.net
Сочетания.
1) Сочетания без повторений.
Определение
3: Сочетания
из 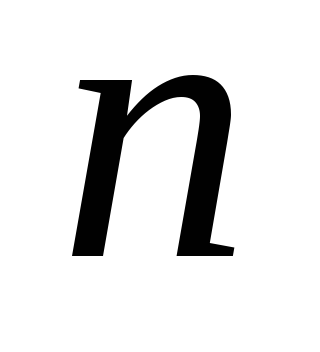 элементов по
элементов по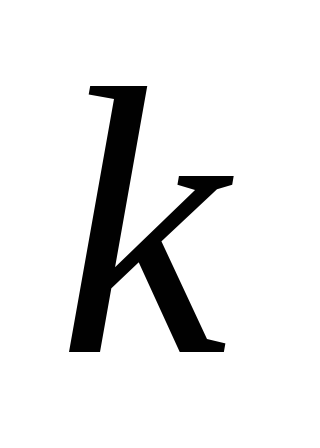 элементов (
элементов (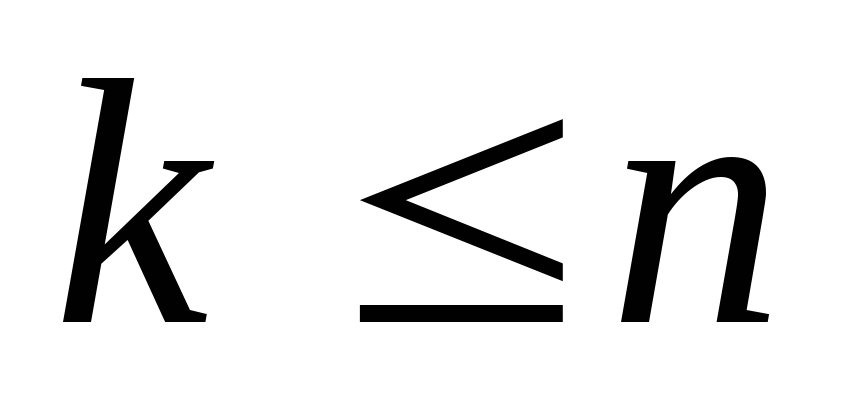 )
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают:
)
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают:  .
.
Теорема 4: Число сочетаний находится по следующей формуле:
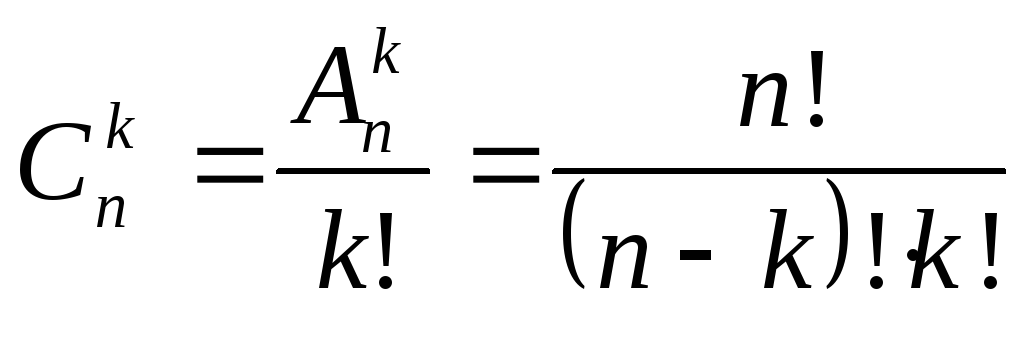 .
.
Доказательство:  .
.
Следствие: Выведенная формула совпадает с формулой
для числа повторений из 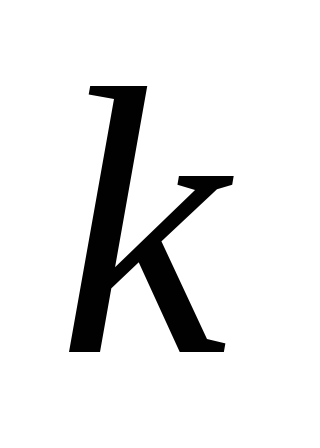 элементов одного типа и
элементов одного типа и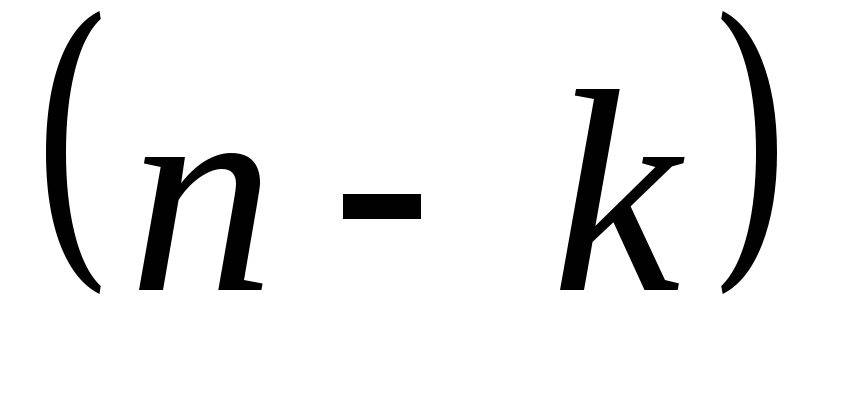 элементов второго типа:
элементов второго типа:
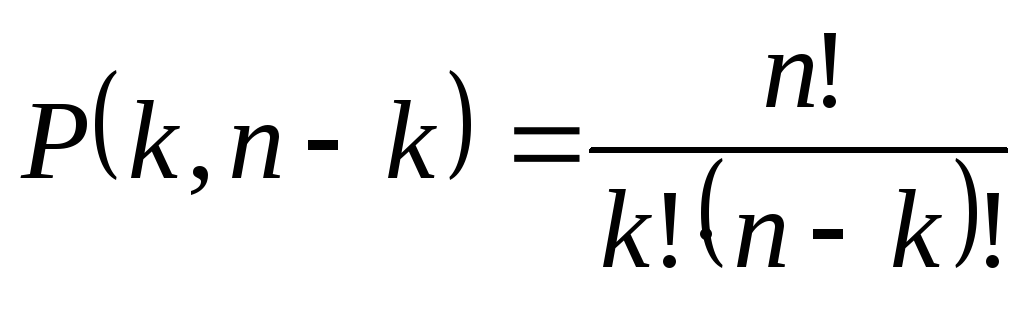 .
.
Иными
словами справедливо равенство: 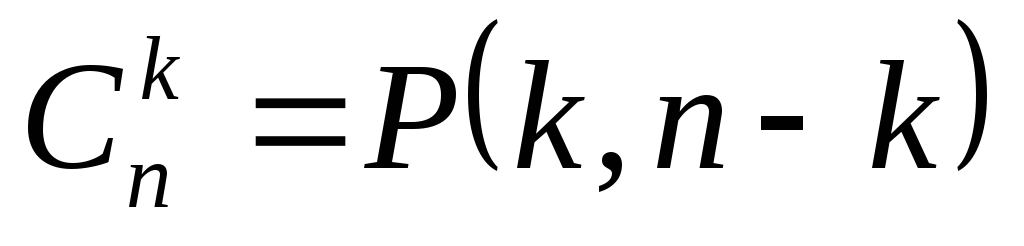 .
.
Примеры: Выбор делегации, число призеров в соревновании и т. д.
Замечание: 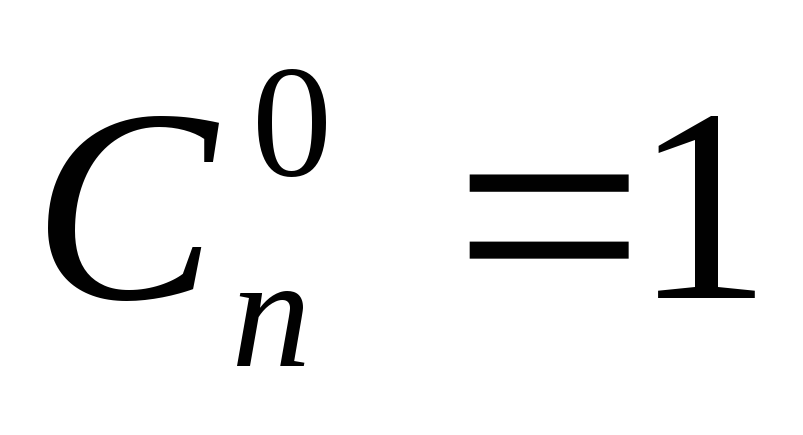 ,
,  .
.
Существенное отличие числа сочетаний от числа соответствующих размещений состоит в том, что для размещений важен состав и порядок элементов в подмножествах, а для сочетаний важен только состав.
2) Сочетания с повторениями.
Пусть
имеется предметы  различных типов. Сколько
различных типов. Сколько комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.
комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.
Задача: В кондитерском магазине продаются пирожные 4 сортов: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Зашифруем каждую покупку с помощью нулей и единиц. Напишем столько единиц, сколько куплено наполеонов, затем пишем 0, чтобы отделить пирожные одного типа от другого и т.д. Тогда каждой покупке будет соответствовать последовательность из семи единиц и трех нулей в различном порядке. Число всех таких покупок тогда будет равно:
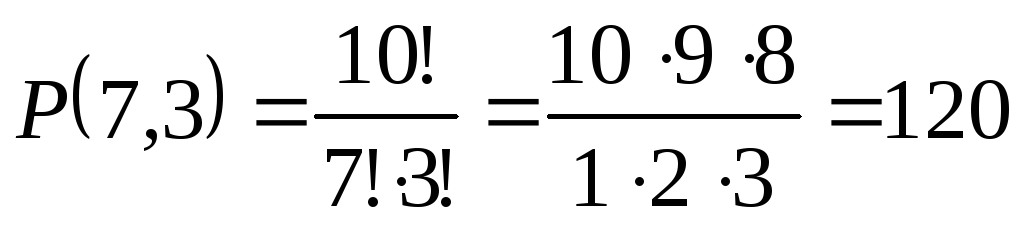 .
.
Для числа сочетаний с повторениями существует формула:
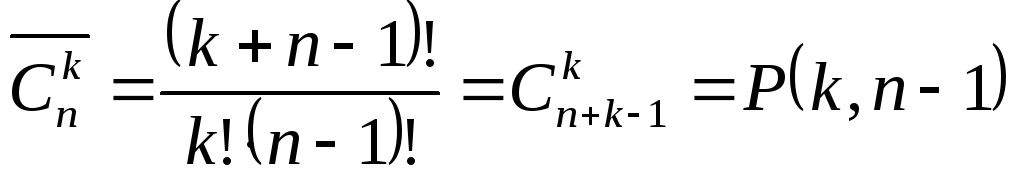 .
.
§2. Свойства сочетаний. Бином Ньютона.
Одной из наиболее распространённых комбинаторных формул является формула числа сочетаний. Для упрощения подсчётов и для доказательства некоторых утверждений удобно использовать следующие свойства сочетаний:
1. 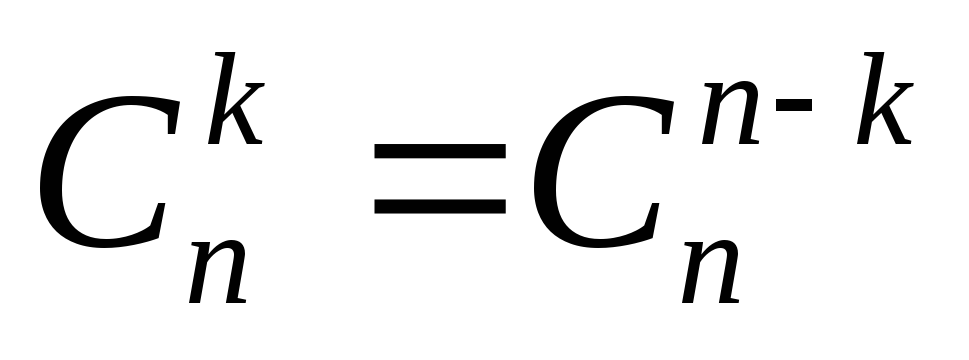 .
.
2. 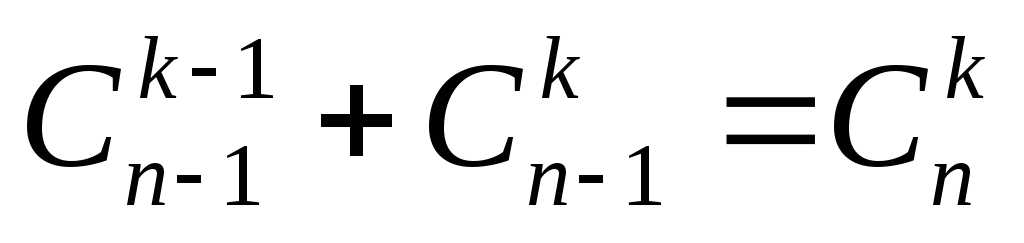 .
.
Доказательство:
1) 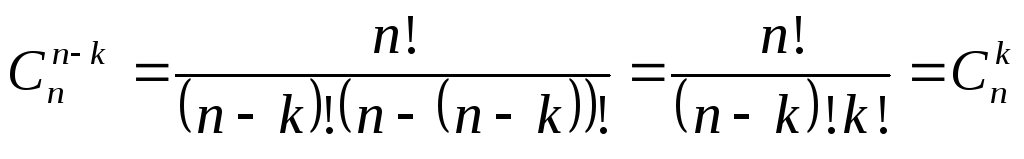 .
.
2) 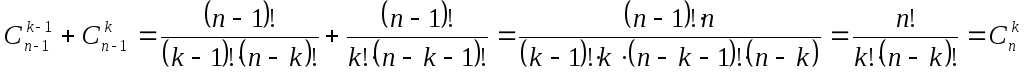 .
.
Сочетания можно встретить и в школьном курсе математики. Например, в качестве коэффициентов бинома Ньютона выступают именно сочетания. Формула бинома Ньютона в общем виде и её доказательство приводятся в следующей теореме.
Теорема
1: 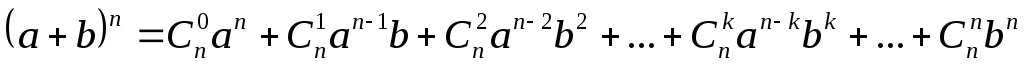 .
.
Доказательство: Применим индукцию по  .
.
При  :
: .
.
Пусть
формула верна, для случая, когда  .
В этом случае следующее равенство будем
считать выполненным:
.
В этом случае следующее равенство будем
считать выполненным:
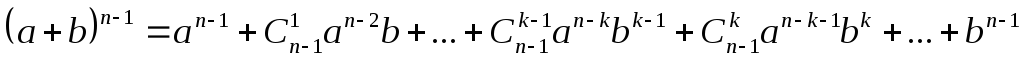 .
.
Покажем,
что формула выполняется для  —
й степени:
—
й степени:
 .
.
В
доказательстве можно также использовать
свойство: 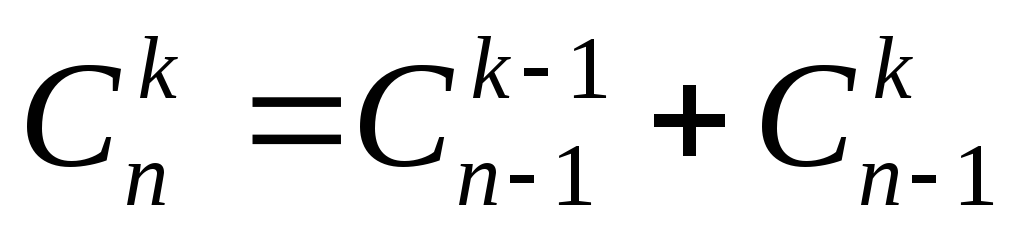 .
.
Следствие: Рассмотрим некоторые частные случаи формулы бинома Ньютона:
1)
если 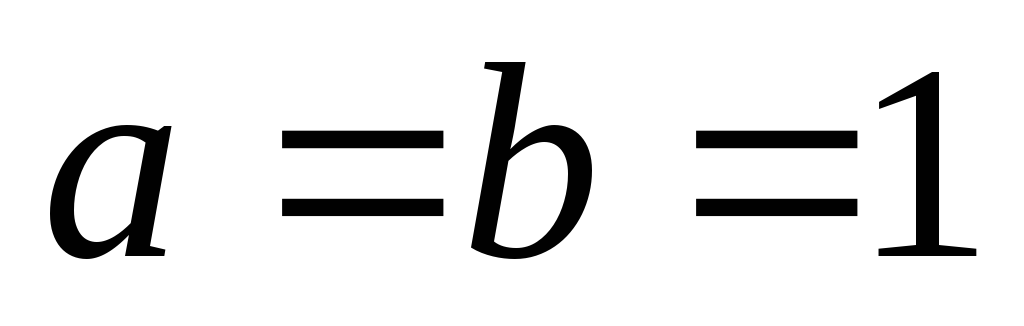 ,
то
,
то .
.
2)
если 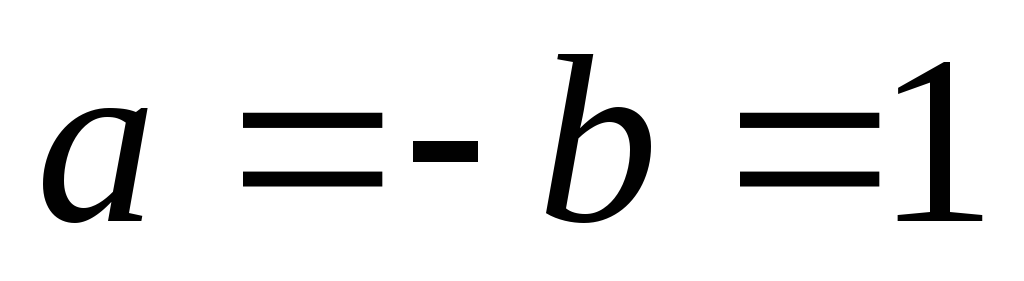 ,
то
,
то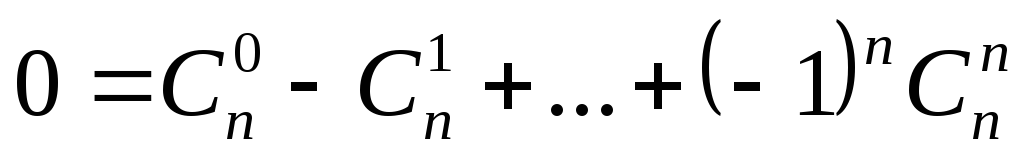 .
.
Определение
1: Коэффициенты 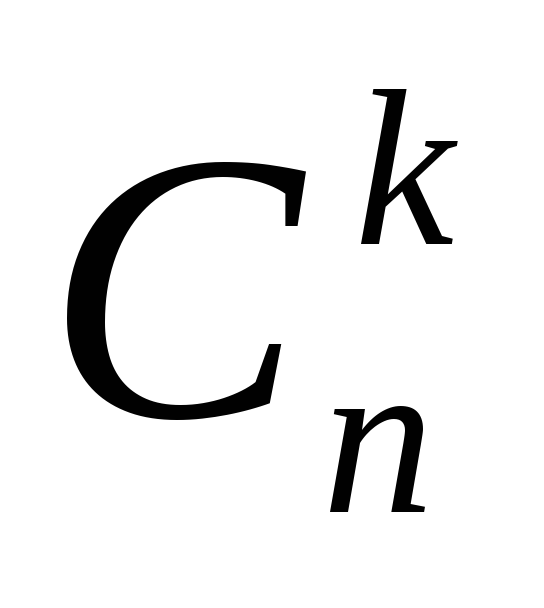 бинома Ньютонаназываются
биномиальными коэффициентами.
бинома Ньютонаназываются
биномиальными коэффициентами.
Числовые
значения биномиальных коэффициентов
вычисляются по формуле числа сочетаний: 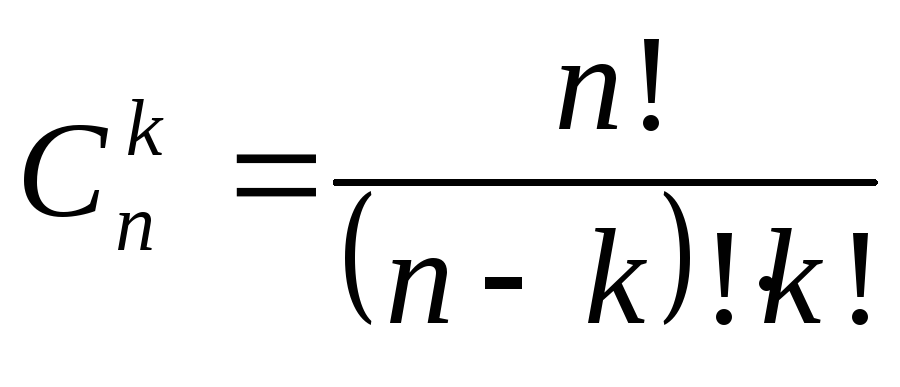 .
Готовые значения этих коэффициентов
располагаются в строкахтреугольника
Паскаля.
.
Готовые значения этих коэффициентов
располагаются в строкахтреугольника
Паскаля.
1 n = 0
1 1 n = 1
1 2 1 n = 2
1 3 3 1 n = 3
1 4 6 4 1 n = 4
1 5 10 10 5 1 n = 5
. . . . . . . . . . . . . . . . . . . . . . . . .
Треугольник
Паскаля строится следующим образом.
Боковые стороны состоят из единиц.
Числа, находящиеся внутри, являются
суммой вышестоящих чисел. Каждая строка
треугольника соответствует некоторой
степени для суммы 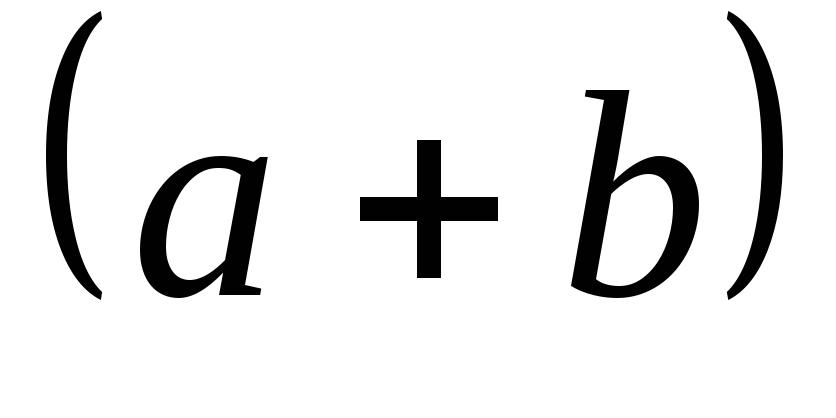 и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы
и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы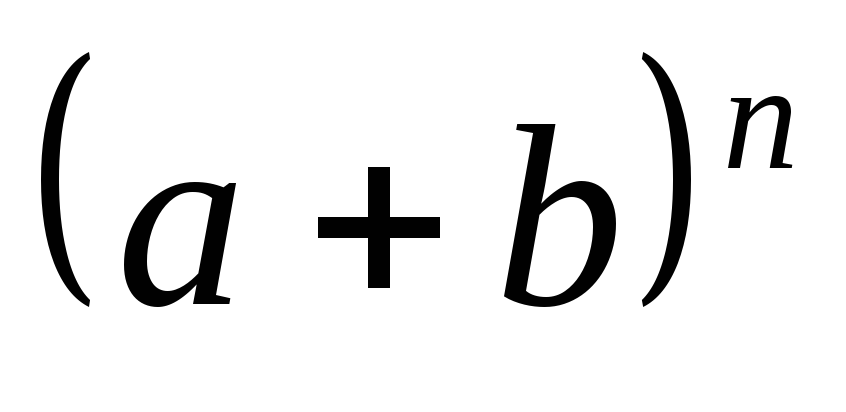 ,
нужно из треугольника Паскаля взять
строку, соответствующую данной степени
,
нужно из треугольника Паскаля взять
строку, соответствующую данной степени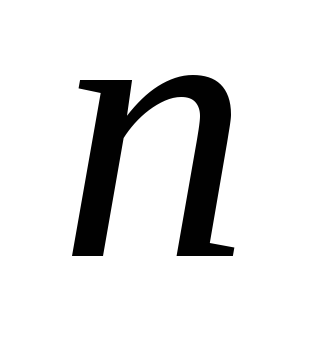 .
Эта строка будет содержать нужные
коэффициенты
.
Эта строка будет содержать нужные
коэффициенты ,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент.
,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент.
Формула бинома Ньютона применяется, когда нужно возвести в целую степень сумму двух слагаемых. Если же это требуется произвести для суммы трёх и более слагаемых, тогда применяют полиномиальную формулу:
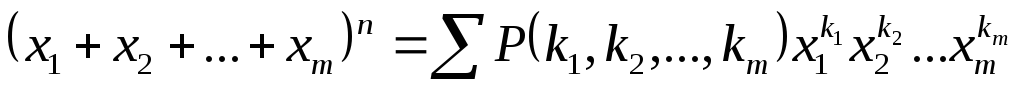
Сумма
в правой части формулы строится по
аналогии с формулой бинома. Она
представляет собой сумму слагаемых,
состоящих из коэффициента 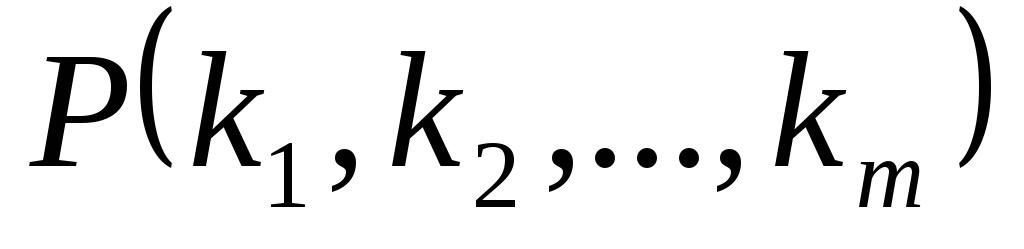 и буквенной части
и буквенной части .
Сумма этих слагаемых берется по
всевозможным разбиениям числа
.
Сумма этих слагаемых берется по
всевозможным разбиениям числа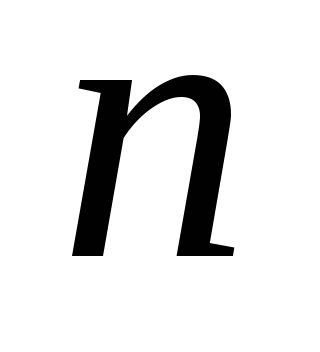 на
на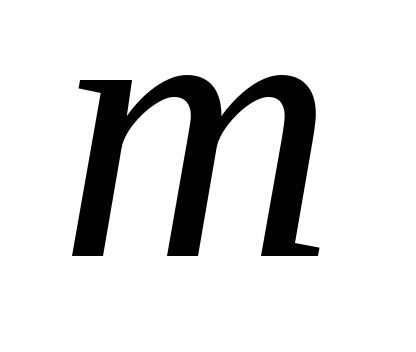 целых неотрицательных слагаемых
целых неотрицательных слагаемых ,
при этом коэффициент находится по
формуле числа перестановок с повторениями:
,
при этом коэффициент находится по
формуле числа перестановок с повторениями:
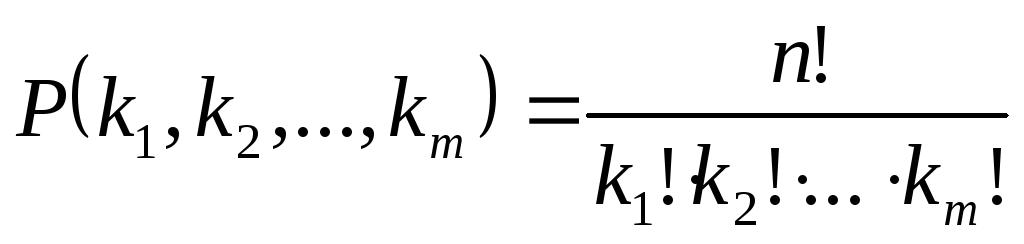 .
.
Если
числа 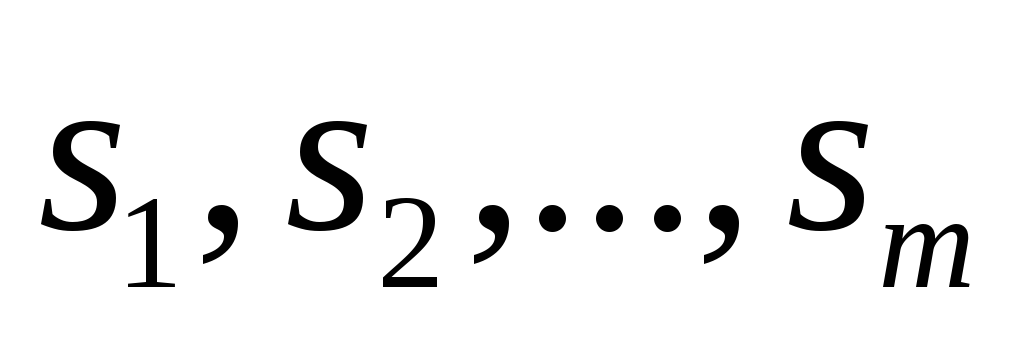 получаются перестановкой из чисел
получаются перестановкой из чисел ,
то считается, что
,
то считается, что
 .
.
Пример: Возвести в пятую степень сумму трёх слагаемых.
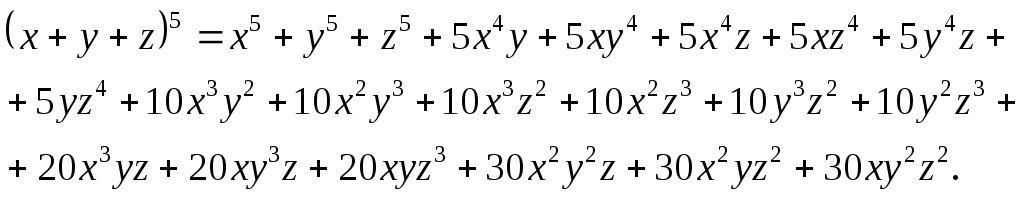
Здесь учитывается, что 5 можно разбить на 3 слагаемых пятью способами:
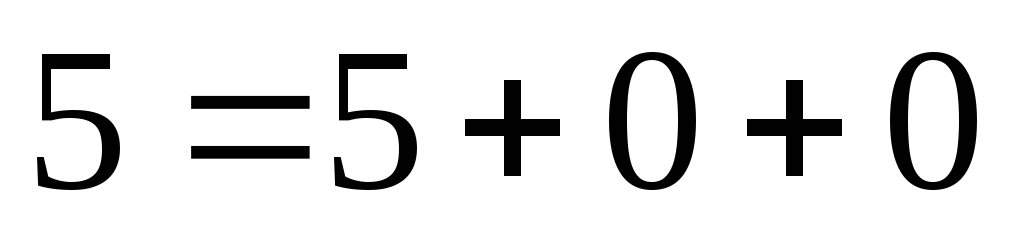 ;
;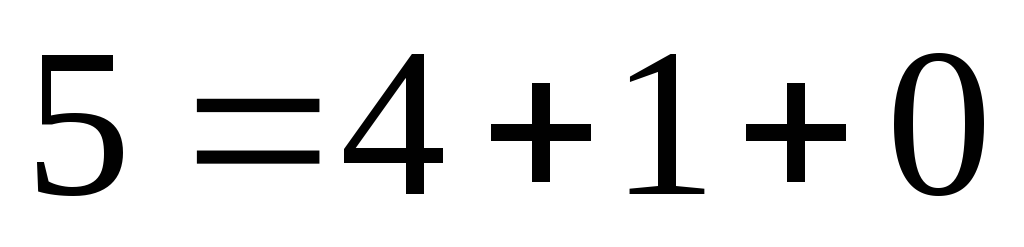 ;
; ;
;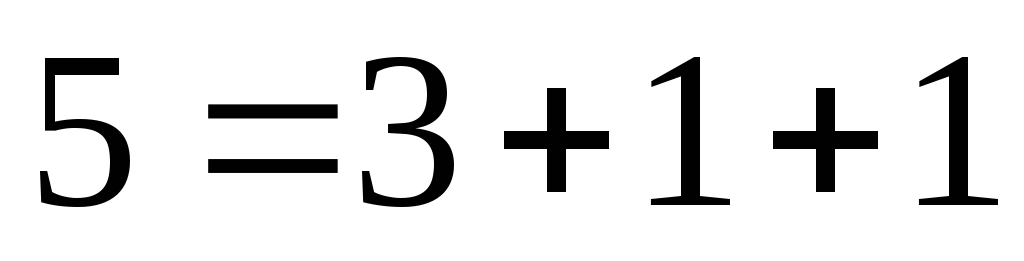 ;
;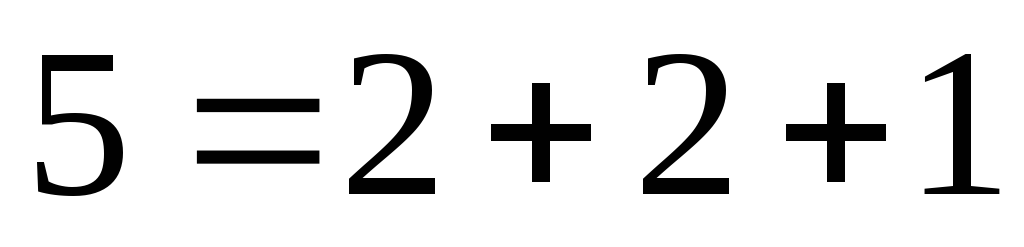 .
.
Тогда
для каждого такого разбиения известны
числа  ,
,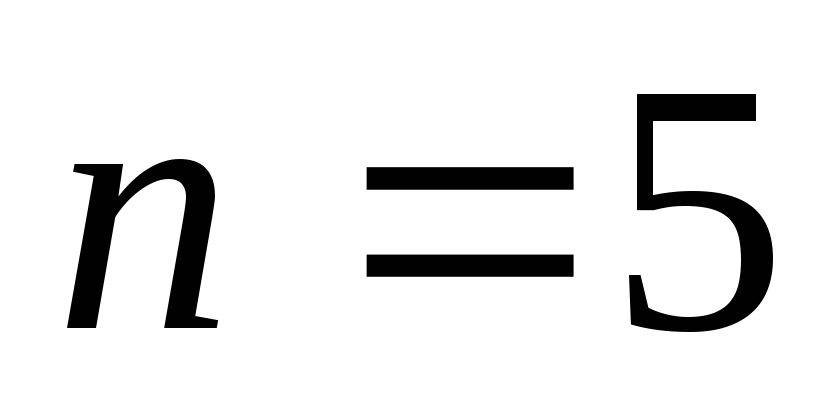 .
Значит, все коэффициенты можно для
каждого случая найти по формуле:
.
Значит, все коэффициенты можно для
каждого случая найти по формуле:
 .
.
Полученные
коэффициенты:  ,
,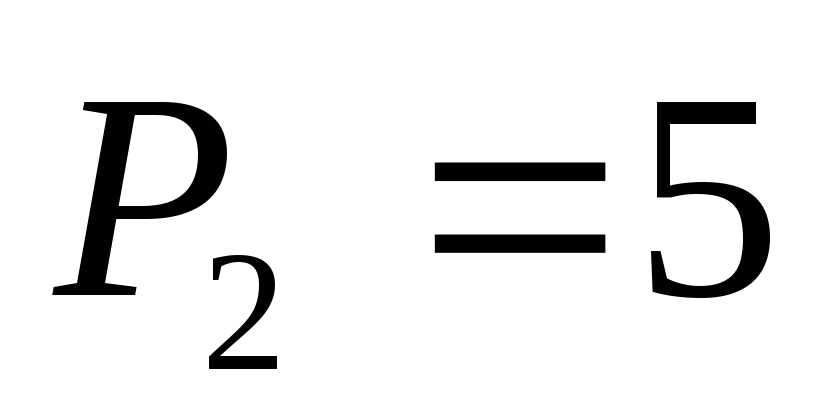 ,
,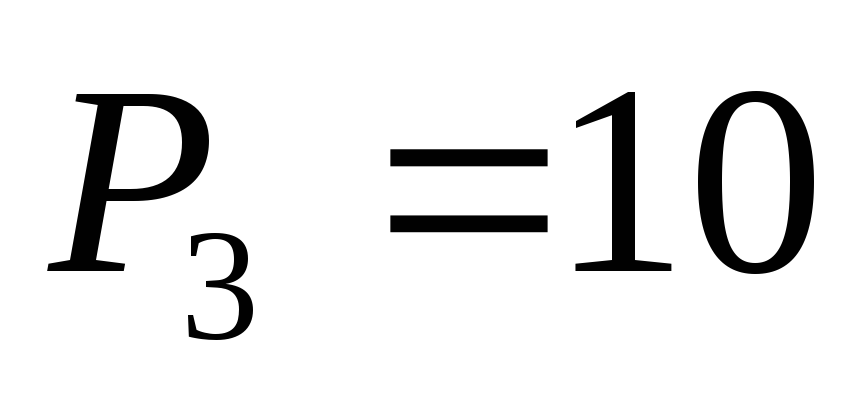 ,
,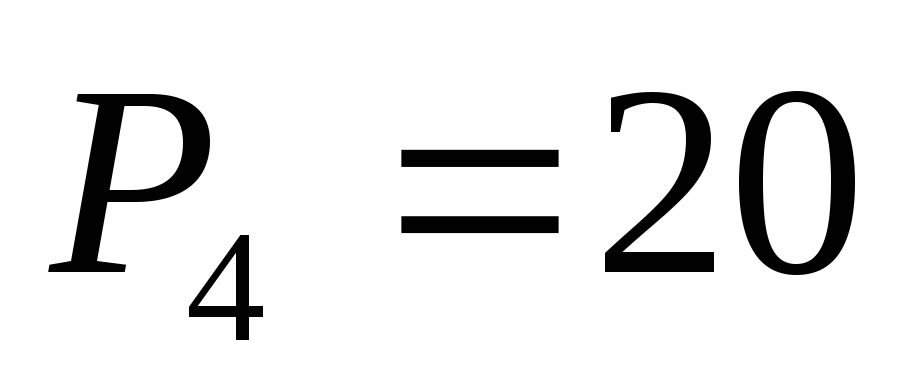 ,
,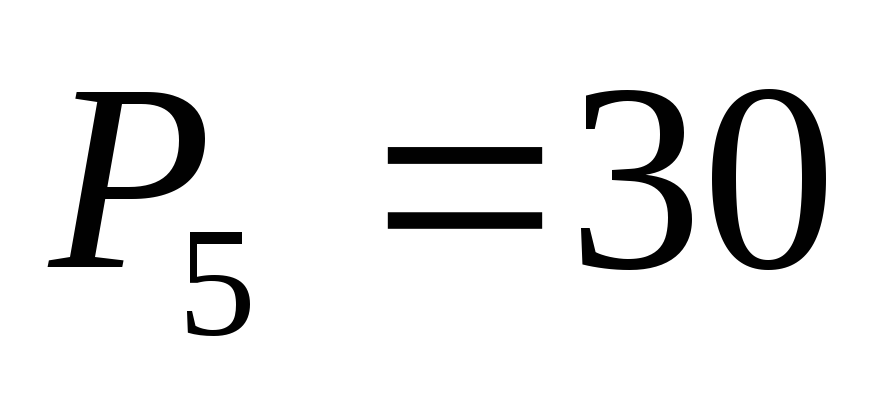 .
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше.
.
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше.
Замечание: Сумма полиномиальных коэффициентов может быть найдена по формуле:
 .
.
Для коэффициентов из рассмотренного примера можно проверить:
 ,
,
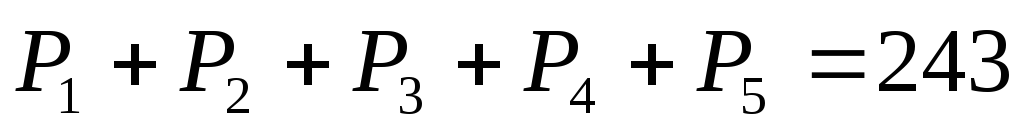 .
.
Рассмотрим  —
сочетания с повторениями, составленные
из элементов
—
сочетания с повторениями, составленные
из элементов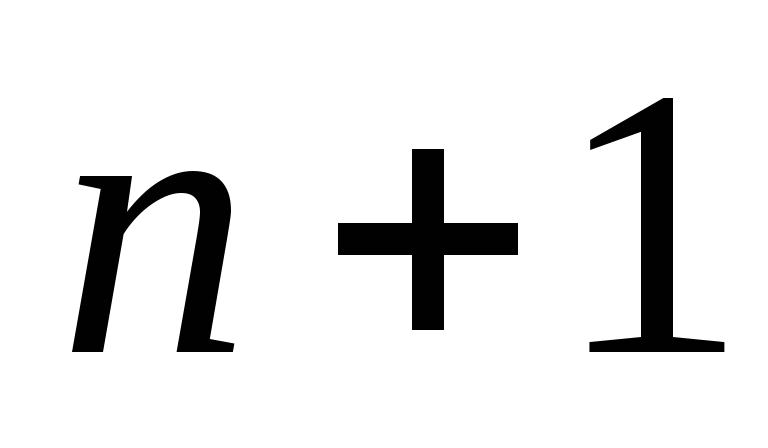 типа, например из
типа, например из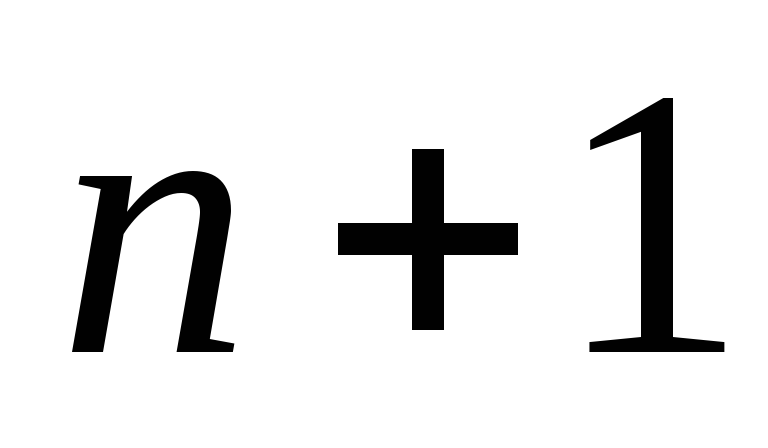 буквы
буквы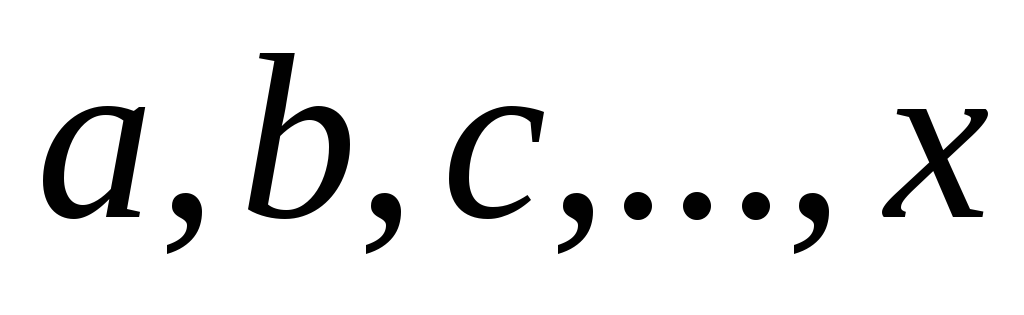 .
Число таких сочетаний равно:
.
Число таких сочетаний равно: .
Разобьём все эти сочетания на классы,
отнеся к
.
Разобьём все эти сочетания на классы,
отнеся к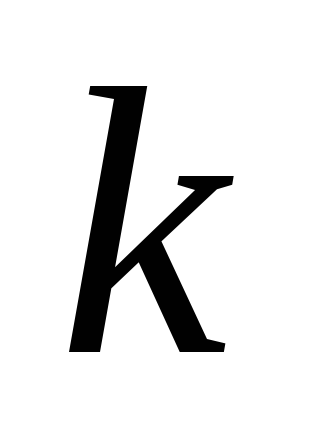 ‑
му классу сочетания, в которых
‑
му классу сочетания, в которых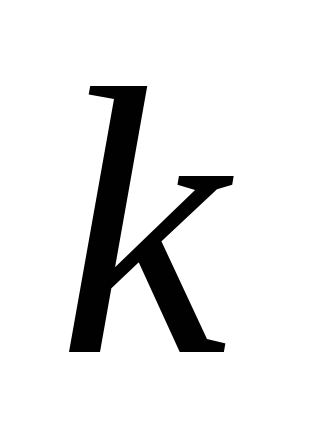 раз входит буква
раз входит буква .
Остальные
.
Остальные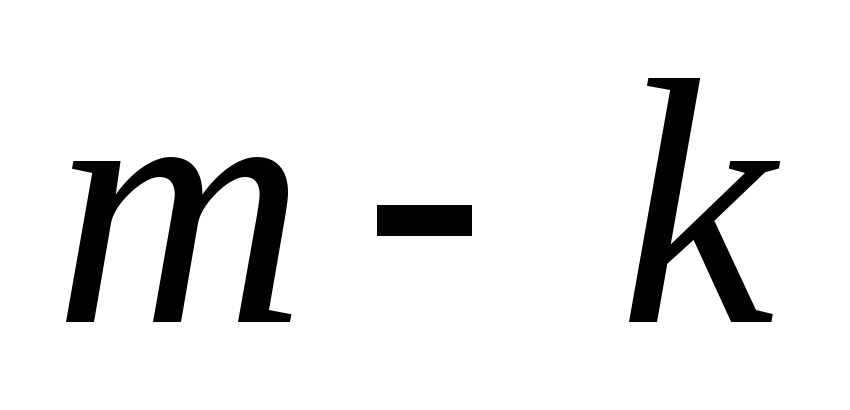 мест могут быть заняты оставшимися
буквами
мест могут быть заняты оставшимися
буквами ,
число которых равно
,
число которых равно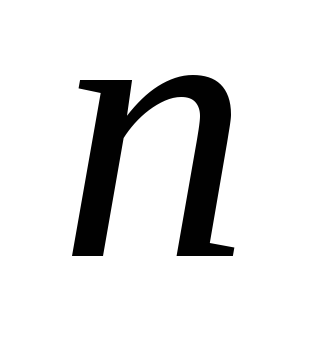 .
Поэтому в
.
Поэтому в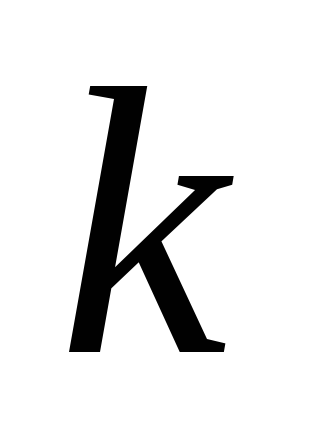 —
й класс входит столько сочетаний, сколько
можно составить
—
й класс входит столько сочетаний, сколько
можно составить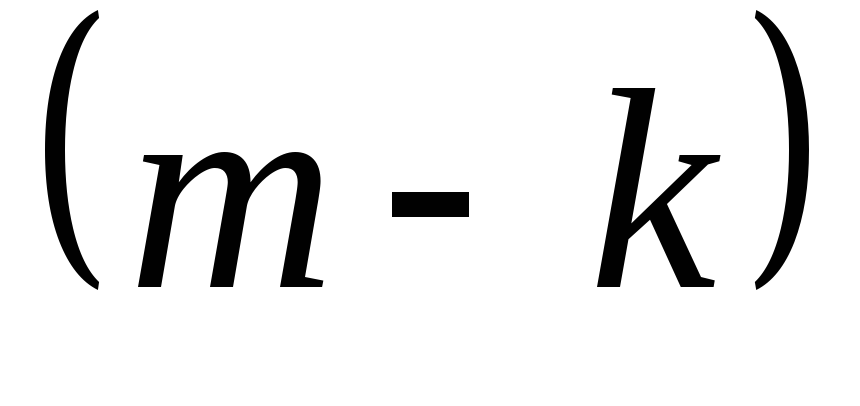 сочетаний с повторениями из элементов
сочетаний с повторениями из элементов типов, т.е.
типов, т.е.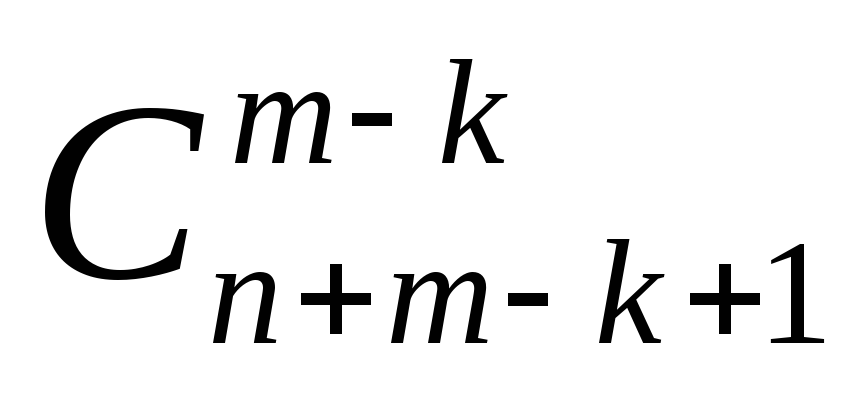 .
.
Значит общее число всех таких сочетаний равно:
 ,
т.е.
,
т.е.
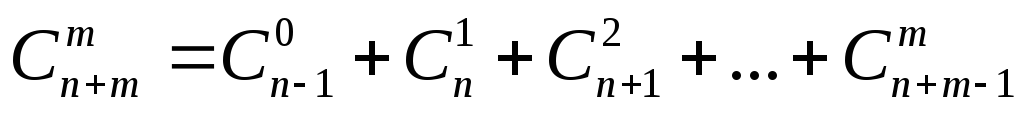 .
.
Меняя
теперь 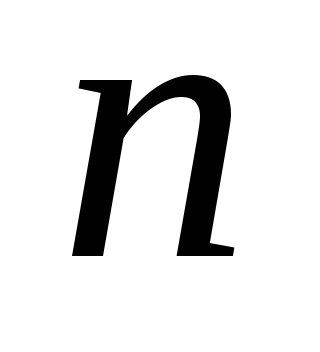 на
на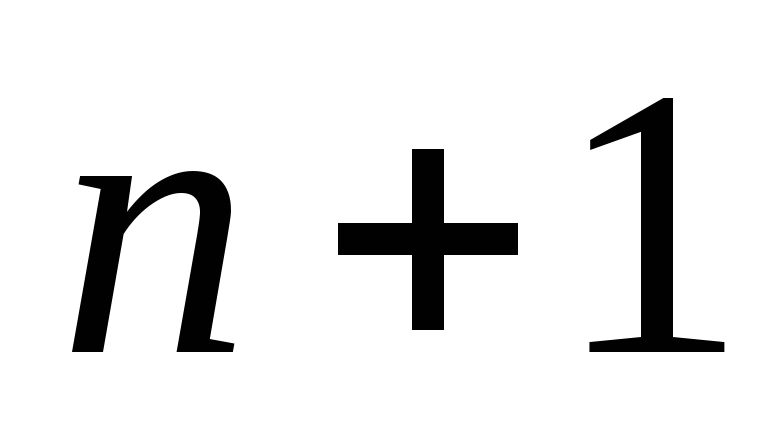 и
и на
на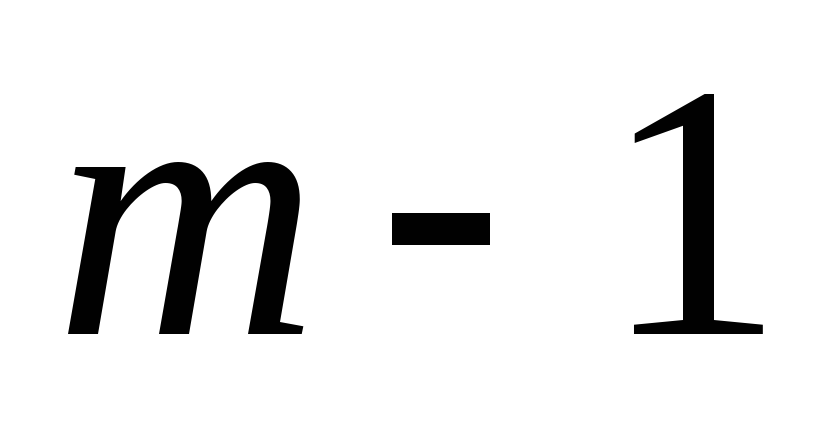 и используя равенство
и используя равенство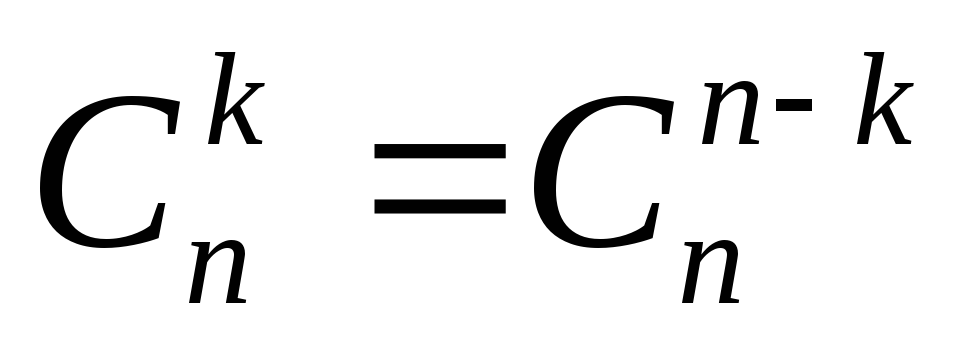 ,
получаем зависимость между биномиальными
коэффициентами:
,
получаем зависимость между биномиальными
коэффициентами:
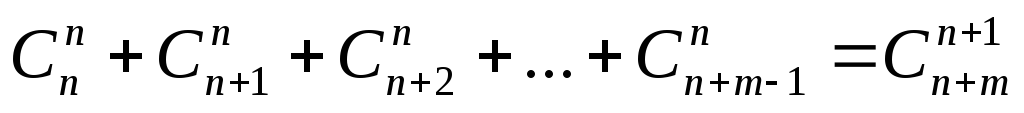 .
.
Доказать
эту формулу можно методом математической
индукции по числу слагаемых в правой
части. Используя эту зависимость, можно
получить формулы для подсчёта суммы
чисел натурального ряда от 1 до  (при
(при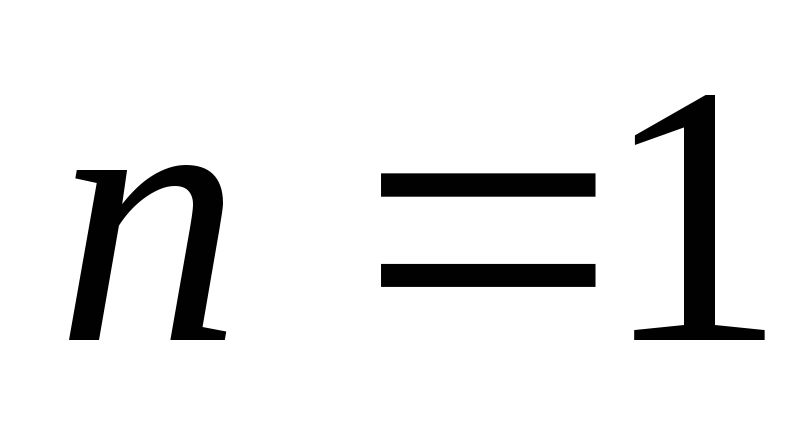 ),
суммы квадратов натуральных чисел (при
),
суммы квадратов натуральных чисел (при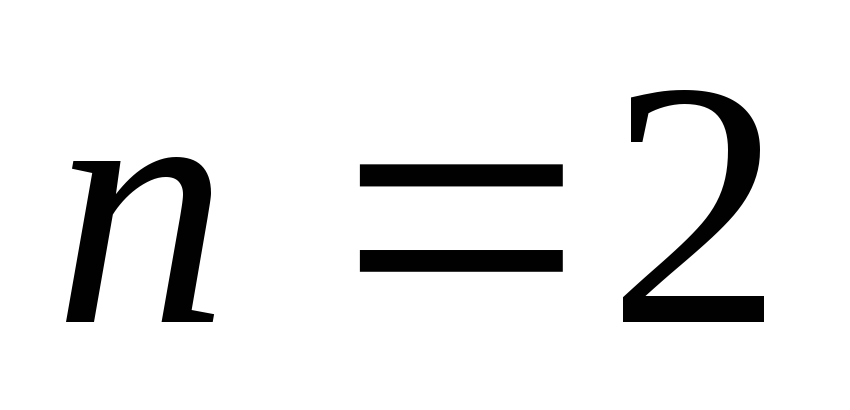 ),
сумму кубов (при
),
сумму кубов (при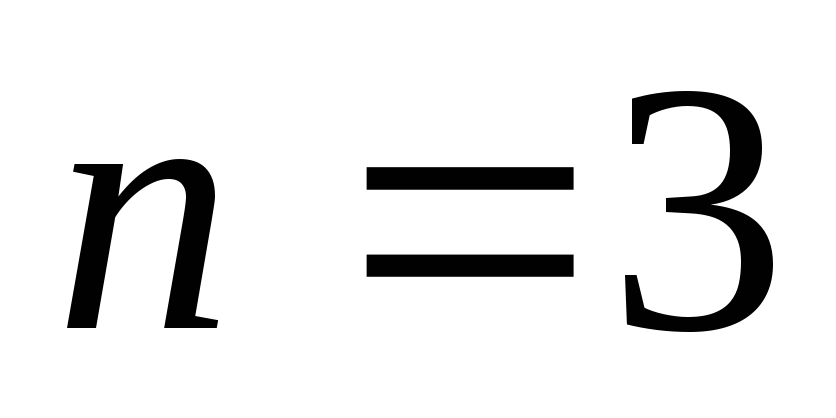 ).
).
Если 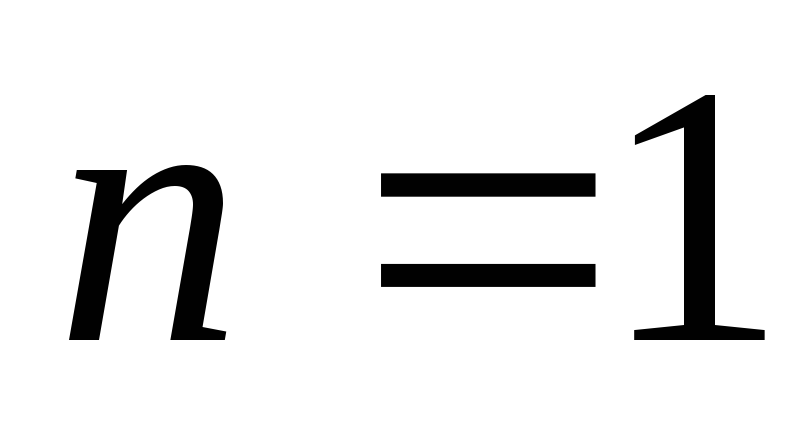 ,
то искомая зависимость имеет вид:
,
то искомая зависимость имеет вид:
 .
.
Для  имеем:
имеем:
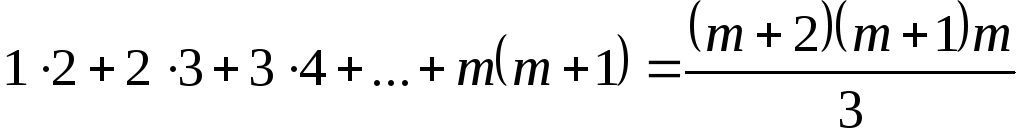 ,
,
или окончательно:
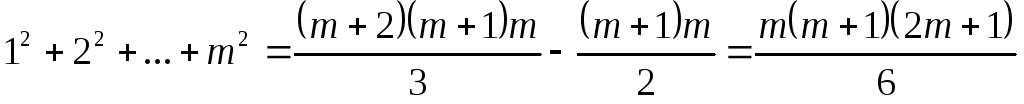 .
.
Для 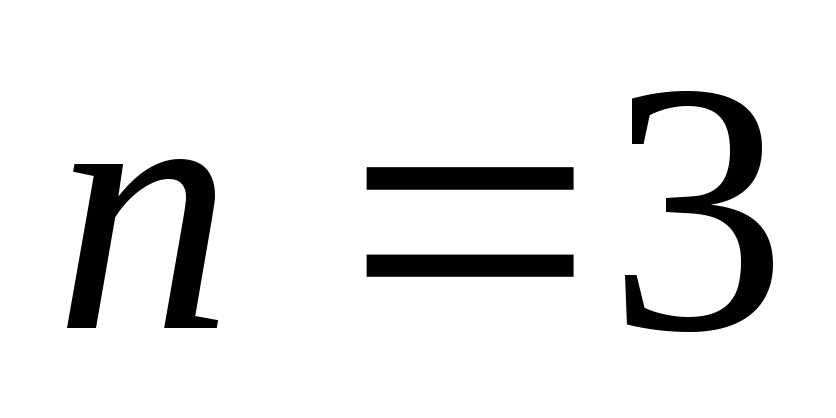 получаем:
получаем:
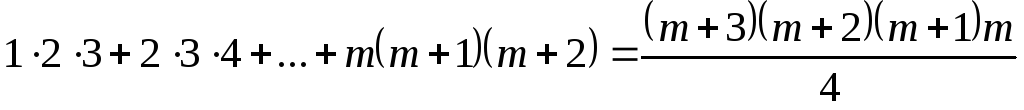 ,
,
или после преобразований:
 .
.
Таким образом, можно получить формулы для сумм более высоких степеней натуральных чисел.
studfile.net
Сочетание без повторений | matematicus.ru
Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.
Обозначение: $С_n^m$
Допустим, имеется три буквы А, В и С.
Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС.
При подсчете числа сочетаний элементов — порядок не важен.
Запишем формулу сочетания

Пример 1
В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем
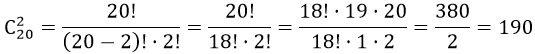
Пример 2
Пусть имеется множество, содержащие 4 буквы: {А,В,С,D}.
Записать все возможные сочетания из указанных букв по три.
Решение
По формуле сочетания имеем,
$C_4^3 =\frac{{4!}}{{\left( {4 — 3} \right)!\cdot3!}} = \frac{{4!}}{{3!}} = \frac{{1\cdot2\cdot3\cdot4}}{{1\cdot2\cdot3}} = 4$
Пример 3
В ящике 15 деталей, среди которых 6 бракованных. Наугад выбирается комплект из 5 деталей. Сколькими способами можно составить такой комплект, в котором 2 детали бракованные?
Решение
$C_{6}^2$ — количество способов выбора двух бракованных деталей из шести
$C_{3}^9$ — количество способов выбора трех исправных деталей из девяти
Тогда количество комбинаций по правилу умножения будет
$C_{6}^2·C_{3}^9=\frac{{6!}}{{(6-2)!2!}}·\frac{{9!}}{{(9-3)!3!}}=15·84=1260$
Пример 4
Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?
Решение
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно
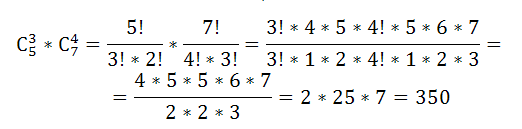
Пример 5
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?
Решение
Из пяти женщин необходимо выбрать по три. Следователь, число таких способов отбора равно $С_5^3$
Число способов отбора мужчин, четырех из семи равно $С_7^4$
По формуле комбинаторики – сочетания, группу можно сформировать способами:
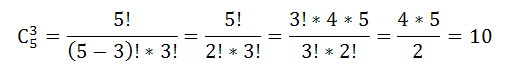
Пример 6
Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?
Решение
Число способов выбора офицера: $С_3^1$
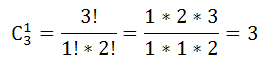
сержантов $С_6^2$
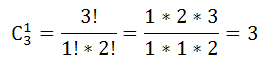
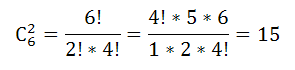
по аналогии, число комбинаций выбора курсантов, получаем $С_30^7$
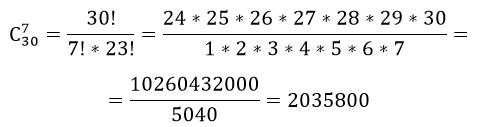
Итак, получаем число способов составления суточного наряда

www.matematicus.ru
35 Элементы комбинаторики-перестановки,размещения, сочетания
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математикисвязано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве 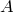
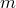 элементов,
а в множестве
элементов,
а в множестве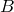 —
—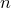 элементов.
Тогда число всех различных пар
элементов.
Тогда число всех различных пар ,
где
,
где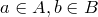 будет
равно
будет
равно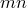 .
.
Доказательство. Действительно,
с одним элементом из множества  мы
можем составить
мы
можем составить таких
различных пар, а всего в множестве
таких
различных пар, а всего в множестве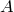
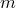 элементов.
элементов.
Размещения, перестановки, сочетания
Пусть
у нас есть множество из трех элементов 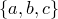 .
Какими способами мы можем выбрать из
этих элементов два?
.
Какими способами мы можем выбрать из
этих элементов два?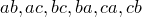 .
.
Определение. Размещениями множества из 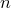 различных
элементов по
различных
элементов по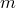 элементов
элементов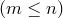 называются
комбинации, которые составлены из данных
называются
комбинации, которые составлены из данных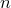 элементов
по
элементов
по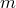 элементов
и отличаются либо самими элементами,
либо порядком элементов.
элементов
и отличаются либо самими элементами,
либо порядком элементов.
Число
всех размещений множества из  элементов
по
элементов
по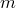 элементов
обозначается через
элементов
обозначается через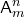 (от
начальной буквы французского слова
“arrangement”, что означает размещение), где
(от
начальной буквы французского слова
“arrangement”, что означает размещение), где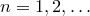 и
и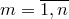 .
.
Теорема. Число размещений множества из 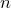 элементов
по
элементов
по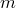 элементов
равно
элементов
равно
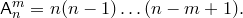
Доказательство. Пусть у нас
есть элементы 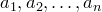 .
Пусть
.
Пусть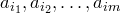 —
возможные размещения. Будем строить
эти размещения последовательно. Сначала
определим
—
возможные размещения. Будем строить
эти размещения последовательно. Сначала
определим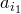 —
первый элемент размещения. Из данной
совокупности
—
первый элемент размещения. Из данной
совокупности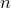 элементов
его можно выбрать
элементов
его можно выбрать различными
способами. После выбора первого элемента
различными
способами. После выбора первого элемента для
второго элемента
для
второго элемента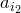 остается
остается способов
выбора и т.д. Так как каждый такой выбор
дает новое размещение, то все эти выборы
можно свободно комбинировать между
собой. Поэтому имеем:
способов
выбора и т.д. Так как каждый такой выбор
дает новое размещение, то все эти выборы
можно свободно комбинировать между
собой. Поэтому имеем:
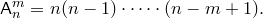
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
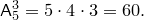
Определение. Перестановкой множества из 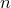 элементов
называется расположение элементов в
определенном порядке.
элементов
называется расположение элементов в
определенном порядке.
Так,
все различные перестановки множества
из трех элементов 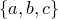 —
это
—
это
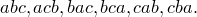
Очевидно,
перестановки можно считать частным
случаем размещений при  .
.
Число
всех перестановок из  элементов
обозначается
элементов
обозначается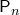 (от
начальной буквы французского слова
“permutation”, что значит “перестановка”,
“перемещение”). Следовательно, число
всех различных перестановок вычисляется
по формуле
(от
начальной буквы французского слова
“permutation”, что значит “перестановка”,
“перемещение”). Следовательно, число
всех различных перестановок вычисляется
по формуле
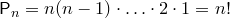
Пример. Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки 8 ладей

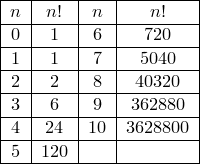
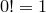 по
определению!
по
определению!
Определение. Сочетаниями из 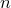 различных
элементов по
различных
элементов по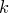 элементов
называются комбинации, которые составлены
из данных
элементов
называются комбинации, которые составлены
из данных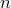 элементов
по
элементов
по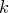 элементов
и отличаются хотя бы одним элементом
(иначе говоря,
элементов
и отличаются хотя бы одним элементом
(иначе говоря,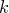 -элементные
подмножества данного множества из
-элементные
подмножества данного множества из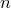 элементов).
элементов).
Как
видим, в сочетаниях в отличие от размещений
не учитывается порядок элементов. Число
всех сочетаний из 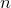 элементов
по
элементов
по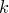 элементов
в каждом обозначается
элементов
в каждом обозначается (от
начальной буквы французского слова
“combinasion”, что значит “сочетание”).
(от
начальной буквы французского слова
“combinasion”, что значит “сочетание”).
Числа 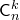

Все
сочетания из множества 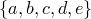 по
два —
по
два — .
.
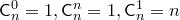 .
.
studfile.net
Комбинаторика. Размещения, перестановки, сочетания | Математика, которая мне нравится
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при >.
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки ладей
по определению!
Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа
Все сочетания из множества по два — .
.
Свойства чисел {\sf C}_n^k
1. .
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
2. .
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .
.
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
hijos.ru