Соотношение между углами и сторонами треугольника — урок. Геометрия, 7 класс.

В треугольнике против большей стороны лежит больший угол.

 

Доказательство

 

Пусть в треугольнике \(ABC\) сторона \(AB\) больше стороны \(AC\).

Докажем, что ∡ \(C >\) ∡ \(B\).

 

Отложим на стороне \(AB\) отрезок, равный стороне \(AC\).

Так как \(AD < AB\), то точка \(D\) лежит между точками \(A\) и \(B\).

Следовательно, угол \(1\) является частью угла \(C\) и, значит, &angmsd; \(C >\) &angmsd; \(1\).

 

Угол \(2\) — внешний угол треугольника \(BDC\), поэтому &angmsd; \(2 >\) &angmsd; \(B\).

&angmsd; \(1 =\) &angmsd; \(2\) как углы при основании равнобедренного треугольника \(ADC\).

Таким образом, &angmsd; \(C >\) &angmsd; \(1 =\) &angmsd; \(2 >\) &angmsd; \(B\).              

 

Отсюда следует, что &angmsd; \(C >\) &angmsd; \(B\).

 

Справедлива и обратная теорема.

В треугольнике против большего угла лежит большая сторона.

 

Следствия

 

Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).

 

Следствие 2. Если три угла треугольника равны, то треугольник равносторонний.

 

Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.

Неравенство треугольника

Каждая сторона треугольника меньше суммы двух других сторон.

 

Доказательство

 

Рассмотрим треугольник \(ABC\) и докажем, что \(AB < AC + BC\).

 

Продолжим сторону \(AC\) и отложим отрезок \(CD = BC\).

Треугольник \(BCD\) — равнобедренный, следовательно, &angmsd; \(1 = \) &angmsd; \(2\).

В треугольнике \(ABD\) очевидно, что &angmsd; \(ABD >\) &angmsd; \(1\), а это значит, что &angmsd; \(ABD >\) &angmsd; \(2\).

 

Так как против большего угла лежит большая сторона, \(AB

 

Следствие 4. Для любых трёх точек \(A\), \(B\) и \(C\), не лежащих на одной прямой, справедливы неравенства:
\(AB < AC + CB,  AC < AB + BC,  BC < AB + AC\).

Теорема о соотношениях между сторонами и углами треугольника

Теорема:

В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.

Доказательство:

1) Дано: АВС, АВАС.

   Доказать: СВ.

   Доказательство:

Отложим на стороне АВ отрезок АD, равный стороне АС.

 АDАВ, т.к. по построению АD = АС, а по условию АСАВ, значит, точка D лежит между точками А и В. Следовательно, 1 является частью С, т.е. С1. Угол 2 внешний угол DBC, поэтому

2В. АDС — равнобедренный с основанием DC, т.к. по построению АD = АС, следовательно, 1 =2 (углы при основании).

Итак, С1,

1 =2, значит, С2, при этом 2В, следовательно, СВ.

2) Дано: АВС,

СВ.

   Доказать: АВАС.

   Доказательство:

Предположим, что это не так. Тогда возможны два варианта:

1. либо АВ = АС, тогда АВС — равнобедренный с основанием ВС, значит, С =В (как углы при основании), что противоречит условию: СВ.
2. либо АВАС, тогда СВ, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию: СВ. 

Значит, наше предположение неверно, следовательно, АВАС. Что и требовалось доказать.

Следствие 1

Доказательство:

Дано:

АВС, ВС — гипотенуза, А — прямой.

Доказать: ВСАС, ВС АВ.

Доказательство:

АВС — прямоугольный, А — прямой, следовательно, углы В и С острые, тогда

АВ и АС, значит, ВСАС, ВСАВ (в треугольнике против большего угла лежит большая сторона). Что и требовалось доказать.

Следствие 2

Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).

Доказательство:

Дано: АВС, В =

С.

Доказать: АС = АВ.

Доказательство:

Предположим, что одна из сторон будет больше, т.е. АСАВ, тогда и угол лежащий против этой стороны будет больше, т.е. ВС (в треугольнике против большей стороны лежит больший угол), а это противоречит условию: В =

С, следовательно, наше предположение неверно, значит АС = АВ.

Итак, в АВС равны две стороны (АС = АВ), следовательно, данный треугольник — равнобедренный. Что и требовалось доказать.

Египетский треугольник — Википедия

Материал из Википедии — свободной энциклопедии

Египетский треугольник

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.

• Особенностью такого треугольника, известной ещё со времён античности, является то, что все три стороны его целочисленны, а по теореме, обратной теореме Пифагора, он прямоуголен.
• Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.
• Радиус вписанной в треугольник окружности равен единице.

Название треугольнику с таким отношением сторон дали эллины: в VII—V веках до нашей эры греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 году до нашей эры по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.

Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид. Историк и математик Ван дер Варден ставил этот факт под сомнение, однако более поздние исследования его подтвердили^[1]. В архитектуре средних веков египетский треугольник применялся для построения схем пропорциональности^[2].

Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.

1. ↑ Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. М.: Физматлит, 1959, С. 13, подстрочное примечание
2. ↑ Египетский треугольник // Юсупов Э. Словарь терминов архитектуры, стр. 121. Издательство: Ленинградская галерея, 1994. ISBN 5-85825-004-1, 432 с.

Обсуждение:Треугольник — Википедия

Исправил некоторые ошибки форматирования и разметки в «Площади Треугольника» и вынес эту тему как заголовок… DiecorD 17:57, 24 апреля 2007 (UTC)

Категория «Треугольники»[править код]

По-моему категория треугольники решена смысла. Она слишком частная. Правильный вариант с моей точки зрения — категории математика и геометрия. halyavin 15:10, 31 Май 2005 (UTC)

Это Ваша личная точка зрения. Вот, например, в английской Википедии есть категория en:Category:Triangles в которой есть десяток статей. А если мы загоним все статьи относящиеся к математике в одну категорию, то там в перспективе будет много тысяч статей. MaxiMaxiMax 15:19, 31 Май 2005 (UTC)

Подумаешь несколько тысяч. Самих категорий намного больше. Зато это лишает недокументированного просмотра всех справок по одной тематике — заходим на страницу Category:Математика и жмем связанные правки. Если страница категории будет долго грузится, то можно использовать прямой url: http://ru.wikipedia.org/w/index.php?title=%D0%A1%D0%BF%D0%B5%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5:Recentchangeslinked&target=Category%3A%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0. Раз уж есть такая категория в английском, то я согласен и на категории математика, геометрия и треугольник вместе. halyavin 15:36, 31 Май 2005 (UTC)

• В разделе «Метрические соотношения в треугольнике» не приведены обозначения:  hc{\displaystyle \ h_{c}},  mc{\displaystyle \ m_{c}},  ac{\displaystyle \ a_{c}},  bc{\displaystyle \ b_{c}},  R{\displaystyle \ R},  r{\displaystyle \ r} (правда, кое-что указано в разделе «Площадь треугольника»). Может быть, следует ввести раздел «обозначения», или что-то типа того.
  Далее,  ac{\displaystyle \ a_{c}} — это что, проекция  a{\displaystyle \ a} на  c{\displaystyle \ c}? В этом случае (если я не туплю) формулы a=acc{\displaystyle a={\sqrt {a_{c}c}}} и b=bcc{\displaystyle b={\sqrt {b_{c}c}}} неверны (c{\displaystyle c} удлинняем,  b{\displaystyle \ b} и  bc{\displaystyle \ b_{c}} остаются).
  — imAnic 20:07, 15 июня 2006 (MSK)

• Успеть все сразу сложно. Обозначения я введу минут через тридцать. Отношения тоже проверю. Мне кажется, ошибки нет. С уважением, Matist Krusoe 17:29, 15 июня 2006 (UTC) (еще картинку нарисую)
  • А, так эти формулы для прямоугольного треугольника. Ну тогда все верно. — imAnic 20:07, 15 июня 2006 (MSK)

Доказательство теорем[править код]

Доказательство теоремы синусов и формулы Герона можно отсюда сносить. Иначе будет две копии. Отсюда лучше сделать ссылки на них. С уважением, Matist Krusoe 04:23, 16 июня 2006 (UTC)

А зачем было добавлять? —Тоша 14:16, 19 июня 2006 (UTC)

Вообще да, доказательства избыточны неон 14:19, 19 июня 2006 (UTC)

Доказательства не избыточны, если это математика. Они просто лежали не по месту. —Matist Krusoe 10:49, 20 июня 2006 (UTC)

По определению, теорема есть утверждение, верность которого устанавливается посредством доказательства. В соответствии с эти определением, следует в статье Википедии о треугольниках, где приводятся теоремы, приводить доказательство — Дмитрий Васильевич 14:21, 18 ноября 2009 (UTC).

Когда говорится про окружности Веррьера, то, вообще говоря, таких окружностей, касающихся двух сторон треугольника и его описанной окружности, не три, а шесть, три внутренних и три внешних. Соответственно, есть две точки Веррьера и т. д. Просьба исправить и дораскрыть тему. Metamatek 15:15, 23 июня 2012 (UTC) Ваше замечание об окружностях Веррьера учтено

Метрические соотношения!!![править код]

Я считаю, что должны быть! Зачем откатили? —Matist Krusoe 10:47, 20 июня 2006 (UTC)

Был не прав, надо вернуть —Тоша 13:08, 20 июня 2006 (UTC)

Все впорядке —Matist Krusoe 15:31, 20 июня 2006 (UTC)

как вам медиана??????????????????????????????

Вроде как небольшой обман для нахождения высоты.. Там ведь просто площадь..

+ Биссектриса через половинный угол. Фил 14:07, 8 мая 2008 (UTC)

+ Формула Эйлера Фил 14:59, 8 мая 2008 (UTC)

+ У высот самую простю вспомнил 😉 + Отношение радиусов вписанной и описанной..Фил 16:49, 8 мая 2008 (UTC)

+ 2 формулы через все углы.. Фил 14:46, 8 мая 2008 (UTC)

S = r²(ctg(α/2)+ctg(β/2)+ctg(γ/2))

S = sqrt(r*r_a*r_b*r_c) = sqrt(r_a*r_b*r_c / (1/r_a + 1/r_b + 1/r_c))

S = (1/4)*sqrt(-a⁴-b⁴-c⁴+2a²b²+2a²c²+2b²c²)

-Talmon-62.219.167.60 20:52, 6 марта 2013 (UTC)

Последняя формула преобразуется в формулу Герона. В таком виде она легче запоминается. Поэтому включать последнюю формуле нет смысла.

«В случае невыполнения одного из неравенств, треугольник называется вырожденным, далее везде предполагается невырожденный случай». Т.е. c>a+b это вырожденный треугольник? По-моему раньше было верно («В случае равенства»).—Фил 07:28, 29 июня 2008 (UTC)

Пропорциональные отрезки в прямоугольном треугольнике

В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов

В прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу

В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов

90.189.165.69 18:58, 13 мая 2009 (UTC)

Надо бы дописать о применении треугольников[править код]

Не хватает энциклопедичного текста в начале статьи, до формул. О применении треугольников, о том, что они везде, о том, кто их изучал и т.п… —Nashev 22:52, 28 февраля 2010 (UTC)

 Не хватает триангуляций (Делоне и прочих). Постараюсь исправить это. Metamatek 10:29, 13 июня 2012 (UTC)

Одна из важнейших тем в математике. С этой целью выношу данную статью на рецензию, чтобы в будущем статья получила статус «Хорошая». Понравились статьи в Английской и Украинской Википедиях, необходимо и в нашем разделе довести статью про треугольник до высокого уровня. —Brateevsky|сказать 10:07, 12 августа 2011 (UTC)

• Нет источников—Meddoc13 14:15, 12 августа 2011 (UTC)

  В принципе вы правы, статью без источников выдвигать в хорошие…А вот тогда где их взять? И что считать АИ — учебник по геометрии? Тут сложно с этим. Здесь в статье очень много утверждений, которые требуют доказательств (теоремы короче). Выходит, одних доказательств мало, нужно ещё и источники привести (возможно литературу). —Brateevsky|сказать 14:56, 12 августа 2011 (UTC)

  А в чем проблема? Учебник это очень хороший источник. 92.62.159.244 20:42, 12 августа 2011 (UTC)

Комментарии Alex-engraver[править код]

• Поддержу предыдущие комментарии в том, что учебник тоже хороший АИ. —Alex-engraver 17:07, 14 августа 2011 (UTC)

Очень приятно видеть, что не один я вынашиваю мысли написать нормальную статусную статью по математике (из существующих разве что Перцептрон кажется приемлемой), но в настоящем виде статья кажется неполной. Почему — далее в списке. P. S. Если нужна будет помощь с построением простых геометрических диаграмм в SVG — обращайтесь. —Alex-engraver 17:07, 14 августа 2011 (UTC)

• Было бы очень полезно дополнить статью доказательствами (как это оформлено в Уравнениях Максвелла, к примеру). —Alex-engraver 17:07, 14 августа 2011 (UTC)
• Сейчас в статье рассматривается исключительно геометрия на плоскости. И в этом определение из преамбулы «часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки» строго говоря не является общим — плоскость не обязательна. У треугольника на сфере сумма углов больше 180° (кривизна положительна). На поверхности с отрицательной кривизной будет наоборот. О подобных свойствах в хорошей статье ИМХО следует хотя бы упомянуть, а в ибранной — осветить настолько подробно, насколько это возможно. —Alex-engraver 17:07, 14 августа 2011 (UTC)

  Контекст предмета данной статьи задан не слишком непосредственно. Статья не начинается словами типа «В планиметрии, треугольником называют…». И, возможно, зря она как-то так не начинается (определённо там вместо планиметрии, правда, нужно что-то шире. Может, евклидова геометрия). Но есть в преамбуле ссылка на многоугольник, одно из определений в которой сужает простор до плоскости. Сферический треугольник есть в своей статье; его надо помянуть в преамбуле данной и/или в самостоятельном разделе о неплоских треугольниках, слегка собезьянничав в этой части относительно англовики. 213.171.63.227 13:34, 25 августа 2011 (UTC)

  С этим совершенно согласен и внизу мне также указали на то, что статья сейчас заявляет о рассмотрении планиметрии. Но тогда её следует переименовать с созданием обобщающей статьи хотя бы в виде стаба. —Alex-engraver 13:52, 25 августа 2011 (UTC)

• Кажется полезным дополнение о нетривиальных свойствах треугольников (из олимпиадных задач, например). А если таковы будут ещё и с доказательствами то вообще супер. —Alex-engraver 17:07, 14 августа 2011 (UTC)
• Хотелось бы почитать о построениях заданных треугольников на плоскости, что-то вроде как здесь, к примеру. —Alex-engraver 17:07, 14 августа 2011 (UTC)
• Существуют «известные» треугольники. Например, определение кривизны пространства построением гигантских треугольников (как пример, описание некоторых экспериментов), тиангуляция поверхностей в компьютерной графике, треугольник у масонов в качестве экзотики. Возможно, это выходит за рамки ХС, но может быть удастся хотя бы упомянуть сделав задел для дальнейшего развития. —Alex-engraver 17:07, 14 августа 2011 (UTC)
• В ЭнВики статья существенно больше, думаю, оттуда можно многое почерпнуть в плане затрагиваемых аспектов. —Alex-engraver 17:07, 14 августа 2011 (UTC)

Отдельная проблема, решения которой пока не могу предложить сам, это вроде как неизбежное множество списков в статье. Может быть на номинации с этим со вздохом смирятся, но замечания по этому поводу будут обоснованными. —Alex-engraver 17:07, 14 августа 2011 (UTC)

По поводу оформления:

• «Типы треугольников» ИМХО лучше загнать не в таблицу, а в {{Gallery}}. —Alex-engraver 17:07, 14 августа 2011 (UTC)
• В «Площадь треугольника» ИМХО будет лучше сначала ввести условные обозначения, а потом перечислить формулы. —Alex-engraver 17:07, 14 августа 2011 (UTC)
• В вычислении площади с помощью векторов необходимо указать что это за таблица в прямых скобках — школьники могут закрыть Википедию навечно увидев в такой статье детерминант без объяснения с чем его едят 🙂 —Alex-engraver 17:07, 14 августа 2011 (UTC)

Комментарий Abeshenkov[править код]

• Что сейчас есть это курс школьной геометрии. С излишними подробностями. Так совершеннно лишне приводить 12 различных формул для площади треугольника. Можно дать одно и указание как из него вывести все остальные.—Abeshenkov 04:35, 17 августа 2011 (UTC)
• Совершенно с этим не согласен. Чем больше формул площади, тем лучше. Не все смогут вывести нужные формулы по этим указаниям. Некоторые люди просто используют готовые формулы, и вывод их абсолютно не интересует. К тому же этих формул не так много. — Эта реплика добавлена с IP 78.132.137.69 (о)
• Разносторонний треугольник — такого термина нет.—Abeshenkov 04:35, 17 августа 2011 (UTC)

Да?? И где?—Abeshenkov 13:05, 1 сентября 2011 (UTC)

Да везде.—Lupus-sapiens 17:58, 5 ноября 2011 (UTC)

• Как уже говорили свойства треугольника выскакивают в разлчных моментах. Геометрия лобачевского и римана лишь часть из этого. К примеру если вместо декартова пространства взять пространство функций, то там тоже появятся некоторые соотношения треугольника.—Abeshenkov 04:35, 17 августа 2011 (UTC)
• Треугольник используется в различных алгоритмах и технологиях в программировании. Ну а про различные построения в стереометрии и высшей математике я уже молчу.—Abeshenkov 04:35, 17 августа 2011 (UTC)

Комментарии Lupus-sapiens[править код]

Статья производит пока впечатление довольно сырой. Сама идея сделать статью о треугольнике хорошей весьма естественна. Однако, во-первых, надо ограничить тему. Даже только в математике треугольник довольно многолик. Я бы назвал статью «треугольник (планиметрия)». Во-вторых, надо стилистически статью к чему-то привязать. Наверное, правильнее всего к школьной программе. По крайней мере, в тех языковых разделах, где статья признана хорошей, сделано именно так (посмотрите грузинскую и португальскую), а вот в английской попытались объять необъятное, получился нечитаемый кошмар. —Lupus-sapiens 10:19, 21 августа 2011 (UTC)

Список формул и свойств выглядит с одной стороны объёмным и пугающим, с другой стороны совершенно бессистемным и произвольным. Я могу привести ещё десятки других формул и указать десятки других точек, прямых, окружностей и прочего, связанного с треугольником. Непонятно, почему выбраны те, а не другие свойства.—Lupus-sapiens 10:19, 21 августа 2011 (UTC)

Точечные замечания:

• иллюстрировать статью о треугольнике изображением равностороннего треугольника странно.
• вырожденный треугольник в ряде источников не считается треугольником
• Фраза «С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве» не имеет смысла.
• Тригонометрия совсем не треугольники изучает (это только название такое; с тем же успехом можно было бы говорить, что геометры занимаются землемерием).
• вырожденный треугольник тоже выпуклый.
• термины «равенство» и «конгруэнтность» используются в статье как попало. Термин «конгруэнтность» не используется в школьных учебниках России уже около 20 лет.
• выводить из теоремы синусов свойство «против большего угла лежит большая сторона» сложно (ведь синус не монотонная функция), и уж заведомо так не делается в школьных учебниках, — это свойство доказывается в 7 классе, когда ни о каких синусах ещё и речи нет.—Lupus-sapiens 10:19, 21 августа 2011 (UTC)

Помещать доказательства в статью, как советуют некоторые комментаторы, означает превратить её в учебник геометрии — непонятно, зачем это нужно. Лучше уж написать хороший Викиучебник. —Lupus-sapiens 10:19, 21 августа 2011 (UTC)

Что непременно нужно в статье о треугольнике — системы координат, связанные с треугольником, барицентрические и плюккеровы. Если, конечно, мы хотим несколько выйти за пределы школьного учебника.—Lupus-sapiens 10:22, 21 августа 2011 (UTC)

BoBink[править код]

Надо или уточнить, что статья сугубо математическая, или вводить огромный новый раздел о культурологическом влиянии. Всё-таки, наравне с кругом или крестом, это один из универсальных символов. Начиная от Треугольник (созвездие), Бермудский треугольник и заканчивая Розовый треугольник. С уважением BoBink 12:32, 8 сентября 2011 (UTC)

Спасибо. Я тогда в начале статьи это напишу; а соответсвующие названия Треугольник (созвездие), Бермудский треугольник и заканчивая Розовый треугольник сделаю как ссылки. —Brateevsky|сказать|$! 15:08, 8 сентября 2011 (UTC)

Надеюсь, Вы пошутили 🙂 —Alex-engraver 19:21, 8 сентября 2011 (UTC)

Deevrod[править код]

В текущем виде статья совершенно неприемлема для того, чтобы быть даже хорошей, поскольку представляет собой груду метрико-алгебраических соотношений. В статье упомянуты лишь самые школьные точки, связанные с треугольником, про изогональное или изотомическое сопряжение ни слова, равно как и про связь коник с треугольником. Попытаюсь исправить это. deevrod (обс) 10:01, 16 сентября 2011 (UTC)

• Дополнил немного, прошу желающих нарисовать иллюстрации. С доказательствами пока повременю. deevrod (обс) 12:47, 16 сентября 2011 (UTC)

Новая редакция (от 16 декабря 20011 года)[править код]

В связи с тем, что статья номинировлась в хорошие, но, по понятным причинам не получила статус хорошей, я взялся за передлку этой статьи, именно для того, чтобы сделать её хорошей. Я надеюсь сделать это вместе с другими участниками и, прежде всего, с участником Deevrod, которому я, собственно и хочу помочь сделать данную статью хорошей. Но это нужно не для, собственно, статуса, а для того, чтобы задать некоторый уровень качества статей в Википедии. Пока я убрал из статьи всё, что совершенно никак не уладывается в представления об энциклопедичности, и существенно отредактирую то, что осталось. Я сделал копию предыдущей версии статьи в Участник:OZH/Статьи/Треугольник, которой я буду пользоваться для пополнения статьи по мере её написания. Пока я предлагаю аккуратно описать описать то, что непосредственно связано с треугольником, а уже потом взяться за другие важные вопросы. Ниже я займусь формированием структуры будущей статьи. —OZH 18:52, 16 декабря 2011 (UTC)

• Я принялся править статью. Но сейчас у меня выходит пауза. Надеюсь, небольшая (одна неделя). Прошу отнестись с пониманием. Я хочу вывести статью в хорошие и очень надеюсь на помощь других участников. Именно, на помощь. И на понимание. 🙂 —OZH 20:19, 5 января 2012 (UTC)

Определение про три отрезка и три точки.[править код]

Это же абсолютно не верно! Как можно найти площадь фигуры, состоящей из трех точек и трех отрезков? Часть плоскости в рамках Евклидовой геометрии вполне корректно Kombi 12:29, 15 октября 2012 (UTC)

Неравенства с площадью треугольника[править код]

Приведенные неравенства, оценивающие снизу и сверху площадь треугольника с заданныим радиусами вписанной и описанной окружностями:
sqrt(27)*r² <= S <= sqrt(27)*R²/4
очень слабые. Написано: «причём оба равенства достижимы». Это не совсем верно. Они достижимы только для равностороннего треугольника, когда R=2r, и никак не достижимы при других соотношениях радиусов.
Более сильные неравенства, в которых равенства достижимы при любых соотношениях радиусов, т.е., определяющие точные границы возможных значений площади при любых заданных допустимых значениях радиусов, являются:
sqrt((R-d+r)³(R+d-r)) <= S <= sqrt((R+d+r)³(R-d-r)),
где d = sqrt(R² — 2Rr) — расстояние между центрами вписанной и описанной окружностями.—Talmon 20:51, 5 марта 2013 (UTC)Talmon—Talmon 20:51, 5 марта 2013 (UTC)

Последняя фраза лишена смысла, так как прямая лежать на прямой не может. Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности (если точка, изогонально (изотомически) сопряжённая точке X, лежит на трилинейной поляре точки Y, то трилинейная поляра точки, изогонально (изотомически) сопряжённой точке Y лежит на трилинейной поляре точки X).

Автор сообщения: Shelomovskii 94.231.169.188 23:26, 11 октября 2014 (UTC)

К обсуждению. Sealle 02:55, 16 октября 2014 (UTC)

В принципе хорошо, когда статья отличается полнотой освещения своей темы. Однако приходится констатировать, что данная статья безобразно разбухла до такой степени, что фактически потеряла практическую ценность. Найти в ней нужные сведения — нелёгкая задача. В интересах читателя предлагаю переформатировать статью следующим образом: сделать первым разделом «Основные сведения» и включить туда весь материал школьного уровня, а затем, в разделе «Дополнительные сведения», изложить более редко используемый коллекционный материал. Сейчас почему-то наоборот, самые важные сведения (теорема синусов, площадь и т. п.) вынесены в конец статьи. Приглашаю участников высказать своё мнение. LGB 16:36, 9 мая 2016 (UTC)

• Да, давно пора. Причем некоторые разделы могут стать отдельными статьями. Например, материала вполне достаточно для статьи Окружности треугольника, в основной статье достаточно только упоминания вписанной и опианной окружности. То же для остальных коник и кубик. Площадь треугольника — тоже может быть отдельной статьей (сейчас перенаправление), а в основной статье только упомянуть основные (школьные) формулы. Alexei Kopylov 17:39, 9 мая 2016 (UTC)
  • Может быть, даже целесообразно сделать общую статью «Вписанные и описанные фигуры для треугольника». Вынести Площадь треугольника как детальную статью — тоже хорошая идея. При этом важно, чтобы все отпочкованные статьи были структурированы в интересах читателя, то есть практически самый важный материал был в начале и удобен для применения (в смысле единства обозначений, удобства поиска по оглавлению и др.). LGB 18:18, 9 мая 2016 (UTC)
    • Конечно, за. Давно уже наблюдаю за превращением этой статьи в свалку склад ценной, значимой, но практически неструктурированной информации. К сожалению, не имею времени на систематизацию, и буду признателен участникам, которые это сделают. DmitTrix 09:01, 10 мая 2016 (UTC)

Я реализовал переделку статьи, о которой говорилось выше. Расцениваю эту корректировку как минимально необходимую, возможно, кто-то захочет продолжить, например, для отделения детальной статьи «Площадь треугольника» и добавления сносок на источники. LGB 17:14, 23 мая 2016 (UTC)

Дуга геодезической — она сама является геодезической? Mx1024 (обс) 20:31, 20 июня 2016 (UTC)

По мнению участника LGB[1], «геодезическая линия по определению не имеет концов, если они специально не заданы».Mx1024 (обс) 20:50, 20 июня 2016 (UTC)

Понятие А является обобщением понятия Б. Это означает Б является частным случаем А. Пример. Многоугольник — обобщение понятия треугольника. (Любой треугольник является многоугольником.) Mx1024 (обс) 09:59, 25 июня 2016 (UTC)

«Замкнутая ломаная из трёх отрезков»? Площадь отрезка равна нулю. Площадь любой замкнутой ломаной из трёх отрезков равна нулю. Mx1024 (обс) 12:08, 25 июня 2016 (UTC)

Золотой треугольник (геометрия) — Википедия

Материал из Википедии — свободной энциклопедии

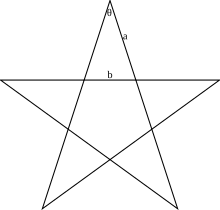Пентаграмма. Каждый угол является золотым треугольником. Фигура также содержит пять золотых гномонов, которые получаются соединением двух несмежных углов с центральным пятиугольником.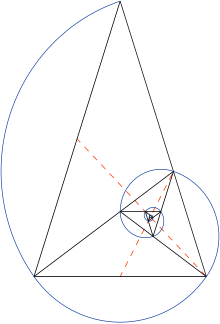

Золотой треугольник^[1] — это равнобедренный треугольник, в котором две боковые (равные) стороны находятся в золотой пропорции с основанием:

ab=φ=1+52.{\displaystyle {a \over b}=\varphi ={1+{\sqrt {5}} \over 2}.}

Золотые треугольники можно обнаружить в развёртках некоторых звёздчатых форм додекаэдра и икосаэдра.

Также, тот же треугольник обнаруживается в вершинах пентаграммы. Угол при вершине равен

θ=cos−1⁡(φ2)=π5=36∘.{\displaystyle \theta =\cos ^{-1}\left({\varphi \over 2}\right)={\pi \over 5}=36^{\circ }.}

Из того, что сумма углов треугольника равна 180°, получаем, что углы при основании равны 72°^[1]. Золотой треугольник можно найти также в десятиугольнике, если соединить две смежные вершины с центром. Полученный треугольник будет золотым, поскольку: 180(10-2)/10=144° является внутренним углом десятиугольника, и деление его отрезком, соединяющим вершину с центром, даст половину, 144/2=72^[1].

Золотой треугольник также замечателен уникальным соотношением углов 2:2:1^[2].

Последовательность золотых треугольников можно вписать в логарифмическую спираль. (Начиная с большого треугольника) делим угол при основании пополам, получаем следующую точку^[3]. Процесс деления может продолжаться бесконечно, создавая бесконечно много золотых треугольников. Логарифмическую спираль можно провести через полученные вершины. Эта спираль известна также как равноугольная спираль. Термин предложил Рене Декарт: «Если провести прямую из полюса к любой точке на кривой, она пересечёт кривую всегда под одним и тем же углом»^[4].

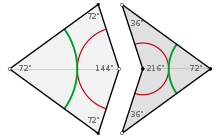
Золотой треугольник разбит на два треугольника Робинсона — золотой треугольник и золотой гномон.

Тесно связан с золотым треугольником золотой гномон, тупоугольный равнобедренный треугольник, в котором отношение длины равных (коротких) сторон к длине третьей стороны (основанию) является обратным к золотому отношению. Золотой гномон является уникальным треугольником с пропорцией углов 1:1:3. Его острые углы составляют 36°, то же значение, что и у угла при вершине золотого треугольника.

Расстояние AX и СX равны φ, что видно на рисунке. «Золотой треугольник имеет отношение основания к стороне, равное золотому отношению φ, в то время как золотой гномон имеет отношение боковой стороны к основанию, равное тому же золотому отношению» ^[5].

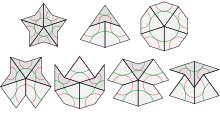
Плитки (сверху) и семь возможных типов вершин (снизу) в мозаике Пенроуза типа P2

Золотой треугольник может быть разрезан на золотой треугольник и золотой гномон. То же самое верно для золотого гномона. Золотой гномон и золотой треугольник с их равными сторонами (сторона гномона равна стороне треугольника) также являются тупым и острым треугольниками Робинсона^[2].

Эти равнобедренные треугольники могут быть использованы для получения мозаик Пенроуза. Плитки Пенроуза состоят из «змеев» и «дротиков». «Змей» представляет собой дельтоид, состоящий из двух золотых треугольников, а «дротик» — дельтоид, состоящий из двух золотых гномонов.

• Kimberly Elam. Geometry of Design. — New York: Princeton Architectural Press, 2001. — ISBN 1-56898-249-6.
• H.E. Huntley. The Divine Proportion: A Study In Mathematical Beauty. — New York: Dover Publications Inc, 1970. — ISBN 0-486-22254-3.
• Mario Livio. The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number. — Broadway Books, 2002. — ISBN 0-7679-0815-5.
• Arthur Loeb. Concepts and Images: Visual Mathematics. — Boston: Birkhäuser Boston, 1992. — ISBN 0-8176-3620-X.

Треугольник Кеплера — Википедия

Материал из Википедии — свободной энциклопедии

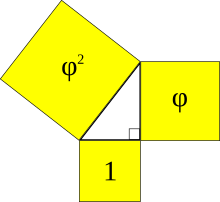Треугольник Кеплера — это прямоугольный треугольник, длины сторон которого составляют геометрическую прогрессию, соответствующую золотому сечению.

Треугольник Кеплера — это прямоугольный треугольник, длины сторон которого составляют геометрическую прогрессию. При этом соотношение длин сторон треугольника Кеплера связано с золотым сечением

φ=1+52{\displaystyle \varphi ={1+{\sqrt {5}} \over 2}}

которое может быть записано в виде : 1:φ:φ{\displaystyle 1:{\sqrt {\varphi }}:\varphi }, или приблизительно 1 : 1.272 : 1.618^[1] Квадраты сторон этого треугольника (см. рисунок) составляют геометрическую прогрессию, соответствующую золотому сечению.

Треугольники с таким соотношением сторон были названы в честь немецкого математика и астронома Иоганна Кеплера (1571—1630), который первым продемонстрировал, что в таких треугольниках отношение длины короткого катета к гипотенузе равно золотому сечению^[2]. Таким образом, треугольник Кеплера объединяет в себе два ключевых математических понятия — теорему Пифагора и золотое сечение, по поводу чего Кеплер отметил:

В геометрии существует два сокровища: одно из них — теорема Пифагора, другое — разделение линии в золотой пропорции. Первое мы можем сравнить с массой золота, второе мы можем назвать драгоценным камнем. Иоганн Кеплер

Некоторые источники утверждают, что соотношение сторон знаменитых пирамид в Гизе приближается к треугольнику Кеплера^[4][5].

Тот факт, что треугольник со сторонами 1{\displaystyle 1}, φ{\displaystyle {\sqrt {\varphi }}} и φ{\displaystyle \varphi } образует прямоугольный треугольник, прямо следует из переписывания квадратного трёхчлена для золотого сечения φ{\displaystyle \varphi }:

φ2=φ+1{\displaystyle \varphi ^{2}=\varphi +1}

в виде теоремы Пифагора:

(φ)2=(φ)2+(1)2.{\displaystyle (\varphi )^{2}=({\sqrt {\varphi }})^{2}+(1)^{2}.}

Отношение к среднему арифметическому, среднему геометрическому и среднему гармоническому[править | править код]

Для положительных вещественных чисел а и b их среднее арифметическое, среднее геометрическое и среднее гармоническое являются длинами сторон прямоугольного треугольника тогда и только тогда, когда треугольник является треугольником Кеплера^[6].

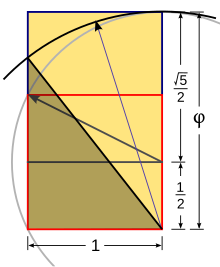
Треугольник Кеплера может быть построен с помощью циркуля и линейки через построение золотого сечения следующим образом:

1. Построить простой квадрат
2. Провести линию от середины одной стороны квадрата к противоположному углу
3. Использовать эту линию в качестве радиуса дуги, определяющей высоту прямоугольника
4. Дополнить до золотого сечения
5. Использовать длинную сторону прямоугольника золотого сечения в качестве радиуса дуги, которая, пересекая противоположную сторону прямоугольника, задаёт длину гипотенузы треугольника Кеплера.

Сам Кеплер строил этот треугольник по-другому. В письме к своему бывшему учителю, профессору Михаэлю Мёстлину, он писал: «Если на линии, которая разделена в крайнем и среднем отношении, построить прямоугольный треугольник таким образом, что прямой угол будет находиться в точке раздела, то меньшая сторона будет равняться большему сегменту разделенной линии.»^[2].

Возьмём треугольник Кеплера со сторонами a,aφ,aφ,{\displaystyle a,a{\sqrt {\varphi }},a\varphi ,} и рассмотрим:

• окружность, которая окружает его, и
• квадрат со стороной, равной средней по величине стороне треугольника.

Тогда периметр квадрата (4aφ{\displaystyle 4a{\sqrt {\varphi }}}) и длина окружности (aπφ{\displaystyle a\pi \varphi }) совпадают с точностью до 0,1 %.

Это математическое совпадение π≈4/φ{\displaystyle \pi \approx 4/{\sqrt {\varphi }}}. Эти квадрат и окружность не могут иметь одинаковую длину периметра, поскольку в этом случае можно было бы решить классическую неразрешимую задачу о квадратуре круга. Другими словами, π≠4/φ{\displaystyle \pi \neq 4/{\sqrt {\varphi }}} поскольку π{\displaystyle \pi } — трансцендентное число.

1. ↑ Roger Herz-Fischler. The Shape of the Great Pyramid (неопр.). — Wilfrid Laurier University Press (англ.)русск., 2000. — ISBN 0-88920-324-5.
2. ↑ ^{1 2} Livio, Mario. The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number (англ.). — New York: Broadway Books (англ.)русск., 2002. — P. 149. — ISBN 0-7679-0815-5.
3. ↑ Karl Fink, Wooster Woodruff Beman, and David Eugene Smith. A Brief History of Mathematics: An Authorized Translation of Dr. Karl Fink’s Geschichte der Elementar-Mathematik (англ.). — 2nd ed.. — Chicago: Open Court Publishing Co, 1903.
4. ↑ The Best of Astraea: 17 Articles on Science, History and Philosophy (англ.). — Astrea Web Radio, 2006. — ISBN 1-4259-7040-0.
5. ↑ Squaring the circle, Paul Calter
6. ↑ Di Domenico, Angelo, «The golden ratio—the right triangle—and the arithmetic, geometric, and harmonic means, » The Mathematical Gazette 89, 2005.

Соотношение между сторонами и углами прямоугольного треугольника. Геометрия, 8 класс: уроки, тесты, задания.

1.	Отношение сторон в прямоугольном треугольнике Сложность: лёгкое
2.	Отношение сторон в прямоугольном треугольнике, теорема Пифагора Сложность: лёгкое
3.	Синус или косинус Сложность: лёгкое
4.	Тангенс, синус или косинус Сложность: лёгкое
5.	Тангенс острого угла прямоугольного треугольника Сложность: лёгкое
6.	Катет прямоугольного треугольника, свойство прямоугольного треугольника Сложность: лёгкое
7.	Диагональ и сторона прямоугольника Сложность: лёгкое
8.	Высота трапеции Сложность: лёгкое
9.	Синус, косинус и тангенс острого угла, гипотенуза прямоугольного треугольника Сложность: среднее
10.	Гипотенуза и катет прямоугольного треугольника Сложность: среднее
11.	Площадь параллелограмма и треугольника, дан острый угол Сложность: среднее
12.	Свойства прямоугольных треугольников, имеющих угол в 30 или 45 градусов. Сложность: среднее
13.	Синус, косинус или тангенс, площадь прямоугольного треугольника Сложность: среднее
14.	Катет прямоугольного треугольника, дан тангенс острого угла Сложность: лёгкое
15.	Синус и косинус острого угла, гипотенуза прямоугольного треугольника Сложность: лёгкое
16.	Катет прямоугольного треугольника, использование синуса или косинуса Сложность: лёгкое
17.	Прямоугольный треугольник, тригонометрия Сложность: лёгкое
18.	Сторона и площадь квадрата, дана его диагональ Сложность: среднее
19.	Сторона равностороннего треугольника Сложность: среднее
20.	Стороны и площадь прямоугольника Сложность: среднее
21.	Площадь равнобедренной трапеции Сложность: среднее
22.	Диагональ и сторона прямоугольника Сложность: среднее
23.	Сторона и площадь квадрата, дана его диагональ Сложность: среднее
24.	Стороны и площадь прямоугольника Сложность: среднее
25.	Диагональ прямоугольной трапеции Сложность: сложное