Нахождение вершины параболы: найти её координаты, способы

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

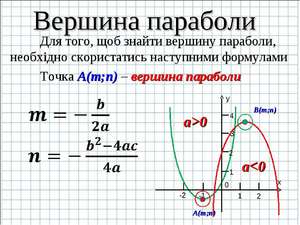
Нахождение вершины параболы: способы, примеры, советы

График функции y = ax²+ bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

Первый способ

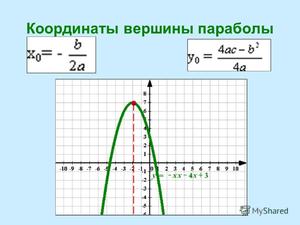
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x²–8 x +15;

находим первый, второй коэффициенты и свободный член;

подставляем значения a и b в формулу;

вычисляем значения y;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x²–6x+5

1) Приравниваем к нулю:

2) Находим дискриминант, используя формулу: D = b

2–4 ac:

3) Находим корни уравнения по формуле (-b±√ D)/2a:

• 1 — первый корень;
• 5 — второй корень.

4) Вычисляем:

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x ²+8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x² + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2)² и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

x² + 8x +16= 6.

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4)² = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

• Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x ²+11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

• Нужно проверять правильно ли ваше решение.
• Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы

liveposts.ru

Как найти вершину параболы и построить ее

В математике есть целый цикл тождеств, среди которых значимое место занимают квадратичные уравнения. Подобные равенства могут решаться как отдельно, так и для построения графиков на оси координат. Корни квадратных уравнений являются точками пересечения параболы и прямой ох.

Общий вид

Квадратное уравнение в общем виде имеет следующую структуру:

ax² +bx+c=0

В роли «икса» могут рассматриваться как отдельные переменные, так и целые выражения. Например:

2x²+5x-4=0;

(x+7)²+3(x+7)+2=0.

В том случае, когда в роли х выступает выражение, необходимо представить его как переменную и найти корни уравнения. После этого к ним приравнять многочлен и найти х.

Так, если (х+7)=а, то уравнение принимает вид а²+3а+2=0.

Д=3²-4*1*2=1;

а₁=(-3-1)/2*1=-2;

а₂=(-3+1)/2*1=-1.

При корнях, равных -2 и -1, получим следующее:

x+7=-2 и x+7=-1;

x=-9 и x=-8.

Корни являются значением х-координаты точки пересечения параболы с осью абсцисс. В принципе, их значение не так уж и важно, если поставлена задача лишь найти вершину параболы. Но для построения графика корни играют важную роль.

Как найти вершину параболы

Вернемся к начальному уравнению. Для ответа на вопрос о том, как найти вершину параболы, необходимо знать следующую формулу:

x_вп=-b/2a,

где х_вп— это значение х-координаты искомой точки.

Но как найти вершину параболы без значения у-координаты? Подставляем полученное значение х в уравнение и находим искомую переменную. Например, решим следующее уравнение:

х²+3х-5=0

Находим значение х-координаты для вершины параболы:

х_вп=-b/2a=-3/2*1;

х_вп=-1,5.

Находим значение у-координаты для вершины параболы:

у=2х²+4х-3=(-1,5)²+3*(-1,5)-5;

у=-7,25.

В результате получаем, что вершина параболы находится в точке с координатами (-1,5;-7,25).

Построение параболы

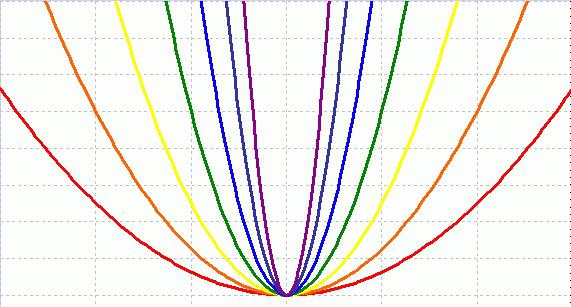Парабола представляет собой соединение точек, имеющее вертикальную ось симметрии. По этой причине само ее построение не представляет особого труда. Самое сложное – это произвести правильные расчеты координат точек.

Стоит обратить особое внимание на коэффициенты квадратного уравнения.

Коэффициент а влияет на направление параболы. В том случае, когда он имеет отрицательное значение, ветви будут направлены вниз, а при положительном знаке – вверх.

Коэффициент b показывает, насколько широк будет рукав параболы. Чем больше его значение, тем он будет шире.

Коэффициент с указывает на смещение параболы по оси ОУ относительно начала координат.

Как найти вершину параболы, мы уже узнали, а чтобы найти корни, следует руководствоваться следующими формулами:

Д=b²-4ac,

где Д – это дискриминант, который необходим для нахождения корней уравнения.

x₁=(-b+V^—Д)/2a

x₂=(-b-V^—Д)/2a

Полученные значения х будут соответствовать нулевым значениям у, т.к. они являются точками пересечения с осью ОХ.

После этого отмечаем на координатной плоскости вершину параболы и полученные значения. Для более детального графика необходимо найти еще несколько точек. Для этого выбираем любое значение х, допустимое областью определения, и подставляем его в уравнение функции. Результатом вычислений будет координата точки по оси ОУ.

Чтобы упростить процесс построения графика, можно провести вертикальную линию через вершину параболы и перпендикулярно оси ОХ. Это будет ось симметрии, при помощи которой, имея одну точку, можно обозначить и вторую, равноудаленную от проведенной линии.

fb.ru

как найти производную в точке х0

Вы искали как найти производную в точке х0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найдите значение производной функции y f x в точке x, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как найти производную в точке х0».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как найти производную в точке х0,найдите значение производной функции y f x в точке x,найдите значение функции в точке x0. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как найти производную в точке х0. Просто введите задачу в окошко и нажмите «решить» здесь (например, найдите значение функции в точке x0).

Где можно решить любую задачу по математике, а так же как найти производную в точке х0 Онлайн?

Решить задачу как найти производную в точке х0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

www.pocketteacher.ru

нули функции. как найти нули функции. график функции y=f(x) как вообще их находить, что это значит?

Нули функции — это такое значение х, при котором функция y=f(x) равна нулю (то есть график функции пересекается с осью Х) . Для того, чтобы найти нули функции, надо функцию приравнять к нулю. Например, дана функция f(x) = х2 – 4 (икс в квадрате минус четыре) Приравниваем к нулю: х2 – 4 = 0 А теперь решаем как квадратное уравнение, находим х (первое) = — 2, х (второе) = 2 При этих значениях х функция y=f(x) = 0 Это можно сделать и графически. Просто построить функцию по точкам и начертить, точки пересечения графика с осью Х и будут нулями функции. Посмотрите еще здесь: <a rel=»nofollow» href=»/» title=»11898030:##:http://www.webmath.ru/poleznoe/svoistva_funcsii.php» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a> <a rel=»nofollow» href=»http://www.mathematics.ru/courses/function/content/chapter1/section3/paragraph4/theory.html» target=»_blank»>http://www.mathematics.ru/courses/function/content/chapter1/section3/paragraph4/theory.html</a> <a rel=»nofollow» href=»http://fgraphiks.narod.ru/svoistva.html» target=»_blank»>http://fgraphiks.narod.ru/svoistva.html</a>

найти при каких х f(х) =0

Ну несколько способов.. Я припоминаю два: 1.Графический. Вы строите график функции и смотрите при каких значениях «х» он пересекает ось «Х» 2.Ну просто f(x)=0 Приравниваем функцию к нулю и считаем «нули» 🙂 Туфтология чутка 🙂

touch.otvet.mail.ru

x нулевое

Вы искали x нулевое? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и игрек нулевое формула, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x нулевое».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как x нулевое,игрек нулевое формула,икс нулевое формула,как найти x нулевое,как найти y нулевое,как найти игрек нулевое,как найти икс нулевое,как найти у нулевое,как найти х нулевое,как найти х0 в физике,формула x нулевое,формула игрек нулевое,формула нулевого х,формула х нулевого,х нулевое,х нулевое как найти,х нулевое формула. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и x нулевое. Просто введите задачу в окошко и нажмите «решить» здесь (например, икс нулевое формула).

Где можно решить любую задачу по математике, а так же x нулевое Онлайн?

Решить задачу x нулевое вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

www.pocketteacher.ru