Простые и составные числа. Видеоурок. Математика 6 Класс

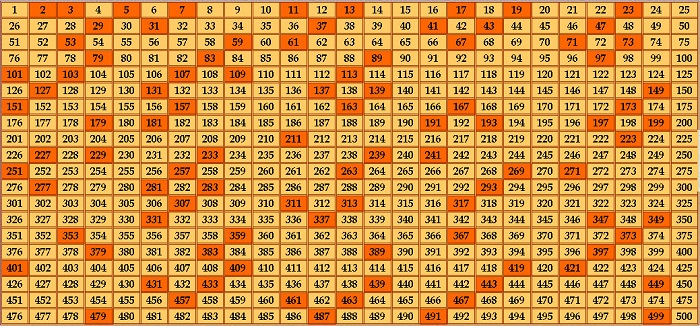
Рассмотрим рисунок 1, на нем выписан натуральный ряд чисел.

Рис. 1. Числа от 1 до 100 (Источник)

Правила игры

1. Берем число, а потом вычеркиваем все числа, которые на него делятся. Начинаем с 2.

Так, каждое второе число будет делиться на два (рис. 2).

Рис. 2. Вычеркивание всех чисел, которые делятся на 2

2. Берем следующее незачеркнутое число и обводим его кружочком. Вычеркиваем числа, которые делятся на три.

Рис. 3. Вычеркивание чисел, которые делятся на 3

3. Следующее незачеркнутое число – пять. Вычеркиваем все числа, делящиеся на пять (рис. 4).

Рис. 4. Вычеркивание чисел, которые делятся на 5

4. Берем число семь и продолжаем зачеркивать числа (рис. 5).

Рис. 5. Вычеркивание чисел, которые делятся на 7

5. Посмотрим, что получилось: зачеркнуты почти все числа. После того как мы подумаем над тем, что объединяет все зачеркнутые числа, ответим: они все на что-то делились. Те числа, которые остались незачеркнутыми (рис. 4), ни на что, кроме себя и единицы, не делятся.

Данное действие называется решето Эратосфена – просеивание натурального ряда в поисках простых чисел. Простые числа – это такие числа, которые делятся на себя и на единицу (например: 2, 3, 5, 7 и т. д.). Те числа, которые делятся не только на себя и на единицу, имеют больше двух делителей, называются

составными.

Есть интересное число, которое делится только на себя (имеет один делитель). Это единица, она не является ни простым, ни составным.

Все натуральные числа – числа, которые мы используем при счете, можно разделить на три группы.

1. Простые – имеют только два делителя: единицу и само себя, например: 2, 3, 5, 7, 11, 17, 19, 23 и т. д.

2. Составные числа – имеют больше двух делителей, например: 4, 6, 8,10,15, 22 и т. д.

3. Единица (1) имеет только один делитель.

Если посмотрим на таблицу простых чисел (рис. 6), то заметим, что все числа, кроме двойки, нечетные. Самое маленькое простое число – два. А самое большое из ныне найденных простых чисел содержит семнадцать миллионов четыреста двадцать пять тысяч сто семьдесят цифр: 17 425 170 цифр.

Рис. 6. Таблица некоторых простых чисел (Источник)

Любое натуральное число можно разложить в произведение простых чисел единственным образом с точностью до порядка сомножителей.

1. Например, число 6 можно получить, если 3 умножить на 2 или 2 умножить на 3.

2. Аналогично раскладываем на простые множители число 48.

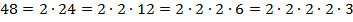
Обратите внимание: каждый раз мы выделяли простой множитель, а потом второй множитель раскладывали на множители и так, пока не получили все простые.

3. Теперь для разложения с помощью основной теоремы арифметики возьмем 122. Данное число делится на два, получаем 61. Так как шестьдесят один – это простое число, то разложение числа 122 на простые множители:

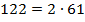
4. Если разложим число 462 на простые множители, получим:

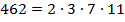
В простых числах интересно то, что иногда они стоят через один (подряд простые числа стоять не могут, потому что каждое второе делится на 2, исключением является пара 2 и 3), например 3 и 5 или 71 и 73, или 461 и 463, такие числа называют «близнецами». Иногда простые числа очень далеко расположены друг от друга и найти каждое следующее простое число с каждым разом все сложнее.

Криптограф – специалист по расшифровке и зашифровыванию информации.

Так, криптографы используют большие простые числа, для того чтобы создавать коды, которые очень сложно взламывать.

В последующих уроках нам потребуются знания о простых числах, чтобы вычислять НОД – наибольший общий делитель и НОК – наименьшее общее кратное.

 

Список литературы

1. Математика. 6 класс. Учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с.: ил.

2. Зубарева И.И., Мордкович А.Г. Математика, 6 класс. – М.: Мнемозина.

3. Истомина Н.Б., Математика, 6 класс. – М.: Ассоциация ХХI век.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «Научная библиотека» (Источник)

2. Интернет портал «Clever Students» (Источник)

3. Интернет портал «Школьный помощник» (Источник)

 

Домашнее задание

1. Математика. 6 класс. Учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013., ст. 17 § 4, № 95, 98, 104.

2. Что такое натуральные числа?

3. Какие группы натуральных чисел вы знаете? 

4.^*Разложите на простые множитель такие числа, воспользовавшись основной теоремой арифметики:

а) 335              б) 892              в) 647             г) 995              д) 44               е) 220

Онлайн урок: Простые и составные числа по предмету Математика 6 класс

Натуральное число можно представить в виде произведения простых чисел.

Такое разложение будет единственным и может отличаться только порядком множителей.

Это понятие носит название основной теоремы арифметики и используется очень часто.

Посмотрим на примерах, как всё тут работает.

Разложить 6 можно двумя способами, расположив по-разному простые множители: 3 умножить на

2 или 2 умножить на 3

\(\mathbf{6 = 3\cdot2 = 2\cdot3}\)

Если попытаемся разложить число 48 на простые множители, то  получим:

\(\mathbf{48 = 2\cdot24 = 2\cdot2\cdot12 = 2\cdot2\cdot2\cdot6= 2\cdot2\cdot2\cdot2\cdot3}\)

Чтобы всё сделать правильно при разложении, нужно выделить простой множитель, с оставшимся числом поступить так же и повторять действия, пока не получатся все простые множители.

Посмотрим еще один пример и возьмем 122.

Это число делится без остатка на два, так как оно чётное, получаем 61. Шестьдесят один — это простое число.

Таким образом, разложение числа 122 на простые множители выглядит так:

\(\mathbf{122 = 2\cdot61}\)

 

Возьмем еще большее число, к примеру, 462. При разложении на простые множители получим:

\(\mathbf{462 = 2\cdot3\cdot7\cdot11}\)

Бывают такие случаи, когда в числовом ряду простые числа стоят через одно составное. Рядом они стоять не могут, ведь каждое второе число будет чётным, значит, оно уже не будет являться простым.

Если простые числа стоят через одно составное, например, 3 и 5 или 71 и 73, или 461 и 463, то они называются «близнецами».

С развитием вычислительной техники было доказано, что простые числа с увеличением располагаются всё дальше друг от друга. Это создаёт проблему при поиске каждого нового простого числа.

 

Пример 1

Используя основную теорему арифметики, разложите на простые множители числа 72, 228, 896, 994, 105, 98

Решение:

$$\mathbf{72 = 8\cdot9=4\cdot2\cdot3\cdot3=2\cdot2\cdot2\cdot3\cdot3}$$

$$\mathbf{228= 12\cdot19 = 4\cdot3\cdot19=2\cdot2\cdot3\cdot19}$$

$$\mathbf{896 = 64\cdot14 = 4\cdot16\cdot2\cdot7= 2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot7}$$

$$\mathbf{994 = 2\cdot7\cdot71}$$

$$\mathbf{105= 3\cdot5\cdot7}$$

$$\mathbf{98 = 2\cdot14 =2\cdot2\cdot7}$$

 

Пример 2

Сколько делителей имеет каждое из чисел: 31, 25, 100, 189, 325, 558, 194?

Решение:

Число 31 имеет два делителя: 1, 31

Число 25 имеет три делителя: 1, 5, 25

Число 100 имеет девять делителей: 1, 2, 4, 5, 10, 20, 25, 50, 100

Число 189 имеет восемь делителей: 1, 3, 7, 9, 21, 27, 63, 189

Число 325 имеет шесть делителей: 1, 5, 13, 25, 65, 325

Число 558 имеет двенадцать делителей: 1, 2, 3, 6, 9, 18, 31, 62, 93, 186, 279, 558

Число 194

имеет четыре делителя: 1, 2, 97, 194

 

Пример 3

Какое из чисел 129, 565, 441, 70, 237, 816 имеет самое большое количество делителей?

Решение:

Число 129 имеет четыре делителя: 1, 3, 43, 129

Число 565 имеет четыре делителя: 1, 5, 113, 565

Число 441 имеет девять делителей: 1, 3, 7, 9, 21, 49, 63, 147, 441

Число 70 имеет восемь делителей: 1, 2, 5, 7, 10, 14, 35, 70

Число 237 имеет четыре делителя: 1, 3, 79, 237

Число 816 имеет двадцать делителей: 1, 2, 3, 4, 6, 8, 12, 16, 17, 24, 34, 48, 51, 68, 102, 136, 204, 272, 408, 816

Самое большое количество делителей имеет число 816

Простые и составные числа | Математика

Натуральные числа, большие единицы, в зависимости от количества их делителей, подразделяются на простые и составные числа.

Простое число – это натуральное число, которое больше единицы и делится только на единицу и само на себя.

Пример.

2, 5, 7, 11 – простые числа.

2 – делится на 1 и на 2.

5 – делится на 1 и на 5.

7 – делится на 1 и на 7.

11 – делится на 1 и на 11.

Составное число – это натуральное число, которое больше единицы, делится не только на единицу и само на себя, но и ещё хотя бы на одно натуральное число.

Пример.

4, 6, 9, 10 – составные числа.

4 – делится на 1, на 2 и на 4.

6 – делится на 1, на 2, на 3 и на 6.

9 – делится на 1, на 3 и на 9.

10 – делится на 1, на 2, на 5 и на 10.

Наименьшее простое число – число 2 (оно же первое простое число). Это единственное чётное простое число. Все остальные простые числа нечётные.

Наименьшее составное число – число 4 (оно же первое составное число).

Простых и составных чисел бесконечно много, есть первое простое и составное число, но нет последнего простого и составного числа.

Единица имеет только один делитель – само число 1. Этим единица отличается от всех остальных натуральных чисел, поэтому условились считать, что единица не является ни простым, ни составным числом.

Не существует простых чисел, оканчивающихся на 4, 6, 8 или 0. Среди простых чисел есть только одно число, оканчивающееся на 2 – само число 2, из оканчивающихся на 5 – тоже есть только одно число – само число 5. Все остальные простые числа, кроме 2 и 5, оканчиваются на 1, 3, 7 или 9. Не все числа, оканчивающиеся на 1, 3, 7, 9, являются простыми, например числа 21, 27, 33, 39 и многие другие – составные.

Как узнать, число простое или составное?

Самый простой способ определить является число простым или составным – посмотреть таблицу простых чисел.

Если под рукой нет таблицы с выписанными простыми числами, то можно попробовать определить с помощью последовательного перебора всех возможных делителей данного числа. Если ни одно число не подойдёт в качестве делителя данного числа, то это число будет простым, в противном случае – составным.

Если данное число превосходит наибольшее число из имеющейся таблицы, то можно попробовать определить с помощью последовательного деления данного числа на простые числа, начиная с числа 2. Если ни одно простое число не подойдёт в качестве делителя данного числа, то это число – простое, в противном случае – составное.

О сайте:	конспекты по математике, русскому языку и химии
Связь:	[email protected]
Новое на сайте | © 2018 – 2019

Простые числа и составные числа. Таблица простых чисел.

Навигация по странице:

Простое число — натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя^[1].

То есть, число x является простым, если оно больше 1 и при этом делится без остатка только на 1 и на x.

Составное число — натуральное число, большее 1, не являющееся простым.

Каждое составное число является произведением двух или более простых чисел.

Таким образом, все натуральные числа разбиваются на три класса:

• единицу — имеет один натуральный делитель,
• простые числа — имеют два натуральных делителя,
• составные числа — имеют больше двух натуральных делителей.

Примеры

2 — простое число (делится на 2 и 1)

3 — простое число (делится на 3 и 1)

4 — составное число (делится на 4, 2 и 1)

5 — простое число (делится на 5 и 1)

6 — составное число (делится на 6, 3, 2 и 1)

7 — простое число (делится на 7 и 1)

8 — составное число (делится на 8, 4, 2 и 1)

9 — составное число (делится на 9, 3 и 1)

10 — составное число (делится на 10, 5, 2 и 1)

Таблица простых чисел от 2 до 1000

2	3	5	7	11	13	17	19	23	29	31	37
41	43	47	53	59	61	67	71	73	79	83	89
97	101	103	107	109	113	127	131	137	139	149	151
157	163	167	173	179	181	191	193	197	199	211	223
227	229	233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409	419	421	431	433
439	443	449	457	461	463	467	479	487	491	499	503
509	521	523	541	547	557	563	569	571	577	587	593
599	601	607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733	739	743
751	757	761	769	773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881	883	887	907	911
919	929	937	941	947	953	967	971	977	983	991	997

Таблица простых чисел от 1000 до 10000

1009	1013	1019	1021	1031	1033	1039	1049	1051	1061	1063	1069
1087	1091	1093	1097	1103	1109	1117	1123	1129	1151	1153	1163
1171	1181	1187	1193	1201	1213	1217	1223	1229	1231	1237	1249
1259	1277	1279	1283	1289	1291	1297	1301	1303	1307	1319	1321
1327	1361	1367	1373	1381	1399	1409	1423	1427	1429	1433	1439
1447	1451	1453	1459	1471	1481	1483	1487	1489	1493	1499	1511
1523	1531	1543	1549	1553	1559	1567	1571	1579	1583	1597	1601
1607	1609	1613	1619	1621	1627	1637	1657	1663	1667	1669	1693
1697	1699	1709	1721	1723	1733	1741	1747	1753	1759	1777	1783
1787	1789	1801	1811	1823	1831	1847	1861	1867	1871	1873	1877
1879	1889	1901	1907	1913	1931	1933	1949	1951	1973	1979	1987
1993	1997	1999	2003	2011	2017	2027	2029	2039	2053	2063	2069
2081	2083	2087	2089	2099	2111	2113	2129	2131	2137	2141	2143
2153	2161	2179	2203	2207	2213	2221	2237	2239	2243	2251	2267
2269	2273	2281	2287	2293	2297	2309	2311	2333	2339	2341	2347
2351	2357	2371	2377	2381	2383	2389	2393	2399	2411	2417	2423
2437	2441	2447	2459	2467	2473	2477	2503	2521	2531	2539	2543
2549	2551	2557	2579	2591	2593	2609	2617	2621	2633	2647	2657
2659	2663	2671	2677	2683	2687	2689	2693	2699	2707	2711	2713
2719	2729	2731	2741	2749	2753	2767	2777	2789	2791	2797	2801
2803	2819	2833	2837	2843	2851	2857	2861	2879	2887	2897	2903
2909	2917	2927	2939	2953	2957	2963	2969	2971	2999	3001	3011
3019	3023	3037	3041	3049	3061	3067	3079	3083	3089	3109	3119
3121	3137	3163	3167	3169	3181	3187	3191	3203	3209	3217	3221
3229	3251	3253	3257	3259	3271	3299	3301	3307	3313	3319	3323
3329	3331	3343	3347	3359	3361	3371	3373	3389	3391	3407	3413
3433	3449	3457	3461	3463	3467	3469	3491	3499	3511	3517	3527
3529	3533	3539	3541	3547	3557	3559	3571	3581	3583	3593	3607
3613	3617	3623	3631	3637	3643	3659	3671	3673	3677	3691	3697
3701	3709	3719	3727	3733	3739	3761	3767	3769	3779	3793	3797
3803	3821	3823	3833	3847	3851	3853	3863	3877	3881	3889	3907
3911	3917	3919	3923	3929	3931	3943	3947	3967	3989	4001	4003
4007	4013	4019	4021	4027	4049	4051	4057	4073	4079	4091	4093
4099	4111	4127	4129	4133	4139	4153	4157	4159	4177	4201	4211
4217	4219	4229	4231	4241	4243	4253	4259	4261	4271	4273	4283
4289	4297	4327	4337	4339	4349	4357	4363	4373	4391	4397	4409
4421	4423	4441	4447	4451	4457	4463	4481	4483	4493	4507	4513
4517	4519	4523	4547	4549	4561	4567	4583	4591	4597	4603	4621
4637	4639	4643	4649	4651	4657	4663	4673	4679	4691	4703	4721
4723	4729	4733	4751	4759	4783	4787	4789	4793	4799	4801	4813
4817	4831	4861	4871	4877	4889	4903	4909	4919	4931	4933	4937
4943	4951	4957	4967	4969	4973	4987	4993	4999	5003	5009	5011
5021	5023	5039	5051	5059	5077	5081	5087	5099	5101	5107	5113
5119	5147	5153	5167	5171	5179	5189	5197	5209	5227	5231	5233
5237	5261	5273	5279	5281	5297	5303	5309	5323	5333	5347	5351
5381	5387	5393	5399	5407	5413	5417	5419	5431	5437	5441	5443
5449	5471	5477	5479	5483	5501	5503	5507	5519	5521	5527	5531
5557	5563	5569	5573	5581	5591	5623	5639	5641	5647	5651	5653
5657	5659	5669	5683	5689	5693	5701	5711	5717	5737	5741	5743
5749	5779	5783	5791	5801	5807	5813	5821	5827	5839	5843	5849
5851	5857	5861	5867	5869	5879	5881	5897	5903	5923	5927	5939
5953	5981	5987	6007	6011	6029	6037	6043	6047	6053	6067	6073
6079	6089	6091	6101	6113	6121	6131	6133	6143	6151	6163	6173
6197	6199	6203	6211	6217	6221	6229	6247	6257	6263	6269	6271
6277	6287	6299	6301	6311	6317	6323	6329	6337	6343	6353	6359
6361	6367	6373	6379	6389	6397	6421	6427	6449	6451	6469	6473
6481	6491	6521	6529	6547	6551	6553	6563	6569	6571	6577	6581
6599	6607	6619	6637	6653	6659	6661	6673	6679	6689	6691	6701
6703	6709	6719	6733	6737	6761	6763	6779	6781	6791	6793	6803
6823	6827	6829	6833	6841	6857	6863	6869	6871	6883	6899	6907
6911	6917	6947	6949	6959	6961	6967	6971	6977	6983	6991	6997
7001	7013	7019	7027	7039	7043	7057	7069	7079	7103	7109	7121
7127	7129	7151	7159	7177	7187	7193	7207	7211	7213	7219	7229
7237	7243	7247	7253	7283	7297	7307	7309	7321	7331	7333	7349
7351	7369	7393	7411	7417	7433	7451	7457	7459	7477	7481	7487
7489	7499	7507	7517	7523	7529	7537	7541	7547	7549	7559	7561
7573	7577	7583	7589	7591	7603	7607	7621	7639	7643	7649	7669
7673	7681	7687	7691	7699	7703	7717	7723	7727	7741	7753	7757
7759	7789	7793	7817	7823	7829	7841	7853	7867	7873	7877	7879
7883	7901	7907	7919	7927	7933	7937	7949	7951	7963	7993	8009
8011	8017	8039	8053	8059	8069	8081	8087	8089	8093	8101	8111
8117	8123	8147	8161	8167	8171	8179	8191	8209	8219	8221	8231
8233	8237	8243	8263	8269	8273	8287	8291	8293	8297	8311	8317
8329	8353	8363	8369	8377	8387	8389	8419	8423	8429	8431	8443
8447	8461	8467	8501	8513	8521	8527	8537	8539	8543	8563	8573
8581	8597	8599	8609	8623	8627	8629	8641	8647	8663	8669	8677
8681	8689	8693	8699	8707	8713	8719	8731	8737	8741	8747	8753
8761	8779	8783	8803	8807	8819	8821	8831	8837	8839	8849	8861
8863	8867	8887	8893	8923	8929	8933	8941	8951	8963	8969	8971
8999	9001	9007	9011	9013	9029	9041	9043	9049	9059	9067	9091
9103	9109	9127	9133	9137	9151	9157	9161	9173	9181	9187	9199
9203	9209	9221	9227	9239	9241	9257	9277	9281	9283	9293	9311
9319	9323	9337	9341	9343	9349	9371	9377	9391	9397	9403	9413
9419	9421	9431	9433	9437	9439	9461	9463	9467	9473	9479	9491
9497	9511	9521	9533	9539	9547	9551	9587	9601	9613	9619	9623
9629	9631	9643	9649	9661	9677	9679	9689	9697	9719	9721	9733
9739	9743	9749	9767	9769	9781	9787	9791	9803	9811	9817	9829
9833	9839	9851	9857	9859	9871	9883	9887	9901	9907	9923	9929
9931	9941	9949	9967	9973

¹Простое число // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 4.

Простые числа 🔢 свойства, формула, последовательность простых и составных чисел, теория, таблица простых чисел до 1000 и до 10000, наибольшое и наименьшее число, примеры

Простые числа – это натуральные числа, их можно разделить только на два значения: единицу и себя. К натуральным относят те, которые используются во время счета, поэтому должно выполняться требование, чтобы они были положительными и целыми. Делители также не должны быть отрицательными и дробными.

Они широко применяются в криптографии, когда необходимо закодировать важную информацию от посторонних глаз. Шифрование касается каждого человека, так как используется в создании электронной почты, банковских карт. Даже мобильная связь защищается кодами. 

Кроме того, используются на системах, защищающих транспортные средства от угонщиков, создают преграду для атак вирусов и взломов компьютерных сайтов. При попытке продолжить разложение простых чисел или определить закономерность появления, возникают новые способы математических расчетов.

Простые и составные числа — что это такое

Математика предлагает начинать знакомиться с данными понятиями в средней школе, в 5 или в 6 классе. 

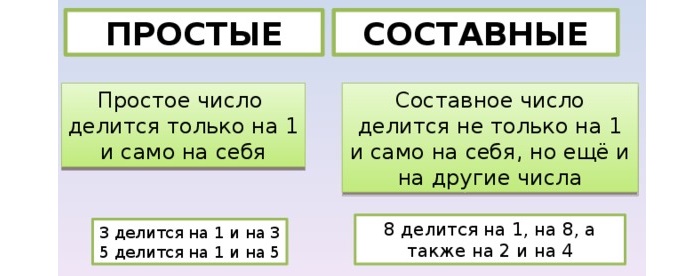
Проверка на принадлежность к определенному множеству достаточно простая:

1. Простые числа можно делить только на 1 и на такое же число. Например 3 и 7 — простые числа, 3 делится на 1 и на 3, 7 делится на 1 и на 7.

2. Составные числа можно делить не только на себя и единицу. При этом не должно получаться остатка. Они делятся на одно или несколько значений. Например, 8 и 6 относят к составным. Восьмерка делится на 1, 2, 4, 8; шестерка – на 1, 2, 3 и 6.

Определение простых чисел позволяет исключить из их ряда единицу. Она характеризуется наличием только одного делителя, не являющегося отрицательным значением. Получить ее можно, используя только один способ, умножив саму на себя.

Простые двузначные числа определяются по внешнему виду:

1. Если оканчиваются четной цифрой, то точно являются составными. То же касается и значений, имеющих больше двух знаков.

2. Если на конце находится цифра 5, то она входит в число делителей.

Такие простые способы помогают легко классифицировать многозначные показатели.

Некоторые двузначные вводят в заблуждение с первого взгляда, если оканчиваются на единицу. Кажется, что разложить на множители их невозможно. Но есть исключения, например: 21, 81. Чем дальше, тем больше отклонений от этой закономерности.

Последовательность простых чисел

Есть целые алгоритмы, помогающие получать новое, ранее неизвестное значение. 

Существуют таблицы, в которых собраны найденные числа, имеющие не больше двух делителей, например, до 200, 1000 или больше. 

Последовательность можно продолжать бесконечно, начинается она так: 2, 3, 5, 7, 11, 13, 17, 19 и т. д.

Наименьшее и наибольшее простое число

Самым меньшим значением, делящимся на себя и 1, является 2. Это единственное простое значение, являющееся четным. Остальные всегда делятся на два, то есть получают третий делитель. 

Простых чисел много и их количество стремится к бесконечности, потому узнать самое большое невозможно.

Нескончаемость ряда была доказана еще до нашей эры Евклидом. Он предложил перемножить все известные исследуемые значения и прибавить к ним единицу. 

При его делении в любом случае будет оставаться остаток, то есть отнести к составным невозможно. Что противоречит тому факту, что были использованы все известные простые числа, в том числе и самое большое. Значит, предположение о конечности ряда является неверным.

В настоящее время известно значение, имеющее около 25 миллионов знаков. Оно относится к наибольшему из открытых наукой, это 2^82589933

Множество простых чисел

Множествами называются совокупности элементов, объединенных в одно целое общими свойствами. 

Для изучаемых объектов к ним относятся:

Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему. 

Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее. 

По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным. 

В итоге, все составные окажутся зачеркнутыми.

Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.

Некоторые свойства простых чисел

Выделяют свойства, объединенные в теоремы, постулаты. Многие являются основой математических правил, используемых в настоящее время. 

Изучением занимается теория чисел, при использовании формул простые числа обозначаются буквой n.

Известны следующие правила:

1. Если рассматривать два простых числа (n), одно из которых делится на другое, то можно утверждать, что они равны.

2. Все являются нечетными, за исключением двойки.

3. Можно выделить пары, разница между которым равна 2. При их сложении получается значение, кратное трем. Их так и называют парными или близнецами. Исключение составляют две первые цифры в ряду, 3 и 5, так как сумму, полученную при их сложении, нельзя разделить на 3.

4. Для каждого натурального значения (N), большего единицы, существует n, превышающее его. При этом удвоенное натуральное будет больше n.

5. Если одно из двух N делится на n, то их произведение также будет делиться на него.

6. Любое N, за исключением единицы, можно отнести к n или представить в виде их произведения.

7. Если взять составное число и разложить его на множители n, то среди них окажется один, квадрат которого будет меньше первоначального составного.

8. Некоторые n имеют пары, которые можно найти, перевернув n наоборот. Например, 13 и 31, 37 и 73. То же самое касается трехзначных n: 107 и 701, 709 и 907.

9. Если N возвести в степень, представленную n, а затем вычесть N, то полученное значение будет делиться на используемое n. Это правило представляет собой малую теорему Ферма.

Действия с простыми числами

Можно использовать разные арифметические действия, складывать, умножать, вычитать, делить. Простые числа могут являться основанием и показателем степени. 

Извлечь корень из них невозможно.

Таблица простых чисел до 1000

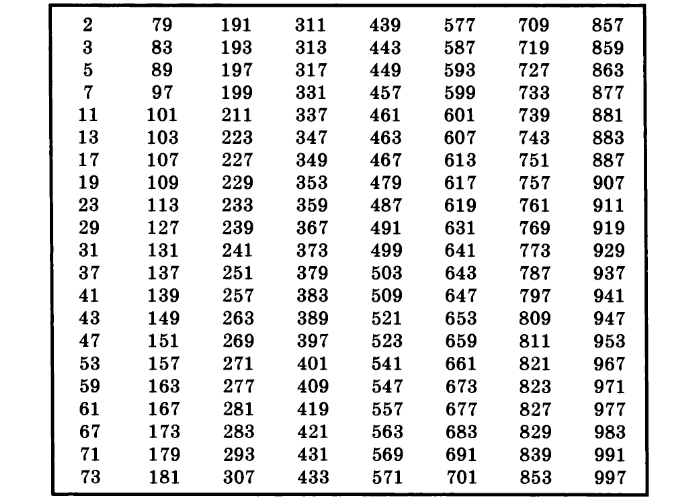
Таблица простых числе до 10000

Простые и составные числа

Определение 9.1. Натуральное число p называется простым, если оно имеет только два различных между собой натуральных делителя: 1 и p.

Примеры. 2, 3, 5, 7, 11, 13 – простые числа.

Определение 9. 2. Натуральное число, большее единицы, называется составным, если оно имеет более двух различных натуральных делителей.

Примеры. 4, 6, 8, 9, 10, 12 – составные числа.

Замечание 1. Из этих определений следует, что множество натуральных чисел можно разбить на три класса:

а) составные числа;

б) простые числа;

в) единица.

Если а – составное, то а = nq, где 1 < n < a, 1 < q < a.

Простейшие свойства простых чисел

1⁰. Если а Z и p – простое, то (а, p) = 1 а p.

Действительно, пусть d = (a, p), тогда (а d) p d, т.к. p – простое число, то оно имеет два делителя 1 и p. Если (а, p) = 1, то а и p взаимно просты, а если (а, p) = p, то а p.

20. Если произведение нескольких сомножителей делится на p, то, по крайней мере, один из сомножителей делится на p.

Действительно, пусть произведение а₁ ∙ а₂ ∙ … ∙ а_n делится на p. Если предположить противное: все а_i не делятся на p, то (а₁ ∙ а₂ ∙ … ∙ а_n, p) = 1, следовательно, какой-то сомножитель делится на p.

30. Различные простые числа взаимно просты.

4⁰. Наименьший простой делитель p натурального числа n > 1 не превосходит .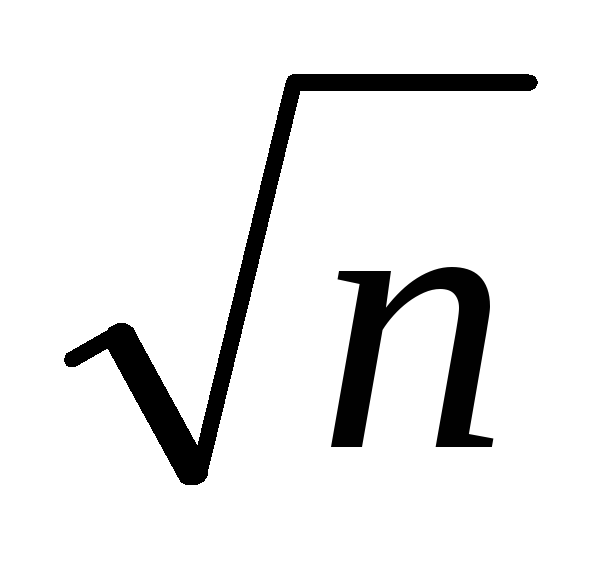

Пусть n = p ∙ n₁, причем p 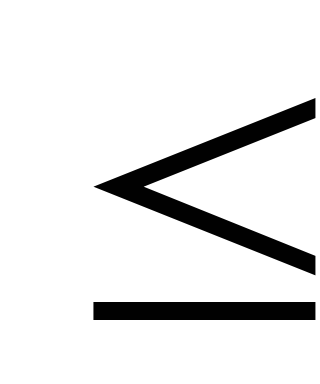n₁ и p – простое. Тогда n 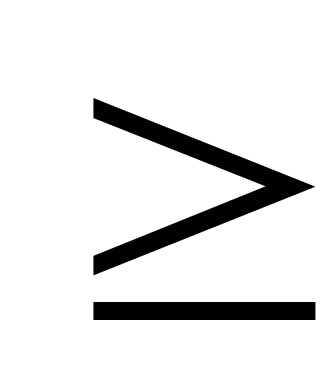p²p .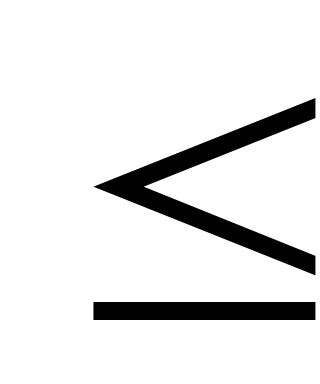

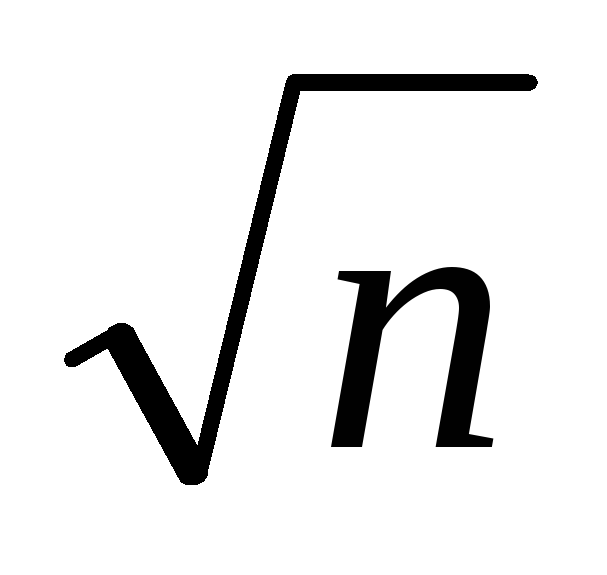50. Если натуральное число n не делится ни на одно простое число p , тоn – простое, в противном случае оно будет составным.

Данное свойство непосредственно следует из свойства 4⁰.

Пример. Выясним, будет ли число 157 простым?

Выпишем простые делители, не превосходящие 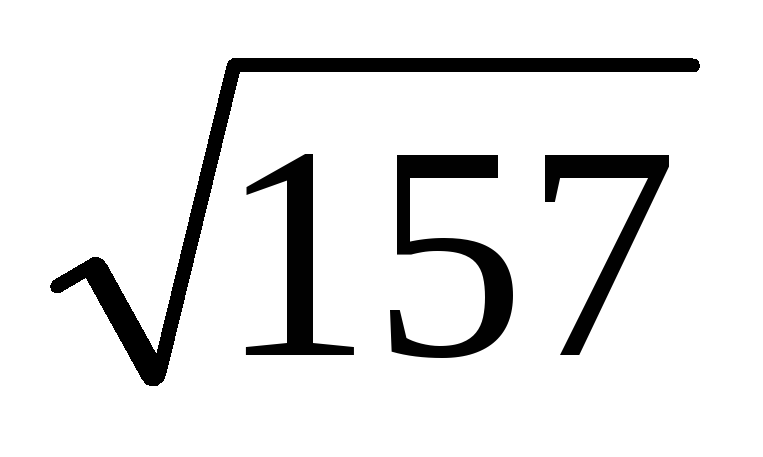: 2, 3, 5, 7, 11. Проверяем, что 157 не делится на 2, на 3, на 5, на 7, на 11. Следовательно, число 157 – простое.

Решето Эратосфена

На свойстве 5⁰ основан метод, позволяющий определить список простых чисел p₁ < p₂ < … до заданной границы n. Этот метод носит название решето Эратосфена, названный в честь древнегреческого математика, географа и астронома.

Шаг 1. Выпишем подряд все натуральные числа 2, … , n – 1, n.

Положим, что p₁ = 2 и вычеркнем все последующие числа, делящиеся на 2, кроме p₁ = 2.

Шаг 2. Пусть k 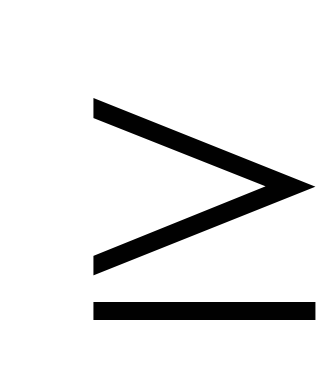2 и уже определены числа p₁,…, p_k-1. Обозначим p_k первое невычеркнутое число, следующее за p_k-1. Если p_k² > n, то обозначим p_k+1, p_k+2, … все оставшиеся невычеркнутыми числа, следующие за p_k, в порядке возрастания. На этом алгоритм завершает свою работу.

Шаг 3. Если p_k²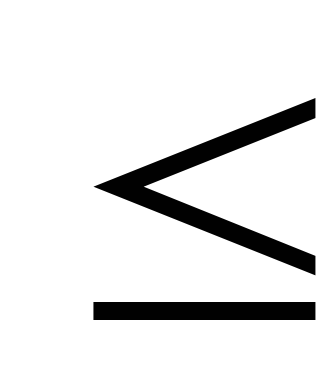n, то вычеркиваем числа, делящиеся на p_k, начиная с p_k² (двигаясь до n с шагом p_k). Вычеркнутые ранее числа также принимаются в учет, но не вычеркиваются еще раз. По завершении процедуры алгоритм увеличивает индекс k на единицу и переходит к шагу 2.

В результате алгоритм оставляет невычеркнутыми только простые числа.

Примеры: 1. Найти все простые числа, меньшие 30.

Применим решето Эратосфена, остановившись, как только найдём простое число, не меньшее 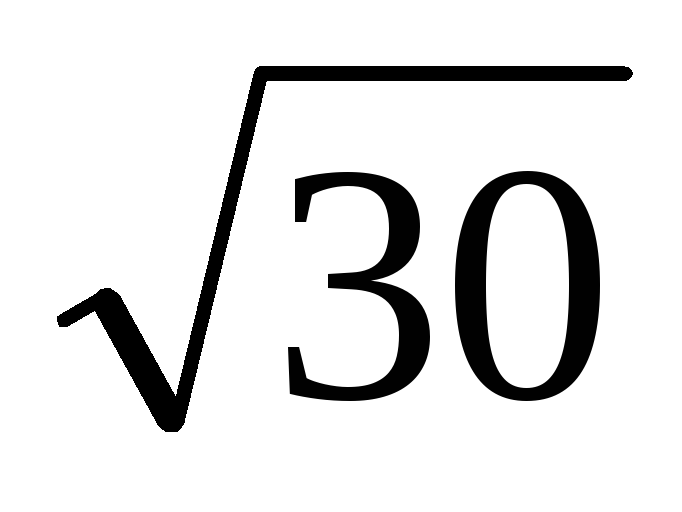=5,… , т.е. простое число 7.

Теорема Евклида. Основная теорема арифметики

Теорема 9.1 (теорема Евклида). Множество простых чисел бесконечно.

Доказательство.

Предположим противное, пусть p₁, p₂, … , p_k – все простые числа, где p₁ = 2, а p_k – самое большое простое число.

Составим натуральное число n = p₁ · p₂ · … · p_k + 1, т.к. n > p_i, то оно должно быть составным. Покажем, что наименьший делитель q1 числа n будет простым. Так как n – составное, то n = n₁ ∙ q, где q < n₁. Если предположить, что q – составное число, то q = q₁ ∙ k и n = n₁ ∙ q₁ ∙ k, так как q₁ < q, то q – уже не будет наименьшим делителем числа n, что противоречит условию. Итак, наименьший делитель числа n будет простым. Однако n не делится ни на p₁, ни на p₂, … , ни на p_k, так как 1 не делится на любое p_i .

Следовательно, наше предположение о конечности множества простых чисел было неверно.

Замечание 2. Простые числа составляют лишь небольшую часть чисел натурального ряда. Доказано, что в натуральном ряду существуют сколь угодно длинные интервалы, не содержащие ни одного простого числа.

Теорема 9. 2 (основная теорема арифметики). Любое натуральное число n > 1 может быть представлено единственным образом в виде произведения простых чисел, с точностью до порядка сомножителей.

Доказательство.

I. Докажем возможность представления методом математической индукции по величине числа. Пусть n N и n > 1.

1) n = 2. Утверждение выполняется, так как 2 – простое число.

2) Предположим, что утверждение теоремы выполнено для всех натуральных чисел,меньших числа k.

3) Покажем, что утверждение выполнено для k.

а) Если k – простое число, то доказывать нечего.

б) Если k – составное число, то оно имеет делитель а, такой, что 1 < a < k . Тогда k = a ∙ b. Очевидно, что 1 < b < k. Согласно предположению, теорема выполнена для чисел а и b, т. е. а = p₁ ∙ p₂ ∙ … ∙ p_s и b = q₁ ∙ q₂ ∙ … ∙ q_m, где p_i, q_j – простые. Тогда k = p₁ ∙ p₂ ∙ … ∙ p_s ∙ q₁ ∙ q₂ ∙ … ∙ q_m. Полученная формула означает, что существует представление числа k в виде произведения простых чисел.

Согласно принципа математической индукции возможность представления в виде произведения простых чисел доказана для любого натурального n > 1.

II. Покажем, что представление числа n в виде произведения простых чисел единственно с точностью до порядка сомножителей.

Пусть n = p₁ ∙ p₂ ∙ … ∙ p_s и n = q₁ ∙ q₂ ∙ … ∙ q_r, где p_i, q_j – простые числа, тогда будет иметь место равенство:

p₁ ∙( p₂ ∙ … ∙ p_s) = q₁ ∙ q₂ ∙ … ∙ q_r(1)

Тогда простое число p₁ делит q₁ ∙ q₂ ∙ … ∙ q_r, так что p₁ делит одно из простых чисел правой части, пусть q₁p₁ , а значит, p₁ = q₁ . Поэтому обе части рассмат­ри­ва­е­мого равенства можно сок­ра­тить на p₁. Разделив обе части равенства (1) на p₁, получим равенство p₂ ∙ … ∙ p_s= q₂ ∙ … ∙ q_r . Повторяя процесс рассуждения еще (s – 1) раз, мы получим равенство:

1 = q_s+1 ∙ q_s+2 ∙ …∙ q_r

Так как все q_i > 1, то это равенство невозможно. Следовательно, в обеих разложениях число сомножителей одинаково (s = r) и сами сомножители одинаковы.

Замечание 3. В разложении числа n на простые сомножители некоторые из них могут повторяться. Обозначим буквами 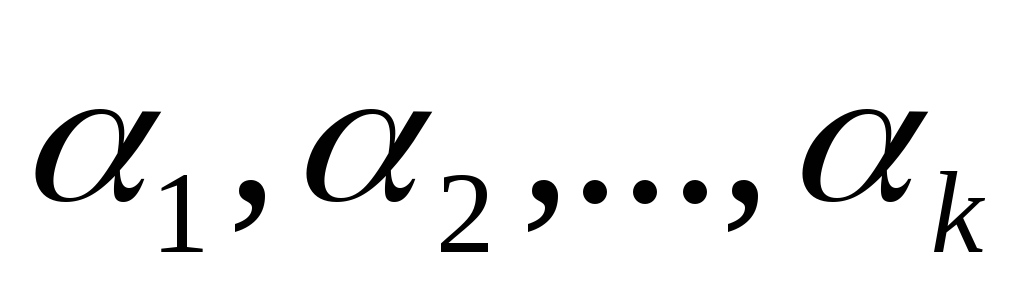кратность их вхождения вn, получим так называемое каноническое разложение числа n:

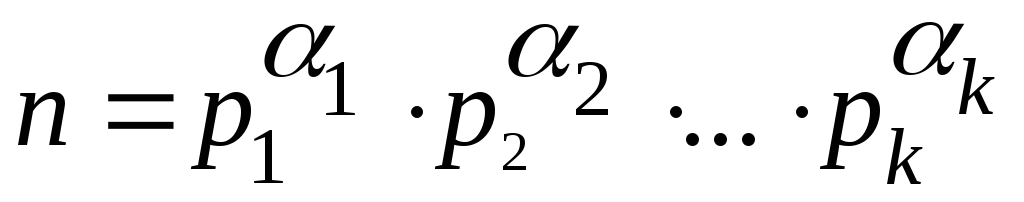
МЕТОДИКА 19. Тема: Простые числа, их свойства. Основная теорема арифметики.

I.Основные понятия: простые числа, составные числа, основная теорема арифметики.

Ранее изученный материал: делители и кратные, признаки делимости.

Теоретический материал темы:

Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число. Натуральное число называют составным, если оно имеет более двух делителей.

Свойства простых чисел:

1⁰. Любое натуральное число либо делится на простое, либо взаимно просто с ним.

2⁰. Произведение натуральных чисел делится на простое тогда и только тогда, когда хотя бы одно из них делится на это простое.

3⁰. Простых чисел бесконечно много (нет самого большого простого числа).

4⁰. Если натуральное число не делится ни на одно простое, квадрат которого не превосходит это натуральное число, то оно само простое.

5⁰. Любое простое число p(p > 3) представимо в виде .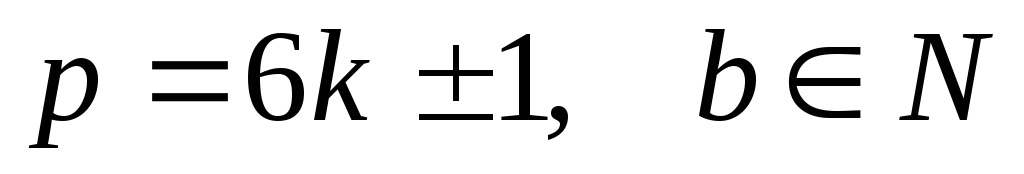

Основная теорема арифметики: всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.

Простые и составные числа

Открытый урок по математике 5 класс по теме

«Простые и составные числа»

Цель: 1)сформировать  понятия  простого  и  составного  числа,  способность  к  установлению  вида  числа  на  основе определения  и  таблицы.

2) повторить  и  закрепить  понятия  классификации, делителя  и  кратного, тренировать  вычислительные  навыки при  решении  уравнений и  примеров.

Структура  урока:

1.Самоопределение  к деятельности (организационный  момент)

2.Актуализация  знаний и  фиксация  затруднений  в  деятельности.

3. Постановка учебной  задачи или  проблемы.

4. «Открытие»  детьми  нового  знания.

5.Первичное  закрепление во  внешней  речи.

6.Самостоятельная  работа  с  самопроверкой  в  классе.

7.Включение  нового знания в систему  знаний  и  повторение.

8.Рефлексия   деятельности. (Итог урока)

Тема: Простые  и  составные  числа

Цель: 1)сформировать  понятия  простого  и  составного  числа,  способность  к  установлению  вида  числа  на  основе определения  и  таблицы.

2) повторить  и  закрепить  понятия  классификации, делителя  и  кратного, тренировать  вычислительные  навыки при  решении  уравнений и  примеров.

Структура  урока:

1.Самоопределение  к деятельности (организационный  момент)

2.Актуализация  знаний и  фиксация  затруднений  в  деятельности.

3. Постановка учебной  задачи или  проблемы.

4. «Открытие»  детьми  нового  знания.

5.Первичное  закрепление во  внешней  речи.

6.Самостоятельная  работа  с  самопроверкой  в  классе.

7.Включение  нового знания в систему  знаний  и  повторение.

8.Рефлексия   деятельности. (Итог урока)

Ход  урока:

1.Орг.  момент

 Итак,  начнём  урок. Ребята, какую  тему  мы  изучали   на  прошлом  уроке?

  -Делители и  кратные

Делители  и  кратные  находят   своё  применение ещё  во многих новых  математических понятиях.

2.Актуализация  знаний.

1. Используя  слова «делится» или  «кратное» и «делитель», что  можно  сказать  о  равенстве?

а=а·1

 21= 3·7,              Д(21)={1,3,7,21}

 21=1·21.  

2.Найдите  делители чисел

I вариант   19, 16, 23,63. ( раздать  листочки)

I вариант  15, 17, 31, 42. (проверить по  листочкам)

Молодцы!!!

—Что  общего  между  данными  числами  и  их   делителями?

— Числа  имеют  по  2  делителя (единицу  и  само   число) или  больше 2  делителей.

— Итак, на  какие  группы    разобьём  эти  числа?

-Числа, имеющие 2  делителя и  больше  двух  делителей.

—Числа  первой  группы  называются  простыми, а  второй — составными.

-Сформулируйте вывод.

-Формулируют определение, т.е.  «открывают»  новое  знание.

—Запишите  тему: «Простые  и составные  числа»

 Какова  наша  цель  урока? Какую  работу  мы  сегодня  должны  провести?

-Найти  способы, как  быстро  определить  простые  и  составные  числа.

—Итак, какие  числа называются  простыми?

— Натуральные числа,  которые  имеют  2 делителя   называются  простыми.

(показать  схему)    Простые числа:  два  делителя ( 1 и само  число)        ***

—Какие  числа  называются  составными?

-Натуральные числа, которые имеют больше двух делителей

-( показать схему)  Составные числа: больше  ДВУХ  делителей  **

-Какие  из чисел являются  простыми, какие  составными?

-19,23,17,31.                16,15,63,42

3. Найдите делители  числа  1

  -1.

-Сколько  делителей?

-1

-Является  простым?

-Нет

-Является составным.

-Нет

-Сформулируйте  вывод.

-1  не  является ни  простым, ни  составным.

4.Определите  какими  являются  числа 8, 11, 12.

Как  быстро  определить,  что  число  составное?

Вывод,  что  определить составное  достаточно  определить  третий  делитель, кроме  1  и  самого  числа.

4.Определите за  30  секунд,  каким   является  число  337?

-Итак, каким  является  число 337?

-Думаем,  что  простое.

-а  почему вы  так  думаете?                     ( Проблема?)

-мы  не  нашли  третий  делитель

—Значит, вы  за  30 секунд успели  перебрать  все  возможные  делители?

-Конечно, нет!

-Тогда  вы  вправе  утверждать, что 337- простое  число?

-Мы  не  можем  этого  утверждать.  (Возникновение  проблемной  ситуации)

-Итак,  что  вы  хотели  сделать  с  числом  337?

-Определить, простым  или  составным  оно  является.

-И  какой  способ  применили?

-Искали  третий  делитель  методом  перебора.

—Удалось  ли вам  это  сделать  быстро? (побуждение  к  осознанию  противоречия )

-Нет (осознание  неприменимости  старого  способа)

-Над  каким  вопросом  будем  дальше  работать? (побуждение  к  формулированию  проблемы)

-Будем  искать  быстрый  способ  определения  простых  составных  чисел.

-Сформулировали  проблему.

-(Проблема  как  вопрос, ответом  на  который  является  таблица  простых  чисел)

-Откройте  учебник на  странице 97, прочитайте,  начиная  со  слова Другой  греческий …

-Итак, придётся  использовать  остроумный способ составления простых  чисел… зафиксируем быстрый  способ определения  простых  чисел.

 -Вот  эта  таблица простых  чисел. Она  даёт  возможность  легко  определить  каким  является число.

Итак,  какой  вывод  можно  сделать?

Способ1            Способ2                                            Способ1           Способ2

Найти

два  делителя: 1 и  само  число

Воспользоваться

таблицей

простых  чисел

Найти

больше

двух делителей

Найти

третий делитель, кроме 1 и самого  числа  и

А теперь  ответьте  на  вопросы, открыв  таблицу  простых  чисел.

1.а) Известно, что  число 809  простое. Делится  ли  оно  на  19?

б)Используя таблицу простых  чисел, определи, являются ли простыми числа:59,83,91, 127,379,511,697,761,803,851,991,997.***

в)Есть ли  чётные  простые  числа?  Сколько  их?  Почему?

г) Есть  ли  простые  числа,  оканчивающиеся  цифрой 0? д)Какими  цифрами  не  может  оканчиваться  многозначное  простое  число?

е)Какими  цифрами  может  оканчиваться  многозначное  простое  число?

Самостоятельная работа с проверкой в классе

2.416а) б)   Записать  на  боковой  доске ***    (карточки)

Докажи, что числа  являются составными:

а)8 ,28, 111                                                б)77 777,1111, 242 242,373 737,111 111 111  

в)111111…1 (1996 цифр)

3.418 1)3)  1вариант (Наташа)                          418 2)4)2 вариант( Ренат)

}

7. Включение нового знания  в  систему  знаний и  повторение

    1 вариант                                                              2вариант

определите, является  ли значение  выражения простым  или  составным

1. .((7777:77+157):86 + 216):219•306            1.((8888:88+136):79 +303):306•219

                       306-составное                                                            219-составное

8.Рефлексия.

-Что  нового  узнали?

—Каким способом  определить является простым  или  составным?

—Как оцениваете  свою деятельность  на  уроке?

-Посмотрите, числа-близнецы …                

   Домашнее  задание  

                                                                                441,442, с451.

Оценки  за урок.                           Спасибо за  урок!