7.1. Степень с натуральным показателем   математика-повторение

I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аⁿ.

Примеры. Записать произведение в виде степени.

1) mmmm;          2) aaabb;         3) 5·5·5·5·ccc;        4) ppkk+pppk-ppkkk.

Решение.

1) mmmm=m⁴, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.

  2) aaabb=a³b²;    3) 5·5·5·5·ccc=5⁴c³;     4) ppkk+pppk-ppkkk=p²k

2+p³k-p²k³.

II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аⁿ – степень, а – основание степени, n – показатель степени. Например:

 2³ — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 2³равно 8, так как 2³=2·2·2=8.

Примеры. Написать следующие выражения без показателя степени.

5) 4³;       6) a³b²

c³;       7) a³-b³;       8 ) 2a⁴+3b².

Решение.

5) 4³=4·4·4;       6) a³b²c³=aaabbccc;       7) a³-b³=aaa-bbb;       8) 2a⁴+3b²=2aaaa+3bb.

 III. а⁰=1  Любое число (кроме нуля) в нулевой степени равно единице. Например, 25⁰=1. 
 IV. а¹=а  Любое число в первой степени равно самому себе. 

 V. a^m∙aⁿ=a^m+n   При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели

складывают.

Примеры. Упростить:

9) a·a³·a⁷;             10) b⁰+b²·b³;             11) c²·c⁰·c·c⁴.

Решение.

9) a·a³·a⁷=a¹⁺³⁺⁷=a¹¹;           10) b⁰+b²·b³=1+b²⁺³=1+b⁵;             

11) c²·c⁰·c·c⁴=1·c²·c·c⁴=c²⁺¹⁺⁴=c⁷.

VI.  a^m:aⁿ=a^m— n  При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры. Упростить:

12) a⁸:a³;       13) m¹¹:m⁴;         14) 5⁶:5⁴.

12) a⁸:a³=a^8-3=a⁵;       13) m¹¹:m⁴=m^11-4=m⁷;         14) 5⁶:5⁴=5²=5·5=25.

VII. (a^m)ⁿ=a^mn   При возведении степени в степень основание оставляют прежним, а показатели перемножают.

Примеры. Упростить:

15) (a³)⁴;         16) (c⁵)².

15) (a³)⁴=a^3·4=a¹²;         16) (c⁵)²=c^5·2=c¹⁰.

Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:

15) (a³)⁴=(a⁴)³;         16) (c⁵)²=(c²)⁵.

 VIII. (a∙b)ⁿ=aⁿ∙bⁿ   При возведении произведения в степень возводят в эту степень каждый из множителей.

Примеры. Упростить:

17) (2a²)⁵;      18) 0,2⁶·5⁶;        19) 0,25²·40².

Решение.

17) (2a²)⁵=2⁵·a^2·5

=32a¹⁰;      18) 0,2⁶·5⁶=(0,2·5)⁶=1⁶=1;

19) 0,25²·40²=(0,25·40)²=10²=100.

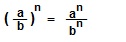       IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.

Примеры. Упростить:

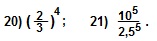
Решение.

 

 

www.mathematics-repetition.com

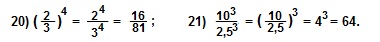
Правила возведения в степень

---

a— основание степени, действительное число ( aϵ R )

n — показатель степени, натуральное число ( n ϵ N )

 

 

 

Произведение степеней с одинаковым основанием:

 

Деление степеней с одинаковым основанием:

если  n > m

 

если  n = m

 

если  n < m

 

Возведение степени в степень:

 

Произведение в степени:

 

Деление в степени:

---

Подробности

Автор: Administrator

Опубликовано: 24 августа 2012

Обновлено: 24 мая 2017

www-formula.ru

Возведение в степень произведения и степени

Вопросы занятия:

·  повторить переместительное и сочетательное свойство умножения;

·  на примере показать, как возвести произведение в степень;

·  сформулировать правило возведения произведения в степень.

Материал урока

Прежде, чем приступить к изучению нового материала, вспомним, что:

Также вспомним переместительное и сочетательное свойства умножения.

А теперь давайте преобразуем выражение:

Вообще, для любых чисел а и b и натурального числа n верно равенство:

Таким образом, можем сформулировать определение.

Чтобы возвести в степень произведение, нужно каждый множитель возвести в эту степень и результаты перемножить.

Например,

Следует также отметить, что свойство степени произведения распространяется на степень трёх и более множителей.

А теперь разберёмся с возведением степени в степень. Для этого рассмотрим выражение, которое представляет собой степень, основание которой само является степенью.

Вообще, для любого числа а и произвольных натуральных чисел m и n верно равенство:

Сформулируем определение.

При возведении степени в степень основание оставляют прежним, а показатели степеней перемножают.

Например,

Пример.

Пример.

videouroki.net