Экспоненциальный рост — Википедия

Материал из Википедии — свободной энциклопедии

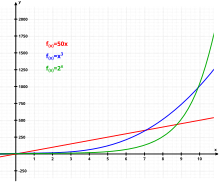Линейная (красная), степенная (синяя) и экспоненциальная (зелёная) зависимости

Экспоненциальный рост — возрастание величины, когда скорость роста пропорциональна значению самой величины. Подчиняется экспоненциальному закону. Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейной или степенной зависимостям. В случае дискретной области определения с равными интервалами его ещё называют геометрическим ростом или геометрическим распадом (значения функции образуют геометрическую прогрессию). Экспоненциальная модель роста также известна как мальтузианская модель роста.

Для любой экспоненциально растущей величины чем большее значение она принимает, тем быстрее растёт. Также это означает, что величина зависимой переменной и скорость её роста прямо пропорциональны. Но при этом, в отличие от гиперболической, экспоненциальная кривая никогда не уходит в бесконечность за конечный промежуток времени.

Экспоненциальный рост в итоге оказывается более быстрым, чем любой степенной и тем более любой линейный рост.

Экспоненциальный рост описывается дифференциальным уравнением:

dxdt=kx{\displaystyle {\frac {dx}{dt}}=kx}

Решение этого дифференциального уравнения — экспонента:

x=aekt{\displaystyle x=ae^{kt}}

Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов. Другим примером экспоненциального роста являются сложные проценты.

Экспоненциальный рост • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Выражение «экспоненциальный рост» вошло в наш лексикон для обозначения быстрого, как правило безудержного увеличения. Оно часто используется, например, при описании стремительного роста числа городов или увеличения численности населения. Однако в математике этот термин имеет точный смысл и обозначает определенный вид роста.

Экспоненциальный рост имеет место в тех популяциях, в которых прирост численности (число рождений минус число смертей) пропорционален числу особей популяции. Для популяции человека, например, коэффициент рождаемости примерно пропорционален количеству репродуктивных пар, а коэффициент смертности примерно пропорционален количеству людей в популяции (обозначим его N). Тогда, в разумном приближении,

прирост населения = число рождений — число смертей

    

    = rN

(Здесь r — так называемый коэффициент пропорциональности, который позволяет нам записать выражение пропорциональности в виде уравнения.)

Пусть dN — число особей, добавившихся к популяции за время dt, тогда если в популяции в общей сложности N особей, то условия для экспоненциального роста будут удовлетворены, если

    dN = rN dt

После того как в XVII веке Исаак Ньютон изобрел дифференциальное исчисление, мы знаем, как решать это уравнение для N — численности популяции в любое заданное время. (Для справки: такое уравнение называется дифференциальным.) Вот его решение:

    N = N₀ e^rt

где N₀ — число особей в популяции на начало отсчета, а t — время, прошедшее с этого момента. Символ е обозначает такое специальное число, оно называется

основание натурального логарифма (и приблизительно равно 2,7), и вся правая часть уравнения называется экспоненциальная функция.

Чтобы лучше понять, что такое экспоненциальный рост, представьте себе популяцию, состоящую изначально из одной бактерии. Через определенное время (через несколько часов или минут) бактерия делится надвое, тем самым удваивая размер популяции. Через следующий промежуток времени каждая из этих двух бактерий снова разделится надвое, и размер популяции вновь удвоится — теперь будет уже четыре бактерии. После десяти таких удвоений будет уже более тысячи бактерий, после двадцати — более миллиона, и так далее. Если с каждым делением популяция будет удваиваться, ее рост будет продолжаться до бесконечности.

Существует легенда (скорее всего, не соответствующая действительности), будто бы человек, который изобрел шахматы, доставил этим такое удовольствие своему султану, что тот пообещал исполнить любую его просьбу. Человек попросил, чтобы султан положил на первую клетку шахматной доски одно зерно пшеницы, на вторую — два, на третью — четыре и так далее. Султан, посчитав это требование ничтожным по сравнению с оказанной им услугой, попросил своего поданного придумать другую просьбу, но тот отказался. Естественно, к 64-му удвоению число зерен стало таким, что во всем мире не нашлось бы нужного количества пшеницы, чтобы удовлетворить эту просьбу. В той версии легенды, которая известна мне, султан в этот момент приказал отрубить голову изобретателю. Мораль, как я говорю моим студентам, такова: иногда не следует быть чересчур умным!

Пример с шахматной доской (как и с воображаемыми бактериями) показывает нам, что никакая популяция не может расти вечно. Рано или поздно она попросту исчерпает ресурсы — пространство, энергию, воду, что угодно. Поэтому популяции могут расти по экспоненциальному закону лишь некоторое время, и рано или поздно их рост должен замедлиться. Для этого нужно изменить уравнение так, чтобы при приближении численности популяции к максимально возможной (которая может поддерживаться внешней средой) скорость роста замедлялась. Назовем эту максимальную численность популяции

K. Тогда видоизмененное уравнение будет выглядеть так:

    dN = rN(1 — (N/K)) dt

Когда N намного меньше K, членом N/K можно пренебречь, и мы возвращаемся к первоначальному уравнению обычного экспоненциального роста. Однако когда N приближается к своему максимальному значению K, значение 1 — (N/K) стремится к нулю, соответственно стремится к нулю и прирост численности популяции. Общая численность популяции в этом случае стабилизируется и остается на уровне K. Кривая, описываемая этим уравнением, а также само уравнение, имеют несколько названий — S-кривая, логистическое уравнение, уравнение Вольтерры, уравнение Лотки—Вольтерры

. (Вито Вольтерра, 1860–1940 — выдающийся итальянский математик и преподаватель; Альфред Лотка, 1880–1949 — американский математик и страховой аналитик.) Как бы она ни называлась, это — достаточно простое выражение численности популяции, резко возрастающей экспоненциально, а затем замедляющейся при приближении к некоему пределу. И она гораздо лучше отражает рост численности реальных популяций, чем обычная экспоненциальная функция.

См. также:

Суммы степеней — арифметические прогрессии, геометрические прогрессии, суммы степеней, различные прогрессии

Арифметические прогрессии

$a+(a+d)+(a+2d)+\cdots+\{a+(n-1)d\}=\left(\frac{1}{2}\right)n\{2a+(n-1)d\}=\left(\frac{1}{2}\right)n(a+l)$
где $l=a+(n-1)d$ есть последним членом.

Некоторые особые случаи есть
$1+2+3+\cdots+n=\left(\frac{1}{2}\right)n(n+1)$
$1+3+5+\cdots+(2n-1)=n^2$

Геометрические прогрессии

$a+ar+ar^2+ar^3+\cdots+ar^n=\frac{a(1-r^n)}{1-r}=\frac{a-rl}{1-r}s$
где $l=ar^{n-1}$ есть последним членом и $r\neq1$.

Если $-1 $a+ar+ar^2+ar^3+\cdots+ar^n=\frac{a}{1 — r}$

Арифметическо-геометрические прогрессии

$a+(a+d)r+(a+2d)r^2+\cdots+\{a+(n-1)d\}r^{n-1}=\frac{a(1-r^n)}{1-r}+\frac{rd\{1-nr^{n-1}+(n-1)r^n\}}{(1-r)^2}$
где $r\neq1$.

Если $-1$a+(a+d)r+(a+2d)r^2+\cdots=\frac{a}{1-r}+\frac{rd}{(1-r)^2}$

Суммы степеней натуральных чисел

$1^p+2^p+3^p+\cdots+n^p=\frac{n^{p+1}}{p+1}+\frac{1}{2}n^p+\frac{B_1pn^{p-1}}{2!}-\frac{B_2p(p-1)(p-2)n^{p-3}}{4!}+\cdots$
где последовательность чисел заканчивается в $n^2$ или $n$ соответственно когда $p$ есть нечетное или четное и $B_k$ есть числа Бернулли.

Некоторые особые случаи есть

$1+2+3+\cdots+n=\frac{n(n+1)}{2}$

$1^2+2^2+3^2+\cdots+n^2=\frac{n(n+1)(2n+1)}{6}$

$1^3+2^3+3^3+\cdots+n^3=\frac{n^2(n+1)^2}{4}=(1+2+3+\cdots+n)^2$

$1^4+2^4+3^4+\cdots+n^4=\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}$

If $S_k=1^k+2^k+3^k+\cdots+n^k$ где $k$ и $n$ есть натуральные числа, тогда
$\binom{k+1}{1}S_1+\binom{k+1}{2}S_2+\cdots+\binom{k+1}{k}S_k=(n+1)^{k+1}-(n+1)$

Прогрессии с обратными степенями натуральных чисел

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots=\ln2$

$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots=\frac{\pi}{4}$

$1-\frac{1}{4}+\frac{1}{7}-\frac{1}{10}+\frac{1}{13}-\cdots=\frac{\pi\sqrt{3}}{9}+\frac{1}{3}\ln2$

$1-\frac{1}{5}+\frac{1}{9}-\frac{1}{13}+\frac{1}{17}-\cdots=\frac{\pi\sqrt{2}}{8}+\frac{\sqrt{2}\ln(1+\sqrt{2})}{4}$

$\frac{1}{2}-\frac{1}{5}+\frac{1}{8}-\frac{1}{11}+\frac{1}{14}-\cdots=\frac{\pi\sqrt{3}}{9}-\frac{1}{3}\ln2$

$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots=\frac{\pi^2}{6}$

$\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\cdots=\frac{\pi^4}{90}$

$\frac{1}{1^6}+\frac{1}{2^6}+\frac{1}{3^6}+\frac{1}{4^6}+\cdots=\frac{\pi^6}{945}$

$\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}-\frac{1}{4^2}+\cdots=\frac{\pi^2}{12}$

$\frac{1}{1^4}-\frac{1}{2^4}+\frac{1}{3^4}-\frac{1}{4^4}+\cdots=\frac{7\pi^4}{720}$

$\frac{1}{1^6}-\frac{1}{2^6}+\frac{1}{3^6}-\frac{1}{4^6}+\cdots=\frac{31\pi^6}{30,240}$

$\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\cdots=\frac{\pi^2}{8}$

$\frac{1}{1^4}+\frac{1}{3^4}+\frac{1}{5^4}+\frac{1}{7^4}+\cdots=\frac{\pi^4}{96}$

$\frac{1}{1^6}+\frac{1}{3^6}+\frac{1}{5^6}+\frac{1}{7^6}+\cdots=\frac{\pi^6}{960}$

$\frac{1}{1^3}-\frac{1}{3^3}+\frac{1}{5^3}-\frac{1}{7^3}+\cdots=\frac{\pi^3}{32}$

$\frac{1}{1^3}+\frac{1}{3^3}-\frac{1}{5^3}-\frac{1}{7^3}+\cdots=\frac{3\pi^3\sqrt{2}}{128}$

$\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+\frac{1}{7\cdot9}+\cdots=\frac{1}{2}$

$\frac{1}{1\cdot3}+\frac{1}{2\cdot4}+\frac{1}{3\cdot5}+\frac{1}{4\cdot6}+\cdots=\frac{3}{4}$

$\frac{1}{1^2\cdot3^2}+\frac{1}{3^2\cdot5^2}+\frac{1}{5^2\cdot7^2}+\frac{1}{7^2\cdot9^2}+\cdots=\frac{\pi^2-8}{16}$

$\frac{1}{1^2\cdot2^2\cdot3^2}+\frac{1}{2^2\cdot3^2\cdot4^2}+\frac{1}{3^2\cdot4^2\cdot5^2}+\cdots=\frac{4\pi^2-39}{16}$

$\frac{1}{a}-\frac{1}{a+d}+\frac{1}{a+2d}-\frac{1}{a+3d}+\cdots=\int\limits_0^1\frac{u^{a-1}\ du}{1+u^d}$

$\frac{1}{1^{2p}}+\frac{1}{2^{2p}}+\frac{1}{3^{2p}}+\frac{1}{4^{2p}}+\cdots=\frac{2^{2p-1}\pi^{2p}B_p}{(2p)!}$

$\frac{1}{1^{2p}}+\frac{1}{3^{2p}}+\frac{1}{5^{2p}}+\frac{1}{7^{2p}}+\cdots=\frac{(2^{2p}-1)\pi^{2p}B_p}{2(2p)!}$

$\frac{1}{1^{2p}}-\frac{1}{2^{2p}}+\frac{1}{3^{2p}}-\frac{1}{4^{2p}}+\cdots=\frac{(2^{2p-1}-1)\pi^{2p}B_p}{(2p)!}$

$\frac{1}{1^{2p+1}}-\frac{1}{3^{2p+1}}+\frac{1}{5^{2p+1}}-\frac{1}{7^{2p+1}}+\cdots=\frac{\pi^{2p+1}E_p}{2^{2p+2}(2p)!}$

Различные прогрессии

$\frac{1}{2}+\cos\alpha+\cos2\alpha+\cdots+\cos n\alpha=\frac{\sin(n+\frac{1}{2})\alpha}{2\sin\frac{\alpha}{2}}$

$\sin\alpha+\sin2\alpha+\sin3\alpha+\cdots+\sin n\alpha=\frac{\sin\left[\frac{1}{2}(n+1)\right]\alpha\sin\frac{1}{2}n\alpha}{\sin\frac{\alpha}{2}}$

$1+r\cos\alpha+r^2\cos2\alpha+r^3\cos3\alpha+\cdots=\frac{1-r\cos\alpha}{1-2r\cos\alpha+r^2}$,   $|r|

$r\sin\alpha+r^2\sin2\alpha+r^3\sin3\alpha+\cdots=\frac{r\sin\alpha}{1-2r\cos\alpha+r^2}$,   $|r|

$1+r\cos\alpha+r^2\cos2\alpha+\cdots+r^n\cos n\alpha=\frac{r^{n+2}\cos n\alpha-r^{n+1}\cos(n+1)\alpha-r\cos\alpha+1}{1-2r\cos\alpha+r^2}$

$r\sin\alpha+r^2\sin2\alpha+\cdots+r^n\sin n\alpha=\frac{r\sin\alpha-r^{n+1}\sin(n+1)\alpha+r^{n+2}\sin n\alpha}{1-2r\cos\alpha+r^2}$

Формулы суммирования Эйлера — Маклорена

$\sum\limits_{k=1}^{n-1}F(k)=\int\limits_0^nF(k)dk-\frac{1}{2}\{F(0)+F(n)\}+\frac{1}{12}\{F'(n)-F'(0)\}-\frac{1}{720}\{F»'(n)-F»’

Гармоническая прогрессия — Википедия

Материал из Википедии — свободной энциклопедии

первые десять членов гармонической последовательности an=1n{\displaystyle a_{n}={\tfrac {1}{n}}}.

В математике гармоническая прогрессия (или гармоническая последовательность) — это прогрессия, образованная обратными элементами арифметической прогрессиии.

Эквивалентное определение — это бесконечная последовательность вида

1a, 1a+d ,1a+2d ,1a+3d ,⋯,{\displaystyle {\frac {1}{a}},\ {\frac {1}{a+d}}\ ,{\frac {1}{a+2d}}\ ,{\frac {1}{a+3d}}\ ,\cdots ,}

где a не равно нулю и −a/d не натуральное число, или конечная последовательность вида

1a, 1a+d ,1a+2d ,1a+3d ,⋯,1a+kd,{\displaystyle {\frac {1}{a}},\ {\frac {1}{a+d}}\ ,{\frac {1}{a+2d}}\ ,{\frac {1}{a+3d}}\ ,\cdots ,{\frac {1}{a+kd}},}

где a≠0, k — натуральное число −a/d — не натуральное число или больше k.

• 1, 1/2, 1/3, 1/4, 1/5, 1/6
• 12, 6, 4, 3, 125{\displaystyle {\tfrac {12}{5}}}, 2, … , 12n{\displaystyle {\tfrac {12}{n}}}, …
• 30, −30, −10, −6, − 307{\displaystyle {\tfrac {30}{7}}}, … , 101−2n3{\displaystyle {\tfrac {10}{1-{\tfrac {2n}{3}}}}}
• 10, 30, −30, −10, −6, − 307{\displaystyle {\tfrac {30}{7}}}, … , 101−2(n−1)3{\displaystyle {\tfrac {10}{1-{\tfrac {2(n-1)}{3}}}}}

Основная статья: Гармонический ряд

Бесконечные гармонические прогрессии не суммируемы (в смысле бесконечной суммы).

Для гармонической прогрессии невозможно при различных единицах дробей (кроме случаев с a = 1 и k = 0) иметь сумму равную целому числу. Причина в том, что по крайней мере один знаменатель прогрессии будет делиться на натуральное число, на которое не делится любой другой знаменатель.^[1]

1. ↑ Erdős, P. (1932), «Egy Kürschák-féle elemi számelméleti tétel általánosítása», Mat. Fiz. Lapok Т. 39: 17–24, <https://www.renyi.hu/~p_erdos/1932-02.pdf> . Цитата по Graham, Ronald L. (2013), «Paul Erdős and Egyptian fractions», Erdős centennial, vol. 25, Bolyai Soc. Math. Stud., János Bolyai Math. Soc., Budapest, с. 289–309, ISBN 978-3-642-39285-6, DOI 10.1007/978-3-642-39286-3_9 .

Экспоненциальный рост Википедия

Линейная (красная), степенная (синяя) и экспоненциальная (зелёная) зависимости

Экспоненциальный рост — возрастание величины, когда скорость роста пропорциональна значению самой величины. Подчиняется экспоненциальному закону. Экспоненциальный рост противопоставляется более медленным (на достаточно длинном промежутке времени) линейной или степенной зависимостям. В случае дискретной области определения с равными интервалами его ещё называют геометрическим ростом или геометрическим распадом (значения функции образуют геометрическую прогрессию). Экспоненциальная модель роста также известна как мальтузианская модель роста.

Свойства[ | ]

Для любой экспоненциально растущей величины чем большее значение она принимает, тем быстрее растёт. Также это означает, что величина зависимой переменной и скорость её роста прямо пропорциональны. Но при этом, в отличие от гиперболической, экспоненциальная кривая никогда не уходит в бесконечность за конечный промежуток времени.

Экспоненциальный рост в итоге оказывается более быстрым, чем любой степенной и тем более любой линейный рост.

Математическая запись[ | ]

Экспоненциальный рост описывается дифференциальным уравнением:

dxdt=kx{\displaystyle {\frac {dx}{dt}}=kx}

Решение этого дифференциального уравнения — экспонента:

x=aekt{\displaystyle x=ae^{kt}}

Примеры[ | ]

Примером экспоненциального роста может быть рост числа бактерий в колонии до наступления ограничения ресурсов. Другим примером экспоненциального роста являются сложные проценты.

См. также[ | ]

Ссылки[ | ]

Проставив сноски, внести более точные указания на источники. Пожалуйста, после исп

Характеристическое свойство показательной прогрессии или новое числовое среднее

Библиографическое описание:

Гульманов Н. К. Характеристическое свойство показательной прогрессии или новое числовое среднее // Молодой ученый. — 2018. — №6. — С. 1-4. — URL https://moluch.ru/archive/192/48026/ (дата обращения: 27.01.2020).



Как известно, числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с некоторым числом, называется арифметической прогрессией [1]. А числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое отличное от нуля постоянное число, называется геометрической прогрессией [1]. Из определения арифметической и геометрической прогрессий мы видим, что они основаны на арифметических действиях суммы (разности) и умножения (деления). Возникает вопрос: существует ли прогрессия, которая основана на действии возведение в степень число. В работе [2] был определен новый вид прогрессии — показательная прогрессия.

Также в работе [2] в качестве характеристического свойства показательной прогрессии рассматривается следующее утверждение. Если 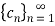— показательная прогрессия, то для любого натурального 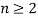выполняется равенство

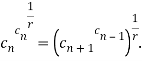
В данном проекте будет доказана другая формула, описывающая характеристическое свойство показательной прогрессии. Также будет рассмотрено неравенство — аналог неравенству Коши [3].

Ключевые слова: числовые последовательности, прогрессия, показательная прогрессия, неравенство Коши.

Докажем следующую теорему, описывающую характеристическое свойство показательной прогрессии.

Теорема 1. Для каждого члена показательной прогрессии, начиная со второго, выполняется равенство:

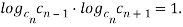
Доказательство. По определению [2] показательной прогрессии

Отсюда следует, что

т. е.

Преобразуем полученное выражение

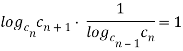
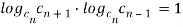(1)

что и требовалось доказать.

Выразим из равенства (1).

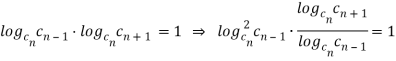
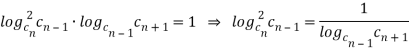
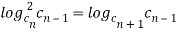
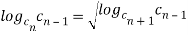
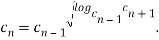
Так как характеристическое свойство арифметической прогрессии построено на основе арифметической средней, а геометрическая прогрессия — на основе геометрической средней, то характеристическое свойство показательной прогрессии должно построено на основе какой-то другой числовой средней. В качестве этой средней будем считать последнее из равенств.

Определение 1. Пусть даны два положительных числа 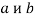. Причем эти числа либо больше единицы, либо меньше единицы одновременно. Средним показательным чисел 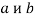называется величина, определяемая следующим образом:

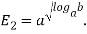(2)

Замечание 1. Если заменить местами 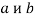, значение средней показательной не изменится.

Доказательство. Преобразуем выражение (2) следующим образом:

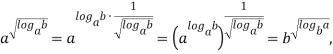
что и требовалось доказать.

Замечание 2. Среднюю показательную можно определить и следующим образом:

где 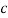— это такое произвольное положительное число, как 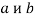, одновременно с ними либо больше единицы, либо — меньше.

Доказательство. Преобразуем выражение (2) следующим образом:

что и требовалось доказать.

Введем обобщенное определение средней показательной для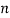

чисел.

Определение 2. Пусть даны положительные числа 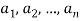и 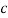. Причем эти числа либо больше единицы, либо меньше единицы одновременно. Средним показательным чисел 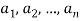называется величина, определяемая следующим образом:

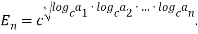
Среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического — это неравенство называется неравенством Коши [3]: если , , 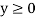то

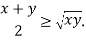
В более общем виде: для неотрицательных чисел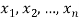

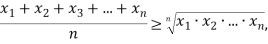
справедливо неравенство между их средним арифметическим и средним геометрическим

причем равенство возможно лишь при условии .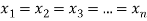

Рассмотрим следующую теорему, описывающую связь между неравенством Коши и средним показательным.

Теорема 2. Пусть даны числа 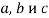, каждое из которых больше единицы. Тогда выполняется следующее неравенство:

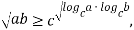
причем равенство возможно лишь при условии

Доказательство. Запишем неравенство Коши для чисел .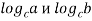

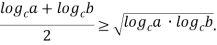
Используя свойства логарифма числа, преобразуем это выражение следующим образом:

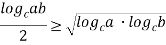
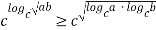
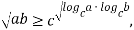
что и требовалось доказать.

Теорема 3. Пусть даны числа 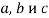, каждое из которых меньше единицы. Тогда выполняется следующее неравенство:

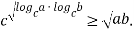
Причем равенство возможно лишь при условии

Доказательство. Запишем неравенство Коши для чисел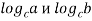

.

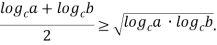
Используя свойства логарифма числа, преобразуем это выражение следующим образом:

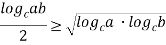
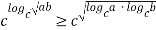
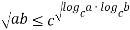
или

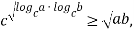
что и требовалось доказать.

Замечание 3. Пусть даны положительные числа 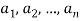и 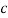. Тогда выполняются неравенства

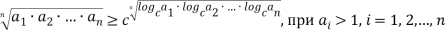
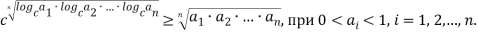
причем равенство возможно лишь при условии .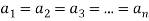

Литература:

1. Н. Я. Виленкин / Алгебра для 9 класса: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математикик / Н. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев / — 3-е изд. — М.: Просвещение, 1999. — С.384: ил. — ISBN 5–09–009020–3
2. Н. К. Гульманов / Определение нового вида прогрессии, основанной на операции возведения в степень, и изучение ее основных свойств / Н. К. Гульманов, Н. А. Марчук // «Высокое качество и лидерство в образовании»: сборник докладов Международной научно-практической конференции (13–15 ноября 2013 года)/ АОО «Назарбаев Интеллектуальные школы». Часть 1. — Астана, 2013. — С. 120–124
3. П. П. Коровкин / Неравенства / Популярные лекции по математике, выпуск № 5/ — М.: Издательство «Наука», 1974. — С. 54
4. И. С. Соминский / Метод математической индукции / Популярные лекции по математике, выпуск № 3/ — М.: Издательство «Наука», 1972. — С. 63

Основные термины (генерируются автоматически): показательная прогрессия, число, характеристическое свойство, неравенство, равенство, геометрическая прогрессия, арифметическая прогрессия, числовая последовательность, свойство логарифма числа, Кош.

Гармонический ряд — Википедия

Гармони́ческий ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:

∑k=1∞1k=1+12+13+14+⋯+1k+⋯{\displaystyle \sum _{k=1}^{\mathcal {\infty }}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{k}}+\cdots }.

Ряд назван гармоническим, так как складывается из «гармоник»: k{\displaystyle k}-я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной 1k{\displaystyle {\frac {1}{k}}} от длины исходной струны^[1]. Кроме того, каждый член ряда, начиная со второго, представляет собой среднее гармоническое двух соседних членов.

Суммы первых n членов ряда (частичные суммы)[править | править код]

Отдельные члены ряда стремятся к нулю, но его сумма расходится. Частичная сумма n первых членов гармонического ряда называется n-м гармоническим числом:

Hn=∑k=1n1k=1+12+13+14+⋯+1n{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}}

Разница между n{\displaystyle n}-м гармоническим числом и натуральным логарифмом n{\displaystyle n} сходится к постоянной Эйлера — Маскерони γ=0,5772…{\displaystyle \gamma =0{,}5772…}.

Разница между различными гармоническими числами никогда не равна целому числу и никакое гармоническое число, кроме h2=1{\displaystyle H_{1}=1}, не является целым: ∀n>1∑k=1n1k∉N{\displaystyle \forall n>1\;\;\;\;\sum _{k=1}^{n}{\frac {1}{k}}\notin \mathbb {N} }^[2].

Некоторые значения частичных сумм[править | править код]

h2=1h3=32=1,5h4=116≈1,833h5=2512≈2,083H5=13760≈2,283{\displaystyle {\begin{matrix}H_{1}&=&1\\\\H_{2}&=&{\frac {3}{2}}&=&1{,}5\\\\H_{3}&=&{\frac {11}{6}}&\approx &1{,}833\\\\H_{4}&=&{\frac {25}{12}}&\approx &2{,}083\\\\H_{5}&=&{\frac {137}{60}}&\approx &2{,}283\end{matrix}}}

H6=4920=2,45H7=363140≈2,593H8=761280≈2,718h203≈7,484h206≈14,393{\displaystyle {\begin{matrix}H_{6}&=&{\frac {49}{20}}&=&2{,}45\\\\H_{7}&=&{\frac {363}{140}}&\approx &2{,}593\\\\H_{8}&=&{\frac {761}{280}}&\approx &2{,}718\\\\H_{10^{3}}&\approx &7{,}484\\\\H_{10^{6}}&\approx &14{,}393\end{matrix}}}

Формула Эйлера[править | править код]

В 1740 году Эйлером было получено асимптотическое выражение для суммы первых n{\displaystyle n} членов ряда:

Hn=ln⁡n+γ+εn{\displaystyle H_{n}=\ln n+\gamma +\varepsilon _{n}},

где γ=0,5772…{\displaystyle \gamma =0{,}5772…} — постоянная Эйлера — Маскерони, а ln{\displaystyle \ln } — натуральный логарифм.

При n→∞{\displaystyle n\rightarrow \infty } значение εn→0,{\displaystyle \varepsilon _{n}\rightarrow 0,} следовательно, для больших n{\displaystyle n}

Hn≈ln⁡n+γ{\displaystyle H_{n}\approx \ln n+\gamma } — формула Эйлера для суммы первых n{\displaystyle n} членов гармонического ряда.

Пример использования формулы Эйлера

n{\displaystyle n}	Hn=∑k=1n1k{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}}	ln⁡n+γ{\displaystyle \ln n+\gamma }	εn{\displaystyle \varepsilon _{n}}, (%)
10	2,93	2,88	1,7
25	3,82	3,80	0,5

Более точная асимптотическая формула для частичной суммы гармонического ряда:

Hn≍ln⁡n+γ+12n−112n2+1120n4−1252n6⋯=ln⁡n+γ+12n−∑k=1∞B2k2kn2k,{\displaystyle H_{n}\asymp \ln n+\gamma +{\frac {1}{2n}}-{\frac {1}{12n^{2}}}+{\frac {1}{120n^{4}}}-{\frac {1}{252n^{6}}}\dots =\ln n+\gamma +{\frac {1}{2n}}-\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k\,n^{2k}}},} где B2k{\displaystyle B_{2k}} — числа Бернулли.

Данный ряд расходится, однако ошибка вычислений по нему никогда не превышает половины первого отброшенного члена^{[источник не указан 482 дня]}.

Гармонический ряд расходится: sn→∞{\displaystyle s_{n}\rightarrow \infty } при n→∞,{\displaystyle n\rightarrow \infty ,} однако очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 10⁴³ элементов ряда).

Расходимость гармонического ряда можно продемонстрировать, сравнив его со следующим телескопическим рядом, который получается из логарифмирования (1+1n)n<e{\displaystyle \left(1+{\frac {1}{n}}\right)^{n}<e}:

vn=ln⁡(n+1)−ln⁡n=ln⁡(1+1n)<1n.{\displaystyle v_{n}=\ln(n+1)-\ln n=\ln \left(1+{\frac {1}{n}}\right)<{\frac {1}{n}}.}

Частичная сумма этого ряда, очевидно, равна ∑i=1nvi=ln⁡(n+1).{\displaystyle \sum _{i=1}^{n}v_{i}=\ln(n+1).} Последовательность таких частичных сумм расходится; следовательно, по определению телескопический ряд расходится, но тогда из признака сравнения рядов следует, что гармонический ряд тоже расходится.

Доказательство через предел последовательности частичных сумм^[3][править | править код]

Рассмотрим последовательность Hn=∑k=1n1k=1+12+13+14+⋯+1n.{\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}.} Покажем, что эта последовательность не является фундаментальной, то есть, что ∃ε>0:∀k∈N ∃n>k,∃p∈N:|Hn+p−Hn|≥ε.{\displaystyle \exists \varepsilon >0:\forall k\in \mathbb {N} \ \exists n>k,\exists p\in \mathbb {N} :\left\vert H_{n+p}-H_{n}\right\vert \geq \varepsilon .} Оценим разность|Hn+p−Hn|=1n+1+⋯+1n+p≥1n+p+⋯+1n+p=pn+p.{\displaystyle \left\vert H_{n+p}-H_{n}\right\vert ={\frac {1}{n+1}}+\cdots +{\frac {1}{n+p}}\geq {\frac {1}{n+p}}+\cdots +{\frac {1}{n+p}}={\frac {p}{n+p}}.} Пусть p≐n.{\displaystyle p\doteq n.} Тогда ∀n∈N:|h3n−Hn|≥12.{\displaystyle \forall n\in \mathbb {N} :\left\vert H_{2n}-H_{n}\right\vert \geq {\frac {1}{2}}.} Следовательно, данная последовательность не является фундаментальной и по критерию Коши расходится. Тогда по определению ряд также расходится.

Доказательство Орема[править | править код]

Доказательство расходимости можно построить, если сравнить гармонический ряд с другим расходящимся рядом, в котором знаменатели дополнены до степени двойки:

∑k=1∞1k=1+[12]+[13+14]+[15+16+17+18]+[19+⋯]+⋯>1+[12]+[14+14]+[18+18+18+18]+[116+⋯]+⋯=1+ 12   +12 + 12  +  12 + ⋯.{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{k}}&{}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right]+\cdots \\&{}>1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right]+\cdots \\&{}=1+\ {\frac {1}{2}}\ \ \ +\quad {\frac {1}{2}}\ \quad +\ \qquad \quad {\frac {1}{2}}\qquad \ \quad \ +\quad \ \ {\frac {1}{2}}\ \quad +\ \cdots .\end{aligned}}}

Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).

Обобщённый гармонический ряд[править | править код]

Обобщённым гармоническим рядом (частный случай ряда Дирихле) называют ряд^[4]

∑k=1∞1kα=1+12α+13α+14α+⋯+1kα+⋯{\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k^{\alpha }}}=1+{\frac {1}{2^{\alpha }}}+{\frac {1}{3^{\alpha }}}+{\frac {1}{4^{\alpha }}}+\cdots +{\frac {1}{k^{\alpha }}}+\cdots }.

Этот ряд расходится при α⩽1{\displaystyle \alpha \leqslant 1} и сходится при α>1{\displaystyle \alpha >1}^[4].

Сумма обобщённого гармонического ряда порядка α{\displaystyle \alpha } равна значению дзета-функции Римана:

∑k=1∞1kα=ζ(α){\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k^{\alpha }}}=\zeta (\alpha )}

Для чётных это значение явно выражается через число пи — например, сумма ряда обратных квадратов ζ(2)=π26{\displaystyle \zeta (2)={\frac {\pi ^{2}}{6}}}. Но уже для α=3 его значение (константа Апери) аналитически неизвестно.

Другой иллюстрацией расходимости гармонического ряда может служить соотношение ζ(1+1n)∼n.{\displaystyle \zeta (1+{\frac {1}{n}})\sim n.}

Знакопеременный ряд[править | править код]

Первые 14 частичных сумм знакочередующегося гармонического ряда (чёрные отрезки), показывающие сходимость к натуральному логарифму от 2 (красная линия)

В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд

∑n=1∞(−1)n+1n=1−12+13−14+15−⋯{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\;=\;1\,-\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,-\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,-\,\cdots }

сходится по признаку Лейбница. Поэтому говорят, что такой ряд обладает условной сходимостью. Его сумма равна натуральному логарифму 2:

1−12+13−14+15−⋯=ln⁡2.{\displaystyle 1\,-\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,-\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,-\,\cdots \;=\;\ln 2.}

Эта формула — частный случай ряда Меркатора, то есть ряда Тейлора для натурального логарифма.

Похожий ряд может быть получен из ряда Тейлора для арктангенса:

∑n=0∞(−1)n2n+1=1−13+15−17+⋯=π4.{\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}\;\;=\;\;1\,-\,{\frac {1}{3}}\,+\,{\frac {1}{5}}\,-\,{\frac {1}{7}}\,+\,\cdots \;\;=\;\;{\frac {\pi }{4}}.}

Это соотношение известно как ряд Лейбница.

Случайный гармонический ряд[править | править код]

В 2003 году изучены^[5][6] свойства случайного ряда

∑n=1∞snn,{\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

где sn{\displaystyle s_{n}} — независимые, одинаково распределённые случайные величины, которые принимают значения +1 и −1 с одинаковой вероятностью ½. Показано, что этот ряд сходится с вероятностью 1, и сумма ряда есть случайная величина с интересными свойствами. Например, функция плотности вероятности, вычисленная в точках +2 или −2 имеет значение:

0,124 999 999 999 999 999 999 999 999 999 999 999 999 999 7 642…,

отличаясь от ⅛ на менее чем 10⁻⁴².

«Истончённый» гармонический ряд[править | править код]

См. Ряд Кемпнера^[en]

Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшийся ряд сходится, и его сумма меньше 80^[7]. Позже была найдена более точная оценка, ряд Кемпнера сходится к 22,92067661926415034816{\displaystyle 22{,}92067661926415034816} (последовательность A082838 в OEIS). Более того, доказано, что если оставить слагаемые, не содержащие любой заранее выбранной последовательности цифр, то полученный ряд будет сходиться. Из этого можно сделать ошибочное заключение о сходимости исходного гармонического ряда, что не верно, поскольку с ростом разрядов в числе n{\displaystyle n} всё меньше слагаемых берётся для суммы «истончённого» ряда. То есть, в конечном счёте отбрасывается подавляющее большинство членов, образующих сумму гармонического ряда, чтобы не превзойти ограничивающую сверху геометрическую прогрессию.

1. ↑ Грэхэм Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики. — М.: Мир; БИНОМ. Лаборатория знаний, 2006. — С. 47. — 703 с. ISBN 5-03-003773-X
2. ↑ Harmonic Number — from Wolfram MathWorld
3. ↑ Кудрявцев Н. Л. Лекции по математическому анализу. — 2013. — С. 35.
4. ↑ ^{1 2} Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. М.: Наука. Главная редакция физико-математической литературы, 1981, 718 с.
5. ↑ «Random Harmonic Series», American Mathematical Monthly 110, 407—416, May 2003
6. ↑ Schmuland’s preprint of Random Harmonic Series
7. ↑ Nick’s Mathematical Puzzles: Solution 72