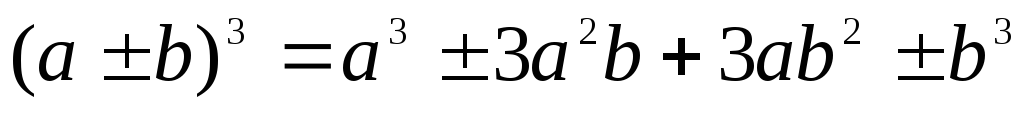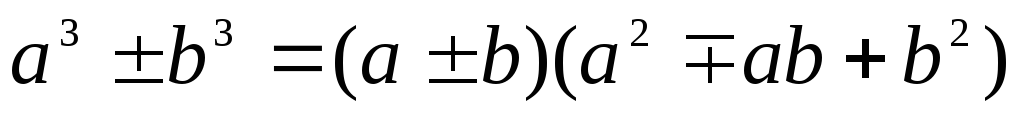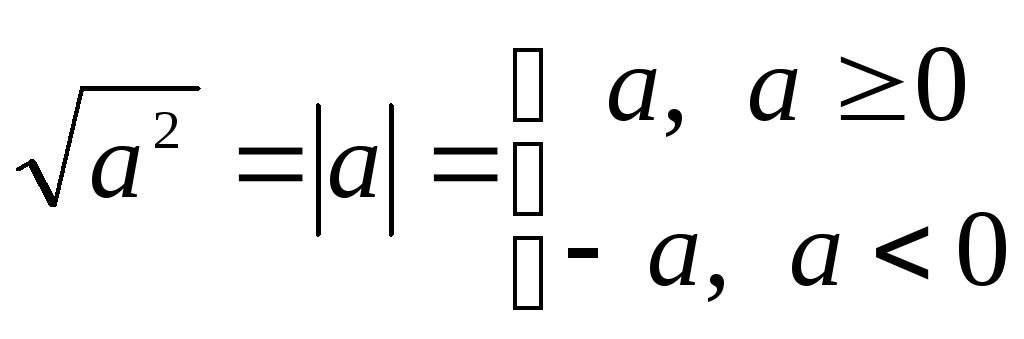Формула суммы членов конечной геометрической прогрессии
Тема: Геометрическая прогрессия
Урок: Формула суммы членов геометрической прогрессии
На уроке повторяется определение геометрической прогрессии, формула общего члена, выводится формула суммы членов конечной геометрической прогрессиии решаются типовые задачи.
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число q, называют геометрической прогрессией. При этом число q называют знаменателем прогрессии.
Математическая запись.
 геометрическая прогрессия, ее члены
геометрическая прогрессия, ее члены 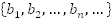 , при этом:
, при этом:

Иная запись: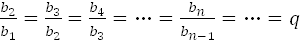 , т.е.
, т.е. 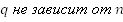 .
. 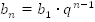 — формула n–го члена геометрической прогрессии, n=1,2,3,…
— формула n–го члена геометрической прогрессии, n=1,2,3,…
 т.е. геометрическую прогрессию можно рассматривать как показательную функцию натурального аргумента.
т.е. геометрическую прогрессию можно рассматривать как показательную функцию натурального аргумента.
Выведем далее формулу суммы конечного числа членов геометрической прогрессии.
Дано: 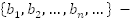
Найти: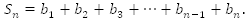
Решение: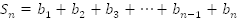 .
.
Умножим обе части этого равенства на q:
 .
.
И вычтем из первого равенства второе:
 ,
,
 ,
,
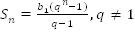
В полученной формуле 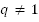 , рассмотрим частный случай
, рассмотрим частный случай
Геометрическая прогрессия 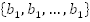 имеет nравных членов, поэтому ее сумма
имеет nравных членов, поэтому ее сумма
Итак, , при
, при 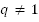 ;
; 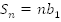
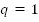 .
.Далее рассмотрим типовые задачи, для решения которых понадобится формула суммы членов геометрической прогрессии:
1. Дано: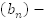 геометрическая прогрессия,
геометрическая прогрессия,  . Найти:
. Найти: 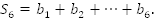 Решение:
Решение: 
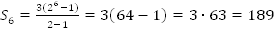 . Ответ:
. Ответ: 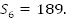
2. Дано: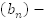 геометрическая прогрессия,
геометрическая прогрессия,  . Найти:
. Найти: 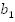 . Решение:
. Решение: 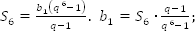
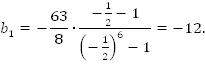

3. «Легенда об изобретателе шахмат». Дано: геометрическая прогрессия,
геометрическая прогрессия, 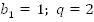 . Найти:
. Найти: 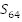 Решение:
Решение: 
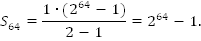 Ответ:
Ответ: 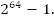
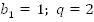 . Мы только что нашли, что
. Мы только что нашли, что  Оказалось, что это число настолько огромно, что у правителя не нашлось столько пшеницы. Возрастающая геометрическая прогрессия возрастает очень быстро и сумма даже не очень большого числа членов – огромное число.
Оказалось, что это число настолько огромно, что у правителя не нашлось столько пшеницы. Возрастающая геометрическая прогрессия возрастает очень быстро и сумма даже не очень большого числа членов – огромное число. 1. Дано: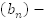 геометрическая прогрессия,
геометрическая прогрессия,  . Найти:
. Найти: 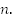 Решение:
Решение: 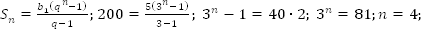
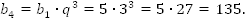 Ответ:
Ответ: 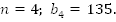
2. Найдите сумму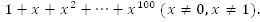
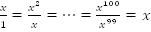 ,отношение не зависит от n, т.е. это геометрическая прогрессия. В этой прогрессии
,отношение не зависит от n, т.е. это геометрическая прогрессия. В этой прогрессии 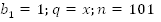 , тогда
, тогда  . Ответ:
. Ответ: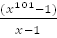 .
.3. Докажите тождество Доказательство: При
Доказательство: При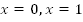
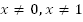 имеем геометрическую прогрессию (
имеем геометрическую прогрессию ( ). В предыдущей задаче мы вычислили
). В предыдущей задаче мы вычислили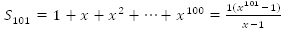 , тогда
, тогда Тождество доказано.
Тождество доказано.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на ресурсы интернет
1. РЕШУ ЕГЭ (Источник).
Рекомендованное домашнее задание
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.
№№ 502 — 505.
interneturok.ru
Сумма геометрической прогрессии | Онлайн калькулятор
Сумма геометрической прогрессии имеет несколько различных представлений, которые зависят от знаменателя прогрессии. Для возрастающей положительной, отрицательной или знакочередующейся прогрессии имеет место исключительно сумма нескольких первых членов геометрической прогрессии, количество которых должно быть ограничено, так как сама последовательность будет бесконечной.
Для прогрессии, знаменатель которой заключен между нулем и единицей, то есть является правильной дробью (0, сумма всей последовательности будет вполне однозначным конкретным числом, так как весь числовой ряд будет убывающим. Сумма бесконечно убывающей геометрической прогрессии имеет свою отдельную формулу, которую можно найти в соответствующем разделе, вместе с калькулятором.
Чтобы найти сумму первых членов геометрической прогрессии, необходимо знать первый член и знаменатель прогрессии. Если по условиям задачи дан какой-либо другой член прогрессии, кроме первого, тогда нужно будет сначала воспользоваться формулой первого члена геометрической прогрессии, чтобы вычислить его, и подставить полученное значение в онлайн калькулятор суммы.
Формула суммы первых трех, четырех или n членов геометрической прогрессии выводится с использованием среднего геометрического, как основного свойства данной прогрессии. Любое из чисел, стоящих в ряду, будет равно среднему геометрическому его соседей: 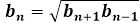
Если объединить это свойство с отношением двух последовательных членов прогрессии, которые неизменно равно одному и тому же числу — знаменателю, то путем нехитрых сокращений, сумма первых нескольких членов геометрической прогрессии приводится к такому виду:

В некоторых источниках встречается похожий вариант, но с другими знаками в скобках — по сути окончательного значения это не меняет, и для ручного расчета, когда даны первые несколько членов, уместно использовать более удобную на момент формулу.
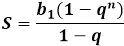
allcalc.ru
Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
О.Геометрической прогрессией называется последовательность, в которой первый член отличен от нуля, а каждый из последующих равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля.
О.Это число называетсязнаменателем геометрической прогрессии q геометрической прогрессии.
Геометрическая
прогрессия задаётся своим первым членом
и знаменателем. Из определения
геометрической прогрессии следует,
что отношение любого её члена, начиная
со второго, к предыдущему члену равно q, т.е. при любом
натуральномnверно
равенство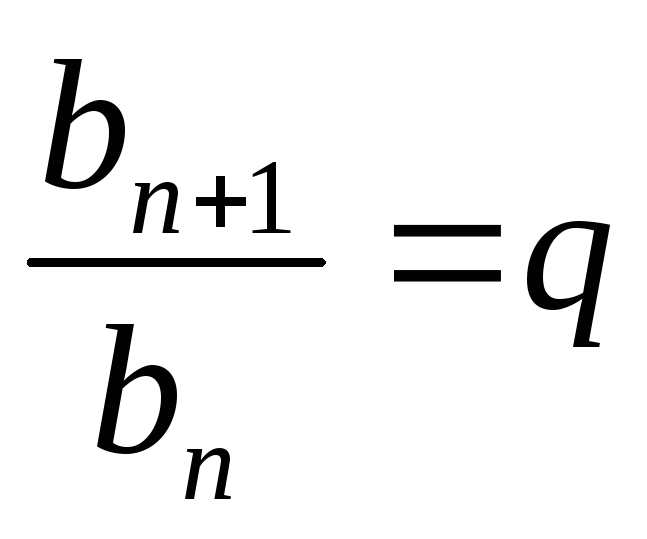 .
.
Формула n-го члена геометрической прогрессии.
Любой член
геометрической прогрессии можно
вычислить по формуле  ,где
,где —
член прогрессии с номеромn,
—
член прогрессии с номеромn, —
первый член иq– её
знаменатель.
—
первый член иq– её
знаменатель.
Возьмём произвольное
натуральное n.Из
определения геометрической прогрессии
следует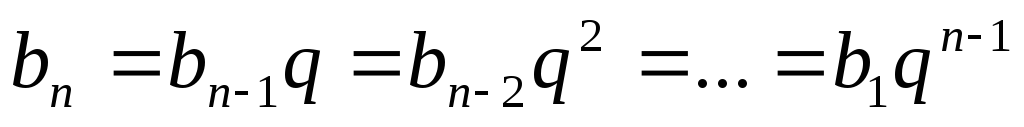 .
.
Эта цепочка состоит из nравенств, поэтому для любого конечногоnона может быть выписана. Следовательно, любой член геометрической прогрессии можно вычислить, зная его номер, первый член прогрессии и её знаменатель.
Характеристическое свойство геометрической прогрессии с положительными членами.
Если последовательность положительных чисел является геометрической прогрессией, то все её члены, начиная со второго, являются средним геометрическим предшествующего и последующего членов.
Доказательство.
Из определения
геометрической прогрессии следует,
что 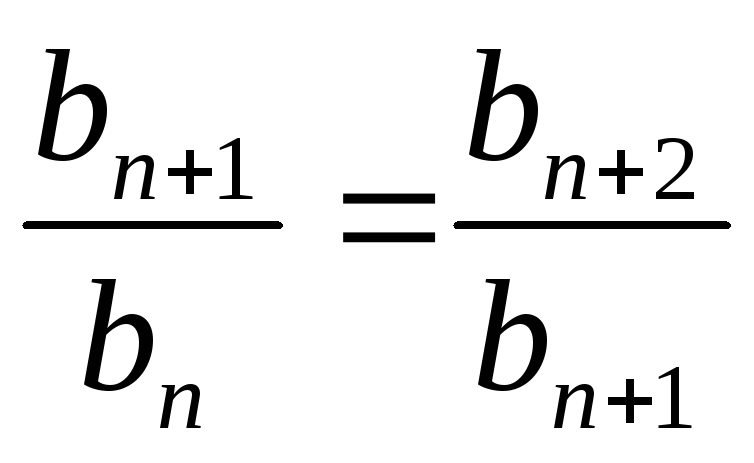 .
.
Выразив из этого
равенства 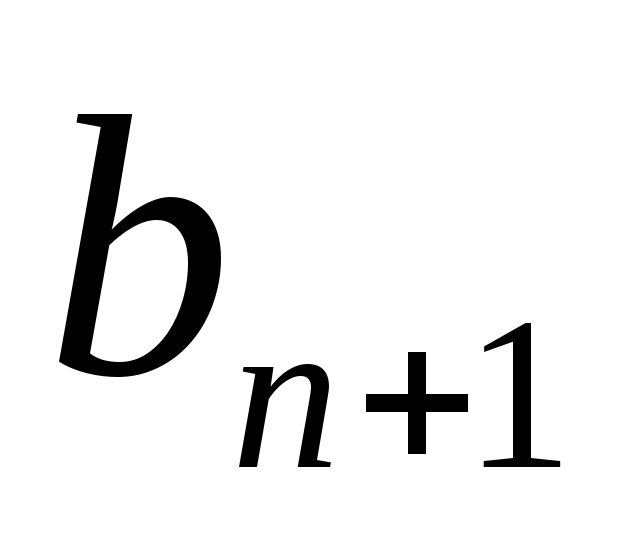 ,
получим
,
получим .
.
Так как все члены
прогрессии положительны, то последнее
равенство равносильно следующему  .
.
Теорема. (формула суммы n первых членов геометрической прогрессии).
Сумма n первых членов геометрической
прогрессии равна  ,при
,при .
.
Доказательство.
Сумма nпервых членов геометрической прогрессии равна
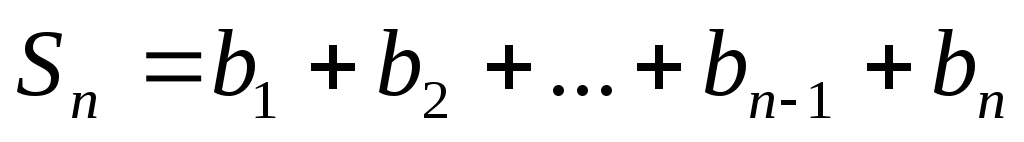 .
. 
Домножим обе части
этого равенства на знаменатель
геометрической прогрессии  .
.
Следовательно, 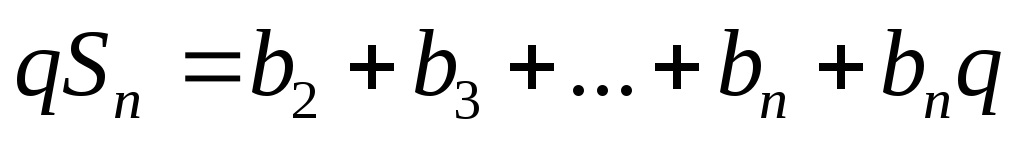 .
Вычтем полученное равенство из
.
Вычтем полученное равенство из .
Получим:
.
Получим:
 .
.
Отсюда следует,
что 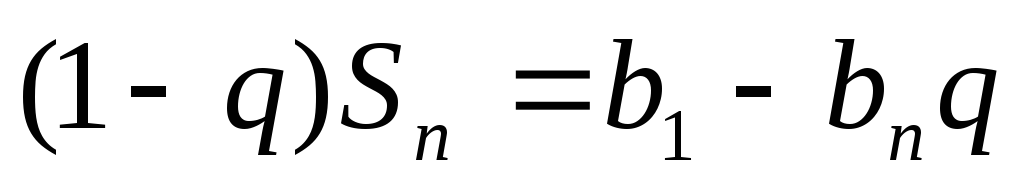 .
При
.
При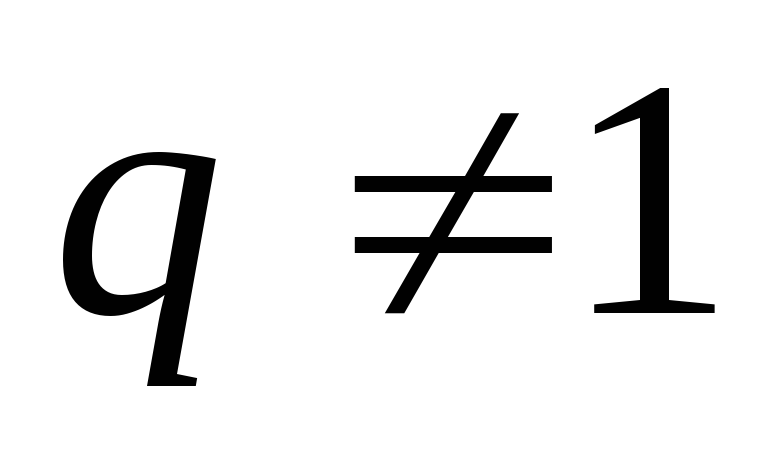 это равенство равносильно доказываемому.
Теорема доказана.
это равенство равносильно доказываемому.
Теорема доказана.
Следствие. 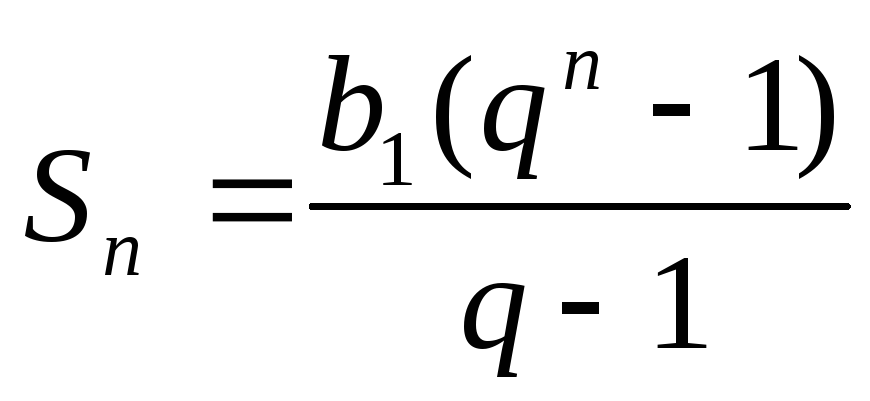 ,при
,при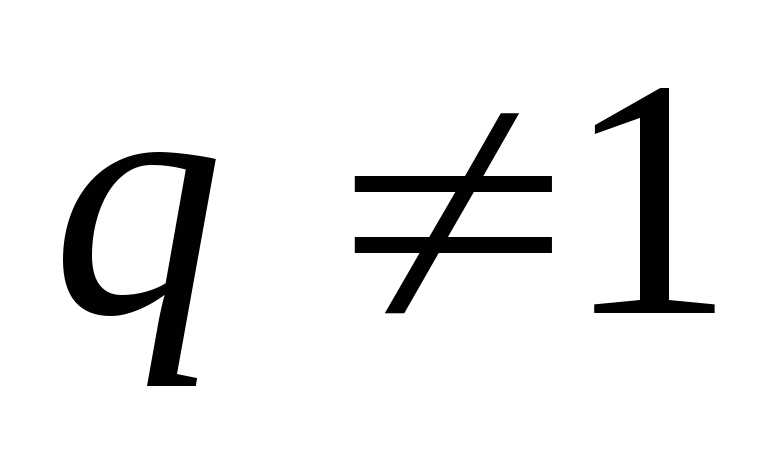 .
.
Доказательство.
Выразим 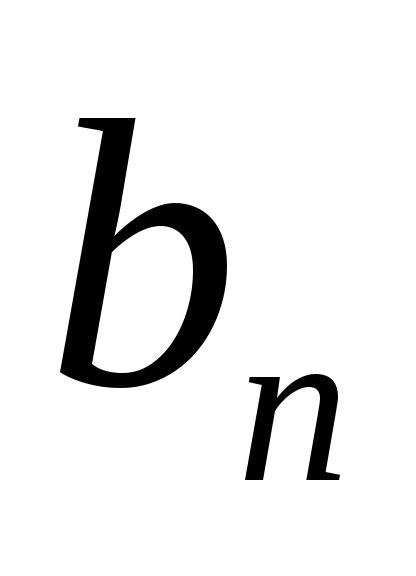 по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
Геометрическая
прогрессия называется бесконечно
убывающей, если её знаменательq по абсолютной величине меньше
единицы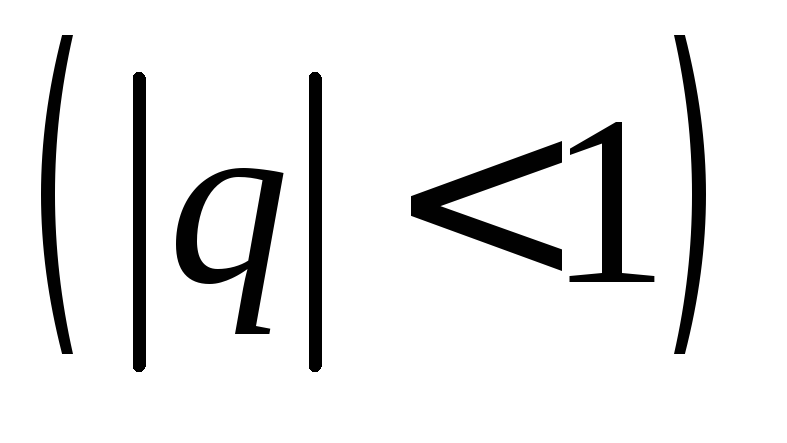 .
.
О.Суммой бесконечно убывающей геометрической прогрессииназывается число, к которому неограниченно приближается суммаnпервых членов бесконечно убывающей геометрической прогрессии при неограниченном увеличенииn.
Сумма
бесконечно убывающей геометрической
прогрессии равна 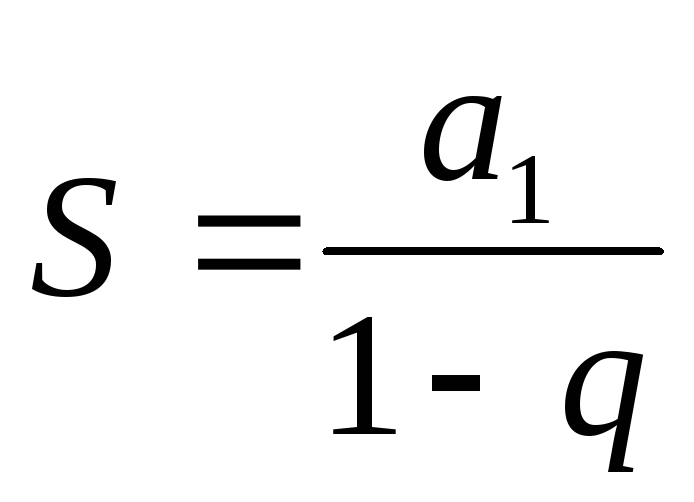 .
.
Приложение
Тригонометрическая окружность

Сборник формул
ТРИГОНОМЕТРИЯ Основные тригонометрические тождества Знаки тригонометрических функций по четвертям Тригонометрические функции отрицательного аргумента Выражение одной функции через другую Обратные функции аргумента Р Функция алгебраической суммы двух аргументов П Функции половинного аргумента | АЛГЕБРА Корни квадратных уравнений Разложение квадратного трехчлена на множители Логарифмы Извлечение квадратного корня из квадрата. Определение модуля числа. |
studfile.net
Арифметическая и геометрическая прогрессии
Арифметическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и некоторого фиксированного числа d:
Фиксированное число d называется разностью арифметической прогрессии.
Формула n-го члена арифметической прогрессии:
Сумма первых n членов арифметической прогрессии вычисляется по формуле:
Каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое соседних:
Геометрическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен произведению предыдущего члена и некоторого фиксированного числа q:
Фиксированное число q называется знаменателем геометрической прогрессии.
Формула n-го члена геометрической прогрессии:
Формула суммы первых n членов геометрической прогрессии вычисляется по формуле:
Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению соседних: .
Для решения задач на нахождение наибольших и наименьших значений функций – повторите тему «Производная».
Примеры решения задач
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru



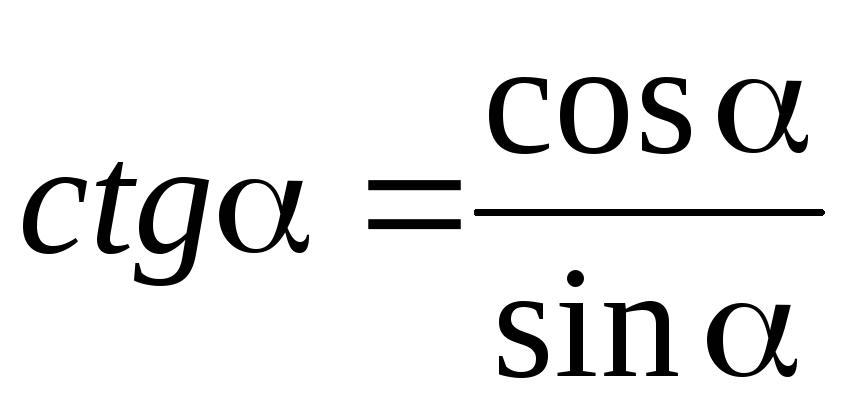

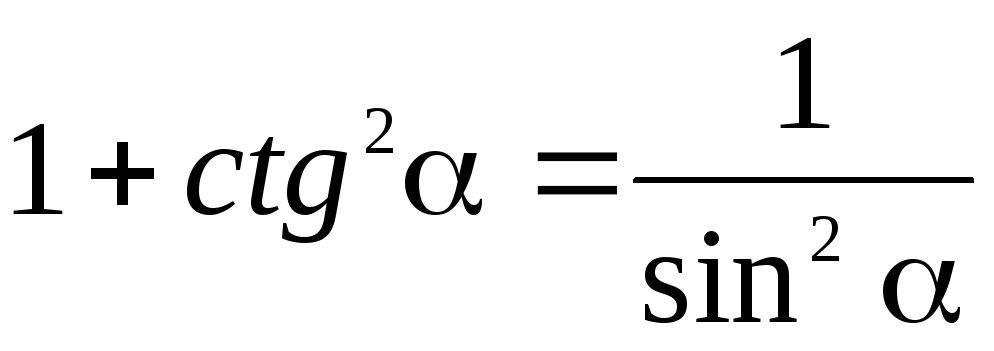














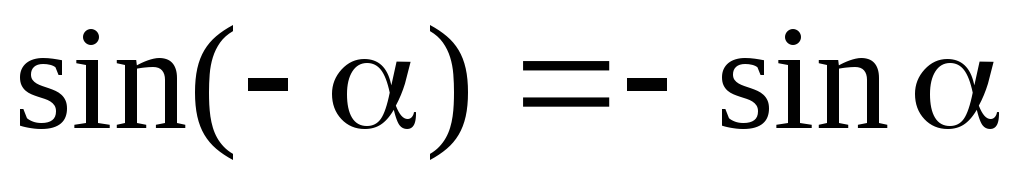
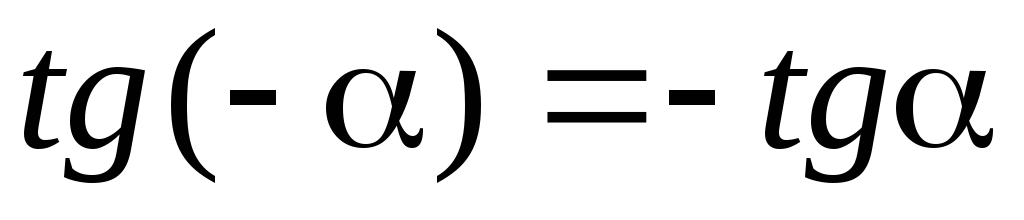

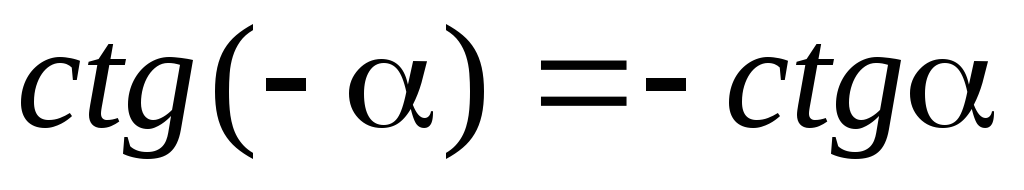


 отрицательного
отрицательного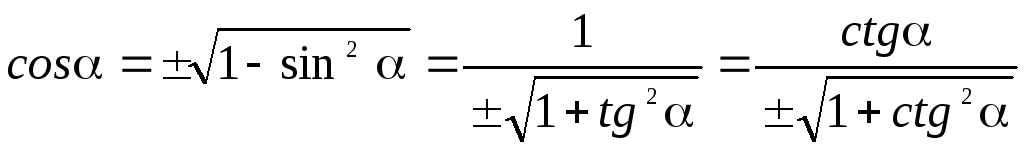
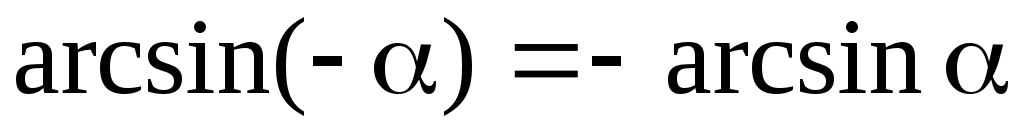

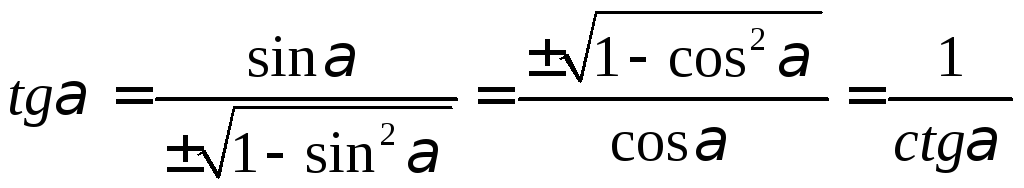

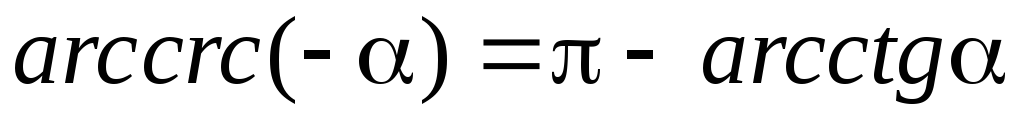
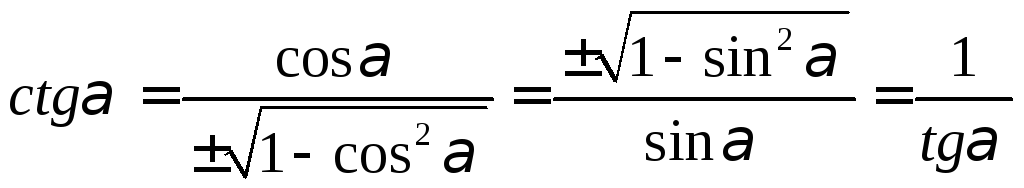
 ешение
простейших тригонометрических
уравнений
ешение
простейших тригонометрических
уравнений

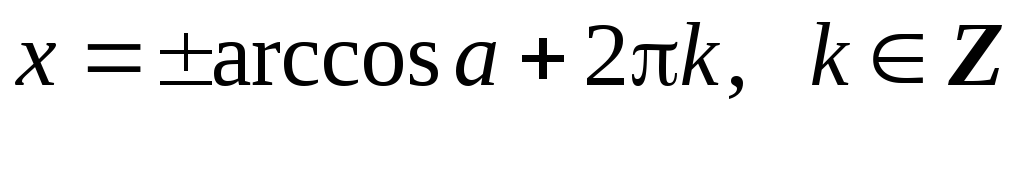

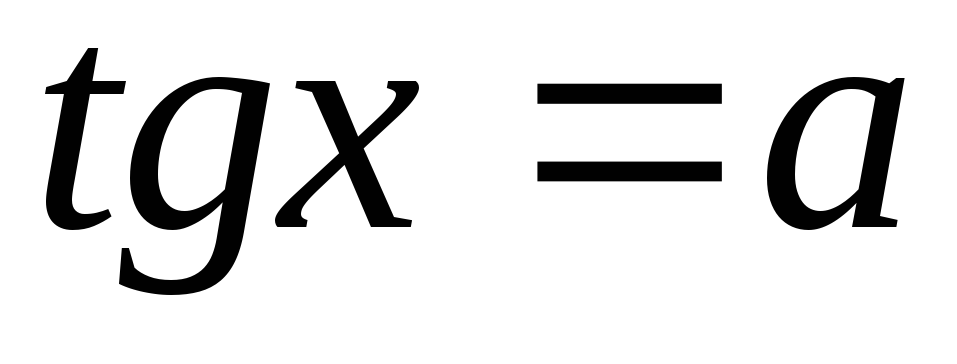
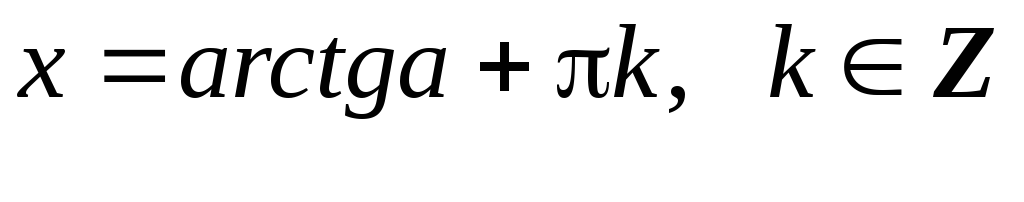
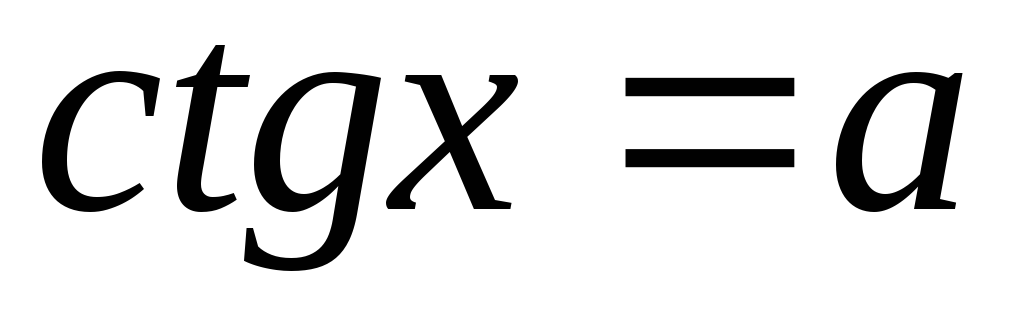
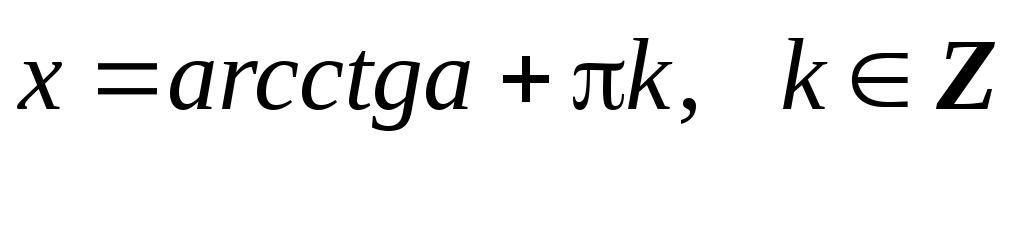

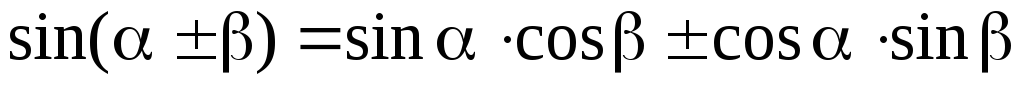
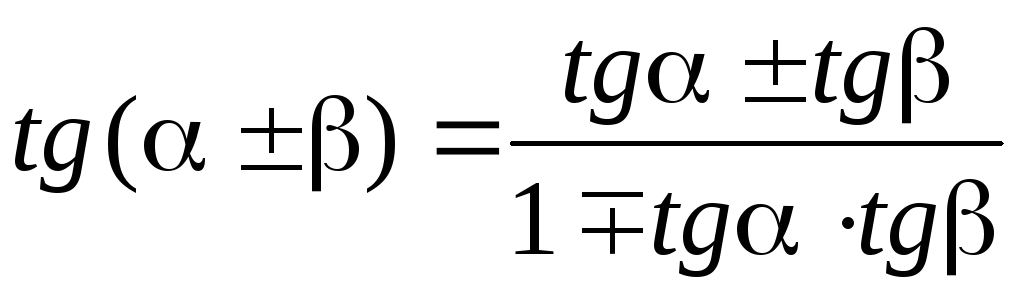


 реобразование
Преобразование
реобразование
Преобразование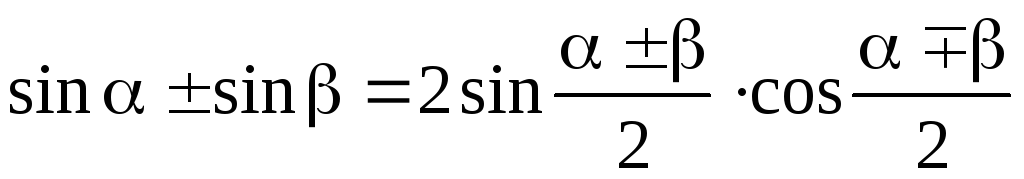 суммы
функций в произведение произведения
функций в сумму
суммы
функций в произведение произведения
функций в сумму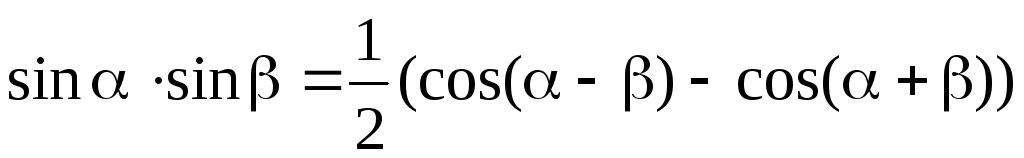
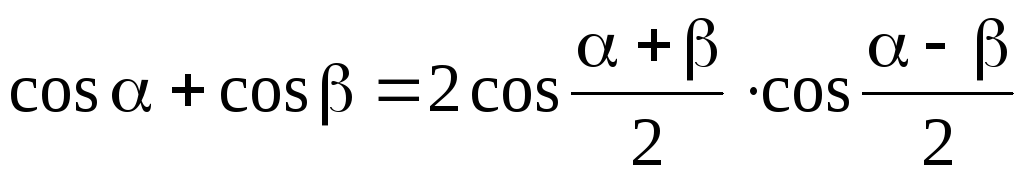
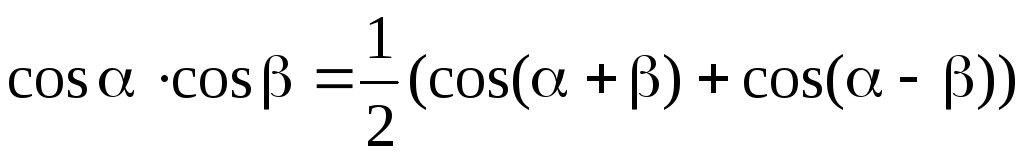
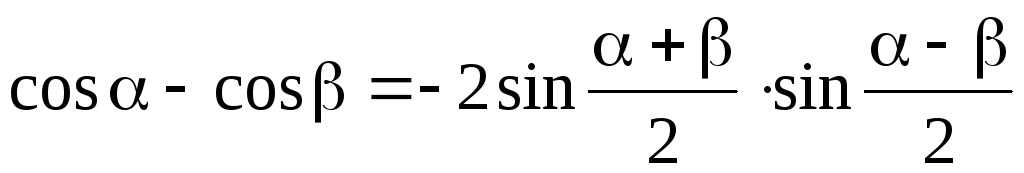

 Ф
Ф ункции
двойного аргумента
ункции
двойного аргумента
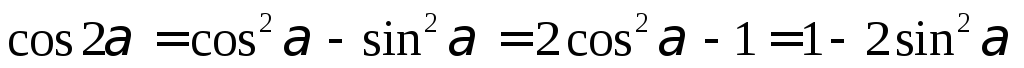


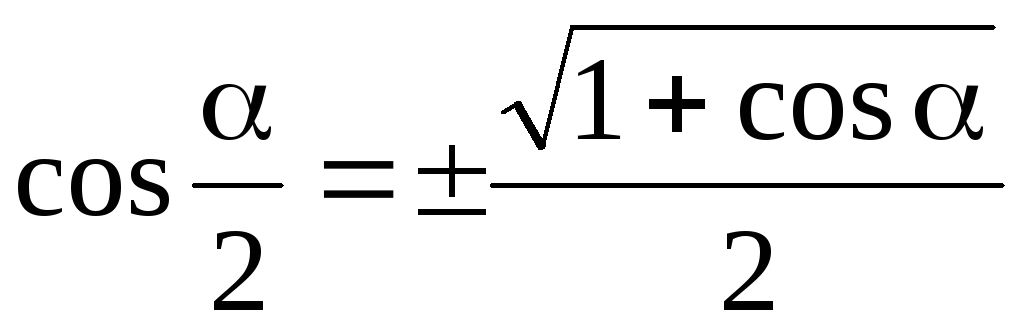


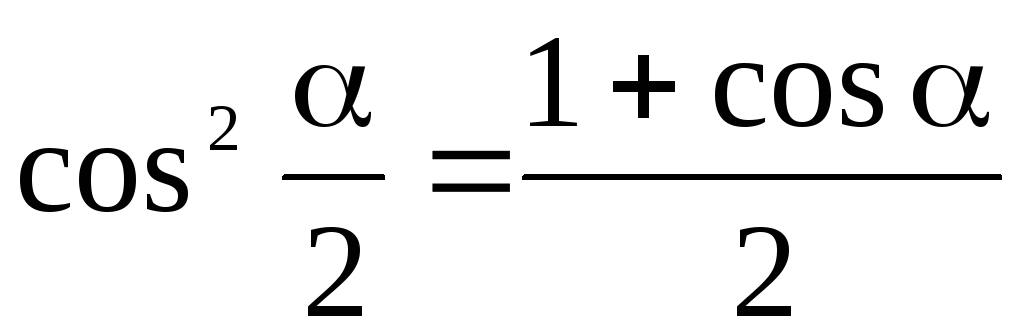
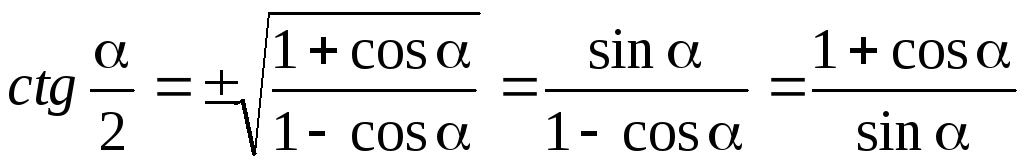

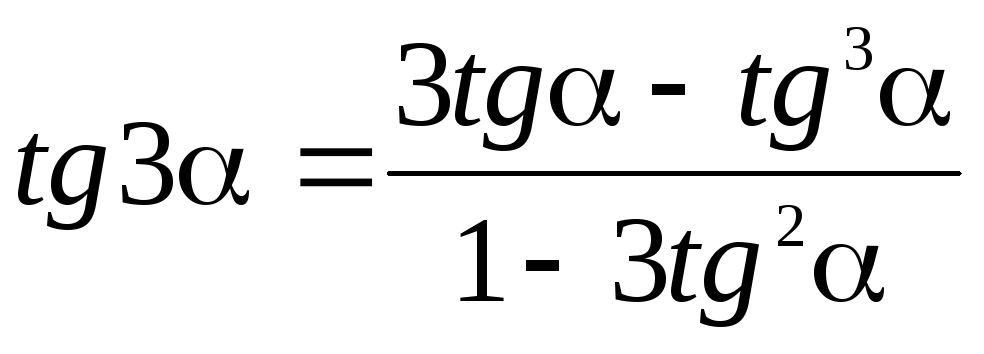 Ф
Ф ункции
тройного аргумента
ункции
тройного аргумента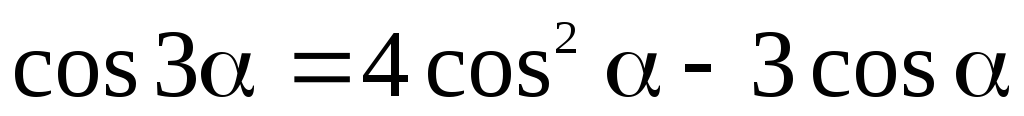

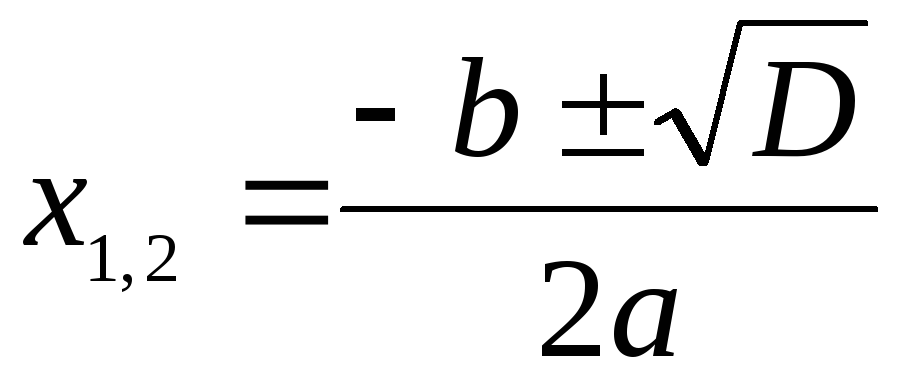

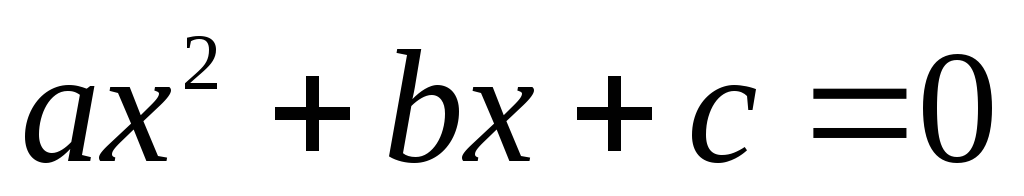 Теорема
Виета
Теорема
Виета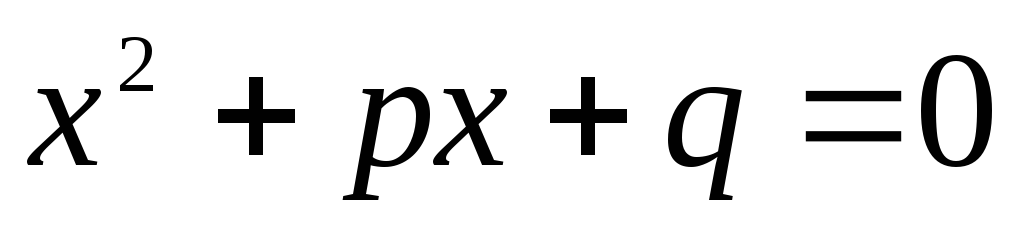






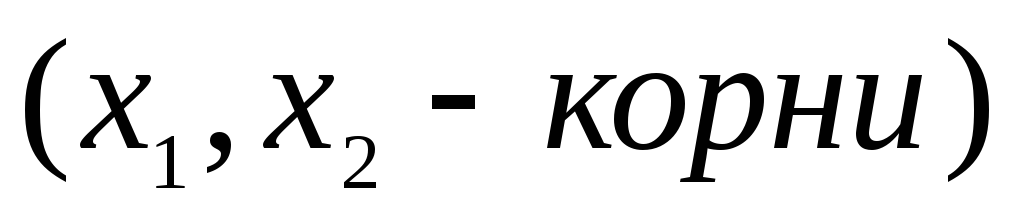
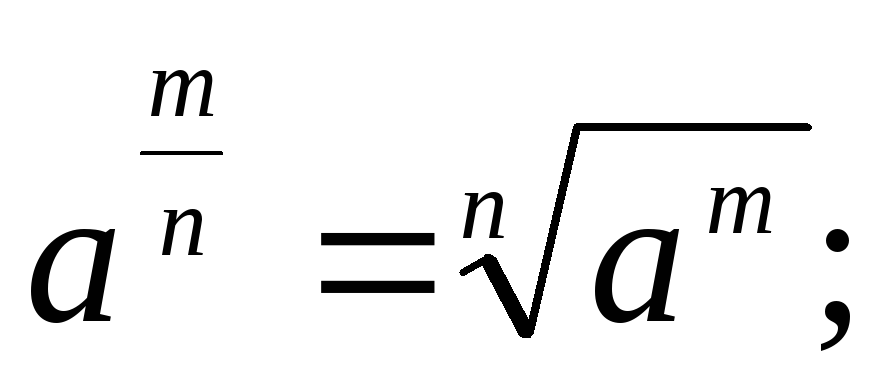 С
С тепени
и корни
тепени
и корни
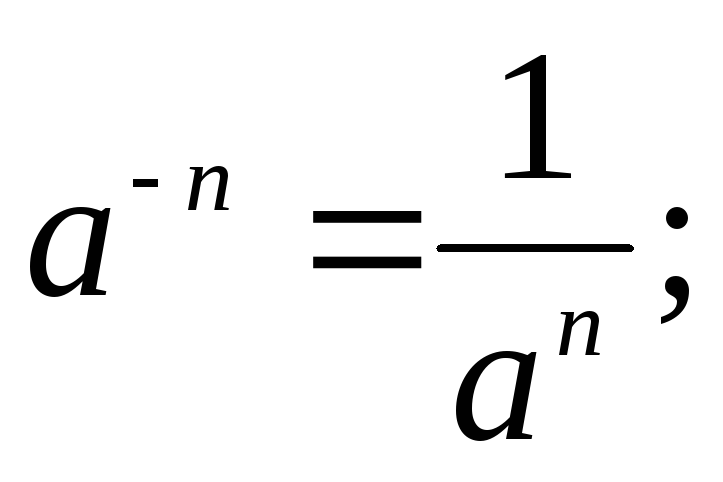



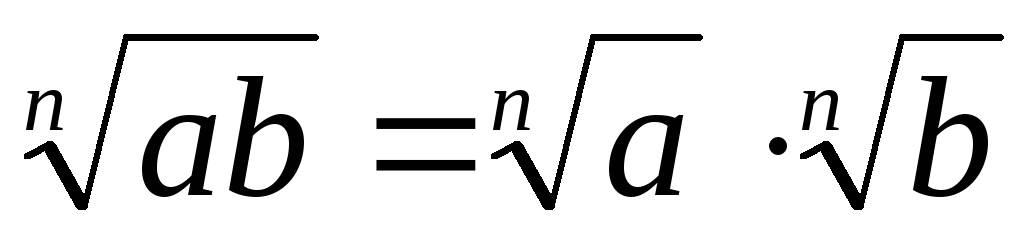
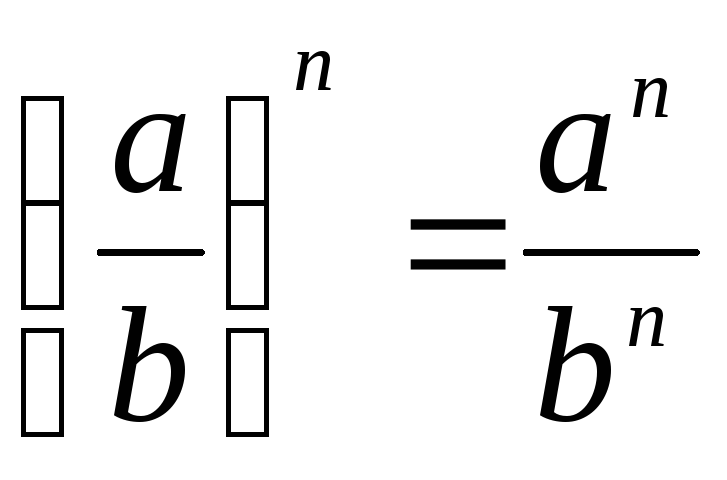



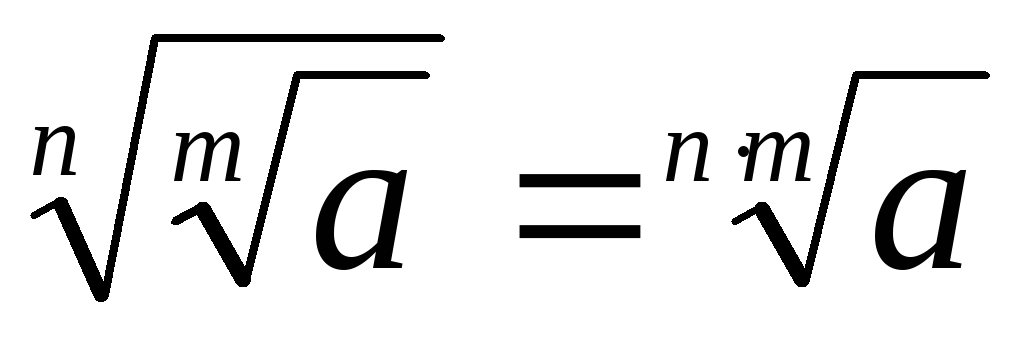

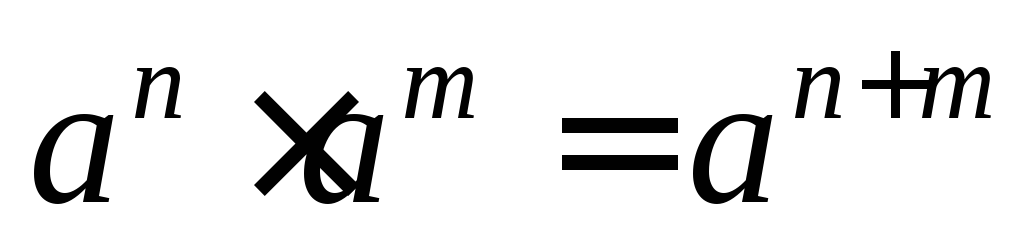

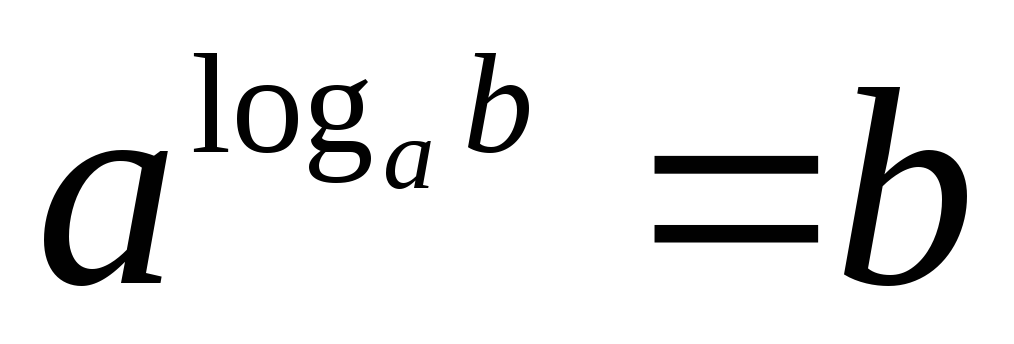


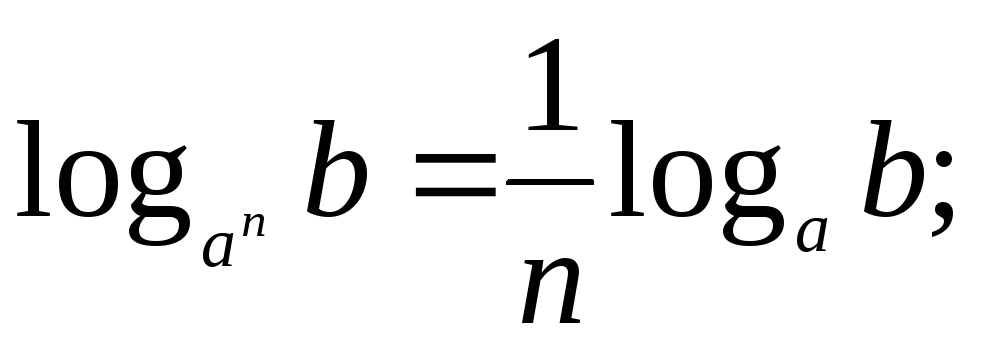
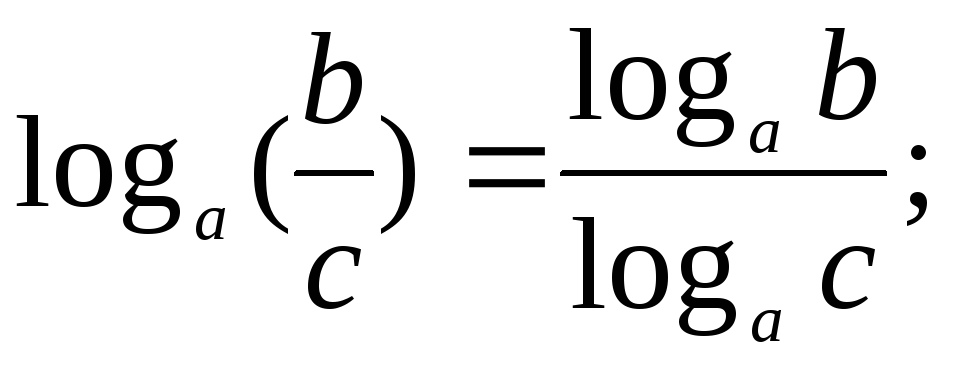
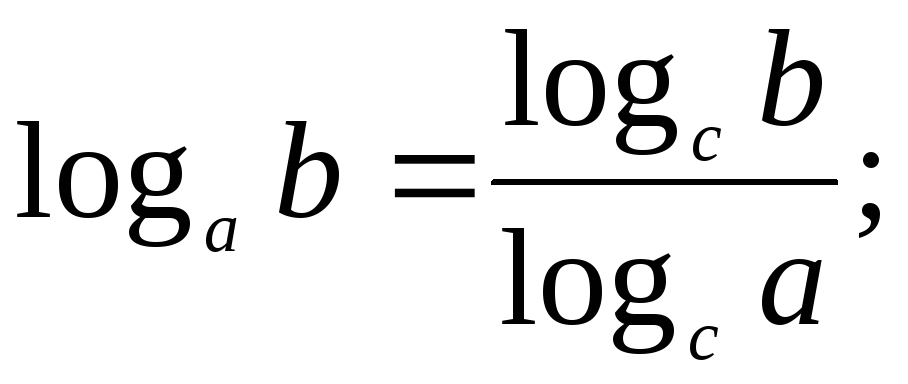
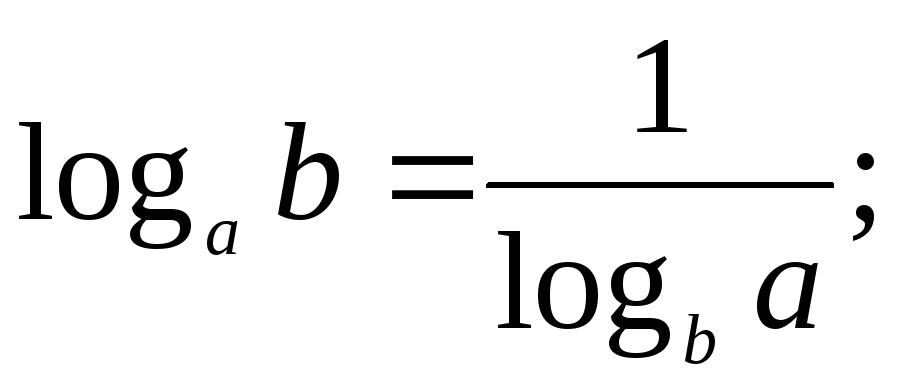
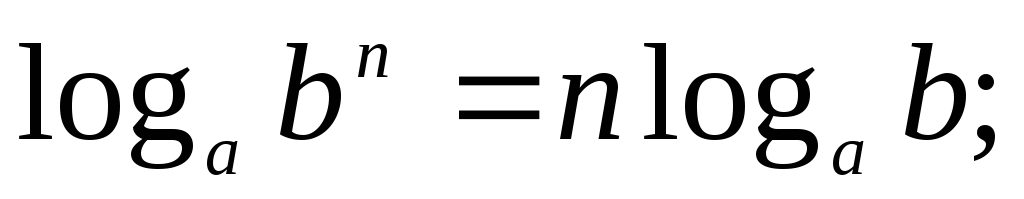

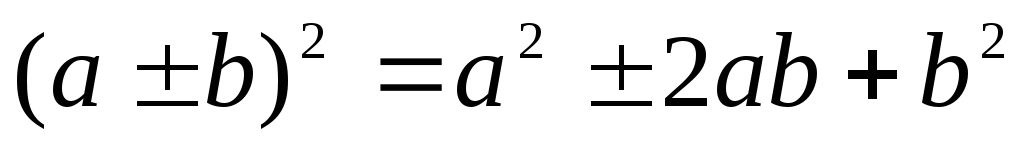 Степень
двучлена
Степень
двучлена