math-public:trapeciya [Президентский ФМЛ №239]
Определение
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Замечание
Сумма углов при боковой стороне трапеции равна $180^\circ$.
Доказательство
Действительно, так как основания трапеции параллельны, а боковая сторона является секущей, то углы при боковой стороне являются внутренними односторонними углами при параллельных прямых, и, следовательно, их сумма равна $180^\circ$.
Определение
Трапеция называется равнобедренной, если ее боковые стороны равны.
Трапеция называется прямоугольной, если один из ее углов равен $90^\circ$.
Свойства равнобедренной трапеции
Углы при основании равнобедренной трапеции равны.
Диагонали равнобедренной трапеции равны.
Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.
Докажем, что $\angle A=\angle D$.
Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.
Треугольники $\triangle ABE$ и $\triangle CFD$ равны по катету и гипотенузе ($AB=CD, BE=CF$).
Следовательно, $\angle A=\angle D$.
Докажем второй пункт теоремы.
В равнобедренной трапеции $ABCD$ рассмотрим треугольники $\triangle ABD$ и $\triangle ACD$.
Они равны по первому признаку ($AB=CD$, $AD$ – общая, $\angle A=\angle D$ по первому пункту).
Следовательно, $AC=BD$.
Докажем третий пункт теоремы.
Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $\triangle AOD$ и $\triangle BOC$ – равнобедренные, а треугольники $\triangle AOB$ и $\triangle COD$ равны.
Действительно, во втором пункте уже было доказано, что $\triangle ABD=\triangle ACD$.
Следовательно, $\angle 1=\angle 2$, а так как они накрест лежащие с углами $\angle 3$ и $\angle 4$ соответственно, то $\angle 3=\angle 4$, что и означает, что треугольники $\triangle AOD$ и $\triangle BOC$ – равнобедренные.
Тогда $AO=OD$ и $BO=OC$, и как следствие, $\triangle AOB=\triangle COD$ по третьему признаку равенства треугольников.
Докажем четвертый пункт теоремы.
Так как $\triangle AEB=\triangle CFD$ (по катету и гипотенузе), то $AE=FD$.
Кроме того, $EF=BC$, следовательно, $AE=\dfrac{AD-BC}{2}$ и $AF=\dfrac{AD-BC}{2}+BC=\dfrac{AD+BC}{2}$.
Признаки равнобедренной трапеции
-
Если углы при основании трапеции равны, то она равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим трапецию $ABCD$, в которой $\angle A=\angle D$.
Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.
Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.
Тогда $\angle A=\angle CED$, как соответственные углы.
Следовательно, $\angle CED=\angle D$, а тогда $\triangle CED$ – равнобедренный.
А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.
Докажем второй пункт теоремы.
Рассмотрим трапецию $ABCD$, у которой $AC=BD$.
Докажем, что тогда $AB=CD$.
Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.
Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.
Тогда $\triangle ACF$ – равнобедренный, так как $AC=CF$.
Следовательно $\angle OAD=\angle ODA$, и $\triangle AOD$ – равнобедренный.
Тогда $AO=OD$ и $BO=OC$.
Следовательно, $\triangle BOA=\triangle COD$ по первому признаку ($\angle BOA=\angle COD$ — как вертикальные).
Следовательно, $AB=CD$.
Теорема (о равнобедренной трапеции с перпендикулярными диагоналями)
В равнобедренной трапеции со взаимно перпендикулярными диагоналями высота равна средней линии.
Доказательство
Рассмотрим равнобедренную трапецию $ABCD$, в которой $AC\perp BD$.
Докажем, что в такой трапеции высота $CH$ равна средней линии то есть полусумме оснований.
Действительно, $\triangle AOD$ – равнобедренный и прямоугольный, следовательно, $\angle OAD = 45^\circ$. Тогда $\triangle AHC$ – равнобедренный, то есть $AH=CH$.
Но отрезок $AH$ равен полусумме оснований.
math-public/trapeciya.txt · Последние изменения: 2016/04/13 23:56 — labreslav
wiki.sch239.net
Трапеция. Видеоурок. Геометрия 8 Класс
Тема: Четырехугольники
Урок: Трапеция
Определение
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие – нет.
На Рис. 1. изображена произвольная трапеция. 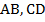 – это боковые стороны (те, которые не параллельны).
– это боковые стороны (те, которые не параллельны). 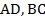 – основания (параллельные стороны).
– основания (параллельные стороны).
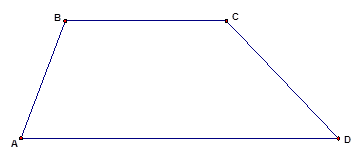
Рис. 1. Трапеция
Если сравнивать трапецию с параллелограммом, то у параллелограмма две пары параллельных сторон. То есть параллелограмм не является частным случаем трапеции, так как в определении трапеции чётко сказано, что две стороны трапеции не параллельны.
Выделим некоторые виды трапеции (частные случаи):
- равнобедренная (равнобокая) трапеция: боковые стороны равны;
- прямоугольная трапеция: один из углов равен
 (из определения трапеции и свойства параллельных прямых следует, что два угла будут по
(из определения трапеции и свойства параллельных прямых следует, что два угла будут по  ).
).
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
На Рис. 2. изображена трапеция со средней линией 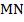 .
.
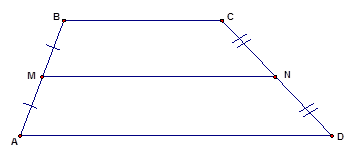
Рис. 2. Средняя линия трапеции
Свойства средней линии трапеции:
1. Средняя линия трапеции параллельна основаниям трапеции.
Доказательство:
Пусть середина боковой стороны 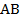 трапеции
трапеции  – точка
– точка  . Проведём через эту точку прямую, параллельную основаниям. Эта прямая пересечёт вторую боковую сторону трапеции
. Проведём через эту точку прямую, параллельную основаниям. Эта прямая пересечёт вторую боковую сторону трапеции 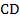 в точке
в точке 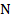 .
.
По построению: 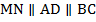 . По теореме Фалеса из этого следует:
. По теореме Фалеса из этого следует: 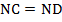 . Значит,
. Значит, 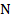 – середина стороны
– середина стороны 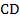
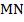 – средняя линия.
– средняя линия.Доказано.
2. Средняя линия трапеции равна полусумме оснований трапеции:  .
.
Доказательство:
Проведём среднюю линию трапеции и одну из диагоналей: например, 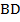 (см. Рис. 3).
(см. Рис. 3).
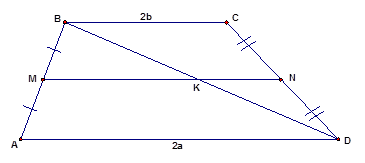
Рис. 3
По теореме Фалеса параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Так как равны отрезки: 
 является средней линией треугольника
является средней линией треугольника  , а отрезок
, а отрезок 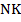 – средней линией треугольника
– средней линией треугольника 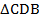 .
.Значит, 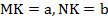 .
.
Примечание: это следует из свойства средней линии треугольника: средняя линия треугольника параллельна основанию и равна его половине. Первая часть этого свойства доказывается аналогично с доказательством первого свойства средней линии трапеции, а вторую часть можно доказать (к примеру, для средней линии 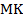
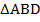 ), проведя через точку
), проведя через точку 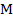 прямую, параллельную
прямую, параллельную 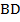 . Из теоремы Фалеса будет следовать, что эта прямая будет являться средней линией, а образованный четырёхугольник – параллелограммом (две пары попарно параллельных сторон). Отсюда уже несложно получить требуемое свойство.
. Из теоремы Фалеса будет следовать, что эта прямая будет являться средней линией, а образованный четырёхугольник – параллелограммом (две пары попарно параллельных сторон). Отсюда уже несложно получить требуемое свойство.Получаем: 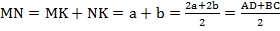 .
.
Доказано.
Рассмотрим теперь подробнее основные виды трапеции и их свойства.
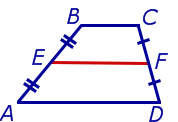
Напомним, что равнобедренная трапеция – трапеция, у которой боковые стороны равны. Рассмотрим свойства боковой трапеции.
1. Углы при основании равнобедренной трапеции равны.
Доказательство:
Выполним стандартное дополнительное построение, которое очень часто используется при решении различных задач на трапецию: проведём прямую 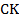 параллельно боковой стороне
параллельно боковой стороне 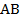 (см. Рис. 4).
(см. Рис. 4).
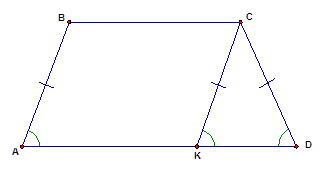
Рис. 4
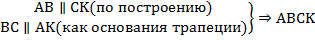 – параллелограмм.
– параллелограмм.
Отсюда следует, что: 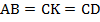 . Значит, треугольник
. Значит, треугольник 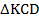 – равнобедренный. А значит, углы при его основании равны, то есть:
– равнобедренный. А значит, углы при его основании равны, то есть: 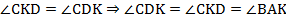 (последние два угла равны, как соответственные при параллельных прямых
(последние два угла равны, как соответственные при параллельных прямых 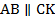 ).
).
Доказано.
2. Диагонали равнобедренной трапеции равны.
Доказательство:
Для доказательства этого свойства воспользуемся предыдущим. Действительно, рассмотрим треугольники: 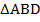 и
и 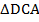 (см. Рис. 5.).
(см. Рис. 5.).

Рис. 5
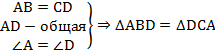 (по первому признаку равенства треугольников: две стороны и угол между ними).
(по первому признаку равенства треугольников: две стороны и угол между ними).
Из этого равенства сразу следует, что: 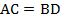
Доказано.
Оказывается, что, как и в случае с параллелограммом, у равнобедренной трапеции свойства одновременно являются и признаками. Сформулируем и докажем эти признаки.
Признаки равнобедренной трапеции
1. Дано: 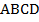 – трапеция;
– трапеция; 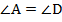 .
.
Доказать: 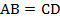
Доказательство:
Доказательство данного признака абсолютно аналогично доказательству соответствующего свойства. Проведём в трапеции 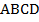 прямую
прямую 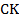
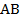 (см. Рис. 6).
(см. Рис. 6).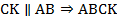 – параллелограмм (две пары попарно параллельных сторон).
– параллелограмм (две пары попарно параллельных сторон).
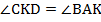 (соответственные углы при параллельных прямых). Откуда, пользуясь условием, получаем:
(соответственные углы при параллельных прямых). Откуда, пользуясь условием, получаем: 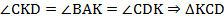 – равнобедренный
– равнобедренный

Рис. 6
(равны углы при основании). Значит: 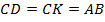 (у параллелограмма противоположные стороны равны).
(у параллелограмма противоположные стороны равны).
Доказано.
2. Дано: 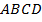 – трапеция;
– трапеция; 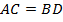 .
.
Доказать: 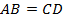 .
.
Доказательство:
Выполним ещё одно стандартное дополнительное построение при решении задач с трапецией: проведём через вершину 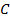 прямую
прямую 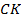 параллельно диагонали
параллельно диагонали 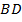 (см. Рис. 7).
(см. Рис. 7).
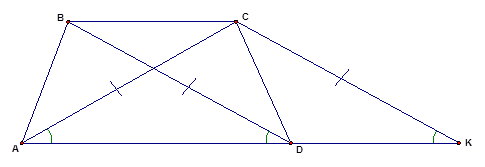
Рис. 7
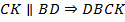 – параллелограмм (две пары попарно параллельных сторон).
– параллелограмм (две пары попарно параллельных сторон).
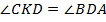 (соответственные углы при параллельных прямых). Кроме того,
(соответственные углы при параллельных прямых). Кроме того, 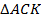 – равнобедренный (
– равнобедренный (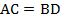 – по условию;
– по условию; 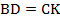 – по свойству параллелограмма). А значит:
– по свойству параллелограмма). А значит: 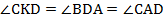 .
.
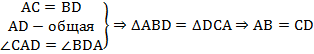
Доказано.
Рассмотрим несколько примеров решения задач с трапецией.
Пример 1.
Дано: 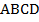 – трапеция;
– трапеция; 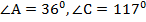 .
.
Найти: 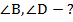
Решение:
Сумма углов при боковой стороне трапеции равна 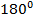 – свойство внутренних односторонних углов при параллельных прямых. Из этого факта можно получить два равенства:
– свойство внутренних односторонних углов при параллельных прямых. Из этого факта можно получить два равенства:
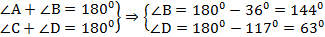
Ответ: 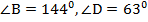 .
.
Пример 2.
Дано:  – трапеция;
– трапеция; 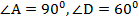 .
. 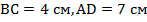 .
.
Найти: 
Решение:
Рис. 8
Проведём высоту  . Получаем четырёхугольник
. Получаем четырёхугольник  , в котором противоположные стороны попарно параллельны, а два углы равны по
, в котором противоположные стороны попарно параллельны, а два углы равны по 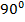 . Значит,
. Значит,  – параллелограмм, а точнее, прямоугольник.
– параллелограмм, а точнее, прямоугольник.
Из этого следует, что 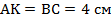 . Откуда:
. Откуда: 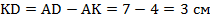 .
.
Рассмотрим прямоугольный треугольник 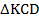 . В нём один из острых углов, по условию, равен
. В нём один из острых углов, по условию, равен 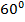 . Значит, второй равен
. Значит, второй равен 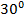 , то есть:
, то есть: 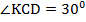 . Воспользуемся свойством катета, лежащего против угла
. Воспользуемся свойством катета, лежащего против угла 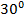 : он в два раза меньше гипотенузы.
: он в два раза меньше гипотенузы.
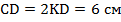 .
.
Ответ: 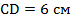 .
.
На этом уроке мы рассмотрели понятие трапеции и её свойства, изучили виды трапеции, а также решили несколько примеров типовых задач.
На следующих уроках мы продолжим изучать различные виды четырёхугольников и их свойства, а также решать различные задачи.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Фестиваль педагогических наук «Открытый урок» (Источник).
- Xvatit.com (Источник).
- Fmclass.ru (Источник).
Домашнее задание
- № 57 (а,б), 58 (а,б) Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Существует ли трапеция, у которой два противоположных угла острые? В случае положительного ответа нарисуйте рисунок.
- Могут ли углы трапеции, взятые в последовательном порядке, относиться как
 ?
? - Высота равнобедренной трапеции, проведённая из вершины тупого угла, делит большее основание на отрезки
 и
и  . Найти основания трапеции и её среднюю линию.
. Найти основания трапеции и её среднюю линию. - На одной из боковых сторон трапеции отмечена середина, через которую проведён отрезок параллельно второй боковой стороне, до пересечения с большим основанием трапеции. Докажите, что длина этого отрезка в два раза меньше длины параллельной ему боковой стороны.
interneturok.ru
Трапеция
Сегодня на уроке мы познакомимся с геометрической фигурой, которую называют трапецией.
Итак, трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны трапеции называются основаниями. А не параллельные – боковыми сторонами.
Перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение, называется высотой трапеции.

Трапеция, у которой есть прямой угол, называется прямоугольной. Следует отметить, что, так как основания AB и CD параллельны, прямая BC – секущая, а сумма односторонних углов равна 180º, то и угол BCD также равен 90º.
Трапеция, у которой боковые стороны равны, называется равнобедренной.
Далее мы рассмотрим некоторые свойства и признаки равнобедренной трапеции.
Теорема. Свойство углов равнобедренной трапеции. Углы при основании равнобедренной трапеции равны.
Доказательство.

Рассмотрим прямоугольные  и
и  .
.
 , так как
, так как  – равнобедр.
трапеция,
– равнобедр.
трапеция,
 .
.
 по катету и
гипотенузе.
по катету и
гипотенузе.
Следовательно,  .
.
Теорема доказана.
Теорема. Свойство диагоналей равнобедренной трапеции. Диагонали равнобедренной трапеции равны.
Доказательство.

Рассмотрим  и
и  .
.
 , так как
, так как  – равнобедр.
трапеция,сторона
– равнобедр.
трапеция,сторона  – общая,
– общая,
 как углы при
основании равнобедр. трапеции.
как углы при
основании равнобедр. трапеции.
 по первому
признаку.
по первому
признаку.
Следовательно,  .
.
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если у трапеции углы при основании равны, то она равнобедренная.
Доказательство.

Рассмотрим прямоугольные  и
и  .
.
 по условию.
по условию.
 .
.
 по катету и
противолежащемуострому углу.
по катету и
противолежащемуострому углу.
Следовательно,  .
.
Тогда трапеция  –
равнобедренная.
–
равнобедренная.
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если у трапеции диагонали равны, то она равнобедренная.
Доказательство.

Рассмотрим прямоугольные  и
и  .
.
 по условию,
по условию, .
.
 по катету и гипотенузе.
по катету и гипотенузе.
Следовательно,  .
.
Рассмотрим  и
и  .
.
 по
условию,сторона
по
условию,сторона  – общая,
– общая, .
.
 по первому
признаку.
по первому
признаку.
Следовательно,  .
.
Тогда трапеция  –
равнобедренная.
–
равнобедренная.
Теорема доказана.
А теперь решим несколько задач.
Задача.  – трапеция, у
которой
– трапеция, у
которой  .
.  . Найдите
градусную меру
. Найдите
градусную меру  .
.
Решение.

Так как  , то трапеция
, то трапеция  –
равнобедренная.
–
равнобедренная.
 как углы при
основании равнобедр. трапеции.
как углы при
основании равнобедр. трапеции.
 ,
,  –
внутр. односторонние при
–
внутр. односторонние при  и секущей
и секущей  , то есть
, то есть
 ,
,
 ,
,
 ,
,
 .
.
Ответ:  .
.
Задача. В прямоугольной
трапеции  проведена
диагональ
проведена
диагональ  .
.  ,
,  . Найдите
градусную меру
. Найдите
градусную меру  .
.
Решение.

 как накр.
лежащие при
как накр.
лежащие при  и секущей
и секущей  ,то есть
,то есть  .
.
 ,следовательно,
,следовательно,  –
равнобедренный, тогда
–
равнобедренный, тогда  .
.
Для  :
:  ,
,
 ,
,
 ,
,
 .
.
Ответ:  .
.
videouroki.net
«Трапеция». 8-й класс
Цель:
- Ввести понятие трапеции, её элементов, виды трапеций.
- Рассмотреть некоторые свойства трапеции.
- Применение знаний при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Кроссворд.
Ключевое слово кроссворда – является темой нашего урока.
- Любой многоугольник разделяет плоскость на две части, одна из которых называется …
- Четырехугольник, у которого противоположные стороны попарно параллельны.
- Отрезок, соединяющий любые две не соседние вершины многоугольника.
- Сумма длин всех сторон многоугольника.
- Две вершины многоугольника, принадлежащие одной стороне, называются…
- В конце урока каждый ученик ждет хорошую …
- Две несмежные стороны четырехугольника называются …
- Любой многоугольник разделяет плоскость на две части, одна из которых внутренняя, а другая
Ответы:
III. Новый материал.
Трапеция – (от греч. trapezion, букв. – столик).
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Виды трапеции.
Равнобедренная – трапеция, у которой равны боковые стороны.
Прямоугольная – трапеция, один из углов которой прямой.
Средняя линия трапеции.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Работа в группах.
Группы с четными номерами – исследуют диагонали равнобедренной трапеции. Группы с нечетными номерами – исследуют углы равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
Свойства равнобедренной трапеции.
Теорема. В равнобедренной трапеции углы при каждом основании равны.
Доказательство.
Проведем СЕ АВ.
ABCD – параллелограмм (АВ СЕ, ВС AD).
CD = AB = CE, СDE – равнобедренный, СDЕ = СЕD.
АВ СЕ, тогда СЕD = ВАЕ, СDЕ = СЕD = ВАЕ.
ABC = 180° – СDЕ = 180° – ВАЕ = BCD.
Теорема. В равнобедренной трапеции диагонали равны.
Доказательство.
ABC = DСВ (АВ = С, ВС – общая сторона, АВС = ВСD) тогда АС = ВD.
Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.
Признаки равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
1. Если углы при основании трапеции равны, то она равнобедренная.
Доказательство.
Проведем ЕС АВ.
ABCЕ – параллелограмм, тогда АВ СЕ, А = СЕD, СЕD – равнобедренный (D = СЕD), тогда СЕ = СD.
АВ = СЕ = СD, тогда АВСD – равнобедренная трапеция.
2. Если диагонали трапеции равны, то она равнобедренная.
Доказательство.
Проведем СК ВD.
ВСКD – параллелограмм (т.к. СК ВD, ВС АК).
АСК – равнобедренный, т.к. АС = ВD = СК, САD = СDА.
СК ВD, ВDА = СКD, тогда САD = СКD.
АВD = DСА, т.к. АС=ВD, АD – общая сторона, САD = СКD, тогда АВ = СD, т.е. АВСD – равнобедренная трапеция.
IV. Закрепление.
Решение задач по готовым чертежам.
V. Итог урока:
VI. Домашнее задание.
Параграф 44, вопросы: 10-11, №386, №388.
urok.1sept.ru
Свойства и признаки равнобедренной трапеции 8 класс

Свойства и признаки
равнобедренной трапеции

Математический диктант
4. Назовите четырехугольник, у которого две стороны параллельны, а две другие нет.
2. Сколько диагоналей можно провести из одной вершины n-угольника, если n = 4, 6.
1. Назовите многоугольник, все виды которого являются выпуклыми многоугольниками.
6. Параллельные стороны в трапеции называются …
3. Чему равна сумма углов выпуклого пятиугольника?
10. В параллелограмме противоположные стороны … и … .
5. Четырехугольник у которого противоположные стороны параллельны ….
8. В четырехугольнике сумма углов равна …
7. В трапеции равные стороны называются …
9. В параллелограмме противоположные углы …

Проверь себя!!!
1. Треугольник
Оценка «5» — 10 баллов.
Оценка «4» — 8-9 баллов.
Оценка «3» — 6-7 баллов.
Менее 5 баллов – учи определения!!!
2. одна, три.
3. 540.
4. трапеция.
5. параллелограмм
6. основания
7. Боковые стороны
8. 360
9. равны
10. Равны и параллельны

Проверка домашнего задания
Трапеция.
1
2
Прямоугольная трапеция.
1 = 2 (внутренние накрест лежащие при // прямых и секущей)
Равнобедренная трапеция.

3
6
Трапеция.
4
5
3 + 4 = 180 (внутренние односторонние при // прямых и секущей)
5 = 6 (соответственные при // прямых и секущей)

Теоремма Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающую вторую прямую, то они пересекут на второй прямой равные между собой отрезки.
Равнобедренная трапеция.

Теоремма средней линии трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.

Самостоятельная работа
- Вариант 1. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120 .
- Вариант 2. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона – 10 см, а один из углов равен 60 .

Проверь себя
8 см
6 см
90
90
30
30
30
30
10 см
60
3 см
8 см
3 см
5 см
5 см
6 см

Самостоятельная работа
- Вариант 3. Диагональ АС равнобедренной трапеции АВСД делит пополам угол ВАД. Найдите периметр трапеции, если основание АД равно 12 см, а угол АСД равен 60 .
90
6 см
30
60
30
12 см

Свойства равнобокой трапеции
1. Углы при основаниях равны.
2. Диагонали равны.
3. Высоты, проведенные из вершин к основанию, делят трапецию на два равных треугольника.
Признаки равнобедренной трапеции.
Запишите самостоятельно.

Решение задач
№ 392(аб), 393(в), 394, 395, 397(а)
Домашнее задание
№ 392(аб), 393(в), 396, 398, 397 (б)
videouroki.net
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Основные определения и свойства трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Трапеция |  | Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Определение | Диагонали трапеции |  | Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Определение | Высота трапеции |  | Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Свойство | Точка пересечения диагоналей |  | Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве |
| Определение | Средняя линия трапеции | 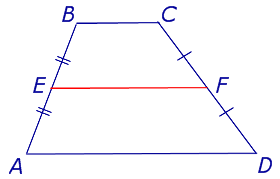 | Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции |
| Свойство | Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство | ||
| Свойство | Биссектрисы углов при боковой стороне трапеции |  | Биссектрисы углов при боковой стороне трапеции перпендикулярны |
| Трапеция |
 Определение: Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Диагонали трапеции |
 Определение: Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Высота трапеции |
 Определение: Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Точка пересечения диагоналей |
 Свойство: Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве |
| Средняя линия трапеции |
 Определение: Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство |
| Биссектрисы углов при боковой стороне трапеции |
 Свойство: Биссектрисы углов при боковой стороне трапеции перпендикулярны |
Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».
В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.
Свойства и признаки равнобедренных трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренная трапеция |  | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Свойство | Равенство углов при основании |  | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. |
| Признак | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | ||
| Свойство | Равенство диагоналей |  | Если трапеция является равнобедренной, то её диагонали равны. |
| Признак | Если у трапеции диагонали равны, то она является равнобедренной | ||
| Свойство | Углы, которые диагонали образуют с основаниями |  | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. |
| Признак | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | ||
| Свойство | Описанная окружность |  | Если трапеция является равнобедренной, то около неё можно описать окружность. |
| Признак | Если около трапеции можно описать окружность, то она является равнобедренной. | ||
| Свойство | Высоты трапеции |  | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Определение: Равнобедренная трапеция | |
 | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Свойство: равенство углов при основании | |
 | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. |
| Признак: равенство углов при основании | |
 | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Свойство: равенство диагоналей | |
 | Если трапеция является равнобедренной, то её диагонали равны. |
| Признак: равенство диагоналей | |
 | Если у трапеции диагонали равны, то она является равнобедренной |
| Свойство: углы, которые диагонали образуют с основаниями | |
 | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. |
| Признак: углы, которые диагонали образуют с основаниями | |
 | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Свойство: описанная окружность | |
 | Если трапеция является равнобедренной, то около неё можно описать окружность. |
| Признак: описанная окружность | |
 | Если около трапеции можно описать окружность, то она является равнобедренной. |
| Свойство: высоты трапеции | |
 | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Равнобедренная трапеция |
 Определение: Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Равенство углов при основании |
 Свойство: Если трапеция является равнобедренной, то углы при каждом из её оснований равны. Признак: Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Равенство диагоналей |
 Свойство: Если трапеция является равнобедренной, то её диагонали равны. Признак: Если у трапеции диагонали равны, то она является равнобедренной. |
| Углы, которые диагонали образуют с основаниями |
 Свойство: Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. Признак: Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Описанная окружность |
 Свойство: Если трапеция является равнобедренной, то около неё можно описать окружность. Признак: Если около трапеции можно описать окружность, то она является равнобедренной. |
| Высоты трапеции |
 Свойство: Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
www.resolventa.ru
Равнобедренная трапеция | Треугольники
Что такое равнобедренная трапеция и каковы ее свойства?
Определение.
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Еще равнобедренную трапецию называют равнобокой (или равнобочной) трапецией.
рисунок
равнобедренной
трапеции
ABCD — равнобедренная трапеция.
AD и BC — основания трапеции,
AB и CD — её боковые стороны,
AB=CD.
Перечислим основные свойства равнобедренной трапеции.
Свойства равнобедренной трапеции:
1) Углы при основании равнобедренной трапеции равны.
∠A=∠D, ∠B=∠C
2) Сумма противолежащих углов равнобедренной трапеции равна 180º.
∠A+∠C=180º, ∠B+∠D=180º
3) Диагонали равнобедренной трапеции равны.
AC=BD
4) Около любой равнобедренной трапеции можно описать окружность.
Кроме основных, у равнобедренной трапеции есть и другие свойства. Например, можно доказать один раз и в дальнейшем использовать при решении задач следующее утверждение:
Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
AD=a, BC=b
Признаки равнобедренной трапеции:
1) Если углы при основании трапеции равны, то она — равнобедренная.
2) Если сумма противолежащих углов трапеции равна 180º, то она — равнобедренная.
3) Если диагонали трапеции равны, то она — равнобедренная.
4) Если около трапеции можно описать окружность, то она — равнобедренная.
www.treugolniki.ru
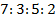 ?
?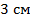 и
и 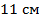 . Найти основания трапеции и её среднюю линию.
. Найти основания трапеции и её среднюю линию.