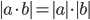Модули — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Базовые сведения о модуле
К оглавлению…
Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:

Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.
Основные свойства модуля:

Некоторые методы решения уравнений с модулями
К оглавлению…
Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:
Предпочтительным способом решения будет переход к совокупности:

А для уравнений вида:

Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:

Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:

Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем:
- Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем.
- Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x
- Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.
educon.by
Доказательства свойств модуля
☰
Существуют следующие свойства модуля действительных чисел:
1) |a + b| ≤ |a| + |b|;
2) |ab| = |a| × |b|;
3) , a ≠ 0;
4) |a – b| ≥ |a| – |b|.
Проведем доказательства, рассматривая различные случаи значений a и b.
Доказательство 1) |a + b| ≤ |a| + |b|:
Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b. Из этого следует, что |a + b| = |a| + |b|.
Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a|. Выражение же |a| + |b| равно сумме абсолютных значений a и b, что больше, чем b – a. Поэтому |a + b| < |a| + |b|.
Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b|, что также меньше суммы модулей |a| + |b|.
Если a и b – отрицательные числа, то получим |–a – b|. Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b|). Но уже было доказано, что |a + b| = |a| + |b|, следовательно и |–a – b| = |a| + |b|.
Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.
Доказательство 3) , a ≠ 0:
Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/a.
Если a – отрицательное число, то имеем . Взятие модуля в обоих выражениях приведет к делению единицы на абсолютное значение a. Значит эти выражения равны друг другу.
Доказательство 4) |a – b| ≥ |a| – |b|:
Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b|, потому что можно не брать модули вообще и тогда с двух сторон получим a – b.
Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b|, что больше, чем |a| – |b|.
Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b|, что больше, чем |a| – |b|.
scienceland.info
Модуль числа и свойства модуля
Определение модуля
Определение: Модулем положительного числа называется само это число, модулем отрицательного числа называется число, ему противоположное, модуль нуля равняется нулю.
Примеры нахождения модуля


Геометрический смысл модуля
Задан отрезок  .
.

Определение: Модуль разности двух чисел  i
i  — это расстояние между точками
— это расстояние между точками  и
и  на координатной прямой.
на координатной прямой.
Свойства модуля
 (Модуль любого числа — неотрицательное число)
(Модуль любого числа — неотрицательное число) (Модули противоположных чисел равны)
(Модули противоположных чисел равны) (Величина числа не превышает величина его модуля)
(Величина числа не превышает величина его модуля) (Модуль произведения дорівнєю произведению модулей сомножителей)
(Модуль произведения дорівнєю произведению модулей сомножителей) (Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))
(Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))




cubens.com
Модуль действительного числа | Формулы с примерами
Модуль действительного числа 8 класс
Определение
 Модуль действительного числа — это же число в абсолютной величине, т.е. без знака «минус».
Модуль действительного числа — это же число в абсолютной величине, т.е. без знака «минус».
Свойства модуля действительного числа
Свойство 1 1. Модуль действительного числа является положительным числом.| a | = ? 0.
Пример | 3 | > 0; | -10 | > 0; | 129 | > 0.
Свойство 2 2. Модули у которых разные знаки — равны.| a | = | — a |.
Пример |4| = |- 4| = 4;|- 3,2| = |3,2| = 3,2;
|4,5| = |- 4,5| = 4,5.
Свойство 3 3. Модуль положительного числа, больше или равен этомуположительному числу. Модуль положительного числа, больше или
равен этому числу со знаком «минус».
|a| ? a; |a| ? — a.
Пример | ? 5 | ? ? 5 и | ? 5 | ? — ? 5, так как | ? 5 | = ? 5;| ? 12 | ? ? 12 и | ? 12 | ? — ? 12, так как | ? 12 | = ? 12;
| ? 32 | ? ? 32 и | ? 32 | ? — ? 32, так как | ? 32 | = ? 32.
Свойство 4 4. Модуль суммы двух и более чисел меньше или равен суммеих модулей.
|a + b| ? |a| + |b|.
Пример |3 + 2| ? |3| + |2| = 5;|1,3 + 4,2| ? |1,3| + |4,2| = 5,5;
|-12,6 + 4,1| ? |-12,2| + |4,1| = 16,3.
Свойство 5 5. Модуль разности двух и более чисел больше или равен разностиих модулей.
|a — b| ? |a| — |b|.
|15 — ( -2 )| ? |15| — |- 2|;
|21 — ( -1,3 )| ? |21| — |-1,3|.
Свойство 6 6. Модуль произведения двух и более чисел равен произведениюих модулей.
|a • b| = |a| • |b|.
Пример |1.2 • 1,3| = |1,2| • |1,3| = 1,56;|2 • ( -2,2 )| = |2| • |-2,2| = 4,4;
|3,1 • ( -6,4 )| = |3,1| • |- 6,4| = 19,84.
Свойство 7 7. Квадрат модуля числа равен квадрату этого числа.|a2| = a2.
Пример |- 4|2 = (- 4)2 = 16;|- 6|2 = (- 6)2 = 36;
|- 1,2|2 = (- 1,2)2 = 1,44.
formula-xyz.ru
Внеклассный урок — Модуль числа
Модуль числа
Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 5 является 5, модулем числа –5 тоже является 5.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |5|, |х|, |а| и т.д.
Правило:
|а| = а, если а ≥ 0. |а| = –а, если а < 0. |
Пояснение:
|5| = 5
Читается так: модулем числа 5 является 5.
|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.
|0| = 0
Читается так: модулем нуля является ноль.
Свойства модуля:
1) Модуль числа есть неотрицательное число: |а| ≥ 0 2) Модули противоположных чисел равны: |а| = |–а| 3) Квадрат модуля числа равен квадрату этого числа: |а|2 = a2 4) Модуль произведения чисел равен произведению модулей этих чисел: |а · b| = |а| · |b| 6) Модуль частного чисел равен отношению модулей этих чисел: |а : b| = |а| : |b| 7) Модуль суммы чисел меньше или равен сумме их модулей: |а + b| ≤ |а| + |b| 8) Модуль разности чисел меньше или равен сумме их модулей: |а – b| ≤ |а| + |b| 9) Модуль суммы/разности чисел больше или равен модулю разности их модулей: |а ± b| ≥ ||а| – |b|| 10) Постоянный положительный множитель можно вынести за знак модуля: |m · a| = m · |а|, m >0 11) Степень числа можно вынести за знак модуля: |аk| = |а|k, если аk существует 12) Если |а| = |b|, то a = ± b |
Геометрический смысл модуля.
Модуль числа – это величина расстояния от нуля до этого числа.
Для примера возьмем снова число 5. Расстояние от 0 до 5 такое же, что и от 0 до –5 (рис.1). И когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Впрочем, не совсем верно: расстояние мы измеряем только положительными числами – или неотрицательными числами. Пусть цена деления нашей шкалы составляет 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до –5 тоже 5 см.
На практике часто расстояние отмеряется не только от нуля – точкой отсчета может быть любое число (рис.2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками а и b на числовой прямой.
Пример 1. Решить уравнение |х – 1| = 3.
Решение.
Смысл уравнения в том, что расстояние между точками х и 1 равно 3 (рис.2). Поэтому от точки 1 отсчитываем три деления влево и три деления вправо – и наглядно видим оба значения х:
х1 = –2, х2 = 4.
Можем и вычислить.
│х – 1 = 3
│х – 1 = –3
↕
│х = 3 + 1
│х = –3 + 1
↕
│х = 4
│ х = –2.
Ответ: х1 = –2; х2 = 4.
Пример 2. Найти модуль выражения:
3√5 – 10.
Решение.
Сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 – это довольно сложно. Поступим проще: возведем в корень 3 и 10. Затем сравним величину чисел, составляющих разность:
3 = √9. Следовательно, 3√5 = √9 · √5 = √45
10 = √100.
Мы видим, что первое число меньше второго. Значит, выражение отрицательное, то есть его ответ меньше нуля:
3√5 – 10 < 0.
Но согласно правилу, модулем отрицательного числа является это же число с противоположным знаком. У нас отрицательное выражение. Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.
Ответ:
|3√5 – 10| = 10 – 3√5.
raal100.narod.ru
Определение модуля
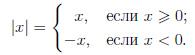
Свойства модуля
1. Модули противоположных чисел равны |
|
2. Квадрат модуля числа равен квадрату этого числа |
|
3. Квадратный корень из квадрата числа есть модуль этого числа | |
4. Модуль числа есть число неотрицательное |
|
5. Постоянный положительный множитель можно выносить за знак модуля |
|
6.
Если |
|
7. Модуль произведения двух (и более) чисел равен произведению их модулей |
|
Числовые промежутки

Окрестность точки Пусть хо—любое действительное число (точка на числовой прямой). Окрестностью точки хо называется любой интервал (a; b), содержащий точку x0. В частности, интервал (хо-ε,хо+ε), где ε >0, называется ε-окрестностью точки хо. Число хо называется центром.
3 ВОПРОС понятие функции Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом.
Переменную у называют зависимой переменной.
Способы задания функции
Табличный способ. заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами — наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.
Аналитический способ. Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х), где f (х) — некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
Для аналитически заданной функции иногда не указывают явно область определения функции. В таком случае подразумевают, что область определения функции у = f (х) совпадает с областью определения выражения f (х), т. е. с множеством тех значений х, при которых выражение f (х) имеет смысл.
Естественная область определения функции
Область определения функции f – это множество X всех значений аргумента x, на котором задается функция.
Для обозначения области определения функции f используется краткая запись вида D(f).
явное неявное параметрическое задание функции
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
studfile.net
Свойства модуля и аргумента комплексного числа
Свойства модуля и аргумента комплексного числа:
1°. $|\bar z| = |z|$
Модуль числа, сопряженного числу $z$ равен модулю самого комплексного числа $z$.
2°. $z \cdot \bar z = |z|^2$
Произведение комплексного числа на сопряжённое ему равно квадрату модуля этого комплексного числа.
3°. $\mathrm{arg} \bar z = -\mathrm{arg} z$, $(\mathrm{arg} z \ne \pi)$
Аргумент числа, сопряжённого комплексному числу $z$ равен отрицательному аргументу комплексного числа $z$.
4°. $\mathrm{max} \{|x|, |y|\} \le |z| \le |x| + |y|$
Модуль комплексного числа больше либо равен наибольшему из модулей его действительной и мнимой части и не превосходит суммы этих модулей.
5°. $|z_1| — |z_2| \le |z_1 + z_2| \le |z_1| + |z_2|$
Модуль суммы двух комплексных чисел больше либо равен разности модулей этих чисел и меньше либо равен сумме модулей этих чисел.
6°. $|z_1 \cdot z_2| = |z_1| \cdot |z_2|$, $\mathrm{Arg} (z_1 \cdot z_2) = \mathrm{Arg} z_1 + \mathrm{Arg} z_2$
Модуль произведения двух комплексных чисел равен произведению модулей этих комплексных чисел, при этом аргумент произведения этих двух чисел равен сумме аргументов этих чисел.
7°. $\left| \frac{z_1}{z_2} \right| = \frac{|z_1|}{|z_2|}$, $\mathrm{Arg} \left( \frac{z_1}{z_2} \right) = \mathrm{Arg} z_1 — \mathrm{Arg} z_2$
Модуль частного двух комплексных чисел равен частности модулей этих комплексных чисел, при этом аргумент частности этих двух чисел равен разности аргументов этих чисел.
8°. $\left| z^n \right| = |z|^n$, $\mathrm{Arg} \left( z^n \right) = n \cdot \mathrm{Arg} z$
Аргумент комплексного числа $z$ в $n$-ой степени равен произведению показателя степени $n$ на аргумент комплексного числа.
9°. $\left| \sqrt[n]{z} \right| = \sqrt[n]{|z|}$, $\mathrm{Arg} \left( \sqrt[n]{z} \right) = \frac{\mathrm{Arg} z}{n}$.
Модуль корня n-ой степени комплексного числа z равен частномум аргумента комплексного числа и показателя степени $n$.
Теорема. Множество комплексных чисел $C$ есть метрическое пространство с метрикой $p(z_1, z_2) = |z_1 — z_2|$.
Следствие. Для множества комлексных чисел $C$ можно ввести все понятия, характерные для метрических пространств:
1) $\varepsilon$ — окружность с центром в точке $z_0$: $\bar u (z_0, \varepsilon) = \{z \in C: \; |z-z_0|< \varepsilon\}$;
2) проколотая $\varepsilon$ — окружность в точке $z_0$: $\bar u (z_0, \varepsilon) = \{z \in C: \; 0<|z-z_0|< \varepsilon\}$;
3) $G \subset C$, понятия внутренней, внешней, граничной точек множества $G$;
4) понятия открытого, замкнутого, связанного множеств.
Определение (предела последовательности $(z_n)$). Число $z_0$ называется пределом последовательности $(z_n)$ $z_0 = \lim_{n \to \infty} z_n$, если $\lim_{n \to \infty} p(z_n, z_0) = 0$ или $\lim_{n \to \infty} |z-z_0| = 0$.
Из соответствующих свойств модуля комплексного числа следует, что сходимость последовательности $(z_n)$ к точке $z_0$ равносильна содимости последовательности $(\mathrm{Re} z_n)$ к $\mathrm {Re} z_0$ и другой последовательнсти $(\mathrm{Im} z_n)$ к $\mathrm{Im} z_0$. Поэтому справедлива следующая теорема.
Теорема (Больцано-Вейерштрасса). Из любой ограниченной последовательности комплексных чисел можно выделить сходящуюся подпоследовательность.
Теорема (Критерий Коши). Для сходимости последовательности $(z_n)$ необходимо и достаточно, чтобы она была фундаментальной, то есть $\forall \varepsilon > 0 \; \exists n_0 \; \forall n, m ((n \le n_0) \& (m \le n_0) \rightarrow |z_n — z_m| < \varepsilon)$.
mathematike.ru
 (Модуль любого числа — неотрицательное число)
(Модуль любого числа — неотрицательное число) (Модули противоположных чисел равны)
(Модули противоположных чисел равны) (Величина числа не превышает величина его модуля)
(Величина числа не превышает величина его модуля) (Модуль произведения дорівнєю произведению модулей сомножителей)
(Модуль произведения дорівнєю произведению модулей сомножителей) (Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))
(Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))






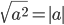


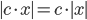 ,
, 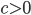
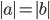 ,
то
,
то