Несобственные интегралы, зависящие от параметра. Равномерная сходимость
Решение.
\(\vartriangle\) Пусть \(y \geq \delta > 0\). Тогда оба интеграла сходятся равномерно по параметру \(y\) на \([\delta, +\infty)\) в силу признака Дирихле: функции \(\cos xy\) и \(\sin xy\) имеют ограниченные первообразные, а функции \(\displaystyle\frac{1}{1+x^{2}}\) и \(\displaystyle\frac{x}{1+x^{2}}\) стремятся к нулю при \(x \rightarrow +\infty\), причем
$$
\frac{d}{dx} \left(\frac{1}{1+x^{2}}\right) = -\frac{2x}{(1+x^{2})^{2}} \leq 0,\quad \frac{d}{dx} \left(\frac{x}{1+x^{2}}\right) = \frac{1-x^{2}}{(1+x^{2})^{2}} \leq 0\nonumber
$$
при \(x \geq 1\).
Дифференцируя \(I_{1}(y)\) по параметру, получаем
$$
\frac{dI_{1}(y)}{dy} = -\int\limits_{0}^{+\infty} \frac{x\sin xy}{1+x^{2}}\ dx = -I_{2}(y),\ \delta \leq y < +\infty.\label{ref26}
$$
Дифференцирование по параметру законно, так как интеграл \(I_{2}(y)\) сходится равномерно по параметру \(y\) при \(y \in [\delta, +\infty)\). Чтобы найти производную \(I_{2}(y)\), заметим, что при \(y \geq \delta > 0\)
$$
I_{2}(y) = \int\limits_{0}^{+\infty} \frac{x\sin xy}{1+x^{2}}\ dx = \int\limits_{0}^{+\infty} \left(\frac{1}{x}-\frac{1}{x(1+x^{2})}\right) \sin xy\ dx =\\= \int\limits_{0}^{+\infty} \frac{\sin xy}{x}\ dx-\int\limits_{0}^{+\infty} \frac{x\sin xy}{x(1+x^{2})}\ dx =\\= \int\limits_{0}^{+\infty} \frac{\sin t}{t}\ dt-\int\limits_{0}^{+\infty} \frac{x\sin xy}{(1+x^{2})x}\ dx = \frac{\pi}{2}-\int\limits_{0}^{+\infty} \frac{x\sin xy}{(1+x^{2})x}\ dx.\nonumber
$$
Применяя теорему 6, получаем
$$
\frac{dI_{2}(y)}{dy} = -\int\limits_{0}^{+\infty} \frac{\cos xy}{1+x^{2}}\ dx = -I_{1}(y),\ y \in [\delta, +\infty).\label{ref27}
$$
Из формул \eqref{ref26} и \eqref{ref27} следует, что при \(y \in [\delta, +\infty)\)
$$
I’_{1}(y) = -I_{2}(y),\ I’_{2}(y) = -I_{1}(y),\ I″_{1}(y)-I_{1}(y) = 0.\label{ref28}
$$
Решая это дифференциальное уравнение, получаем
$$
I_{1}(y) = C_{1}e^{-y}+C_{2}e^{y}\ \mbox{при}\ y \in [\delta, +\infty),\label{ref29}
$$
где \(C_{1}\) и \(C2\) — произвольные постоянные.
Покажем, что \(C_{2} = 0\). Так как
$$
|I_{1}(y)| = \left|\int\limits_{0}^{+\infty} \frac{\cos xy}{1+x^{2}}\ dx\right| \leq \int\limits_{0}^{+\infty} \frac{|\cos xy|}{1+x^{2}}\ dx \leq \int\limits_{0}^{+\infty} \frac{dx}{1+x^{2}} = \frac{\pi}{2},\nonumber
$$
то \(I_{1}(y)\) есть ограниченная функция на \([\delta, +\infty)\). Так как \(e^{y}\) — неограниченная функция на \([\delta, +\infty)\), то в формуле \eqref{ref29} нужно принять \(C_{2} = 0\).
Итак,
$$
I_{1}(y) = C_{1}e^{-y},\ I_{2}(y) = -I’_{1}(y) = C_{1}e^{-y}\ \mbox{при}\ y \in [\delta, +\infty).\label{ref30}
$$
Так как \(\delta\) — произвольное положительное число, то из \eqref{ref30} следует, что
$$
I_{1}(y) = C_{1}e^{-y} = I_{2}(y)\ \mbox{при}\ y > 0.\label{ref31}
$$
Замечая, что интеграл Лапласа \(I_{1}(y)\) есть четная функция на \((-\infty, +\infty)\), а интеграл \(I_{2}(y)\) есть нечетная функция на \((-\infty, +\infty)\), перепишем равенство \eqref{ref31} в следующем виде:
$$
I_{1}(y) = C_{1}e^{-|y|},\ I_{2}(y) = C_{1}\ \operatorname{sign}\ ye^{-|y|}\ \mbox{при}\ y \neq 0.\label{ref32}
$$
Для определения произвольной постоянной \(C_{1}\) воспользуемся тем, что интеграл Лапласа \(I_{1}(y)\) сходится равномерно по параметру \(y\) на \((-\infty, +\infty)\) (пример 3). Поэтому \(I_{1}(y)\) есть непрерывная функция в точке \(y = 0\). Следовательно,
$$
\frac{\pi}{2} = \int\limits_{0}^{+\infty} \frac{dx}{1+x^{2}} = I_{1}(0) = \lim_{y \rightarrow +0} I_{1}(y) = \lim_{y \rightarrow +0} C_{1}e^{-y} = C_{1}.\nonumber
$$
Теперь формулы \eqref{ref32} дают, что при любом \(y \in \boldsymbol{R}\)
$$
\int\limits_{0}^{+\infty} \frac{\cos xy}{1+x^{2}}\ dx = \frac{\pi}{2}e^{-|y|},\\ \int\limits_{0}^{+\infty} \frac{x\sin xy}{1+x^{2}}\ dx = \frac{\pi}{2}\ \operatorname{sign}\ ye^{-|y|}.\label{ref33}
$$
То, что формулы \eqref{ref33} справедливы при \(y = 0\), проверяется непосредственно. \(\blacktriangle\)
univerlib.com
3.3 Признаки сходимости несобственных интегралов
Рассмотрим достаточные признаки сходимости несобственных интегралов (признаки сравнения), позволяющие выяснить вопрос о сходимости несобственного интеграла без знания первообразной его подынтегральной функции.
Признак
сравнения 1 (без доказательства). Пусть
на промежутке 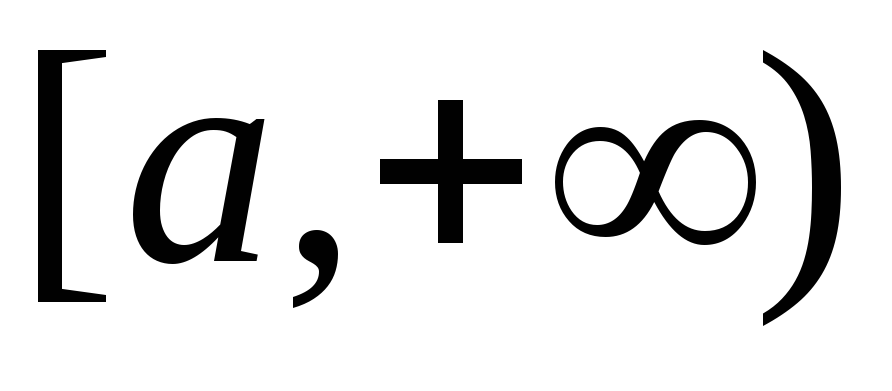 функции
функции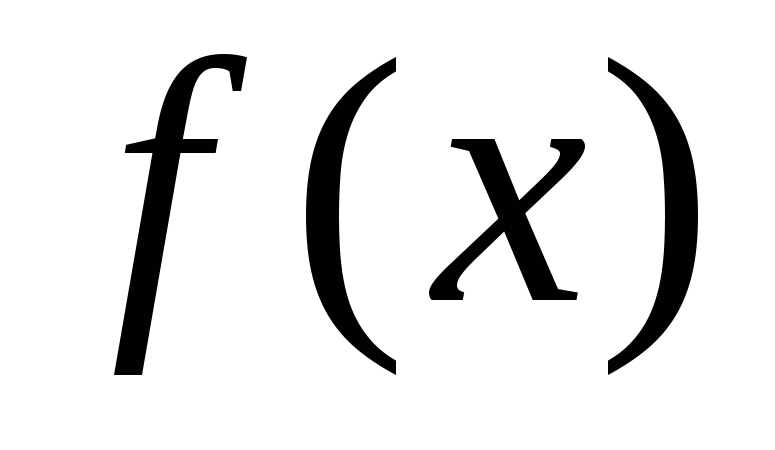 и
и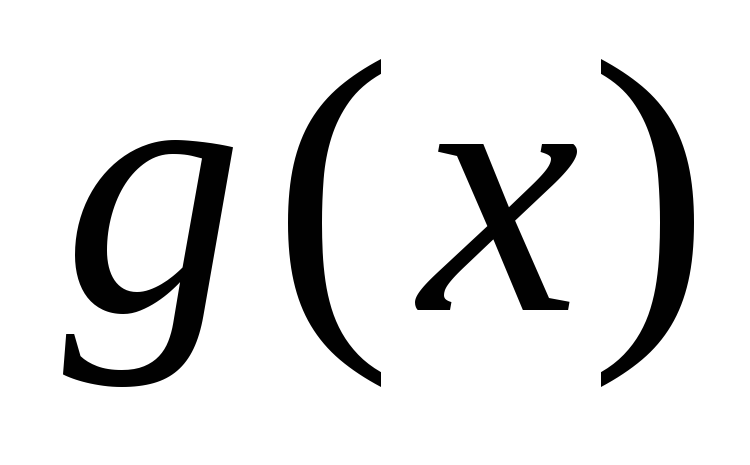
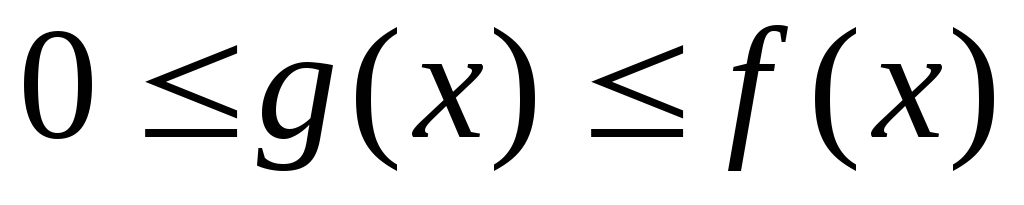 .
Тогда:
.
Тогда: 1) если интеграл 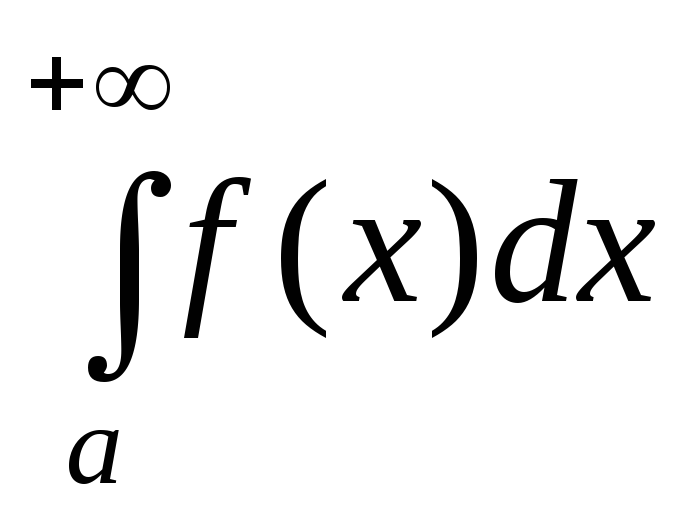 сходится, то сходится и интеграл
сходится, то сходится и интеграл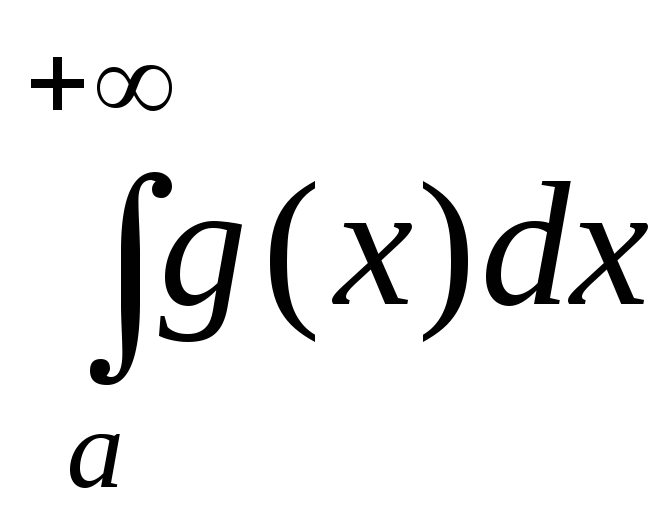 ;
;
2) если интеграл 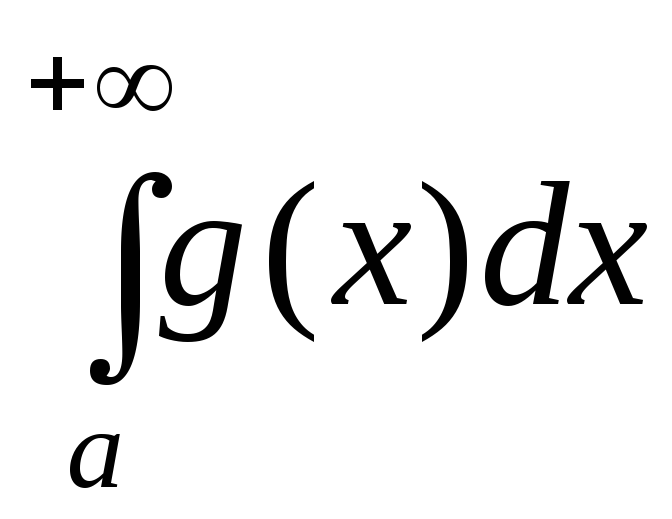 расходится, то расходится и интеграл
расходится, то расходится и интеграл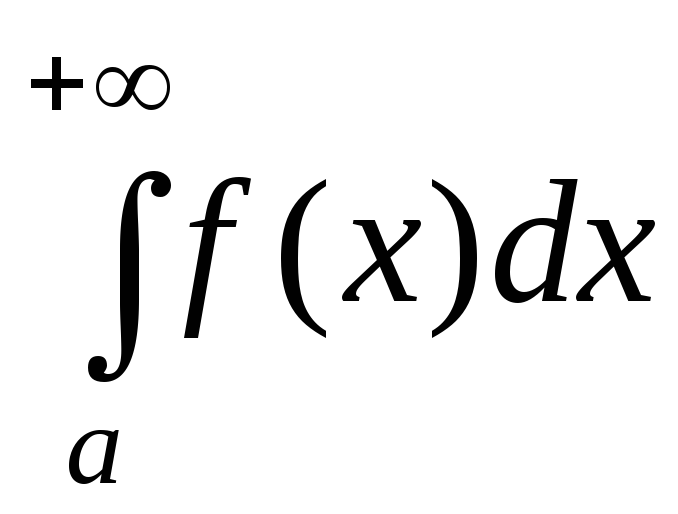 .
.
Признак
сравнения 2 (без доказательства). Пусть
на промежутке 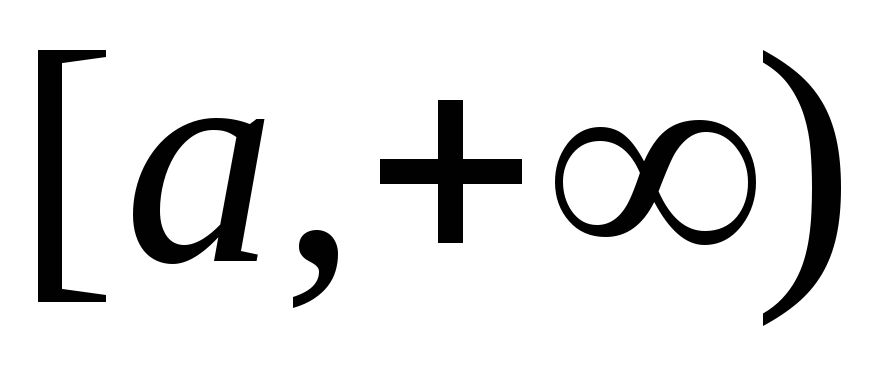 функции
функции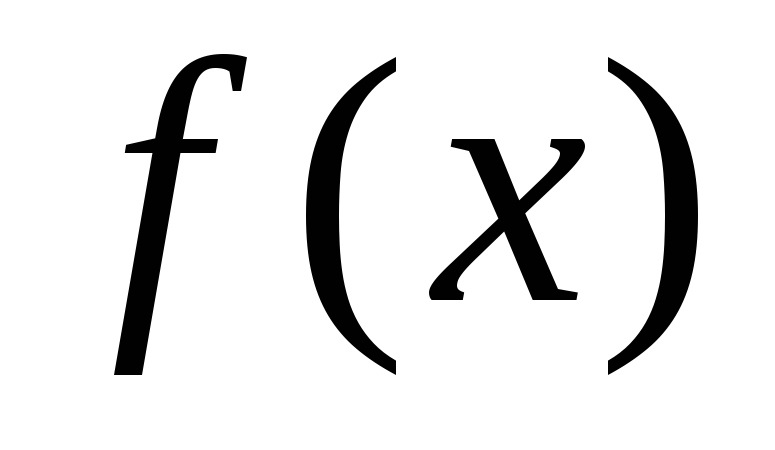
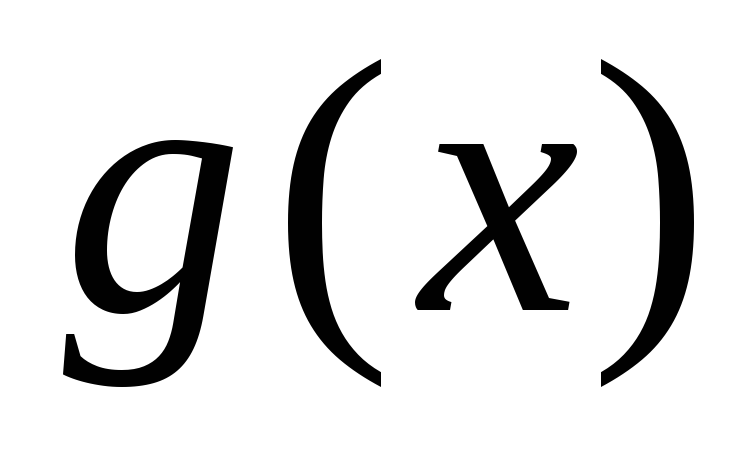 непрерывны и удовлетворяют неравенствам
непрерывны и удовлетворяют неравенствам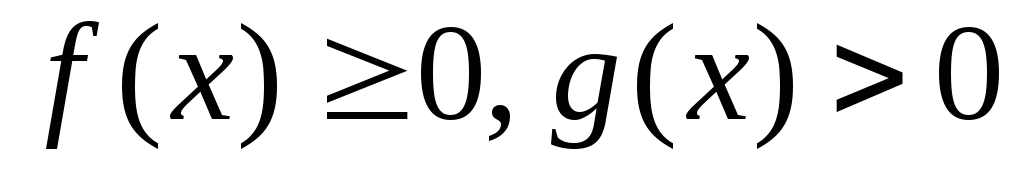 .
Тогда, если существует конечный и
отличный от нуля предел
.
Тогда, если существует конечный и
отличный от нуля предел  ,
,
то несобственные
интегралы 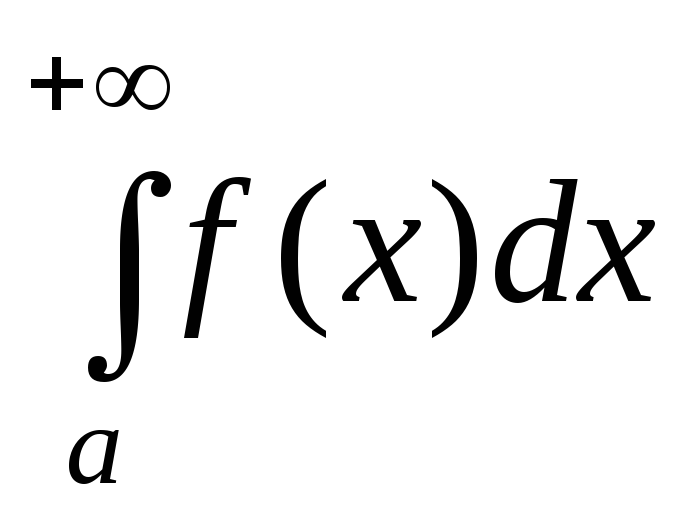 и
и оба сходятся или оба расходятся.
оба сходятся или оба расходятся.
Замечание 1. Аналогичные признаки сравнения справедливы и для других видов несобственного интеграла первого рода, а также для несобственных интегралов второго рода.
Замечание 2. При применении признаков сравнения требуется знать несобственные интегралы, относительно которых заранее известно, сходятся они или расходятся. В качестве таких «эталонных» интегралов на практике часто используются следующие несобственные интегралы:
1) несобственный интеграл первого рода

 ,
,
который сходится
при 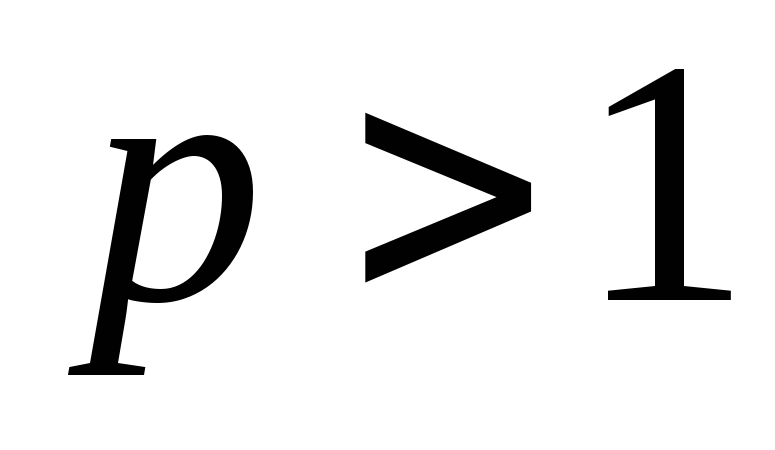 и расходится при
и расходится при ;
;
2) несобственный интеграл второго рода
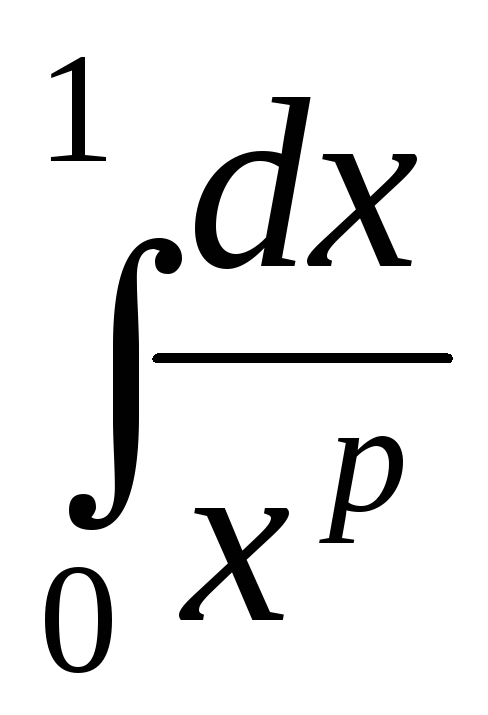
 ,
,
который сходится
при 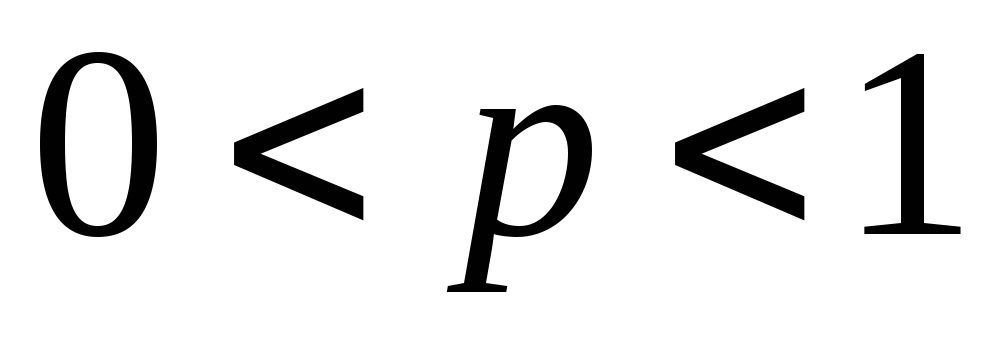
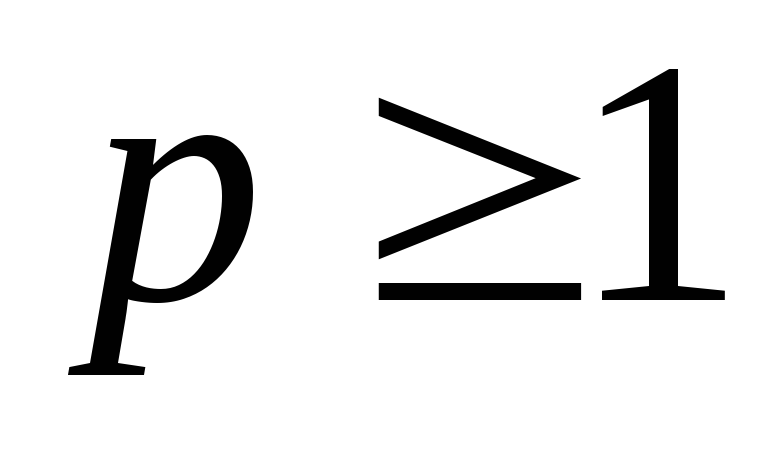 .
.Пример. Исследуем на сходимость несобственный интеграл первого рода
 .
.
Так как на промежутке 
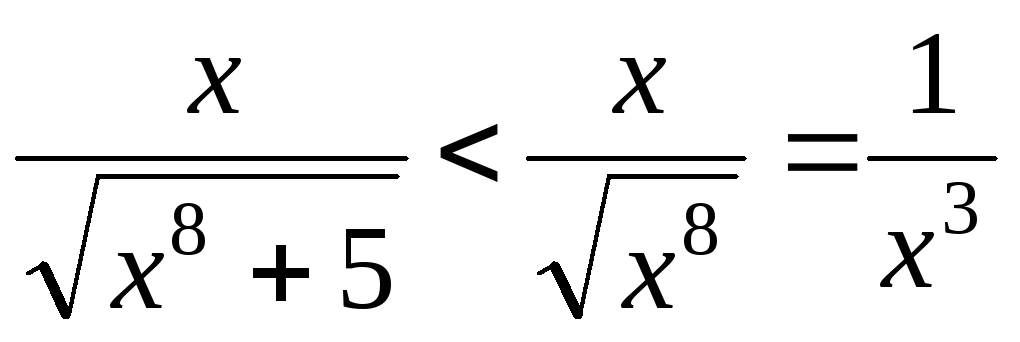 ,
,
а интеграл 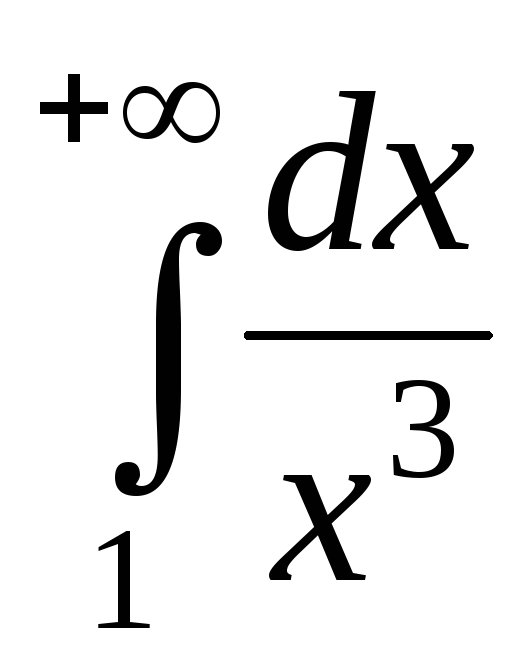 сходится
сходится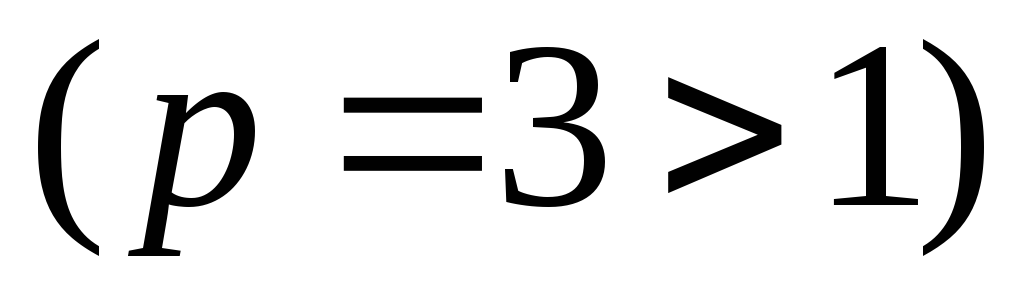 ,
то по признаку сравнения 1 исходный
интеграл также сходится.
,
то по признаку сравнения 1 исходный
интеграл также сходится.
3.4 Абсолютная и условная сходимости
Определение. Несобственный интеграл называется
Несобственный интеграл называется условно сходящимся, если он сходится, а несобственный интеграл от абсолютной величины подынтегральной функции расходится.
Теорема 3.1 (без доказательства). Абсолютно сходящийся интеграл сходится.
Используя понятие абсолютной сходимости и данную теорему, можно исследовать сходимость несобственных интегралов от знакопеременных функций, применяя признаки сравнения.
Пример. Исследуем на сходимость несобственный интеграл первого рода
от знакопеременной функции
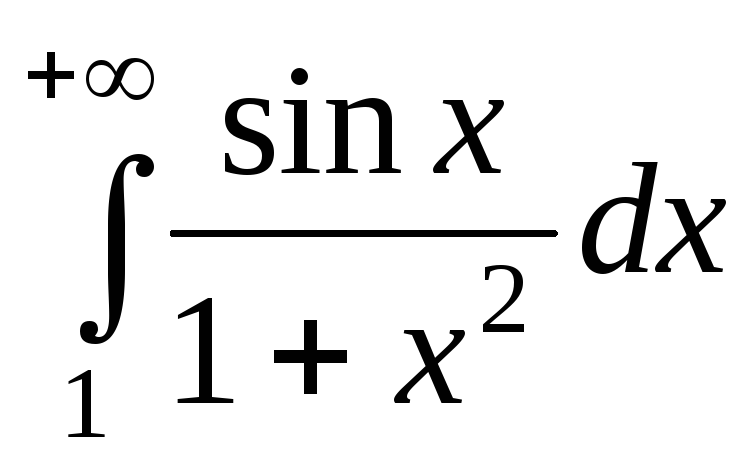 .
.
Так как на промежутке 
 ,
, и интеграл 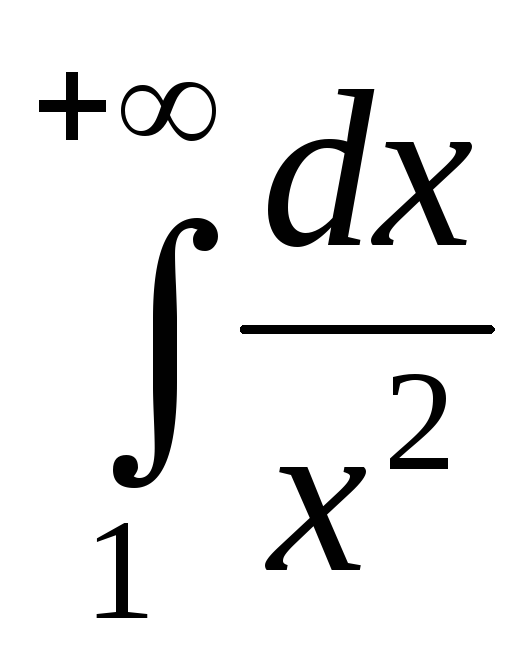 сходится
сходится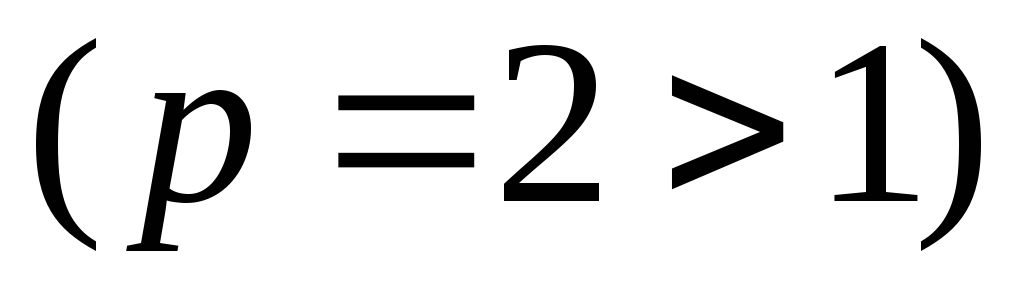 ,
то по признаку сравнения 1 исходный
интеграл также сходится (абсолютно).
,
то по признаку сравнения 1 исходный
интеграл также сходится (абсолютно).
4 Обыкновенные дифференциальные уравнения
4.1 Общие понятия
Определение. Дифференциальным уравнением называется уравнение, содержащее производные или дифференциалы неизвестной функции.
Если неизвестная функция зависит только от одного аргумента, то дифференциальное уравнение называется обыкновенным.
Если же неизвестная функция зависит от двух или большего числа независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.
Определение. Порядком n дифференциального уравнения называется порядок наивысшей производной или наивысшего дифференциала, входящих в уравнение.
В данном разделе
будем изучать только обыкновенные
дифференциальные уравнения, как правило,
относительно неизвестной функции 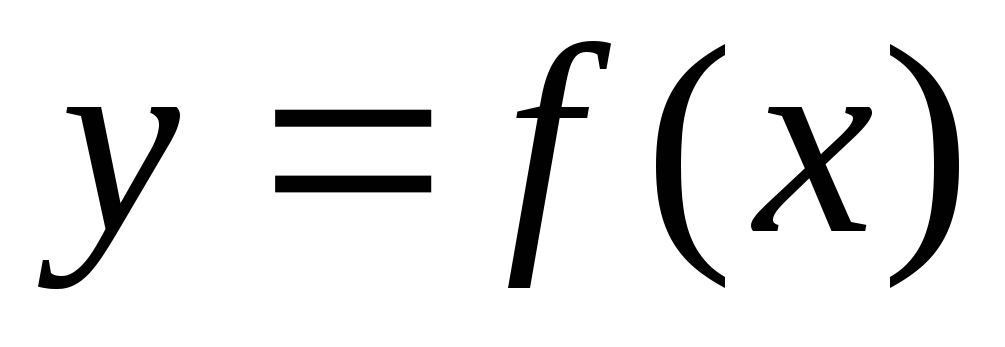 аргументаx.
аргументаx.
Примеры
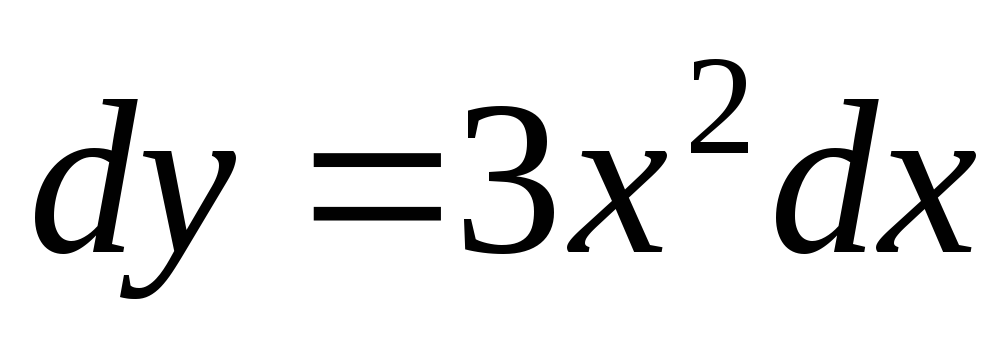 ,
, 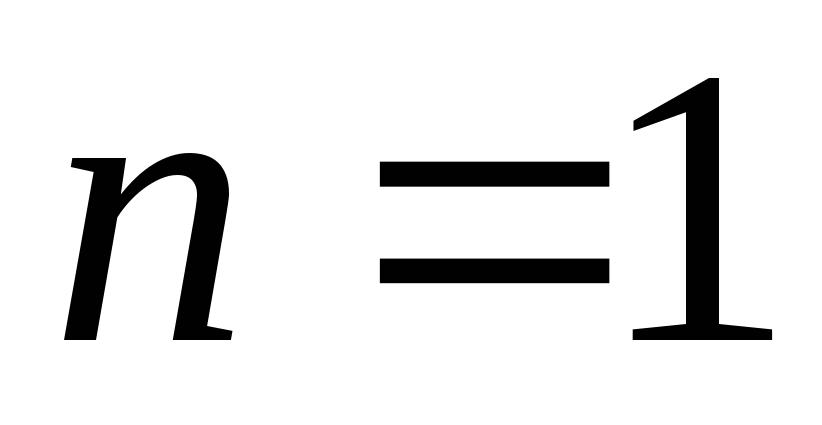 , уравнение 1-го порядка;
, уравнение 1-го порядка;
 ,
,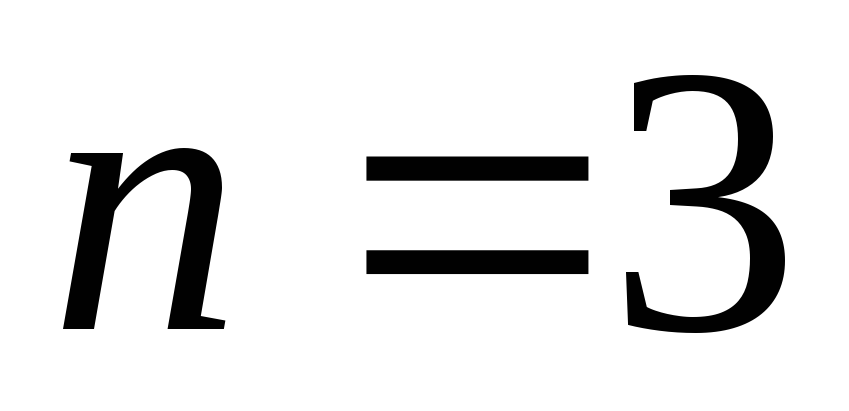 , уравнение 3-го порядка;
, уравнение 3-го порядка;
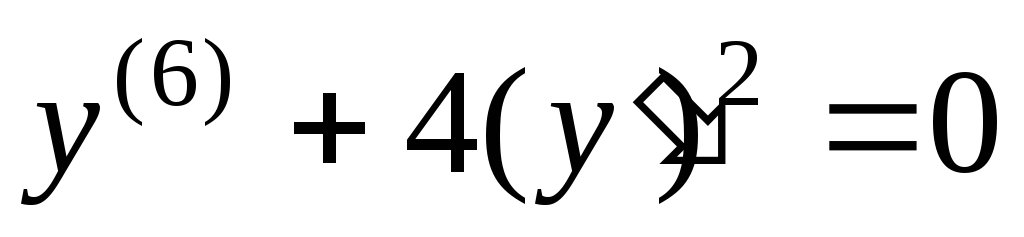 ,
,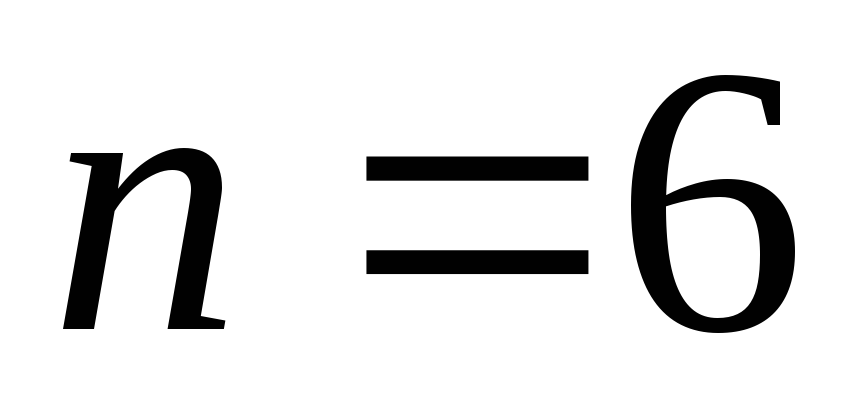 , уравнение 6-го порядка.
, уравнение 6-го порядка.
Определение. Решением дифференциального
уравнения называется функция  ,
которая при подстановке в дифференциальное
уравнение обращает его в верное равенство
(тождество).
,
которая при подстановке в дифференциальное
уравнение обращает его в верное равенство
(тождество).
Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения, а действие интегрирования функций называется квадратурой.
При этом под
квадратурой 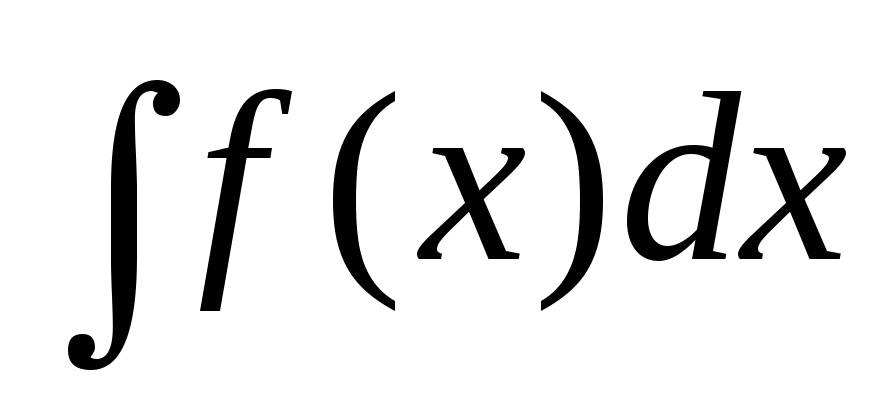 всегда будем понимать какую-либоодну первообразную.
всегда будем понимать какую-либоодну первообразную.
Однако не всегда
решение дифференциального уравнения
может быть получено в виде явно заданной
функции 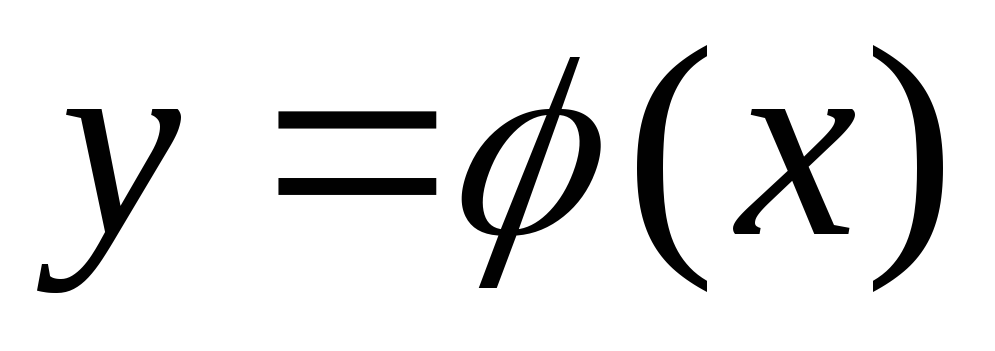
Пример
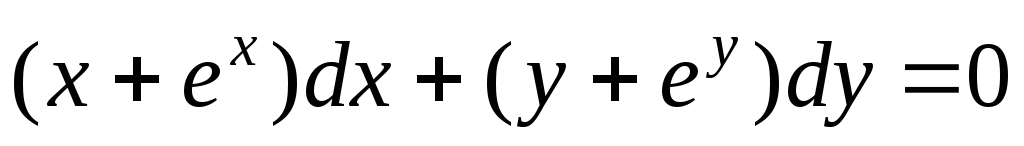 ;
;
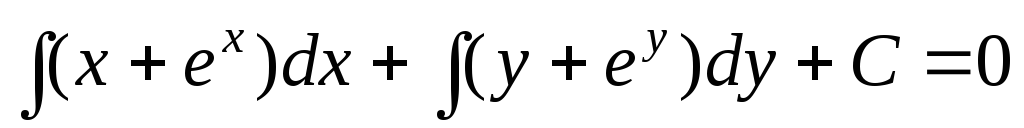 ;
;
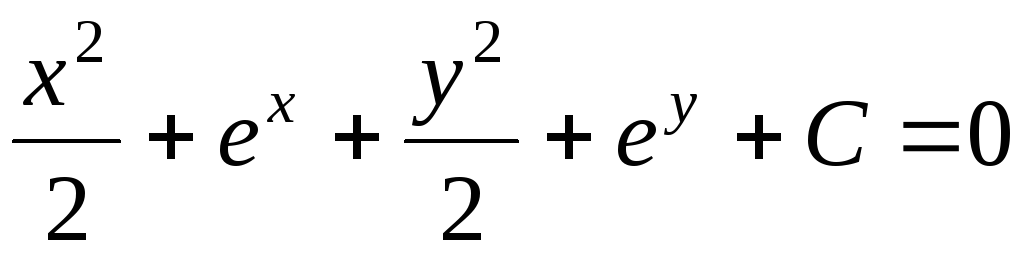 .
.
Обозначим
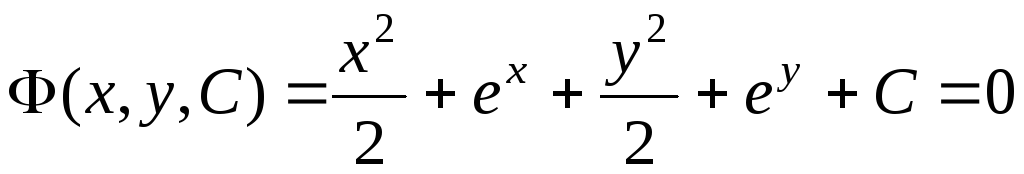 .
.
Определение.
Уравнение 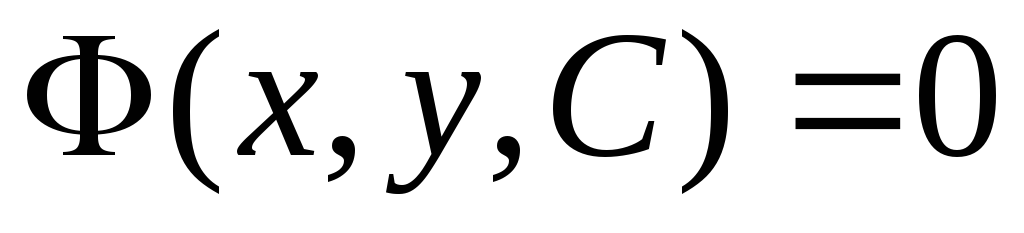 ,которое
определяет решение
,которое
определяет решение  дифференциального уравнения как неявную
функциюx,
называется интегралом рассматриваемого
дифференциального уравнения.
дифференциального уравнения как неявную
функциюx,
называется интегралом рассматриваемого
дифференциального уравнения.
studfile.net
Примеры исследования несобственных интегралов на сходимость
Примеры исследования несобственных интегралов на сходимость
Пример 1 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a>1 и расходится при a£1.
Пример 2 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a<1 и расходится при a³1.
Пример 3 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два
.
Сходимость первого интеграла I1 исследуем с помощью эквивалентной функции: ( т. к. n>0), а интеграл сходится при m>-1 (пример 2). Аналогично, для интеграла I2 :
, а интеграл сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.
Пример 4 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:
.
Так как arctgx »x при x®0, то интеграл I1 эквивалентен интегралу , который сходится при m+1>-1 т. е. при m>-2 (пример1).
Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:
т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
Объединяя условия сходимости интегралов I1 и I2 получим условия сходимости исходного интеграла: m>-2 и m+n<-1 одновременно.
Замечание. В примерах 2-4 использовался 2 признак сравнения, который обеспечивает необходимые и достаточные условия сходимости, что позволяет, установив сходимость при некотором условии на значения параметров, не доказывать расходимость интеграла при нарушении полученных условий сходимости.
Пример 5 Исследовать на сходимость .
Данный интеграл содержит особую точку 0, в которой подынтегральная функция может обращается в бесконечность при p<0, поэтому снова разобьем исходный интеграл на два:
.
Интеграл I1 является несобственным интегралом второго рода, и подынтегральная функция эквивалентна при x®0 функции xp (e-x ®1 при x®0), т. е. I1 сходится при p>-1 (пример 1).
Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается. Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
,
Т. е. интеграл I2 сходится при любом p.
Таким образом, исходный интеграл сходится при p>-1.
Пример 6 Исследовать на сходимость .
Проведем замену переменной: t = lnx, и получим
.
Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q<1.
Рассмотрим интеграл I2 . При условии 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения и a=(1-p)/2. ).
Итак, I2 сходится при p>1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.
Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
При p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T—QE(1-P)T ³ M=const>0. Тогда для интеграла I2 справедлива оценка
,
Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .
Суммируя полученные результаты, получаем что исходный интеграл сходится при q<1 и p>1, в противном случае интеграл расходится.
Пример 6 Исследовать на абсолютную и условную сходимость .
Разобьем исходный интеграл на два:
.
Сходимость. Интеграл I1 эквивалентен , т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
Интеграл I2 сходится про признаку Дирихле-Абеля при p>0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.
Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием
.
Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда
, при p>0.
Таким образом, интеграл сходится при 0<p<1.
Абсолютная сходимость Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху:
, т. е. интеграл сходится при p>1.
Для доказательства расходимости при p£1 оценим интеграл снизу
.
Разобьем последний интеграл от разности функций на разность интегралов
.
Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится — то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев.
расходится (пример 1) при p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (см. Сходимость), следовательно интеграл оценивается снизу расходящимся интегралом, т. е. расходится.
Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл расходится.
Таким образом, исходный интеграл сходится абсолютно при 0<p<1, сходится условно при 1£p<2.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
сходимость интегралов — ПриМат
Пусть функция $f$ задана на промежутке $[a, +\infty)$, где $a \in R$, и интегрируема по Риману на каждом отрезке $[a, \xi)$, где $a \lt \xi \lt +\infty$. Выражение $\int_a^{+\infty} f(x) dx$ называют несобственным интегралом I рода. Если существует $\lim\limits_{\xi\to +\infty}\int_a^\xi f(x) dx$ то этот несобственный интеграл называют сходящимся, а его значение полагают равным:
$$\int_{a}^{\infty}f(x)dx=\lim_{\xi \to +\infty}\int_{a}^{\xi}f(x)dx.$$
Если же не существует конечного предела, то несобственный интеграл называют расходящимся.
Аналогично определяется несобственный интеграл:
$$\int_{-\infty}^{a}f(x)dx = \lim_{\eta\to -\infty}\int_{\eta}^{a}f(x)dx.$$
Пусть теперь функция $f$ задана на всей действительной прямой и интегрируема по Риману на любом отрезке $\left[\eta, \xi\right]$, где $ -\infty \lt \eta \lt \xi \lt +\infty.$
Если существует конечный двойной предел $\lim\limits_{\substack{\xi\to +\infty \\ \eta\to-\infty}}\int_\eta^\xi f(x) dx$,то несобственный интеграл $\int_{-\infty}^{+\infty} f(x) dx$ называется сходящимся, а его значение полагают равным $$\int_{-\infty}^{+\infty}f(x)dx = \lim_{\substack{\xi\to +\infty\\ \eta\to-\infty}}\int_{\eta}^{\xi}f(x)dx.$$
Утверждение. Сходимость интеграла $\int_{-\infty}^{+\infty}f(x)dx$ равносильна тому, что сходятся оба интеграла $\int_{a}^{+\infty}f(x)dx$ и $\int_{-\infty}^{a}f(x)dx$, причем имеет место равенство $$\int_{-\infty}^{+\infty}f(x)dx = \int_{-\infty}^{a}f(x)dx + \int_{a}^{+\infty}f(x)dx$$
где a – произвольное действительное число.
$$\int_{\eta}^{\xi}f(x)dx = \int_{\eta}^{a}f(x)dx + \int_{a}^{\xi}f(x)dx$$
Отсюда, переходя к пределам при $\xi → +\infty$ и $\eta → -\infty$, получаем
$$\lim_{\substack{\xi\to +\infty \\ \eta\to-\infty}}\int_{\eta}^{\xi}f(x)dx = \lim_{\substack{\xi\to +\infty \\ \eta\to-\infty}}\int_{\eta}^{a}f(x)dx + \lim_{\substack{\xi\to +\infty \\ \eta\to-\infty}}\int_{a}^{\xi}f(x)dx=\\
= \int_{-\infty}^{a}f(x)dx + \int_{a}^{+\infty}f(x)dx$$
т. е. интеграл $\int_{-\infty}^{+\infty}f(x)dx$ сходится и для него справедливо равенство $\int_{-\infty}^{+\infty}f(x)dx = \int_{-\infty}^{a}f(x)dx + \int_{a}^{+\infty}f(x)dx$.
Для доказательства обратного утверждения зафиксируем произвольное $a \in R$ и предположим, что существует
$$\int_{-\infty}^{+\infty}f(x)dx=\lim_{\substack{\xi\to +\infty \\ \eta\to-\infty}}\int_{\eta}^{\xi}f(x)dx.$$
Тогда, в силу критерия Коши существования двойного предела, отсюда
следует, что для любого $ \eps\gt 0$ найдется такое $A$, что для любых $\xi^{\prime}, \xi^{\prime\prime} \gt A$ и для любых $\eta^{\prime},\eta^{\prime\prime}\lt −A$ справедливо неравенство
$$\left|\displaystyle\int_{\eta^{\prime}}^{\xi^{\prime}}f(x)dx — \int_{\eta^{\prime\prime}}^{\xi^{\prime\prime}}f(x)dx\right|\lt \eps $$
Зафиксируем $\eps\gt 0$ и найдем такое $A$. Можем считать, что $A\gt|a|$. Выберем $\eta=\eta^{\prime}=\eta^{\prime\prime}\lt −A$ и $\xi^{\prime}, \xi^{\prime\prime}\gt A$. Тогда получим
$$\left|\displaystyle\int_{\xi^{\prime}}^{\xi^{\prime\prime}}f(x)dx\right| = \left|\displaystyle\int_{\eta}^{\xi^{\prime}}f(x)dx — \int_{\eta}^{\xi^{\prime\prime}}f(x)dx\right|\lt \eps, $$
т. е. выполнено условие критерия Коши существования предела
$$\lim_{\xi\to +\infty}\int_{a}^{\xi}f(x)dx.$$
Отсюда следует, что интеграл $\int_{a}^{+\infty}f(x)dx$ сходится. Аналогично получаем, что и интеграл $\int_{-\infty}^{a}f(x)dx$ также сходится. Имеем
$$\int_{-\infty}^{a}f(x)dx + \int_{a}^{+\infty}f(x)dx = \lim_{\eta\to -\infty}\int_{\eta}^{a}f(x)dx + \lim_{\xi\to +\infty}\int_{a}^{\xi}f(x)dx =\\
= \lim_{\substack{\xi\to +\infty \\ \eta\to-\infty}}\left(\displaystyle\int_{\eta}^{a}f(x)dx + \int_{a}^{\xi}f(x)dx\right) = \lim_{\substack{\xi\to +\infty \\ \eta\to-\infty}}\int_{\eta}^{\xi}f(x)dx = \int_{-\infty}^{+\infty}f(x)dx$$ Последний предел существует в силу условия, а выражение справа не
зависит от $a$. Тем самым доказано $\int_{-\infty}^{+\infty}f(x)dx = \int_{-\infty}^{a}f(x)dx + \int_{a}^{+\infty}f(x)dx$ для любого $a \in R$.
Пример 1. Вычислим $$\int_0^{+\infty}\frac{dx}{1+x^2} = \lim_{\xi\to +\infty}\int_{0}^{\xi}\frac{dx}{1+x^2}=\lim_{\xi\to +\infty} {\mathrm {arctg}}\,x\bigg|_0^{\xi} = \lim_{\xi\to +\infty}{\mathrm {arctg}}\,x=\frac{\pi}{2}.$$
Пример 2. Несобственный интеграл $\int_0^{+\infty}\sin x dx.$ расходится. В самом деле, $$\int_0^{\xi}\sin x dx =-\cos x \bigg|_0^{\xi}= 1-cos {\xi} $$ не имеет предела.
Примеры решения задач
Пример 1
Вычислить $\int_0^{+\infty}e^{-px}dx.$
Решение:
$$\int_0^{+\infty}e^{-px}dx= -\frac{1}{p}e^{-px}\bigg|_0^{+\infty}=-\frac{1}{p}\lim_{x\to +\infty}(e^{-px}-1)= \begin{cases}
\frac{1}{p}, \text{если $p \gt 0$;} \\
+\infty, \text{если $p\lt 0$.}
\end{cases}$$ При $p \gt 0 \lim\limits_{x\to +\infty}e^{-px}= \lim\limits_{x\to +\infty}\frac{1}{e^{px}}=0$, так как $e^{px}\to+\infty$ при $x\to+\infty.$ При $p\lt 0 \lim\limits_{x\to +\infty}e^{-px} = +\infty.$
Таким образом, интеграл $\int_0^{+\infty}e^{-px}dx$ сходится при $p \gt 0$ и расходится при $p\lt 0.$
[свернуть]
Пример 2
При каких значениях показателя $\lambda \gt 0$ существует несобственный интеграл $\int_a^{+\infty}\frac{dx}{x^\lambda}, (a\gt 0).$
Решение:
Пусть $\lambda\neq1$, тогда $$\int_a^{\xi}\frac{dx}{x^\lambda}=\frac{1}{1-\lambda}x^{1-\lambda}\bigg|_a^\xi=\frac{1}{1-\lambda} (\xi^{1-\lambda} — a^{1-\lambda}).$$
Это выражение при $\xi\to+\infty$ имеет предел $\infty$ ( $\lambda \lt 1$) или конечное число $\frac{1}{1-\lambda} a^{1-\lambda}$ ($\lambda \gt 1$).
Если $\lambda=1$, имеем $$\int_a^{\xi}\frac{dx}{x}=\ln(x)\bigg|_a^\xi=\ln(\xi)-\ln(a)$$ и при $\xi\to+\infty$ в пределе получается $+\infty$. Таким образом, интеграл $\int_a^{+\infty}\frac{dx}{x^\lambda}$ при $\lambda\gt 1$ сходится (и равен $\frac{1}{1-\lambda} a^{1-\lambda}$), а при $\lambda\leq 1$ расходится.
[свернуть]
Пример 3
Вычислить $\int_{-\infty}^{+\infty}\frac{dx}{1+x^2}.$
Решение:
$$\int_{-\infty}^{+\infty}\frac{dx}{1+x^2}=\lim\limits_{x\to{+\infty}} {\mathrm {arctg}}\,x -\lim\limits_{x\to{-\infty}} {\mathrm {arctg}}\,x = \frac{\pi}{2} -(-\frac{\pi}{2})=\pi.$$
Интеграл $\int_{-\infty}^{+\infty}\frac{dx}{1+x^2}$ сходится и равен $\pi$.
[свернуть]
Несобственные интегралы по неограниченным промежуткам
Лимит времени: 0
Информация
Для закрепления пройденного материала предлагается пройти тест.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 5
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Литература
- Коляда В.И.,Кореновский А.А. Курс лекций по математическому анализу / В.И.Коляда.-Одесса: Изд-во «Астропринт», 2010. т.2. -С.102-105.
- Каплан И.А. Практические занятия по высшей математике / И.А.Каплан. -Харьков: Изд-во Харьковского университета, 1967. ч.3. -С.760-761.
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления/ Г.М.Фихтенгольц -Москва: Изд-во «Наука», 1969. т.2. -С.553.
- Лысенко З.М. Конспект лекций по математическому анализу.
Поделиться ссылкой:
ib.mazurok.com
Определение определенного интеграла. Основные свойства определенного интеграла. Приложения определенного интеграла, страница 7
7. Несобственные интегралы
Рассмотрим так называемые несобственные интегралы, т.е. определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования (несобственный интеграл I рода), или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв (несобственный интеграл II рода).
Рассмотрим, как вычисляются несобственные интегралы I рода. Здесь возможны три варианта:
1) Пусть функция  непрерывна
на промежутке
непрерывна
на промежутке 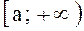 , тогда
, тогда
0 а х Рисунок 19 |
Если этот предел существует, то говорят, что интеграл сходится; если же предел не существует или бесконечен, то говорят, что интеграл расходится. |
2) Если функция  непрерывна
на промежутке
непрерывна
на промежутке 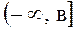 , тогда
, тогда
в 0 х Рисунок 20 |
Сходимость и расходимость такого интеграла определяется аналогично. |
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется формулой
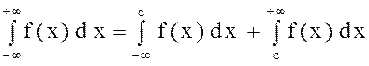 ,
,
где с – произвольное число.
у
0 с х Рисунок 21 | Интеграл, стоящий в левой части равенства, сходится лишь тогда, когда сходятся оба интеграла, стоящие в правой части равенства. |
Вычислить несобственные интегралы или установить их расходимость :
1.  данный интеграл
сходится.
данный интеграл
сходится.
2.  т. к. при
т. к. при 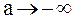
 не существует,
не существует,  данный интеграл расходится.
данный интеграл расходится.
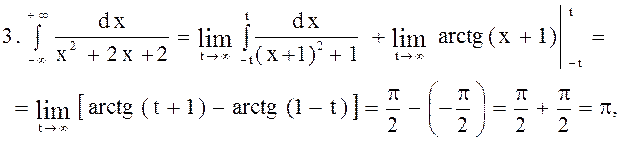
следовательно, данный интеграл сходится.
В некоторых задачах нет необходимости вычислять интеграл, достаточно лишь знать, сходится он или нет.
Сформулируем признак сходимости:
Интеграл  : 1) сходится, если
: 1) сходится, если 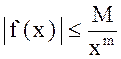 и
и  ;
;
2) расходится, если  и
и 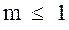 , где М, m — постоянные.
, где М, m — постоянные.
Пример.
Установить, сходится или расходится интеграл 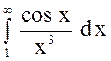 ,
используя признак сходимости.
,
используя признак сходимости.
Решение. Так как 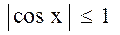 , то
, то  , т.е. подынтегральная функция
удовлетворяет условию (1) при
, т.е. подынтегральная функция
удовлетворяет условию (1) при  ,
,  данный интеграл сходится.
данный интеграл сходится.
Теперь рассмотрим, как вычисляются несобственные интегралы II рода.
Если функция  терпит бесконечный
разрыв в точках
терпит бесконечный
разрыв в точках  , или
, или  ,
или
,
или  , то интеграл
, то интеграл 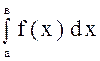 называется несобственным интегралом II рода.
называется несобственным интегралом II рода.
Таким образом, при вычислении таких интегралов также возможны три варианта:
Если хотя бы один из пределов не существует или равен бесконечности, несобственный интеграл II рода расходится. В противном случае – сходится.
Вычислить несобственные интегралы или установить их расходимость:
1. 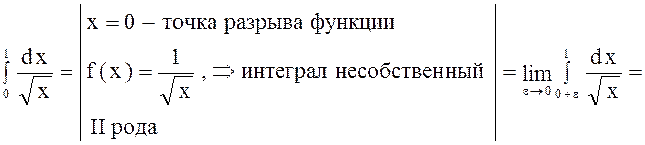
 ,
,
следовательно, данный интеграл сходится.
2. 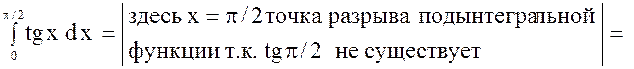

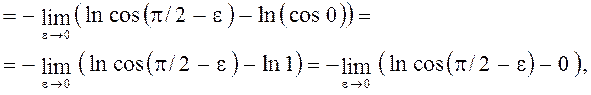
так как этот предел не существует, следовательно, данный интеграл расходится.
3. 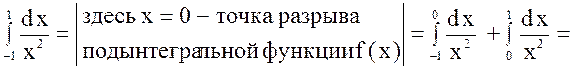

следовательно,
данный интеграл расходится  .
.
Задания для самостоятельной работы
Вычислить несобственные интегралы или установить их расходимость:
Ответы:
1. |
|
2. | 1. |
3. | Расходится. |
4. | 6. |
5. | 1. |
6. |
|
vunivere.ru
сходимость интеграла — это… Что такое сходимость интеграла?
- сходимость измерений
- сходимость на бесконечности
Смотреть что такое «сходимость интеграла» в других словарях:
СХОДИМОСТЬ — одно из основных понятий математич. анализа, означающее, что нек рый математич. объект имеет предел. В этом смысле говорят о С. последовательности каких либо элементов, С. ряда, С. бесконечного произведения, С. цепной дроби, С. интеграла и т. п.… … Математическая энциклопедия
Сходимость — математическое понятие, означающее, что некоторая переменная величина имеет Предел. В этом смысле говорят о С. последовательности, С. ряда, С. бесконечного произведения, С. непрерывной дроби, С. интеграла и т. д. Понятие С. возникает,… … Большая советская энциклопедия
Абсолютная сходимость — У этого термина существуют и другие значения, см. Сходимость. Сходящийся ряд называется сходящимся абсолютно, если сходится ряд из модулей , иначе сходящимся условно. Аналогично, если несобственный интеграл от функции сходится, то он… … Википедия
НОРМАЛЬНАЯ СХОДИМОСТЬ — сходимость ряда оставленного из ограниченных отображений множества в нормированное пространство Y, такая, что сходится ряд с положительными членами составленный из норм отображений Из Н. с. ряда (1) вытекает абсолютная и равномерная сходимость… … Математическая энциклопедия
РАВНОМЕРНАЯ СХОДИМОСТЬ — последовательности функций (отображений) свойство последовательности , где X произвольное множество, Y метрич. пространство, n=1,2,…, к функции (отображению) , означающее, что для любого e>0 существует такой номер п e , что для всех номеров… … Математическая энциклопедия
АБСОЛЮТНО СХОДЯЩИЙСЯ НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — несобственный интеграл, для к рого интеграл от абсолютной величины подинтегральной функции сходится. Если несобственный интеграл абсолютно сходится, то он и просто сходится. Пусть дан (для определенности) несобственный интеграл вида: где функция… … Математическая энциклопедия
Сильные взаимодействия — одно из основных фундаментальных (элементарных) взаимодействий природы (наряду с электромагнитным, гравитационным и слабым взаимодействиями). Частицы, участвующие в С. в., называются адронами, в отличие от Фотона и лептонов (См. Лептоны)… … Большая советская энциклопедия
ОПЕРАТОР — отображение одного множества на другое, каждое из к рых наделено нек рой структурой (алгебраич. операциями, топологией, отношением порядка). Общее определение О. совпадает с определением отображения или функции: пусть Xи Y два множества;… … Математическая энциклопедия
ФУНКЦИЙ ТЕОРИЯ — раздел математики, занимающийся изучением свойств различных функций. Теория функций распадается на две области: теорию функций действительного переменного и теорию функций комплексного переменного, различие между которыми настолько велико, что… … Энциклопедия Кольера
Интеграл Лебега — Стилтьеса — Интеграл Лебега это обобщение интеграла Римана на более широкий класс функций. Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла… … Википедия
Лебега интеграл — Интеграл Лебега это обобщение интеграла Римана на более широкий класс функций. Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла… … Википедия
dic.academic.ru
20. Несобственные интегралы, зависящие от параметра. Равномерная сходимость. Признак Вейерштрасса.
Рассм. интеграл (1)  ,yєY,a<b<+
,yєY,a<b<+ ,
где для
,
где для фиксир.
фиксир.
интеграл (1) несобств.
Тогда интеграл (1) наз. несобств. инт-лом,
зависящим от параметра, 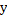 —
параметр. Далее рассм. несобств. инт-л,
зависящ от параметра вида (2)
—
параметр. Далее рассм. несобств. инт-л,
зависящ от параметра вида (2) ,
зависящий от параметраyєYНесобств. инт-лы (1), гдеb– конеч. число, рассм-ся анал-но.
,
зависящий от параметраyєYНесобств. инт-лы (1), гдеb– конеч. число, рассм-ся анал-но.
Предположим, что для 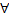 фиксир
фиксир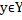 ф-я
ф-я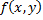 интегрируема на
интегрируема на конечном промежутке
конечном промежутке
Опр. Инт-л (2) сх-ся на мн-ве У, если для  фиксир.
фиксир. интеграл
интеграл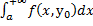 сх-ся, т.е. для
сх-ся, т.е. для
 фиксир.
фиксир.
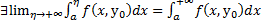 (обозн)
(обозн)
Другими словами 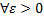
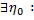
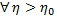

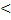

Равномерная сходимость несобственных интегралов, зависящих от параметра.
Опр. Инт-л (2) сх-ся равномерно на мн-ве
У, если 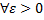

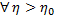
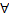
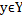
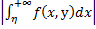

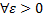
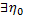
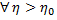
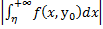
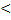
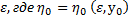
Замечание. Если инт-л (2) сх-ся равномерно на У, то он сх-ся на У. Обратное неверно.
Т. (Критерий Коши равномер. сх-сти)
Инт-л (2) сх-ся равном на S
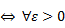


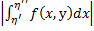
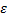
Для доказательства критерия Коши необх. рассм. единство функций
Ф (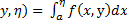 и док-ся Крит.Коши равном сх-ти сем-ва
ф-ий,из кот след.крит.Коши равном сх-ти
несобств.инт-лов.
и док-ся Крит.Коши равном сх-ти сем-ва
ф-ий,из кот след.крит.Коши равном сх-ти
несобств.инт-лов.
Теорема.(Критерий Коши для ФП)
Функциональная последовательность
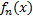 сходится равномерно на Е
сходится равномерно на Е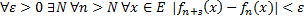
Доказательство
=>
{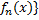 Сходится равномерно на Е =
Сходится равномерно на Е =
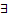 функция
функция ,определена на Е, т.ч.
,определена на Е, т.ч.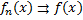 на Е
Фиксируем
на Е
Фиксируем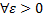
Для 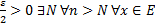
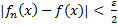
=> 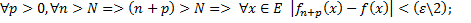
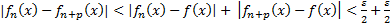 =
=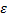

<=
 для
для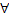 фиксированного
фиксированного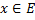 для числовой последовательности{
для числовой последовательности{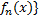 выполнен Критерий Коши => для
выполнен Критерий Коши => для фиксированного
фиксированного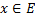 числовая последовательность{
числовая последовательность{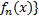 сходится к некоторому числу =>
функциональная последовательность{
сходится к некоторому числу =>
функциональная последовательность{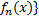 сходится к некоторой функции
сходится к некоторой функции 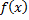 на множестве Е. Докажем что функц.
Последовательность
на множестве Е. Докажем что функц.
Последовательность на Е
на Е
Имеем по условию: 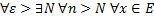
 (1*)
(1*)
Т.к 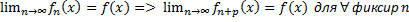
Для 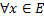
 Переходим в неравенство(1*)к
Переходим в неравенство(1*)к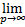 =>
=>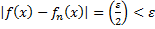

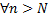 => ФП
=> ФП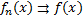 на Е.
на Е.
Док-во крит Коши для ед-ва ф-й полностью анал-но док-ву крит Коши для ф-й послед-сти.
Т. (признак Вейерштрасса)
Пусть  неотриц ф-я
неотриц ф-я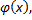 т.ч.
т.ч.
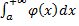 сх-ся и
сх-ся и
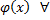
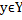 ,
,
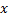 є
є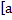 , +
, + Тогда
Тогда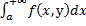 сх-ся равномерно на У.
сх-ся равномерно на У.
Д.1) Д-м, что сх-ся на У.
сх-ся на У.
т.к. 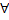

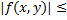
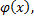
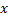 є
є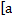 , +
, +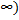 и
и
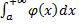 сх-ся, то призн сравнения для
сх-ся, то призн сравнения для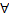 фикс
фикс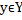 сх-ся инт-л
сх-ся инт-л

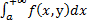 сх-ся
(абсол)
сх-ся
(абсол)
для 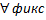 У
У
(3) 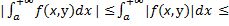
Т.к. ф-и 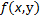 (для фикс у) и
(для фикс у) и инт-мы на
инт-мы на [a,η]⊂[a,+
[a,η]⊂[a,+ ],
то
],
то η
η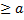 инт-лы
инт-лы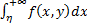 ,
, ,
,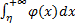 сх-ся (для
сх-ся (для фикс.y
фикс.y Y)
и справедливы нер-ва
Y)
и справедливы нер-ва
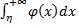
 y
y Y(4).
2)Д-м,что
Y(4).
2)Д-м,что сх-ся равномерно неY.
имеем
сх-ся равномерно неY.
имеем сх-ся
равномерно наY. Имеем
сх-ся
равномерно наY. Имеем сх-ся
сх-ся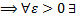 η0
η0 η> η0
η> η0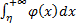 <
<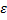 .
Из (4)получ., что
.
Из (4)получ., что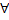 y
y Y
Y <
<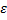
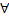 η> η0
η> η0 η0
η0 η> η0
η> η0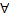 y
y Y
Y

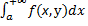 сх-ся равномерно наY.
сх-ся равномерно наY.
21. Непрерывность несобственного интеграла, зависящего от параметра.
Т.Пусть непрерывна (по совокупности переменных)
на
непрерывна (по совокупности переменных)
на х
х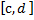 (декартово произведение) и интеграл
(декартово произведение) и интеграл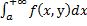 сходится равномерно на
сходится равномерно на , тогда ф-ция
, тогда ф-ция
Ф(у)= непрерывна на
непрерывна на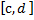
Д .Рассмотрим посл-сть точек
.Рассмотрим посл-сть точек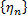 ,
такую что
,
такую что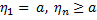
Рассмотрим функц. ряд 

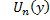
Докажем, что ряд (5) сходится на  .
.
Рассмотрим частную сумму ряда: 
Т.к. 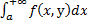 сходится равномерно на
сходится равномерно на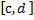 ,
,
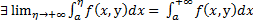
Последовательность 
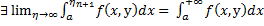



ряд 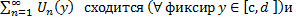
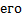 сумма
сумма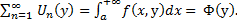 Докажем, что ф-ция
Докажем, что ф-ция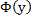 непрерывна на
непрерывна на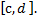
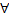 nф-ияUn(y)=
nф-ияUn(y)=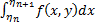 — собств. инт-л , зависящий от парам-ра.
— собств. инт-л , зависящий от парам-ра.
Т.к. f(x,y)
непрер. на мн-ве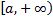 х
х f(x,y)
неперер.на
f(x,y)
неперер.на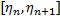 х
х
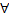 n
n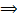 по теор. о непрер-ти собств. инт-ла,
зависящего от параметра, все ф-ииUn(y)
непрер. на [c,d]Докажем,
что
по теор. о непрер-ти собств. инт-ла,
зависящего от параметра, все ф-ииUn(y)
непрер. на [c,d]Докажем,
что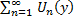 сх-ся
равномерно на [c,d].
сх-ся
равномерно на [c,d].
Т.к 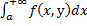 сх-ся равномерно на [c,d]
сх-ся равномерно на [c,d] >0
>0 :
: η>η0
η>η0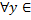 [c,d]
|
[c,d]
|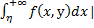 <
<
Т.к. функц.ряд 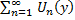 сх-ся
на [c,d]
сх-ся
на [c,d]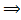 сх-ся
сх-ся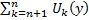 на [c,d]
на [c,d] ,
причем
,
причем =
=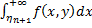 .
.
Т.к

studfile.net
 у
у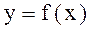
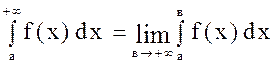 .
. у
у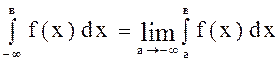 .
.
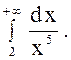
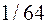 .
.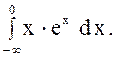
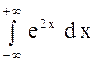 .
. .
.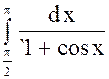 .
.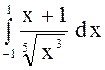 .
.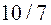 .
.