Таблица интегралов (неопределенных и т.д.)
Интегрирование — это одна из основных операций в матанализе. Таблицы известных первообразных могут быть полезны, но сейчас они, после появления систем компьютерной алгебры, теряют свою значимость. Ниже находится список больше всего встречающихся первообразных.
Таблица основных интегралов
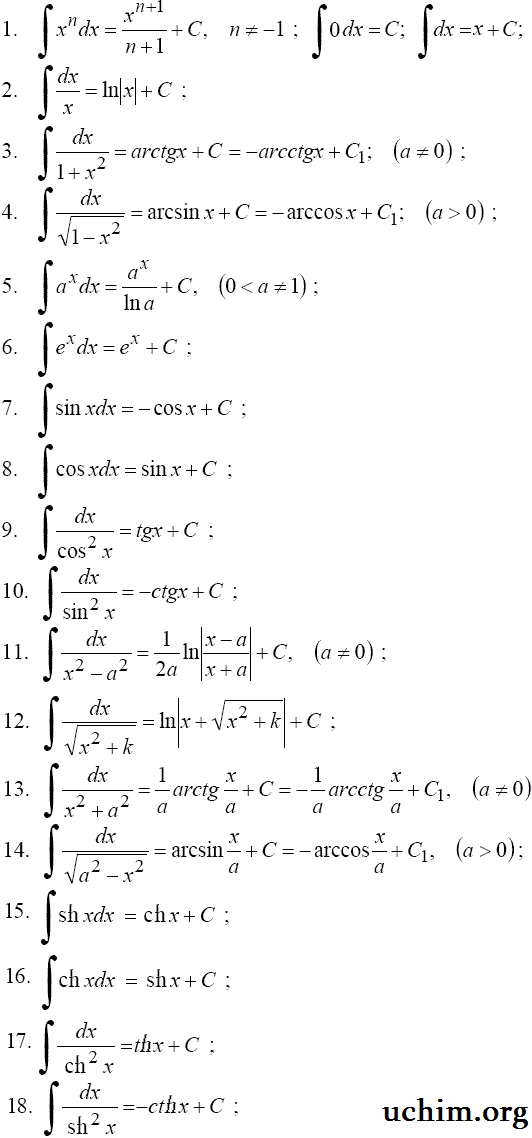
Другой, компактный вариант
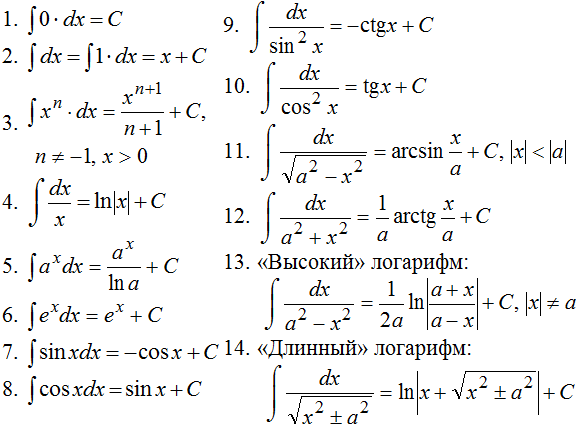
Таблица интегралов от тригонометрических функций
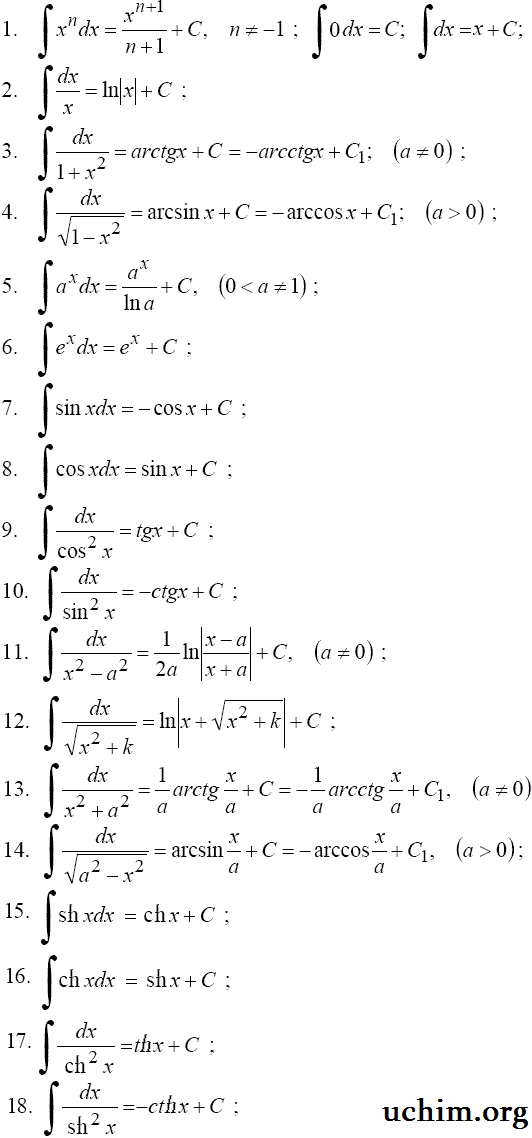
От рациональных функций
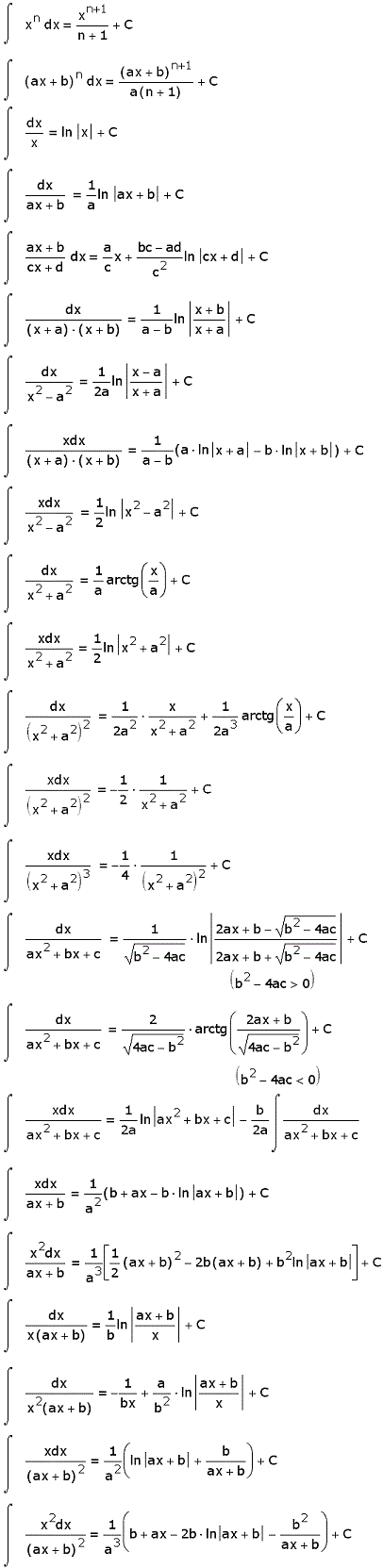
От иррациональных функций
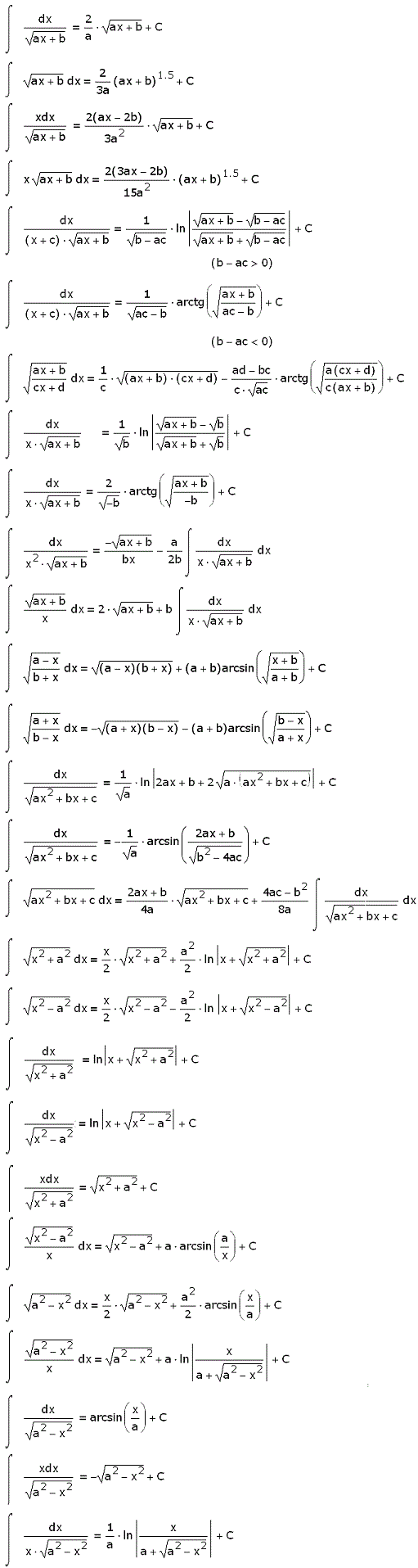
https://uchim.org/matematika/tablica-integralov — uchim.org
Интегралы от трансцендентных функций
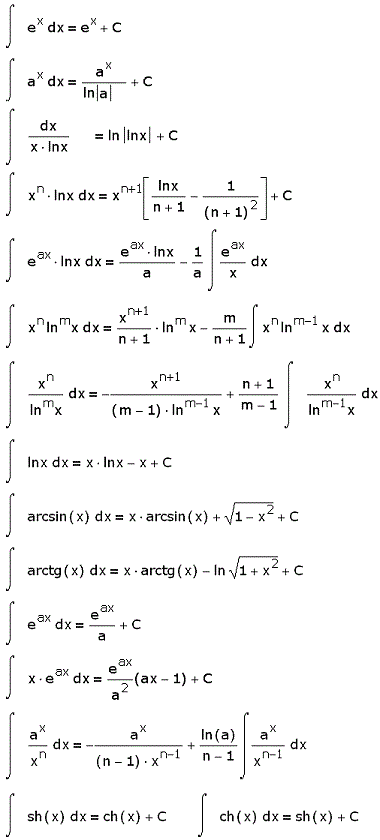
«C» – произвольная константа интегрирования, которая определяется, если известно значение интеграла в какой-либо точке. Каждая функция имеет бесконечное число первообразных.
У большинства школьников и студентов бывают проблемы с вычислением интегралов. На этой странице собраны таблицы интегралов от тригонометрических, рациональных, иррациональных и трансцендентных функций, которые помогут в решении. Еще вам поможет таблица производных.
Видео — как находить интегралы
Если вам не совсем понятна данная тема, посмотрите видео, в котором всё подробно объясняется.Всё для учебы » Математика в школе » Таблица интегралов (неопределенных и т.д.)
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-integralov
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
uchim.org
Интеграл степенной функции. |
Интеграл степенной функции. |
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
Интеграл экспоненциальной функции. |
Интеграл экспоненты, где a-постоянное число. |
Интеграл сложной экспоненциальной функции. |
Интеграл экспоненциальной функции. |
| — | |
| Интеграл, равняющийся натуральному логарифму. |
Интеграл : «Длинный логарифм». |
| Интеграл : «Длинный логарифм». |
|
| Интеграл : «Высокий логарифм». |
|
dpva.ru
Таблица интегралов
$$\int 0\, dx = C$$Интеграл от нуля равен постоянной C
$$\int a\, dx = a*x + C$$
Интеграл от постоянной a равен этой постоянной, умноженной на x и плюс постоянная C
$$\int x^{n}\, dx = \frac{x^{n}}{n + 1} + C$$ при $n \ne 1$
Интеграл x в степени n (n не равна единице), равен x в степени n плюс один и все это деленное на n плюс один и все это плюс постоянная C
$$\int \frac{dx}{x} = \int x^{-1}\, dx = \ln{\left (x \right )} + C$$
Интеграл от единицы, деленной на x равен натуральному логарифму от x плюс постоянная C
$$\int \frac{dx}{x^{2} + a^{2}} = \frac{1}{a}\operatorname{arctg}{\left (\frac{x}{a} \right )} + C$$ $$ = -\frac{1}{a}\operatorname{arcctg}{\left (\frac{x}{a} \right )} + C$$
Интеграл от единицы, деленной на сумму x в квадрате плюс a в квадрате равен арктангенсу от x, деленному на a и все это разделено на a
$$\int \frac{dx}{x^{2} — a^{2}} = \frac{1}{2 a} \operatorname{ln}\left|{\frac{- a + x}{a + x}}\right| + C$$
Интеграл от единицы, деленной на разницу x в квадрате минус a в квадрате равен натуральному логарифму от модуля деления x-a на x + a и весь этот логарифм делен на произведение 2a
$$\int \operatorname{ln}\left(x\right)\,dx = x \operatorname{ln}\left(x\right) — x + C$$
Интеграл от натуральной логарифической функции равен произведению x на натуральный логарифм и минус переменная x
$$\int \frac{dx}{x \operatorname{ln}\left(x\right)} = \operatorname{ln}\left(\operatorname{ln}\left(x\right)\right) + C$$
Integral от единицы, деленной на произведение x на натуральный логарифм равняется логарифму от логарифма от x — по сути получается такая сложная функция
$$\int \operatorname{log}_{b}\left(x\right)\,dx = x \operatorname{log}_{b}\left(x\right) — \operatorname{log}_{b}\left(e\right) + C$$
Интеграл от логарифма от x по основанию b равен произведению x на логарифм от x по основанию b минус логарифм от экспоненты по основанию b
$$\int e^{x}\,dx = e^{x} + C$$
Значение интеграла от экспоненты в степени x равно самой экспоненте от x плюс константа C
$$\int a^{x}\,dx = \frac{a^{x}}{\operatorname{ln}\left(a\right)} + C$$
Интеграл от числа a в степени x равняется a в степени x, деленное на натуральный логарифм от a
$$\int \frac{dx}{\sqrt{a^{2} — x^{2}}} = \operatorname{arcsin}\left(\frac{x}{a}\right) + C$$
Интегральное выражение от 1 деленного на корень квадратный из разницы a в квадрате минус x в квадрате равняется арксинусу от деления x на a
$$\int \frac{- dx}{\sqrt{a^{2} — x^{2}}} = \operatorname{arccos}\left(\frac{x}{a}\right) + C$$
Этот же интеграл, но со знаком минус равен арккосинусу от деления x на a
$$\int \frac{dx}{x \sqrt{x^{2} — a^{2}}} = \frac{1}{a} \operatorname{arcsec} \frac{\left|x\right|}{a} + C$$
$$\int \frac{dx}{\sqrt{x^{2} \pm a^{2}}} = \operatorname{ln}\left| x + \sqrt{x^{2} \pm a^{2}}\right| + C$$
$$\int \operatorname{sin}\left(x\right)\,dx = — \operatorname{cos}\left(x\right) + C$$
Интеграл от функции синус от x равен минус косинусу от того же x
$$\int \operatorname{cos}\left(x\right)\,dx = \operatorname{sin}\left(x\right) + C$$
Интеграл от функции косинус от x равен синусу от x
$$\int \operatorname{tg}\left(x\right)\,dx = \frac{1}{2} \operatorname{ln}\left(\operatorname{tg}^{2}\left(x\right) + 1\right) + C$$
Интегральное от тангенса от x равно одной второй от логарифма от суммы тангенса в квадрате от x плюс один
$$\int \frac{dx}{\operatorname{tg}\left(x\right)} = — \frac{1}{2} \operatorname{ln}\left(\operatorname{tg}^{2}\left(x\right) + 1\right) + \operatorname{ln}\left(\operatorname{tg}\left(x\right)\right) + C$$
$$\int \frac{dx}{\operatorname{cos}\left(x\right)} = — \frac{1}{2} \operatorname{ln}\left(\operatorname{sin}\left(x\right) -1\right) + \frac{1}{2} \operatorname{ln}\left(\operatorname{sin}\left(x\right) + 1\right) + C$$
$$\int \frac{dx}{\operatorname{sin}\left(x\right)} = \frac{1}{2} \operatorname{ln}\left(\operatorname{cos}\left(x\right) -1\right) — \frac{1}{2} \operatorname{ln}\left(\operatorname{cos}\left(x\right) + 1\right) + C$$
$$\int \frac{dx}{\operatorname{cos}^{2}\left(x\right)} = \frac{\operatorname{sin}\left(x\right)}{\operatorname{cos}\left(x\right)} + C$$
интегралиус от 1 деленной на косинус в квадрате от x равен синусу от x, деленному на косинус от x
$$\int \frac{dx}{\operatorname{sin}^{2}\left(x\right)} = — \frac{\operatorname{cos}\left(x\right)}{\operatorname{sin}\left(x\right)} + C$$
интегрализэ от единицы, деленной на синус в квадрате от x равен минус косинусу от x, деленному на синус от x
$$\int \frac{\operatorname{tg}\left(x\right)}{\operatorname{cos}\left(x\right)}\,dx = \frac{1}{\operatorname{cos}\left(x\right)} + C$$
$$\int \frac{dx}{\operatorname{sin}\left(x\right) \operatorname{tg}\left(x\right)} = \frac{1}{\operatorname{sin}\left(x\right)} + C$$
$$\int \operatorname{sin}^{2}\left(x\right)\,dx = \frac{1}{2} x — \frac{1}{2} \operatorname{sin}\left(x\right) \operatorname{cos}\left(x\right) + C$$
$$\int \operatorname{cos}^{2}\left(x\right)\,dx = \frac{1}{2} x + \frac{1}{2} \operatorname{sin}\left(x\right) \operatorname{cos}\left(x\right) + C$$
$$\int \operatorname{arctg}\left(x\right)\,dx = x \operatorname{arctg}\left(x\right) — \frac{1}{2} \operatorname{ln}\left(x^{2} + 1\right) + C$$
$$\int \operatorname{sin}^{n} \left(x\right)\,dx = — \frac{\operatorname{sin}^{n-1}\left(x\right)*x*\operatorname{cos}\left(x\right)}{n} + \frac{n-1}{n} \int \operatorname{sin}^{n-2}\left(x\right)\,dx$$ при $n \geq 2, n \in \mathbb{N}$
$$\int \operatorname{cos}^{n} \left(x\right)\,dx = \frac{\operatorname{cos}^{n-1}\left(x\right)*x*\operatorname{sin}\left(x\right)}{n} + \frac{n-1}{n} \int \operatorname{cos}^{n-2}\left(x\right)\,dx$$ при $n \geq 2, n \in \mathbb{N}$
$$\int \operatorname{sh}\left(x\right)\,dx = \operatorname{ch}\left(x\right) + C$$
Интеграл от гипорболического синуса от x равен гиперболическому косинусу от x
$$\int \operatorname{ch}\left(x\right)\,dx = \operatorname{sh}\left(x\right) + C$$
Интеграл от гипорболического косинуса от x равен гиперболическому синусу от x
$$\int \frac{dx}{\operatorname{ch}^{2}\left(x\right)} = \frac{2 \operatorname{th}\left(\frac{x}{2}\right)}{\operatorname{th}^{2}\left(\frac{x}{2}\right) + 1} + C$$
$$\int \frac{dx}{\operatorname{sh}^{2}\left(x\right)} = — \frac{1}{2} \operatorname{th}\left(\frac{x}{2}\right) — \frac{1}{2 \operatorname{th}\left(\frac{x}{2}\right)} + C$$
$$\int \operatorname{th}\left(x\right)\,dx = x — \operatorname{ln}\left(\operatorname{th}\left(x\right) + 1\right) + C$$
$$\int \frac{dx}{\operatorname{sh}\left(x\right)} = \operatorname{ln}\left(\operatorname{th} \frac{x}{2}\right) + C$$
$$\int \frac{dx}{\operatorname{ch}\left(x\right)} = \operatorname{arctg}\left(\operatorname{sh}\left(x\right)\right) + C$$
$$\int \frac{dx}{\operatorname{th}\left(x\right)} = x — \operatorname{ln}\left(\operatorname{th}\left(x\right) + 1\right) + \operatorname{ln}\left(\operatorname{th}\left(x\right)\right) + C$$
www.kontrolnaya-rabota.ru
Основные формулы и методы интегрирования
Методы интегрирования
Ниже перечислены четыре основных метода интегрирования.
1) Правило интегрирования суммы или разности.
.
Здесь и далее u, v, w – функции от переменной интегрирования x.
2) Вынесение постоянной за знак интеграла.
Пусть c – постоянная, не зависящая от x. Тогда ее можно вынести за знак интеграла.
См. подробнее: Вычисление интегралов от многочленов >>>
3) Метод замены переменной.
Рассмотрим неопределенный интеграл .
Если удастся подобрать такую функцию φ(x) от x, так что
,
то, выполнив замену переменной t = φ(x), имеем
.
См. подробнее: Интегрирование методом замены переменной >>>
4) Формула интегрирования по частям.
,
где u и v – это функции от переменной интегрирования.
См. подробнее: Метод интегрирования неопределенного интеграла по частям >>>
Конечная цель вычисления неопределенных интегралов – это, путем преобразований, привести заданный интеграл к простейшим интегралам, которые называются табличными. Табличные интегралы выражаются через элементарные функции по известным формулам.
См. Таблица интегралов >>>
Пример
Вычислить неопределенный интеграл
Решение
Замечаем, что подынтегральная функция является суммой и разностью трех членов:
, и .
Применяем метод 1.
Далее замечаем, что подынтегральные функции новых интегралов умножены на постоянные 5, 4, и 2, соответственно. Применяем метод 2.
В таблице интегралов находим формулу
.
Полагая n = 2, находим первый интеграл.
Перепишем второй интеграл в виде
.
Замечаем, что . Тогда
Применяем третий метод. Делаем замену переменной t = φ(x) = ln x.
.
В таблице интегралов находим формулу
Поскольку переменная интегрирования может обозначаться любой буквой, то
Перепишем третий интеграл в виде
.
Применяем формулу интегрирования по частям.
Положим .
Тогда
;
;
;
;
.
Окончательно имеем
.
Соберем члены с x3.
.
Ответ
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Таблица неопределенных интегралов для студентов

Представлена таблица основных неопределенных интегралов для студентов, а также интегралы, связанные с гиперболическими функциями. Приводится таблица интегралов в дифференциальной форме и основные методы интегрирования.
СодержаниеТаблица неопределенных интегралов ⇓
Интегралы, связанные с гиперболическими функциями ⇓
Таблица интегралов в дифференциальной форме ⇓
Основные методы интегрирования ⇓
См. также: Таблица производных
Основные элементарные функции и их свойства
Таблица неопределенных интегралов
Ниже приводится таблица основных неопределенных интегралов. Эта таблица является основой, используемой для нахождения более сложных интегралов.
;
;
; ;
;
;
;
;
;
;
;
.
Интегралы, связанные с гиперболическими функциями
Дополнительные формулы, имеющие отношение к гиперболическим функциям:
;
;
;
;
;
;
;
;
.
Таблица интегралов в дифференциальной форме
В математическом анализе большое значение имеет преобразование дифференциалов. Задачей интегрирования является сведение функции за знак дифференциала. Ниже приводится таблица интегралов в дифференциальной форме, устанавливающая связь между дифференциалами – бесконечно малыми приращениями.
;
;
; ;
;
;
;
;
;
;
;
.
Формулы, связанные с гиперболическими функциями:
;
;
;
;
;
;
;
;
.
Основные методы интегрирования
Далее f, u, v – это функции от x; c – постоянная.
;
;
;
;
.
Автор: Олег Одинцов. Опубликовано: Изменено:
См. также: Таблица производныхОсновные элементарные функции и их свойства
1cov-edu.ru
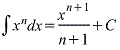
Интеграл степенной функции. |
Интеграл степенной функции. |
|
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
|
Интеграл экспоненциальной функции. |
Интеграл экспоненты, где a-постоянное число. |
|
Интеграл сложной экспоненциальной функции. |
Интеграл экспоненциальной функции. |
|
Интеграл, равняющийся натуральному логарифму. |
|
|
|
Интеграл : «Длинный логарифм». |
|
|
Интеграл, где х в числителе заводится под знак дифференциала |
|
Интеграл : «Высокий логарифм». |
|
|
Интеграл косинуса. |
Интеграл синуса. |
|
Интеграл, равный тангенсу. |
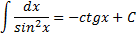
Интеграл, равный котангенсу. |
|
Интеграл, равный как арксинусу, так и арккосинусу |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
Интеграл, равный как арксинусу, так и арккосинусу. |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
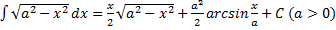 |
|
|
Интеграл равный косекансу. |
Интеграл, равный секансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арккосекансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арксекансу. |
|
Интеграл, равный гиперболическому синусу. |
Интеграл, равный гиперболическому косинусу. |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому синусу, где sinhx |
Интеграл, равный гиперболическому косинусу, где sinhx |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому секансу. |
Интеграл, равный гиперболическому косекансу. |
tehtab.ru
53)Вывести таблицу интегралов из определения неопределенного интеграла .
Таблица интегралов.
1)
∫xαdx
= 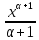 +C
(α≠-1)
+C
(α≠-1)
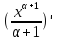 =
=  =xα
=xα
2)
α=-1
=> ∫x-1dx
= ∫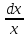 =ln|x|+C
=ln|x|+C
ln|x|=ln(x) при x>0 и ln(-x) при x<0
(ln|x|)’= 1/x при x>0 и 1/x при x<0
∫
 =
arctgx
+ C
или –arctgx
+ C
=
arctgx
+ C
или –arctgx
+ C∫
 =
= 
∫
 =
arcsinx + C или
–arcsinx + C
=
arcsinx + C или
–arcsinx + C∫
 =
ln|x+
=
ln|x+ |+C
= (+)Arshx + Cили
(-) Archx + C
|+C
= (+)Arshx + Cили
(-) Archx + C∫axdx =
 + C
+ C∫exdx = ex + C
∫sinxdx = -cosx + C
∫cosxdx = sinx + C
∫
 =
tgx + C
=
tgx + C∫
 =
ctgx
+ С
=
ctgx
+ С∫shxdx = chx + C
∫chxdx = shx + C
∫
 =
thx + C
=
thx + C∫
 =
-cthx + C
=
-cthx + C
Дополнение к таблице интегралов.
1)
∫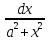 =
=
∫ =
∫
=
∫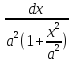 =
= =
=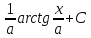
2)
∫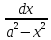 =
=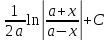
∫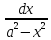 =
= 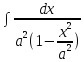 =
=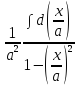 =
=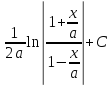 =
=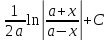
∫
 =
= 
∫ =
= 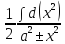 =
=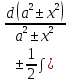 =
=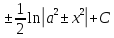
4)  = arcsin
= arcsin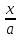 + C
+ C
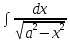 =
= 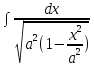 =
= = arcsin
= arcsin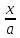 + C
+ C
5) 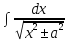 = ln|x +
= ln|x +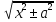 |
+ C
|
+ C
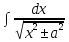 =
= 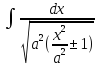 =
=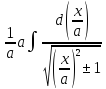 =
=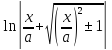 + C =
+ C =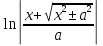 +C=
ln|x +
+C=
ln|x +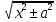 |
— lna + C = ln|x +
|
— lna + C = ln|x +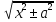 |
+ C1
|
+ C1
6)  = ±
= ±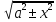 + C
+ C
 =
= 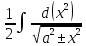 =
= =
=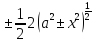 + C = =±
+ C = =±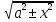 + C
+ C
7) 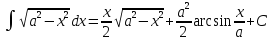
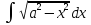 =
|x=asint, dx=acostdt,
=
|x=asint, dx=acostdt,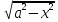 =acost|
=
=acost|
=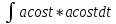 = =
= =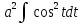 =
=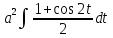 =
=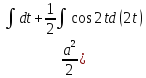 =
=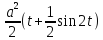 + C = =
+ C = = + C =
+ C =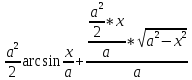 + C =
+ C =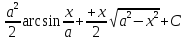 ,при
cos2t=
,при
cos2t=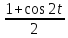 ,
sint=x/a, cost=
,
sint=x/a, cost= ,
t=arcsin(x/a).
,
t=arcsin(x/a).
8)  dx
=
dx
=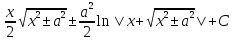
________________________________________________________________________
54) Замена переменной в неопределенном интеграле.
Теорема: пусть ф-я x=ϕ(t) определена и дифференцируема на (α;β), а мн-во ее значений есть (a,b).
Пусть для ф-и f(x) на (a,b) существует первообразная F(x), т.е. ∫f(x)dx= F(x)+C.Тогда всюду на (α;β) существует первообразная для ф-и f(ϕ(t))*ϕ’(t) и имеет место ф-ла
∫f(x)dx = ∫f(ϕ(t))*ϕ’(t)dt = F(ϕ(t)) + C
Док-во: F(x) – первообразная для f(x). найдем дифференциал d(F(ϕ(t))+C)=(F(ϕ(t))+C)t’dt = =F’(ϕ(t))*ϕ’(t)dt = f(ϕ(t))*ϕ’(t)dt => ∫f(ϕ(t))*ϕ’(t)dt = F(ϕ(t))+C (1)
d(F(ϕ(t))+C)=f(ϕ(t))*ϕ’(t)dt=f(x)dx при x=ϕ(t), ϕ’(t)dt=xt’dt=dx
∫f(x)dx=f(ϕ(t))+C (2)
Объединяя (1) и (2)б, получаем:
∫f(x)dx=∫f(ϕ(t))*ϕ’(t)dt=F(ϕ(t))+C. полученная ф-ла назыв. ф-лой замены переменной в неопределенном интеграле.
В некоторых примерах, когда под знаком корня стоят выр-я, содержащие x2б аналогичные замены ен приводят к верному решению. Для интегралов такого вида сещуствуют спец. Замены:
∫R(x,
 )dx
=>замена
x=asint, dx=arccost+dt(a>0)
)dx
=>замена
x=asint, dx=arccost+dt(a>0)
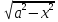 =
= 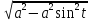 =
=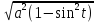 =
=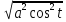 = a|cost| = acost
= a|cost| = acost
x=asint
=> sint = 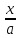 => t=arcsin
=> t=arcsin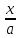 ,
tϵ[
,
tϵ[ ], cost>0
], cost>0
∫R(x, )dx
= ∫R(asint, acost)*acostdt
)dx
= ∫R(asint, acost)*acostdt
∫R(x,
 )dx
=>замена
x=asht, dx=acht+dt(a>0)
)dx
=>замена
x=asht, dx=acht+dt(a>0)
= 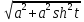 =
=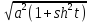 =
=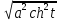 = a|cht| = acht
= a|cht| = acht
ch2t – sh2t = 1
∫R(x, )dx
= ∫R(asht, acht)*achtdt
)dx
= ∫R(asht, acht)*achtdt
Либо:
x=atgt,
dx=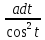
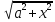 =
= 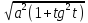 =
= =
=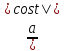 =
=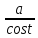
1
+ tg2t
= 1 +  =
=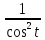
x=atgt
=> tgt = 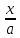 => t = arctg
=> t = arctg ,
tϵ[
,
tϵ[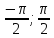 ]
]
∫R(x,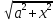 )dx
= ∫R(atgt,
)dx
= ∫R(atgt,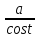 )
)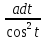
∫R(x,
 )dx
=>замена
x=acht, dx=ashtdtб
либо
x=
)dx
=>замена
x=acht, dx=ashtdtб
либо
x=
 =
= 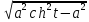 =
=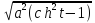 =
=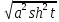 = a|sht| = asht
= a|sht| = asht
∫R(x,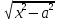 )dx
= ∫R(acht, asht)*ashtdt
)dx
= ∫R(acht, asht)*ashtdt
Либо:
x=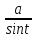 ,dx=
,dx=
 =
= 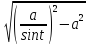 =
= =
=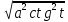 = a|ctgt|= actgt.
= a|ctgt|= actgt.
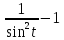 =
= =
=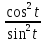 = ctg2t
= ctg2t
∫R(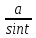 ,actgt)actgtdt.
,actgt)actgtdt.
________________________________________________________________________
55)Интегрирование по частям в неопределенном интеграле.
Теор.: пусть каждая из ф-й u(x) и v(x) определены и диффер. на (a,b) и пусть на этом мн-ве сущ. первообразная для ф-и u(x)*v’(x). Тогда на (a,b) сущ. первообразная для ф-и v(x)*u‘(x) и имеет место ф-ла ∫u(x)*v’(x)dx = uv — ∫v(x)*u’(x)dx или ∫udv = uv — ∫vdu.
Док-во: рассмотрим дифференциал d(uv) = vdu + udv
udv = d(uv) – vdu |∫ => ∫udv = ∫d(uv) — ∫vdu
∫udv = uv — ∫vdu – формула интегрирования по частям
Для применения этой формулы подынтегральные выр-я нужно представить в виде одной ф-и на дифференциал другой ф-и.
Применяется к ∫ след вида:
∫f(x)dx, где f(x) – обратная ф-я
f(x)
= {lnx, 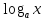 ,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
dx=dv
,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
dx=dv
∫f(x)P(x)dx, где f(x)= {lnx,
 ,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
P(x)dx=dv,
P(x)
– рациональная или иррациональная
ф-я.
,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
P(x)dx=dv,
P(x)
– рациональная или иррациональная
ф-я.∫P(x)f(x)dx, где P(x)-многочлен, f(x) = {ex, ax, sinx, cosx, tgx, ctgx}, P(x)=г
∫eaxcosbxdx и ∫eaxsinbxdx – круговые интегралы.
Эти интегралы вычисляются 2 раза по частям. В результате двукратного применения ф-лы интегрирования по частям, в правой части получаем такой же интеграл, что и в левой. Вычисляем этот интеграл, решая алгебраическое уравнение. В круговых интегралах не важно, какую из ф-й обозначить за u.
eiϕ=cosϕ+isinϕ, cosϕ=Re eiϕ, sinϕ=Im eiϕ. Re-действительная часть, Im-мнимая часть.
________________________________________________________________________
studfile.net
(1).gif)
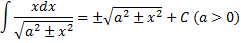
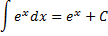
.gif)
.gif)
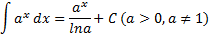
.gif)
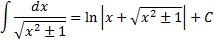
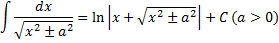
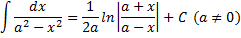
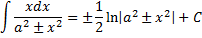
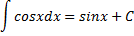
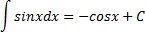
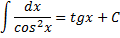
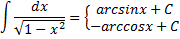
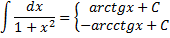
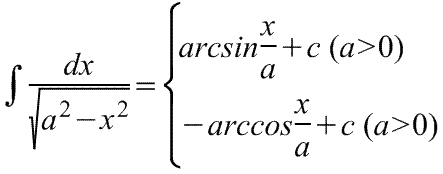
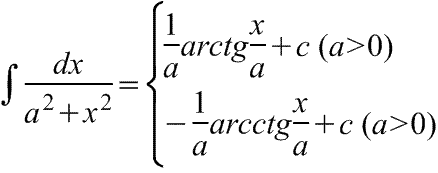
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
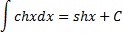
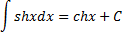
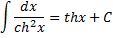
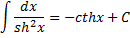
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
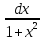 =
arctgx
+ C
или –arctgx
+ C
=
arctgx
+ C
или –arctgx
+ C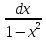 =
= 
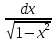 =
arcsinx + C или
–arcsinx + C
=
arcsinx + C или
–arcsinx + C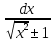 =
ln|x+
=
ln|x+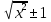 |+C
= (+)Arshx + Cили
(-) Archx + C
|+C
= (+)Arshx + Cили
(-) Archx + C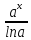 + C
+ C =
tgx + C
=
tgx + C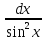 =
ctgx
+ С
=
ctgx
+ С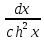 =
thx + C
=
thx + C =
-cthx + C
=
-cthx + C =
= 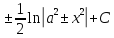
 )dx
=>замена
x=asint, dx=arccost+dt(a>0)
)dx
=>замена
x=asint, dx=arccost+dt(a>0)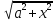 )dx
=>замена
x=asht, dx=acht+dt(a>0)
)dx
=>замена
x=asht, dx=acht+dt(a>0)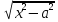 )dx
=>замена
x=acht, dx=ashtdtб
либо
x=
)dx
=>замена
x=acht, dx=ashtdtб
либо
x=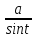
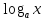 ,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
P(x)dx=dv,
P(x)
– рациональная или иррациональная
ф-я.
,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
P(x)dx=dv,
P(x)
– рациональная или иррациональная
ф-я.