Теорема Пифагора. 8-й класс

Цели урока:

1. Образовательная цель: познакомится с биографией Пифагора, изучить теорему Пифагора.
2. Развивающая цель: развитие у учащихся исследовательских способностей; познавательного интереса, логического мышления; внимания, наблюдательности.
3. Воспитательная цель: воспитывать устойчивый интерес к предмету.

План урока:

• Организационный момент.
• Актуализация знаний.
• Историческая справка о Пифагоре (Презентация 1)
• Изучение нового материала (Презентация 2).
• Первичное закрепление знаний.
• «Теорема Пифагора в природе» (Презентация 3), «Это интересно» (Презентация 4).
• Итоги урока.
• Домашнее задание.

Оборудование:

• демонстрационный компьютер;
• мультимедийный проектор;
• портрет Пифагора;
• высказывания Пифагорейцев.

Ход урока

Организационный момент.

Учитель: Сегодня на уроке мы познакомимся с биографией Пифагора, изучим одну из самых известных геометрических теорем древности, называемую теоремой Пифагора, одну из главных теорем планиметрии.

(На доске в центре портрет Пифагора, вокруг портрета, высказывания Пифагорейцев – приложение 1.)

I. Актуализация знаний.

1) Ребята укажите лишнюю геометрическую фигуру из предложенного ряда (макеты из картона прикреплены на магнитной доске).

2) Вопросы:

1. Дать определение квадрата?
2. Как найти площадь квадрата?
3. Какой треугольник называют прямоугольным?
4. Как называются стороны прямоугольного треугольника?
5. Как найти площадь прямоугольного треугольника?

Формулировка темы и целей урока.

II. Изучение нового материала.

1. Историческая справка (см. Презентация 1).
2. Доказательство теоремы (см. Презентация 2).

Достроим прямоугольник до квадрата со стороной a + b.

Ребята по чертежу доказывают теорему, проводится проверка результатов с помощью компьютера.

S = (a + b)²
S = S1 + 4 S2
(a + b)² = 4 * 1/2 ab + с²
a² + 2 ab + b² = 2 ab+ с²
a² + b² = с² – теорема доказана.

Теорема формулируется и проговаривается учащимися.

III. Первичное закрепление знаний.

1) Применение теоремы Пифагора к решению задач.

С помощью теоремы Пифагора можно решать два вида задач.

1. Найти гипотенузу прямоугольного треугольника, если известны катеты.

Дано: ∆АВС – прямоугольный треугольник, С = 90°, a, b – катеты.

Найти: с – гипотенуза.
Решение: .

2. Найти катет, если известна гипотенуза и другой катет.

Дано:∆АВС – прямоугольный треугольник, С = 90°, с – гипотенуза, а – катет.
Найти: b – катет.
Решение: .

2) Решение задач (см. Презентация 2).

IV. «Теорема Пифагора в природе» (см. Презентация 3). «Это интересно» (см. Презентация 4).

V. Итог урока.

• Что нового вы узнали сегодня на уроке?
• Для каких треугольников применяется теорема Пифагора?
• В чём заключается теорема Пифагора?

VI. Домашнее задание: П 54, № 483 (б,.в), 486 (а).

В качестве домашнего задания по этой теме можно предложить исследовательскую работу со следующей мотивирующей задачей: «Почему теорему Пифагора называют «теоремой невесты»? Существуют ли другие доказательства теоремы?»

urok.1sept.ru

Теорема Пифагора

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока: изучение теоремы Пифагора и ее применение.

Задачи:

• Познакомить учащихся с жизнью Пифагора, его школой.
• Доказать теорему и показать различные способы доказательства.
• Показать применение теоремы  в жизни
  (флеш-проекты учащихся).
• Развивать логическое мышление, самостоятельность и воображение учащихся.
• Поддерживать интерес к предмету.

Оборудование и материалы: мультимедийный проектор, РС, учебник, раздаточный материал презентация к уроку и флеш проекты учащихся.
Особенностью урока является то, что он  базируется на флеш – проектах учащихся.с использованием РС.

ХОД УРОКА

«Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!»

1. Пифагор Самосский и история  доказательства  теоремы (5 мин.)  (слайды 5-9)

Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко недостоверны. С его именем связано много легенд.
Достоверно известно, что Пифагор много путешествовал по странам Востока, посещал Египет, Индию и Вавилон, изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии, куда принимались с большими церемониями после долгих испытаний.

В результате первой же прочитанной лекции Пифагор приобрел 2000 учеников, которые не вернулись домой, а вместе со своими женами и детьми образовали громадную школу. Теоремой Пифагора и пифагорейской школой восхищается человечество на протяжении всей истории, им посвящают стихи, песни, рисунки, картины. Так художник Ф.А. Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу»
В Греции была выпущена почтовая марка по случаю переименования острова Самос в остров Пифагорейон. 
На марке надпись: «Теорема Пифагора. Эллас. 350 драхм».
Эта красивая марка – почти единственная среди многих тысяч существующих, на которой изображен математический факт

Пифагор – это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор – «убеждающий речью».)
Сохранилась легенда, которая гласит, что, доказав свою знаменитую теорему, Пифагор принес богам в жертву быка, а по другим источникам, даже 100 быков .

2. Различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков (3 мин.) (слайды 10-16)

У Евклида эта теорема гласит (дословный перевод):
«В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».

Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Кремонским (начало 12 в.), в переводе на русский гласит:
«Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол».

В Geometria Culmonensis (около 1400 г.) теорема читается так:
Also, wird das vierecke Feld, gemessen an der langen Wand, so also gross ist als bei beide Vierecke, bei zwei werden gemessen von den zwei Wanden des deren, bei zwei gemeinde, tretten in dem rechten Winkel. В переводе это означает:
«Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу».
Современная формулировка теоремы Пифагора  «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

3. Доказательсто теоремы Пифагора (5 мин.)  (слайды 17-20)

Доказательство:

1. (а + b

)² = 4S + c²
2. 4S= 4 · 1/2 ab = 2 ab
3. а² + 2ab + b² = 2ab + c²
4. а² + b² = c²

Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum – ослиный мост, или elefuga – бегство “убогих”, так как некоторые “убогие” ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозваны по этому “ослами”, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.

4. Примеры различных способов доказательства теоремы (5 мин.)

(слайды 21-29)

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса».

• Древнекитайское доказательство.
• Доказательство Евклида.
• Доказательство Вальдхайма
• Доказательство Хоукинса.
• Доказательство Гутхейля.
• Доказательство  Перигаля.
• Доказательство основанное на теории подобия.
• Луночки Гиппократа.
• Доказательство на китайском, 1670 г.
• Доказательство из сочинений Бхаскары.
• Доказательство – модель (видеоролик).

5. Примеры  применения  теоремы Пифагора на практике (18 мин.) (слайды 30-31)  

Пифагора замечательна тем, что она проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное практическое значение: она применяется в геометрии буквально на каждом шагуТеорема Пифагора – одна из самых главных теорем геометрии. Из нее или с ее помощью можно вывести большинство теорем. Сама же теорема

• в планиметрии
• в стереометрии
• в архитектуре
• в строительстве
• в физике
• в астрономии
• в литературе

В планиметрии:

1. Квадрат со стороной а и диагональю d.

Рассмотрим применение теоремы Пифагора для нахождения диагонали квадрата со стороной а.
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, тогда  d² = a² + a² откуда: d² = 2a²d = а 2

2. Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b.
По теореме Пифагора: d² = a² + b²

Рассмотрим пример вычисления диагонали прямоугольника со сторонами 5 см и 12 см.

3. Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом по теореме Пифагора

а² = h² + (1/2a)²
h² = a² – (1/2a)²  h = 1/2a3

Рассмотрим пример вычисления длины высоты в равностороннем треугольнике со стороной 4 см.

В стереометрии:

Вычисление длины диагонали прямоугольного параллелепипеда

В архитектуре:

В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле.
Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.
В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b/2 и r = b/4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4 + p, один катет равен b/4, а другой b/2 – p.
По теореме Пифагора имеем: (b/4 + p)² = (b/4)² + (b/2 – p)²
Решив данное уравнение, легко найти радиус внутренней окружности р = b/6

В строительстве:

Возможно, кто-то сочтёт приложения теоремы Пифагора сугубо теоретическими. Но это не так. Если, например, рассматривать треугольную призму  как крышу башни, то в первом нашем вопросе речь идёт о том, какой длины нужно сделать боковые рёбра, чтобы при данной площади чердака была выдержана предписанная высота крыши. Заметим, что расчёт площади кровли можно сильно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит:
Чтобы найти площадь поверхности двухскатной крыши, все скаты которой имеют равный уклон, нужно умножить площадь чердака Sч на длину стропила и разделить на половину ширины дома.
Например, при строительстве любого сооружения рассчитывают расстояния, центры тяжести, размещение опор, балок и т.д. В целом значение теоремы кроме вышесказанного в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых.

В физике:

Молниеотвод, громоотвод, устройство для защиты зданий, промышленных, транспортных, коммунальных, с-х. и других сооружений от ударов молнии.  
Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

• По теореме Пифагора h²> a² + b²,
• значит h >  a² + b²

В астрономии:

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. Это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы, которые долгое время считались искусственными)и др. Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100 000 франков  тому, кто первый установит связь с каким – нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса Световой сигнал  в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора,  имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

В литературе:

Многие при имени Пифагор вспоминают его теорему, но мало кто знает, что он имел отношение не только к математике, но и к литературе….
Великий математик был еще и великим философом своего времени
Вот некоторые его высказывания:

• Делая великое, не обещай великого.
• Как ни коротки слова «да» и «нет», все же они требуют самого серьезного размышления.
• Ни  делай ничего постыдного ни в присутствии других, ни в тайне.
• Первым твоим законом должно быть уважение к самому себе
• Не закрывай глаз, когда хочешь спать, не разобравши всех своих поступков за прошедший день.
• По торной дороге не ходи.

Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни.
О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист o Плутарх, греческий ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.
Легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков, послужила поводом для юмора в рассказах писателей и в стихах поэтов. Так, например, немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в кругосветном путешествии на русском корабле «Рюрик», написал следующие стихи:

Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них П

urok.1sept.ru

Эпонимы в классе: как связаны теорема Пифагора и русский язык

Метапредметность вызывает много вопросов у педагогов. Как объединить физику и пение или географию и физкультуру? А вот с русским языком всё легко объединяется эпонимами! Наш блогер Марк Блау рассказывает, что это такое и как связать географию, физику, биологию и другие науки с русским языком.

Рассылка «Мела»

Мы отправляем нашу интересную и очень полезную рассылку два раза в неделю: во вторник и пятницу

С точки зрения школьника, скучнее занятия, чем изучение грамматики, не придумаешь. Особенно грамматики такого языка, как русский, где на каждое правило по нескольку исключений. В конце концов, оказывается, что, если много читал или памятью обладаешь фотографической, никакие правила тебе не нужны. Смотришь на слово и видишь, правильно или неправильно оно написано. Ну а если не повезло, вряд ли спасёт свод правил с прилагаемым к нему сводом исключений. Учи его или не учи — результат один, и результат грустный: «Как ниграмотно песал, так песать и будиш»!

Хорошо, что всё чаще приходится писать не рукой и не ручкой, а с помощью компьютера или телефона. В этом случае к нашим услугам различные программы-корректоры, которые и правописание поправят, а иногда и покажут, как лучше построить предложение. Ещё чуть-чуть, и письма за нас станет писать искусственный интеллект. То-то станет весело, то-то хорошо!

Впрочем, языкознание изучением грамматики не исчерпывается. Есть в нём очень интересные разделы. Один из таких разделов — этимология, наука о происхождении слов. Будет время (а оно будет!) — расскажу об этом разделе подробнее. А пока о самом интересном, пожалуй, — о способе образования новых слов, об эпонимии.

Что такое эпонимия

Этим красивым термином называется процесс словообразования, при котором имя нарицательное образуется из имени собственного. Имена людей (знаменитых и не очень) переходят на те предметы, которые эти люди изобрели, создали, построили, а иной раз просто пользовались ими, как, например, граф Сэндвич, придумавший способ наскоро перекусить. В результате появляется целый класс имён нарицательных, образовавшихся из имён собственных. Такие слова называются эпонимами.

Здесь стоит ненадолго остановиться и попытаться придумать несколько слов, названных по имени людей. Сразу приходят в голову рентген, автомат Калашникова, а также его коллега и, скорее всего, старший брат «шмайсер». А марки многих современных автомобилей, от простодушной «Шкоды» до роскошного «Роллс-Ройса»? А единицы измерения: джоули, ватты, амперы и омы? В общем, современный человек без особенного напряжения составит весьма большой список таких слов.

Доблестные предки

«Эпоним» — это слово древнегреческого происхождения. ἐπώνῠμος в буквальном переводе означает «давший имя». Древние греки называли города, реки, горы и другие географические объекты именами богов, легендарных героев или реальных людей.

Например, город Византий, согласно легенде, основал герой-мореплаватель Визант, которого мифы называли сыном бога Посейдона. Визант, таким образом, стал эпонимом Византия, а через него также и эпонимом Византийской империи, возникшей на том же месте гораздо позже.

Геенна огненная сейчас место совершенно идиллическое

Ещё один пример из совсем другого времени и совсем другого языка. У подножия Иерусалима находится долина Гей Бен Хинном, что в переводе с иврита означает «долина сынов Еннома». Во времена царя Соломона и библейских пророков эта долина пользовалась нехорошей славой: здесь приносили человеческие жертвы языческим богам. Позже долина стала муниципальной территорией, свалкой. Сюда свозили из города и сжигали мусор. Огонь горел здесь и днём, и ночью. Зрелище пугающее и дурнопахнущее! Так иерусалимская мусорка, находившаяся на земле, названной по имени давно, казалось бы, забытого Еннома, стала прообразом вечно пылающего ада, геенной огненной. Этот пример показывает, какой извилистой может быть жизнь обычного слова-эпонима.

К легендарным предкам-эпонимам различные народы и племена зачастую возводили свои названия. Например, эпонимом племени латинян считают мифического царя Латина. По другой легенде, названия народов чехов и поляков (ляхов) происходят от имён легендарных князей Чеха и Леха.

Памятник основателям Киева на берегу Днепра

Эпонимом города Киева стал легендарный князь Кий. Один из братьев Кия, Щек, стал эпонимом горы Щекавица, возвышающейся над Подолом, а их сестра Лыбедь — эпонимом реки Лыбедь (правого притока Днепра), которая протекает по территории нынешнего Киева.

Имена собственные становились также названиями промежутков времени. Так, в античных Афинах год назывался по имени первого из девяти правителей-архонтов, который поэтому назывался «архонтом-эпонимом». По этой причине в официальных хрониках датировка была такой: «в год, когда архонтом был такой-то». В истории Китая выделяются времена правления различных императорских династий (например, Цинь, Хань, Мин).

Слишком много эпонимов?

Со временем появлялось всё большее количество понятий и явлений, наименования которых образовывали от имён собственных самых разных людей. Всё чаще эпонимами становились реальные, а не легендарные личности. Так, уже в 332 году до нашей эры в Египте на берегу Средиземного моря был построен город Александрия, эпонимом которого стал Александр Македонский. В 330 году нашей эры уже упомянутый Византий переименовали в Константинополь. Таким образом, произошла смена эпонима, старый город принял новое имя, имя императора Константина.

Количество географических объектов, для которых понадобилось придумывать названия, резко возросло в эпоху Великих географических открытий. Когда началась научно-техническая революция, появилось огромное число новых предметов, явлений и понятий. Всем им требовались наименования, и их стали называть по имени реальных людей: первооткрывателей, изобретателей, учёных, предпринимателей, владельцев или властителей.

Почему эпонимы

Эверест — самая высокая гора в мире

Иной раз кажется, что эпонимы — это только дань человеческому тщеславию. Самую высокую вершину мира британские геодезисты, работавшие в Индии, назвали в честь начальника всей геодезической службы колонии сэра Джорджа Эвереста. Ещё чаще (особенно в биологических науках, где количество обнаруженных человеком живых организмов упрямо стремится к бесконечности) называют не ради славы, а просто для того, чтобы назвать. Ведь у всякого предмета должно быть название, и желательно короткое. Так что «эффект Мёссбауэра», без сомнения, более удачный научный термин, чем «резонансное поглощение гамма-фотонов». Во-первых, на два слова короче, а во-вторых, хоть какая-то информация для профанов: этот непонятный широкой публике эффект открыл Рудольф Мёссбауэр.

Как язык производит эпонимы

Эпонимия оказалась удачным способом образования слов. Эпоним может быть не одним словом, а парой слов (болезнь Боткина, теорема Пифагора) или даже несколькими словами. В русском языке эпонимия совершила интересный кульбит. Если раньше эпонимом называлась персона, дававшая своё имя некоторому предмету или понятию, то сейчас эпонимом чаще всего называют само слово, имя нарицательное, произведённое от имени собственного. То есть сейчас эпонимами являются джоуль, а не Джоуль, рентген, а не Рентген, и «Форд», а не Форд.

Эпонимы — удивительные кентавры

Эпонимы — тема интересная ещё и потому, что один эпоним всегда объединяет некоторую персону и некоторый материальный или духовный объект. Сам по себе объект может быть весьма интересным. Например, автомобили, компьютеры, оружие — о них можно говорить бесконечно. Но ведь и биография человека-эпонима может быть потрясающей. Цветок бугенвиллия красив, но и биография капитана Бугенвилля, в честь которого этот цветок назван, может быть основой интереснейшего сериала. Жюль Верн эту биографию оценил и подробно описал.

Бугенвиллея — тропическое растение с красивыми цветками

Поэтому эпонимы — одна из самых интересных для учащихся тем в изучении языка. Одна из возможностей показать им, что языкознание — не набор скучных и ненужных правил.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

mel.fm

Урок по теме «Теорема Пифагора»

Геометрия обладает двумя великими сокровищами.
Первое — это теорема Пифагора, которую можно
сравнить с мерой золота: Кеплер.

Цель урока: совершенствовать навыки решения задач на применение теоремы Пифагора и теоремы, обратной теореме Пифагора.

Задачи урока:

• образовательные: закрепить навыки решения задач на применение теоремы Пифагора;
• развивающие: развивать умения в применении знаний в конкретной и проблемной ситуации, самостоятельность в решении задач;
• воспитательные: воспитывать интерес к геометрии через содержание учебного материала.

Оборудование: интерактивная доска, презентация, плакаты, карточки с заданиями.

Подготовительная работа: Из класса выбрать 2 ученика, которые в течение урока помогут группам учащимся вести поисковую работу, проведут консультации по решению задач по карточкам. Эти учащиеся заранее готовят на ватманах доказательство теоремы Пифагора двумя способами. При входе в класс каждый ученик получает карточку красного, желтого или зеленого цвета. Ребята рассаживаются за парты в любом порядке. Во время урока учитель предлагает собраться группам по цвету карточек и начать поисковую работу. Для усиления драматизации урока класс попадает в детективное агентство, на урок приглашены Пифагор (ученик 11 класса), его дочь Теорема Пифагора (ученица 5 класса), пират Джек-Воробей (ученик 11 класса).Все герои появляются в ходе урока и вносят оживление и неожиданный поворот урока.

Ход урока

I. Организационный момент.

Учитель: Добрый день, ребята! Сегодня мы находимся в детективном агентстве » Истина». Его президент — я, у меня в штате — два помощника. Они у меня грамотные и умные специалисты. Сейчас у доски оба помощника подготовят доказательство теоремы Пифагора. Но мне бы хотелось пополнить свой штат новыми сотрудниками и поэтому хочу узнать, готовы ли вы к проверке своих возможностей. У нас сегодня присутствуют представители Детективного агентства «Мудрость» (учителя, родители) и они так же хотят выяснить: насколько вы грамотные и компетентные ребята. Итак, у нас урок решения задач по теореме Пифагора, а цель урока — закрепить знания, умения и навыки при решении задач с использованием теоремы Пифагора, а также решение старинных математических задач с использованием теоремы Пифагора..

II. Итак, устная разминка. (презентация на интерактивной доске)

1. Какой треугольник называется прямоугольным? Как называются его стороны? (катеты, гипотенуза лежит против угла в 90°)

2. Продолжите предложение: В прямоугольном треугольнике любой катет

а) равен гипотенузе;

б) меньше гипотенузы;

в) больше гипотенузы;

г) определить нельзя.

3. В прямоугольном треугольнике один из острых углов равен 20°.Найдите второй острый угол. (90°-20°=70°)

4. Один из катетов прямоугольного треугольника равен половине гипотенузы, острые углы равны:

а) 60° и 30°;

б) по 45°;

в) однозначно определить нельзя.

5. Сформулируйте теорему Пифагора.(В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов).

6. Решите устно задачи по чертежу.

Найдите неизвестную сторону треугольника.

(Как иначе называют треугольник со сторонами 3, 4 и 5? (египетским).

ответ к задаче 2: v13²-5² = v144=12 )

Учитель: Молодцы, а сейчас с вами заслушаем два доказательства теоремы Пифагора.

1 ученик. Теорема Пифагора гласит «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». На сегодняшний день в мире известно около 150 способов доказательства этого утверждения. Я докажу теорему способом, предложенным в учебнике геометрии Атанасяна.

Теорема: Во всяком прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано:  АВС, угол С=90°. АС, СВ — катеты, АВ - гипотенуза.

АС=b; СВ=а; АВ=с.

Доказать: а² +b² =с²

Доказательство: Достроим АВС до квадрата.

Получим четыре равных прямоугольных треугольника (по 2-м катетам), отсюда следует, что гипотенузы равны. Четырехугольник АВМК — ромб.

т.к. r АВС - прямоугольный.

^l, следовательно,

Если у ромба есть угол 90°, то такой ромб является квадратом: АВМК -квадрат.

S_б.кв.=(a+b)²=a²+2ab+b²

S_б.кв.=4Sr +S_ABKM= 4Y l/2Y aY b +c² =2ab+c².

Имеем: a²+2ab+b²=2ab+c², т.е. a²+b²=c²

Теорема доказана.

2 ученик.

Я расскажу о другом способе доказательства теоремы Пифагора.

Пусть дан треугольник АВС с прямым углом С, гипотенузой с и катетами a и b, такими, что b>a. Продолжим отрезок СВ за точку В и построим треугольник BMD так, чтобы точки М и А лежали по одну сторону от прямой СD и, кроме того, BD=b, <BDM =90⁰, DM = a, тогда треугольники BMD и ABC равны по двум сторонам и углу между ними. Точки А и М соединим отрезком АМ. Имеем МD+СD и AС+CD, прямая АС параллельна прямой МD. Так как МD<AC, то прямые CD и AM не параллельны. Следовательно, AMDC - прямоугольная трапеция.

В прямоугольных треугольниках ABC и BMD <1 + <2 =90⁰ и <3+<4=90⁰, но так как <1 = <3, то <3 + <2 = 90⁰; тогда <ABM = 180⁰ — 90⁰ = 90⁰. Оказалось, что трапеция AMDC разбита на три неперекрывающихся прямоугольных треугольника, тогда по аксиомам площадей имеем S_ABC +_{S ABM +S BMD =Sтрап , или}

1/2 ab + 1/2 с² + 1/2 ab = 1/2 (a+b)(a+b).

Умножив обе части равенства на 2, получим

ab + c² + ab = (a + b)², 2ab + c²= a² + 2ab + b², откуда c² = a² + b². (5 минут)

Учитель: Откройте тетради. Запишите число и тему урока.

III этап урока. Решение исторических задач.

Стук в дверь. Входит Пифагор.

Пифагор. Это детективное агенство «Истина»?

Учитель. Да. А вы кто и что вас к нам привело?

Пифагор. Кто я? Неважно! Главное то — что пропало мое любимое дитя. Я сколько лет был с ней рядом, и она мне во всем помогала, а теперь её нет. Что мне делать и как я вернусь к своим ученикам без неё?!

Учитель: Ребята, как вы думаете, кто к нам пришел?

Ученик: Я думаю, что к нам пришел Пифагор, и он потерял теорему Пифагора.

Учитель: Уважаемый Пифагор, присядьте, не волнуйтесь, мы немедленно отправляемся в путь на поиски вашей любимицы.Ребята, я отправляю вас в разные страны: Китай, Индию и Россию. Прошу всех занять места по цветам карточек.

Прошу каждую группу получить задание. (группа - по 1 задаче с чертежом)

1) Индийская задача.В древней Индии был обычай предлагать задачи в стихах. Я предлагаю вам решить одну из таких задач.

Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
«Как озера вода здесь глубока?»

Решение: Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда

AD = AB = Х + 0,5 .

Из треугольника ACB по теореме Пифагора имеем AB² — AC² = BC²,

(Х + 0,5 )² — Х² = 2²,

Х² + Х + 0,25 — Х² = 4, Х = 3,75.

Таким образом, глубина озера составляет 3,75 фута.(Какова глубина в современных единицах длины (1 фут приближенно равен 0,3 м) ?

3, 75 * 0,3 = 1,125 (м)

Ответ: 3,75 фута или 1, 125 м.

2) Китайская задача.

Задача о бамбуке из древнекитайского трактата «Гоу-гу»

Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи). Какова высота бамбука после сгибания?

Решение: 1) Выполним чертеж к задаче и обозначим высоту бамбука после сгибания ВС= х чи. Тогда ВD=АВ=10-х(чи).

Из треугольника АВС по теореме Пифагора имеем АВ²=АС²+ВС²

(10-х)² =х²+3² ,

100-20х+ х²= х² + 9,

-20х=9-100,

-20х=-91,

х=4,55

2) 10-4,55=5,45.

Таким образом, высота бамбука после сгибания равна 5,45 чи.

Задача №3 Задача из первого учебника математики на Руси. Назывался этот учебник «Арифметика».

Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.

Задача 4 Задача арабского математика XI в.

На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой — 20 локтей. Расстояние между их основаниями — 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

Решение. Пусть АD=Х, тогда АЕ= 50-Х

Итак, в треугольнике АDВ: АВ² =ВD² +АD² =30² +Х²=900+Х²;

в треугольнике АЕС: АС²= СЕ²+АЕ² =202+(50 — Х)² =400+2500 — 100Х+Х²=2900 — 100Х+Х².

Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время. Поэтому АВ² =АС² ,

900+Х² =2900 — 100Х+Х²,

100Х=2000,

Х=20,

АD=20.

Значит, рыба была на расстоянии 20 локтей от большой пальмы.

Ответ: 20 локтей.

Учитель. Уважаемый Пифагор. К нам поступило сообщение, что видели вашу дочь в тридевятом царстве, тридесятом государстве. Внимание, мы отправляемся в сказку!

Сказка-клип на интерактивной доске.

Задача — сказка.

Давным-давно в некоторой стране жила прекрасная принцесса. Она затмевала красотой всех подруг и свою старшую сестру, которая красотой не блистала. Старшая сестра решила ей отомстить. Она пошла к ведьме и попросила ее заколдовать принцессу. Ведьма не смогла ей отказать, и придумала усыпить принцессу в башне до той поры, пока какой-нибудь принц не посмотрит на окно башни с такого места, чтобы расстояние от глаз принца до окна было 50 шагов.

Принцесса заснула крепким сном. Прошло много лет, но никто мне смог расколдовать принцессу. И вот, в один прекрасный день в этом городе появляется на белом прекрасном коне молодой принц. Узнав, какое несчастье произошло с принцессой, молодой принц берется расколдовать ее. Для этого он измеряет длину от основания башни до окна, за которым скрывается принцесса. У него получается 30 шагов. Затем что-то прикидывает в уме и отходит на несколько шагов, поднимает голову и вдруг…башня озаряется светом и через мгновенье навстречу принцу выбегает еще более прекрасная принцесса… На сколько же шагов отошел принц от башни?

Решение:

50²-30²=40²

2500-900=1600

v1600=40(шагов)

Учитель: Пифагор, видно ваша дочь побывала и здесь, но снова отправилась в путь. Мы подумаем, где её еще можно поискать. А пока проведем динамическую паузу.

Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.

Учитель:Внимание, к нам прибыла шифровка. Ребята, помогите узнать, о чем идет речь. Самостоятельная работа: математическое лото. На обычной доске табло для каждой группы. Задание группа получает в конверте. Каждый ученик получает индивидуальное задание: решить задачу с применением теоремы Пифагора, найти ответ, с обратной стороны — буква, которую надо прикрепить в табло на доске. Кто решит раньше, помогает ребятам по команде.

(ответ: найдите остров сокровищ)

Учитель: Ребята, возможно, это подсказка, что теорема Пифагора на острове сокровищ. Вбегает в класс Джек-воробей.

Джек-воробей. Это детективное агентство?

Учитель. Да, а что вы хотели?

Джек-воробей. Я отправляюсь на остров сокровищ и хочу на нем поставить флагшток. Для этого я купил 50 метров троса. Как вы думаете, мне хватит троса, если флагшток высотой 12 метров, а растяжки на земле 5 метров.

Если поможете, я вам верну ваше сокровище-теорему Пифагора.(практическая задача, устно).

Решение:

12²+5²=144+25=169

=13

13*4=52 (м)

Ответ: Троса не хватит.

Учитель. Глупый ты Джек-воробей. Придется тебе отдать нашу теорему Пифагора. Где же она.

Джек-воробей. Да вот она.(Девочка весь урок сидела в классе у компьютера).

Выходит девочка-Теорема Пифагора , одетая в тунику, на голове треугольник и написано:а²+в²=с² .Она подбегает к Пифагору. Он благодарит всех ребят за помощь в поиске.

Учитель: Уважаемый Пифагор не уходите. Мы хотим подарить вам шуточную песню про прямоугольный треугольник.

Текст песни «Прямоугольный треугольник».
Это все так схоже с детскою игрой —
Сами треугольник мы сложили снова:
Первый катет — Витька, я второй,
А гипотенуза — Светка Иванова.

Припев:
И не можем мы поделать ничего.
Напрасно геометрию ругая,
Я люблю ее, она — его,
А ему, как видно, нравится другая.

Милый математик, добрый Пифагор,
Раз уж речь зашла у нас на эту тему,
Ты нас извини, но до сих пор
Мы твою понять не можем теорему.

Припев.

Ни один учебник так и не успел
Чуточку помочь нам в этом трудном деле.
Зря в руках крошился белый мел,
Зря в тетрадках наших перышки скрипели.

Припев.

Учитель: Ребята, вы отлично поработали на уроке, я вас всех возьму в штат агентства «Истина». Слово предоставляется детективному агентству «Мудрость».

Домашнее задание.

Фронтон Большого театра в Москве имеет форму равнобедренного треугольника с боковыми сторонами по 21,5 м и основанием 42 м (размеры приближены). Вычислите площадь фронтона.

Даны отрезки a и b, а = 5 см, b = 7 см. Постройте отрезокvа²+в².

Найдите ещё одно доказательство теоремы Пифагора(по выбору). Урок окончен.

Литература:

1. Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. Геометрия 7-9. Учебник для 7-9 классов средней школы. М.: Просвещение, 2007

urok.1sept.ru

Теорема Пифагора

Цели урока:

• Образовательная: добиться усвоения теоремы Пифагора, привить навыки вычисления неизвестной стороны прямоугольного треугольника по двум известным, научить применять теорему Пифагора при решении простейших задач.
• Развивающая: развивать способности к сопоставлению, к аналитико-синтетическому мышлению, способствовать развитию наблюдательности, внимания, расширение кругозора.
• Воспитательная: формирование потребности в знаниях, интереса к математике.

Тип урока: урок изложения нового материала.

Оборудование: компьютер, мультимедийный проектор, презентация к уроку в программе “Живая математика”.

План урока:

1. Организационный момент
2. Устные упражнения
3. Исследовательская работа, выдвижение гипотезы и проверка ее на частных случаях
4. Объяснение нового материала
   а) О Пифагоре
   b) Формулировка и доказательство теоремы
5. Закрепление изложенного через решение задач
6. Задание на дом, подведение итогов урока.

Ход урока

Слайд 1 (Приложение 1): Выполните упражнения.

1. Раскройте скобки: (3 + х)²
2. Вычислите 3² + х² при х = 1, 2, 3, 4.
   – Существует ли натуральное число, квадрат которого равен 10, 13, 18, 25?
3. Найдите площадь квадрата со стороной 11 см, 50 см, 7 дм.
   – По какой формуле находится площадь квадрата?
   – А как найти площадь прямоугольного треугольника?

Вопрос-ответ

– Угол, градусная мера которого равна 90° (прямой).
– Сторона, лежащая напротив прямого угла треугольника (гипотенуза).
– Треугольник, квадрат, трапеция, круг – это геометрические … (фигуры).
– Меньшая сторона прямоугольного треугольника (катет).
– Фигура, образованная двумя лучами, исходящими из одной точки (угол).
– Отрезок перпендикуляра, проведенный из вершины треугольника к прямой, содержащей противоположную сторону (высота).
– Треугольник, у которого две стороны равны (равнобедренный).

Слайд 2 (приложение 1). Задачи по готовым чертежам.

Слайд 3. Задача.

Построить прямоугольный треугольник со сторонами 3 см, 4 см и 6 см.

Задание разбивается по рядам.

	1 ряд	2 ряд	3 ряд
Катет a	3	3
Катет b	4		4
Гипотенуза с		6	6

Вопросы:

– Получился ли у кого-нибудь треугольник с заданными сторонами?
– Какой можно сделать вывод? (Прямоугольный треугольник нельзя задать произвольным образом. Между его сторонами существует зависимость.)
– Измерьте получившиеся стороны. (Примерный средний результат от каждого ряда заносится в таблицу.)

	1 ряд	2 ряд	3 ряд
Катет a	3	3	~4,5
Катет b	4	~5,2	4
Гипотенуза с	~5	6	6

– Да, действительно, между гипотенузой и катетами существует зависимость, давайте попробуем выяснить какая.

Слайд 4. Практическое исследование.

Построим на сторонах прямоугольного треугольника квадраты и посчитаем их площади.

Найдем сумму площадей квадратов, построенных на катетах. Что вы заметили?

Изменим размеры нашего треугольника. Что мы видим?

Обозначим катеты и гипотенузу треугольника через а, в и с.

Какой можно сделать вывод?

Да, действительно, квадрат гипотенузы равен сумме квадратов катетов, и этот факт доказал ученый, имя которого Пифагор. В честь него эта теорема и названа.

Слайд 5. Пифагор Самосский.

Далее ученик (или группа учащихся), заранее подготовивший доклад и презентацию о Пифагоре, рассказывает о нем классу.

Слайд 6. Тема урока

– Кто назовет тему сегодняшнего урока?

Учащиеся в тетрадях записывают тему урока: “Теорема Пифагора”.

Давайте сформулируем цели нашего урока:

1) доказать теорему Пифагора;
2) научиться применять ее в различных ситуациях;
3) учиться логически мыслить, анализировать, рассуждать, выделять главное и делать выводы.

– Теорема Пифагора – одна из главных теорем геометрии. С ее помощью доказываются многие другие теоремы и решаются задачи из различных областей: физики, астрономии, строительства и др. Она была известна задолго до того, как ее доказал Пифагор. Древние египтяне использовали ее при построении прямоугольного треугольника со сторонами 3, 4 и 5 единиц с помощью веревки для построения прямых углов при закладке зданий, пирамид. Поэтому такой треугольник называют египетским треугольником.

Существует более трехсот способов доказательства этой теоремы. Мы рассмотрим сегодня один из них.

Слайд 7. Теорема Пифагора (может быть использовано Приложение 2).

Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано:

Прямоугольный треугольник,

a, b – катеты, с – гипотенуза

Доказать:

c² = a² + b²

Доказательство.

1. Продолжим катеты прямоугольного треугольника: катет а – на длину b, катет b – на длину а.

– До какой фигуры можно достроить треугольник? Почему до квадрата? Чему будет равна сторона квадрата?

2. Достроим треугольник до квадрата со сторонойа + b.

– Как можно найти площадь этого квадрата?

3. Площадь квадрата равна.

S = (a + b)²

S = a² + 2ab + b²

– Разобьем квадрат на части: 4 треугольника и квадрат со стороной с.
– Каким образом еще можно найти площадь исходного квадрата?
– Почему равны получившиеся прямоугольные треугольники?

4. С другой стороны,

Приравняем получившиеся равенства:

Теорема доказана.

Существует шуточная формулировка этой теоремы: “Пифагоровы штаны во все стороны равны”. Вероятно, такая формулировка связана с тем, что первоначально эта теорема была установлена для равнобедренного прямоугольного треугольника. Причем, звучала она немного по-другому: “Площадь квадрата, построенного на гипотенузе прямоугольного треугольника равна сумме площадей квадратов, построенных на его катетах”.

А я приведу вам еще одну формулировку этой теоремы в стихах:

Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путем
К результату мы придем.

– Итак, сегодня вы познакомились с самой известной теоремой планиметрии – теоремой Пифагора. Как же формулируется теорема Пифагора?

Слайд 8. Следствие.

Слайд 9. Решение задач по готовым чертежам.

 

Слайд 10. Решение задач в тетради.

Один ученик на закрытой доске.

Для сильных учащихся можно предложить дополнительную задачу. (Проверить решение индивидуально в тетрадях)

Слайд 11. Домашнее задание.

Домашнее задание. п. 54, вопрос 8, докажите следствие из теоремы Пифагора, задачи № 483(б), 484(б), 486(а).
Подготовить сообщение о теореме Пифагора или о Пифагоре.

Подведение итогов урока:

– Что нового вы узнали сегодня на уроке?
– Сформулируйте теорему Пифагора.
– Что вы научились делать на уроке?

Оценивается работа класса в целом, выделяя отдельных учеников.

urok.1sept.ru

Тема урока: «Теорема Пифагора»

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

• изучение теоремы Пифагора, ее роли в геометрии; использование теоремы в решении задач;
• развитие логическое мышление, познавательного интереса, творческого поиска, самостоятельности;
• воспитание у обучающихся ответственного отношения к учению, культуры математической речи.

Ход урока

Слайд 3

“Да, путь познания не гладок. 
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!”

И я предлагаю вам разгадать одну из таких загадок.

Слайд 2

Сегодня на уроке мы познакомимся с одной из важнейших теорем геометрии – теоремой Пифагора. Она является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем. Докажем эту теорему, решим несколько задач с ее применением, ответим на вопросы теста.

Откройте тетради, запишите число и тему урока “Теорема Пифагора”.

Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко недостоверны. С его именем связано много легенд.

Родился Пифагор на острове Самос в Эгейском море, в семье купца Мнезарха. Путешествуя с отцом, будто бы в возрасте 18–20 лет он посетил старого тогда уже Фалеса (о. Самос почти рядом с Милетом!), который и пробудил интерес юноши к математике и астрономии, посоветовал ему поехать для основательного образования в Египет. Пифагор последовал совету. Затем были Вавилон, Индия…

Слайд 4

По возвращении на Самос Пифагор основал свою школу, но затем покинул остров. В южноиталийском г. Кротоне им был основан знаменитый пифагорейский союз, бывший одновременно и научной школой, и политическим и религиозным сообществом, в котором Пифагор почитался чуть ли не божеством…

В школе Пифагора рассматривались четыре mathema (науки): арифметика, музыка (гармония), геометрия и астрономия с астрологией. Пифагорейцы считали, что в основе всего лежат числа и гармония, ими поддерживаемая, но что все в математике нужно доказывать. Изучению математики придавался мистический характер, что не помешало найти доказательство теоремы Пифагора, а из нее получить (доказать!) иррациональность корня из двух! Это были великие математические открытия… Однако в школе существовал Декрет, по которому авторство всех математических работ приписывалось Пифагору.

Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили тайной имя своего учителя, так что установить правду о Пифагоре невозможно.

Без преувеличения можно сказать, что это самая известная теорема геометрии, ибо о ней знает подавляющее большинство населения планеты, хотя доказать ее способна лишь очень незначительная его часть.

Иоганн Кеплер писал: “Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора”.

Слайд 5

Ребята, а вы когда-нибудь слышали о теореме Пифагора?

Наверняка многие из вас слышали шутливый стишок:

“Пифагоровы штаны
Во все стороны равны”.

Смотрите, а вот и “Пифагоровы штаны”. Такие стишки придумывали учащиеся средних веков при изучении теоремы.

Слайд 6

На самом деле теорема звучит совсем иначе.

Предполагают, что во времена Пифагора теорема звучала по-другому.

Слайд 7

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum «ослиный мост» или elefuga – «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.

Слайд 8

Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.

Слайд 9

В некоторых списках «Начал» Евклида теорема Пифагора называлась теоремой Нимфы, «теорема-бабочка», по-видимому из-за сходства чертежа с бабочкой, поскольку словом «нимфа» греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь.

При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» не как «бабочка», а как «невеста». Так и появилось ласковое название знаменитой теоремы – «Теорема Невесты».

Итак, теорема Пифагора.

Запишите в тетрадях формулировку теоремы: “В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов”.

Слайд 10

Для доказательства теоремы рассмотрим прямоугольный треугольник с катетами равными а и b, и гипотенузой равной с. Для простоты построения, пусть a= 3 см, b = 2 см.

Слайд 11

Достроим треугольник до квадрата со стороной  так, как показано на чертеже.

Площадь этого квадрата равна 

С другой стороны этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна , и квадрата со стороной с, поэтому .

Таким образом , .

Теорема доказана.

Предлагаю вашему вниманию еще одно доказательство теоремы Пифагора, которое состоит из одного-единственного слова: “Смотри”.

Слайд 12

 

Физкультминутка.

Слайд 13

I. Решение задач с применением теоремы.

А сейчас рассмотрим решение задачи с применением теоремы Пифагора.

Задача 1. Найдите медиану равнобедренного треугольника с основанием а и боковой стороной в, проведенную к основании.

II. Пифагоровы тройки чисел.

Слайд 15

III. «Золотые стихи» Пифагора.

Слайды 16–18

IV. Применение теоремы Пифагора.

Итак, сегодня на уроке мы познакомились с одной из главных теорем геометрии: “теоремой Пифагора”, ее доказательством, решили задачу.

Слайд 19

Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство.

V. Тест.

Слайды 20–24

В завершении хотелось бы сказать: Причина популярности теоремы Пифагора триедина – это красота, простота и значимость!

urok.1sept.ru

«Теорема Пифагора» 8 класс

Урок по теме: «Теорема Пифагора»

Тип урока: урок изучения нового материала. ( по учебнику “Геометрия, 7–9”, учебник для общеобразовательных учреждений; Л.С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2009).

Цель:

познакомить учащихся с теоремой Пифагора и историческими сведениями, связанными с этой теоремой; развивать интерес к изучению математики, логическое мышление; внимание.

Ход урока:

1. Организационный момент.

СЛАЙД 2 Сказка « Дом».

Тема нашего урока «Теорема Пифагора». Сегодня на уроке мы познакомимся с биографией Пифагора, изучим одну из самых известных геометрических теорем древности, называемую теоремой Пифагора, одну из главных теорем планиметрии.

2. Актуализация знаний. (Подготовка к изучению нового материала, повторяется тот материал, который нужен будет при доказательстве теоремы)

1) Вопросы:

Какой четырехугольник называется квадратом?

Как найти площадь квадрата?

Какой треугольник называют прямоугольным?

Как называются стороны прямоугольного треугольника?

Как найти площадь прямоугольного треугольника?

3. Изучение нового материала.

1) Историческая справка.

СЛАЙД 3 и 4.

Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Как всякий отец, Мнесарх мечтал, что сын будет продолжать его дело — ремесло золотых дел мастера. Жизнь рассудила иначе. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам.

Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др. Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор — «убеждающий речью».)

Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством.

Излюбленной геометрической фигурой пифагорейцев была пентаграмма, называемая также пифагорейской звездой. Пифагорейцы пользовались этой фигурой, вычерчивая ее на песке, чтобы приветствовать и узнавать друг друга. Пентаграмма служила им паролем и была символом здоровья и счастья.

Предание гласит, что когда Пифагор пришёл к теореме, носящей его имя, он принёс богам 100 быков. В пятисотых годах до нашей эры Пифагор был убит в уличной схватке во время народного восстания. В настоящее время известно около 200 доказательств теоремы Пифагора.

Формулировка теоремы

Слайд 5.

2) Доказательство теоремы.

Достроим прямоугольник до квадрата со стороной a + b.

Ребята с помощью учителя по чертежу доказывают теорему, затем записывают доказательство в тетради.

Доказательство:

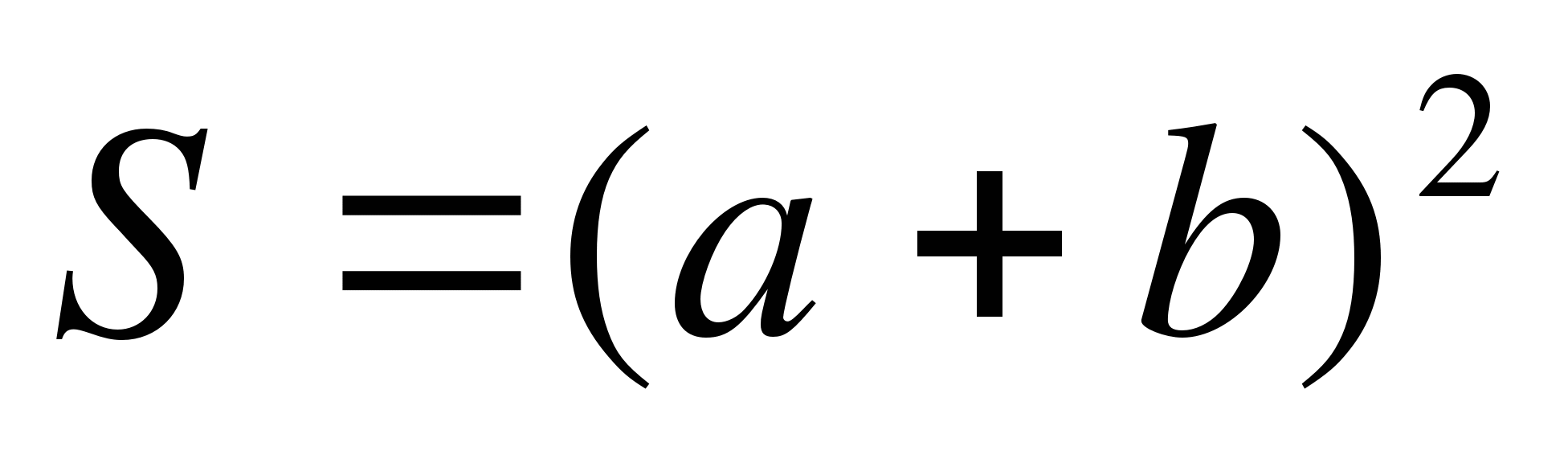— площадь квадрата

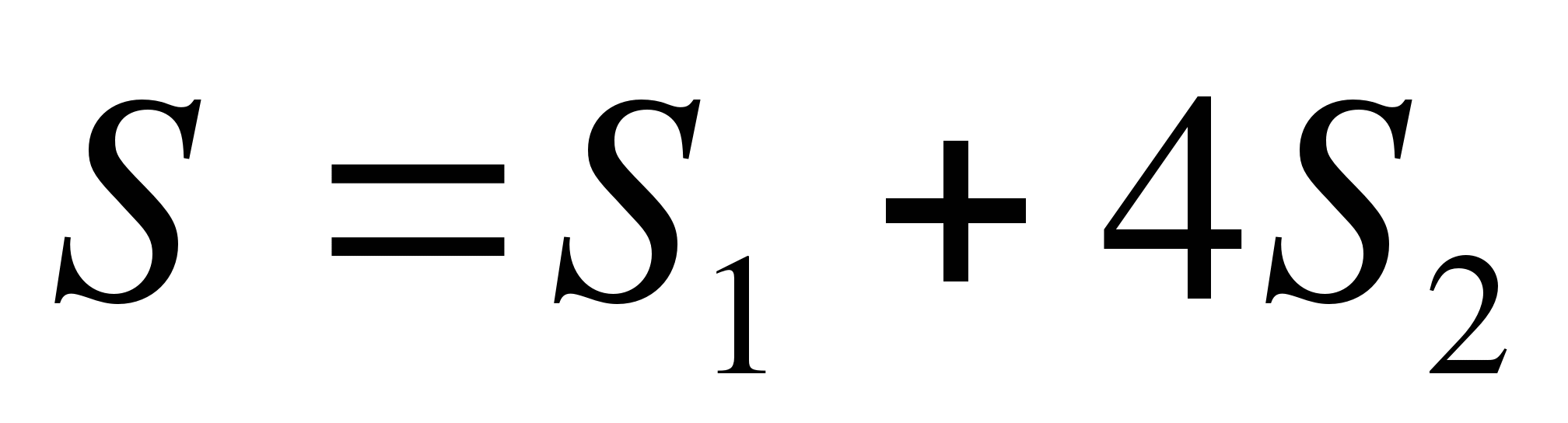
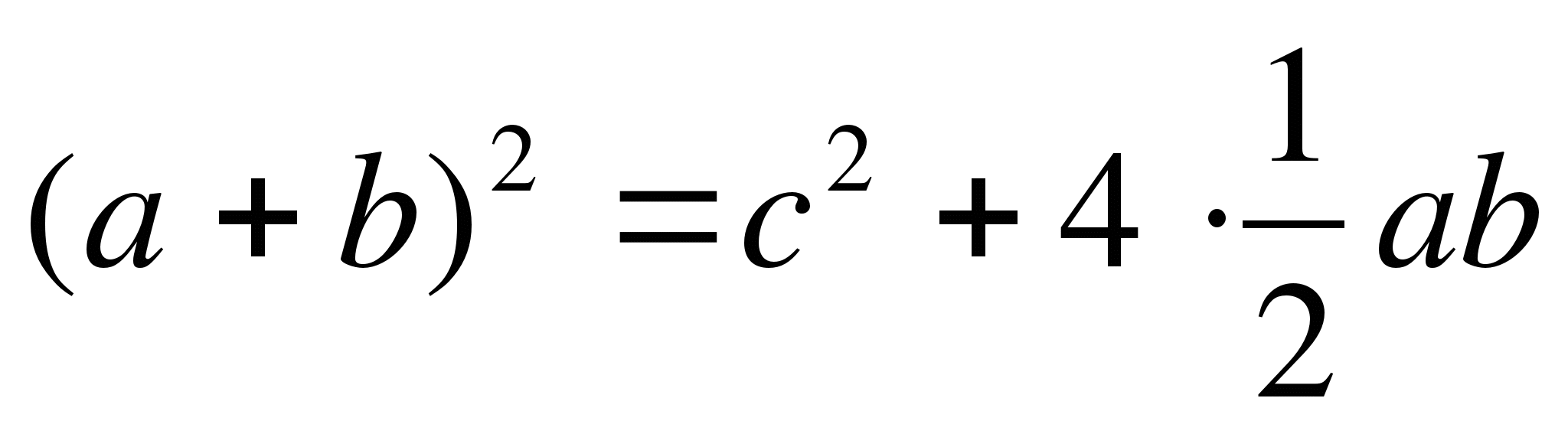
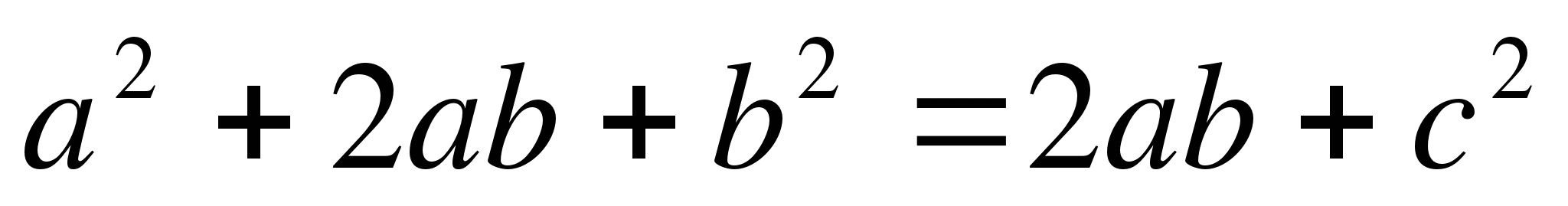
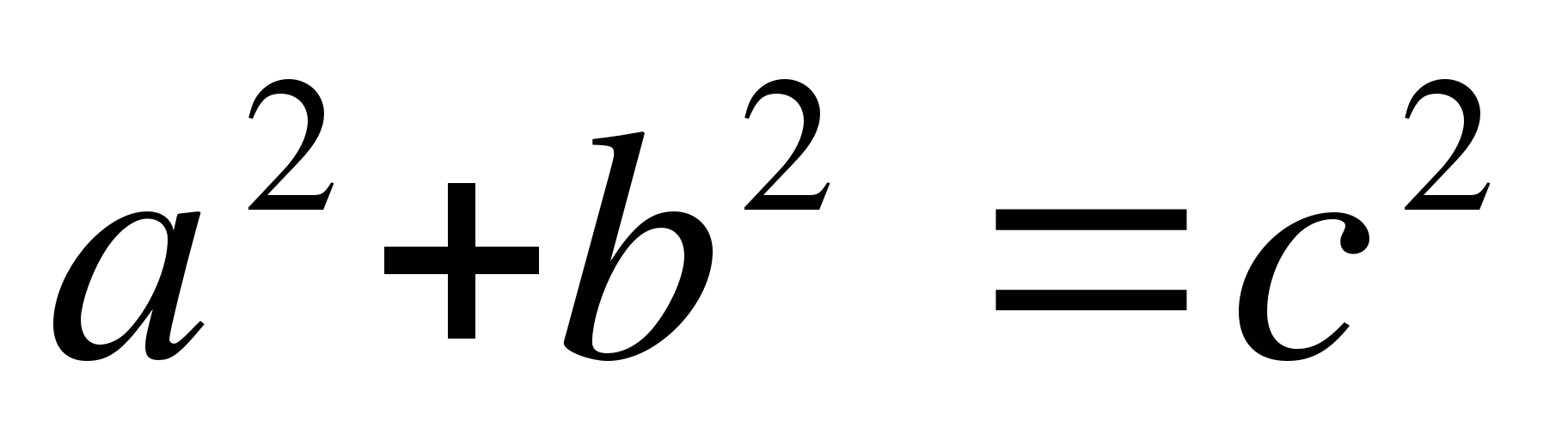— теорема доказана.

4. Первичное закрепление знаний.

Работа по учебнику (Применение теоремы Пифагора к решению задач).

Задачи решаются на доске и в тетрадях.

№ 483 (а),

№ 484 (а).

Вывод: с помощью теоремы Пифагора можно решать два вида задач:

1. Найти гипотенузу прямоугольного треугольника, если известны катеты.

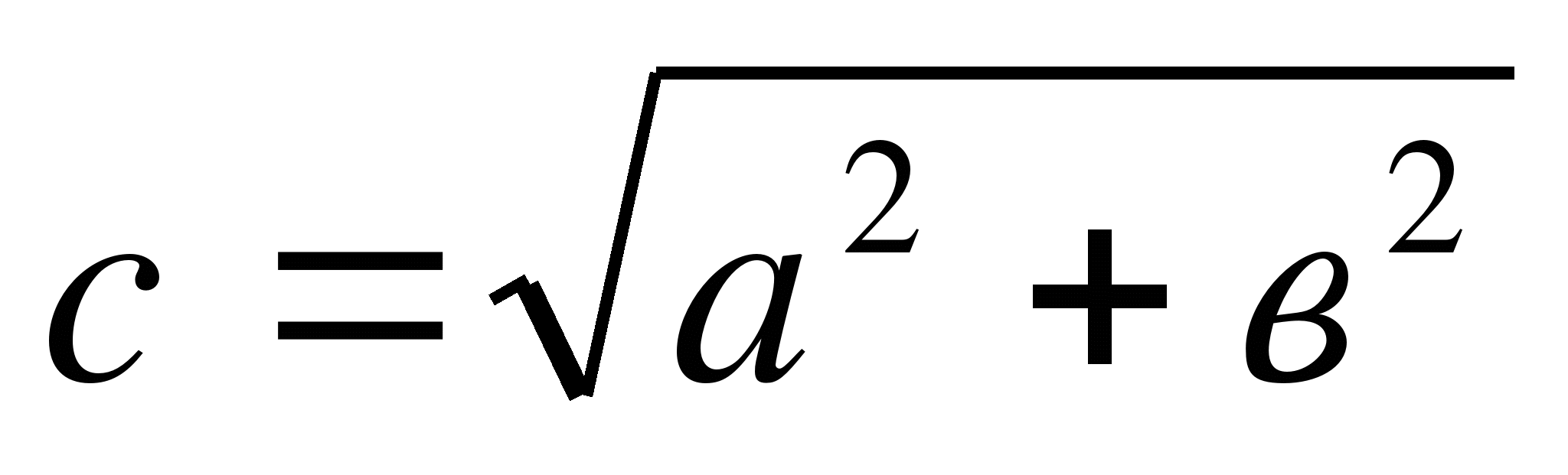
2. Найти катет, если известна гипотенуза и другой катет.

.

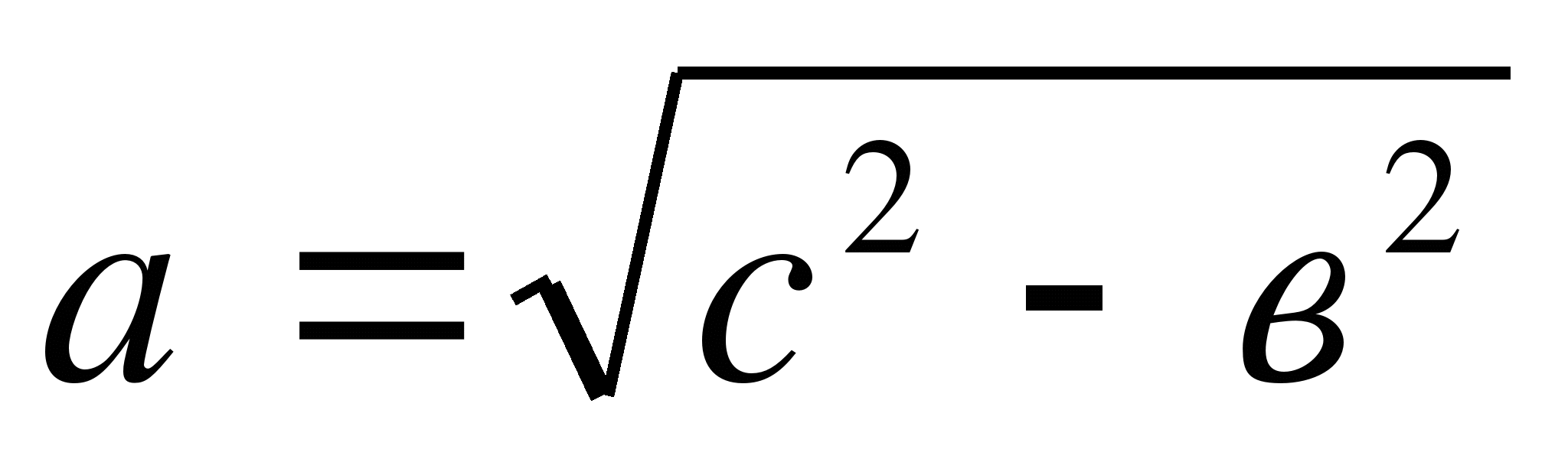
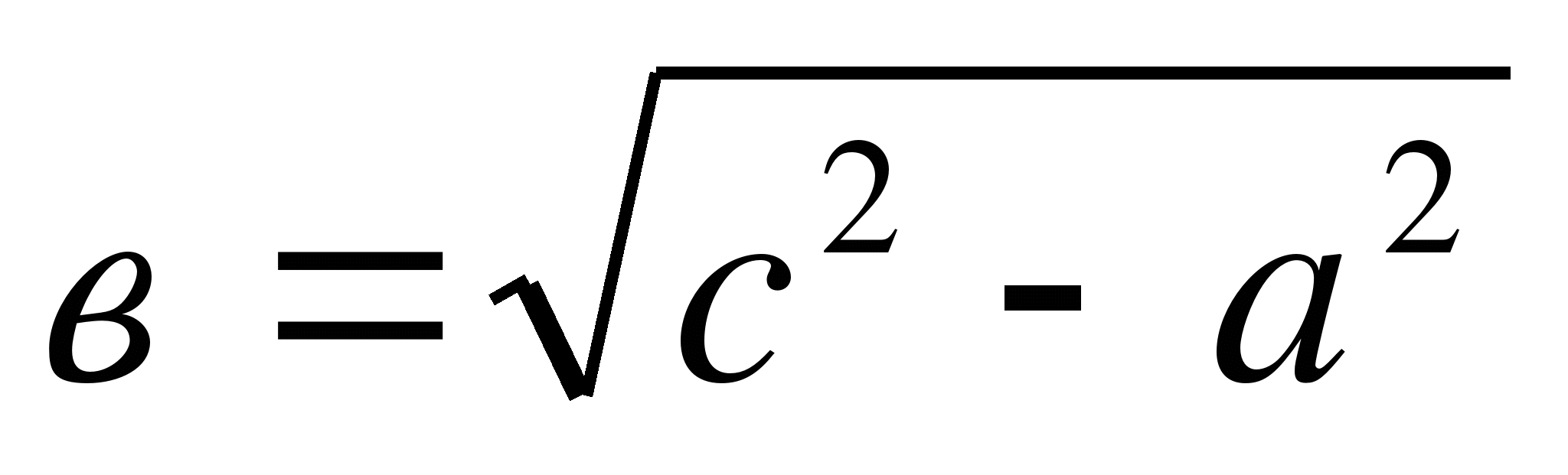5. Самостоятельное решение задач.

№483(б), 484 (б)

6. Домашнее задание: П 54, № 483 (г), 484 (г).

7. Итог урока.

Что нового вы узнали сегодня на уроке?

Для каких треугольников применяется теорема Пифагора?

В чём заключается теорема Пифагора?( Прочитать шуточную формулировку теоремы слайд 6).

Закончить урок стихотворением.

Многим известен сонет Шамиссо:

Пребудет вечной истина, как скоро

Ее познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Обильно было жертвопринашенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За света луч, пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут, ее почуя ,вслед.

Они не в силах свету помешать ,

А могут лишь закрыв глаза дрожать

От страха, что вселил в них Пифагор.

infourok.ru