Теорема косинусов и синусов треугольника. Формулы и примеры
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
cos2α + sin2α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b2 + c2 — a2 > 0, угол α будет острым.
- Когда b2 + c2 — a2 = 0, угол α будет прямым.
- Когда b2 + c2 — a2 < 0, угол α будет тупым.
Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b 2 — (b × cos α)2
- h2 = a2 — (c – b × cos α)2
Приравниваем правые части уравнений:
- b2 — (b × cos α)2 = a2 — (c — b × cos α)2
либо
- a2 = b2 + c2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b2 = a2 + c2 — 2ac × cos β;
- c2 = a2 + b2 — 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Аналогично:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).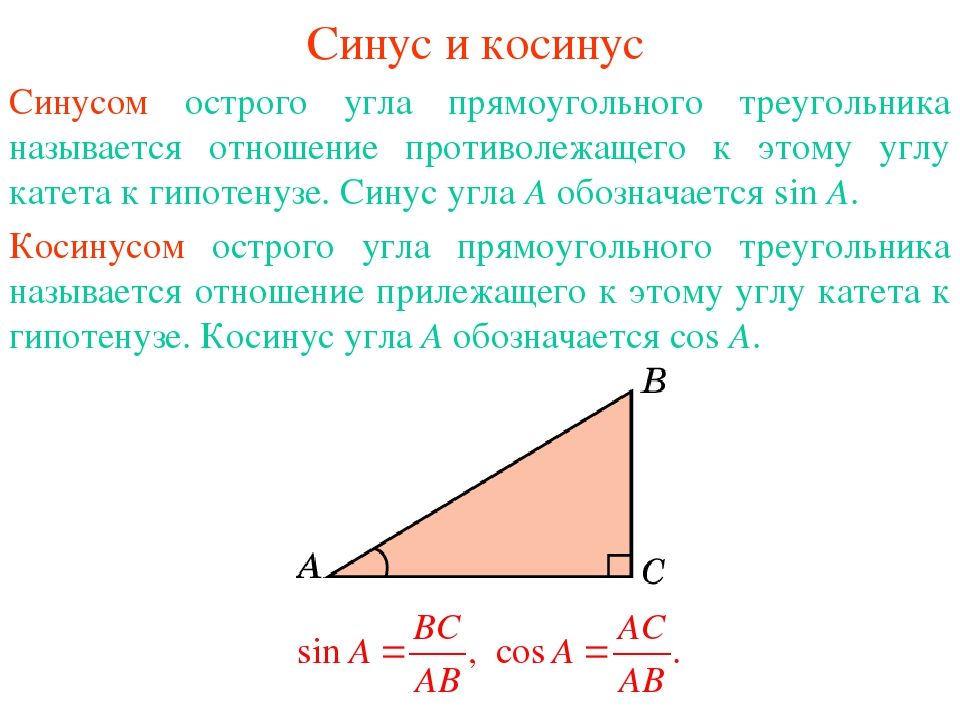
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = .
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.
- Если c2 < a2 + b2, то ∠C — острый.

Теорема синусов. Формулы и доказательства
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.

- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
α = 2R sinα
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Следовательно:
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2,…,Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
∠A + ∠C = 180°
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Как решаем:
Ответ: AC = 12.
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
Как решаем:
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Следовательно:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов. > |
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение: > |
Теорема синусов
Примечание. В данной главе приводится формулировка и доказательство теоремы синусов. В уроках главы приведены задачи по геометрии с решениями на эту же тему. См. также Теорема косинусов.
В данной главе приводится формулировка и доказательство теоремы синусов. В уроках главы приведены задачи по геометрии с решениями на эту же тему. См. также Теорема косинусов.
Формулировка теоремы синусов:
Стороны треугольника пропорциональны синусам противолежащих углов
или,
где
R — радиус описанной вокруг треугольника окружности
a, b, c — стороны треугольника
α, β, γ — величины противолежащих этим сторонам углов
Доказательство теоремы синусов
Доказательство теоремы синусов происходит с помощью дополнительных построений.
Построим произвольный треугольник, вписанный в окружность. Обозначим его как ABC.
Дополнительно построим диаметр окружности, в который вписан произвольный треугольник, но так, чтобы он проходил через один из его углов. Диаметр равен двойному радиусу окружности (2R).
Диаметр равен двойному радиусу окружности (2R).
Примем во внимание, что одним из свойств прямоугольного треугольника, вписанного в окружность является то, что его гипотенуза, является диаметром окружности, в которую он вписан.
Обозначим диаметр для описанной окружности как BD. Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность).
Таким образом, дополнительно построенный треугольник, у которого одна общая сторона с построенным ранее произвольным треугольником, а гипотенуза совпадает с диаметром окружности — является прямоугольным. То есть треугольник DBC — прямоугольный.
Для доказательства всей теоремы, поскольку размеры треугольника ABC выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R.
Пусть это будет 2R = a / sin α, то есть если взять по чертежу 2R = BC / sin A.
Поскольку, углы, вписанные в окружность, опирающиеся на одну и ту же дугу, равны, то угол CDB либо равен углу CAB (если точки A и D лежат по одну сторону от прямой BC), либо равен π — CAB (в противном случае).
Обратимся к свойствам тригонометрических функций. Поскольку sin( π − α ) = sin α, то указанные варианты построения треугольника все равно приведут к одному результату.
Вычислим значение 2R = a / sin α, по чертежу 2R = BC / sin A. Для этого заменим sin A на соотношение соответствующих сторон прямоугольного треугольника.
2R = BC / sin A
2R = BC / ( BC / DB )
2R = DB
А, поскольку, DB строился как диаметр окружности, то равенство выполняется.
Повторив то же рассуждение для двух других сторон треугольника, получаем:
Теорема синусов доказана.
Содержание главы:Синус | Описание курса | Задачи на решение с помощью теоремы синусов
Синус, косинус угла треугольника
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Если у нас есть треугольник \(ABC\), рисунок выше, для которого \(С\)- прямой угол, то сторонами \(BC\) и \(AC\) будут катеты, а сторона \(AB\) — гипотенуза. Следовательно, по определению, синус угла \(ABC\) равен отношению катета \(АС\) к гипотенузе: синус угла \(ABC=\frac{AC}{AB}\) и синус угла \(BAC=\frac{BC}{AB}\).
косинус угла \(ABC=\frac{BC}{AB}\) и косинус угла \(BAC=\frac{AC}{AB}\).
Чаще всего известно лишь часть данных, например катет и угол, нужно выразить неизвестную величину. Подумайте, как это сделать.
Пример 1. Вычислим синус по двум катетам.
Берем тот же треугольник \(ACB\) с прямым углом \(С\) в котором мы знаем катеты: \(BC = 3\), \(AC = 4\). Для вычисления синуса угла с необходимо разделить катет на гипотенузу: \(sin ∠BAC = \frac{BC} { AB}\).
Гипотенузу вычислим из теоремы Пифагора: \(AC^2+BC^2=AB^2\) \(9+16=25\) \(AB=5\) откуда синус равен:
\(sin ∠ BAC = \frac{3}{5}\)
Пример 2. Вычислим синус угла \(ABC\) по углу\( BAC \) 30° градусов в прямоугольном треугольнике \(ACB\).
Вычислим синус угла \(ABC\) по углу\( BAC \) 30° градусов в прямоугольном треугольнике \(ACB\).
Самое главное помнить, что сумма всех углов в треугольнике равна 180 °.Найдем угол \(ABC\):
\(180\)° \(-30\)° \(-90\)°\(=60\)°.
\(sin\) \(60\)° возьмем из табличного значения: \(\frac{ \sqrt{3}} { 2}\)
Табличные значения \(sin\) и \(cos\):
Чтобы лучше понимать значения табличные значения синуса и косинуса представим их на координатной окружности: где ось ординат \((y)\) линия синуса, ось абсцисс \((x)\) – линия косинуса. Если вы забыли значения синуса и косинуса \(90\) и \(180\) можно нарисовать рисунок и посмотреть значения, не забывая, что на первом месте стоит \(x\), на втором \(y\) \((x,y)\);
Теорема синусов:
Теорема косинусов:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Барановичский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-4 классов. Сложной математика кажется только на первый взгляд. Немного желания и внимания — и все становится понятным, а самое главное хочется изучать дальше. Математика развивает логику и мышление, а значит помогает во всех сферах нашей жизни. Сделаю математику понятной и интересной для вашего ребенка, учитывая его индивидуальность.
Сложной математика кажется только на первый взгляд. Немного желания и внимания — и все становится понятным, а самое главное хочется изучать дальше. Математика развивает логику и мышление, а значит помогает во всех сферах нашей жизни. Сделаю математику понятной и интересной для вашего ребенка, учитывая его индивидуальность.
Репетитор по математике
МГУ имени А. А.Кулешова
А.Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 4-9 классов. “В математике есть своя красота, как в живописи и поэзии“
Математику люблю за ее точность и простоту.
Методика крупноблочного изложения учебного материала и внедрение ИКТ в уроки математики.
Могу с лёгкостью найти контакт с ребёнком, заинтересовать в математике.
“В математике есть своя красота, как в живописи и поэзии“
Математику люблю за ее точность и простоту.
Методика крупноблочного изложения учебного материала и внедрение ИКТ в уроки математики.
Могу с лёгкостью найти контакт с ребёнком, заинтересовать в математике.
Репетитор по математике
Международный независимый эколого-политологический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку 1-11 классов. Работаю по классической и коммуникативной методикам, активно применяя интерактивные материалы: упражнения, игры, видео и тд. Имею обширный опыт преподавания в государственных школах и на курсах, в том числе за рубежом. Окончил ряд курсов повышения уровня владения языком и преподавательской квалификации: CAE, TKT (модули 1,3), TEFL и TOEIC.
Работаю по классической и коммуникативной методикам, активно применяя интерактивные материалы: упражнения, игры, видео и тд. Имею обширный опыт преподавания в государственных школах и на курсах, в том числе за рубежом. Окончил ряд курсов повышения уровня владения языком и преподавательской квалификации: CAE, TKT (модули 1,3), TEFL и TOEIC.
Курсы ЕГЭ
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Векторы
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Теорема косинусов.
 Доказательство 1 — МАТВОКС
Доказательство 1 — МАТВОКСТеорема косинусов (теорема, обобщающая теорему Пифагора)
Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:
Классическое доказательство теоремы косинусов
Шаг 1
Докажем теорему косинусов.
Возможны три варианта треугольника:
- Рассматриваемый треугольник – остроугольный.
- Рассматриваемый треугольник – тупоугольный.
- Рассматриваемый треугольник – прямоугольный.
Рассмотрим первый вариант, когда:
Рассматриваемый треугольник ABC – остроугольныйВведем следующие обозначения:
- Сторону ВС обозначим через а.
- Сторону АС обозначим через b.
- Сторону AB обозначим через c.
- Угол А обозначим через α.
- Угол В обозначим через β.
- Угол С обозначим через γ.
Опустим высоту h на сторону АВ из вершины С.
Высота разобьет треугольник АВС на два прямоугольных треугольника: ADC и BDC.
Рассмотрим прямоугольный треугольник ADC.
CD – высота, которая делит сторону с на две части:
По определению косинуса – косинус угла – это отношение прилежащего катета к гипотенузе.
Следовательно, из прямоугольного треугольника АDС имеем:
Отсюда:
Так как:
то:
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Следовательно, квадрат катета равен: квадрат гипотенузы минус квадрат другого катета.
В треугольнике ADC:
В треугольнике BDC:
Так как левые части записанных выше уравнений равны, то равны и правые части:
Воспользуемся формулой квадрата разности двух выражений и раскроем скобки:
Выразим а2 из полученного уравнения:
Аналогичным образом выводятся:
и:
Теорема синусов.
 Теорема косинусов
Теорема косинусовПри решении прямоугольных треугольников используются только основные тригонометрические функции. Для решения же косоугольных треугольников потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.
В дальнейшем мы будем пользоваться следующими обозначениями: a, b и c — стороны треугольника; А, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; r — радиус вписанного круга; hа, lа и mа — высота, биссектриса и медиана, соответствующие стороне а.
Теорема синусов
Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:
$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} $$Доказательство. Опишем круг около данного треугольника ABC. Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА описанного круга. Вспомогательный треугольник АВС прямоугольный, так как вписанный угол АСВ опирается на диаметр. Из вспомогательного треугольника найдём:
Опишем круг около данного треугольника ABC. Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА описанного круга. Вспомогательный треугольник АВС прямоугольный, так как вписанный угол АСВ опирается на диаметр. Из вспомогательного треугольника найдём:
а = 2Rsin A.
Если угол А острый, то А = А, так как вписанные углы A и A опираются на одну и ту же дугу.
Если угол А тупой, то угол А острый, измеряющийся половиной дуги ВАС:
Итак, или A= А, или A =\(\pi\) — A, в обоих случаях sin A = sin A, а потому
а = 2R sin A. (1)
Если угол Aпрямой, то а = 2R, sin A= 1 и равенство (1) также справедливо.
Аналогичные равенства найдём и для прочих углов В и С. Итак,
а =2R sin A; b =2R sin В; с = 2R sin С, откуда
$$ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R $$Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.
Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.
Теорема косинусов
Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
а2 =b2 + с2 — 2bccosА
b2 =c2 + a2 — 2cacosB
c2 =a2 + b2 — 2abcosC
Доказательство. Докажем первое равенство.
Случай 1. Угол A острый.
Пусть ВН — высота, опущенная из вершины В ; из геометрии известно, что
а2 = b2 + с2—2b · АН. (1)
Из прямоугольного треугольника АВН найдём
АН = с cos А; подставив в формулу (1), получим доказываемое равенство.
Случай 2. Угол A тупой.
В этом случае а2 = b2 + с2 +2b · АН. (2)
Из треугольника АВН найдём:
АН = с cos∠BAH = с cos(\(\pi\) — A) = — с cosA.
Подставив в формулу (2), получим доказываемое равенство.
Случай 3. Угол А прямой.
В этом случае (по теореме Пифагора):
а2 = b2 + с2= b2 + с2 — 2bccosА
(так как cos А = 0).
Итак, во всех случаях
а2 = b2 + с2 — 2bccosА
Теорема синусов и теорема косинусов
Содержание:
Теорема синусов, теорема косинусов:
Теорема синусовВы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
Пусть
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
Доказательство:
Пусть дан треугольник АВС, ВС = — радиус его описанной окружности. Угол а может быть острым, тупым или прямым. Рассмотрим эти случаи отдельно.
1) Угол острый (рис. 152, а). Проведя диаметр BD и отрезок DC, получим прямоугольный треугольник BCD, в котором как вписанный угол, опирающийся на диаметр. Заметим, что как вписанные углы, опирающиеся на одну и ту же дугу ВС. Из прямоугольного треугольника BCD находим т. е. откуда
2) Угол тупой (рис. 152, б). Проведем диаметр BD и отрезок DC. В четырехугольнике ABDC по свойству вписанного четырехугольника Из прямоугольного треугольника как вписанный угол, опирающийся на диаметр) Поскольку то откуда
3) Для справедливость равенства докажите самостоятельно, В силу доказанного откуда
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция позволяет решить две следующие задачи:
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы можно решить еще три задачи (рис. 153):
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
Пример:
В остроугольном треугольнике известны стороны и угол Найти два других угла округлив их значения до 1°, и третью сторону треугольника, округлив ее длину до 0,1.
Решение:
По теореме синусов откуда При помощи калькулятора (таблиц). находим Тогда По теореме синусов откуда
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом то, зная вначале мы нашли бы острый угол А затем, используя формулу получили бы, что
Пример:
Доказать справедливость формулы площади треугольника где — его стороны, R — радиус описанной окружности.
Доказательство:
Воспользуемся известной формулой площади треугольника: По теореме синусов откуда Тогда Что и требовалось доказать.
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
Пример:
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
Решение:
Способ 1. Из формулы следует, что Найдем . Для этого в треугольнике АВС проведем высоту ВК, которая будет и медианой, откуда Из по теореме Пифагора откуда
Из формулы следует, что Найдем . Для этого в треугольнике АВС проведем высоту ВК, которая будет и медианой, откуда Из по теореме Пифагора откуда
Тогда
Способ 2. Используем формулу из которой Так как то
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу где — боковая сторона, — высота, проведенная к основанию
Заменив в формуле получим — формулу радиуса описанной окружности для произвольного треугольника. Итак, мы имеем четыре формулы для нахождения радиуса R описанной окружности треугольника:
Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны треугольника АВС (рис. 165) через длины сторон ). Теорему косинусов можно назвать самой «работающей» в геометрии. Она имеет многочисленные следствия, которые часто используются при решении задач.
165) через длины сторон ). Теорему косинусов можно назвать самой «работающей» в геометрии. Она имеет многочисленные следствия, которые часто используются при решении задач.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из находим откуда
Из по теореме Пифагора
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда или тупой или прямой, докажите самостоятельно. Теорема доказана.
Для сторон теорема косинусов запишется так:
Замечание. Если , то по теореме Пифагора Так как то Таким образом, теорема Пифагора — частный случай теоремы косинусов.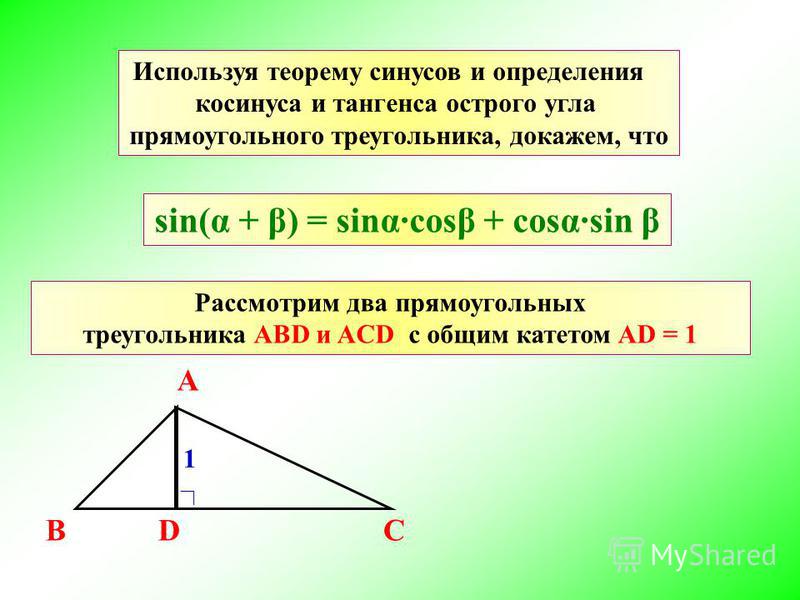
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства следует формула
Для углов получим:
Пример:
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы с учетом того, что следует:
- если то и угол острый;
- если то и угол тупой;
- если то и угол прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как то угол тупой и данный треугольник тупоугольный.
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD — острый, откуда — тупой (рис. 169). По теореме косинусов из
169). По теореме косинусов из
(1)
Из Поскольку cos то
(2)
Сложив почленно равенство (1) и равенство (2), получим что и требовалось доказать.
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
Медиану треугольника со сторонами а, b и с можно найти по формуле
Доказательство:
Рассмотрим — медиана треугольника (рис. 170). Продлим медиану AM за точку М на ее длину:
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма Отсюда следует, что
Утверждение доказано.
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, Найти сторону с. б) Дан треугольник АВС, а = 7, с = 8, а = 60°. Найти сторону Ь.
Решение:
а) По теореме косинусов
Отсюда б) Пусть По теореме косинусов то есть Отсюда или так как для наборов длин отрезков 7, 3, 8 и 7, 5, 8 выполняется неравенство треугольника.
Ответ: а) 7; б) 3 или 5.
Пример:
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в стороны АВ = 6, ВС = 10 и (рис. 171).
171).
Поскольку то откуда
Так как и по условию — тупой, то . Для нахождения стороны АС применим теорему косинусов:
Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника Пусть — медиана (рис. 172).
По формуле медианы откуда По обратной теореме Пифагора данный треугольник со сторонами 6, 8 и 10 — прямоугольный, его площадь равна половине произведения катетов:
Ответ: 24.
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: а также по двум сторонам и углу между ними: Теперь мы выведем формулу нахождения площади треугольника по трем сторонам.
Теорема (формула Герона).
Площадь треугольника со сторонами можно найти по формуле где — полупериметр треугольника.
Доказательство:
(рис. 183). Из основного тригонометрического тождества следует, что Для синус положительный. Поэтому Из теоремы косинусов откуда
Тогда
Так как
Теорема доказана.
Решение треугольниковРешением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
Дано: (рис. 184).
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол находим при помощи калькулятора или таблиц.
4) Угол
Замечание. Нахождение угла по теореме синусов требует выяснения того, острый или тупой угол
Нахождение угла по теореме синусов требует выяснения того, острый или тупой угол
Дано: (рис. 185).
Найти:
Решение:
1) Угол
2) По теореме синусов (sin и sin находим при помощи калькулятора или таблиц).
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: или (cos и sin находим при помощи калькулятора или таблиц).
Пример №3 (решение треугольника по трем сторонам).Дано: (рис. 186).
Найти: и радиус R описанной окружности.
Решение:
1) По следствию из теоремы косинусов
2) Зная угол находим при помощи калькулятора или таблиц.
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле где
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов затем нахождение по косинусу угла его синуса и, наконец, использование теоремы синусов для нахождения R.
Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов затем нахождение по косинусу угла его синуса и, наконец, использование теоремы синусов для нахождения R.
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
Тогда
Радиус R описанной окружности найдем из формулы Имеем:
Ответ:
Способ 2. Так как поскольку то треугольник — прямоугольный по обратной теореме Пифагора. Его площадь равна половине произведения катетов: а радиус описанной окружности равен половине гипотенузы:
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и Проведем (рис. 187). Так как АВСК — параллелограмм, то СК = АВ = 10, АК = ВС = 5, откуда KD = AD — АК = 9. Найдем высоту СН треугольника KCD, которая равна высоте трапеции. Площадь треугольника KCD найдем по формуле Герона, обозначив его стороны а = 10, b = 17, с = 9. Получим:
187). Так как АВСК — параллелограмм, то СК = АВ = 10, АК = ВС = 5, откуда KD = AD — АК = 9. Найдем высоту СН треугольника KCD, которая равна высоте трапеции. Площадь треугольника KCD найдем по формуле Герона, обозначив его стороны а = 10, b = 17, с = 9. Получим:
Так как СН = 8. Площадь трапеции
Ответ: 76.
Пример:
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть Найдем
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС , то около него можно описать окружность по признаку вписанного четырехугольника (рис. 189, б). Поскольку прямой вписанный угол опирается на диаметр, то отрезок AM — диаметр этой окружности, т. е. где R — радиус. Из по теореме косинусов Из по теореме синусов откуда
189, б). Поскольку прямой вписанный угол опирается на диаметр, то отрезок AM — диаметр этой окружности, т. е. где R — радиус. Из по теореме косинусов Из по теореме синусов откуда
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
В прямоугольном треугольнике АВС известно: высота СН = 2 (рис. 190). Найти гипотенузу АВ.
Решение:
Построим симметричный относительно прямой АВ (см. рис. 190).
Поскольку то вокруг четырехугольника можно описать окружность, где АВ — диаметр этой окружности (прямой вписанный угол опирается на диаметр). Треугольник вписан в эту окружность, По теореме синусов откуда
Ответ: 8.
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = На гипотенузе АВ как на стороне построен квадрат ADFB (рис. 191). Найти расстояние от центра О этого квадрата до вершины С прямого угла, т. е. отрезок СО.
191). Найти расстояние от центра О этого квадрата до вершины С прямого угла, т. е. отрезок СО.
Решение:
Способ 1. Так как (диагонали квадрата ADFB взаимно перпендикулярны), то поэтому четырехугольник АОВС является вписанным в окружность, ее диаметр Тогда
Пусть СО = х. По теореме косинусов из находим
из находим
По свойству вписанного четырехугольника Поскольку то откуда находим Тогда .
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим до квадрата CMNK, как показано на рисунке 192. Можно показать, что центр квадрата CMNK совпадет с центром квадрата ADFB, т. е. с точкой О (точки В и D симметричны относительно центров обоих квадратов). Тогда
Тогда
Ответ:
Точка О — центр окружности, вписанной в треугольник АВС, Найти стороны треугольника (см. задачу 232*).
Решение:
Пусть и
— радиус вписанной окружности (рис. 193).
Тогда
Отсюда Применим формулу Герона:
С другой стороны, Из уравнения находим = 2. Откуда (см), (см), (см).
Ответ: 15 см; 20 см; 7 см.
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из и (см. рис. 194) следует:
(1)
(2)
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
Теорема доказана.
Следствие:
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника Разделив сторону с в отношении получим:
По теореме Стюарта
Пример №9Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, — биссектрисы, проведенные к сторонам ВС = а и АС = b соответственно, и (рис. 196). Нужно доказать, что Выразим и через и приравняем полученные выражения. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому откуда откуда
По формуле биссектрисы треугольника
Из условия следует: Перенеся слагаемые в одну сторону равенства и разложив на множители (проделайте это самостоятельно), получим: Отсюда (второй множитель при положительных больше нуля).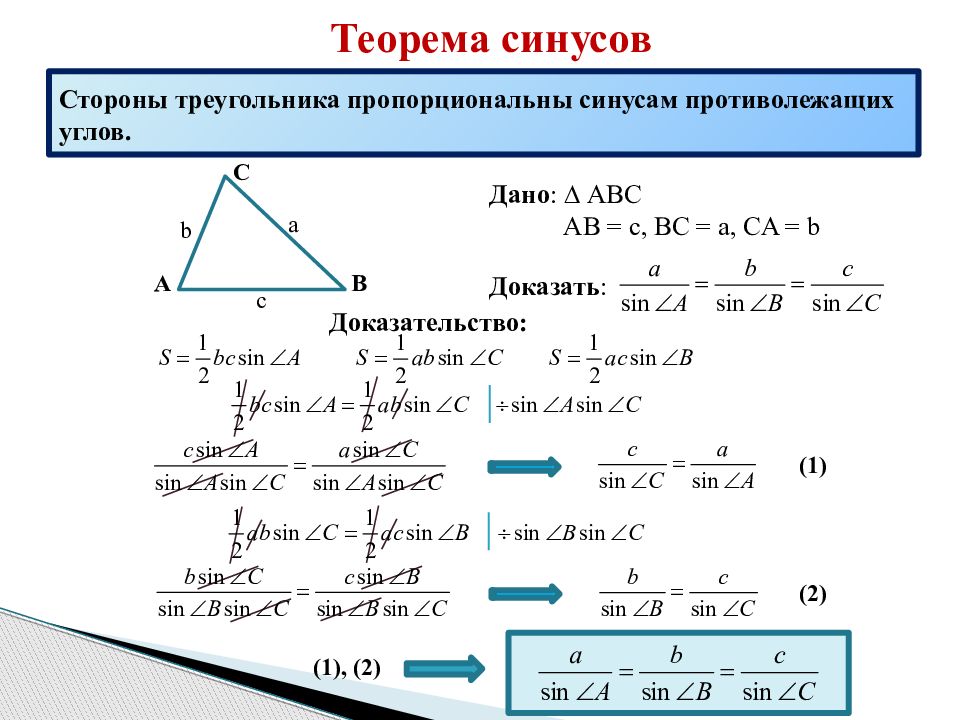 Утверждение доказано.
Утверждение доказано.
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е. (рис. 197).
Доказательство:
Из по теореме косинусов
Так как (по свойству вписанного четырехугольника) и откуда
Аналогично из получим Тогда Теорема доказана.
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть — стороны треугольника и с — большая сторона.
 Если , то треугольник тупоугольный, если то треугольник остроугольный, если , то треугольник прямоугольный.
Если , то треугольник тупоугольный, если то треугольник остроугольный, если , то треугольник прямоугольный. - Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
Синус-косинус-касательная
Чтобы лучше понять некоторые проблемы, связанные с самолетами и двигательная установка необходимо использовать некоторые математические идеи из тригонометрия, изучение треугольников. Начнем с некоторых определений и терминологии. который мы будем использовать на этом слайде. Прямоугольный треугольник — это трехсторонняя фигура с одним углом, равным 90 градусам. Угол 90 градусов называется прямым углом , что дает название прямоугольному треугольнику.Выбираем один из двух оставшихся углов и маркируем его c а третий угол обозначим d . Сумма углов любого треугольника равна 180 градусам. Если мы знаем значение c , тогда мы знаем, что значение d :
90 + с + г = 180
г = 180 — 90 — в
г = 90 — с
Определим сторону треугольника противоположную от прямого угла к
— гипотенуза . Это самая длинная из трех сторон.
прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов.
означает «растягивать», так как это самая длинная сторона. Обозначим гипотенузу символом h .
Есть сторона, противоположная углу c , которую мы обозначаем o .
для «противоположного». Оставшуюся сторону мы помечаем как для «смежных».
Угол c образован пересечением гипотенузы h .
и соседняя сторона а .
Это самая длинная из трех сторон.
прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов.
означает «растягивать», так как это самая длинная сторона. Обозначим гипотенузу символом h .
Есть сторона, противоположная углу c , которую мы обозначаем o .
для «противоположного». Оставшуюся сторону мы помечаем как для «смежных».
Угол c образован пересечением гипотенузы h .
и соседняя сторона а .
Нас интересует соотношение сторон и углов прямоугольный треугольник. Начнем с некоторых определений. Мы будем называть соотношение стороны прямоугольного треугольника гипотенузы синус и присвоить ему символ sin .
грех = о / ч
Отношение смежной стороны прямоугольного треугольника к гипотенузе называется косинус и обозначен символом cos .
cos = а / ч
Наконец, отношение противоположной стороны к соседней стороне называется
касательная и обозначена символом tan .
загар = о / а
Мы утверждаем, что значение каждого коэффициента зависит только от значения
угол c , образованный смежной и гипотенузой.
Чтобы продемонстрировать этот факт,
давайте изучим три фигуры в середине страницы.В этом примере у нас есть
8-футовая лестница, которую мы собираемся прислонить к стене. Стена
8 футов высотой, и мы нарисовали белые линии на стене
и синие линии на земле с интервалом в один фут.
Длина лестницы фиксированная.
Если наклонить лестницу так, чтобы ее основание находилось на расстоянии 2 фута от стены,
лестница образует угол около 75,5 градусов с землей.
Лестница, земля и стена образуют прямоугольный треугольник. Соотношение расстояния от
стены (а — прилегающая) к длине лестницы (h — гипотенуза) составляет 2/8 =.25.
Это определено как косинус c = 75,5 градуса. (На
другая страница
покажем, что если бы лестница была вдвое длиннее (16 футов),
и наклонена под тем же углом (75,5 градуса), чтобы он сидел вдвое
далеко (4 фута) от стены. 2 = 64 — 4 = 60
2 = 64 — 4 = 60
о = 7.745
Отношение противоположности гипотенузы составляет 0,967 и определяется как синус угла c = 75,5 градуса.
Теперь предположим, что мы наклоняем 8-футовую лестницу так, чтобы ее основание находилось на 4 футах от стены.
Как показано на рисунке, теперь лестница наклонена под меньшим углом, чем в
первый пример. Угол составляет 60 градусов, а соотношение прилегающих к
гипотенуза теперь 4/8 = 0,5. Уменьшение угла c увеличивает косинус угла, потому что гипотенуза фиксирована
а соседний увеличивается с уменьшением угла.Если мы наклоним 8 футов
лестнице так, чтобы ее основание находилось на расстоянии 6 футов от стены, угол уменьшается до
около 41,4 градуса, и соотношение увеличивается до 6/8, что составляет 0,75.
Как видите, для каждого угла
на земле есть уникальная точка, которой соприкасается 8-футовая лестница,
И это одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом. Математики называют эту ситуацию
функция.
Соотношение соседних
сторона гипотенузы является функцией угла c , поэтому мы можем записать
символ как cos (c) = значение .
Математики называют эту ситуацию
функция.
Соотношение соседних
сторона гипотенузы является функцией угла c , поэтому мы можем записать
символ как cos (c) = значение .
Также обратите внимание, что по мере увеличения cos (c) уменьшается sin (c) . Если мы наклоним лестницу так, чтобы основание находилось на расстоянии 6,938 фута от стены, угол c становится 30 градусов, а отношение соседнего к гипотенуза 0,866. Сравнивая этот результат со вторым примером, мы обнаруживаем, что:
cos (c = 60 градусов) = sin (c = 30 градусов)
sin (c = 60 градусов) = cos (c = 30 градусов)
Мы можем обобщить это соотношение:
sin (c) = cos (90 — c)
90 — c — величина угла d .Вот почему мы назовем соотношение смежного и гипотенузы «косинусом» угла.
sin (c) = cos (d)
Поскольку синус, косинус и тангенс являются функциями угла c , мы можем
определить (измерить) коэффициенты один раз и составить таблицы значений
синус, косинус и тангенс для различных значений c . Позже, если мы узнаем
значение угла в прямоугольном треугольнике, таблицы покажут нам соотношение
сторон треугольника.Если мы знаем длину одной стороны, мы можем найти длину другой.
стороны.
Или, если мы знаем соотношение любых двух сторон прямоугольного треугольника, мы можем
найти значение угла между сторонами. Мы можем использовать таблицы для решения проблем. Некоторые примеры проблем, связанных с треугольниками и углами, включают
силы
на самолете в полете,
приложение крутящих моментов,
и разрешение
компоненты
вектора.
Позже, если мы узнаем
значение угла в прямоугольном треугольнике, таблицы покажут нам соотношение
сторон треугольника.Если мы знаем длину одной стороны, мы можем найти длину другой.
стороны.
Или, если мы знаем соотношение любых двух сторон прямоугольного треугольника, мы можем
найти значение угла между сторонами. Мы можем использовать таблицы для решения проблем. Некоторые примеры проблем, связанных с треугольниками и углами, включают
силы
на самолете в полете,
приложение крутящих моментов,
и разрешение
компоненты
вектора.
Вот таблицы синуса, косинуса и тангенса, которые вы можете использовать для решения проблемы.
Действия:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
Синус, косинус и теорема Птолемея
Из теоремы Птолемея следует теорема Пифагора. Последний служит основой тригонометрии, раздела математики, который занимается отношениями между сторонами и углами треугольника. {2} (A) = 1, $
{2} (A) = 1, $
, где $ A $ — один из внутренних углов прямоугольного треугольника. Если гипотенуза треугольника имеет длину $ 1, $, то $ \ sin (A) $ — длина стороны, противоположной углу $ A, $ $ \ cos (A) $ — длина соседней стороны.
Теорема Птолемея также предоставляет элегантный способ доказательства других тригонометрических тождеств. Через некоторое время я докажу формулы сложения и вычитания для синуса :
.(1)
$ \ sin (A + B) = \ sin (A) \ cos (B) + \ cos (A) \ sin (B) $
(2)
$ \ sin (A — B) = \ sin (A) \ cos (B) — \ cos (A) \ sin (B).$
Но сначала давайте рассмотрим простое доказательство закона синуса .
Предложение III.20 из Евклида Элементы говорит:
В круге угол в центре вдвое больше угла на окружности, когда углы имеют ту же длину окружности, что и основание. Более распространенная формулировка утверждает, что угол, описанный в окружности, равен половине центрального угла, который образует ту же хорду. (Как следствие, отсюда следует, что все описанные углы, соединяющие одну и ту же дугу, равны независимо от их положения на окружности. Это предложение III.21) На диаграмме $ \ angle BOC = 2 \ angle BAC (= 2A .) $
(Как следствие, отсюда следует, что все описанные углы, соединяющие одну и ту же дугу, равны независимо от их положения на окружности. Это предложение III.21) На диаграмме $ \ angle BOC = 2 \ angle BAC (= 2A .) $
Опустите перпендикуляр из $ O $ на сторону $ BC. $ Предполагая, что радиус окружности равен $ R, $ $ OB = OC = R. $ Кроме того, $ \ angle BOP = \ angle POC. $ In $ \ Delta BOP, $ $ \ sin (\ angle BOP) = BP / OB = BC / 2R. $ Следовательно, $ BC / \ sin (\ angle BOP) = 2R. $ Когда угол $ A $ тупой, центр $ O $ находится вне $ \ Delta ABC $ и диаграмма выглядит иначе.Однако в результате идентичность остается прежней. Повторяя эти шаги с двумя другими углами $ B $ и $ C $ в $ \ Delta ABC $, мы получаем закон синусов , который в стандартных обозначениях выглядит как
(3)
$ \ displaystyle \ frac {a} {\ sin (A)} = \ frac {b} {\ cos (B)} = \ frac {c} {\ sin (A)} = 2R. $
В случае, когда диаметр описанной окружности равен 1, мы имеем $ a = \ sin (A), $ $ b = \ sin (B), $ и $ c = \ sin (C). $ Это все, что нам нужно, чтобы применить теорему Птолемея.Конечно, полезно помнить об определении функций синуса и косинуса. В прямоугольном треугольнике синус острого угла — это отношение противоположного катета к гипотенузе; его косинус — это отношение соседнего катета к гипотенузе.
$ Это все, что нам нужно, чтобы применить теорему Птолемея.Конечно, полезно помнить об определении функций синуса и косинуса. В прямоугольном треугольнике синус острого угла — это отношение противоположного катета к гипотенузе; его косинус — это отношение соседнего катета к гипотенузе.
Рассмотрим четырехугольник $ ABDC $, вписанный в окружность диаметра $ 1 $, так что диагональ $ BC $ служит диаметром.
Из определения синуса и косинуса мы определяем стороны четырехугольника. Закон синуса определяет длину оставшейся диагонали.Формула сложения для синуса — это просто переформулировка теоремы Птолемея.
Для доказательства формулы вычитания пусть сторона $ BC $ служит диаметром.
Как следствие, получаем формулы для синуса (за один шаг) и косинуса (за два шага) дополнительных углов:
$ \ begin {align}
\ sin (\ frac {\ pi} {2} — \ alpha) & = \ cos \ alpha, \\
\ cos (\ frac {\ pi} {2} — \ alpha) & = \ sin \ alpha. \ end {align} $
\ end {align} $
Из этих формул и формул сложения для синуса нетрудно вывести формулы сложения для косинуса:
$ \ begin {align} \ cos (\ alpha + \ beta) & = \ cos (\ alpha) \ cos (\ beta) — \ sin (\ alpha) \ sin (\ beta), \\ \ соз (\ альфа — \ бета) & = \ соз (\ альфа) \ соз (\ бета) + \ грех (\ альфа) \ грех (\ бета).\ end {align} $
(Есть дополнительные простые доказательства этих формул.)
Список литературы
- Э. Маор, Тригонометрические наслаждения , Princeton University Press, 1998
Тригонометрия
| Контакты | | Первая страница | | Содержание | | Геометрия | | Вверх |
Copyright © 1996-2018 Александр Богомольный
Синус, косинус, тангенс
Три функции, но та же идея.
Правый треугольник
Синус, косинус и тангенс — основные функции, используемые в тригонометрии, они основаны на прямоугольном треугольнике.
Прежде чем углубляться в функции, полезно присвоить имя каждой стороне прямоугольного треугольника:
- «Противоположно» противоположно углу θ
- «Соседний» примыкает (рядом) к углу θ
- «Гипотенуза» длинная
Соседний всегда находится рядом с углом
И Напротив , напротив угла
Синус, косинус и тангенс
Синус , Косинус и Касательная (часто сокращается до sin , cos и tan ), каждая из которых имеет отношение сторон прямоугольного треугольника :
Для заданного угла θ каждое отношение остается неизменным
независимо от того, насколько большой или малый треугольник
Для их расчета:
Разделите длину одной стороны на другую
Пример: Что такое синус 35 °?
Используя этот треугольник (длины до одного десятичного знака):
| sin (35 °) | = Напротив Гипотенуза |
= 2. 8 4,9 8 4,9 | |
| = 0,57 … | |
| cos (35 °) | = Соседний Гипотенуза |
| = 4,0 4,9 | |
| = 0,82 … | |
| желто-коричневый (35 °) | = Напротив Соседний |
| = 2.8 4,0 | |
| = 0,70 … |
Размер не имеет значения
Треугольник может быть большим или маленьким, а соотношение сторон остается неизменным .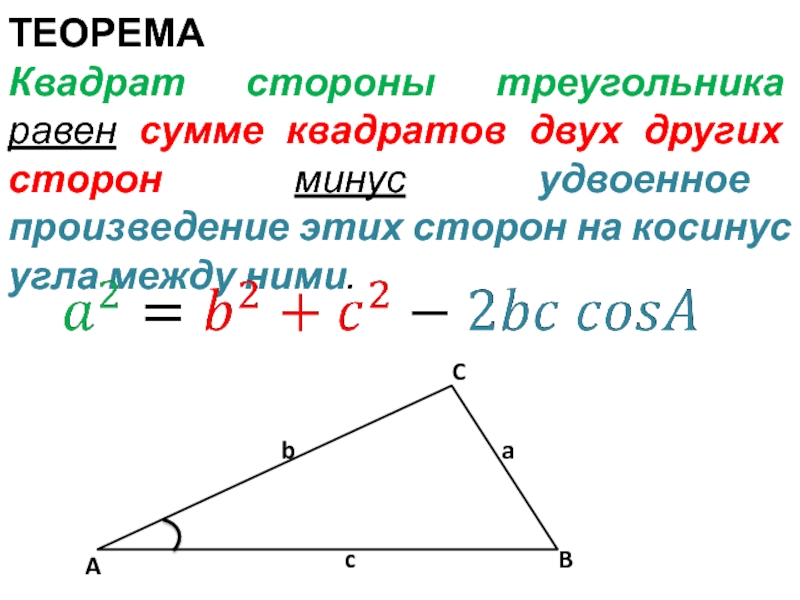
Только угол меняет соотношение.
Попробуйте перетащить точку «A», чтобы изменить угол, и точку «B», чтобы изменить размер:
На хороших калькуляторах есть sin, cos и tan, чтобы облегчить вам задачу.Просто вставьте угол и нажмите кнопку.
Но все же нужно помнить , что означает !
В форме изображения:
Практика здесь:
Sohcahtoa
Как запомнить? Думайте «Sohcahtoa» !
Работает так:
Soh … | S ine = O pposite / H ypotenuse |
…ка … | C осин = A djacent / H ypotenuse |
… toa | T angent = O pposite / A djacent |
Вы можете узнать больше о sohcahtoa . .. пожалуйста, запомните это, это может помочь на экзамене!
.. пожалуйста, запомните это, это может помочь на экзамене!
Углы от 0 ° до 360 °
Перемещайте мышь, чтобы увидеть, как разные углы (в радианах или градусах) влияют на синус, косинус и тангенс.
алгебра / изображения / круг-треугольник.js
На этой анимации гипотенуза равна 1, образуя единичную окружность.
Обратите внимание, что соседняя сторона и противоположная сторона могут быть положительными или отрицательными, что также приводит к изменению синуса, косинуса и тангенса между положительными и отрицательными значениями.
| «Почему sin и tan не пошли на вечеринку?» «… всего cos !» |
Примеры
Пример: каковы синус, косинус и тангенс 30 °?
Классический треугольник 30 ° имеет гипотенузу длины 2, противоположную сторону длины 1 и смежную сторону √3:
Теперь мы знаем длины, можем вычислить функции:
синус | грех (30 °) = 1/2 = 0.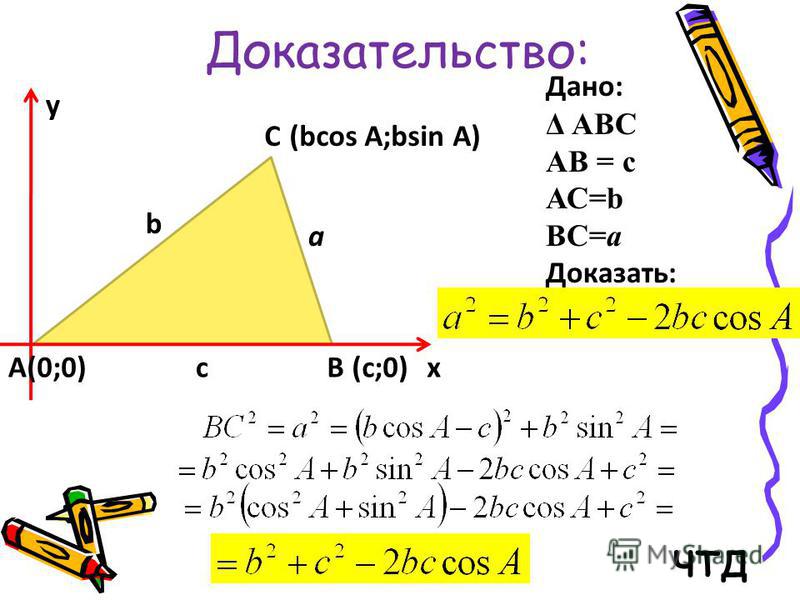 5 5 | |
Косинус | cos (30 °) = 1,732 / 2 = 0,866 … | |
Касательная | тангенс угла (30 °) = 1 / 1,732 = 0,577 … |
(возьмите калькулятор и проверьте его!)
Пример: каковы синус, косинус и тангенс угла 45 °?
Классический треугольник 45 ° имеет две стороны 1 и гипотенузу √2:
синус | sin (45 °) = 1/1.414 = 0,707 … | |
Косинус | cos (45 °) = 1 / 1,414 = 0,707 … | |
Касательная | загар (45 °) = 1/1 = 1 |
Почему?
Почему эти функции важны?
- Потому что они позволяют нам вычислять углы, когда мы знаем стороны
- И они позволяют нам определять стороны, когда мы знаем углы
Пример: используйте синусоидальную функцию
, чтобы найти «d»Мы знаем:
- Кабель образует угол 39 ° с морским дном
- Кабель длиной 30 метров .

И мы хотим знать «d» (расстояние вниз).
Начать с: sin 39 ° = противоположно / гипотенуза
sin 39 ° = d / 30
Поменять местами стороны: d / 30 = sin 39 °
С помощью калькулятора найдите sin 39 °: d / 30 = 0,6293 …
Умножаем обе стороны на 30: d = 0,6293… x 30
d = 18,88 с точностью до 2 десятичных знаков.
Глубина «d» 18,88 м
Упражнение
Попробуйте это бумажное упражнение, в котором вы можете вычислить синусоидальную функцию. для всех углов от 0 ° до 360 °, а затем нарисуйте результат.Это поможет вам понять эти относительно простые функции.
Вы также можете увидеть графики синуса, косинуса и тангенса.
И поиграйте с пружиной, создающей синусоидальную волну.
Менее распространенные функции
Чтобы завершить картину, есть еще 3 функции, в которых мы разделяем одну сторону на другую, но они не так часто используются.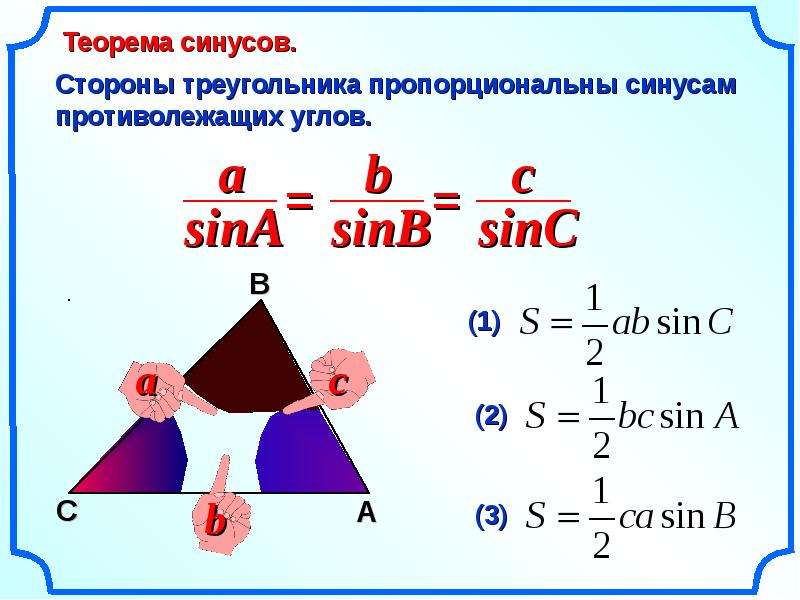
Они равны 1, разделенному на cos , 1, разделенному на sin , и 1, разделенному на tan :
Секущая функция: | сек ( θ ) = Гипотенуза Соседний | (= 1 / cos) | ||
Косеканс, функция: | csc ( θ ) = Гипотенуза Напротив | (= 1 / sin) | ||
Функция котангенса: | детская кроватка ( θ ) = Соседний Напротив | (= 1 / tan) |
1494, 1495, 724, 725, 1492, 1493, 726, 727, 2362, 2363
Закон косинусов
В Закон косинусов используется для поиска оставшихся частей наклонной (не правой)
треугольник
когда известны либо длины двух сторон и мера включенного угла (SAS), либо длины трех сторон (SSS). В любом из этих случаев невозможно использовать
Закон синуса
потому что мы не можем установить решаемую пропорцию.
В любом из этих случаев невозможно использовать
Закон синуса
потому что мы не можем установить решаемую пропорцию.
Закон косинусов гласит:
c 2 знак равно а 2 + б 2 — 2 а б потому что C .
Это похоже на Теорема Пифагора кроме третьего срока и если C — прямой угол, третий член равен 0 потому что косинус 90 ° является 0 и мы получаем теорему Пифагора.Итак, теорема Пифагора — это частный случай закона косинусов.
Закон косинусов также можно сформулировать как
б 2 знак равно а 2 + c 2 — 2 а c потому что B или
а
2
знак равно
б
2
+
c
2
—
2
б
c
потому что
А
.
Пример 1: Две стороны и прилагаемый Angle-SAS
Данный а знак равно 11 , б знак равно 5 и м ∠ C знак равно 20 ° . Найдите оставшуюся сторону и углы.
c 2 знак равно а 2 + б 2 — 2 а б потому что C
c знак равно а 2 + б 2 — 2 а б потому что C
знак равно 11 2 + 5 2 — 2 ( 11 ) ( 5 ) ( потому что 20 ° )
≈
6. 53
53
Чтобы найти оставшиеся углы, теперь проще всего воспользоваться законом синусов.
грех А ≈ 11 грех 20 ° 6.53
А ≈ 144,82 °
грех B ≈ 5 грех 20 ° 6.53
B ≈ 15,2 °
Обратите внимание, что угол
А
противоположна самой длинной стороне, и треугольник не является прямоугольным. Итак, когда вы берете обратное, вам нужно учитывать тупой угол, синус которого равен
11
грех
(
20
°
)
6. 53
≈
0,5761
.
53
≈
0,5761
.
Пример 2: Три стороны-ССС
Данный а знак равно 8 , б знак равно 19 и c знак равно 14 . Найдите размеры углов.
Лучше сначала найти угол, противоположный самой длинной стороне.В данном случае это сторона б .
потому что
B
знак равно
б
2
—
а
2
—
c
2
—
2
а
c
знак равно
19
2
—
8
2
—
14
2
—
2
(
8
)
(
14
)
≈
—
0. 45089
45089
С потому что B отрицательно, мы знаем, что B — тупой угол.
B ≈ 116,80 °
С B — тупой угол, а у треугольника не более одного тупого угла, мы знаем, что угол А и угол C оба острые.
Чтобы найти два других угла, проще всего использовать закон синуса.
а грех А знак равно б грех B знак равно c грех C
8
грех
А
≈
19
грех
116. 80
°
≈
14
грех
C
80
°
≈
14
грех
C
грех А ≈ 8 грех 116,80 ° 19
А ≈ 22.08 °
грех C ≈ 14 грех 116,80 ° 19
C ≈ 41,12 °
2.1.1: Тригонометрия прямоугольного треугольника — K12 LibreTexts
Синус, косинус, тангенс и другие отношения сторон прямоугольного треугольника.
Тригонометрия — это исследование отношений между сторонами и углами прямоугольных треугольников. Ноги называются смежными или напротив в зависимости от того, какой острый угол используется.
Рисунок \ (\ PageIndex {1} \)\ (\ begin {align} a \ text {примыкает к} \ angle B \ qquad a \ text {противоположно} \ angle A \\ b \ text {примыкает к } \ angle A \ qquad b \ text {противоположен} \ angle B \\ c \ text {гипотенуза} \ end {выравнивается} \)
Три основных тригонометрических отношения называются синусом, косинусом и тангенсом.Для прямоугольного треугольника △ ABC имеем:
\ (\ begin {align}
\ text {sine Ratio:} \ dfrac {\ text {противоположная нога}} {\ text {hypotenuse}} \ qquad \ sin A = \ dfrac {a} {c} \ text { или} \ sin B = \ dfrac {b} {c} \\
\ text {Коэффициент косинуса:} \ dfrac {\ text {смежная нога}} {\ text {hypotenuse}} \ qquad \ cos A = \ dfrac { b} {c} \ text {или} \ cos B = \ dfrac {a} {c} \\
\ text {Коэффициент касания:} \ dfrac {\ text {противоположная нога}} {\ text {смежная нога}} \ qquad \ tan A = \ dfrac {a} {b} \ text {или} \ tan B = \ dfrac {b} {a}
\ end {align} \)
Простой способ запомнить отношения — использовать SOH-CAH-TOA.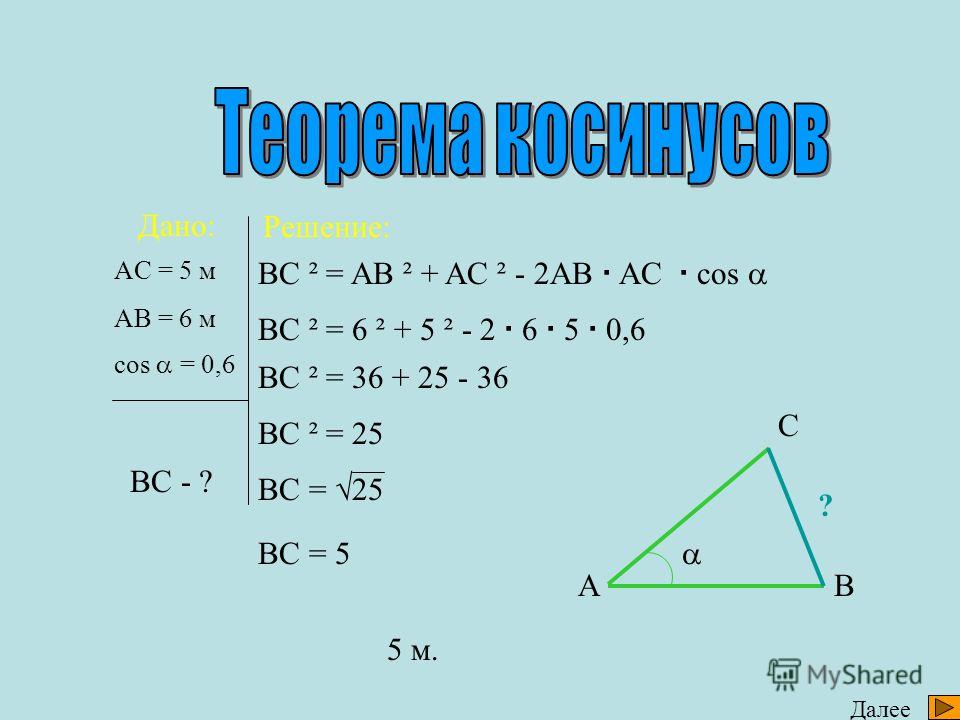
Несколько важных моментов:
- Всегда уменьшайте передаточные числа (дроби), когда можете.
- Используйте теорему Пифагора , чтобы найти недостающую сторону (если она есть).
- Если в знаменателе стоит радикал , то рационализируют знаменатель.
Что, если бы вам дали прямоугольный треугольник и сказали, что его стороны имеют размер 3, 4 и 5 дюймов? Как найти синус, косинус и тангенс одного из непрямых углов треугольника?
Пример \ (\ PageIndex {1} \)
Найдите отношения синуса, косинуса и тангенса \ (\ angle A \).{2} \\
13 & = c \ end {align} \)
\ (\ begin {align}
\ sin A & = \ dfrac {leg \ text {напротив} \ angle A} {\ text {hypotenuse}} = \ dfrac {12} {13} & \ cos A = \ dfrac {\ text {нога, прилегающая к} \ angle A} {\ text {hypotenuse}} = \ dfrac {5} {13}, \\
\ tan A & = \ dfrac {\ text {leg Against} \ angle A} {\ text {нога, прилегающая к} \ angle A} = \ dfrac {12} {5}
\ end {align} \)
Пример \ (\ PageIndex {2} \)
Найдите синус, косинус и тангенс \ (\ angle B \). {\ circ} = \ dfrac {6} {6 \ sqrt {3}} = \ dfrac {1} {\ sqrt {3}} \ cdot \ dfrac {\ sqrt {3}} {\ sqrt {3}} = \ dfrac {\ sqrt {3}} {3} \)
{\ circ} = \ dfrac {6} {6 \ sqrt {3}} = \ dfrac {1} {\ sqrt {3}} \ cdot \ dfrac {\ sqrt {3}} {\ sqrt {3}} = \ dfrac {\ sqrt {3}} {3} \)
Пример \ (\ PageIndex {4} \)
Ответьте на вопросы о следующем изображении. Уменьшить все фракции.
Рисунок \ (\ PageIndex {6} \)Что такое \ (\ sin A \), \ (\ cos A \) и \ (\ tan A \)?
Решение
\ (\ begin {array} {l}
\ sin A = \ dfrac {16} {20} = \ dfrac {4} {5} \\
\ cos A = \ dfrac {12} {20} = \ dfrac {3} {5} \\
\ tan A = \ dfrac {16} {12} = \ dfrac {4} {3}
\ end {array} \)
Чтобы увидеть ответы на обзор, откройте этот PDF-файл и найдите раздел 8.7.
Закон косинусов — алгебра и тригонометрия
Цели обучения
В этом разделе вы:
- Используйте закон косинусов для решения наклонных треугольников.
- Решайте прикладные задачи с помощью закона косинусов.

- Используйте формулу Герона, чтобы найти площадь треугольника.
Предположим, что лодка покидает порт, проходит 10 миль, разворачивается на 20 градусов и проходит еще 8 миль, как показано на (Рисунок). Как далеко от порта находится лодка?
Рисунок 1.К сожалению, хотя закон синусов позволяет нам рассматривать многие случаи неправильных треугольников, он не помогает нам с треугольниками, в которых известный угол находится между двумя известными сторонами, треугольником SAS (сторона-угол-сторона) или когда все известны три стороны, но не известны углы, это треугольник SSS (сторона-сторона-сторона). В этом разделе мы исследуем другой инструмент для решения наклонных треугольников, описанных этими двумя последними случаями.
Использование закона косинусов для решения наклонных треугольников
Инструмент, который нам нужен для решения проблемы расстояния лодки от порта, — это закон косинусов , который определяет соотношение между угловыми измерениями и длинами сторон в наклонных треугольниках. Три формулы составляют Закон косинусов. На первый взгляд формулы могут показаться сложными, потому что они включают много переменных. Однако, как только схема будет понята, с законом косинусов легче работать, чем с большинством формул на этом математическом уровне.
Три формулы составляют Закон косинусов. На первый взгляд формулы могут показаться сложными, потому что они включают много переменных. Однако, как только схема будет понята, с законом косинусов легче работать, чем с большинством формул на этом математическом уровне.
Понимание того, как выводится закон косинусов, будет полезно при использовании формул. Вывод начинается с Обобщенной теоремы Пифагора, которая является расширением теоремы Пифагора на неправильные треугольники.Вот как это работает: произвольный непрямоугольный треугольник помещается в координатную плоскость с вершиной в начале координат, проходит вдоль оси x , а вершина располагается в некоторой точке плоскости, как показано на (Рисунок). Обычно треугольники существуют где угодно на плоскости, но для этого объяснения мы разместим треугольник, как указано.
Рисунок 2.Мы можем опустить перпендикуляр к оси x — (это высота или высота). Вспоминая основные тригонометрические тождества, мы знаем, что
В терминах и Точка, расположенная в, имеет координаты.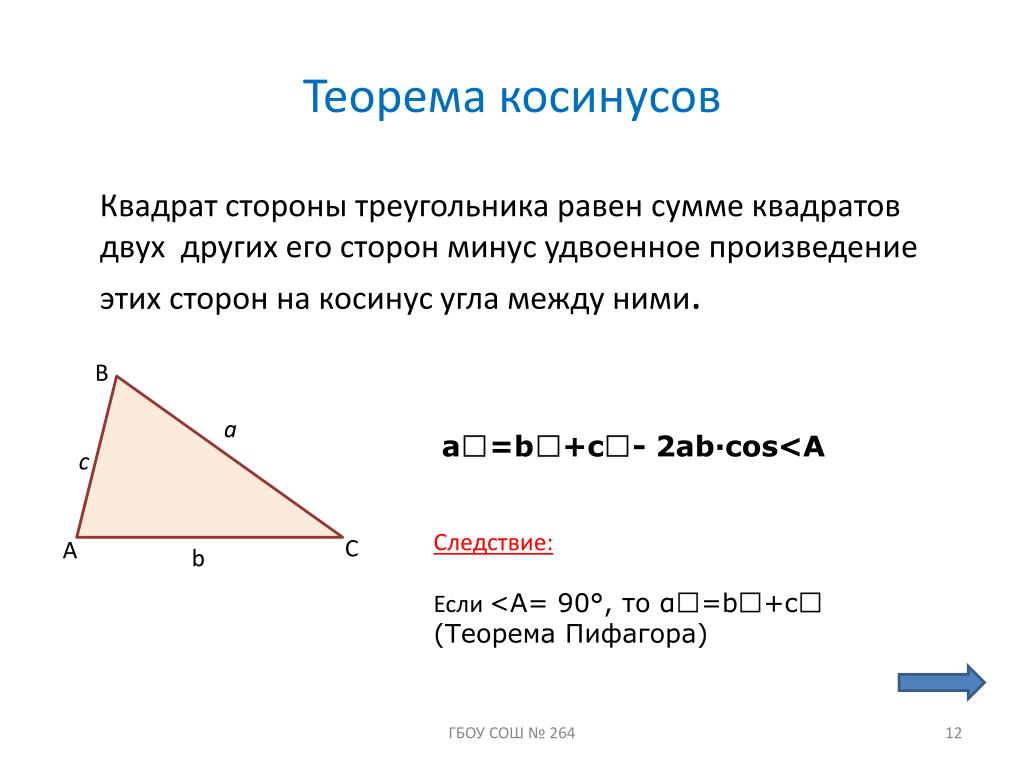 Используя сторону в качестве одного катета прямоугольного треугольника и в качестве второго катета, мы можем найти длину гипотенузы, используя теорему Пифагора.Таким образом,
Используя сторону в качестве одного катета прямоугольного треугольника и в качестве второго катета, мы можем найти длину гипотенузы, используя теорему Пифагора.Таким образом,
Полученная формула является одним из трех уравнений закона косинусов. Остальные уравнения находятся аналогичным образом.
Имейте в виду, что всегда полезно рисовать треугольник при решении углов или сторон. В реальном сценарии попробуйте нарисовать схему ситуации. По мере появления дополнительной информации диаграмму, возможно, придется изменить. Внесите эти изменения в схему и, в конце концов, проблему будет легче решить.
Зная две стороны и угол между ними (SAS), найдите размеры оставшейся стороны и углы треугольника.
- Нарисуйте треугольник. Определите размеры известных сторон и углов. Используйте переменные для представления размеров неизвестных сторон и углов.
- Примените закон косинусов, чтобы найти длину неизвестной стороны или угла.

- Примените закон синусов или косинусов, чтобы найти величину второго угла.
- Вычислите величину оставшегося угла.
Нахождение неизвестной стороны и углов треугольника SAS
Найдите неизвестную сторону и углы треугольника на (Рисунок).
Рисунок 4.Попробуй
Найдите недостающую сторону и углы данного треугольника:
[show-answer q = ”fs-id1165135360387 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135360387 ″]
[/ hidden-answer]
Попробуй
Дайте и найдите недостающие углы.
[show-answer q = ”fs-id1165133210042 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133210042 ″]
[/ hidden-answer]
Решение прикладных задач с использованием закона косинусов
Так же, как Закон синусов предоставил соответствующие уравнения для решения ряда приложений, Закон косинусов применим к ситуациям, в которых данные соответствуют моделям косинусов. Мы можем увидеть это в областях навигации, геодезии, астрономии и геометрии, и это лишь некоторые из них.
Мы можем увидеть это в областях навигации, геодезии, астрономии и геометрии, и это лишь некоторые из них.
Использование закона косинусов для решения проблемы связи
На многих сотовых телефонах с GPS приблизительное местоположение можно указать до приема сигнала GPS. Это достигается с помощью процесса, называемого триангуляцией, который работает с использованием расстояний от двух известных точек. Предположим, что есть две вышки сотовой связи в пределах досягаемости сотового телефона. Две башни расположены на расстоянии 6000 футов друг от друга по прямому шоссе, идущему с востока на запад, а сотовый телефон находится к северу от шоссе.На основании задержки сигнала можно определить, что сигнал находится на расстоянии 5050 футов от первой башни и 2420 футов от второй башни. Определите положение сотового телефона к северу и востоку от первой вышки и определите, как далеко он находится от шоссе.
[show-answer q = ”fs-id1165137419121 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137419121 ″]
Для простоты мы начнем с рисования диаграммы, подобной (Рисунок), и пометить данную информацию.
Используя закон косинусов, мы можем найти угол. Помните, что закон косинусов использует квадрат одной стороны для нахождения косинуса противоположного угла. В этом примере letandThus соответствует противоположной стороне
Чтобы ответить на вопросы о положении телефона к северу и востоку от вышки, а также о расстоянии до шоссе, опустите перпендикуляр от положения мобильного телефона, как показано на (Рисунок). Это формирует два прямоугольных треугольника, хотя для этой задачи нам нужен только прямоугольный треугольник, включающий первую башню.
Рисунок 7.Используя угол и основные тригонометрические тождества, мы можем найти решения. Таким образом,
Сотовый телефон находится примерно в 4638 футах к востоку и 1998 футах к северу от первой башни и в 1998 футах от шоссе. [/ Hidden-answer]
Расчет пройденного расстояния с помощью треугольника SAS
Возвращаясь к нашей задаче в начале этого раздела, предположим, что лодка покидает порт, проходит 10 миль, разворачивается на 20 градусов и проходит еще 8 миль. Как далеко от порта находится лодка? Схема повторяется здесь на (Рисунок).
Как далеко от порта находится лодка? Схема повторяется здесь на (Рисунок).
[скрытый-ответ a = ”fs-id1165134282021 ″]
Лодка повернулась на 20 градусов, поэтому тупой угол непрямого треугольника является дополнительным углом. С этим мы можем использовать закон косинусов, чтобы найти недостающую сторону тупого треугольника — расстояние от лодки до порта. .
Судно находится примерно в 17,7 милях от порта.[/ hidden-answer]
Использование формулы Герона для определения площади треугольника
Мы уже научились определять площадь наклонного треугольника, зная две стороны и угол. Мы также знаем формулу для определения площади треугольника по основанию и высоте. Однако, зная три стороны, мы можем использовать формулу Герона вместо определения высоты. Герон Александрийский был геометром, жившим в первом веке нашей эры.Он открыл формулу для определения площади наклонных треугольников, когда известны три стороны.
Формула Герона
Формула Герона находит площадь наклонных треугольников, в которых известны стороны и.
, где — половина периметра треугольника, иногда называемая полупериметром.
Использование формулы Герона для определения площади заданного треугольника
Найдите площадь треугольника на (рисунке), используя формулу Герона.
Рисунок 9. [show-answer q = ”611728 ″] Показать решение [/ show-answer][hidden-answer a = ”611728 ″]
Сначала вычисляем
Затем применяем формулу.
Площадь примерно 29,4 кв.
[/ hidden-answer]
Попробуй
Воспользуйтесь формулой Герона, чтобы найти площадь треугольника со сторонами длины и
[show-answer q = ”fs-id1165134102074 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134102074 ″]
Площадь = 552 квадратных фута
[/ hidden-answer]
Применение формулы Герона к реальной проблеме
Городской застройщик Чикаго хочет построить здание, состоящее из чердаков художников, на треугольном участке, граничащем с Раш-стрит, Вабаш-авеню и Пирсон-стрит. Фасад по Раш-стрит составляет примерно 62,4 метра, по Вабаш-авеню — примерно 43,5 метра, а по Пирсон-стрит — примерно 34,1 метра. Сколько квадратных метров доступно застройщику? См. (Рисунок) вид на собственность города.
Фасад по Раш-стрит составляет примерно 62,4 метра, по Вабаш-авеню — примерно 43,5 метра, а по Пирсон-стрит — примерно 34,1 метра. Сколько квадратных метров доступно застройщику? См. (Рисунок) вид на собственность города.
[скрытый-ответ a = ”fs-id1165135518137 ″]
Найдите размер, равный половине периметра.
Примените формулу Герона.
У девелопера около 711,4 кв. М. [/ Hidden-answer]
Попробуй
Найдите площадь данного треугольника и
[show-answer q = ”fs-id1165137394207 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137394207 ″]
около 8,15 квадратных футов
[/ hidden-answer]
Ключевые уравнения
| Закон косинусов | |
| Формула Герона |
Ключевые понятия
- Закон косинусов определяет соотношение между измерениями углов и длинами сторон в наклонных треугольниках.

- Обобщенная теорема Пифагора — это закон косинусов для двух случаев наклонных треугольников: SAS и SSS. При падении воображаемого перпендикуляра наклонный треугольник разбивается на два прямоугольных или образуется один прямоугольный треугольник, что позволяет связать стороны и рассчитать размеры. См. (Рисунок) и (Рисунок).
- Закон косинусов полезен для решения многих типов прикладных задач. Первым шагом в решении таких проблем обычно является набросок представленной проблемы.Если предоставленная информация соответствует одной из трех моделей (трех уравнений), примените закон косинусов, чтобы найти решение. См. (Рисунок) и (Рисунок). Формула
- Герона позволяет вычислять площадь в наклонных треугольниках. Чтобы применить формулу Герона, необходимо знать все три стороны. См. (Рисунок) и См. (Рисунок).
Упражнения по разделам
Устный
Если вы ищете недостающую сторону треугольника, что вам нужно знать при использовании закона косинусов?
[show-answer q = ”fs-id1165137887398 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137887398 ″]
две стороны и угол, противоположный отсутствующей стороне.
[/ hidden-answer]
Если вы ищете недостающий угол треугольника, что вам нужно знать при использовании закона косинусов?
Объясните, что представляет собой формула Герона.
[show-answer q = ”fs-id1165133143109 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133143109 ″]
— это полупериметр, который составляет половину периметра треугольника.
[/ hidden-answer]
Объясните связь между теоремой Пифагора и законом косинусов.
Когда нужно использовать закон косинусов вместо теоремы Пифагора?
[show-answer q = ”fs-id1165135518102 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135518102 ″]
Закон косинусов должен использоваться для любого наклонного (непрямого) треугольника.
[/ hidden-answer]
Алгебраические
В следующих упражнениях предположим, что противоположная сторона является противоположной стороной, а противоположная сторона — если возможно, решите каждый треугольник относительно неизвестной стороны. Округлите до ближайшей десятой.
Округлите до ближайшей десятой.
[скрытый-ответ a = ”fs-id1165133359517 ″] 11,3
[/ hidden-answer]
[show-answer q = ”fs-id1165134574953 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134574953 ″]
34,7
[/ hidden-answer]
[show-answer q = ”fs-id1165135354970 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135354970 ″]
26.7
[/ hidden-answer]
[show-answer q = ”fs-id1165137938467 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137938467 ″]
257,4
[/ hidden-answer]
[show-answer q = ”fs-id1165135515881 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135515881 ″]
невозможно
[/ hidden-answer]
В следующих упражнениях используйте закон косинусов, чтобы найти недостающий угол наклонного треугольника. Округлите до ближайшей десятой.
Округлите до ближайшей десятой.
найти угол
найти угол
[show-answer q = ”fs-id1165135208492 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135208492 ″]
95,5 °
[/ hidden-answer]
найти угол
найти угол
[show-answer q = ”fs-id1165137899963 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137899963 ″]
26,9 °
[/ hidden-answer]
найти угол
Для следующих упражнений решите треугольник.Округлите до ближайшей десятой.
[show-answer q = ”fs-id1165133199358 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133199358 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165137765785 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137765785 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165137643163 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165137643163 ″]
[/ hidden-answer]
Для следующих упражнений используйте формулу Герона, чтобы найти площадь треугольника. Округлить до ближайшей сотой.
Округлить до ближайшей сотой.
Найдите площадь треугольника со сторонами длиной 18, 21 и 32 дюйма. Округлите до ближайшей десятой.
[show-answer q = ”fs-id1165134201647 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134201647 ″]
177,56 дюйм2
[/ hidden-answer]
Найдите площадь треугольника со сторонами длиной 20, 26 и 37 см. Округлите до ближайшей десятой.
[show-answer q = ”fs-id1165134328321 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134328321 ″]
0.04 кв.м
[/ hidden-answer]
[show-answer q = ”fs-id1165133365504 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133365504 ″]
0,91 ярда2
[/ hidden-answer]
Графический
Для следующих упражнений найдите длину стороны Округлите до ближайшей десятой.
[show-answer q = ”fs-id1165135505463 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135505463 ″]
3. 0
0
[/ hidden-answer]
[show-answer q = ”fs-id1165133249132 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133249132 ″]
29,1
[/ hidden-answer]
[show-answer q = ”fs-id1165134370025 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134370025 ″]
0,5
[/ hidden-answer]
Для следующих упражнений найдите измерение угла
[show-answer q = ”fs-id1165135545523 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135545523 ″]
70.7 °
[/ hidden-answer]
[show-answer q = ”fs-id1165134401621 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134401621 ″]
77,4 °
[/ hidden-answer]
Найдите размер каждого угла в треугольнике, показанном на (Рисунок). Округлите до ближайшей десятой.
Рисунок 11. Для следующих упражнений решите неизвестную сторону. Округлите до ближайшей десятой.
[скрытый-ответ a = ”fs-id1165133236451 ″]
25.0
[/ hidden-answer]
[show-answer q = ”fs-id1165135698477 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135698477 ″]
9,3
[/ hidden-answer]
Для следующих упражнений найдите площадь треугольника. Округлить до ближайшей сотой.
[show-answer q = ”fs-id1165135525901 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135525901 ″]
43,52
[/ hidden-answer]
[show-answer q = ”fs-id1165134239622 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134239622 ″]
1.41
[/ hidden-answer]
[show-answer q = ”fs-id1165134263937 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134263937 ″]
0,14
[/ hidden-answer]
Расширения
У параллелограмма длина сторон 16 единиц и 10 единиц. Более короткая диагональ — 12 единиц. Найдите размер более длинной диагонали.
Более короткая диагональ — 12 единиц. Найдите размер более длинной диагонали.
Стороны параллелограмма 11 футов 17 футов. Более длинная диагональ — 22 фута. Найдите длину более короткой диагонали.
[show-answer q = ”fs-id11651330″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id11651330
″]
18,3
[/ hidden-answer]
Стороны параллелограмма равны 28 см и 40 см. Размер большего угла составляет 100 °. Найдите длину более короткой диагонали.
Правильный восьмиугольник вписан в круг радиусом 8 дюймов. (См. (Рисунок).) Найдите периметр восьмиугольника.
Рисунок 12. [show-answer q = ”fs-id1165135697763 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135697763 ″]
48.98
[/ hidden-answer]
Правильный пятиугольник вписан в круг радиусом 12 см. (См. (Рисунок).) Найдите периметр пятиугольника. Округлите до ближайшей десятой доли сантиметра.
Рисунок 13.
Для следующих упражнений предположим, что это представляет собой отношение трех сторон треугольника и косинуса угла.
[show-answer q = ”fs-id1165131837019 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165131837019 ″] [/ скрытый-ответ]
Найдите длину третьей стороны.
Для следующих упражнений найдите площадь треугольника.
[show-answer q = ”fs-id1165134130014 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134130014 ″]
7,62
[/ hidden-answer]
[show-answer q = ”fs-id1165135633910 ″] Показать решение [/ show-answer][hidden-answer a = ”fs-id1165135633910 ″] 85,1
[/ hidden-answer]
Реальные приложения
Инспектор провел измерения, показанные на (Рисунок).Найдите расстояние через озеро. Округлите ответы до ближайшей десятой.
Рисунок 14. Спутник вычисляет расстояния и угол, показанные на (Рисунок) (не в масштабе). Найдите расстояние между двумя городами. Округлите ответы до ближайшей десятой.
Найдите расстояние между двумя городами. Округлите ответы до ближайшей десятой.
[скрытый-ответ a = ”fs-id1165137827744 ″]
24,0 км
[/ hidden-answer]
Самолет пролетает 220 миль с курсом 40 °, а затем 180 миль с курсом 170 °.Как далеко самолет от начальной точки и по какому курсу? Округлите ответы до ближайшей десятой.
113-футовая башня расположена на холме, который наклонен на 34 ° к горизонтали, как показано на (Рисунок). Оттяжка должна быть прикреплена к вершине башни и закреплена в точке на высоте 98 футов от основания башни. Найдите нужную длину провода.
Рисунок 16. [show-answer q = ”fs-id1165135500669 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135500669 ″]
99.9 футов
[/ hidden-answer]
Два корабля вышли из порта одновременно. Одно судно двигалось со скоростью 18 миль в час при курсе 320 °. Другой корабль двигался со скоростью 22 мили в час при курсе 194 °. Найдите расстояние между двумя кораблями после 10 часов пути.
Другой корабль двигался со скоростью 22 мили в час при курсе 194 °. Найдите расстояние между двумя кораблями после 10 часов пути.
График на (Рисунок) представляет две лодки, одновременно отходящие от одного и того же причала. Первая лодка движется со скоростью 18 миль в час с курсом 327 °, а вторая лодка движется со скоростью 4 мили в час с курсом 60 °.Найдите расстояние между двумя лодками через 2 часа.
Рисунок 17. [show-answer q = ”fs-id1165135695099 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135695099 ″]
37,3 миль
[/ hidden-answer]
Треугольный бассейн имеет размеры 40 футов с одной стороны и 65 футов с другой стороны. Эти стороны образуют угол в 50 °. Какова длина третьей стороны (с точностью до десятых)?
Пилот летит по прямой 1 час 30 мин.Затем она корректирует курс, отклоняясь на 10 ° вправо от своего первоначального курса, и летит 2 часа в новом направлении. Если она поддерживает постоянную скорость 680 миль в час, как далеко она от исходной позиции?
[show-answer q = ”fs-id1165135453158 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135453158 ″]
2371 миль
[/ hidden-answer]
Лос-Анджелес находится в 1744 милях от Чикаго, Чикаго находится в 714 милях от Нью-Йорка, а Нью-Йорк находится в 2451 милях от Лос-Анджелеса. Нарисуйте треугольник, соединяющий эти три города, и найдите углы в треугольнике.
Нарисуйте треугольник, соединяющий эти три города, и найдите углы в треугольнике.
Филадельфия находится в 140 милях от Вашингтона, округ Колумбия, Вашингтон, округ Колумбия, находится в 442 милях от Бостона, а Бостон находится в 50 км от Филадельфии. Нарисуйте треугольник, соединяющий эти три города, и найдите углы в треугольнике.
[show-answer q = ”fs-id1165135200381 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135200381 ″] [/ скрытый-ответ]
Два самолета одновременно вылетают из одного аэропорта.Один летит под углом 20 ° к востоку от севера со скоростью 500 миль в час. Второй летит под углом 30 ° к востоку от юга со скоростью 600 миль в час. Как далеко друг от друга разойдутся самолеты через 2 часа?
Два самолета взлетают в разные стороны. Один движется на 300 миль в час строго на запад, а другой на 25 ° к северу от запада со скоростью 420 миль в час. Как далеко они разойдутся по прошествии 90 минут при условии, что они летят на одной высоте?
[show-answer q = ”fs-id1165135694395 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135694395 ″] 599.
 8 миль
8 миль[/ hidden-answer]
У параллелограмма длина сторон составляет 15,4 единицы и 9,8 единицы. Его площадь составляет 72,9 кв. Найдите размер более длинной диагонали.
Четыре последовательные стороны четырехугольника имеют длину 4,5 см, 7,9 см, 9,4 см и 12,9 см. Угол между двумя наименьшими сторонами составляет 117 °. Какова площадь этого четырехугольника?
[show-answer q = ”fs-id1165134408492 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134408492 ″]
65.4 см2
[/ hidden-answer]
Четыре последовательные стороны четырехугольника имеют длину 5,7 см, 7,2 см, 9,4 см и 12,8 см. Угол между двумя наименьшими сторонами составляет 106 °. Какова площадь этого четырехугольника?
Найдите площадь треугольного участка земли размером 30 футов с одной стороны и 42 фута с другой; Включенный угол составляет 132 °. Округлить до ближайшего целого квадратного фута.
[show-answer q = ”fs-id1165135506390 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135506390 ″]
468 фут2
[/ hidden-answer]
Найдите площадь треугольного участка земли размером 110 футов с одной стороны и 250 футов с другой; включенный угол составляет 85 °. Округлить до ближайшего целого квадратного фута.
Округлить до ближайшего целого квадратного фута.
Глоссарий
- Закон косинусов
- утверждает, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение двух других сторон и косинус включенного угла
- Обобщенная теорема Пифагора
- расширение закона косинусов; связывает стороны наклонного треугольника и используется для треугольников SAS и SSS
Sin Cos Tan — значения, формулы, таблица, примеры
В тригонометрии sin, cos и tan являются основными тригонометрическими отношениями, используемыми для изучения взаимосвязи между углами и сторонами треугольника (особенно прямоугольного).Пифагор работал над взаимосвязью между сторонами прямоугольного треугольника с помощью теоремы Пифагора, в то время как Гиппаркус работал над установлением взаимосвязи между сторонами и углами прямоугольного треугольника, используя концепции тригонометрии. Формулы sin, cos и tan в тригонометрии используются для нахождения недостающих сторон или углов прямоугольного треугольника.
Давайте разберемся с sin, cos и tan в тригонометрии, используя формулы и примеры.
Что такое Sin Cos Tan в тригонометрии?
Sin, cos и tan — это три основных тригонометрических отношения, а именно синус, косинус и тангенс соответственно, где каждое из которых дает отношение двух сторон прямоугольного треугольника.Мы знаем, что самая длинная сторона прямоугольного треугольника известна как «гипотенуза», а две другие стороны известны как «катеты». Это означает, что в тригонометрии самая длинная сторона прямоугольного треугольника все еще известна как «гипотенуза», но два других катета имеют следующие названия:
- противоположная сторона и
- смежная сторона
Мы определяем «противоположную» и «смежную» стороны, исходя из угла, о котором мы говорим.
- «Противоположная сторона» или перпендикуляр — это сторона, которая просто «противоположна» углу.
- «Смежная сторона» или основание — это сторона (кроме гипотенузы), которая «касается» угла.

Sin Cos Tan Значения
Значения Sin, Cos и Tan в тригонометрии относятся к значениям соответствующей тригонометрической функции для данного угла. Мы можем найти значения sin, cos и tan для данного прямоугольного треугольника, найдя необходимое соотношение сторон. Давайте разберемся с формулами, чтобы найти эти соотношения подробно в следующих разделах.
Формулы для загара Sin Cos Tan
Функции Sin, cos и tan в тригонометрии определяются в терминах двух из трех сторон (противоположной, смежной и гипотенузы) прямоугольного треугольника.Вот формулы sin, cos и tan.
sin θ = Противоположно / Гипотенуза
cos θ = Соседний / Гипотенуза
тангенс угла θ = напротив / рядом
Помимо этих трех тригонометрических соотношений, у нас есть еще три соотношения, называемые csc, sec и cot, которые являются обратными величинами sin, cos и tan соответственно. Давайте разберемся с этими формулами sin, cos и tan на примере, приведенном ниже.
Пример: Найдите sin, cos и tan треугольника для заданного угла θ.
Раствор:
В треугольнике самая длинная сторона (или) сторона, противоположная прямому углу, является гипотенузой. Сторона, противоположная θ, является противоположной стороной или перпендикулярной. Сторона, смежная с θ, является смежной стороной или основанием.
Теперь мы находим sin θ, cos θ и tan θ, используя приведенные выше формулы:
sin θ = Противоположно / Гипотенуза = 3/5
cos θ = прилегающая / гипотенуза = 4/5
тангенс угла θ = напротив / рядом = 3/4
Уловка для запоминания формул sin cos tan в тригонометрии: Вот уловка для запоминания формул sin, cos и tan.Мы можем использовать аббревиатуру «SOHCAHTOA», как показано ниже,
Стол Sin Cos Tan
Тригонометрические отношения sin, cos и tan не зависят в точности от длин сторон треугольника, а, скорее, от угла, потому что в конечном итоге мы берем соотношение сторон. Таблица Sin, cos и tan используется для нахождения значений этих тригонометрических функций для стандартных углов. Во время расчетов с использованием синусоидальных, косинусных или тангенциальных соотношений мы можем напрямую обращаться к триггерной диаграмме, приведенной в следующем разделе, чтобы упростить выводы.
Таблица Sin, cos и tan используется для нахождения значений этих тригонометрических функций для стандартных углов. Во время расчетов с использованием синусоидальных, косинусных или тангенциальных соотношений мы можем напрямую обращаться к триггерной диаграмме, приведенной в следующем разделе, чтобы упростить выводы.
Sin Cos Tan Диаграмма
Sin cos tan диаграмма / таблица — это диаграмма с тригонометрическими значениями синуса, косинуса и тангенса для некоторых стандартных углов 0 o , 30 o , 45 o , 60 o и 90 o . Мы можем обратиться к приведенной ниже таблице триггеров, чтобы напрямую выбрать значения sin, cos и tan для стандартных углов.
Полезные советы Sin Cos Tan Table
Советы, которые вам нужно запомнить из этой таблицы:
- Углы 0 o , 30 o , 45 o , 60 o и 90 o по порядку.
- Первую строку (sin) можно запомнить так: 0/2, √1 / 2, √2 / 2, √3 / 2.

- Это все, что вам нужно запомнить, потому что:
Строка cos такая же, как и строка sin, только в обратном порядке. - Каждое значение в строке tan получается делением соответствующих значений sin на cos, поскольку tan = sin / cos.
Вы можете увидеть, как tan = sin / cos здесь:
sin θ / cos θ = (Противоположный / Гипотенуза) ÷ (Соседний / Гипотенуза) = (Противоположный / Гипотенуза) × (Гипотенуза / Соседний) = Противоположный / Соседний = tan θ
Sin Cos Tan на единичном круге
Значения sin, cos и tan можно вычислить для любого заданного угла с помощью единичной окружности.Единичный круг в координатной плоскости — это круг с единичным радиусом 1, часто с центром в начале координат (0, 0) в декартовой системе координат в евклидовой плоскости, особенно в тригонометрии. Для любой точки на единичной окружности, заданной с координатами (x, y), отношения sin, cos и tan могут быть заданы как
- грех θ = y / 1
- cos θ = x / 1
- тангенс угла θ = y / x
где θ — это угол, который линия, соединяющая точку и начало координат, образует с положительной осью x.
Применение Sin Cos Tan в реальной жизни
Тригонометрические соотношения sin, cos, tan находят применение в нашей повседневной жизни для определения высоты и расстояния. Мы используем sin, cos и tan для решения многих реальных проблем. Вот пример, чтобы понять применение sin, cos и tan.
Пример: Лестница прислоняется к кирпичной стене под углом 50 o к горизонту. Если лестница находится на расстоянии 10 футов от стены, то до какой высоты стены она достигает?
Раствор:
Предположим, что лестница достигает x футов стены.
Используя предоставленную информацию:
Здесь мы знаем соседнюю сторону (которая составляет 10 футов), и мы должны найти противоположную сторону (которая равна x ft). Таким образом, мы используем отношение между противоположной и смежной сторонами, которое является желтовато-коричневым.
загар 50 o = x / 10
x = 10 загар 50 o
x ≈ 11. 9 футов
9 футов
Здесь tan 50 o рассчитывается с помощью калькулятора, а окончательный ответ округляется до 1 десятичного знака. Следовательно, лестница доходит до 11.9 футов стены.
Темы, связанные с Sin Cos Tan:
Часто задаваемые вопросы о Sin Cos Tan
Что означает Sin Cos Tan в тригонометрии?
Sin, cos и tan — основные тригонометрические соотношения в тригонометрии, используемые для изучения взаимосвязи между углами и сторонами треугольника (особенно прямоугольного).
Как использовать Sin Cos Tan?
Мы можем использовать sin cos и tan для решения реальных проблем.Чтобы решить любую проблему, мы сначала рисуем фигуру, описывающую проблему, и используем соответствующее тригонометрическое соотношение для решения проблемы.
Как найти ценности Sin Cos Tan?
Чтобы найти sin, cos и tan, мы используем следующие формулы:
- sin θ = Противоположно / Гипотенуза
- cos θ = Соседний / Гипотенуза
- тангенс угла θ = напротив / рядом
Чтобы найти sin, cos и tan стандартных углов, вы можете использовать таблицу тригонометрии.
Что такое таблица синуса, косинуса и тангенса в тригонометрии?
Тригонометрическая таблица или диаграмма для sin, cos и tan используются для нахождения этих тригонометрических значений для стандартных углов 0 o , 30 o , 45 o , 60 o и 90 o . Используя таблицу sin cos tan, мы можем напрямую найти значения sin cos tan для этих углов и использовать их в задачах.
Как определить ценность загара с помощью греха и сознавания?
Значение функции загара для любого угла θ в терминах sin и cos может быть задано с помощью формулы: tan θ = sin θ / cos θ.
Каков трюк, чтобы запомнить формулу для поиска Sin Cos Tan?
Мы можем вспомнить формулы sin cos tan, используя слово «SOHCAHTOA». Это слово можно использовать для запоминания соотношений сторон, участвующих в вычислении значений sin, cos и tan в тригонометрии, как указано ниже,
- S дюйм θ = O pposite / H ypotenuse
- C os θ = A djacent / H ypotenuse
- T an θ = O pposite / A djacent
Где используется Sin Cos Tan?
Sin, cos и tan находят применение в тригонометрии для вычисления значений этих функций при установлении взаимосвязи между углами и сторонами треугольника (особенно прямоугольного).


 Если , то треугольник тупоугольный, если то треугольник остроугольный, если , то треугольник прямоугольный.
Если , то треугольник тупоугольный, если то треугольник остроугольный, если , то треугольник прямоугольный.