Ромб и квадрат / Четырехугольники / Справочник по геометрии 7-9 класс
Частным видом параллелограмма является ромб.
| Ромбом называется параллелограмм, у которого все стороны равны |
ABCD — ромб.
Ромб обладает всеми свойствами параллелограмма.
Особое свойство ромба
Доказательство
Дано: ABCD — ромб
Доказать: ACBD, ADO = CDO
Доказательство:
AD = DC (по определению ромба), значит, ADC — равнобедренный.
AO = OC (по свойству диагоналей параллелограмма), DO — медиана ADC , а в 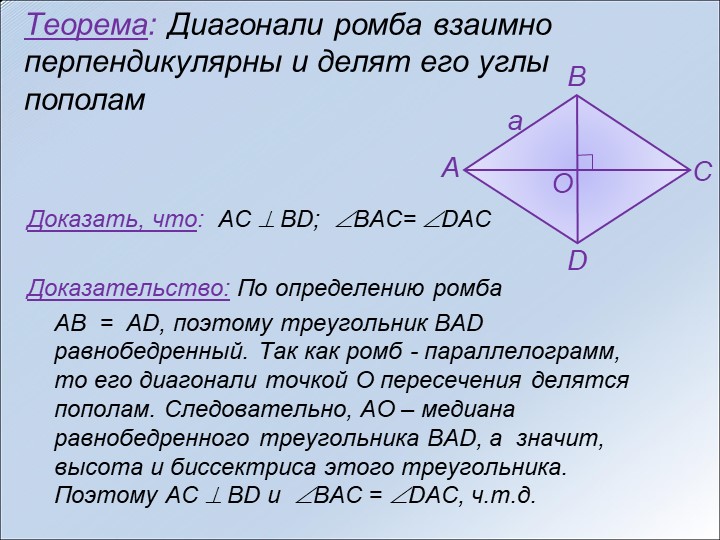
Теорема
Доказательство
Дано: ABCD — параллелограмм, ACBD
Доказать: ABCD — ромб
Доказательство:
Рассмотрим AOВ и COВ:
Т.к. ACBD, тоAOВ = COВ = 900;
AO = OC (по свойству диагоналей параллелограмма), ОВ — общий катет, AOВ = COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны, ВС = ВА.
В параллелограмме противоположные стороны равны, AD = BC, AB = DC
Итак: ABCD — параллелограмм (по условию) AD = BC = AB = DC (по доказанному). ABCD — ромб, что и требовалось доказать.
ABCD — ромб, что и требовалось доказать.
Теорема
Доказательство
Дано: ABCD — параллелограмм, АС — диагональ и биссектриса DAB иDCB
Доказать: ABCD — ромб
Доказательство:
DAB =DCB (по свойству параллелограмма), а АС -биссектриса DAB иDCB (т.е. АС делит эти углы на два равных угла), DAC = BAC =DCA = BCA
Рассмотрим ADC : DAC =DCA, ADC — равнобедренный с основанием AC, и AD = DC.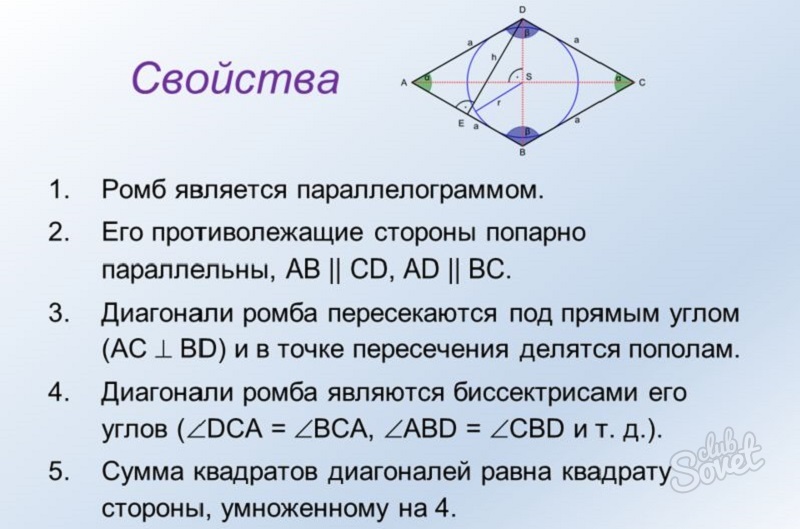 В параллелограмме противоположные стороны равны, AD = BC, AB = DC
В параллелограмме противоположные стороны равны, AD = BC, AB = DC
Итак: ABCD — параллелограмм (по условию) AD = BC = AB = DC (по доказанному). ABCD — ромб, что и требовалось доказать.
Две теоремы, доказанные выше, называют признаками ромба.
Основные свойства квадрата:
1. Все углы квадрата прямые
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
math-public:romb [Президентский ФМЛ №239]
Определение
Ромб – это четырехугольник, у которого все стороны равны. \circ$, так как это смежные
углы.
\circ$, так как это смежные
углы.
Кроме того, $\angle 3=\angle 4=\angle 5=\angle 6$, $\angle 7=\angle 8=\angle 9=\angle 10$.
Таким образом диагонали перпендикулярны и являются биссектрисами углов ромба.
Следствие
Диагонали ромба разбивают его на четыре равных прямоугольных треугольника.
Признаки ромба
Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб.
Если одна из диагоналей параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Если в четырёхугольнике $ABCD$ диагональ $AC$ является биссектрисой углов $\angle A$ и $\angle C$, а диагональ $BD$ является биссектрисой углов $B$ и $D$, то $ABCD$ – ромб.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим параллелограмм $ABCD$, в котором $AC\perp BD$.
Докажем, что $ABCD$ – ромб.
В параллелограмме диагонали точкой пересечения делятся
пополам, следовательно, $AO=OC, BO=OD$.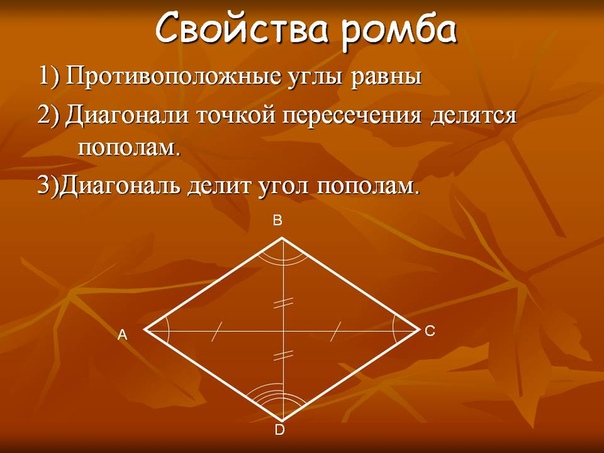 \circ$.
\circ$.
Тогда $\triangle AOB=\triangle AOD$ по первому признаку равенства.
Следовательно $AB=AD$.
А так как $ABCD$ – параллелограмм, то $BC=AD=AB=CD$, то есть $ABCD$ – ромб.
Докажем второй пункт теоремы.
Рассмотрим параллелограмм $ABCD$, в котором диагональ $AC$ является биссектрисой угла $\angle A$, то есть $\angle 1=\angle 2$.
Докажем, что $ABCD$ – ромб.
То есть $\triangle ABC$ – равнобедренный и $AB=BC$.
А так как $ABCD$ – параллелограмм, то $AB=CD, BC=AD$, то есть $AB=BC=CD=AD$, и $ABCD$ – ромб.
Докажем третий пункт теоремы
Заметим, что $\triangle ABC=\triangle ADC$ по второму признаку ($\angle 1=\angle 2, \angle 3=\angle 4$, $AC$ – общая).
Тогда $\angle B=\angle D$, а следовательно, равны и их половины: $\angle 5=\angle 6=\angle7=\angle 8$.
Но тогда треугольники $\triangle ABD$ и $\triangle BCD$ – равнобедренные: $AB=AD, BC=CD$.
Кроме того $\triangle ABD=\triangle BCD$ по второму признаку ($BD$ – общая, $\angle 5=\angle6, \angle 7=\angle 8$).
А значит $AB=BC$ и $AD=CD$.
Таким образом все стороны четырёхугольника равны между собой: $AB=BC=CD=DA$.
math-public/romb.txt · Последнее изменение: 2016/04/17 00:55 — labreslav
Как находится диагональ ромба. Ромб. Полные уроки — Гипермаркет знаний
Определение
Ромб – это четырехугольник, у которого все стороны равны.
Замечание
Ромб является частным случаем параллелограмма, так как его противоположные стороны попарно равны (третий признак).
Замечание
Ромб наследует все свойства параллелограмма.
Свойства ромба
Диагонали ромба взаимно перпендикулярны.
Диагонали ромба являются биссектрисами его углов.
Доказательство
Рассмотрим ромб $ABCD$, в котором диагонали $AC$ и $BD$ пересекаются
в точке $O$. \circ$, так как это смежные
углы.
\circ$, так как это смежные
углы.
Кроме того, $\angle 3=\angle 4=\angle 5=\angle 6$, $\angle 7=\angle 8=\angle 9=\angle 10$.
Таким образом диагонали перпендикулярны и являются биссектрисами углов ромба.
Следствие
Диагонали ромба разбивают его на четыре равных прямоугольных треугольника.
Признаки ромба
Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб.
Если одна из диагоналей параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Если в четырёхугольнике $ABCD$ диагональ $AC$ является биссектрисой углов $\angle A$ и $\angle C$, а диагональ $BD$ является биссектрисой углов $B$ и $D$, то $ABCD$ – ромб.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим параллелограмм $ABCD$, в котором $AC\perp BD$.
Докажем, что $ABCD$ – ромб.
В параллелограмме диагонали точкой пересечения делятся
пополам, следовательно, $AO=OC, BO=OD$.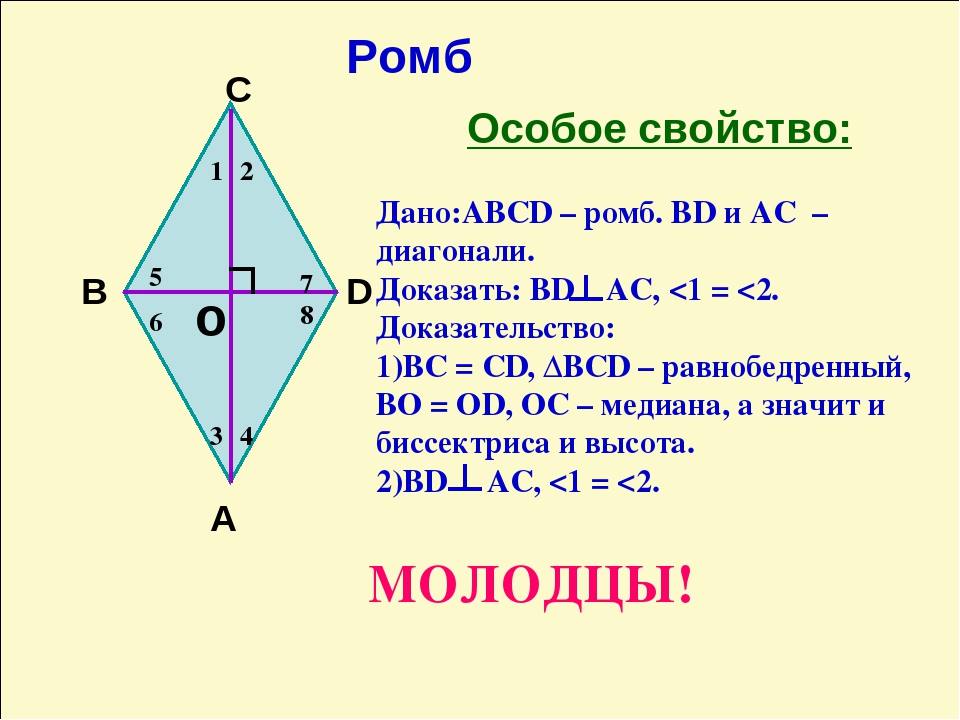 \circ$.
\circ$.
Тогда $\triangle AOB=\triangle AOD$ по первому признаку равенства.
Следовательно $AB=AD$.
А так как $ABCD$ – параллелограмм, то $BC=AD=AB=CD$, то есть $ABCD$ – ромб.
Докажем второй пункт теоремы.
Рассмотрим параллелограмм $ABCD$, в котором диагональ $AC$ является биссектрисой угла $\angle A$, то есть $\angle 1=\angle 2$.
Докажем, что $ABCD$ – ромб.
$\angle 2=\angle 3$, как накрест лежащие, следовательно, $\angle 1=\angle 3$.
То есть $\triangle ABC$ – равнобедренный и $AB=BC$.
А так как $ABCD$ – параллелограмм, то $AB=CD, BC=AD$, то есть $AB=BC=CD=AD$, и $ABCD$ – ромб.
Докажем третий пункт теоремы
Заметим, что $\triangle ABC=\triangle ADC$ по второму признаку ($\angle 1=\angle 2, \angle 3=\angle 4$, $AC$ – общая).
Тогда $\angle B=\angle D$, а следовательно, равны и их половины: $\angle 5=\angle 6=\angle7=\angle 8$.
Но тогда треугольники $\triangle ABD$ и $\triangle BCD$ – равнобедренные: $AB=AD, BC=CD$.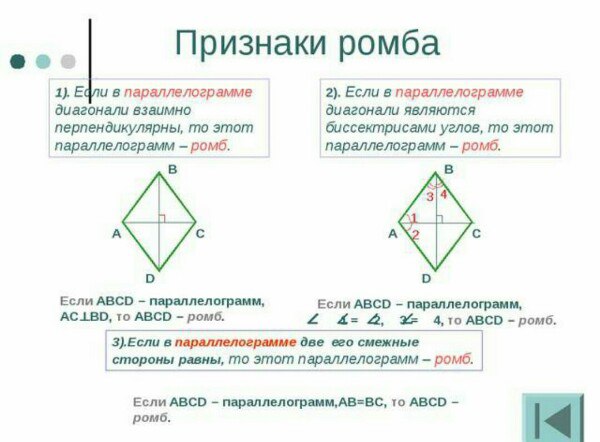
Кроме того $\triangle ABD=\triangle BCD$ по второму признаку ($BD$ – общая, $\angle 5=\angle6, \angle 7=\angle 8$).
А значит $AB=BC$ и $AD=CD$.
Таким образом все стороны четырёхугольника равны между собой: $AB=BC=CD=DA$.
В. А. С. D. Особое свойство ромба. Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Дано: ABCD ромб. Так как ромб – параллелограмм, то ВО=DО. Тогда, АО – медиана. АО – высота. АО — биссектриса.
Слайд 11 из презентации «Виды прямоугольников» . Размер архива с презентацией 275 КБ.Геометрия 8 класс
краткое содержание других презентаций««Подобные треугольники» 8 класс» — Среднее пропорциональное. Признаки подобия треугольников. Подобные треугольники. Второй признак. Косинус. О – пересечение медиан. В повседневной жизни встречаются предметы одинаковой формы. Задача. Катет прямоугольного треугольника. Отрезки. Средняя линия. АСН и ВСН – прямоугольные. Медианы в треугольнике. Высота в треугольнике. Синус острого угла прямоугольного треугольника. Определение подобных треугольников.
Синус острого угла прямоугольного треугольника. Определение подобных треугольников.
«Теоремы Чевы и Менелая» — Точки. Теорема Чевы. Биография ученого. Теорема Менелая. Точка К. Теоремы Чевы и Менелая. Проведем прямые. Прямая, параллельная биссектрисе. Решение. Менелай Александрийский. Точка. Отрезки. Равенство. ВМ-медиана. Середина стороны. Утверждение обратное теореме.
«Нахождение площади параллелограмма» — Найдите площадь параллелограмма. Признаки равенства прямоугольных треугольников. Площадь треугольника. Высота. Определение высоты параллелограмма. Найдите площадь прямоугольника. Свойства площадей. Найдите площадь треугольника. Площадь квадрата. Найдите площадь квадрата. Площадь параллелограмма. Высоты параллелограмма. Устные упражнения. Найдите периметр квадрата. Основание.
«Построение касательной к окружности» — Теорема об отрезках касательных. Окружность и прямая имеют одну общую точку. Повторение. Окружность. Общие точки. Решение. Взаимное расположение прямой и окружности. Диаметр. Окружность и прямая. Хорда. Касательная к окружности.
Диаметр. Окружность и прямая. Хорда. Касательная к окружности.
««Окружность» геометрия» — Теорема об окружности, вписанной в треугольник. Биссектрисы треугольника. Касательная к окружности. Свойства сторон четырехугольника, описанного около окружности. Теорема о серединном перпендикуляре. Угол, вершина которого лежит на окружности. Теорема о биссектрисе угла. Центральный угол. Прямая, имеющая с окружностью только одну общую точку. Свойства углов четырехугольника, вписанного в окружность.
«Решение теоремы Пифагора» — Хаммураби. Квадрат. Диаметр. Площадь квадрата. Шестиугольники. Геометрия. Приложения теоремы Пифагора. Высота. Доказательство Эпштейна. Треугольники. Биография Пифагора. Доказательство методом вычитания. Полноценное доказательство. Доказательство методом разложения. Доказательство 9 века н.э. Мотив. Теорема Пифагора. Кантор. Доказательство Гутхейля. Доказательство Нильсена. Формулировка теоремы. Пифагорейцы.
Ромб — четырехугольник, стороны которого равны и попарно параллельны. 1/2=6 см.
1/2=6 см.
Несмотря на кажущуюся простоту такой геометрической фигуры, как ромб, он таит в себе много интересных моментов. К нему применимы свойства параллелограмма, биссектрисы, прямоугольного, а иногда и равнобедренного треугольника. Зная формулы, легко можно решить задачи по нахождению диагоналей ромба.
Цели урока
Продолжать знакомить учеников о такой геометрической фигуре, как ромб;
Закрепить знания о таких понятиях, как ромб и квадрат, а также научиться определять их разницу;
Освежить знания школьников о свойствах и признаках ромба;
Продолжать совершенствовать знания учащихся о геометрических фигурах в процессе решения задач.
Вызвать заинтересованность к урокам геометрии.
Задачи урока
Повторить, обобщить и закрепить полученные знания о такой геометрической фигуре, как ромб;
Продолжать формировать умения и навыки построения геометрических фигур;
Усовершенствовать навыки построения ромба с помощью чертежных инструментов;
Продолжать закреплять знания школьников с использованием практических заданий;
Продолжать развивать внимание, усидчивость и стремление к познавательному процессу.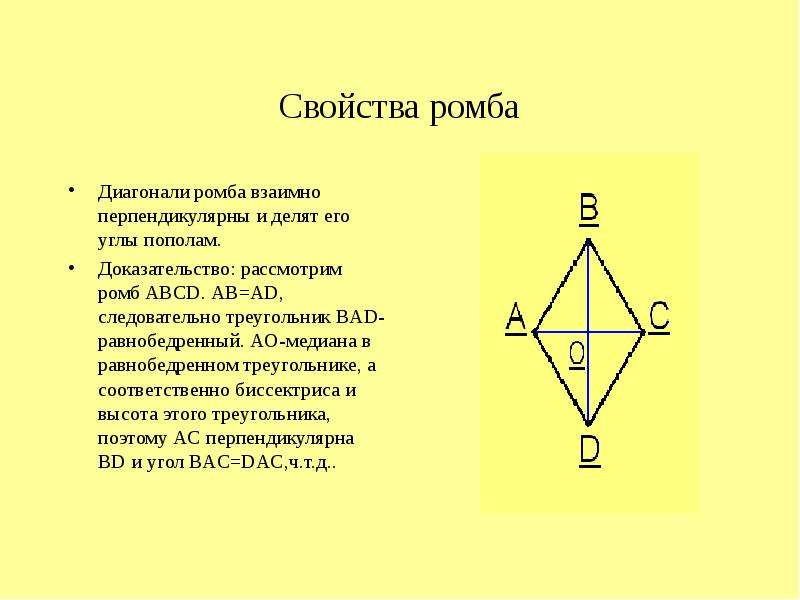
План урока
1. Раскрытие главное темы урока, определение геометрической фигуры «Ромб».
2. Ознакомление со свойствами и признаками ромба.
3. Теоремы и их доказательство.
4. Как нарисовать ромб. Способы изображения ромба.
5. Как найти площадь ромба?
6. Повторение пройденного материала.
7. Интересные факты.
8. Домашнее задание.
Определение ромба, как геометрической фигуры
Ромб — это такой параллелограмм, у которого все стороны равны. Если же ромб имеет прямые углы, то он называется квадратом.
Сам термин «Ромб» в переводе с греческого языка, обозначает «бубен». Конечно же в нашем понимании бубен, как музыкальный инструмент, имеет круглую форму. Но это сейчас бубны делают круглыми, а в древние времена он как раз и имел квадратную форму или форму ромба.
Давайте остановимся на основных определениях ромба и попробуем понять, что же являет собой эта геометрическая фигура.
Ромб – это такой равносторонний параллелограмм, у которого равные стороны, но неравные углы.
В отличие от квадрата, ромб – это равносторонний косоугольник.
Как всегда мы получаем множество определений той или иной геометрической фигуры, но это не означает, что каждый ученик должен сесть и «зазубрить» именно эти определения. Отличие в определениях – это насколько широко они описывают нашу геометрическую фигуру. Самое главное, это понимание о чем говориться в определении и возможность представить фигуру. Если вы будете придерживаться этих двух правил, то и сами сможете написать или дополнить парочку определений.
Свойства ромба
2. Вторым его свойством является то, что все диагонали ромба пересекаются под прямым углом. В точке пересечения диагонали ромба делятся пополам.
3. Биссектрисами углов ромба являются его диагонали.
4. Чтобы найти сумму квадратов диагоналей ромба, необходимо квадрат его стороны умножить на четыре.
5. Противолежащие стороны ромба равны;
6. Сумма углов ромба, которые прилежат к одной его стороне, равна 180 градусов.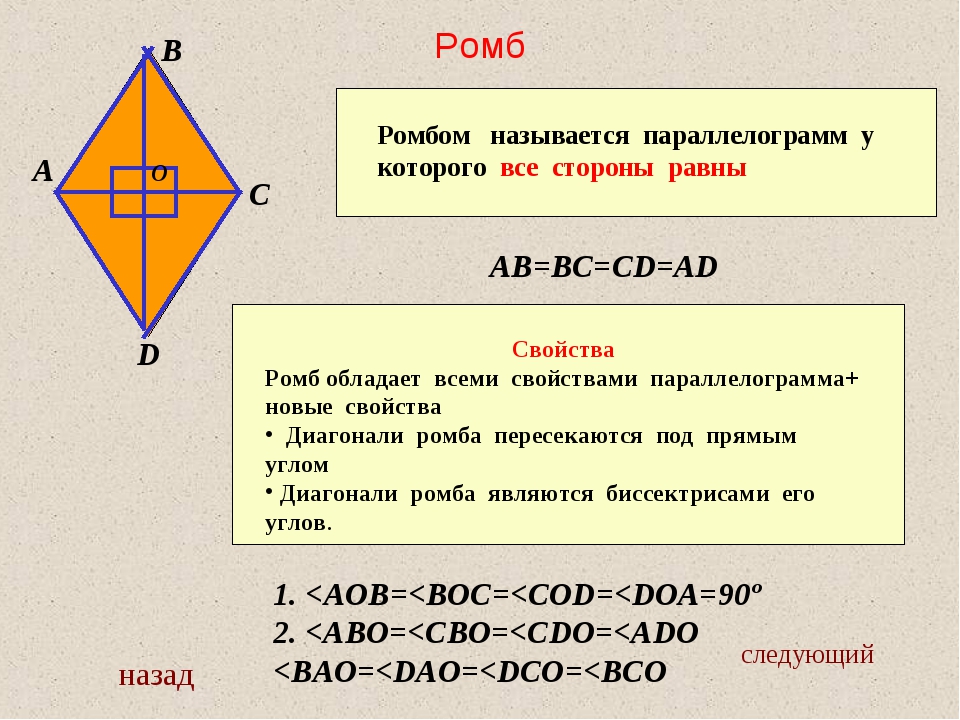
Признаки ромба
Параллелограмм является ромбом в том случае, если он соответствует следующим условиям:
1. Во-первых, у него все стороны равны между собой;
2. Во-вторых, диагонали ромба пересекаются под прямым углом.
3. В-третьих, если диагонали его углов являются биссектрисами.
4. В-четвертых, если его две смежные стороны равны между собой.
5. В-пятых, если хотя бы одна из диагоналей является биссектрисой параллелограмма.
Теоремы и их доказательство
Теперь давайте более подробно рассмотрим свойства и признаки ромба, доказав теоремы:
Теорема 1
Теорема 2
Из этого следует, что:
1. У ромба две оси симметрии – диагонали AC и BD.
2. Его диагонали взаимно перпендикулярны.
3. А также являются биссектрисами его углов.
Площадь ромба
Площадь ромба равна половине произведения его диагоналей. Но так как ромб, по сути, это параллелограмм, то его площадь можно узнать, умножив его стороны на высоту.
Формулы площади ромба:
Где:
a – является стороной ромба
D – обозначается его большая диагональ
d – имеет обозначение меньшая диагональ
α – это острый угол
β – является тупым углом
Площадь любой геометрической фигуры является частью поверхности, которая ограничивается замкнутым контуром данной фигуры. А величина площади ромба выражается числом заключающихся в него квадратных единиц.
Как нарисовать ромб
Чтобы нарисовать ромб воспользуемся свойствами диагоналей ромба. Нам уже известно, что диагонали нашей геометрической фигуры взаимно перпендикулярны и делятся пополам в точке пересечения. Поэтому построение ромба проще всего начать с построения его диагоналей.
Первый способ
И так, в первую очередь выбираем точку, от которой откладываем влево и право отрезки одной длины, в вверх и вниз одинаковые отрезки другой длины.
Теперь нам остается только соединить концы этих отрезков, и в результате мы получим ромб.
Второй способ
Ромб можно еще начертить без использования диагоналей. В этом случае нужно определить лишь концы диагоналей и потом соединить точки отрезками.
Третий способ
И наконец, третий способ, черчения ромба можно выполнить при помощи линейки. Так как мы с вами знаем, что ромб имеет равные стороны, то вначале нужно нарисовать его нижнюю часть. Затем необходимо отложить от нее равный отрезок. А так как третья сторона параллельна первой, то соединив концы первого и третьего отрезков, мы получим ромб.
Повторение
Вы уже познакомились с такой геометрической фигурой, как ромб и понимаете, что квадрат является его частным случаем.
1. Поэтому давайте вспомним определение, что такое квадрат? Дайте самостоятельно определение квадрата.
2. Какими свойствами обладает квадрат? Назовите их.
3. В чем все-таки разница между ромбом и квадратом, если квадрат является его частным случаем?
4. Какую фигуру называют четырехугольником, и относится ли ромб к этой геометрической фигуре?
5. Какие виды четырехугольников вы уже изучали? Назовите их.
Какие виды четырехугольников вы уже изучали? Назовите их.
6. Какие между ними существуют отличия?
Это интересно знать
Известно ли вам, что если взять прямоугольник и соединить отрезками середины его сторон, то в итоге мы получим ромб.
А если, наоборот, мы с вами возьмем ромб и попробуем соединить его середины сторон отрезками, то мы получим такую геометрическую фигуру, как прямоугольник.
Если вы возьмете параллелограмм с равными высотами, то такой параллелограмм является ромбом.
А знаете ли вы, что названием карточной масти бубны, имеющего ромбическую форму, появилось еще в те времена, когда бубен имел далеко не круглую форму, а вид ромба или квадрата.
Впервые слово «ромб» в своем лексиконе был использован Герроном и Паппой Александрийским.
Домашнее задание
1. Как вы думаете, является ли ромбом параллелограмм, который имеет хотя бы один прямой угол?
2. Верно ли утверждение, что каждый параллелограмм является ромбом?
3. Если диагонали параллелограмма равны 5 см и 7см, может ли быть ромбом этот параллелограмм?
Если диагонали параллелограмма равны 5 см и 7см, может ли быть ромбом этот параллелограмм?
4. Если диагонали параллелограмма равны, то может ли он быть ромбом?
5. Назовите особое свойство ромба, которым обладают его диагонали, помимо того, что они точкой пересечения делятся пополам?
6. Подумайте, где в повседневной жизни применяется такая геометрическая фигура, как ромб?
Среди многообразия геометрических фигур заметно выделяется такой четырехугольник, как ромб. Даже само его название не типично для обозначения четырехугольников. И хотя в геометрии он встречается значительно реже, чем такие простые фигуры, как круг, треугольник, квадрат или прямоугольник, его также нельзя оставлять без внимания.
Ниже представлены определение, свойства и признаки ромбов.
Определение
Ромб — это параллелограмм, имеющий равные стороны. Ромб называется квадратом, если все его углы прямые. Наиболее ярким примером ромба является изображение бубновой масти на игральной карте.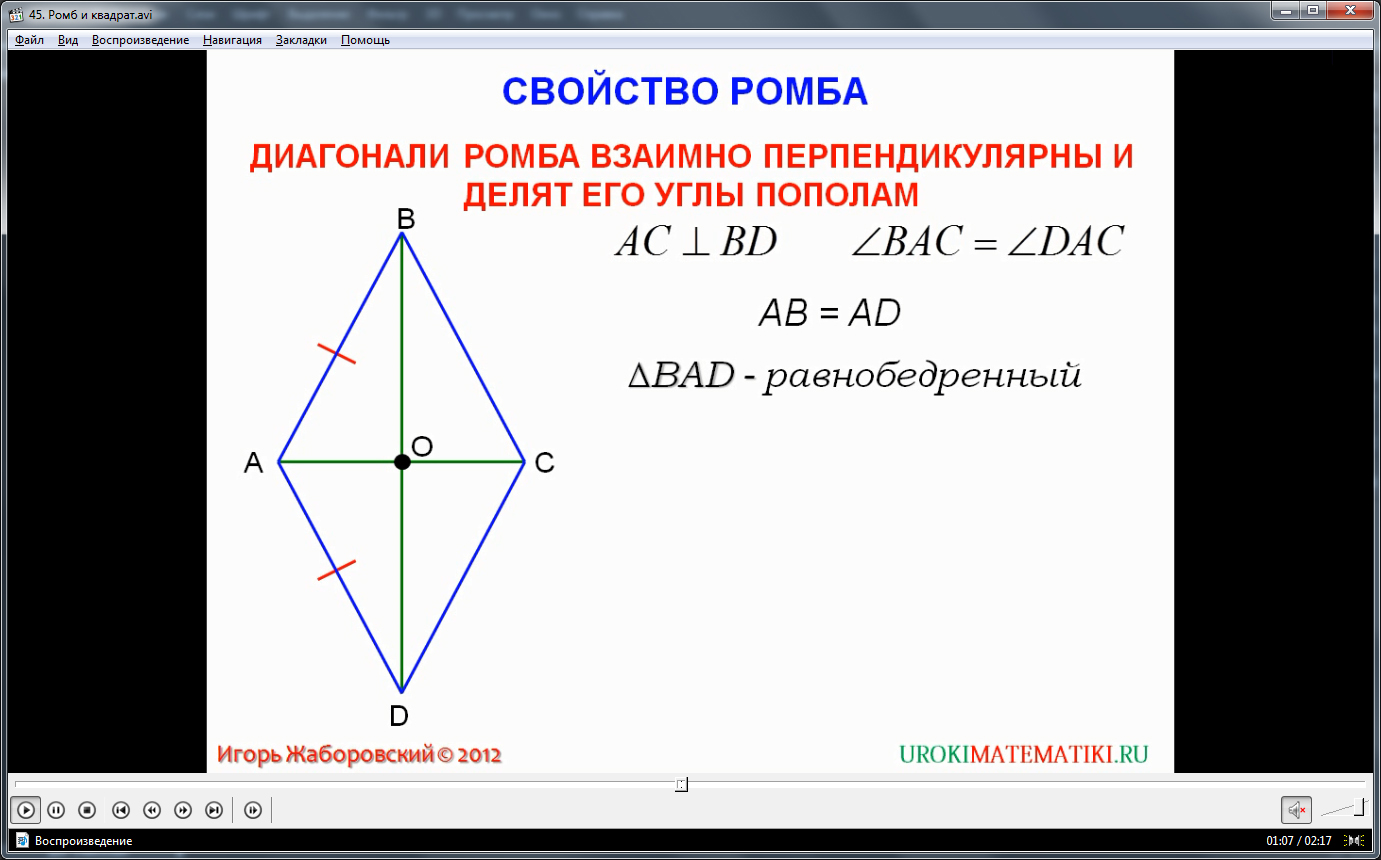 Кроме того, ромб часто изображали на различных гербах. Примером ромба в повседневной жизни может служить баскетбольное поле.
Кроме того, ромб часто изображали на различных гербах. Примером ромба в повседневной жизни может служить баскетбольное поле.
Свойства
- Противолежащие стороны ромба лежат на параллельных прямых и имеют одинаковую длину.
- Пересечение диагоналей ромба происходит под углом 90 о в одной точке, которая является их серединой.
- Диагонали ромба делят угол, из вершины которого они вышли, пополам.
- Исходя из свойств параллелограмма, можно вывести сумму квадратов диагоналей. Согласно формуле она равна стороне, возведенной в квадратичную степень и умноженной на четыре.
Признаки
Мы должны четко понимать, что любой ромб является параллелограммом, но в то же время не любой параллелограмм обладает всеми показателями ромба. Чтобы отличать эти две геометрические фигуры, нужно знать признаки ромба. Ниже перечислены характерные признаки данной геометрической фигуры:
- Две любые стороны с общей вершиной равны.
- Диагонали пересекаются под углом 90 о С.

- Хотя бы одна диагональ делит углы, из точек вершин которых она выходит, пополам.
Формулы площади
Основная формула:
Исходя из свойств параллелограмма:
Исходя из величины угла между двумя смежными сторонами ромба:
Если нам известна длина радиуса окружности, вписанной в ромб:
- S = 4r 2 /(sinα), где:
- S — площадь;
- AB, AC, BD — обозначение сторон;
- H — высота;
- r — радиус окружности;
- sinα — синус альфа.
Периметр
Чтобы вычислить периметр ромба, достаточно лишь умножить длину любой из его сторон на четыре.
Построение рисунка
У некоторых возникают трудности с построением рисунка ромба. Даже если вы уже разобрались с тем, что такое ромб, не всегда ясно, как построить его рисунок аккуратно и с соблюдением необходимых пропорций.
Есть два способа построения рисунка ромба:
- Построить вначале одну диагональ, затем перпендикулярно к ней вторую диагональ, а потом соединить концы отрезков смежных попарно параллельных сторон ромба.

- Отложить вначале одну сторону ромба, затем параллельно ей построить отрезок, равный по длине, и соединить концы этих отрезков также попарно параллельно.
Будьте внимательны при построении — если на рисунке сделаете длину всех сторон ромба одинаковой, вы получите не ромб, а квадрат.
Подписаться на еженедельную рассылку eduction.ru
Теорема о нахождении площади ромба. Четыре формулы, по которым можно вычислить площадь ромба. Свойства ромба. В задаче даны сторона ромба и его высота
Несмотря на то, что математика – царица наук, а арифметика – царица математики, самую большую сложность в изучении у школьников вызывает геометрия. Планиметрия – раздел геометрии, который изучает плоские фигуры. Одной из таких фигур является ромб. Большинство задач по решению четырехугольников сводятся к нахождению их площадей. Систематизируем известные формулы и различные способы расчета площади ромба.
Ромб – это параллелограмм, все четыре стороны которого равны.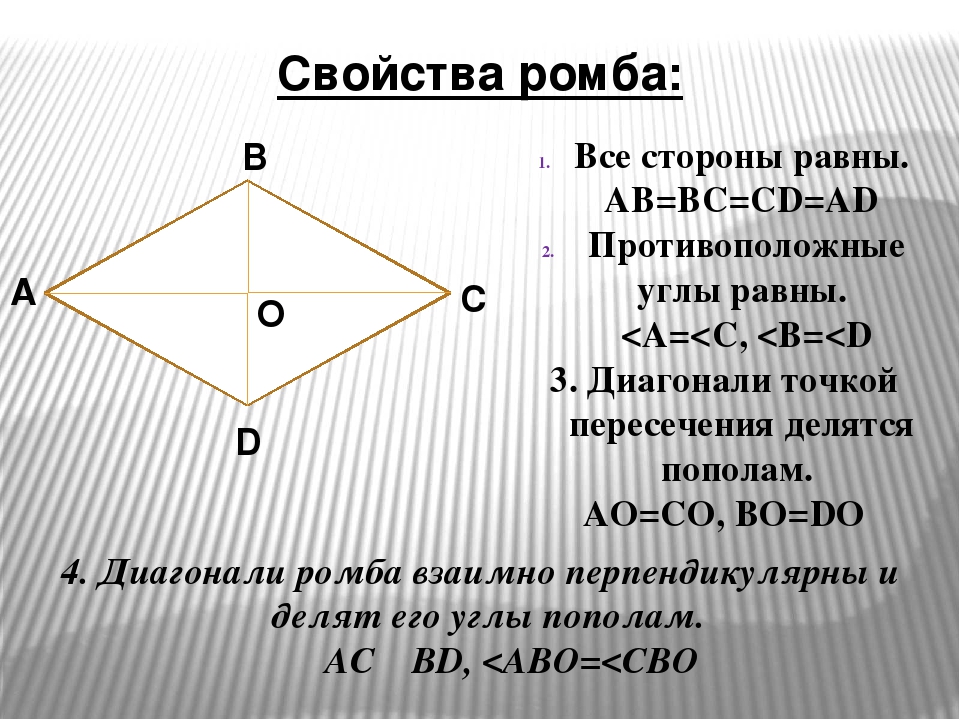 Напомним, что у параллелограмма есть четыре угла и четыре попарно параллельные равные стороны. Как любой четырехугольник, ромб имеет ряд свойств, которые сводятся к следующим: при пересечении диагонали образуют угол, равный 90 градусов (AC ⊥ BD), точка пересечения делит каждую на два равных отрезка. Диагонали ромба также являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого.
Напомним, что у параллелограмма есть четыре угла и четыре попарно параллельные равные стороны. Как любой четырехугольник, ромб имеет ряд свойств, которые сводятся к следующим: при пересечении диагонали образуют угол, равный 90 градусов (AC ⊥ BD), точка пересечения делит каждую на два равных отрезка. Диагонали ромба также являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей. При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты.
Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей. При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты.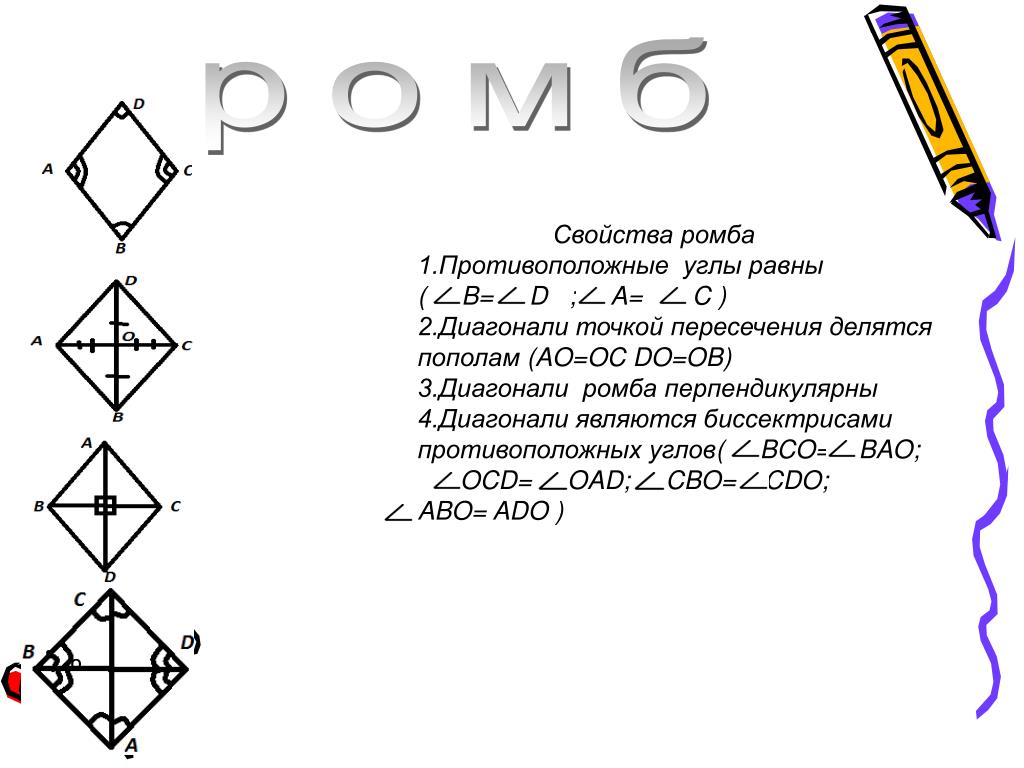 Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.
Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.Как видите, существует множество способов для нахождения площади ромба. Конечно, чтобы запомнить каждый из них, потребуется терпение, внимательность и, конечно же, время. Но в дальнейшем вы сможете легко выбрать метод, подходящий для вашей задачи, и убедитесь, что геометрия – это несложно.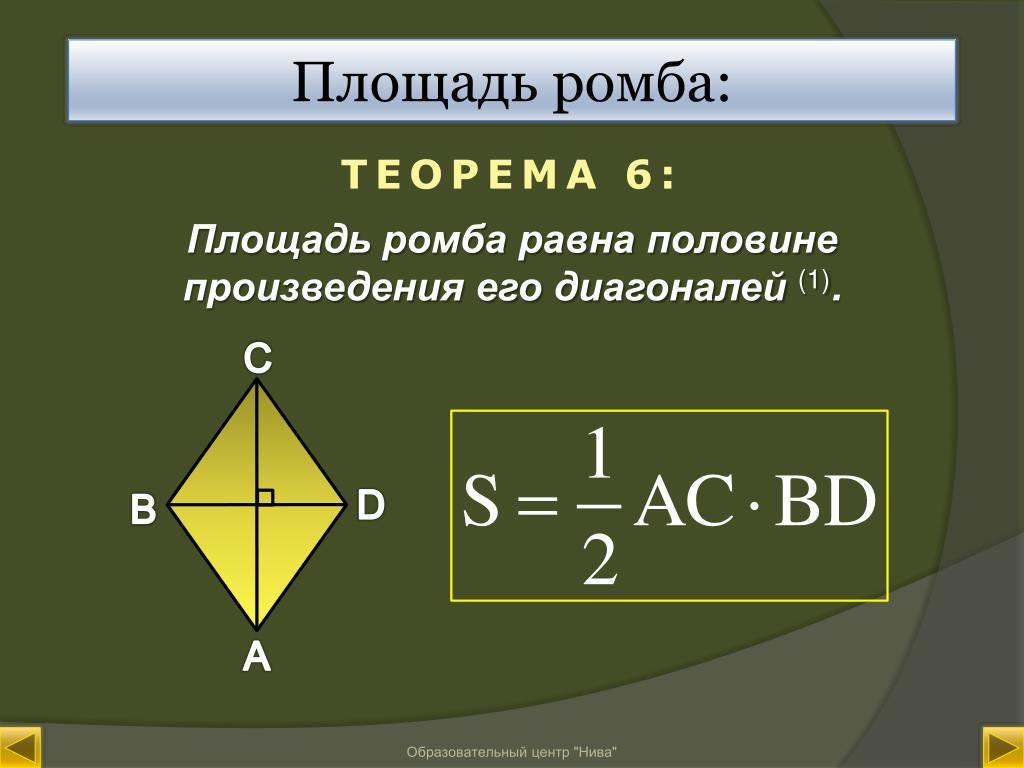
– это параллелограмм, у которого все стороны равны.
Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1
=5 см и d2
=4. Найдем площадь.
Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост.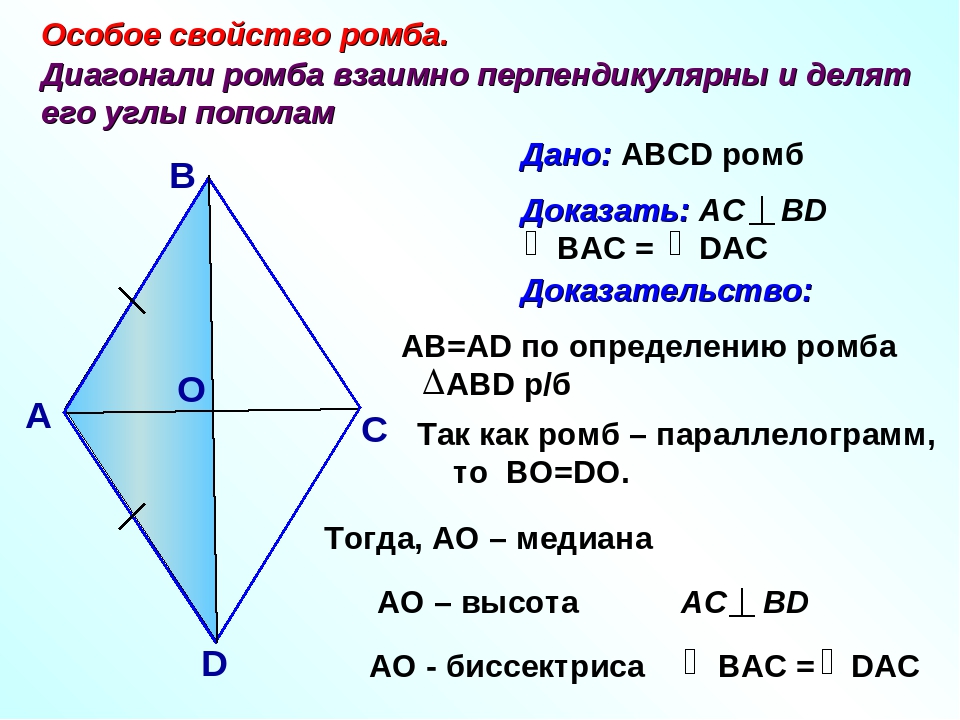 Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Площади ромба через сторону и угол
Формула площади ромба через сторону и угол используется очень часто.
Рассмотрим пример расчета площади ромба через сторону и угол.
Задача: Дан ромб, диагонали которого равны d1
=4 см,d2
=6 см. Острый угол равен α
= 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:
Математика — школьный предмет, который изучается всеми, независимо от профиля класса. Однако она не всеми любима. Порой незаслуженно. Эта наука постоянно подбрасывает ученикам задачи, которые позволяют их мозгу развиваться. Математика отлично справляется с тем, чтобы не дать мыслительным возможностям детей угаснуть. Особенно хорошо с этим справляется один из ее разделов — геометрия.
Особенно хорошо с этим справляется один из ее разделов — геометрия.
Любая из тем, которые в ней изучаются, достойна внимания и уважения. Геометрия — это способ развить пространственное воображение. Примером может служить тема о площадях фигур, в частности ромбов. Эти задачки могут завести в тупик, если не разобраться в деталях. Потому что возможны разные подходы к поиску ответа. Кому-то проще запомнить разные варианты формул, которые написаны ниже, а кто-то способен сам их получить из ранее усвоенного материала. В любом случае безвыходных ситуаций не бывает. Если немного подумать, то решение обязательно найдется.
Ответить на этот вопрос нужно, чтобы понять принципы получения формул и ход рассуждения в задачах. Ведь чтобы разобраться в том, как найти площадь ромба, нужно отчетливо понимать, что это за фигура и каковы ее свойства.
Для удобства рассмотрения параллелограмм, который является четырехугольником с попарно параллельными сторонами, примем за «родителя». У него есть двое «детей»: прямоугольник и ромб.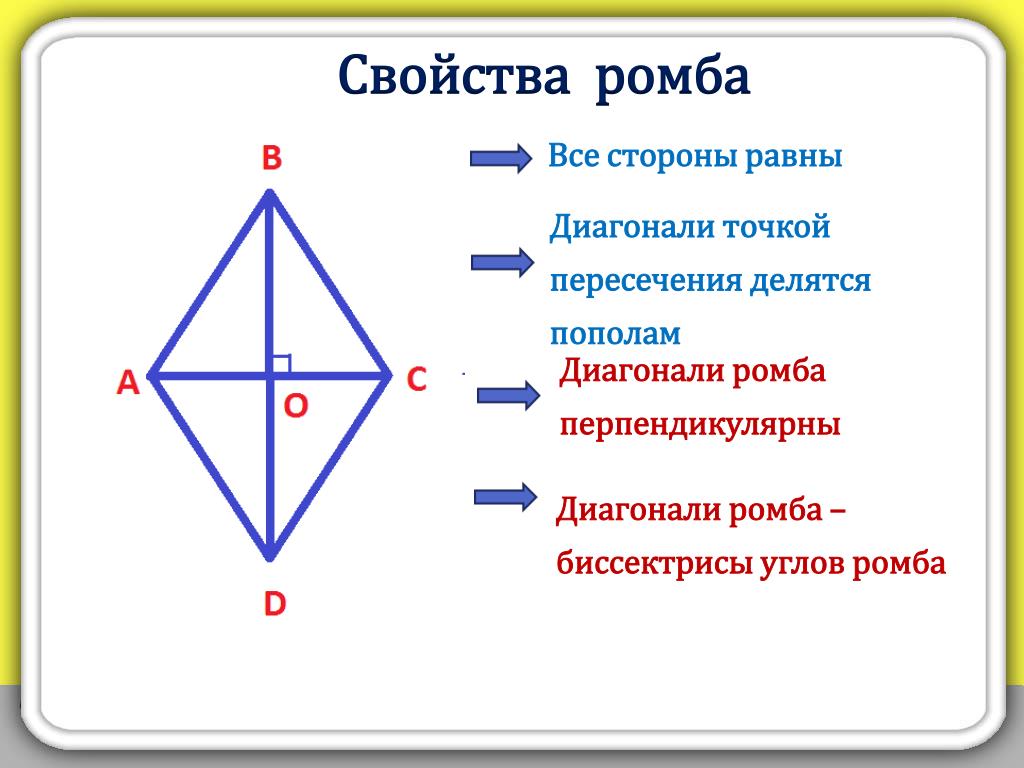 Оба они являются параллелограммами. Если продолжать параллели, то это — «фамилия». Значит, для того чтобы найти площадь ромба, можно воспользоваться уже изученной формулой для параллелограмма.
Оба они являются параллелограммами. Если продолжать параллели, то это — «фамилия». Значит, для того чтобы найти площадь ромба, можно воспользоваться уже изученной формулой для параллелограмма.
Но, как и все дети, ромб имеет и нечто свое. Это немного отличает его от «родителя» и позволяет рассматривать как отдельную фигуру. Ведь прямоугольник не ромб. Возвращаясь к параллелям — они как брат и сестра. В них много общего, но они все же различаются. Эти отличия — их особенные свойства, которыми нужно пользоваться. Было бы странно знать о них и не применять в решении задач.
Если продолжить аналогии и вспомнить еще одну фигуру — квадрат, то она будет продолжением ромба и прямоугольника. В этой фигуре объединены все свойства и одного, и другого.
Свойства ромба
Их пять и они перечислены ниже. Причем некоторые из них повторяют свойства параллелограмма, а какие-то присущи только рассматриваемой фигуре.
- Ромб — это параллелограмм, который принял особую форму.
 Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата. - Диагонали этого четырехугольника пересекаются под углом, который равен 90º. Это удобно и во многом упрощает ход рассуждений при решении задач.
- Другое свойство диагоналей: каждая из них делится точкой пересечения на равные отрезки.
- Лежащие друг напротив друга углы у этой фигуры равны.
- И последнее свойство: диагонали ромба совпадают с биссектрисами углов.
Обозначения, которые приняты в рассмотренных формулах
В математике полагается решать задачи с использованием общих буквенных выражений, которые называются формулами. Тема про площади не является исключением.
Для того чтобы перейти к записям, которые расскажут, как найти площадь ромба, нужно договориться о буквах, которыми заменены все числовые значения элементов фигуры.
Теперь пришла пора написания формул.
Среди данных задачи — только диагонали ромба
Правило утверждает, что для нахождения неизвестной величины нужно перемножить длины диагоналей, а потом произведение разделить пополам. Результат деления — это и есть площадь ромба через диагонали.
Результат деления — это и есть площадь ромба через диагонали.
Формула для этого случая будет выглядеть так:
Пусть эта формула будет идти под номером 1.
В задаче даны сторона ромба и его высота
Чтобы вычислить площадь, потребуется найти произведение этих двух величин. Пожалуй, это самая простая формула. Причем она известна еще из темы про площадь параллелограмма. Там такая формула уже изучалась.
Математическая запись:
Номер этой формулы — 2.
Известны сторона и острый угол
В этом случае нужно возвести в квадрат величину стороны ромба. Потом найти синус угла. И третьим действием вычислить произведение двух образовавшихся величин. Ответом будет площадь ромба.
Буквенное выражение:
Его порядковый номер — 3.
Данные величины: радиус вписанной окружности и острый угол
Для вычисления площади ромба нужно найти квадрат радиуса и умножить его на 4. Определить значение синуса угла. Потом разделить произведение на вторую величину.
Формула принимает такой вид:
Она будет пронумерована цифрой 4.
В задаче фигурируют сторона и радиус вписанной окружности
Чтобы определить, как найти площадь ромба, потребуется вычислить произведение данных величин и числа 2.
Формула для этой задачи будет выглядеть так:
Ее номер по порядку — 5.
Примеры возможных заданий
Задача 1
Одна из диагоналей ромба равна 8, а другая — 14 см. Требуется найти площадь фигуры и длину ее стороны.
Решение
Для нахождения первой величины потребуется формула 1, в которой Д 1 = 8, Д 2 = 14. Тогда площадь вычисляется так: (8 * 14) / 2 = 56 (см 2).
Диагонали делят ромб на 4 треугольника. Каждый из них обязательно будет прямоугольным. Этим нужно воспользоваться, чтобы определить значение второй неизвестной. Сторона ромба станет гипотенузой треугольника, а катетами будут половины диагоналей.
Тогда а 2 = (Д 1 /2) 2 + (Д 2 /2) 2 . После подстановки всех значений получается: а 2 = (8 / 2) 2 + (14 / 2) 2 = 16 + 49 = 65..jpg) Но это квадрат стороны. Значит, нужно извлечь квадратный корень из 65. Тогда длина стороны будет приблизительно равна 8,06 см.
Но это квадрат стороны. Значит, нужно извлечь квадратный корень из 65. Тогда длина стороны будет приблизительно равна 8,06 см.
Ответ: площадь 56 см 2 , а сторона 8,06 см.
Задача 2
Сторона ромба имеет значение, равное 5,5 дм, а его высота — 3,5 дм. Найти площадь фигуры.
Решение
Для того чтобы найти ответ нужна будет формула 2. В ней а = 5,5, Н = 3,5. Тогда, заменив в формуле буквы на числа, получим, что искомая величина равна 5,5 * 3,5 = 19,25 (дм 2).
Ответ: площадь ромба равна 19,25 дм 2 .
Задача 3
Острый угол у некоторого ромба равен 60º, а его меньшая диагональ — 12 см. Требуется вычислить его площадь.
Решение
Чтобы получить результат, нужна будет формула под номером 3. В ней вместо А будет 60, а значение а неизвестно.
Для нахождения стороны ромба потребуется вспомнить теорему синусов. В прямоугольном треугольнике а будет гипотенузой, меньший катет равен половине диагонали, а угол делится пополам (известно из свойства, где упоминается биссектриса).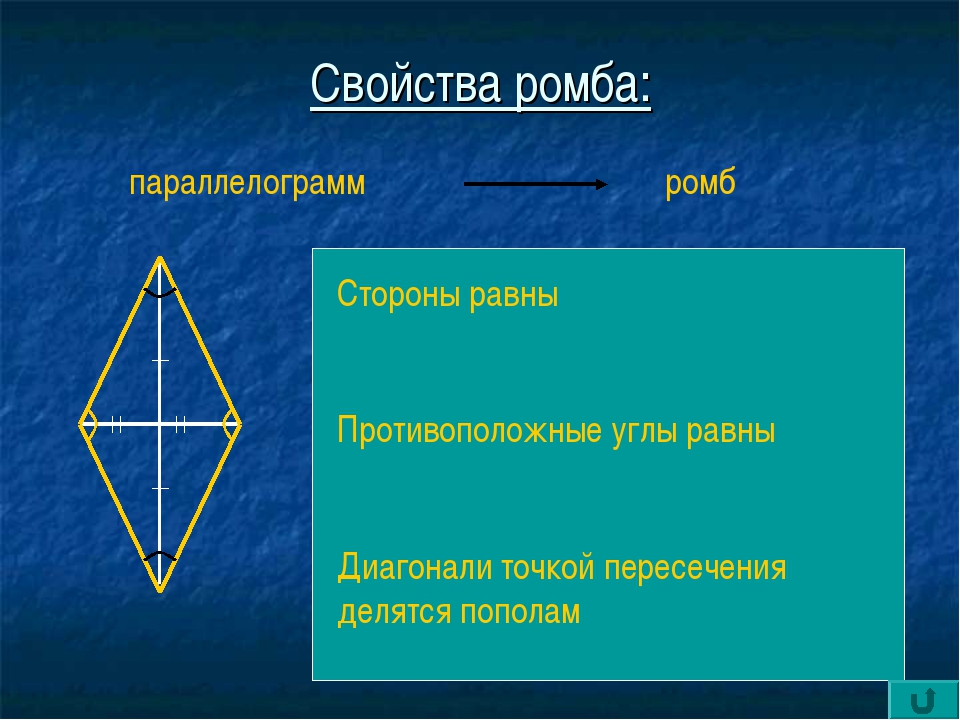
Тогда сторона а будет равна произведению катета на синус угла.
Катет нужно вычислить как Д/2 = 12/2 = 6 (см). Синус(А/2) будет равен его значению для угла 30º, то есть 1/2.
Выполнив несложные вычисления, получим такое значение стороны ромба: а = 3 (см).
Теперь площадь — это произведение 3 2 и синуса 60º, то есть 9 * (√3)/2 = (9√3)/2 (см 2).
Ответ: искомая величина равна (9√3)/2 см 2 .
Итоги: все возможно
Здесь были рассмотрены некоторые варианты того, как найти площадь ромба. Если в задаче напрямую непонятно, какую формулу использовать, то нужно немного подумать и попробовать связать ранее изученные темы. В других темах обязательно найдется подсказка, которая поможет связать известные величины с теми, что есть в формулах. И задача решится. Главное — помнить, что все раньше изученное можно и нужно использовать.
Кроме предложенных заданий, возможны и обратные задачи, когда по площади фигуры нужно вычислить значение какого-либо элемента ромба. Тогда нужно воспользоваться тем уравнением, которое ближе всего к условию. А потом преобразовать формулу, оставив в левой части равенства неизвестную величину.
Тогда нужно воспользоваться тем уравнением, которое ближе всего к условию. А потом преобразовать формулу, оставив в левой части равенства неизвестную величину.
– это параллелограмм , у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны .
Площадь ромба можно найти, также зная его диагонали . Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника . Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если в распоряжении только угол и сторона , то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба.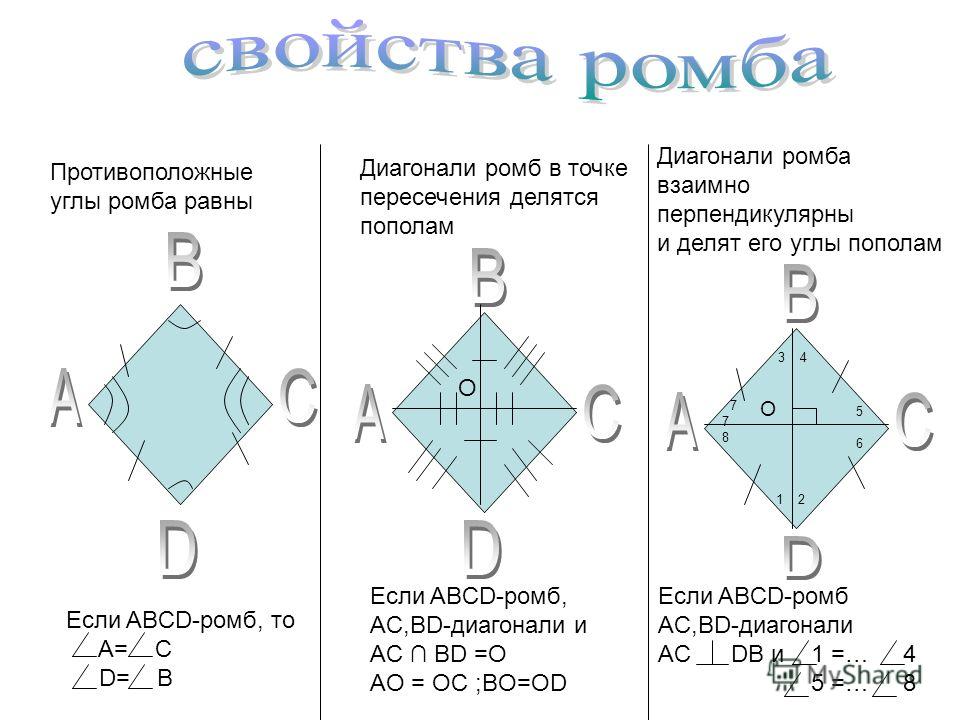 Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника . Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:
Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника . Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:
Если внутри ромба вписать окружность , то его радиус будет относиться к стороне под углом 90° , что значит, что удвоенный радиус будет равен высоте ромба . Подставив вместо высоты h=2r в предыдущую формулу, получим площадь S=ha=2ra
Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом. Тогда сторона a может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит
В школьном курсе в геометрии среди основных задач значительное внимание уделено примерам вычисления площади и периметра ромба. Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD
. Ниже приведен рисунок на котором изображен ромб.
Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD
. Ниже приведен рисунок на котором изображен ромб.
Поскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.

- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.
- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а ).
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S)
ромба и величина острого угла (alpha)
то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
Она достаточно проста для того чтобы запомнить, а также — для вычислений.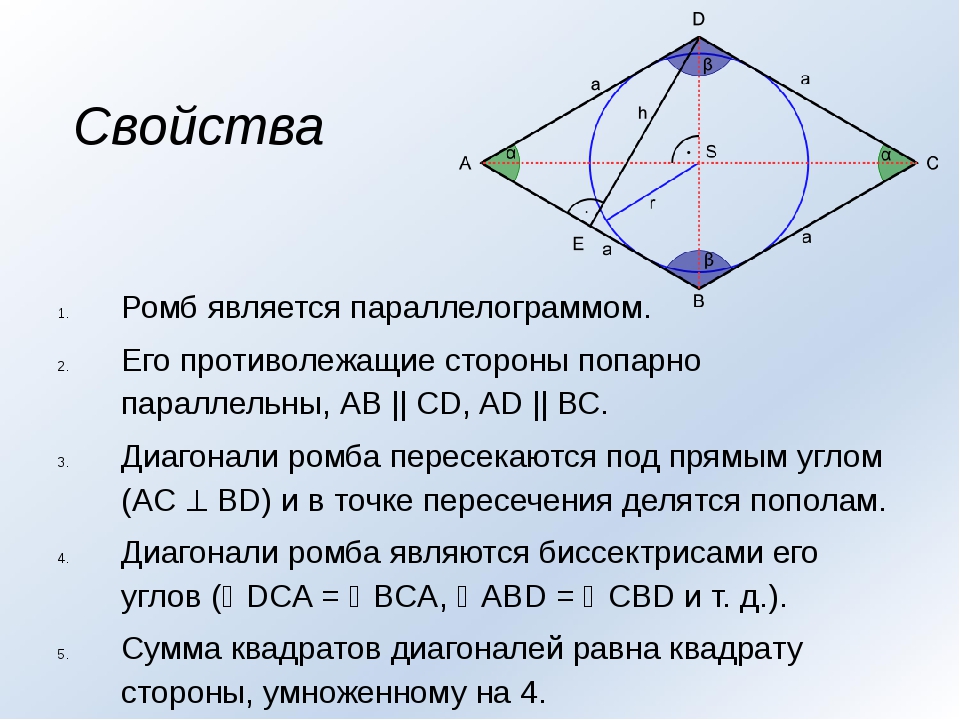
Третья формула площади имеет смысл когда известен угол между сторонами. Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Ромб и квадрат
Давайте ещё раз вспомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. А прямоугольник – это параллелограмм, у которого все углы прямые.
На этом уроке мы поговорим о таких геометрических фигурах как ромб и квадрат.
Итак, ромб – это параллелограмм, у которого все стороны равны.
Так как ромб является параллелограммом, то он обладает всеми его свойствами, о которых мы с вами говорили на предыдущих уроках.
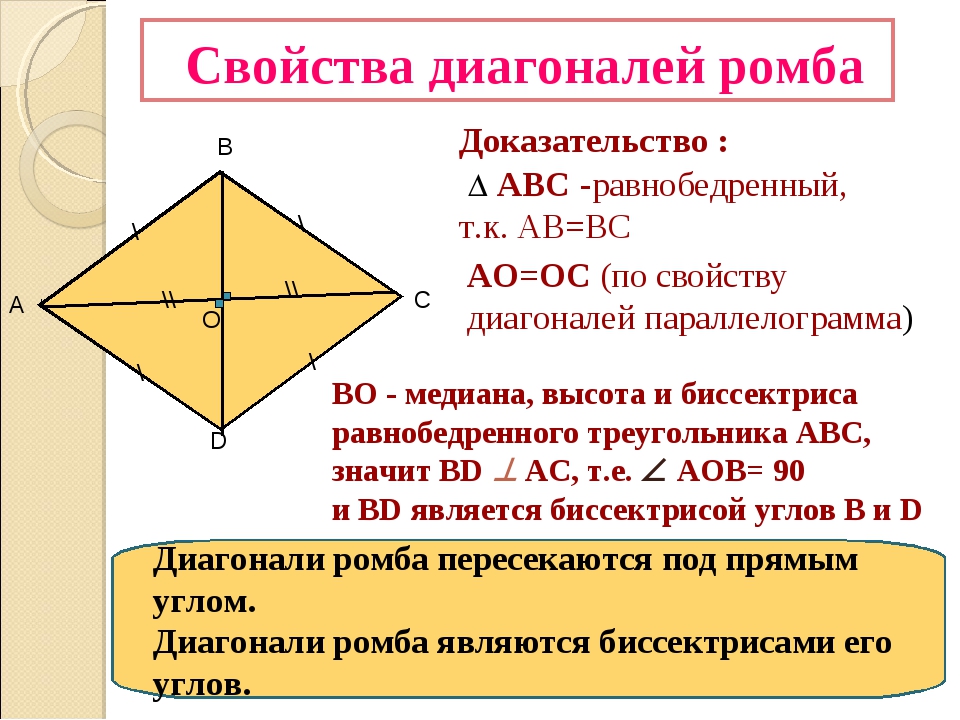
Теорема. Свойства диагоналей ромба. У
ромба диагонали взаимно перпендикулярны и лежат на биссектрисах его углов.
Доказательство.
Рассмотрим .
, следовательно, – медиана.
.
– равнобедренный.
Медиана – биссектриса, высота.
Следовательно, диагональ и лежит на биссектрисе .
Что и требовалось доказать.
Теперь сформулируем и докажем признаки ромба.
Теорема. Признак ромба. Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм – ромб.
Доказательство.
Рассмотрим и .
Сторона – общая, , так как диагонали т. делятся пополам
по двум катетам.
Следовательно, .
, .
Следовательно, .
– ромб.
Что и требовалось доказать.
И ещё один признак.
Теорема. Признак ромба. Если у параллелограмма одна из диагоналей лежит на биссектрисе угла, то этот параллелограмм – ромб.
Доказательство.
.
как накр. лежащие при и секущей .
Следовательно, .
– равнобедренный, то есть .
,.
Следовательно, .
– ромб.
Что и требовалось доказать.
Задача. Чему равны углы ромба, если его меньшая диагональ равна стороне?
Решение.
– равносторонний.
.
,
.
Ответ: , , , .
Решим ещё одну задачу.
Задача. В ромбе перпендикуляр , проведённый из вершины делит сторону пополам. Найдите градусную меру .
Решение.
– прямоугольный.
.
, то есть .
.
, – внутр. одностор. при и секущей .
.
Так как , то .
.
.
Ответ: .
Теперь поговорим о квадрате.
Квадрат – это
прямоугольник, у которого все стороны равны. Также можно сказать, что квадрат
– это ромб, у которого все углы прямые.
Также можно сказать, что квадрат
– это ромб, у которого все углы прямые.
Эти два определения равносильны. Из каждого следует, что квадрат – это параллелограмм, который одновременно является и прямоугольником, и ромбом.
Следовательно, квадрат обладает всеми свойствами и прямоугольника, и ромба.
Основные свойства квадрата:
1.Все углы квадрата прямые.
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и лежат на биссектрисах его углов.
Задача. На рисунке – квадрат, . Найдите .
Решение.
.
, – смежные, то есть .
Так как , то .
.
– равнобедренный, тогда .
,
,
,
.
,,
то есть ,.
Ответ: ,.
Основание ромба формула.
 Как найти площадь ромба
Как найти площадь ромба– это параллелограмм, у которого все стороны равны.
Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1
=5 см и d2
=4. Найдем площадь.
Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост.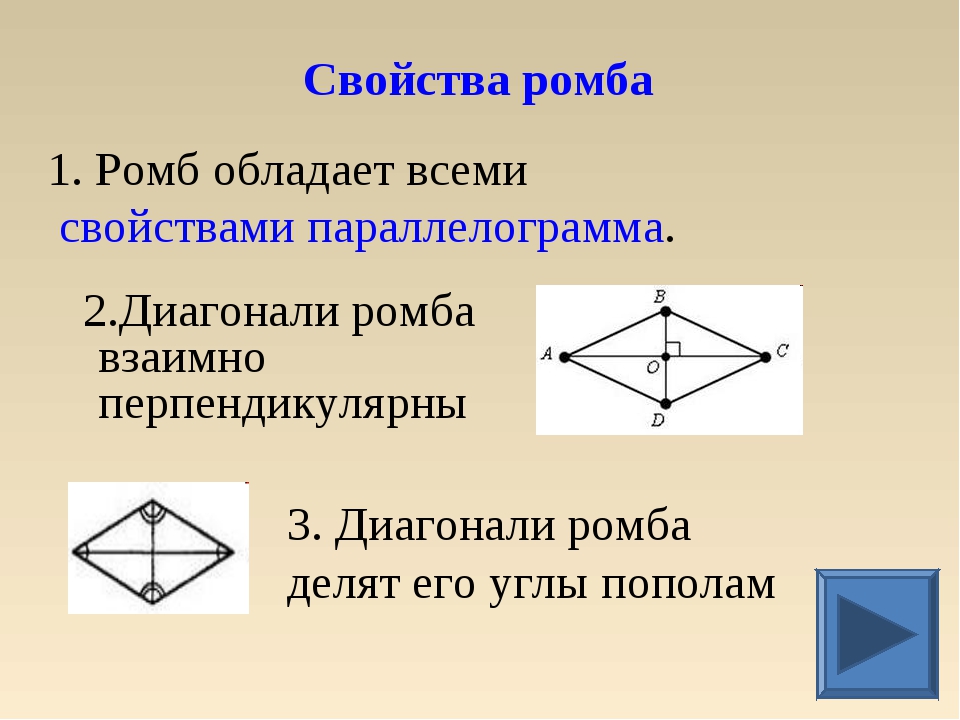 Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Площади ромба через сторону и угол
Формула площади ромба через сторону и угол используется очень часто.
Рассмотрим пример расчета площади ромба через сторону и угол.
Задача: Дан ромб, диагонали которого равны d1
=4 см,d2
=6 см. Острый угол равен α
= 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:
Математика — школьный предмет, который изучается всеми, независимо от профиля класса. Однако она не всеми любима. Порой незаслуженно. Эта наука постоянно подбрасывает ученикам задачи, которые позволяют их мозгу развиваться. Математика отлично справляется с тем, чтобы не дать мыслительным возможностям детей угаснуть.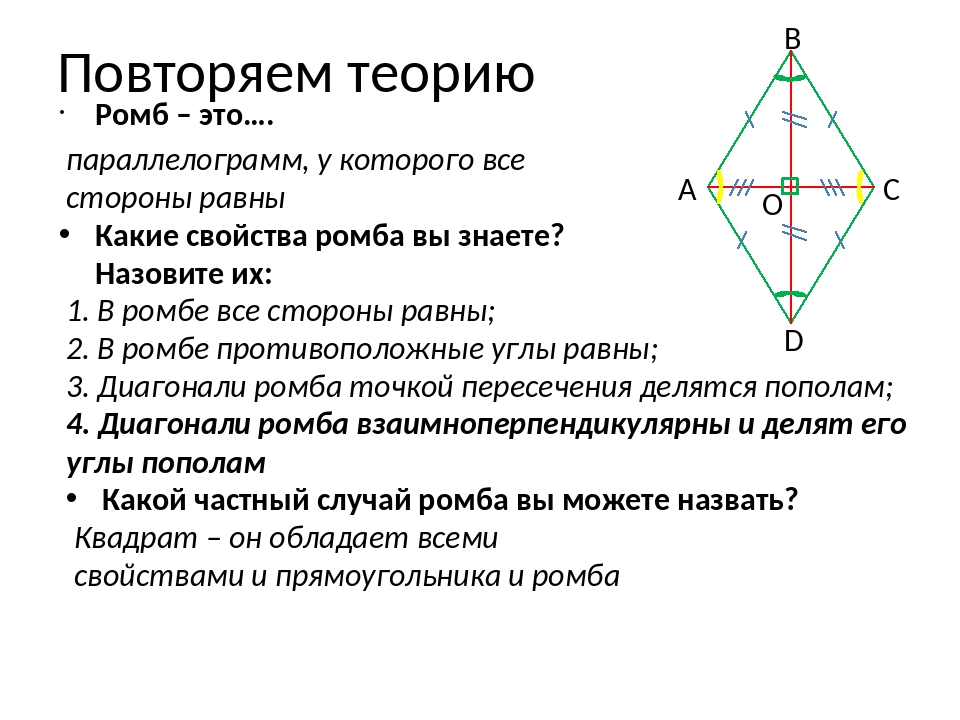 Особенно хорошо с этим справляется один из ее разделов — геометрия.
Особенно хорошо с этим справляется один из ее разделов — геометрия.
Любая из тем, которые в ней изучаются, достойна внимания и уважения. Геометрия — это способ развить пространственное воображение. Примером может служить тема о площадях фигур, в частности ромбов. Эти задачки могут завести в тупик, если не разобраться в деталях. Потому что возможны разные подходы к поиску ответа. Кому-то проще запомнить разные варианты формул, которые написаны ниже, а кто-то способен сам их получить из ранее усвоенного материала. В любом случае безвыходных ситуаций не бывает. Если немного подумать, то решение обязательно найдется.
Ответить на этот вопрос нужно, чтобы понять принципы получения формул и ход рассуждения в задачах. Ведь чтобы разобраться в том, как найти площадь ромба, нужно отчетливо понимать, что это за фигура и каковы ее свойства.
Для удобства рассмотрения параллелограмм, который является четырехугольником с попарно параллельными сторонами, примем за «родителя». У него есть двое «детей»: прямоугольник и ромб. Оба они являются параллелограммами. Если продолжать параллели, то это — «фамилия». Значит, для того чтобы найти площадь ромба, можно воспользоваться уже изученной формулой для параллелограмма.
Оба они являются параллелограммами. Если продолжать параллели, то это — «фамилия». Значит, для того чтобы найти площадь ромба, можно воспользоваться уже изученной формулой для параллелограмма.
Но, как и все дети, ромб имеет и нечто свое. Это немного отличает его от «родителя» и позволяет рассматривать как отдельную фигуру. Ведь прямоугольник не ромб. Возвращаясь к параллелям — они как брат и сестра. В них много общего, но они все же различаются. Эти отличия — их особенные свойства, которыми нужно пользоваться. Было бы странно знать о них и не применять в решении задач.
Если продолжить аналогии и вспомнить еще одну фигуру — квадрат, то она будет продолжением ромба и прямоугольника. В этой фигуре объединены все свойства и одного, и другого.
Свойства ромба
Их пять и они перечислены ниже. Причем некоторые из них повторяют свойства параллелограмма, а какие-то присущи только рассматриваемой фигуре.
- Ромб — это параллелограмм, который принял особую форму.
 Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата. - Диагонали этого четырехугольника пересекаются под углом, который равен 90º. Это удобно и во многом упрощает ход рассуждений при решении задач.
- Другое свойство диагоналей: каждая из них делится точкой пересечения на равные отрезки.
- Лежащие друг напротив друга углы у этой фигуры равны.
- И последнее свойство: диагонали ромба совпадают с биссектрисами углов.
Обозначения, которые приняты в рассмотренных формулах
В математике полагается решать задачи с использованием общих буквенных выражений, которые называются формулами. Тема про площади не является исключением.
Для того чтобы перейти к записям, которые расскажут, как найти площадь ромба, нужно договориться о буквах, которыми заменены все числовые значения элементов фигуры.
Теперь пришла пора написания формул.
Среди данных задачи — только диагонали ромба
Правило утверждает, что для нахождения неизвестной величины нужно перемножить длины диагоналей, а потом произведение разделить пополам.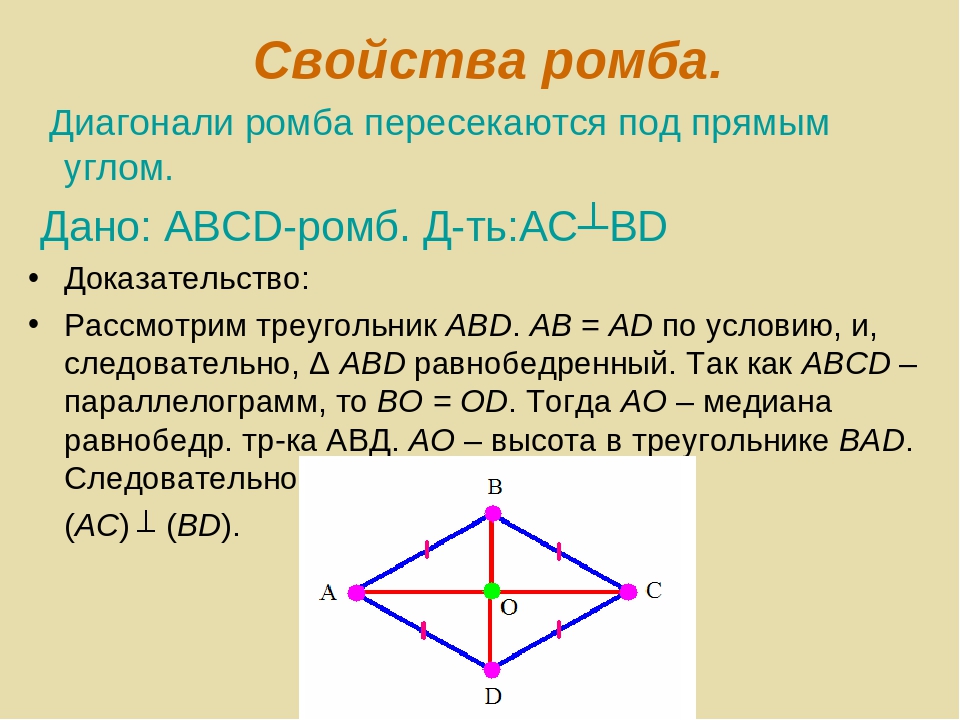 Результат деления — это и есть площадь ромба через диагонали.
Результат деления — это и есть площадь ромба через диагонали.
Формула для этого случая будет выглядеть так:
Пусть эта формула будет идти под номером 1.
В задаче даны сторона ромба и его высота
Чтобы вычислить площадь, потребуется найти произведение этих двух величин. Пожалуй, это самая простая формула. Причем она известна еще из темы про площадь параллелограмма. Там такая формула уже изучалась.
Математическая запись:
Номер этой формулы — 2.
Известны сторона и острый угол
В этом случае нужно возвести в квадрат величину стороны ромба. Потом найти синус угла. И третьим действием вычислить произведение двух образовавшихся величин. Ответом будет площадь ромба.
Буквенное выражение:
Его порядковый номер — 3.
Данные величины: радиус вписанной окружности и острый угол
Для вычисления площади ромба нужно найти квадрат радиуса и умножить его на 4. Определить значение синуса угла. Потом разделить произведение на вторую величину.
Формула принимает такой вид:
Она будет пронумерована цифрой 4.
В задаче фигурируют сторона и радиус вписанной окружности
Чтобы определить, как найти площадь ромба, потребуется вычислить произведение данных величин и числа 2.
Формула для этой задачи будет выглядеть так:
Ее номер по порядку — 5.
Примеры возможных заданий
Задача 1
Одна из диагоналей ромба равна 8, а другая — 14 см. Требуется найти площадь фигуры и длину ее стороны.
Решение
Для нахождения первой величины потребуется формула 1, в которой Д 1 = 8, Д 2 = 14. Тогда площадь вычисляется так: (8 * 14) / 2 = 56 (см 2).
Диагонали делят ромб на 4 треугольника. Каждый из них обязательно будет прямоугольным. Этим нужно воспользоваться, чтобы определить значение второй неизвестной. Сторона ромба станет гипотенузой треугольника, а катетами будут половины диагоналей.
Тогда а 2 = (Д 1 /2) 2 + (Д 2 /2) 2 . После подстановки всех значений получается: а 2 = (8 / 2) 2 + (14 / 2) 2 = 16 + 49 = 65. Но это квадрат стороны. Значит, нужно извлечь квадратный корень из 65. Тогда длина стороны будет приблизительно равна 8,06 см.
Но это квадрат стороны. Значит, нужно извлечь квадратный корень из 65. Тогда длина стороны будет приблизительно равна 8,06 см.
Ответ: площадь 56 см 2 , а сторона 8,06 см.
Задача 2
Сторона ромба имеет значение, равное 5,5 дм, а его высота — 3,5 дм. Найти площадь фигуры.
Решение
Для того чтобы найти ответ нужна будет формула 2. В ней а = 5,5, Н = 3,5. Тогда, заменив в формуле буквы на числа, получим, что искомая величина равна 5,5 * 3,5 = 19,25 (дм 2).
Ответ: площадь ромба равна 19,25 дм 2 .
Задача 3
Острый угол у некоторого ромба равен 60º, а его меньшая диагональ — 12 см. Требуется вычислить его площадь.
Решение
Чтобы получить результат, нужна будет формула под номером 3. В ней вместо А будет 60, а значение а неизвестно.
Для нахождения стороны ромба потребуется вспомнить теорему синусов. В прямоугольном треугольнике а будет гипотенузой, меньший катет равен половине диагонали, а угол делится пополам (известно из свойства, где упоминается биссектриса).
Тогда сторона а будет равна произведению катета на синус угла.
Катет нужно вычислить как Д/2 = 12/2 = 6 (см). Синус(А/2) будет равен его значению для угла 30º, то есть 1/2.
Выполнив несложные вычисления, получим такое значение стороны ромба: а = 3 (см).
Теперь площадь — это произведение 3 2 и синуса 60º, то есть 9 * (√3)/2 = (9√3)/2 (см 2).
Ответ: искомая величина равна (9√3)/2 см 2 .
Итоги: все возможно
Здесь были рассмотрены некоторые варианты того, как найти площадь ромба. Если в задаче напрямую непонятно, какую формулу использовать, то нужно немного подумать и попробовать связать ранее изученные темы. В других темах обязательно найдется подсказка, которая поможет связать известные величины с теми, что есть в формулах. И задача решится. Главное — помнить, что все раньше изученное можно и нужно использовать.
Кроме предложенных заданий, возможны и обратные задачи, когда по площади фигуры нужно вычислить значение какого-либо элемента ромба.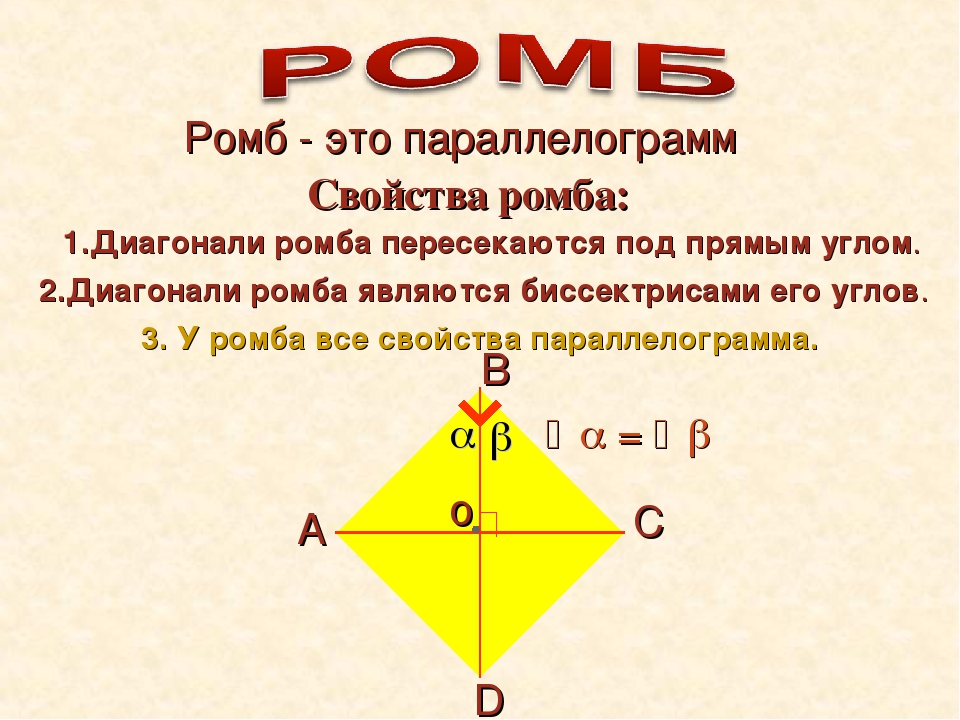 Тогда нужно воспользоваться тем уравнением, которое ближе всего к условию. А потом преобразовать формулу, оставив в левой части равенства неизвестную величину.
Тогда нужно воспользоваться тем уравнением, которое ближе всего к условию. А потом преобразовать формулу, оставив в левой части равенства неизвестную величину.
Несмотря на то, что математика – царица наук, а арифметика – царица математики, самую большую сложность в изучении у школьников вызывает геометрия. Планиметрия – раздел геометрии, который изучает плоские фигуры. Одной из таких фигур является ромб. Большинство задач по решению четырехугольников сводятся к нахождению их площадей. Систематизируем известные формулы и различные способы расчета площади ромба.
Ромб – это параллелограмм, все четыре стороны которого равны. Напомним, что у параллелограмма есть четыре угла и четыре попарно параллельные равные стороны. Как любой четырехугольник, ромб имеет ряд свойств, которые сводятся к следующим: при пересечении диагонали образуют угол, равный 90 градусов (AC ⊥ BD), точка пересечения делит каждую на два равных отрезка. Диагонали ромба также являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей.
д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень. Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей. При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета.
При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 . Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла. Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.
Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.Как видите, существует множество способов для нахождения площади ромба. Конечно, чтобы запомнить каждый из них, потребуется терпение, внимательность и, конечно же, время. Но в дальнейшем вы сможете легко выбрать метод, подходящий для вашей задачи, и убедитесь, что геометрия – это несложно.
В школьном курсе в геометрии среди основных задач значительное внимание уделено примерам вычисления площади и периметра ромба. Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD
. Ниже приведен рисунок на котором изображен ромб.
Ниже приведен рисунок на котором изображен ромб.
Поскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.
- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.

- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а ).
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.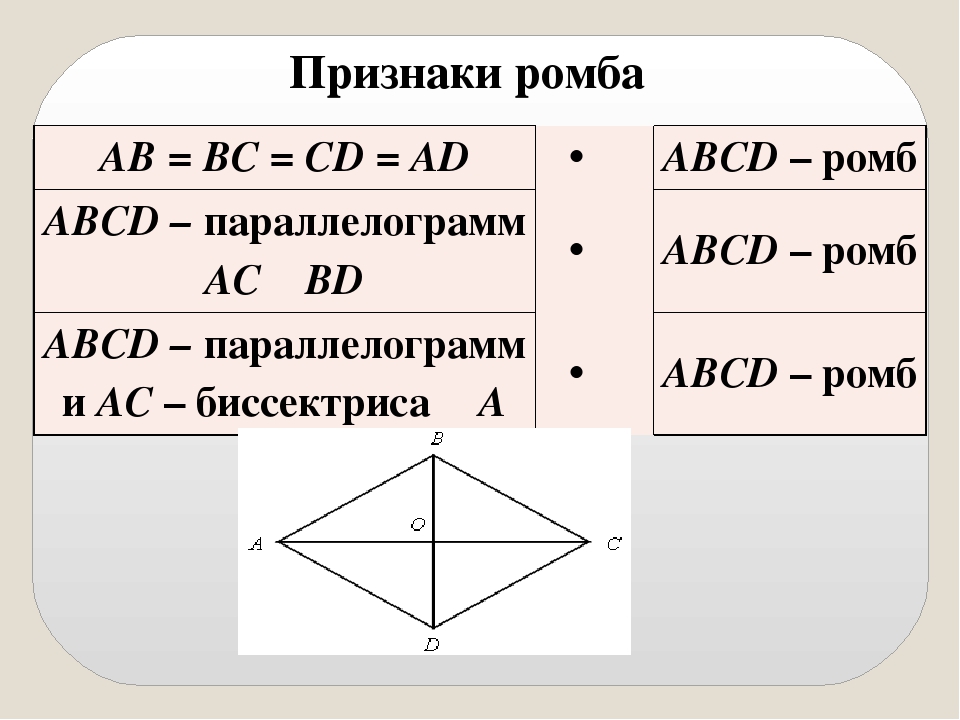
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S)
ромба и величина острого угла (alpha)
то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
Она достаточно проста для того чтобы запомнить, а также — для вычислений.
Третья формула площади имеет смысл когда известен угол между сторонами. {2} \cdot sin(\alpha) \]
{2} \cdot sin(\alpha) \]
3. Площадь ромба также равна полупроизведению диагоналей, то есть:
\[ S = \dfrac{d_{1} \cdot d_{2} }{2} \]
4. Если известен радиус r окружности, вписанной в ромб, и сторона ромба a , то его площадь вычисляется по формуле:
\[ S = 2 \cdot a \cdot R \]
Свойства ромба
На рисунке выше \(ABCD \) — ромб, \(AC = DB = CD = AD \) . Так как ромб — это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:
\[ r = \frac{ AH }{2} \]
Свойства ромба
Диагонали ромба перпендикулярны;
Диагонали ромба являются биссектрисами его углов.
Признаки ромба
Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Вершины ромба свойства. Ромб как геометрическая фигура. Краткое изложение и основные формулы
краткое содержание других презентаций«Задачи на признаки подобия треугольников» — Подобие треугольников. Определение высоты предмета по зеркалу. Определение высоты предмета по луже. Решение практических задач. Тень от палки. Определение высоты предмета. Измерение высоты больших объектов. Девиз урока. Решение задач по готовым чертежам. Самостоятельная работа. Гимнастика для глаз. Способ Фалеса. Индивидуальная карта. Определение высоты пирамиды. Назвать подобные треугольники.
«Свойства четырёхугольников» — Названия четырехугольников. Все углы прямые. Свойства четырехугольников. Трапеция. Квадратом называется прямоугольник, у которого все стороны равны. Элементы параллелограмма. Диагонали делят углы пополам. Четырехугольник. Диктант. Диагональ. Противоположные углы. Помогите Незнайке исправить двойку. Исторические сведения. Четырехугольники и их свойства. Диагонали. Ромб. Противоположные стороны. Стороны.
Противоположные углы. Помогите Незнайке исправить двойку. Исторические сведения. Четырехугольники и их свойства. Диагонали. Ромб. Противоположные стороны. Стороны.
«Ромб» — Признаки. Периметр. Появление ромба. Сказка про ромб. Ромб. Ромб, в котором проведены диагонали. Что такое ромб. Формула площади. Интересные факты. Свойства ромба. Ромб в жизни.
«Решение теоремы Пифагора» — Доказательство методом разложения. Площадь квадрата. Простейшее доказательство. Доказательство Перигаля. Пифагорейцы. Диагональ. Доказательство 9 века н.э. Последователи. Высота. Диаметр. Полноценное доказательство. Мотив. Шестиугольники. Доказательство методом вычитания. Квадрат. Прямоугольник. Возможности применения теоремы. Доказательство Гутхейля. Применение теоремы. Задача о лотосе. История теоремы.
««Площадь прямоугольника» 8 класс» — Площадь квадрата равна квадрату его стороны. Площадь. Найдите площадь и периметр квадрата. Единицы измерения площадей. Многоугольник составлен из нескольких многоугольников. Найти площадь треугольника. Стороны каждого из прямоугольников. Единицы. Найдите площадь квадрата. АBCD и DСМK – квадраты. Площадь ромба равна половине произведения его диагоналей. На стороне АВ построен параллелограмм. Найдите площадь шестиугольника.
Найти площадь треугольника. Стороны каждого из прямоугольников. Единицы. Найдите площадь квадрата. АBCD и DСМK – квадраты. Площадь ромба равна половине произведения его диагоналей. На стороне АВ построен параллелограмм. Найдите площадь шестиугольника.
««Трапеция» 8 класс» — Трапециевидные мышцы обеих сторон спины вместе имеют форму трапеции. Задания для устной работы. Являются ли четырёхугольники трапециями. Свойства равнобедренной трапеции. Признаки равнобедренной трапеции. Виды трапеций. Площадь трапеции. Элементы трапеции. Определение. Средняя линия трапеции. Трапеция. Геометрическая фигура была названа так по внешнему сходству с маленьким столом.
Ромб – одна из простейших геометрических фигур. Мы настолько часто встречаемся с ромбом в геометрических задачках, что слова «фантастика» и «ромб» кажутся для нас несовместимыми понятиями. А между тем, удивительное, как говорится, рядом… в Британии. Но для начала, давайте вспомним, что же такое «ромб», его признаки и свойства.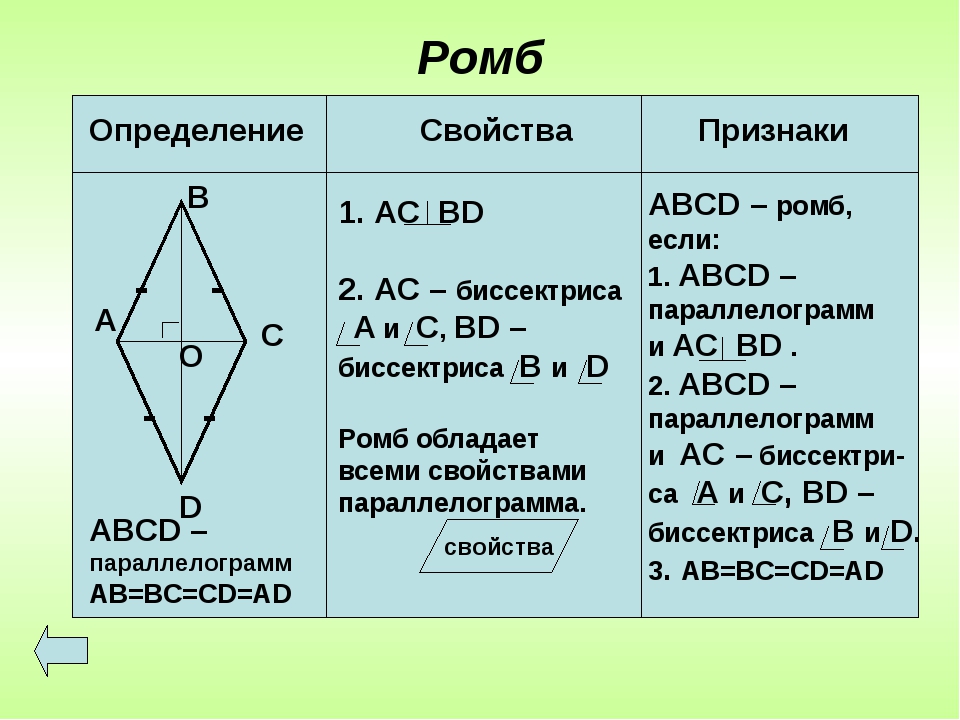
Термин «ромб» в переводе с древнегреческого означает «бубен». И это не случайно. А дело вот в чем. Бубен хоть раз в жизни, но видели все. И все знают, что он круглый. Но давным-давно бубны делали как раз в форме квадрата или ромба. Более того, название масти бубны также связанно именно с этим фактом.
Из геометрии мы представляем, как выглядит ромб. Это четырехугольник, который изображается в виде как бы наклоненного квадрата. Но путать ромб и квадрат ни в коем случае нельзя. Правильнее сказать, что ромб – это частный случай параллелограмма. Отличие лишь в том, что все стороны ромба равны. Чтобы быстро и верно решать задачи по геометрии, необходимо помнить о свойствах ромба. К слову, ромб обладает всеми свойствами параллелограмма. Итак:
Свойства ромба:
- противолежащие стороны равны;
- противоположные углы равны;
- диагонали ромба пересекаются под прямым и в точке пересечения делятся пополам;
- сумма углов, прилежащих к одной стороне, равна 180°;
- сумма квадратов диагоналей равна сумме квадратов всех сторон;
- диагонали являются биссектрисами его углов.

Признаки ромба:
- если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб;
- если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.
И еще один важный момент, без знания которого не возможно успешно решить задачку, – формулы. Ниже представлены формулы для нахождения площади любого ромба, которые употребляются в зависимости от известных данных: высота, диагональ, сторона, радиус вписанной окружности. В следующих формулах приняты условные обозначения: a – сторона ромба, h a – высота, проведенная к стороне а, а – угол между сторонами, d 1 d 2 – диагонали ромба.
Основные формулы:
S = a 2 sin а
S = 1/2 (d 1 d 2)
S = 4r 2 / sin a
Есть еще одна формула, которая употребляется не так часто, но полезна:
d 1 2 + d 2 2 = 4a 2 или сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
А теперь самое время вернуться к самому началу. Что же такого удивительного может быть в этой фигурке? Оказывается, в XIX веке при археологических раскопках был найден ромб. Да не простой, а золотой, при чем, в самом прямом смысле этого слова! Эта находка из великобританского кургана Баш была найдена в районе Уилсфорда, неподалёку от знаменитого Стоунхенджа. Загадочный ромб представляет собой отполированную пластинку, на которой выгравированы необычные узоры. Размер его 15,2 х 17,8 см (ромб лишь с небольшой оговоркой). У пластины кроме окантовки есть еще три меньших ромбовидных узора, которые якобы вложены друг в друга. При этом, в центре последнего выгравирована ромбическая сетка. По краям ромба изображен шевронный рисунок – по девять символов на каждой стороне ромба. Всего таких треугольников тридцать шесть.
Что же такого удивительного может быть в этой фигурке? Оказывается, в XIX веке при археологических раскопках был найден ромб. Да не простой, а золотой, при чем, в самом прямом смысле этого слова! Эта находка из великобританского кургана Баш была найдена в районе Уилсфорда, неподалёку от знаменитого Стоунхенджа. Загадочный ромб представляет собой отполированную пластинку, на которой выгравированы необычные узоры. Размер его 15,2 х 17,8 см (ромб лишь с небольшой оговоркой). У пластины кроме окантовки есть еще три меньших ромбовидных узора, которые якобы вложены друг в друга. При этом, в центре последнего выгравирована ромбическая сетка. По краям ромба изображен шевронный рисунок – по девять символов на каждой стороне ромба. Всего таких треугольников тридцать шесть.
Безусловно, данное изделие очень дорого стоит, но также очевидно, что создание такого ромба преследовало какую-то определенную цель. Вот только какую, ученые долго не могли разгадать.
Одна из более правдоподобных и принятых версий касается непосредственно Стоунхенджа.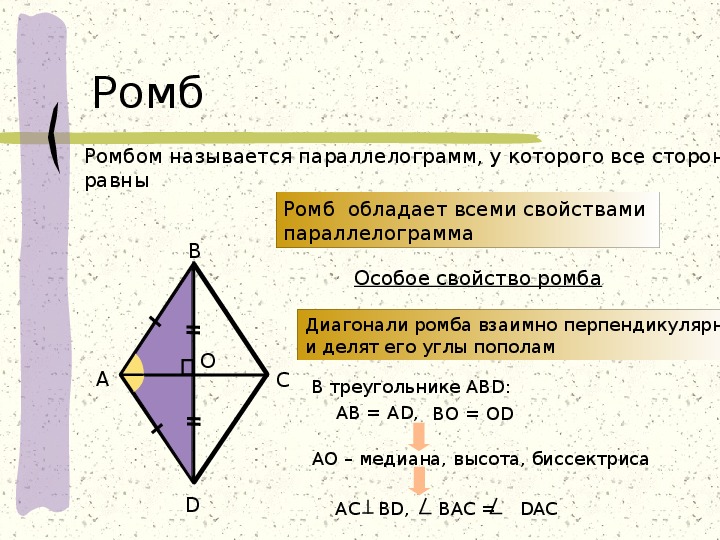 Известно, что сооружения Стоунхенджа возводились постепенно, в течение нескольких столетий. Считается, что строительство началось около 3000 года до н.э. Следует учесть, что золото в Британии стало известно уже где-то с 2800 года до н.э. Отсюда можно сделать предположение, что золотой ромб вполне мог быть инструментом жреца. В частности, визира. Такую гипотезу предложил вниманию современных ученых профессор А. Том, известный исследователь Стоунхенджа, в последней четверти ХХ века.
Известно, что сооружения Стоунхенджа возводились постепенно, в течение нескольких столетий. Считается, что строительство началось около 3000 года до н.э. Следует учесть, что золото в Британии стало известно уже где-то с 2800 года до н.э. Отсюда можно сделать предположение, что золотой ромб вполне мог быть инструментом жреца. В частности, визира. Такую гипотезу предложил вниманию современных ученых профессор А. Том, известный исследователь Стоунхенджа, в последней четверти ХХ века.
Не все могут себе представить, что древние строители могли с точностью определить углы на местности. Тем не менее, английский исследователь Д. Фарлонг предложил метод, которым, по его мнению, могли пользоваться древние египтяне. Фарлонг считал, что наши предки использовали заранее подобранные соотношения сторон в прямоугольных треугольниках. Ведь давно известно, что египтяне широко применяли треугольник со сторонами в три, четыре и пять мерных единиц. Видимо, множество подобных приёмов знали и древние жители Британских островов.
Что ж, даже если представить, что люди, которые строили Стоунхендж, были отличнейшими геодезистами, как в этом мог помочь им золотой ромб? Едва ли какой-нибудь современный геодезист сможет ответить на этот вопрос. Вероятнее всего, тот факт, что Фарлонг был геодезистом по профессии, дал возможность ему разгадать эту загадку. После внимательного изучения исследователь пришел к выводу, что отполированный золотой ромб с разметкой отлично подходит для применения его в качестве отражателя солнечных лучей, иначе говоря, особого мерного зеркала.
Было доказано, что для быстрого определения азимута на местности с достаточно небольшими погрешностями необходимо было использовать два подобные зеркала. Схема же была такова: один жрец, например, становился на вершине одного холма, а другой в прилегающей долине. Нужно было также предварительно установить расстояние между жрецами. Это можно сделать просто шагами. Хотя обычно пользовались мерной тростью, так как результаты были более достоверны. Два ромбовидных металлических зеркалаобеспечиваютпрямой угол. А потом уже легко отмерить практически любые требуемые углы. Д. Фарлонг привел даже таблицу таких пар целых чисел, которая позволяет задать любой угол с погрешностью в один градус. Вероятнее всего, что именно таким способом пользовались жрецы эпохи Стоунхенджа. Конечно, для подтверждения этой гипотезы нужно было бы найти второй, парный золотой ромб, но, по всей видимости, это того не стоит. Ведь доказательства и так вполне очевидны. Кроме вычисления азимутов на местности была обнаружена и еще одна способность удивительного золотого ромба. Эта удивительная вещица позволяется вычислять моменты зимнего и летнего солнцестояния, весеннего и осеннего равноденствия. Это являлось незаменимым качеством для жизни древних египтян, которые поклонялись тогда в первую очередь Солнцу.
Два ромбовидных металлических зеркалаобеспечиваютпрямой угол. А потом уже легко отмерить практически любые требуемые углы. Д. Фарлонг привел даже таблицу таких пар целых чисел, которая позволяет задать любой угол с погрешностью в один градус. Вероятнее всего, что именно таким способом пользовались жрецы эпохи Стоунхенджа. Конечно, для подтверждения этой гипотезы нужно было бы найти второй, парный золотой ромб, но, по всей видимости, это того не стоит. Ведь доказательства и так вполне очевидны. Кроме вычисления азимутов на местности была обнаружена и еще одна способность удивительного золотого ромба. Эта удивительная вещица позволяется вычислять моменты зимнего и летнего солнцестояния, весеннего и осеннего равноденствия. Это являлось незаменимым качеством для жизни древних египтян, которые поклонялись тогда в первую очередь Солнцу.
Вполне вероятно, что внушительный вид ромба являлся не только незаменимым инструментом для жрецов, но был также и эффектным украшением для его владельца.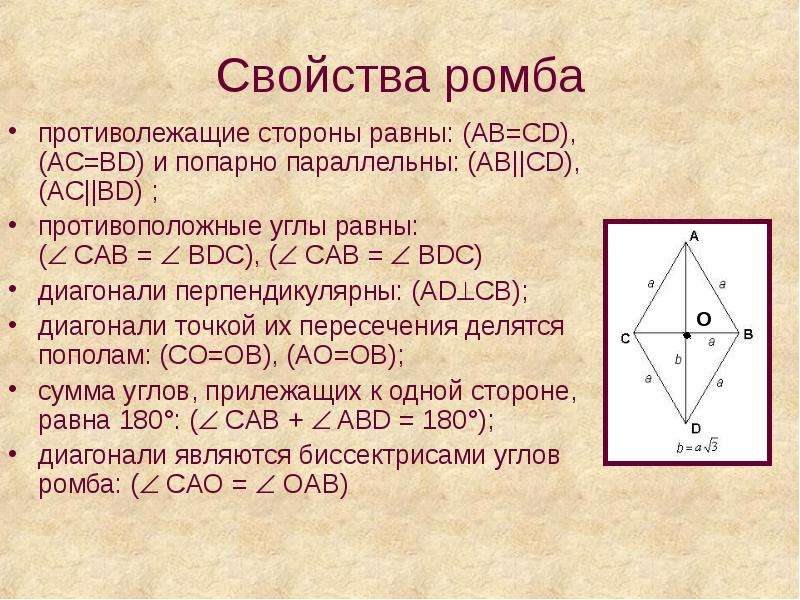 Вообще говоря, абсолютное большинство найденных на первый вид дорогостоящий на сегодняшний день украшений, являются, как узнается позже, измерительными инструментами.
Вообще говоря, абсолютное большинство найденных на первый вид дорогостоящий на сегодняшний день украшений, являются, как узнается позже, измерительными инструментами.
Итак, людей всегда притягивала неизвестность. И, судя по тому, что так много остается загадочного и не доказанного в нашем мире, человек еще долго будет пытаться отыскать разгадки древности. И это очень здорово! Ведь у наших предков можно многому научиться. Для этого нужно много знать, уметь и учиться. А ведь невозможно стать таким высококвалифицированным специалистом без базовых знаний. В конце концов, ведь каждый великий археолог, открыватель когда-то ходил в школу!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
AB \parallel CD,\;BC \parallel AD
AB = CD,\;BC = AD
2. Диагонали ромба перпендикулярны.
AC\perp BD
Доказательство
Так как ромб является параллелограммом, то его диагонали делятся пополам.
Значит, \triangle BOC = \triangle DOC
по трем сторонам (BO = OD
, OC
— совместная, BC = CD
).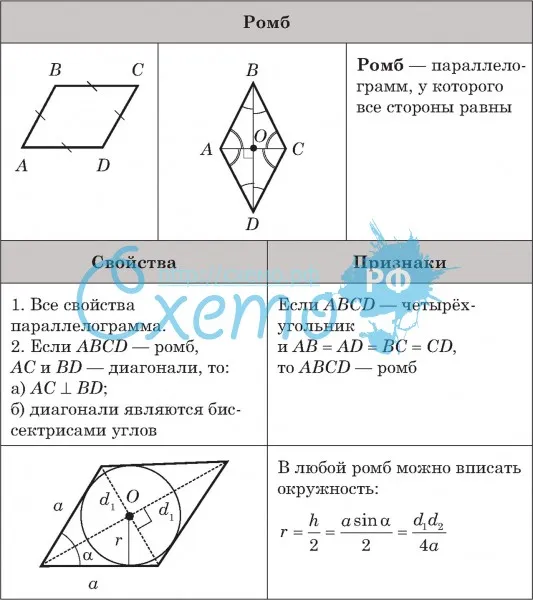 2
2
Признаки ромба
1. Параллелограмм с перпендикулярными диагоналями является ромбом.
\begin{cases} AC \perp BD \\ ABCD \end{cases} — параллелограмм, \Rightarrow ABCD — ромб.
Доказательство
ABCD является параллелограммом \Rightarrow AO = CO ; BO = OD . Также указано, что AC \perp BD \Rightarrow \triangle AOB = \triangle BOC = \triangle COD = \triangle AOD — по 2-м катетам.
Получается, что AB = BC = CD = AD .
Доказано!
2. Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то этой фигурой будет ромб.
Доказательство
На заметку: не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом.
К примеру:
Это уже не ромб, не смотря на перпендикулярность диагоналей.
Для отличия стоит запомнить, что сначала четырехугольник должен быть параллелограммом и иметь
1. — прямая. Соответственно, решением неравенства
, является полуплоскость, лежащая ниже или выше этой прямой.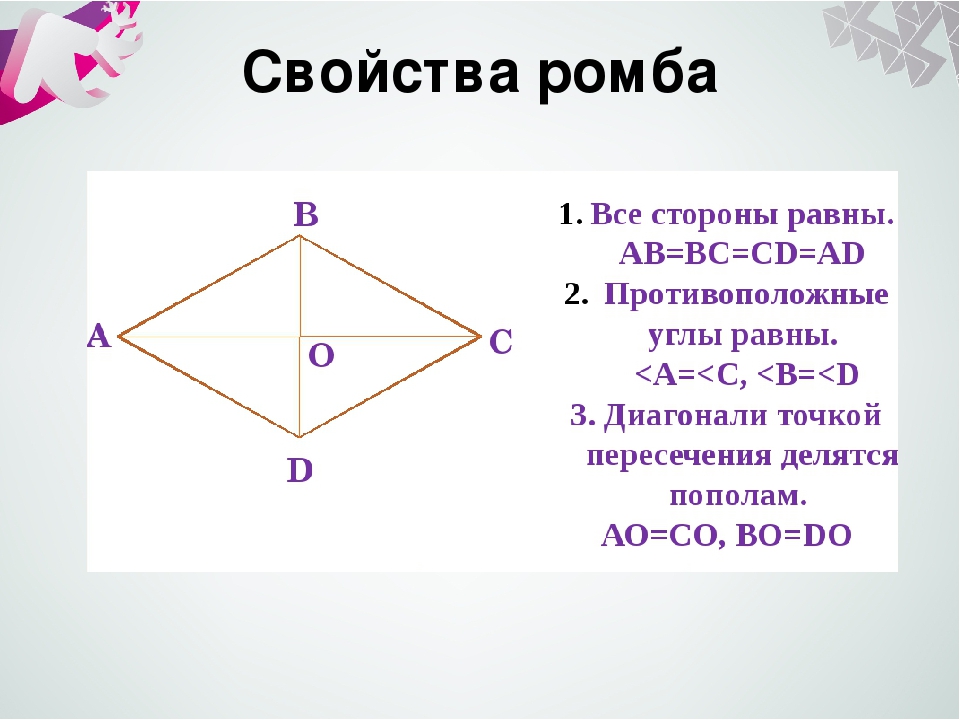
2.
— гипербола, т.к. отсюда
. Эта гипербола делит плоскость на 3 (!!!) области, поэтому знак неравенства надо проверять в каждой из них.
3.
— «лежачая парабола», т.е. парабола, повернутая на 90 по часовой стрелке. Делит плоскость на 2 части (внутри параболы и вне ее.)
4.
— окружность с центром в начале координат, радиуса R (где R>0). Решением неравенства
является круг (т.е. вся область, лежащая внутри окружности, вместе с границей), а неравенства
— область вне круга.
5.
— при а > 0 – квадрат с вершинами в точках (а;0), (0; а), (-а; 0), (0; -а). Соответственно, решением неравенства
является область внутри квадрата, а неравенства
— область вне квадрата.
Преобразования графиков:
1 f(x-a; y-b)=0, надо сначала построить график уравнения f(x; y)=0, а затем сместить его на а единиц по оси Ох, и на b единиц по оси Оy.
2 . Чтобы построить график уравнения
, надо выполнить симметрию графика уравнения f(x; y)=0 относительно оси Оy (не забыв при этом стереть часть исходного графика, лежащую левее оси Оy).
3 . Чтобы построить график уравнения
, надо выполнить симметрию графика уравнения f(x; y)=0 относительно оси Ох (не забыв при этом стереть часть исходного графика, лежащую ниже оси Ох).
4. Соответственно, чтобы построить график уравнения
, надо сначала построить график уравнения f(x; y)=0 (т.е. убрать все модули) в первой четверти , а затем выполнить симметрию этого графика относительно всех осей.
Неравенства с двумя переменными.
Чаще всего для решения используют «метод областей». То есть сначала в неравенстве заменяют знак неравенства на знак «=» и изображают полученный график на координатной плоскости. Затем «методом пробной точки» проверяют знак неравенства в каждой из образовавшихся областей.
Кроме этого, отдельно можно рассмотреть неравенства вида
и
. Для их решения сначала строят график функции
. Тогда решением первого неравенства будут точки, лежащие ниже этого графика, а решением второго, соответственно, точки, лежащие выше.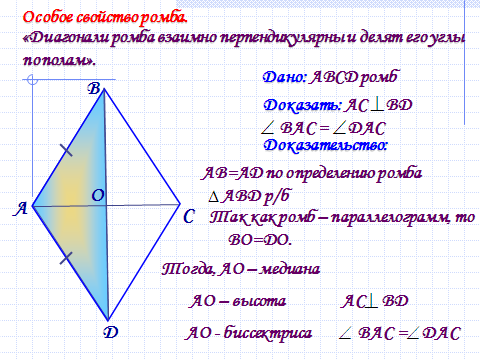
Можно еще выделить неравенства вида
. (Знак неравенства может быть и другим). Чтобы его решить, нужно сплошной линией изобразить график уравнения
и пунктирной линией — график уравнения
и проверить знак неравенства в каждой получившейся области(выбрав любую точку из каждой области).
Пример 1.
№ 9.20 (г)
Изобразите решение неравенства
и определите все значения а, при которых данное неравенство имеет хотя бы одно решение.
Решение.
Данное неравенство равносильно следующему:
.
Для этого сначала построим график уравнения
.
а) В свою очередь, для построения этого графика воспользуемся правилом 4 преобразования графиков. Здесь f(x; a) = 5x + 2a . Графиком этого уравнения является прямая, пересекающая оси координат в точках (2, 0) и (0, 5). Т.к. мы рассматриваем случай без модулей (т.е. x
и y), то возьмем только часть этой прямой, лежащую в первой четверти.
б) чтобы построить график уравнения , выполним симметрию полученного отрезка относительно всех координатных осей и начала координат. Получим ромб с «центром» в начале координат.
б) Теперь сместим этот график на 3 единицы вправо и на 1 единицу вниз.
Получили график уравнения
Видим, что координатная плоскость оказалась разбита на 2 области, внутри ромба и вне его. Видим, что, например, точка (3,-1) принадлежит внутренней области. Подставим ее координаты в неравенство . Убеждаемся, что неравенство в данной точке выполнено. Значит, все точки этой области удовлетворяют неравенству. Для проверки подставим и точку из внешней области в неравенство. Например, это точка (0, 8). При данных значениях переменных неравенство обращается в неверное числовое неравенство, а, значит, никакая точка из внешней области не удовлетворяет неравенству. Окончательно получаем, что решением неравенства является «внутренность» ромба. Показываем это штриховкой.
Ответ: данное неравенство имеет решение при
Пример 2 . Изобразить на координатной плоскости множество точек, удовлетворяющих неравенству
.
Решение
1. Построим линии, ограничивающие график неравенства. Это будут линии, которые являются изображением множеств тех точек, в которых числитель и знаменатель обращаются в 0. Т.е. построим графики уравнений
(А)
и
(Б)
А) Графиком данного уравнения является окружность с центром в точке (2, -3) и радиусом, равным 4 – изображается сплошной линией, т.к. неравенство нестрогое.
Б) График этого уравнения – «лежачая парабола», опущенная на 1 единицу вниз – изображается пунктирной линией в силу область определения неравенства.
2. Пусть ,
. Тогда наше неравенство принимает вид
.
Окружность и парабола разбивают координатную плоскость на 4 области.
Заметим, что область внутри окружности соответствует неравенству
, т.
 е.
е. . Область вне окружности – неравенству
, т.е.
.
Аналогично, область «внутри», или правее параболы соответствует неравенству
или
, а область «вне», или левее параболы – неравенству
или
.
И, наконец, в области IV и , т.е. дробь неположительна и неравенство не выполнено.
Таким образом, решением неравенства является объединение областей I и III.
ромб и его теоремы
Мы в ask-math считаем, что учебные материалы должны быть бесплатными для всех. Пожалуйста, используйте содержимое этого веб-сайта для более глубокого понимания концепций. Кроме того, мы создали и разместили видеоролики на нашем YouTube.
Мы также предлагаем индивидуальные занятия / групповые занятия / помощь в выполнении домашних заданий по математике с 4 по 12 классы по алгебре, геометрии, тригонометрии, предварительному исчислению и исчислению для учащихся из США, Великобритании, Европы, Юго-Восточной Азии и ОАЭ.
Также приветствуются связи со школами и образовательными учреждениями.
Пожалуйста, свяжитесь с нами по [email protected] / Whatsapp +919998367796 / Skype ID: anitagovilkar.abhijit
Мы также будем рады разместить видео в соответствии с вашими требованиями. Напишите нам.
В этом разделе мы обсудим ромб и его теоремы.Ромб – это параллелограмм, у которого все стороны равны и параллельны.
Ромб и его теоремы :
Теорема 1 : Диагонали ромба перпендикулярны друг другу.
Ромб ABCD, диагонали, чей AC и BD пересекаются на O.
Докажите, что: ∠boc = ∠doc = ∠aod = ∠aob = 90 0
| Отчеты | Причины |
| 1) ABCD — ромб. | 1) Дано |
| 2) AB = BC = CD = DA | 2) Свойства ромба. |
| 3) OB = OD и OA = OC | 3) Поскольку параллелограмм является ромбом, его диагонали делят друг друга пополам. |
| 4) ДВ = НД | 4) Из (3) |
| 5) ВС = DC | 5) Свойства ромба. |
| 6) ОС = ОС | 6) Рефлекторный (общая сторона) |
| 7) ΔBOC ≅ ΔDOC | 7) Постулат ССС. |
| 8) ∠BOC = ≅ ∠DOC | 8) ЦПКТС |
| 9)∠BOC + ∠DOC = 180 | 9) Линейные парные углы являются дополнительными. |
| 10) 2∠ВОС = 180 | 10) Дополнительное свойство |
| 11) ∠ВОС = 90 | 11) Имущество отдела |
| 12) ∠BOC = ∠DOC = 90 | 12) Так как эти два угла равны. |
Следовательно, ∠AOB = ∠BOC = ∠COD = ∠DOA = 90 0
Обратное утверждение теоремы также верно ⇒ Если диагонали параллелограмма перпендикулярны, то это ромб.
Пример:
1) ABCD — ромб с ∠ABC = 56. Определить ∠ACD.
Решение: ABCD — ромб.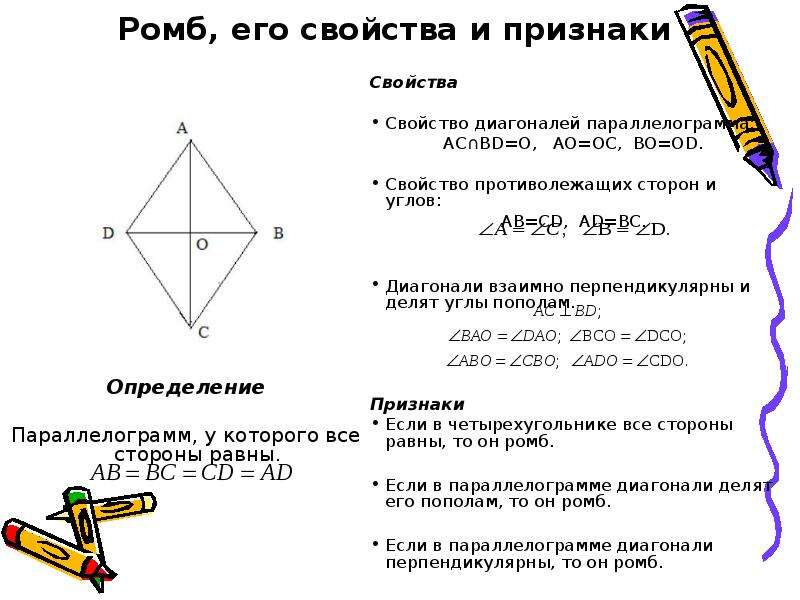
∠ ABC = ∠ADC (противоположные углы равны)
∠ADC = 56 0
∴ ∠ ODC = ½ ∠Adc (диагонали ромба бисекты угол)
⇒ ∠ODC = ½ x 56
⇒ ∠ODC = 28 0
∠OCD + ∠ODC + ∠COD = 180 (В ΔOCD сумма всех углов треугольника равна 180)
∠OCD + 28 + 90 = 180 OCD
∠D + 118 = 180⇒ ∠OCD = 180-118
∠OCD = 62 0
0Quadrilatoral
• Введение в четырехугольник
• Типы четырехсторонних
• Свойства четырехугольника
• Параллелограмма и его теоремы
• Прямоугольник и его теоремы
• Квадрат и его теоремы
• Ромб и его теоремы
• Трапеция (трапеция) и его теоремы
• Воздушный змей и его теоремы
• Теорема о средней точке
Covid-19 повлиял на физическое взаимодействие между людьми .
Не позволяйте этому влиять на ваше обучение.
Теоремы о прямоугольниках, ромбах, квадратах
Теоремы о прямоугольниках, ромбах, квадратах
Прямоугольник
Определение: Прямоугольник — это параллелограмм с четырьмя прямыми углами.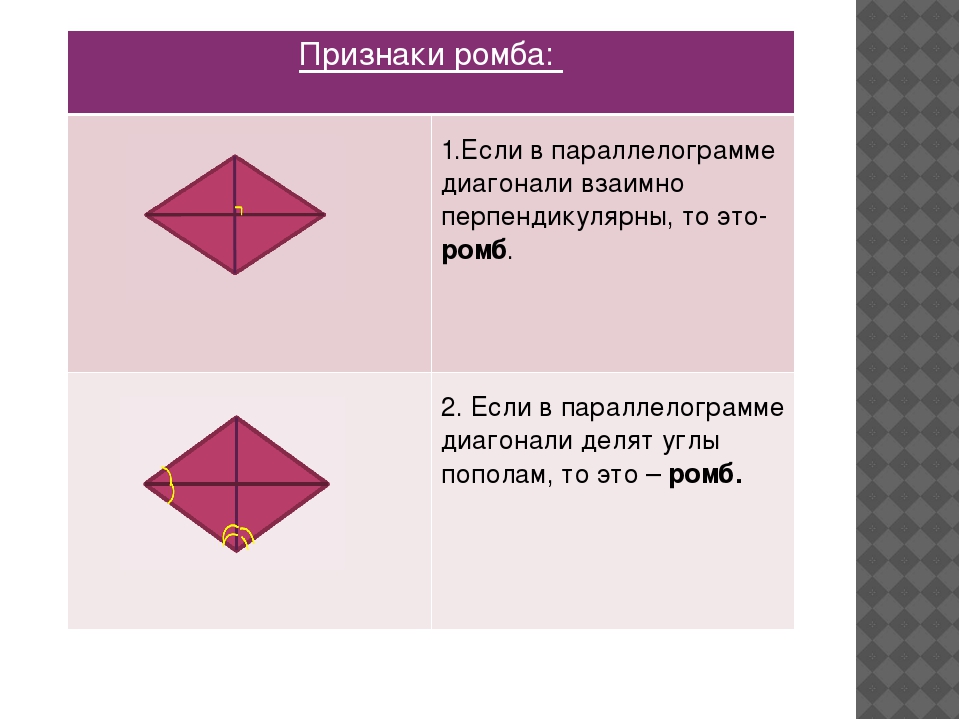
Свойства:
- Прямоугольник обладает всеми свойствами параллелограмма.
- 4 прямых угла
- диагонали равны
Используя определение, можно «доказать» истинность свойств прямоугольника и превратить их в теоремы.
При работе с прямоугольником определение и теоремы формулируются как …
- Прямоугольник представляет собой параллелограмм с четырьмя прямыми углами.
Хотя в определении указано «параллелограмм», достаточно сказать: «Четырехугольник является прямоугольником тогда и только тогда, когда он имеет четыре прямых угла», поскольку любой четырехугольник с четырьмя прямыми углами является параллелограммом. - Если параллелограмм имеет один прямой угол, он является прямоугольником.
- Параллелограмм является прямоугольником тогда и только тогда, когда его диагонали равны.
Строители используют тот факт, что диагонали прямоугольника конгруэнтны (равны), когда пытаются построить «квадратное» основание для здания, патио, огороженной территории, столешницы и т. д. Рабочие измеряют диагонали. Когда диагонали проекта равны, линия здания называется квадратной.
д. Рабочие измеряют диагонали. Когда диагонали проекта равны, линия здания называется квадратной.
Ромб
Определение: Ромб – это параллелограмм с четырьмя конгруэнтными сторонами.
Свойства:
- Ромб обладает всеми свойствами параллелограмма.
- 4 конгруэнтные стороны
- диагонали делят углы пополам
- диагонали перпендикулярны
Используя определение, свойства ромба могут быть «доказаны» истинными и стать теоремами.
При работе с ромбом определение и теоремы формулируются как …
- Ромб представляет собой параллелограмм с четырьмя конгруэнтными сторонами.
Хотя в определении говорится «параллелограмм», достаточно сказать: «Четырехугольник является ромбом тогда и только тогда, когда у него четыре конгруэнтные стороны.», так как любой четырехугольник с четырьмя конгруэнтными сторонами является параллелограммом. - Если у параллелограмма две последовательные стороны конгруэнтны, то это ромб.

- Параллелограмм является ромбом тогда и только тогда, когда каждая диагональ делит пополам пару противоположных углов.
- Параллелограмм является ромбом тогда и только тогда, когда его диагонали перпендикулярны. (Доказательство теоремы приведено ниже.)
Квадрат
Определение: Квадрат — это параллелограмм с четырьмя конгруэнтными сторонами и четырьмя прямыми углами.
Квадрат обладает всеми свойствами параллелограмма И прямоугольника И ромба.
Используя определение, можно «доказать» истинность свойств ромба и превратить их в теоремы.
Когда речь идет о квадрате, определение формулируется как …
Квадрат – это параллелограмм с четырьмя конгруэнтными сторонами и четырьмя прямыми углами.
Это определение можно также сформулировать так: Четырехугольник является квадратом тогда и только тогда, когда он является ромбом и прямоугольником.
Доказательство теоремы: Если параллелограмм является ромбом, то его диагонали перпендикулярны.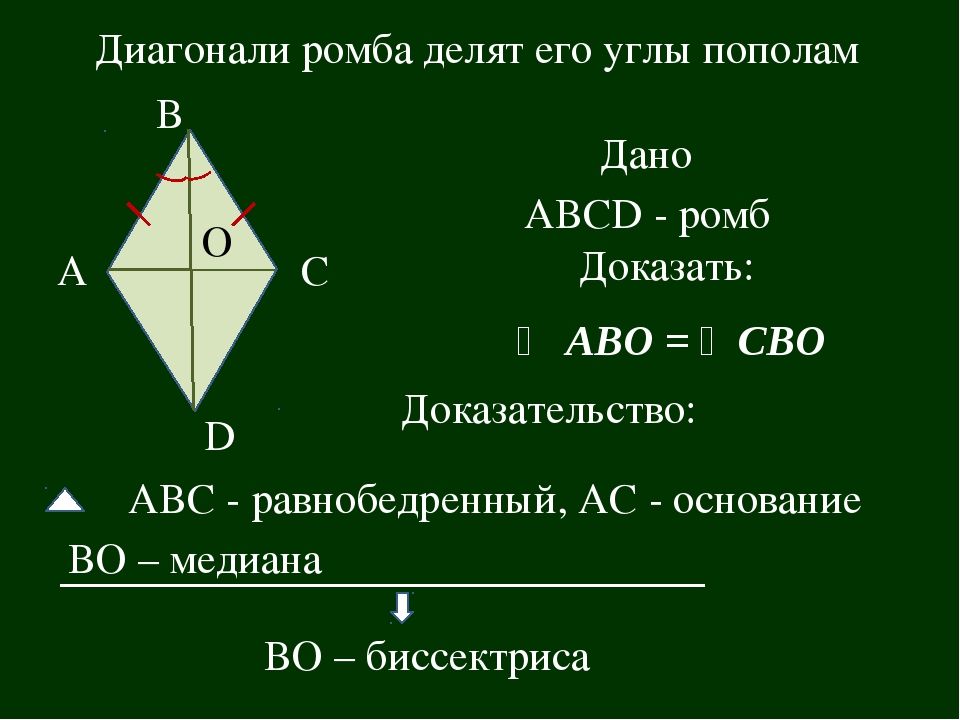
(Помните: когда вы пытаетесь доказать истинность теоремы, вы не можете использовать теорему в качестве аргумента в своем доказательстве.)
Свойства специальных параллелограммов
ромб – четырехугольник, все стороны которого равны. Это также параллелограмм со всеми связанными свойствами. Однако у ромба есть и дополнительные свойства.
Теорема 52: Диагонали ромба делят противоположные углы пополам.
Теорема 53: Диагонали ромба перпендикулярны друг другу.
В ромбе CAND (рисунок 2), по теореме 52 , CN делит пополам ∠ DCA и ∠ ДНК. Кроме того, AD делит пополам ∠ CAN и ∠ CDN и по Теореме 53 , CN ⊥ AD .7 .
Рисунок 2 Диагонали ромба перпендикулярны друг другу и делят противоположные углы пополам.
Квадрат это четырехугольник со всеми прямыми углами и равными сторонами. Квадрат также является параллелограммом, прямоугольником и ромбом и обладает всеми свойствами всех этих специальных четырехугольников. На рис. 3 показан квадрат.
Квадрат также является параллелограммом, прямоугольником и ромбом и обладает всеми свойствами всех этих специальных четырехугольников. На рис. 3 показан квадрат.
Рисунок 3 Квадрат имеет четыре прямых угла и четыре равные стороны.
На рис. 4 показаны отношения этих четырехугольников друг к другу.
Рисунок 4 Отношения между различными типами четырехугольников.
Пример 1: Найдите следующие цифры 5.
Рисунок 5 Идентифицируйте эти многоугольники.
(а) пятиугольник, (б) прямоугольник, (в) шестиугольник, (г) параллелограмм, (д) треугольник, (е) квадрат, (ж) ромб, (з) четырехугольник, (и) восьмиугольник, и (к) правильный пятиугольник
Пример 2 : На рисунке 6 находятся м ∠ A, M ∠ C, C, M ∠ D, CD, и AD .
Рисунок 6 Параллелограмм с одним заданным углом.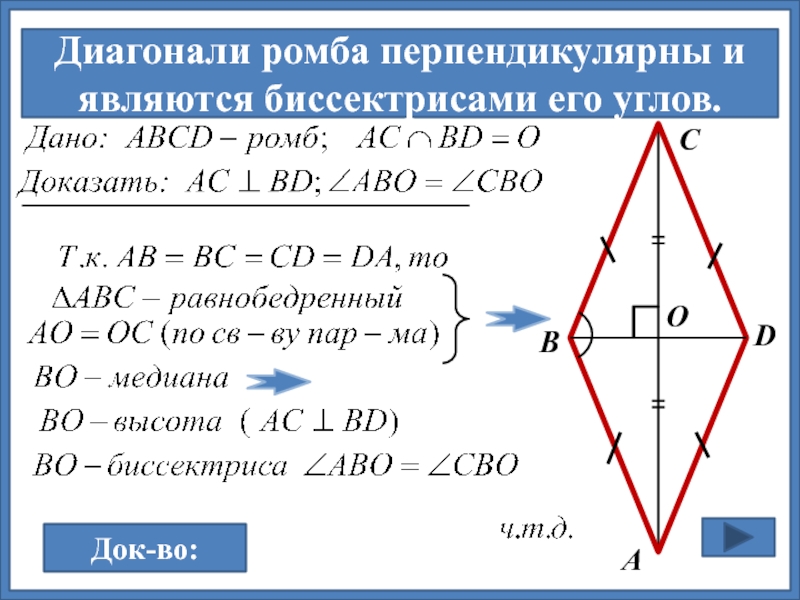
м ∠ A = м ∠ C = 80°, так как последовательные углы параллелограмма являются дополнительными.
м ∠ D = 100°, так как противоположные углы параллелограмма равны.
CD = 8 и AD = 4, потому что противоположные стороны параллелограмма равны.
Пример 3: На рисунке 7 найдите TR, QP, PS, TP, и PR .
Рисунок 7 Прямоугольник с одной заданной диагональю.
TR = 15, так как диагонали прямоугольника равны.
QP = PS = TP = PR = 7,5, потому что диагонали прямоугольника делят друг друга пополам.
Пример 4: На рисунке 8 найдите m ∠ MOE, m ∠ NOE, и m ∠ MYO MYO.
Рисунок 8 Ромб с одним указанным углом.
м ∠ МОЭ = м ∠ НОЭ = 70°, потому что диагонали ромба делят противоположные углы пополам.
м ∠ MYO = 90°, так как диагонали ромба перпендикулярны.
Геометрия: самые популярные параллелограммы
Самые популярные параллелограммы
Прямоугольники, ромбы и квадраты — это три конкретных вида параллелограммов. Все они обладают свойствами параллелограмма: их противоположные стороны параллельны, их диагонали делят друг друга пополам и делят параллелограмм на два конгруэнтных треугольника, а противоположные стороны и углы конгруэнтны.Но у прямоугольников, ромбов и квадратов есть дополнительные характеристики, которых нет у других параллелограммов.
Прямоугольники
Прямоугольник представляет собой параллелограмм с прямым углом. На самом деле, из этого небольшого количества информации вы знаете обо всех четырех углах прямоугольника. Прямоугольник является параллелограммом, поэтому его противоположные углы конгруэнтны, а смежные углы смежны. Напомним, что дополнением к прямому углу является еще один прямой угол. Таким образом, у прямоугольника на самом деле четыре прямых угла.
Таким образом, у прямоугольника на самом деле четыре прямых угла.
Надежные факты
Прямоугольник — это параллелограмм с прямым углом.
Прямоугольники обладают некоторыми свойствами, которых нет у общих параллелограммов. Одним из таких свойств является то, что диагонали прямоугольника равны. Я сформулирую это как теорему и обсужу план ее доказательства. Я оставлю детали на ваше усмотрение.
- Теорема 15.9 : Диагонали прямоугольника равны.
Чтобы доказать эту теорему, взгляните на прямоугольник на рисунке 15.9. Прямоугольник ABCD имеет диагонали AC и BD. Чтобы доказать, что они конгруэнтны, вы захотите использовать CPOCTAC. Но какие два треугольника, как вы показываете, равны? Я бы порекомендовал вам показать ?ADC ~= ?DAB. Разделите эти два треугольника и соедините их. Они оба прямоугольные, так что это одна пара конгруэнтных углов. Поскольку противоположные стороны конгруэнтны, вы сможете использовать наш постулат SAS, чтобы показать ?ADC ~= ?DAB.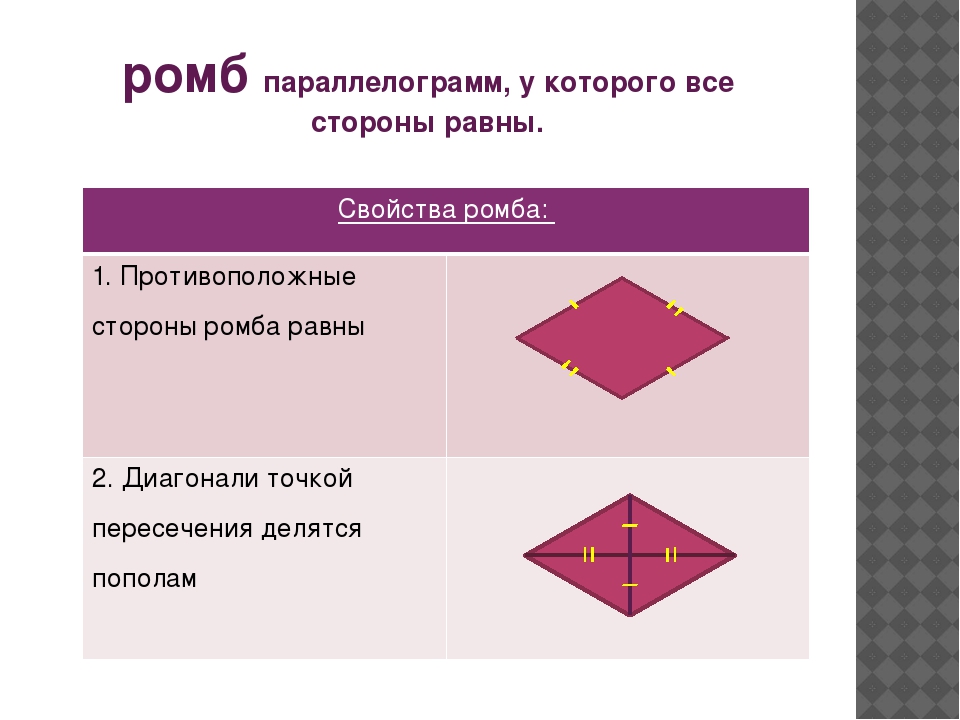
Рис. 15.9 Прямоугольник ABCD имеет диагонали AC и BD .
Ромб
Ромб представляет собой параллелограмм с двумя конгруэнтными смежными сторонами. Как и в случае с прямоугольником, ромб наследует все желаемые свойства параллелограмма. А ромбы обладают особыми свойствами, которых нет у общих параллелограммов и прямоугольников. Я запишу эти специальные свойства в виде теорем, на которые вы сможете ссылаться позже.
Первое свойство ромба состоит в том, что все его стороны равны. Это неудивительно, ведь вы уже знаете, что противоположные стороны ромба конгруэнтны (потому что это параллелограмм).Если противоположные стороны и смежные стороны конгруэнтны, то они конгруэнтны. Не все параллелограммы и прямоугольники обладают этим особым свойством.
Solid Facts
Ромб представляет собой параллелограмм с двумя конгруэнтными смежными сторонами.
- Теорема 15.
 10 : Все стороны ромба равны.
10 : Все стороны ромба равны.
Следующее свойство ромба, о котором стоит упомянуть, это то, что его диагонали перпендикулярны. Это может быть не так очевидно, и стоит написать формальное доказательство.
- Теорема 15.11 : Диагонали ромба перпендикулярны.
- Пример 4 : Напишите формальное доказательство теоремы 15.11.
- Решение : Как обычно, я напишу формальное доказательство шаг за шагом. На рис. 15.10 изображен ромб ABCD с диагоналями AC и BD, пересекающимися в точке M.
Рис. 15.10 Ромб ABCD с диагоналями AC и BD, пересекающимися в точке M.
- Дано: ромб ABCD с диагоналями AC и BD.
- Доказать: AC ? БД.
- Доказательство: вам нужен план игры. Держитесь за свою шляпу, потому что это довольно сложно. Чтобы показать, что AC ? BD, нужно показать, что AC и BD пересекаются и образуют прямой угол. Итак, вам нужно показать, что угол ?AMB прямой.
 Поскольку ?AMB и ?BMC образуют прямой угол, они являются дополнительными. Если бы вы могли показать, что они конгруэнтны, то они должны были бы быть прямыми углами. Самый простой способ показать ?AMB ~= ?BMC — показать ?AMB ~= ?CMB и использовать CPOCTAC.Теперь, поскольку вы имеете дело с ромбом, AB ~= BC. По рефлексивному свойству ~= вы знаете, что BM ~= BM. Поскольку ромб является параллелограммом, и показано, что диагонали параллелограмма делят друг друга пополам, AM ~= MC. Вы можете использовать наш постулат SSS, чтобы заключить, что ?AMB ~= ?CMB. Давайте запишем это.
Поскольку ?AMB и ?BMC образуют прямой угол, они являются дополнительными. Если бы вы могли показать, что они конгруэнтны, то они должны были бы быть прямыми углами. Самый простой способ показать ?AMB ~= ?BMC — показать ?AMB ~= ?CMB и использовать CPOCTAC.Теперь, поскольку вы имеете дело с ромбом, AB ~= BC. По рефлексивному свойству ~= вы знаете, что BM ~= BM. Поскольку ромб является параллелограммом, и показано, что диагонали параллелограмма делят друг друга пополам, AM ~= MC. Вы можете использовать наш постулат SSS, чтобы заключить, что ?AMB ~= ?CMB. Давайте запишем это.
| Заявления | Причины | ||
|---|---|---|---|
| 1. | Параллелограмма ABCD имеет диагонали AC и BD, что пересекается на M | , данном | |
| 2. | ~ = MC | Теорема 15.6 | |
| 3. | AB ~ = BC | Определение Rhombus | |
| 4. | BM ~ = BM | Рефлексивное свойство ~ = | |
5. | ? Amb ~ =? CMB | SSS Postulate | |
| 6. | ? Amb ~ =? BMC | CPOCTAC | |
| 7. | |||
| 7. | ? AMM и? BMC образуют прямой угол | Определение прямого угла | |
| 8. | м? Amb + M? BMC = 180 | And Apply Postulate | |
| 9. | м? Amb + M? Amb = 180 | Замена (шаги 6 и 8) | |
| 10. | ?AMB правильный | Алгебра | |
| 11. | ?AMB правильный | Определение прямого угла | |
| 12. | AC ? BD | Определение ? |
Квадраты
Квадрат является и прямоугольником, и ромбом.Квадрат можно определить как прямоугольник с конгруэнтными смежными сторонами или как ромб с прямым углом. Я выберу прежнее описание в качестве официального определения. Квадрат наследует все свойства параллелограмма, прямоугольника и ромба. Квадрат имеет лучшее из всех миров. Он обладает свойствами параллелограмма (противоположные стороны конгруэнтны, противоположные углы конгруэнтны, противоположные стороны параллельны, а диагонали делят друг друга пополам), прямоугольника (диагонали конгруэнтны и все четыре угла равны) и ромба (диагонали перпендикулярны и все четыре угла равны). стороны равны).
Квадрат имеет лучшее из всех миров. Он обладает свойствами параллелограмма (противоположные стороны конгруэнтны, противоположные углы конгруэнтны, противоположные стороны параллельны, а диагонали делят друг друга пополам), прямоугольника (диагонали конгруэнтны и все четыре угла равны) и ромба (диагонали перпендикулярны и все четыре угла равны). стороны равны).
Solid Facts
Квадрат представляет собой прямоугольник с конгруэнтными смежными сторонами.
Выдержки из The Complete Idiot’s Guide to Geometry 2004 Denise Szecsei, Ph.D. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476.Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
Формула вероятности: Знайте формулу, определение здесь
Вероятность наступления события определяется вероятностью. Есть много сценариев, в которых мы должны предсказать исход события в реальной жизни. Мы можем быть уверены или не уверены в исходе события. В таких случаях мы говорим, что событие имеет шанс произойти или не произойти. Вероятность имеет множество применений в играх, в бизнесе для создания прогнозов, основанных на вероятности, и в этой новой области искусственного интеллекта.Разделив количество благоприятных возможностей на общее количество возможных исходов, можно оценить вероятность события, используя формулу вероятности . Поскольку число благоприятных исходов никогда не может превышать полного числа исходов, вероятность наступления события может находиться в диапазоне от 0 до 1. Кроме того, число благоприятных исходов не может быть отрицательным.
Есть много сценариев, в которых мы должны предсказать исход события в реальной жизни. Мы можем быть уверены или не уверены в исходе события. В таких случаях мы говорим, что событие имеет шанс произойти или не произойти. Вероятность имеет множество применений в играх, в бизнесе для создания прогнозов, основанных на вероятности, и в этой новой области искусственного интеллекта.Разделив количество благоприятных возможностей на общее количество возможных исходов, можно оценить вероятность события, используя формулу вероятности . Поскольку число благоприятных исходов никогда не может превышать полного числа исходов, вероятность наступления события может находиться в диапазоне от 0 до 1. Кроме того, число благоприятных исходов не может быть отрицательным.
Формулы вероятности можно использовать для расчета вероятности наступления события.Вероятность — это раздел математики, связанный с числовым представлением вероятности наступления события. Вероятность события всегда находится в диапазоне от 0 до 1, где 0 означает невозможность, а 1 — уверенность.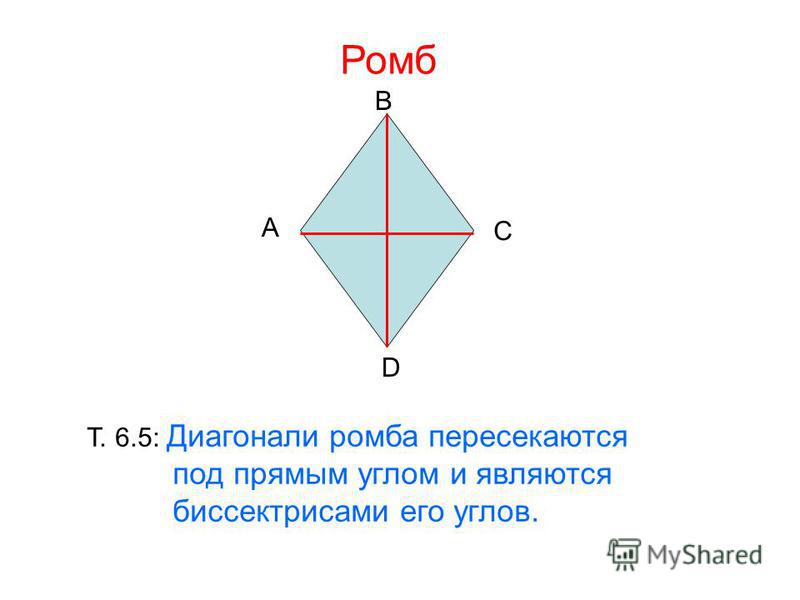 В следующих разделах мы рассмотрим основы вероятности более подробно.
В следующих разделах мы рассмотрим основы вероятности более подробно.
Формула вероятности: определение вероятности
Неопределенность/определенность возникновения события измеряется вероятностью. Хотя вероятность началась с азартных игр, сейчас она широко используется в областях физических наук, коммерции, биологических наук, медицинских наук, прогнозирования погоды и т. д.Вероятность для 10-го класса — важная глава для учащихся, объясняющая все основные понятия.
Изучите концепции 10-го экзамена CBSE
Чтобы найти вероятность возникновения одного события, сначала нам нужно знать общее количество возможных исходов. Например, когда мы подбрасываем монету, выпадает либо орел, либо решка, т.е. возможны только два возможных исхода (H, T). Если мы хотим, чтобы выпал орел, наш благоприятный исход равен H. Итак, мы обозначаем вероятность выпадения орла при подбрасывании монеты:
= 1/2
Как найти вероятность?
Формула вероятности дает вероятность того, что событие произойдет.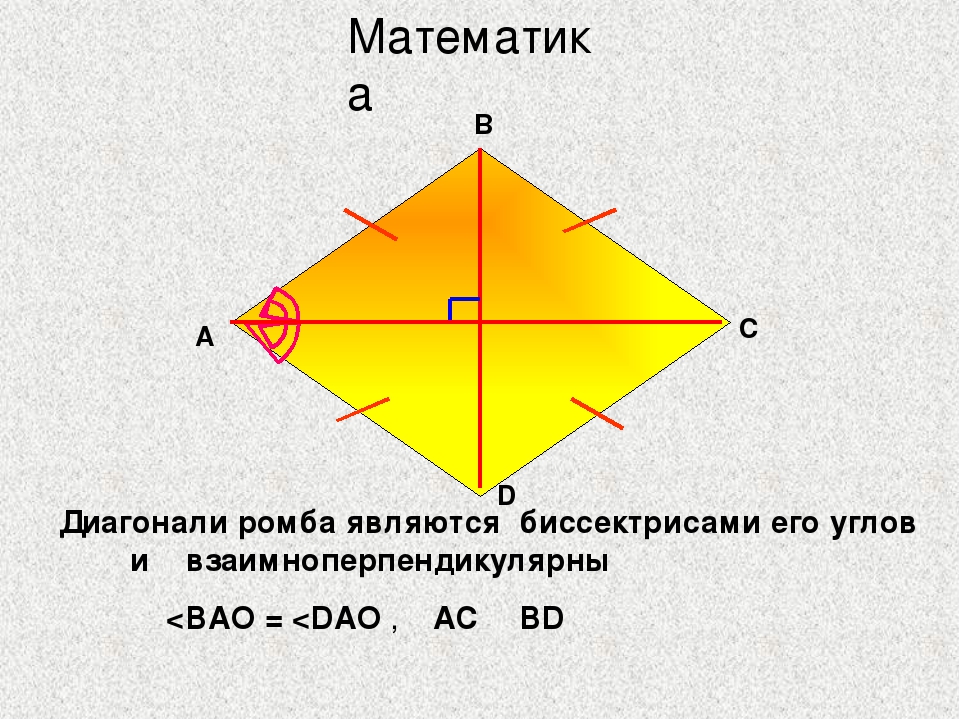 Он равен отношению числа благоприятных исходов к общему числу исходов. Мы привели формулы вероятности с примерами.
Он равен отношению числа благоприятных исходов к общему числу исходов. Мы привели формулы вероятности с примерами.
| Вероятность наступления события P(E) = количество благоприятных исходов/общее число исходов |
или,
P(A) — вероятность события «A»
n(A) — количество благоприятных исходов
n(S) — общее количество событий в пространстве выборки
Мы используем два термина — «благоприятный исход» и «желательный исход» в контексте вероятности.Иногда студенты путают эти два термина. В некоторых требованиях проигрыш в определенном тесте или появление нежелательного результата может быть благоприятным событием для проведения экспериментов.
Основные формулы вероятности
Здесь мы предоставили некоторые математические формулы вероятности, которые будут очень полезны для учащихся:
| Диапазон вероятности | 0 ≤ p (A) ≤ 1 |
| Правило дополнительных событий | P (A C ) + P (A) = 1 |
| Настройка добавления | P (A∪B) = P(A) + P(B) – P(A∩B) |
| Непересекающиеся события – события A и B не пересекаются, если | P(A∩B) = 0 |
| Условная вероятность | P(A|B) = P(A∩B) / P(B) |
| Формула Байеса | P(A|B) = P(B|A) ⋅ P(A) / P (B) |
| Независимые события – События A и B независимы тогда и только тогда, когда | P(A∩B) = P(A) ⋅ P(B) |
| Кумулятивная функция распределения | |
Практические вопросы 10-го экзамена CBSE
Помимо этих формул вероятности класса 10, есть еще несколько важных уравнений вероятности:
Функция массы вероятности
Функция массы вероятности (PMF) (или функция частоты) дискретной случайной величины X присваивает вероятности возможным значениям случайной величины.
Кроме того, если A является подмножеством возможных значений X, то вероятность того, что X примет значение в A , определяется как:
Функция плотности вероятности
Функция плотности вероятности (PDF) , обозначенная f, непрерывной случайной величины X удовлетворяет следующему:
Ковариация
Ковариация — это мера совместной изменчивости двух случайных величин.Обозначается следующей формулой:
Здесь,
COV X, Y = =
x I = значение данных x
y I
= значение данных Yx ̄ = = ȳ = среднее значение Y
N = Количество значений данных
Скачать – Формулы вероятности PDF
Попытка 10-го пробного экзамена CBSE
Другие важные статьи по математике:
Решенные примеры по формулам вероятности класс 12
Здесь мы предоставили несколько примеров вероятностного решения.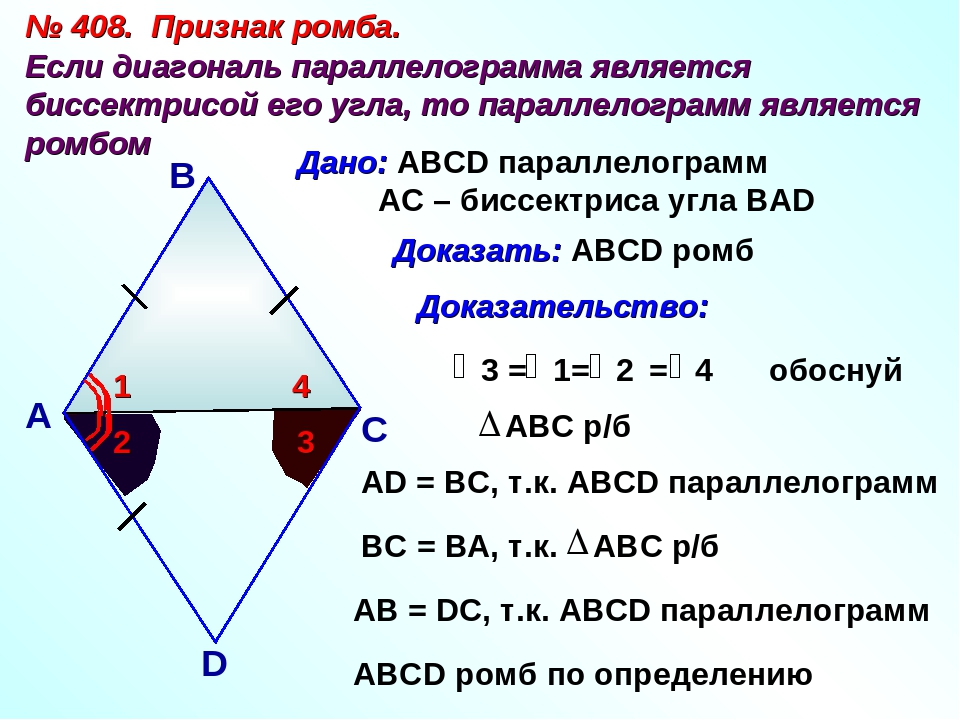
Вопрос 1: Монету подбрасывают 3 раза. Какова вероятность того, что выпадет хотя бы одна голова?
Решение: Пример пространства = [HHH, HHT, HTH, THH, TTH, THT, HTT, TTT]
Общее количество способов = 2 × 2 × 2 = 8.
Благоприятные варианты = 7 [Требуется хотя бы 1 голова ]
P (A) = количество благоприятных исходов/общее число исходов
= 7/8
Вопрос 2: Из колоды в 52 карты берутся две карты. Найдите вероятность того, что оба бубны или оба короли.
Решение: Всего № Слуки = 52 C 2 C 2
9
Дело Я: Оба Diamonds = 13 C 2
Case II: Оба коробки = 4 C 2
P (оба являются бриллиантами или оба короля) = ( 13 C 2 + 4 C 2 ) / 52 C 2 = 14/221
Вопрос 3. Рассчитайте вероятность выпадения четного числа при бросании игральной кости.
Рассчитайте вероятность выпадения четного числа при бросании игральной кости.
Решение: Выборочное пространство (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Пусть «E» — событие получения нечетного числа, E = {2, 4, 6}
n(E) = 3
Итак, Вероятность выпадения нечетного числа:
P(E) = (Количество благоприятных исходов)/(Общее количество исходов)
= n(E)/n (S)
= 3/6
= 1/2
Вопрос 4. Какова вероятность того, что при подбрасывании четырех костей выпадет 22 или более?
Решение: Общее количество способов = 6 4
= 1296
(i) Количество способов получить сумму 22 равно 6,6,6,4 = 4! / 3!
= 4 и 6,6,5,5 = 4! / 2!2!
= 6.
(ii) Количество способов получить сумму 23 равно 6,6,6,5 = 4! / 3! = 4
(iii) Количество способов получить сумму 24 равно 6,6,6,6 = 1.
Изб. Количество случаев = 4 + 6 + 4 + 1 = 15 способов.
P (получение суммы 22 и более) = 15/1296
= 5/432
Вопрос 5.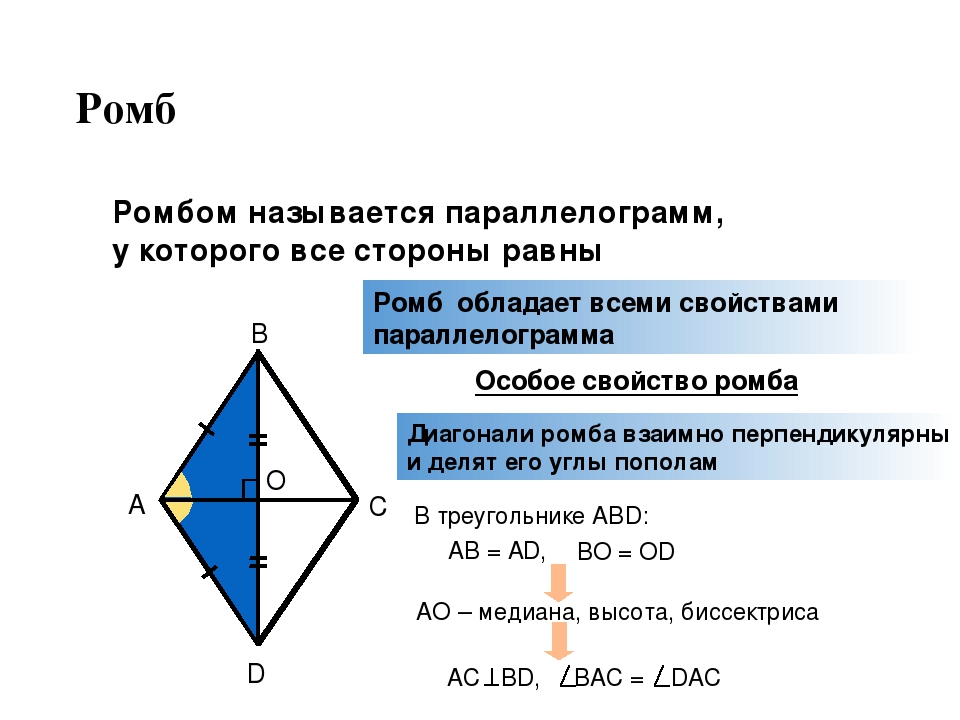 Найдите вероятность того, что в високосном году 52 воскресенья.
Найдите вероятность того, что в високосном году 52 воскресенья.
Решение: В високосном году может быть 52 воскресенья или 53 воскресенья.
В високосном году 366 дней, из которых 52 полных недели и 2 оставшихся дня.
Теперь эти два дня могут быть (сб, вс), (вс, пн), (пн, вт), (вт, ср), (ср, чт), (чт, пт), (пт, сб).
Таким образом, всего 7 случаев, из которых (Сб, Вс) (Вс, Пн) два благоприятных случая.
Итак, P (53 воскресенья) = 2/7
Теперь P(52 воскресенья) + P(53 воскресенья) = 1
Итак, P (52 воскресенья) = 1 – P(53 воскресенья) = 1 – (2/ 7) = (5/7)
Также проверьте:
Практические вопросы по всем формулам вероятности
Здесь мы подготовили для вас несколько практических вопросов по формулам вероятности для класса 7:
Вопрос 1: В трех пакетах 3 красных, 7 черных; 8 красных, 2 черных и 4 красных и 6 черных шаров соответственно.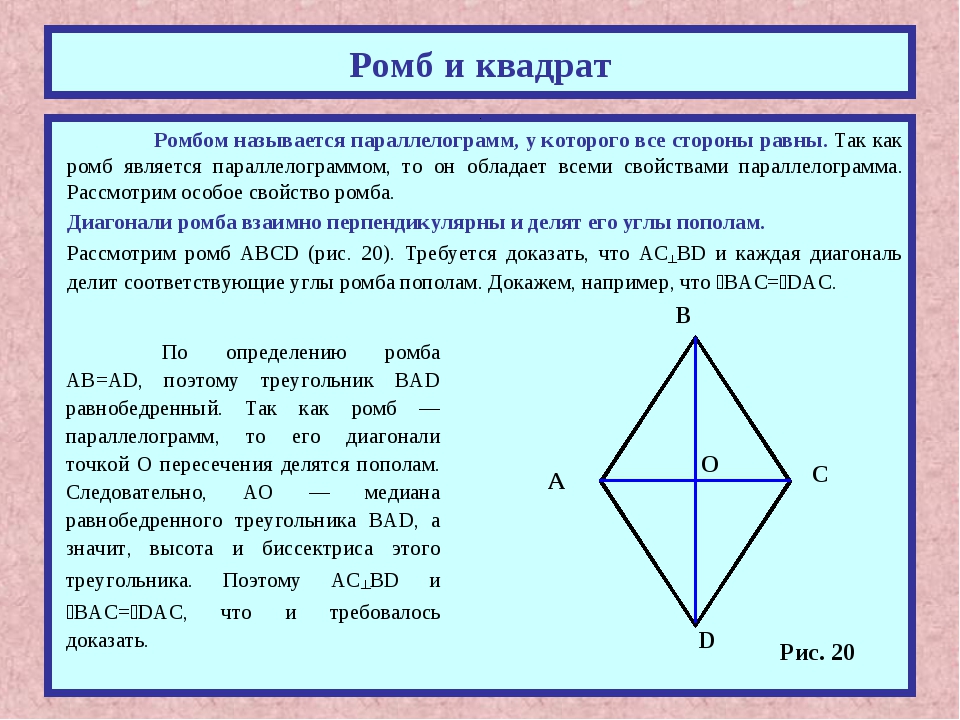 Наугад выбирается 1 из мешков и из него вынимается шар. Если вынутый шар красный, найти вероятность того, что он вынут из третьего мешка. Наугад выбирается 1 из мешков и из него вынимается шар. Если вынутый шар красный, найти вероятность того, что он вынут из третьего мешка.Вопрос 2: Пятнадцать человек сидят за круглым столом. Каковы шансы против двух конкретных людей, сидящих вместе? Вопрос 3: Из колоды карт наугад берутся три карты. Найдите вероятность того, что все карты принадлежат разной масти. Вопрос 4: Два игральных кубика брошены вместе.Какова вероятность того, что число, выпавшее на одном из кубиков, будет кратно числу, выпавшему на другом кубике? Вопрос 5: Из колоды в 52 карты случайным образом вытягивается 1 карта. Вопрос 6: Есть 5 зеленых 7 красных шаров. Два шара выбираются один за другим без замены. Найти вероятность того, что первый зеленый, а второй красный. Вопрос 7: Рассмотрим еще один пример: в упаковке 4 синих, 2 красных и 3 черных ручки. Вопрос 8: В классе 40% учеников изучают математику и естественные науки. 60% студентов изучают математику. Какова вероятность того, что студент будет изучать естественные науки, если он уже изучает математику? |
Часто задаваемые вопросы
Здесь мы предоставили некоторые из часто задаваемых вопросов, связанных с формулами статистической вероятности:
Q1: Где я могу скачать формулы вероятности для способностей?
О: Вы можете скачать формулы вероятности для aptitude в формате PDF с Embibe.Мы предоставили все основные формулы вместе с уравнениями вероятности на этой странице.
Q2: Какая платформа лучше всего подходит для начинающих, чтобы изучить основы вероятностей?
A: Embibe — одна из лучших образовательных технологий, предлагающая обучающие материалы по теории вероятностей от начального до следующего уровня для учащихся. Студенты также могут получить доступ к списку всех формул вероятности на Embibe и попробовать некоторые пробные тесты, чтобы подготовиться к экзаменам.
Студенты также могут получить доступ к списку всех формул вероятности на Embibe и попробовать некоторые пробные тесты, чтобы подготовиться к экзаменам.
Q3: Как проще всего понять вероятность?
A: Самый простой способ понять вероятность — это сначала взглянуть на решенные вопросы и примеры вероятности.После этого учащиеся должны начать с основ вероятности. На Embibe доступно множество пробных тестов на вероятность того, что учащиеся могут попытаться развеять свои сомнения относительно вероятности.
Q4: Что такое формула вероятности?
A: Вероятность события равна количеству благоприятных исходов, деленному на общее число возможных исходов. Это базовое определение вероятности предполагает, что все исходы имеют одинаковую вероятность.
Q5: Какие существуют 3 типа вероятности?
О: Существует 3 типа вероятности:
(i) Теоретическая вероятность.
(ii) Экспериментальная вероятность.
(iii) Аксиоматическая вероятность.
Q6: Что означает P (AUB)?
A: P(AUB) — это вероятность суммы всех точек выборки в AU B. Она определяется как P(A) + P(B), которая представляет собой сумму вероятностей точек выборки в A и B.
Q7: Что означает P (A|B)?
A: P(A|B) — условная вероятность. Это вероятность наступления события А при условии, что произошло событие В.
Теперь у вас есть вся необходимая информация по всем вероятностным формулам класса 9.Мы надеемся, что вы загрузили PDF-формулы вероятности, доступные на этой странице. Практикуйте больше вопросов и осваивайте эту концепцию.
Учащиеся могут использовать NCERT Solutions для математики, предоставленные Embibe, для подготовки к экзамену.
Мы надеемся, что эта подробная статья о формулах статистической вероятности поможет вам. Если у вас есть какие-либо вопросы относительно этой статьи, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.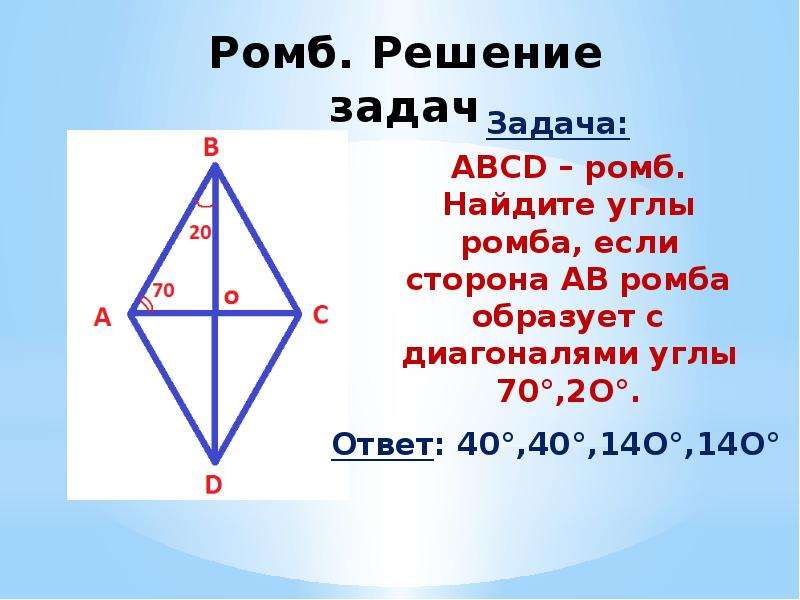
2001 Просмотров
Формулы дифференциации: Формулы производных — Embibe
Формулы дифференциации: Дифференциация – одна из самых важных тем для учащихся 11 и 12 классов. В колледжах преподается множество концепций дифференциации более высокого уровня. Таким образом, каждый студент, обучающийся в потоке естественных наук, должен хорошо знать эти формулы дифференцирования и правила, которые всегда под рукой. Мы предоставили список формул дифференцирования для справки студентов, чтобы они могли использовать его для решения задач, основанных на дифференциальных уравнениях.Производная представлена как d/dx.
Мы дали список формул, который включает производные для постоянных, тригонометрических функций, многочленов, логарифмических функций, экспоненциальных, гиперболических, обратных тригонометрических функций и т. д. В программе 11 и 12 классов есть ряд примеров и задач. Учащиеся могут легко ответить на эти вопросы, используя решения, которые мы предоставили здесь.
В этой статье мы предоставили вам список формул полного дифференцирования , а также тригонометрические формулы, формулы для логарифмических, полиномиальных, обратных тригонометрических и гиперболических функций.Эти производные формулы помогут вам решить различные задачи, связанные с дифференцированием.
Практика JEE Основные вопросы сейчас
Формулы дифференциации: что такое дифференциация? | Формулы дифференциации
Дифференцирование — это процесс вычисления функции, представляющей скорость изменения одной переменной по отношению к другой. Дифференциация и производные имеют огромное применение не только в нашей повседневной жизни, но и в высшей математике.
Определение дифференциации : Предположим, что y является функцией x и выражается как \(y=f(x)\). Тогда скорость изменения «y» на единицу изменения «x» определяется выражением \(\frac{dy}{dx} \).
Здесь \(\frac{dy}{dx} \) известно как дифференцирование y по x . {2} }}\)
{2} }}\)
\(\frac{d}{dx}f(x)=\frac{d}{dx}\left[ a(x)\pm b(x) \right]=\frac{d }{dx}a(x)\pm \frac{d}{dx}b(x)\)
Предположим, \(f(x)=c\), где c — константа. У нас есть
\(\frac{d}{dx}f(x)=\frac{d}{dx}(c)=0\)
\(\frac{d}{dx} \left[ c\times f(x) \right]=c\times \frac{d}{dx}f(x)\)
\(\frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}\)
Список формул дифференциации
В таблице ниже представлены производные основных функций, константа, константа, умноженная на функцию, правило степени, правило суммы и разности, правило произведения и частного и т. 2}}\)
2}}\)
Практические экзаменационные вопросы
Итак, теперь вы знакомы с формулами дифференцирования, т.е.е. производные популярных тригонометрических, полиномиальных, обратных тригонометрических, логарифмических и гиперболических функций.
Попытка пробных тестов
Важные часто задаваемые вопросы о списке формул дифференциации
Вы можете найти ответы на важные часто задаваемые вопросы, на которые наши специалисты ответили ниже:
| Q1: Каковы формулы дифференцирования? Ответ: Когда вы вычисляете функцию, представляющую скорость изменения одной переменной по отношению к другой, используется дифференцирование, а связанные с ним формулы являются формулами дифференцирования. |
| Q2: Как запомнить все формулы интегрирования и дифференцирования для тригонометрии? Ответ: Лучший способ запомнить сложные формулы интегрирования и дифференцирования — решать вопросы.  Начните с тем, а затем последовательно продвигайтесь к концу главы. Продолжайте обращаться к этим формулам всякий раз, когда вы застряли на вопросе. Со временем вы станете лучше и вам больше не потребуется формуляр. Начните с тем, а затем последовательно продвигайтесь к концу главы. Продолжайте обращаться к этим формулам всякий раз, когда вы застряли на вопросе. Со временем вы станете лучше и вам больше не потребуется формуляр. |
| Вопрос 3. Есть ли какой-либо веб-сайт, на котором я могу бесплатно практиковать формулы дифференцирования? Ответ: На Embibe можно бесплатно попрактиковаться в вопросах дифференциального исчисления. |
| Q4. Каковы общие формулы дифференцирования? Ответ: Общие формулы дифференцирования включают: производные основных функций, производные логарифмических и экспоненциальных функций, производные тригонометрических функций, производные обратных тригонометрических функций, правила дифференцирования.2 x (d/dx) cosec x = -cosec x cot x |
Q7.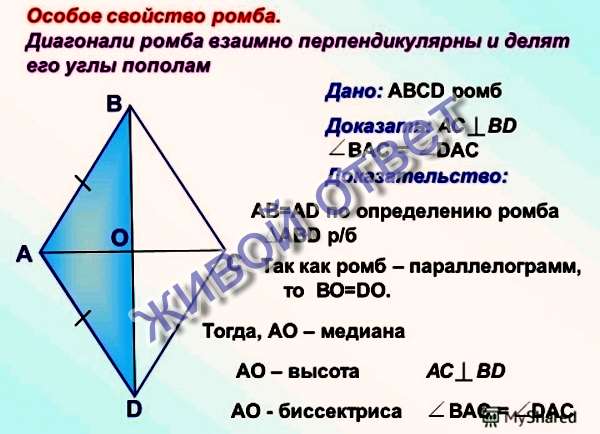 Что такое д/дх? Что такое д/дх? Ответ: d/dx является общим представлением производной функции. d/dx обозначает дифференцирование по переменной x. |
| Q8. Что такое формула УФ? Ответ: (d/dx)(uv) = v(du/dx) + u(dv/dx) Эта формула используется для нахождения производной произведения двух функций. |
Учащиеся могут использовать NCERT Solutions for Maths, предоставленные Embibe, для подготовки к экзаменам.
Бесплатные практические вопросы и пробные тесты по математике (с 8 по 12 классы)
Мы надеемся, что этот полный список формул дифференцирования поможет вам. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев ниже. Мы свяжемся с вами в ближайшее время.
1722 просмотров
ромбы с первого взгляда
Теперь, когда мы рассмотрели самый распространенный тип четырехугольника, с которым мы сталкиваемся, мы можем вытащить наши лопаты и копнуть немного глубже в поисках более редких четырехугольников.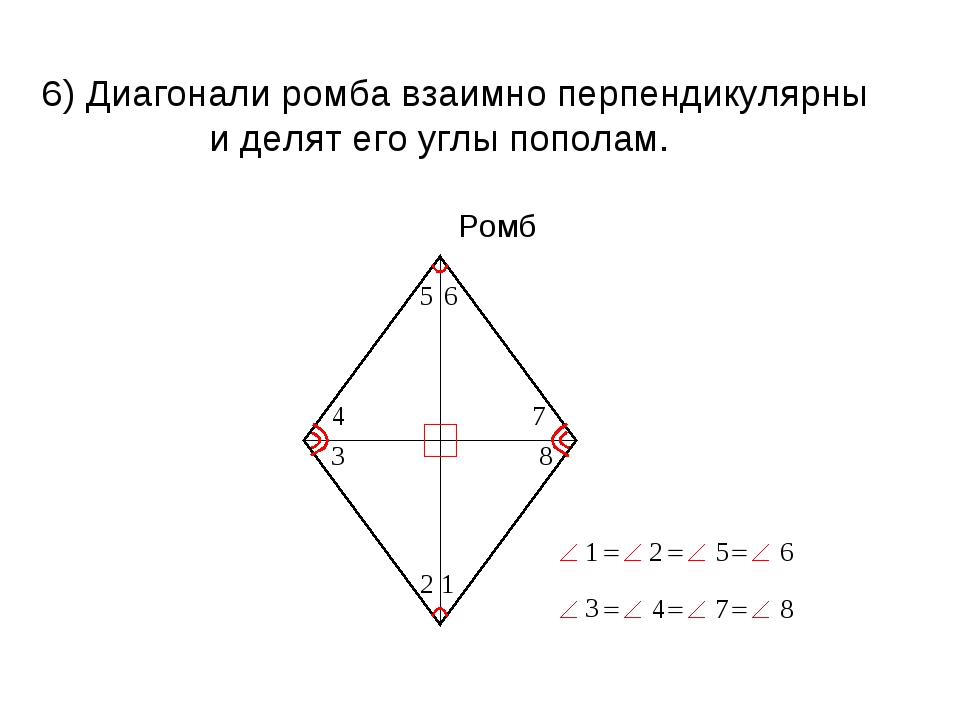 Как мы узнаем, является ли четырехугольник обычным или редким? Что ж, нам следует искать четырехугольники, которые чем-то отличаются и обладают особыми свойствами. Они будут выделяться, как оперный певец на съезде пантомимы.
Как мы узнаем, является ли четырехугольник обычным или редким? Что ж, нам следует искать четырехугольники, которые чем-то отличаются и обладают особыми свойствами. Они будут выделяться, как оперный певец на съезде пантомимы.
Первым из этих параллелограммов является ромб, или ромбы во множественном числе. Если это сбивает с толку, подумайте «осьминог → осьминог». Конечно, весь спор об осьминогах и осьминогах еще более сбивает с толку. Мы бы предпочли не вникать в это.
Ромб — это тип параллелограмма, у которого четыре конгруэнтные стороны.На нашем рисунке WX || YZ и XY || ZW (что делает его параллелограммом) и WX ≅ XY ≅ YZ ≅ ZW (что делает его ромбом).
Пример задачи
Является ли четырехугольник PQRS ромбом?
PQRS — параллелограмм, но конгруэнтны только противоположные стороны. Поскольку PQ ≅ RS ≇ QR ≅ PS , этот параллелограмм не является ромбом.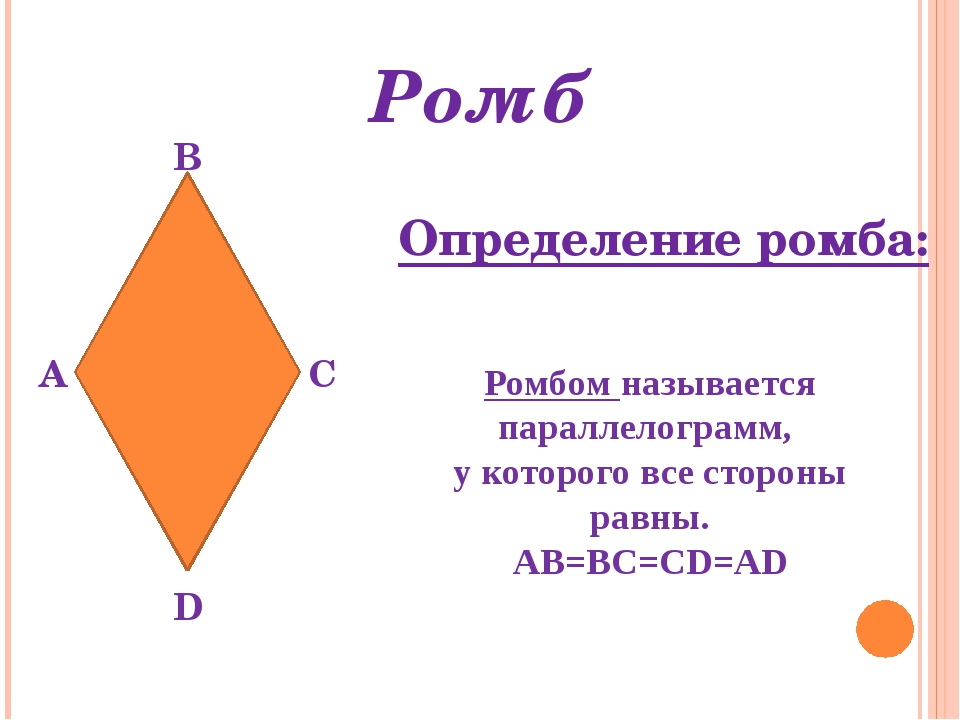
Ромбы превосходят ожидания параллелограммов. Они обладают всеми свойствами параллелограмма и даже больше. Гораздо больше.
Общеизвестно, что диагонали параллелограмма делят друг друга пополам. Это все хорошо, но диагонали ромбов делают этот хет-трик еще дальше. Они не только являются биссектрисами друг друга; они же перпендикулярны. Оооо, да.
Еще одна удивительная особенность диагоналей ромба заключается в том, что они делят его углы пополам.Другими словами, диагонали ромба также являются биссектрисами угла.
В ромбе ABCD , ∠1 ≅ ∠2 ≅ ∠3 ≅ ∠4 и ∠5 ≅ ∠6 ≅ ∠7 ≅ ∠8. Итак, диагонали ромба — это биссектрисы угла и серединные перпендикуляры. Расскажите о многозадачности.
Пример задачи
Какова мера ∠ HIA в ромбе HIJK ?
Нам дано, что m∠ AHI = 80°, и мы знаем, что диагонали ромба перпендикулярны друг другу.Это означает, что ∠ HAI составляет 90°. Эти три угла образуют внутренние углы треугольника, которые в сумме должны составлять 180° в соответствии с теоремой о сумме углов для треугольников. Это означает, что ∠ HIA равно 180 – 80 – 90 = 10°.
Эти три угла образуют внутренние углы треугольника, которые в сумме должны составлять 180° в соответствии с теоремой о сумме углов для треугольников. Это означает, что ∠ HIA равно 180 – 80 – 90 = 10°.
Пример задачи
Докажите, что диагонали ромба делят его на четыре равных треугольника.
Естественно, это можно сделать несколькими способами. Мы могли бы использовать любое количество различных теорем и определений о ромбах, но прежде чем мы это сделаем, почему бы нам не провести диагонали? Возможно, это нам немного поможет.
Теперь приступим к доказательству.
| Заявления | Причины |
| 1. ABCD является ромбом | |
| 2. AB ≅ BC ≅ CD ≅ DA | Определение ромба (1) |
| 3. ABCD является параллелограммом | Ромб также является параллелограммом (1) |
4. AE ≅ CE и CE и BE и DE ≅ de AE ≅ CE и CE и BE и DE ≅ de | диагонали параллелограммы бислект друг друга (3) |
| 5. Δ BEC ≅ δ ≅ Δ Bea ≅ δ DEA | Постулат SSS (2, 4) |
Все, что нам нужно сделать, чтобы доказать наши теоремы о том, что диагонали перпендикулярны друг другу и делят внутренние углы пополам, это продолжить это доказательство, используя CPCTC и зная несколько определений. .Вы, вероятно, можете сделать это сами, поэтому мы не будем тратить на это ваше время.
Но что, если четырехугольникам нужно доказать, что они ромбы? Например, MARK отчаянно пытается доказать Четырехстороннему комитету, что он больше, чем просто предсказуемый параллелограмм. Он ромб, но как ему проявить себя?
МАРК нужно будет спуститься к его вершинам и умолять. Но члены Четырехстороннего комитета довольно прямолинейны.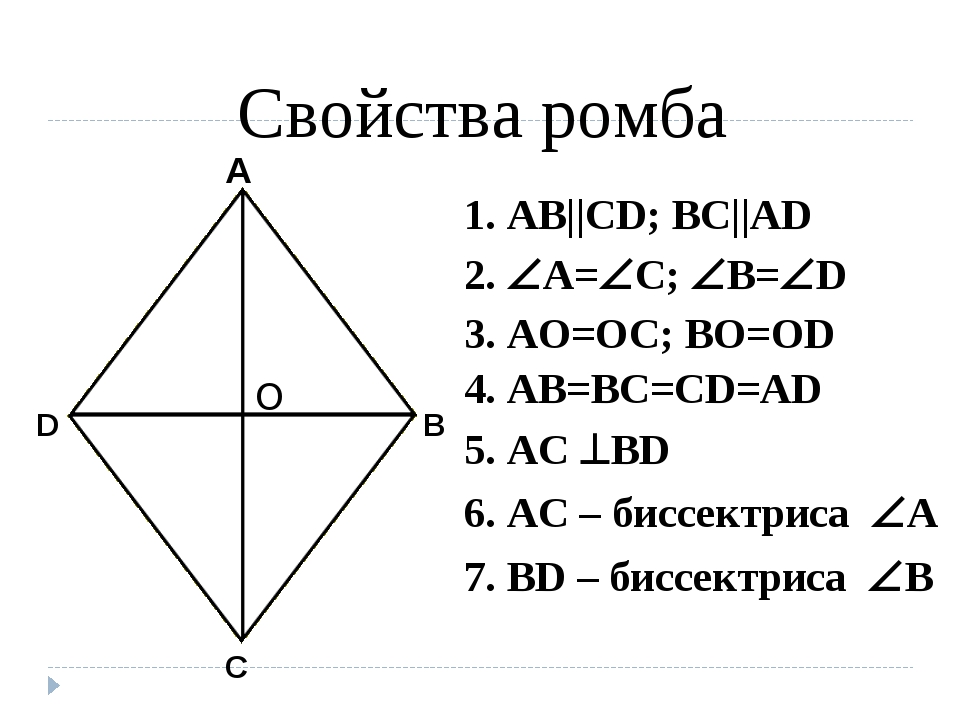 Их ничуть не смущает его низкопоклонство.Им потребуются доказательства того, что он настоящий ромб, поэтому сумма внутренних углов, равная 360°, или диагонали, разделенные пополам, не помогут. Любой старый параллелограмм мог бы так же легко удовлетворить этим требованиям, верно? А вот MARK придется доказывать еще немного, чтобы добиться ромбовидности. Ему нужно убедить их одним из следующих способов:
Их ничуть не смущает его низкопоклонство.Им потребуются доказательства того, что он настоящий ромб, поэтому сумма внутренних углов, равная 360°, или диагонали, разделенные пополам, не помогут. Любой старый параллелограмм мог бы так же легко удовлетворить этим требованиям, верно? А вот MARK придется доказывать еще немного, чтобы добиться ромбовидности. Ему нужно убедить их одним из следующих способов:
- Докажите, что он параллелограмм с 4 конгруэнтными сторонами.
- Докажите, что он параллелограмм с перпендикулярными диагоналями.
Например, MARK может доказать, что он ромб следующим образом:
| Утверждения | Причины 9 1 Mark — параллелограмма | дано |
| 2 мА ≅ RK и ar ≅ км | напротив параллелограммы конгруэнтны (1) | |
3.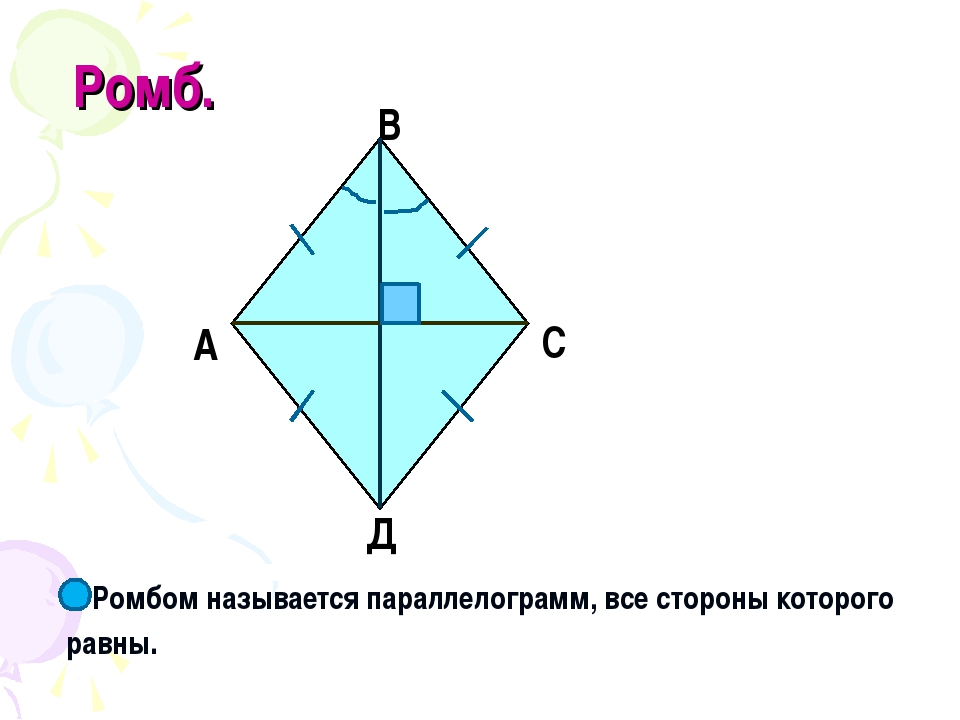 |


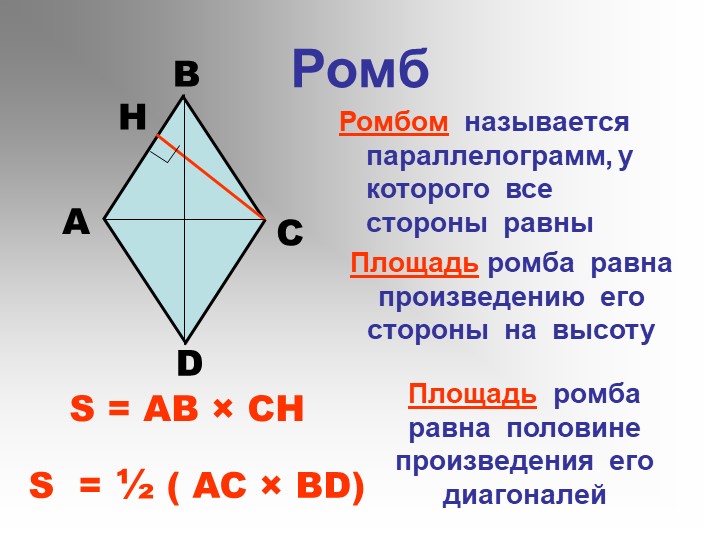 Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.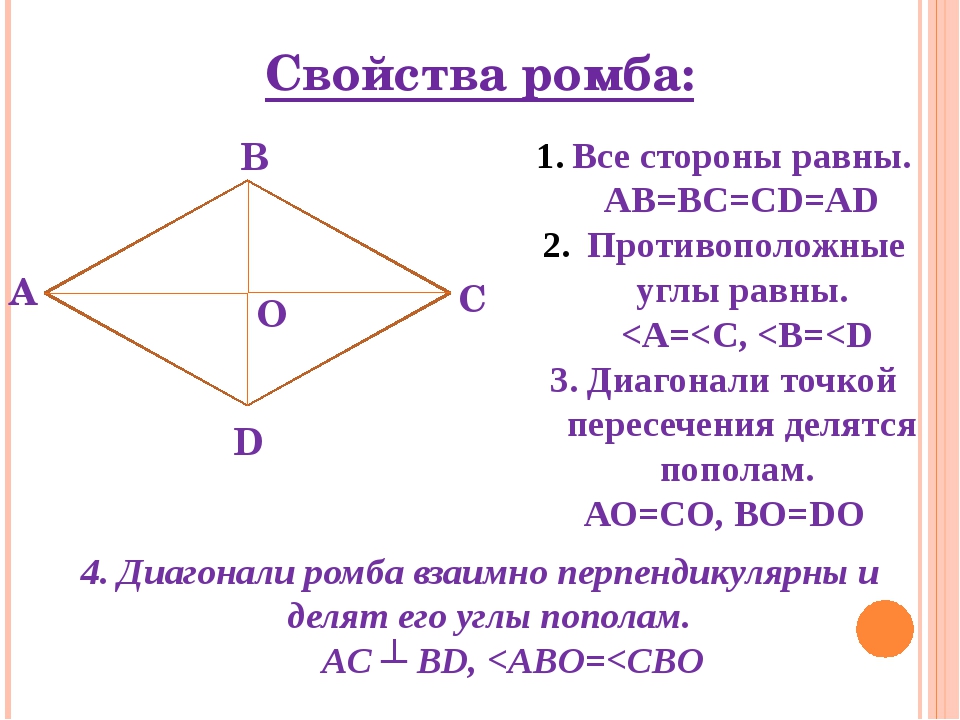
 Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
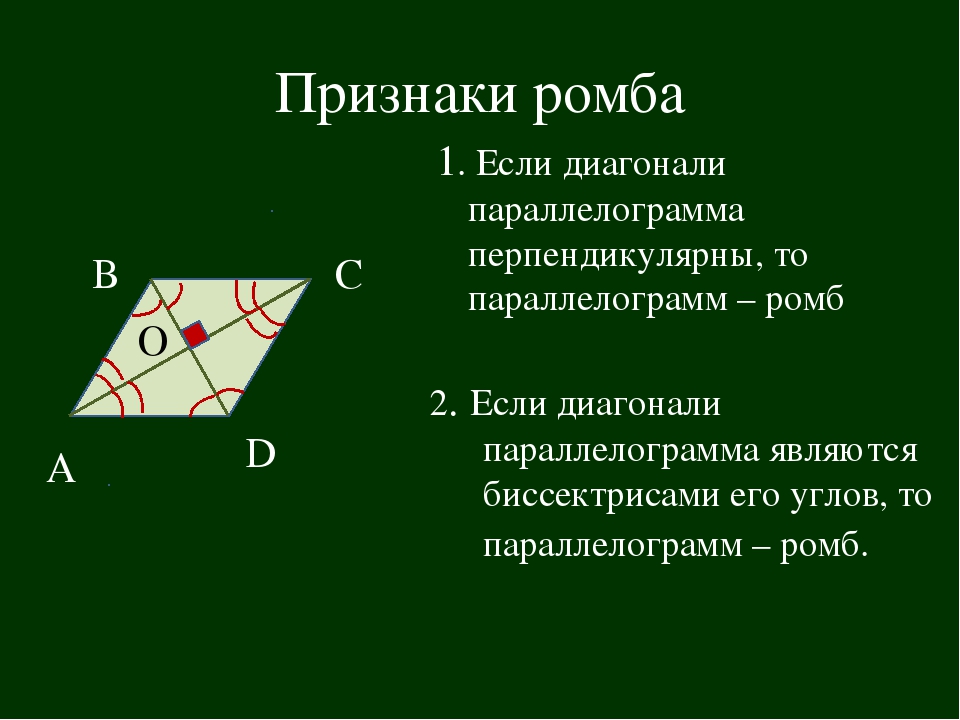


 10 : Все стороны ромба равны.
10 : Все стороны ромба равны. Поскольку ?AMB и ?BMC образуют прямой угол, они являются дополнительными. Если бы вы могли показать, что они конгруэнтны, то они должны были бы быть прямыми углами. Самый простой способ показать ?AMB ~= ?BMC — показать ?AMB ~= ?CMB и использовать CPOCTAC.Теперь, поскольку вы имеете дело с ромбом, AB ~= BC. По рефлексивному свойству ~= вы знаете, что BM ~= BM. Поскольку ромб является параллелограммом, и показано, что диагонали параллелограмма делят друг друга пополам, AM ~= MC. Вы можете использовать наш постулат SSS, чтобы заключить, что ?AMB ~= ?CMB. Давайте запишем это.
Поскольку ?AMB и ?BMC образуют прямой угол, они являются дополнительными. Если бы вы могли показать, что они конгруэнтны, то они должны были бы быть прямыми углами. Самый простой способ показать ?AMB ~= ?BMC — показать ?AMB ~= ?CMB и использовать CPOCTAC.Теперь, поскольку вы имеете дело с ромбом, AB ~= BC. По рефлексивному свойству ~= вы знаете, что BM ~= BM. Поскольку ромб является параллелограммом, и показано, что диагонали параллелограмма делят друг друга пополам, AM ~= MC. Вы можете использовать наш постулат SSS, чтобы заключить, что ?AMB ~= ?CMB. Давайте запишем это.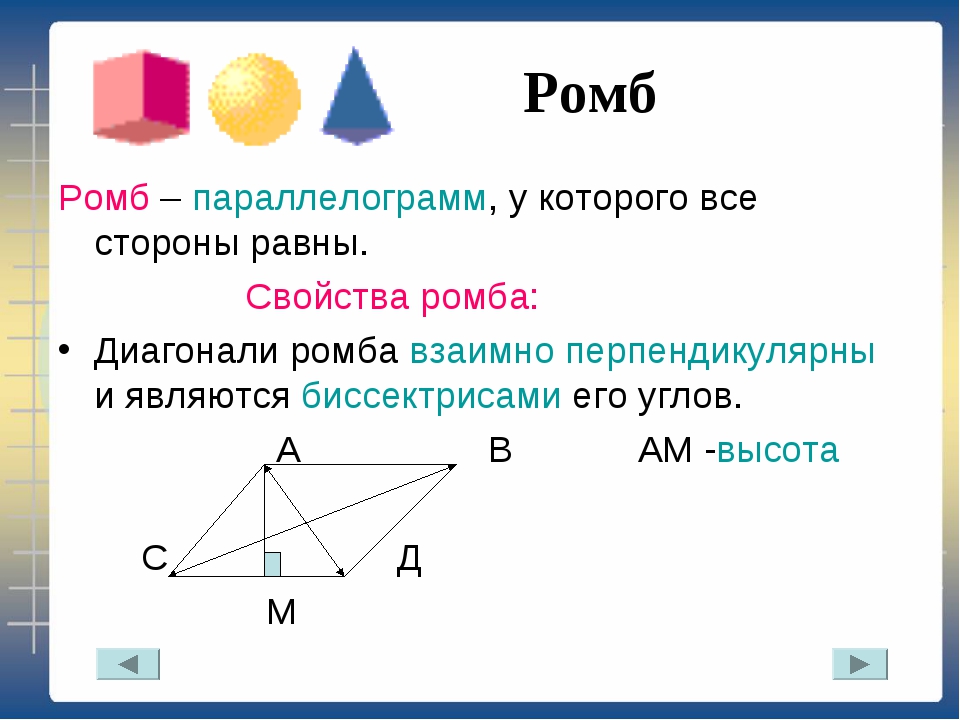 Если из пачки наугад взять ручку, заменить ее и повторить процесс еще 2 раза, какова вероятность того, что вытащите 2 синие ручки и 1 черную ручку?
Если из пачки наугад взять ручку, заменить ее и повторить процесс еще 2 раза, какова вероятность того, что вытащите 2 синие ручки и 1 черную ручку?