Тесты Геометрия 11 класс | Социальная сеть работников образования
Тест 3: «Компланарные векторы»
№ п/п вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | В1 | В2 | В3 |
1 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 2 | комп. | не комп. | 4 |
2 | 1 | 2 | 3 | 1 | 2 | 2 | 1 | 1 | комп. | не комп. | 3 |
ТЕСТ 3: «КОМПЛАНАРНЫЕ ВЕКТОРЫ»
Вариант №1
Уровень А
1. Какое утверждение верное?
1) Любые два вектора компланарны.
2) Любые три вектора компланарны.
3) Три нулевых вектора компланарны.
2. Какое утверждение верное?
1) Если один из трёх векторов нулевой, то векторы компланарны.
2) Если векторы компланарны, то один из них нулевой.
3) Если векторы компланарны, то они равны.
3. ABCDA1B1C1D1 – параллелепипед. Являются компланарными векторы…
1)
2)
3)
4. Известно, что
Тогда векторы и являются…
1) коллинеарными;
2) компланарными;
3) некомпланарными.
5. Векторы и некомпланарны, если…
1)
2)
3)
6. DABC – тетраэдр. О – точка пересечения медиан грани ABD.
Тогда …
1)
2)
3)
7. Диагонали параллелограмма ABCD пересекаются в точке M. Точка О – произвольная точка пространства.
Тогда k = …
1)
2) 2
3)
8. Какое утверждение неверное?
1) Коллинеарные векторы компланарны.
2) Если векторы компланарны, то они коллинеарны.
3) Векторы компланарны, если имеются равные им векторы, лежащие в одной плоскости.
Уровень В
1. Векторы …
2. Точки А, В и С лежат на окружности, а точка О не лежит в плоскости этой окружности. Тогда векторы и …
3. ABCDA1B1C1D1 – прямой параллелепипед, см. ABCD – квадрат, АВ = 2 см. Тогда …
ТЕСТ 3: «КОМПЛАНАРНЫЕ ВЕКТОРЫ»
Вариант №2
Уровень А
1. Какое утверждение верное?
1) Любые два вектора не могут не быть компланарными.
2) Любые три вектора некомпланарны.
3) Только нулевые три вектора компланарны.
2. Какое утверждение неверное?
1) Три вектора компланарны, если любые два из них коллинеарны.
2) Если векторы компланарны, то любые два из них коллинеарны.
3) Любые три равных вектора компланарны.
3. FABCD – пирамида. ABCD – параллелограмм.
Не являются компланарными векторы…
1)
2)
3)
4. Тогда прямые АС и BD…
1) пересекаются;
2) скрещиваются;
3) параллельные.
5. Векторы и некомпланарны, если…
1)
2)
3)
6. DABC – тетраэдр. О – точка пересечения медиан грани BDC. Тогда …
1)
2)
3)
7. Точки M, N, P, K – середины сторон четырёхугольника ABCD. Точка О – произвольная точка пространства.
Тогда …
1)
2)
3)
8. Какое утверждение неверное?
1) Прямые, содержащие компланарные векторы, лежат в одной плоскости.
2) Если векторы лежат в одной плоскости, то они компланарны.
3) Если вектор можно разложить по векторам и , то векторы и компланарны.
Уровень В
1. Известно, что векторы и компланарны. Тогда векторы …
2. Точки А, В и С не лежат на одной прямой, а точка О не лежит в плоскости (АВС). Тогда векторы и …
3. ABCDA1B1C1D1 – куб. АВ = см.
Тогда …
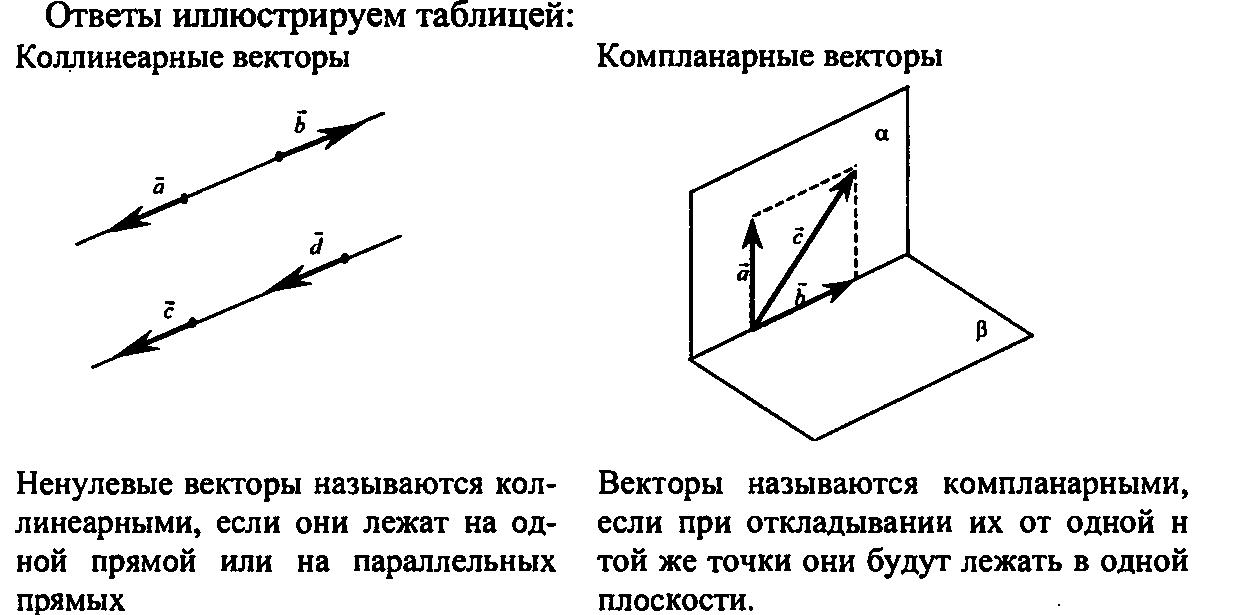
Связь между координатами вектора и координатами его начала и конца
Цель данного урока – научиться находить координаты произвольного вектора, зная координаты его начала и конца. Здесь мы вспомним, как вектор раскладывается по двум неколлинеарным векторам, найдем координаты вектора через это разложение. Поймем, как получить координаты любого вектора и решим типовые примеры.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Напомним, что любой вектор на плоскости можно однозначно выразить через два неколлинеарных вектора  и
и  . Это значит, что векторы
. Это значит, что векторы  и
и  задают координатную плоскость, в которой будут рассматриваться все остальные векторы (см. рис. 1).
задают координатную плоскость, в которой будут рассматриваться все остальные векторы (см. рис. 1).
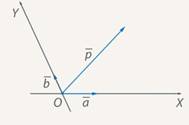
Рис. 1. Разложение вектора по двум неколлинеарным векторам
Так, найдутся такие числа 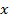 ,
, 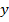 , что:
, что:
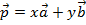
Для конкретного вектора пара чисел 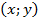
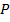 – конца вектора.
– конца вектора.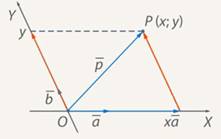
Рис. 2. Координаты вектора
Из точки 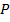 проведем прямые, параллельные осям координат (см. рис. 2). По правилу треугольника имеем:
проведем прямые, параллельные осям координат (см. рис. 2). По правилу треугольника имеем:
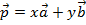
Дано: 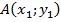 ;
; 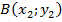 .
.
Найти координаты вектора 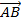 .
.
Решение
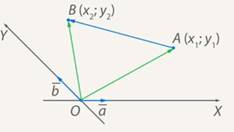
Рис. 3. Координаты вектора
Мы можем найти координаты вектора, построенного из начала координат. Далее применим правило треугольника (см. рис. 3):
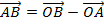
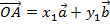 ;
; 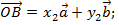
Тогда:
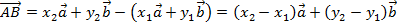
Так, искомые координаты вектора: 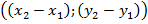 , каждая координата вектора равна разности соответствующих координат его конца и начала.
, каждая координата вектора равна разности соответствующих координат его конца и начала.
Пример
Дано: 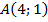 ;
; 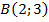
Найти координаты вектора 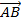 ;
; 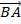 .
.
Решение
По формуле:
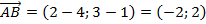
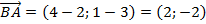
Напомним, что векторы 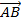
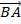 являются противоположными и их координаты противоположны.
являются противоположными и их координаты противоположны.
Пример
Дано: 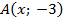 ;
; 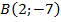 ;
; 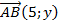 .
.
Найти числа 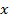 ,
, 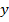
Решение
По формуле:
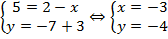
Пример
Дано: параллелограмм 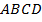 ;
; 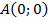 ;
; 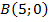 ;
; 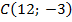
Найти координаты вершины 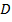 параллелограмма (см. рис. 4).
параллелограмма (см. рис. 4).
Решение
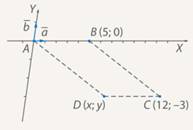
Рис. 4. Иллюстрация к задаче
Построим заданные точки в системе координат, построим параллелограмм. Чтобы найти координаты точки 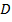 воспользуемся равенством векторов
воспользуемся равенством векторов 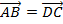 .
.
Найдем координаты векторов:
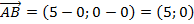
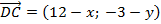
Из равенства векторов следует равенство их координат:
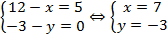
Итак, мы научились находить координаты вектора по координатам его начала и конца.
Список литературы
- Атанасян Л.С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
- Фарков А.В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А.В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Onlinemschool.com (Источник).
- Mathprofi.ru (Источник).
- Make-me-smart.com (Источник).
Домашнее задание
- Найти координаты вектора
 :
:
 ,
,  ;
;
 ;
; ,
,  .
.
- Найти числа
 ,
,  :
:
 ,
,  ,
,  ;
; ,
,  ,
,  .
.
- Найти координаты недостающей вершины параллелограмма:
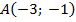 ;
; 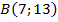 ;
; 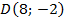
Конспект урока по геометрии по теме «Связь между координатами векторов и координат точек», 11 класс


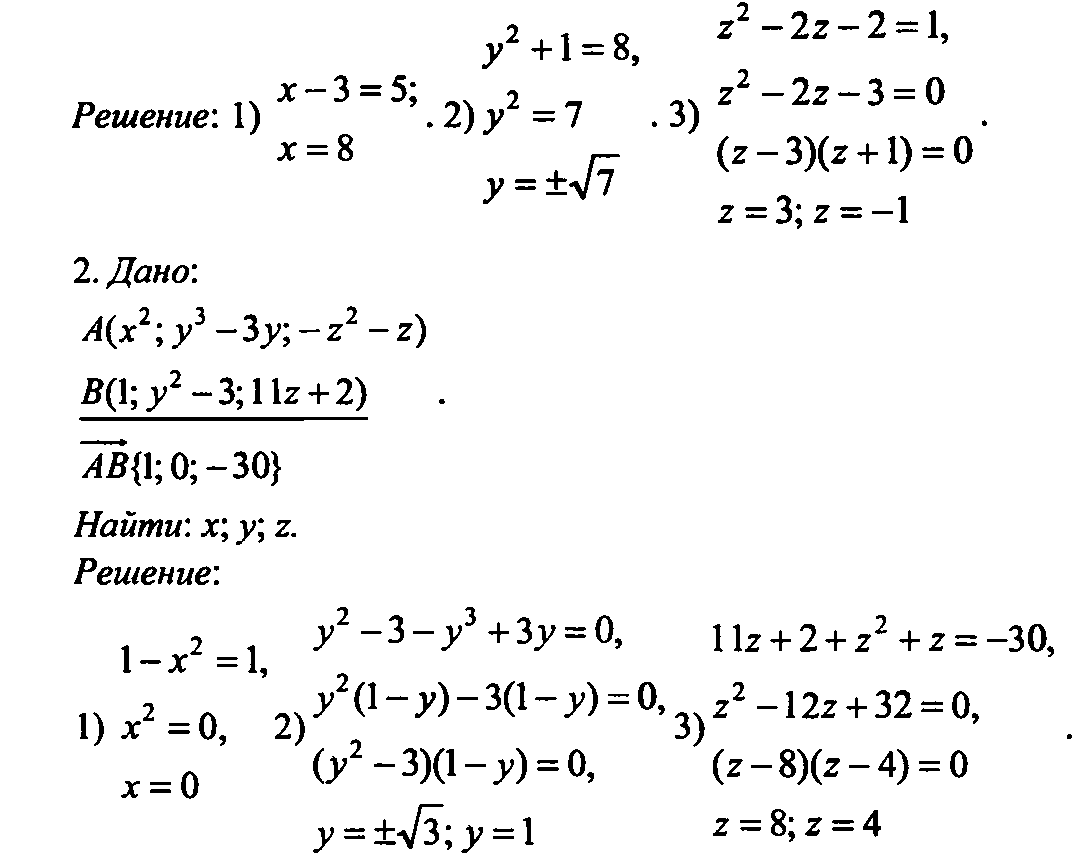


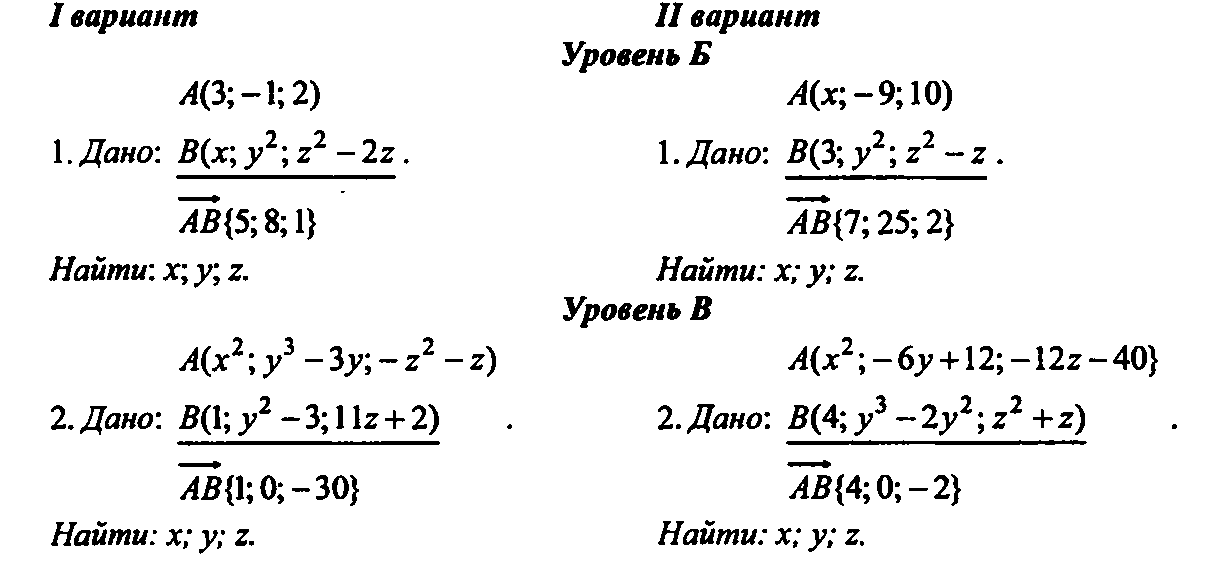
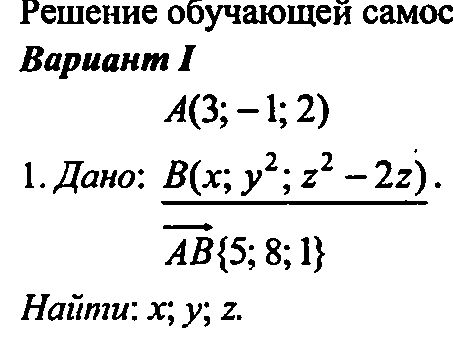
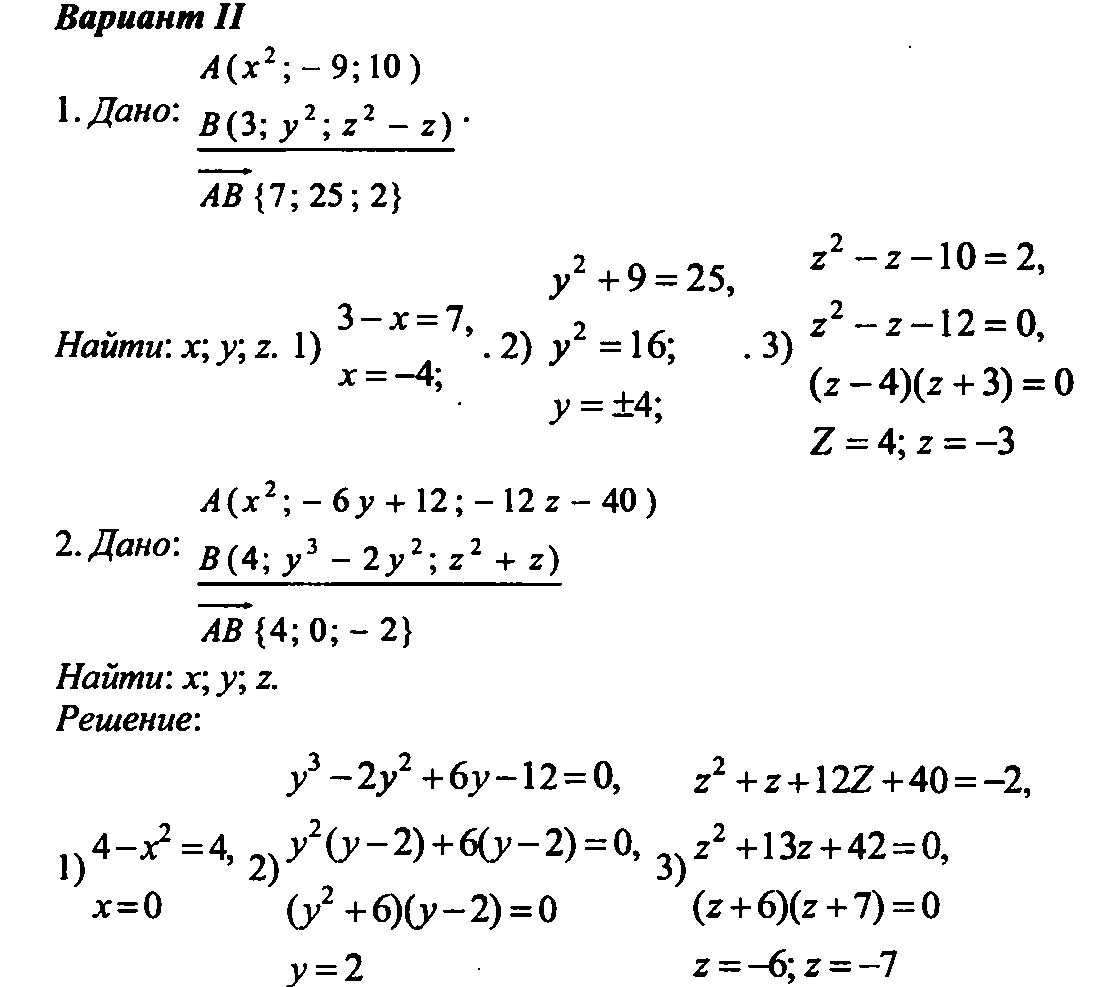
III. Изучение нового материала
1. Ввести понятие многоугольника, его сторон, вершин, диагоналей.
На доске и в тетрадях учащихся сделать краткую запись и
выполнить рисунки.
а) Рис. 70. ABCDEKF -многоугольник (семиугольник), АВ, ВС,CD, DE, EF, FK, KA —
стороны многоугольника, А, В, С, D, Е,F, К —
вершины многоугольника, А, В -соседние вершины,AC, AD, AE, AF- диагонали многоугольника.
б) Рис. 1X.ABCDEF- не многоугольник (CE0AD =В).
2. Ввести понятие внутренней и внешней областей
многоугольника (рис. 72).
3. Ввести определение выпуклого многоугольника.
Многоугольник называется выпуклым, если он лежит поодну сторону от каждой прямой, проходящей через две его соседние вершины.
Выпуклые многоугольники: рис. 73.
Невыпуклый многоугольник: рис. 74.
2Фронтальная работа с классом
1. Среди всех фигур, изображенных на рис. 75, укажите те,
которые являются:
а) многоугольниками;б) выпуклыми многоугольниками;
в) невыпуклыми многоугольниками.
2. Начертите:
/ вариант -выпуклый пятиугольник ABCDE.
II вариант -выпуклый шестиугольник ABCDEF.
(У доски работают два ученика.)
Запишите в тетрадях:
а) вершины многоугольника;
б) стороны многоугольника;
в) диагонали многоугольника;
г) вычислите сумму углов многоугольника.
Обсудить решение задачи 2 (г): —
Сумму углов какой геометрической фигуры мы умеем вычислять?
Чему равна сумма углов прямоугольника? —
Чему равна сумма углов выпуклого четырехугольника? —
Найдите сумму углов своей фигуры.
3. Чему равна сумма углов десятиугольника?
4. Чему равна сумма углов я-угольника? (Работа в группах.)
Учащиеся работают самостоятельно в группах по 3-4 ученика в
течение 3-5 минут, затем заслушиваются 2-3 решения и
обсуждается их правильность.
Наводящие вопросы (на случай, если никто из учащихся не
справился с решением задачи):
Сколько треугольников получится, если провести все
диагонали, выходящие из одной вершины? —
Чему равна сумма углов каждого из полученных
треугольников?
Что вы можете сказать о сумме углов всех треугольников? —
Чему равна сумма углов выпуклого я-угольника?
IV. Закрепление изученного материала
1. Работа в рабочих тетрадях. (Один из учащихся вслух читает
задачу и ее решение, заполняя пропуски, остальные
внимательно следят за его работой. Если ученик допускает при этом
ошибку, то класс исправляет ее.)
Задача № 3. Ответ: а) 5; б) 900°.
Задача № 4. Ответ: а) 1620°; б) 3600°.
2. Решить письменно № 365 (в).
Один из учащихся вызывается к доске для решения задачи,
остальные работают в тетрадях.
Решить задачи № 364 (а, б), 365 (а, б, г), 368. Решить задачи № 1, 2 из рабочей тетради
Связь между координатами вектора и координатами его начала и конца
Вы
уже знакомы с понятием координат вектора. Ими называют коэффициенты разложения
данного вектора по единичным координатным векторам  и
и
 .
.
Сегодня мы ответим на вопрос «Как связаны координаты вектора с координатами его начала и конца?».
Но для начала вернёмся к координатам точки в прямоугольной системе координат.

Напомним, что для их определения нужно опустить перпендикуляры из данной точки к осям.
Точки пересечения данных прямых с осями обозначим как М1 и М2.
Абсциссой точки М
является число x, которое является длиной
отрезка ОМ1. А ординатой — число y,
которое является длиной отрезка ОМ2. ,
,
 ,
,
 .
.
Определим координаты точек А, B, C, D, Е и F.

 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
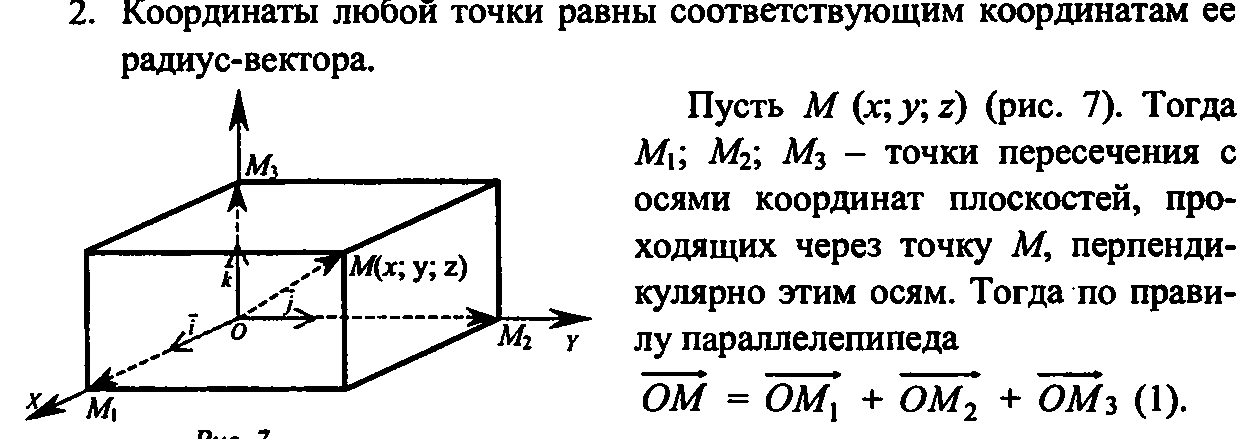
Мы вспомнили, как определять координаты точек, а теперь вернёмся к общему случаю и, уже рассмотренной, точке М.
Проведём вектор из точки О к точке М. Запомните, вектор ОМ называют радиус-вектором точки М.

Для
точки А радиус-вектором будет вектор  ,
для точки B — вектор
,
для точки B — вектор  ,
для точки C —
,
для точки C —  ,
для точки D —
,
для точки D —  ,
радиус-вектором точки Е является вектор
,
радиус-вектором точки Е является вектор  ,
а радиус-вектором точки F
— вектор
,
а радиус-вектором точки F
— вектор  .
.

Сейчас докажем следующее утверждение: координаты точки М равны соответствующим координатам её радиус-вектора.
Доказать:
 .
.
Доказательство.


Понятно, что вектор  по
правилу параллелограмма.
по
правилу параллелограмма.
Теперь необходимо
доказать, что вектор  ,
а
вектор
,
а
вектор  .
Тем самым мы докажем, что вектор
.
Тем самым мы докажем, что вектор  .
.

 ,
, 

 ,
, 

 ,
, 


Итак, мы доказали, что вектор  . То есть координаты
вектора
. То есть координаты
вектора  ,
так же как и у точки М.
,
так же как и у точки М.
Что и требовалось доказать.
Вернёмся к нашим векторам из примера.

Можем сказать, что
координаты точки  равны
соответствующим координатам радиус-вектора
равны
соответствующим координатам радиус-вектора  .
Значит, вектор
.
Значит, вектор  .
.
Аналогично,  ,
,
 ,
,
 ,
,
 ,
,
 .
.
Обратите внимание, что координаты точек помогают определить их расположение в пределах координатной плоскости, а вот координаты векторов указывают на перемещение относительно осей x и y.
Если взять две несовпадающие точки, то они однозначно имеют различные координаты.
А вот два несовпадающих вектора могут иметь одинаковые координаты в том случае, если векторы равны.
Итак, мы доказали, что координаты точки М равны соответствующим координатам её радиус-вектора. Радиус-вектором точки называют вектор, начало которого совпадает с точкой начала координат, а конец — с данной точкой.
Пользуясь
этим утверждением, выразим координаты вектора  через
координаты его начала и конца.
через
координаты его начала и конца.

Пусть точка А имеет
координаты  ,
а точка B имеет координаты
,
а точка B имеет координаты  .
.
Вектор  .
А они в свою очередь являются радиус-векторами точек B
и А соответственно.
.
А они в свою очередь являются радиус-векторами точек B
и А соответственно.
А
это значит, что координаты вектора  ,
а координаты вектора
,
а координаты вектора 
 .
.
Можем найти координаты
вектора разности: 
 ,
,

 .
.
Понятно,
что эти значения и будут координатами вектора  .
.
Так мы доказали, что каждая координата вектора равна разности соответствующих координат его конца и начала.
Задача.
По координатам точек  и
и
 найти
координаты вектора
найти
координаты вектора  .
.






Решение.
 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

 ,
,

Задача. Дописать в таблицу недостающие координаты.

Решение











На примере этого задания вы увидели, как находить ту или иную координату начала и конца вектора, а также самого вектора.
Далее решим задачу.
Задача.  —
параллелограмм. Найти координаты точки
—
параллелограмм. Найти координаты точки  ,
если
,
если  ,
,
 ,
,
 .
.
Решение

1 способ

 ,
,

 ,
,

 ,
,



2 способ




Ответ:  .
.
Подведём итоги урока. Сегодня мы установили связь между координатами вектора и координатами его начала и конца.
Перед этим ввели понятие радиус-вектора точки и доказали, что координаты точки равны соответствующим координатам её радиус-вектора.
Далее рассмотрели произвольный вектор и выразили его координаты как разности соответствующих координат его конца и начала. Это утверждение и помогло нам успешно справиться с решением задач.
Тест 2 координаты точки и координаты вектора
Тест 2: «Координаты точки и координаты вектора»
№ п/п вариант А1А2А3 А4А5 А6А7А8 А9В1В2В3 В4В5
1 1 3 3 1 3 1 1 1 2 (0;0;5) 3 (2;2;0)
2 1 3 1 3 3 1 1 1 2 (–1;0;0) {-1;-1;6} 5 (–1;0; 1)
Тест 2: «Координаты точки и координаты вектора»
Вариант №1
Уровень А1. Точка M (–2; 3; –7) находится от плоскости XOY на расстоянии, равном…
1) 7;
2) 2;
3) 3.
2. Тогда вектор имеет координаты…
1)
2)
3)
3. Тогда коллинеарными будут векторы…
1) и
2) и
3) и
4. Первая и третья координаты ненулевого вектора равны нулю. Тогда неверно, что…
1)
2)
3)
5. Первая координата ненулевого вектора равна нулю. Тогда неверно, что…
1)
2)
3)
6. А (1; 2; 3), В (1; 5; 4), С (4; 5; 3). Тогда верно, что…
1)
2)
3)
7. Ордината точки А равна 3, ордината точки В равна 6. Длина отрезка АВ равна 3. Тогда прямая АВ и ось OY…
1) параллельны;
2) перпендикулярны;
3) скрещиваются.
8. M (x1; y1; z1), K (x2; y2; z2). Тогда координаты вектора равны…
1)
2)
3)
9. Тогда верно, что…
1)
2)
3)
Уровень В1. Дана точка А (–1; 2; 5). Тогда координаты точки – проекции точки А на ось OZ равны…
2. Даны точки M (–1; 2; 3) и В (1; –1; 5). Тогда координаты вектора равны…
3. А (–1; 0; 2), В (1; –2; 3). Тогда …
4. ABCD – параллелограмм, В (–2; 1; 0), О (0; 1,5; 0). Тогда координаты точки D равны…
5. Вектор сонаправлен с вектором Тогда координаты вектора равны…
Тест 2: «Координаты точки и координаты вектора»
Вариант №2
Уровень А1. Точка А (–1; 2; –3) находится от плоскости YOZ на расстоянии, равном…
1) 1;
2) 2;
3) 3.
2. Тогда вектор имеет координаты…
1)
2)
3)
3. Координаты равных векторов…
1) равны;
2) противоположны;
1) пропорциональны.
4. Первая и вторая координаты ненулевого вектора равны нулю. Тогда верно, что…
1)
2)
3)
5. Третья координата ненулевого вектора равна нулю. Тогда неверно, что…
1)
2)
3)
6. А (2; 3; 4), В (2; 5; 6), С (5; 3; 6). Тогда верно, что…
1)
2)
3)
7. Абсцисса точки А равна 3, абсцисса точки В равна 6. Длина отрезка АВ равна 3. Тогда прямая АВ и ось OX…
1) параллельны;
2) пересекаются;
3) скрещиваются.
8. M (x1; y1; z1), K (x2; y2; z2). Тогда длина вектора равна…
1)
2)
3)
9. A (x1; y1; z1), B (x2; y2; z2). Тогда координаты точки – середины отрезка АВ равны…
1)
2)
3)
Уровень В1. Дана точка А (–1; 2; 5). Тогда координаты точки – проекции точки А на плоскость OYZ равны…
2. Даны точки K (2; –1; –3) и M (1; –2; 3). Тогда координаты вектора равны…
3. А (7; 1; –5), В (4; –3; –5). Тогда …
4. В параллелограмме ABCD диагонали пересекаются в точке О. А (1; 3; –1), О (0; 1,5; 0). Тогда координаты точки С равны…
5. Вектор противоположно направлен вектору Тогда координаты вектора равны…
Тест по теме «Координаты и векторы»
Тест для самоконтроля
Тема: «Координаты и векторы»
Вариант № ___
Задание 1. (выберите один вариант ответа) Укажите координаты вектора .
Варианты ответов:
1) (0; 1; 3) 2) (1; 0; 3) 3) (1; 3; 0)
Задание 2. (выберите один вариант ответа) Укажите, при каких значениях n и p векторы и коллинеарные.
Варианты ответов:
1) 2) 3)
Задание 3. (выберите один вариант ответа) Укажите координаты вектора , если А(2; — 3; 4) и В(- 8; 4; 6).
Варианты ответов:
1) (1; 3,5; — 5) 2) (- 5; 3,5; 1) 3) (5; — 3,5; — 1)
Задание 4. (выберите один вариант ответа) Укажите координаты суммы векторов , если и .
Варианты ответов:
1) 2) (0; — 11; — 7) 3) (0; — 11; — 5)
Задание 5. (выберите один вариант ответа) Укажите, чему равно скалярное произведение векторов, если и угол между векторами 30°.
Варианты ответов:
1) 2) 6 3)
Задание 6. (выберите один вариант ответа) Найдите скалярное произведение векторов и .
Варианты ответов:
1) — 2 2) (0; 0; — 2) 3) – 4
Задание 7. (выберите один вариант ответа) Укажите, при каком значениях z векторы и перпендикулярные.
Варианты ответов:
1) 2) 3)
Задание 8. (выберите один вариант ответа) Укажите длину вектора , если
А(5; 3; 1), В(4; 5; 1).
Варианты ответов:
1) 3 2) 3)
Задание 9. (выберите варианты ответов согласно тексту задания) Установите соответствие между векторами и их длинами.
А) Б) В)
Варианты ответов:
1) 2) 3)
Задание 10. (выберите один вариант ответа) Укажите середину отрезка АВ, заданного точками А(3; — 7; 11) и В(- 1; 3; — 3).
Варианты ответов:
1) (- 2; 5; — 7) 2) (4; — 2; 1) 3) (1; — 2; 4)
Задание 11. (выберите два варианта ответов) Установите, какие из точек принадлежат прямой .
Варианты ответов:
1) (2; 3) 2) (- 4; — 6) 3) (- 2; 3)
Задание 12. (выберите один вариант ответа) Какой нормальный вектор имеет прямая, заданная уравнением у – 2х + 5 = 0?
Варианты ответов:
1) (- 2; 1) 2) (- 2; — 1) 3) (1; — 2)
Задание 13. (выберите один вариант ответа) Укажите уравнение окружности с центром в точке А(5; — 3) и радиусом R = 2.
Варианты ответов:
1) (х + 5)2 + (у — 3)2 = 4 2) (х — 5)2 + (у + 3)2 = 2 3) (х — 5)2 + (у + 3)2 = 4
Тест для самоконтроля
Тема: «Координаты и векторы»
Вариант № ___
Задание 1. (выберите варианты ответов согласно тексту задания) Установите соответствие между векторами и их координатами.
А) Б) В)
Варианты ответов:
1) (1; 0; -1) 2) (1; -1; 0) 3) (0; 1; -1)
Задание 2. (выберите один вариант ответа) Укажите, при каких значениях n и p векторы и коллинеарные.
Варианты ответов:
1) 2) 3)
Задание 3. (выберите один вариант ответа) Найдите координаты вектора 0,2 если
А(5; 0; — 8) и В(15; — 10; — 28).
Варианты ответов:
1) (- 4; — 2; 2) 2) (- 2; 2; 4) 3) (2; — 2; — 4)
Задание 4. (выберите один вариант ответа) Чему равны координаты разности векторов , если и .
Варианты ответов:
1) (3; — 3; — 1) 2) (3; 3; 1) 3) (- 3; — 9; 1)
Задание 5. (выберите один вариант ответа) Укажите, чему равно скалярное произведение векторов, если и угол между векторами 60°.
Варианты ответов:
1) 4 2) 3) 2
Задание 6. (выберите один вариант ответа) Найдите скалярное произведение векторов и ?
Варианты ответов:
1) (- 2; 0; 0) 2) — 2 3)
Задание 7. (выберите один вариант ответа) Укажите, при каком значении у векторы и перпендикулярные.
Варианты ответов:
1) 2) 3)
Задание 8. (выберите один вариант ответа) Найдите длину вектора , если С(3; -2; — 5) и Д(7; 6; — 1).
Варианты ответов:
1) 2) 3)
Задание 9. (выберите один вариант ответа) Расположите векторы в порядке увеличения их длин.
А) Б) В)
Варианты ответов:
1) Б; В; А 2) В; А; Б 3) А; В; Б
Задание 10. (выберите один вариант ответа) Укажите середину отрезка АВ, заданного точками А(4; 2; — 3) и В(6; — 4; — 1).
Варианты ответов:
1) (1;- 3; 1) 2) (5; — 1; — 2) 3) (- 2; — 1; 5)
Задание 11. (выберите два варианта ответов) Установите, какие из точек принадлежат прямой .
Варианты ответов:
1) (- 6; 8) 2) (- 3; — 4) 3) (3; — 4)
Задание 12. (выберите один вариант ответа) Какой нормальный вектор имеет прямая, заданная уравнением 2у – х – 7 = 0?
Варианты ответов:
1) (- 2; 1) 2) (1; — 2) 3) (- 2; — 1)
Задание 13. (выберите один вариант ответа) Укажите уравнение окружности с центром в точке А(- 2; 1) и радиусом R = .
Варианты ответов:
1) (х + 2)2 + (у — 1)2 = 3 2) (х — 2)2 + (у + 1)2 = 3 3) (х + 2)2 + (у — 1)2 =
Тест для самоконтроля
Тема: «Координаты и векторы»
Вариант № ___
Задание 1. (выберите варианты ответов согласно тексту задания) Установите соответствие между векторами и их координатами.
А) Б) В)
Варианты ответов:
1) (0; -1; 2) 2) (1; 0,5; 0) 3) (-0,5; 0; 1)
Задание 2. (выберите один вариант ответа) Укажите, при каких значениях n и p векторы и коллинеарные.
Варианты ответов:
1) 2) 3)
Задание 3. (выберите один вариант ответа) Укажите координаты вектора – 2 , если А(- 3; 4; 0) и В(- 5; 4; — 3).
Варианты ответов:
1) (4; 0; 6) 2) (- 4; 0; — 6) 3) (4; 0; — 6)
Задание 4. (выберите один вариант ответа) Укажите координаты суммы векторов , если и .
Варианты ответов:
1) (2; -1; -5) 2) (-5; -1; 2) 3) (2; -5; 1)
Задание 5. Чему равно скалярное произведение векторов, если и угол между векторами 30°?
Варианты ответов:
1) 2) 18 3)
Задание 6. (выберите один вариант ответа) Найдите скалярное произведение векторов и .
Варианты ответов:
1) (- 1; 0; 4) 2) 0 3) 3
Задание 7. (выберите один вариант ответа) Укажите значение n, при котором векторы и перпендикулярны.
Варианты ответов:
1) 2) 3)
Задание 8. (выберите один вариант ответа) Чему равна длина вектора , если А(3; — 2; 8) и С(5; 1; — 7).
Варианты ответов:
1) 2) 3)
Задание 9. (выберите один вариант ответа) Расположите векторы в порядке уменьшения их длин.
А) Б) В)
Варианты ответов:
1) Б; В; А 2) В; А; Б 3) Б; А; В
Задание 10. (выберите один вариант ответа) Укажите координаты середины отрезка, заданного точками M(2; — 3; 0,5) и N(- 6; — 7; — 2,5).
Варианты ответов:
1) (- 2; — 5; — 1) 2) (- 2; 2; 1) 3) (2; 5; — 1)
Задание 11. (выберите два варианта ответов) Установите, какие из точек принадлежат прямой .
Варианты ответов:
1) (1; 4) 2) (4; 1) 3) (- 4; — 1)
Задание 12. (выберите один вариант ответа) Какой нормальный вектор имеет прямая, заданная уравнением 5х + 3у – 4 = 0?
Варианты ответов:
1) (3; 5) 2) (5; — 3) 3) (5; 3)
Задание 13. (выберите один вариант ответа) Укажите уравнение окружности с центром в точке А(- 1; 3) и радиусом R = .
Варианты ответов:
1) (х — 1)2 + (у + 3)2 = 25 2) (х + 1)2 + (у — 3)2 = 25 3) (х + 1)2 — (у — 3)2 = 25
Тест для самоконтроля
Тема: «Координаты и векторы»
Вариант № ___
Задание 1. (выберите один вариант ответа) Чему равны координаты вектора .
Варианты ответов:
1) (0; — 4; 2) 2) (- 4; 0; 2) 3) (- 4; 2; 0)
Задание 2. (выберите один вариант ответа) Укажите, при каких значениях n и p векторы и коллинеарные.
Варианты ответов:
1) 2) 3)
Задание 3. (выберите один вариант ответа) Найдите координаты вектора , если А(- 3; 5;0) и В(2; 3; — 1).
Варианты ответов:
1) (0,5; 1; — 2,5) 2) (- 2,5; 1; 0,5) 3) (2,5; 1; 0,5)
Задание 4. (выберите один вариант ответа) Укажите координаты разности векторов , если и .
Варианты ответов:
1) (11; 6; -5) 2) (9; 6; -5) 3) (11; 6; -3)
Задание 5. (выберите один вариант ответа) Укажите, чему равно скалярное произведение векторов, если и угол между векторами 60°.
Варианты ответов:
1) 6 2) 3 3)
Задание 6. (выберите один вариант ответа) Найдите скалярное произведение векторов и ?
Варианты ответов:
1) 10 2) 6 3) — 6
Задание 7. (выберите один вариант ответа) Укажите значение n, при котором векторы и перпендикулярны.
Варианты ответов:
1) 2) 3)
Задание 8. (выберите один вариант ответа) Найдите длину вектора , если
В(- 1; 0; 6) и С(5; 1; — 7).
Варианты ответов:
1) 2) 3)
Задание 9. (выберите варианты ответов согласно тексту задания) Установите соответствие между векторами и их длинами.
А) Б) В)
Варианты ответов:
1) 2) 3)
Задание 10. (выберите один вариант ответа) Укажите середину отрезка АВ, заданного точками А(3; — 7; 5) и В(5; 3; — 3).
Варианты ответов:
1) (4; — 5; — 7) 2) (1; — 2; 4) 3) (4; — 2; 1)
Задание 11. (выберите два варианта ответов) Установите, какие из точек принадлежат прямой .
Варианты ответов:
1) (5; 2) 2) (2; 5) 3) (2,5; 1)
Задание 12. (выберите один вариант ответа) Какой нормальный вектор имеет прямая, заданная уравнением — х + 5у + 2 = 0?
Варианты ответов:
1) (1; — 5) 2) (1; 5) 3) (5; — 1)
Задание 13. (выберите один вариант ответа) Укажите уравнение окружности с центром в точке А(4; — 1) и радиусом R = .
Варианты ответов:
1) (х — 4)2 — (у + 1)2 = 49 2) (х — 4)2 + (у + 1)2 = 49 3) (х + 4)2 + (у — 1)2 = 49
Ответы на тест
15 баллов
«5» — 14, 15 баллов
«4» — 11, 12, 13 баллов
«3» — 8, 9,10 баллов
«2» — 7 и менее баллов
«Связь между координатами вектора и координатами его начала и конца»
Тема урока: «Связь между координатами вектора
и координатами его начала и конца»
Тип урока: урок «открытия» нового знания
9 класс
Продолжительность урока: 45 минут
Учебник: Л.С. Атанасян и др. Геометрия 7-9.
Учитель: Андреева О.А.
Цели и задачи урока:
Образовательные: ввести понятие радиус — вектора и связь между координатами его начала и конца;
Развивающие: развитие внимания, памяти, речи, логического мышления, самостоятельности;
Воспитательные: воспитание дисциплины, аккуратности, чувства ответственности, уверенности в себе
Методы обучения: дедуктивно-репродуктивный, дедуктивно-исследовательский.
Оборудование: учебники, тетради, меловая доска, линейка, циркуль.
План урока:
1. Организационный момент (2 мин.)
2. Актуализация опорных знаний (10 мин.)
3. Изучение нового материала (15 мин.)
4. Закрепление изученного материала (10 мин.)
5. Итог урока (6 мин.)
6. Домашнее задание (2 мин)
Ход урока.
I. Организационный момент
Приветствие учителем учащихся, проверка готовности класса к уроку и проверка отсутствующих.
II. Актуализация опорных знаний.
Работа в классе: повторение пройденного материала по теме «Координаты вектора»:
1. Найдите координаты вектора а+в, если:
а) а{3; 2} и в{1; 5} а + в {3+1; 4+5}, а+в{4; 9}
б) а{-4; -2} и {5; 3} а + в {-4+5; -2+3}, а+в{1; 1}
в) а{2; 7} и {-3; -7} а + в {2-3; 7-7}, а+в{-1; 0}
2. Найдите координаты вектора а-в, если:
а) а{3; 2} и в{-3; 2} а – в{3+3; 2-2}, а-в{6; 0}
б) а{3; 6} и в{4; -3} а – в{3-4; 6+3}, а-в{-1; 9}
в) а{-5; -6} и в{2; -4} а – в {-5-2; -6+4}, а-в{-7; -2}
3. Найдите координаты векторов, если а{3; 2}
3а{3*3; 3*2}, 3а; 6} -а {-3; -2} -3а{-9;-6}
Опрос учащихся по правилам
1. Как найти координаты суммы двух и более векторов?
Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
2. Как найти координаты разности двух векторов?
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
3.Как найти координаты вектора умноженного на число?
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Ⅲ. Изучение нового материала
На этом уроке мы выясним, как найти координаты вектора, зная координаты его начала и конца.
Рассмотрим рисунок 277 на странице 229.
Покажем связь между координатами вектора и координатами его начала и конца.
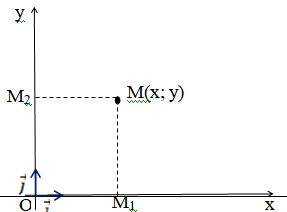
Рассмотрим прямоугольную систему координат и какую-нибудь точку М с координатами x и y. Чтобы определить числа x и y, проведём через точку М прямые, перпендикулярные к осям координат, и обозначим через M1 и M2 точки пересечения этих прямых с осями Оx и Оy .
Число x – абсцисса точки М, равно отрезку ОМ1, если M1 – точка положительной полуоси: х = ОМ1. Если точка M1 – точка отрицательной полуоси, то х = –ОМ1. Если точка M1 совпадает с точкой О, то икс в этом случае равен нулю.
Аналогично определяется число y – ордината точки M2.
Докажем, что координаты точки М равны соответствующим координатам её радиус-вектора. Вектор назовем радиус-вектором точки М. Координаты точки М равны соответствующим координатам ее радиус-вектора.
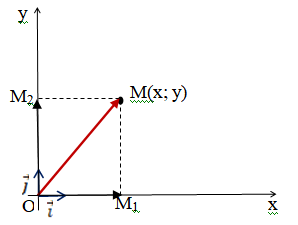
Радиус-вектор точки М – это вектор, соединяющий начало координат и точку М.
Докажем следующие равенства
и
Действительно, , то , и справедливо равенство:
Если x < 0, то и справедливо следующее равенство:
Наконец, если , то и равенство в этом случает также справедливо:
Таким образом, в любом случае равенство справедливо.
Аналогично доказывается и второе равенство
Следовательно,
А это значит, что координаты радиус вектора OM равны соответствующим координатам точки
M:
Рассмотрим рисунок 279, выразим координаты вектора через координаты его начала А (х1; у1) и конца В (х2;у2). Вектор равен разности векторов и .
Точка А (х₁; у₁) и точка В (х₂; у₂), тогда вектор имеет координаты {х₂ — х₁; у₂ — у₁}
Каждая координата вектора равна разности соответствующих координат его конца и начала.
IV. Закрепление изученного материала
№933
№934 (а,б)
Дано: А(2; 7), В(-2; 7)
Найти: {?; ?}
Решение: {-2-2; 7-7}={-4; 0} Ответ: {-4; 0}.
V. Итог урока
Сегодня на уроке мы рассмотрели понятие радиус – вектора, связь между координатами его начала и конца.
Закончить предложение:
1. Вектор, длина которого равна единице называется … (единичным)
2. Любой вектор можно представить в виде …
(, то есть разложить по двум неколлинеарным векторам)
3. Радиус – вектор – это вектор … (начало которого в начале координат)
4. Как связаны координаты радиус вектора и координаты конца вектора? (они равны)
5. Как найти координаты вектора, не являющегося радиус – вектором? (найти координаты соответственно равного ему радиус – вектора)
VI. Домашнее задание.
§2, п.91 , №934(в, г )
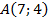 ,
, 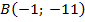 ;
;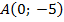
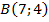 ;
;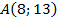 ,
, 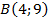 .
.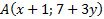 ,
, 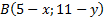 ,
, 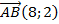 ;
;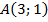 ,
, 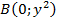 ,
, 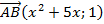 .
.