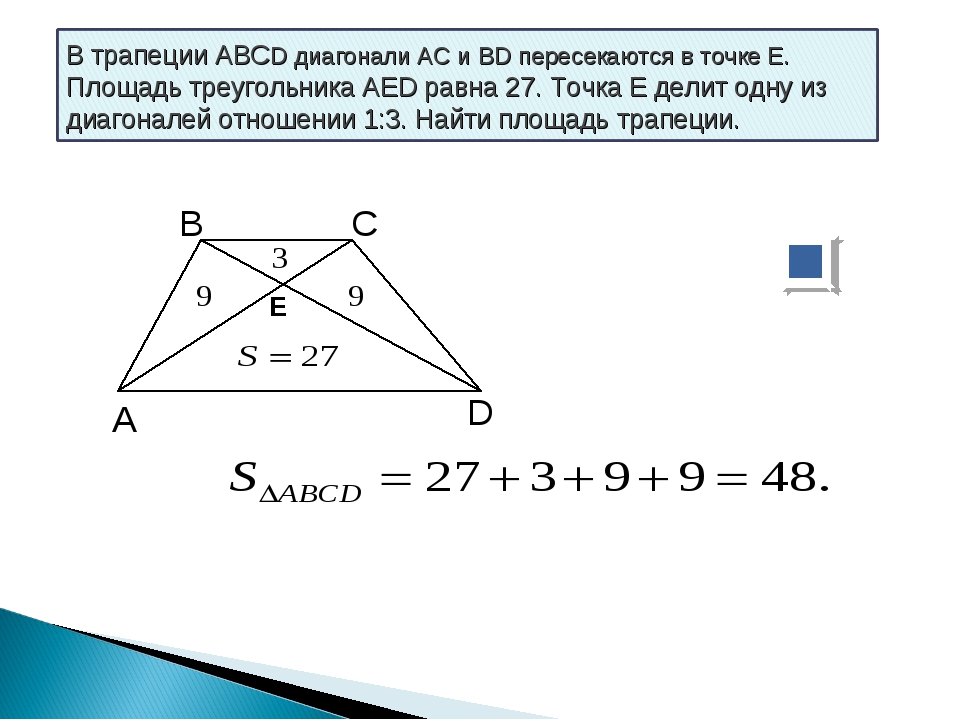
\(ABCD\) – трапеция \(\Rightarrow \, \angle{CAD}=\angle{ACB}, \, \angle{BDA}=\angle{DBC};\)
\(ABCD\) – трапеция, \(AC \cap BD=O\) \(\Rightarrow \, \triangle{AOD} \backsim \triangle{COB};\)
\(ABCD\) – трапеция, \(AB \cap CD=E\) \(\Rightarrow \, \triangle{AED} \backsim \triangle{BEC}\)
Средняя линия трапеции
Определение. Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$
Свойства равнобедренной трапеции
1. В равнобедренной трапеции углы при каждом основании равны.
2. Диагонали равнобедренной трапеции равны.
3. Ранобедренную трапецию можно вписать в окружность.
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, \angle{ABC}=\angle{DCB}, \, \angle{BAD}=\angle{CDA}; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, ABCD\) вписанная
Признаки равнобедренной трапеции
1. Если углы при некотором основании трапеции равны, то эта трапеция равнобедренная.
Если углы при некотором основании трапеции равны, то эта трапеция равнобедренная.
2. Если диагонали трапеции равны, то эта трапеция равнобедренная.
3. Если трапецию можно вписать в окружность, то эта трапеция равнобедренная.
\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$
Площадь трапеции
1. Площадь трапеции равна половине произведения суммы её оснований на высоту трапеции.
2. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.
$$ S=\frac{1}{2}(a+b)h$$ | $$ S=\frac{1}{2} d_1d_2\sin{\varphi}$$ |
Формулы и свойства трапеции
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 5
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ город – курорт АНАПА
Рассмотрено и
рекомендовано к использованию
на заседании МО от _______________
Протокол №______
Подготовка к ОГЭ и ЕГЭ.
«Формулы и свойства трапеции»
Методическая разработка
учителя математики
Снегуровой Амины Мугиновны
2018 год.
Введение 3
Определения 4
Частные случаи трапеции 5
Свойства произвольной трапеции 6-7
Свойства равнобедренной трапеции 8-10
Свойства биссектрисы угла трапеции 10-12
Свойства треугольников, образованных диагоналями трапеции 12-13
Формулы нахождения диагоналей трапеции 13-14
Трапеция и окружность 14-17
Дополнительные построения в трапеции 17-23
Для тех, кому интересно. Теоремы.
 23-27
23-27Задачи с решениями.27-35
Список используемой литературы .
Дорогой ученик!
В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует от учащихся знаний «непрограммных» свойств трапеции. (Программными считаются свойство средней линии трапеции, свойства диагоналей и углов
равнобедренной трапеции.) Свойства, необходимые для решения задач, отсутствуют в учебниках или перенесены в задачи и не воспринимаются как теоретические положения.
Какими же замечательными свойствами обладает трапеция? Как решать геометрические задачи, требующие глубоких знаний? Трапеция обладает рядом интересных и полезных для решения задач свойствами. Если овладеть ими и рассмотреть дополнительные построения в трапеции, то возникает объективная возможность для решения задач повышенной сложности.
В планиметрии существует целый класс таких задач, к которым традиционные методы (метод цепочек равных треугольников, метод геометрических преобразований, векторный метод и др.) либо вовсе не применимы, либо дают сложные и громоздкие решения. Во многих случаях решать такого рода задачи помогает введение в чертеж дополнительных линий – так называемое дополнительное построение. В одних случаях эти построения напрашиваются сами собой, в других они не так очевидны и требуют от решающего достаточно большого опыта, изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно достраивать до фигуры другого типа, можно с многоугольной фигурой связывать окружность, а можно целью дополнительного построения ставить выделение на чертеже равных, равновеликих или подобных фигур.
Знание метода дополнительных построений в большинстве случаев позволяет решать, казалось бы, сложные геометрические задачи просто, понятно и красиво.
В этой разработке собраны формулы, свойства и подсказки для решения задач связанных с трапецией. Надеюсь, что ты здесь найдешь для себя много полезной информации.
1.Определения.
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
Параллельные стороны
называются её основаниями, а две другие стороны — боковыми
сторонами.
Высотой трапеции называется расстояние между основаниями.
Kаждый из этих отрезков EF, BM, DK, PQ является высотой трапеции ABCD.
В формулах используются следующие обозначения:
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота.
2.Частные случаи трапеции.
Прямоугольной трапецией называется трапециия, в которой одна из боковых сторон перпендикулярна основаниям.
У нее два прямых угла при меньшей боковой стороне.
Эта сторона одновременно является и высотой трапеции.
произвольная
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
У равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при основании равны.
Трапеция, у которой боковые стороны равны, называется равнобедренной
(равнобокой, равнобочной).
3.Свойства произвольной трапеции.
1. Во всякой трапеции сумма углов , прилежащих к одной ее боковой стороне, равна 1800.
2. Во всякой трапеции средняя линия параллельна ее основаниям, равна полусумме этих оснований и делит диагонали трапеции пополам.
MК =
3.Четыре замечательные точки трапеции:
Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
4. Во всякой трапеции если сумма углов при большем основании равна 900, то боковые стороны лежат на перпендикулярных прямых. Длина отрезка, соединяющего середины оснований, равна полуразности оснований.
5. Свойства отрезка, соединяющего основания трапеции
Отрезок, соединяющий основания всякой трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции.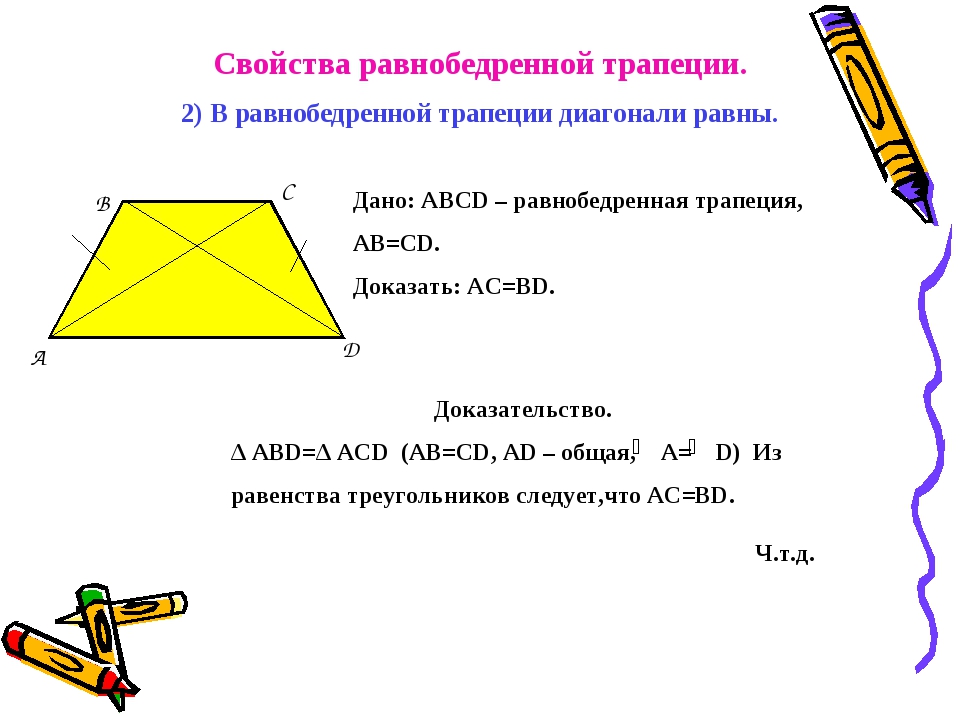
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношение составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции:
6.Свойства отрезка, параллельного основаниям всякой трапеции.Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
*Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам, то есть КО=ОМ
*Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна
KM = .
7.Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему геометрическому оснований, если он делит трапецию на две трапеции, подобные между собой.
8. Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему квадратичному оснований, если он делит трапецию на две трапеции равной площади (
9.Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований.
d12 + d22 = c2 + d2+ 2ab, d- боковая сторона. d1 и d2 – диагонали.
Свойства равнобедренной трапеции.
Трапеция является равнобедренной тогда и только тогда, когда
*углы, прилежащие к одному основанию, равны
*сумма противолежащих углов 1800;
*диагонали равны;
AC = BD
*отрезки диагоналей, соединяющих точку пересечения с концами одного основания, равны; BO = OC, AO = OD.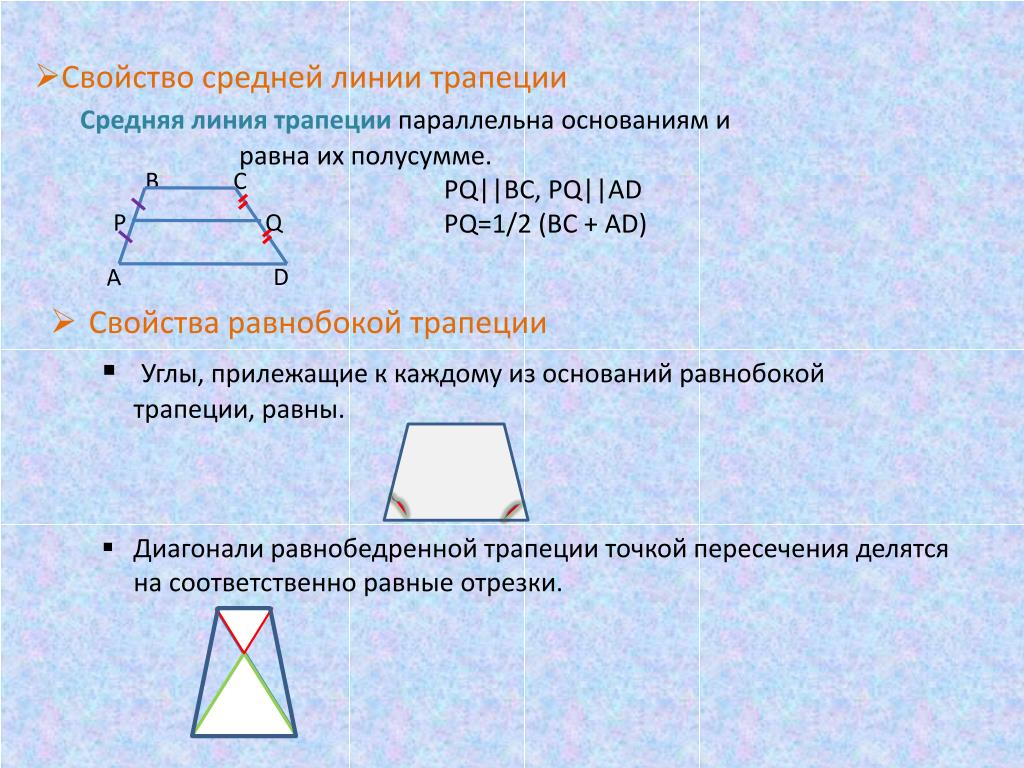
*вокруг этой трапеции можно описать окружность.
BC // AD, AB = CD. ABCD – вписанная трапеция.
* высота, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
*если в равнобедренной трапеции диагонали перпендикулярны, то
1)квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
2)высота трапеции равна полусумме оснований.
3)ее высота равна средней линии.
4) площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты.
(или квадрату полусуммы оснований, или квадрату средней линии).
*если в равнобокой трапеции высота равна средней линии, то диагонали трапеции взаимно перпендикулярны.
BH = HD = h =.
*высота, проведённая через точку пересечения диагоналей, в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
*в равнобедренной трапеции прямая, проходящая через середины оснований, перпендикулярна им и является осью симметрии трапеции.
*отрезки, последовательно соединяющие середины смежных сторон равнобедренной трапеции, образуют ромб.
MNKE – ромб, то есть
MN=NK=KE= ME.
*в равнобедренной трапеции квадрат диагонали равен квадрату его боковой стороны плюс произведение оснований: d2 = c2 + a b
*площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
S =
Свойства биссектрисы угла трапеции.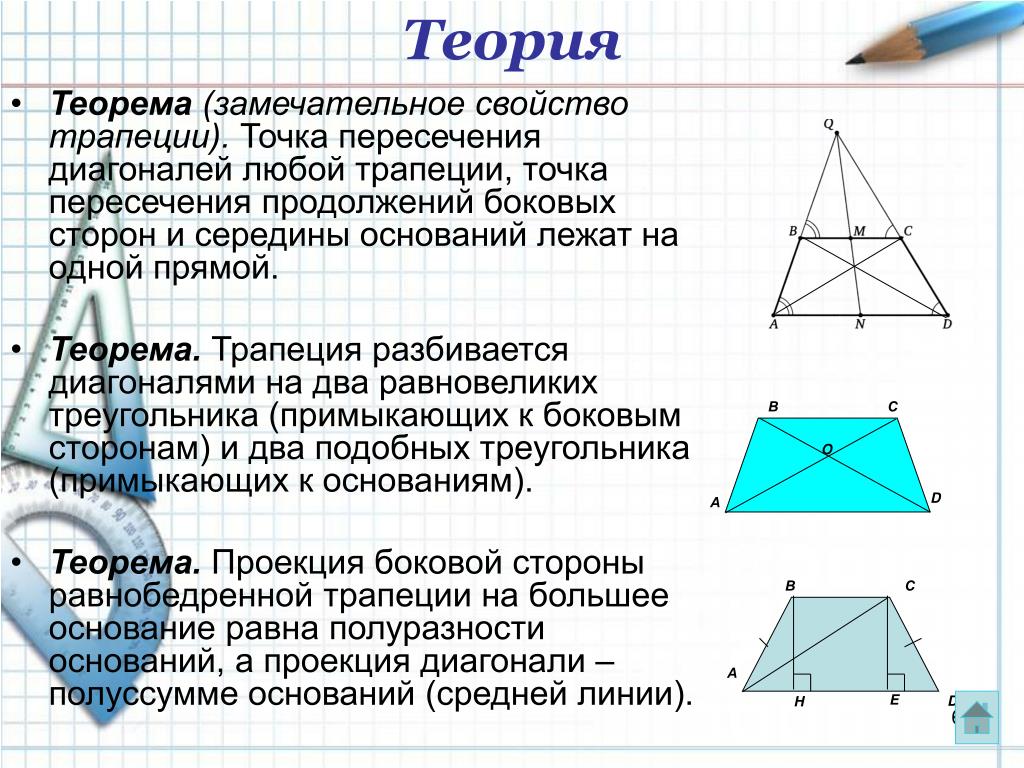
*биссектриса угла отсекает от трапеции равнобедренный треугольник.
*точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
*если диагональ трапеции является биссектрисой ее острого угла, то меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.
*биссектриса угла трапеции, пересекающая основание, отсекает от трапеции равнобедренный треугольник.
*биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
* точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
*если биссектриса тупого угла трапеции является диагональю, то боковая сторона равна большему основанию трапеции.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
*если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
* если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.
* если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
* если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
* если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.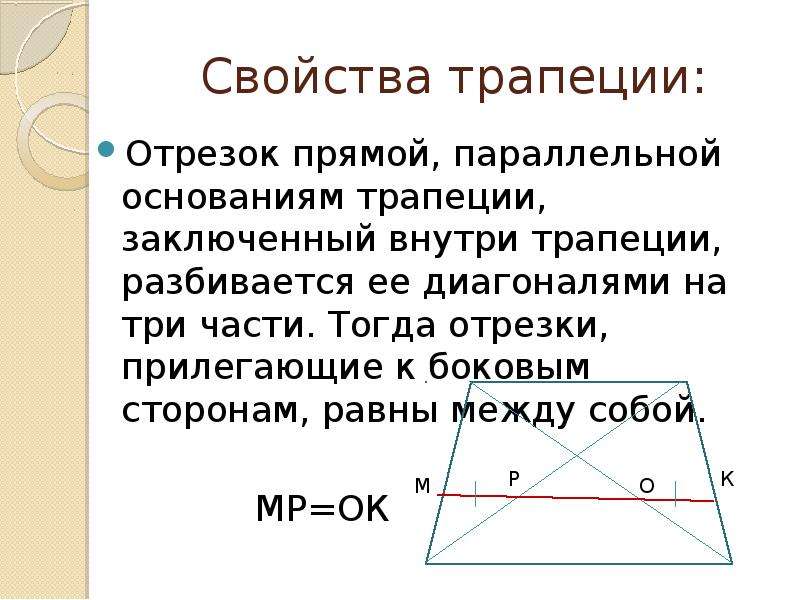
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом.
*Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
*В подобных треугольниках длины всех линейных элементов пропорциональны, а именно:
отношения периметров, радиусы вписанных окружностей, радиусы описанных окружностей, соответствующих высот, биссектрис, медиан (проведенных из равных углов) подобных треугольников равны отношению соответствующих сторон (лежащих против равных углов) или равны коэффициенту подобия.
*Площади подобных треугольников относятся как квадраты соответствующих сторон или равно квадрату коэффициента подобия.
*Площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
S12= S2 S3
S3: S2 = 2
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Эта группа формул отражает одно из основных свойств диагоналей трапеции:
*Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Используем теорему косинусов.
*Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
*Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
4.В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований
d12 — d22 = a2 – b2
*Если диагонали трапеции взаимно перпендикулярны, то длина отрезка, соединяющего середины оснований трапеции равна полусумме оснований.
MH =
BDCE и FAOD прямоугольники, а диагонали прямоугольника равны.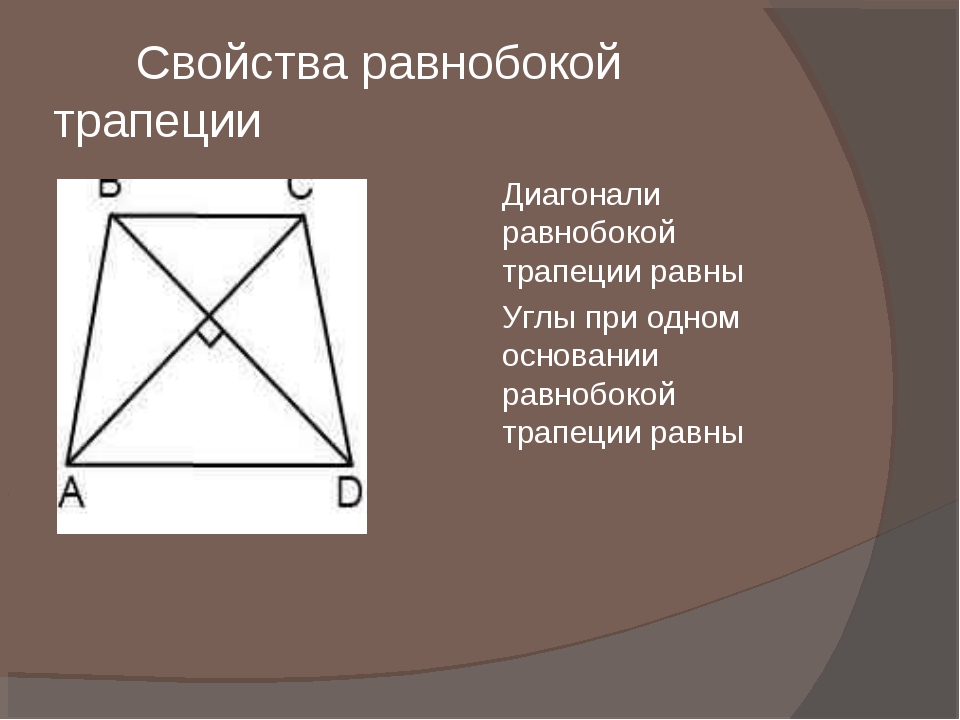
Трапеция и окружность.
1) Если в равнобокую трапецию можно вписать окружность, то средняя линия трапеции равна боковой стороне.
Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований
h2 = a ∙ b
2) Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии. Площадь трапеции определяется произведением средней линии на высоту трапеции.
3. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
. CF =m, FD =n, OF = r.
∠COD=90º, т.к. ∠ADC+∠BCD=180º — так
как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD равна 1800.
Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как r = .
А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков: h = 2 .
5.Если в трапецию можно вписать окружность и около трапеции можно описать окружность, то проекция диагонали на большее основание, равна боковой стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, в задаче появляется несколько путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.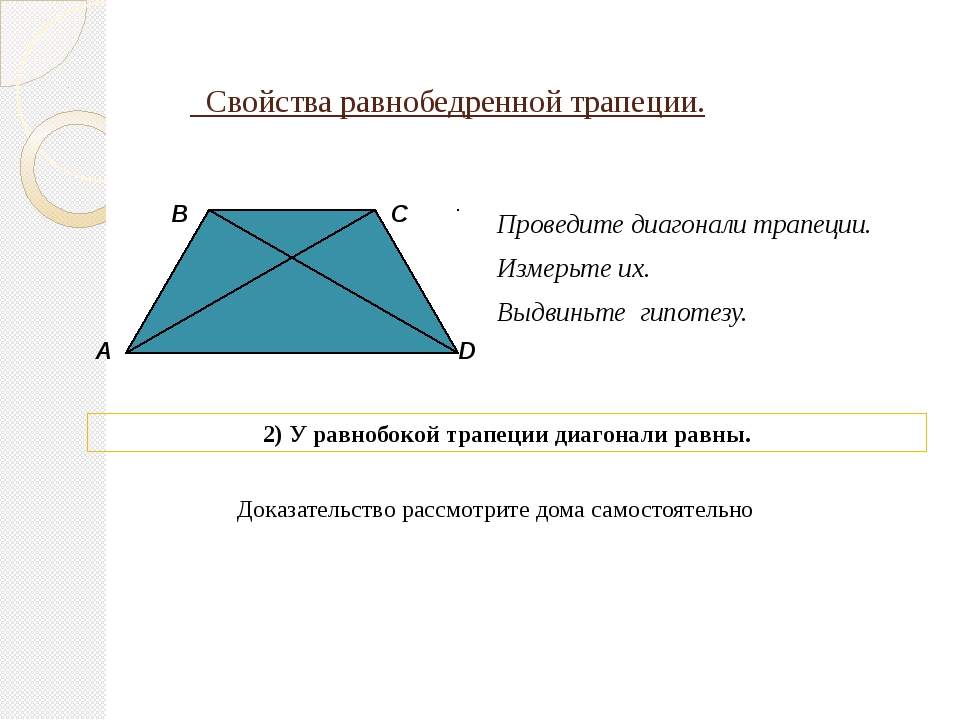
AB+CD=AD+BC
2. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что
AL=AK BL=BM
CM=CF DF=DK
Описанная окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
1)Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
2) Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции.
3) Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
4)Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Например,
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
5)Если диагонали вписанной в окружность трапеции (четырехугольника) взаимно перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности или удвоенному квадрату боковой стороны:
a2 + b2 = 4R2 = 2c2.
6) Если в трапецию вписана окружность, то вершина трапеции, центр вписанной в нее окружности и основание перпендикуляра, опущенного из другой вершины на основание, лежат на одной прямой.
Дополнительные построения как прием при решении задач
Дополнительные построения являются эффективным методом решения геометрических задач.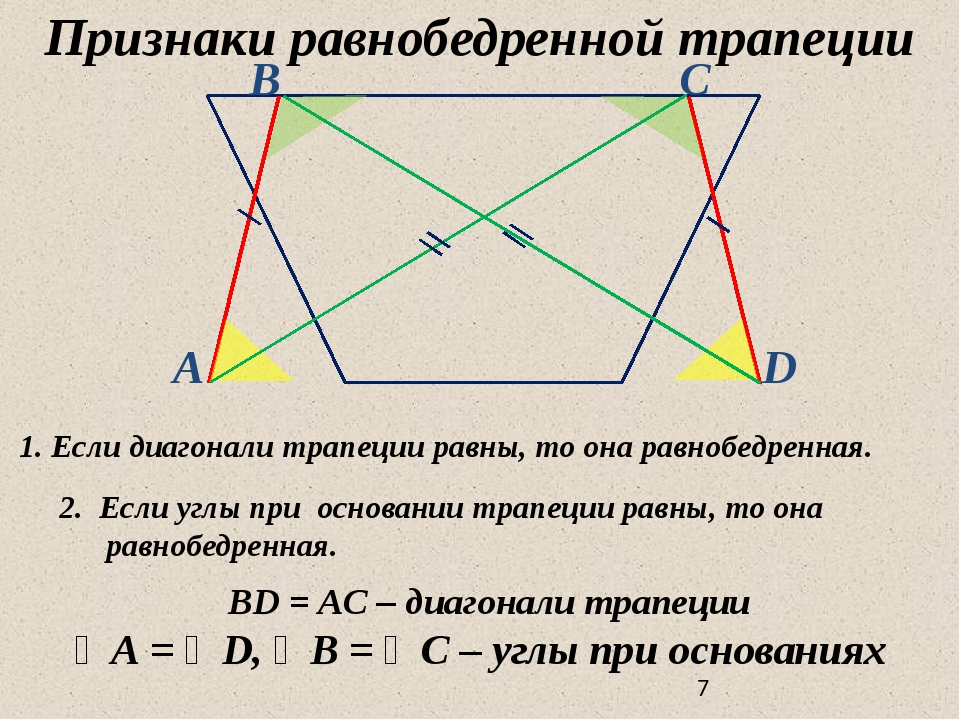 Наиболее часто используются при решении задач:
Наиболее часто используются при решении задач:
1. Опускание высот из концов одного основания на другое основание
2. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину
3. Проведение через середину меньшего основания прямых, параллельных боковым сторонам
4. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину .
5. Продолжение боковых сторон до пересечения.
Рассмотрим каждое их них.
При решении задач на отыскание площади дополнительным построением считается построение ее высоты или высот. Если построение высоты не помогает решить задачу, то нужно построить прямую, параллельную одной из ее диагоналей. Потом найти площадь полученного треугольника, который будет равновеликим исходной трапеции.
1. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину.
При дополнительном построении, когда переносится диагональ, образуется треугольник, площадь которого равна площади трапеции.
S1 = S2
Задача.
Найдите площадь трапеции, дмагонали которой равны 8 и 15, а средняя линия равна 8,5.
Решение.
Построим CF // BD и получим SACF = SABCD. Почему?
ABC = CDF, так как DF = BC и эти треугольники имеют одинаковую высоту.
Значит, для того, чтобы найти площадь трапеции нам достаточно найти площадь ACF.
АF = АD + ВС — сумма оснований трапеции. По условию задачи средняя линия трапеции 8,5. Значит сумма оснований АF = 8,52=17.
Рассмотрим ACF. Проверим, является ли он прямоугольным? В этом нам поможет теорема Пифагора:
172 = 82 + 152
289 = 64 + 225.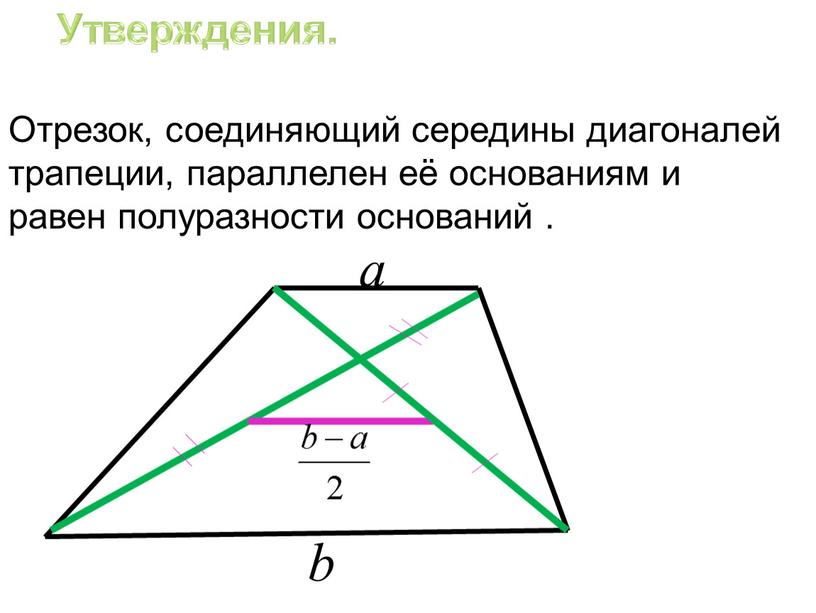
289 = 289.
ACF – прямоугольный. SACF = AC*CF = 8*15 = 60. SABCD= 60.
Если ACF разносторонний, то его площадь вычислим по формуле Герона.
Ответ:60.
2. Продолжение боковых сторон до пересечения.
Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
*Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
*Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника..jpg)
*Если ABCD равнобедренная трапеция, то KL является биссектрисой, медианой и высотой одновременно.
Это дополнительное построение позволяет перейти от трапеции к треугольнику. Если сумма углов при большем основании равна 900, топродолжив боковые стороны мы получим прямоугольный треугольник.
Задача.
В трапеции ABCD основания АD и ВС равны соответственно 72 и 18, а сумма углов при основании АD равна 900. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой CD, если АВ = 18.
Решение.
Центром О данной окружности будет точка пересечения серединного перпендикуляра к АВ и перпендикуляра, возведенного к стороне CD из точки касания окружности. АВО равнобедренный: АО = ВО. Продлим боковые стороны трапеции и получим прямоугольный треугольник АМD. KMNO – прямоугольник, где KM = MN = NO =КО = R.
BMC AMD.
= , то есть и x = 6. Тогда R = КВ + 6 = 9 + 6 = 15.
Ответ:15.
3. Опускание высот из концов одного основания на другое основание.
Дополнительное построение 1,2 позволяет разбить трапецию на прямоугольник (стороны которого — одно из оснований и высота трапеции) и два прямоугольных треугольника (в которых один из катетов – высота трапеции, а гипотенузы – боковые стороны трапеции)
Построение 1 Построение 2
Задача. Найдите площадь трапеции с основаниями 8 и 13 и боковыми сторонами 3 и 4.
Решение.
Проведем ВН и СM — высоты и получим ABD (египетский треугольник) со сторонами 3,4,5, так как АD – ВС=13 – 8=5.
S= АВ* BD= 6.
Найдем высоту трапеции: h= 2S:5 = 2*6:5= 2,4.
SABCD= 6+2,4*8=25,2. Ответ:25,2.
4. Проведение через середину меньшего основания прямых, параллельных боковым сторонам.
Дополнительное построение 4 делит трапецию на параллелограммы и треугольник. Боковые стороны соединяются в треугольник.
5. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину.
Задача. Основания трапеции равны 30см и 15см, а боковые стороны равны 9 см и 12 см. Найдите высоту трапеции.
Решение. Пусть АВСД трапеция, заданная в условии.
Проведем через вершину С прямую, которая параллельна АВ. Пусть эта прямая пересекает АД в точке М.
Тогда АВСМ – параллелограмм и СМ=9, АМ=ДМ=15.
Так как 92+122=152, то, применив обратную теорему Пифагора, приходим к выводу, что СМ перпендикулярна СД.
Заметим, что высота трапеции и треугольника МСД, проведенная из вершины С, совпадают. Для определения искомой высоты применим метод площадей. Пусть искомая высота равна х. Тогда для определения х составим уравнение, дважды вычислив площадь треугольника МСД:
.
Решив это уравнение находим: х=7,2. Ответ: 7,2.
Задача. Боковые стороны AB и CD трапеции ABCD равны 15 и 12 соответственно. Найдите градусную величину угла D, если одно из оснований трапеции на 9 больше другого.
Решение.
Из вершины угла проведем прямую линию, параллельную стороне. Трапеция разделена данной прямой линией на параллелограмм и треугольник. Противоположные стороны параллелограмма равны, значит, длина стороны треугольника равна разности длин оснований трапеции. Данный треугольник определен по трем сторонам. По теореме косинусов определим искомый угол. Вычисления показывают, что боковая сторона перпендикулярна к основанию, искомый угол прямой.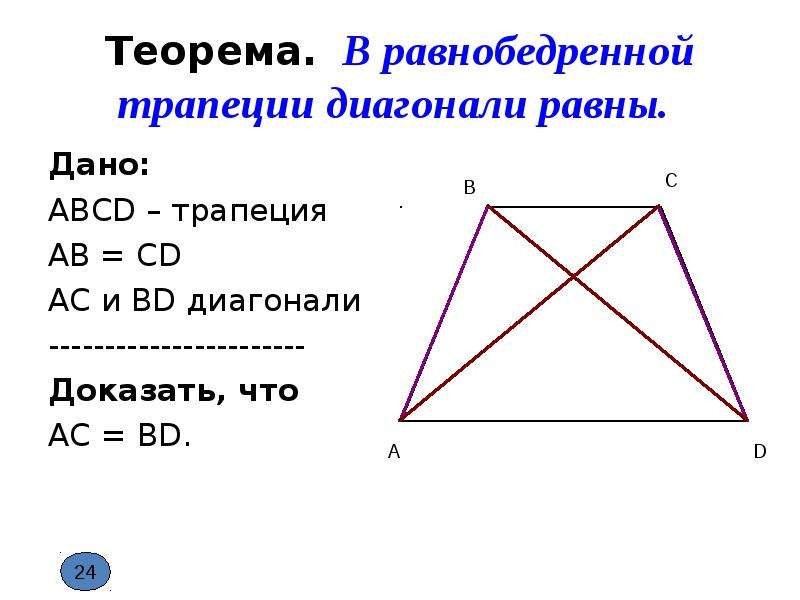
Ответ:
Для тех, кому интересно.
Теорема.
Задачи с решениями.
Пример 1.Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD — равнобедренная трапеция, r = 4, AB = 10
Найти: SABCD
AB = CD = 10 по условию.
AB + CD = AD + BC по свойству вписанной окружности.
AD + BC = 10 + 10 = 20.
FE = 2r = 2 · 4 = 8.
SABCD=1/2(BC + AD)·FE, SABCD = 1/2 · 20 · 8 = 20/2 · 8 = 10 · 8 = 80.

Пример 2.Основания трапеции равны 10 м и 31 м, а боковые стороны — 20 м и 13 м. Найдите высоту трапеции.
Решение.
Пусть HK = BC = 10 м, BH = CK = x, AH = y, тогда KD = 21 – y
По теореме Пифагора:x2 + y2 = 132x2 + (21 – y)2 = 202x2 + y2 = 169 (1)
x2 + 441 – 42y + y2 = 400 (2)
Вычтем из (2) уравнения (1):441 – 42y = 23142y = 210y = 5AH = 5 м
По теореме Пифагора:BH2 = AB2 – AH2BH2 = 132 – 52BH2 = 169 – 25BH2 = 144
BH = 12
Пример 3.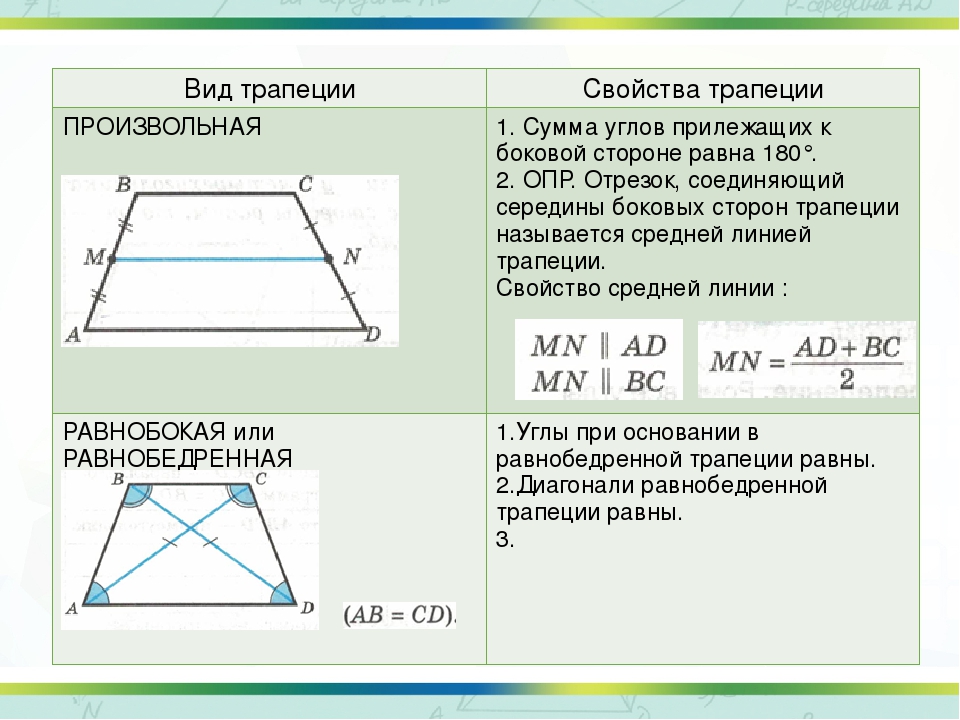 Большее основание трапеции равно 24. Найдите длину меньшего основания, если расстояние между серединами диагоналей равно 4.
Большее основание трапеции равно 24. Найдите длину меньшего основания, если расстояние между серединами диагоналей равно 4.
Решение.
Пример 4.Диагонали AC и BD трапеции ABCD пересекаются в точке O.
Найдите площадь трапеции, если BC < AD и площади треугольников BOC и ABO равны соответственно равны 2 и 8.
Анализ.
Рассмотреть подобие треугольников.
Квадраты соответствующих сторон относятся как площади треугольников.
Введем параметры треугольников: стороны оснований и высоты треугольников.
Площади трапеции и треугольников определим по известным формулам.
Решение.
Ответ:
Пример 5.В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны боковым сторонам. Найдите площадь трапеции.
Найдите площадь трапеции.
Анализ.
Длины диагоналей равны и перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников по катету и гипотенузе: ABD = ACD, поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для определения боковой стороны трапеции.
Высоту трапеции определим из равенства площадей.
Проекцию боковой стороны на большее основание легче определить из подобия треугольников, чем по теореме Пифагора.
Длину средней линии в равнобокой трапеции можно определять как разность большего основания и проекции боковой стороны на основание.
Площадь трапеции находим как площадь прямоугольника АМСК, который получим, если достроим трапецию.
Пример 6.Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9.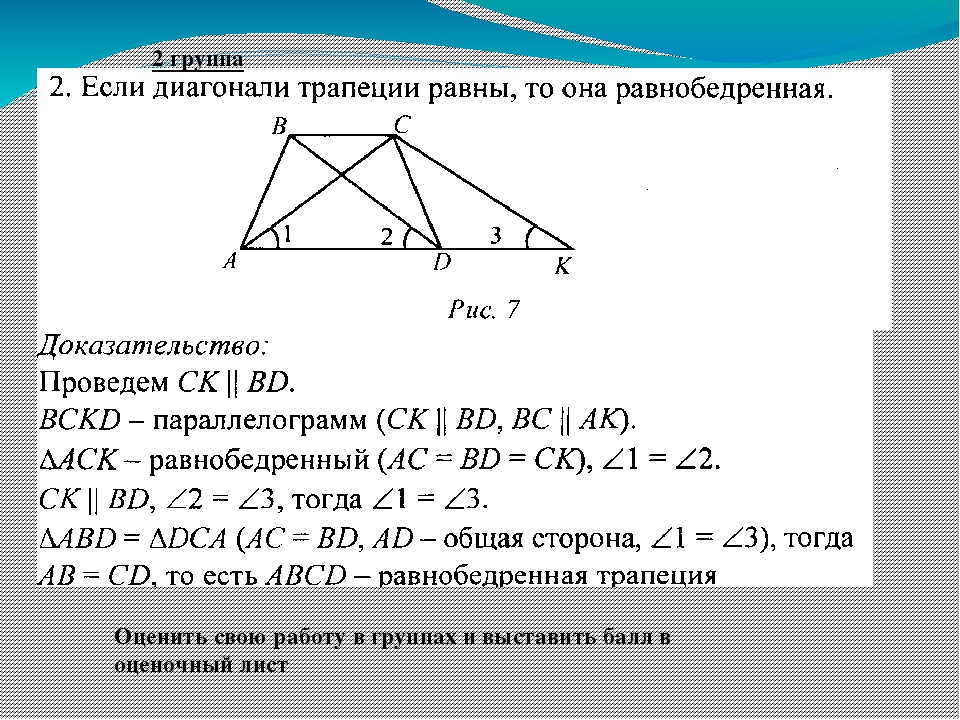 Найдите длину отрезка, соединяющего середины оснований трапеции.
Найдите длину отрезка, соединяющего середины оснований трапеции.
Анализ.
Задача решается построением.
Достроим прямоугольники и используем свойство прямоугольника: диагонали прямоугольника равны и в точке пересечения делятся пополам.
Длина средней линии равна полусумме длин оснований.
Длина отрезка, соединяющая середины оснований, равна полусумме длин диагоналей двух построенных треугольников.
Пример 7.Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного основаниям и заключенного между боковыми сторонами, который делит трапецию на две равновеликие части.
Анализ.
Провести из вершины тупого угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей трапеций.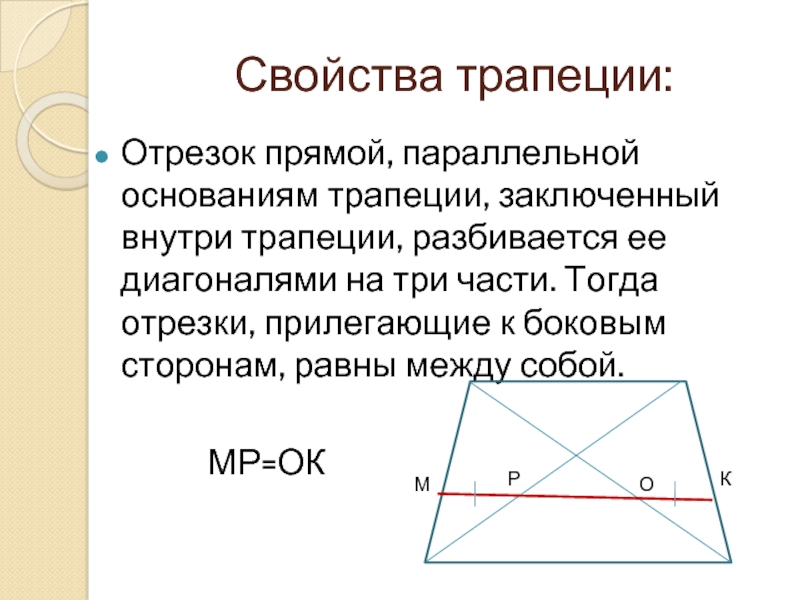
Определить отношение при подобии треугольников.
Рациональные алгебраические преобразования приведут к результату.
Решение.Ответ:
Пример 11.Равнобедренная трапеция ABCD описана около окружности. Боковая сторона трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
Анализ.
Сумма противоположных сторон трапеции равна между собой — свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине средней линии.
Применяем теорему Пифагора для нахождения высоты трапеции.
Площадь трапеции определяем по доступной формуле.
Пример 8.Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно вписать окружность, а средняя линия делит ее на части, площади которых относятся как 5: 11. Найдите длину большего основания трапеции.
Найдите длину большего основания трапеции.
Анализ.
Трапеция является описанной.
Сумма длин оснований равна сумме боковых сторон.
Средняя линия делит трапецию на две трапеции, высоты которых равны.
Задача сводится к системе уравнений.
Длина средней линии равна половине суммы длин боковых сторон.
Пример 9.Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.
Анализ.
Трапеция равнобедренная.
Длина средней линии равна боковой стороне.
Площадь трапеции определяется произведением средней линии на высоту трапеции.
Опустим высоту трапеции из тупого угла..jpg) Через заданный косинус угла определим синус угла.
Через заданный косинус угла определим синус угла.
По синусу угла выразим высоту трапеции через боковую сторону.
Пример 10.В прямоугольной трапеции, описанной около окружности, большая боковая сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание трапеции.
Анализ.
Необходимо использовать свойство сторон четырехугольника, описанной около окружности: сумма длин противоположных сторон равна между собой.
Кроме того, длина средней линии равна полусумме длин сторон оснований.
Проведем из вершины тупого угла высоту трапеции.
Воспользуемся теоремой Пифагора и определим проекцию наклонной боковой стороны на основание.
Пример 11.В равнобедренную трапецию, один из углов которой равен 60°, а площадь равна , вписана окружность. Найдите радиус этой окружности.
Найдите радиус этой окружности.
Анализ.
Важное положение, что трапеция является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны равна длине средней линии.
Введем параметр боковой стороны, из прямоугольного треугольника по заданному углу определим высоту трапеции, которая является диаметром вписанной окружности. Площадь трапеции определяется как произведение средней линии на высоту трапеции.
.
Пример 12.Найдите площадь равнобедренной трапеции, у которой большее основание равно 13, средняя линия равна 8, а биссектриса тупого угла является диагональю трапеции.
Анализ.
При проведении биссектрисы тупого угла боковая сторона равна большему основанию трапеции. Проекция боковой стороны равнобедренной трапеции равна полуразности длин оснований.
По теореме Пифагора найдем высоту трапеции.
Площадь трапеции находим по формул.
Список используемой литературы
Когда около трапеции можно описать окружность. Диагонали трапеции
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами.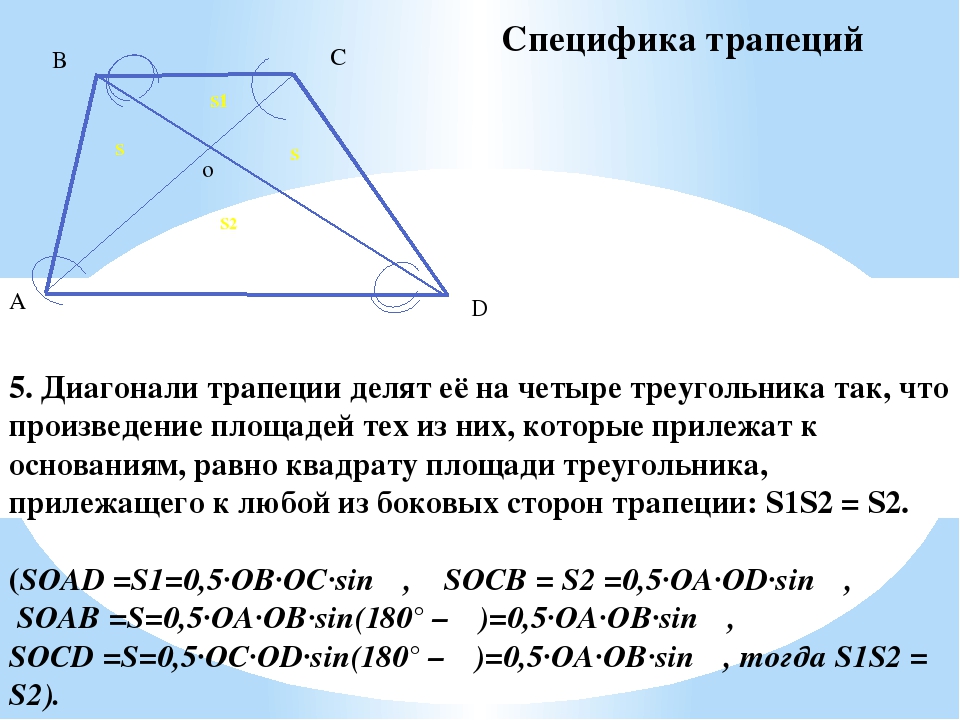 При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°.
 Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .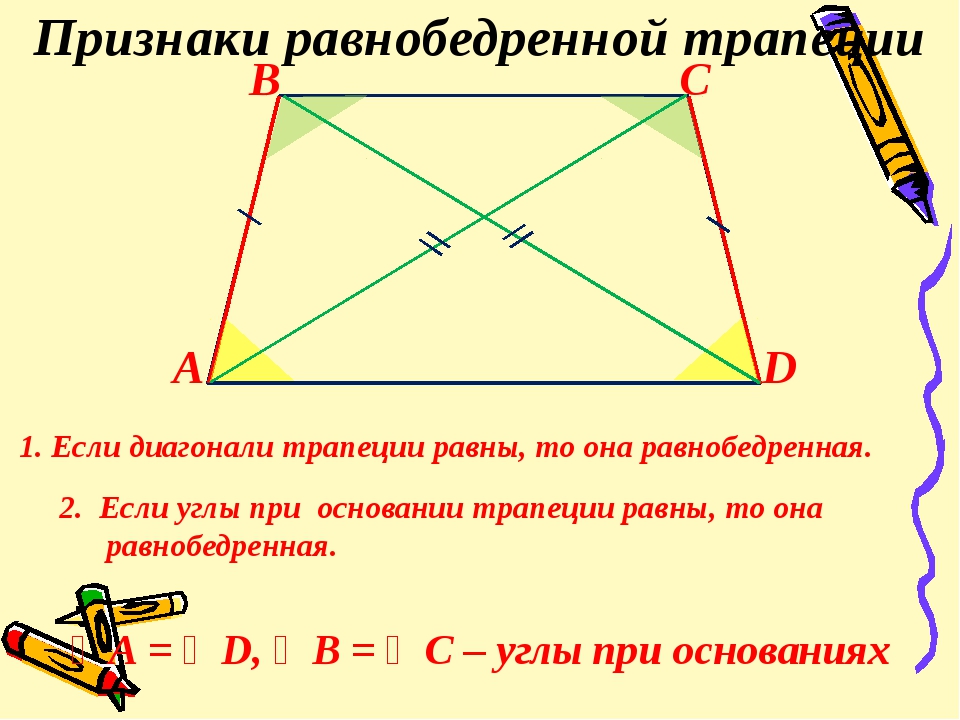
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .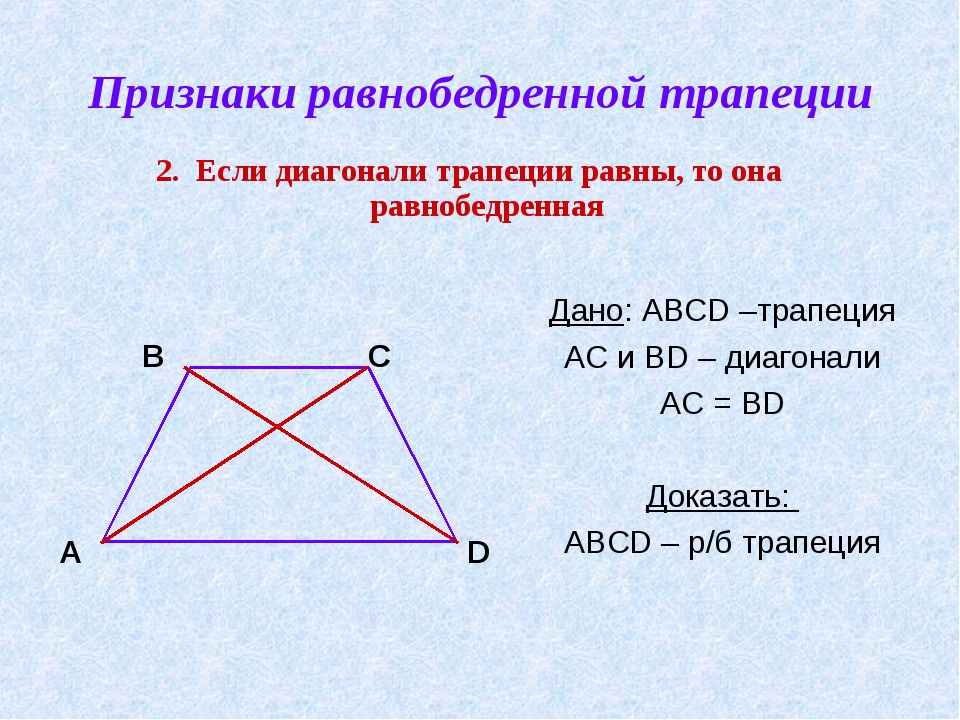
Проектная работа « Интересные свойства трапеции » Выполнили: ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года
Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства.
Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к
Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с
Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К
МР=ОК Р М О К
Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д. Е О
Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д
Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h
1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен
Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
(AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
Доказательство: Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.
I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.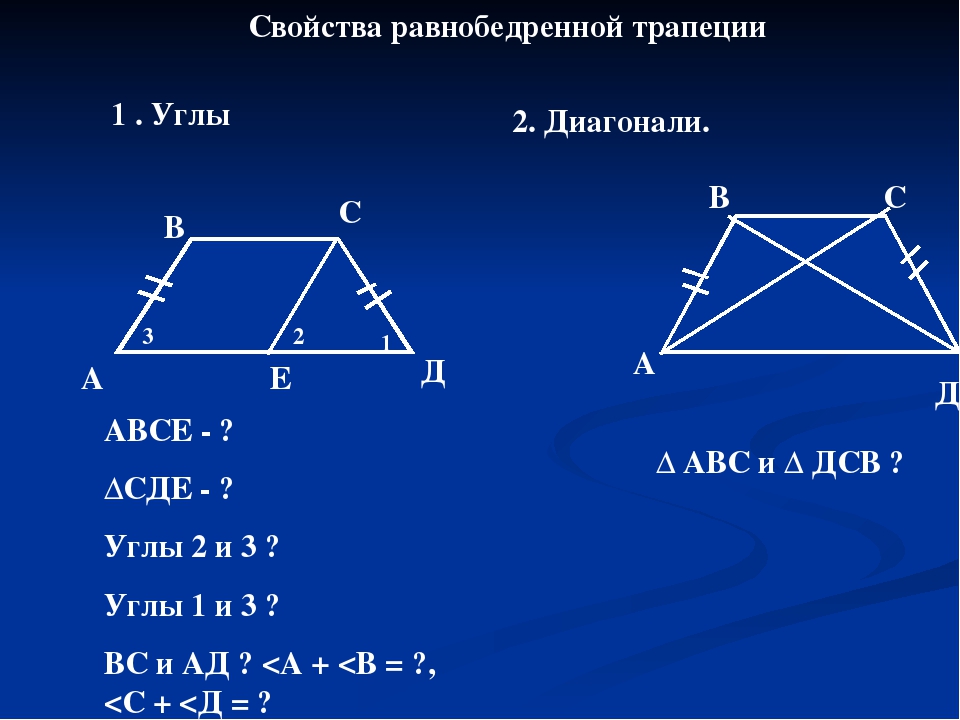 Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Если равнобедеренную трапецию со сторонами а,в,с, d можно вписать и около неё можно описать окружности, то площадь трапеции равна
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности.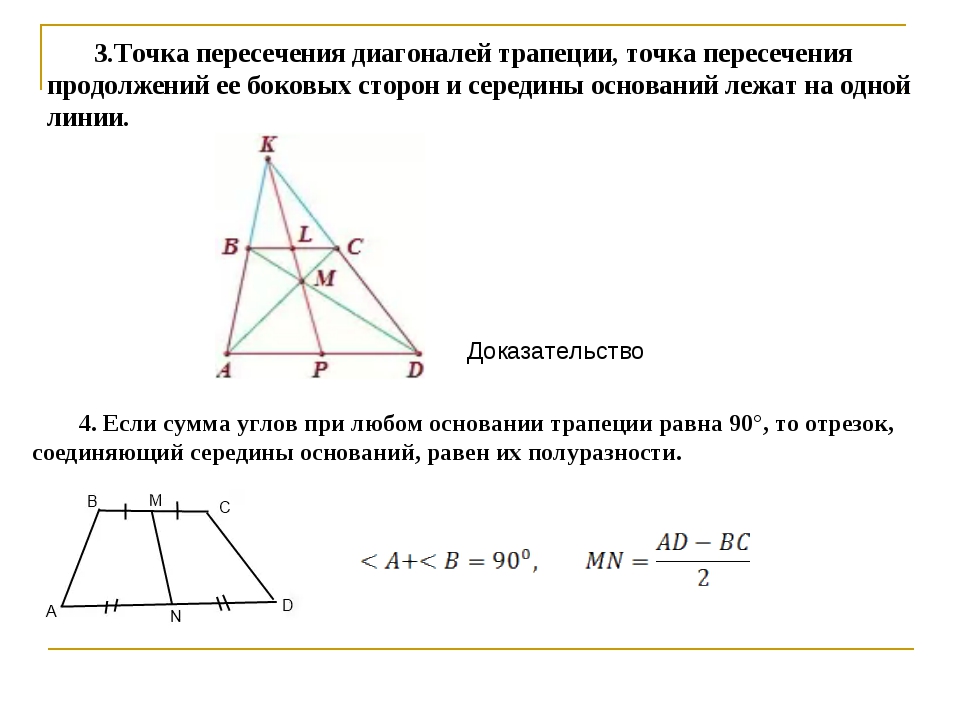 *Центр шестиугольника и центр окружности совпадают, подробнее
*Центр шестиугольника и центр окружности совпадают, подробнее
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.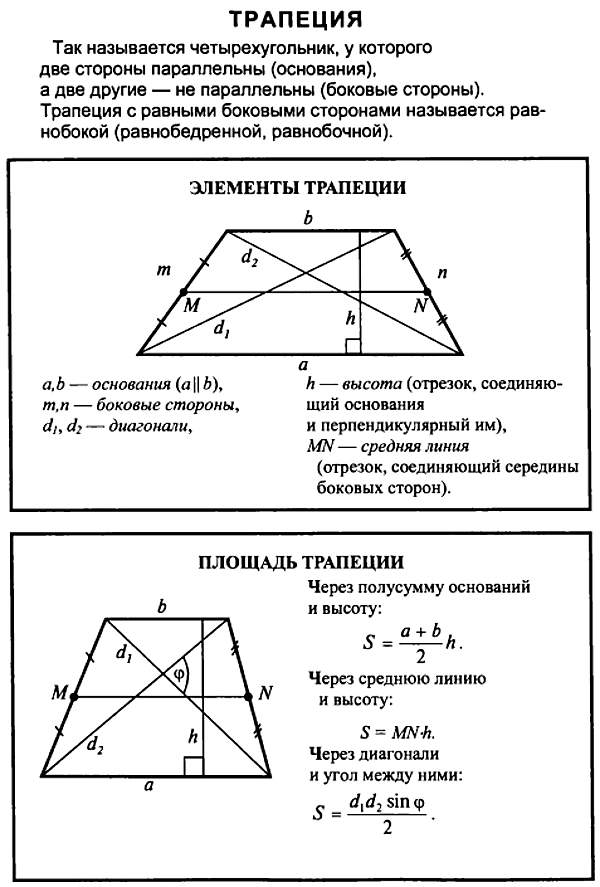
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Трапеция определение свойства. Диагонали трапеции
Проектная работа « Интересные свойства трапеции » Выполнили: ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года
Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства.
Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к
Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с
Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с
Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К
Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д. Е О
Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д
Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h
1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен
2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен
Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
Доказательство: Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.
1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.
I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции. Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Если равнобедеренную трапецию со сторонами а,в,с, d можно вписать и около неё можно описать окружности, то площадь трапеции равна
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.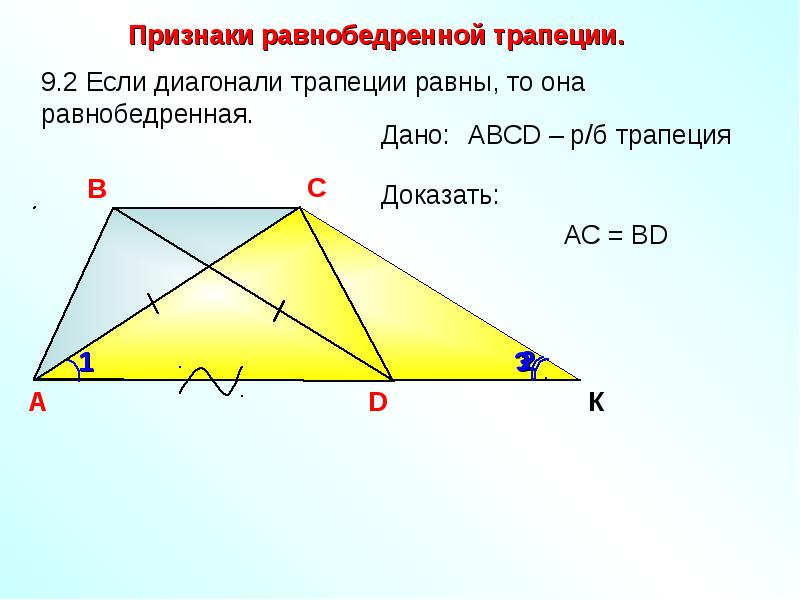 \circ\)
.
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN»\parallel AD\) (\(N»\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\) ) точка \(N»\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
.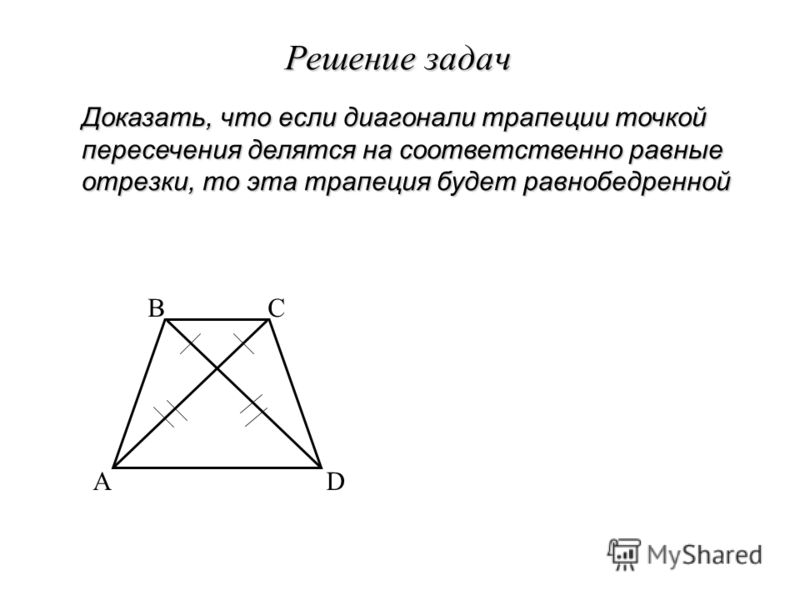 Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\) и \(N»\) — середины отрезков \(BB»\) и \(CC»\) соответственно. Значит, \(MM»\) – средняя линия \(\triangle ABB»\) , \(NN»\) — средняя линия \(\triangle DCC»\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Значит, \(B»M»N»C»\) и \(BM»N»C\) – равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\) , \(N\) и \(M\) лежат на одной прямой.
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.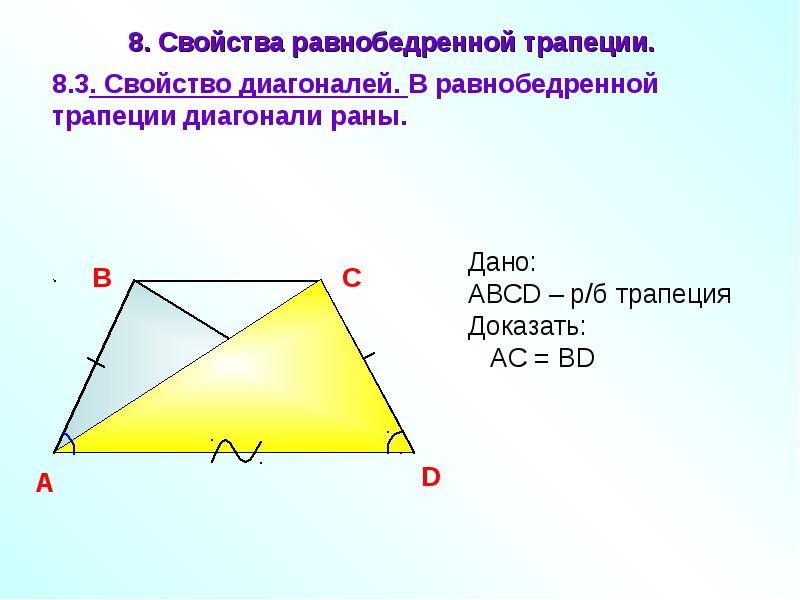
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\) .
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.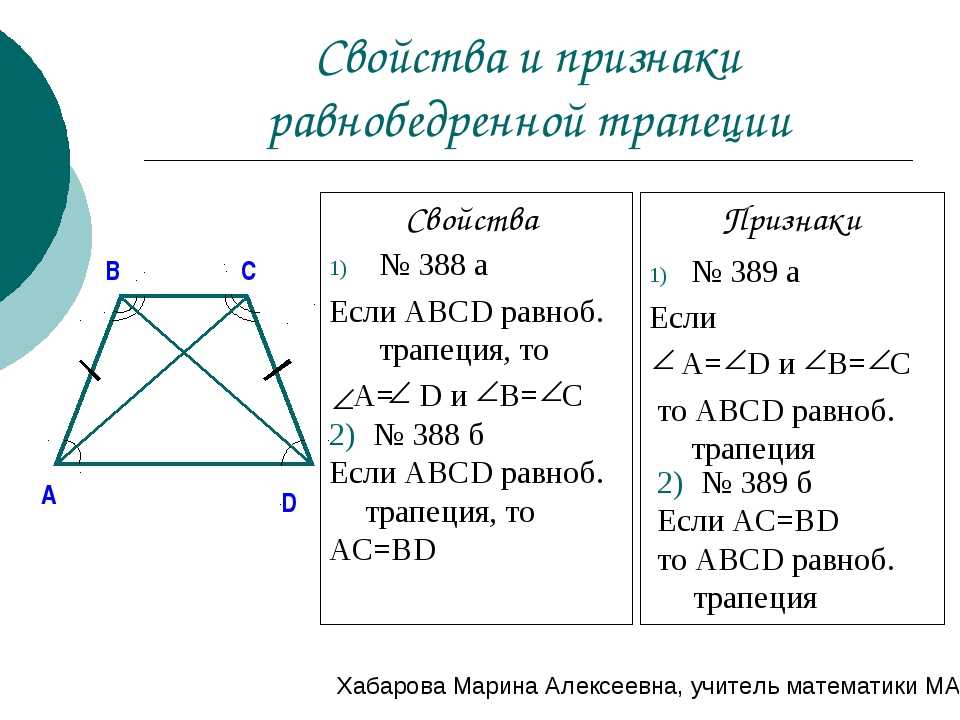
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE — BE = DE — CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
.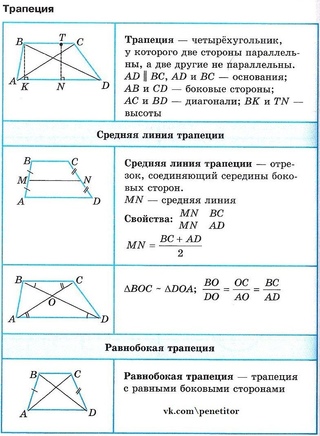 Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии.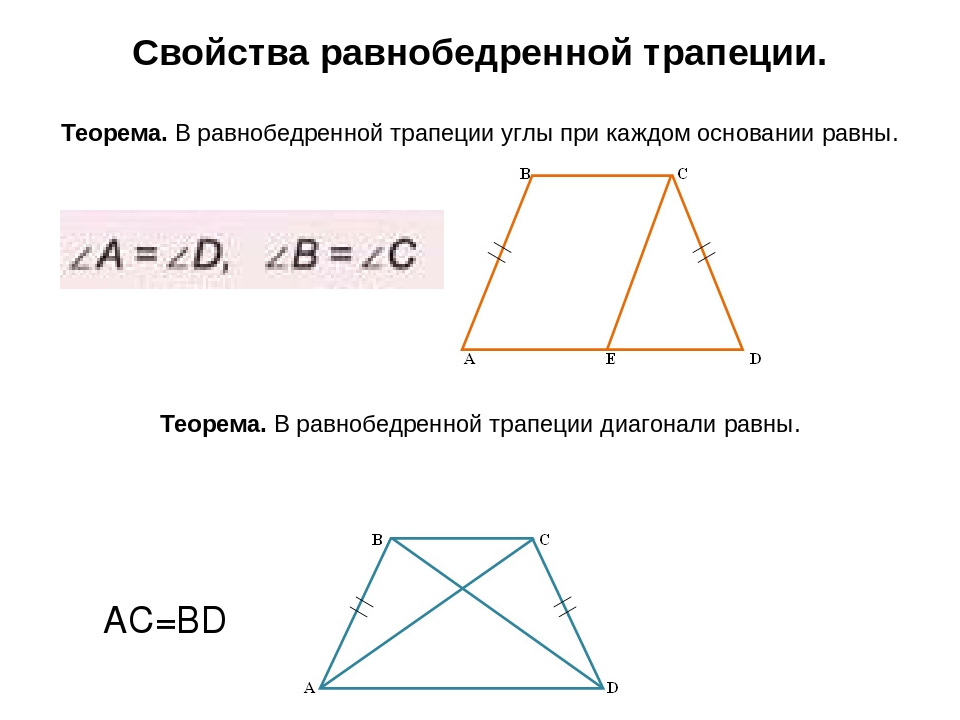 Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .

- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
- Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ.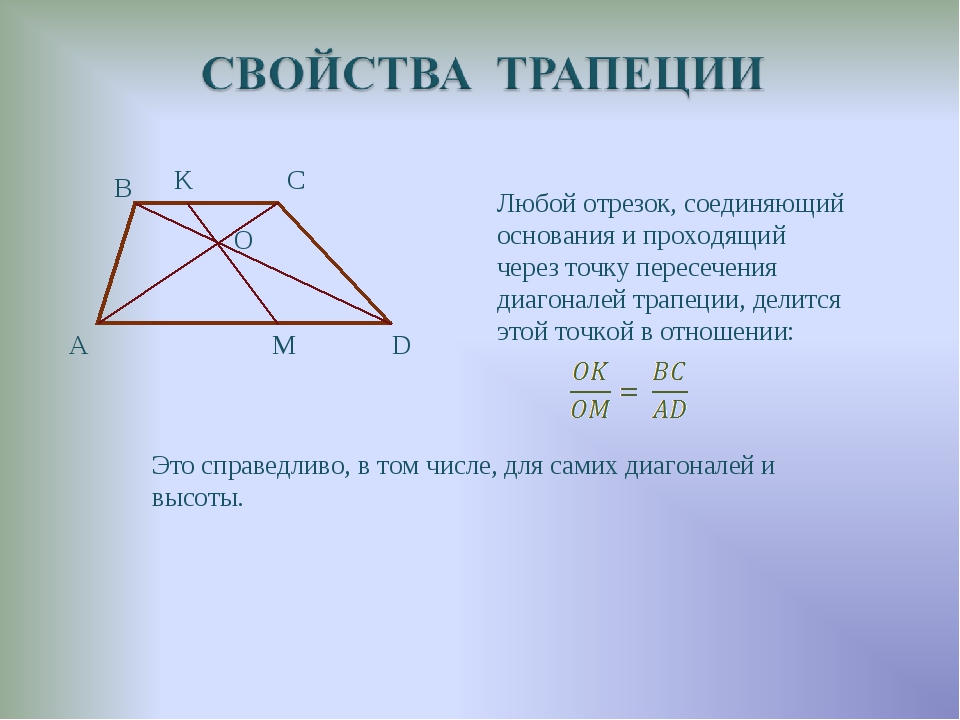 Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь.
 Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны. - Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям.
 И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции. - На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).

- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .

Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности.
 В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию.
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5.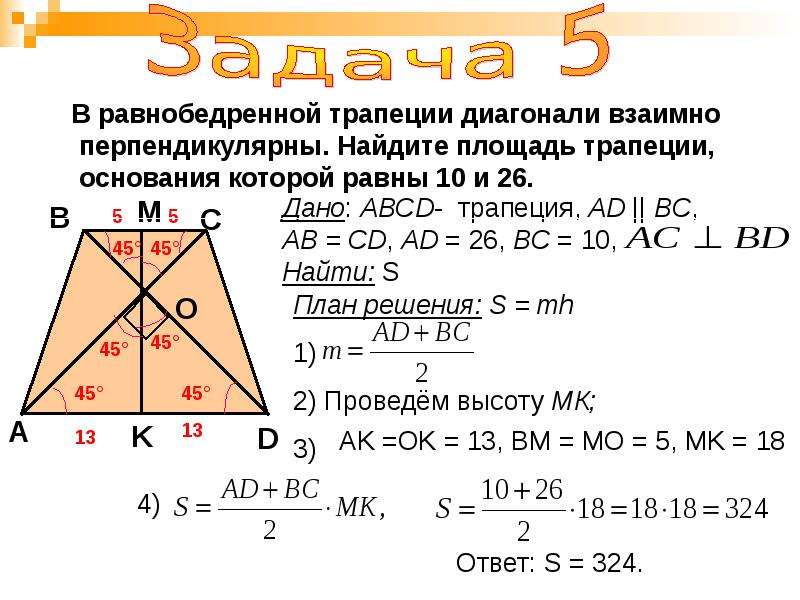 Найдите боковую сторону трапеции.
Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.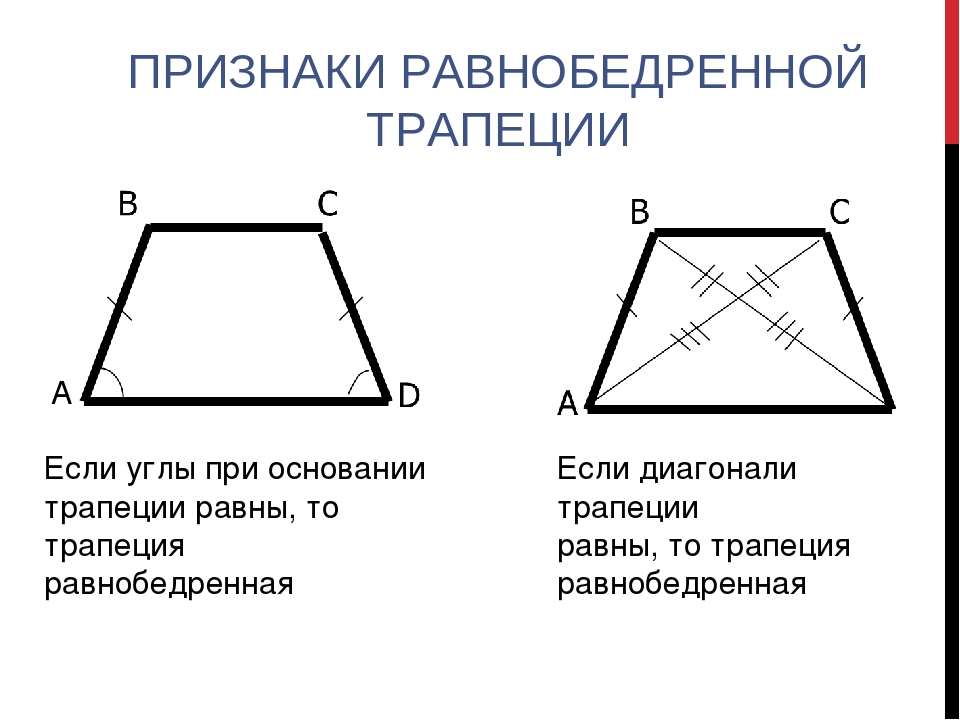
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
Четырехугольники
Параллелограмм
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
- Диагональ разбивает параллелограмм на два равных треугольника.
- Противоположные стороны параллелограмма попарно равны.
- Противоположные углы параллелограмма попарно равны.
- Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
- Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм.

- Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник – параллелограмм.
- Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник – параллелограмм.
Свойство середин сторон четырёхугольника
Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника.
Прямоугольник
Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
- Диагонали прямоугольника равны.
- Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.
Квадрат
Квадратом называется прямоугольник, все стороны которого равны.
Ромб
Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба
- Диагонали ромба перпендикулярны.
- Диагонали ромба делят его углы пополам.
- Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.
- Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.
Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны.
Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
Теорема о средней линии трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция
Трапеция называется равнобедренной, если ее боковые стороны равны.
Свойства и признаки равнобедренной трапеции
- Углы при основании равнобедренной трапеции равны.
- Диагонали равнобедренной трапеции равны.
- Если углы при основании трапеции равны, то она равнобедренная.
- Если диагонали трапеции равны, то она равнобедренная.
- Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Замечательные свойства трапеции
I.Замечательные отрезки в трапеции.
Для начала я обозначу некоторые очень важные факты об отрезках в трапеции.
1. Во
всякой трапеции середины оснований, точка пересечения диагоналей и точка
пересечения продолжения боковых сторон лежат на одной прямой.
2. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой, называемой средней линией трапеции или среднем арифметическим оснований.
3. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
4. Отрезок, параллельный основаниям и разбивающий трапецию на две равновеликие трапеции, равен среднему квадратичному оснований:
5. Отрезок,разбивающий трапецию на две подобные трапеции, имеет длину, равную среднему геометрическому длин оснований.
6. Отрезок, проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому оснований.
Между средними отрезками выполняются следующие соотношения
Доказательства этих фактов я не считаю нужным и уместным приводить в докладе, так как любой уважающий себя школьник должен их знать и уметь делать самостоятельно
Теперь,
когда мы знаем эти, весьма важные, факты преступим к решению поистине
прекрасных задач.
Задача 1:ABCD- трапеция, отрезок MN параллелен основаниям трапеции; AD=11,BC=3,MN=8.Может ли быть x:y=4:3?
Решение:
Применим приём достраивания.
Построим CF║BA, NE║BA. По построению MBCF и AMNE- параллелограммы, тогда имеем MF=3,FN=5,AE=8 и ED=3.
Рассмотрим ∆FCN ~∆END( ∟FCN=∟END, ∟FNC=∟EDN, как накрестлежащие). Из подобия следует, что x:y=5:3, следовательно такого соотношения, как указанно в условии не может быть.
Ответ: не может быть.
Задача 2
ABCD- трапеция,MN║AD, MN=4; точка О ,пересечения диагоналей, находится вдвое дальше от меньшего основания, чем от средней линии. Чему равны основания трапеции?
Решение
ПустьAD=a, BC=b.
1. Из 6 свойства трапеции, а именно, отрезок , проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому длин оснований трапеции. Следовательно, MN=.
2. Пусть
ST- средняя линия и через точку О
проведена прямая EF, перпендикулярная к
основаниям.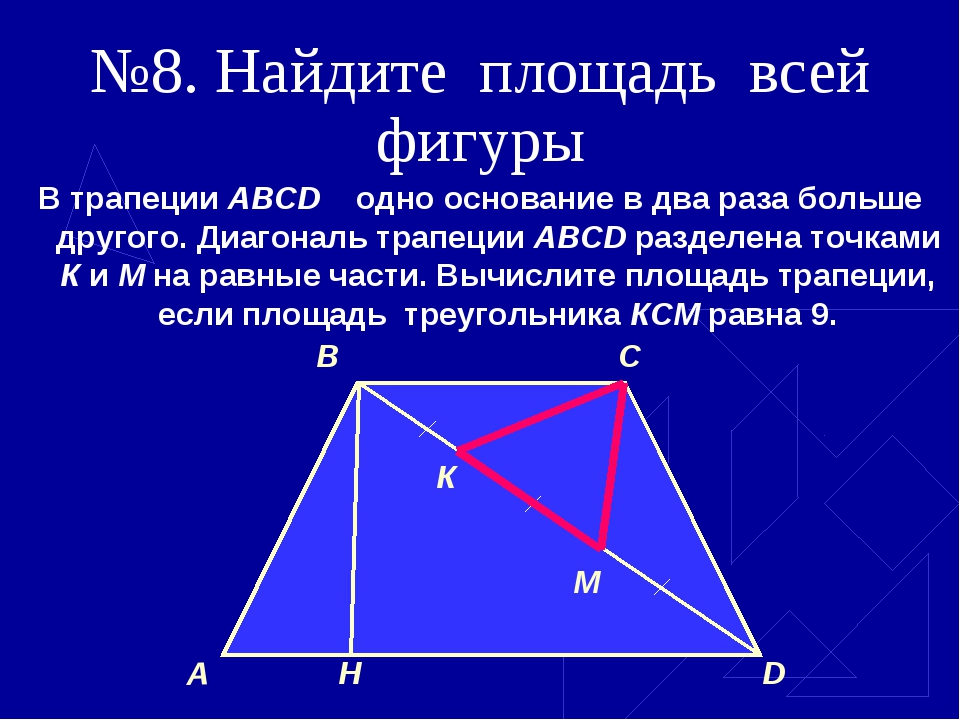
EF- высота трапеции, обозначим EF=h. Очевидно, что средняя линия делит высоту трапеции пополам EH=FH=h
∆BOC~∆DOA(по двум накрестлежащим углам)→
∆OFC~∆OEA(по двум углам)→
FO+OE=h, OE=, тогда находим FO=. По условию FH=FO+½FO=FO, следовательноFO= и тогда , откуда имеем a=2b.
3. Подставляем a=2b в равенство , находим b=3 и а=6.
Ответ: a=6;b=3.
II Метод площадей
Для того, чтобы решать задачи, где рассматривается площадь трапеции, необходимо помнить несколько очень важных утверждений:
1.Если прямаяL1║L2, то S∆ABC=S∆AC1B=S∆AC2B.
Доказательство:
Это
очень легко доказать: площадь треугольника можно вычислить по формуле . Высоты у всех
треугольников одинаковы, так как расстояние между параллельными прямыми всегда
одинаково; треугольники имеют общее основание.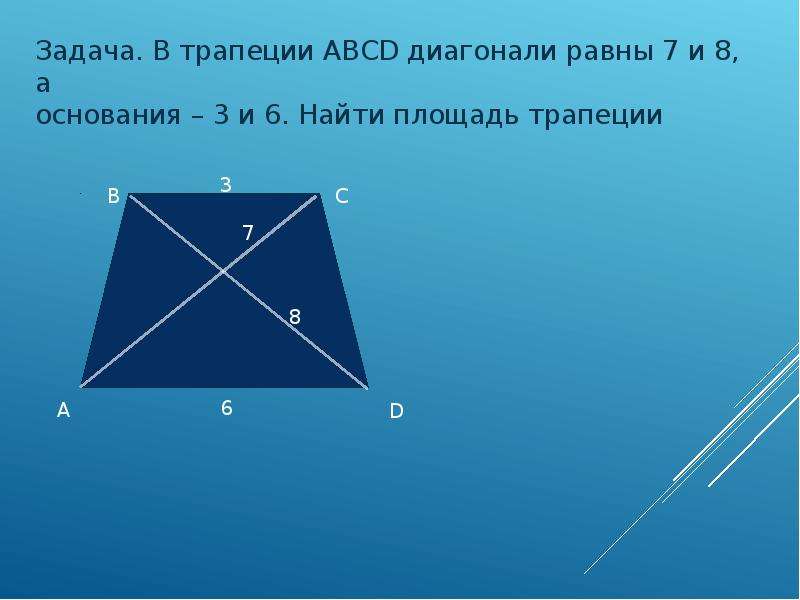 Из этих двух фактов следует, что
S∆ABC=S∆AC1B=S∆AC2B.
Из этих двух фактов следует, что
S∆ABC=S∆AC1B=S∆AC2B.
2.Если прямаяL1║L2 и треугольники не имеют общегооснования, то
.
Доказательство:
Высоты у этих треугольников равные, следовательно, площади этих треугольников относятся, как их снования.
А сейчас немного отвлечёмся от трапеции и перенесёмся в треугольник. Возьмём на рассмотрение одну очень красивую и важную задачу, которая поможет нам в понимании следующей задачи с трапецией. Когда я первый раз увидела эту задачу , она мне сразу же понравилась своей изящностью рисунка и простой гениальностью решения.
Задача 3:
Через точку М, лежащую внутри треугольника АВС проведены три прямые, параллельные его сторонам. При этом образовались три треугольника(см.рис.), площади которых равны S1,S2,S3. Найдите площадь треугольника АВС.
Решение:
Легко
видеть, что ∆EKM,∆MQF
и ∆PMNподобны ∆АВС. Пусть
Sплощадь треугольника АВС, тогда ;; .
Пусть
Sплощадь треугольника АВС, тогда ;; .
Отсюда находим
Так какEM=AP, MF=NC , тоEM+PN+MF=AP+PN+NC=AC. Таким образом ,, откуда следует
Ответ:
Мне захотелось убедиться, возможно ли в трапеции похожее соотношение площадей. И действительно в трапеции нашёлся похожий случай. Рассмотрим его в следующей задачи.
Задача 4:
Дана трапеция ABCD; в трапеции проведены диагонали, пересекающиеся в точке О. Выразите площадь трапеции из площадей образовавшихся треугольников.
Решение:
1.Пусть площадь ∆AOB и ∆CODравныS. Площадь треугольника BOC равна S1 , а площадь треугольника DOA равна S2.
2. Докажем, что S∆AOB=S∆COD.
∆ABC
и ∆DBC имеют общее основание BCи
общую высотуh (т.к.BC║AD
по свойству трапеции). Поскольку мы уже знаем , что треугольники имеющие общее
основание и высоту имеют равные площади, следовательно, S∆ABC=S∆DBC . Заметим, что ∆ABC
и ∆DBC имеют один общий
элемент- ∆BOC, следовательно,
если вычесть из площадей искомых треугольников площадь ∆BOC
мы получим два, равных по площади треугольника. Значит, S∆AOB=S∆COD.
Заметим, что ∆ABC
и ∆DBC имеют один общий
элемент- ∆BOC, следовательно,
если вычесть из площадей искомых треугольников площадь ∆BOC
мы получим два, равных по площади треугольника. Значит, S∆AOB=S∆COD.
3. Рассмотрим ∆AOB и ∆BOC, они имеют общую высоту h2, но имеют различные основания, поскольку мы знаем, что площади треугольников имеющих общую высоты относятся как их основания:
4. Рассмотрим ∆AOD и ∆ COD, они имеют общую высоту h3, но имеют различные основания, поскольку мы знаем, что площади треугольников имеющих общую высоты относятся как их основания:
5. Правые части равенств (1) и (2) одинаковы, следовательно одинаковы и правые части:
Ответ: площадь трапеции равна .
III Замечательные задачи
Планиметрические
задачи с трапецией встречаются не только в 9 и 10 классе, но и в 11. Для того,
чтобы в 11 классе решать более сложные задачи необходимо получить базовые
знания ещё в самом начале изучения планиметрии. Необходимо ещё с самых азов
стараться полностью вникнуть в суть предложенных в учебнике задач. Ведь именно
они есть основа других задач, более сложных и увлекательных. А теперь после
такого небольшого лирического отступления рассмотрим задачу, которая
встретилась на диагностической работе по математике в 11 классе.
Для того,
чтобы в 11 классе решать более сложные задачи необходимо получить базовые
знания ещё в самом начале изучения планиметрии. Необходимо ещё с самых азов
стараться полностью вникнуть в суть предложенных в учебнике задач. Ведь именно
они есть основа других задач, более сложных и увлекательных. А теперь после
такого небольшого лирического отступления рассмотрим задачу, которая
встретилась на диагностической работе по математике в 11 классе.
Задача 5:Площадь трапеции ABCD равна 810. Диагонали пересекаются в точке O. Отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого.
Рассмотрим первый случай.
1.Пусть AD=2BC.
2. ABCP и BCDP – параллелограммы (по построению), поэтому M и N– середины BP и CP, значит, CM и BN — медианы ∆BPC
3. Пусть h – высота трапеции, ВС=a, AD=2a, OM=x. Тогда
4. ОС=2х
(т.к. О- точка пересечения медиан треугольника BPC),
поэтому AM=MC=3x,
OA=AM+OM=3x+x=4x
ОС=2х
(т.к. О- точка пересечения медиан треугольника BPC),
поэтому AM=MC=3x,
OA=AM+OM=3x+x=4x
Аналогично, , значит, ∆ MON~∆AOD с коэффициентом подобия. Следовательно,
Рассмотрим 2 случай:
1.ПустьВС=2AD, h- высота трапеции, AD=a, BC=2a, AM=3t.Тогда ah=540( см. 1 случай)
2.∆AOD~∆COB с коэффициентом подобия, а ∆AMP~∆CMB с коэффициентом подобия . Тогда,
, значит
Аналогично,
Следовательно,
Ответ:S∆mon=22.5 или14.4
Задача 6
Я не могла удержаться от соблазна представить моим слушателям решение одной из самых красивых и простых задач о трапеции . Она была представлена в методичке УРЭК « Трапеция. Некоторые методы решения задач»
Дано:
Диагонали трапеции равны 3 и 5 см , а отрезок, соединяющий середины оснований, равен 2 см . Найти площадь трапеции.
Решение
Выполним дополнительные
построения: проведём отрезок CF,
параллельный диагонали BD,
проведём отрезок СКǁ MN.
Получим параллелограммы MCKN и BCFD, следовательно, CK=MN, MC=NK , BC=DF , BD=CF. Тогда
Значит, СК- медиана треугольника ACF.
Докажем, что площадь исходной трапеции равна площади треугольника ACF.
Для вычисления площади треугольника ACF проведём следующие дополнительные построения: на прямой СК отложим КН=СК.
Тогда ∆CKF=∆HKA ( по двум сторонам и углу между ними). Поэтому AH=CF и площадь треугольника ACF равна площади треугольника ACH. По теореме обратной теореме Пифагора , убеждаемся, что треугольник АСН – прямоугольный. Находим его площадь
Ответ : S=6 см.
Это короткое и изящное решение приносит эстетическое удовольствие!
Задача 7
Дано:
В четырёхугольнике ABCD
сторона АВ равна стороне ВС, диагональ АС равна стороне CD
а ∟АСВ=∟ACD. Радиусы
окружностей вписанных в треугольники АСВ и ACD,
относятся как 3:4. Найдите отношение площадей этих треугольников.
Решение
Обозначим ∟АСВ=∟ACD=α. Прямые AB и CDпараллельны, так как ∟ВАС=∟АСВ=∟ACD, значит ABCD — трапеция.
Высоты треугольников АВС и ACD, проведённые и з вершин соответственно С и А , равны, поэтому отношение площадей треугольников АВС и ACD равно отношению оснований АВ и CD трапеции.
Центры O и Q окружностей, вписанных в треугольники соответственно АВС и ACD, — точки пересечения биссектрис этих треугольников, поэтому ∟АСО=∟ACQ.
Пусть ОМ и QK – радиусы окружностей, проведённые в точки касания окружностей со стороной АС, N- середина основания AD равнобедренного треугольника ACD.
Прямоугольные треугольники CKQ и СМО подобны по двум углам, причём коэффициент подобия равен
Значит
Положим СК= 4х, СМ=3х. Точка М- середина основания АС равнобедренного треугольника АВС, поэтому
По теореме косинусов
Из прямоугольного треугольника ВМС находим, что
Значит, АВ=ВС= . Следовательно
Следовательно
Ответ : 9:14
Эта задача поистине прекрасна! В ней есть абсолютно всё: и подобие и и свойства фигур и даже тригонометрия!
А теперь напоследок мне хочется рассмотреть задачу по стереометрии, которая решается с помощью планиметрии. И как решается- просто блеск! Решение этой, казалось бы, сложной задачи оказывает весьма простым, но очень красивым.
Задача 8
Дано:
О- центр шара, вписанного в усечённый конус, ABCD- осевое сечение конуса, ОЕ┴CD , МК┴AD, MC=r, KD=R, OM=rш.
Доказать, что r 2ш=R*r.
1. Поскольку ОЕ┴ CD, то ОЕ=rш, поскольку радиус окружности — это перпендикуляр в точку касания.
2. Отрезки касательных, проведённые и з одной точки равны, следовательно, МС=СЕ, KD=DE.
3. Докажем что треугольник OCD прямоугольный.
Во-первых, СО и DO биссектрисы по определению. Тогда пусть угол МСО=α , а угол KDO=β
Сумма односторонних углов
при параллельных прямых BC
и AD равна 180◦, то есть
2α+2β=180◦ ,следовательно α+β=90◦,
следовательно треугольник OCD
прямоугольный.
4. Рассмотрим треугольник OCD.
ОЕ- высота в прямоугольном треугольнике , по определению ОЕ2=DE*EC, то есть r2ш=R*r .
ЧТД
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четыреугольник у котрого две стороны паралельны, а две другие стороны не паралельны.Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четыреугольник у которого одна пара противоположных сторон паралельна и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие строрны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция — трапеция у которой боковые стороны равны
- Прямоугольная трапеция — трапеция у которой одна из боковых сторон перпендикулярна основам
Рис.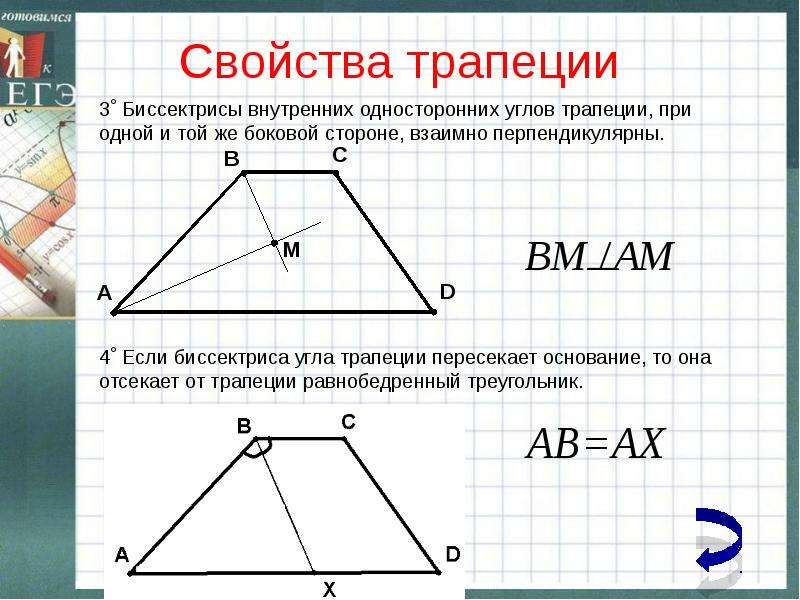 1 1 | Рис.2 |
Основные свойства трапеции
1. В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок который соединяет основы, так же делит диагонали пополам:AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции паралельна основаниям и равна их полусумме:4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины как сотношение между основаниями:BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через середнюю линию и другую основу:
Формула длины оснований трапеции через середнюю линию и другую основу:a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:| с = | h | d = | h |
| sin α | sin β |
Средняя линия трапеции
Определение.
Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1.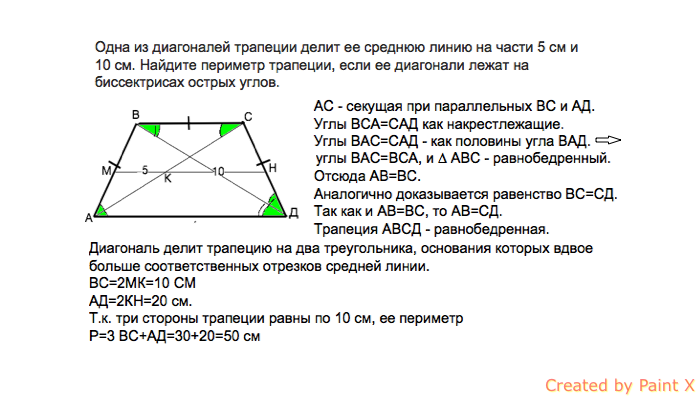 Формула высоты через сторону и прилегающий угол при основании:
Формула высоты через сторону и прилегающий угол при основании:h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:| h = | sin γ · | d1d2 | = | sin δ · | d1d2 |
| a + b | a + b |
| h = | sin γ · | d1d2 | = | sin δ · | d1d2 |
| 2m | 2m |
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:d1 = √a2 + d2 — 2ad·cos β
d2 = √a2 + c2 — 2ac·cos β
2. Формулы диагоналей через четыре стороны:
Формулы диагоналей через четыре стороны:| d1 = | √ | d 2 + ab — | a(d 2 — c2) | d2 = | √ | c2 + ab — | a(c2 — d 2) |
| a — b | a — b |
d1 = √h2 + (a — h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a — h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:d1 = √c2 + d 2 + 2ab — d22
d2 = √c2 + d 2 + 2ab — d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту: 2. Формула площади через среднюю линию и высоту:
Формула площади через основания и высоту: 2. Формула площади через среднюю линию и высоту:S = m · h
3. Формула площади через через диагонали и угол между ними:| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
| S = | a + b | √(p — a)(p — b)(p — a — c)(p — a — d) |
| |a — b| |
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
Окружность вписанная в трапецию
В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
Формула определения длин отрезков проходящих через трапецию:| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Что такое трапеция? (Определение, свойства и видео) // Tutors.com
Содержание
- Что такое трапеция?
- Определения трапеций
- Уголки трапеции
- Свойства трапеции
- Трапеции
- Типы трапеций
Что такое трапеция?
Трапеция — четырехугольник с одной парой параллельных сторон. Трапеция — это:
- Фигурка плоская (плоская)
- Замкнутая фигура (имеет внутреннюю и внешнюю)
- Многоугольник (прямые стороны)
- Четырехугольник (четыре прямые стороны)
Чтобы сделать трапецию, понадобится треугольник. Подойдет любой треугольник: прямой, тупой, равнобедренный, разносторонний. Отрежьте верхнюю часть треугольника так, чтобы разрез был параллелен основанию треугольника. Теперь у вас есть более крошечный треугольник и трапеция.
Подойдет любой треугольник: прямой, тупой, равнобедренный, разносторонний. Отрежьте верхнюю часть треугольника так, чтобы разрез был параллелен основанию треугольника. Теперь у вас есть более крошечный треугольник и трапеция.
Поскольку для определения требуется только одна пара параллельных сторон, две другие стороны можно расположить разными способами, создавая четыре внутренних угла, которые всегда в сумме составляют 360 °.
Определения трапеций
Мы уже знаем, что трапеция похожа на нижнюю часть треугольника, если от нее отрезать меньший треугольник.Вы также можете сделать трапецию из четырех отрезков или четырех прямых объектов.
Используйте все, что вам нравится: сырые спагетти, карандаши, леденцы; все, что у вас есть под рукой. Четыре прямых (линейных) объекта могут быть четырех разных длин или трех разных длин (два из них могут быть одинаковыми).
Положите два объекта вниз или нарисуйте два отрезка линии, чтобы они были параллельны (равноудалены). Сделайте их горизонтально по отношению к вам. Поместите два других объекта слева и справа от этих двух или нарисуйте их так, чтобы все восемь конечных точек соприкасались.
Сделайте их горизонтально по отношению к вам. Поместите два других объекта слева и справа от этих двух или нарисуйте их так, чтобы все восемь конечных точек соприкасались.
Вот и все, трапеция! Горизонтальные части — это основания . Последние две части, которые вы нарисовали или положили (на левом и правом концах), называются ногами трапеции .
Уголки трапеции
Обратите внимание, что мы не беспокоились ни о каком из внутренних углов, так как при сохранении параллельности двух сторон остальная часть трапеции встала на свои места. Углы сортируются и складываются в 360 °.
Высота трапеции — это ее высота.Пусть вас не обманывают покатые ножки — если они наклонены, то длиннее высоты. Высота всегда измеряется от основания (любой параллельной стороны) до другой стороны под прямым углом к основанию.
Вы можете провести перпендикулярную линию где угодно вдоль основания трапеции, и когда она касается противоположной, параллельной стороны, ее длина равна высоте.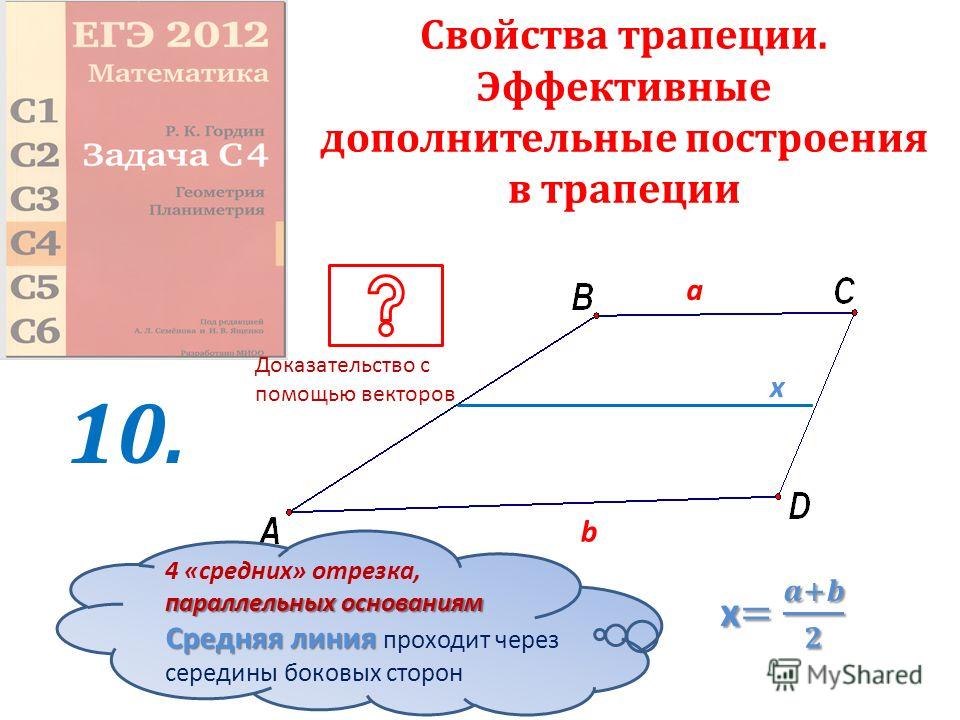
Свойства трапеции
Трапеция — это параллелограмм?
Вы можете определить любую трапецию, если это четырехугольник с одной парой параллельных сторон.Многие математики включают параллелограммы как типы трапеций, потому что, конечно, параллелограмм имеет по крайней мере одну пару параллельных сторон. Другие математики исключают параллелограммы, говоря, что трапеция должна иметь ровно одну пару параллельных сторон.
Еще одним отличительным свойством всех трапеций является то, что любые два смежных внутренних угла будут дополнительными (добавить к 180 °).
Трапеции
Обычно для максимальной ясности на изображениях и рисунках трапеций показаны две параллельные стороны, идущие горизонтально, причем более длинная сторона обращена вниз в качестве основания.Однако будьте готовы увидеть трапеции в при любой ориентации . Трапецию можно нарисовать или изобразить либо с ногой внизу, либо с более короткой параллельной стороной внизу.
Поскольку параллельные стороны — единственные, которые могут быть основаниями, даже когда трапеция рисуется с ногой внизу и горизонтально, это , а не основание. Это все еще нога.
Основание обычно представляет собой более длинную параллельную сторону, но если трапеция рисуется с более короткой параллельной стороной внизу, то это основание.
Типы трапеций
Поскольку трапеции могут возникать в виде треугольников, они имеют общие названия, полученные от типов треугольников:
- Scalene trapezoid — Начинается как разносторонний треугольник
- Равнобедренная трапеция — Начиналась как равнобедренный треугольник
- Правая трапеция — Когда-то был прямоугольный треугольник
- Тупая трапеция — Как тупой треугольник
- Острая трапеция — как острый треугольник
Скаленовая трапеция
Разносторонняя трапеция имеет четыре стороны неравной длины.Основания параллельны, но разной длины. Две ножки разной длины.
Две ножки разной длины.
Равнобедренная трапеция
Равнобедренная трапеция имеет ножки одинаковой длины. Основания параллельны, но разной длины.
Трапеция правая
Прямая трапеция имеет один прямой угол (90 °) между основанием и ножкой.
Тупая трапеция
Тупая трапеция имеет один внутренний угол (созданный либо основанием , либо ножкой) больше 90 °.
Острая трапеция
Острая трапеция имеет оба внутренних угла (образованные более длинным основанием и ножками ) размером менее 90 °.
Краткое содержание урока
Используя всего четыре линии и четыре внутренних угла, мы построили трапецию , узнали, что делает трапецию уникальной (пара параллельных сторон), каковы различные части трапеции и названия пяти специальных трапеций.
Следующий урок:
Как найти площадь трапеции
Трапеции и ее свойства
Освойте 7 столпов успеха в школе
Повысьте успеваемость и снизьте уровень стресса
Срединное сечение трапеции (также называемое средним) создается путем проведения линии из середины единицы.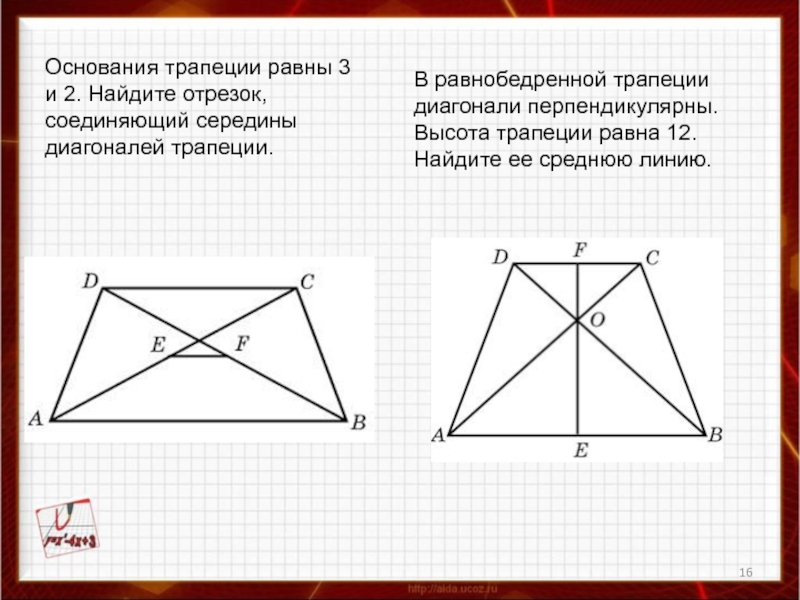 ногу до середины другой ноги.
ногу до середины другой ноги.
Длину средней части можно рассчитать, сложив длину двух оснований и разделив ее на два.
Средняя часть EF = AB + DC / 2
Трапеция может иметь прямой угол
Базовые углы равнобедренной трапеции совпадают, а противоположные углы являются дополнительными.
∠A и ∠B и ∠D и ∠C совпадают
A и ∠C и ∠B и ∠D дополнительные
Углы, образованные ножками на одной стороне трапеции, смежны углы, и являются дополнительными. (добавить к 180 градусам)
∠A и ∠D и ∠B и ∠C смежные и дополнительные
- Трапеция — это четырехугольник с ровно одной парой параллельных сторон.
- Параллельные стороны трапеции образуют основания.
- Сумма внутренних углов трапеции равна 360 градусам, а углы с каждой стороны трапеции являются дополнительными.
- Трапеция имеет четыре вершины, также называемые углами.

- Медиана трапеции — это линия, соединяющая середину двух сторон.
- Трапеция имеет одну пару параллельных сторон.У параллелограмма две пары параллельных сторон.
- Дополнительно есть прямые трапеции и равнобедренные трапеции.
- Равнобедренная трапеция — это трапеция с двумя параллельными сторонами, причем две другие стороны совпадают.
- Кроме того, диагонали равнобедренного треугольника совпадают.
- Базовые углы равнобедренной трапеции совпадают.
- У правой трапеции два прямых угла.
- В Великобритании трапеция называется трапецией
Common Core Standard. 7.G.6
Трапеция — это четырехугольник.
| |
Трапеция имеет две параллельные
стороны и две непараллельные стороны.
| |
Внутренние углы а трапеции складываются в 360 градусов, а углы с каждой стороны являются дополнительными.
| |
Формула площади трапеция равна Площадь = 1/2 (b1 + b2) h h = высота b = основание | |
Формула периметра a трапеция равна Периметр = b1 + b2 + s1 + s2 | |
Высота Трапеция ч = г * SinB или h = w * SinA | |
Диагонали длина
| |
youtube.com/embed/J3Qh2TTIKkM?autoplay=0&color1=0x999999&color2=0xe8e8e8&wmode=transparent» allowfullscreen=»»/>
Вам также может понравиться……
Из этого видео вы узнаете ….
Формула для определения периметра трапеции
Пошаговая инструкция для определения периметра
Видео отрабатывает высоту проблема
Какова высота равнобедренной трапеции с основанием 10 и 18 единиц, длиной стороны 4 единицы и углом наклона 50 градусов? (см. рисунок)
Внутренние углы трапеции складываются в 360 градусов.
Углы трапеции
Трапеция — определение, свойства, формулы и примеры
Определение
Трапеция — это плоская геометрическая форма с четырьмя прямыми сторонами, имеющая по крайней мере одну пару противоположных параллельных сторон.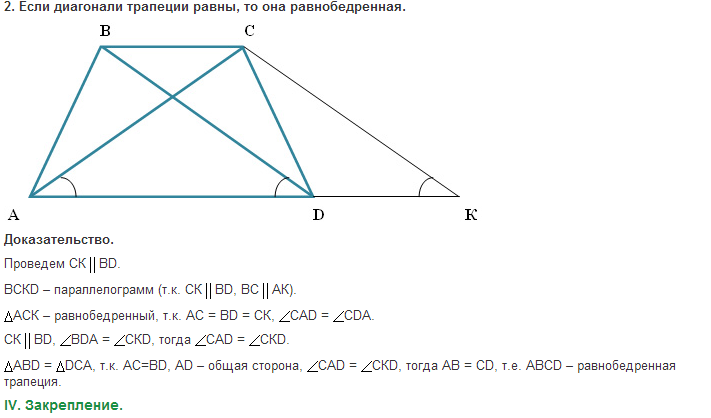 Это похоже на треугольник, у которого срезана верхняя часть.
Это похоже на треугольник, у которого срезана верхняя часть.
Параллельные стороны являются основаниями, а две другие стороны называются ножками или боковыми сторонами. Его также называют трапецией в Великобритании и некоторых других частях света.
ТрапецияНедвижимость
Свойства трапеции- Имеет четыре стороны и четыре угла; в трапеции ABCD, AB, BC, CD и DA — четыре стороны, составляющие углы ∠DAB, ∠ABC, ∠BCD, и ∠CDA
- Имеет одну пару параллельных сторон. Две параллельные стороны — это основания, а непараллельные стороны — ноги; здесь AD = короткое основание, BC = длинное основание, в то время как AB = отрезок 1 и CD = отрезок 2, и AD ∥ BC
- Смежные углы в сумме составляют 180 °; Итак, ∠DAB + ∠ABC = 180 °, ∠ABC + ∠BCD = 180 °, ∠BCD + ∠CDA = 180 ° и ∠CDA + ∠DAB = 180 °
- Медиана параллельна двум основаниям и делит непараллельные стороны на две равные части; Итак, EF ∥ AD и EF ∥ BC
Формулы
Медиана
Это отрезок линии посередине между двумя основаниями. Его еще называют средней линией или средним сегментом. Формула приведена ниже:
Его еще называют средней линией или средним сегментом. Формула приведена ниже:
Найдите середину трапеции с основаниями размером 7 м и 9 м.
Решение:
Как известно,
Медиана ( M ) = ½ ( a + b ) , здесь a = 9 м и b = 7 м
= ½ (9 + 7) м
= 16/2 м
= 8 м
Площадь
Общее пространство, ограниченное трапецией.Формула приведена ниже:
Найдите площадь трапеции, когда два основания составляют 8 см и 6 см, а высота равна 10 см
Решение:
Как известно,
Площадь ( A ) = ½ ( a + b ) × h , здесь a = 8 см, b = 6 см и h = 10 см
= 1/2 × (8 + 6) × 10 см 2
= ½ × 14 × 10 см 2
= 70 см 2
Задача: Нахождение площади трапеции, когда известны значения MEDIAN и HEIGHT
Найдите площадь трапеции со средним значением 5 см и высотой 11 см
Решение:
Здесь мы воспользуемся альтернативной формулой,
A = м × h , здесь м = медиана и h = высота
В этой трапеции м = 5 см и h = 11 см
Т. к., A = м × h
к., A = м × h
= 5 × 11 см 2
= 55 см 2
Периметр
Общее расстояние, пройденное по краю трапеции.Формула приведена ниже:
Найдите периметр трапеции со сторонами 6 м, 8 м, 12 м и 15 м.
Решение:
Как известно,
Периметр ( P ) = a + b + c + d , здесь a = 15 м, b = 12 м, c = 6 м и d = 8 м
= 15 м + 12 м + 6 м + 8 м
= 41 м
Типы
Трапеции подразделяются на две группы: по сторонам : 1) разносторонняя и 2) равнобедренная трапеция; на основе углов : 1) острый, 2) тупой и 3) правая трапеция.
Различия между типами приведены ниже:
Типы трапецииГеометрия: свойства трапеций
Свойства трапеций
Трапеция представляет собой четырехугольник с ровно двумя параллельными сторонами. На рисунке 15.1 изображена трапеция ABCD. Помните соглашения об именах для многоугольников. Вы должны перечислить вершины в последовательном порядке. В трапеции ABCD, BC? ? ОБЪЯВЛЕНИЕ. Параллельные стороны BC и AD называются основаниями , а непараллельные стороны AB и CD — ножками . Базовые углы — это пара углов, имеющих общую основу. На рисунке 15.1? A и? D образуют один набор базовых углов.
Рисунок 15.1 Трапеция ABCD.
Когда средние точки двух сторон трапеции соединяются вместе, результирующий сегмент называется медианной трапеции. На рисунке 15.2 R и S — середины AB и CD, а RS — медиана трапеции ABCD. Медиана трапеции параллельна каждому основанию. Как ни странно, длина медианы трапеции равна половине суммы длин двух оснований.Примите эти утверждения как теоремы (без доказательства) и используйте их при необходимости.
Рис. 15.2 R и S — это середины AB и CD, а RS — это медиана трапеции ABCD.
- Теорема 15.1 : Медиана трапеции параллельна каждому основанию.
- Теорема 15.2 : Длина медианы трапеции равна половине суммы длин двух оснований.
- Пример 1 : Трапеция ABCD, BC? ? AD, R — это середина AB, а S — середина CD, как показано на рисунке 15.3. Найдите AD, BC и RS, если BC = 2x, RX = 4x? 25 и AD = 3x? 5.
Рисунок 15.3 Трапеция ABCD, BC? ? AD AB имеет среднюю точку R, а CD — среднюю точку S.
- Решение : Поскольку RS = 1 / 2 (AD + BC), вы можете подставить значения для каждой длины сегмента:
- 4x? 25 = 1 / 2 (3x? 5 + 2x)
- Перестановка и упрощение дает:
- 4x? 25 = 5 / 2 x — 5 / 2
- 4x? 5 / 2 x = 25 — 5 / 2
- 3 / 2 x = 45 / 2
- x = 15
- Итак, x = 15, BC = 30, RS = 35 и AD = 40.
Высота трапеции — это отрезок перпендикулярной линии от вершины одного основания до другого основания (или до продолжения этого основания). На рисунке 15.4 BT — это высота трапеции ABCD.
Рисунок 15.4 Трапеция ABCD с высотой BT.
Solid Facts
Трапеция — это четырехугольник с ровно двумя параллельными сторонами.
Основания трапеции — это параллельные стороны.
Ноги трапеции — непараллельные стороны.
Медиана трапеции — это отрезок прямой, соединяющий средние точки двух сторон.
Высота трапеции — это отрезок перпендикулярной линии от вершины одного основания до другого основания (или до продолжения этого основания).
Углы основания трапеции — это пара углов, имеющих общее основание.
В трапецию встроены две параллельные линии (основания BC и AD), пересеченные поперечиной (одна из опор, AB или CD).Вы знаете, что два внутренних угла на одной стороне трансверсали являются дополнительными углами (теорема 10.5), поэтому? A и? B являются дополнительными углами, как и? C и? D.
Выдержка из The Complete Idiot’s Guide to Geometry 2004 Дениз Сечей, доктор философии. Все права защищены, включая право на воспроизведение полностью или частично в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476.\ circ. \ _\квадратный \ end {align} ∠D = 360∘− (∠A + ∠B + ∠C) = 360∘ − 290∘ = 70∘. □
ParallelAngleBisector
На рисунке выше изображена равнобедренная трапеция.
Если длина AB‾ \ overline {AB} AB равна 5, какова длина CD‾? \ overline {CD}? CD?
Равнобедренная трапеция — это трапеция с конгруэнтными ногами. {‘} D ′ — перпендикулярные основания на BC‾ \ overline {BC} BC из точек AAA и D, D, D соответственно.\ circ. \ _ \ square30∘. □
Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция
В евклидовой геометрии четырехугольник — это четырехсторонняя двумерная фигура, сумма внутренних углов которой равна 360 °. Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Итак, каковы свойства четырехугольника? Четырехугольники обладают двумя свойствами:
- Четырехугольник должен быть замкнутой формы с 4 сторонами
- Сумма всех внутренних углов четырехугольника составляет 360 °
В этой статье вы получите представление о 5 типах четырехугольников (прямоугольник, квадрат, параллелограмм, Ромб и Трапеция) и познакомьтесь со свойствами четырехугольников.
Вот пять типов четырехугольников, обсуждаемых в этой статье:
- Прямоугольник
- Квадрат
- Параллелограмм
- Ромб
- Трапеция
Вот видео, объясняющее свойства четырехугольника:
Свойства четырехугольников — Обзор
На приведенной ниже схеме показан четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов составляет 360 °.Таким образом, A + ∠B + ∠C + ∠D = 360 °
| Свойства четырехугольника | Прямоугольник | Квадрат | Параллелограмм | Ромб | Да | Нет | |||||
| Противоположные стороны равны | Да | Да | Да | Да | Нет | ||||||
| Противоположные стороны параллельны | Да | Да | Да | Да | Да | Да | Да | ||||
| Все углы равны | Да | Да | Нет | Нет | Нет | ||||||
| Противоположные углы равны | Да | Да | Да | Да | Да | Да | Да | Да | Да | Да | |
| Сумма двух смежных углов равна 180 | 9097 2 ДаДа | Да | Да | Нет | |||||||
| Разделить пополам | Да | Да | Да | Да | Нет | ||||||
| Пополам Нет | Да | Нет |
Давайте подробно обсудим каждый из этих 5 четырехугольников:
Вот вопросы, которые научат вас применять свойства всех пяти четырехугольников, которые вы узнаете в этой статье.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами. Таким образом, все углы в прямоугольнике равны (360 ° / 4 = 90 °). Причем противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.
Вот три свойства прямоугольника:
- Все углы прямоугольника равны 90 °
- Противоположные стороны прямоугольника равны и параллельны
- Диагонали прямоугольника делят друг друга пополам
Формула прямоугольника — площадь и периметр прямоугольника
Если длина прямоугольника L, а ширина B, то
- Площадь прямоугольника = длина × ширина или длина × ширина
- Периметр прямоугольника = 2 × (L + B)
Эти практические вопросы помогут вам закрепить свойства прямоугольников
Планируете ли вы поступать в лучшие бизнес-школы? Позвольте нам помочь вам пройти первый этап процесса i.е., сдавая GMAT. Пройдите бесплатный тест GMAT, чтобы понять свой базовый результат, и начните подготовку к GMAT с нашей бесплатной пробной версии. По состоянию на 4 октября 2021 года мы являемся самой популярной онлайн-компанией по подготовке к GMAT: 2200+ отзывов на GMATClub.
Знаете ли вы, что участники программы e-GMAT набрали более 700 баллов, чем когда-либо за всю историю GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг такого рекордного результата благодаря инвестициям и инновациям с единственной целью — создать платформу, которая дает учащимся возможность добиваться наилучших результатов.
Площадь
Квадрат — четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.
Вот три свойства квадрата:
- Все углы квадрата равны 90 °
- Все стороны квадрата равны и параллельны друг другу
- Диагонали делят друг друга пополам перпендикулярно
Формула квадрата — площадь и периметр квадрата
Если сторона квадрата — «а», тогда
- Площадь квадрата = a × a = a²
- Периметр квадрата = 2 × (a + a) = 4a
Эти практические вопросы помогут вам закрепить свойства квадратов
Если вы набрали Q50-51 за GMAT, вы сможете набрать 700+ баллов за GMAT.Начните свой путь к получению Q50-51 по GMAT с онлайн-курса подготовки e-GMAT, основанного на искусственном интеллекте. Наш xPERT не только подбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого количественного балла. Посмотрите это видео, чтобы узнать больше:
Параллелограмм
Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, у него две пары параллельных сторон. Причем противоположные углы в параллелограмме равны, а их диагонали делят друг друга пополам.
Вот четыре свойства параллелограмма:
- Противоположные углы равны
- Противоположные стороны равны и параллельны
- Диагонали делят друг друга пополам
- Сумма любых двух смежных углов равна 180 °
Формулы параллелограмма — площадь и периметр параллелограмма
Если длина параллелограмма равна «l», ширина — «b», а высота — «h», тогда:
- Периметр параллелограмма = 2 × (l + b)
- Площадь параллелограмма = l × h
Эти практические вопросы помогут вам закрепить свойства параллелограмма
Ромб
Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу.Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», так как он похож на ромб в игральных картах.
Вот четыре свойства ромба:
- Противоположные углы равны
- Все стороны равны и противоположные стороны параллельны друг другу
- Диагонали делят друг друга перпендикулярно
- Сумма любых двух смежных углов составляет 180 °
Формулы ромба — площадь и периметр ромб
Если сторона ромба — это, то периметр ромба = 4a
Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Эти практические вопросы помогут вам закрепить свойства ромба
Трапеция
Трапеция (в США ее называют трапецией) — это четырехугольник, у которого есть только одна пара параллельных сторон.Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.
Трапеция — это четырехугольник, в котором одно свойство:
- Только одна пара противоположных сторон параллельна друг другу
Формулы трапеции — площадь и периметр трапеции
Если высота трапеции « h» (как показано на диаграмме выше), то:
- Периметр трапеции = Сумма длин всех сторон = AB + BC + CD + DA
- Площадь трапеции = ½ × (Сумма длин параллельных сторон) × h = ½ × (AB + CD) × h
Эти практические вопросы помогут вам закрепить свойства трапеции
Свойства четырехугольников — сводка
На изображении ниже также показаны свойства четырехугольника
.Важные формулы четырехугольника
В таблице ниже приведены формулы площади и периметра четырехугольников различных типов:
| Четырехугольные формулы | Прямоугольник | Квадрат | Параллелограмм | Ромб | 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 l × h½ × d1 × d2 | ½ × (Сумма параллельных сторон) × высота |
| Периметр | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Сумма всех сторон |
Дополнительная литература:
Чтобы успешно сдать GMAT, необходим четко определенный учебный план.Сэкономьте 60+ часов на подготовке к GMAT, выполнив следующие три шага:
Четырехсторонний практический вопрос
Попрактикуемся в применении свойств четырехугольника на следующих типовых вопросах:
GMAT Quadrilaterials Практический вопрос 1
Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров. Сколько метров забора нужно купить, чтобы оградить весь сад?
- 20 метров
- 25 метров
- 30 метров
- 40 метров
- 50 метров
Решение
Шаг 1: Дано
- У Адама прямоугольный сад.
- Имеет длину 10 метров и ширину 15 метров.
- Он хочет построить вокруг него забор.
Шаг 2: найти
- Длина, необходимая для ограждения всего сада.
Шаг 3: подход и разработка
Забор можно строить только вокруг внешней стороны сада.
- Итак, общая необходимая длина забора = Сумма длин всех сторон сада.
- Так как сад прямоугольный, сумма длин всех сторон — это не что иное, как периметр сада.
- Периметр = 2 × (10 + 15) = 50 метров
Следовательно, необходимая длина забора — 50 метров.
Следовательно, вариант E — правильный ответ.
GMAT Quadrilaterials Практический вопрос 2
Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стены — 1,5 доллара за квадратный метр.Если стена 25 метров в длину и 18 метров в ширину, то какова общая стоимость покраски стены?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Решение
Шаг 1: Дано
- Стив хочет покрасить одну стену своей комнаты.
- Стена 25 метров в длину и 18 метров в ширину.
- Стоимость покраски стены — 1,5 доллара за квадратный метр.
Шаг 2: найти
- Полная стоимость покраски стены.
Шаг 3: подход и разработка
- Стена окрашена по всей площади.
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, то мы сможем получить общую стоимость.
- Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
- Общая стоимость покраски стены = 450 × 1,5 $ = 675 $
Следовательно, правильный ответ — вариант E.
Мы надеемся, что к настоящему времени вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти концепции для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT. Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить доступ бесплатно, зарегистрировавшись здесь.
Вот еще несколько статей по математике:
- Повысьте точность в вопросах по математике по многоугольникам
- Вопросы по геометрии — наиболее распространенные ошибки | GMAT Quant Prep
Посмотрите этот веб-семинар без геометрии GMAT, где мы обсуждаем, как решать вопросы о достаточности данных на уровне 700 и проблемные вопросы в четырехугольниках GMAT:
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки.По состоянию на 4 октября 2021 года наша компания по подготовке к GMAT является самой обсуждаемой компанией по подготовке к GMAT с более чем 2200 отзывами.
Напишите нам по адресу [email protected] в случае возникновения каких-либо вопросов.
Часто задаваемые вопросы
Какие бывают четырехугольники?Есть 5 типов четырехугольников — прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб.
Где я могу найти несколько практических вопросов по четырехугольникам?В этой статье вы можете найти несколько практических вопросов о четырехугольниках.
Какова сумма внутренних углов четырехугольника?Сумма внутренних углов четырехугольника равна 360 °.
Площадь формулы трапеции: определение, типы, примеры, свойства
Площадь трапеции Формула: Трапеция — это четырехугольник, две стороны которого параллельны. Представьте себе трапецию \ (ABCD \) такую, что \ (AB \) и \ (CD \) — две ее параллельные стороны, а \ (AD \) и \ (BC \) — ее непараллельные стороны. Основание трапеции — две параллельные стороны трапеции.Расстояние между двумя параллельными сторонами называется высотой трапеции.
В этой статье мы изучим формулу площади трапеции, используя основание и высоту трапеции, а также два треугольника, образованных, когда мы соединяем два угла трапеции.
Изучите все концепции на площади трапеции
Что такое трапеция?
Трапеция или трапеция — это четырехугольник, определяемый как форма с четырьмя сторонами и одним набором параллельных сторон.Параллельные стороны называются основаниями, а непараллельные стороны — ножками трапеции.
Изучите концепции экзамена на Embibe
Линия, соединяющая середины непараллельных сторон трапеции, называется средним сегментом.
Проверьте выше различные типы изображений трапеции, где стрелка представляет их параллельную сторону. На всех трех изображениях мы видим, что две стороны параллельны друг другу, тогда как две другие стороны не параллельны
Если мы проведем отрезок прямой между двумя непараллельными сторонами, трапеция будет разделена на две неравные части.
Равнобедренная трапеция
Мы изучили концепцию равнобедренных треугольников, в которой две стороны треугольника равны, и углы, противоположные равным сторонам, также равны. Таким же образом у нас есть равнобедренная трапеция, у которой две непараллельные стороны равны и образуют равные углы у одного из оснований. Мы можем увидеть пример этого на приведенном ниже рисунке. Ее еще называют равнобедренной трапецией.
Вопросы для практического экзамена
Прямоугольная трапеция
Правая трапеция (также называемая прямоугольной трапецией) имеет два смежных прямых угла.\ circ} \).
Площадь трапеции можно вычислить, используя длины двух ее параллельных сторон и высоту между ними.Формула для расчета площади \ ((A) \) трапеции с использованием базы и высоты задается как
\ (A = \ frac {1} {2} (a + b) \ times h \)
где \ (a \) и \ (b \) — длины параллельных сторон трапеции, а \ (h \) — высота.
Попытка пробного тестирования
Расчет площади трапеции по формуле
Пусть \ (ABCD \) — трапеция такая, что \ (AB \) и \ (CD \) — две ее параллельные стороны, а \ (AD \) и \ (BC \) — ее непараллельные стороны.
Пусть \ (DL = h \) будет высотой трапеции \ (ABCD. AC \), разделенной на два треугольника \ (ABC \) и \ (ACD \).
Следовательно, Площадь трапеции \ (ABCD = {\ text {Area}} \, {\ text {of}} \, \ Delta ABC + {\ text {Area}} \, {\ text {of}} \, ACD \)… (I)
Так как \ (h \) — высота трапеции \ (ABCD \). Следовательно, это также высота \ (\ Delta ABC \) и \ (\ Delta ACD \).
Следовательно, площадь \ (\ Delta ABC = \ frac {1} {2} \ times AB \ times h \)
и площадь \ (\ Delta ACD = \ frac {1} {2} \ times ДК \ раз ч \)
Подставляя эти значения в (i), мы получаем
Площадь трапеции \ (ABCD = \ left ({\ frac {1} {2} \ times AB \ times h} \ right) + \ left ({\ frac {1 } {2} \ times DC \ times h} \ right) \)
\ (= \ frac {1} {2} \ times (AB + DC) \ times h \)
\ (= \ frac {1} { 2} \ times \ left ({{\ rm {Сумма \; \; параллельных \; сторон}}} \ right) \ times \ left ({{\ rm {расстояние \; между \; параллельными \; сторонами}} } \ right) \)
Следовательно, площадь трапеции равна половине суммы параллельных сторон, умноженной на высоту.
Площадь трапеции с использованием двух трапеций
Чтобы вывести формулу площади трапеции с использованием параллелограмма, мы рассмотрим две идентичные трапеции, каждая с основаниями \ (a \) и \ (b \) и высотой \ (h \). Пусть \ (A \) — площадь каждой трапеции. Представьте, что вторая трапеция перевернута, как показано на рисунке ниже.
Соединяя две трапеции, получаем
Мы видим, что новая фигура, полученная путем соединения двух трапеций, представляет собой параллелограмм с основанием \ (a + b \) и высотой \ (h \).Мы знаем, что
Площадь параллелограмма \ (= {\ rm {base}} \ times {\ rm {height}} \)
Площадь приведенного выше параллелограмма равна \ (A + A = 2A \).
Следовательно, \ (2 {\ rm {}} A = (a + b) {\ rm {}} h \)
\ (\ Rightarrow A = \ frac {1} {2} (a + b) \ times в \)
Таким образом, мы получили площадь трапеции.
Призма трапециевидная
Трехмерное тело, состоящее из двух трапеций на противоположных гранях, соединенных четырьмя параллелограммами, называемыми боковыми гранями, называется трапециевидной призмой.
Если \ (a, b \) — стороны основания, \ (h \) — высота, а \ (l \) — длина. Тогда объем трапециевидной призмы равен
\ (V = \ frac {1} {2} (a + b) \ times h \ times l \)
Площадь поверхности трапециевидной призмы \ (= 2 \ times {\ rm {area \; of \; base}} + {\ rm {lateral \; surface \; area}} \)
\ (= 2 \ times \ frac {1} {2} (a + b) h + (a \ times l) + (b \ times l) + (c \ times l) + (d \ times l) \)
\ (= h (a + b) + l (a + b + c + d ) \)
Следовательно, общая площадь поверхности трапециевидной призмы равна \ (h (a + b) + l (a + b + c + d) \)
Решенные примеры — Площадь трапеции, формула
В.2} \), а длина параллельных сторон равна \ (30 \; {\ rm {cm}} \) и \ (14 \; {\ rm {cm}} \) соответственно.
Мы знаем, что, площадь трапеции
\ (= \ frac {1} {2} \ times \ left ({{\ rm {sum \; of \; the \; parallel \; sizes}}} \ right) \ times \ left ({{\ rm {Расстояние \; между \; \; параллельными \; сторонами}}} \ right) \)
\ (\ Rightarrow 440 = \ frac {1} {2} \ times (30 + 14) \ times h \)
\ (\ Rightarrow h = \ frac {{440 \ times 2}} {{44}} \; {\ rm {cm}} \)
\ (\ Rightarrow h = 10 \ умножить на 2 \; {\ rm {cm}} \)
\ (\ Rightarrow h = 20 \; {\ rm {cm}} \)
Следовательно, высота трапеции равна \ (20 \; {\ rm { см}} \)
В.2} \)
Мы знаем, что, площадь трапеции
\ (= \ frac {1} {2} \ times \ left ({{\ rm {сумма \; of \; \; параллельные \; стороны}} } \ right) \ times \ left ({{\ rm {Расстояние \; между \; \; параллельными \; сторонами}}} \ right) \)
\ (\ Rightarrow 480 = \ frac {1} {2} \ times (AB + CD) \ times AL \)
\ (\ Rightarrow 480 = \ frac {1} {2} \ times (20 + CD) \ times 15 \)
\ (\ Rightarrow 20 + CD = \ frac {{480 \ times 2}} {{15}} \)
\ (\ Rightarrow 20 + CD = 32 \ times 2 \)
\ (\ Rightarrow 20 + CD = 64 \)
\ (\ Rightarrow CD = 44 \; {\ rm {cm}} \)
Следовательно, обратная сторона данной трапеции равна \ (44 \; {\ rm {cm}} \)
В.2} \).
Мы знаем, что, площадь трапеции
\ (= \ frac {1} {2} \ times \ left ({{\ rm {sum \; of \; the \; parallel \; sizes}}} \ right) \ times \ left ({{\ rm {Расстояние \; между \; \; параллельными \; сторонами}}} \ right) \)
\ (\ Rightarrow 0.55 = \ frac {1} {2} \ times \ left ({{\ rm {сумма \; из \; \; параллельных \; сторон}}} \ справа) \ times \ left ({{\ rm {Расстояние \; между \; \; параллельными \; сторонами}} } \ right) \)
\ (\ Rightarrow \ frac {1} {2} \ times \ left ({{\ rm {сумма \; из \; \; параллельные \; стороны}}} \ right) \ times \ frac {{11}} {{100}} = 0.2} \)
Мы знаем, что, площадь трапеции
\ (= \ frac {1} {2} \ times \ left ({{\ rm {sum}} \, {\ rm {of}} \, { \ rm {the}} \, {\ rm {parallel}} \, {\ rm {сторон}}} \ right) \ times \ left ({{\ rm {Distance}} \, {\ rm {between}} \, {\ rm {the}} \, {\ rm {parallel}} \, {\ rm {side}}} \ right) \)
\ (\ Rightarrow 105 = \ frac {1} {2} \ times \ left ({{\ rm {sum}} \, {\ rm {of}} \, {\ rm {the}} \, {\ rm {parallel}} \, {\ rm {side}}} \ right ) \ times 7 \)
\ (\ Rightarrow 105 = \ frac {1} {2} \ times (x + 6 + x) \ times 7 \)
\ (\ Rightarrow 2x + 6 = \ frac {{105 \ раз 2}} {7} \)
\ (\ Rightarrow 2x + 6 = 30 \)
\ (\ Rightarrow 2x = 24 \)
\ (\ Rightarrow x = 12 \; {\ rm {cm}} \)
Следовательно, длина параллельных сторон равна \ (12 \, {\ rm {cm}} \) и \ (\ left ({12 + 6} \ right) \, {\ rm {cm = 18}} \ , {\ rm {cm}} \)
В приведенной выше статье мы изучили определение трапеции, свойства трапеции и формулу для определения площади трапеции.Кроме того, мы вывели формулу площади трапеции, используя треугольники и две трапеции.
Изучите все концепции на трапеции
Часто задаваемые вопросы — Область формулы трапеции
Q.1. Какова формула площади трапеции?
Ответ: Площадь трапеции определяется как
\ (= \ frac {1} {2} \ times \ left ({{\ rm {сумма \; из \; \; параллельных \; сторон}} } \ right) \ times \ left ({{\ rm {Расстояние \; между \; \; параллельными \; сторонами}}} \ right) \)
В.2. Каковы формулы площади и периметра трапеции?
Ответ: Площадь трапеции определяется как
\ (= \ frac {1} {2} \ times \ left ({{\ rm {сумма \; из \; \; параллельных \; сторон}} } \ right) \ times \ left ({{\ rm {Расстояние \; между \; \; параллельными \; сторонами}}} \ right) \) и периметром трапеции \ (= a + b + c + d \)
Где \ (a, b, c \) и \ (d \) — длина сторон трапеции.
Q.3. Какие свойства у трапеции?
Ответ: Свойства трапеции:
1.\ circ} \).
2. Трапеция имеет две параллельные стороны и две непараллельные стороны.
3. Диагонали равнобедренной трапеции пересекают друг друга пополам.
4. Длина среднего сегмента равна половине суммы параллельных оснований трапеции.
5. Две пары смежных углов трапеции, образованной между параллельными сторонами, и одна из непараллельных сторон являются дополнительными.
Q.4. Какая связь между диагоналями трапеции?
Ответ: Диагонали равнобедренной трапеции пересекают друг друга пополам.Длина среднего сегмента равна половине суммы параллельных оснований трапеции. Две пары смежных углов трапеции, образованной между параллельными сторонами, и одна из непараллельных сторон являются дополнительными.
Q.5. Что такое равнобедренная и правосторонняя трапеция?
Ответ: У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла.
 23-27
23-27
 Отрезок, соединяющий основания, будет равен 1/2 их разности.
Отрезок, соединяющий основания, будет равен 1/2 их разности.
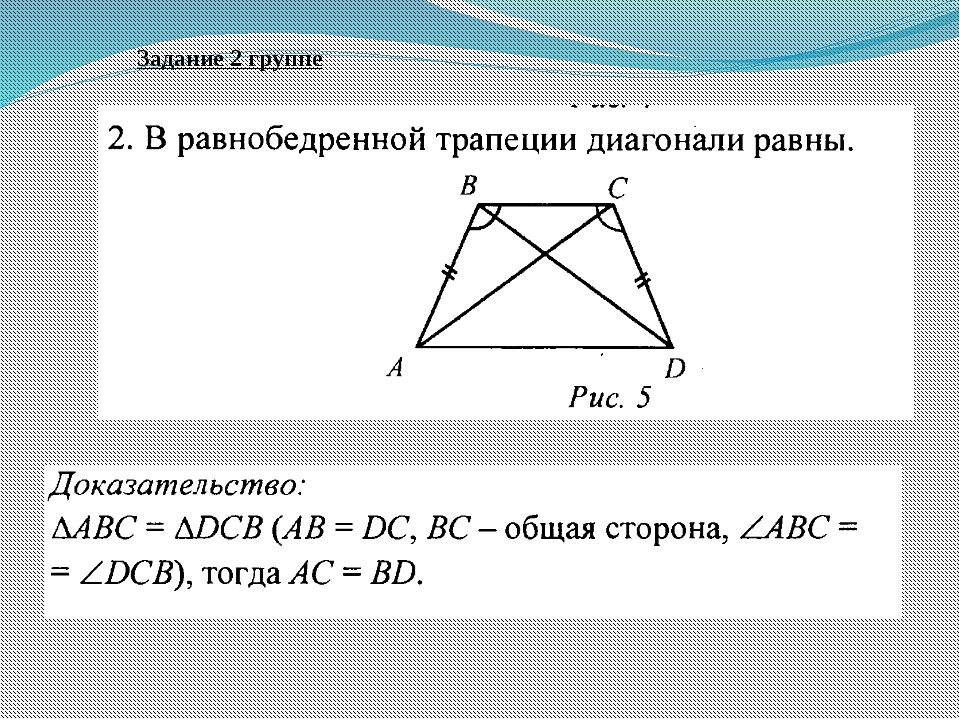

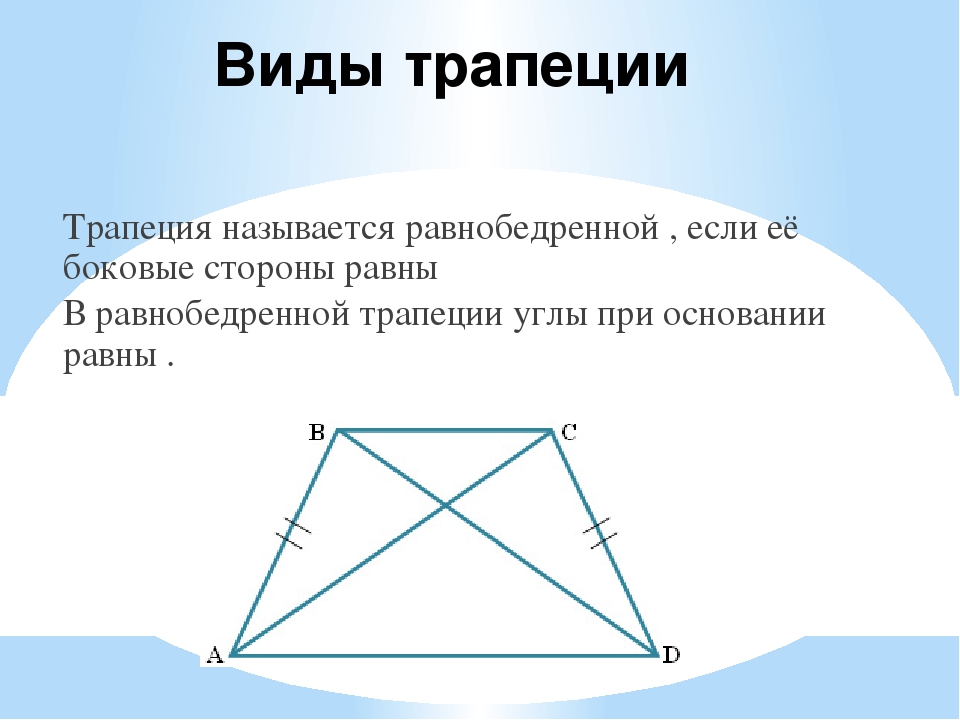
 Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны. И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции.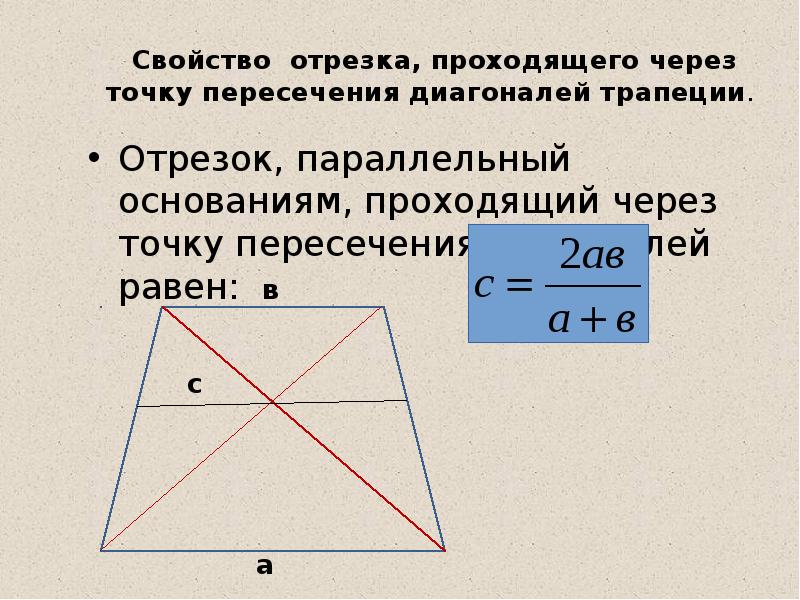

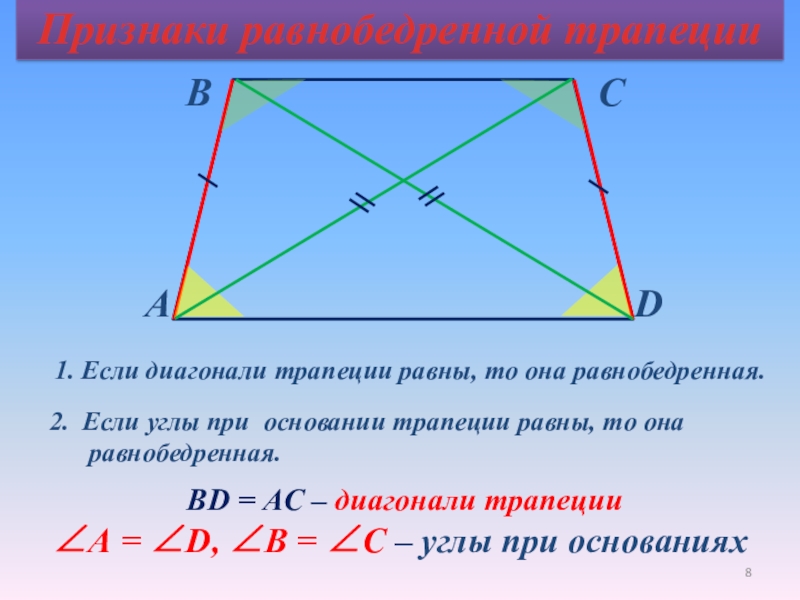 В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.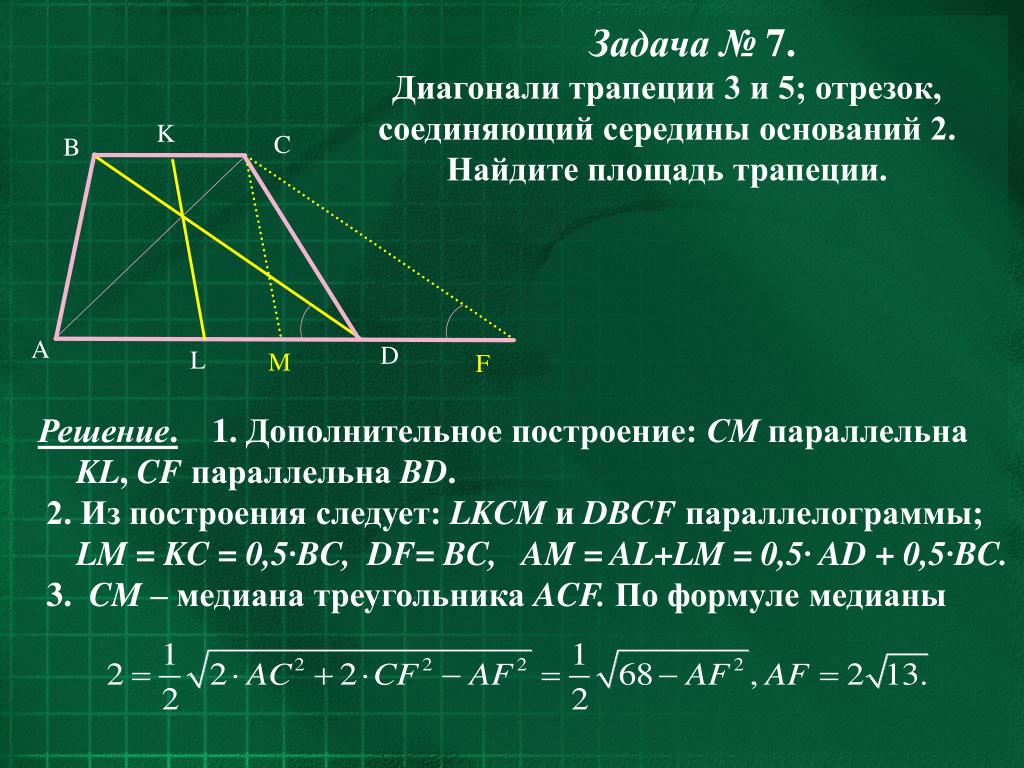 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).