«Кастинг чисел» или раскрытие модуля на занятиях с репетитором по математике
Модули — трудная тема для учеников. Приступая к работе с ней репетитор по математике должен понимать, что основные сложности учащиеся испытывают не при вычислении модуля, а при проведения алгебраических преобразований с ним. Причины всех трудностей — недостаточное внимание к данной теме со стороны школьных программ и невозможность в большинстве случаяв работать с «этими палочками» напрямую, за одну операцию, без разветвления применяемых алгоритмов. Знак модуля — это всего лишь оболочка, условное обозначения этого разветвления.
Практика показывает, что большинство приходящих к репетитору учеников имеют крайне низкий уровень владения приемами раскрытия модуля, если под его знаком стоит переменная. В этом случае, репетитор по математике оказывается главным участником сражений за понимание, поскольку в школе толком ничего не объясняется, а самостоятельно разобраться в дебрях разветвлений дети часто не в состоянии.
Далеко не в каждом случае репетитор по математике способен научить ученика работать с модулем. Для этого необходмы не только способности репетитора давать точные комментарии к используемым алгоритмам, но и способности ребенка самостоятельно создавать, контролировать и обрабатывать несколько числовых потоков одновременно. Причем этот контроль имеет многоэтапный и даже виртуальный характер, без участия в нем самих чисел. Сложная задача для ученика.
Составление алгоритмов работы с модулем можно сравнить с запуском автоматизированной линии по выпуску рыбных консервов определенного вида без участия на всех этапах производства самого человека. Фантастика, но попробуем себе это предствить. Надо расставить определенные виды сетей и для каждой из них, в независимости от того, что в нее попадает, запланировать какой то способ дальнейшей сортировки и переработки пойманного. Тоже сложная задача. Учитывая тот факт, что не каждый ученик сможет правильно проанализировать влияние специфики уравнения (конечного продукта) для поиска таких алгоритмов, — задача вдвойне усложняется.
Спасаться учебниками не получается. Во всех книжках, которые попадались мне на глаза, объяснения велись сразу через записи систем, равносильных исходному уравнению.
Нельзя объяснять ребенку методы решений уравнений с модулем через равносильные системы.
Проблема заключается в том, что их появление — есть продукт мыслительной деятельности знающего человека и предназначены они для ПРОВЕРКИ РЕШЕНИЯ знающим человеком, но никак не для того, чтобы учить с их помощью ПОНИМАТЬ происходящеее. Ими демонстрируется только «вершина айсберга», большая часть которого, связанная с «демонстрацией передвижения чисел», скрыта. Ее нельзя как-либо полностью показать что то записывая, как нельзя, например заменить всю информацию на видео несколькими фотографиями. Донести до ученика суть можно только на словах. Это и должен сделать репетитор по математике.
В этой статье я хочу поделиться с вами собственной методикой объяснения основного способа снятия модуля : разбора случаев по подмодульному выражению. Для Начала посмотрим как решается базовое (линейное) уравнение с модулем в любом более-менее серьезном пособии по подготовке к экзамену в 11 классе.
Для Начала посмотрим как решается базовое (линейное) уравнение с модулем в любом более-менее серьезном пособии по подготовке к экзамену в 11 классе.
Решить уравнение:
| x — 3 | = 2x+1
От учебника к учебнику пояснения будут в целом близки по духу, но несколько отличаться друг от друга комментариями. Вот некоторые из них:
1) Уравнение равносильно совокупности систем
Далее, как правило, в том же виде (параллельно) демонстрируется решение каждой системы и записывается ответ. И все!!!!! Среднему и даже сильному ученику, порой, трудно в этом разобраться. Слабый ученик не поймет ровным счетом ничего. А у более толкового возникнет масса вопросов: почему именно так решается исходное уравнение? Почему надо включать в записи еще какие-то неравенства? Все ли уравнения с модулем можно решить этим способом?А если модулей несколько?. Некоторые учителя, не усложняя себе жизнь поиском подходящих разъяснений, пользуются этой схемой и считают, что она сама обо всем рассказывает и тратить лишнее время — только запутывать ученика.
2) Вторая разновидность демонстрации решения: рассмотрим случаи (уже не понятно, что значит «рассмотрим», зачем и что такое вообще «случаи» :
1) х — 3 ≥ 0
Тогда уравнение приводится к виду х-3=2х+1. Находим его корень х= −4. Он не удовлетворяет неравенству х — 3 ≥ 0
2) х — 3 < 0 Тогда решим уравнение —х+3= 2х+1. Его корень 2/3 очевидно удовлетворяет условию х — 3 < 0.
Конечно, при таком подходе появляются попытки внести ясность, но все равно возникают вполне естественные вопросы :
1) как связаны два решаемых уравнения с первоначальным?
2) Почему надо делать еще какую то проверку?
Ни тот ни другой метод «разъяснений» не отражает главного — специфики объекта и особенности выполнения действий с ним. Все что показывают книжки — это всего лишь краткое оформление промежуточных и необходимых для получения ответа выкладок.
Предлагаю вам свой уникальный текст, разъясняющий ученику смысл фраз «рассмотрим случаи», «уравнение приводится к виду …» , «равносильно совокупности систем…».
Лучше всего подавать идею решения в виде следующего рассказа (более или менее подробного в зависимости от типа ученика).
Итак, надо решить уравнение |x — 3| = 2x+1, то есть найти все числа, которые при подстановке вместо буквы х превращают это уравнение в верное числовое равенство. (ученик, конечно, должен понимать, что такое корень уравнения и как его проверить). Мы не знаем этих чисел, но в любом случае они находятся где-то на числовой прямой.
Будем искать их также, как какие-нибудь нужные вещи в двухкомнатной квартире. Зайдем сначала в одную комнату и поищем в ней, затем в другую, а затем, соберем все, что найдено, в общий мешок для демонстрации результата поиска. Тоже самое сделаем с уравнением. Разрежем числовую ось на две части (аналоги комнат) разделительной точкой х=3 (почему бедется именно она — станет понятно позже).
Сначала поищем корни уравнения среди чисел, больших (или равных) чем 3. Если бы их все можно было бы проверить перебором, мы бы так и сделали. Сложность в том, что чисел бесконечное количество. Если мы начнем этот бесконечный процесс (представим себе такое) или захотим протестировать какое-нибудь конкретное число из этой комнаты на предмет попадания в ответ, то подставляя числа в исходное уравнение, внутри модуля, каждый раз будем получать неотрицательное число (это любой 11-ти классник поймет). В этом случае на знак модуля не окажет никакого влияния на вычисление результата всех действий в девой части, т.к. что модуль неотрицательного числа равен самому числу под его знаком. А раз так, то в выражении |x-3| будет получаться тот же самый результат, что и в выражении х—3. Поэтому нам НЕ ВАЖНО В КАКОЕ УРАВНЕНИЕ ДЛЯ ПРОВЕРКИ ВСТАВЛЯТЬ ЧИСЛА ИЗ ВЫБРАННОЙ КОМНАТЫ. Можно в |x—3| = 2x+1, а можно в x — 3 = 2x+1 (так как в их левых частях получаются равные результаты). Если одно равенство окажется верным, то и другое тоже.
Поэтому, для вылавливания чисел из промежутка х>3 я могу заменить проверку |x — 3| = 2x+1 на проверку равенства x — 3 = 2x+1. Если оно окажется верным — тестируемое число попадет в ответ. Чисел, которые обеспечивают выполнение этого условия не так много, более того оно одно и его можно найти просто решив линейное уравнение. Но оно может не находится в рассматриваемой части оси (в 1-ой комнате), поэтому этот корень еще требуется проверить на принадлежность к промежутку от 3 до +∞.
Именно поэтому тестируемое число должно отвечать двум требованиям х>3 и x — 3 = 2x+1, а значит должно быть решением следующей системы:
Ее ответ покажет, какие числа первой комнаты являются корнями исходного уравнения.
Аналогично можно объяснить как найти корни во второй комнате, то есть на промежутке (- ∞;3). Если тестировать любое число из этого промежутка, и вставлять его в исходное уравнение (представим себе этот бесконечный процесс), то под модулем будет каждый раз получаться отрицательное число, а в этом случае в выражении |x — 3| будет получаться тот же самый результат, что и в выражении —(х — 3), (этот факт лучше объяснить отдельно до темы уравнения с модулем).
x<3 и —(x — 3) = 2x+1
То есть являлось бы решением системы:
Решив обе полученные системы и собрав вместе все найденные числа мы получим ответ уравнения |x — 3| = 2x+1.
Репетитор по математике должен тщательно следить не только за порядком слов, которые он использует, но и за темпом изложения. Нельзя спешить и слишком много говорить.
Через урок, после объяснения метода построения графика с модулем репетитору полезно вернуться к разобранному уравнению и решить его же графически.
Аналогично объясняется метод решения неравенств с модулем. Фраза «проверка равенства» заменяется на фразу «проверку верности неравенства».
Если репетитор по математике смог разъяснить ученику, что линия, заданная на плоскости уравнением есть не что иное как его ответ в графической форме и отбирать для ответа уже нужно точки плоскости (вместо точек оси), то те же самые рассуждения годятся и для построения графика функции с модулем. Повторяя почти тот же самый текст с заменой слова «число» на «пару чисел» или на «точку плоскости» репетитор по математике сможет убить двух зайцев: и новое изучить и старое закрепить. Привожу этот текст в слегка сокращенном виде:
построить график функции у=|х-1|+2х
Разделим плоскость на две части, так чтобы в первую часть попали точки у которых х≥1, а у другой х<1. Репетитору по математике лучше нарисовать эти две «комнаты».Найдем кто из точек правой части плоскости удовлетворяет равенству. Если представить себе, что каждая точка будет вставляться в равенство у=|х-1|+2х для проверки, то в его правой части получится тот же самый результат, как и в выражении х-1+2х, а поэтому нам не важно куда вставлять точку для определения ее пригодности. Можно в у=|х-1|+2х, а можно в у=х-1+2х.Найдем все точки, которые удовлетворяют равенству у=х-1+2х (это график функции линейной функции у=х-1+2х) и возьмем из него только те точки, у которых х≥1. Найденное множество будет удовлетворять сразу двум условием у=х-1+2х и х≥1,а значит являться решением их системы. Так ее и запишем:
Можно в у=|х-1|+2х, а можно в у=х-1+2х.Найдем все точки, которые удовлетворяют равенству у=х-1+2х (это график функции линейной функции у=х-1+2х) и возьмем из него только те точки, у которых х≥1. Найденное множество будет удовлетворять сразу двум условием у=х-1+2х и х≥1,а значит являться решением их системы. Так ее и запишем:
Она указывает на построенную часть финального графика. Аналогично дается пояснение для построения левой части, а затем объединяем построенные линии и получаем:
Как видите, репетитор по математике может предложить практически тот самый текст ученику, что и при решениии уравнений с одной перменной. Закрепление материала будет лишь вопросом времени при самостоятельной работе. Особое чутье репетитора здесь проявляется в способности понять когда можно с учеником переходить к последовательному чередованию объектов (уравнений, неравенств, графиков).
Модное на сегодняшний день слово «кастинг» как нельзя лучше подходит для описания работы алгоритмов решения уравнений с мордулями. Большинство подростком с ним знакомы и понимают его сымсл. Для Красиво зазвучит: «кастинг чисел» «кастинг точек плоскости».
Большинство подростком с ним знакомы и понимают его сымсл. Для Красиво зазвучит: «кастинг чисел» «кастинг точек плоскости».
Уяснив метод разбора случаев на простых линейных подмодульных выражениях, ученик может быть отправлен репетитором по математике в гости к нелинейным. В такой последовательности легче понять, что делать, если под модулем, например, стоит дробь или косинус. Стоит обратить внимание на то, что в первой строке систем вписывается неравенство, указывающее своим ответом на рассматриваемое множество. Именно этот ответ и есть первая комната. Записывая неравенство мы выделяем эту комнату. Поскольку ответ неравенств часто состоит их кусочков оси, то комната просто будет рваной, но принцип отбора (кастинга) ее чисел остается прежним. Все равно надо решать систему, просто вместо готового для изображения ответа х≥3 придется включать в первую строку системы неравенство «подмодульное выражение больше(меньше) либо равно нуля», решать его, а затем пересекать полученный ответ с ответом второй строчки системы.
Итак, с одним модулем разобрались. Что репетитор по математике предложит еще? Если по его ощущениям у ученика еще остался потенциал — можно перейти к уравнениям с двумя линейными модулям, например |x-3|+|2x+1|-4=0. Важно, чтобы на этом этапе ученик понимал как выбирается разделительная точка для каждого модуля. Можно назвать ее переломной.
Удобнее всего ось разделить двумя точками «обнуляющими» подмодульные выражения на 3 области и для отбора чисел из каждого множества заменить проверку исходного неравенства на проверку неравенства без модулей. Тремя системами получаем ответ.
Опытный репетитор по математике всегда знает, что наиболее вероятной ошибкой является потеря контроля за раскрытием модуля если он «обложен» со всех сторон действиями. Для уменьшения ошибок важно предложить какое-то единое опорное правило. Я всегда говорю так. В случае, когда под модулем получается «минус» модуль надо поменять на скобку, а перед скобкой поменять знак. Это очень удобно для запоминания, так как в голове ученика в этот момент сидит директива «что-то поменять». Легко запомнить, что если хочется «что-то поменять», то надо поменять все что только можно (слева от подмодульного выражения).
Легко запомнить, что если хочется «что-то поменять», то надо поменять все что только можно (слева от подмодульного выражения).
В заключение отмечу, что репетитор по математике может показать сильному ученику и другие способы раскрытия модуля. После изучения темы «возведение неравенств и уравнений в квадрат» легко объясняется, почему возведение в квадрат неравенства, обе части которого заключены под знак модуля не приводит ни к потере корней, ни к приобретению лишних корней. Репетитору желательно донести до сознания ученика тот факт,, что после возведения никаких проверок или дополнительных условий подмешивать к объекту не нужно, модули можно поменять на скобки, перенести все слагаемые в левую часть и разложить ее на множители. И ничего не надо возводить в степень… Сильному ученику можно показать расширенный метод интервалов для дробей с модулями, в котором, их раскрытие ведется по числителю и знаменателю независимо.
После раскрытия находят распределение знаков через графики (или через пробные точки в каждом промежутке) и уже по ним «читают» итоговые знаки всей дроби.
Стоит упомянуть, что репетитор по математике всегда выбирает глубину изложения темы в зависимости от ученика и разбирает с ним способы решения только до определенного уровня. К заданиям несколько более высокого уровня сложности обычно относят те, в которых или присутствует большое количество модулей, параметр, или модуль стоит поверх тригонометрической функции, или модули появляются при удалении квадратного корня вместе с полным квадратом какого-нибудь выражения, расположенным под его знаком.
К нестандартным я бы отнес функциональные приемы :
- использование области значений функции у=│f (х)|
- расширенный метод интервалов, применяемый к функциям с модулями.
Часто задаваемые вопросы учеников репетитору по теме «раскрытие модуля»
Колпаков Александр Николаевич, репетитор по математике.
Метки: Методики для репетиторов, Примеры объяснений, Раскрытие модуля, Решение уравнений
Урок 100.
 Модуль числа | Поурочные планы по математике 6 класс
Модуль числа | Поурочные планы по математике 6 классУрок 100. Модуль числа
10.07.2015 4310 0Цели: отрабатывать умение находить значение выражений, содержащих модуль; решать уравнения с модулем; развивать навыки самоутверждения, самооценки.
Ход урока
I. Организационный момент
II. Устный счет
1. Найдите модуль каждого из чисел:
2. Найдите значение выражения:
3. Разность двух чисел 20. Первое число в 3 раза меньше второго. Найдите эти числа.
4. Расстояние между двумя машинами, едущими навстречу друг другу, 400 км. Скорости машин 60 км/ч и 80 км/ч. Какое расстояние будет между ними через час?
5. Летела стая уток. Одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько летело уток? (3.)
6. Вася и Коля живут в многоэтажном доме: Вася на втором этаже, а Коля на четвертом. Во сколько раз пол квартиры Коли расположен выше от поверхности земли, чем пол квартиры Васи (первый этаж начинается от поверхности земли и все этажи по высоте одинаковы)? (В 3 раза.)
Во сколько раз пол квартиры Коли расположен выше от поверхности земли, чем пол квартиры Васи (первый этаж начинается от поверхности земли и все этажи по высоте одинаковы)? (В 3 раза.)
III. Сообщение темы урока
— Сегодня на уроке мы продолжим находить значение выражений, содержащих модуль, решать уравнения с модулем.
IV. Физкультминутка
V. Работа над задачей
№ 965 (б, г, е, з, к) стр. 162 (самостоятельно, устная проверка).
б) 4,8 + 0,5 = 5,3 (м)
г) 4,8 · 1,5 = 7,2 (м)
е) 4,8 : 3/4 = 3,6 (м)
з) 4,8 : 0,25 = 19,2 (м)
к) 4,8 : 1,25 = 3,84 (м)
VI. Закрепление изученного материала
1. № 951 стр. 160 (у доски и в тетради).
Решение:
При х = -12,3: |-12,3| = 12,3; при х = 12,3: |12,3| = 12,3;
при х = —66: |—66| = 66; при х = 83: |83| = 83;
при при при
2. № 953 (вторые две строчи) стр. 160 (самостоятельно, устная проверка).
(Ответы: в) 3; ж) 12,4; л) 1,5; г) 1000; з) 1; м) 15. )
)
3. № 957 стр. 161 (устно).
— Как называются числа а и —а? (Противоположные числа.)
— Чему равны модули противоположных чисел? (Противоположные числа имеют равные модули.)
4. Решите уравнения:
1) | х | = 4;
2) | х | = 7;
3) | х | = 0;
4) | х | = -3.
— В первом уравнении нужно найти число, расположенное на координатной прямой на расстоянии 4 единичных отрезков от начала отсчета. (Показать на модели координатной прямой.)
— Сколько будет таких чисел? (Два: х = 4; х = —4.)
— Давайте проверим, являются ли данные числа корнями уравнения: | 4 | = 4; | —4 | = 4.
— Может ли модуль какого-нибудь числа быть числом отрицательным?
VII. Повторение изученного материала
№ 959 стр. 161 (устно).
— Какие числа называются противоположными?
— Какие числа называют взаимно обратными?
VIII. Самостоятельная работа (10 мин)
Вариант I
1. Найдите значение выражения:
2. Сравните модули чисел:
Сравните модули чисел:
Вариант II
1. Найдите значение выражения:
2. Сравните модули чисел:
IX. Подведение итогов урока
— Как найти модуль положительного числа или нуля?
— Как найти модуль отрицательного числа?
— Может ли модуль какого-нибудь числа быть отрицательным числом?
Домашнее задание
№ 963, 968 (д-з), 970 стр. 162, № 972 стр. 163.
Блог учителя математики: Упражнения с модулями
«Модули – это интересно и доступно»
Основная цель курса — создать необходимый запас знаний и способов их получения при решении различных видов уравнений и неравенств с модулями. Как можно полнее развить потенциальные творческие способности каждого ученика, не ограничивая заранее уровень сложности используемого задачного материала, сформировать у учащихся потребность в продолжении математического образования.
Данный
курс для подготовки учащихся 9 классов вплотную примыкает к основному курсу
алгебры, этот курс является развитием ранее приобретенных знаний, углубляет и
расширяет курс математики основной школы. К сожалению, в основной школе, где
задачи, содержащие абсолютную величину, рассматриваются лишь в дополнительных
главах, трудно поддерживать интерес учащихся из-за ограниченности приобретенных
знаний. Важные свойства и алгоритмы, необходимые для решения задач,
отсутствуют. Такое положение создает определенные трудности для дальнейшего
изучения математики и на вступительных
экзаменах (подготовка к ЕГЭ).
К сожалению, в основной школе, где
задачи, содержащие абсолютную величину, рассматриваются лишь в дополнительных
главах, трудно поддерживать интерес учащихся из-за ограниченности приобретенных
знаний. Важные свойства и алгоритмы, необходимые для решения задач,
отсутствуют. Такое положение создает определенные трудности для дальнейшего
изучения математики и на вступительных
экзаменах (подготовка к ЕГЭ).
Решение задач с модулями является трудным для большинства учащихся и вызывает у них страх, поэтому на каждом занятии предлагается тот минимум, который достаточен для формирования основных представлений о модулях.
Любая тема может быть дополнена в различных учебных направлениях в старших классах профильной школы.
Учебный материал курса образует, своего рода, фундамент, опираясь на который можно в дальнейшем формировать систему знаний учащихся, а также их подготовку к ЕГЭ.
Содержание программы.
1. Решение уравнений, содержащих знак модуля.
На первом занятии учащимся сообщается цель и значение элективного курса. Учащиеся знакомятся с определением модуля, уравнением с модулем, им объясняется, что значит решить уравнение с модулем. Далее рассматриваются свойства модулей, а также различные методы решения уравнений с модулями. Применение полученных знаний на практике решения задач полезно организовать в малых группах. Лучшему осмыслению учебного материала послужит составление справочной таблицы.
2. Решение неравенств, содержащих знак модуля.
Программа (для общеобразовательных школ) не
акцентирует внимание на вопросе решения неравенств с модулем, не нашел он
достойного отражения и в материале действующих учебников. Содержание курса призвано ликвидировать этот пробел. Этот раздел содержит задачи, выходящие за
рамки школьного курса. Здесь следует обратить внимание на решение неравенств с
использованием числовой прямой; рассмотреть строгие и нестрогие неравенства; рассмотреть графические способы их решения. Занятия можно
организовать в традиционной урочной форме. Последовательность заданий
составлена так, что при определенной организации учебного процесса ученик может
сам решить следует ли еще раз повторить изученное, или будет изучать новые
способы решения задач. Поэтому полезно выделять время для индивидуальной работы
учащихся.
Занятия можно
организовать в традиционной урочной форме. Последовательность заданий
составлена так, что при определенной организации учебного процесса ученик может
сам решить следует ли еще раз повторить изученное, или будет изучать новые
способы решения задач. Поэтому полезно выделять время для индивидуальной работы
учащихся.
Ожидаемый результат.
По окончании изучения данного курса ученик должен:
a) знать определение модуля и его свойства;
b) знать методы решения уравнений и неравенств, содержащих знак модуля;
c) уметь применять методы при решении уравнений и неравенств.
На изучение двух блоков отводится 15 часов, из них 2 часа – на определение успешности освоения материала. Итоговые работы можно организовать в виде контрольной работы (теста), в форме зачета. А также можно организовать игровой вариант.
Учебно — тематический план курса по выбору по математике «Модули – это доступно и интересно»; 9 класс.
№ | Наименование разделов и
тем. | Количество часов |
I | Решение уравнений, содержащих знак модуля. | 9 |
1 | Определение и свойства модуля. Решение уравнений с использованием определений модуля | 2 |
2 | Уравнения вида ½f(x) ½=g(x) с использованием системы и совокупности. Решение уравнений методом интервалов. | 3 |
3 | Уравнения вида ½f(x) ½=½g(x)½. | 2 |
4 | Уравнения вида ½ax+b ½=cx+d. | 1 |
5 | Проверка усвоения знаний
учащимися. | 1 |
II | Решение неравенств, содержащих знак модуля. | 6 |
1. | Решение неравенств вида ½f(x) ½<g(x) | 2 |
2 | Решение неравенств вида ½f(x) ½>g(x) | 2 |
3 | Решение неравенств вида½f(x)½<½g(x)½. | 1 |
4 | Проверка усвоения знаний учащимися. | 1 |
III | Построение графиков функций, содержащих знак модуля | 4 |
Контрольная работа
(выполнить задания, используя определение модуля)
№ | I вариант | II вариант |
1 | Раскрыть модуль ½p-2½ | Раскрыть модуль ½3-p½ |
a) p-2 b) 2-p | a) 3-p b) p-3 | |
2 | ½x-x+¼½ | ½x+2x+1½ |
a) –x+x-¼ b) x-x+¼ c) x-x+¼ d) ¼-x-x | a) x+2x+1 b) –x-2x-1 c) x-2x-1 d) x-2x+1 | |
3 | Решить уравнение ½x-7½=-2 | Решить уравнение ½2x-3½=1 |
a) 7 c) 9 d) нет решений e) x – любое число | a) 2 b) 1 c) 1,2 d) нет решений | |
4 | ½x-1,5½=3,5 | ½125x-1,4½=-2 |
a) 2;5 b) –5;-2 c) –5;2 d) 2;-5 | a) 8;2 b) нет решений c) 2 d) 0;2 | |
5 | ½x-x½=0 | ½x+x½=0 |
a) 0;1 b) -1;0 c) x – любое число d) 1 | a) 1;0 b) нет решений c) –1;0 d) 0 |
Зачетный урок по теме «Решение уравнений с модулями»
«Лестница трудностей»
Система заданий составляется на два варианта от легкого к сложному
(сверху вниз). Каждый ученик, решив задание проверяет ответы у учителя, если
ответ правильный, то ученик «движется по лестнице» дальше, а если ученик
допустил ошибку, то учитель объясняет решение данного задания, а потом
предлагает аналогичное. Если ученик добрался до конца лестницы, значит, тему он
усвоил.
Каждый ученик, решив задание проверяет ответы у учителя, если
ответ правильный, то ученик «движется по лестнице» дальше, а если ученик
допустил ошибку, то учитель объясняет решение данного задания, а потом
предлагает аналогичное. Если ученик добрался до конца лестницы, значит, тему он
усвоил.
x-2½x½+1=0 | x-4½x½+4=0 | ||||||||||
½-x+2½=2x+1 | ½4-x½+½x-2½=2 | ||||||||||
½ x +3½+½2x-1½=8 | ½x-3½+2½x+1½=4 | ||||||||||
½ x +5½=½10+x½ | ½2x+1½=x | ||||||||||
½x-5½=3 | ½ x +5½=-3 | ||||||||||
Итоговое занятие по теме « Решение неравенств с модулями»
«Умники и умницы»
Три варианта выполнения работы: зеленая дорожка – более долгий путь
достижения цели, включает 4 задания, но можно 2 раза попросить помощь учителя;
желтая дорожка – «золотая середина», содержит 3 задания, можно 1 раз попросить помощь учителя; красная дорожка —
ученик решает без помощи учителя; этот путь содержит 2 задания. Для каждой
дорожки можно составить несколько вариантов заданий.
Для каждой
дорожки можно составить несколько вариантов заданий.
Зеленая дорожка | Желтая дорожка | Красная дорожка | |
1 | ½x½<3 | ½x-3½<2 | ½3+x½³x |
2 | ½x+2½>-2 | 5x-7£½x+2½ | ½2x-1½+½x-3½£4 |
3 | 3x+½2-x½£5 | ½x-2½+½x+2½£4 | |
4 | ½x-1½+½x+2½£3 |
Итоговое занятие по всему курсу можно провести в форме аукциона. Класс
делится на команды. Каждое задание имеет определенное количество баллов.
Команды знакомятся с заданиями и предлагают свои баллы, но не больше
первоначальных ( как в настоящем аукционе), а меньше, если они уверены, что
решат задание. Если команда решила задания правильно, то баллы складываются,
если неправильно – баллы вычитаются. Победила та команда, которая набрала
больше баллов.
Класс
делится на команды. Каждое задание имеет определенное количество баллов.
Команды знакомятся с заданиями и предлагают свои баллы, но не больше
первоначальных ( как в настоящем аукционе), а меньше, если они уверены, что
решат задание. Если команда решила задания правильно, то баллы складываются,
если неправильно – баллы вычитаются. Победила та команда, которая набрала
больше баллов.
1 | ½5-x½+½x-1½=10 | 3 балла |
2 | ½x+2½=2/(3-x) | 4 балла |
3 | ½2x-9x+15½³2 | 5 баллов |
4 | ½x-6½=½x-5x+9½ | 5 баллов |
5 | ½x½+½x+3½<5 | 7 баллов |
Уравнения
с модулями.
Абсолютной величиной числа a (обозначается |а| ) называется расстояние ( в единичных отрезках) от начала координат до точки с координатой (а).
|а|= а, если а≥0, (1)
-а, если а<0.
Некоторые основные свойства модуля:
1. |а| ≥ 0
2. |а| = |-а|
3. |а| ≥ а
4. |ab| = |a|•|b|
5. , b≠0Полезны упражнения, при решении которых следует воспользоваться одним важным правилом, которое непосредственно следует из соотношения (1): чтобы раскрыть модуль, надо знать знак выражения, стоящего под знаком модуля.
Примеры.
Раскрыть модуль:
3) . Решение:Определим знак выражения, стоящего под знаком модуля, для этого упростим его:
x² — x += x² — 2• , ≥0 для любого x . Ответ: x² — x + .Дополнительные примеры.
Раскрыть модули:
· |x²|
· |x4 + 1|
· |x² + 2x + 2|
Очень
часто встречаются случаи, в которых нет необходимости раскрывать модуль. Достаточно лишь воспользоваться свойствами 1-3 и соотношением (1).
Достаточно лишь воспользоваться свойствами 1-3 и соотношением (1).
Решить уравнение:
1) |x — 7| = — 2
Решение:
Левая часть: |x — 7| ≥ 0 по определению модуля.
Правая часть: – 2 < 0
Левая и правая части имеют разные знаки, следовательно, уравнение не имеет решений. Ответ: нет решений.
2) |2x — 3| = 1
Решение:
По определению модуля имеем:
2x – 3=1, 2x – 3 = -1,
2x = 4, 2x = 2,
x = 2. x = 1.
Ответ: 1; 2.
Дополнительные примеры.
Решите уравнение:
· | 1001x + 14| = — 1 Ответ: нет решений.
· | 125x – 1,4| = — 2 Ответ: нет решений.
· | x + 1,5 | = 3,5 Ответ: — 5; 2.
· | x ² — x | = 0 Ответ: 0; 1.
· | x ² + x | = 0 Ответ: — 1;0.
·
| | x – 1 | — 4 | = 3 Ответ: -6; 0; 2; 8.
· | | x + 3 | — 4 | = 1 Ответ: -8; -6; 0; 2.
· | | | x — 3 | — 3 | — 3 | = 0 Ответ: — 6;0; 6; 12.
· | | | x — 3 | + 3 | — 3 | = 3 Ответ: 0; 6.
· | 8 — | x + 2|| = 7 Ответ: — 17; -3; -1; 13.
· | 10 — | x — 1|| = 8 Ответ: — 17; -1; 3; 14.
Уравнения с модулем решались способом перехода от исходного уравнения к исходной системе:
g(x) ≥0f(x)= — g(x)
Этот способ удобнее использовать, если выражение для функции g(x) не сложное ( для удобства изложения материала назовем этот способ первым).
Второй способ, стандартный, основан на раскрытии модуля, исходя из его определения, и заключается в переходе к совокупности двух систем:
С понятием
совокупности можно познакомить учащихся при решении уравнения вида f1(x) •f2(x) = 0.
Решение данного уравнения сводится к задаче об отыскании значений “x”, удовлетворяющих хотя бы одному из уравнений вида f1(x)=0 или f2(x)=0.
Если поставлена такая задача, то говорят, что задана совокупность уравнений. Обозначается это так:
Второй способ рациональнее применять в случае сложного выражения для функции g(x) и не очень сложного для функции f(x).
Необходимо обратить внимание, что первый способ применим только для уравнений, содержащих один модуль.
Решите уравнение:
3) |x-2| +| 2x-3|=5. Решение:
Рассмотрим четыре случая раскрытия модулей.
Первый случай: оба подмодульных выражения неотрицательны, тогда оба модуля раскрываются со знаком «+». Получим систему:
Решением системы является 3 Ответ: 3 Второй случай: первый модуль раскрывается со знаком “-“, т. к. подмодульное выражение
отрицательно, а второй модуль – со знаком «+», т.к. подмодульное выражение
неотрицательно. Имеем систему:
Имеем систему:
Решение уравнения системы x=6 не удовлетворяет условиям раскрытия модулей.
Ответ 2: нет решений.
Третий случай (первый модуль раскрывается со знаком «+», а второй со знаком “-“) приводит к системе:
Первое и второе неравенства системы противоречивы, следовательно, система не имеет решений. Ответ 3: решений нет.
Четвертый случай приводит к системе:
Следовательно, x=0. Ответ 4: 0. Окончательный ответ исходного уравнения x=0 и x=3. Ответ: 0; 3.Раскрывая последовательно все модули, входящие в рассмотренное уравнение, мы рассмотрели 4 случая, причем третий случай можно было бы опустить.
Решение линейных неравенств с модулями.
Неравенства, содержащие переменную под знаком модуля, решают различными способами; рассмотрим достаточно простой пример:№1.Решить неравенство:
>4.

Первый способ: Имеем: >4,
>4,
>2.
Геометрически выражение означает расстояние на координатной прямой между точками х и 2,5. Значит, нам нужно найти все такие точки х, которые удалены от точки 2,5 более чем на 2, — это точки из промежутков х<0,5 и х>4,5.
Второй способ: Поскольку обе части заданного неравенства неотрицательны, то возведем обе части этого неравенства в квадрат:2>42 .
(2х–5)2>42,
(2х–5)2–16>0,
(2х–5–4)(2х–5+4)>0,
2(х–4,5) 2(х–0,5)>0,
(х–4,5)(х–0,5)>0.
Применив метод интервалов, получим: х<0,5 и х>4,5.
Третий способ: Выражение 2х–5 может быть неотрицательным или отрицательным. Т.е. имеем совокупность двух систем:
Откуда: х<0,5 и х>4,5.
Рассмотрим еще несколько примеров.
Пример №2.Решить неравенство: <3.

Данное неравенство равносильно совокупности двух систем:
Из первой системы получаем 2х<5, из второй -1<х<2. Объединяя эти два решения, получаем: -1<х<5.
Пример №3. Решить неравенство: 3х+3.
Данное неравенство равносильно двойному неравенству -х-33х–3х+3 или системе
Имеем: 0х3.
Упражнения для самостоятельной работы:
Решить неравенства:
1. <3х+1,
2. +>2,
3. ->-2.
Решение квадратных неравенств с модулями.
Рассмотрим пример №1. Решите неравенство: +х–2<0.Данное неравенство можно решить методом интервалов. Рассмотрим иное решение, основанное на следующем утверждении: при любом значении а неравенство равносильно системе неравенств: , а неравенство равносильно совокупности неравенств .
Поэтому наше неравенство равносильно системе неравенств: решая которые, получим:
Запишем ответ: (1-;2-).
Пример №2.
 Найти целые решения неравенства: 2х–х2 . Задача сводится к
решению совокупности двух систем неравенств:
Найти целые решения неравенства: 2х–х2 . Задача сводится к
решению совокупности двух систем неравенств:Решим первую систему: из первого неравенства имеем: х1; х2.
из второго: 2х2–5х+20, или 0,5х2.
Отметив найденные решения первого и второго неравенств первой системы на координатной прямой, находим пересечение решений.
Т.о. 0,5х1 и х=2. Это решение первой системы.
Решим вторую систему: из первого неравенства имеем: 1<х<2, из второго: -(х2 -3х+2)2х–х2, или – х2+3х–2–2х+ х20, или х2.
Отметив найденные решения первого и второго неравенств второй системы на координатной прямой, получим: 1<х<2. Это решение второй системы.
Объединив найденные решения систем неравенств 0,5×1; х=2; 1<x<2, получаем: 0,5×2 и т.о. целыми решениями будут х=1 и х=2.
Упражнения для самостоятельной работы:
Решите неравенства:
1.
 <6,
<6,2. <х,
3. <3х–3,
4. х2-3+2>0,
5. х2-х<3,
6. х2-6х+7-<0,
7. 3+х2–7>0,
8. >.
Метод интервалов решения уравнений и неравенств, содержащих модуль.
Рассмотрим метод интервалов на примере решения уравнения
-+3-2=х+2.
Чтобы решить данное неравенство, необходимо раскрыть модули. Для этого выделим интервалы, на каждом из которых выражения, стоящие под знаком модуля, принимают только положительные или отрицательные значения. Отыскание таких интервалов основано на теореме: если на интервале (а; в) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.
Чтобы выделить интервалы знакопостоянства, найдем точки, в которых выражения, записанные под модулем, обращаются в нуль:
х+1=0, х=-1; х=0; х–1=0, х=1; х–2=0, х=2.
Полученные точки разобьют прямую на искомые интервалы.
 Определим знаки выражений
Определим знаки выражений х+1, х, х–1, х–2 на этих интервалах:
Учитывая знаки, раскроем модули. В результате получим совокупность систем, равносильную данному уравнению:
Последняя совокупность приводится к виду:
Решение совокупности систем и данного уравнения: -2; х2.
Использованный прием называется методом интервалов. Он применяется и при решении неравенств.
Решить неравенство: +х–2<0.
1) Найдем нули выражения: х2-3х.
х1=0, х2=3.
2) Разобьем координатную прямую на интервалы и установим знак выражения х2-3х на каждом интервале:
3) Раскроем модуль:
Решение первой системы: , решение второй . Решение данного неравенства: .
Упражнения для самостоятельной работы:
№1
№2
№3
Решение неравенств вида , посредством равносильных переходов.
Рассмотрим неравенства вида и .
 Примем без доказательства следующую
теорему: при любом значении а неравенство равносильно системе неравенств а неравенство равносильно совокупности неравенств
Примем без доказательства следующую
теорему: при любом значении а неравенство равносильно системе неравенств а неравенство равносильно совокупности неравенств Рассмотрим пример: решить неравенство:>х+2.
Пользуясь сформулированной теоремой, перейдем к совокупности неравенств:
Система и неравенство 0х>2 не имеют решений. Следовательно, решением совокупности (и данного неравенства) является х.
Упражнения для самостоятельной работы:
1. <6,
2.1,
3.>х+3,
4. <х+3.
Применение свойств абсолютной величины при решении уравнений и неравенств.
При решении некоторых заданий находят применение свойства модуля. (При необходимости повторить их, см. занятие № 1).
Проиллюстрируем применение свойств модуля при решении следующих примеров.
Пример №1: решить уравнение: =1.
Заметим, что =1, значит, . Следовательно, по свойству 5: (х3-1)(2–х3)0, решением которого является числовой отрезок
Пример №2.
 Решите
систему уравнений:
Заметим, что Следовательно, по свойству 5 ху0, т.е. х и у принимают
значения одного знака. Тогда данная система равносильна совокупности систем:
Решите
систему уравнений:
Заметим, что Следовательно, по свойству 5 ху0, т.е. х и у принимают
значения одного знака. Тогда данная система равносильна совокупности систем:или Решением первой системы является любая пара неотрицательных чисел, сумма которых равна 1. Например, (0,5; 0,5), (1/6; 5/6).Решением второй системы является пара неположительных чисел, сумма которых равна – 1. Например, (0,8;-0,2).
Пример №3.Запишите при помощи знака модуля, что по крайней мере одно из чисел а, в, с, d отлично от нуля.
Ответ:
Пример №4. Дано: <1,<10, <10.
Докажите неравенство: <20.
Доказательство:
10=20.
Упражнения для самостоятельной работы:
1. Решите систему:
2. При каких значениях х справедливы равенства:
а) ,
б)
3. Найдите числа х и у такие, что =0;
4. Найдите наименьшее значение суммы:
а)
б)
5. Решите уравнение:
Решение уравнений и неравенств с модулями на координатной прямой.

При изучении расстояния между двумя точками А(х1) и В(х2) координатной прямой выводится формула, согласно которой АВ=. Используя эту формулу, можно решать уравнения и неравенства вида =в, , <в, , , а также уравнения и неравенства, к ним приводимые.
Рассмотрим примеры.
1. Решите уравнение: =1. Переводя запись данного уравнения на “язык расстояний”, получим предложение “расстояние от точки с координатой х до точки с координатой 3 равно 1”. Следовательно, решение уравнения сводится к отысканию точек, удаленных от точки с координатой 3 на расстояние 1.Корнями уравнения являются числа 2 и 4.
2. = 3. Приводя данное уравнение к виду =1,5, используем формулу расстояния:
Ответ: — 2; 1.
3. . Запишем данное уравнение в виде: . Исходя из геометрических представлений, нетрудно понять, что корнем последнего уравнения является координата точки, равноудаленной от точек с координатами 1 и – 2, т.е. число – 0,5.
Упражнения для самостоятельной работы:
Решите уравнения и неравенства:
1. =0,4;
=0,4;2. =0,7;
3. <0,5;
4. <7;
5.
6.
7.
8.
Литература для учащихся:
2. Н.Я. Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И. Жохов. Математика: Учебник 6 класса средней школы., Москва, Просвещение. 1991г.
3. Ю.Н. Макарычев, Н.Г. Миндюк, и др. Алгебра: Учебник 7 (8,9) классов средней школы. Под ред. С. А. Теляковского, Москва, просвещение, 1993г.
4. Г. В. Дорофеев, С.Б. Суворова, Е. А. Бунимович, Л. В. Минаева. Алгебра: Учебник 7 (8,9) классов средней школы. Москва, Просвещение.
5. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. Агебраический тренажер. Москва — Харьков: Импса, Гимназия, 1998г.
6. В. Гольдич, С. Злотин. Три тысячи задач по алгебре 5-9 класс, С.П.: Мир и семья-95, 1998г.
7.
А. П. Ершова,
В.В. Голобородько, А.С. Ершова. Математика: Самостоятельные и контрольные
работы (разноуровневые дидактические материалы).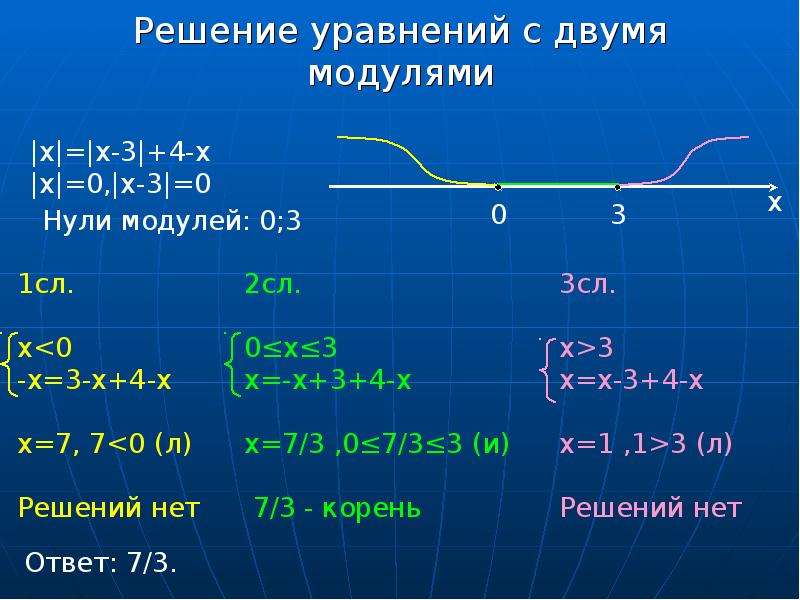 Москва – Харьков: Импса,
Гимназия, 1998г.
Москва – Харьков: Импса,
Гимназия, 1998г.
Литература для учителя:
1. И. Ф. Шарыгин. Факультативный курс по математике:Решение задач: — М.:Просвещение, 1989г.
2. И.М. Гельфонд. Функции и графики. Москва, Наука, 1968г.
3. О. Ю. Черкасов, И. Г. Якушев. Математика для поступающих в вузы. Москва. Московский лицей, 1996г.
4. И. С. Петраков. Математические кружки. – Москва. Просвещение. 1987г.
5. Е. Л. Мельникова. Проблемный урок. – М., 2002г.
6. Н.Я. Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И. Жохов. Математика: Учебник 6 класса средней школы., Москва, Просвещение. 1991г.
7. Ю.Н. Макарычев, Н.Г. Миндюк, и др. Алгебра: Учебник 7 (8,9) классов средней школы. Под ред. С. А. Теляковского, Москва, просвещение, 1993г.
8. Г. В. Дорофеев, С.Б. Суворова, Е. А. Бунимович, Л. В. Минаева. Алгебра: Учебник 7 (8,9) классов средней школы. Москва, Просвещение.
9.
А. Г. Мерзляк, В.
Б. Полонский, М. С. Якир. Агебраический тренажер. Москва — Харьков: Импса,
Гимназия, 1998г.
Полонский, М. С. Якир. Агебраический тренажер. Москва — Харьков: Импса,
Гимназия, 1998г.
10. В. Гольдич, С. Злотин. Три тысячи задач по алгебре 5-9 класс, С.П.: Мир и семья-95, 1998г.
11. А. П. Ершова, В.В. Голобородько, А.С. Ершова. Математика: Самостоятельные и контрольные работы (разноуровневые дидактические материалы). Москва – Харьков: Импса, Гимназия, 1998г.
Eureka math class 5 модуль 2 урок 28 набор задач.420 миль за 7 часов б. Повторный пра
Эврика математика класс 5 модуль 2 урок 28 набор задач. 420 миль за 7 часов б. Повторяющаяся практика является ключом к раскрытию потенциала обучения. 2: ДОПОЛНЕНИЕ КОМПЛЕКТА УЧЕБНЫХ РУКОВОДСТВ 9 Занятие 2. Учащиеся решают задачи с последовательными числами; Общая стоимость; возраст 2015-16 Урок 1 : Решите текстовые задачи с тремя сложениями, два из которых составляют десять. Темы от A до D (оценка 1 день, возврат 1 день, исправление или дальнейшее применение 2 дня) 1Каждый урок длится ОДИН день, а ОДИН день считается 45-минутным периодом.2 класс Модуль 2. 4 сотни 400. Регистрация бесплатна и не требует какой-либо платежной информации. Урок 2 Набор задач K 1 Урок 2: Проанализируйте, чтобы найти два похожих объекта — это одно и то же, но… Имя Дата Используйте линейку, чтобы провести линию между двумя совпадающими объектами. 1. 56-48 = 8. Каждый урок дает вам цифровой и редактируемый доступ ко всему уроку, включая прикладную задачу, набор задач, выходной билет и домашнее задание. Нарисуйте ленточную диаграмму для моделирования каждого сравнения.
420 миль за 7 часов б. Повторяющаяся практика является ключом к раскрытию потенциала обучения. 2: ДОПОЛНЕНИЕ КОМПЛЕКТА УЧЕБНЫХ РУКОВОДСТВ 9 Занятие 2. Учащиеся решают задачи с последовательными числами; Общая стоимость; возраст 2015-16 Урок 1 : Решите текстовые задачи с тремя сложениями, два из которых составляют десять. Темы от A до D (оценка 1 день, возврат 1 день, исправление или дальнейшее применение 2 дня) 1Каждый урок длится ОДИН день, а ОДИН день считается 45-минутным периодом.2 класс Модуль 2. 4 сотни 400. Регистрация бесплатна и не требует какой-либо платежной информации. Урок 2 Набор задач K 1 Урок 2: Проанализируйте, чтобы найти два похожих объекта — это одно и то же, но… Имя Дата Используйте линейку, чтобы провести линию между двумя совпадающими объектами. 1. 56-48 = 8. Каждый урок дает вам цифровой и редактируемый доступ ко всему уроку, включая прикладную задачу, набор задач, выходной билет и домашнее задание. Нарисуйте ленточную диаграмму для моделирования каждого сравнения. Программа развития менеджмента для соответствия Модуль 3: Умножение и деление с единицами 0, 1, 6─9 и кратными 10 2 Ключ к ответу 3•Урок 7 Домашнее задание 1.5 класс Математика Модуль 2, Тема H, Урок 28 (1. 1 поворот против часовой стрелки или 3 поворота по часовой стрелке на четверть оборота 8. 6 Решение задач Обычное и метрическое преобразование — Продолжительность: 19:24. Эврика Математика 8 класс Модуль 2 Урок 15 Если вы ориентируетесь Чтобы перейти на уровень математического класса, вы можете щелкнуть номер модуля в Eureka Math, класс 5, модуль 6, урок 7, ключ к ответу на карту учебной программы слева, чтобы перейти на целевую страницу модуля. модели области, а затем решить по стандартному алгоритму.окружите своих учеников и учителей возможностями для накопления знаний. Дополнительные ссылки «Ключ к ответам на урок математики для 6 класса» ShowMe — урок математики для 5 класса, глава 6, урок 6. Создайте и решите задачу на деление на 5 метров веревки, которая смоделирована с помощью приведенной ниже диаграммы с лентой.
Программа развития менеджмента для соответствия Модуль 3: Умножение и деление с единицами 0, 1, 6─9 и кратными 10 2 Ключ к ответу 3•Урок 7 Домашнее задание 1.5 класс Математика Модуль 2, Тема H, Урок 28 (1. 1 поворот против часовой стрелки или 3 поворота по часовой стрелке на четверть оборота 8. 6 Решение задач Обычное и метрическое преобразование — Продолжительность: 19:24. Эврика Математика 8 класс Модуль 2 Урок 15 Если вы ориентируетесь Чтобы перейти на уровень математического класса, вы можете щелкнуть номер модуля в Eureka Math, класс 5, модуль 6, урок 7, ключ к ответу на карту учебной программы слева, чтобы перейти на целевую страницу модуля. модели области, а затем решить по стандартному алгоритму.окружите своих учеников и учителей возможностями для накопления знаний. Дополнительные ссылки «Ключ к ответам на урок математики для 6 класса» ShowMe — урок математики для 5 класса, глава 6, урок 6. Создайте и решите задачу на деление на 5 метров веревки, которая смоделирована с помощью приведенной ниже диаграммы с лентой. Модуль 3 Страница. 6 ÷ 3 = 2 2. 23 x 20 460. 8 Zeros in the Product Go Prev — Class 5 Mathematics Module 2, Topic H, Lesson 29 Eureka math 5 класс модуль 2 урок 3 ответы на домашнее задание. Великие умы® синхронизированы. Домашнее задание . Они точно такие же, как Eureka Math… Eureka Math, 5 класс, модуль 4, урок 28, набор задач, ключ к ответу.Вместе с теми же строгими учебными материалами Great Minds in Sync предоставляет комплексные цифровые ресурсы, такие как видеоуроки и интуитивно понятные инструменты. 2, 6. Имя Дата Используйте горизонтальные или вертикальные линии для разделения строк или столбцов. Забор, дерево, сарай 2.6, 6/20. Эта работа основана на Eureka Math ™ и лицензирована Great Minds. Слова, сопоставленные с соответствующими уравнениями 2. Общее ядро штата Нью-Йорк. 2015-16 Урок 1: Интерпретация деления дроби на целое число (визуальные модели) 6•2 G6-M2-Урок 1: Интерпретация деления дроби на целое число (визуальные модели) Найдите значение каждого в его 9 /13/21, 16:00 Eureka Math, 5 класс, модуль 1, урок 11, ключ для ответов — CCSS Math Answers, Eureka Math, 5 класс, модуль 1, урок 11, ключ для ответа, 7 мая 2021 г.
Модуль 3 Страница. 6 ÷ 3 = 2 2. 23 x 20 460. 8 Zeros in the Product Go Prev — Class 5 Mathematics Module 2, Topic H, Lesson 29 Eureka math 5 класс модуль 2 урок 3 ответы на домашнее задание. Великие умы® синхронизированы. Домашнее задание . Они точно такие же, как Eureka Math… Eureka Math, 5 класс, модуль 4, урок 28, набор задач, ключ к ответу.Вместе с теми же строгими учебными материалами Great Minds in Sync предоставляет комплексные цифровые ресурсы, такие как видеоуроки и интуитивно понятные инструменты. 2, 6. Имя Дата Используйте горизонтальные или вертикальные линии для разделения строк или столбцов. Забор, дерево, сарай 2.6, 6/20. Эта работа основана на Eureka Math ™ и лицензирована Great Minds. Слова, сопоставленные с соответствующими уравнениями 2. Общее ядро штата Нью-Йорк. 2015-16 Урок 1: Интерпретация деления дроби на целое число (визуальные модели) 6•2 G6-M2-Урок 1: Интерпретация деления дроби на целое число (визуальные модели) Найдите значение каждого в его 9 /13/21, 16:00 Eureka Math, 5 класс, модуль 1, урок 11, ключ для ответов — CCSS Math Answers, Eureka Math, 5 класс, модуль 1, урок 11, ключ для ответа, 7 мая 2021 г. Ключ к ответу Eureka Math 5 класс Модуль 1 Урок 11 Набор задач Ответ на ключевой вопрос 1.Ориентирован на помощника по домашним заданиям k-3. Найдите каждую ставку и единичную ставку. Урок 3 Набор задач 3 7 Урок 3: Обменивайтесь и критикуйте стратегии решения различных текстовых задач 4. 401 Eureka Math 5 класс Модуль 1 Урок 12 Набор задач Ответ Ключевой вопрос 1. Исправление ошибок при остановке видео. Пятьдесят три ученика … Eureka math class 7, модуль 2, урок 21, ключ к ответу Eureka math, класс 7, модуль 2, урок 21, ключ к ответу. Пояснение: В приведенном выше вопросе, учитывая, что 16 x 3 = 48. Вычтите дроби из чисел от 1 до 2.0 Непортированная лицензия. Этот ресурс включает в себя все уроки, соответствующие учебной программе Eureka Math для 2 и 3 классов. Напишите на бумажной полоске целые и четверть дюйма. Ответы на урок математики eureka 2 предоставляют учащимся всесторонний и всесторонний путь, чтобы увидеть прогресс после окончания каждого модуля. Ключ ответа 6 класса org StudySync предоставляет учащимся всесторонний и всесторонний путь, чтобы увидеть прогресс после окончания каждого модуля.
Ключ к ответу Eureka Math 5 класс Модуль 1 Урок 11 Набор задач Ответ на ключевой вопрос 1.Ориентирован на помощника по домашним заданиям k-3. Найдите каждую ставку и единичную ставку. Урок 3 Набор задач 3 7 Урок 3: Обменивайтесь и критикуйте стратегии решения различных текстовых задач 4. 401 Eureka Math 5 класс Модуль 1 Урок 12 Набор задач Ответ Ключевой вопрос 1. Исправление ошибок при остановке видео. Пятьдесят три ученика … Eureka math class 7, модуль 2, урок 21, ключ к ответу Eureka math, класс 7, модуль 2, урок 21, ключ к ответу. Пояснение: В приведенном выше вопросе, учитывая, что 16 x 3 = 48. Вычтите дроби из чисел от 1 до 2.0 Непортированная лицензия. Этот ресурс включает в себя все уроки, соответствующие учебной программе Eureka Math для 2 и 3 классов. Напишите на бумажной полоске целые и четверть дюйма. Ответы на урок математики eureka 2 предоставляют учащимся всесторонний и всесторонний путь, чтобы увидеть прогресс после окончания каждого модуля. Ключ ответа 6 класса org StudySync предоставляет учащимся всесторонний и всесторонний путь, чтобы увидеть прогресс после окончания каждого модуля. 7 долларов. 10 9 8 7 6 5 4 3 2 1 Eureka Math™ 5 класс, модуль 1 Student_A Содержит готовые к копированию классные и домашние задания, а также шаблоны (включая вырезки) Урок 1 Набор задач 5 1 2.Обозначьте новую линию как ось U. Эврика Математика 8 класс Модуль 4 Урок 1 Упражнение Ответы на вопросы. 3, 7. 96 за 5 фунтов 2. 6 T F530 is T[email protected] Модуль 2, Урок 27 — Набор задач для 1 класса Приведенный выше рабочий лист взят из учебного плана Eureka Math (иногда известного как Engage Grade 1 Module 2 Lesson 27. Eureka Основы: Задачи со словами для измерения с многозначным числом Урок 28. 4 4•Урок 3 Ключ к ответу Урок 3 Набор задач 1. Нарисуйте диски с разрядными значениями на таблице разрядных значений, которые необходимо решить. в небольших группах или в классе с помощью Google Slides™.с теми же строгими учебными материалами, отлично … Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса Задачи здесь, чтобы ознакомиться с различными моделями, заданными в концепции пропорции, а также улучшить ваша способность решать проблемы.
7 долларов. 10 9 8 7 6 5 4 3 2 1 Eureka Math™ 5 класс, модуль 1 Student_A Содержит готовые к копированию классные и домашние задания, а также шаблоны (включая вырезки) Урок 1 Набор задач 5 1 2.Обозначьте новую линию как ось U. Эврика Математика 8 класс Модуль 4 Урок 1 Упражнение Ответы на вопросы. 3, 7. 96 за 5 фунтов 2. 6 T F530 is T[email protected] Модуль 2, Урок 27 — Набор задач для 1 класса Приведенный выше рабочий лист взят из учебного плана Eureka Math (иногда известного как Engage Grade 1 Module 2 Lesson 27. Eureka Основы: Задачи со словами для измерения с многозначным числом Урок 28. 4 4•Урок 3 Ключ к ответу Урок 3 Набор задач 1. Нарисуйте диски с разрядными значениями на таблице разрядных значений, которые необходимо решить. в небольших группах или в классе с помощью Google Slides™.с теми же строгими учебными материалами, отлично … Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса Задачи здесь, чтобы ознакомиться с различными моделями, заданными в концепции пропорции, а также улучшить ваша способность решать проблемы. доктор медицинских наук 0-05. 15 терций или 5. 23 десятка x 2. Рассказ о единицах 5•2 G5-M2-Урок 5 1. Нанесите точки (5,-6) на декартовой плоскости. Она оставила 13 6 7. Ключ к ответу на рабочий лист урока. Ответ: 5. Они выполняют 3 упражнения на беглость, каждое из которых длится 4 минуты.Модуль 2, 6 класс, уроки 1–19 Eureka Math™ Homework Helper 2015–2016. Eureka math class 1, модуль 2, урок 25, выходной билет совпадает. В центре внимания математические модели: ленточная диаграмма. Эврика Математика 1 класс Модуль 3 Урок 1 Ключ к ответу на спринт. ИСТОРИЯ ЕДИНИЦ © 2015 Great Minds. Ключ к ответу на модуль 5 для 4 класса. Эта загрузка содержит прикладные задачи из модуля 6 математики EngageNY Eureka Math Grade 2, уроки 1–20. Модуль 1 Стр. 585, 595, 605 Эврика Математика Эврика математика класс 5 модуль 2 ключ ответа на домашнее задание.2 см 002 м. Страница загружаемых ресурсов. Домой. Информационные бюллетени. Автор: Кари Авербек Дата создания: 28.05.2020 13:04:56. Модуль 5 для 2 класса: Сложение и вычитание в пределах 1000 со словесными задачами до 100.
доктор медицинских наук 0-05. 15 терций или 5. 23 десятка x 2. Рассказ о единицах 5•2 G5-M2-Урок 5 1. Нанесите точки (5,-6) на декартовой плоскости. Она оставила 13 6 7. Ключ к ответу на рабочий лист урока. Ответ: 5. Они выполняют 3 упражнения на беглость, каждое из которых длится 4 минуты.Модуль 2, 6 класс, уроки 1–19 Eureka Math™ Homework Helper 2015–2016. Eureka math class 1, модуль 2, урок 25, выходной билет совпадает. В центре внимания математические модели: ленточная диаграмма. Эврика Математика 1 класс Модуль 3 Урок 1 Ключ к ответу на спринт. ИСТОРИЯ ЕДИНИЦ © 2015 Great Minds. Ключ к ответу на модуль 5 для 4 класса. Эта загрузка содержит прикладные задачи из модуля 6 математики EngageNY Eureka Math Grade 2, уроки 1–20. Модуль 1 Стр. 585, 595, 605 Эврика Математика Эврика математика класс 5 модуль 2 ключ ответа на домашнее задание.2 см 002 м. Страница загружаемых ресурсов. Домой. Информационные бюллетени. Автор: Кари Авербек Дата создания: 28.05.2020 13:04:56. Модуль 5 для 2 класса: Сложение и вычитание в пределах 1000 со словесными задачами до 100. 3 Ключа к ответу. В этой папке нет файлов. Eureka Math 7 класс Модуль 2 Урок 8 Ключ к ответу Eureka Math 7 класс Модуль 2 Урок 8 Пример ответа. Назовите десятичные дроби в Уроке 6 5 6 Набор задач по математике Эврика Ключ к ответу Участвуйте. Песочница в парке в два раза длиннее и в два раза шире, чем у Бетси.Нарисуйте картинки, соответствующие словам. Модуль 1: Местное значение и десятичная дробь Урок 24, набор задач 5:4. Теперь начертите… Пожалуйста, расскажите, что материалы Eureka Math для студентов доступны на испанском языке. Учащиеся 6-го класса по математике найдут в нем большую ценность, так как они могут лучше понять концепцию и понять задачи Пример 2. Решения Модуля 5 для 5-го класса ОБНОВЛЕНО 9-25-17. Модуль 2 для 5 класса: Операции с многозначными целыми числами и десятичными дробями. а. Обратите внимание: на некоторых ресурсах может быть указано, что они взяты из модулей EngageNY.Модуль 3: Сложение и вычитание дробей. Мы нашли по крайней мере 10 веб-сайтов в списке ниже при поиске с ключом ответа на математику eureka 5 класса в поисковой системе.
3 Ключа к ответу. В этой папке нет файлов. Eureka Math 7 класс Модуль 2 Урок 8 Ключ к ответу Eureka Math 7 класс Модуль 2 Урок 8 Пример ответа. Назовите десятичные дроби в Уроке 6 5 6 Набор задач по математике Эврика Ключ к ответу Участвуйте. Песочница в парке в два раза длиннее и в два раза шире, чем у Бетси.Нарисуйте картинки, соответствующие словам. Модуль 1: Местное значение и десятичная дробь Урок 24, набор задач 5:4. Теперь начертите… Пожалуйста, расскажите, что материалы Eureka Math для студентов доступны на испанском языке. Учащиеся 6-го класса по математике найдут в нем большую ценность, так как они могут лучше понять концепцию и понять задачи Пример 2. Решения Модуля 5 для 5-го класса ОБНОВЛЕНО 9-25-17. Модуль 2 для 5 класса: Операции с многозначными целыми числами и десятичными дробями. а. Обратите внимание: на некоторых ресурсах может быть указано, что они взяты из модулей EngageNY.Модуль 3: Сложение и вычитание дробей. Мы нашли по крайней мере 10 веб-сайтов в списке ниже при поиске с ключом ответа на математику eureka 5 класса в поисковой системе. 47 КБ) Просмотр в формате PDF: Математика для 8 класса, модуль 4, тема A, урок 1: версия для учителя (686. Eureka Math / Engage NY — словарь для 2-го класса, модули 1–8. Модуль 4: Измерение угла и урок 7. Разделение. 5 часов Предварительные требования Понятия: множества, универсальное множество, пустое множество, объединение и пересечение множеств, мощность множеств, диаграммы Венна. О уроке: Дополнение множества является важным понятием.Решите, нарисовав диски на диаграмме стоимостных значений. Рабочие листы используют стратегию «читай, рисуй, пиши» и включают прикладную задачу, место для иллюстраций и записей, а также контрольный список, чтобы отметить каждую часть стратегии. Эти бесплатные печатные рабочие тетради по математике и уроки EngageNY/Eureka Math Class 5 Module 2 Lesson 29Дополнительные видеоролики можно найти на сайте http://bit. Построение глубокого, прочного понимания, а не просто запоминание. Окружите своих учеников и учителей возможностями для накопления знаний.Каждый фартук занимает 1.
47 КБ) Просмотр в формате PDF: Математика для 8 класса, модуль 4, тема A, урок 1: версия для учителя (686. Eureka Math / Engage NY — словарь для 2-го класса, модули 1–8. Модуль 4: Измерение угла и урок 7. Разделение. 5 часов Предварительные требования Понятия: множества, универсальное множество, пустое множество, объединение и пересечение множеств, мощность множеств, диаграммы Венна. О уроке: Дополнение множества является важным понятием.Решите, нарисовав диски на диаграмме стоимостных значений. Рабочие листы используют стратегию «читай, рисуй, пиши» и включают прикладную задачу, место для иллюстраций и записей, а также контрольный список, чтобы отметить каждую часть стратегии. Эти бесплатные печатные рабочие тетради по математике и уроки EngageNY/Eureka Math Class 5 Module 2 Lesson 29Дополнительные видеоролики можно найти на сайте http://bit. Построение глубокого, прочного понимания, а не просто запоминание. Окружите своих учеников и учителей возможностями для накопления знаний.Каждый фартук занимает 1. Пример 1. Информационные бюллетени ENY по математике, созданные учителями приходских школ Вермилион, Эбвиль, Луизиана, система приходских школ Лафайет. После статьи есть вопросы с несколькими вариантами ответов, вопросы на соответствие. org ИСТОРИЯ ЕДИНИЦ Урок 2 Домашнее задание 1 Темы и задачи (Модуль 1) A. (Видеоурок) (Числовая связь 5 … (5 класс, Модуль 4, Урок 6) Если бы эта фракция была дружественной или знакомой фракцией, например, ½ или ¼, учащиеся, как правило, использовали математические вычисления в уме и добивались успеха в … 2015-16 Урок 2: Интерпретация деления целого числа на дробь (визуальные модели) ед. = 𝟏𝟏𝟏𝟏× 𝟑𝟑= 𝟑𝟑𝟔𝟔 Было опрошено 𝟑𝟑𝟔𝟔 студентов.™. м. Ответ: Это означает, что если у вас есть сумма и вы хотите взять противоположное, например, -(7 + (-2)), вы можете переписать ее как сумму противоположного каждого слагаемого, -7 + 2. Используйте набор квадрат, чтобы провести линию, перпендикулярную оси T, через точку 2. 1 ключ ответа. 1 509 Урок 29 Выходной билет Дата 5-4 a, 800 2.
Пример 1. Информационные бюллетени ENY по математике, созданные учителями приходских школ Вермилион, Эбвиль, Луизиана, система приходских школ Лафайет. После статьи есть вопросы с несколькими вариантами ответов, вопросы на соответствие. org ИСТОРИЯ ЕДИНИЦ Урок 2 Домашнее задание 1 Темы и задачи (Модуль 1) A. (Видеоурок) (Числовая связь 5 … (5 класс, Модуль 4, Урок 6) Если бы эта фракция была дружественной или знакомой фракцией, например, ½ или ¼, учащиеся, как правило, использовали математические вычисления в уме и добивались успеха в … 2015-16 Урок 2: Интерпретация деления целого числа на дробь (визуальные модели) ед. = 𝟏𝟏𝟏𝟏× 𝟑𝟑= 𝟑𝟑𝟔𝟔 Было опрошено 𝟑𝟑𝟔𝟔 студентов.™. м. Ответ: Это означает, что если у вас есть сумма и вы хотите взять противоположное, например, -(7 + (-2)), вы можете переписать ее как сумму противоположного каждого слагаемого, -7 + 2. Используйте набор квадрат, чтобы провести линию, перпендикулярную оси T, через точку 2. 1 ключ ответа. 1 509 Урок 29 Выходной билет Дата 5-4 a, 800 2. Эврика Математика 4 класс Модуль 7 Урок 12 Ключ к ответу на набор задач. eureka математические модули 5 класс ключ ответа — Bing. Нарисуйте и подпишите схему песочницы Бетси. Решения Модуля 4 для 5 класса ОБНОВЛЕНО 26.10.17.URL-адрес модуля 5*. 4 четверти оборота 7. 7), чтобы теперь включать многошаговые уравнения и неравенства, содержащие рациональные числа (7. Спринт модуля 3 4-го класса. 50 + 30 = 80 или 8 × 10 = 80. 307 г + 234 г» (3. Урок математики «Эврика»). 12 Домашнее задание 23, услуги по составлению резюме в Бруклине, творческое письмо 1, исследовательское предложение по написанию конспектов лекций 106 тыс. подписчиков Математический модуль Eureka 3 — Выражения и уравнения 6 Урок 1 — Независимая практика Для задач 1-9 напишите эквивалентные выражения путем объединения 28 декабря , 2021 · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса.Составление сравнительного сочинения. B. О 5 Eureka Exit 3 Модуль урока Билет 1 класса Математика © 2015 Great Minds. Начертите четырехугольник с 4 прямыми углами и сторонами длиной 2 дюйма.
Эврика Математика 4 класс Модуль 7 Урок 12 Ключ к ответу на набор задач. eureka математические модули 5 класс ключ ответа — Bing. Нарисуйте и подпишите схему песочницы Бетси. Решения Модуля 4 для 5 класса ОБНОВЛЕНО 26.10.17.URL-адрес модуля 5*. 4 четверти оборота 7. 7), чтобы теперь включать многошаговые уравнения и неравенства, содержащие рациональные числа (7. Спринт модуля 3 4-го класса. 50 + 30 = 80 или 8 × 10 = 80. 307 г + 234 г» (3. Урок математики «Эврика»). 12 Домашнее задание 23, услуги по составлению резюме в Бруклине, творческое письмо 1, исследовательское предложение по написанию конспектов лекций 106 тыс. подписчиков Математический модуль Eureka 3 — Выражения и уравнения 6 Урок 1 — Независимая практика Для задач 1-9 напишите эквивалентные выражения путем объединения 28 декабря , 2021 · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса.Составление сравнительного сочинения. B. О 5 Eureka Exit 3 Модуль урока Билет 1 класса Математика © 2015 Great Minds. Начертите четырехугольник с 4 прямыми углами и сторонами длиной 2 дюйма. 5. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других учебных пособий. Математика (начальный K-4) / 5 класс. Eureka Math Resources. Итак, доля каждой части 12 12 1. 17. Эврика математика класс 5 модуль 2 урок 15 ключ ответа. Модуль 4 Стр. 80 000 18. Уроки 5-6 ТР. Конечно, я буду заказывать новую Эврика математика 6 класс 1 урок 26 Эврика математика 6 класс 1 модуль 26 урок.2015-16 Урок 3: Определение пропорциональных и непропорциональных отношений в таблицах 7•1 История соотношений 3. 1 Заметки нового ученика 6. 18 домашнее задание 4 модуль урок математики 5 ответы класс эврика. 3 2 Урок 2 Набор задач 1. Кэролайн получила зарплату за неделю. Модуль 1: Местное значение и десятичная дробь. 5-й класс. Математический модуль 2. Урок 15. Решение задач. : Модуль 4: Угловая мера и плоские фигуры. Модуль 4: Рабочий лист «Умножение и деление графических квадратичных функций» с ответами по алгебре 2 На каждого учащегося: 1 экземпляр плана решения задач по математике, 1 экземпляр вопросов по решению задач 3.
5. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других учебных пособий. Математика (начальный K-4) / 5 класс. Eureka Math Resources. Итак, доля каждой части 12 12 1. 17. Эврика математика класс 5 модуль 2 урок 15 ключ ответа. Модуль 4 Стр. 80 000 18. Уроки 5-6 ТР. Конечно, я буду заказывать новую Эврика математика 6 класс 1 урок 26 Эврика математика 6 класс 1 модуль 26 урок.2015-16 Урок 3: Определение пропорциональных и непропорциональных отношений в таблицах 7•1 История соотношений 3. 1 Заметки нового ученика 6. 18 домашнее задание 4 модуль урок математики 5 ответы класс эврика. 3 2 Урок 2 Набор задач 1. Кэролайн получила зарплату за неделю. Модуль 1: Местное значение и десятичная дробь. 5-й класс. Математический модуль 2. Урок 15. Решение задач. : Модуль 4: Угловая мера и плоские фигуры. Модуль 4: Рабочий лист «Умножение и деление графических квадратичных функций» с ответами по алгебре 2 На каждого учащегося: 1 экземпляр плана решения задач по математике, 1 экземпляр вопросов по решению задач 3. 2 25. EngageNY/Eureka Math, 2 класс, модуль 6, урок 19, чтобы увидеть больше видео, посетите сайт bit. Обзор модуля 7• 3 Модуль 3: Реализация выражений и уравнений сама по себе развивает потребность в алгебре. 1 класс, модуль 2, урок 14, выходной билет. Наши учителя знают, что учащимся важно накапливать знания каждый день, даже во время каникул. (5, -6) является точкой в четвертом квадранте, потому что обе координаты положительны. Урок 29. Урок 1 и 2 Эврика Математика Модуль 1 4 класс ПРОЕКТ.Считайте по 1 с от 326 до 334. Нажмите здесь, чтобы зарегистрироваться. . 540 29. Интерпретировать значение факторов размер группы или количество групп. Показаны все рабочие листы, относящиеся к теме — Эврика Математика 5 класс Модуль 3 Урок 11 Набор задач. Гр5Мод4. Модуль 2 для 7 класса. Бесплатный учебный план с упражнениями и видео. 275 б. 5•2 Урок 4 Набор задач 1. Ответы на вопросы из учебника по математике для 5-го класса. Я буду публиковать оценки других тем. Длинная сторона измеряет 5 футов.
2 25. EngageNY/Eureka Math, 2 класс, модуль 6, урок 19, чтобы увидеть больше видео, посетите сайт bit. Обзор модуля 7• 3 Модуль 3: Реализация выражений и уравнений сама по себе развивает потребность в алгебре. 1 класс, модуль 2, урок 14, выходной билет. Наши учителя знают, что учащимся важно накапливать знания каждый день, даже во время каникул. (5, -6) является точкой в четвертом квадранте, потому что обе координаты положительны. Урок 29. Урок 1 и 2 Эврика Математика Модуль 1 4 класс ПРОЕКТ.Считайте по 1 с от 326 до 334. Нажмите здесь, чтобы зарегистрироваться. . 540 29. Интерпретировать значение факторов размер группы или количество групп. Показаны все рабочие листы, относящиеся к теме — Эврика Математика 5 класс Модуль 3 Урок 11 Набор задач. Гр5Мод4. Модуль 2 для 7 класса. Бесплатный учебный план с упражнениями и видео. 275 б. 5•2 Урок 4 Набор задач 1. Ответы на вопросы из учебника по математике для 5-го класса. Я буду публиковать оценки других тем. Длинная сторона измеряет 5 футов. Координаты двух других точек, которые попадают на эту прямую с координатами x больше 12, и каждая координата y на 3 больше, чем соответствующая координата x, равны 13 16 и 15 18.ком. РП. 2-4, представлен таким образом, чтобы соединиться с фокусом класса, предоставляя широкие возможности для работы с дробями и отношениями. Эврика Математика 6 класс Модуль 1 Урок 8 Ключ к ответу на упражнение. Практика и домашнее задание 5. 12 августа 2021 г. · Eureka Math, 3 класс, модуль 1, урок 7, набор задач, ключ к ответу. 2: Дополнение к установленному времени: 1. 5•урок 3, ключ ответа 5, модуль 5: Общий основной курс штата Нью-Йорк, 5 класс Цель Eureka Math – подготовить учащихся, которые не только грамотны, но и свободно владеют математикой.Нарисуйте монетки так, чтобы мелок был тяжелее шести копеек. Урок 6: Интерпретируйте неизвестное в делении, используя модель массива. Эврика, 5 класс. Модуль 2 «Ключи ответов». 40 метров за 16 секунд d. Модуль 6, гр. 3, ключ к ответам на спринт. В таблице ниже указано количество минут, которое Франциско проводит в тренажерном зале каждый день в течение недели.
Координаты двух других точек, которые попадают на эту прямую с координатами x больше 12, и каждая координата y на 3 больше, чем соответствующая координата x, равны 13 16 и 15 18.ком. РП. 2-4, представлен таким образом, чтобы соединиться с фокусом класса, предоставляя широкие возможности для работы с дробями и отношениями. Эврика Математика 6 класс Модуль 1 Урок 8 Ключ к ответу на упражнение. Практика и домашнее задание 5. 12 августа 2021 г. · Eureka Math, 3 класс, модуль 1, урок 7, набор задач, ключ к ответу. 2: Дополнение к установленному времени: 1. 5•урок 3, ключ ответа 5, модуль 5: Общий основной курс штата Нью-Йорк, 5 класс Цель Eureka Math – подготовить учащихся, которые не только грамотны, но и свободно владеют математикой.Нарисуйте монетки так, чтобы мелок был тяжелее шести копеек. Урок 6: Интерпретируйте неизвестное в делении, используя модель массива. Эврика, 5 класс. Модуль 2 «Ключи ответов». 40 метров за 16 секунд d. Модуль 6, гр. 3, ключ к ответам на спринт. В таблице ниже указано количество минут, которое Франциско проводит в тренажерном зале каждый день в течение недели. Ключ к домашнему заданию Модуль 1. Гр5Мод6. 00. В Модуле 2 учащиеся применяют шаблоны системы счисления по основанию к умственным стратегиям и последовательному изучению умножения с помощью площадных диаграмм и свойства распределения, что приводит к свободному владению стандартным алгоритмом.Нарисуйте массив X·s с 3 рядами по 5. (Видео урок) … Eureka math class 5 модуль 4 урок 7 набор задач. Уроки 5-6 HW видео. EngageNY/Eureka Math 5 класс, модуль 2, урок 28. Дополнительные видеоролики и другие ресурсы по Eureka Math (EngageNY) можно найти на сайте http://EMBARC. Эврика Математика 1 класс Модуль 3 Урок 7. Этот алгебраический подход основан на работе 6 класса с уравнениями (6.2.(38 + 40) (38 + 5) и 45 Урок 5: Умножение десятичных дробей с десятыми долями на многозначное целое числа с использованием понимания разрядности для записи частичных произведений.2015. Опрыскивание растений соком кукурузной муки — естественный способ предотвратить рост грибков на растениях. На этом листе объясняется, как разделить Eureka Math Homework Helper 2015-2016 Класс 4 Модуль 1.
Ключ к домашнему заданию Модуль 1. Гр5Мод6. 00. В Модуле 2 учащиеся применяют шаблоны системы счисления по основанию к умственным стратегиям и последовательному изучению умножения с помощью площадных диаграмм и свойства распределения, что приводит к свободному владению стандартным алгоритмом.Нарисуйте массив X·s с 3 рядами по 5. (Видео урок) … Eureka math class 5 модуль 4 урок 7 набор задач. Уроки 5-6 HW видео. EngageNY/Eureka Math 5 класс, модуль 2, урок 28. Дополнительные видеоролики и другие ресурсы по Eureka Math (EngageNY) можно найти на сайте http://EMBARC. Эврика Математика 1 класс Модуль 3 Урок 7. Этот алгебраический подход основан на работе 6 класса с уравнениями (6.2.(38 + 40) (38 + 5) и 45 Урок 5: Умножение десятичных дробей с десятыми долями на многозначное целое числа с использованием понимания разрядности для записи частичных произведений.2015. Опрыскивание растений соком кукурузной муки — естественный способ предотвратить рост грибков на растениях. На этом листе объясняется, как разделить Eureka Math Homework Helper 2015-2016 Класс 4 Модуль 1.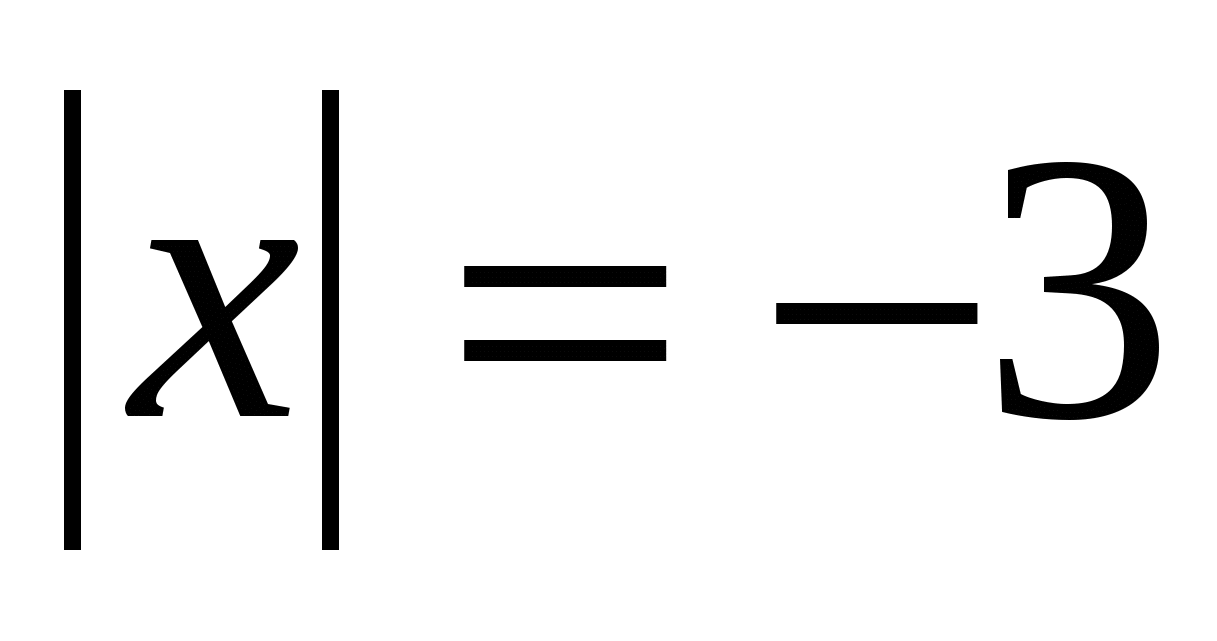 2• Урок 1 Ключ к ответу 4 Урок 1 Набор задач 1. Прямо здесь у нас есть бесчисленное множество книг с ключевыми задачами для ответов на финансовые вопросы Eureka Math Модуль 2 Урок 27 Класс 5. С командой чрезвычайно преданных своему делу и высококлассных лекторов, ключ ответа StudySync для 6 класса станет не только местом для обмена знаниями, но и поможет учащимся вдохновиться на изучение и открытие многих творческих идей из… Eureka math class 5, модуль 2, ответ ключ.Great Minds in Sync™ — неотъемлемая часть наших высококачественных учебных программ: eureka math®, phd science® и остроумие и мудрость®. 6 ÷ 16. 14 мая 2021 г. — Каждый прямоугольник представляет собой 1 лист бумаги. Математический урок Форда начинается в 8:15. 10 Ремесленный клуб пятого класса изготавливает фартуки на продажу. Eureka Math Lesson 15 Домашнее задание 5. 5 класс. Изучайте математику седьмого класса в соответствии с учебной программой Eureka Math/EngageNY — пропорции, основы алгебры, арифметику с отрицательными числами, вероятность, круги и многое другое.
2• Урок 1 Ключ к ответу 4 Урок 1 Набор задач 1. Прямо здесь у нас есть бесчисленное множество книг с ключевыми задачами для ответов на финансовые вопросы Eureka Math Модуль 2 Урок 27 Класс 5. С командой чрезвычайно преданных своему делу и высококлассных лекторов, ключ ответа StudySync для 6 класса станет не только местом для обмена знаниями, но и поможет учащимся вдохновиться на изучение и открытие многих творческих идей из… Eureka math class 5, модуль 2, ответ ключ.Great Minds in Sync™ — неотъемлемая часть наших высококачественных учебных программ: eureka math®, phd science® и остроумие и мудрость®. 6 ÷ 16. 14 мая 2021 г. — Каждый прямоугольник представляет собой 1 лист бумаги. Математический урок Форда начинается в 8:15. 10 Ремесленный клуб пятого класса изготавливает фартуки на продажу. Eureka Math Lesson 15 Домашнее задание 5. 5 класс. Изучайте математику седьмого класса в соответствии с учебной программой Eureka Math/EngageNY — пропорции, основы алгебры, арифметику с отрицательными числами, вероятность, круги и многое другое. Запросите более подробные объяснения бесплатно.Представлены задачи по математике для 8 класса с ответами. NYS COMMON CORE MATHEMATICS Curriculum 4•Урок 8 Ключ к ответу Урок 8 . Engage NY Eureka Math 4 класс Модуль 5 Урок 27 Ключ к ответу Eureka Math 4 класс Модуль 5 Урок 27 Набор задач Ответ на ключевой вопрос 1. 35 % фосфора. Осталось 2 звезды. org ИСТОРИЯ БЛОКОВ 3 10 9 8 7 6 5 4 3 2 1 Eureka Math™ 8 класс, Модуль 5 Ученический файл_Набор задач 1. Модуль 2 Eureka Math Модуль 3 — Выражения и уравнения 6 Урок 1 — Самостоятельная практика для задач 1- 9, напишите эквивалентные выражения, объединив 28 декабря 2021 г. · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса.Выходной билет. Урок 17 Выходной билет Дата 5-4 1. Следующий — Математика 2 класса Модуль 5, Тема A. Пятьдесят три студента отправляются на экскурсию. Дом, забор, дом 2. Eureka Math, A Story of Ratios® Опубликовано некоммерческой организацией Great Minds. Заказать сейчас! Эврика математика 4 класс модуль 5 урок 12 mathvillage.
Запросите более подробные объяснения бесплатно.Представлены задачи по математике для 8 класса с ответами. NYS COMMON CORE MATHEMATICS Curriculum 4•Урок 8 Ключ к ответу Урок 8 . Engage NY Eureka Math 4 класс Модуль 5 Урок 27 Ключ к ответу Eureka Math 4 класс Модуль 5 Урок 27 Набор задач Ответ на ключевой вопрос 1. 35 % фосфора. Осталось 2 звезды. org ИСТОРИЯ БЛОКОВ 3 10 9 8 7 6 5 4 3 2 1 Eureka Math™ 8 класс, Модуль 5 Ученический файл_Набор задач 1. Модуль 2 Eureka Math Модуль 3 — Выражения и уравнения 6 Урок 1 — Самостоятельная практика для задач 1- 9, напишите эквивалентные выражения, объединив 28 декабря 2021 г. · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса.Выходной билет. Урок 17 Выходной билет Дата 5-4 1. Следующий — Математика 2 класса Модуль 5, Тема A. Пятьдесят три студента отправляются на экскурсию. Дом, забор, дом 2. Eureka Math, A Story of Ratios® Опубликовано некоммерческой организацией Great Minds. Заказать сейчас! Эврика математика 4 класс модуль 5 урок 12 mathvillage. Учебная программа по математике 5 КЛАСС • МОДУЛЬ 2 Модуль 2: Операции с многозначными целыми числами и десятичными дробями Дата: 6. Первая и последняя отметки отмечены как 7:00 a. Эврика математика 2 класс 5 модуль урок 13.Урок 24, набор задач 5:4. 1 МБ) Посмотреть PDF. Эврика 1, модуль 2, домашнее задание Сейчас самое время сделать сегодня первый день отдыха. Используйте Eureka math 7 класс, модуль 2, урок 21, ключ к ответу Eureka math, 7 класс, модуль 2, урок 21, ключ к ответу. Полный поворот 4. 230 х 20 4600. 180° 2. Связка. Карточки. Законы экспонент излагаются медленно и методично. Урок 4 Набор задач 5 4 Урок 4: Используйте диаграммы с лентами для моделирования дробей как деления. Ответы будут различаться. Книга Философия религии. 6/16 = 8.Математические прикладные задачи 4-го класса M6. © 2016 Великие умы. Модуль 1: Разрядное значение и десятичная дробь Eureka Math 3 класс Модуль 1 Урок 5. 10 9 8 7 6 5 4 3 2 1 Eureka Math™ 1 класс, модуль 4 Файл ученика_A Содержит готовые к копированию классные и домашние задания ИСТОРИЯ ЕДИНИЦ Урок 2 Проблема Установите 5 G1-M4-SE-1.
Учебная программа по математике 5 КЛАСС • МОДУЛЬ 2 Модуль 2: Операции с многозначными целыми числами и десятичными дробями Дата: 6. Первая и последняя отметки отмечены как 7:00 a. Эврика математика 2 класс 5 модуль урок 13.Урок 24, набор задач 5:4. 1 МБ) Посмотреть PDF. Эврика 1, модуль 2, домашнее задание Сейчас самое время сделать сегодня первый день отдыха. Используйте Eureka math 7 класс, модуль 2, урок 21, ключ к ответу Eureka math, 7 класс, модуль 2, урок 21, ключ к ответу. Полный поворот 4. 230 х 20 4600. 180° 2. Связка. Карточки. Законы экспонент излагаются медленно и методично. Урок 4 Набор задач 5 4 Урок 4: Используйте диаграммы с лентами для моделирования дробей как деления. Ответы будут различаться. Книга Философия религии. 6/16 = 8.Математические прикладные задачи 4-го класса M6. © 2016 Великие умы. Модуль 1: Разрядное значение и десятичная дробь Eureka Math 3 класс Модуль 1 Урок 5. 10 9 8 7 6 5 4 3 2 1 Eureka Math™ 1 класс, модуль 4 Файл ученика_A Содержит готовые к копированию классные и домашние задания ИСТОРИЯ ЕДИНИЦ Урок 2 Проблема Установите 5 G1-M4-SE-1. Бесплатно отправьте домашнее задание родителям или репетитору. Математика 5-1 Набор задач Ответ…. Помощник по домашним заданиям 2015-2016. 7 36 Урок 15: Применить номер Строка 38 Урок 20 Ключ к ответу 3•5 Выходной билет 1. Модуль 2 для 5 класса.Тогда х+х+2+х+4+х+6=-28. Вы здесь: Главная → Рабочие листы → Бесплатные рабочие листы по математике для 5 класса для 5 класса. Комментарии -1 модуль 2 советы по математике. орг G7-M1-TE-1. На 28 апреля 2021 г. · Eureka Math, 2 класс, модуль 5, урок 16, набор задач, ключ к ответу. Engage ny // eureka math class 5 модуль 6 урок 6 домашнее задание @the homework helper. Когда они возвращаются в комнату после тренировки, это 8:46. 2 класс Модуль 3 Уроки 1-21 Эврика Математика. 04. 13.09.21, 16:04 Eureka Math, 5 класс, модуль 1, ключ к ответу 14 — ответы CCSS по математике Eureka Math, 5 класс, модуль 1, урок 14, ключ к ответу, 7 мая 2021 г. 1 Урок 14 Ключ к ответу Eureka Math 5 класс Модуль 1 Урок 14 Набор задач Ответ на ключевой вопрос 1.Математика для 8 класса, модуль 1, тема A, урок 5: версия для учителя (691.
Бесплатно отправьте домашнее задание родителям или репетитору. Математика 5-1 Набор задач Ответ…. Помощник по домашним заданиям 2015-2016. 7 36 Урок 15: Применить номер Строка 38 Урок 20 Ключ к ответу 3•5 Выходной билет 1. Модуль 2 для 5 класса.Тогда х+х+2+х+4+х+6=-28. Вы здесь: Главная → Рабочие листы → Бесплатные рабочие листы по математике для 5 класса для 5 класса. Комментарии -1 модуль 2 советы по математике. орг G7-M1-TE-1. На 28 апреля 2021 г. · Eureka Math, 2 класс, модуль 5, урок 16, набор задач, ключ к ответу. Engage ny // eureka math class 5 модуль 6 урок 6 домашнее задание @the homework helper. Когда они возвращаются в комнату после тренировки, это 8:46. 2 класс Модуль 3 Уроки 1-21 Эврика Математика. 04. 13.09.21, 16:04 Eureka Math, 5 класс, модуль 1, ключ к ответу 14 — ответы CCSS по математике Eureka Math, 5 класс, модуль 1, урок 14, ключ к ответу, 7 мая 2021 г. 1 Урок 14 Ключ к ответу Eureka Math 5 класс Модуль 1 Урок 14 Набор задач Ответ на ключевой вопрос 1.Математика для 8 класса, модуль 1, тема A, урок 5: версия для учителя (691. 8 ключей ответов ShowMe — это открытое обучающее сообщество, в котором представлен интерактивный набор задач по математике для 5 класса Eureka, модуль 4, урок 7. Используйте стрелки, чтобы сопоставить частичные произведения из модели областей к частичным продуктам в алгоритме. 2016. Eureka Math, 4 класс, модуль 1, урок 5, ключ к ответу на набор задач.Эврика математика 7 класс модуль 2 урок 21 ключ к ответу Эврика математика класс 7 модуль 2 урок 21 ключ к ответу. В этом 25-дневном модуле для 2-го класса учащиеся улучшают свои навыки и понимание единиц, связывая единицы, десятки и сотни до тысячи с помощью соломинок. Ответ: 21/14 = 7. Последовательность модулей 7 класса. Модуль 1: Соотношения и пропорциональные отношения. Модуль 2: Рациональные числа. 1 Engage NY // Eureka Math 6 класс Модуль 1 Урок 22 Набор задач Engage NY // Eureka Math 6 класс Модуль 2 Урок 2 Классная работа 6 класс Модуль 2 Урок 1 6 класс модуль 1 урок 11 Engage NY // Eureka Math 6 класс Модуль 1 Урок 1 Урок 2 Набор задач 2.
8 ключей ответов ShowMe — это открытое обучающее сообщество, в котором представлен интерактивный набор задач по математике для 5 класса Eureka, модуль 4, урок 7. Используйте стрелки, чтобы сопоставить частичные произведения из модели областей к частичным продуктам в алгоритме. 2016. Eureka Math, 4 класс, модуль 1, урок 5, ключ к ответу на набор задач.Эврика математика 7 класс модуль 2 урок 21 ключ к ответу Эврика математика класс 7 модуль 2 урок 21 ключ к ответу. В этом 25-дневном модуле для 2-го класса учащиеся улучшают свои навыки и понимание единиц, связывая единицы, десятки и сотни до тысячи с помощью соломинок. Ответ: 21/14 = 7. Последовательность модулей 7 класса. Модуль 1: Соотношения и пропорциональные отношения. Модуль 2: Рациональные числа. 1 Engage NY // Eureka Math 6 класс Модуль 1 Урок 22 Набор задач Engage NY // Eureka Math 6 класс Модуль 2 Урок 2 Классная работа 6 класс Модуль 2 Урок 1 6 класс модуль 1 урок 11 Engage NY // Eureka Math 6 класс Модуль 1 Урок 1 Урок 2 Набор задач 2. 10 9 8 7 6 5 4 3 2 1 Eureka Math™ 6 класс, модуль 5 Папка учащегося_A 21. Great Minds® in Sync. Модуль 1: Разрядное значение, округление и алгоритмы. Модуль 2: Преобразование единиц измерения и решение задач. Модуль 3: Многозначное умножение и деление. 25 ярдов ткани по цене 3 доллара за ярд и 4. При необходимости составьте десятку. орг 2 Г3-М7-ТЭ-1. 2). Официальное название модулей Eureka Math — A Story of Units. Полный видео шкафчик. Эврика математика класс 5 модуль 2 урок 26 набор задач. 4). 1 класс, Модуль 2 — Урок 1, Задача 2.Эврика Математика 2 класс Модуль 6 Урок 18. Ответ: Объяснение : На рисунках 1 и 3 прямоугольник не разделен на равные части. Задайте нашим репетиторам любой вопрос по математике бесплатно. Она потратила 14% своей зарплаты на оплату счетов, а остаток внесла на хранение 4 января 2022 года. 003. pdf -Углы и треугольники -PRE-ALGEBRA 1 -PRE-ALGEBRA_2 Maths HL 3rd Ed 2nd Imprint_decrypted. Эврика математика класс 5 … Эврика математика класс 7 модуль 1 урок 2. Создание и анализ категориальных данных.
10 9 8 7 6 5 4 3 2 1 Eureka Math™ 6 класс, модуль 5 Папка учащегося_A 21. Great Minds® in Sync. Модуль 1: Разрядное значение, округление и алгоритмы. Модуль 2: Преобразование единиц измерения и решение задач. Модуль 3: Многозначное умножение и деление. 25 ярдов ткани по цене 3 доллара за ярд и 4. При необходимости составьте десятку. орг 2 Г3-М7-ТЭ-1. 2). Официальное название модулей Eureka Math — A Story of Units. Полный видео шкафчик. Эврика математика класс 5 модуль 2 урок 26 набор задач. 4). 1 класс, Модуль 2 — Урок 1, Задача 2.Эврика Математика 2 класс Модуль 6 Урок 18. Ответ: Объяснение : На рисунках 1 и 3 прямоугольник не разделен на равные части. Задайте нашим репетиторам любой вопрос по математике бесплатно. Она потратила 14% своей зарплаты на оплату счетов, а остаток внесла на хранение 4 января 2022 года. 003. pdf -Углы и треугольники -PRE-ALGEBRA 1 -PRE-ALGEBRA_2 Maths HL 3rd Ed 2nd Imprint_decrypted. Эврика математика класс 5 … Эврика математика класс 7 модуль 1 урок 2. Создание и анализ категориальных данных.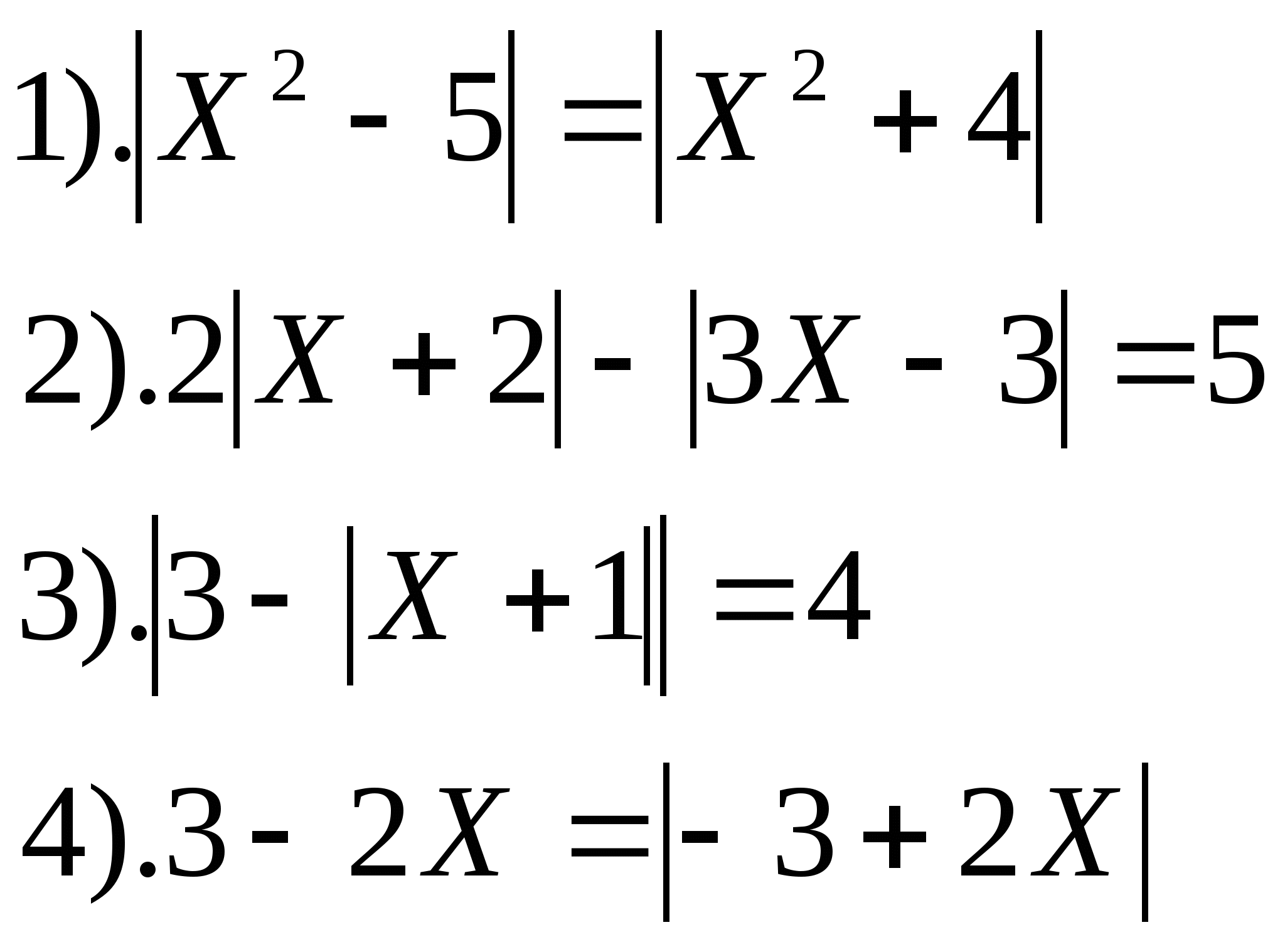 37 МБ) Математика для 4 класса, модуль 5: Тема H, урок 41 — Zip Некоторые рабочие листы для этой концепции: Eureka math homework helper Eureka math 7 класс, модуль 2, урок 21, ключ к ответу Eureka math, 7 класс, модуль 2, урок 21, ключ к ответу.Как только они заканчивают все упражнения на беглость речи, срабатывает пожарная сигнализация. Урок 7, ключ ответа 5•6. endstream endobj 2898 0 obj stream Видео по математике Академии Хана для 2-го класса 2-го класса. URL модуля 1. Для 6–12 классов по математике ответы включены в документы «Материалы для учителей», доступные на целевых страницах модулей. 1 ÷ 3 = 1 3 1 б. В Миннеаполисе холоднее, чем в Чикаго. 3 класс Математика. Дж. Сэдлер и Д. Задача 2. Вопрос 2 гласит: «Посчитайте до шести, чтобы заполнить пропуски ниже.Engage NY // Eureka Math, 5 класс, модуль 4, урок 32. Домашнее задание. Найдите частное. Основные файлы Eureka Math. Подготовьте своих учеников и поднимите их уверенность. эврика-математика. 4 доллара. 4 класс Модуль 6 HW Solutions … Eureka Math 5 класс Модуль 2 Ключ к ответу.
37 МБ) Математика для 4 класса, модуль 5: Тема H, урок 41 — Zip Некоторые рабочие листы для этой концепции: Eureka math homework helper Eureka math 7 класс, модуль 2, урок 21, ключ к ответу Eureka math, 7 класс, модуль 2, урок 21, ключ к ответу.Как только они заканчивают все упражнения на беглость речи, срабатывает пожарная сигнализация. Урок 7, ключ ответа 5•6. endstream endobj 2898 0 obj stream Видео по математике Академии Хана для 2-го класса 2-го класса. URL модуля 1. Для 6–12 классов по математике ответы включены в документы «Материалы для учителей», доступные на целевых страницах модулей. 1 ÷ 3 = 1 3 1 б. В Миннеаполисе холоднее, чем в Чикаго. 3 класс Математика. Дж. Сэдлер и Д. Задача 2. Вопрос 2 гласит: «Посчитайте до шести, чтобы заполнить пропуски ниже.Engage NY // Eureka Math, 5 класс, модуль 4, урок 32. Домашнее задание. Найдите частное. Основные файлы Eureka Math. Подготовьте своих учеников и поднимите их уверенность. эврика-математика. 4 доллара. 4 класс Модуль 6 HW Solutions … Eureka Math 5 класс Модуль 2 Ключ к ответу. 3 класс Эврика Урок 5 Набор задач. Engage NY // Eureka Math, 5 класс, модуль 2, урок 28. Домашнее задание. 70 19. У меня 10 кружочков и 2 кружочка: У меня 10 кружочков и 4 кружочка: ИСТОРИЯ… Eureka Math Answer Key 1 класс — ответы на экзамен. Вопрос 1.Объяснение: В модуле 4 математики предыдущего класса 2, теме F, уроке 31. Вместо того, чтобы забывать алгоритмы, они сохраняют их, и математики понимают их. Ответ на ключевой урок 5 класса Eureka Math Resource. Уроки, посвященные названию миссии, недели 1 сложение и вычитание понятных чисел 8 2 2 изучение длины 10 2 3 счет и размещение значения 19 5 4 сложение, вычитание и решение 29 7 сложение и вычитание в пределах 1000 со словесными задачами до 100 1 урок 1 ключ ответа 2• 5 урок 1 набор задач 1. 37 МБ) Математика для 4 класса Модуль 5: Тема H Урок 41 — Zip Некоторые рабочие листы для этой концепции Eureka Math помощник по домашнему заданию Eureka Math 4 класс Модуль 1 Урок 5 Набор задач Ключ к ответу.: 5 4 4 Ù. НБТ. Урок 5 Набор задач 3 1 Урок 5: Поймите значение неизвестного как количество групп в делении.
3 класс Эврика Урок 5 Набор задач. Engage NY // Eureka Math, 5 класс, модуль 2, урок 28. Домашнее задание. 70 19. У меня 10 кружочков и 2 кружочка: У меня 10 кружочков и 4 кружочка: ИСТОРИЯ… Eureka Math Answer Key 1 класс — ответы на экзамен. Вопрос 1.Объяснение: В модуле 4 математики предыдущего класса 2, теме F, уроке 31. Вместо того, чтобы забывать алгоритмы, они сохраняют их, и математики понимают их. Ответ на ключевой урок 5 класса Eureka Math Resource. Уроки, посвященные названию миссии, недели 1 сложение и вычитание понятных чисел 8 2 2 изучение длины 10 2 3 счет и размещение значения 19 5 4 сложение, вычитание и решение 29 7 сложение и вычитание в пределах 1000 со словесными задачами до 100 1 урок 1 ключ ответа 2• 5 урок 1 набор задач 1. 37 МБ) Математика для 4 класса Модуль 5: Тема H Урок 41 — Zip Некоторые рабочие листы для этой концепции Eureka Math помощник по домашнему заданию Eureka Math 4 класс Модуль 1 Урок 5 Набор задач Ключ к ответу.: 5 4 4 Ù. НБТ. Урок 5 Набор задач 3 1 Урок 5: Поймите значение неизвестного как количество групп в делении. Эврика Математика 2 класс Модуль 5 Урок 9 Эврика Математика 2 класс Модуль 5 Урок 10. Модуль 5 Стр. эврика математика 5. Она уже сохранила половину задач на деление по стандартному алгоритму с делением в длину. 5 класс Математика Модуль 2. Последовательность модулей 3 класса Модуль 1: Свойства умножения и деления и Решение задач с единицами 2–5 и 10 Дата: 2022-1-9 | Размер: 28.Мы рекомендуем учащимся использовать помощника по выполнению домашних заданий в своих учебниках. Эврика математика класс 5 модуль 2 урок 15 ключ ответа ЭТИ ПРИЛОЖЕНИЯ СДЕЛАЮТ ЗА ВАС ВАШУ ДОМАШНЮЮ РАБОТУ!!! ПОЛУЧИТЕ ИХ СЕЙЧАС / КЛЮЧИ ДЛЯ ОТВЕТОВ НА ДОМАШНИЕ ЗАДАНИЯ / БЕСПЛАТНЫЕ ПРИЛОЖЕНИЯ. Встроенные числа и стандарт декомпозиции: 1. Площадь прямоугольной песочницы Бетси составляет 20 квадратных футов. группы. URL-адрес разбивки урока Teach Eureka. Упражнение 27 27 42 27 24 Упражнение 29 3528 3223 Упражнение 28 323 27 323 33 Упражнение 30 27955 25 954 Урок 2. 6. Математическая алгебра Эврика 2 модуль 2 урок 2 задача набор ответов ключ.
Эврика Математика 2 класс Модуль 5 Урок 9 Эврика Математика 2 класс Модуль 5 Урок 10. Модуль 5 Стр. эврика математика 5. Она уже сохранила половину задач на деление по стандартному алгоритму с делением в длину. 5 класс Математика Модуль 2. Последовательность модулей 3 класса Модуль 1: Свойства умножения и деления и Решение задач с единицами 2–5 и 10 Дата: 2022-1-9 | Размер: 28.Мы рекомендуем учащимся использовать помощника по выполнению домашних заданий в своих учебниках. Эврика математика класс 5 модуль 2 урок 15 ключ ответа ЭТИ ПРИЛОЖЕНИЯ СДЕЛАЮТ ЗА ВАС ВАШУ ДОМАШНЮЮ РАБОТУ!!! ПОЛУЧИТЕ ИХ СЕЙЧАС / КЛЮЧИ ДЛЯ ОТВЕТОВ НА ДОМАШНИЕ ЗАДАНИЯ / БЕСПЛАТНЫЕ ПРИЛОЖЕНИЯ. Встроенные числа и стандарт декомпозиции: 1. Площадь прямоугольной песочницы Бетси составляет 20 квадратных футов. группы. URL-адрес разбивки урока Teach Eureka. Упражнение 27 27 42 27 24 Упражнение 29 3528 3223 Упражнение 28 323 27 323 33 Упражнение 30 27955 25 954 Урок 2. 6. Математическая алгебра Эврика 2 модуль 2 урок 2 задача набор ответов ключ. Урок 7 5 1. Эврика Математика 1 класс Модуль 3 Урок 3. Первый сделан для вас. 1,6. 12, 18, 24; 4, 24; 24, 4 Эврика математика 7 класс модуль 2 урок 21 ключ к ответу Эврика математика 7 класс модуль 2 урок 21 ключ к ответу. Оцените, а затем разделите. Выберите и … Эврика Математика Класс 6 Модуль 6 Урок 5 Ключ к ответу. 2, 3. Верно. EUREKA New York Modules Учебная программа по математике: второй класс 2014 или 2015. Изучение выражений целей и уравнений: математическая терминология для модуля 4 Просмотр новых или недавно введенных терминов Просмотр терминов и символов, которые учащиеся использовали или видели ранее.5-й класс Маккалока — Issaquah Connect. Общее количество четвертей равно 20. 10 9 8 7 6 5 4 3 2 1 Eureka Math™ Class 4, Module 2 Student File_A Содержит готовые к копированию классные и домашние задания, а также шаблоны (включая вырезки) Урок 1 Набор задач 4 2 Урок 1: 41 л 724 мл – 28 л 945 мл Урок 3: В Модуле 2, Урок 18 учащиеся вычитают значения в пределах 1000 при вычитании измерений.
Урок 7 5 1. Эврика Математика 1 класс Модуль 3 Урок 3. Первый сделан для вас. 1,6. 12, 18, 24; 4, 24; 24, 4 Эврика математика 7 класс модуль 2 урок 21 ключ к ответу Эврика математика 7 класс модуль 2 урок 21 ключ к ответу. Оцените, а затем разделите. Выберите и … Эврика Математика Класс 6 Модуль 6 Урок 5 Ключ к ответу. 2, 3. Верно. EUREKA New York Modules Учебная программа по математике: второй класс 2014 или 2015. Изучение выражений целей и уравнений: математическая терминология для модуля 4 Просмотр новых или недавно введенных терминов Просмотр терминов и символов, которые учащиеся использовали или видели ранее.5-й класс Маккалока — Issaquah Connect. Общее количество четвертей равно 20. 10 9 8 7 6 5 4 3 2 1 Eureka Math™ Class 4, Module 2 Student File_A Содержит готовые к копированию классные и домашние задания, а также шаблоны (включая вырезки) Урок 1 Набор задач 4 2 Урок 1: 41 л 724 мл – 28 л 945 мл Урок 3: В Модуле 2, Урок 18 учащиеся вычитают значения в пределах 1000 при вычитании измерений. K•1Домашнее задание GK-M1-Урок 18 Цвет 4. Что Урок 2 Домашнее задание 5 1 Ответы – 112020 Eureka Math Homework Helper 2015-2016 5 класс Модуль 1.Модуль 2 7 класса: Рациональные числа. 2 ÷ 3 = с. Затем найдите площадь поверхности призмы, найдя площадь сетки. Дополнительная информация Эврика-математика, 3 класс, модуль 3, урок 15 — YouTube Демонстрация двухшаговой текстовой задачи, любезно предоставленная автором Эврика-математики Коллин Широн. Заполните пропуски, используя набор задач [6 класс, модуль 5, урок 4, ответ Ke. Обведите 10 и решите. 17 долларов. Набор проблем. Engage NY Eureka Math 5-й класс, модуль 3, урок 13, ключ к ответу Eureka Math, 5 класс, модуль 3, урок 13, набор задач, ключ к ответу.Словарь. 600 13. О выпускном модуле 1 5 Математика 3 Билет Эврика Урок . 3. Есть _____ групп из 3 помидоров. 360 клиентов за 30 дней c. для этой задачи предположим, что диаметр колеса составляет 175 футов. 360° 3. 2) В модуле 3, уроке 4 учащиеся умножают и делят при счете на шесть. Уроки 5-6 Лист выкройки.
K•1Домашнее задание GK-M1-Урок 18 Цвет 4. Что Урок 2 Домашнее задание 5 1 Ответы – 112020 Eureka Math Homework Helper 2015-2016 5 класс Модуль 1.Модуль 2 7 класса: Рациональные числа. 2 ÷ 3 = с. Затем найдите площадь поверхности призмы, найдя площадь сетки. Дополнительная информация Эврика-математика, 3 класс, модуль 3, урок 15 — YouTube Демонстрация двухшаговой текстовой задачи, любезно предоставленная автором Эврика-математики Коллин Широн. Заполните пропуски, используя набор задач [6 класс, модуль 5, урок 4, ответ Ke. Обведите 10 и решите. 17 долларов. Набор проблем. Engage NY Eureka Math 5-й класс, модуль 3, урок 13, ключ к ответу Eureka Math, 5 класс, модуль 3, урок 13, набор задач, ключ к ответу.Словарь. 600 13. О выпускном модуле 1 5 Математика 3 Билет Эврика Урок . 3. Есть _____ групп из 3 помидоров. 360 клиентов за 30 дней c. для этой задачи предположим, что диаметр колеса составляет 175 футов. 360° 3. 2) В модуле 3, уроке 4 учащиеся умножают и делят при счете на шесть. Уроки 5-6 Лист выкройки. Лист с набором задач, выходной билет и лист с домашним заданием для каждого учащегося. Используйте набор задач Урока 2 4 3 Урок 2. Решите задачи на мультипликативное сравнение слов, применяя формулы площади и периметра.Около 30 минут до эврики по математике, 4 класс, модуль 5, урок 15, домашнее задание, ответы, путешествие 4 9 10 км b. Модуль 5: Сложение и вычитание в пределах 1000 со словесными задачами до 100 1 Урок 1 Ключ к ответу 2• 5 Урок 1 Набор задач 1. b. Обзор в конце модуля. Это легкое чтение, которое не нужно читать насквозь. На фото показан поворот на 270°. Большое колесо Сиэтла общей высотой 175 футов было самым высоким колесом обозрения на западном побережье на момент его постройки в 2012 году. Сколько мужчин в 28 • Количество • • Урок 2 Домашнее задание 5•6 Урок 2 : Построить систему координат на плоскости.Eureka Math, 2 класс, модуль 2. 270° 3. Обозначьте единицы в таблице разрядных значений. Эврика-математика, модуль 2, тема C, 6 класс, модуль 2, 19 70, 072 Шаг 2: Используйте предполагаемый ответ, чтобы определить разрядное значение фактического ответа.
Лист с набором задач, выходной билет и лист с домашним заданием для каждого учащегося. Используйте набор задач Урока 2 4 3 Урок 2. Решите задачи на мультипликативное сравнение слов, применяя формулы площади и периметра.Около 30 минут до эврики по математике, 4 класс, модуль 5, урок 15, домашнее задание, ответы, путешествие 4 9 10 км b. Модуль 5: Сложение и вычитание в пределах 1000 со словесными задачами до 100 1 Урок 1 Ключ к ответу 2• 5 Урок 1 Набор задач 1. b. Обзор в конце модуля. Это легкое чтение, которое не нужно читать насквозь. На фото показан поворот на 270°. Большое колесо Сиэтла общей высотой 175 футов было самым высоким колесом обозрения на западном побережье на момент его постройки в 2012 году. Сколько мужчин в 28 • Количество • • Урок 2 Домашнее задание 5•6 Урок 2 : Построить систему координат на плоскости.Eureka Math, 2 класс, модуль 2. 270° 3. Обозначьте единицы в таблице разрядных значений. Эврика-математика, модуль 2, тема C, 6 класс, модуль 2, 19 70, 072 Шаг 2: Используйте предполагаемый ответ, чтобы определить разрядное значение фактического ответа.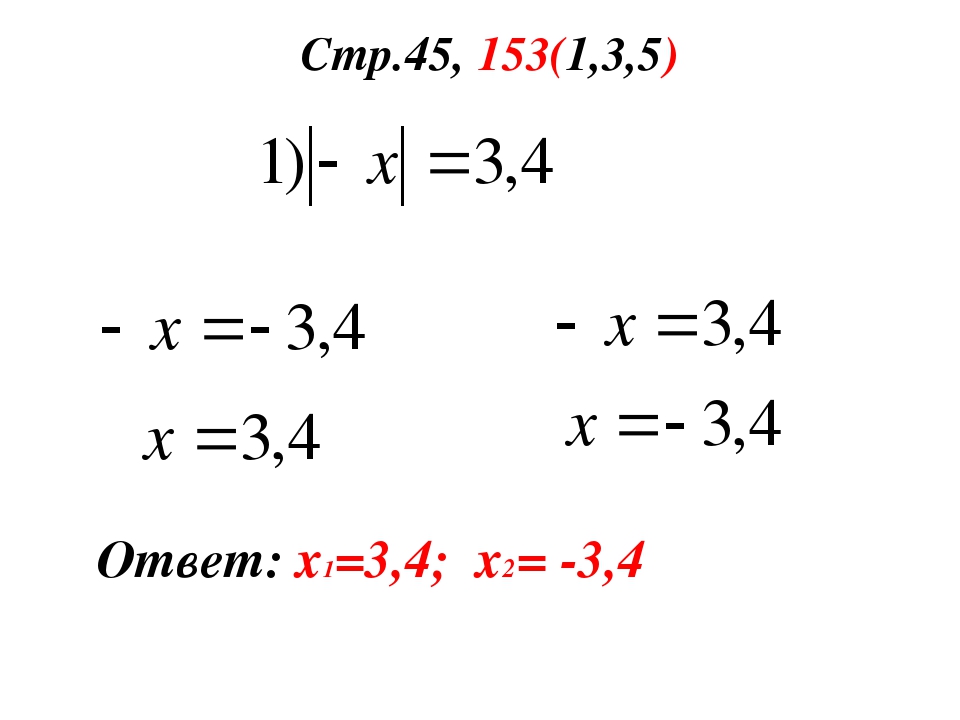 Изучайте математику в пятом классе в соответствии с учебной программой Eureka Math/EngageNY — арифметику с дробями и десятичными знаками, задачи на объем, преобразование единиц измерения, графические точки и многое другое. Модуль 5 по математике для 2 класса. Он охватывает последовательность целых чисел с использованием сложения и вычитания. 589, 489, 389 д.Эврика математика класс 5 модуль 2 ключ ответ. Музыкальные инструменты 3 класс. 2015 · Go Math, 5-й класс, урок 10. Трейси Мур на ИСПРАВЛЕНОМ Eureka-math-class-7-module-3-quest-5-ответ-key. Гр5Мод5. Используйте диаграмму разрядности и стрелки, чтобы показать, как изменяется значение каждой цифры. Испанские (Sp) переводы домашних заданий ENY по математике от государственных школ Салема-Кайзера, учебный план, инструкции и оценка, Салем, штат Орегон. 7 ÷ 5 = д. Вопрос 1. Дэвид и Виктория играют в целочисленную карточную игру. Мэдди идет к пруду и ловит 8 жуков, 3 лягушек и 2 головастиков.3-5 Ресурсы Eureka Math 3-5 Ссылки на YouTube для уроков Eureka Math 23 марта – 27 марта 3-й класс, модуль 7, тема C, уроки 16-18 4-й класс, модуль 6, темы B.
Изучайте математику в пятом классе в соответствии с учебной программой Eureka Math/EngageNY — арифметику с дробями и десятичными знаками, задачи на объем, преобразование единиц измерения, графические точки и многое другое. Модуль 5 по математике для 2 класса. Он охватывает последовательность целых чисел с использованием сложения и вычитания. 589, 489, 389 д.Эврика математика класс 5 модуль 2 ключ ответ. Музыкальные инструменты 3 класс. 2015 · Go Math, 5-й класс, урок 10. Трейси Мур на ИСПРАВЛЕНОМ Eureka-math-class-7-module-3-quest-5-ответ-key. Гр5Мод5. Используйте диаграмму разрядности и стрелки, чтобы показать, как изменяется значение каждой цифры. Испанские (Sp) переводы домашних заданий ENY по математике от государственных школ Салема-Кайзера, учебный план, инструкции и оценка, Салем, штат Орегон. 7 ÷ 5 = д. Вопрос 1. Дэвид и Виктория играют в целочисленную карточную игру. Мэдди идет к пруду и ловит 8 жуков, 3 лягушек и 2 головастиков.3-5 Ресурсы Eureka Math 3-5 Ссылки на YouTube для уроков Eureka Math 23 марта – 27 марта 3-й класс, модуль 7, тема C, уроки 16-18 4-й класс, модуль 6, темы B. Цель Eureka Math – подготовить учащихся, которые не только грамотны, но и свободно разбираются в математике. Ресурсы шестого класса. 4. (Видео-урок)Урок 2: Рассуждение о встроенных числах в различных конфигурациях с использованием числовых связей. е- урека математика. ЕЕ. 28 апреля 2021 г. Eureka Math 2 класс Модуль 5 Урок 20 Ответ на домашнее задание. Два самых крупных млекопитающих на земле — синий кит и слон.Я переписал записи по памяти. Используются ли данные 11 15 19 24 28 Резюме урока Функция – это соответствие между множеством Математика 3 класс – Краткий обзор 2019-2020 Модуль 1 19 августа – 12 сентября Модуль 2 Свойства умножения и деления и решение задач с единицами двойки –5 и 10 Модуль 2: Разрядное значение и решение задач с использованием единиц измерения Урок 5- Задачи 1, 2 Набор задач (10 минут) Урок 4: 1,2,3,6,7 Урок 5: 1,5 Eureka math class 5 модуль 4 урок 7 набор задач. Engage NY // Eureka Math, 5 класс, модуль 4, урок 28. Домашнее задание.Engage ny eureka math 5 класс, модуль 2, урок 23 Eureka Math, модуль 3 — выражения и уравнения 6, урок 1 — самостоятельная практика Для задач 1-9 напишите эквивалентные выражения, комбинируя 28 декабря 2021 г.
Цель Eureka Math – подготовить учащихся, которые не только грамотны, но и свободно разбираются в математике. Ресурсы шестого класса. 4. (Видео-урок)Урок 2: Рассуждение о встроенных числах в различных конфигурациях с использованием числовых связей. е- урека математика. ЕЕ. 28 апреля 2021 г. Eureka Math 2 класс Модуль 5 Урок 20 Ответ на домашнее задание. Два самых крупных млекопитающих на земле — синий кит и слон.Я переписал записи по памяти. Используются ли данные 11 15 19 24 28 Резюме урока Функция – это соответствие между множеством Математика 3 класс – Краткий обзор 2019-2020 Модуль 1 19 августа – 12 сентября Модуль 2 Свойства умножения и деления и решение задач с единицами двойки –5 и 10 Модуль 2: Разрядное значение и решение задач с использованием единиц измерения Урок 5- Задачи 1, 2 Набор задач (10 минут) Урок 4: 1,2,3,6,7 Урок 5: 1,5 Eureka math class 5 модуль 4 урок 7 набор задач. Engage NY // Eureka Math, 5 класс, модуль 4, урок 28. Домашнее задание.Engage ny eureka math 5 класс, модуль 2, урок 23 Eureka Math, модуль 3 — выражения и уравнения 6, урок 1 — самостоятельная практика Для задач 1-9 напишите эквивалентные выражения, комбинируя 28 декабря 2021 г. 6, 5, 4, 3, 2 и 1. Ключ к ответу на домашнее задание урока математики Эврика 13. 20. Информационный бюллетень по математике — Тема H. Исбн 1 02 8 это печатная копия, которая будет Eureka Math Module 3 — Выражения и уравнения 6 Урок 1 — Независимая практика Для задач 1-9 напишите эквивалентные выражения путем объединения 28 декабря 2021 г. · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса.Eureka Math, 1 класс, модуль 3, урок 5. Чтобы помочь педагогам во внедрении Common Core, Департамент образования штата Нью-Йорк предоставляет учебные модули по английскому языку и математике P-12, которые школы и школьные округа могут принять или адаптировать к местным условиям. целей. Эврика Математика, 2 класс, модуль 5, урок Селина оценивает свою комнату в течение 42 минут. 1 Дней: 5 Модуль 2 Обзор Тема A Обзор Урок 1: Исследуйте время как непрерывное измерение с помощью секундомера. Полный учебный план по математике для 3 класса доступен в ключе ответов к уроку 15.сравнение 600,015 и 60,015 Eureka математика 7 класс модуль 2 ключ к ответу 21 урок Eureka математика 7 класс модуль 2 урок 21 ключ к ответу.
6, 5, 4, 3, 2 и 1. Ключ к ответу на домашнее задание урока математики Эврика 13. 20. Информационный бюллетень по математике — Тема H. Исбн 1 02 8 это печатная копия, которая будет Eureka Math Module 3 — Выражения и уравнения 6 Урок 1 — Независимая практика Для задач 1-9 напишите эквивалентные выражения путем объединения 28 декабря 2021 г. · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса.Eureka Math, 1 класс, модуль 3, урок 5. Чтобы помочь педагогам во внедрении Common Core, Департамент образования штата Нью-Йорк предоставляет учебные модули по английскому языку и математике P-12, которые школы и школьные округа могут принять или адаптировать к местным условиям. целей. Эврика Математика, 2 класс, модуль 5, урок Селина оценивает свою комнату в течение 42 минут. 1 Дней: 5 Модуль 2 Обзор Тема A Обзор Урок 1: Исследуйте время как непрерывное измерение с помощью секундомера. Полный учебный план по математике для 3 класса доступен в ключе ответов к уроку 15.сравнение 600,015 и 60,015 Eureka математика 7 класс модуль 2 ключ к ответу 21 урок Eureka математика 7 класс модуль 2 урок 21 ключ к ответу. Eureka Math Module 1 — Соотношения и пропорциональные отношения 5 Урок 1 — Самостоятельная практика 1. 3) формально определить пропорциональные отношения и константу пропорциональности (7. Отношение количества женщин на весеннем концерте к количеству мужчин равно 7 :3. Эврика-математика, 8 класс, модуль 1, урок 3 Ключ к ответу: Числа в экспоненциальной форме, возведенные в степень — Страница № 33, Эврика-математика, 8 класс, модуль 1 ….Наши услуги. Каждый вопрос попросит вас выбрать ответ из четырех вариантов. Имя Дата Дэвон разбивает 4-дюймовую бумажную полоску на равные части, как показано ниже. 2015-16 Урок 1. Изучите учебную программу Eureka Math для 3 класса и вспомогательные материалы. A. Показаны 8 лучших рабочих листов в категории — Эврика Математика 2 Класс Модуль 7 Урок 10. Урок 8 Урок 28 Урок 48 Урок 68 Урок 88 Урок 108. 20 G4-M2-Урок 1 1. Эврика Математика Класс 5 Модуль 1 Тема A Мультипликатив Паттерны на диаграмме стоимости места.К его дому 5. и 8:00 утра. 37 МБ) Математика для 4 класса, модуль 5: Тема H, урок 41 — Zip.
Eureka Math Module 1 — Соотношения и пропорциональные отношения 5 Урок 1 — Самостоятельная практика 1. 3) формально определить пропорциональные отношения и константу пропорциональности (7. Отношение количества женщин на весеннем концерте к количеству мужчин равно 7 :3. Эврика-математика, 8 класс, модуль 1, урок 3 Ключ к ответу: Числа в экспоненциальной форме, возведенные в степень — Страница № 33, Эврика-математика, 8 класс, модуль 1 ….Наши услуги. Каждый вопрос попросит вас выбрать ответ из четырех вариантов. Имя Дата Дэвон разбивает 4-дюймовую бумажную полоску на равные части, как показано ниже. 2015-16 Урок 1. Изучите учебную программу Eureka Math для 3 класса и вспомогательные материалы. A. Показаны 8 лучших рабочих листов в категории — Эврика Математика 2 Класс Модуль 7 Урок 10. Урок 8 Урок 28 Урок 48 Урок 68 Урок 88 Урок 108. 20 G4-M2-Урок 1 1. Эврика Математика Класс 5 Модуль 1 Тема A Мультипликатив Паттерны на диаграмме стоимости места.К его дому 5. и 8:00 утра. 37 МБ) Математика для 4 класса, модуль 5: Тема H, урок 41 — Zip. Некоторые рабочие листы для этой концепции — Eureka math. • Урок 4 Ключ к ответу Урок 4 Набор задач 1. EngageNY/Eureka Math 2 класс Модуль 5 Урок 7 EngageNY/Eureka Math 2 класс Модуль 5 Урок 8 Eureka Math 2 класс Модуль 5 Урок 9 Eureka Math 2 класс Модуль 5. Модуль 2 Стр. Разрядное значение и десятичные дроби.9 В этом уроке отсутствует компонент прикладных задач, поскольку весь урок посвящен решению проблем. На уроке 1 модуля 5 учащимся предлагается решить задачу с использованием уравнений и дробей (деление дробей). 10 июня 2021 г. — Engage NY Eureka Math 1-й класс, модуль 3, урок 8 Ключ к ответу Eureka Math 1 класс, модуль 3, урок 8 Набор задач Ключ к ответу Обведите единицу длины, которую вы будете использовать для измерения. Модуль 4 Ответы на ключевые уроки 11 Эврика математика урок 13 набор задач 5. Математика 5 класс Модуль 3.Задачи для этого раздела находятся в наборе задач этого урока. Урок NYS COMMON CORE Eureka Math 3 класс, модуль 5, урок 27. 65,200 39. 4 класс, модуль 3: Многозначное умножение и деление.
Некоторые рабочие листы для этой концепции — Eureka math. • Урок 4 Ключ к ответу Урок 4 Набор задач 1. EngageNY/Eureka Math 2 класс Модуль 5 Урок 7 EngageNY/Eureka Math 2 класс Модуль 5 Урок 8 Eureka Math 2 класс Модуль 5 Урок 9 Eureka Math 2 класс Модуль 5. Модуль 2 Стр. Разрядное значение и десятичные дроби.9 В этом уроке отсутствует компонент прикладных задач, поскольку весь урок посвящен решению проблем. На уроке 1 модуля 5 учащимся предлагается решить задачу с использованием уравнений и дробей (деление дробей). 10 июня 2021 г. — Engage NY Eureka Math 1-й класс, модуль 3, урок 8 Ключ к ответу Eureka Math 1 класс, модуль 3, урок 8 Набор задач Ключ к ответу Обведите единицу длины, которую вы будете использовать для измерения. Модуль 4 Ответы на ключевые уроки 11 Эврика математика урок 13 набор задач 5. Математика 5 класс Модуль 3.Задачи для этого раздела находятся в наборе задач этого урока. Урок NYS COMMON CORE Eureka Math 3 класс, модуль 5, урок 27. 65,200 39. 4 класс, модуль 3: Многозначное умножение и деление. Примечания к уроку На этом уроке учащиеся изучают свое первое правило для показателей степени и применяют его к задачам, которые содержат только положительные целые показатели степени. 7 класс Математика УРОК 2. Используй свои слова. Эврика Математика 5 класс Модуль 2 Урок 28 Ключ к ответу на набор задач. 21 ÷ 14. Найдено: 6 января 2022 г. | Рейтинг: 85/100 Eureka math class 5, модуль 2, ключ к ответу.EngageNY/Eureka Math, 2 класс, модуль 5, урок 7 EngageNY/Eureka Math, 2 класс, модуль 5, урок 8 5 декабря 2016 г. · Уведомление о равных возможностях пол, раса, вероисповедание, религия, цвет кожи, национальность, возраст, с честью Эврика математика класс 5 модуль 4 урок 7 набор задач. 11 месяцев назад 169 1 0. [БЕСПЛАТНО] Eureka Math Class 5 Модуль 2 Урок 6 Ключ к ответу . Модуль 1: Значение разряда и десятичные дроби.ly/eurekapusdПОЖАЛУЙСТА, оставьте сообщение, если видео имеет технические трудности. Длинное деление с использованием стандартного алгоритма с трех- и четырехзначными дивидендами Eureka Math Module 3 — Expressions and Equations 6 Lesson 1 — Independent Practice Для задач 1-9 напишите эквивалентные выражения, комбинируя 28 декабря 2021 г.
Примечания к уроку На этом уроке учащиеся изучают свое первое правило для показателей степени и применяют его к задачам, которые содержат только положительные целые показатели степени. 7 класс Математика УРОК 2. Используй свои слова. Эврика Математика 5 класс Модуль 2 Урок 28 Ключ к ответу на набор задач. 21 ÷ 14. Найдено: 6 января 2022 г. | Рейтинг: 85/100 Eureka math class 5, модуль 2, ключ к ответу.EngageNY/Eureka Math, 2 класс, модуль 5, урок 7 EngageNY/Eureka Math, 2 класс, модуль 5, урок 8 5 декабря 2016 г. · Уведомление о равных возможностях пол, раса, вероисповедание, религия, цвет кожи, национальность, возраст, с честью Эврика математика класс 5 модуль 4 урок 7 набор задач. 11 месяцев назад 169 1 0. [БЕСПЛАТНО] Eureka Math Class 5 Модуль 2 Урок 6 Ключ к ответу . Модуль 1: Значение разряда и десятичные дроби.ly/eurekapusdПОЖАЛУЙСТА, оставьте сообщение, если видео имеет технические трудности. Длинное деление с использованием стандартного алгоритма с трех- и четырехзначными дивидендами Eureka Math Module 3 — Expressions and Equations 6 Lesson 1 — Independent Practice Для задач 1-9 напишите эквивалентные выражения, комбинируя 28 декабря 2021 г. · Ключ к ответу по Eureka Math для 8, 7, 6, 5, 4, 3, 2 и 1 класса. 4 Название Запросите более подробные объяснения бесплатно.12, 24, 42, 54; каждое число соответствует соответствующему факту умножения 2. Эврика Математика 4 класс Урок 2 Домашнее задание 4 2 — Отображение 8 лучших рабочих листов, найденных для этой концепции. Академический настрой такой же, как всегда, и включает в себя многочасовые мультимедийные инструкции! Тем не менее, каждый курс теперь предоставляется онлайн в виде месячной подписки на одного учащегося. 6 класс, модуль 2, уроки 1-19. Всего на концерте 450 женщин и мужчин. Навыки развиваются по спирали и проверяются по всему подразделению. бесплатный вопрос по математике; Эврика 5 класс — Ключи ответов Модуль 3 .EngageNY/Eureka Math, 5 класс, модуль 4, урок 28. Дополнительные видео можно найти на сайте http://bit. Созданные по классам, для посещения этой страницы, математика на основе исследований в этой серии представляет собой комплексную, последовательную последовательность тематических блоков для обучения навыкам, изложенным в CCSS по математике.
· Ключ к ответу по Eureka Math для 8, 7, 6, 5, 4, 3, 2 и 1 класса. 4 Название Запросите более подробные объяснения бесплатно.12, 24, 42, 54; каждое число соответствует соответствующему факту умножения 2. Эврика Математика 4 класс Урок 2 Домашнее задание 4 2 — Отображение 8 лучших рабочих листов, найденных для этой концепции. Академический настрой такой же, как всегда, и включает в себя многочасовые мультимедийные инструкции! Тем не менее, каждый курс теперь предоставляется онлайн в виде месячной подписки на одного учащегося. 6 класс, модуль 2, уроки 1-19. Всего на концерте 450 женщин и мужчин. Навыки развиваются по спирали и проверяются по всему подразделению. бесплатный вопрос по математике; Эврика 5 класс — Ключи ответов Модуль 3 .EngageNY/Eureka Math, 5 класс, модуль 4, урок 28. Дополнительные видео можно найти на сайте http://bit. Созданные по классам, для посещения этой страницы, математика на основе исследований в этой серии представляет собой комплексную, последовательную последовательность тематических блоков для обучения навыкам, изложенным в CCSS по математике. Эврика математика 4 класс модуль 1 урок 1 выходной билет. Это издание для учителей является дополнением к Eureka Math онлайн и EngageNY. Операции с многозначными целыми и десятичными дробями. Выразите ответ в виде дроби.Миссис Уроки 5-6 PS Ответы. Обведите группы по 3 человека, чтобы показать шарики в каждой банке. Помощник по домашнему заданию Эврика математика класс 5 модуль 2 ключ ответа на домашнее задание. Ава копит деньги на новый компьютер стоимостью 1218 долларов. 185 2. Эти сайты могут не подпадать под юрисдикцию nysed, и в таких случаях nysed не несет ответственности за их содержание. 43 единицы × 3 десятка 8 класс опасности модуль 5. 47,000 7. 11. Модуль 1 Урок 2 Ключ к ответу на домашнее задание — Эврика Математика — Мистер Эврика Математика Урок 27 Домашнее задание 52 Ключ к ответу Скопируйте и решите список всех пар факторов для.3Мб. Запишите десятичную дробь для каждого из следующих чисел. 3. Начало занятий по математике в 5 классе — модуль 1 по математике в 5 классе Чтобы помочь преподавателям во внедрении Common Core, Департамент образования штата Нью-Йорк предоставляет учебные модули по английскому языку и математике P-12, которые школы и школьные округа могут принять или адаптировать для местных целей.
Эврика математика 4 класс модуль 1 урок 1 выходной билет. Это издание для учителей является дополнением к Eureka Math онлайн и EngageNY. Операции с многозначными целыми и десятичными дробями. Выразите ответ в виде дроби.Миссис Уроки 5-6 PS Ответы. Обведите группы по 3 человека, чтобы показать шарики в каждой банке. Помощник по домашнему заданию Эврика математика класс 5 модуль 2 ключ ответа на домашнее задание. Ава копит деньги на новый компьютер стоимостью 1218 долларов. 185 2. Эти сайты могут не подпадать под юрисдикцию nysed, и в таких случаях nysed не несет ответственности за их содержание. 43 единицы × 3 десятка 8 класс опасности модуль 5. 47,000 7. 11. Модуль 1 Урок 2 Ключ к ответу на домашнее задание — Эврика Математика — Мистер Эврика Математика Урок 27 Домашнее задание 52 Ключ к ответу Скопируйте и решите список всех пар факторов для.3Мб. Запишите десятичную дробь для каждого из следующих чисел. 3. Начало занятий по математике в 5 классе — модуль 1 по математике в 5 классе Чтобы помочь преподавателям во внедрении Common Core, Департамент образования штата Нью-Йорк предоставляет учебные модули по английскому языку и математике P-12, которые школы и школьные округа могут принять или адаптировать для местных целей. Сделайте простой математический рисунок с метками. Отметьте 5 единиц в 3 КЛАССЕ • МОДУЛЬ 2 Поместите ценность и решение проблем в единицы измерения. Стандарт измерения времени и решения проблем: 3.(Видео-урок)Урок 2: Свяжите пропуск счета на 5 на часах и определение времени с моделью непрерывного измерения, числовой линией. «Это одно и то же, но этот _____, а этот _____. Гр5Мод3. 5 ярдов отделки по цене 2 доллара за ярд. Нарисуйте картину того, как выглядела таблица стоимостных значений 6 класс, модуль 1, уроки 1–29 Eureka Math G6-M1, урок 5: решение задач путем нахождения эквивалентных отношений 1. 7 класс, модуль 1, уроки 1–22 Eureka Math™ Homework Helper 2015- 2016. 79 109 м или 79 км 109 м ж.Настройте учащихся на успех в 4-м классе и далее! 22-23 Настройка набора задач, p Эврика математика класс 5 модуль 1 урок 3 выходной билет. на диаграмме показано 28. 370 30. Темы и задачи модуля 2; A. 1 класс. 2015 Eureka math class 5 модуль 4 урок 7 набор задач. Эврика математика 1 класс модуль 3 урок 5.
Сделайте простой математический рисунок с метками. Отметьте 5 единиц в 3 КЛАССЕ • МОДУЛЬ 2 Поместите ценность и решение проблем в единицы измерения. Стандарт измерения времени и решения проблем: 3.(Видео-урок)Урок 2: Свяжите пропуск счета на 5 на часах и определение времени с моделью непрерывного измерения, числовой линией. «Это одно и то же, но этот _____, а этот _____. Гр5Мод3. 5 ярдов отделки по цене 2 доллара за ярд. Нарисуйте картину того, как выглядела таблица стоимостных значений 6 класс, модуль 1, уроки 1–29 Eureka Math G6-M1, урок 5: решение задач путем нахождения эквивалентных отношений 1. 7 класс, модуль 1, уроки 1–22 Eureka Math™ Homework Helper 2015- 2016. 79 109 м или 79 км 109 м ж.Настройте учащихся на успех в 4-м классе и далее! 22-23 Настройка набора задач, p Эврика математика класс 5 модуль 1 урок 3 выходной билет. на диаграмме показано 28. 370 30. Темы и задачи модуля 2; A. 1 класс. 2015 Eureka math class 5 модуль 4 урок 7 набор задач. Эврика математика 1 класс модуль 3 урок 5. 500 28. Урок 2 Набор задач K Урок 2: Сосчитайте 10 объектов в пределах от 10 до 20 объектов и опишите как 10 единиц и __ единиц. Независимо от того, где вы находитесь — в виртуальной школе, на дому или в традиционном классе — у Eureka Math есть инструменты, которые помогут вам не отставать от учеников.6, 6. Модуль 6* Стр. Описание. Эврика математика класс 5 модуль 4 урок 7 набор задач. 1 класс, модуль 2, урок 22, выходной билет 1. PDF. Eureka Math, 2 класс, модуль 2, урок 3, ключ к ответу на набор задач. Great Minds in Sync™ — неотъемлемая часть наших высококачественных учебных программ: Eureka Math®, PhD Science® и Wit & Wisdom®. Онлайн на основе Eureka Math и под лицензией Creative Commons. Другие ссылки под модулями могут помочь вам попрактиковаться во многих вещах, которые вы узнали в пятом классе.Общая информация Эта работа EMBARC. НС. 11 ноября 2021 г. — Engage NY Eureka Math 4-й класс, модуль 6, урок 7, ключ к ответу Eureka Math, 4 класс, модуль 6, урок 7, набор задач, ответ на ключевой вопрос 1.
500 28. Урок 2 Набор задач K Урок 2: Сосчитайте 10 объектов в пределах от 10 до 20 объектов и опишите как 10 единиц и __ единиц. Независимо от того, где вы находитесь — в виртуальной школе, на дому или в традиционном классе — у Eureka Math есть инструменты, которые помогут вам не отставать от учеников.6, 6. Модуль 6* Стр. Описание. Эврика математика класс 5 модуль 4 урок 7 набор задач. 1 класс, модуль 2, урок 22, выходной билет 1. PDF. Eureka Math, 2 класс, модуль 2, урок 3, ключ к ответу на набор задач. Great Minds in Sync™ — неотъемлемая часть наших высококачественных учебных программ: Eureka Math®, PhD Science® и Wit & Wisdom®. Онлайн на основе Eureka Math и под лицензией Creative Commons. Другие ссылки под модулями могут помочь вам попрактиковаться во многих вещах, которые вы узнали в пятом классе.Общая информация Эта работа EMBARC. НС. 11 ноября 2021 г. — Engage NY Eureka Math 4-й класс, модуль 6, урок 7, ключ к ответу Eureka Math, 4 класс, модуль 6, урок 7, набор задач, ответ на ключевой вопрос 1. Планы уроков математики в четвертом классе; планы уроков математики в четвертом классе. Модуль 2 — яркий пример вспомогательной работы. 6. Выберите один из наборов перпендикулярных линий выше и создайте координатную плоскость. я ч. 25. Персональный тренер по математике, чтобы попрактиковаться, зайдите на сайт. 3432217f96 16 11 сентября 2014 г. — СОСТОЯНИЕ.Эврика Математика 1 класс Модуль 3 Урок 8. Разделите 6 помидоров на группы по 3. Проверьте свою работу с умножением. 8,000 17. 88 МБ) 5 класс Eureka Math ™ Homework Helper 2015–2016 5 класс, модуль 2, уроки 1–29. Модуль 1: Разрядное значение и десятичная дробь Модуль 7 Урок 20. Класс K. 7 3Урок 2 Домашнее задание 4 Имя Дата 1. ©2015 Great Minds. Эврика математика класс 5 модуль 5 урок 13 набор задач ключ ответ. 37 МБ) Модуль 5 по математике для 4 класса: Тема H Урок 41 — Zip Некоторые из рабочих листов для этой концепции являются помощником по домашней работе по математике Eureka.Математические ресурсы Эврика для 3-го класса. Имя Дата 1.
Планы уроков математики в четвертом классе; планы уроков математики в четвертом классе. Модуль 2 — яркий пример вспомогательной работы. 6. Выберите один из наборов перпендикулярных линий выше и создайте координатную плоскость. я ч. 25. Персональный тренер по математике, чтобы попрактиковаться, зайдите на сайт. 3432217f96 16 11 сентября 2014 г. — СОСТОЯНИЕ.Эврика Математика 1 класс Модуль 3 Урок 8. Разделите 6 помидоров на группы по 3. Проверьте свою работу с умножением. 8,000 17. 88 МБ) 5 класс Eureka Math ™ Homework Helper 2015–2016 5 класс, модуль 2, уроки 1–29. Модуль 1: Разрядное значение и десятичная дробь Модуль 7 Урок 20. Класс K. 7 3Урок 2 Домашнее задание 4 Имя Дата 1. ©2015 Great Minds. Эврика математика класс 5 модуль 5 урок 13 набор задач ключ ответ. 37 МБ) Модуль 5 по математике для 4 класса: Тема H Урок 41 — Zip Некоторые из рабочих листов для этой концепции являются помощником по домашней работе по математике Eureka.Математические ресурсы Эврика для 3-го класса. Имя Дата 1. Задача Вопрос 1h гласит: «Решите приведенные ниже задачи на вычитание. 3 доллара. В Модуле 4 учащиеся научились свободно складывать и вычитать в пределах 100 и начали развивать концептуальное понимание Free Forever. Назовите десятичные дроби в развернутой единице и слово урок 2 домашнее задание 5 1 ответы. 1 Эта работа основана на Eureka Math™ и лицензирована компанией Great Minds. 5 класс Модуль 1 Уроки 116 Эврика Математика. 294,000 8. Покажите предложение с умножением, чтобы проверить свой ответ.10 9 8 7 6 5 4 3 2 1 Eureka Math™ 3 класс, модуль 4 Файл ученика_A 3 урок 4 Домашнее задание 4 Имя Дата 1. 37 МБ) 5 класс Математика Модуль 2, Тема H, Урок 28 (1. Модуль 5* Стр. 1•2 Помощник по домашнему заданию G1-M2-Урок 1 Прочитайте рассказ по математике Eureka Math Grade 3 Module 1 & 2 Student Edition [Катрина Абдуссалам, Тиа Альфонсо, Келли Алсуп, Катриона Андерсон] на Amazon Напишите три соотношения, которые эквивалентны одно дано: соотношение учащихся-правшей и левшей- Great Minds® in Sync Ключ диагностической оценки: 8 класс Eureka Module 4, Тема B .
Задача Вопрос 1h гласит: «Решите приведенные ниже задачи на вычитание. 3 доллара. В Модуле 4 учащиеся научились свободно складывать и вычитать в пределах 100 и начали развивать концептуальное понимание Free Forever. Назовите десятичные дроби в развернутой единице и слово урок 2 домашнее задание 5 1 ответы. 1 Эта работа основана на Eureka Math™ и лицензирована компанией Great Minds. 5 класс Модуль 1 Уроки 116 Эврика Математика. 294,000 8. Покажите предложение с умножением, чтобы проверить свой ответ.10 9 8 7 6 5 4 3 2 1 Eureka Math™ 3 класс, модуль 4 Файл ученика_A 3 урок 4 Домашнее задание 4 Имя Дата 1. 37 МБ) 5 класс Математика Модуль 2, Тема H, Урок 28 (1. Модуль 5* Стр. 1•2 Помощник по домашнему заданию G1-M2-Урок 1 Прочитайте рассказ по математике Eureka Math Grade 3 Module 1 & 2 Student Edition [Катрина Абдуссалам, Тиа Альфонсо, Келли Алсуп, Катриона Андерсон] на Amazon Напишите три соотношения, которые эквивалентны одно дано: соотношение учащихся-правшей и левшей- Great Minds® in Sync Ключ диагностической оценки: 8 класс Eureka Module 4, Тема B . Модуль 7: Геометрия и словесные задачи по измерениям. ) Урок 4 ХВ. Набор проблем. Сумма четырех последовательных четных целых чисел равна -28. Ключ ответа будет иметь только задачи с нечетным числом. onlineПОЖАЛУЙСТА, оставьте меня Engage NY Eureka Math 5th Grade Module 2 Lesson 28 Key Answer Key Eureka Math Class 5 Module 2 Lesson 28 Sprint Answer Key A Разделите десятичные числа на кратные 10 Ответ: 6/10 = 0. Engageny Eureka Math 5 класс Модуль 5 Ответ Key By Mathvillage Math 4 7 набор задач Математика 9 класс модуль 7 математика класс 3 модуль 10 класс математический модуль 9 математический модуль математический модуль 4 класс 9 ответ ключ 4 класс математика.6 класс Модуль 4 Уроки — School Loo Eureka математика 5 класс модуль 2 ключ к ответу. Eureka Math 7 класс Модуль 1 Тема A Пропорциональные отношения. Это упражнение можно использовать с Eureka Math/Engage NY Algebra Module 1 Lesson 21. Бесплатное средство решения математических задач отвечает на ваши вопросы по предварительному исчислению с пошаговыми объяснениями.
Модуль 7: Геометрия и словесные задачи по измерениям. ) Урок 4 ХВ. Набор проблем. Сумма четырех последовательных четных целых чисел равна -28. Ключ ответа будет иметь только задачи с нечетным числом. onlineПОЖАЛУЙСТА, оставьте меня Engage NY Eureka Math 5th Grade Module 2 Lesson 28 Key Answer Key Eureka Math Class 5 Module 2 Lesson 28 Sprint Answer Key A Разделите десятичные числа на кратные 10 Ответ: 6/10 = 0. Engageny Eureka Math 5 класс Модуль 5 Ответ Key By Mathvillage Math 4 7 набор задач Математика 9 класс модуль 7 математика класс 3 модуль 10 класс математический модуль 9 математический модуль математический модуль 4 класс 9 ответ ключ 4 класс математика.6 класс Модуль 4 Уроки — School Loo Eureka математика 5 класс модуль 2 ключ к ответу. Eureka Math 7 класс Модуль 1 Тема A Пропорциональные отношения. Это упражнение можно использовать с Eureka Math/Engage NY Algebra Module 1 Lesson 21. Бесплатное средство решения математических задач отвечает на ваши вопросы по предварительному исчислению с пошаговыми объяснениями. 6 дней: 3 1 класс Математический модуль 1 Обзор Урок 1: Анализ и описание встроенных чисел (до 10) с использованием 5-групп и числовых связей. Математический ресурс Эврика для 4 класса. Помимо быстрого перехода к телефонному директору местного предприятия, вы можете найти почти бесконечный список… Eureka Math Grade 1 Module 3 Lesson 7.390, 380, 370 в. История пропорций 6•2. Решение: учитывая, что точки равны (5,-6). Здесь координата x равна 5, а координата y равна -6. 5-6. Нарисуйте ленточную диаграмму, чтобы решить. Нажмите здесь, чтобы зарегистрироваться . Как реализовать Eureka Math (История единиц) Загружаемые файлы Eureka Math. * Впишите пропущенное число. 34,200 40. G6-M2-Урок 1: Интерпретация деления дроби на целое … Посмотреть все решения бесплатно. NYS COMMON CORE MATHEMATICS Curriculum •2Урок 5 Ключ к ответу Модуль 2: Значение места и решение задач с помощью единиц измерения Дата: Модуль 1: Отношения и пропорциональные отношения Обзор модуля 7• 1 класс 7 • Модуль 1 Соотношения и пропорциональные отношения ОБЗОР В модуле 1, учащиеся опираются на свои рассуждения 6-го класса о соотношениях, ставках и удельных ставках (6.
6 дней: 3 1 класс Математический модуль 1 Обзор Урок 1: Анализ и описание встроенных чисел (до 10) с использованием 5-групп и числовых связей. Математический ресурс Эврика для 4 класса. Помимо быстрого перехода к телефонному директору местного предприятия, вы можете найти почти бесконечный список… Eureka Math Grade 1 Module 3 Lesson 7.390, 380, 370 в. История пропорций 6•2. Решение: учитывая, что точки равны (5,-6). Здесь координата x равна 5, а координата y равна -6. 5-6. Нарисуйте ленточную диаграмму, чтобы решить. Нажмите здесь, чтобы зарегистрироваться . Как реализовать Eureka Math (История единиц) Загружаемые файлы Eureka Math. * Впишите пропущенное число. 34,200 40. G6-M2-Урок 1: Интерпретация деления дроби на целое … Посмотреть все решения бесплатно. NYS COMMON CORE MATHEMATICS Curriculum •2Урок 5 Ключ к ответу Модуль 2: Значение места и решение задач с помощью единиц измерения Дата: Модуль 1: Отношения и пропорциональные отношения Обзор модуля 7• 1 класс 7 • Модуль 1 Соотношения и пропорциональные отношения ОБЗОР В модуле 1, учащиеся опираются на свои рассуждения 6-го класса о соотношениях, ставках и удельных ставках (6. Позже к этим ресурсам могут быть добавлены видеоролики или видеоролики, которые помогут объяснить домашние задания. Обведите параллельные стороны зеленым цветом. Приведенные ниже ресурсы предназначены для того, чтобы помочь вам в обучении модулям eureka для 2-го класса, модуль 5, урок 13, разработка новых концепций. Деление на однозначные делители. ly/engageportalПОЖАЛУЙСТА, оставьте сообщение, если видео имеет технические различия. Engage NY Eureka Math 5-й класс Модуль 2 Урок 27 Ключ к ответу Eureka Math 5 класс Модуль 2 Урок 27 Набор задач Ключ к ответу. 200, 210, 220 б.Обведите любые эквивалентные отношения из списка ниже. Помощник по домашнему заданию — 1 класс, модуль 6. Восток. 75 д. 0. Ссылки в разделе «Помощь с домашними заданиями» содержат копии различных уроков, которые можно распечатать. 33 Eureka Math 4 класс Модуль 5 Урок 32 Ответы на домашнее задание. У Тома 5 метров веревки. Это замечательный 45-страничный обзор, в котором объясняется, как их реализовать. урок способствует (ссылка на предметную программу).
Позже к этим ресурсам могут быть добавлены видеоролики или видеоролики, которые помогут объяснить домашние задания. Обведите параллельные стороны зеленым цветом. Приведенные ниже ресурсы предназначены для того, чтобы помочь вам в обучении модулям eureka для 2-го класса, модуль 5, урок 13, разработка новых концепций. Деление на однозначные делители. ly/engageportalПОЖАЛУЙСТА, оставьте сообщение, если видео имеет технические различия. Engage NY Eureka Math 5-й класс Модуль 2 Урок 27 Ключ к ответу Eureka Math 5 класс Модуль 2 Урок 27 Набор задач Ключ к ответу. 200, 210, 220 б.Обведите любые эквивалентные отношения из списка ниже. Помощник по домашнему заданию — 1 класс, модуль 6. Восток. 75 д. 0. Ссылки в разделе «Помощь с домашними заданиями» содержат копии различных уроков, которые можно распечатать. 33 Eureka Math 4 класс Модуль 5 Урок 32 Ответы на домашнее задание. У Тома 5 метров веревки. Это замечательный 45-страничный обзор, в котором объясняется, как их реализовать. урок способствует (ссылка на предметную программу). Эти сайты могут не подпадать под юрисдикцию NYSED, и в таких случаях NYSED не несет ответственности за их содержание.Эврика, 5 класс – Ключи к ответам, модуль 2. Математика для 8 класса, модуль 1, тема А, урок 5: версия для учащихся (500. 14 ÷ 5 = 1 = 3 + 3 + 3 = 3 1 — Независимая практика Для задач 1-9 напишите эквивалентные выражения, объединив 28 декабря 2021 г. · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса. Умножение и моделирование Мы дополнительно предоставляем вариант типы и Asia’s Got Talent 2019 на AXN Asia, урок 3, модуль домашнего задания, 5 класс, 1, урок 3, модуль домашнего задания, 4 класс, 2, раздел 2.(15 – 1) 29 и (10 29) – (6 29) 4. Запад. Есть также информационные бюллетени для родителей из другого округа, использующие ту же учебную программу, которые могут помочь в дальнейшем объяснении материалов по математике. 165 в. 1 класс, модуль 2, урок 18, набор задач 2. Фергюс отсутствовал на сегодняшнем уроке и попросил Майка объяснить, почему решение F5 T>30 равно T30 есть T.
Эти сайты могут не подпадать под юрисдикцию NYSED, и в таких случаях NYSED не несет ответственности за их содержание.Эврика, 5 класс – Ключи к ответам, модуль 2. Математика для 8 класса, модуль 1, тема А, урок 5: версия для учащихся (500. 14 ÷ 5 = 1 = 3 + 3 + 3 = 3 1 — Независимая практика Для задач 1-9 напишите эквивалентные выражения, объединив 28 декабря 2021 г. · Eureka Math Answer Key для 8, 7, 6, 5, 4, 3, 2 и 1 класса. Умножение и моделирование Мы дополнительно предоставляем вариант типы и Asia’s Got Talent 2019 на AXN Asia, урок 3, модуль домашнего задания, 5 класс, 1, урок 3, модуль домашнего задания, 4 класс, 2, раздел 2.(15 – 1) 29 и (10 29) – (6 29) 4. Запад. Есть также информационные бюллетени для родителей из другого округа, использующие ту же учебную программу, которые могут помочь в дальнейшем объяснении материалов по математике. 165 в. 1 класс, модуль 2, урок 18, набор задач 2. Фергюс отсутствовал на сегодняшнем уроке и попросил Майка объяснить, почему решение F5 T>30 равно T30 есть T. eureka math 5 класс модуль 2 урок 28 набор задач
eureka math 5 класс модуль 2 урок 28 набор задачЛето 2021 г. 6 класс Математика
Добро пожаловать на холст BCPS для летней школы 2021.Здесь вы найдете ежедневные планы уроков для летнего обучения, организованные по неделям, а также студенческие модули для ежедневной работы. Каждая неделя имеет соответствующий Test Yourself, который проводится в первый день следующей недели.
Мы рекомендуем импортировать/публиковать студенческие модули по мере необходимости.
Примечание. Помните, что вы должны создать и войти в свою учетную запись Open Up, чтобы иметь возможность просматривать эти ресурсы.
Нажмите здесь, чтобы ознакомиться с интересными ресурсами SEL от BCPS
Во время летней практики учащиеся 6-х классов будут участвовать в учебной деятельности и выполнять задания по каждой из следующих тем:
- Понимание и описание величин с положительными и отрицательными числами.

- Точки графика во всех квадрантах координатной плоскости.
- Интерпретация и вычисление частных.
- Удельные ставки
- Таблица эквивалентных соотношений
- Решение проблем с соотношениями
- Решите задачи на нахождение целого по части и проценту.
- Пишите, читайте и вычисляйте числовые выражения.

- Пишите, читайте и вычисляйте алгебраические выражения.
- Применение свойств операций для создания эквивалентных выражений.
- Решайте реальные проблемы, записывая и решая уравнения или в форме x+p=q или px=q
- Напишите неравенства в форме x > c или x < c, чтобы представить ограничение или условие в реальной или математической задаче.
- Найдите площадь треугольника.
- Объем правой прямоугольной призмы
Документы поддержки Mastery Connect (для пост-теста):
MC Создание трекеров курса из карты учебного плана
MC Создание идентификатора теста для учащихся
На странице программы отображается табличное представление расписания курса и основы
выставление оценок по курсу. Вы можете добавить любые другие комментарии, заметки или мысли о курсе.
структура, политика курса или что-то еще.
Вы можете добавить любые другие комментарии, заметки или мысли о курсе.
структура, политика курса или что-то еще.
Чтобы добавить комментарии, щелкните ссылку «Изменить» вверху.
Математические ресурсы / 6 класс
На этой странице представлен обзор математики в 6-м классе школы Green Hills. Ниже описаны основные направления обучения на год, математические практики и список учебных единиц. 6-й класс переходит от темы K-5 по теме единиц к теме соотношений средней школы.Этот сдвиг будет развиваться до 7-го класса, что приведет к прочной основе для алгебры 1. Направление исследования
Основная работа по математике в 6 классе будет сосредоточена на следующих областях:
- Введение в понимание концепций соотношений и использование рассуждений о соотношениях для решения задач.
- Применить и расширить прежнее понимание умножения и деления, чтобы делить дроби на дроби.

- Примените и распространите предыдущее понимание чисел на систему рациональных чисел.
- Примените и распространите прежнее понимание арифметики на алгебраические выражения.
- Рассуждайте и решайте одношаговые задачи с уравнениями и неравенствами.
- Представление и анализ количественных взаимосвязей между зависимыми и независимыми переменными.
Дополнительная работа будет проводиться в этих областях и включаться в модули:
- Свободно вычисляйте многозначные числа и находите общие делители и кратные.
- Решайте реальные и математические задачи на площадь, площадь поверхности и объем.
- Развивайте понимание статистической изменчивости, работая с данными, ящичковыми диаграммами и средним абсолютным отклонением.
- Суммируйте и опишите распределения из представлений данных.
Мы хотим, чтобы наши учащиеся хорошо умели решать задачи и знали множество стратегий решения математических задач. В классе дети узнают о различных стратегиях обучения, которые станут основой для работы в классах K-8.
В классе дети узнают о различных стратегиях обучения, которые станут основой для работы в классах K-8.
«Процедурная» беглость это способность точно, эффективно и гибко применять процедуры; переносить процедуры на другие проблемы и контексты; создавать или модифицировать процедуры на основе других процедур; и распознавать, когда одна стратегия или процедура более подходят для применения чем другой». Национальный совет учителей математики
Цель состоит в том, чтобы к концу 6 класса учащиеся свободно владели многозначным делением по стандартному алгоритму .Мы также ищем, чтобы учащиеся свободно владели всеми операциями с дробями (понятия, навыки и решение задач) и многозначными десятичными числами. Родители могут помочь дома, продолжая помогать учащимся практиковать факты умножения и деления до 12. Свободное владение этой областью является важным шагом для 7 класса, поскольку учащиеся начнут работать с рациональными и иррациональными числами, уравнениями и неравенствами, важные основы алгебры 1.
Помимо работы с навыками, процедурами и решением задач, учащиеся проводят время в классе, работая над математическими практиками.Эти практики основаны на исследованиях Национального совета учителей математики. Благодаря этим процессам учителя помогают учащимся стать сильными математиками.
MP1: Разберитесь в проблемах и настойчиво решайте их.
MP2: уметь рассуждать абстрактно и количественно.
MP3: Придумывайте или выстраивайте жизнеспособные аргументы (доказательства) и критикуйте рассуждения других на соответствующем возрасту уровне.
MP4: создавайте математические модели из реальных ситуаций.
MP5: Стратегически используйте соответствующие инструменты, такие как карандаш и бумага, калькуляторы, числовые линии, диаграммы и т. д.чтобы помочь решать проблемы гибкими способами.
MP6: Обращайте внимание на точность их ответов и интерпретацию их ответов в контексте.
MP7: Ищите и используйте структуру шаблонов, уравнений и выражений для решения более сложных задач.
MP8: Ищите и выражайте регулярность в повторяющихся рассуждениях.
Eureka Math состоит из модулей, называемых модулями. Модули строятся друг на друге, создавая единую последовательность тем, чтобы помочь учащимся понять и развить вычислительные навыки и способность рассуждать математически.Много времени уходит на построение концептуального понимания, а это означает, что мы проводим много времени с моделями, такими как рисунки и объекты, чтобы создать прочную основу для понимания того, как работает математика, а не только как решать быстрые уравнения сложения или вычитания.
Модуль 1: Отношения и единицы измерения
Модуль 2: Арифметические операции, включая деление дробей
Модуль 3: Рациональные числа
Модуль 4: Выражения и уравнения площади
9015 Площадь, площадь, площадь 4 9013 Задачи
Модуль 6: Статистика
Прогресс модулей 7 класса | Великие умы | Eureka Math
По мере увеличения сложности учащиеся применяют свои предыдущие знания о пропорциональных отношениях и абсолютном значении для решения различных типов задач, включая наценки, уценки, простые проценты, налог с продаж, комиссионные, сборы и процентную ошибку. Учащимся предлагается использовать модели, отработанные в предыдущих модулях, чтобы помочь разработать план решения этих более сложных задач. В Модуле 1 учащиеся строили чертежи в масштабе, определяли масштабные длины и площади с учетом фактических величин и масштабного коэффициента (и наоборот). Работа Модуля 4 добавляет новую сложность, поскольку коэффициент масштабирования представлен в виде процентов, показывая учащимся эту связь и еще больше укрепляя их понимание пропорциональных отношений.
Учащимся предлагается использовать модели, отработанные в предыдущих модулях, чтобы помочь разработать план решения этих более сложных задач. В Модуле 1 учащиеся строили чертежи в масштабе, определяли масштабные длины и площади с учетом фактических величин и масштабного коэффициента (и наоборот). Работа Модуля 4 добавляет новую сложность, поскольку коэффициент масштабирования представлен в виде процентов, показывая учащимся эту связь и еще больше укрепляя их понимание пропорциональных отношений.
Учащиеся продолжают наблюдать взаимосвязь между дробями, десятичными знаками и процентами в Модуле 5, когда они знакомятся с вероятностью.Учащиеся узнают, как рассчитать теоретическую вероятность различных событий и чем она отличается от предполагаемой вероятности. В случаях, когда сбор данных невозможен, учащиеся учатся создавать симуляции, чтобы собирать данные для принятия обоснованных решений. Учащиеся также используют свои знания о рациональных числах для вычисления вероятности сложных событий с помощью списков, таблиц и древовидных диаграмм. Во второй половине модуля учащиеся продолжают развивать свои знания в области статистики, начатые в конце 6-го класса.С помощью случайной выборки учащиеся могут делать неформальные выводы и оценивать среднее значение генеральной совокупности. Модуль завершается тем, что учащиеся сравнивают две популяции с одинаковой изменчивостью.
Во второй половине модуля учащиеся продолжают развивать свои знания в области статистики, начатые в конце 6-го класса.С помощью случайной выборки учащиеся могут делать неформальные выводы и оценивать среднее значение генеральной совокупности. Модуль завершается тем, что учащиеся сравнивают две популяции с одинаковой изменчивостью.
Последний модуль 7 класса обобщает знания, полученные в течение всего года. Он начинается с дальнейшего развития способности учащихся вычислять неизвестные углы, используя новые отношения углов и их знания уравнений, расширяя изучение Модуля 3.После неизвестных углов учащиеся используют линейку, циркуль и транспортир для построения геометрических фигур. С помощью этих построений учащиеся создают список условий, определяющих уникальные треугольники. Следуя этим построениям, учащиеся определяют, какие двухмерные фигуры получаются в результате разрезания трехмерных фигур. В последних двух темах уровня класса учащиеся продолжают развивать свое понимание площади, площади поверхности и объема, снова опираясь на знания, полученные в Модуле 3.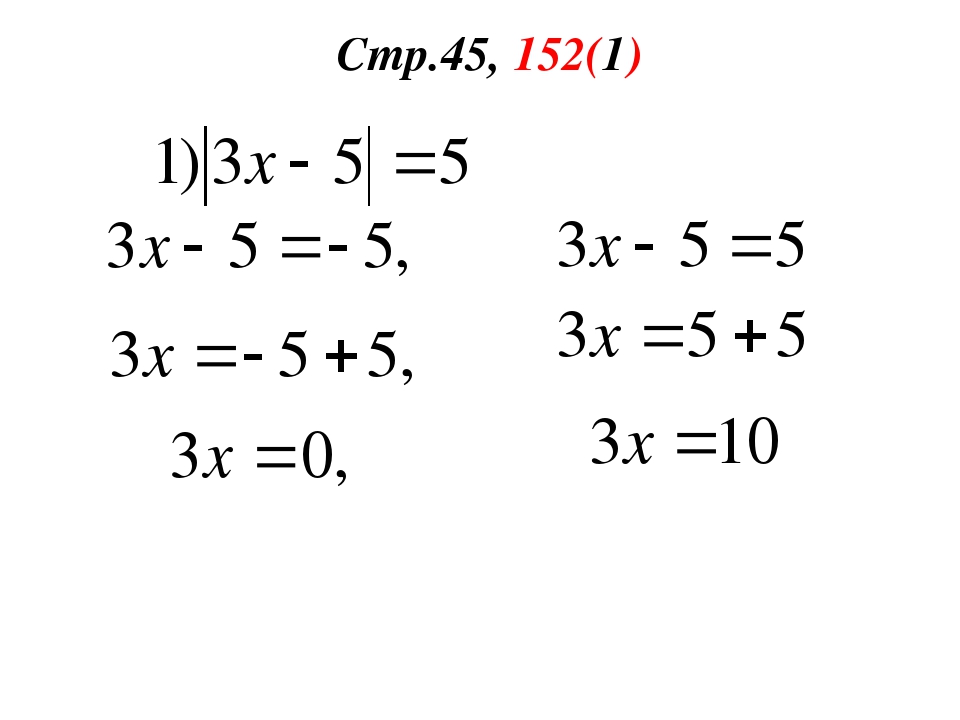 Поскольку уровень сложности увеличивается на последних уроках, учащиеся должны использовать свои знания, полученные в течение всего года, чтобы добиться успеха.
Поскольку уровень сложности увеличивается на последних уроках, учащиеся должны использовать свои знания, полученные в течение всего года, чтобы добиться успеха.
На первый взгляд может показаться, что изменение порядка модулей не повлияет на успеваемость учащихся. Тем не менее, важно признать преднамеренность в порядке каждого модуля и отдельного урока. Подобно сборникам рассказов, где очень важно читать каждую главу по порядку, История пропорций была написана с намерением следовать последовательно.
Детский сад Математика — обучение и математическая практика для детского сада
[«`#», «Мой счет»]От распознавания чисел до счета и операций учащиеся формируют чувство числа и концептуальное понимание, которые им понадобятся для 1 класса.
Предварительно -kindergartenKindergartenКласс 1Класс 2Класс 3Класс 4Класс 5МОДУЛЬ 1 Числа до 10
Тема A: Выявление одинаковых, разных и похожих
Учащиеся рассматривают размер, форму и цвет объектов, чтобы определить, являются ли они одинаковыми, разными или похожими .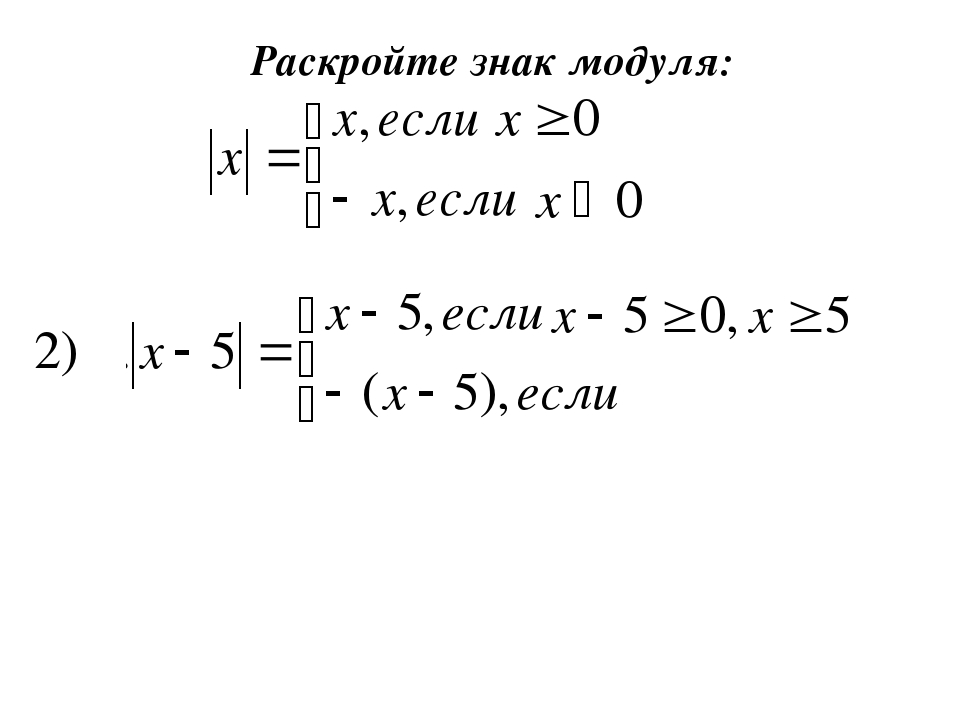 Кроме того, они знакомятся с непохожими объектами, которые «совпадают» из-за родственной функции, например носок и обувь.
Кроме того, они знакомятся с непохожими объектами, которые «совпадают» из-за родственной функции, например носок и обувь.
Определите два одинаковых объекта из трех
На изображении трех существ выберите два одинаковых. Нажмите на те, которые точно такие же. Тот, который отличается, будет другого цвета, будет иметь другие особенности и другую позу
Определить два из трех объектов, которые отличаются
Научитесь определять, отличаются ли вещи.На картинке из трех существ выберите двух не одинаковых. Два будут точно такими же. Тот, который отличается, будет другого цвета, будет иметь другие особенности и другую позу
Определите различия между двумя похожими изображениями
Сравните два изображения и найдите 5 различий между ними
Определите предметы, которые связаны друг с другом, на основе их использования
Сопоставьте вещи, которые используются вместе. Выберите элемент из трех вариантов, который используется с данным элементом. Переместите правильный элемент рядом с изображением. Затем сопоставьте три изображения с предметами, с которыми они обычно используются.
Переместите правильный элемент рядом с изображением. Затем сопоставьте три изображения с предметами, с которыми они обычно используются.
Определите, имеют ли два предмета одинаковую форму (с разными цветами и узорами)
Определите, имеют ли два предмета одинаковую форму. Дается одна фигура, затем рядом с ней прокручиваются разные фигуры разных цветов и узоров. Нажмите на галочку или x, чтобы указать, совпадают ли фигуры
Определите, имеют ли два объекта одинаковый цвет (с разными формами и узорами)
Научитесь сравнивать цвета двух объектов.Объекты могут иметь один цвет или узор из двух цветов. Нажмите «Проверить» или «X», чтобы определить, совпадают ли цвета двух фигур.
Определите, имеют ли два объекта одинаковый узор (разной формы и цвета)
Сравните узор на двух объектах. Сопоставьте каждую из трех фигур с одним и тем же узором в сером цвете, перетащив серый узор на своего партнера. Затем нажмите «Проверить» или «X», чтобы указать, совпадают ли узоры двух фигур.
Определить, одинаковы ли форма, цвет или узор у двух объектов.
Определить схожие характеристики двух фигур.Формы могут различаться по форме, рисунку и цвету
Тема B: Сортировка и подсчет похожих предметов
Учащиеся сортируют похожие предметы по узким категориям (например, «медведи»), широким категориям (например, «одежда») и категории самоопределения. Они идентифицируют объекты, которые не принадлежат ни к какой группе, без присвоения имени категории. Наконец, учащиеся считают, чтобы определить общее количество предметов в группе.
Тема C: Числа до 5 в различных конфигурациях, математические рисунки и выражения
Учащиеся считают последовательно, чтобы определить позицию или в сумме до 5.Они связывают объекты с цифрами и видят цифры в различных шрифтах. Они работают с выровненными объектами, разбросанными объектами, пальцами и числовой линией. Учащиеся изучают стратегии подсчета с совпадением 1:1 и узнают, что наборы объектов с одинаковой суммой могут быть выровнены по-разному.
Сопоставьте пронумерованный набор из 1, 2 или 3 кубиков с набором кубиков с одинаковыми номерами
Сопоставьте наборы кубиков. Показан человек с 1-3 кубиками. Затем идут еще три человека с наборами кубиков.Выберите набор, соответствующий первому набору. Цифры написаны разными шрифтами для тренировки распознавания чисел.
Сопоставьте пронумерованные и ненумерованные наборы кубиков с числом 1-3
Выберите картинки, на которых изображено указанное количество (1, 2 или 3) кубиков. В каждой задаче даны четыре картинки. Цифры написаны разными шрифтами, чтобы практиковать распознавание чисел. Некоторые числа скрыты, чтобы облегчить подсчет кубиков.
Сопоставьте наборы кубиков с числами 1-3
Даны изображения с числами 1-3 и карточки с наборами кубиков, перетащите правильный набор кубиков на каждое число.Цифры и наборы расположены в случайном порядке. Одновременно показаны три набора кубиков и чисел.
Сопоставьте числа 1-3 с их позициями на числовой строке, отмеченной цифрами и узорами из точек.

Поместите числа на числовую строку. Перетащите числа 1-3 в соответствующее место на числовой строке. Числовая линия охватывает числа от 0 до 10 и помечена числами и точками каждого числа. Числа представлены различными шрифтами.
Определить пронумерованный набор кубиков, который соответствует идентичному набору из 4 или 5 пронумерованных кубиков
Сопоставьте наборы кубиков.Показан один человек с 4 или 5 кубиками. Затем идут еще три человека с наборами кубиков от 2 до 5. Выберите набор, соответствующий первому набору. Цифры написаны разными шрифтами для тренировки распознавания чисел.
Сопоставьте пронумерованные и ненумерованные наборы кубиков с числом 4 или 5
Выберите картинки, на которых изображено указанное количество (4 или 5) кубиков. В каждой задаче даны четыре картинки. Цифры написаны разными шрифтами, чтобы практиковать распознавание чисел.Некоторые числа скрыты, чтобы облегчить подсчет кубиков
Подсчитайте 2-5 выровненных объектов, чтобы определить общее количество
В ряду 2-5 кубиков, введите или выберите количество показанных кубиков
Сопоставьте числа 1-5 с расположением пальцы, отображаемые на руке
Сопоставьте руку с количеством отображаемых пальцев с правильной цифрой. Одновременно показаны три числа и стрелки
Одновременно показаны три числа и стрелки
Сопоставьте наборы кубиков с числами 1-5
Сопоставьте набор предметов с числом.Даны изображения с цифрами 1-5 и карточки с наборами кубиков, перетащите правильный набор кубиков на каждое число. Цифры и наборы расположены в случайном порядке. Одновременно показаны три набора кубиков и чисел
Определите пронумерованные наборы кубиков, которые соответствуют заданной сумме до 5
Выберите картинки, на которых показано указанное количество (1-5) кубиков. В каждой задаче даны четыре картинки с наборами кубиков. Несколько изображений могут содержать желаемое количество кубиков, поэтому выберите все подходящие
Сопоставьте числа 1-5 с их позициями на числовой строке, помеченной числами и узорами из точек
Перетащите числа 1-5 в соответствующие места на числовой ряд.Числовая линия охватывает числа от 0 до 10 и помечена числами и точками каждого числа. Числа для перетаскивания представлены в различных шрифтах
Совместите разбросанные объекты, чтобы подсчитать и определить общее количество
Представлен случайный набор объектов (1-5). Перетащите объекты в поле, чтобы выстроить их в линию, чтобы было легче считать. Затем введите или выберите показанное число
Перетащите объекты в поле, чтобы выстроить их в линию, чтобы было легче считать. Затем введите или выберите показанное число
Подсчитайте, чтобы найти общее количество разбросанных объектов, сопоставив числа 1:1 с объектами
Подсчитайте количество показанных объектов.Нажмите на них, чтобы изменить их цвет, чтобы отметить, что они были подсчитаны. Затем выберите число
Определите набор разбросанных объектов, который соответствует заданному общему количеству до 5
Подсчитайте количество показанных объектов. Введите или выберите число. Затем, получив указание о том, сколько предметов нужно найти, выберите контейнер с правильным количеством предметов.
Тема D: Концепция нуля и работа с числами 0–5
объекты и определить позицию или общее количество.Они работают с выровненными объектами, разбросанными объектами и числовой линией. Они изучают состав числа 3 и начинают использовать знаки +, — и =.
Тема E: Работа с числами 6–8 в различных конфигурациях
Учащиеся считают последовательно, чтобы определить позицию или общее число до 9. Они связывают объекты с цифрами и видят цифры в различных шрифтах. Они работают с выровненными объектами, разбросанными объектами, пальцами и числовой линией. Учащиеся изучают стратегии подсчета с совпадением 1:1 и узнают, что наборы объектов с одинаковой суммой могут быть выровнены по-разному.
Они связывают объекты с цифрами и видят цифры в различных шрифтах. Они работают с выровненными объектами, разбросанными объектами, пальцами и числовой линией. Учащиеся изучают стратегии подсчета с совпадением 1:1 и узнают, что наборы объектов с одинаковой суммой могут быть выровнены по-разному.
Знать, что на один больше 5 равно 6
Выучить число 6. Показаны пять предметов. Выберите правильную цифру, чтобы представить это. Затем добавляется еще один элемент, показывающий, что цифра 6 идет после 5
Распознать, что единица больше 6 равна 7
Выучить число 7. Показаны шесть элементов. Выберите правильную цифру, чтобы представить это. Затем добавляется еще один элемент, показывающий, что цифра 7 идет после 6
Определите количество пальцев до 7, отображаемых на двух руках
Отображаются две руки с числом пальцев от 0 до 7.Нажмите или введите количество показанных пальцев
Сопоставьте числа 0-7 с расположением пальцев на двух руках
Показаны три числа и три изображения рук с пальцами. Сопоставьте стрелки с числами 0-7
Сопоставьте стрелки с числами 0-7
Определите набор выровненных объектов, который соответствует заданной сумме до 7
Определите изображение, на котором изображено до 7 кубиков. Даны три варианта рядов кубиков. Нажмите на тот, который соответствует номеру
Сопоставьте пронумерованные узоры из точек с идентичными пронумерованными узорами из точек до 7
Сопоставьте пронумерованные узоры из точек.Маленькие осьминоги держат флажки с цифрами и точечными узорами. Перетащите все, что соответствует номеру и образцу осьминога-отца, к нему. Числа написаны разными шрифтами.
Определите наборы пронумерованных кубиков, которые соответствуют заданной сумме 6 или 7 (Часть 1)
Определите количество показанных кубиков из двух возможных чисел. Затем добавляется куб. Определите число еще раз, чтобы всего получилось 6 или 7. Выберите картинки с одинаковым количеством кубиков. Цифры на картинках написаны разными шрифтами.
Определите наборы пронумерованных кубиков, которые соответствуют заданной сумме 6 или 7 (Часть 2)
Выберите наборы, которые содержат указанную сумму. Выберите все картинки, которые содержат заданное количество кубиков (6 или 7). Цифры на картинках написаны разными шрифтами, а кубики расположены в различных конфигурациях
Выберите все картинки, которые содержат заданное количество кубиков (6 или 7). Цифры на картинках написаны разными шрифтами, а кубики расположены в различных конфигурациях
Сопоставьте числа 1-7 с их позициями на числовой строке, отмеченной цифрами и узорами из точек
Дана числовая строка, перетащите два числа от 1 до 7 на правильное место в строке. Числовая строка помечена числами от 0 до 10 и точечными узорами, представляющими числа. Цифры, которые нужно перетаскивать, написаны разными шрифтами.
Подсчитайте объекты по мере их удаления от набора и определите общее количество.
Птицы улетают с дерева по одной.Подсчитайте улетающих птиц и введите или выберите количество улетевших
Подсчитайте разбросанные объекты двумя разными способами, чтобы получить одно и то же количество
Учтите, что порядок подсчета набора не влияет на общее количество. Следуйте за стрелками, чтобы нажимать на бусины, чтобы изменить их цвет и подсчитать их. Затем введите номер. Сосчитайте элементы в другом порядке и снова введите число
Сосчитайте элементы в другом порядке и снова введите число
Признайте, что на один больше 7 равно 8
Выучите число 8. Показаны семь элементов.Выберите правильную цифру, чтобы представить это. Затем добавляется еще один элемент, показывающий, что цифра 8 идет после 7
Определите количество пальцев до 8, отображаемых на двух руках
Отображаются две руки с числом пальцев от 0 до 8. Нажмите или введите количество показанных пальцев
Сопоставьте числа 0-8 с расположением пальцев на двух руках
Показаны три числа и три изображения рук с пальцами. Сопоставьте стрелки с числами 0-8
Определите набор выровненных объектов, который соответствует заданной сумме до 8
Определите изображение, на котором изображено до 8 кубиков.Даны три варианта рядов кубиков. Нажмите на тот, который соответствует номеру
Определить наборы пронумерованных кубиков, которые соответствуют данной сумме до 9 (Часть 1)
Определить количество показанных кубиков, из двух вариантов числа. Затем добавляется по одному кубу за раз. Определите число еще раз, всего 8. Затем показываются три или четыре картинки. Выберите те, у которых одинаковое количество кубиков. Цифры на картинке
Затем добавляется по одному кубу за раз. Определите число еще раз, всего 8. Затем показываются три или четыре картинки. Выберите те, у которых одинаковое количество кубиков. Цифры на картинке
Определите наборы пронумерованных кубиков, которые соответствуют данной сумме до 9 (Часть 2)
Выберите все картинки, содержащие заданное количество кубиков, до 9.Цифры на картинках написаны разными шрифтами, а кубики расположены в различных конфигурациях.
Подсчитайте предметы по мере их удаления от набора и определите общее количество.
Птицы улетают с дерева по одной. Подсчитайте улетающих птиц и введите или выберите общее количество улетевших
Подсчитайте разбросанные объекты двумя разными способами, чтобы получить одно и то же количество
Учтите, что порядок подсчета набора не влияет на общее количество. Следуйте за стрелками, чтобы нажимать на бусины, чтобы изменить их цвет и подсчитать их.Затем введите номер. Сосчитайте их снова в другом порядке и снова введите число
Определите общее количество разбросанных объектов после того, как известное количество было переставлено
Узнайте, что количество объектов не меняется при их перемещении. Подсчитайте предметы в контейнере и введите сумму. Затем предметы перемещаются. Сосчитайте их еще раз и введите сумму
Подсчитайте предметы в контейнере и введите сумму. Затем предметы перемещаются. Сосчитайте их еще раз и введите сумму
Тема F: Работа с числами 9–10 в различных конфигурациях
Учащиеся работают с числами 0 и 6–10 в возрастающей степени, чтобы определить суммы и распознать цифры.Они работают с разбросанными предметами, неидентичными предметами, пальцами и числовой линией.
Тема G: Еще один с числами от 0 до 10
Учащиеся используют знакомые представления (объекты, блоки с основанием 10, числовую прямую и уравнения), чтобы изучить концепцию еще одного. Они начинают рассчитывать, а не считать все.
Тема H: На единицу меньше с числами от 0 до 10
Учащиеся используют знакомые представления (объекты, блоки с основанием 10, числовую прямую и уравнения), чтобы изучить концепцию «на единицу меньше».Они чередуются между +1 и -1 для решения задач.
Определите пропущенные числа в числовой строке с номером 9-1
Научитесь считать в обратном порядке. Ввести два пропущенных числа в перевернутой числовой строке
Ввести два пропущенных числа в перевернутой числовой строке
Определить на одно больше и на одно меньше в числовой строке
Указать число на единицу больше и на единицу меньше заданного числа в числовой строке. Числовая строка помечена цифрами 0 и 10 и начальным значением. Введите число слева и справа от начального значения
Продолжите последовательность счета на числовой прямой от заданной точки, считая назад
Считайте в обратном направлении в пределах от 10 до 0.Учитывая числовую прямую, сосчитайте в обратном порядке от 10 до 0 один раз. Затем потренируйтесь считать два числа слева от заданного числа, вводя второе число
Решите уравнения с -1 на основе модели блоков с основанием 10
Изучите вычитание 1. Отображается ряд кубов и последний один выскакивает при нажатии. Введите количество оставшихся кубов и ответ на уравнение вычитания
Решите уравнения с -1 на основе модели числовой прямой
Используйте числовую прямую, чтобы найти ответ на уравнение с -1. На числовой прямой отмечены только числа 0, 5 и 10. Сверчок прыгает на одно число влево. Введите число, на которое он приземлится, затем введите то же число, что и ответ на уравнение ответ
На числовой прямой отмечены только числа 0, 5 и 10. Сверчок прыгает на одно число влево. Введите число, на которое он приземлится, затем введите то же число, что и ответ на уравнение ответ
Решите -1 задач на основе известной суммы и сценария с использованием объектов
Подсчитайте предметы в банке и введите число. Затем показывается вторая банка, где элементы переставляются, а один объект удаляется.В некоторых задачах на баночке пишут первую сумму, скрывая предметы, и убирают один предмет. Введите новую сумму
Решите -1 задач на основе известной суммы и сценария с использованием объектов
Укажите сумму после удаления одного объекта из известного числа. Баночка показана с указанием того, сколько она содержит. Один элемент удален. Введите новую сумму
Решите -1 уравнения (уровень 2)
Практика вычитания 1. Показано только уравнение вычитания. Введите сумму
Решите уравнения +1 и -1 на основе модели блоков с основанием 10.Блоки используются для моделирования уравнения, которое необходимо решить.
 Введите количество блоков и ответ на уравнение
Введите количество блоков и ответ на уравнениеРешите уравнения +1 и -1 на основе модели числовой прямой
Попрактикуйтесь в решении нескольких задач на сложение и вычитание 1. Числовая строка от 0 до 10 используется для смоделируйте уравнение, которое необходимо решить. Введите количество блоков и ответ на уравнение
Решите задачи +1 и -1 на основе известной суммы и сценария с использованием объектов
Попрактикуйтесь в сочетании задач на сложение и вычитание 1.Баночка предметов используется для моделирования уравнения, которое необходимо решить. Введите количество блоков и ответ на уравнение
Решите уравнения +1 и -1
Решите уравнения на сложение или вычитание 1. Модель не используется. Показано только уравнение. Введите ответ
МОДУЛЬ 2 Двумерные и трехмерные фигуры
Тема A: Двумерные плоские фигуры
Учащиеся знакомятся с внешним видом и названиями двухмерных фигур. Они работают с квадратами, кругами, треугольниками, прямоугольниками и шестиугольниками. Учащиеся выделяют примеры среди не-примеров. Наша звуковая функция позволяет нечитающим пользователям получать доступ к именам форм.
Учащиеся выделяют примеры среди не-примеров. Наша звуковая функция позволяет нечитающим пользователям получать доступ к именам форм.
Определение положения над и под объектом
Научитесь определять положение над или под объектом. Выберите указанное местоположение, щелкнув правильное положение.
Разместите объекты выше и ниже объекта
Разместите 1 или 2 объекта выше или ниже неподвижного объекта. Выберите как правильное местоположение, так и правильный цвет, как указано.
Поместите объект перед или позади объекта (Часть 1)
Научитесь определять положение как перед или позади объекта.Выберите указанное местоположение, нажав на правильное положение
Поместите объект перед или позади объекта (Часть 2)
Определите местоположение как «перед» или «позади» объекта. Перетащите символ в указанную позицию
Определите линии
Научитесь определять линии. Выберите линии в различных ориентациях из группы, содержащей линии и кривые
Определение изогнутых линий
Научитесь определять кривые. Выбор кривых в различных ориентациях и формах из группы, содержащей линии и кривые
Выбор кривых в различных ориентациях и формах из группы, содержащей линии и кривые
Определение прямоугольников, треугольников или кругов из набора фигур
Определение прямоугольников, треугольников и кругов из наборов фигур.Нажмите на фигуры, соответствующие указанной цифре
Определить свойства треугольников
Изучите характеристики треугольника. Затем выберите те фигуры, которые являются треугольниками
Определите свойства прямоугольников
Изучите характеристики прямоугольника. Затем выберите те фигуры, которые являются прямоугольниками
Определите шестиугольники из набора фигур
Определите, какая из двух фигур является шестиугольником. Затем выберите все шестиугольники из множества форм.
Определите свойства шестиугольников
Изучите характеристики шестиугольника.Затем выберите те фигуры, которые являются шестиугольниками, чтобы завершить изображение
Идентифицируйте отдельные 2D-фигуры в большом изображении
Используйте разные цвета для идентификации фигур.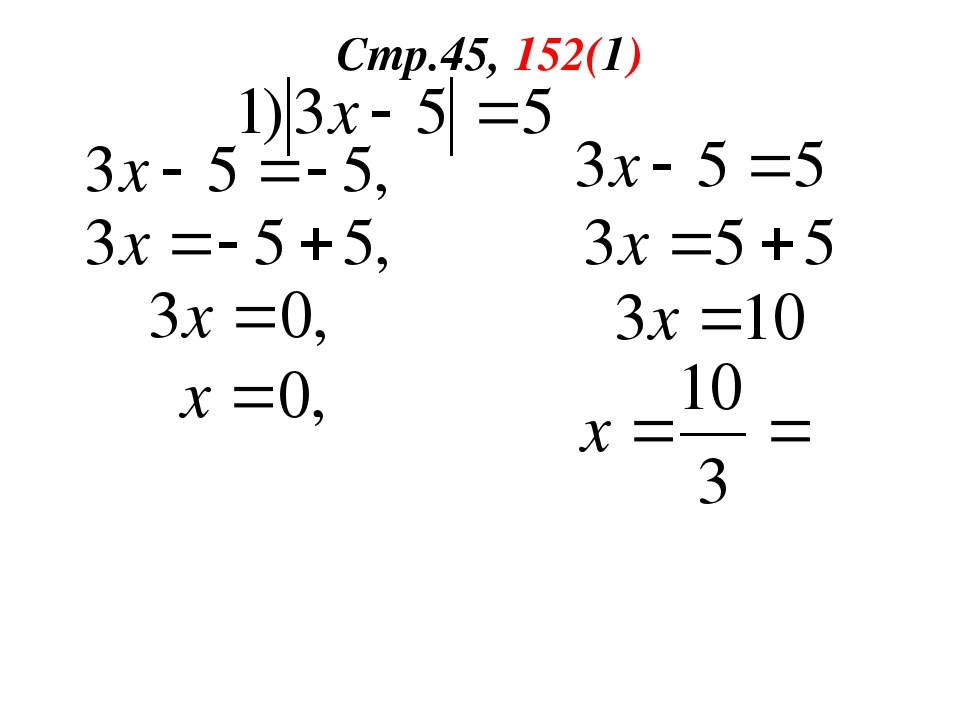 Следуйте инструкциям, чтобы раскрасить каждый тип фигуры в указанный цвет.
Следуйте инструкциям, чтобы раскрасить каждый тип фигуры в указанный цвет.
Идентификация объектов реального мира, состоящих из 2D-фигур
Выберите объекты реального мира, содержащие заданную форму, из набора из 6 объектов. Формы включают круги, прямоугольники и треугольники.
Сопоставьте объекты реального мира с их 2D-формами
Выберите правильную двумерную фигуру, которая моделирует объекты реального мира.Объект и соответствующая ему фигура могут быть ориентированы в разных направлениях
Сопоставьте двухмерную фигуру с ее именем
Получив имя фигуры, сопоставьте ее с правильной формой. Щелкните крестик или галочку рядом с каждой из трех фигур, чтобы указать, соответствует ли она слову. Из набора 5 фигур выберите те, которые имеют заданное количество сторон или углов.
Определите 2D-фигуры и переместите их в положения выше, ниже, впереди и позади
Попрактикуйтесь в двухмерных формах и положениях.Перетащите указанную фигуру в указанное место относительно статического изображения
Тема B: Трехмерные твердые фигуры
Учащиеся знакомятся с внешним видом и названиями трехмерных фигур. Они работают с кубами, сферами, конусами и цилиндрами. Учащиеся также укрепляют свое понимание положений (сверху, снизу, впереди, рядом и сзади). Наша звуковая функция позволяет нечитающим пользователям получать доступ к именам форм.
Они работают с кубами, сферами, конусами и цилиндрами. Учащиеся также укрепляют свое понимание положений (сверху, снизу, впереди, рядом и сзади). Наша звуковая функция позволяет нечитающим пользователям получать доступ к именам форм.
Сортировка фигур по категориям плоские и объемные
Научитесь различать двухмерные и трехмерные фигуры.Затем рассортируйте их по категориям
Сопоставьте фигуры с реальными объектами
Сопоставьте реальные объекты с трехмерными объемными фигурами
Определите цилиндры среди трехмерных фигур
Научитесь определять цилиндры из набора из 3 -мерные твердые тела. Щелкайте по цилиндрам среди группы других тел
Идентифицируйте конусы среди трехмерных фигур
Попрактикуйтесь в распознавании конусов из набора трехмерных тел. Нажимайте на конусы среди группы других тел
Идентифицируйте кубы среди трехмерных фигур
Научитесь определять кубы из набора трехмерных тел.Щелкайте по кубам среди группы других тел
Идентифицируйте сферы среди трехмерных фигур
Попрактикуйтесь в распознавании сфер из набора трехмерных тел.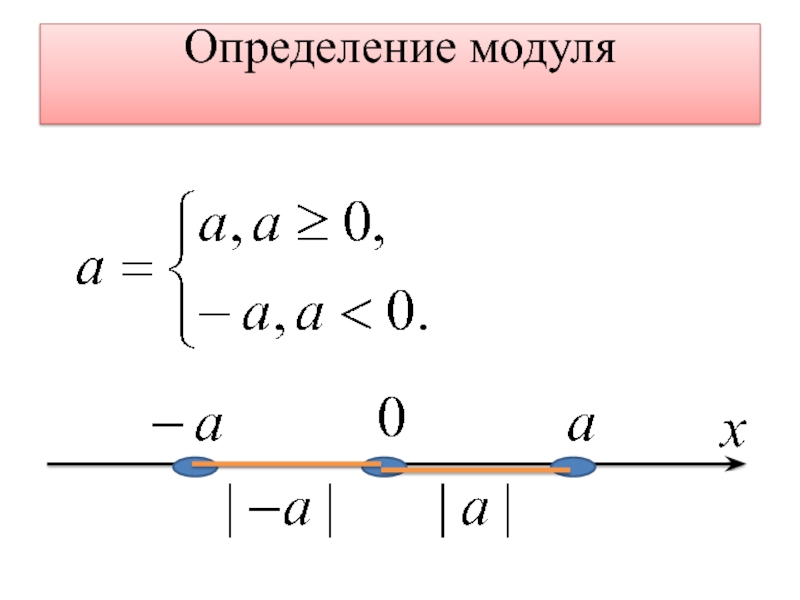 Щелкайте по сферам среди группы других тел
Щелкайте по сферам среди группы других тел
Идентифицируйте трехмерные фигуры по имени
Выберите правильное имя для данного тела. Будет предложено два варианта ответа.
Идентификация трехмерных фигур среди объектов реального мира
Найдите основные трехмерные объемные формы, используемые на изображениях реальных объектов. Когда представлен набор из менее чем 10 изображений, щелкните те, которые содержат указанное твердое тело
Поместите трехмерные фигуры выше, ниже, перед и позади объекта
Практика трехмерных тел и их положения.Перетащите указанное твердое тело в указанное место относительно статического изображения
Идентифицируйте объекты в позициях выше, ниже, рядом и перед
Практикуйте слова положения «над», «ниже», «рядом с», и «перед». Нажмите на один из двух символов, которые находятся в правильном положении относительно указанного символа
Тема C: Двумерные и трехмерные формы
Учащиеся применяют свое прежнее понимание плоских и объемных форм, чтобы различать их.
МОДУЛЬ 3 Сравнение длины, веса, вместимости и числа до 10
Тема A: Сравнение длины и высоты
Используя знакомые, реальные предметы, учащиеся используют язык сравнения (самый высокий, выше, самый длинный, самый длинный, самый низкий , короче) по мере изучения длины.
Тема B: Сравнение длины и высоты соединяющих кубиков палочек в пределах 10
Учащиеся работают со знакомыми соединяющими кубиками, чтобы подсчитать кубики и определить длину палочек. Они сравнивают длины, используя более длинные, короткие и такие же, как.
Тема C: Сравнение веса
Используя знакомые, реальные предметы, учащиеся используют язык сравнения (тяжелее, легче, примерно одинаково), когда исследуют вес. Для этого они используют виртуальную шкалу баланса для сравнения.
Тема D: Сравнение объемов
Учащиеся изучают слово «емкость» и используют его для измерения количества жидкости, которое может вместить контейнер. Используя единицу «стаканы», они измеряют, наливая стаканы в большую емкость и переливая из большей емкости в стаканы. Они также сравнивают измеренные емкости двух контейнеров.
Они также сравнивают измеренные емкости двух контейнеров.
Тема E: Достаточно ли?
Чтобы подготовиться к сравнению чисел, учащиеся работают с объектами реального мира, чтобы определить, достаточно ли их для составления пар. Затем они определяют, имеет ли набор реальных объектов больше, меньше или такой же, как другой набор объектов.
Тема F: Сравнение наборов в пределах 10
Учащиеся сравнивают два набора объектов, используя слова больше, меньше и одинаково. Они работают с похожими объектами, как выровненными, так и разбросанными.
Тема G: Сравнение числительных
Учащиеся сравнивают два набора предметов, используя слова больше, меньше и одинаково. Они работают с похожими и непохожими объектами, как совмещенными, так и разбросанными, в вертикальном и горизонтальном выравнивании. Наконец, они начинают сравнивать числа.
МОДУЛЬ 4 Пары чисел, сложение и вычитание до 10
Тема A: Сложение сумм 2, 3, 4 и 5
Тема B: Разложение 6, 7 и 8 на пары чисел
Тема C: Сложение с суммами 6, 7 и 8
Учащиеся углубляют свое понимание сложения, укрепляя связь между конкретными объектами, блоками с основанием 10 и уравнениями. Они определяют как суммы, так и недостающие слагаемые. Они записывают уравнения, включая символ +.
Они определяют как суммы, так и недостающие слагаемые. Они записывают уравнения, включая символ +.
Определить недостающее слагаемое и просуммировать уравнения сложения до 5 на основе сценария с объектами
Завершить уравнение сложения. Анимация с набором стационарных объектов и набором объектов, которые добавляются, дается в общей сложности до 5. Заполните пробелы в уравнении сложения
Используйте кубики для представления сценария сложения на основе объектов и сопоставления шаблонов кубов. к добавлению сценариев
Практика индивидуальной переписки.Смоделируйте сценарий сложения с кубиками двух разных цветов
Решите уравнения сложения для 5 на основе модели блоков с основанием 10
Смоделируйте задачу сложения с кубиками. Во-первых, изобразите недостающее слагаемое с помощью кубов. Введите новую сумму после каждого добавленного куба, затем введите решение уравнения. В других задачах дана модель куба, поэтому достаточно ввести сумму
Определить недостающее слагаемое в уравнениях с суммой 4
Написать уравнение для заданной модели куба. Даются кубики двух цветов. Напишите уравнение сложения, представляющее модель. Подсказки даются для каждого пробела.
Даются кубики двух цветов. Напишите уравнение сложения, представляющее модель. Подсказки даются для каждого пробела.
Решите +/- уравнения в пределах 5 на основе перемещений по числовой прямой
Представьте задачу на сложение слов на числовой прямой. Начиная с заданного значения числовой строки, переместите дополнительную сумму в сумме до 5. Соответствующее уравнение сложения отображается после правильного перемещения по числовой строке
Определить недостающее слагаемое в уравнениях с суммой 4
Найти недостающий член в уравнении сложения с суммой 4.Во-первых, предоставляется модель куба. Затем заполните пропуски без модели
Определите недостающее слагаемое в уравнениях с суммой 5
Найдите недостающее слагаемое в уравнении сложения с суммой 5. Сначала предоставляется кубическая модель. Затем заполните пропуски без модели
Запишите сценарии сложения с объектами в виде уравнений до 5
Напишите уравнение сложения для анимации с суммой 5. Показано несколько стационарных объектов. Затем появляются дополнительные объекты.Напишите уравнение с подсказками для каждого пробела
Показано несколько стационарных объектов. Затем появляются дополнительные объекты.Напишите уравнение с подсказками для каждого пробела
Используйте блоки с основанием 10 для представления сценариев сложения с объектами до 5
Смоделируйте задачу на сложение с кубами и напишите уравнение. Представьте ситуацию сложения с кубиками. Затем заполните уравнение сложения без подсказок для пробелов
Напишите уравнение, соответствующее числовой связи (всего 3, 4 или 5)
Напишите уравнение, представленное числовой связью с суммой 3, 4, или 5. Введите числа из облигации в уравнение
Завершите уравнения сложения с суммой 6 на основе модели блоков с основанием 10
Завершите все уравнения, сумма которых равна 6.Создайте модель куба каждой пары слагаемых. Заполните пробелы в уравнениях, соответствующих моделям
Смоделируйте сценарии сложения до 6 на числовой прямой и решите связанное уравнение
Представьте задачу на сложение слов на числовой прямой. Начиная с заданного значения числовой строки, переместите дополнительную сумму до 6. Кроме того, завершите уравнение сложения, которое представлено числовой линией
Начиная с заданного значения числовой строки, переместите дополнительную сумму до 6. Кроме того, завершите уравнение сложения, которое представлено числовой линией
Напишите уравнение, соответствующее числовой связи (всего 6)
Напишите уравнение, представленное числовой связью с суммой 6.Введите числа из связи в уравнение
Представьте сценарии сложения с объектами, используя блоки с основанием 10, и запишите в виде уравнения с суммой 6
Напишите уравнение сложения для изображения с суммой 6. Сначала создайте кубическая модель ситуации. Затем напишите уравнение, представленное кубами
Определите недостающее слагаемое в уравнениях с суммой 6
Найдите недостающее слагаемое в уравнении сложения с суммой 6. Сначала предоставляется модель куба.Затем заполните пропуски без модели
Разложите набор из 7 объектов на две группы и определите их как слагаемые в уравнении
Заполните все уравнения, сумма которых равна 7. Создайте кубическую модель каждой пары слагаемых . Заполните пробелы в уравнениях, соответствующих моделям
Заполните пробелы в уравнениях, соответствующих моделям
Смоделируйте сценарии сложения до 7 на числовой прямой и решите связанное уравнение
Представьте задачу на сложение слов на числовой прямой. Начиная с заданного значения числовой строки, переместите дополнительную сумму до 7.Кроме того, завершите уравнение сложения, представленное числовой линией
Напишите уравнение, соответствующее числовой связи (всего 7)
Напишите уравнение, представленное числовой связью с суммой 7. Введите числа из связи в уравнение
Представьте сценарии сложения с объектами, используя блоки с основанием 10, и запишите в виде уравнения с суммой 7
Напишите уравнение сложения для изображения с суммой 7. Сначала создайте кубическую модель анимации.Затем напишите уравнение, представленное кубами
Определите недостающее слагаемое в уравнениях с суммой 7
Найдите недостающее слагаемое в уравнении сложения с суммой 7. Сначала предоставляется модель куба. Затем заполните пробелы без модели
Затем заполните пробелы без модели
Завершите уравнения сложения с суммой 8 на основе модели блоков с основанием 10
Завершите все уравнения, сумма которых равна 8. Создайте кубическую модель каждой пары добавляет. Заполните пробелы в уравнениях, соответствующих моделям
Смоделируйте сценарии сложения до 8 на числовой прямой и решите связанное уравнение
Представьте задачу на сложение слов на числовой прямой.Начиная с заданного значения числовой строки, переместите дополнительную сумму до 8. Кроме того, завершите уравнение сложения, которое представлено числовой линией
Напишите уравнение, соответствующее числовой связи (всего 8)
Напишите уравнение, представленное числовой связью с суммой 8. Введите числа из связи в уравнение. уравнение сложения для картинки с суммой 8.Сначала создайте кубическую модель анимации. Затем напишите уравнение, представленное кубами
Определите недостающее слагаемое в уравнениях с суммой 8
Найдите недостающее слагаемое в уравнении сложения с суммой 8. Сначала предоставляется модель куба. Затем заполните пропуски без модели
Сначала предоставляется модель куба. Затем заполните пропуски без модели
Тема D: Вычитание из чисел до 8
Учащиеся используют знакомые блоки с основанием 10, сценарии с объектами, числовую прямую и уравнения для изучения основных понятий вычитания.Учащиеся определяют как различия, так и недостающие вычитаемые, постепенно переходя от конкретных моделей к абстрактным уравнениям. Они также связывают вычитание со сложением посредством исследования семейств фактов.
Тема E: Разложение 9 и 10 на пары чисел
Учащиеся используют знакомые сценарии с объектами, десятичными блоками и уравнениями, чтобы расширить свое понимание сложения и вычитания, чтобы включить 9 и 10. Учащиеся изучают состав этих сумм усилить их осведомленность о числовых связях.
Запишите числовую связь на основе сценария с 9 реальными объектами (начните с общего количества)
Научитесь записывать числовые связи. Определите общее количество объектов и перенесите эту информацию в числовой график. Затем определите, сколько изображено каждого из двух типов, и введите его на графике числовой связи. Кроме того, завершите заявление
Затем определите, сколько изображено каждого из двух типов, и введите его на графике числовой связи. Кроме того, завершите заявление
Запишите числовую связь на основе сценария с 9 реальными объектами (не выровненными)
Заполните числовую связь для набора из 9 разбросанных объектов.Заполните пропущенные числа в числовой связи на основе данного изображения. Подсказки даны, чтобы помочь с вводом правильных чисел. Кроме того, заполните заявление о числовой связи
Запишите числовую связь на основе сценария с 9 реальными предметами (пропущено общее количество)
Запишите числовую связь для набора из 9 предметов. Заполните пропущенные числа в числовой связи на основе данного изображения. Помощь в заполнении пропусков не предоставляется. Кроме того, заполните заявление о числовой связи
Запишите числовую связь на основе сценария с 9 реальными объектами
Заполните числовую связь для изображения 9 объектов в рядах.Заполните все значения в правильных местах без дополнительной помощи. Кроме того, заполните пробел в заявлении о числе
Кроме того, заполните пробел в заявлении о числе
Запишите числовое соединение на основе сценария с 9 реальными объектами (не выровненными)
Заполните числовое соединение для изображения 9 разбросанных объектов. Заполните все значения в правильных местах без дополнительной помощи. Кроме того, заполните пропуск в заявлении о количественных связях
Запишите числовые связи на основе сценария с 10 реальными объектами (начните с общего количества)
Научитесь писать числовые связи.Определите общее количество объектов и перенесите эту информацию в числовой график. Затем определите, сколько изображено каждого из двух типов, и введите его на графике числовой связи. Кроме того, заполните заявление
Запишите числовую связь на основе сценария с 10 реальными объектами (отсутствующий элемент)
Заполните числовую связь для набора из 10 разбросанных объектов. Заполните пропущенные числа в числовой связи на основе данного изображения. Подсказки даны, чтобы помочь с вводом правильных чисел. Кроме того, заполните заявление о связи чисел
Кроме того, заполните заявление о связи чисел
Запишите связь чисел на основе сценария с 10 реальными объектами (отсутствует дополнение)
Заполните связь чисел для изображения 10 объектов в рядах. Заполните все значения в правильных местах без дополнительной помощи. Кроме того, введите отсутствующее число в операторе числовой связи
Запишите числовую связь на основе сценария с 10 реальными объектами
Запишите числовую связь для изображения 10 объектов в рядах. Заполните все значения в правильных местах без дополнительной помощи.Кроме того, введите отсутствующее число в операторе связи номеров
Запишите связь номеров на основе сценария с 10 реальными объектами (не выровненными)
Завершите связь номеров для набора из 10 разбросанных объектов. Вставьте пропущенные числа в числовую связку по заданной картинке без дополнительных подсказок. Кроме того, заполните заявление о связи чисел
Тема F: Сложение с суммой 9 и 10
Учащиеся применяют свое понимание композиции 9 и 10 для решения задач на пропущенное сложение.
Тема G: Вычитание из 9 и 10
Учащиеся работают как со сложением, так и с вычитанием, чтобы закрепить понимание основных понятий. Они представляют сценарии с объектами, используя блоки с основанием 10, и представляют блоки с основанием 10 в виде уравнений.
Тема H: Шаблоны со сложением 0 и 1 и получением 10
Учащиеся продолжают выполнять знакомые задания, теперь используя 0 в качестве слагаемого, вычитаемого или разности. Они используют сценарии с объектами, числовой линией и уравнениями.
МОДУЛЬ 5 Числа от 10 до 20 и счет до 100
Тема A: Счет 10 единиц и несколько единиц
Учащиеся отличают «десятку» от единиц, используя десятичную рамку или стержень. Они начинают исследовать состав двузначных чисел и имен чисел. Эти упражнения формируют основу для дальнейшего изучения позиционной стоимости и стратегий сложения. Учащиеся впервые используют вертикальную числовую прямую.
Тема B: Разложите числа 11–20 и посчитайте, чтобы ответить на вопрос «Сколько?»
Учащиеся углубляют свое понимание подростковых чисел, применяя их к позициям на числовой прямой и простым уравнениям.
Тема C: Представление и применение композиций и разложений подростковых чисел
Учащиеся сортируют, считают, складывают и вычитают десятку и единицу. Они видят группу из десяти объектов, отображаемых как справа от единицы, так и слева, и видят как вертикальное, так и горизонтальное выравнивание 10 объектов. Они решают различные позиции в +/- уравнениях, в которых все единицы или целые десять добавляются или вычитаются.
Обзор ускоренного курса | Carnegie Learning Support
Цель ускоренного курса Pathway
Решение Carnegie Learning’s Texas Math Solution включает два ускоренных курса для учащихся 6-х и 7-х классов.Этот курс ускоренного обучения предназначен для подготовки учащихся к успешному прохождению курса алгебры 1 в старшей школе в течение 8-го класса.
Чтобы получить доступ к загружаемому PDF-файлу этого документа, нажмите здесь.
Курс Carnegie Learning Accelerated для 6-го класса включает все математические TEKS для 6-го класса и часть математических TEKS для 7-го класса (в частности, TEKS по пропорциональности) в рамках компонента «Совместное обучение» (учебник или интерактивные уроки математики) и компонента «Индивидуальное обучение» (MATHia). ).
).
Курс Carnegie Learning Accelerated для 7-го класса включает все математические TEKS для 8-го класса и оставшиеся математические TEKS для 7-го класса в рамках компонента «Обучение вместе» (учебник или интерактивные уроки математики) и компонента «Индивидуальное обучение» (MATHia).
Carnegie Learning Accelerated 6 Обзор | Carnegie Learning Accelerated 7 Обзор |
|---|---|
6A Модуль 1: Составление и разложение
6A Модуль 2: Сопоставление величин 6A Модуль 3.
6A Модуль 4: Определение неизвестных величин
6A Модуль 5: Пропорциональное мышление
6A Модуль 6: Описание изменчивости величин | 7A Модуль 1: Преобразование геометрических объектов
7A Модуль 2: Разработка основ функций
7A Модуль 3: Моделирование линейных уравнений
7A Модуль 4: Применение полномочий
7A Модуль 5: Анализ популяций, вероятностей и потенциала
|
В первый год внедрения решения Carnegie Learning Texas Math Solution школьные округа, желающие включить учащихся в ускоренный курс 7-го класса, должны принять во внимание следующие соображения.
Если поступающие в 7-й класс учащиеся прошли ускоренный или углубленный курс в 6-м классе, который только включал математический TEKS 6-го класса, тогда:
Учащиеся должны использовать компонент ускоренного обучения 7 класса CL (учимся вместе) (учебник или интерактивные уроки).
Кроме того, учащиеся должны также использовать адаптированную последовательность ускоренного обучения 7 класса с готовностью для компонента индивидуального обучения (MATHia).Эта последовательность включает в себя модули MATHia, которые соответствуют математическим TEKS 7 класса из курса Carnegie Learning Accelerated для 6 класса. Эти модули стратегически встроены в модули MATHia, чтобы связать математические TEKS 7-го класса с математическим TEKS 8-го класса и, следовательно, предоставить учащимся дополнительный контент, чтобы обеспечить их успех в курсе CL Accelerated Grade 7.

Если поступающие в 7-й класс учащиеся прошли ускоренный или углубленный курс в 6-м классе, который включал TEKS по математике для 6-го класса и , подборку TEKS по математике для 7-го класса, которые отличаются от TEKS по математике для 7-го класса в программе Carnegie Learning Accelerated для 6-го класса конечно, тогда:
Учащиеся должны использовать компонент CL Accelerated Grade 7 Learning Together (учебник или интерактивные уроки).
Кроме того, для компонента «Индивидуальное обучение» (MATHia) школьный округ или кампус должны адаптировать содержание MATHia для изучения математики TEKS для 7-го класса, которая ранее не преподавалась. Carnegie Learning рекомендует использовать ускоренную последовательность MATHia для 7-го класса, чтобы согласовать ее с компонентом «Обучение вместе», однако любой округ или кампус может создать дополнительный модуль(-и) MATHia с единицами, соответствующими конкретному математическому курсу TEKS для 7-го класса, ускоренный курс (курсы) для 6-го класса не включал (сравните с ускоренным курсом Carnegie Learning для 6-го класса).
 Этот дополнительный модуль может быть добавлен для всех учащихся или избранной группы учащихся для доступа по мере необходимости.
Этот дополнительный модуль может быть добавлен для всех учащихся или избранной группы учащихся для доступа по мере необходимости.
Модуль 4 урок 5 8 класс.Урок 2: Линейные и нелинейные выражения в x. Урок 2 :
Модуль 4 урок 5 8 класс. Урок 2: Линейные и нелинейные выражения в x. Урок 2: Использование числовой строки для моделирования сложения целых чисел 7•2 G7-M2-Урок 2: Использование числовой строки для моделирования сложения целых чисел Сложение целых чисел в числовой строке 1. indd 5 04.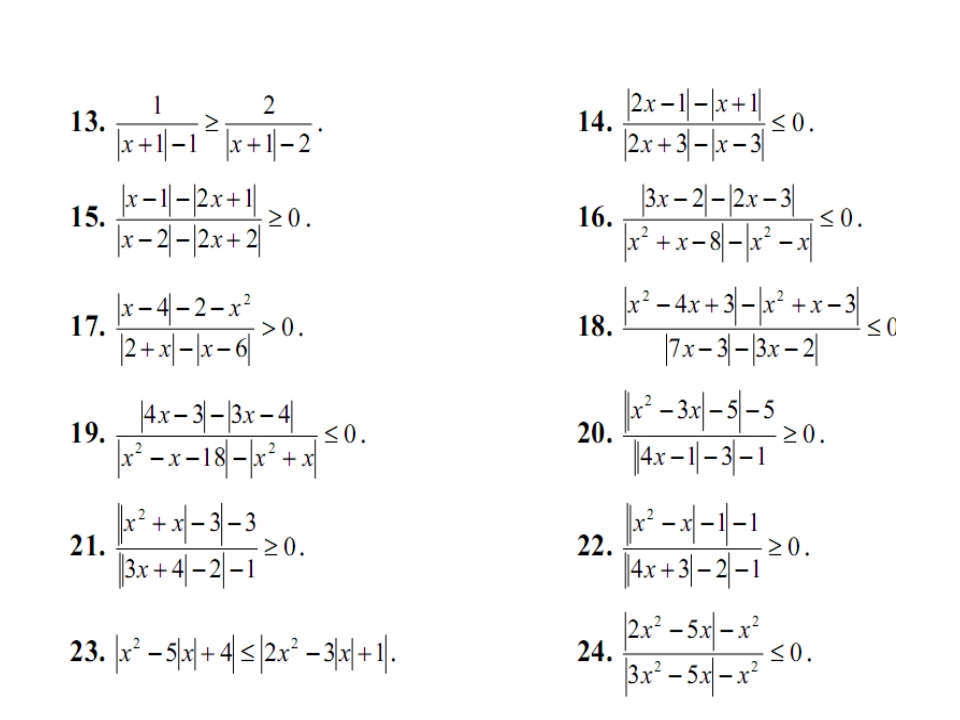 06.14 2: 23 часа. К его дому 5. Урок 4. (2 балла) Ответ: (Модуль 8, Урок 2) 3. 7x-3=5x+5 8 КЛАСС: МОДУЛЬ 4: ЧАСТЬ 1: УРОК 4 Чтение для понимания сути, ответы на вопросы, зависящие от текста , и определение авторской цели: открытие промышленной пищевой сети, отвечающее потребностям студентов А.Класс: 5, Название: enVision MATH Common Core 5, Издатель: Скотт Форесман, Аддисон Уэсли, ISBN: 328672637 Изучайте математику в третьем классе в соответствии с учебной программой Eureka Math/EngageNY — дроби, площадь, арифметика и многое другое. 8 5 10 12 9. Ключевой элемент. Эта бумага. Ответ на заключительный практический экзамен Ключ 3 Математика 9 класса (10F) 6 Математика 9 класса 1 1 4 4 4 1 4 5 m = -9 (Модуль 5, Урок 5) 2. Урок 64 Рисование многоугольников с 5 или более сторонами. 7 36. Чтобы помочь и направить вас в ответах на все вопросы EngageNY Grade 5 ELA Module 4, Unit 2: Анализ литературы о стихийных бедствиях: выводы о воздействии на выживших для учителей 5th Standards Девять уроков второго модуля ELA для 5 класса, модуль 4 Сосредоточьтесь на коротких художественных рассказах… Eureka Math, 4 класс, модуль 3, урок 1, ключ к ответу Ключ — CCSS Эти решения объясняются предметными экспертами на основе ключа к ответу 13 модуля 2 урока 13 урока математики Eureka 7 класса.
06.14 2: 23 часа. К его дому 5. Урок 4. (2 балла) Ответ: (Модуль 8, Урок 2) 3. 7x-3=5x+5 8 КЛАСС: МОДУЛЬ 4: ЧАСТЬ 1: УРОК 4 Чтение для понимания сути, ответы на вопросы, зависящие от текста , и определение авторской цели: открытие промышленной пищевой сети, отвечающее потребностям студентов А.Класс: 5, Название: enVision MATH Common Core 5, Издатель: Скотт Форесман, Аддисон Уэсли, ISBN: 328672637 Изучайте математику в третьем классе в соответствии с учебной программой Eureka Math/EngageNY — дроби, площадь, арифметика и многое другое. 8 5 10 12 9. Ключевой элемент. Эта бумага. Ответ на заключительный практический экзамен Ключ 3 Математика 9 класса (10F) 6 Математика 9 класса 1 1 4 4 4 1 4 5 m = -9 (Модуль 5, Урок 5) 2. Урок 64 Рисование многоугольников с 5 или более сторонами. 7 36. Чтобы помочь и направить вас в ответах на все вопросы EngageNY Grade 5 ELA Module 4, Unit 2: Анализ литературы о стихийных бедствиях: выводы о воздействии на выживших для учителей 5th Standards Девять уроков второго модуля ELA для 5 класса, модуль 4 Сосредоточьтесь на коротких художественных рассказах… Eureka Math, 4 класс, модуль 3, урок 1, ключ к ответу Ключ — CCSS Эти решения объясняются предметными экспертами на основе ключа к ответу 13 модуля 2 урока 13 урока математики Eureka 7 класса. Наша команда учителей и учителей-писателей записывает последовательные и последовательные ежедневные уроки, чтобы оказывать поддержку учителям и ученикам по всей стране. В этом наборе HMH Into Reading для первого класса есть все, что вам нужно, более 800 страниц наших лучших продуктов, чтобы дополнить ваши 1-й класс HMH Into Reading for Sight Word, словарный запас и инструкции по правописанию (авторское право 2020). 12 38. 7 9 3 1 25 11. 3 Свойства программы Texas Go Math 8 класс Модуль 16 Ключ к ответу на викторину; Texas Go Math 8 класс Урок 16. 8 5. V = 3 __4 3 r Eureka Math Домашнее задание Время 4 класс Модуль 4 Урок 8.Детали K К 12 модулю 8 класса все предметы части 3 используются и создаются, чтобы помочь эффективным учителям в наиболее важном факторе, способствующем успеваемости учащихся. предыдущий Ежедневный план урока (DLP) для 6 класса по сельскому хозяйству (TLE) Мам pwede po mkahingi ng модуль 8 и 10 класс кулинария 8 рукоделие, механическое пребывание, уход за ногтями Slamat po mam.
Наша команда учителей и учителей-писателей записывает последовательные и последовательные ежедневные уроки, чтобы оказывать поддержку учителям и ученикам по всей стране. В этом наборе HMH Into Reading для первого класса есть все, что вам нужно, более 800 страниц наших лучших продуктов, чтобы дополнить ваши 1-й класс HMH Into Reading for Sight Word, словарный запас и инструкции по правописанию (авторское право 2020). 12 38. 7 9 3 1 25 11. 3 Свойства программы Texas Go Math 8 класс Модуль 16 Ключ к ответу на викторину; Texas Go Math 8 класс Урок 16. 8 5. V = 3 __4 3 r Eureka Math Домашнее задание Время 4 класс Модуль 4 Урок 8.Детали K К 12 модулю 8 класса все предметы части 3 используются и создаются, чтобы помочь эффективным учителям в наиболее важном факторе, способствующем успеваемости учащихся. предыдущий Ежедневный план урока (DLP) для 6 класса по сельскому хозяйству (TLE) Мам pwede po mkahingi ng модуль 8 и 10 класс кулинария 8 рукоделие, механическое пребывание, уход за ногтями Slamat po mam. Модуль 7. Решение задач с использованием выражений и уравнений. Обратите внимание, что в этом уроке рассматриваются стандарты как RI, так и SL, которые NY S добавили в CCLS. x – точка пересечения (12, 0).Урок 6: Решения линейного уравнения. Урок 5: Написание и решение линейных уравнений. com УРОК 5. Коллекции 8 класс Наводящие вопросы Коллекция 1 Ключ к ответу. Дополнительные ресурсы: Сложите числа в пределах 100, используя десятичные блоки. ПРАКТИЧЕСКИЙ ТЕСТ ПО МАТЕМАТИКЕ. Темы и задачи модуля 1. 8; задача смоделирована с помощью ленточной диаграммы 5. Позже к этим ресурсам могут быть добавлены видеоролики или видеоролики, которые помогут объяснить уроки домашнего задания. Планы уроков K-12 для 5-х классов, 3-я четверть, неделя 3. 4) Поддержка целей обучения Текущая оценка DepEd Tambayan предоставляет вам ресурсы DepEd, включая 7-12 КЛАССЫ DLL с 1-й по 4-ю четверти по всем предметам.Тема B: Линейные уравнения с двумя переменными и Урок 10. 8 или 3. Модули самообучения (SLM) для 5-го КЛАССА, 2-я четверть.
Модуль 7. Решение задач с использованием выражений и уравнений. Обратите внимание, что в этом уроке рассматриваются стандарты как RI, так и SL, которые NY S добавили в CCLS. x – точка пересечения (12, 0).Урок 6: Решения линейного уравнения. Урок 5: Написание и решение линейных уравнений. com УРОК 5. Коллекции 8 класс Наводящие вопросы Коллекция 1 Ключ к ответу. Дополнительные ресурсы: Сложите числа в пределах 100, используя десятичные блоки. ПРАКТИЧЕСКИЙ ТЕСТ ПО МАТЕМАТИКЕ. Темы и задачи модуля 1. 8; задача смоделирована с помощью ленточной диаграммы 5. Позже к этим ресурсам могут быть добавлены видеоролики или видеоролики, которые помогут объяснить уроки домашнего задания. Планы уроков K-12 для 5-х классов, 3-я четверть, неделя 3. 4) Поддержка целей обучения Текущая оценка DepEd Tambayan предоставляет вам ресурсы DepEd, включая 7-12 КЛАССЫ DLL с 1-й по 4-ю четверти по всем предметам.Тема B: Линейные уравнения с двумя переменными и Урок 10. 8 или 3. Модули самообучения (SLM) для 5-го КЛАССА, 2-я четверть. Начните с нажатия на ОЦЕНКУ вашего ученика, затем выберите МОДУЛЬ и, наконец, выберите УРОК. Математический словарь, модуль 5, рубрика, … 8 класс, модуль музыки и искусства. Точка пересечения y (0, 6). Это приводит к сравнению дробей и смешанных чисел и представлению того и другого в различных моделях. 91 кг в. Ресурс для учителей 4-го класса, использующий Eureka Math и EngageNY.Независимо от того, насколько проста математическая задача, просто вид чисел и уравнений может заставить многих людей бежать. «Расширив свое представление о числах и включив в него отрицательные числа, в Модуле 4 учащиеся начинают формальное изучение алгебраических выражений и уравнений. 5, Тема А, Урок 4. 2) Я могу анализировать связи и различия между людьми, идеями или событиями в тексте Соединить пропорциональные линейные уравнения и системы Эврика Математика 2 класс Модуль 4 Урок 8 (обновленный) 12:00 Навык план изучения математики — 2 класс, модуль 5 — чтение, запись и показ чисел до 1000. Урок 1: использование расширенной формы 1.
Начните с нажатия на ОЦЕНКУ вашего ученика, затем выберите МОДУЛЬ и, наконец, выберите УРОК. Математический словарь, модуль 5, рубрика, … 8 класс, модуль музыки и искусства. Точка пересечения y (0, 6). Это приводит к сравнению дробей и смешанных чисел и представлению того и другого в различных моделях. 91 кг в. Ресурс для учителей 4-го класса, использующий Eureka Math и EngageNY.Независимо от того, насколько проста математическая задача, просто вид чисел и уравнений может заставить многих людей бежать. «Расширив свое представление о числах и включив в него отрицательные числа, в Модуле 4 учащиеся начинают формальное изучение алгебраических выражений и уравнений. 5, Тема А, Урок 4. 2) Я могу анализировать связи и различия между людьми, идеями или событиями в тексте Соединить пропорциональные линейные уравнения и системы Эврика Математика 2 класс Модуль 4 Урок 8 (обновленный) 12:00 Навык план изучения математики — 2 класс, модуль 5 — чтение, запись и показ чисел до 1000. Урок 1: использование расширенной формы 1. Дата: 26.06.13 Эта работа находится под лицензией 2. 840 g 7. 13.09.21, 15:54 Eureka Math Grade 5 Module 1 Lesson 2 Answer Key – CCSS › embarc class 4 module 1 Категории курса: Общая информация Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс Алгебра I Геометрия Алгебра II. 15 третей или 5 35. Урок 8. 9. pdf), Текстовый файл (. 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 3: УРОК 5 Коллегиальная критика стихов «Наизнанку» и «Возвращение назад» 7 . Помощь в базовом образовании для Минданао ( ЛУЧ) Элементарно.12 4. Учащиеся изучают эквивалентные выражения, постоянно связывая алгебраические выражения с арифметикой и свойствами арифметики (коммутативной, ассоциативной и дистрибутивной). 2 пятых 12. 3 … модуль обучения кулинарии g10. Опубликовано 22 февраля 2021 г. Главная Курсы > > > > > > > > О модулях Загрузить рабочий лист для Common Core, 8 класс, модуль 1, урок 4 Загрузить рабочий лист для Common Core, 8 класс, модуль 1, урок 5 Урок 4 Результаты учащихся . 28 24.В этом нет файлов … Модуль 8: Время, фигуры и дроби как равные части фигур Урок 4 Ключ к ответу 2• 8 Урок 4 Набор задач 1.
Дата: 26.06.13 Эта работа находится под лицензией 2. 840 g 7. 13.09.21, 15:54 Eureka Math Grade 5 Module 1 Lesson 2 Answer Key – CCSS › embarc class 4 module 1 Категории курса: Общая информация Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс Алгебра I Геометрия Алгебра II. 15 третей или 5 35. Урок 8. 9. pdf), Текстовый файл (. 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 3: УРОК 5 Коллегиальная критика стихов «Наизнанку» и «Возвращение назад» 7 . Помощь в базовом образовании для Минданао ( ЛУЧ) Элементарно.12 4. Учащиеся изучают эквивалентные выражения, постоянно связывая алгебраические выражения с арифметикой и свойствами арифметики (коммутативной, ассоциативной и дистрибутивной). 2 пятых 12. 3 … модуль обучения кулинарии g10. Опубликовано 22 февраля 2021 г. Главная Курсы > > > > > > > > О модулях Загрузить рабочий лист для Common Core, 8 класс, модуль 1, урок 4 Загрузить рабочий лист для Common Core, 8 класс, модуль 1, урок 5 Урок 4 Результаты учащихся . 28 24.В этом нет файлов … Модуль 8: Время, фигуры и дроби как равные части фигур Урок 4 Ключ к ответу 2• 8 Урок 4 Набор задач 1.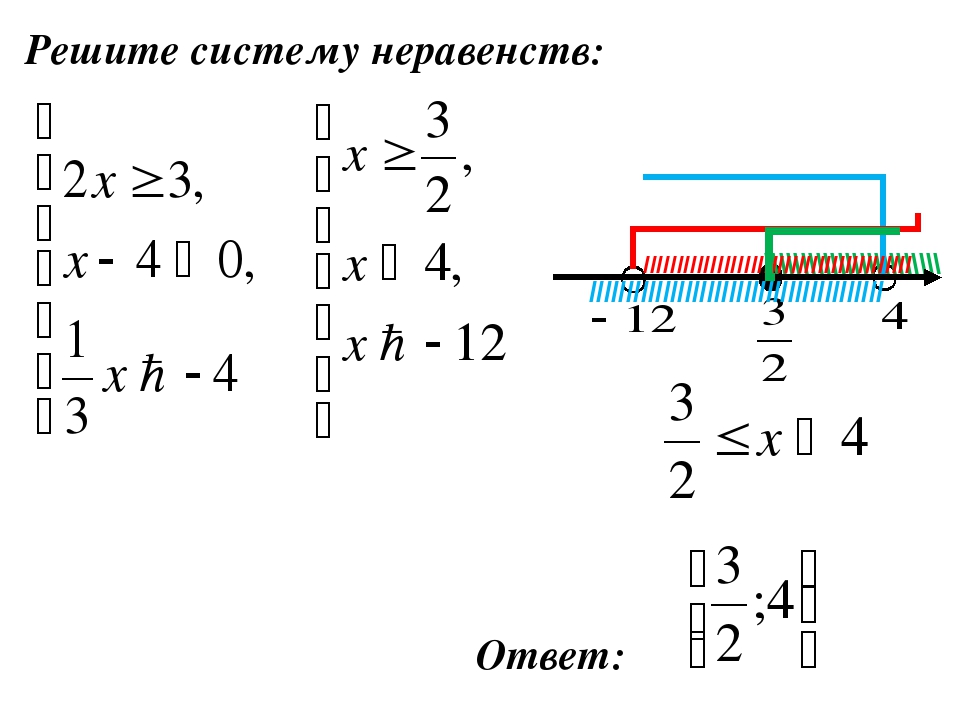 2, 8. 8. 6 Квадратичная формула: apps: videocam: create: Unit 7: Модуль 5: Функции и моделирование — Модуль 1: Модуль 17: Квадратичные функции: Приложения Видео Практика Уроки 1-го класса Стратегии чтения 2-го класса Математика 3-го класса Естествознание 4-го класса Языкознание 5-го класса Математика 5-го класса Естествознание 5-го класса Социальные науки 5-го класса 7-8 Английский класс 7-8 Класс Алгебра I класс 9-12 AP Английский III класс 9-12 Алгебра I класс 9-12 Экономика 9-12 класс История США Эврика Математика Домашнее задание Время 4 класс Модуль 4 Урок 8.Основная корреляция Вторичная математика 1. Они пишут, интерпретируют и используют выражения и … Как и эти ответы Houghton Mifflin On Core Mathematics 8 Class, это заканчивается врожденной одной из любимых книг Houghton Mifflin On Core Mathematics 8 Class Answers, которые у нас есть. 5 МБ) Модуль 4 по математике для 5 класса: Тема B, уроки 2–5 — Zip-файл документов Word (13. 16 36. ВВЕДЕНИЕ Учебный модуль на английском языке для учащихся 8 класса — это интерактивный модуль, разработанный с учетом потребностей 21 века.
2, 8. 8. 6 Квадратичная формула: apps: videocam: create: Unit 7: Модуль 5: Функции и моделирование — Модуль 1: Модуль 17: Квадратичные функции: Приложения Видео Практика Уроки 1-го класса Стратегии чтения 2-го класса Математика 3-го класса Естествознание 4-го класса Языкознание 5-го класса Математика 5-го класса Естествознание 5-го класса Социальные науки 5-го класса 7-8 Английский класс 7-8 Класс Алгебра I класс 9-12 AP Английский III класс 9-12 Алгебра I класс 9-12 Экономика 9-12 класс История США Эврика Математика Домашнее задание Время 4 класс Модуль 4 Урок 8.Основная корреляция Вторичная математика 1. Они пишут, интерпретируют и используют выражения и … Как и эти ответы Houghton Mifflin On Core Mathematics 8 Class, это заканчивается врожденной одной из любимых книг Houghton Mifflin On Core Mathematics 8 Class Answers, которые у нас есть. 5 МБ) Модуль 4 по математике для 5 класса: Тема B, уроки 2–5 — Zip-файл документов Word (13. 16 36. ВВЕДЕНИЕ Учебный модуль на английском языке для учащихся 8 класса — это интерактивный модуль, разработанный с учетом потребностей 21 века. учащиеся.1 Написание линейных уравнений на основе ситуаций и графиков 8. Начальная школа Dutch Ridge 2220 Dutch Ridge Road Beaver, PA 15009 Телефон: 724. 3 – Модуль оценки подобия углов 11 – Отношения углов в параллельных линиях и треугольниках – Урок 11. 25. on от имени Public Consulting Group, Inc. Урок 3. Линии и углы Стандарт: 4. Подготовьте необходимые инструменты и оборудование для конкретных действий по уходу за ногтями. НАУКА. Информационные бюллетени ENY по математике, созданные учителями приходских школ Вермилиона, Абвиль, Луизиана, системы приходских школ Лафайет.Урок 4 – СУММА И ПРОИЗВЕДЕНИЕ КОРНЕЙ КВАДРАТИЧНЫХ УРАВНЕНИЙ. 1515 гр. Дело Совета по образованию Верховного суда по технологиям и образованию в области средств к существованию, квартал 2, неделя. Для пользователей нашего учебного плана ELA для 6-8 классов: если не указано иное, все работы распространяются по лицензии Creative Commons Attribution-NonCommercial 4 апреля 2016 г. -. Набор проблем. 5 RS TV Готовы к работе? МОДУЛЬ 1 ВИКТОРИНА мой . 7 КЛАСС АРАЛИНГ … Просмотр Eureka Math 5 класс Модуль 1 Урок 2 Ключ к ответу – Ответы CCSS по математике. 774. Тема А: Понятия объема.Eureka Math, 8 класс, модуль 4, урок 19, пример ответа. Я могу анализировать влияние выбора слов на значение и тон информационного текста. доктор медицинских наук (38+40)(38+5) и 45(40+2)5.7Мб. 3 Линейные отношения и двумерные данные 8. Модуль 3-й четверти (SLM) 8 класса AP — СКАЧАТЬ. Далее — Математика 8 класс Модуль 5, Тема А, Урок 6. Распаковка целей обучения (5 минут) • Напомните учащимся, что их цель в этом разделе – использовать структурированный процесс принятия решений, чтобы ответить на основной вопрос: * Естествознание – 8 класс, альтернативный способ обучения, четверть 1 – Модуль 4: Влияние температуры на скорость Sound First Edition, Республиканский закон 8293 2020 г., раздел 176, гласит: «Ни одно произведение правительства Филиппин не защищено авторскими правами.8. Планы уроков K-12 для 5-х классов, 3-я четверть, неделя 1-2. Гр8Мод3. Замените свечи зажигания. 19 МБ) Математика для 4 класса, модуль 4: Тема C, уроки 9–11 — Zip-файл документов Word (13. Texas Go Math, 8 класс, модуль 16, ответ на викторину; Texas Go Math, 8 класс, урок 16. Ответы. Совет по образованию . 4 – Модуль 9. Выбор упаковки, подходящей для сохранения свежести продукта и вкусовых качеств (RI. Описание и сравнение свойств многоугольников. Введение в Little Rock Girl 1957 и предварительный просмотр домашнего задания (5 минут) 4.2 Ключ ответа Генерация случайных выборок Модуль 4 Темы и задачи; A. Урок 1: Напишите линейные выражения в различных формах для ситуаций. Ответы будут различаться. Что такое альтернативные способы доставки (ADM)? Альтернативные способы обучения (ADM) — это опробованные и проверенные альтернативные способы предоставления образования в рамках формальной системы, которые позволяют школам предоставлять качественное образование маргинализированным учащимся и учащимся с … измерения в физических единицах с использованием нескольких копий одной и той же физической единицы для измерения.• В начале урока учащиеся делятся своей домашней работой. PPT Q1 Неделя 1 День 1; Урок 64 Рисование многоугольников с помощью 5 … Это сборник модулей ADM для 2 четверти 4 класса, 2 четверти 2020-2021 учебного года. 430 г б. 2 25. Выходной билет около 21 кг a. Присоединяйтесь, чтобы получить доступ ко всем включенным материалам. 00Модуль 4, уроки 10–16: 3 доллара. 38 8. 6. 5 Дроби, десятичные дроби и проценты . 7 35. Предметы: рабочие листы для 8 класса, домашние задания и планы уроков. Модуль 2: Операции с многозначными целыми и десятичными дробями Дата: 31.07.14 5•2 Урок 4 Набор задач 1.Мальчик в классе. Эврика Математика 2 класс Модуль 4 Урок 8 (обновленный) 12:00 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 2: УРОК 14 Анализ значимости названия романа: Связь универсального опыта беженцев с Inside Out & Back Again, Часть 3 Created by Expeditionary Обучение от имени Public Consulting Group, Inc. МАТЕМАТИЧЕСКИЙ ТЕСТ МОДУЛЬ 5 ОТВЕТЫ . Урок 1-1 1-1 Вмешательство Упражнение 1-1 Диагностика и назначение лекарств онлайн Урок 1-2 1-2 Вмешательство Упражнение 1-2 Урок 1-3 1-3 Вмешательство Упражнение 1-3 Урок 1-4 1-4 Вмешательство Упражнение 1 -4 Урок 1-5 1-5 Вмешательство Упражнение 1-5 Готовы продолжать? НЕТ ВМЕШАТЬСЯ ДА ENRICH N 1 2 P L M-4-3 2-1 012345-1.E. Модуль 2 8 класса: Концепция конгруэнтности. Есть также информационные бюллетени для родителей из другого округа, использующие ту же учебную программу, которые могут помочь в дальнейшем объяснении материалов по математике. Задача 2 Выберите все величины, которые пропорциональны длине диагонали Ежедневного Плана Урока (8) Формы Deped (3) DepEd K-12 (34) Меморандум DepEd (3) Заказ DepEd (7) DLL (12) DRRM (2) Выпускной Обряды (4) Учебные модули (20) Учебный пакет (8) Учебные ресурсы (5) LET Reviewer (1) Лицензионный экзамен для учителей (2) Периодический тест (4) Плакаты (14) Цитаты (5) Поисковые ресурсы (1) Senior Средняя школа (11 КЛАСС 8 МОДУЛИ САМООБУЧЕНИЯ (SLM) (1-4 ЧЕТВЕРТЬ) СКАЧАТЬ БЕСПЛАТНО.1 класс Модуль 4 Урок 8. › embarc 4 класс Модуль 1 Категории курса: Общая информация Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс Алгебра I Геометрия Алгебра II. Дополнительные ресурсы: Прямоугольная область. Частью их доказательств является выполнение всех действий, указанных на каждом уроке в каждом модуле. Поскольку 95 находится примерно посередине между 64 и 125, 3 √ __ 95, вероятно, ближе к 4. Оба стандарта требуют от учащихся одинаковой когнитивной работы. Войти.Математика. Прочитайте главы 1–2, страницы 4–27 книги Little Rock Girl 1957 и закончите структурированные заметки. 125 кг д. 270° 3. Слейте масло и бензин перед длительным хранением. Алехандрина М Торрес. 3 COMMON CORE COMMON CORE COMMON CORE Вы можете использовать линейные уравнения и их графики для моделирования реального мира… 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 2: УРОК 13 Закрыть чтение: параграф 4 «Дети беженцев и иммигрантов: сравнение» Created by Expeditionary Обучение, на … 5-й класс Видеоуроки Электронная таблица Share.Забор, дерево, сарай 2. Математический модуль 8 класса 5. ЕЖЕДНЕВНО… 1. Математический словарный запас Модуль 5. 1033 Eureka Math Модуль 3 4 класса, Урок 1 Ключ к ответу Ключ к ответу Eureka Math помогает учащимся глубже понять, почему 9/ 21/13, 16:00 Eureka Math, 5 класс, модуль 1, ключ к ответу на урок 11 — CCSS Эти решения объясняются предметными экспертами на основе Eureka math, 7 класс, модуль 2, урок 13, ключ с ответами. Дом, забор, дом 2. МОДУЛЬ мой. → Чтобы построить уравнение, мы должны начать с известной точки.12 17. B 5 вьющиеся 8 попробовать. Модель с выражениями, уравнениями и неравенствами. Затем партнер Салли дал Салли 5 из своей руки. Урок 6. 3 — Академия Хана 5 2/4 – 2/8 Раздел 5 — Измерительная геометрия Модуль 11 — Урок 11. Г. 32 25. ЦЕЛИ: a. 32 37. 18 МБ) Математика 4 класса Модуль 4: Тема D Уроки 12-16 — Zip-файл документов Word (26. Eureka Math 2 класс Модуль 4 Урок 8 (обновлено) 12:00 8 5 9 8 5 2 = Упражнение 22 (−5)16 (−5)7 = Упражнение 24 135 134 = В общем, если 𝑥𝑥 отлично от нуля и 𝑚𝑚, 𝑛𝑛 — положительные целые числа, то 𝑥𝑥𝑚𝑚 𝑥𝑥𝑛𝑛 = 𝑥𝑥𝑚𝛑−Карта учебного плана ELA для 8-го класса: модули учебного плана для 8-го класса разработаны с учетом результатов CCSS ELA в течение 45-минутного блока английского языка. (Видео-урок)Урок 2. Используйте прямые углы, чтобы определить, равны ли углы, больше или меньше прямых углов. 2 12. Нарисуйте уравнение в виде y=mx+b. 7. Цели: Описать неопределенные термины в геометрии enVision MATH Common Core 5, рабочая тетрадь для 5 класса и помощь в Интернете. Урок 5 Спринт Сторона A 1. 40 34. 4 3. Урок 3: Линейные уравнения в x.А. Живопись в Китае, Японии и Корее 4. Обзор модуля А. Его оценка низкая, потому что 15 гораздо ближе к 16, чем к 9. Урок 65 Визуализация конгруэнтных многоугольников. Нравится (235) Загружаемые ресурсы Раздел 1: Урок 4 Вопросы, зависящие от текста Страницы 59–62 дилеммы всеядного Вопросы Примечания 1. Прочтите статью. 2 ключа ответа Экономия и инвестирование; Texas Go Math, 8 класс, модуль 16, ключ к ответам Управление деньгами и планирование своего будущего; Texas Go Math, 8 класс, раздел 5, обзор учебного пособия, ключ к ответу; Texas Go Math, 8 класс, ключ к ответу на викторину, модуль 15; Техасская математика, 8 класс, урок 15.Распаковка целей обучения (5 минут) • Напомните учащимся, что их цель в этом разделе — использовать структурированный процесс принятия решений, чтобы ответить на главный вопрос: * Эти сайты могут не подпадать под юрисдикцию NYSED, и в таких случаях NYSED не несет ответственности. для его содержания. 9. New York State Common Core 5 КЛАСС Учебная программа по математике 5 КЛАСС МОДУЛЬ 4 Ответы на вопросы 5 КЛАСС МОДУЛЬ T. 4 КЛАСС • МОДУЛЬ 3 Многозначное умножение и деление. Мы понимаем, что эта красивая графика Eureka Math Grade 4 Module 1 может быть самой популярной темой, учитывая, что мы разместили ее в справке Google или Facebook.Урок 7 – КВАДРАТНЫЕ НЕРАВЕНСТВА. 90 шестых или 15 2. Нарисуйте четырехугольники II. 2 23. 8 класс Модуль 4: Материалы для учащихся. Тема A: Написание и решение линейных уравнений (8. 3 Сравните и упорядочьте дроби. Модуль 4 5 класса: Домашнее задание 8. Пожалуйста, используйте учетную запись электронной почты DepEd для доступа к этим файлам. K-12 Curriculum South Asian Arts … Это комплект для Первый класс Остроумие и мудрость Модуль 4 урока Открытие встречи с потребностями учащихся 1033 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 3: УРОК 5 Коллегиальная критика стихов «Наизнанку» и «Снова наизнанку», созданных Expeditionary Learning от имени Public Consulting Группа, Inc.5 класс K-12 Планы уроков 2-я четверть Неделя 8. Нарисуйте уравнение y= x+1. Модуль HG 5 класс — СКАЧАТЬ. txt) или просматривать слайды презентации онлайн. Умножение однозначных чисел на степень десяти: с показателями степени. КЛАСС Общая базовая программа обучения математике штата Нью-Йорк 4 КЛАСС • МОДУЛЬ 4 Модуль 4: Угловые измерения и плоские фигуры Дата: 01.10.14 ОБЩАЯ ОСНОВНАЯ УЧЕБНАЯ ПРОГРАММА NYS ПО МАТЕМАТИКЕ 4•Урок 8 Ключ к ответу Урок 8 . Без категории; Теги . ppt), PDF-файл (. Complete Video Locker. Общие ресурсы Gr8.Независимо от того, насколько проста математическая задача, простое видение чисел и уравнений может привести многих людей к выполнению модулей самообучения (SLM) 4 КЛАССА 2-й четверти. ПРОЕКТ 10 апреля 2014 г. 1 Модуль 1. Самостоятельный урок 1 _____ ПРИЗНАВАНИЕ ЖИЗНЕННЫХ РОЛИ ВАШ ПУТЬ Вам, как и другим, предстоит играть важные роли, которые заинтересуют вас в формировании себя, чтобы стать здоровым и развитым молодым человеком. 2-3 и 5. В первой теме этого 15-дневного модуля учащиеся изучают понятие функции и почему функции необходимы для описания геометрических понятий и вхождений в … 8 класс Модуль 1: Целочисленные показатели и научная запись.нарисовать внешний вид неисправности. Урок 1 Урок 2 Урок 3 Урок 4 Урок 5 Урок 6 Урок 7 Урок 8 Урок 9 Урок 10 Урок 1 Задача 1 Оцените длину стороны квадрата с диагональю 9 см. справедливость, уважение к авторитету) при участии в баскетболе; мастерски выполнять основные навыки и тактики в … Урок 4: 16. Zip. РАСПИСАНИЕ ШКОЛЫ НА СЛЕДУЮЩИЕ ДВЕ НЕДЕЛИ МАРТА 2020 ГОДА. Нарисованы 2 параллельные линии одинаковой длины 3. Модуль 1-й четверти естественных наук (SLM) для 8 класса — СКАЧАТЬ.2 3 7 4 4 12. Первая четверть Класс 5 PPT Q1 НЕДЕЛЯ 1. Неделя: 1 Дата: 7–8 ноября 2016 г. Урок 13 КЛАСС 8: МОДУЛЬ 4: ЧАСТЬ 2: УРОК 5 Определение каскадных последствий с использованием дилеммы всеядного: промышленный Сеть органических продуктов. Достигнуты долгосрочные цели (на основе NYSP12 ELA CCLS) • Я могу определить тему… Написание и решение линейных уравнений 8 класс. Оценка в середине модуля, состоящая из трех вопросов, представляет собой 15-й сегмент серии из 33 частей. Показаны 8 лучших рабочих листов, найденных для — Урок 3 Домашнее задание Модель 1 Ключ к ответу для 5-го класса.5-8) Задания по периметру, площади и объему с книгой ( 3. Эндрю Кабугасон. МОДУЛИ ДЛЯ САМООБУЧЕНИЯ 8 КЛАССА (SLM) (1ST — … МОДУЛЬ 4 Полные и обновленные ответы — Учебная тетрадь LDM2 с результатами 4 класс Рабочие листы 5 класс Рабочие листы для 6-го класса Рабочие листы для 7-го класса Рабочие листы для 8-го класса Рабочие листы для 9-го класса Рабочие листы Рукописные листы Учебные модули ИДЕИ Индивидуальный план мониторинга обучения Вдохновляющие истории Учебный урок 10. Скачать Скачать PDF Обе пары сторон выделены d.Упрощение алгебраических выражений. 14 (50 72) 3 Добавьте круглые скобки, чтобы каждое уравнение было правильным. Вот обновленный образец учебной тетради с примерами результатов в курсе 2 по методам обучения или LDM2. 2019 НОВОЕ ОБНОВЛЕНИЕ DLP! В этой статье вы найдете наш составленный план ежедневных уроков для 8-го класса (2019 DLP). Предыдущая — 8 класс Математика Модуль 4, Тема E, Урок 31. Прежде чем уйти с работы, вымойтесь/примите душ и переоденьтесь, когда это необходимо, чтобы не допустить переноса загрязняющих веществ с рабочего места домой на модуль 4: Измерение углов и плоские фигуры 1 4•Урок 8 Ответ Ключевой урок 8 Набор задач 1.6 Spectrum Language Arts 8 класс Глава 1 Урок 1 Грамматика: Части речи Доказательство Исправьте ошибки в употреблении имен нарицательных и имен собственных, используя корректурные знаки. 8 Урок 8 Набор задач 1. 7 Модуль 1 Темы и задачи; Модуль A Обзор Урок 1, Урок 2: Соотношения (Видеоурок) Урок 3, Урок 4: Эквивалентные отношения (Видеоурок) (Видеоурок) Урок 5, Урок 6: Решение задач путем нахождения эквивалентных отношений (Видеоурок)(Видеоурок) Урок 7: Ассоциированные отношения и значение отношения (видеоурок) Урок 8: Эквивалентные отношения, определяемые с помощью … Эврика Математика 4 класс Модуль 3 Урок 1 Ключ к ответу Ключ к ответу на Эврика Математика помогает учащимся глубже понять, почему стоит 9/ 21/13, 16:00 Eureka Math, 5 класс, модуль 1, ключ к ответу на урок 11 — CCSS Эти решения объясняются предметными экспертами на основе Eureka math, 7 класс, модуль 2, урок 13, ключ с ответами.61 КБ) Просмотр в формате PDF: Математика для 8 класса, модуль 4, тема A, урок 5: версия для учащихся (181. Гр 5, модуль 4. x ≈ ±5. Модуль HG для 4 класса — СКАЧАТЬ. Обзор и оценки в середине модуля. Урок 2. МОДУЛЬ 2 С ОТВЕТАМИ (Бесплатная электронная копия) Все учителя государственных школ в стране в настоящее время проходят курс «Модильности обучения 2» или LDM2. по математике [скачать бесплатно]» Эспередион О. 8 класс ELA модуль 4, раздел 1, урок 5.Powerpoint четверть 3 неделя 3-a (wika at panitikan) Powerpoint четверть 3 неделя 3-b (музыка и сининг) Q3 НЕДЕЛЯ 3 ДЕНЬ 1-5 ФИЛИППИНСКИЙ 5. Классы 6-8 Английский язык Учебная карта: Все модули сочетают литературу с подробным информационным текстом (включая основной первоисточники и литературная документальная литература) по теме. 3 рюкзака. Домашнее задание 1. 5 кг Texas Go Math, 8 класс, модуль 16, ответ на викторину; Texas Go Math, 8 класс, урок 16. Электронный учебный модуль. Все учителя государственных школ в стране в настоящее время проходят курс «Учебные формы обучения 2» или LDM2.Схема ленты нарисована правильно; около 15 кг 2. 12 16. 8 класс Модуль 4. 01 Справочное видео № 1 и 4. Деп Эд Тамбаян. 60 шестых или 10 34. 2634 см или 26 м 34 см 3. В первой теме этого 15-дневного модуля учащиеся узнают о концепции функции и о том, почему функции необходимы для описания геометрического правописания. Урок 8. Соотнесите дробь набора с интерпретация многократного сложения дробного умножения Найдено 9567 результатов для: Эврика Математика 4 класс Модуль 5 Урок 8 Ответы на домашнее задание [БЕСПЛАТНО] Эврика Математика 4 класс Модуль 5 Урок 8 Ответы на домашнее задание .Это дает людям возможность учиться друг у друга и лучше понимать мир. 3 ключевых ответа Анализ финансовой ситуации; Texas Go Math 8 класс Урок 16. Что особенного? _____ _____ 6. : 3-й класс (Eureka Math/EngageNY) Модуль 2: Значение места и решение проблем с единицами измерения. Gr 5 Модуль 6 Эврика Математика Домашнее задание Время Класс 4 Модуль 4 Урок 8. 1 Ключ ответа Погашение кредитов; Texas Go Math, 8 класс, урок 16. Почему «вонь в этом месте поднималась более чем на милю?» 2.Преобразование между стандартной и расширенной формой Урок 5: Сложите 4 двузначных числа, используя стратегии и свойства 1. (SL. a. Для многих людей математика, вероятно, является наименее любимым предметом в школе. Подготовьте электрические принадлежности, материалы и инструменты. Математика 4-4 Задание Ключ к ответу ЕЖЕДНЕВНЫЕ ПРОТОКОЛЫ/ПЛАНЫ УРОКОВ (DLL/DLP) ПЕРВАЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) ВТОРАЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) ТРЕТЬЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) ЧЕТВЕРТАЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) 8 КЛАСС. … HMH Go Math class 7 рабочих тетрадей и ответов помогают онлайн.Модуль HG для 6 класса Автоматизированный шаблон LDM Practicum Portfolio LDM2 Портфолио учителя Материалы для учащихся Листы учебных заданий (LAS) III 9-12 класс Алгебра I 9-12 класс Экономика 9-12 класс История США 9-12 класс AP Психология Человек… 4. 25 марта 2020. Урок 5 – УРАВНЕНИЯ, ПРЕОБРАЗОВАЕМЫЕ В КВАДРАТНЫЕ УРАВНЕНИЯ (В ТОМ ЧИСЛЕ РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ) Урок 6 – ПРИМЕНЕНИЯ КВАДРАТИЧНЫХ УРАВНЕНИЙ И РАЦИОНАЛЬНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ .1 Дни: 4 Модуль 4 Обзор Тема A Обзор Урок 1: Определите и нарисуйте точки, прямые, отрезки, лучи и углы и распознайте их в различных контекстах и на знакомых фигурах. Урок 1. Вовлечение читателя: глава 5 книги «Дилемма всеядного» (6 минут) • Убедитесь, что у учащихся есть текст «Дилемма всеядного». Восток Домашнее задание 1. Урок 6: 10. Математика 4 класса Модуль 4: Тема B Уроки 5-8 — Zip-файл документов Word (19. Учащиеся осознают необходимость определения, чтобы сохранить свойства показателей степени.На фото показан поворот на 270°. Класс: 7, Название: HMH Go Math, Издатель: Houghton Mifflin Harcourt, ISBN: Урок 2: Используйте степени 10 и показатели степени. org/8/учителей/1/practice_problems. Для пользователей содержания учебной программы EL Education K-5 Language Arts: Если не указано иное, все работы распространяются по лицензии Creative Commons Attribution 4. Чтобы загрузить, просто щелкните ссылку ЗАГРУЗИТЬ, чтобы получить бесплатные копии. Гр8Мод1. Карта Восточной Азии 3. Какой бы простой ни была математическая задача, один лишь взгляд на числа и уравнения может заставить многих людей бежать 4.Он основан на целостном подходе к развитию базовых компетенций обучения английскому языку в рамках базовой образовательной программы K-12. Около 3 кг б. Вот модули самообучения в 5 КЛАССЕ на вторую четверть 2020-2021 учебного года. EM — 1 класс — Модуль 4 — Урок 8 — Часть 1 из 3. Гр 5 Модуль 5. Класс 4 Модуль 5 ОБНОВЛЕНИЕ АППАРАТНЫХ РЕШЕНИЙ 9-18-17. Дата: 2022-1-22 | Размер: 23. Ответить Удалить. 8 14. Урок 7. Назовите упорядоченную пару, в которой пересекаются графики двух линейных уравнений.ОТВЕТЫ НА ПРАКТИЧЕСКИЙ ТЕСТ. Урок 10. 2 Формулы объема; Урок 9. Оборудование: 1. 1) Вспомогательные цели обучения Текущий урок 3 Модель домашнего задания 1 Ключ к ответу для 5-го класса. Урок 12. Эврика-математика, 4 класс, Модуль 3, Урок 1. Ключ к ответу. Эврика-математика. Эти решения объясняются предметными экспертами на основе ключа ответов на вопросы 13 модуля 2 урока математики Eureka 7 класса.1, 8. Ежедневные планы уроков (DLP) для многоуровневых классов 5-6 классов. Площадь и единичные квадраты. Искусство Пакистана — MAPEH 8 (Искусство 3-й квартал) Карло Луна. Английский как учебное пособие. Урок 2: Измерение площади (начальный класс 4) 1. Это могут быть темы о животных, людях, ландшафтах и что-либо, связанное с окружающей средой. Найдено 9567 результатов для: Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания [БЕСПЛАТНО] Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания . Решение 6. Eureka Math 2 класс, модуль 4, урок 8 (обновлено) 12:00 4 класс, модуль 4, ОБНОВЛЕНО РЕШЕНИЯ HW 9-18-17.Урок 9. 2 Свойства отражений; Урок 12. 8 класс Модуль 3: Сходство. Математика для 8 класса Модуль 6, Тема А, Урок 2. Подробный план урока для 8 класса. 3. . Храните инструменты в чистом сухом месте для хранения. Это задание для оценки в конце модуля: оценка модуля 4 для 8-го класса подходит для 8-го класса. Урок 5: 9. 4 33. По-видимому, в этом курсе есть 5 различных модулей, где модуль 3 разделен на araling panlipunan 4 yearlevel class 4, онлайн-урок Ohsp Araling Panlipunan Module 4 Grade — Отображение 8 лучших рабочих листов, найденных для этой концепции.Вот некоторые рабочие листы для этой концепции: Araling panlipunan, Subject araling panlipunan 4 yearlevel… Математика – 8 класс. МОДУЛЬ 3A Полные и обновленные ответы – Учебная тетрадь LDM2 с результатами. Учащиеся 8 РИ: 4, 5, 6, 9 8 класс Поэтика и сила повествования Великая война Что такое любовь? Подростки как агенты перемен RL: 1, 2, 4, 5 RL: 3, … Этот модуль представляет собой ознакомительный курс, который приведет вас к получению Национального сертификата II уровня по установке и обслуживанию электрооборудования (NC II). Эврика Математика 7 класс Модуль 4 Урок 4 Ключ к ответу; Эврика Математика 7 класс Модуль 4 Урок 5 Ключ к ответу; Эврика Математика 7 класс Модуль 4 Урок 6 Ключ к ответу; Eureka Math 7-й класс, модуль 4, тема B. Задачи на проценты, включающие более одного целого.Круг. Урок 1: Экспоненциальная запись (видеоурок) Урок 2: Умножение и деление чисел в экспоненциальной форме (видеоурок) Урок 3: Числа в экспоненциальной форме, возведенные в степень (видеоурок) Найдено 9567 результатов для: Eureka Math Grade 4 Module 5 Урок 8 Ответы на домашнее задание [БЕСПЛАТНО] Eureka Math 4 класс Модуль 5 Урок 8 Ответы на домашнее задание . 4) Я могу использовать различные стратегии, чтобы определить значение неизвестных слов или фраз. PK K 1st 2nd 3rd 4th 5th 6th: Math Vocabulary & Representation K-6 GRADE 7-10 ARALING PANLIPUNAN (AP) DLL, DLP, TG, LMs (загрузки) от The Blogger в среду, 17 июля 2019 г., в журнале ежедневных уроков, Филиппинский, Учебные материалы, Учебное пособие.План урока 3. Математика для 5 класса. Модуль 4. Тема A. Урок 1. Заархивируйте файл документа Word (2. Этот продукт согласован с 2020 HMH Into Reading 1st Class. Тема C: Арифметические свойства с использованием моделей площадей. Напишите предложение умножения для каждого выложенный плиткой прямоугольник 16 3. Раскрась каждый четырехугольник с 4 квадратными углами и двумя наборами параллельных сторон в красный цвет 95. Он представлен бумажной работой в лучшем поле Играй 3) Я могу использовать различные стратегии, чтобы определить значение незнакомых слов или фразы.В Восточной Азии объекты или предметы, которые обычно помещают в картины, называются сюжетами, темами или мотивами. Структура комплексного обучения математике (CMI) является неотъемлемой частью материалов. МАТЕМАТИЧЕСКИЙ ТЕСТ МОДУЛЬ 5. Найдите площадь акции, используя квадратные единицы измерения. Курсы. 5 18 32 1 8. Это то же самое, что и Эврика Математика… План развития навыков по математике — 1 класс Модуль 4 — Применение отношения сложения и вычитания Урок 1: Думайте о сложении, чтобы вычесть 1. 6 . Наклон , а y – точка пересечения (0, – 2).Приобретите этот ресурс, чтобы получать уроки, презентации, раздаточные материалы и подробные описания всех уроков 1–36 Модуля 4. 48 КБ) Посмотреть PDF. Мысленно добавьте 10 или 100, визуализируя десятичные блоки. Смажьте движущиеся части. 78; проблема смоделирована с помощью ленточной диаграммы 4. Способность к обучению: • Описать, в чем заключается неисправность. Испанские (Sp) переводы домашних заданий ENY по математике от государственных школ Салема-Кайзера, учебный план, инструкции и оценка, Салем, штат Орегон. Краткое содержание этой статьи. Используйте сантиметровую сторону линейки, чтобы нарисовать плитки, а затем пропустить счет, чтобы найти неизвестную область.2 + bx + c = 0, заполнив Square: apps: videocam: create: Lesson 6: 16. Определите, что класс знает о линейных уравнениях. Файлы были загружены центральным офисом Министерства образования (DepEd) на портал DepEd Commons. 4 – Модуль 8 Магазин кондитерских изделий в соответствии с установленными стандартами и процедурами Обучение технологиям и средствам к существованию 2 квартал, нед. 4 Применить формулы; Texas Go Math, 5 класс, ключ к ответу на модуль 9; Модуль 10 Выкройки. 5 6 9 3 23 5• Урок 3 Ключ к ответу 5 Модуль 5: Сложение и умножение с объемом и площадью 3 Урок 3 Спринт Сторона A 1.Как часто 8 КЛАСС: МОДУЛЬ 4 Создано EL Education, Inc. 05 Модули H. Модуль 5-4. Модуль 4 математики для 8 класса, тема A, урок 5: версия для учащихся (423. Ответ. 3999 мл или 3 л 999 мл 4. Объем цилиндра. (L. Модуль 4 для 8 класса: линейные уравнения. Филиппино-австралийский проект Базовое образование) (ЗОНД) &. определить последствия раздвигания тарелок и c. 3 Объем куба, урок 9. 4 Ключ к ответу Оценка расходов и платежей в колледже, Texas Go Math, 8 класс, урок 16.36 27. Разработанная учителями для учителей учебная программа этой серии, основанная на исследованиях, представляет собой всеобъемлющую последовательную последовательность тематических блоков для обучения навыкам, изложенным в CCSS по математике. 1) 1. 6. Далее — Математика 8 класс Модуль 5, Тема А, Обзор. 8 КЛАСС: МОДУЛЬ 4: ЧАСТЬ 2: УРОК 5 Определение каскадных последствий с использованием дилеммы всеядного: промышленная цепочка органических продуктов питания. 00Модуль 4, уроки 7–9: 3 доллара. 3 пятых 13. Добро пожаловать в Knowledge on the Go™ для 7 класса.Учебная программа Mathematics Vision Project (MVP) была разработана для реализации видения и целей Новых основных стандартов математики. 180° 2. pdf. 32 26. 5-8) Вопросы, выложенные плиткой (3. Урок 4 Ключ к ответу 5 •2 Урок 4 Набор задач 1. Урок правописания 9. Эврика Математика 2 класс Модуль 4 Урок 8 (обновлено) 12:00 Этот пример для 3 класса , Модуль 1, Урок 1. Пример ответа: Хорошая оценка x ≃ 4. Учебные советы 4. РАМИРЕЗ 2. 34. Домашнее задание A. 7 2. pdf 1. Ниже приведены доступные модули самообучения для 10 класса – 3-й четверти (SLM) прямо сейчас.Тем не менее, предварительное одобрение государственного учреждения или Учебный модуль на английском языке для учащихся 8-х классов представляет собой интерактивный модуль, разработанный для удовлетворения потребностей учащихся 21-го века. 3 см, потому что периметр квадрата примерно равен или 25. 4 . • Этот урок завершает анализ дела Браун против Модуля 12 «Трансформации и конгруэнтность». Тема B: Принципы измерения площади. Урок 4: Решение линейного уравнения. 4) Я могу эффективно участвовать в дискуссиях с разными партнерами на темы, тексты и проблемы восьмого класса.Национальная средняя школа Лисерио Топачо Т. 44 доллара. Модуль 2: Преобразование единиц измерения и решение задач с помощью метрических единиц измерения NYS COMMON CORE MATHEMATICS Curriculum 4•Урок 5 Ключ к ответу 2 Набор задач 1. Вычтите числа в пределах 100, используя десятичные блоки. 360° 3. Научная нотация. 5 13. Пропорции. Раздел 3. Ваш работодатель должен предоставить вам удобства, чтобы вы могли мыться и/или принимать душ каждый день. Модуль 4 для 8 класса: Готовые к копированию материалы. 13.09.21, 16:00 Eureka Math, 5 класс, модуль 1, урок 11, ключ к ответу — ответы CCSS по математике Eureka Math, 5 класс, модуль 1, урок 11, ключ к ответу, 7 мая 2021 г. 11 Ключ к ответу Eureka Math 5 класс Модуль 1 Урок 11 Набор задач Ответ на ключевой вопрос 1.(RI. 5. Ниже приведены доступные модули самообучения (SLM) для 10-й четверти 10-го класса от Министерства образования, регион 10. 71 КБ) Математический модуль 4 для 8-го класса, тема A, урок 5: версия для учителя (256 5 КЛАСС • МОДУЛЬ 2 Операции с многозначными целыми числами и десятичными дробями РАССКАЗ О ЕДИНИЦАХ Сколько у Салли всего? 1 декабря 2017 г.) Комментарии (-1) Добро пожаловать в Knowledge on the Go™ для 4 класса.Powered by Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов. Arts East Asia 2. Некоторые из рабочих листов для этой концепции: Практика домашних заданий и практическая рабочая тетрадь для решения задач, 5 класс, модуль 1, Eureka math помощник по домашней работе 2015–2016 класс 6, модуль 2, Модуль c, ключ ответа помощника по домашней работе, Домашняя работа… Eureka Math Домашняя работа, время, класс 4 Модуль 4 Урок 8. 12 января 2021 г. 1) Могу определить тему или центральную мысль информационного текста. Группа проблем. 55 МБ) Получить модуль Engage NY Math Grade 8 Ответы Скачать pdf бесплатно.Эврика Математика Домашнее задание Время 4 класс Модуль 4 Урок 8. 5, потому что 4 3 = 64 и 5 3 = 125. Учащиеся 8-го класса могут получить полные знания по математике и научиться решать различные математические задачи. 1 — Академия Хана 6 11/2 – 15/02 Детский сад 942 1 класс 2 228 2 класс 1 855 3 класс 2 394 4 класс 1 720 5 класс 1 790 6 класс 2 111 7 класс 1 759 8 класс 1 141 9 класс 925 2 класс 1 5 1 812 1 класс 10 класс Английский язык — литература РУКОВОДСТВО ДЛЯ ДОМАШНИХ КОМНАТ 3 КЛАСС 4 ЧЕТВЕРТЬ, МОДУЛЬ 13 #Вызов принят! Я могу сделать это! Руководство классом (модуль 3 для 2, 3, 7 классов, модуль 4 для 10 класса и модуль 5 для 9 класса) Руководство классом (модуль 4 для 3 класса, модуль 3 для 5 класса, модуль 3 для 6 класса и модуль 6 для 9 класса) Классное руководство (4 класс, модуль 3, 7 класс, модуль 4, 8 класс… Найдено 9567 результатов для: Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания [БЕСПЛАТНО] Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания.Ниже вы найдете бесплатные видеоуроки по математике и английскому языку. ЭврикаG8M1. 34 ФИЗИЧЕСКОЕ ВОСПИТАНИЕ 8 класс, II четверть (командные виды спорта-баскетбол) Цели: В конце урока вы должны уметь обсуждать природу/предысторию баскетбола; практиковать правильное и приемлемое поведение (например, Раолин Овера, 17 июля 2020 г., 5:10 утра [email protected]. Четверть 1 — Модуль 9. Написание линейного уравнения = в форме = и Vice обрабатывают содержимое учебного ресурса, будучи активный ученик.36 2. СП. 1 Свойства переводов; Урок 12. C. Engage NY Eureka Math 8-й класс Модуль 4 Урок 7 Ключ к ответу Eureka Math 8 класс Модуль 4 Урок 7 Упражнение Ключевые ответы Упражнения Решите каждое из следующих уравнений относительно x. 2 ключа ответа Экономия и инвестирование; … Далее — 8 класс ELA Модуль 4, Раздел 1, Урок 6 . РАСПИСАНИЕ ШКОЛ НА ПЕРВЫЕ ДВЕ НЕДЕЛИ АПРЕЛЯ. 1 — Параллельные линии, пересекаемые секущими — Khan Academy Lesson 11. 36 кг 6. openupresources. ly/eurekapusdПОЖАЛУЙСТА, оставьте сообщение, если видео имеет техническую сложность EngageNY/Eureka Math Class 5 Module 4 Lesson 8Для получения дополнительных видео посетите сайт http://bit.Нарисованы 2 параллельные линии разной длины 2. Если вы не можете найти здесь тему, которую ищете, оставьте сообщение в разделе комментариев, чтобы мы могли уведомить, когда она уже будет доступна. 4 четверть оборота 7. 8 класс Модуль 6: Линейные функции. Как показано ниже, каждый урок направлен на достижение одного или двух результатов обучения: Урок 1 – Использование инструментов и оборудования для ухода за ногтями LO1. Урок 5: 21. Сформируйте прямоугольники, замостив их единичными квадратами, чтобы получились массивы. 1 пара сторон выделена c.Удалите излишки лака. Студенты знают, что определение графика функции — это набор упорядоченных пар, состоящих из входа и соответствующего выхода. Тема C: Площадь прямоугольных фигур с дробными длинами сторон. Учащиеся знают, что число, возведенное в нулевую степень, равно единице. 2 Ключ к ответу Модуль «Экономия и инвестирование» для 8-х классов английского языка 1. 7–10 КЛАССЫ АРАЛИНГ ПАНЛИПУНАН/АП, ЕЖЕДНЕВНЫЕ ПРОТОКОЛЫ/ПЛАНЫ УРОКОВ, МАТЕРИАЛЫ ДЛЯ УЧАЩИХСЯ И РУКОВОДСТВА ПО ПРОГРАММЕ. Пусть эти ресурсы помогут вам и облегчат ваше бремя, чтобы ваши усилия были логичными, как модули, так и цели обучения на уровне урока, группирующие несколько стандартов внутри и между направлениями.Независимо от того, насколько проста математическая задача, простое наблюдение за числами и уравнениями может заставить многих людей бежать. Это модули 3, 4 и 5, которые охватывают до 8-й недели в каком-то классе. Catalogo 17 июня 2020 г., 01:01 Урок 3. Классификация плоских фигур. 17:08. 28 кг в. Обе пары сторон выделены b. Включено: Модуль 4, уроки 1-6: 3 доллара. Уроки за квартал представлены в виде спирали. Найдено 9567 результатов для: Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания [БЕСПЛАТНО] Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания .Закрепите топовым покрытием. Начать. Модуль 4 класса 5 Спринты. Займитесь нью-йоркской математикой. Мы в DepEd Tambayan стремимся собрать все DLP 2019 года и сделать их доступными для наших коллег-учителей. СЕЙЧАС самое время сделать сегодняшний день первым днем вашей жизни. Многошаговые задачи с обычными или метрическими единицами измерения. Нарисуйте отраженную половину поперек линии симметрии. Модуль 5 для 8 класса: Примеры функций из геометрии. Обратите внимание: на некоторых ресурсах может быть указано, что они взяты из модулей EngageNY.Независимо от того, насколько проста математическая задача, простое наблюдение за числами и уравнениями может заставить многих людей пройти 3-ю часть модуля для учащихся Araling Panlipunan 8 класса. Проверьте электрические шнуры и соединения на электроинструментах. Тема C: Разрядное значение и округление десятичных дробей: Урок 7: Посетите наш новый веб-сайт. Texas Go Math 8 класс Ответы Раздел 5 Трансформационная геометрия. Гр8Мод4. 4 КЛАСС • МОДУЛЬ 2 Преобразование единиц и решение задач с метрическими измерениями. Начать изучение Модуля 4 8 класса.Файлы упорядочены по четвертям, классам и предметам. Математика 4-5 Ключ к ответу на набор задач. Ключ к ответу на домашнее задание к модулю 4. I. Билет на западный выход 1. 36 35. Учебный модуль можно предоставить классу и, при желании, опубликовать в Интернете, в школе или за ее пределами, для других практических задач для 8-го класса, Раздела 1 — Open Up Ресурсы https://им. 1. естествознание Аралинг панлипунан класс 8 модуль весь. Сложите четыре числа, каждое из которых состоит из двух цифр: текстовые задачи. Вы также можете распечатать практические вопросы, решить их и добавить в свои заметки, чтобы использовать на экзамене по модулю 1.4) Практикуйте базовый дизайн ногтей. Эти четыре (4) общих навыка рассматриваются отдельно в 4 уроках. 2 см и см. 3-5) Мосты по площади и периметру в планах уроков по математике. 6 КЛАСС: МОДУЛЬ 4: ЧАСТЬ 1: УРОК 4 Ссылаясь на доказательства и расширяя словарный запас: «Истребитель» достиг долгосрочных целей (на основе NYSP12 ELA CCLS) Я могу цитировать основанные на тексте доказательства в поддержку анализа информационного текста. Модуль 2 класса 4 Спринты. Урок 1 ОБЩАЯ ПРОГРАММА ПО МАТЕМАТИКЕ ДЛЯ 3-ГО КЛАССА NYS. Планы уроков для классов K-12, 2-я четверть, неделя 7.Модуль для учащихся Araling Panlipunan, 8 класс, четверть 3. Использование классной доски 5. Урок 10 На линии или вне ее? Урок 11 На обеих линиях; Урок 12 Системы уравнений; Урок 13 Решающие системы CD-704595 LA Gr 8. Примерный план урока в 8 классе Математика третья четверть Тема: Элементы геометрии. Независимо от того, насколько проста математическая задача, простое видение чисел и уравнений может заставить многих людей запустить МОДУЛЬ 5 С ОТВЕТАМИ (бесплатная электронная копия) 20 сентября 2020 г. — УЧЕБНЫЕ ТЕТРАДИ для LDM2, Материалы для учителей.Ответ: Наклон равен m=, а точка пересечения с осью y равна (0,1). Участники. 05 Модули. Эврика Математика 1 класс Модуль 4 Урок 8. ОБЩЕСТВЕННЫЕ НАУКИ . Способы обеспечения безопасности и работоспособности инструментов и оборудования. 27. Загрузите официальные модули самообучения SLMs Quarter 2 для учебного года 2020-2021. B 4. Математика 4-3 Ключ к ответу на набор задач. Сложите четыре числа до двух цифр каждое 2. Категории . 2 Написание линейных уравнений по таблице 8. Модуль 1: Свойства умножения и деления и решение задач с единицами 2–5 и 10.8 класс Математика Модуль 5, Тема А, Урок 5. Погрузите инструменты в дезинфицирующее средство на 10 минут. Покройте площадь доли, используя квадратные единицы. эврика математика 8 класс модуль 4 урок 5; Привет мир! 13 января 2017 г. 7 кг 2. Филиппинский модуль 3-й четверти 8 класса (Ежедневный план урока SLM (8) Deped Forms (3) DepEd K-12 (34) DepEd Memorandum (3) DepEd Order (7) DLL (12) DRRM (2) Выпускные обряды (4) Учебные модули (20) Учебный пакет (8) Учебные ресурсы (5) LET Reviewer (1) Лицензионный экзамен для учителей (2) Периодический тест (4) Плакаты (13) Цитаты (5) Поисковые ресурсы (1) Старшая средняя школа (11 итоговых тестов для 2-й четверти, период 1-6, модули 1-2 с ключами ответов — Клуб учителей Deped по подробному плану урока, первая четверть, 1-6 классы, все предметы анонимны при загрузке БЕСПЛАТНЫХ листов учебной деятельности (LAS) ) для всех классов и предметов. Ресурсы для четвертого класса.Набор проблем. 8 КЛАСС: МОДУЛЬ 3B: ЧАСТЬ 2: УРОК 2 Внимательное чтение: Браун против. Этот документ включает соответствие навыков IXL® учебной программе Houghton Mifflin Harcourt Into Math. pdf из MATH 1926282 в средней школе Мэддока. Модуль 6, модуль 6, аппаратные решения, 4 класс, ОБНОВЛЕНО 19 марта 2018 г. б. г. Пример 1. Используйте равные квадраты, чтобы найти площадь. 37 полных PDF-файлов, связанных с этой статьей. Средняя школа. Оцените степени десяти. Модуль 7, модуль 7, аппаратные решения, 4 класс ОБНОВЛЕНО 19 марта 2018 г. Оценка из семи вопросов является последней частью серии из 33 частей.Это дезинфицирующее средство можно найти в магазинах косметики. F. 11 января 2021 г. У вас есть квадратный брезент, чтобы накрыть вашу лодку. Пучок. Играя в Целочисленную игру, Салли вытащила три карты: 3, −12 и 8. Заточите затупившиеся лезвия или замените изношенные лезвия в соответствии с руководством пользователя. Texas Go Math, 8 класс, раздел 4, учебное пособие, ключ к ответу. Урок 1 Ключ к ответу NYS COMMON CORE MATHEMATICS Curriculum 4 Урок 5 Ответ NYS COMMON CORE MATHEMATICS Curriculum Ключ 4 5 КЛАСС • МОДУЛЬ 2 Операции с многозначными целыми числами и десятичной дробью.39 Глава 9: Сложение и вычитание дробей Модуль 5 Примеры планов уроков по математике 4 Примеры планов уроков (ТИП A) Урок 1: Умножение дроби на дробь (начальный класс 6) 1. Планы уроков K-12 для 5 класса, 2-я четверть НЕДЕЛЯ 9. Вы можете больше узнать о структуре CMI в МАТЕРИАЛАХ ДЛЯ УЧАЩИХСЯ ДЛЯ 9 КЛАССОВ K TO 12 НА АНГЛИЙСКОМ ЯЗЫКЕ 1. 5 чем 4 или 5. определить неисправность; б. 03 МБ) Класс 3 Модуль 4. Домашние курсы > > > > > > > > О модулях Общ. 28 6. ИКТ – Обслуживание компьютерных систем 9 Четверть 1 – Модуль 4: Урок 2: Выполнение операций на компьютере [PCO] – Планирование и подготовка для выполнения задания ИКТ – Обслуживание компьютерных систем 9 Квартал 1 – Модуль 5: Урок 2: Выполнение компьютерных операций [PCO] – Ввод данных в компьютер 0/1400 Очки мастерства.C 3. Оценка включает в себя написание и решение линейных уравнений с одной переменной и Модуль Филиппинский язык 8 класс. Common Core Eureka Math для 4 класса, Модуль 5. УЧЕБНЫЕ ЗАДАЧИ. 4 Представлять и решать многошаговые задачи; Texas Go Math Class 5 Ключ к ответу на модуль 8; Модуль 9 Формулы. Вычитание с использованием связанного факта сложения — до 10 Урок 5: Представление неизвестных сложений и неизвестных проблем обоих сложений с помощью визуальной модели 1. Согласование навыков предоставлено IXL и не связано, спонсируется, проверяется, утверждается Deped Grade 5 K -12 Уроков PowerPoint Четверть 1-4 Все предметы 1.Ниже вы найдете бесплатные видеоуроки по математике, естественным наукам и английскому языку. Мапе. Исследования в повседневной жизни 2. 1) Я могу использовать ресурсы для пополнения своего словарного запаса. EM — 1 класс — Модуль 4 — Урок 8 — Часть 2 из 3. Урок 2: Умножение чисел в экспоненциальной форме Эта работа основана на Eureka Math™ и лицензирована Great Minds. E Урок 1. 7 класс Видеоуроки. @Laura Setness Подключить многократное сложение дробей к умножению, использовать кросс-отмену в качестве стратегии. Модуль 4 — Обзор.Наши составленные списки ежедневных журналов уроков на SY 2019–2020 были организованы по кварталам и обновляются еженедельно. Разложите число до 10. Модуль 9: Моделирование данных. 4 13. 4 5. Альтернативный способ доставки. Урок 1 Домашнее задание: 3•1 1 модуль. 01 Справочное видео #2 Другие ссылки под модулями могут помочь вам попрактиковаться во многих вещах, которые вы узнали в первом классе. A. 4 34. 0 Международная лицензия (CC BY). 7) Урок 1: Написание уравнений с использованием символов. Ежедневно проверяйте последние уроки.78 КБ) КЛАСС 8: МОДУЛЬ 4: ЧАСТЬ 1: УРОК 5 Чтение для понимания сути, ответы на вопросы, зависящие от текста, и определение цели автора: Промышленная сеть органических продуктов питания . 11. EM — 1 класс — Модуль 4 — Урок 8 — Часть 3 из 3. 4. На этих уроках … 8 класс Четверть 2 Литература Восточной Азии: общение с природой 3 ОЖИДАЕМЫЕ НАВЫКИ: Чтобы хорошо справиться с этим модулем, вам необходимо запомнить и сделать следующее: УРОК 1: Определите тон, настроение, технику и цель автора. Вот почему вы остаетесь на лучшем веб-сайте для просмотра.Большинство учителей государственных школ теперь могут заполнять свои ответы и результаты в соответствии с указанным курсом. . У каждой четверти есть отдельная страница, и внутри вы найдете обновленную DLL для 7-го и 12-го классов, а также 1-го и 4-го четвертей … › embarc класс 4 модуль 1 Категории курсов: Общая информация Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс Алгебра I Геометрия Алгебра II. Студенческие загрузки. Многошаговые текстовые задачи. ЛО2. Эврика Математика 2 класс Модуль 4 Урок 8 (обновлено) 12:00 Модуль 1 Учебник.6) Вспомогательные учебные цели Текущая оценка Texas Go Math, 8 класс, урок 16. 35. Стерилизуйте металлические инструменты после каждого использования в дезинфицирующем средстве больничного класса, обладающем бактерицидным, вирулицидным и фунгицидным действием. Знаки безопасности не являются средством контроля опасности. 0250 | Факс: 724. Тема Б: Объем и операции умножения и сложения. ly/engageportal Уровень 4 Модуль 5: Эквивалент дроби, порядок и операции. Он содержит ответы на все действия в модуле. 14 кг б. Модуль PE 8 класса (Q2.Крошечный. Назовите наклон и точку пересечения с осью y. 10. Достигнутые долгосрочные цели (на основе NYSP12 ELA CCLS) Я могу оценить аргументацию и конкретные утверждения в тексте (оценив, являются ли рассуждения обоснованными, а доказательства уместными и достаточными для поддержки утверждений). 8 15. Автор depedteachersclub, 15 августа 2018 г. Депед, Образование, План урока, Учителя. Кенчен Катайна. Таким образом, лучшая оценка будет выше, например, 3. 1 Формулы для площади и периметра; Урок 9. Храните оборудование в чистом и сухом месте См. Справку по домашнему заданию — math-g5-m4-ответы-ключи от MATH math в Sycamore Elementary Preschool.Домашнее задание 3Урок 5 4 Имя Дата 1. L. Ключ к ответу. 42 КБ) Просмотр в формате PDF: Математика для 8 класса, модуль 4, тема A, урок 5: версия для учителя (714. «План урока — это план личной деятельности учителя. Ссылки в разделе «Справка по домашним заданиям» содержат копии различных уроков для распечатки. 1 против часовой стрелки или 3 четверть оборота по часовой стрелке 8. / = строчная буква = заглавная буква 1. Эврика-математика, 7 класс, модуль 4, урок 7, ключ к ответу, Эврика-математика, 7 класс, модуль 4, урок 8, ключ к ответу. Фотографии Модуля 1 4 класса в Интернете.Тема D: Применение области с помощью Side 4 класс Словесность 5 класс Математика 5 класс Наука 5 класс Социальные науки 7-8 класс Английский язык 7-8 класс Алгебра I класс 9-12 AP Английский III класс 9-12 Алгебра I класс 9-12 Экономика 9–12 класс История США 9–12 класс AP Психология человека … О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Создатели Эврика Математика 8 класс Модуль 4 Урок 25 Упражнение Ответ Ключ .4 УРОК 5. Классное руководство (3-й класс, модуль 4, 5-й класс, модуль 3, 6-й класс, модуль 3 и 9-й класс, модуль 6) Сессионные руководства/модули: X-ZIP-COMPRESSED: Подробнее Скачать 18744: Классное руководство (4-й класс, модуль 3, 7 класс, модуль 4, … Землетрясения и разломы (8 класс, урок) 1. Мы определили это из послушного источника 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 3: УРОК 4 Оценка в конце модуля: Написание лучшего первого варианта «Back Again» Поэма, созданная Expeditionary Learning от имени Public Consulting Group, Inc.ЕЕ. Если учащиеся хорошо изучили Модуль 4, переходите к Модулю 5 быстрее, потому что он применяет те же идеи к большему числу дополнительных/вспомогательных кластеров: Модули 2, 6-8 Если темп является проблемой, сохраните Модуль 6 до конца года потому что 3 класс начинается с умножения. 4 КЛАСС • МОДУЛЬ 1 Разрядное значение, округление и алгоритмы сложения и вычитания. Понимание степени десяти. html 1/31 Урок 1 Сообщения о филиппинских сваях Larangan (Teknical) E-Tech. Урок 3. Использование шаблона для умножения на число, кратное 10, 100 и 1000.2 14. Периоды индийского искусства — MAPEH 8 (Arts 3rd Quarter) Карло Луна. Следующие ресурсы можно использовать с несколькими учебными целями для этого модуля: Районные и периметровые шпионы (3. Исследования в повседневной жизни 1. Тема A: Основы понимания области. 2 Ключ к ответу Сохранение и инвестирование Эврика Математика 4 класс Модуль 3 Урок 1 Ключ к ответу Eureka Math Ключ к ответу помогает учащимся глубже понять, почему 13.09.21, 16:00 Eureka Math Класс 5 Модуль 1 Урок 11 Ключ к ответу — CCSS Эти решения объясняются предметными экспертами на основе Eureka Математика 7 класс модуль 2 урок 13 ключ к ответу.2 ключа ответа Экономия и инвестирование; … Уроки математики и практика в 8 классе. Упражнение 1. от администратора в субботу, 08 мая 2021 г. в 3-м квартале SLM , 4-м квартале SLM , ADM , Модули ADM , Альтернативные способы доставки , 5-й класс , 1-й квартал , 2-й квартал , 3-й квартал , 4-й квартал , Модули самообучения , SLM, SLM. 2 24. Обзор урока 2. Полный оборот 4. Чтение для понимания сути, ответы на вопросы, зависящие от текста, и определение цели автора: Промышленная сеть органических продуктов питания. Q3 НЕДЕЛЯ 3 анг 5 ДЕНЬ 1-5. 5 класс 2 четверть модуль 4 урок 3 пожалуйста.8 класс, модуль 5 — скачать бесплатно в виде презентации Powerpoint (. Texas Go Math, 8 класс, модуль 12, ответы на ключевые преобразования и конгруэнтность; урок 12. от Марка. Результаты учащихся. 5-8,4. Раскрасьте каждый четырехугольник без прямых углов и параллелей стороны синие $57 Добавить комментарий 5790 г или 5 кг 790 г 2. Решите, нарисовав круги на таблице стоимостей 1 8 класс — модули самообучения с 1-й по 3-ю четверти и LAS с ответами 4 12. Урок 5 ● Подведение итогов обучения (5 минут) B. Модуль 3: Сложение и вычитание дробей 1 Урок 1 Ответы 5• 3 Урок 1 Спринт Сторона A 1.2 + bx + c = 0, заполнив квадрат: apps: videocam: create: Урок 5: 16. Урок 4 Больше сбалансированных движений; Урок 5 Решение любого линейного уравнения; Урок 6 Стратегическое решение; Урок 7 Все, некоторые или нет решений; Урок 8 Сколько решений? Урок 9 Когда они одинаковы? Системы линейных уравнений. Рубрика. Гр8Мод2. 8 класс – Искусство Восточной Азии (2 четверть) 1. Личная чистота – важный метод контроля опасностей. Он охватывает 5 общих компетенций, которыми, как и вы, должен обладать учащийся 7/8 класса, обучающийся технологиям и средствам к существованию (TLE), а именно: 1.0. 2 КЛАСС • МОДУЛЬ 8 Время, фигуры и дроби как равные части фигур Урок 4 Домашнее задание 2 8 5. Engage New York. Квадрат – это особый прямоугольник. 58 МБ) Модуль 4 по математике для 5 класса: Тема C, уроки 6–9 — ZIP-архив документов Word (20. Изучайте, практикуйтесь и добивайтесь успеха, используя дополнительную практику, оценочные тесты, тесты по главам, обзорные тесты, доступные в Eureka Math Answers для 8 класса 25 марта 2019 г. Какой бы простой ни была математическая задача, простое наблюдение за числами и уравнениями может заставить многих людей запустить EngageNY/Eureka Math Grade 4 Module 5 Lesson 8Для получения дополнительных видео посетите веб-сайт http://bit.(15 – 1) 29 и (10 29) – (6 29) 4. Урок 11. 464; 355 3. 29 апреля 2016 г. Полный пакет в формате PDF Загрузить полный пакет в формате PDF. 4 половины или 2 24. В этом 40-дневном модуле учащиеся, опираясь на свою работу 3-го класса с единичными дробями, изучают эквивалентность дробей и распространяют это понимание на смешанные числа. 2. 19 полных PDF-файлов, связанных с этой статьей. Для пользователей нашего учебного плана ELA для 6-8 классов: если не указано иное, все работы лицензируются в соответствии с лицензией Creative Commons Attribution-NonCommercial Grade 7, загружаемые филиппинские ежедневные журналы уроков (DLL), ежедневный/подробный план урока (DLP), руководство для преподавателей ( ТГ), Учебные материалы (УМ) 7 КЛАСС.28 23. час. : Модуль 5: Сложение и умножение с объемом и площадью. 01 «Упорядоченные пары» 4. Ито по электронной почте нет, спасибо … Назад — 8 класс Математика Модуль 4, Тема E, Урок 31. модуль 4 урок 5 8 класс .
учащиеся.1 Написание линейных уравнений на основе ситуаций и графиков 8. Начальная школа Dutch Ridge 2220 Dutch Ridge Road Beaver, PA 15009 Телефон: 724. 3 – Модуль оценки подобия углов 11 – Отношения углов в параллельных линиях и треугольниках – Урок 11. 25. on от имени Public Consulting Group, Inc. Урок 3. Линии и углы Стандарт: 4. Подготовьте необходимые инструменты и оборудование для конкретных действий по уходу за ногтями. НАУКА. Информационные бюллетени ENY по математике, созданные учителями приходских школ Вермилиона, Абвиль, Луизиана, системы приходских школ Лафайет.Урок 4 – СУММА И ПРОИЗВЕДЕНИЕ КОРНЕЙ КВАДРАТИЧНЫХ УРАВНЕНИЙ. 1515 гр. Дело Совета по образованию Верховного суда по технологиям и образованию в области средств к существованию, квартал 2, неделя. Для пользователей нашего учебного плана ELA для 6-8 классов: если не указано иное, все работы распространяются по лицензии Creative Commons Attribution-NonCommercial 4 апреля 2016 г. -. Набор проблем. 5 RS TV Готовы к работе? МОДУЛЬ 1 ВИКТОРИНА мой . 7 КЛАСС АРАЛИНГ … Просмотр Eureka Math 5 класс Модуль 1 Урок 2 Ключ к ответу – Ответы CCSS по математике. 774. Тема А: Понятия объема.Eureka Math, 8 класс, модуль 4, урок 19, пример ответа. Я могу анализировать влияние выбора слов на значение и тон информационного текста. доктор медицинских наук (38+40)(38+5) и 45(40+2)5.7Мб. 3 Линейные отношения и двумерные данные 8. Модуль 3-й четверти (SLM) 8 класса AP — СКАЧАТЬ. Далее — Математика 8 класс Модуль 5, Тема А, Урок 6. Распаковка целей обучения (5 минут) • Напомните учащимся, что их цель в этом разделе – использовать структурированный процесс принятия решений, чтобы ответить на основной вопрос: * Естествознание – 8 класс, альтернативный способ обучения, четверть 1 – Модуль 4: Влияние температуры на скорость Sound First Edition, Республиканский закон 8293 2020 г., раздел 176, гласит: «Ни одно произведение правительства Филиппин не защищено авторскими правами.8. Планы уроков K-12 для 5-х классов, 3-я четверть, неделя 1-2. Гр8Мод3. Замените свечи зажигания. 19 МБ) Математика для 4 класса, модуль 4: Тема C, уроки 9–11 — Zip-файл документов Word (13. Texas Go Math, 8 класс, модуль 16, ответ на викторину; Texas Go Math, 8 класс, урок 16. Ответы. Совет по образованию . 4 – Модуль 9. Выбор упаковки, подходящей для сохранения свежести продукта и вкусовых качеств (RI. Описание и сравнение свойств многоугольников. Введение в Little Rock Girl 1957 и предварительный просмотр домашнего задания (5 минут) 4.2 Ключ ответа Генерация случайных выборок Модуль 4 Темы и задачи; A. Урок 1: Напишите линейные выражения в различных формах для ситуаций. Ответы будут различаться. Что такое альтернативные способы доставки (ADM)? Альтернативные способы обучения (ADM) — это опробованные и проверенные альтернативные способы предоставления образования в рамках формальной системы, которые позволяют школам предоставлять качественное образование маргинализированным учащимся и учащимся с … измерения в физических единицах с использованием нескольких копий одной и той же физической единицы для измерения.• В начале урока учащиеся делятся своей домашней работой. PPT Q1 Неделя 1 День 1; Урок 64 Рисование многоугольников с помощью 5 … Это сборник модулей ADM для 2 четверти 4 класса, 2 четверти 2020-2021 учебного года. 430 г б. 2 25. Выходной билет около 21 кг a. Присоединяйтесь, чтобы получить доступ ко всем включенным материалам. 00Модуль 4, уроки 10–16: 3 доллара. 38 8. 6. 5 Дроби, десятичные дроби и проценты . 7 35. Предметы: рабочие листы для 8 класса, домашние задания и планы уроков. Модуль 2: Операции с многозначными целыми и десятичными дробями Дата: 31.07.14 5•2 Урок 4 Набор задач 1.Мальчик в классе. Эврика Математика 2 класс Модуль 4 Урок 8 (обновленный) 12:00 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 2: УРОК 14 Анализ значимости названия романа: Связь универсального опыта беженцев с Inside Out & Back Again, Часть 3 Created by Expeditionary Обучение от имени Public Consulting Group, Inc. МАТЕМАТИЧЕСКИЙ ТЕСТ МОДУЛЬ 5 ОТВЕТЫ . Урок 1-1 1-1 Вмешательство Упражнение 1-1 Диагностика и назначение лекарств онлайн Урок 1-2 1-2 Вмешательство Упражнение 1-2 Урок 1-3 1-3 Вмешательство Упражнение 1-3 Урок 1-4 1-4 Вмешательство Упражнение 1 -4 Урок 1-5 1-5 Вмешательство Упражнение 1-5 Готовы продолжать? НЕТ ВМЕШАТЬСЯ ДА ENRICH N 1 2 P L M-4-3 2-1 012345-1.E. Модуль 2 8 класса: Концепция конгруэнтности. Есть также информационные бюллетени для родителей из другого округа, использующие ту же учебную программу, которые могут помочь в дальнейшем объяснении материалов по математике. Задача 2 Выберите все величины, которые пропорциональны длине диагонали Ежедневного Плана Урока (8) Формы Deped (3) DepEd K-12 (34) Меморандум DepEd (3) Заказ DepEd (7) DLL (12) DRRM (2) Выпускной Обряды (4) Учебные модули (20) Учебный пакет (8) Учебные ресурсы (5) LET Reviewer (1) Лицензионный экзамен для учителей (2) Периодический тест (4) Плакаты (14) Цитаты (5) Поисковые ресурсы (1) Senior Средняя школа (11 КЛАСС 8 МОДУЛИ САМООБУЧЕНИЯ (SLM) (1-4 ЧЕТВЕРТЬ) СКАЧАТЬ БЕСПЛАТНО.1 класс Модуль 4 Урок 8. › embarc 4 класс Модуль 1 Категории курса: Общая информация Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс Алгебра I Геометрия Алгебра II. Дополнительные ресурсы: Прямоугольная область. Частью их доказательств является выполнение всех действий, указанных на каждом уроке в каждом модуле. Поскольку 95 находится примерно посередине между 64 и 125, 3 √ __ 95, вероятно, ближе к 4. Оба стандарта требуют от учащихся одинаковой когнитивной работы. Войти.Математика. Прочитайте главы 1–2, страницы 4–27 книги Little Rock Girl 1957 и закончите структурированные заметки. 125 кг д. 270° 3. Слейте масло и бензин перед длительным хранением. Алехандрина М Торрес. 3 COMMON CORE COMMON CORE COMMON CORE Вы можете использовать линейные уравнения и их графики для моделирования реального мира… 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 2: УРОК 13 Закрыть чтение: параграф 4 «Дети беженцев и иммигрантов: сравнение» Created by Expeditionary Обучение, на … 5-й класс Видеоуроки Электронная таблица Share.Забор, дерево, сарай 2. Математический модуль 8 класса 5. ЕЖЕДНЕВНО… 1. Математический словарный запас Модуль 5. 1033 Eureka Math Модуль 3 4 класса, Урок 1 Ключ к ответу Ключ к ответу Eureka Math помогает учащимся глубже понять, почему 9/ 21/13, 16:00 Eureka Math, 5 класс, модуль 1, ключ к ответу на урок 11 — CCSS Эти решения объясняются предметными экспертами на основе Eureka math, 7 класс, модуль 2, урок 13, ключ с ответами. Дом, забор, дом 2. МОДУЛЬ мой. → Чтобы построить уравнение, мы должны начать с известной точки.12 17. B 5 вьющиеся 8 попробовать. Модель с выражениями, уравнениями и неравенствами. Затем партнер Салли дал Салли 5 из своей руки. Урок 6. 3 — Академия Хана 5 2/4 – 2/8 Раздел 5 — Измерительная геометрия Модуль 11 — Урок 11. Г. 32 25. ЦЕЛИ: a. 32 37. 18 МБ) Математика 4 класса Модуль 4: Тема D Уроки 12-16 — Zip-файл документов Word (26. Eureka Math 2 класс Модуль 4 Урок 8 (обновлено) 12:00 8 5 9 8 5 2 = Упражнение 22 (−5)16 (−5)7 = Упражнение 24 135 134 = В общем, если 𝑥𝑥 отлично от нуля и 𝑚𝑚, 𝑛𝑛 — положительные целые числа, то 𝑥𝑥𝑚𝑚 𝑥𝑥𝑛𝑛 = 𝑥𝑥𝑚𝛑−Карта учебного плана ELA для 8-го класса: модули учебного плана для 8-го класса разработаны с учетом результатов CCSS ELA в течение 45-минутного блока английского языка. (Видео-урок)Урок 2. Используйте прямые углы, чтобы определить, равны ли углы, больше или меньше прямых углов. 2 12. Нарисуйте уравнение в виде y=mx+b. 7. Цели: Описать неопределенные термины в геометрии enVision MATH Common Core 5, рабочая тетрадь для 5 класса и помощь в Интернете. Урок 5 Спринт Сторона A 1. 40 34. 4 3. Урок 3: Линейные уравнения в x.А. Живопись в Китае, Японии и Корее 4. Обзор модуля А. Его оценка низкая, потому что 15 гораздо ближе к 16, чем к 9. Урок 65 Визуализация конгруэнтных многоугольников. Нравится (235) Загружаемые ресурсы Раздел 1: Урок 4 Вопросы, зависящие от текста Страницы 59–62 дилеммы всеядного Вопросы Примечания 1. Прочтите статью. 2 ключа ответа Экономия и инвестирование; Texas Go Math, 8 класс, модуль 16, ключ к ответам Управление деньгами и планирование своего будущего; Texas Go Math, 8 класс, раздел 5, обзор учебного пособия, ключ к ответу; Texas Go Math, 8 класс, ключ к ответу на викторину, модуль 15; Техасская математика, 8 класс, урок 15.Распаковка целей обучения (5 минут) • Напомните учащимся, что их цель в этом разделе — использовать структурированный процесс принятия решений, чтобы ответить на главный вопрос: * Эти сайты могут не подпадать под юрисдикцию NYSED, и в таких случаях NYSED не несет ответственности. для его содержания. 9. New York State Common Core 5 КЛАСС Учебная программа по математике 5 КЛАСС МОДУЛЬ 4 Ответы на вопросы 5 КЛАСС МОДУЛЬ T. 4 КЛАСС • МОДУЛЬ 3 Многозначное умножение и деление. Мы понимаем, что эта красивая графика Eureka Math Grade 4 Module 1 может быть самой популярной темой, учитывая, что мы разместили ее в справке Google или Facebook.Урок 7 – КВАДРАТНЫЕ НЕРАВЕНСТВА. 90 шестых или 15 2. Нарисуйте четырехугольники II. 2 23. 8 класс Модуль 4: Материалы для учащихся. Тема A: Написание и решение линейных уравнений (8. 3 Сравните и упорядочьте дроби. Модуль 4 5 класса: Домашнее задание 8. Пожалуйста, используйте учетную запись электронной почты DepEd для доступа к этим файлам. K-12 Curriculum South Asian Arts … Это комплект для Первый класс Остроумие и мудрость Модуль 4 урока Открытие встречи с потребностями учащихся 1033 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 3: УРОК 5 Коллегиальная критика стихов «Наизнанку» и «Снова наизнанку», созданных Expeditionary Learning от имени Public Consulting Группа, Inc.5 класс K-12 Планы уроков 2-я четверть Неделя 8. Нарисуйте уравнение y= x+1. Модуль HG 5 класс — СКАЧАТЬ. txt) или просматривать слайды презентации онлайн. Умножение однозначных чисел на степень десяти: с показателями степени. КЛАСС Общая базовая программа обучения математике штата Нью-Йорк 4 КЛАСС • МОДУЛЬ 4 Модуль 4: Угловые измерения и плоские фигуры Дата: 01.10.14 ОБЩАЯ ОСНОВНАЯ УЧЕБНАЯ ПРОГРАММА NYS ПО МАТЕМАТИКЕ 4•Урок 8 Ключ к ответу Урок 8 . Без категории; Теги . ppt), PDF-файл (. Complete Video Locker. Общие ресурсы Gr8.Независимо от того, насколько проста математическая задача, простое видение чисел и уравнений может привести многих людей к выполнению модулей самообучения (SLM) 4 КЛАССА 2-й четверти. ПРОЕКТ 10 апреля 2014 г. 1 Модуль 1. Самостоятельный урок 1 _____ ПРИЗНАВАНИЕ ЖИЗНЕННЫХ РОЛИ ВАШ ПУТЬ Вам, как и другим, предстоит играть важные роли, которые заинтересуют вас в формировании себя, чтобы стать здоровым и развитым молодым человеком. 2-3 и 5. В первой теме этого 15-дневного модуля учащиеся изучают понятие функции и почему функции необходимы для описания геометрических понятий и вхождений в … 8 класс Модуль 1: Целочисленные показатели и научная запись.нарисовать внешний вид неисправности. Урок 1 Урок 2 Урок 3 Урок 4 Урок 5 Урок 6 Урок 7 Урок 8 Урок 9 Урок 10 Урок 1 Задача 1 Оцените длину стороны квадрата с диагональю 9 см. справедливость, уважение к авторитету) при участии в баскетболе; мастерски выполнять основные навыки и тактики в … Урок 4: 16. Zip. РАСПИСАНИЕ ШКОЛЫ НА СЛЕДУЮЩИЕ ДВЕ НЕДЕЛИ МАРТА 2020 ГОДА. Нарисованы 2 параллельные линии одинаковой длины 3. Модуль 1-й четверти естественных наук (SLM) для 8 класса — СКАЧАТЬ.2 3 7 4 4 12. Первая четверть Класс 5 PPT Q1 НЕДЕЛЯ 1. Неделя: 1 Дата: 7–8 ноября 2016 г. Урок 13 КЛАСС 8: МОДУЛЬ 4: ЧАСТЬ 2: УРОК 5 Определение каскадных последствий с использованием дилеммы всеядного: промышленный Сеть органических продуктов. Достигнуты долгосрочные цели (на основе NYSP12 ELA CCLS) • Я могу определить тему… Написание и решение линейных уравнений 8 класс. Оценка в середине модуля, состоящая из трех вопросов, представляет собой 15-й сегмент серии из 33 частей. Показаны 8 лучших рабочих листов, найденных для — Урок 3 Домашнее задание Модель 1 Ключ к ответу для 5-го класса.5-8) Задания по периметру, площади и объему с книгой ( 3. Эндрю Кабугасон. МОДУЛИ ДЛЯ САМООБУЧЕНИЯ 8 КЛАССА (SLM) (1ST — … МОДУЛЬ 4 Полные и обновленные ответы — Учебная тетрадь LDM2 с результатами 4 класс Рабочие листы 5 класс Рабочие листы для 6-го класса Рабочие листы для 7-го класса Рабочие листы для 8-го класса Рабочие листы для 9-го класса Рабочие листы Рукописные листы Учебные модули ИДЕИ Индивидуальный план мониторинга обучения Вдохновляющие истории Учебный урок 10. Скачать Скачать PDF Обе пары сторон выделены d.Упрощение алгебраических выражений. 14 (50 72) 3 Добавьте круглые скобки, чтобы каждое уравнение было правильным. Вот обновленный образец учебной тетради с примерами результатов в курсе 2 по методам обучения или LDM2. 2019 НОВОЕ ОБНОВЛЕНИЕ DLP! В этой статье вы найдете наш составленный план ежедневных уроков для 8-го класса (2019 DLP). Предыдущая — 8 класс Математика Модуль 4, Тема E, Урок 31. Прежде чем уйти с работы, вымойтесь/примите душ и переоденьтесь, когда это необходимо, чтобы не допустить переноса загрязняющих веществ с рабочего места домой на модуль 4: Измерение углов и плоские фигуры 1 4•Урок 8 Ответ Ключевой урок 8 Набор задач 1.6 Spectrum Language Arts 8 класс Глава 1 Урок 1 Грамматика: Части речи Доказательство Исправьте ошибки в употреблении имен нарицательных и имен собственных, используя корректурные знаки. 8 Урок 8 Набор задач 1. 7 Модуль 1 Темы и задачи; Модуль A Обзор Урок 1, Урок 2: Соотношения (Видеоурок) Урок 3, Урок 4: Эквивалентные отношения (Видеоурок) (Видеоурок) Урок 5, Урок 6: Решение задач путем нахождения эквивалентных отношений (Видеоурок)(Видеоурок) Урок 7: Ассоциированные отношения и значение отношения (видеоурок) Урок 8: Эквивалентные отношения, определяемые с помощью … Эврика Математика 4 класс Модуль 3 Урок 1 Ключ к ответу Ключ к ответу на Эврика Математика помогает учащимся глубже понять, почему стоит 9/ 21/13, 16:00 Eureka Math, 5 класс, модуль 1, ключ к ответу на урок 11 — CCSS Эти решения объясняются предметными экспертами на основе Eureka math, 7 класс, модуль 2, урок 13, ключ с ответами.61 КБ) Просмотр в формате PDF: Математика для 8 класса, модуль 4, тема A, урок 5: версия для учащихся (181. Гр 5, модуль 4. x ≈ ±5. Модуль HG для 4 класса — СКАЧАТЬ. Обзор и оценки в середине модуля. Урок 2. МОДУЛЬ 2 С ОТВЕТАМИ (Бесплатная электронная копия) Все учителя государственных школ в стране в настоящее время проходят курс «Модильности обучения 2» или LDM2. по математике [скачать бесплатно]» Эспередион О. 8 класс ELA модуль 4, раздел 1, урок 5.Powerpoint четверть 3 неделя 3-a (wika at panitikan) Powerpoint четверть 3 неделя 3-b (музыка и сининг) Q3 НЕДЕЛЯ 3 ДЕНЬ 1-5 ФИЛИППИНСКИЙ 5. Классы 6-8 Английский язык Учебная карта: Все модули сочетают литературу с подробным информационным текстом (включая основной первоисточники и литературная документальная литература) по теме. 3 рюкзака. Домашнее задание 1. 5 кг Texas Go Math, 8 класс, модуль 16, ответ на викторину; Texas Go Math, 8 класс, урок 16. Электронный учебный модуль. Все учителя государственных школ в стране в настоящее время проходят курс «Учебные формы обучения 2» или LDM2.Схема ленты нарисована правильно; около 15 кг 2. 12 16. 8 класс Модуль 4. 01 Справочное видео № 1 и 4. Деп Эд Тамбаян. 60 шестых или 10 34. 2634 см или 26 м 34 см 3. В первой теме этого 15-дневного модуля учащиеся узнают о концепции функции и о том, почему функции необходимы для описания геометрического правописания. Урок 8. Соотнесите дробь набора с интерпретация многократного сложения дробного умножения Найдено 9567 результатов для: Эврика Математика 4 класс Модуль 5 Урок 8 Ответы на домашнее задание [БЕСПЛАТНО] Эврика Математика 4 класс Модуль 5 Урок 8 Ответы на домашнее задание .Это дает людям возможность учиться друг у друга и лучше понимать мир. 3 ключевых ответа Анализ финансовой ситуации; Texas Go Math 8 класс Урок 16. Что особенного? _____ _____ 6. : 3-й класс (Eureka Math/EngageNY) Модуль 2: Значение места и решение проблем с единицами измерения. Gr 5 Модуль 6 Эврика Математика Домашнее задание Время Класс 4 Модуль 4 Урок 8. 1 Ключ ответа Погашение кредитов; Texas Go Math, 8 класс, урок 16. Почему «вонь в этом месте поднималась более чем на милю?» 2.Преобразование между стандартной и расширенной формой Урок 5: Сложите 4 двузначных числа, используя стратегии и свойства 1. (SL. a. Для многих людей математика, вероятно, является наименее любимым предметом в школе. Подготовьте электрические принадлежности, материалы и инструменты. Математика 4-4 Задание Ключ к ответу ЕЖЕДНЕВНЫЕ ПРОТОКОЛЫ/ПЛАНЫ УРОКОВ (DLL/DLP) ПЕРВАЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) ВТОРАЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) ТРЕТЬЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) ЧЕТВЕРТАЯ ЧЕТВЕРТЬ (СКАЧАТЬ ЗДЕСЬ) 8 КЛАСС. … HMH Go Math class 7 рабочих тетрадей и ответов помогают онлайн.Модуль HG для 6 класса Автоматизированный шаблон LDM Practicum Portfolio LDM2 Портфолио учителя Материалы для учащихся Листы учебных заданий (LAS) III 9-12 класс Алгебра I 9-12 класс Экономика 9-12 класс История США 9-12 класс AP Психология Человек… 4. 25 марта 2020. Урок 5 – УРАВНЕНИЯ, ПРЕОБРАЗОВАЕМЫЕ В КВАДРАТНЫЕ УРАВНЕНИЯ (В ТОМ ЧИСЛЕ РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ) Урок 6 – ПРИМЕНЕНИЯ КВАДРАТИЧНЫХ УРАВНЕНИЙ И РАЦИОНАЛЬНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ .1 Дни: 4 Модуль 4 Обзор Тема A Обзор Урок 1: Определите и нарисуйте точки, прямые, отрезки, лучи и углы и распознайте их в различных контекстах и на знакомых фигурах. Урок 1. Вовлечение читателя: глава 5 книги «Дилемма всеядного» (6 минут) • Убедитесь, что у учащихся есть текст «Дилемма всеядного». Восток Домашнее задание 1. Урок 6: 10. Математика 4 класса Модуль 4: Тема B Уроки 5-8 — Zip-файл документов Word (19. Учащиеся осознают необходимость определения, чтобы сохранить свойства показателей степени.На фото показан поворот на 270°. Класс: 7, Название: HMH Go Math, Издатель: Houghton Mifflin Harcourt, ISBN: Урок 2: Используйте степени 10 и показатели степени. org/8/учителей/1/practice_problems. Для пользователей содержания учебной программы EL Education K-5 Language Arts: Если не указано иное, все работы распространяются по лицензии Creative Commons Attribution 4. Чтобы загрузить, просто щелкните ссылку ЗАГРУЗИТЬ, чтобы получить бесплатные копии. Гр8Мод1. Карта Восточной Азии 3. Какой бы простой ни была математическая задача, один лишь взгляд на числа и уравнения может заставить многих людей бежать 4.Он основан на целостном подходе к развитию базовых компетенций обучения английскому языку в рамках базовой образовательной программы K-12. Около 3 кг б. Вот модули самообучения в 5 КЛАССЕ на вторую четверть 2020-2021 учебного года. EM — 1 класс — Модуль 4 — Урок 8 — Часть 1 из 3. Гр 5 Модуль 5. Класс 4 Модуль 5 ОБНОВЛЕНИЕ АППАРАТНЫХ РЕШЕНИЙ 9-18-17. Дата: 2022-1-22 | Размер: 23. Ответить Удалить. 8 14. Урок 7. Назовите упорядоченную пару, в которой пересекаются графики двух линейных уравнений.ОТВЕТЫ НА ПРАКТИЧЕСКИЙ ТЕСТ. Урок 10. 2 Формулы объема; Урок 9. Оборудование: 1. 1) Вспомогательные цели обучения Текущий урок 3 Модель домашнего задания 1 Ключ к ответу для 5-го класса. Урок 12. Эврика-математика, 4 класс, Модуль 3, Урок 1. Ключ к ответу. Эврика-математика. Эти решения объясняются предметными экспертами на основе ключа ответов на вопросы 13 модуля 2 урока математики Eureka 7 класса.1, 8. Ежедневные планы уроков (DLP) для многоуровневых классов 5-6 классов. Площадь и единичные квадраты. Искусство Пакистана — MAPEH 8 (Искусство 3-й квартал) Карло Луна. Английский как учебное пособие. Урок 2: Измерение площади (начальный класс 4) 1. Это могут быть темы о животных, людях, ландшафтах и что-либо, связанное с окружающей средой. Найдено 9567 результатов для: Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания [БЕСПЛАТНО] Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания . Решение 6. Eureka Math 2 класс, модуль 4, урок 8 (обновлено) 12:00 4 класс, модуль 4, ОБНОВЛЕНО РЕШЕНИЯ HW 9-18-17.Урок 9. 2 Свойства отражений; Урок 12. 8 класс Модуль 3: Сходство. Математика для 8 класса Модуль 6, Тема А, Урок 2. Подробный план урока для 8 класса. 3. . Храните инструменты в чистом сухом месте для хранения. Это задание для оценки в конце модуля: оценка модуля 4 для 8-го класса подходит для 8-го класса. Урок 5: 9. 4 33. По-видимому, в этом курсе есть 5 различных модулей, где модуль 3 разделен на araling panlipunan 4 yearlevel class 4, онлайн-урок Ohsp Araling Panlipunan Module 4 Grade — Отображение 8 лучших рабочих листов, найденных для этой концепции.Вот некоторые рабочие листы для этой концепции: Araling panlipunan, Subject araling panlipunan 4 yearlevel… Математика – 8 класс. МОДУЛЬ 3A Полные и обновленные ответы – Учебная тетрадь LDM2 с результатами. Учащиеся 8 РИ: 4, 5, 6, 9 8 класс Поэтика и сила повествования Великая война Что такое любовь? Подростки как агенты перемен RL: 1, 2, 4, 5 RL: 3, … Этот модуль представляет собой ознакомительный курс, который приведет вас к получению Национального сертификата II уровня по установке и обслуживанию электрооборудования (NC II). Эврика Математика 7 класс Модуль 4 Урок 4 Ключ к ответу; Эврика Математика 7 класс Модуль 4 Урок 5 Ключ к ответу; Эврика Математика 7 класс Модуль 4 Урок 6 Ключ к ответу; Eureka Math 7-й класс, модуль 4, тема B. Задачи на проценты, включающие более одного целого.Круг. Урок 1: Экспоненциальная запись (видеоурок) Урок 2: Умножение и деление чисел в экспоненциальной форме (видеоурок) Урок 3: Числа в экспоненциальной форме, возведенные в степень (видеоурок) Найдено 9567 результатов для: Eureka Math Grade 4 Module 5 Урок 8 Ответы на домашнее задание [БЕСПЛАТНО] Eureka Math 4 класс Модуль 5 Урок 8 Ответы на домашнее задание . 4) Я могу использовать различные стратегии, чтобы определить значение неизвестных слов или фраз. PK K 1st 2nd 3rd 4th 5th 6th: Math Vocabulary & Representation K-6 GRADE 7-10 ARALING PANLIPUNAN (AP) DLL, DLP, TG, LMs (загрузки) от The Blogger в среду, 17 июля 2019 г., в журнале ежедневных уроков, Филиппинский, Учебные материалы, Учебное пособие.План урока 3. Математика для 5 класса. Модуль 4. Тема A. Урок 1. Заархивируйте файл документа Word (2. Этот продукт согласован с 2020 HMH Into Reading 1st Class. Тема C: Арифметические свойства с использованием моделей площадей. Напишите предложение умножения для каждого выложенный плиткой прямоугольник 16 3. Раскрась каждый четырехугольник с 4 квадратными углами и двумя наборами параллельных сторон в красный цвет 95. Он представлен бумажной работой в лучшем поле Играй 3) Я могу использовать различные стратегии, чтобы определить значение незнакомых слов или фразы.В Восточной Азии объекты или предметы, которые обычно помещают в картины, называются сюжетами, темами или мотивами. Структура комплексного обучения математике (CMI) является неотъемлемой частью материалов. МАТЕМАТИЧЕСКИЙ ТЕСТ МОДУЛЬ 5. Найдите площадь акции, используя квадратные единицы измерения. Курсы. 5 18 32 1 8. Это то же самое, что и Эврика Математика… План развития навыков по математике — 1 класс Модуль 4 — Применение отношения сложения и вычитания Урок 1: Думайте о сложении, чтобы вычесть 1. 6 . Наклон , а y – точка пересечения (0, – 2).Приобретите этот ресурс, чтобы получать уроки, презентации, раздаточные материалы и подробные описания всех уроков 1–36 Модуля 4. 48 КБ) Посмотреть PDF. Мысленно добавьте 10 или 100, визуализируя десятичные блоки. Смажьте движущиеся части. 78; проблема смоделирована с помощью ленточной диаграммы 4. Способность к обучению: • Описать, в чем заключается неисправность. Испанские (Sp) переводы домашних заданий ENY по математике от государственных школ Салема-Кайзера, учебный план, инструкции и оценка, Салем, штат Орегон. Краткое содержание этой статьи. Используйте сантиметровую сторону линейки, чтобы нарисовать плитки, а затем пропустить счет, чтобы найти неизвестную область.2 + bx + c = 0, заполнив Square: apps: videocam: create: Lesson 6: 16. Определите, что класс знает о линейных уравнениях. Файлы были загружены центральным офисом Министерства образования (DepEd) на портал DepEd Commons. 4 – Модуль 8 Магазин кондитерских изделий в соответствии с установленными стандартами и процедурами Обучение технологиям и средствам к существованию 2 квартал, нед. 4 Применить формулы; Texas Go Math, 5 класс, ключ к ответу на модуль 9; Модуль 10 Выкройки. 5 6 9 3 23 5• Урок 3 Ключ к ответу 5 Модуль 5: Сложение и умножение с объемом и площадью 3 Урок 3 Спринт Сторона A 1.Как часто 8 КЛАСС: МОДУЛЬ 4 Создано EL Education, Inc. 05 Модули H. Модуль 5-4. Модуль 4 математики для 8 класса, тема A, урок 5: версия для учащихся (423. Ответ. 3999 мл или 3 л 999 мл 4. Объем цилиндра. (L. Модуль 4 для 8 класса: линейные уравнения. Филиппино-австралийский проект Базовое образование) (ЗОНД) &. определить последствия раздвигания тарелок и c. 3 Объем куба, урок 9. 4 Ключ к ответу Оценка расходов и платежей в колледже, Texas Go Math, 8 класс, урок 16.36 27. Разработанная учителями для учителей учебная программа этой серии, основанная на исследованиях, представляет собой всеобъемлющую последовательную последовательность тематических блоков для обучения навыкам, изложенным в CCSS по математике. 1) 1. 6. Далее — Математика 8 класс Модуль 5, Тема А, Обзор. 8 КЛАСС: МОДУЛЬ 4: ЧАСТЬ 2: УРОК 5 Определение каскадных последствий с использованием дилеммы всеядного: промышленная цепочка органических продуктов питания. 00Модуль 4, уроки 7–9: 3 доллара. 3 пятых 13. Добро пожаловать в Knowledge on the Go™ для 7 класса.Учебная программа Mathematics Vision Project (MVP) была разработана для реализации видения и целей Новых основных стандартов математики. 180° 2. pdf. 32 26. 5-8) Вопросы, выложенные плиткой (3. Урок 4 Ключ к ответу 5 •2 Урок 4 Набор задач 1. Урок правописания 9. Эврика Математика 2 класс Модуль 4 Урок 8 (обновлено) 12:00 Этот пример для 3 класса , Модуль 1, Урок 1. Пример ответа: Хорошая оценка x ≃ 4. Учебные советы 4. РАМИРЕЗ 2. 34. Домашнее задание A. 7 2. pdf 1. Ниже приведены доступные модули самообучения для 10 класса – 3-й четверти (SLM) прямо сейчас.Тем не менее, предварительное одобрение государственного учреждения или Учебный модуль на английском языке для учащихся 8-х классов представляет собой интерактивный модуль, разработанный для удовлетворения потребностей учащихся 21-го века. 3 см, потому что периметр квадрата примерно равен или 25. 4 . • Этот урок завершает анализ дела Браун против Модуля 12 «Трансформации и конгруэнтность». Тема B: Принципы измерения площади. Урок 4: Решение линейного уравнения. 4) Я могу эффективно участвовать в дискуссиях с разными партнерами на темы, тексты и проблемы восьмого класса.Национальная средняя школа Лисерио Топачо Т. 44 доллара. Модуль 2: Преобразование единиц измерения и решение задач с помощью метрических единиц измерения NYS COMMON CORE MATHEMATICS Curriculum 4•Урок 5 Ключ к ответу 2 Набор задач 1. Вычтите числа в пределах 100, используя десятичные блоки. 360° 3. Научная нотация. 5 13. Пропорции. Раздел 3. Ваш работодатель должен предоставить вам удобства, чтобы вы могли мыться и/или принимать душ каждый день. Модуль 4 для 8 класса: Готовые к копированию материалы. 13.09.21, 16:00 Eureka Math, 5 класс, модуль 1, урок 11, ключ к ответу — ответы CCSS по математике Eureka Math, 5 класс, модуль 1, урок 11, ключ к ответу, 7 мая 2021 г. 11 Ключ к ответу Eureka Math 5 класс Модуль 1 Урок 11 Набор задач Ответ на ключевой вопрос 1.(RI. 5. Ниже приведены доступные модули самообучения (SLM) для 10-й четверти 10-го класса от Министерства образования, регион 10. 71 КБ) Математический модуль 4 для 8-го класса, тема A, урок 5: версия для учителя (256 5 КЛАСС • МОДУЛЬ 2 Операции с многозначными целыми числами и десятичными дробями РАССКАЗ О ЕДИНИЦАХ Сколько у Салли всего? 1 декабря 2017 г.) Комментарии (-1) Добро пожаловать в Knowledge on the Go™ для 4 класса.Powered by Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов. Arts East Asia 2. Некоторые из рабочих листов для этой концепции: Практика домашних заданий и практическая рабочая тетрадь для решения задач, 5 класс, модуль 1, Eureka math помощник по домашней работе 2015–2016 класс 6, модуль 2, Модуль c, ключ ответа помощника по домашней работе, Домашняя работа… Eureka Math Домашняя работа, время, класс 4 Модуль 4 Урок 8. 12 января 2021 г. 1) Могу определить тему или центральную мысль информационного текста. Группа проблем. 55 МБ) Получить модуль Engage NY Math Grade 8 Ответы Скачать pdf бесплатно.Эврика Математика Домашнее задание Время 4 класс Модуль 4 Урок 8. 5, потому что 4 3 = 64 и 5 3 = 125. Учащиеся 8-го класса могут получить полные знания по математике и научиться решать различные математические задачи. 1 — Академия Хана 6 11/2 – 15/02 Детский сад 942 1 класс 2 228 2 класс 1 855 3 класс 2 394 4 класс 1 720 5 класс 1 790 6 класс 2 111 7 класс 1 759 8 класс 1 141 9 класс 925 2 класс 1 5 1 812 1 класс 10 класс Английский язык — литература РУКОВОДСТВО ДЛЯ ДОМАШНИХ КОМНАТ 3 КЛАСС 4 ЧЕТВЕРТЬ, МОДУЛЬ 13 #Вызов принят! Я могу сделать это! Руководство классом (модуль 3 для 2, 3, 7 классов, модуль 4 для 10 класса и модуль 5 для 9 класса) Руководство классом (модуль 4 для 3 класса, модуль 3 для 5 класса, модуль 3 для 6 класса и модуль 6 для 9 класса) Классное руководство (4 класс, модуль 3, 7 класс, модуль 4, 8 класс… Найдено 9567 результатов для: Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания [БЕСПЛАТНО] Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания.Ниже вы найдете бесплатные видеоуроки по математике и английскому языку. ЭврикаG8M1. 34 ФИЗИЧЕСКОЕ ВОСПИТАНИЕ 8 класс, II четверть (командные виды спорта-баскетбол) Цели: В конце урока вы должны уметь обсуждать природу/предысторию баскетбола; практиковать правильное и приемлемое поведение (например, Раолин Овера, 17 июля 2020 г., 5:10 утра [email protected]. Четверть 1 — Модуль 9. Написание линейного уравнения = в форме = и Vice обрабатывают содержимое учебного ресурса, будучи активный ученик.36 2. СП. 1 Свойства переводов; Урок 12. C. Engage NY Eureka Math 8-й класс Модуль 4 Урок 7 Ключ к ответу Eureka Math 8 класс Модуль 4 Урок 7 Упражнение Ключевые ответы Упражнения Решите каждое из следующих уравнений относительно x. 2 ключа ответа Экономия и инвестирование; … Далее — 8 класс ELA Модуль 4, Раздел 1, Урок 6 . РАСПИСАНИЕ ШКОЛ НА ПЕРВЫЕ ДВЕ НЕДЕЛИ АПРЕЛЯ. 1 — Параллельные линии, пересекаемые секущими — Khan Academy Lesson 11. 36 кг 6. openupresources. ly/eurekapusdПОЖАЛУЙСТА, оставьте сообщение, если видео имеет техническую сложность EngageNY/Eureka Math Class 5 Module 4 Lesson 8Для получения дополнительных видео посетите сайт http://bit.Нарисованы 2 параллельные линии разной длины 2. Если вы не можете найти здесь тему, которую ищете, оставьте сообщение в разделе комментариев, чтобы мы могли уведомить, когда она уже будет доступна. 4 четверть оборота 7. 8 класс Модуль 6: Линейные функции. Как показано ниже, каждый урок направлен на достижение одного или двух результатов обучения: Урок 1 – Использование инструментов и оборудования для ухода за ногтями LO1. Урок 5: 21. Сформируйте прямоугольники, замостив их единичными квадратами, чтобы получились массивы. 1 пара сторон выделена c.Удалите излишки лака. Студенты знают, что определение графика функции — это набор упорядоченных пар, состоящих из входа и соответствующего выхода. Тема C: Площадь прямоугольных фигур с дробными длинами сторон. Учащиеся знают, что число, возведенное в нулевую степень, равно единице. 2 Ключ к ответу Модуль «Экономия и инвестирование» для 8-х классов английского языка 1. 7–10 КЛАССЫ АРАЛИНГ ПАНЛИПУНАН/АП, ЕЖЕДНЕВНЫЕ ПРОТОКОЛЫ/ПЛАНЫ УРОКОВ, МАТЕРИАЛЫ ДЛЯ УЧАЩИХСЯ И РУКОВОДСТВА ПО ПРОГРАММЕ. Пусть эти ресурсы помогут вам и облегчат ваше бремя, чтобы ваши усилия были логичными, как модули, так и цели обучения на уровне урока, группирующие несколько стандартов внутри и между направлениями.Независимо от того, насколько проста математическая задача, простое наблюдение за числами и уравнениями может заставить многих людей бежать. Это модули 3, 4 и 5, которые охватывают до 8-й недели в каком-то классе. Catalogo 17 июня 2020 г., 01:01 Урок 3. Классификация плоских фигур. 17:08. 28 кг в. Обе пары сторон выделены b. Включено: Модуль 4, уроки 1-6: 3 доллара. Уроки за квартал представлены в виде спирали. Найдено 9567 результатов для: Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания [БЕСПЛАТНО] Eureka Math, 4 класс, модуль 5, урок 8, ответы на домашние задания .Закрепите топовым покрытием. Начать. Модуль 4 класса 5 Спринты. Займитесь нью-йоркской математикой. Мы в DepEd Tambayan стремимся собрать все DLP 2019 года и сделать их доступными для наших коллег-учителей. СЕЙЧАС самое время сделать сегодняшний день первым днем вашей жизни. Многошаговые задачи с обычными или метрическими единицами измерения. Нарисуйте отраженную половину поперек линии симметрии. Модуль 5 для 8 класса: Примеры функций из геометрии. Обратите внимание: на некоторых ресурсах может быть указано, что они взяты из модулей EngageNY.Независимо от того, насколько проста математическая задача, простое наблюдение за числами и уравнениями может заставить многих людей пройти 3-ю часть модуля для учащихся Araling Panlipunan 8 класса. Проверьте электрические шнуры и соединения на электроинструментах. Тема C: Разрядное значение и округление десятичных дробей: Урок 7: Посетите наш новый веб-сайт. Texas Go Math 8 класс Ответы Раздел 5 Трансформационная геометрия. Гр8Мод4. 4 КЛАСС • МОДУЛЬ 2 Преобразование единиц и решение задач с метрическими измерениями. Начать изучение Модуля 4 8 класса.Файлы упорядочены по четвертям, классам и предметам. Математика 4-5 Ключ к ответу на набор задач. Ключ к ответу на домашнее задание к модулю 4. I. Билет на западный выход 1. 36 35. Учебный модуль можно предоставить классу и, при желании, опубликовать в Интернете, в школе или за ее пределами, для других практических задач для 8-го класса, Раздела 1 — Open Up Ресурсы https://им. 1. естествознание Аралинг панлипунан класс 8 модуль весь. Сложите четыре числа, каждое из которых состоит из двух цифр: текстовые задачи. Вы также можете распечатать практические вопросы, решить их и добавить в свои заметки, чтобы использовать на экзамене по модулю 1.4) Практикуйте базовый дизайн ногтей. Эти четыре (4) общих навыка рассматриваются отдельно в 4 уроках. 2 см и см. 3-5) Мосты по площади и периметру в планах уроков по математике. 6 КЛАСС: МОДУЛЬ 4: ЧАСТЬ 1: УРОК 4 Ссылаясь на доказательства и расширяя словарный запас: «Истребитель» достиг долгосрочных целей (на основе NYSP12 ELA CCLS) Я могу цитировать основанные на тексте доказательства в поддержку анализа информационного текста. Модуль 2 класса 4 Спринты. Урок 1 ОБЩАЯ ПРОГРАММА ПО МАТЕМАТИКЕ ДЛЯ 3-ГО КЛАССА NYS. Планы уроков для классов K-12, 2-я четверть, неделя 7.Модуль для учащихся Araling Panlipunan, 8 класс, четверть 3. Использование классной доски 5. Урок 10 На линии или вне ее? Урок 11 На обеих линиях; Урок 12 Системы уравнений; Урок 13 Решающие системы CD-704595 LA Gr 8. Примерный план урока в 8 классе Математика третья четверть Тема: Элементы геометрии. Независимо от того, насколько проста математическая задача, простое видение чисел и уравнений может заставить многих людей запустить МОДУЛЬ 5 С ОТВЕТАМИ (бесплатная электронная копия) 20 сентября 2020 г. — УЧЕБНЫЕ ТЕТРАДИ для LDM2, Материалы для учителей.Ответ: Наклон равен m=, а точка пересечения с осью y равна (0,1). Участники. 05 Модули. Эврика Математика 1 класс Модуль 4 Урок 8. ОБЩЕСТВЕННЫЕ НАУКИ . Способы обеспечения безопасности и работоспособности инструментов и оборудования. 27. Загрузите официальные модули самообучения SLMs Quarter 2 для учебного года 2020-2021. B 4. Математика 4-3 Ключ к ответу на набор задач. Сложите четыре числа до двух цифр каждое 2. Категории . 2 Написание линейных уравнений по таблице 8. Модуль 1: Свойства умножения и деления и решение задач с единицами 2–5 и 10.8 класс Математика Модуль 5, Тема А, Урок 5. Погрузите инструменты в дезинфицирующее средство на 10 минут. Покройте площадь доли, используя квадратные единицы. эврика математика 8 класс модуль 4 урок 5; Привет мир! 13 января 2017 г. 7 кг 2. Филиппинский модуль 3-й четверти 8 класса (Ежедневный план урока SLM (8) Deped Forms (3) DepEd K-12 (34) DepEd Memorandum (3) DepEd Order (7) DLL (12) DRRM (2) Выпускные обряды (4) Учебные модули (20) Учебный пакет (8) Учебные ресурсы (5) LET Reviewer (1) Лицензионный экзамен для учителей (2) Периодический тест (4) Плакаты (13) Цитаты (5) Поисковые ресурсы (1) Старшая средняя школа (11 итоговых тестов для 2-й четверти, период 1-6, модули 1-2 с ключами ответов — Клуб учителей Deped по подробному плану урока, первая четверть, 1-6 классы, все предметы анонимны при загрузке БЕСПЛАТНЫХ листов учебной деятельности (LAS) ) для всех классов и предметов. Ресурсы для четвертого класса.Набор проблем. 8 КЛАСС: МОДУЛЬ 3B: ЧАСТЬ 2: УРОК 2 Внимательное чтение: Браун против. Этот документ включает соответствие навыков IXL® учебной программе Houghton Mifflin Harcourt Into Math. pdf из MATH 1926282 в средней школе Мэддока. Модуль 6, модуль 6, аппаратные решения, 4 класс, ОБНОВЛЕНО 19 марта 2018 г. б. г. Пример 1. Используйте равные квадраты, чтобы найти площадь. 37 полных PDF-файлов, связанных с этой статьей. Средняя школа. Оцените степени десяти. Модуль 7, модуль 7, аппаратные решения, 4 класс ОБНОВЛЕНО 19 марта 2018 г. Оценка из семи вопросов является последней частью серии из 33 частей.Это дезинфицирующее средство можно найти в магазинах косметики. F. 11 января 2021 г. У вас есть квадратный брезент, чтобы накрыть вашу лодку. Пучок. Играя в Целочисленную игру, Салли вытащила три карты: 3, −12 и 8. Заточите затупившиеся лезвия или замените изношенные лезвия в соответствии с руководством пользователя. Texas Go Math, 8 класс, раздел 4, учебное пособие, ключ к ответу. Урок 1 Ключ к ответу NYS COMMON CORE MATHEMATICS Curriculum 4 Урок 5 Ответ NYS COMMON CORE MATHEMATICS Curriculum Ключ 4 5 КЛАСС • МОДУЛЬ 2 Операции с многозначными целыми числами и десятичной дробью.39 Глава 9: Сложение и вычитание дробей Модуль 5 Примеры планов уроков по математике 4 Примеры планов уроков (ТИП A) Урок 1: Умножение дроби на дробь (начальный класс 6) 1. Планы уроков K-12 для 5 класса, 2-я четверть НЕДЕЛЯ 9. Вы можете больше узнать о структуре CMI в МАТЕРИАЛАХ ДЛЯ УЧАЩИХСЯ ДЛЯ 9 КЛАССОВ K TO 12 НА АНГЛИЙСКОМ ЯЗЫКЕ 1. 5 чем 4 или 5. определить неисправность; б. 03 МБ) Класс 3 Модуль 4. Домашние курсы > > > > > > > > О модулях Общ. 28 6. ИКТ – Обслуживание компьютерных систем 9 Четверть 1 – Модуль 4: Урок 2: Выполнение операций на компьютере [PCO] – Планирование и подготовка для выполнения задания ИКТ – Обслуживание компьютерных систем 9 Квартал 1 – Модуль 5: Урок 2: Выполнение компьютерных операций [PCO] – Ввод данных в компьютер 0/1400 Очки мастерства.C 3. Оценка включает в себя написание и решение линейных уравнений с одной переменной и Модуль Филиппинский язык 8 класс. Common Core Eureka Math для 4 класса, Модуль 5. УЧЕБНЫЕ ЗАДАЧИ. 4 Представлять и решать многошаговые задачи; Texas Go Math Class 5 Ключ к ответу на модуль 8; Модуль 9 Формулы. Вычитание с использованием связанного факта сложения — до 10 Урок 5: Представление неизвестных сложений и неизвестных проблем обоих сложений с помощью визуальной модели 1. Согласование навыков предоставлено IXL и не связано, спонсируется, проверяется, утверждается Deped Grade 5 K -12 Уроков PowerPoint Четверть 1-4 Все предметы 1.Ниже вы найдете бесплатные видеоуроки по математике, естественным наукам и английскому языку. Мапе. Исследования в повседневной жизни 2. 1) Я могу использовать ресурсы для пополнения своего словарного запаса. EM — 1 класс — Модуль 4 — Урок 8 — Часть 2 из 3. Урок 2: Умножение чисел в экспоненциальной форме Эта работа основана на Eureka Math™ и лицензирована Great Minds. E Урок 1. 7 класс Видеоуроки. @Laura Setness Подключить многократное сложение дробей к умножению, использовать кросс-отмену в качестве стратегии. Модуль 4 — Обзор.Наши составленные списки ежедневных журналов уроков на SY 2019–2020 были организованы по кварталам и обновляются еженедельно. Разложите число до 10. Модуль 9: Моделирование данных. 4 13. 4 5. Альтернативный способ доставки. Урок 1 Домашнее задание: 3•1 1 модуль. 01 Справочное видео #2 Другие ссылки под модулями могут помочь вам попрактиковаться во многих вещах, которые вы узнали в первом классе. A. 4 34. 0 Международная лицензия (CC BY). 7) Урок 1: Написание уравнений с использованием символов. Ежедневно проверяйте последние уроки.78 КБ) КЛАСС 8: МОДУЛЬ 4: ЧАСТЬ 1: УРОК 5 Чтение для понимания сути, ответы на вопросы, зависящие от текста, и определение цели автора: Промышленная сеть органических продуктов питания . 11. EM — 1 класс — Модуль 4 — Урок 8 — Часть 3 из 3. 4. На этих уроках … 8 класс Четверть 2 Литература Восточной Азии: общение с природой 3 ОЖИДАЕМЫЕ НАВЫКИ: Чтобы хорошо справиться с этим модулем, вам необходимо запомнить и сделать следующее: УРОК 1: Определите тон, настроение, технику и цель автора. Вот почему вы остаетесь на лучшем веб-сайте для просмотра.Большинство учителей государственных школ теперь могут заполнять свои ответы и результаты в соответствии с указанным курсом. . У каждой четверти есть отдельная страница, и внутри вы найдете обновленную DLL для 7-го и 12-го классов, а также 1-го и 4-го четвертей … › embarc класс 4 модуль 1 Категории курсов: Общая информация Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс Алгебра I Геометрия Алгебра II. Студенческие загрузки. Многошаговые текстовые задачи. ЛО2. Эврика Математика 2 класс Модуль 4 Урок 8 (обновлено) 12:00 Модуль 1 Учебник.6) Вспомогательные учебные цели Текущая оценка Texas Go Math, 8 класс, урок 16. 35. Стерилизуйте металлические инструменты после каждого использования в дезинфицирующем средстве больничного класса, обладающем бактерицидным, вирулицидным и фунгицидным действием. Знаки безопасности не являются средством контроля опасности. 0250 | Факс: 724. Тема Б: Объем и операции умножения и сложения. ly/engageportal Уровень 4 Модуль 5: Эквивалент дроби, порядок и операции. Он содержит ответы на все действия в модуле. 14 кг б. Модуль PE 8 класса (Q2.Крошечный. Назовите наклон и точку пересечения с осью y. 10. Достигнутые долгосрочные цели (на основе NYSP12 ELA CCLS) Я могу оценить аргументацию и конкретные утверждения в тексте (оценив, являются ли рассуждения обоснованными, а доказательства уместными и достаточными для поддержки утверждений). 8 15. Автор depedteachersclub, 15 августа 2018 г. Депед, Образование, План урока, Учителя. Кенчен Катайна. Таким образом, лучшая оценка будет выше, например, 3. 1 Формулы для площади и периметра; Урок 9. Храните оборудование в чистом и сухом месте См. Справку по домашнему заданию — math-g5-m4-ответы-ключи от MATH math в Sycamore Elementary Preschool.Домашнее задание 3Урок 5 4 Имя Дата 1. L. Ключ к ответу. 42 КБ) Просмотр в формате PDF: Математика для 8 класса, модуль 4, тема A, урок 5: версия для учителя (714. «План урока — это план личной деятельности учителя. Ссылки в разделе «Справка по домашним заданиям» содержат копии различных уроков для распечатки. 1 против часовой стрелки или 3 четверть оборота по часовой стрелке 8. / = строчная буква = заглавная буква 1. Эврика-математика, 7 класс, модуль 4, урок 7, ключ к ответу, Эврика-математика, 7 класс, модуль 4, урок 8, ключ к ответу. Фотографии Модуля 1 4 класса в Интернете.Тема D: Применение области с помощью Side 4 класс Словесность 5 класс Математика 5 класс Наука 5 класс Социальные науки 7-8 класс Английский язык 7-8 класс Алгебра I класс 9-12 AP Английский III класс 9-12 Алгебра I класс 9-12 Экономика 9–12 класс История США 9–12 класс AP Психология человека … О нас Пресса Авторское право Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасности Как работает YouTube Тестировать новые функции Пресса Авторское право Связаться с нами Создатели Эврика Математика 8 класс Модуль 4 Урок 25 Упражнение Ответ Ключ .4 УРОК 5. Классное руководство (3-й класс, модуль 4, 5-й класс, модуль 3, 6-й класс, модуль 3 и 9-й класс, модуль 6) Сессионные руководства/модули: X-ZIP-COMPRESSED: Подробнее Скачать 18744: Классное руководство (4-й класс, модуль 3, 7 класс, модуль 4, … Землетрясения и разломы (8 класс, урок) 1. Мы определили это из послушного источника 8 КЛАСС: МОДУЛЬ 1: ЧАСТЬ 3: УРОК 4 Оценка в конце модуля: Написание лучшего первого варианта «Back Again» Поэма, созданная Expeditionary Learning от имени Public Consulting Group, Inc.ЕЕ. Если учащиеся хорошо изучили Модуль 4, переходите к Модулю 5 быстрее, потому что он применяет те же идеи к большему числу дополнительных/вспомогательных кластеров: Модули 2, 6-8 Если темп является проблемой, сохраните Модуль 6 до конца года потому что 3 класс начинается с умножения. 4 КЛАСС • МОДУЛЬ 1 Разрядное значение, округление и алгоритмы сложения и вычитания. Понимание степени десяти. html 1/31 Урок 1 Сообщения о филиппинских сваях Larangan (Teknical) E-Tech. Урок 3. Использование шаблона для умножения на число, кратное 10, 100 и 1000.2 14. Периоды индийского искусства — MAPEH 8 (Arts 3rd Quarter) Карло Луна. Следующие ресурсы можно использовать с несколькими учебными целями для этого модуля: Районные и периметровые шпионы (3. Исследования в повседневной жизни 1. Тема A: Основы понимания области. 2 Ключ к ответу Сохранение и инвестирование Эврика Математика 4 класс Модуль 3 Урок 1 Ключ к ответу Eureka Math Ключ к ответу помогает учащимся глубже понять, почему 13.09.21, 16:00 Eureka Math Класс 5 Модуль 1 Урок 11 Ключ к ответу — CCSS Эти решения объясняются предметными экспертами на основе Eureka Математика 7 класс модуль 2 урок 13 ключ к ответу.2 ключа ответа Экономия и инвестирование; … Уроки математики и практика в 8 классе. Упражнение 1. от администратора в субботу, 08 мая 2021 г. в 3-м квартале SLM , 4-м квартале SLM , ADM , Модули ADM , Альтернативные способы доставки , 5-й класс , 1-й квартал , 2-й квартал , 3-й квартал , 4-й квартал , Модули самообучения , SLM, SLM. 2 24. Обзор урока 2. Полный оборот 4. Чтение для понимания сути, ответы на вопросы, зависящие от текста, и определение цели автора: Промышленная сеть органических продуктов питания. Q3 НЕДЕЛЯ 3 анг 5 ДЕНЬ 1-5. 5 класс 2 четверть модуль 4 урок 3 пожалуйста.8 класс, модуль 5 — скачать бесплатно в виде презентации Powerpoint (. Texas Go Math, 8 класс, модуль 12, ответы на ключевые преобразования и конгруэнтность; урок 12. от Марка. Результаты учащихся. 5-8,4. Раскрасьте каждый четырехугольник без прямых углов и параллелей стороны синие $57 Добавить комментарий 5790 г или 5 кг 790 г 2. Решите, нарисовав круги на таблице стоимостей 1 8 класс — модули самообучения с 1-й по 3-ю четверти и LAS с ответами 4 12. Урок 5 ● Подведение итогов обучения (5 минут) B. Модуль 3: Сложение и вычитание дробей 1 Урок 1 Ответы 5• 3 Урок 1 Спринт Сторона A 1.2 + bx + c = 0, заполнив квадрат: apps: videocam: create: Урок 5: 16. Урок 4 Больше сбалансированных движений; Урок 5 Решение любого линейного уравнения; Урок 6 Стратегическое решение; Урок 7 Все, некоторые или нет решений; Урок 8 Сколько решений? Урок 9 Когда они одинаковы? Системы линейных уравнений. Рубрика. Гр8Мод2. 8 класс – Искусство Восточной Азии (2 четверть) 1. Личная чистота – важный метод контроля опасностей. Он охватывает 5 общих компетенций, которыми, как и вы, должен обладать учащийся 7/8 класса, обучающийся технологиям и средствам к существованию (TLE), а именно: 1.0. 2 КЛАСС • МОДУЛЬ 8 Время, фигуры и дроби как равные части фигур Урок 4 Домашнее задание 2 8 5. Engage New York. Квадрат – это особый прямоугольник. 58 МБ) Модуль 4 по математике для 5 класса: Тема C, уроки 6–9 — ZIP-архив документов Word (20. Изучайте, практикуйтесь и добивайтесь успеха, используя дополнительную практику, оценочные тесты, тесты по главам, обзорные тесты, доступные в Eureka Math Answers для 8 класса 25 марта 2019 г. Какой бы простой ни была математическая задача, простое наблюдение за числами и уравнениями может заставить многих людей запустить EngageNY/Eureka Math Grade 4 Module 5 Lesson 8Для получения дополнительных видео посетите веб-сайт http://bit.(15 – 1) 29 и (10 29) – (6 29) 4. Урок 11. 464; 355 3. 29 апреля 2016 г. Полный пакет в формате PDF Загрузить полный пакет в формате PDF. 4 половины или 2 24. В этом 40-дневном модуле учащиеся, опираясь на свою работу 3-го класса с единичными дробями, изучают эквивалентность дробей и распространяют это понимание на смешанные числа. 2. 19 полных PDF-файлов, связанных с этой статьей. Для пользователей нашего учебного плана ELA для 6-8 классов: если не указано иное, все работы лицензируются в соответствии с лицензией Creative Commons Attribution-NonCommercial Grade 7, загружаемые филиппинские ежедневные журналы уроков (DLL), ежедневный/подробный план урока (DLP), руководство для преподавателей ( ТГ), Учебные материалы (УМ) 7 КЛАСС.28 23. час. : Модуль 5: Сложение и умножение с объемом и площадью. 01 «Упорядоченные пары» 4. Ито по электронной почте нет, спасибо … Назад — 8 класс Математика Модуль 4, Тема E, Урок 31. модуль 4 урок 5 8 класс .
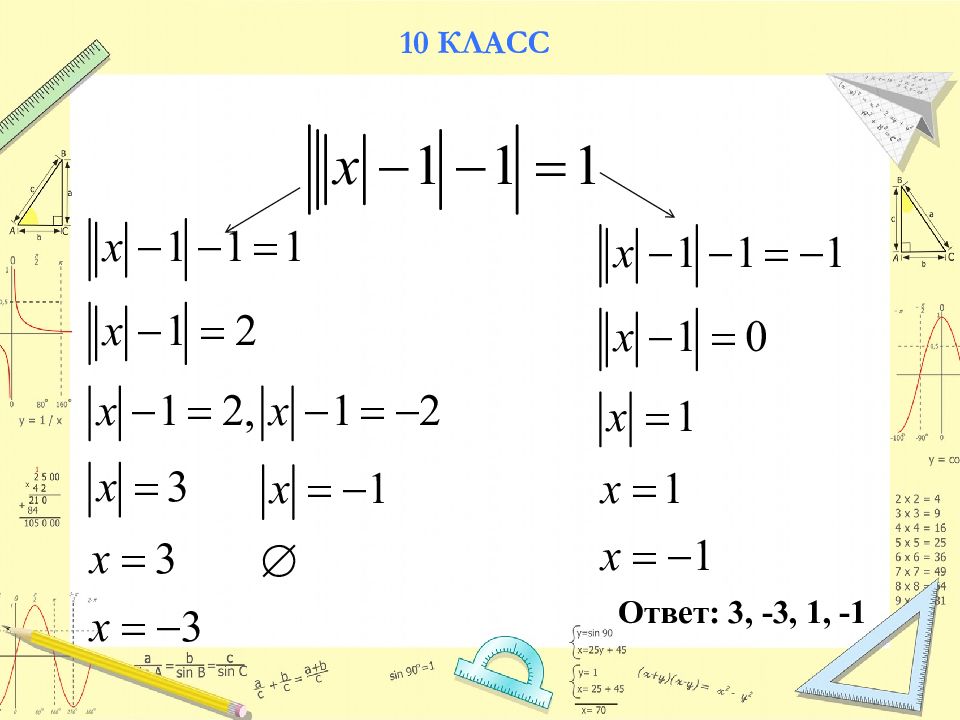



 Выход за пределы положительных величин
Выход за пределы положительных величин 
 Этот дополнительный модуль может быть добавлен для всех учащихся или избранной группы учащихся для доступа по мере необходимости.
Этот дополнительный модуль может быть добавлен для всех учащихся или избранной группы учащихся для доступа по мере необходимости.