Уравнение касательной и уравнение нормали к графику функции

Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой.

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

Значение производной f ‘(x0) функции y = f(x) в точке x0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку

M0(x0, y0), где y0 = f(x0). В этом состоит геометрический смысл производной.

Таким образом, можем заменить k на f ‘(x0) и получить следующее уравнение касательной к графику функции:

y — y0 = f ‘(x0)(x — x0).

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной.

Уравнение нормали:

(x — x0) + f ‘(x0)(y — y0) = 0

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

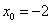Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

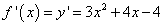Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

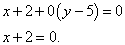
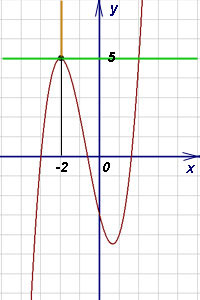
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции 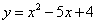, если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

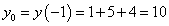Найдём производную функции:

.

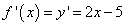Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

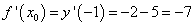Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

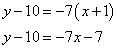
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

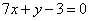
Составляем уравнение нормали:

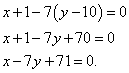
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции 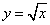, если абсцисса точки касания .

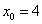Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

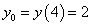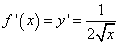Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

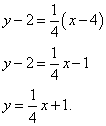
Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

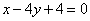
Составляем уравнение нормали:

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции

, если абсцисса точки касания .

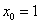Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

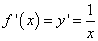Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

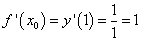Получаем уравнение касательной:

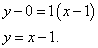
Приводим уравнение к общему виду:

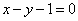
Составляем уравнение нормали:

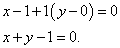
Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции 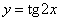, если абсцисса точки касания .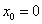

Решение. Найдём ординату точки касания:

.

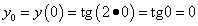Внимание! Данная функция — сложная, так как аргумент тангенса (2x) сам является функцией. Поэтому найдём производную функции как производную сложной функции:

.

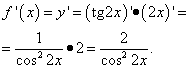Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

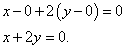
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции 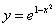, если абсцисса точки касания

.

Решение. Найдём ординату точки касания:

.

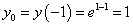Как и в предыдущем примере, данная функция — сложная, так как степень (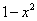) сама является функцией. Поэтому найдём производную функции как производную сложной функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

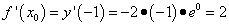Получаем уравнение касательной:

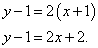
Приводим уравнение к общему виду:

Составляем уравнение нормали:

Поделиться с друзьями

Весь блок «Производная»

function-x.ru

как составить и решить задачу с его помощью

Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Как составлять уравнение касательной в заданной точке

При написании уравнения будем использовать следующие обозначения:

• x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
• f(x) — исходная функция;
• f'(x) — производная от функции;
• k — угловой коэффициент.

Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.

Алгоритм написания уравнения

После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:

1. Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
2. Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
3. Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
4. Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.

В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.

Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.

Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.

Задачи на написание уравнения касательной

Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.

Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.

Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.

• Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
• Возьмем от функции производную: f'(x) = 4x.
• Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
• Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
• Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.

В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.

Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).

• Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
• Запишем производную: g'(x) = 6x².
• Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
• Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
• Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
• В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.

Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.

Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.

Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.

Видео

Закрепить это тему вам поможет видео.

liveposts.ru

Уравнение касательной

Вспомним определение секущей для лучшего понимания что такое касательная.

Определение 1

Секущей называют прямую, пересекающую график кривой в двух точках одновременно.

Касательной прямой к графику кривой называют прямую, проходящую через некую точку кривой и совпадающую с ней в этой точке так, что это прямая лишь касается кривой.

Другое и более ёмкое определение касательной дал Лейбниц.

Определение 2

Лейбниц касательной называл прямую, проведённую через пару точек на рассматриваемой кривой, не совпадающих между собой, но находящихся бесконечно близко друг к другу. Из определения Лейбница видно, что касательная является частным случаем секущей.

Геометрический смысл производной в точке и касательной

Рассмотрим определение касательной подробнее.

Рисунок 1. Касательная и секущая к графику. Автор24 — интернет-биржа студенческих работ

Пусть дана некая кривая $L$, а на ней выбрана произвольная точка $M$. Возьмём ещё одну точку $P$, расположенную также на этой кривой и проведём через точки $M$ и $P$ секущую. Теперь поставим точку $P$ ещё ближе к точке $M$ и проведём новую секущую.

Проделаем так ещё несколько раз, каждый раз получая новую секущую, как бы поворачивающуюся вокруг точки $M$.

В момент, когда очередная точка $P$ находится бесконечно близко к точке $M$, секущая как бы достигает своего предельного положения, в котором по сути она лишь касается графика.

Это положение называется касательной к графику кривой $L$ в точке $M$.

Уравнение касательной через производную

Теперь узнаем, как найти уравнение касательной.

Рассмотрим некую функцию $y(x)$ и выберем на ней точку $M$ с координатами $(a; y(a))$.

Сделаем приращение к аргументу $x$ в этой точке, равное $Δx$ и рассмотрим точку $P$ на графике функции с абсциссой, равной $x=x+Δx$. Значение функции в этой точке будет равно $y(a+ Δx)$. Проведём через точки $M$ и $P$ секущую.

Как мы помним из курса математики, угловой коэффициент равен тангенсу угла прямой с осью абсцисс. Это значит, что угловой коэффициент рассматриваемой нами секущей равен приращению функции $y$ к приращению функции $x$:

$k_{секущ.}=\frac{Δy}{Δx}\left(1\right)$.

Теперь рассмотрим приращение $Δx$ как бесконечно малую величину. В этом случае точка $P$ с координатами $(a; y(a)+ Δy)$ будет приближаться к точке $M$, стремясь к ней. Следовательно, угловой коэффициент нашей секущей, которая в данном случае является касательной, равен пределу:

$k_{кас.}=lim_{ Δx \to 0}(k_{секущ.})$

Воспользуемся формулой $(1)$ для секущей:

$k_{кас.}=lim_{ Δx \to 0} \frac{Δy}{Δx}$

Данный предел также носит название производной функции $y=f(x)$ в точке $x$ и обозначается как $y’(x)$.

Определение 3

Геометрический смысл производной состоит в том, что при условии возможности проведения касательной в точке $x$ к графику исследуемой кривой, такой, что эта касательная не параллельна оси $OX$, значение производной является угловым коэффициентом проведённой касательной в этой точке.

Иначе данное утверждение можно записать как

$k_{кас.}(a)=f’(a)$.

То есть, при составлении уравнения касательной через производную, производная функции является угловым коэффициентом.

Заметим на всякий случай, что сама функция $y=f(x)$ и её производная $y’(x)$ — две разные функции, равные между собой в точке $x$.

Таким образом, в общем виде уравнение касательной будет иметь вид:

$y=f(x_0)+f’(x_0)(x-x_0) \left(2\right)$,

где $f(x_0)$ — значение функции в точке $x_0$, а $f’(x_0)$ — её производная.

Уравнение касательной для параболы

Рисунок 2. Уравнение касательной к графику параболической функции. Автор24 — интернет-биржа студенческих работ

Рассмотрим получение уравнения касательной к графику функции на параболе $y=ax^2$ в точке $M$ c координатами $(x; y)$.

Придадим этой точке приращение по оси $OX$, равное $Δx$, приращение по оси $y$ тогда составит $y+Δy=a(x+ Δx)^2$. Точку с координатами $(x+ Δx; y+Δy)$ назовём $P$.

Теперь чтобы определить тангенс угла секущей $MP$с осью абсцисс, рассмотрим прямоугольный треугольник $\triangle MNP$. В нём катет $MN$ равен $Δx$, а второй катет $Δy$ — это приращение ординаты, равное $Δy=a(2x \cdot Δx + Δx^2)$.

Выразим используя эти данные тангенс угла $φ$.

$\mathrm{tg}φ=\frac{Δy}{Δx}=2ax + a \cdot Δx$

Теперь для получения углового коэффициента рассмотрим это отношение при бесконечно малой величине $Δx$. Как известно, в этом случае мы имеем дело с пределом:

$\mathrm{tg}φ= \lim_{Δx \to 0}(2ax+a \cdot x)=2ax$.

Благодаря такому соотношению становится легко построить касательную к параболе (рис. 2, б).

Для этого достаточно рассмотреть треугольник $\triangle MPT$, так как отрезок $TP$ будет равен:

$TP=\frac{y}{\mathrm{tg}α}=\frac{ax^2}{2ax}=\frac{x}{2}$

То есть, для того чтобы получить касательную, необходимо соединить середину отрезка $OP$ с точкой $M$.

Расположение касательной в зависимости от значения её углового коэффициента

Рассмотрим несколько различных случаев значения углового коэффициента для касательной.

Если её угловой коэффициент, то есть, тангенс, равен нулю, то касательная расположена параллельно оси $OX$, а сама прямая принимает вид $y=b$.

Если тангенс положительный, то касательная образует острый угол с осью абсцисс, что значит, что вместе с ростом $x$ растёт и $y$.

В случае если тангенс отрицательный, прямая образует тупой угол с горизонтальной осью, а это значит, что с увеличением значения икса происходит уменьшение значения игрека.

Есть ещё один случай расположения касательной — параллельно оси $OY$, в этом случае её уравнение описывается как $x=c$, где $c$ — некая константа.

Другим числом, определяющим положение касательной, является число $b$, являющееся свободным членом в уравнении прямой $y=kx+b$. Число $b$ характеризует значение функции $y(x)$ в точке её пересечения с осью ординат, иначе говоря, оно есть не что иное, как значение уравнения касательной к графику функции в точке $x=0$.

Пример 1

Составить уравнение касательной в точке $x=3$ для графика функции $y(x)=2x^2+3x-6$.

Сначала найдём значение функции в точке $x=3$:

$y=2 \cdot 3^2 +3 \cdot 3 – 6 = 21$

Теперь определим значение производной для исследуемой функции:

$(2x^2+3x-6)’=4x+3$

Теперь получим значение углового коэффициента, для этого подставим $x=3$ в производную:

$y’(x)=4 \cdot 3 + 3 = 15$

Подставим это значение в формулу для касательной $(2)$:

$y_{кас.}=21+15 \cdot (x-3)$

$y=15x-24$ — уравнение касательной получено.

spravochnick.ru

9. Уравнения касательной и нормали.

Рассмотрим кривую, уравнение которой имеет вид

Уравнение касательной к данной кривой в точке 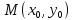имеет вид:

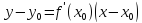(34)

Нормалью к кривой в данной точке называется прямая, проходящая через данную точку, перпендикулярную к касательной в этой точке.

Уравнение нормали к данной кривой в точке 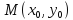имеет вид:

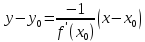(35)

_{Длина отрезка касательной, заключенного между точкой касания и осью абсцисс называется длиной касательной, проекция этого отрезка на ось абсцисс называется подкасательной.}

_{Длина отрезка нормали, заключенного между точкой касания и осью абсцисс называется длиной нормали,проекция этого отрезка на ось абсцисс называется поднормалью.}

Пример 17

Написать уравнения касательной и нормали к кривой в точке, абсцисса которой равна.

Решение:

Найдем значение функции в точке :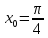

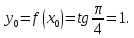
Найдем производную заданной функции в точке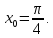

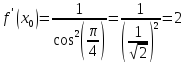
Уравнение касательной найдем по формуле (34):

Уравнение нормали найдем по формуле (35):

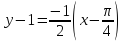
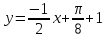
Ответ: Уравнение касательной :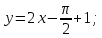

Уравнение нормали :.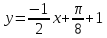

Пример 18

Написать уравнения касательной и нормали, длины касательной и подкасательной, длины нормали и поднормали для эллипса

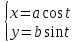
в точке 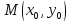, для которой.

Решение:

Найдем как производную функции, заданной параметрически по формуле (10):

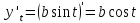
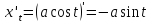
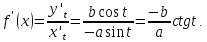
Найдем координаты точки касания : и значение производной в точке касания :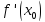

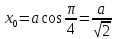
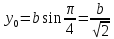
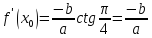
Уравнение касательной найдем по формуле (34):

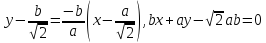
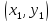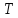Найдем координаты точкипересечения касательной с осью: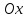

Длина касательной равна длине отрезка :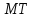

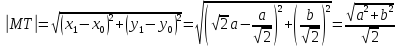
Согласно определению, подкасательная равна

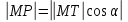
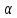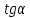Где угол – угол между касательной и осью. Поэтому,— угловой коэффициент касательной, равный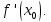

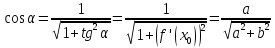
Таким образом, подкасательная 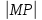равна

Уравнение нормали найдем по формуле (35):

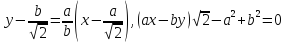
Найдем координаты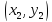точкипересечения нормали с осью:

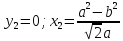
Длина нормали равна длине отрезка :

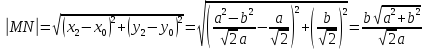
Согласно определению, поднормаль 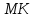равна

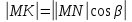
Где угол 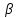– угол между нормалью и осью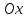. Поэтому,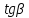— угловой коэффициент нормали, равный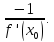

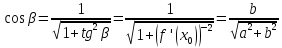
Поэтому, поднормаль 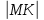равна:

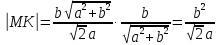
Ответ: Уравнение касательной :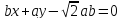

Уравнение нормали :

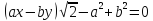
Длина касательной 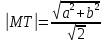; подкасательная;

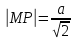Длина нормали 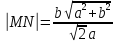; поднормаль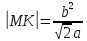

Задания 7. Написать уравнения касательной и нормали:

1. К параболе в точке, абсцисса которой

.

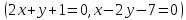2. К окружности 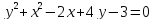в точках пересечения её с осью абсцисс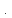

.

3. К циклоиде 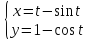в точке, для которой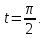

.

4. В каких точках кривой 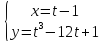касательная параллельна:

а) оси Оx; б) прямой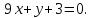

.

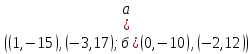10. Промежутки монотонности функции. Экстремумы функции.

Условие монотонности функции:

Для того, чтобы дифференцируемая на функция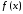не возрастала, необходимо и достаточно, чтобы во всех точках, принадлежащих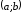ее производная была неположительна .

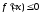(36)

Для того, чтобы дифференцируемая на 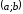функция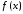не убывала, необходимо и достаточно, чтобы во всех точках, принадлежащихее производная была неотрицательна.

(37)

Промежутки, на которых производная функции сохраняет определенный знак, называются промежутками монотонности функции

Пример 19

Найти промежутки монотонности функции .

Решение:

Найдем производную функции .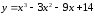

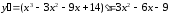
Найдем промежутки знакопостоянства полученной производной. Для этого

разложим полученный квадратный трехчлен на множители:

.

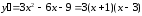Исследуем знак полученного выражения, используя метод интервалов.

Таким образом, получаем согласно (36), (37),что заданная функция возрастает на и убывает на.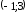

Ответ: Заданная функция 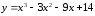возрастает на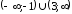и убывает на.

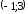_{Определение} Функция имеет в точке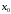локальный максимум (минимум), если существует такая окрестность точки , что для всех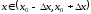выполняется условие

().

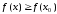Локальный минимум или максимум функции 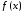называетсялокальным экстремумом.

Необходимое условие существования экстремума.

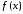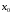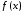Пусть функция определена в некоторой окрестности точки. Если функцияимеет в точке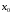экстремумом, то производная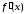в точке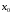либо равна нулю, либо не существует.

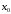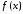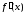Точка называетсякритической точкой функции , если производнаяв точке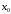либо равна нулю, либо не существует.

Достаточные условия наличия экстремума в критической точке .

Пусть точка 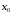является критической.

Первое достаточное условие экстремума:

Пусть функция 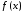непрерывна в некоторой окрестност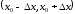иточки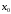и дифференцируема в каждой точке.

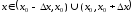Точка 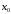является локальным максимумом, если при переходе через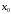

производная функции меняет знак с плюса на минус.

Точка 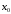является локальным минимумом, если при переходе через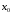

производная функции меняет знак с минуса на плюс.

Пример 20

Найти экстремумы функции .

Решение:

Найдем производную заданной функции

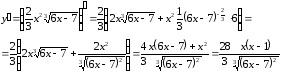
Приравнивая в полученной производной к нулю числитель и знаменатель, найдем критические точки:

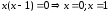
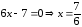
Исследуем знак производной, используя метод интервалов.

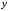
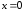Из рисунка видно, что при переходе через точку производная меняет знак с плюса на минус. Следовательно, в точке— локальный максимум.

При переходе через точку 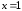производная меняет знак с минуса на плюс.

Следовательно, в точке 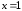— локальный минимум.

При переходе через точку производная не меняет знак. Следовательно, критическая точка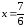не является экстремумом заданной функции.

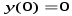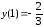Ответ: — локальный максимум, — локальный минимум.

Второе достаточное условие экстремума:

Если первые 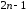производные функции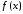в точке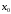равны нулю, а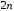-ная производная функции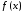в точке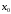отлична от нуля, то точка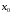является экстремумом функции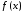, причем,

если

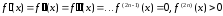, (38)

то 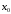-локальный минимум

если

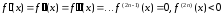, (39)

то 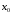-локальный максимум.

Пример 21

Найти экстремумы функции, пользуясь второй производной .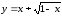

Решение:

ОДЗ: .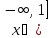

Найдем первую производную заданной функции

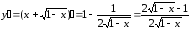
Найдем критические точки функции:

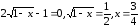
Точку 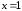мы не рассматриваем, так как функция определена только в левой окрестности.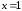

Найдем вторую производную

Находим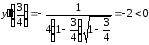

Таким образом, на основании (39) делаем вывод о том, что при 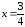— локальный максимум.

Ответ: 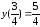— локальный максимум.

Задания 8.

Исследовать на возростание и убывание функции:

Исследовать на экстремумы функции:

studfile.net

Уравнение касательной — 14 Октября 2015 — Примеры решений задач

Здесь необходимо отсеять неверные определения касательной.

Толковый словарь Ушакова; Касательная — прямая линия, имеющая одну общую точку с кривой.

Определение верно для окружности рис.1, в общем случае неверно рис.2.

Академический словарь, за ним повторяет толковый словарь Кузнецова, Ефремовой и т.д.: Касательная — Прямая, имеющая общую точку с кривой, но не пересекающая её.

Определение  в общем случае неверно рис.3.

 

 

Определение: Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

 

Формула уравнения касательной

Если существует конечная производная f'(x₀) то уравнение касательной к графику функции y=f(x) выражается следующим уравнением:

Особый случай когда   f'(x₀) бесконечна, разберем отдельно.

Пример 1. Найти уравнение касательной к графику функции y=x² в точке 2.

Алгоритм решения следующий:

1. Находим производную функции:

2. Находим значение производной в точке x₀=2:

3. Находим значение функции в точке x₀=2:

4. Найденные значения подставляем в формулу уравнения касательной:

5. Получаем уравнение касательной в точке x₀=2:

Получить уравнение касательной онлайн, а также графическое решение, можно с помощью данного калькулятора.

 

www.reshim.su

Урок по теме «Касательная. Уравнение касательной»

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Тип урока: изучение нового материала.

Методы обучения: наглядный, частично поисковый.

Цель урока:

1. Ввести понятие касательной к графику функции в точке, выяснить, в чём состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.
2. Развитие логического мышления, исследовательских навыков, функционального мышления, математической речи.
3. Выработка коммуникативных навыков в работе, способствовать развитию самостоятельной деятельности учащихся.

Оборудование: компьютер, мультимедийный проектор, раздаточный материал.

План урока

I Организационный момент.
<слайд 2, 3> Проверка готовности учащихся к уроку. Сообщение темы и девиза урока.

II Актуализация материала.
(Активизировать внимание, показать недостаточность знаний о касательной, сформулировать цели и задачи урока.) <слайд 5>

Давайте обсудим, что такое касательная к графику функции? Согласны ли вы с утверждением, что «Касательная – это прямая, имеющая с данной кривой одну общую точку»?
Идёт обсуждение. Высказывания детей (да и почему, нет и почему). В процессе обсуждения приходим к выводу, что данное утверждение не верно.

Примеры. <слайд 6>
1) Прямая x = 1 имеет с параболой y = x2 одну общую точку M(1; 1), однако не является касательной к параболе. Прямая же y = 2x – 1, проходящая через ту же точку, является касательной к данной параболе <рисунок 1>.
 2) Аналогично, прямая x = π не является касательной к графику y = cos x, хотя имеет с ним единственную общую точку K(π; 1). С другой стороны, прямая y = — 1, проходящая через ту же точку, является касательной к графику, хотя имеет с ним бесконечно много общих точек вида

(π+2 πk; 1), где k – целое число, в каждой из которых она касается графика <рисунок 2>.

Рисунок 1

Рисунок 2

Постановка цели и задачи перед детьми на уроке: <слайд 7> выяснить, что такое касательная к графику функции в точке, как составить уравнение касательной?
Что нам для этого понадобиться?
Вспомнить общий вид уравнения прямой, условия параллельности прямых, определение производной, правила дифференцирования.

III Подготовительная работа к изучению нового материала.
Опрос материала по карточкам: (задания выполняются на доске)
1 ученик: заполнить таблицу производных элементарных функций

2 ученик: вспомни правила дифференцирования

3 ученик: составьте уравнение прямой y = kx + 4, проходящей через точку А(3; -2).
(y = -2x+4)

4 ученик: составьте уравнение прямей y = 3x + b, проходящей через точку С(4; 2).
(y = 3x – 2).

С остальными фронтальная работа. <слайд 8>

1. Сформулируйте определение производной.
2. Какие из указанных  прямых параллельны? у = 0,5х; у = — 0,5х; у = — 0,5х + 2. Почему?

Отгадай фамилию учёного <слайд 9>:

Ключ к ответам

Кем был этот учёный, с чем связаны его работы, мы узнаем на следующем уроке.
Проверка ответов учащихся по карточкам. <слайд 10>

IV Изучение нового материала.
Чтобы задать уравнение прямой на плоскости нам достаточно знать её угловой
коэффициент и координаты одной точки.

• Начнём с углового коэффициента <слайд 11>

Рисунок 3

Рассмотрим график функции y = f(x)  дифференцируемой в точке А(x₀, f(x₀)) <рисунок 3>.
Выберем на нём точку M (x₀ + Δх, f(x₀+ Δх)) и проведем секущую AM.
Вопрос: чему равен угловой коэффициент секущей? (∆f/∆x=tgβ)

Будем приближать по дуге точку M к точке A. В этом случае прямая AM будет поворачиваться вокруг точки A, приближаясь (для гладких линий) к некоторому предельному положению — прямой AT. Другими словами < TAM → 0 если длина АМ → 0. Прямую AT, обладающую таким свойством, называют касательной к графику функции y = f(x) в точке А(x₀, f(x₀)). <слайд 12>

Угловой коэффициент секущей AM при AM → 0 стремится к угловому коэффициенту касательной AT Δf/Δx → f ‘(x₀). Значение производной в точке х₀ примем за угловой коэффициент касательной. Говорят, что касательная есть предельное положение секущей  при ∆х → 0.

Существование производной функции в точке x₀ эквивалентно существованию (невертикальной) касательной в точке (x₀, f(x₀)) графика, при этом угловой коэффициент касательной равен f ‘(x₀) . В этом состоит геометрический смысл производной. <слайд 13>

Определение касательной: <слайд 14> Касательная    к    графику   дифференцируемой    в точке х₀функции f  — это прямая, проходящая через точку (x₀, f(x₀)) и имеющая угловой коэффициент f ‘(х₀).
Проведем касательные к графику функции y = f(x)  в точках х₁, х₂, х₃,  <рисунок 4> и отметим углы, которые они образуют с осью абсцисс. (Это угол, отсчитываемый в положительном направ­лении от положительного направления оси до прямой.)

Рисунок 4

Мы видим, что угол α₁ острый, угол α₃ тупой, а угол α₂ равен нулю, так как прямая l параллельна оси Ох. Тангенс острого угла   положителен,   тупого — отрицателен. Поэтому  f ‘(х₁)>0, f ‘(х₂) = 0, f ‘(х₃) < 0. <слайд 15, 16>

• Выведем теперь уравнение касательной <слайд 17, 18> к графику функцииf в точке А(x₀, f(x₀)).

Общий вид уравнения прямой y = kx + b.

1. Найдём угловой коэффициент k = f ‘(х₀), получим y = f ‘(х0)∙x + b, f(x) = f ‘(х₀)∙x + b
2. Найдём b.  b = f(x₀) — f ‘(х₀)∙x₀.
3. Подставим полученные значения k и b в уравнение прямой: y = f ‘(х₀)∙x + f(x₀) — f ‘(х₀)∙x₀ или  y = f(x₀) + f ‘(х₀)(x — x₀)

•  Обобщение материала лекции. <слайд 19>

— что называется касательной к графику функции в точке?
— в чём заключается геометрический смысл производной?
— сформулируйте алгоритм нахождения уравнения касательной в точке?

1. Значение функции в точке касания
2. Общую производную функции
3. Значение производной в точке касания
4. Подставить найденные значения в общее уравнение касательной.

V Закрепление изученного материала.

1. Устная работа:
1) <слайд 20> В  каких точках графика <рисунок 5> касательная к нему
а) горизонтальна;
б) образует с осью абсцисс острый угол;
в) образует с осью абсцисс тупой угол?
2)  <слайд 21> При каких значениях аргумента производная функции, заданной графиком <рисунок 6>
а) равна 0;
б) больше 0;
в) меньше 0?

Рисунок 5

Рисунок 6

3) <слайд 22> На рисунке изображён график функцииf(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f ‘(x) в точке x₀<рисунок 7>.

Рисунок 7

 2. Письменная работа.
№ 253 (а, б), № 254 (а, б). (работа на местах, с комментарием)

3. Решение опорных задач. <слайд 23>
Рассмотрим четыре типа задач. Дети читают условие задачи, предлагают алгоритм решения, один из учеников оформляет его на доске, остальные записывают в тетрадь.
1. Если задана точка касания
Составить уравнение касательной к графику функции f(x) = x³ – 3x – 1 в точке М с абсциссой –2.
Решение: 

1. Вычислим значение функции: f(-2) =(-2)³ – 3(-2) – 1 = -3;
2. найдём производную функции:  f ‘(х) = 3х² – 3;
3. вычислим значение производной:  f ‘(-2) = — 9.;
4. подставим эти значения в уравнение касательной: y = 9(x + 2) – 3 = 9x + 15.

Ответ: y = 9x + 15.

2. По ординате точки касания.
Составить уравнение касательной в точке графика с ординатой y₀  = 1.
Решение:

1. Найдем абсциссу точки касания: , х₀ = 1.
2. Найдём производную функции: f ‘(х) = .
3. Найдем угловой коэффициент касательной f ‘(х₀) : f ‘(1)= — 1
4. Теперь можно записать уравнение касательной:  y = –1(x – 1) + 1 = –x + 2.

Ответ: y = –x + 2.

3. Заданного направления.
Написать уравнения касательной к графику y = x³ – 2x + 7, параллельной прямой у = х.
Решение.
Искомая касательная параллельна прямой y = x.  Значит, они имеют один и тот же угловой коэффициент k = 1,  y‘(х) = 3х2 – 2. Абсцисса х₀ точек касания удовлетворяет уравнению 3х² – 2 = 1, откуда х₀ = ±1.
Теперь можно написать уравнения касательных: y = x + 5 и y = x + 9.
Ответ: y = x + 5,  y = x + 9.

4. Условия касания графика и прямой.
Задача. При каких b прямая  y = 0,5x + b является касательной к графику функции f(х) = ?
Решение.
Вспомним, что угловой коэффициент касательной – это значение производной в точке касания. Угловой коэффициент данной прямой равен k = 0,5. Отсюда получаем уравнение для определения абсциссы x точки касания: f ‘(х) = = 0,5. Очевидно, его единственный корень  –х = 1. Значение данной функции в этой точке у(1) = 1. Итак, координаты точки касания (1; 1). Теперь остается подобрать такое значение параметра b, при котором прямая проходит через эту точку, то есть координаты точки удовлетворяют уравнению прямой: 1 = 0,5 ·1 + b, откуда b = 0,5.

5. Самостоятельная работа обучающего характера. <слайд 24>

Работа в парах.

Проверка: результаты решения заносятся в таблицу на доске (от каждой пары один ответ), обсуждение ответов.

6. Нахождение угла пересечения графика функции и прямой.  <слайд 25>
Углом пересечения графика функции y = f(x) и прямой l называют угол, под которым в этой же точке прямую пересекает касательная к графику функции.
№ 259 (а, б), № 260 (а) – разобрать у доски.

7. Самостоятельная работа контролирующего характера. <слайд 26> (работа дифференцированная, проверяет учитель к следующему уроку)
1 вариант.

1. Найдите тангенс угла наклона касательной к графику функции f(x)= х³+ 27 в точке х₀= -3.
2. Напишите уравнение касательной к графику функции  в точке с абсциссой  х₀= 3. Выполните рисунок.
3. Выясните, является ли прямая у = 0,5х + 0,5 касательной к графику функции у = .

2 вариант.

1. В каких точках касательная к графику функции f(x) = 3х² — 12х + 7 параллельна оси х?
2. Составьте уравнение касательной к графику функции f(x)= х² — 4 в точке с абсциссой х₀ =  — 2. Выполните рисунок.
3. Выясните, является ли прямая у = 12х – 10 касательной к графику функции у = 4х³.

3 вариант.

1. В какой точке графика функции у = . касательная наклонена к оси абсцисс под углом 60°?
2. Составьте уравнение касательной к графику функции  , параллельно прямой у = 3х.
3. Выясните, является ли прямая у = х касательной к графику функции у = sin x.

VI Подведение итогов урока. <слайд 27>
1. Ответы на вопросы
— что называется касательной к графику функции в точке?
— в чём заключается геометрический смысл производной?
— сформулируйте алгоритм нахождения уравнения касательной в точке?
2. Вспомните цели и задачи урока, достигли ли мы данной цели?
3. В чём были трудности на уроке, какие моменты урока наиболее понравились?
4. Выставление отметок за урок.
VII Комментарий домашнего задания: п. 19 (1, 2), № 253 (в), № 255 (г), № 256 (г), № 257 (г), № 259 (г). Подготовить сообщение о Лейбнице <слайд 28>.

Литература <слайд 29>

1. Алгебра и начала анализа: Учеб. для 10—11 кл. общеобразоват. учреждений / А.Н.Колмогоров, А.М.Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н.Колмогорова. — М.: Просвещение, 2004.
2. Дидактические материалы по алгебре и нача­лам анализа для 10 класса / Б.М.Ивлев, С.М.Саакян, С.И. Шварцбурд. — М.: Просвещение, 2003.
3. Мультимедийный диск  фирмы «1С». 1С: Репетитор. Математика (ч. 1) + Варианты ЕГЭ. 2006.
4. Открытый банк заданий по математике/ http://mathege.ru/

urok.1sept.ru