6.2.4. Модуль числа математика-повторение
Модулем числа а (записывают |a|) называют расстояние от начала отсчета до точки, соответствующей данному числу а.
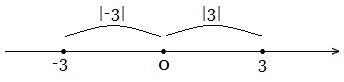
Значение модуля любого числа неотрицательно. |3|=3; |-3|=3, т.к. расстояние от начала отсчета и до числа -3, и до числа 3 равно трем единичным отрезкам. Противоположные числа имеют равные модули. Модуль нуля равен нулю: |0|=0.
По определению модуля числа: |a|=a, если a≥0 и |a|=-a, если а<0. Читают: модуль неотрицательного числа равен самому этому числу; модуль отрицательного числа равен противоположному числу.
Примеры.
1. Вычислить: а) |5|-2; б) |-12| : 6; в) |-24| + |13|;
Решение. а) |5|-2=5-2=3;
б) |-12| : 6=12 : 6=2;
в) |-24|+|13|=24+13=37;
г) |65|-|-45|=65-45=20.
2. Решить уравнение: а) |m|+4=10; б) 6-|x|=2.
Решение.
а) |m|+4=10;
|m|=10-4; из суммы вычли известное слагаемое;
|m|=6. Так как |-6|=6 и |6|=6, то m=-6 или m=6.
Ответ: -6; 6.
б) 6-|x|=2.
|x|=6-2;
|x|=4, отсюда х=-4 или х=4.
Ответ: -4; 4.
3. Записать перечислением элементов множество целых чисел А, модуль которых меньше числа 5.
Решение. По определению модуля числа 5 искомые числа должны отстоять от начала отсчета как вправо, так и влево на расстояние, меньшее пяти единичных отрезков. В этом промежутке (показан штриховкой на рисунке) бесконечно много чисел, но нам нужно выбрать из них лишь все целые числа. Берем числа: -4, -3, -2, -1, 0, 1, 2, 3, 4. Числа -5 и 5 не подходят по условию.
Ответ: множество А={-4, -3, -2, -1, 0, 1, 2, 3, 4}.
4. Записать перечислением множество натуральных чисел В, модуль которых меньше числа 5.
Решение. Из всех чисел, показанных на рисунке штриховкой, нам нужно выбрать натуральные, т.е. только те числа, которые употребляются при счете предметов. Ответ: B={1, 2, 3, 4}.
www.mathematics-repetition.com
Решение уравнений с модулем в 6 классе
Покропаева О.Б.,
учитель математики
г. Санкт-Петербурга
Решение уравнений с модулем в 6 классе
В учебнике Н.Я. Виленкина и др. «Математика, 6» очень мало внимания уделено решению уравнений с модулем. Тогда как в 6 классе, при формировании понятия «модуль числа», есть возможность уделить больше внимания уравнениям данного вида. На трёх уроках после изучения понятия модуля я рассматриваю с учащимися уравнения со знаком модуля, переходя от самых простых к более сложным:
;
При решении данных уравнений шестиклассники учатся применять определение модуля; получают навыки элементарных операций с модулем; привыкают к мысли о том, что под знаком модуля могут быть как положительные, так и отрицательные выражения, но сам модуль может быть только неотрицательным числом; тренируются в применении свойств уравнений.
При изучении данной темы мы опираемся на общепринятое определение модуля числа:
Это определение даёт учащимся более чёткое представление о том, что им надо делать в каждом конкретном случае: сменить ли знак у числа или оставить его без изменения.
Приведу несколько примеров решений уравнений такого типа.
Решить уравнение
ПРОВЕРКА:
В обоих случаях значения модуля оказались отрицательными, что противоречит определению модуля числа. Значит, числа и 3 не являются корнями данного уравнения.
ОТВЕТ: нет решений.
Решить уравнение
ПРОВЕРКА:
1 = 1 — верно
5 = 5 – верно
ОТВЕТ: 0; 2..
Решить уравнение
Нет решений.
2 = 2 – верно 2 = 2 – верно ОТВЕТ: -2; 4.
Рассмотренные уравнения развивают у учащихся умение анализировать полученное решение. Они позволяют показать, что уравнение может и не иметь корней или иметь посторонние корни. Эти наблюдения существенно расширяют представления школьников об уравнении.
educontest.net
Урок-путешествие по теме: «Решение уравнений», 6 класс
Форма проведения: урок-путешествие.
Цели урока:
- закрепить и совершенствовать умения и навыки учащихся при решении уравнений;
- продолжить формирование вычислительных навыков с рациональными числами и умений контролировать деятельность по конечному результату;
- возбудить интерес к содержанию учебного материала и способам деятельности.
ХОД УРОКА
I. Актуализация опорных знаний.
Сегодня мы отправляемся на остров Сокровищ на поиски клада. Трудное путешествие может выдержать не каждый. Поэтому начинаем набор команды следующими испытаниями:
1. Определите знак:
| – 5 – 3 –3 + 9 –7 – 6 22 – 11 |
– 5 . (– 3) – 3 . 9 – 7 . (– 6) 22 : (– 11) |
2. Вычислите:
– .
– : (–)
(– 2)3
(– 0,1)2
3. Раскройте скобки:
– 2(x
+ 3)
4(a + 4)
5 – (x + 6)
4 + (2 – b)
3(y – 4)
II. Работа по теме урока.
1. Управляемая самостоятельная работа с последующей проверкой.
Итак, испытания выдержали все. На каком судне отправимся в далёкое путешествие? Ответ на этот вопрос нам поможет получить тест.
| 1. – 2,5 . (– 0,2) 2. 2,5 – 8,5 3. – 4 . 2,5 4. – 5. – : 6. (– 0,3)2 |
а) – 5; о) – 6; л) – 8,5; д) ; е) – 1; н) 0,6; |
к) 0,5; г) – 6,5; з) 8,2; в) –; у) – ; ф) 0,9; |
б) 50. и) 11. р) – 10. ж) – . х) . т) 0,09. |
Вы правильно угадали название судна, на котором мы сейчас отправимся в путешествие. Это КОРВЕТ – трехмачтовое военное судно.
2. Команда и судно готовы к отплытию, но на карте временем стёрты координаты местонахождение клада.
Чтобы восстановить их, нужно решить уравнения. (На доске и в тетрадях решаются уравнения двумя вариантами одновременно. Первый вариант находит координату X, второй вариант–Y ).
I вариант |
II вариант |
| 5(x – 9) = 3(3x – 3) (x = – 9) | |
| – 0,2x + 2,3 = – 0,7x – 3,2 (x = – 11) | 0,25 + 0,1(y + 0,5) = 0,4y (y = 1) |
| 0,1x – 0,3(x + 3) = 0,3 (x = – 6) | – 5(13 – 2y) = – 30 + 5y (y = 7) |
| 0,2(x + 2) = 0,6(x – 2) (x = 4) | – 7,6 – (y – 2,75) = – 1,85 (y = – 7) |
| – 1,3 – 3(0,5x + 2) = – 1,3 (x = – 4) | 8,8 + (y – 3,1) = 8,7 (y = 3) |
| – 4(– x + 7) = x – 40 (x = – 4) | 2,1(4 – 6y) = – 4,2 (y = 1) |
Ура! Координаты восстановлены. Вот они: (– 9; – 3) (– 11; 1) (– 6; 7) (4; – 3) (– 4; 3) (– 4; 1).
3. Что же кроется в этой карте? Построив фигуру в координатной плоскости, мы об этом узнаем.
(В конце построения должен получиться СУНДУК.)
III. Подведение итогов урока.
Что за сокровища оказались в сундуке? (Знания)
urok.1sept.ru