Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
средняя линия
трапеции ABCD,
AD||BC, то
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.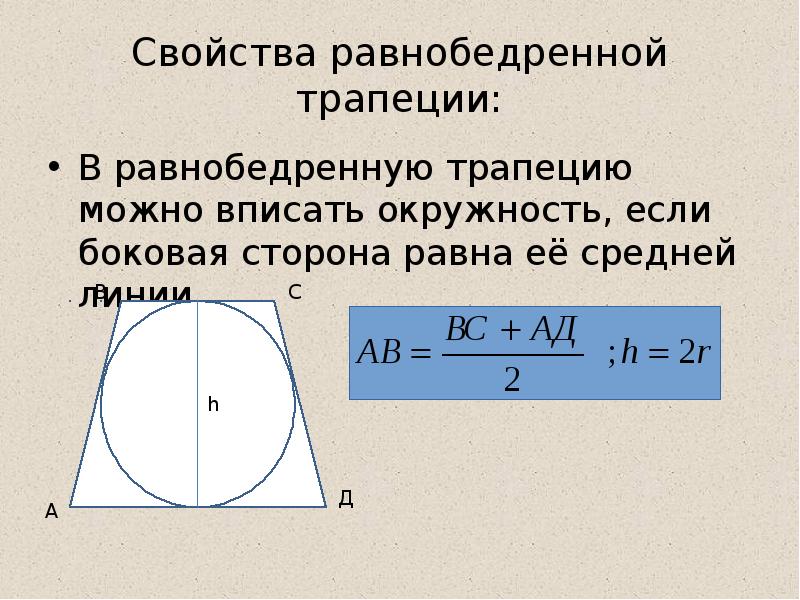
По свойству равнобедренной трапеции,
Если AD=a, BC=b,
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
AK=AP=DP=DN,
BK=BF=CF=CN.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
Значит, треугольник COD — прямоугольный,
(как радиус, проведенный в точку касания).
Следовательно, ON — высота, проведённая к гипотенузе,
В равнобедренную трапецию вписана окружность
Рассмотрим частный случай вписанной в трапецию окружности.
Если в равнобедренную трапецию вписана окружность, существует несколько направлений, по которым можно повести решение задачи.
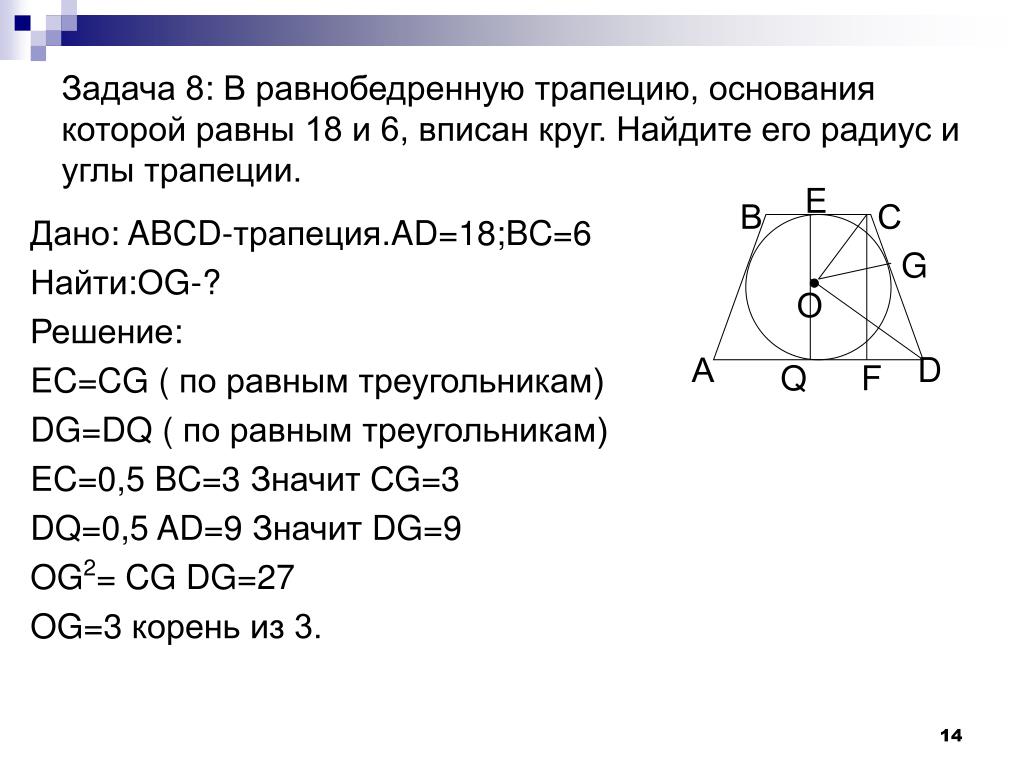
1. В равнобедренную трапецию вписана окружность, которая в точке касания делит боковую сторону на отрезки m и n. Найти площадь трапеции.
Решение:
1)∠ADC+∠BCD=180º(как внутренние односторонние при AD∥BC и секущей CD).
2) Так как центр вписанной окружности — точка пересечения биссектрис трапеции, то
∠OCD+∠ODC=90º.
3) Так как сумма углов треугольника равна 180º, в треугольнике OCD ∠COD=90º.
4) OF перпендикулярен CD (как радиус, проведенный в точку касания), следовательно, в треугольнике OCD OF — высота, проведенная к гипотенузе. По свойству прямоугольного треугольника,
Так как высота трапеции равна диаметру вписанной окружности, то
5) Формула для нахождения площади трапеции
Так как в трапецию вписана окружность, суммы ее противолежащих сторон равны:
Таким образом, площадь трапеции равна
2.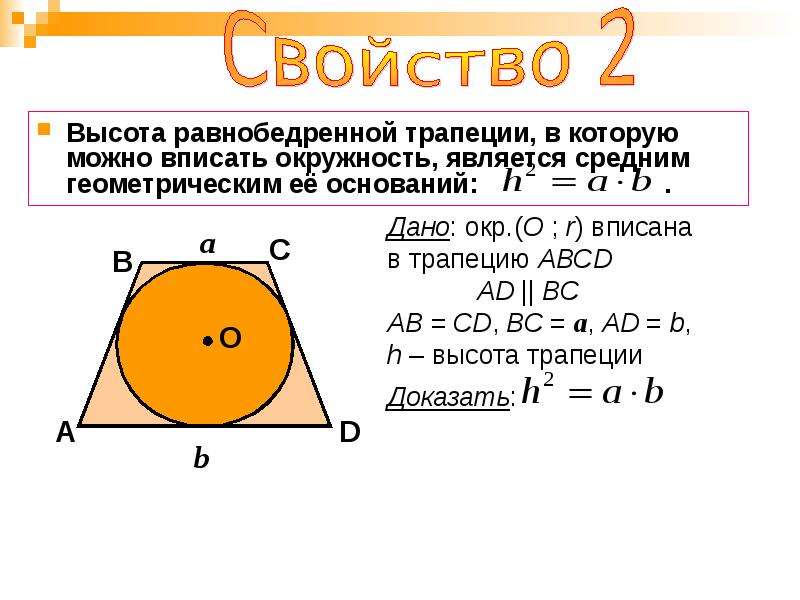 В равнобедренную трапецию вписана окружность, которая в точке касания делит боковую сторону на отрезки m и n.Найти периметр трапеции.
В равнобедренную трапецию вписана окружность, которая в точке касания делит боковую сторону на отрезки m и n.Найти периметр трапеции.
Решение:
CD=CF+FD=m+n.
AB=CD (по условию).
AD+BC=AB+CD (так как в трапецию вписана окружность).
P=AD+BC+AB+CD=4(m+n).
3.В равнобедренную трапецию вписана окружность. Найти высоту трапеции, если известны ее основания: AD=a, BC=b.
Решение:
Проведем высоты трапеции BP и CE. Четырехугольник BCEP- прямоугольник (так как у него все углы прямые). Следовательно, PE=BC=b.
Прямоугольные треугольники треугольники ABP и DCE равны по катету и гипотенузе. Отсюда,
Поскольку в трапецию вписана окружность, AB+CD=AD+BC=a+b,
Из треугольника ABPпо теореме Пифагора
Таким образом,
Вывод:
Если в равнобедренную трапецию вписана окружность, высота трапеции есть среднее пропорциональное между ее основаниями.
Практикум по решению многовариантных задач. тема «Трапеция»
Многовариантные задачи
Задача 1.
В окружность радиуса R
Решение:
Пусть трапеция с основаниями BC=10 и AD=24 вписана в окружность с центром O радиуса R=3. Опустим перпендикуляры OP и OQ из центра окружности на основания BC и AD соответственно. Тогда P и Q – середины этих оснований , а так как BCIIAD, то точки O, P и Q лежат на одной прямой.
По теореме Пифагора
Либо точка O лежит на отрезке PQ, либо вне его. В первом случае PQ=OP+OQ=12+5=17. Во втором случае PQ=IOP-OQI=I12-5I=7. Значит либо высота трапеции равна 17, либо 7.
В первом случае PQ=OP+OQ=12+5=17. Во втором случае PQ=IOP-OQI=I12-5I=7. Значит либо высота трапеции равна 17, либо 7.
Следовательно,
Ответ:119, 289
Задача 2.
Точка касания окружности, вписанной в равнобедренную трапецию, делит боковую сторону на отрезки 1 и 4. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите его площадь.
Решение:
Пусть окружность радиуса R с центром O, вписанная в равнобедренную трапецию ABCD, касается боковой стороны AB в точке M , причем AM=4 и BM=1. Тогда OM – высота прямоугольного треугольника AOB, проведенная из вершины прямого угла AOB, поэтому
Если h – высота трапеции, то h=2R=4.
Пусть прямая, о которой говорится в условии задачи, проходит через вершину B и пересекает основание AD трапеции в точке P.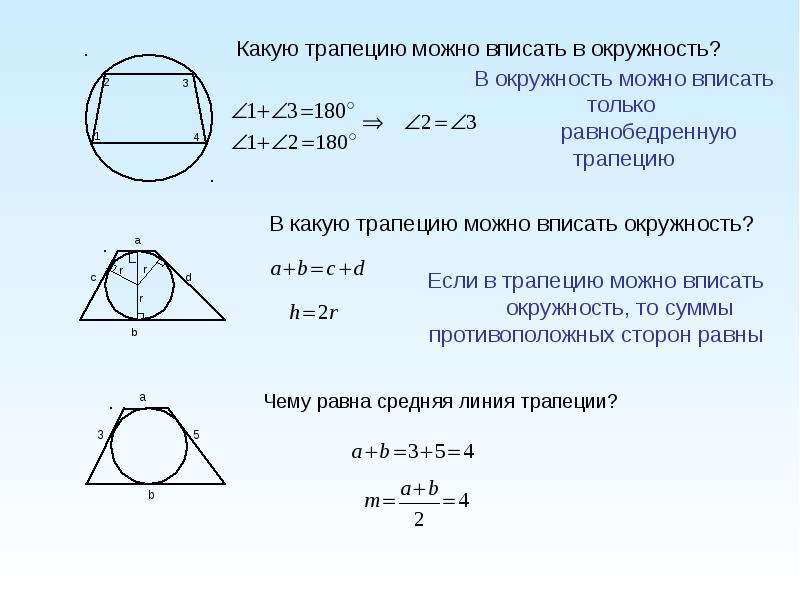 Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому значит треугольник ABP – равнобедренный, AP=AB=5. Следовательно,.
Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому значит треугольник ABP – равнобедренный, AP=AB=5. Следовательно,.
Площадь треугольника ABP можно вычислить и так. Пусть K и L – точки касания вписанной в трапецию окружности с основаниями BC и AD соответственно. Тогда K и L – середины оснований, прямоугольные треугольники POL и BOK равны по катету и прилежащему острому углу, поэтому треугольник ABP равновелик прямоугольной трапеции ABKL. Следовательно,
Поскольку трапеция равнобедренная, для прямой, проходящей через C, получим тот же результат. Пусть теперь, указанная прямая проходит через вершину A, пересекает боковую сторону CD в точке Q, а продолжение основания BC – в точке Е. Треугольник ABE – равнобедренный , поэтому BE=AB=5, CE=BE-BC=AB-BC=5-2=3. Треугольник AQD подобен треугольнику EQC с коэффициентом значит, если QH – высота треугольника AQD, то
Следовательно,
Ответ: 10;
Задача 3.
Окружность радиуса 6 вписана в равнобедренную трапецию, большее основание которой равно 18. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Решение:
Пусть окружность радиуса R с центром O, вписанная в равнобедренную трапецию ABCD, касается боковой стороны AB в точке M, причем R=6 и AD=18. Тогда OM – высота прямоугольного треугольника AOB, проведенная из вершины прямого угла AOB, поэтому
Пусть прямая, о которой говорится в условии задачи, проходит через вершину B и пересекает основание AD трапеции в точке P (рис.1). Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому значит треугольник ABP – равнобедренный, AP=AB=13, поэтому .
Если S – площадь трапеции ABCD, h – высота трапеции, то
Следовательно,
Искомое отношение можно вычислить и так. Пусть K и L – точки касания вписанной в трапецию окружности с основаниями BC и AD соответственно. Тогда K и L – середины оснований, прямоугольные треугольники POL и BOK равны по катету и прилежащему острому углу, поэтому треугольник ABP равновелик прямоугольной трапеции ABKL. Следовательно, )
Пусть K и L – точки касания вписанной в трапецию окружности с основаниями BC и AD соответственно. Тогда K и L – середины оснований, прямоугольные треугольники POL и BOK равны по катету и прилежащему острому углу, поэтому треугольник ABP равновелик прямоугольной трапеции ABKL. Следовательно, )
Поскольку трапеция равнобедренная, для прямой, проходящей через C, получим тот же результат. Пусть теперь, указанная прямая проходит через вершину A (рис.2), пересекает боковую сторону CD в точке Q, а продолжение основания BC – в точке Е. Треугольник ABE – равнобедренный , поэтому BE=AB=13, CE=BE-BC=AB-BC=13-8=5. Треугольник AQD подобен треугольнику EQC с коэффициентом значит, если QH – высота треугольника AQD, то
Следовательно,
Следовательно,
Ответ:
Задача 4.
Окружность вписана в равнобедренную трапецию, большее основание которой равно 24, а синус угла при большем основании равен.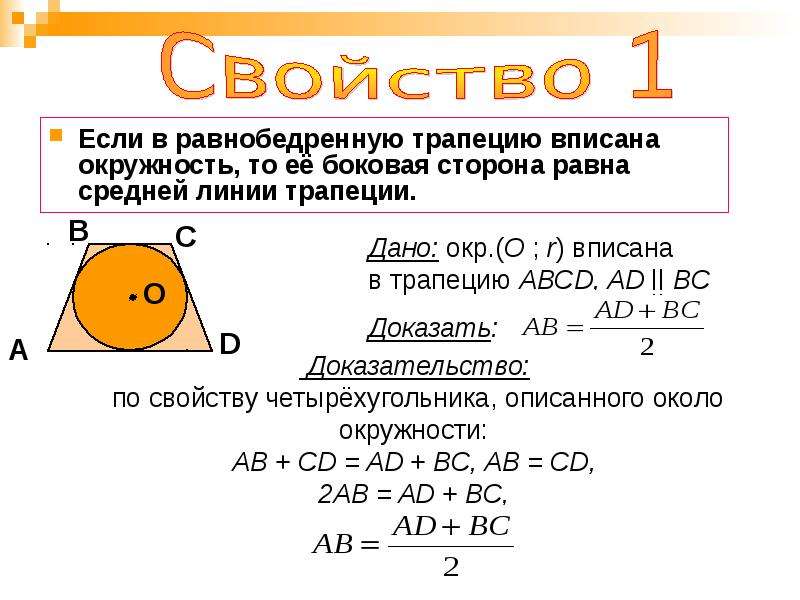 Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Решение:
Пусть окружность радиуса R с центром O, вписанная в равнобедренную трапецию ABCD, с углом при большем основании, касается боковой стороны AB в точке M, большего основания AD в точке N. Причем AD=24 и . Тогда AM=AN=.
.
BC=2BM=2(.
Пусть прямая, проходящая через центр окружности и через вершину B и пересекает основание AD трапеции в точке P(рис.1). Тогда значит треугольник ABP – равнобедренный, AP=AB=, поэтому
Если S – площадь трапеции ABCD, то . Следовательно,
Искомое отношение можно вычислить и так. Пусть K — точка касания вписанной в трапецию окружности с основанием BC. Тогда K и N — середины оснований, прямоугольные треугольники PON и BOK равны по катету и прилежащему острому углу, поэтому треугольник ABP равновелик прямоугольной трапеции ABKN. Следовательно, .
Пусть K — точка касания вписанной в трапецию окружности с основанием BC. Тогда K и N — середины оснований, прямоугольные треугольники PON и BOK равны по катету и прилежащему острому углу, поэтому треугольник ABP равновелик прямоугольной трапеции ABKN. Следовательно, .
Поскольку трапеция равнобедренная, для прямой, проходящей через C, получим тот же результат. Пусть теперь, указанная прямая проходит через вершину A (рис.2), пересекает боковую сторону CD в точке Q, а продолжение основания BC – в точке Е. Треугольник ABE – равнобедренный , поэтому BE=AB=, CE=BE-BC=AB-BC= Треугольник AQD подобен треугольнику EQC с коэффициентом значит, если QH – высота треугольника AQD, то . Следовательно,
Ответ:
Задача 5.
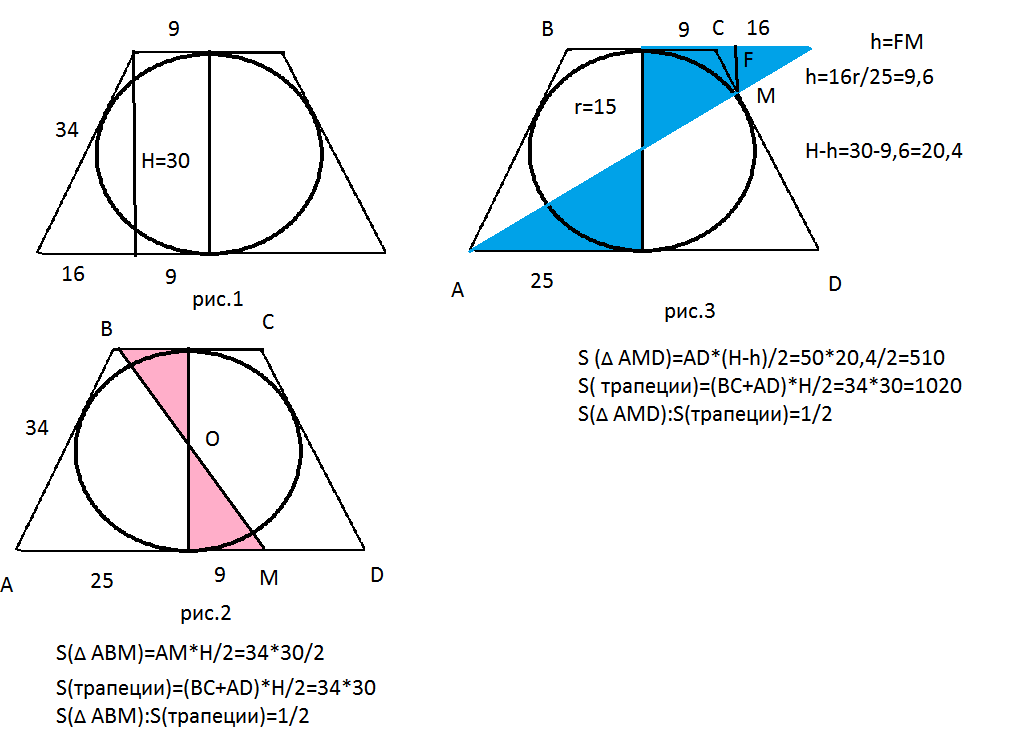
Окружность вписана в равнобедренную трапецию, основания которой равны 18 и 50. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Найдите отношение площади этого треугольника к площади трапеции.
Решение:
Пусть окружность радиуса R с центром O, вписанная в равнобедренную трапецию ABCD, с основаниями BC=18 и AD=50. Касается боковой стороны AB в точке M,а оснований AD и BC – в точках K и L соответственно. Тогда , AB=AM+BM=25=9=34. Отрезок OM – высота прямоугольного треугольника AOB, проведенная из вершины прямого угла AOB, поэтому. Пусть прямая, о которой говорится в условии задачи, проходит через вершину B и пересекает основание AD трапеции в точке P(рис.1). Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому значит треугольник ABP – равнобедренный, AP=AB=34. . Если S – площадь трапеции ABCD, a h – ее высота, то h=2R=30, Следовательно, Искомое отношение можно вычислить и так. Пусть K и L – точки касания вписанной в трапецию окружности с основанием BC и AD соответственно. Тогда K и L – середины оснований, прямоугольные треугольники POL и BOK равны по катету и прилежащему острому углу, поэтому треугольник ABP равновелик прямоугольной трапеции ABKL. Следовательно,.
Следовательно,.
Поскольку трапеция равнобедренная, для прямой, проходящей через C, получим тот же результат. Пусть теперь, указанная прямая проходит через вершину A (рис.2), пересекает боковую сторону CD в точке Q, а продолжение основания BC – в точке Е. Треугольник ABE – равнобедренный , поэтому BE=AB=34, CE=BE-BC=AB-BC=34-18=16. Треугольник AQD подобен треугольнику EQC с коэффициентом значит, если QH – высота треугольника AQD, то . Следовательно,
Ответ:
Задача 6.
В трапеции ABCD, у которой ADIIBC и AD:BC=2:1, на боковых сторонах AB и CD выбраны соответственно точки E и F так, что Отрезки AF и DEпересекаются в точке G. Площадь треугольника ADG в 6 раз меньше площади трапеции ABCD. В каком отношении точка E делит боковую сторону AB?
Площадь треугольника ADG в 6 раз меньше площади трапеции ABCD. В каком отношении точка E делит боковую сторону AB?
Решение:
Пусть продолжения боковых сторон AB и BC трапеции ABCD пересекаются в точке O. Тогда BC – средняя линия треугольника AOD (BCIIAD и ). По условию задачи . Поэтому . Обозначим AE=a, BE=b, DF=c, CF=d,. Тогда a=bx, d=cx. Через вершину A проведем прямую, параллельную CD. Пусть эта прямая пересекается с прямой DG в точке T. Из подобия треугольников AET и OED следует, что . А из подобия треугольников AGT и FGD Тогда
Пусть площадь трапеции равна S, высота трапеции h, а высота треугольника AFD, опущенная на сторону AD равна h1. Тогда
Из этого уравнения находим, что x=2 или x=. Следовательно, или .
Ответ: 2:1; 1:2
Задача 7.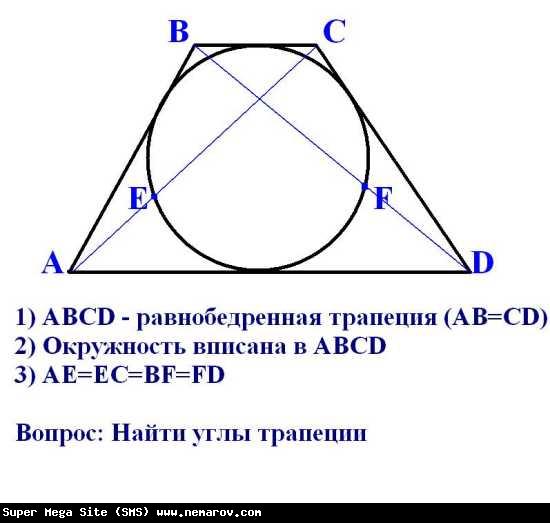
Площадь трапеции ABCD равна 810. Диагонали пересекаются в точке O, отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого.
Решение:
Пусть AD=2BC (рис.1). Четырехугольники ABCP и BCDP-параллелограммы, поэтому M и N – середины сторон BP и CP, значит CM и BN- медианы треугольника BPC. Пусть h- высота трапеции. Положим BC=a, AD=2a, OM=x. Тогда a OC=2x, т.к. O- точка пересечения медиан треугольника BPC. Поэтому AM=MC=3x, OA=AM+OM=3x+x=4x, . Аналогично,, значит треугольник MON, подобен треугольнику AOD с коэффициентом 2, высота треугольника AOD вдвое больше высоты треугольника BOC и составляет высоты трапеции. Имеем:
Пусть BC=2AD(рис.2). Пусть h- высота трапеции. Положим AD =a, BC =2a, АM=3t. Тогда. Треугольник AOD подобен треугольнику COB с коэффициентом ½. А
Положим AD =a, BC =2a, АM=3t. Тогда. Треугольник AOD подобен треугольнику COB с коэффициентом ½. А
Треугольник AMP подобен треугольнику CMB с коэффициентом. Тогда
, , MC=12t, AC=AM+MC=15t, AO=5t, MO=2t, значит . Аналогично. Следовательно,
Ответ:
Задача 7a.
Площадь трапеции ABCD равна 405. Диагонали пересекаются в точке O, отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого.
Решение:
Рис.1Рис.2
Решение:
Пусть AD=2BC (рис. 1). Четырёхугольники ABCP и BCDP—параллелограммы, поэтому M и N—середины BP и CP, значит, CM и BN—медианы треугольника BPC. Пусть h—высота трапеции. Положим BC=a, AD=2a, OM=x. Тогда , а так как O – точка пересечения медиан треугольника BPC, то OC=2x, поэтому AM=MC=3x, OA=AM+OM=3x+x=4x, значит с коэффициентом равным . Следовательно,
Пусть h—высота трапеции. Положим BC=a, AD=2a, OM=x. Тогда , а так как O – точка пересечения медиан треугольника BPC, то OC=2x, поэтому AM=MC=3x, OA=AM+OM=3x+x=4x, значит с коэффициентом равным . Следовательно,
Рассмотрим случай, когда BC=2AD (рис. 2). Пусть h—высота трапеции. Положим AD=a, BC=2a, AM=3t. Тогда ah=270. , с коэффициентом , ас коэффициентом.Тогда, аналогично.Следовательно,
Ответ:
Задача 8.
Площадь трапеции ABCD равна 240. Диагонали пересекаются в точке O, отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции втрое больше другого.
Решение:
Рис.1 РИС.2
Пусть AD=3BC (рис. 1). Положим BC=a, AD=3a, OC=x. с коэффициентом, а с коэффициентом,поэтому OA=3x, AC=OA+OC=3x+x=4x,OM=MC-OC=значит, Аналогично,Пусть h- высота трапеции. Тогда, а так как с коэффициентом то
с коэффициентом, а с коэффициентом,поэтому OA=3x, AC=OA+OC=3x+x=4x,OM=MC-OC=значит, Аналогично,Пусть h- высота трапеции. Тогда, а так как с коэффициентом то
Рассмотрим случай, когда BC=3AD(рис.2) Аналогично предыдущему получим, что и . Следовательно
Ответ:
Задача 9.
Площадь трапеции ABCD равна 240. Диагонали пересекаются в точке O, отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь четырёхугольника OMPN, если одно из оснований трапеции втрое больше другого.
рис.1рис.2
Решение:
Пусть AD=3BC (рис. 1). Положим BC=a, AD=3a, OC=x. с коэффициентом, а с коэффициентом, поэтому OA=3x, AC=OA+OC=3x+x=4x, OM=MC-OC=значит,
Аналогично,Пусть h- высота трапеции. Тогда .
Следовательно,
Рассмотрим случай, когда BC=3AD(рис. 2). Положим BC=3a, AD=a, AM=t. с коэффициентом , а с коэффициентом, поэтому MC=6t, AC=AM+MC=6t+t=7t, значит Аналогично, Пусть h – высота трапеции. Тогда
2). Положим BC=3a, AD=a, AM=t. с коэффициентом , а с коэффициентом, поэтому MC=6t, AC=AM+MC=6t+t=7t, значит Аналогично, Пусть h – высота трапеции. Тогда
Следовательно,
Ответ:
Задача 10.
Площадь трапеции ABCD равна 90. Диагонали пересекаются в точке O, отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь четырёхугольника OMPN, если одно из оснований трапеции вдвое больше другого.
Ответ. 10 или 4.
Задача 11.
Площадь трапеции ABCD равна S, отношение оснований На прямой, пересекающей продолжение основания AD за точку D, расположен отрезок EF, причем A E I I DF, BE I ICF и Найти площадь треугольникa EFD.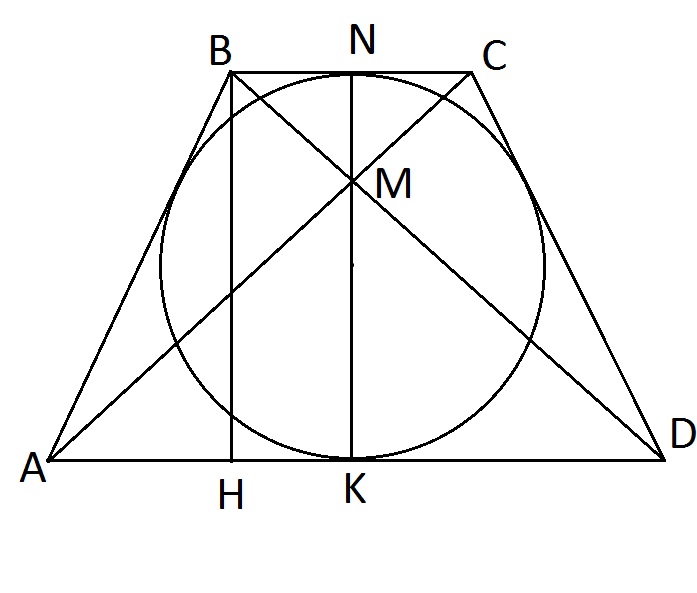
Решение:
рис.1 рис.2
Пусть M—точка пересечения прямых EF и AD. Поскольку точка D лежит между точками A и M, то из условия задачи следует, что D — середина отрезка AM. Пусть N — точка пересечения прямых EF и BC. Возможны два её положения: либо B — середина отрезка NC (рис. 1), либо N лежит на отрезке BC и (рис.2). Обозначим BC=a. Тогда AD=DM=3a. В первом случае NE=EF =FM. Поэтому, если провести высоту трапеции через точку E, то она разделится этой точкой в отношении 1:2. Пусть h — высота трапеции. Тогда высота треугольника AEM, поэтому =2ah, то
Во втором случае EF=FM, EN= . Поэтому высота треугольника DEM, опущенная из вершины E, равна S,
Ответ:
Задача 12.
Площадь трапеции ABCD равна S, отношение оснований Отрезок MN расположен так, что он параллелен стороне CD, пересекает сторону AB, а отрезок AM параллелен отрезку BN.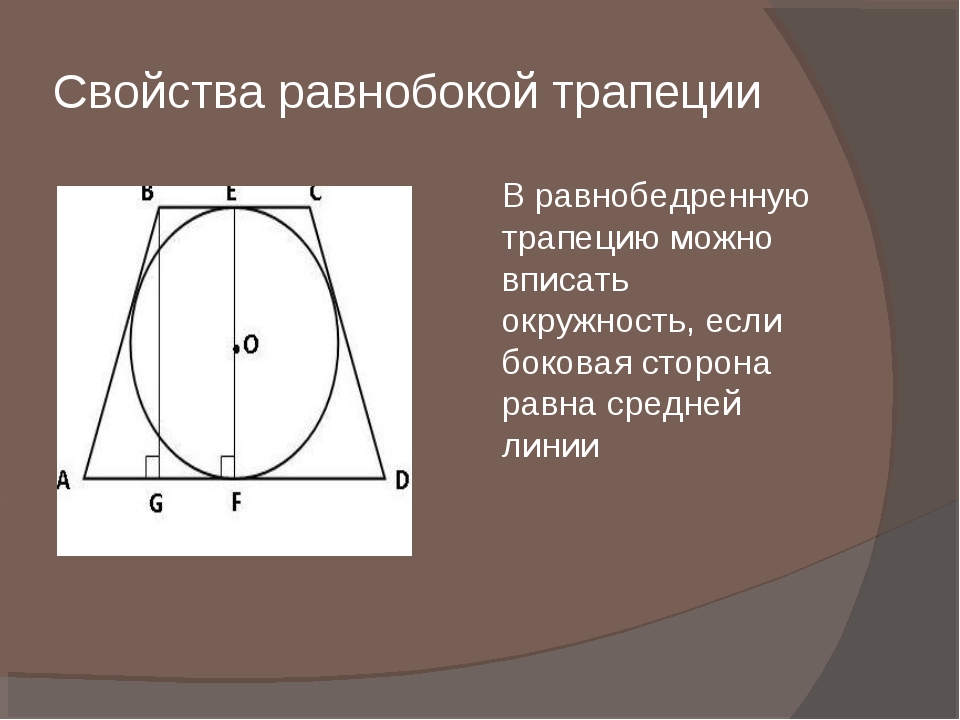 Найдите площадь треугольника BNC, если .
Найдите площадь треугольника BNC, если .
Ответ:
Задача 13.
Площадь трапеции ABCD равна S, отношение оснований Отрезок MN расположен так, что он параллелен диагонали BD, пересекает диагональ AC, а отрезок AM параллелен отрезку СN. Найдите площадь четырехугольника AMND , если .
Ответ:
Задача 14.
Площадь трапеции ABCD равна S, отношение оснований На прямой, пересекающей отрезок AD, расположен отрезок EF, причем AEIIDF, BEIICF и Найти площадь треугольникa EFD.
Ответ:
Задача 15.
Площадь равнобедренной трапеции равна . Угол между диагональю и основанием на больше угла между диагональю и боковой стороной. Найдите острый угол трапеции, если её диагональ равна 2.
рис.1 рис.2
Решение:
Пусть AD – большее основание равнобедренной трапеции ABCD. Тогда ∟BAD –острый. Если CH – высота трапеции, то , поэтому . Обозначим ∟BAC=α. Тогда ∟CAH=α+200. Из прямоугольного треугольника AHC находим, что , , поэтому . Значит, 2α+400=600 или 2α+400=1200. Отсюда находим, что α=100 или α=400, а ∟BAD=2α+200=400 или ∟BAD=1000. Поскольку ∟BAD – острый, подходит только 400. Если AD – меньшее основание, то аналогично находим, что ∟ABC = 800.
Ответ: 400; 800
Задача 16.
Найдите площадь трапеции, если её диагонали равны 17 и 113, а высота равна 15.
Решение:
рис.1 рис.2
Через вершину C меньшего основания трапеции ABCD (AC=17, BD=113) проведём прямую, параллельную диагонали BD. Пусть K—точка пересечения этой прямой с прямой AD. Тогда данная трапеция равновелика треугольнику ACK. Известны стороны AC=17, CK =113 и высота CM=15 этого треугольника. Из прямоугольных треугольников ACM и KCM находим, что , Если точка M лежит между точками A и K (рис.1), то . Если же точка A лежит между точками M и K (рис.2), то
Ответ: 900; 780
Задача 17.
Прямая, параллельная основаниям трапеции, делит ее на две трапеции, площади которых относятся как 1:2. Найдите отрезок этой прямой, заключенный внутри трапеции, если основания трапеции равны a и b.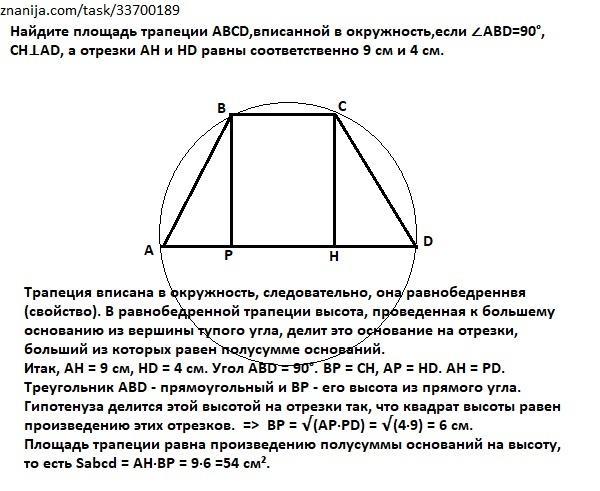
Ответ:
Задача 18.
Основания трапеции равны a и b. Прямая, параллельная основаниям, разбивает трапецию на две трапеции, площади которых относятся как 2: 3. Найти длину отрезка этой прямой, заключенного внутри трапеции.
Решение:
Неизвестно как относятся площади трапеций BCFE и AEFD — как 2:3 или как 3:2.
Поэтому эту задачу будем решать в общем виде.
Обозначим искомый отрезок ЕF=х. Пусть . , выразим отношение высот трапеций , где h1 и h2 – высоты этих трапеций. Через точку F проведем отрезок PH, параллельный AB. Тогда по двум углам и , . Используя предыдущее равенство, имеем . Решая полученное уравнение относительно переменной x. Получаем, . Если площади трапеций относятся, как 2:3. То n=2, m=3, искомый ответ будет. Если площади трапеций относятся, как 3:2, то n=3, m=2, искомый ответ будет .
Ответ:;.
Задача 19.
Периметр равнобедренной трапеции равен 52. Известно, что в эту трапецию можно вписать окружность, причем боковая сторона делится точкой касания в отношении 4 : 9. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.
Решение:
По теореме об отрезках касательных KB = BP = PC = CQ = 4x, QD = DL =LA = AK = 9x, тогда периметр трапеции равен 4 · (9x + 4x) = 52, откуда x = 1. Отсюда вычисляем боковые стороны AB = CD = 13 и основания BC = 8, AD= 18. Тогда AH = (AD — BC)/2 = 5. Из прямоугольного треугольника BHA по теореме Пифагора находим высоту трапеции BH = 12, . Площадь трапеции тогда равна S = (BC + AD) · BH/2 = 156. В зависимости от того, о какой прямой говорится в условии задачи, возможны два случая:
Площадь трапеции тогда равна S = (BC + AD) · BH/2 = 156. В зависимости от того, о какой прямой говорится в условии задачи, возможны два случая:
1) Пусть данная прямая проходит через вершину, содержащую меньшее основание трапеции (на рисунке прямая BM). Центр вписанной в угол окружности лежит на его биссектрисе, то есть ∠ABM = ∠MBC, ∠MBC= ∠AMB (как накрест лежащие при параллельных прямых BC, AD и секущей BM), значит ∠ABM = ∠AMB и ABM — равнобедренный, AM =AB = 13. Тогда, а искомое отношение равно
2) Пусть теперь прямая, о которой говорится в условии, проходит через вершину, содержащую меньшее основание трапеции (на рисунке прямая AN). Выполним дополнительное построение: продлим основание BC и прямую AN до пересечения в точке Y. Аналогично доказываем, что ABY — равнобедренный, AB = BY = 13, CY = BY — BC = 5. CNY и AND подобны по двум углам (∠AND = ∠CNY как вертикальные, ∠CYA = ∠YAD как накрест лежащие при параллельных прямых BC, AD и секущей AY), значит DN : NC = AD : CY = 18 : 5, значит DN = 18/23 CD = 18/23, AB = 234/23. Тогда, а искомое отношение равно .
CNY и AND подобны по двум углам (∠AND = ∠CNY как вертикальные, ∠CYA = ∠YAD как накрест лежащие при параллельных прямых BC, AD и секущей AY), значит DN : NC = AD : CY = 18 : 5, значит DN = 18/23 CD = 18/23, AB = 234/23. Тогда, а искомое отношение равно .
Ответ:
Задача 21.
Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке М, найдите радиус окружности, вписанной в треугольник ВМС.
Решение:
В любой трапеции отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований трапеции, а средняя линия — полусумме оснований трапеции. В нашем случае полуразность оснований равна 5, а полусумма оснований равна 25, поэтому основания трапеции равны 20 и 30. Предположим что BC=30, AD=20 (рис. 1). Стороны BС и АD треугольников МВС и MAD параллельны, поэтому эти треугольники подобны с коэффициентом . Значит, ,. Заметим, что , поэтому треугольник прямоугольный с гипотенузой BC . Радиус его вписанной окружности равен: . Пусть теперь AD=30, BC=20 (Рис.2). Аналогично предыдущему случаю можно показать, что радиус вписанной окружности треугольника MAD равен 6. Треугольники MAD и МВС подобные. Коэффициент . Значит, радиус вписанной окружности МВС, .
В нашем случае полуразность оснований равна 5, а полусумма оснований равна 25, поэтому основания трапеции равны 20 и 30. Предположим что BC=30, AD=20 (рис. 1). Стороны BС и АD треугольников МВС и MAD параллельны, поэтому эти треугольники подобны с коэффициентом . Значит, ,. Заметим, что , поэтому треугольник прямоугольный с гипотенузой BC . Радиус его вписанной окружности равен: . Пусть теперь AD=30, BC=20 (Рис.2). Аналогично предыдущему случаю можно показать, что радиус вписанной окружности треугольника MAD равен 6. Треугольники MAD и МВС подобные. Коэффициент . Значит, радиус вписанной окружности МВС, .
Ответ: 6;4
Задача 25.
Диагонали АС и BD трапеции ABCD пересекаются в точке Е. Найти площадь трапеции, если площадь треугольника AED равна 9, а точка Е делит одну из диагоналей в отношении 1 : 3.
Найти площадь трапеции, если площадь треугольника AED равна 9, а точка Е делит одну из диагоналей в отношении 1 : 3.
Решение:
При решении данной задачи неоднозначность состоит в выборе варианта буквенного обозначения вершин трапеции и, дополнительно к этому, в выборе большего основания. Пусть точка E делит каждую диагональ в отношении 1 : 3, считая от вершины верхнего основания.
Рассмотрим трапецию с основаниями ВС и AD. Треугольники ВЕС и АED подобны (по двум углам) с коэффициентом подобия k=EC/AE=1/3. Значит, отношение площадей SBEC/SAED=1/9. Отсюда SBEC=1. Треугольники АВE и ВЕС имеют общую высоту, поэтому SABE/SBEC=AE/EC=3, SABE=3*SBEC=3. Аналогично SDEC = 3*SBEC = 3. Следовательно, SABCD = 1 + 3 + 3 + 9 = 16. В остальных случаях, решая аналогично, получим: SABCD = 3 + 9 + 9 + 27 = 48; SABCD = 9 + 27 + 27 + 81 = 144
Следовательно, SABCD = 1 + 3 + 3 + 9 = 16. В остальных случаях, решая аналогично, получим: SABCD = 3 + 9 + 9 + 27 = 48; SABCD = 9 + 27 + 27 + 81 = 144
Ответ: 16,48,144
Задача 26.
Дана трапеция ABCD, в которой BC = a, AD = b. Параллельно основаниям трапеции BC и AD проведена прямая, пересекающая сторону AB в точке P, диагональ AC в точке L, диагональ BD в точке R и сторону CD в точке Q. Известно, что PL = LR. Найдите PQ.
Известно, что PL = LR. Найдите PQ.
Решение:
Пусть M — точка пересечения диагоналей данной трапеции. Предположим, что точка L
лежит между точками A и M. Обозначим PL = x. Из подобия треугольников APL и ABC следует, что . Поэтому; . Пусть K – точка пересечения прямой BL с основанием AD . Тогда;. Поскольку
; PL=LR, то . Поэтому; . Поскольку, то . Следовательно, . Если точка L лежит между точками M и C , то аналогично находим .
(Ответ: )
Элективный курс «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов»
О.П. Иванченко |
ГЕОМЕТРИЯ
Вписанная и описанная окружность в трапецию»
в рамках курса по выбору
по геометрии для обучающихся 9 классов
Управление образования администрации
Ангарского городского округа
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №15»
О. П. Иванченко
П. Иванченко
Вписанная и описанная окружность в трапецию»
в рамках курса по выбору
по геометрии для обучающихся 9 классов
Элективный курс
Ангарск
2017
Автор-составитель Иванченко Ольга Петровна, учитель математики МБОУ «СОШ №15» г. Ангарск
Иванченко О.П.
Вписанная и описанная окружность в трапецию» в рамках курса по выбору
по геометрии для обучающихся 9 классов: Элективный курс / О.П. Иванченко. – Ангарск: МБОУ «СОШ №15», 2017. – 50с.
СОДЕРЖАНИЕ
Введение ……………………………………………………………………….…… 5
Глава 1. Трапеция, вписанная в окружность и трапеция, описанная около окружности …………………………………..…………………………….………. 8
1.1. Вписанные и описанные четырехугольники ………….……………… 8
1.2. Трапеция …………………………………………..………………….. 9
Трапеция …………………………………………..………………….. 9
1.3. Анализ учебной литературы ……………..………..………………..10
1.4. Трапеция, вписанная в окружность …………………………………12
1.5. Трапеция, описанная около окружности …..……………………… 13
Глава 2. Содержание занятий по теме «Трапеция, вписанная в окружность и трапеция, описанная около окружности» в рамках курса по выбору по геометрии для обучающихся 9 классов ………………………………………..….20
2.1. Пояснительная записка ………………………………………………20
2.2. Содержание занятий по теме: «Трапеция, вписанная в окружность и трапеция, описанная около окружности» ………………………………………22
Заключение ……………………………………………………………….44
Литература ………………………………………………………………..45
Приложение 1 (Входная самостоятельная работа) …………………….47
Приложение 2 (Итоговая самостоятельная работа) ……………………49
ВВЕДЕНИЕ
Геоме́трия (от γη — Земля и μετρεω — мера, измерение) — наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела; раздел математики, изучающий пространственные отношения и их обобщения. [1]
[1]
В общеобразовательной школе предмет «Геометрия» изучается с 7 класса и, по мнению многих обучающихся, является одним из сложнейших школьных предметов. Многие обучающиеся не понимают назначения геометрии в жизни, так как не собираются связывать свою будущую профессию с математикой вообще.
Основой курса геометрии является принцип доказательности всех утверждений. И это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на последовательном выводе всех утверждений. Людьми, понимающими, что такое доказательство, трудно и даже невозможно манипулировать.[1]
Итак, Геометрия — один из важнейших предметов, причем не только среди предметов математического цикла, но и вообще среди всех школьных предметов. Ее целевой потенциал охватывает необычайно широкий арсенал, включает в себя чуть ли не все мыслимые цели образования.
Куда бы мы ни повернулись в нашей жизни, повсюду мы видим применение принципов геометрии. Она может быть в строительстве сооружений и оформлении их, в архитектуре, устройстве интерьеров, даже в создании ландшафта.[2]
Она может быть в строительстве сооружений и оформлении их, в архитектуре, устройстве интерьеров, даже в создании ландшафта.[2]
Каждый день, идя по улице, мы начинаем замечать, что мир состоит из разных геометрических фигур. Окна домов – квадраты или прямоугольники, дорожные знаки – круги, треугольники или прямоугольники. Но иногда встречаются такие фигуры, и даже очень часто, у которых две противоположные стороны параллельны, а две нет – предметы обихода, лобовые и боковые стекла у машин, крыши домов, тротуарная плитка, религиозные знаки и, даже, силуэты одежды.
Эти фигуры похожи на треугольник, у которого срезали вершину. Иногда они правильной формы, иногда – нет. Это трапеции.
В принципе, это давно известная фигура, свойства которой исследовали еще и Евклид, и Архимед.
«Трапецией» называются не только геометрические фигуры, но и спортивный снаряд, и мышцы атлета, и система тросов на яхтах, и женские юбки.
В настоящей работе рассмотрим трапецию, вписанную в окружность и трапецию, описанную около окружности.
Объект исследования: трапеция, вписанная в окружность и трапеция, описанная около нее.
Предмет исследования: содержание занятий по теме «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов.
Цель работы: разработка занятий по теме «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов.
Задачи:
1. анализ учебной и методической литературы по теме исследования;
2. подбор теоретического и практического материала;
3. разработка практического и контрольно-измерительного материала.
Структура работы:
Работа состоит из введения, 2-х глав, заключения, списка литературы и 2 приложений, в которых представлено решение входной и итоговой самостоятельных работ. Общий объем работы 48 страниц.
Общий объем работы 48 страниц.
Глава 1. Трапеция, вписанная в окружность и трапеция, описанная около окружности
1.1. Вписанные и описанные четырехугольники
Четырёхугольник — это геометрическая фигура (многоугольник), которая состоит из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. [3]
Виды четырехугольников:
— параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
— прямоугольник — четырёхугольник, у которого все углы прямые;
— ромб — четырёхугольник, у которого все стороны равны;
— квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
— трапеция — четырёхугольник, у которого две противоположные стороны параллельны. [4]
[4]
Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности, которая будет называться описанной вокруг четырехугольника. [5]
Теорема 1. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180. Отсюда следует, что вписать в окружность можно только равнобокую трапецию. [6] | |
Площадь где (полупериметр) |
Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник. [5]
Теорема 2. | |
Площадь , где (полупериметр) r – радиус вписанной окружности |
1.2. Трапеция
Понятие трапеции формировалось в течение длительного периода времени. Сначала трапецией называли любой четырехугольник, не являющийся параллелограммом. [7]
Именно в таком смысле термин «трапеция» использовал Евклид в своих «Началах».
В XVIII веке понятие трапеции приобрело современные определения:
— «Трапецией называется четырехугольник, у которого две противоположные стороны параллельны, а две другие нет»;
— «Трапеция в геометрии – четырехугольник, с парой параллельных сторон, и с другой парой непараллельных»;
— «Трапеция – четырехугольник, в котором две противоположные стороны параллельны, называемые основаниями трапеции, а другие две – непараллельные»;
— «Трапеция – четырёхугольник, у которого только одна пара противолежащих сторон параллельна».
Таким образом, трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два противоположных из которых параллельны между собой и называются основаниями трапеции.
Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Две параллельные стороны называются основаниями трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции. [8]
1.3. Анализ учебной литературы
Приведем анализ школьных учебников по геометрии на выявление особенностей темы: «Трапеция, вписанная в окружность и трапеция, описанная около окружности».
Особенности изложения темы в учебнике Л.С. Атанасян и др.
Тема: «Трапеция, вписанная в окружность и трапеция, описанная около окружности» не достаточно рассматриваются данными авторами. Авторы в учебнике за 8 класс в параграфе «Вписанная и описанная окружность» дают определение окружности вписанной в многоугольник, и многоугольника описанного около окружности. Доказывается теорема: Около любого треугольника можно описать окружность. На основании, которой авторы приводят замечания, одно из которых:
— не во всякий четырехугольник можно вписать окружность, доказательство которого учащимся предлагается привести самостоятельно.
Авторы предлагают обучающимся в задаче 710 (стр. 187) выполнить доказательство свойства трапеции вписанной в окружность. Так токовые свойства трапеции вписанной в окружность, и трапеции описанной около окружность авторами не рассматриваются и в 9 классе. [10]
Особенности изложения темы в учебнике А.В. Погорелова
Темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не рассматриваются данным автором.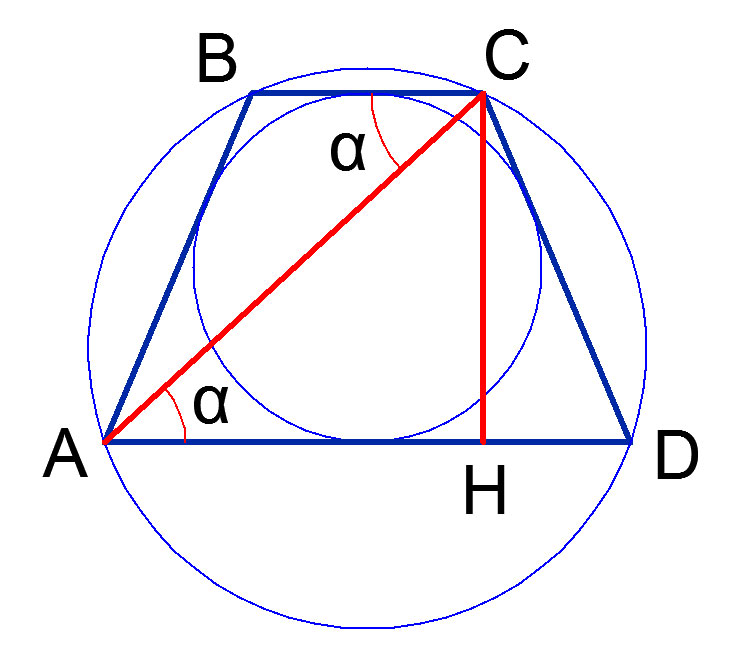 Автор дает определение трапеции в разделе за 8 класс и рассматривает ее свойства с доказательством. Но о вписанной трапеции в окружность, и трапеции описанной около окружности он не упоминает и в представленных задачах за 8 класс, а так, же и в разделе за 9 класс. [9]
Автор дает определение трапеции в разделе за 8 класс и рассматривает ее свойства с доказательством. Но о вписанной трапеции в окружность, и трапеции описанной около окружности он не упоминает и в представленных задачах за 8 класс, а так, же и в разделе за 9 класс. [9]
Особенности изложения тем в учебнике Г.П. Бевз и др.
Темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не достаточно рассматриваются данными авторами. Авторы в разделе за 8 класс в параграфе «Вписанные и описанные многоугольники» дают определение окружности вписанной в многоугольник, и многоугольника описанного около окружности. Доказывают теоремы:
— Около любого треугольника можно описать окружность, и только одну.
— Во всякий треугольник можно вписать окружность, и только одну.
На основании, которых авторы приводят следствия, одно из которых:
— если четырехугольник вписан в окружность, то сумма его противолежащих углов равна 1800. Если четырехугольник описан около окружности, то суммы длин его противолежащих сторон равны.
Если четырехугольник описан около окружности, то суммы длин его противолежащих сторон равны.
Авторы предлагают обучающимся в задаче 803 (стр. 146) выполнить доказательство свойства трапеции вписанной в окружность. Так токовые свойства трапеции вписанной в окружность, и трапеции описанной около окружность авторами не рассматриваются в достаточном объеме. [11]
Особенности изложения тем в учебнике А.Л. Вернер и др.
Темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не достаточно рассматриваются данными авторами. Автор в учебнике за 8 класс дает определение трапеции в 8 классе и рассматривает ее свойства с доказательством в параграфе «Четырехугольники с параллельными сторонами». Но о вписанной трапеции в окружность, и трапеции описанной около окружности он не упоминает и в представленных задачах за 8 класс, а так, же и в разделе за 9 класс. [12, 13, 14]
Вывод: В учебниках школьного курса геометрии тема «Трапеция» изучается в 8 классе. Вводятся понятия «трапеция», «равнобокая трапеция», «прямоугольная трапеция», «средняя линия трапеции». Так же в учебниках предлагается серия задач по данной теме.
Вводятся понятия «трапеция», «равнобокая трапеция», «прямоугольная трапеция», «средняя линия трапеции». Так же в учебниках предлагается серия задач по данной теме.
Тема «Трапеция, вписанная в окружность и трапеция, описанная около окружности» входит в тему «Вписанные и описанные многоугольники» и рассматривается в учебниках Г.П. Бевз и др., Л.С. Атанасян и др. в 8 классе при решении небольшого количества задач на доказательство.
1.4. Трапеция, вписанная в окружность
На основании определения четырехугольника вписанного в окружность можно сформулировать определение трапеции вписанной в окружность.
Трапеция называется вписанной в окружность, если все вершины ее лежат на одной окружности, которая будет называться описанной около трапеции.
Трапецию можно вписать в окружность, если она равнобокая.
Теорема 3. | |
Доказательство Так как ΔАСD – прямоугольный, вписанный в окружность, то AD – диагональ => | |
Теорема 4. Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции. [15] | |
Теорема 5. Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием. | |
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. [15] | |
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним: Отсюда: [15] | |
1.5. Трапеция, описанная около окружности
На основании определения четырехугольника описанного около окружности можно сформулировать определение трапеции описанной около окружности.
Трапеция называется описанной около окружности, если все ее стороны касаются одной окружности.
Теорема 6. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что [15] AL = AK, BL = BM, CM = CF, DF = DK | |
Доказательство Обозначим точки касания буквами L, M, F, K. На основании свойства касательных (Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными), проведенных к окружности из одной точки, имеем: AL = AK, BL = BM, CM = CF, DF = DK Ч.Т.Д. | |
Теорема 7. MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности. [15] | |
Доказательство 1) Пусть отрезок КМ – диаметр вписанной окружности в трапецию. d = 2r = KM 2) Проведем высоту трапеции так, чтобы она проходила через центр окружности, тогда высота КМ = МО + ОК. Следовательно, KM = 2r Ч.Т.Д. | |
Теорема 8. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. [15] | |
Теорема 9. Боковая сторона описанной трапеции видна из центра описанной окружности под прямым углом. | |
Доказательство 1) ADC + BCD = 180º (так как сумма внутренних односторонних углов при параллельных прямых AD и ВС и секущей CD) 2) так как точка O — точка пересечения биссектрис углов трапеции, то ODF + OCF = (ADC + BCD) = 90º 3) так как сумма углов треугольника равна 180º, то в ΔCOD COD = 90º Ч.Т.Д. | |
Теорема 10. Если точка касания трапеции описанной около окружности делит боковую сторону на отрезки длиной m и n (CF=m, FD=n), высота трапеции равна ее диаметру, то высоту трапеции можно выразить через длины этих отрезков. [15] | |
Доказательство Точка касания делит боковую сторону на отрезки длиной m и n (CF=m, FD=n). 1) ADC + BCD = 180º (так как сумма внутренних односторонних углов при параллельных прямых AD и ВС и секущей CD) 2) так как точка O — точка пересечения биссектрис углов трапеции, то ODF + OCF = (ADC + BCD) = 90º 3) так как сумма углов треугольника равна 180º, то в ΔCOD COD = 90º 4) таким образом, COD прямоугольный, а OF — высота, проведенная к гипотенузе, CF и FD — проекции катета OC и OD на гипотенузу. Поскольку высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков: Ч. | |
Теорема 11. Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. [15] | |
Доказательство Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF = m, FD = n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
Ч.Т.Д. | |
Таким образом, в первой главе рассмотрели теоретические сведения о трапеции, вписанной в окружность и трапеции, описанной около окружности.
Сведем все основные свойства трапеции (рассмотренные в школьном курсе геометрии и нет) в таблицу.
Трапеция, вписанная в окружность и трапеция, описанная около нее
Трапеция, вписанная в окружность | |
Теорема 3. | |
Теорема 4. Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции. [15] | |
Теорема 5. Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием. [15] | |
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. | |
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним: Отсюда: [15] | |
Трапеция, описанная около окружности | |
Теорема 6. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что [15] AL = AK, BL = BM, CM = CF, DF = DK | |
Теорема 7. MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности. [15] | |
Теорема 8. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. [15] | |
Теорема 9. Боковая сторона описанной трапеции видна из центра описанной окружности под прямым углом. [15] | |
Теорема 10. Если точка касания трапеции описанной около окружности делит боковую сторону на отрезки длиной m и n (CF=m, FD=n), высота трапеции равна ее диаметру, то высоту трапеции можно выразить через длины этих отрезков. [15] | |
Теорема 11. | |
Глава 2.
Содержание занятий по теме «Трапеция, вписанная в окружность и трапеция, описанная около окружности» в рамках курса по выбору по геометрии для обучающихся 9 классов
В данной главе разработаны содержания занятия по теме: «Трапеция, вписанная в окружность и трапеция, описанная около окружности» в рамках курса по выбору по геометрии для обучающихся 9 классов.
2.1. Пояснительная записка
Организационно-методический раздел
Цель занятий: расширить геометрическое представление обучающихся о вписанной и описанной окружности в трапецию.
Задачи занятий:
1. Расширить знания учащихся связанные со свойствами вписанной трапеции;
2. Расширить знания обучающихся связанные со свойствами описанной трапеции;
Расширить знания обучающихся связанные со свойствами описанной трапеции;
3. Овладение дополнительными знаниями при решении заданий уровня повышенной сложности итоговой государственной аттестации;
4. Предоставить обучающимся возможность проанализировать свои способности к математической деятельности.
Требования к подготовке учащихся
В результате проведенных дополнительных занятий по теме: «Вписанная и описанная окружность в трапецию» ученик должен:
Знать/понимать
— понятие математического доказательства, примеры доказательств;
— как используются теоремы и свойства при решении заданий повышенной сложности;
— свойства трапеции вписанной в окружность;
— свойства трапеции описанной около окружности.
Уметь
— проводить сложные доказательства, получать следствия, оценивать логическую правильность рассуждений;
— распознавать геометрические фигуры, различать их взаимное расположение;
— изображать геометрические фигуры; выполнять чертежи по условию задач;
— решать геометрические задачи, опираясь на изученные дополнительные свойства вписанной и описанной трапеции;
— проводить доказательные рассуждения при решении задач, используя теоремы, обнаруживая возможности для их использования.
Количество часов всего – 6 часов (2 часа в неделю, 3 недели).
Самостоятельных работ – 1 час (входная – 0,5 часа, итоговая – 0,5 часа).
Календарно-тематическое планирование
№ п/п | Содержание урока | Количество часов |
1 | Вписанная и описанная окружность в трапецию | 0,5 |
Входная самостоятельная работа | 0,5 | |
2 | Трапеция, вписанная в окружность. Решение задач. | 1 |
3 | Трапеция, описанная около окружности. | 1 |
4 | Трапеция, вписанная и описанная около окружности. Решение задач | 1 |
5 | Трапеция, вписанная и описанная около окружности. Решение задач | 1 |
6 | Трапеция, вписанная и описанная около окружности. | 0,5 |
Итоговая самостоятельная работа | 0,5 |
2.2. Содержание занятий по теме: «Трапеция, вписанная в окружность и трапеция, описанная около окружности»
Занятие 1
Тема: Вписанная и описанная окружность в трапецию
Цель: расширение знаний обучающихся о вписанной и описанной трапеции в окружность, ее свойства.
Тип урока: урок закрепления знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение видов четырехугольников, какой четырехугольник можно вписать и описать около окружности, основные свойства вписанной и описанной окружности в трапецию.
Рассмотрение свойств с доказательством.
Теорема (о вписанной трапеции). Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.В
С
Дано:
– трапеция
W – описанная окружность
Доказать: — равнобедренная
А
D
Доказательство.
1) – вписанная трапеция, следовательно
(1)
Так же: (2)
(по свойству углов при параллельных сторонах).
2) Сравниваем (1) и (2) выражения, получаем:
т.е.
, т.е.
Углы при верхнем и нижнем основаниях попарно равны => АВСD – равнобедренная трапеция.
Ч.Т.Д.
Т
Дано:
– трапеция, описанная около окружности
Доказать:
еорема (об описанной трапеции). Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.
Доказательство.
Пусть трапеция описана около окружности.
Точки E, F, G, H – точки касания.
Тогда
Если сложить попарно получим равенство
Ч. Т.Д.
Т.Д.
3. Закрепление
Выполнение входной контрольной работы рассчитанной на 15-20 мин.
Входная самостоятельная работа
Задача 1. В равнобедренной трапеции основания 21 и 9 сантиметров, высота — 8 сантиметров. Найти радиус описанной окружности.
Задача 2. Прямоугольная трапеция описана около окружности. Найти радиус этой окружности, если длины оснований трапеции равны a и b.
4. Итог урока
Занятие 2
Тема: Трапеция, вписанная в окружность. Решение задач
Цель: расширение знаний обучающихся о вписанной трапеции в окружность, ее свойств и теорем.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
Знакомство с содержанием занятий по теме: «Вписанная и описанная окружность в трапецию»
2. Актуализация знаний
Повторение основных свойств трапеции вписанной в окружность школьного курса геометрии, а так же рассмотрение дополнительных теорем. (Глава 1, п.1.4)
3. Закрепление
Решение задач.
Задача 1. Трапеция с основаниями см и см и диагональю см вписана в окружность. На окружности взята точка K, отличная от точки D, так что см. Найдите длину отрезка AK.
На основании свойства вписанной трапеции .
Из
Из
Если то => равны углы и , что невозможно, так как первый угол меньше второго. Значит, значение 6 не подходит. Остается только 4.
Значит, значение 6 не подходит. Остается только 4.
Ответ: 4
Задача 2. В окружности радиуса вписана трапеция с основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции.
В данной задаче возможны только 2 случая решения. Первый, когда нижнее основание ниже центра окружности, второй случай, когда нижнее основание выше центра окружности. Третий невозможен, так как большее основание .
1 случай
Дано:
– вписанная трапеция
Найти: OG
Решение.
Рассмотрим по теореме Пифагора
Рассмотрим по теореме Пифагора
Рассмотрим и
~
2 случай
Дано:
– вписанная трапеция
Найти: OG
Решение.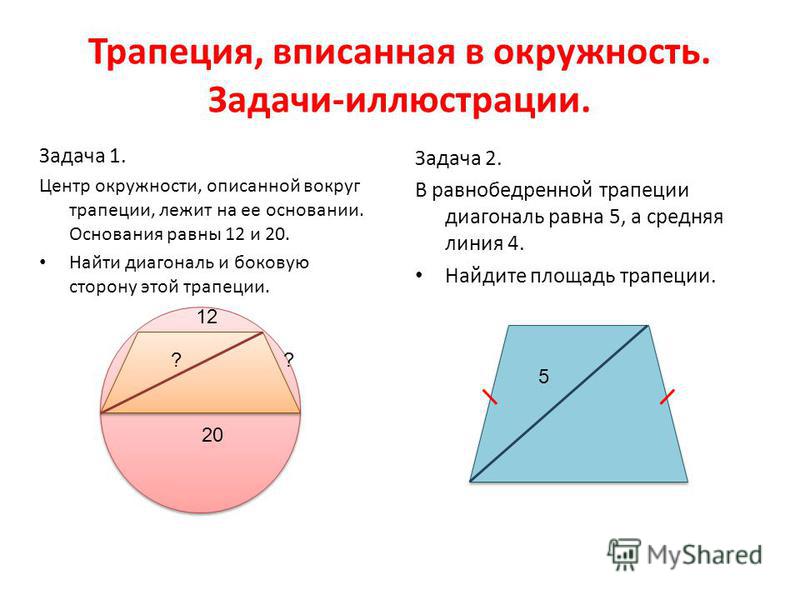
Рассмотрим по теореме Пифагора
Рассмотрим ΔAFO по теореме Пифагора
Рассмотрим и
~
Ответ:
4. Итог урока
Анализ: В данном занятии применяются Теорема 1, Теорема 3, Теорема 4, Теорема 5.
Занятие 3
Тема: Трапеция, описанная около окружности. Решение задач
Цель: расширение знаний обучающихся об описанной трапеции около окружности, ее свойств.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение основных свойств и теорем о трапеции, описанной около окружности школьного курса геометрии, а так же рассмотрение дополнительных и теорем. (Глава 1, п.1.5)
3. Закрепление
Решение задач
Задача 1. В описанной около окружности равнобокой трапеции основания относятся как 3:5. Из вершины меньшего основания опущена высота на большее основание; точка H — основание высоты. Из точки H опущен перпендикуляр HE на боковую сторону трапеции. В каком отношении точка E делит боковую сторону?
1 случай | 2 случай |
Дано:
– равнобокая описанная трапеция около окружности
ВС : AD = 3 : 5
BH – высота
EH ⊥AB
Найти: АЕ : ЕВ = ?
Дано:
– равнобокая описанная трапеция около окружности
ВС : AD = 3 : 5
BH – высота
EH ⊥CD
Найти: DE : ЕC = ?
Решение.
Пусть из вершины В трапеции ABCD опущена высота ВН на основание AD.
Пусть основания равны AD = 5x и ВС = 3х
Суммы противоположных сторон трапеции равны, поэтому
Рассмотри 1 случай.
Точка Е лежит на стороне АВ.
Катет прямоугольного треугольника равен среднему геометрическому между гипотенузой и своей проекцией на гипотенузу:
АН2 = АЕ · АВ, откуда
АЕ : ВЕ = 1: 15
Рассмотрим 2 случай.
Точка Е лежит на стороне CD.
ΔDEH = ΔAHB (по гипотенузе и острому углу)
Поэтому DE = AH = x
CE = CD – DE = 3x
Откуда DE : CE = 1 : 3
Ответ: 1 : 15 и 1 : 3
Задача 2.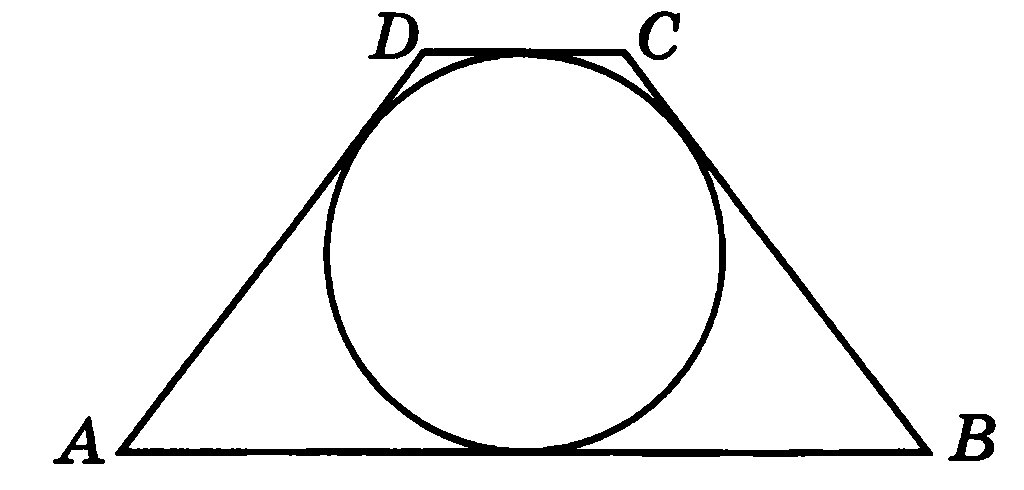 Периметр трапеции равен 112. Точка касания вписанной в трапецию окружности делит одну из боковых сторон на отрезки, равные 8 и 18 см. Найдите основания этой трапеции.
Периметр трапеции равен 112. Точка касания вписанной в трапецию окружности делит одну из боковых сторон на отрезки, равные 8 и 18 см. Найдите основания этой трапеции.
Дано:
ABCD – трапеция описная около окружности
РABCD = 112
a = 8
b = 18
Найти: ВС и ВD
Решение.
Так как в трапецию вписана окружность, то АВ + СD = BC + AD = 112 : 2 = 56
АВ = а + b = 18 + 8 = 26 =>
CD = 30
Если в трапецию вписана окружность с радиусом r и она делит боковую сторону на отрезки а и b, то
Высота трапеции 2r = 24, тогда ВН = СН = 24
Из ΔАВН по теореме Пифагора
Из ΔНСD по теореме Пифагора
ВС = НН = 56 – ( АН + НD) : 2 = (56 – 28) : 2 = 14
Тогда AD = АН + НН + НD = 10 + 14 + 18 = 42
Ответ: 14 и 42
4. Итог урока
Итог урока
Анализ: В данном занятии применяются Теорема 2, Теорема 7.
Занятие 4
Тема: Трапеция, вписанная и описанная около окружности. Решение задач
Цель: расширение знаний обучающихся о вписанной и описанной трапеции около окружности, ее свойств и теорем.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение основных свойств трапеции вписанной и описанной около окружности школьного курса геометрии, а так же применение рассмотренных дополнительных теорем. (Глава 1, п. 1.4, п.1.5)
1.4, п.1.5)
3. Закрепление
Решение задач
Задача 1. Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.
Дано:
ABCD – трапеция
BC = 14
AD = 40
R = 25
Найти: h
Решение.
Трапеция вписана в окружность, поэтому она равнобедренная.
Пусть ВС = 14 – хорда окружности радиуса 25. Существует две хорды, параллельные BC и равные 40. Соответственно, в окружность можно вписать две трапеции с основаниями 14 и 40.
Центр O на серединном перпендикуляре к BC.
1 случай.
В трапеции ABCD центр О окружности лежит внутри трапеции.
В этом случае высота EF = EO + OF
Из прямоугольного ΔАОЕ, в котором АО = 25
по теореме Пифагора, получаем
Из прямоугольного ΔВFO, в котором BО = 25
по теореме Пифагора, получаем
Тогда EF = EO + OF = 39
2 случай.
В трапеции A1BCD1 центр О окружности лежит вне трапеции.
Аналогично, находим
Ответ: 39 и 9
Задача 2. На основании ВС трапеции АВСD взята точка Е, лежащая на одной окружности с точками А, С и D. Другая окружность проходящая через точки А, В, и С, касается прямой CD. АВ=12, ВЕ : ЕС = 4 : 5.
а) Докажите, что треугольник АСD подобен треугольнику АВЕ.
б) Найдите ВС.
Дано:
АВСD – трапеция
Е ϵ ВС
АВ = 12
ВЕ : ЕС = 4 : 5
а) Доказать: ΔACD ~ ΔABE
б) Найти: ВС
Решение.
Рассмотрим АЕСD – равнобедренную трапецию вписанную в окружность =>
АЕС + ADC = 1800
Значит, угол ВЕА, смежный с углом АЕС, равен углу АDС
Опишем окружность около ΔАВС.
По условию CD касается окружности, а значит СD ⊥ OC, где О – центр окружности.
Угол между хордой АС и касательной CD равен половине дуги АС второй окружности.
Половине этой же дуги равен вписанный АВС. Найдена вторая пара равных углов. Найдя две пары равных углов, мы доказали подобие треугольников АСD и АВЕ.
Из подобия следует равенство третьей пары углов, ВАЕ = САD
Кроме того равны дуги АЕ и СD, заключенные между параллельными прямыми ЕС и АD
Вписанный CAD равен половине дуги CD, а значит, ВАЕ равен половине дуги АЕ.
ВАЕ – это угол между хордой АЕ и прямой АВ, проходящей через конец хорды А. Значит прямая АВ – касательная ко второй окружности.
Воспользуется свойством секущей и касательной, проведенных к окружности из точки В.
ВА2 = ВЕ · ВС
122 = (4х) · (9х)
36х2 = 144
х2 = 4
х = 2
ВС = 9х = 9 · 2 = 18
Ответ: 18
4. Итог урока
Итог урока
Анализ: В данном занятии применяются Теорема 1, Теорема 4, Теорема 5.
Занятие 5.
Тема: Трапеция, вписанная и описанная около окружности. Решение задач
Цель: расширение знаний обучающихся о вписанной и описанной трапеции около окружности, ее свойств.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение основных свойств трапеции вписанной и описанной около окружности школьного курса геометрии, а так же применение рассмотренных дополнительных свойств. (Глава 1, п.2.1, п.2.2)
(Глава 1, п.2.1, п.2.2)
3. Закрепление
Решение задач
Задача 1. Окружность, вписанная в равнобедренную трапецию с основаниями а и b. Найдите диагональ трапеции.
Дано:
АВСD – равнобедренная трапеция
AD = b
BC = a
Найти: BD
Решение.
Пусть окружность с центром О, вписанная в равнобедренную трапецию АВСD, касается боковой стороны АВ в точке М, а оснований ВС и АD – в точке N и L соответственно.
Поскольку ОМ – высота прямоугольного ΔАОВ, опущенная из вершины прямого угла, то
Опустим перпендикуляр ВН на AD. Тогда
Из прямоугольного ΔBHD находим, что
Ответ:
Задача 2.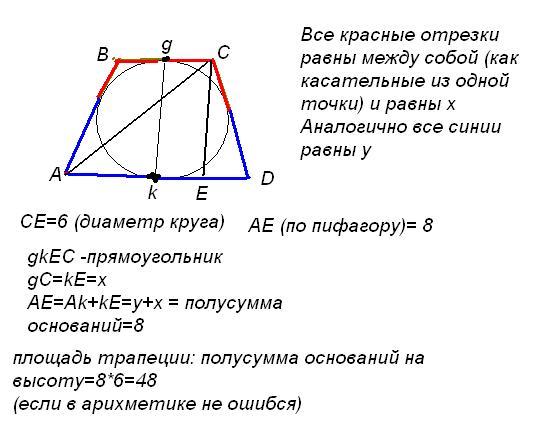 Трапеция с высотой h вписана в окружность. Боковая сторона трапеции видна из центра окружности под углом 1200. Найдите среднюю линию трапеции.
Трапеция с высотой h вписана в окружность. Боковая сторона трапеции видна из центра окружности под углом 1200. Найдите среднюю линию трапеции.
Дано:
АВСD – трапеция
АОВ = 1200
Найти: среднюю линию трапеции
Решение.
Пусть О – центр окружности, описанной около трапеции АВСD с основаниями AD > BC. Трапеция АВСD – равнобедренная, поэтому
Пусть СК – высота трапеции, тогда АК = h·ctg600 = ,
а так как трапеция равнобедренная, то отрезок АК равен ее средней линии.
Ответ:
Задача 3. Около окружности описана равнобедренная трапеция АВСD. Боковые стороны АВ и СD касаются окружности в точках М и N, К – середина АD. В каком отношении прямая ВК делит отрезок МN?
Дано:
АВСD – равнобедренная трапеция
М ϵ АВ
N ϵ СD
AK = KD
Найти: МР : РN = ?
Решение.
Обозначим х = АК, у = ВF, где F – середина ВС. Пусть Q – точка пересечения KF и MN, а Р – точка пересечения MN и ВК. Тогда
АМ = АК = х, ВМ = ВF = у
и Q – середина MN.
Поскольку MN параллельно основаниям трапеции, треугольник ВМР подобен треугольнику ВАК, а треугольник КРQ подобен треугольнику КВF. Поэтому
, значит, РМ = PQ и PM = MN =>
Ответ: 1 : 3
Задача 4. В прямоугольной трапеции меньшее основание равно высоте, а большее основание равно а. Найдите боковые стороны трапеции, если известно, что одна из них касается окружности, проходящей через концы меньшего основания и касающееся большего основания.
Дано: АВСD – прямоугольная трапеция
АВ = ВС
AD = a
Найти: AB, CD
Решение.
Обозначим меньшее основание ВС и меньшую боковую сторону трапеции АВСD через х. Пусть М – точка касания окружности с большим основанием AD. Тогда точка М лежит на серединном перпендикуляре к отрезку ВС, поэтому
Тогда точка М лежит на серединном перпендикуляре к отрезку ВС, поэтому
Пусть К – проекция вершины С на AD. Тогда KD = a – x, CK = x
По теореме Пифагора
Отсюда находим, что
Тогда
Ответ:
Задача 5. В равнобедренной трапеции с острым угломпри основании окружность, построенная на боковой стороне как на диаметре, касается другой боковой стороны. В каком отношении она делит большее основание трапеции?
Дано:
АВСD — равнобедренная трапеция
BAD = ADC =
Найти: АК : КD
Решение.
Пусть О – центр окружности (середина боковой стороны АВ трапеции АВСD), ОР – средняя линия трапеции, К – точка пересечения указанной окружности с большим основанием AD. Тогда ВК – перпендикуляр к AD и .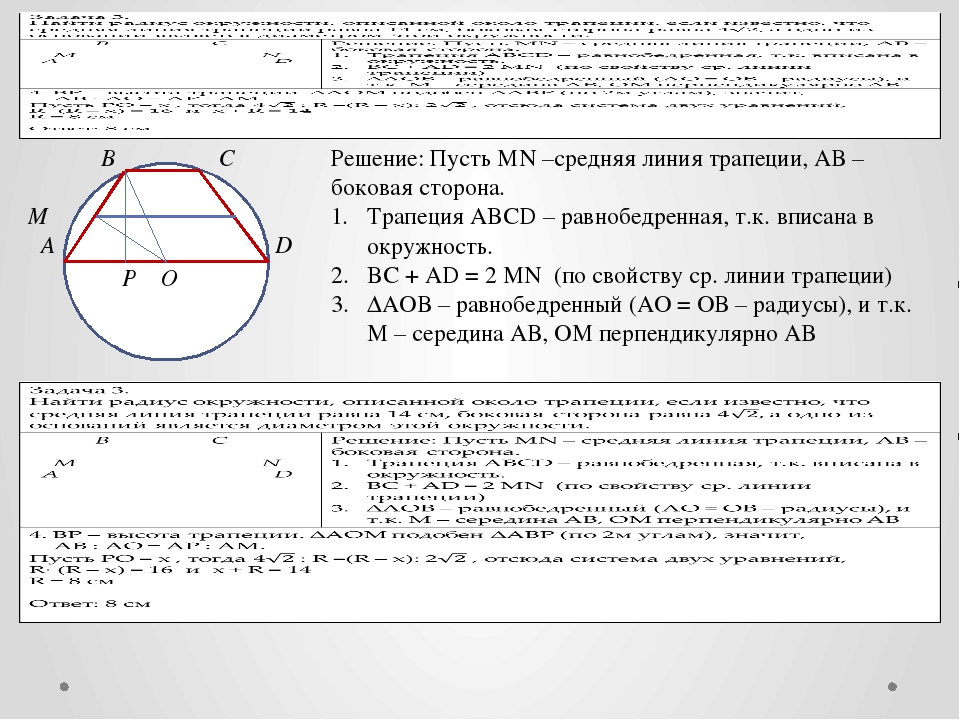 Если М – точка касания окружности с боковой стороной CD, то
Если М – точка касания окружности с боковой стороной CD, то
Следовательно,
Ответ: sin2
4. Итог урока
Анализ: В данном занятии применяются Теорема 1, Теорема 3, Теорема 4, Теорема 6, Теорема 7, Теорема 8, Теорема 9, Теорема 10, Теорема 11
Занятие 6.
Тема: Итоговое занятие.
Цель: проверка усвоения знаний обучающихся по теме курса «Вписанная и описанная окружность в трапецию»
Тип урока: закрепление
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Закрепление
Закрепление
Обучающимся предлагается, ответит на вопросы (устно):
1. Вопрос: Определение четырехугольника?
Ответ: Четырёхугольник — это геометрическая фигура (многоугольник), которая состоит из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки.
2. Вопрос: Виды четырехугольников?
Ответ: Виды четырехугольников:
— параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
— прямоугольник — четырёхугольник, у которого все углы прямые;
— ромб — четырёхугольник, у которого все стороны равны;
— квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
— трапеция — четырёхугольник, у которого две противоположные стороны параллельны.
3. Вопрос: Какая окружность называется вписанной в четырехугольник? Какой четырехугольник называется описанным около окружности?
Вопрос: Какая окружность называется вписанной в четырехугольник? Какой четырехугольник называется описанным около окружности?
Ответ: Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности, которая будет называться описанной вокруг четырехугольника. Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.
4. Вопрос: В какой четырехугольник можно вписать окружность?
Ответ: Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы его длин противоположных сторон равны. а + с = b+ d
5. Вопрос: Около какого четырехугольника можно описать окружность?
Ответ: Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180.
6. Вопрос: Можно ли описать окружность около трапеции?
Ответ: Вписать в окружность можно только равнобокую трапецию.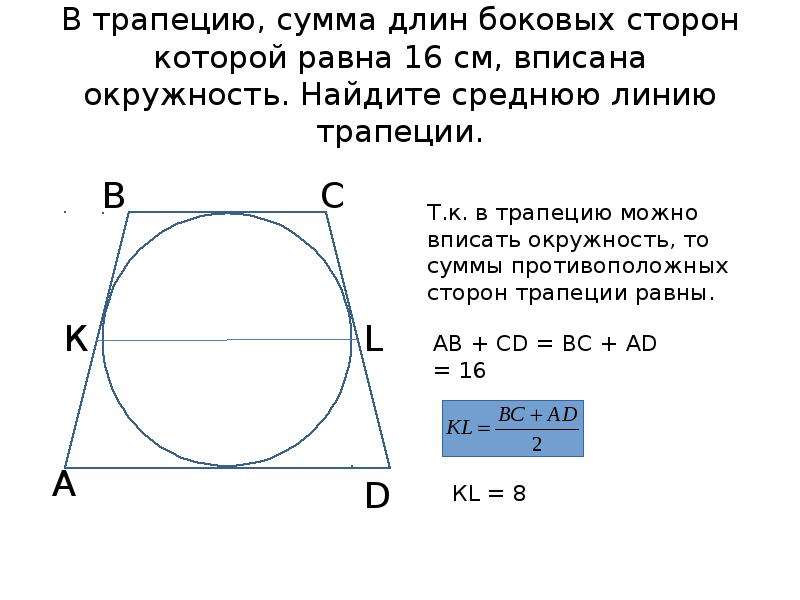
7. Вопрос: Можно ли вписать окружность в трапецию?
Ответ: Если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон. АВ + CD = AD + BC
8. Вопрос: Какими свойствами обладает трапеция, вписанная в окружность?
Ответ: 1) Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
2) Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции.
3) Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
9. Вопрос: Какими свойствами обладает трапеция, описанная около окружности?
Ответ: 1) Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию
окружности.
2) Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
3) Боковая сторона описанной трапеции видна из центра описанной окружности под прямым углом.
4) Высота трапеции равна ее диаметру, то высоту трапеции можно выразить через длины этих отрезков.
Самостоятельная работа
Выполнение итоговой самостоятельной работы для обучающихся предлагается в виде выполнения теста.
1. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
2. В четырехугольник можно вписать окружность, если __________________________________________________________.
3. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
а) AB + BC = AD + CD
б) AB + CD = BC + AD
в) AB + AD = BC + CD
г) AD·BC = AB·CD
4. Вписанная в четырехугольник окружность изображена на рисунке:
Вписанная в четырехугольник окружность изображена на рисунке:
5. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
а)
б) AB+CD=BC+AD
в)
г) AD·BC=AB·CD
6. Описанная около четырехугольника окружность изображена на рисунке:
7. В любом описанном четырехугольнике суммы длин противолежащих сторон:
а) равны между собой
б) равны радиусу окружности
в) равны диаметру окружности
г) равны периметру
8. Углы А, В и С четырехугольника ABCD относятся как 1 : 2 : 3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
а) 1350 б) 1200 в) 900 г) 600
9. Трапеция описана около окружности. Чему равен ее периметр, если средняя линия равна 7 см?
а) 25 см б) 28 см в) 30 см г) 32 см
10. Чему равна площадь прямоугольной трапеции с тупым углом, равным 1500, если радиус вписанной в него окружности равен 2?
Чему равна площадь прямоугольной трапеции с тупым углом, равным 1500, если радиус вписанной в него окружности равен 2?
а) 18 б) 20 в) 22 г) 24
11. Выпуклый четырехугольник АВСD вписан в окружность. При этом величины углов АВС и ВСD соответственно равны 700 и 600. Тогда величина угла ВАD равна:
а) 1200 б) 1100 в) 650 г) 500
Заключение
В настоящей работе по теме: «Содержание занятий по теме: «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов» в первой главе приведены основные теоретические сведения темы исследования, основные свойства и теоремы сведены в таблицу. Проанализированы учебники школьного курса геометрии для обучающихся в 7, 8, 9-х классах, на основании, которых сделан вывод, что темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не достаточно рассматриваются в школьном курсе геометрии в 7, 8, 9-х классах для решения задач повышенной сложности.
Во второй главе работы приведены разработки содержания 6 занятий по теме исследования; разработаны входящая и итоговая самостоятельные работы. В приложениях приведены решения данных работ.
Результаты работы могут быть использованы в рамках курса по выбору на дополнительных занятиях по геометрии или для подготовки к итоговой государственной аттестации, так как при проведении государственной итоговой аттестации среди 9-х классов общеобразовательных школ в части С геометрии часто встречается задание по теме «Трапеция вписанная в окружность или трапеция описанная около окружности».
Таким образом, поставленные задачи выполнены, цель достигнута.
Литература
1. http://nsportal.ru/ap/drugoe/library/referat-znachenie-geometrii-v-zhizni-lyudei
2. http://www.kniga.es/articles/article637.shtml
3. http://ru.wikipedia. org/wiki /%D7%E5%F2%FB%F0%B8%F5%F3%E3%EE%EB
org/wiki /%D7%E5%F2%FB%F0%B8%F5%F3%E3%EE%EB
4. http://free.megacampus.ru/xbookM0005/index.html ?go=part-021*page.htm
5. http://ege- study.ru/materialy-ege/vpisannyj-i-opisannyj-chetyrexugolniki-i-ix-svojstva /
6. http://free.megacampus.ru/xbookM0001/index.html ?go=part-034*page.htm
7. http://otvet.mail.ru/question/47745330
8. http://www.smekalka.pp.ru/node/1586
9. Погорелов А.В., Геометрия: Учебник для 7-11 классов средних школ – 2-е издание – М.: Просвещение, 1991 – 384 с.
10 Атанасян Л.С. и др., Геометрия 7-9 классы: учебник для общеобразовательных учреждений / [Л.С. Атанасян, В.Ф. Бутусов, С.Б. Кадомцев и др.] – 21-е издание – М.: Просвещение, 2011 – 384 с.
11. Бевз Г.П., Геометрия: Учебник для 7-11 классов средних школ / Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова. – М.: Просвещение, 1992 – 352 с.
12. Вернер А.Л. и др., Геометрия: Учебник для 7 класса общеобразовательных учреждений / А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. – М.: Просвещение, 1999 – 192 с.
13. Вернер А.Л. и др., Геометрия: Учебное пособие для 8 класса общеобразовательных учреждений / А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. – М.: Просвещение, 2001 – 192 с.
14. Вернер А.Л. и др., Геометрия: Учебное пособие для 9 класса общеобразовательных учреждений / А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. – М.: Просвещение, 2001 – 207 с.
15. http://www.uznateshe.ru/trapetsiya-vpisana-v-okruzhnost/
16. http:// www.alexlarin.narod.ru
17. Корянов А.Г. Математика. ЕГЭ 2010. Задания типа С4. Многовариантные задачи по планиметрии http://www.alexlarin.narod.ru/ege/2010/C4a
gk.pdf
18. Созоненко Р.С., Теоремы и задачи по планиметрии с перекрестными ссылками. – 2-е издание, исправлено и дополнено – Новосибирск: Издательство ИМ СО РАН, 1998 – 209 с.
– 2-е издание, исправлено и дополнено – Новосибирск: Издательство ИМ СО РАН, 1998 – 209 с.
19. Гордин Р.К., ЕГЭ 2012 Математика. Решение задач С4. – М.: МЦНМО, 2012 – 328 с.
20. Никитин Н.Н., Геометрия: Учебник для 6-8 классов / Н.Н. Никитин. – М.: Просвещение, 1971 – 209 с.
Приложение 1
Входная самостоятельная работа
Задача 1. В равнобедренной трапеции основания 21 и 9 сантиметров, высота — 8 сантиметров. Найти радиус описанной окружности.
Дано:
ABCD – равнобедренная трапеция
ВС = 9 см
AD = 21 см
h = 8 см
Найти: R
Решение.
Пусть EF – серединный перпендикуляр c основаниями EF , тогда О – центр окружности лежит на прямой EF.
ОА = ОВ = R.
О делит EF на две части: пусть OF = х, тогда OE = 8-х.
По теореме Пифагора получаем,
АО2 = АF2 + FО2
ОВ2 = ВE2 + EО2.
Так как ОА2 = ОВ2, получим:
АF2 + FО2 = ВE2 + EО2
Ответ: 10,625 см
Задача 2. Прямоугольная трапеция описана около окружности. Найти радиус этой окружности, если длины оснований трапеции равны a и b.
Дано:
АВСD – прямоугольная трапеция
АВ = а
АD = b
Найти: r
Решение.
Пусть r – радиус окружности вписанной в трапецию ABCD.
Так как трапеция прямоугольная, то АВ = 2r.
Так как трапеция описана около окружности, то AD + BC = AB + CD.
Тогда а + b = 2r + CD.
CD = a + b – 2r
Пусть СЕ – высота, тогда СЕ ⊥ АD и СЕ = АВ = 2r.
ED = b – a.
По теореме Пифагора для треугольника ЕСD имеем
СD2 = CE2 + ED2
или
(а + b – 2r)2 = 4r2 + (b – a)2
Ответ:
Приложение 2
Итоговая самостоятельная работа
1. Вокруг четырехугольника можно описать окружность, если (суммы его противоположных углов равны 180, )
2. В четырехугольник можно вписать окружность, если (суммы его длин противоположных сторон равны, а + с = b+ d)
3. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
а) AB + BC = AD + CD
б) AB + CD = BC + AD
в) AB + AD = BC + CD
г) AD·BC = AB·CD
Ответ: б)
4. Вписанная в четырехугольник окружность изображена на рисунке:
Ответ: б)
5. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
а)
б) AB+CD=BC+AD
в)
г) AD·BC=AB·CD
Ответ: в)
6. Описанная около четырехугольника окружность изображена на рисунке:
Ответ: в)
7. В любом описанном четырехугольнике суммы длин противолежащих сторон:
а) равны между собой
б) равны радиусу окружности
в) равны диаметру окружности
г) равны периметру
Ответ: а)
8. Углы А, В и С четырехугольника ABCD относятся как 1 : 2 : 3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
а) 1350 б) 1200 в) 900 г) 600
Ответ: в)
9. Трапеция описана около окружности. Чему равен ее периметр, если средняя линия равна 7 см?
Чему равен ее периметр, если средняя линия равна 7 см?
а) 25 см б) 28 см в) 30 см г) 32 см
Ответ: б)
10. Чему равна площадь прямоугольной трапеции с тупым углом, равным 1500, если радиус вписанной в него окружности равен 2?
а) 18 б) 20 в) 22 г) 24
Ответ: г)
11. Выпуклый четырехугольник АВСД вписан в окружность. При этом величины углов АВС и ВСД соответственно равны 700 и 600. Тогда величина угла ВАД равна:
а) 1200 б) 1100 в) 650 г) 500
Ответ: а)
Как найти центр окружности описанной около трапеции. Материал по геометрии на тему «трапеция и ее свойства»
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.

- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 .
- Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .

- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .

- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.

- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .

Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .

- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .

- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
ФГКОУ «МКК «Пансион воспитанниц МО РФ»«УТВЕРЖДАЮ»
Руководитель отдельной дисциплины
(математика, информатика и ИКТ)
Ю. В. Крылова _____________
«___» _____________ 2015 г.
«Трапеция и ее свойства »
Методическая разработка
преподавателя математики
Шаталиной Елены Дмитриевны
Рассмотрено и
на заседании ПМО от _______________
Протокол №______
Москва
2015 год
Оглавление
Введение 2
Определения 3
Свойства равнобедренной трапеции 4
Вписанные и описанные окружности 7
Свойства вписанных и описанных трапеций 8
Средние величины в трапеции 12
Свойства произвольной трапеции 15
Признаки трапеции 18
Дополнительные построения в трапеции 20
Площадь трапеции 25
10. Заключение
Заключение
Список используемой литературы
Приложение
Доказательства некоторых свойств трапеции 27
Задачи для самостоятельных работ
Задачи по теме «Трапеция» повышенной сложности
Проверочный тест по теме «Трапеция»
Введение
Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.
Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.
Трапеция.
Определения
Трапеция
– четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Расстояние между основаниями называется высотой трапеции .
2 . Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны.
4
1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
3. Вписанная и описанная окружность
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
Е
сли трапеция равнобедренная, то около неё можно описать окружность.
4 . Свойства вписанных и описанных трапеций
2.Если в равнобедренную трапецию можно вписать окружность, то
сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.
4 . Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
Е сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m и n, тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.
1
0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.
5. Средние величины в трапеции
Среднее геометрическое
В любой трапеции с основаниями a и b для a > b справедливо неравенство :
b
˂
h
˂
g
˂
m
˂
s
˂
a
6.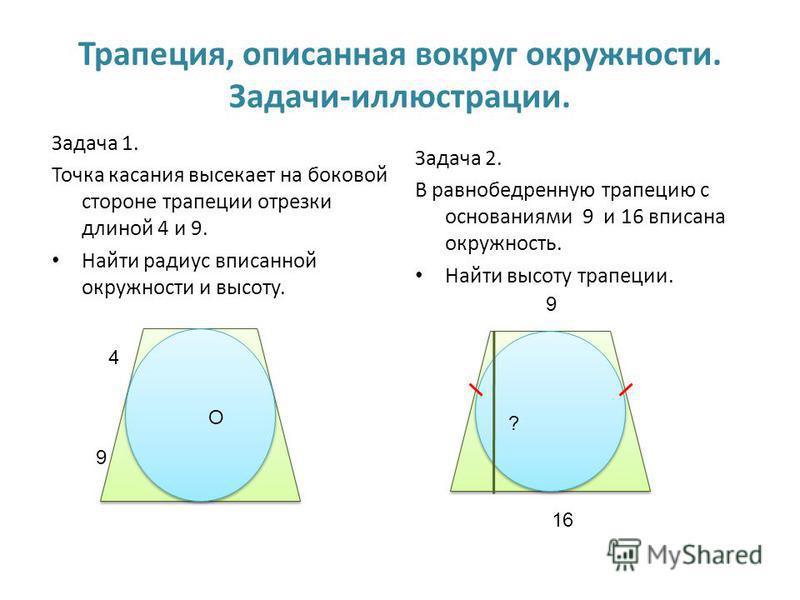 Свойства произвольной трапеции
Свойства произвольной трапеции
1
. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.
2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.
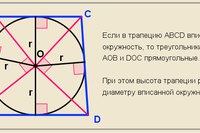 е. имеют равные площади).
е. имеют равные площади). 6. Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
d 1 2 + d 2 2 = c 2 + d 2 + 2 ab
7
. В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований d 1 2 — d 2 2 = a 2 – b 2
8 . Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.
7 . Признаки трапеции
8 . Дополнительные построения в трапеции
1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.
3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.
4
. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.
6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований
7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.
8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
9. Биссектриса угла трапеции отсекает равнобедренный треугольник.
1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.
13. Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.
9. Площадь трапеции
1 . Площадь трапеции равна произведению полусуммы оснований на высоту S = ½(a + b ) h или
П
лощадь трапеции равна произведению средней линии трапеции на высоту S = m h .
2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.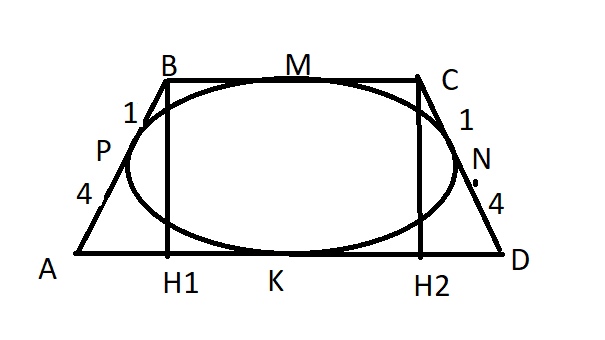
Площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
10. Заключение
ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?
Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.
Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.
Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.
Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.
Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн
В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.
Список используемой литературы
Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.
Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004
Гордин Р.К. Планиметрия. Задачник.
Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN 5-89155-188-3
Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).
Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.
Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.
Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.
Приложение
1. Доказательство некоторых свойств трапеции.
Доказательство некоторых свойств трапеции.
1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L . Доказать, что если основания трапеции равны а и b , то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство
Пусть О — точка пересечения диагоналей, AD = а, ВС = b . Прямая KL параллельна основанию AD , следовательно, K О ║ AD , треугольники В K О и BAD подобны, поэтому
(1)
(2)
Подставим (2) в (1) , получим KO =
Аналогично LO = Тогда K L = KO + LO =
В о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.
Доказательство: Пусть продолжения боковых сторон пересекаются в точке К. Через точку К и точку О пересечения диагоналей проведём прямую КО.
K
Окажем, что эта прямая делит основания пополам.
Обозначим ВМ = х, МС = у, AN = и, ND = v . Имеем:
∆ ВКМ ~ ∆AKN →
M
x
B
C
Y
∆ MК C ~ ∆NKD → →В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.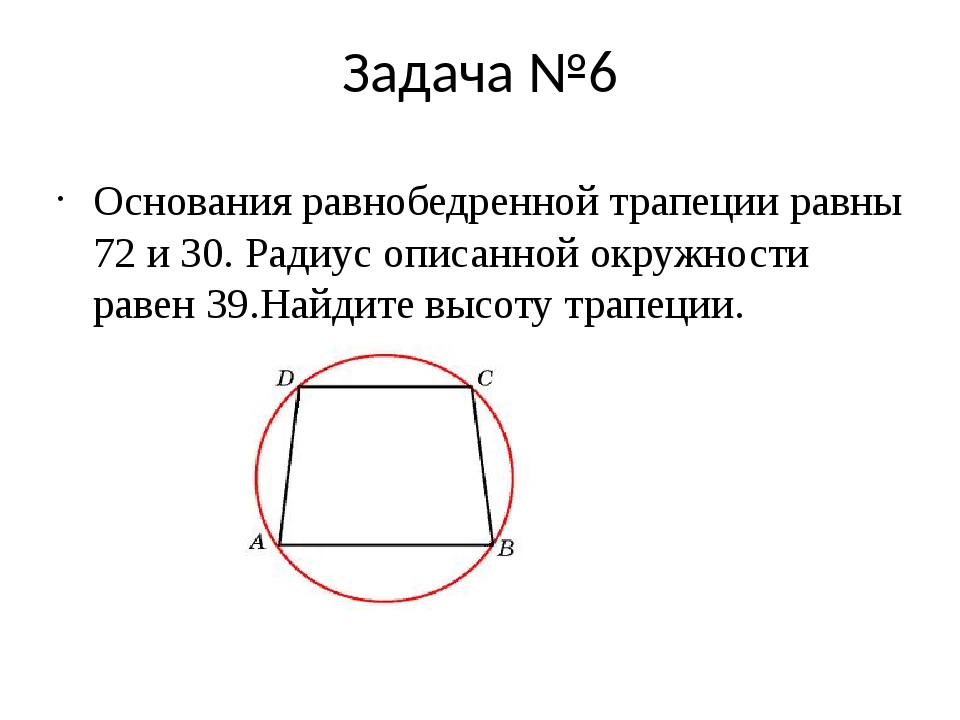
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии.
 А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 . - Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую.
 Она пересекает основания в точках Х и Т.
Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.

- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям.
 И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции. - На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).

- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .

Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности.
 В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию.
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. \circ\)
.
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN»\parallel AD\) (\(N»\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\) ) точка \(N»\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\) и \(N»\) — середины отрезков \(BB»\) и \(CC»\) соответственно. Значит, \(MM»\) – средняя линия \(\triangle ABB»\) , \(NN»\) — средняя линия \(\triangle DCC»\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Значит, \(B»M»N»C»\) и \(BM»N»C\) – равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE — BE = DE — CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Окружность описанная около трапеции. Описанная окружность и трапеция
Добрый вечер! Ох уж эти описанные, или вписанные окружности, геометрические фигуры. Так сложно запутаться. что да когда.
Давайте попробуем разобраться для начала с формулировкой. Нам дана окружность описанная около . Иными словами — данная трапеция вписана в окружность.
Давайте вспомним, что описать окружность мы можем только вокруг . А равнобедренная трапеция в свою очередь — это трапеция, у которой боковые стороны равны.
Давайте попробуем решить задачку. Нам известно, что основания равнобедренной трапеции ADCB равны 6 (DC) и 4 (AB). А радиус описанной окружности равен 4. Нужно найдите высоту трапеции FK.
FK — высота трапеции. её нам нужно найти, но перед этим вспомним, что точка О — это центр окружности. А ОС, ОD, OA, OB — известные радиусы .
В OFC нам известна гипотенуза, которая является радиусом окружности, а катет FC = половине основания DC = 3 см (так как DF = FC).
Теперь по найдём OF:
А в прямоугольном треугольнике OKB нам тоже известна гипотенуза, так как это радиус окружности. А KB равняется половине AB; KB = 2 см. И, используя теорему Пифагора вычислим отрезок OK:
Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Общие сведения
Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.
Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Виды трапеции
Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.
1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.
Главные принципы методики изучения свойств трапеции
К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры.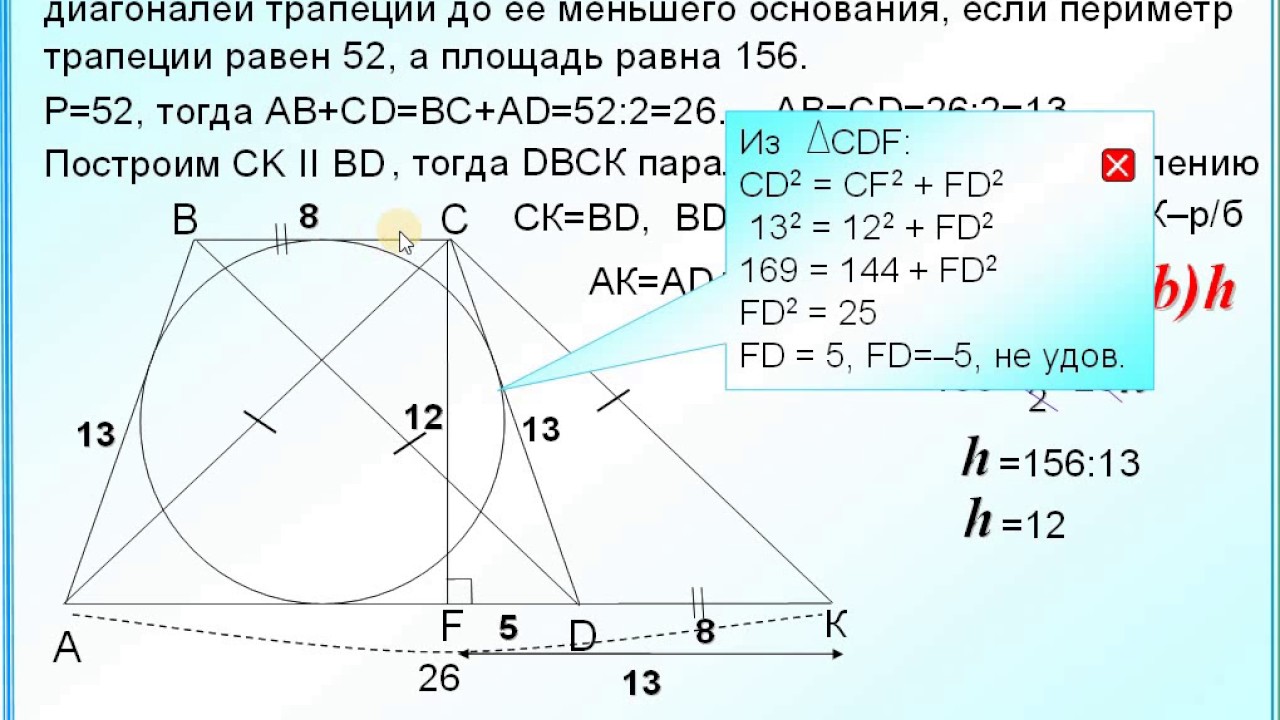 Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg.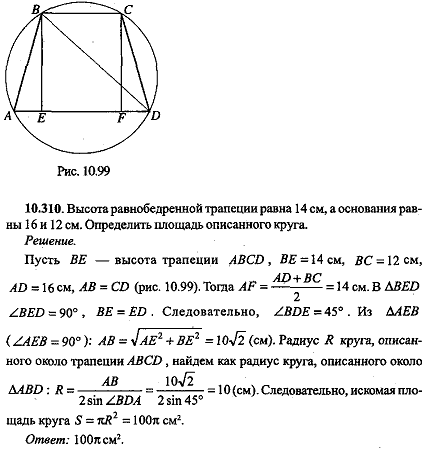 В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Ее высота и средняя линия равны;
Центр окружности является точкой, в которой пересекаются ;
Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;
Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.
Подобные трапеции
Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Доказательство теоремы
Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Свойства подобия
Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям.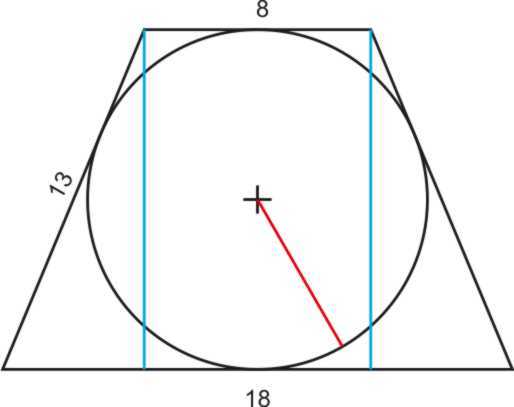 Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).
2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.
Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Центр тяжести
Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.
Вписанные и описанные трапеции
Давайте перечислим особенности таких фигур:
1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.
2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Следствия вписанной окружности:
1.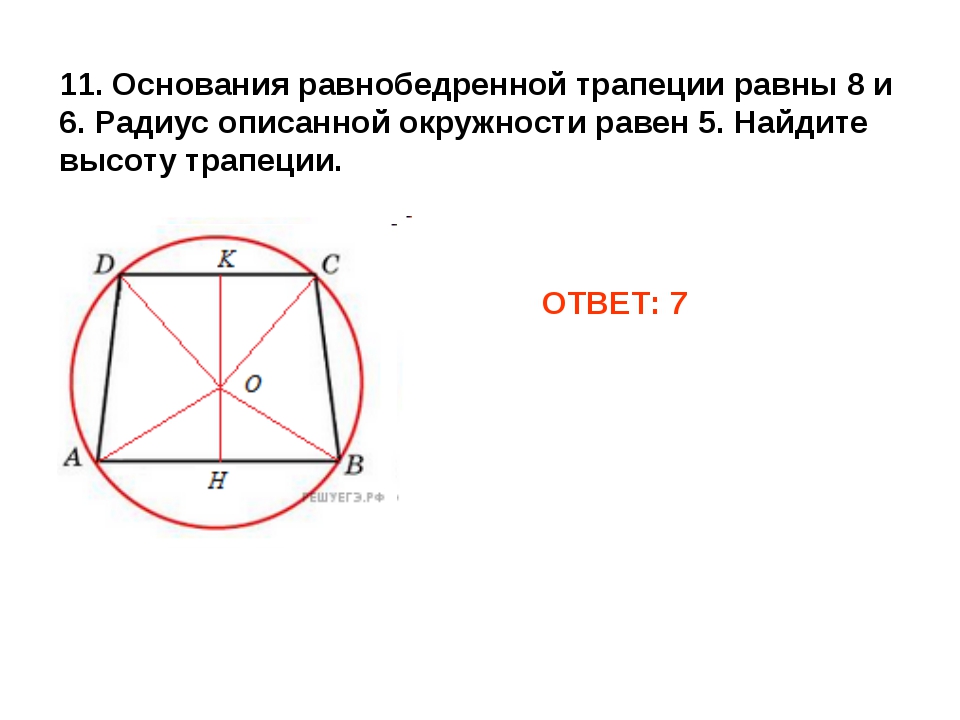 Высота описанной трапеции всегда равна двум радиусам.
Высота описанной трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.
Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+Б)/2.
2. Через высоту, основание и углы:
М = А-Н*(ctgα+ctgβ)/2;
М = Б+Н*(ctgα+ctgβ)/2.
3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:
М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.
4. Через площадь и высоту: М = П/Н.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии.
 А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 . - Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую.
 Она пересекает основания в точках Х и Т.
Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.

- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям.
 И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции. - На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).

- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .

Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности.
 В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию.
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.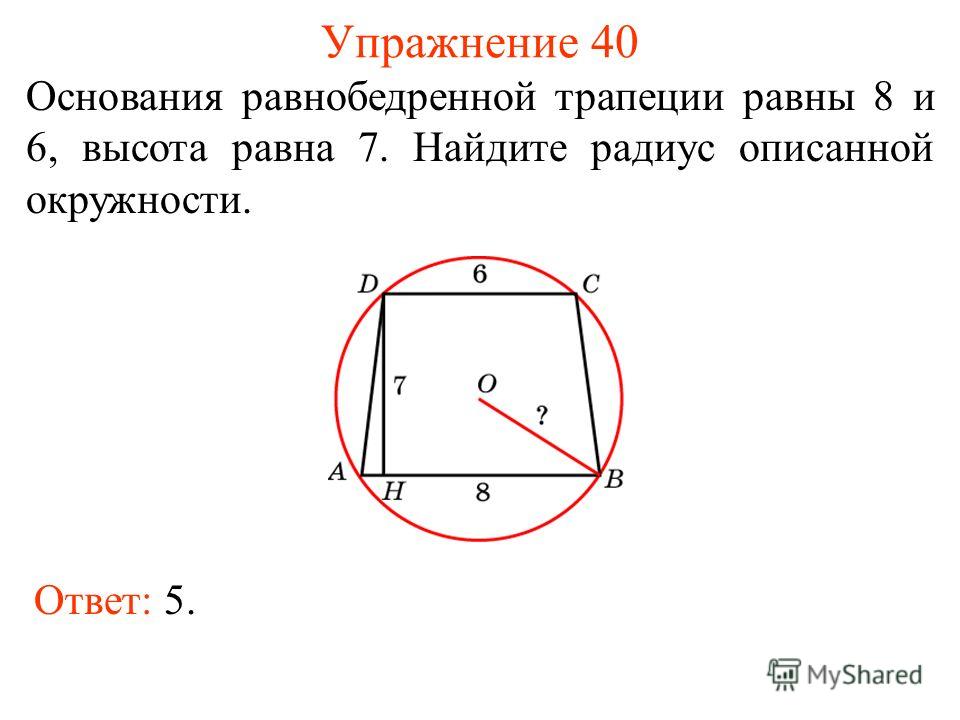
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.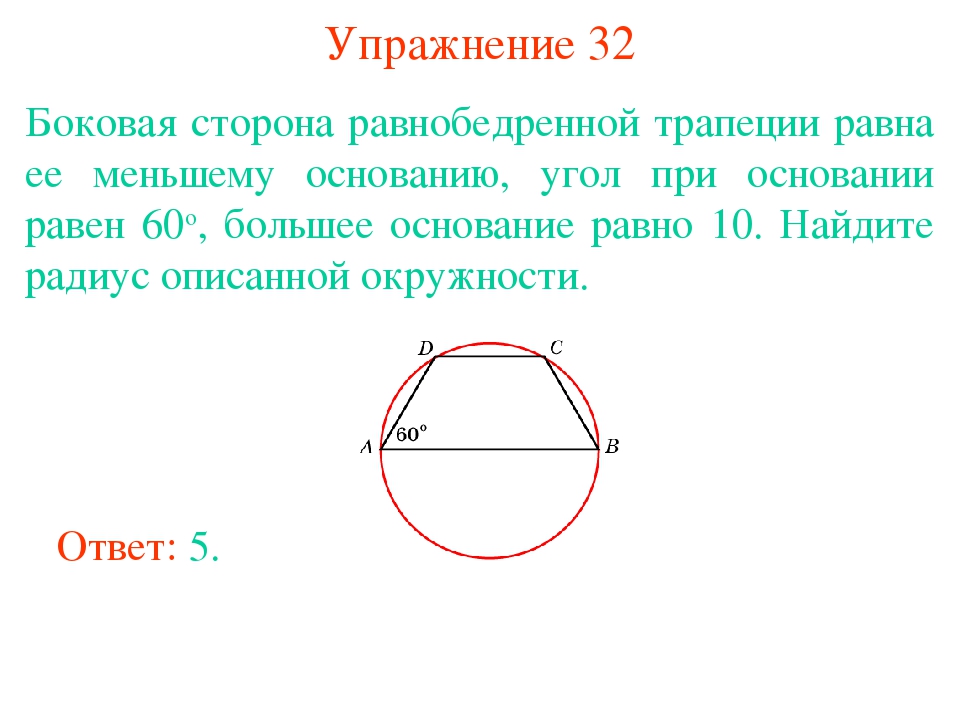 Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .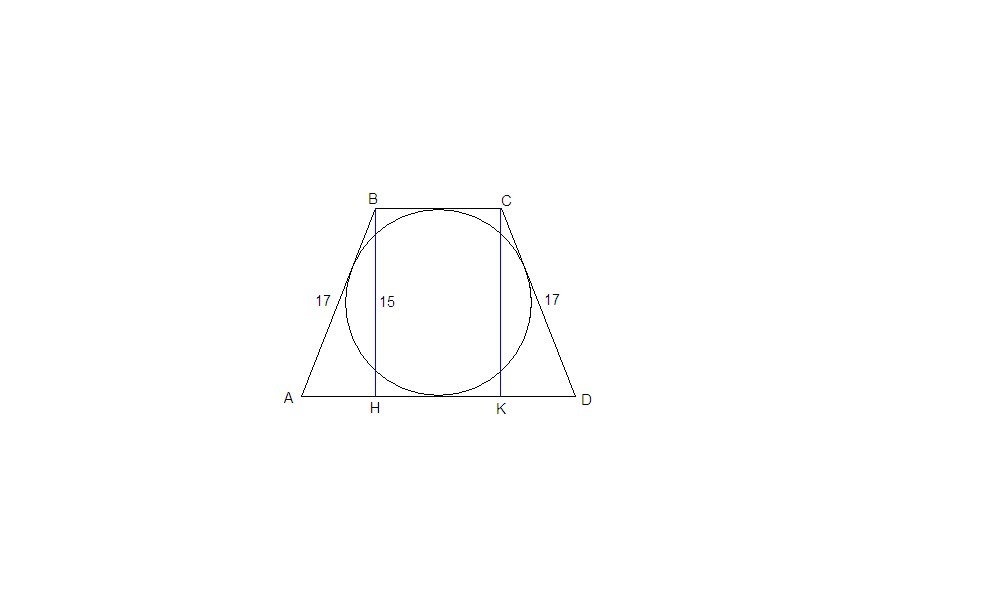
Как доказать, что трапеция, вписанная в круг, равнобедренная? — Реабилитацияrobotics.net
Как доказать, что трапеция, вписанная в круг, равнобедренная?
Чтобы доказать, что трапеция ABCD равнобедренная, вам нужно показать, что непараллельные стороны BD и AC имеют одинаковую длину. Это можно сделать следующим образом. Сотрите линии, идущие к центру круга. Проведите одну линию от точки A до точки C.
Все ли равнобедренные трапеции цикличны?
Равнобедренная трапеция всегда циклична.
Можно ли вписать равнобедренный треугольник в круг?
Равнобедренный треугольник, вписанный в круг — Math Central. треугольник как функция от h, где h обозначает высоту треугольника ». Поскольку треугольник равнобедренный, A — середина основания. пусть b = | AB | тогда b составляет половину длины основания равнобедренного треугольника.
Как найти вписанный круг треугольника?
Для вписанной окружности треугольника нужны только две биссектрисы; их пересечение будет центром круга. Найдите радиус r вписанной окружности для треугольника △ ABC из примера 2.6 раздела 2.2: a = 2, b = 3 и c = 4.
Найдите радиус r вписанной окружности для треугольника △ ABC из примера 2.6 раздела 2.2: a = 2, b = 3 и c = 4.
Каков радиус окружности, вписанной в треугольник со сторонами длиной 12 см, 35 и 37 см?
Ответ. Нам нужно найти радиус вписанной окружности в треугольник со сторонами длиной 12 см, 35 см и 37 см. Решение: см. диаграмму, пусть O — центр вписанной окружности в треугольник ∆ABC. Следовательно, радиус круга равен 5 см.
Каков радиус окружности, вписанной в треугольник с длинами сторон 35 см, 44 см и 75 см?
Следовательно, радиус круга равен 6 см.
Когда круг вписан в треугольник?
Окружность вписана в треугольник, если все три стороны треугольника касаются окружности. В этой ситуации круг называется вписанным кругом, а его центр — внутренним центром или центром.
Как найти диаметр вписанной окружности?
Когда круг вписан в квадрат, длина каждой стороны квадрата равна диаметру круга. То есть диаметр вписанной окружности равен 8 единицам и, следовательно, радиус равен 4 единицам. Площадь круга радиусом r единиц равна A = πr2. Подставим в формулу r = 4.
Площадь круга радиусом r единиц равна A = πr2. Подставим в формулу r = 4.
Сколько треугольников можно вписать в круг?
Каждый круг имеет вписанный треугольник с любыми тремя заданными углами (суммируя, конечно, 180 °), и каждый треугольник может быть вписан в некоторый круг (который называется его описанным кругом или описанным кругом).
Есть ли у воздушного змея равные стороны?
Воздушный змей с парами сторон равной длины и вписанным кругом.В евклидовой геометрии воздушный змей — это четырехугольник, четыре стороны которого могут быть сгруппированы в две пары сторон равной длины, которые примыкают друг к другу.
У ромба четыре равные стороны?
Ромб — это параллелограмм с четырьмя равными сторонами. Множественное число ромба — ромб.
У каждой трапеции 2 пары противоположных параллельных сторон?
Некоторые люди определяют трапеции, чтобы иметь одну и только одну пару противоположных сторон, параллельных, в то время как некоторые люди определяют трапеции, чтобы иметь, по крайней мере, одну пару противоположных сторон, параллельных.
У трапеции 1 пара равных сторон?
Есть два конкурирующих определения «трапеции»: Исключительное определение трапеции гласит, что трапеция имеет ровно одну пару параллельных противоположных сторон. Включенное определение гласит, что трапеция имеет по крайней мере одну пару параллельных противоположных сторон.
Как найти угол в трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Geometry Problem Solver — трапеция
Они дают трекам, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.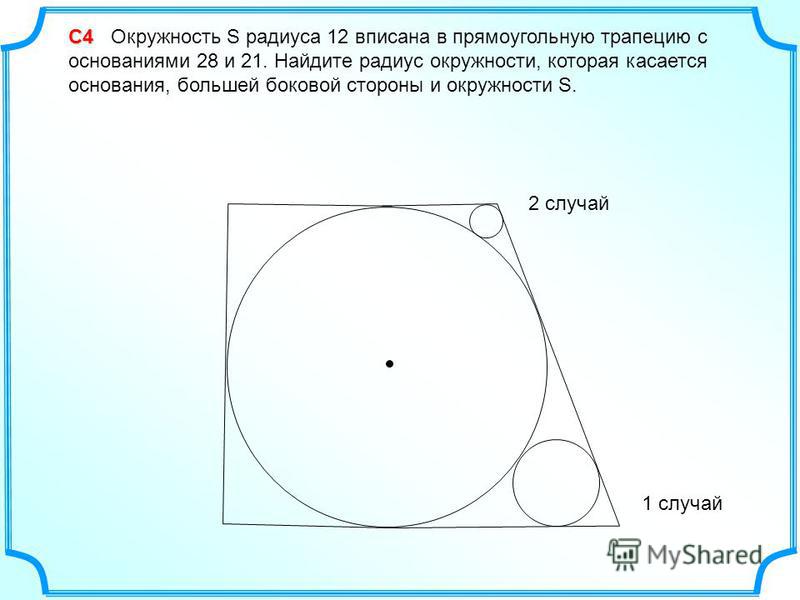
Трасса 1
Равнобедренная трапеция имеет высоту 20 м, большее основание 80 м, меньшее основание 50 м. Рассчитайте периметр и площадь трапеции.
Колея 2
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание большее 80 см, имеет меньшее основание 50 см. Рассчитайте периметр.
Трасса 3
Прямоугольная трапеция имеет высоту 40 м, основание большее 80 м, меньшее основание 50 м.Рассчитайте периметр и площадь трапеции.
Колея 4
Равнобедренная трапеция с основанием больше 80 см, имеет меньшее основание 50 см, имеет площадь 1300 см. Рассчитайте высоту трапеции.
Колея 5
Прямоугольник в форме трапеции имеет площадь 1500 см; имеет высоту 30 см. Вычисляет сумму двух оснований.
Колея 6
Равнобедренная трапеция имеет площадь 1500 см; имеет высоту 30 см.Вычисляет сумму двух оснований.
Колея 7
Равнобедренная трапеция имеет периметр 150 см; имеет основание больше 50 см; имеет меньшую базу 30 см. Рассчитайте длину скошенной стороны.
Направляющая 8
Равнобедренная трапеция имеет периметр 150 см, меньшее основание 30 см, наклонную сторону 35 см. Рассчитайте длину более длинного основания.
Колея 9
Равнобедренная трапеция имеет периметр 150 см, основание больше 50 см, наклонную сторону 35 см.Рассчитайте длину более короткого основания.
Колея 10
Прямоугольная трапеция имеет основание больше 50 см, имеет меньшее основание 30 см; имеет наклонную сторону 35 см. Рассчитайте периметр и площадь.
Колея 11
Прямоугольник трапеции имеет периметр 180 см; имеет основание больше 60 см, имеет наклонную сторону 50 см; имеет высоту 40 см. Рассчитайте длину более короткого основания.
Колея 12
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет высоту 40 см. Рассчитайте длину более длинного основания.
Рассчитайте длину более длинного основания.
Колея 13
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет высоту 40 см; имеет базу больше 60 см. Рассчитайте длину скошенной стороны.
Колея 14
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет базу больше 60 см. Рассчитывает длину высоты.
Колея 15
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет высоту 4 см.Рассчитайте меньшую базу.
Колея 16
Равнобедренная трапеция имеет меньшее основание 14 см; имеет скошенную сторону 5 см; имеет высоту 4 см. Вычисляет большую базу.
Колея 17
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет выступ скошенной стороны на большее основание 3 см. Рассчитайте периметр.
Колея 18
Равнобедренный треугольник имеет меньшее основание 14 см; имеет наклонную сторону 5 см. Имеет экранирование наклонной стороны на большем основании 3 см.Рассчитайте периметр.
Трасса 19
Равнобедренная трапеция имеет площадь 2400 см, высоту 40 см, основы составляют треть от другой. Определите периметр.
Дорожка 20
Трапеция образована квадратом и треугольником. Учитывая, что площадь треугольника составляет 6 см, а разница между основаниями трапеции составляет 4 см, рассчитайте площадь трапеции.
Колея 21
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание большее 90 см, имеет меньшее основание, равное 2/3 большего основания.Рассчитайте периметр.
Колея 22
Прямоугольная трапеция эквивалентна 1/4 квадрата с периметром 160 см. Учитывая, что высота трапеции составляет 20 см и 6 см, рассчитайте площадь прямоугольника, размеры которого совпадают с размерами оснований трапеции.
Направляющая 23
Прямоугольник в форме трапеции, описанный по кругу, длина скошенной стороны составляет 40 см, а высота равна 3/5 наклонной стороны.Рассчитайте периметр и площадь трапеции.
Дорожка 24
Площадь трапециевидного прямоугольника составляет 2250 см. Зная, что разница размеров проекции наклонной стороны на большее основание и высоты составляет 15 см, а их соотношение составляет 3/4, рассчитайте периметр трапеции.
Трасса 25
Периметр равнобедренной трапеции 250 см, высота 30 см, меньшее основание на 4/7 большего, чем косая сторона.Вычислите площадь трапеции.
Колея 26
Большая база прямоугольной формы трапеции со скошенной стороной под углом 45; зная, что основания 25 см и 15 см, вычисляет площадь трапеции.
Трасса 27
Равнобедренная трапеция ABCD образована тремя равнобедренными равнобедренными треугольниками, периметр каждого из которых равен 170 см, а наклонная сторона составляет 6/5 основания. Рассчитайте периметр трапеции.
Рассчитайте периметр трапеции.
Дорожка 28
Равнобедренная трапеция ABCD имеет площадь 900 см. Основание AB является двойным, его высота составляет 20 см. Определите площадь треугольника ACD
Track 29
В равнобедренной трапеции площадь равна 1032 см, а два основания имеют размер 61 см и 25 см соответственно. Вычислите меру высоты и периметра.
Колея 30
В прямоугольной трапеции со скошенной стороной образует большое основание под широким углом 30.Две базы размером 50 см и 30 см соответственно определяют периметр и площадь трапеции.
Track 31
В равнобедренной трапеции сумма и разница размеров двух оснований составляет соответственно 74 см и 14 см. Вычисляет площадь и периметр трапеции, зная, что наклонная сторона равна 25 см.
Колея 32
Периметр равнобедренной трапеции 176 см. Зная, что меньшее основание составляет 4/3 наклонной стороны, а большее основание составляет 19/10 меньшего основания, вычисляется площадь трапеции.
Трасса 33
Каждая из наклонных сторон равнобедренной трапеции составляет треть меньшего основания. Зная, что периметр равен 230 см, а наибольшее основание — 105 см, вычисляется размер меньшего основания и площадь трапеции.
Колея 34
В прямоугольной трапеции нижняя диагональ перпендикулярна наклонной стороне. Зная, что эта диагональная линия и наклонная сторона 24 см и 18 см соответственно, найдите периметр и площадь трапеции.
Колея 35
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30. Рассчитайте периметр трапеции, зная, что высота 11,56 см, а площадь 462,42 см.
Направляющая 36
В трапеции главное основание и вспомогательное основание имеют длину 55 см и 30 см, а периметр — 140 см. Определяет длину наклонных сторон, зная, что одна составляет 6/5 другой.
Колея 37
Разница между основаниями равнобедренной трапеции составляет 30 см, меньшее основание — 5/8 большего основания, периметр — 180 см.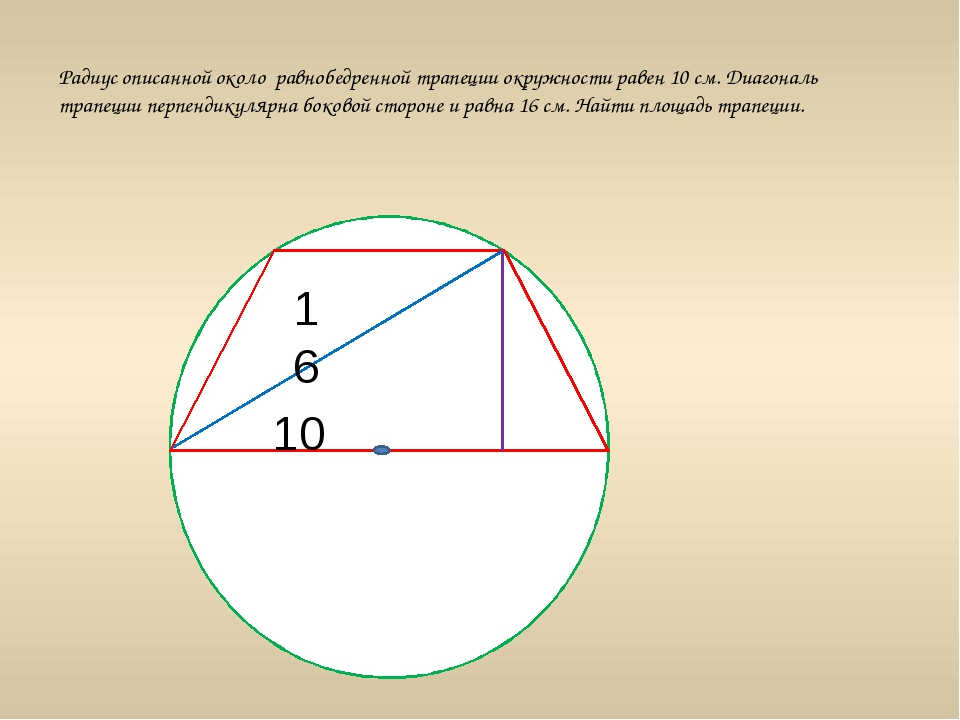 Рассчитывает размер наклонных сторон.
Рассчитывает размер наклонных сторон.
Track 38
Вы знаете, что у равнобедренной трапеции: а) высота составляет 20 см. б) разница между двумя базами 30 см. в) основание больше 80 см. Рассчитайте периметр и площадь трапеции.
Колея 39
Периметр трапеции, имеющей высоту 34,60 см, составляет 203,49 см. Вычислите площадь трапеции, зная, что наклонные стороны образуют с большим основанием острые углы шириной 45 и 60.
Дорожка 40
Площадь трапециевидного прямоугольника составляет 1080 квадратных сантиметров, а высота — 24 см. Вычислите размеры двух оснований, зная, что периметр равен 140 см.
Колея 41
Периметр равнобедренной трапеции составляет 152 см, а длина скошенной стороны — 26 см. Вычислите высоту и площадь трапеции, зная, что меньшее основание имеет длину 40 см.
Направляющая 42
В прямоугольной трапеции основное основание, меньшее основание и высота имеют длину соответственно 60 см, 50 см и 24 см.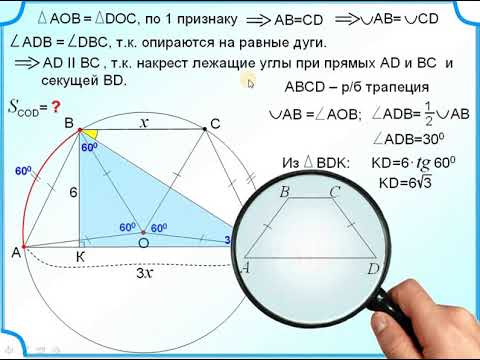 Вычисляет площадь и периметр трапеции.
Вычисляет площадь и периметр трапеции.
Track 43
Вычислите площадь трапеции, у которой большее основание составляет 8/5 меньшего основания, что, в свою очередь, равно высоте, составляющей 50 см.
Колея 44
Сумма оснований трапеции 80 см, основание 5/3 другого, высота 2/3 вспомогательного основания. Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что одна диагональ равна 25/16 другой.
Дорожка 45
Трапеция образована квадратом со стороной 48 см и двумя треугольниками, катет которых совпадает с одной из двух противоположных сторон квадрата. Гипотенуза двух треугольников составляет 60 см и 50 см соответственно. Рассчитайте периметр и площадь трапеции.
Колея 46
Разносторонняя трапеция имеет периметр 180 см; вычисляет все стороны, зная, что AB = 8/5 DC, DC — AB = 30 см, AD = 2/5 DC.
Track 47
У равнобедренной трапеции ABCD основание CD составляет 15/22 большего основания, наклонные стороны превышают 7 см 3/5 меньшего основания, периметр составляет 124 см. Какой район?
Какой район?
Направляющая 48
Увеличенное основание, высота и наклонная сторона прямоугольника до трапеции размером 80 см, 48 см и 50 см соответственно. Рассчитайте периметр и площадь трапеции.
Колея 49
Окружность имеет радиус 50 см; две параллельные хорды AB и CD расположены на противоположных частях относительно центра и имеют размер соответственно 96 см и 28 см.Вычисляет площадь и периметр трапеции, в основе которой лежат две хорды.
Колея 50
Равнобедренная трапеция имеет высоту 20 м, основание большее 80 м, меньшее основание 50 м. Вычислите радиус окружности, описанной трапецией.
Дорожка 51
Трапеция имеет основания для диаметра окружности длиной 50 см и параллельной ей веревкой длиной 30 см. Рассчитайте периметр и площадь трапеции.
Дорожка 52
В круге с радиусом 50 см сделайте две параллельные хорды, расположенные на противоположных сторонах относительно центра и на расстоянии 14 см и 48 см от него соответственно. Вычисляет площадь и периметр трапеции, у которой есть основания для двух струн.
Колея 53
Прямоугольник и равнобедренная трапеция равны по высоте, периметр прямоугольника 140 см, разница размеров прямоугольника между ними 30 см, наклонная сторона трапеции 25 см.Вычислить:
размер оснований прямоугольника;
протяженность оснований трапеции;
площадь трапеции и прямоугольника;
периметр трапеции.
Направляющая 54
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует наклонной стороне, зная, что площадь трапеции составляет 1320 см.
Направляющая 55
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 28 и 8 см.Вычислите периметр, площадь и две диагонали.
Направляющая 56
Прямоугольная трапеция имеет высоту 24 см и основания соответственно 18 и 10 см. Вычислите периметр, площадь и две диагонали.
Колея 57
Прямоугольная трапеция, сумма оснований 110 см, высота 24 см. Рассчитывает площадь.
Трасса 58
Равнобедренная трапеция, сумма оснований 110 см, высота 24 см.Рассчитывает площадь.
Трасса 59
Равнобедренная трапеция имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Дорожка 60
Прямоугольник трапеции имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Колея 61
Равнобедренная трапеция имеет большее основание 50 см, меньшее основание 30 см. Рассчитайте высоту, зная, что наклонная сторона равна 26 см.
Колея 62
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Вычислите радиус круга, вписанного в трапецию, зная, что высота равна 24 см.
Колея 63
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 64
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см.Вычислите радиус круга, вписанного в трапецию, зная, что высота равна 24 см.
Колея 65
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 66
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Рассчитайте диаметр круга на трапеции, зная, что высота равна 48.75 дюймов.
Колея 67
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите длину круга, окружающего трапецию, зная, что высота составляет 48,75 дюйма.
Колея 68
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите площадь описанной круговой трапеции, зная, что высота составляет 48,75 дюйма.
Колея 69
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см.Вычислите:
площадь круга, описанного трапецией, зная, что высота составляет 48,75 дюйма;
расстояние от центра хорды AB;
расстояние каната от центра CD;
длина дуги АВ;
длина дуги CD;
центральный угол АОБ;
центральный угол ХПК;
площадь кругового сектора AOB; площадь кругового сектора наложенным платежом.
Направляющая 70
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1320 см.
Направляющая 71
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого равен диагонали, зная, что площадь трапеции составляет 1320 см.
Направляющая 72
Прямоугольная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см.Вычислите радиус окружности, соответствующей трапеции.
Направляющая 73
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Колея 74
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 75
Прямоугольник трапеции имеет периметр 160 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Колея 76
Прямоугольник трапеции имеет основное основание 60 см, меньшее основание 50 см и высоту 24 см. Вычислите площадь окружности, имеющей изопериметрическую длину окружности трапеции.
Направляющая 77
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1320 см.
Колея 78
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1440 см.
Трасса 79
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 80
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует малой диагонали, зная, что площадь трапеции составляет 1320 см.
Трасса 81
Равнобедренная трапеция имеет высоту 10 см и основания, которые являются одним из 7/17 другого.Вычислите площадь круга, радиус которого равен диагонали, зная, что площадь трапеции составляет 240 см.
Дорожка 82
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Трасса 83
Равнобедренная трапеция имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Направляющая 84
Прямоугольник в форме трапеции имеет площадь 360 см и основания соответственно 10 см и 20 см. Вычислите площадь круга, диаметр которого меньше диагонали трапеции.
Track 85
Равнобедренная трапеция имеет площадь 240 см и основания соответственно 34 см и 14 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 86
Равнобедренная трапеция имеет периметр 186 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см.Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Трасса 87
Равнобедренная трапеция имеет большое основание 70 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь окружности, имеющей изопериметрическую длину окружности трапеции.
Track 88
Рассчитайте площадь и периметр разносторонней трапеции, зная, что большее основание составляет 80 см, а меньшее основание — 50 см, а наклонные стороны имеют длину соответственно 30 см и 20 см.
Колея 89
Равнобедренная трапеция имеет меньшее основание 8,4 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 90
Прямоугольная трапеция имеет меньшее основание 19,2 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 91
Прямоугольник в форме трапеции имеет наклонную сторону 18 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 92
Равнобедренная трапеция имеет наклонную сторону 18 см и выступание наклонной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 93
Равнобедренная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 94
Прямоугольная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 95
Прямоугольная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 96
Равнобедренная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 97
Периметр равнобедренной трапеции составляет 204 см, а каждая наклонная сторона — 30 см.Вычислите площадь и протяженность оснований, зная, что большее — это 5/3 второстепенного.
Колея 98
Основание большей формы равнобедренной трапеции с косой стороной под углом 45; зная, что основания 35 см и 15 см, вычисляет площадь и периметр трапеции.
***********
Оптимизация. После того, как вы освоите деривативы… | Соломон Се | Основы исчисления
Как только вы освоите производные, вы поймете, что задачи оптимизации просты.
Это просто прогресс, чтобы получить максимальных или минимальных баллов для данной функции.
Решить:
- Разобраться в вопросе непросто.
- Сформируйте функцию:
P (x) = x (a-x) = ax - x² - Чтобы получить максимум, необходимо сначала найти критические точки.
- Установите
P '(x) = 0, затем получитеx = a / 2. - Для выполнения второго производного теста:
P '' (x) = -2, означает, что это вогнутая вниз - Таким образом, критическая точка
a / 2является максимумом.
Q: Какова площадь самой большой трапеции, которую можно вписать в полукруг с радиусом r = 1 ?
См. Видео Кристакинга: Наибольшая область прямоугольника, вписанного в полукруг
Понимание:
- Для этой задачи
Трапеция, вписанная в круг, вы действительно хотите нарисовать ее прежде всего. Обратитесь к этому анимированному инструменту из Геогебра, которую я создал для этой задачи. - Помните, что трапеция
- Знайте, что четырехугольник
- Трапеция максимальной площади, вписанная в полукруг, будет иметь основание на оси X. Это означает, что длина нижнего основания
b₁ = 2 · r - Поскольку это трапеция
- Зная все вышеперечисленные условия, вы можете начать абстрагировать информацию в уравнения.
- Сначала получите представление о результате, затем посмотрите, чего не хватает, и найдите способ получить это.
Решите:
- Сначала сформируйте уравнение площади трапеции:
A = 1/2 · (b₁ + b₂) · h -
b₁— нижнее основание, которое равно2r = 2, потому что трапеция с наибольшей площадью, вписанная в круг, ДОЛЖНА: - положить свое основание на ось X
- , равное диаметру (потому что это самая длинная длина основания)
- симметрично относительно оси Y (потому что два основания параллельны )
- Предположим, что одна из
вершинна верхнем основании —(x, y). - Поскольку два основания параллельны, поэтому верхнее основание также симметрично, это означает, что оно имеет одинаковое расстояние до вершин обеих сторон, из чего можно сделать вывод, что:
- Другая вершина
(- х, у). - Длина верхнего основания должна быть
b₂ = x - (-x) = 2x -
h— высота трапеции, которая равна значениюyверхней вершины. - Таким образом, уравнение принимает следующий вид:
A = 1/2 · (2r + 2x) · y. - Нам нужно сформировать функцию как
Area в x, это означает, что Area изменится с изменениемx. Таким образом,yдолжно преобразоваться в членx. - Поскольку
(x, y)— точка окружности, стандартная формула окружности должна работать:x² + y² = r² - Тогда мы получаем:
y = √ (r²-x²) = √ (1-x²) - Итак, окончательная функция выглядит так:
A (x) = 1/2 · (2r + 2x) · √ (r²-x²) = (1 + x) · √ (1- x²) - Вернемся к началу, поскольку мы должны найти наибольшую площадь, поэтому он говорит, что мы должны найти максимальное значение функции
A (x). - Установите
A '(x) = 0, чтобы сначала найти критическую точку. После решения первой производной, применяя правило произведения, мы получаем:x = -1 или 1/2. - Поскольку
x— это длина, это положительное значение, поэтомуx = 1/2. Тогдаy = √ (1-x²) = √3 / 2 - Выполните тест второй производной
A '' (x) <0. - Подставляем значения обратно в уравнение площади, получаем
A = 3√3 / 4
Решаем:
- Предположим, что площадь внутреннего прямоугольника (тексты) равна
T = w · h = 150 - Таким образом, площадь бумаги должна быть
A = (w + 2) · (h + 3) - Пусть
h = T / w = 150 / w - Таким образом, функция площади должна быть
A (w) = (w + 2) · (150 / w +3) - Для получения наименьшего значения площади нам нужно сначала найти критические точки:
- Установите
A '(w) = 0, и дифференцируя функцию, получаем:A '(w) = 3 - 300 / w²иw = 10.
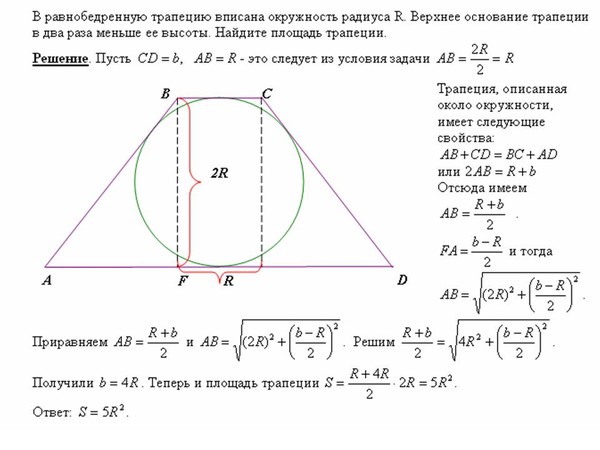 Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы его длин противоположных сторон равны. [6]
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы его длин противоположных сторон равны. [6]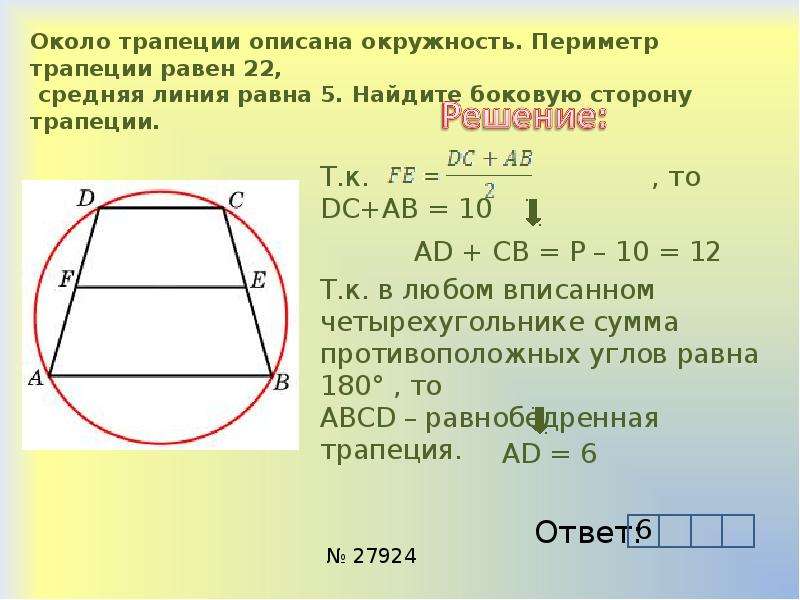 Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: [15]
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: [15]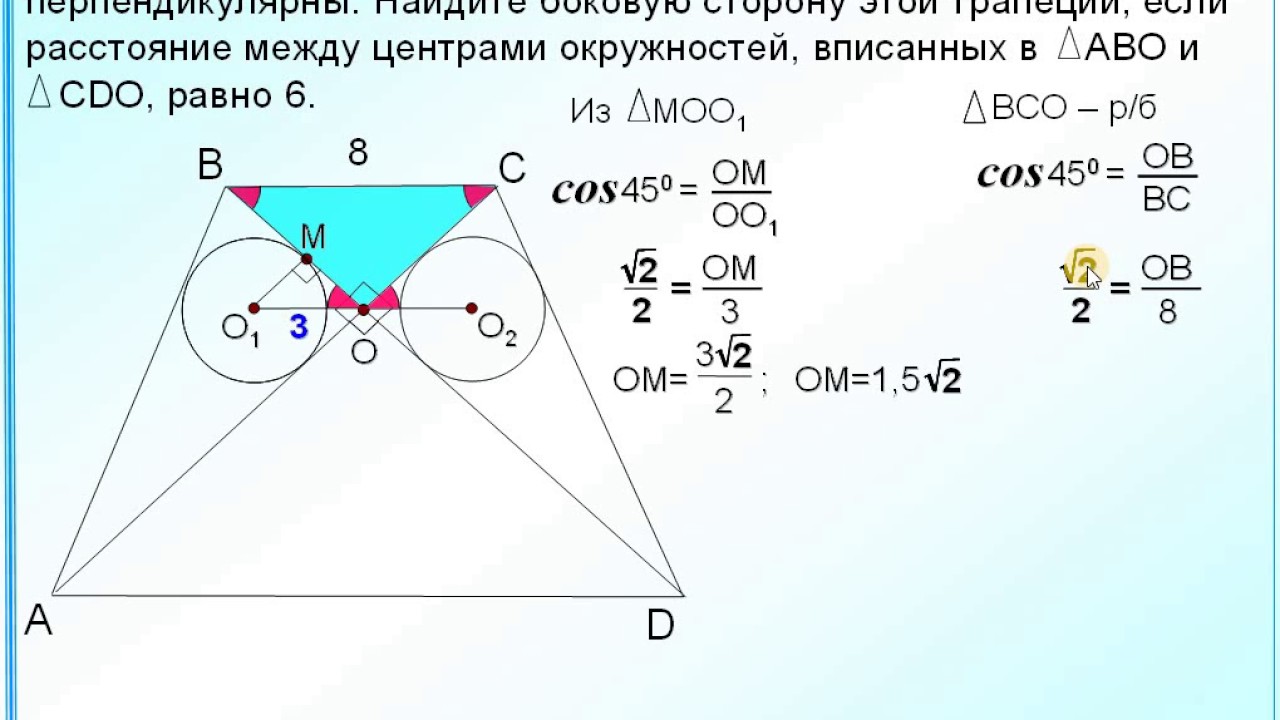 [15]
[15] Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.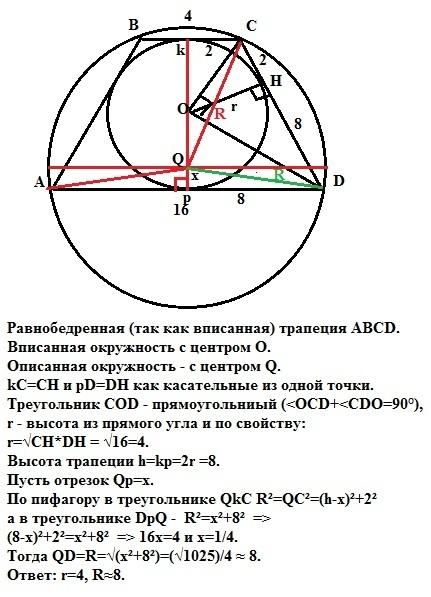 [15]
[15]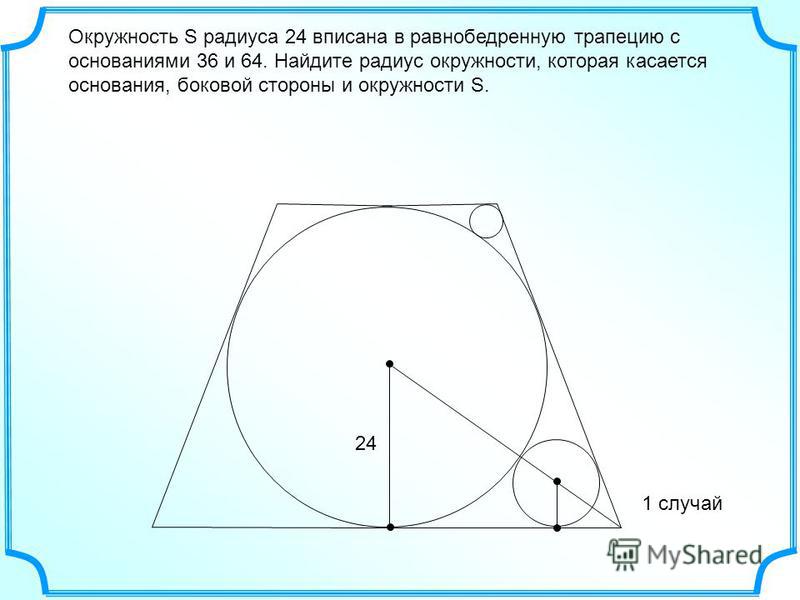
 Т.Д.
Т.Д. Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: [15]
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: [15] [15]
[15] Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.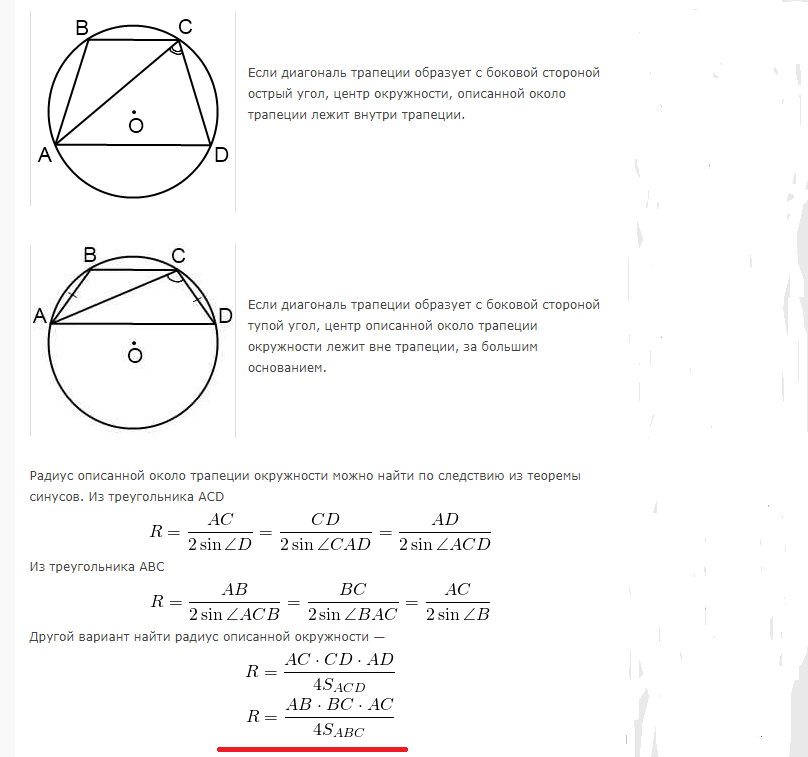 Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. [15]
Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. [15] Решение задач.
Решение задач.








 А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 . Она пересекает основания в точках Х и Т.
Она пересекает основания в точках Х и Т.

 И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции.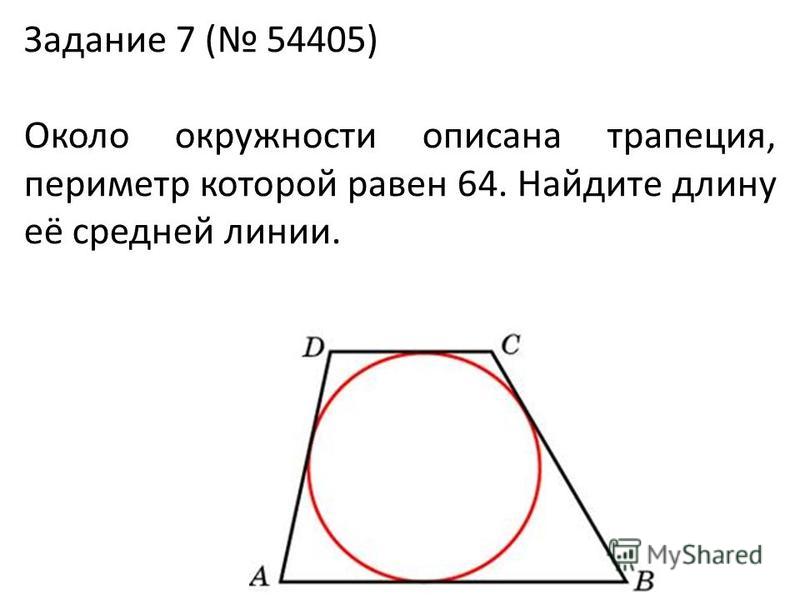

 В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).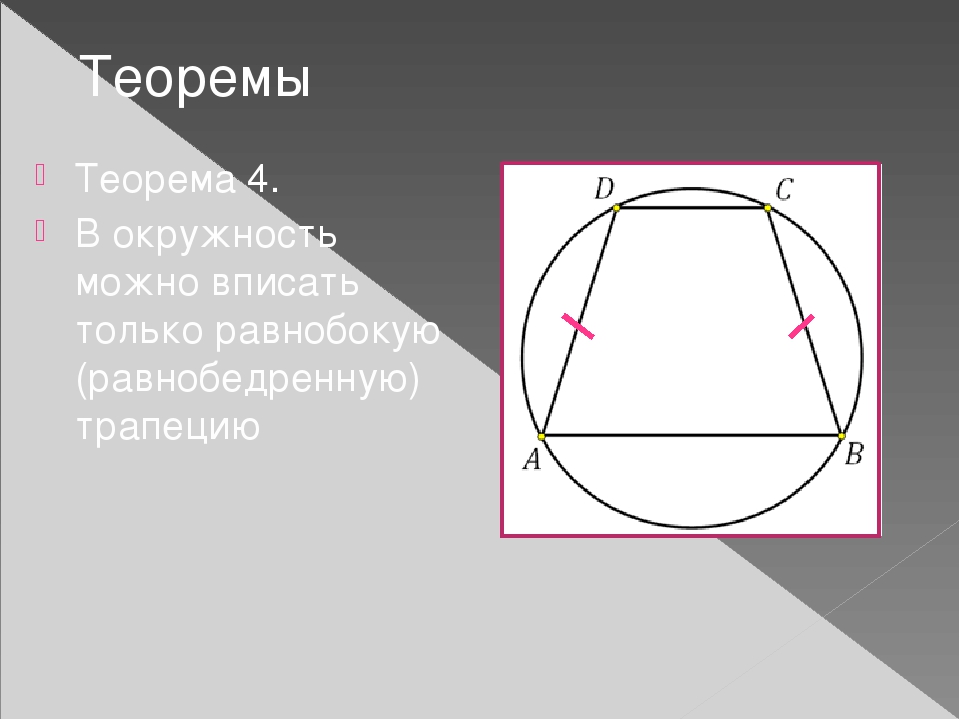 А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .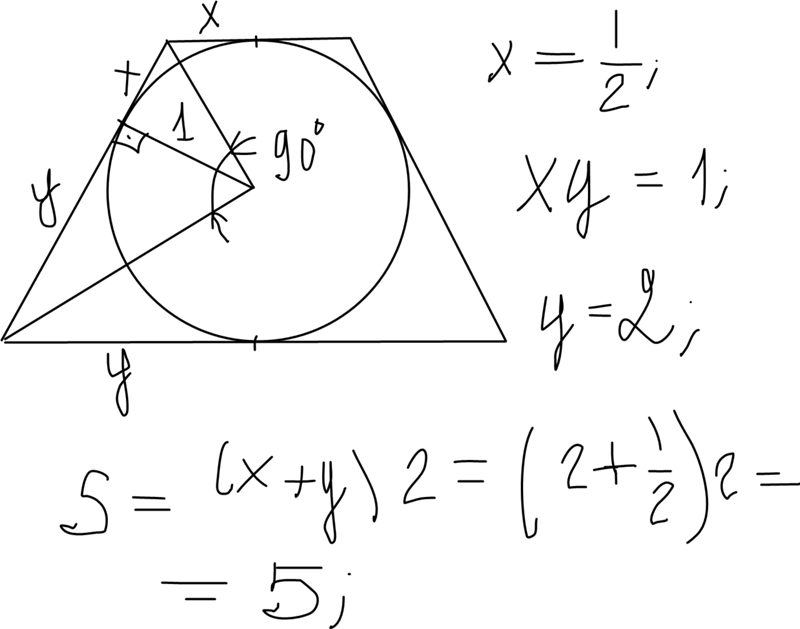 Она пересекает основания в точках Х и Т.
Она пересекает основания в точках Х и Т.
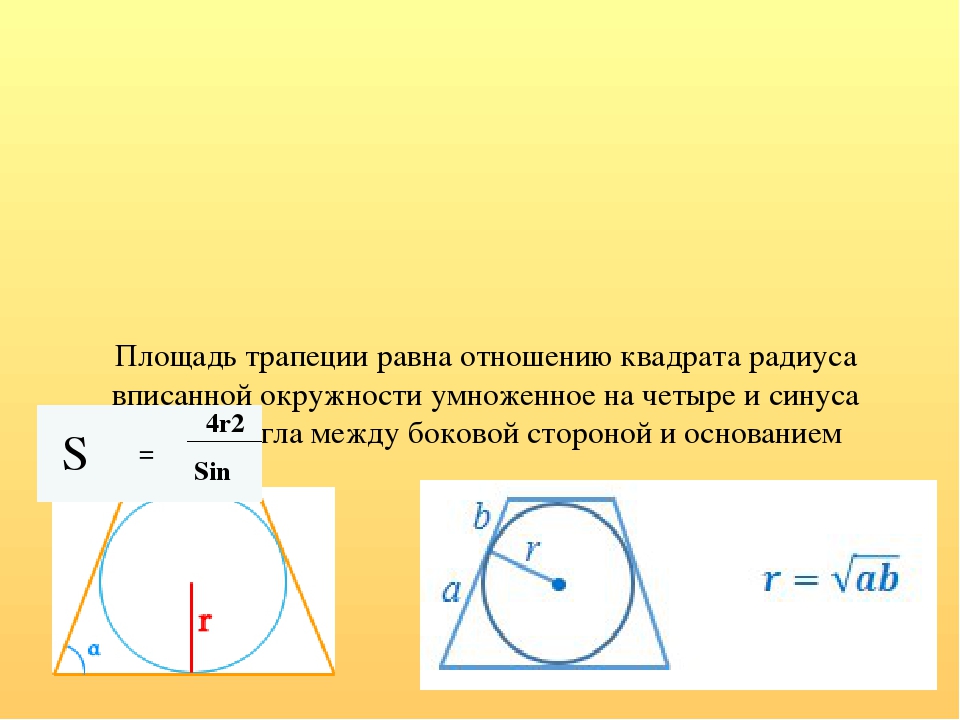
 И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции.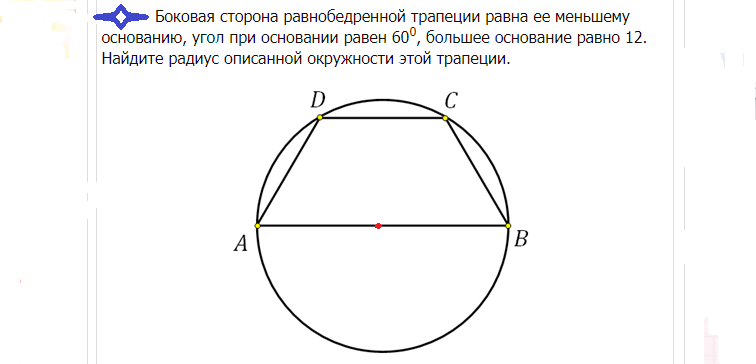

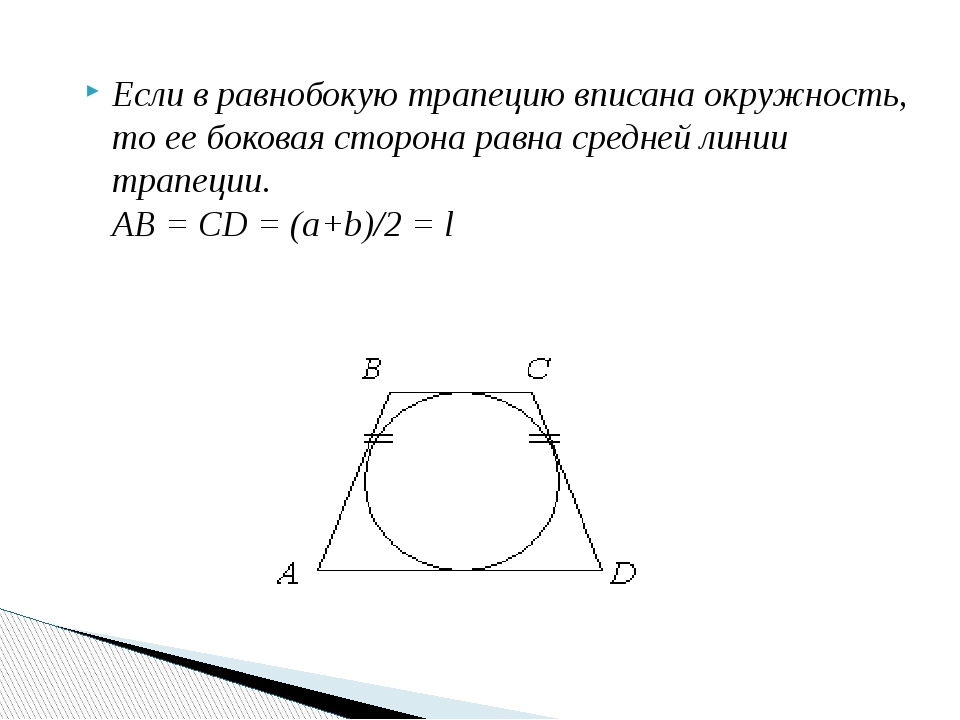 В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).