морфемный разбор — Какой корень в слове «мальчик»?
Это не совсем моя тема, но всё-таки у меня есть вопросы к первому ответу.
Я сомневаюсь, что в этом слове корень МАЛ, скорее здесь верна информация из словаря Тихонова: корень «мальчик».
Надо хотя бы дать определение корня. Допустим, это наименьшая общая часть родственных слов, передающая его основное значение.
МАЛ – это действительно наименьшая общая часть исторически родственных слов, но вот значение слов маленький и мальчик в современном языке не совпадают. Прилагательное маленький может даже определять существительное мальчик: маленький мальчик.
Слово малый в словаре также отодвинули на задний план, оно чаще употребляется в краткой форме. Теперь на непроизводное слово с основным значением «небольшой» больше претендует прилагательное маленький
МАЛЬЧИК, м. 1. Ребёнок, подросток мужского пола.
МАЛЕНЬКИЙ, 1. Незначительный по величине, размерам (противоп.: большой). М-ая комната. М. стол. // Невысокого роста. (противоп.: высокий). М. человек. М. мальчик. М-ая лошадка.
Что касается формального словообразования, то верно мал/ец – мальч/ик, здесь суффикс ИК, а не ЧИК. Суффикс ЧИК используется для образования существительных от существительных.
«Малец» и «мальчуган» (в современном языке) образуются от слова «мальчик» при усечении основы, это его стилистические варианты: МАЛЕЦ, м. Разг. Мальчик, подросток.
А история такая: «малый» известно с XI века, «маленький» – с XVII века, а «мальчик» (в форме малчик) зафиксировано в словаре в 1731 году.
ДОПОЛНЕНИЕ
Разыскала я старый словарь Тихонова (1978 год), где слова расположены по гнездам. Там всё убедительно выглядит.
Там всё убедительно выглядит.
Обозначены два гнезда: малый и мальчик. Это непроизводные основы, в них суффикс не выделяется.
Далее от малый образуются слова с корнем МАЛ: маленький, мало, малыш, малютка, умалить, а также сложные слова (малолюдный, маломощный).
От мальчик образуются слова с корнем МАЛЬЧ: мальчишка, мальчонка, мальчишеский и т.д.
перевод, произношение, транскрипция, примеры использования
Он не располагал никакой ценной информацией.
Она ценит время которое проводит со своей семьей.
Они возместили ему стоимость пропавшего имущества.
Шелли дорожила своим личным пространством.
Это красивый ковёр — он не должен падать в цене.
Практическая ценность его исследований незначительна.
The herbs are valued for their medicinal properties.
Эти травы ценятся за их целебные свойства.
The home has a value of $1,000,000.
Этот дом стоит миллион долларов.
You may exchange the item for something of equal value.
Товар можно обменять на что-то равной стоимости /равноценное/.
Every one is in danger of valuing himself for what he does. (J. H. Newman)
В жизни каждого человека есть опасность возгордиться в связи с тем, что он делает.
The lunch special is really good value.
Спецменю — очень выгодная вещь.
No one can deny the value of a good education.
Никто не может отрицать ценность хорошего образования.
The dollar has been steadily increasing in value.
Доллар неуклонно растёт в цене.
An economist knows the value of everything and the cost of nothing.
Экономист отлично знает ценность любой вещи, но о ее цене не имеет ни малейшего представления.
The items are highly valued by collectors.
Эти предметы высоко ценятся коллекционерами.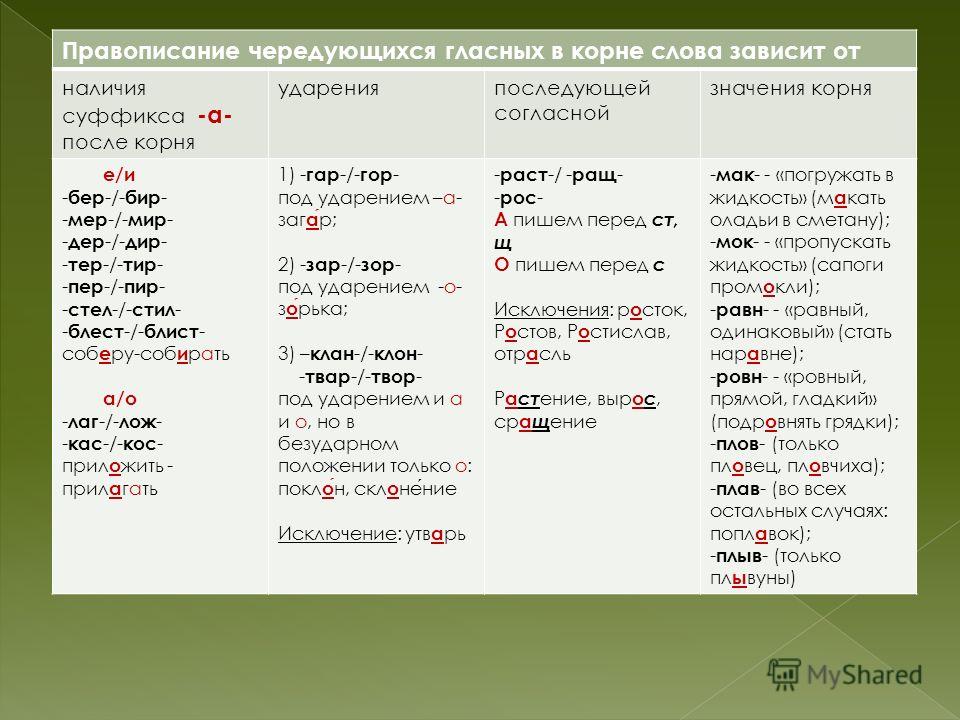
The parties agreed to employ an appraiser to value the company.
Стороны согласились нанять оценщика, чтобы оценить компанию.
We sold the home for less than its full value.
Мы продали дом дешевле его полной стоимости.
Let x have the value 25.
Пусть x равен двадцати пяти.
A group of athletes spoke to the students about the value of a college education.
Группа спортсменов рассказала студентам о важности университетского образования.
We decided to get the house valued.
Мы решили произвести оценку дома.
The company’s stock continues to decline in value.
Акции компании продолжают падать в цене.
Every customer is looking for value for money.
Каждый покупатель хочет, чтобы купленный товар стоил своих денег.
an increase in the value of the dollar
увеличение стоимости доллара
The alterations doubled the value of the house.
Эти изменения удвоили стоимость дома.
The locket has great sentimental value (=importance because it was a gift, it reminds you of someone etc).
Этот медальон очень дорог (моему) сердцу (т.е. он важен, потому что это был подарок, он напоминает о ком-то и т.д).
The store advertises great values.
Магазин рекламирует товары по отличным ценам.
Mr. Yeo valued Jan for her hard work.
Мистер Йо ценил Джен за её нелегкий труд.
value the jewelry and art work in the estate
оценить стоимость ювелирных изделий и произведений искусства в имении
The Sioux Indians placed a high value on generosity.
Индейцы сиу придавали большое значение щедрости.
Презентация к уроку русского языка 3 класса по теме «Корень слова»
Подготовила : Артемьева Н.А. учитель начальных классов
С. Красные Четаи 2020 г.
»
Орфографическая минутка
К расная площадь, м о роз, Р о сс ия, м е тро, м

К О Р Е Н Ь
Величина в
математике
Начало, происхождение рода, поколения
БУДЕМ УЧИТЬСЯ:
1 .ОПРЕДЕЛЯТЬ ЛЕКСИЧЕСКОЕ ЗНАЧЕНИЕ СЛОВА
2.ПОДБИРАТЬ РОДСТВЕННЫЕ СЛОВА
3.НАХОДИТЬ ОБЩУЮ ЧАСТЬ СЛОВ(КОРЕНЬ).
ПРОВЕРКА
осиновый
осинник
осинки
осины
подосиновик
18 октября.
Классная работа .
У у
Ученик
Словарный диктант
АЛГОРИТМ
- 1.Подобрать однокоренные слова.
- 2. Выделить общую главную часть- корень.
- 3.Корень в однокоренных словах пишется одинаково.
1
2
3
4
Сегодня на уроке я узнал … Урок заставил меня задуматься о … Я понял, что … Мне было интересно, потому что…
Спиши 1 из высказываний и продолжи предложение
»
Домашнее задание: выучить правила стр.56,59 упр.133
Запишите на листочек любые
1-2 цепочки однокоренных слов
Спасибо
за урок !
Основы теории вероятностей для актуариев
Вероятность: основные правила
Формула полной вероятности
Формула Байеса
Случайные величины и их характеристики
Время жизни как случайная величина
Функция выживания
Характеристики продолжительности жизни
Аналитические законы смертности
Все на свете происходит детерминировано или случайно…
Аристотель
Вероятность: основные правила
Теория вероятностей вычисляет вероятности различных событий. Основным в теории вероятностей является понятие случайного события.
Основным в теории вероятностей является понятие случайного события.
Например, вы бросаете монету, она случайным образом падает на герб или решку. Заранее вы не знаете, на какую сторону монета упадет. Вы заключаете договор страхования, заранее вы не знаете, будут или нет проводиться выплаты.
В актуарных расчетах нужно уметь оценивать вероятность различных событий, поэтому теория вероятностей играет ключевую роль. Ни одна другая область математики не может оперировать с вероятностями событий.
Рассмотрим более подробно подбрасывание монеты. Имеется 2 взаимно исключающих исхода: выпадение герба или выпадение решки. Исход бросания является случайным, так как наблюдатель не может проанализировать и учесть все факторы, которые влияют на результат. Какова вероятность выпадения герба? Большинство ответит ½, но почему?
Пусть формально А обозначает выпадение герба. Пусть монета бросается n раз. Тогда вероятность события А можно определить как долю тех бросков, в результате которых выпадает герб:
(1)
где n общее количество бросков, n(A) число выпадений герба.
Отношение (1) называется частотой события А в длинной серии испытаний.
Оказывается, в различных сериях испытаний соответствующая частота при больших n группируется около некоторой постоянной величины Р(А). Эта величина называется вероятностью события
Формально имеем:
(2)
Этот закон называется законом больших чисел.
Если монета правильная (симметричная), то вероятность выпадения герба равняется вероятности выпадения решки и равняется ½.
Пусть А и В некоторые события, например, произошел или нет страховой случай. Объединением двух событий называется событие, состоящее в выполнении события А, события В, или обоих событий вместе. Пересечением двух событий А и В называется событие, состоящее в осуществлении как события А, так и события В.
Пересечением двух событий А и В называется событие, состоящее в осуществлении как события А, так и события В.
Основные правила исчисления вероятностей событий следующие:
1. Вероятность любого события заключена между нулем и единицей:
2. Пусть А и В два события, тогда:
(3)
Читается так: вероятность объединения двух событий равна сумме вероятностей этих событий минус вероятность пересечения событий. Если события являются несовместными или непересекающимися, то вероятность объединения (суммы) двух событий равна сумме вероятностей. Этот закон называется законом сложения вероятностей.
Мы говорим, что события является достоверным, если его вероятность равна 1. При анализе тех или иных явлений возникает вопрос, как влияет наступление события В на наступление события А. Для этого вводится условная вероятность:
(4)
Читается так: вероятность наступления А при условии В равняется вероятности пересечения А и В, деленной на вероятность события В.
В формуле (4) предполагается, что вероятность события
Формулу (4) можно записать также в виде:
(5)
Это формула умножения вероятностей.
Условную вероятность называют также апостериорной вероятностью события А – вероятность наступления А после наступления В.
В этом случае саму вероятность называют априорной вероятностью. Имеется еще несколько важных формул, которые интенсивно используются в актуарных расчетах.
Формула полной вероятности
Допустим, что проводится опыт, об условиях которого можно заранее сделать взаимно исключающие друг друга предположения (гипотезы):
Мы предполагаем, что имеет место либо гипотеза , либо … либо. Вероятности этих гипотез известны и равны:
Вероятности этих гипотез известны и равны:
Тогда имеет место формула полной вероятности:
(6)
Вероятность наступления события А равна сумме произведений вероятности наступления А при каждой гипотезе на вероятность этой гипотезы.
Формула Байеса
Формула Байеса позволяет пересчитывать вероятность гипотез в свете новой информации, которую дал результат А.
Формула Байеса в известном смысле является обратной к формуле полной вероятности.
(7)
Рассмотрим следующую практическую задачу.
Задача 1
Предположим, произошла авиакатастрофа и эксперты заняты исследованием ее причин. Заранее известны 4 причины, по которым произошла катастрофа: либо причина, либо , либо , либо . По имеющейся статистике эти причины имеют следующие вероятности:
При осмотре места катастрофы найдены следы воспламенения горючего, согласно статистике вероятность этого события при тех или иных причинах такая:
Вопрос: какая причина катастрофы наиболее вероятна?
Вычислим вероятности причин при условия наступления события А.
Отсюда видно, что наиболее вероятной является первая причина, так как ее вероятность максимальна.
Задача 2
Рассмотрим посадку самолета на аэродром.
При посадке погодные условия могут быть такими: низкой облачности нет (), низкая облачность есть (). В первом случае вероятность благополучной посадки равна P1. Во втором случае – Р2. Ясно, что P1>P2.
Приборы, обеспечивающие слепую посадку, имеют вероятность безотказной работы Р. Если есть низкая облачность и приборы слепой посадки отказали, вероятность удачного приземления равна Р3, причем Р3<Р2. Известно, что для данного аэродрома доля дней в году с низкой облачностью равна .
Известно, что для данного аэродрома доля дней в году с низкой облачностью равна .
Найти вероятность благополучной посадки самолета.
Имеем:
Нужно найти вероятность .
Имеются два взаимно исключающих варианта: приборы слепой посадки действуют, приборы слепой посадки отказали, поэтому имеем:
Отсюда по формуле полной вероятности:
Задача 3
Страховая компания занимается страхованием жизни. 10% застрахованных в этой компании являются курильщиками. Если застрахованный не курит, вероятность его смерти на протяжении года равна 0.01 Если же он курильщик, то эта вероятность равна 0.05.
Какова доля курильщиков среди тех застрахованных, которые умерли в течение года?
Варианты ответов: (А) 5%, (Б) 20%, (В) 36 %, (Г) 56%, (Д) 90%.
Решение
Введём события:
-
= {застрахованный – курильщик}
-
= {застрахованный – не курильщик}
-
= {застрахованный умер в течение года}
Условие задачи означает, что
Кроме того, поскольку события и образуют полную группу попарно несовместимых событий, то .
Интересующая нас вероятность – это .
Используя формулу Байеса, мы имеем:
поэтому верным является вариант (В).
Задача 4
Страховая компания продаёт договора страхования жизни трёх категорий: стандартные, привилегированные и ультрапривилегированные.
50% всех застрахованных являются стандартными, 40% — привилегированными и 10% — ультрапривилегированными.
Вероятность смерти в течение года для стандартного застрахованного равна 0.010, для привилегированного – 0.005, а для ультра привилегированного – 0. 001.
001.
Чему равна вероятность того, что умерший застрахованный является ультрапривилегированным?
Решение
Введем в рассмотрение следующие события:
-
= {застрахованный является стандартным}
-
= {застрахованный является привилегированным}
-
= {застрахованный является ультрапривилегированным}
-
= {застрахованный умер в течение года}
В терминах этих событий интересующая нас вероятность – это . По условию:
Поскольку события , , образуют полную группу попарно несовместимых событий, используя формулу Байеса мы имеем:
Случайные величины и их характеристики
Пусть некоторая случайная величина, например, ущерб от пожара или величина страховых выплат.
Случайная величина полностью характеризуется своей функцией распределения.
Определение. Функция называется функцией распределения случайной величины ξ.
Определение. Если существует такая функция , что для произвольных a<b выполнено
,
то говорят, что случайная величина ξ имеет плотность распределения вероятности f(x).
Определение. Пусть . Для непрерывной функции распределения F теоретической α-квантилью называется решение уравнения .
Такое решение может быть не единственным.
Квантиль уровня ½ называется теоретической медианой, квантили уровней ¼ и ¾ — нижней и верхней квартилями соответственно.
В актуарных приложениях важную роль играет неравенство Чебышева:
при любом
— символ математического ожидания.
Читается так: вероятность того, что модуль больше меньше или равняется математическому ожиданию величины модуль , деленному на .
Время жизни как случайная величина
Неопределенность момента смерти является основным фактором риска при страховании жизни.
Относительно момента смерти отдельного человека нельзя сказать ничего определенного. Однако если мы имеем дело с большой однородной группой людей и не интересуемся судьбой отдельных людей из этой группы, то мы находимся в рамках теории вероятностей как науки о массовых случайных явлениях, обладающих свойством устойчивости частот.
Соответственно, мы можем говорить о продолжительности жизни как о случайной величине Т.
Функция выживания
В теории вероятностей описывают стохастическую природу любой случайной величины Т функцией распределения F (x), которая определяется как вероятность того, что случайная величина Т меньше, чем число x:
.
В актуарной математике приятно работать не с функцией распределения, а с дополнительной функцией распределения . Применительно к продолжительной жизни – это вероятность того, что человек доживет до возраста x лет.
Функция
называется функцией выживания (survival function):
Функция выживания обладает следующими свойствами:
- убывает при ;
- ;
- ;
- непрерывна.
В таблицах продолжительности жизни обычно считают, что существует некоторый предельный возраст (limiting age) (как правило, лет) и соответственно при x >.
При описании смертности аналитическими законами обычно считают, что время жизни неограниченно, однако подбирают вид и параметры законов так, чтобы вероятность жизни свыше некоторого возраста была пренебрежимо мала.
Функция выживания имеет простой статистический смысл.
Допустим, что мы наблюдаем за группой из новорожденных (как правило, ), которых мы наблюдаем и можем фиксировать моменты их смерти.
Обозначим число живых представителей этой группы в возрасте через . Тогда:
.
Символ E здесь и ниже используется для обозначения математического ожидания.
Итак, функция выживания равна средней доле доживших до возраста из некоторой фиксированной группы новорожденных.
В актуарной математике часто работают не с функцией выживания , а с только что введенной величиной (зафиксировав начальный размер группы ).
Функция выживания может быть восстановлена по плотности:
Характеристики продолжительности жизни
С практической точки зрения важны следующие характеристики:
1. Среднее время жизни
,
2. Дисперсия времени жизни
,
где
,
Корень квадратный из дисперсии называется стандартным отклонением (standard deviation). Это более удобная величина, чем дисперсия, так как имеет ту же размерность, что исходные данные.
3. Медиана времени жизни , которая определяется как корень уравнения
.
Медиана времени жизни – это возраст, до которого доживает ровно половина представителей исходной группы новорожденных.
Аналитические законы смертности
Для упрощения расчетов, теоретического анализа и т.д. естественно попытаться описать получаемые эмпирическим путем данные о функции выживания или интенсивности смертности с помощью простых аналитических формул.
Простейшее приближение было введено в 1729 году де Муавром (de Moivre), который предложил считать, что время жизни равномерно распределено на интервале , где — предельный возраст.
В модели де Муавра при 0<x<
Сравнение графиков этих функций с реальными графиками функции выживания , функции смертей , интенсивности смертности , показывает, что закон де Муавра является не очень хорошим приближением.
Например, первая формула означает, что кривая смертей является горизонтальной линией, в то время как эмпирические данные указывают на пик в районе 80 лет.
В модели, которую предложил в 1825 году Гомпертц (Gompertz), интенсивность смертности приближается показательной функцией вида , где >0 и B>0 – некоторые параметры. Соответствующая функция выживания имеет вид
,
а кривая смертей:
.
Мэйкхам (Makeham) в 1860 году обобщил предыдущую модель, приблизив интенсивность смертности функцией вида .
Постоянное слагаемое позволяет учесть риски для жизни, связанные с несчастными случаями (которые мало зависят от возраста), в то время как член учитывает влияние возраста на смертность.
В этой модели
,
.
Второй закон Мэйкхама, введенный в 1889 году, приближает интенсивность смертности функцией вида . В этой модели
,
.
Вейбулл (Weibull) в 1939 году предложил приближать интенсивность смертности более простой степенной функцией вида . В этой модели
, .
В практике страхования эти параметры неизвестны и оцениваются по реальным данным.
Связанные определения:
Вероятность события
Независимые повторные испытания Бернулли
Независимые события
В начало
Содержание портала
что это такое, как ее рассчитать, как использовать при оптимизации конверсии
Статистическая значимость часто применяется в маркетинге. С ее помощью определяют правильность выдвинутых предположений и вероятность их результатов. Она позволяет сделать выбор среди представленных теорий, что приводит к получению отличных результатов на практике.
Что такое статистическая значимость
Суть статистической значимости состоит в определении того, существует ли реальное основание в разнице между выбранными для исследования показателями, или это случайность? С данным понятием тесно связаны «нулевая» и «альтернативная» гипотезы.
Для лучшего понимания термина «статистическая значимость» необходимо понять, что такое «проверка гипотез». Эти два термина тесно взаимосвязаны.
Гипотеза иначе называется теорией. После окончания ее разработки требуется установить порядок по сбору достаточного количества доказательств этой теории и собрать их. Существует два типа гипотез: нулевая и альтернативная.
Нулевая гипотеза представляет собой теорию, которая гласит, что внесение коррективов ничего не поменяет, то есть сравниваемые объекты равнозначны в своих свойствах и нет смысла что-либо менять. Суть исследования заключается в опровержении гипотезы.
Альтернативная (исследовательская) гипотеза подразумевает сравнение, в результате которого один объект показывает себя эффективнее, чем другой.
Статистическая значимость как количественный показатель требует оценки. Оценка проходит поэтапно.
Постановка эксперимента
Все начинается с формулировки гипотезы. При этом должно быть выдвижение и нулевой, и альтернативной гипотезы. Придется сравнивать два набора данных для выяснения схожести и отличий. Эти утверждения требуют подтверждения с помощью экспериментальных данных.
Установка уровня
Данный уровень представляет собой порог статистической значимости, который каждый устанавливает сам. Этот уровень носит название displaystyle \alpha }\alpha – уровня. Чаще всего, устанавливают значение в 0,05. Вероятность найти разницу составляет 5%. Чем выше уровень, тем достовернее результаты.
Когда нужна максимальная достоверность, стоит снизить значение с 0,05 до 0,01. Чаще всего, такие показатели применяют в производстве для выявления брака. Однако для большинства экспериментов достаточно значения в 0,05.
Чаще всего, такие показатели применяют в производстве для выявления брака. Однако для большинства экспериментов достаточно значения в 0,05.
Решение об используемом критерии
После установки уровня требуется определить, какой критерий использовать: одно- или двусторонний. Здесь стоит опираться на t-критерии Стьюдента. Они показывают, насколько нормально распределены данные. Графически они представлены в виде колоколообразной кривой. Большее количество результатов расположено в середине.
Критерий Стьюдента позволяет математически проверить расположены ли данные в установленных пределах или же выпадают из нормального распределения.
Двусторонний критерий нужен, когда нет уверенности в том, что показатели находятся выше или ниже установленной нормы распределения.
Когда есть точная уверенность, в каком направлении может наблюдаться выход за пределы нормы, нужно использовать односторонний критерий.
Определение объема выборки
Здесь потребуется статистическая мощность. Она представляет собой вероятность, что при выбранном объеме будет получен ожидаемый результат. Распространенный порог — 80%. Для анализа можно использовать специальные онлайн-калькуляторы. Это позволит определить оптимальный объем выборки.
Часто проводят пробное исследование, которое позволяет получить данные для анализа и установить объем выборки. Когда такой возможности нет, стоит поискать в тематической литературе усредненные значения.
Вычисление стандартного отклонения
Стандартное отклонение показывает величину разброса данных. Оно позволяет сделать выбор о близости или отдаленности данных. Их вычисляют по следующей формуле: s = √∑((xi – µ)2/(N – 1)).
-
s — стандартное отклонение;
-
∑ указывает на необходимость суммировать полученные данные по выборке;
-
xi соответствует значению i, то есть отдельному полученному результату;
-
µ — это среднее значение для данной группы;
-
N — общее число данных в выборке.

Теперь потребуется отыскать среднее значение для каждой группы. Для этого суммируют средние значения каждой группы и делят на объем выборки.
Далее необходимо определить разницу (xi – µ). Для этого следует вычесть из найденной средней величины каждое полученное значение.
Теперь каждую полученную величину умножают на саму себя или возводят во вторую степень и суммируют величины. После этой операции не должно остаться отрицательных значений.
Следующий шаг — деление объема минус один. Делят полученную в предыдущем шаге сумму на величину, полученную от вычитания единицы. После этого извлекают квадратный корень из величины. Это и будет нужная величина стандартного отклонения.
Определение значимости
Для определения значимости потребуется взять две группы данных. Для последней вычисляют стандартное отклонение, после чего вычисляют дисперсию между обеими группами по формуле:
sd = √((s1/N1) + (s2/N2)).
-
sd — дисперсия между двумя группами;
-
s1 — стандартное отклонение в группе 1, N1 — объем выборки в группе 1;
-
s2 — стандартное отклонение в группе 2, N2 — объем выборки в группе 2.
Необходимо определить t-оценку показателей для перевода полученных данных в стандартизированную форму, которая позволить провести сравнение с другими данными. Эта оценка делает возможным проверку t-критерия, а также выяснение величины отличия одной группы от другой. Для определения t-оценки применяют формулу: t = (µ1 – µ2)/sd:
-
µ1 — среднее значение для первой группы;
-
µ2 — среднее значение для второй группы;
-
sd — дисперсия между двумя выборками.

Совет: первым используют большее среднее значение, чтобы итоговая величина не была отрицательной.
Далее требуется определить степень свободы выборки. Для этого вычисляют объем: суммируют объемы двух выборок и вычитают 2. Полученная величина станет окончательной. Ее оценивают по таблице значений критерия Стьюдента (t-критерия). Таблица представлена ниже.
Пользоваться представленной таблицей просто: находите строку в соответствии с полученной степенью свободы и определяете соответствующее t-оценке Р-значение.
Например, при степени свободы 8 и t-оценке 2,61 Р-значение для одностороннего критерия попадает между 0,01 и 0,025. При выбранном показателе в 0,05 эти данные попадают в категорию «статистически значимые». Это помогает сделать выбор в пользу альтернативной гипотезы и отказаться от нулевой.
Заключение
Определение статистической значимости помогает решать маркетинговые задачи и минимизировать риски. Такие расчеты часто проводятся при A/B тестированиях и помогают узнать, как будет вести себя клиент в будущем, окупится ли товар и т.д.
Веласкес в натуральную величину – Газета Коммерсантъ № 208 (5481) от 18.11.2014
В Вене, в Музее истории искусства (Kunsthistorisches Museum) открыта выставка с немудреным названием «Веласкес», первая монографическая в немецкоязычном мире и, вероятно, одна из самых больших за пределами Испании. Работы Диего Родригеса де Сильвы-и-Веласкеса (1599-1660) предоставили помимо Прадо, главного партнера Кунстхисторишес, музеи, фонды и частные коллекции Севильи, Барселоны, Валенсии, Парижа, Лондона, Берлина, Дрездена, Рима, Флоренции, Будапешта, Орлеана, Руана, Бостона, Далласа и Нью-Йорка. Кажется, только Эрмитаж не участвует в этом интернациональном блокбастере. Из Вены — АННА ТОЛСТОВА.
Выставка живопись
Благодаря тесным связям испанских и австрийских Габсбургов венский Кунстхисторишес сделался вторым в мире после Прадо собранием Веласкеса — и по количеству картин, и по безупречности их происхождения. Однако благодаря все тем же обстоятельствам собрание Веласкеса в Кунстхисторишес односторонне — оно состоит из парадных портретов королей и инфантов. Понятно, что «Менины», «Пряхи» и «Сдача Бреды» не гастролируют и что собрать всего движимого Веласкеса в одном месте не представляется возможным. Что в отсутствие многих шедевров художника может стать сюжетом сенсационной выставки, а она, безусловно, гвоздь сезона? Банальный и универсальный сюжет — Веласкес и модернизм, стоит лишь подхватить песню про «живописца живописцев», затянутую Мане, рассказывать о мазке и всех оттенках серого, о Веласкесе как предтече импрессионистов, как предмете размышлений Уистлера, Пикассо, Бэкона, Ортеги-и-Гассета и Фуко. Банальный и напрашивающийся именно в венском музее сюжет — Веласкес и Рубенс, ведь «великий фламандец» в его постоянной экспозиции то и дело напоминает о «великом испанце». Но Кунстхисторишес, возможно, один из последних музеев на земле, где умеют рассказывать небанальные истории искусства практически без слов — одними изобразительными рядами. И выставка с немудреным названием «Веласкес» говорит о нем самом, исходя из него самого.
Однако благодаря все тем же обстоятельствам собрание Веласкеса в Кунстхисторишес односторонне — оно состоит из парадных портретов королей и инфантов. Понятно, что «Менины», «Пряхи» и «Сдача Бреды» не гастролируют и что собрать всего движимого Веласкеса в одном месте не представляется возможным. Что в отсутствие многих шедевров художника может стать сюжетом сенсационной выставки, а она, безусловно, гвоздь сезона? Банальный и универсальный сюжет — Веласкес и модернизм, стоит лишь подхватить песню про «живописца живописцев», затянутую Мане, рассказывать о мазке и всех оттенках серого, о Веласкесе как предтече импрессионистов, как предмете размышлений Уистлера, Пикассо, Бэкона, Ортеги-и-Гассета и Фуко. Банальный и напрашивающийся именно в венском музее сюжет — Веласкес и Рубенс, ведь «великий фламандец» в его постоянной экспозиции то и дело напоминает о «великом испанце». Но Кунстхисторишес, возможно, один из последних музеев на земле, где умеют рассказывать небанальные истории искусства практически без слов — одними изобразительными рядами. И выставка с немудреным названием «Веласкес» говорит о нем самом, исходя из него самого.
В первом разделе собраны вещи севильского периода, отмеченные влиянием учителя, Франсиско Пачеко, влиянием не только и не столько ремесленным, сколько духовным, ведь школа Пачеко, «севильского Вазари», слыла самым утонченным и самым интеллектуальным кругом живописцев испанского золотого века. Шесть алтарных картин и три бодегона (разновидность бытового жанра с элементами натюрморта, сценка в трактире или лавке) говорят о Веласкесовом отроческом караваджизме, понятом столь юным художником с удивительной для его возраста зрелостью. То есть не как набор уже изрядно затертых, дошедших до Севильи в весьма приблизительных пересказах приемов, но как философская, платоновская проблема — проблема конфликта земного и небесного, возвышенных образов и низменной натуры. Он пытается решать ее, проводя жанровую границу между тем и этим, оставляя небесную красоту Пречистой Деве — в «Непорочных зачатиях» и «Поклонении волхвов», а земные инстинкты — завсегдатаям трактиров. И даже если они, как «Три музыканта» из Берлинской картинной галереи, самозабвенно музицируют, резонер-мальчишка на первом плане, подняв бокал, намекает, что на его коллег не то чтобы вдохновение снизошло, а вино ударило в голову. Однако конфликт не снимается, и величественный «Водонос» из Эпсли-хаус — при всей предполагаемой скабрезности этого комедийного сюжета — кажется апостолом, несущим в мир святую воду учения Христова.
И даже если они, как «Три музыканта» из Берлинской картинной галереи, самозабвенно музицируют, резонер-мальчишка на первом плане, подняв бокал, намекает, что на его коллег не то чтобы вдохновение снизошло, а вино ударило в голову. Однако конфликт не снимается, и величественный «Водонос» из Эпсли-хаус — при всей предполагаемой скабрезности этого комедийного сюжета — кажется апостолом, несущим в мир святую воду учения Христова.
Второй раздел посвящен мадридскому, придворному и портретному по преимуществу периоду, и в качестве вступления к нему даны контрастом два — одного формата и композиции — погрудных портрета. Один — бесподобный «Дон Луис де Гонгора» из Бостона, сам интеллект, отлитый в скульптурных формах высокого, светлого лба. Второй — позднее многократно повторенный в разных вариантах «Король Филипп IV» из Далласа, считающийся самым первым портретом монарха, который, очаровавшись картиной, пообещал Веласкесу, что никому, кроме него, позировать не будет. Роковой портрет Филиппа IV, его жен, первую, Изабеллу, и вторую, Марию Анну, их многочисленных, больных и рано умирающих детей мы не раз увидим далее — конных, пеших, в рост, поколенных, погрудных. Веласкеса тут принято жалеть — натура ему, и правда, досталась не самая удачная, с признаками фамильного вырождения в лицах. И принято объяснять его так называемый импрессионизм, его свободный мазок, его уистлеровские гармонии в сером, розовом и голубом однообразием и скукой этой натуры, что, дескать, и спровоцировало все формальные эксперименты.
Но, не заглядывая в далекое импрессионистическое будущее, венская выставка показывает, как Веласкес переизобретает формулу придворного портрета: отказывается от старинной черно-белой схемы, переступает через вакхического Рубенса и восходит к их общим с Рубенсом кумирам, Тициану и ученикам, так что некогда охристую, почвенную испанскую гамму теперь озаряет венецианский пламенеющий алый. Меж тем конфликт натуры и идеала, слегка лошадиных испано-габсбургских физиономий и необходимости их идеализации не снят, но смягчается в детских — совершенно ангельских — образах, которыми и знаменит Кунстхисторишес. Придворный портретист успевает поймать ряд волшебных возрастных изменений нежного личика трех-, пяти- и восьмилетней инфанты Маргариты, он может сыграть на противопоставлении двухлетнего инфанта Бальтасара Карлоса и уродца-карлика — сводные брат и сестра умрут в юности, не успев превратиться в таких же уродцев. Финалом портретному разделу служит остроумно подобранный ряд картин из Кунстхисторишес: последние представители испанских Габсбургов кисти последователей Веласкеса — особенно хорош и страшен портрет Карла II работы Хуана Карреньо де Миранды, зримое свидетельство двойного вырождения, королевского дома и высокого стиля.
Придворный портретист успевает поймать ряд волшебных возрастных изменений нежного личика трех-, пяти- и восьмилетней инфанты Маргариты, он может сыграть на противопоставлении двухлетнего инфанта Бальтасара Карлоса и уродца-карлика — сводные брат и сестра умрут в юности, не успев превратиться в таких же уродцев. Финалом портретному разделу служит остроумно подобранный ряд картин из Кунстхисторишес: последние представители испанских Габсбургов кисти последователей Веласкеса — особенно хорош и страшен портрет Карла II работы Хуана Карреньо де Миранды, зримое свидетельство двойного вырождения, королевского дома и высокого стиля.
Однако выставка не заканчивается «Аллегорией бренности» Антонио де Переды-и-Сальгадо — в качестве весьма уместной для барокко точки. За нею следует раздел, который можно было бы назвать «Веласкес сам по себе». Веласкес — итальянский и мадридский, не придворный и относительно свободный в выборе тем и моделей для портретов, «Кузницы Вулкана», «Венеры с зеркалом» и «Демокрита», высоких философских материй и игр в мифологические подтексты, портретов придворных шутов и автопортретов, что неизбежно рифмуются друг с другом. Веласкес как вольный художник, живописец для живописцев, свершивший в своем искусстве, казалось бы, невозможный брак между Караваджо и Тицианом. Веласкес как мастер династических браков, не хуже Габсбургов: женатый на дочери своего учителя Пачеко, выхлопотавшего зятю придворное место, он выдал любимую дочь за лучшего из своих учеников, Хуана Баутисту Мартинеса дель Масо, который впоследствии получит придворную должность тестя. И даже отчасти займет его место в истории искусства: «Семью художника» кисти дель Масо, неловко копирующую композицию «Менин», до самого конца XIX века считали чуть ли не лучшим полотном Веласкеса — гордым ответом габсбургскому самодержавию, высказыванием о королевском месте художника в мире. Сейчас мы знаем, что весь пафос этой картины-манифеста — на совести романтических зрителей, что если тут и есть Веласкес — так только в роли основателя династии, которая, однако, не выродилась. На самом деле Веласкес не был так уж прочно и безнадежно забыт вплоть до Мане и импрессионистов: его помнили итальянцы, признавая единственным наследником Тициана в живописи барокко, его знал и любил любимец Винкельмана Менгс, его боготворил Гойя. Его картины, наконец, вывез во Францию Наполеон — на распродаже Испанской галереи Лувра как раз и озарило Мане. Славная династия, словом, все же продолжалась.
На самом деле Веласкес не был так уж прочно и безнадежно забыт вплоть до Мане и импрессионистов: его помнили итальянцы, признавая единственным наследником Тициана в живописи барокко, его знал и любил любимец Винкельмана Менгс, его боготворил Гойя. Его картины, наконец, вывез во Францию Наполеон — на распродаже Испанской галереи Лувра как раз и озарило Мане. Славная династия, словом, все же продолжалась.
Математические понятия | Немецкий язык онлайн. Изучение, уроки.
Расширенный список математических определений, действий, фигур и др. Термины из школьной программы.
| Немецкое имя существительное | Русский перевод | Немецкое имя существительное | Русский перевод |
| die Zahl | цифра, число, количество | das Quadrat | квадрат |
| die Anzahl | количество | das Rechteck | прямоугольник |
| das Plus | плюс | das Vieleck | многоугольник |
| das Minus | минус | das Dreieck | треугольник |
| die Gleichung | уравнение | das Viereck | четырехугольник |
| die Summe | сумма | das Fünfeck | пятиугольник |
| die Addition, das Addieren | сложение | das Sechseck | шестиугольник |
| der Summand | слагаемое | der Rhombus | ромб |
| die Subtraktion, das Subtrahieren | вычитание | das Trapez | трапеция |
| der Subtrahend | вычитаемое | der Konus | конус |
| der Minuend | уменьшаемое | der Zylinder | цилиндр |
| die Differenz | разность | das Oval | овал |
| das Teilen, die Division | деление | der Umkreis | круг |
| der Dividend, die Teilungszahl | делимое | der Halbkreis | полукруг |
| der Teiler, der Divisor | делитель | die Kreislinie | окружность |
| der Quotient | частное | die Kurve | кривая (линия) |
| der Rest, das Residuum | остаток | die gebrochene Linie | ломаная (линия) |
| der Multiplikator | множитель | die Ebene, die Fläche | плоскость |
| die Multiplikation, das Multiplizieren | умножение | die Diagonalebene | диагональная плоскость |
| das Produkt | произведение | die Normalebene | нормальная плоскость |
| der Wert | величина | die Linie | линия |
| die Wurzel | корень | die Gerade | прямая (линия) |
| die Quadratwurzel | квадратный корень | die Normale, die Senkrechte | перпендикуляр, нормаль |
| das Wurzelzeichen | знак корня | die Achse | ось |
| die Funktion | функция | das Zentrum | центр |
| der Grad | степень | der Punkt | точка |
| der Tangens | тангенс | das Segment, der Abschnitt | отрезок |
| der Kotangens | котангенс | die Unendlichkeit | бесконечность |
| der Sinus | синус | der Winkel | угол |
| der Kosinus | косинус | der rechte Winkel | прямой угол |
| das Verhältnis | соотношение | der spitze Winkel | острый угол |
| der Unbekannte, die unbekannte Größe | неизвестный, неизвестная величина | der stumpfe Winkel | тупой угол |
| die Algebra | алгебра | der Durchmesser | диаметр |
| die Geometrie | геометрия | der Radius | радиус |
| die Trigonometrie | тригонометрия | der Perimeter | периметр |
| die höhere Mathematik | высшая математика | die Fläche | площадь |
| der Faktor | коэффициент | der Querschnitt | сечение |
| die Variable, die variable Größe | переменная величина | die Maßeinheit | единица измерения |
| die Fixgröße | постоянная величина | der Logarithmus | логарифм |
| die gerade Zahl | четное число | der Rechenstab | логарифмическая линейка |
| die ungerade Zahl | нечетное число | die Umkehrfunktion | обратная функция |
корней | Безграничная биология
Типы корневых систем и зоны роста
Кончик корня имеет три основные зоны: зону деления клеток, зону растяжения и зону созревания.
Цели обучения
Опишите три зоны верхушки корня и резюмируйте роль каждой зоны в росте корня
Основные выводы
Ключевые моменты
- Верхушки корней в конечном итоге образуют два основных типа корневой системы: стержневые и волокнистые корни.
- Отрастающая верхушка корня защищена корневым покровом.
- Внутри кончика корня клетки дифференцируются, активно делятся и увеличиваются в длине, в зависимости от того, в какой зоне расположены клетки.
- Делящиеся клетки составляют зону деления клеток прорастающего растения.
- Новообразованный корень увеличивается в размерах в зоне растяжения.
- Дифференцирующиеся клетки составляют зону созревания клеток.
Ключевые термины
- корешок : рудиментарный побег растения, поддерживающий семядоли в семени и от которого корень развивается вниз; корень зародыша
- меристема : ткань растения, состоящая из тотипотентных клеток, обеспечивающая рост растений
- прорастание : начало вегетации или роста из семян или спор
Типы корневых систем
Есть два основных типа корневых систем.У двудольных растений стержневая корневая система, а у однодольных — мочковатая корневая система, также известная как придаточная корневая система. Система стержневого корня имеет основной корень, который растет вертикально вниз, из которого возникает множество более мелких боковых корней. Одуванчики — распространенный пример; их стержневые корни обычно отламываются, когда эти сорняки вырываются из земли; они могут вырастить еще один побег из оставшегося корня. Система стержневого корня глубоко проникает в почву. В отличие от этого мочковатая корневая система расположена ближе к поверхности почвы, где она образует плотную сеть корней, которая также помогает предотвратить эрозию почвы (хорошим примером являются газонные травы, а также пшеница, рис и кукуруза). Некоторые растения имеют сочетание стержневых и волокнистых корней. Растения, произрастающие в засушливых районах, часто имеют глубокую корневую систему, тогда как растения, которые растут в районах с обильным количеством воды, скорее всего, имеют более мелкую корневую систему.
Некоторые растения имеют сочетание стержневых и волокнистых корней. Растения, произрастающие в засушливых районах, часто имеют глубокую корневую систему, тогда как растения, которые растут в районах с обильным количеством воды, скорее всего, имеют более мелкую корневую систему.
Основные типы корневых систем : (а) Системы стержневых корней имеют главный корень, который растет вниз, в то время как (б) волокнистые корневые системы состоят из множества мелких корней.
Зоны корневого кончика
Рост корней начинается с прорастания семян. Когда зародыш растения выходит из семени, корешок зародыша образует корневую систему.Кончик корня защищен корневым покровом, структурой, характерной только для корней и не похожей на любую другую структуру растения. Корневой покров постоянно заменяется, потому что он легко повреждается, когда корень проталкивается через почву. Кончик корня можно разделить на три зоны: зону деления клеток, зону растяжения и зону созревания. Зона деления клеток находится ближе всего к кончику корня и состоит из активно делящихся клеток корневой меристемы, содержащей недифференцированные клетки прорастающего растения.Зона удлинения — это место, где новообразованные клетки увеличиваются в длине, тем самым удлиняя корень. Начиная с первых корневых волосков, это зона созревания клеток, где корневые клетки дифференцируются на специализированные типы клеток. Все три зоны находятся примерно в первом сантиметре кончика корня.
Зоны кончика корня : Продольный вид корня показывает зоны деления, удлинения и созревания клеток. Деление клеток происходит в апикальной меристеме.
Модификации корня
У растений есть самые разные корни для таких разнообразных функций, как структурная поддержка, хранение пищи и паразитизм.
Цели обучения
Объясните причины модификации рута
Основные выводы
Ключевые моменты
- Хранящие корнеплоды, в состав которых входит большое количество съедобных овощей, таких как картофель и морковь, являются одними из наиболее широко известных типов модифицированных корнеплодов.

- Воздушные корни бывают самых разных форм, но действуют одинаково как структурная опора для растения.
- У паразитических растений есть особые гаусториальные корни, которые позволяют растению поглощать питательные вещества из растения-хозяина.
Ключевые термины
- сочные : с мясистыми листьями или другими тканями, в которых накапливается вода
- эпифит : растение, которое растет на другом, использует его в качестве физической поддержки, но не получает от него питательных веществ и не причиняет ему никакого вреда, если также не приносит пользы
Модификации корня
У растений есть разные корневые структуры для определенных целей.Есть много различных типов специализированных корней, но два из наиболее известных типов корней включают воздушные корни и корни хранения. Воздушные корни растут над землей, обычно обеспечивая структурную опору. Хранящие корни (например, стержневые и клубневые корни) модифицируются для хранения пищевых продуктов.
Воздушные корни встречаются у многих различных видов растений, выполняя различные функции в зависимости от местоположения растения. Эпифитные корни — это тип воздушного корня, который позволяет растению расти на другом растении без паразитарных воздействий.Баньяновое дерево начинается как эпифит, прорастающий в ветвях дерева-хозяина. Воздушные корни опоры развиваются из веток и в конечном итоге достигают земли, обеспечивая дополнительную поддержку. Со временем многие корни сойдутся, образуя ствол. Эпифитные корни орхидей образуют губчатую ткань, поглощающую влагу и питательные вещества из любого органического материала на своих корнях. У винта, похожего на пальму дерева, произрастающего на песчаных тропических почвах, развиваются воздушные корни, которые обеспечивают дополнительную поддержку, которая помогает дереву оставаться в вертикальном положении в зыбучих условиях песка и воды.
Воздушные корни : (а) баньяновое дерево, также известное как фиговый душитель, начинает жизнь как эпифит в дереве-хозяине. Воздушные корни доходят до земли, поддерживая растущее растение, которое в конечном итоге задыхает дерево-хозяин. (B) винт развивает воздушные корни, которые помогают поддерживать растение в песчаных почвах.
Воздушные корни доходят до земли, поддерживая растущее растение, которое в конечном итоге задыхает дерево-хозяин. (B) винт развивает воздушные корни, которые помогают поддерживать растение в песчаных почвах.
Хранящие корнеплоды, такие как морковь, свекла и сладкий картофель, являются примерами корнеплодов, специально модифицированных для хранения крахмала и воды. Обычно они растут под землей в качестве защиты от животных, питающихся растениями.Однако некоторые растения, такие как листовые суккуленты и кактусы, накапливают энергию в своих листьях и стеблях, а не в корнях.
Хранящие корнеплоды : Многие овощи, такие как морковь и свекла, представляют собой модифицированные корнеплоды, в которых хранится еда и вода.
Другими примерами модифицированных корней являются аэрирующие корни и гаусториальные корни. Аэрирующие корни, которые возвышаются над землей, особенно над водой, обычно встречаются в мангровых лесах, которые растут вдоль береговой линии с соленой водой.Гаусториальные корни часто встречаются у растений-паразитов, таких как омела. Их корни позволяют растениям поглощать воду и питательные вещества из других растений.
Насколько далеко распространяются корни больших деревьев? — Глубокая зеленая пермакультура
Лесоводство — это выращивание, управление и изучение деревьев и кустарников, и арбористы используют несколько формул для расчета того, насколько далеко простираются корни деревьев, чтобы защитить здоровье деревьев, когда поблизости происходят строительные работы и нарушение почвы.
Знание того, насколько далеко простираются корни деревьев, может быть важно для расположения больших тенистых деревьев, чтобы их корни не заходили в соседние грядки и не влияли на рост растений, поглощая их воду и питательные вещества.
Также важно уметь определить, где можно прорезать корни деревьев при установке корневых барьеров, не убивая дерево или не заставляя его упасть!
Что такое Root Spread
Вычислить, насколько далеко простираются корни дерева, довольно просто.
Большинство корней деревьев распространяются в 2–3 раза больше радиуса кроны деревьев, а в засушливых условиях часто достигают в 5 раз больше радиуса кроны деревьев.
Так, например, если дерево шириной 6 м, радиус навеса составляет 3 м.
Ширина корня = 2 (до 3) x радиус купола = 2 (до 3) x 3 м = 6 м (до 9 м).
Следовательно, корни будут расходиться от ствола на расстояние от 6 до 9 м, и до 5 x 3 м = 15 м!
Итак, если вам интересно, почему ваши недавно посаженные деревья не растут, а соседние гигантские деревья находятся в пределах этого корневого диапазона, тогда есть ответ.Корни больших деревьев могут распространяться на значительные расстояния, поглощая воду и питательные вещества, необходимые для роста молодых деревьев. Установка корневого барьера вдоль линии забора может дать новым деревьям шанс снизить конкуренцию со стороны крупных деревьев поблизости.
Вы можете использовать эту формулу, чтобы определить, насколько далеко могут простираться корни ближайшего дерева, прежде чем вырыть яму для посадки нового дерева или выбрать место для новой грядки.
Что такое лесозащитная зона (TPZ)
Зона защиты деревьев (TPZ) — это территория, определенная лесоводами как запрещенная для любого строительства из-за расположения корней, которые имеют решающее значение для здоровья дерева.
TPZ указывает зону, которая должна быть защищена от развития со всех сторон, если дерево должно быть сохранено, и только с одобрения лесовода строительство может посягать на эту область, так как повреждение корней приведет к стрессу от засухи и возможной гибели дерева. дерево, и последствия такого повреждения могут проявиться в кроне дерева через несколько лет.
Существует три правила расчета зоны защиты деревьев (TPZ):
- TPZ = капельная линия навеса + 1 м
Это менее точный метод, при котором край ствола дерева (известный как капельная линия навеса) идентифицируется и выдвигается на один метр дальше, чтобы определить границу TPZ. .
. - TPZ = DBH x 12 , где DBH (Диаметр на высоте груди) = диаметр ствола, измеренный на высоте 1,4 м над землей
Это более часто используемый метод, при котором радиус TPZ рассчитывается для дерева путем умножения его ствола. ширина (диаметр) на высоте груди, 1,4 м над землей (DBH) и умноженная на 12.
Обратите внимание, радиус измеряется от центра стержня на уровне земли. - TPZ = 1/2 x Высота
Этот метод используется только для высоких узких деревьев, TPZ определяется как простирающаяся до половины высоты дерева.
Примечание: Раздел 3.2 Австралийского стандарта AS4970–2009 (Защита деревьев на участках застройки) гласит, что TPZ пальм и других однодольных, саговников и древовидных папоротников (pachycauls) не должна находиться на расстоянии менее 1 м от выступа кроны (капельный полог). линия).
Что такое структурная корневая зона (SRZ)
Структурная корневая зона (SRZ) — это область вокруг ствола дерева, которая важна для устойчивости дерева. Повреждение корней в этой области, скорее всего, приведет к тому, что дерево станет неустойчивым в земле, что означает, что дерево может упасть.
TPZ, который важен для здоровья дерева, имеет большую площадь, чем SRZ, что важно для устойчивости дерева.
Если строительство или земляные работы будут значительно нарушать Зону защиты деревьев (TPZ), то Корневая структурная зона (SRZ) рассчитывается, чтобы гарантировать, что работы не приведут к тому, что дерево станет неустойчивым и не упадет.
Расчет структурной корневой зоны (SRZ) немного сложнее.
DRC (Диаметр над корневой кроной) — это ширина (диаметр) ствола дерева, измеренная непосредственно над корневой кроной или корневым контрфорсом.0,42 х 0,64
Где
- DRC (Диаметр над корневой коронкой) = диаметр ствола в метрах, измеренный над корневой коронкой
- Радиус измеряется от центра штанги на уровне земли.
 0.0,42 * 0,64
0.0,42 * 0,64 В этом примере будет возвращено значение 2,67 м при правильном вводе.
Примечание: SRZ для деревьев с диаметром ствола (DRC) менее 0,15 м будет составлять 1,5 м.
Формула SRZ не используется для пальм, однодольных, саговников и древовидных папоротников. Кроме того, pachycauls — деревья с толстыми толстыми стеблями / стволами с небольшим количеством ветвей, такие как баобабы и брахихитоны, технически не соответствуют определению деревьев по мнению лесоводов, и поэтому технически не имеют SRZ, хотя в реальном мире это деревья. и имеют структурные корни!
Установка барьеров для корней деревьев
Барьеры для корней деревьев должны быть установлены за пределами SRZ для поддержания устойчивости деревьев.
Простая формула для оценки минимального расстояния, на котором могут быть размещены преграды для корней дерева, выглядит следующим образом:
Минимальное расстояние до корневого барьера = 3,5 x DBH
Где
- Минимальное расстояние измеряется от центра стержня до корневого барьера
- DBH (Диаметр на высоте груди) = диаметр ствола, измеренный на высоте 1,4 м над уровнем земли во время созревания.
Примечание: минимальное расстояние должно составлять 1,5 м, если расчетное значение меньше этого.
Нравится:
Нравится Загрузка …
СвязанныеОпубликовано Анджело (администратор)
Анджело Элиадес — ведущий, тренер, писатель, консультант по пермакультуре, пионер городской пермакультуры и специалист по пищевым лесам. Просмотреть все сообщения Анджело (администратор)
разделов — Какого размера я должен сделать разделы root, home и swap?
Раздел : A H.Д.Д. можно разделить на несколько частей в цифровом виде. Эти части известны как разделы / диски.
Точка крепления : Проще говоря, это флаг / имя / тип, присвоенный разделу.

FileSys. Тип : Тип раздела. В Linux в основном используются ExtX (X = 1,2,3,4) и NTFS.
Первичный раздел : Максимальное количество первичных разделов в накопителе H.D.D. Первичный раздел может содержать один или несколько логических разделов.
Логический раздел : виртуальный раздел в основном разделе.
SDA : Носители данных, такие как H.D.D. или другие СМИ. Если у вас больше дисков, то он будет называться SDA, SDB, SDC, ++
.Устройство для установки загрузчика : —-
Boot Loader : Как мы знаем, BootLoader — это программа который загружен на носитель, которым управляет B.I.O.S. после выполнения P.O.S.T..BootLoader загружает операционную систему или предоставляет меню, если более одного O.S. установлен в СМИ.
Выбор устройства : если у вас ранее установлен O.S. что означает у него есть собственная программа BootLoader, которая устанавливается в MBR (главный загрузчик) HDDN. Теперь, когда вы устанавливаете Linux, он спросит вас, где установить GRUB (Grand Unified Boot Loader) или Linux BootLoader. Это дает вам варианты. установить его в MBR который закончится напишите существующий загрузчик или установите его в любой из разделов, который добавит эту точку входа Linux в существующий загрузчик загрузчика. твой.
Для установки любого дистрибутива Linux вам потребуется как минимум 3 раздела..
Достаточно 100 ГБ. диска / раздела для приличной установки Linux.
Раздел 1 : Корень (/): Для файлов ядра Linux: 20 G.B. (Минимум 15 ГБ)
Раздел 2 : Дом (/ home): Диск для данных пользователя: 70 G.B. (Минимум 30 ГБ)
Раздел 3 : Область подкачки: Пространство, которое действует как дополнительный R.A.M. : 2 x R.A.M. Размер.
Примечание : пространство подкачки ведет себя как дополнительный R.
 A.M. когда R.A.M. полный.
A.M. когда R.A.M. полный.корень | Определение, типы, морфология и функции
Корень , в ботанике — та часть сосудистого растения, которая обычно находится под землей. Его основные функции — закрепление растения, поглощение воды и растворенных минералов и их отвод к стеблю, а также хранение резервных кормов. Корень отличается от стебля, главным образом, отсутствием рубцов и почек на листьях, наличием корневой шляпки и ветвями, которые происходят из внутренней ткани, а не из почек.
Подробнее по этой теме
покрытосеменных: корневые системы
Корни закрепляют растение, впитывают воду и минералы и служат местом для хранения пищи.Два основных типа корневых систем являются первичными …
Виды корней и корневых систем
Первичный корень или корешок — это первый орган, который появляется при прорастании семян. Он прорастает вниз в почву, закрепляя саженец. У голосеменных и двудольных (покрытосеменных с двумя семенными листами) корешок становится стержневым корнем. Он растет вниз, а вторичные корни растут сбоку от него, образуя систему стержневых корней. У некоторых растений, таких как морковь и репа, стержневой корень также служит хранилищем пищи.
Два типа корневой системы: (слева) волокнистые корни травы и (справа) мясистый стержневой корень сахарной свеклы.
Британская энциклопедия, Inc.Травы и другие однодольные растения (покрытосеменные растения с одним семенным листом) имеют мочковатую корневую систему, характеризующуюся массой корней примерно одинакового диаметра. Эта сеть корней возникает не как ветви основного корня, а состоит из множества ветвящихся корней, выходящих из основания стебля.
Некоторые корни, называемые придаточными корнями, возникают не из корня, а из другого органа — обычно стебля, иногда листа.Они особенно многочисленны на подземных стеблях, таких как корневища, клубнелуковицы и клубни, и позволяют вегетативно размножать многие растения из стебля или листовых черенков.
Воздушный корень Некоторые придаточные корни, известные как воздушные корни, либо проходят некоторое расстояние по воздуху, прежде чем достигают почвы, либо остаются висящими в воздухе. Некоторые из них, такие как кукуруза (кукуруза), винтовая сосна и баньян, в конечном итоге помогают поддерживать растение в почве. У многих эпифитных растений, таких как различные орхидеи и виды Tillandsia , воздушные корни являются основным средством прикрепления к непочвенным поверхностям, таким как другие растения и камни.
Некоторые придаточные корни, известные как воздушные корни, либо проходят некоторое расстояние по воздуху, прежде чем достигают почвы, либо остаются висящими в воздухе. Некоторые из них, такие как кукуруза (кукуруза), винтовая сосна и баньян, в конечном итоге помогают поддерживать растение в почве. У многих эпифитных растений, таких как различные орхидеи и виды Tillandsia , воздушные корни являются основным средством прикрепления к непочвенным поверхностям, таким как другие растения и камни.Баньяновое дерево ( видов фикусов ) с воздушными корнями, выходящими из ветвей.
© Андрей Слиозберг / Fotolia Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасСреди сосудистых растений существует ряд других специализированных корней. Пневматофоры, обычно встречающиеся у видов мангровых деревьев, которые растут на солончаках, представляют собой боковые корни, которые растут вверх из ила и воды и служат местом поступления кислорода для погруженной в воду первичной корневой системы.Корни некоторых паразитических растений сильно видоизменяются в гаустории, которые внедряются в сосудистую систему растения-хозяина, чтобы прокормить паразита. Узловатые корни многих членов семейства гороховых (Fabaceae) являются хозяевами симбиотических азотфиксирующих бактерий, а корни многих растений также образуют сложные ассоциации с микоризными почвенными грибами; ряд нефотосинтезирующих микогетеротрофных растений, таких как индийская трубка, питаются исключительно этими грибами.
Морфология и рост
Корни растут в длину только от концов.Самый верхушка корня покрыта корнем в форме наперстка, который защищает верхушку роста, когда она пробивается через почву. Сразу за корневой крышкой находится апикальная меристема, ткань активно делящихся клеток. Некоторые из клеток, продуцируемых апикальной меристемой, добавляются к корневому покрову, но большинство из них добавляются в область удлинения, которая лежит чуть выше меристематической области.
корень и апикальная меристема побега Именно в области удлинения происходит рост длины. Выше этой зоны растяжения находится область созревания, где созревают первичные ткани корня, завершая процесс дифференцировки клеток, который фактически начинается в верхней части меристематической области.
Именно в области удлинения происходит рост длины. Выше этой зоны растяжения находится область созревания, где созревают первичные ткани корня, завершая процесс дифференцировки клеток, который фактически начинается в верхней части меристематической области.Апикальная меристема побега Hypericum uralum (слева) появляется на самой верхней части стебля. Сразу за апикальной меристемой находятся три области первичных меристематических тканей. Апикальная меристема корня (справа) появляется сразу за защитной крышкой корня. Сразу за апикальной меристемой отчетливо видны три первичные меристемы.
Британская энциклопедия, Inc.Основными тканями корня являются эпидермис, кора и сосудистый цилиндр, от самого внешнего до самого внутреннего.Эпидермис состоит из тонкостенных клеток и обычно имеет толщину всего в один клеточный слой. Поглощение воды и растворенных минералов происходит через эпидермис, и этот процесс значительно усиливается у большинства наземных растений из-за наличия корневых волосков — тонких трубчатых расширений стенки эпидермальных клеток, которые встречаются только в области созревания. Поглощение воды происходит главным образом за счет осмоса, который происходит потому, что (1) вода присутствует в почве в более высоких концентрациях, чем в клетках эпидермиса (где она содержит соли, сахара и другие растворенные органические продукты) и (2) мембрана клетки эпидермиса проницаемы для воды, но не для многих веществ, растворенных во внутренней жидкости.Эти условия создают осмотический градиент, благодаря которому вода проникает в клетки эпидермиса. Этот поток создает силу, называемую давлением корней, которая помогает продвигать воду через корни. Давление на корни частично отвечает за подъем воды в растениях, но оно не может самостоятельно объяснять перенос воды к вершинам высоких деревьев.
корень в разрезеПоперечный разрез типичного корня, показывающий первичную ксилему и первичную флоэму, расположенные в центральном цилиндре.
Британская энциклопедия, Inc.
Кора головного мозга проводит воду и растворенные минералы через корень от эпидермиса к сосудистому цилиндру, откуда они транспортируются к остальной части растения. Кора также хранит пищу, транспортируемую вниз от листьев через сосудистые ткани. Самый внутренний слой коры обычно состоит из плотно упакованного слоя клеток, называемого энтодермой, который регулирует поток материалов между корой и тканями сосудов.
Сосудистый цилиндр находится внутри энтодермы и окружен перициклом, слоем клеток, который дает начало корням ветвей.Проводящие ткани сосудистого цилиндра обычно расположены в форме звезды. Ткань ксилемы, которая несет воду и растворенные минералы, составляет ядро звезды; ткань флоэмы, несущая пищу, расположена небольшими группами между остриями звезды.
Более старые корни древесных растений образуют вторичные ткани, которые приводят к увеличению обхвата. Эти вторичные ткани производятся сосудистым камбием и пробковым камбием. Первые возникают из меристематических клеток, лежащих между первичной ксилемой и флоэмой.По мере развития сосудистый камбий образует кольцо вокруг первичного сосудистого цилиндра. При делении клеток в сосудистом камбии образуется вторичная ксилема (древесина) внутри кольца и вторичная флоэма снаружи. Рост этих вторичных сосудистых тканей выталкивает перицикл наружу и разделяет кору и эпидермис. Перицикл становится пробковым камбием, производящим пробковые клетки (внешнюю кору), которые заменяют кору и эпидермис.
The Editors of Encyclopaedia Britannica Эта статья была недавно отредактирована и обновлена Мелиссой Петруццелло, помощником редактора.Узнайте больше в этих связанных статьях Britannica:
Взаимосвязь между диаметром корня, длиной корня и ветвлением корней вдоль боковых корней взрослой кукурузы, выращиваемой в полевых условиях | Летопись ботаники
Аннотация
Предпосылки и цели Диаметр корня, особенно апикальный диаметр, играет важную роль в развитии и функционировании корня.
 Различия в диаметре между корнями и вдоль корней влияют на структуру корней и, таким образом, на общую эффективность кормодобывания корневой системы.Однако влияние изменения диаметра на удлинение корня, ветвление и топологические связи не исследовалось систематически ни в популяции корней высокого порядка, ни вдоль корней, особенно для зрелых растений, выращиваемых в поле.
Различия в диаметре между корнями и вдоль корней влияют на структуру корней и, таким образом, на общую эффективность кормодобывания корневой системы.Однако влияние изменения диаметра на удлинение корня, ветвление и топологические связи не исследовалось систематически ни в популяции корней высокого порядка, ни вдоль корней, особенно для зрелых растений, выращиваемых в поле.Методы Метод, сочетающий выемку грунта и анализ, был применен для извлечения и количественной оценки архитектурных особенностей корней взрослых, выращиваемых в поле растений кукурузы. Взаимосвязь между диаметром корня и другими архитектурными характеристиками корня анализируется для двух сортов кукурузы.
Ключевые результаты Базальный диаметр боковых корней (порядки 1–3) сильно варьировался. Диаметр базальной частично определяется диаметром сегмента подшипника. Базальный диаметр определял потенциальную длину корня, но длина большинства корней намного меньше этой длины. Частично это объясняется различиями в характере изменения диаметра корней. Диаметр имел тенденцию к уменьшению вдоль большинства корней с крутизной градиента уменьшения в зависимости от базального диаметра.Самыми длинными корнями были те, которые сохраняли (или иногда увеличивали) свой диаметр при удлинении. Плотность разветвления (–1 см) боковых сторон также определялась диаметром несущего сегмента. Однако положение этого несущего сегмента вдоль материнского корня также имело значение — промежуточные положения были связаны с более высокой плотностью боковых сторон.
Выводы Используемый здесь метод позволяет нам получить очень подробные записи геометрии и топологии сложной корневой системы.Базальный диаметр и характер изменения диаметра вдоль корня были связаны с его окончательной длиной. Эти соотношения особенно полезны при моделировании удлинения и ветвления корней в моделях источник-сток.
ВВЕДЕНИЕ
Удлинение и ветвление корня — повторяющиеся процессы в развитии корня (Malamy and Benfey, 1997; Nibau et al .
 , 2008; Atkinson et al ., 2014). Вариации в атрибутах удлинения и ветвления создают морфологические различия в длине, количестве и диаметре корней разного порядка в корневой системе (Fitter, 1987; Gruber et al ., 2013).
, 2008; Atkinson et al ., 2014). Вариации в атрибутах удлинения и ветвления создают морфологические различия в длине, количестве и диаметре корней разного порядка в корневой системе (Fitter, 1987; Gruber et al ., 2013).Для понимания итоговой архитектуры корневой системы записи диаметров корней — особенно их более молодых частей (диаметр кончика или апикальной части) — являются ключевыми характеристиками по нескольким причинам. С экономической точки зрения диаметр корня напрямую связан с вложением растением биомассы в его корни (Eissenstat, 1992), потому что в первом приближении биомасса корня заданной длины зависит от квадрата его диаметра. . Следовательно, для данного вложения углеводов диаметр корня влияет на возможную длину × количество корней в системе (Bidel et al ., 2000). Как и ожидалось, многие виды растений имеют архитектуру корневой системы, в большинстве своем состоящую из очень тонких корней. Они имеют тенденцию оптимизировать соотношение длины корня (и, следовательно, площади поверхности корня для поглощения) к весу корня (паковка). Однако уменьшенный диаметр корня ограничивает проникновение корня в почву (Materechera et al ., 1992; Clark et al ., 2008), и корни также должны развивать внутренние структуры, предназначенные для транспортировки воды и питательных веществ (Jordan et al ., 1993; Jaramillo и др. ., 2013). С точки зрения развития апикальный диаметр отражает размер апикальной меристемы. У многих видов была обнаружена положительная взаимосвязь между размером корневой меристемы (и, следовательно, апикальным диаметром) и несколькими важными характеристиками развития, включая скорость удлинения (Cahn et al ., 1989; Thaler and Pagès, 1996, a) ), продолжительность роста (Cahn et al ., 1989; Pregitzer et al ., 1993; Pagès, 1995; Wells and Eissenstat, 2001) и гравитропизм (Oyanagi et al ., 1993; Абэ и Морита, 1994; Singh et al .
 , 2011).
, 2011).Есть несколько других аллометрических отношений внутри корневой системы, которые влияют на ее функцию. Диапазон изменения диаметра корня внутри корневой системы также варьируется (Pagès, 1995; Thaler and Pagès, 1996 a ; Wu et al ., 2014), и это может иметь первостепенное значение для продуктивности кормления, как показано Пажеса (2011). Корневая система также является сетью, проводящей сок, иногда с большим количеством порядков ветвления (например,грамм. до четырех или даже пяти) (Wu, Guo, 2014). Гидравлические и пищевые ограничения также могут влиять на диаметр корня и относительное расположение анатомических характеристик (North and Nobel, 1991; Steudle, 2000; Fan et al ., 2003; Saengwilai et al ., 2014; Lynch et al ). ., 2014) и, следовательно, топологические связи между диаметрами. Таким образом, точная взаимосвязь между диаметром и удлинением, с одной стороны, и топологическими связями корней разного диаметра, с другой, являются важными вопросами, которые мы стремимся решить для выращиваемых в поле растений кукурузы.
В большинстве работ, посвященных влиянию диаметра корня на рост корня, предполагается (часто неявно), что диаметр корня в момент прорастания (базальный диаметр) остается постоянным на протяжении всего развития корня (Hackett, 1969; Cahn et al ., 1989). Однако этот упрощенный взгляд заслуживает дальнейшего изучения. Некоторые авторы недавно показали, что апикальный диаметр корня может колебаться во время удлинения или быть неоднородным вдоль некоторых корней (Pagès, 1995; Thaler and Pagès, 1996 a ; Wu et al ., 2014). Эта возможность предоставит дополнительные степени свободы для роста корней. Было показано, что у некоторых видов временные вариации доступности ассимилятов синхронизируются с вариациями диаметра корня (Thaler and Pagès, 1996, a , b ) и, следовательно, могут вводить несколько моделей удлинения (Thaler and Pagès, 1996 a ).
 . Этот фактор сделает модели развития более сложными, но также и более адаптивными, поскольку диаметр корня может регулироваться во время удлинения корня.Тем не менее, общность некоторых из этих результатов заслуживает оценки с другими видами, а также должна быть оценена в полевых условиях. Следует напомнить, что изменения диаметра корня во времени были впервые зарегистрированы путем мониторинга апикального диаметра отдельных корней через окна наблюдения (Pagès, 1995; Thaler and Pagès, 1996 a ). Хотя этот метод дает прямой доступ к динамике диаметра корня, он очень ограничен и требует специального оборудования, что делает невозможными измерения в более естественных условиях почвы.У однодольных видов, у которых вторичный рост корня не изменяет диаметр корня, можно заменить временной мониторинг диаметра изучением продольного профиля диаметра корня вдоль вынутого корня. Этот метод следует применять незамедлительно к тщательно вынутым корням, прежде чем произойдет какое-либо ухудшение диаметра из-за старения после травмы.
. Этот фактор сделает модели развития более сложными, но также и более адаптивными, поскольку диаметр корня может регулироваться во время удлинения корня.Тем не менее, общность некоторых из этих результатов заслуживает оценки с другими видами, а также должна быть оценена в полевых условиях. Следует напомнить, что изменения диаметра корня во времени были впервые зарегистрированы путем мониторинга апикального диаметра отдельных корней через окна наблюдения (Pagès, 1995; Thaler and Pagès, 1996 a ). Хотя этот метод дает прямой доступ к динамике диаметра корня, он очень ограничен и требует специального оборудования, что делает невозможными измерения в более естественных условиях почвы.У однодольных видов, у которых вторичный рост корня не изменяет диаметр корня, можно заменить временной мониторинг диаметра изучением продольного профиля диаметра корня вдоль вынутого корня. Этот метод следует применять незамедлительно к тщательно вынутым корням, прежде чем произойдет какое-либо ухудшение диаметра из-за старения после травмы.Плотность разветвлений также является важным компонентом архитектуры корневой системы, и возможно, что это может быть связано с диаметром корня (Draye, 2002; Lecompte and Pagès, 2007; Bécel et al ., 2012). Однако соотношение ветвления и диаметра корня остается неопределенным, с противоречивыми результатами даже у одного и того же вида (Draye, 2002; Lecompte and Pagès, 2007). По-прежнему трудно определить из литературы, в какой степени эти различия связаны с видовым разнообразием, а какие — с разнообразием окружающей среды. Из-за продольных вариаций как диаметра корня, так и плотности ветвления (Lecompte et al ., 2005), для дальнейшего разъяснения этого важного нового аспекта развития корня предлагается рассматривать эти отношения в масштабе корневого сегмента, а не как обычно (Draye, 2002; Lecompte and Pagès, 2007; Bécel et al., ., 2012).
Таким образом, наше исследование основано на анализе большого количества корней и нескольких порядков ветвления у выращиваемых в поле растений кукурузы.
 Мы также используем два генотипа в одном сезоне и один генотип в течение двух сезонов, чтобы лучше оценить общность наших результатов. Растения были тщательно вырыты с помощью специального устройства, описанного в предыдущей статье (Wu and Guo, 2014). Основные цели состояли в том, чтобы охарактеризовать: (1) распределение диаметров корней в системе, изучая отношения диаметров через точки ветвления (поперечный диаметр по сравнению с диаметром родителей) и изменение продольного диаметра вдоль отдельных корней; (2) соотношение между диаметром корня и общей длиной корня с учетом как базального (начального) диаметра, так и возможных продольных изменений; и (3) взаимосвязь между диаметром и плотностью ветвления в локальном масштабе корневого сегмента, чтобы проверить наличие положительной взаимосвязи или отчетливого распределения плотности ветвления вдоль корней.В частности, мы проверили гипотезу о том, что конечная длина бокового корня (LR) была связана с размером базального корня и степенью изменения диаметра вдоль корня.
Мы также используем два генотипа в одном сезоне и один генотип в течение двух сезонов, чтобы лучше оценить общность наших результатов. Растения были тщательно вырыты с помощью специального устройства, описанного в предыдущей статье (Wu and Guo, 2014). Основные цели состояли в том, чтобы охарактеризовать: (1) распределение диаметров корней в системе, изучая отношения диаметров через точки ветвления (поперечный диаметр по сравнению с диаметром родителей) и изменение продольного диаметра вдоль отдельных корней; (2) соотношение между диаметром корня и общей длиной корня с учетом как базального (начального) диаметра, так и возможных продольных изменений; и (3) взаимосвязь между диаметром и плотностью ветвления в локальном масштабе корневого сегмента, чтобы проверить наличие положительной взаимосвязи или отчетливого распределения плотности ветвления вдоль корней.В частности, мы проверили гипотезу о том, что конечная длина бокового корня (LR) была связана с размером базального корня и степенью изменения диаметра вдоль корня.МАТЕРИАЛЫ И МЕТОДЫ
Полевые эксперименты
Полевые эксперименты проводились на экспериментальной станции Шанчжуан Китайского сельскохозяйственного университета, Пекин, Китай (40 ° 8′N, 116 ° 10′E). Тип почвы — водный камбизол со структурой супеси суглинка (ФАО).Использовали два гибрида кукурузы ( Zea mays L.), «ND108» и «ZD958». «ND108» и ZD958 последовательно занимали самые большие посевные площади в качестве коммерческого гибрида в Китае за последние годы. В 2009 г. оба гибрида были посеяны 8 мая. В 2011 году использовался только «ZD958», и он был посеян 15 мая. Плотность посадки составила 5 · 8 растений на метр −2 с междурядьями 60 и 30 см соответственно (каждый квартал 16 × 6 · 5 м, восток – запад × север – юг). План эксперимента представлял собой рандомизированный блок с двумя повторениями блоков.Чтобы избежать потенциального воздействия возвращенной срезанной соломы на рост корней, в предыдущие годы солому убирали с поля после сбора урожая.
 За пятнадцать дней до посева был проведен полив затоплением.
За пятнадцать дней до посева был проведен полив затоплением.В соответствии с местной практикой для кукурузы было внесено базовое удобрение 120 кг P 2 O 5 га -1 (суперфосфат) и 100 кг K 2 O га -1 (сульфат калия). перед посевом. Это было внесено в верхний слой почвы 0–15 см с помощью отвального плуга и роторного культиватора.На оба сорта было внесено в общей сложности 120 кг N га -1 ; 30% общего азота в виде мочевины было внесено в качестве подкормки на стадии с четырьмя листами при орошении 5 мм с использованием ленты для микрораспыления, а 70% общего азота в виде мочевины было внесено на стадии с 11 листами. Сорняки удаляли вручную, чтобы избежать воздействия гербицидов на рост сельскохозяйственных культур.
Выборка корня в поле
Корневые системы отдельных растений кукурузы отбирали на стадии насыпки зерна. Перед отбором образцов был проведен скрининг растений.Каждое отобранное растение было выбрано из группы из девяти растений (3 ряда × 3 растения в ряду). Расстояние между рядами и растениями между соседними растениями в каждой группе должно быть в пределах 58–62 и 28–32 см соответственно. Растения в каждой группе были одинаковой высоты, высоты колоса и толщины базальных междоузлий. В качестве пробы была взята корневая система растения, расположенного в центре группы.
В 2009 г. из четырех корневых систем «ZD958» (Z09) и «ND108» (N09) были взяты пробы через 24 и 27 дней после шелушения, соответственно.Для отбора корней сначала срезали побег. Затем был изготовлен заказной «секторный пробоотборник», состоящий из двух съемных частей. Сначала лист 4-миллиметровой мягкой стали (70 × 50 см) был сложен поперек его длинной оси, чтобы образовалось V-образное лезвие с центральным углом 120 ° и сторонами шириной 35 см (радиус) и высотой 50 см (глубина). ). К этому «V» при помощи 3-миллиметровой проволоки из мягкого железа была прикреплена внешняя панель, сделанная из листа 5-миллиметровой мягкой стали (105 × 50 см), изогнутая в виде гладкой дуги, которая едва касалась краев пластины.
 V-образное лезвие под прямым углом.Два компонента включали фланцы, приваренные вдоль их стыковых кромок для облегчения сборки. Секторный пробоотборник помещали на поверхность почвы так, чтобы его длинная ось была вертикальной, и выровняли так, чтобы его вершина входила только в пень кукурузы (с зазором около 5 см). Образцы корней выбранных растений собирали в междурядьях и внутри рядах соответственно. Затем секторный пробоотборник забивали в почву с помощью горизонтального деревянного бруска и кувалды. Окружающий грунт постепенно выкапывался, чтобы облегчить установку.Когда пробоотборник был погружен на полную глубину (примерно 50 см) и окружающий грунт был полностью выкопан, два стальных троса были прикреплены к приварным проушинам на пробоотборнике, и он и содержащийся в нем клиновидный монолит грунта были осторожно поднял. Затем тангенциальные стальные листы были удалены и заменены крупной сеткой из стальной проволоки (10 × 10 мм), чтобы свести к минимуму поломку корней во время последующего вымывания монолита почвы с использованием тонких водяных струй. После промывки беспочвенный сектор корневой системы хранили в прохладном помещении при 3 ° С.Из-за формы и размера секторного пробоотборника было неизбежно, что некоторые узловые корни пересекали наклонные стороны, и поэтому они были вырезаны. Следовательно, в каждом монолите было ограниченное количество неповрежденных узловых корней.
V-образное лезвие под прямым углом.Два компонента включали фланцы, приваренные вдоль их стыковых кромок для облегчения сборки. Секторный пробоотборник помещали на поверхность почвы так, чтобы его длинная ось была вертикальной, и выровняли так, чтобы его вершина входила только в пень кукурузы (с зазором около 5 см). Образцы корней выбранных растений собирали в междурядьях и внутри рядах соответственно. Затем секторный пробоотборник забивали в почву с помощью горизонтального деревянного бруска и кувалды. Окружающий грунт постепенно выкапывался, чтобы облегчить установку.Когда пробоотборник был погружен на полную глубину (примерно 50 см) и окружающий грунт был полностью выкопан, два стальных троса были прикреплены к приварным проушинам на пробоотборнике, и он и содержащийся в нем клиновидный монолит грунта были осторожно поднял. Затем тангенциальные стальные листы были удалены и заменены крупной сеткой из стальной проволоки (10 × 10 мм), чтобы свести к минимуму поломку корней во время последующего вымывания монолита почвы с использованием тонких водяных струй. После промывки беспочвенный сектор корневой системы хранили в прохладном помещении при 3 ° С.Из-за формы и размера секторного пробоотборника было неизбежно, что некоторые узловые корни пересекали наклонные стороны, и поэтому они были вырезаны. Следовательно, в каждом монолите было ограниченное количество неповрежденных узловых корней.В 2011 году образцы трех корневых систем «ZD958» (Z11) были взяты через 19 дней после шелушения. Чтобы повысить эффективность отбора проб корней и получить более полную корневую систему, была разработана новая система отбора проб (Wu and Guo, 2014). В новой системе использовалась труба из мягкой стали (толщина 4 мм; диаметр 50 см, высота 55 см), состоящая из двух съемных полутрубок, соединенных болтами.Трубка для отбора проб была размещена на поверхности почвы соосно с пнем кукурузы, а наверху была прикреплена крестовина. Затем использовали электрический молоток, чтобы вдавить цилиндр для отбора проб в почву на желаемую глубину (примерно 50 см).
 Затем пробоотборная трубка вместе с цилиндрическим монолитом грунта была поднята из грунта с помощью цепного блока, соединенного со стальной портальной рамой. Затем удалили две полутрубки и промыли почвенный монолит тонкой струей воды. Чтобы свести к минимуму поломку корня, стальная трубка (диаметр 50 см, высота 10 см), состоящая из двух съемных полутрубок, была закреплена вокруг основания сердцевины корня, а углы и давление форсунок были оптимизированы.Подробная информация о системе отбора проб корня представлена в Wu and Guo (2014).
Затем пробоотборная трубка вместе с цилиндрическим монолитом грунта была поднята из грунта с помощью цепного блока, соединенного со стальной портальной рамой. Затем удалили две полутрубки и промыли почвенный монолит тонкой струей воды. Чтобы свести к минимуму поломку корня, стальная трубка (диаметр 50 см, высота 10 см), состоящая из двух съемных полутрубок, была закреплена вокруг основания сердцевины корня, а углы и давление форсунок были оптимизированы.Подробная информация о системе отбора проб корня представлена в Wu and Guo (2014).Отделение корней и сканирование
Только две корневые системы были проанализированы после простого визуального сравнения формы корня трех корневых систем. Каждый узловой корень, отделенный от отобранной корневой системы, хранили в отдельном пластиковом ящике. В каждой корневой системе насчитывалось до семи оборотов узловых корней. Только узловые корни, отходящие от 4-го до 7-го узловых корневых мутовок, были сравнительно неповрежденными и пригодными для измерения.Затем узловые корни из каждого из оборотов были сгруппированы в соответствии с их визуальным сходством (то есть диаметром и длиной их подмышечных корней, длиной неразветвленных зон, количеством и длиной LR первого порядка). Репрезентативные узловые корни в каждой группе были выбраны для дальнейшего анализа.
Зона ветвления подмышечного корня каждого из выбранных узловых корней была разрезана на 5-сантиметровые секции. В зависимости от сложности участков осевого разветвления применялись три различных стратегии сканирования.Для сечений невысокой сложности осевое разветвление сканировалось напрямую, включая его LR. Для участков средней сложности LR первого порядка были вырезаны из корня оси, а затем сканированы вместе. Для участков высокой сложности LR первого порядка сначала были вырезаны из корня оси, а затем каждый LR был разрезан на несколько частей. После этих процессов LR были разложены вручную перед сканированием, чтобы минимизировать перекрытие корней.
 Все корни сканировали планшетным сканером (i800 Plus, Microtek, Шанхай, Китай) с разрешением 400 d.Пи.
Все корни сканировали планшетным сканером (i800 Plus, Microtek, Шанхай, Китай) с разрешением 400 d.Пи.Обработка изображений и данных
Для анализа сканированных изображений корня использовалась система анализа изображений WinRHIZO Pro 2009b (Régent Instruments Inc., Квебек, Канада). Шум в исходных изображениях был удален с помощью инструмента стирания программного обеспечения. Бледные корни, не распознаваемые программой, были подчеркнуты с помощью инструмента заливки. Также были выявлены и исправлены неправильные топологические соединения. Система упорядочивания сегментов развития (Berntson, 1997) использовалась для записи корневой топологии.«Связь», определяемая как линейная (неразветвленная) часть корневого раздела, ограниченная на каждом конце либо другим корневым разделом, либо верхушкой корня, считалась базовой единицей измерения с использованием программного обеспечения WinRHIZO. Смежные группы звеньев одного порядка рассматривались как ось (Berntson, 1997). Программное обеспечение организует геометрию (длина и диаметр) и топологическое соединение (порядок ветвления, последовательность осей, последовательность связей на текущей оси, последовательность ее материнской оси) отдельных связей.Блок LR (LRU), LR первого порядка с LR более высокого порядка, использовался в качестве блока для группировки данных, полученных из одного и того же LR первого порядка.
В соответствии с тремя различными стратегиями корневого сканирования, соответствующие стратегии применялись для анализа изображений с помощью WinRHIZO. Для разреза оси с низкой сложностью был выбран и отмечен весь корневой разрез оси. Для осевого разреза средней сложности был выбран каждый корень первого порядка и отмечен порядковыми номерами. Для LRU высокой сложности последовательные части каждого разреза LR первого порядка были отмечены последовательными номерами.После анализа отсканированного изображения данные были выведены программой в текстовый файл.
 Сценарий, основанный на языке Visual Basic Application (VBA), встроенный в Microsoft Excel, использовался для пакетной обработки файлов для извлечения топологических соединений и геометрических данных отдельных LRU (Wu and Guo, 2014). Для LRU высокой сложности, который был разрезан на части для сканирования, эти части были последовательно объединены для восстановления полного LRU с помощью сценария. Наконец, сценарий экспортировал файл, содержащий значения, разделенные запятыми, для отдельных узловых корней.Подробную информацию о сценарии можно найти в Wu and Guo (2014).
Сценарий, основанный на языке Visual Basic Application (VBA), встроенный в Microsoft Excel, использовался для пакетной обработки файлов для извлечения топологических соединений и геометрических данных отдельных LRU (Wu and Guo, 2014). Для LRU высокой сложности, который был разрезан на части для сканирования, эти части были последовательно объединены для восстановления полного LRU с помощью сценария. Наконец, сценарий экспортировал файл, содержащий значения, разделенные запятыми, для отдельных узловых корней.Подробную информацию о сценарии можно найти в Wu and Guo (2014).Расчеты
Всего было сканировано 25 узловых корней N09, 19 из Z09 и 28 из Z11. Всего было 22 880 LR первого порядка, 144 624 второго порядка, 25 650 третьего порядка и 1941 четвертого порядка. Каждый LR был разделен на сегменты длиной 1 мм с помощью линейной интерполяции, диаметр каждого был равен диаметру его звена. Базальные диаметры LR первого порядка относились к диаметрам базального сегмента корня длиной не более 0,5 см, а длина базального сегмента для LR более высокого порядка составляла 0,1 см (рис.1). Для анализа данных использовалось программное обеспечение R (R Development Core Team, 2014), в котором для визуализации данных использовался пакет ggplot2 (http://ggplot2.org/).
Рис. 1.
Схема описания терминологии корней и определения корневых признаков.
Рис. 1.
Схема описания терминологии корней и определения корневых признаков.
РЕЗУЛЬТАТЫ
Вариация диаметров и топологические связи диаметров в пределах корневой системы
Средний базальный диаметр уменьшался с увеличением порядка ветвления.Исключение составляют LR четвертого порядка N09 (рис. 2). Средние базальные диаметры LR первого порядка были существенно больше, чем LR второго порядка, в то время как различия в среднем базальном диаметре между LR другого порядка были намного меньше.
 Вариации диаметра также уменьшались с увеличением порядка ветвления. Этот эффект все еще был заметен в логарифмическом масштабе. Однако вариации диаметра не сильно различались ни для двух сортов в один сезон (Z09 и N09), ни для одного и того же сорта в два разных сезона (Z09 и Z11).
Вариации диаметра также уменьшались с увеличением порядка ветвления. Этот эффект все еще был заметен в логарифмическом масштабе. Однако вариации диаметра не сильно различались ни для двух сортов в один сезон (Z09 и N09), ни для одного и того же сорта в два разных сезона (Z09 и Z11).Рис. 2.
Вариация базального диаметра боковых корней разного порядка разного порядка комбинаций обработки сорта кукурузы × год. N09, Z09 и Z11 обозначают «ND108» в 2009 году, «ZD958» в 2009 году и «ZD958» в 2011 году соответственно. Показаны медианы (сплошные, горизонтальные толстые линии), средние значения (пунктирные горизонтальные линии) и 25 и 75% квартили (нижнее и верхнее поля прямоугольников) диаметров боковых сторон разного порядка. Верхние / нижние усы простираются от шарнира до самого высокого / самого низкого значения, которое находится в пределах 1,5 × IQR (межквартильный диапазон) шарнира, где IQR — это расстояние между первым и третьим квартилями.Выбросы — это любые данные, лежащие за пределами усов. Масштаб оси y преобразуется логарифмически. Общее количество корней и выбросов (в скобках) каждого порядка LR указано в ключе.
Рис. 2.
Вариация базального диаметра боковых корней разного порядка разного порядка комбинаций обработок сорта кукурузы × год. N09, Z09 и Z11 обозначают «ND108» в 2009 году, «ZD958» в 2009 году и «ZD958» в 2011 году соответственно. Показаны медианы (сплошные, горизонтальные толстые линии), средние значения (пунктирные горизонтальные линии) и 25 и 75% квартили (нижнее и верхнее поля прямоугольников) диаметров боковых сторон разного порядка.Верхние / нижние усы простираются от шарнира до самого высокого / самого низкого значения, которое находится в пределах 1,5 × IQR (межквартильный диапазон) шарнира, где IQR — это расстояние между первым и третьим квартилями. Выбросы — это любые данные, лежащие за пределами усов. Масштаб оси y преобразуется логарифмически. Общее количество корней и выбросов (в скобках) каждого порядка LR указано в ключе.

На рис. 3 приведены зависимость между средним диаметром ЛРП и диаметра сегмента подшипника, для трех комбинаций лечения по отдельности, а также объединение всех корневых заказов.Корреляция была высокозначимой, но ниже для сорта N ( R 2 = 0,26 для N09), чем для сорта Z ( R 2 = 0,4 для Z09 и R 2 = 0 · 45 для Z11). И точки пересечения, и наклоны существенно не различались для трех комбинаций обработки. Положение точек зависело от корневого порядка, особенно для боковых линий первого порядка, которые, как правило, располагались выше общих линий регрессии. По этой причине мы повторно проанализировали взаимосвязь для различных корневых порядков, смешав три комбинации лечения.Эти корреляции были значительными, но были высокими только для опорных сегментов ( R 2 = 0,35 для корней подмышек и R 2 <0,1 для LR второго и третьего порядка). Таким образом, простая линейная регрессия не может удовлетворительно описать взаимосвязь из-за большого разброса диаметра дочернего корня для данного класса диаметров. Вместо этого мы рассчитали и построили квантили среднего базального диаметра дочерних корней на основе классов опорных диаметров (рис.3Б). Наивысшая кривая (квантиль 99%) определяет потенциальный средний базальный диаметр дочерних корней для данного диаметра опоры. С увеличением диаметра несущего корня увеличение потенциального диаметра дочерних корней было более крутым, чем для среднего диаметра. Для аналогичных диапазонов опорных диаметров корни более низкого порядка имели тенденцию давать дочерние корни с большим потенциальным базальным диаметром.
Рис. 3.
Зависимость базального диаметра дочерних корней от диаметра несущих сегментов корня.Различные критерии были установлены для длины подшипника корневого сегмента и его разветвленности номер: длина сегмента axile корня 5 см; длина сегмента LR первого порядка 2 см, число ветвлений не менее 4; длина сегмента LR второго порядка составляла 1 см, а его число разветвлений было не менее 2.
 (A) LR разного порядка разветвления были объединены для каждой комбинации обработки. (B) Для каждого порядка ветвления объединение трех комбинаций лечения. Кривые разной толщины указывают на квантильные кривые 50% (тонкие) и 99% (толстые).Общее количество корней для LR каждого порядка указывается в ключе.
(A) LR разного порядка разветвления были объединены для каждой комбинации обработки. (B) Для каждого порядка ветвления объединение трех комбинаций лечения. Кривые разной толщины указывают на квантильные кривые 50% (тонкие) и 99% (толстые).Общее количество корней для LR каждого порядка указывается в ключе.Рис. 3.
Взаимосвязь между базальным диаметром дочерних корней и диаметром несущих сегментов корня. Различные критерии были установлены для длины подшипника корневого сегмента и его разветвленности номер: длина сегмента axile корня 5 см; длина сегмента LR первого порядка 2 см, число ветвлений не менее 4; Длина сегмента LR второго порядка составляла 1 см, а число его ветвлений — не менее 2.(A) LR разного порядка ветвления были объединены для каждой комбинации лечения. (B) Для каждого порядка ветвления объединение трех комбинаций лечения. Кривые разной толщины указывают на квантильные кривые 50% (тонкие) и 99% (толстые). Общее количество корней для LR каждого порядка указывается в ключе.
Взаимосвязь диаметра и конечной длины отдельного корня
Длина корня имела тенденцию к увеличению с увеличением базального диаметра (рис. 4). Корреляция между этими переменными была значимой для всех комбинаций лечения ( P <0 0001), а коэффициенты детерминации ( R 2 ) всегда были больше 0,39.Вариации пересечений (от -0,46 до -0,86 мм) и наклонов (от 83 до 96) линий регрессии для трех комбинаций лечения были небольшими. Поскольку вариации длины были высокими для каждого класса диаметра, мы рассчитали и построили квантили длины для классов диаметра (рис. 4). Кривые, соединяющие эти квантили, увеличивались, особенно в диапазоне 0–0,9 мм, а затем стабилизировались на плато от 25 до 35 см (рис. 4A). Более высокие кривые (квантили 95 и 99%) определяют потенциальную длину для данного диаметра.Поскольку линии регрессии и вариации кривых квантилей были подобны для трех комбинаций лечения, данные для трех комбинаций лечения были объединены и исследованы для различных порядков (рис.
 4B). В пределах того же диапазона базального диаметра корни более низкого порядка имели большую длину корня. Однако с увеличением базального диаметра скорость увеличения потенциальной длины была ниже для корней с большим диаметром, более 0,6 мм (рис. 4A).
4B). В пределах того же диапазона базального диаметра корни более низкого порядка имели большую длину корня. Однако с увеличением базального диаметра скорость увеличения потенциальной длины была ниже для корней с большим диаметром, более 0,6 мм (рис. 4A).Рис. 4.
Зависимость длин от базального диаметра LR разного порядка.Базальные диаметры были разделены на 25 классов. (A) Объединение заказов ветвления для каждой комбинации лечения. (B) Для каждого порядка корней объединение трех комбинаций обработки. Общее количество корней для каждого заказа LR указывается в ключе.
Рис. 4.
Зависимость длин от базального диаметра LR разного порядка. Базальные диаметры были разделены на 25 классов. (A) Объединение заказов ветвления для каждой комбинации лечения. (B) Для каждого порядка корней объединение трех комбинаций обработки.Общее количество корней для каждого заказа LR указывается в ключе.
Мы заметили, что диаметр изменялся вдоль LR первого порядка (вспомогательная информация, рис. S1). Поэтому мы провели более систематическое исследование картины изменения диаметра LR первого порядка для разных классов длины и базального диаметра (рис. 5). У подавляющего большинства корней диаметр уменьшался от проксимального к дистальному концу. Также ясно, что вариации базального диаметра были намного больше, чем вариации дистального диаметра.Дистальный диаметр оставался в пределах 0,25–0,55 мм для медианных значений. Для того же класса длины корни с большим базальным диаметром показали более резкое уменьшение диаметра. Это указывает на то, что для данного класса длины изменение диаметра связано с базальным диаметром. Причем для каждого класса базального диаметра это уменьшение было более крутым для коротких корней. И наоборот, длинные корни лучше сохраняли свой больший диаметр. Диаметр корня даже увеличивался в промежуточном положении для корней в классе малого диаметра (0,01–0,4 мм), но имеющих большую длину (15–20 см).Следовательно, характер изменения диаметра вдоль корней был связан с базальным диаметром и длиной, а скорость уменьшения диаметра была связана с конечной длиной.

Рис. 5.
Вариации диаметра по LR первого порядка для разных классов длины и базального диаметра. Классы длины составляли 5–6, 8–10, 15–20 и 25–30 см, а классы диаметра — 0 · 01–0 · 4, 0 · 4–0 · 8, 0 · 8–1 · 2 и 1. · 2–2 · 0 мм. Для каждой позиции (каждые 1 см) вдоль корня диаграмма показывает значения 50% (линия), 25% и 75% (поля прямоугольника).Значение усов и выбросов показано на рис. 2. Число корней, используемых на каждой панели, указано в верхнем левом углу.
Рис. 5.
Вариации диаметра по LR первого порядка для разных классов длины и базального диаметра. Классы длины составляли 5–6, 8–10, 15–20 и 25–30 см, а классы диаметра — 0 · 01–0 · 4, 0 · 4–0 · 8, 0 · 8–1 · 2 и 1. · 2–2 · 0 мм. Для каждой позиции (каждые 1 см) вдоль корня диаграмма показывает значения 50% (линия), 25% и 75% (поля прямоугольника). Значение усов и выбросов такое же, как на рис.2. Количество корней, используемых на каждой панели, указано в верхнем левом углу.
Чтобы понять эту тенденцию с более синтетической точки зрения, мы построили график зависимости расстояния до потенциальной длины (95% квантиль) от скорости изменения диаметра для каждого класса базального диаметра (рис. 6). Расстояние до потенциальной длины рассчитывается для отдельных корней как потенциальная длина минус наблюдаемая длина. Скорость изменения диаметра рассчитывается как разница между дистальным диаметром и базальным диаметром, деленная на длину.Были включены корни первого порядка размером более 5 см, независимо от их классификации по длине и базальному диаметру. Левая часть рис. 6 подтверждает явление, показанное на рис. 5, т. Е. Чем ниже скорость уменьшения диаметра, тем ближе корень к его потенциальной длине (для его класса базального диаметра). Напротив, правая часть не показывает явной тенденции. Нижняя правая часть рисунка показывает корни, диаметр которых увеличился и достиг большей длины, чем ожидалось, в то время как правая верхняя часть показывает корни, диаметр которых увеличился, но длина которых сильно отличалась от их потенциальной длины.
 Мы предполагаем, что корни в верхней правой части могли столкнуться с объемом уплотненной почвы (имеющей низкую проницаемость), поскольку их рост прекратился, а их апикальный диаметр увеличился (рис. S2). Некоторые из этих корней также давали толстые LR (рис. S2).
Мы предполагаем, что корни в верхней правой части могли столкнуться с объемом уплотненной почвы (имеющей низкую проницаемость), поскольку их рост прекратился, а их апикальный диаметр увеличился (рис. S2). Некоторые из этих корней также давали толстые LR (рис. S2).Рис. 6.
Зависимость расстояния до потенциальной длины от скорости изменения диаметра для различных классов базального диаметра LR первого порядка. Скорость изменения диаметра рассчитывается как: дистальный диаметр минус базальный диаметр, разделенный на длину.Потенциальная длина указывает длину в пределах 95% квантиля. Расстояние до потенциальной длины рассчитывается как: потенциальная длина минус длина отдельного корня. Корни длиной <5 см не учитывались в этом расчете.
Рис. 6.
Зависимость расстояния до потенциальной длины от скорости изменения диаметра для различных классов базального диаметра LR первого порядка. Скорость изменения диаметра рассчитывается как: дистальный диаметр минус базальный диаметр, разделенный на длину. Потенциальная длина указывает длину в пределах 95% квантиля.Расстояние до потенциальной длины рассчитывается как: потенциальная длина минус длина отдельного корня. Корни длиной <5 см не учитывались в этом расчете.
Взаимосвязь между диаметром и плотностью ветвления в масштабе корневого сегмента
Взаимосвязи между количеством дочерних корней и диаметрами сегментов несущих корней представлены на рис. 7. Корреляции были значительными ( P <0 · 0001) для трех комбинаций обработки, но коэффициенты детерминации были низкими ( R 2 <0,16).Опять же, мы использовали кривые, соединяющие квантили, чтобы помочь интерпретировать эти слабые взаимосвязи (рис. 7). Плотность ветвления увеличивалась с увеличением диаметра корневого сегмента подшипника, особенно при малых значениях диаметра сегмента, то есть менее 0,5 мм (рис. 7А). Выше этого значения увеличение было нулевым или умеренным.
 Потенциальная плотность ветвления (представленная квантилями 95 и 99%) была достигнута для корней среднего диаметра. Плотность ветвления также анализировалась по порядку ветвления (рис. 7B). Согласно этим графикам, плотность ветвления зависела от порядка ветвления.Плотность разветвления была выше у несущих корней более низкого порядка того же диапазона диаметров. Плато было достигнуто за счет более толстых опорных корней (1 мм для осевых корней, 0,5 мм для LR первого порядка и 0,3 мм для LR второго порядка).
Потенциальная плотность ветвления (представленная квантилями 95 и 99%) была достигнута для корней среднего диаметра. Плотность ветвления также анализировалась по порядку ветвления (рис. 7B). Согласно этим графикам, плотность ветвления зависела от порядка ветвления.Плотность разветвления была выше у несущих корней более низкого порядка того же диапазона диаметров. Плато было достигнуто за счет более толстых опорных корней (1 мм для осевых корней, 0,5 мм для LR первого порядка и 0,3 мм для LR второго порядка).Рис. 7.
Зависимость плотности ветвления от диаметра корневых сегментов разного порядка. Неразветвленные сегменты в рисунки не вошли. Различные критерии были установлены для длины корневого сегмента подшипника и его разветвленность числа, как показано на рисе.3. (A) Объединение заказов на ветвление для каждой комбинации лечения; базальные диаметры были разделены на 25 классов. (B) Для каждого порядка ветвления объединение трех комбинаций лечения; Базальные диаметры были разделены на пять классов для подмышечных корней и на 25 классов для LR. Общее количество корней для каждого заказа LR указано в ключе.
Рис. 7.
Зависимость плотности ветвления от диаметра корневых сегментов разного порядка. Неразветвленные сегменты в рисунки не вошли.Различные критерии были установлены для длины корневого сегмента подшипника и его разветвленность числа, как показано на рис 3. (А) Аккумулирование ветвления заказов для каждой комбинации лечения. базальные диаметры были разделены на 25 классов. (B) Для каждого порядка ветвления объединение трех комбинаций лечения; Базальные диаметры были разделены на пять классов для подмышечных корней и на 25 классов для LR. Общее количество корней для каждого заказа LR указано в ключе.
Далее мы проанализировали характер изменения плотности ветвления в зависимости от категорий длины и базального диаметра (рис.8). В классе малого диаметра (0,01–0,4 мм) плотность ветвления не изменялась равномерно вдоль корней независимо от их длины.
 Однако для классов большего диаметра плотность ветвления увеличивалась от основания и достигала максимальных значений в промежуточных положениях. Чем толще и длиннее корень, тем сильнее была эта тенденция. Как на рис. 7, так и на рис. 8, соотношение между диаметром и плотностью разветвлений было искажено расположением этого сегмента вдоль корня. Действительно, толстые сегменты около проксимальной части корня разветвлялись не так плотно.Этот эффект «положение» частично объясняет свободную взаимосвязь между плотностью ветвления и диаметра сегмента подшипника.
Однако для классов большего диаметра плотность ветвления увеличивалась от основания и достигала максимальных значений в промежуточных положениях. Чем толще и длиннее корень, тем сильнее была эта тенденция. Как на рис. 7, так и на рис. 8, соотношение между диаметром и плотностью разветвлений было искажено расположением этого сегмента вдоль корня. Действительно, толстые сегменты около проксимальной части корня разветвлялись не так плотно.Этот эффект «положение» частично объясняет свободную взаимосвязь между плотностью ветвления и диаметра сегмента подшипника.Рис. 8.
Изменение плотности разветвления вдоль LR первого порядка для разных классов длины и базального диаметра. Классы длины составляли 5–6, 8–10, 15–20 и 25–30 см, а классы диаметра — 0 · 01–0 · 4, 0 · 4–0 · 8, 0 · 8–1 · 2 и 1. · 2–2 · 0 мм. Для каждой позиции (каждые 1 см) вдоль корня диаграмма показывает значения 50% (линия), 25% и 75% (поля прямоугольника).Значение усов и выбросов показано на рис. 2. Число корней, используемых на каждой панели, указано в верхнем левом углу.
Рис. 8.
Изменение плотности разветвления вдоль LR первого порядка для разных классов длины и базального диаметра. Классы длины составляли 5–6, 8–10, 15–20 и 25–30 см, а классы диаметра — 0 · 01–0 · 4, 0 · 4–0 · 8, 0 · 8–1 · 2 и 1. · 2–2 · 0 мм. Для каждой позиции (каждые 1 см) вдоль корня диаграмма показывает значения 50% (линия), 25% и 75% (поля прямоугольника).Значение усов и выбросов показано на рис. 2. Число корней, используемых на каждой панели, указано в верхнем левом углу.
ОБСУЖДЕНИЕ
В этом исследовании мы применили индивидуальный метод отбора проб корней и комбинированную процедуру обработки изображений и программу анализа данных для изучения диаметра корня и разветвления в масштабе корневого сегмента у зрелых, выращиваемых в поле растений кукурузы. Этот комбинированный метод позволяет очень подробно изучить геометрию и топологию корневой системы зрелых растений, выращиваемых в полевых условиях, таких как кукуруза.
 Простая схема была использована для иллюстрации общего строения корней, имеющих увеличивающийся базальный диаметр (рис. 9). Корни с большим базальным диаметром имеют тенденцию расти длиннее и иметь больше ветвей с большим базальным диаметром и большей длиной. Несмотря на большие различия в их базальных диаметрах, их дистальные диаметры не сильно различались. Однако некоторые отчетливые паттерны ветвления все же имели место. В этом исследовании мы обнаружили, что LR первого порядка с аналогичным базальным диаметром имели несколько паттернов изменения диаметра, что приводило к разной длине корня.Базальный диаметр дополнительно определял степень изменения диаметра. В частности, для корней, имеющих одинаковую классификацию длины, корни, имеющие больший базальный диаметр, показали более высокую скорость уменьшения диаметра вдоль корней; в то же время для корней, имеющих одинаковую классификацию диаметра, корни с более длинными корнями показывают меньшую скорость уменьшения диаметра (рис. 5). Таким образом, изменение диаметра сегментов корня влияло на базальный диаметр и количество дочерних корней (рис. 3 и 7). Отношения между диаметром, длиной и плотностью ветвления и их иерархические связи обсуждаются ниже.
Простая схема была использована для иллюстрации общего строения корней, имеющих увеличивающийся базальный диаметр (рис. 9). Корни с большим базальным диаметром имеют тенденцию расти длиннее и иметь больше ветвей с большим базальным диаметром и большей длиной. Несмотря на большие различия в их базальных диаметрах, их дистальные диаметры не сильно различались. Однако некоторые отчетливые паттерны ветвления все же имели место. В этом исследовании мы обнаружили, что LR первого порядка с аналогичным базальным диаметром имели несколько паттернов изменения диаметра, что приводило к разной длине корня.Базальный диаметр дополнительно определял степень изменения диаметра. В частности, для корней, имеющих одинаковую классификацию длины, корни, имеющие больший базальный диаметр, показали более высокую скорость уменьшения диаметра вдоль корней; в то же время для корней, имеющих одинаковую классификацию диаметра, корни с более длинными корнями показывают меньшую скорость уменьшения диаметра (рис. 5). Таким образом, изменение диаметра сегментов корня влияло на базальный диаметр и количество дочерних корней (рис. 3 и 7). Отношения между диаметром, длиной и плотностью ветвления и их иерархические связи обсуждаются ниже.Рис. 9.
Четыре сканированных корня первого порядка с увеличивающимися базальным диаметром, длиной и плотностью ветвления, но с аналогичными дистальными диаметрами.
Рис. 9.
Четыре сканированных корня первого порядка с увеличивающимися базальным диаметром, длиной и плотностью ветвления, но с одинаковыми дистальными диаметрами.
Положительная корреляция между диаметром дочернего корня и диаметром материнского корня уже отмечена и количественно определена для нескольких видов (Bouma et al ., 2001; Lecompte и др. , 2005; Бесель и др. , 2012; Pagès et al ., 2013, 2014). Тем не менее, в этих исследованиях методы и определения корня дочернего и диаметра подшипника корневой выборки были в основном отличаются от тех, которые используются здесь.
 Более ранние исследования обычно связывали средний апикальный диаметр дочерних корней в целом или дистального несущего корня с апикальным или средним диаметром несущего корня для различных двудольных и однодольных видов (Lecompte et al ., 2005; Бесель и др. , 2012; Pagès et al ., 2013, 2014). Чтобы учесть изменение диаметра вдоль опорных корней, которое не рассматривалось в предыдущих исследованиях, мы связали средние базальные диаметры дочерних корней в последовательных опорных сегментах корня с диаметрами этих сегментов для подмышечных корней и LR более высокого порядка (рис. . 3А). Зависимость между шоу диаметра диаметра дочери корня и матери корня, что значительная часть изменения базального диаметра можно объяснить диаметр сегмента подшипника.Распределение диаметров дочерних корней в каждом классе диаметров несущих корней было просто описано с помощью квантильных кривых с различными значениями вероятности (рис. 3B). Более толстые несущие сегменты корня имели больший разброс диаметров дочерних корней. Это может указывать на то, что дочерние корни толстого несущего сегмента корня обладают большей способностью реагировать на местные почвенные условия или на общее состояние растения. Эта способность важна, если растения хотят расширяться и совершенствовать свое исследование почвы.Таким образом, корни с большим базальным диаметром будут иметь большую способность как расти дольше (чтобы достигать более отдаленных ресурсов) (рис.4), так и генерировать более обильные ветви более высокого порядка (для увеличения площади контакта с почвой) (рис.3 и 7. ). Обратное также верно. Малый диаметр основания корня позволяет эффективно использовать местные ресурсы и сводит к минимуму инвестиции, необходимые для создания и поддержания корневой системы, чтобы другие части корневой системы могли использовать внешние ресурсы почвы (воду, минералы и т. Д.).) более эффективно.
Более ранние исследования обычно связывали средний апикальный диаметр дочерних корней в целом или дистального несущего корня с апикальным или средним диаметром несущего корня для различных двудольных и однодольных видов (Lecompte et al ., 2005; Бесель и др. , 2012; Pagès et al ., 2013, 2014). Чтобы учесть изменение диаметра вдоль опорных корней, которое не рассматривалось в предыдущих исследованиях, мы связали средние базальные диаметры дочерних корней в последовательных опорных сегментах корня с диаметрами этих сегментов для подмышечных корней и LR более высокого порядка (рис. . 3А). Зависимость между шоу диаметра диаметра дочери корня и матери корня, что значительная часть изменения базального диаметра можно объяснить диаметр сегмента подшипника.Распределение диаметров дочерних корней в каждом классе диаметров несущих корней было просто описано с помощью квантильных кривых с различными значениями вероятности (рис. 3B). Более толстые несущие сегменты корня имели больший разброс диаметров дочерних корней. Это может указывать на то, что дочерние корни толстого несущего сегмента корня обладают большей способностью реагировать на местные почвенные условия или на общее состояние растения. Эта способность важна, если растения хотят расширяться и совершенствовать свое исследование почвы.Таким образом, корни с большим базальным диаметром будут иметь большую способность как расти дольше (чтобы достигать более отдаленных ресурсов) (рис.4), так и генерировать более обильные ветви более высокого порядка (для увеличения площади контакта с почвой) (рис.3 и 7. ). Обратное также верно. Малый диаметр основания корня позволяет эффективно использовать местные ресурсы и сводит к минимуму инвестиции, необходимые для создания и поддержания корневой системы, чтобы другие части корневой системы могли использовать внешние ресурсы почвы (воду, минералы и т. Д.).) более эффективно.Соотношение между базальным диаметром и конечной длиной корня у корней разного порядка показывает, что только корни с большим базальным диаметром имеют шанс стать длинными (рис.
 4). Эта взаимосвязь была подтверждена и уточнена в более ранних исследованиях кукурузы на корреляции между апикальным диаметром корня и скоростью роста и продолжительностью роста (Cahn et al ., 1989). Однако в нашем исследовании мы наблюдали очень большие различия в длине корней (особенно для толстых корней), которые не были учтены Cahn et al .(1989), и большинство корней не достигают своей потенциальной длины. Несколько предыдущих исследований зафиксировали временные вариации апикального диаметра (Pagès, 1995; Thaler and Pagès, 1996 a , b ; Lecompte et al ., 2001). Они обнаружили, что апикальный диаметр не является фиксированным атрибутом корня и может изменяться параллельно со скоростью роста во время удлинения отдельного корня. Такие колебания апикального диаметра и скорости роста были связаны с вариациями в доступности ассимилятов (Pagès, 1995; Thaler and Pagès, 1996, a , b ; Lecompte et al ., 2001). Корни однодольных не растут радиально, поэтому изменение апикального диаметра во времени представлено в профиле проксимально-дистального диаметра корня. Конечно, местные вариации факторов почвы, таких как проницаемость, также будут влиять на эту картину продольного диаметра (Bécel et al ., 2012). Согласно профилю диаметра LR первого порядка с различным базальным диаметром (0–2 мм) (рис. 5), мы обнаружили, что большинство корней уменьшилось в диаметре, в то время как другие увеличились, а затем уменьшились в диаметре.Это явление также наблюдалось у проростков двудольных растений (например, у дуба и каучуковых деревьев) для корней с небольшим диапазоном базального диаметра (0,4–0,8 мм) (Pagès, 1995; Thaler and Pagès, 1996, a ). Мы обнаружили, что изменение структурированного диаметра вдоль корня также вызывает изменение длины (рис. 5 и 6). При заданном базальном диаметре те корни, которые становились длинными, также могли каким-то образом сохранять свой диаметр. Это свойство было похоже на то, что наблюдалось у саженцев деревьев (Pagès, 1995).
4). Эта взаимосвязь была подтверждена и уточнена в более ранних исследованиях кукурузы на корреляции между апикальным диаметром корня и скоростью роста и продолжительностью роста (Cahn et al ., 1989). Однако в нашем исследовании мы наблюдали очень большие различия в длине корней (особенно для толстых корней), которые не были учтены Cahn et al .(1989), и большинство корней не достигают своей потенциальной длины. Несколько предыдущих исследований зафиксировали временные вариации апикального диаметра (Pagès, 1995; Thaler and Pagès, 1996 a , b ; Lecompte et al ., 2001). Они обнаружили, что апикальный диаметр не является фиксированным атрибутом корня и может изменяться параллельно со скоростью роста во время удлинения отдельного корня. Такие колебания апикального диаметра и скорости роста были связаны с вариациями в доступности ассимилятов (Pagès, 1995; Thaler and Pagès, 1996, a , b ; Lecompte et al ., 2001). Корни однодольных не растут радиально, поэтому изменение апикального диаметра во времени представлено в профиле проксимально-дистального диаметра корня. Конечно, местные вариации факторов почвы, таких как проницаемость, также будут влиять на эту картину продольного диаметра (Bécel et al ., 2012). Согласно профилю диаметра LR первого порядка с различным базальным диаметром (0–2 мм) (рис. 5), мы обнаружили, что большинство корней уменьшилось в диаметре, в то время как другие увеличились, а затем уменьшились в диаметре.Это явление также наблюдалось у проростков двудольных растений (например, у дуба и каучуковых деревьев) для корней с небольшим диапазоном базального диаметра (0,4–0,8 мм) (Pagès, 1995; Thaler and Pagès, 1996, a ). Мы обнаружили, что изменение структурированного диаметра вдоль корня также вызывает изменение длины (рис. 5 и 6). При заданном базальном диаметре те корни, которые становились длинными, также могли каким-то образом сохранять свой диаметр. Это свойство было похоже на то, что наблюдалось у саженцев деревьев (Pagès, 1995). Тем не менее, увеличение апикального диаметра не всегда приводило к увеличению длины корня, поскольку физические характеристики почвы могут вызывать увеличение диаметра дистальных частей корней, в то же время препятствуя их удлинению (рис.S2). Это явление наблюдалось ранее (Atwell, 1993; Croser et al ., 2000; Bengough et al ., 2006). Базальный диаметр повлиял не только на конечную длину корня (рис. 4), но и на продольную картину изменения диаметра (рис. 5). Для данной длины корни, имеющие больший базальный диаметр, имели более резкое уменьшение продольного диаметра. Морфологически как базальный диаметр, так и характер изменения диаметра определяли окончательную длину корня. В дополнение к влиянию диаметра корня, несколько внешних факторов также влияют на скорость роста корня и продолжительность роста корня, и, следовательно, на конечную длину корня.Эти внешние факторы включают температуру почвы (Tardieu and Pellerin, 1991; Nagel et al ., 2009), проницаемость почвы (Bécel et al ., 2012), глобальную доступность питательных веществ и неоднородность питательных веществ (Yu et al ., 2015). Несмотря на большие различия в базальном диаметре и заметную картину изменения диаметра среди LR первого порядка, дистальный диаметр был гораздо менее изменчивым. Это, по-видимому, подразумевает наличие минимального порога для дистального диаметра.
Тем не менее, увеличение апикального диаметра не всегда приводило к увеличению длины корня, поскольку физические характеристики почвы могут вызывать увеличение диаметра дистальных частей корней, в то же время препятствуя их удлинению (рис.S2). Это явление наблюдалось ранее (Atwell, 1993; Croser et al ., 2000; Bengough et al ., 2006). Базальный диаметр повлиял не только на конечную длину корня (рис. 4), но и на продольную картину изменения диаметра (рис. 5). Для данной длины корни, имеющие больший базальный диаметр, имели более резкое уменьшение продольного диаметра. Морфологически как базальный диаметр, так и характер изменения диаметра определяли окончательную длину корня. В дополнение к влиянию диаметра корня, несколько внешних факторов также влияют на скорость роста корня и продолжительность роста корня, и, следовательно, на конечную длину корня.Эти внешние факторы включают температуру почвы (Tardieu and Pellerin, 1991; Nagel et al ., 2009), проницаемость почвы (Bécel et al ., 2012), глобальную доступность питательных веществ и неоднородность питательных веществ (Yu et al ., 2015). Несмотря на большие различия в базальном диаметре и заметную картину изменения диаметра среди LR первого порядка, дистальный диаметр был гораздо менее изменчивым. Это, по-видимому, подразумевает наличие минимального порога для дистального диаметра.Плотность ветвления сильно различалась, особенно вдоль корней оси.Наибольшая плотность ветвления вдоль пазовых сегментов корня составила почти 45 см -1 в 5-сантиметровых сегментах (рис. 7). Это выше, чем наблюдается у выращиваемой в поле кукурузы (35 см -1 в сегментах по 2 см) (Pagès and Pellerin, 1994), у выращиваемых в горшках проростков кукурузы (30 см -1 в сегментах по 5 см). (Varney et al ., 1991) и в банане (20 см -1 в сегментах по 2 см) (Lecompte and Pagès, 2007). Наибольшая плотность ветвления наших сегментов LR первого порядка составила 24 см −1 (рис.
 7). Это не сильно отличается от самых высоких значений 23 см -1 для банана (Lecompte and Pagès, 2007). В отличие от общепринятого мнения о том, что существует положительная взаимосвязь между диаметром дочернего корня и диаметром несущего корня, существуют противоречивые представления о взаимосвязи между плотностью ветвления и диаметром несущего корня. Бесель и др. . (2012) наблюдали уменьшение плотности ветвления с уменьшением среднего диаметра несущего корня у персика. Lecompte и Pagès (2007) также обнаружили у банана, что LR первого порядка меньшего диаметра имеют тенденцию иметь более высокую плотность ветвления, чем осевые корни большего диаметра.Для банана Draye (2002) также наблюдал для аксильных корней, что плотность ветвления увеличивается с увеличением апикального диаметра. Эти разные отношения, наблюдаемые у банана, могут быть приписаны разной скорости удлинения среди корневых порядков, что может вызывать различия в расстоянии дочерних корней вдоль файлов на основе протоксилемы, а также вариации в количестве полюсов протоксилемы (Draye, 2002; Lecompte and Pagès , 2007). Уменьшение плотности ветвления вдоль узловых корней наблюдается у кукурузы, выращиваемой в полевых условиях (Pagès and Pellerin, 1994).По мере уменьшения диаметра вдоль узлового корня можно сделать вывод, что плотность ветвления уменьшается с уменьшением диаметра корня. В нашем исследовании мы разделили корень подшипника на последовательные сегменты, так что изменение плотности ветвления в разных частях корня подшипника может быть записано. Мы заметили, что плотность ветвления увеличивается с увеличением диаметра несущего корневого сегмента для всех корневых порядков. Взаимосвязь была относительно плотной для подмышечных корней, хотя раннее плато было достигнуто сегментами подмышечных корней промежуточных диаметров (рис.7). Большинство исследователей измеряли плотность ветвления у молодых растений (Varney et al ., 1991; Lecompte et al ., 2005; Ito et al .
7). Это не сильно отличается от самых высоких значений 23 см -1 для банана (Lecompte and Pagès, 2007). В отличие от общепринятого мнения о том, что существует положительная взаимосвязь между диаметром дочернего корня и диаметром несущего корня, существуют противоречивые представления о взаимосвязи между плотностью ветвления и диаметром несущего корня. Бесель и др. . (2012) наблюдали уменьшение плотности ветвления с уменьшением среднего диаметра несущего корня у персика. Lecompte и Pagès (2007) также обнаружили у банана, что LR первого порядка меньшего диаметра имеют тенденцию иметь более высокую плотность ветвления, чем осевые корни большего диаметра.Для банана Draye (2002) также наблюдал для аксильных корней, что плотность ветвления увеличивается с увеличением апикального диаметра. Эти разные отношения, наблюдаемые у банана, могут быть приписаны разной скорости удлинения среди корневых порядков, что может вызывать различия в расстоянии дочерних корней вдоль файлов на основе протоксилемы, а также вариации в количестве полюсов протоксилемы (Draye, 2002; Lecompte and Pagès , 2007). Уменьшение плотности ветвления вдоль узловых корней наблюдается у кукурузы, выращиваемой в полевых условиях (Pagès and Pellerin, 1994).По мере уменьшения диаметра вдоль узлового корня можно сделать вывод, что плотность ветвления уменьшается с уменьшением диаметра корня. В нашем исследовании мы разделили корень подшипника на последовательные сегменты, так что изменение плотности ветвления в разных частях корня подшипника может быть записано. Мы заметили, что плотность ветвления увеличивается с увеличением диаметра несущего корневого сегмента для всех корневых порядков. Взаимосвязь была относительно плотной для подмышечных корней, хотя раннее плато было достигнуто сегментами подмышечных корней промежуточных диаметров (рис.7). Большинство исследователей измеряли плотность ветвления у молодых растений (Varney et al ., 1991; Lecompte et al ., 2005; Ito et al . , 2006), в то время как наше исследование рассматривает узловые корни высоких мутовок на зрелых растениях. . Уже было показано, что уменьшение диаметра намного сильнее на узловых корнях, происходящих от более высоких оборотов (Wu et al ., 2014). Близость к основанию корня и, следовательно, (предположительно) обильное поступление углеводов из побега может позволить крупным базальным сегментам подмышечных корней прорваться больше дочерних корней, которые в большинстве своем все еще имеют большой базальный диаметр.Феномен того, что сегменты осевых корней обычно имеют большее количество дочерних корней с большим диаметром основания, не согласуется с идеей компромисса между количеством и диаметром дочерних корней молодых проростков (Lecompte et al ., 2005 ; Pagès, 2014). Противоположное наблюдение этих авторов может относиться к ограничению поступления ассимилятов из небольших надземных побегов их растений. Следовательно, осевые корни, появляющиеся на разных стадиях роста, вполне могли иметь разные характеристики ветвления.
, 2006), в то время как наше исследование рассматривает узловые корни высоких мутовок на зрелых растениях. . Уже было показано, что уменьшение диаметра намного сильнее на узловых корнях, происходящих от более высоких оборотов (Wu et al ., 2014). Близость к основанию корня и, следовательно, (предположительно) обильное поступление углеводов из побега может позволить крупным базальным сегментам подмышечных корней прорваться больше дочерних корней, которые в большинстве своем все еще имеют большой базальный диаметр.Феномен того, что сегменты осевых корней обычно имеют большее количество дочерних корней с большим диаметром основания, не согласуется с идеей компромисса между количеством и диаметром дочерних корней молодых проростков (Lecompte et al ., 2005 ; Pagès, 2014). Противоположное наблюдение этих авторов может относиться к ограничению поступления ассимилятов из небольших надземных побегов их растений. Следовательно, осевые корни, появляющиеся на разных стадиях роста, вполне могли иметь разные характеристики ветвления.По сравнению с осевыми корнями, плотности ветвления вдоль LR уделялось меньше внимания (Lecompte et al ., 2005; Ito et al ., 2006; Gaudin et al ., 2011; Gruber et al ., 2013). Структурированный профиль плотности разветвлений вдоль LR первого порядка — новая находка (рис. 8). Хотя потенциальная плотность ветвления корневых сегментов кукурузы обычно может быть связана с их диаметром, наибольшее количество дочерних корней часто находилось в промежуточных положениях и с корнями среднего диаметра.Особенно это касалось толстых LR первого порядка. Диаметр обычно резко уменьшается в проксимальной части, в то время как полюса протоксилемы уменьшаются с умеренной скоростью (Draye, 2002). Было обнаружено, что продольное расстояние дочерних корней в файлах на основе протоксилемы положительно коррелирует с апикальным диаметром (Draye, 2002). Уменьшение полюсов протоксилемы может вызывать снижение плотности ветвления, тогда как уменьшение продольного расстояния внутри файлов на основе протоксилемы может вызывать увеличение плотности ветвления (Draye, 2002).
 Когда уменьшение продольного расстояния в файлах на основе протоксилемы превышает уменьшение полюсов протоксилемы, это, вероятно, приведет к увеличению плотности ветвления с уменьшением апикального диаметра. Следовательно, самая высокая плотность ветвления часто может быть обнаружена в средней и / или проксимальной части корня. По мере увеличения расстояния до основания корня (а также до источника ассимилятов) поступление ассимилятов из надземных побегов может не удовлетворить потребность в увеличении плотности ветвления, вызванную прогрессивным уменьшением как апикального диаметра, так и скорости удлинения.Таким образом, плотность ветвления имеет тенденцию к снижению в дистальной части корня. Различия в плотности ветвления также можно отнести к факторам почвы, таким как градиенты объемной плотности почвы (Konôpka et al ., 2009), влажности почвы (Johnson and Aguirre, 1991; Ito et al ., 2006). ), температурой почвы (Sattelmacher et al ., 1990) и питательными веществами почвы (Gruber et al ., 2013), в том числе по мере прохождения корнями питательных пятен (Hodge, 2004; Yu et al ., 2014). Однако, поскольку эти LR первого порядка расположены в разных положениях вдоль узловых корней, а узловые корни из более высоких оборотов имеют более крутые углы корня, так что они проникают в почву более вертикально, LR первого порядка будут испытывать разнообразие местных почвенная среда, поэтому на нее с большей вероятностью будет влиять ряд почвенных факторов. Несмотря на влияние этих факторов, профиль плотности разветвлений на LR первого порядка относительно стабилен. Следовательно, профиль плотности ветвления на LR первого порядка определяется как их базальным диаметром, так и их удлинением и может быть неотъемлемой особенностью растений кукурузы.
Когда уменьшение продольного расстояния в файлах на основе протоксилемы превышает уменьшение полюсов протоксилемы, это, вероятно, приведет к увеличению плотности ветвления с уменьшением апикального диаметра. Следовательно, самая высокая плотность ветвления часто может быть обнаружена в средней и / или проксимальной части корня. По мере увеличения расстояния до основания корня (а также до источника ассимилятов) поступление ассимилятов из надземных побегов может не удовлетворить потребность в увеличении плотности ветвления, вызванную прогрессивным уменьшением как апикального диаметра, так и скорости удлинения.Таким образом, плотность ветвления имеет тенденцию к снижению в дистальной части корня. Различия в плотности ветвления также можно отнести к факторам почвы, таким как градиенты объемной плотности почвы (Konôpka et al ., 2009), влажности почвы (Johnson and Aguirre, 1991; Ito et al ., 2006). ), температурой почвы (Sattelmacher et al ., 1990) и питательными веществами почвы (Gruber et al ., 2013), в том числе по мере прохождения корнями питательных пятен (Hodge, 2004; Yu et al ., 2014). Однако, поскольку эти LR первого порядка расположены в разных положениях вдоль узловых корней, а узловые корни из более высоких оборотов имеют более крутые углы корня, так что они проникают в почву более вертикально, LR первого порядка будут испытывать разнообразие местных почвенная среда, поэтому на нее с большей вероятностью будет влиять ряд почвенных факторов. Несмотря на влияние этих факторов, профиль плотности разветвлений на LR первого порядка относительно стабилен. Следовательно, профиль плотности ветвления на LR первого порядка определяется как их базальным диаметром, так и их удлинением и может быть неотъемлемой особенностью растений кукурузы.Подробные признаки корней были извлечены в основном для корневых систем сеянцев с использованием недавно разработанных автоматизированных / полуавтоматических методов в двух или трех измерениях (Iyer-Pascuzzi et al .
 , 2010; Clark et al ., 2011, 2012 ; Mairhofer et al ., 2012; Nagel et al ., 2012; Tracy et al ., 2012). Эти результаты в сочетании с исследованиями корневой функции облегчают параметризацию корневых архитектурных моделей, используемых для моделирования всей корневой системы молодых растений.Напротив, эти подробные результаты по архитектуре взрослых корней, особенно растений, выращиваемых в поле, все еще в значительной степени отсутствуют (Fiorani and Schurr, 2013). Наиболее подробными измерениями зрелых корневых систем в поле были траектории осевых корней в двух / трех измерениях (Tardieu and Pellerin, 1990; Wu et al ., 2014). Диаметры вдоль корней подмышек также измерялись по траектории (Wu et al ., 2014). Напротив, информации о ветвлении корней особенно не хватало даже для ветвления аксильных корней (Pagès and Pellerin, 1994; Pagès, 2014; Wu and Guo, 2014).В этом исследовании мы начали с анализа ветвления LR первого порядка полевых растений кукурузы, включая изменения их диаметра. Диаметр корня является незаменимым морфологическим параметром архитектурной модели корня (Dunbabin et al ., 2013). Для упрощения вычислений в большинстве моделей корней диаметр LR обычно считается постоянным для молодых растений, поскольку диаметры мелких LR не сильно различаются (рис. 5). При моделировании взрослых корневых систем изменение диаметра вдоль подмышечных корней и вдоль LR первого порядка нельзя игнорировать (Pagès, 1995; Thaler and Pagès, 1996 a ; Wu et al ., 2014), поскольку это изменение диаметра сильно коррелирует с анатомическими особенностями, диаметром и количеством дочерних боковых стволов (рис. 3 и рис. 7), и, следовательно, их продолжительностью жизни и функциями в поглощении ресурсов. Взаимосвязи характеристик ветвления, полученные в этом исследовании, не исключают влияния внешних факторов на ветвление, таких как доступность N и P (Postma et al ., 2014), неоднородность питательных веществ (Yu et al .
, 2010; Clark et al ., 2011, 2012 ; Mairhofer et al ., 2012; Nagel et al ., 2012; Tracy et al ., 2012). Эти результаты в сочетании с исследованиями корневой функции облегчают параметризацию корневых архитектурных моделей, используемых для моделирования всей корневой системы молодых растений.Напротив, эти подробные результаты по архитектуре взрослых корней, особенно растений, выращиваемых в поле, все еще в значительной степени отсутствуют (Fiorani and Schurr, 2013). Наиболее подробными измерениями зрелых корневых систем в поле были траектории осевых корней в двух / трех измерениях (Tardieu and Pellerin, 1990; Wu et al ., 2014). Диаметры вдоль корней подмышек также измерялись по траектории (Wu et al ., 2014). Напротив, информации о ветвлении корней особенно не хватало даже для ветвления аксильных корней (Pagès and Pellerin, 1994; Pagès, 2014; Wu and Guo, 2014).В этом исследовании мы начали с анализа ветвления LR первого порядка полевых растений кукурузы, включая изменения их диаметра. Диаметр корня является незаменимым морфологическим параметром архитектурной модели корня (Dunbabin et al ., 2013). Для упрощения вычислений в большинстве моделей корней диаметр LR обычно считается постоянным для молодых растений, поскольку диаметры мелких LR не сильно различаются (рис. 5). При моделировании взрослых корневых систем изменение диаметра вдоль подмышечных корней и вдоль LR первого порядка нельзя игнорировать (Pagès, 1995; Thaler and Pagès, 1996 a ; Wu et al ., 2014), поскольку это изменение диаметра сильно коррелирует с анатомическими особенностями, диаметром и количеством дочерних боковых стволов (рис. 3 и рис. 7), и, следовательно, их продолжительностью жизни и функциями в поглощении ресурсов. Взаимосвязи характеристик ветвления, полученные в этом исследовании, не исключают влияния внешних факторов на ветвление, таких как доступность N и P (Postma et al ., 2014), неоднородность питательных веществ (Yu et al . , 2015 ) и проницаемости почвы (Bécel et al ., 2012), поскольку большие различия в плотности ветвления действительно существовали среди корней даже в одних и тех же группах (рис. 8). Несмотря на это, общие паттерны ветвления должны быть основным ориентиром для получения морфологических параметров корня для моделей корня, используемых для моделирования больших корневых систем.
, 2015 ) и проницаемости почвы (Bécel et al ., 2012), поскольку большие различия в плотности ветвления действительно существовали среди корней даже в одних и тех же группах (рис. 8). Несмотря на это, общие паттерны ветвления должны быть основным ориентиром для получения морфологических параметров корня для моделей корня, используемых для моделирования больших корневых систем.БЛАГОДАРНОСТИ
Эта работа была поддержана Национальным фондом естественных наук Китая (41471235) и Китайским фондом постдокторантуры (2015M571167).Мы благодарим Цзе Чжоу и Кай Бая за их помощь в проведении экспериментов и доктора Сэнди Лэнга за его ценные комментарии к рукописи.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
.
1994
.Направление роста узловых корней риса: его вариации и вклад в формирование корневой системы
.Растения и почвы
165
:333
—337
.и другие. .
2014
.Разветвление в корнях: раскрытие формы, функции и регулирования
.Физиология растений
166
:538
—550
..
1993
.Реакция корней на механическое сопротивление
.Экологическая и экспериментальная ботаника
33
:27
—40
..
2012
.Сопротивление проникновению в почву, подходящее свойство почвы для учета отклонений в удлинении и ветвлении корней
.Растения и почвы
353
:169
—180
..
2006
.Реакция корней на физические условия почвы; динамика роста от поля к ячейке
.
Журнал экспериментальной ботаники
57
:437
—447
..
1997
.Топологическое масштабирование и архитектура корневой системы растений: иерархии развития и функциональные иерархии
.Новый фитолог
135
:621
—634
..
2000
.MassFlowDyn I: модель переноса и разделения углерода для архитектуры корневой системы
.Анналы ботаники
85
:869
—886
..
2001
.Топология корневой системы и распределение по диаметру видов из местообитаний, различающихся частотой затопления
.Функциональная экология
15
:360
—369
..
1989
.Взаимосвязь между степенью удлинения корня и диаметром и продолжительностью роста боковых корней кукурузы
.Растения и почвы
119
:271
—279
..
2008
.Доказательства по почти изогенным линиям, что глубина проникновения корней увеличивается с увеличением диаметра корня и жесткости на изгиб у риса
.Функциональная биология растений
35
:1163
—1171
.и другие. .
2011
.Трехмерное фенотипирование корня с помощью новой платформы визуализации и программного обеспечения
.Физиология растений
156
:455
—465
.и другие. .
2012
.Высокопроизводительная платформа для двумерного фенотипирования корневой системы облегчает генетический анализ роста и развития корней
.
Завод, клетки и окружающая среда
36
:454
—466
..
2000
.Влияние механического сопротивления на рост корней гороха ( Pisum sativum ).II. Расширение клеток и реология стенок во время восстановления
.Physiologia Plantarum
109
:150
—159
..
2002
.Влияние кинетики роста корней и структуры сосудов на распределение боковых корней
.Завод, клетки и окружающая среда
25
:1463
—1474
.и другие. .
2013
.Моделирование взаимодействия корней и почвы с использованием трехмерных моделей роста, архитектуры и функции корней
.Растения и почвы
372
:93
—124
..
1992
.Стоимость и выгода построения корней малого диаметра
.Журнал питания растений
15
:763
—782
..
2003
.Физиологическая роль аэренхимы в корнях, подвергшихся стрессу фосфором
.Функциональная биология растений
30
:493
—506
..
2013
.Будущие сценарии фенотипирования растений
.Ежегодный обзор биологии растений
64
:267
—291
..
1987
.Архитектурный подход к сравнительной экологии корневых систем растений
.Новый фитолог
106
:61
—77
..
2011
.Новые фенотипы временной, мелкомасштабной и изменчивой роста в корнях взрослой кукурузы (Zea mays L.
. ) в ответ на низкий азотный стресс
) в ответ на низкий азотный стрессЗавод, клетки и окружающая среда
34
:2122
—2137
..
2013
.Пластичность корневой системы арабидопсиса при недостатке питательных веществ
.Физиология растений
163
:161
—179
..
1969
.Количественные аспекты роста корневой системы злаковых
. В:, под ред.Рост корня
.Лондон
:Баттерворт и Ко
,134
—147
..
2004
.Пластичное растение: реакция корней на неоднородные запасы питательных веществ
.Новый фитолог
162
:9
—24
..
2006
.Боковое развитие корней, включая реакцию на высыхание почвы, семенных корней кукурузы ( Zea mays ) и пшеницы ( Triticum aestivum )
.Physiologia Plantarum
127
:260
—267
.и другие. .
2010
.Платформа визуализации и анализа для автоматического фенотипирования и ранжирования признаков корневых систем растений
.Физиология растений
152
:1148
—1157
..
2013
.Корковая нагрузка корня влияет на засухоустойчивость кукурузы
.Анналы ботаники
112
:429
—437
..
1991
.Влияние воды на морфологическое развитие проростков трех сорных трав: особенности ветвления корней
.Журнал управления диапазоном
44
:355
—360
.
.
1993
.Узловое ветвление корней кукурузы: отсутствие покоящихся зачатков, классификация корней по гистологическим параметрам и влияние на сокопроводимость
.Растения и почвы
153
:125
—143
..
2009
.Уплотнение почвы изменяет морфологические характеристики корней семенной кукурузы
.Почвенная среда растений
55
:1
—10
..
2007
.Апикальный диаметр и плотность ветвления влияют на скорость удлинения боковых корней банана
.Экологическая и экспериментальная ботаника
59
:243
—251
..
2001
.Отношения между статическими и динамическими переменными в описании роста корня. Последствия для полевой интерпретации изменчивости укоренения
.Растения и почвы
236
:19
—31
..
2005
.Закономерности изменчивости диаметра боковых корней корневой системы банана
.Новый фитолог
167
:841
—850
..
2014
.Анатомические фены корней, связанные с поглощением воды из высыхающей почвы: цели для улучшения сельскохозяйственных культур
.Журнал экспериментальной ботаники
65
:6155
—6166
.и другие. .
2012
.RooTrak: автоматическое восстановление трехмерной структуры корней растений в почве по изображениям рентгеновской микрокомпьютерной томографии с использованием визуального отслеживания
.
Физиология растений
158
:561
—569
..
1997
.Организация и дифференцировка клеток боковых корней Arabidopsis thaliana
.Девелопмент
124
:33
—44
..
1992
.Влияние диаметра корня на проникновение семенных корней в уплотненный грунт
.Растения и почвы
144
:297
—303
.и другие. .
2009
.Температурные реакции корней: влияние на рост, архитектуру корневой системы и последствия для фенотипирования
.Функциональная биология растений
36
:947
—959
.и другие. .
2012
.GROWSCREEN-Rhizo — это новый фенотипический робот, позволяющий одновременно измерять рост корней и побегов растений, выращиваемых в ризотронах
, заполненных почвой.Функциональная биология растений
39
:891
—904
..
2008
.Разветвление в новых направлениях: контроль архитектуры корня путем формирования бокового корня
.Новый фитолог
179
:595
—614
..
1991
.Изменения гидравлической проводимости и анатомии, вызванные высыханием и повторным увлажнением корней Agave deserti (Agavaceae)
.Американский журнал ботаники
78
:906
—915
..
1993
.Гравитропный ответ корней и формирование корневой системы злаковых растений
.Экологическая и экспериментальная ботаника
33
:141
—158
.
.
1995
.Характер роста боковых корней молодых сеянцев дуба ( Quercus robur ) в соотношении с апикальным диаметром
.Новый фитолог
130
:503
—509
..
2011
.Связь между корневыми особенностями развития и продуктивностью кормления
.Завод, клетки и окружающая среда
34
:1749
—1760
..
2014
.Типы ветвления корневых систем: количественный анализ разнообразия двудольных видов
.Анналы ботаники
114
:591
—598
..
1994
.Оценка параметров, описывающих архитектуру корневой системы растений кукурузы, выращиваемых в поле II. Плотность, длина и ветвление боковых корней первого порядка
.Растения и почвы
164
:169
—176
..
2013
.Возможные и фактические вариации роста корней в корневых системах: моделирование с помощью двухэтапного стохастического подхода
.Растения и почвы
373
:723
—735
..
2014
.Калибровка и оценка ArchiSimple, простой модели архитектуры корневой системы
.Экологическое моделирование
290
:76
—84
..
2014
.Оптимальная плотность боковых корней кукурузы зависит от наличия азота и фосфора.
.Физиология растений
166
:590
—602
..
1993
.Демография тонких корней в ответ на пятна воды и азота
.
Новый фитолог
125
:575
—580
.Основная группа разработчиков R
.2014
.R: язык и среда для статистических вычислений
.Вена
:R Фонд статистических вычислений
..
2014
.Кортикальная аэренхима корня увеличивает усвоение азота кукурузой из почв с низким содержанием азота.
.Физиология растений
166
:726
—735
..
1990
.Влияние температуры зоны укоренения на рост и развитие корней картофеля ( Solanum tuberosum )
.Анналы ботаники
65
:27
—36
..
2011
.Генетическая изменчивость и контроль узлового корневого угла у сорго
.Crop Science
51
:2011
..
2000
.Поглощение воды корнями: последствия водного дефицита
.Журнал экспериментальной ботаники
51
:1531
..
1990
.Траектория узловых корней кукурузы на полях с низкими механическими ограничениями
.Растения и почвы
124
:39
—45
..
1991
.Влияние температуры почвы при появлении корней на траекторию движения узловых корней полевой кукурузы
.Растения и почва
131
:207
—214
..
1996а
.Апикальный диаметр корня и степень удлинения корня проростков каучука ( Hevea brasiliensis ) показывают параллельные реакции на доступность фотоассимилятов
.
Physiologia Plantarum
97
:365
—371
..
1996b
.Периодичность развития корневой системы молодых каучуковых деревьев ( Hevea brasiliensis Müell. Arg.): Взаимосвязь с развитием побегов
.Завод, клетки и окружающая среда
19
:56
—64
.и другие. .
2012
.Количественная оценка воздействия уплотнения почвы на структуру корневой системы томата ( Solanum lycopersicum ) с помощью рентгеновской микрокомпьютерной томографии
.Анналы ботаники
110
:511
—519
..
1991
.Корни ветви Zea . I. Ветви первого порядка, их количество, размеры и деление на классы
.Анналы ботаники
67
:357
..
2001
.Заметные различия в выживаемости корней яблони разного диаметра
.Экология
82
:882
—892
..
2014
.Интегрированный метод количественной оценки корневой архитектуры выращиваемой в поле кукурузы
.Анналы ботаники
114
:841
—851
..
2014
.Трехмерная архитектура пазовых корней полевой кукурузы
.Растения и почвы
387
:363
—377
..
2014
.Фенотипическая пластичность корневой системы кукурузы в ответ на неоднородную доступность азота
.Planta
240
:667
—678
.
.
2015
.Пластичность корней в ответ на локализованное высокое содержание нитратов в кукурузе ( Zea mays )
.Анналы ботаники
116
:751
—762
.© Автор, 2016. Опубликовано издательством Oxford University Press от имени компании Annals of Botany. Все права защищены. Для получения разрешений, пожалуйста, напишите в журналы[email protected]
Проксимальный диаметр корня как предиктор общего размера корня для моделей фрактального ветвления.
Белл, А. Д., Робертс, Д. и Смит, А., 1979 г. Паттерны ветвления: моделирование архитектуры растений. J. Theor. Биол. 81, 351–375.
PubMed CAS Статья Google Scholar
Браун, С., Гиллеспи, А. Дж. И Луго, А. Е. 1989 Процедуры оценки биомассы для тропических лесов с приложениями к данным лесной инвентаризации.Для. Sci. 35, 889–902.
Google Scholar
Cayley, A 1875 Об аналитических формах, называемых деревьями. Филос. Mag. 18, 374–378.
Google Scholar
Де Виллиген П. и Ван Нордвейк М. 1987 Корни для производства растений и эффективности использования питательных веществ, докторская диссертация в сельскохозяйственном университете, Вагенинген, 282 стр.
Ericsson, T 1981 Влияние различного азотного стресса на рост и питание трех клонов Salix .Physiol. Растение. 51, 423–429.
CAS Статья Google Scholar
Монтажник, А. Х. 1988 Топология и геометрия корневых систем растений: влияние нормы полива на топологию корневой системы у Trifolium pratense . Аня. Бот. 58, 91–101.
Google Scholar
Монтажник, А.
 Х, Николас, Р. и Харви, М. Л., 1988 Архитектура корневой системы в связи с жизненным циклом и питательными веществами.Funct. Ecol. 2, 345–351.
Х, Николас, Р. и Харви, М. Л., 1988 Архитектура корневой системы в связи с жизненным циклом и питательными веществами.Funct. Ecol. 2, 345–351.Артикул Google Scholar
Fitter, A H 1991 Характеристики и функции корневых систем. В корнях растений, скрытая половина. Ред. Ю. Вайсель, А. Эшель, У. Кафкафи. стр. 3–25 Marchel Dekker Inc., Нью-Йорк.
Google Scholar
Фиттер, А. Х. и Стикленд, Т. Р. 1991 Архитектурный анализ корневой системы растений 2. Влияние поступления питательных веществ на архитектурно контрастирующие виды растений.Новый Фитол. 118, 383–389.
Артикул Google Scholar
Установщик, А. Х. и Стикленд, Т. Р. 1992 Фрактальная характеристика корневой архитектуры. Funct. Ecol. 6, 632–635.
Артикул Google Scholar
Койпер Л.К., Баккер А.Дж. и Ван Дейк Г.Дж. 1990 Параметры стебля и кроны, связанные со структурной корневой системой пихты Дугласовой. Wageningen Agric. Univ. Статьи 90–6, 57–67.
Lyford, WH 1975 Ризография недревесных корней деревьев в полу. С. 179–197. В Развитие и функции корней. Ред. Дж. Г. Горри и Д. Т. Кларксон. Третий симпозиум Кэбота, Academic Press, Лондон.
Google Scholar
Мандельброт Б. Б. 1983 Фрактальная геометрия природы. Фриман, Нью-Йорк.
Google Scholar
Marcelis-VanAcker, C. A. M, Keijzer, C. J. и Van dePol, P. A. 1993 Ксилемные пути у растений розы в связи с развитием базальных побегов.Acta Bot. Neerl. 42, 313–318.
Google Scholar
Милберн Дж. Поток воды в растениях, 1979 г., Лонгман, Лондон.
Google Scholar
Пажес, Л.
 и Кервелла, Дж. 1990 Рост и развитие корневой системы: геометрические и структурные аспекты. Acta Biotheor. 38, 289–302.
и Кервелла, Дж. 1990 Рост и развитие корневой системы: геометрические и структурные аспекты. Acta Biotheor. 38, 289–302.Артикул Google Scholar
Rayner, RJ 1983 Новые наблюдения за Sawdonia ornata из Шотландии.Пер. R. Soc. Эдинбург: Науки о Земле 74, 79–93.
Google Scholar
Райнер, Р. Дж. 1984 Новые находки Drepanophycus spinaeformis Goppert из нижнего девона в Шотландии. Пер. R. Soc. Эдинбург: Науки о Земле 75, 353–363.
Google Scholar
Спек, Л. И и Ван Нордвейк, М. 1994 Проксимальный диаметр корня как предиктор общего размера корневой системы для моделей фрактального ветвления.II. Численная модель. Растения и почва 164, 119–127.
CAS Google Scholar
Сугихара, Дж. И Мэй, Р. М. 1990 Применение фракталов в экологии. Trends Ecol. Evol. 5, 79–86.
Артикул Google Scholar
Тацуми, Дж. Т., Ямаути, А. и Коно, Ю. 1989 Фрактальный анализ корневых систем растений. Аня. Бот. 64, 499–503.
Google Scholar
Ван Нордвейк М. 1987 Методы количественной оценки структуры распределения корней и динамики корней в полевых условиях.pp 263–281. 20-й Международный институт калийных удобрений, Берн.
Ван Нордвейк, М. и ДеВиллиген, П. 1991 Корневые функции в сельскохозяйственных системах. В корнях растений и окружающей их среде. Ред. HPersson и B LMcMichael. pp 381–395, Elsevier, Amsterdam.
Google Scholar
VanNoordwijk, M, Hairiah, K, Syekhfani, M. S. и Flach, B. 1991 Peltophorum pterocarpa дерево с распределением корней, подходящее для выращивания аллей. В корнях растений и окружающей их среде.
 Ред. HPersson и B LMcMichael. pp 526–532, Elsevier, Amsterdam.
Ред. HPersson и B LMcMichael. pp 526–532, Elsevier, Amsterdam.Google Scholar
Уоринг Р. Х. и Шлезингер В. Х. 1985 Углеродный баланс деревьев. В Лесные экосистемы, концепции и управление. Academic Press, Орландо, Флорида.
Google Scholar
Вернер С. и Смарт Дж. С. 1973 Некоторые новые методы топологической классификации канальных сетей.Геогр. Анальный. 5, 271–295.
Артикул Google Scholar
- Корневая крышка
- Меристематический регион
- Область удлинения
- Область созревания
- Волокнистые корни растут от основания стебля
- Они подземные
- Они представлены в виде скоплений корней одинакового размера
- Основной корень заменен придаточными корнями
- Не проникают глубоко в почву.
- Стержневые корни развиваются из корня эмбриона
- Они всегда находятся под поверхностью почвы
- У них один главный корень (первичный корень) с ветвями, которые растут акропетально.
- Первичный корень остается у растения на протяжении всей жизни
- Они действуют как глубокие питатели, то есть проникают глубоко в почву.
- У большинства растений рост под землей (в виде корней) такой же, как и над землей.
- У сельскохозяйственных культур, выращиваемых на суше, 90% корней находятся в верхних 10 см почвы. Оставшиеся 10% корней вырастают на глубину до 2 м, чтобы достичь глубокой воды и выжить.
- В идеальных условиях корни могут расти со скоростью до 1 см в день.
- Почва прочностью менее 3 мегапаскалей подходит для роста корней.
- Корни разрастаются случайным образом, но они растут быстрее и сильнее разветвляются на участках с благоприятными почвенными условиями.
- Рост корней идет не в сторону воды или удобрений. Вместо этого они растут вокруг этих областей, поскольку это способствует росту.
- Большая часть воды и удобрений впитывается корнями на несколько миллиметров выше кончика роста.
- Старые корни служат трубой для передачи воды и питательных веществ другим частям растения.
- В областях, где болезнь поражает кончик корня или где рост ограничен, потребление воды и питательных веществ будет ограничено.
- Многие корни используются человеком в пищу. Эти корни включают морковь, батат, картофель и редис.
- Корни являются источником некоторых важных лекарств, которые могут спасти жизнь. Растительные лекарства, такие как женьшень, ипекака, раувольфия, ашваганда, получают из корней.
- Корни содержат много клетчатки. Волокно из корней используется для изготовления веников, корзин, щеток и т. Д.
- Корни помогают предотвратить эрозию почвы путем сохранения почвы.
- Предотвращая эрозию почвы, они играют важную роль в предотвращении опустынивания.
9 типов корней деревьев, растений и цветов
Вот ваше полное руководство по корням … корневым системам деревьев, растений и цветов. Мы излагаем и объясняем различные типы корней, а также функции корней (что они делают) и включаем иллюстрацию, показывающую анатомию корневой системы.
Корни — это нелистовая часть тела растения, на которой нет узлов.Это орган, который находится под поверхностью почвы. Корни также могут быть воздушными, то есть растущими над поверхностью земли, или аэрированными, что означает, что они плавают над поверхностью воды. Корни отвечают за обеспечение стеблей и листьев достаточным количеством воды и питательных веществ для их роста.
Связанные: Виды растений в горошек | Типы газовых заводов | Инструменты для обрезки растений | Виды нефритовых растений
Корневые функцииКорни составляют основную часть тела растения с точки зрения объема и функций.Основные функции корней следующие:
Анкер и опораКорневая система растения обеспечивает физическую поддержку, прикрепляя тело растения к почве. Многие растения могут стоять прямо в течение сотен лет, потому что их корни глубоко уходят в почву и надежно удерживают растения на месте.
Поглощение и проводимость Корни имеют корневые волоски, через которые корни поглощают воду и питательные вещества из почвы, необходимые для роста растений. Корни обладают способностью поглощать неорганические питательные вещества против градиента концентрации. После того, как вода и питательные вещества впитаются, они перемещаются вверх к стеблю и листьям.
Корни обладают способностью поглощать неорганические питательные вещества против градиента концентрации. После того, как вода и питательные вещества впитаются, они перемещаются вверх к стеблю и листьям.
В пустынях корни уходят глубоко в постоянные запасы воды. Считается, что пустынные районы, где растут растения, имеют запасы подземных вод. Это очень помогает в принятии решения, где копать колодец.
Транспорт У корнейесть специально разработанные каналы для транспортировки поглощенных питательных веществ и воды к стеблям и листьям.Кроме того, у них также есть каналы, по которым органические продукты могут транспортироваться от надземных частей растения к корням.
СкладНекоторые корнеплоды, такие как морковь и сладкий картофель, служат хранилищем. В них хранятся углеводы и вода. В корнях некоторых растений, содержащихся в десертах, может храниться до 70 кг воды.
ФотосинтезФотосинтез — это процесс, с помощью которого растения готовят себе пищу.Некоторые корни способны к фотосинтезу, как, например, воздушные корни мангровых растений и эпифитных орхидей.
АэрацияУ растений, которые растут на поверхности стоячей воды, есть специальные корни, называемые пневматофорами, которые распространяют кислород из воздуха.
МеханизмСокращающиеся корни многих луковичных растений втягивают растение в почву. Подземная среда более благоприятна для луковичных растений.
РепродукцияНекоторые особые корни способны к размножению. Они служат средством сохранения вида. У некоторых растений, таких как зрелый агохо, вокруг ствола видны обильно растущие побеги от корней, которые растут горизонтально.
Анатомия корнейКорень имеет четыре основных региона :
Корневой колпачок находится на вершине корня. Это структура, похожая на наперсток. Верхушка корня нежная. Корневая шляпка защищает этот нежный конец и помогает корню глубже проникнуть в почву. Корневая шляпка выделяет слизь, которая отвечает за смазку прохода корня в почве. Эта слизь также способствует усвоению воды и питательных веществ. Корневой колпачок изнашивается, но его постоянно обновляют.
Это структура, похожая на наперсток. Верхушка корня нежная. Корневая шляпка защищает этот нежный конец и помогает корню глубже проникнуть в почву. Корневая шляпка выделяет слизь, которая отвечает за смазку прохода корня в почве. Эта слизь также способствует усвоению воды и питательных веществ. Корневой колпачок изнашивается, но его постоянно обновляют.
Термин «меристематический» означает быстрый рост.Эта область находится чуть выше корневой крышечки. Клетки в этой области быстро растут. Они очень маленькие и очень тонкостенные. У них плотная протоплазма.
Область удлиненияКлетки в области удлинения быстро увеличиваются и удлиняются. Клетки в этой области отвечают за рост длины корня.
Область созреванияКлетки в области удлинения после дифференцировки постепенно созревают и образуют область созревания.Клетки дифференцируются, образуя различные специализированные ткани, такие как постоянная область и корневые волоски.
Корни однодольных и корни двудольныхКорни однодольных растений называются корнями однодольных, а корни двудольных растений называются корнями двудольных.
Однодольные растения имеют в зародышах одну семядолю. У однодольных корней ксилема и флоэма расположены по кругу. У двудольных растений в зародышах есть две семядоли. У двудольных корней ксилема находится в середине, а флоэма ее окружает.
Разница между корнями однодольных и двудольныхРазличия между корнями однодольных и двудольных корней составляют:
Корни однодольныхПерицикл дает начало только боковым корням. Сердцевина хорошо развита, крупная. В корнях однодольных растений много ксилемы и флоэмы. Вторичного роста нет.
Двоякие корни Перицикл дает начало нескольким боковым корням, пробковому камбию и некоторой части сосудистого камбия. Шаг отсутствует. Количество ксилемы и флоэмы ограничено. Вторичный рост происходит в корне двудольного дерева.
Шаг отсутствует. Количество ксилемы и флоэмы ограничено. Вторичный рост происходит в корне двудольного дерева.
Существуют разные типы корней в зависимости от типа и вида растений. Основные типы:
1. Волокнистые корниВолокнистые корни встречаются у однодольных растений. Они тонкие, разветвленные, растут прямо из стебля. Эти корни имеют тенденцию расти близко к поверхности и распространяться горизонтально.Они имеют гроздевидный вид с многочисленными корнями, вместе почти одинаковыми по размеру. В мочковатой корневой системе первичный корень недолговечен. Его заменяют многочисленные корни.
Волокнистая корневая система не обеспечивает прочного закрепления растений, так как они не проникают глубоко в почву.
Характеристики:
Стержневой корень встречается у большинства двудольных растений. Этот тип корня представляет собой прямое удлинение корня. В отличие от волокнистых корней, стержневые корни не являются ветвями. Вместо этого они представляют собой единственный первичный корень, который прорастает глубоко в почву. Главный корень дает начало боковым ветвям (вторичным и третичным корням), что приводит к образованию системы стержневых корней.
Ветви стержневого корня растут в акропетальной последовательности, что означает, что более длинные и старые находятся у основания, а более новые, более короткие — около вершины основного корня.
Система Taproot обеспечивает очень прочное закрепление. Причина такой сильной опоры в том, что они глубоко проникают в почву.
У некоторых растений стержневой корень не зарастает слишком глубоко. Вместо этого его боковые ветви растут горизонтально по поверхности. Эти типы корней называются фидерными корнями.
Характеристики:
Придаточные корни подобны волокнистым корням. Однако они могут быть подземными или воздушными (над землей). Они могут расти из любой части растения, кроме прикорневой. Обычно они растут из интермодальных узлов, стеблевых узлов и листьев. Эти корни могут быть толстыми, тонкими или модифицированными в зависимости от вида. Придаточные корни возникают в стрессовых условиях, например, при заболачивании после паводков.
Обрезки листьев и отводок у таких растений, как роза, могут привести к развитию придаточных корней.Также они развиваются при повреждении растений. Они могут увеличить шансы растения на выживание, поскольку растение размножается с помощью придаточных корней.
4. Ползучие корниПолзучие корни — это те корни, которые не проникают глубоко в почву. Они неглубокие и широко распространены по горизонтали от основания растения. У многих деревьев ползучие корни .
5. Клубневые корниКлубневые корни — очень толстые корни.В них хранится значительное количество пищи, чтобы прокормить все растение. Это мясистый, увеличенный и видоизмененный накопительный орган. Они модифицированы из стебля.
Размножение клубневых корней осуществляется делением кроны, при котором на каждом делении кроны имеется несколько почек и достаточно места для хранения, чтобы образовалось новое растение.
Водные корни — это типы корней, которые растут в воде у растений. Они более тонкие и хрупкие.У них есть способность пропускать кислород из атмосферы, который затем используется корнями для обмена веществ и роста. Они морфологически отличаются от почвенных корней.
7. Корни паразитовКорни паразитов — это типы корней, которые прикрепляются к другому растению и высасывают из него питательные вещества. Они не приносят никакой пользы растению-хозяину. Вместо этого они наносят серьезный ущерб, отсюда и название, корни паразита.
Основные фактыФакты о корнях о корнях, перечисленные ниже, — это несколько удивительных указателей, о которых, мы уверены, вы никогда раньше не слышали:
Корни широко используются человеком. Некоторые из наиболее известных применений корней для человека:
Некоторые из наиболее известных применений корней для человека:
Как упоминалось ранее, корни являются источником некоторых очень важных лекарств .Мы перечислили для вас самые известные.
1. КуркумаКорень куркумы способен лечить все, от боли в желудке до артрита, заболеваний желчного пузыря и печени, менструальных спазмов, инфекций и головных болей. Куркума в основном используется в качестве специи, но в лечебных целях корень куркумы просто феноменален.
2. ИмбирьИмбирь эффективен при диарее, тошноте и расстройстве желудка.Его также можно использовать для облегчения простуды, заложенности носа, гриппа и головных болей.
3. СолодкаСолодка издавна использовалась для лечения язвы желудка, бронхита и ангины. Согласно некоторым исследованиям, солодка также может быть полезна при лечении гепатита С.
4. АшвагандаЭтот лекарственный корень можно использовать для лечения артрита, заболеваний печени и фибромиалгии.
5. Валериан Валериана используется для лечения нарушений сна. Многие люди, которые пытаются избавиться от привычки употреблять снотворное, получили пользу от валерианы.



 .
. 0.0,42 * 0,64
0.0,42 * 0,64 
 A.M. когда R.A.M. полный.
A.M. когда R.A.M. полный. Некоторые придаточные корни, известные как воздушные корни, либо проходят некоторое расстояние по воздуху, прежде чем достигают почвы, либо остаются висящими в воздухе. Некоторые из них, такие как кукуруза (кукуруза), винтовая сосна и баньян, в конечном итоге помогают поддерживать растение в почве. У многих эпифитных растений, таких как различные орхидеи и виды Tillandsia , воздушные корни являются основным средством прикрепления к непочвенным поверхностям, таким как другие растения и камни.
Некоторые придаточные корни, известные как воздушные корни, либо проходят некоторое расстояние по воздуху, прежде чем достигают почвы, либо остаются висящими в воздухе. Некоторые из них, такие как кукуруза (кукуруза), винтовая сосна и баньян, в конечном итоге помогают поддерживать растение в почве. У многих эпифитных растений, таких как различные орхидеи и виды Tillandsia , воздушные корни являются основным средством прикрепления к непочвенным поверхностям, таким как другие растения и камни. Именно в области удлинения происходит рост длины. Выше этой зоны растяжения находится область созревания, где созревают первичные ткани корня, завершая процесс дифференцировки клеток, который фактически начинается в верхней части меристематической области.
Именно в области удлинения происходит рост длины. Выше этой зоны растяжения находится область созревания, где созревают первичные ткани корня, завершая процесс дифференцировки клеток, который фактически начинается в верхней части меристематической области.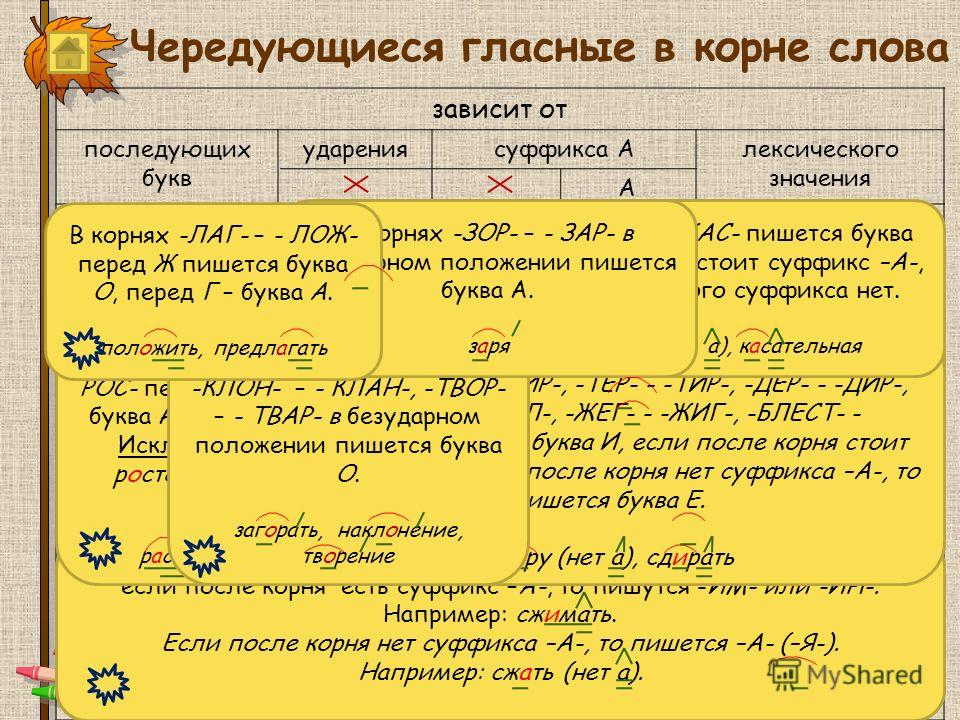
 Различия в диаметре между корнями и вдоль корней влияют на структуру корней и, таким образом, на общую эффективность кормодобывания корневой системы.Однако влияние изменения диаметра на удлинение корня, ветвление и топологические связи не исследовалось систематически ни в популяции корней высокого порядка, ни вдоль корней, особенно для зрелых растений, выращиваемых в поле.
Различия в диаметре между корнями и вдоль корней влияют на структуру корней и, таким образом, на общую эффективность кормодобывания корневой системы.Однако влияние изменения диаметра на удлинение корня, ветвление и топологические связи не исследовалось систематически ни в популяции корней высокого порядка, ни вдоль корней, особенно для зрелых растений, выращиваемых в поле. , 2008; Atkinson et al ., 2014). Вариации в атрибутах удлинения и ветвления создают морфологические различия в длине, количестве и диаметре корней разного порядка в корневой системе (Fitter, 1987; Gruber et al ., 2013).
, 2008; Atkinson et al ., 2014). Вариации в атрибутах удлинения и ветвления создают морфологические различия в длине, количестве и диаметре корней разного порядка в корневой системе (Fitter, 1987; Gruber et al ., 2013). , 2011).
, 2011). . Этот фактор сделает модели развития более сложными, но также и более адаптивными, поскольку диаметр корня может регулироваться во время удлинения корня.Тем не менее, общность некоторых из этих результатов заслуживает оценки с другими видами, а также должна быть оценена в полевых условиях. Следует напомнить, что изменения диаметра корня во времени были впервые зарегистрированы путем мониторинга апикального диаметра отдельных корней через окна наблюдения (Pagès, 1995; Thaler and Pagès, 1996 a ). Хотя этот метод дает прямой доступ к динамике диаметра корня, он очень ограничен и требует специального оборудования, что делает невозможными измерения в более естественных условиях почвы.У однодольных видов, у которых вторичный рост корня не изменяет диаметр корня, можно заменить временной мониторинг диаметра изучением продольного профиля диаметра корня вдоль вынутого корня. Этот метод следует применять незамедлительно к тщательно вынутым корням, прежде чем произойдет какое-либо ухудшение диаметра из-за старения после травмы.
. Этот фактор сделает модели развития более сложными, но также и более адаптивными, поскольку диаметр корня может регулироваться во время удлинения корня.Тем не менее, общность некоторых из этих результатов заслуживает оценки с другими видами, а также должна быть оценена в полевых условиях. Следует напомнить, что изменения диаметра корня во времени были впервые зарегистрированы путем мониторинга апикального диаметра отдельных корней через окна наблюдения (Pagès, 1995; Thaler and Pagès, 1996 a ). Хотя этот метод дает прямой доступ к динамике диаметра корня, он очень ограничен и требует специального оборудования, что делает невозможными измерения в более естественных условиях почвы.У однодольных видов, у которых вторичный рост корня не изменяет диаметр корня, можно заменить временной мониторинг диаметра изучением продольного профиля диаметра корня вдоль вынутого корня. Этот метод следует применять незамедлительно к тщательно вынутым корням, прежде чем произойдет какое-либо ухудшение диаметра из-за старения после травмы. Мы также используем два генотипа в одном сезоне и один генотип в течение двух сезонов, чтобы лучше оценить общность наших результатов. Растения были тщательно вырыты с помощью специального устройства, описанного в предыдущей статье (Wu and Guo, 2014). Основные цели состояли в том, чтобы охарактеризовать: (1) распределение диаметров корней в системе, изучая отношения диаметров через точки ветвления (поперечный диаметр по сравнению с диаметром родителей) и изменение продольного диаметра вдоль отдельных корней; (2) соотношение между диаметром корня и общей длиной корня с учетом как базального (начального) диаметра, так и возможных продольных изменений; и (3) взаимосвязь между диаметром и плотностью ветвления в локальном масштабе корневого сегмента, чтобы проверить наличие положительной взаимосвязи или отчетливого распределения плотности ветвления вдоль корней.В частности, мы проверили гипотезу о том, что конечная длина бокового корня (LR) была связана с размером базального корня и степенью изменения диаметра вдоль корня.
Мы также используем два генотипа в одном сезоне и один генотип в течение двух сезонов, чтобы лучше оценить общность наших результатов. Растения были тщательно вырыты с помощью специального устройства, описанного в предыдущей статье (Wu and Guo, 2014). Основные цели состояли в том, чтобы охарактеризовать: (1) распределение диаметров корней в системе, изучая отношения диаметров через точки ветвления (поперечный диаметр по сравнению с диаметром родителей) и изменение продольного диаметра вдоль отдельных корней; (2) соотношение между диаметром корня и общей длиной корня с учетом как базального (начального) диаметра, так и возможных продольных изменений; и (3) взаимосвязь между диаметром и плотностью ветвления в локальном масштабе корневого сегмента, чтобы проверить наличие положительной взаимосвязи или отчетливого распределения плотности ветвления вдоль корней.В частности, мы проверили гипотезу о том, что конечная длина бокового корня (LR) была связана с размером базального корня и степенью изменения диаметра вдоль корня. За пятнадцать дней до посева был проведен полив затоплением.
За пятнадцать дней до посева был проведен полив затоплением. V-образное лезвие под прямым углом.Два компонента включали фланцы, приваренные вдоль их стыковых кромок для облегчения сборки. Секторный пробоотборник помещали на поверхность почвы так, чтобы его длинная ось была вертикальной, и выровняли так, чтобы его вершина входила только в пень кукурузы (с зазором около 5 см). Образцы корней выбранных растений собирали в междурядьях и внутри рядах соответственно. Затем секторный пробоотборник забивали в почву с помощью горизонтального деревянного бруска и кувалды. Окружающий грунт постепенно выкапывался, чтобы облегчить установку.Когда пробоотборник был погружен на полную глубину (примерно 50 см) и окружающий грунт был полностью выкопан, два стальных троса были прикреплены к приварным проушинам на пробоотборнике, и он и содержащийся в нем клиновидный монолит грунта были осторожно поднял. Затем тангенциальные стальные листы были удалены и заменены крупной сеткой из стальной проволоки (10 × 10 мм), чтобы свести к минимуму поломку корней во время последующего вымывания монолита почвы с использованием тонких водяных струй. После промывки беспочвенный сектор корневой системы хранили в прохладном помещении при 3 ° С.Из-за формы и размера секторного пробоотборника было неизбежно, что некоторые узловые корни пересекали наклонные стороны, и поэтому они были вырезаны. Следовательно, в каждом монолите было ограниченное количество неповрежденных узловых корней.
V-образное лезвие под прямым углом.Два компонента включали фланцы, приваренные вдоль их стыковых кромок для облегчения сборки. Секторный пробоотборник помещали на поверхность почвы так, чтобы его длинная ось была вертикальной, и выровняли так, чтобы его вершина входила только в пень кукурузы (с зазором около 5 см). Образцы корней выбранных растений собирали в междурядьях и внутри рядах соответственно. Затем секторный пробоотборник забивали в почву с помощью горизонтального деревянного бруска и кувалды. Окружающий грунт постепенно выкапывался, чтобы облегчить установку.Когда пробоотборник был погружен на полную глубину (примерно 50 см) и окружающий грунт был полностью выкопан, два стальных троса были прикреплены к приварным проушинам на пробоотборнике, и он и содержащийся в нем клиновидный монолит грунта были осторожно поднял. Затем тангенциальные стальные листы были удалены и заменены крупной сеткой из стальной проволоки (10 × 10 мм), чтобы свести к минимуму поломку корней во время последующего вымывания монолита почвы с использованием тонких водяных струй. После промывки беспочвенный сектор корневой системы хранили в прохладном помещении при 3 ° С.Из-за формы и размера секторного пробоотборника было неизбежно, что некоторые узловые корни пересекали наклонные стороны, и поэтому они были вырезаны. Следовательно, в каждом монолите было ограниченное количество неповрежденных узловых корней. Затем пробоотборная трубка вместе с цилиндрическим монолитом грунта была поднята из грунта с помощью цепного блока, соединенного со стальной портальной рамой. Затем удалили две полутрубки и промыли почвенный монолит тонкой струей воды. Чтобы свести к минимуму поломку корня, стальная трубка (диаметр 50 см, высота 10 см), состоящая из двух съемных полутрубок, была закреплена вокруг основания сердцевины корня, а углы и давление форсунок были оптимизированы.Подробная информация о системе отбора проб корня представлена в Wu and Guo (2014).
Затем пробоотборная трубка вместе с цилиндрическим монолитом грунта была поднята из грунта с помощью цепного блока, соединенного со стальной портальной рамой. Затем удалили две полутрубки и промыли почвенный монолит тонкой струей воды. Чтобы свести к минимуму поломку корня, стальная трубка (диаметр 50 см, высота 10 см), состоящая из двух съемных полутрубок, была закреплена вокруг основания сердцевины корня, а углы и давление форсунок были оптимизированы.Подробная информация о системе отбора проб корня представлена в Wu and Guo (2014). Все корни сканировали планшетным сканером (i800 Plus, Microtek, Шанхай, Китай) с разрешением 400 d.Пи.
Все корни сканировали планшетным сканером (i800 Plus, Microtek, Шанхай, Китай) с разрешением 400 d.Пи. Сценарий, основанный на языке Visual Basic Application (VBA), встроенный в Microsoft Excel, использовался для пакетной обработки файлов для извлечения топологических соединений и геометрических данных отдельных LRU (Wu and Guo, 2014). Для LRU высокой сложности, который был разрезан на части для сканирования, эти части были последовательно объединены для восстановления полного LRU с помощью сценария. Наконец, сценарий экспортировал файл, содержащий значения, разделенные запятыми, для отдельных узловых корней.Подробную информацию о сценарии можно найти в Wu and Guo (2014).
Сценарий, основанный на языке Visual Basic Application (VBA), встроенный в Microsoft Excel, использовался для пакетной обработки файлов для извлечения топологических соединений и геометрических данных отдельных LRU (Wu and Guo, 2014). Для LRU высокой сложности, который был разрезан на части для сканирования, эти части были последовательно объединены для восстановления полного LRU с помощью сценария. Наконец, сценарий экспортировал файл, содержащий значения, разделенные запятыми, для отдельных узловых корней.Подробную информацию о сценарии можно найти в Wu and Guo (2014). Вариации диаметра также уменьшались с увеличением порядка ветвления. Этот эффект все еще был заметен в логарифмическом масштабе. Однако вариации диаметра не сильно различались ни для двух сортов в один сезон (Z09 и N09), ни для одного и того же сорта в два разных сезона (Z09 и Z11).
Вариации диаметра также уменьшались с увеличением порядка ветвления. Этот эффект все еще был заметен в логарифмическом масштабе. Однако вариации диаметра не сильно различались ни для двух сортов в один сезон (Z09 и N09), ни для одного и того же сорта в два разных сезона (Z09 и Z11).
 (A) LR разного порядка разветвления были объединены для каждой комбинации обработки. (B) Для каждого порядка ветвления объединение трех комбинаций лечения. Кривые разной толщины указывают на квантильные кривые 50% (тонкие) и 99% (толстые).Общее количество корней для LR каждого порядка указывается в ключе.
(A) LR разного порядка разветвления были объединены для каждой комбинации обработки. (B) Для каждого порядка ветвления объединение трех комбинаций лечения. Кривые разной толщины указывают на квантильные кривые 50% (тонкие) и 99% (толстые).Общее количество корней для LR каждого порядка указывается в ключе. 4B). В пределах того же диапазона базального диаметра корни более низкого порядка имели большую длину корня. Однако с увеличением базального диаметра скорость увеличения потенциальной длины была ниже для корней с большим диаметром, более 0,6 мм (рис. 4A).
4B). В пределах того же диапазона базального диаметра корни более низкого порядка имели большую длину корня. Однако с увеличением базального диаметра скорость увеличения потенциальной длины была ниже для корней с большим диаметром, более 0,6 мм (рис. 4A).
 Мы предполагаем, что корни в верхней правой части могли столкнуться с объемом уплотненной почвы (имеющей низкую проницаемость), поскольку их рост прекратился, а их апикальный диаметр увеличился (рис. S2). Некоторые из этих корней также давали толстые LR (рис. S2).
Мы предполагаем, что корни в верхней правой части могли столкнуться с объемом уплотненной почвы (имеющей низкую проницаемость), поскольку их рост прекратился, а их апикальный диаметр увеличился (рис. S2). Некоторые из этих корней также давали толстые LR (рис. S2). Потенциальная плотность ветвления (представленная квантилями 95 и 99%) была достигнута для корней среднего диаметра. Плотность ветвления также анализировалась по порядку ветвления (рис. 7B). Согласно этим графикам, плотность ветвления зависела от порядка ветвления.Плотность разветвления была выше у несущих корней более низкого порядка того же диапазона диаметров. Плато было достигнуто за счет более толстых опорных корней (1 мм для осевых корней, 0,5 мм для LR первого порядка и 0,3 мм для LR второго порядка).
Потенциальная плотность ветвления (представленная квантилями 95 и 99%) была достигнута для корней среднего диаметра. Плотность ветвления также анализировалась по порядку ветвления (рис. 7B). Согласно этим графикам, плотность ветвления зависела от порядка ветвления.Плотность разветвления была выше у несущих корней более низкого порядка того же диапазона диаметров. Плато было достигнуто за счет более толстых опорных корней (1 мм для осевых корней, 0,5 мм для LR первого порядка и 0,3 мм для LR второго порядка). Однако для классов большего диаметра плотность ветвления увеличивалась от основания и достигала максимальных значений в промежуточных положениях. Чем толще и длиннее корень, тем сильнее была эта тенденция. Как на рис. 7, так и на рис. 8, соотношение между диаметром и плотностью разветвлений было искажено расположением этого сегмента вдоль корня. Действительно, толстые сегменты около проксимальной части корня разветвлялись не так плотно.Этот эффект «положение» частично объясняет свободную взаимосвязь между плотностью ветвления и диаметра сегмента подшипника.
Однако для классов большего диаметра плотность ветвления увеличивалась от основания и достигала максимальных значений в промежуточных положениях. Чем толще и длиннее корень, тем сильнее была эта тенденция. Как на рис. 7, так и на рис. 8, соотношение между диаметром и плотностью разветвлений было искажено расположением этого сегмента вдоль корня. Действительно, толстые сегменты около проксимальной части корня разветвлялись не так плотно.Этот эффект «положение» частично объясняет свободную взаимосвязь между плотностью ветвления и диаметра сегмента подшипника. Простая схема была использована для иллюстрации общего строения корней, имеющих увеличивающийся базальный диаметр (рис. 9). Корни с большим базальным диаметром имеют тенденцию расти длиннее и иметь больше ветвей с большим базальным диаметром и большей длиной. Несмотря на большие различия в их базальных диаметрах, их дистальные диаметры не сильно различались. Однако некоторые отчетливые паттерны ветвления все же имели место. В этом исследовании мы обнаружили, что LR первого порядка с аналогичным базальным диаметром имели несколько паттернов изменения диаметра, что приводило к разной длине корня.Базальный диаметр дополнительно определял степень изменения диаметра. В частности, для корней, имеющих одинаковую классификацию длины, корни, имеющие больший базальный диаметр, показали более высокую скорость уменьшения диаметра вдоль корней; в то же время для корней, имеющих одинаковую классификацию диаметра, корни с более длинными корнями показывают меньшую скорость уменьшения диаметра (рис. 5). Таким образом, изменение диаметра сегментов корня влияло на базальный диаметр и количество дочерних корней (рис. 3 и 7). Отношения между диаметром, длиной и плотностью ветвления и их иерархические связи обсуждаются ниже.
Простая схема была использована для иллюстрации общего строения корней, имеющих увеличивающийся базальный диаметр (рис. 9). Корни с большим базальным диаметром имеют тенденцию расти длиннее и иметь больше ветвей с большим базальным диаметром и большей длиной. Несмотря на большие различия в их базальных диаметрах, их дистальные диаметры не сильно различались. Однако некоторые отчетливые паттерны ветвления все же имели место. В этом исследовании мы обнаружили, что LR первого порядка с аналогичным базальным диаметром имели несколько паттернов изменения диаметра, что приводило к разной длине корня.Базальный диаметр дополнительно определял степень изменения диаметра. В частности, для корней, имеющих одинаковую классификацию длины, корни, имеющие больший базальный диаметр, показали более высокую скорость уменьшения диаметра вдоль корней; в то же время для корней, имеющих одинаковую классификацию диаметра, корни с более длинными корнями показывают меньшую скорость уменьшения диаметра (рис. 5). Таким образом, изменение диаметра сегментов корня влияло на базальный диаметр и количество дочерних корней (рис. 3 и 7). Отношения между диаметром, длиной и плотностью ветвления и их иерархические связи обсуждаются ниже. Более ранние исследования обычно связывали средний апикальный диаметр дочерних корней в целом или дистального несущего корня с апикальным или средним диаметром несущего корня для различных двудольных и однодольных видов (Lecompte et al ., 2005; Бесель и др. , 2012; Pagès et al ., 2013, 2014). Чтобы учесть изменение диаметра вдоль опорных корней, которое не рассматривалось в предыдущих исследованиях, мы связали средние базальные диаметры дочерних корней в последовательных опорных сегментах корня с диаметрами этих сегментов для подмышечных корней и LR более высокого порядка (рис. . 3А). Зависимость между шоу диаметра диаметра дочери корня и матери корня, что значительная часть изменения базального диаметра можно объяснить диаметр сегмента подшипника.Распределение диаметров дочерних корней в каждом классе диаметров несущих корней было просто описано с помощью квантильных кривых с различными значениями вероятности (рис. 3B). Более толстые несущие сегменты корня имели больший разброс диаметров дочерних корней. Это может указывать на то, что дочерние корни толстого несущего сегмента корня обладают большей способностью реагировать на местные почвенные условия или на общее состояние растения. Эта способность важна, если растения хотят расширяться и совершенствовать свое исследование почвы.Таким образом, корни с большим базальным диаметром будут иметь большую способность как расти дольше (чтобы достигать более отдаленных ресурсов) (рис.4), так и генерировать более обильные ветви более высокого порядка (для увеличения площади контакта с почвой) (рис.3 и 7. ). Обратное также верно. Малый диаметр основания корня позволяет эффективно использовать местные ресурсы и сводит к минимуму инвестиции, необходимые для создания и поддержания корневой системы, чтобы другие части корневой системы могли использовать внешние ресурсы почвы (воду, минералы и т. Д.).) более эффективно.
Более ранние исследования обычно связывали средний апикальный диаметр дочерних корней в целом или дистального несущего корня с апикальным или средним диаметром несущего корня для различных двудольных и однодольных видов (Lecompte et al ., 2005; Бесель и др. , 2012; Pagès et al ., 2013, 2014). Чтобы учесть изменение диаметра вдоль опорных корней, которое не рассматривалось в предыдущих исследованиях, мы связали средние базальные диаметры дочерних корней в последовательных опорных сегментах корня с диаметрами этих сегментов для подмышечных корней и LR более высокого порядка (рис. . 3А). Зависимость между шоу диаметра диаметра дочери корня и матери корня, что значительная часть изменения базального диаметра можно объяснить диаметр сегмента подшипника.Распределение диаметров дочерних корней в каждом классе диаметров несущих корней было просто описано с помощью квантильных кривых с различными значениями вероятности (рис. 3B). Более толстые несущие сегменты корня имели больший разброс диаметров дочерних корней. Это может указывать на то, что дочерние корни толстого несущего сегмента корня обладают большей способностью реагировать на местные почвенные условия или на общее состояние растения. Эта способность важна, если растения хотят расширяться и совершенствовать свое исследование почвы.Таким образом, корни с большим базальным диаметром будут иметь большую способность как расти дольше (чтобы достигать более отдаленных ресурсов) (рис.4), так и генерировать более обильные ветви более высокого порядка (для увеличения площади контакта с почвой) (рис.3 и 7. ). Обратное также верно. Малый диаметр основания корня позволяет эффективно использовать местные ресурсы и сводит к минимуму инвестиции, необходимые для создания и поддержания корневой системы, чтобы другие части корневой системы могли использовать внешние ресурсы почвы (воду, минералы и т. Д.).) более эффективно. 4). Эта взаимосвязь была подтверждена и уточнена в более ранних исследованиях кукурузы на корреляции между апикальным диаметром корня и скоростью роста и продолжительностью роста (Cahn et al ., 1989). Однако в нашем исследовании мы наблюдали очень большие различия в длине корней (особенно для толстых корней), которые не были учтены Cahn et al .(1989), и большинство корней не достигают своей потенциальной длины. Несколько предыдущих исследований зафиксировали временные вариации апикального диаметра (Pagès, 1995; Thaler and Pagès, 1996 a , b ; Lecompte et al ., 2001). Они обнаружили, что апикальный диаметр не является фиксированным атрибутом корня и может изменяться параллельно со скоростью роста во время удлинения отдельного корня. Такие колебания апикального диаметра и скорости роста были связаны с вариациями в доступности ассимилятов (Pagès, 1995; Thaler and Pagès, 1996, a , b ; Lecompte et al ., 2001). Корни однодольных не растут радиально, поэтому изменение апикального диаметра во времени представлено в профиле проксимально-дистального диаметра корня. Конечно, местные вариации факторов почвы, таких как проницаемость, также будут влиять на эту картину продольного диаметра (Bécel et al ., 2012). Согласно профилю диаметра LR первого порядка с различным базальным диаметром (0–2 мм) (рис. 5), мы обнаружили, что большинство корней уменьшилось в диаметре, в то время как другие увеличились, а затем уменьшились в диаметре.Это явление также наблюдалось у проростков двудольных растений (например, у дуба и каучуковых деревьев) для корней с небольшим диапазоном базального диаметра (0,4–0,8 мм) (Pagès, 1995; Thaler and Pagès, 1996, a ). Мы обнаружили, что изменение структурированного диаметра вдоль корня также вызывает изменение длины (рис. 5 и 6). При заданном базальном диаметре те корни, которые становились длинными, также могли каким-то образом сохранять свой диаметр. Это свойство было похоже на то, что наблюдалось у саженцев деревьев (Pagès, 1995).
4). Эта взаимосвязь была подтверждена и уточнена в более ранних исследованиях кукурузы на корреляции между апикальным диаметром корня и скоростью роста и продолжительностью роста (Cahn et al ., 1989). Однако в нашем исследовании мы наблюдали очень большие различия в длине корней (особенно для толстых корней), которые не были учтены Cahn et al .(1989), и большинство корней не достигают своей потенциальной длины. Несколько предыдущих исследований зафиксировали временные вариации апикального диаметра (Pagès, 1995; Thaler and Pagès, 1996 a , b ; Lecompte et al ., 2001). Они обнаружили, что апикальный диаметр не является фиксированным атрибутом корня и может изменяться параллельно со скоростью роста во время удлинения отдельного корня. Такие колебания апикального диаметра и скорости роста были связаны с вариациями в доступности ассимилятов (Pagès, 1995; Thaler and Pagès, 1996, a , b ; Lecompte et al ., 2001). Корни однодольных не растут радиально, поэтому изменение апикального диаметра во времени представлено в профиле проксимально-дистального диаметра корня. Конечно, местные вариации факторов почвы, таких как проницаемость, также будут влиять на эту картину продольного диаметра (Bécel et al ., 2012). Согласно профилю диаметра LR первого порядка с различным базальным диаметром (0–2 мм) (рис. 5), мы обнаружили, что большинство корней уменьшилось в диаметре, в то время как другие увеличились, а затем уменьшились в диаметре.Это явление также наблюдалось у проростков двудольных растений (например, у дуба и каучуковых деревьев) для корней с небольшим диапазоном базального диаметра (0,4–0,8 мм) (Pagès, 1995; Thaler and Pagès, 1996, a ). Мы обнаружили, что изменение структурированного диаметра вдоль корня также вызывает изменение длины (рис. 5 и 6). При заданном базальном диаметре те корни, которые становились длинными, также могли каким-то образом сохранять свой диаметр. Это свойство было похоже на то, что наблюдалось у саженцев деревьев (Pagès, 1995). Тем не менее, увеличение апикального диаметра не всегда приводило к увеличению длины корня, поскольку физические характеристики почвы могут вызывать увеличение диаметра дистальных частей корней, в то же время препятствуя их удлинению (рис.S2). Это явление наблюдалось ранее (Atwell, 1993; Croser et al ., 2000; Bengough et al ., 2006). Базальный диаметр повлиял не только на конечную длину корня (рис. 4), но и на продольную картину изменения диаметра (рис. 5). Для данной длины корни, имеющие больший базальный диаметр, имели более резкое уменьшение продольного диаметра. Морфологически как базальный диаметр, так и характер изменения диаметра определяли окончательную длину корня. В дополнение к влиянию диаметра корня, несколько внешних факторов также влияют на скорость роста корня и продолжительность роста корня, и, следовательно, на конечную длину корня.Эти внешние факторы включают температуру почвы (Tardieu and Pellerin, 1991; Nagel et al ., 2009), проницаемость почвы (Bécel et al ., 2012), глобальную доступность питательных веществ и неоднородность питательных веществ (Yu et al ., 2015). Несмотря на большие различия в базальном диаметре и заметную картину изменения диаметра среди LR первого порядка, дистальный диаметр был гораздо менее изменчивым. Это, по-видимому, подразумевает наличие минимального порога для дистального диаметра.
Тем не менее, увеличение апикального диаметра не всегда приводило к увеличению длины корня, поскольку физические характеристики почвы могут вызывать увеличение диаметра дистальных частей корней, в то же время препятствуя их удлинению (рис.S2). Это явление наблюдалось ранее (Atwell, 1993; Croser et al ., 2000; Bengough et al ., 2006). Базальный диаметр повлиял не только на конечную длину корня (рис. 4), но и на продольную картину изменения диаметра (рис. 5). Для данной длины корни, имеющие больший базальный диаметр, имели более резкое уменьшение продольного диаметра. Морфологически как базальный диаметр, так и характер изменения диаметра определяли окончательную длину корня. В дополнение к влиянию диаметра корня, несколько внешних факторов также влияют на скорость роста корня и продолжительность роста корня, и, следовательно, на конечную длину корня.Эти внешние факторы включают температуру почвы (Tardieu and Pellerin, 1991; Nagel et al ., 2009), проницаемость почвы (Bécel et al ., 2012), глобальную доступность питательных веществ и неоднородность питательных веществ (Yu et al ., 2015). Несмотря на большие различия в базальном диаметре и заметную картину изменения диаметра среди LR первого порядка, дистальный диаметр был гораздо менее изменчивым. Это, по-видимому, подразумевает наличие минимального порога для дистального диаметра. 7). Это не сильно отличается от самых высоких значений 23 см -1 для банана (Lecompte and Pagès, 2007). В отличие от общепринятого мнения о том, что существует положительная взаимосвязь между диаметром дочернего корня и диаметром несущего корня, существуют противоречивые представления о взаимосвязи между плотностью ветвления и диаметром несущего корня. Бесель и др. . (2012) наблюдали уменьшение плотности ветвления с уменьшением среднего диаметра несущего корня у персика. Lecompte и Pagès (2007) также обнаружили у банана, что LR первого порядка меньшего диаметра имеют тенденцию иметь более высокую плотность ветвления, чем осевые корни большего диаметра.Для банана Draye (2002) также наблюдал для аксильных корней, что плотность ветвления увеличивается с увеличением апикального диаметра. Эти разные отношения, наблюдаемые у банана, могут быть приписаны разной скорости удлинения среди корневых порядков, что может вызывать различия в расстоянии дочерних корней вдоль файлов на основе протоксилемы, а также вариации в количестве полюсов протоксилемы (Draye, 2002; Lecompte and Pagès , 2007). Уменьшение плотности ветвления вдоль узловых корней наблюдается у кукурузы, выращиваемой в полевых условиях (Pagès and Pellerin, 1994).По мере уменьшения диаметра вдоль узлового корня можно сделать вывод, что плотность ветвления уменьшается с уменьшением диаметра корня. В нашем исследовании мы разделили корень подшипника на последовательные сегменты, так что изменение плотности ветвления в разных частях корня подшипника может быть записано. Мы заметили, что плотность ветвления увеличивается с увеличением диаметра несущего корневого сегмента для всех корневых порядков. Взаимосвязь была относительно плотной для подмышечных корней, хотя раннее плато было достигнуто сегментами подмышечных корней промежуточных диаметров (рис.7). Большинство исследователей измеряли плотность ветвления у молодых растений (Varney et al ., 1991; Lecompte et al ., 2005; Ito et al .
7). Это не сильно отличается от самых высоких значений 23 см -1 для банана (Lecompte and Pagès, 2007). В отличие от общепринятого мнения о том, что существует положительная взаимосвязь между диаметром дочернего корня и диаметром несущего корня, существуют противоречивые представления о взаимосвязи между плотностью ветвления и диаметром несущего корня. Бесель и др. . (2012) наблюдали уменьшение плотности ветвления с уменьшением среднего диаметра несущего корня у персика. Lecompte и Pagès (2007) также обнаружили у банана, что LR первого порядка меньшего диаметра имеют тенденцию иметь более высокую плотность ветвления, чем осевые корни большего диаметра.Для банана Draye (2002) также наблюдал для аксильных корней, что плотность ветвления увеличивается с увеличением апикального диаметра. Эти разные отношения, наблюдаемые у банана, могут быть приписаны разной скорости удлинения среди корневых порядков, что может вызывать различия в расстоянии дочерних корней вдоль файлов на основе протоксилемы, а также вариации в количестве полюсов протоксилемы (Draye, 2002; Lecompte and Pagès , 2007). Уменьшение плотности ветвления вдоль узловых корней наблюдается у кукурузы, выращиваемой в полевых условиях (Pagès and Pellerin, 1994).По мере уменьшения диаметра вдоль узлового корня можно сделать вывод, что плотность ветвления уменьшается с уменьшением диаметра корня. В нашем исследовании мы разделили корень подшипника на последовательные сегменты, так что изменение плотности ветвления в разных частях корня подшипника может быть записано. Мы заметили, что плотность ветвления увеличивается с увеличением диаметра несущего корневого сегмента для всех корневых порядков. Взаимосвязь была относительно плотной для подмышечных корней, хотя раннее плато было достигнуто сегментами подмышечных корней промежуточных диаметров (рис.7). Большинство исследователей измеряли плотность ветвления у молодых растений (Varney et al ., 1991; Lecompte et al ., 2005; Ito et al . , 2006), в то время как наше исследование рассматривает узловые корни высоких мутовок на зрелых растениях. . Уже было показано, что уменьшение диаметра намного сильнее на узловых корнях, происходящих от более высоких оборотов (Wu et al ., 2014). Близость к основанию корня и, следовательно, (предположительно) обильное поступление углеводов из побега может позволить крупным базальным сегментам подмышечных корней прорваться больше дочерних корней, которые в большинстве своем все еще имеют большой базальный диаметр.Феномен того, что сегменты осевых корней обычно имеют большее количество дочерних корней с большим диаметром основания, не согласуется с идеей компромисса между количеством и диаметром дочерних корней молодых проростков (Lecompte et al ., 2005 ; Pagès, 2014). Противоположное наблюдение этих авторов может относиться к ограничению поступления ассимилятов из небольших надземных побегов их растений. Следовательно, осевые корни, появляющиеся на разных стадиях роста, вполне могли иметь разные характеристики ветвления.
, 2006), в то время как наше исследование рассматривает узловые корни высоких мутовок на зрелых растениях. . Уже было показано, что уменьшение диаметра намного сильнее на узловых корнях, происходящих от более высоких оборотов (Wu et al ., 2014). Близость к основанию корня и, следовательно, (предположительно) обильное поступление углеводов из побега может позволить крупным базальным сегментам подмышечных корней прорваться больше дочерних корней, которые в большинстве своем все еще имеют большой базальный диаметр.Феномен того, что сегменты осевых корней обычно имеют большее количество дочерних корней с большим диаметром основания, не согласуется с идеей компромисса между количеством и диаметром дочерних корней молодых проростков (Lecompte et al ., 2005 ; Pagès, 2014). Противоположное наблюдение этих авторов может относиться к ограничению поступления ассимилятов из небольших надземных побегов их растений. Следовательно, осевые корни, появляющиеся на разных стадиях роста, вполне могли иметь разные характеристики ветвления. Когда уменьшение продольного расстояния в файлах на основе протоксилемы превышает уменьшение полюсов протоксилемы, это, вероятно, приведет к увеличению плотности ветвления с уменьшением апикального диаметра. Следовательно, самая высокая плотность ветвления часто может быть обнаружена в средней и / или проксимальной части корня. По мере увеличения расстояния до основания корня (а также до источника ассимилятов) поступление ассимилятов из надземных побегов может не удовлетворить потребность в увеличении плотности ветвления, вызванную прогрессивным уменьшением как апикального диаметра, так и скорости удлинения.Таким образом, плотность ветвления имеет тенденцию к снижению в дистальной части корня. Различия в плотности ветвления также можно отнести к факторам почвы, таким как градиенты объемной плотности почвы (Konôpka et al ., 2009), влажности почвы (Johnson and Aguirre, 1991; Ito et al ., 2006). ), температурой почвы (Sattelmacher et al ., 1990) и питательными веществами почвы (Gruber et al ., 2013), в том числе по мере прохождения корнями питательных пятен (Hodge, 2004; Yu et al ., 2014). Однако, поскольку эти LR первого порядка расположены в разных положениях вдоль узловых корней, а узловые корни из более высоких оборотов имеют более крутые углы корня, так что они проникают в почву более вертикально, LR первого порядка будут испытывать разнообразие местных почвенная среда, поэтому на нее с большей вероятностью будет влиять ряд почвенных факторов. Несмотря на влияние этих факторов, профиль плотности разветвлений на LR первого порядка относительно стабилен. Следовательно, профиль плотности ветвления на LR первого порядка определяется как их базальным диаметром, так и их удлинением и может быть неотъемлемой особенностью растений кукурузы.
Когда уменьшение продольного расстояния в файлах на основе протоксилемы превышает уменьшение полюсов протоксилемы, это, вероятно, приведет к увеличению плотности ветвления с уменьшением апикального диаметра. Следовательно, самая высокая плотность ветвления часто может быть обнаружена в средней и / или проксимальной части корня. По мере увеличения расстояния до основания корня (а также до источника ассимилятов) поступление ассимилятов из надземных побегов может не удовлетворить потребность в увеличении плотности ветвления, вызванную прогрессивным уменьшением как апикального диаметра, так и скорости удлинения.Таким образом, плотность ветвления имеет тенденцию к снижению в дистальной части корня. Различия в плотности ветвления также можно отнести к факторам почвы, таким как градиенты объемной плотности почвы (Konôpka et al ., 2009), влажности почвы (Johnson and Aguirre, 1991; Ito et al ., 2006). ), температурой почвы (Sattelmacher et al ., 1990) и питательными веществами почвы (Gruber et al ., 2013), в том числе по мере прохождения корнями питательных пятен (Hodge, 2004; Yu et al ., 2014). Однако, поскольку эти LR первого порядка расположены в разных положениях вдоль узловых корней, а узловые корни из более высоких оборотов имеют более крутые углы корня, так что они проникают в почву более вертикально, LR первого порядка будут испытывать разнообразие местных почвенная среда, поэтому на нее с большей вероятностью будет влиять ряд почвенных факторов. Несмотря на влияние этих факторов, профиль плотности разветвлений на LR первого порядка относительно стабилен. Следовательно, профиль плотности ветвления на LR первого порядка определяется как их базальным диаметром, так и их удлинением и может быть неотъемлемой особенностью растений кукурузы. , 2010; Clark et al ., 2011, 2012 ; Mairhofer et al ., 2012; Nagel et al ., 2012; Tracy et al ., 2012). Эти результаты в сочетании с исследованиями корневой функции облегчают параметризацию корневых архитектурных моделей, используемых для моделирования всей корневой системы молодых растений.Напротив, эти подробные результаты по архитектуре взрослых корней, особенно растений, выращиваемых в поле, все еще в значительной степени отсутствуют (Fiorani and Schurr, 2013). Наиболее подробными измерениями зрелых корневых систем в поле были траектории осевых корней в двух / трех измерениях (Tardieu and Pellerin, 1990; Wu et al ., 2014). Диаметры вдоль корней подмышек также измерялись по траектории (Wu et al ., 2014). Напротив, информации о ветвлении корней особенно не хватало даже для ветвления аксильных корней (Pagès and Pellerin, 1994; Pagès, 2014; Wu and Guo, 2014).В этом исследовании мы начали с анализа ветвления LR первого порядка полевых растений кукурузы, включая изменения их диаметра. Диаметр корня является незаменимым морфологическим параметром архитектурной модели корня (Dunbabin et al ., 2013). Для упрощения вычислений в большинстве моделей корней диаметр LR обычно считается постоянным для молодых растений, поскольку диаметры мелких LR не сильно различаются (рис. 5). При моделировании взрослых корневых систем изменение диаметра вдоль подмышечных корней и вдоль LR первого порядка нельзя игнорировать (Pagès, 1995; Thaler and Pagès, 1996 a ; Wu et al ., 2014), поскольку это изменение диаметра сильно коррелирует с анатомическими особенностями, диаметром и количеством дочерних боковых стволов (рис. 3 и рис. 7), и, следовательно, их продолжительностью жизни и функциями в поглощении ресурсов. Взаимосвязи характеристик ветвления, полученные в этом исследовании, не исключают влияния внешних факторов на ветвление, таких как доступность N и P (Postma et al ., 2014), неоднородность питательных веществ (Yu et al .
, 2010; Clark et al ., 2011, 2012 ; Mairhofer et al ., 2012; Nagel et al ., 2012; Tracy et al ., 2012). Эти результаты в сочетании с исследованиями корневой функции облегчают параметризацию корневых архитектурных моделей, используемых для моделирования всей корневой системы молодых растений.Напротив, эти подробные результаты по архитектуре взрослых корней, особенно растений, выращиваемых в поле, все еще в значительной степени отсутствуют (Fiorani and Schurr, 2013). Наиболее подробными измерениями зрелых корневых систем в поле были траектории осевых корней в двух / трех измерениях (Tardieu and Pellerin, 1990; Wu et al ., 2014). Диаметры вдоль корней подмышек также измерялись по траектории (Wu et al ., 2014). Напротив, информации о ветвлении корней особенно не хватало даже для ветвления аксильных корней (Pagès and Pellerin, 1994; Pagès, 2014; Wu and Guo, 2014).В этом исследовании мы начали с анализа ветвления LR первого порядка полевых растений кукурузы, включая изменения их диаметра. Диаметр корня является незаменимым морфологическим параметром архитектурной модели корня (Dunbabin et al ., 2013). Для упрощения вычислений в большинстве моделей корней диаметр LR обычно считается постоянным для молодых растений, поскольку диаметры мелких LR не сильно различаются (рис. 5). При моделировании взрослых корневых систем изменение диаметра вдоль подмышечных корней и вдоль LR первого порядка нельзя игнорировать (Pagès, 1995; Thaler and Pagès, 1996 a ; Wu et al ., 2014), поскольку это изменение диаметра сильно коррелирует с анатомическими особенностями, диаметром и количеством дочерних боковых стволов (рис. 3 и рис. 7), и, следовательно, их продолжительностью жизни и функциями в поглощении ресурсов. Взаимосвязи характеристик ветвления, полученные в этом исследовании, не исключают влияния внешних факторов на ветвление, таких как доступность N и P (Postma et al ., 2014), неоднородность питательных веществ (Yu et al . , 2015 ) и проницаемости почвы (Bécel et al ., 2012), поскольку большие различия в плотности ветвления действительно существовали среди корней даже в одних и тех же группах (рис. 8). Несмотря на это, общие паттерны ветвления должны быть основным ориентиром для получения морфологических параметров корня для моделей корня, используемых для моделирования больших корневых систем.
, 2015 ) и проницаемости почвы (Bécel et al ., 2012), поскольку большие различия в плотности ветвления действительно существовали среди корней даже в одних и тех же группах (рис. 8). Несмотря на это, общие паттерны ветвления должны быть основным ориентиром для получения морфологических параметров корня для моделей корня, используемых для моделирования больших корневых систем.

 ) в ответ на низкий азотный стресс
) в ответ на низкий азотный стресс





 Х, Николас, Р. и Харви, М. Л., 1988 Архитектура корневой системы в связи с жизненным циклом и питательными веществами.Funct. Ecol. 2, 345–351.
Х, Николас, Р. и Харви, М. Л., 1988 Архитектура корневой системы в связи с жизненным циклом и питательными веществами.Funct. Ecol. 2, 345–351. и Кервелла, Дж. 1990 Рост и развитие корневой системы: геометрические и структурные аспекты. Acta Biotheor. 38, 289–302.
и Кервелла, Дж. 1990 Рост и развитие корневой системы: геометрические и структурные аспекты. Acta Biotheor. 38, 289–302. Ред. HPersson и B LMcMichael. pp 526–532, Elsevier, Amsterdam.
Ред. HPersson и B LMcMichael. pp 526–532, Elsevier, Amsterdam.