Смежные и вертикальные углы | Геометрия

Смежные углы

Смежные углы – это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны (только в том случае, когда смежные углы не равны).

∠ABD  и  ∠DBC  – это смежные углы, AC  – прямая, луч  BD  – общая сторона углов и наклонная к прямой  AC, ∠ABC  – развёрнутый угол, B  – основание наклонной.

Чтобы построить угол, смежный с данным углом, нужно одну из сторон угла продлить за вершину:

Сумма смежных углов

Любые два смежных угла составляют в сумме развёрнутый угол. Развёрнутый угол равен двум прямым углам, поэтому можно сказать, что сумма двух смежных углов равна двум прямым углам.

∠ABD + ∠DBC = 2d,

где d – это обозначение прямого угла (d = 90°).

Вертикальные углы

Вертикальные углы – это пара углов, у которых стороны одного угла являются продолжением сторон другого угла. Пересечение двух прямых линий образует две пары вертикальных углов:

∠AOB  и  ∠COD, а также  ∠AOD  и  ∠BOC  – вертикальные углы.

Равенство вертикальных углов

Вертикальные углы равны между собой.

Рассмотрим вертикальные углы 1 и 3:

Сумма  ∠1  и  ∠2  равна развёрнутому углу (180°). Сумма  ∠2  и  ∠3  тоже равна развёрнутому углу (180°). Значит:

∠1 + ∠2 = ∠2 + ∠3

Следовательно, ∠1 = ∠3. Равенство вертикальных углов доказано.

Урок 6. смежные и вертикальные углы. аксиомы и теоремы. — Геометрия — 7 класс

Геометрия

7 класс

Урок № 6

Смежные и вертикальные углы. Аксиомы и теоремы

Перечень вопросов, рассматриваемых в теме:

• Понятие смежных и вертикальных углов
• Свойства смежных и вертикальных углов
• Отличие аксиомы от теоремы

Тезаурус

Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются

смежными.

Свойства смежных углов:

• Сумма смежных углов равна 180⁰.
• Если два угла равны, то и смежные с ними углы равны.
• Угол, смежный с прямым углом, есть прямой угол.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Свойство вертикальных углов: вертикальные углы равны.

Аксиома– положение, принимаемое без доказательств.

Основная литература:

1. Атанасян Л. С. Геометрия: 7 – 9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

1. Погорелов А. В. Геометрия: 7 – 9 класс. // Погорелов А. В. – М.: Просвещение, 2017. – 224 с.

Теоретический материал для самостоятельного изучения

Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это

смежные углы. На основании этого сформулируем определение смежных углов.

Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.

Обратите, внимание, что смежные углы АОВ и ВОС лежат на развёрнутом угле АОС. Отсюда можно сделать вывод: сумма смежных углов равна 180^о.

Свойство смежных углов: сумма смежных углов равна 180^о.

Давайте докажем это свойство.

Доказательство. Пусть углы ∠АОВ и ∠ВОС – смежные, луч ОВ – проходит между сторонами развёрнутого угла ∠АОС. Поэтому, сумма углов ∠АОВ и ∠ВОС равна ∠АОС, а этот угол развёрнутый, он равен 180^о. Свойство доказано.

Укажем ещё одно свойство смежных углов.

• Если два угла равны, то и смежные с ними углы равны.

Сейчас давайте вспомним определение прямого угла: угол, равный 90

0, называется прямым углом. Опираясь на свойство суммы смежных углов, можно сделать вывод: угол, смежный с прямым углом, есть прямой угол.

Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.

Углы, которые не являются смежными:

∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.

Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов

∠1+ ∠2= 180⁰ и ∠3+ ∠2= 180

0. Получаем, что ∠1+ ∠2= ∠3+ ∠2, значит, ∠1= ∠3. Углы ∠1 и ∠3 – вертикальные. Мы доказали справедливость этого свойства.

Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.

На предыдущих уроках вы познакомились с понятием аксиомы.

В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Используя чертёж, найдите угол ∠ВОК.

Ответ: ∠ВОК=____⁰

Решение. Воспользуемся свойством смежных углов: сумма смежных углов равна 180⁰. По условию задачи ∠АОК= 11

0, то ∠ВОК+ ∠АОК= 180⁰

∠ВОК+ 11⁰= 180⁰

∠ВОК= 180⁰– 11⁰= 169⁰.

Ответ: ∠ВОК= 169⁰

№2. Тип задания: единичный / множественный выбор.

Используя чертёж, найдите угол ∠AOD.

Варианты ответов:

1. 112⁰
2. 64⁰
3. 116⁰
4. 68⁰

Решение. На чертеже указано, что углы ∠СОЕ= ∠DOE. Значит, ∠COD= ∠СОЕ+ ∠DOE= 32⁰+ 32⁰= 64⁰. ∠AOD смежный с углом ∠COD, по свойству смежных углов: ∠AOD= 180⁰–∠COD= 180⁰– 64⁰=116⁰.

Ответ: 116⁰

№3. Тип задания: выделение цветом.

Используя чертёж, найдите градусную меру угла ∠BMD, если ∠AMD= 125⁰, ∠BMC= 115⁰.

∠BМD=____⁰.

Выделите верный ответ из списка:

60⁰

; 30⁰; 75⁰; 90⁰

Решение. По чертежу можно увидеть, что ∠BМD является частью ∠AMD и ∠BMC. Рассмотрим ∠DMC и ∠AMD. Эти углы – смежные, т.е. их сумма равна 180⁰. Значит, зная градусную меру ∠AMD, мы сможем найти градусную меру ∠DMC= 180⁰–∠AMD= 180⁰-–125⁰= 55⁰. Теперь рассмотрим ∠BMC= ∠BMD+ ∠DMC. Мы знаем градусные меры ∠BMC и ∠DMC, значит, мы сможем найти градусную меру ∠BMD.

∠BMD= ∠BMC–∠DMC= 115⁰– 55⁰= 60⁰.

Верный ответ: 60⁰

Поурочные планы по геометрии «Смежные и вертикальные углы»

Поурочные планы по геометрии 7 класс по теме «Смежные и вертикальные углы»

Смежные и вертикальные углы (7 часов)

Цели: ввести понятия смежных и вертикальных углов; научить применять свойства этих углов при решение задач и различать их.

Урок 16
Смежные углы

Цели: дать определение смежных углов; научить применять теорему о смежных углах при решении задач.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ контрольной работы.

III. Проверка домашнего задания.

Во время проверки домашнего задания два ученика решают задачи по карточкам, затем всем классом разбирают правильность решения и оценивают ответы одноклассников.

Карточка 1

Известно, что  МРК =  CDE. Запишите все равные стороны и углы этих треугольников.

Карточка 2

Дано:  МВЕ =  КОР, DE = 4,5 см, DB = 9 см, D = 60°, В = 30°.

Найти соответствующие стороны и углы треугольника. Чему они равны?

IV. Изучение нового материала.

1. На доске нарисованы смежные углы, по ним дается определение:

Два угла называются смежными, если у них одна общая сторона, а другие стороны являются дополнительными полупрямыми.

2. Сформулировать теорему о смежных углах.

Сумма смежных углов равна 180°.

Вынести доказательство на доску.

3. Записать следствия из данной теоремы.

Если два угла равны, то смежные с ними углы равны.

Если угол не развернутый, то его градусная мера меньше 180°.

Угол, смежный с прямым углом, есть прямой угол.

V. Решение задач.

1. Решение задач по готовым чертежам.

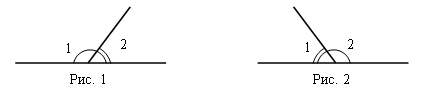
Дано: 1 –  2 = 30°. Дано: 1 = 2 – 90°.

Найдите: 1, 2. Найдите: 1, 2.

Решение:

Выразим угол 1 через угол 2, получим 1 = 30 ° + 2. Так как сумма смежных углов равна 180°, то получим уравнение, где 2 примем за новую переменную х. Решим полученное уравнение:

30° + х + х = 180°

2х = 150°

х = 75°

2 = 75°, значит, 1 = 30° + 75° =
= 105°.

Ответ: 1 = 105°, 2 = 75°.

Вторая задача решается аналогично.

Ответ: 1 = 45°,

2 = 135°.

2. Решение задач 3, 4, 5 по учебнику.

VI. Итог урока.

Задание на дом: пункты 14; вопросы 1, 4, 5; задачи 1, 2, 6.

Дополнительная задача.

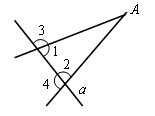
Прямая а пересекает стороны угла А. Докажите, что 1 = 2, если известно, что 3 = 4.

Урок 17
Смежные углы

Цели: закрепить полученные знания о смежных углах; научить применять теорему о смежных углах при решении задач.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Проверка домашней работы.

III. Решение задач.

1) Смежные углы относятся как 1 : 2 . Найдите эти смежные углы.

2) Один из смежных углов больше другого на 20°. Найдите эти углы.

3) Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.

4) Меньший из смежных углов в 4 раза меньше разности этих смежных углов. Найдите эти смежные углы.

5) Докажите, что сумма каждых трех углов, не прилежащих один к другому и образуемых тремя прямыми, проходящими через одну точку, равна двум прямым углам.

IV. Итог урока.

– Могут ли два смежных угла быть оба:

1) острыми;

2) тупыми;

3) прямыми?

– Какой вывод можно сделать из этого?

Задание на дом: пункт 14.

Дополнительные задачи.

1. Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы.

2. Один из четырех углов, образовавшихся при пересечении двух прямых, в 11 раз меньше суммы трех остальных углов. Найдите эти четыре угла.

Урок 18
Вертикальные углы

Цели: ввести понятие вертикальных углов; доказать теорему о вертикальных углах; научить применять знания о вертикальных углах при решении задач.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Устная работа.

Задача 1.

Один из углов, полученный при пересечении двух прямых, равен 118°. Найдите остальные три угла.

Задача 2.

Дополните рисунок, чтобы образовалось четыре смежных угла.

III. Изучение нового материала.

1. Вспомнить, что такое дополнительные прямые, после чего дать определение вертикального угла.

2. Записать теорему: Вертикальные углы равны. Доказательство разбирается всем классом, оформляется на доске и записывается учащимися в тетрадь.

IV. Решение задач.

1. Коллективный разбор задачи.

Найти: АОВ, АОD, CОВ.

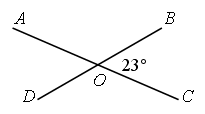
2. Решение задач 7, 9 по учебнику.

V. Итог урока.

– Что такое вертикальные углы?

– Какими свойствами они обладают?

– В чем различие между вертикальными и смежными углами?

Задание на дом: пункты 15; задачи 8, 10, 12.

Урок 19
Перпендикулярные прямые.
Доказательство от противного

Цели: ввести понятие перпендикулярной прямой, перпендикуляра; познакомить с методом доказательства от противного.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Проверка домашнего задания.

Один ученик решает задачу 11, затем проводится коллективное обсуждение решения этой задачи.

III. Изучение нового материала.

1. Ввести понятия перпендикуляра, перпендикулярной прямой, основания перпендикуляра, обозначения перпендикуляра.

Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

На рисунке ас.

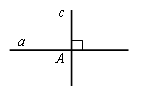
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец называется основанием перпендикуляра.

2. Прочитать пункт 17, сделать выводы и записать их в тетрадь.

Доказательство от противного состоит в том, что нужно сделать предположение, противоположное тому, которое утверждается в теореме. Затем путем рассуждений, опираясь на аксиомы и ранее доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо какой-то аксиоме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

3. Доказать теорему о перпендикулярных прямых.

Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

Для доказательства использовать метод от противного.

4. Показать, как строить перпендикулярные прямые.

IV. Решение задач.

1. Дополнительная задача.

Даны АОЕ – развернутый, АОВ на 40° меньше, чем DOE, ВОС на 40° больше, чем DOС. Доказать, что СО || АЕ.

2. Решить задачи 13, 14.

V. Практическая работа.

Необходимо построить произвольный треугольник, отметить на каждой стороне точку, назвать ее и провести перпендикуляры через эти точки к сторонам треугольника.

VI. Итог урока.

– Что такое перпендикулярные прямые?

– Что называется перпендикуляром?

– Что такое основание перпендикуляра?

– В чем заключается смысл доказательства от противного?

Задание на дом: пункты 16, 17, 19; задачи 23, 24.

Урок 20
Решение задач

Цель: выработать у учащихся умение применять полученные знания при решении задач.

Ход урока

I.Организационный момент.

Формулировка темы и постановка цели урока.

II. Анализ практической работы.

Объявить результаты, выявить ошибки, сделать работу над ошибками.

III. Решение задач.

1. Три точки В, С, D лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?

2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.

3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла.

4. Лежат ли точки M, N, P на одной прямой, если МР = 5 см, MN = 12 см, PN = 8 см. В каком случае это возможно?

5. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 83° больше другого.

IV. Итог урока.

Задание на дом: решить задачи.

1) Сумма углов равна 178°. Докажите, что эти углы не могут быть смежными.

2) Разность смежных углов равна 54°. Определите величину другого угла.

Урок 21
Решение задач

Цели: повторить, систематизировать и обобщить знания по теме.

Ход урока

I. Организационный момент.

Формулировка темы и постановка цели урока.

II. Решение задач.

1. Сумма трех углов, образованных при пересечении двух прямых, на 280° больше четвертого угла. Найдите эти углы.

2. Сумма вертикальных углов в 5 раз меньше угла, смежного с каждым из них. Найдите эти вертикальные углы.

3. Какое наименьшее число лучей можно провести из одной точки, чтобы все углы, ограниченные соседними лучами, были острыми?

4. Точки А, В и С лежат на одной прямой, причем длина отрезка ВС больше длины отрезка АС в 3 раза, а длина отрезка АВ меньше длины ВС на 3,6 см. Найдите длину отрезка АС.

Задание на дом: повторить изученный материал, подготовиться к контрольной работе. Решить задачи:

1) Найдите неразвернутые углы, образованные при пересечении двух прямых, если разность двух из них равна .

2) Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.

Урок 22
Контрольная работа № 2 по теме
«Смежные и вертикальные углы»

Цель: проверить знания, умения и навыки учащихся.

Контрольную работу можно провести по вариантам.

Ход урока

I. Организационный момент.

II. Выполнение работы.

Вариант 1

1. Прямые АВ и СD пересекаются в точке О.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов в 3 раза меньше другого. Найдите эти углы.

б) Могут ли два смежных угла быть тупыми? Ответ обоснуйте.

Вариант 2

1. Прямые РН и ОМ пересекаются в точке Х.

а) Выпишите две пары смежных углов. Каким свойством они обладают?

б) Какие из углов, образовавшихся при пересечении этих прямых, равны? Как они называются?

2. а) Один из смежных углов на 50° меньше другого. Найдите эти углы.

б) Может ли один из вертикальных углов быть тупым? Ответ обоснуйте.

III. Итог урока.

Задание на дом: повторить § 1, 2; вопросы на с. 15–16, 26.

Можно провести контрольную работу с использованием дифференцированных заданий.

Задания на оценку «3»

Карточка 1

1. Известно, что АВС = KHP. Запишите равные углы и стороны в данных треугольниках.

2. Сформулируйте основные свойства принадлежности точек и прямых на плоскости.

3. По рисунку выполните задания.

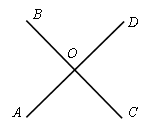
а) Среди углов, полученных при пересечении прямых АD и ВС, найдите и запишите углы, смежные с АОС.

б) Дайте определение смежных углов.

4. а) Постройте отрезок АВ = 3 см.

б) На отрезке АВ отметьте точку С так, чтобы АС = 3 см.

в) Найдите длину отрезка ВС.

Карточка 2

1. По рисунку ответьте на вопросы.

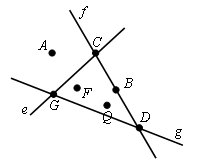
а) Через какие точки проходит прямая g?

б) Какие точки лежат на прямой f?

в) Каким прямым принадлежит точка Q?

2. а) Назовите все углы, изображенные на рисунке.

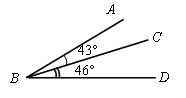
б) Назовите луч, проходящий между сторонами угла АВD.

в) Чему равна градусная мера угла ABD?

3. Проведите полупрямую АВ. Отложите от этой полупрямой угол ВАС, равный 70°, причем точки С и D лежат в одной полуплоскости. Определите взаимное расположение полупрямых АС и АВ.

4. Прямые ВD и АС пересекаются в точке О. Найдите градусную меру угла СОD, если АОД = 138°.

Задания на оценку «4»

Карточка 1

1. Сформулируйте основное свойство принадлежности точек и прямой на плоскости.

2. Сформулируйте определение равных треугольников.

3. Сформулируйте и докажите теорему о вертикальных углах.

4. Разность смежных углов равна 40°. Определите величину большего угла.

5. Точка С лежит на прямой АВ между А и В. Известно, что отрезок АС на 6 см меньше отрезка ВС. Найдите длину отрезков АС и ВС, если АВ = 24 см.

Карточка 2

1. Сформулируйте и докажите теорему о смежных углах.

2. Сформулируйте основное свойство существования треугольника, равного данному.

3. Сформулируйте основное свойство расположения точек на прямой.

4. На отрезке АС, длина которого равна 24 см, отмечена точка В. Найдите расстояние между серединами отрезков АВ и ВС.

5. Прямые АВ и СD перпендикулярны и пересекаются в точке О. Найдите угол между биссектрисой АОС и полупрямой, дополнительной к ОС.

Карточка 3

1. Сформулируйте основное свойство измерения углов.

2. Сформулируйте основное свойство откладывания углов.

3. Докажите, что если два угла равны, то смежные с ними углы равны.

4. Градусные меры двух углов относятся как 2 : 3. Могут ли эти углы быть вертикальными?

5. От данной полупрямой отложены АВС = 56° и ABD = 43°. Найдите DCB.

Карточка 4

1. Сформулируйте основное свойство измерения углов.

2. Докажите, что если два смежных угла равны, то вертикальные им углы равны.

3. Какими свойствами обладает разбиение плоскости на две полуплоскости?

4. Градусные меры двух углов, которые получаются при пересечении двух прямых, относятся как 11 : 9. Найдите эти углы.

5. Луч c проходит между сторонами угла (аb), равного 120°. Чему равны углы (ас) и (bс), если угол (ас) в три раза больше угла (bс)?

Задания на оценку «5»

Карточка 1

1. Точки А и В принадлежат прямой с. Различны ли прямые АВ и с?

2. Верно ли утверждение: На полупрямой от данной точки можно отложить только один отрезок, равный данному? Объясните ответ.

3. Сумма двух углов равна 178°. Докажите, что эти углы не могут быть смежными.

4. Длина отрезка АВ равна 5 см. На отрезке отмечены точки М и Р так, что АМ = 3,1 см и РВ = 2,6 см. Найдите длину отрезка МР.

5. Может ли луч с проходить между сторонами угла (аb), если (ас) = 27°, (сd) = 73°, (аb) = 70°?

Карточка 2

1. Ответьте на вопросы и выполните задания:

а) На сколько частей разделят плоскость три прямые, пересекающиеся в одной точке?

б) На сколько частей разделят плоскость три попарно пересекающиеся прямые?

в) На плоскости отмечены семь точек. Любые четыре из них не лежат на одной прямой. Проведите три прямые так, чтобы в каждой части плоскости оказалось ровно по одной точке. Покажите на рисунке, как это можно сделать.

2. Верно ли утверждение: На одной полупрямой от ее начала можно отложить только один угол, равный данному? Ответ объясните.

3. Докажите, что биссектрисы углов, образовавшихся при пересечении двух прямых, перпендикулярны или образуют развернутый угол.

4. Разность двух углов равна 178°. Докажите, что эти углы могут быть вертикальными.

5. Длина отрезка АВ равна 1,5 см, на луче АВ отмечена точка М так, что АМ = 0,7 см, а на луче ВА отмечена точка Р так, что ВР = 2,1 см. Найдите длину отрезка МР.

Углы при параллельных прямых и их свойства

Пусть прямая с пересекает параллельные прямые  и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы  и  — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы  и ,  и  — тоже вертикальные.

Углы  и  — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы  и  (а также  и ,  и ,  и ) — накрест лежащие. Накрест лежащие углы равны.

,

,

,

.

Углы  и  — односторонние. Они лежат по одну сторону от всей «конструкции». Углы  и  — тоже односторонние. Сумма односторонних углов равна , то есть

,

.

Углы  и  (а также  и ,  и ,  и ) называются соответственными.

Соответственные углы равны, то есть

,

.

Углы  и  (а также  и ,  и ,  и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

,

,

,

.

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть  — биссектриса тупого угла . По условию, отрезки и  равны  и  соответственно.

Рассмотрим углы и . Поскольку и  параллельны,  — секущая, углы и  являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник  — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

.

Отсюда , .

Ответ: .

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы  и  — односторонние при параллельных прямых и секущей, следовательно,

°.

Итак,

, тогда .

Ответ: .

Ответы Mail.ru: докажите свойство вертикальных углов

Два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Теперь доказательство теоремы: Вертикальные углы равны! Представь углы 1, 3 и 2, 4. Угол 2 является смежным как с углом 1 так и с углом 3. Два угла, у которых одна сторона общая а две другие являются продолжениями одна другой, называються смежными. По свойству смежных углов < 1+<2=180градусов. <3+<2=180градусов Отсюда получаем <1=180-<2. <3=180-<2 таким образом, градусные меры углов 1 и 3 равны. Значит и сами углы равны. Теорема доказана

Два угла называются вертикальными, если стороны одного составляют продолжение сторон другого. Так, при пересечении двух прямых AB и СD образуются две пары вертикальных углов: AOD и СOB; AOС и DOB . Теорема. Два вертикальных угла равны. Свойства смежных и вертикальных углов. Пусть даны два вертикальных угла: AOD и СOB т. е. OB есть продолжение OA, а OС продолжение OD. Требуется доказать, что AOD = СOB. По свойству смежных углов можем написать: AOD + DOB = 2d DOB + BOС = 2d Значит: AOD + DOB = DOB + BOС. Если вычесть из обеих частей этого равенства по углу DOB, получим: AOD = BOС, что и требовалось доказать. Аналогично докажем, что AOС = DOB. на рисунке поменяйте В и С местами <img src=»//otvet.imgsmail.ru/download/247168206_c6d3bac30a6cd1eccaf90906d4c1ec73_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/247168206_c6d3bac30a6cd1eccaf90906d4c1ec73_120x120.jpg» data-big=»1″>