Урок 33. угол. виды углов: прямой, острый, тупой — Математика — 2 класс
Математика, 2 класс
Урок № 33. Угол. Виды углов: прямой, острый, тупой
Перечень вопросов, рассматриваемых в теме:
— Какие бывают углы?
— Как распознавать углы?
Глоссарий по теме:
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.8-9.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова – 6-е изд.

- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.16.
Теоретический материал для самостоятельного изучения
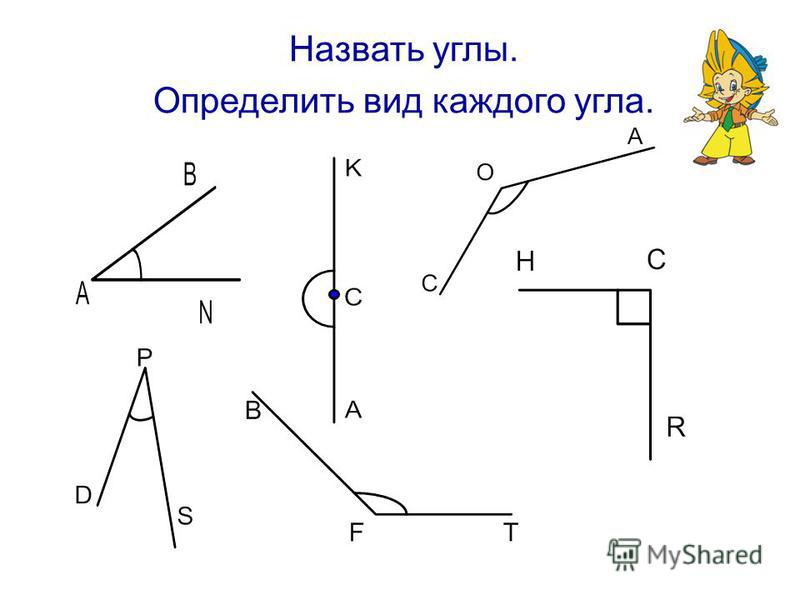
Рассмотрите фигуры и выберите лишнюю.
Лишняя фигура под номером 2. Она образована незамкнутой линией.
Она называется угол.
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Посмотрите на рисунки: по-разному открытый веер, образует разные углы.
У каждого угла есть две стороны и вершина. Углы бывают прямые, острые и тупые. Углы определить можно помощью чертежного угольника.
Прямой угол определяем с помощью чертежного угольника.
Угол, который меньше прямого угла называется острым углом.
Угол, который больше прямого угла называется тупым углом.
Посмотрите, как из обычного листа бумаги можно сделать модель прямого угла.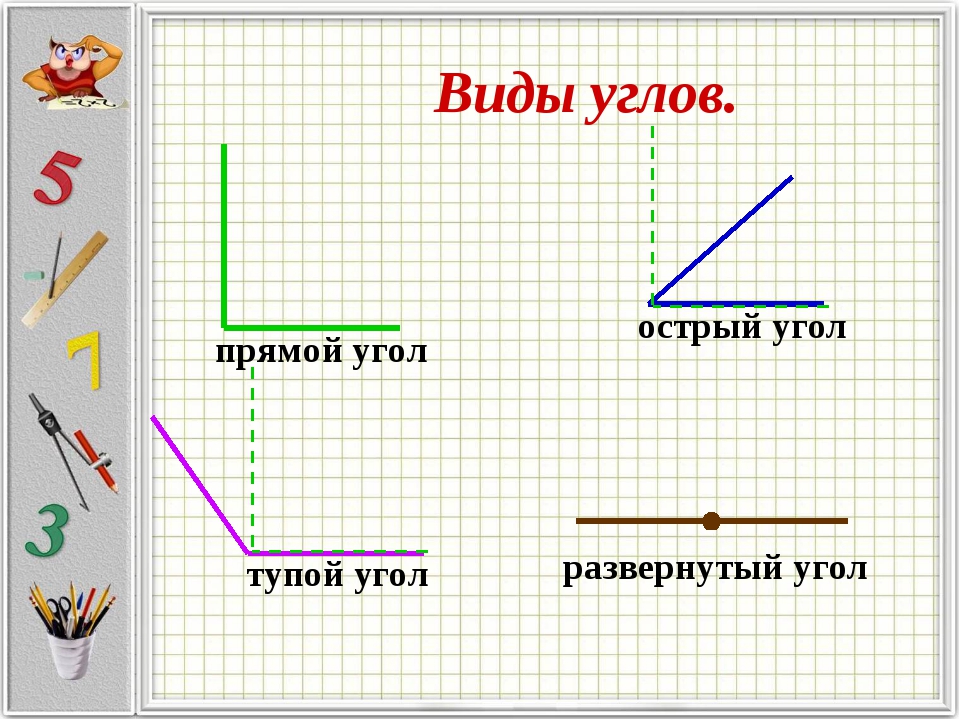
Разверните лист. Линии сгиба образовали 4 прямых угла.
Чтобы определить, какой угол начерчен, на него накладывают угольник или модель прямого угла.
Вывод: Углы могут быть прямыми и непрямыми. Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник. Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол – прямой. Не совпадут – непрямой. Непрямые углы делятся на: тупые и острые. Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.
Тренировочные задания.
1.Посмотрите на крыши домов и домиков. Какие углы ты видишь на рисунке? Соотнесите вид угла с изображением домика.
Правильные ответы:
2. Выберите цифры, в записи которых присутствуют только прямые углы.
Правильные ответы:
Угол. Виды углов / Основы геометрии / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Угол. Виды углов
Мы узнаем, что углы бывают, острыми, прямыми и тупыми.
Вспомни, чтобы начертить угол, нужно поставить точку и из неё провести два луча в разные стороны.
Луч — это сторона угла.
Вершина — это точка, из которой выходят лучи.
Прямой угол
Прямой угол — это угол в 90о (90 градусов). Его легко определять по треугольнику, например, такому:
Острый угол
Острый угол — это угол, который МЕНЬШЕ прямого угла, меньше 90о.
м
Тупой угол
Острый угол — это угол, который БОЛЬШЕ прямого угла, больше 90о.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Круг. Шар. Овал
Треугольники
Многоугольники
Обозначение геометрических фигур буквами
Периметр многоугольника
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 45. Вариант 2. № 2, Моро, Волкова, Проверочные работы
Страница 72. Вариант 1. Тест 3, Моро, Волкова, Проверочные работы
Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 45, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 76, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 12, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 36, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 35. Урок 14,
Петерсон, Учебник, часть 2
Урок 14,
Петерсон, Учебник, часть 2
Страница 45. Урок 15, Петерсон, Учебник, часть 3
3 класс
Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 43, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 86, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 102, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
4 класс
Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 18, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 24, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 45, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 50, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
© budu5. com, 2022
com, 2022
Пользовательское соглашение
Copyright
Угол. Обозначение углов / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Угол. Обозначение углов
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т. к. точки В и С
к. точки В и С
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.
Прямой угол — угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На рис. 6 АОВ и ВОС — прямые, АОС — развернутый.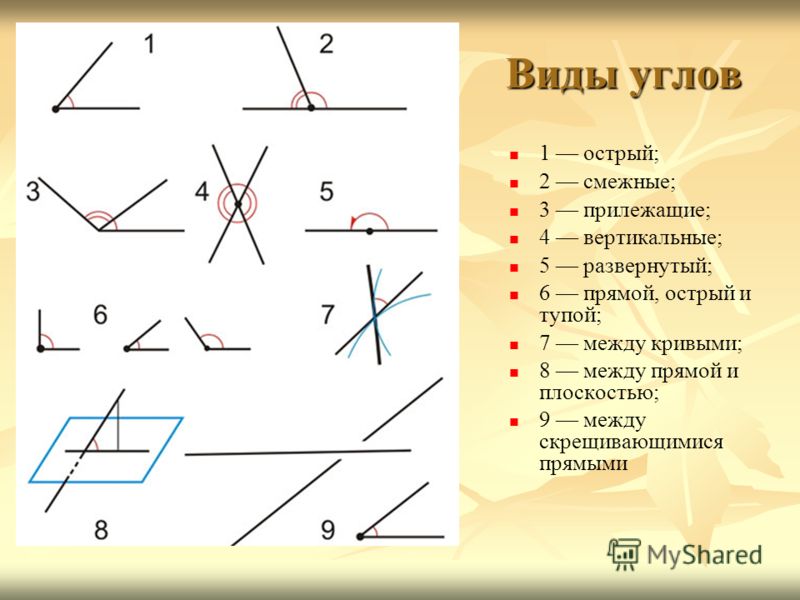
Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
Острый угол — угол, который меньше прямого угла. На рис. 7 МОN — острый.
Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК — тупой.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1617, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1659, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 288, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 297, Мерзляк, Полонский, Якир, Учебник
Номер 304, Мерзляк, Полонский, Якир, Учебник
Номер 312, Мерзляк, Полонский, Якир, Учебник
Номер 330, Мерзляк, Полонский, Якир, Учебник
Номер 443, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 206, Мерзляк, Полонский, Якир, Учебник
Номер 219, Мерзляк, Полонский, Якир, Учебник
Номер 220, Мерзляк, Полонский, Якир, Учебник
Номер 1217, Мерзляк, Полонский, Якир, Учебник
Номер 1220, Мерзляк, Полонский, Якир, Учебник
Номер 1226, Мерзляк, Полонский, Якир, Учебник
Номер 1234, Мерзляк, Полонский, Якир, Учебник
Задание 611, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1375, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1546, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Задание 81, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5. com, 2022
com, 2022
Пользовательское соглашение
Copyright
Виды углов по градусной мере. Какие есть углы? Измерение углов транспортиром
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т. е. их сумма 90 о.
е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.

- В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.
Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию.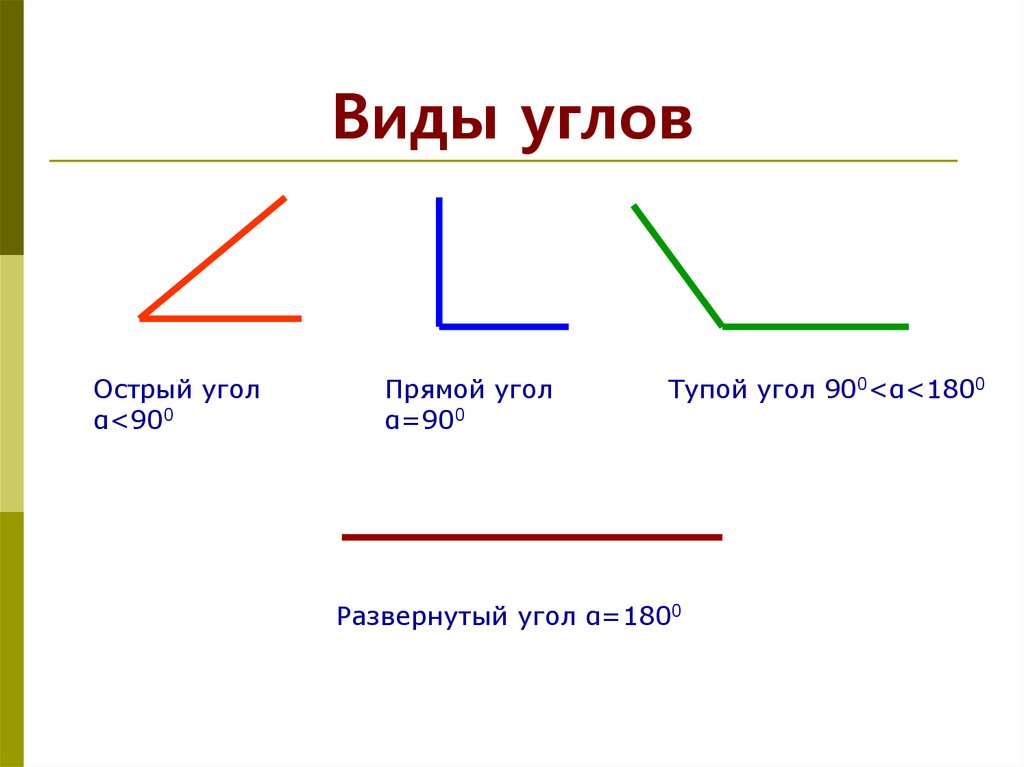 Неразвернутый угол это все остальные случаи.
Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.
Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов. Их называют выпуклыми.
Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две прямые, все эти пары углов имеют определённые свойства:
- Внутренние накрест лежащие и соответственные фигуры между собой равны.
- Внутренние односторонние элементы в сумме дают 180 градусов.
Изучаем углы в геометрии, их свойства
Виды углов в математике
Вывод
В этой статье представлены все основные виды углов, которые встречаются в планиметрии и изучаются в седьмом классе. Во всех последующих курсах свойства, касающихся всех рассмотренных элементов, являются основой для дальнейшего изучения геометрии. К примеру, изучая , необходимо будет вспомнить все свойства углов, образованных при пересечении двух параллельных прямых секущей. При изучении особенностей треугольников, необходимо вспомнить, что такое смежные углы. Перейдя в стереометрию, все объёмные фигуры будут изучаться и строиться, опираясь на планиметрические фигуры.
К примеру, изучая , необходимо будет вспомнить все свойства углов, образованных при пересечении двух параллельных прямых секущей. При изучении особенностей треугольников, необходимо вспомнить, что такое смежные углы. Перейдя в стереометрию, все объёмные фигуры будут изучаться и строиться, опираясь на планиметрические фигуры.
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.

- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов.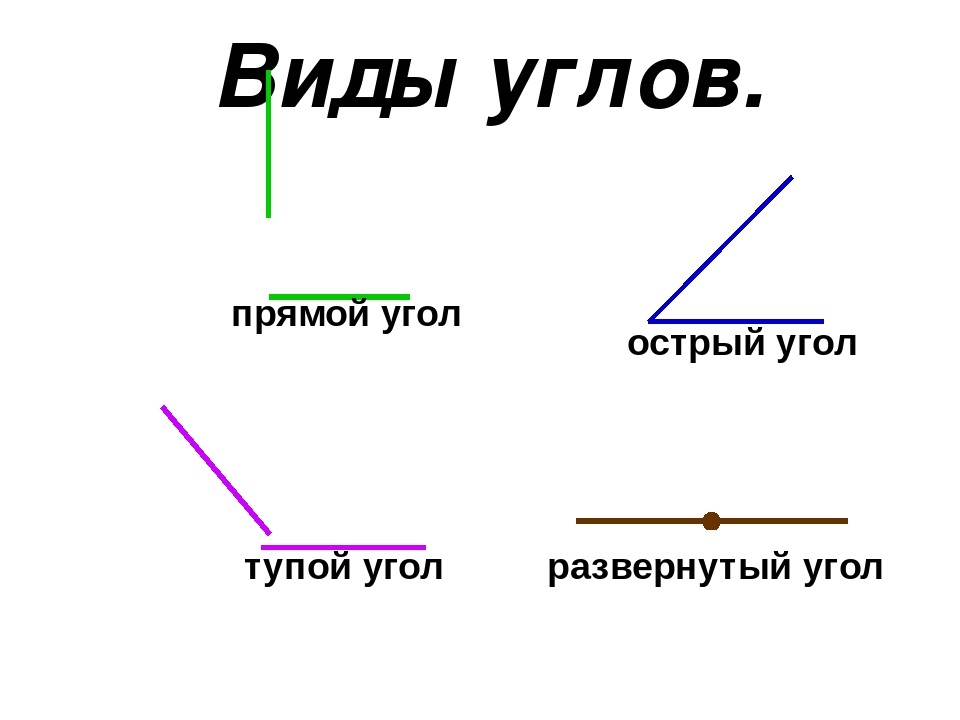 Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х.
 Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Измерение углов сводится к измерению соответствующих им дуг следующим образом. За единицу углов принимают угол, составляющий 1/90 часть прямого угла. Эту единицу называют угловым градусом .
За единицу дуг одинакового радиуса принимают такую дугу того же радиуса, которая соответствует центральному углу , равному угловому градусу. Такая дуга называется дуговым градусом .
Так как прямому центральному углу соответствует 1/4 окружности, то угловому градусу соответствует 1/90 четверти окружности. Значит, дуговой градус составляет 1/360 целой окружности.
Значит, дуговой градус составляет 1/360 целой окружности.
Пусть требуется измерить угол AOB, то есть найти отношение этого угла к угловому градусу MNP.Для этого опишем из вершин углов дуги СD и EF произвольным, но одинаковым радиусом.
Тогда будем иметь:
Левое отношение этой пропорции — число, измеряющее угол AOB в угловых градусах Правое отношение — число, измеряющее дугу СD в дуговых градусах.
Следовательно, эту пропорцию можно выразить так: число, измеряющее угол в угловых градусах, равно числу, измеряющему соответствующую дугу в дуговых градусах.
Для краткости эту фразу выражают обыкновенно так: Угол измеряется соответствующей ему дугой.
Градусы угла или дуги подразделяются на 60 равных частей, называемых минутами (угловыми или дуговыми).
Минуту разделяют на 60 равных частей, называемых секундами (угловыми или дуговыми).
Из сказанного выше следует, что в угле содержится столько угловых градусов, минут и секунд, сколько в соответствующей ему дуге заключается дуговых градусов, минут и секунд.
Если, например, в дуге СD содержится 40 град. 25 мин. и 13,5 секунды (дуговых), то и в угле AOB заключается 40 град. 25 мин. 13,5 сек. (угловых). Это выражают сокращенно так:
∠AOB = 40°25’ 13,5’’,
обозначая значками (°), (‘), (‘’) соответственно градусы, минуты и секунды.
Так как прямой угол содержит 90°, то:
1. сумма углов всякого треугольника равна 180 °;
2. сумма острых углов прямоугольного треугольника равна 90°;
3. каждый угол равностороннего треугольника равен 60°;
4. сумма углов выпуклого многоугольника , имеющего n сторон, равна 180° (n — 2).
Транспортир — это прибор, употребляемый для измерения углов, представляет собой полукруг, дуга которого разделена на 180 градусов.
Чтобы измерить угол AOB, накладывают на него прибор так, чтобы центр полукруга совпал с вершиной угла, а радиусом OM совпал со стороной AO. Тогда число градусов, содержащееся в дуге PN, покажет величину угла AOB. При помощи транспортира можно также начертить угол, содержащий данное число градусов.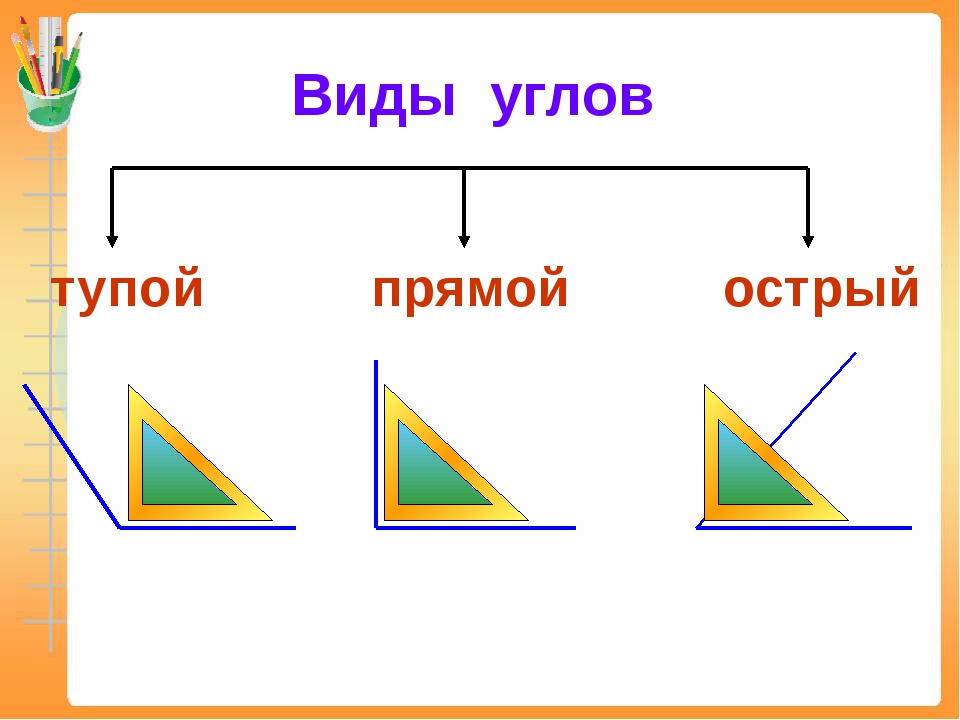
Конечно, на таком приборе нет возможности отсчитывать не только секунды, но и минуты. Измерение и построение можно выполнить только приближенно.
Игро+матика: Виды углов
Угол называется РАЗВЕРНУТЫМ, если его стороны вместе образуют прямую.
Величина развернутого угла равна 180°.
Угол, который равен половине развернутого угла, называется ПРЯМЫМ.Величина прямого угла равна 90°.
ОСТРЫЙ угол — это угол, который меньше прямого.
Величина острого угла < 90°.ТУПОЙ угол — это угол, который больше прямого, но меньше развернутого.
Величина тупого угла > 90° и < 180°Обобщим все сказанное, на рисунке:
А теперь с помощью несложных тестов и тренажеров проверьте, насколько хорошо вы усвоили данные понятия.
Какой это угол?
Посмотрите на чертеж и определите, какой это угол: острый, прямой или тупой. Еще один, очень похожий тренажер, в котором для узнавания добавлен еще и развернутый угол.
Еще один, очень похожий тренажер, в котором для узнавания добавлен еще и развернутый угол.А это аналогичный русскоязычный ресурс, но для работы с ним требуется регистрация
Попади в нужный угол
Для работы с этим тренажером выберите верхний раздел меню. В открывшемся окне, вы должны выбрать угол, тип которого указан на прицеле, навести на него курсор и кликнуть мышкой. В случае правильного попадания, угол исчезнет. Типы углов указаны по английски, но можно легко запомнить, что RIGHT — это прямой угол, ACUTE — острый, OBTUSE — тупой.
В этой флеш игре вы должны показать насколько хорошо вы знакомы с такими понятиями как острый, тупой и прямой угол. Робот будет задавать вам задания. Постарайтесь каждый раз выбирать правильный ответ. Игра на английском языке. Заодно можно подтянуть свои знания языка.
Играть втроем и вдвоем тоже можно!
Робот передвигается к нужному углу с помощью стрелок управления курсором; выстрел — клавиша — «Пробел». Acute — острый угол; Obtuse — тупой угол; Right -прямой угол.
Acute — острый угол; Obtuse — тупой угол; Right -прямой угол.
Ответь на вопросы.
При работе с этим тестом, включите автоматический перевод страниц, чтобы вопросы отображались по-русски
Презентация «Угол. Прямой угол. Виды углов.»
библиотека
материалов
Содержание слайдов
Номер слайда 1
Угол. Прямой угол. Виды углов. Учитель начальных классов Солдатова. Наталья Николаевна
Номер слайда 2
Цели: Научить учащихсястроить углы, различать их по видам. Развивать пространственное воображение, внимание, мышление, память. Формировать графические умения и навыки.
Развивать пространственное воображение, внимание, мышление, память. Формировать графические умения и навыки.
Номер слайда 3
Устный счет. Игра «Истина – ложь». Разность чисел 16 и 6 равна 9. 9 увеличить на 5 равно 14. 100 – это самое большое трёхзначное число. 8 – это четное число. Куб – это объёмная фигура. Прямоугольник – это плоская фигура.
Номер слайда 4
Задание на смекалку. К количеству пальцев на одной руке прибавить количество дней в декаде. К любимой оценке ученика прибавить количество цветов радуги. К количеству месяцев в году прибавить число дней в неделе. Из количества пальцев на двух руках вычесть количество колес у автомобиля.5 + 10 = 155 + 7 = 1212 + 7 = 1910 – 4 = 6
К количеству пальцев на одной руке прибавить количество дней в декаде. К любимой оценке ученика прибавить количество цветов радуги. К количеству месяцев в году прибавить число дней в неделе. Из количества пальцев на двух руках вычесть количество колес у автомобиля.5 + 10 = 155 + 7 = 1212 + 7 = 1910 – 4 = 6
Номер слайда 5
В саду росли 2 березы, 4 яблони, 5 вишен. Сколько всего фруктовых деревьев росло в саду?Сестре 9 лет, брату 3 года. На сколько сестра будет старше брата через пять лет?9 фруктовых деревьевна 6 лет сестра старше брата
Номер слайда 6
Актуализация знаний за 60 секунд.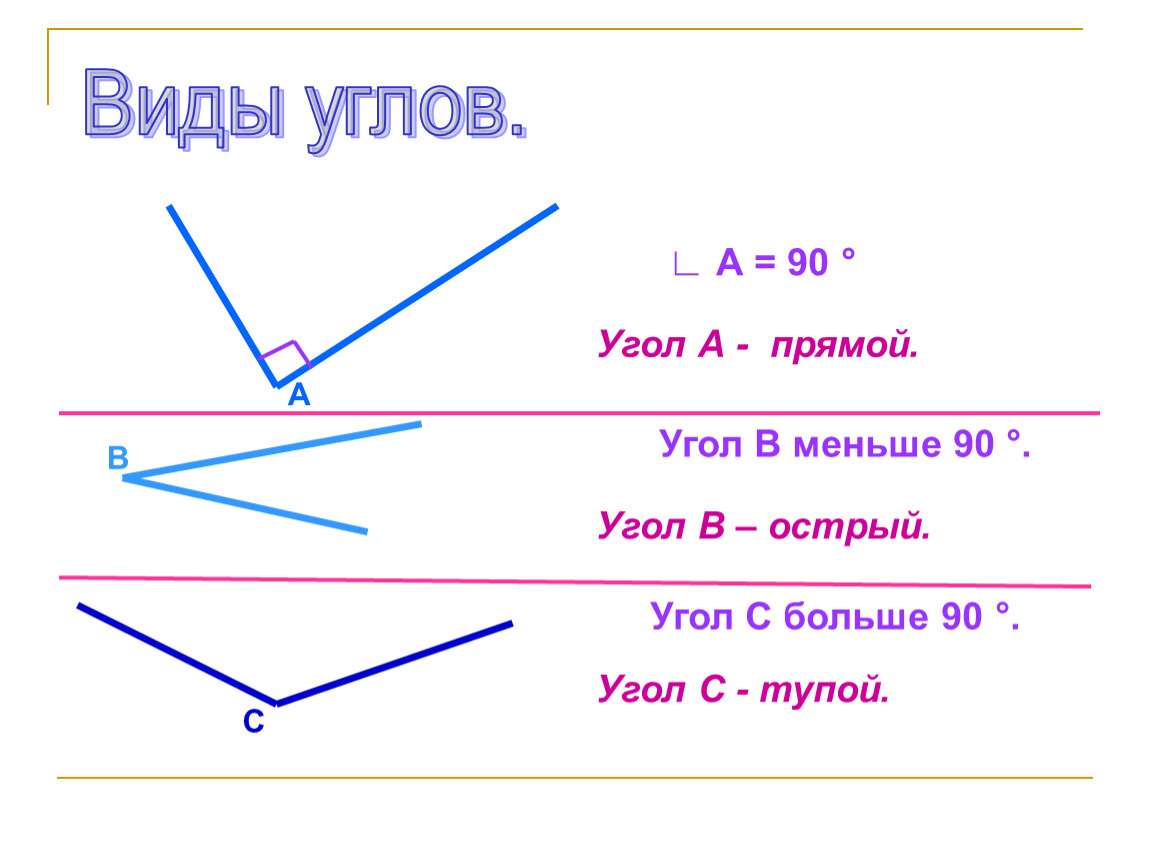 Сколько треугольников на рисунке?Открываем букву У.?
Сколько треугольников на рисунке?Открываем букву У.?
Номер слайда 7
В чем различие этих фигур?? Открываем букву Г.
Номер слайда 8
«Четвертый лишний». Открываем букву О.?
Открываем букву О.?
Номер слайда 9
Указать сходства геометрических фигур. Имеют:сторонывершиныуглы. Открываем букву Л.
Номер слайда 10
Что такое угол?Угол – это фигура, образованная двумя лучами, выходящими из одной точки.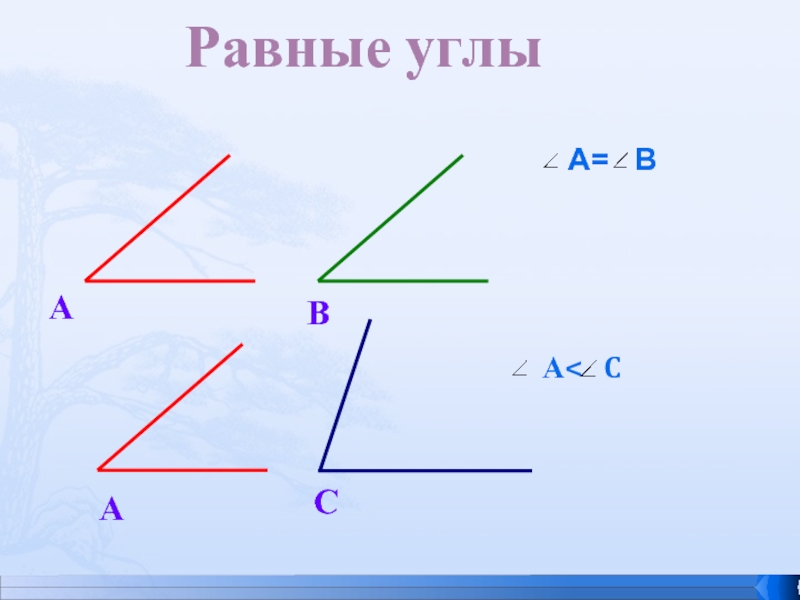
Номер слайда 11
Стороны угла – это лучи, которые образуют угол. Вершина угла – это точка, из которой выходят лучи.
Номер слайда 12
Виды углов. прямой уголострый уголтупой уголразвернутый угол
прямой уголострый уголтупой уголразвернутый угол
Номер слайда 13
Практическая работа. Шаг № 1 Шаг № 2 Шаг № 3
Номер слайда 14
Модель прямого угла сторонасторонавершина
Номер слайда 15
Модель прямого угла прямой угол
Номер слайда 16
Модель прямого угла острый угол
Номер слайда 17
Модель прямого угла острый угол
Номер слайда 18
Модель прямого угла острый уголострый уголпрямой угол
Номер слайда 19
Прямой угол
Номер слайда 20
Острый угол
Номер слайда 21
Тупой угол
Номер слайда 22
Номер слайда 23
Номер слайда 24
Номер слайда 25
Номер слайда 26
Номер слайда 27
Поднимает руки класс- это «раз».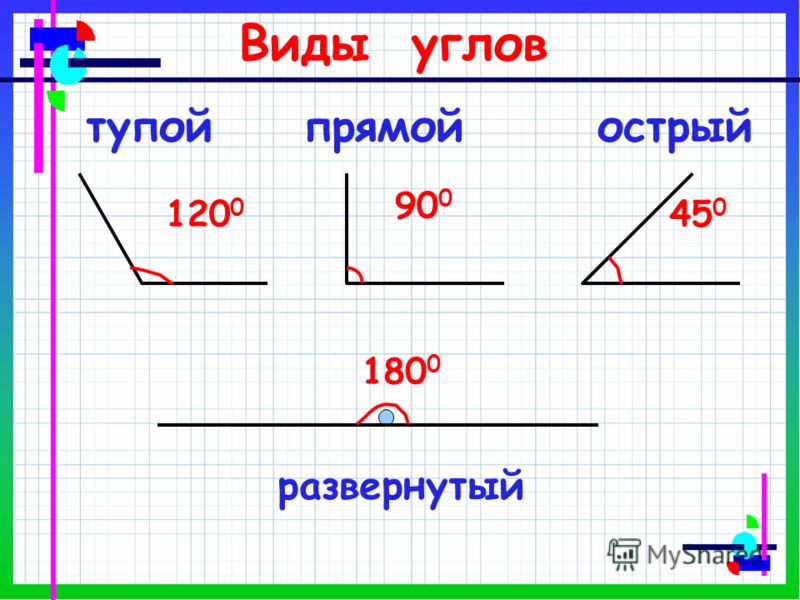 Повернулась голова – это «два». Руки вниз, вперед смотри- это «три». Руки в стороны пошире развернули на «четыре». С силой их к плечам прижать- это «пять». Всем ребятам тихо сесть- Это «шесть»!ФИЗКУЛЬТМИНУТКА
Повернулась голова – это «два». Руки вниз, вперед смотри- это «три». Руки в стороны пошире развернули на «четыре». С силой их к плечам прижать- это «пять». Всем ребятам тихо сесть- Это «шесть»!ФИЗКУЛЬТМИНУТКА
Номер слайда 28
З а д а ч а. У одного многоугольника 5 углов. У другого на 8 больше. А у третьего на 6 углов меньше, чем у второго. — Поставьте вопрос так, чтобы задача решалась в два действия. Сколько углов у третьего многоугольника?1). 5 + 8 = 13 (уг.)2). 13 – 6 = 7 (уг.)5 + 8 – 6 = 7 (уг.)
Номер слайда 29
Из каких фигур состоит дворец?Дома сделать аппликацию дворца, используя геометрические фигуры с разными углами.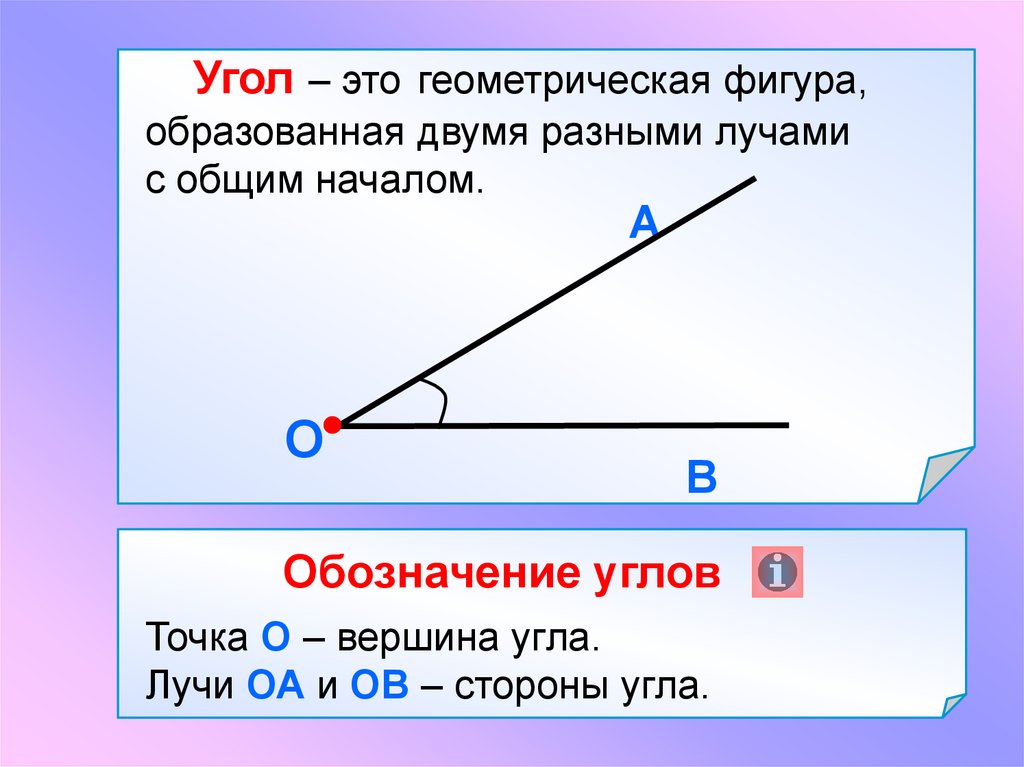
Номер слайда 30
Рефлексия. Яузналсмогвыполнил
Номер слайда 31
Номер слайда 32
Источники. Интернет – ресурсы.
Интернет – ресурсы.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings. DRAG_TEXT_HELP}}
DRAG_TEXT_HELP}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings. CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}типов углов — примеры
Когда два луча или линии встречаются в одной точке, образуется угол, и каждый угол отличается по своей величине. Существуют различные типы углов в геометрии, такие как острый угол, тупой угол, прямой угол, рефлекторный угол и прямой угол. Например, острый угол — это угол, который меньше 90°, а тупой угол — это угол, который больше 90°. Существуют также некоторые специальные типы пар углов. Давайте узнаем о различных типах углов в деталях.
Типы углов на основе измерения
Пространство, образованное при встрече двух лучей в одной точке, называется углом. Углы можно классифицировать как по их измерению, так и по способу их вращения. В зависимости от размера углы классифицируют следующим образом. На следующем рисунке показаны различные виды углов, описанные ниже.
Острый угол
Любой угол меньше 90° является острым.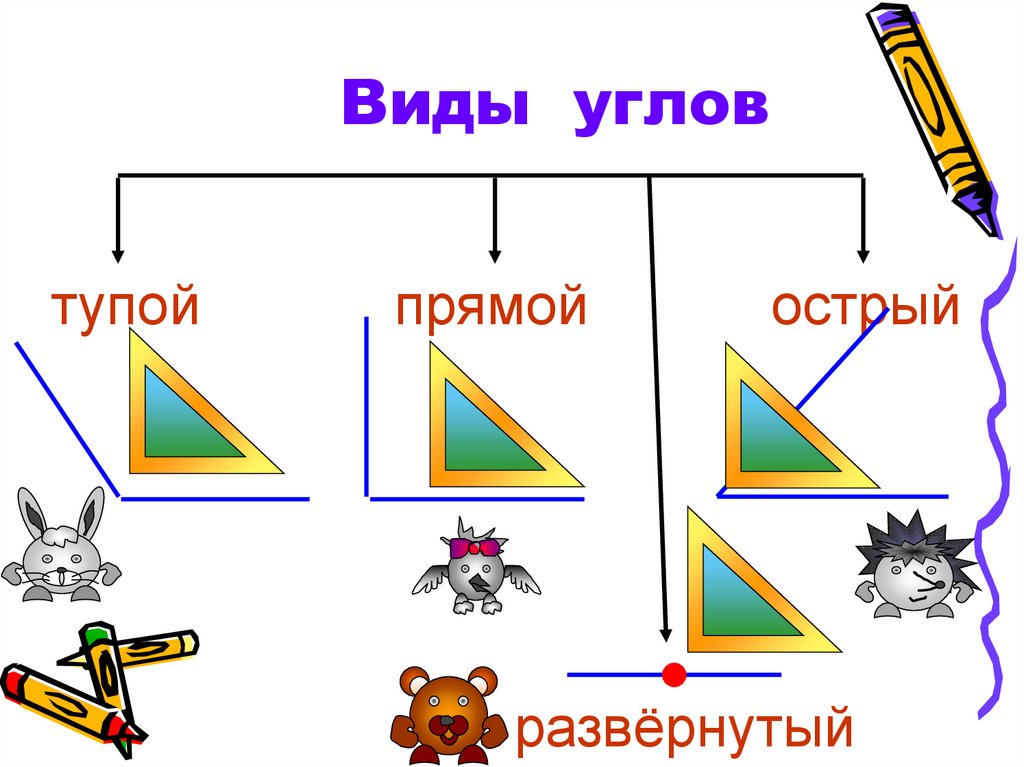 Если два луча пересекаются в вершине, образуя угол, меньший 90°, то образуется острый угол. Некоторые примеры острого угла: 20°, 30°, 45°, 60°. Обратите внимание на рисунок, на котором показано, что угол ∠XYZ острый.
Если два луча пересекаются в вершине, образуя угол, меньший 90°, то образуется острый угол. Некоторые примеры острого угла: 20°, 30°, 45°, 60°. Обратите внимание на рисунок, на котором показано, что угол ∠XYZ острый.
Прямой угол
Если угол между двумя лучами равен 90°, то он называется прямым углом или углом 90°. Обратите внимание на рисунок, который показывает, что ∠AOB является прямым углом или углом 90°.
Тупой угол
Любой угол, который больше 90°, но меньше 180°, является тупым углом.Угол, образованный лучами PQ и QR на рисунке, является тупым углом. Некоторые примеры тупых углов: 110°, 130°, 145°, 165°.
Прямоугольный
Как следует из названия, прямой угол — это прямая линия, а угол, образованный между двумя лучами, точно равен 180°. Под прямым углом два луча противоположны друг другу. Прямой угол может быть образован путем соединения двух смежных прямых углов или, другими словами, два прямых угла составляют прямой угол.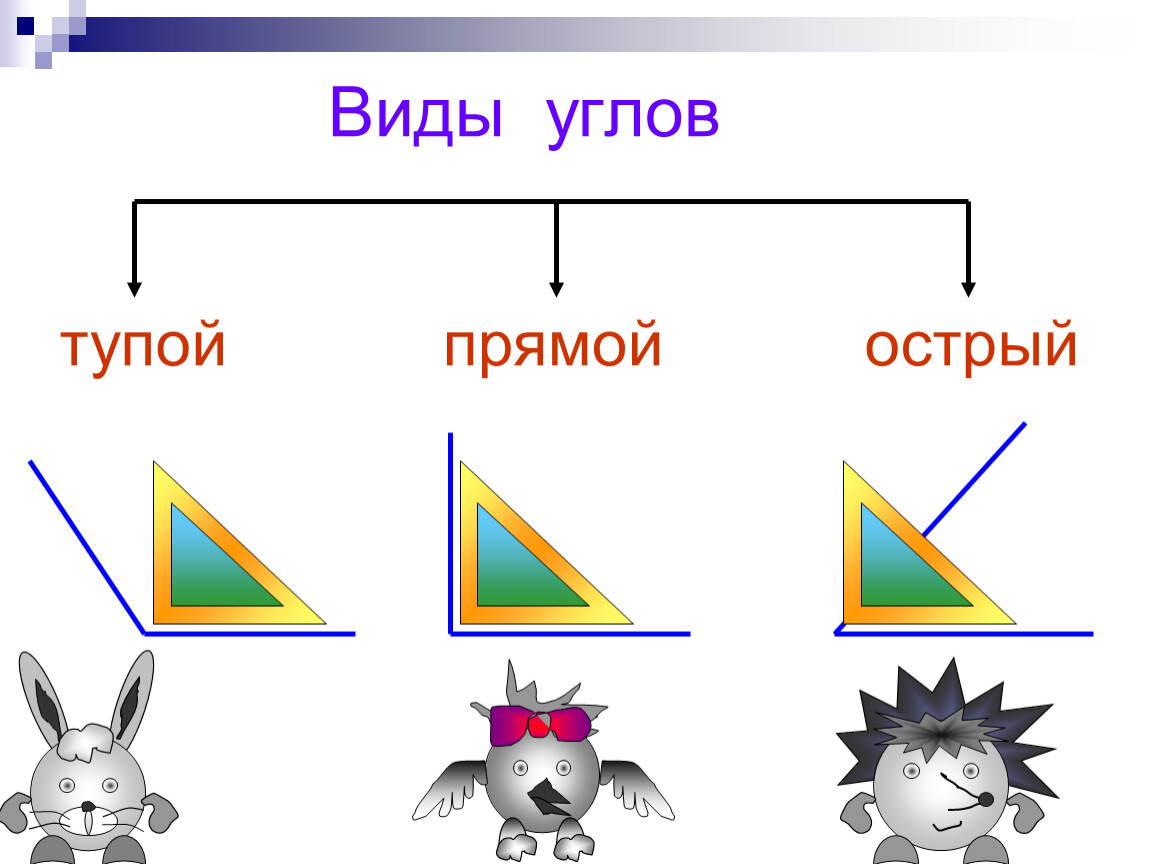 На рисунке ∠SRT представляет собой угол 180° или прямой угол.
На рисунке ∠SRT представляет собой угол 180° или прямой угол.
Угол рефлекса
Угол больше 180° и меньше 360° называется рефлекторным углом. На рисунке ∠ABC — угол рефлекса. Примеры углов рефлекса: 210°, 250°, 310°.
Полный угол поворота
Полный угол поворота образуется, когда одно из плеч угла совершает полный оборот или делает 360°. На рисунке ∠MNR = 360° и называется полным углом поворота.
Типы углов на основе вращения
Следующий тип уголков основан на направлении вращения одного плеча угла.Когда две прямые пересекаются и встречаются в одной точке, образуется угол. Давайте обсудим типы углов на основе вращения.
Положительные углы
Положительные углы — это углы, в которых углы поворачиваются от основания против часовой стрелки или против часовой стрелки. На рисунке ниже при повороте стороны 1(AB) против часовой стрелки на угол θ образуется положительный угол.
Отрицательные углы
Отрицательные углы — это углы, в которых углы поворачиваются от основания по часовой стрелке. На рисунке ниже при повороте стороны 1 (DE) по часовой стрелке на угол θ образуется отрицательный угол.
На рисунке ниже при повороте стороны 1 (DE) по часовой стрелке на угол θ образуется отрицательный угол.
Типы угловых пар
Пара углов обозначает два угла. Давайте прочитаем о различных парах углов в геометрии.
Смежные углы
Чтобы два угла были смежными, должны выполняться следующие условия.
- Два угла имеют общую вершину.
- Два угла имеют общее плечо.
- Есть две руки, которые не являются обычными.
Дополнительные углы
Когда сумма двух углов равна 90°, они называются дополнительными углами. Два угла могут быть любой величины, чтобы в сумме они составляли 90°. Например, два угла могут быть равны 30° и 60°. Здесь один угол является дополнением другого угла.
Дополнительные уголки
Когда сумма двух углов равна 180°, они называются дополнительными углами.Два угла при сложении составляют 180°. Например, 110° и 70° составляют 180°.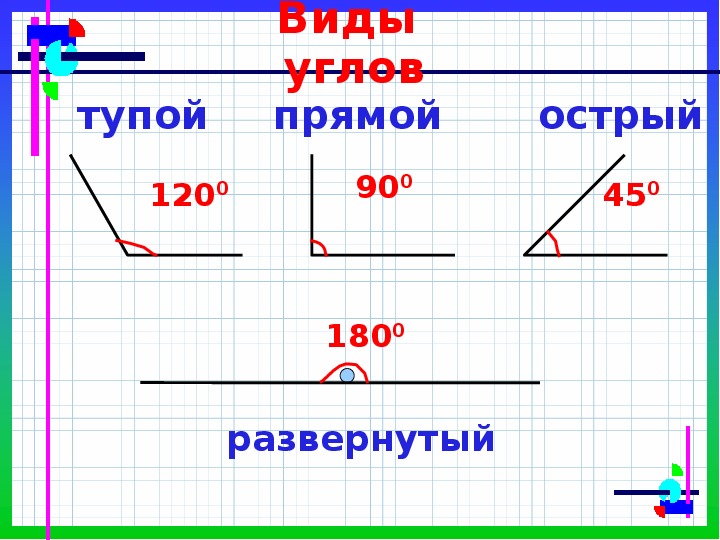 Поэтому эти два угла называются дополнительными. Здесь один угол является дополнением другого угла. Например, дополнение к 60° равно (180° — 60°), что составляет 120°.
Поэтому эти два угла называются дополнительными. Здесь один угол является дополнением другого угла. Например, дополнение к 60° равно (180° — 60°), что составляет 120°.
Альтернативные внутренние углы
Когда прямая или секущая проходит через две параллельные прямые, углы, образованные на противоположных сторонах линии или секущей, называются параллельными внутренними углами, которые равны.
Альтернативные внешние углы
Когда прямая или секущая проходит через две параллельные прямые, углы, образованные на внешней стороне линии или секущей, называются параллельными внешними углами, которые равны.
Соответствующие углы
Когда прямая или секущая проходит через две параллельные прямые, углы, образованные в одном и том же месте или по одну сторону от секущей, являются соответствующими углами, и эти углы конгруэнтны.
Вертикальные углы
Когда две линии пересекаются друг с другом, углы, противоположные друг другу, равны и называются вертикальными углами или вертикально противоположными углами.
Обратите внимание на следующий рисунок, чтобы соотнести углы, указанные выше.
Темы, относящиеся к типам углов
Ознакомьтесь с интересными статьями об углах.
Как классифицируются типы углов?
Угол образуется при пересечении двух лучей или прямых в одной точке. Типы углов классифицируются на основе различных факторов, таких как их размеры или способ их вращения. Учитывая эти факты, типы углов, основанные на измерениях, – это острый угол, тупой угол, прямой угол, прямой угол, угол полного поворота, угол отражения.В зависимости от поворота углы делятся на положительные и отрицательные.
Какие существуют типы пар углов?
Типы угловых пар следующие.
- Смежные углы: имеют общую вершину и одно плечо. Два других плеча не пересекаются.
- Дополнительные углы: когда сумма двух углов равна 90°, такие углы называются дополнительными углами. Каждый угол называется дополнением другого угла.

- Дополнительные углы: два угла считаются дополнительными, если их сумма составляет 180°.Каждый угол называется дополнением другого угла.
- Альтернативные внутренние углы: Углы, образованные, когда секущая проходит через две параллельные линии на внутренних сторонах секущей, называются альтернативными внутренними углами, и они конгруэнтны.
- Альтернативные внешние углы: Углы, образованные при прохождении секущей через две параллельные прямые на внешних сторонах секущей, называются альтернативными внешними углами, и они конгруэнтны.
- Соответствующие углы: Углы, образованные с одной стороны, когда секущая проходит через две параллельные прямые, называются соответственными углами, которые равны.
- Вертикальные углы: Углы, образованные при пересечении двух прямых, являются вертикальными углами. Противоположные углы, образованные этим пересечением, равны по размеру и также известны как вертикально противоположные углы.
Какие типы углов меньше 180°?
Острые и тупые углы — это типы углов, градусная мера которых меньше 180°.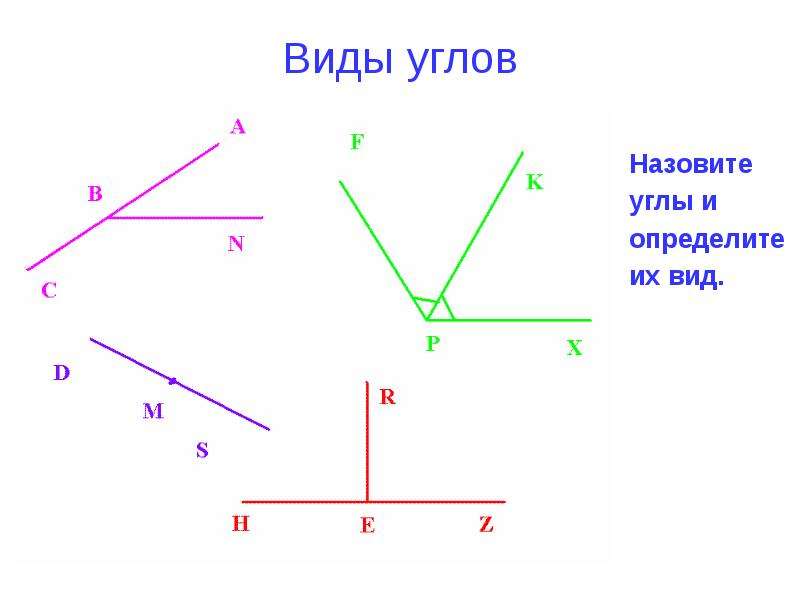 Острые углы всегда меньше 90°, а тупые углы больше 90°, но всегда меньше 180°. Примеры острых углов: 60°, 70°, тупые углы: 110°, 125°.
Острые углы всегда меньше 90°, а тупые углы больше 90°, но всегда меньше 180°. Примеры острых углов: 60°, 70°, тупые углы: 110°, 125°.
Какие виды углов образуются при прохождении секущей через две параллельные прямые?
Когда секущая проходит через две параллельные прямые, образуется много пар углов, таких как чередующиеся внутренние углы, чередующиеся внешние углы и соответствующие углы. Все эти пары углов равны по размеру.
Какой тип угла больше 180°, но меньше 360°?
Рефлекторный угол – это угол, величина которого больше 180°, но меньше 360°.Например, угол измерения 270° является углом отражения.
Как называются типы углов, сумма которых составляет 90° и 180°?
Когда два угла в сумме составляют 90°, они называются дополнительными углами. Два угла могут быть любой величины, чтобы в сумме они составляли 90°. Например, 20° и 70° являются дополнительными углами, потому что в сумме они дают 90°. Когда сумма двух углов равна 180°, они называются дополнительными углами. Два угла всегда в сумме дают 180°. Например, 105° и 75° являются дополнительными, поскольку в сумме дают 180°.
Два угла всегда в сумме дают 180°. Например, 105° и 75° являются дополнительными, поскольку в сумме дают 180°.
Типы углов — Острые, прямые, тупые, прямые и обратные Углы
Углы — одна из фундаментальных единиц геометрии, которую можно найти даже в природе. Для человека углы являются важным аспектом архитектуры и инженерии. Без него невозможно строить здания, производить машины, строить дороги и плотины и многие другие сооружения. Углы можно найти везде, от кусочка пиццы до плотницких эскизов и дизайна одежды.
Типы углов — острые, прямые, тупые, прямые и обратные углы
Изучение углов очень важно, так как они составляют основу геометрии.В следующей статье мы рассмотрим различные типы и важность углов применительно к задачам геометрии. Простой способ начать с концепции состоит в том, что при пересечении двух прямых в точке их пересечения образуется угол. Два луча, образующие угол, называются сторонами угла. Необязательно, чтобы угол образовывался при пересечении двух прямых; он также может быть образован пересечением двух изогнутых линий. Прежде чем понять типы углов, давайте сначала сосредоточимся на том, как их измерять.
Прежде чем понять типы углов, давайте сначала сосредоточимся на том, как их измерять.
Части угла
(Изображение скоро будет загружено)
Угол образуется при пересечении двух лучей в одной точке. При измерении угла одна рука фиксируется в качестве основания, а другая движется по часовой стрелке или против часовой стрелки, образуя угол между ними. Следовательно, все углы имеют две «стороны» или «плеча» и одну «вершину».
Как маркировать углы?
Существует два основных способа обозначения угла:
Как показано на рисунке, углу присваивается греческий алфавит, например альфа (α) или тета (θ).Вы также можете пометить их строчными буквами.
При работе над геометрическими задачами со сложными фигурами углы можно обозначать с помощью маркировки фигуры. Рассмотрим приведенный выше рисунок; например, угол α также можно назвать углом PQR.

Положительные и отрицательные углы
В зависимости от направления вращения можно классифицировать углы как положительные и отрицательные.
(Изображение скоро будет загружено)
Положительные углы: Углы измеряются в направлении против часовой стрелки (противоположном направлению вращения часов), начиная с основания угла.
Отрицательные углы: эти углы измеряются по часовой стрелке, начиная с основания угла.
Величина угла
Величина угла — это вращение вокруг вершины, при котором одно из плеч образует угол. Говорят, что чем больше вращение или раскрытие между плечами, тем большую величину оно имеет. Например-
(Изображение скоро будет загружено)
Существуют различные типы углов в зависимости от их меры угла.Типы:
1. Острый угол
2. Прямой угол
3. Тупой угол
4. Прямой угол
Прямой угол
5. Рефлекторный угол
Как измерить различные типы углов?
1. Острый угол
Угол, величина которого меньше 90°, называется острым углом. Измерение от 0° до 90°. На рисунке ниже угол, образованный пересечением PQ и QR в точке Q, образует угол PQR, равный 45°. Таким образом, PQR называется острым углом.
(Изображение скоро будет загружено)
2. Прямой угол
Угол, равный ровно 90°, называется прямым. Обычно он образуется, когда две линии перпендикулярны друг другу. На рисунке ниже линия AB пересекает линию BC в точке B и образует угол ABC, равный 90°.
(Изображение скоро будет загружено)
3. Тупой угол
Угол, величина которого превышает 90°, называется тупым углом. Диапазон измерения угла составляет от 90° до 180°.Тупой угол также можно найти, если у нас есть мера острого угла.
Мера тупого угла = (180 — мера острого угла)
На рисунке выше отрезок прямой DO пересекает отрезок прямой OQ в точке O и образует угол DOQ размером 120°.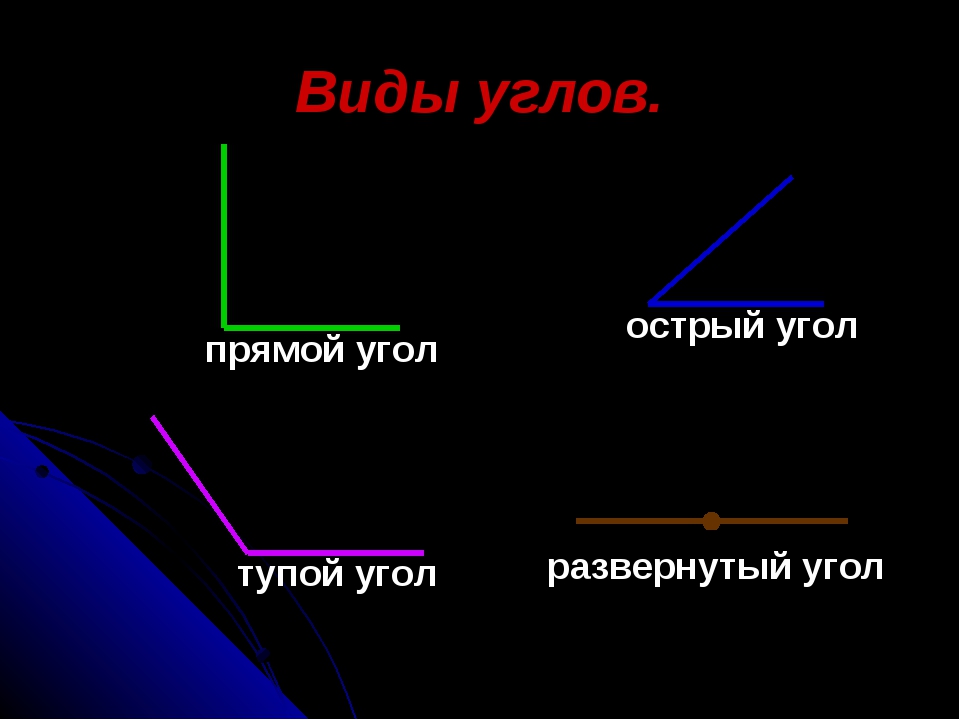 Таким образом, это тупой угол.
Таким образом, это тупой угол.
(Изображение скоро будет загружено)
Кроме того, если мы продолжим линию OQ до OP, то сможем найти меру острого угла.
DOP = 180° — DOQ = 180° — 120° = 60°
4.Прямой угол
Угол, который составляет ровно 180°, называется прямым углом. Это похоже на прямую линию, отсюда и название прямого угла.
Прямой угол есть не что иное, как смесь тупого угла и острого угла на прямой.
5. Угол рефлекса
Угол, который больше 180° и меньше 360°, называется углом рефлекса. Угол рефлекса можно рассчитать, если указана мера острого угла, поскольку он дополняет острый угол на другой стороне линии.
(Изображение скоро будет загружено)
Используя угол отражения, мы можем найти меру острого угла.
Мера острого угла = 360° – мера рефлекторного угла
6. Дополнительные и дополнительные углы
Дополнительный угол
Если сумма двух углов составляет 90°, то они называются дополнительными углами. Углы не обязательно должны быть смежными друг с другом, чтобы считаться дополнительными. Если в сумме они составляют 90°, их называют дополнительными углами.
Углы не обязательно должны быть смежными друг с другом, чтобы считаться дополнительными. Если в сумме они составляют 90°, их называют дополнительными углами.
(Изображение скоро будет загружено)
На приведенном выше рисунке углы расположены рядом друг с другом и в сумме составляют 90°, поэтому их называют дополнительными углами. На рисунках c и d углы не примыкают друг к другу, но в сумме дают 90° и поэтому называются дополнительными углами.
Дополнительные углы
Когда два угла в сумме составляют 180°, они называются дополнительными углами. Существуют различные типы дополнительных углов.
Эти углы имеют общую сторону и вершину, т.е.д., угловая точка. Однако эти точки никак не пересекаются. Проще говоря, смежные углы — это два угла рядом друг с другом.
(Изображение скоро будет загружено)
Эти углы не имеют общего конца, т.е. обычно не имеют общей вершины.
(Изображение скоро будет загружено)
Типы несмежных углов-
Углы, которые имеют общую вершину и стороны угла образованы одними и теми же прямыми, называются вертикальными углами.Вертикальные углы равны между собой.
(Изображение скоро будет загружено)
На приведенном выше рисунке 1 и 3, 2 и 4, 6 и 8, 5 и 7 являются вертикальными углами. Кроме того, 3, 4, 5, 6 известны как внутренние углы, а 1, 2, 7, 8 известны как внешние углы.
Это пара внутренних углов на противоположной стороне поперечной. Самый простой способ обнаружить альтернативные внутренние углы — это определить букву «Z» на внутренней стороне.
На приведенном выше рисунке 3 и 5, 4 и 6 — внутренние углы.Внутренние углы равны между собой.
Аналогично альтернативным внутренним углам; только то, что он присутствует на внешней стороне. На приведенном выше рисунке 1 и 7, 2 и 8 — это пара чередующихся внешних углов. Подобно альтернативным внутренним углам, даже альтернативные внешние углы равны друг другу.
Подобно альтернативным внутренним углам, даже альтернативные внешние углы равны друг другу.
Углы, находящиеся в одинаковом положении, называются соответствующими углами. На приведенном выше рисунке 1 и 5 — соответствующие углы, и они равны друг другу.
Summary
Угол мера | |||
Острый угол | больше чем на 0 °, менее 90 ° | ||
прямой угол | 90 ° | ||
Тупые угол | больше 90 °, менее 180 ° | ||
180 ° | 180 ° | ||
Reflex Угол | Больше 180°, меньше 360° |
Основой геометрии являются углы. Углы находят свое применение практически во всех типах вопросов, будь то тригонометрия или замкнутые фигуры. Понимание углов и типов углов поможет в решении многих каверзных вопросов. Таким образом, убедитесь, что вы понимаете это хорошо.
Углы находят свое применение практически во всех типах вопросов, будь то тригонометрия или замкнутые фигуры. Понимание углов и типов углов поможет в решении многих каверзных вопросов. Таким образом, убедитесь, что вы понимаете это хорошо.
Острый, тупой, прямой и правый
Угол измеряет величину поворота
Имена углов
По мере увеличения угла имя меняется:
Попробуйте сами:
геометрия/изображения/угол-перетаскивание.js
В одной диаграммеЭта диаграмма может облегчить запоминание: Также: острый, тупой и рефлекторный расположены в алфавитном порядке. |
Еще: у буквы «А» острый угол.
Будь осторожен с тем, что измеряешь
| Меньший угол — это Тупой угол , , а больший угол — это Угол отражения |
Итак, называя углы, убедитесь, что что вы знаете под каким углом попросил !
Положительные и отрицательные углы
При измерении от линии:
- a положительный угол идет против часовой стрелки (направление, противоположное ходу часов)
- a отрицательный угол идет по часовой стрелке
Пример: −67°
Части угла
Угловая точка угла называется вершиной
А две прямые стороны называются руками
Угол равен количеству поворотов между каждым рычагом.
Как маркировать углы
Существует два основных способа маркировки углов:
1. Дайте углу имя, обычно строчную букву, например a или b , или иногда греческую букву, например α (альфа) или θ (тета)
2. или тремя буквами на фигуре, определяющими угол, причем средняя буква соответствует тому месту, где на самом деле находится угол (его вершине).
Пример угла « a » равен « BAC «, а угол « θ » равен « BCD »
800, 801, 802, 803, 804, 805, 3276, 3277, 3278, 3279
типов угловых отношений | Соответствующий, альтернативный интерьер и многое другое
Типы уголков
Изучая геометрию, вы обнаружили острые, прямые и тупые углы.Возможно, вы даже узнали о прямых и рефлекторных углах, но если вы хотите узнать еще больше, вы можете исследовать многие другие виды углов, такие как внешние и внутренние углы. Вы также можете узнать о конгруэнтных, смежных, вертикальных, соответствующих и переменных углах.
Вы также можете узнать о конгруэнтных, смежных, вертикальных, соответствующих и переменных углах.
Различные типы уголков
Прежде чем углубиться, давайте наметим различные углы, которые мы можем изучить:
- Равные углы
- Смежные углы
- Вертикальные уголки
- Соответствующие углы
- Наружные углы
- Последовательные внешние углы
- Альтернативные внешние углы
- Последовательные внутренние углы
- Альтернативные внутренние углы
Соотношение углов
Помимо измерения градусов или радианов, вы также можете сравнивать углы и учитывать их взаимосвязь с другими углами.Мы говорим об отношениях углов, потому что мы сравниваем положение, измерение и конгруэнтность между двумя или более углами.
Например, при пересечении двух линий или отрезков они образуют две пары вертикальных углов. Когда две параллельные прямые пересекаются секущей, образуются сложные отношения углов, такие как чередующиеся внутренние углы, соответствующие углы и т. Д.
Д.
Умение определять взаимосвязь углов и уверенно находить конгруэнтные углы при пересечении прямых сделает вас лучшим учеником геометрии.Вы будете решать сложные задачи быстрее, когда будете досконально знакомы со всеми типами взаимосвязей углов.
Равные углы
Любые два угла, независимо от их ориентации, которые имеют одинаковую меру (в радианах или градусах), конгруэнтны . Они показывают одинаковую «открытость» между двумя лучами, отрезками или линиями, которые их образуют. Таким образом, эти два угла в 35° равны, даже если они представлены не одинаково и образованы разными конструкциями:
Смежные углы
Когда две прямые пересекаются, они образуют четыре угла.Любые два угла, имеющие общий луч, отрезок или прямую, являются смежными . На следующем рисунке линия JC пересекает линию OK, образуя четыре смежные пары и пересекаясь в точке Y. Сможете ли вы найти их все?
- Вы нашли ∠JYO рядом с ∠OYC?
- Как насчет ∠OYC рядом с ∠KYC?
- Вы видели ∠KYC рядом с ∠KYJ, верно?
- И вы наверняка нашли ∠KYJ рядом с ∠JYO!
Уголки вертикальные
На том же рисунке выше углы, которые пропускают угол, то есть углы, которые не касаются друг друга, кроме своей вершины, являются вертикальными углами . Здесь слово «вертикальный» означает «относящийся к вершине», а не «вверх и вниз». Вертикальные углы являются противоположными углами; они разделяют только свою точку вершины.
Здесь слово «вертикальный» означает «относящийся к вершине», а не «вверх и вниз». Вертикальные углы являются противоположными углами; они разделяют только свою точку вершины.
Две пересекающиеся линии образуют две пары вертикальных углов. Посмотрите, сможете ли вы найти их на нашем рисунке.
- Вы нашли пару ∠JYO и ∠KYC? Они соприкасаются только в точке Y .
- Вы обнаружили, что ∠KYJ и ∠OYC составили другую пару? Они также соприкасаются только в точке Y .
Вы можете задаться вопросом, почему смежные углы не являются также и вертикальными углами, ведь они тоже имеют общую вершину.Смежные углы имеют больше общего, чем вершина; они имеют общую сторону с углом.
Соответствующие углы
Каждый раз, когда секущая пересекает две другие прямые, мы получаем соответствующие углы. Чем более ограниченными становятся наши пересекающиеся линии, тем более ограниченными являются их угловые отношения. Когда линия пересекает две параллельные линии (поперечную), открывается совершенно новый уровень угловых отношений:
Мы можем ловко вытянуть из этой фигуры углы, похожие друг на друга. Углы, которые имеют одинаковое положение относительно друг друга в двух наборах из четырех углов (четыре вверху, линия AR; четыре внизу, линия TO), являются соответствующими углами. Когда соответствующие углы лежат на параллельных прямых, они равны.
Углы, которые имеют одинаковое положение относительно друг друга в двух наборах из четырех углов (четыре вверху, линия AR; четыре внизу, линия TO), являются соответствующими углами. Когда соответствующие углы лежат на параллельных прямых, они равны.
Наши поперечные и параллельные линии образуют четыре пары соответствующих углов. Можете назвать их всех?
- Вы нашли, что ∠AYD соответствует ∠TLY?
- Как насчет того, чтобы ∠DYR соответствовал &∠YLO?
- Вы нашли, что ∠RYL соответствует ∠OLI, верно?
- И вы не забыли, что ∠AYL соответствует ∠TLI, не так ли?
Во всех случаях, поскольку наши прямые AR и TO параллельны, их соответствующие углы равны.
Наружные углы
Те же самые параллельные прямые и их поперечные образуют внешние углы. Внешний угол среди линейных построений (не многоугольников) — это угол, лежащий вне параллельных прямых. Вы можете увидеть два типа взаимосвязей внешних углов:
Последовательные внешние углы
Когда внешние углы лежат по одну сторону от поперечной, они представляют собой последовательных внешних углов, и дополнительных (прибавляя к 180°). На нашем рисунке выше ∠AYD и ∠TLI — последовательные внешние углы. Единственная другая пара последовательных внешних углов равна …
На нашем рисунке выше ∠AYD и ∠TLI — последовательные внешние углы. Единственная другая пара последовательных внешних углов равна …
Вы сказали ∠DYR и ∠OLI? Мы надеемся на это, потому что это правильно!
Альтернативные внешние углы
Альтернативные внешние углы аналогичны углам при вершине тем, что они являются противоположными углами (по обе стороны от поперечной). Альтернативные внешние углы находятся на противоположных сторонах поперечной (это альтернативная часть) и вне параллельных прямых (это внешняя часть).Сможете ли вы найти на нашем рисунке две пары альтернативных внешних углов?
Вы записали ∠AYD и ∠OLI, а потом написали ∠DYR в паре с ∠TLI, несомненно!
Конгруэнтные альтернативные внешние углы используются для доказательства того, что прямые параллельны, с использованием (подходящей) теоремы о альтернативных внешних углах.
Внутренние углы
Углы между границами двух параллельных прямых составляют внутренних углов , снова образованных секущей. Как и в случае с внешними углами, у нас могут быть последовательные внутренние углы и чередующиеся внутренние углы.
Как и в случае с внешними углами, у нас могут быть последовательные внутренние углы и чередующиеся внутренние углы.
Последовательные внутренние углы
Внутренние углы по одну сторону от секущей составляют последовательных внутренних углов . На нашем рисунке вы можете найти две пары? Вы нашли пару ∠RYL с ∠YLO? Вы видели, что ∠AYL объединился с ∠TLY?
В параллельных прямых последовательные внутренние углы являются дополнительными.
Альтернативные внутренние углы
Когда внутренние углы находятся на противоположных сторонах поперечной, они являются альтернативными внутренними углами .Они поддаются теореме о чередующихся внутренних углах, которая утверждает, что конгруэнтные чередующиеся внутренние углы доказывают параллельность прямых (так же, как это сделала теорема о чередующихся внешних углах).
На нашем рисунке ∠ALY является альтернативным внутренним углом для ∠YLO, что делает их конгруэнтными.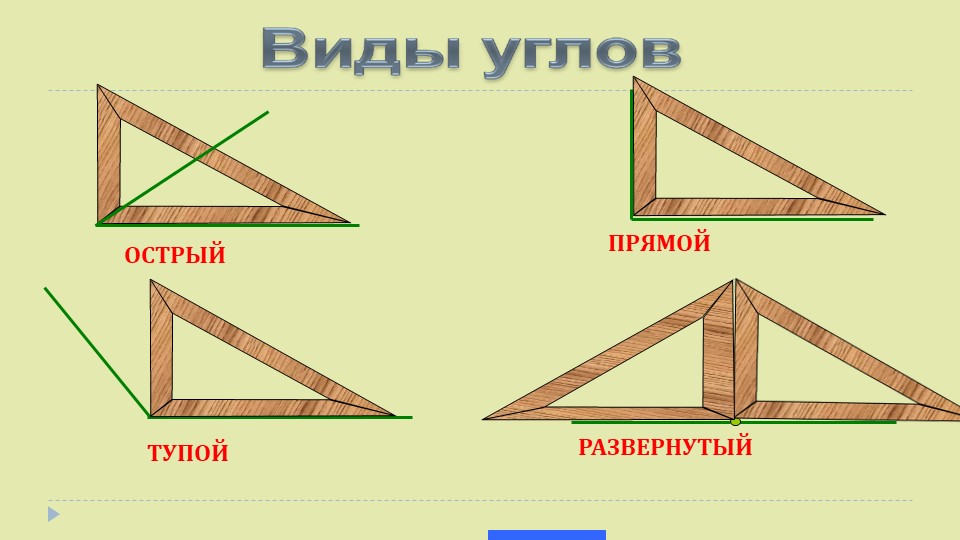 И, конечно же, ∠RYL представляет собой альтернативный внутренний угол ∠TLY.
И, конечно же, ∠RYL представляет собой альтернативный внутренний угол ∠TLY.
Примеры соотношения углов
Вы можете использовать свои новые знания об отношениях углов для решения алгебраических задач о геометрических фигурах.При просмотре любой новой цифры просмотрите свой список и определите три вещи:
- Взаимное расположение двух рассматриваемых углов
- Находятся ли углы вне параллельных прямых (внешние) или внутри параллельных прямых (внутренние)
- Находятся ли два исследуемых угла на одной стороне поперечной (последовательные) или на противоположных сторонах поперечной (альтернативные)
Как только вы поймете взаимосвязь между двумя углами, вы сможете предположить некоторые основные факты, такие как их совпадение или то, что они могут быть дополнительными.
Вы можете использовать эту осведомленность для решения кажущихся сложными алгебраических задач, таких как эта:
[вставьте параллельные линии MJ и TE и поперечные AS с пересечением точки C на линии MJ и точкой пересечения I на линии TE, написав по кругу MAJESTIC; пусть ∠MCA = 123°]
По фигуре найдите значение x, если ∠MCA = 4x + 3°, а ∠EIS = 5x — 27°.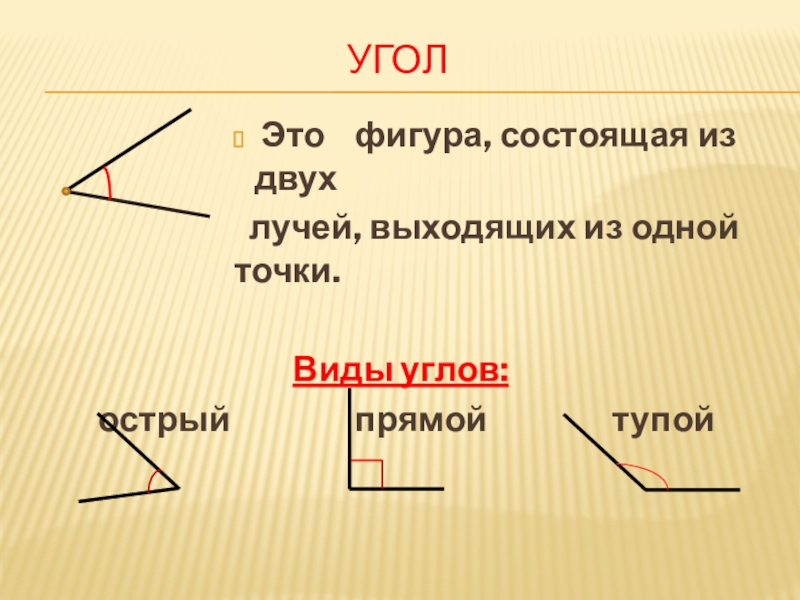
Сразу видно, что эти два угла, ∠MCA и ∠EIS, являются внешними углами, лежащими по разные стороны от трансверсали.Таким образом, они являются альтернативными внешними углами, что делает их конгруэнтными и позволяет составить простое алгебраическое уравнение:
4x + 3° = 5x — 27°
3° = x — 27° (вычесть 4x с обеих сторон)
30° = x (добавьте 27° к обеим сторонам)
Чтобы найти наши углы, подставьте 30° вместо x:
∠MCA = 4x + 3°
∠MCA = 4(30°) + 3°
∠MCA = 120° + 3°
∠MCA = 123°
Хотя ∠EIS предполагается конгруэнтным , вы все равно можете проверить это:
∠EIS = 5x — 27°
∠EIS = 5(30°) — 27°
∠EIS = 150° – 27°
∠EIS = 123°
Давайте попробуем выполнить второе упражнение, используя ту же фигуру.Если вы сможете решить это, вы добились ВЕЛИКИХ математических результатов!
Что вы можете рассказать нам о ∠JCI и ∠TIS?
Что если мы скажем вам, что ∠JCI = 2y — 7°, а ∠TIS = y — 8°?
Можете ли вы найти у?
Ни один из углов не лежит по одну сторону от секущей, и оба они не лежат вне параллельных прямых. Они оба не находятся внутри параллельных линий! Кажется, что у них вообще нет отношений!
Они оба не находятся внутри параллельных линий! Кажется, что у них вообще нет отношений!
И все же по дедукции можно увидеть взаимосвязь:
- ∠JCI является последовательным партнером по внутреннему уголку ∠EIC .
- ∠EIC является партнером ∠TIS по вертикальным углам.
Это означает, что наши два проблематичных угла на самом деле дополняют друг друга, что является отличным намеком.Вместе их два уравнения должны составлять 180°:
.2y — 7° + y — 8° = 180° (упростить)
3 г – 15 ° = 180 ° (теперь добавьте 15 ° в обе стороны)
3y = 195° (теперь разделите на 3)
г = 65°
Если вернуться к решению задачи, вы обнаружите, что ∠JCI = 123° и ∠TIS = 57°. Успех! Потренируйтесь сами, построив параллельные линии с пересечениями и определяя все отношения углов, которые они создают. Помните также, что отношения остаются в силе, когда линии, пересекаемые секущей, не параллельны; вы просто не можете использовать теоремы, чтобы делать предположения об углах.
Следующий урок:
Конструкция углов 30°, 60°, 90° и 120°
типов углов: вертикальные, соответствующие, альтернативные внутренние и другие — видео и стенограмма урока
Типы углов
Первое соотношение углов, которое мы обсудим, это вертикальных углов . Они определяются как пара несмежных углов, образованных только двумя пересекающимися прямыми. Они известны как «Поцелуи против» и всегда имеют конгруэнтные измерения. На рисунке ниже углы 1 и 3 вертикальны, как и углы 2 и 4.
Второе соотношение соответствующих углов . Считается, что они находятся в одном и том же месте в каждой точке пересечения. Например, взгляните на углы 1 и 3 ниже. Они оба в верхнем левом углу. Другая пара соответствующих углов — это углы 6 и 8, которые находятся в правом нижнем углу.
Далее у нас есть альтернативных внутренних углов . Расположенные между двумя пересекающимися прямыми, эти углы находятся по разные стороны от секущей. Углы 2 и 7 выше, а также углы 3 и 6 являются примерами чередующихся внутренних углов.
Точно так же у нас также есть альтернативных внешних углов , которые расположены вне двух пересекающихся линий и на противоположных сторонах секущей. Примером этой связи могут быть углы 1 и 8, а также углы 4 и 5.
Последнее отношение углов составляет последовательных внутренних углов . Эти углы расположены по одну сторону от секущей и внутри двух прямых. На приведенной выше диаграмме углы 2 и 3 являются последовательными внутренними углами, а также углы 6 и 7.
За исключением вертикальных углов, все эти отношения могут быть образованы только при пересечении двух прямых секущей.
Определение отношения углов
При таком большом количестве сходств вам может быть интересно, как определить отношение между углами, образованными секущими и пересекающимися линиями. Все, что вам нужно сделать, это задать себе три основных вопроса:
Все, что вам нужно сделать, это задать себе три основных вопроса:
- Находятся ли углы в одном и том же месте в обеих точках пересечения? Это означает, что мы хотим знать, находятся ли они оба в верхнем левом, верхнем правом, нижнем левом или нижнем правом углах перекрестков. Если вы определите, что они находятся в одном и том же месте, то эти углы должны быть соответствующими углами, и все готово. Если это не соответствующие углы, переходите к вопросам 2 и 3.
- Углы по одну сторону или по разные стороны от поперечной? Если они находятся на одной стороне, то углы считаются последовательными.Если они находятся на противоположных сторонах, то углы считаются параллельными.
- Углы находятся внутри или снаружи двух пересекающихся линий? Если они находятся внутри двух линий, то они будут классифицироваться как внутренние. Если они расположены вне двух прямых, то углы считаются внешними.
Отсюда мы объединим наши ответы на вопросы 2 и 3, чтобы определить взаимосвязь между углами.
Прежде чем мы перейдем к нашим примерам, давайте продолжим и обсудим взаимосвязь между величинами этих углов.
Угловые меры
Как упоминалось ранее, пара вертикальных углов всегда будет конгруэнтной. Независимо от того, как выглядит диаграмма, каждая пара вертикальных углов всегда будет иметь одно и то же измерение. Но история немного отличается при наблюдении за соответствующими альтернативными внутренними, альтернативными внешними или последовательными внутренними углами. Мы не можем делать никаких предположений об их значениях, если у нас нет одного конкретного условия: параллельных линий.
Когда две прямые, пересекаемые секущей, параллельны, соответствующие углы конгруэнтны, альтернативные внутренние углы конгруэнтны, альтернативные внешние углы конгруэнтны, а последовательные внутренние углы становятся дополнительными, что означает, что их сумма равна 180 градусам.
Собираем все вместе
Теперь, когда мы знаем об этих отношениях и их измерениях, давайте свяжем всю эту информацию вместе, исследуя пару основных проблем.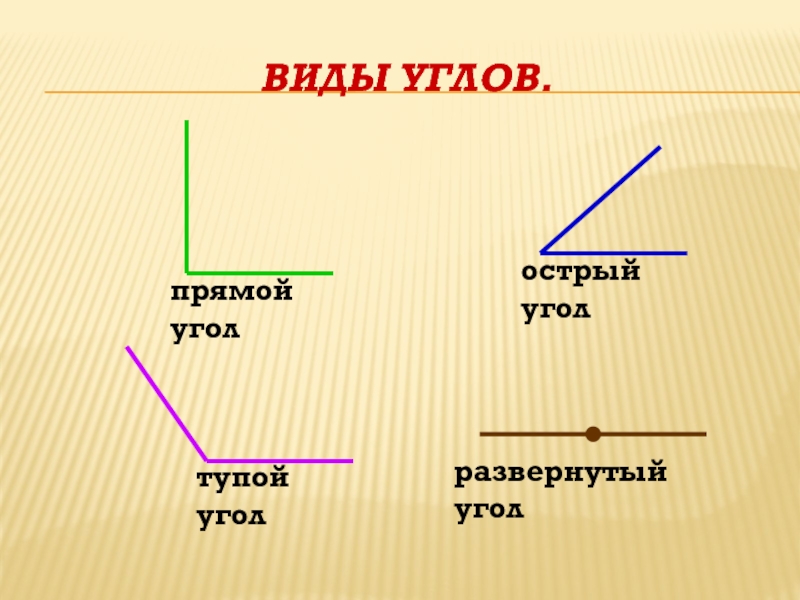
Обратите внимание, что на приведенной ниже диаграмме линия a параллельна линии b . Линия c является поперечной. В нашем первом примере мера угла 1 = 6 x — 3, а мера угла 8 = 4 x + 33. Каково значение x ?
Прежде чем мы сможем решить эту задачу, мы должны определить соотношение между этими двумя углами.Давайте ответим на эти три вопроса, заданные ранее. Что касается вопроса 1, мы замечаем, что эти углы не находятся в одном и том же месте. Угол 1 находится в верхнем левом углу верхнего пересечения, а угол 8 — в нижнем правом углу нижнего пересечения, поэтому они не могут быть соответствующими углами. Давайте перейдем к вопросу 2. Мы видим, что эти два угла находятся на противоположных сторонах секущей, поэтому мы можем классифицировать их как альтернативные углы. В ответ на вопрос 3 оба угла находятся вне двух прямых и должны быть внешними углами. Когда мы комбинируем наши ответы на эти вопросы, мы можем заключить, что это альтернативные внешние углы.
Когда мы комбинируем наши ответы на эти вопросы, мы можем заключить, что это альтернативные внешние углы.
Поскольку две прямые параллельны, мы знаем, что их размеры должны быть равны. Итак, чтобы найти x , мы установим 6 x — 3 = 4 x + 33. Отсюда мы вычтем 4 x с обеих сторон, а затем прибавим 3 к обеим сторонам, чтобы получить 2 . x = 36. Как только мы разделим обе части на 2, мы обнаружим, что значение x = 18.
Для нашего следующего примера пусть угол 6 = 15 y — 11 и угол 4 = 20 y + 16.Чему равен угол 7?
Прежде чем мы сможем найти меру угла, мы должны сначала найти y . Для этого начнем с определения отношения между двумя углами. Мы вернемся к трем вопросам, заданным ранее. Отвечая на вопрос 1, мы видим, что угол 4 и угол 6 не находятся в одном и том же месте на каждом пересечении, поэтому они не являются соответствующими углами. Чтобы ответить на вопрос 2, они находятся на одной стороне поперечной, что делает их последовательными углами.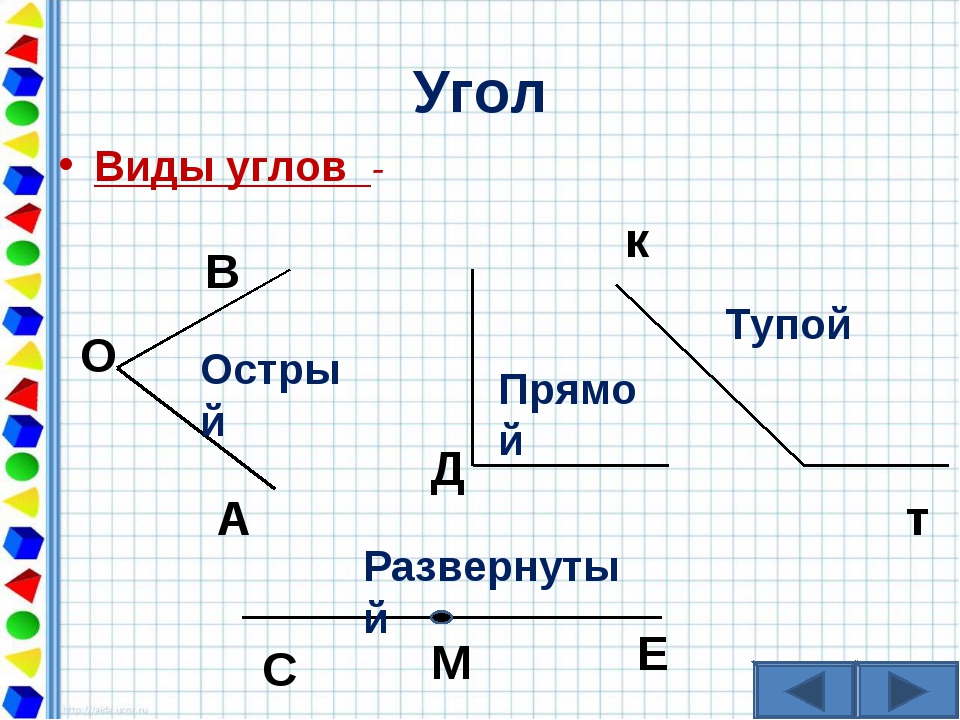 И, чтобы ответить на вопрос 3, они оба находятся внутри двух строк, что делает их внутренними. Следовательно, мы видим, что углы 4 и 6 являются последовательными внутренними углами.
И, чтобы ответить на вопрос 3, они оба находятся внутри двух строк, что делает их внутренними. Следовательно, мы видим, что углы 4 и 6 являются последовательными внутренними углами.
Так как две прямые параллельны, мы знаем, что мы должны сложить эти углы вместе и установить их равными 180. Когда мы это сделаем, мы получим 15 y — 11 + 20 y + 16 = 180. Как только мы объединим наши подобные условия, мы имеем 35 y + 5 = 180. Отсюда мы вычтем 5 с обеих сторон, чтобы получить 35 y = 175, а затем мы разделим обе части на 35, чтобы получить y = 5 .
Хотя это отличное начало нашей проблемы, мы еще не закончили. Нас попросили определить меру угла 7, хотя нам дали информацию только об углах 6 и 4. Найдем связь между углами.
Рассматривая рисунок, мы замечаем, что вершина угла 7 пересекается с вершиной угла 6. Эти два угла несмежны и образованы всего двумя пересекающимися прямыми. По определению, это вертикальные углы, и их меры должны быть конгруэнтны. Следовательно, если мы найдем меру угла 6, мы также будем знать меру угла 7.
Следовательно, если мы найдем меру угла 6, мы также будем знать меру угла 7.
Поскольку мы знаем, что y имеет значение 5, мы подставим это в уравнение для угла 6. Мы увидим этот угол 6 = 15(5) — 11. После упрощения мы видим, что угол 6 равен 64 градусам. Как мы уже говорили ранее, угол 6 и угол 7 равны, потому что они вертикальные углы. Следовательно, мы можем сделать вывод, что угол 7 также равен 64 градусам.
Резюме урока
В обзоре вертикальных углов являются углами, образованными пересечением двух прямых, в то время как чередующихся внутренних углов , альтернативных внешних углов , соответствующих углов и последовательных внутренних углов образуются пересечением из двух прямых и секущей.
Определение того, являются ли углы вертикальными, требует простого наблюдения, в то время как определение других взаимосвязей углов можно выполнить, задав себе три вопроса:
- Находятся ли углы в одном и том же месте?
- Находятся ли они на одной или противоположных сторонах поперечной?
- Они внутри или снаружи двух линий?
Говоря о мерах углов, мы знаем, что меры вертикальных углов всегда конгруэнтны; однако отношения мер для других углов определяются тем, параллельны ли две пересекающиеся линии или нет.
Результаты обучения
По окончании этого урока вы сможете:
- Описывать вертикальные, альтернативные внутренние, альтернативные внешние, соответствующие и последовательные внутренние углы
- Объясните, как определить тип вашего угла
- Определить важность знания того, параллельны ли две пересекающиеся прямые, для определения углов
- Вычислить градусы угла с помощью соотношения углов
Тип углов: свойства и решаемые вопросы
Угол образуется при пересечении двух лучей или прямых в одной точке.Согласно измерению, в геометрии существует несколько типов углов , включая нулевые углы, острые углы, тупые углы, прямые углы, отраженные углы и прямые углы. Углы — это фундаментальная единица геометрии, встречающаяся в природе и используемая в качестве важного аспекта архитектуры и инженерии с незапамятных времен.
Мы используем Углы при строительстве зданий, дорог, плотин, производственных машин и т. д. Углы встречаются везде, от кусочка пиццы до плотницких эскизов и дизайна одежды.Более того, мы используем понятие углов для измерения изменений траектории движения кораблей, самолетов, звезд и т. д. Познакомимся с семью видами углов, их свойствами и способами их измерения. Мы также предоставили несколько решенных примеров для общих математических задач, включая углы. Читайте дальше, чтобы глубже понять концепцию углов и узнать важные определения и формулы.
д. Углы встречаются везде, от кусочка пиццы до плотницких эскизов и дизайна одежды.Более того, мы используем понятие углов для измерения изменений траектории движения кораблей, самолетов, звезд и т. д. Познакомимся с семью видами углов, их свойствами и способами их измерения. Мы также предоставили несколько решенных примеров для общих математических задач, включая углы. Читайте дальше, чтобы глубже понять концепцию углов и узнать важные определения и формулы.
Угол образуется, когда 2 луча исходят из одной исходной точки.Такие лучи образуют угол, который называется плечом угла, а точка их начала называется вершиной угла.
Угол, представленный символом \(\угол \). Здесь на приведенной выше диаграмме образованный угол представлен (\угол PQR\). Этот же угол можно также представить как \(\угол RQP\). Угол измеряется градусов.
Вышеуказанные два луча могут комбинироваться несколькими способами, образуя различные типы углов в геометрии. Давайте начнем с изучения этих различных типов углов.
Давайте начнем с изучения этих различных типов углов.
Типы углов
Углы можно разделить на два основных типа:
- На основе величины
- На основе вращения
Существует \(7\) типов углов, основанных на величине или измерениях угла.
Они перечислены ниже:
1. Нулевые углы
2. Острый угол
3. Прямые углы
4.\цирк\). Его еще называют полным углом. На рисунке ниже показан полный/полный угол.
Загрузите математические формулы для класса 6 отсюда
Типы углов на основе поворотаВ зависимости от направления измерения или направления вращения углы бывают \(2\) типов:
- Положительные углы
- Отрицательные углы
Углы, измеренные против часовой стрелки (или против часовой стрелки), называются положительными углами.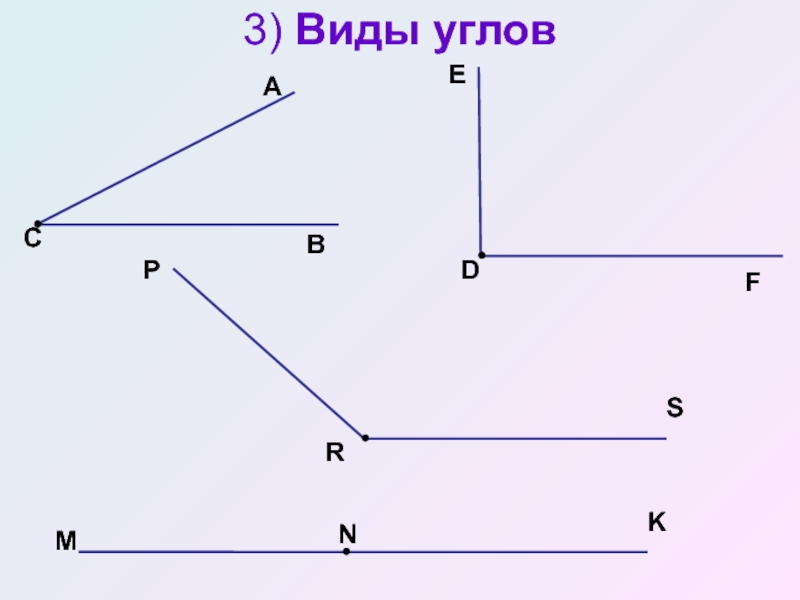 \circ \), называются дополнительными углами.\цирк\).
\circ \), называются дополнительными углами.\цирк\).
На приведенном ниже рисунке \(\угол 1\) и \(\угол 2\) называются линейной парой углов.
Разница между парами дополнительных углов и линейными парами угловПара дополнительных углов может иметь или не иметь общую вершину, но линейная пара углов всегда должна иметь общую вершину.
Смежные углыСмежные углы — это два угла, которые имеют общую вершину и общую сторону, но не пересекаются.На приведенном ниже рисунке \(\угол 1\) и \(\угол 2\) являются смежными углами. Они имеют одну и ту же вершину и одну общую сторону.
Вертикально противоположные углы При пересечении двух прямых противоположные углы равны. На диаграмме ниже углы \(\угол 1\) и \(\угол 2\) равны. Эти углы \(\угол 1\) и \(\угол 2\) называются вертикально противоположными углами, поскольку они противоположны друг другу в вершине.
Линия, которая пересекает две или более прямых в разных точках, называется секущей.Углы, образованные в точке пересечения, равны
.- Внутренние углы : внутренний из двух углов, образованный там, где сходятся две стороны многоугольника. \(\угол 3,\,\угол 4,\,\угол 5\) и \(\угол 6\) — внутренние углы.
- Внешние углы : Внешний угол – это угол между любой стороной фигуры и линией, продолжающейся от следующей стороны. \(\угол 1,\угол 2,\,\угол 7\) и \(\угол 8\) — внешние углы.
- Пары чередующихся внутренних углов : Пары чередующихся внутренних углов — это парные углы, образованные при пересечении одной прямой двух параллельных прямых.Альтернативные внутренние углы всегда равны. \(\угол 3\,\& \,\угол 6\) и \(\угол 4\,\& \,\угол 5\) две пары чередующихся внутренних углов. \(\угол 3 = \угол 6\) и \(\угол 4 = \угол 5\)
- Пары альтернативных внешних углов : Пары альтернативных внешних углов — это просто вертикальные углы альтернативных внутренних углов.
 Альтернативные внешние углы равны. \(\угол 1\,\& \,\угол 8\) и \(\угол 2\,\& \,\угол 7\) две пары чередующихся внешних углов.\(\угол 1 = \угол 8\) и \(\угол 2 = \угол 7\)
Альтернативные внешние углы равны. \(\угол 1\,\& \,\угол 8\) и \(\угол 2\,\& \,\угол 7\) две пары чередующихся внешних углов.\(\угол 1 = \угол 8\) и \(\угол 2 = \угол 7\) - Пары соответствующих углов : Соответствующие углы — это парные углы, образованные при пересечении прямой с парой параллельных прямых. Соответственные углы также равны. \(\угол 1 = \угол 5,\,\угол 3 = \угол 7,\,\угол 2 = \угол 6\) и \(\угол 4 = \угол 8\) — четыре пары соответствующих углов
- Пары внутренних углов на одной стороне поперечной : \(\угол 3\,\& \,\угол 5\) и \(\угол 4\,\& \,\угол 6\) два пары внутренних углов по одну сторону от секущей.\цирк\). Типы углов – Пример s a) Пример нулевого угла
Угол между часовой и минутной стрелками, как показано на часах выше, образует нулевой угол.
b) Пример острого углаУгол между часовой и минутной стрелками, как показано на часах выше, образует острый угол.
c) Пример прямого угла
Угол между часовой и минутной стрелками, как показано на часах выше, образует прямой угол.
d) Пример тупого углаУгол между часовой и минутной стрелками, как показано на часах выше, образует тупой угол.
e) Пример прямого угла
Угол между часовой и минутной стрелками, как показано на часах выше, образует прямой угол.
Попытка пробных тестов
f) Пример угла рефлексаУгол между часовой и минутной стрелками, как показано на часах выше, образует рефлекторный угол.\цирк\) .
СводкаИз этой статьи мы узнали, что угол – это геометрическая фигура, образованная с помощью двух лучей. Здесь обсуждались такие типы углов, как нулевой, острый, прямой, тупой, отраженный, прямой, полный, положительный и отрицательный углы, дополнительные углы, дополнительные углы, поперечные углы и т.
Часто задаваемые вопросы Д. Углы, образованные секущей, являются соответствующими чередующимися внутренними углами. Также обсуждались чередующиеся внешние углы, внутренние углы, внешние углы и вертикально противоположные углы.
Д. Углы, образованные секущей, являются соответствующими чередующимися внутренними углами. Также обсуждались чередующиеся внешние углы, внутренние углы, внешние углы и вертикально противоположные углы.Q.1. Как описать углы?
Ответ: Угол можно описать как фигуру, образованную двумя лучами, встречающимися в общей точке. Угол обозначается символом \(\angle .\). Углы измеряются в градусах с помощью транспортира.Q.2. Что такое угол и его виды?
Ответ: Угол образуется, когда два луча пересекаются в одной точке.\цирк\). Его еще называют полным углом. Таким образом, полный угол является наибольшим.Q.4. Как определить углы?
Ответ: Мы можем определить угол, визуализируя фигуру или измеряя углы с помощью транспортира.
Q.5. Что такое вертикальный угол?
Ответ: Углы, имеющие общую вершину и стороны угла образованы одними и теми же прямыми, называются вертикальными углами.Вертикальные углы равны.Учащиеся также могут использовать Решения NCERT по практической геометрии для 6 класса , которые будут полезны при подготовке.
Теперь, когда вы получили всю необходимую информацию о типах углов, мы надеемся, что эта статья будет вам полезна. Если у вас есть какие-либо вопросы, отправьте нам сообщение через поле для комментариев ниже, и мы свяжемся с вами как можно скорее.
461 вид
Типы углов: острый, прямой, тупой, прямой и рефлекторный
Уголок:
В геометрии две стрелки представляют собой два луча, сходящихся в одной точке, и когда два луча имеют общий конец, они образуют угол.Два луча, образующие угол, называются плечами угла или отрезками угла, а их общая точка называется вершиной угла.
 Углы обычно измеряются в градусах. Для измерения углов мы обычно используем инструмент, называемый транспортиром, он имеет форму полукруга, а середина транспортира называется центральной точкой, от которой мы измеряем угол. Угол в центре разделен на 180 равных делений. Если мы сделаем полный оборот, то получится 360 равных делений, и каждая из этих частей называется степенью.Степень обозначается °. Градусы указывают, насколько открыт каждый угол, и по их открытию мы классифицируем эти углы. Угол обозначается символом ∠. Существуют различные типы углов в зависимости от положения рук.
Углы обычно измеряются в градусах. Для измерения углов мы обычно используем инструмент, называемый транспортиром, он имеет форму полукруга, а середина транспортира называется центральной точкой, от которой мы измеряем угол. Угол в центре разделен на 180 равных делений. Если мы сделаем полный оборот, то получится 360 равных делений, и каждая из этих частей называется степенью.Степень обозначается °. Градусы указывают, насколько открыт каждый угол, и по их открытию мы классифицируем эти углы. Угол обозначается символом ∠. Существуют различные типы углов в зависимости от положения рук.Связанное чтение: https://mytutorsource.com/blog/how-mts-tutors-can-help-you-in-improving-your-mathematics/
Типы уголков:
Различные типы уголков:
- Острый угол
- Прямоугольный
- Тупой угол
- Прямоугольный
- Угол рефлекса
- Полный оборот
Угол, величина которого больше нуля градусов 0° и меньше девяноста градусов 90°, называется острым углом.
 Острые углы меньше других углов. Если у нас есть треугольник ABC с углом B 50 °, то можно сказать, что треугольник ABC остроугольный. ∠B — острый угол, так как при пересечении AB и CB в точке B угол меньше 90°.
Острые углы меньше других углов. Если у нас есть треугольник ABC с углом B 50 °, то можно сказать, что треугольник ABC остроугольный. ∠B — острый угол, так как при пересечении AB и CB в точке B угол меньше 90°.Угол, градусная мера которого составляет девяносто градусов (90°), называется прямым углом, и он больше острого угла. Когда стороны угла перпендикулярны друг другу, они образуют прямой угол. Однако, если угол больше девяноста градусов (90°), то это не будет прямым углом.Если у нас есть треугольник PQR, PQ и QR перпендикулярны друг другу или пересекаются друг с другом в Q, образуя угол ∠Q = 90 °, что делает его прямым углом.
Угол, градусная мера которого больше девяноста градусов (90°) и меньше ста восьмидесяти градусов (180°), называется тупым углом. Тупой угол больше прямого угла и острого угла. Тупой угол имеет размеры от девяноста градусов (90°) до ста восьмидесяти градусов (180°). Один из способов вычислить тупой угол — это знать значение острых углов.Например,
Тупой угол = 180° – значение острого угла
Угол, если стороны угла направлены в противоположные друг другу стороны, называется прямым углом.
 Проще говоря, тип угла, который измеряет 180 градусов (180 °), называется прямым углом. Если мера угла больше 180° или меньше 180°, то он не может быть прямым углом. Более того, он образует полный полукруг.
Проще говоря, тип угла, который измеряет 180 градусов (180 °), называется прямым углом. Если мера угла больше 180° или меньше 180°, то он не может быть прямым углом. Более того, он образует полный полукруг.Угол, величина которого больше ста восьмидесяти градусов (180°) и меньше трехсот шестидесяти градусов (360°), называется рефлекторным углом.Угол рефлекса больше прямого угла, но меньше полного оборота, так как угол рефлекса не равен тремстам шестидесяти градусам (360°). Угол рефлекса измеряется от ста восьмидесяти градусов (180°) до трехсот шестидесяти градусов (360°). Один из способов вычислить тупой угол, если мы знаем значение острого угла или тупого угла. Например,
Угол рефлекса = 360° – значение острого или тупого угла
Если оба плеча угла накладываются друг на друга, то они образуют угол в триста шестьдесят градусов, известный как полный поворот.Проще говоря, угол, который измеряется или равен тремстам шестидесяти градусам (360°), называется полным поворотом.
 Он также известен как полный угол из-за того, что он образует полный круг.
Он также известен как полный угол из-за того, что он образует полный круг.Кроме того, углы можно разделить на два типа в зависимости от их вращения: положительные и отрицательные углы.
Положительный угол:
Положительный угол — это угол, который направлен против часовой стрелки от основания и обычно используется для обозначения углов в математике, геометрии и т. д.
Отрицательный угол:
Отрицательный угол — это угол, который направлен по часовой стрелке от основания и обычно используется для обозначения отрицательных углов в математике, геометрии и т. д.
Чтобы вам было легче, мы сделаем таблицу, с помощью которой вы сможете запомнить эти углы!
ТИПЫ УГЛОВ ОСТРЫЙ УГОЛ Более 0° Меньше 90°
ПРЯМОЙ УГОЛ Равен 90° ТУПОЙ УГОЛ Более 90° Менее 180°
ПРЯМОЙ УГОЛ Равен 180° УГОЛ ОТРАЖЕНИЯ Более 180° Менее 360°
ПОЛНЫЙ ВРАЩ Равен 360° Найдите лучших репетиторов в вашем регионе
.

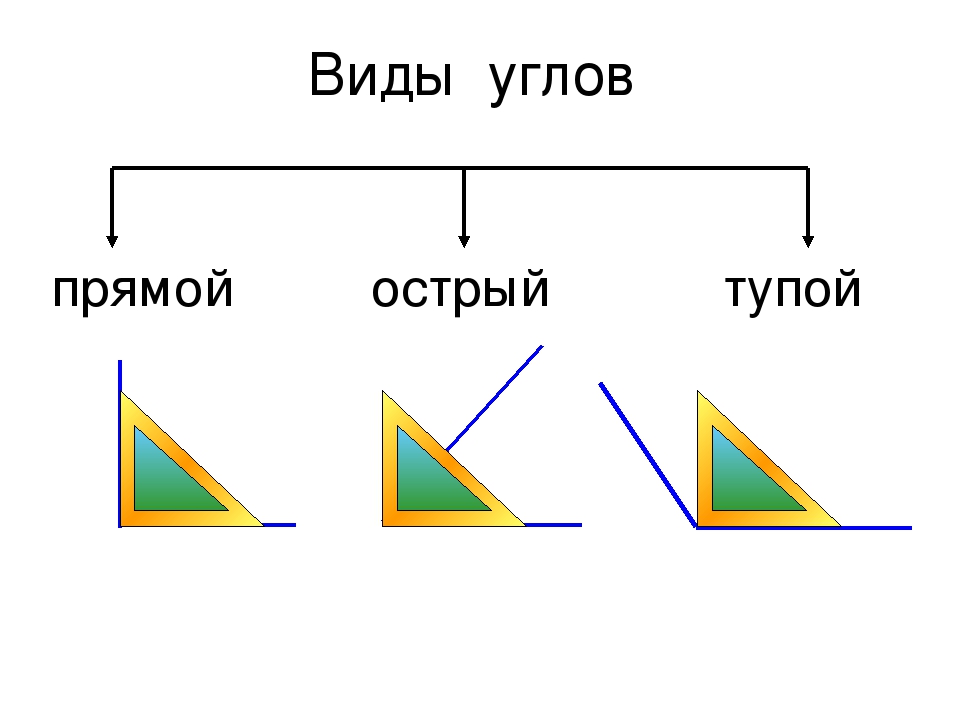

 Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.


 Альтернативные внешние углы равны. \(\угол 1\,\& \,\угол 8\) и \(\угол 2\,\& \,\угол 7\) две пары чередующихся внешних углов.\(\угол 1 = \угол 8\) и \(\угол 2 = \угол 7\)
Альтернативные внешние углы равны. \(\угол 1\,\& \,\угол 8\) и \(\угол 2\,\& \,\угол 7\) две пары чередующихся внешних углов.\(\угол 1 = \угол 8\) и \(\угол 2 = \угол 7\)
 Д. Углы, образованные секущей, являются соответствующими чередующимися внутренними углами. Также обсуждались чередующиеся внешние углы, внутренние углы, внешние углы и вертикально противоположные углы.
Д. Углы, образованные секущей, являются соответствующими чередующимися внутренними углами. Также обсуждались чередующиеся внешние углы, внутренние углы, внешние углы и вертикально противоположные углы.
 Углы обычно измеряются в градусах. Для измерения углов мы обычно используем инструмент, называемый транспортиром, он имеет форму полукруга, а середина транспортира называется центральной точкой, от которой мы измеряем угол. Угол в центре разделен на 180 равных делений. Если мы сделаем полный оборот, то получится 360 равных делений, и каждая из этих частей называется степенью.Степень обозначается °. Градусы указывают, насколько открыт каждый угол, и по их открытию мы классифицируем эти углы. Угол обозначается символом ∠. Существуют различные типы углов в зависимости от положения рук.
Углы обычно измеряются в градусах. Для измерения углов мы обычно используем инструмент, называемый транспортиром, он имеет форму полукруга, а середина транспортира называется центральной точкой, от которой мы измеряем угол. Угол в центре разделен на 180 равных делений. Если мы сделаем полный оборот, то получится 360 равных делений, и каждая из этих частей называется степенью.Степень обозначается °. Градусы указывают, насколько открыт каждый угол, и по их открытию мы классифицируем эти углы. Угол обозначается символом ∠. Существуют различные типы углов в зависимости от положения рук. Острые углы меньше других углов. Если у нас есть треугольник ABC с углом B 50 °, то можно сказать, что треугольник ABC остроугольный. ∠B — острый угол, так как при пересечении AB и CB в точке B угол меньше 90°.
Острые углы меньше других углов. Если у нас есть треугольник ABC с углом B 50 °, то можно сказать, что треугольник ABC остроугольный. ∠B — острый угол, так как при пересечении AB и CB в точке B угол меньше 90°. Проще говоря, тип угла, который измеряет 180 градусов (180 °), называется прямым углом. Если мера угла больше 180° или меньше 180°, то он не может быть прямым углом. Более того, он образует полный полукруг.
Проще говоря, тип угла, который измеряет 180 градусов (180 °), называется прямым углом. Если мера угла больше 180° или меньше 180°, то он не может быть прямым углом. Более того, он образует полный полукруг.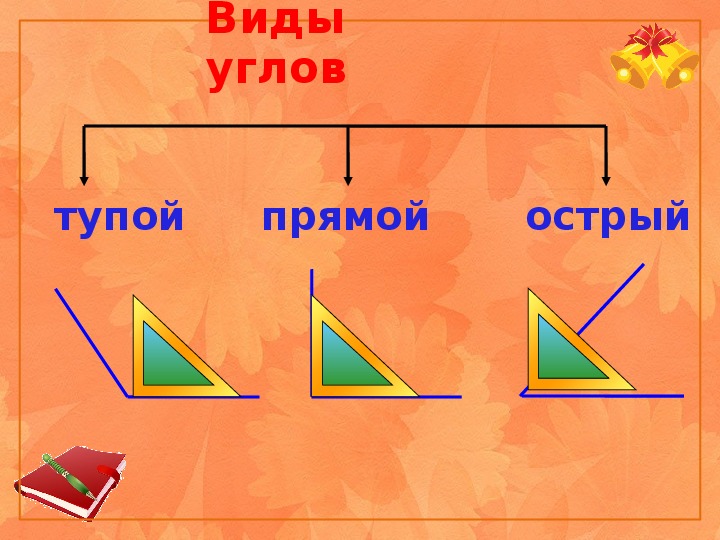 Он также известен как полный угол из-за того, что он образует полный круг.
Он также известен как полный угол из-за того, что он образует полный круг.