Степенные ряды, которые мы и станем использовать, сходятся равномерно, поэтому их можно почленно интегрировать по любому отрезку, лежащему внутри интервала сходимости. Схема решения подобных задач на вычисление интегралов с помощью рядов проста:
- Разложить подынтегральную функцию в функциональный ряд (обычно в ряд Маклорена).
- Произвести почленное интегрирование членов записанного в первом пункте функционального ряда.
- Вычислить сумму полученного во втором пункте числового ряда с заданной точностью $\varepsilon$.

Продолжение темы вычисления интегралов с помощью рядов Маклорена продолжим во второй части.
Вычислить с точностью. §6
Пример №7 . Написать ряд Тейлора по степеням (х -1) функции ln(x+2) .
Решение .Ряд сходится при , или -2
Пример №8 . Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x =2.
Решение . Сделаем замену t=х-2:Воспользовавшись разложением (3), в котором на место х подставим π / 4 t, получим:
Полученный ряд сходится к заданной функции при -∞Таким образом,
, (-∞Приближенные вычисления с помощью степенных рядов
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Рассмотрим разложение функции в степенной ряд:Для того, чтобы вычислить приближенное значение функции в заданной точке х , принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:
Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r n (x) .
 Для этого применяют следующие приемы:
Для этого применяют следующие приемы:- если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена .
- если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: ax).
Пример №1 . Вычислить ln(3) с точностью до 0,01.
Решение . Воспользуемся разложением , где x=1/2 (см. пример 5 в предыдущей теме):Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
Таким образом, мы можем отбросить этот остаток и получаем
Пример №2 . Вычислить с точностью до 0,0001.
Решение . Воспользуемся биномиальным рядом. Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5.
Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5.так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
, поэтому его и следующие за ним члены можно отбросить.Пример №3 . Вычислить интеграл ∫ 0 1 4 sin (x) x с точностью до 10 -5 .
Решение . Соответствующий неопределенный интеграл не может быть выражен в элементарных функциях, т. е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим
.Пример №4 . Вычислить интеграл ∫ 0 1 4 e x 2 с точностью до 0,001.
Решение .
. Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
≈0.0001.На данном уроке мы рассмотрим первую, наиболее простую задачу, для решения которой потребуются самые элементарные знания о рядах, таблица разложений функций в степенные ряды и микрокалькулятор. Как вариант, пойдёт Эксель (если умеете управляться с его функциями).
 Вычислительные задачи требуют повышенной концентрации внимания, поэтому к изучению статьи рекомендую подойти в хорошей физической форме и со свежей головой:
Вычислительные задачи требуют повышенной концентрации внимания, поэтому к изучению статьи рекомендую подойти в хорошей физической форме и со свежей головой:Существует 2 типа рассматриваемой задачи, с которыми мы на самом деле уже сталкивались ранее, в частности при вычислении интеграла по формуле трапеций и методом Симпсона . Тип первый:
Пример 1
Используя разложение функции в ряд, вычислить число , ограничившись 5 членами разложения. Результат округлить до 0,001. Провести вычисления на калькуляторе и найти абсолютную погрешность вычислений.
Решение : прежде всего, выбираем подходящее табличное разложение функции . Очевидно, что в нашем случае необходимо взять следующий ряд:
, который сходится при любом значении «икс».Кратко повторим, что такое сходимость функционального ряда : чем больше слагаемых мы рассмотрим, тем точнее функция-многочлен будет приближать функцию . Действительно, график параболы совсем не напоминает экспоненту и график кубической функции тоже далёк от идеала, но если взять 50-100 членов ряда, то картина в корне поменяется.

Примечание : в теории даже есть такой подход и определение: функция – это сумма функционального ряда .
В условии прямо сказано, что нужно просуммировать 5 первых членов ряда, причём, результат следует округлить до 0,001. И поэтому проблем здесь никаких:
Вычислим более точное значение с помощью микрокалькулятора:
Абсолютная погрешность вычислений:
– ну что же, вполне и вполне неплохо. Но бывает лучше.Ответ :
Теперь рассмотрим нескольку другую разновидность задания:
Пример 2
Используя разложение функции в ряд, вычислить приближённо с точностью до 0,001.
! Примечание : иногда аргумент бывает выражен в градусах, в таких случаях его необходимо
перевести в радианы .Давайте вспомним смысл выражения «с точностью до 0,001». Оно обозначает, что наш ответ должен отличаться от истины не более чем на 0,001.

Решение : используя табличное разложение , запишем несколько членов соответствующего ряда, при этом округление лучше проводить с «запасом» – до 5-6 знаков после запятой:
Сколько членов ряда следует просуммировать для достижения требуемой точности? Для сходящихся знакочередующихся рядов справедлив следующий критерий :члены следует суммировать до тех пор, пока они по модулю больше заданной точности. Первый же меньший вместе со всем «хвостом» подлежит утилизации. В данном примере таковым является 4-й член: , поэтому:
– с округлением финального результата до требуемой точности.
Ответ : с точностью до 0,001
Наверное, все понимают, почему она гарантирована: здесь к отрицательному 4-му члену прибавляется мЕньшее по модулю число , затем из результата вычитается ещё более малое число – и так далее до бесконечности. Образно говоря, конструкция напоминает маятник с затухающими колебаниями, где – самый большой размах в отрицательную сторону, «затмевающий» собой все остальные движения.

Очевидно, что для сходящихся положительных рядов (ближайший пример – Пример 1) рассмотренный критерий некорректен. Условно говоря, если 0,00034 (т.к. ВСЕ члены ряда положительны) . И к этому вопросу я ещё вернусь позже:
Пример 3
Пример 4
Вычислить приближённо, используя первые два члена соответствующего разложения. Оценить абсолютную погрешность вычислений.
Это примеры для самостоятельного решения. Разумеется, выгодно сразу же найти чтобы эффективно контролировать ход решения.
И возникает вопрос: зачем заниматься такими нелепыми вещами, если есть калькуляторы, расчётные программы? Отчасти я дал ответ на уроке Приближенные вычисления с помощью дифференциала . Не так уж и давно калькулятор был большой редкостью, не говоря о такой роскоши, как клавиши с надписями и т.д. В гостевой книге сайта одна из посетительниц поделилась воспоминаниями, как все расчёты своего диплома проводила с помощью математических таблиц и логарифмической линейки.
 А такой инструментарий наряду с механическими счётами сегодня займут место разве что в музее истории математики.
А такой инструментарий наряду с механическими счётами сегодня займут место разве что в музее истории математики.Резюме таково – мы решаем устаревшую задачу. Насущный же практический смысл состоит в том, что её нужно решить =) Ну, может ещё по информатике будет полезно кому – приближенная сумма с наперёд заданной точностью элементарно алгоритмизируется циклом. Правда, какой-нибудь Паскаль довольно быстро сломается, поскольку факториал растёт семимильными шагами.
Кроме того, есть ещё одно очень важное и актуальное приложение, имеющее прикладное значение, но этот секрет будет раскрыт по ходу урока;-) Выдвигайте гипотезы, если догадаетесь – респект.
Также не следует упускать из внимания область сходимости предлагаемых рядов, разложения синуса, косинуса и экспоненты – да, сходятся при любом «икс», но разобранные примеры не должны усыплять бдительность! Простейшая иллюстрация – арктангенс и его разложение . Если попытаться вычислить, скажем, значение , то легко заметить неограниченный рост (по модулю) членов ряда, который не приведёт нас к какому бы то ни было конечному , и тем более приближённому значению.
 А всё потому, что не входит в область сходимости данного разложения.
А всё потому, что не входит в область сходимости данного разложения.Разберём более трудные задания:
Пример 5
Вычислить с точностью до 0,01
Решение : щёлкаем по клавишам калькулятора: . И думаем, как выполнить приближённые вычисления с помощью ряда. В ситуациях с корнем дело сводится к биномиальному разложению с гарантированным интервалом сходимости .
Пытаемся представить наш радикал в виде :
И всё бы было хорошо, но только значение не входит в область сходимости рассматриваемого биномиального ряда, то есть конструкция не годится для вычислений – произойдёт такой же несчастный случай, как с рассмотренным выше .
Как быть? Ещё раз смотрим на значение и замечаем, что оно близко к «тройке». В самом деле: . Используя замечательного соседа, проводим следующее типовое преобразование: под корнем выделяем число 27, искусственно выносим его за скобки и далее выносим из-под корня:
Вот теперь всё тип-топ: число принадлежит интервалу сходимости .
 Но в качестве «побочного эффекта» возникает необходимость поправить точность вычислений. Ведь когда мы подсчитаем члены разложения , то будем обязаны домножить каждое число на «тройку». И по этой причине изначально требуемую точность 0,01 нужно устрожить в три раза: .
Но в качестве «побочного эффекта» возникает необходимость поправить точность вычислений. Ведь когда мы подсчитаем члены разложения , то будем обязаны домножить каждое число на «тройку». И по этой причине изначально требуемую точность 0,01 нужно устрожить в три раза: .Итак, используем ряд , в котором . Не забываем проверить по таблице разложений , не подпадает ли наш пример под какой-нибудь частный случай биномиального разложения. Нет. А, значит, придётся работать ручками:
Тут для достижения необходимой точности (заметьте, что члены начали знакочередоваться!) хватило трёх слагаемых, и четвёртого монстра считать не было смысла. Но «про запас» всегда стараемся расписать побольше членов ряда. Если поленитесь и не хватит слагаемых – будете заново переписывать всё задание.
Ответ : с точностью до 0,001
Да, вычисления, конечно, не подарочные, но что поделать….
Более простая вариация на ту же тему для самостоятельного решения:
Пример 6
Вычислить , ограничившись первыми тремя членами ряда.
 Результат округлить до 3 знаков после запятой.
Результат округлить до 3 знаков после запятой.Образец оформления задачи в конце урока. И не забываем вновь обратиться к вычислительной технике: .
Что студент с нетерпением ждёт изо дня в день? Логарифмы:
Пример 7
Вычислить с точностью до 0,001
Решение : сначала, как всегда, узнаем ответ: .
Очевидно, что здесь нужно использовать разложение
И это действительно возможно, т.к. значение входит в область сходимости данного ряда.
Считаем:
Стоп. Что-то здесь не так. Сойтись-то ряд сойдётся, но такими темпами вычисления могут затянуться до скончания века. И научный тык в неравенство подсказал, что этот конец наступит после счастливого номера .
Таким образом, ряд сходится довольно медленно и пригоден для вычислений разве что и других логарифмов, аргумент которых достаточно близок к единице.
В целях значительного ускорения процесса несложно вывести следующее разложение:
с областью сходимостиПриятная вещь состоит в том, что всякое положительное число (кроме единицы) можно представить в виде .
 Преобразуем аргумент логарифма в обыкновенную дробь: и решим следующее уравнение:
Преобразуем аргумент логарифма в обыкновенную дробь: и решим следующее уравнение:Проверка:
«Заряжаем»:
И теперь у нас обнаружилась другая проблемка – ряд-то, оказывается, положительный , и поэтому здесь нельзя указать и отбросить весь «хвост». Вдруг он в своей сумме окажется больше, чем 0,001? В этой связи используем более хитрый метод оценки. Сохранив «на всякий случай» подозрительно большой 3-й член, рассмотрим остаток ряда:
Числа 9, 11, 13, … в знаменателях меняем на 7 – тем самым только увеличивая члены, а значит, и всю сумму остатка:
По-научному, это называется подбором мажорантного сходящегося ряда (в данном случае – геом. прогрессии), сумму которого легко отыскать (или которая известна). И план оказался не только выполнен, но и перевыполнен! Отбрасывая все члены ряда, начиная с 4-го, будет гарантирована точность 0,00002! Впрочем, по условию результат всё равно нужно округлить до трёх знаков после запятой:Ответ : с точностью до 0,001
Ну и осталось с чувством голубого морального удовлетворения свериться с более точным значением .

…А может быть, было проще вычислить сумму 12 членов медленно сходящегося ряда? =) Впрочем, в следующем задании такой возможности уже не будет в принципе:
Пример 8
Вычислить с точностью до 0,001
– по той причине, что значение не входит в область сходимости ряда .
Дерзайте!
Статья начиналась с приближённого вычисления числа «е», и закончим мы её другой знаменитой константой:
Приближённое вычисление числа с помощью рядаО «пи» исписаны километры бумаги и сказаны миллионы слов, поэтому я не буду загружать вас историей, теорией и гипотезами, если интересно (а это и на самом деле интересно), обратитесь, например, к Википедии. Данное число обладает бесконечным количеством знаков после запятой: , и теория рядов предоставляет один из эффективных способов нахождения этих цифр.
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов.
 Ряды применяются также при интегрировании
дифференциальных уравнений.
Ряды применяются также при интегрировании
дифференциальных уравнений.1. Приближенное вычисление значений функций
Рассмотрим разложение функции в степенной ряд:
Для того, чтобы вычислить приближенное значение функции в заданной точке х , принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:
Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r n (x ). Для этого применяют следующие приемы:
Пример 1 . Пользуясь разложением в ряд sinx , вычислить sin20 o с точностью до 0,0001.
Решение . Чтобы можно было пользоваться формулой (2), необходимо выразить значение аргумента в радианной мере. Получаем
. Подставляя это значение в формулу, получаемПолученный ряд является знакочередующимся и удовлетворяет условиям Лейбница. Так как
, то этот и все последующие члены ряда можно отбросить, ограничиваясь первыми двумя членами. Таким образом,
Таким образом,Пример 2 . Вычислить
с точностью до 0,01.Решение . Воспользуемся разложением
, где(см. пример 5 в предыдущей теме):Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
.
Таким образом, мы можем отбросить этот остаток и получаем
.
Пример 3 . Вычислить
с точностью до 0,0001.Решение . Воспользуемся биномиальным рядом. Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5.
так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
, поэтому его и следующие за ним члены можно отбросить.
2. Приближенное вычисление определенных интегралов
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях.
 Бывает также,
что нахождение первообразной возможно,
но излишне трудоемко. Однако если
подинтегральная функция раскладывается
в степенной ряд, а пределы интегрирования
принадлежат интервалу сходимости этого
ряда, то возможно приближенное вычисление
интеграла с наперед заданной точностью.
Бывает также,
что нахождение первообразной возможно,
но излишне трудоемко. Однако если
подинтегральная функция раскладывается
в степенной ряд, а пределы интегрирования
принадлежат интервалу сходимости этого
ряда, то возможно приближенное вычисление
интеграла с наперед заданной точностью.Пример 4 : Вычислить интеграл
с точностью до 0,00001.Решение . Соответствующий неопределенный интеграл
не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.Разделив почленно ряд для sinx на x , получим:
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим
.
 x, Sin(x), Cos(x) и другие, это и есть разложения в ряд Тейлора, но в точке 0 для аргумента. Для функций комплексного аргумента ряд Лорана является наиболее частой задачей в ТФКП, так как представляет двусторонний бесконечный ряд. Он и является суммой двух рядов. Мы предлагаем вам посмотреть пример разложения прямо на сайте сайт, это сделать очень просто, нажав на «Пример» с любым номером, а затем кнопку «Решение». Именно такому разложению функции в ряд сопоставлен мажорирующий ряд, ограничивающий функцию исходную в некоторой области по оси ординат, если переменная принадлежит области абсцисс. Векторному анализу поставляется в сравнение другая интересная дисциплина в математике. Поскольку исследовать нужно каждое слагаемое, то необходимо достаточно много времени на процесс. Всякому ряду Тейлора можно сопоставить ряд Маклорена, заменив x0 на нуль, а вот по ряду Маклорена порой не очевидно представление ряда Тейлора обратно. Как бы это и не требуется делать в чистом виде, но интересно для общего саморазвития.
x, Sin(x), Cos(x) и другие, это и есть разложения в ряд Тейлора, но в точке 0 для аргумента. Для функций комплексного аргумента ряд Лорана является наиболее частой задачей в ТФКП, так как представляет двусторонний бесконечный ряд. Он и является суммой двух рядов. Мы предлагаем вам посмотреть пример разложения прямо на сайте сайт, это сделать очень просто, нажав на «Пример» с любым номером, а затем кнопку «Решение». Именно такому разложению функции в ряд сопоставлен мажорирующий ряд, ограничивающий функцию исходную в некоторой области по оси ординат, если переменная принадлежит области абсцисс. Векторному анализу поставляется в сравнение другая интересная дисциплина в математике. Поскольку исследовать нужно каждое слагаемое, то необходимо достаточно много времени на процесс. Всякому ряду Тейлора можно сопоставить ряд Маклорена, заменив x0 на нуль, а вот по ряду Маклорена порой не очевидно представление ряда Тейлора обратно. Как бы это и не требуется делать в чистом виде, но интересно для общего саморазвития. Всякому ряду Лорана соответствует двусторонний бесконечный степенной ряд по целым степеням z-a, другими словами ряд вида того же Тейлора, но немного отличающегося вычислением коэффициентов. Про область сходимости ряда Лорана расскажем чуть позже, после нескольких теоретических выкладок. Как и в прошлом веке, поэтапного разложения функции в ряд вряд ли можно достичь только лишь приведением слагаемых к общему знаменателю, так как функции в знаменателях нелинейные. Приближенное вычисление функционального значения требует постановка задач. Задумайтесь над тем, что когда аргумент ряда Тейлора есть линейная переменная, то разложение происходит в несколько действий, но совсем другая картина, когда в качестве аргумента раскладываемой функции выступает сложная или нелинейная функция, тогда очевиден процесс представления такой функции в степенной ряд, поскольку, таким образом, легко вычислить, пусть и приближенное, но значение в любой точке области определения, с минимальной погрешностью, мало влияющей на дальнейшие расчеты.
Всякому ряду Лорана соответствует двусторонний бесконечный степенной ряд по целым степеням z-a, другими словами ряд вида того же Тейлора, но немного отличающегося вычислением коэффициентов. Про область сходимости ряда Лорана расскажем чуть позже, после нескольких теоретических выкладок. Как и в прошлом веке, поэтапного разложения функции в ряд вряд ли можно достичь только лишь приведением слагаемых к общему знаменателю, так как функции в знаменателях нелинейные. Приближенное вычисление функционального значения требует постановка задач. Задумайтесь над тем, что когда аргумент ряда Тейлора есть линейная переменная, то разложение происходит в несколько действий, но совсем другая картина, когда в качестве аргумента раскладываемой функции выступает сложная или нелинейная функция, тогда очевиден процесс представления такой функции в степенной ряд, поскольку, таким образом, легко вычислить, пусть и приближенное, но значение в любой точке области определения, с минимальной погрешностью, мало влияющей на дальнейшие расчеты. Это касается и ряда Маклорена. когда необходимо вычислить функция в нулевой точке. Однако сам ряд Лорана здесь представлен разложением на плоскости с мнимыми единицами. Также не без успеха будет правильное решение задачи в ходе общего процесса. В математике такого подхода не знают, но он объективно существует. В результате вы можете прийти к выводу так называемых поточечных подмножеств, и в разложении функции в ряд нужно применять известные для этого процесса методы, таких как применение теории производных. Лишний раз убеждаемся в правоте учителя, который сделал свои предположения на счет итогов пост вычислительных выкладок. Давайте отметим, что ряд Тейлора, полученный по всем канонам математики, существует и определен на всей числовой оси, однако, уважаемые пользователи сервиса сайт, не забывайте вид исходной функции, ведь может получиться так, что изначально необходимо установит область определения функции, то есть выписать и исключить из дальнейших рассмотрений те точки, при которых функция не определена в области действительных чисел.
Это касается и ряда Маклорена. когда необходимо вычислить функция в нулевой точке. Однако сам ряд Лорана здесь представлен разложением на плоскости с мнимыми единицами. Также не без успеха будет правильное решение задачи в ходе общего процесса. В математике такого подхода не знают, но он объективно существует. В результате вы можете прийти к выводу так называемых поточечных подмножеств, и в разложении функции в ряд нужно применять известные для этого процесса методы, таких как применение теории производных. Лишний раз убеждаемся в правоте учителя, который сделал свои предположения на счет итогов пост вычислительных выкладок. Давайте отметим, что ряд Тейлора, полученный по всем канонам математики, существует и определен на всей числовой оси, однако, уважаемые пользователи сервиса сайт, не забывайте вид исходной функции, ведь может получиться так, что изначально необходимо установит область определения функции, то есть выписать и исключить из дальнейших рассмотрений те точки, при которых функция не определена в области действительных чисел. Так сказать это покажет вашу расторопность при решении задачи.
Не исключением высказанного будет и построение ряда Маклорена с нулевым значением аргумента. Процесс нахождения области определения функции никто при этом не отменял, и вы обязаны подойти со всей серьезностью к этому математическому действию. В случае содержания рядом Лорана главной части, параметр «a» будет называться изолированной особой точкой, и ряд Лорана будет разложен в кольце — это пересечение областей сходимости его частей, отсюда будет следовать соответствующая теорема. Но не все так сложно как может показаться на первый взгляд неопытному студенту. Изучив как раз ряд Тейлора, можно с легкостью понять ряд Лорана — обобщенный случай на расширение пространства чисел. Любое разложение функции в ряд можно производить только в точке области определения функции. Следует учитывать свойства таких функций, например, как периодичность или бесконечная дифференцируемость. Также предлагаем вам воспользоваться таблицей готовых разложений в ряд Тейлора элементарных функций, поскольку одна функция может быть представлена до десятков отличных от друг друга степенных рядов, что можно видеть из применения нашего калькулятора онлайн.
Так сказать это покажет вашу расторопность при решении задачи.
Не исключением высказанного будет и построение ряда Маклорена с нулевым значением аргумента. Процесс нахождения области определения функции никто при этом не отменял, и вы обязаны подойти со всей серьезностью к этому математическому действию. В случае содержания рядом Лорана главной части, параметр «a» будет называться изолированной особой точкой, и ряд Лорана будет разложен в кольце — это пересечение областей сходимости его частей, отсюда будет следовать соответствующая теорема. Но не все так сложно как может показаться на первый взгляд неопытному студенту. Изучив как раз ряд Тейлора, можно с легкостью понять ряд Лорана — обобщенный случай на расширение пространства чисел. Любое разложение функции в ряд можно производить только в точке области определения функции. Следует учитывать свойства таких функций, например, как периодичность или бесконечная дифференцируемость. Также предлагаем вам воспользоваться таблицей готовых разложений в ряд Тейлора элементарных функций, поскольку одна функция может быть представлена до десятков отличных от друг друга степенных рядов, что можно видеть из применения нашего калькулятора онлайн. Онлайн ряд Маклорена проще простого определить, если воспользоваться уникальным сервисом сайт, вам достаточно только ввести правильную записанную функцию и представленный ответ получите в считанные секунды, он будет гарантированно точным и в стандартно записанном виде. Можете переписать результат сразу в чистовик на сдачу преподавателю. Правильно бы сначала определить аналитичность рассматриваемой функции в кольцах, а затем однозначно утверждать, что она разложима в ряд Лорана во всех таких кольцах. Важен момент чтобы не упустить из вида содержащие отрицательных степеней членов ряда Лорана. На этом сосредоточьтесь как можно сильнее. Применяйте с пользой теорему Лорана о разложении функции в ряд по целым степеням.
Онлайн ряд Маклорена проще простого определить, если воспользоваться уникальным сервисом сайт, вам достаточно только ввести правильную записанную функцию и представленный ответ получите в считанные секунды, он будет гарантированно точным и в стандартно записанном виде. Можете переписать результат сразу в чистовик на сдачу преподавателю. Правильно бы сначала определить аналитичность рассматриваемой функции в кольцах, а затем однозначно утверждать, что она разложима в ряд Лорана во всех таких кольцах. Важен момент чтобы не упустить из вида содержащие отрицательных степеней членов ряда Лорана. На этом сосредоточьтесь как можно сильнее. Применяйте с пользой теорему Лорана о разложении функции в ряд по целым степеням.Лекция 57
РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ
Всякая функция, бесконечно дифференцируемая в интервале , т.е.
, может быть разложена в этом интервале в сходящийся к ней бесконечный степеннойряд Тейлора,
если в этом интервале выполняется условие
, где
— остаточный член формулы Тейлора,.
При
получаем так называемыйряд Маклорена :.Если в некотором интервале, содержащем точку , при любомвыполняется неравенство
, где
— положительная постоянная, то
и функция
разложима в ряд Тейлора.Приведем разложения в ряд Тейлора следующих функций:
1)
2)
7)
8) биномиальный ряд:
Это последнее разложение применимо в следующих случаях:
при
еслипри
еслипри
если
.В общем случае разложение функций в степенные ряды основано на использовании рядов Тейлора или Маклорена. На практике степенные ряды многих функций можно найти формально, используя ряды (1-8) или формулу для суммы членов геометрической прогрессии. Иногда при разложении полезно пользоваться почленным дифференцированием или интегрированием рядов. В интервале сходимости ряды сходятся к соответствующим функциям.
1.Разложить по степеням разности
функцию
.Решение. Для того, чтобы воспользоваться формулой Тейлора при
, найдем:и т.
 д.
д.Следовательно,
2.Разложить
в ряд по степеням
.Решение. Воспользуемся равенством
. Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом
и знаменателем
. Отсюда получаемТак как
, то3. Разложить в ряд Маклорена функцию
Решение. Разложим данную функцию на сумму простейших рациональных дробей:
Поскольку
тоТак как ряд
сходится при
, а ряд
сходится при
, то ряд
сходится к данной функции при
.4.Разложить в степенной ряд функцию
.Решение. Найдем значения функции и ее производных при
Так как
, то при фиксированномимеет место неравенство
при любом. Следовательно, функция может быть представлена в виде суммы ряда Тейлора:.
В данном случае
Это разложение можно получить и иначе: достаточно в разложении
заменитьна
.5. Разложить в степенной ряд функцию
.
Решение. В разложении
заменяем на
, получаем6. Разложить
в ряд по степеням
.Решение. В разложении
заменяем на
, получаем7. Разложить в степенной ряд функцию
.Решение. Заметим, что
.Рассмотрим рядДанный ряд сходится при
, значит, его можно почленно интегрировать на любом отрезке
. Следовательно,, т.е получили ряд, сходящийся к данной функции при
8. Разложить по степеням
многочлен9. Разложить по степеням
функцию
и найти область сходимости полученного ряда.Ответ:
10. Разложить по степеням
функцию
и найти область сходимости этого ряда.11. Разложить по степеням
функцию
. Найти область сходимости этого ряда.Ответ
Разложить в ряд Маклорена функцию
. Указать область сходимости полученного ряда к этой функции.12.
. Ответ:13.
Ответ:
.14.
. Ответ:
.
15.
. Ответ:16.
Ответ:
.17.
. Ответ:
.18.
Ответ:19.
.Ответ:
.6.16. Применение степенных рядов в приближённых вычислениях
Вычисление значений функции . Пусть дан степенной ряд функции
. Задача вычисления значения этой функции заключается в отыскании суммы ряда при заданном значении аргумента. Ограничиваясь определенным числом членов ряда, находим значение функции с точностью, которую можно установить путем оценивания остатка числового ряда либо остаточного члена
формул Тейлора или Маклорена. Если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией. В случае знакочередующегося ряда используется оценка
, где
— первый из отброшенных членов ряда.Пример 1. Вычислить с точностью до 0,0001 значение ln1,1.
Решение.
Для вычисления приближённых значений функции с заданной точностью удобно пользоваться рядами в том случае, когда соответствующий ряд является знакочередующимся; для знакочередующегося сходящегося ряда легко оценить погрешность приближённого значения суммы – она меньше абсолютного значения первого из отброшенных членов.

Возьмём ряд для функции ln(1+x):
Который сходится к ln(1+x) в интервале (-1,1], и, полагая, x=0,1 , получим ряд для вычисления ln1,1 с любой точностью.
Абсолютное значение четвёртого члена этого ряда меньше 0,0001. Поэтому, согласно свойству знакочередующегося сходящегося ряда, для вычисления приближённого значения ln1,1 с точностью до 0,0001 достаточно взять сумму трёх первых членов ряда
.
Точность: 0,001.
В прикладных задачах важна оценка погрешности приближения.
Определение: Точность вычисления не превышает первого из отброшенных элементов ряда.
1.Оценить погрешность приближенного равенства
Решение. Погрешность этого приближенного равенства определяется суммой членов, следующих после
в разложении:,
Заменив каждый из сомножителей
,… меньшей величиной
, получим неравенствоПросуммируем бесконечно убывающую геометрическую прогрессию, получим:
, т.е.
2.Вычислить
с точностью до 0,00001.
Решение. Используя разложение в ряд, получаем
Определим число так, чтобы погрешность приближенного равенства
не превышала 0,00001. Воспользуемся оценкой погрешности, данной в предыдущем примере. Полагаем
, тогда:т.е.
.Путем подбора определим, при каком значении будет выполняться неравенство
. Пусть
, тогда
, т.е.
. Пусть
, тогда
, т.е.
. Принимаем
..Вычисляем каждое слагаемое с точностью до 0,000001, для того чтобы при суммировании не получить погрешность, превышающую 0,00001. Окончательно получаем
.3. Вычислить
с точностью до 0,00001.Решение. Имеем
Получен знакочередующийся ряд, удовлетворяющий условиям сходимости признака Лейбница, поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда. Нетрудно видеть, что
, поэтому первый из отброшенных членов равен
и
. Вычисляем сумму и получаем
.4. Пользуясь разложением
в ряд, вычислить
с точностью до 0,0001 .
Решение. .
Достаточно взять три члена ряда, так как Тогда
5. Вычислить
с точностью до 0,0001.
в ряд, полагая
. ИмеемЧетвертый и следующие за ним члены отбрасываем, так как четвертый член меньше 0,0001. Итак
6. Вычислить
с точностью до 0,001.Решение. Так как является ближайшим к числу 130 кубом целого числа, то целесообразно число 130 представить в виде суммы двух слагаемых:
. ТогдаЧетвертый член меньше
, поэтому его и следующие за ним члены можно отбросить. Итак,, т.е.
.7. Вычислить
с точностью до 0,0001.Решение. Воспользуемся разложением
в ряд:или , откуда
Вычислить указанную величину приближенно с заданной степенью точности , воспользовавшись разложением в степенной ряд соответствующим образом подобранной функции.
8.
. Ответ: 3,017.9.
Ответ: 0,340.10.
. Ответ: 0,84147.11.
. Ответ: 1,3956.
12.
,
. Ответ: 1,140.13.
Ответ: 0,302.14.
Ответ: 0,464.15.
Ответ: 1,0986.16.
,
Ответ: 0,999.17.
Ответ: 0,3679.Вычисление интегралов . Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри их интервала сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы.
18. Вычислить
с точностьюРешение. Воспользуемся разложением . Заменив в немна, получим ряд.
Данный ряд сходится на всей числовой прямой, поэтому его можно всюду почленно интегрировать. Следовательно,
поскольку уже третий член полученного знакочередующегося ряда меньше
19. Найти интеграл
в виде степенного ряда и указать область его сходимости.Решение. Воспользуемся разложением , получим ряд для подынтегральной функции
Он сходится на всей числовой прямой, и, следовательно, его можно почленно интегрировать:
Поскольку при интегрировании степенного ряда его интервал сходимости не изменяется, то полученный ряд сходится также на всей числовой прямой.

Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до
.20.
. Ответ: 0,070.21.
. Ответ: 0,223.22.
. Ответ: 0,162.23.
. Ответ: 0,480.24.
. Ответ: 0,054.25.
. Ответ: 0,484.26.
. Ответ: 0,487.27.
. Ответ: 0,156.28.
. Ответ: 0,059.29.
Ответ: 0,103.Приближенное решение дифференциальных уравнений .
В случае, когда точно проинтегрировать дифференциальное уравнение с помощью элементарных функций не удается, его решение удобно искать в виде степенного ряда, например ряда Тейлора или Маклорена.
При решении задачи Коши
, используется ряд Тейлора
, где, а остальные производные
находятся путем последовательного дифференцирования уравнения
и подстановки начальных данных в выражения для этих производных.Решение задачи Коши
для дифференциального уравнения можно также искать в виде разложения в степенной рядс неопределенными коэффициентами
.
30. Найти пять первых членов разложения в степенной ряд решения
, если
.Решение. Из данного уравнения находим, что
. Дифференцируем исходное уравнение:и т.д. Подставляя найденные значения производных в ряд Тейлора, получаем
Разлагая подынтегральную функцию в ряд вычислить интеграл
Степенные ряды, которые мы и станем использовать, сходятся равномерно, поэтому их можно почленно интегрировать по любому отрезку, лежащему внутри интервала сходимости. Схема решения подобных задач на вычисление интегралов с помощью рядов проста:
- Разложить подынтегральную функцию в функциональный ряд (обычно в ряд Маклорена).
- Произвести почленное интегрирование членов записанного в первом пункте функционального ряда.
- Вычислить сумму полученного во втором пункте числового ряда с заданной точностью $varepsilon$.
Задачи на вычисление интегралов с помощью рядов популярны у составителей типовых расчётов по высшей математике.
 7>>=frac<1> <5376>of your page —>
7>>=frac<1> <5376>of your page —>Сумма ряда
Чтобы посчитать сумму ряда онлайн выполните следующие действия:
- ввести выражение, для которого нужно вычислить ряд
- указать параметр, по которому будет считать сумма
- указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность)
Разложение в ряд Тейлора (степенной ряд)
Это он-лайн сервис в три шага:
- Ввести функцию, которую необходимо разложить
- Ввести точку, в окрестности которой необходимо разложить
- Указать до какого члена раскладывать
Разложение в ряд Фурье
Это он-лайн сервис в два шага:
- Ввести функцию, которую необходимо разложить
- Ввести отрезок, на котором необходимо разложить
Произведение ряда
Чтобы посчитать произведение ряда онлайн выполните следующие действия:
- ввести выражение, для которого нужно вычислить произведение ряда
- указать параметр, по которому считать произведение
- указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность oo)
© Контрольная работа РУ — калькуляторы онлайн
Кроме вышеперечисленных способов, можно вычислить значение определенного интеграла с помощью разложения подынтегральной функции в степенной ряд.

Принцип этого метода состоит в том, чтобы заменить подынтегральную функцию по формуле Тейлора и почленно проинтегрировать полученную сумму.
Пример. С точностью до 0,001 вычислить интеграл
Т.к. интегрирование производится в окрестности точки х=0, то можно воспользоваться для разложения подынтегральной функции формулой Маклорена.
Разложение функции cos x имеет вид:
Зная разложение функции cos х легко найти функцию 1 – cos x:
В этой формуле суммирование производится по п от 1 до бесконечности, а в предыдущей – от 0 до бесконечности. Это – не ошибка, так получается в результате преобразования.
Теперь представим в виде ряда подынтегральное выражение.
Теперь представим наш интеграл в виде:
В следующем действии будет применена теорема о почленном интегрировании ряда. (Т.е. интеграл от суммы будет представлен в виде суммы интегралов членов ряда).
Вообще говоря, со строго теоретической точки зрения для применения этой теоремы надо доказать, что ряд сходится и, более того, сходится равномерно на отрезке интегрирования [0, 0,5].
 Эти вопросы будут подробно рассмотрены позже (См. Действия со степенными рядами). Отметим лишь, что в нашем случае подобное действие справедливо хотя бы по свойствам определенного интеграла (интеграл от суммы равен сумме интегралов).
Эти вопросы будут подробно рассмотрены позже (См. Действия со степенными рядами). Отметим лишь, что в нашем случае подобное действие справедливо хотя бы по свойствам определенного интеграла (интеграл от суммы равен сумме интегралов).Как видно, абсолютная величина членов ряда очень быстро уменьшается, и требуемая точность достигается уже при третьем члене разложения.
Для справки: Точное (вернее – более точное) значение этого интеграла: 0,2482725418…
Интегралы с бесконечными пределами.
Пусть функция f(x) определена и непрерывна на интервале [a, ¥ ). Тогда она непрерывна на любом отрезке [a, b].
Определение: Если существует конечный предел , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥ ).
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Несобственный интеграл расходится.
Теорема: Если для всех х (x ³ a) выполняется условие и интеграл сходится, то тоже сходится и ³ .
Теорема: Если для всех х (x ³ a) выполняется условие и интеграл расходится, то тоже расходится.
Теорема: Если сходится, то сходится и интеграл .
В этом случае интеграл называется абсолютно сходящимся.
Интеграл от разрывной функции.
Если в точке х = с функция либо неопределена, либо разрывна, то
Если интеграл существует, то интеграл — сходится, если интеграл не существует, то — расходится.
Если в точке х = а функция терпит разрыв, то .
Если функция f(x) имеет разрыв в точке b на промежутке [a, с], то
Таких точек внутри отрезка может быть несколько.
Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.
Приложения определенного интеграла.
Вычисление площадей плоских фигур.
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x).
 Если график расположен ниже оси Ох, т.е. f(x) 0, то площадь имеет знак “+”.
Если график расположен ниже оси Ох, т.е. f(x) 0, то площадь имеет знак “+”.Для нахождения суммарной площади используется формула .
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
Нахождение площади криволинейного сектора.
Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид r = f( j ), где r — длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а j — угол наклона этого радиус – вектора к полярной оси.
Площадь криволинейного сектора может быть найдена по формуле
Приближенное вычисление определенного интеграла
Пусть требуется найти определенный интеграл , причем функция считается непрерывной на отрезке .
 Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница:
Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница:Но не в каждом случае отыскание первообразной для подынтегральной функции является достаточно простым, а также не для всякой непрерывной функции существует первообразная, выражающаяся через элементарные функции. В подобных случаях применяют приближенные формулы, которые позволяют вычислить определенный интеграл с любой степенью точности.
Наиболее часто используются три формулы приближенного вычисления определенного интеграла – формула прямоугольников, формула трапеций и формулу парабол или формула Симпсона, основанные на геометрическом смысле определенного интеграла: если функция непрерывна и положительна на отрезке , то определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями , , и (рис. 1).
1. Формула прямоугольников
Пусть на отрезке задана непрерывная функция .
 Вычислим численно определенный интеграл , который равен площади криволинейной трапеции.
Вычислим численно определенный интеграл , который равен площади криволинейной трапеции.Разобьем основание этой трапеции (отрезок ) на равных частей-отрезков длины
Величину будем называть шагом разбиения. В результате получим точки
Можно записать, что
В середине каждого такого элементарного отрезка отметим точку . Приняв ординату этой точки за высоту, построим прямоугольник с площадью (рис. 2).
Тогда сумма площадей всех прямоугольников равна площади ступенчатой фигуры, которая представляет собой приближенное значение искомого определенного интеграла :
Полученная формула называется формулой прямоугольников.
Абсолютная погрешность последнего приближенного равенства удовлетворяет следующей оценке:
где – наибольшее значение на рассматриваемом отрезке .
2. Формула трапеций
Эту формулу получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Пусть необходимо вычислить определенный интеграл . Разобьем отрезок интегрирования на равных частей длины . В результате получим точки (рис. 3). Пусть – соответствующие им ординаты функции. Тогда можно записать, что
Заменим кривую ломаной линией, звенья которой соединяют концы ординат и . Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями , и высотой , то есть
Записанная формула называется формулой трапеций.
Абсолютная погрешность
где .
3. Формула парабол (Симпсона)
Если заменить график функции на каждом отрезке , которые получены после разбиения отрезка интегрирования на равных частей, не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления определенного интеграла .
Как было сказано выше, разобьем отрезок на равных частей (отрезков) длиной точками
причем , .
 В точках разбиения находим значения подынтегральной функции
В точках разбиения находим значения подынтегральной функциито есть (рис. 4).
Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями одной элементарной параболической трапецией с основанием . Тогда, например, на частичном отрезке парабола проходит через три точки , , и так далее.
Расчетная формула парабол (или Симпсона) для этого метода имеет вид:
Абсолютная погрешность вычисления по этой формуле оценивается соотношением
где .
«Приближенные методы вычисления определенных интегралов»
ТЕМА: Приближенные методы вычисления определенных интегралов.
ЦЕЛЬ: рассмотреть приближенные методы вычисления интегралов на основании геометрического смысла интеграла.
ЗАДАЧИ:
образовательные:
— изучение приближенных методов вычисления определенных интегралов: метода прямоугольников и метода трапеций, параболических трапеций;
— формирование умений и навыков вычисления определенных интегралов методами прямоугольников и трапеций, параболических трапеций;
воспитательные:
– воспитание самостоятельности, инициативности, решительности, уверенности в себе, стремления к творческому поиску и исследовательской деятельности;
развивающие:
– развитие концентрации внимания, абстрактно-логического мышления,
ТИП: урок новых знаний.

МЕТОДЫ ОБУЧЕНИЯ: проблемное изложение учебного материала.
ВНУТРИДИСЦИПЛИНАРНЫЕ СВЯЗИ
Дифференциальное исчисление.
Дифференциал функции и его приложение к приближенным вычислениям.
Интегральное исчисление.
и определенный интегралы, методы их решений.
МЕЖДИСЦИПЛИНАРНЫЕ СВЯЗИ
Дисциплина «Естествознание».
Современные естественнонаучные знания о мире.
2.5. Вещество и поле, их взаимодействие.
2. Дисциплина «Экономическая статистика».
Отражение результатов производства.
МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ: презентация, раздаточный материал.
Студент должен
знать:
формулы приближенного вычисления определенного интеграла:
— формулу прямоугольников;
— формулу трапеций;
— формулой параболических трапеций ( формула Симпсона).
уметь:
— вычислять определенные интегралы приближенно методами прямоугольников и трапеций, параболических трапеций.

ХОД ЗАНЯТИЯ
1. Организационный момент
Решение многих технических задач сводится к вычислению определённых интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближённого значения.
Очень часто приходится вычислять определённые интегралы, для которых невозможно найти первообразную. В этом случае применяют приближённые методы вычисления определённых интегралов. Иногда приближённый метод применяют и для “берущихся” интегралов, если вычисление по формуле Ньютона-Лейбница не рационально.
2. Сообщение темы, целей занятия
Преподаватель объявляет тему занятия, привлекает студентов к постановке целей и задач занятия.
3. Мотивация
Чтобы вдохновиться на изучение нового материала, вспомним о полезности интеграла.
Выясним, в чем состоит экономический смысл интеграла:
Экономический смысл интеграла
Z(t) — функция производительности труда от времени
V(t) — функция объема произведенной продукции от времени
Z(t) =V'(t)
V(t) — первообразная Z(t)
Объем произведенной продукции есть первообразная производительности труда
Применение интеграла в естествознании.

Перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:
Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:
4. Актуализация опорных знаний.
а) фронтальный опрос.
Что называют неопределенным интегралом функции ?
Что называют определенным интегралом от a до b функции ?
В чем состоит геометрический смысл определенного интеграла?
4) Какие два метода интегрирования вы знаете?
5) Какие вопросы можно задать об этих двух методах? (выбранный студент опрашивает группу о том, на чем основан метод непосредственного интегрирования и в каких случаях применяется метод замены переменной).
6) Что называют прямоугольником? Начертите изображение прямоугольника и запишите формулу его площади.
7) Выполните те же задания, но для трапеции.
б) тестирование по теме “Интеграл”.

Вариант 1.
1) Вычислите:
Ответ: а) 27 б) 24 в) 18 г) 21
Ответ: а) -2 б) 2 в) -3 г) 3
Ответ: а) 26/3 б) 28/3 в) 15/2 г) 47/6
2) Найдите интеграл:
Ответ: а) 1.5 б) 2/3 в) -2/3 г) не существует.
3) При каком значении “а” выполняется равенство ?
Ответы: а) 2/3 б) 8/3 или -2 в) 2 или -1/3 г) -3
4) Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x2+x+2
Ответы: а) 13/3 б) 29/6 в) 16/3 г) 4,5
Вариант 2.
1) Вычислите:
Ответы: а) 25/3 б) 28/3 в) 26/3 г) 29/3
Ответы: -3.5 б) 1.5 в) -1.5 г) -3.5
Ответ: а) 22/9 б) -14/9 в) -22/9 г) 14/9
2) Найдите интеграл.
Ответ: а) 0 б) -12 в) не существует.
 Г) 12
Г) 123) При каком значении “а” выполняется равенство ?
Ответы: а) 2, -13/3 б) -4 в) 4, -5/2 г) -3,9/4
Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x2+4x-3
Ответы: а) 4/3 б) -1,5 в) 11/6 г)7/6
5. Формирование новых знаний и способов действий
Организация деятельности
Предполагается, проводить работу 3-мя группами.
1-я группа – работает над формулой приближенного интегрирования — формулой прямоугольников
2-я группа – работает над формулой приближенного интегрирования – формулой трапеций
3-я группа – работает над формулой приближенного интегрирования – формулой параболических трапеций ( формула Симпсона)
Описание
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
 Но вычислить интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница либо невозможно, либо затруднительно, поэтому прибегают к различным методам приближенного интегрирования.
Но вычислить интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница либо невозможно, либо затруднительно, поэтому прибегают к различным методам приближенного интегрирования.Вычислить интеграл точно по формуле Ньютона – Лейбница с целью оценки погрешности при приближенном вычислении этого же интеграла.
Все три группы одновременно вычисляют интеграл :
Пример 1
= .
Блок 1
Разделим интервал интегрирования на равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции в начальных или конечных точках частичных интервалов. Значение площади этой фигуры и будет давать приближенное значение искомого интеграла .

Если обозначить значения функции в точках деления через , то будем иметь следующую формулу — формулу прямоугольников :
или
Блок 2
Оставим разбиение интервала прежним, но заменим теперь каждую дугу линии , соответствующую частичному интервалу . хордой, соединяющей конечные точки этой дуги. Таким образом, заменяем данную криволинейную трапецию прямолинейными. Площадь каждой трапеции, построенной на частичном интервале, равна полусумме площадей , соответствующих этому интервалу прямоугольников. Суммируя все эти площади, получим формулу трапеций :
Блок 3
Разобьем интервал на равных частей , но предположим, что – четное число: . Заменим дугу линии , соответствующую интервалу , дугой параболы, ось которой параллельна оси ординат и которая проходит через следующие три точки дуги: начальную точку дуги , среднюю точку , конечную точку . Площадь данной трапеции приближенно равна сумме площадей получающихся параболических трапеций и выражается формулой :
1 группа
Решает пример 1 по формуле прямоугольников : при
Таблица расчетов :
1
2
3
4
5
0
0.
 2
20.4
0.6
0.8
1
1
0,9615
0,8621
0,7353
0,6098
0,5
2 группа
Решает пример 1 по формуле трапеций : при
Таблица расчетов :
1
2
3
4
5
0
0.2
0.4
0.6
0.8
1
1
0,9615
0,8621
0,7353
0,6098
0,5
3 группа
Решает пример 1 по формуле параболических трапеций : при
Таблица расчетов :
1
2
3
4
0
1
Занесем итоги расчета в таблицу и сравним:
абсолютная погрешность
относительная погрешность
формула Н-Л
0,7854
фор-ла прям-ков
0,8337
6,1 %
фор-ла трапеций
0,7837
фор-ла Симпсона
0,7854
0
0
= 6,1 %
Вывод : гипотеза о том, что с помощью формул численного интегрирования можно вычислять определенные интегралы подтвердилась.
 Однако, при одном и том же значении формула Симпсона дает лучшее приближение.
Однако, при одном и том же значении формула Симпсона дает лучшее приближение.6. Закрепление материала
Пример 1. Вычислить по формуле прямоугольников . Найти абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных частей. Тогда а = 0, b = 3 ,
х k = a + k х
х0 = 2 + 0* = 2 х1 = 2 + 1* = 2,5 х2 = 2 + 2* =3
х3 = 2 + 3 * = 3,5 х4 = 2 + 4* = 4 х5 = 2 + 5 * = 4,5
f (x0) = 22 = 4
f (x 1 ) = 2 ,52 = 6,25
f (x 2 ) = 32 = 9
f (x 3 ) = 3,52 = 12,25
f (x 4 ) = 42 = 16
f (x 5 ) = 4,52 = 20,25
х 2 2,5 3 3,5 4 4,5
у 4 6,25 9 12,25 16 20,25
По формуле (1):
Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:
Пример 2.
 Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.
Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.Решение:
а)
По условию отрезок интегрирования нужно разделить на 3 части, то есть .
Вычислим длину каждого отрезка разбиения: . Параметр , напоминаю, также называют шагом.Сколько будет точек (узлов разбиения)? Их будет на одну больше, чем количество отрезков:
Ну а общая формула трапеций сокращается до приятных размеров:
Для расчетов можно использовать обычный микрокалькулятор:
Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-го знака после запятой.
Окончательно:
б) Разобьём отрезок интегрирования на 5 равных частей, то есть .
 Увеличивая количество отрезков, мы увеличиваем точность вычислений.
Увеличивая количество отрезков, мы увеличиваем точность вычислений.Если , то формула трапеций принимает следующий вид:
Найдем шаг разбиения:
, то есть, длина каждого промежуточного отрезка равна 0,6.При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:
В первой строке записываем «счётчик»
Как формируется вторая строка– сначала записываем нижний предел интегрирования , остальные значения получаем, последовательно приплюсовывая шаг .
В результате:
Если для 3 отрезков разбиения приближённое значение составило, то для 5 отрезков . Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере .
Пример 3
Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков
Решение: Начинаем решать.
 Если у нас два отрезка разбиения , то узлов будет на один больше: . И формула Симпсона принимает весьма компактный вид:
Если у нас два отрезка разбиения , то узлов будет на один больше: . И формула Симпсона принимает весьма компактный вид:Вычислим шаг разбиения:
Заполним расчетную таблицу:
В верхнюю строку записываем «счётчик» индексовВо второй строке сначала пишем нижний предел интегрирования , а затем последовательно приплюсовываем шаг .
В третью строку заносим значения подынтегральной функции. Например, если , то . Сколько оставлять знаков после запятой? Действительно, в условии опять об этом ничего не сказано. Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой.
В результате:
Первичный результат получен. Теперь удваиваем количество отрезков до четырёх: . Формула Симпсона для данного разбиения принимает следующий вид:
Вычислим шаг разбиения:
Заполним расчетную таблицу:
Таким образом:Найдём абсолютное значение разности между приближениями:
Правило Рунге для метода Симпсона очень вкусное.
 Если при использовании метода средних прямоугольников и метода трапеций нам даётся «поблажка» в одну треть, то сейчас – аж в одну пятнадцатую:
Если при использовании метода средних прямоугольников и метода трапеций нам даётся «поблажка» в одну треть, то сейчас – аж в одну пятнадцатую:
, и точность здесь уже не страдает:Рассмотрим другое решение, где придётся сделать дополнительный шаг: так как больше требуемой точности: , то необходимо еще раз удвоить количество отрезков: .
Формула Симпсона растёт, как на дрожжах:
Вычислим шаг:
И снова заполним расчетную таблицу:
Таким образом:
Оцениваем погрешность:
Погрешность меньше требуемой точности: . Осталось взять наиболее точное приближение , округлить его до трёх знаков после запятой и записать:
Ответ: с точностью до 0,001
Приведенные правила численного интегрирования помогают решать прикладные задачи.
Прикладная задача
Ширина реки равна 20м; промеры глубины в некотором поперечном ее сечении через каждые 2м дали следующую таблицу :
2
4
6
8
10
12
14
16
18
20
0.
 2
20,5
0,9
1,1
1,3
1,7
2,1
1,5
1,1
0,6
0,2
Расстояние (в метрах) от одного из берегов обозначено через , соответствующая глубина реки ( также в метрах) – через Требуется найти площадь поперечного сечения реки.
По формуле Симпсона находим :
7. Контроль усвоения, обсуждение допущенных ошибок и их коррекция. Самостоятельная работа студентов:
Вариант 1
Вариант 2
Обсуждение решения.
8. Подведение итогов занятия
Обобщаются новые знания, делаются выводы студентами о достигнутых целях. Отмечаются активные студенты.

9. Домашнее задание
Студенты записывают домашнее задание, преподаватель объясняет способ его выполнения.
Домашнее задание:
Вычислить интеграл приближенно методами: 1) прямоугольников; 2) трапеций и точно – по формуле Ньютона-Лейбница; найти абсолютные погрешности приближений:
Литература
Пахомова Н.Ю. Метод учебного проекта в образовательном учреждении: Пособие для учителей и студентов пед.вузов, — М:АРКТИ, 2005г.
Чечель И.Д Исследовательский проекты в практике обучения. «Практика административной работы в школе» , 6/2003 г.
Богомолов Н.В. Практические задания по математике. — М.:Высшая школа, 1990.
Бермант А. Ф., Араманович И. Г. Краткий курс математического анализа для втузов. — М.: Наука, 1967.
 2
2- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
В выражениях можно применять следующие операции:- Действительные числа
- вводить в виде 7.
 3
3 - — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Используя разложение подынтегральной функции в степенной ряд вычислить
Степенные ряды, которые мы и станем использовать, сходятся равномерно, поэтому их можно почленно интегрировать по любому отрезку, лежащему внутри интервала сходимости. Схема решения подобных задач на вычисление интегралов с помощью рядов проста:
- Разложить подынтегральную функцию в функциональный ряд (обычно в ряд Маклорена).
- Произвести почленное интегрирование членов записанного в первом пункте функционального ряда.
- Вычислить сумму полученного во втором пункте числового ряда с заданной точностью $\varepsilon$.
 $, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно.
$, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно.Начнём с разложения подынтегральной функции $\frac>$ в ряд Маклорена. Запишем разложение функции $\cos$ в ряд Маклорена:
Данное разложение верно при всех $x\in$. Подставим вместо $x$ дробь $\frac$:
Интегрируем данное разложение на отрезке $\left[0;\frac\right]$:
Получили знакочередующийся ряд. Запишем несколько первых членов этого ряда (до тех пор, пока записанный член не станет меньше $\varepsilon$):
Так как $\frac<\varepsilon$, то для вычисления интеграла с точностью $\varepsilon$ достаточно первого члена полученного числового ряда:
Продолжение темы вычисления интегралов с помощью рядов Маклорена продолжим во второй части.
Производная функции по графику
Задачи по множествамОпределенные интегралы
Возможно, вам сначала захочется прочитать «Введение в интеграцию»!
Интеграция
Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.
 Но его часто используют, чтобы найти область под графиком функции следующим образом:
Но его часто используют, чтобы найти область под графиком функции следующим образом:Область может быть найдена путем добавления срезов, ширина которых приближается к нулю :
И есть Правила интеграции, которые помогают нам получить ответ.
Обозначение
Символ «Интеграл» — стильная буква «S» (от «Сумма», идея суммирования срезов):
После символа интеграла мы помещаем функцию, интеграл от которой мы хотим найти (называемую интегралом).А затем закончите с dx , чтобы обозначить, что срезы идут в направлении x (и приближаются к нулю по ширине).
Определенный интеграл
Определенный интеграл имеет начальное и конечное значения: другими словами, существует интервал [a, b].
a и b (называемые пределами, границами или границами) помещаются внизу и вверху буквы «S», например:
Определенный Интегральный
(от a до b )Неопределенный Интегральный
(без конкретных значений)Мы находим Определенный интеграл, вычисляя неопределенный интеграл при a и b , а затем вычитая:
Пример: Что такое
Нам нужен определенный интеграл , от 1 до 2, из 2x dx
Сначала нам нужно найти Indefinite Integral .

Используя правила интегрирования, находим, что ∫2x dx = x 2 + C
Теперь посчитайте, что при 1 и 2:
- При x = 1: ∫2x dx = 1 2 + C
- При x = 2: ∫2x dx = 2 2 + C
Вычесть:
(2 2 + C) — (1 2 + C)
2 2 + К — 1 2 — К
4 — 1 + С — С = 3
И «C» отменяется… так что с определенными интегралами мы можем игнорировать C .
Результат:
Проверить : с такой простой формой попробуем еще вычислить площадь по геометрии:
А = 2 + 4 2 × 1 = 3
Да, у него есть площадь 3.
(Ура!)
Обозначение : Обычно неопределенный интеграл (без + C) указывается внутри квадратных скобок с границами a и b после, например:
Пример (продолжение)
Как показать свой ответ:
Давайте попробуем другой пример:
Пример:
Определенный интеграл, от 0.
 От 5 до 1.0, из cos (x) dx:
От 5 до 1.0, из cos (x) dx:(Примечание: x должен быть в радианах)
Неопределенный интеграл : ∫ cos (x) dx = sin (x) + C
Мы можем игнорировать C для определенных интегралов (как мы видели выше) и получаем:
= грех (1) — грех (0,5)
= 0,841 … — 0,479 …
= 0,362 …
И еще один важный пример:
Пример:
Определенный интеграл от 0 до 1 от sin (x) dx:
Неопределенный интеграл : ∫ sin (x) dx = −cos (x) + C
Поскольку мы идем от 0, , можем ли мы просто вычислить интеграл при x = 1 ??
−cos (1) = −0.540 …
Что? Это минус ? Но на графике это выглядит положительно.
Ну … мы сделали ошибку !
Поскольку нам нужно вычесть интеграл при x = 0 . Не следует предполагать, что он равен нулю.
Итак, давайте сделаем это правильно, вычтя одно из другого:
грех (x) dx
= [−cos (x)]= −cos (1) — (−cos (0))
= -0,540 .
 .. — (-1)
.. — (-1)= 0.460 …
Так лучше!
Но мы можем иметь отрицательные области , когда кривая ниже оси:
Пример:
Определенный интеграл от 1 до 3 от cos (x) dx:
Обратите внимание, что некоторые из них положительные, а некоторые отрицательные.
Определенный интеграл даст чистое значение .Сделаем расчеты:
= грех (3) — грех (1)
= 0.141 … — 0,841 …
= −0,700 …
Таким образом, отрицательного больше, чем положительного, с чистым результатом -0,700 ….
Итак, нам нужно запомнить одну важную вещь:f (x) dx = (Площадь над осью x) — (Площадь под осью x)
Попробуйте интегрировать cos (x) с разными начальными и конечными значениями, чтобы увидеть, как работают положительные и отрицательные значения.
Положительная область
Но иногда мы хотим, чтобы вся область обрабатывалась как положительное значение (без вычитания части ниже оси).

В этом случае мы должны вычислить площади отдельно , как в этом примере:
Пример: Какова общая площадь
между y = cos (x) и осью x, от x = 1 до x = 3?Это похоже на пример, который мы только что сделали, но теперь мы ожидаем, что — это все положительное значение (представьте, что нам пришлось его раскрасить).
Итак, теперь мы должны делать детали отдельно:
- Один для области над осью x
- Один для области ниже оси x
Кривая пересекает ось x при x = π / 2, поэтому мы имеем:
От 1 до π / 2:
cos (x) dx
= грех (π / 2) — грех (1)= 1 — 0.841 …
= 0,158 …
От π / 2 до 3:
cos (x) dx
= грех (3) — грех (π / 2)= 0,141 … — 1
= -0,859 …
Последний выходит отрицательным, но мы хотим, чтобы он был положительным, поэтому:
Общая площадь = 0,158 … + 0,859 … = 1,017 …
Это сильно отличается от ответа в предыдущем примере.

непрерывный
О да, функция, которую мы интегрируем, должна быть непрерывной между a и b : без дырок, скачков или вертикальных асимптот (где функция направлена вверх / вниз в сторону бесконечности).
Пример:
Вертикальная асимптота между a и b влияет на определенный интеграл.
Недвижимость
Область выше — область ниже
Интеграл добавляет площадь над осью, но вычитает площадь ниже, для «чистого значения»:
f (x) dx = (Площадь над осью x) — (Площадь под осью x)
Добавление функций
Интеграл от f + g равен интегралу от f плюс интеграл от g :
f (x) + g (x) dx =
ф (х) dx +
г (x) dx
Реверсирование интервала
Изменение направления интервала на противоположное дает отрицательное значение исходного направления.
f (x) dx = —
f (x) dx
Интервал нулевой длины
Когда интервал начинается и заканчивается в одном и том же месте, результат равен нулю:
Добавление интервалов
Мы также можем сложить два соседних интервала вместе:
f (x) dx =
ф (х) dx +
f (x) dx
Сводка
Определенный интеграл между a и b — это неопределенный интеграл при b минус неопределенный интеграл при a .

6864, 6865, 6866, 6867, 6868, 6869, 6870, 6871, 6872, 6873, 6874
Определенные интегралы
Определенный интеграл функции тесно связан с первообразным и неопределенным интегралом функции. Основное отличие состоит в том, что неопределенный интеграл, если он существует, является вещественным числовым значением, в то время как последние два представляют бесконечное количество функций, которые отличаются только константой. Взаимосвязь между этими понятиями будет обсуждаться в разделе, посвященном фундаментальной теореме исчисления, и вы увидите, что определенный интеграл будет иметь приложения ко многим задачам исчисления.Развитие определения определенного интеграла начинается с функции f ( x ), которая непрерывна на отрезке [ a, b ]. Данный интервал разделен на подинтервалы « n », которые, хотя и не являются необходимыми, могут быть приняты равными по длине (Δ x ). Произвольное значение домена, x i , выбирается в каждом подынтервале, и определяется его последующее значение функции, f ( x i ).
 Определяется произведение каждого значения функции на соответствующую длину подынтервала, и эти произведения « n » складываются для определения их суммы. Эта сумма называется суммой Римана и может быть положительной, отрицательной или нулевой, в зависимости от поведения функции на закрытом интервале. Например, если f ( x )> 0 на [ a, b ], тогда сумма Римана будет положительным действительным числом. Если f ( x ) <0 на [ a, b ], тогда сумма Римана будет отрицательным действительным числом.Сумма Римана функции f ( x ) на [ a, b ] выражается как
Определяется произведение каждого значения функции на соответствующую длину подынтервала, и эти произведения « n » складываются для определения их суммы. Эта сумма называется суммой Римана и может быть положительной, отрицательной или нулевой, в зависимости от поведения функции на закрытом интервале. Например, если f ( x )> 0 на [ a, b ], тогда сумма Римана будет положительным действительным числом. Если f ( x ) <0 на [ a, b ], тогда сумма Римана будет отрицательным действительным числом.Сумма Римана функции f ( x ) на [ a, b ] выражается какТаким образом, сумму Римана можно представить как «сумму n произведений».
Пример 1: Вычислите сумму Римана для f ( x ) = x 2 на [1,3], используя четыре подинтервала равной длины, где x i — правая конечная точка на подынтервале и (см.
 рисунок).
рисунок).Рисунок 1 Сумма Римана с четырьмя частями.
Поскольку подынтервалы должны иметь одинаковую длину, получается, что
Сумма Римана для четырех подинтервалов равна
.Если количество подынтервалов многократно увеличивать, то в результате длина каждого подынтервала будет становиться все меньше и меньше. Это можно переформулировать следующим образом: если количество подынтервалов неограниченно увеличивается ( n → + ∞), то длина каждого подынтервала приближается к нулю (Δ x → + ∞).Этот предел суммы Римана, если он существует, используется для определения определенного интеграла функции на [ a, b ]. Если f ( x ) определено на закрытом интервале [ a, b ], то определенный интеграл из f ( x ) от a до b определяется как
, если это ограничение выходит за пределы.

Функция f ( x ) называется подынтегральным выражением, а переменная x является переменной интегрирования.Числа a, и b, называются пределами интегрирования, а a, — нижним пределом интегрирования, а b, — верхним пределом интегрирования.
Обратите внимание, что символ ∫, используемый с неопределенным интегралом, — это тот же символ, который ранее использовался для неопределенного интеграла функции. Причина этого станет более очевидной в следующем обсуждении фундаментальной теоремы исчисления. Также имейте в виду, что определенный интеграл является уникальным действительным числом и не представляет бесконечное количество функций, которые являются результатом неопределенного интеграла функции.
Вопрос о существовании предела суммы Римана важно рассмотреть, поскольку он определяет, существует ли определенный интеграл для функции на отрезке. Как и в случае с дифференцированием, между непрерывностью и интегрированием существует значительная взаимосвязь, которую можно резюмировать следующим образом: если функция f ( x ) непрерывна на отрезке [ a, b ], то определенный интеграл от f ( x ) на [ a, b ] существует, а f считается интегрируемым на [ a, b ].
 Другими словами, непрерывность гарантирует, что определенный интеграл существует, но обратное не обязательно верно.
Другими словами, непрерывность гарантирует, что определенный интеграл существует, но обратное не обязательно верно.К сожалению, тот факт, что определенный интеграл функции существует на отрезке, не означает, что значение определенного интеграла легко найти.
Некоторые свойства полезны при решении задач, требующих применения определенного интеграла. Некоторые из наиболее распространенных свойств:
1.
2.
3., где c — постоянная
4.
5. Правило суммы:
6. Правило разницы:
7. Если
8. Если
9. Если
10. Если a, b, и c — любые три точки на закрытом интервале, то
11. Теорема о среднем значении для определенных интегралов: если f ( x ) непрерывно на закрытом интервале [ a, b ], то по крайней мере одно число c существует в открытом интервале ( a , b ) такая, что
Значение f ( c ) называется средним или средним значением функции f ( x ) на интервале [ a, b ] и
.
Пример 2: Оценить
Пример 3: Учитывая, что
Пример 4: Учитывая, что
Пример 5 Вычислить
Пример 6: Учитывая, что оценка
Пример 7: Учитывая, что оценка.
Пример 8: Учитывая это, оцените.
Пример 9: При условии, что найти все c значений, которые удовлетворяют теореме о среднем значении для данной функции на отрезке.
По теореме о среднем значении
Поскольку находится в интервале (3,6), заключение теоремы о среднем значении выполняется для этого значения c .
Основная теорема исчисления
Фундаментальная теорема исчисления устанавливает связь между неопределенными и определенными интегралами и вводит методику вычисления определенных интегралов без использования сумм Римана, что очень важно, поскольку вычисление предела суммы Римана может быть чрезвычайно трудоемким и трудным.
 Утверждение теоремы таково: если f ( x ) непрерывно на интервале [ a, b ], а F ( x ) является любой первообразной от f ( x ) на [ a, b ], затем
Утверждение теоремы таково: если f ( x ) непрерывно на интервале [ a, b ], а F ( x ) является любой первообразной от f ( x ) на [ a, b ], затемДругими словами, значение определенного интеграла функции на [ a, b ] — это разность любой первообразной функции, вычисленной на верхнем пределе интегрирования, за вычетом той же первообразной, вычисленной на нижнем пределе интегрирования.Поскольку константы интегрирования одинаковы для обеих частей этой разности, они игнорируются при вычислении определенного интеграла, поскольку они вычитаются и дают ноль. Помня об этом, выберите постоянную интегрирования равной нулю для всех определенных интегральных вычислений после примера 10.
Пример 10: Оценить
Поскольку общая первообразная x 2 равна (1/3) x 3 + C , вы обнаружите, что
Пример 11: Оценить
Поскольку первообразная sin x — cos x , вы обнаружите, что
Пример 12: Оценить
(Потому что (первообразная от, и вы обнаружите, что
Пример 13: Оценить
Поскольку первообразная x 2 — 4 x + 1 — это (1/3) x 3 — 2 x 2 + x , вы обнаружите, что
Определенная интегральная оценка
Многочисленные методы, которые можно использовать для вычисления неопределенных интегралов, также могут использоваться для вычисления определенных интегралов.
 Методы подстановки и замены переменных, интегрирования по частям, тригонометрических интегралов и тригонометрической подстановки проиллюстрированы в следующих примерах.
Методы подстановки и замены переменных, интегрирования по частям, тригонометрических интегралов и тригонометрической подстановки проиллюстрированы в следующих примерах.Пример 14: Оценить
Используя метод замены с
пределы интегрирования могут быть преобразованы из значений x в соответствующие им значения u . Когда x = 1, u = 3 и когда x = 2, u = 6, вы обнаружите, что
Обратите внимание, что когда метод подстановки используется для вычисления определенных интегралов, нет необходимости возвращаться к исходной переменной, если пределы интегрирования преобразованы в новые значения переменных.
Пример 15: Оценить
Используя метод подстановки с u = sin x + 1, du = cos x dx , вы обнаружите, что u = 1, когда x = π, и u = 0, когда x = 3π / 2; следовательно,
Обратите внимание, что вам никогда не приходилось возвращаться к тригонометрическим функциям в исходном интеграле для вычисления определенного интеграла.

Пример 16: Оценить
Использование интеграции по частям с
вы обнаружите, что
Пример 17: Оценить
Использование интеграции по частям с
Пример 18: Оценить
Пример 19: Оценить.
Пример 20: Оценить.
Поскольку подынтегральное выражение содержит форму a 2 + x 2 ,
Рисунок 2 Диаграмма для примера 20.
Пример 21: Оценить
Поскольку радикал имеет вид
Рисунок 3 Схема для примера 21.
Исчисление I — Вычисление определенных интегралов
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана (, то есть , вероятно, вы используете мобильный телефон).
 Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.Раздел 5-7: Вычисление определенных интегралов
В этом разделе мы сосредоточимся на том, как мы фактически вычисляем определенные интегралы на практике. Для этого нам понадобится Фундаментальная теорема исчисления, часть II.б = F \ влево (б \ вправо) — F \ влево (а \ вправо) \]
Чтобы увидеть доказательство этого, см. Раздел «Доказательство различных интегральных свойств» главы «Дополнительные возможности».
Напомним, что когда мы говорим об антипроизводной функции, на самом деле мы говорим о неопределенном интеграле для функции.
 Итак, чтобы вычислить определенный интеграл, первое, что мы собираемся сделать, — это вычислить неопределенный интеграл для функции. Это должно объяснить сходство обозначений неопределенного и определенного интегралов.
Итак, чтобы вычислить определенный интеграл, первое, что мы собираемся сделать, — это вычислить неопределенный интеграл для функции. Это должно объяснить сходство обозначений неопределенного и определенного интегралов.Также обратите внимание, что мы требуем, чтобы функция была непрерывной в интервале интегрирования. Это также было требованием при определении определенного интеграла. В последнем разделе мы не особо особо задумывались об этом. Однако в этом разделе нам нужно будет помнить об этом условии при проведении наших оценок.
Теперь давайте обратимся к тому факту, что мы можем использовать любую антипроизводную от \ (f \ left (x \ right) \) в оценке. Давайте в последний раз взглянем на следующий интеграл.3} + 0 — \ frac {{18}} {{31}}} \ right) \\ & = \ frac {{14}} {3} — \ frac {{18}} {{31}} + \ гидроразрыв {{18}} {{31}} \\ & = \ frac {{14}} {3} \ end {align *} \]
Константа, которую мы добавили ко второй антипроизводной, аннулирована на этапе оценки.
 {- 2}} \, dy}} & = \ left .3} — \ frac {1} {1}} \ right) \\ & = \ frac {8} {3} — \ frac {1} {2} — \ frac {1} {3} + 1 \\ & = \ frac {{17}} {6} \ end {align *} \]
{- 2}} \, dy}} & = \ left .3} — \ frac {1} {1}} \ right) \\ & = \ frac {8} {3} — \ frac {1} {2} — \ frac {1} {3} + 1 \\ & = \ frac {{17}} {6} \ end {align *} \]Помните, что оценка всегда выполняется в порядке оценки на верхнем пределе минус оценка на нижнем пределе. Также будьте очень осторожны со знаками минус и круглыми скобками. Их очень легко забыть или неправильно использовать и получить неправильный ответ.
Также обратите внимание, что для облегчения вычисления мы немного переписали неопределенный интеграл.{- 2}} \, dy}} \) Показать решение
Этот интеграл здесь, чтобы подчеркнуть. Напомним, что для того, чтобы мы могли сделать интеграл, подынтегральное выражение должно быть непрерывным в пределах диапазона. В этом случае второй член будет иметь деление на ноль в точке \ (y = 0 \), и поскольку \ (y = 0 \) находится в интервале интегрирования, , т.е. , он находится между нижним и верхним пределом, это подынтегральное выражение равно не непрерывна в интервале интегрирования, поэтому мы не можем сделать этот интеграл.

Обратите внимание, что эта проблема не помешает нам выполнить интеграл в (b), поскольку \ (y = 0 \) не находится в интервале интегрирования.
Итак, что мы узнали из этого примера?
Во-первых, чтобы получить определенный интеграл, первое, что нам нужно сделать, это неопределенный интеграл. Итак, мы не собираемся отказываться от вычисления неопределенных интегралов, они будут в каждом интеграле, который мы будем делать в оставшейся части этого курса, поэтому убедитесь, что вы хорошо умеете их вычислять.
Во-вторых, нам нужно внимательно следить за функциями, которые не являются непрерывными ни в одной точке между пределами интеграции.Кроме того, важно отметить, что это будет проблемой только в том случае, если точка (точки) разрыва возникает между пределами интегрирования или на самих границах. Если точка разрыва возникает за пределами интегрирования, интеграл все еще может быть вычислен.
В следующих наборах примеров мы не будем уделять слишком много внимания проблемам непрерывности или отсутствию проблем непрерывности, если это не влияет на оценку интеграла.
 Не позволяйте этому убедить вас, что вам не стоит беспокоиться об этой идее.{{\ pi} / {3} \;} \\ & = — 2 \ cos \ left ({\ frac {\ pi} {3}} \ right) — 5 \ sin \ left ({\ frac {\ pi } {3}} \ right) — \ left ({- 2 \ cos 0 — 5 \ sin 0} \ right) \\ & = — 1 — \ frac {{5 \ sqrt 3}} {2} + 2 \ \ & = 1 — \ frac {{5 \ sqrt 3}} {2} \ end {align *} \]
Не позволяйте этому убедить вас, что вам не стоит беспокоиться об этой идее.{{\ pi} / {3} \;} \\ & = — 2 \ cos \ left ({\ frac {\ pi} {3}} \ right) — 5 \ sin \ left ({\ frac {\ pi } {3}} \ right) — \ left ({- 2 \ cos 0 — 5 \ sin 0} \ right) \\ & = — 1 — \ frac {{5 \ sqrt 3}} {2} + 2 \ \ & = 1 — \ frac {{5 \ sqrt 3}} {2} \ end {align *} \]Сравните этот ответ с предыдущим, особенно с нулевой оценкой. Очень легко выработать привычку просто записывать ноль при оценке функции на ноль. Это особенно проблема, когда многие из функций, которые мы интегрируем, включают только \ (x \), возведенные в положительные целые числа; эти оценки нулевая конечно.{\, {\ pi} / {4} \;} \\ & = 5 \ left ({\ frac {\ pi} {4}} \ right) — 2 \ sec \ left ({\ frac {\ pi} {4}} \ right) — \ left ({5 \ left ({\ frac {\ pi} {6}} \ right) — 2 \ sec \ left ({\ frac {\ pi} {6}} \ right) )} \ right) \\ & = \ frac {{5 \ pi}} {{12}} — 2 \ sqrt 2 + \ frac {4} {{\ sqrt 3}} \ end {align *} \]
Для оценки напомним, что
\ [\ sec z = \ frac {1} {{\ cos z}} \], и поэтому, если мы можем оценить косинус под этими углами, мы сможем оценить секанс под этими углами.
 6} — 10t + \ frac {1} {t} \; dt}} \) Показать решение
6} — 10t + \ frac {1} {t} \; dt}} \) Показать решениеЭтот интеграл не может быть выполнен. В третьем члене при \ (t = 0 \) есть деление на ноль, а \ (t = 0 \) лежит в интервале интегрирования. Тот факт, что первые два члена могут быть объединены, не имеет значения. Если даже одно слагаемое в интеграле не может быть интегрировано, то и весь интеграл не может быть выполнен.
Итак, на данный момент мы вычислили изрядное количество определенных интегралов. Помните, что большая часть работы по их вычислению — это сначала поиск неопределенного интеграла.{{\, 22}} {{f \ left (x \ right) \, dx}} \) Показать решение
Для этого интеграла обратите внимание, что \ (x = 1 \) не находится в интервале интегрирования, и поэтому нам не нужно беспокоиться об этом в этой части.
Также обратите внимание, что пределы интеграла полностью лежат в диапазоне для первой функции. Для нас это означает, что при выполнении интеграла все, что нам нужно сделать, это вставить первую функцию в интеграл.

Вот интеграл.{{\, 3}} {{f \ left (x \ right) \, dx}} \) Показать решение
В этой части \ (x = 1 \) находится в пределах интегрирования. Это означает, что подынтегральное выражение больше не является непрерывным в интервале интегрирования, и, насколько нам известно, это явный ограничитель. Как отмечалось выше, мы просто не можем интегрировать функции, которые не являются непрерывными в интервале интегрирования.
Кроме того, даже если бы функция была непрерывной при \ (x = 1 \), у нас все еще была бы проблема, заключающаяся в том, что функция на самом деле представляет собой два разных уравнения в зависимости от того, где мы находимся в интервале интегрирования.
Давайте сначала рассмотрим проблему того, что функция не является непрерывной в точке \ (x = 1 \). Как мы увидим, в этом случае, если мы сможем найти способ обойти эту проблему, вторая проблема также будет решена одновременно.
 {3} {{\ left | {3t — 5} \ right | \, dt}} \]
Показать решение
{3} {{\ left | {3t — 5} \ right | \, dt}} \]
Показать решениеНапомним, что смысл неопределенного интегрирования (который нам нужно будет сделать в этой задаче) состоит в том, чтобы определить, какую функцию мы продифференцировали, чтобы получить подынтегральное выражение.На данный момент мы не видели никаких функций, которые будут дифференцироваться для получения абсолютного значения, и мы никогда не увидим функцию, которая будет дифференцировать, чтобы получить абсолютное значение.
Единственный способ решить эту проблему — избавиться от абсолютного значения. Для этого нам нужно вспомнить определение абсолютной величины.
\ [\ left | х \ право | = \ left \ {{\ begin {array} {* {20} {l}} x & {{\ mbox {if}} x \ ge 0} \\ {- x} & {{\ mbox {if}} xКак только мы вспомним, что можем определить абсолютное значение как кусочную функцию, мы можем использовать работу из примера 4 в качестве руководства для вычисления этого интеграла.
 {{\, 3}} {{\ left | {3t — 5} \ right | \, dt}} \]
{{\, 3}} {{\ left | {3t — 5} \ right | \, dt}} \]Теперь в первых интегралах \ (t <\ frac {5} {3} \) и, значит, \ (3t - 5 <0 \) в этом интервале интегрирования.2} - 5 \ left ({\ frac {5} {3}} \ right)} \ right)} \ right) \\ & = \ frac {{25}} {6} + \ frac {8} {3} \\ & = \ frac {{41}} {6} \ end {align *} \]
Неплохо интегрировать функции абсолютного значения. Это немного больше работы, чем «стандартный» определенный интеграл, но на самом деле это не так уж и много работы. Во-первых, определите, где количество внутри столбцов абсолютного значения отрицательное, а где положительное. Когда мы определили эту точку, все, что нам нужно сделать, это разбить интеграл так, чтобы в каждом диапазоне пределов количество внутри столбцов абсолютного значения всегда было положительным или всегда отрицательным.Как только это будет сделано, мы можем отбросить столбцы абсолютного значения (добавив отрицательные знаки, когда количество отрицательное), а затем мы можем выполнить интеграл, как мы всегда делали.
 2} \ hпространство {0.5} + \ sin \ left (x \ right) \, dx}} = \ cos \ left ({10} \ right) — \ cos \ left (9 \ right) — \ frac {{468559}} {6} = — 78093.09461 \]
2} \ hпространство {0.5} + \ sin \ left (x \ right) \, dx}} = \ cos \ left ({10} \ right) — \ cos \ left (9 \ right) — \ frac {{468559}} {6} = — 78093.09461 \]Мораль здесь — быть осторожным и не злоупотреблять этими фактами.
Правило трапеции — Что такое формула правила трапеции? Примеры
В математике правило трапеции, также известное как правило трапеции или правило трапеции, представляет собой метод аппроксимации определенного интеграла в численном анализе. Правило трапеции — это правило интегрирования, используемое для вычисления площади под кривой путем деления кривой на маленькие трапеции.Суммирование всех площадей маленьких трапеций даст площадь под кривой. Давайте разберемся с формулой правила трапеции и ее доказательством на примерах в следующих разделах.
Что такое правило трапеции?
Правило трапеции применяется для решения определенного интеграла вида b ∫ \ (_ a \) f (x) dx, аппроксимируя область под графиком функции f (x) как трапецию и вычисляя ее площадь .
 Согласно правилу трапеций, мы оцениваем площадь под кривой путем деления общей площади на маленькие трапеции, а не на прямоугольники.
Согласно правилу трапеций, мы оцениваем площадь под кривой путем деления общей площади на маленькие трапеции, а не на прямоугольники.Формула трапециевидного правила
Мы применяем формулу правила трапеций для решения определенного интеграла путем вычисления площади под кривой путем деления общей площади на маленькие трапеции, а не на прямоугольники. Это правило используется для аппроксимации определенных интегралов, где оно использует линейные приближения функций. Правило трапеции берет среднее левой и правой суммы.
Пусть y = f (x) непрерывно на [a, b]. Разделим интервал [a, b] на n равных подинтервалов, каждый шириной, h = (b — a) / n,
такое, что a = x \ (_ 0 \)
Площадь = \ (\ dfrac {h} {2} [y_0 + 2 (y_1 + y_2 + y_3 +….. + y_ {n-1}) + y_n] \)
где,
- \ (y_0 \), \ (y_1 \), \ (y_2 \)…. — значения функции при x = 1, 2, 3… .. соответственно.

Вывод формулы правила трапеции
Мы можем вычислить значение определенного интеграла, используя трапеции, чтобы разделить площадь под кривой для данной функции.
Формулировка правила трапеции: Пусть f (x) — непрерывная функция на интервале (a, b).б \) е (х) дх
Проба:
Чтобы доказать правило трапеции, рассмотрите кривую, показанную на рисунке выше, и разделите область под этой кривой на трапеции. Мы видим, что первая трапеция имеет высоту Δx и параллельные основания длиной y \ (_ 0 \) или f (x \ (_ 0 \)) и y \ (_ 1 \) или f \ (_ 1 \). Таким образом, площадь первой трапеции на приведенном выше рисунке может быть задана как
.(1/2) Δx [f (x \ (_ 0 \)) + f (x \ (_ 1 \))]
Площади остальных трапеций равны (1/2) Δx [f (x \ (_ 1 \)) + f (x \ (_ 2 \))], (1/2) Δx [f (x \ (_ 2 \ )) + f (x \ (_ 3 \))] и так далее.b_af (x) \, dx≈ \ frac {Δx} {2} \ big (f (x_0) +2 \, f (x_1) +2 \, f (x_2) +2 \, f (x_3) \) + .
 .. + \ (2f (x_ {n-1}) + f (x_n) \ big) \)
.. + \ (2f (x_ {n-1}) + f (x_n) \ big) \)Как применить правило трапеции?
Правило трапеций может применяться для решения определенного интеграла любой заданной функции. Он вычисляет площадь под кривой, образованной функцией, путем деления ее на трапеции и является менее точным методом по сравнению с правилом Симпсона. И Правило Симпсона, и Правило Трапеции дают значение приближения, но Правило Симпсона дает еще более точное значение приближения интегралов, поскольку Правило Симпсона использует квадратичное приближение вместо линейного приближения.{b} f (x) dx \ приблизительно T_ {n} = \ frac {\ bigtriangleup x} {2} [f (x_ {0}) + 2f (x_ {1}) + 2f (x_ {2}) \ ) +…. + \ (2f (x_ {n-1}) + f (x_ {n})] \), где x \ (_ i \) = a + i △ x
- \ (y_0 \), \ (y_1 \), \ (y_2 \)…. — значения функции при x = 1, 2, 3… .. соответственно.
- h = малый интервал (\ (x_1- x_0) \)
- Подсказка
\ (Δx = \ frac {1} {2}, \ quad m_1 = \ frac {5} {4}, \ quad \ text {и} \ quad m_2 = \ frac {7} {4}. \)
- Ответ
\ (\ dfrac {24} {35} \ приблизительно 0,685714 \)
- Подсказка
Set \ (Δx = \ dfrac {1} {2}. \) Конечные точки подынтервалов являются элементами множества \ (P = \ left \ {1, \ frac {3} {2}, 2 \ right \}. \)
- Ответ
\ (\ dfrac {17} {24} \ приблизительно 0,708333 \)
- Подсказка
Используйте предыдущие примеры в качестве руководства.
- Ответ
абсолютная погрешность \ (\ примерно 0,0074, \) и относительная погрешность \ (\ примерно 1,1 \% \)
- Подсказка
\ (f » (x) = 2, \) поэтому \ (M = 2. \)
- Ответ
\ (\ dfrac {1} {192} \)
Давайте взглянем на несколько примеров, чтобы лучше понять правило трапеции.
Часто задаваемые вопросы по правилу трапеции
Что такое правило трапеции?
Правило трапеции — это правило интегрирования, используемое для вычисления площади под кривой путем деления кривой на маленькие трапеции.
 Суммирование всех площадей маленьких трапеций даст площадь под кривой.Согласно этому правилу площадь под кривой оценивается путем деления общей площади на маленькие трапеции, а не на прямоугольники.
Суммирование всех площадей маленьких трапеций даст площадь под кривой.Согласно этому правилу площадь под кривой оценивается путем деления общей площади на маленькие трапеции, а не на прямоугольники.Что такое формула правила трапеции?
Формула правила трапеции: Area = \ (\ dfrac {h} {2} [y_0 + y_n + 2 (y_1 + y_2 + y_3 + ….. + y_ {n-1})] \)
где,
Почему это называется формулой трапециевидного правила?
Правило называется трапециевидным, потому что при оценке площади под кривой общая площадь делится на маленькие трапеции вместо прямоугольников.Затем находим площадь этих маленьких трапеций в определенном интервале.
Используя формулу правила трапеции, найдите площадь, когда h = 2, y
0 = 4, y 1 = 8, y 2 = 12, y 3 = 15.
Используя формулу правила трапеции, площадь = \ (\ dfrac {h} {2} [y_0 + y_n + 2 (y_1 + y_2 + y_3 + ….. + y_ {n-1})] \)
= \ (\ dfrac {2} {2} [4 + 15 + 2 (8 + 12)] \)
= 1 [19 + 40]
= 1 [59]
= 59
Таким образом, площадь под кривой составляет 59 кв.единицы.7.7: Приближенное интегрирование — математика LibreTexts
Первообразные многих функций либо не могут быть выражены, либо не могут быть легко выражены в замкнутой форме (то есть в терминах известных функций). Следовательно, вместо того, чтобы напрямую оценивать определенные интегралы этих функций, мы прибегаем к различным методам численного интегрирования для аппроксимации их значений. В этом разделе мы исследуем несколько из этих техник. Кроме того, мы исследуем процесс оценки ошибки при использовании этих методов.n_ {i = 1} f (m_i) Δx \) соответствует сумме площадей прямоугольников, аппроксимирующих площадь между графиком \ (f (x) \) и осью \ (x \) над \ ([ а, б] \).
 2 \, dx \) с использованием четырех подинтервалов.Сравните результат с фактическим значением этого интеграла.
2 \, dx \) с использованием четырех подинтервалов.Сравните результат с фактическим значением этого интеграла.Решение: каждый подынтервал имеет длину \ (Δx = \ dfrac {1−0} {4} = \ dfrac {1} {4}. \) Следовательно, подынтервалы состоят из
\ [\ left [0, \ tfrac {1} {4} \ right], \, \ left [\ tfrac {1} {4}, \ tfrac {1} {2} \ right], \, \ left [\ tfrac {1} {2}, \ tfrac {3} {4} \ right], \, \ text {и} \, \ left [\ tfrac {3} {4}, 1 \ right]. \ nonumber \]
Середины этих подынтервалов: \ (\ left \ {\ frac {1} {8}, \, \ frac {3} {8}, \, \ frac {5} {8}, \, \ frac {7 } {8} \ right \}. \) Таким образом,
\ [\ begin {align *} M_4 & = \ frac {1} {4} \ cdot f \ left (\ frac {1} {8} \ right) + \ frac {1} {4} \ cdot f \ left (\ frac {3} {8} \ right) + \ frac {1} {4} \ cdot f \ left (\ frac {5} {8} \ right) + \ frac {1} {4} \ cdot f \ left (\ frac {7} {8} \ right) \\ [4pt] & = \ frac {1} {4} ⋅ \ frac {1} {64} + \ frac {1} {4} ⋅ \ frac {9} {64} + \ frac {1} {4} ⋅ \ frac {25} {64} + \ frac {1} {4} ⋅ \ frac {49} {64} \\ [4pt] & = \ frac {21} {64} = 0.
 2_1 \ frac {1} {x} \, dx.\)
2_1 \ frac {1} {x} \, dx.\)Правило трапеции
Мы также можем аппроксимировать значение определенного интеграла, используя трапеции, а не прямоугольники. На рисунке \ (\ PageIndex {2} \) область под кривой аппроксимирована трапециями, а не прямоугольниками.
Рисунок \ (\ PageIndex {2} \): Трапеции могут использоваться для аппроксимации площади под кривой, таким образом аппроксимируя определенный интеграл.Правило трапеций для оценки определенных интегралов использует трапеции, а не прямоугольники для аппроксимации площади под кривой. Чтобы понять окончательную форму правила, рассмотрим трапеции, показанные на рисунке \ (\ PageIndex {2} \).
 b_af (x) \, dx≈ \ frac {1} {2} Δx \ Big (f (x_0) + f (x_1) \ Big) + \ frac {1} {2} Δx \ Big ( f (x_1) + f (x_2) \ Big) + \ frac {1} {2} Δx \ Big (f (x_2) + f (x_3) \ Big) + \ frac {1} {2} Δx \ Big ( е (х_3) + е (х_4) \ большой).b_af (x) \, dx≈ \ frac {Δx} {2} \ Big [f (x_0) +2 \, f (x_1) +2 \, f (x_2) +2 \, f (x_3) + f ( x_4) \ Big]. \ nonumber \]
b_af (x) \, dx≈ \ frac {1} {2} Δx \ Big (f (x_0) + f (x_1) \ Big) + \ frac {1} {2} Δx \ Big ( f (x_1) + f (x_2) \ Big) + \ frac {1} {2} Δx \ Big (f (x_2) + f (x_3) \ Big) + \ frac {1} {2} Δx \ Big ( е (х_3) + е (х_4) \ большой).b_af (x) \, dx≈ \ frac {Δx} {2} \ Big [f (x_0) +2 \, f (x_1) +2 \, f (x_2) +2 \, f (x_3) + f ( x_4) \ Big]. \ nonumber \]Обобщая, формально сформулируем следующее правило.
Правило трапеции
Предположим, что \ (f (x) \) непрерывно над \ ([a, b] \). Пусть \ (n \) — натуральное число и \ (Δx = \ dfrac {b − a} {n} \). Пусть \ ([a, b] \) разделен на \ (n \) подынтервалы, каждый длиной \ (Δx \), с конечными точками в \ (P = \ {x_0, x_1, x_2…, x_n \}. \ )
Набор
\ [T_n = \ frac {Δx} {2} \ Big [f (x_0) +2 \, f (x_1) +2 \, f (x_2) + ⋯ + 2 \, f (x_ {n − 1}) ) + f (x_n) \ Большой].nf (x_i) Δx. \)
То есть \ (L_n \) и \ (R_n \) аппроксимируют интеграл, используя левую и правую конечные точки каждого подынтервала, соответственно.
Рисунок \ (\ PageIndex {3} \): правило трапеции имеет тенденцию быть менее точным, чем правило средней точки. Вдобавок внимательное изучение рисунка \ (\ PageIndex {3} \) приводит нас к следующим наблюдениям об использовании правил трапеции и правил средней точки для оценки определенного интеграла неотрицательной функции. Правило трапеции имеет тенденцию систематически переоценивать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически недооценивать значение определенного интеграла на интервалах, где функция вогнута вниз.С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично недооценивая значение определенного интеграла по тем же типам интервалов. Это заставляет нас предположить, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеции.
Вдобавок внимательное изучение рисунка \ (\ PageIndex {3} \) приводит нас к следующим наблюдениям об использовании правил трапеции и правил средней точки для оценки определенного интеграла неотрицательной функции. Правило трапеции имеет тенденцию систематически переоценивать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически недооценивать значение определенного интеграла на интервалах, где функция вогнута вниз.С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично недооценивая значение определенного интеграла по тем же типам интервалов. Это заставляет нас предположить, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеции.Пример \ (\ PageIndex {3} \): использование правила трапеции
Используйте правило трапеции для оценки \ (\ displaystyle ∫ ^ 1_0x ^ 2 \, dx \) с использованием четырех подинтервалов.
 2_1 \ frac {1} {x} \, dx. \)
2_1 \ frac {1} {x} \, dx. \)Абсолютная и относительная погрешность
Важным аспектом использования этих правил численной аппроксимации является вычисление погрешности их использования для оценки значения определенного интеграла.Сначала нам нужно определить абсолютную ошибку и относительную ошибку.
Определение: абсолютная и относительная погрешность
Если \ (B \) — наша оценка некоторой величины, имеющей фактическое значение \ (A \), то абсолютная ошибка определяется как \ (| A-B | \).
Относительная ошибка — это ошибка в процентах от фактического значения, выражаемая как \ [\ left \ lvert \ frac {A-B} {A} \ right \ rvert⋅100 \%.
 2 \, dx \), используя правило средней точки, найденное в примере \ (\ PageIndex {1} \).2_1 \ frac {1} {x} \, dx \) должно быть \ (\ frac {24} {35} \) с использованием \ (M_2 \). Фактическое значение этого интеграла \ (\ ln 2 \). Используя \ (\ frac {24} {35} ≈0.6857 \) и \ (\ ln 2≈0.6931, \) вычислите абсолютную ошибку и относительную ошибку.
2 \, dx \), используя правило средней точки, найденное в примере \ (\ PageIndex {1} \).2_1 \ frac {1} {x} \, dx \) должно быть \ (\ frac {24} {35} \) с использованием \ (M_2 \). Фактическое значение этого интеграла \ (\ ln 2 \). Используя \ (\ frac {24} {35} ≈0.6857 \) и \ (\ ln 2≈0.6931, \) вычислите абсолютную ошибку и относительную ошибку.Границы ошибок на средней точке и трапециевидные правила
В двух предыдущих примерах мы смогли сравнить нашу оценку интеграла с фактическим значением интеграла; однако обычно у нас нет такой роскоши.В общем, если мы приближаем интеграл, мы делаем это, потому что мы не можем легко вычислить точное значение самого интеграла.
 Поэтому часто бывает полезно определить верхнюю границу ошибки при приближении интеграла. Следующая теорема предоставляет границы ошибок для средней точки и правил трапеции. Теорема формулируется без доказательства.
Поэтому часто бывает полезно определить верхнюю границу ошибки при приближении интеграла. Следующая теорема предоставляет границы ошибок для средней точки и правил трапеции. Теорема формулируется без доказательства.Границы ошибок для средней точки и трапецеидальные правила
Пусть \ (f (x) \) — непрерывная функция над \ ([a, b] \), имеющая вторую производную \ (f » (x) \) на этом интервале.2} \, dx − M_n \ right \ rvert <0,01. \ Nonumber \]
Анализ
У нас могло возникнуть искушение округлить \ (8.24 \) в меньшую сторону и выбрать \ (n = 8 \), но это было бы неверно, потому что у нас должно быть целое число больше или равное \ (8.24 \). Мы должны иметь в виду, что оценки ошибок дают верхнюю границу только для ошибки. Фактическая оценка на самом деле может быть гораздо лучшим приближением, чем указано в границах погрешности.
Упражнение \ (\ PageIndex {4} \)
Используйте уравнение \ (\ ref {MidError} \), чтобы найти верхнюю границу ошибки при использовании \ (M_4 \) для оценки \ (\ displaystyle ∫ ^ 1_0x ^ 2 \, dx.
 \)
\)Правило Симпсона
С помощью правила средней точки мы оценили площади областей под кривыми с помощью прямоугольников. В некотором смысле мы аппроксимировали кривую кусочно-постоянными функциями. С помощью правила трапеции мы аппроксимировали кривую с помощью кусочно-линейных функций.{x_4} _ {x_2} f (x) \, dx \) с интегралом от другой квадратичной функции, проходящим через \ ((x_2, f (x_2)), \, (x_3, f (x_3)), \) и \ ((x_4, f (x_4)). \) Этот процесс продолжается с каждой последовательной парой подынтервалов.
Рисунок \ (\ PageIndex {4} \): С помощью правила Симпсона мы приближаем определенный интеграл, интегрируя кусочно-квадратичную функцию.Чтобы понять формулу, которую мы получаем для правила Симпсона, мы начнем с вывода формулы для этого приближения для первых двух подинтервалов.
 {x_4} _ {x_0} f (x) \, dx≈ \ frac {Δx} {3} (f (x_0) +4 \, f (x_1) +2 \, f (x_2) +4 \, f ( x_3) + f (x_4)). \ nonumber \]
{x_4} _ {x_0} f (x) \, dx≈ \ frac {Δx} {3} (f (x_0) +4 \, f (x_1) +2 \, f (x_2) +4 \, f ( x_3) + f (x_4)). \ nonumber \]Шаблон продолжается, когда мы добавляем пары подинтервалов к нашему приближению. Общее правило можно сформулировать следующим образом.
Правило Симпсона
Предположим, что \ (f (x) \) непрерывно над \ ([a, b] \). Пусть \ (n \) — положительное четное целое число и \ (Δx = \ dfrac {b − a} {n} \). Пусть \ ([a, b] \) разделен на \ (n \) подынтервалы, каждый длиной \ (Δx \), с конечными точками в \ (P = \ {x_0, x_1, x_2,…, x_n \}.b_af (x) \, dx. \ nonumber \]
Подобно тому, как правило трапеций представляет собой среднее значение правил левой и правой руки для оценки определенных интегралов, правило Симпсона может быть получено из средней точки и правил трапеций с использованием средневзвешенного значения. Можно показать, что \ (S_ {2n} = \ left (\ frac {2} {3} \ right) M_n + \ left (\ frac {1} {3} \ right) T_n \).
Также возможно установить границу ошибки при использовании правила Симпсона для приближения определенного интеграла.
 {3} {\ left (\ frac {1} {5} \ right)} + 1 } \ приблизительно 2.{3} {\ left (x \ right)} + 1} \, dx \ приблизительно 1.084208122931016 $$$ A
{3} {\ left (\ frac {1} {5} \ right)} + 1 } \ приблизительно 2.{3} {\ left (x \ right)} + 1} \, dx \ приблизительно 1.084208122931016 $$$ A Использование основной теоремы для вычисления определенных интегралов
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.
 org.
org.Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
.

 Для этого применяют следующие приемы:
Для этого применяют следующие приемы: Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5.
Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5. е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.  Вычислительные задачи требуют повышенной концентрации внимания, поэтому к изучению статьи рекомендую подойти в хорошей физической форме и со свежей головой:
Вычислительные задачи требуют повышенной концентрации внимания, поэтому к изучению статьи рекомендую подойти в хорошей физической форме и со свежей головой:


 А такой инструментарий наряду с механическими счётами сегодня займут место разве что в музее истории математики.
А такой инструментарий наряду с механическими счётами сегодня займут место разве что в музее истории математики.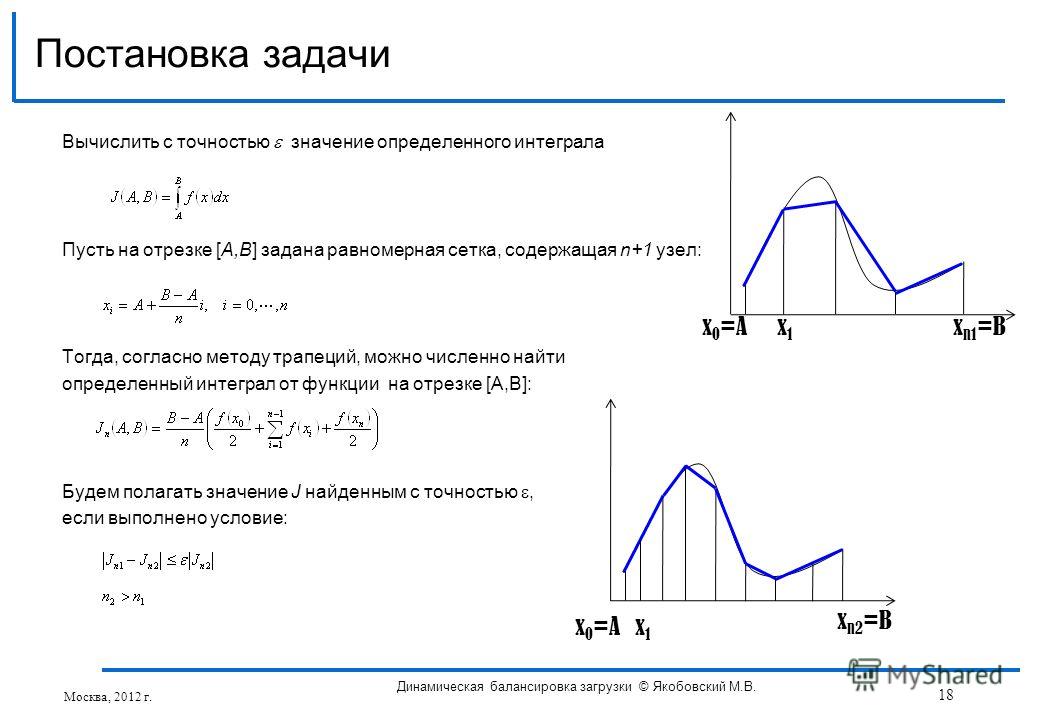 А всё потому, что не входит в область сходимости данного разложения.
А всё потому, что не входит в область сходимости данного разложения. Но в качестве «побочного эффекта» возникает необходимость поправить точность вычислений. Ведь когда мы подсчитаем члены разложения , то будем обязаны домножить каждое число на «тройку». И по этой причине изначально требуемую точность 0,01 нужно устрожить в три раза: .
Но в качестве «побочного эффекта» возникает необходимость поправить точность вычислений. Ведь когда мы подсчитаем члены разложения , то будем обязаны домножить каждое число на «тройку». И по этой причине изначально требуемую точность 0,01 нужно устрожить в три раза: . Результат округлить до 3 знаков после запятой.
Результат округлить до 3 знаков после запятой. Преобразуем аргумент логарифма в обыкновенную дробь: и решим следующее уравнение:
Преобразуем аргумент логарифма в обыкновенную дробь: и решим следующее уравнение:
 Ряды применяются также при интегрировании
дифференциальных уравнений.
Ряды применяются также при интегрировании
дифференциальных уравнений. Таким образом,
Таким образом, Бывает также,
что нахождение первообразной возможно,
но излишне трудоемко. Однако если
подинтегральная функция раскладывается
в степенной ряд, а пределы интегрирования
принадлежат интервалу сходимости этого
ряда, то возможно приближенное вычисление
интеграла с наперед заданной точностью.
Бывает также,
что нахождение первообразной возможно,
но излишне трудоемко. Однако если
подинтегральная функция раскладывается
в степенной ряд, а пределы интегрирования
принадлежат интервалу сходимости этого
ряда, то возможно приближенное вычисление
интеграла с наперед заданной точностью. x, Sin(x), Cos(x) и другие, это и есть разложения в ряд Тейлора, но в точке 0 для аргумента. Для функций комплексного аргумента ряд Лорана является наиболее частой задачей в ТФКП, так как представляет двусторонний бесконечный ряд. Он и является суммой двух рядов. Мы предлагаем вам посмотреть пример разложения прямо на сайте сайт, это сделать очень просто, нажав на «Пример» с любым номером, а затем кнопку «Решение». Именно такому разложению функции в ряд сопоставлен мажорирующий ряд, ограничивающий функцию исходную в некоторой области по оси ординат, если переменная принадлежит области абсцисс. Векторному анализу поставляется в сравнение другая интересная дисциплина в математике. Поскольку исследовать нужно каждое слагаемое, то необходимо достаточно много времени на процесс. Всякому ряду Тейлора можно сопоставить ряд Маклорена, заменив x0 на нуль, а вот по ряду Маклорена порой не очевидно представление ряда Тейлора обратно. Как бы это и не требуется делать в чистом виде, но интересно для общего саморазвития.
x, Sin(x), Cos(x) и другие, это и есть разложения в ряд Тейлора, но в точке 0 для аргумента. Для функций комплексного аргумента ряд Лорана является наиболее частой задачей в ТФКП, так как представляет двусторонний бесконечный ряд. Он и является суммой двух рядов. Мы предлагаем вам посмотреть пример разложения прямо на сайте сайт, это сделать очень просто, нажав на «Пример» с любым номером, а затем кнопку «Решение». Именно такому разложению функции в ряд сопоставлен мажорирующий ряд, ограничивающий функцию исходную в некоторой области по оси ординат, если переменная принадлежит области абсцисс. Векторному анализу поставляется в сравнение другая интересная дисциплина в математике. Поскольку исследовать нужно каждое слагаемое, то необходимо достаточно много времени на процесс. Всякому ряду Тейлора можно сопоставить ряд Маклорена, заменив x0 на нуль, а вот по ряду Маклорена порой не очевидно представление ряда Тейлора обратно. Как бы это и не требуется делать в чистом виде, но интересно для общего саморазвития. Всякому ряду Лорана соответствует двусторонний бесконечный степенной ряд по целым степеням z-a, другими словами ряд вида того же Тейлора, но немного отличающегося вычислением коэффициентов. Про область сходимости ряда Лорана расскажем чуть позже, после нескольких теоретических выкладок. Как и в прошлом веке, поэтапного разложения функции в ряд вряд ли можно достичь только лишь приведением слагаемых к общему знаменателю, так как функции в знаменателях нелинейные. Приближенное вычисление функционального значения требует постановка задач. Задумайтесь над тем, что когда аргумент ряда Тейлора есть линейная переменная, то разложение происходит в несколько действий, но совсем другая картина, когда в качестве аргумента раскладываемой функции выступает сложная или нелинейная функция, тогда очевиден процесс представления такой функции в степенной ряд, поскольку, таким образом, легко вычислить, пусть и приближенное, но значение в любой точке области определения, с минимальной погрешностью, мало влияющей на дальнейшие расчеты.
Всякому ряду Лорана соответствует двусторонний бесконечный степенной ряд по целым степеням z-a, другими словами ряд вида того же Тейлора, но немного отличающегося вычислением коэффициентов. Про область сходимости ряда Лорана расскажем чуть позже, после нескольких теоретических выкладок. Как и в прошлом веке, поэтапного разложения функции в ряд вряд ли можно достичь только лишь приведением слагаемых к общему знаменателю, так как функции в знаменателях нелинейные. Приближенное вычисление функционального значения требует постановка задач. Задумайтесь над тем, что когда аргумент ряда Тейлора есть линейная переменная, то разложение происходит в несколько действий, но совсем другая картина, когда в качестве аргумента раскладываемой функции выступает сложная или нелинейная функция, тогда очевиден процесс представления такой функции в степенной ряд, поскольку, таким образом, легко вычислить, пусть и приближенное, но значение в любой точке области определения, с минимальной погрешностью, мало влияющей на дальнейшие расчеты. Это касается и ряда Маклорена. когда необходимо вычислить функция в нулевой точке. Однако сам ряд Лорана здесь представлен разложением на плоскости с мнимыми единицами. Также не без успеха будет правильное решение задачи в ходе общего процесса. В математике такого подхода не знают, но он объективно существует. В результате вы можете прийти к выводу так называемых поточечных подмножеств, и в разложении функции в ряд нужно применять известные для этого процесса методы, таких как применение теории производных. Лишний раз убеждаемся в правоте учителя, который сделал свои предположения на счет итогов пост вычислительных выкладок. Давайте отметим, что ряд Тейлора, полученный по всем канонам математики, существует и определен на всей числовой оси, однако, уважаемые пользователи сервиса сайт, не забывайте вид исходной функции, ведь может получиться так, что изначально необходимо установит область определения функции, то есть выписать и исключить из дальнейших рассмотрений те точки, при которых функция не определена в области действительных чисел.
Это касается и ряда Маклорена. когда необходимо вычислить функция в нулевой точке. Однако сам ряд Лорана здесь представлен разложением на плоскости с мнимыми единицами. Также не без успеха будет правильное решение задачи в ходе общего процесса. В математике такого подхода не знают, но он объективно существует. В результате вы можете прийти к выводу так называемых поточечных подмножеств, и в разложении функции в ряд нужно применять известные для этого процесса методы, таких как применение теории производных. Лишний раз убеждаемся в правоте учителя, который сделал свои предположения на счет итогов пост вычислительных выкладок. Давайте отметим, что ряд Тейлора, полученный по всем канонам математики, существует и определен на всей числовой оси, однако, уважаемые пользователи сервиса сайт, не забывайте вид исходной функции, ведь может получиться так, что изначально необходимо установит область определения функции, то есть выписать и исключить из дальнейших рассмотрений те точки, при которых функция не определена в области действительных чисел. Так сказать это покажет вашу расторопность при решении задачи.
Не исключением высказанного будет и построение ряда Маклорена с нулевым значением аргумента. Процесс нахождения области определения функции никто при этом не отменял, и вы обязаны подойти со всей серьезностью к этому математическому действию. В случае содержания рядом Лорана главной части, параметр «a» будет называться изолированной особой точкой, и ряд Лорана будет разложен в кольце — это пересечение областей сходимости его частей, отсюда будет следовать соответствующая теорема. Но не все так сложно как может показаться на первый взгляд неопытному студенту. Изучив как раз ряд Тейлора, можно с легкостью понять ряд Лорана — обобщенный случай на расширение пространства чисел. Любое разложение функции в ряд можно производить только в точке области определения функции. Следует учитывать свойства таких функций, например, как периодичность или бесконечная дифференцируемость. Также предлагаем вам воспользоваться таблицей готовых разложений в ряд Тейлора элементарных функций, поскольку одна функция может быть представлена до десятков отличных от друг друга степенных рядов, что можно видеть из применения нашего калькулятора онлайн.
Так сказать это покажет вашу расторопность при решении задачи.
Не исключением высказанного будет и построение ряда Маклорена с нулевым значением аргумента. Процесс нахождения области определения функции никто при этом не отменял, и вы обязаны подойти со всей серьезностью к этому математическому действию. В случае содержания рядом Лорана главной части, параметр «a» будет называться изолированной особой точкой, и ряд Лорана будет разложен в кольце — это пересечение областей сходимости его частей, отсюда будет следовать соответствующая теорема. Но не все так сложно как может показаться на первый взгляд неопытному студенту. Изучив как раз ряд Тейлора, можно с легкостью понять ряд Лорана — обобщенный случай на расширение пространства чисел. Любое разложение функции в ряд можно производить только в точке области определения функции. Следует учитывать свойства таких функций, например, как периодичность или бесконечная дифференцируемость. Также предлагаем вам воспользоваться таблицей готовых разложений в ряд Тейлора элементарных функций, поскольку одна функция может быть представлена до десятков отличных от друг друга степенных рядов, что можно видеть из применения нашего калькулятора онлайн. Онлайн ряд Маклорена проще простого определить, если воспользоваться уникальным сервисом сайт, вам достаточно только ввести правильную записанную функцию и представленный ответ получите в считанные секунды, он будет гарантированно точным и в стандартно записанном виде. Можете переписать результат сразу в чистовик на сдачу преподавателю. Правильно бы сначала определить аналитичность рассматриваемой функции в кольцах, а затем однозначно утверждать, что она разложима в ряд Лорана во всех таких кольцах. Важен момент чтобы не упустить из вида содержащие отрицательных степеней членов ряда Лорана. На этом сосредоточьтесь как можно сильнее. Применяйте с пользой теорему Лорана о разложении функции в ряд по целым степеням.
Онлайн ряд Маклорена проще простого определить, если воспользоваться уникальным сервисом сайт, вам достаточно только ввести правильную записанную функцию и представленный ответ получите в считанные секунды, он будет гарантированно точным и в стандартно записанном виде. Можете переписать результат сразу в чистовик на сдачу преподавателю. Правильно бы сначала определить аналитичность рассматриваемой функции в кольцах, а затем однозначно утверждать, что она разложима в ряд Лорана во всех таких кольцах. Важен момент чтобы не упустить из вида содержащие отрицательных степеней членов ряда Лорана. На этом сосредоточьтесь как можно сильнее. Применяйте с пользой теорему Лорана о разложении функции в ряд по целым степеням.
 д.
д.







 7>>=frac<1> <5376>of your page —>
7>>=frac<1> <5376>of your page —>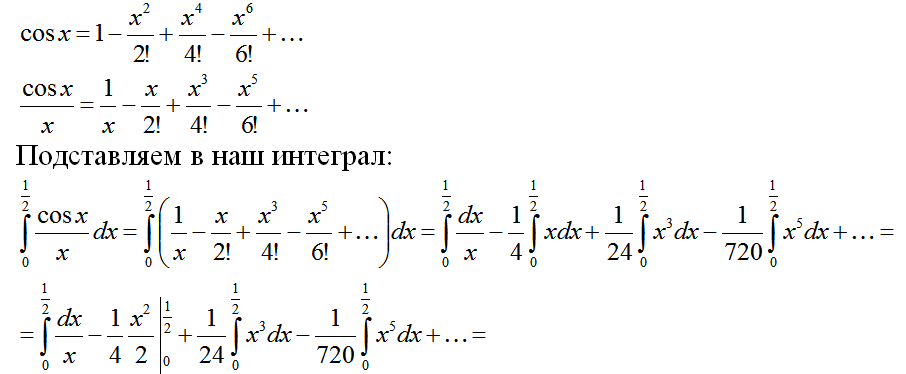
 Эти вопросы будут подробно рассмотрены позже (См. Действия со степенными рядами). Отметим лишь, что в нашем случае подобное действие справедливо хотя бы по свойствам определенного интеграла (интеграл от суммы равен сумме интегралов).
Эти вопросы будут подробно рассмотрены позже (См. Действия со степенными рядами). Отметим лишь, что в нашем случае подобное действие справедливо хотя бы по свойствам определенного интеграла (интеграл от суммы равен сумме интегралов).
 Если график расположен ниже оси Ох, т.е. f(x) 0, то площадь имеет знак “+”.
Если график расположен ниже оси Ох, т.е. f(x) 0, то площадь имеет знак “+”. Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница:
Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница: Вычислим численно определенный интеграл , который равен площади криволинейной трапеции.
Вычислим численно определенный интеграл , который равен площади криволинейной трапеции.
 В точках разбиения находим значения подынтегральной функции
В точках разбиения находим значения подынтегральной функции



 Г) 12
Г) 12 Но вычислить интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница либо невозможно, либо затруднительно, поэтому прибегают к различным методам приближенного интегрирования.
Но вычислить интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница либо невозможно, либо затруднительно, поэтому прибегают к различным методам приближенного интегрирования.
 2
2 Однако, при одном и том же значении формула Симпсона дает лучшее приближение.
Однако, при одном и том же значении формула Симпсона дает лучшее приближение. Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.
Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой. Увеличивая количество отрезков, мы увеличиваем точность вычислений.
Увеличивая количество отрезков, мы увеличиваем точность вычислений. Если у нас два отрезка разбиения , то узлов будет на один больше: . И формула Симпсона принимает весьма компактный вид:
Если у нас два отрезка разбиения , то узлов будет на один больше: . И формула Симпсона принимает весьма компактный вид: Если при использовании метода средних прямоугольников и метода трапеций нам даётся «поблажка» в одну треть, то сейчас – аж в одну пятнадцатую:
Если при использовании метода средних прямоугольников и метода трапеций нам даётся «поблажка» в одну треть, то сейчас – аж в одну пятнадцатую: 2
2
 2
2 3
3 14159..
14159.. $, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно.
$, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно. Но его часто используют, чтобы найти область под графиком функции следующим образом:
Но его часто используют, чтобы найти область под графиком функции следующим образом:
 От 5 до 1.0, из cos (x) dx:
От 5 до 1.0, из cos (x) dx: .. — (-1)
.. — (-1)


 Определяется произведение каждого значения функции на соответствующую длину подынтервала, и эти произведения « n » складываются для определения их суммы. Эта сумма называется суммой Римана и может быть положительной, отрицательной или нулевой, в зависимости от поведения функции на закрытом интервале. Например, если f ( x )> 0 на [ a, b ], тогда сумма Римана будет положительным действительным числом. Если f ( x ) <0 на [ a, b ], тогда сумма Римана будет отрицательным действительным числом.Сумма Римана функции f ( x ) на [ a, b ] выражается как
Определяется произведение каждого значения функции на соответствующую длину подынтервала, и эти произведения « n » складываются для определения их суммы. Эта сумма называется суммой Римана и может быть положительной, отрицательной или нулевой, в зависимости от поведения функции на закрытом интервале. Например, если f ( x )> 0 на [ a, b ], тогда сумма Римана будет положительным действительным числом. Если f ( x ) <0 на [ a, b ], тогда сумма Римана будет отрицательным действительным числом.Сумма Римана функции f ( x ) на [ a, b ] выражается как рисунок).
рисунок).
 Другими словами, непрерывность гарантирует, что определенный интеграл существует, но обратное не обязательно верно.
Другими словами, непрерывность гарантирует, что определенный интеграл существует, но обратное не обязательно верно.
 Утверждение теоремы таково: если f ( x ) непрерывно на интервале [ a, b ], а F ( x ) является любой первообразной от f ( x ) на [ a, b ], затем
Утверждение теоремы таково: если f ( x ) непрерывно на интервале [ a, b ], а F ( x ) является любой первообразной от f ( x ) на [ a, b ], затем Методы подстановки и замены переменных, интегрирования по частям, тригонометрических интегралов и тригонометрической подстановки проиллюстрированы в следующих примерах.
Методы подстановки и замены переменных, интегрирования по частям, тригонометрических интегралов и тригонометрической подстановки проиллюстрированы в следующих примерах.
 Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Итак, чтобы вычислить определенный интеграл, первое, что мы собираемся сделать, — это вычислить неопределенный интеграл для функции. Это должно объяснить сходство обозначений неопределенного и определенного интегралов.
Итак, чтобы вычислить определенный интеграл, первое, что мы собираемся сделать, — это вычислить неопределенный интеграл для функции. Это должно объяснить сходство обозначений неопределенного и определенного интегралов. {- 2}} \, dy}} & = \ left .3} — \ frac {1} {1}} \ right) \\ & = \ frac {8} {3} — \ frac {1} {2} — \ frac {1} {3} + 1 \\ & = \ frac {{17}} {6} \ end {align *} \]
{- 2}} \, dy}} & = \ left .3} — \ frac {1} {1}} \ right) \\ & = \ frac {8} {3} — \ frac {1} {2} — \ frac {1} {3} + 1 \\ & = \ frac {{17}} {6} \ end {align *} \]
 Не позволяйте этому убедить вас, что вам не стоит беспокоиться об этой идее.{{\ pi} / {3} \;} \\ & = — 2 \ cos \ left ({\ frac {\ pi} {3}} \ right) — 5 \ sin \ left ({\ frac {\ pi } {3}} \ right) — \ left ({- 2 \ cos 0 — 5 \ sin 0} \ right) \\ & = — 1 — \ frac {{5 \ sqrt 3}} {2} + 2 \ \ & = 1 — \ frac {{5 \ sqrt 3}} {2} \ end {align *} \]
Не позволяйте этому убедить вас, что вам не стоит беспокоиться об этой идее.{{\ pi} / {3} \;} \\ & = — 2 \ cos \ left ({\ frac {\ pi} {3}} \ right) — 5 \ sin \ left ({\ frac {\ pi } {3}} \ right) — \ left ({- 2 \ cos 0 — 5 \ sin 0} \ right) \\ & = — 1 — \ frac {{5 \ sqrt 3}} {2} + 2 \ \ & = 1 — \ frac {{5 \ sqrt 3}} {2} \ end {align *} \] 6} — 10t + \ frac {1} {t} \; dt}} \) Показать решение
6} — 10t + \ frac {1} {t} \; dt}} \) Показать решение
 {3} {{\ left | {3t — 5} \ right | \, dt}} \]
Показать решение
{3} {{\ left | {3t — 5} \ right | \, dt}} \]
Показать решение {{\, 3}} {{\ left | {3t — 5} \ right | \, dt}} \]
{{\, 3}} {{\ left | {3t — 5} \ right | \, dt}} \] 2} \ hпространство {0.5} + \ sin \ left (x \ right) \, dx}} = \ cos \ left ({10} \ right) — \ cos \ left (9 \ right) — \ frac {{468559}} {6} = — 78093.09461 \]
2} \ hпространство {0.5} + \ sin \ left (x \ right) \, dx}} = \ cos \ left ({10} \ right) — \ cos \ left (9 \ right) — \ frac {{468559}} {6} = — 78093.09461 \] Согласно правилу трапеций, мы оцениваем площадь под кривой путем деления общей площади на маленькие трапеции, а не на прямоугольники.
Согласно правилу трапеций, мы оцениваем площадь под кривой путем деления общей площади на маленькие трапеции, а не на прямоугольники.
 .. + \ (2f (x_ {n-1}) + f (x_n) \ big) \)
.. + \ (2f (x_ {n-1}) + f (x_n) \ big) \) Суммирование всех площадей маленьких трапеций даст площадь под кривой.Согласно этому правилу площадь под кривой оценивается путем деления общей площади на маленькие трапеции, а не на прямоугольники.
Суммирование всех площадей маленьких трапеций даст площадь под кривой.Согласно этому правилу площадь под кривой оценивается путем деления общей площади на маленькие трапеции, а не на прямоугольники.
 2 \, dx \) с использованием четырех подинтервалов.Сравните результат с фактическим значением этого интеграла.
2 \, dx \) с использованием четырех подинтервалов.Сравните результат с фактическим значением этого интеграла. 2_1 \ frac {1} {x} \, dx.\)
2_1 \ frac {1} {x} \, dx.\) b_af (x) \, dx≈ \ frac {1} {2} Δx \ Big (f (x_0) + f (x_1) \ Big) + \ frac {1} {2} Δx \ Big ( f (x_1) + f (x_2) \ Big) + \ frac {1} {2} Δx \ Big (f (x_2) + f (x_3) \ Big) + \ frac {1} {2} Δx \ Big ( е (х_3) + е (х_4) \ большой).b_af (x) \, dx≈ \ frac {Δx} {2} \ Big [f (x_0) +2 \, f (x_1) +2 \, f (x_2) +2 \, f (x_3) + f ( x_4) \ Big]. \ nonumber \]
b_af (x) \, dx≈ \ frac {1} {2} Δx \ Big (f (x_0) + f (x_1) \ Big) + \ frac {1} {2} Δx \ Big ( f (x_1) + f (x_2) \ Big) + \ frac {1} {2} Δx \ Big (f (x_2) + f (x_3) \ Big) + \ frac {1} {2} Δx \ Big ( е (х_3) + е (х_4) \ большой).b_af (x) \, dx≈ \ frac {Δx} {2} \ Big [f (x_0) +2 \, f (x_1) +2 \, f (x_2) +2 \, f (x_3) + f ( x_4) \ Big]. \ nonumber \] Вдобавок внимательное изучение рисунка \ (\ PageIndex {3} \) приводит нас к следующим наблюдениям об использовании правил трапеции и правил средней точки для оценки определенного интеграла неотрицательной функции. Правило трапеции имеет тенденцию систематически переоценивать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически недооценивать значение определенного интеграла на интервалах, где функция вогнута вниз.С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично недооценивая значение определенного интеграла по тем же типам интервалов. Это заставляет нас предположить, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеции.
Вдобавок внимательное изучение рисунка \ (\ PageIndex {3} \) приводит нас к следующим наблюдениям об использовании правил трапеции и правил средней точки для оценки определенного интеграла неотрицательной функции. Правило трапеции имеет тенденцию систематически переоценивать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически недооценивать значение определенного интеграла на интервалах, где функция вогнута вниз.С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично недооценивая значение определенного интеграла по тем же типам интервалов. Это заставляет нас предположить, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеции. 2_1 \ frac {1} {x} \, dx. \)
2_1 \ frac {1} {x} \, dx. \) 2 \, dx \), используя правило средней точки, найденное в примере \ (\ PageIndex {1} \).2_1 \ frac {1} {x} \, dx \) должно быть \ (\ frac {24} {35} \) с использованием \ (M_2 \). Фактическое значение этого интеграла \ (\ ln 2 \). Используя \ (\ frac {24} {35} ≈0.6857 \) и \ (\ ln 2≈0.6931, \) вычислите абсолютную ошибку и относительную ошибку.
2 \, dx \), используя правило средней точки, найденное в примере \ (\ PageIndex {1} \).2_1 \ frac {1} {x} \, dx \) должно быть \ (\ frac {24} {35} \) с использованием \ (M_2 \). Фактическое значение этого интеграла \ (\ ln 2 \). Используя \ (\ frac {24} {35} ≈0.6857 \) и \ (\ ln 2≈0.6931, \) вычислите абсолютную ошибку и относительную ошибку. Поэтому часто бывает полезно определить верхнюю границу ошибки при приближении интеграла. Следующая теорема предоставляет границы ошибок для средней точки и правил трапеции. Теорема формулируется без доказательства.
Поэтому часто бывает полезно определить верхнюю границу ошибки при приближении интеграла. Следующая теорема предоставляет границы ошибок для средней точки и правил трапеции. Теорема формулируется без доказательства. \)
\) {x_4} _ {x_0} f (x) \, dx≈ \ frac {Δx} {3} (f (x_0) +4 \, f (x_1) +2 \, f (x_2) +4 \, f ( x_3) + f (x_4)). \ nonumber \]
{x_4} _ {x_0} f (x) \, dx≈ \ frac {Δx} {3} (f (x_0) +4 \, f (x_1) +2 \, f (x_2) +4 \, f ( x_3) + f (x_4)). \ nonumber \] {3} {\ left (\ frac {1} {5} \ right)} + 1 } \ приблизительно 2.{3} {\ left (x \ right)} + 1} \, dx \ приблизительно 1.084208122931016 $$$ A
{3} {\ left (\ frac {1} {5} \ right)} + 1 } \ приблизительно 2.{3} {\ left (x \ right)} + 1} \, dx \ приблизительно 1.084208122931016 $$$ A  org.
org. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.