Десятичный логарифм
Навигация по странице:
Определение. Логарифмом числа b по основанию a, где a > 0, a ≠ 1, b > 0, называется показатель степени, в которую нужно возвести основание a, чтоб получить число b.
Определение. Десятичный логарифм — логарифм по основанию 10.
Другими словами, десятичный логарифм числа b является решением уравнения 10x = b.
Обозначение. Десятичный логарифм обозначается lg x или log x.
Калькулятор десятичных логарифмов
lg 2Свойства десятичного логарифмов
Для любых x > 0 и y > 0 выполняются следующие свойства десятичных логарифмов.
lg x = log10x — так как основание десятичного логарифма равно 10.
10lg b = b.
lg 1 = 0
lg 10 = 1
lg 10n = n
lg(x · y) = lg x + lg y
lg xy = lg x — lg y
lg xn = n lg x
- График функции y = lg x
(lg x)′ = 1x ln 10
∫ lg x dx = x lg x — xln 10 + C
 Найти значения десятичного логарифма от чисел 100, 1000, 0.1, 0.01, 0.001.
Найти значения десятичного логарифма от чисел 100, 1000, 0.1, 0.01, 0.001.lg 100 = lg 102 = 2
lg 1000 = lg 103 = 3
lg 0.1 = lg 10-1 = -1
lg 0.01 = lg 10-2 = -2
lg 0.001 = lg 10-3 = -3
Пример 2.Доказать равенство: a lg b = b lg a.
Запишем очевидное равенство:
lg b · lg a = lg a · lg ab
Возведем 10 в соответствующие степени
10lg b · lg a = 10lg a · lg b
(10lg b)lg a = (10lg a)lg b
blg a = alg b
Равенство доказано.
Пример 3.Зная, что lg 2 = a, lg 3 = b, lg 5 = c, выразить lg 6; lg 30; lg 16 через a, b, c.
Используем формулы логарифма произведения и степени получим:
lg 6 = lg (2·3)= lg 2 + lg 3 = a + b;
lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c;
lg 16 = lg 24= 4 · lg 2 = 4a.
Вычислить log9 5 · log25 27.
Перейдем к основе 10:
log9 5 · log25 27 = lg 5lg 9 · lg 27lg 25
Используем свойство логарифма степени lg xn = n lg x:
lg 5lg 9 · lg 27lg 25 = lg 5lg 32 · lg 33lg 52 = lg 52 lg 3 · 3 lg 32 lg 5 = 34
Пример 5.Вычислить log30 8, если lg 5 = a, lg 3 = b.
Перейдем к основе 10:
log 30 8 = lg 8lg 30 = lg 23lg (3 · 10) =
Используем свойство логарифма степени, произведения, частного и то что 2= 105:
= 3 lg 2lg 3 + lg 10 = 3 lg 2lg 3 + 1 = 3 lg 105lg 3 + 1 = 3(lg 10 — lg 5)lg 3 + 1 = 3(1 — lg 5)lg 3 + 1 =
Подставим lg 5 = a, lg 3 = b:
= 3(1 — a)b + 1
Ответ:
log30 8 = 3(1 — a)b + 1
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни. / / Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
| ||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | |||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | ||||||||||||||||||||||||||
Функция LN — Служба поддержки Office
В этой статье описан синтаксис формулы и использование функции LN в Microsoft Excel.
Описание
 Натуральный логарифм — это логарифм по основанию e (2,71828182845904).
Натуральный логарифм — это логарифм по основанию e (2,71828182845904).
Синтаксис
LN(число)
Аргументы функции LN описаны ниже.
Замечание
LN является обратной функцией к EXP.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|---|---|---|
|
=LN(86) |
Натуральный логарифм числа 86 |
4,4543473 |
|
=LN(2,7182818) |
Натуральный логарифм числа e |
1 |
|
=LN(EXP(3)) |
Натуральный логарифм числа e, возведенного в третью степень |
3 |
Изучение логарифмов в старшей школе – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)
- Интернет-магазин
- Где купить
- Аудио
- Новости
- LECTA
- Программа лояльности
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни. / / Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln). Поделиться:
 Введите свой запрос: Введите свой запрос: | ||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||
45. Понятие логарифма и его свойства
Логарифмом числа B (B > 0) По основанию а (А > 0, А ¹ 1) называют показатель степени, в которую нужно возвести число А, чтобы получить число B:
(6. 1)
1)
Формулу (6.1) называют Основным логарифмическим тождеством.
Логарифм числа B по основанию 10 называется Десятичным логарифмом И обозначается
Логарифм по основанию E (E = 2,71828…) называется Натуральным логарифмом и обозначается
Свойства логарифмов
Пусть Тогда:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11) Тогда и только тогда, когда
12) тогда и только тогда, когда
13) тогда и только тогда, когда
Обобщенные свойства логарифмов
Пусть и – выражения с переменной. Тогда:
3*) где
4*) где
5*) где
6*) где
З а м е ч а н и е 1. Следует различать произведение логарифмов и повторный логарифм
З а м е ч а н и е 2. Степень логарифма может быть записана двумя способами:
или
Логарифмированием называется операция нахождения логарифма числа или выражения.
Потенцированием называют действие, обратное логарифмированию, т. е. потенцирование – это операция нахождения числа (выражения) по его логарифму. При выполнении этих операций пользуются свойствами логарифмов.
Пример 1. Упростить выражение
Решение. Преобразуем каждое слагаемое отдельно. При этом сделаем ссылку на конкретные свойства логарифмов, приведенные выше.
|используем свойство 9| |по свойству 5|= |по основному логарифмическому тождеству|
|по свойству 10|
Тогда
|по свойству 5| =
= |по свойству 2| =
|по свойству 8|
Таким образом:
З а м е ч а н и е 3. Решение этого примера при одновременном преобразовании всех слагаемых (что и следует делать) выглядит так:
Пример 2. Вычислить
Решение. Для преобразования первого и второго слагаемых используем формулу изменения основания логарифма (свойство 9), а затем свойства 3 и 5.
= |по свойствам 5 и 2| =
Для преобразования третьего слагаемого используем свойства 3–5:
Тогда получаем:
З а м е ч а н и е 4. Подробное описание решения и преобразование всех слагаемых отдельно приведено исходя из соображений доступности объяснений. Целесообразно делать преобразования всего выражения сразу, аналогично тому, как сделано в замечании 1.
Пример 3. Прологарифмировать по основанию 10 выражение
Решение. Замечаем, что сделать это можно, если Тогда
Пример 4. Выполнить потенцирование выражения
Решение. Используем свойства логарифмов 3–5 («справа–налево»):
Получаем ответ:
Пример 5. Выразить через и
Решение.
| < Предыдущая | Следующая > |
|---|
Pascal.
 Стандартные функции и выражения
Стандартные функции и выраженияСтандартные функции.
В программировании, довольно часто приходиться выполнять однотипные действия, причем в задачах разного уровня и класса. И для ускорения процесса написания кода эти действия выносят в специальные подпрограммы – стандартные функции. Обращение к такой подпрограмме происходит по ее имени, а в скобках указывается значение аргумента. В следующей таблице указаны те стандартные функции, которые используются в языке программирования Pascal.
| Функция | Назначение |
| ABS(x) | Вычисление абсолютного значения x: |х| |
| SQR(x) | Вычисление квадрата x: x*x |
| SIN(x) | Вычисление синуса x: sin x |
| COS(x) | Вычисление косинуса x: cos x |
| ARCTAN(x) | Вычисление арктангенса x: arctg x |
| EXP(x) | Вычисление экспоненты (числа Е) в степени x |
| EXP10(x) | Вычисление 10 в степени x |
| LN(x) | Вычисление натурального логарифма x |
| LOG(x) | Вычисление десятичного логарифма x |
| SQRT(x) | Вычисление квадратного корня из x |
| A DIV B | Вычисление частного при делении А на В с отбрасыванием остатка |
| A MOD B | Нахождение остатка от делении А на В |
| TRUNC(x) | Нахождение целой части x |
| RANDOM(x) | Псевдослучайное число в интервале [0, x] |
| ROUND(x) | Округление значения x в сторону ближайшего целого |
| ODD(x) | Проверяет аргумент на нечетность. Результат TRUE, если аргумент нечетный, FALSE – если четный. Результат TRUE, если аргумент нечетный, FALSE – если четный. |
| ORD(x) | Возвращает порядковый номер аргумента и, как следствие, преобразует величину порядкового типа в величину целого типа. |
| CHR(x) | Определение символа языка Паскаль по его порядковому номеру |
| SUCC(x) | Нахождение элемента, идущего после данного в перечне допустимых элементов |
| PRED(x) | Нахождение элемента, идущего перед данным в перечне допустимых элементов |
| FRAC(X) | Возвращает дробную часть x |
| INT(X) | Возвращает целую часть x |
| Pi | Значение математической постоянной π |
| EOF(x) | Возвращает TRUE, если файл находится в стоянии “конец файла”, иначе FALSE, если нет конца файла |
Выражения
Выражение состоит из переменных, констант, полей в записях, указателей функций, круглых скобок и знаков операций. Для корректной записи выражений необходимо знать не только как обозначаются те или иные операции, функции и т. п., но также стоит предусмотреть приоритеты их выполнения, математические и логические правила, а также некоторые тонкости самого языка. Для более углубленного изучения выражений, стоит рассмотреть несколько примеров.
Для корректной записи выражений необходимо знать не только как обозначаются те или иные операции, функции и т. п., но также стоит предусмотреть приоритеты их выполнения, математические и логические правила, а также некоторые тонкости самого языка. Для более углубленного изучения выражений, стоит рассмотреть несколько примеров.
1) 12+3*3=21 (12+3)*3=45
Как видите выражения в Pascal, имеют такой же приоритет, как и в математике, а с помощью круглых скобок его можно изменить.
2) (a>1) and (a<=20)
Такое логическое выражение возвращает истину, лишь в том случае, когда истинны оба выражения, т. е. если a входит в диапазон от 1 до 20 включительно. Стоит обратить внимание на скобки, здесь они необходимы для изменения приоритета, так как у операторов сравнения он низший.
3) (a+3>0) and (a+3<15) or (b>1) and (b<10)
Условие вернет истину, тогда когда истинными будут два условия слева или справа от OR, а также если они оба будут истинными. (a) = exp(a*ln(x))
(a) = exp(a*ln(x))
В Pascal нет функции возведения числа в степень (кроме степени 2), поэтому существует два пути:
1 — умножать число само на себя, какое то количество раз;
2 — воспользоваться функциями экспоненты и натурального логарифма.
В этом примере использованы оба варианта, но если степень, в которую необходимо возвести число, достаточно велика, то предпочтение следует отдать второму способу.
Похожие записи:
Базовые правила журнала и расширяющиеся выражения журнала
Purplemath
Вы изучили различные правила для манипулирования и упрощения выражений с показателями, например, правило, которое гласит, что x 3 × x 5 равно x 8 , потому что вы можете складывать экспоненты. Аналогичные правила для логарифмов.
Аналогичные правила для логарифмов.
Правила журнала:
1) журнал b ( mn ) = журнал b ( m ) + журнал b ( n )
2) бревно b ( м / n ) = бревно b ( м ) — бревно b ( n )
3) журнал b ( м n ) = n · журнал b ( м )
MathHelp.com
Менее формально правила журнала могут быть выражены как:
1) Умножение внутри журнала можно превратить в сложение вне журнала, и наоборот.
2) Деление внутри журнала можно превратить в вычитание вне журнала, и наоборот.
3) Показатель для всего, что находится внутри бревна, можно вынести вперед как множитель, и наоборот.
Предупреждение: как и в случае с экспонентами, приведенные выше правила работают только , если основания совпадают. Например, выражение «log d ( m ) + log b ( n )» нельзя упростить, потому что основания («d» и «b») не совпадают, просто как x 2 × y 3 нельзя упростить, потому что основания ( x и y ) не совпадают.
Расширяющиеся логарифмы
Правила журнала могут использоваться для упрощения (или, точнее, для «уплотнения») выражений, для «расширения» выражений или для поиска значений. Начнем с расширения.
Когда в инструкциях говорится «расширить», они означают, что они дали мне одно выражение журнала с большим количеством информации внутри него, и они хотят, чтобы я использовал правила журнала, чтобы разбить журнал на множество отдельных терминов журнала, каждый из которых имеет только одна вещь внутри его конкретного журнала. То есть они дали мне , один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .
То есть они дали мне , один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .
В этом случае у меня внутри журнала есть «2 x ». Поскольку «2 x » — это умножение, я могу разделить это выражение в соответствии с первым из приведенных выше правил журнала и превратить его в сложение вне журнала:
журнал 3 (2 x ) = журнал 3 (2) + журнал 3 ( x )
Тогда ответ, который они ищут:
Примечание: не пытайтесь вычислить «log 3 (2)» в вашем калькуляторе.Хотя вы были бы правы, если бы сказали, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить на своем калькуляторе), что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Если вы дадите «ответ» в виде десятичного приближения, вы должны ожидать потерю баллов.
У меня внутри бревна деление.Согласно второму правилу журнала, приведенному выше, его можно разделить на части как вычитание вне журнала, поэтому:
журнал 4 ( 16 / x ) = журнал 4 (16) — журнал 4 ( x )
Первый член в правой части приведенного выше уравнения можно упростить до точного значения, применив основное определение логарифма. В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
Затем исходное выражение полностью раскрывается как:
журнал 4 ( 16 / x ) = 2 — журнал 4 ( x )
Всегда не забывайте находить время, чтобы проверить, можно ли упростить какие-либо термины в вашем расширении (например, журнал 4 (16) выше).
Показатель внутри бревна можно вынести как множитель:
log 5 ( x 3 ) = 3 · log 5 ( x ) = 3log 5 ( x )
Приведенные выше примеры представляют собой очень простое использование правил журнала применительно к раскрытию выражений журнала. На следующей странице мы рассмотрим, какие упражнения вы будете выполнять в своем домашнем задании и на следующем тесте.
URL: https://www.purplemath.com/modules/logrules.htm
Работа с логарифмами | Безграничная алгебра
Логарифмы произведений
Полезное свойство логарифмов гласит, что логарифм произведения двух величин является суммой логарифмов двух множителей. В символах [латекс] \ log_b (xy) = \ log_b (x) + \ log_b (y). [/ Latex]
В символах [латекс] \ log_b (xy) = \ log_b (x) + \ log_b (y). [/ Latex]
Цели обучения
Свяжите правило продукта для логарифмов с правилами работы с показателями степени и используйте это правило для перезаписи логарифмов продуктов
Основные выводы
Ключевые моменты
- Логарифм произведения — это сумма логарифмов факторов.
- Правило произведения не применяется, если основания двух логарифмов различаются.
Ключевые термины
- показатель степени : Степень возведения числа, символа или выражения.{\ log_b (z)} = z [/ латекс]
Правило произведения для логарифмов
Логарифмы были введены Джоном Нэпиром в начале 17 века как средство упрощения вычислений. Логарифмы были быстро приняты навигаторами, учеными, инженерами и другими, чтобы упростить вычисления с помощью правил скольжения и таблиц логарифмов. Утомительные шаги многозначного умножения могут быть заменены поиском в таблице и более простым сложением, поскольку логарифм произведения является суммой логарифмов множителей:
[латекс] \ displaystyle log_b (xy) = log_b (x) + log_b (y) [/ latex]
Мы можем убедиться, что это правило верно, если записать логарифмы в виде экспонент.
 p) = p \ log_b (x). [/ latex]
p) = p \ log_b (x). [/ latex]Цели обучения
Свяжите правило степени для логарифмов с правилами работы с показателями степени и используйте это правило для перезаписи логарифмов степеней
Основные выводы
Ключевые моменты
- Логарифм произведения — это сумма логарифмов факторов.
- Показатель степени [латекс] p [/ latex] означает, что число умножается само на себя [latex] p [/ latex] количество раз. Поскольку логарифм продукта является суммой логарифмов факторов, логарифм числа [латекс] x [/ латекс] до степени [латекс] p [/ латекс] совпадает с логарифмом of [latex] x [/ latex] сложено вместе [latex] p [/ latex] раз, так что оно равно [latex] p \ log_b (x).3) \\ x + 1 & = 3 \ log_2 (10) \\ x & = 3 \ log_2 (10) -1 \ end {align} [/ latex]
Следовательно, решением будет [латекс] x = 3 \ log_2 (10) -1. [/ латекс]
Логарифмы частных
Логарифм отношения двух величин — это разность логарифмов величин.
 В символах [латекс] \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — \ log_by. [/ Latex]
В символах [латекс] \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — \ log_by. [/ Latex]Цели обучения
Свяжите правило частного для логарифмов с правилами работы с показателями и используйте это правило для переписывания логарифмов частных
Основные выводы
Ключевые моменты
- Логарифм числа — это показатель степени, на который нужно возвести другое фиксированное значение, основание, чтобы получить это число.3 [/ латекс].
Мы уже видели, что логарифм произведения — это сумма логарифмов множителей:
[латекс] \ displaystyle \ log_b (xy) = \ log_bx + \ log_by [/ latex]
Точно так же логарифм отношения двух величин есть разность логарифмов:
[латекс] \ displaystyle \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — log_by. [/ Latex]
Мы можем показать, что это правда, на следующем примере:
Пусть [латекс] u = \ log_b x [/ latex] и [латекс] v = \ log_b y [/ latex].
 {100}) = 4 \ log_2x + 9 \ log_2y-100 \ log_2z. [/ Латекс]
{100}) = 4 \ log_2x + 9 \ log_2y-100 \ log_2z. [/ Латекс]Изменение логарифмического основания
Логарифм, записанный с одним основанием, может быть преобразован в равную величину, записанную с другим основанием.
Цели обучения
Используйте изменение базовой формулы для преобразования логарифмов в разные основания
Основные выводы
Ключевые моменты
- Основание логарифма можно изменить, выразив его как частное двух логарифмов с общим основанием.
- Изменение основания логарифма на [латекс] 10 [/ латекс] значительно упрощает вычисление; это можно сделать на калькуляторе.
Ключевые термины
- логарифм : Логарифм числа — это показатель степени, на который необходимо увеличить другое фиксированное значение, основание, чтобы получить это число.
- с основанием : Число в степени экспоненты.
Большинство обычных научных калькуляторов имеют ключ для вычисления логарифмов с основанием [латекс] 10 [/ latex], но не имеют ключей для других оснований.
 z = \ log_bx [/ latex]
z = \ log_bx [/ latex]Использование правила мощности дает:
[латекс] \ Displaystyle Z \ cdot \ log_ba = \ log_b x [/ латекс]
Разделив обе стороны на [latex] \ log_ba [/ latex], получим:
[латекс] \ displaystyle z = {\ log_b x \ over \ log_ba}.2 + 1 \ over \ log_ {10} 5}. [/ латекс]
РЕШЕНИЕ: Выразите y через x log base 4 y = log base 2 x + log base 2 9
Чтобы выразить y через x, нам нужно получить y из аргумента логарифма. И чтобы получить переменную из аргумента логарифма, вы обычно начинаете с преобразования уравнения в одну из следующих форм:
log (выражение-переменная) = выражение-другое
или
log (выражение-переменное) = log (другое- выражение)
(с одинаковыми основаниями логарифмов во второй форме).Чтобы получить любую из этих форм из вашего уравнения, нам необходимо иметь одинаковые основания для каждого логарифма. Итак, нам нужно:
- Сделать основания логарифмов равными.
- Преобразуйте новое уравнение в одну из приведенных выше форм.

- Решите уравнение для y из шага 2.
Давайте посмотрим на это в действии.
1. Базы одинаковые. Поскольку существует только один логарифм с основанием 4, мы изменим его, чтобы он соответствовал основанию других (основание 2). Есть формула преобразования основ логарифмов.Чтобы заменить логарифм с основанием «a» на выражение с логарифмом с основанием «b»:. Чтобы преобразовать в эквивалентное выражение логарифмов с основанием 2:. Подставив это выражение с основанием 2 вместо логарифма с основанием 4, мы получим уравнение:
К счастью, с тех пор. Таким образом, наше уравнение упрощается до:2. Преобразуйте уравнение в одну из приведенных выше форм. Поскольку каждый член нашего уравнения является логарифмом, я буду работать над второй формой. Для этого потребуется объединить три логарифма справа в один логарифм.К счастью, у нас есть свойства логарифмов, которые позволяют нам это делать:
Поскольку между первыми двумя логарифмами стоит знак «+», мы будем использовать первое свойство для их объединения:
или
Поскольку между двумя оставшимися логарифмами стоит знак «-», я буду использовать второе свойство, чтобы объединить их:
, что упрощается до
Мы близки ко второй форме. Но 2 в знаменателе нужно убрать. Если мы умножим обе стороны на 2, получим:
Но 2 в знаменателе нужно убрать. Если мы умножим обе стороны на 2, получим:
2 все еще мешает, но находится в лучшем месте.Теперь мы можем использовать третье свойство логарифмов, которое позволяет нам переместить коэффициент в аргумент как показатель степени:
, что упрощается до
Мы наконец достигли второй формы (log (…) = log (. ..)).3. Решите уравнение относительно y. Это требует, чтобы мы получили y из аргумента слева. Со второй формой это довольно просто. Уравнение говорит, что логарифм y по основанию 2 равен логарифму по основанию 2. Если их бревна равны, то они равны. Другими словами:
, который выражает y через x.логарифмов
логарифмовЛогарифм — показатель степени. Логарифм — это показатель степени, который указывает, в какой степени для получения заданного числа необходимо поднять базу.
г = b x экспоненциальная форма
х = журнал b y логарифмический форма
x — логарифм y по основанию b
log b y — это степень, в которую мы должны возвести b, чтобы получить y
Мы выражаем x через y
Примеры
x = журнал b y
x = журнал 2 8 Это означает логарифм 8 по основанию 2.  Это
экспонента, до которой нужно возвести 2, чтобы получить 8. Мы знаем, что 2 (2) (2)
= 8. Следовательно, x = 3.
Это
экспонента, до которой нужно возвести 2, чтобы получить 8. Мы знаем, что 2 (2) (2)
= 8. Следовательно, x = 3.x = журнал 6 36 Это означает логарифм 36 по основанию 6. Это показатель степени, до которого нужно возвести 6, чтобы получить 36. Мы знаем, что 6 (6) = 36. Следовательно, x = 2. x = журнал 10 10,000 Это означает логарифм 10000 с основанием 10.Это — показатель степени, до которого нужно поднять 10, чтобы получить 10 000. Мы знаем что 10 (10) (10) (10) = 10,000. Следовательно, x = 4. журнал b b = 1 Логарифм любого числа по одному основанию равен 1. x = журнал 11 11 Это означает логарифм 11 по основанию 11.  Это показатель степени.
на которое нужно поднять 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, x = 1.
Это показатель степени.
на которое нужно поднять 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, x = 1.журнал b 1 = 0 Логарифм 1 всегда равен 0.
Любое число может служить базой b.
Общий (Бриггсиан) логарифмы Основание 10.логарифмов к базе 10 широко используются. Таким образом, обычно опускают нижний индекс.Если база не указана, значит, база равна 10.
журнал 10 y = журнал y
Натуральный (Наперианские) логарифмы Основание — e.
Помнить e — иррациональное число, где e = 2,71828 … Символ «ln» относится к натуральным логарифмам.журнал e x = ln x ln x — показатель степени, до которого необходимо возвести e, чтобы получить x. 
Почему мы хотим использовать логарифмы? Для упрощения расчетов во многих случаях.
Правила логарифмовПравило продукта Правило частных Power rule Это правило полезно, потому что оно позволяет нам решать уравнения где переменная — показатель степени.
Экспоненциальные и логарифмические функции являются обратными функциямиРассмотрим следующие таблицы и связанные графики:
x
f (x) = e x
x
f (x) = ln x
0
1
1
0
1
2.
 7
72,7
1
2
7,39
7,39
2
3
20
20
3
[индекс]
% PDF-1.4 % 240 0 объект > эндобдж xref 240 64 0000000016 00000 н. 0000001649 00000 н. 0000001913 00000 н. 0000002065 00000 н. 0000002140 00000 н. 0000002402 00000 п. 0000003686 00000 н. 0000004107 00000 п. 0000004186 00000 п. 0000004513 00000 н. 0000004908 00000 н. 0000005315 00000 н. 0000005337 00000 н. 0000005446 00000 н. 0000006796 00000 н. 0000006818 00000 н. 0000007016 00000 н. 0000007213 00000 н. 0000007411 00000 н.
Логарифм 0000007609 00000 н.
0000007807 00000 н.
0000008080 00000 н.
0000008387 00000 н.
0000008743 00000 н.
0000009013 00000 н.
0000009034 00000 н.
0000024051 00000 п.
0000024075 00000 п.
0000024128 00000 п.
0000024341 00000 п.
0000024522 00000 п.
0000025371 00000 п.
0000026217 00000 п.
0000026425 00000 н.
0000026455 00000 п.
0000027362 00000 п.
0000027384 00000 п.
0000027746 00000 п.
0000028077 00000 п.
0000028270 00000 п.
0000030317 00000 п.
0000030781 00000 п.
0000031632 00000 п.
0000031835 00000 п.
0000032685 00000 п.
0000032897 00000 н.
0000033016 00000 п.
0000033318 00000 п.
0000033402 00000 п.
0000034191 00000 п.
0000034395 00000 п.
0000034457 00000 п.
0000034567 00000 п.
0000034594 00000 п.
0000034621 00000 п.
0000034648 00000 п.
0000034799 00000 н.
0000034943 00000 п.
0000035011 00000 п.
0000035079 00000 п.
0000035147 00000 п.
0000035215 00000 п.
0000002443 00000 н.
0000003663 00000 н.
трейлер
]
>>
startxref
0
%% EOF
241 0 объект
>
/ Имена 245 0 руб.
0000007609 00000 н.
0000007807 00000 н.
0000008080 00000 н.
0000008387 00000 н.
0000008743 00000 н.
0000009013 00000 н.
0000009034 00000 н.
0000024051 00000 п.
0000024075 00000 п.
0000024128 00000 п.
0000024341 00000 п.
0000024522 00000 п.
0000025371 00000 п.
0000026217 00000 п.
0000026425 00000 н.
0000026455 00000 п.
0000027362 00000 п.
0000027384 00000 п.
0000027746 00000 п.
0000028077 00000 п.
0000028270 00000 п.
0000030317 00000 п.
0000030781 00000 п.
0000031632 00000 п.
0000031835 00000 п.
0000032685 00000 п.
0000032897 00000 н.
0000033016 00000 п.
0000033318 00000 п.
0000033402 00000 п.
0000034191 00000 п.
0000034395 00000 п.
0000034457 00000 п.
0000034567 00000 п.
0000034594 00000 п.
0000034621 00000 п.
0000034648 00000 п.
0000034799 00000 н.
0000034943 00000 п.
0000035011 00000 п.
0000035079 00000 п.
0000035147 00000 п.
0000035215 00000 п.
0000002443 00000 н.
0000003663 00000 н.
трейлер
]
>>
startxref
0
%% EOF
241 0 объект
>
/ Имена 245 0 руб. YVxp @ => A} ĽXP {Ȇqup>% Qz
YVxp @ => A} ĽXP {Ȇqup>% Qz| Правила, примеры и формулы
Логарифм , показатель степени или степень, до которой необходимо возвести основание, чтобы получить данное число.Выражаясь математически, x — это логарифм n по основанию b , если b x = n , и в этом случае записывается x = log b n . Например, 2 3 = 8; следовательно, 3 — это логарифм 8 с основанием 2, или 3 = log 2 8. Таким же образом, поскольку 10 2 = 100, тогда 2 = log 10 100. Логарифмы последнего вида (что (логарифмы с основанием 10) называются обычными, или бриггсовскими, логарифмами и записываются просто log n .
Логарифмы, изобретенные в 17 веке для ускорения вычислений, значительно сократили время, необходимое для умножения чисел на многозначные числа. Они были основой численной работы более 300 лет, пока совершенствование механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделало их устаревшими для крупномасштабных вычислений.
 Натуральный логарифм (с основанием e ≅ 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из самых полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.
Натуральный логарифм (с основанием e ≅ 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из самых полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.Свойства логарифмов
Логарифмыбыли быстро приняты учеными из-за различных полезных свойств, которые упростили долгие и утомительные вычисления. В частности, ученые могли найти произведение двух чисел m и n , просмотрев логарифм каждого числа в специальной таблице, сложив логарифмы вместе, а затем снова просмотрев таблицу, чтобы найти число с вычисленным логарифмом (известным как его антилогарифм). Выраженное в терминах десятичных логарифмов, это соотношение определяется как log m n = log m + log n .Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы вместе (5), а затем найдя его антилогарифм (100000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с помощью логарифмов: log m / n = log m — log n .
 Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться как основание, поскольку все его степени равны 1), как показано в таблице логарифмических законов.
Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться как основание, поскольку все его степени равны 1), как показано в таблице логарифмических законов.В таблицы логарифмов обычно включались только логарифмы для чисел от 0 до 10. Чтобы получить логарифм некоторого числа за пределами этого диапазона, число сначала было записано в экспоненциальной форме как произведение его значащих цифр и его экспоненциальной степени — например, 358 будет записано как 3,58 × 10 2 , а 0,0046 будет можно записать как 4,6 × 10 −3 . Тогда логарифм значащих цифр — десятичная дробь от 0 до 1, известная как мантисса, — будет найден в таблице.Например, чтобы найти логарифм 358, нужно найти log 3,58 ≅ 0,55388. Следовательно, журнал 358 = журнал 3,58 + журнал 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательной экспонентой, например 0,0046, можно найти log 4,6 ≅ 0,66276.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724.
Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724.История логарифмов
Изобретение логарифмов было предсказано сравнением арифметических и геометрических последовательностей.В геометрической последовательности каждый член образует постоянное отношение со своим последователем; Например, … 1/1000, 1/100, 1/10, 1, 10, 100, 1000… имеет общее отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как общая разница; Например, … −3, −2, −1, 0, 1, 2, 3… имеет общее различие 1. Обратите внимание, что геометрическая последовательность может быть записана в терминах ее общего отношения; для примера геометрической последовательности, приведенной выше: … 10 −3 , 10 −2 , 10 −1 , 10 0 , 10 1 , 10 2 , 10 3 ….Умножение двух чисел в геометрической последовательности, скажем 1/10 и 100, равносильно сложению соответствующих показателей общего отношения, -1 и 2, чтобы получить 10 1 = 10.
 Таким образом, умножение преобразуется в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.
Таким образом, умножение преобразуется в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.Шотландский математик Джон Напьер опубликовал свое открытие логарифмов в 1614 году. Его цель заключалась в том, чтобы помочь в умножении величин, которые тогда назывались синусами. Полный синус был величиной стороны прямоугольного треугольника с большой гипотенузой. (Первоначальная гипотенуза Нэпьера была 10 7 .) Его определение было дано в терминах относительных скоростей.
Логарифм, следовательно, любого синуса — это число, очень точно выражающее линию, которая одинаково увеличивалась за определенное время, в то время как линия всего синуса пропорционально уменьшалась до этого синуса, причем оба движения равны по времени и начало одинаково сдвигается.

В сотрудничестве с английским математиком Генри Бриггсом Нэпьер привел свой логарифм в его современную форму. Для логарифма Напериана сравнение будет происходить между точками, движущимися по градуированной прямой, точка L (для логарифма) равномерно перемещается от минус бесконечности к плюс бесконечности, точка X (для синуса) движется от нуля до бесконечность со скоростью, пропорциональной ее расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице и их скорость в этот момент равна.Суть открытия Напьера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; т.е. умножение и возведение в степень значений точки X соответствуют сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0.
 Это изменение привело к появлению бриггсовского, или обыкновенного, логарифма.
Это изменение привело к появлению бриггсовского, или обыкновенного, логарифма.Нэпир умер в 1617 году, и Бриггс продолжал работать в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанных до 14 десятичных знаков для чисел от 1 до 20 000 и от 90 000 до 100 000. В 1628 году голландский издатель Адриан Влак составил 10-местную таблицу для значений от 1 до 100 000, добавив недостающие 70 000 значений. И Бриггс, и Влакк занимались настройкой тригонометрических таблиц журнала. Такие ранние таблицы были либо с точностью до одной сотой градуса, либо до одной угловой минуты.В 18 веке таблицы публиковались с интервалом в 10 секунд, что было удобно для таблиц с семью знаками после запятой. Как правило, более мелкие интервалы требуются для вычисления логарифмических функций меньших чисел — например, при вычислении функций log sin x и log tan x .
Наличие логарифмов сильно повлияло на форму плоской и сферической тригонометрии. Процедуры тригонометрии были переработаны для создания формул, в которых операции, зависящие от логарифмов, выполняются одновременно.
Фрэнсис Дж. Мюррей Обращение к таблицам тогда состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.
Обращение к таблицам тогда состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.Узнайте больше в этих связанных статьях Britannica:
Свойства логарифма
Логарифмы и их обратные свойства
Напомним определение логарифма по основанию b : дано b> 0, где b ≠ 1,
y = logb x тогда и только тогда, когда x = на
Используйте это определение для преобразования логарифмов в экспоненциальную форму.Поступая так, мы можем получить несколько свойств:
logb 1 = 0, потому что b0 = 1 logb b = 1, потому что b1 = blogb (1b) = — 1, потому что b − 1 = 1b
Пример 1
Оценить:
- журнал 1
- ln e
- журнал5 (15)
Решение:
Если основание не записано, предполагается, что оно равно 10.
. Это десятичный логарифм
Это десятичный логарифмжурнал 1 = журнал10 1 = 0
Натуральный логарифм по определению имеет основание e ,
ln e = loge = 1
Поскольку 5−1 = 15, получаем
log5 (15) = — 1
Кроме того, рассмотрим дробное основание вида 1 / b, где b> 1.
log1 / b b = −1, поскольку (1b) −1 = 1−1b − 1 = b1 = b
Пример 2
Оценить:
- лог1 / 4 4
- журнал2 / 3 (32)
Решение:
- log1 / 4 4 = −1, поскольку (14) −1 = 4
- log2 / 3 (32) = — 1, поскольку (23) −1 = 32
Для экспоненциальной функции, определяемой формулой f (x) = bx, где b> 0 и b 1, обратным ей является логарифм с основанием b , f − 1 (x) = logb x.
 И поскольку f (f − 1 (x)) = x и f − 1 (f (x)) = x, у нас есть следующие обратные свойства логарифма, заданного b> 0, мы имеем logb bx = x и blogb x = x, когда х> 0 .:
И поскольку f (f − 1 (x)) = x и f − 1 (f (x)) = x, у нас есть следующие обратные свойства логарифма, заданного b> 0, мы имеем logb bx = x и blogb x = x, когда х> 0 .:f − 1 (f (x)) = logb bx = xandf (f − 1 (x)) = blogb x = x, x> 0
Поскольку f − 1 (x) = logb x имеет область, состоящую из положительных значений (0, ∞), свойство blogb x = x ограничено значениями, где x> 0.
Пример 3
Оценить:
- журнал 5625
- 5log5 3
- элн 5
Решение:
Примените обратные свойства логарифма.
- log5 625 = log5 54 = 4
- 5log5 3 = 3
- eln 5 = 5
Таким образом, когда b> 0 и b ≠ 1, мы имеем следующие свойства:
logb 1 = 0
logb b = 1
log1 / b b = -1
logb (1b) = — 1
logb bx = x
блогb x = x, x> 0
Попробуй! Вычислить: журнал 0.
 00001
00001Ответ: −5
Произведение, частное и степенные свойства логарифмов
В этом разделе описаны три очень важных свойства логарифма. Эти свойства позволят нам расширить нашу способность решать гораздо больше уравнений. Мы начинаем с присвоения u и v следующим логарифмам, а затем записываем их в экспоненциальной форме:
logb x = u ⇒ bu = xlogb y = v ⇒ bv = y
Подставляем вместо x = bu и y = bv логарифм произведения logb (xy) и логарифм частного logb (xy).Затем упростите, используя правила экспонент и обратные свойства логарифма.
Логарифм продукта
Логарифм частного
logb (xy) = logb (bubv) = logb bu + v = u + v = logb x + logb y
logb (xy) = logb (bubv) = logb bu − v = u − v = logb x − logb y
Это дает нам два важных свойства: свойство произведения logarithmslogb (xy) = logb x + logb y; логарифм продукта равен сумме логарифма факторов.
 ,
,logb (xy) = logb x + logb y
и факторное свойство logarithmslogb (xy) = logb x − logb y; логарифм частного равен разности логарифма числителя и логарифма знаменателя.,
logb (xy) = logb x − logb y
Проще говоря, логарифм продукта равен сумме логарифма факторов. Точно так же логарифм частного равен разности логарифма числителя и логарифма знаменателя.
Пример 4
Запишите как сумму: log2 (8x).
Решение:
Примените свойство произведения логарифмов, а затем упростите.
log2 (8x) = log2 8 + log2 x = log2 23 + log2 x = 3 + log2 x
Ответ: 3 + log2 x
Пример 5
Запишите как разницу: журнал (x10).
Решение:
Примените свойство логарифмов частного, а затем упростите.
журнал (x10) = журнал x − log 10 = журнал x − 1
Ответ: log x − 1
Затем мы начинаем с logb x = u и переписываем его в экспоненциальной форме.
 После возведения обеих сторон в степень n преобразовать обратно в логарифмическую форму, а затем обратно подставить.
После возведения обеих сторон в степень n преобразовать обратно в логарифмическую форму, а затем обратно подставить.logb x = u ⇒ bu = x (bu) n = (x) nlogb xn = nu ⇐ bnu = xnlogb xn = nlogb x
Это приводит нас к свойству мощности logarithmslogb xn = nlogb x; логарифм величины, возведенный в степень, равен этой степени, умноженной на логарифм количества.,
logb xn = nlogb x
Словами, логарифм величины в степени равен этой степени, умноженной на логарифм величины.
Пример 6
Напишите как продукт:
- журнал2 x4
- log5 (х).
Решение:
Примените свойство логарифмов мощности.
log2 x4 = 4 log2 x
Напомним, что квадратный корень можно выразить с помощью рациональных показателей x = x1 / 2.
 Сделайте эту замену, а затем примените степенное свойство логарифмов.
Сделайте эту замену, а затем примените степенное свойство логарифмов.log5 (x) = log5 x1 / 2 = 12 log5 x
Таким образом,
Свойство продукта логарифмов
logb (xy) = logb x + logb y
Частное свойство логарифмов
logb (xy) = logb x − logb y
Силовые свойства логарифмов
logb xn = nlogb x
Мы можем использовать эти свойства для раскрытия логарифмов, включающих произведения, частные и степени, используя суммы, разности и коэффициенты.
 Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.Внимание! Важно отметить следующее:
журнал (xy) ≠ журнал x⋅log y и журнал (xy) ≠ журнал xlog y
Пример 7
Полностью развернуть: ln (2×3).
Решение:
Напомним, что натуральный логарифм является основанием логарифма e , ln x = loge x.Следовательно, применяются все свойства логарифма.
ln (2×3) = ln 2 + ln x3 Правило произведения для логарифмов = ln 2 + 3ln x Правило степени для логарифмов
Ответ: ln 2 + 3ln x
Пример 8
Полностью развернуть: журнал 10xy23.
Решение:
Начните с переписывания корня куба, используя рациональную экспоненту 13, а затем примените свойства логарифма.
журнал 10xy23 = журнал (10xy2) 1/3 = 13log (10xy2) = 13 (журнал 10 + журнал x + журнал y2) = 13 (1 + журнал x + 2log y) = 13 + 13log x + 23log y
Ответ: 13 + 13log x + 23log y
Пример 9
Полностью развернуть: log2 ((x + 1) 25y).

Решение:
Применяя свойство продукта к знаменателю, позаботьтесь о распределении отрицательного значения, полученного в результате применения свойства частного.
log2 ((x + 1) 25y) = log2 (x + 1) 2 − log2 (5y) = log2 (x + 1) 2− (log2 5 + log2 y) Распределить. = Log2 (x + 1) 2− log2 5 − log2 y = 2 log2 (x + 1) −log2 5 − log2 y
Ответ: 2log2 (x + 1) −log2 5 − log2 y
Осторожно : Нет правила, позволяющего расширить логарифм суммы или разницы.Другими словами,
журнал (x ± y) ≠ журнал x ± журнал y
Попробуй! Полностью развернуть: ln (5y4x).
Ответ: ln 5 + 4ln y − 12ln x
Пример 10
Учитывая, что log2 x = a, log2 y = b и log2 z = c, запишите следующее в терминах a , b и c :
а.
 log2 (8x2y)
log2 (8x2y)г.log2 (2x4z)
Решение:
Начните с расширения с использованием сумм и коэффициентов, а затем замените a и b соответствующим логарифмом.
log2 (8x2y) = log2 8 + log2 x2 + log2 y = log2 8 + 2log2 x + log2 y = 3 + 2a + b
Разверните, а затем замените на , b и c , где это необходимо.
log2 (2x4z) = log2 (2×4) −log2 z1 / 2 = log2 2 + log2 x4 − log2 z1 / 2 = log2 2 + 4log2 x − 12log2 z = 1 + 4a − 12b
Далее мы упростим логарифмические выражения. Как мы увидим, важно иметь возможность объединить выражение, содержащее логарифмы, в единый логарифм с коэффициентом 1. Это будет одним из первых шагов при решении логарифмических уравнений.

Пример 11
Запишите как один логарифм с коэффициентом 1: 3log3 x − log3 y + 2log3 5.
Решение:
Начните с переписывания всех логарифмических членов с коэффициентом 1. Используйте для этого правило степени. Затем используйте правила произведения и частного для дальнейшего упрощения.
3log3x − log3y + 2log35 = {log3x3 − log3y} + log352 свойство частного = {log3 (x3y) + log325} свойство продукта = log3 (x3y⋅25) = log3 (25x3y)Ответ: log3 (25x3y)
Пример 12
Запишем одним логарифмом с коэффициентом 1: 12ln x − 3ln y − ln z.
Решение:
Начнем с записи коэффициентов логарифмов в виде степеней их аргумента, после чего мы дважды применим правило частного, работая слева направо.
12ln x − 3ln y − ln z = ln x1 / 2 − ln y3 − ln z = ln (x1 / 2y3) −ln z = ln (x1 / 2y3 ÷ z) = ln (x1 / 2y3⋅1z) = ln (x1 / 2y3z) или = ln (xy3z)
Ответ: ln (xy3z)
Попробуй! Запишите как один логарифм с коэффициентом 1: 3log (x + y) −6log z + 2log 5.

Ответ: log (25 (x + y) 3z6)
Основные выводы
- Для любого основания b> 0 и b ≠ 1 мы можем сказать, что logb 1 = 0, logb b = 1, log1 / b b = −1 и что logb (1b) = — 1.
- Обратные свойства логарифма: logb bx = x и blogb x = x, где x> 0.
- Свойство произведения логарифма позволяет нам записать произведение в виде суммы: logb (xy) = logb x + logb y.
- Факторное свойство логарифма позволяет нам записать частное как разность: logb (xy) = logb x − logb y.
- Степенное свойство логарифма позволяет нам записывать показатели в виде коэффициентов: logb xn = nlogb x.
- Поскольку натуральный логарифм является логарифмом по основанию e , ln x = loge x, к нему применяются все свойства логарифма.
- Мы можем использовать свойства логарифма для расширения логарифмических выражений, используя суммы, разности и коэффициенты.
 Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены. - Мы можем использовать свойства логарифма, чтобы объединить выражения, содержащие логарифмы, в единый логарифм с коэффициентом 1. Это важный навык, который необходимо изучить в этой главе.
Тематические упражнения
ln (1e)
log1 / 2 (12)
Часть A: Логарифмы и их обратные свойства
Вычислить:
Найдите a :
log2 (xy2)
log5 (25x)
log3 (x3yz2)
журнал (xy3z2)
log5 (1x2yz)
log4 (116x2z3)
log3 (x2y3z)
журнал (2 (x + y) 3z2)
журнал (100×3 (y + 10) 3)
log7 (х (у + z) 35)
log5 (x3yz23)
журнал (x2y3z25)
log3 (27x2y3z)
log3 (xy3z)
log3 (9x2yz3)
log3 (x3yz2)
log2 5 + 2log2 x + log2 y
log3 4 + 3log3 x + 12log3 y
3log2 x − 2log2 y + 12log2 z
4log x − log y − log 2
log3 x − 2log3 y + 5log3 z
7log x − log y − 2log z
2ln x − 3ln y − ln z
23log3 x − 12 (log3 y + log3 z)
15 (log7 x + 2log7 y) −2log7 (z + 1)
−ln 2 + 2ln (x + y) −ln z
−3ln (x − y) −ln z + ln 5
13 (ln x + 2ln y) — (3ln 2 + ln z)
4log 2 + 23log x − 4log (y + z)
log2 3−2log2 x + 12log2 y − 4log2 z
2log5 4 − log5 x − 3log5 y + 23log5 z
журнал (x + 1) + журнал (x − 1)
журнал2 (x + 2) + журнал2 (x + 1)
лин (x2 + 2x + 1) −ln (x + 1)
лин (x2−9) −ln (x + 3)
log5 (x3-8) −log5 (x − 2)
log3 (x3 + 1) −log3 (x + 1)
журнал x + журнал (x + 5) −log (x2−25)
журнал (2x + 1) + журнал (x − 3) −log (2×2−5x − 3)
Часть B: Произведение, частное и степенные свойства логарифмов
Полностью развернуть.

Учитывая log3 x = a, log3 y = b и log3 z = c, запишите следующие логарифмы в единицах a , b и c .

Дано logb 2 = 0.43, logb 3 = 0,68 и logb 7 = 1,21, рассчитайте следующее. (Подсказка: разверните, используя суммы, разности и частные множителей 2, 3 и 7.)
Разверните, используя свойства логарифма, а затем приблизьте с помощью калькулятора до ближайшей десятой.

Записать в виде единственного логарифма с коэффициентом 1.
Выразите как единственный логарифм и упростите.

ответы
3log3 x − log3 y − 2log3 z
−2log5 x − log5 y − log5 z
log7 2 + 12log7 x + 12log7 y
2log3 x + 13log3 y − log3 z
2 + 3log x − 3log (y + 10)
3log5 x − 13log5 y − 23log5 z
лн (6.
 2) −15≈ − 13,2
2) −15≈ − 13,2log2 (x3zy2)
ln (xzy6)
журнал (x7yz2)
log3 (x23yz)
log2 (2xy)
log2 (xy23)
ln ((x + y) 22z)
ln (xy238z)
log2 (3yx2z4)
журнал (xx − 5)


 Но ряд:
Но ряд: Десятичные (lg) и натуральные логарифмы (ln).
Десятичные (lg) и натуральные логарифмы (ln). Но ряд:
Но ряд: p) = p \ log_b (x). [/ latex]
p) = p \ log_b (x). [/ latex] В символах [латекс] \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — \ log_by. [/ Latex]
В символах [латекс] \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — \ log_by. [/ Latex] {100}) = 4 \ log_2x + 9 \ log_2y-100 \ log_2z. [/ Латекс]
{100}) = 4 \ log_2x + 9 \ log_2y-100 \ log_2z. [/ Латекс] z = \ log_bx [/ latex]
z = \ log_bx [/ latex]
 Но 2 в знаменателе нужно убрать. Если мы умножим обе стороны на 2, получим:
Но 2 в знаменателе нужно убрать. Если мы умножим обе стороны на 2, получим:  Это
экспонента, до которой нужно возвести 2, чтобы получить 8. Мы знаем, что 2 (2) (2)
= 8. Следовательно, x = 3.
Это
экспонента, до которой нужно возвести 2, чтобы получить 8. Мы знаем, что 2 (2) (2)
= 8. Следовательно, x = 3. Это показатель степени.
на которое нужно поднять 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, x = 1.
Это показатель степени.
на которое нужно поднять 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, x = 1.
 7
7 0000007609 00000 н.
0000007807 00000 н.
0000008080 00000 н.
0000008387 00000 н.
0000008743 00000 н.
0000009013 00000 н.
0000009034 00000 н.
0000024051 00000 п.
0000024075 00000 п.
0000024128 00000 п.
0000024341 00000 п.
0000024522 00000 п.
0000025371 00000 п.
0000026217 00000 п.
0000026425 00000 н.
0000026455 00000 п.
0000027362 00000 п.
0000027384 00000 п.
0000027746 00000 п.
0000028077 00000 п.
0000028270 00000 п.
0000030317 00000 п.
0000030781 00000 п.
0000031632 00000 п.
0000031835 00000 п.
0000032685 00000 п.
0000032897 00000 н.
0000033016 00000 п.
0000033318 00000 п.
0000033402 00000 п.
0000034191 00000 п.
0000034395 00000 п.
0000034457 00000 п.
0000034567 00000 п.
0000034594 00000 п.
0000034621 00000 п.
0000034648 00000 п.
0000034799 00000 н.
0000034943 00000 п.
0000035011 00000 п.
0000035079 00000 п.
0000035147 00000 п.
0000035215 00000 п.
0000002443 00000 н.
0000003663 00000 н.
трейлер
]
>>
startxref
0
%% EOF
241 0 объект
>
/ Имена 245 0 руб.
0000007609 00000 н.
0000007807 00000 н.
0000008080 00000 н.
0000008387 00000 н.
0000008743 00000 н.
0000009013 00000 н.
0000009034 00000 н.
0000024051 00000 п.
0000024075 00000 п.
0000024128 00000 п.
0000024341 00000 п.
0000024522 00000 п.
0000025371 00000 п.
0000026217 00000 п.
0000026425 00000 н.
0000026455 00000 п.
0000027362 00000 п.
0000027384 00000 п.
0000027746 00000 п.
0000028077 00000 п.
0000028270 00000 п.
0000030317 00000 п.
0000030781 00000 п.
0000031632 00000 п.
0000031835 00000 п.
0000032685 00000 п.
0000032897 00000 н.
0000033016 00000 п.
0000033318 00000 п.
0000033402 00000 п.
0000034191 00000 п.
0000034395 00000 п.
0000034457 00000 п.
0000034567 00000 п.
0000034594 00000 п.
0000034621 00000 п.
0000034648 00000 п.
0000034799 00000 н.
0000034943 00000 п.
0000035011 00000 п.
0000035079 00000 п.
0000035147 00000 п.
0000035215 00000 п.
0000002443 00000 н.
0000003663 00000 н.
трейлер
]
>>
startxref
0
%% EOF
241 0 объект
>
/ Имена 245 0 руб. YVxp @ => A} ĽXP {Ȇqup>% Qz
YVxp @ => A} ĽXP {Ȇqup>% Qz Натуральный логарифм (с основанием e ≅ 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из самых полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.
Натуральный логарифм (с основанием e ≅ 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из самых полезных функций в математике с приложениями к математическим моделям в физических и биологических науках. Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться как основание, поскольку все его степени равны 1), как показано в таблице логарифмических законов.
Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться как основание, поскольку все его степени равны 1), как показано в таблице логарифмических законов. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724.
Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724. Таким образом, умножение преобразуется в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.
Таким образом, умножение преобразуется в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.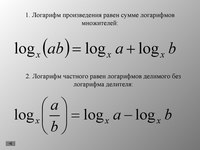
 Это изменение привело к появлению бриггсовского, или обыкновенного, логарифма.
Это изменение привело к появлению бриггсовского, или обыкновенного, логарифма. Обращение к таблицам тогда состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.
Обращение к таблицам тогда состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов. Это десятичный логарифм
Это десятичный логарифм И поскольку f (f − 1 (x)) = x и f − 1 (f (x)) = x, у нас есть следующие обратные свойства логарифма, заданного b> 0, мы имеем logb bx = x и blogb x = x, когда х> 0 .:
И поскольку f (f − 1 (x)) = x и f − 1 (f (x)) = x, у нас есть следующие обратные свойства логарифма, заданного b> 0, мы имеем logb bx = x и blogb x = x, когда х> 0 .: 00001
00001 ,
, После возведения обеих сторон в степень n преобразовать обратно в логарифмическую форму, а затем обратно подставить.
После возведения обеих сторон в степень n преобразовать обратно в логарифмическую форму, а затем обратно подставить. Сделайте эту замену, а затем примените степенное свойство логарифмов.
Сделайте эту замену, а затем примените степенное свойство логарифмов. Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
 log2 (8x2y)
log2 (8x2y)

 Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.



 2) −15≈ − 13,2
2) −15≈ − 13,2