3.Линейная функция вида y = kx + b

Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.

В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).

Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.

Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.

Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.

Свойства линейной функции:

1) Область определения линейной функции есть вся вещественная ось;

2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b;

3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.

a) b ≠ 0, k = 0, следовательно, y = b – четная;

b) b = 0, k ≠ 0, следовательно y = kx – нечетная;

c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;

d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.

4) Свойством периодичности линейная функция не обладает;

5) Точки пересечения с осями координат:

Ox:  y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.

Oy:  y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.

Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.

6) Промежутки знакопостоянства зависят от коэффициента k.

a) k > 0;  kx + b > 0, kx > -b, x > -b/k.

y = kx + b – положительна при x  из (-b/k; +∞),

y = kx + b – отрицательна при x  из (-∞; -b/k).

b) k < 0; kx + b < 0, kx < -b, x < -b/k.

y = kx + b – положительна при x  из (-∞; -b/k),

y = kx + b – отрицательна при x  из (-b/k; +∞).

c) k = 0, b > 0; y = kx + b положительна на всей области определения,

k = 0, b < 0; y = kx + b

отрицательна на всей области определения.

7) Промежутки монотонности линейной функции зависят от коэффициента k.

k > 0, следовательно y = kx + b возрастает на всей области определения,

k < 0, следовательно y = kx + b убывает на всей области определения.

8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b. Ниже приведена таблица, которая наглядно это иллюстрирует.

Линейная функция y = kx — урок. Алгебра, 7 класс.

Рассматривая линейную функцию вида \(y=kx + m\), особо выделяют случай, когда \(m=0\).

Тогда линейная функция принимает вид \(y=kx\).

Графиком линейной функции \(y=kx\) является прямая, проходящая через начало координат.

Важно уметь переходить от аналитической модели \(y=kx\) к геометрической и, наоборот, от геометрической к аналитической модели.

 

Например, рассмотрим прямую, изображённую на рисунке.

 

 

Эта прямая является графиком линейной функции \(y=kx\), так как проходит через начало координат. Нужно лишь определить значение коэффициента \(k\).

Из формулы линейной функции \(y=kx\) получим, что k=yx.

 

Чтобы определить коэффициент \(k\), необходимо выбрать некоторую точку на прямой и вычислить частное ординаты и абсциссы заданной точки.

 

Прямая проходит через точку \(M(4; 2)\), следовательно получим 24=0,5. Значит, \(k=0,5\), и данная прямая является графиком линейной функции \(y=0,5x\).

 

Если в формуле \(y=kx\) вместо \(x\) подставим \(1\), то получим \(y=k\). Это означает, что прямая  \(y=kx\) проходит через точку \((1; k)\). Поэтому график линейной функции можно строить по двум точкам: \((0;0)\) и \((1; k)\).

Иногда вместо точки \((1; k)\) удобнее взять другую точку.

Коэффициент \(k\) определяет угол между прямой и положительным направлением оси \(x\).

 

Если \(k>0\), то этот угол острый (как на первом рисунке), а

если \(k<0\), то этот угол тупой (как на втором рисунке).

 

Поэтому коэффициент \(k\) в записи \(y=kx\) называют угловым коэффициентом.

 

Обобщая сведения о линейных функциях, можно сделать вывод:

прямая, служащая графиком линейной функции \(y=kx + m\), параллельна прямой, служащей графиком линейной функции \(y=kx\).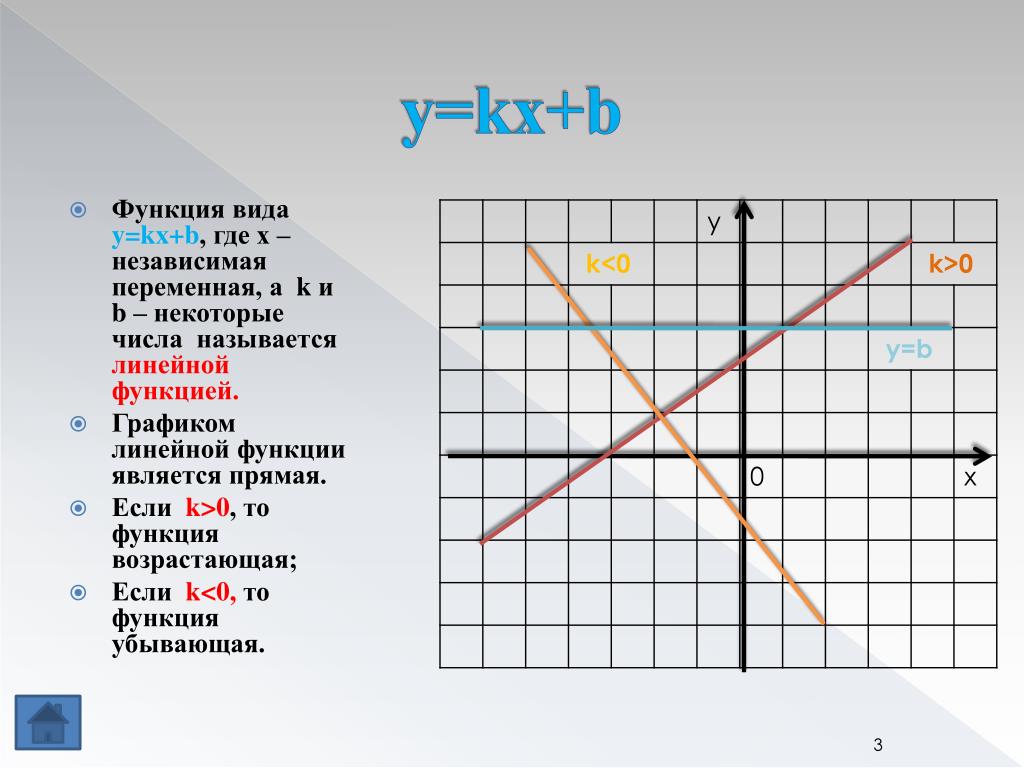

 

На рисунке показаны параллельные прямые с одним и тем же коэффициентом \(k = 4\).

Поэтому коэффициент \(k\) в записи \(y=kx + m\) также называют угловым коэффициентом, и

если \(k>0\), то прямая \(y=kx + m\) образует с положительным направлением оси \(x\) острый угол;

если \(k<0\), то этот угол тупой.

8 КЛАСС АЛГЕБРА Линейная функция y kx b

8 КЛАСС. АЛГЕБРА. Линейная функция. y = kx+b Савченко Е. М. МОУ гимназия № 1, г. Полярные Зори, Мурманская обл.

Линейной функцией называется функция вида у = kx + b где k и b – заданные числа у = kx + b Графиком линейной функции является прямая 1 способ построения – по двум точкам

2 x +3 2 x – 4 y= (0 ; 0 ), (- 2; — 4 ) 2 x y=2 x у y= Прямая пропорциональность y = 2 x +3 y=2 x– 4 (0 ; 3 ), ( — 4 ; — 5 ) (0; — 4), y= Линейная функция 0 1 (4; 4 ) Если угловые коэффициенты равны, то прямые параллельны. х

2 способ построения – с помощью параллельного переноса у y 4 x+ , 5 =0 y y =0, 5 x +4 0 1 y 5 x , =0 , 5 =0 y y = 0, 5 x — 2 y = 0, 5 x – 3, 5 Это важно! 2 , 5 – 3 x x 0, 5 = х

Определите знаки коэффициентов k и b у =k y y=kx+b k>0 b>0 0 1 +b x х

у Определите знаки коэффициентов k и b y=kx+b k>0 0 b

Определите знаки коэффициентов k и b у y=kx+b k

Определите знаки коэффициентов k и b у y=kx+b k0 0 1 y х = k x + b

у y = 0, 5 x+3 (0 ; 3 ), (- 4; 1 ) y= Точки y = − 2 х — 1 (0 ; — 1 ), (- 3; 5 ) 3 + , 5 x 0 0 1 х Точки y= − 2 х1 Это важно! Если , то прямые перпендикулярны.

у y=3 (0 ; 3 ), (- 4; 3 ) y=3 Точки x=4 0 ( 4 ; 2), ( 4 ; — 5 ) 1 х Точки x =4 Прямая y = b параллельна оси абсцисс. Прямая х = а параллельна оси ординат.

y = 3, 5 у y = 3, 5 y = 0, 5 y=-5 y = 0, 5 x=-3 1 x=0 0 x =- 3 x=4 y=-5 у=0 Ось абсцисс х=0 Ось ординат х x =4 y=0

у Построение графиков функций с помощью преобразований. y =0, 5 x− 3 План построения y =x y = 0, 5 x – 3 0 1 y= 0 − , 5 x 3 х

у 2 x y= План построения +3 y = 2 x + 3 0 y =x y = 2 x + 3 1 х

у y = − 2 x + 3 План построения 0 y =x y = 2 x y = − 2 x + 3 1 х

Быстрый способ построения графика y=kx+b

у 1 0 -2 1 х

у 2 1 0 1 х

у 1 0 -1 1 3 х

у 1 0 -2, 5 1 5 х

Постройте самостоятельно графики указанных функций

Top 18 y=kx+b k больше 0 mới nhất 2021

1.

График линейной функции. Свойства и Формулы — Skysmart

Tác giả: skysmart.ru

Ngày đăng: 28/4/2021

Đánh giá: 3 ⭐ ( 30033 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 2 ⭐

Tóm tắt: Построение графика линейной функции, свойства, формулы и наглядные примеры. Математика 7 класс

Khớp với kết quả tìm kiếm: 30 thg 11, 2020 Если b = 0, то уравнение примет вид «y = kx». Такая функция называется прямой пропорциональностью. График прямая, которая проходит через …… xem ngay

2. Варианты заданий — OГЭ–2021, математика: задания …

Tác giả: oge.sdamgia.ru

Ngày đăng: 6/6/2021

Đánh giá:

4 ⭐ ( 38232 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 4 ⭐

Tóm tắt: Тысячи заданий с решениями для подготовки к OГЭ

Khớp với kết quả tìm kiếm: А) k меньше 0, b больше 0. Б) k больше 0, b больше 0. В) k больше 0, b меньше 0. ГРАФИКИ … На рисунке изображены графики функций вида y = kx плюс b …. xem ngay

3. 3.Линейная функция вида y = kx + b — Google Sites

Tác giả: sites.google.com

Ngày đăng: 3/2/2021

Đánh giá: 4 ⭐ ( 38019 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 1 ⭐

Tóm tắt: Bài viết về 3.Линейная функция вида y = kx + b — Функции и их графики. Đang cập nhật…

Khớp với kết quả tìm kiếm: Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью. Геометрический смысл коэффициента b – длина отрезка, который отсекает …… xem ngay

4. Линейная функция и ее график

Tác giả: ege-ok.ru

Ngày đăng: 11/1/2021

Đánh giá: 3 ⭐ ( 95763 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 5 ⭐

Tóm tắt: Линейная функция и ее график.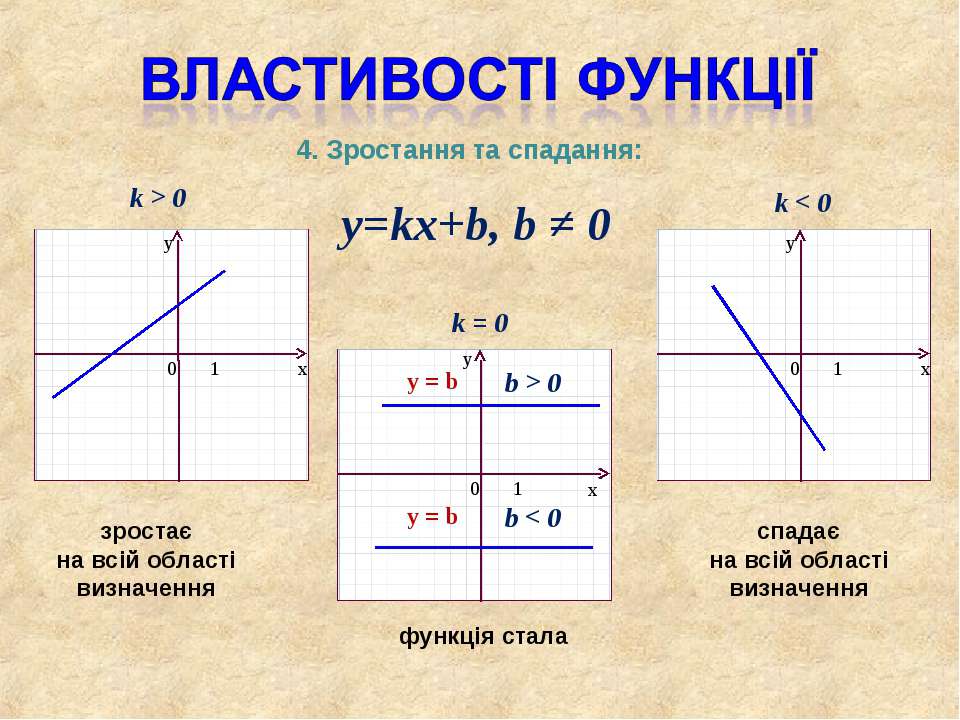 Все о линейной функции и ее графике. Просто. Доступно. Для вас репетитор по математике Инна Фельдман

Khớp với kết quả tìm kiếm: 3 thg 4, 2012 больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение k … Если k<0 и b>0, то график функции y=kx+b имеет вид:…. xem ngay

5. Линейная функция y = kx — урок. Алгебра, 7 класс. — ЯКласс

Tác giả: www.yaklass.ru

Ngày đăng: 14/3/2021

Đánh giá: 3 ⭐ ( 17537 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 1 ⭐

Tóm tắt: Bài viết về Линейная функция y = kx — урок. Алгебра, 7 класс.. Đang cập nhật…

Khớp với kết quả tìm kiếm: Значит, k=0,5, и данная прямая является графиком линейной функции y=0,5x. Если в формуле y=kx вместо x подставим 1, то получим …… xem ngay

6. § Линейная функция y = kx + b и её график

Tác giả: math-prosto.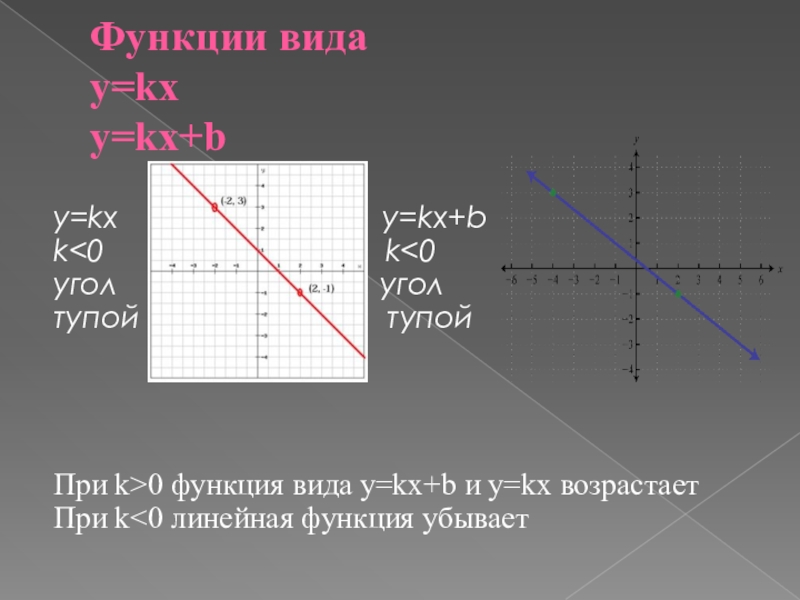 ru

Ngày đăng: 2/3/2021

Đánh giá: 5 ⭐ ( 62004 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 5 ⭐

Tóm tắt: Bài viết về § Линейная функция y = kx + b и её график. Đang cập nhật…

Khớp với kết quả tìm kiếm: Рассматривая функцию «y = 0,5x», неверно утверждать, что числового коэффициента «b» в функции нет. Числовый коэффициент «b» присутствет в функции типа «y = kx + …… xem ngay

7. K больше 0 b меньше 0 график

Tác giả: kztarif.ru

Ngày đăng: 18/3/2021

Đánh giá: 4 ⭐ ( 23755 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 2 ⭐

Tóm tắt: Bài viết về K больше 0 b меньше 0 график – Тарифы на сотовую связь. Đang cập nhật…

Khớp với kết quả tìm kiếm: Как решать задачи на линейную функцию « y = kx + b » Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые . ….. xem ngay

8. Решение 4445. На рисунках изображены графики функций …

Tác giả: self-edu.ru

Ngày đăng: 24/2/2021

Đánh giá:

4 ⭐ ( 89666 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 5 ⭐

Tóm tắt: Bài viết về Решение 4445. На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b. ГРАФИКИ КОЭФФИЦИЕНТЫ: 1) k>0, b<0; 2) k<0, b<0; 3). Đang cập nhật…

Khớp với kết quả tìm kiếm: … вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b. ГРАФИКИ КОЭФФИЦИЕНТЫ: 1) k>0, b<0; 2) k<0, b<0; 3)…. xem ngay

9. Решение 5346. На рисунках изображены графики функций …

Tác giả: self-edu.ru

Ngày đăng: 22/7/2021

Đánh giá: 2 ⭐ ( 24896 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 3 ⭐

Tóm tắt: Bài viết về Решение 5346. На рисунках изображены графики функций вида у = kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций. КОЭФФИЦИЕНТЫ А) k < 0, b < 0; Б) k < 0, b > 0; В) k >. Đang cập nhật…

Khớp với kết quả tìm kiếm: Если угловой коэффициент k прямой y=kx+b больше 0, то прямая образует с осью Ox острый угол, а при k<0 – тупой угол. Коэффициент b показывает насколько …… xem ngay

10. * На рисунке изображены графики функций вида y=kx+b …

Tác giả: school.umk-spo.biz

Ngày đăng: 4/3/2021

Đánh giá: 2 ⭐ ( 71136 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 4 ⭐

Tóm tắt: Bài viết về . Đang cập nhật…

Khớp với kết quả tìm kiếm: На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэф-тов * МАТЕМАТИКА — Графики ОГЭ — РЕШЕНИЯ ЗАДАНИЙ. … xem ngay

11. Срочно! Дана функция y = kx + b. На каком из рисунков …

Tác giả: znanija.com

Ngày đăng: 20/3/2021

Đánh giá: 2 ⭐ ( 72846 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 4 ⭐

Tóm tắt: Школьные знания.com это сервис в котором пользователи бесплатно помогают друг другу с учебой, обмениваются знаниями, опытом и взглядами.

Khớp với kết quả tìm kiếm: 27 thg 4, 2016 Ответ: 1)(k<0 -угол тупой , b>0 — идём наверх по оси Oy.1 câu trả lời · 17 bình chọn: Ответ: 1)(k<0 -угол тупой , b>0 — идём наверх по оси Oy… xem ngay

12. Как расположен в координатной плоскости график …

Tác giả: znanija.com

Ngày đăng: 19/6/2021

Đánh giá: 4 ⭐ ( 36509 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 1 ⭐

Tóm tắt: Школьные знания. com это сервис в котором пользователи бесплатно помогают друг другу с учебой, обмениваются знаниями, опытом и взглядами.

Khớp với kết quả tìm kiếm: 24 thg 10, 2014 Найди ответ на свой вопрос: Как расположен в координатной плоскости график функции y=kx при k больше 0 и при k меньше 0?… xem ngay

13. Линейная функция, график — прямая. Нули, промежутки …

Tác giả: fizmat.by

Ngày đăng: 10/1/2021

Đánh giá: 3 ⭐ ( 53088 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 4 ⭐

Tóm tắt: Bài viết về Линейная функция, график — прямая. Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты — курсы. Đang cập nhật…

Khớp với kết quả tìm kiếm: Особые случаи. 1) Если b=0, получим уравнение y=kx. Функция такого вида называется прямой пропорциональностью.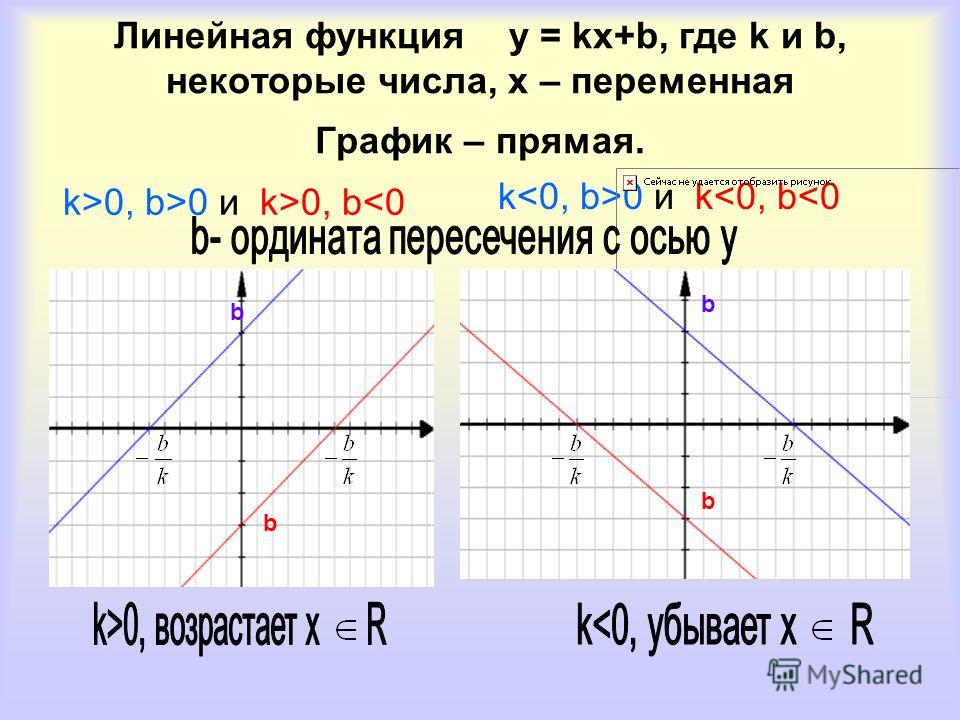 Графиком является прямая, проходящая через начало …… xem ngay

14. На рисунках изображены графики функций вида у = kx + b …

Tác giả: otvet.mail.ru

Ngày đăng: 7/2/2021

Đánh giá: 4 ⭐ ( 90239 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 5 ⭐

Tóm tắt: коэффициентов k и b и графиками функций. ГРАФИКИ КОЭФФИЦИЕНТЫ а) k < 0, b < 0 б) k < 0, b > 0 в) k > 0, b > 0

Khớp với kết quả tìm kiếm: ГРАФИКИ КОЭФФИЦИЕНТЫ а) k < 0, b < 0 б) k < 0, b > 0 в) k > 0, b > 0. … Используя график функции y=kx, изображённый на рисунке, определите знак k.4 câu trả lời · Câu trả lời hàng đầu: все возможные варианты… xem ngay

15. Расположение графика линейной функции y=kx+b в за…

Tác giả: www.mindmeister.com

Ngày đăng: 16/7/2021

Đánh giá: 4 ⭐ ( 36523 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 1 ⭐

Tóm tắt: Открытая карта от T E.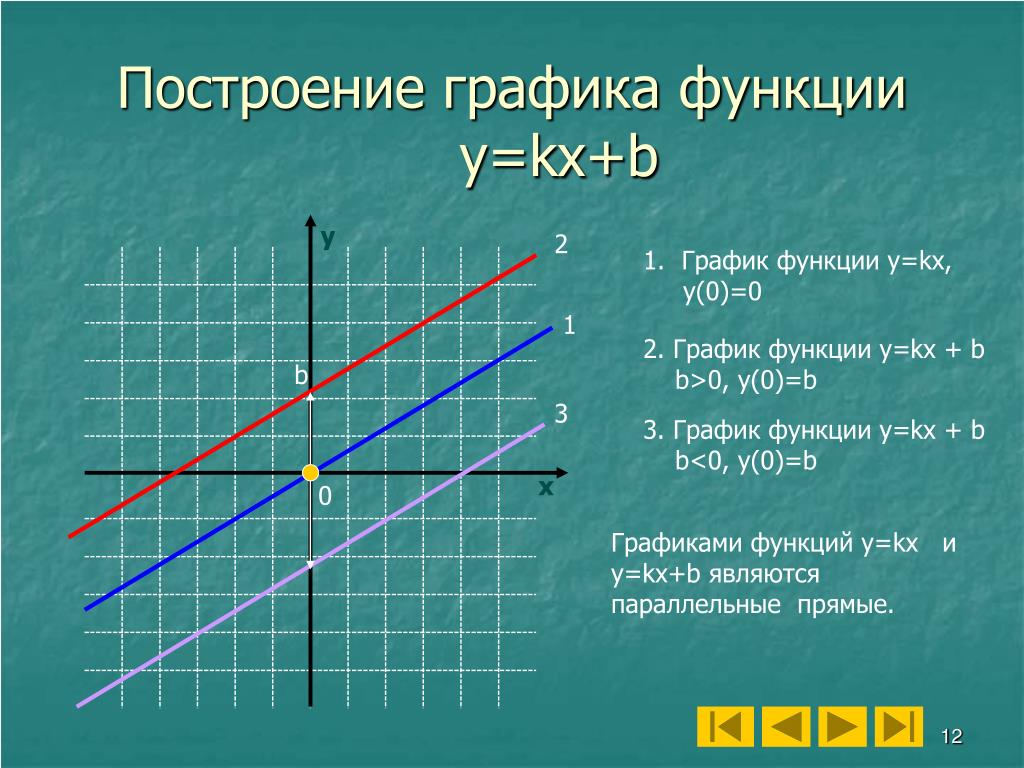 Создавайте свои собственные коллективные ментальные карты бесплатно на www.mindmeister.com

Khớp với kết quả tìm kiếm: k<0, b>0. Угол тупой. ✓ k=0, b>0. Прямые параллельны. ✓ k=0… … Расположение графика линейной функции y=kx+b в зависимости от коэффициентов k и b.Bị thiếu: bk ‎| Phải bao gồm: bk… xem ngay

16. Угловой коэффициент — Википедия

Tác giả: ru.wikipedia.org

Ngày đăng: 18/5/2021

Đánh giá: 2 ⭐ ( 22137 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 1 ⭐

Tóm tắt: Bài viết về Угловой коэффициент — Википедия. Đang cập nhật…

Khớp với kết quả tìm kiếm: Угловой коэффициент прямой (также наклон) коэффициент k {\displaystyle k} k в уравнении y = k x + b {\displaystyle y=kx+b} y=kx+b …… xem ngay

17. Khi có (y = k.x ) (với k # 0) ta nói

Tác giả: vungoi. vn

Ngày đăng: 18/8/2021

Đánh giá: 2 ⭐ ( 71528 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 3 ⭐

Tóm tắt: Khi có (y = k.x ) (với k # 0) ta nói

Khớp với kết quả tìm kiếm: Khi có (y = k.x ) (với k # 0) ta nói.Bị thiếu: bk ‎больше… xem ngay

18. Степенные ряды одной переменной с условием …

Tác giả: dspace.spbu.ru

Ngày đăng: 24/6/2021

Đánh giá: 1 ⭐ ( 63294 lượt đánh giá )

Đánh giá cao nhất: 5 ⭐

Đánh giá thấp nhất: 4 ⭐

Tóm tắt: null

Khớp với kết quả tìm kiếm: viết bởi AV Zheleznyak · 2020 · Trích dẫn 1 bài viết aK+l. aK+l−1 ≤ M. Коэффициент при bK+l−1 больше 0, так как. aK+la0 − aK+l−1.11 trang

Как решать график функции y kx b.

Что такое угловой коэффициент линейной функции? Сбор и использование персональной информации

Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
Графиком линейной функции является прямая.

1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции y= &frac13; x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3. Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= &frac13; x+2:

2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½ x+3; y=x+3

Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.

Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3

На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3; y=2x; y=2x-3

Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k 0

Если k>0 и b>0 , то график функции y=kx+b имеет вид:

Если k>0 и b , то график функции y=kx+b имеет вид:

Если k, то график функции y=kx+b имеет вид:

Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:

3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.

Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2

5. Условие перепендикулярности двух прямых:

График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2

6. Точки пересечения графика функции y=kx+b с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):

«Критические точки функции» — Критические точки. Среди критических точек есть точки экстремума. Необходимое условие экстремума. Ответ: 2. Определение. Но, если f» (х0) = 0, то необязательно, что точка х0 будет точкой экстремума. Точки экстремума (повторение). Критические точки функции Точки экстремумов.

«Координатная плоскость 6 класс» — Математика 6 класс. 1. Х. 1.Найдите и запишите координаты точек A,B, C,D: -6. Координатная плоскость. О. -3. 7. У.

«Функции и их графики» — Непрерывность. Наибольшее и наименьшее значение функции. Понятие обратной функции. Линейная. Логарифмическая. Монотонность. Если k > 0, то образованный угол острый, если k

«Функции 9 класс» — Допустимые арифметические действия над функциями. [+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.

«Урок Уравнение касательной» — 1. Уточнить понятие касательной к графику функции. Лейбниц рассматривал задачу о проведении касательной к произвольной кривой. АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у=f(x). Тема урока: Тест: найти производную функции. Уравнение касательной. Флюксия. 10 класс. Расшифруйте, как исаак ньютон назвал производную функцию.

«Построить график функции» — Дана функция y=3cosx. График функции y=m*sin x. Постройте график функции. Содержание: Дана функция: y=sin (x+?/2). Растяжение графика y=cosx по оси y. Чтобы продолжить нажмите на л. Кнопку мыши. Дана функция y=cosx+1. Смещения графика y=sinx по вертикали. Дана функция y=3sinx. Смещение графика y=cosx по горизонтали.

Всего в теме 25 презентаций

Линейная функция – это функция вида

x-аргумент (независимая переменная),

y- функция (зависимая переменная),

k и b- некоторые постоянные числа

Графиком линейной функции является прямая .

Для построения графика достаточно двух точек, т.к. через две точки можно провести прямую и притом только одну.

Если k˃0, то график расположен в 1-й и 3-й координатных четвертях. Если k˂0, то график расположен в 2-й и 4-й координатных четвертях.

Число k называют угловым коэффициентом прямой графика функции y(x)=kx+b. Если k˃0, то угол наклона прямой y(x)= kx+b к положительному направлению Ох — острый; если k˂0, то этот угол- тупой.

Коэффициент b показывает точку пересечения графика с осью ОУ (0; b).

y(x)=k∙x— частный случай типичной функции носит название прямая пропорциональность. Графиком является прямая, проходящая через начало координат, поэтому для построения этого графика достаточно одной точки.

График линейной функции

Где коэффициент k = 3, следовательно

График функции будет возрастать и иметь острый угол с осью Ох т.к. коэффициент k имеет знак плюс.

ООФ линейной функции

ОЗФ линейной функции

Кроме случая, где

Так же линейная функция вида

Является функцией общего вида.

Б) Если k=0; b≠0,

В этом случае графиком является прямая параллельная оси Ох и проходящая через точку (0;b).

В) Если k≠0; b≠0, то линейная функция имеет вид y(x)=k∙x+b.

Пример 1 . Построить график функции y(x)= -2x+5

Пример 2 . Найдём нули функции у=3х+1, у=0;

– нули функции.

Ответ: или (;0)

Пример 3 . Определить значение функции y=-x+3 для x=1 и x=-1

y(-1)=-(-1)+3=1+3=4

Ответ: y_1=2; y_2=4.

Пример 4 . Определить координаты их точки пересечения или доказать, что графики не пересекаются. Пусть даны функции y 1 =10∙x-8 и y 2 =-3∙x+5.

Если графики функций пересекаются, то значение функций в этой точке равны

Подставим х=1, то y 1 (1)=10∙1-8=2.

Замечание. Подставить полученное значение аргумента можно и в функцию y 2 =-3∙x+5, тогда получим тот же самый ответ y 2 (1)=-3∙1+5=2.

y=2- ордината точки пересечения.

(1;2)- точка пересечения графиков функций у=10х-8 и у=-3х+5.

Ответ: (1;2)

Пример 5 .

Построить графики функций y 1 (x)= x+3 и y 2 (x)= x-1.

Можно заметить, что коэффициент k=1 для обеих функций.

Из выше сказанного следует, что если коэффициенты линейной функции равны, то их графики в системе координат расположены параллельно.

Пример 6 .

Построим два графика функции.

Первый график имеет формулу

Второй график имеет формулу

В данном случае перед нами график двух прямых, пересекающихся в точке (0;4). Это значит, что коэффициент b, отвечающий за высоту подъёма графика над осью Ох, если х=0. Значит мы может полагать, что коэффициент bу обоих графиков равен 4.

Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.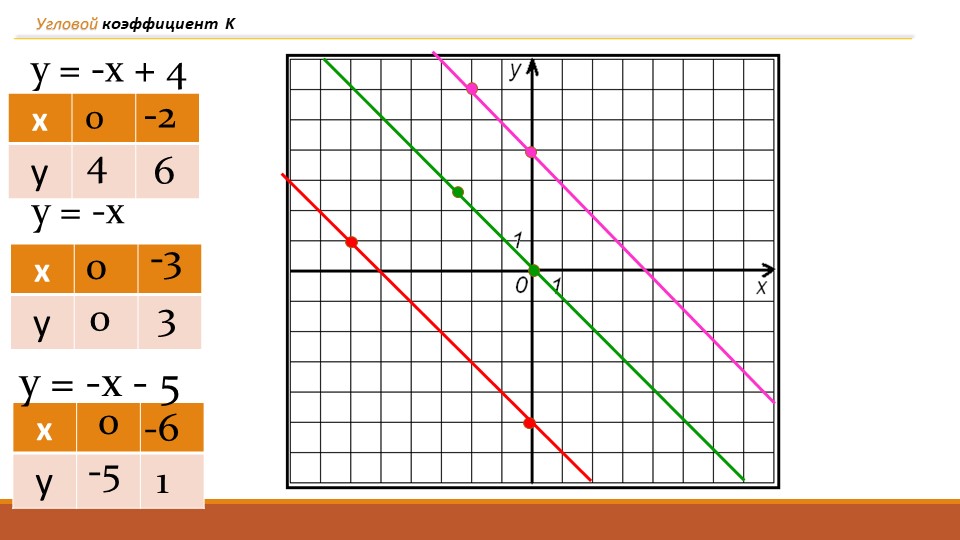

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

PPT — Линейная функция. y = kx+b Обратная пропорциональность. y = PowerPoint Presentation

7 КЛАСС. АЛГЕБРА. Линейная функция. y = kx+b Обратная пропорциональность.y = k x Савченко Е.М. МОУ гимназия №1, г. Полярные Зори, Мурманская обл.

у = kx + b Графиком линейной функции является прямая Линейной функцией называется функция вида у = kx + b гдеkи b– заданные числа 1 способ построения – по двум точкам

у х Прямая пропорциональность y = 2x y =2x+3 y = 2 x (0 ; ), (- 2; ) 0 — 4 y = 2x – 4 Линейная функция y = 2 x +3 (0 ; ), ( — 4 ; ) 3 — 5 0 1 (0; ), (4; ) y = 2x – 4 — 4 4 Если угловые коэффициенты равны, то прямые параллельны.

у х 2 способ построения – с помощью параллельного переноса y =0,5x+4 y = 0,5x y =0,5x 0 1 y =0,5x +4 y = 0,5x — 2 y = 0,5x – 3,5 y = 0,5x — 2 y = 0,5x – 3,5 Это важно!

у х Определите знаки коэффициентов k и b y = k x + b y = k x + b k > 0 0 1 b > 0

у х Определите знаки коэффициентов k и b y = k x + b k > 0 0 1 b < 0 y = k x + b

у х Определите знаки коэффициентов k и b y = k x + b k < 0 0 1 b < 0 y = k x + b

у х Определите знаки коэффициентов k и b y = k x + b k < 0 0 1 b > 0 y = k x + b

у х y =x+3 0,5 y = 0,5x+3 (0 ; ), (- 4; ) 3 1 Точки y = х — 1 −2 0 1 Точки (0 ; ), (- 3; ) — 1 5 y =−2х — 1 Это важно! Если , то прямые перпендикулярны.

у х y = 3 y = 3 (0 ; ), (- 4; ) 3 3 Точки x = 4 0 1 Точки ( ; 2), (; — 5 ) 4 4 x =4 Прямая y = b параллельна оси абсцисс. Прямая х = а параллельна оси ординат.

у х y = 3,5 y = 3,5 y = 0,5 y = — 5 y = 0,5 y = 0 0 1 x = 4 x = 0 x =- 3 x =4 x = — 3 y = — 5 Ось абсцисс у = 0 Ось ординат х = 0

у х Построение графиков функций с помощью преобразований. y =0,5x− 3 План построения 0 1 y =0,5x− 3 y =x y = 0,5x y = 0,5x – 3

у х y =2x+ 3 План построения y = 2x + 3 0 1 y =x y = 2x y = 2x + 3

у х y =−2x+ 3 План построения 0 1 y =x y = 2x y =−2x y =−2x + 3

4 т 15 рейсов х 12 рейсов № 568 Для перевозки некоторого количества зерна автомашина, имеющая грузоподъемность 4 т, сделала 15 рейсов. Какую грузоподъемность должна иметь автомашина, чтобы такое же количество зерна перевезти за 12 рейсов?

700 t = v Москва 700 t(v) = Санкт-Петербург v Поезд движется из Москвы в Санкт-Петербург со скоростью vкм/ч. За какое время поезд пройдет путь 700 км?

k y = x Графиком является гипербола Обратная пропорциональность – функция вида гдеk– заданное число

у х 0 1 – – – – – – – – 4 2 1 0,5 Гипербола в I и III координатных четвертях.

у х 0 1 – – – – – 4 –2 –1 – 0,5 Гипербола в II и IV координатных четвертях.

у х у = х у = — х у = х IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 у = — х

у х 0 1

Лінійна функція y = kx — урок. Алгебра, 7 клас.

Розглядаючи лінійну функцію виду \(y = kx + b\), особливо виділяють випадок, коли \(b = 0\).
Тоді лінійна функція набуває вигляду \(y = kx\).

 

Графіком лінійної функції \(y = kx\) є пряма, що проходить через початок координат.

 

Важливо вміти переходити від аналітичної моделі \(y = kx\) до геометричної і, навпаки, від геометричної до аналітичної моделі.

 

Наприклад, розглянемо пряму, зображену на рисунку.

 

 

Ця пряма є графіком лінійної функції \(y = kx\), оскільки проходить через початок координат. Потрібно лише визначити значення коефіцієнта \(k\).
З формули лінійної функції \(y = kx\) отримаємо, що k=yx.

 

Тому для визначення коефіцієнта \(k\) досить узяти будь-яку точку на прямій і знайти відношення ординати цієї точки до її абсциси.

 

Пряма проходить через точку \(M (4; 2)\), а для цієї точки маємо 24=0,5. Отже, \(k = 0,5\) і дана пряма є графіком лінійної функції \(y = 0,5 x\).

 

Графік лінійної функції \(y = kx\) будують так: беруть точку \((1; k)\) (якщо \(x = 1\), то з рівності \(y = kx\) знаходять, що \(y = k\)) і проводять пряму через цю точку і початок координат.
Іноді замість точки \((1; k)\) можна взяти іншу точку, більш зручну.

 

Від коефіцієнта \(k\) залежить кут, який побудована пряма утворює з додатним напрямком осі \(x\).

 

Якщо \(k> 0\), тоді цей кут гострий (як на рисунку вище), а
якщо \(k <0\), тоді цей кут тупий (як на наступному рисунку)

 

 

Тому коефіцієнт \(k\) у записі \(y = kx\) називають кутовим коефіцієнтом.

 

Узагальнюючи відомості про лінійні функції, можна зробити висновок:

 

Пряма, що служить графіком лінійної функції \(y=kx + b\), паралельна прямій, що служить графіком лінійної функції \(y=kx\).

 

 

На рисунку показано паралельні прямі з одним і тим самим кутовим коефіцієнтом \(k = 4\).

 

Отже,  коефіцієнт \(k\) у записі \(y = kx + b\) також називають кутовим коефіцієнтом, і якщо \(k> 0\), тоді пряма \(y = kx + b\) утворює з додатним напрямком осі \(x\) гострий кут, якщо \(k <0\), тоді цей кут тупий.

Под каким углом пересекаются прямые y = Kx + B и y = Bx + K? — The Beat Форум GMAT

M7MBA написал: Под каким углом пересекаются прямые y = Kx + B и y = Bx + K?

(1) B + K = 1

(2) BK = 0

OA — C.

Как я могу найти угол? Я не понимаю, как мне решить этот вопрос DS. Может мне кто-нибудь поможет? Пожалуйста.

Нам нужно найти угол между двумя линиями y = Kx + B и y = Bx + K.

Давайте рассмотрим каждое утверждение по очереди.

(1) B + K = 1

Случай 1: Скажем, B = K = 1/2

Это означает, что линии имеют вид y = x / 2 + 1/2 и y = x / 2 + 1/2 . На самом деле это одни и те же строки. Угол между ними равен 0.

Случай 2: Скажем, B = 0 и K = 1

Это означает, что линии имеют вид y = x и y = 1. Угол y = x при y = 1 составляет 45 градусов. Если вы не знаете, как его рассчитать, ничего страшного. Не нужно этого знать. Все, что вы можете вывести из уравнений, — это то, что наклон линий неодинаков; таким образом, они составляют угол больше 0.

Нет однозначного ответа. Недостаточный.

(2) BK = 0

=> По крайней мере один из B и K равен 0.

Если оба они равны 0, уравнение будет y = 0. Две строки будут одной и той же строкой, что означает, что угол между ними равен 0. Однако, если, скажем, B = 0 и K = 1, то две линии будут иметь угол больше 0.

Нет однозначного ответа. Недостаточный.

(1) и (2) вместе

Из двух утверждений мы имеем либо B = 0, либо K = 1, либо B = 1 и K = 0.В любом случае уравнения имеют вид y = x и y = 1. Поскольку наклон двух линий известен, угол между ними может быть вычислен. Достаточный.

Вычисление угла между двумя линиями не входит в задачи GMAT. Поскольку это вопрос DS, и нужно только быть уверенным, возможно ли значение unqiue, нам не обязательно его вычислять.

Правильный ответ: C

Надеюсь, это поможет!

-Jay
_________________
Manhattan Review GMAT Prep

Местоположение: Нью-Хейвен | Доха | Стокгольм | Претория | и многое другое…

Запишитесь на бесплатную консультацию с опытным консультантом по подготовке к GMAT! Кликните сюда.

Обратное изменение

Пока прямая вариация описывает линейную связь между двумя переменные , обратная вариация описывает другой вид отношений.

Для двух величин с обратным изменением, когда одна величина увеличивается, другая величина уменьшается.

Например, когда вы путешествуете в определенное место, по мере увеличения вашей скорости время, необходимое для прибытия в это место, уменьшается.Когда вы уменьшаете скорость, время, необходимое для прибытия в это место, увеличивается. Итак, количества обратно пропорциональны.

Обратную вариацию можно представить уравнением Икс у знак равно k или у знак равно k Икс .

Это, у изменяется обратно пропорционально Икс если есть некоторая ненулевая константа k такой, что, Икс у знак равно k или у знак равно k Икс где Икс ≠ 0 , у ≠ 0 .

Предполагать у изменяется обратно пропорционально Икс такой, что Икс у знак равно 3 или у знак равно 3 Икс . Этот график этого уравнения показан.

С k является положительным значением, так как значения Икс увеличиваются, значения у снижаться.

Примечание. Для уравнений прямой вариации вы говорите, что у изменяется прямо как Икс .Для обратных уравнений вариации вы говорите, что у изменяется обратно пропорционально Икс .

Правило произведения для обратной вариации

Если ( Икс 1 , у 1 ) и ( Икс 2 , у 2 ) являются решениями обратной вариации, то Икс 1 у 1 знак равно k и Икс 2 у 2 знак равно k .

Заменять Икс 1 у 1 за k .

Икс 1 у 1 знак равно Икс 2 у 2 или Икс 1 Икс 2 знак равно у 2 у 1

Уравнение Икс 1 у 1 знак равно Икс 2 у 2 называется правилом произведения для обратных вариаций.

Пример:

На заводе, 10 мужчины могут делать работу в 30 дней. Сколько дней потребуется, если 20 мужчины делают ту же работу?

Здесь, когда численность персонала увеличится, им потребуется меньше, чем 30 дней на выполнение той же работы. Итак, это обратная вариация.

Позволять Икс быть числом рабочих, и пусть у быть количеством дней на выполнение работы.

Так, Икс 1 знак равно 10 , Икс 2 знак равно 20 и у 1 знак равно 30 .

По правилу произведения обратной вариации,

( 10 ) ( 30 ) знак равно ( 20 ) ( у 2 ) 300 знак равно 20 у 2

Решить для у 2 .

у 2 знак равно 300 20 знак равно 15

Следовательно, 20 мужчины могут делать ту же работу в 15 дней.

% PDF-1.6 % 179 0 объектов> эндобдж xref 179 101 0000000016 00000 н. 0000003852 00000 н. 0000003917 00000 н. 0000004536 00000 н. 0000005414 00000 н. 0000005822 00000 н. 0000006311 00000 н. 0000009158 00000 п. 0000009534 00000 п. 0000009880 00000 н. 0000010210 00000 п. 0000010646 00000 п. 0000011399 00000 п. 0000012546 00000 п. 0000012844 00000 п. 0000013727 00000 п. 0000014375 00000 п. 0000015025 00000 п. 0000015904 00000 п. 0000016513 00000 п. 0000016939 00000 п. 0000017425 00000 п. 0000028477 00000 п. 0000028966 00000 п. 0000035473 00000 п. 0000035919 00000 п. 0000036284 00000 п. 0000036848 00000 н. 0000037289 00000 п. 0000037965 00000 п. 0000047832 00000 п. 0000057779 00000 п. 0000058241 00000 п. 0000058655 00000 п. 0000058972 00000 п. 0000065296 00000 п. 0000065633 00000 п. 0000066055 00000 п. 0000066277 00000 н. 0000074648 00000 п. 0000074725 00000 п. 0000075642 00000 п. 0000076523 00000 п. 0000084824 00000 п. 0000085269 00000 п. 0000085669 00000 п. 0000085998 00000 п. 0000086631 00000 н. 0000091542 00000 п. 0000091935 00000 п. 0000092362 00000 п. 0000092660 00000 п. 0000099740 00000 п. 0000100292 00000 н. 0000100693 00000 п. 0000101116 00000 н. 0000101991 00000 н. 0000102737 00000 н. 0000103658 00000 п. 0000103992 00000 н. 0000104768 00000 н. 0000105124 00000 п. 0000105325 00000 н. 0000105969 00000 н. 0000106345 00000 п. 0000106959 00000 п. 0000107337 00000 н. 0000111882 00000 н. 0000113322 00000 н. 0000121297 00000 н. 0000121624 00000 н. 0000122067 00000 н. 0000122328 00000 н. 0000122895 00000 н. 0000123524 00000 н. 0000124168 00000 н. 0000124817 00000 н. 0000129665 00000 н. 0000130055 00000 н. 0000130243 00000 н. 0000130645 00000 н. 0000130900 00000 н. 0000135250 00000 н. 0000135573 00000 н. 0000135946 00000 н. 0000136737 00000 н. 0000137325 00000 н. 0000137438 00000 н. 0000138320 00000 н. 0000138568 00000 н. 0000138999 00000 н. 0000139360 00000 п. 0000145999 00000 н. 0000146119 00000 н. 0000146921 00000 н. 0000147050 00000 п. 0000147698 00000 п. 0000150964 00000 н. 0000151258 00000 н. 0000151578 00000 н. 0000002316 00000 н. трейлер ] >> startxref 0 %% EOF 279 0 obj> поток x ڴ VkL [eNiwsJ٠lr + [k c2h] t]; c`: P7qKe͹˙o & [? Ęh: 4 $> @ QLV «\ $ Y.() u

Найдите значения k и b, если известно, что график y = kx + b проходит через точки (2, 10) и (−7, −10)

Сай 9.

спросил • 17.10.17

найдите Найдите значения k и b

Артуро О. ответил • 18.10.17

Опытный учитель физики Репетиторство по физике

k = наклон = (-10-10) / (- 7-2) = -20 / -9 = 20/9

10 = (20/9) (2) + b

b = 10-40/9 = (90-40) / 9 = 50/9

к = 20/9

b = 50/9

Проверьте ответы.

Все еще ищете помощь? Получите правильный ответ быстро.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.

---

¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊

Напишите уравнение в виде y = kx, где k — постоянная вариации, если y изменяется прямо как x и x = -1, когда y = -4

Ахбрейона В.

задано • 24.07.19

для y = kx k = y / x = -4 / -1 = 4

Итак, y = 4x

Все еще ищете помощь? Получите правильный ответ быстро.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и познакомьтесь онлайн.Никаких пакетов или подписок, платите только за необходимое время.

---

¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊

y = kx bk! = 0 上 有 几个 点 _ 一次 函数 y = kx bk ， = 0 的 图像 是 什么 因此 画 一次 函数 图像 时 只需 确定 几个 过 这个 _ 作业 九九 网 _www.

zuoye99.com

作业解析

y=kx+b k=根3时 求与坐标轴的夹角度数!我知道k=1时是45° 根3时是几?

回答作者：柔声娇喘-柔声娇喘

采纳时间：2021-10-22 00:33

根3的反正切为60°斜率就是角度的正切值,所以为60°!

作业解析

y+kx=b k怎么画图 比如 K=3/5
Y=KX+B 打错了

回答作者：不喜暧昧-不喜暧昧

采纳时间：2021-10-21 00:33

以K=0,k=1,k=-1时为参照

作业解析

已知一次函数y等于kx加b k不等于0.的图像经过点（负二,4）和直线y等于负三x加1与y轴的交点 求一次函数的h解析式 当a为何值时,点p（负二 a,4a减4）在这个一次函数图像上

回答作者：饮酒作詩-饮酒作詩

采纳时间：2021-10-20 00:33

因为一次函数y=kx+b的图象经过直线y=-3x+1与y轴的交点,
所以两直线在y轴上的截距相等,即b=1.
把(-2,4)代入y=kx+1,得-2k+1=4,解得k=-3/2,
所以函数的解析式为y=-3/2x+1.
把点P的坐标(-2a,4a-4)代入y=-3/2x+1,得-3/2×(-2a)+1=4a-4,解得a=5.

作业解析

一次函数表达式y=kx+b k怎么求
我是初二的学生 最近教函数了 可是一点都听不懂
我知道一次函数公式好像是y=kx+b
b就是图像直线与Y轴的交点
K要怎么求啊

回答作者：北栀海-北栀海

采纳时间：2021-10-19 00:33

一次函数的表达式（也称为函数解析式,或函数关系式）是y=kx+b；
b是图像直线与Y轴交点的纵坐标,
如果b的值已经求出,要再求出K的值,则要有一个X与Y的对应值（可以是一个点的坐标）,将X、Y的值代进去,就可以解出K了.

作业解析

一次函数y=kx+b k不等于0的图像是一条经过——和——两点的直线

回答作者：1am-1am

采纳时间：2021-10-18 00:33

就是最简单的一次函数 当k>0时 图像经过一 三象限 当k

作业解析

y=kx+b k的绝对值越大 越靠近y轴:越小,反之

回答作者：人间风雅客-人间风雅客

采纳时间：2021-10-17 00:33

答：
一次函数y=kx+b
当k绝对值越大,即k趋于无穷,则直线越倾斜,倾斜角越大,接近垂直,因此约靠近y轴
当k绝对值越小,即k趋于0时,则直线越接近水平,从而趋于垂直y轴
因此是对的.

作业解析

一次函数 y=kx+b k代表什么值?
比如说：给你一个坐标点（6.2）我怎么根据这个坐标点来写它的函数表达式?

回答作者：你知我几分-你知我几分

采纳时间：2021-10-16 00:33

k代表常数,表现在平面坐标系中就是,直线的斜率,
一个坐标是不可能求出函数表达式的!

作业解析

y=kx＋b k,b分别代表什么

回答作者：关于昨天-关于昨天

采纳时间：2021-10-15 00:33

k表示一次函数的倾斜程度
b表示y轴上的截距

作业解析

关于一次函数画图
y=kx+b k代表什么 x代表什么 代表什么

回答作者：风中花-风中花

采纳时间：2021-10-14 00:33

k代表直线的倾斜程度,k的绝对值越小,直线越接近于与x 轴平行,k的绝对值越大,直线越接近于与y轴平行;b直线与y轴交点的纵坐标.

网友问题：一次函数y=kx bk，=0的图像是什么因此画一次函数图像时只需确定几个点在过这个 ？

回答作者：林间独角兽-林间独角兽

采纳时间：2021-10-12 00:33

　　一次函数y=kx+ b(k≠0)的图像是一条直线 　　因此画一次函数图像时只需确定两个点在过这个直线上。

网友问题：从数的方面看当一次函数y=kx bk，=0的y值为零时相应的什么值就是方程kx b=0的 ？

回答作者：人间有味清欢-人间有味清欢

采纳时间：2021-10-11 00:33

　　在一次函数y=kx+b中， 　　当x为0时，y=0k+b 　　即y（0，b） 当y=0时，0=kx+b 　　即 x（-b/k，0）

网友问题：函数中y=kx+bk是什么啊有什么作用决定什么 ？

回答作者：不归客-不归客

采纳时间：2021-10-10 00:33

　　一般地，形如y=kx+b（k,b是常数，k≠0）的函数叫做一次函数（linear function）。其中x是自变量，y是因变量。特别地，当b=0时，y=kx（k为常数，k≠0），y叫做x的正比例函数 　　一次函数,表示在坐标轴上就是一条直线,该直线跟X轴夹角的正切值（tan）是k,与Y轴交点的纵坐标是b,通过这两个参数确定了一条直线的“斜截式”.

网友问题：y=kx+bK的意思 ？

回答作者：被神偏爱-被神偏爱

采纳时间：2021-10-09 00:33

网友问题：一次函数ｙ等于ｋｘ加ｂｋ不等于零的图像如图所示则关于ｘ的方程ｋｘ加ｂ等于零的解是多少方程ｋｘ加ｂ等 ？

回答作者：中意独享-中意独享

采纳时间：2021-10-08 00:33

　　没有图像，没法解

网友问题：如果kb＞0，且不等式kx+b＞0的解集是x＜bk，那么函数y=kx+b的图象只可能是（　　）A．B．C．D ？

回答作者：情场缉捕官-情场缉捕官

采纳时间：2021-10-07 00:33

　　由kb＞0，可知（1）k＞0，b＞0；（2）k＜0，b＜0；显然B、D不符合题意，∵不等式kx+b＞0的解集是：x＜?bk，∴k＜0，第一种情况不合题意，显然A不符合．故选C．

网友问题：在平面直角坐标系xOy中，已知一次函数y=kx+b（k≠0）的图象过点P（1，1），与x轴交于点A，与y轴交于点B， ？

回答作者：多球善感-多球善感

采纳时间：2021-10-06 00:33

　　解：令x=0，则y=b； 令y=0，则x=-bk．所以A（-bk，0），B（0，b）．∵一次函数y=kx+b（k≠0）的图象过点P（1，1），∴k+b=1．①若直线在l1位置，则OA=bk，OB=b．根据题意有OAOB=bkb=1k=3，∴k=13．∴b=1-13=23．∴A点坐标为A（-2，0）；②若直线在l2位置，则OA=-bk，OB=b．根据题意有-1k=3，∴k=-13．∴b=1-（-13）=43．∴A点坐标为A（4，0）．故答案为（-2，0）或（4，0）． 　　

网友问题：抛物线y=ax2（a＞0）与直线y=kx+b（k≠0）有两个公共点，其横坐标分别是x1，x2；而直线y=kx+b与x轴焦点的 ？

回答作者：少女二三事-少女二三事

采纳时间：2021-10-05 00:33

　　由题意x3＝?bk，联立抛物线y=ax2（a＞0）与直线y=kx+b得ax2-kx-b=0，∴x1 +x2＝ka，x1x2＝?ba，∴1×1+1×2＝?kb，∴x1x2=x1x3+x2x3，故选D．

网友问题：一次函数y=kx+b（k≠0）的图象是一条直线，它与x轴的交点坐标是（bk，0），与y轴的交点坐标是（0，b）， ？

回答作者：赤脚孤儿-赤脚孤儿

采纳时间：2021-10-04 00:33

　　（1）写出一次函数y=-2x-3与坐标轴的交点；当y=0，解得：x=-32，∴与x轴的交点坐标是：（-32，0），与y轴的交点坐标是：（0，-3）；故答案为：（-32，0），（0，-3）；（2）∵把?bk叫做一次函数图象在x轴上的截距m，∴m=-?3?2=-32，∵把b叫做一次函数图象在y轴上的截距n，∴n=b=-3；故答案为：-32，-3；（3）∵把?nm叫做一次函数图象的斜率，∴-nm=-?3?32=-2，∴该图象的斜率为：-2；（4）∵把?bk叫做一次函数图象在x轴上的截距m，把b叫做一次函数图象在y轴上的截距n；而把?nm叫做一次函数图象的斜率．∴一次函数y=3x+5中m=-53，n=5，∴一次函数y=3x+5的图象的斜率是：-5?53=3．故答案为：3．

网友问题：如果实数k，b满足kb＜0且不等式kx＜b的解集是x＞bk，那么函数y=kx+b的图象只可能是（　　）A．B．C．D ？

回答作者：衬衣如雪-衬衣如雪

采纳时间：2021-10-03 00:33

　　∵不等式kx＜b的解集是x＞bk，∴k＜0，∵kb＜0，∴b＞0，∴函数y=kx+b的图象过一、二、四象限．故选A．

What does it mean when y varies inversely with x? – Book Vea

What does it mean when y varies inversely with x?

The phrase y varies inversely as x or y is inversely proportional to x means that as x gets bigger, y gets smaller, or vice versa. Это понятие переводится двояко. yx k для некоторой константы k, называемой константой пропорциональности.

Как вы решаете, что y изменяется обратно пропорционально x?

1 Ответ

• Напомним, что общий вид моделей обратной вариации — ykx. Вы также можете написать его как xyk, что более четко объясняет обратное имя.
• ykx.
• (3,24) лежит на кривой. Уравнение должно выполняться для x3 и y24.
• 24к3.
• И изолирующий к:
• 72к.

06 апреля 2018

Как найти k, если y изменяется обратно пропорционально x, а если y 24, когда x 3?

Например, когда вы путешествуете в определенное место, по мере увеличения вашей скорости время, необходимое для прибытия в это место, уменьшается. Когда вы уменьшаете скорость, время, необходимое для прибытия в это место, увеличивается. Итак, количества обратно пропорциональны.

Что значит y обратно пропорционально значению X?

Выражение y изменяется обратно пропорционально, поскольку x означает, что , когда x увеличивается, y уменьшается в тот же коэффициент.

Что означает, когда Y обратно пропорционально x?

Какова формула обратно пропорционального? Предположим, что две переменные x и y обратно пропорциональны; тогда мы можем представить их как x ∝ 1 / y . Это означает, что если значение x увеличивается, значение y уменьшается, и наоборот.

Что это значит, когда y изменяется вместе с X?

(Некоторые учебники описывают прямое изменение, говоря, что y изменяется прямо как x, y изменяется пропорционально x, или y прямо пропорционально x.) Это означает, что при увеличении x увеличивается y, а при уменьшении x уменьшается y, и соотношение между ними всегда остается неизменным.

Что означает, когда y изменяется обратно пропорционально x?

Обратное изменение

Как найти k, если y изменяется обратно пропорционально x?

Поскольку k является постоянным, мы можем найти k для любой точки , умножив координату x на координату y. Например, если y изменяется обратно пропорционально x, а x 5, когда y 2, то постоянная изменения равна k xy 5 (2) 10. Таким образом, уравнение, описывающее эту обратную вариацию, будет xy 10 или y.

Что такое уравнение, когда y 12 x 2?

Фраза y изменяется обратно пропорционально x или y обратно пропорционально x означает, что , когда x становится больше, y становится меньше, или наоборот. Это понятие переводится двояко. yx k для некоторой константы k, называемой константой пропорциональности.

Каково уравнение обратной связи?

Обратное изменение может быть представлено уравнением xy = k или y = kx .То есть y изменяется обратно пропорционально x, если существует некоторая ненулевая константа k такая, что xy = k или y = kx, где x ≠ 0, y ≠ 0. Предположим, y изменяется обратно пропорционально x, так что xy = 3 или y = 3x. Этот график этого уравнения показан.

Что это значит, если y изменяется обратно пропорционально x?

Фраза y изменяется обратно пропорционально x или y обратно пропорционально x означает, что , когда x становится больше, y становится меньше, или наоборот. Это понятие переводится двояко. yx k для некоторой константы k, называемой константой пропорциональности.Используйте этот перевод, если требуется константа.

Что означает обратная вариация?

(Некоторые учебники описывают прямое изменение, говоря, что y изменяется прямо как x, y изменяется пропорционально x, или y прямо пропорционально x.) Это означает, что при увеличении x y увеличивается, а при уменьшении x y уменьшается, и что соотношение между ними всегда остается неизменным.

Что это значит, если Y обратно пропорционально x?

Фраза y изменяется обратно пропорционально x или y обратно пропорционально x означает , что чем больше x, тем меньше y, или наоборот.Это понятие переводится двояко. yx k для некоторой константы k, называемой константой пропорциональности. Используйте этот перевод, если требуется константа.

Как узнать, обратно ли y обратно пропорционально x?

Когда одна переменная увеличивается, другая пропорционально уменьшается, так что продукт остается неизменным. Если b обратно пропорционально a, уравнение имеет вид b k / a (где k — постоянная). y обратно пропорционален x.

Что означает, когда что-то обратно пропорционально?

Если одно значение обратно пропорционально другому, то оно записывается с использованием символа пропорциональности по-другому.Обратная пропорция возникает , когда одно значение увеличивается, а другое уменьшается . Например, большее количество рабочих сократит время на выполнение задачи. Они обратно пропорциональны.

Что означает, когда y пропорционально x?

(Некоторые учебники описывают пропорциональную зависимость, говоря, что y изменяется пропорционально x или что y прямо пропорционально x.) Это означает, что по мере увеличения x y увеличивается, а по мере уменьшения x y уменьшается — и что отношение между ними всегда остается прежним

Как узнать, изменяется ли y вместе с X?

Поскольку k является постоянным (одинаковым для каждой точки), мы можем найти k, когда задана для любой точки, разделив координату y на координату x . Например, если y изменяется прямо как x, а y = 6, когда x = 2, постоянная вариации равна k = = 3. Таким образом, уравнение, описывающее это прямое изменение, будет y = 3x.

Показывают ли x и y прямое изменение?

(Некоторые учебники описывают прямое изменение, говоря, что « y изменяется прямо как x» , y изменяется пропорционально x »или« y прямо пропорционально x ».) Это означает, что по мере увеличения x, y увеличивается и как x уменьшается, y уменьшается — и соотношение между ними всегда остается неизменным.

Как узнать, изменяется ли y обратно пропорционально x?

Обратное изменение может быть представлено уравнением xy = k или y = kx . То есть y изменяется обратно пропорционально x, если существует некоторая ненулевая константа k такая, что xy = k или y = kx, где x ≠ 0, y ≠ 0.

Когда y изменяется обратно пропорционально квадрату x?

Определение обратной вариации 1: математическая связь между двумя переменными, которая может быть выражена уравнением, в котором произведение двух переменных равно константе. 2: уравнение или функция, выражающая обратную вариацию сравните прямую вариацию

По какой формуле y изменяется обратно пропорционально x?

Обратное изменение может быть представлено уравнением xy = k или y = kx . То есть y изменяется обратно пропорционально x, если существует некоторая ненулевая константа k такая, что xy = k или y = kx, где x ≠ 0, y ≠ 0.

Что такое K в прямой и обратной вариациях?

Фраза y изменяется обратно пропорционально x или y обратно пропорционально x означает, что , когда x становится больше, y становится меньше, или наоборот.Это понятие переводится двояко. yx k для некоторой константы k, называемой константой пропорциональности.

Как X и Y называются в уравнении x / y 12?

Переменная x называется независимой переменной (также иногда называемой аргументом функции), а переменная y называется зависимой переменной (также иногда называемой изображением функции). Для y12 существует два возможных значения x. х-4 и х4.

Что это значит, если y напрямую зависит от x?

Формула обратной связи помогает математически представить обратно пропорциональную зависимость.Формула обратной вариации: x xd7 y k или y k / x, где x и y — две переменные, а k — константа пропорциональности.

В каком уравнении y изменяется прямо как x?

(Некоторые учебники описывают прямое изменение, говоря, что y изменяется прямо как x, y изменяется пропорционально x, или y прямо пропорционально x.) Это означает, что при увеличении x y увеличивается, а при уменьшении x y уменьшается, и что соотношение между ними всегда остается неизменным.

.