Задачи на расстояние и скорость 5 класс с решением и ответами

15 Яблонский Д15. Применение принципа возможных перемещений к определению реакций опор составной конструкции — Яблонский — условие и подробное решение задачи № 15026 бесплатно — bambookes.ru.

Задачи на движение

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.

Задача на нахождение расстояния/скорости/времени

Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?

Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)

Ответ: за 3 часа автомобиль проедет 240 километров.

Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?

Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.

Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:

Ответ: скорость автомобиля составляет 60 км/ч

Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?

Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)

Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)

Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12

Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.

Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?

Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения

600 : 120 = 5 часов

Ответ: вертолет был в пути 5 часов.

Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?

Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время

Ответ: за 6 часов вертолет преодолел 960 км.

Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.

Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9

Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения

723 − 495 = 228 км

Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:

Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч

Скорость сближения

Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100+105, то есть 205 м/м. Значит каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.

Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, мы сможем определить расстояние между двумя пунктами:

205 × 3 = 615 метров

Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.

Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100×3 метров

100 × 3 = 300 метров

А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105×3 метров

105 × 3 = 315 метров

Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:

300 м + 315 м = 615 м

Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами

Найдем скорость сближения велосипедистов

10 км/ч + 12 км/ч = 22 км/ч

Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения

Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.

Найдем расстояние, пройденное первым велосипедистом:

Найдем расстояние, пройденное вторым велосипедистом:

Сложим полученные расстояния:

20 км + 24 км = 44 км

Ответ: расстояние между населенными пунктами составляет 44 км.

Задача 2. Из двух на

Задачи 5 класс на скорость время расстояние с решением

Основания равнобедренной трапеции равны 23 и 27. Косинус острого угла трапеции равен Найдите боковую сторону. Решается аналогично прототипу: Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен Найдите боковую сторону. Решение: Ответ: 21.

Задачи на движения (5 класс)

УЖЕ ЧЕРЕЗ 10 МИНУТ ВЫ МОЖЕТЕ ПОЛУЧИТЬ ДИПЛОМ

От проекта «Инфоурок» с указанием данных образовательной лицензии, что важно при прохождении аттестации.

Если Вы учитель или воспитатель, то можете прямо сейчас получить документ, подтверждающий Ваши профессиональные компетенции. Выдаваемые дипломы и сертификаты помогут Вам наполнить собственное портфолио и успешно пройти аттестацию.

Список всех тестов можно посмотреть тут — https://infourok. ru/tests

Описание презентации по отдельным слайдам:

Урок математики в 5 классе «Решение задач на движение»

Цели урока: Закрепить и развивать навыки решения задач на движение; Закрепить знание единиц измерения расстояний, времени, скорости; Воспитывать самостоятельность, аккуратность, внимательность; Развивать память, наблюдательность, мышление; Оборудование: экран, компьютер, мультимедийный проектор

I. РАЗМИНКА 1. Выберите правильное утверждение: А) Скорость – это расстояние между двумя точками; Б) Скорость – это расстояние, пройденное телом за единицу времени; В) Скорость – это быстрая езда. 2. Заполните таблицу Скорость Время Расстояние 15 км/ч 3 ч 9 ч 270 км 45 км/ч 180 км 50 км/ч 1 сут

Движение в противоположном направлении – на удаление Движение в противоположном направлении – навстречу друг другу Движение в одном направлении – с отставанием Движение в одном направлении – вдогонку Что общего? есть объекты движения, есть величины: скорость, время, расстояние В чём различия? направление движения объектов пункт отправления объектов время отправления значения величин и единицы их измерения Какие виды задач на движение существуют? Что общего и в чём различие этих движений?

СКОРОСТЬ V= S : t ВРЕМЯ t = S : V РАССТОЯНИЕ S = V × t Основные формулы:

Движение навстречу друг другу Скорость сближения показывает на сколько километров в час объекты, о которых идет речь в задаче сближаются друг с другом: vсбл.= v1 + v2

Из двух сел, расстояние между которыми 130 км, одновременно навстречу друг другу вышли два спортсмена. Их скорости 14 км/ч и 16 км/ч. На сколько километров в час спортсмены сближаются друг с другом? 130 км Решение: vсбл.= v1 + v2 = 14 + 16 = 30 км/ч

560 м t = 560 / 80 = 7 мин vсбл. = v1+v2 vсбл.= 30 + 50 = 80 м/мин

Из двух городов, расстояние между которым 1800 км, одновременно навстречу друг другу вылетели два вертолёта. Скорость первого вертолёта равна 200км/ч, а скорость второго составляет 80% скорости первого. Через сколько времени после вылета расстояние между вертолётами сократится до 720 км. 200км/ч 80% 1800 км. t =? V1 = 200 /100 х 80 = 160 – скорость 2 вертолёта S = 1800 – 720 = 1080 vсбл. = v1+v2 vсбл.= 200 + 160 = 360 км/час t = 1080 / 360 = 3 часа

Из двух посёлков выехали одновременно навстречу друг другу два всадника. Первый ехал со средней скоростью 200м/мин, а второй проезжал в минуту на 20м меньше. Всадники встретились через 50 мин. Найди расстояние между посёлками? Решение: v2 = 200 – 20 = 180 м/мин – скорость 2 всадника vсбл. = v1+v2 vсбл. = 180 + 200 = 380 м/мин S = 380 * 50 = 19000 метров = 19 км.

Движение в одном направлении. Движение вдогонку. Скорость сближения равна разности скоростей объектов vсбл.= v2 — v1 , (v2 > v1 )

Сороконожка поползла за муравьём, когда расстояние между ними было 50 м. Скорость сороконожки 8 м/мин, а скорость муравья – 6 м/мин. Через сколько времени сороконожка догонит муравья? t =?

Решение: 204 : 51 = 4 (время пути трактора) 4 – 1 = 3 (время пути автомобиля) 51 : 3 = 17 (скорость сближения) 17 * 4 = 68 (скорость автомобиля) Из города со скоростью 51 км/ч выехал трактор, а через час следом за ним выехал автомобиль, который догнал трактор в 204 км от города. С какой скоростью ехал автомобиль?

Из села вышел пешеход со скоростью 4 км/ч. Через 3 ч вслед за ним выехал велосипедист со скоростью 10 км/ч. За сколько часов велосипедист догонит пешехода? v= 4км/ч v= 10км/ч t – 3ч v= 4км/ч

Движение в противоположных направлениях из одного пункта. Скорость удаления показывает на сколько километров в час объекты, о которых идет речь в задаче, удаляются друг от друга: vудал.= v1 + v2

Два туриста одновременно вышли в противоположных направлениях из одной турбазы. Скорость первого 4 км/ч, скорость второго 5 км/ч. Какое расстояние будет между ними через 3 ч? Задача № 5 5 км/ч 4 км/ч 3 ч 5 км/ч S = ? Решение: vудал.= v1 + v2 = 5 + 4 = 9 км/ч (скорость удаления) S = 9*3 = 27 км

Два скакуна одновременно понеслись в противоположных направлениях из одной фермы. Скорость первого 15 км/ч, скорость второго 18 км/ч. Через сколько времени расстояние между ними будет равно 165 км? Задача № 6 15 км/ч 18 км/ч 165 км t = ? Решение: vудал.= v1 + v2 = 15 + 18 = 33 км/ч (скорость удаления) t = S/ vудал.= 165/ 33 = 5 часов

Из двух городов, расстояние между которым 110 км. Одновременно в противоположных направлениях выехали 2 автобуса. Первый автобус ехал со скоростью 60 км/ч. С какой скоростью ехал второй автобус, если через 3 ч после выезда расстояние между ними было равно 500 км. Задача № 7 500 – 110 = 390 км 390:3 = 130 км/ч (скорость удаления) v2 = 130 – 60 = 70 км/ч

От станции одновременно в противоположных направлениях отошли два мотоциклиста со скоростями 40 км/ч и 35 км/ч. Какое расстояние будет между ними через 6 часов? Задача № 8 40 км/ч 35 км/ч 6 ч? км. Решение: vудал.= v1 + v2 = 40 + 35 = 75 км/ч (скорость удаления) S = 75*6 = 450 км

Два катера отошли от одной пристани в противоположных направлениях. Первый катер прошёл 56 км, а второй катер – в 2 раза меньше, чем первый. Какое расстояние стало между катерами? На сколько километров больше прошёл первый катер? Задача

скорость, время, расстояние» (5 класс)

Дидактическая карточка по теме

«Решение задач на движение с величинами: скорость, время, расстояние»

(5 класс)

Цель: отработка навыков применения изученных правил на практике.  

Задачи: формировать математические знания;

побуждать к чёткой, последовательной и аккуратной деятельности;

развивать логическое мышление, творческие способности;

прививать интерес к предмету.

Универсальные учебные действия:

Познавательные УУД:

— овладение основами логического и алгоритмического мышления;

— контроль и оценка процесса и результата деятельности.

Коммуникативные УУД:

— определять общую цель и пути её достижения;

— осуществлять самоконтроль, взаимный контроль;

— строить высказывания, аргументировано доказывать свою точку зрения;

— обращаться за помощью, предлагать помощь и сотрудничество.

Регулятивные УУД:

— развивать умение читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;

— адекватно воспринимать предложения учителя, товарищей по исправлению допущенных ошибок.

Ожидаемые результаты:

— у обучающихся сформируется навык самоконтроля;

— систематизируются знания по изученному материалу.

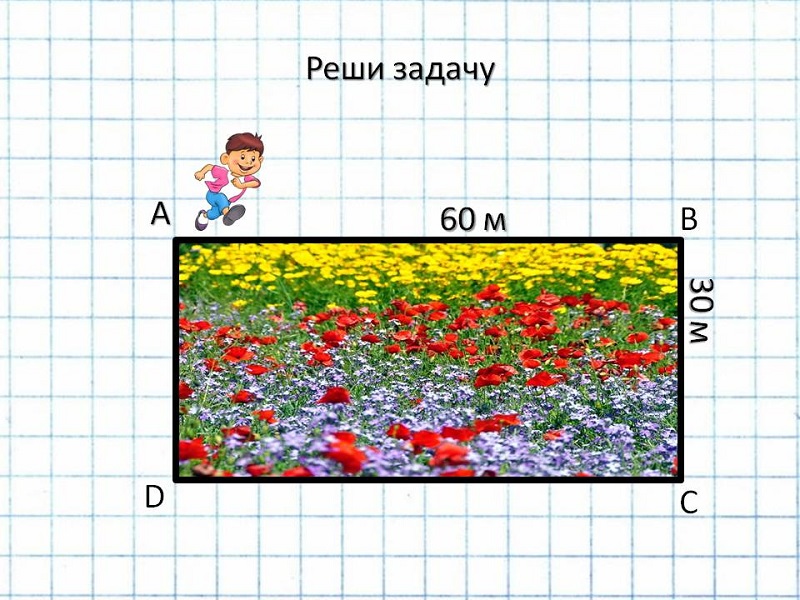
Петя Иванов бегает вокруг площадки со скоростью 45 м/мин.

Где будет находиться Петя:

— через две минуты после начала движения, если он будет бежать из точки А по часовой стрелке; против часовой стрелки;

— через 4 мин после начала движения?

Сколько потребуется времени, чтобы обежать площадку 3 раза?

С какой скоростью надо бежать Пете, чтобы обежать площадку за 3 минуты?

Ответы к задаче: С; С; А; 12 мин; 60 м/мин.

Используемые интернет-ресурсы:

https://forum.materinstvo.ru/uploads/1296476411/post-280722-1296563285.png