Задачи на движение с решением 8 класс – Тематическая тренировочная работа №11 по теме «Решение текстовых задач на движение по воде, на работу, на концентрацию, смеси и сплавы, на движение по прямой, » для подготовки к региональному экзамену по математике в 8 классе.

Posted on by alexxlab

Тематическая тренировочная работа №11 по теме «Решение текстовых задач на движение по воде, на работу, на концентрацию, смеси и сплавы, на движение по прямой, » для подготовки к региональному экзамену по математике в 8 классе.

Тренировочная работа. Задание №11. Умение решать текстовые задачи. (С ответами)

Задачи на движение по воде

1. Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?

2. Расстояние между пристанями А и В равно 80 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 22 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

3. Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.

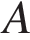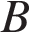4. Пристани hello_html_m72b00d28.pngи hello_html_102cce21.pngрасположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.

5. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отдалился, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?

6. Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?

7. Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?

8. Катер прошёл от одной пристани до другой, расстояние между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся обратно через 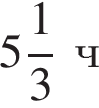hello_html_2325f94a.pngпосле начала поездки. Найдите скорость течения реки, если известно, что скорость катера в стоячей воде равна 20 км/ч.

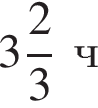9. Моторная лодка прошла от одной пристани до другой, расстояние между которыми по реке равно 16 км, сделала стоянку на 40 мин и вернулась обратно через hello_html_m7ab628a6.pngпосле начала поездки. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 12 км/ч.

10. Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.

11. Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

12. От пристани А к пристани В, расстояние между которыми равно 70 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью, на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.

13. Расстояние между пристанями А и В равно 99 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 22 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч.

14. Расстояние между пристанями А и В равно 75 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 44 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.

15. Теплоход проходит по течению реки до пункта назначения 76 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.

16. От пристани А к пристани В, расстояние между которыми равно 153 км, отправился с постоянной скоростью первый теплоход, а через 4 часа после этого следом за ним, со скоростью, на 16 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.

17. Баржа прошла по течению реки 48 км и, повернув обратно, прошла ещё 36 км, затратив на весь путь 6 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

18. Расстояние между пристанями А и В равно 63 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 20 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.

Задачи на проценты, сплавы и смеси

1. Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?

2. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?

3. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

4. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?

5. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

6. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?

7. Смешали некоторое количество 10-процентного раствора некоторого вещества с таким же количеством 12-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

8. Свежие фрукты содержат 86 % воды, а высушенные — 23 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?

9. Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?

10. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?

11. Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?

12. Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?

13. Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?

14. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?

15. Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?

16. Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?

17. Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?

18. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?

19. Свежие фрукты содержат 88 % воды, а высушенные — 30 %. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?

20. Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

21. Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?

Задачи на совместную работу

1. Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?

2. На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?

3. Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?

4. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?

5. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 часов. За сколько часов наполняет бассейн одна вторая труба?

6. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объёмом 136 литров?

7. Две трубы наполняют бассейн за 6 часов 18 минут, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?

8. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

9. Три бригады изготовили вместе 266 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.

10. Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?

11. Три бригады вместе изготовили 114 карданных валов. Известно, что вторая бригада изготовила карданных валов в 3 раза больше, чем первая, и на 16 карданных валов меньше, чем третья. На сколько карданных валов больше изготовила третья бригада, чем первая?

12. Три бригады изготовили вместе 114 деталей. Известно, что вторая бригада изготовила деталей в 3 раза больше, чем первая, и на 16 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.

13. Три бригады вместе изготовили 114 синхронизаторов передач. Известно, что вторая бригада изготовила синхронизаторов в 3 раза больше, чем первая, и на 16 синхронизаторов меньше, чем третья. На сколько синхронизаторов передач больше изготовила третья бригада, чем первая.

14. Игорь и Паша красят забор за 18 часов. Паша и Володя красят этот же забор за 20 часа, а Володя и Игорь — за 30 часов. За сколько минут мальчики покрасят забор, работая втроём?

15. Три бригады изготовили вместе 248 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.

16. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

Движение по прямой

1. Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шёл со скоростью, на 1 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку.

2. Из пункта А в пункт В, расстояние между которыми 19 км, вышел пешеход. Через полчаса навстречу ему из пункта В вышел турист и встретил пешехода в 9 км от В. Турист шёл со скоростью, на 1 км/ч большей, чем пешеход. Найдите скорость пешехода, шедшего из А.

3. Расстояние между городами А и В равно 375 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 1 час 30 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С.

4. Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

5. Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

6. Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

7. Железнодорожный состав длиной в 1 км прошёл бы мимо столба за 1 мин., а через туннель (от входа локомотива до выхода последнего вагона) при той же скорости — за 3 мин. Какова длина туннеля (в км)?

8. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.

9. Из пункта А в пункт В, расстояние между которыми 27 км, вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что она была на 2 км/ч меньше скорости пешехода.

10. Из пункта А в пункт В, расстояние между которыми 34 км, выехал велосипедист. Одновременно с ним из В в А вышел пешеход. Велосипедист ехал со скоростью, на 8 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость велосипедиста, если известно, что они встретились в 10 км от пункта В.

11. Из пункта А в пункт В, расстояние между которыми 19 км, вышел пешеход. Через полчаса навстречу ему из пункта В вышел турист и встретил пешехода в 9 км от В. Турист шёл со скоростью, на 1 км/ч большей, чем пешеход. Найдите скорость пешехода, шедшего из А.

12. Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.

13. Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 45 секунд. Найдите длину поезда в метрах.

14. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 30 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 144 км, скорость первого велосипедиста равна 24 км/ч, скорость второго — 28 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

15. Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

16. Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.

17. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.

18. Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 40 минут раньше, чем велосипедист приехал в А, а встретились они через 15 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

19. Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

20. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

21. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.

22. Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

23. Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 90 минут следом за ним со скоростью 100 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

24. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

25. Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью, на 20 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.

26. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

27. Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?

28. Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 14 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 3 км/ч?

29. Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 4 км от места отправления. Один идёт со скоростью 2,7 км/ч, а другой — со скоростью 4,5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

30. Поезд, двигаясь равномерно со скоростью 86 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 18 секунд. Найдите длину поезда в метрах.

31. Поезд, двигаясь равномерно со скоростью 44 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 4 км/ч, за 81 секунду. Найдите длину поезда в метрах.

32. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 3 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 9 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.

33. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 30 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 9 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.

34. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 57 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 38 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.

35. Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 33 минуты раньше, чем велосипедист приехал в А, а встретились они через 22 минуты после выезда. Сколько часов затратил на путь из В в А велосипедист?

36. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 100 км. Отдохнув, он отправился обратно в А, увеличив скорость на 15 км/ч. По пути он сделал остановку на 6 часов, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

37. Теплоход проходит по течению реки до пункта назначения 285 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 34 км/ч, стоянка длится 19 часов, а в пункт отправления теплоход возвращается через 36 часов после отплытия из него.

38. Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 27 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

39. Расстояние между городами А и В равно 120 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 36 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из C в А, автомобиль прибыл в В. Найдите расстояние от А до С.

40. Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

41. Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 15 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него.

42. Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.

43. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 15 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.

44. Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,7 км от места отправления. Один идёт со скоростью 3,3 км/ч, а другой — со скоростью 4,1 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

45. Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью, на 24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого автомобиля.

46. Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 6 км/ч пешехода за 8 секунд. Найдите длину поезда в метрах.

Урок математики в коррекционной школе 8 вида по теме «Задачи на движение»

Конспект открытого урока по математике

в 7 классе коррекционной школы 8 вида по теме:

«Задачи на движение»

Цель урока:

  • комплексное изучение теоретического материала и способов деятельности учащихся по теме «Задачи на движение».

  • Тип урока: урок обобщения и систематизации знаний по данной теме

  • Оборудование : доска, ПК, интерактивная доска, листы с заданиями для самостоятельной работы, таблицы для заполнения, памятки «Схема решения задач на движение».

  • Формирование УУД:

  • Познавательные: умение работать с текстом, ставить цели, отвечать на вопросы, использовать уже изученный материал при решении задач, работа с текстом задачи;

  • Регулятивные: постановка личных целей, технология оценивания, действия по плану;

  • Коммуникативные: совместное решение задач ( в парах), оценивание

полученных результатов.

Планируемые образовательные результаты:

  • личностные: развивать активность, находчивость при решении задач; уметь общаться в коллективе и в паре, способствовать эмоциональному восприятию математических задач;

  • метапредметные: уметь видеть использование задач на движение в науке, технике, в других дисциплинах и в окружающей жизни;

  • предметные: уметь читать задачи, записывать условие и требование задачи; определять тип задачи, решать задачи на движение.

Основные понятия, изучаемые на уроке: задача на движение, скорость, время, расстояние.

Формы работы: фронтальная, парная, индивидуальная.

Этапы урока:

  1. Актуализация знаний

  1. Этап работы с информацией

  2. Этап закрепления полученных знаний

  3. Этап контроля усвоения знаний

  4. Подведение итогов урока.

ХОД УРОКА

  1. Актуализация знаний (5)

Организационный момент. Мотивация учебной деятельности учащихся

Вы уже умеете решать некоторые задачи на движение. В них рассматриваются три взаимосвязанных величины:

v – скорость движения (расстояние, пройденное за единицу времени),

t – время движения,

s – пройденный путь.

Эта взаимосвязь выражается формулами:

2. Этап работы с информацией (5 мин)

В начальной школе вы научились решать задачи, в которых рассматривалось движение одного объекта: пешехода, велосипедиста, автомобиля и т.д.

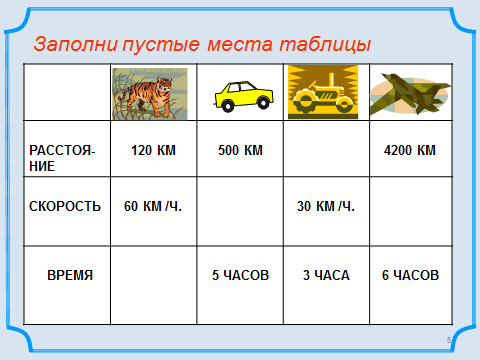
Составьте и решите задачи, используя данные в таблице.

Задачи решаем в парах, потом обсуждаем вместе.

Давайте договоримся, как мы будем решать все задачи:

  1. Находим формулу для нахождения неизвестной величины.

  2. Подставляем числовые значения и вычисляем.

hello_html_m2e011f49.png

3. Этап закрепления полученных знаний (20 мин)

Давайте вспомним, как решаются задачи, в которых два участника движения, стартовав одновременно, двигались навстречу друг другу, двигались в противоположных направлениях, двигались в одном направлении.

Физминутка

ПАМЯТКА «Схема решения задач на движение»

1. Определить вид движения объектов

в данной задаче

2. Составить схему к данной задаче

3. Подобрать формулу к задаче

4. Правильно решить задачу.

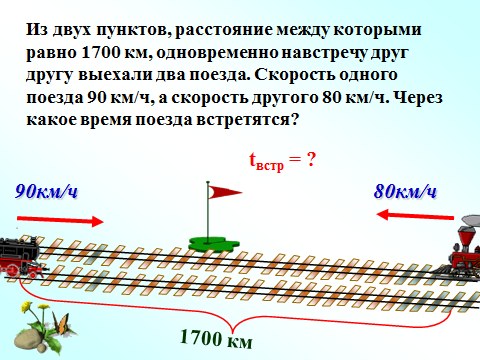
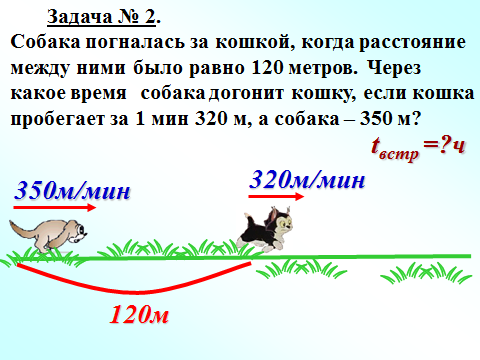
Решаем 2 задачи у доски, используя памятку!

hello_html_5981222e.png

hello_html_m50c893b9.png

Производим целеполагание, планирование, распределение времени, задаём необходимость самооценки и коррекции результатов.

На этом этапе урока мы формируем:

–  по использованию математических знаний для решения различных математических задач и оценки полученных результатов;

–  по использованию доказательной математической речи;

–  по работе с информацией, в том числе и с различными математическими текстами;

  • регулятивные УУД – формирование умений ставить личные цели деятельности, планировать свою работу, действовать по плану, оценивать полученные результаты;

  • коммуникативные УУД – формирование умений совместно с другими детьми в группе находить решение задачи и оценивать полученные результаты.

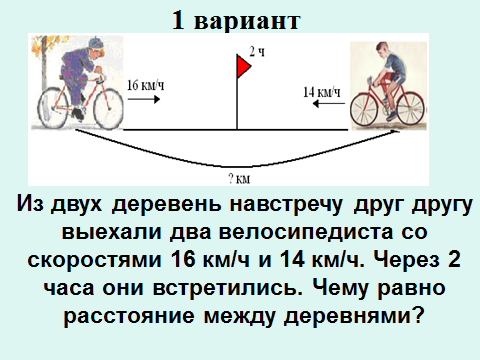
4.Этап контроля усвоения знаний (5)

Форма работы: индивидуальная самостоятельная.

hello_html_m6e9563b6.png

hello_html_4bba2f2.png

hello_html_m6e5f8a74.png

5. Подведение итогов урока (5)

Рефлексия

hello_html_m44a549ff.png

Домашнее задание

Оценки за урок

«Решение задач на движение в одном направлении с помощью квадратных уравнений» (для 8-9 классов)

Система тренировочных упражнений по теме: «Решение задач на движение в одном направлении с помощью квадратных уравнений» (для 8-9 классов)

Два автомобиля одновременно отправляются в 660-километровый пробег. Первый едет со скоростью на 11 км/ч больше, чем второй и прибывает к финишу на 2ч раньше второго. Найдите скорость первого автомобиля.

Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью на 14 км/ч больше, чем второй и прибывает к финишу на 5 часов раньше второго. Найдите скорость велосипедиста, прибывшего к финишу вторым.

Два автомобиля одновременно отправляются в 950-километровый пробег. Первый едет со скоростью на 18 км/ч больше, чем второй и прибывает к финишу на 4 часа раньше второго. Найдите скорость первого автомобиля.

Два велосипедиста одновременно отправляются в 208-километровый пробег. Первый едет со скоростью на 3 км/ч больше, чем второй и прибывает к финишу на 3 часа раньше второго. Найдите скорость второго велосипедиста, пришедшего к финишу вторым.

  1. Два автомобиля одновременно отправляются в 660-километровый пробег. Первый едет со скоростью на 11 км/ч больше, чем второй и прибывает к финишу на 2ч раньше второго. Найдите скорость первого автомобиля.

  2. Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью на 14 км/ч больше, чем второй и прибывает к финишу на 5 часов раньше второго. Найдите скорость велосипедиста, прибывшего к финишу вторым.

  3. Два автомобиля одновременно отправляются в 950-километровый пробег. Первый едет со скоростью на 18 км/ч больше, чем второй и прибывает к финишу на 4 часа раньше второго. Найдите скорость первого автомобиля.

  4. Два велосипедиста одновременно отправляются в 208-километровый пробег. Первый едет со скоростью на 3 км/ч больше, чем второй и прибывает к финишу на 3 часа раньше второго. Найдите скорость второго велосипедиста, пришедшего к финишу вторым

  1. Два автомобиля одновременно отправляются в 660-километровый пробег. Первый едет со скоростью на 11 км/ч больше, чем второй и прибывает к финишу на 2ч раньше второго. Найдите скорость первого автомобиля.

  2. Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью на 14 км/ч больше, чем второй и прибывает к финишу на 5 часов раньше второго. Найдите скорость велосипедиста, прибывшего к финишу вторым.

  3. Два автомобиля одновременно отправляются в 950-километровый пробег. Первый едет со скоростью на 18 км/ч больше, чем второй и прибывает к финишу на 4 часа раньше второго. Найдите скорость первого автомобиля.

  4. Два велосипедиста одновременно отправляются в 208-километровый пробег. Первый едет со скоростью на 3 км/ч больше, чем второй и прибывает к финишу на 3 часа раньше второго. Найдите скорость второго велосипедиста, пришедшего к финишу вторым

Проверочная по алгебре для 8 класса по теме «Задачи на движение»

Проверочная работа. Задачи на движение.

Вариант 1

1. Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

2. Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью, на 24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого автомобиля.

_____________________________________________________________________________________

Вариант 2

1. Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 15 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него.

2. Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

_____________________________________________________________________________________

Проверочная работа. Задачи на движение.

Вариант 1

1. Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

2. Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью, на 24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого автомобиля.

_____________________________________________________________________________________

Вариант 2

1. Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 15 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него.

2. Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

Проверочная работа. Задачи на движение.

Вариант 1

1. Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.

2. Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью, на 24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого автомобиля.

_____________________________________________________________________________________

Вариант 2

1. Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 15 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него.

2. Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

Методическая разработка по математике (8 класс) на тему: Решение задач на движение.

                                                     Задача

Два автомобиля одновременно отправляются в 660-километровый пробег. Первый едет со скоростью на 11 км/ч больше, чем второй, и прибывает к финишу на 2ч. Раньше второго. Найдите скорость первого автомобиля

  1. Внимательно читаем задачу. (О чем идет речь в задачи)

О двух автомобилях.

1 автомобиль

2 автомобиль

  1. Так как задача на движение, у движения есть три характеристики. Какие?

Скорость

Время

Расстояние

1 автомобиль

2 автомобиль

  1. Читаем задачу до точки или до запятой и заполняем таблицу.

Скорость

Время

Расстояние

1 автомобиль

На 11 км/ч больше

На 2ч. раньше.

660 км

2 автомобиль

660 км

  1. Ищем неизвестный компонент и обозначаем за Х

Скорость

Время

Расстояние

1 автомобиль

На 11 км/ч больше

На 2ч. раньше.

660 км

2 автомобиль

      х

660 км

  1. Заполняем все возможные ячейки , через х

Скорость

Время

Расстояние

1 автомобиль

На 11 км/ч больше

Х+11

На 2ч. раньше.

660/х+11

660 км

2 автомобиль

      х

660/х

660 км

  1. Составляем Уравнение:

 —  = 2

  1. Решаем уравнение и записываем

 

План-конспект урока по алгебре (8 класс) на тему: Решение задач на движение методом подобия

Решетова Марина Георгиевна. Учитель математики МКОУ «ООШ № 164» Таштагольский район Кемеровской области.

Урок математики в 8 классе.

Тема урока: «Решение задач на движение методом подобия».

Цели урока:

  • Воспитание воли и настойчивости для достижения поставленной задачи.
  • Научиться применять знания о подобных треугольниках при решении текстовых задач на движение.
  • Закрепить умение выбора способа решения текстовой задачи.
  • Развитие пространственного мышления.
  • Развитие умений обобщать и конкретизировать свойства изучаемых объектов и отношений.

Оборудование:

  • технические средства – мультипроектор,
  • раздаточный материал (карточки с заданиями)

Приложение: Презентация.

Структура урока:

  1. Сообщение темы и цели урока. (2 минуты)
  2. Актуализация опорных знаний. (5 минут)
  3. Разбор домашнего задания. (5 минут)
  4. Объяснение применения метода подобия треугольников при решении задач на движение. (10 минут)
  5. Решение задач в парах. (10 минут)
  6. Обсуждение результатов. (5 минут)
  7. Постановка домашнего задания. (5 минут)
  8. Подведение итогов урока. (3 минуты)

Ход урока

  1. Сообщение темы и цели урока.

Тема урока: «Решение задач на движение методом подобия».

Цель урока:  

Научиться применять знания о подобных треугольниках при решении текстовых задач на движение.

(Тема и цели урока, а так же все последующие иллюстрации  проецируются на экран при помощи мультипроектора)

 

  1. Актуализация опорных знаний.

Фронтальный опрос:

  • Какие треугольники называются подобными?
  • Какие признаки подобия вы знаете?
  • Устное решение задач по готовым чертежам.

 

  • Какое движение называется равномерным?
  • Какая зависимость между основными характеристиками прямолинейного равномерного движения?
  • Как выглядит график равномерного прямолинейного движения?
  • Сравните скорости тел по графикам их движения.

  1. Разбор домашнего задания.

Два автомобиля выехали одновременно из своих городов А и В навстречу друг другу. После встречи первый ехал 45 минут до города В, а второй ехал 60 минут до города А. Сколько минут они ехали до встречи?

Один из учащихся записывает решение задачи на доске.

  1. Объяснение применения метода подобия треугольников при решении задач на движение.

Учитель: Предлагаю рассмотреть другой способ решения этой задачи.

 Построим схематически графики движения первого и второго автомобилей :CD и EF соответственно в одной системе координат.

Обозначим момент встречи автомобилей точкой М.

Проведем через точку М  отрезок PN перпендикулярный оси времени.

Подпишем на графике время движения каждого автомобиля после встречи.

Обозначим через Х время движения автомобилей до встречи.

Вопросы:  

  • Есть ли на полученном рисунке подобные треугольники?
  • Назовите их.
  • Докажите их подобие.

Учитель: таким образом, на рисунке мы видим две пары подобных треугольников 1) DMN и CMP, 2)  EMN и  FMP.

Вопрос: Составьте  пропорции для каждой пары. (CP÷DN= МР÷ МN   и    FP÷ EN= МР÷ МN)

Учитель: из этих двух пропорций следует: CP÷DN= FP÷ EN

 или Х÷ 49 = 64÷ Х.

 Учащиеся решают полученное уравнение.

Уравнение имеет единственный положительный корень Х=56

Ответ: Автомобили ехали до встречи 56 минут.

Учитель: Предлагаю вам сравнить два способа решения одной и той же задачи.

 

Учащиеся сравнивают способы и делают вывод.

Учитель: Предлагаю вам решить еще одну задачу этим же способом.

Задача №2

В один и тот же час навстречу друг другу из посёлков М и N должны были выйти два пешехода. Однако первый задержался и вышел позже на 8 ч. При встрече выяснилось, что он прошёл на 8 км меньше, чем второй. Отдохнув, они одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате первый пришёл в N через 4 ч, а второй пришёл в М через 5 ч после встречи. Определите расстояние между посёлками MN и скорости пешеходов.

Чертеж к задаче помогает выполнить учитель.

При обсуждении работает весь класс. После того, как будет выработано решение задачи, один ученик выполняет решение на доске, остальные работают в тетрадях. Сравнивается ответ. Делаются выводы.

  1. Решение задач в парах.

Класс разбивается на пары (сильный – слабый). На доске демонстрируется условие задачи.

  1. Обсуждение результатов.

Учащиеся сравнивают ответы, делают вывод, обсуждают ход решения.

  1. Постановка домашнего задания.

Ученикам предлагаются индивидуальные карточки с тремя  задачами.

Первая и вторая задачи аналогичны тем, которые были решены на уроке, третья задача немного отличается.

Ход решения и чертеж к этой задаче обсуждаются на уроке.

Ход обсуждения

Вопрос

Ответ

На какой вопрос нужно ответить в задаче?

Сколько времени потратил турист на весь путь?

Как обозначено на рисунке время туриста в пути?

BS

На рисунке есть подобные треугольники?

AOC  и BOD

Докажите их подобие.

Учащиеся доказывают

Что показывает отрезок DЕ?

Путь, который осталось пройти туристу.

Сколько времени потратил пешеход на этот путь?

2 часа

Из какого условия можно получить ответ на вопрос, поставленный в задаче?

После встречи с автобусом туристу осталось пройти еще половину пути.

На этом обсуждение заканчивается.

Выполнить письменно решение всех трех задач учащиеся должны дома.

  1. Подведение итогов урока.

Учитель:  Прошу вас ответить на два вопроса:

  1. Оцените  насколько хорошо вы поняли ,  как решаются задачи на движение с применением метода подобия.
  2. Как вы думаете, пригодится ли он вам владение этим методом  при решении задач?

Учащиеся отвечают на вопросы.

Учитель выставляет оценки за работу на уроке.

Используемая литература: 

  1. А.В. Шевкин. Текстовые задачи в школьном курсе математики. – М.: Педагогический университет “Первое сентября”, 2011г.
  2. Ю.Н.Макарычев и др. Алгебра 8,9 – М.: Просвещение, 2008 г.
  3. Л.В. Кузнецов, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 класс. – М.: Дрофа, 2007.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *