«Задачи на производительность» (4 класс)
Задачи на производительность 4 класс. УМК «Планета знаний»
На лодочной станции надо покрасить 168 лодок. Один мастер может выполнить эту работу за 28 дней, а другой – за 21 день. За сколько дней они могут выполнить эту работу, работая вместе?
Одна бригада рабочих может построить 15 км шоссейной дороги за 30 дней, а другая – за 60 дней. За сколько дней могут построить эту дорогу обе бригады, работая вместе?
Одна бригада рабочих может посадить 600 плодовых деревьев за 10 дней, а другая — за 15 дней. За сколько дней могут посадить эти деревья две бригады, работая вместе?
На швейной фабрике два одинаковых автомата пришивают пуговицы к пальто. Один автомат работал 50 минут, другой 40 минут. Сколько пуговиц пришил каждый автомат, если вместе они пришили 1.350 пуговиц?
Библиотеке нужно переплести 4500 книг. Одна мастерская может переплести эти книги за 30 дней, а другая – за 45. За сколько дней могут выполнить заказ обе эти мастерские, работая одновременно?
Один трубоукладчик прокладывает 24 м труб в час. Другой 32 м труб в час. Сколько метров труб уложат обе машины за 6 часов, работая одновременно?
Один мастер ремонтирует 20 пар обуви в день. Другой – 18 пар обуви в день. Сколько пар обуви отремонтируют оба мастера за 4 дня?
Производительность первого насоса 180 л/ч, второго – 140 л/ч. Сколько воды перекачают два насоса за 3 часа, работая одновременно?
На первой скорости станок изготавливает 200 деталей в час. На второй скорости 260 деталей в час. Станок работал 2 ч на первой скорости и 3 ч на второй. Сколько деталей было изготовлено за это время?
Станок штампует 1000 пластиковых тарелок в час. На новом станке стали выпускать на 600 тарелок в час больше. Сколько тарелок выпустят на новом станке за 8-часовой рабочий день?
Два корректора должны прочесть 720 страниц рукописи за 5 дней. Один корректор прочитывает 64 страницы в день. Сколько страниц в день должен читать второй корректор, чтобы закончить рукописи в срок?
Мастер и ученик получили заказ на изготовление 72 табуреток. Мастер может сделать эту работу за 6 дней, а ученик за 12 дней. За сколько дней они выполнят эту работу вместе?
Через кран с горячей водой наливается 10 л в минуту, а через кран с холодной водой – 8 л в минуту. Сколько нужно времени, чтобы наполнить ванну, которая вмещает 360 литров?
Фабрика получила заказ на пошив 168 платьев. Одна бригада может выполнить его за 28 дней, а другая – за 21 день. За сколько дней обе бригады выполнят заказ, если будут работать вместе?
Мастер производил на 5 изделий в час больше, чем его ученик. За 2 часа совместной работы они произвели 58 изделий . Сколько изделий за семичасовую смену произведет каждый из них?
Двумя автомобилями необходимо вывезти из леса на станцию 420 бревен. Первый автомобиль за 5 рейсов перевез третью часть всех бревен. Остальные бревна перевез второй автомобиль, который вывозил на 42 бревна больше за 1 рейс. Какое число рейсов совершил второй автомобиль?
По плану слесарю необходимо сделать 120 гаек за 5 часов. Но он в час делал на 8 деталей больше нормы. Сколько гаек слесарь изготовил за это время?
infourok.ru
Решение текстовых задач на совместную работу. 6-й класс
Цели:
- научить находить способ решения задач с помощью использования опорных задач на совместную работу;
- научить использовать арифметический способ решения текстовых задач,
- развивать смекалку и сообразительность, умение ставить вопросы и отвечать на них.
Ход урока
1. Организационный момент.
Учитель: Добрый день, ребята! Самое главное в математике – умение решать текстовые задачи. Эпиграфом к сегодняшнему уроку будут слова Д. Пойа: “Умение решать задачи – практическое искусство, подобное плаванию или катанию на лыжах, или игре на фортепиано…”.
2. Этап подготовки к активному усвоению знаний.
Учитель: У каждого из вас лежат карточки с опорными задачами типа А (задача 1), В (задача 2), С (задача 3). Ученики читают опорные задачи.
Задача 1 (тип задачи А). Бассейн наполняется за 10 часов. Какая часть бассейна наполняется за 1 час?
Решение: 1 : 10 = часть бассейна наполнится за 1 час. Ответ: .
Задача 2 (тип задачи В). В каждый час первая труба наполняет бассейн бассейна, а вторая – бассейна. Какую часть бассейна наполняют обе трубы за 1 час совместной работы?
Решение: часть бассейна наполняют обе трубы за 1 час.
Ответ: .
Задача 3 (тип задачи С). В каждый час труба наполняет бассейна. За сколько часов она наполнит бассейн?
Решение: 1: = 6 часов – время для наполнения бассейна. Ответ: 6 часов.
Учитель: Итак, отправляемся в путь. Учитель задает вопросы, а учащиеся отвечают.
- Сколько минут содержится в половине, в трети, в четверти часа?
- Работу выполнили за 4 часа. Какую часть работы выполняли в каждый час?
- Путник проходит в час пути. За сколько часов он пройдет весь путь?
- Два путника вышли одновременно навстречу друг другу и встретились через 3 часа. На какую часть первоначального расстояния они сближались в каждый час?
3. Этап закрепления знаний.
Учитель: Есть много старинных задач на совместную работу, вот одна из них.
Старинная задача из математической рукописи XVII века: “Два плотника
рядились двор ставить. И говорит первый:
– Только бы мне одному двор ставить, то я бы поставил в 3 года.
А другой молвил:
– Я бы поставил его в шесть лет.
Оба решили сообща ставить двор. Сколь долга они ставили двор?”
Выслушать мнение ребят по поводу решения старинной задачи, разобрать затруднения, возникшие у ребят, при решении задачи на совместную работу.
Учитель: При совместной работе складывается не время работы, а часть работы, которую делают ее участники.
Решение задачи:
Ответ: 2 года.
Вывод: при решении задач на совместную работу вся выполненная работа принимается за 1 – “целое”, а часть работы, выполненная за единицу времени, находится по формуле.
Учитель: Разберем решение двух задач (текст задач на карточках).
Задача 1. В городе есть водоем. Одна из труб может заполнить его за 4 часа, вторая – за 8 часов, а третья – за 24 часа. За сколько времени наполнится водоем, если открыть сразу 3 трубы?
Решение задачи:
- 1: 4 = (водоема) наполнится через 1 трубу за 1 час;
- 1 : 8 = (водоема) наполнится через 2 трубу за 1 час;
- 1 : 24 = (водоема) наполнится через 3 трубу за 1 час; (водоема) наполнится через 3 трубы за 1 час; (часа) время наполнения водоема через 3 трубы.
Ответ: через 3 трубы, работающие одновременно, водоем наполнится за часа.
Задача 2. Два пешехода вышли одновременно из двух поселков навстречу друг другу. Один пешеход может пройти весь путь за 3 часа, а другой – за часа. Через сколько времени они встретятся?
Решение задачи: это тоже задача на “совместную работу”, хотя никто не работает. Но можно считать, что “работа” пешеходов – это прохождение пути. Поэтому весь путь принимается за “единицу” и вычисляется часть пути, пройденная каждым пешеходом.
- 1: 3 = (расстояния) проходит 1 пешеход за 1 час;
- 1 : (расстояния) проходит 2 пешеход за 1 час; (расстояния) сближаются оба пешехода за 1 час; (часа) пешеходы встретятся.
Ответ: через часа.
4. Рейтинговая самостоятельная работа.
Учитель: На карточках условия текстовых задач. Вы можете решить одну из предложенных задач по выбору. Решения задач проверяется через проектор.
1) Задача 1 (3 балла) Мастер делает всю работу за 3 часа, а его ученик – за 6 часов.
а) Какую часть работы делает каждый из них за 1 час?
б) Какую часть работы сделают они вместе за 1 час?
в) За сколько времени сделают они всю работу, если будут работать совместно?
2) Задача 2 (4 балла) Бассейн заполняется через 2 трубы за 3 часа. Если открыть одну первую трубу, то бассейн наполнится за 6 часов. За сколько времени наполнится бассейн через одну вторую трубу?
3) Задача 3 (5 баллов) Чтобы выкачать из цистерны нефть, поставили два насоса различной мощности. Если бы действовали оба насоса, цистерна оказалась бы пуста через 12 минут. Оба действовали в течение 4 минут, после чего работал только второй насос, который через 24 минуты выкачал всю остальную нефть. За сколько минут каждый насос, действуя один, мог бы качать всю нефть?
5. Рефлексия.
1) Достаточно ли знаний было, чтобы решить задачи?
2) Какие пробелы в знаниях выявились на уроке?
3) Какое открытие вы сделали для себя?
6. Задание на дом: составить по схемам текст задачи с решением.
Литература:
- Дорофеев Г. В., Петерсон Л. Г. Математика. 5 класс. Часть 2 [Текст]: учебник / Г. В. Дорофеев, Л. Г. Петерсон – М.: Издательство “Ювента”, 2008. – 240 с.
- Петерсон Л. Г. Математика. 4 класс. Часть 3 [Текст]: учебник / Л. Г. Петерсон – М.: Издательство “Ювента”, 2005. – с. 59
- Шевкин, А. В. Материалы курса “Текстовые задачи в школьном курсе математики” [Текст]: лекции 1-4. / А. В. Шевкин – М.: Педагогический университет “Первое сентября”, 2006. – 88 с.
- Шевкин, А. В. Материалы курса “Текстовые задачи в школьном курсе математики” [Текст]: лекции 5-8. / А. В. Шевкин – М.: Педагогический университет “Первое сентября”, 2006. – 80 с.
urok.1sept.ru
Задачи на работу. (9 класс)
Тема урока: Задачи на работу.
Цели и задачи: развить навыки решения задач ЕГЭ на работу; развить логическое мышление, внимание, память; воспитывать самостоятельность учащихся.
Ход урока:
Организационный момент.
Проверка знаний
А) д/з
Б) карточки3) Решение задач.
Еще один тип задач В13, встречающийся в вариантах ЕГЭ по математике — это задачи на работу.
Задачи на работу также решаются с помощью формулы: A 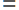 p
p 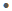 t. Здесь A — работа, t — время, а величина p, которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, продавец в супермаркете надувает воздушные шарики. Количество шариков, которые он надует за час — это и есть его производительность.
t. Здесь A — работа, t — время, а величина p, которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, продавец в супермаркете надувает воздушные шарики. Количество шариков, которые он надует за час — это и есть его производительность.
Правила решения задач на работу очень просты.
A

 t, то есть работа
t, то есть работа  производительность
производительность  время. Из этой формулы легко найти t или p.
время. Из этой формулы легко найти t или p.Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один). Написана книга (одна). А вот если речь идет о количестве кирпичей, страниц или построенных домов — работа как раз и равна этому количеству.
Если трудятся двое рабочих (два экскаватора, два завода…) — их производительности складываются.
В качестве переменной 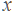
Задача 1. (разбор всем классом)
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
В колонке «работа» и для первого, и для второго рабочего запишем: 110. В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем ее за 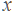 . Тогда производительность первого рабочего равна
. Тогда производительность первого рабочего равна 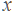
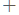
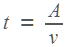 , время работы первого рабочего равно
, время работы первого рабочего равно 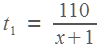 , время работы второго равно
, время работы второго равно 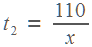 . Первый рабочий выполнил заказ на час быстрее. Следовательно,
. Первый рабочий выполнил заказ на час быстрее. Следовательно, 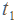 на 1 меньше, чем
на 1 меньше, чем 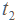 , то есть
, то есть 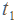
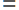
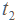
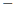 1
1
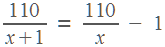 .
.
Мы уже решали такие уравнения. Оно легко сводится к квадратному:
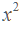
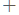
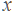
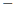 110
110 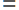 0
0
Дискриминант равен 441. Корни уравнения: 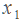
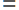 10,
10, 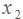
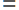
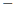 11. Очевидно, производительность рабочего не может быть отрицательной — ведь он производит детали, а не уничтожает их 🙂 Значит, отрицательный корень не подходит.
11. Очевидно, производительность рабочего не может быть отрицательной — ведь он производит детали, а не уничтожает их 🙂 Значит, отрицательный корень не подходит.
Ответ: 10.
2. (самостоятельная работа). Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
В этой задаче (в отличие от предыдущей) ничего не сказано о том, какая это работа, чему равен ее объем. Значит, работу можем принять за единицу.
А что же обозначить за переменные? Мы уже говорили, что за переменную 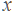 удобно обозначить производительность. Пусть
удобно обозначить производительность. Пусть 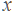 — производительность первого рабочего. Но тогда производительность второго нам тоже понадобится, и ее мы обозначим за
— производительность первого рабочего. Но тогда производительность второго нам тоже понадобится, и ее мы обозначим за 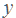 .
.
По условию, первый рабочий за два дня делает такую же часть работы, какую второй — за три дня. Значит, 2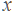
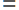 3
3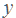 . Отсюда
. Отсюда 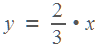 .
.
Работая вместе, эти двое сделали всю работу за 12 дней. При совместной работе производительности складываются, значит,
(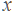
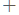
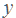 )
) 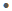 12
12 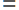 1,
1,
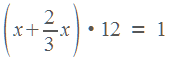 ,
,
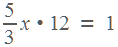 ,
,
20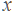
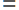 1,
1,
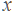
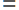
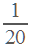 .
.
Итак, первый рабочий за день выполняет 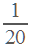 всей работы. Значит, на всю работу ему понадобится 20 дней.
всей работы. Значит, на всю работу ему понадобится 20 дней.
Ответ: 20.
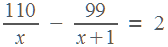
(разбор с комментированием учеником у доски). Два фермера, работая вместе, могут вспахать поле за 25 часов.
Производительность труда у первого и второго относятся как 2:5.
Фермеры планируют работать поочередно.
Сколько времени должен проработать второй фермер, чтобы поле было вспахано за 45,5 часов?
Решение | —
Пусть Х-производительность 1-го, У-производительность 2-го.
Система:
х+у=125
2х=5у
Последовательно:
2х+2у=225
2х-5у=0
7у=225 и у=2175
Тогда х=135
Итак, производительности мы нашли.
Поочередно фермеры работали 45,5 часа = 91/2 часа.
Пусть из этого времени 2-ой работал Т часов, тогда 1-ый работал 912-Т часов.
Уравнение:
(912-Т)⋅(135)+Т⋅(2175)=1
имеет корень Т=17,5
Проверка.
1. проверим , что х+у=125
135+2175=70+175175⋅35=7175=125
2. проверим, что 2х=3у:
235=5⋅2175
3. Проверим уравнение при поочередной работе:
Если 2-ой работал 17,5 часов, то 1-ый работал 45,5-17,5=28 часов
28⋅135+(352)⋅(2175)=2835+15=1
ОТВЕТ: 17,5
Задача 4 (Объяснение учителя) Заказ по выпуску машин завод должен выполнить за 20 дней, но уже за 18 дней завод перевыполнил план на 6 машин, так как ежедневно выпускал на 3 машины сверх плана. Сколько машин выпустил завод?
1способ
Пусть х машин выпустил завод.
А (шт.)
N (шт. в день)
t (дни)
По плану
x-6
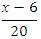
20
Фактически
х
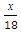 (на 3 шт больше, чем по плану)
(на 3 шт больше, чем по плану)
18
Тогда
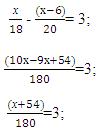
х+54=3·180; х+54=540; х=540-54; х=486
Ответ: 486 штук.
способ
Пусть х – количество машин в день по плану.
А (шт.)
N(шт. в день)
t(дни)
По плану
20х
х
20
Фактически
18(х+3) (на 6 больше чем по плану)
х+3
18
Тогда
18∙(x+3) – 20x = 6;
18x + 54 – 20x=6;
-2x=-54+6;
-2x = -48;
x=24;
18∙(24+3)=18∙27=486.
Ответ: 486 штук.
Задача 5. (самостоятельная работа). Две бригады, работая вместе, могут закончить уборку урожая за 8 дней. Если ервая бригада будет работать 3 дня, а вторая 12 дней, то они выполнят 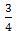 всей работы. За сколько дней может закончить уборку урожая каждая бригада, работая отдельно?
всей работы. За сколько дней может закончить уборку урожая каждая бригада, работая отдельно?
Решение:
Примем весь объем работы за 1. Тогда две бригады, работая вместе за один день выполнят 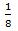 часть работы. Это их общая производительность.
часть работы. Это их общая производительность.
Пусть производительность первой бригады равна х, тогда второй 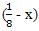 . (Это часть работы, выполненная за 1 день).
. (Это часть работы, выполненная за 1 день).
За три дня, работая отдельно первая бригада сделает 3х часть работы, а вторая за 12 дней: 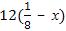 . Обе бригады при этом выполнят
. Обе бригады при этом выполнят 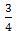 от 1.
от 1.
Составляем уравнение:
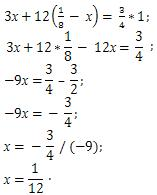
Так как А=p·t, то 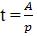 p– производительность.
p– производительность.
Время работы первой бригады: 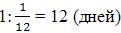 отдельно.
отдельно.
Вторая бригада, работая сама, потратит время: 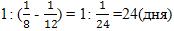
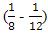 производительность второй бригады.
производительность второй бригады.
Ответ: 12 дней, 24 дня.

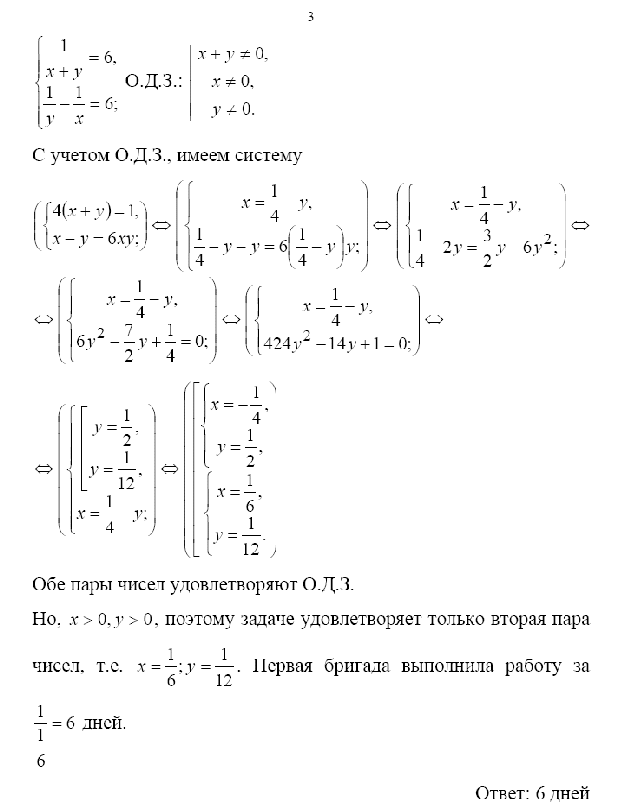


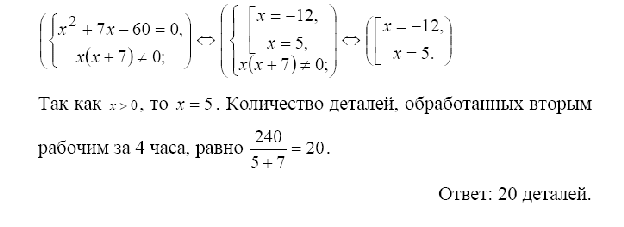
Рефлексия (заполнение оценочных листов)
Итог урока (учитель смотрит оценочные листы, комментирует оценки).
Домашнее задание (на слайде презентации).
infourok.ru
Задачи на производительность труда, с решением
Показатели производительности труда
Прежде чем начать решение задачи на производительность труда, необходимо дать определение и формулу расчета. Производительность труда в целом является мерой результативности и эффективности человеческого производительного труда.
Для решения задачи на производительность труда, ее можно выразить через два показателя:
- выработки каждого работника,
- трудоемкости по единице продукции.
Выработка представляет собой объем продукции, которая выпускается одним работником за определенную единицу времени. Решим несколько задач на выработку.
Решение по выработке
Показатель трудоемкости
Трудоемкость можно определить количеством времени, которое затрачивается на выпуск единицы изделия. Задачи на производительность труда по трудоемкости используются для формирования плана производства, обоснования бизнес-планов, анализа и эффективности работы персонала в производстве.
Основные показатели, воздействующие на трудоёмкость, представлены квалификацией, сложностью выпуска готовых изделий, степенью автоматизации и условиями труда. Общая формула трудоемкости выглядит таким образом:
Тр = РВ / ВП
РВ – рабочее время по изготовлению определенного количества товаров,
ВП – количество выпущенных товаров.
Решение по трудоемкости
Задачи на производительность труда
Можно сказать, что производительность труда представляет собой объем, который выпускается работником за единицу времени или время, которое потрачено на выпуск единицы продукции. Показатели производительности рассчитываются как на отдельных рабочих местах, так и в среднем по всей организации.
Примеры задач на производительность
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
«Задачи на определение производительности, времени работы, объёма работы» для работы в классе
«Задачи на определение производительности, времени работы, объёма работы»
Фамилия, имя_______________________________________________________________
1 вариант
Определи производительность бригады, если за 8-часовую рабочую смену бригада производит 160 т кирпича.
_____________________________________________________________________________
Ответ:______________________________________________________________________
За 4 часа художник оформил 12 страниц. Определи, сколько таких страниц оформит художник за 6 часов.
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
Ответ: __________________________________________________________________
Реши задачу. Вычисли и запиши ответ. Экскаватор за 4 часа вырыл 120 м траншеи. Сколько времени ему потребуется, чтобы при той же производительности вырыть 210 м траншеи?
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
Ответ:______________________________________________________________________
4. Ответь на следующие вопросы.
а) За смену завод выпускает 16.000 т кирпича. Уменьшится или увеличится производительность завода, если за смену будет выпущено 32.000 т кирпича? Во сколько раз изменится производительность завода?
_____________________________________________________________________________
Ответ: _____________________________________________________________________
б) Мальчик прочитывает несколько страниц за 40 мин. Уменьшится или увеличится скорость чтения мальчика, если то же количество страниц он прочитает за 20 мин? Во сколько раз изменится его скорость чтения?
_____________________________________________________________________________
Ответ: _____________________________________________________________________
Производительность первого насоса 150 л/ч, второго – 130 л/ч. Сколько литров воды смогут перекачать два насоса за 3 часа, работая одновременно?
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
Ответ: _____________________________________________________________________
На стройке 120 т кирпича. Первый кран может поднять весь кирпич за 60 мин, а второй – за 12 мин. Сколько времени потребуется двум кранам, чтобы поднять весь кирпич, работая одновременно?
_____________________________________________________________________________
_____________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________
Фамилия, имя_______________________________________________________________
«Задачи на определение производительности, времени работы, объёма работы»
2 вариант
Определи производительность бригады, если за 6 дней бригада асфальтирует 5400 м дороги.
_______________________________________________________________________________
Ответ: ____________________________________________________________________
За 3 дня мельница перемалывает 24 мешка. Определи, сколько таких мешков смелет мельница за 7 дней.
__________________________________________________________________________________________________________________________________________________________
_____________________________________________________________________________
Ответ: ____________________________________________________________________
Реши задачу. Вычисли и запиши ответ.
Рабочий за 5 часов собирает 75 деталей. Сколько времени ему потребуется, чтобы при той же производительности собрать 120 деталей?
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
Ответ: ____________________________________________________________________
Ответь на следующие вопросы.
а) За несколько часов на электрической плите можно вскипятить 250 л воды. Уменьшится или увеличится производительность плиты, если за это время на ней вскипит 750 л воды? Во сколько раз изменится производительность плиты?
____________________________________________________________________________
Ответ: ____________________________________________________________________
б) Мальчик прочитывает несколько страниц за 60 мин. Уменьшится или увеличится скорость чтения мальчика, если то же количество страниц он прочитает за 30 мин? Во сколько раз изменится его скорость чтения?
_____________________________________________________________________________
Ответ: ____________________________________________________________________
Производительность первого станка 75 дет./ч, второго – 35 дет./ч. Сколько деталей смогут произвести два станка за 2 часа, работая одновременно?
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
Ответ: ____________________________________________________________________
В зале 150 лампочек. Первый электрик может поменять все лампочки за 15 ч, а второй – за 30 ч. Сколько времени потребуется двум электрикам, чтобы поменять все лампочки, работая одновременно?
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
infourok.ru
Решение задач на производительность
Муниципальное бюджетное образовательное учреждение «Лицей» города Абакана
Решение задач на производительность
Автор: ученик 8Г класса Кожуховский Максим Руководитель: Казакова Наталья Андреевна |
Абакан,2017
СодержаниеВведение 3
1. Способы решения текстовых задач 4
2. Виды задач на производительность 4
3. Способы решения текстовых задач 5
Заключение 10
Список литературы 11
ВведениеУмение решать задачи является одним из основных показателей математического развития, глубины освоения учебного материала. Текстовые задачи – традиционно трудный для значительной части школьников материал. С этим столкнулся я и мои одноклассники при решении 22 задачи из ОГЭ. Поэтому я решил свою работу посветить задачам на производительность из ОГЭ.
Цель: создание методического пособия для подготовки к успешному решению задач на производительность.
Объект: задачи на производительность.
Предмет: методы решения текстовых задач на производительность.
Для реализации поставленной цели поставлены следующие задачи:
изучить литературу по данной теме;
изучить методику решения текстовых задач на производительность;
описать методы решения задач на производительность;
составить подборку задач для самостоятельного решения.
- Способы решения текстовых задач
Арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой.
Алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств.
Геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний.
Схематический способ – это способ решения текстовой задачи с помощью схем.
Графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.
- Виды задач на производительность
Текстовые задачи на производительность наряду с задачами на движение являются одними из наиболее популярных видов задач на экзаменах разного уровня. Как в задачах на движение, в которых присутствуют элементы v –скорость, t –время и S – расстояние, так и в задачах на производительность и грузоперевозки есть аналогичные элементы.
В задачах на производительность существуют:
р – производительность, аналог скорости, то есть количество работы, производимой в единицу времени;
t – время работы;
А – объём работы, аналог расстояния.
.
В основном в экзаменационных тестах есть 2 вида задач на производительность и они различаются количеством рабочих , задачи с 2 рабочими и с 3.
Пример: 2 рабочих. На изготовление 231 детали ученик тратит на 11 часов больше , чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на детали меньше, чем мастер. Сколько деталей в час делает ученик?
- Способы решения текстовых задач
При решении задач на производительность в основном используют 2 способа – алгебраический и арифметический. При чем арифметический способ встречается очень редко, потому что в ОГЭ обычно не известно 2 пункта из 3, и без использования переменной не возможно решить задачу.
Примечание. В задач с совместной работой производительности складываются.
Пример: Паша с Витей красят забор за 2 часа 1/(П+В)= ½ (П и В – время за которое каждый красит забор один).
Если объем работы неизвестен и его не нужно найти по условия задачи, то берем его за единицу.
Рассмотрим несколько задач на производительность.
Задача 1 .На изготовление 231 детали ученик тратит на 11 часов больше , чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на детали меньше, чем мастер. Сколько деталей в час делает ученик?
Решение:
1. Нам известен объем работы 231 деталь делает ученик и 462 детали делает учитель A1= 231 , A2= 462.
2.Производительность неизвестна , но мы знаем что ученик за 4 детали за час делает меньше чем учитель
Обозначим за x производительность ученика за час, значит производительность мастера будет x+4 . p1=x ,p2=x+4.
3. Время не известно, но мы знаем, что ученик на изготовление 231 детали тратит на 11 часов больше чем мастер на 462 ,т.к. t = A/p ,то t1=231/x, t2=462/x+4.
Составим уравнение.
Т.к. ученик тратит на 11 часов больше , то 231/x – 462/x+4 = 11 = 231x + 924 – 462x = 11x² + 44x =-275x + 924 = 11x² = 11x² + 275x — 924 = 0 = x² + 25x – 84 = 0 . По теореме Виета x1 = -28 и x2 = 3 .
-28 не подходит т.к. невозможно делать отрицательное кол-во деталей . Ответ : 3 детали за час делает ученик
Задача 2.
Игорь и Паша красят забор за 18 часов. Паша и Володя красят этот же забор за 20 часов, а Володя и Игорь — за 30 часов. За сколько минут мальчики покрасят забор, работая втроём?
1.Т.к. объем работы неизвестен , то обозначим его за единицу . A = 1
2.Время каждого нам неизвестно , но в парах
Известно , поэтому время каждого обозначим
Игорь – И , Паша – П , Володя – В , тогда И + П = 18 часов , П + В = 20, В + И = 30.
3. Покраска забора за час ,то есть производительность p = 1/И+П = 1/18 , 1/П+В = 1/20 и 1/В+И = 1/30
Т.к. нам нужно найти их время работая втроем , то есть за сколько они покрасят забор в 3 , то просто сложим их производительности , а позже зная их совместную производительность можно будет узнать время .
1/18 + 1/20 + 1/30 =25/180 = 5/36 . т.к. сложив их производительности по парам получилось что работает 2 Игоря, Паши и Володи поэтому разделим их производительность на 2 .5/72 забора они покрасят за час , а т.к. A = 1 то 1/(5/72) = 14,4 часов они покрасят весь забор т.к. нам надо найти в минутах, то умножим на 14,4 часа на 60 . 14,4 * 60 = 864 мин.
Ответ : За 864 мин они покрасят забор.
Задача 3.Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
Решение:
Обозначим за x объем работы , т.к. они выполняют один и тот же тест . Производительность Димы равна 12 вопросов в час , а Саши 22. Время Димы x/12 , а Саши x/22. Зная что Дима закончил тест позже Саши на 75 минут или 1,25 часа составим уравнение
x/12 – x/22 = 1,25 = (11x – 6x)/132 = 1,25 = 5x/165 = x= 33
Ответ 33 вопроса.
Задача 4. Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Обозначим производительность накачивания за x , тогда производительность выкачивания будет x+3.
Объем работы накачивания 117 литров , а выкачивания 96.t= A/p . Время накачивания 117/x , а выкачивания 96/x+3.
Зная что чтобы накачать в бак 117 воды ,требуется на 5 минут больше времени ,чем на то , чтобы накачать составим уравнение. 117/x – 96/x+3 = 5 =21x+351 = 5x² + 15x = 5x² — 6x – 351 = 0 = x1 = 9 ,x2 = -7.8 .и получаем 9 литров в минуту накачивается в минуту.
Задача 5.
Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
Решение:
Объем работы неизвестен поэтому возьмём его за единицу , обозначим за x время за которое выполнит работу 1 оператор ,а за y время второго. Тогда их производительность будет 1/x и 1/y , если мы поделим время за которое по они выполняют ¾ работы ,то есть 3 и 12 часов , на время которое они выполняют полную работу , то есть на x и y ,то мы получим объем работы каждого оператора , и из полученных данных мы сможем составить систему уравнений.
1/x+1/y = 1/8 и 3/x + 12/y =3/4 = 1/x+1/y = 1/8 и 1/x = ¼ — 4/y = 3/y =1/8 = y=24 . 1/x = 2/24 = 2x = 24 = x=12.
Ответ: за 12 часов выполнит работу 1 оператор и за 24 второй.
Перейдем к задачам с 3 рабочими .
Задача 6 . Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?
Решение:
Объем работы единица . Обозначим каждого мальчика 1 именем его буквы . tИ+П = 20 , tП+В = 24 , tВ+И = 30 .И производительность pИ+П = 1/20 , pП+В = 1/24 , pВ+И =1/30 . Сложим их производительность и получим общую производительность , а позже разделим объем работы на общую производительность. Т.к. мы сложили попарно , то разделим на 2 их производительность. 1/20 + 1/24 + 1/30 = 15/120 = 5/40 = 1/8 . 1/(1/16) = 16 часов.
Ответ: За 16 часов они покрасят забор.
4. Задачи для самостоятельного решения
1.Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая труба. Сколько литров в минуту пропускает вторая труба, если резервуар объёмом 400 литров она заполняет на 2 часа 20 минут быстрее, чем первая труба заполняет резервуар объёмом 900 литров?
2. Две бригады, работая вместе, могут выполнить некоторую работу за 12 часов. Первая бригада, работая одна, могла бы выполнить эту работу на 10 часов быстрее, чем вторая. Сколько часов потребовалось бы первой бригаде для выполнения этой работы?
3. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 часов. За сколько часов наполняет бассейн одна вторая труба?
4. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
5. На изготовление 180 деталей первый рабочий тратит на 3 часа меньше. чем второй рабочий, если известно, что первый за час делает на 3 детали больше.
6. Первый кран разгрузит баржу за 3 часа, второй кран разгрузит сухогруз за 8 часов. Во сколько раз производительность первого крана больше производительности второго, если первый кран разгрузит сухогруз на 10 часов быстрее, чем второй кран баржу?
7. Игорь и Паша красят забор за 10 часов. Паша и Володя красят этот же забор за 15 часов, а Володя и Игорь — за 21 час. За сколько часов мальчики покрасят забор, работая втроём?
8. Три бригады вместе изготовили 114 синхронизаторов передач. Известно, что вторая бригада изготовила синхронизаторов в 3 раза больше, чем первая, и на 16 синхронизаторов меньше, чем третья. На сколько синхронизаторов передач больше изготовила третья бригада, чем первая.
9. Три бригады изготовили вместе 248 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
ЗаключениеЦель и задачи поставленные в работе выполнены. В частности изучили литературу по данной теме, методику и методы решения и составил подборку заданий для самостоятельного решения. Не секрет что очень важно сдать экзаменационные тесты и после изучения данной методики вы сможете решить 22 задачу из ОГЭ . Умение решать текстовые задачи очень пригодится в жизни и как говорилось в начале , является одним из основных показателей математического развития , именно поэтому время , усилия и внимание потраченное на изучение данной темы не напрасно , а даже на оборот .
Список литературыhttps://oge.sdamgia.ru/test?theme=77
http://www.fipi.ru/
Задачи на работу и производительность
http://www.egesdam.ru/page242.php
https://examer.ru/ege_po_matematike/teoriya/zadachi_na_proizvoditelnost
http://matematika-doma.ru/tematicheskie-9/278-oge-2015-reshenie-zadach-modul-algebra-2-chast-zadanie-22-povyshennyy-uroven.html
https://matematikalegko.ru/rabota/zadachi-na-rabotu-chast-1.html
multiurok.ru
Презентация к уроку по алгебре (9 класс) на тему: Готовимся к ГИА. «Задачи на совместную работу»
Слайд 1
Краснодарский край г.Армавир МБОУ – СОШ №8 учитель Черноус Ольга Шамильевна.Слайд 2
Что необходимо знать? 1. Объём, выполняемой работы! (A) 3 . Производительность! (N) 2 . Время работы! (t) Что необходимо делать?
Слайд 3
Задачу прочти Немного помолчи Про себя повтори Ещё раз прочти Нет объёма работы, за 1 прими Данные в таблицу занеси Уравнение запиши Уравнение реши! Что необходимо делать?
Слайд 4
Мастер, работая самостоятельно, может изго- товить партию из 200 деталей за некоторое время. Ученик за это же время может изготовить только половину всех деталей. Работая вместе, они могут изготовить всю партию деталей за 4 ч. За какое время мастер может изготовить все детали, работая самостоятельно? мастер ученик Время ( t) х 200 Объем работы 100 Производительность Объем работы = производительность ⋅ время . х 4 вместе 200 Составим и решим уравнение. ⋅ = Ответ: 6 часов.
Слайд 5
Саша и Маша решают задачи. Саша может решить 20 задач за то время, за которое Маша может решить в 2 раза меньше задач. Саша и Маша вместе могут решить 20 этих задач за 2 ч. За сколько часов Саша самостоятельно может решить 20 задач? C аша Маша t х 20 А 10 N Объем работы = производительность ⋅ время . х 2 вместе 20 Составим и решим уравнение. Ответ: 3 часов.
Слайд 6
Ученик, работая самостоятельно, может поштукатурить всю стену площадью 10 м 2 за то время, за которое мастер может поштукатурить две таких стены. Мастер и ученик, работая вместе, могут поштукатурить всю стену за 6 ч. За какое время ученик может поштукатурить всю стену, работая самостоятельно? ученик мастер t х 10 А 20 N Объем работы = производительность ⋅ время . х 6 вместе 10 Составим и решим уравнение. Ответ: 18 часов.
Слайд 7
Токарь четвёртого разряда и его ученик за час вместе изготавливают 50 деталей. Ученику для изгото- вления 50 деталей требуется времени на 2 часа больше, чем требуется токарю для изготовления 120 деталей. Сколько деталей в час изготовляет токарь? токарь ученик N х 120 A 50 t Составим и решим уравнение. Ответ: 40 деталей в час. вместе 50 х+2 5х 2 – 7х – 24 = 0 х = 3 =3 N = 40
Слайд 8
Один мастер может выполнить заказ за 12 часов, а другой – за 18 часов. За сколько часов выполнят заказ эти мастера, работая вместе? мастер ученик t 12 1 А 1 N Объем работы = производительность ⋅ время . 18 х вместе 1 ⋅ = Ответ: 7,2 часа. Составим и решим уравнение.
Слайд 9
Первая труба и вторая, работая вместе, наполняют бассейн за 36 часов, первая и третья – за 30 часов, вторая и третья – за 20 часов. За сколько часов наполнят бассейн три трубы, работая вместе? 1 т 2 т х 1 1 Объем работы = производительность ⋅ время . у z Вместе 1 и 2 1 = Ответ: 18 часов. 3 т + 36 1 Вместе 1 и 3 1 + Вместе 2 и 3 + 1 3 0 20 ⋅ 36 = + 1 + ⋅ 3 0= 1 + ⋅ 20= 1 А N t
Слайд 10
Токари выходят на работу с интервалом в 1 час производительность труда первого токаря равна шести деталям в час, а второго – пяти деталям в час. Третий токарь догоняет второго по числу изготовленных деталей, а ешё через 2 часа догоняет первого. Какова производительность труда третьего токаря? 1 т 2 т х 3 т 6 5 Пусть третий токарь догоняет второго по числу деталей через t часов Составим и решим систему уравнений N t 1 t +1 А 1 (Кол-во деталей.) х⋅ t 5(t +1 ) =х t Получаем первое уравнение. t +2 А 2 (Кол-во деталей) x(t +2) t+4 6(t+4) Получаем второе уравнение. 6 (t +4 ) =х( t +2) 5( t +1) t t 2 2х 2 – 29х + 90 = 0 Ответ: 10 деталей в час
nsportal.ru