Задачи на скорость движения – Задачи на движение — Детская игровая комната «Волшебный лес»

Posted on 14.01.202023.12.2019 by alexxlab

Содержание

Решение задач на расчёт скорости. Видеоурок. Физика 7 Класс

Тема: Взаимодействие тел

Урок: Решение задач на расчет скорости

Автомобиль движется с севера на юг со скоростью 90 км/ч. Необходимо выразить эту скорость в метрах в секунду и изобразить графически.

Рис. 1. К условию задачи № 1

Условие и решение данной задачи не требуют специального оформления. Вначале нужно перевести скорость 90 км/ч в метры в секунду, в СИ. 90 км/ч можно записать как 90 000 метров, деленные на 3600 секунд. Если провести математический расчет, то мы получим, что 90 км/ч соответствует 25 м/с.

Затем выберем масштаб изображение вектора скорости автомобиля. Например, одна клеточка вашей тетради будет соответствовать 5 м/с. Тогда, чтобы изобразить вектор скорости, численно равный 25 м/с, в выбранном масштабе нужно изобразить стрелку, направленную с севера на юг (т.е., сверху вниз), длиной в 5 клеточек. Рядом ставим обозначение: символ v, обозначающий скорость, с маленькой стрелкой над ним – знаком вектора.

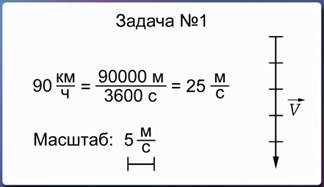
Рис. 2. К решению задачи № 1

За 20 минут тело переместилось на 6000 см. Необходимо определить скорость движения данного тела.

Такие задачи в физике называются количественными, потому что как условие, так и ответ содержат числовые данные. Решение подобных задач требует специального оформления, с которым мы сейчас познакомимся.

В левом углу тетрадного листа записываем слово «Дано:», ставим двоеточие и ниже в столбик перечисляем заданные величины и через знак равенства их числовые значения с размерностью. Далее отчеркиваем данные вертикальной и перпендикулярной ей горизонтальной чертой, под чертой пишем слово «Найти:», указываем, какую физическую величину нам необходимо найти в этой задаче, ставим знак равенства и знак вопроса.

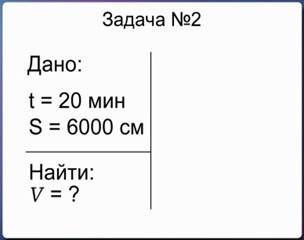
Рис. 3. Оформление краткого условия задачи

Величины в условии данной задачи заданы во внесистемных единицах – сантиметрах и минутах. Поэтому справа от вертикальной черты мы ставим обозначение «СИ» (интернациональная система) и производим перевод единиц в СИ. 20 мин – это 1200 с, а 6000 см – это 60 м. Правее колонки чисел ставим еще одну вертикальную черту.

Рис. 4. Перевод единиц в СИ

На оставшемся справа свободном пространстве сверху пишем слово «Решение:».

В физике принято сначала записывать формулу, с помощью которой будут производиться расчеты. Чтобы найти скорость, необходимо пройденный телом путь разделить на время движения тела. Затем принято делать проверку размерности (единиц измерения) полученного результата. Размерности величин, входящих в формулы, записывают в квадратных скобках. Мы получаем, что скорость измеряется в метрах в секунду.

Следующий этап – подстановка в формулу числовых данных. Еще раз записываем букву, обозначающую скорость, но вместо букв, обозначающих путь и время, записываем численные значения этих величин и выполняем вычисления. Деля 60 на 1200, получаем значение 0,05 – это и есть искомое значение скорости. В круглых скобках мы записываем размерность получившейся величины (метры в секунду).

Внизу пишем слово «Ответ», ставим двоеточие и еще раз указываем числовое значение скорости с размерностью.

Рис 5. Полностью оформленное решение задачи № 2

Задачи, подобные этой, часто используются при выполнении тестовых заданий. В них есть условие и несколько вариантов ответов, из которых необходимо выбрать правильный.

По графику зависимости пути, пройденного телом, от времени, необходимо определить скорость тела, движущегося равномерно и прямолинейно.

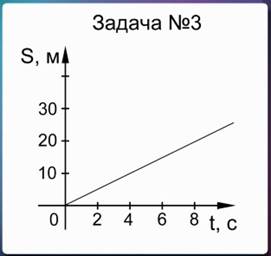
Рис. 6. К условию задачи № 3

Так как в условии задачи указано, что движение равномерное, то можно взять любую точку на графике. Лучше всего выбирать точку, которая расположена против штрихов на осях графика. Проведем пунктирные линии перпендикулярно осям пути и времени, чтобы найти, какой путь прошло тело за определенный промежуток времени. В нашем случае, например, за 4 секунды тело прошло путь 10 метров. Затем по формуле рассчитаем значение скорости. Разделив 10 м на 4 с, получим, что скорость тела равна 2,5 м/с. Следовательно, правильным является ответ «В».

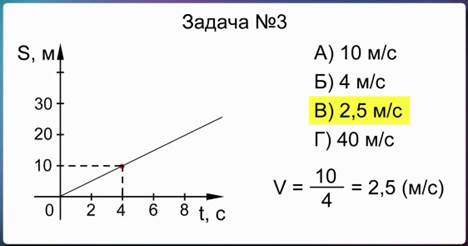
Рис. 7. Решение задачи № 3

Список литературы

1. Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.

2. Перышкин А.В. Сборник задач по физике, 7 – 9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.

3. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7 – 9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Единая коллекция Цифровых Образовательных Ресурсов (Источник).

2. Единая коллекция Цифровых Образовательных Ресурсов (Источник).

Домашнее задание

Перышкин А.В. Сборник задач по физике, 7 – 9 кл. №№ 75–77, 93–95, 96.

interneturok.ru

Тренажёр по математике (3, 4 класс) на тему: Простые задачи на движение (12 вариантов)

Вариант 1.

1.Лыжник прошёл дистанцию 24 км за три часа. С какой скоростью он шёл?

2. Самолёт летел 4 часа со скоростью

600 км/ч. Какое расстояние он пролетит?

3. Скорость звука в воздухе 330 м/с. Через какое время мы услышим звук выстрела, произведённого на расстоянии 990 м?

Вариант 2.

1. Мотоциклист ехал 4 часа со скоростью

80 км/ч. Какое расстояние он проехал?

2. За какое время пешеход пройдёт 15 км, идя со скоростью 5 км/ч?

3.Гепард пробежал 6000 м за 4 минуты.

С какой скоростью он бежал?

Вариант 3.

1. Лодка проплыла 28 км со скоростью

7 км/ч. Какое время она была в пути?

2. С какой скоростью должен ехать велоси педист, чтобы за 3 часа проехать 33 км?

3. Спасаясь от собаки, кошка вскарабкалась на дерево со скоростью 2 м/с за 3 секунды. На какую высоту забралась кошка?

Вариант 4.

1. Мышка, убегая от кота, пробежала 12 метров до совей норки за 4 секунды. С какой скоростью она бежала?

2. За какое время прошёл турист 28 км, если он шёл со скоростью 4 км/ч?

3. Почтовый голубь летел 3 часа со скоростью 90 км/ч. Какое расстояние он пролетел?

Вариант 5.

1. Бамбук за 24 часа вырос на 72 см.

С какой скоростью рос бамбук?

2. Какое расстояние проплывёт катер за

4 ч, если он движется со скоростью 32 км/ч?

3. Охотник верхом на лошади проехал

28 км со скоростью 14 км/ч. Сколько времени он потратил на дорогу?

Вариант 6.

1. За 3 часа поезд прошёл 210 км. Чему равна скорость поезда?

2. Расстояние от города до посёлка 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью

6 км/ч?

3.Муха летела 15 секунд со скоростью

5 м/с. Какое расстояние она пролетела?

Вариант 7.

1.Расстояние до школы 1200 м мальчик прошёл за 20 минут. С какой скоростью он шёл в школу?

2. Скорость грузового поезда 35 км/ч. Поезд был в пути 2 часа. Какое расстояние он прошёл?

3. Крейсер проплыл 80 км со скоростью 40 км/ч. Сколько времени он затратил?

Вариант 8.

1. Плот проплыл по течению реки 18 км за 6 часов. Какова скорость течения реки?

2. Грач пролетел 100 м со скоростью

10 м/с. Сколько времени он был в пути?

3. Мотоциклист ехал 6 часов со скоростью 40 км/ч. Какое расстояние он проехал?

Вариант 9.

1. Велосипедист проехал 36 км за 2 часа.

С какой скоростью он двигался?

2. Орёл летел 6 секунд со скоростью

30 м/с. Сколько метров пролетел орёл?

3. Туристы прошли 60 км, двигаясь со скоростью 12 км/ч. Сколько времени они были в пути?

Вариант 10.

1. Мальчик пробежал 20 метров за

10 секунд. С какой скоростью бежал мальчик?

2. Сокол пролетел 78 метров со скоростью 26 м/с. Сколько времени он летел?

3. Скорость пешехода 60 м/мин. Какой путь он пройдёт за 30 минут?

Вариант 11.

1.Расстояние между городами 366 км поезд прошёл за 6 часов. Чему равна скорость поезда?

2. За какое время самолёт пролетит

1200 км, если его скорость 300 км/ч?

3. Автомобиль проехал от города до посёлка за 3 часа со скоростью 55 км/ч. Какое расстояние от города до посёлка?

Вариант 12.

1. Расстояние в 450 км скорый поезд проехал за 5 часов. С какой скоростью ехал скорый поезд?

2. Теплоход плыл 4 часа со скоростью

45 км/ч. Какое расстояние он проплыл?

3. Самолёт пролетел 4800 км со скоростью 800 км/ч. Сколько времени он был в пути?

nsportal.ru

Простые задачи на движение

Задачи по математике для 4 класса.

Задача 1

С какой скоростью летел вертолет, если за 2 часа он пролетел расстояние в 600 километров?

Решение:
1) 600 : 2 = 300

Ответ: 300 километров.

Задача 2

Скорость орла 30 метров в секунду. Какое расстояние пролетит орел за 5 секунд?

Решение:
1) 30 * 5 = 150

Ответ: 150 метров.

Задача 3

Авианосец проплыл 90 км со скоростью 30 км/чес. Сколько времени он затратил?

Решение:
1) 90 : 30 = 3

Ответ: 30 часа.

Задача 4

Мотоциклист двигался со скоростью 35 км/час В пути он был 2 часа Какое расстояние он преодолел за это время?

Решение:
1) 2 * 35 = 70

Ответ: 70 километров.

Задача 5

Улитка проползла 36 метров за 2 часа. Сколько всего метров проползла улитка?

Решение:
1) 36 : 2 = 18

Ответ: 18 километров в час.

Задача 6

Велосипедист проехал 28 км со скоростью 14 км/час. Сколько времени у него заняла дорога?

Решение:
28 : 14 = 2

Ответ: 2 часа.

Задача 7

Деревня от города находится на расстоянии 30 км. Сколько времени будет идти пешеход из деревни в город, если его скорость 6 км/час?

Решение:
1) 30 : 6 = 5

Ответ: 5 часов.

Задача 8

Какое расстояние пролетит комар за 19 секунд, если его скорость 4 метра в секунду?

Решение:
1) 4 * 19 = 76

Ответ: 76 метров.

Задача 9

Ворона пролетела 150 м со скоростью 10 метров в секунду. Сколько времени она потратила на полет

Решение:
1) 150 : 10 = 10

Ответ: 15 секунд.

Задача 10

Скорый поезд проезжает за 5 часов расстояние в 450 километров. С какой скоростью движется поезд?

Решение:
1) 450 : 5 = 90

Ответ: 90 километров в час.

Задача 11

Велосипедист проехал с одинаковой скоростью 70 км за 5 часов. Какова скорость велосипедиста?

Решение:
70 : 5 = 14

Ответ: 14 километров в час.

Задача 12

Рыбаки прошли на лодке 12 километров со скоростью 12 км/час. Какое расстояние они преодолели?

Решение:
1) 12 * 5 = 60

Ответ: 60 километров.

mat-zadachi.ru

Задачи на движение

Задачи на движение — один из самых распространенных видов задач алгебры. Простейшие задачи на движение изучаются еще в начальной школе. В 6-7 классах решение задач на движение сводится к линейному уравнению либо системе линейных уравнений. Здесь мы рассмотрим задачи на движение, которые можно решить с помощью дробного рационального уравнения. При решении задач на движение используем формулу пути:

где s — путь, v — скорость, t — время. Как правило, в задачах на движение в 8 классе нужно выразить время через путь и скорость:

Чаще всего путь измеряется в километрах, скорость — в километрах в час, время — в часах. Время, заданное в минутах, нужно перевести в часы. Так как в 1 часе 60 минут, то 1 минута — это одна шестидесятая часа, а t минут — t шестидесятых часа:

1 (мин)=1/60(часа). t (мин)=t/60 (часа).

1) Из пункта А в пункт В автомобиль ехал по шоссе протяженностью 210 километров, а возвращался назад по грунтовой дороге протяженность. 160 километров, затратив на обратный путь на 1 час больше, чем на путь из А в В. Найти, с какой скоростью автомобиль двигался по грунтовой дороге, если она на 30 километров в час меньше его скорости по шоссе.

Решение:

Пусть х км/ч — скорость автомобиля по грунтовой дороге, тогда его скорость по шоссе равна (х+30) км/ч.

Составим и решим уравнение:

Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, автомобиль по грунтовой дороге двигался со скоростью 40 км/ч.

Ответ: 40 км/ч.

2) Первые 20 км пути велосипедист двигался со скоростью, на 5 км/ч большей скорости, с которой он ехал последние 20 км. С какой скоростью велосипедист проехал вторую половину пути, если на весь путь он затратил 3 часа 20 минут?

Решение:

Пусть II половину пути велосипедист двигался со скоростью х км/ч, тогда его скорость на I половине пути была (х+5)км/ч.

3 часа 20 минут = 3 20/60 =3 1/3 = 10/3 часа.

Составим и решим уравнение:

Упростим уравнение, разделив почленно обе его части на 10:

Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, II половину пути велосипедист проехал со скоростью 10 км/ч.

Ответ: 10 км/ч.

www.uznateshe.ru

Решение задач на определение ускорения, мгновенной скорости и перемещения при равноускоренном прямолинейном движении

Задача 1 посвящена исследованию пути и перемещения.

Условие: тело движется по окружности, проходя ее половину. Необходимо определить отношение пройденного пути к модулю перемещения (рис. 1).

Обратите внимание: дано условие задачи, но нет ни одного числа. Такие задачи будут встречаться в курсе физики довольно часто.

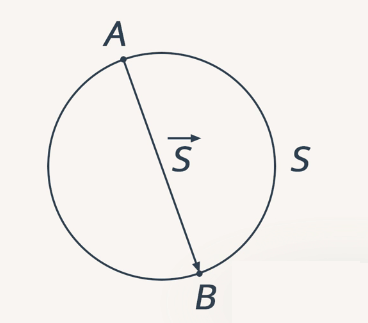
Рис. 1. Путь и перемещение тела

Решение

Введем обозначения. Радиус окружности, по которой движется тело, обозначим 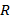. При решении задачи удобно сделать рисунок, на котором изобразим окружность. Произвольную точку, из которой движется тело, обозначим 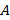; точку, в которую переместилось тело, – . – это дуга половина окружности, 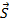– это перемещение, соединяющее начальную точку движения с конечной.

Найдем половину длины окружности:

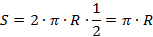
С другой стороны модуль перемещения равен диаметру окружности (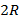). Найдем отношение этих величин:

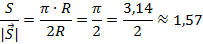
Ответ:.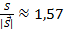

Несмотря на то что в задаче ни одного числа нет, тем не менее в ответе мы получаем вполне определенное число.

Ветка. Задача на нахождения средней скорости

Задача.Автомобиль первую половину времени двигался со скорость 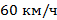, а вторую – со скоростью 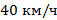(рис. 2). Определите среднюю скорость автомобиля.

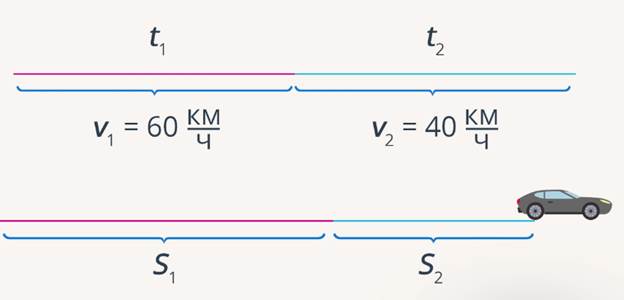
Рис. 2. Рисунок к задаче

Решение

Средняя скорость равна отношению пройденного пути ко времени, за которое произошло движение:

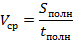
Полное перемещение состоит из двух частей: 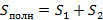. Аналогично и время состоит из двух частей: 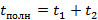. Промежутки времени у нас одинаковы: .

Перемещение при равномерном движении равно произведению скорости на время. Следовательно:

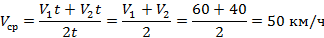
Ответ: .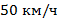

Задача 2 будет посвящена графикам скорости.

Условие: Два поезда движутся навстречу друг другу по параллельным путям, скорость первого поезда – 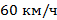, скорость второго – (рис. 3). Ниже представлены 4 графика (рис. 4), и нужно выбрать те, на которых правильно изображены графики проекции скорости движения этих поездов.

Рис. 3. Рисунок к задаче 2

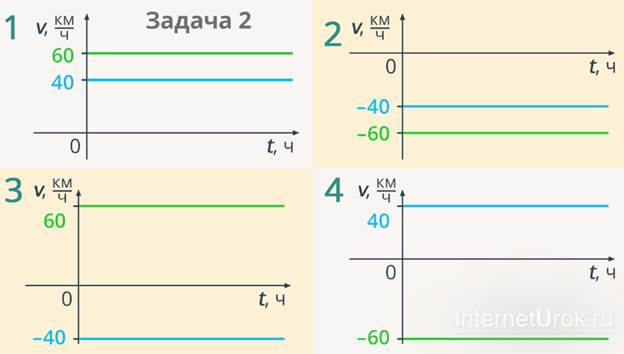
Рис. 4. Графики к задаче 2

Решение

Ось скорости – вертикальная (км/ч), а ось времени – горизонтальная (время в часах).

На 1-м графике две параллельные прямые, это модули скорости движения тела – 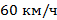и 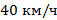. Если вы посмотрите на график, под номером 2, то увидите то же самое, только в отрицательной област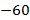и: и 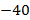. На двух других графиках 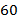сверху и 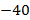снизу. На 4-м графике 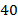в верхней части, а 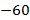внизу. Что же можно сказать об этих графиках?

Согласно условию задачи два поезда едут навстречу друг другу, по параллельным путям, поэтому если мы выберем ось, связанную с направлением скорости одного из поездов, то проекция скорости одного тела будет положительной, а проекция скорости другого – отрицательной (поскольку сама скорость направлена против выбранной оси). Поэтому ни первый график, ни второй к ответу не подходят. Когда проекция скорости имеет одинаковый знак, нужно говорить о том, что два поезда движутся в одну сторону. Если мы выбираем систему отсчета, связанную с первым поездом, то тогда проекция скорости первого поезда 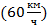будет положительной, а второго 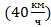– отрицательной, поезд едет навстречу. Или наоборот, если мы связываем систему отчета со вторым поездом, то у одного из них проекция скорости 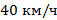, а у другого 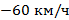, отрицательная. Таким образом, подходят оба графика (3 и 4).

Ответ: 3-й и 4-й графики.

Ветка. Задача на нахождения средней скорости (продолжение)

Поменяем в предыдущей задаче всего одно слово.

Задача:

Автомобиль первую половину пути двигался со скоростью 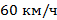, а вторую – со скоростью 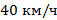(рис. 5). Определите среднюю скорость автомобиля.

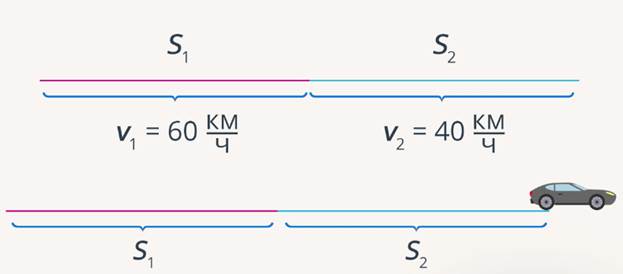
Рис. 5. Рисунок к задаче

Решение

По аналогии с предыдущей задачей запишем выражение для средней скорости:

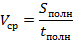
Полное перемещение состоит из двух частей: 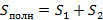, причем 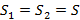. Аналогично и время состоит из двух частей: .

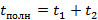Вспомним, что для равномерного движения время равно отношению перемещения ко времени. Тогда:

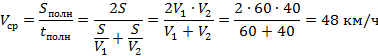
Ответ: .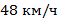

Задача 3.

Условие: автомобиль движется со скоростью 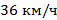и в течение 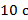тормозит с ускорением 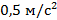. Необходимо определить его скорость в конце торможения.

Решение

В данном случае удобнее выбрать ось 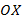и направить начальную скорость вдоль этой оси, т. е. вектор начальной скорости будет направлен в ту же сторону, что и ось. Ускорение будет направлено в противоположную сторону, ведь автомобиль замедляет свое движение. Проекция ускорения на ось 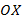будет со знаком минус (рис. 6).

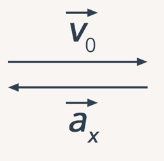
Рис. 6. Рисунок к задаче 3

Для нахождения мгновенной конечной скорости воспользуемся уравнением проекции скорости: . Время и ускорение заданы в СИ, поэтому начальную скорость также переведем в СИ: 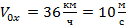. Подставляя значения, получаем конечную скорость:

Значит, через 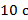после торможения скорость будет .

Ответ: .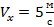

Задача 4.

Условие: на графике (рис. 7) представлены 4 зависимости скорости от времени. Необходимо определить, у какого из этих тел максимальный, а у какого минимальный модуль ускорения.

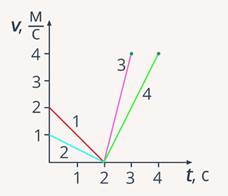
Рис. 7. Графики к задаче 4

Решение

Для решения необходимо рассмотреть все 4 графика поочередно.

Для сравнения ускорений нужно определить их значения. Для каждого тела ускорение будет определяться как отношение изменения скорости ко времени, в течение которого это изменение произошло.

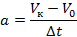
Ниже проведены расчеты ускорения для всех четырех тел:

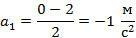
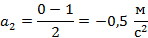
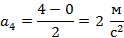
Как видим, у второго тела модуль ускорения минимальный, а у трет

interneturok.ru

Тренажёр по математике (4 класс): Задачи на движение 4 класс

По теме: методические разработки, презентации и конспекты

Презентация по математике 4 класс «Устный счёт по теме:Решение задач на движение»
Презентация создана в Microsoft Office PowerPoint 2007…
Урок математики «Подкормка птиц» для 4 класса. Задачи на движение
Урок-путешествие (марш-бросок) в зимний лес «Подкормка птиц». На уроке решаются задачи экологического воспитания, учебные — решение задач на движение и др. Цель: закрепить умение решать зад…
Урок математики в 4 классе по теме «Решение задач на движение»
Урок математики с использованием презентации. В течении всего урока учащиеся отмечают на маршрутном листе свои успехи, тем самым оценивают каждый участок пройденного пути….
урок математики 4 класс специализированного (коррекционного) класса VII вида «Решение задач на движение в противоположных направлениях»
данный урок был дан в 4 коррекционном классе 7 вида в МБОУСОШ № 17 г. Смоленска Ошметковой Н.В.. Также этот урок был опубликован в «сборнике уроков и статей»….
Урок математики по теме «Задачи на движение. Движение — жизнь».
Урок интегрированный, интересный, нестандартный, увлекательный. Детям показано, что не только двигается человек и транспорт, но и растения. Присутствует здоровьесберегающий аспект, всё-таки: движение …
Урок математики по теме «Решение задач на движение. Нахождение скорости изменения движения»
Урок математики «Решение задач на движение. Нахождение скорости изменения движения» для 4 класса по программе «Перспективная начальная школа»…
Урок математики в 4 классе по теме: «Задачи на движение. Движение вдогонку». Образовательная система «Школа 2100»
Урок открытия новых знаний. Цели урока: Формирование умения проводить исследования значения расстояния между движущимися объектами в заданный момент времени при движении вдогонку, фиксировать результа…
nsportal.ru
Относительность движения — простые задачи
Начинать такую сложную тему, как относительность движения, нужно с простых задач. Тема и правда непростая, нужно усвоить хорошо закон сложения классических скоростей (то есть не релятивистских). Правильно выбрали неподвижную систему отсчета, правильно определили скорость подвижной системы отсчета, не забыли про векторное сложение скоростей – и все должно получиться.
Задача 1. Скорость велосипедиста равна м/с, а скорость встречного ветра – $\upsilon= 4$ м/с. Какова скорость ветра относительно велосипедиста? Какой была бы скорость ветра относительно него, если бы ветер был попутный?
Наверное, все замечали, как сильно развевается на ветру одежда и волосы, если мы выглянем в окно несущегося поезда, или поднимемся на палубу мощного корабля. Нам кажется, что ветер усилился, но на самом деле это наша собственная скорость увеличилась, и к скорости встречного ветра добавилась скорость транспортного средства. Чтобы найти скорость ветра относительно велосипедиста (скорость в подвижной системе отсчета), нужно вычесть из скорости ветра (скорость в неподвижной системе) скорость велосипедиста (скорость системы отсчета). Не забываем, что скорости – это вектора, поэтому вычитание будем производить векторное, с учетом направлений скоростей. Тогда при встречном ветре получим:
$\vec{u_1}=\vec{\upsilon}-\vec{u}$
$\mid u_1 \mid=\mid -4-10 \mid=14$
А при попутном:
$u_1=4-10=6$
Ответ: при встречном ветре – 14 м/с, при попутном – 6 м/с.

Задача 2. Нарисовать траекторию движения точки обода колеса велосипеда при его движении относительно: а) рамы велосипеда; б) земли. Зависит ли вид траектории от выбора тела отсчета? Зависят ли путь и перемещение от выбора системы отсчета?
Траекторией движения в первом случае будет окружность. Во втором случае траектория будет выглядеть так:
Теперь просто ответить на вопросы задачи: да, вид траектории зависит от выбора тела отсчета (если бы за точку отсчета выбрали точку на ободе, то траектория обратилась бы в точку – относительно такой точки отсчета движения не было бы). Также и путь, и перемещение зависят от выбранной точки отсчета.
Задача 3. Самолет поднимается с аэродрома под углом $20^{\circ}$ к горизонту со скоростью $\upsilon=216$ км/ч. Найти вертикальную и горизонтальную составляющие скорости. Какой высоты достигнет самолет за с подъема? Как изменится скорость самолета при встречном ветре 20 м/с?
Сначала найдем вертикальную и горизонтальную составляющие скорости самолета:
$\upsilon_{gor}=\upsilon \cdot \cos{\alpha}=\frac{216000}{3600}\cdot \cos{20^{\circ}}=60 \cdot 0,939=56,34$
$\upsilon_{vert}=\upsilon \cdot \sin{\alpha}=\frac{216000}{3600}\cdot \sin{20^{\circ}}=60 \cdot 0,342=20,52$
Самолет поднимется на 20,5 м за 1 секунду. Теперь определим, как изменится скорость самолета со встречным ветром. Ветер, очевидно, уменьшит горизонтальную составляющую:
$\upsilon_{1gor}=\upsilon_{gor}-\upsilon_{v}=56,34-20=36,34$
Скорость самолета при встречном ветре найдем, воспользовавшись теоремой Пифагора:
$\upsilon_1=\sqrt{{\upsilon_{1gor}}^2+{\upsilon_{vert}}^2}=\sqrt{1741}=41,7$
Получается, что скорость самолета упала почти на 20 м/с. Вылет, скорее всего, отменят.
Ответ: самолет поднимется на 20,5 м за 1 секунду. При встречном ветре скорость самолета станет равна 41,7 м/с.

Задача 4. Теплоход длиной м движется прямолинейно по озеру со скоростью $\upsilon_1$ . Катер, имеющий скорость $\upsilon_2=90$ км/ч, проходит расстояние от кормы до носа движущегося теплохода и обратно за время с. Найти скорость теплохода.
Когда катер обгоняет теплоход (движется от кормы к носу), скорость обгона равна $\upsilon_2-\upsilon_1$ . При движении катера от носа к корме скорость сближения катера и теплохода равна: $\upsilon_2+\upsilon_1$ . Тогда время движения от кормы к носу равно:
$t_1=\frac{l}{\upsilon_2-\upsilon_1}$
А время движения от носа к корме:
$t_2=\frac{l}{\upsilon_2+\upsilon_1}$
В сумме эти два времени дадут с:
$\frac{l}{\upsilon_2-\upsilon_1}+\frac{l}{\upsilon_2+\upsilon_1}=37,5$
Прежде чем решать, переведем скорость катера в м/с:
$\upsilon_2=\frac{90000}{3600}=25$
Теперь решаем уравнение:
$\frac{300}{25-\upsilon_1}+\frac{300}{25+\upsilon_1}=37,5$
$\frac{300(25+\upsilon_1)+300(25-\upsilon_1)}{25^2-\upsilon_1^2}=37,5$
После переноса влево и приведения к общему знаменателю имеем квадратное уравнение:
$25^2-\upsilon_1^2=400$
Откуда
$\upsilon_1^2=225$
$\upsilon_1=15$
Ответ: скорость теплохода равна 15 м/с.

Задача 5. Пролетая над пунктом А, пилот вертолета догнал воздушный шар, который сносило ветром по курсу вертолета. Через полчаса пилот повернул обратно и встретил воздушный шар в 30 км от пункта А. Чему равна скорость ветра, если мощность двигателя вертолета оставалась постоянной?
Задача не требует решения: шар снесло за час на 30 км, следовательно, скорость ветра 30 км/ч. Хотя, конечно, можно было бы определить скорость удаления шара и вертолета на пути туда, затем скорость сближения на пути обратно… Записать разность расстояний, которые пролетел пилот туда и обратно и приравнять эту разность к 30 км… Но ответ будет тот же самый, тогда зачем усложнять?
easy-physic.ru