Задачи на тему ромб – План-конспект урока по геометрии (8 класс) по теме: Прямоугольник. Ромб. Квадрат. Решение задач. Разработка урока геометрии в 8 классе

Posted on by alexxlab

Задания категории В5. Ромб | Подготовка к ЕГЭ по математике

В этой статье работаем с Задачами №3 ЕГЭ по математике, которые связаны с ромбом.

Смотрите в других статьях разбор Задачи №3, в которых фигурирует:v

– треугольник;
– прямоугольник;
– параллелограмм;
– произвольный четырехугольник;
– трапеция;
– многоугольник;
– круг;
– векторы;
– координатная плоскость;

Задача 1. Найдите площадь ромба, если его стороны равны 7, а один из углов равен 150°.

ромб

Решение: + показать

Задача 2. Найдите площадь ромба, если его диагонали равны 45 и 2.

be23f541c0d4e9b51c76ec43a963075b

Решение: + показать

Задача 3. Площадь ромба равна 361. Одна из его диагоналей в 2 раза больше другой. Найдите меньшую диагональ.

be23f541c0d4e9b51c76ec43a963075b

Решение: + показать

Пусть меньшая диагональ ромба равна x, тогда большая – 2x.

Так как S=\frac{d_1\cdot d_2}{2}, то

361=\frac{x\cdot 2x}{2};

361=x^2;

x=19 – длина меньшей диагонали.

Ответ: 19. 

Задача 4. Диагонали ромба ABCD равны 40 и 42. Найдите длину вектора \vec{AB}.

pic

Решение: + показать

Задача 5. Диагонали ромба ABCD равны 11 и 59. Найдите длину вектора \vec{AB}+\vec{AD}.

pic-1

Решение: + показать

Задача 6. Диагонали ромба ABCD равны 26 и 20. Найдите длину вектора \vec{AB}-\vec{AD}.

pic-1

Решение: + показать

Заменим разность векторов суммой, введя противоположный вектор:

\vec{AB}-\vec{AD}=\vec{AB}+\vec{DA};

Поменяем для удобства слагаемые:

\vec{AB}+\vec{DA}=\vec{DA}+\vec{AB}=\vec{DB}.

Длина вектора \vec{DB}, равная длине отрезка DB,  равна 20.

Ответ: 20. 

Задача 7. Диагонали ромба ABCD пересекаются в точке O

 и равны 3 и 4. Найдите скалярное произведение векторов \vec{AO}  и  \vec{BO}.

pic-2

Решение: + показать

Скалярное произведение двух векторов равно произведению их длин на косинус угла между ними.

Диагонали же  в ромбе перпендикулярны. Следовательно угол между векторами \vec{AO}  и  \vec{BO}

– прямой.

Значит, поскольку  косинус  90^{\circ} равен нулю, скалярное произведение тоже равно нулю.

Ответ: 0. 

Задача 8. Диагонали ромба относятся как 1:3. Периметр ромба равен 90. Найдите высоту ромба.

pic-3

Решение: + показать

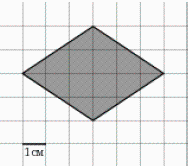
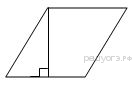
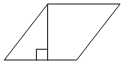
Задача 9. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

f2eb64cad19324dd2e3ebdf50d6db4dc

Решение: + показать

гнНапример, из равнобедренного прямоугольного треугольника с катетами 6, помеченного на чертеже зеленым цветом, находим гипотенузу: \sqrt{6^2+6^2}=6\sqrt{2}.

Аналогично находим меньшую диагональ ромба: \sqrt{4^2+4^2}=4\sqrt2.

Площадь ромба ищем по формуле S=\frac{d_1d_2}{2}.

S=\frac{6\sqrt2\cdot 4\sqrt2}{2}=24.

Ответ: 24. 

тест

 

Вы можете пройти тест «Задачи №3. Ромб»

Ромб

Примечание. Это часть урока с задачами по геометрии (раздел ромб). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √  или sqrt(), при чем в скобках указано подкоренное выражение.

Задача

Найдите периметр ромба ABCD, если угол B равен 60градусов, а длина AC составляет  10,5 см.

Решение.

Поскольку AC является диагональю ромба, все стороны ромба равны, то ABC — равнобедренный треугольник. Поэтому углы ABC и ACB равны (углы при основаниях равнобедренного треугольника).

Поскольку сумма углов треугольника равна 180 градусам, то каждый из этих углов будет равен (180° — 60°) / 2 = 60° .

Треугольник, все углы которого равны, является равносторонним. Таким образом,  AB = BC = AC.

Зная сторону ромба, найдем его периметр. P = 10,5 * 4 = 42 см

Ответ: 42 см

Задача

У ромба ABCD диагональ BD равна 14 см, длина диагонали AC равна 48 см. Найти длину стороны АВ

Решение.
Поскольку диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам, то

DO = OB = BD / 2
DO = OB = 24 см

AO = OC = AC /2
AO = OC = 7 см

Исходя из того, что диагонали ромба пересекаются под прямім углом, треугольники AOD и AOB — прямоугольные. Откуда

AO2 + OB2 = AB2
откуда
72 + 242 =  AB2
49 + 576 =
625 = AB2
AB =25 см

Ответ: 25 см

 Правильный четырехугольник (квадрат). Правильний чотирикутник (квадрат) | Описание курса | Трапеция 

   

Решение задач по теме «Прямоугольник. Квадрат. Ромб»

Цель урока: закрепить в процессе решения задач полученные знания и навыки.

Задачи урока:

  • закрепить теоретический материал по теме “Прямоугольник. Ромб. Квадрат”;
  • совершенствовать навыки решения задач;
  • развитие элементов геометрического мышления и воспитание интереса к оперированию геометрическими понятиями;
  • умение выполнять и оценивать выполненную работу;
  • расширение кругозора, развитие чувства взаимопомощи, совершенствование навыков работы с компьютером.

Оборудование: доска, компьютеры, карточки с заданиями, тесты, справочный материал, таблицы.

Ход урока

1. Организационный момент.

– Сообщить тему урока, сформулировать цели урока.

  • Какую тему мы изучаем?
  • В процессе изучения темы вы должны знать:

Уметь:

Учащиеся должны:

Знать: определение прямоугольника и его свойства, определение и свойства ромба, определение квадрата и все его свойства.
Уметь: доказывать особое свойство прямоугольника и ромба, применять свойства прямоугольника, ромба и квадрата при решении задач, решать задачи, в которых рассматриваются параллелограмм, прямоугольник, ромб, квадрат.

На сегодняшний день мы

знаем: определение прямоугольника и его свойства, определение и свойства ромба, определение квадрата и все его свойства;
умеем: доказывать особое свойство прямоугольника и ромба.

Что не умеем? применять свойства прямоугольника, ромба и квадрата при решении задач, решать задачи, в которых рассматриваются параллелограмм, прямоугольник, ромб, квадрат.

Поэтому целью нашего урока будет закрепить в процессе решения задач полученные знания и навыки.

2. Актуализация знаний учащихся.

Повторим знания, полученные на прошлом уроке. Предлагаю вам, работая в парах, дать определения параллелограмма, прямоугольника, ромба, квадрата и, вспомнив их свойства заполнить таблицу.

Теоретический опрос (работа в парах).

  1. Дать определения понятиям: параллелограмм, прямоугольник, ромб, квадрат.
  2. Вспомнить свойства и заполнить таблицу, отметив знаки + (да) и — (нет).

По первому вопросу оценить друг друга. Оценки выставляем в лист учета.

Свойство Параллелограмм Прямоугольник Ромб Квадрат
Противолежащие стороны параллельны и равны.
Все стороны равны.
Противолежащие углы равны, сумма соседних углов равна 180.
Все углы прямые.
Диагонали пересекаются и точкой пересечения делятся пополам.
Диагонали равны.
Диагонали взаимно перпендикулярны и являются биссектрисами его углов.

Произведите взаимопроверку и оцените друг друга.

Используя определения и свойства фигур, выполните математический диктант.

Математический диктант (графический).

Вариант 1.

  1. Является ли прямоугольником параллелограмм, у которого есть прямой угол?
  2. Верно ли, что каждый параллелограмм является прямоугольником?
  3. Диагонали параллелограмма равны 3 см и 5 см. Является и этот параллелограмм прямоугольником?
  4. Верно ли, что каждый ромб является параллелограммом?
  5. Ромб АВСD имеет прямой угол. Является ли этот ромб квадратом?

Вариант 2.

  1. Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?
  2. Верно ли, что каждый прямоугольник является параллелограммом?
  3. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник – прямоугольник?
  4. Верно ли, что каждый параллелограмм является ромбом?
  5. Две соседние стороны параллелограмма равны и образуют прямой угол. Называется ли такой параллелограмм — квадратом?

Проверьте правильность своих ответов и оцените свой диктант.

Итак, мы повторили определения и свойства параллелограмма, прямоугольника, квадрата, ромба. Но основной нашей целью является закрепить в процессе решения задач, полученные знания и навыки, научиться применять свойства прямоугольника, ромба и квадрата при решении задач.

Поэтому перейдем к решению задач с использованием теоретического материала.

3. Формирование умений и навыков. Решение задач.

Решение задач (устно и по готовым чертежам).(таблица 5).

1. Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.

Всегда ли при решении задач используем свойства?

(Определение).

Значит, для решения задач надо знать и свойства, и определения.

Выполнение задания – карточки с печатной основой (для коррекции знаний учащихся).

№ 11, 12, 14.

Решение задачи с комментированием.

1. В прямоугольнике АВСD диагонали АС и ВD пересекаются в точке О, причем, угол АОВ равен 40. Найдите угол DАО.

Обратите внимание на правильное оформление решения задачи. А теперь решим задачу с записью в тетради.

Решение задачи с комментированием в тетради. Учебник № 403.

4. Контроль за знаниями, умениями и навыками решения задач.

Мы повторили теоретический материал, разобрали решение задач с применением свойств фигур. А теперь предлагаю вам, решить самостоятельно задачи теста и задачи, предложенные компьютером.

1 вариант – у компьютера,

2 вариант – выполняет тест; затем поменялись местами.

Задания на карточках (тест, 2 варианта).

Вариант 1.

А1. Диагональ ромба образует с его стороной угол 26. Найдите наибольший угол ромба.

1) 128; 2) 154; 3) 104; 4) 52.

А2. Периметр параллелограмма равен 42 см, а одна из его сторон на 5 см больше другой. Найдите меньшую сторону параллелограмма.

1) 5 см; 2) 9 см; 3) 13 см; 4) 8 см.

А3. В прямоугольнике АВСD :  ВD = 10 см, периметр треугольника ВОС равен 16 см. Найдите длину стороны ВС.

1) 5 см; 2) 6 см; 3) 7 см; 4) 8 см.

Вариант 2.

А1. Диагональ ромба образует с его стороной угол 32. Найдите наибольший угол ромба.

1) 148; 2) 64; 3) 126; 4) 116.

А2. Периметр параллелограмма равен 56 см, а одна из его сторон в 3 раза больше другой. Найдите большую сторону параллелограмма.

1) 14 см; 2) 12 см; 3) 21 см; 4) 16 см.

А3. В прямоугольнике АВСD : АВ = 5 см, АС = 12 см. Найдите периметр треугольника АОВ.

1) 15 см; 2) 25 см; 3) 17 см; 4) 7 см.

Оцените правильность ответов теста.

Проверка верных ответов.

Вариант 1: А1. – 1), А2 – 4), А3 – 2).

Вариант 2: А1 – 4), А2 – 3), А3 – 3).

Задания на компьютере.

В программе “ Планиметрия” открыть тему “ Четырехугольники”.

В разделе “ Контрольные вопросы” решить задачу. (3, 4, 7, 8, 11).

В журнале узнать свой средний бал и записать его в лист учета.

5. Итог урока.

Самооценка своей деятельности на уроке.

Урок подходит к концу, давайте подведем итоги. Посмотрим, удалось ли нам реализовать поставленную цель?

Какая была цель?

(Закрепить в процессе решения задач полученные знания и навыки, научиться применять свойства прямоугольника, ромба и квадрата при решении задач.)

Достигли ли мы ее?

Оцените, на сколько успешно каждый из вас справился с поставленной целью. Каждый, работая на уроке, оценивал свои знания теоретического материала.

У кого оценка “5”? “4”? “3”?, а есть оценка “2”?

Если ваши знания не на “5”, то дома вам еще раз необходимо проработать п. 45, 46, и ответить на вопросы 12–15.

Оценим свои умения по решению задач.

У кого оценка “5”? “4”? “3”?, а есть оценка “2”?

Для того, чтобы вы могли лучше решать задачи, дома необходимо решить следующие задачи № 405, 401 (а).

Запишите домашнее задание в дневник.

6. Домашнее задание.

Повторить п. 45, 46, вопросы 12–15, № 405, 401 (а).

Урок окончен. Спасибо за урок.

Литература

  1. Рабочая тетрадь по геометрии для 8 класса / Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина — М.: Просвещение, 2003.
  2. Геометрия, 7–9: Учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2003.
  3. Современный учебно-методический комплекс “Планиметрия” 7–9. Просвещение – Медиа, 2003.
  4. Упражнения по планиметрии на готовых чертежах: Пособие для учителя / С. М. Саврасова, Г. А. Ястребинецкий. – М.: Просвещение, 1987.

Задания для подготовки и самостоятельная работа по теме: «Ромб»

1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см)

2) Точка O — центр окружности, на которой лежат точки H, I и K таким образом, что OHIK — ромб. Найдите угол HIK. Ответ дайте в градусах.

3) В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.

4) Сторона ромба равна 4, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.

5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба.

(В от­ве­те за­пи­ши­те ве­ли­чи­ны раз­лич­ных углов в по­ряд­ке воз­рас­та­ния без пробелов.)

6) Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=1. Найдите высоту ромба.

7) Найдите площадь ромба, если его диагонали равны 4 и 6.

8) Периметр ромба равен 36, а один из углов равен 30°. Найдите площадь этого ромба.

9) Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба.

10) Сто­ро­на ромба равна 34, а ост­рый угол равен 60° . Вы­со­та ромба, опу­щен­ная из вер­ши­ны ту­по­го угла, делит сто­ро­ну на два от­рез­ка. Ка­ко­вы длины этих от­рез­ков?

11) Площадь ромба равна 6, а пе­ри­метр равен 24. Най­ди­те высоту ромба.

1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см)

2) Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол STV. Ответ дайте в градусах.

3) В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.

4) Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.

5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите углы ромба. (В от­ве­те за­пи­ши­те ве­ли­чи­ны раз­лич­ных углов в по­ряд­ке воз­рас­та­ния без пробелов.)

6) Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=3. Найдите высоту ромба.

7) Найдите площадь ромба, если его диагонали равны 19 и 6.

8) Периметр ромба равен 60, а один из углов равен 30°. Найдите площадь этого ромба.

9) Сторона ромба равна 7, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.

10) Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

11) Площадь ромба равна 18, а пе­ри­метр равен 36. Най­ди­те высоту ромба.

1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см)

2) Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.

3) В ромбе ABCD угол ABC равен 84°. Найдите угол ACD. Ответ дайте в градусах.

4) Сторона ромба равна 54, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.

5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба. (В от­ве­те за­пи­ши­те ве­ли­чи­ны раз­лич­ных углов в по­ряд­ке воз­рас­та­ния без пробелов.)

6) Высота AH ромба ABCD делит сторону CD на отрезки DH=20 и CH=5. Найдите высоту ромба.

7) Найдите площадь ромба, если его диагонали равны 5 и 6.

8) Периметр ромба равен 12, а один из углов равен 30°. Найдите площадь этого ромба.

9) Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.

10) Сто­ро­на ромба равна 30, а ост­рый угол равен 60°. Вы­со­та ромба, опу­щен­ная из вер­ши­ны ту­по­го угла, делит сто­ро­ну на два от­рез­ка. Ка­ко­вы длины этих от­рез­ков?

11) Пло­щадь ромба равна 27, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба

 

1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см)

2) Точка O — центр окружности, на которой лежат точки E, F и G таким образом, что OEFG — ромб. Найдите угол OEF. Ответ дайте в градусах.

3) В ромбе ABCD угол ABC равен 102°. Найдите угол ACD. Ответ дайте в градусах.

4) Сторона ромба равна 14, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.

5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба. (В от­ве­те за­пи­ши­те ве­ли­чи­ны раз­лич­ных углов в по­ряд­ке воз­рас­та­ния без пробелов.)

6) Высота AH ромба ABCD делит сторону CD на отрезки DH=15 и CH=2. Найдите высоту ромба.

7) Найдите площадь ромба, если его диагонали равны 32 и 4.

8) Периметр ромба равен 88, а один из углов равен 30°. Найдите площадь этого ромба.

9) Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 4. Найдите площадь этого ромба.

10) Сто­ро­на ромба равна 40, а ост­рый угол равен 60° . Вы­со­та ромба, опу­щен­ная из вер­ши­ны ту­по­го угла, делит сто­ро­ну на два от­рез­ка. Ка­ко­вы длины этих от­рез­ков?

11) Пло­щадь ромба равна 63, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.

 

Задачи на прямоугольник, ромб, квадрат

Задачи на прямоугольник, ромб, квадрат

к содержанию задачника

  1. В прямоугольнике, длины сторон которого равны 8 и 2, проведены биссектрисы всех углов до взаимного пересечения. Найдите площадь четырехугольника, который образован биссектрисами. ответ: 18
  2. Перпендикуляр, проведенный из вершины прямоугольника на диагональ, делит ее в отношении 1 : 3. Найдите длину диагонали, если известно, что точка ее пересечения с другой диагональю находится от большей стороны на расстоянии 4. ответ: 16
  3. В прямоугольнике АВCD биссектриса угла С пересекает сторону АВ в точке Е, а прямую DA в точке F. Найдите площадь прямоугольника, если СЕ равно 4 и CF равно 6. ответ:  12
  4. Стороны АВ и ВС прямоугольника ABCD равны 12 и 16 соответственно. Окружности, вписанные в треугольники АВС и ADC, касаются диагонали АС в точках К и Т. Найдите расстояние между точками К и Т. ответ: 4
  5. Длины сторон АВ и ВС прямоугольника ABCD равны 12 и 5 соответственно. Найдите расстояние от точки пересечения диагоналей О до центра окружности, вписанной в треугольник AOD. ответ: 13/3
  6. В прямоугольнике ABCD длины сторон AB и ВС равны 6 и 8 соответственно, а диагонали пересекаются в точке О. Окружности, вписанные в треугольники АОВ и DOC, касаются диагонали DB в точках К и Е. Найдите длину отрезка КЕ. ответ:  4
  7. В прямоугольнике АВСD диагонали пересекаются в точке О. Периметры треугольников AOD и DOC равны и соответственно. Найдите радиус окружности, вписанной в треугольник AOD, если радиус окружности, вписанной в треугольник DOC, равен . ответ:
  8. Площадь круга, вписанного в ромб, равна половине площади ромба. Найдите синус угла при вершине ромба. ответ:
  9. На сторону ВС ромба ABCD опущена высота DK. Диагональ АС пересекает высоту DK в точке М так, что DM : MK = 13 : 7.  Найдите DK, если известно, что АК равно 17. ответ:
  10. В ромб, сторона которого равна и острый угол равен 60о, вписана окружность. Найдите площадь четырехугольника, вершины которого совпадают с точками, в которых окружность касается сторон ромба. ответ:
  11. Периметр ромба равен , а длины диагоналей находятся в отношении . Найдите площадь ромба. ответ:  
  12. Высота ромба равна 12, а одна из его диагоналей равна 15. Найдите площадь ромба. ответ: 150
  13. Найдите площадь ромба ABCD с острым углом , если радиус окружности, вписанной в треугольник ABD, равен . ответ:
  14. Ромб, у которого сторона равна меньшей диагонали, равновелик кругу радиуса R. Найдите сторону ромба. ответ:
  15. Из вершины В острого угла ромба ABCD проведены перпендикуляры ВЕ и  ВК к прямым CD и AD соответственно. Длина каждого перпендикуляра равна 3, а длина отрезка КЕ равна . Найдите диагональ ромба. ответ: 6;
  16. Диагонали АС и BD ромба ABCD пересекаются в точке О. Найдите площадь ромба, если известно, что высота ромба равна 24, а радиус окружности, вписанной в треугольник ВОС, равен 5. ответ:  600
  17. Длина стороны ромба ABCD равна 15. Найдите диагонали ромба, если известно, что радиус окружности, вписанной в треугольник АВС, равен 4. ответ: 18; 24
  18. Диагонали ромба АВСD пересекаются в точке О. Найдите высоту ромба, если известно, что площадь треугольника ВОС равна 24, и периметр этого треугольника равен 24. ответ: 48/5
  19. Площадь ромба равна S, а диагонали находятся в отношении m : n. Найдите сторону ромба. ответ:
  20. Диагонали ромба ABCD пересекаются в точке О. Полуокружность, построенная на отрезке ВО как на диаметре, пересекает сторону ВС в точке Е. Найдите площадь ромба, если ОЕ равно 12, АС равно 30. ответ: 600

 

Метки задачи, параллелограмм. Смотреть запись.

Презентация к уроку по геометрии (8 класс) на тему: задачи на готовых чертежах по теме: «Ромб»

Слайд 1

Подготовила: Наседкина О.А., учитель математики 1 кв. категории МКОУ Квитокская СОШ№1 п.Квиток, Тайшетского района, Иркутской области Задачи на готовых Чертежах Ромб

Слайд 2

Ромб O D C B A Свойства: Диагонали в точке пересечения делятся пополам C тороны равны Противолежащие углы равны Диагонали пересекаются под прямым углом Диагонали являются биссектрисами углов 6 7 8 9 11 10 12 13 14 1 2 3 4 5 15 16 17 18 19

Слайд 3

Задача 1 A D C B Дано: ABCD — ромб Найти: ∠ BDC

Слайд 4

Задача 2 Найти: ∠ ABC A D C B Дано: ABCD — ромб

Слайд 5

Задача 3 A B C D Дано: ABCD — ромб Найти: ∠ BAD

Слайд 6

Задача 4 A C D B E Дано: ABCD — ромб Найти: ∠ BAD

Слайд 7

Задача 5 A F E D C B Дано: ABCD — ромб Доказать : BE = DF

Слайд 8

Задача 6 A K P B C D Дано: ABCD — ромб Доказать : OK = OP

Слайд 9

Задача 7 K D C B A Дано: ABCD — ромб Доказать : KB = KD

Слайд 10

Задача 8 Дано : ABCD – ромб Диагонали составляют с его сторонами углы, один из которых на 30° меньше другого Найти : углы ромба C A B D O

Слайд 11

Задача 9 A N M O D B C Дано : ABCD – ромб AM – биссектриса ∠ BAC пересекает сторону ВС в точке М и диагональ BD в точке N , ∠ AMC = 120° Найти : ∠ ANB

Слайд 12

Задача 10 A B C D F E Дано : ABCD – ромб Доказать : ∠ ABF =∠CBE

Слайд 13

Задача 1 1 A B D C Дано : ABCD – ромб Найти : углы ромба

Слайд 14

Задача 12 A D C B E Дано : ABCD – ромб Найти : ∠ BAD

Слайд 15

Задача 13 A D C B F E Дано : ABCD – параллелограмм Доказать : ABCD – ромб

Слайд 16

Задача 1 4 6 см A M N B C D Дано : ABCD – ромб Найти : MD + DN

Слайд 17

Задача 1 5 A K B D C Дано : ABCD – ромб Найти : ∠ ABC

Слайд 18

Задача 16 A O D C B Дано : ABCD – ромб, ∠А = 31° Найти : углы ∆ B О C

Слайд 19

Задача 1 7 A D C B Дано: ABCD – ромб, АВ = , ∠А =60° Найти : большую диагональ ромба

Слайд 20

Задача 1 8 A M K D C B O Дано : ABCD – ромб, BD : AC = 3 : 4, Р ABCD = 200 Найти : высоту ромба МК

Слайд 21

Задача 1 9 A D C B Дано : ABCD – ромб, Длина квадратных клеток равна Найти : периметр ABCD

Слайд 22

Список литературы 1.Смирнов В.А. Геометрия (планиметрия) Готовимся к ЕГЭ Москва Издательство МЦНМО 2009 г. Под редакцией И.В.Ященко, А.В. Семенова. 2. Зив Б.Г. и др. Задачи по геометрии: Пособие для учащихся 7-11 кл . Общеобразоват . учреждений. — М .: Просвещение , 2000.-271 с.: ил . 3. Рабинович Е.М. Сборник задач на готовых чертежах.-К.:1996.-56с. 4. Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс.-2-е изд., перераб . и доп.-М.: ВАКО,2008.-368 с.

Конспект «ЗАДАЧИ по теме Квадрат»

«ЗАДАЧИ по теме Квадрат»

КВАДРАТ определение

свойства квадрата

Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны. Квадрат является одновременно частным случаем ромба и прямоугольника. Длины всех сторон равны. Все углы квадрата прямые.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Задача № 1. Дано: ABCD — квадрат; AC и BD — диагонали; AC = 4 см; BC — диагональ квадрата OBKC.  Найти: BK.

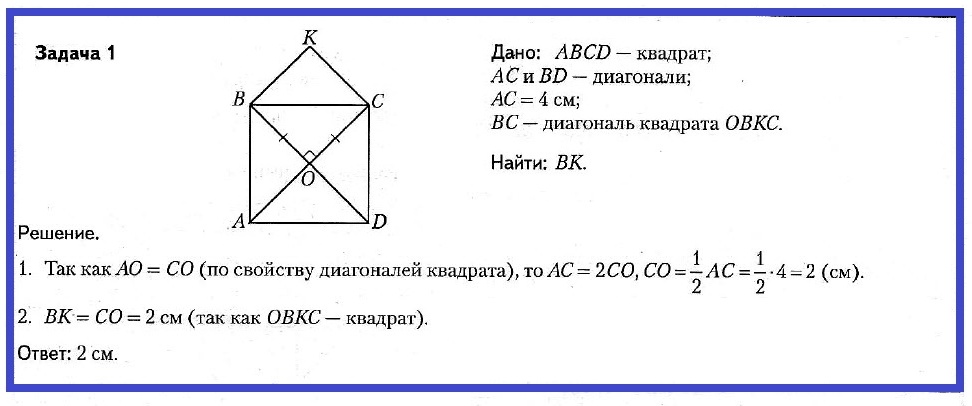
ЗАДАЧИ по теме Квадрат. Задача 1

 

Задача № 2. Дано: ΔABC — равнобедренный, прямоугольный; AB1DC1 — квадрат;  ∠A — общий; AB = 2 см.   Найти: PAB1DC1 

задача 2

 

Задача № 3. Дано: ΔABC — равнобедренный, прямоугольный; LEKD — квадрат;  L ∈ AB; D ∈ AC; E ∈ BC; K ∈ BC; BC = 3 см.   Найти: LD.

ЗАДАЧИ по теме Квадрат. Задача 3

 

Задача № 4. Дано: ABCD — квадрат; AC = 18,4 см; A ∈ l;  l ⟂ AC;  l ∩ BC = M;  l ∩ CD = N.  Найти: MN.

задача 4

Это конспект по теме «ЗАДАЧИ по теме Квадрат». Выберите дальнейшие действия:

 

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *